因式分解 课后训练
七年级因式分解刷题练习92题-答案版

第X 讲因式分解刷题练习(92题)-7上复习用【例题1】()()()()23222336x y x y y x y x x y -++---+【分析】 原式()()3221x y x =--【例题2】222944a b bc c -+-【分析】 原式()()()()22222944923232a b bc c a b c a b c a b c =--+=--=+--+【例题3】3223x x xy y y ----【分析】 原式()()221x xy y x y =++--【例题4】54323331x x x x x -+-+-【分析】 原式()()()223111x x x x x =-++-+【例题5】222595121824x y z xy yz zx --+-+【分析】 原式()()3553x y z x y z =++--【例题6】22121115x xy y --【分析】 原式()()4335x y x y =+-【例题7】2408124848x x --【分析】 原式()()204612x x =+-【例题8】633619216x x y y --【分析】 原式()()()()2222232439x y x y x xy y x xy y =+--+++【例题9】2222x yz axyz yz xy xz az ++---【分析】 原式()()xy z az xz y =-+-【例题10】222222444222a b b c c a a b c ++---原式()()()()b c a b c a c a b a b c =+++-+-+-【例题11】22015201420162015x x -⨯-【分析】 原式()()201512015x x =+-【例题12】()()()22592791a a a +---【分析】 原式()()()242728a a a a =-+--【例题13】()()()()26121311x x x x x ----+【分析】 原式()22661x x =-+【例题14】()()()()461413119x x x x x ----+【分析】 原式()22971x x =-+【例题15】343115x x -+【分析】 原式()()()21253x x x =--+【例题16】322772x x x -+-【分析】 原式()()()1221x x x =---【例题17】3331x y xy ++-【分析】 原式()()2211x y x y xy x y =+-++-++【例题18】432655x x x x ++++【分析】 原式()()2251x x x =+++【例题19】()()()()222222261561121x x x x x x ++++++++ 【分析】 原式()()229141x x x =+++【例题20】()()()322223a b c a a c b a b c abc +-+-++-【分析】 原式()()()a b a c a b c =+-+-【例题21】322222422x x z x y xyz xy y z --++-【分析】 原式()()22x z x y =--【例题22】()()()2122xy x y x y xy -++-+-【分析】 原式()()2211x y =--【例题23】32542071227x y x xy --【分析】 原式()()22223293293x x xy y x xy y =-++-+【例题24】43241x x x x +-++【分析】 原式()()22131x x x =-++【例题25】()()22222a a b b ab a -+--【分析】 原式()222a b b =-【例题26】43214599448x x x x -+-+【分析】 原式()()()()1238x x x x =----【例题27】432673676x x x x +--+【分析】 原式=()()()()221331x x x x -++-【例题28】()22223122331x x x x -+-+- 【分析】 原式()()()23323x x x x =--+【例题29】2244661124864x y x y x y -+-【分析】 原式()()331212xy xy =+-【例题30】()()()333222222x y z x y z ++--+ 【分析】 原式()()()()22223x y y z z x z x =-+++-【例题31】32221x ax ax a --+-【分析】 原式()()211x a x x a =--+-+【例题32】42201520142015x x x +++【分析】 原式()()2212015x x x x =++-+【例题33】22()()1ab a b a b +-++【分析】 原式22(1)(1)a ab b ab =+-+-【例题34】()()66x x y z y z y x +-+--【分析】 原式()()()()()2222x y z x y x y x xy y x xy y =+--+++-+【例题35】432227447x x x x ---+【例题36】()()()2222223241x x x x x x -+++-++ 【分析】 原式()()()2112x x x x =--++【例题37】323233332a a a b b b ++++++【分析】 原式()()222a b a b ab a b =+++-++【例题38】()322312b a a b a a -++--++【分析】 ()()212a b ab a b b =-+-+++【例题39】()()211ab ab ab a b a b +-+--+【分析】 原式()()()2111ab ab a b ab =+-+++(以1ab +为主元) ()()()()22111111a ab b ab a b a ab b =+-+-⎡⎤⎡⎤⎣⎦⎣⎦=+-+-【例题40】()()()333222x y z y z x z x y -+-+-【分析】 原式()()()()x y y z z x xy yz zx =---++【例题41】()()()()3311x a xy x y a b y b +---++【分析】 原式()()22x xy y ax x y by =-++++【例题42】22()()()()ax by ay bx ay ax by ay bx ay +++-+++-原式2222()()a ab b x xy y =++++【例题43】22222612523171319322312520a b c d ab ac ad bc bd cd a b c d ---+--+-+-+-+-【分析】 原式()()23423455a b c d a b c d =+-+--+-+【例题44】()()()()()()2222326232x y a b m n xy a b m n xy a b m n ++-+++++【分析】 原式()()()32421xy a b m n ax bx my ny =+++--+【例题45】22223273x xy y xz yz z ---+-【分析】 原式()()232x y z x y z =+--+【例题46】2299x x +-【分析】 原式()()119x x =+-【例题49】632827x x -+【分析】 原式()()()()2211339x x x x x x =-++-++【例题50】32374a a +-【分析】 原式()()()1322a a a =+-+【例题51】4464a b +【分析】 原式()()22224848a ab b a ab b =++-+【例题52】()()3211x y xy x y ++---【分析】 原式()()2211x y x y x y =+-++++【例题53】()()()2113212xy xy xy x y x y ⎛⎫+++-++-+- ⎪⎝⎭ 【分析】 原式()()()()1111x y x y =++--【例题54】22243x y x y ----【分析】 原式()()13x y x y =++--【例题55】2231032x xy y x y ---++【分析】 原式()()5221x y x y =--+-【例题56】32256x x x +--【分析】 原式()()()123x x x =+-+【例题57】4322111236x x x x --++【分析】 原式()()2223x x =+-【例题58】432262x x x x ---+【分析】 原式()()()22121x x x =--+【例题59】()()22213260x x x x -+-+ 【分析】 原式()()()()2165x x x x =-+-+【例题60】()()222248415x x x x x x ++++++ 【分析】 原式()()22264x x x =+++【例题62】()()()()11359x x x x -+++-【分析】 原式()()22246x x x =++-【例题63】()()()()245610123x x x x x ++++-【分析】 原式()()()22158235120x x x x =++++【例题64】()()42424413110x x x x x -++++【分析】 原式()()()()22221111x x x x x x =+-++-+【例题65】2222232a x acx bcx b x c ++--【分析】 原式()()2ax bx c ax bx c =-++-【例题66】()()()2222a b a b c a b ++-++ 【分析】 原式()()222a b c =++【例题67】()()()3332a b c a b b c ++-+-+【分析】 原式()()()32a b b c a b c =++++【例题68】()()ab bc ca a b c abc ++++-【分析】 原式()()()a b b c c a =+++【例题69】86421x x x x ++++【分析】 86421x x x x ++++()()()4322221x x x =+++()()()()551111x x x x +-=+-551111x x x x +-=⋅+- ()()43243211x x x x x x x x =-+-+++++【例题70】已知2220x y z --=,试将333x y z --分解成一次因式之积.【分析】 由已知,222z x y =-,222y x z =-,故()3333322x y z x y z x y --=---()()()()22x y x xy y x y x y z =-++--+()()22x y x xy y x y z ⎡⎤=-++-+⎣⎦()()222x y x xy z xz yz =-+---()()()()2x y x z x z y x z =--++-⎡⎤【例题71】证明:220162014201520172018+⨯⨯⨯是一个完全平方数【分析】 设2016x =,故原式()()()()22112x x x x x =+--++()()22222x x x x x =+--+-()222x =-()2220162=-,得证.【例题72】证明:20132014201520172018201936⨯⨯⨯⨯⨯+是一个完全平方数【分析】 设2016n =,则原式()()()()()()32112336n n n n n n =---++++()()()22214936n n n =---+()()42254936n n n =-+-+6421449n n n =-+()2227n n =-()227n n ⎡⎤=-⎣⎦ ()22201620167⎡⎤=⨯-⎣⎦,得证.【例题73】证明:22222016201620172017+⨯+是一个完全平方数【分析】 令2016n =,则2222(1)(1)a n n n n =++++()2432223211n n n n n n =++++=++, 故()22201620161a =++【例题74】证明:3320162016201620182016201720162015⨯-⨯是一个完全立方数【分析】 令20162016m =,则原数()()()()333323211812612140324033m m m m m m m m =+-+-=+++=+=【例题75】333333()()()a b b c c a a b c ++++++++【解析】 原式333333222[()][()][()]3()()a b c b c a c a b a b c a b c =++++++++=++++;【例题76】42222222()()x a b x a b -++-.【解析】 ()()()()()222242222222222222x a b x a b x a b a b a b ⎡⎤-++-=-+-++-⎣⎦ ()222224x a b a b =---()()22222222x a b ab x a b ab =--+---()()2222x a b x a b ⎡⎤⎡⎤=---+⎣⎦⎣⎦()()()()x a b x a b x a b x a b =+--+--++【例题77】()()()()()2222221ab x y a b xy a b x y ---+-++【解析】 原式2222[(1)()]()[()(1)]b xy x y ab x y a x y xy =+-++--+++2222(1)(1)()(1)(1)b x y ab x y a x y =--+--++[(1)(1)][(1)(1)]x b y a y b x a =--+-++【解析】 2227()()ab a b a ab b +++【例题79】33(1)()()(1)x a xy x y a b y b +---++ 【解析】33(1)()()(1)x a xy x y a b y b +---++33(1)()[(1)(1)](1)x a xy x y a b y b =+--+-+++ 322322(1)()(1)()a x x y xy b y x y xy =+-++++-2222(1)()(1)()x a x xy y b x xy y =+-+++-+ 22()()x xy y ax by x y =-++++【例题80】32()(32)(23)2()l m x l m n x l m n x m n +++-+---+【解析】 如果多项式的系数的和等于0,那么1一定是它的根;如果多项式的偶次项系数的和减去奇次项系数的和等于0,那么1-一定是它的根.现在正是这样:()(32)(23)2()0l n l m n l m n m n -+++-----+=所以1x +是原式的因式,并且32()(32)(23)2()l m x l m n x l m n x m n +++-+---+322[()()][(2)(2)][2()2()]l m x l m x l m n x l m n x m n x m n =+++++-++--+++ 2(1)[()(2)2()]x l m x l m n x m n =++++--+(1)(2)()x x lx mx m n =+++--【例题81】21(1)(3)2()(1)2xy xy xy x y x y +++-++-+- 【解析】 设xy u =,x y v +=,原式(1)(1)(1)(1)(1)(1)u v u v y x x y =+--+=++--【例题82】()()()()22222222ab cd a b c d ac bd a b c d +-+-+++--【分析】 原式()()()()()()()()22222222ab cd a d ab cd b c ac bd a d ac bd b c =+--+-++-++-()()()()()()()()()()()()()()()()()()()()222222ab cd ac bd a d ac bd ab cd b c a d b c a d a d b c d a b c b c a d b c a d b c a d b c a d b c a d b c =+++-++---=+++-+---+⎡⎤=-++--⎣⎦=-++-+++-【例题83】432234a b a b a b ab +--【分析】 ⑴原式432234332()()()()()()a b a b a b ab a b a b ab a b ab a b a b =+-+=+-+=-+【例题84】22(2)9x x -- 【分析】 原式222(23)(23)(23)(1)(3)x x x x x x x x =-+--=-++-【例题85】3139k +()1【分析】 原式2221(44)1(2)(12)(12)x xy y x y x y x y =--+=--=+--+【例题87】()()()333ax by by cz ax cz -+---【分析】 原式()()()333ax by bx cz cz ax =-+-+- ()()()3ax by bx cz cz ax =---【例题88】333()()()a b c bc b c ca c a ab a b ++++++++【分析】 原式222()()a b c a b c =++++【例题89】326116x x x +++【分析】 原式326126x x x x =-+++()()()21161x x x x =+-++()()()()22166156x x x x x x x =+-++=+++()()()()()21236123x x x x x x x =++++=+++【例题90】32254x x x +--【分析】 ()()()()232225515115x x x x x x x x x x =++--=+-+=++-【例题91】521171x x x +-+【分析】 设522321171(1)(1)x x x x ax x bx cx +-+=+-++-展开得5254321171()(1)(1)()1x x x x a b x ab c x ac b x a c x +-+=++++-+---++比较对应系数得0101117a b ab c ac b a c +=⎧⎪+-=⎪⎨--=⎪⎪+=⎩,解得225a b c =⎧⎪=-⎨⎪=⎩,∴原式232(21)(251)x x x x x =+--+-【例题92】54321x x x +-+【分析】 设()()5423232111x x x x ax x bx cx +-+=+++++展开得()()()()545432321111x x x x a b x ab c x b ac x a c x +-+=+++++++++++比较对应系数得31010a b ab c b ac +=⎧⎪++=⎪⎨++=⎪,解得12a b =⎧⎪=⎨⎪,∴原式()()2321231x x x x x =+++-+。
因式分解课后补习
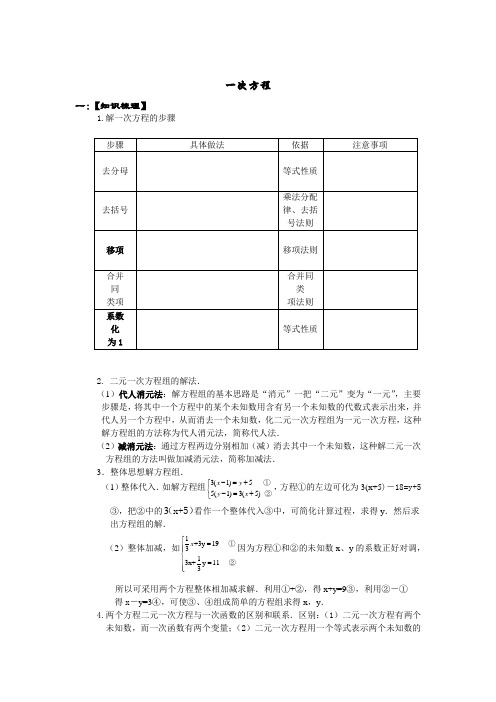
一次方程一:【知识梳理】1.解一次方程的步骤2. 二元一次方程组的解法.(1)代人消元法:解方程组的基本思路是“消元”一把“二元”变为“一元”,主要步骤是,将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代人另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代人消元法,简称代人法.(2)减消元法:通过方程两边分别相加(减)消去其中一个未知数,这种解二元一次方程组的方法叫做加减消元法,简称加减法. 3.整体思想解方程组. (1)整体代入.如解方程组3(1) 5 5(1)3(5) x y y x -=+⎧⎨-=+⎩①②,方程①的左边可化为3(x+5)-18=y+5③,把②中的3(x+5)看作一个整体代入③中,可简化计算过程,求得y .然后求出方程组的解.(2)整体加减,如1+3y 19 313x+y 11 3x ⎧=⎪⎪⎨⎪=⎪⎩①②因为方程①和②的未知数x 、y 的系数正好对调,所以可采用两个方程整体相加减求解.利用①+②,得x+y=9③,利用②-①得x -y=3④,可使③、④组成简单的方程组求得x ,y . 4.两个方程二元一次方程与一次函数的区别和联系.区别:(1)二元一次方程有两个未知数,而一次函数有两个变量;(2)二元一次方程用一个等式表示两个未知数的关系,而一次函数既可以用一个等式表示两个变量之间的关系,又可以用列表或图象来表示两个变量之间的关系. 联系:(1)在直角坐标系中分别描出以二元一次方程的解为坐标的点,这些点都在相应的一次函数的图象上;(2)在一次函数的图象上任取一点,它的坐标都适合相应的二元一次方程.(二):【课前练习】1. 若(32)x -∶2=(32)x +∶5,则x = 。
2. 如果235x -与233x -的值互为相反数,则x = 。
3. 已知11x y =⎧⎨=-⎩是方程组1242ax by x by +=⎧⎨-=⎩的解,则b a += 。
三十道因式分解练习题

三十道因式分解练习题一、提取公因式类1. 因式分解:$6x^2 + 9x$2. 因式分解:$8a^3 12a^2$3. 因式分解:$15xy 20xz$4. 因式分解:$21m^2n 35mn^2$5. 因式分解:$4ab^2 + 6a^2b$二、公式法类6. 因式分解:$x^2 9$7. 因式分解:$a^2 4$8. 因式分解:$4x^2 25y^2$9. 因式分解:$9m^2 16n^2$10. 因式分解:$25p^2 49q^2$三、分组分解类11. 因式分解:$x^3 + x^2 2x 2$12. 因式分解:$a^3 a^2 3a + 3$13. 因式分解:$3x^2 + 3x 2x 2$14. 因式分解:$4m^2 4m 3m + 3$15. 因式分解:$5n^3 10n^2 + 3n 6$四、十字相乘法类16. 因式分解:$x^2 + 5x + 6$17. 因式分解:$a^2 7a + 10$18. 因式分解:$2x^2 9x 5$20. 因式分解:$4n^2 13n + 3$五、综合运用类21. 因式分解:$x^3 2x^2 5x + 10$22. 因式分解:$a^3 + 3a^2 4a 12$23. 因式分解:$2x^2 + 5x 3$24. 因式分解:$3m^2 7m + 2$25. 因式分解:$4n^2 + 10n 6$六、特殊因式分解类26. 因式分解:$x^4 16$27. 因式分解:$a^4 81$28. 因式分解:$16x^4 81y^4$29. 因式分解:$25m^4 49n^4$30. 因式分解:$64p^4 81q^4$一、平方差公式类1. 因式分解:$x^2 25$2. 因式分解:$4y^2 9$3. 因式分解:$49z^2 100$4. 因式分解:$25a^2 121b^2$5. 因式分解:$16m^2 36n^2$二、完全平方公式类6. 因式分解:$x^2 + 8x + 16$7. 因式分解:$y^2 10y + 25$8. 因式分解:$z^2 + 14z + 49$10. 因式分解:$b^2 + 22b + 121$三、交叉相乘法类11. 因式分解:$x^2 + 7x + 12$12. 因式分解:$y^2 5y 14$13. 因式分解:$z^2 + 11z + 30$14. 因式分解:$a^2 13a 42$15. 因式分解:$b^2 + 17b + 60$四、多项式乘法公式类16. 因式分解:$x^3 + 3x^2 + 3x + 1$17. 因式分解:$y^3 3y^2 + 3y 1$18. 因式分解:$z^3 + 6z^2 + 12z + 8$19. 因式分解:$a^3 6a^2 + 12a 8$20. 因式分解:$b^3 + 9b^2 + 27b + 27$五、分组分解法类21. 因式分解:$x^4 + 4x^3 + 6x^2 + 4x + 1$22. 因式分解:$y^4 4y^3 + 6y^2 4y + 1$23. 因式分解:$z^4 + 8z^3 + 18z^2 + 8z + 1$24. 因式分解:$a^4 8a^3 + 18a^2 8a + 1$25. 因式分解:$b^4 + 12b^3 + 54b^2 + 108b + 81$六、多项式长除法类26. 因式分解:$x^5 x^4 2x^3 + 2x^2 + x 1$27. 因式分解:$y^5 + y^4 + 2y^3 2y^2 y + 1$28. 因式分解:$z^5 3z^4 + 3z^3 z^2 + z 1$29. 因式分解:$a^5 + 3a^4 3a^3 + a^2 a + 1$30. 因式分解:$b^5 5b^4 + 10b^3 10b^2 + 5b 1$答案一、提取公因式类1. $6x^2 + 9x = 3x(2x + 3)$2. $8a^3 12a^2 = 4a^2(2a 3)$3. $15xy 20xz = 5x(3y 4z)$4. $21m^2n 35mn^2 = 7mn(3m 5n)$5. $4ab^2 + 6a^2b = 2ab(2b + 3a)$二、公式法类6. $x^2 9 = (x + 3)(x 3)$7. $a^2 4 = (a + 2)(a 2)$8. $4x^2 25y^2 = (2x + 5y)(2x 5y)$9. $9m^2 16n^2 = (3m + 4n)(3m 4n)$10. $25p^2 49q^2 = (5p + 7q)(5p 7q)$三、分组分解类11. $x^3 + x^2 2x 2 = (x^2 + 2)(x 1)$12. $a^3 a^2 3a + 3 = (a^2 3)(a 1)$13. $3x^2 + 3x 2x 2 = (3x 2)(x + 1)$14. $4m^2 4m 3m + 3 = (4m 3)(m 1)$15. $5n^3 10n^2 + 3n 6 = (5n^2 3)(n 2)$四、十字相乘法类16. $x^2 + 5x + 6 = (x + 2)(x + 3)$17. $a^2 7a + 10 = (a 2)(a 5)$18. $2x^2 9x 5 = (2x + 1)(x 5)$19. $3m^2 + 11m + 4 = (3m + 1)(m + 4)$20. $4n^2 13n + 3 = (4n 1)(n 3)$五、综合运用类21. $x^3 2x^2 5x + 10 = (x^2 5)(x 2)$22. $a^3 + 3a^2 4a 12 = (a^2 + 4)(a 3)$23. $2x^2 + 5x 3 = (2x 1)(x + 3)$24. $3m^2 7m + 2 = (3m 1)(m 2)$25. $4n^2 + 10n 6 = (2n 1)(2n + 6)$六、特殊因式分解类26. $x^4 16 = (x^2 + 4)(x + 2)(x 2)$27. $a^4 81 = (a^2 + 9)(a + 3)(a 3)$28. $16x^4 81y^4 = (4x^2 + 9y^2)(2x + 3y)(2x 3y)$29. $25m^4 49n^4 = (5m^2 + 7n^2)(5m + 7n)(5m 7n)$30. $64p^4 81q^4 = (8p^2 + 9q^2)(4p + 3q)(4p 3q)$一、平方差公式类1. $x^2 25 = (x + 5)(x 5)$2. $4y^2 9 = (2y + 3)(2y 3)$3. $49z^2 100 = (7z + 10)(7z 10)$4. $25a。
《因式分解专题训练》有答案

因式分解专题训练一、整式有关概念:1.单项式(单个字母或数)(次数,系数);2.多项式(次数,项数)3.同类项与合并同类项二、幂的运算性质:1. n m n m aa a +=⋅ 2. ()mn n m a a = 3. ()n n nb a ab = 4. n n n b a b a =⎪⎭⎫ ⎝⎛ 5. n m n m a a a -=÷ 6. 10=a 7.p p a a 1=- 8. pp b a a b ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛- 三、整式的运算:加、减、乘、除(乘方、开方) 1. m (a+b+c )=ma+mb+mc 2. (a+b )(m+n )=am+an+bm+bn3. (a+b )(a-b )=22b a -4. ()2222a b ab a b +±=± 5. ()ca bc ab c b a c b a 2222222+++++=++ 6.()()3322b a b ab a b a ±=+± 7. ()()()ca bc ab c b a a c c b b a 222222222222+++++=+++++ 四、因式分解:1.把一个多项式化成几个整式的积的形式. 2.方法(一提二套三分组) (套公式包括十字相乘法)五、方法·规律·技巧:1.性质、公式的逆向使用;2.整体代入(配方、换元)3.非负数 的运用(配方)六、实际运用1.下列变形中,正确的是( )A. ()123422+-=+-x x xB. ()112+=+÷xx x x C. ()()22y x y x y x -=+--- D. xx x x -=-11 2.若n m n m b b a ++-224a 52与可以合并成一项,则nm 的值是( ) A. 2 B. 0 C. -1 D. 13.若22=+b a ,ab =2,则22b a +的值为( ) A. 6 B. 4 C. 23 D. 324.把多项式x x x 1212323+-分解因式,结果正解的是( )A. ()4432+-x x x B. ()243-x x C. ()()223-+x x x D. ()223-x x 5.已知0322=--x x ,则x x 422-的值为( )A. -6B. 6C. -2或6D. -2或306.下列等式从左到右的的变形,属于因式分解的是( )A. a (x-y )=ax-ayB.()12122++=++x x x xC. ()()34312++=++x x x xD. ()()11x 3-+=-x x x x7.因式分解:()()21622---x x x = .8.分解因式:(a-b )(a-4b )+ab = .9.分解因式:()9332--+x x x = . 10.分解因式:22my mx -= .11.多项式4x 2+1加上一个单项式后能成为一个完全平方式,请你写出符合条件的所有的单 项式: .12.计算:()20172016201642125.0⨯⨯-= . 13.已知===-n m n m a a a 4323,16,64则 .14.已知=+-=+-634x 964322x x x ,则 . 15.若()()222222,121y x y x y x +=-++= . 16、将下列各式分解因式:(1)x ax x 2842+-- (2)xy xy y x 2712322-+-(3)()b a b a +--22 (4)()()321612-+-x a x 17.将下列各式分解因式:(1)42161259y x - (2) 3394xy y x - (3)()()221162-++-x x (4)()()222516b a b a +--(5)2244y xy x -+- (6)22363ay axy ax ++(7)172x 4912+-x (8)()()9326322++-+y x y x (9)()()()()222510b a b a b a b a -+-+++ (10)()()1222222+-+-x x x x18.将下列各式分解因式: (1)232+-x x (2)1322++x x(3)22144y xy x -- (4)()()()32212-+-+-m x m x m 19.将下列各式分解因式:(1)()()a b y b a x -+-2249 (2)212+++-n n n x x x(3)()()xy y x41122--- (4)()133********-+-+-x x x x (5)()()15222222--+-x x x x (6)(x+1)(x+2)(x+3)(x+4)-12020.将下列各式分解因式:(1)9622-++-y x x (2)ab b a 44422-+-(3)2212b a a +--- (4)3223y xy y x x --+21.简便计算:(1)1323.16523.14823.1⨯⨯+⨯- (2)814.13125.06.18⨯+⨯ (3)2.48.1425.042.032⨯+⨯+⨯ (4)7582-2582 (5)99992+19998+1 (6)20162-2015×2017 (7)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-2222201611411311211 (8)420172014201320132016201420142016222-⨯-⨯-+ 22.已知()()()()137373212-----x x x x 可分解因式为()()b x a x ++3,其中a 、b 都是整数,求a+3b 的值.23.已知2222912x 4,010644y xy y x y x +-=++-+求的值.24.已知13,022232++=-+x x x x 求的值.25.已知n 为正整数,试说明n n 332-+能被24整除. 26.若()5522,,1,1n m n m n n m m +≠+=+=求的值.27.设()()222222211212,...,35,13--+=-=-=n n a a a n (n 是大于0的自然数)。
因式分解练习题及答案

因式分解练习题及答案在初中数学学习中,因式分解是一个重要的概念和技巧。
因式分解是将一个代数式写成若干个因式的乘积的过程,对于解决代数方程、简化复杂的代数式以及寻找多项式的零点都有重要的作用。
为了帮助大家更好地掌握因式分解的方法和技巧,以下是一些因式分解的练习题及答案。
练习题1:因式分解基础1. 将代数式完全分解:a) 4x^2 - 9b) x^2 - 6x + 9c) 2x^3 - 8x^2 + 8x - 322. 将代数式因式分解:a) x^2 - 5x + 6b) 9x^2 - 16c) x^3 + 83. 判断以下代数式是否可以进一步因式分解:a) 3x^2 - 3x + 1b) 4x^3 + 2x^2 + 4x + 2c) x^4 - 81练习题2:因式分解中的公式1. 利用差平方公式,将以下代数式因式分解:a) x^2 - 16b) 4x^2 - 9c) 16x^2 - 4y^22. 利用完全平方公式,将以下代数式因式分解:a) x^2 + 2x + 1b) x^2 - 10x + 25c) 4x^2 + 12x + 93. 利用立方差公式,将以下代数式因式分解:a) 27 - 8x^3b) 8x^3 - 27答案:练习题1:1. a) (2x + 3)(2x - 3)b) (x - 3)^2c) 2(x - 4)(x^2 + x + 4)2. a) (x - 2)(x - 3)b) (3x - 4)(3x + 4)c) (x + 2)(x^2 - 2x + 4)3. a) 不可以进一步因式分解b) 不可以进一步因式分解c) (x^2 + 9)(x - 3)(x + 3)练习题2:1. a) (x - 4)(x + 4)b) (2x - 3)(2x + 3)c) 4(x + y)(4x - y)2. a) (x + 1)^2b) (x - 5)^2c) (2x + 3)^23. a) (3 - 2x)(9 + 4x + 2x^2)b) (2x - 3)^3通过这些练习题和答案,你可以更好地掌握因式分解的方法和技巧。
因式分解专项练习100题及答案

因式分解专项练习100题及答案一、提取公因式(1) (61)(53)(61)(23)(61)(62)m n m n m n -++---+---(2) 424266x yz x y -(3) (72)(81)(72)(74)(72)(41)x x x x x x --++--++--(4) 444245a a x y -(5) 233332361515x y z x z x z ++(6) (53)(34)(53)(33)a b a b -----+(7) 323515a c bc +(8) 431216xyz xyz -(9) 431025c b c +(10) 3333189ax y a x y +(11) 324226a bc a b c -(12) 23341435a x y x -(13) (61)(25)(91)(61)x x x x -+-+-(14) 33434332816x y z y z y z ++(15) (32)(41)(32)(75)(32)(21)x x x x x x -++-++-+(16) (52)(2)(25)(52)m n n m +-++-+(17) (65)(43)(65)(64)x x x x +--+-(18) (85)(91)(85)(94)(85)(42)a b a b a b +--+++++-+(19) (23)(35)(23)(71)(23)(93)m n m n m n --+--++---(20) (35)(32)(35)(4)(35)(1)x x x x x x ---+-++-+二、公式法(21) 2212122x xy y -+(22) 22481a b -(23) 22784529x y -(24) 212396324x x -+(25) 22289121x y -(26) 2290064a b -(27) 2281450625m mn n -+(28) 2249238289m mn n ++(29) 225628881x x ++(30) 257664x -三、分组分解法(31) 281040xy x y --+(32) 8122842ab a b --+(33) 221635262124x y xy yz zx-++-(34) 21187060ax ay bx by +--(35) 2294221469a c ab bc ca ++--(36) 45352721mx my nx ny -+-(37) 2212621728a b ab bc ca --++(38) 863224xy x y -+-+(39) 4102870ab a b +++(40) 142070100ax ay bx by +--(41) 222720452057x z xy yz zx++--(42) 2273554426a b ab bc ca ++++(43) 302064xy x y ----(44) 4101640ax ay bx by --+(45) 2212354928x y xy yz zx -+--(46) 363060mx my nx ny --+(47) 424954xy x y -++-(48) 18168172ab a b --+(49) 2438010ab a b +++(50) 819182ax ay bx by -+-四、拆添项(51) 2281491268413a b a b -+++(52) 229143024m n m n -+++(53) 4224363316x x y y -+(54) 4224364716m m n n ++(55) 228191621277m n m n ---+(56) 22449249813x y x y ----(57) 422493364m m n n -+(58) 2264251289017m n m n -+--(59) 229643611213x y x y ----(60) 2281610827x y x y -+--五、十字相乘法(61) 223579424942x xy y x y ++--(62) 2228114254545x y z xy yz ---+(63) 22458835434510x xy y x y -++-+ (64) 22145521455025x xy y x y -++-+ (65) 2221261539236x xy y x y -----(66) 2216232876a ab b a b --+++(67) 22225424450x y z yz xz -++-(68) 2243014192912m mn n m n +++++(69) 221526713152m mn n m n ++--+(70) 222523x xy y x y +-+++(71) 22228630463111x y z xy yz xz +-+-+(72) 2222415821432x y z xy yz xz -+--+(73) 2285921556742m mn n m n -+-++(74) 22915412133x xy y x y ++--+(75) 22232237a b c ab bc ac -+---(76) 2159341515x xy x y ++++(77) 226271510174x xy y x y +---+(78) 22241128602624x xy y x y --+++(79) 22812839228x xy y x y +--++(80) 23036553025p pq p q --++六、双十字相乘法(81) 2223520245342x y z xy yz xz +--+-(82) 22273422113x y z xy yz xz +-+-+(83) 22256356212910x y z xy yz xz -----(84) 22228282065198a b c ab bc ac +-+-+(85) 22264212946x y z xy yz xz -----(86) 2214133592635x xy y x y -+-++(87) 22227493042769x y z xy yz xz -+-++(88) 2226184242711x y z xy yz xz +++--(89) 22243110472921x xy y x y ++---(90) 22228101827354a b c ab bc ac -++++七、因式定理 (91) 3222x x x +--(92) 321845192a a a -+-(93) 323744x x x +++(94) 3228115x x x +++(95)32--+671510y y y (96)3212351710++-x x x (97)32x x x+++526356 (98)32+++x x x157911745 (99)32-+-522236x x x (100)32--+35159x x x因式分解专项练习100题答案一、提取公因式 (1) (61)(32)m n --- (2) 426()x y z y - (3) (72)(114)x x --+ (4) 442(45)a x y - (5) 2333(255)x z y x ++ (6) (53)(67)a b --+ (7) 235(3)c a bc + (8) 34(34)xyz z - (9) 425(25)c b c + (10) 3229(2)ax y a y + (11) 32(3)a bc c ab - (12) 3237(25)x a y x - (13) (61)(74)x x --- (14) 33338(42)y z x z z ++ (15) (32)(137)x x -+ (16) (52)(3)m n +- (17) (65)(21)x x -+- (18) (85)(45)a b +-+ (19) (23)(137)m n ---(20) (35)(3)x x --+ 二、公式法 (21) 2(11)x y - (22) (29)(29)a b a b +- (23) (2823)(2823)x y x y +- (24) 2(1118)x - (25) (17)(17)x y x y +- (26) (308)(308)a b a b +- (27) 2(925)m n - (28) 2(717)m n + (29) 2(169)x + (30) (248)(248)x x +- 三、分组分解法 (31) 2(5)(4)x y -- (32) 2(27)(23)a b -- (33) (87)(253)x y x y z -+- (34) (310)(76)a b x y -+ (35) (7)(926)a c a b c -+- (36) (53)(97)m n x y +- (37) (4)(367)a b a b c +-+ (38) 2(4)(43)x y -+-(39) 2(7)(25)a b ++ (40) 2(5)(710)a b x y -+ (41) (94)(355)x z x y z -+- (42) (7)(756)a b a b c +++ (43) 2(51)(32)x y -++ (44) 2(4)(25)a b x y -- (45) (357)(47)x y z x y --+ (46) 3(10)(2)m n x y -- (47) (49)(6)x y --- (48) (29)(98)a b -- (49) (310)(81)a b ++ (50) (92)(9)a b x y +- 四、拆添项(51) (971)(9713)a b a b ++-+ (52) (32)(312)m n m n ++-+(53) 2222(694)(694)x xy y x xy y ++-+ (54) 2222(64)(64)m mn n m mn n ++-+ (55) (937)(9311)m n m n +--- (56) (271)(2713)x y x y ++-- (57) 2222(398)(398)m mn n m mn n ++-+ (58) (8517)(851)m n m n ++--(59) (381)(3813)x y x y ++-- (60) (99)(93)x y x y ++-- 五、十字相乘法 (61) (577)(76)x y x y +-+ (62) (925)(975)x y z x y z +--+ (63) (955)(572)x y x y -+-+ (64) (275)(735)x y x y -+-+ (65) (731)(356)x y x y ++-- (66) (832)(23)a b a b ++-+ (67) (524)(526)x y z x y z --+- (68) (423)(74)m n m n ++++ (69) (32)(571)m n m n +-+- (70) (23)(1)x y x y -+++ (71) (465)(76)x y z x y z +++- (72) (434)(652)x y z x y z ++-+ (73) (76)(837)m n m n ---- (74) (33)(341)x y x y +-+- (75) (2)(32)a b c a b c --+- (76) (533)(35)x y x +++ (77) (634)(51)x y x y --+- (78) (346)(874)x y x y -+++(79)(847)(24)x y x y--+-(80)(65)(565)p p q---六、双十字相乘法(81)(544)(756)x y z x y z-+--(82)(3)(74)x y z x y z+++-(83)(852)(773)x y z x y z++--(84)(745)(474)a b c a b c+-++ (85)(273)(364)x y z x y z--++ (86)(27)(735)x y x y----(87)(975)(376)x y z x y z++-+ (88)(334)(26)x y z x y z+-+-(89)(853)(327)x y x y+++-(90)(456)(723)a b c a b c++-+七、因式定理(91)(1)(1)(2)x x x+-+(92)(2)(61)(31)a a a---(93)2(2)(32)x x x+++(94)2(1)(265)x x x+++(95)2(2)(655)y y y-+-(96)(2)(31)(45)x x x+-+ (97)(3)(51)(2)x x x+++(98)(3)(35)(53)x x x+++ (99)(1)(52)(3)x x x---(100)2(3)(343)x x x-+-。
因式分解全章练习题

因式分解练习题一、提取公因式专项训练一:确定下列各多项式的公因式。
1、ay ax +2、36mx my -3、2410a ab +4、2155a a +5、22x y xy -6、22129xyz x y -7、()()m x y n x y -+-8、()()2x m n y m n +++9、3()()abc m n ab m n --- 10、2312()9()x a b m b a --- 专项训练二:利用乘法分配律的逆运算填空。
1、22____()R r R r ππ+=+2、222(______)R r πππ+=3、2222121211___()22gt gt t t +=+ 4、2215255(_______)a ab a +=专项训练三、在下列各式左边的括号前填上“+”或“-”,使等式成立。
1、__()x y x y +=+ 2、__()b a a b -=- 3、__()z y y z -+=- 4、()22___()y x x y -=- 5、33()__()y x x y -=- 6、44()__()x y y x --=- 7、22()___()()n n a b b a n -=-为自然数 8、2121()___()()n n a b b a n ++-=-为自然数9、()1(2)___(1)(2)x y x y --=-- 10、()1(2)___(1)(2)x y x y --=-- 11、23()()___()a b b a a b --=- 12、246()()___()a b b a a b --=- 专项训练四、把下列各式分解因式。
(单项式因式分解)1、23222515x y x y - 6、22129xyz x y - 7、2336a y ay y -+8、259a b ab b -+ 9、2x xy xz -+- 10、223241228x y xy y --+11、323612ma ma ma -+- 12、32222561421x yz x y z xy z +-13、3222315520x y x y x y +- 14、432163256x x x --+专项训练五:把下列各式分解因式。
人教版八年级数学上册因式分解课后训练

人教版八年级数学上册因式分解课后训练基础巩固1.下列各式从左到右的变形中,是因式分解的为〖〗.A.x〖a-b〗=ax-bx B.x2-1+y2=〖x-1〗〖x+1〗+y2C.x2-1=〖x+1〗〖x-1〗D.ax+bx+c=x〖a+b〗+c2.把x3-xy2分解因式,正确的结果是〖〗.A.〖x+xy〗〖x-xy〗B.x〖x2-y2〗C.x〖x-y〗2 D.x〖x-y〗〖x+y〗3.下列多项式能进行因式分解的是〖〗.A.x2-y B.x2+1C.x2+y+y2D.x2-4x+44.把多项式m2〖a-2〗+m〖2-a〗分解因式等于〖〗.A.〖a-2〗〖m2+m〗B.〖a-2〗〖m2-m〗C.m〖a-2〗〖m-1〗D.m〖a-2〗〖m+1〗5.下列各式中不能用平方差公式分解的是〖〗.A.-a2+b2B.-x2-y2C.49x2y2-z2D.16m4-25n26.下列各式中能用完全平方公式分解的是〖〗.①x2-4x+4;②6x2+3x+1;③4x2-4x+1;④x2+4xy+2y2;⑤9x2-20xy+16y2‘A.①②B.①③C.②③D.①⑤7.把下列各式分解因式:〖1〗9x3y2-12x2y2z+3x2y2;〖2〗2a〖x+1〗2-2ax;〖3〗16x2-9y2;〖4〗〖x+2〗〖x+3〗+x2-4‘能力提升8.若m-n=-6,mn=7,则mn2-m2n的值是〖〗.A.-13 B.13 C.42 D.-429.若x2+mx-15=〖x+3〗〖x+n〗,则m的值为〖〗.A.-5 B.5 C.-2 D.210.若x2-ax-1可以分解为〖x-2〗〖x+b〗,则a+b的值为〖〗.A.-1 B.1 C.-2 D.211.若16x2+mxy+9y2是一个完全平方式,那么m的值是〖〗.A.12 B.24 C.±12 D.±2412.分解因式〖x-3〗〖x-5〗+1的结果是〖〗.A.x2-8x+16 B.〖x-4〗2 C.〖x+4〗2 D.〖x-7〗〖x-3〗13.分解因式3x2-3y4的结果是〖〗.A.3〖x+y2〗〖x-y2〗B.3〖x+y2〗〖x+y〗〖x-y〗C.3〖x-y2〗2 D.3〖x-y〗2〖x+y〗214.若a+b=-1,则3a2+3b2+6ab的值是〖〗.A.-1 B.1 C.3 D.-315.-6x n-3x2n分解因式正确的是〖〗.A.3〖-2x n-x2n〗B.-3x n〖2+x n〗C.-3〖2x n+x2n〗D.-3x n〖x n+2〗16.把下列各式分解因式:〖1〗x〖x-5〗2+x〖-5+x〗〖x+5〗;〖2〗〖a+2b〗2-a2-2ab;〖3〗-2〖m-n〗2+32;〖4〗-x3+2x2-x;〖5〗4a〖b-a〗-b2;〖6〗2x3y+8x2y2+8xy3‘17.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.〖1〗28和2 012这两个数是神秘数吗?为什么?〖2〗设两个连续偶数为2k+2和2k 〖其中k取非负整数〗,由这两个连续偶数构造的神秘数是4的倍数吗?为什么?〖3〗两个连续奇数的平方差〖取正数〗是神秘数吗?为什么?参考答案1.C 2‘D 3‘D 4‘C 5‘B 6‘B7.解:〖1〗原式=3x2y2〖3x-4z+1〗;〖2〗原式=2a〖x2+x+1〗.〖3〗原式=〖4x+3y〗〖4x-3y〗;〖4〗方法一:原式=〖x+2〗〖x+3〗+〖x+2〗〖x-2〗=〖x+2〗〖x+3+x-2〗=〖x+2〗〖2x+1〗方法二:原式=x2+5x+6+x2-4=2x2+5x+2=〖x+2〗〖2x+1〗.8.C 9‘C 10‘D 11‘D 12‘B 13‘A 14‘C 15‘B16.解:〖1〗原式=x〖x-5〗2+x〖x-5〗〖x+5〗=x〖x-5〗[〖x-5〗+〖x+5〗]=2x2〖x-5〗;〖2〗原式=a2+4ab+4b2-a2-2ab=2ab+4b2=2b〖a+2b〗;〖3〗原式=-2[〖m-n〗2-16]=-2〖m-n+4〗〖m-n-4〗;〖4〗原式=-x〖x2-2x+1〗=-x〖x-1〗2;〖5〗原式=4ab-4a2-b2=-〖4a2-4ab+b2〗=-〖2a-b〗2‘〖6〗原式=2xy〖x2+4xy+4y2〗=2xy〖x+2y〗2‘17.解:〖1〗因为28=82-62;2 012=5042-5022,所以28和2 012是神秘数.〖2〗因为〖2k+2〗2-〖2k〗2=4〖2k+1〗,所以由2k+2和2k构造的神秘数是4的倍数.〖3〗由〖2〗知神秘数可表示为4的倍数,但一定不是8的倍数,设两个连续奇数为2k +1和2k-1〖k取正整数〗,而〖2k+1〗2-〖2k-1〗2=8k,即两个连续奇数的平方差不是神秘数.。
因式分解经典练习100道及答案

因式分解经典练习100道及答案一、提取公因式(1)3332-4518ab c a b c(2)334434343++243024x y z x y z x y z(3)(94)(92)(1)(94)--+----x x x x(4)(83)(2)(83)(75)-+---m x m x(5)(51)(5)(51)(54)(51)(31)--++--++---m n m n m n(6)344c b c+630(7)(3)(52)(3)(51)(3)(93)---+--++-+x x x x x x(8)334+412ac a c(9)2443+x y ax y(10)(54)(95)(54)(21)(54)(35)x x x x x x+-+++--+++ (11)44324++142835x z x yz x yz(12)2342-a x y a xy1220(13)2423+2012a b c a bc(14)43242-+20520x y x y z xyz(15)(41)(31)(41)(84)---+-+a b a b(16)33-xz y4016(17)(41)(45)(41)(52)+++++m x m x(18)(94)(83)(55)(94)m n n m ----+-(19)2232718x y z xyz-(20)222242x z x y z+二、公式法(21)2249369849x y x -+-(22)22144600625a ab b -+(23)228114464m n m -+-(24)224001160841a ab b ++(25)22361529a b -(26)22x y-121289(27)2x-814(28)212136x-(29)22-+78428025a ab b(30)22-+m mn n48422025三、分组分解法(31)48321812--++xy x y(32)22----a c ab bc ca5435543033 (33)221+--ab a b(34)22+-+-7653043a c ab bc ca(35)22x y xy yz zx+--+3512443035 (36)35257050+--ax ay bx by (37)3287218xy x y-++-(38)20410020+--ax ay bx by (39)48564856-+-mx my nx ny (40)40408080--+xy x y(41)22x y xy yz zx-++-2430163542 (42)22---+x y xy yz zx2449144928 (43)8756-+-ax ay bx by(44)2216538216a b ab bc ca----(45)2212353541a c ab bc ca+-+-(46)81648ax ay bx by+--(47)227228271231a c ab bc ca-+-+(48)224220591221a b ab bc ca++++(49)221851249x z xy yz zx----(50)63362112mx my nx ny--+四、拆添项(51)424169x x -+(52)2216162455a b a b --++(53)22362524305x y x y --+-(54)2281161081632a b a b --++(55)222581609011m n m n ---+(56)422442125x x y y -+(57)226469627x y x y ----(58)42244910516x x y y -+(59)4225111x x -+(60)42246416149m m n n -+五、十字相乘法(61)22+-+++x xy y x y20196441824 (62)222+-+++x y z xy yz xz3621575841 (63)22---+x xy y x y251083528 (64)222x y z xy yz xz-+--+635826646 (65)22--+++x xy y x y24112847820 (66)22x xy y x y+--++4536831328 (67)22x xy y x y---++1612422127 (68)22++--+ 284715654128x xy y x y(69)22569359192m mn n m n ---+-(70)22491435145824p pq q p q --++-(71)2235692829296x xy y x y -++-+(72)2221401627206x xy y x y +++++(73)22921101576x xy y x y ++++-(74)22213723112x xy y x y --++-(75)22228216612329a b c ab bc ac+++--(76)2225421221218x y z xy yz xz+-+++(77)2225465602921a b c ab bc ac+-+--(78)222204912634932x y z xy yz xz++--+(79)2282620324930x xy y x y -++-+(80)2223018621328x y z xy yz xz-+--+六、双十字相乘法(81)2291481586x xy y x y ---++(82)2228152537512x xy y x y +-+++(83)22251418173627a b c ab bc ac+--+-(84)22104121284016x xy y x y +++++(85)2224652137x xy y x y-++-(86)22291216243224a b c ab bc ac+++++(87)22991024337a ab b a b ---++(88)222091943x xy y x y +++++(89)2236306242521x xy y x y -----(90)225272822368x xy y x y -+-++七、因式定理(91)33112x x --(92)322163a a a --+(93)321257360x x x +-+(94)3266132x x x --+(95)32331315x x x ---(96)321624196x x x --+(97)321037960x x x +--(98)324721x x x ++-(99)32472x x x ---(100)324x x -+因式分解经典练习100道答案一、提取公因式(1)2229(52)ab c bc a-(2)3336(454)x y z z xz y++ (3)(94)(103)x x---(4)(83)(67)m x---(5)(51)(98)m n--+(6)346(15)c b c+(7)(3)(2)x x--+(8)324(13)ac a c+(9)232()x y y ax+(10)(54)(89)x x+-+ (11)22337(245)x z x z xy yz++ (12)2224(35)a xy x a y-(13)2324(53)a bcb c+(14)32325(44)xy x y xy z z-+(15)(41)(53)a b-+(16)338(52)xz y-(17)(41)(97)m x++(18)(94)(138)m n--+ (19)29(32)xyz xyz-(20)222(2)x z z y+二、公式法(21)(767)(767)x y x y++-+ (22)2(1225)a b-(23)(98)(98)m n m n++-+ (24)2(2029)a b+(25)(1923)(1923)a b a b+-(26)(1117)(1117)x y x y+-(27)(92)(92)x x+-(28)(116)(116)x x+-(29)2(285)a b-(30)2(225)m n-三、分组分解法(31)2(83)(32)x y--+(32)(667)(95)a b c a c--+(33)(21)(1)a b-+(34)(6)(75)a c ab c---(35)(76)(525)x y x y z--+(36)5(2)(75)a b x y-+ (37)2(49)(41)x y---(38)4(5)(5)a b x y-+(39)8()(67)m n x y+-(40)40(2)(1)x y--(41)(467)(65)x y z x y+--(42)(677)(47)x y z x y++-(43)(7)(8)a b x y+-(44)(252)(8)a b c a b--+(45)(35)(47)a c ab c---(46)4(2)(2)a b x y-+(47)(94)(837)a c ab c-++(48)(74)(653)a b a b c+++(49)(3)(645)x z x y z+--(50)3(3)(74)m n x y--四、拆添项(51)22(223)(223)x x x x+---(52)(411)(45)a b a b+---(53)(655)(651)x y x y+--+(54)(948)(944)a b a b+---(55)(591)(5911)m n m n+---(56)2222(25)(25)x xy y x xy y+---(57)(83)(89)x y x y++--(58)2222(774)(774)x xy y x xy y+---(59)22(51)(51)x x x x+---(60)2222(877)(877)m mn n m mn n+---五、十字相乘法(61)(44)(566)x y x y-+++(62)(93)(475)x y z x y z+-++(63)(54)(527)x y x y-+-(64)(72)(954)x y z x y z++-+(65)(344)(875)x y x y-+++(66)(934)(527)x y x y--+-(67)(221)(827)x y x y--+-(68)(734)(457)x y x y+-+-(69)(752)(871)m n m n+--+(70)(776)(754)p q p q-++-(71)(743)(572)x y x y-+-+(72)(742)(343)x y x y++++(73)(356)(321)x y x y+++-(74)(24)(73)x y x y+--+(75)(473)(732)a b c a b c+-+-(76)(62)(926)x y z x y z+-++(77)(66)(95)a b c a b c+++-(78)(573)(474)x y z x y z-+-+(79)(456)(245)x y x y-+-+ (80)(563)(632)x y z x y z-+++六、双十字相乘法(81)(946)(21)x y x y+---(82)(453)(754)x y x y++-+(83)(26)(573)a b c a b c---+ (84)(534)(274)x y x y++++ (85)(831)(37)x y x y-+-(86)(364)(324)a b c a b c++++(87)(327)(351)a b a b+---(88)(51)(43)x y x y++++ (89)(667)(63)x y x y--++(90)(44)(572)x y x y----七、因式定理(91)2(2)(361)x x x-++ (92)2(3)(251)a a a-+-(93)(3)(34)(45)x x x+--(94)2(2)(661)x x x-+-(95)2(3)(365)x x x-++ (96)(2)(43)(41)x x x-+-(97)(3)(54)(25)x x x-++ (98)2(1)(41)x x+-(99)2(2)(41)x x x-++ (100)2(2)(22)x x x+-+。
21.2.3因式分解法课后练「含答案」

1.一元二次方程(1)2(1)x x x -=-的解完全正确的是( )A .2x =B .122,1x x ==C .122,1x x =-=D .123,1x x ==-2.方程23x x =的解是( )A .0x =B .13x =C .113x =-,20x =D .113x =,20x =3.已知a b c ,,满足0,420a b c a b c ++=++=,则关于x 的一元二次方程20(0)ax bx c a ++=¹的解的情况为( )A .121,2x x ==B .121,2x x =-=-C .方程的解与a b ,的取值有关D .方程的解与a b c ,,的取值有关4.若实数x 满足方程()()22280x x x x +×+--=,那么2x x +的值为( )A .2-B .4C .2-或4D .2或4-5.如图,在ABCD Y 中,AE BC ^于点E ,BE a =,2AE CE a ==,且a 是一元二次方程2340x x +-=的根,则ABCD Y 的周长为( )A .6+B .8C .10D .4+6.如果2368x x +-的值与221x -的值相等,则x = .7.一元二次方程()()240x x --=的较大的根是 .8.定义:如果关于x 的一元二次方程20ax bx c ++=有两个实数根为a b ,,且满足2a b =,则称这样的方程为“倍根方程”.(1)方程 29180x x -+= (选填“是”或“不是”)“倍根方程”.(2)若()()50x x a --=是“倍根方程”,则=a9.一个菱形的边长是方程29180x x -+=的一个根其中一条对角线长为6,则该菱形的面积为 .10.解方程.(1)220x -=(公式法);(2)22330x x +-=(配方法);(3)()()22221y y +=+(因式分解法).11.已知关于x 的一元二次方程()22210x k x k k -+++=.(1)求证:方程有两个不相等的实数根;(2)若ABC V 的两边,AB AC 的长是这个方程的两个实数根,第三边BC 的长为5,当ABC V 是直角三角形时,求k 的值.12.阅读下面的材料,回答问题:解方程42540x x -+=,这是一个一元四次方程,根据该方程的特点,它的解法通常是:设2x y =,那么42x y =,于是原方程可变为2540y y -+=①,解得11y =,24y =.当1y =时,21x =,1x \=±;当4y =时,24x =,2x \=±;\原方程有四个根:11x =,21x =-,32x =,42x =-.这一方法,在由原方程得到方程①的过程中,利用“换元法”达到降次的目的,体现了数学的转化思想.(1)方程4260x x --=的解为________.(2)仿照材料中的方法,尝试解方程()()2224120x x x x +-+-=.【分析】此题考查了解一元二次方程,利用因式分解法解一元二次方程即可得到答案.【详解】解:∵(1)2(1)x x x -=-,∴(1)(2)0x x --=,∴20x -=或10x -=,∴1221x x ==,,故选:B .2.D【分析】本题考查了一元二次方程的解法,熟悉其解法是解决问题的关键.利用因式分解法解一元二次方程即可.【详解】解:Q 23x x =,\ 230x x -=,即(31)0x x -=,\ 113x =,20x =,故选:D .3.A【分析】根据已知条件求出a b c 、、之间的关系,代入方程即可解答.本题考查了一元二次方程的概念及利用因式分解法解一元二次方程,理解一元二次方程的概念是解题的关键.【详解】解:∵0a b c ++=,420a b c ++=,∴a c b +=-①,42a c b +=-②,∴-②①得3b a =-,将3b a =-代入0a b c ++=得:30a a c -+=,∴2c a =,将3b a =-,2c a =代入20(0)ax bx c a ++=¹得:()2320a x x -+=,∵0a ¹,∴2320x x -+=,∴()()120x x --=,解得121,2x x ==,故选A .【分析】此题考查了换元法解一元二次方程.设2y x x =+,则原方程转化为关于y 的新方程,通过解新方程来求y 的值,即2x x +的值.【详解】解:设2y x x =+,原方程变形为()280y y --=,整理得:2280y y --=,解得:1242y y ==-,,当14y =时,24x x +=,即240x x +-=,此时()21414170D =-´´-=>;当22y =-时,22x x +=-,即220x x ++=,此时2141270D =´´=-<-;此时方程220x x ++=无解;∴24x x +=.故选:B5.A【分析】本题考查了平行四边形的性质,勾股定理,以及用因式分解法解一元二次方程,是基础知识要熟练掌握.先解方程求得a ,再根据勾股定理求得AB ,从而计算出ABCD Y 的周长即可.【详解】解:a Q 是一元二次方程2340x x +-=的根,2340a a \+-=,即()()140a a -+=,解得,1a =或4a =-(不合题意,舍去).∴1BE =,2AE CE ==,在Rt ABE △中,AB ===,3BC EB EC \=+=,ABCD \Y 的周长())2236AB BC =+==+故选:A .6.7-或1【分析】本题主要考查解一元二次方程,解一元一次方程,等式的性质等知识,根据题意得到方程2236821x x x +-=-,求出方程的解即可.【详解】解:根据题意得:2236821x x x +-=-,∴2670x x +-=,分解因式得:(7)(1)0x x +-=,∴70x +=,10x -=,解方程得:17x =-,21x =.故答案为:7-或1.7.4x =【分析】本题主要考查了用因式分解法解一元二次方程,先运用因式分解法解一元二次方程,再根据两根的大小得到较大的根,这种方法简便易用,是解一元二次方程最常用的方法.【详解】解:(2)(4)0x x --=20x \-=或40x -=,解得12x =,24x =,\较大的根是4x =,故答案为:4x =.8. 是 10或52【分析】本题主要考查了解一元二次方程,新定义:(1)利用因式分解法求出方程的两个根,再根据“倍根方程”的定义求解即可;(2)先解方程得到125x a x ==,,再根据“倍根方程”的定义求解即可.【详解】解:(1)∵29180x x -+=,∴()()360x x --=,解得1236x x ==,,∴212x x =,∴方程 29180x x -+=是 “倍根方程”.故答案为:是;(2)解方程()()50x x a --=得125x a x ==,,∵()()50x x a --=是“倍根方程”,∴2510a =´=或15522a =´=,故答案为:10或52.9.【分析】本题考查了因式分解法解一元二次方程、菱形的性质、勾股定理,先解方程得出16x =,23x =,结合一条对角线长为6得出菱形的边长为6,利用勾股定理得出菱形的另一条对角线为=,再由面积公式计算即可.【详解】解:29180x x -+=Q ,()()630x x \--=,解得:16x =,23x =,Q 菱形一条对角线长为6,\菱形的边长为6,\菱形的另一条对角线为=\菱形的面积为162´´=故答案为:10.(1)12x x ==(2)1x =2x =(3)11y =-,21y =.【分析】本题考查解一元二次方程,(1)根据公式法直接求解即可;(2)先将二次项系数化为1,再移项,再进行配方,最后开平方即可求解;(3)先进行移项,再利用平方差公式进行因式分解即可求解.【详解】(1)解:220x -=,1a =,b =-2c =,∵2244120b ac -=--´´=,∴x ==,∴12x x ==(2)解:22330x x +-=两边都除以2,得233022x x +-=.移项,得23322x x +=.配方,得22233332424x x æöæö++=+ç÷ç÷èøèø,即2333416x æö+=ç÷èø,开平方,得34x +=即x x ∴1x =2x (3)解:原方程可变形为()()222210y y +-+=.∴()()2212210y y y y ++++--=.∴330y +=,10y -=,∴11y =-,21y =.11.(1)见解析(2)k 的值为12或3【分析】本题考查一元二次方程综合,涉及一元二次方程根的情况与判别式关系,一元二次方程根与直角三角形结合等,熟练掌握一元二次方程相关定义与性质是解决问题的关键.(1)根据方程的系数结合根的判别式,可得出10D =>进而可证出方程有两个不相等的实数根;(2)利用因式分解法可求出,AB AC 的长,分BC 为直角边及BC 为斜边两种情况,利用勾股定理可得出关于k 的一元一次方程或一元二次方程解之即可得出k 值,取其正值(利用三角形的三边关系判定其是否构成三角形)即可得出结论.【详解】(1)由题意得:22[(21)]4()10k k k D =-+-´+=>∴方程有两个不相等的实数根(2)∵()22210x k x k k -+++=,即()[(1)]0x k x k --+=解得:12,1x k x k ==+当BC 为直角边时,2225(1)k k +=+,解得:12k =当BC 为斜边时,222(1)5k k ++=,解得:123,4k k ==-(不合题意,舍)综上:k 的值为12或312.(1)1x =2x =(2)13x =-,22x =;【分析】本题考查了根的判别式,换元法解一元二次方程,能够正确换元是解此题的关键.(1)结合材料,利用2x m =,再换元,求出m 的值,再代入求出x 即可;(2)结合材料,利用2x x n +=,再换元,求出n 的值,再代入求出x 即可.【详解】(1)解:设2x m =,则原方程变为260m m --=,解得:13m =,22m =-,当3m =时,23x =,解得x =当2m =-时,22x =-,方程无解;故原方程的解为:1x =2x =,故答案为:1x =2x =.(2)解:设2x x n +=,则原方程变为24120--=n n ,解得:16n =,22n =-,当6n =时,26x x +=,解得:13x =-,22x =;当2n =-时,22x x +=-,即220x x ++=,Q 2141270D =´´=-<-,\方程无解;故原方程的解为:13x =-,22x =.。
人教版八年级上册数学《第十四章 14.3 因式分解》课后练习(含答案)

八年级上册数学《第十四章14.3因式分解》课后练习一、单选题1.下列各选项中因式分解正确的是()A.B.C.D.2.下列运算不正确的是()A.B.C.D.3.下列各式中,哪项可以使用平方差公式分解因式()A.B.C.D.4.多项式12ab3c+8a3b的公因式是()A.4ab2B.4abc C.2ab2D.4ab5.若,则().A.是完全平方数,还是奇数B.是完全平方数,还是偶数C.不是完全平方数,但是奇数D.不是完全平方数,但是偶数6.设,,则,的大小关系是().A.B.C.D.无法确定二、填空题7.因式分解:______.8.因式分解:﹣x2﹣4y2+4xy=_____.9.若整式(为常数,且)能在有理数范围内分解因式,则的值可以是_____(写一个即可).10.若,则的值为_____.11.因式分解:_____.12.当时,代数式的值是_____.13.满足的整数对,共有______对.三、解答题14.分解因式:(1);(2);(3).15.先化简,再求值:,其中16.解下列各题:(1)分解因式:9a2(x﹣y)+4b2(y﹣x);(2)甲,乙两同学分解因式x2+mx+n,甲看错了n,分解结果为(x+2)(x+4);乙看错了m,分解结果为(x+1)(x+9),请分析一下m,n的值及正确的分解过程.17.在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的6位数密码就很有必要了.有一种用“因式分解法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x3+2x2﹣x﹣2因式分解的结果为(x﹣1)(x+1)(x+2),当x=18时,x﹣1=17,x+1=19,x+2=20,此时可以得到数字密码171920.(1)根据上述方法,当x=21,y=7时,对于多项式x3﹣xy2分解因式后可以形成哪些数字密码?(写出两个)(2)若多项式x3+(m﹣3n)x2﹣nx﹣21因式分解后,利用本题的方法,当x=27时可以得到其中一个密码为242834,求m、n的值.18.阅读材料:把形ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2.请根据阅读材料解决下列问题:(1)填空:a2﹣4a+4=.(2)若a2+2a+b2﹣6b+10=0,求a+b的值.(3)若a、b、c分别是△ABC的三边,且a2+4b2+c2﹣2ab﹣6b﹣2c+4=0,试判断△ABC 的形状,并说明理由.19.仔细阅读下面例题,解答问题:例题,已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.解:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),则x2-4x+m=x2+(n+3)x+3n.∴,解得n=-7,m=-21,∴另一个因式为(x-7),m的值为-21.问题:仿照以上方法解答下面问题:已知二次三项式3x2+5x-m有一个因式是(3x-1),求另一个因式以及m的值.20.阅读下列材料解决问题:将下图一个正方形和三个长方形拼成一个大长方形,观察这四个图形的面积与拼成的大长方形的面积之间的关系.∵用间接法表示大长方形的面积为:,用直接法表示面积为:∴于是我们得到了可以进行因式分解的公式:(1)运用公式将下列多项式分解因式:①,②;(2)如果二次三项式“”中的“”只能填入有理数1,2,3,4,并且填入后的二次三项式能进行因式分解,请你写出所有的二次三项式.答案1.D2.B3.B4.D5.A6.B 7.8.﹣(x﹣2y)29.-110.411.12.13.314.解(1)原式=x4+2x2+1-x2=(x2+1)2-x2=(x2+1+x)(x2+1-x)(2)原式=x3-16x+5x+20=x(x+4)(x-4)+5(x+4)=(x+4)(x2-4x+5).(3)原式=a3+3a2b+3ab2+b3+c3-3abc-3a2b-3ab2=(a+b)3+c3-3ab(a+b+c)=(a+b+c)[(a+b)2-(a+b)c+c2]-3(a+b+c)ab=(a+b+c)[(a+b)2-ac-bc+c2-3ab]=(a+b+c)(a2+b2+c2-ab-bc-ca).15.解:原式.∵,∴原式.16.解:(1)原式=9a2(x﹣y)﹣4b2(x﹣y)=(x﹣y)(9a2﹣4b2)=(x﹣y)(3a+2b)(3a﹣2b);(2)∵(x+2)(x+4)=x2+6x+8,甲看错了n,∴m=6.∵(x+1)(x+9)=x2+10x+9,乙看错了m,∴n=9,∴x2+mx+n=x2+6x+9=(x+3)2.17.解(1)x3﹣xy2=x(x2﹣y2)=x(x+y)(x﹣y),当x=21,y=7时,x+y=28,x﹣y=14,∴可以形成的数字密码是:212814、211428;(2)设x3+(m﹣3n)x2﹣nx﹣21=(x+p)(x+q)(x+r),∵当x=27时可以得到其中一个密码为242834,∴27+p=24,27+q=28,27+r=34,解得,p=﹣3,q=1,r=7,∴x3+(m﹣3n)x2﹣nx﹣21=(x﹣3)(x+1)(x+7),∴x3+(m﹣3n)x2﹣nx﹣21=x3+5x2﹣17x﹣21,∴得,即m的值是56,n的值是17.18.解:,故答案为:;,,,,;为等边三角形,理由如下:,,,,,为等边三角形.19.解:设另一个因式为(x+n),则3x2+5x-m=(3x-1)(x+n),则3x2+5x-m=3x2+(3n-1)x-n,∴,解得n=2,m=2,∴另一个因式为(x+2),m的值为2. 20.解(1)①=;=;(2),。
专题14.6 因式分解专项训练(30道)

专题14.6 因式分解专项训练(30道)【人教版】1.(2021春•拱墅区校级期中)因式分解(1)﹣a2+1;(2)2x3y+4x2y2+2xy3;(3)4(x+2y)2﹣25(x﹣y)2;(4)(a2+a)2﹣8(a2+a)+12.【解题思路】(1)逆用平方差公式进行因式分解.(2)先逆用平方差公式,再提公因式.(3)先逆用平方差公式,再提公因式.(4)运用十字相乘法进行因式分解,注意分解彻底.【解答过程】解:(1)﹣a2+1=(1+a)(1﹣a).(2)2x3y+4x2y2+2xy3=2xy(x2+2xy+y2)=2xy(x+y)2.(3)4(x+2y)2﹣25(x﹣y)2=[2(x+2y)+5(x﹣y)][2(x+2y)﹣5(x﹣y)]=(2x+4y+5x﹣5y)(2x+4y﹣5x+5y)=(7x﹣y)(﹣3x+9y)=﹣3(7x﹣y)(x﹣3y).(4)(a2+a)2﹣8(a2+a)+12=(a2+a﹣2)(a2+a﹣6)=(a+2)(a﹣1)(a+3)(a﹣2).2.(2021秋•拜泉县期中)因式分解(1)6x2﹣3x;(2)16m3﹣mn2;(3)25m2﹣10mn+n2;(4)9a2(x﹣y)+4b2(y﹣x).【解题思路】(1)原式提取公因式3x,分解即可;(2)原式提取公因式m,再利用平方差公式分解即可;(3)原式利用完全平方公式分解即可;(4)原式变形后,提取公因式(x﹣y),再利用平方差公式分解即可.【解答过程】解:(1)6x2﹣3x=3x(2x﹣1);(2)16m3﹣mn2=m(16m2﹣n2)=m(4m+n)(4m﹣n);(3)25m2﹣10mn+n2=(5m﹣n)2;(4)9a2(x﹣y)+4b2(y﹣x)=9a2(x﹣y)﹣4b2(x﹣y)=(x﹣y)(9a2﹣4b2)=(x﹣y)(3a+2b)(3a﹣2b).3.(2021秋•浠水县月考)分解因式:(1)3pq3+15p3q;(2)ab2﹣a;(3)4xy2﹣4x2y﹣y3;(4)(a2+1)2﹣4a2.【解题思路】(1)原式提取公因式3pq即可;(2)原式提取公因式a,再利用平方差公式分解即可;(3)原式提取公因式﹣y,再利用完全平方公式分解即可;(4)原式利用平方差公式,以及完全平方公式分解即可.【解答过程】解:(1)3pq3+15p3q=3pq(q2+5p2);(2)ab2﹣a=a(b2﹣1)=a(b+1)(b﹣1);(3)4xy2﹣4x2y﹣y3=﹣y(2x﹣y)2;(4)(a2+1)2﹣4a2=(a2+1+2a)(a2+1﹣2a)=(a+1)2(a﹣1)2.4.(2021秋•绿园区校级月考)把下列多项式分解因式.(1)3x2﹣3y2.(2)a2b+2ab2+b3.(3)(m﹣1)(m﹣3)+1.(4)2a2+4ab+2b2.【解题思路】(1)先提公因式,再利用平方差公式即可;(2)先提公因式,再利用完全平方公式即可;(3)先计算多项式乘多项式,整理后,再利用完全平方公式即可;(4)先提公因式,再利用完全平方公式即可;【解答过程】解:(1)原式=3(x2﹣y2)=3(x+y)(x﹣y);(2)原式=b(a2+2ab+b2)=b(a+b)2;(3)原式=m2﹣4m+4=(m﹣2)2;(4)原式=2(a2+2ab+b2)=2(a+b)2.5.(2021春•东昌府区期末)把下列各式进行因式分解:(1)2(x﹣y)﹣(x﹣y)2;(2)﹣x2+8x﹣15;(3)8m3n+40m2n2+50mn3;(4)a4﹣b4.【解题思路】(1)直接提取公因式;(2)先加上负括号,再利用十字相乘法;(3)先提取公因式2mn,再利用完全平方公式;(4)利用平方差公式因式分解.【解答过程】解:(1)2(x﹣y)﹣(x﹣y)2=(x﹣y)[2﹣(x﹣y)](2)﹣x2+8x﹣15=﹣(x2﹣8x+15)=﹣(x﹣5)(x﹣3);(3)8m3n+40m2n2+50mn3=2mn(4m2+20mn+25n2)=2mn(2m+5n)2;(4)a4﹣b4=(a2+b2)(a2﹣b2)=(a2+b2)(a+b)(a﹣b).6.(2021春•南山区校级期中)分解因式:(1)12ab2﹣6ab;(2)a2﹣6ab+9b2;(3)x4﹣1;(4)n2(m﹣2)+(2﹣m).【解题思路】(1)直接提取公因式6ab,进而分解因式即可;(2)直接利用完全平方公式分解因式得出答案;(3)直接利用平方差公式分解因式得出答案;(4)直接提取公因式(m﹣2),再利用平方差公式分解因式即可.【解答过程】解:(1)12ab2﹣6ab=6ab(2b﹣1);(2)a2﹣6ab+9b2=(a﹣3b)2;(3)x4﹣1=(x2+1)(x2﹣1)=(x2+1)(x﹣1)(x+1);(4)n2(m﹣2)+(2﹣m)=n2(m﹣2)﹣(m﹣2)=(m﹣2)(n2﹣1)=(m﹣2)(n+1)(n﹣1).7.(2021春•邗江区期中)分解因式:(2)a3﹣a;(3)4ab2﹣4a2b﹣b3;(4)m3(a﹣2)+m(2﹣a).【解题思路】(1)首先提公因式2,再利用完全平方公式进行分解即可;(2)首先提公因式a,再利用平方差公式进行分解即可;(3)首先提公因式﹣b,再利用完全平方公式进行分解即可;(4)首先提公因式m(a﹣2),再利用平方差公式进行分解即可.【解答过程】解:(1)原式=2(x2﹣6x+9)=2(x﹣3)2;(2)原式=a(a2﹣1)=a(a+1)(a﹣1);(3)原式=﹣b(b2﹣4ab+4a2)=﹣b(b﹣2a)2;(4)原式=m(a﹣2)(m2﹣1)=m(a﹣2)(m﹣1)(m+1).8.(2020秋•丛台区期末)因式分解(1)(a﹣b)2+4ab;(2)x2﹣2x﹣8;(3)x4﹣6x3+9x2﹣16;(4)(x2+3x+5)(x2+3x+1)+3.【解题思路】(1)先根据完全平方公式展开,再根据完全平方公式分解因式即可;(2)根据十字相乘法分解因式即可;(3)先分组,根据完全平方公式进行计算,再根据平方差公式分解因式,最后根据“十字相乘法”分解因式即可;(4)把x2+3x当作一个整体展开,再根据“十字相乘法”分解因式即可.【解答过程】解:(1)(a﹣b)2+4ab=a2﹣2ab+b2+4ab=a2+2ab+b2=(a+b)2;(2)x2﹣2x﹣8=(x﹣4)(x+2);=(x4﹣6x3+9x2)﹣16=x2(x﹣3)2﹣42=[x(x﹣3)+4][x(x﹣3)﹣4]=(x2﹣3x+4)(x2﹣3x﹣4)=(x2﹣3x+4)(x﹣4)(x+1);(4)(x2+3x+5)(x2+3x+1)+3=(x2+3x)2+6(x2+3x)+5+3=(x2+3x)2+6(x2+3x)+8=(x2+3x+2)(x2+3x+4)=(x+1)(x+2)(x2+3x+4).9.(2021春•江北区校级期中)因式分解:(1)﹣8ab2+6a2b﹣2ab;(2)4a2﹣(a2+1)2;(3)x4﹣8x2﹣9;(4)(2﹣x2)2+2x(x2﹣2)+x2.【解题思路】(1)原式提取﹣2ab,利用提公因式法因式分解即可;(2)原式利用平方差公式化简,再利用完全平方公式分解即可;(3)原式利用十字相乘法分解,再利用平方差公式分解即可;(4)利用完全平方公式变形,再利用提公因式分解即可.【解答过程】解:(1)原式=﹣2ab(4b﹣3a+1);(2)原式(2a)2﹣(a2+1)2=(2a+a2+1)(2a﹣a2﹣1)=﹣(a+1)2(a﹣1)2;(3)原式=(x2+1)(x2﹣9)=(x2+1)(x+3)(x﹣3);(4)原式=(x2﹣2)2+2x(x2﹣2)+x2=(x2+x﹣2)2=(x+2)2(x﹣1)2.10.(2021春•福田区校级期中)因式分解:(1)ab2﹣a;(2)2xy2﹣12x2y+18x3;(3)a4﹣8a2+16;(4)(x﹣4)(x+1)+3x.【解题思路】(1)提公因式后再利用平方差公式即可;(2)提公因式后再利用完全平方公式即可;(3)利用完全平方公式后再利用平方差公式;(4)根据多项式乘法计算,再利用平方差公式.【解答过程】解:(1)ab2﹣a=a(b2﹣1)=a(b+1)(b﹣1);(2)原式=2x(y2﹣6xy+9x2)=2x(y﹣3x)2;(3)原式=(a2﹣4)2=(a﹣2)2(a+2)2;(4)原式=x2﹣3x﹣4+3x=x2﹣4=(x+2)(x﹣2).11.(2021秋•姜堰区月考)因式分解:(1)a4﹣1;(2)x3﹣2x2y+xy2.【解题思路】(1)原式利用平方差公式分解即可;(2)原式提取公因式x,再利用完全平方公式分解即可.【解答过程】解:(1)原式=(a2+1)(a2﹣1)=(a2+1)(a+1)(a﹣1);(2)原式=x(x2﹣2xy+y2)=x(x﹣y)2.12.(2021春•平山区校级期中)分解因式:(1)x2(m﹣n)+y2(n﹣m);(2)3x2﹣18xy+27y2.【解题思路】(1)首先提取公因式(m﹣n),然后利用平方差公式继续进行因式分解;(2)先提取公因式,再利用完全平方公式把原式进行因式分解即可.【解答过程】解:(1)x2(m﹣n)+y2(n﹣m)=(m﹣n)(x2﹣y2)=(m﹣n)(x+y)(x﹣y);(2)3x2﹣18xy+27y2=3(x2﹣6xy+9y2)=3(x﹣3y)2.13.(2021春•鄄城县期末)因式分解:(1)(a﹣b)(x﹣y)﹣(b﹣a)(x+y);(2)(x2+1)2﹣4x2.【解题思路】(1)用提取公因式法分解因式;(2)用平方差公式、完全平方公式分解因式.【解答过程】解:(1)原式=(a﹣b)(x﹣y)+(a﹣b)(x+y)=(a﹣b)[(x﹣y)+(x+y)]=2x(a﹣b),(2)原式=(x2+1)2﹣(2x)2=(x2+1+2x)(x2+1﹣2x)=(x+1)2(x﹣1)2.14.(2021春•福田区校级期中)分解因式:(1)4x2﹣(x2+1)2;(2)3(x﹣1)2﹣18(x﹣1)+27.【解题思路】(1)先选择平方差公式分解因式,再运用完全平方公式进行因式分解;(2)先运用提取公因式法分解因式,再运用完全平方公式分解因式.【解答过程】解:(1)原式=(2x)2﹣(x2+1)2=(2x+x2+1)(2x﹣x2﹣1)=﹣(x+1)2(x﹣1)2;(2)原式=3[(x﹣1)2﹣6(x﹣1)+9]=3[(x﹣1)﹣3]2=3(x﹣4)2.15.(2021春•凤翔县期末)分解因式:(1)9a2(x﹣y)+y﹣x;(2)(x2﹣2xy+y2)+(﹣2x+2y)+1.【解题思路】(1)原式变形后,提取公因式,再利用平方差公式分解即可;(2)原式整理后,利用完全平方公式分解即可.【解答过程】解:(1)原式=9a2(x﹣y)﹣(x﹣y)=(x﹣y)(9a2﹣1)=(x﹣y)(3a+1)(3a﹣1);(2)原式=(x﹣y)2﹣2(x﹣y)+1=(x﹣y﹣1)2.16.(2021春•沈北新区期末)因式分解:(1)﹣10a2bc+15bc2﹣20ab2c;(2)(x2+1)2﹣4x2.【解题思路】(1)直接提公因式﹣5bc即可;(2)先利用平方差公式,将原式化为(x2+1+2x)(x2+1﹣2x),再利用完全平方公式得出答案.【解答过程】解:(1)原式=﹣5bc(2a2﹣3c+4ab);(2)原式=(x2+1+2x)(x2+1﹣2x)=(x+1)2(x﹣1)2.17.(2021春•平顶山期末)把下列各式因式分解:(1)x2+2xy+y2﹣c2;(2)b2(a﹣2)+b(2﹣a).【解题思路】(1)先分组,再分解.(2)先将b2(a﹣2)+b(2﹣a)变形为b2(a﹣2)﹣b(a﹣2),再运用提公因式法.【解答过程】解:(1)x2+2xy+y2﹣c2=(x+y)2﹣c2=(x+y+c)(x+y﹣c).(2)b2(a﹣2)+b(2﹣a)=b2(a﹣2)﹣b(a﹣2)=b(a﹣2)(b﹣1).18.(2021春•覃塘区期末)因式分解:(1)3x3﹣12x;(2)1﹣2x+2y+(x﹣y)2.【解题思路】(1)先提公因式,再用公式法进行因式分解.(2)先将1﹣2x+2y+(x﹣y)2变形为=1﹣(2x﹣2y)+(x﹣y)2,再用公式法进行因式分解.【解答过程】解:(1)3x3﹣12x=3x(x2﹣4)=3x(x+2)(x﹣2).(2)1﹣2x+2y+(x﹣y)2=1﹣(2x﹣2y)+(x﹣y)2=1﹣2(x﹣y)+(x﹣y)2=[1﹣(x﹣y)]2=(1﹣x+y)2.19.(2021春•江宁区月考)分解因式:(1)4x2(x﹣y)+(y﹣x);(2)(x2﹣5)2+8(x2﹣5)+16.【解题思路】(1)可先将(y﹣x)变形为﹣(x﹣y),再根据因式分解的步骤进行分解即可;(2)将(x2﹣5)看作一个整体,利用完全平方公式进行因式分解,最后再利用平方差公式因式分解即可.【解答过程】解:(1)4x2(x﹣y)+(y﹣x)=4x2(x﹣y)﹣(x﹣y)=(x﹣y)(4x2﹣1)=(x﹣y)(2x+1)(2x﹣1);(2)(x2﹣5)2+8(x2﹣5)+16=(x2﹣5+4)2=(x2﹣1)2=(x+1)2(x﹣1)2.20.(2021春•汉寿县期中)分解因式:3x2﹣xy﹣2y2﹣x+y.【解题思路】先将3x2﹣xy﹣2y2﹣x+y分组整理,然后利用公式即可解答.【解答过程】解:原式=(3x2﹣xy﹣2y2)﹣(x﹣y)=(3x+2y)(x﹣y)﹣(x﹣y)=(x﹣y)(3x+2y﹣1).21.(2020秋•浦东新区期末)因式分解(1)5x2+6y﹣15x﹣2xy;(2)(1+ab)2﹣(a+b)2.【解题思路】(1)将原式分为两组:(5x2﹣15x)、﹣(2xy﹣6y),然后利用提取公因式法进行因式分解;(2)利用平方差公式进行因式分解.【解答过程】解:(1)原式=(5x2﹣15x)﹣(2xy﹣6y)=5x(x﹣3)﹣2y(x﹣3)=(x﹣3)(5x﹣2y);(2)原式=(1+ab﹣a﹣b)(1+ab+a+b)=[(1﹣a)﹣b(1﹣a)][(1+a)+b(1+a)]=(1﹣a)(1﹣b)(1+a)(1+b).22.(2020春•市南区校级期中)因式分解:4(x+y)2﹣16(x﹣y)2.【解题思路】首先提公因式4,再利用平方差公式进行分解即可.【解答过程】解:4(x+y)2﹣16(x﹣y)2=4[(x+y)2﹣4(x﹣y)2]=4(x+y+2x﹣2y)(x+y﹣2x+2y)=4(3x﹣y)(3y﹣x).23.(2020秋•宝山区期末)分解因式:2x3﹣2x2y+8y﹣8x.【解题思路】两两分组:先分别提取公因式2x2,8;再提取公因式2(y﹣x)进行二次分解;最后利用平方差公式再次进行因式分解即可求得答案.【解答过程】解:原式=2x2(x﹣y)﹣8(x﹣y)=2(x﹣y)(x2﹣4)=2(x﹣y)(x+2)(x﹣2).24.(2020秋•上海期末)分解因式:a4+4b2c2﹣a2b2﹣4a2c2.【解题思路】先利用分组分解法进行恰当的分组,再利用提公因式法和公式法进行因式分解即可.【解答过程】解:原式=(a4﹣a2b2)﹣(4a2c2﹣4b2c2)=a2(a2﹣b2)﹣4c2(a2﹣b2)=(a2﹣b2)(a2﹣4c2)=(a+b)(a﹣b)(a+2c)(a﹣2c).25.(2020秋•松江区期末)因式分解:x3+3x2y﹣4x﹣12y.【解题思路】分为两组:(x3+3x2y)和(﹣4x﹣12y),然后运用完全平方公式和平方差公式进行因式分解.【解答过程】解:x3+3x2y﹣4x﹣12y=(x3+3x2y)﹣(4x+12y)=x2(x+3y)﹣4(x+3y)=(x+3y)(x2﹣4)=(x+3y)(x+2)(x﹣2).26.(2020秋•浦东新区期末)分解因式:a4+4b2c2﹣a2b2﹣4a2c2.【解题思路】利用加法的结合律和交换律,把整式的第一项和第三项,第四项和第二项分组,提取公因式后再利用公式.【解答过程】解:原式=(a4﹣a2b2)﹣(4a2c2﹣4b2c2)=a2(a2﹣b2)+4c2(a2﹣b2)=(a2﹣b2)(a2﹣4c2)=(a+b)(a﹣b)(a+2c)(a﹣2c).27.(2020秋•浦东新区期末)因式分解:(x2+2x)2﹣7(x2+2x)﹣8.【解题思路】原式利用十字相乘法分解后,再利用完全平方公式分解即可.【解答过程】解:原式=(x2+2x﹣8)(x2+2x+1)=(x﹣2)(x+4)(x+1)2.28.(2021秋•浦东新区校级期中)分解因式:(x2+x+1)(x2+x+2)﹣12.【解题思路】将原式展开,是关于x的四次多项式,分解因式较困难.我们不妨将x2+x看作一个整体,并用字母y来替代,于是原题转化为关于y的二次三项式的因式分解问题了.【解答过程】解:设x2+x=y,则原式=(y+1)(y+2)﹣12=y2+3y﹣10=(y﹣2)(y+5)=(x2+x﹣2)(x2+x+5)=(x﹣1)(x+2)(x2+x+5).说明本题也可将x2+x+1看作一个整体,比如令x2+x+1=u,一样可以得到同样的结果,有兴趣的同学不妨试一试.故答案为(x﹣1)(x+2)(x2+x+5)29.(2020秋•海淀区校级期中)因式分解:64a6﹣48a4b2+12a2b4﹣b6.【解题思路】先利用分组分解法分解,再分别利用公式法和提取公因式法分解即可得出答案.【解答过程】解:64a6﹣48a4b2+12a2b4﹣b6=(64a6﹣b6)﹣(48a4b2﹣12a2b4)=(8a3+b3)(8a3﹣b3)﹣12a2b2(4a2﹣b2)=(2a+b)(4a2﹣2ab+b2)(2a﹣b)(4a2+2ab+b2)﹣12a2b2(2a+b)(2a﹣b)=(2a+b)(2a﹣b)[(4a2﹣2ab+b2)(4a2+2ab+b2)﹣12a2b2]=(2a+b)(2a﹣b)[(4a2+b2)2﹣4a2b2﹣12a2b2]=(2a+b)(2a﹣b)[(4a2+b2)2﹣16a2b2]=(2a+b)(2a﹣b)(4a2﹣b2)2=(2a+b)3(2a﹣b)3.30.(2020秋•海淀区校级期中)请用两种方法对多项式x3﹣4x2+6x﹣4进行因式分解.(拆添项算一种方法)【解题思路】分别利用拆添项及配方法和提取公因式法进行分解即可.【解答过程】解:方法一:x3﹣4x2+6x﹣4=(x3﹣2x2)﹣(2x2﹣4x)+(2x﹣4)=x2(x﹣2)﹣2x(x﹣2)+2(x﹣2)=(x﹣2)(x2﹣2x+2);方法二:x3﹣4x2+6x﹣4=x(x2﹣4x2+4+2)﹣4=x(x﹣2)2+2x﹣4=(x﹣2)(x2﹣2x+2).。
八年级数学上册14.3因式分解14.3.2公式法(2)课后练习新人教版(new)

14。
3.2公式法(2)-—完全平方公式班级:___________ 姓名:___________ 得分:___________一、 选择题(每小题6分,共30分)1。
下列各式能用完全平方式进行分解因式的是( )A 。
21x - B. 221x x +- C 。
221x x ++ D. 21x x ++2。
下列分解因式错误的是( )A 。
()2155531a a a a +=+B. ()()()2222x y x y x y x y --=--=-+-C. ()()()1k x y x y k x y +++=++D. ()23221a a a a a -+=-3.把8a 3-8a 2+2a 进行因式分解,结果正确的是( )A 。
2a (4a 2-4a +1)B 。
8a 2(a -1)C 。
2a (2a +1)2D. 2a (2a -1)2 4.把x 2y ﹣2y 2x +y 3分解因式正确的是( )A. y (x ﹣y )2B. x 2y ﹣y 2(2x ﹣y ) C 。
y (x 2﹣2xy +y 2)D 。
y (x +y )2 5.下列多项式,能用公式法分解因式的有( )①22x y +② 22x y -+ ③ 22x y -- ④ 22x xy y ++ ⑤222x xy y +- ⑥ 2244x xy y -+-A 。
2个B 。
3个 C. 4个 D 。
5个二、填空题(每小题6分,共30分)6.x 2+4x +4=(___________)2.7.分解因式: 2269ax axy ay -+= ________________。
8。
若x +y =2,则代数式14x 2+12xy +14y 2=________。
9.已知正方形的面积是9x 2+6xy +y 2(x >0,y >0),则该正方形的边长用代数式表示为_____________.10。
若,则的值为___________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础巩固
1.下列各式从左到右的变形中,是因式分解的为().
A.x(a-b)=ax-bx B.x2-1+y2=(x-1)(x+1)+y2
C.x2-1=(x+1)(x-1) D.ax+bx+c=x(a+b)+c
2.把x3-xy2分解因式,正确的结果是().
A.(x+xy)(x-xy) B.x(x2-y2)
C.x(x-y)2 D.x(x-y)(x+y)
3.下列多项式能进行因式分解的是().
A.x2-y B.x2+1
C.x2+y+y2D.x2-4x+4
4.把多项式m2(a-2)+m(2-a)分解因式等于().
A.(a-2)(m2+m) B.(a-2)(m2-m)
C.m(a-2)(m-1) D.m(a-2)(m+1)
5.下列各式中不能用平方差公式分解的是().
A.-a2+b2B.-x2-y2
C.49x2y2-z2D.16m4-25n2
6.下列各式中能用完全平方公式分解的是().
①x2-4x+4;②6x2+3x+1;③4x2-4x+1;④x2+4xy+2y2;⑤9x2-20xy+16y2. A.①②B.①③
C.②③D.①⑤
7.把下列各式分解因式:
(1)9x3y2-12x2y2z+3x2y2;
(2)2a(x+1)2-2ax;
(3)16x2-9y2;
(4)(x+2)(x+3)+x2-4.
能力提升
8.若m-n=-6,mn=7,则mn2-m2n的值是().
A.-13 B.13 C.42 D.-42
9.若x2+mx-15=(x+3)(x+n),则m的值为().
A.-5 B.5 C.-2 D.2
10.若x2-ax-1可以分解为(x-2)(x+b),则a+b的值为().
A.-1 B.1 C.-2 D.2
11.若16x2+mxy+9y2是一个完全平方式,那么m的值是().
A.12 B.24 C.±12 D.±24
12.分解因式(x-3)(x-5)+1的结果是().
A.x2-8x+16 B.(x-4)2 C.(x+4)2 D.(x-7)(x-3) 13.分解因式3x2-3y4的结果是().
A.3(x+y2)(x-y2) B.3(x+y2)(x+y)(x-y)
C.3(x-y2)2 D.3(x-y)2(x+y)2
14.若a+b=-1,则3a2+3b2+6ab的值是().
A.-1 B.1 C.3 D.-3
15.-6x n-3x2n分解因式正确的是().
A.3(-2x n-x2n) B.-3x n(2+x n)
C.-3(2x n+x2n) D.-3x n(x n+2)
16.把下列各式分解因式:
(1)x(x-5)2+x(-5+x)(x+5);
(2)(a+2b)2-a2-2ab;
(3)-2(m-n)2+32;
(4)-x3+2x2-x;
(5)4a(b-a)-b2;
(6)2x3y+8x2y2+8xy3.
17.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.
(1)28和2 012这两个数是神秘数吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
参考答案
1.C 2.D 3.D 4.C 5.B 6.B
7.解:(1)原式=3x2y2(3x-4z+1);
(2)原式=2a(x2+x+1).
(3)原式=(4x+3y)(4x-3y);
(4)方法一:原式=(x+2)(x+3)+(x+2)(x-2)=(x+2)(x+3+x-2)=(x+2)(2x+1)
方法二:原式=x2+5x+6+x2-4=2x2+5x+2=(x+2)(2x+1).
8.C9.C10.D11.D12.B13.A14.C15.B
16.解:(1)原式=x(x-5)2+x(x-5)(x+5)
=x(x-5)[(x-5)+(x+5)]
=2x2(x-5);
(2)原式=a2+4ab+4b2-a2-2ab
=2ab+4b2
=2b(a+2b);
(3)原式=-2[(m-n)2-16]=-2(m-n+4)(m-n-4);
(4)原式=-x(x2-2x+1)=-x(x-1)2;
(5)原式=4ab-4a2-b2=-(4a2-4ab+b2)=-(2a-b)2.
(6)原式=2xy(x2+4xy+4y2)=2xy(x+2y)2.
17.解:(1)因为28=82-62;2 012=5042-5022,所以28和2 012是神秘数.
(2)因为(2k+2)2-(2k)2=4(2k+1),所以由2k+2和2k构造的神秘数是4的倍数.
(3)由(2)知神秘数可表示为4的倍数,但一定不是8的倍数,设两个连续奇数为2k+1和2k-1(k取正整数),而(2k+1)2-(2k-1)2=8k,即两个连续奇数的平方差不是神秘数.。
