2010初中数学联赛
2010年全国初中竞赛获奖情况公报

2010年全国初中竞赛获奖情况公报现将2010年全国初中数学竞赛(南昌赛区)获奖情况予以公报。
请市区有关学校在5月28日—6月8日上班期间到南昌市教研室511室领取获奖证书。
(如学校需要了解学生竞赛成绩,可自带U盘来拷贝本校成绩,该成绩仅供教师了解情况使用,不得予以公布)县(区)学校到各县(区)教研室领取获奖证书。
南昌市中学数学教学研究专业委员会2010年5月6日江西省2010年全国初中数学联赛获奖名单一等奖(全省63名)南昌大学附中谢睿123分南昌十中黄炜琛113分南昌大学附中车希明111分南昌十中廖羽晨111分二等奖(全省126名)南昌十中雷霆108分南昌十中黄越106分南昌十中周智鑫103分南昌二中涂文涛101分南昌二中黎爱迪101分南昌外国语学校陈毓芮96分南昌大学附中罗艺康96分南昌外国语学校余鹏94分南昌十中章俊彦92分南昌十中龚子恒92分南昌十中易加诺91分南昌十中彭渤91分南昌大学附中陈际宇91分南昌外国语学校雷旸90分江西师大附中熊一帆89分南昌十中刘怡慧89分江西师大附中董明海87分南昌十中谢旸晖87分南昌十中杜苏怀87分南昌广福二中欧阳柳87分三等奖(全省245名)南昌十中毛启东81分南昌十中杨云帆79分南昌十中魏啸宸79分南昌一中顾砾天77分南大附中梅源77分南昌外国语学校章灵兮76分南昌莲一直升刘祥74分南昌十中刘云哲74分南昌二中刘逸豪72分南昌南新中学龚宇翔72分南昌八一中学万强71分南昌十中张超70分南昌三中罗逸轩70分南昌外国语学校王竞成70分南昌十中段兆錚69分南昌三中陈佳明67分南昌十中张鑫67分南昌十中刘坤元67分南昌二中帅冲67分生米中学谭文根67分南昌十中胡文凯65分流湖二中宋彬65分南昌外国语学校张歆哲65分进贤一中万剑涛62分南昌市2010年全国初中数学联赛获奖名单(市区学校)七年级学校姓名成绩获奖等级南昌外国语学校王勃竣140 1南昌外国语学校俞晨露139 1南昌十中邓奭炎135 1南昌外国语学校余子恒132 1南昌十中邝明125 1南昌十中胡煜炜121 1南昌外国语学校李想121 1南昌二中万圣杰120 1南昌十中李均祥119 1南昌十中肖立恒117 1南昌十中张浩鹏116 1南昌外国语学校杨宇杰116 1南昌十中李尚武115 1江西师大附中万睿之114 1南昌十中徐彪114 1南昌十中卢振元114 1江西师大附中朱海东113 1南昌十中李能群113 1南昌十中周忆鹤113 1南昌十中龚子轩113 1南昌外国语学校肖霈113 1南昌外国语学校魏道鑫113 1南昌市育新学校余翰良112 1南昌外国语学校付嘉裕111 1南昌十中夏子超109 1南昌十中熊一昕108 1南昌十中李雨曦108 1南昌十中周鑫源107 1江西师大附中夏子哲106 1江西师大附中奚睿哲106 1 南昌三中曾益106 1 南昌十中肖奕恒106 1 南昌十中张学圣106 1 南昌十中陆忠涛106 1 南昌十中黄旭106 1 南昌市洪都中学陈涵晟106 1 南昌外国语学校肖云桓106 1 南昌十中廖溥昀103 1 南昌十中章昉103 1 南昌二十六中黄文瑞102 2 南昌二中胡宇琦102 2 南昌二中朱松102 2 南昌二中左永强102 2 南昌三中章誉怀102 2 南昌外国语学校徐梦瑶102 2 江西师大附中余翘楚101 2 南昌二中肖铭101 2 南昌十中尹子霄101 2 南昌十中余秋雨101 2 南昌外国语学校高天杰101 2 江西师大附中何天豪99 2 江西师大附中廖正99 2 江西师大附中张震宇99 2 南昌二中余孟超99 2 南昌二中程盛淦99 2 南昌二中芦强辉99 2 南昌三中刘德韦华99 2 南昌十中刘伟99 2 南昌十中王逸哲99 2 南昌十中王今99 2 南昌十中邓悦99 2 南昌十中胡浩铭99 2 南昌十中宋文99 2 南昌市八一中学付程远99 2 南昌市育新学校揭华敏99 2 南昌二十七中万文韬98 2 南昌三中李睿杰98 2 南昌十中李俊驰98 2 江西师大附中邓镔97 2 江西师大附中陈浩97 2 江西师大附中蔡玖宇97 2 南昌二十八中黄雅坤97 2 南昌三中徐政奇97 2 南昌外国语学校糜江涛97 2江西师大附中刘亦奇96 2 南昌二中何文若96 2 南昌十中胡煜镁96 2 南昌十中杨文超96 2 南昌十中艾佳媛96 2 南昌十中周立勤96 2 南昌市实验中学薛涵96 2 南昌十中熊诗雨95 2 南昌市洪都中学刘志95 2 南昌大学附中刘文聪94 2 南昌二十八中徐彦平94 2 南昌二十七中万家兴94 2 南昌二中万鸣晨94 2 南昌三中李昊伦94 2 南昌三中杨天94 2 南昌十九中熊泽亚94 2 南昌十中胡辰阳94 2 南昌十中杨晟韬94 2 南昌十中曾宪林94 2 南昌十中林辰正94 2 南昌十中黄浩94 2 南昌市洪都中学熊光劲94 2 南昌市洪都中学陈金金94 2 南昌市育新学校胡瀚文94 2 南昌市豫章中学俞希94 2 南昌外国语学校欧阳文露94 2 南昌外国语学校曹威94 2 南昌外国语学校钟静文94 2 南昌外国语学校金静94 2 南昌外国语学校严斯惟94 2 南昌外国语学校何心怡94 2 南昌外国语学校周嘉坤94 2 南昌二中邹丽93 2 南昌市育新学校王祺林93 2 南昌外国语学校薛睿93 2 江西师大附中彭雨欣92 2 江西师大附中吴乔逸92 2 江西师大附中刘治宇92 2 江西师大附中刘畅92 2 南昌二十八中徐景灏92 2 南昌二十七中涂勇峰92 2 南昌二中张政92 2 南昌二中王铭豪92 2 南昌三中肖烁羽92 2 南昌三中余涛92 2南昌三中邓志鹏92 2 南昌三中衷斯扬92 2 南昌十中杜凯92 2 南昌十中胡文鑫92 2 南昌十中谭智健92 2 南昌十中徐明萱92 2 南昌十中周嘉惠92 2 南昌十中饶熠92 2 南昌十中杨舒涵92 2 南昌外国语学校孙玥92 2 南昌外国语学校屠婕妤92 2 南昌外国语学校谭一铭92 2 南昌外国语学校陈祯祺92 2 南昌外国语学校曾子玲92 2 南航附中徐婉蓉92 2 南昌二十八中万子祥91 2 南昌二中王超91 2 南昌二中王新宇91 2 南昌十中涂泽中91 2 南昌十中王浩宇91 2 南昌十中张明轩91 2 南昌市实验中学杨凯91 2 江西师大附中涂雨晨90 2 南昌十中张海珮90 2 南昌外国语学校程达轩90 2 南昌外国语学校徐健90 2 南昌外国语学校万加宏90 2 江西师大附中曾霄89 3 南昌大学附中熊洁旖89 3 南昌二十七中万超辉89 3 南昌二十七中张钰敏89 3 南昌二中钟昊89 3 南昌二中刘名扬89 3 南昌二中邹凯欣89 3 南昌三中米家天89 3 南昌十中朱宇斌89 3 南昌十中李希文89 3 南昌十中胡冠午89 3 南昌十中万萦菲89 3 南昌十中陈任懿89 3 南昌十中朱益璋89 3 南昌十中殷欣89 3 南昌十中皮奕杰89 3 南昌市八一中学郑文峰89 3 南昌市洪都中学陈庭阳89 3南昌市育新学校郑星89 3 南昌外国语学校张鹤显89 3 南昌外国语学校徐炜杰89 3 南昌外国语学校肖艺帆89 3 南昌外国语学校伍绍文89 3 江西师大附中熊益群88 3 南昌二十八中曾明杰88 3 南昌二十七中甘唯嘉88 3 南昌二十七中熊晨志88 3 南昌外国语学校吴迪88 3 江西师大附中张馨予87 3 江西师大附中徐则林87 3 南昌大学附中龚嘉承87 3 南昌二十八中陶聪87 3 南昌二十八中万志翀87 3 南昌二十七中程龙87 3 南昌二十七中罗浩奇87 3 南昌二十三中黄文翔87 3 南昌二中徐诗雯87 3 南昌二中饶晶辉87 3 南昌十中张佳程87 3 南昌十中陈煜东87 3 南昌十中赵昱辰87 3 南昌市育新学校张驰87 3 南昌市豫章中学柳雨铭87 3 南昌外国语学校陈文慧87 3 南昌外国语学校毛瑞盈87 3 南昌外国语学校彭悦来87 3 南昌外国语学校董治87 3 南昌外国语学校熊婕滢87 3 南昌外国语学校陈唯佳87 3 南昌外国语学校万其至87 3 南昌外国语学校简曲87 3 南昌大学附中何立晗86 3 南昌市八一中学蔡雅文86 3 红谷滩实验学校杨伟杰85 3 江西教育学院附中刘诚85 3 江西师大附中吴天85 3 江西师大附中蒋雨馨85 3 江西师大附中胡人俊85 3 江西师大附中段舒尹85 3 江西师大附中黄泽寰85 3 南昌二十二中陈思婕85 3 南昌二十七中闻泓祥85 3 南昌二十七中刘俊85 3南昌二十七中马文君85 3 南昌三中林捃彦85 3 南昌十中徐嵩85 3 南昌十中俞晓聪85 3 南昌十中黄巍85 3 南昌十中陶嘉琦85 3 南昌十中文康85 3 南昌十中陈祥序85 3 南昌市洪都中学张泓苇85 3 南昌市洪都中学谭正洋85 3 南昌市实验中学李媛媛85 3 南昌市育新学校胡赟豪85 3 南昌市育英学校徐瀚欣85 3 南昌市豫章中学叶一阳85 3 南昌外国语学校朱雅婕85 3 南昌外国语学校涂浩凯85 3 南航附中卢思瑶85 3 南航附中刘明威85 3 江西师大附中方奕真84 3 江西师大附中占恩佐84 3 南昌二十七中王龙84 3 南昌二中付娟84 3 南昌二中黄祁明84 3 南昌二中于龙84 3 南昌十四中左琪84 3 南昌十中罗凯文84 3 南昌市洪都中学张松毅84 3 南昌市育新学校李希84 3 桑海中学闵鹏飞84 3 南昌大学附中胡正阳83 3 南昌二中徐立飞83 3 南昌二中万博文83 3 南昌市八一中学胡振涛83 3 南昌外国语学校李浩楠83 3 南昌外国语学校章亦弛83 3 南昌外国语学校丁泽凯83 3 江西师大附中饶馨怡82 3 江西师大附中万缘强82 3 江西师大附中钟元浩82 3 南昌大学附中周天骏82 3 南昌大学附中聂菲82 3 南昌二十八中周韬82 3 南昌二十七中蒋超群82 3 南昌二十七中张苇82 3 南昌二十七中蔡久通82 3南昌二中王一钒82 3 南昌三中秦玥82 3 南昌三中黎士韬82 3 南昌三中濮俊松82 3 南昌十九中黄逗82 3 南昌十中金融82 3 南昌十中涂文睿82 3 南昌十中戴伯璇82 3 南昌十中匡迪82 3 南昌十中左浩宇82 3 南昌十中魏薇82 3 南昌十中梁文奕82 3 南昌市洪都中学赖晨欣82 3 南昌市洪都中学万伊82 3 南昌市新才学校颜港生82 3 南昌市育新学校唐颖蔚82 3 南昌市育英学校陈明行82 3 南昌五中龚宇星82 3 江西师大附中陈尚钧81 3 南昌大学附中樊志兴81 3 南昌十中杨一鸣81 3 南昌十中沈鑫宏81 3 南昌十中黄铸君81 3 南昌外国语学校袁珺一81 3 江西师大附中蒋剑飞80 3 南昌二十七中刘泽宇80 3 南昌二十七中胡超超80 3 南昌二十三中胡雲鹤80 3 南昌二中张皓天80 3 南昌三中罗欣月80 3 南昌三中李毅恒80 3 南昌十中王炜程80 3 南昌市育新学校李青涵80 3 南昌市育新学校黄柳青80 3 南昌市育英学校周一鸣80 3 南昌外国语学校万佳艺80 3 南昌外国语学校严海洋80 3 南昌外国语学校李峰远80 3 南昌外国语学校黄敏80 3 南昌外国语学校吴耀刚80 3 南昌外国语学校彭小宝80 3 南昌外国语学校黄熠权80 3 南航附中辛琨80 3 江西师大附中童昱杰79 3 江西师大附中支亦杰79 3南昌大学附中李铭洋79 3 南昌二十八中姜晨昊79 3 南昌二十七中谌凌睿79 3 南昌三中扈洪志79 3 南昌三中魏子豪79 3 南昌十中贾亚俊79 3 南昌十中黄越79 3 南昌十中郭宽逵79 3 南昌市联立学校方成79 3 南昌市水电中学龚浩昌79 3 南昌外国语学校胡溪玮79 3 南昌外国语学校邓日昇79 3 南昌外国语学校邓世杰79 3 江西师大附中文雨78 3 南昌大学附中陈曦78 3 南昌大学附中彭柏文78 3 南昌大学附中刘达琳78 3 南昌大学附中王展鹏78 3 南昌二十七中闵鹏宇78 3 南昌二中周雨萌78 3 南昌三中张博鑫78 3 南昌十九中刘宇鑫78 3 南昌十四中万如梦78 3 南昌十中李澄曜78 3 南昌十中袁瑞彬78 3 南昌十中余成越78 3 南昌市育新学校姜通昊78 3 南昌市育英学校黄晨欣78 3 南昌外国语学校陈思思78 3 南昌外国语学校胡伯晨78 3 南昌外国语学校徐艺78 3 南昌外国语学校杨菁华78 3 南昌外国语学校曾大智78 3 南昌外国语学校易帆78 3 南昌外国语学校朱晨悦78 3 南航附中徐翀78 3 红谷滩实验学校危文文77 3 江西师大附中甘嘉伟77 3 江西师大附中杜曦越77 3 江西师大附中熊煦77 3 南昌八中谢天77 3 南昌大学附中腾晓锟77 3 南昌二中李博77 3 南昌二中贺琼慧77 3 南昌二中王蔚杰77 3南昌三中蔡沁明77 3 南昌三中陈琰昱77 3 南昌三中叶文杰77 3 南昌三中黄晟77 3 南昌三中杨洋77 3 南昌三中甘云鹏77 3 南昌三中熊涵磊77 3 南昌三中李芷薇77 3 南昌十九中张子康77 3 南昌十中陈子雨77 3 南昌市八一中学徐阳屹77 3 南昌市洪都中学杨林立77 3 南昌市建设路学校饶鹏程77 3 南昌市新才学校蒋明轩77 3 南昌市育新学校谢泽熙77 3 南昌外国语学校陈曦远77 3 南昌外国语学校薛良犇77 3 南昌外国语学校谌鑫77 3 江西师大附中王逸民76 3 南昌二十八中郎羽寅76 3 南昌二十八中万清宇76 3 南昌二中赵殷东76 3 南昌二中王瀚棠76 3 南昌外国语学校邓斌76 3 南昌外国语学校万昊76 3 江铃学校龚琪75 3 江西师大附中杨馥维75 3 江西师大附中胡凯巽75 3 江西师大附中杜万琛75 3 江西师大附中钱明康75 3 江西师大附中万震远75 3 江西师大附中高嘉年75 3 江西师大附中陈楚钰75 3 经开区新城学校涂曾瑜75 3 经开区新城学校孙光凡75 3 南昌八中王安75 3 南昌八中姜忆来75 3 南昌二十八中支卓75 3 南昌二十八中刘雨乔75 3 南昌二十八中谭卓然75 3 南昌二十七中魏志成75 3 南昌二十七中魏伟75 3 南昌二十七中李磊钦75 3 南昌二十七中丁志伟75 3 南昌二十七中徐昊75 3南昌二十三中王子正75 3 南昌二中马凌坤75 3 南昌二中赖博轩75 3 南昌二中戴宸煜75 3 南昌三中周玥75 3 南昌三中张嘉敏75 3 南昌三中胡雨宽75 3 南昌三中罗序达75 3 南昌三中董昊75 3 南昌三中龚力伟75 3 南昌三中蒋凯75 3 南昌三中连昀泽75 3 南昌十二中戴逸凡75 3 南昌十二中杨隆涛75 3 南昌十二中杨波75 3 南昌十九中尹文昊75 3 南昌十九中徐齐昆75 3 南昌十中熊子达75 3 南昌十中宋嘉峰75 3 南昌十中金妍文75 3 南昌十中万鸿宇75 3 南昌十中雷政75 3 南昌十中魏晨燕75 3 南昌十中杨夕宜75 3 南昌市洪都中学聂舒悦75 3 南昌市京东学校罗云昌75 3 南昌市培英学校樊启祥75 3 南昌市培英学校陈佳鸣75 3 南昌市新才学校贾子豪75 3 南昌市育新学校章思菀75 3 南昌市豫东学校杨强75 3 南昌市豫章中学熊文晖75 3 南昌外国语学校郑芙蓉75 3 南昌外国语学校尹梦涵75 3 南昌外国语学校郭志勇75 3 南昌外国语学校刘海75 3 南昌外国语学校龚徐成75 3 南昌市育新学校郭云婕75 3 南航附中贺睿75 3 南昌二中潘晖75 3八年级学校姓名成绩获奖等级江西师大附中杨欢94 1江西师大附中付志强93 1南昌二十八中李超91 1南昌二十七中杨云天90 1南昌三中李夏涵89 1南昌三中陈逸彬89 1南昌外国语学校胡恩文87 1南昌二十七中饶明磊86 1南昌外国语学校王昕悦83 1江西财大附中邹驰原82 1江西师大附中易卓然82 1南昌二十七中王康81 1南昌市铁路一中邓立81 1南昌外国语学校熊雨蓉81 1江西师大附中王晚晴81 1江西师大附中于太典81 1南昌二中盛澴81 1江西师大附中舒皓祥79 1南昌十中刘根宇78 1南昌外国语学校谭雪婧77 1南昌二十八中缪嘉诚77 1南昌三中刘翔宇76 1南昌二十八中夏天颢76 1南昌市育新学校陈婳76 1江西师大附中张李巽76 1南昌市洪都中学熊达文76 1南昌大学附中张蒙75 1红谷滩实验学校裘宗平74 1南昌二十七中李伟74 1桑海中学余昊74 1南昌十中刘子彧74 1南昌八中蔡万城74 1南昌二十七中李媛媛74 1南昌市南钢学校余冠东74 1南昌十中芦柯宇74 1南昌外国语学校魏明扬74 1南昌二十八中魏昺卿74 1南昌二十七中范亦文74 1南昌大学附中林定浩74 1江西师大附中王晨74 1江西师大附中卢翔72 1南昌市京东学校熊娇娇71 2桑海中学熊宏71 2 南昌市迎宾中学朱冨艳71 2 南昌八中张莹71 2 南昌市育英学校徐璐瑶71 2 南昌外国语学校王家琪71 2 南昌二十八中陈俊橦71 2 南昌外国语学校杨文豪71 2 江西师大附中戴一鸣71 2 江西师大附中褚晨亮69 2 江西师大附中王斐侦69 2 江西师大附中黄晨曦69 2 南昌外国语学校陈佳69 2 南昌二十八中熊羽69 2 江西师大附中朱洪毅69 2 江西师大附中万鹏68 2 南昌外国语学校冯晨辉68 2 南昌二中陈实68 2 南昌十九中钟恺67 2 南昌大学附中吴晨卉67 2 南昌市洪都中学郭珈旭67 2 南昌二中徐艺珺67 2 南昌外国语学校沙里洲67 2 南昌十中涂皓67 2 南昌大学附中贾书豪67 2 南昌二十八中王昊东67 2 江西师大附中刘阳67 2 江西师大附中章启峰67 2 南昌二十八中吴安琪67 2 南昌二十八中章睿67 2 江西师大附中康可凡67 2 南昌二十七中徐歆尧67 2 南昌二十七中万坤67 2 江西教育学院附中高俊67 2 江西师大附中陈子昊67 2 南昌外国语学校胡博66 2 南昌十中陈其斌65 2 南昌外国语学校张浩川65 2 南昌外国语学校李垚钰65 2 南昌二十七中吴振松65 2 南昌二中刘洋64 2 南昌十中饶晟锐64 2 南昌二中余希恺64 2 江西师大附中李日炫64 2 南昌外国语学校陈伊滢64 2 南昌大学附中毛尔谦64 2南昌外国语学校胡天庆64 2 江西省农科院中学邓静宇64 2 南昌十九中肖尧64 2 南昌二十二中周雯雯64 2 江西财大附中黄蓉菲63 2 江西师大附中许瑞卿63 2 江西师大附中周路漫63 2 南昌市联立学校胡丽云62 2 南昌外国语学校李佳祺62 2 江西师大附中李可怿62 2 江西师大附中李思颖62 2 南昌三中肖伟62 2 南昌八中熊晨宇62 2 南昌外国语学校林芃61 2 南昌二十七中谢锍锴61 2 南昌十九中李松61 2 南昌三中熊鹏伟61 2 南昌外国语学校陈星宇61 2 江西师大附中谭畅61 2 南昌十二中杨宇恒61 2 南昌市豫章中学江子艺60 2 江西师大附中罗钰婷60 2 南昌市江安学校欧阳冲60 2 南昌外国语学校廖宸睿60 2 南昌外国语学校金程60 2 南昌八中程宇轩60 2 江西省农科院中学朱博成60 2 南昌外国语学校徐家炜60 2 南昌二中余雪君60 2 南昌市育新学校熊英豪60 2 江西师大附中宁志天60 2 南昌二十八中胡奇隆60 2 南昌大学附中樊龙豪60 2 南昌十九中魏长鑫60 2 江西师大附中雷子健60 2 南昌二十七中辜丹晨60 2 经开区新城学校邓康60 2 南昌二十八中徐力60 2 江西师大附中彭迎丰60 2 南昌市江安学校樊浩南59 3 江西师大附中陈景松59 3 南昌外国语学校郑伟昊59 3 南昌二十八中刘书伟59 3 南昌八中喻阳59 3 南昌二十八中周润倩59 3罗家一中凌志刚59 3 南昌市育英学校刘松松58 3 南昌市铁路一中张逸晗58 3 南昌外国语学校邓宸翰58 3 南航附中徐悦58 3 罗家一中吴传龙58 3 南昌三中赵天博57 3 南昌市铁路一中王佳琦57 3 南昌外国语学校殷豪57 3 南昌外国语学校李广瑞57 3 南昌外国语学校倪安松57 3 南昌大学附中魏璇琳57 3 南昌二中邹乐57 3 南昌三中龚昕蓓57 3 南昌十九中徐世哲57 3 南昌外国语学校刘奕君56 3 南昌市洪都中学熊立伟56 3 南昌三中熊睿志56 3 南昌市江安学校万云飞56 3 江西师大附中赵子聪56 3 南昌二中阎晁昕56 3 南昌外国语学校李响56 3 南昌二十八中鞠凌鹏56 3 江西师大附中付翔飞56 3 南昌十九中易昕杰56 3 南昌外国语学校龚喆欣55 3 桑海中学付方超55 3 南昌八中丁一55 3 南昌外国语学校吕梦阳55 3 南昌二十八中袁泉55 3 南昌外国语学校万雪莹55 3 南昌市洪都中学罗晶55 3 南昌市豫章中学谢煜东55 3 南昌外国语学校李兴艺55 3 南昌市铁路一中黄傲寒55 3 南昌外国语学校曾思源55 3 南昌市水电中学杨涵55 3 南昌市江安学校吴奇艳55 3 南昌现代外国语学校吴振华55 3南昌市新才学校黄魏灵思55 3南昌市江安学校万思敏55 3 南昌市英雄一中王振宇55 3 江西农大附中郑威55 3 南昌外国语学校范孟阳55 3南昌市江安学校万煚55 3 南昌二十八中朱越55 3 南昌二中晏星光55 3 南昌二十七中康子浩55 3 南昌八中姚萌55 3 南昌三中李子潇55 3 南昌二十八中黄冠迪54 3 南昌市铁路一中张麟翼54 3 南昌二中舒晨浩54 3 江西省农科院中学郭天54 3 南昌外国语学校张翀54 3 南昌外国语学校朱小宇54 3 南昌外国语学校段谟斌54 3 南昌外国语学校邓文琦54 3 南昌外国语学校杨佳蔚54 3 南昌二中卢瑜54 3 南昌八中周宁54 3 南昌二十七中潘高源54 3 南昌外国语学校陈奕铭54 3 南昌市江安学校章岚54 3 南昌外国语学校吴旭莹54 3 南昌十七中王海旭54 3 南昌二中雷杨54 3 南昌大学附中张昊泽54 3 南昌十二中涂聪54 3 南昌三中陈嘉旭54 3 南昌十九中叶子睿54 3 南昌二十六中熊佳玉54 3 南昌市洪都中学廖聃54 3 南昌二十七中胡之豪54 3 南昌大学附中杜仁杰54 3 南昌大学附中万雨轩54 3 南昌二中刘柏君54 3 南昌市育新学校刘新海53 3 南昌外国语学校杨文逸53 3 南昌三中谢雅嵘53 3 南昌市江安学校吴祖斌53 3 江西师大附中钱楠53 3 江西教育学院附中王楷53 3 南昌十中万慧杰53 3 南昌十中何昕53 3 南昌市联立学校胡洋53 3 江西师大附中黄茂然53 3 南昌大学附中何霁53 3 南昌二十八中黄沁仪53 3江西教育学院附中黄鑫53 3 江西师大附中徐睿53 3 南昌八中刘嘉明53 3 江西师大附中胡玥莹53 3 南昌三中王弼晟53 3 南昌二十七中江宇薇53 3 南昌大学附中武圣53 3 江西师大附中庄子烜53 3 南昌市实验中学郑寓升52 3 南昌市育新学校(二部)熊颖52 3 南昌市豫章中学李轲52 3 南昌外国语学校徐晓霜52 3 南昌大学附中樊庆翀52 3 南昌二十二中史婧婷52 3 红谷滩实验学校徐天雄52 3 南昌市育新学校卢东昊52 3 经开区新城学校邓立52 3 红谷滩实验学校刘露露52 3 南昌二十七中魏伊宁52 3 南昌二十七中刘元亨52 3 南昌市洪都中学艾婧52 3 红谷滩实验学校聂月52 3 南昌二十八中万文灏52 3 南昌三中熊智星52 3 南昌二十八中姜纹昕51 3 桑海中学于超伟51 3 南昌二中胡亮平51 3 南昌八中胡南辉51 3 南昌三中陈捷彬51 3 南昌市洪都中学章魏婷51 3 南昌市育新学校陈昌炜51 3 南航附中熊启阳50 3 南昌外国语学校裘昕玥50 3 南昌市豫章中学刘百里50 3 南昌市南钢学校熊定华50 3 南昌二十七中王姿人50 3 江西省农科院中学熊耀婷50 3 南昌市豫章中学陶博洋50 3 南昌外国语学校邹秉承50 3 南昌外国语学校朱煚50 3 南航附中刘陈柠50 3 南昌二中张官熙50 3 南昌外国语学校余海鹏50 3 经开区新城学校穆文珺50 3 南昌三中李曦晖50 3南昌二十七中刘星宇50 3 南昌市培英学校张子欣50 3 南昌外国语学校龚浩良50 3 南昌二中刘洋滔50 3 南昌三中何俊良50 3 南昌二十七中胡侨宇50 3 南昌市培英学校杨岚49 3 南昌外国语学校何佳宸49 3 江铃学校龚俊杰49 3 南昌外国语学校李佳49 3 江西师大附中高麒49 3 南昌市豫章中学陶宇婷49 3 水文学校沈志坚49 3 南昌外国语学校毛嘉敏49 3 南昌市迎宾中学王艺瑒49 3 南昌外国语学校熊能越49 3 南昌市育英学校龚敏49 3 南昌二十八中余晓春49 3 南昌二中胡程远49 3 南昌二中朱彦49 3 南昌外国语学校郑涵49 3 南昌市豫章中学杨东辰49 3 南昌二十七中黄政伟49 3 南昌外国语学校张书培49 3 江西师大附中晏子豪49 3 南昌十九中魏政国49 3 南昌外国语学校黄璐49 3 南昌市南钢学校陈一豪49 3 南昌外国语学校詹敏慧49 3 南昌十二中李均旺49 3 南昌市豫章中学黄光舟49 3 南昌二十七中缪新柯49 3 南昌三中吴迪49 3 南昌三中李犇49 3 南昌大学附中陈子循49 3 南昌八中吕俊杰49 3 南昌市育英学校黄家欣49 3 南昌市京东学校曹鑫49 3 南昌八中胡华龙49 3 南昌十二中杨宏49 3 南昌二十二中周瞾49 3 南昌市培英学校熊悦49 3 南昌二十七中何子畅49 3 南昌市洪都中学黄卓然49 3 南昌八中廖千姿49 3南昌二十七中邹震坤49 3 江西师大附中甘家宁49 3 南昌二十八中薜柏才49 3 红谷滩实验学校周原49 3 南昌十五中邓嘉辉49 3 南昌市洪都中学吴嘉豪49 3 江西师大附中陈贵越49 3 南昌三中甘婉坍49 3 南昌二十八中邹梦佳49 3 南昌市育新学校朱思全48 3 南昌市新才学校金舒雯48 3 南昌市江安学校罗志伟48 3 南昌外国语学校周宇婷48 3 南昌市豫章中学李文宇48 3 南昌市滨江学校彭乐48 3 南昌二中李青48 3 南昌市铁路一中刘思民48 3 南昌市洪都中学艾斌48 3 南昌市洪都中学熊日48 3 南昌外国语学校涂翔鹏48 3 南昌外国语学校王律锟48 3 南航附中吴颖48 3 南昌市洪都中学徐李恒48 3 南昌市铁路一中龚鑫宇48 3 南昌外国语学校史文超48 3 南昌八中王菲48 3 南昌大学附中汪径慈48 3 南昌二十八中江佳钰48 3 南昌市江安学校钟山48 3 南昌外国语学校夏月48 3 桑海中学朱敏48 3 南昌二中邹先立48 3 江西财大附中胡本源48 3 南昌市豫章中学张子越48 3 南昌二中曾涵48 3 南昌市八一中学李宸48 3 经开区新城学校胡雨霞48 3 南昌二十七中姚聪48 3 南昌市江安学校吴宇轩48 3 南昌外国语学校孔祥懿48 3 南昌市青云谱中学胡莎莎48 3 南昌三中周舟48 3 南昌市联立学校吴能亨48 3 南航附中杨慧琴48 3 南昌二中梁恺48 3。
2010年全国初中数学联赛试题

2010年全国初中数学联赛试题说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( )A .1.B .2.C .3.D .4.【答】B.因为,,a b c 均为整数,所以a b -和a c -均为整数,从而由1010()()1a b a c -+-=可得 ||1,||0a b a c -=⎧⎨-=⎩或||0,|| 1.a b a c -=⎧⎨-=⎩ 若||1,||0,a b a c -=⎧⎨-=⎩则a c =,从而|||a b b c c -+-=|||a b b a a a -+-+-=. 若||0,||1,a b a c -=⎧⎨-=⎩则a b =,从而||||||a b b c c a -+-+-=||||||2||2a a a c c a a c -+-+-=-=.因此,||||||a b b c c a -+-+-=2.2.若实数,,a b c 满足等式3||6b =,9||6b c =,则c 可能取的最大值为 ( )A .0.B .1.C .2.D .3.【答】C.32(3),||(2)55c b c =+=-,而||0b ≥,所以2c ≤. 当2c =时,可得9,0a b ==,满足已知等式.所以c 可能取的最大值为2.3.若b a ,是两个正数,且 ,0111=+-+-a b b a 则 ( )A .103a b <+≤. B .113a b <+≤. C .413a b <+≤. D .423a b <+≤. 【答】C. 由1110a b b a--++=可得b a b ab a +=++22,则 2()()()(1)ab a b a b a b a b =+-+=++-①由于b a ,是两个正数,所以,0>ab 0a b +>,所以10a b +->,从而.1>+b a 另一方面,由22()()44a b a b ab ab +=-+≥可得4)(2b a ab +≤,结合①式可得14a b a b +≥+-,所以.34≤+b a 因此,413a b <+≤.4.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( )A .-13.B .-9.C .6.D . 0.【答】A.设m 是方程2310x x --=的一个根,则2310m m --=,所以231m m =+.由题意,m 也是方程420x ax bx c +++=的根,所以420m am bm c +++=,把231m m =+代入此式,得22(31)0m am bm c ++++=,整理得2(9)(6)10a m b m c +++++=. 从而可知:方程2310x x --=的两根也是方程2(9)(6)10a x b x c +++++=的根,这两个方程实质上应该是同一个一元二次方程,从而有22(9)(6)1(31)a x b x c k x x +++++=--(其中k 为常数),故961131a b c +++==--,所以333,10b a c a =--=--.因此,2(333)2(10)13a b c a a a +-=+-----=-.5.在△ABC 中,已知︒=∠60CAB ,D ,E 分别是边AB ,AC 上的点,且︒=∠60AED ,CE DB ED =+,CDE CDB ∠=∠2,则=∠DCB( )A .15°.B .20°.C .25°.D .30°.【答】 B.如图,延长AB 到F ,使BF =ED ,连CF ,EF .∵ ︒=∠=∠60AED EAB ,∴︒=∠60EDA ,︒=∠=∠120CED EDB ,BF ED AE AD ===,DF BF DB DB ED CE =+=+=,于是,AF AC =,︒=∠=∠60AFC ACF .又∵︒=∠120EDB ,CDE CDB ∠=∠2,∴ ︒=∠︒=∠80,40CDB CDE ,︒=∠-∠-︒=∠20180EDC CED ECD .在△CDA 和△CBF 中,CA=CF ,︒=∠=∠60CFB CAD ,AD=BF ,∴ △CDA ≌△CBF , ∴ ︒=∠=∠20ACD FCB .于是,︒=∠-∠-︒=∠2060FCB CDE DCB .6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则123a a a a ++++( ) A .28062. B .28065. C .28067. D .28068.【答】D.把1到2010之间的所有自然数均看作四位数(如果不足四位,则在前面加0,补足四位,这样做不会改变n a 的值).1在千位上出现的次数为310,1在百位上出现的次数为2210⨯,1在十位和个位上出现的次数均为22101⨯+,因此,1出现的总次数为3210210321602+⨯⨯+=.2在千位上出现的次数为11,2在百位和十位上出现的次数均为2210⨯,2在个位上出现的次数为22101⨯+,因此,2出现的总次数为21121031612+⨯⨯+=.类似的,可求得(3,4,5,6,7,8,9)k k =出现的总次数均为221031601⨯⨯+=.因此11a a ++=28068.二、填空题:(本题满分28分,每小题7分)1.已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += .【答】 13.由3319x y +=得2()[()3]19x y x y xy ++-=,把1x y +=代入,可得6xy =-. 因此,,x y 是一元二次方程260t t --=的两个实数根,易求得这两个实数根分别为3和2-,所以22223(2)13x y +=+-=.2.二次函数c bx x y ++=2的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知AC AB 3=,︒=∠30CAO ,则c = . 【答】 19. 由题意知,点C 的坐标为),0(c ,c OC =.设B A ,两点的坐标分别为)0,(1x ,)0,(2x ,则21,x x 是方程02=++c bx x 的两根. 由根与系数的关系得c x x b x x =-=+2121,.又︒=∠30CAO ,则c AC AB c AC 323,2===. 于是,c AC OA x 330cos 1=︒==,c AB OA OB x 332=+==. 由c c x x ==2219,得91=c . 3.在等腰直角△ABC 中,AB =BC =5,P 是△ABC 内一点,且PAPC =5,则PB =______.【答】作P E ⊥AB ,交AB 于点E ,作P F ⊥BC ,交BC 于点F ,设,PE mPF n ==,分别在△PAE 、△PCF 中利用勾股定理,得22(5)5m n +-= ①22(5)25m n -+= ②②-①,得10()20n m -=,所以2m n =-,代入①中,得27120n n +-=,解得13n =,24n =. 当3n =时,21m n =-=,在Rt △PAE中,由勾股定理可得PB ==当4n =时,22m n =-=,此时PE AE >,所以点P 在△ABC 的外面,不符合题意,舍去.因此PB =4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放_______个球.【答】 15.将这些球的位置按顺序标号为1,2,3,4,…….由于1号球与7号球中间夹有5个球,1号球与12号球中间夹有10个球,12号球与6号球中间夹有5个球,7号球与13号球中间夹有5个球,13号球与2号球中间夹有10个球,2号球与8号球中间夹有5个球,8号球与14号球中间夹有5个球,14号球与3号球中间夹有10个球,3号球与9号球中间夹有5个球,9号球与15号球中间夹有5个球,15号球与4号球中间夹有10个球,4号球与10号球中间夹有5个球,因此,编号为1,7,12,6, 13,2,8,14,3,9,15,4,10的球颜色相同,编号为5,11的球可以为另外的一种颜色.因此,可以按照要求摆放15个球.如果球的个数多于15个,则一方面,16号球与10号球应同色,另一方面,5号球与16号球中间夹有10个球,所以5号球与16号球同色,从而1到16号球的颜色都相同,进一步可以知道:所有的球的颜色都相同,与要求不符.因此,按这种要求摆放,最多可以摆放15个球.第二试 (A )一.(本题满分20分)设整数,,a b c (a b c ≥≥)为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数.解 由已知等式可得222()()()26a b b c a c -+-+-=①令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.C于是,等式①变为222()26m n m n +++=,即 2213m n mn ++=②由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ …………10分 (1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形. …………15分(2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5+6=11. ……………………20分二.(本题满分25分)已知等腰三角形△ABC 中,AB =AC ,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD//AC ,交⊙I 于点D.证明:PD 是⊙I 的切线.证明 过点P 作⊙I 的切线PQ (切点为Q )并延长,交BC 于点N.因为CP 为∠ACB 的平分线,所以∠ACP =∠BCP.又因为PA 、PQ 均为⊙I 的切线,所以∠APC =∠NPC.又CP 公共,所以△ACP ≌△NCP , …………10分所以∠PAC =∠PNC.由NM =QN ,BA =BC ,所以△QNM ∽△BAC ,故∠NMQ =∠ACB ,所以MQ//AC.………………………………20分又因为MD//AC ,所以MD 和MQ 为同一条直线. NCA又点Q 、D 均在⊙I 上,所以点Q 和点D 重合,故PD 是⊙I 的切线. ……………………………25分三.(本题满分25分)已知二次函数2y x bx c =+-错误!未找到引用源。
全国初中数学联赛试题及详解

∴
(3a
b
33)
x
(a
c
10)
0
,故
3a b 33 0 a c 10 0
a
b
2c
13
5. 在△ ABC 中,已知 CAB 60 ,D,E 分别是边 AB,AC 上的点,且 AED 60 ,
ED DB CE , CDB 2CDE ,则 DCB
(B)
A.15°.
B.20°. C.25°.
D.30°.
解:如图,由已知,ADE 是正三角形。作 BF∥DE 交
AC 于 F,则 BD=EF,从而 EC=DE+BD=AB=BF,DE=FC,
又∠1=∠2=120○,故ΔEDC≌ΔFCB.故 x .
∵∠CDB=2 ,∠BDE=120○,∴ 40 ,故 x 40
由 40 60 20 ,得: x 20 .
(2,997)、…、(499,500).注意到:这 500 个数组中,每个数组的两个自然数各位数字之和均为 9+9
+9=27,故 0,1,2,…,999 这 1000 个自然数各位数字之和等于 27500 13500 .
于是,1000,1001,1002,…,1999 这 1000 个自然数各位数字之和等于 13500+1000
个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放 15 个球.
解:先画一个“初始图”:
○ABCDE○ABCDE○
按照题目要求,逐一确定各个字母的颜色,得到:
○○○○D○○○○○D○
显然,D 应为黑色。即:
○○○○●○○○○○●○
再按要求尝试增加小球,确定最后结果如下:
○○○○●○○○○○●○○○○
3.若 a, b 是两个正数,且 a 1 b 1 1 0, 则 ba
2010年数学竞赛获奖名单

张藩藉 兰彧 唐利彬 唐媛艺 万奇挧
荣县中学 荣县中学 荣县中学 荣 王县 大中 山学 中 学
李劲松 李劲松 李劲松 李劲松 万永利
赵逸飞 钟豪 钟远志 周婧珂 邹俊志
田家炳中学 田家炳中学 江姐中学 自贡28中 解放路中学
第 1 页,共 8 页
周浪 周浪 宋生贵
田华
夏青 谢津宝 徐敏 周慎博 程瑞静 范皓然 高华礼 胡体彬 姜文浩 刘一霖 郑剑 雷茂林 涂小波 晏粮清 余涵知 曾真 郑月 罗钞予 邓青清 邓志聪 龚雅琼 桂源
杨倩
王大山学校: 陈 勇 自贡34中: 邵丹银 回龙中学: 王 浩
邱彦 李杭雨 曹 罗
旭川中学: 范婷婷 自贡11中: 张 杰
熊智临 何 浩
陈雨佳
自贡18中: 李 雪
仙市中学:
王杨嵌 宇
赖弈昆 钟慧 聂檄晨
陈静 邹胜 李祥林
管其舜 邱柏森 何 倩
江 雪 付程晗 李志超 富顺二职中: 舒 俊 童寺中心校: 郭 桃 长滩乡中: 伍晋衡
指导教师 田华 周浪 周勇 李劲松 周浪 范其金 王小惠 李劲松 魏明全 李劲松 李劲松
代高声
全国二等奖(74人)
姓名
刘书言 倪雪珂 涂珊珊 李昕 邓棼木 郝祎婷 梁茂 胡采曦 王银季 赵梓涵
学校
荣县中学 自贡28中 自 解贡 放1路9中中 学 解放路中 学 荣县中学 板 解桥 放中 路学 中 学 蜀光中学 荣县中学
杰 张光雨 刘雨杰
周锋
古文强 周夕寒
钟春燕 徐娜
金珂 杜丽双 黄蓉
曾彦俊 刘庆宇 高逸雯 赵梦寒 刘郑健 喻晨峰
王俊杰 项瑞麟 车怡 朱寒迪 刘钰婷 罗凌杰
朱寒迪 蒋沁吟 陈衍瑜 余唯唯 刘洋铭 邹森
2010年全国 初中数学联赛(含答案)

12010年全国初中数学联合竞赛试题参考答案第一试一、选择题:(本题满分42分,每小题7分)1.若a ,b ,c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-=( )A .1B .2C .3D .4【答案】 B【解析】 因为()()10101a b a c ---=,而左边的两个加数都是非负整数,所以一个等于0,另一个等于1,也就是说,a ,b ,c 三个数中有两个相等,另一个和它们相差1.因此,所求的和式中,两项等于1,另一项等于2,结果为2.2.若实数a ,b ,c 满足等式3||6a b =,49||6a b c =,则c 可能取的最大值为( )A .0B .1C .2D .3【答案】 C【解析】 为了使c 尽量大,a 应该尽量大,b 应该尽量小.因为它们都是非负数,3a ,0b =,不难观察到所求答案为2.3.若a ,b 是两个正数,且1110,a b b a--++= 则( )2A .103a b <+≤B .113a b <+≤C .413a b <+≤D .423a b <+≤. 【答案】 C【解析】 去分母之后得到()()110a a b b ab -+-+=,即220a ab b a b ++--=.给定a 和b 是两个正数,那么如果让它们中的一个等于0,则另一个等于0或14.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( )A .13-B .9-C .6D .0【答案】 A【解析】 这需要使得前者是后者的因式,用综合除法可得,余式为()()33310a b x a c +++++,它应该等于0.所以两个系数都为0,特别地,()()333210a b a c ++-++,所以所求答案为13-.5.在ABC △中,已知60CAB ∠=︒,D ,E 分别是边AB ,AC 上的点,且60AED ∠=︒,ED DB CE +=,2CDB CDE ∠=∠,则DCB ∠= ( )A .15oB .20oC .25oD .30o【答案】 B【解析】 观察可得ADE △为正三角形,6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则312320092010a a a a a +++++=L ( )A .28062B .28065C .28067D .28068.【答案】 D【解析】 根据弃九法,它和1到2010的和被9除的余数相等.每连续9个自然数之和被9整除,2010被9除余3,1236++=,所以只有D 符合.二、填空题:(本题满分28分,每小题7分)1.已知实数x ,y 满足方程组33191x y x y ⎧+=⎨+=⎩,,则22x y += .【答案】 13【解析】 第一式除以第二式可得2219x xy y -+=,第二式平方可得2221x xy y ++=,那么所求答案就是()1921313⨯+÷=.2.二次函数2y x bx c =++的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知3AB ,30CAO ∠=︒,则c = .【答案】 19【解析】 观察可知A 必须在B 左边,否则B 会跑到x 轴负半轴上.设A 的横坐标为a ,则C 的纵坐标3,23AC =,2AB a =.因此,考虑两根之积,33a a ⨯,3a =319=. 3.在等腰直角ABC △中,5AB BC ==,P 是ABC △内一点,且5PA ,5PC =,则PB = .4【答案】 10【解析】 设()00B ,,()50A ,,()05C ,,根据熟知的勾三股四弦五,可观察到()31P ,,(另一个点在三角形外,不符合),所以10PB =.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放 个球.【答案】 15【解析】 也就是说,编号之差为6或11的两个球颜色相同.下面从1号球开始,依次写出颜色相同的球的编号:11261711516104159314821371→→→→→→→→→→→→→→→→→也就是说,如果有17个球,则全部同色;如果超过17个,则任何连续17个同色,也不行.如果有16个,则上面的圈去掉17号球仍然是一条链,仍然不行;如果有15个,则上面的圈去掉17号球和16号球后断成两部分,所以可以.第二试 (A )一.(本题满分20分)设整数()a b c a b c ≥≥,,为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长5不超过30的三角形的个数.【解析】 由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤, 所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.6⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)已知等腰三角形ABC △中,AB AC =,C ∠的平分线与AB 边交于点P ,M 为ABC △的内切圆I e 与BC 边的切点,作MD AC ∥,交I e 于点D .证明:PD 是I e 的切线.【解析】 过点P 作I e 的切线PQ (切点为Q )并延长,交BC 于点N .因为CP 为ACB ∠的平分线,所以ACP BCP ∠=∠.又因为PA 、PQ 均为I e 的切线,所以APC NPC ∠=∠.IP QNB7又CP 公共,所以ACP NCP △≌△,所以PAC PNC ∠=∠.由NM QN =,BA BC =,所以QNM BAC △≌△,故NMQ ACB ∠=∠,所以MQ AC ∥.又因为MD AC ∥,所以MD 和MQ 为同一条直线.又点Q 、D 均在I e 上,所以点Q 和点D 重合,故PD 是I e 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点()1P a ,,()210Q a ,. ⑴ 如果a ,b ,c 都是整数,且8c b a <<,求a ,b ,c 的值.⑵ 设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为C .如果关于x 的方程20x bx c +-=的两个根都是整数,求ABC △的面积.【解析】 点()1P a ,、()210Q a ,在二次函数2y x bx c =+-的图象上,故1b c a +-=,4210a c a +-=,解得93b a =-,82c a =-.⑴ 由8c b a <<知8293938a a a a -<-⎧⎨-<⎩,,解得13a <<.又a 为整数,所以2a =,9315b a =-=,8214c a =-=.⑵ 设m ,n 是方程的两个整数根,且m n ≤,旗开得胜8由根与系数的关系可得39m n b a +=-=-,28mn c a =-=-,消去a ,得98()6mn m n -+=-,两边同时乘以9,得8172()54mn m n -+=-,分解因式,得(98)(98)10m n --=.所以9819810m n -=⎧⎨-=⎩,,或982985m n -=⎧⎨-=⎩,,或9810981m n -=-⎧⎨-=-⎩,,或985982m n -=-⎧⎨-=-⎩,,解得12m n =⎧⎨=⎩,,或109139m n ⎧=⎪⎪⎨⎪=⎪⎩,,或2979m n ⎧=-⎪⎪⎨⎪=⎪⎩,,或19323m n ⎧=⎪⎪⎨⎪=⎪⎩,,又m ,n 是整数,所以后面三组解舍去,故1m =,2n =.因此,()3b m n =-+=-,2c mn =-=-,二次函数的解析式为232y x x =-+.易求得点A 、B 的坐标为()10,和()20,,点C 的坐标为()02,, 所以ABC △的面积为1(21)212⨯-⨯=.第二试 (B )旗开得胜9一.(本题满分20分)设整数a ,b ,c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).【解析】 不妨设a b c ≥≥,由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤,旗开得胜10所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )11一.(本题满分20分)题目和解答与(B )卷第一题相同.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数2(1)4y x px k p =+++-的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.【解析】 由题意知,方程2(1)40x px k p +++-=的两根1x ,2x 中至少有一个为整数.由根与系数的关系可得12x x p +=-,12(1)4x x k p =+-,从而有()()()()12121222241x x x x x x k p ++=+++=- ①⑴ 若1k =,则方程为22(2)0x px p ++-=,它有两个整数根2-和2p -.⑵ 若1k >,则10k ->.因为12x x p +=-为整数,如果1x ,2x 中至少有一个为整数,则1x ,2x 都是整数.又因为p 为质数,由①式知1|2p x +或2|2p x +.不妨设1|2p x +,则可设12x mp +=(其中m 为非零整数),则由①式可得212k x m-+=,12故()()12122k x x mp m -+++=+,即1214k x x mp m-++=+. 又12x x p +=-,所以14k p mp m--+=+, 即1(1)4k m p m-++= ② 如果m 为正整数,则(1)(11)36m p ++⨯=≥,10k m->, 从而1(1)6k m p m-++>,与②式矛盾. 如果m 为负整数,则(1)0m p +<,10k m-<, 从而1(1)0k m p m-++<,与②式矛盾. 因此,1k >时,方程2(1)40x px k p +++-=不可能有整数根.综上所述,1k =.旗开得胜13。
2010年数学竞赛获奖名单

邓贤模 张皓 王晨伟 王玲 黄昊皓 邹寒乔 何婷逸 黄喆威
李淮旭 曾雨 椰林
杨曦 代珊
林伊陶 赵晴
徐铖敏 黄戈 黄思源 杨榆 罗清扬
曾子航 蔡林 阳清
余悦琪
门璐 熊慧
陈柯宇 刘彦均 钟旺
桂瑞良
龚宇 王凯加 王思贤
李欧艺阳周秋 张砚嘉芮
廖留尘 刘婧媛
绿盛学 校:
彭
璐
自贡六中: 伍金顺
余川
赖琬婷 陈 艳自 贡34中:回 龙中学:
郝祎婷 荣县中学
梁 茂 板桥中学
胡采曦 解放路中学
王银季 蜀光中学
赵梓涵 荣县中学
张藩藉 荣县中学
兰 彧 荣县中学
唐利彬 荣县中学
唐媛艺 荣县中学
万奇挧 王大山中学
夏 青 荣县中学
谢津宝 富南学校
涂珊珊 自贡19中
指导教师 李斌 田华 李劲松 刘瑞洪 李斌 王小惠 李劲松 李劲松 李劲松 李劲松 李劲松 万永利 曹晴 范荣华 刘方利
李瑞杰 吴雨潼 刘朔源
张洛源
刘亚萍 陈隽豪
富顺二中: 富顺三中: 骑龙镇中心: 东湖镇中: 互助乡中: 板桥中心校: 童寺中心校: 永年中心校: 东湖观音寺: 富顺城关: 赵化中学:
荣县: 荣县中学: 旭东中学: 富南中学: 长山镇中学: 双古中学:
李志强 陈孟旸 胡丹 杨兴广 何俊 丁启航 吴茂 钟泽彬 曾建 陈银杰 李胜 刘道林 22人 刘如鑫 代玉霞 吴艾株 但利波 王皓宇
朱侯睿 蔡林玉 官子欣 范婷婷 张慧 黄志东
市一等
板桥中心校: 李宇洪
赵颖 丁威戈 黄昌彬
赵曙熙 王 阳 粟 邱 刘诒嘉 蔡定芸 刘才国 金正垚 吴 恒
双古中学: 朱 强 过水中学: 刘 琴 高山中学: 杨 通 留佳中学: 袁德能
2010年数学联赛成绩

2010全国初中联赛获奖名单公示数奥研究中心 发表于2010年05月10日 17:06 阅读(27) 评论(0) 分类: 个人日记 2010全国初中联赛获奖名单姓名 学校 奖次一等奖陆禹十四中一黄雨杨十四中一廖亦阳十四中一黄冬三十六中一黄钲麟新民中学一邹凯三十六中一梁钧十四中一杨昊旸二十六中一张正威 天桃实验中学 一梁 沁 三美学校 一刘甘霖 二十六中 一韦博文 新民中学 一申雯霞 广西民大附中 一二等奖何新磊 三美学校 二黄云昊 三美学校 二吴 凯 十四中 二唐乾洋 十四中 二李彦孜 二十六中 二陈丹雯 天桃实验中学 二苏子畅 十四中 二陈 典 十四中 二陈昙天 十四中 二莫文杰 新民 二蒲启迪 新民 二吴佳燕 天桃 二刘尔帅 十四中 二黄华仪 十四中 二吴伊芸 十四中 二周 旻 新民 二龙志洋 二十六中 二黄婧欢 南宁外国语学校 二罗 程 南宁外国语学校 二廖启承 新民 二杨福恒 广西民大附中 二王 也 新民中学 二李晨怡 天桃实验中学 二王天乐 新民中学 二陈俊铭 新民 二廖逸飞 三十七中 二冷雨遥 新民中学 二李培滔 十四中 二周铭锴 三十六中 二龙宇森 十四中 二黄俊尧 十四中 二梁健玮 三美学校 二林家鑫 三美 二农璧源 三美 二潘圳辉 新民中学 二罗华亮 二十六中 二三等奖罗 悦 外国语学校 三伦颖慧 民大附中 三苏巧欣 外国语学校 三韦启锋 民大附中 三陈兴和 二十六中 三覃冠麟 新兴 三罗宗保 十四中 三李 博 十三中 三陶俊元 外国语学校 三卓肖航 十四中 三任智桂 十四中 三米小倩 外国语学校 三王 硕 十四中 三秦 依 新民中学 三王仲凌 三美学校 三廖宇盛 十三中 三韦 悦 十四中 三邓组铭 新民中学 三韦星宇 三美学校 三李梓民 二十六中 三莫弘杨 十四中 三杨昭华 新民中学 三黄 钧 三美学校 三左 罗 新民中学 三黄幸璐 三美学校 三谭黎睿 新民中学 三秦元睿 十四中 三秦凯鹏 新民中学 三罗彬彬 三美学校 三陆 远 二十六中 三马诗域 育才实验中学 三葛章明 十四中 三余恩岑 育才实验中学 三黄柯颖 十四中 三罗希晨 三美学校 三梁立忠 外国语学校 三何 山 十四中 三侯茵茵 二十六中 三钟欣原 十四中 三蒋清宇 二十六中 三刘佳莹 十四中 三滕 悦 外国语学校 三叶子霄 十四中 三钟佳玲 二十六中 三幸荣堃 三美学校 三郑 喆 十四中 三韦兆劼 十四中 三覃 稆 十四中 三李沅泽 十四中 三黄佳杰 新民中学 三林康健 民大附中 三张凯程 外国语学校 三伍杨柳 民大附中 三乐昌来 外国语学校 三李沅泽 民大附中 三施展欣 外国语学校 三杨建雄 民大附中 三李 泽 外国语学校 三李剑秋 民大附中 三慕俊豪 二十六中 三个人日记。
2010年九年级数学联赛试卷(十六)及答案

AB CD2010年九年级数学联赛试卷(十六)班级______ 姓名_____________ 一、选择题1.已知一个多边形的内角和是外角和的4倍,则这个多边形是( ) A.八边形 B. 十二边形 C. 十边形 D. 九边形2.若(2,k )是双曲线xy 1=上的一点,则函数x k y )1(-=的图象经过( ) A.一、三象限 B.二、四象限 C.一、二象限 D.三、四象限 3.如图,∠BDC =98°,∠C =38°,∠B =23°,则∠A =( ) A .61° B .60° C .37° D .39°4.如图是由四个全等的直角三角形围成的,若两条直角边分别为3和4,则向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率(不考虑落在线上的情形)是( A . 3 5 B . 4 5 C . 16 25 D . 25495.如图,在△ABC 中,AB =AC ,M 、N 分别是AB 、AC 的中点,D 、E 为BC 上的点,连接DN 、=8cm ,DE =4cm A .1cm 2 B .1.5cm 2 C .6.已知二次函数0(2≠++=a c bx ax y 下列4A. 0<abc C. 02=-b a 7.如图,在梯形ABCD 中,AB ∥CD ,垂足为O .若CD =3,AB =5,则AC A .24 B .4 C .33 D .52 8.如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为4的概率是O ABCDA 1B 1C 1A 2C 2B 2xyA .21 B .31 C .41 D .519.如图所示,∠E=∠F=90°, ∠B=∠C ,AE=AF ,结论:○1 EM=FN ;○2 CD=DN ;○3 ∠F AN=∠EAM ; ○4△CAN ≌△ABM.其中正确的有( ) A. 1个 B. 2个 C.3个 D.4个10.在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2).延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ;延长C 1B 1交x 轴于点A 2,作正方形A 2B 2C 2C 1…按这样的规律进行下去,第2010个正方形的面积为 A .2009235⎪⎭⎫⎝⎛B .2010495⎪⎭⎫ ⎝⎛ C .2008495⎪⎭⎫ ⎝⎛D .4018235⎪⎭⎫ ⎝⎛二、填空题(共5个小题,每小题4分,共20分) 11.已知:442+-x x 与1-y 互为相反数, 则式子)((y x xyy x +÷-的值等于 . 12.已知三角形两边长是方程0652=+-x x 的两个根,则三角形的第三边c 的取值范围是 .13.2010年上海世博会的园区规划用地面积约为5280000m 2.将5280000用科学记数法表示为 .14.在一次数学测验中,某小组5名学生的成绩(单位:分)如下:72、68、86、92、82.这组数据的中位数是 .15.在四边形ABCD 中,已知AD ∥BC .若再添加一个条件,能使四边形ABCD 成为平行四边形,则这个条件可以是 (写一个即可,但不能添加任何辅助线). 16.在一个不透明的口袋中,装有5个红球和n 个黄球,它们除颜色外其余均相同.若从中随机摸出一个球,摸到黄球的概率为 34,则口袋中球的总数为 个.17.如图,在梯形ABCD 中,AB ∥CD ,∠C =90º,AB =25,BC =24.若将该梯形沿BD 折叠,点C 恰好与腰AD 上的点E 重合,则AE 的长为 .第17题 第18题 第19题18.如图,AB 为半圆O 的直径,C 、D 、E 、F 是AB ⌒的五等分点,P 是AB 上的任意一点.若AB =4,则图中阴影部分的面积为 .19.如图,O 是四边形ABCD 内的一点,OB =OC =OD ,∠BCD =∠BAD =75º,则∠ADO +∠ABO = 度.20.二次函数y =ax 2+bx +c 的图象如图所示,给出下列说法:①abc <0;②方程ax 2+bx +c =0的根为x 1=-1、x 2=3;③当x >1时,y 随x 值的增大而减小;④当y >0时,-1<x <3. 其中正确的说法是( )A .①B .①②C .①②③D .①②③④三、解答题(共2个小题,每小题7分,共14分)21.(9分)先化简,再求值:⎝⎛⎭⎫ 1a -2-1a +2÷ 2 2-a,其中a =3-1.AB CDOAB CD EABCDEF GHO22.(13分)如图,O 是矩形ABCD 的对角线的交点,E 、F 、G 、H 分别是OA 、OB 、OC 、OD 上的点,且AE =BF =CG =DH . (1)求证:四边形EFGH 是矩形;(2)若E 、F 、G 、H 分别是OA 、OB 、OC 、OD 的中点,且DG ⊥AC ,OF =2cm ,求矩形ABCD 的面积.23.(9分)如图,ACD △和BCE △都是等腰直角三角形,90ACD BCE AE ∠=∠=°,交CD 于点F BD ,分别交CE AE 、于点.G H 、试猜测线段AE 和BD 的数量和位置关系,并说明理由.24.(16分)如图,在平面直角坐标系中,直线AB与x、y轴分别交于点A(3,0)、B(0,3),点C在线段AB上,过点C作CD⊥x轴于点D.(1)求直线AB的解析式;(2)若S四边形OBCD=433,求点C的坐标;(3)在第一象限内是否存在点P,使得以P、O、B为顶点的三角形与△OBA相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.25.(12分)如图,抛物线()2230y mx mx m m =-->与x 轴交于A B 、两点,与y 轴交于C 点. (1)请求出抛物线顶点M 的坐标(用含m 的代数式表示),A B 、两点的坐标; (2)经探究可知,BCM △与ABC △的面积比不变,试求出这个比值;(3)是否存在使BCM △为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.参考答案一、选择题(每小题3分,共30分)二 、填空题(每小题3分,共30分)11、 ; 12、 ; 13、 ; ; 14、 ; 15 ; 16、 ; 17、 ;18、 ;19、 ; 20、 。
2010年全国初中数学竞赛获奖名单
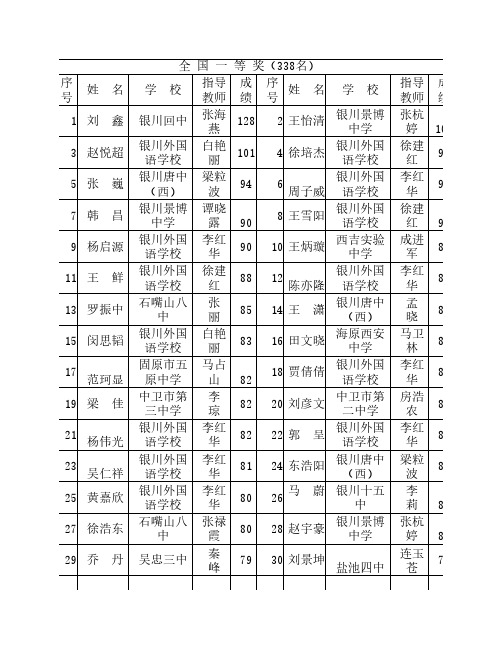
徐建 红
76
46 程玄玲
海原西安 中学
马卫 林
75
48 李 杰
海原西安 中学
马卫 林
75
50 曹成翔
海原西安 中学
方建 永
74
52 卢 焱 贺兰四中
何丽 娟
74
54 郭文涛
中卫市第 三中学
黄鸿 文
73
56 侯泽成
石嘴山惠 农中学
董学 英
73
58 王
萌
中卫市第 五中学
段学 英
73
60 徐伟润
石嘴山九 中
航
银川外国 语学校
徐建 红
65
165 樊 璟
隆德二中
王升 利
65
166 李怀翔
中卫市第 四中学
王玉 珍
65
167 刘 浩
平罗四中
张文 兵
65
168 马
政
银川外国 语学校
吴晓 灵
65
169 孟嘉诚
银川唐中 (西)
王丽 敏
65
170 任兴华
中卫市第 四中学
张国 华
65
171 孙 阳
银川景博 中学
张杭 婷
62
226 杜佳欣
银川景博 中学
谭晓 露
62
227 龚俊峰
中卫市东 月学校
刘志 艳
62 228 郭 恺 贺兰四中
何丽 娟
62
229 郭禹辰
银川唐中 (西)
王丽 敏
62
230 季
亮
石嘴山十 五中学
张云 宾
62
231 贾梦霄 银川外国 吴晓 62 232 蒋超达 中卫市第 刘荣 62
2010年全国初中数学联赛武汉选拔赛试题

2010年全国初中数学联赛武汉选拔赛试题悬赏分:0 |解决时间:2010-8-9 21:51 |提问者:高中新菜求2010年全国初中数学联赛武汉选拔赛(一般称作CASIO杯)试题,有附答案当然更好啦比赛进行时间为2009年12月,我说的不是2010年4月11日的全国初中数学联赛啊!(其中有几个题我不会做,所以想现在重新把题目弄出来再研究研究)问题补充:啊,真可惜,都不是啊最佳答案是这个吧??一、选择题(满分30分)1.如图a,ABCD是一矩形纸片,AB=6cm,AD=8cm,E是AD上一点,且AE=6cm,操作:⑴将AB向AE折过去,使AB与AE重合,得折痕AF,如图b;⑵将△AFB以BF为折痕向右折过去,得图c,则△GFC的面积为( )A.2B.3C.4D.52.若M=3x2-8xy+9y2-4x+6y+13(x,y是实数),则M的值一定是( )A.正数B.负数C.零D.整数3.已知点I是锐角△ABC的内心,A1,B1,C1分别是点I关于边BC,CA,AB 的对称点。
若点B在△A1B1C1的外接圆上,则∠ABC等于( )A.30°B.45°C.60°D.90°4.设,则与A最接近的正整数是( )A.18B.20C.24D.255.设a、b都是正数,且满足56≤a+b≤59,0.9<a/b<0.91,则b2-a2等于( )A.171B.177C.180D.182二、填空题(满分30分)6.在一个圆形的时钟的表面,OA表示秒针,OB表示分针(O为两针的旋转中心)。
若现在时间恰好是12点整,则经过_____秒后,△OAB的面积第一次达到最大。
7.在直角坐标系中,抛物线与x轴交于A,B的两点。
若A,B两点到原点的距离分别为OA,OB,且满足,则m=_____.8.有两幅扑克牌,每幅的排列顺序是:第一张是大王,第二张是小王,然后是黑桃、红桃、方块、梅花四种花色排列,每种花色的牌又按A,2,3,…,J,Q,K的顺序排列。
2010年全国初中数学联赛江西省初赛试题及解答

2010年全国初中数学联赛江西省初赛试题解答第 一 试一. 选择题(每小题7分,共42分)1的结果是( ).()A()B、2; ()C 、2; ()D 、12.答案:D解:22131(1=++=+,25(141)-+=-=,2241)31)2222⎛++=+=== ⎝⎭,因此原式12=. 2、ABC ∆是一个等腰直角三角形,DEFG 是其内接正方形,H 是正方形的对角线交点;那么,由图中的线段所构成的三角形中相互全等的三角形的对数为( ).()A 、12; ()B 、13; ()C 、26; ()D 、30.答案:C .解:设3AB =,图中所有三角形均为等腰直角三角形,其中,斜边长为1的有5个,它们组成10对全等三角形;6个,它们组成15对全等三角形;斜边长为2的有2个,它们组成1对全等三角形;共计26对.3、设0ab ≠,且函数21()24f x x ax b =++与22()42f x x ax b =++有相同的最小值u ;函数23()24f x x bx a =-++与24()42f x x bx a =-++有相同的最大值v ;则u v +的值( ).()A 、必为正数; ()B 、必为负数; ()C 、必为0; ()D 、符号不能确定.答案:C .解:2221()()44f x x a b a b a =++-≥-,2222()(2)2424f x x a b a b a =++-≥-, 由22424b a u b a -==-,得223b a -= ……①2223()()44f x x b a b a b =--++≤+,2224()(2)2424f x x b a b a b =--++≤+;由22424a b v a b +==+,得223a b = ……②②-①得,222()3()a b b a +=-,所以0a b += ……③,或23b a -=……④ 若0a b +=,则222()(65)(65)()[65()]0u v b a a b a b b a +=-++=++-=;若23b a -=,据②④,222()33b b -=,即2(31)30b -+=,矛盾! 4、若关于x 的方程227100x ax a ++-=没有实根,那么,必有实根的方程是( ).()A 、22320x ax a ++-=; ()B 、22560x ax a ++-=; ()C 、2210210x ax a ++-=; ()D 、22230x ax a +++=.答案:A .解:由方程227100x ax a ++-=无实根,得其判别式Δ0<,于是25a <<,方程,,,A B C D 的判别式分别是:4(1)(2)A a a ∆=--,4(2)(3)B a a ∆=--,4(3)(7)C a a ∆=--,4(1)(3)D a a ∆=+-,显然,对于满足25a <<的每个a 值,可以确保0A ∆>,但不能保证,,B C D ∆∆∆非负,(即使得方程,,B C D 无实根的a 的区间与区间(2,7)都有重叠部分,而使方程A 无实根的a 的区间(1,2)与区间(2,7)无重叠部分),所以A 必有实根,其余方程不一定有实根.5、正方形ABCD 中,,E F 分别是,AB BC 上的点,DE 交AC 于M ,AF 交BD 于N ;若AF 平分BAC ∠,DE AF ⊥;记BE x OM =,BNy ON=, CFz BF=,则有( ).()A 、x y z >>; ()B 、x y z ==;()C 、x y z =>; ()D 、x y z >=. 答案:D解:由角平分线,BN AB AC CFON AO AB BF====,即y z =,又AME ∆的角分线与高重合,则AME ∆为等腰三角形,AM AE =,作OP ∥AB ,交OE 于P ,则OP 为DBE ∆的中位线,OMP ∆∽AME ∆,2BE BEx OM OP===,所以x y z >=.6、将1,2,3,4,5,6,7,8这八个数分别填写于一个圆周八等分点上,使得圆周上任两个相邻位置的数之和为质数, 如果圆周旋转后能重合的算作相同填法,那么不同的填法有( ). ()A 、4种; ()B 、 8种; ()C 12种、; ()D 、16种. 答案:B解:相邻两数和为奇质数,则圆周上的数奇偶相间,于是8的两侧为3,5,而7的两侧为4,6;剩下两数1,2必相邻,且1与4,6之一邻接;考虑三个模块[4,7,6],[5,8,3],[1,2]的邻接情况,得到8种填法.EFDBE二、 填空题(每小题7分,共28分)1、若k 个连续正整数之和为2010,则k 的最大值是 . 答案:60.解:设(1)2010(1)(2)()2k k n n n k kn +=++++++=+,则(21)4020k n k ++=, 注意21k n k <++,而2402023567=⨯⨯⨯,为使k 值最大,当把4020表成最接近的一对因数之积,为40206067=⨯,所以60k =.2、单位正三角形中,将其内切圆及三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则三角形剩下部分的面积为 .答案:49S π=-解:单位正三角形内切圆半径为r =其面积为212s r ππ==,而O 为其中心,故OD OH AH r ===,因此,AEF ∆与ABC ∆的相似比为1:3,于是每个小圆面积等于⊙O 面积的19,故四个圆面积之和为439s π=,因此,所求三角形剩下部分的面积为9S π=. 3、圆内接四边形A B C D 的四条边长顺次为:2,7,6,9AB BC CD DA ====,则四边形的面积为 . 答案:30.解:由于2222768592+==+,即2222BC CD DA AB +=+,所以BCD ∆与DAB ∆都是直角三角形,因此,四边形面积1(7692)302BCD DAB S S =+=⋅⨯+⨯=. 4、在123520±±±±±中,适当选择+、-号,可以得到不同代数和的个数是 . 答案:24个.解:1,2,3,5,20中,有奇数三个,故其代数和必为奇数;由1,2,3,5可以得到绝对值11≤的所有奇数:这是由于11235=--+,31235=-+-+,51235=+-+,71235=-++,91235=-+++,111235=+++;以上各式通乘1-,可得1,3,5,7,9,11------的表达式;而据题意,表达式中,1,2,3,5及20都必须参与,那么,能得到的整数应是±20加或减135,7,9,11,,,即得到十二个正奇数9,11,13,,31 和十二个负奇数9,11,,31--- ;因此可表出的数共计24个.第 二 试一、(20分)边长为整数的直角三角形,若其两直角边长是方程2(2)40x k x k -++=的两根,求k 的值并确定直角三角形三边之长.解:设直角边为,a b ,(a b <)则2,4a b k ab k +=+=,因方程的根为整数,故其判别式为平方数,设()()22(2)166613221648k k n k n k n +-=⇒-+--=⨯=⨯=⨯,66,k n k n -+>--63261k n k n -+=⎧∴⎨--=⎩或61662k n k n -+=⎧⎨--=⎩或63261k n k n -+=⎧⎨--=⎩解得1452k =(不是整数,舍去),2315,12k k == 215k =时,17,605,12,13a b ab a b c +==⇒=== 312k =时,14,486,8,10a b ab a b c +==⇒===二、(25分)如图,自ABC ∆内的任一点P ,作三角形三条边的垂线:,,PD BC PE CA PF AB ⊥⊥⊥,若,BD BF CD CE ==;证明:AE AF =.证:注意如下事实:若四边形的两条对角线互相垂直,则其两组对边的平方和相等. 连,,PA PB PC ,则有2222PA BF PB AF +=+;2222PB CD PC BD +=+,2222PC AE PA CE +=+;三式相加得222222AE CD BF AF CE BD ++=++, 利用条件,BD BF CD CE ==,代入上式,得AE AF =.三、(25分)已知,,a b c222a b c a b c ++++为整数.0c -≠,而==20b ac -=,于是 222222()2()()2()a b c a b c ab bc ac a b c ab bc b ++=++-++=++-++2()2()()()a b c b a c b a b c a b c =++-++=++-+, 因此,222a b c a b c a b c++=-+++为整数.。
全国初中数学联赛试题及答案(2010年).doc

2010年全国初中数学联合竞赛试题第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( B )A .1.B .2.C .3.D .4.2.若实数,,a b c 满足等式3||6b =,9||6b c =,则c 可能取的最大值为 ( C )A .0.B .1.C .2.D .3.3.若b a ,是两个正数,且 ,0111=+-+-a b b a 则 ( C )A .103a b <+≤. B .113a b <+≤. C .413a b <+≤. D .423a b <+≤. 4.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为( A )A .-13.B .-9.C .6.D . 0.5.在△ABC 中,已知︒=∠60CAB ,D ,E 分别是边AB ,AC 上的点,且︒=∠60AED ,CEDB ED =+,CDE CDB ∠=∠2,则=∠DCB( B ) A .15°. B .20°. C .25°. D .30°.6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则123a a a a ++++( D ) A .28062. B .28065. C .28067. D .28068.二、填空题:(本题满分28分,每小题7分)1.已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += 13 .2.二次函数c bx x y ++=2的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知AC AB 3=,︒=∠30CAO ,则c = 19 .3.在等腰直角△ABC 中,AB =BC =5,P 是△ABC 内一点,且PA ,PC =5,则PB =.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放____15___个球.第二试 (A )一.(本题满分20分)设整数,,a b c (a b c ≥≥)为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数.解 由已知等式可得222()()()26a b b c a c -+-+-= ① 令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.于是,等式①变为222()26m n m n +++=,即 2213m n mn ++= ② 由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ (1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.(2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.二.(本题满分25分)已知等腰三角形△ABC 中,AB =AC ,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD//AC ,交⊙I 于点D.证明:PD 是⊙I 的切线.证明 过点P 作⊙I 的切线PQ (切点为Q )并延长,交BC 于点N.因为CP 为∠ACB 的平分线,所以∠ACP =∠BCP.又因为PA 、PQ 均为⊙I 的切线,所以∠APC =∠NPC.又CP 公共,所以△A CP ≌△NCP ,所以∠PAC =∠PNC.由NM =QN ,BA =BC ,所以△QNM ∽△BAC ,故∠NMQ =∠ACB ,所以MQ//AC.又因为MD//AC ,所以MD 和MQ 为同一条直线.又点Q 、D 均在⊙I 上,所以点Q 和点D 重合,故PD 是⊙I 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点P (1,)a ,Q (2,10)a .(1)如果,,a b c 都是整数,且8c b a <<,求,,a b c 的值.(2)设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为C.如果关于x 的方程20x bx c +-=的两个根都是整数,求△ABC 的面积.解 点P (1,)a 、Q (2,10)a 在二次函数2y x bx c =+-的图象上,故1b c a +-=,4210a c a +-=,解得93b a =-,82c a =-.(1)由8c b a <<知8293,938,a a a a -<-⎧⎨-<⎩解得13a <<.又a 为整数,所以2a =,9315b a =-=,8214c a =-=.(2) 设,m n 是方程的两个整数根,且m n ≤.由根与系数的关系可得39m n b a +=-=-,28mn c a =-=-,消去a ,得98()6m n m n -+=-,NC A两边同时乘以9,得8172()54mn m n -+=-,分解因式,得(98)(98)10m n --=. 所以981,9810,m n -=⎧⎨-=⎩或982,985,m n -=⎧⎨-=⎩或9810,981,m n -=-⎧⎨-=-⎩或985,982,m n -=-⎧⎨-=-⎩解得1,2,m n =⎧⎨=⎩或10,913,9m n ⎧=⎪⎪⎨⎪=⎪⎩或2,97,9m n ⎧=-⎪⎪⎨⎪=⎪⎩或1,932,3m n ⎧=⎪⎪⎨⎪=⎪⎩又,m n 是整数,所以后面三组解舍去,故1,2m n ==.因此,()3b m n =-+=-,2c mn =-=-,二次函数的解析式为232y x x =-+. 易求得点A 、B 的坐标为(1,0)和(2,0),点C 的坐标为(0,2),所以△ABC 的面积为1(21)212⨯-⨯=.第二试 (B )一.(本题满分20分)设整数,,a b c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).解 不妨设a b c ≥≥,由已知等式可得222()()()26a b b c a c -+-+-= ① 令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.于是,等式①变为222()26m n m n +++=,即 2213m n mn ++= ② 由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩(1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.(2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )一.(本题满分20分)题目和解答与(B )卷第一题相同.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数4)1(2-+++=p k px x y 的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.解 由题意知,方程04)1(2=-+++p k px x 的两根21,x x 中至少有一个为整数.由根与系数的关系可得4)1(,2121-+=-=+p k x x p x x ,从而有p k x x x x x x )1(4)(2)2)(2(212121-=+++=++ ①(1)若1k =,则方程为0)2(22=-++p px x ,它有两个整数根2-和2p -.(2)若1k >,则01>-k .因为12x x p +=-为整数,如果21,x x 中至少有一个为整数,则21,x x 都是整数.又因为p 为质数,由①式知2|1+x p 或2|2+x p .不妨设2|1+x p ,则可设12x mp +=(其中m 为非零整数),则由①式可得212k x m -+=, 故121(2)(2)k x x mp m -+++=+,即1214k x x mp m-++=+. 又12x x p +=-,所以14k p mp m--+=+,即 41)1(=-++mk p m ② 如果m 为正整数,则(1)(11)36m p +≥+⨯=,10k m ->,从而1(1)6k m p m-++>,与②式矛盾.如果m 为负整数,则(1)0m p +<,10k m -<,从而1(1)0k m p m -++<,与②式矛盾. 因此,1>k 时,方程04)1(2=-+++p k px x 不可能有整数根.综上所述,1=k .。
2010年全国 初中数学联赛(含答案)

12010年全国初中数学联合竞赛试题参考答案第一试一、选择题:(本题满分42分,每小题7分)1.若a ,b ,c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-=( )A .1B .2C .3D .4【答案】 B【解析】 因为()()10101a b a c ---=,而左边的两个加数都是非负整数,所以一个等于0,另一个等于1,也就是说,a ,b ,c 三个数中有两个相等,另一个和它们相差1.因此,所求的和式中,两项等于1,另一项等于2,结果为2.2.若实数a ,b ,c 满足等式3||6a b =,49||6a b c =,则c 可能取的最大值为( )A .0B .1C .2D .3【答案】 C【解析】 为了使c 尽量大,a 应该尽量大,b 应该尽量小.因为它们都是非负数,3a ,0b =,不难观察到所求答案为2.3.若a ,b 是两个正数,且1110,a b b a--++= 则( )2A .103a b <+≤B .113a b <+≤C .413a b <+≤D .423a b <+≤. 【答案】 C【解析】 去分母之后得到()()110a a b b ab -+-+=,即220a ab b a b ++--=.给定a 和b 是两个正数,那么如果让它们中的一个等于0,则另一个等于0或14.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( )A .13-B .9-C .6D .0【答案】 A【解析】 这需要使得前者是后者的因式,用综合除法可得,余式为()()33310a b x a c +++++,它应该等于0.所以两个系数都为0,特别地,()()333210a b a c ++-++,所以所求答案为13-.5.在ABC △中,已知60CAB ∠=︒,D ,E 分别是边AB ,AC 上的点,且60AED ∠=︒,ED DB CE +=,2CDB CDE ∠=∠,则DCB ∠= ( )A .15oB .20oC .25oD .30o【答案】 B【解析】 观察可得ADE △为正三角形,6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则312320092010a a a a a +++++=L ( )A .28062B .28065C .28067D .28068.【答案】 D【解析】 根据弃九法,它和1到2010的和被9除的余数相等.每连续9个自然数之和被9整除,2010被9除余3,1236++=,所以只有D 符合.二、填空题:(本题满分28分,每小题7分)1.已知实数x ,y 满足方程组33191x y x y ⎧+=⎨+=⎩,,则22x y += .【答案】 13【解析】 第一式除以第二式可得2219x xy y -+=,第二式平方可得2221x xy y ++=,那么所求答案就是()1921313⨯+÷=.2.二次函数2y x bx c =++的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知3AB ,30CAO ∠=︒,则c = .【答案】 19【解析】 观察可知A 必须在B 左边,否则B 会跑到x 轴负半轴上.设A 的横坐标为a ,则C 的纵坐标3,23AC =,2AB a =.因此,考虑两根之积,33a a ⨯,3a =319=. 3.在等腰直角ABC △中,5AB BC ==,P 是ABC △内一点,且5PA ,5PC =,则PB = .4【答案】 10【解析】 设()00B ,,()50A ,,()05C ,,根据熟知的勾三股四弦五,可观察到()31P ,,(另一个点在三角形外,不符合),所以10PB =.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放 个球.【答案】 15【解析】 也就是说,编号之差为6或11的两个球颜色相同.下面从1号球开始,依次写出颜色相同的球的编号:11261711516104159314821371→→→→→→→→→→→→→→→→→也就是说,如果有17个球,则全部同色;如果超过17个,则任何连续17个同色,也不行.如果有16个,则上面的圈去掉17号球仍然是一条链,仍然不行;如果有15个,则上面的圈去掉17号球和16号球后断成两部分,所以可以.第二试 (A )一.(本题满分20分)设整数()a b c a b c ≥≥,,为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长5不超过30的三角形的个数.【解析】 由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤, 所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.6⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)已知等腰三角形ABC △中,AB AC =,C ∠的平分线与AB 边交于点P ,M 为ABC △的内切圆I e 与BC 边的切点,作MD AC ∥,交I e 于点D .证明:PD 是I e 的切线.【解析】 过点P 作I e 的切线PQ (切点为Q )并延长,交BC 于点N .因为CP 为ACB ∠的平分线,所以ACP BCP ∠=∠.又因为PA 、PQ 均为I e 的切线,所以APC NPC ∠=∠.IP QNB7又CP 公共,所以ACP NCP △≌△,所以PAC PNC ∠=∠.由NM QN =,BA BC =,所以QNM BAC △≌△,故NMQ ACB ∠=∠,所以MQ AC ∥.又因为MD AC ∥,所以MD 和MQ 为同一条直线.又点Q 、D 均在I e 上,所以点Q 和点D 重合,故PD 是I e 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点()1P a ,,()210Q a ,. ⑴ 如果a ,b ,c 都是整数,且8c b a <<,求a ,b ,c 的值.⑵ 设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为C .如果关于x 的方程20x bx c +-=的两个根都是整数,求ABC △的面积.【解析】 点()1P a ,、()210Q a ,在二次函数2y x bx c =+-的图象上,故1b c a +-=,4210a c a +-=,解得93b a =-,82c a =-.⑴ 由8c b a <<知8293938a a a a -<-⎧⎨-<⎩,,解得13a <<.又a 为整数,所以2a =,9315b a =-=,8214c a =-=.⑵ 设m ,n 是方程的两个整数根,且m n ≤,旗开得胜8由根与系数的关系可得39m n b a +=-=-,28mn c a =-=-,消去a ,得98()6mn m n -+=-,两边同时乘以9,得8172()54mn m n -+=-,分解因式,得(98)(98)10m n --=.所以9819810m n -=⎧⎨-=⎩,,或982985m n -=⎧⎨-=⎩,,或9810981m n -=-⎧⎨-=-⎩,,或985982m n -=-⎧⎨-=-⎩,,解得12m n =⎧⎨=⎩,,或109139m n ⎧=⎪⎪⎨⎪=⎪⎩,,或2979m n ⎧=-⎪⎪⎨⎪=⎪⎩,,或19323m n ⎧=⎪⎪⎨⎪=⎪⎩,,又m ,n 是整数,所以后面三组解舍去,故1m =,2n =.因此,()3b m n =-+=-,2c mn =-=-,二次函数的解析式为232y x x =-+.易求得点A 、B 的坐标为()10,和()20,,点C 的坐标为()02,, 所以ABC △的面积为1(21)212⨯-⨯=.第二试 (B )旗开得胜9一.(本题满分20分)设整数a ,b ,c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).【解析】 不妨设a b c ≥≥,由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤,旗开得胜10所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )11一.(本题满分20分)题目和解答与(B )卷第一题相同.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数2(1)4y x px k p =+++-的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.【解析】 由题意知,方程2(1)40x px k p +++-=的两根1x ,2x 中至少有一个为整数.由根与系数的关系可得12x x p +=-,12(1)4x x k p =+-,从而有()()()()12121222241x x x x x x k p ++=+++=- ①⑴ 若1k =,则方程为22(2)0x px p ++-=,它有两个整数根2-和2p -.⑵ 若1k >,则10k ->.因为12x x p +=-为整数,如果1x ,2x 中至少有一个为整数,则1x ,2x 都是整数.又因为p 为质数,由①式知1|2p x +或2|2p x +.不妨设1|2p x +,则可设12x mp +=(其中m 为非零整数),则由①式可得212k x m-+=,12故()()12122k x x mp m -+++=+,即1214k x x mp m-++=+. 又12x x p +=-,所以14k p mp m--+=+, 即1(1)4k m p m-++= ② 如果m 为正整数,则(1)(11)36m p ++⨯=≥,10k m->, 从而1(1)6k m p m-++>,与②式矛盾. 如果m 为负整数,则(1)0m p +<,10k m-<, 从而1(1)0k m p m-++<,与②式矛盾. 因此,1k >时,方程2(1)40x px k p +++-=不可能有整数根.综上所述,1k =.旗开得胜13。
2010年全国初中数学联赛

2010年 全 国 初 中 数 学 联 赛
中图分类号:G424.79 文献标识码:A 文章编号:1005—6416( 2mo) 10—0023—04
第一试
一、选择题( 每小题7分,共42分)
1.已知a、b、C均为整数,且满足
( a—b) 10+(a—c) 10=1.
贝4 l 口一bI +I b—Cl +I c—a l =(
B卷
一、( 20分)设正整数a、6、c为三角形的 三边长,且满足
口2+62+c 2一 口b一∞ 一6c =13. 求 符合 条 件且 周长 不 超过 30 的三 角形 的个数( 全等的三角形只计算1次) . 二、( 25分) 同A卷第二题. 三、( 25分) 同A卷第三题.
C卷
一、( 20分) 同B卷第一题. 二、(25分) 同A卷第二题. 三、( 25分) 设P是大于2的质数,七为正 整数.若函数y=石2+肛+( 矗+1) P一4的图 像与戈轴的两个交点的横坐标至少有一个为 整数,求后 的值.
P是/hABC内一点, 且PA=怕, PC=5.则
PB=————_. 4.将若干个红、黑两种颜色的球摆成一
行,要求两种颜色的球都要出现,且任意中间 夹有5个或10个球的两个球必为同一种颜 色的球.按这种要求摆放,最多可以摆放
个球.
第二试
A卷
一、( 20分) 设正整数口、6、c( a≥b≥c)
为三角形的三边长,且满足
6.D.
把l 到2 010之间的所有自然数均看作 四位数( 如果n不足四位,则在前面加0补足 四位,这样做不会改变口。的值) .
注意到,l 在千位、百位、十位、个位上 出现的次数依次为103、2 X 102、2 X102+l 、 2×102+1.因此,1出现的总次数为
2010年全国初中数学竞赛获奖名单

田晨光 马占山 李学智 白艳丽 贾正龙 徐 静 杨永兴 刘志艳 王丽敏 吴晓灵 刘淑霞 徐 张 静 丽
序 号
姓 刘 张 韩 王
名 鑫 巍 昌 鲜
学
校
全 国 一 等 奖(338 名) 指导 成 序 姓 名 教师 绩 号 张海燕 白艳丽 梁粒波 谭晓露 李红华 徐建红 张 丽 白艳丽 马占山 李 琼 李红华 李红华 李红华 张禄霞 秦 峰 李淑梅 马跃兵 王学霞 王学霞 李红华 徐建红 石秀梅 徐建红 吴玉霞 张翰河 李红华 徐建红 王学霞 李红华 白艳丽 张玉海 麦吉红 左亚虹 白艳丽 128 101 94 90 90 88 85 83 82 82 82 81 80 80 79 77 77 77 77 77 76 76 76 75 75 74 74 73 73 73 73 72 72 72
李红华 吴佳丽 高永宁 李红华 田 静 刘玉梅 张桂琴 白艳丽 白占玉 成进军
杨晓楠 朱佳兴 陈 灿 丁璐瑶 李兰君 刘丹阳 倪天资 王 洁
王绍先
王晓蕾
王学霞
213 215 217 219 221 223 225 227 229 231 233 235 237 239 241 243 245 247 249 251 253 255 257 259 261 263 265 267 269 271 273 275 277 279 281 283
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67
银川回中 银川外国语学校 银川唐中(西) 银川景博中学 银川外国语学校 银川外国语学校 石嘴山八中 银川外国语学校 固原市五原中学 中卫市第三中学 银川外国语学校 银川外国语学校 银川外国语学校 石嘴山八中 吴忠三中 石嘴山八中 平罗四中 银川十八中 银川十八中 银川外国语学校 银川外国语学校 石嘴山八中 银川外国语学校 石嘴山六中 银川英才学校 银川外国语学校 银川外国语学校 银川十八中 银川外国语学校 银川外国语学校 中卫市常乐中学 中宁二中 银川十三中 银川外国语学校
2010年全国初中数学联赛
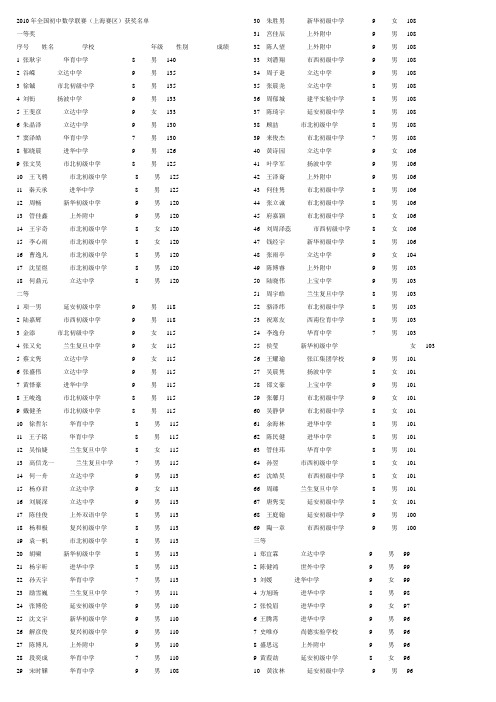
2010年全国初中数学联赛(上海赛区)获奖名单一等奖序号姓名学校年级性别成绩1 张耿宇华育中学8 男1402 谷嵘立达中学9 男1353 徐铖市北初级中学8 男1354 刘衒扬波中学9 男1335 王斐彦立达中学9 女1336 朱晶泽立达中学9 男1307 窦泽皓华育中学7 男1308 郁晓晨进华中学9 男1269 张文昊市北初级中学8 男12510 王飞骋市北初级中学8 男12511 秦天承进华中学8 男12512 周畅新华初级中学9 男12013 管佳鑫上外附中9 男12014 王宇奇市北初级中学8 女12015 李心雨市北初级中学8 女12016 曹逸凡市北初级中学8 男12017 沈星煜市北初级中学8 男12018 何鼎元立达中学8 男120二等1 项一男延安初级中学9 男1182 陆嘉辉市西初级中学9 男1183 金添市北初级中学9 女1154 张又允兰生复旦中学9 女1155 蔡文隽立达中学9 女1156 张盛伟立达中学9 男1157 黄怿豪进华中学9 男1158 王峻逸市北初级中学8 男1159 戴健圣市北初级中学8 男11510 徐哲尔华育中学8 男11511 王子铭华育中学8 男11512 吴怡婕兰生复旦中学8 女11513 高信龙一兰生复旦中学7 男11514 何一舟立达中学9 男11315 杨亦君立达中学9 女11316 刘展深立达中学9 男11317 陈佳俊上外双语中学8 男11318 杨和极复兴初级中学8 男11319 袁一帆市北初级中学8 男11320 胡啸新华初级中学8 男11321 杨宇昕进华中学8 男11322 孙天宇华育中学7 男11323 励雪巍兰生复旦中学7 男11124 张博伦延安初级中学9 男11025 沈文宇新华初级中学9 男11026 解彦俊复兴初级中学9 男11027 陈博凡上外附中9 男11028 段奕成华育中学7 男11029 宋时韡华育中学9 男108 30 朱胜男新华初级中学9 女10831 宫佳辰上外附中9 男10832 陈人望上外附中9 男10833 刘潜翔市西初级中学9 男10834 周子疌立达中学9 男10835 张晨尧立达中学8 男10836 周郁城建平实验中学8 男10837 陈琦宇延安初级中学8 男10838 顾喆市北初级中学8 男10839 来俊杰市北初级中学7 男10840 黄诗园立达中学9 女10641 叶学军扬波中学9 男10642 王泽裔上外附中9 男10643 何佳隽市北初级中学8 男10644 张立诚市北初级中学8 男10645 府嘉颖市北初级中学8 女10646 刘周泽蕊市西初级中学8 女10647 钱经宇新华初级中学8 男10648 张雨亭立达中学9 女10449 陈博睿上外附中9 男10350 陆晓伟上宝中学9 男10351 周宇皓兰生复旦中学8 男10352 骆泽纬市北初级中学8 男10353 祝寒友西南位育中学8 男10354 李逸舟华育中学7 男10355 侯莹新华初级中学女10356 王耀瑜张江集团学校9 男10157 吴晨隽扬波中学8 女10158 邵文豪上宝中学9 男10159 张馨月市北初级中学9 女10160 吴静伊市北初级中学8 女10161 余海林进华中学8 男10162 陈民健进华中学8 男10163 管佳玮华育中学8 男10164 孙翌市西初级中学8 女10165 沈皓昊市西初级中学8 女10166 周臻兰生复旦中学8 男10167 唐隽雯延安初级中学8 女10168 王庭翰延安初级中学9 男10069 陶一章市西初级中学9 男100三等1 郑宜霖立达中学9 男992 陈健鸿世外中学9 男993 刘媛进华中学9 女994 方旭旸进华中学8 男985 张悦眉进华中学9 女976 王腾霄进华中学9 男967 史唯亦尚德实验学校9 男968 盛思远上外附中9 男969 黄葭劼延安初级中学8 女9610 黄汝林延安初级中学9 男9611 华雯婷新华初级中学女9612 周君铭扬波中学9 男9513 杨易宁立达中学9 男9514 高晓耕立达中学8 男9515 胡瀛华育中学8 男9516 陈飞雄上宝中学8 男9417 虞珏钦向明初级中学8 男9418 王佳祺立达中学8 男9319 章展宏扬波中学8 男9320 黄濛婷华育中学9 女9321 周诗婕进华中学9 女9122 肖珺上宝中学9 男9123 陈孟起延安初级中学8 男9124 马志贤兰生复旦中学7 男9125 吴鑫鑫尚德实验学校9 男9026 戴镇建平西校9 男9027 蔡迥盛进华中学8 男9028 严凯华育中学8 男9029 钱汉森进才中学北校8 男9030 竺旭亮市北初级中学8 男9031 吴驿光市北初级中学7 男9032 朱文耀立达中学8 男9033 马可玮新华初级中学8 男8934 李岳融新华初级中学8 男8935 乐嘉盈新华初级中学9 女8836 丁馨宁立达中学9 女8837 李焱立达中学9 男8838 沈哲卿立达中学8 男8839 张文浩扬波中学8 男8840 陈子恒华育中学7 男8841 曹馨元华育中学8 女8842 曹喆焱华育中学8 男8843 胡泽欧延安初级中学8 男8844 周晟宇进华中学8 男8845 孙君劼进华中学8 男8846 崔羽琪进华中学8 男8847 宓金泓市西初级中学8 男8848 王宗怡上外附中7 男8749 胡逸豪市北初级中学7 男8650 宋艾伦华育中学9 男8651 赵展成兰生复旦中学9 男8652 金梦媛新华初级中学9 女8553 李天宇上外附中9 男8554 黄成瑶立达中学8 男8555 葛泽浩凯慧中学7 男8556 刘志健延安初级中学8 男8457 马渊培上外附中9 男8358 朱晨烨上外附中9 男8359 顾文灏华育中学9 男8360 倪馨仪上海市实验学校9 女8361 薛宋恺进华中学9 男83 62 谷峥立达中学9 男8363 沈佳卿立达中学8 男8364 王唯怡扬波中学8 女8365 蒋唯真市北初级中学8 男8366 刘传市北初级中学8 男8367 何思凡市北初级中学7 男8368 郑重市北初级中学8 男8369 李佳颖兰生复旦中学8 女8370 顾有为兰生复旦中学8 男8371 谢逸维市西初级中学8 男8372 毛书南新华初级中学8 男8373 丁允梓延安初级中学8 男8374 张梦晓延安初级中学8 男8275 金艳上外第一实验学校9 女8276 陆俊一立达中学8 男8277 汪阅进华中学8 男8278 沈思旸格致初级中学9 男8179 张安东上宝中学9 女8180 张家录复兴初级中学9 男8181 李嘉瑞立达中学9 男8182 汤晟皓立达中学9 男8183 顾文渊华育中学9 男8184 宋彦帆市北初级中学9 女8185 顾佳莉市北初级中学8 女8186 周立东市北初级中学8 男8187 肖栎婳兰生复旦中学8 女8188 朱兆成华育中学8 男8189 胡恺元静安教师进修学院附中8 男8190 施毅喆延安初级中学9 男8091 潘斐然尚德实验学校9 男8092 潘圣杰上外附中9 男7993 张核豪静安教师进修学院附中7 男7994 王道烨静安教师进修学院附中8 男7995 许东徐汇中学7 男7996 龚译凡尚德实验学校9 男7897 袁鸿翔进才中学北校9 男7898 刘澄新华初级中学9 男7899 李昂兰生复旦中学9 男78 100 钱列兰生复旦中学8 男78 101 高匀丰兰生复旦中学7 男78 102 沈智成市西初级中学8 男78。
2010年全国初中数学竞赛试题及参考答案

2010年全国初中数学竞赛试题参考答案一、选择题(共5小题,每小题7分,共35分.其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若20 10a b b c ==,,则a b b c++的值为( ). (A )1121 (B )2111 (C )11021 (D )21011解:D 由题设得12012101111110a ab bc b c b +++===+++. 2.若实数a ,b 满足21202a ab b -++=,则a 的取值范围是 ( ).(A )a ≤2- (B )a ≥4 (C )a ≤2-或 a ≥4 (D )2-≤a ≤4 解.C因为b20=的判别式 2()a ∆-=a ≥4.3.如图,在四边形=BC =4-CD =则AD (A)AE ,DF 垂直于直线BC ,BE =AE ,CF =DF =于是 EF =4+过点A 作AG ⊥DF ,垂足为G .在Rt △ADG 中,根据勾股定理得AD ==2+4.在一列数123x x x ,,,……中,已知11=x ,且当k ≥2时,1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭(取整符号[]a 表示不超过实数a 的最大整数,例如[]2.62=,[]0.20=),则2010x 等于( ).(A) 1 (B) 2 (C) 3 (D) 4 解:B由11=x 和1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭可得 11x =,22x =,33x =,44x =,51x =,62x =,73x =,84x =,……因为2010=4×502+2,所以2010x =2.5.如图,在平面直角坐标系xOy 中,等腰梯形ABCD 的顶点坐标分别为A (1,1),B (2,-1),C (-2,-1),D (-1,1).y 轴上一点P (0,2)绕点A 180°得点P 1,点P 1绕点B 旋转180°得点P 2,点P 2绕点C 旋转180°得点P 3,点P 3绕点D 旋转180°得点P 4,……,重复操作依次得到点P 1,P 2,…, 则点P 2010的坐标是( ).(A )(2010,2) (B )(2010,2-) (C )(2012,2-) (D )(0,2)解:B 由已知可以得到,点1P ,2P 的坐标分别为(2,0),(2,2-).记222 )P a b (,,其中222,2a b ==-. 根据对称关系,依次可以求得:322(42)P a b --,--,422(2)P a b ++,4,522(2)P a b ---,,622(4)P a b +,. 令662(,)P a b ,同样可以求得,点10P 的坐标为(624,a b +),即10P (2242,a b ⨯+), 由于2010=4⨯502+2,所以点2010P 的坐标为(2010,2-). 二、填空题6.已知a =5-1,则2a 3+7a 2-2a -12 的值等于 .解:由已知得 (a +1)2=5,所以a 2+2a =4,于是2a 3+7a 2-2a -12=2a 3+4a 2+3a 2-2a -12=3a 2+6a -12=0.7.一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶.在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间.过了10分钟,小轿车追上了货车;又过了5分钟,小轿车追上了客车;再过t 分钟,货车追上了客车,则t = .解:15设在某一时刻,货车与客车、小轿车的距离均为S 千米,小轿车、货车、客车的速度分别为a b c ,,(千米/分),并设货车经x 分钟追上客车,由题意得()10a b S -=, ①()152a c S -=, ② ()x b c S -=.③ 由①②,得30b c S -=(),所以,x =30. 故 3010515t =--=(分).8.如图,在平面直角坐标系xOy 中,多边形OABCDE 的顶点坐标分别是O (0,0),A (0,6),B (4,6),C (4,4),D (6,4),E (6,0).若直线l 经过点M (2,3),且将多边形OABCDE 分割成面积相等的两部分,则直线l 的函数表达式是 .x 轴于点F ;连接OB ,AF ;连接CE ,DF ,且相交于点N . 由已知得点M (2,3)是OB ,AF 的中点,即点M 为矩形ABFO 的中心,所以直线l 把矩形ABFO 分成面积相等的两部分.又因为点N (5,2)是矩形CDEF 的中心,所以,过点N (5,2)的直线把矩形CDEF 分成面积相等的两部分.于是,直线MN 即为所求的直线l .设直线l 的函数表达式为y kx b =+,则2352k b k b =⎧⎨+=⎩+,,(第8题解得 1311.3k b ⎧=-⎪⎪⎨⎪=⎪⎩,,故所求直线l 的函数表达式为11133y x =-+.9.如图,射线AM ,BN 都垂直于线段AB ,点E 为AM 上一点,过点A 作BE 的垂线AC 分别交BE ,BN 于点F ,C ,过点C 作AM 的垂线CD ,垂足为D .若CD =CF ,则AEAD= . 解:215- 见题图,设,FC m AF n ==.因为Rt △AFB ∽又因为 FC=DC 210n m+-=, 解得12n m =,或n m 又Rt △AFE ∽Rt △ 即AE AD =12.10.对于i =2,3,…,k n 的最小值0n 满足020003000n <<,则正整数k 的最小值为 .解:9 因为1n +为2 3 k ,,,的倍数,所以n 的最小值0n 满足 []012 3 n k += ,,,,其中[]2 3 k ,,,表示2 3 k ,,,的最小公倍数. 由于[][]2 3 88402 3 92520 == ,,,,,,,, [][]2 3 1025202 3 1127720== ,,,,,,,, 因此满足020003000n <<的正整数k 的最小值为9.(第9题)三、解答题(共4题,每题20分,共80分)11.如图,△ABC 为等腰三角形,AP 是底边BC 上的高,点D 是线段PC 上的一点,BE 和CF 分别是△ABD 和△ACD 的外接圆直径,连接EF . 求证: tan EFPAD BC∠=.证明:如图,连接ED ,FD . 因为BE 和CF 都是直径,所以ED ⊥BC , FD ⊥BC ,因此D ,E ,F 三点共线. …………(5分) 连接AE ,AF ,则AEF ABC ACB AFD ∠=∠=∠=∠,所以,△ABC ∽△AEF . …………(10分)作AH ⊥EF ,垂足为H ,则AH =PD . 由△ABC ∽△AEF 可得EFAHBC AP =, 从而E FP DB CA P=, 所以 t a n P D E FPAD AP BC∠==. …………(20分)12.如图,抛物线2y ax bx =+(a >0)与双曲线ky x=相交于点A ,B . 已知点A 的坐标为(1,4),点B 在第三象限内,且△AOB 的面积为3(O 为坐标原点).(1)求实数a ,b ,k 的值;(2)过抛物线上点A 作直线AC ∥x 轴,交抛物线于另一点C ,求所有满足△EOC ∽△AOB 的点E 的坐标.解:(1)因为点A (1,4)在双曲线k y x =上,所以k=4. 故双曲线的函数表达式为xy 4=.设点B (t ,4t),0t <,AB 所在直线的函数表达式为y mx n =+,则有44m n mt n t =+⎧⎪⎨=+⎪⎩,, 解得4m t =-,4(1)t n t +=. 于是,直线12AOB S ∆=解得2t =-,或t因为点A ,B 44a b +=⎧⎨⎩, 3.=x 轴,所以C (4-,4),于是CO =42=BOCO. (a >0)与x 轴负半轴相交于点D , 则点D 的坐标为(3-,0).因为∠COD =∠BOD =45︒,所以∠COB =90︒.(i )将△BOA 绕点O 顺时针旋转90︒,得到△1B OA '.这时,点B '(2-,2)是CO 的中点,点1A 的坐标为(4,1-). 延长1OA 到点1E ,使得1OE =12OA ,这时点1E (8,2-)是符合条件的点.(ii )作△BOA 关于x 轴的对称图形△2B OA ',得到点2A (1,4-);延长2OA 到点2E ,使得2OE =22OA ,这时点E 2(2,8-)是符合条件的点.所以,点E 的坐标是(8,2-),或(2,8-). …………(20分)13.求满足22282p p m m ++=-的所有素数p 和正整数m ..解:由题设得(21)(4)(2)p p m m +=-+,所以(4)(2)p m m -+,由于p 是素数,故(4)p m -,或(2)p m +. ……(5分) (1)若(4)p m -,令4m kp -=,k 是正整数,于是2m kp +>,2223(21)(4)(2)p p p m m k p >+=-+>,故23k <,从而1k =.所以4221m p m p -=⎧⎨+=+⎩,,解得59.p m =⎧⎨=⎩, …………(10分)(2)若(2)p m +,令2m kp +=,k 是正整数. 当5p >时,有46(1)m kp kp p p k -=->-=-,223(21)(4)(2)(1)p p p m m k k p >+=-+>-,故(1)3k k -<,从而1k =,或2.由于(21)(4)(2)p p m m +=-+是奇数,所以2k ≠,从而1k =.于是4212m p m p -=+⎧⎨+=⎩,,这不可能.当5p =时,2263m m -=,9m =;当3p =,2229m m -=,无正整数解;当2p =时,2218m m -=,无正整数解.综上所述,所求素数p =5,正整数m =9. …………(20分)14.从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?解:首先,如下61个数:11,1133+,11233+⨯,…,116033+⨯(即1991)满足题设条件. …………(5分)另一方面,设12n a a a <<< 是从1,2,…,2010中取出的满足题设条件的数,对于这n 个数中的任意4个数i j k m a a a a ,,,,因为33()i k m a a a ++, 33()j k m a a a ++,所以10分) 设133i i a a d =+,i =由12333()a a a ++所以1333a ,1115分)故n d ≤60. 所以,n ≤61.综上所述,n 的最大值为61. …………(20分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年全国初中数学联合竞赛试题参考答案第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( B )A .1.B .2.C .3.D .4.2.若实数,,a b c 满足等式3||6b =,9||6b c =,则c 可能取的最大值为 ( C )A .0.B .1.C .2.D .3.3.若b a ,是两个正数,且,0111=+-+-ab b a 则 ( C ) A .103a b <+≤. B .113a b <+≤. C .413a b <+≤. D .423a b <+≤. 4.若方程2310x x --=的两根也是方程420x ax bxc +++=的根,则2a b c +-的值为 ( A )A .-13.B .-9.C .6.D . 0.5.在△ABC 中,已知︒=∠60CAB ,D ,E 分别是边AB ,AC 上的点,且︒=∠60AED ,CE DB ED =+,CDE CDB ∠=∠2,则=∠DCB ( B )A .15°.B .20°.C .25°.D .30°.6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则12320092010a a a a a +++++= ( D )A .28062.B .28065.C .28067.D .28068.二、填空题:(本题满分28分,每小题7分)1.已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += 13 .2.二次函数c bx x y ++=2的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知AC AB 3=,︒=∠30CAO ,则c = 19.3.在等腰直角△ABC 中,AB =BC =5,P 是△ABC 内一点,且PA PC =5,则PB =.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放____15___个球.第二试 (A )一.(本题满分20分)设整数,,a b c (a b c ≥≥)为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数.解 由已知等式可得 222()()()26a b b c a c -+-+-= ①令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ (1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形. (2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形. 综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.二.(本题满分25分)已知等腰三角形△ABC 中,AB =AC ,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD//AC ,交⊙I 于点D.证明:PD 是⊙I 的切线. 证明 过点P 作⊙I 的切线PQ (切点为Q )并延长,交BC 于点N. 因为CP 为∠ACB 的平分线,所以∠ACP =∠BCP. 又因为PA 、PQ 均为⊙I 的切线,所以∠APC =∠NPC. 又CP 公共,所以△ACP ≌△NCP ,所以∠PAC =∠PNC.由NM =QN ,BA =BC ,所以△QNM ∽△BAC ,故∠NMQ =∠ACB ,所以MQ//AC.又因为MD//AC ,所以MD 和MQ 为同一条直线.又点Q 、D 均在⊙I 上,所以点Q 和点D 重合,故PD 是⊙I 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点P (1,)a ,Q (2,10)a .(1)如果,,a b c 都是整数,且8c b a <<,求,,a b c 的值.(2)设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为 C.如果关于x 的方程20x bx c +-=的两个根都是整数,求△ABC 的面积.解 点P (1,)a 、Q (2,10)a 在二次函数2y x bx c =+-的图象上,故1b c a +-=,4210a c a +-=, 解得93b a =-,82c a =-.(1)由8c b a <<知8293,938,a a a a -<-⎧⎨-<⎩解得13a <<. 又a 为整数,所以2a =,9315b a =-=,8214c a =-=.(2) 设,m n 是方程的两个整数根,且m n ≤.NC A由根与系数的关系可得39m n b a +=-=-,28mn c a =-=-,消去a ,得98()6mn m n -+=-, 两边同时乘以9,得8172()54mn m n -+=-,分解因式,得(98)(98)10m n --=.所以981,9810,m n -=⎧⎨-=⎩或982,985,m n -=⎧⎨-=⎩或9810,981,m n -=-⎧⎨-=-⎩或985,982,m n -=-⎧⎨-=-⎩解得1,2,m n =⎧⎨=⎩或10,913,9m n ⎧=⎪⎪⎨⎪=⎪⎩或2,97,9m n ⎧=-⎪⎪⎨⎪=⎪⎩或1,932,3m n ⎧=⎪⎪⎨⎪=⎪⎩又,m n 是整数,所以后面三组解舍去,故1,2m n ==.因此,()3b m n =-+=-,2c mn =-=-,二次函数的解析式为232y x x =-+.易求得点A 、B 的坐标为(1,0)和(2,0),点C 的坐标为(0,2),所以△ABC 的面积为1(21)212⨯-⨯=. 第二试 (B )一.(本题满分20分)设整数,,a b c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).解 不妨设a b c ≥≥,由已知等式可得 222()()()26a b b c a c -+-+-= ①令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.于是,等式①变为222()26m n m n +++=,即 2213m n mn ++= ②由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ (1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形. (2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形. 综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )一.(本题满分20分)题目和解答与(B )卷第一题相同.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数4)1(2-+++=p k px x y 的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.解 由题意知,方程04)1(2=-+++p k px x 的两根21,x x 中至少有一个为整数.由根与系数的关系可得4)1(,2121-+=-=+p k x x p x x ,从而有p k x x x x x x )1(4)(2)2)(2(212121-=+++=++ ①(1)若1k =,则方程为0)2(22=-++p px x ,它有两个整数根2-和2p -.(2)若1k >,则01>-k .因为12x x p +=-为整数,如果21,x x 中至少有一个为整数,则21,x x 都是整数.又因为p 为质数,由①式知2|1+x p 或2|2+x p .不妨设2|1+x p ,则可设12x mp +=(其中m 为非零整数),则由①式可得212k x m -+=, 故121(2)(2)k x x mp m -+++=+,即1214k x x mp m-++=+. 又12x x p +=-,所以14k p mp m--+=+,即 41)1(=-++mk p m ② 如果m 为正整数,则(1)(11)36m p +≥+⨯=,10k m ->,从而1(1)6k m p m-++>,与②式矛盾. 如果m 为负整数,则(1)0m p +<,10k m -<,从而1(1)0k m p m-++<,与②式矛盾. 因此,1>k 时,方程04)1(2=-+++p k px x 不可能有整数根.综上所述,1=k .。
