脉冲压缩 雷达方程
雷达波形设计与LFM信号处理(雷达脉冲压缩)

雷达波形设计与LFM信号处理(雷达脉冲压缩)本文关键词:雷达脉冲压缩,波形设计,二相编码信号,旁瓣抑制,检测与参数估计,反辐射导弹,抑制滤波器,分数阶,线性调频,回波,变换,多普勒频移,脉压,信噪比损失,时域信号,匹配滤波,模糊函数,联合分辨,距离旁瓣,峰值旁瓣电平雷达波形设计与线性调频(LFM)信号的处理在雷达系统中占有重要的位置。
本文主要研究了雷达脉冲压缩波形的设计、脉压旁瓣抑制体制的性能分析与改进、旁瓣抑制滤波器的设计、LFM信号的分析与处理特别是反辐射导弹的检测与参数估计。
现代雷达技术中广泛使用LFM信号,对LFM信号的处理至关重要。
雷达信号中线性调频项的产生有两种原因,一是人为因素有意产生的,如脉冲压缩技术中使用的LFM信号;二是目标本身客观存在的,如导弹的主动飞行段、飞机的机动飞行等产生的加速度,以及目标与雷达平台相对运动所产生的雷达回波信号中的线性调频项,如合成孔径雷达(SAR)回波、反辐射导弹回波等。
常规的雷达脉冲压缩波形有LFM信号和相位编码信号。
LFM信号的模糊函数为斜刀刃形,优点是对多普勒频移不敏感,但时频联合分辨率差,脉压输出的峰值旁瓣电平高达-13.2dB;二相编码信号如13位Barkei。
码具有图钉状的模糊函数,因而时频联合分辨率好,且脉压输出的峰值旁瓣电平相对较低,为-22.2dB,但对多普勒频移敏感。
本文提出了一类新的脉压信号——二次伸缩二相编码信号,将具有特定Fourier级数展开系数的波形在时域进行二次伸缩,采样,并符号化为二值序列,即得到这类二次伸缩二相编码信号。
信号本身兼有线性调频和调相,因而其模糊函数为刀刃型和图钉型的复合形状,对多普勒频移不敏感及有较好的距离一速度联合分辨率,且其峰值旁瓣可低于-30dB。
脉压波形经匹配滤波后,除了主瓣,尚存在不希望的距离旁瓣,影响了雷达对多目标的探测。
对于LFM这类复信号,传统的旁瓣抑制方法是在匹配滤波后引入加权网络,在频域进行加权处理,使旁瓣降低。
脉冲压缩雷达..

'
T P , D ' P T
'
可见输出脉冲的峰值功率增大了D倍。 若输入脉冲幅度为A,输出脉冲幅度为A’,则:
A T ' D A T
'
,
A A D
'
因为噪声通过压缩滤波器后,噪声不会被压 缩,其噪声电平仍保持在接收机原有的噪声电平
上,所以输出信噪比也提高了D倍:
(S / N )0 D ( S / N )i
t
td 2 td 1
T ' T
f1
td1
f2
T’ td2
f
t
(3) 同相位矢量相加方法
f
压缩前信号频谱矢量图
f
压缩后信号频谱矢量图
6 脉冲压缩雷达信号处理方式(1)
中频 信号
匹配滤波 脉冲压缩
I/Q 解调
采样 保持
窄带A/D 转换
高速 存储
信号 滤波器
频谱 分析
检测器 CFAR
检测 结果
模拟脉冲压缩方式
1 4
增加雷达系统发射信号脉冲宽度有利于提高的雷达 发射平均功率,但影响雷达系统的带宽和距离分辨率。
压缩后与压缩前雷达信号时宽之比为:
T 1 ' T TB
定义雷达信号时宽与带宽的乘积为脉冲压缩比:
'
D TB
'
如果压缩滤波器是无源的,它本身不消耗 能量也不产生能量,满足能量守恒原理:
E P T P T
相位编码脉冲压缩雷达有二相制、多相制以及巴克码、伪随机 码等类型。在二相制相位编码脉冲压缩体制中,宽度为T的宽脉冲 被划分为N个宽度为τ的子脉冲,每个子脉冲的相位按0°、180° 两相编码。经过压缩滤波器后,输出的是一个主瓣宽度为τ、幅度 为宽脉冲回波幅度N倍的窄脉冲。在要求大脉冲压缩比的场合,相 位的编码通常采用伪随机码,对于同一码长,可以得到多种不同的 编码。相位编码脉冲压缩雷达多采用数字技术进行压缩滤波处理。 数字处理方法的优点是在计算机控制下可以快速改变发射波形,相 应地改变信号处理,以适应不同的战术要求。 脉冲压缩雷达采用的宽频带信号有利于反噪声干扰。在相位编 码脉冲压缩雷达中,还可以方便地选择不同的编码,来对付欺骗干 扰。脉冲压缩技术可与动目标显示、单脉冲测角、相控阵天线等雷 达技术兼容,因而在超远程警戒雷达、远程跟踪雷达、三坐标雷达、 合成孔径雷达、精密测量雷达以及相控阵雷达中都得到广泛应用。
脉冲压缩技术研究

脉冲压缩技术在雷达信号处理中的应用姓名郭帅王继鹏学号 02103032 02103031脉冲压缩技术研究一、引言脉冲压缩技术是雷达信号处理的关键技术之一。
主要是通过发射许多具有脉内调制的足够宽的脉冲,从而在峰值功率不太高的情况下也能给出所需的平均功率,然后,在接收时用解调办法将收到的回波“压缩”起来,解决了距离分辨率与作用距离之间的矛盾。
现代雷达信号处理中常用的脉冲压缩主要有应用最广的线性调频信号脉压、巴克码信号脉压、多相码信号脉压、非线性调频信号脉压等几类。
本文在首先总结了脉冲压缩的基本原理的基础上从信号形式、优势和不足、应用场合等方面介绍这几类常用脉冲压缩信号。
最后就最为普遍的线性调频信号经行了进一步分析,利用Matlab对某个雷达的回波经行了仿真,对比脉冲压缩前后的回波信号,加深了对脉冲压缩的认识。
脉冲压缩的定义脉冲压缩即pulse compression,它是指发射宽编码脉冲并对回波进行处理以获得窄脉冲,因此脉冲压缩雷达既保持了窄脉冲的高距离分辨力,又能获得宽脉冲的强检测能力。
1.2脉冲压缩的主要手段目前的脉冲压缩的手段主要有线性调频、非线性调频与相位编码等。
1)线性调频是最简单的脉冲压缩信号,容易产生,而且其压缩脉冲形状和信噪比对多普勒频移不敏感,因而得到了广泛的应用,但是,在利用多普勒频率测量目标方位和距离的情况下很少使用;2)非线性调频非线性调频具有几个明显的优点,不需要对时间和频率加权,但是系统复杂。
为了达到所需的旁瓣电平,需要对每个幅度频谱分别进行调频设计,因而在实际中很少应用;3)相位编码相位编码波形不同于调频波形,它将宽脉冲分为许多短的子脉冲。
这些子脉冲宽度相等,其相位通过编码后被发射。
根据所选编码的类型,包括巴克码、伪随机序列编码以及多项制编码等。
二、脉冲压缩的基本原理随着雷达技术的发展和雷达应用领域的不断扩大,雷达的作用距离、分辨能力和测量精度等性能指标必须得到相应的提高。
第4章脉冲压缩雷达

因此要对滤波器系数加权,减小副瓣。加权函数通常用海明权 函数进行加权。海明函数为:
πt ) T 加权以后的失配滤波器的冲激响应为: w(t ) = 0.08 + 0.92 cos 2 ( t≤ T 2
h(t ) = s ∗ (t0 − t ) w(t )
海明加权以后,失配将导致主瓣信噪比增益下降,主瓣宽度增 加等。 匹配滤波器可用数字方法实现,结果就是一个横向滤波器。 线性调频信号还可以在频域进行压缩。 2.线性调频信号的模拟产生 见教材p127-p130
脉冲压缩的实现: 1. 发射脉冲应按一定规则编码,以获得较大带宽。 2. 接收机中应有一个压缩网络, 脉冲压缩网络实际上是一个匹配滤波器。脉冲压缩常用 的四种 调制方式: 1. 线性调频脉冲压缩 2. 非线性调频 3. 相位编码脉冲压缩 4. 时间频率编码脉冲压缩 能够进行脉冲压缩的波形:
调制类型 伪随机二进制序列 线性调频扫描 非线性调频扫描 噪声
带宽 比特率 |f2-f1| |f2-f1| B
分辨率 1/比特率 1/|f2-f1| 1/|f2-f1| 1/B
脉冲压缩匹配滤波器可以用数字电路实现,也 可以用模拟电路实现。 脉冲压缩原理: 设信号函数为s(t),对应的匹配滤波器的冲激响 应为: h(t)=s*(t0-t) 经过匹配滤波器的输出信号y(t)为:
上-章小结 1. 多普勒效应、正频率、负频率。 2. 脉冲雷达与连续波雷达(单频、调频)。 3. 脉冲雷达与距离模糊、速度模糊。 4. 脉冲雷达与速度模糊。 5. PD雷达按重频分类及其特性。 6. PD雷达的三种杂波。 7. PD雷达信号处理:单边带滤波、多普勒滤波、主瓣杂波滤波、距 离选通等。 8. 圆锥扫描跟踪。 9. 单脉冲体制雷达跟踪。 10.边扫描边跟踪。 11.解距离模糊。 12.解速度模糊。 13.影响PD雷达距离方程的主要因素。
脉冲压缩原理

脉冲压缩原理
1.脉冲压缩的目的和意义
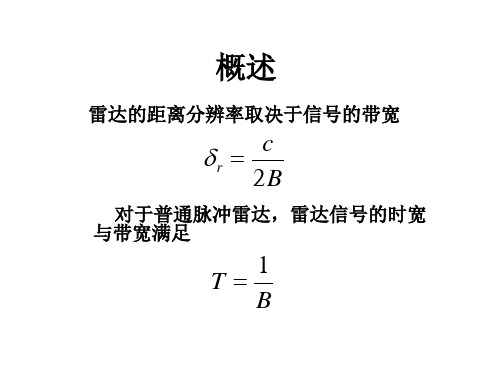
雷达距离分辨率
δ = c τ 2 \delta=\frac{c\tau}{2}δ=2cτ
c是光速,τ \tauτ是矩形脉冲的时宽,从上式中,我们不难看出决定雷达的距离分辨率的是脉冲信号的时宽,所以,如果我们想要得到高的距离分辨率,就必须要发射更窄的脉冲,但是窄脉冲意味着发射信号的能量小,就会导致雷达的探测距离变短。
对于一般的脉冲信号(时宽*带宽=常数),比如矩形脉冲信号的时宽和带宽不能同时增大,因此,距离分辨率和探测距离是一对矛盾。
脉冲压缩技术就能够很好的处理上述的这组矛盾,首先,发射宽脉冲信号保证雷达的探测距离,其次,将回波信号经过一个匹配滤波器(脉冲压缩),得到窄脉宽信号,提高了雷达的分辨率。
2.脉冲压缩的优点:提高信噪比、压缩信号的时宽
3.线性调频(Linear Frequency Modulation,LFM)信号是一种大时宽的宽频信号,LFM信号的时宽和带宽都可以自己选择,不像矩形脉冲那样时宽和带宽相互抑制。
4.由于脉冲压缩要在雷达接收机的数字处理器件完成,由于受到器件的约束,脉冲压缩通常要在零中频进行(接收信号与本振信号下变频后进行脉冲压缩)。
线性调频(LFM)脉冲压缩雷达仿真.

线性调频(LFM )脉冲压缩雷达仿真一. 雷达工作原理雷达是Radar (RAdio Detection And Ranging )的音译词,意为“无线电检测和测距”,即利用无线电波来检测目标并测定目标的位置,这也是雷达设备在最初阶段的功能。
典型的雷达系统如图1.1,它主要由发射机,天线,接收机,数据处理,定时控制,显示等设备组成。
利用雷达可以获知目标的有无,目标斜距,目标角位置,目标相对速度等。
现代高分辨雷达扩展了原始雷达概念,使它具有对运动目标(飞机,导弹等)和区域目标(地面等)成像和识别的能力。
雷达的应用越来越广泛。
图1.1:简单脉冲雷达系统框图雷达发射机的任务是产生符合要求的雷达波形(Radar Waveform ),然后经馈线和收发开关由发射天线辐射出去,遇到目标后,电磁波一部分反射,经接收天线和收发开关由接收机接收,对雷达回波信号做适当的处理就可以获知目标的相关信息。
假设理想点目标与雷达的相对距离为R ,为了探测这个目标,雷达发射信号()s t ,电磁波以光速C 向四周传播,经过时间R C 后电磁波到达目标,照射到目标上的电磁波可写成:()Rs t C -。
电磁波与目标相互作用,一部分电磁波被目标散射,被反射的电磁波为()Rs t Cσ⋅-,其中σ为目标的雷达散射截面(Radar Cross Section ,简称RCS ),反映目标对电磁波的散射能力。
再经过时间R C 后,被雷达接收天线接收的信号为(2)Rs t C σ⋅-。
如果将雷达天线和目标看作一个系统,便得到如图1.2的等效,而且这是一个LTI (线性时不变)系统。
图1.2:雷达等效于LTI 系统等效LTI 系统的冲击响应可写成: 1()()Miii h t t σδτ==-∑ (1.1)M 表示目标的个数,i σ是目标散射特性,i τ是光速在雷达与目标之间往返一次的时间,2ii R cτ=(1.2) 式中,i R 为第i 个目标与雷达的相对距离。
雷达中的线性调频脉冲压缩
dt]
T / 2
dt
T
均方根时宽:
2
( 2 )
2
2
t | u (t ) | dt
2
2
2
| u (t ) | dt 1 (T ) 2 3
( 2 )
T /2
T / 2
t 2 dt
T /2
T / 2
dt
调频常数:
2
T /2
T /2
T / 2 T /2
时间轴上的切面:
sin K (T | |) | ( ,0) || (T | |) | K (T | |)
sin B (1 | / T |) | ( ,0) | T | | B sin B | ( ,0) | T | | B | | T
1 f H( f ) rect( )e B K 1 d 2 f td ( f ) 2 df K K
j
2 f K
幅度频谱:
1 f | u( f ) | rect( ) B K
相位频谱:
2 ( f ) f /4 K
线性调频信号的近似匹配滤波器的频谱特性应满足:
1 幅度谱与信号的频谱相同,即带宽为B的矩形谱 2 相位谱是信号相位谱的共轭
2 ( f ) f K
压缩滤波器的频谱应该是:
| | T
| | T
频率轴上的切面:
sin T | (0, ) | T | | T
特点: 1 随着多普勒频移,主峰值降低。
2 随着多普勒频移,主峰值产生时移。
3 随着多普勒频移,切割图与辛克函数的失真进一步加大。
第三章 脉冲压缩雷达简介

∂∇第三章 脉冲紧缩雷达简介脉冲紧缩简介雷达的分辩理论标明:要得到高的测距精度亲睦的距离分辩力,发射旌旗灯号必须具有大的带宽;要得到高的测速精度亲睦的速度分辩力,旌旗灯号必须具有大的时宽.是以,要使感化距离远,又具有高的测距.测速精度亲睦的距离.速度分辩力,起首发射旌旗灯号必须是大带宽.长脉冲的情势.显然,单载频矩形脉冲雷达不克不及知足现代雷达提出的请求.而脉冲紧缩技巧可以获得大时宽带宽旌旗灯号,使雷达同时具有感化距离远.高测距.测速精度亲睦的距离.速度分辩力.具有大时宽带宽的旌旗灯号平日被称作脉冲紧缩旌旗灯号.脉冲紧缩技巧包含两部分:脉冲紧缩旌旗灯号的产生.发射部分和为获得较窄的脉冲对吸收回波的处理部分.在发射端,它经由过程对相对较宽的脉冲进行调制使其同时具有大的带宽,在吸收端对吸收的回波波形进行紧缩处理得到较窄的脉冲.脉冲紧缩道理时宽-带宽积的概念发射脉冲宽度τ和体系有用(经紧缩的)脉冲宽度0τ的比值称为脉冲紧缩比,即 0D ττ=(3-1) 因为01B τ=,所以,式(3-1)可写成D B τ=(3-2)即紧缩比等于旌旗灯号的时宽-带宽积.在很多运用处合,脉冲紧缩体系经常运用当时宽-带宽积暗示.大时宽带宽矩形脉冲旌旗灯号的复包络表达式可以写成:(),/2/2()0,j t Ae T t T u t θ⎧-<<=⎨⎩其他(3-3)匹配滤波器输出端的信噪比为:()00S N EN = (3-4)个中旌旗灯号能量为[13] :212E A T =(3-5)这种体系体例的旌旗灯号具有以下几个明显的特色:(1)在峰值功率受限的前提下,进步了发射机的平均功率av P ,加强了发射旌旗灯号的能量,是以扩大了探测距离.(2)在吸收机中设置一个与发射旌旗灯号频谱相匹配的紧缩收集,使宽脉冲的发射旌旗灯号变成窄脉冲,是以保持了优胜的距离分辩力.(3)有利于进步体系的抗干扰才能.当然,采取大时宽带宽旌旗灯号也会带来一些缺陷[14][15],这重要有:(1)最小感化距离受脉冲宽度τ的限制.(2)收发体系比较庞杂,在旌旗灯号产生和处理进程中的任何掉真,都将增大旁瓣高度.(3)消失距离旁瓣.一般采取掉配加权以克制旁瓣,主旁瓣比可达30dB ~35dB 以上,但将有1 dB ~3 dB 的信噪比损掉.(4)消失必定的距离和速度测定隐约.恰当选择旌旗灯号参数和情势可以减小隐约.但脉冲紧缩体系体例的优胜性超出了它的缺陷,已成为近代雷达普遍运用的一种体系体例.3.2.2 线性调频脉冲旌旗灯号线性调频脉冲紧缩体系体例的发射旌旗灯号,其频谱在脉冲宽度内按线性纪律变更,即用对载频进行调制的办法展宽发射旌旗灯号的频谱,使其相位具有色散.同时,在t P 受限情形下为了充分运用发射机的功率,往往采取矩形宽脉冲包络,线性调频脉冲旌旗灯号的复数表达式可写成[16][17]:200()2()()()t j t j t t s t u t e Arect e μωωτ+== (3-6)式(3-6)中u(t)为旌旗灯号复包络:22()()t j t u t Arect e μτ= (3-7)若令B 为频率变更规模,则21B f f f =∆=-,而2fωπμττ∆∆==为调制斜率.若旌旗灯号的载波中间角频率为002f ωπ=,则线性调频旌旗灯号的角频率变更纪律为:0t ωωμ=+, 2|t |τ≤(3-8)因而旌旗灯号的瞬时相位: 201()()2i t dt t dt t t C ωωμωμφ==+=++⎰⎰ (3-9) 如图3-1所示,图3-1(a )为线性调频脉冲旌旗灯号的波形;图3-1(b )为旌旗灯号的包络幅度为A,图3-1(c)为载频的调制特征,在τ内由低频端1f 至高频端2f 按线性纪律变更.图3-1 线性调频旌旗灯号波形.包络及频率变更图脉冲紧缩雷达脉冲紧缩雷达经由过程发射宽脉冲以进步发射旌旗灯号的平均功率,包管足够的最大感化距离,而在吸收时则采取响应的脉冲紧缩法获得窄脉冲,以进步距离分辩力,从而较好地解决了感化距离和分辩才能之间的抵触.给定雷达体系的距离分辩力为: 2r c B δ=(3-10)个中,c 为光速,B f =∆为发射波形带宽.对于简略的脉冲雷达,1B f T =∆=,T 为发射脉冲宽度,则有 2r cT δ=(3-11)而在脉冲紧缩体系中,发射波形往往在相位上或频率长进行调制,吸收时将回波旌旗灯号加以紧缩,使其等效带宽B 知足1B f T =∆.令脉冲紧缩后的有用脉冲宽度1B τ=,则2r c τδ=(3-12)由此可见,脉冲紧缩雷达可用宽度T 的发射脉冲来获得相当于发射脉冲有用宽度为τ的简略脉冲体系的距离分辩力.则脉冲紧缩比(发射脉冲宽度T 跟体系有用脉冲宽度τ的比值)为TD τ= (3-13)又因为1B τ=,则D TB = (3-14)即紧缩比等于旌旗灯号的时宽-带宽积.在很多运用处合,脉冲紧缩体系经常运用当时宽-带宽积表征.实现脉冲紧缩的前提如下:(1)发射脉冲的脉冲宽度与有用频谱宽度的乘积弘远于1.(2)吸收机中必须具有一个紧缩收集,其相频特征应与发射旌旗灯号实现“相位共扼匹配”,即相位色散绝对值雷同而符号相反,以清除输入回波旌旗灯号的相位色散.脉冲紧缩按发射旌旗灯号的调制纪律(调频或调相)分类,可以分为以下四种:(1)线性调频脉冲紧缩;(2)非线性调频脉冲紧缩;(3)相位编码脉冲紧缩;(4)时光频率编码脉冲紧缩.本文重要评论辩论较罕有的线性调频脉冲紧缩.线性调频脉冲紧缩雷达线性调频旌旗灯号(LFM)在二十世纪四十年月后期就被起首提出来,是研讨最早.运用最普遍的一种脉压旌旗灯号[18].线性调频经由过程对雷达的载波频率进行调制以增长雷达的发射带宽并在吸收时实现脉冲紧缩,线性调频脉压的基起源基础理如图3-2所示.图3-2 线性调频脉冲紧缩基起源基础理图线性调频波形由宽度为T 的矩形发射脉冲构成,如图3-2 (a)所示.载波频率f 在脉冲宽度内按照21f f f ∆=-做线性增长变更,调制斜率2f T μπ=∆,如图3-2(b)所示.图3-2 (c)为紧缩收集的频率-延迟特征,按照线性递减变更,与旌旗灯号的线性调频斜率相反,滤波器对线性调频旌旗灯号中最先辈入的低端频率为延时长(1d t ),对经由T 时光最落后入的高端频率2f 分量延时短(2d t ).如许,旌旗灯号中不合频率分量经由过程这一滤波器后几乎同时到达输出端,从而获得幅度增大宽度变窄的脉冲旌旗灯号,其幻想包络如图3-2(d )所示.依据图3-1(b),有12B f f f =∆=-和2f T Tωπμ∆∆==,若旌旗灯号的载波中间角频率为002f ωπ=,则线性调频旌旗灯号的角频率变更纪律为:0t ωωμ=+,2Tt ≤(3-15)因而旌旗灯号的瞬时相位为: 2001()()2i t dt t dt t t C φωωμωμ==+=++⎰⎰(3-16)则线性调频脉冲紧缩雷达的发射旌旗灯号为:201cos(),22()0,2i T A t t t u t T t ωμ⎧+≤⎪⎪=⎨⎪>⎪⎩(3-17)个中A 为旌旗灯号幅度.或者将上式暗示成:201()cos()2i t u t Arect t t T ωμ=+ (3-18)个中,t rect T为矩形函数,即:为便利剖析和盘算,用复数情势来暗示()i u t ,即: 201()2()()j t t i t u t Arect e T ωμ+= (3-19)则()i u t 的复频谱为:2200112()()222()()()T j t t j t t j t j t i i Tt U u t e dt Arect e e dt A e dt T ωμωωμωωω∞∞+-+---∞-∞-===⎰⎰⎰(3-20)因为平日运用的线性调频脉冲旌旗灯号均知足1D TB =,其频谱的振幅散布很接近矩形,()i U ω可近似地暗示为:002()0,2i U ωωωωωωω⎧∆-≤⎪⎪=⎨∆⎪->⎪⎩(3-21)()i U ω的相频特征可近似地暗示为: 20()()24i ωωπφωμ-=-+ (3-22)综上所述,线性调频旌旗灯号在D 很大时的频谱表达式为:20()2400,2()0,2j i U ωωπμωωωωωωω⎡⎤--+⎢⎥⎢⎥⎣⎦⎧∆⎪-≤⎪=⎨⎪∆->⎪⎩ (3-23)设匹配滤波器频率特征为()H ω,那么依据匹配前提应知足如下关系: ()()()i dj j t i H k U e e φωωωω--= (3-24)个中,k 为归一化系数,使幅频特征归一化,d t 为匹配滤波器的固定延时[19].是以线性调频脉冲旌旗灯号的匹配滤波器频率特征可近似为: 20()240(),2d j t H eωωπωμωωωω⎡⎤---⎢⎥⎢⎥⎣⎦∆=-≤ (3-25)设线性调频脉冲旌旗灯号经匹配滤波后的输出旌旗灯号为0()u t ,则其频谱()o U ω为:0()()(),2d j t o i U U H ωωωωωωω-∆==-≤ (3-26)则匹配滤波器输出的旌旗灯号为:02()001()()2d j f t t j t d u t U e d πωωωπ∞--∞==⎰(3-27)上式暗示的旌旗灯号是复数,而现实的旌旗灯号应为实数,是以取其实部得到输出旌旗灯号为:00()2()d d u t f t t π=- (3-28)因为0f B ,故输出旌旗灯号的载波为: 而旌旗灯号的包络为:二相编码脉冲紧缩雷达线性调频旌旗灯号的频率调制函数是中断函数,而相位编码旌旗灯号的相位调制函数是离散的有限状况.因为相位编码采取伪随机序列,亦称为伪随机编码旌旗灯号.伪随机相位编码旌旗灯号按相移取值数量分类,假如相移只取0,π两个数值,称二相编码旌旗灯号.假如相移取两个以上的数值,则称多相编码旌旗灯号.一般相位编码旌旗灯号的复数表达式为:2()()()j f t j t s t a t e e πϕ= (3-29)则旌旗灯号的复包络函数为:()()()j t u t a t e ϕ= (3-30)个中,()t ϕ为相位调制函数.对于二相编码旌旗灯号来说,()t ϕ只有0或者π两种取值.可用二进制相位序列{}0,k ϕπ=暗示,也可以用二进制序列{}1,1kj k c e ϕ==+-暗示. 假如二相编码旌旗灯号的包络为矩形,即:()0,t NT a t <<∆==⎩其他 (3-31)则二相编码旌旗灯号的复包络可写成:10()N k k c v t kT -=-⎩1u(t)=0,其他 (3-32)个中,k c 为二进制序列,v(t)为子脉冲函数,T 为子脉冲宽度,N 为码长,NT ∆=为编码旌旗灯号中断期.运用δ函数性质,式(3-32)还可写成:1120()()()()()N k k u t v t c t kT u t u t δ-==-=⊗1 (3-33)个中,⊗暗示卷积运算,且1()()0,t T u t v t <<==⎩其他 (3-34)120()()N kk u t c t kT δ-==-1(3-35)依据傅里叶变换对:sin ()trect T c fT T⇔ (3-36)2()j fkT T kT e πδ--⇔ (3-37)则式(3-33)中1()u t 和2()u t 对应的频谱分离为:112()()()j fTt T u t U f c fT e T π--=⇔=(3-38)11222()()()N N j fkTk k k k u t c t kT U f c eπδ---===-⇔=1(3-39)是以,依据傅里叶变换卷积规矩,由式(3-33),可得二相编码旌旗灯号的频谱为:12120()()()()N j fT j fkT k k U f U f U f c fT e c e ππ---=⎡⎤==⎢⎥⎣⎦∑ (3-40) 盘算标明,二相编码旌旗灯号的频谱重要取决于子脉冲频谱1()U f ,至于附加因子120N j fkT k k c e π--=∑的感化则与所采取码的情势有关.二相编码旌旗灯号的带宽B 与子脉冲带宽异常接近,有:1NB T ≈=∆(3-41)则旌旗灯号的脉冲紧缩比为:ND B N =∆⋅=∆⋅=∆(3-42)由此可见,采取长的二元序列,就能得到大时宽-带宽积的编码脉冲紧缩旌旗灯号经常运用的二相编码旌旗灯号有巴克码序列.m 序列.L 序列.双素数序列等.这里重要介绍巴克码序列和m 序列.巴克码是一种二元伪随机序列码{}k c ,(1,1),0,1,2,1k c k N ∈+-=-,其非周期自相干函数知足:10,0(,0)01,0N mk k m k N m m c c m χ--+==⎧==⎨±≠⎩∑或(3-43)表3-1 巴克码序列长度N{}k c 序列(,0),0,1,,1m m N χ=-主旁瓣比/dB2 + +;- + 2,+1;2,-1 63 + + - 3,0,-14 + + - +;+ + + - 4,-1,0,+1,;4,+1,0,-1 125 + + + - + 5,0,+1,0,+1 14 7 + + + - - + - 7,0,-1,0,-1,0,-1 17 11 + + + - - - + - - + - 11,0,-1,0,-1,0,-1,0,-1,0,-113+ + + + + - - + + - + -+13,0,+1,0,+1,0,+1,0,+1,0,+1,0,+1巴克码自相干函数的主旁瓣比等于紧缩比,即为码长N .巴克码是一种较幻想的编码紧缩旌旗灯号,惋惜其长度有限.已经证实,对于奇数长度,13N ≤;对于偶数长度,N 为一完全平方数,但已证实N 在4到6084之间不消失,超出6084的码一般不采取.今朝只找到下列几种巴克码序列,最长的是13位,如表3-1所示.在现实运用中,可以采取组合巴克码序列以扩大长度.组合巴克码序列是以长度为1k 的巴克码序列作为长度为2k 的巴克码序列的码元,结构长度为12k k ⋅的组合巴克码序列[21].m 序列也是一种二元伪随机序列,它的周期自相干函数很幻想.但m 序列在非周期工作时,其自相干函数将有较高的旁瓣,当1N时,.m序列是一种周期为21n -的轮回二进制序列,n 为整数.它的产生办法比较简略,现实运用中多采取n 阶线性逻辑反馈移位存放器来产生序列,且各个移位存放器的初始状况不克不及全体为零.图3-3示出了一般线性反馈移位存放器的构成[22].图3-3 线性反馈移位存放器图3-3中一级移位存放器的状况用i a 暗示,01i a =或,i 是整数.反馈线的衔接状况用i c 暗示,1i c =暗示此线接通(介入反馈),0i c =暗示此线断开.表2列出10n ≤时m 序列的反馈衔接.表3-2 m 序列的反馈衔接级数n 长度N 序列个数反馈衔接 2 3 1 2,1 3 7 2 3,2 4 15 2 4,3或4,1 5 31 6 5,3 6 63 6 6,5 7 127 18 7,6或7,4 8 255 16 8,6,5,4 9 511 48 9,5或9,4 1010236010,7值得指出的是m序列的非周期自相干函数不如巴克码序列幻想.作为脉冲紧缩旌旗灯号,序列的非周期自相干函数更令人存眷.具有优胜的周期自相干特征的序列不必定具有优胜的非周期特征.本章小结本章重要讲述了雷达的根本构成以及扼要概述了脉冲紧缩理论,雷达为了加大发射脉冲的能量,只有增大脉冲宽度,但通例脉冲的时宽-带宽积约等于1,增大脉冲宽度会下降脉冲的有用带宽,使雷达的测距精度下降,也就是说,通例脉冲旌旗灯号体系体例雷达消失着感化距离和测距精度的抵触,为解决这一抵触,就要对脉冲频率进行调制,是以,脉冲紧缩技巧显然成为雷达发射较宽脉冲和恢复测距精度请求的脉冲宽度程度的重要办法.为包治理论研讨的完全性,特在本章参加了二相编码脉冲紧缩雷达的介绍,但是因为我们的雷达获取的目的一般为中断旌旗灯号,采取线性调频脉冲紧缩雷达比较适合,而二相编码脉冲紧缩雷达实用于离散旌旗灯号,故对二相编码脉冲紧缩雷达只做简略介绍,而线性调频脉冲雷达才是本文重点部分.第四章雷达脉冲紧缩技巧的MATLAB实现线性调频脉冲旌旗灯号脉冲紧缩雷达能同时进步雷达的感化距离和距离分辩率.这种体系体例采取宽脉冲发射以进步发射的平均功率,包管足够大的感化距离;而接收时采取响应的脉冲紧缩算法获得窄脉冲,以进步距离分辩率,较好的解决雷达感化距离与距离分辩率之间的抵触.脉冲紧缩雷达最罕有的调制旌旗灯号是线性调频(Linear Frequency Modulation )旌旗灯号,吸收时采取匹配滤波器(Matched Filter )紧缩脉冲.LFM 旌旗灯号(也称Chirp 旌旗灯号)的数学表达式为:22()2()()c K j f t t t s t rect Te π±=(4-1)式中c f 为载波频率,()t rect T为矩形旌旗灯号,11()0,t t rect TT ⎧ , ≤⎪=⎨⎪ ⎩其他(4-2)B K T=,是调频斜率,于是,旌旗灯号的瞬时频率为()22c T T f Kt t ± -≤≤,如图4-1图4-1 典范的chirp 旌旗灯号(a )up-chirp (b )down-chirp 将(4-1)式中的up-chirp 旌旗灯号重写为:2()()cj f t s t S t e π=(4-3) 式中,2()()j Kt tS t rect e Tπ= (4-4)是旌旗灯号s(t)的复包络.由傅立叶变换性质,S(t)与s(t)具有雷同的幅频特征,只是中间频率不合而以,是以,MATLAB 仿真时,只需产生S(t).MATLAB 程序1(附录1)产生(4-4)式的chirp 旌旗灯号,并作出当时域波形和幅频特征,见仿真成果. 4.2 匹配滤波道理设吸收滤波器[22]的传输函数为()H f ,冲激响应为()h t ,滤波器输入码元()s t 的中断时光为s T ,旌旗灯号和噪声之和()r t 为()()(),0s r t s t n t t T =+≤≤ (4-5)式中:()s t 为旌旗灯号码元,()n t 为高斯白噪声.并设旌旗灯号码元()s t 的频谱密度函数为()S f ,噪声()n t 的双边功率谱密度为0()2n P f n =,0n 为噪声单边功率谱密度.因为假定滤波器是线性的,依据线性电路叠加定理,当滤波器输入电压()r t 中包含旌旗灯号和噪声两部分时,滤波器的输出电压()y t 中夜包含响应的输出旌旗灯号0()s t 和输出噪声0()n t 两部分,即:00()()()y t s t n t =+ (4-6) 个中,20()()()j ft s t H f S f e dfπ∞-∞=⎰(4-7)为了求出输出噪声功率,由式2*0()()()()()()i i P f H f H f P f H f P f =⋅⋅=可知,一个随机进程经由过程线性体系时,其输出功率谱密度0()P f 等于输入功率谱密度()i P f 乘以体系传输函数()H f 的模的平方.所以,这时的输出噪声功率0N 等于:22000()()22n n N H f df H f df∞∞-∞-∞=⋅=⎰⎰(4-8)是以,在抽样时刻0t 上,输出旌旗灯号瞬时功率与噪声平均功率之比为:2220002()()()()2j ft H f S f e dfs t r n N H f dfπ∞-∞∞-∞==⎰⎰(4-9)为了求出0r 的最大值,我们运用施瓦兹不等式:2221212()()()()f x f x dx f x dx f x dx∞∞∞-∞-∞-∞≤⎰⎰⎰(4-10)若*12()()f x kf x =,个中k 为随意率性常数,则式(4-10)的等号成立.将式(4-9)右端的分子看作是式(4-10)的左端,并令: 则有:22202000()()()2()22H f df S f dfS f df E r n n n H f df∞∞∞-∞-∞-∞∞-∞≤==⎰⎰⎰⎰(4-11)式中:2()E S f df ∞-∞=⎰,为旌旗灯号码元能量.并且当2*()()j ft H f kS f e π-=(4-12)时,式(4-11)的等号成立,即得到最大输出信噪比02E n .式(4-12)标明,()H f 就是我们要找的最佳吸收滤波器传输特征,它等于旌旗灯号码元频谱的复共轭.故称此滤波器为匹配滤波器.4.3 LFM 脉冲的匹配滤波旌旗灯号()s t 的匹配滤波器的时域脉冲响应为:*0()()h t s t t =- (4-13)0t 是使滤波器物理可实现所附加的时延.理论剖析时,可令0t =0,则:*()()h t s t =-(4-14)将4-13式代入4-14式得:22()()c j f t j Kt t h t rect e e Tππ-=⨯(4-15)图4-2 LFM 旌旗灯号的匹配滤波如图4-2,()s t 经由体系()h t 得输出旌旗灯号()o s t ,2222()()()()*()()()()()()()c c o j f u j f t u j Ku j K t u s t s t h t s u h t u du h u s t u du u t u erect e e rect e du T Tππππ∞∞-∞-∞∞----∞= =- =-- =⨯⎰⎰⎰(4-16)当0t T ≤≤时,22222022222()2sin ()T T c c j Kt j Ktu t j Ktu T j f tj Kt T j f ts t e e du e ee t j Kt K T t t eKtπππππππππ---==⨯--- =⎰(4-17) 当0T t -≤≤时,22222022222()2sin ()T T c c t j Kt j Ktu j Ktu T j f tj Kt T j f ts t ee dut e eej Kt K T t t eKtπππππππππ+---=+ =⨯--+ =⎰(4-18)归并(4-17)和(4-18)两式:20sin (1)()()2c j f t tKT tt T s t Trect e KTt Tπππ-= (4-19)(4-19)式即为LFM 脉冲旌旗灯号经匹配滤波器得输出,它是一固定载频c f 的旌旗灯号.当t T ≤时,包络近似为辛克(sinc )函数.0()()()()()22t tS t TSa KTt rect TSa Bt rect T Tππ== (4-20)图4-3 匹配滤波的输出旌旗灯号如图4-3,当Bt ππ=±时,1t B=±为其第一零点坐标;当2Bt ππ=±时,12t B=±,习惯上,将此时的脉冲宽度界说为紧缩脉冲宽度. 1122B Bτ=⨯=(4-21)LFM 旌旗灯号的紧缩前脉冲宽度T 和紧缩后的脉冲宽度τ之比平日称为紧缩比D,TD TB τ==(4-22)上式标明,紧缩比也就是LFM 旌旗灯号的时宽频宽积.因为s(t),h(t),so(t)均为复旌旗灯号情势,MATLAB 仿真时,只需斟酌它们的复包络S(t),H(t),So(t).MATLAB 程序2(附录2)仿真了图4-2所示的进程,并将仿真成果和理论进行对比.仿真成果见图4-4,4-5. 4.4 MATLAB 仿真成果仿真一:线性调频脉冲紧缩旌旗灯号(1) 体系模子:图4-4 线性调频脉冲紧缩旌旗灯号体系框图(2) 仿真成果:图4-5 LFM 旌旗灯号的时域波形和幅频特征(3) 成果剖析:如图4-5所示,图中为典范的线性调频旌旗灯号的时域和频域特征,经调制,旌旗灯号带宽为30MHz ,旌旗灯号周期为10us.仿真二:匹配滤波吸收回波旌旗灯号(1)体系模子:图4-6 匹配滤波体系框图(2)仿真成果:图4-7 脉冲紧缩后的回波图4-8 脉冲紧缩后的回波(局部图)(3)成果剖析:如图4-8,对时光轴进行了归一化,(/(1/)t B t B =⨯).图中反应出理论与仿真成果吻合优胜.第一零点出如今1±(即1B ±)处,此时相对幅度.紧缩后的脉冲宽度近似为1B (12B ±),此时相对幅度-4dB,这与理论剖析(图4-3)一致.上面只是对各个旌旗灯号复包络的仿真,现实雷达体系中,LFM脉冲的处理进程如图4-6.雷达回波旌旗灯号()r s t 经由正交解调后,得到基带旌旗灯号,再经由匹配滤波脉冲紧缩后就可以作出判决.正交解调道理如图4-9,雷达回波旌旗灯号经正交解调后得两路互相正交的旌旗灯号I(t)和Q(t).一种数字办法处理的的匹配滤波道理如图4-10.图4-9 正交解调道理图4-10 一种脉冲紧缩雷达的数字处理方法仿真三:脉冲紧缩前后的回波仿真(1)体系模子:联合以上剖析,用MATLAB 仿真雷达发射旌旗灯号,回波旌旗灯号和紧缩后的旌旗灯号的复包络特征,其载频不予斟酌(现实中需加调制和正交解调环节),仿真旌旗灯号与体系模子如图4-11.图4-11 雷达仿真等效旌旗灯号与体系模子(2)在MATLAB指令窗中键入:LFM_radar(10e-6,30e6,10000,15000,[10500,11000,12000,12008,13000,13005], [1,1,1,1,1,1])得到的仿真成果如下:图4-12 仿真成果(3)成果剖析:由图4-12可以看出,旌旗灯号回波在紧缩之前,目的难以分辩,在旌旗灯号回波经由紧缩之后,带宽变大,目的的相对距离也扩大,当T=10us,B=30MHz时,雷达的距离分辩率为:(4-23)当两目的相距5m时,现实上是两目的的输出sinc包络叠加,他们的副瓣互相抵消;而当两目的距离大于雷达的距离分辩率时可以分辩出,并且,跟着目的距离越大,雷达越轻易区分. 本章小结本章重要介绍了雷达在传输以及吸收旌旗灯号中所采取的不合技巧,个中,因为旌旗灯号发射时须要有较大的带宽,为了实现这一目的,我们将旌旗灯号进行线性调频,脉冲紧缩,如许扩大了带宽,有利于旌旗灯号的传输,同时也包管了较大的感化距离.在接收进程中,采取匹配滤波,可以得到较大的信噪比,包管紧缩比.。
线性调频脉冲压缩雷达的设计报告ppt

-3
-2
0 1 t/s chirp信 号 的 虚 部
-1
2
3
4
5
4 2
时宽T为10us 0 带宽为B为40MHz
-2 -4 -5
-4 -3 -2 0 1 t/s chirp信 号 的45 虚部
40
-1
2
3
4
5
chirp信 号 的 幅 频 特 性
-4
-3
-2
-1
0 t/s
1
2
3
4
5
4 2 0 -2 -4 -5
总括
线 性 调 频 脉 冲 压 缩 雷 达 仿 真
• 雷达的基本原理
• 线性调频信号
• 脉冲压缩过程 • 加权抑制旁瓣技术
• 雷达系统 的仿真过程
雷达基本原理
天线 收发转换开关 发射机 接收的电磁波 R 噪声 接收机 信号 处理机 显示器
发射的电磁波 目标
抽象出来的流程图
雷达的基本原理
Tr (a )
可以独立选取脉冲宽度与有 效频谱宽度这两个参数,从而增 加雷达波形设计的灵活性。 • 通过匹配压缩处理,获得较 高的距离分辨率。
• 宽带信号有利于提高系统的 抗干扰能力。
旁瓣抑制技术
• 目标的反射面差别很大。强信号的压缩脉 冲的副瓣可能覆盖或者干扰弱信号的反射 波形。在这个时候就需要用加权技术来抑 制旁瓣,使得弱信号的波形显现出来。
• 加权技术的做法通常是用匹配滤波器的频 率响应乘上某个适当的函数。例如窗函数, 常用的窗有: 矩形窗、三角窗、汉宁窗、汉 明窗。
旁瓣抑制
• 框图 :
• 使用加权函数来降低脉冲压缩谱的旁瓣电 平,其代价是主瓣分辨率的损失和峰值的 降低(即SNR的损失)。
气象雷达用的脉冲压缩技术

图 1 L 3
采 用 脉压波 形 和 相 控 阵 电 扫 天 线 的 先进 高分 辨 力 雷 达 系 统
气 象 目标 特 性
与 其 他 扩 展 的 散 射 体 (如 昆 虫 ) 和 折 射 系 数 梯 度 一 样
,
气 象是 由 许 多 小 散 射 体构 成
, .
它可 在 机 场 终端 区 迅 速 造成 致 命 的 航
,
气象空域扫描时 间 为
2 5~
.
0 1
分钟 的 情 况 下
TD
WR
.
和 N EX R A D 雷 达 的 特性
.
不具 备 足 够 的时 间分 辨 力 来 采 集 精 确 微 暴 危 害 预 报 所 需 要 的 数 据 达 用 现 有 方 式 在 机场 终 端 区 搜 索 预 报 特 征 是 极 为 困 难 的 描 时 间可 明显 减 少
9 9 万年
第
了期
现代 电子
总第
2期
*
气 象 雷 达 用 的脉 冲 压 缩 技 术
摘要
形 包括
下 世 纪 的 先 进 气 象雷 达 将 能 采 纳脉 冲 压缩波 形 和 相 控 阵电 扫 天 线
.
,
以满 足 更高 的 时
.
间 与空 间 分辨 力 要求
Ba r
,
我 们 已 研 究 出 几 种 用 于气 象 雷 达 的 编 码波 形 和 脉 压 滤 波 器
;
t h mi
9 7 1 4
K e
l e e r
与
F
r h u s
9 8 1 3 a )
:
脉冲压缩

雷达分辨率分辨力是指雷达对两个相邻目标的分辨能力。
分为四个方面:距离向、横向(方位向)、纵向和多普勒频移[1],对进场转台目标成像主要考虑距离向和方位向的分辨力。
距离向分辨力定义为两个目标处于同一方位角但不在同一距离时,雷达能够区分它们的能力。
通常表示为:当较近的目标回波脉冲的后沿与较远目标回波的前沿刚好重合时,作为可分辨的极限。
此时两个目标的距离就是距离分辨力,从上图看,距离分辨力ΔR 为:2c R τ∆= C 为电磁波的传播速度(8310/m s ⨯),τ为处理后的信号在显示屏上的脉冲宽度(s )。
由于c 为常数,距离分辨力由脉冲宽度决定。
宽度越小,分辨力越好。
搞分辨力要求窄脉冲宽度,雷达波形设计中的一对矛盾是:我们希望同时得到宽发射脉冲和大发射带宽。
前者有理由目标检测,而后者有利于距离分辨。
这个矛盾可以通过对发射信号进行调制,然后再接收端压缩信号来调节。
发射信号为宽脉冲,而在接受端经过压缩成为窄脉冲。
许多信号都具有这种特性,其中最为常用的就是线性调频(LFM )信号。
线性调频脉冲(LFM )信号的数学表达式为: 201()()cos(2())2t S t rect j f t T πα=+ 写成复数形式即为2012()2()()j f t t S t rect e Tπα+= 式中,α为调频率,T 为脉冲宽度,()t rect T为矩形窗函数,定义为: 1...2()0 (2)T t t rect T T t ⎧≤⎪⎪=⎨⎪>⎪⎩ LFM 信号如图所示,图中B=αT 为发射信号的频率变化范围,它近似于信号的带宽。
根据模糊函数理论,雷达的距离分辨力与发射信号的复自相关函数有关。
自相关函数的主瓣宽度越窄,距离分辨率越好。
S (t )的复自相关函数为:*sin()()()()T C S t S t dt T T πατττπατ∞-∞=+≈⎰ ()C τ具有sinc 函数的形式,如图。
主瓣宽度(半功率主瓣宽度)可以从图上得到(近似为第一零点距离的一半),也可以通过求解函数第一次过零点的值近似推出:011T Bτα≈= 距离分辨率为:022r c c Bτρ≈= 显然,信号带宽越大,自相关函数的主瓣宽度就越窄,雷达的距离分辨率就越高,分辨相邻目标的能力越强。
雷达脉冲压缩信号基本理论

雷达脉冲压缩信号基本理论第二章 雷达脉冲压缩信号基本理论在介绍脉冲压缩之前,首先要了解关于雷达信号处理的基本基本理论,为研究雷达信号的脉冲压缩技术奠定理论基础。
2.1雷达信号处理基本理论简介 匹配滤波匹配滤波(matched filtering )是最佳滤波的一种。
当输入信号具有某一特殊波形时,其输出达到最大。
在形式上,一个匹配滤波器由以按时间反序排列的输入信号构成。
且滤波器的振幅特性与信号的振幅谱一致。
因此,对信号的匹配滤波相当于对信号进行自相关运算。
配滤波器是一种非常重要的滤波器,广泛应用与通信、雷达等系统中。
现假设一雷达输入信号为()x t ,其中已知的雷达信号为()s t ,噪声信号为()n t 。
那么有()()()x t s t n t =+(2.1)其中雷达信号()s t 的频谱表达式和能量表达式分别可以用式2.2和2.3表示。
()()exp(2)S f s t j ft dtπ∝-∝=⋅-⎰ (2.2)2|()|E S f df∝-∝=⎰(2.3)假设匹配滤波器的冲激响应为h(t),那么滤波器的输出响应为:()()()s n y t y t y t =+(2.4)其中滤波器对()s t 的响应函数()s y t 的表达式为:()()()exp(2)s y t H f S f j ft dfπ∝-∝=⎰(2.5)再假设滤波器的输出信号成分在0t 时刻会得到一个峰值,那么输出信号的峰值功率为:200()|()()exp(2)|s y t H f S f j ft df π∝-∝=⎰(2.6)此外,噪声的平均功率为:22()|()|2n Ny t H f df∝-∝=⎰(2.7)因此可以得到信噪比:2202022000|()()exp(2)||()||()|2|()|/2|()|2s n H f S f j ft df S f df y t ESNR y t N N N H f df π∝∝-∝-∝∝-∝==≤=⎰⎰⎰(2.8)当式2.8满足信噪比最大值的时候,则有:*0()()exp(2)H f KS f j ft π=-(2.9)转换为时域,则有*0()()h t Ks t t =-(2.10)从上面的理论推导可以看到,当输出信噪比为最大值的时候,滤波器的传递函数与输入信号的频谱函数满足特定的关系,式2.10就反映了这个关系。
04(雷达方程)

十一, 十一,体目标和杂波的雷达方程
S / CV =
2π Bσ Deff ( AZ ) Deff ( EL ) ∑σ cλ 2 R 2
S / CV =
2π Bσ Deff ( AZ ) Deff ( EL ) ( MTI IV ) 4 ∑σ cλ 2 R 2
�
二,雷达方程概述
PT G λ σ S/N = 3 4 (4π ) R LS LA KT0 BF
2 2
PT = 发射的峰值功率 σ = 目标的雷达散射截面积 λ= 波长 Ls = 系统损耗 B = 带宽
G = 天线增益
R = 雷达到目标的单程距离 LA = 传播损耗 T0 = 290K F = 接收机噪声系数
PGσ AE t (4π R 2 ) 2
三,噪声中的点目标
PR PT Gσ AE S/I = = PI (4π ) 2 R 4 PI
PI = 系统接收功率处的干扰功率
λ2 AE = G 4π
PT G λ σ S/I = 3 4 (4π ) R PI
2 2
噪声中的点目标 考虑损耗
PT G 2 λ 2σ S/I = (4π )3 R 4 PI LS LA LGP
GP ( N ) NL = Li
积累损失
噪声中的点目标
观测能量和平均功率
B ≈ 1/ τ
PTτ N LG 2 λ 2σ S/N = (4π )3 R 4 KT0 FLS LA LGP Li W L G 2 λ 2σ S/N = (4π ) 3 R 4 KT0 FLS L A LGP Li
PAVGTD G 2 λ 2σ S/N = (4π )3 R 4 KT0 FLS LA LGP Li
积累时间由信号处理机或伺服带宽决定
脉冲压缩技术在雷达系统中的应用

(2)
其中,u 为瞬时频率的变化率,他与脉冲宽度 与 内的频率变化范围 B 有 如下关系: u B / 。 对式(1)做傅立叶变换得到:
S LMF (f ) A 2 e
2 j(f f 0 )2
j 2(f0 ut 2 )
1 2
e j 2ftdt dt
电子工程学院
脉冲压缩技 术在雷达系统中 的应用
雷达原理
狄冲 陈维森 赵禹慕尘 吕凯
02123071 02123008 02123089 02123094
摘要
对目前在雷达信号处理系统中应用较为广泛的脉冲压缩技术进行了介绍, 主 要是线性调频的脉冲压缩信号。 首先对脉冲压缩和线性调频脉冲信号进行了介绍, 然后研究了线性调频信号的压缩过程及其压缩方法。 关键词:脉冲压缩;线性调频;匹配滤波
subplot(212) plot(t*1e6,x); xlabel('t/us'); title('线性调频加噪后'); grid on;axis tight; plot(freq*1e-6,fftshift(abs(fft(St)))); xlabel('Frequency in MHz'); title('Magnitude spectrum of chirp signal'); grid on;axis tight; 信噪比为 6 时的仿真结果
时,信号能量绝大部分集中在 f f0 <
义为 0.5, s(u1 ) s(u 2 )定义为 0.5,由此得到
S LMF(f )
A f f0 rect( ) B u
(f f0 )2 LMF(f ) u 4
经典雷达资料-第10章 脉 冲 压 缩-3汇总

变换对3通过在频域引入一个幅度波动而得到锥状递减的函数W1(f)。
根据变换对1和2,它的时间函数是三个时间位置不同并经加权的(sin x)/x函数之和[39]。
若选择适当的系数F1,合成函数w1(t)可获得低的时间副瓣。
特别是,F1=0.426对应于海明加权[40]~[42],它的时间函数的幅度曲线如图10.15所示的实线B。
变换对4频域加权函数是包括n-1个余弦项的傅里叶级数,其中n由所要求的压缩脉冲宽度和期望的副瓣衰减决定。
根据变换对1和2,它的时间函数是2(n-1)个回波的叠加,并且有n-1个对称回波对。
如果可选系数F m选定为泰勒加权函数[39][42][43]W Tay(f),并根据给定副瓣电平的小主瓣宽度准则,合成的时间函数w Tay(t)具有好的分辨特性。
副瓣电平为-40d B,n等于6时选出的泰勒系数可得到的主副瓣结构如图10.15所示的曲线C。
图10.15 三种频率加权函数脉冲压缩形状的比较第10章脉冲压缩·385·变换对5~7根据对偶定理5,上述每一个变换对的时域函数和频域函数可互换。
如果参数t的符号相反,则函数可互换。
例如,用T(s)代替B(Hz),变换对6和7可由变换对2和4得到。
若系数是根据给定的副瓣电平选择的,那么泰勒时域加权可应用于变换对7,并能达到良好的频率分辨力。
变换对8与变换对1的幅度变化相似,通带上相位的正弦变化在时域上产生主信号g(t)和对称的回波对。
回波为主信号的复制,只是时间上滞后和超前n/B s,幅度上缩小b n/2,并且极性相反。
加权函数的比较表10.8归纳出各种频域加权函数所能达到的性能。
通过变换参数,该表也可用于时域加权(或天线孔径分布加权)。
若加权函数在频带中心(f=0)的幅度归一化为1,那么在各种情况下,基座高度H就是加权函数在频带边沿(f = ±B/2)时的幅度。
信噪比损失是根据发射幅度谱是矩形谱的假设计算的。
脉冲压缩雷达(2)

N 1 m k 0
c
k
ck m
其中 ( N 1) m N 1。当m=0时,非归一化伪随机序列的 非周期自相关函数取得最大值。 由匹配滤波器理论知道,信号通过匹配滤波器的输出 就是信号的自相关函数。因此,在雷达信号中所用的二相 编码信号,应要求其非周期自相关函数具有高的主峰和低 的副瓣。
信号频谱表示为:
1
N sin c( f 1 )e jf1 ck e j 2f1
k 0 N 1
二相编码信号的带宽B与子脉冲带宽相近,即
N B 1 T
信号的时宽带宽乘积或脉冲压缩比为
1
N D TB T N T
3 巴克序列码和组合巴克序列码
巴克序列是一种二元伪随机序列{cn}
5
-10
-5
0
5
10
图5
N=7的巴克序列
图6
N=11的巴克序列
10 5 0
-10
图7
-5
0
5
10
N=13的巴克序列
由于巴克序列长度有限,可以通过组合巴克序列来增 加长度,但组合巴克序列不再保持原巴克序列的旁瓣特性。 有两种组合法,例如(1)以4位巴克序列作为13位的巴克码 的码元,(2)以13位巴克序列作为4位巴克码的码元。
1 u (t ) N
0 t 其他
则二相编码信号的复包络可写成
c v(t k
k 0 k
N 1
1
)
0 t 其他
0
式中v(t)为子脉冲函数, 1 为子脉冲宽度, N为码长
振幅
N 1
+ + + - 1
t
可用离散形式写出自相关函数为:
脉冲压缩公式

脉冲压缩公式
脉冲压缩公式是一种处理雷达或声纳中脉冲信号的方法,用于提高脉冲信号的信噪比。
脉冲压缩公式可以表示为:
$c(t) = x(t) * h(t)$
其中,$c(t)$表示压缩后的脉冲信号,$x(t)$表示原始脉冲信号,$h(t)$表示脉冲压缩滤波器的冲激响应。
脉冲压缩滤波器的冲激响应$h(t)$通常是一种特定的函数,例
如MatchedFilter,具有与原始脉冲信号$x(t)$的自相关函数最
大化的性质。
这样,信号通过脉冲压缩滤波器后,可以使得信号的功率被集中到较短的时间间隔内,从而提高信号的信噪比。
脉冲压缩公式应用于雷达或声纳等领域,用于从噪声背景中提取出目标信号,提高目标检测和跟踪的性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
脉冲压缩雷达方程
脉冲压缩雷达方程是雷达技术中的重要概念,它是一种通过处理雷达回波信号的方法,可以提高雷达系统的距离分辨率。
本文将介绍脉冲压缩雷达方程的原理和应用。
脉冲压缩雷达方程是指通过对雷达回波信号进行特定的处理,使得雷达系统可以在较短的脉冲宽度内获得较高的距离分辨率。
在传统的雷达系统中,由于脉冲宽度较宽,导致雷达无法准确地分辨目标之间的距离。
而脉冲压缩雷达方程通过对回波信号进行复杂的信号处理,可以降低脉冲宽度,从而提高距离分辨率。
脉冲压缩雷达方程的实现需要利用雷达的发射和接收系统。
在发射端,雷达发射窄脉冲信号,脉冲宽度通常很宽。
然后,在接收端,雷达接收回波信号,并进行一系列的信号处理步骤。
其中,最关键的步骤是压缩滤波器的应用。
压缩滤波器是脉冲压缩雷达方程中的核心部分。
它的作用是对接收到的回波信号进行滤波,使得脉冲宽度变窄。
具体来说,压缩滤波器利用了信号的自相关性质,通过与发射信号进行相关运算,将回波信号的脉冲宽度压缩到较窄的范围内。
这样,雷达系统就能够在较短的时间内获取到高分辨率的距离信息。
脉冲压缩雷达方程的应用非常广泛。
首先,在军事领域,脉冲压缩雷达方程可以提高雷达系统对目标的探测和识别能力。
它可以有效
地区分目标之间的距离,提供更准确的目标定位信息。
因此,在雷达导航、目标跟踪和导弹制导等军事应用中,脉冲压缩雷达方程被广泛采用。
脉冲压缩雷达方程还在民用领域得到了广泛应用。
例如,在航空领域,脉冲压缩雷达方程可以提高飞机的导航安全性,确保飞行器与其他目标之间的安全距离。
在气象领域,脉冲压缩雷达方程可以用于天气预测和气象观测,提供更准确的降水和风速信息。
脉冲压缩雷达方程是一种能够提高雷达系统距离分辨率的重要方法。
通过对回波信号进行特定的信号处理,脉冲压缩雷达方程可以使雷达系统在较短的时间内获取到更准确的距离信息。
它在军事和民用领域都有广泛的应用,为各种应用场景提供了更高的探测和识别能力。
随着雷达技术的不断发展,脉冲压缩雷达方程将继续发挥重要作用,为各个领域的应用提供更高的性能和效果。
