和退火算法类似的算法
十大经典数学模型

1、蒙特卡罗算法(该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,是比赛时必用的方法)2、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具)3、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo软件实现)4、图论算法(这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备)5、动态规划、回溯搜索、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法(这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用)元胞自动机7、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)8、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)9、数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用)10、图象处理算法(赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理)以上为各类算法的大致介绍,下面的内容是详细讲解,原文措辞详略得当,虽然不是面面俱到,但是已经阐述了主要内容,简略之处还望大家多多讨论。
数值优化算法

数值优化算法在现代科学和工程中,数值优化算法被广泛应用于解决各种复杂问题。
数值优化算法是一种寻找函数极值的方法,这些函数可能具有多个自变量和约束条件。
数值优化算法对于在实际问题中找到最佳解决方案至关重要。
本文将介绍几种常见的数值优化算法及其应用。
一、梯度下降法梯度下降法是一种常用的数值优化方法。
它通过寻找损失函数的梯度来更新参数,以在每次迭代中逐步接近极值点。
梯度下降法的优势在于简单易实现,并且在大规模数据集上的表现良好。
这使得它成为许多机器学习算法中参数优化的首选方法。
二、牛顿法牛顿法是一种用于寻找函数极值点的迭代优化算法。
它利用函数的一阶导数和二阶导数信息来逼近极值点。
与梯度下降法相比,牛顿法的收敛速度更快,但它的计算复杂度更高。
牛顿法在求解高维问题或拟合复杂曲线时表现出色。
三、遗传算法遗传算法是一种模拟生物遗传和进化过程的优化算法。
它通过使用选择、交叉和变异等操作,模拟自然界的进化规律,来寻找函数的最优解。
遗传算法适用于复杂问题,能够在搜索空间中找到全局最优解。
在函数不可导或离散问题中,遗传算法能够提供有效的解决方案。
四、模拟退火算法模拟退火算法是一种启发式搜索算法,模拟了金属退火过程中原子随温度变化的行为。
模拟退火算法以一定的概率接受更差的解,并以较低的概率逐渐收敛到全局最优解。
模拟退火算法对局部极小点有一定的免疫能力,并且在大规模离散优化问题中表现出优越性。
五、粒子群算法粒子群算法是一种基于群体行为的优化算法。
它模拟了鸟群觅食的行为,通过迭代寻找问题的最优解。
粒子群算法通过评估适应度函数来引导粒子的移动,从而逐渐靠近最优解。
这种算法适用于多目标优化问题和高维函数优化。
结论数值优化算法在科学和工程领域扮演着至关重要的角色。
梯度下降法、牛顿法、遗传算法、模拟退火算法和粒子群算法是几种常见的数值优化方法。
它们各自具有不同的优势和适用范围,可以根据问题的特点选择合适的优化算法。
通过应用这些优化算法,可以帮助科学家和工程师在实际问题中找到最佳解决方案,推动技术的进步和创新。
五大常用算法 模拟退火算法

五大常用算法模拟退火算法
模拟退火算法是一种常用的求解优化问题的算法,它可以用于解决各种实际问题。
本文将介绍模拟退火算法及其应用,同时还会介绍其他四种常用的算法。
一、模拟退火算法
模拟退火算法是一种启发式算法,适用于求解复杂的优化问题。
它源于固体物理学中的退火过程,通过模拟退火过程来寻求最优解。
模拟退火算法通过随机跳出局部最优解的过程,寻找全局最优解。
二、其他四种常用算法
1.遗传算法
遗传算法是一种模拟自然进化过程的优化方法。
它通过对可行解进行适应度评价、选择、交叉和变异等操作,将优秀的个体遗传给下一代,从而不断优化解的质量。
2.蚁群算法
蚁群算法是一种模拟蚂蚁寻找食物的行为而发展出来的算法。
它通过模拟蚂蚁在搜索过程中的信息素沉积和信息素挥发,不断优化搜索路径,从而找到最优解。
3.粒子群算法
粒子群算法是一种模拟粒子在空间中移动的算法。
它通过模拟粒子在搜索空间中的移动和互相协作,不断优化搜索路径,从而找到最优解。
4.人工神经网络
人工神经网络是一种模拟人脑神经元工作原理的算法。
它通过构建神经元之间的连接和权重来实现对输入信息的处理和输出结果的预测,可以用于分类、回归等问题的求解。
三、总结
以上介绍了五种常用的算法,它们都可以用于解决不同类型的优化问题。
在实际应用中,需要根据具体问题的特点选择合适的算法。
模拟退火算法是其中一种常用算法,具有较为广泛的应用。
供应链管理中配送路线规划算法的使用教程

供应链管理中配送路线规划算法的使用教程随着电子商务的兴起和物流行业的快速发展,供应链管理中的配送路线规划算法变得尤为重要。
准确的配送路线规划能够提高物流效率,降低成本,为企业节约时间和资源。
本文将介绍供应链管理中常用的一些配送路线规划算法,并详细说明它们的使用教程。
一、贪心算法贪心算法是一种简单而常用的算法,它在每一步都做出当前最优的选择,但并不保证全局最优解。
在配送路线规划中,贪心算法可以按照以下步骤进行:1.确定起点和终点:首先确定货物的起点和终点,通常是仓库和客户的地址。
2.计算距离矩阵:根据起点、终点和中间所有点的地址,计算出它们之间的距离矩阵。
3.选择最近邻居:从起点开始,选择距离最近的邻居作为下一个节点,将其添加到路径中。
4.更新路径和距离:将新节点添加到路径中,更新距离矩阵,重复步骤3,直到到达终点。
5.输出最优路径:输出路径和距离,路径即为货物的配送路线。
贪心算法的优点在于简单易懂,计算速度快。
然而,它的缺点是可能陷入局部最优解,不能保证得到最优的配送路线。
二、遗传算法遗传算法是一种模拟自然界进化过程的启发式优化算法。
在配送路线规划中,遗传算法可以按照以下步骤进行:1.初始化种群:根据货物的起点和终点,随机生成初始解作为种群。
2.计算适应度:根据候选解的质量,计算每个解的适应度值,一般可以使用总路程作为适应度函数。
3.选择操作:根据适应度值,按照一定的选择策略选出优秀的个体作为父代。
4.交叉操作:通过交叉操作生成新的子代个体,将父代的染色体片段互换,并保留优秀的基因。
5.变异操作:对子代个体进行变异操作,引入新的基因,增加算法的搜索空间。
6.更新种群:将父代和子代个体结合,形成新的种群。
7.重复步骤3-6:重复执行3-6步骤,直到满足停止准则。
8.输出最优解:输出适应度最优的个体,作为货物的配送路线。
遗传算法的优点在于能够全局搜索和优化,有较高的收敛性和适应性。
然而,它的缺点是计算复杂度较高,需要耗费更多的时间和计算资源。
模拟退火算法与遗传算法

模拟退火算法与遗传算法
模拟退火算法(Simulated Annealing,SA)和遗传算法(Genetic Algorithms,GA)是两种常用的优化算法,分别简要介绍如下:
1. 模拟退火算法(Simulated Annealing,SA):模拟退火是一种基于物理退火原理的优化算法。
该算法在搜索过程中,根据某一概率接受一个比当前解要差的解,因此有可能会跳出局部最优解,达到全局最优解。
它的优点是能够在全局范围内搜索到最优解,具有较好的鲁棒性,适用于多峰值、非线性、离散、连续等问题的优化。
在求解组合优化问题和离散优化问题上模拟退火表现良好。
2. 遗传算法(Genetic Algorithms,GA):遗传算法是一种基于自然选择和遗传学原理的优化算法。
它通过模拟生物进化过程中的自然选择和遗传机制,如选择、交叉、变异等操作,在解空间内搜索最优解。
遗传算法具有较好的全局搜索能力,能够处理复杂的、非线性的、离散的优化问题。
在求解连续函数优化问题和组合优化问题上表现良好。
总之,模拟退火算法和遗传算法都是非常有效的优化算法,各有其适用范围和优点。
在实际应用中,可以根据问题的类型和特点选择合适的算法进行优化求解。
爬山算法与模拟退火比较

爬山算法与模拟退火比较在计算机科学领域,寻找最优解是一项常见的任务。
爬山算法和模拟退火算法是两种常用的优化算法,本文将对这两种算法进行比较。
一、爬山算法爬山算法是一种局部搜索算法,常用于解决最优化问题。
它的基本思想是从当前解出发,沿着梯度方向不断地移动,直到达到一个局部最优解。
爬山算法具有以下特点:1. 简单直观:爬山算法的实现相对简单,容易理解和实现。
2. 局部搜索:由于爬山算法只关注当前解的邻域,并不会全局搜索解空间,因此容易陷入局部最优解。
3. 容易受到初始解的影响:由于算法在初始解附近进行局部搜索,因此初始解的选择会直接影响搜索结果。
4. 高计算效率:爬山算法通过不断地调整当前解,找到更优的解。
由于只需计算当前解的邻域,所以计算效率较高。
二、模拟退火算法模拟退火算法是一种全局优化算法,它通过模拟固体退火的过程来进行搜索。
模拟退火算法具有以下特点:1. 全局搜索:模拟退火算法通过接受劣解的概率来跳出局部最优解,从而有机会搜索到全局最优解。
2. 逐步降温:模拟退火算法在搜索过程中逐渐减小退火温度,降低随机性,以便更好地接受优解。
3. 较复杂的参数设置:模拟退火算法需要合理地设置参数,如初始温度、退火速率等,而且不同问题可能需要不同的参数配置。
4. 高计算复杂度:由于模拟退火算法涉及到接受劣解的概率计算和随机跳转,因此其计算复杂度较高。
三、比较分析1. 搜索范围:- 爬山算法只在当前解的邻域内进行搜索,易陷入局部最优解。
- 模拟退火算法可以全局搜索,有机会找到全局最优解。
2. 算法复杂度:- 爬山算法的计算复杂度较低,因为它只需计算当前解的邻域。
- 模拟退火算法的计算复杂度较高,因为它需要多次重复计算接受劣解的概率和随机跳转。
3. 对初始解的依赖:- 爬山算法对初始解的依赖较大,不同的初始解可能导致不同的搜索结果。
- 模拟退火算法对初始解不敏感,因为算法会通过温度的逐渐降低逐渐摆脱初始解的影响。
遗传算法与模拟退火算法的比较分析

遗传算法与模拟退火算法的比较分析在计算机科学领域,遗传算法和模拟退火算法是两种常用的优化算法。
它们都能够在寻找最优解的问题中发挥重要作用。
然而,这两种算法在原理和应用方面存在着一些差异。
本文将对遗传算法和模拟退火算法进行比较分析,以便更好地了解它们的特点和适用场景。
首先,我们来看一下遗传算法。
遗传算法的灵感来源于生物进化的过程。
它通过模拟遗传、变异和选择的机制来搜索最优解。
遗传算法的基本步骤包括初始化种群、选择操作、交叉操作和变异操作。
在选择操作中,适应度较高的个体被选择作为父代,通过交叉和变异操作产生新的个体。
这个过程模拟了自然界中的基因传递和变异。
通过多代的迭代,遗传算法能够逐渐优化个体,并找到最优解。
相比之下,模拟退火算法是一种基于物理退火原理的优化算法。
它模拟了金属冶炼中的退火过程。
在退火过程中,金属被加热然后缓慢冷却,以使其达到最佳的结晶状态。
模拟退火算法通过随机搜索和接受劣解的策略来避免陷入局部最优解。
算法开始时,通过随机生成一个初始解,并随机选择一个邻域解。
然后,根据一定的概率接受邻域解,以便在搜索空间中进行更广泛的探索。
随着退火过程的进行,概率逐渐降低,使得算法趋向于收敛到全局最优解。
在实际应用中,遗传算法和模拟退火算法各有其优势和适用场景。
遗传算法适用于问题空间较大、复杂度较高的情况。
它能够通过种群的多样性来避免陷入局部最优解,并且能够在搜索空间中进行全局搜索。
遗传算法在组合优化、路径规划和参数优化等问题中表现出色。
例如,在旅行商问题中,遗传算法能够找到最短路径的近似解。
而模拟退火算法适用于问题空间较小、复杂度较低的情况。
它通过接受劣解的策略来避免陷入局部最优解,并能够在搜索空间中进行局部搜索。
模拟退火算法在组合优化、图着色和函数优化等问题中表现出色。
例如,在图着色问题中,模拟退火算法能够找到最少颜色的解。
此外,遗传算法和模拟退火算法在时间复杂度和收敛速度上也存在差异。
遗传算法的时间复杂度较高,因为它需要进行多次迭代和多次操作。
十大经典数学模型
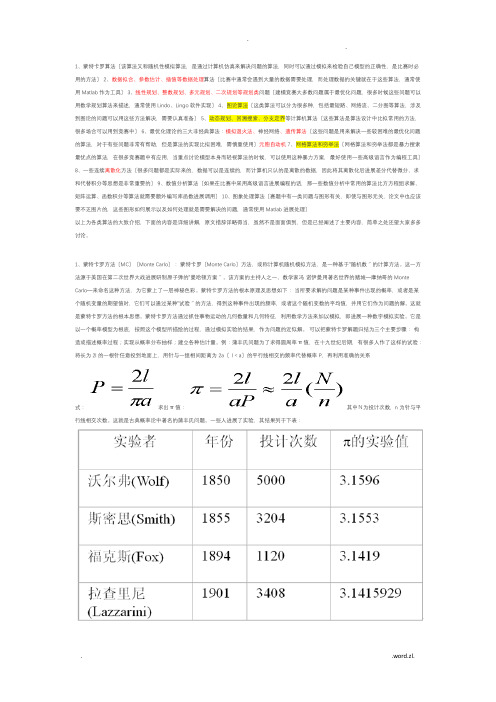
1、蒙特卡罗算法〔该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,是比赛时必用的方法〕2、数据拟合、参数估计、插值等数据处理算法〔比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具〕3、线性规划、整数规划、多元规划、二次规划等规划类问题〔建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo软件实现〕4、图论算法〔这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备〕5、动态规划、回溯搜索、分支定界等计算机算法〔这些算法是算法设计中比拟常用的方法,很多场合可以用到竞赛中〕6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法〔这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比拟困难,需慎重使用〕元胞自动机7、网格算法和穷举法〔网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具〕8、一些连续离散化方法〔很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进展差分代替微分、求和代替积分等思想是非常重要的〕9、数值分析算法〔如果在比赛中采用高级语言进展编程的话,那一些数值分析中常用的算法比方方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进展调用〕10、图象处理算法〔赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进展处理〕以上为各类算法的大致介绍,下面的内容是详细讲解,原文措辞详略得当,虽然不是面面俱到,但是已经阐述了主要内容,简单之处还望大家多多讨论。
数学建模常用算法

数学建模常用算法数学建模是指将实际问题转化为数学模型,并通过数学方法进行求解的过程。
在数学建模中,常用的算法有很多种,下面将介绍一些常见的数学建模算法。
1.最优化算法:-线性规划算法:如单纯形法、内点法等,用于求解线性规划问题。
-非线性规划算法:如最速下降法、牛顿法等,用于求解非线性规划问题。
-整数规划算法:如分支定界法、割平面法等,用于求解整数规划问题。
2.概率统计算法:-蒙特卡洛模拟:通过模拟随机事件的方式,得出问题的概率分布。
-贝叶斯统计:利用先验概率和条件概率,通过数据更新后验概率。
-马尔可夫链蒙特卡洛:用马尔可夫链的方法求解复杂的概率问题。
3.图论算法:-最短路径算法:如迪杰斯特拉算法、弗洛伊德算法等,用于求解两点之间的最短路径。
-最小生成树算法:如普里姆算法、克鲁斯卡尔算法等,用于求解图中的最小生成树。
- 最大流最小割算法: 如Edmonds-Karp算法、Dinic算法等,用于求解网络流问题。
4.插值和拟合算法:-多项式插值:如拉格朗日插值、牛顿插值等,用于通过已知数据点拟合出多项式模型。
-最小二乘法拟合:通过最小化实际数据与拟合模型之间的差异来确定模型参数。
-样条插值:通过使用多段低次多项式逼近实际数据,构造连续的插值函数。
5.遗传算法和模拟退火算法:-遗传算法:通过模拟自然选择、遗传变异和交叉等过程,优化问题的解。
-模拟退火算法:模拟固体退火过程,通过随机策略进行,逐步靠近全局最优解。
6.数据挖掘算法:- 聚类算法: 如K-means算法、DBSCAN算法等,用于将数据分为不同的类别。
-分类算法:如朴素贝叶斯算法、决策树算法等,用于通过已知数据的类别预测新数据的类别。
- 关联分析算法: 如Apriori算法、FP-growth算法等,用于发现数据集中的关联规则。
以上只是数学建模中常用的一些算法,实际上还有很多其他算法也可以应用于数学建模中,具体使用哪种算法取决于问题的性质和要求。
数学优化问题的求解方法

数学优化问题的求解方法数学优化问题是数学中的一个重要分支,它在各个领域都有广泛的应用。
解决数学优化问题的方法多种多样,下面将介绍几种常见的求解方法。
一、暴力搜索法暴力搜索法也称为穷举法,是最简单直接的求解数学优化问题的方法之一。
它通过枚举问题的所有可能解,并计算得出每个解对应的目标函数值,最后找到最优解。
但此方法在问题规模较大时无法满足实际需求,因为其时间复杂度过高。
二、单纯形法单纯形法是一种经典的线性规划求解算法,主要用于求解线性优化问题。
它通过在顶点集合内移动,不断寻找更优解的方法。
单纯形法具有高效性和可靠性,并且可以处理大规模的线性规划问题,成为了一种常用的求解方法。
三、梯度下降法梯度下降法是一种常见的非线性优化求解算法,主要用于求解无约束的最优化问题。
它通过迭代的方式逐步接近最优解,通过计算目标函数的梯度方向来确定搜索方向。
梯度下降法易于理解和实现,但在复杂的非凸问题中可能会陷入局部最优解。
四、遗传算法遗传算法是一种基于自然选择和遗传机制的优化算法,主要应用于复杂的非线性优化问题。
它通过模拟进化过程,利用选择、交叉和变异等操作,生成新的解,并根据适应度评估函数筛选出最优解。
遗传算法适用于多模态和多目标优化问题,但其计算量较大。
五、模拟退火算法模拟退火算法是一种随机搜索算法,主要应用于组合优化和全局优化问题。
它通过模拟固体物质退火过程中的晶格结构演化,寻找出合适的解。
模拟退火算法能够跳出局部最优解,找到全局最优解,但其收敛速度较慢。
六、动态规划法动态规划法适用于具有最优子结构的问题,通过将原问题划分为多个子问题,利用子问题的最优解推导出原问题的最优解。
动态规划法通常需要建立状态转移方程和选择最优策略,通过填表法来计算最优解。
动态规划法的时间复杂度通常较低,适用于一些具有递推性质的优化问题。
总结而言,数学优化问题的求解方法有很多种,每种方法都有其适用范围和特点。
选择合适的求解方法需要根据问题的具体情况来决定,包括约束条件、问题规模、目标函数形式等。
数学建模中常见的十大模型

数学建模常用的十大算法==转(2011-07-24 16:13:14)转载▼1. 蒙特卡罗算法。
该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,几乎是比赛时必用的方法。
2. 数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用MA TLAB 作为工具。
3. 线性规划、整数规划、多元规划、二次规划等规划类算法。
建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo 软件求解。
4. 图论算法。
这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备。
5. 动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法,竞赛中很多场合会用到。
6. 最优化理论的三大非经典算法:模拟退火算法、神经网络算法、遗传算法。
这些问题是用来解决一些较困难的最优化问题的,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用。
7. 网格算法和穷举法。
两者都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具。
8. 一些连续数据离散化方法。
很多问题都是实际来的,数据可以是连续的,而计算机只能处理离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9. 数值分析算法。
如果在比赛中采用高级语言进行编程的话,那些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10. 图象处理算法。
赛题中有一类问题与图形有关,即使问题与图形无关,论文中也会需要图片来说明问题,这些图形如何展示以及如何处理就是需要解决的问题,通常使用MA TLAB 进行处理。
常用优化计算方法

常用优化计算方法
计算是现代科学和技术发展的基础,而优化计算方法则是提高计算效率和精度的关键。
优化计算方法可以应用于各个领域,包括工程、经济、医学等等。
本文将介绍几种常用的优化计算方法,包括贪婪算法、遗传算法、模拟退火算法和粒子群算法。
贪婪算法是一种简单而有效的优化方法。
它通过每次选择当前最优解来逐步构建整体最优解。
贪婪算法的优势在于其高效性和易于实现,但也存在局限性,可能无法得到整体最优解。
遗传算法是一种模拟生物进化过程的优化计算方法。
遗传算法通过模拟自然选择、交叉和变异等过程,逐步优化解的质量。
遗传算法具有较强的全局搜索能力,但对问题的建模和参数的选择要求较高。
第三,模拟退火算法是一种基于物理退火过程的优化方法。
模拟退火算法通过模拟固体物质退火时的温度变化,使解能够从局部最优逃脱并逐步趋于全局最优。
模拟退火算法可以灵活地调整搜索策略,但需要合理设置退火参数。
粒子群算法是一种模拟鸟群觅食行为的优化计算方法。
粒子群算法通过模拟粒子在解空间中的搜索和交流行为,逐步优化解的质量。
粒子群算法具有较强的全局搜索能力和较快的收敛速度,但对问题的建模和参数的选择也有一定要求。
贪婪算法、遗传算法、模拟退火算法和粒子群算法是常用的优化计算方法。
它们各自具有特点和适用范围,可以根据问题的性质选择合适的方法。
在实际应用中,还可以结合多种优化计算方法,以进一步提高计算效率和精度。
不同的方法有不同的适用场景,研究者和工程师可以根据具体问题的特点选择合适的方法。
通过不断优化计算方法,我们将能够更好地解决实际问题,推动科学技术的发展。
通俗解释爬山法模拟退火遗传算法贝叶斯算法

通俗解释爬山法模拟退火遗传算法贝叶斯算法
爬山法:
爬山法是一种简单的优化算法,用于寻找一个问题的局部最优解。
这个方法模拟了爬山的过程,从一个起点开始,每次选择一个相邻点,并沿着该方向移动,直到无法继续移动为止。
爬山法的基本思想是通过比较邻近点的目标函数值,选择一个比当前点更好的点,然后以这个点为新的起点,继续向更好的方向移动,直到找到一个不能被改进的局部最优解。
模拟退火:
遗传算法:
遗传算法是一种模拟自然进化过程的算法。
它通过模拟遗传操作,如选择、交叉和变异,以及适应度的评估,来逐代问题的解空间。
遗传算法的基本思想是通过不断的演化,将种群中较好的个体遗传下去,并通过选择和交叉操作来生成新的个体,以适应环境的变化并优化问题的解。
通过这种方式,遗传算法可以在一个大的解空间中找到问题的全局最优解。
贝叶斯算法:
贝叶斯算法是一种基于贝叶斯定理的统计推断方法。
它通过将先验知识和新的观察结果结合起来,更新问题的概率分布,从而得到最接近真实情况的后验概率分布。
贝叶斯算法的基本思想是根据已有的知识(先验概率)和新的观测数据(似然度)来推断参数的概率分布(后验概率)。
通过迭代的方式,不断更新后验概率分布,贝叶斯算法可以更好地利用已有的知识和新的观测数据,得到更准确的结果。
贝叶斯算法在概率推断、数据挖掘和机器学习等领域得到了广泛的应用。
以上是对爬山法、模拟退火、遗传算法和贝叶斯算法的通俗解释。
它们分别是解决不同类型问题的优化算法,通过模拟不同的自然过程和统计推断方法,以达到在复杂的解空间中找到问题最优解的目的。
优化算法-模拟退火-粒子群-遗传算法
粒子群算法
二、粒子群算法求解最优解
D维空间中,有m个粒子; 粒子i位置:xi=(xi1,xi2,…xiD),将xi代入适应函数F(xi)求适应值; 粒子i速度:vi=(vi1,vi2,…viD) 粒子i个体经历过的最好位置:pbesti=(pi1,pi2,…piD) 种群所经历过的最好位置:gbest=(g1,g2,…gD)
粒子群算法
每个寻优的问题解都被想像成一只鸟, 称为“粒子;
所有的粒子都由一个Fitness Function 确定适应值以判断目前的位置好坏;
每一个粒子必须赋予记忆功能,能记住 所搜寻到的最佳位置;
每一个粒子还有一个速度以决定飞行的 距离和方向,这个速度根据它本身的飞 行经验以及同伴的飞行经验进行动态调 整。
模拟退火算法
四、模拟退火算法特点
一.最终求得的解与初始值无关,与初始解状 态S无关;
二.具有渐近收敛性,在理论上是一种以概率 1收敛于全局最优解的全局优化算法;
三.具有并行性。
遗传算法
一.遗传算法概念
遗传算法简称GA,是模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优 化方法。遗传算法将“优胜劣汰,适者生存”的生物进化原理引入优化参数形成的编 码串联群体中,按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行 筛选,使适应度高的个体被保留下来,组成新的群体,新的群体既继承了上一代的信 息,又优于上一代。这样周而复始,群体中个体适应度不断提高,直到满足一定的条 件。
遗传算法
一.遗传算法基本操作 1. 复制:复制操作可以通过随机方法来实现。首先产生0~1之间均 匀分布的随机数,若某串的复制概率为40%,则当产生的随机数 在0.40~1.0之间时,该串被复制,否则被淘汰 2. 交叉:在匹配池中任选两个染色体,随机选择一点或多点交换点 位置;交换双亲染色体交换点右边的部分,即可得到两个新的染 色体数字串。 3. 变异:在染色体以二进制编码的系统中,它随机地将染色体的某 一个基因由1变为0,或由0变为1。
三种常见现代优化算法的比较

三种常见现代优化算法的比较作者:郝思齐池慧来源:《价值工程》2014年第27期摘要:现代最优化算法比较常见的有遗传算法、蚁群算法、粒子群算法、鱼群算法和模拟退火算法。
这些算法主要是解决优化问题中的难解问题。
文章主要是对遗传算法、粒子群算法和模拟退火算法三个算法的优化性能进行比较。
首先介绍了三个算法的基本思想,以此可以了解三种算法有着自身的特点和优势,而后用这三种算法对典型函数进行计算,并对优化结果比较分析,提出了今后研究的方向。
Abstract: Modern optimization includes genetic algorithm (GA), ant colony algorithm (ACO), particle swarm algorithm optimization (PSO), fish-swarm algorithm and simulated annealing algorithm (SA) and so on. They are mainly applied to solve some difficult optimization problems. The paper mainly makes a comparative study of the optimization performance of GA,PSO and SA. First the basic principles of the three algorithms are introduced, and the characteristics and advantages of these algorithms are understood. At last, the three algorithms are used for typical functions calculation, and comparative analysis is made to the results. And the future research directions are put forward.关键词:遗传算法;粒子群算法;模拟退火算法;比较;优化Key words: genetic algorithm(GA);particle swarm algorithm optimization(PSO);simulated annealing algorithm(SA);comparison;optimization中图分类号:TP301.6 文献标识码:A 文章编号:1006-4311(2014)27-0301-020 引言传统的优化算法在优化时可以解决一些比较简单的线性问题,但优化一些非线性的复杂问题时,往往会需要很长时间,并且经常不能优化到最优解,甚至无法知道所得解同最优解的近似程度。
A星算法八数码问题和SA算法模拟退火算法旅行商问题

A*算法&SA算法A*算法&SA算法 (1)A*算法 (1)【算法简介】 (1)【算法流程】 (1)【问题描述】 (1)【核心代码】 (2)【实验结果】 (2)【实验思考】 (6)SA算法 (7)【算法简介】 (7)【算法流程】 (7)【问题描述】 (7)【核心代码】 (7)【实验结果】 (8)【实验思考】 (9)附录 (10)【A*算法解决八数码问题代码】 (10)【SA算法解决旅行商问题代码】 (23)A*算法【算法简介】A*搜索算法是对A搜索算法的改进,从而不仅能得到目标解,而且还一定能找到最优解。
当然是问题有节的前提下。
定义最优估价函数f*(n)=g*(n)+h*(n)。
其中n为状态空间图中的一个状态,g*(n)为起点到n状态的最短路径代价值,h*(n)为n状态到目的状态的最短路径的代价值。
这样f*(n)就是从起点出发通过n状态而到达目的状态的最佳路径的总代价。
A*搜索中用个个个g(n)和h(n)作为g*(n)和h*(n)的估计,使其尽量接近,从而提高效率。
【算法流程】•初始化open、closed链表•判断此问题是否有解:无解,则打印信息退出;有解,则继续•Repeatopen表为空→查找失败open表不空,从open表中拿出f min(记为Bestnode)放入closed表若Bestnode是目标结点→成功求解break若Bestnode不是目标结点,产生它的后继→succeed链表对每个后继,Repeat建立此结点到Bestnode的parent指针结点在open表中,将open表中结点加入Bestnode后继结点链,若此结点g值小于open表中结点g值,open表中结点改变parent指针,并删除此点结点在closed表中,将closed表中结点加入Bestnode后继结点链,若此结点g值小于closed表中结点g值,closed表中结点改变parent指针,closed表中结点重新加入open表中,并删除此点open表和closed表中均无此点,将此点加入Bestnode后继结点链,并按一定规则的加入到open表中【问题描述】在一个3*3的方棋盘上放着1,2,3,4,5,6,7,8八个数码,每个数码各占一格,且有一个空格。
几种常见的智能调度算法

几种常见的智能调度算法
常见的智能调度算法包括:
1. 遗传算法:该算法模拟生物进化过程中的自然选择和遗传机制,通过不断迭代搜索问题的解空间,最终找到最优解。
2. 蚁群算法:该算法模拟蚂蚁觅食过程中的行为规律,通过正
反馈机制不断优化解的质量,从而在寻找最短路径等问题上表现出色。
3. 模拟退火算法:该算法类似于物理中的退火过程,通过随机
搜索解空间,在一定概率下接受劣解,从而达到全局最优解。
4. 粒子群算法:该算法模拟鸟群、鱼群等生物群体的行为规律,通过个体之间的信息共享和协作,最终找到问题的最优解。
5. 神经网络算法:该算法模拟人脑神经元的工作原理,通过训
练神经网络来识别和解码输入的信息,从而完成智能调度任务。
这些智能调度算法在具体应用中可以根据问题的特点和要求进
行选择和调整。
五大常用算法 模拟退火算法

五大常用算法模拟退火算法随着科技的不断发展,算法在实际应用中也变得越来越多样。
其中“五大常用算法”是解决问题最常用的算法之一,而模拟退火算法更是在优化问题中独具一格。
什么是“五大常用算法”?“五大常用算法”是指在计算机科学中,被认为是解决问题最常用的五种基本算法,即贪心算法、分治算法、回溯算法、动态规划算法和分支限界算法。
这五种算法在解决不同类型的问题时,各有特点和优缺点。
如何使用“五大常用算法”?1.贪心算法在贪心算法中,每一步都选择当时看起来最好的选择,即以局部最优解为出发点,通过相邻的两个最优点组成的最优解,最终求得全局最优解。
贪心算法适用于解决最优化问题。
2.分治算法分治算法是将问题拆分成小问题解决,再合并进行更高级别的解决,直至最终得到全局解决方案。
其中,子问题规模往往比原问题规模小。
分治算法适用于求解大规模问题。
3.回溯算法回溯算法也称试探算法,通过逐步试探所有可行解,找到最优解。
在回溯算法中,随着搜索的进行,每次通常只需要记录子问题的局部解,直至最终解决全局问题。
回溯算法适用于要求全部解的问题。
4.动态规划算法动态规划算法是通过将问题拆分成相对独立的子问题进行求解,以解决复杂问题。
动态规划算法中往往需要用到子问题之间的重叠,通过记录下最优解,得到全局的最优解。
5.分支限界算法分支限界算法是将问题的状态空间树划分成多个子树,然后用估价函数来找到最有希望到的子树,将其转化成下一个问题的状态,然后进行搜索。
分支限界算法主要用于求解最优解或全部解的问题。
什么是“模拟退火算法”?模拟退火算法(Simulated Annealing)是一种通用性很强的优化算法,能在较短时间内求得大规模复杂问题的较优解。
该算法来源于固体物理中的“退火”过程,也称为“模拟退火算法”。
模拟退火算法对遗传算法和其他优化算法有着很好的补充作用。
如何使用模拟退火算法?1.初始化问题首先,需要初始化初始解和初始温度。
初始解和初始温度决定了模拟退火算法是否会找到全局最优解。
切割的优化方法有哪些?

切割的优化方法有哪些?面对日益复杂的生产和加工需求,切割技术在各类行业中变得越来越重要。
无论是金属切割、激光切割还是木材切割,优化切割方法对于提高效率和降低成本具有重要意义。
本文将介绍切割的优化方法,并从三个方面进行讨论。
一、切割路径的优化切割路径的优化是提高切割效率和降低切割时间的关键。
在切割路径的规划中,常用的方法有以下几种:1. 最短路径算法:通过求解最短路问题,确定切割路径中各个点的次序。
最短路径算法包括贪心算法、动态规划算法和遗传算法等。
这些算法能够有效地减少切割路径的长度,从而提高切割效率。
2. 车辆路径优化算法:与最短路径算法类似,车辆路径优化算法的目标是确定车辆在切割过程中的最佳路径。
例如,通过考虑车辆的载重、运输时间和耗能等因素,可以采用启发式算法和模拟退火算法等来优化切割路径。
3. 多切割刀具的使用:对于某些需求较高的切割任务,可以尝试使用多个切割刀具同时工作。
通过合理分配多个刀具的位置和数量,可以大大提高切割效率,减少等待时间。
二、材料利用率的优化材料利用率的优化是切割过程中不可忽视的方面。
在一些对材料消耗较大的行业,如钢铁制造和纺织制品等,提高材料利用率可以有效降低成本。
以下是几种常见的优化方法:1. 材料排版优化:通过合理排列待切割零件,使之在材料平板上布局最为紧密,减少材料的浪费。
这需要考虑零件的形状、大小和数量等因素,结合排样算法和填充算法等进行布局。
2. 自适应切割宽度:通过根据材料切割轮廓的特点,自动调整切割宽度,减小切割过程中的浪费。
这一优化方法一方面可以节约材料,另一方面可以减轻切割刀具的磨损。
三、切割质量的优化切割质量是无论在工业生产还是个人加工时都需要考虑的一项指标。
切割质量的好坏直接影响到产品的合格率和外观质量。
1. 切割速度的优化:在保证切割质量的前提下,尽可能提高切割速度,减少切割过程中的时间消耗。
这需要根据切割材料的硬度和密度等特性,选择适当的切割参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和退火算法类似的算法
模拟退火算法是一种启发式优化算法,常用于解决组合优化问题,也
可以用于近似求解连续优化问题。
退火算法通过模拟固体退火过程中晶体
粒子的行为,随机解空间,以寻找到更优的解。
然而,除了退火算法之外,还有一些类似的启发式优化算法,它们也可以被用于解决类似问题。
1. 遗传算法(Genetic Algorithm,GA)
遗传算法是受到自然进化理论启发的一种优化算法。
它通过模拟生物
进化过程中的选择、交叉和变异等操作,通过不断迭代的方式逐步优化解。
遗传算法的思想是将问题的解表示为染色体,并将其编码为二进制字符串。
通过选择、交叉和变异等遗传操作,从而获得更好的解。
遗传算法常用于
求解复杂的组合优化问题,例如旅行商问题、背包问题等。
2. 蚁群算法(Ant Colony Optimization,ACO)
蚁群算法受到蚂蚁找食觅食行为的启发,是一种模拟退火算法的变种。
蚁群算法通过模拟自然界蚂蚁的觅食行为,在解空间中随机,并通过信息
素的传递和更新,引导蚁群发现更优的解。
蚁群算法适用于求解TSP (Traveling Salesman Problem)等具有组合性质的问题。
3. 粒子群优化算法(Particle Swarm Optimization,PSO)
粒子群优化算法是一种启发式优化算法,模拟了鸟群或鱼群等集体行
为中的协同过程。
粒子群优化算法通过不断调整粒子的位置和速度,使得
粒子不断向全局最优解靠近。
粒子群优化算法适用于求解连续优化问题,
如函数最优化、神经网络等。
4. 混沌优化算法(Chaos Optimization Algorithm,COA)
混沌优化算法受到混沌理论启发,通过利用混沌映射的随机性和确定性特性,在解空间进行随机,以寻找更优的解。
混沌优化算法适用于求解连续优化问题,如神经网络权重优化、函数最优化等。
5. 频域优化算法(Frequency Domain Optimization,FDO)
频域优化算法是一种基于频率域的优化算法,利用傅立叶变换将优化问题转化为频域上的问题,通过在频域上,以获得更优的解。
频域优化算法适用于求解连续优化问题,如信号重构、滤波器设计等。
这些算法和模拟退火算法一样都是启发式优化算法,它们通过不同的方式对解空间进行,以寻找到更优的解。
虽然这些算法在原理和应用领域上有所差异,但它们在求解优化问题时都具有一定的优势,可以根据具体问题的特点选择相应的算法。
