初二数学最新教案-八年级数学相似多边形的性质2 精品
27.1相似多边形(教案)

(五)总结回顾(用时5分钟)
今天的学习,我们了解了相似多边形的定义、性质和在实际生活中的应用。同时,我们也通过实践活动和小组讨论加深了对相似多边形的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“相似多边形在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
-解决实际问题中相似多边形的计算和应用。
举例解释:
a.理解相似多边形的性质:教师需要引导学生通过实际操作、观察和推导,理解并掌握相似多边形的性质。例如,通过比较相似多边形的对应边长、对应角度、周长和面积等,让学生深刻理解相似多边形的性质。
b.判断相似性:针对不规则多边形的相似性判断,教师可以引导学生运用对应角和对应边成比例的原则,通过画图、测量和计算等方法,进行相似性判断。同时,可以举例说明如何将不规则多边形转化为规则多边形,以便更容易地进行相似性判断。
3.增强学生的几何直观和几何建模能力:让学生在实际问题中运用相似多边形知识,培养几何直观,提高解决几何问题的建模能力。
三、教学难点与重点
1.教学重点
-理解相似多边形的定义:对应角相等,对应边成比例。
-掌握相似多边形的性质:包括对应角相等、对应边成比例、对应周长比相等、对应面积比相等。
初中相似多边形的数学教案

初中相似多边形的数学教案一、教学目标:1. 让学生理解相似多边形的概念,掌握相似多边形的性质和判定方法。
2. 培养学生运用相似多边形的知识解决实际问题的能力。
3. 提高学生对数学的兴趣,培养学生的观察能力、推理能力和思维能力。
二、教学内容:1. 相似多边形的定义和性质2. 相似多边形的判定方法3. 相似多边形在实际问题中的应用三、教学重点与难点:1. 重点:相似多边形的概念、性质和判定方法。
2. 难点:相似多边形在实际问题中的应用。
四、教学方法:1. 采用问题驱动法,引导学生通过观察、思考、讨论,自主探索相似多边形的性质和判定方法。
2. 利用多媒体课件辅助教学,生动展示相似多边形的图形变化,增强学生的直观感受。
3. 结合实际例子,让学生运用相似多边形的知识解决实际问题,提高学生的应用能力。
五、教学过程:1. 引入:通过展示一些相似的图形,如树叶、五星红旗等,引导学生观察相似现象,激发学生的兴趣。
2. 讲解:讲解相似多边形的定义、性质和判定方法,结合PPT演示,让学生清晰理解相似多边形的概念。
3. 练习:布置一些相关的练习题,让学生巩固所学知识,提高解题能力。
4. 应用:结合实际问题,让学生运用相似多边形的知识解决问题,培养学生的应用能力。
5. 总结:对本节课的内容进行总结,强调相似多边形的性质和判定方法,以及其在实际问题中的应用。
6. 作业:布置一些课后作业,让学生进一步巩固所学知识。
六、教学评价:1. 通过课堂提问、练习和作业,评估学生对相似多边形概念、性质和判定方法的理解程度。
2. 观察学生在解决实际问题时的应用能力,评价其对相似多边形知识的掌握情况。
3. 收集学生课堂参与度、提问反馈,了解学生对教学方法的接受程度和兴趣。
七、教学反思:1. 课后回顾教学过程,评估教学目标的达成情况。
2. 根据学生的反馈和表现,反思教学方法和策略的有效性,提出改进措施。
3. 考虑如何在后续教学中更好地激发学生的学习兴趣和主动性,提高教学效果。
初中老师优秀教案数学范文

教案名称:初中数学《相似多边形的性质》优秀教案一、教学目标:1. 让学生理解相似多边形的概念,掌握相似多边形的性质。
2. 培养学生观察、分析、推理的能力,提高学生的数学思维水平。
3. 通过对相似多边形的性质的学习,培养学生对数学的兴趣和探究精神。
二、教学内容:1. 相似多边形的定义2. 相似多边形的性质3. 相似多边形的判定三、教学重点与难点:1. 教学重点:相似多边形的性质及其应用。
2. 教学难点:相似多边形的判定。
四、教学过程:1. 导入新课:通过展示两幅相似的图形,引导学生观察、分析,从而引出相似多边形的概念。
2. 自主学习:让学生自主阅读教材,理解相似多边形的定义及性质,并在课堂上进行讨论、交流,加深对知识的理解。
3. 课堂讲解:详细讲解相似多边形的性质,通过实例分析,让学生掌握相似多边形的判定方法。
4. 课堂练习:设计一些具有代表性的练习题,让学生在课堂上进行练习,巩固所学知识。
5. 总结提升:对本节课的知识进行总结,引导学生思考相似多边形在实际生活中的应用。
6. 课后作业:布置一些相关的作业,让学生进一步巩固所学知识。
五、教学策略:1. 采用问题驱动的教学方法,引导学生主动探究相似多边形的性质。
2. 利用多媒体手段,展示相似多边形的实例,提高学生的学习兴趣。
3. 注重个体差异,给予学生充分的思考时间,鼓励学生提出不同的观点。
4. 创设生活情境,让学生体会相似多边形在实际生活中的应用。
六、教学评价:1. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态。
2. 作业完成情况:检查学生作业的完成质量,评估学生对知识的掌握程度。
3. 课后访谈:与学生进行交流,了解学生对相似多边形知识的理解和应用情况。
4. 单元测试:通过单元测试,全面评估学生对本节课知识的掌握情况。
通过以上教学设计,希望能够有效地帮助学生掌握相似多边形的知识,提高学生的数学素养。
在实际教学过程中,教师还需根据学生的实际情况灵活调整教学策略,以达到最佳教学效果。
相似多边形及性质-优秀教案

23.4 相似多边形及性质(第1课时,共2课时)【教学目标】1.相似多边形的周长比,面积比与相似比的关系.2.经历探索相似多边形的性质的过程,培养学生的探索能力. 【教学重点】相似多边形的周长比、面积比与相似比的关系. 【教学难点】相似多边形周长比、面积比与相似比的关系的推导. 【教学过程】一.引入新课 听故事 想问题很久以前,某地发生大旱,地里的庄稼都干死了,于是大家到庙里向神祈求下雨.神说,如果你们做一个比现在的方桌大一倍的方桌来祭我,我就给你们降水.于是大家重新做了一个摆设祭品的方桌.新方桌的边长是原来的2倍.可是神愈发怒了.想一想如果△ABC ∽△A ′B ′C ′,相似比为k ,那么△ABC 与△A ′B ′C ′的周长比和面积比分别是多少? [生]△ABC 与△A ′B ′C ′的周长比为k ,面积比为k 2. 二、新课如图4-45,四边形A 1B 1C 1D 1∽四边形A 2B 2C 2D 2,相似比为k .(1)四边形A 1B 1C 1D 1与四边形A 2B 2C 2D 2的周长比是多少?(2)连接相应的对角线A 1C 1,A 2C 2,所得的△A 1B 1C 1与△A 2B 2C 2相似吗? △A 1C 1D 1与△A 2C 2D 2呢?如果相似,它们的相似各是多少?为什么?(3)设△A 1B 1C 1,△A 1C 1D 1,△A 2B 2C 2,△A 2C 2D 2的面积分别是,111C B A S ∆ 222222111,,D C A C B A D C A S S S ∆∆∆ 那么222111222111D C A D C A C B A C B A S S S S ∆∆∆∆=各是多少?(4)四边形A 1B 1C 1D 1与四边形A 2B 2C 2D 2的面积比是多少?提示:△A 1B 1C 1∽△A 2B 2C 2、△A 1C 1D 1∽△A 2C 2D 2,且相似比都为k . ∵四边形A 1B 1C 1D 1∽四边形A 2B 2C 2D 2 ∴2211221122112211D A DA D C D C CBC B B A B A === ∠D 1A 1B 1=∠D 2A 2B 2,∠B 1=∠B 2. ∠B 1C 1D 1=∠B 2C 2D 2,∠D 1=∠D 2. 在△A 1B 1C 1与△A 2B 2C 2中∵22112211C B CB B A B A = ∠B 1=∠B 2. ∴△A 1B 1C 1∽△A 2B 2C 2. ∴2211B A B A =k . 同理可知,△A 1C 1D 1∽△A 2C 2D 2,且相似比为k . 发现得:(3)提示:△A 1B 1C 1∽△A 2B 2C 2,△A 1C 1D 1∽△A 2C 2D 2.得其面积之比等于相似比的平方,再利用等比性质得:22222222222222)(k S S S S k D C A C B A D C A C B A =++∆∆∆∆,得相似四边形的面积之比等于相似比的平方.如果把四边形换成五边形,那么结论又如何呢?让学生完成相似五边形的周长比等于相似比;面积比等于相似比的平方的证明 照此方法,将四边形换成五边形,那么也有相同的结论. 由此可知:相似多边形对应对角线之比等于相似比. 相似多边形的周长比等于相似比.相似多边形的面积比等于相似比的平方. 三.练习1.课本P90第7题2、课本P89 练习题1、2 四.小结相似多边形对应对角线之比等于相似比. 相似多边形的周长比等于相似比. 相似多边形的面积比等于相似比的平方. 五.作业 课本P89习题23.4第2、5题 课后作业:习题23.4第1、4题同步练习六.反思23.4 相似多边形及性质(第2课时,共2课时)授课人: 刘华 教学时间:【教学目标】1.相似多边形的周长比,面积比在实际中的应用.2.经历探索相似多边形的性质的过程,培养学生的探索能力. 【教学重点】相似多边形的周长比、面积比与相似比关系的归纳. 【教学难点】相似多边形周长比、面积比与相似比的关系的应用. 【教学过程】 一.知识点回顾:相似多边形的性质:● 相似三角形对应高的比,对应角平分线的比,对应中线的比, ● 相似三角形的周长的比都等于相似比. ● 相似三角形面积的比等于相似比的平方. ● 相似比等于1的两个三角形全等.● 相似多边形对应对角线的比等于相似比. ● 相似多边形的周长等于相似比.● 相似多边形面积的比等于相似比的平方.二.例题讲解例1如图,在梯形ABCD 中,ADBC ,AD =2,BC =8,EF‖BC ,且EF 分别交AB 、DC 于E 、F . (1)若梯形AEFD ∽梯形EBFD ,求EF 的长;(2)求满足(1)条件下的梯形AEFD 与梯形EBFD 的周长比. 分析:(1)由相似得相似比可求线段的长;(2)由相似多边形的性质可求周长比.由学生完成求解过程. 解:(1)∵梯形AEFD ∽梯形EBFD∴BCEFEF AD =得:16822=⨯=*=BC AD EFEF 的长是非曲4;(2)∵梯形AEFD ∽梯形EBFD∴2142===++++++EF AD CF BC EB EF FD EF AE AD∴梯形AEFD 与梯形EBFD 的周长比等于1:2.例2.如图,在△ABC 中,∠C =90°,以它的边为对应边,在三角形外分别作三个相似多边形.问斜边上多边形的面积S1与两直角边上多边形面积之和(S2+S3)有什么关系?为什么?解:根据相似多边形性质,得A EB CFD232221AC S BC S AB S ==由等比性质,得223221AC BC S S ABS ++= 又 ∵222AC BC AB +=∴ S 1=S 2+S 3三.练习:补例1、同步练习P75第8题。
2021年八年级数学下册 4.8. 相似多边形的性质(二)示范教案 北师大版

2021年八年级数学下册 4.8.2 相似多边形的性质(二)示范教案1 北师大版●课题§4.8.2 相似多边形的性质(二)●教学目标(一)教学知识点1.相似多边形的周长比,面积比与相似比的关系.2.相似多边形的周长比,面积比在实际中的应用.(二)能力训练要求1.经历探索相似多边形的性质的过程,培养学生的探索能力.2.利用相似多边形的性质解决实际问题训练学生的运用能力.(三)情感与价值观要求1.学生通过交流、归纳,总结相似多边形的周长比、面积比与相似比的关系,体会知识迁移、温故知新的好处.2.运用相似多边形的周长比,面积比解决实际问题,增强学生对知识的应用意识.●教学重点1.相似多边形的周长比、面积比与相似比关系的推导.2.运用相似多边形的比例关系解决实际问题.●教学难点相似多边形周长比、面积比与相似比的关系的推导及运用.●教学方法引导启发式通过温故知新,知识迁移,引导学生发现新的结论,通过比较、分析,应用获得的知识达到理解并掌握的目的.●教具准备投影片四张第一张:(记作§4.8.2 A)第二张:(记作§4.8.2 B)第三张:(记作§4.8.2 C)第四张:(记作§4.8.2 D)●教学过程Ⅰ.创设问题情境,引入新课[师](拿大小不同的两个等腰直角三角形三角板).我手中拿着两名同学的两个大小不同的三角板.请同学们观察其形状,并请两位同学来量一量它们的边长分别是多少.然后告诉大家数据.(让学生把数据写在黑板上)[师]同学们通过观察和计算来回答下列问题.1.两三角形是否相似.2.两三角形的周长比和面积比分别是多少?它们与相似比的关系如何?与同伴交流.[生]因为两三角形都是等腰直角三角形,其对应角分别相等,所以它们是相似三角形.周长比与相似比相等,而面积比与相似比却不相等.[师]能不能找到面积比与相似比的量化关系呢?[生]面积比与相似比的平方相等.[师]老师为你的重大发现感到骄傲.但这是特殊三角形,对一般三角形、多边形,我们发现的结论成立吗?这正是我们本节课要解决的问题.Ⅱ.新课讲解投影片(§4.8.2 A)图4-44在图4-44中,△ABC∽△A′B′C′,相似比为.(1)请你写出图中所有成比例的线段.(2)△ABC与△A′B′C′的周长比是多少?你是怎么做的?(3)△ABC的面积如何表示?△A′B′C′的面积呢?△ABC与△A′B′C′的面积比是多少?与同伴交流.∴======.(2).∵===.∴CACBBAACBCABllCBAABC''+''+''++='''∆∆==.(3)S△ABC=AB·C D.S△A′B′C′=A′B′·C′D′.∴2)43(2121=''⋅''=''⋅''⋅='''∆∆DCCDBAABDCBACDABSSCBAABC.2.想一想如果△ABC∽△A′B′C′,相似比为k,那么△ABC与△A′B′C′的周长比和面积比分别是多少?[生]由上可知若△ABC∽△A′B′C′,相似比为k,那么△ABC与△A′B′C′的周长比为k,面积比为k2.3.议一议如图4-45,四边形A1B1C1D1∽四边形A2B2C2D2,相似比为k.图4-45(1)四边形A 1B 1C 1D 1与四边形A 2B 2C 2D 2的周长比是多少?(2)连接相应的对角线A 1C 1,A 2C 2,所得的△A 1B 1C 1与△A 2B 2C 2相似吗?△A 1C 1D 1与△A 2C 2D 2呢?如果相似,它们的相似各是多少?为什么?(3)设△A 1B 1C 1,△A 1C 1D 1,△A 2B 2C 2,△A 2C 2D 2的面积分别是那么各是多少?(4)四边形A 1B 1C 1D 1与四边形A 2B 2C 2D 2的面积比是多少?如果把四边形换成五边形,那么结论又如何呢?[生]解:(1)∵四边形A 1B 1C 1D 1∽四边形A 2B 2C 2D 2.相似比为k .(2)△A 1B 1C 1∽△A 2B 2C 2、△A 1C 1D 1∽△A 2C 2D 2,且相似比都为k .∵四边形A 1B 1C 1D 1∽四边形A 2B 2C 2D 2∴2211221122112211D A D A D C D C C B C B B A B A === ∠D 1A 1B 1=∠D 2A 2B 2,∠B 1=∠B 2.∠B 1C 1D 1=∠B 2C 2D 2,∠D 1=∠D 2.在△A 1B 1C 1与△A 2B 2C 2中∵ ∠B 1=∠B 2.∴△A 1B 1C 1∽△A 2B 2C 2.∴=k .同理可知,△A 1C 1D 1∽△A 2C 2D 2,且相似比为k .(3)∵△A 1B 1C 1∽△A 2B 2C 2,△A 1C 1D 1∽△A 2C 2D 2.22222222222222)(k S S S S k D C A C B A D C A C B A =++∆∆∆∆照此方法,将四边形换成五边形,那么也有相同的结论.由此可知:相似多边形的周长比等于相似比,面积比等于相似比的平方.4.做一做图4-46是某城市地图的一部分,比例尺为1∶100000.(1)设法求出图上环形快速路的总长度,并由此求出环形快速路的实际长度.(2)估计环形快速路所围成的区域的面积,你是怎样做的?与同伴交流.图4-46解:(1)量出图上距离约为20 cm ,则实际长度约为20千米.(2)图上区域围成的面积约为23.7 cm 2.根据相似多边形面积的比等于相似比1∶100000的平方,则实际区域的面积约为23.7平方千米.在设计图上,某城市中心有一个矩形广场,设计图的比例尺是1∶10000,图上矩形与实际矩形相似吗?如果相似,它们的相似比是多少?图上矩形与实际矩形的周长比是多少?面积比呢?答案:相似,相似比是1∶10000.周长比是1∶10000.面积比是1∶100002.本节课我们重点研究了相似多边形的对应线段(高、中线、角平分线)的比,周长比都等于相似比,面积比等于相似比的平方.Ⅴ.课后作业习题4.11预习位似图形的定义、性质.Ⅵ.活动与探究如图4-47已知,M 是□ABCD 的AB 边的中点,CM 交BD 于点E ,则图中阴影部分的面积与平行四边形ABCD 的面积比是多少?图4-47过程:这是一道综合性较高的题目,它考查了相似三角形的性质、面积计算及等积定理等,所以让学生进行讨论、总结,利用所学知识解决这个问题.讨论结果:作DN⊥AB于N,过E作GF⊥AB于F.∵M为AB中点∴S△AMD=S△DMB=S△ABD=S□ABCD∵S△MBD=S△MBC(同底等高的两个三角形面积相等).∴S△MBD-S△MBE=S△MBC-S△MBE即S△DME=S△CBE因此图中阴影部分的面积与平行四边形的面积之比是.§4.8.2 相似多边形的性质(二)一、1.做一做2.想一想3.议一议4.做一做二、课堂练习三、课时小结四、课后作业25658 643A 携S22255 56EF 囯A37714 9352 鍒Mg。
(人教版八年级数学教案) 相似多边形(2)
相似多边形(二)目的要求:1、使学生掌握相似多边形性质定理1,理解性质定理2。
2、进一步培养和巩固学生类比的数学思想。
3、进一步巩固将复杂的问题转化成简单的问题的研究方法。
教学重点:相似多边形性质定理1、2及简单应用。
教学难点:利用相似三角形的性质推出相似多边形的有关性质的方法。
教具准备:一副三角板教学方法: 探索发现法教学过程:复习提问:1、什么是相似多边形?什么是相似多边形的相似比?2、什么是相似三角形的性质定理?新课讲解:根据相似多边形的定义,可知相似多边形的对应角相等、对应边成比例。
那么相似多边形还有哪些性质呢?让学生类比相似三角形的性质定理1、2 导出相似多边形的性质定理。
性质定理1: 相似多边形的周长比等于相似比。
性质定理2: 相似多边形对应对角线的比等于相似比。
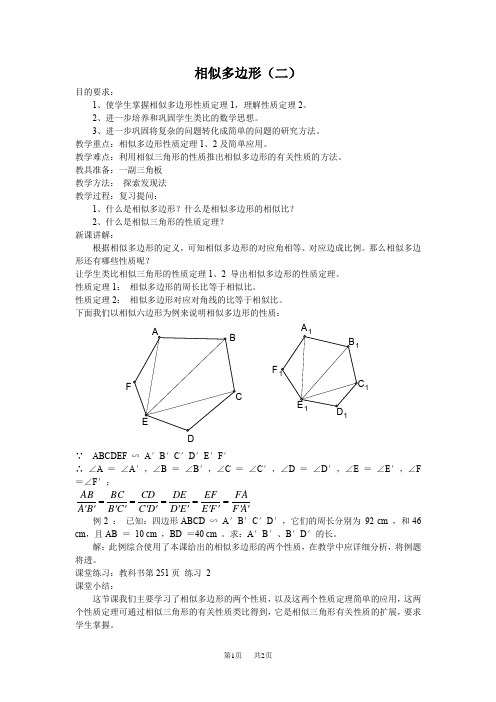
下面我们以相似六边形为例来说明相似多边形的性质:∵ ABCDEF ∽ A ′B ′C ′D ′E ′F ′∴ ∠A = ∠A ′,∠B = ∠B ′,∠C = ∠C ′,∠D = ∠D ′,∠E = ∠E ′,∠F =∠F ′;A F FA F E EF E D DE D C CD CB BC B A AB ''=''=''=''=''='' 例2 : 已知:四边形ABCD ∽ A ′B ′C ′D ′,它们的周长分别为 92 cm ,和46 cm ,且AB = 10 cm ,BD =40 cm 。
求:A ′B ′、B ′D ′的长。
解:此例综合使用了本课给出的相似多边形的两个性质,在教学中应详细分析,将例题将透。
课堂练习:教科书第251页 练习 2课堂小结:这节课我们主要学习了相似多边形的两个性质,以及这两个性质定理简单的应用,这两个性质定理可通过相似三角形的有关性质类比得到,它是相似三角形有关性质的扩展,要求学生掌握。
F11AF D课外作业:教科书第255 页习题B 组1、2同步精练练习(二)。
初中相似教案数学

初中相似教案数学教学目标:1. 理解相似多边形的概念,掌握相似多边形的性质;2. 学会使用尺规作图找出多边形的相似图形;3. 能够运用相似多边形的性质解决实际问题。
教学内容:1. 相似多边形的定义及性质;2. 相似多边形的判定方法;3. 尺规作图找出多边形的相似图形;4. 实际问题中的应用。
教学过程:一、导入(5分钟)1. 引导学生回顾之前学过的图形变换知识,如平移、旋转等;2. 提问:同学们,你们知道吗?在数学中,有一种特殊的图形变换,它可以让两个多边形完全重合,但形状不变,你们能猜到是什么吗?二、新课讲解(15分钟)1. 引入相似多边形的概念,通过示例讲解相似多边形的定义及性质;2. 讲解相似多边形的判定方法,如AA相似定理、相似比等;3. 结合实例,演示如何使用尺规作图找出多边形的相似图形。
三、课堂练习(15分钟)1. 让学生独立完成练习题,巩固相似多边形的性质及判定方法;2. 引导学生思考如何将相似多边形的性质应用于实际问题中。
四、课后作业(5分钟)1. 布置适量作业,让学生巩固所学知识;2. 鼓励学生自主探究,发现相似多边形在实际生活中的应用。
五、总结与反思(5分钟)1. 让学生回顾本节课所学内容,总结相似多边形的性质及判定方法;2. 引导学生思考如何将相似多边形的知识应用于实际问题中,提高解决实际问题的能力。
教学评价:1. 课堂讲解是否清晰,学生是否掌握相似多边形的性质及判定方法;2. 学生是否能独立完成练习题,运用相似多边形的知识解决实际问题;3. 学生对课后作业的完成情况,以及对相似多边形知识的深入探究程度。
教学资源:1. 教学PPT;2. 练习题;3. 尺规作图工具。
教学建议:1. 在讲解相似多边形的性质及判定方法时,要注意示例的选取,让学生直观地理解;2. 课堂练习环节,要及时解答学生的疑问,帮助学生巩固知识;3. 鼓励学生在课后自主探究,发现相似多边形在实际生活中的应用,提高学习兴趣。
数学初中第2单元教案

数学初中第2单元教案一、教学目标1. 让学生掌握相似多边形的定义及其性质。
2. 培养学生运用相似多边形解决实际问题的能力。
3. 培养学生合作学习、积极思考的良好学习习惯。
二、教学内容1. 相似多边形的定义:在平面内,如果两个多边形对应角相等,对应边成比例,那么这两个多边形叫做相似多边形。
2. 相似多边形的性质:(1)相似多边形的对应角相等。
(2)相似多边形的对应边成比例。
(3)相似多边形的面积比等于相似比的平方。
3. 相似多边形的应用:解决实际问题。
三、教学重点与难点1. 教学重点:相似多边形的定义及其性质。
2. 教学难点:相似多边形的应用。
四、教学方法1. 采用问题驱动法,引导学生主动探究相似多边形的定义和性质。
2. 利用多媒体课件,直观展示相似多边形的图形,增强学生的空间观念。
3. 结合实例,让学生亲身体验相似多边形的应用,提高解决实际问题的能力。
4. 组织小组讨论,培养学生的合作意识和团队精神。
五、教学过程1. 导入:通过展示一些相似的图形,如树叶、卫星图片等,引导学生思考:这些图形有什么共同特点?2. 探究相似多边形的定义:让学生尝试用自己的语言描述相似多边形的特点,然后给出正式的定义。
3. 探究相似多边形的性质:引导学生通过观察、操作、猜想等方法,发现相似多边形的性质。
4. 验证相似多边形的性质:让学生运用几何画板等软件,自行验证相似多边形的性质。
5. 应用相似多边形解决实际问题:出示一些实际问题,让学生运用相似多边形的知识解决。
6. 总结与评价:对本节课的内容进行总结,对学生的学习情况进行评价。
六、课后作业1. 完成教材上的练习题。
2. 选取一个实际问题,运用相似多边形的知识解决。
七、教学反思本节课通过问题驱动法、多媒体展示、实例分析等方法,引导学生主动探究相似多边形的定义、性质和应用。
在教学过程中,要注意关注学生的学习情况,及时给予指导和帮助。
同时,要培养学生合作学习、积极思考的良好学习习惯,提高学生的数学素养。
初中相似多边形的概念教案

初中相似多边形的概念教案教学目标:1. 知识与技能:理解相似多边形的概念,掌握相似多边形的性质,能够判断两个多边形是否相似。
2. 过程与方法:通过观察、操作、交流等活动,培养学生的几何思维能力和逻辑推理能力。
3. 情感态度价值观:激发学生对数学的兴趣,培养学生的探索精神和合作意识。
教学重点:相似多边形的概念和性质。
教学难点:相似多边形的判断和应用。
教学准备:多媒体课件、几何图形、剪刀、直尺等。
教学过程:一、导入(5分钟)1. 引导学生回顾已学的多边形的相关知识,如多边形的定义、性质等。
2. 提问:同学们,你们知道吗?在数学中,有一种特殊的多边形,它们的大小不一样,但是形状相同。
你们能猜到是什么吗?二、新课导入(10分钟)1. 介绍相似多边形的概念:各角对应相等,各边对应成比例的两个多边形叫做相似多边形。
2. 讲解相似多边形的性质:相似多边形的对应角相等,对应边成比例。
3. 举例说明相似多边形的性质,如相似三角形、相似矩形等。
三、实践活动(10分钟)1. 学生分组,每组提供一些几何图形,如三角形、矩形等。
2. 要求学生通过剪切、拼接等方法,创造出相似多边形。
3. 学生展示自己的作品,并解释相似多边形的性质。
四、巩固练习(10分钟)1. 给出一些几何图形,要求学生判断它们是否相似。
2. 解决问题:一个矩形的长是10cm,宽是5cm,如果从中截去一个相似矩形,剩下的矩形的长和宽分别是多少?五、总结与反思(5分钟)1. 学生总结相似多边形的概念和性质。
2. 教师强调相似多边形在实际生活中的应用,如建筑设计、工程测量等。
教学反思:本节课通过引导学生观察、操作、交流等活动,让学生掌握了相似多边形的概念和性质。
在实践活动环节,学生通过剪切、拼接等方法,亲手创造了相似多边形,加深了对相似多边形性质的理解。
在巩固练习环节,学生通过判断和解决问题,提高了运用相似多边形解决实际问题的能力。
总体来说,本节课达到了预期的教学目标,学生对相似多边形的概念有了深入的理解。
初中相似多边形的数学教案

初中相似多边形的数学教案一、教学目标1. 让学生理解相似多边形的概念,掌握相似多边形的性质和判定方法。
2. 培养学生运用相似多边形的知识解决实际问题的能力。
3. 发展学生的逻辑思维能力和合作交流能力。
二、教学内容1. 相似多边形的定义2. 相似多边形的性质3. 相似多边形的判定方法4. 相似多边形在实际问题中的应用三、教学重点与难点1. 教学重点:相似多边形的概念、性质、判定方法及应用。
2. 教学难点:相似多边形的判定方法及在实际问题中的应用。
四、教学方法1. 采用直观演示法、讲解法、引导发现法、实践操作法等多种教学方法。
2. 利用多媒体课件、模型、图片等教学资源,增强学生对相似多边形概念的理解。
3. 组织学生进行小组讨论、探究活动,培养学生的合作交流能力。
五、教学过程1. 引入新课:通过展示一些相似图形,引导学生发现它们的共同特征,从而引出相似多边形的概念。
2. 讲解相似多边形的定义:讲解相似多边形的定义,让学生理解相似多边形的性质和判定方法。
3. 相似多边形的性质:引导学生发现相似多边形的一些性质,如对应角相等、对应边成比例等。
4. 相似多边形的判定方法:讲解相似多边形的判定方法,让学生能够运用判定方法判断两个多边形是否相似。
5. 实际问题中的应用:出示一些实际问题,让学生运用相似多边形的知识解决问题,巩固所学知识。
6. 课堂小结:对本节课的内容进行总结,强调相似多边形的概念、性质和判定方法。
7. 布置作业:设计一些有关相似多边形的练习题,巩固所学知识。
六、教学评价1. 通过课堂讲解、练习和小组讨论,评价学生对相似多边形概念、性质和判定方法的理解程度。
2. 评估学生在解决实际问题中运用相似多边形知识的熟练程度。
3. 观察学生在课堂活动中的参与程度、合作交流能力和创新思维能力。
七、教学反馈1. 课后收集学生作业,分析其对相似多边形知识的掌握情况。
2. 在课堂上抽取学生回答问题,了解其对相似多边形知识的理解程度。
初中数学最新-相似多边形及性质教案2 精品

课题
3.4相似多边形及性质(第2课时)
教学目标
1.使学生掌握相似多边形性质定理1,理解性质定理2.
2.进一步培养和巩固学生类比的数学思想.
3.进一步巩固将复杂问题转化成简单问题的教学难点
利用相似三角形的性质推出相似多边形的有关性质的方法
教学用具
探索发现法
执教者
教学内容
共案
个案
(一)复习提问
1.什么是相似多边形?什么是相似多边形的相似比?
2.什么是相似三角形的性质定理1、2?
(二)讲解新课
让学生类比相似三角形的性质定理1、2,导出相似多边形的性质定理,这里教师要提示相似多边形的对应线段是“对应对角线”.
性质定理1:相似多边形周长的比等于相似比.
性质定理2:相似多边形对应对角线的比等于相似比.
以五边形为例,让学生利用等比性质证明定理1.
以六边形为例,教师和学生共同探讨由学生类比过来的性质定理2的正确性.教师要讲清楚什么是“对应对角线”,对应对角线就是指连结对应顶点而设的对角线.
例2已知四边形ABCD~四边形A′B′C′D′,它们的周长分别为92cm和46cm,且AB=10cm,BD=40cm.
(五)作业
教材B组1(教师可仿照2自编一题)
板书设计
教学反思
相似多边形
(一)复习提问
(二)讲解新课
(三)练习
(四)作业
求A′B′、B′D′的长.
此例综合使用了本课结出的相似多边形的两个性质,在教学中应详细分析,将例题讲细讲好.
(三)小结:
本节课主要学习了相似多边形的两个性质定理,以及这两个性质定理简单的应用,这两个性质定理可通过相似三角形的有关性质类比得到,它是相似三角形有关性质的扩展,要求学生掌握.
相似多边形教案

相似多边形教案教案标题:相似多边形教案教案目标:1. 理解相似多边形的概念和性质。
2. 能够识别相似多边形,并找出它们之间的相似关系。
3. 掌握相似多边形的比例关系和性质。
4. 能够应用相似多边形的知识解决实际问题。
教学准备:1. 教师准备:投影仪、白板、彩色笔、相似多边形的示例图片、实际生活中的相似多边形图片。
2. 学生准备:铅笔、直尺、量角器。
教学过程:步骤一:引入1. 教师通过投影仪展示一些相似多边形的示例图片,并引导学生观察并描述它们之间的相似关系。
2. 教师解释相似多边形的概念,即具有相同形状但大小不同的多边形。
步骤二:相似多边形的性质1. 教师引导学生发现相似多边形之间的比例关系,如边长比例、角度比例等。
2. 教师通过示例和图示解释相似多边形的性质,如对应角相等、对应边成比例等。
步骤三:相似多边形的判定1. 教师给出一些多边形,要求学生判断它们是否相似,并解释判断的依据。
2. 学生进行小组讨论,然后展示并解释自己的判断结果。
步骤四:相似多边形的应用1. 教师给出一些实际生活中的相似多边形的图片,如建筑物、地图等。
2. 学生观察并讨论这些图片中的相似多边形,并分析它们之间的相似关系。
3. 学生尝试应用相似多边形的知识解决一些实际问题,如计算高楼的高度、估算地图上的距离等。
步骤五:总结和拓展1. 教师与学生一起总结相似多边形的概念、性质和应用。
2. 学生通过练习题巩固所学知识,并尝试拓展更复杂的相似多边形问题。
教学延伸:1. 学生可以用几何软件绘制相似多边形,并观察它们之间的性质和关系。
2. 学生可以进行实地考察,寻找并记录实际生活中的相似多边形,并分析它们之间的相似关系。
教学评估:1. 教师观察学生在课堂上的参与和回答问题的能力。
2. 教师布置相似多边形的练习题,检查学生对知识的掌握情况。
3. 学生通过解决实际问题展示他们对相似多边形的应用能力。
教学反思:1. 教师根据学生的反馈和表现,及时调整教学步骤和策略。
初中数学教案备课

教案标题:初中数学《相似多边形的性质》备课一、教学目标1. 让学生掌握相似多边形的定义及其性质。
2. 培养学生运用相似多边形解决实际问题的能力。
3. 提高学生的逻辑思维能力和团队合作能力。
二、教学内容1. 相似多边形的定义2. 相似多边形的性质3. 相似多边形的应用三、教学重点与难点1. 重点:相似多边形的定义及其性质。
2. 难点:相似多边形的性质在实际问题中的应用。
四、教学方法1. 采用问题驱动法,引导学生主动探究相似多边形的性质。
2. 利用多媒体辅助教学,直观展示相似多边形的图形变化。
3. 采用案例分析法,让学生通过解决实际问题,巩固相似多边形的知识。
五、教学步骤1. 导入新课:1.1 复习相关知识:回顾上一节课所学的多边形的相关知识。
1.2 提出问题:什么是相似多边形?相似多边形有哪些性质?2. 自主学习:2.1 让学生通过阅读教材,自主学习相似多边形的定义及其性质。
2.2 学生分享学习心得,教师点评并总结。
3. 案例分析:3.1 教师展示一系列相似多边形的图形,让学生观察并分析。
3.2 学生分组讨论,总结相似多边形的性质。
3.3 各组汇报讨论成果,教师点评并总结。
4. 课堂练习:4.1 教师布置练习题,让学生运用相似多边形的性质解决问题。
4.2 学生独立完成练习,教师批改并给予反馈。
5. 拓展与应用:5.1 教师提出实际问题,让学生运用相似多边形的知识解决。
5.2 学生分组讨论,提出解决方案,教师点评并总结。
6. 课堂小结:6.1 教师引导学生总结本节课所学内容。
6.2 学生分享学习收获,教师给予鼓励和评价。
六、课后作业1. 复习本节课所学知识,整理笔记。
2. 完成课后练习题,巩固相似多边形的性质。
3. 收集实际问题,准备下一节课的讨论。
七、教学反思本节课结束后,教师应认真反思教学效果,针对学生的掌握情况,调整教学策略,以提高学生对相似多边形的理解和应用能力。
同时,关注学生的学习兴趣,激发学生主动探究数学知识的欲望。
初中相似多边形的性质教案

初中相似多边形的性质教案教学目标:1. 知识与技能:使学生掌握相似多边形的定义和性质,能够运用相似多边形的性质解决一些实际问题。
2. 情感与态度:培养学生的探索精神和合作意识,通过运用相似多边形的性质,增强学生的应用意识。
教学重难点:1. 重点:相似多边形的性质及其应用。
2. 难点:相似多边形的性质的灵活运用。
教学准备:1. 教学工具:黑板、粉笔、多媒体教学设备。
2. 教学素材:相关例题和练习题。
教学过程:一、创设情境,引入新课1. 复习已学知识:回顾多边形的定义和性质,复习三角形的相关知识。
2. 提出问题:在两个相似多边形中,它们的对应边和对应角有什么关系?二、自主探究,揭示相似多边形的性质1. 引导学生通过观察、分析、归纳相似多边形的性质。
2. 学生汇报探究结果,教师进行总结,得出相似多边形的性质:a. 相似多边形的对应边成比例。
b. 相似多边形的对应角相等。
c. 相似多边形的面积比等于相似比的平方。
三、巩固新知,运用性质解决实际问题1. 通过幻灯片展示一些实际问题,引导学生运用相似多边形的性质进行解决。
2. 学生独立解答问题,教师进行讲解和指导。
四、课堂练习,巩固提高1. 布置一些相关的练习题,让学生独立完成。
2. 教师对学生的解答进行点评和指导。
五、总结反思,拓展延伸1. 让学生回顾本节课所学的内容,总结相似多边形的性质及其应用。
2. 提出一些拓展性问题,激发学生的学习兴趣。
教学反思:本节课通过创设问题情境,引导学生自主探究相似多边形的性质,并通过实际问题让学生运用性质进行解决。
在教学过程中,注意引导学生积极参与,培养学生的探索精神和合作意识。
通过课堂练习和总结反思,巩固提高学生对相似多边形性质的理解和应用。
总体来说,本节课达到了预期的教学目标。
初中八年级数学 §4.8.2相似多边形的性质(二)教学设计

§4.8.2 相似多边形的性质(二)教学目标(一)知识认知要求1.相似多边形的周长比,面积比与相似比的关系.2.相似多边形的周长比,面积比在实际中的应用. (二)能力训练要求1.经历探索相似多边形的性质的过程,培养学生的探索能力.2.利用相似多边形的性质解决实际问题训练学生的运用能力. (三)情感与价值观要求1.学生通过交流、归纳,总结相似多边形的周长比、面积比与相似比的关系,体会知识迁移、温故知新的好处.2.运用相似多边形的周长比,面积比解决实际问题,增强学生对知识的应用意识. 教学重点1.相似多边形的周长比、面积比与相似比关系的推导.2.用相似多边形的比例关系解决实际问题. 教学难点相似多边形周长比、面积比与相似比的关系的推导及运用. 教学过程一、创设问题情境,引入新课(拿大小不同的两个等腰直角三角形三角板).我手中拿着两名同学的两个大小不同的三角板.请同学们观察其形状,并请两位同学来量一量它们的边长分别是多少.然后告诉大家数据.(让学生把数据写在黑板上)通过观察和计算来回答下列问题. 1.两三角形是否相似.2.两三角形的周长比和面积比分别是多少?它们与相似比的关系如何?与同伴交流. 因为两三角形都是等腰直角三角形,其对应角分别相等,所以它们是相似三角形. 周长比与相似比相等,而面积比与相似比却不相等. 能不能找到面积比与相似比的量化关系呢?面积比与相似比的平方相等.对一般三角形、多边形,我们发现的结论成立吗?这正是我们本节课要解决的问题. 二、新课讲解 1.做一做在图中,△ABC ∽△A ′B ′C ′,相似比为43. (1)请你写出图中所有成比例的线段.(2)△ABC 与△A ′B ′C ′的周长比是多少?你是怎么做的?(3)△ABC 的面积如何表示?△A ′B ′C ′的面积呢?△ABC 与△A ′B ′C ′的面积比是多少?与同伴交流.(1)∵△ABC ∽△A ′B ′C ′∴B A AB ''=C B BC ''=C A AC ''=D C CD ''=D B BD''= D A AD ''=43. (2)43='''∆∆的周长的周长C B A ABC .∵B A AB ''=C B BC ''=C A AC ''=43. ∴C A C B B A ACBC AB l l C B A ABC ''+''+''++='''∆∆ =C A C B B A C A C B B A ''+''+''''+''+''434343 =43)(43=''+''+''''+''+''C A C B B A C A C B B A . (3)S △ABC =21AB ·CD. S △A ′B ′C ′=21A ′B ′·C ′D ′. ∴2)43(2121=''⋅''=''⋅''⋅='''∆∆D C CD B A AB D C B A CDAB S S C B A ABC . 2.想一想如果△ABC ∽△A ′B ′C ′,相似比为k ,那么△ABC 与△A ′B ′C ′的周长比和面积比分别是多少?若△ABC ∽△A ′B ′C ′,相似比为k ,那么△ABC 与△A ′B ′C ′的周长比为k ,面积比为k 2.3.议一议如图四边形A 1B 1C 1D 1∽四边形A 2B 2C 2D 2,相似比为k.(1)四边形A 1B 1C 1D 1与四边形A 2B 2C 2D 2的周长比是多少?(2)连接相应的对角线A 1C 1,A 2C 2,所得的△A 1B 1C 1与△A 2B 2C 2相似吗?△A 1C 1D 1与△A 2C 2D 2呢?如果相似,它们的相似各是多少?为什么?(3)设△A 1B 1C 1,△A 1C 1D 1,△A 2B 2C 2,△A 2C 2D 2的面积分别是,111C B A S ∆ 222222111,,D C A C B A D C A S S S ∆∆∆那么222111222111D C A D C A C B A C B A S S S S ∆∆∆∆=各是多少?(4)四边形A 1B 1C 1D 1与四边形A 2B 2C 2D 2的面积比是多少?如果把四边形换成五边形,那么结论又如何呢?解:(1)∵四边形A 1B 1C 1D 1∽四边形A 2B 2C 2D 2.相似比为k.(2)△A 1B 1C 1∽△A 2B 2C 2、△A 1C 1D 1∽△A 2C 2D 2,且相似比都为k. ∵四边形A 1B 1C 1D 1∽四边形A 2B 2C 2D 2 ∴2211221122112211D A DA D C D C CBC B B A B A === ∠D 1A 1B 1=∠D 2A 2B 2,∠B 1=∠B 2. ∠B 1C 1D 1=∠B 2C 2D 2,∠D 1=∠D 2. 在△A 1B 1C 1与△A 2B 2C 2中 ∵22112211C B CB B A B A = ∠B 1=∠B 2. ∴△A 1B 1C 1∽△A 2B 2C 2. ∴2211B A B A =k. 同理可知,△A 1C 1D 1∽△A 2C 2D 2,且相似比为k. (3)∵△A 1B 1C 1∽△A 2B 2C 2,△A 1C 1D 1∽△A 2C 2D 2.22222222222222)(k S S S S k D C A C B A D C A C B A =++∆∆∆∆照此方法,将四边形换成五边形,那么也有相同的结论. 由此可知:相似多边形的周长比等于相似比,面积比等于相似比的平方. 4.做一做图是某城市地图的一部分,比例尺为1∶100000.(1)设法求出图上环形快速路的总长度,并由此求出环形快速路的实际长度. (2)估计环形快速路所围成的区域的面积,你是怎样做的?与同伴交流.解:(1)量出图上距离约为20 cm ,则实际长度约为20千米.(2)图上区域围成的面积约为23.7 cm 2.根据相似多边形面积的比等于相似比1∶100000的平方,则实际区域的面积约为23.7平方千米. 三.随堂练习在设计图上,某城市中心有一个矩形广场,设计图的比例尺是1∶10000,图上矩形与实际矩形相似吗?如果相似,它们的相似比是多少?图上矩形与实际矩形的周长比是多少?面积比呢?答案:相似,相似比是1∶10000. 周长比是1∶10000.面积比是1∶100002. 四.课时小结本节课我们重点研究了相似多边形的对应线段(高、中线、角平分线)的比,周长比都等于相似比,面积比等于相似比的平方.五.课后作业 习题4.11 六、活动与探究如图已知,M 是□ABCD 的AB 边的中点,CM 交BD 于点E ,则图中阴影部分的面积与平行四边形ABCD 的面积比是多少?过程:这是一道综合性较高的题目,它考查了相似三角形的性质、面积计算及等积定理等,所以让学生进行讨论、总结,利用所学知识解决这个问题. 讨论结果:作DN ⊥AB 于N ,过E 作GF ⊥AB 于F.∵M 为AB 中点 ∴S △AMD =S △DMB =21S △ABD =41S □ABCD ∵S △MBD =S △MBC (同底等高的两个三角形面积相等).∴S △MBD -S △MBE =S △MBC -S △MBE 即S △DME =S △CBE因此图中阴影部分的面积与平行四边形的面积之比是31.。
最新版初中数学教案《相似多边形2 2》精品教案(2022年创作)

对应练习如下列图的两个梯形相似,求出未知的x ,y ,z 的长和∠α,∠β的度数.四、总结 1. 知识点 2. 方法和技巧 五、作业1.两个多边形相似的条件是〔 〕A .对应角相等B .对应边相等C .对应角相等,对应边相等D .对应角相等,对应边成比例 2.以下列图形是相似多边形的是〔 〕A .所有的平行四边形;B .所有的矩形C .所有的菱形;D .所有的正方形3.E,F 分别为矩形ABCD 的边AD ,BC 的中点,假设矩形ABCD ∽矩形EABF ,AB =1,求矩形ABCD 的面积。
4.把一个矩形剪去一个正方形,假设剩余的矩形和原矩形相似,求原矩形的长与宽的比.5. 如图,矩形的草坪长20m ,宽10m ,沿草坪四周外围有1m 的环行小路, 小路的内外边缘所成的矩形相似吗?圆周角 教学目标(1)通过本节的教学使学生理解圆周角的概念,掌握圆周角的性质;(2)准确地运用圆周角性质进行简单的证明计算。
通过观察、思考实验探索等活动,分情况证明圆周角定理。
向学生渗透由特殊到一般的数学思想方法。
3.情感、态度与价值观在活动中获取成功的体验,提高学习数学的兴趣。
教学重点难点1.重点 圆周角的概念和圆周角性质;2.难点 认识圆周角性质需要分三种情况逐一证明的必要性。
教与学互动设计〔一〕创设情景,导入新课如下列图,A 、B 两点为足球球门的两端,现有三名运动锅分别站在C 、D 、E 的位置,且A 、B 、C 、D 、E 五点在以O 点为圆心的同一圆上,请问:运发动完整地看见球门的视角一样大吗? 〔二〕合作交流,解读探究 【思考】观察下面两组图形: 第一组: 第二组:让学生指出第一组图中角的两边、第二组图中角的顶点的特点,找一找哪几个图同时具备两组图形的特点。
得出结论:像〔2〕、〔6〕中的两条线段所成的角叫做圆周角。
【做一做】〔学生独立完成〕作⊙O 的直径AB ,在⊙O 上任取一点C 〔除点A 、B 〕,连结AC 、AB ,量出∠ACB 的OCA度数,记录下来。
2022年数学精品初中教学设计《相似多边形2 (2)》特色教案

4.3 相似多边形一、教学目标1.知道相似多边形的主要特征, 即:相似多边形的对应角相等, 对应边的比相等.2.会根据相似多边形的特征识别两个多边形是否相似, 并会运用其性质进行相关的计算.二、重点、难点1.重点:相似多边形的主要特征与识别.2.难点:运用相似多边形的特征进行相关的计算.三、探索新知1、观察图片, 体会相似图形性质(1) 图 (1)中的△A 1B 1C 1是由正△ABC 放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边又有什么关系呢?(2)对于图 (2)中两个相似的正六边形, 是否也能得到类似的结论?2 、如图的左边格点图中有一个四边形, 请在右边的格点图中画出一个与该四边形相似的图形.问题:对于图中两个相似的四边形, 它们的对应角, 对应边的比是否相等.3.【结论】:〔1〕相似多边形的特征:相似多边形的对应角______, 对应边的比_______. 反之, 如果两个多边形的对应角______, 对应边的比_______, 那么这两个多边形_______.几何语言:在⊿ABC 和⊿A 1B 1C 1中假设111;;C C B B A A ∠=∠∠=∠∠=∠.那么⊿ABC 和⊿A 1B 1C 1相似〔2〕相似比:相似多边形________的比称为相似比.问题:相似比为1时, 相似的两个图形有什么关系?结论:相似比为1时, 相似的两个图形______, 因此________形是一种特殊的相似形.四、例题讲解例1〔补充〕〔选择题〕以下说法正确的选项是〔 〕A .所有的平行四边形都相似B .所有的矩形都相似C .所有的菱形都相似D .所有的正方形都相似分析:A 中平行四边形各角不一定对应相等, 因此所有的平行四边形不一定都相似, 故A 错;B 中矩形虽然各角都相等, 但是各对应边的比不一定相等, 因此所有的矩形不一定都相似, 故B 错;C 中菱形虽然各对应边的比相等, 但是各角不一定对应相等, 因此所有的菱形不一定都相似, 故C 也错;D 中任两个正方形的各角都相等, 且各边都对应成比例, 因此所有的正方形都相似, 故D 说法正确, 因此此题应选D .例2、如图, 四边形ABCD 和EFGH 相似, 求角βα和的大小和EH 的长度x . 例3〔补充〕四边形ABCD 与四边形A 1B 1C 1D 1相似, 且A 1B 1:B 1C 1:C 1D 1:D 1A 1=7:8:11:14, 假设四边形ABCD 的周长为40, 求四边形ABCD 的各边的长.分析:因为两个四边形相似, 因此可根据相似多边形的对应边的比相等来解题.分析:因为两个四边形相似, 因此可根据相似多边形的对应边的比相等来解题. 解:∵ 四边形ABCD 与四边形A 1B 1C 1D 1相似,∴ AB :BC :CD :DA= A 1B 1:B 1C 1:C 1D 1:D 1A 1.∵ A 1B 1:B 1C 1:C 1D 1:D 1A 1=7:8:11:14,∴ AB :BC :CD :DA= 7:8:11:14.设AB=7m, 那么BC=8m, CD=11m, DA=14m .∵ 四边形ABCD 的周长为40,∴ 7m+8m+11m+14m=40.∴ m=1.∴ AB=7, 那么BC=8, CD=11, DA=14.五、课堂练习1.在比例尺为1﹕10 000 000的地图上, 量得甲、乙两地的距离是30 cm, 求两地的实际距离.2.如下图的两个直角三角形相似吗?为什么?3.如下图的两个五边形相似, 求未知边a 、b 、c 、d 的长度.六、当堂检测1.〔选择题〕△ABC 与△DEF 相似, 且相似比是32, 那么△DEF 与△ABC 与的相似比是〔 〕.A .32B .23C .52D .942.〔选择题〕以下所给的条件中, 能确定相似的有〔 〕〔1〕两个半径不相等的圆;〔2〕所有的正方形;〔3〕所有的等腰三角形;〔4〕所有的等边三角形;〔5〕所有的等腰梯形;〔6〕所有的正六边形.A .3个B .4个C .5个D .6个3.四边形ABCD 和四边形A 1B 1C 1D 1相似, 四边形ABCD 的最长边和最短边的长分别是10cm 和4cm, 如果四边形A 1B 1C 1D 1的最短边的长是6cm, 那么四边形A 1B 1C 1D 1中最长的边长是多少?4.如图, AB ∥EF ∥CD, CD=4, AB=9, 假设梯形CDEF 与梯形EFAB 相似, 求EF 的长.5.如图, 一个矩形ABCD的长AD= a cm, 宽AB= b cm, E、F分别是AD、BC的中点, 连接E、F, 所得新矩形ABFE与原矩形ABCD相似, 求a:b的值.〔2:1〕6.3 从统计图分析数据的集中趋势一、学生知识状况分析学生的知识技能根底:学生在前面的数学学习中, 已掌握了条形统计图、扇形统计图等统计图的画法, 并能从条形统计图、扇形统计图等统计图表中获取信息, 解决一些相关问题.学生活动经验根底:学生在前面的数学学习活动中, 已获得了从事统计活动所必须的数学方法, 形成了动手实践、自主探索、合作交流的学习方式, 积累了一些数学活动经验.二、教学任务分析本节课的教学任务是:学生进一步理解平均数、中位数、众数的实际含义;能从条形统计图、扇形统计图等统计图表中获取信息, 求出或估计相关数据的平均数、中位数、众数. 通过例题和习题的学习, 加强知识之间的联系, 稳固对各种图表信息的识别和评判能力, 开展学生初步的统计意识和数据处理能力, 达成有关的情感态度目标. 为此, 本节课的教学目标是:1. 知识与技能:进一步理解平均数、中位数、众数等的实际含义;能从条形统计图、扇形统计图等统计图表中获取信息, 求出或估计相关数据的平均数、中位数、众数.2. 过程与方法:初步经历数据的获取, 并求出或估计相关数据的平均数、中位数、众数的过程, 开展学生初步的统计意识和数据处理能力.3.情感与态度:通过探索活动, 培养学生的探索精神和创新意识;通过相互间合作交流, 让所有学生都有所获, 共同开展.三、教学过程设计本节课设计了五个教学环节:第一环节:情境引入;第二环节:活动探究;第三环节:运用提高;第四环节:课堂小结;第五环节:布置作业.第一环节:情境引入内容:为了检查面包的质量是否达标, 随机抽取了同种规格的面包10个, 这10个面包的质量如以下图所示.〔1〕这10个面包质量的众数、中位数分别是多少?〔2〕估计这10个面包的平均质量, 再具体算一算, 看看你的估计水平如何. 目的:通过学生读取随机抽取了同种规格面包的统计图的信息, 复习平均数、中位数、众数的概念, 初步体会估计相关数据的平均数、中位数、众数的过程, 从而引入新课.考前须知:引例的解答要让学生自主参与, 带着积极的状态进入新课的学习.第二环节:活动探究内容1:试一试:某次射击比赛, 甲队员的成绩如下:〔1〕根据统计图, 确定10次射击成绩的众数、中位数, 说说你的做法, 与同伴交流. 〔210次射击成绩的平均数, 再具体算一算, 看看你的估计水平如何. 内容2:议一议:甲、乙、丙三支青年排球队各有12名队员, 三队队员的 〔1〕观察三幅图, 你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?〔2〕根据图表, 你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?与同伴交流.〔3〕计算出三支球队队员的平均年龄, 看看你上面的估计是否准确? 内容3:做一做:小明调查了班级里20位同学本学期方案购置课外书的花费情况, 并将结果绘制成了下面的统计图.〔1〕在这20位同学中, 本学期方案购置课外书的花费的众数是多少? 〔2〕计算这20位同学方案购置课外书的平均花费是多少?你是怎么计算的?与同伴交流.〔3〕在上面的问题, 如果不知道调查的总人数, 你还能求平均数吗? 目的:以上“试一试〞、 “议一议〞、 “做一做〞的活动, 让学生经历数据的收集、加工与整理的过程, 分别从折线图、条形图、扇形图中获取信息, 估计数据的平均数、中位数、众数, 并与同伴交流, 学生能都有所获, 形成学习经88.28.48.68.899.29.49.69.81012345678910成绩次数甲队员10次射击成绩初三(1)班体育成绩102010550510152025不及格及格中良好优秀成绩人数验, 进一步开展初步的统计意识和数据处理能力, 培养学生的探索精神和创新意识;考前须知:注重学生读图、估计的过程、方法与结果, 及时评价矫正. 第三环节:运用提高内容:1. 以下图反映了初三〔1〕班、〔2〕班的体育成绩.〔1〕不计算, 根据条形统计图, 你能判断哪个班学生的体育成绩好一些吗? 〔2〕你能从图中观察出各班学生体育成绩等级的“众数〞吗? 〔3〕如果依次将不及格、及格、中、良好、优秀记为55、65、75、85、95分, 分别估算一下, 两个班学生体育成绩的平均值大致是多少?算一算, 看看你估计的结果怎么样?〔4〕初三〔1〕班学生体育成绩的有什么关系?你能说说其中的理由吗? 目的:通过学生的反应练习, 使教师及时了解学生从统计图估计数据的平均数、中位数和众数的情况, 及分析数据的能力, 以便教师及时对学生进行矫正.考前须知:教师除了掌握学生从统计图估计数据的平均数、中位数和众数的情况, 还要关注学生分析数据的能力, 帮助学生提高认识.第四环节:课堂小结内容:在本节课的学习中, 你通过从统计图估计数据的平均数、中位数和众数的学习有什么认识, 有什么经验?〔学生交流, 教师小结〕.目的: 发挥学生的主观能动性, 提高学生整理归纳的能力.考前须知:在发挥学生的主观能动性的同时, 不要忽略教师的主导作用. 第五环节:布置作业课本习题6.4的第1、2、3、4、5题.四、教学反思本节课以数学活动为主, 通过情境导入的引例和课堂评价, 激发学生的学习积极性. 通过的“想一想〞、 “议一议〞、 “做一做〞的探究活动和运用提高, 向学生提供充分从事数学活动的时机, 使他们在自主探索和合作交流的过程中进一步理解平均数、中位数、众数的实际含义;学会从条形统计图、扇形统计图等统计图表中获取信息, 估计相关数据的平均数、中位数、众数;从而增强统计意识和数据处理能力, 培养探索精神和创新意识. 教师一定要鼓励学生积极探索, 体验数学活动的趣味与应用价值, 让学生在相互间交流中, 互相启发, 共同进步.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面积:0.5AB*HC/0.5EDGF=16/9
所以面积之比是16/9
(1)四边形A1B1C1D1和A2B2C2D2相似.连接对角线A1C1和A2C2所得的ΔA1B1C1与ΔA2B2C2相似吗?
(2)ΔA1C1D1与ΔA2C2D2呢?如果相似,它们相似比是否相等?为什么?相等,
(3)四边形A1B1C1D1和A2B2C2D2的周长比,面积比与相似比有什么关系?
教学流程
(内容概要)
师生互动
(问题设计,情景创设)
引入
体会面积与边长的关系.
具体讨论三角形
A B若正方形ABCD边长为1周长为4,面积为1
若边长增大一倍,变为2.周长为8,面积为4
若边长,变为3.周长为12,面积为9
C D若边长,变为N.周长为4N,面积为NN
钳工小王准备按照比例尺3:4的图纸制作三角形零件,该零件的横截面为ΔABC画在图纸上是ΔDEF, CH,FG分别是它们的高.
C1 C2
D1 A2 B2
A1 B1
相似多边形的周长等于相似比,面积比等于相似比的平方.
练习:P79习题2.10
放缩比例是1:4.面积变为原来的16倍
教学流程
(内容概要)
师生互动
(问题设计,情景创设)
做一做
周长和面积比的应用
随堂练习
小结
作业
左图是某城市地图的一部分,比例尺
1:6000
(1)设法求出图上环形快速路的总长度,并由此求出环形快速路的实际长度.
P79习题2.10 3.4
课后记:
课题名称
相似多边形的性质(二)
新授
教材分析
德育点
发展学生积极的情感,态度,价值观.
创新点
体验解决问题策略的多样性.
能力点
培养学生的分析能力和数形结合的能力.
知识点
掌握相似多边形周长,面积的比.
学情ห้องสมุดไป่ตู้析
由相似比得出周长和面积的比需要一定的推理过程,但本书没有介绍等比定理,因此要引导学生引入比值K,要给学生的思考和交流留有充分的时间和空间.
C
F
A H B E G D
(1)找出图中的相似三角形,并简述理由.
ΔABC∽ΔDEF,
ΔAHc∽ΔGFE
ΔHCBΔDGFΔABC∽ΔDEF,
教学流程
(内容概要)
师生互动
(问题设计,情景创设)
议一议
CH与FG的比是多少? 3:4
ΔABC与DEF,的周长比和面积比分别是多少?
你是怎么想的?与同伴交流.
(AB+AC+BC)/(EF+ED+FD)=4:3
(2)估计环形快速路所围成的区域的面积,你怎么想的?与同伴交流.
(3)有人认为,两个相似三角对应角平分线的比等于周长的比,你认为对吗?
若比例尺是1:10000.图上图形与实际图形相似吗?求相似比?周长比,面积比.
(1)本节课你最成功的是什么?
(2)你认为你下节课应该注意什么?
(3)今天回家应对本节哪个知识点进行练习?
