一次函数面积问题.doc
一次函数之面积问题(与坐标轴围成的面积)(人教版)(含答案)

一次函数之面积问题(与坐标轴围成的面积)(人教版)一、单选题(共8道,每道12分)1.已知一次函数和的图象都经过点A(2,0),且与y轴分别交于B,C两点,则△ABC的面积是( )A.1B.2C.4D.8答案:C解题思路:试题难度:三颗星知识点:坐标线段长互转2.已知一次函数y=kx+(k-3)与一次函数y=2x+b交于点C(1,3),则两条直线的函数图象与x 轴所围成的三角形的面积是( )A.1B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积3.已知一次函数y=kx+b的图象经过点B(0,10),且与正比例函数y=2x的图象相交于点A(2,a),则这两个函数图象与y轴所围成的三角形的面积是( )A.5B.10C.20D.40答案:B解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积4.已知一次函数y=kx+b的图象经过点(3,-3),且与直线y=4x-3的交点在x轴上,则此函数的图象与坐标轴围成的三角形的面积为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积5.已知一次函数的图象经过点(-2,0),它与坐标轴围成的三角形面积等于1,则这个一次函数的函数表达式是( )A. B.C.或D.或答案:D解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积6.已知一次函数的图象过点(3,0),且与两坐标轴围成的三角形面积为3,则一次函数的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积7.若直线y=kx+b与直线y=4x平行,且直线y=kx+b与两坐标轴围成的三角形的面积为2,则直线y=kx+b与x轴的交点坐标是( ).A.(1,0)B.(1,0)或(-1,0)C.(2,0)D.(2,0)或(-2,0)答案:B解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积8.若直线y=x+k,x=1,x=4和x轴围成的直角梯形的面积等于9,则k的值为( )A. B.C.或D.或答案:C解题思路:试题难度:三颗星知识点:一次函数与坐标轴围成的图形面积。
一次函数中的面积问题

一次函数中的面积问题学习目标:1.通过复习使学生熟悉直线与坐标轴的交点坐标的求法,会求出两直线交点坐标,会求一次函数的解析式。
2.初步掌握由若干条直线所围成的图形的面积的计算方法。
一、探究新知例1:已知直线l :22+-=x y ,(1)求直线l 与两坐标轴的交点坐标;(2)求此一次函数的图象与两坐标轴所围成的三角形的面积。
变式1:已知直线l :22+-=x y ,且点T )32,(t 在直线l 上, (1) 求OT 所在直线的解析式;(2) 求直线l 和直线OT 与x 轴所围成的图形面积。
变式2:如图,已知直线l :22+-=x y 与x 轴、y 轴分别交于点B 、M,,将变式1中的直线OT 向上平移1个单位长度得到直线PA ,点Q 是直线PA 与y 轴的交点,求四边形PQOB 的面积。
变式3:如图,已知直线PA 是一次函数)0(>+=n n x y 的图象,直线PB 是一次函数)(2n m m x y +-=的图象。
(1)用m 、n 表示出A 、B 、P 点的坐标;(2)若点Q 是直线PA 与y 轴的交点,且四边形PQOB 的面积65,AB=2,试求点P 的坐标,并写出直线PA 与PB 的解析式。
例2:如图,已知直线1l 经过点)1,0()0,2(B A 与点,另一条直线2l 经过点B ,且与x 轴相交于点P(a,0),若APB ∆的面积为3,求a 的值。
变式:如图,已知直线1l 经过点)1,0()0,2(B A 与点,如果在第二象限内有一点)21,(a P ,且APB ∆的面积为3,求a 的值。
三、提升训练1:如图,点m x y C B A +-=2在一次函数、、的图象上,它们的横坐标依次为,211、、-分别过这些点作x 轴与y 轴的垂线,求图中阴影部分的面积之和。
2:设直线1l :1-+=k kx y 和直线2l :k x k y ++=)1((k 为正整数)及x 轴围成的三角形面积为k S ,求200621S S S +++ 的值。
一次函数面积问题专题(含答案解析)

一次函數面積問題1、如图,一次函数的图像与X轴交于点B (- 6 , 0),交正比例函数的图像于点A,点A的横坐标为-4,△ ABC的面积为15,求直线OA的解析式。
2、直线y=x+3的图像与X轴、y轴分别交于A B两点,直线a经过原点与线段AB 交于。
,把厶ABO勺面积分为2:1的两部分,求直线a的函数解析式。
3、直线PA是一次函数y=x+n的图像,直线PB是一次函数y=-2x+m (m>n>0的图像,(1) 用m n表示A、B、P的坐标(2) 四边形PQoB勺面积是',AB=2求点P的坐标4、A AOB的顶点0( 0, 0) A (2, 1)、B (10, 1),直线CDL X 轴且△ AOB面积二等分,若D (m, 0),求m的值5、点B在直线y=-x+1上,且点B在第四象限,点A(2, 0)、0(0, 0),A ABo 的面积为2,求点B的坐标。
6直线y=- x+1与X轴y轴分别交点A B,以线段AB为直角边在第一象限内作等腰直角△ ABC N BAC=90 ,点P( a,])在第二象限,△ ABP勺面积与△ ABC7、如图,已知两直线y=0.5x+2.5和y=-x+1分别与X轴交于A、B两点,这两直线的交点为P(1)求点P的坐标(2)求厶PAB的面积8、已知直线y=ax+b (b>0)与y轴交于点N,与X轴交于点A且与直线y=kx交于点M (2, 3),如图它们与y轴围成的厶MoN勺面积为5,求(1)这两条直线的函数关系式(2)它们与X轴围成的三角形面积9、已知两条直线y=2x-3和y=5-x(1)求出它们的交点A的坐标(2)求出这两条直线与X轴围成的三角形的面积10、已知直线y=x+3的图像与X轴、y轴交于A B两点,直线I经过原点,与线段AB 交于点。
,把厶AoB的面积分为2:1的两部分,求直线I的解析式。
11、已知直线y=2x+3与直线y=-2x-1与y轴分别交于点A B(1)求两直线交点C的坐标(2)求厶ABe的面积(3)在直线BC上能否找到点P,使得△ APC的面积為6,求出点P的坐标,12、已知直线y=-x+2与X轴、y轴分别交于点A和点B,另一直线y=kx+b(k≠ 0)经过点C(1,0),且把△ AOB分为两部分,(1)若厶AOB被分成的两部分面积相等,求k和b的值(2)若厶AOB被分成的两部分面积为1:5,求k和b的值13、直线y=- x+3交X, y坐标轴分别为点A B,交直线y=2x-1于点P,直线-Iy=2x-1交X, y坐标轴分别为C。
一次函数面积专题附答案

一次函数面积专题学校:___________姓名:___________班级:___________考号:___________ 一、解答题1.如图,在平面直角坐标系中,△ABC 三个顶点的坐标分别是A (1,5),B (-3,-3)和C (7,2),求△ABC 的面积.【答案】30 【解析】 【分析】解法1:延长AC 交x 轴于点D ,先求出直线AC 的解析式,从而得出点D 的坐标,再利用=+-ABCAEDBEFCFDSSSS即可.解法2:分别过点A ,B ,C 向坐标轴作垂线,得到矩形BEFG ,然后利用矩形=---ABCBEACFACBGBEFG SS SSS就可得到所求三角形的面积.解法3:分别过点A ,B ,C 向坐标轴作垂线,得到矩形BEFG ,据勾股定理求得45AB =同理可得35AC =55BC =由勾股定理逆定理和三角形的面积公式即可得出答案. 解法4:作AM//y 轴交BC 于M ,先得出直线BC 解析式为1322y x =-,然后得出点M (1,-1),从而确定水平宽a =10,铅垂高h =6,再利用=+ABCABMACMS SS即可;【详解】解法1:如图2,延长AC 交x 轴于点D . 因为A (1,5),C (7,2),所以直线AC 的解析式为11122y x =-+,所以点D 的坐标为D (11,0).同理,可以求出点E 3,02⎛⎫- ⎪⎝⎭,点F (3,0),所以DE =252,EF =92,DF =8,所以1252783044ABCAEDBEFCFDSSSS=+-=+-=.解法2:如图3,分别过点A ,B ,C 向坐标轴作垂线,得到矩形BEFG . 因为A (1,5),B (-3,-3),C (7,2), 所以E (-3,5),F (7,5),G (7,-3),所以BE =8,BG =10,AE =4,AF =6,CF =3,CG =5, 所以801692530ABCBEACFACBGBEFG SS SSS=---=---=矩形.解法3:如图4,在Rt △ABE 中,因为A (1,5),B (-3,-3),E (-3,5), 所以根据勾股定理求得45AB = 同理可得35AC =55BC = 因为2224580125AC AB BC +=+==, 所以由勾股定理逆定理得90BAC ∠=︒. 所以1145353022ABCSAB AC =⋅=⨯=.解法4:如图5,由B (-3,-3),C (7,2)容易得到水平宽a =10, 所以直线BC 解析式为1322y x =-. 作AM//y 轴交BC 于M , 令x =1,代入1322y x =-得y =-1,则M (1,-1). 此时,可以得到铅垂高h =5+1=6. 所以1211130222ABCABMACMSSSAM h AM h a h =+=⋅+⋅=⋅=.2.如图,已知直线AB 经过A (2,0),B (0,1)两点,点P 的坐标为(-2,a ),且0<a <2.若△ABP 的面积是1,求a 的值.【答案】1 【解析】 【分析】方法1:先根据A 、B 两点坐标求出直线AB 的解析式为112y x =-+,再过点P 作QN x⊥轴,交直线AB 于点Q ,交x 轴于点N ,利用割补法建立关于a 的方程,求解即可;方法2:设直线BP 交x 轴于点Q ,利用P 、B 两点坐标求出直线PB 的解析式为112a y x -=+,进而求出Q 2,01a ⎛⎫⎪-⎝⎭,利用割补法建立关于a 的方程,求解即可; 方法3:过点O 作AB 的平行线于直线x =-2交于点P ,根据A 、B 两点坐标求出直线AB 的解析式为112y x =-+,由直线OP 与直线AB 平行,且过原点,得到直线OP 的解析式即可求解. 【详解】 方法1:如答图所示,过点P 作QN x ⊥轴,交直线AB 于点Q ,交x 轴于点N . 设直线AB 的解析式为y kx b =+.将A (2,0),B (0,1)两点坐标代入可得201k b b +=⎧⎨=⎩,解得121k b ⎧=-⎪⎨⎪=⎩. 则直线AB 的解析式为112y x =-+,令x =-2得y =2,则Q (-2,2). 由42(2)1ABPAQNPNAPQBSSSSa a =--=---=,解得a =1.方法2:设直线BP 交x 轴于点Q ,直线PB 的解析式为y kx b =+.将P (-2,a),B (0,1)两点坐标代入可得21k b ab -+=⎧⎨=⎩,解得121a k b -⎧=⎪⎨⎪=⎩. 则直线PB 的解析式为112ay x -=+.a =1时,显然成立; 1a ≠时,令y =0得x =2a 1-,则Q 2,01a ⎛⎫⎪-⎝⎭.如图所示,121212212121ABPABQPQASSSa a a ⎛⎫⎛⎫=-=⨯⨯--⨯⨯-= ⎪ ⎪--⎝⎭⎝⎭, 解得a =1,又1a ≠,故此时a 不存在.综上得a =1.方法3:如答图所示,过点O 作AB 的平行线于直线x =-2交于点P ,连接AP ,BP . 因为“平行线间的距离处处相等”,所以△ABP 与△AOB 同底等高,面积都是1. 设直线AB 的解析式为y kx b =+.将A (2,0),B (0,1)两点坐标代入可得201k b b +=⎧⎨=⎩,解得121k b ⎧=-⎪⎨⎪=⎩,则直线AB 的解析式为112y x =-+. 因为直线OP 与直线AB 平行,且过原点,所以直线OP 的解析式为12y x =-.令x =-2得a =1.3.如图,在平面直角坐标系中,一次函数y x b =-+的图象与正比例函数y kx =的图象都经过点()3,1B .(1)求一次函数和正比例函数的解析式;(2)若点(),P x y 是线段AB 上一点,且在第一象限内,连接OP ,设APO ∆的面积为S ,求面积S 关于x 的函数解析式. 【答案】(1)y =﹣x +4,13y x =;(2)S =2x (0<x ≤3). 【解析】 【分析】(1)把B (3,1)分别代入y =﹣x +b 和y =kx 即可得到结论; (2)根据三角形的面积公式即可得到结论. 【详解】(1)把B (3,1)分别代入y =﹣x +b 和y =kx 得1=﹣3+b ,1=3k ,解得:b =4,k 13=,∴y =﹣x +4,y 13=x ;(2)∵点P (x ,y )是线段AB 上一点,∴S 12OA =•xP 142x =⋅⋅=2x (0<x ≤3).【点睛】本题考查了两直线相交或平行,三角形面积的求法,待定系数法确定函数关系式,正确的理解题意是解题的关键.4.如图,在平面直角坐标系中,一次函数12y x m =-+的图象1l 分别与x ,y 轴交于A ,B 两点,正比例函数的图象2l 与1l 交于点()2,4C .(1)求m 的值及2l 的解析式;(2)若点M 是直线12y x m =-+上的一个动点,连接OM ,当AOM 的面积是BOC 面积的2倍时,请求出符合条件的点M 的坐标;(3)一次函数2y kx =+的图象为3l ,且1l ,2l ,3l 不能围成三角形,直接写出k 的值.【答案】(1)5m =,2l 的解析式为2y x =(2)()6,2M 或()142,(3)12k =-或2或1【解析】 【分析】(1)设2l 的解析式为1y k x =,将点C 的坐标代入12,l l 的解析式,即可求解;(2)设1(,5)2M a a -+,进而根据题意列出方程,解方程求解即可;(3)根据题意,则31l l ∥或32l l ∥,进而即可求得k 的值 (1)2l 与1l 交于点()2,4C .设2l 的解析式为1y k x =,将点C 的坐标代入12,l l 的解析式,可得, 1422m =-⨯+,142k =,解得5m =,12k =,∴2l 的解析式为2y x = (2)设1(,5)2M a a -+,152y x =-+,令0x =,则5y =,令0y =,则10x =()0,5B ∴,()10,0A又()2,4C∴11111525,105522222BOCC AOMM M SBO x S OA y y a =⨯=⨯⨯==⨯=⨯⨯=⨯-+ AOM 的面积是BOC 面积的2倍,∴1552a ⨯-+2=⨯5即1522a -+=解得6a =或14∴()6,2M 或()142, (3)一次函数2y kx =+的图象为3l ,且1l ,2l ,3l 不能围成三角形,∴31l l ∥或32l l ∥当3l 过点C (2,4)时,将点C 坐标代入y =kx +2并解得:k =l ,∴12k =-或2或1【点睛】本题考查了一次函数综合,求一次函数解析式,求一次函数与坐标轴围成的三角形面积,一次函数与坐标轴的交点问题,一次函数的平移,掌握一次函数的性质是解题的关键. 5.如图,在平面直角坐标系中,一次函数332y x =-+与y 轴交于点A ,与x 轴交于点B ,过点B 作AB 的垂线,垂线与反比例函数()10my m x=≠交于C 、D 两点,且AB BC =.(1)求反比例函数()10my m x=≠的表达式,及经过点C 、D 的一次函数表达式()20y kx b k =+≠;(2)请直接写出使12y y >的x 取值范围; (3)求出ABD △的面积. 【答案】(1)110y x =,22433y x =- (2)3x <-或05x << (3)656【解析】 【分析】(1)由一次函数y =﹣32x +3求得A 、B 的坐标,然后通过证得△ABO ≌△BCF ,求得C(5,2),然后利用待定系数法即可求得函数的解析式; (2)求得D 的坐标,然后根据图象即可求得;(3)利用三角形面积公式,根据S △ABD =S △ABE +S △ADE 求得即可. (1)解:∵332y x =-+ 与y 轴交于点A ,与x 轴交于点B ,∴A (0,3),B (2,0), 如图,过点C 作CF ⊥x 轴于点F ,∵AB ⊥CD ,∴∠ABO +∠CBF =90°, ∵∠ABO +∠BAO =90°, ∴∠BAO =∠CBF , 在△ABO 和△BCF 中,BAO CBF AOB BFC AB BC =⎧⎪=⎨⎪=⎩∠∠∠∠ , ∴△ABO ≌△BCF (AAS ), ∴BF =AO =3,CF =OB =2, ∴C (5,2), ∵反比例函数y 1=mx(m ≠0)过点C , ∴m =5×2=10, ∴反比例函数110y x=, 将B (2,0),C (5,2)代入y 2=kx +b (k ≠0)得2052k b k b +=⎧⎨+=⎩,解得2343k b ⎧=⎪⎪⎨⎪=-⎪⎩,∴经过点C 、D 的一次函数表达式为22433y x =- ; (2)由102433y xy x ⎧=⎪⎪⎨⎪=-⎪⎩, 解得52=⎧⎨=⎩x y 或3103x y =-⎧⎪⎨=-⎪⎩,∴D 横坐标为﹣3.∴y 1>y 2的x 取值范围:x <﹣3或0<x <5; (3)ABD ADE ABE S S S =+△△△ 12D AE x =1·2B AE x + 656=. 【点睛】本题主要考查了反比例函数与一次函数交点问题,求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.6.如图,已知一次函数1y k x b =+与反比例函数2k y x=的图象交于第一象限内的点()1,6A 和()6,B m ,与x 轴交于点C .(1)分别求出这两个函数的表达式;(2)①观察图象,直接写出不等式21k k x b x+≥的解集;②请连接OA 、OB ,并计算△AOB 的面积;(3)是否存在坐标平面内的点P ,使得由点O ,A ,C ,P 组成的四边形是平行四边形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.【答案】(1)反比例函数的表达式是:y =6x ,一次函数表达式是:y =﹣x +7 (2)①x <0或1≤x ≤6;352(3)存在点P 的坐标为(8,6)或(﹣6,6)或(6,﹣6)使得由点O ,A ,C ,P 组成的四边形是平行四边形【解析】【分析】(1)直接利用待定系数法分别求出一次函数与反比例函数解析式;(2)①利用函数图象结合其交点得出不等式k 1x +b ≥2k x的解集;②如图所示,过点A 作AD ⊥x 轴于D ,过点B 作BE ⊥x 轴于B ,则2==32AOD BOE k S S =△△,再根据=AOB BOE AOD ADEB S S S S ++△△△梯形进行求解即可;(3)利用平行四边形的性质结合当AP 为边和AP 为对角线两种情况分别得出答案即可.(1)解:∵点A (1,6)在反比例函数y =2k x 的图象上, ∴6=21k , 解得:k 2=6,∴反比例函数的表达式是:y =6x; ∵B (6,m )在反比例函数y =6x的图象上, ∴m =66=1,∴B (6,1),将点A (1,6),B (6,1)代入y =k 1x +b ,可得: 11616k b k b =+⎧⎨=+⎩, 解得:117k b =-⎧⎨=⎩, ∴一次函数表达式是:y =﹣x +7;(2)解:①∵点A (1,6),B (6,1),∴不等式k 1x +b ≥2k x的解集是:x <0或1≤x ≤6; 故答案为:x <0或1≤x ≤6;②如图所示,过点A 作AD ⊥x 轴于D ,过点B 作BE ⊥x 轴于B , ∴2==32AOD BOE k S S =△△, ∵A (1,6),B (6,1),∴OD =1,AD =6,OE =6,BE =1,∴DE =5,∵=AOB BOE AOD ADEB S S S S ++△△△梯形,∴()35===22AOB ADEB AD BE DE S S +⋅△梯形;(3)解:∵C是直线AB与x轴的交点,∴点C的坐标为(7,0),如图3-1所示:当AP为边时,∴AP∥OC,AP=OC=7,∵A(1,6),∴P点坐标为:(8,6)或(-6,6);当AP为对角线时,如图3-2所示,∵AP与OC的中点坐标相同,∴1072260022PPxy++⎧=⎪⎪⎨++⎪=⎪⎩,∴66PPxy=⎧⎨=-⎩,∴点P的坐标为(6,-6);综上所述存在点P的坐标为(8,6)或(﹣6,6)或(6,﹣6)使得由点O,A,C,P 组成的四边形是平行四边形.【点睛】此题主要考查了反比例函数的综合以及待定系数法求一次函数解析式、平行四边形的性质等知识,正确数形结合分析是解题关键.7.如图,一次函数y=kx+b(k>0)的图象经过点C(−3,0),且与两坐标轴围成的三角形的面积为3.(1)求一次函数的解析式;(2)若反比例函数myx的图象与该一次函数的图象交于一、三象限内的A,B两点,且AC=2BC,求m的值.【答案】(1)一次函数的解析式为y=23x+2;(2)m的值为12.【解析】【分析】(1)根据一次函数y=kx+b(k>0)的图象经过点C(-3,0),得到-3k+b=0①,点C到y轴的距离是3,解方程即可得到结论;(2)如图,作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.根据相似三角形的性质得到AD=2BE.设B点纵坐标为-n,则A点纵坐标为2n.求得A(3n-3,2n),B(-3-32 n,-n),根据反比例函数y=mx的图象经过A、B两点,列方程即可得到结论.(1)解:∵一次函数y=kx+b(k>0)的图象经过点C(-3,0),∴-3k+b=0①,点C到y轴的距离是3,∵k>0,∴b>0,∵一次函数y=kx+b的图象与y轴的交点是(0,b),∴12×3×b=3,解得:b=2.把b=2代入①,解得:k=23,则函数的解析式是y=23x+2.故这个函数的解析式为y=23x+2;(2)解:如图,作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.∵AD∥BE,∴△ACD∽△BCE,∴AD ACBE BC=2,∴AD=2BE.设B点纵坐标为-n,则A点纵坐标为2n.∵直线AB的解析式为y=23x+2,∴A(3n-3,2n),B(-3-32n,-n),∵反比例函数y=mx的图象经过A、B两点,∴(3n-3)•2n=(-3-32n)•(-n),解得n1=2,n2=0(不合题意舍去),∴m=(3n-3)•2n=3×4=12.【点睛】本题考查了反比例函数与一次函数的交点问题,待定系数法求一次函数的解析式,三角形的面积,相似三角形的判定与性质,一次函数、反比例函数图象上点的坐标特征,难度适中.正确求出一次函数的解析式是解题的关键.8.如图,反比例函数kyx=的图象与一次函数12y x=-的图象分别交于M,N两点,已知点M(-2,m).(1)求反比例函数的表达式;(2)点P为y轴上的一点,当点P的坐标为(5时,求△MPN的面积.【答案】(1)2 yx =-(2)5【解析】【分析】(1)把M(-2,m)代入函数式y=-12x中,求得m的值,从而求得M的坐标,代入y=kx可求出函数解析式;(2)根据反比例函数与正比例函数的中心对称性求得N的坐标,然后利用S△MPN=S△MOP+S△NOP求得即可.(1)解:∵点M(-2,m)在一次函数y=-12x的图象上,∴m=-12×(-2)=1.∴M(-2,1).∵反比例函数y=kx的图象经过点M(-2,1),∴k=-2×1=-2.∴反比例函数的表达式为y=-2x;(2)解:∵反比例函数y=kx的图象与一次函数y=-12x的图象分别交于M,N两点,M(-2,1),∴N(2,-1),∵点P为y轴上的一点,点P的坐标为(0,5),∴OP=5,∴S△MPN=S△MOP+S△NOP=12×5×2+12×5×2=25.【点睛】本题考查了反比例函数与一次函数的交点问题,本题利用了待定系数法求函数解析式以及利用中心对称求两个函数的交点,三角形的面积等知识.9.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数ymx(m≠0)的图象相交于A,B两点,过点A作AD⊥x轴于点D,AO=5,OD:AD=3:4,B点的坐标为(﹣6,n)(1)求一次函数和反比例函数的表达式;(2)求△AOB的面积;(3)P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.【答案】(1)y23=x+2,y12x=;(2)△AOB的面积S9=;(3)P点坐标为:(0,8)或(0,5)或(0,﹣5)或(0,258)【解析】【分析】(1)设OD=3a,AD=4a,则AO=5a=5,解得:a=1,故点A(3,4),故反比例函数的表达式为:y=12x,故B(-6,2),将点A、B的坐标代入一次函数表达式,即可求解;(2)△AOB的面积S=12×OM×(xA-xB)=12×2×(3+6)=9;(3)分AP=AO、AO=PO、AP=PO三种情况,分别求解即可.(1)解:AO=5,OD:AD=3:4,设:OD=3a,AD=4a,则AD=5a=5,解得:a=1,故点A(3,4),则m=3×4=12,故反比例函数的表达式为:y12x=,故B(﹣6,﹣2),将点A、B的坐标代入一次函数表达式y=kx+b得:4326k bk b=+⎧⎨-=-+⎩,解得:232kb⎧=⎪⎨⎪=⎩,故一次函数的表达式为:y23=x+2;(2)解:设一次函数y23=x+2交y轴于点M(0,2),∵点A(3,4),B(﹣6,﹣2),∴△AOB的面积S12=⨯OM×(xA﹣xB)12=⨯2×(3+6)=9;(3)解:设点P(0,m),而点A、O的坐标分别为:(3,4)、(0,0),AP2=9+(m﹣4)2,AO2=25,PO2=m2,当AP=AO时,9+(m﹣4)2=25,解得:m=8或0(舍去0);当AO=PO时,同理可得:m=±5;当AP=PO时,同理可得:m258 =;综上,P点坐标为:(0,8)或(0,5)或(0,﹣5)或(0,258).【点睛】本题考查了反比例函数与一次函数综合,等腰三角形的判定与性质,利用形数结合解决此类问题,是非常有效的方法.10.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=mx(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(−3,4),点B的坐标为(6,n).(1)求该反比例函数和一次函数的解析式;(2)连接OB,求△AOB的面积;(3)在x轴上是否存在点P,使△APC是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)反比例函数的解析式为y=-12x;一次函数的解析式为y=-23x+2;(2)S△AOB=9;(3)存在.P点坐标为(-3,0)、(-173,0).【解析】【分析】(1)先把A(-3,4)代入反比例函数解析式得到m的值,从而确定反比例函数的解析式为y =-12x;再利用反比例函数解析式确定B 点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y =-23x +2; (2)先依据一次函数求得点C 的坐标,进而得到△AOB 的面积;(3)过A 点作AP 1⊥x 轴于P 1,AP 2⊥AC 交x 轴于P 2,可得P 1点的坐标为(-3,0);再证明Rt △AP 2P 1∽Rt △CAP 1,利用相似比计算出P 1P 2的长度,进而得到OP 2的长度,可得P 2点的坐标为(-173,0),于是得到满足条件的P 点坐标. (1)解:将A (-3,4)代入y =m x ,得m =-3×4=-12, ∴反比例函数的解析式为y =-12x ; 将B (6,n )代入y =-12x,得6n =-12, 解得n =-2,∴B (6,-2), 将A (-3,4)和B (6,-2)分别代入y =kx +b (k ≠0),得3462k b k b -+=⎧⎨+=-⎩, 解得232k b ⎧=-⎪⎨⎪=⎩, ∴所求的一次函数的解析式为y =-23x +2; (2)解:当y =0时,-23x +2=0, 解得:x =3,∴C (3,0),∴S △AOC =12×3×4=6,S △BOC =12×3×2=3, ∴S △AOB =6+3=9;(3)解:存在.过A 点作AP 1⊥x 轴于P 1,AP 2⊥AC 交x 轴于P 2,如图,∴∠AP 1C =90°,∵A 点坐标为(-3,4),∴P 1点的坐标为(-3,0);∵∠P 2AC =90°,∴∠P 2AP 1+∠P 1AC =90°,而∠AP 2P 1+∠P 2AP 1=90°,∴∠AP 2P 1=∠P 1AC ,∴Rt △AP 2P 1∽Rt △CAP 1, ∴11211AP PP CP AP =,即12464PP =, ∴P 1P 2=83, ∴OP 2=3+83=173, ∴P 2点的坐标为(-173,0), ∴满足条件的P 点坐标为(-3,0)、(-173,0). 【点睛】本题考查了反比例函数与一次函数交点问题,解决问题的关键是了解反比例函数图象上点的坐标特征和待定系数法确定函数解析式;会运用三角形相似知识求线段的长度.。
一次函数与面积问题

一次函数常与三角形或四边形的面积相结合进行考查,两种类型的题目比较常见:(1)由函数图像求面积;(2)由面积求点坐标。
遇到第一种类型题目时,找准三角形的底和高是解题的关键,特别是遇到钝角三角形。
如果无法直接求解,可以利用割补法、铅锤法等方法进行转化。
遇到第二种类型题目时,要特别注意,很容易出错,不要忘记使用绝对值。
01类型一:由函数图像求图形面积例题1:如图,直线l1:y=-3x+3与x轴交于点A,直线l2经过点B(4,0),C(3,-1.5),并与直线l2交于点D.(1)求直线l2的函数解析式;(2)求△ABD的面积.分析:求l2的函数解析式,利用待定系数法,已知点B(4,0)、点C (3,-1.5),代入解析式中求出K、b得值即可得到一次函数解析式。
求△ABD的面积,三角形有一边在x轴上,求三角形的面积可直接利用三角形的面积公式,选择x轴上的线段AB为底,那么点D纵坐标的绝对值即为三角形的高,因此需要求出点B坐标。
点B是两直线的交点,联立方程组即可求得点B坐标。
本题主要是有函数图像求得三角形的面积,属于基础题。
02类型二:由面积求点坐标例题2:如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2).(1)求直线AC的表达式;(2)求△OAC的面积;(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC 的面积是△OAC的面积的14?若存在,求出此时点M的坐标;若不存在,请说明理由.分析:(1)由点C和点A的坐标,利用待定系数法即可求得函数的解析式;(2)求△AOC的面积,由题可知该三角形可选OC作为底,点A的横坐标的绝对值即为该三角形的高,点A与点C坐标已知,可通过三角形的面积公式直接求出。
(3)当△OMC的面积是△OAC的面积的1/4时,根据面积公式即可求得M的横坐标的绝对值,然后代入解析式即可求得M的坐标.由面积求点坐标时,一定要注意绝对值的使用,注意分情况进行讨论。
一次函数图象中的面积问题

例 4 已知直线 Y :一 +2与 轴 、 Y轴分别交于点 A、 点 B, 另一直线 Y=k x+b ( k ≠0 ) 经过点 C ( 1 , 0 ) 与直
.
.
s ∞ = + S A A o B  ̄ - 了 1
S A A C D: c・ DE, A C =I , DE =y 0 ,
・ . .
即(
丽
・ .
+v / 芝
+
) < 8
> 0, 点评此题 中用 Nhomakorabea 替 换
T, 缩小分 母 , 放 大分
数, 问题获解.
.
+
_ 『< = z / Y
+
一
总之 , 利用放缩法 解题 时 , 应 把握 住放 缩 的 目标 和 放缩 的适度 , 问题才能得到合理解决. ) 放
k+b=0,
4 了 2)
,
/ c E A\
r
‘ ・
i 争 号 . 解 之 尼 2 ,
T— z / h - - -  ̄= 1的大小.
√n
( 上接 6 6页 )
应 用相 关知识使问题迅速获解.
≠ 丽 , 于是 ( 丽
解
一
。 . ‘ o ≠b , . ・ . 丽 r ) > O .
) 并
点评
大为 ( 丽
解 题 的关键 是 将 (
+ 丽 ) +( 丽
珏
氯
J
/
\/ B
~
其坐标为 ( ‰, Y o ) .
・ . ’
点A 、 点 B是 直线 Y= 一 + 2与 轴 、 Y轴 的交
点,
‘ . .
点A ( 2 , 0 ) , 点n ( o , 2 ) .
与一次函数有关的面积问题

知识拓展
拓展一 如图,点E(1 ,3) ,点F( 3 ,1) ,在直线 y=-2x+4上,求△EO2F的面积(2多种方法).
B
E (1 ,3) 2 F ( 3 ,1)
A2
B
H
K
G
H
L
G
A
知识拓展
拓展二 点Q在y轴上,且△QPB与△CPB 面积相等,求点Q的坐标.
分类讨论
知识拓展
拓展三 如图,直线y 2x 4 与x轴、y轴分
2.已知直线y=kx+2与两坐标轴围成的三角形面 积是2,求k的值.
3.已知点P是一次函数y=-x+2的图象上一点,如 果图象与x轴交于A点,且△OAP的面积等于3, 求P点的坐标.
课后巩固
4.如图(4),已知直线经过点 A(2,0)与点B(0,1),
如果在坐标平面内有一点 P(t, 1) . (1)求△BPA的面积S与t的函数2关系. (2) 当△BPA的面积为3时,求t的值.
别交于点A、B,点T是直线AB上的一个动点,
连结CT.设T点横坐标为t. (1)求△CAT的面积S与t的 函数关系式.
(t,-2t+4)
T
(2)当点T运动到什么位置
时△CAT的面积为6.
-1
-1
P(1,2)
2 2
课堂小结
谈一谈这节课的收获!
课后巩固
1.直线y=x和直线y=-x+2与y轴围成的面积是 .
武义县实验中学 周 东
知识回顾
y B(0,4)
(1)点M(a,b)到x轴的 距离为 b ,到y轴的距
P
离为 a .
(1,2)
(2)一次函数y=kx+b与
一次函数面积问题专题(含答案解析)

一次函數面積問題1、如图,一次函数的图像与*轴交于点B〔-6,0〕,交正比例函数的图像于点A,点A的横坐标为-4,△ABC的面积为15,求直线OA的解析式。
2、直线y=*+3的图像与*轴、y轴分别交于A、B两点,直线a经过原点与线段AB交于C,把△ABO的面积分为2:1的两局部,求直线a的函数解析式。
3、直线PA是一次函数y=*+n的图像,直线PB是一次函数y=-2*+m〔m>n>0〕的图像,〔1〕用m、n表示A、B、P的坐标〔2〕四边形PQOB的面积是,AB=2,求点P的坐标4、△AOB的顶点O〔0,0〕、A〔2,1〕、B〔10,1〕,直线CD⊥*轴且△AOB面积二等分,假设D〔m,0〕,求m的值5、点B在直线y=-*+1上,且点B在第四象限,点A〔2,0〕、O〔0,0〕,△ABO的面积为2,求点B的坐标。
6、直线y=-*+1与*轴y轴分别交点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC, BAC=90°,点P〔a,〕在第二象限,△ABP的面积与△ABC 面积相等,求a的值.7、如图,两直线y=0.5*+2.5和y=-*+1分别与*轴交于A、B两点,这两直线的交点为P〔1〕求点P的坐标〔2〕求△PAB的面积8、直线y=a*+b〔b>0〕与y轴交于点N,与*轴交于点A且与直线y=k*交于点M 〔2,3〕,如图它们与y轴围成的△MON的面积为5,求〔1〕这两条直线的函数关系式〔2〕它们与*轴围成的三角形面积9、两条直线y=2*-3和y=5-*〔1〕求出它们的交点A的坐标〔2〕求出这两条直线与*轴围成的三角形的面积10、直线y=*+3的图像与*轴、y轴交于A、B两点,直线l经过原点,与线段AB 交于点C,把△AOB的面积分为2:1的两局部,求直线l的解析式。
11、直线y=2*+3与直线y=-2*-1与y轴分别交于点A、B〔1〕求两直线交点C的坐标〔2〕求△ABC的面积〔3〕在直线BC上能否找到点P,使得△APC的面积為6,求出点P的坐标,假设不能请说明理由。
复习课件一次函数交点与面积问题.doc

y Ox yO教师姓名学科校区上课时间:学生姓名性别年级学校课题一次函数交点问题及直线围成的面积问题计划课时本节课为第课时教学目标掌握一次函数面积的计算方法难点重点求相关点的坐标,割补法求面积教学过程知识点及例题设计1.y=-x+2与x轴的交点坐标是______,与y轴的交点坐标是_____2.直线y=2x+5与y= x+5的交点坐标______.3.函数y=3x-2与函数y=2x+1的交点坐标______.4.点A(-1,2)到x轴距离___,到y轴距离____。
任意一点P(x,y)到x轴距离___,到y轴距离____。
5.在x轴上点M(-3,0),点N(5,0),则MN的长度____。
6.在y轴上点P(0,3),点Q(0,-2),则PQ的长度____例1:已知一次函数.(1)求图象与x 轴交点A, 与y 轴交点B的坐标.(2)求图象与坐标轴所围成的三角形面积.例2:已知直线y=2x+3、y=-2x-1求:(1)两直线与y轴围成的三角形的面积(2)两直线与x轴围成的三角形的面积(3)求四边形APDO的面积练习:已知直线y=x+3、y=-x+1(1)两直线与x轴围成的三角形的面积(2)两直线与y轴围成的三角形的面积(3)求四边形AOCP的面积Oy4xy=2x+4-3-2-1321-4-2-3432-11AB24y x=+x。
一次函数面积问题

一次函数面积问题
一次函数是指形如y = kx + b 的函数,其中k 和 b 是常数。
如果我们将这个函数画成图像,可以得到一条直线。
一次函数的面积问题通常指的是求解一条直线与坐标轴所围成的面积。
具体来说,如果我们有一个一次函数y = kx + b,我们可以将其表示为一条直线。
这条直线与x 轴和y 轴交于两个点,分别为(0, b) 和(-b/k, 0)。
这两个点就是直线所围成的矩形的两个顶点,我们可以计算出这个矩形的面积。
矩形的面积等于矩形的长乘以宽。
在这个问题中,矩形的长就是直线与x 轴的交点的x 坐标的绝对值,即|-b/k|。
矩形的宽就是直线与y 轴的交点的y 坐标的绝对值,即|b|。
因此,我们可以将这个矩形的面积表示为:
```
A = |-b/k| * |b|
```
需要注意的是,如果直线的斜率k 是正数,那么这个矩形的面积就是正值。
如果直线的斜率k 是负数,那么这个矩形的面积就是负值,但是我们通常会取其绝对值。
这就是一次函数面积问题的解法。
需要注意的是,这个问题只适用于一次函数,对于其他类型的函数,可能需要使用其他的方法来计算面积。
一次函数面积问题专题(含答案)

一次函數面積問題1、如图,一次函数的图像与x轴交于点B(-6,0),交正比例函数的图像于点A,点A的横坐标为-4,△ABC的面积为15,求直线OA的解析式。
2、直线y=x+3的图像与x轴、y轴分别交于A、B两点,直线a经过原点与线段AB交于C,把△ABO的面积分为2:1的两部分,求直线a的函数解析式。
3、直线PA是一次函数y=x+n的图像,直线PB是一次函数y=-2x+m(m>n>0)的图像,(1)用m、n表示A、B、P的坐标(2)四边形PQOB的面积是,AB=2,求点P的坐标4、△AOB的顶点O(0,0)、A(2,1)、B(10,1),直线CD⊥x轴且△AOB面积二等分,若D(m,0),求m的值5、点B在直线y=-x+1上,且点B在第四象限,点A(2,0)、O(0,0),△ABO 的面积为2,求点B的坐标。
6、直线y=-x+1与x轴y轴分别交点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC, BAC=90°,点P(a,)在第二象限,△ABP的面积与△A BC 面积相等,求a的值.7、如图,已知两直线y=0.5x+2.5和y=-x+1分别与x轴交于A、B两点,这两直线的交点为P(1)求点P的坐标(2)求△PAB的面积8、已知直线y=ax+b(b>0)与y轴交于点N,与x轴交于点A且与直线y=kx交于点M(2,3),如图它们与y轴围成的△MON的面积为5,求(1)这两条直线的函数关系式(2)它们与x轴围成的三角形面积9、已知两条直线y=2x-3和y=5-x(1)求出它们的交点A的坐标(2)求出这两条直线与x轴围成的三角形的面积10、已知直线y=x+3的图像与x轴、y轴交于A、B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线l的解析式。
11、已知直线y=2x+3与直线y=-2x-1与y轴分别交于点A、B(1)求两直线交点C的坐标(2)求△ABC的面积(3)在直线BC上能否找到点P,使得△APC的面积為6,求出点P的坐标,若不能请说明理由。
一次函数之面积问题 (习题及答案).

一次函数之面积问题(习题)1.如图,一次函数y=kx+b 的图象经过A(-2,-1),B(1,3)两点,并且与x 轴交于点C,与y 轴交于点D,则△AOB 的面积为.第1 题图第2 题图2.如图,直线y =1x +1 经过点A(1,m),B(4,n),点C 的坐2标为(2,5),则△ABC 的面积为.3.如图,直线y=-x+3 经过点A(4,m),B(-1,n),若点P 的坐标为(6,2),则S△ABP= .4.如图,直线l1:y=x-3 与直线l2:y=2x 交于点A,点B(5,m)在直线l1 上,点C(2,n)在直线l2 上,则△ABC 的面积为.5.如图,直线y =1x +1 与x 轴、y 轴分别交于点A,B,直线2y=kx-3 与x 轴、y 轴分别交于点C,D,两直线相交于点P,若S△ADP=20,则k 的值为.6.如图,在平面直角坐标系中,已知A(2,4),B(10,5),C(8,2),则四边形OABC 的面积为.7.如图,在平面直角坐标系中,已知直线l1,l2 相交于点A(2,1),点B(8,4)在直线l1 上,直线l2 的表达式为y=3x-5.C 为直线l2 上的一个动点,且在点A 右侧,若△ABC 的面积为15,则点C 的坐标为.8. 如图,直线 y =-x +2 与 x 轴、y 轴分别交于点 A ,B ,以 A 为直角顶点,线段 AB 为腰在第一象限内作等腰 Rt △ABC ,点 P 为直线 x =1 上的一点,若 S △ABP =S △ABC ,则点 P 的坐标为 .9. 如图,已知直线 y = - 1 x + 4 与 x 轴、y 轴分别相交于点 A ,B , 2再将△AOB 折叠,使点 A 与点 B 重合,折痕与 x 轴交于点 C , 与 AB 交于点 D .(1) 点 A 的坐标为 ,点 B 的坐标为 .(2) 求线段 OC 的长及直线 BC 的表达式.(3) 直线 BC 上是否存在一点 M ,使△ABM 的面积与△ABO 的面积相等?若存在,请直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.【参考答案】1.522.923. 25 24. 205. 16. 257. (4,7)8. (1,5)或(1,-3)9. (1)(8,0),(0,4);(2)线段OC 的长为3,直线BC 的表达式为y =-4x + 4 ;3(3)存在,点M 的坐标为( 24,-12)或( -24,52).5 5 5 5。
一次函数之面积问题(铅垂法)(人教版)(含答案)

一次函数之面积问题(铅垂法)(人教版)一、单选题(共8道,每道11分)1.如图,已知一次函数的图象经过A(5,-1),B(-3,-5)两点,则△AOB的面积为( )A. B.C.14D.28答案:C解题思路:试题难度:三颗星知识点:铅垂法求面积2.如图,已知一次函数的图象经过A(2,a),B(-1,b)两点,则△AOB的面积为( )A. B.5C.3D.答案:A解题思路:试题难度:三颗星知识点:铅垂法求面积3.如图,已知一次函数y=x-1的图象经过A(m,1),B(n,-2)两点,则△AOB的面积为( )A.3B.C.2D.答案:D解题思路:试题难度:三颗星知识点:铅垂法求面积4.如图,△ABC三个顶点的坐标分别为A(4,1),B(5,5),C(-1,2),则三角形的面积为( )A. B.C.21D.答案:D解题思路:试题难度:三颗星知识点:铅垂法求面积5.如图,已知一次函数的图象经过A(5,m),B(1,n)两点,点C(3,4),则△ABC 的面积为( )A.8B.4C.5D.6答案:B解题思路:试题难度:三颗星知识点:铅垂法求面积6.如图,已知一次函数的图象经过A(-5,-1),B(-1,n)两点,点C(-3,0),则△ABC的面积为( )A.8B.4C.5D.7答案:B解题思路:试题难度:三颗星知识点:铅垂法求面积7.如图,直线AB:分别与x轴、y轴交于点A,B,直线CD:y=x+b分别与x轴、y轴交于点C,D,直线AB与CD交于点P(8,5),则的面积为( )A.12B.16C.18D.20答案:D解题思路:试题难度:三颗星知识点:铅垂法求面积8.如图,直线与x轴、y轴分别交于A,B两点,直线与x 轴、y轴分别交于C,D两点.设直线,交于点P,则△PAD的面积为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:铅垂法求面积二、填空题(共1道,每道12分)9.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别为A(-1,3),B(-3,-2),C(4,-3),D(3,2),则四边形ABCD的面积是____.答案:28 解题思路:试题难度:知识点:铅垂法求面积。
一次函数面积问题总结
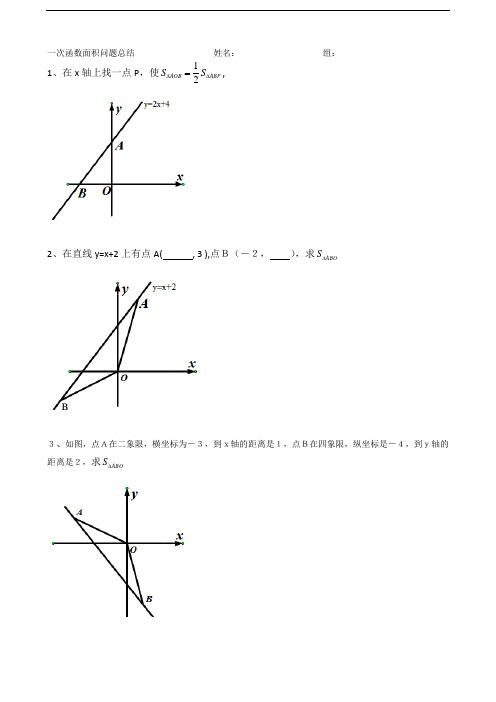
一次函数面积问题总结 姓名: 组:
1、在x 轴上找一点P ,使ABP AOB S S ∆∆=2
1,
2、在直线y=x+2上有点A( , 3 ),点B(-2, ),求ABO S ∆
3、如图,点A在二象限,横坐标为-3,到x轴的距离是1,点B在四象限,纵坐标是-4,到y轴的距离是2,求ABO S ∆
4、写出A\B的坐标,求ABC S ∆
5\如图,在平面直角坐标系中,直线y =﹣2x +10与y 轴交于点A ,与x 轴交于点B ,另一条直线经过点A
和点C (﹣2,8),且与x 轴交于点D .(1)求直线AD 的解析式;(2)求△ABC 的面积.(3)在线段AB 上找一点P ,使得ABD ABP S S ∆∆=3
1,求P 的坐标
6、如图1,在平面直角坐标系中,等腰Rt △AOB 直角边OA ,OB 与坐标轴重合,且OA =3,直线BC 与
x 轴交于点C ,且OC
OB =.(1)求直线BC 函数表达式;(2)如图2,点D 是直线BC 上一动点, 当S △ABD =时,求点D 的坐标;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学【一次函数面积问题】
一﹑要点回顾
1. 直线 y= -2x - 1 与 x 轴相交于点 ,与 y 轴相交于点 。
2. 直线 y
3x 4与 y 2x 1相交于点 P ,则点 P 的坐标为。
3. 一次函数的图象经过 (3, 5), (-4 ,-9) ,则此一次函数的解析式为 。
4、距离问题
(一)两点之间的距离
( 1)类型 1:A ( x 1,0), B ( x 2, 0), AB= ; C ( x 1, y ), D ( x 2, y ),则 CD= ; ( 2)类型 2:A ( 0, y 1), B ( 0, y 2), AB= ; C ( x , y 1), D ( x , y 2),则 CD= ;
( 3)类型 3:A ( x , 0), B ( 0, y ), AB= ;
( 4)类型 4:A ( x 1,y 1), B ( x 2, y 2), AB= ;
(二)点到坐标轴的距离 A(x,y) 到 x 轴的距离为 ,到 y 轴的距离为。
二、培优讲解 例 1:已知直线 l : y
2x 2 ,
( 1)求直线 l 与坐标轴的交点坐标分别为
;
(2)此一次函数的图象与两坐标轴所围成的三角形的面积 。
变式 1:已知直线 l : y
2 x 2 ,且点 T (t , 2
) 在直线 l 上,
3
(1) 求 OT 所在直线的解析式;
(2) 求直线 l 和直线 OT 与 x 轴所围成的图形面积。
y
变式 2:如图,已知直线
l : y 2x 2 与 x 轴、 y 轴分别交于点 B 、
M, ,将变式 1 中的直线 OT 向上平移 1 个单位长度得到直线 PA ,点 Q 是直线 PA 与 y 轴的交点,求四边形 PQOB 的面积。
M
P
Q
A O B
x
变式 3:如图,已知直线 PA 是一次函数 y x n( n 0) 的图像,直线
y PB 是一次函数 y2x
m( m n) 的图象。
M
( 1)用 m 、 n 表示出 A 、 B 、P 点的坐标;
P ( 2)若点 Q 是直线 PA 与 y 轴的交点,且四边形
PQOB 的面积
5
,AB=2 ,
Q
6
AO
B
试求点 P 的坐标,并写出直线 PA 与 PB 的解析式。
例 2:如图, 已知直线 l 1 经过点 A(2,0)与点 B(0,1) ,另一条直线 l 2 经过点 B ,且与 x 轴相交于点 P(m,0),
若
APB 的面积为 3,求 m 的值。
y
B
A
O
x
3:如图,已知直线 l 1 经过点 A(2,0)与点 B(0,1) ,如果在第二象限内有一点
1 例 P( 5, ) ,
2
求
APB 的面积。
y
B
P
A
O
x
x
l1经过点 A(2,0)与点 B(0,1) ,如果在第二象限内有一点1
APB 的面
变式:如图,已知直线P(a, ) ,且
2
积为 4,求a的值。
y
B
P
A
O x
例 4、直线y kx 6 与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。
( 1)求k的值;
( 2)若点 P(x,y)是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积
S 与 x 的函数关系式,并写出自变量x 的取值范围;画出S 与 x 的图象。
( 3)探究:当点P 运动到什么位置时,△ OPA 的面积为
27
8
,并说明理由。
y
F
E
A o x。
