几何体中的截面问题复习课程
几何体中的截面问题(修订版)精选-共6页

几何体中的的截面问题1.定义及相关要素用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线.此平面与几何体的棱的交集(交点)叫做截点. 2.作多面体的截面方法(交线法):该作图关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.题型一、截面的形状1.P 、Q 、R 三点分别在直四棱柱AC 1的棱BB 1、CC 1和DD 1上,试画出过P 、Q 、R 三点的截面.1解答:(1)连接QP 、QR 并延长,分别交CB 、CD 的延长线于E 、F . (2)连接EF 交AB 于T,交AD 于S .(3)连接RS 、TP 。
则多边形PQRST 即为所求截面。
2.已知P 、Q 、R 分别是四棱柱ABCD ―A 1B 1C 1D 1的棱CD 、DD 1和AA 1上的点,且QR 与AD 不平行,求作过这三点的截面.2解答: (1)连接QP 并延长交DA 延长线于点I 。
(2)在平面ABCD 内连接PI 交AB 于点M 。
(3)连接QP、RM。
则四边形PQRM即为所求。
注:①若已知两点在同一平面内,只要连接这两点,就可以得到截面与多面体的一个面的截线。
②若面上只有一个已知点,应设法在同一平面上再找出第二确定的点。
③若两个已知点分别在相邻的面上,应找出这两个平面的交线与截面的交点。
3.一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是ACBD3答案:D解析:考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D 。
题型二、截面面积、长度等计算4.过正方体1111D C B A ABCD -的对角线1BD 的截面面积为S ,S max 和S min 分别为S 的最大值和最小值,则m inm axS S 的值为 ( ) A .23 B .26 C .332 D .362 4答案:C解析:设M 、N 分别为AA 1、CC 1的中点.易证截面BMD 1N1D1D 5. 如图,已知球O 是棱长为1 的正方体ABCD ﹣A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为 . 5答案:解析:平面ACD 1是边长为的正三角形,且球与以点D 为公共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积,则由图得,△ACD 1内切圆的半径是×tan30°=,则所求的截面圆的面积是π××=.6.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )A .1BCD .26答案:C解析:1O 与2O 的公共弦为AB ,球心为O,AB 中点为C , 则四边形C OO O 21为矩形,12||||,O O OC =||2,OA = 所以||1,||AC AC OC OC =⊥∴==7.已知正四棱锥P —ABCD 的棱长都等于a ,侧棱PB 、PD 的中点分别为M 、N ,则截面AMN 与底面ABCD 所成二面角大小的正切值为 . 7答案:12O2OCO2解析:过A 在平面ABCD 内作直线l BD //,连接AC,BD 交于O ,连接PO ,MN .记PO 、MN 交于O‘.因为PB 、PD 的中点分别为M 、N ,所以MN //BD ,因为l BD //,所以l MN //,A l ∈,所以l ⊂平面AMN , l =平面AMN∩平面ABCD .易知O AO '∠即为面AMN 与底面ABCD 所成二面角的平面角.1tan 242AO PO a O O O AO ''==⇒=⇒= 8.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S 。
2024版高考数学二轮复习专题3立体几何培优拓展五立体几何中的截面交线问题课件

1.正方体的斜截面
方式
正六面体
横截
正方形
竖截
正方形/矩形
斜截
如上图所示
2.圆柱体的基本截面
方式
圆柱体
横截
圆形
竖截
矩形
斜截
如上图③④⑤所示
考点一
确定截面形状
角度1 直接法
例1在正方体ABCD-A1B1C1D1中,P为BB1的中点,画出过点A1,C1,P的截面.
解 因为此三点在几何体的棱上,且两两在一个平面内,直接连接
2
2
2
4
2
4
2
13
2
13
2
2
则 A1P= ,AP= ,故 D1P= 2 +
=
,EP= 1 +
=
,
3
3
3
3
3
3
2 13
13
同理可得 D1Q= 3 ,FQ= 3 ,而 EF= 2,
2 13
13
则五边形 D1QFEP 的周长为 2×( 3 + 3 )+ 2=2 13 + 2.
增分技巧若截面上的点中至少有两个在一个几何体的一个表面上,可以借
2
ABC距离的 3
,过点M作一个平面,使其平行于直线PB和AC,则这个平面与
三棱锥表面交线的总长为( B )
24+16 3
A. 9
12+16 3
B. 9
12+8 3
C. 9
24+8 3
D. 9
解析 因为三棱锥P-ABC为正三棱锥,所以△ABC为等边三角形且边长为2,
即AB=AC=BC=2.
因为三棱锥P-ABC为正三棱锥,因此过点P作底面ABC的垂线于点O,则点O
2024年高考数学复习拓展考点精讲精练讲义 25 立体几何中的截面问题含详解

【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结(新高考通用)素养拓展25立体几何中的截面问题(精讲+精练)一、截面问题的理论依据(1)确定平面的条件①不在同一平面的三点确定一个平面;②两条平行线确定一个平面(2)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线(3)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内(4)如果一条直线平行于一个平面,且经过这条直线的平面与这个平面相交,那么这条直线就和交线平行(5)如果两个平面平行,第三个平面和它们相交,那么两条交线平行二、截面问题的基本思路1.定义相关要素①用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.②此平面与几何体表面的交集(交线)叫做截线.③此平面与几何体的棱(或面)的交集(交点)叫做实截点.④此平面与几何体的棱(或面)的延长线的交点叫做虚截点.⑤截面中能够确定的一部分平面叫做截小面.2.作截面的基本逻辑:找截点→连截线→围截面3.作截面的具体步骤(1)找截点:方式1:延长截小面上的一条直线,与几何体的棱、面(或其延长部分)相交,交点即截点方式2:过一截点作另外两截点连线的平行线,交几何体的棱于截点(2)连截线:连接同一平面内的两个截点,成截线(3)围截面:将各截线首尾相连,围成截面三、作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程。
(2)延长线法:同一个平面有两个点,可以连线并延长至与其他平面相交找到交点。
(3)平行线法:过直线与直线外一点作截面,拖直线所在的面与点所在的平面平行,可以通过过点找直线的平行线找到几何体的截面的交线。
模型演练:如下图E、F是几等分点,不影响作图。
可以先默认为中点,等完全理解了,再改成任意等分点一、知识点梳理方法:两点成线相交法或者平行法特征:1.三点中,有两点连线在表面上.本题如下图是EF (这类型的关键);2.“第三点”是在外棱上,如C 1,注意:此时合格C 1点特殊,在于它是几何体顶点,实际上无论它在何处,只要在棱上就可以.方法一:相交法,做法如下图.方法二:平行线法,做法如下图.四、正方体中的基本截面类型【典例1】用一个平面去截正方体,所得截面不.可能是()A .直角三角形B .直角梯形C .正五边形D .正六边形【答案】ABC 【分析】二、题型精讲精练根据正方体的几何特征,我们可分别画出用一个平面去截正方体得到的几何体的图形,然后逐一与四个答案中的图形进行比照,即可判断选项.【详解】当截面为三角形时,可能出现正三角形,但不可能出现直角三角形;截面为四边形时,可能出现矩形,平行四边形,等腰梯形,但不可能出现直角梯形;当截面为五边形时,不可能出现正五边形;截面为六边形时,可能出现正六边形,故选:ABC .【典例2】已知正四棱柱1111ABCD A B C D -中,1124BE BB ==,143AB AA =,则该四棱柱被过点1A ,C ,E 的平面截得的截面面积为______.【典例3】如图,在正方体1111ABCD A B C D -中,4AB =,E 为棱BC 的中点,F 为棱11A D 的四等分点(靠近点1D ),过点,,A E F 作该正方体的截面,则该截面的周长是___________.连接,,,,AE EG GHHF FA ,易证因为4AB =,所以BE CE =中点,若平面α截三棱锥A BCD -和球O 所得的截面面积分别为1S ,2S ,则12S S =()A .8πB .16πC .38πD .364π【题型训练-刷模拟】1.截面形状问题一、单选题1.(2023·全国·高三专题练习)用一平面去截一长方体,则截面的形状不可能是()A .四边形B .五边形C .六边形D .七边形2.(2023·全国·高三专题练习)已知在正方体1111ABCD A B C D -中,E ,F ,G 分别是AB ,1BB ,11B C 的中点,则过这三点的截面图的形状是()A .三角形B .四边形C .五边形D .六边形3.(2023·全国·高三专题练习)已知在长方体1111ABCD A B C D -中,12AB BB BC ==,点P ,Q ,T 分别在棱1BB ,1CC 和AB 上,且13B P BP =,13CQ C Q =,3BT AT =,则平面PQT 截长方体所得的截面形状为()A .三角形B .四边形C .五边形D .六边形4.(2023秋·江苏南京·高三统考开学考试)在正方体1111ABCD A B C D -中,过点B 的平面α与直线1AC 垂直,则α截该正方体所得截面的形状为()A .三角形B .四边形C .五边形D .六边形5.(2023·河南·模拟预测)在正方体1111ABCD A B C D -中,M ,N 分别为AD ,11C D 的中点,过M ,N ,1B 三点的平面截正方体1111ABCD A B C D -所得的截面形状为()A .六边形B .五边形C .四边形D .三角形6.(2023·全国·高三专题练习)在如图所示的棱长为20的正方体1111ABCD A B C D -中,点M 为CD 的中点,点P 在侧面11ADD A 上,且到11A D 的距离为6,到1AA 的距离为5,则过点P 且与1A M 垂直的正方体截面的形状是()A .三角形B .四边形C .五边形D .六边形7.(2023·上海·高三统考学业考试)如图是长方体被一平面所截得到的几何体,四边形EFGH 为截面,长方形ABCD 为底面,则四边形EFGH 的形状为()A .梯形B .平行四边形C .可能是梯形也可能是平行四边形D .不确定2.求截面的面积一、单选题A .23B .4.(2023春·全国·高一专题练习)已知三棱锥ABC 被球O 截得的截面面积为A .1B .5.(2023·吉林通化·梅河口市第五中学校考模拟预测)若球E 在线段BA 上,3BA BE =A .8π3B .2π6.(2023·四川内江·四川省内江市第六中学校考模拟预测)已知球在底面的射影为底面中心)的外接球,得截面面积的最小值是(A.π68.(2023·四川成都·校联考模拟预测)点F为棱AV上一点,二、填空题16.(2023·江苏常州·江苏省前黄高级中学校考二模)在正四棱台为棱11B C的中点,当正四棱台的体积最大时,平面17.(2023·江西吉安·吉安三中校考一模)如图,正方体的动点,过点,,A P Q的平面截该正方体所得的截面记为题的编号)①当12CQ=时,S为等腰梯形;②当34CQ=时,S与11C D的交点③当314CQ<<时,S为六边形;3.求截面的周长一、单选题A.3225+B.22.(2023春·四川南充·高三阆中中学校考阶段练习)AA的中点,则平面E是侧棱1A.32252++C.3252++3.(2023·江西鹰潭·贵溪市实验中学校考模拟预测)已知正方体点,若点P∈平面α,且AC+B.A.35225.(2023·全国·高三专题练习)在正方体棱A D''的四等分点(靠近点A.9225+B.42A.2+25B7.(2023春·广西南宁·高三南宁三中校考专题练习)已知正方体BC的中点,则平面1D EFA.6B二、填空题10.(2023春·上海黄浦·高三格致中学校考开学考试)正三棱柱棱1BB 、11AC 的中点,若过点11.(2023·山东泰安·统考模拟预测)在棱长为中点,则过线段AG 且平行于平面4.圆柱、圆锥、球的截面问题一、单选题1.(2023·山西阳泉·阳泉市第一中学校校考模拟预测)圆锥的母线长为母线作圆锥的截面,则该截面面积的最大值是(A .8B .2.(2023·广西·统考模拟预测)表面积为16π,O 到圆锥底面圆的距离为A .6πB .3.(2023·天津红桥·统考二模)用与球心距离为A .43π3C .83π3....2023秋·陕西西安高三西安市铁一中学校考期末)如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是(A.①②B.①③C.①④D.①⑤7.(2023·全国·高三专题练习)从一个底面圆半径与高均为2的圆柱中挖去一个正四棱锥(以圆柱的上底面为正四棱锥底面的外接圆,下底面圆心为顶点)而得到的几何体如图所示,今用一个平行于底面且距底面为π-A.448.(2023·全国·高三专题练习)B,C,D在圆锥底面上,A.22A .2πB 10.(2023·江西南昌·江西师大附中校考三模)已知正方体足平面BDE ⊥平面1A BDA .136πB 的最大值为(二、填空题18.(2023·陕西西安·校联考一模)某圆锥的底面半径为柱体积的最大值为19.(2023·上海·高三专题练习)在圆柱中,底面圆半径为个动点,绕着底面圆周转,则20.(2023·重庆·统考模拟预测)底面ABC,则过点Q的平面截该三棱锥外接球所得截面面积的取值范围为21.(2023·江西上饶·校联考模拟预测)已知四棱锥面ABCD是等腰梯形,AD点M作球O的截面,所得截面圆面积的最小值为22.(2023春·重庆万州·==,面上,PA PB PC平面截球O所得截面面积的最小值是【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结(新高考通用)素养拓展25立体几何中的截面问题(精讲+精练)一、截面问题的理论依据(1)确定平面的条件①不在同一平面的三点确定一个平面;②两条平行线确定一个平面(2)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线(3)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内(4)如果一条直线平行于一个平面,且经过这条直线的平面与这个平面相交,那么这条直线就和交线平行(5)如果两个平面平行,第三个平面和它们相交,那么两条交线平行二、截面问题的基本思路1.定义相关要素①用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.②此平面与几何体表面的交集(交线)叫做截线.③此平面与几何体的棱(或面)的交集(交点)叫做实截点.④此平面与几何体的棱(或面)的延长线的交点叫做虚截点.⑤截面中能够确定的一部分平面叫做截小面.2.作截面的基本逻辑:找截点→连截线→围截面3.作截面的具体步骤(1)找截点:方式1:延长截小面上的一条直线,与几何体的棱、面(或其延长部分)相交,交点即截点方式2:过一截点作另外两截点连线的平行线,交几何体的棱于截点(2)连截线:连接同一平面内的两个截点,成截线(3)围截面:将各截线首尾相连,围成截面三、作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程。
立体几何中的截面(解析版)
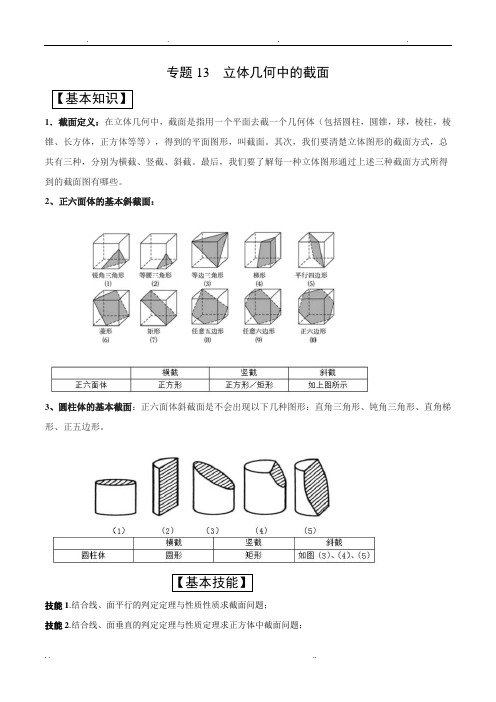
专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体接于一个球,过这个球的球心作一平面,则截面图形不可能...是( )分析 考虑过球心的平面在转动过中,平面在球的接正方体上截得的截面不可能是大圆的接正方形,故选D 。
例2 如图,在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器灌进一些水,固定容器底面一边BC 于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:① 水的部分始终呈棱柱状; ② 水面EFGH 的面积不改变; ③ 棱A 1D 1始终与水面EFGH 平行;④ 当容器倾斜到如图5(2)时,BE·BF 是定值; 其中正确的命题序号是______________分析 当长方体容器绕BC 边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BC BF BE V ⋅⋅=21水是定值,又BC 是定值,所以BE·BF 是定值,即④正确。
强基专题--立体几何中的截面问题

强基专题3 立体几何中的截面问题
[跟进训练]
1.(2021·重庆模拟)在三棱锥 P-ABC 中,PA,PB,PC 两两垂直,
PA=3,PB=4,PC=5,点 E 为线段 PC 的中点,过点 E 作该三棱
锥外接球的截面,则所得截面圆的面积不可能为( )
A.6π
B.8π
C.10π
D.12π
1234 5
(2)当π2<θ<π时,0<α<θ<π,此时sin θ<1,sin α可以取到最 大值1,
此时过圆锥母线的截面面积最大,最大值为S=12l2.
1234 5
强基专题3 立体几何中的截面问题
综上所述,过圆锥母线的截面面积的最大值与轴截面顶角θ的范 围有关,
当0<θ≤π2时,轴截面面积最大,最大值为S=12l2sin θ. 当π2<θ<π时,过圆锥母线的截面面积最大,最大值为S=12l2.
同理 FG∥EH,所以四边形 EFGH 为平行四边形,又 AD⊥BC, 所以四边形 EFGH 为矩形.
1234 5
强基专题3 立体几何中的截面问题
由相似三角形的性质得BECF=AACF,FACC=AFDG, 所以BECF+FAGD=AACF+FACC,BC=AD=2, 所以 EF+FG=2,所以四边形 EFGH 的周长为定值 4,S 四边形 EFGH =EF×FG≤EF+2 FG2=1, 所以四边形 EFGH 的面积有最大值 1.故选 B.]
1 2
l2sin θ.截面VCD的面积S′=12l2sin α.在△V强基专题3 立体几何中的截面问题
(1)当0<θ≤π2时,0<α<θ≤π2,sin α<sin θ⇒S′<S,此时过圆 锥母线的截面面积最大为轴截面面积S=12l2sin θ.
截面形状及相应面积的求法 (1)结合线、面平行的判定定理与性质定理求截面问题; (2)结合线、面垂直的判定定理与性质定理求正方体中截面问题; (3)猜想法求最值问题:“要灵活运用一些特殊图形与几何体的 特征,“动中找静”,如正三角形、正六边形、正三棱锥等; (4)建立函数模型求最值问题:①设元;②建立二次函数模型; ③求最值.
立体几何中截面问题重难考点归纳总结

高三二轮专题复习立体几何中截面问题重难考点归纳总结作空间几何体截面的常见方法:(1)直接连接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面就是找交线的过程;(2)作平行线法:过直线与直线外一点作截面,若直线所在的平面与点所在的平面平行,可以通过过点找直线的平行线找到几何体与截面的交线;(3) 作延长线找交点法:若直线相交但是立体图形中未体现,可通过作延长线的方法先找到交点,然后借助交点找到截面形成的交线;(4)辅助平面法:若三个点两两都不在一个侧面或者底面中,则在作截面时需要作一个辅助平面.考点一:截面形状的判断1.在立体几何中,用一个平面去截一个几何体得到的平面图形叫截面.平面以任意角度截正方体,所截得的截面图形不可能为() A .等腰梯形B .非矩形的平行四边形C .正五边形D .正六边形2.在立体几何中,用一个平面去截一个几何体得到的平面图形叫截面,如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点E 、F 分别是棱B 1B 、B 1C 中点,点G 是棱CC 1的中点,则过线段AG 且平行于平面A 1EF 的截面图形为( )A .矩形B .三角形C .正方形D .等腰梯形3.如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个垂直于圆柱底面的平面去截这个组合体﹐则截面图形可能是______(填序号).4.(多选题)一个正方体内有一个内切球,用一个平面去截,所得截面图形可能是图中的( )A .AB .BC .CD .D5.在正方体中,M ,N ,Q 分别为棱AB ,的中点,过点M ,N ,Q 作该正方体的截面,则所得截面的形状是() A .三角形B .四边形C .五边形D .六边形考点二:求截面面积6.已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为16的正方形,则该圆柱的表面积为() A . B . C . D . 7.已知球O 的表面积为,则过球Q 一条半径的中点,且与该半径垂直的截面圆的面积为___________. 8.已知圆锥的侧面积为,若其过轴的截面为正三角形,则该圆锥的母线的长为___________. 9.已知正四棱柱中、的交点为,AC 、BD 的交点为,连接,点为的中点.过点且与直线AB 平行的平面截这个正四棱柱所得截面面积的最小值和最大值分别为1,则正四棱柱的体积为______________.111-ABCD A B CD 111,B B C D 1O 2O 12O O 24π20π8π29π11A C 11B D 1O 2O 12O O O 12O O O 1111ABCD A B C D -10.已知正四棱柱中,,,则该四棱柱被过点,C ,E 的平面截得的截面面积为______. 11.已知圆锥的侧面积为20π,底面圆O 的直径为8,当过圆锥顶点的平面截该圆锥所得的截面面积最大时,则点O 到截面的距离为______________.12.在立体几何中,用一个平面去截一个几何体得到的平面图形叫截面. 如图,在棱长为1的正方体中,点分别是棱的中点,点是棱的中点,则过线段且平行于平面的截面的面积为A . B. C . D13.已知棱长为的正四面体,,,分别是棱,,的中点,则正四面体的外接球被三角形所在的平面截得的截面面积是( )A .B .C .D . 14.已知三棱锥的所有棱长均相等,四个顶点在球的球面上,平面经过棱,,的中点,若平面截三棱锥和球所得的截面面积分别为,,则( ) ABC .D . 15.已知正方体的长为2,直线平面,下列有关平面截此正方体所得截面的结论中,说法正确的序号为______.①截面形状一定是等边三角形:②截面形状可能为五边形;③截面面积的最大值为④存在唯一截面,使得正方体的体积被分成相等的两部分.16.已知某圆锥轴截面的顶角为,过圆锥顶点的平面截此圆锥所得截面面积的最大值为,则该圆锥的1111ABCD A B C D -1124BE BB ==143AB AA =1A 1111ABCD A B C D -,E F 111,B B B C G 1CC AG 1A EF 198894ABCD E F N AB AC AD ABCD EFN 73π83π103π163πA BCD -O αAB AC AD αA BCD -O 1S 2S 12S S =38π364π1111ABCD A B C D -1AC ⊥αα120 2底面半径为() ABC .D .17.在长方体中,已知,,分别为,的中点,则平面被三棱锥外接球截得的截面圆面积为___________.考点三:求截面周长18.如图,在正方体中,,为棱的中点,为棱的四等分点(靠近点),过点作该正方体的截面,则该截面的周长是___________.19.已知在棱长为6的正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是棱C 1D 1,B 1C 1的中点,过A ,E ,F 三点作该正方体的截面,则截面的周长为________.20.正三棱柱ABC ﹣A 1B 1C 1中,所有棱长均为2,点E ,F 分别为棱BB 1,A 1C 1的中点,若过点A ,E ,F 作一截面,则截面的周长为( )1111ABCD A B C D -122AA AB AD ===E F 1BB 11D C 11A BCD 1C CEF -1111ABCD A B C D -4AB =E BC F 11A D 1D ,,A E FA .B .C .D .21.在三棱锥中,,截面与,都平行,则截面的周长等于( )A .B .C .D .无法确定考点四:截面最值问题22.已知三棱锥的四个顶点在球的球面上,,的正三角形,三棱锥的体积为,为的中点,则过点的平面截球所得截面面积的取值范围是( ) A . B . C . D . 23.正四面体ABCD 的棱长为4,E 为棱AB 的中点,过E 作此正四面体的外接球的截面,则该截面面积的取值范围是( ) A . B . C . D . 24.已知球O 是正三棱锥A -BCD (底面是正三角形,顶点在底面的射影为底面中心)的外接球,BC =3,AB =E 在线段BD 上,且BD =3BE .过点E 作球O 的截面,则所得截面面积的最小值是( ) A . B. C . D .25.如图,四边形为四面体的一个截面,若四边形为平行四边形,,,则四边形的周长的取值范围是___________.26.如图,设正三棱锥的侧棱长为,,分别是上的点,过作三棱锥的截面,则截面周长的最小值为________.+A BCD -AB CD a ==MNPQ AB CD MNPQ 2a 4a a P ABC -O PA PB PC ==ABC ∆P ABC -16Q BC Q O 13,24ππ⎡⎤⎢⎥⎣⎦12,23ππ⎡⎤⎢⎥⎣⎦13,44ππ⎡⎤⎢⎥⎣⎦12,43ππ⎡⎤⎢⎥⎣⎦[]46ππ,[]412ππ,[]4ππ,[]6ππ,2π3π4π5πEFGH ABCD EFGH 4AB =6CD =EFGH P ABC -240APB ∠=︒,E F ,BP CP ,,A E F AEF27.正三棱锥,点在棱上,且,已知点都在球的表面上,过点作球的截面,则截球所得截面面积的最小值为___________.考点五:有关截面的综合问题28.如图,在正方体中,点P 为线段上的动点(点与,不重合),则下列说法不正确的是( )A .B .三棱锥的体积为定值C .过,,三点作正方体的截面,截面图形为三角形或梯形D .DP 与平面所成角的正弦值最大为 29.(多选题)在棱长为2的正方体中,以下结论正确的有()A .三棱锥外接球的体积是B .当点在直线上运动时,的最小值是P ABC -AB ==E PA 3PE EA =P A B C 、、、O E O ααO 1111ABCD A B C D -11A C P 1A 1C BD CP ⊥C BPD -P C 1D 1111D C B A 131111ABCD A B C D -11B A DC -Q 1BC 1A Q QC +8+C .若棱,,的中点分别是,,,过,,三点作正方体的截面,则所得截面面积为D .若点是平面上到点和距离相等的点,则点的轨迹是直线30.(多选题)如图,正方体的棱长为1,P 为的中点,Q 为线段上的动点,过点A ,P ,Q 的平面截该正方体所得的截面多边形记为S ,则下列命题正确的是( )A .当时,S 为等腰梯形B .当时,S 与的交点R 满足C .当时,S 为六边形D .当时,S31.(多选题)在正方体中,,点E ,F 分别为,中点,点P 满足,,则( )A .当时,平面截正方体的截面面积为B .三棱锥体积为定值 AB 1AA 11CDEFG E F G M 1111D C B A D 1C M 11A D 1111ABCD A B C D -BC 1CC 12CQ =34CQ =11C D 113C R =314CQ <<1CQ =1111ABCD A B C D -2AB =AB BC 1AP AA λ= [0,1]λ∈1λ=PEF 941P ECC -C .当时,平面截正方体的截面形状为五边形D .存在点P ,二面角为45°10,3λ⎛⎤∈ ⎥⎝⎦PEF P EF A --Word 版见:高考高中资料无水印无广告word 群559164877详细解析1.C 【详解】画出截面图形如图:可以画出等腰梯形,故A 正确;在正方体中,作截面(如图所示)交,,,分别于点,,,,根据平面平行的性质定理可得四边形中,,且,故四边形是平行四边形,此四边形不一定是矩形,故B 正确;经过正方体的一个顶点去切就可得到五边形.但此时不可能是正五边形,故C 错误;正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,且可以画出正六边形,故D 正确. 故选:C1111ABCD A B C D EFGH 11C D 11A B AB CD E F G H EFGH //EF HG //EH FGEFGH高中数学教研群 QQ 群号929518278 精品资料每天更新2.D 【详解】取的中点,如图连接、、、,由题意得:,, 不在平面内,平面内,∴平面.不在平面内,平面内,∴平面.,平面,平面平面,过线段且平行于平面的截面图形为等腰梯形.故选:.3.①⑤【详解】由题意,当截面过旋转轴时,圆锥的轴截面为等腰三角形,此时①符合条件; 当截面不过旋转轴时,圆锥的轴截面为双曲线的一支,此时⑤符合条件, 综上可知截面的图形可能是①⑤.故答案为:①⑤4.AB 【详解】由组合体的结构特征可知:当截面过球与正方体切点时可知A 正确、C 错误;当截面过正方体的对角面时可知B 正确;此题是正方体的内切球,可知D 错误.故选:AB5.D 【详解】如图所示:分别为中点,M ,N ,Q 确定平面, 且,故,,故,同理可得,,,故截面为六边形.故选:D. BC H AH GH 1D G 1AD //GH EF 1//AH A F GH 1A EF EF ⊆1A EF ||GH 1A EF AH 1A EF 1A F ⊆1A EF ||AH 1A EF GH AH H = ,GH AH ⊆1AHGD ∴1//AHGD 1A EF AG AEF 1AHGDD ,,EF H 111,,AD DD B C αNH MQ ∥N α∈NH α⊂,Q H αα∈∈QH α⊂FQ α⊂EF α⊂EM α⊂6.B 【详解】根据题意,所得截面是边长为4的正方形,结合圆柱的特征,可知该圆柱的底面是半径为的圆,且高为4,所以其表面积.故选:B. 7.【详解】 设球的半径为,则,解得.设截面圆的半径为,由题知:, 所以截面圆的面积.故答案为: 8.【详解】 设圆锥的底面半径为r ,圆锥的母线为l ,又圆锥过轴的截面为正三角形,圆锥的侧面积为, ∴, ∴.故答案为:. 9.3【详解】设正四棱柱的底面边长为a ,高为h ,由题知当截面平行于平面时,截面面积最小;当截面为平面时,截面面积最大,2()22222424S =⨯+⨯⨯=πππ32ππR 248R ππ=R =r r ==232S ππ==32π2329π22,9l r rl ππ==23l =23ABCD 11A B CD因为过点且与直线AB 平行的平面截这个正四棱柱所得截面面积的最小值和最大值分别为1,所以, 于是正四棱柱的体积为.故答案为:3.10.由题意,正四棱柱中,,, 可得,在上取点,使得,连接,则有, 所以四边形是平行四边形,由勾股定理可得,所以所以, 所以四边形是平行四边形的面积为, 故答案为:O 21a ⎧=⎪⎨=⎪⎩13a h =⎧⎨=⎩1111ABCD A B C D -23a h =1111ABCD A B C D -1124BE BB ==143AB AA =1118,2AA BB CC BE ====1DD F 12D F =1,A F CF 11,//A F CE A F CE =1A ECF 11A E CE A C ====2221111cos 2A E CE A C A EC A E CE +-∠===⨯1sin A EC ∠=1A ECF 11sin A E EC A EC ⨯⨯∠==11设圆锥的底面圆的半径为r ,高为h ,母线长为l ,则,∴,h =3,由于h<r ,所以圆锥的轴截面为钝角三角形,所以过圆锥顶点的平面截该圆锥所得的截面为直角三角形时面积最大,如图,△SAB 为截面三角形,SO 为圆锥的高,设点O 到截面的距离为d ,则∴,即, ∴,即点O. 12.B 【详解】取BC 的中点H ,连接,4,20r rl ππ==5l =25,2SAB AB S == 14,2AOB OA OB S ===⨯= 1133SAB AOB S d S h ⋅=⋅ 12513323d ⨯⋅=d =,AH GH因为面AHGD1,面AHGD1,面AHGD1,同理,面AHGD1,又,则平面AHGD1∥平面A1EF,等腰梯形AHGD1,,故选B.13.D【详解】过点作平面的垂线,垂足为,交平面于点,设该四面体外接球球心为,连接,作图如下所示:因为四面体为正四面体,且面,故点为△的外心,则该四面体的球心一定在上,不妨设外接球球心为;因为分别为的中点,则//,//,又,且面,面,故平面//平面,故面,又为中点,故也为中点.因为正四面体的所有棱长为,故1,EF BC GH EF⊄GH⊂EF∴∥1A E∥1A E EF E⋂=98A BCD H EFN'O O,OB BHABCD AH⊥BCDH BCD AH O,,E F N,,AB AC AD EF BC FN CD,EF FN F BC CD C⋂=⋂= ,EF FN⊂EFN,BC CD⊂BCD EFN BCDAO'⊥EFN E AB'O AHABCD4243BH==则设该四面体的外接球半径为,即,则, 在△中,,即, 解得即外接球球心到平面, 设平面截外接球所得圆的半径为,则,解得,故截面圆的面积为.故选:D. 14.B 【详解】设平面截三棱锥所得正三角边长为a ,截面圆的半径为r ,则, 由正弦定理可得, ,故选:B15.④【详解】如图可知,截面形状可以是等边三角形、六边形、正六边形,∴①②明显错误;截面面积的最小值可以趋向于零,故③错误;当截面为正六边形时,截面过正方体的中心,此时正方体的体积被分成相等的两部分.故④正确.故答案为:④AH ===12O H AH ='=R OA OB R ==OH AH R R =-=Rt OHB 222OH BH OB +=222R R ⎫+=⎪⎪⎭R =OO R AO =-==''O EFN EFN r 222r +=2163r =163παA BCD -21S =sin 60a r ==︒22243πa S πr ∴==12S S =∴16.A 【详解】如图,由题可知,,又过圆锥顶点的平面截此圆锥所得截面面积的最大值为,∴,即, 在中,.故选:A. 17.【详解】 以点为原点建立空间直角坐标系如图所示:120APB ∠= 30ABP ∠= 22122l =2l =Rt POB cos302r l === 98πD依题意得:,,,则,,所以,则;设为中点,因为则,所以点为三棱锥外接球的球心,则设球心到平面的距离为,又因为为中点,所以点到平面的距离为,由于,所以故截面圆的半径为,所以截面圆面积为. 故答案为:18如图,取的中点,取上靠近点的三等分点,()0,2,0C ()1,2,1E ()0,1,2F ()1,0,1EC =-- ()111EF ,,=-- 1010EC EF ⋅=+-= EF EC ⊥O CF EF EC ⊥1EO OC FO C O ===O 1C CEF -12R CF ==O 11A BCD h O CF F 11A BCD 2h 111244h C D ==⨯=h =r ==98π98π11C D H 1CC 1C G连接,易证,则五边形为所求截面.因为,所以, 则, 故该截面的周长是.19.如图,延长EF ,A 1B 1,相交于点M ,连接AM ,交BB 1于点H ,延长FE ,A 1D1,相交于点N ,连接AN,交DD 1于点G ,连接FH,EG,可得截面为五边形AHFEG .因为ABCD-A 1B 1C 1D1是棱长为6的正方体,且E ,F 分别是棱C 1D 1,B 1C 1的中点,由中位线定理易得:EF =:AG =AH =EG =FH AH +HF +EF +EG +AG =故答案为:20.B 【详解】如图,在正三棱柱中,延长AF 与CC 1的延长线交于M ,连接EM 交B 1C 1于P ,连接FP ,则四边形AEPF 为所求截面.,,,,AE EG GH HF FA //,//AE HF AF EG AEGHF 4AB =111182,3,1,3BE CE C H D H A F D F CG =======143C G =103AE EG ==5,GH HF AF ===AE EG GH HF AF ++++=+111ABC A B C -过E 作EN 平行于BC 交CC 1于N ,则N 为线段CC 1的中点,由相似于可得MC 1=2,由相似于可得:, 在中,,则,在中,,则在中,,则在中,, 由余弦定理:,则故选:B.21.A 【详解】 设,因为平面,平面平面,平面,所以,同理可得,,,故四边形为平行四边形, 所以,. 因为,所以,, 1MFC MAC △1MPC △MEN 111242,2333PC PC B P =⇒==1Rt AA F 112,1AA A F ==AF ==Rt ABE △2,1AB BE ==AE ==1Rt B EP 1121,3B E B P ==PE ==1C FP 11141,,603C F C P FC P ==∠=︒2224413121cos 60339PF ⎛⎫=+-⨯⨯⨯︒= ⎪⎝⎭PF ==AM k CM=//AB MNPQ ABC MNPQ MN =AB ÌABC //MN AB //PQ AB //MQ CD //NP CD MNPQ 11MN PQ AB AB k ==+1MQ NP k CD CD k==+AB CD a ==1a MN PQ k ==+1ak MQ NP k==+所以四边形的周长为. 故选:A.22.A 【详解】设在底面上的射影为,因为,所以为的中心,由题可知,,由,解得 在正中,可得.从而直角在中解得. 进而可得,,,因此正三棱锥可看作正方体的一角, 正方体的外接球与三棱锥的外接球相同,正方体对角线的中点为球心. 记外接球半径为,则所以过的平面截球所得截面的面积最大为; 又为中点,由正方体结构特征可得 由球的结构特征可知,当垂直于过的截面时, MNPQ 2211a ak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭P ABC M PA PB PC ==M ABC ∆ABC S ∆1136P ABC ABC V PM S -∆=⨯⨯=PM =ABC ∆AM =ABC 1PA =PA PB ⊥PB PC ⊥PC PA ⊥P ABC -P ABC -O R R Q O 2max 34S R ππ==Q BC 1122OQ PA ==OQ Q截面圆半径最小为. 因此,过的平面截球所得截面的面积范围为. 故选:A.23.A 【详解】如图,将正四面体补为边长是ABCD 的外接球为正方体 的外接球,球心O在体对角线的中点,且球的半径;当OE 垂直于截面时,截面面积最小,截面圆的半径为面积为;当截面过球心O 时,截面面积最大,截面圆的半径为,面积为故选:A24.A【详解】解:如图,O 1是A 在底面的射影,由正弦定理得,△BCD 的外接圆半径r ==2min 12S r ππ==Q O 13,24ππ⎡⎤⎢⎥⎣⎦R =12r ==4π1r R =6π1031sin 602r =⨯=由勾股定理得棱锥的高AO 1;设球O 的半径为R ,则,解得,所以OO 1=1;在△BO 1E 中,由余弦定理得 所以O 1E =1;所以在△OEO 1中,OE;当截面垂直于OE. 故选:A25.【详解】解:四边形为平行四边形,;平面,平面, 平面;又平面,平面平面,,同理可得;设,, ,, ; 又,,, ,且; 四边形的周长为 ,;四边形周长的取值范围是.故答案为:26.将正三棱锥的三个侧面展开如图,由图可知,为使的周长最小,只需让四点共线即可,则当为与交点时,的周长最小,由题意,,∴,得的周长3==()223R R =-2R =2113211,O E =+-⨯==2π(8,12) EFGH //EH FG ∴EH ⊂/ ABD FG ⊂ABD //EH ∴ABD EH ⊂ ABC ABC ABD AB =//EH AB ∴//EF CD EH x =EF y =∴EH CE AB CA =EF AE CD AC =∴1EH EF CE AE AC AB CD CA AC AC+=+==4AB =Q 6CD =∴146x y +=614x y ⎛⎫∴=- ⎪⎝⎭04x <<∴EFGH 2()2[6(1)]4xl x y x =+=+-12x =-81212x ∴<-<∴EFGH (8,12)(8,12)AEF 1,,,A E F A ,E F 1AA ,BP CP AEF 140BPC CPA APB ∠=∠=∠=︒1120APA ∠=︒1AA ===AEF的最小值为故答案为:27.【详解】,,, 同理,故可把正三棱锥补成正方体(如图所示),其外接球即为球,直径为正方体的体对角线,故,设的中点为,连接,则.所以,当平面时,平面截球O 的截面面积最小,,故截面的面积为.故答案为:28.D 【详解】由题可知平面,所以,故A 正确; 由等体积法得为定值,故B 正确; 设的中点为,当时,如下图所示:3π4PA PC PB === AB AC BC ===222PA PC AC ∴+=2CPA π∴∠=2CPB BPA π∠=∠=O 2R =PA F OF OF =OF PA ⊥3OE ==OE ⊥αα=3π3πBD ⊥11ACC A BD CP ⊥113C BPD P BCD BCD V V S AA --==⋅⋅ 11A C M 1P MC ∈此时截面是三角形,当时,如下图所示:此时截面是梯形,故C 正确;选项D ,在正方体中,连接,则为在平面上的射影,则为与平面所成的角,设正方体的棱长为1,,则当取得最小值时,的值最大,即时,, 所以D 不正确. 故选:D.29.ACD 【详解】对于A :三棱锥的外接球即为正方体的外接球,因为正方体的外接球的直径即为正方体的体对角线,即所以外接球的体积是,故选项A 正确;1D QC 1PMA ∈1D QRC 1D P 1D P DP 1111D C B A 1D PD ∠DP 1111D C B A 1PD x =DP =1sin D PD ∠x 1sin D PD ∠111D P A C ⊥x 1sin D PD ∠11B A DC -1111ABCD A B C D -2R =R 34π3V =´=对于B :把沿翻折到与在同一个平面(如图所示),连接,则是的最小值,其中是边长为的等边三角形,是直角边为的等腰直角三角形,所以, 即故选项B 错误;对于C :分别取棱,,的中点,,,连接,,,,,,则易知过,,三点的截面是正六边形,1BCC 1BC 11A C B △1A C 1A C 1A Q QC +11A C B △1BCC 211A C A Q QC =+==1A Q QC +11A D 1CC BC H M N EF FH HG GM MN NE E F G EFHGMN所以截面面积为故选项C 正确;对于D :因为是平面上到点和距离相等的点,所以点的轨迹是平面与线段的垂直平分平面的交线,即点的轨迹是平面与平面的交线,所以点的轨迹是直线,即选项D 正确.故选:ACD.30.ABD 【详解】解:过点A ,P ,Q 的平面截正方体,当时,其截面形状为梯形如图1,特别地当时,截面形状为等腰梯形, 当时,其截面形状为五边形如图2. 若,则,所以. 当时,与重合,其截面形状为四边形如图3,此时,因为P 为的中点,且,所以为的中点,所以,同理,所以四边形为平行四边形,所以四边形为菱形,其面积为ABD 正确. 故选:ABD.31.BCD 【详解】A 选项中,当时,与重合,则截面为等腰梯形,其面积为,故A 选项错误; 1(62⨯=M 1111D C B A D 1C M 1111D C B A 1DC 11A BCD M 1111D C B A 11A BCD 11A D M 11A D 102CQ <≤12CQ =112CQ <<34CQ =1113C Q C R QC CM ==113C R =1CQ =Q 1C PQ AP =BC CP AD ∕∕Q MN PC AE ∕∕QE AP ∕∕APQE APQE 112AC PE ⋅==1λ=P 1A 92B 选项中,因为平面,故P 到平面的距离不变,故三棱锥体积为定值.故B 选项正确:C 选项中,当时,其截面刚好为五边形,时,截面为五边形;故C 选项正确;D 选项中,当点P 与重合时,其二面角正切值为,此时二面角大于45°, 所以存在点P ,二面角为45°,D 选项正确;故选:BCD .1//AA 1ECC 1ECC 1P ECC -13λ=103λ<<1A P EF A --。
高中总复习二轮数学精品课件 专题四 立体几何 素养提升微专题(五) 截面问题

21
3
2
-12
=
2 3
>1,故球
3
O 与正方体 ABCD-A1B1C1D1 的每个面的交线均为四段圆弧,易求得每段圆
π
π
2π
弧所对的圆心角为6,故每个面上的四段圆弧所对的圆心角之和为6 ×4= 3 ,
2π
2 3
故每个面上的交线长为 3 × 3
4 3π
|1 |sin∠CA1N=
时,Smin=
6
2
< 2.
6
综上所述,截面面积的最小值为 2 .
2( 2 -
+ 1) =
2
1 2
- 2
3
+4
,当
1
t=2
4.如图,正方体ABCD-A1B1C1D1的棱长为2,P为BC的中点,Q为CC1的中点,则
过点A,P,Q的平面α截该正方体所得截面的周长为
.
答案 2 5+3 2
A.1
5
B.4
)
6
C. 2
D. 2
答案 C
解析 以A为坐标原点,AB,AD,AA1所在直线分别为x轴、y轴、z轴,建立空间
直角坐标系如图所示,则
A(0,0,0),A1(0,0,1),B(1,0,0),B1(1,0,1),C(1,1,0),C1(1,1,1),D(0,1,0),D1(0,1,1).
设点P(1,t,t),其中0≤t≤1.
· =-1+tz=0,得
1
z= >1,不合题意.
设平面 α 交棱 AB 于点 M(x,0,0),则=(x-1,-1,0),由 ·=x-1-(t-1)=0,得
空间几何体的截面及交线问题课件-2025届高三数学一轮复习

B1C1,C1D1 的中点,故 BD=2 2,MN= 2,且 BM=
DN= 5,所以等腰梯形 MNDB 的高为 h=
(
5)2-
222=32 2,所
以Hale Waihona Puke 梯形 MNDB 的面积为12×( 2+2 2)×322=92.
对点练2.(1)过正方体ABCD -A1B1C1D1的体对角线BD1的截面面积为S,Smax
√D. 3π 2
由题意得△ACD,△ABC 为等腰直角三角形. 设球 C 与 Rt△ACD 的边 CD,AD 分别交于点 M,N,如图①所示,设球 C 与 Rt△ABC 的边 AB,CB 分别交于点 H,G,如图②所示.易得 cos∠ACN= 23,则∠ACN=π6,AN=AC·tanπ6=1,所以∠NCM=∠ACD -∠ACN=π4-π6=1π2,所以M︵N的长=2×1π2=π6,同理,G︵H的长=π6.
二、多面体中的截面问题
知识链接
1.正方体中的基本斜截面
2. 多面体中找截面的几种方法 (1) 直接法:有两点在多面体的同一个面上,连接这两点即为多面体与截 面的交线,找截面实际就是找交线的过程. (2) 延长线法:若直线相交,但在多面体中未体现,可以通过作延长线的 方法找到交点,然后借助交点找到交线. (3) 平行线法:过直线与直线外一点作截面,若直线所在的平面与点所在 的平面平行,可以通过过点作直线的平行线找到多面体与截面的交线.
2=2 6
3 3.故选
C.
2
(2)[多选题]正方体ABCD -A1B1C1D1的棱长为2,已知平面α⊥AC1,则关于α 截此正方体所得截面的判断正确的是
√A.截面形状可能为正三角形
B.截面形状可能为正方形
√C.截面形状可能为正六边形 √D.截面面积最大值为3 3
立体几何中的截面问题及球的切接问题--备战2022年高考数学一轮复习配套(创新设计版)

(2)(2020·名校仿真训练五)棱长为 2 的正方体 ABCD-A1B1C1D1 中,E,F 分别 为棱 C1D1 与 C1B1 的中点,则经过点 B,E,F 的平面截正方体所得的封闭图
形的面积为( A )
A.92 B.3 10 C.32 D. 10 解析 (2)
如图,经过点 B,E,F 的平面 BEF 截正方体所得截面为四边形 BDEF, 因为 E,F 分别是 C1D1,C1B1 的中点,正方体的棱长为 2, 所以 EF∥BD,且 EF=12BD, 所以四边形 BDEF 是下底为 BD=2 2,上底为 EF= 2的等腰梯形.
|OM|
23
解得|ON|= 3,
则圆 N 的半径 r= 42-( 3)2= 13,圆 N 的面积为πr2=13π,故选 D.
感悟升华
此类题主要考查空间想象能力及空间几何体的结构特征,解题时可寻找特 殊情况使问题得到简化.
【训练 1】 (1)已知圆柱的上、下底面的中心分别为 O1,O2,过直线 O1O2 的平
2.构造正方体、长方体、直棱柱等用上述结论确定外接球的球心 (1)同一个顶点上的三条棱两两垂直的四面体,求其外接球问题可构造正 方体或长方体. (2)相对的棱长相等的三棱锥,求其外接球问题可构造正方体或长方体.
【训练 2】(1)一个四面体的所有棱长都为 2,四个顶点在同一球面上,则此球的
表面积为( A )
感悟升华
求内切球的半径常用等积法 (1)正多面体内切球的球心与其外接球的球心重合,内切球的半径为球心 到多面体任一面的距离. (2)正棱锥的内切球与外接球的球心都在其高线上,但不一定重合.
【训练 3】 (1)(2020·全国Ⅲ卷)已知圆锥的底面半径为 1,母线长为 3,则该圆
立体几何中的截面(解析版)
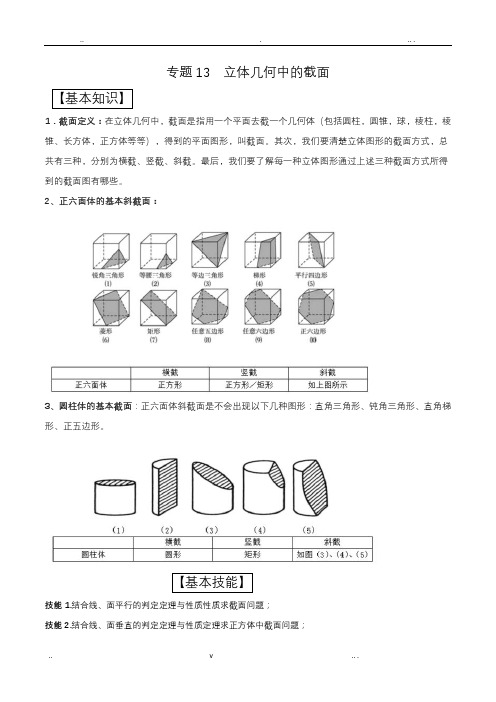
专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________分析当长方体容器绕BC边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG,但EH与FG的距离EF在变,所以水面EFGH的面积在改变,故②错误;在转动过程中,始终有BC//FG//A1D1,所以A1D1//面EFGH,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BCBFBEV⋅⋅=21水是定值,又BC是定值,所以BE·BF是定值,即④正确。
立体几何中的截面问题

立体几何中的截面问题一.基本原理:过正方体(长方体)上三点做截面.1.三点中有两点共面例1.如图,在正方体ABCD-A 1B 1C 1D 1中,E,F,G 分别在AB,BC,DD 1上,求作过E,F,G 三点的截面.思路:当三点中有两点共面时,做截面的思路就是先找共面两点所在直线与该平面所有的棱交点,而这些交点由同时在另外一个平面中,即该截面和正方体某个侧面的交点,这样利用公理1,逐次相连找到所有的交点,即可得到截面.解析:作法:①.由于F E ,共面,在底面AC 内,过F E ,作直线EF ,与DA 于L ,显然,此时L 即在侧面D A 1内,又在欲求截面内,而该截面与侧面D A 1又交于点G ,根据公理1,截面与侧面D A 1交于L .同理,过F E ,作直线EF 与DC 的延长线交于M ,此时M 即在侧面1DC 内,又在欲求截面内,根据公理1,截面与侧面1DC 交于M .②在侧面D A 1内,连接LG 交1AA 于K .③在侧面1DC 内,连接GM 交1CC 于H .④连接FH KE ,.则五边形EFHGK EFHGK 即为所求的截面.练习1.(三点两两共面)P,Q,R 三点分别在直四棱柱AC 1的棱BB 1,CC 1和DD 1上,试画出过P,Q,R 三点的截面作法.解析:作法:(1)连接QP,QR 并延长,分别交CB,CD 的延长线于E,F.(2)连接EF 交AB 于T,交AD 于S.(3)连接RS,TP.则五边形PQRST 即为所求截面.例2.(三点所在的棱两两异面)如图,长方体1111D C B A ABCD -中,R Q P ,,分别为111,,CC AB D A 上三点,求过这三点的截面.分析:此题的难点在于R Q P ,,三点均不在同一个侧面(底面)中,这样我们就暂时无法通过侧面(底面)中连线与棱的交点来找到截面的边界点,于是需要先做出一个平面来,让上面三点RQ P ,,中有两点共面,这就转化成例1的情形,从而解决问题.解:如图,作1//BB QE 交11B A 与E ,则1,RC QE 确定一个平面,转化为例1的情形.连接QR EC ,1,交于点F ;连接PF 交1111,B A D C 延长线于H G ,;连接HQ 交11,BB AA 延长线于J I ,;连接JR 交BC 于K .则KRGPIQK 为所作截面.例3.利用平行关系确定截面在三棱锥A BCD -中,AB CD a ==,截面MNPQ 与AB ,CD 都平行,则截面MNPQ 的周长等于()A.2a B.4a C.a D.无法确定解析:设AM k CM=,因为//AB 平面MNPQ ,平面ABC 平面MNPQ MN =,AB Ì平面ABC ,所以//MN AB ,同理可得//PQ AB ,//MQ CD ,//NP CD ,故四边形MNPQ 为平行四边形,所以11MN PQ AB AB k ==+,1MQ NP k CD CD k ==+.因为AB CD a ==,所以1a MN PQ k==+,1ak MQ NP k ==+,所以四边形MNPQ 的周长为2211a ak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭.故选:A.二.截面的的画法小结1.确定截面的主要依据有(1)平面的四个公理及推论.(2)直线和平面平行的判定和性质.(3)两个平面平行的性质.2.作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程。
高三培优讲义18---立体几何体中的截面问题(1)

专题3-4 立体几何体中的截面问题(常考题型梳理)一、如何做截面?作出过EFG 三点的截面C 1DABB 1A GC 1DABB 1A G二、如何确定截面是否已经“搞定”?题型一 作截面类型1:三个点在棱上 1.作出过EFG 三点的截面2.作出过EFG 三点的截面,EFG 为所在棱上中点(三条边都在正方体内部)ED 1C 1CGD FABA 1B 1EF D 1C 1CG D ABA 1B 1GF ED 1C 1CDABA 1B 1ED 1C 1CDFABA 1B 1G 重点题型·归类精讲3.如图①,正方体1111ABCD A B C D −的棱长为2,P 为线段BC 的中点,Q 为线段1CC 上的动点,过点A 、P 、Q 的平面截该正方体所得的截面记为S ,若12CQ <<,请在图中作出截面S (保留尺规作图痕迹);4.如图,已知正方体1111ABCD A B C D −,点E 为棱1CC 的中点,在图中作出平面1BED 截正方体所得的截面图形(如需用到其它点,需用字母标记并说明位置),并说明理由.类型二:两个点在棱上,一个点在面上5.已知G 是底面ABCD 上一点,E,F 为棱上的点,作出过EFG 三点的截面1C DBA B 1GE F题型二 补全截面再判断位置关系武汉调研&浙江杭州二模6.(多选)如图,点A ,B ,C ,M ,N 为正方体的顶点或所在棱的中点,则下列各图中,满足直线MN //平面ABC 的是( )2023·温州模拟7.下列正方体中,A ,B 为正方体的两个顶点,M ,N ,P 分别为其所在棱的中点,则能满足//AB 平面MNP的是( )A .B .C .D .题型三 确定截面形状8.在正方体1111ABCD A B C D −中,1BB 和11C D 的中点分别为M ,N .如图,若以A ,M ,N 所确定的平面将正方体截为两个部分,则所得截面的形状为( )A .六边形B .五边形C .四边形D .三角形AAMCBBCAB MC BNCMDCAB M9.如图,在正方体1111ABCD A B C D −中,2AB =,E 为棱BC 的中点,F 为棱11A D 上的一动点,过点A ,E ,F 作该正方体的截面,则该截面不可能是( )A .平行四边形B .等腰梯形C .五边形D .六边形2023·重庆巴蜀中学高三校考10.(多选)已知截面定义:用一个平面去截一个几何体,得到的平面图形(包含图形内部)称为这个几何体的一个截面.则下列关于正方体截面的说法,正确的是( ) A .截面图形可以是七边形B .若正方体的截面为三角形,则只能为锐角三角形C .当截面是五边形时,截面可以是正五边形D .当截面是梯形时,截面不可能为直角梯形2024届雅礼中学月考(二)11.如图所示,在棱长为2的正方体1111ABCD A B C D −中,点M ,N 分别为棱11B C ,CD 上的动点(包含端点),当M ,N 分别为棱11B C ,CD 的中点时,则过1A ,M ,N 三点作正方体的截面,所得截面为______边形12.如图正方体1111ABCD A B C D −,棱长为1,P 为BC 中点,Q 为线段1CC 上的动点,过A 、P 、Q 的平面截该正方体所得的截面记为Ω.若1CQ CC λ→→=,则下列结论错误的是( )A .当102λ∈⎛⎫⎪⎝⎭,时,Ω为四边形B .当12λ=时,Ω为等腰梯形 C .当3,14λ⎛⎫∈ ⎪⎝⎭时,Ω为六边形D .当1λ=时,Ω6题型四 截面周长,面积相关计算13.如图,在棱长为1的正方体1111ABCD A B C D −中,点EF 分别是棱111,B B B C 的中点,点G 是棱1C C 中点,则过线段AG 且平行于平面1A EF 的截面的面积为________.14.如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 是棱CC 1的中点,则过三点A,D 1,E 的截面面积等于( )FED 11CDBA B 1A .3 2B .3 102C .92D .315.如图,在棱长为4的正方体1111ABCD A B C D −中,M ,N 分别为棱AB ,11B C 的中点,过C ,M ,N 三点作正方体的截面,则以B 点为顶点,以该截面为底面的棱锥的体积为( )A .83B .8C 83D 163162ABCD A B C D −''''中,点E 、F 、G 分别是棱A B ''、B C ''、CD 的中点,则由点E 、F 、G 确定的平面截正方体所得的截面多边形的面积等于 .17.如图,在正方1111ABCD A B C D −中,2,,,,,AB E F P M N =分别是11,,,,AB CC DD AD CD 的中点,存在过点,E F 的平面α与平面P MN 平行,平面α截该正方体得到的截面面积为______D1C CDBB 1A题型五 球的截面计算计算球截面基本规律 1.确定球心和半径2.寻找做出并计算截面与球心的距离3.要充分利用“球心做弦的垂直垂足是弦的中点”这个性质4.强调弦的中点,不一定是几何体线段的中点。
北师版高考总复习一轮理科数精品课件 第8章 立体几何 指点迷津(八) 空间几何体的截面问题

因为 4
>
2 3
3
>
3 2
4
>
1
S=6·2
3
,选项
2
·
2
3 3
·sin 60° = 4 .
B,C,D 错误,故选 A.
(方法2)B1A1,B1B,B1C1与平面A1BC1所成的角都相等,如图所示,
在AB,BC,CC1,C1D1,D1A1,A1A上分别取点E,F,G,H,K,L.
设BE=BF=C1G=C1H=A1K=A1L=x,则CF=CG=D1H=D1K
第八章
指点迷津(八) 空间几何体的截面问题
空间几何体的截面问题
用平面去截一个几何体,所截出的面叫作截面.我们可以想象,类似于用刀
去切(截)几何体,把几何体分成两部分,刀在几何体上留下的痕迹就是截面
的形状,截面是一个平面图形.空间几何体的截面问题涉及平面的基本事实、
空间线面的位置关系、点线共面、线共点等问题,综合性较强,对直观想象
2
则 S=
2+ 2
2
2
·h2.点 E 到 LG 的距离 h1= [ 2(1-)] -
H 到 LG 的距离
6
2(1-)+ 2
· 2 (1-x)+
2
2- 2
2
6
h2= 2 x,
6
3
· 2 x= 2 (-2x2+2x+1).当
1
3 3
x=2时,Smax= 4 .
2
解题心得作出截面的关键是找到截线,作出截线的主要根据有:(1)确定平
=AE=AL=1-x,易证点E,F,G,H,K,L共面.因为BE=BF,
2025年新人教版高考数学一轮复习讲义 第七章 §7.9 立体几何中的截面、交线问题

2025年新人教版高考数学一轮复习讲义第七章§7.9 立体几何中的截面、交线问题“截面、交线”问题是高考立体几何问题中最具创新意识的题型,它渗透了一些动态的线、面等元素,给静态的立体几何题赋予了活力.求截面、交线问题,一是与解三角形、多边形面积、周长、扇形弧长、面积等相结合求解,二是利用空间向量的坐标运算求解.题型一 截面作图例1 如图,在正方体ABCD-A1B1C1D1中,M是A1B1的中点,N在棱CC1上,且CN=2NC1.作出过点D,M,N的平面截正方体ABCD-A1B1C1D1所得的截面,写出作法.如图所示,五边形DQMFN即为所求截面.作法如下:连接DN并延长交D1C1的延长线于点E,连接ME交B1C1于点F,交D1A1的延长线于点H,连接DH交AA1于点Q,连接QM,FN,则五边形DQMFN即为所求截面.思维升华作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程.(2)延长线法:同一个平面有两个点,可以连线并延长至与其他平面相交找到交点.(3)平行线法:过直线与直线外一点作截面,若直线所在的面与点所在的平面平行,可以通过过点找直线的平行线找到几何体与截面的交线.作出这个截面图,写出作法.CD1MP为过C,D1,M三点的正方体的截面.例2 (多选)在正方体ABCD -A 1B 1C 1D 1中,点E 是线段DD 1上的动点,若过A ,B 1,E 三点的平面将正方体截为两个部分,则所得截面的形状可能为A.等边三角形B.矩形C.菱形D.等腰梯形题型二 截面图形的形状判断√√√当点E与D1重合时,过A,B1,E三点的截面是等边三角形AB1D1,故A正确;当点E与D重合时,过A,B1,E三点的截面为矩形AB1C1D,故B正确;若截面为菱形,则必有AB1=AE,此时点E与D1重合,故C错误;当点E与DD1中点重合时,记C1D1的中点为F,连接EF,FB1,C1D(图略),易知EF∥DC1,由正方体性质可知,AD∥B1C1且AD=B1C1,所以四边形AB1C1D为平行四边形,所以DC1∥AB1,所以过A,B1,E三点的截面为等腰梯形AB1FE,故D正确.思维升华判断几何体被一个平面所截的截面形状,关键在于弄清这个平面与几何体的面相交成线的形状和位置.跟踪训练2 已知一个棱柱的底面是正六边形,侧面都是正方形,用至少过该棱柱三个顶点(不在同一侧面或同一底面内)的平面去截这个棱柱,所得截面的形状不可能是A.等腰三角形B.等腰梯形√C.五边形D.正六边形三角形,选项A可能;截面ABEF为等腰梯形,选项B可能;如图②,截面AMDEN为五边形,选项C可能;因为侧面是正方形,只有平行于底面的截面才可能是正六边形,故过两底的顶点不可能得到正六边形,选项D不可能.题型三 截面图形的周长或面积例3 (2024·朔州模拟)在正方体ABCD-A1B1C1D1中,棱长为3,E为棱BB1上靠近B1的三等分点,则平面AED1截正方体ABCD-A1B1C1D1的截面面积为√B1交于点F,连接D1F交B1C1于点G,延长AE,A如图,在正方体ABCD-A1B1C1D1中,平面ADD1A1∥平面BCC1B1,∵平面AFD1∩平面ADD1A1=AD1,平面AFD1∩平面BCC1B1=EG,方体ABCD-A1B1C1D1的截面.思维升华几何体的截面的相关计算,关键在于根据公理作出所求的截面,再运用解三角形的相关知识得以解决.跟踪训练3 (2023·新乡模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,过A,D1,E三点的截面把正方体ABCD-A1B1C1D1分成两部分,则该截面的周长为√如图,取BC的中点F,连接EF,AF,BC1,E,F分别为棱CC1,BC的中点,则EF∥BC1,又在正方体中BC1∥AD1,则有EF∥AD1,所以平面AFED1为所求截面,因为正方体ABCD-A1B1C1D1的棱长为2,一、单项选择题1.过正方体ABCD-A1B1C1D1的棱AB,BC的中点E,F作一个截面,使截面与底面ABCD所成二面角为45°,则此截面的形状为A.三角形或五边形B.三角形或四边形√C.正六边形D.三角形或六边形12345678910B1-EF-B都大于45°,∴当截面为EFHJIG时,如图所示,为六边形;当截面为EFM时,如图所示,为三角形.2.在长方体ABCD-A1B1C1D1中,若AB=2,AD=AA1=4,E,F分别为BB1,A1D1的中点,过点A,E,F作长方体ABCD-A1B1C1D1的一个截面,则该截面的周长为√如图,连接AF,过点E作EP∥AF交B1C1于点P,连接FP,AE,即可得到截面AFPE,因为E为BB1的中点,EP∥AF,因为AB=2,AD=AA1=4,3.(2023·承德模拟)在三棱锥P-ABC中,AB+2PC=9,E为线段AP上更靠近P的三等分点,过E作平行于AB,PC的平面,则该平面截三棱锥P-ABC所得截面的周长为√A.5B.6C.8D.9EF∥AB,EH∥PC,再分别过点H,F作HG∥AB,FG∥PC,可得E,F,G,H四点共面,因为AB⊄平面EFGH,EF⊂平面EFGH,所以AB∥平面EFGH,同理可证,PC∥平面EFGH,所以截面即为平行四边形EFGH,2PC=9,4.已知正方体ABCD-A1B1C1D1的棱长为2,M,N分别为A1B1,B1C1的中点,过M,N的平面所得截面为四边形,则该截面的最大面积为√5.从一个底面圆半径与高均为2的圆柱中挖去一个正四棱锥(以圆柱的上底面为正四棱锥底面的外接圆,下底面圆心为顶点)而得到的几何体如图所示,用一个平行于底面且距底面为1的平面去截这个几何体,则截面图形的面积为A.4π-4B.4π√C.4π-2D.2π-2且圆的半径是2,则截面圆的面积为4π,正方形相似,所以截面图形的面积为4π-2.6.在正方体ABCD-A1B1C1D1中,M,N分别为AD,C1D1的中点,过M,N,B1三点的平面截正方体ABCD-A1B1C1D1所得的截面形状为√A.六边形B.五边形C.四边形D.三角形如图,在AB上取点Q,且BQ=3AQ,取CD的中点P,连接QM,BP,NP,B1Q.在DD1上取点R,且D1R=3DR,连接NR,MR.所以△QAM∽△PCB,所以∠AQM=∠BPC.又AB∥CD,所以∠ABP=∠BPC,所以∠ABP=∠AQM,所以QM∥BP.所以PN∥CC1,且PN=CC1.根据正方体的性质,可知BB1∥CC1,且BB1=CC1,所以PN∥BB1,且PN=BB1,所以四边形BPNB1是平行四边形,所以B1N∥BP,所以B1N∥QM.同理可得NR∥B1Q.所以五边形QMRNB1即为所求正方体的截面.二、多项选择题7.用一个平面截正方体,则截面的形状不可能是A.锐角三角形B.直角梯形C.正五边形D.正六边形√√三角形,不可能是直角三角形和钝角三角形.如图所示的截面为△ABC.设DA=a,DB=b,DC=c,所以AC2=a2+c2,AB2=a2+b2,BC2=b2+c2.所以∠CAB为锐角.同理可求,∠ACB为锐角,∠CBA为锐角.所以△ABC为锐角三角形,故A不符合题意;对于B ,如图,截面图形如果是四边形,可能是正方形、矩形、菱形、一般梯形、等腰梯形,不可能是直角梯形,故B 符合题意;对于C ,如图,当截面为五边形时,不可能出现正五边形,故C 符合题意;对于D ,当截面过棱的中点时,如图,即截面为正六边形,故D 不符合题意.8.已知正方体ABCD-A1B1C1D1的棱长为2,E,F,H是棱BC,D1C1,AA1上的动点(包含端点),且满足CE=D1F=AH,则下列结论正确的是A.DB1⊥平面EFHB.存在E,F,H,使得点D到平面EFH的距离为1C.平面EFH截此正方体所得截面面积的最大值为D.平面EFH截此正方体所得截面的周长为定值√√√=AH=m,m∈[0,2],则D(0,0,0),E(m,2,0),F(0,m,2),H(2,0,m),B1(2,2,2),同理可得DB1⊥EH,EF∩EH=E,EF,EH⊂平面EFH,故DB1⊥平面EFH,故A正确;设平面EFH分别与A1D1,AB,CC1交于P,Q,R,设P(p,0,2),如图,过点P作PM⊥HR于M,EN⊥HR于N,三、填空题9.(2024·曲靖模拟)“中国天眼”(如图1)是世界最大单口径、最灵敏的射电望远镜,其形状可近似地看成一个球冠(球冠是球面被平面所截的一部分,如图2所示,截得的圆叫做球冠的底,垂直于截面的直径被截得的线段叫做球冠的高.若球面的半径是R,球冠的高度是h,则球冠的面积S=2πRh).已知天眼的球冠的底的半径约为250米,天眼的反射面总面积(球冠面积)约为25万平方米,则130天眼的球冠高度约为________米.则2Rh=h2+2502,则S=2πRh=πh2+2502π=250 000,10.如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=,AA1=3,M为线段BB1上的一动点,则过A,M,C1三点的平面截该三棱柱所得截面的最小周长为___________.所得截面的周长即△AMC1的周长,直三棱柱ABC-A1B1C1的侧面部分展开图如图所示,本课结束。
高中数学截面面积问题教案

高中数学截面面积问题教案
教学目标:
1. 掌握截面面积的计算方法
2. 能够应用截面面积问题解决实际问题
教学重点:
1. 掌握不同截面面积的计算方法
2. 理解截面面积问题的解题思路
教学难点:
1. 理解复杂几何图形的截面面积计算方法
2. 掌握截面面积问题的解题技巧
教学过程:
一、导入(5分钟)
通过展示一个三维几何图形,引入截面面积的概念,让学生思考如何计算这个图形的截面面积。
二、讲解(15分钟)
1. 讲解截面面积的定义和计算方法。
2. 以直角圆柱体、正方体等几何体为例,详细介绍其截面面积的计算方法。
三、示范(10分钟)
以几个实际问题为例,演示如何应用截面面积解题,让学生跟随思路,掌握解题方法。
四、练习(15分钟)
1. 让学生在小组内完成几道截面面积问题的练习题。
2. 整理学生答案,对犯错的地方进行详细解析。
五、讨论(10分钟)
1. 让学生分享自己的解题思路和方法。
2. 引导学生讨论截面面积问题的解题技巧。
六、作业布置(5分钟)
布置一些截面面积问题的作业,要求学生认真完成并及时交上。
七、小结(5分钟)
总结本节课的内容,强调截面面积问题的重要性和解题技巧,激发学生学习兴趣。
教学反思:
通过本节课的教学,我发现学生对截面面积的理解和应用还有些困难,下节课我将更加注重实例分析,帮助学生掌握解题思路。
同时,我还需要关注学生的反馈和思考,及时帮助他们解决困惑。
初中截面研究教案数学

初中截面研究教案数学一、教学目标:1. 让学生掌握截面的基本概念,了解截面的性质和特点。
2. 培养学生运用几何知识解决实际问题的能力。
3. 培养学生的空间想象能力和动手操作能力。
二、教学内容:1. 截面的定义及性质2. 不同几何体的截面特点3. 截面的作图方法及实际应用三、教学重点与难点:1. 截面的定义及性质2. 不同几何体的截面特点3. 截面的作图方法及实际应用四、教学过程:1. 导入:利用多媒体展示各种几何体的图片,引导学生观察并思考:这些几何体如果被一个平面切割,会形成怎样的图形?2. 新课讲解:(1)截面的定义:用一个平面去截一个几何体,截出的图形叫做这个几何体的截面。
(2)截面的性质:截面与几何体的表面相交,且截面上的每一条线段都是几何体表面的线段。
(3)不同几何体的截面特点:① 立方体:截面可能是正方形、长方形、三角形等。
② 球体:截面一定是圆。
③ 圆柱体:截面可能是圆、椭圆、矩形等。
④ 圆锥体:截面可能是圆、椭圆、三角形等。
3. 实践操作:让学生利用手中的几何体模型,自己尝试进行截面操作,观察并记录不同几何体的截面特点。
4. 应用拓展:出示一些实际问题,让学生运用截面知识解决:(1)一个长方体木块,被一个平面从中间切开,求切开的截面面积。
(2)一个圆锥体铁块,被一个平面从顶部切开,求切开的截面面积。
5. 总结:本节课我们学习了截面的定义、性质和不同几何体的截面特点,通过实践操作和应用拓展,提高了我们的空间想象能力和解决问题的能力。
五、课后作业:1. 复习本节课的内容,巩固截面的基本概念和性质。
2. 完成课后练习题,提高运用截面知识解决问题的能力。
3. 预习下一节课的内容,了解截面的作图方法。
六、教学反思:本节课通过展示几何体图片、讲解截面定义和性质、实践操作、应用拓展等环节,让学生掌握了截面的基本知识和应用。
在教学过程中,要注意关注学生的学习情况,及时解答学生的疑问,提高学生的学习兴趣和积极性。
空间几何体的截面、球的切接问题课件-2025届高三数学一轮总复习

【对点训练】
(2023·广东开平模拟)如图所示,在等腰直角三角形 中, 为直角, , ,沿 把面 折起,使平面 平面 ,当四棱锥 的体积最大时, 的长为____.
,即外接球的半径 .则该正六棱柱的外接球和内切球的表面积的比值为 ,故选C.
2.(2023·山东临沂模拟)如图,已知球 与圆锥 的侧面和底面均相切,且球心 在线段 上,圆锥 的底面半径为1,母线长为2,则球 的表面积为_ __.
解析:设球 的半径为 ,因为圆锥 的底面半径为1,母线长为2,所以 .设球 与圆锥 的侧面的一个切点为 ,如图所示,所以有 , .在 中,
A. B. C. D.
√
解析:由题意得如图所示的截面五边形 .易知 , , ,设 , , 相交于点 , 易得 ,则截面将正方体分成的两部分中“后面”
部分的体积 , 故“前面”部分的体积为 ,则 , ,结合选项知选A.
利用平面的性质确定截面的形状是解决问题的关键. 作截面应遵循的三个原则:①在同一平面上的两点可作直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线.
第1讲 基本立体图形及其表面积与体积
第2课时 空间几何体的截面、球的切接问题
核心考点 师生共研
核心考点 师生共研
01
考点一 空间几何体的截面问题(师生共研)
例1 如图,正方体 的棱长为 , , 分别为棱 , 的中点,过 , , 作正方体的截面,将正方体分成的两部分体积之比最接近( )
连接 ,则 .连接 , ,易得 ,故可知以 为圆心, 为半径的圆弧 为球面与侧面 的交线.由 知 ,所以 的长为 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FE 1Q1几何体中的的截面问题1.定义及相关要素用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线.此平面与几何体的棱的交集(交点)叫做截点. 2.作多面体的截面方法(交线法):该作图关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.题型一、截面的形状1.P 、Q 、R 三点分别在直四棱柱AC 1的棱BB 1、CC 1和DD 1上,试画出过P 、Q 、R 三点的截面.1解答:(1)连接QP 、QR 并延长,分别交CB 、CD (2)连接EF 交AB 于T,交AD 于S .(3)连接RS 、TP 。
则多边形PQRST 即为所求截面。
2.已知P 、Q 、R 分别是四棱柱ABCD ―A 1B 1C 1D 1的棱CD 、DD 1和AA 1上的点,且QR与AD 不平行,求作过这三点的截面.2解答: (1)连接QP 并延长交DA 延长线于点I 。
(2)在平面ABCD 内连接PI 交AB 于点M 。
(3)连接QP、RM 。
则四边形PQRM 即为所求。
注:①若已知两点在同一平面内,只要连接这两点,就可以得到截面与多面体的一个面的截线。
②若面上只有一个已知点,应设法在同一平面上再找出第二确定的点。
③若两个已知点分别在相邻的面上,应找出这两个平面的交线与截面的交点。
3.一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能是3答案:D解析:考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D 。
题型二、截面面积、长度等计算4.过正方体1111D C B A ABCD -的对角线1BD 的截面面积为S ,S max 和S min 分别为S 的最大值和最小值,则m inm axS S 的值为 ( ) A .23 B .26 C .332 D .362 4答案:C解析:设M 、N 分别为AA 1、CC 1的中点.易证截面BMD 1N 是边长为52的菱形(正方体棱长设为1),其面积S(min)=62. 而截面BB 1D 1D 是矩形,其面积S(max)=2. 5. 如图,已知球O 是棱长为1 的正方体ABCD ﹣A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为 . 5答案:解析:平面ACD 1是边长为的正三角形,且球与以点D 为公共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积,则由图得,△ACD 1内切圆的半径是×tan30°=,则所求的截面圆的面积是π××=.6.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )A .1B .2C .3D .26答案:C解析:1O 与2O 的公共弦为AB ,球心为O,AB 中点为C , 则四边形C OO O 21为矩形,12||||,O O OC =||2,OA =Q 所以22||1,||||||3AC AC OC OC OA AC =⊥∴=-=7.已知正四棱锥P —ABCD 的棱长都等于a ,侧棱PB 、PD 的中点分别为M 、N ,则截面AMN 与底面ABCD 所成二面角大小的正切值为 . 7答案:12O2OCO2解析:过A 在平面ABCD 内作直线l BD //,连接AC,BD 交于O ,连接PO ,MN .记PO 、MN 交于O‘.因为PB 、PD 的中点分别为M 、N ,所以MN //BD ,因为l BD //,所以l MN //,A l ∈,所以l ⊂平面AMN , l =平面AMN∩平面ABCD .易知O AO '∠即为面AMN 与底面ABCD 所成二面角的平面角.221tan 242AO PO a O O a O AO ''==⇒=⇒= 8.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S 。
则下列命题正确的是_____ ①当102CQ <<时,S 为四边形 ②当12CQ =时,S 为等腰梯形 ③当34CQ =时,S 与11C D 的交点R 满足1113C R =④当314CQ <<时,S 为六边形⑤当1CQ =时,S 的面积为6 8答案: ①②③⑤解析:CQ DT PQ AT PQ AT T D D 22//1=⇒=且,则相交于设截面与. 对①,时当210.<<CQ ,则.10<<DT 所以截面S 为四边形,且S 为梯形.所以为真. 对②, 1 = DT ,21.时当=CQ 重合与1,D T ,截面S 为四边形.,11Q D AP APQD =所以截面S 为等腰梯形. 所以为真. 对③, 时当43.=CQ .31.21,23,411111====⇒R C T D DT QC 利用三角形相似解得所以为真. 对④, 2 DT 23,143.<<<<时当CQ .截面S 与线段1111C D ,D A 相交,所以四边形S 为五边形.所以为假.对⑤,A G APC G D A S C CQ 111111,Q 1.即为菱形相交于中点与线段截面重合与时,当=.对角线长度分别为.2632的面积为,和S 所以为真.9.如图,1111D C B A ABCD -为正方体。
任作平面α与对角线C A '垂直,使得α与正方体的每个面都有公共点,记这样得到 的截面多边形的面积为S ,周长为l .则( ) A .S 为定值,l 不为定值 B .S 不为定值,l 为定值 C .S 与l 均为定值D .S 与l 均不为定值9答案:B解析:将正方体切去两个正三棱锥A A BD '-与C D B C '''-后,得到一个以平行平面A BD '与D B C ''为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱A B ''剪开,展平在一张平面上,得到一个平行四边形11A B B A '',而多边形W 的周界展开后便成为一条与1A A '平行的线段(如图中1E E '),显然11A A E E ''=,故l 为定值。
当E '位于A B ''中点时,多边形W 为正六边形,而当E '移至A '处时,W 为正三角形,易知周长为定值l 的正六边形与正三角形面积分别为2324l 与2336l ,故S 不为定值。
题型三、截面图形的计数10.设四棱锥 P ABCD - 的底面不是平行四边形, 用平面α去截此四棱锥, 使得截面四边形是平行四边形, 则这样的平面α( )A. 不存在B. 只有1个C. 恰有4个D. 有无数多个 10答案:D解析:设四棱锥的两组不相邻的侧面的交线为m ,n ,直线m 、n 确定了平面β,作与β平行的平面α与四棱锥侧棱相截,则截得的四边形是平行四边形.这样的平面α有无数多个. 11.过正四面体ABCD 的顶点A 做一个形状为等腰三角形的截面,且使截面与底面BCD 成75o 角,问这样的截面可作几个?11答案:6个.解析:可以证明正四面体的棱、侧面与底面成角均小于75度,这样过顶点与底面成75度角,且平行与底面一条边的 截面也就是符合题意的截面,有两个。
三条边就是6个。
题型四、截面图形的性质12.如图4,在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器内灌进一些水,固定容器底面一边BC 于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:① 水的部分始终呈棱柱状; ② 水面EFGH 的面积不改变; ③ 棱A 1D 1始终与水面EFGH 平行;④ 当容器倾斜到如图4(2)时,BE ·BF 是定值; 其中正确的命题序号是______________ 12答案:①③④解析 当长方体容器绕BC 边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BC BF BE V ⋅⋅=21水是定值,又BC 是定值,所以BE ·BF 是定值,即④正确。
13.有一容积为1 立方单位的正方体容器ABCD-A 1B 1C 1D 1,在棱AB 、BB 1及对角线B 1C 的中点各有一小孔E 、F 、G ,若此容器可以任意放置,则该容器可装水的最大容积是 A .21 B .87 C .1211D .484713答案:C解析:本题很容易认为当水面是过E 、F 、G 三点的截面时容器可装水的容积最大图6(1),最大值为8712121211=⋅⋅⋅-=V 立方单位,这是一种错误的解法,错误原因是对题中“容器是可以任意放置”的理解不够,其实,当水平面调整为图6(2)△EB 1C 时容器的容积最大,最大容积为1211112121311=⋅⋅⋅⋅-=V . 14.(08年江西)如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a 升水时,水面恰好经过正四棱锥的顶点P 。
如果将容器倒置,水面也恰好过点P (图2)。
有下列四个命题: A .正四棱锥的高等于正四棱柱高的一半 B .将容器侧面水平放置时,水面也恰好过点PC .任意摆放该容器,当水面静止时,水面都恰好经过点PD .若往容器内再注入a 升水,则容器恰好能装满 其中真命题是: 14答案:BD解析:a 升水对应的体积为V ,则正四棱锥的体积2V,正四棱柱的体积为522V V V V ++=AB C HA 1B 1C 1D 1E FGDA B CD A 1B 1C 1D 1EFG H图4(2)图4(1)C 1ABCDA 1D 1B 1E GF 图(2)C 1A B C D A 1D 1 B 1EGF 图(1)图12图容器的盛水量为2V.易知所盛水的容积为容器容量的一半,故D正确,于是A错误;水平放置时由容器形状的对称性知水面经过点P,故B正确;C的错误可由图1中容器位置向右边倾斜一些可推知点P将露出水面。
