立体几何中的截面(解析版)
立体几何中的截面(解析版)

专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________A CBD分析 当长方体容器绕BC 边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BC BF BE V ⋅⋅=21水是定值,又BC 是定值,所以BE ·BF 是定值,即④正确。
立体几何中的截面(解析版)

立体几何中的截面(解析版)在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱、圆锥、球、棱柱、棱锥、长方体、正方体等),得到的平面图形。
总共有三种截面方式,分别为横截、竖截、斜截。
我们需要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
正六面体的基本斜截面不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
圆柱体的基本截面也有其特殊性质。
我们可以运用线、面平行的判定定理与性质求截面问题,或者结合线、面垂直的判定定理与性质定理求正方体中截面问题。
此外,我们还可以灵活运用一些特殊图形与几何体的特征,“动中找静”,如正三角形、正六边形、正三棱锥等。
建立函数模型也是求最值问题的一种方法。
在一个透明的塑料制成的长方体内灌进一些水,固定底面一边于地面上,再将倾斜,有四个命题。
其中,水的部分始终呈棱柱状,棱AD始终与水面平行,当倾斜到如图5(2)时,BE·BF是定值。
水面的面积在转动过程中会改变,而BC//FG//A1D1,所以A1D1//面EFGH。
因此,正确的命题序号为①③④。
一个容积为1立方单位的正方体,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G。
若此可以任意放置,则该可装水的最大容积是多少?分析本题,不能用一个平面去截一个正方体,使得截面为五边形。
进一步地,截面也不能为正五边形。
这是因为正方体的每个面都是正方形,而五边形无法与正方形相切。
因此,无论如何调整平面的位置,都不能得到五边形的截面。
而且OE=OC是抛物线的直线准线,所以焦点F在OC上,且OF=OC=1.故选:D二、完形填空在数学课上,老师讲到一个有趣的问题:如何用一个平面去截一个正方体所得截面不能是一个正五边形。
这个问题引起了我的思考,我开始想象一个平面在正方体中穿过的情景。
我发现,如果截面是一个正五边形,那么这个五边形的五条边必须分属于正方体的五个不同的面。
但是,正方体的每两个相对的面是平行的,所以这五条边中必有两条边是平行的。
立体几何中的 截面问题

立体几何中的截面问题立体几何中的截面问题⒈引言立体几何是研究空间之中各种几何体的形态、位置、运动和性质的数学学科。
在立体几何中,截面问题是一个重要的研究方向。
本文将介绍截面问题的基本概念、解题方法以及应用领域。
⒉基本概念⑴截面的定义截面是指将一个立体体积由一个或多个平面切割所得到的平面图形。
⑵截面的种类常见的截面包括平行截面、垂直截面、倾斜截面等。
平行截面是指与立体体积的底面平行的截面,垂直截面是指与立体体积的底面垂直的截面,倾斜截面是指与立体体积的底面既不平行也不垂直的截面。
⒊解题方法⑴平行截面的求解方法平行截面与底面平行,因此可以通过计算底面的面积和位于底面高度上的平行截面与底面的比例关系来求解平行截面的面积。
⑵垂直截面的求解方法垂直截面与底面垂直,因此可以通过计算底面的面积和垂直截面的高度来求解垂直截面的面积。
⑶倾斜截面的求解方法倾斜截面与底面既不平行也不垂直,因此求解倾斜截面的面积需要考虑其与底面的夹角以及截面的形状。
可以通过投影的方法或截面形状的几何关系来求解倾斜截面的面积。
⒋应用领域⑴建筑设计在建筑设计中,截面问题常常用于计算建筑物的横截面积,从而确定建筑物的结构稳定性和负荷承受能力。
⑵工程力学在工程力学中,截面问题常常用于计算结构件的截面形状和尺寸,从而确定结构件的刚度和强度。
⑶生物学在生物学中,截面问题常常用于计算生物体的截面积,从而确定生物体的体积和表面积,进而研究生物体的生理功能和生物学特性。
附件:本文档涉及的附件包括:⒈示例图片:包括平行截面、垂直截面和倾斜截面的示意图。
⒉计算表格:包括计算平行截面、垂直截面和倾斜截面面积的示例表格。
法律名词及注释:⒈立体几何:是数学学科中研究空间中各种几何体的形态、位置、运动和性质的学科。
⒉截面:把立体体积由一个或多个平面切割所得到的平面图形。
立体几何中的截面(解析版)

专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________分析当长方体容器绕BC边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EHA CBDBC BF BE V ⋅⋅=21水例3 有一容积为1 立方单位的正方体容器ABCD-A 1B 1C 1D 1,在棱AB 、BB 1及对角线B 1C 的中点各有一小孔E 、F 、G ,若此容器可以任意放置,则该容器可装水的最大容积是( )A .21 B .87 C .1211 D .4847 分析 本题很容易认为当水面是过E 、F 、G 三点的截面时容器可装水的容积最大图(1),最大值为8712121211=⋅⋅⋅-=V 立方单位,这是一种错误的解法,错误原因是对题中“容器是可以任意放置”的理解不够,其实,当水平面调整为图(2)△EB 1C 时容器的容积最大,最大容积为1211112121311=⋅⋅⋅⋅-=V ,故选C 。
立体几何中的 截面问题

立体几何中的截面问题本文档旨在介绍立体几何中的截面问题,包括截面的定义、性质、计算方法等方面的内容。
通过对截面问题的介绍和详细解析,读者可以更好地理解和应用相关知识。
1、截面的定义在立体几何中,截面是指一个平面和立体图形相交而形成的曲线或平面部分。
截面可以是二维的曲线,也可以是三维的平面。
截面问题主要研究在不同情况下的截面形状、面积、体积等性质。
2、截面的性质截面的性质取决于所截图形的性质以及截面的位置和方向。
主要包括以下几个方面:2.1 几何形状:截面可以是点、线段、圆、椭圆、抛物线等各种几何形状。
2.2 面积:截面的面积可能是有限的,也可能是无限的。
2.3 体积:截面可以用来计算图形的体积,从而解决与立体几何有关的问题。
2.4 位置和方向:不同位置和方向的截面可以得到不同的结果,需要根据具体问题进行分析和计算。
3、截面的计算方法根据截面的性质和具体问题的要求,有多种不同的计算方法可以用来求解截面问题。
常用的计算方法包括以下几种:3.1 几何分析法:通过几何分析截面的形状和性质,利用几何定理和方法计算截面的面积、体积等。
3.2 数学建模法:将截面问题转化为数学模型,利用数学方法和计算机技术进行计算和求解。
3.3 数值模拟法:通过数值模拟和计算机仿真,模拟和计算截面问题的解答。
3.4 实验测量法:通过实际测量和实验,获取截面的相关数据和性质进行计算和分析。
附件:本文档无附件。
法律名词及注释:1、立体几何:研究三维空间中点、线、面等几何图形的性质和变换的数学学科。
2、截面:一个平面和立体图形相交而形成的曲线或平面部分。
立体几何中的 截面问题

立体几何中的截面问题立体几何中的截面问题⒈简介立体几何是研究物体的形状、尺寸和空间关系的一门学科。
在立体几何中,截面问题是一个重要的研究方向。
截面问题指的是在一个立体物体中,通过给定的切割平面,研究切割所得的平面图形与原立体物体的关系。
⒉切割平面的表示方法在研究截面问题时,我们通常将切割所用的平面表示为一个方程。
常见的表示方法有点法式、一般式和截距式等。
⑴点法式点法式是通过给定平面上的一点和法向量来表示平面的方程。
设平面上一点为P(x0, y0, z0),法向量为n(n1, n2, n3),则平面的点法式为:n1(x ●x0) + n2(y ●y0) + n3(z ●z0) = 0⑵一般式一般式将平面的方程表示为一个二次齐次方程,形式为Ax +By + Cz + D = 0。
其中A、B、C是平面的法向量的坐标,D是一个与平面有关的常数。
⑶截距式截距式是通过平面与坐标轴交点的位置来表示平面的方程。
设平面与x轴、y轴、z轴的交点分别为(x0, 0, 0),(0, y0, 0),(0, 0, z0),则平面的截距式为:x/x0 + y/y0 + z/z0 = 1⒊平面与立体物体的相交及分类当给定切割平面后,它可能与立体物体相交于不同的方式。
根据相交情况的不同,我们将平面与立体物体的相交分为以下几类:⑴完全相交当切割平面与立体物体完全相交时,即切割平面穿过了立体物体的内部,并将其分成两个或多个部分。
⑵部分相交当切割平面与立体物体部分相交时,即切割平面与立体物体的边界相交。
⑶不相交当切割平面与立体物体不相交时,即切割平面与立体物体没有交点。
⒋截面图形的性质通过研究切割平面与立体物体的相交情况,可以得到截面图形的一些性质。
⑴形状截面图形的形状与切割平面的位置和方向有关。
在同一个立体物体中,不同位置和方向的切割平面可能得到不同形状的截面图形。
⑵面积截面图形的面积可以通过计算得到。
对于平面图形,常用的计算方法有面积公式和积分法。
强基专题--立体几何中的截面问题

强基专题3 立体几何中的截面问题
[跟进训练]
1.(2021·重庆模拟)在三棱锥 P-ABC 中,PA,PB,PC 两两垂直,
PA=3,PB=4,PC=5,点 E 为线段 PC 的中点,过点 E 作该三棱
锥外接球的截面,则所得截面圆的面积不可能为( )
A.6π
B.8π
C.10π
D.12π
1234 5
(2)当π2<θ<π时,0<α<θ<π,此时sin θ<1,sin α可以取到最 大值1,
此时过圆锥母线的截面面积最大,最大值为S=12l2.
1234 5
强基专题3 立体几何中的截面问题
综上所述,过圆锥母线的截面面积的最大值与轴截面顶角θ的范 围有关,
当0<θ≤π2时,轴截面面积最大,最大值为S=12l2sin θ. 当π2<θ<π时,过圆锥母线的截面面积最大,最大值为S=12l2.
同理 FG∥EH,所以四边形 EFGH 为平行四边形,又 AD⊥BC, 所以四边形 EFGH 为矩形.
1234 5
强基专题3 立体几何中的截面问题
由相似三角形的性质得BECF=AACF,FACC=AFDG, 所以BECF+FAGD=AACF+FACC,BC=AD=2, 所以 EF+FG=2,所以四边形 EFGH 的周长为定值 4,S 四边形 EFGH =EF×FG≤EF+2 FG2=1, 所以四边形 EFGH 的面积有最大值 1.故选 B.]
1 2
l2sin θ.截面VCD的面积S′=12l2sin α.在△V强基专题3 立体几何中的截面问题
(1)当0<θ≤π2时,0<α<θ≤π2,sin α<sin θ⇒S′<S,此时过圆 锥母线的截面面积最大为轴截面面积S=12l2sin θ.
截面形状及相应面积的求法 (1)结合线、面平行的判定定理与性质定理求截面问题; (2)结合线、面垂直的判定定理与性质定理求正方体中截面问题; (3)猜想法求最值问题:“要灵活运用一些特殊图形与几何体的 特征,“动中找静”,如正三角形、正六边形、正三棱锥等; (4)建立函数模型求最值问题:①设元;②建立二次函数模型; ③求最值.
专题38 立体几何中的距离、截面、折叠问题(解析版)

结合图1可知, 为 中点,故 ,从而
所以 ,所以二面角 的平面角的余弦值为 .
向量法:以 点为原点,建立空间直角坐标系 如图所示,
则 , , ,所以 ,
设 为平面 的法向量,则 ,即 ,
解得 ,令 ,得 ,由(Ⅰ)知, 为平面 的一个法向量,
所以 ,即二面角 的平面角的余弦值为 .
2、平面外一点P到平面α的距离:如图,已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点,过点P作平面α的垂线l,交平面α于点Q,则n是直线l的方向向量,且点P到平面α的距离PQ= = =
基本题型:
1.(多选)已知正方体ABCD-A1B1C1D1的棱长为1,点E,O分别是A1B1,A1C1的中点,点P在正方体内部且满足 = + + ,则下列说法正确的是()
【解析二】由题意可知,该平面与在正方体的截面为对边平行的六边形,如图所示,则截面面积为
所以当 时,
7.(2017新课标Ⅰ)如图,圆形纸片的圆心为 ,半径为5 cm,该纸片上的等边三角形 的中心为 . 、 、 为圆 上的点, , , 分别是以 , , 为底边的等腰三角形。沿虚线剪开后,分别以 , , 为折痕折起 , , ,使得 、 、 重合,得到三棱锥。当 的边长变化时,所得三棱锥体积(单位: )的最大值为_______。
所以 , , , .
得 , .
设平面 的法向量 ,平面 的法向量 ,
平面 与平面 夹角为 ,则 ,得 ,取 ,
,得 ,取 ,从而 ,
即平面 与平面 夹角的余弦值为 .
9.(2015浙江)如图,已知 , 是 的中点,沿直线 将 翻折成 ,所成二面角 的平面角为 ,则
10.(2012浙江)已知矩形 , , .将 沿矩形的对角线 所在的直线进行翻折,在翻折过程中,
立体几何如何作截面

D1 A1
Q C1
RD
B1
D1
A1
Q
C1
RD
B1
A
P
A
C
I
M
P C
B
B
作法:(1)连接QP并延长交DA延长线于点I。 (2)在平面ABCD内连接PI交AB于点M。 (3)连接QP、RM。则四边形PQRM即为所求。
2°截面经过的三个已知点至少有一点在多面体的面上, 其余点在棱上.
作图题5.如图,正方体ABCD―A1B1C1D1中,E、F在两
底中心连线OO1中点的截面。
A1
O1 D1 C1
A1 G E
F O1
D1 C1
B1
B1
M
M
A
C
O
D
B
A
C
O
D
B
作法:(1)过A1A和OO1作平面AOO1A1,交BC于D,交B1C1于D1,则D、 D1分别为BC、B1C1的中点。 (2)在平面A1AM内,作直线DM交上底面A1B1C1于点G。 (3)在平面A1B1C1内,过G作EF∥B1C1交A1B1于E,交A1C1于F。 (4)连接BE,CF。则多边形BCFE为所求。
条棱上,G在底面A1C1内,求过E、F、G的截面.
D1
C1
D1
C1
F1
G
A1
B1
A1 M
G
N
B1
P
E
E
D
C F
D
C F
A
B
。在面BC1内,过F作FF1∥BB1, 交B1C1于点F1,则面AFF1A1为所作的辅助面. (2)在面AFF1A1内,延长F1A1交FE的延长线于P.
立体几何中的截面(解析版)
专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________分析当长方体容器绕BC边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG,但EH与FG的距离EF在变,所以水面EFGH的面积在改变,故②错误;在转动过程中,始终有BC//FG//A1D1,所以A1D1//面EFGH,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BCBFBEV⋅⋅=21水是定值,又BC是定值,所以BE·BF是定值,即④正确。
立体几何中的截面问题

立体几何中的截面问题一.基本原理:过正方体(长方体)上三点做截面.1.三点中有两点共面例1.如图,在正方体ABCD-A 1B 1C 1D 1中,E,F,G 分别在AB,BC,DD 1上,求作过E,F,G 三点的截面.思路:当三点中有两点共面时,做截面的思路就是先找共面两点所在直线与该平面所有的棱交点,而这些交点由同时在另外一个平面中,即该截面和正方体某个侧面的交点,这样利用公理1,逐次相连找到所有的交点,即可得到截面.解析:作法:①.由于F E ,共面,在底面AC 内,过F E ,作直线EF ,与DA 于L ,显然,此时L 即在侧面D A 1内,又在欲求截面内,而该截面与侧面D A 1又交于点G ,根据公理1,截面与侧面D A 1交于L .同理,过F E ,作直线EF 与DC 的延长线交于M ,此时M 即在侧面1DC 内,又在欲求截面内,根据公理1,截面与侧面1DC 交于M .②在侧面D A 1内,连接LG 交1AA 于K .③在侧面1DC 内,连接GM 交1CC 于H .④连接FH KE ,.则五边形EFHGK EFHGK 即为所求的截面.练习1.(三点两两共面)P,Q,R 三点分别在直四棱柱AC 1的棱BB 1,CC 1和DD 1上,试画出过P,Q,R 三点的截面作法.解析:作法:(1)连接QP,QR 并延长,分别交CB,CD 的延长线于E,F.(2)连接EF 交AB 于T,交AD 于S.(3)连接RS,TP.则五边形PQRST 即为所求截面.例2.(三点所在的棱两两异面)如图,长方体1111D C B A ABCD -中,R Q P ,,分别为111,,CC AB D A 上三点,求过这三点的截面.分析:此题的难点在于R Q P ,,三点均不在同一个侧面(底面)中,这样我们就暂时无法通过侧面(底面)中连线与棱的交点来找到截面的边界点,于是需要先做出一个平面来,让上面三点RQ P ,,中有两点共面,这就转化成例1的情形,从而解决问题.解:如图,作1//BB QE 交11B A 与E ,则1,RC QE 确定一个平面,转化为例1的情形.连接QR EC ,1,交于点F ;连接PF 交1111,B A D C 延长线于H G ,;连接HQ 交11,BB AA 延长线于J I ,;连接JR 交BC 于K .则KRGPIQK 为所作截面.例3.利用平行关系确定截面在三棱锥A BCD -中,AB CD a ==,截面MNPQ 与AB ,CD 都平行,则截面MNPQ 的周长等于()A.2a B.4a C.a D.无法确定解析:设AM k CM=,因为//AB 平面MNPQ ,平面ABC 平面MNPQ MN =,AB Ì平面ABC ,所以//MN AB ,同理可得//PQ AB ,//MQ CD ,//NP CD ,故四边形MNPQ 为平行四边形,所以11MN PQ AB AB k ==+,1MQ NP k CD CD k ==+.因为AB CD a ==,所以1a MN PQ k==+,1ak MQ NP k ==+,所以四边形MNPQ 的周长为2211a ak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭.故选:A.二.截面的的画法小结1.确定截面的主要依据有(1)平面的四个公理及推论.(2)直线和平面平行的判定和性质.(3)两个平面平行的性质.2.作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程。
第9讲 立体几何截面和交线问题(解析版)

第9讲 立体几何截面和交线问题1.在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为11A D ,11D C 的中点,则过B ,E ,F 三点的平面截该正方体,所得截面的周长为( )A .52B .62C 2213D 2413【解答】解:如图,延长EF ,FE ,分别交11B C ,11B A 的延长线于点H ,G 连结BG ,BH , 分别交1AA ,1CC 于点I ,J ,则五边形BIEFJ 为所求截面.平面1//B C 平面1A D ,∴平面BGH 与之交线//IE BJ ,棱长为2的正方体1111ADCB A D C B -中,可得2242132()3BI GJ ==+,222131()3EI FJ ∴==+=2EF ,∴则过D ,E ,F 三点的平面截该正方体, 1321322(2213C .2.已知正方体1111ABCD A B C D -的棱长为2,M 为1CC 的中点,若AM ⊥平面α,且B ∈平面α,则平面α截正方体所得截面的周长为( )A .3225B .442+C .2225D .2【解答】解:正方体1111ABCD A B C D -中BD AC ⊥, BD AM ∴⊥(三垂线定理), 取1BB 中点N ,11A B 中点E ,连MN ,AN ,BE , 可知BE AN ⊥,BE AM ∴⊥(三垂线定理), AM ∴⊥平面DBE , 取11A D 中点F , 则α即为截面BEFD , 易求周长为3225, 故选:A .3.正方体1111ABCD A B C D -的棱长为4,E ,F 分别是BC 和11C D 的中点,经过点A ,E ,F 的平面把正方体1111ABCD A B C D -截成两部分,则截面的周长为1053++. 【解答】解:如图所示:过点F 作//FH AE 交11A D 于H ,由题意可得AE == 易知11D H =,可得HF =所以点H 为11A D的四等分点,可得5AH ===, 所以11114D H A D =, 过点E 作//EP AH 交1CC 于点P , 则△1AA H PCE ∆∽, 所以11AA CP A H CE =,解得83CP =, 所以截面与11BCC B的交线段长为103PE =,PF ,可得截面的周长10105533L AE EP PF FH HA =++++==++故答案为:1053+4.如图正方体1111ABCD A B C D -的棱长为2,P 为BC 的中点,Q 为线段1CC 的中点,过点A ,P ,Q 的平面α截该正方体所得的截面的周长为 2532 .【解答】解:正方体1111ABCD A B C D -的棱长为2,P 为BC 的中点,Q 为线段1CC 的中点, ∴过点A ,P ,Q 的平面α截该正方体所得的截面为梯形1APQD , 22122222AD PQ ==+, 221215AP D Q ==+∴过点A ,P ,Q 的平面α截该正方体所得的截面的周长为:11532L AP PQ QD AD =+++=故答案为:2532.18.已知正方体1111ABCD A B C D -的棱长为2,M 为1CC 的中点,若AM ⊥平面α,且B ∈平面α,则平面α截正方体所得截面的周长为 3225 .【解答】解:正方体1111ABCD A B C D -中BD AC ⊥, BD AM ∴⊥(三垂线定理), 取1BB 中点N ,11A B 中点E ,连MN ,AN ,BE , 可知BE AN ⊥,BE AM ∴⊥(三垂线定理),AM ∴⊥平面DBE , 取11A D 中点F ,则α即为截面BEFD ,易求周长为3225故答案为32252.已知圆22:(2)4M x y -+=,过点(1,1)的直线中被圆M 截得的最短弦长为O 是棱长为4的正方体的外接球,过该正方体的棱的中点作球O 的截面,则最小截面的面积为( ) A .3πB .4πC .5πD .6π【解答】解:由题意,正方体的棱的中点与O 的距离为,∴2=, ∴最小截面的面积为224ππ=, 故选:B .4.正方体1111ABCD A B C D -棱长为4,M ,N ,P 分别是棱11A D ,1A A ,11D C 的中点,则过M ,N ,P 三点的平面截正方体所得截面的面积为( )A .B .C .D .【解答】解:如图所示;取正方体1111ABCD A B C D -棱AB 、BC 、1CC 的中点L 、K 、Q , 连接NL ,LK 、KQ 、QP ,则六边形PQKLNM 是过M ,N ,P 三点的平面截正方体所得的截面,该六边形是正六边形,其边长为12NQ =其面积为2162⨯⨯=故选:D .5.已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A 33B 23C 32D 3【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且正六边形时,α截此正方体所得截面面积的最大, 22, α截此正方体所得截面最大值为:232336(). 故选:A .6.体积为183的正三棱锥A BCD -的每个顶点都在半径为R 的球O 的球面上,球心O在此三棱锥内部,且:2:3R BC =,点E 为线段BD 上一点,且2DE EB =,过点E 作球O 的截面,则所得截面圆面积的取值范围是( )A .[4π,12]πB .[8π,16]πC .[8π,12]πD .[12π,16]π【解答】解:设3BC a =,则2R a =,体积为183的正三棱锥A BCD -的每个顶点都在半径为R 的球O 的球面上,∴21391833a h =224h a ∴=, 222()(3)R h R a =-+,2222244(2)3a a a a∴=-+,2a ∴=,6BC ∴=,4R =, 点E 为线段BD 上一点,且2DE EB =,ODB ∴∆中,4OD OB ==,6DB =,3cos 4ODB ∠=, 31616244224OE ∴=+-⨯⨯⨯,截面垂直于OE 时,16822-,截面圆面积为8π, 以OE 所在直线为直径时,截面圆的半径为4,截面圆面积为16π, ∴所得截面圆面积的取值范围是[8π,16]π. 故选:B .7.圆锥的母线长为2,其侧面展开图的中心角为θ弧度,过圆锥顶点的截面中,面积的最大值为2;则θ的取值范围是( ) A .[2,2)ππB .[2]ππC .{2}πD .2[)ππ 【解答】解:圆锥的母线长为2,其侧面展开图的中心角为θ弧度, 过圆锥顶点的截面中,面积的最大值为2, 设轴截面的中心角为2α,由条件得:42ππα<,2sin 22r r l α==, 解得2r,22222r l ππθπ==,∴22πθπ<, θ∴的取值范围是[2,2)ππ.故选:A .8.如图,已知四面体ABCD 为正四面体,1AB =,E ,F 分别是AD ,BC 中点.若用一个与直线EF 垂直,且与四面体的每一个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为( )A .14B 2C 3D .1【解答】解:补成正方体如图:由于EF α⊥,故截面为平行四边形MNKL ,可得1KL KN +=;又//KL BC ,//KN AD ,且AD BC ⊥;KN KL ∴⊥,(2MNKL NK KL S NK KL +∴=⋅四边形21)4=, 当且仅当NK KL =时取等号.故选:A .19.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 12π . 【解答】解:设圆柱的轴截面的边长为x , 则由28x =,解得22x =222 其表面积为:222(2)22212S S S πππ=+=⨯⨯+=侧圆柱表底.故答案为:12π.20.正方体1111ABCD A B C D -棱长为4,M ,N ,P 分别是棱11A D ,1A A ,11D C 的中点,则过M ,N ,P三点的平面截正方体所得截面的面积为 【解答】解:如图所示;取正方体1111ABCD A B C D -棱AB 、BC 、1CC 的中点L 、K 、Q , 连接NL ,LK 、KQ 、QP ,则六边形PQKLNM 是过M ,N ,P 三点的平面截正方体所得的截面,该六边形是正六边形,其边长为12NQ =其面积为162⨯⨯=.故答案为:.21.已知棱长为2的正方体1111ABCD A B C D -,球O 与该正方体的各个面相切,则平面1ACB 截此球所得的截面的面积为23π. 【解答】解:正方体1111ABCD A B C D -的棱长为2,球O 与该正方体的各个面相切,则球O 的半径为1,如图,设E 、F 、G 分别为球O 与平面ABCD 、平面11BB C C 、11AA B B 的切点, 则等边三角形EFG 为平面1ACB 截此球所得的截面圆的内接三角形,由已知可得EF EG GF ===∴平面1ACB 截此球所得的截面圆的半径r =.∴截面的面积为223ππ⨯=. 故答案为:23π.9.设四棱锥P ABCD -的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面(α )A .不存在B .只有1个C .恰有4个D .有无数多个【解答】证明:由侧面PAD 与侧面PBC 相交,侧面PAB 与侧面PCD 相交, 设两组相交平面的交线分别为m ,n , 由m ,n 确定的平面为β,作α与β平行且与四条侧棱相交, 交点分别为1A ,1B ,1C ,1D 则由面面平行的性质定理得:1111////A B m D C ,1111////A D n B C , 从而得截面必为平行四边形.由于平面α可以上下移动,则这样的平面α有无数多个. 故选:D .10.如图,在棱长为1的正方体1111ABCD A B C D -的对角线1AC 上任取一点P ,以A 为球心,AP 为半径作一个球.设AP x =,记该球面与正方体表面的交线的长度和为()f x ,则函数()f x 的图象最有可能的是( )A .B .C .D .【解答】解:如图,球面与正方体的表面都相交,根据选项的特点,我们考虑三个特殊情形:①当1x =;②当12x =;③当2x ①当1x =时,以A 为球心,1为半径作一个球,该球面与正方体表面的交线分别是图中的红色的弧线,其弧长为:1332142ππ⨯⨯⨯=,且为函数()f x 的最大值;②当12x =时,以A 为球心,12为半径作一个球,该球面与正方体表面的交线分别是图中的兰色的弧线,根据图形的相似,其弧长为①中弧长的一半;③当2x =.以A 2其弧长为:1332142ππ⨯⨯⨯=,且为函数()f x 的最大值;对照选项,B 正确. 故选:B .11.如图,正方体1111ABCD A B C D -A 为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )A .56π B .23π C .π D .76π 【解答】解:如图,球面与正方体的六个面都相交,所得的交线分为两类:一类在顶点A 所在的三个面上,即面11AA B B 、面ABCD 和面11AA D D 上; 另一类在不过顶点A 的三个面上,即面11BB C C 、面11CC D D 和面1111A B C D 上.在面11AA B B 上,交线为弧EF 且在过球心A 的大圆上,因为2AE =,1AA =, 则16A AE π∠=.同理6BAF π∠=,所以6EAF π∠=,故弧EF 的长为:263ππ⨯=,而这样的弧共有三条. 在面11BB C C 上,交线为弧FG 且在距球心为1的平面与球面相交所得的小圆上,此时,小圆的圆心为B ,半径为1,2FBG π∠=,所以弧FG 的长为:122ππ⨯=.于是,所得的曲线长为:5326πππ+=. 故选:A .12.已知三棱锥P ABC -的棱AP 、AB 、AC P 为球心2为半径作一个球,则球面与三棱锥的表面相交所得到的四段弧长之和等于( ) A .23π B .56π C .π D .32π【解答】解:如图,AP 1AN =,6APN π∠=,12NPM π∠=,∴2126MN ππ=⨯=.同理6GH π=,122HN ππ=⨯=,2233GM ππ=⨯=,球面与三棱锥的表面相交所得到的四段弧长之和等于2366232πππππ+++=. 故选:D .13.已知底面为正方形的四棱锥O ABCD -,各侧棱长都为16,以O 为球心,以2为半径作一个球,则这个球与四棱锥O ABCD -相交部分的体积是( ) A .29π B .89πC .169πD .43π 【解答】解:连接正方体的对角线根据交点得出正方体可以分割成6个相同的四棱锥,∴四棱锥O ABCD -的底面ABCD 是边长为4的正方形,各侧棱长均为以O 为中心,将6个这样的四棱锥放在一起,会得到一个正方体;而以O 为球心,2为半径的球正好在正方体的内部;则球与该四棱锥重叠部分的体积为球体积的16; 因此以O 为球心,2为半径的球与该四棱锥重叠部分的体积是314162639V ππ=⨯⨯⨯=,故选:C .22.球O 为正方体1111ABCD A B C D -的内切球,2AB =,E ,F 分别为棱AD ,1CC 的中点,则直线EF 被球O【解答】解:连结OE ,OF ,取EF 的中点M ,连结OM . O 是正方体的中心,E ,F 是AD ,1CC 的中点,OE OF ∴=OM EF ∴⊥.又EF ==OM ∴. 球O 的半径为1r =,EF ∴被球O 截得弦长为23.如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上,过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M ,N 两点,设BP x =,MN y =,则函数()y f x =的图象大致是 ② .(在横线上填上正确的序号,多选少选都不得分)【解答】解:由题意知,MN ⊥平面11BB D D ,则MN 在底面ABCD 上的射影是与对角线AC 平行的直线,故当动点P 在对角线1BD 上从点B 向1D 运动时,x 变大y 变大,直到P 为1BD 的中点时,y 最大为AC ; 然后x 变小y 变小,直到y 变为0,因底面ABCD 为正方形,故变化速度是均匀的,且两边一样. 故答案为:②.24.如图,正方体1111ABCD A B C D -A 为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和()GF EF +等于56π.【解答】解:如图,球面与正方体的六个面都相交,所得的交线分为两类:一类在顶点A 所在的三个面上,即面11AA B B 、面ABCD 和面11AA D D 上; 另一类在不过顶点A 的三个面上,即面11BB C C 、面11CC D D 和面1111A B C D 上.在面11AA B B 上,交线为弧EF 且在过球心A 的大圆上,因为2AE =,1AA =, 则16A AE π∠=.同理6BAF π∠=,所以6EAF π∠=,故弧EF 的长为:263ππ⨯=,而这样的弧共有三条.在面11BB C C 上,交线为弧FG 且在距球心为1的平面与球面相交所得的小圆上, 此时,小圆的圆心为B ,半径为1,2FBG π∠=,所以弧FG 的长为:122ππ⨯=.于是,所得的曲线长为5326GF EF πππ+=+=. 故答案为:56π.25.已知正方体1111ABCD A B C D -的棱长为1,以顶点A表面相交所得到的曲线的长等于. 【解答】解:如图,球面与正方体的六个面都相交,所得的交线分为两类:一类在顶点A 所在的三个面上,即面11AA B B 、面ABCD 和面11AA D D 上;另一类在不过顶点A 的三个面上,即面11BB C C 、面11CC D D 和面1111A B C D 上.在面11AA B B 上,交线为弧EF 且在过球心A的大圆上,因为AE =,11AA =,则16A AE π∠=.同理6BAF π∠=,所以6EAF π∠=,故弧EF6π=,而这样的弧共有三条.在面11BB C C 上,交线为弧FG 且在距球心为1的平面与球面相交所得的小圆上,此时,小圆的圆心为B ,半,2FBG π∠=,所以弧FG2π=.这样的弧也有三条.于是,所得的曲线长为33+=.26.已知正三棱锥P ABC -侧棱长为1,且PA 、PB 、PC 两两垂直,以顶点A个球,则球面与正三棱锥的表面相交得到一条封闭的曲线,则这条封闭曲线的长度为. 【解答】解:设以顶点A线是EFNM ,如图所示.则AE AF AM AN ====, 在直角三角形APE中,cos PAE ∠=,6PAE π∴∠=,∴()46ME ππ=-=,同理NF =; 在直角三角形PBC 中,2BPC π∠=,PE PF ==∴2EF π==在等边三角形ABC 中,MN AM ==,3MAN π∠=,∴3MN π==.则这条封闭曲线的长度为ME NF EF MN +++=..28.正方体1111ABCD A B C D -棱长为2,以其体对角线的交点O 为半径的球与正方体表面的交线长为. 【解答】解:依题意,球心O 到正方体表面的距离为1, 设正方形ABCD 的中心为1O ,正方形ABCD 所在平面裁球O 所得的圆的半径1r =>. 故球O 与每一个面的交线均为四段圆弧,且13EO F π∠=.故四段圆弧的圆心角之和为2()4233πππ-⨯=,故一个面上的交线长23l π==,则66⨯=,29.已知正方体的棱长为4,以该正方体的一个顶点为球心,以表面所截得的所有弧长的和为 6π .【解答】解:如图,不妨以D 为球心,则正方体的表面被该球面所截得的弧长有相等的三部分, 与上底面截得的弧长,是以1D 为圆心,以4为半径的四分之一圆周, 则弧长:111824AC ππ=⨯=. ∴该球面被正方体表面所截得的所有的弧长和为6π.故答案为:6π.30.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截该正方体所得截面记为S ,则下列命题正确的是 ①②③⑤ (写出所有正确命题的编号) ①当102CQ <<时,S 为四边形 ②当12CQ =时,S 为等腰梯形 ③当34CQ =时,S 与11C D 的交点R 满足1113C R = ④当314CQ <<时,S 为四边形⑤当1CQ =时,S【解答】解:如图当12CQ =时,即Q 为1CC 中点,此时可得1//PQ AD ,1AP QD ==,故可得截面1APQD 为等腰梯形,故②正确;由上图当点Q 向C 移动时,满足102CQ <<,只需在1DD 上取点M 满足//AM PQ , 即可得截面为四边形APQM ,故①正确;③当34CQ =时,如图,延长1DD 至N ,使112D N =,连接AN 交11A D 于S ,连接NQ 交11C D 于R ,连接SR , 可证//AN PQ ,由11NRD QRC ∆∆∽,可得1111::1:2C R D R C Q D N ==,故可得113C R =,故③正确;④由③可知当314CQ <<时,只需点Q 上移即可,此时的截面形状仍然上图所示的APQRS ,显然为五边形,故④错误;⑤当1CQ =时,Q 与1C 重合,取11A D 的中点F ,连接AF ,可证1//PC AF ,且1PC AF =,可知截面为1APC F 为菱形,故其面积为112AC PF ⋅,故⑤正确. 故答案为:①②③⑤.31.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S ,若102CQ<,则S 的面积取值范围是 3(4,9]8.【解答】解:在1CC 上取点M 使得2CM CQ =,在1DD 上取点N ,使得DN CM =,连接BM ,AN ,MN ,CN ,AP ,则PQ 为BCM ∆的中位线,//PQ BM ∴,//DN CM =,CD CM ⊥,∴四边形CDNM 是矩形, ////MN CD AB ∴==,∴四边形ABMN 是平行四边形,//AN BM ∴,//AN PQ ∴,故截面多边形为梯形APQN , 设CQ x =,则PQ =,2AN BM PQ ===, 取AD 的中点O ,过O 作OE AN ⊥,过D 作DF AN ⊥,则可证PE AN ⊥,则DF =,12OE DF ∴=,PE ∴∴梯形APQN的面积为S =102x<,∴3948S <.故答案为:3(4,9]8.32.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截正方体所得的截面为S ,当1CQ =时,S 的面积为.【解答】解:当1CQ =时,1C 与Q 重合,取11A D 中点E ,则菱形1APC E 就是过点A ,P,Q 的平面截正方体所得的截面, 1AC =PE =∴过点A ,P ,Q的平面截正方体所得的截面为:112S AC PE =⨯⨯=..14.如图,在正方体1111ABCD A B C D -中,M ,N ,P ,Q 分别是所在棱的中点,则下列结论正确的是( )A .点1C ,1D 到平面PMN 的距离相等B .PN 与QM 为异面直线C .90PNM ∠=︒D .平面PMN 截该正方体的截面为正六边形【解答】解:如图,取BC 中点E ,1CC 中点F ,则有六边形MQNPEF 为正六边形, 对于A ,根据正方体的对称性,可得点1C ,1D 到平面MQNPEF 的距离相等,A ∴正确; 对于B ,PN 与QM 为共面直线,故B 错;对于C ,在正六边形MQNPEF 中,设1PN =,则2PM =,MN =222MN PN PM ∴+=,则MN PN ⊥,故C 正确;对于D ,平面PMN 截该正方体的截面为正六边形,故D 正确. 故选:ACD .15.如图,棱长为2的正方体1111ABCD A B C D -的内切球为球O ,E 、F 分别是棱AB 和棱1CC 的中点,G 在棱BC 上移动,则下列结论成立的有( )A .存在点G ,使OD 垂直于平面EFGB .对于任意点G ,//OA 平面EFGC .直线EF 的被球O 2D .过直线EF 的平面截球O 所得的所有圆中,半径最小的圆的面积为2π 【解答】解:正方体的内切球的球心即正方体的中心O ,1R =, 对于A ,当G 为BC 的中点时,EG BD ⊥,1BB EG ⊥, 1BB BD B =,EG ∴⊥平面1BB D ,而1B D ⊂平面1BB D ,则1EG B D ⊥, 同理,FG ⊥平面1B CD ,可得1FG B D ⊥,EG FG G =,1B D ∴⊥平面EFG ,即OD 垂直于平面EFG ,故A 正确;对于B ,当G 与B 重合时,A ∈平面EFB ,O ∉平面EFB , OA ∴与平面EFG 相交,此时//OA 平面EFG 不成立,故B 错误; 对于C ,22516EF EC FC =+=+=EF 的中点M , 由对称性可知,OE OF =,OM EF ∴⊥, 2OE =2222OM OE EM ∴=-O 到EF 的距离为22, ∴直线EF 的被球O 截得的弦长为22221()22R OM -=-故C 正确; 对于D ,设截面圆的半径为r ,O 到平面的距离为d ,则222r d R +=, 当O 到平面的距离最大时,截面圆的半径r 最小, O 到平面的距离小于等于O 到EF 的距离,∴当22d =时,2221()2min r =-= ∴半径最小的圆的面积为22r ππ=,故D 正确.故选:ACD .。
立体几何截面问题的十种题型(解析版)
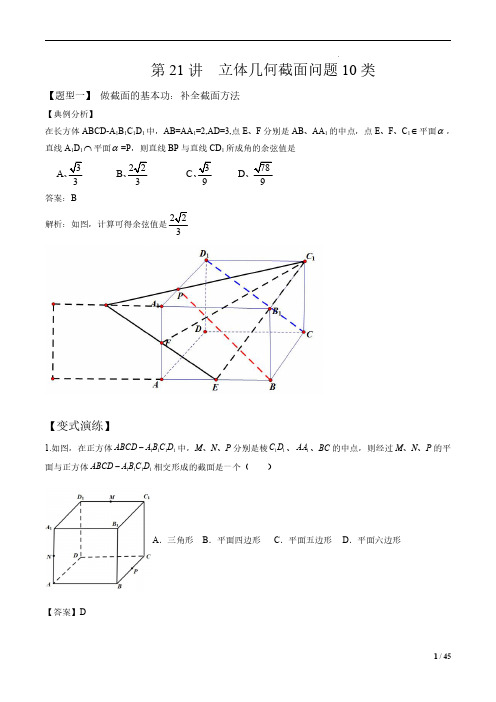
第21讲立体几何截面问题10类【题型一】做截面的基本功:补全截面方法【典例分析】在长方体ABCD-A 1B 1C 1D 1中,AB=AA 1=2,AD=3,点E 、F 分别是AB 、AA 1的中点,点E 、F 、C 1∈平面α,直线A 1D 1⋂平面α=P ,则直线BP 与直线CD 1所成角的余弦值是3378 A22 C B 3 D 3 99、、、、答案:B解析:如图,计算可得余弦值是3【变式演练】1.如图,在正方体1111ABCD A B C D -中,M 、N 、P 分别是棱11C D 、1AA 、BC 的中点,则经过M 、N 、P 的平面与正方体1111ABCD A B C D -相交形成的截面是一个()A .三角形B .平面四边形C .平面五边形D .平面六边形【答案】D分别取11A D 、AB 、1C C 的中点、、F H E ,连接MF 、FN 、NH 、HP 、PE 、EM 、11A C 、AC 、NE 、1A B ,先证明、、、H P M F 四点共面,再证明N ∈平面HPMF ,P ∈平面HPMF 可得答案.【详解】如图,分别取11A D 、AB 、1C C 的中点、、F H E ,连接MF 、FN 、NH 、HP 、PE 、EM 、11A C 、AC 、NE 、1A B ,且M 、N 、P 分别是棱11C D 、1AA 、BC 的中点,所以11//A C FM 、//HP AC ,且11//A C AC ,所以//HP FM ,即、、、H P M F 四点共面,因为11//=,F BP F BP A A ,所以四边形1A FPB 是平行四边形,所以1//A B FP ,又因为1//A B NH ,得//NH FP ,且FP ⊂平面HPMF ,H ∈平面HPMF ,所以NH ⊂平面HPMF ,得N ∈平面HPMF ,因为11//=,M H MC B C BH ,所以四边形1C MHB 是平行四边形,所以1//C B MH ,又因为1//C B EP ,得//MH EP ,又MH ⊂平面HPMF ,P ∈平面HPMF ,所以PE ⊂平面HPMF ,得E ∈平面HPMF ,所以、、、、、H P E M F N 六点共面,平面六边形HPEMFN 即为经过M 、N 、P 与正方体1111ABCD A B C D -相交形成的截面,故选:D.2.如图,在正方体1111ABCD A B C D -中,E 是棱1CC 的中点,则过三点A 、D1、E 的截面过()A .AB 中点B .BC 中点C .CD 中点D .BB1中点【答案】B根据截面特点结合正方形结构性质求解.【详解】取BC 的中点F ,连接EF ,AF ,如图,则1EF AD ∥,所以F 在截面上,故选:B3.如图正方体1111ABCD A B C D -,棱长为1,P 为BC 中点,Q 为线段1CC 上的动点,过A 、P 、Q 的平面截该正方体所得的截面记为Ω.若1CQ CC λ→→=,则下列结论错误的是()A .当102λ∈⎛⎫⎪⎝⎭,时,Ω为四边形B .当12λ=时,Ω为等腰梯形C .当3,14λ⎛⎫∈ ⎪⎝⎭时,Ω为六边形D .当1λ=时,Ω的面积为2【答案】C 【分析】根据题意,依次讨论各选项,作出相应的截面,再判断即可.【详解】解:当102λ<<时,如下图1,Ω是四边形,故A 正确;当12λ=时,如下图2,Ω为等腰梯形,B 正确:当314λ<<时,如下图3,Ω是五边形,C 错误;当1λ=时,Q 与1C 重合,取11A D 的中点F ,连接AF ,如下图4,由正方体的性质易得1////BM PC AF ,且=1PC AF ,截面Ω为1APC F 为菱形,其面积为112AC PF ⋅,D 正确.故选:C【题型二】截面形状的判断【典例分析】一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是()A .B .C .D .【答案】B 【分析】根据题意可知,该三棱锥为正四面体,内切球与各面相切于各个面的中心,即可判断出选项B 正确.【详解】如图所示:因为三棱锥的各棱长均相等,所以该三棱锥为正四面体,内切球与各面相切于各个面的中心,即可知过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是.故选:B .【变式演练】1.如图,正四棱锥P ABCD -的高为12,AB =E ,F 分别为PA ,PC 的中点,过点B ,E ,F 的截面交PD 于点M ,截面EBFM 将四棱锥分成上下两个部分,规定BD为主视图方向,则几何体CDAB FME -的俯视图为()A .B .C .D .【答案】C 【分析】根据主视图所给方向即可知俯视图中底面正方形,计算可知M 点投影位置,即可得出答案.【详解】研究平面DPB ,设AC 与BD 的交点为O ,BM 与EF 交点为N,,E F 为,PA PC 的中点,N ∴为PO 的中点,12PO =,6ON OB ∴==,又因为12tan 26PO PDB OD ∠===,过点M 作MG DB ⊥,设GB x =,45NBO ∠=︒ ,GB MG x ∴==,又12DB = ,12DG x ∴=-,tan 212xPDB x∠==-,8x GB ∴==,DG ∴为4个格,GB 为8个格,故选:C 2.用一个平面去截正方体,所得截面不.可能是()A .直角三角形B .直角梯形C .正五边形D .正六边形【答案】ABC 【分析】根据正方体的几何特征,我们可分别画出用一个平面去截正方体得到的几何体的图形,然后逐一与四个答案中的图形进行比照,即可判断选项.【详解】当截面为三角形时,可能出现正三角形,但不可能出现直角三角形;截面为四边形时,可能出现矩形,平行四边形,等腰梯形,但不可能出现直角梯形;当截面为五边形时,不可能出现正五边形;截面为六边形时,可能出现正六边形,故选:ABC.3.在正方体1AC 中,M 为AB 中点,N 为BC 中点,P 为线段1CC 上一动点(不含C )过M 、N 、P 与正方体的截面记为α,则下面三个判断,其中正确判断的序号有______.①当P 为1CC 中点时,截面α为六边形;②当112CP CC <时,截面α为五边形;③当截面α为四边形时,它一定是等腰梯形;【答案】①③.【分析】①延长MN 交AD 于M ',交CD 于N ',延长N P '交11C D 于T ,取11A D 的中点S ,连接M S '交1AA 于P ',连接11,AC A C ,结合图形即可判断;②延长MN 交AD 于M ',交CD 于N ',连接1N D '交1CC 于P ,连接1M D '交1AA 于P ',此时截面α为五边形,求出1CPCC 即可判断;③当截面α为四边形时,点P 与点1C 重合,判断四边形11A MNC 的形状即可.【详解】解:如图①,延长MN 交AD 于M ',交CD 于N ',延长N P '交11C D 于T ,取11A D 的中点S ,连接M S '交1AA 于P ',连接11,AC A C ,因为M 为AB 中点,N 为BC 中点,所以MN AC ∕∕,同理11ST A C ∕∕,又因11AC A C ∕∕,所以ST MN ∕∕,同理,SP PN MP PT ''∕∕∕∕,所以,,,,,S T P N M P '共面,此时六边形STPNMP '为截面α,所以截面α为六边形;故①正确;如图②,延长MN 交AD 于M ',交CD 于N ',连接1N D '交1CC 于P ,连接1M D '交1AA 于P ',此时截面α为五边形因为11CD C D ∕∕,所以11CPN C PD ' ∽,所以11112CP CN C P C D '==,即113CP CC =,所以当113CP CC ≤时,截面α为五边形;故②错误;当截面α为四边形时,点P 与点1C 重合,如图,由①得,11MN A C ∕∕,所以四边形11A MNC 即为截面α,设正方体的棱长为1,则12NC =,12MA =,所以11NC MA =,所以四边形11A MNC 是等腰梯形;故③正确.故答案为:①③.【题型三】平行关系确定截面【典例分析】在三棱锥A BCD -中,AB CD a ==,截面MNPQ 与AB ,CD 都平行,则截面MNPQ 的周长等于()A .2aB .4aC .aD .无法确定【答案】A 【分析】由线面平行的性质定理确定截面MNPQ 的形状,再利用三角形相似的性质求截面MNPQ 的周长.【详解】设AMk CM=,因为//AB 平面MNPQ ,平面ABC 平面MNPQ MN =,AB Ì平面ABC ,所以//MN AB ,同理可得//PQ AB ,//MQ CD ,//NP CD ,故四边形MNPQ 为平行四边形,所以11MN PQ AB AB k ==+,1MQ NP k CD CD k==+.因为AB CD a ==,所以1aMN PQ k ==+,1ak MQ NP k==+,所以四边形MNPQ 的周长为2211aak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭.故选:A.【变式演练】1.在正方体1111ABCD A B C D -中,与AC 平行,且过正方体三个顶点的截面是___________和___________.【答案】平面11AC D 平面11A C B【分析】根据题意,结合图形,得出与AC 平行,且过正方体三个顶点的截面是平面11AC D ,平面11A C B .【详解】解:在正方体1111ABCD A B C D -中,与AC 平行,且过正方体三个顶点的截面是平面11AC D ,平面11A C B .11//AA CC ,11AA CC =,∴四边形11ACC A 是平行四边形;11//AC A C ∴,又AC ⊂/平面11AC D ,11AC ⊂平面11ACD ,//AC ∴平面11AC D ;同理//AC 平面11A C B .故答案为:平面11AC D ,平面11A CB .2.若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有()A .0条B .1条C .2条D .4条【答案】C 【分析】由平行四边形的性质有两对边平行且相等,再应用线面平行的判定可确定线面平行,由线面平行的性质、判定即可知有几条棱与平面α平行.【详解】如下图示,若平面α即为面HEGF 为平行四边形,即//HE FG 且HE FG =,//EG HF 且EG HF =,又HE ⊂面ACD ,FG ⊄面ACD ,则//FG 面ACD ,而FG ⊂面ABD ,面ABD ⋂面ACD AD =,∴//FG AD ,由线面平行判定易知://AD 平面α;同理可得//EG BC ,易得//BC 平面α.∴该三棱锥与平面α平行的棱有AD 、BC ,共2条.故选:C3.如图是一个以 A 1B 1C 1为底面的直三棱柱被一平面所截得的几何体,截面为 ABC .已知AA 1=4,BB 1=2,CC 1=3.在边AB 上是否存在一点O ,使得OC ∥平面A 1B 1C 1.【答案】存在【分析】取AB 的中点O ,连接OC ,可证明11//,OD CC OD CC =,即四边形ODC 1C 是平行四边形,所以OC ∥C 1D ,由线线平行证明线面平行,即得证【详解】存在,取AB 的中点O ,连接OC ,作OD ∥AA 1交A 1B 1于点D ,连接C 1D ,则OD ∥BB 1∥CC 1.因为O 是AB 的中点,所以OD=12(AA 1+BB 1)=3=CC 1,则四边形ODC 1C 是平行四边形,所以OC ∥C 1D.又C 1D ⊂平面C B 1A 1,且OC ⊄平面C 1B 1A 1,所以OC ∥平面A 1B 1C 1.即在边AB 上存在一点O ,使得OC ∥平面A 1B 1C 1.【题型四】垂直关系确定的截面【典例分析】已知正三棱柱(底面为正三角形的直棱柱)111ABC A B C -的体积为AB =D 是11B C 的中点,点P 是线段1A D 上的动点,过BC 且与AP 垂直的截面α与AP 交于点E ,则三棱锥P BCE -的体积的最小值为A 2B .32C .2D .52【答案】A 【分析】由正三棱柱111ABC A B C -的体积为AB =12AA =,由于P ABC P BCE A BCE V V V ---==+,所以要使三棱锥P BCE -的体积最小,则三棱锥E ABC -的体积最大,设BC 的中点为F ,作出截面如图所示,可得点E 在以AF 为直径的圆上,从而可求出点E 到底面ABC 距离的最大值,进而可求得三棱锥P BCE -的体积的最小值【详解】如图所示,因为正三棱柱111ABC A B C -的体积为AB =(214AA ⨯⨯=,即12AA =,因为(21234P ABC P BCE A BCE V V V ---=⨯⨯=+,所以要使三棱锥P BCE -的体积最小,则三棱锥E ABC -的体积最大,设BC 的中点为F ,作出截面如图所示,因为AP α⊥,所以AE EF ⊥,所以点E 在以AF 为直径的圆上,所以点E 到底面ABC 1322=,所以三棱锥P BCE -的体积的最小值为(21332-⨯⨯=.故选:A.【变式演练】1.如图,ABCD A B C D ''''-为正方体,任作平面α与对角线AC '垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l ,则()A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值【答案】B【分析】将正方体切去两个正三棱锥'A A BD -与'''C D B C -后,得到一个以平行平面'A BD 与''D B C 为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱''A B 剪开,展开在一个平面上,得到一个平行四边形''11A B B A ,考查'E 的位置,确定,S l【详解】解:将正方体切去两个正三棱锥'A A BD -与'''C D B C -后,得到一个以平行平面'A BD 与''D B C 为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱''A B 剪开,展开在一个平面上,得到一个平行四边形''11A B B A ,如图所示而多边形W 的周界展开后便成为一条与'1A A 平行的线段(如图中'1E E ),显然,''11E E A A =,所以l 为定值,当'E 位于''A B 中点时,多边形W 为正六边形,而当'E 称到'A 时,W 为正三角形,则当周长这定值l 的正六22,所以S 不是定值,故选:B 2.正方体1111ABCD A B C D -,的棱长为4,已知1AC ⊥平面α,1AC β⊂,则关于α、β截此正方体所得截面的判断正确的是()A .α截得的截面形状可能为正三角形B .1AA 与截面αC .α截得的截面形状可能为正六边形D .β截得的截面形状可能为正方形【答案】ABC【分析】首先根据已知条件确定截面,αβ,然后根据选项依次判断正误即可.【详解】如图因为正方体1111ABCD A B C D -∴AC BD ⊥,1BD CC ⊥,又∵1AC CC C = ∴BD ⊥平面11ACC A 又∵1AC ⊂平面11ACC A ∴1AC BD ⊥同理:11AC A D ⊥又∵1A D BD D ⋂=∴1AC ⊥平面1A BD ∴平面α可以是平面1A BD ,又因为11A D BD A B ==∴1A BD 为等边三角形,故A 正确取111111,,,,,A D D D CD CB BB A B 的中点,,,,,E G P K H F 并依次连接易知11=2EG A D ∥,因为EG ⊄平面1A BD ,1A D ⊂平面1A BD ∴=EG ∥平面1A BD 同理:GP 平面1A BD 又因为EG GP G = 且EG ⊂平面EGPKHF ,GP ⊂平面EGPKHF ∴平面EGPKHF ∥平面1A BD ∴平面α可以是平面EGPKHF ∵=EG GP PK KH HF FE ====∴六边形EGPKHF 是正六边形,故C 正确以平面α是平面1A BD 为例计算:设A 到平面1A BD 的距离为h等体积法求距离∵11A A BD A ABD V V --=,∴111133A BD ABD h S AA S ⋅⋅=⋅⋅又因为11=2A BD S ⨯ ,1=44=82ABD S ⨯⨯∴=3h 则1AA 与平面1A BD所成角的正弦值为1=3h AAB 正确对于D 选项:由于直线1AC β⊂,在正方体上任取点但异于1,A C ,与1,A C 可构成平面β,但是截面的形状都不是正方形,故D 错误故选:ABC3.已知正方体1111ABCD A B C D -的棱长为2,M 为1AA 的中点,平面α过点1D 且与CM 垂直,则()A .CM BD⊥B .//BD 平面αC .平面1//C BD 平面αD .平面α截正方体所得的截面面积为92【答案】ABD【分析】分析出BD ⊥面ACM ,可判断选项A ;取AD 的中点E ,由平面几何知识可知,1DM D E ⊥,从而判断出CM ⊥面11B D EF ,即平面α截正方体所得的截面为梯形11B D EF ,从而可判断剩余的三个选项.【详解】连接AC ,则AC BD ⊥,又因为BD AM ⊥,AC AM A ⊥=,所以BD ⊥面ACM ,又因为CM ⊂面ACM ,所以BD ⊥CM ,故选项A 正确;取AD 的中点E ,AB 的中点F ,连接1D F ,EF ,1B F ,DM ,11B D ,在正方形11ADD A 中,由平面几何知识可知,1DM D E ⊥,又因为1CD D E ⊥,CD DM D ⋂=,所以1D E ⊥面CDM ,所以1D E CM ⊥,又因为BD ⊥CM ,所以11B D CM ⊥,又因为1111D E B D D ⋂=,所以CM ⊥面11B D EF ,即平面α截正方体所得的截面为梯形11B D EF ,所以显然//BD 平面α,选项B 正确;平面1C BD 与平面α不平行,选项C 错误;在梯形11B D EF 中,11B D =EF =11B F D E ==所以梯形的高为2,所以梯形11B D EF 的面积为92,即平面α截正方体所得的截面面积为92,故选项D 正确.故选:ABD.【题型五】求截面周长【典例分析】如图,在正方体1111ABCD A B C D -中,4AB =,E 为棱BC 的中点,F 为棱11A D 的四等分点(靠近点1D ),过点,,A E F 作该正方体的截面,则该截面的周长是___________.【分析】首先根据面面平行的性质定理作出过点,,A E F 的正方体的截面,从而求截面的周长.【详解】如图,取11C D 的中点H ,取1CC 上靠近点1C 的三等分点G ,连接,,,,AE EG GH HF FA ,易证//,//AE HF AF EG ,则五边形AEGHF 为所求截面.因为4AB =,所以111182,3,1,3BE CE C H D H A F D F CG =======,143C G =则103AE EG ==,5,GH HF AF ===故该截面的周长是AE EG GH HF AF ++++【变式演练】1.正三棱柱ABC ﹣A 1B 1C 1中,所有棱长均为2,点E ,F 分别为棱BB 1,A 1C 1的中点,若过点A ,E ,F 作一截面,则截面的周长为()A .B .C .D .2【答案】B【分析】根据题意先作出截面,进而算出截面各边的长度,最后得到答案.【详解】如图,在正三棱柱111ABC A B C -中,延长AF 与CC 1的延长线交于M ,连接EM 交B 1C 1于P ,连接FP ,则四边形AEPF 为所求截面.过E 作EN 平行于BC 交CC 1于N ,则N 为线段CC 1的中点,由1MFC 相似于MAC △可得MC 1=2,由1MPC △相似于MEN 可得:111242,2333PC PC B P =⇒==,在1Rt AA F 中,112,1AA A F ==,则AF ==,在Rt ABE △中,2,1AB BE ==,则AE ==1Rt B EP 中,1121,3B E B P ==,则PE =在1C FP 中,11141,,603C F C P FC P ==∠=︒,由余弦定理:2224413121cos 60339PF ⎛⎫=+-⨯⨯⨯︒= ⎪⎝⎭,则PF ==故选:B.2.已知在棱长为6的正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是棱C 1D 1,B 1C 1的中点,过A ,E ,F 三点作该正方体的截面,则截面的周长为________.【答案】【分析】根据正方体的性质作出截面图形,进而算出周长.【详解】如图,延长EF ,A 1B 1,相交于点M ,连接AM ,交BB 1于点H ,延长FE ,A 1D 1,相交于点N ,连接AN ,交DD 1于点G ,连接FH ,EG ,可得截面为五边形AHFEG .因为ABCD -A 1B 1C 1D 1是棱长为6的正方体,且E ,F 分别是棱C1D 1,B 1C 1的中点,由中位线定理易得:EF =AG =AH =EG=FH AH +HF +EF +EG +AG =故答案为:+3.已知直三棱柱111ABC A B C -的侧棱长为2,AB BC ⊥,2AB BC ==.过AB 、1BB 的中点E 、F 作平面α与平面11AA C C 垂直,则所得截面周长为()A .+B C .D .【答案】C【分析】确定平面α与各棱的交点位置,计算出截面各边边长,由此可得出所得截面周长.【详解】如下图所示,取AC 的中点J ,连接BJ ,取AJ 的D ,连接DE ,取11A C 的中点K ,连接KJ 、1B K ,AB BC = ,J 为AC 的中点,则BJ AC ⊥,1AA ⊥ 平面ABC ,BJ ⊂平面ABC ,1BJ AA ∴⊥,1AC AA A ⋂=,BJ ∴⊥平面11AA C C ,D Q 、E 分别为AJ 、AB 的中点,则//DE BJ 且12DE BJ =,DE ∴⊥平面11AA C C ,DE ⊂ 平面DEF ,所以,平面DEF ⊥平面11AA C C ,所以,平面α即为平面DEF ,设平面α交11B C 于点I ,在直棱柱111ABC A B C -中,11//AA CC 且11AA CC =,所以,四边形11AA C C 为平行四边形,11//AC A C ∴且11AC A C =,J 、K 分别为AC 、11A C 的中点,1//AJ A K 且1AJ A K =,所以,四边形1AA KJ 为平行四边形,1//KJ AA ∴且1KJ AA =,11//BB AA 且11BB AA =,1//KJ BB ∴且1KJ BB =,所以,四边形1BB KJ 为平行四边形,//DE BJ ,DE ⊄平面1BB KJ ,BJ ⊂平面1BB KJ ,//DE ∴平面1BB KJ ,设平面α 平面1BB KJ FG =,DE ⊂ 平面α,所以,//DE FG ,//FG BJ ∴,//BF GJ ,所以,四边形BFGJ 为平行四边形,可得11122GJ BF BB KJ ===,所以,G 为KJ 的中点,延长DG 交11A C 于点H ,//DJ KH ,所以,DJG HKG ∠=∠,JDG KHG ∠=∠,又JG KG = ,所以,DJG HKG ≅△△,11122HK DJ AJ KC ∴===,H ∴为1KC 的中点,因为平面//ABC 平面111A B C ,平面α 平面ABC DE =,平面α 平面111A B C IH =,//DE IH ∴,//DE BJ ,1//BJ B K ,//DE IH ,1//IH B K ∴,I ∴为11B C 的中点,AB BC ⊥,2AB BC ==,则AC ==J 为AC的中点,12BJ AC ∴==122DE BJ ==,同理2IH =,因为直棱柱111ABC A B C -的棱长为2,F 为1BB 的中点,1112BF BB ∴==,由勾股定理可得EF ==IF =,1//KJ BB 且12KJ BB ==,1BB ⊥平面ABC ,KJ ∴⊥平面ABC ,AC ⊂ 平面ABC ,KJ AC ∴⊥,G 、D 分别为KJ 、AJ 的中点,则112GJ KJ ==,122DJ AJ ==,由勾股定理可得DG,同理GH =因此,截面的周长为22DE IH EF IF DH ++++=++.故选:C.【题型六】求截面面积【典例分析】已知正四棱柱1111ABCD A B C D -中,1124BE BB ==,143AB AA =,则该四棱柱被过点1A ,C ,E 的平面截得的截面面积为______.【答案】【分析】在1DD 上取点F ,使得12D F =,连接1,A F CF ,则四边形1A ECF 是平行四边形,由勾股定理可得11,,A E CE A C ,再结合余弦定理与面积公式即可求解【详解】由题意,正四棱柱1111ABCD A B C D -中,1124BE BB ==,143AB AA =,可得1118,2AA BB CC BE ====,在1DD 上取点F ,使得12D F =,连接1,A F CF ,则有11,//A F CE A F CE =,所以四边形1A ECF是平行四边形,由勾股定理可得11A E CE A C ======所以2221111cos 210A E CE A C A EC A E CE +-∠==-⨯,所以1sin 10A EC ∠=,所以四边形1A ECF 是平行四边形的面积为11sin 1210A E EC A EC ⨯⨯∠==,故答案为:【变式演练】1.正方体1111ABCD A B C D -的棱长为2,E 是棱1DD 的中点,则平面1AC E 截该正方体所得的截面面积为()A .5B .C .D .【答案】D【分析】作出示意图,设F 为1BB 的中点,连接1,,AF FC EF ,易得平面1AC E 截该正方体所得的截面为1AFC E ,再计算其面积.【详解】如图所示,设F 为1BB 的中点,连接1,AF FC ,设G 为1CC 的中点,连接,EG GB ,由//EG AB 且EG AB =,得ABGE 是平行四边形,则//AE BG 且AE BG =,又1//BG C F 且1BG C F =,得1//AE C F 且1AE C F =,则1,,,A E C F 共面,故平面1AC E 截该正方体所得的截面为1AFC E .又正方体1111ABCD A B C D -的棱长为2,11AF FC EC EA ===,1AC =EF =1EF AC ⊥,故1AFC E 的面积为12S =⨯=故选:D.2.在棱长为a 的正方体1111ABCD A B C D -中,E 为1AA 的中点,则过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面面积为()A 2B .298aC .24aD 2【答案】B【分析】取11A D 中点F ,连接BE 、EF 、1C F 、1BC 、1AD ,证明出1//EF BC ,故四点B 、1C 、E 、F 共面,所以过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面为等腰梯形1EFC B ,根据已知,即可求解.【详解】取11A D 中点F ,连接BE 、EF 、1C F 、1BC 、1AD ,因为11//AB C D 且11AB C D =,所以,四边形11ABC D 为平行四边形,所以,11//AD BC ,E 、F 分别为1AA 、11A D 的中点,所以,1//EF AD 且112EF AD a =,所以,1//EF BC ,故B 、1C 、E 、F 四点共面,所以过B 、1C 、E 三点的平面截正方体1111ABCD A B C D -所得的截面为等腰梯形1EFC B ,其中2EF a =,1BC =,12BE C F a =,过点E 、F 在平面1BC FE 内分别作1BC 的垂线,垂足点分别为G 、H ,因为1BE C F =,1EBG FC H ∠=∠,12EGB FHC π∠=∠=,所以,1Rt EBG Rt FHC ≅△△,故1BG C H =,在平面1BC FE 内,因为1EG BC ⊥,1FH BC ⊥,1//EF BC ,所以,四边形EFHG 为矩形,则GH EF a =,所以,112BC EF BG C H a -==,所以,梯形1BC FE 的高4h a ==,梯形1B CFE 的面积2192428a S a a ⎫=⨯⨯=⎪⎪⎭.故选:B.3.已知正方体1111ABCD A B C D -的棱长为2,点P 在线段1CB 上,且12B P PC =,平面α经过点1,,A P C ,则正方体1111ABCD A B C D -被平面α截得的截面为___________,其面积为___________.【答案】四边形1AECQ 【分析】第一空,先画出1,,A P C 所在平面,由平面11//AA DD 平面11BB CC 得出1//AQ EC ,1//AQ EC ,1A E C Q ,,,四点共面,即为所求截面;第二空由已知条件可求出11AE EC AC ==1AEC 的面积,再乘以2可得截面的面积.【详解】如图所示:1,,A P C 确定一个平面α,因为平面11//AA DD 平面11BB CC ,所以1//AQ EC ,同理1//AQ EC ,所以四边形1AEC Q 是平行四边形.即正方体被平面截的截面.因为12B P PC =,所以112C B CE =,即1EC EB ==所以11AE EC AC ===由余弦定理得:22211111cos 25AE EC AC AEC AE EC +-∠==⨯,所以1sin AEC ∠,所以1AEC Q S四边形1112sin 22AE EC AEC =⨯⨯⨯∠=故答案为:四边形1AEC Q。
立体几何的截面问题

立体几何的截面问题
嘿,咱来聊聊立体几何的截面问题啊!比如说,你怎么知道一个几何体被某个平面截了之后,截面会是什么形状呢?这就好像你切一块蛋糕,你能想象出不同的切法会得到什么样的切面吗?这多有意思呀!
再想想,如何找到截面与几何体各个面的交线呢?这不就像是在一个复杂的迷宫里找特定的通道一样吗?
还有哦,截面面积怎么求呢?哇,这可不是个简单的事儿呢,就像要算出一个奇形怪状的图形有多大一样难。
比如说一个三棱锥,它的截面面积能那么容易就求出来吗?
而且呀,截面问题里还常常会有最值问题呢!哎呀呀,就好像要在一堆选择里找到那个最棒的、最特别的一样,得绞尽脑汁去思考呢!
不同的几何体,截面的情况也完全不同呢!这就像不同性格的人面对同样的事情会有不同的反应,你说神奇不神奇?咱可不能小瞧了这立体几何的截面问题呀!。
《立体几何》微专题3 空间中的截面

《立体几何》微专题3 空间中的截面一、内容解析在立体几何中,截面是指用一个平面去截一个几何体(如圆柱、圆锥、球、棱柱、棱锥、长方体等)所得的平面图形.高考中涉及空间几何体截面的地方较多,如:判断截面图形的形状,判断截面与其他直线(平面)的位置关系,计算截面的边长、周长和面积(或者求相关几何体的表面积、体积)等.在破解较复杂的综合问题的过程中,要把握好“定位”、“定形”、“定量”这三个环节.首先,由已知条件作出截面与空间几何体的交线;其次,根据线面位置关系相关定理确定截面的基本特征;再次,运用平面几何的有关知识计算截面的边长、周长、面积等.其中,作出空间几何体的截面图形是解决问题的关键.现将空间几何体中截面作图的主要原理(三个公理+两个定理)梳理如下:1.三个公理ABPPA唯一的注:平面的三公理说明了三个问题:(1)平面是平的,平面是无限延展的;(2)要确定两平面交线,可以找两个两平面的交点;(3)确定一个平面的4种方法.【应用举例】如图所示,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.(1)过点G及AC;(2)过三点E,F,D1.【分析】我们可以将截面与空间几何体表面的交集(交线)叫做截线,将截面与空间几何体的棱的交集(交点)叫做截点.本题的关键在于确定截点,有了位于多面体同一表面上的两个截点即可连接成截线,从而得到截面.【作法】(1)连接GA交A1D1于点M,连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.(2)连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.2.两个定理则过这条直线的任一平面与此平面的交【应用举例】(1)在三棱锥P-ABC中,G为△PAC的重心,过点G作三棱锥的截面α,使其平行于PB 和AC,请画出截面α与三棱锥表面的交线.【分析】若截面α与PB和AC平行,则交线分别与PB和AC中的一条平行.【作法】如图,过G作EF∥AC,分别交PA,PC于点E,F,过点F作FM∥PB交BC于点M,过点E作EN∥PB交AB于点N,连接MN,可知EN∥FM,所以E、F、M、N四点共面,且MN∥AC∥EF,EN∥PB∥FM,则EF,FM,MN,EN即为截面α与三棱锥表面的交线.(2)如图,一个四面体木块ABCD,在△ABC的面内有一点P,过点P作一个截面α,使其垂直于直线AD,请画出截面α与四面体表面的交线.【分析】若截面α与AD垂直,则交线与AD垂直.由于在平面ABD和平面ACD内垂直于AD的直线有无数条,故根据面面平行的性质定理,可采用平移法,先作出AD的一个垂面,再平移至点P.【作法】如图,在AD上任取异于A,D的一点Q,过点Q分别在平面ABD和平面ACD 内作QR⊥AD,QS⊥AD,分别交AB,AC于R,S两点.连接RS,过点P在平面ABC内作EF∥RS交AB,AC于E,F两点.过F在平面ACD内作FG∥SQ交AD于G,连接EG,可先证明平面QRS∥平面EFG,再由面面平行的性质定理证明RQ∥EG,从而可证直线AD垂直于平面EFG,则EF,FG,GE即为截面α与四面体表面的交线.【注】截面问题中与平行有关的定理不仅可以用于在截面作图的过程中确定截面的交线,还可以判断截面图形的形状.有关线面、面面垂直的定理在解题时主要用于确定截面的位置关系,故不再专门列出.通过上述分析,可以将空间几何体中截面作图方法小结如下:① 若已知两点在同一平面内,只要连接这两点,就可以得到截面与多面体的一个面的截线; ② 若面上只有一个已知点,应设法在同一平面内再找出第二个确定的点; ③ 若已知两个点分别在两个相邻的面上,应找出这两个平面的交线与截面的交点; ④ 若所做截面要求与多面体的某一条棱平行,则由一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行的性质,可得截面与平面的交线; ⑤ 若两平行平面中的一个平面与截面有交线,另一个面上只有一个已知点,则由平行平面与第三个平面相交,那么它们的交线互相平行的性质,可得截面与平面的交线; ⑥ 若有一个点在面上而不在棱上,则可通过作辅助平面转化为棱上的点的问题;同理,若已知点在体内,则可通过辅助平面使它转化为面上的点,再转化为棱上的点的问题来解决.下面以正方体为例,列举其基本斜截面图形如下(横截面和竖截面均为正方形): ① 三角形(锐角三角形) (等腰三角形) (等边三角形)注:可以分别用反证法和余弦定理证明,不可能出现直角三角形和钝角三角形截面. ② 四边形(梯形) (平行四边形) (菱形) (矩形) 注:可以用反证法证明,不可能出现直角梯形截面. ③ 五边形1A1A1A1A1A1A1A(普通五边形)注:可以用反证法证明,不可能出现正五边形截面. ④ 六边形(普通六边形) (正六边形)其他空间多面体和旋转体的截面也可以类似作出,并进行分类研究. 二、典型例题题型一、判断截面图形的形状例1 过正方体ABCD -A 1B 1C 1D 1的棱AB ,BC 的中点E ,F 作一个截面使截面与底面所成的角为45o ,则此截面的形状为( )A .三角形或五边形B .三角形或六边形C .六边形D .三角形 【分析】此题中可以直接去找与底面成45o 角的截面,也可以找一些特殊位置的截面,通过计算其与底面所成角得出所求截面的相对位置,体现了运动变化的动态探究. 【答案】B 【解析】如图,显然,本题中的截面有两个,其中一个与线段B 1B 相交,截面为三角形,故只需判断另一个截面的位置和形状.111A1A A连接BD 交EF 于G ,设上下底面中心分别为O 1,O ,设过点D 1的截面与底面的所成角为α,易得tan α=tan ∠D 1GD =223<1, 故α<45o ;设过棱A 1C 1的截面与底面的所成角为β,易得tan β=tan ∠O 1GO =22>1,故α>45o , 故所求截面应与A 1D 1,C 1D 1都相交(不过其端点),为六边形. 故选B .【注】若截面与棱D 1D 相交,则截面为五边形;若截面与棱A 1D 1,C 1D 1都相交(不过其端点),则截面为六边形;若截面与棱A 1B 1,B 1C 1都相交(不过点B 1),则截面为四边形.题型二、判断截面与其他直线(平面)的位置关系例2 如图,在下列三个正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 均为所在棱的中点,过E ,F ,G 作正方体的截面.在各正方体中,直线BD 1与平面EFG 的位置关系描述正确的是( )① ② ③ A . BD 1∥平面EFG 的有且只有①;BD 1⊥平面EFG 的有且只有② B . BD 1∥平面EFG 的有且只有②;BD 1⊥平面EFG 的有且只有① C . BD 1∥平面EFG 的有且只有①;BD 1⊥平面EFG 的有且只有②③ D . BD 1∥平面EFG 的有且只有②;BD 1⊥平面EFG 的有且只有③【分析】无论是线面位置关系,还是面面位置关系,归根结底都应转化为对线线位置关系的探求.在判断截面与其他直线(平面)的位置关系的问题中,可以借助截面图形中现有的直线探寻位置关系,也可以将截面进行延展,作出与空间几何体的交线,通过交线(也可以是截面中的其他直线)探寻位置关系. 【答案】C【解析】若从图①研究起,取A 1D 1中点H ,通过截面EFHG 与对角面BDD 1B 1平行,可得BD 1∥面EFG ,从而排除B ,D 选项;1A1A1A若从图②研究起,可通过证明BD 1⊥EF ,BD 1⊥EG ,得证BD 1⊥平面EFG ,从而排除B ,D 选项;对比A ,C 选项,只需考查图③对应的结论:取AA 1中点M ,连EM ,FM ,仿图②,可证BD 1⊥平面EFM ,故BD 1⊥EF ;类似可证得BD 1⊥GF (BD 1⊥EG ) .从而BD 1⊥平面EFG ,排除A . 故选C .题型三、计算截面的面积和周长例3 有一正三棱柱(底面为正三角形的直棱柱)木料ABC -A 1B 1C 1,各棱长都为2.已知O 1,O 2分别为上,下底面的中心,M 为O 1O 2的中点,过A ,B ,M 三点的截面把该木料截成两部分,则截面面积为( )A . 7B . 1639C . 3194D . 2【分析】本题中构造截面并发现截面的特征是解决问题的关键,而构造截面的过程需运用面面平行的性质定理. 【答案】 B【解析】如图,在正三棱柱ABC -A 1B 1C 1中,各棱长都为2,M 为O 1O 2的中点, 由面面平行的性质定理,可知过A ,B ,M 三点的截面为等腰梯形ABEF , 则EF =13A 1B 1=23,梯形的高为PD =22+(233)2=433,则截面面积为S =12×(23+2)×433=1639. 故选B .例4 已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 为CC 1的中点,若AM ⊥平面α,且B ∈平面α,则平面α截正方体所得截面的周长为( )1AA . 32+2 5B . 4+4 2C . 22+2 5D . 6 2【分析】本题中构造与AM 垂直的截面是解决问题的关键,而构造截面的过程需运用线面垂直的判定定理(定义)和面面平行的性质定理. 【答案】A【解析】如图,取BB 1中点N ,A 1B 1中点E ,连接MN ,AN ,BE ,可证AM ⊥面DBE , 由面面平行的性质定理可知截面α与正方体的上下底面的交线平行.由E 为A 1B 1中点可取A 1D 1中点F ,则α即为截面BEFD ,易求周长为32+25,故选A .三、反馈练习A 组(一)单选题:1.截一个几何体,所得各截面都是圆面,则这个几何体一定是( )A. 圆柱B. 圆锥C. 球D. 圆台【答案】C【解析】A.圆柱的轴截面是一个矩形,此选项错误; B.圆锥的轴截面是一个三角形,此选项错误; C.球的截面是一个圆面,此选项正确; D.圆台的轴截面一个梯形,此选项错误. 故选C .2.如图,在四棱锥P -ABCD 中,AD 与BC 相交.若平面α截此四棱锥得到的截面是一个平行四边形,则这样的平面α的个数是( )A .不存在B .恰有1个C .恰有5个D .有无数个1A【答案】D【解析】 在平面ABCD 中作直线MN ∥AB ,交AD 、BC 于点M 、N ,在平面PAB 中作EF ∥AB ,交PA 、PB 于点E 、F ,使MN =EF ,由线面平行的性质定理可知四边形EFNM 为平行四边形,这样的平行四边形显然可以做无数个,且平行四边形所在平面即为所求的平面α. 故选D .(二)多选题:3. (多选题)过正方体中心的截面图形可以是( )A .三角形B .四边形C .五边形D .六边形 【答案】BD【解析】过正方体中心的截面图形至少与正方体的四个面相交,所以不可能是三角形.又因为截面是五边形时不过正方体的中心.过正方体一面上相邻两边的中点及正方体的中心的截面形状为正六边形. 故答案为BD .4.(多选题)用一个平面截正四面体,下列结论中正确的是( ) A .正四面体的截面不可能是正方形; B .正四面体的截面可能是等腰梯形; C .正四面体的截面可能是直角三角形;D .若正四面体的截面是三角形,一定是等腰三角形. 【答案】BC【解析】利用正四面体的性质,分析4个选项,取正四面体各条棱的中点连接而成的截面图形是正方形,故选项A 错误;当截面只与正四面体对棱中的一条平行时,截面为等腰梯形,故选项B 正确;对于选项C 、D ,正四面体的截面可以是三角形,但不一定为等腰三角形,A如下图,过点A 作AO ⊥平面BCD ,要构造截面直角三角形APQ ,只需先在底面BCD 内构造直角三角形OPQ ,故选项C 正确,选项D 错误,故答案为BC .(三)填空题:5.过正方体ABCD -A 1B 1C 1D 1的顶点A 1,C 1,B 的平面与底面ABCD 所在的平面的交线为l ,则l 与A 1C 1的位置关系是________. 【答案】平行【解析】由于平面ABCD ∥平面A 1B 1C 1D 1,平面A 1B 1C 1D 1∩平面A 1C 1B =A 1C 1,平面ABCD ∩平面A 1C 1B =l ,所以l ∥A 1C 1.6.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,平面α与正方体每条棱所成的角均相等,则平面α截正方体所形成的三角形截面中,截面面积的最大值为_____________;平面α与正方体每条棱所成的角的正弦值为_____________. 【答案】32,33 【解析】如图,在正方体ABCD -A 1B 1C 1D 1中,与A 1B 1,A 1D 1, A 1A 平行的直线各有4条, ∵A 1B 1=A 1D 1=A 1A ,∴三棱锥A 1-AB 1D 1是正三棱锥,∴A 1B 1,A 1D 1,A 1A 与平面AB 1D 1所成角相等,∴与正方体的12条棱所在直线所成角均相等的一个平面α是平面A 1BD 1(或平面AB 1C 或平面ACD 1),且截面面积最大,1A由棱长为1,故AB 1=2,再由三角形AB 1D 1为正三角形,其面积为34×(2)2=32,故答案为32. 由顶点A 1到平面AB 1D 1的距离为体对角线的13,则平面α与正方体每条棱所成的角的正弦值为33a a =33.(四)解答题:7.如图所示,在正方体ABCD −A 1B 1C 1D 1中,试作出过AC 且与直线D 1B 平行的截面,并说明理由.【解答】如图,连接DB 交AC 于点O ,取D 1D 的中点M ,连接MA ,MC ,MO ,则截面MAC 即为所求作的截面.证明:∵MO 为△D 1DB 的中位线,∴D 1B ∥MO .∵D 1B ⊄平面MAC ,MO ⊂平面MAC ,∴D 1B ∥平面MAC ,则截面MAC 为过AC 且与直线D 1B 平行的截面.8.下图表示以AB =4,BC =3的矩形ABCD 为底面的长方体被一平面斜截所得的几何体,其中四边形EFGH 为截面.已知AE =5,BF =8,CG =12,1A A1A(1)截面四边形EFGH 是否为菱形?证明你的结论;(2) 求DH 的长. 【解答】(1)截面EFGH 为菱形.证明如下:∵平面ABFE ∥平面DCGH ,且平面EFGH 分别截平面ABFE 与平面DCGH 得直线EF 与直线GH ,∴EF ∥GH .同理,FG ∥EH ,∴四边形EFGH 为平行四边形.又∵EF 2=AB 2+(BF -AE )2=25,FG 2=BC 2+(CG -BF )2=25,∴EF =FG =5, ∴四边形EFGH 为菱形.(2) ∵几何体是长方体被一平面斜截所得的,∴AE +CG =BF +DH ,将AE =5,BF =8,CG =12代入得,DH 的长为9.B 组填空题:9.各面均为等边三角形的四面体ABCD 的外接球的表面积为12π,过棱AB 作球的截面,则截面面积的最小值为________. 【答案】2π【解析】根据题意,球的半径为3,面积最小的截面是以AB 为直径的截面,将四面体ABCD 放置于正方体中,可得正方体的外接球就是四面体ABCD 的外接球,设AB =a ,则△ABC 的外接圆半径为32a ×23=33a ,可求得三棱锥的高为a 2-13a 2=63a 2,则63a -32+33a 2=32,解得a =2,进而截面面积的最小值为π×22=2π.故答案为2π.10.如图,已知球O 是棱长为1的正方体ABCD -A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为________.AE【答案】π6 【解析】根据题意知,平面ACD 1是边长为2的正三角形,且球与以点D 为公共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积,则由上图得,△ACD 1内切圆的半径是22×tan30o =66, 则所求的截面圆的面积是π×(66)2=π6.故答案为66.11. 如图,正方体ABCD -A 1B 1C 1D 1的棱长为a ,动点P 在对角线BD 1上,过点P 作垂直于BD 1的平面γ,记这样得到的截面多边形(含三角形)的周长为y ,设BP=x ,则当x ∈[33a ,233 a ]时,函数y=f (x )的值域为________.【答案】{32a } 【解析】1AA1A如图,当x ∈[33a ,233 a ]时,截面多边形为六边形HIJKLM , 设11111B I HIA CBC λ==,则11111C I IJ B C B C λ==-,故HI+IJ=2a 为定值,从而截面多边形(含三角形)的周长为32a .12.如图,在四面体ABCD 中,AB =CD =2,AC =BD =3,AD =BC =5,E ,F 分别是AD ,BC 的中点.若用一个与直线EF 垂直,且与四面体的每个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积的最大值为________.【答案】62 【解析】将四面体补成长、宽、高分别为3,2,1的长方体,如图,∵EF ⊥α,∴截面为平行四边形MNKL ,可得KL +KN =5,G 1A ABGHDA设异面直线BC 与AD 所成的角为θ,则sin θ=sin ∠HFB =sin ∠LKN ,可得sin θ=265, S MNKL =NK ·KL sin ∠NKL ≤62(NK +KL 2)2=62,当且仅当KL =KN 时取等号,故该多边形截面面积的最大值为62.四、真题再现1. (2015全国2文 19)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16,BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说明画法和理由); (Ⅱ)求平面α把该长方体分成的两部分体积的比值. 【解答】(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作EM ⊥AB ,垂足为M ,则AM =A 1E =4,EB 1=12,EM =AA 1=8.因为EHGF 为正方形,所以EH =EF =BC =10.于是MH =EH 2-EM 2=6,AH =10,HB =6. 因为长方形被平面α分成两个高为10的直棱柱,所以其体积的比值为97(79也正确).2. (2016年全国1文 11)平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α∥平面CB 1D 1,α∩平面ABCD =m ,α∩平面ABB 1A 1=n ,则m ,n 所成角的正弦值为A .32 B .22 C .33 D .13【答案】A1A AAA 1【解析】因为过点A 的平面α与平面CB 1D 1平行,平面ABCD ∥平面A 1B 1C 1D 1,所以m ∥B 1D 1∥BD ,又A 1B ∥平面CB 1D 1,所以n ∥A 1B ,则BD 与A 1B 所成的角为所求角,所以m ,n 所成角的正弦值为32,选A .3. (2018全国1理 12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A .334B .233C .324D .32【答案】A【解析】记该正方体为ABCD -A'B'C'D',正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱A'A ,A'B',A'D'与平面α所成的角都相等,如图,连接AB',AD',B'D',因为三棱锥A'-AB'D'是正三棱锥,所以A'A ,A'B',A'D'与平面AB'D'所成的角都相等,分别取C'D',B'C',BB',AB ,AD ,DD'的中点E ,F ,G ,H ,I ,J ,连接EF ,FG .GH ,IH ,IJ ,IE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面AB'D'平行,且截正方体所得截面的面积最大,又EF =FG =GH =IH =IJ =JE =22,所以该正六边形的面积为6×34×(23)2=334,所以α截此正方体所得截面面积的最大值为334,故选A .4.(2019全国2文 16)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)【答案】26,2-1.【解析】如图,依题意知,题中的半正多面体的上、下、左、右、前、后6个面都在正方体的表面上,且该半正多面体的表面由18个正方形,8个正三角形组成,故该半正多面体共有18+8=26个面,或者逐层计算得8+8+8+2=26个面.关注到该半正多面体的俯视图(或水平截面、竖直截面)的轮廓是一个正八边形,设该半正多面体的棱长为x,则x+22x+22x=1,解得x=2-1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体接于一个球,过这个球的球心作一平面,则截面图形不可能...是( )分析 考虑过球心的平面在转动过中,平面在球的接正方体上截得的截面不可能是大圆的接正方形,故选D 。
例2 如图,在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器灌进一些水,固定容器底面一边BC 于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:① 水的部分始终呈棱柱状; ② 水面EFGH 的面积不改变; ③ 棱A 1D 1始终与水面EFGH 平行;④ 当容器倾斜到如图5(2)时,BE·BF 是定值; 其中正确的命题序号是______________分析 当长方体容器绕BC 边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BC BF BE V ⋅⋅=21水是定值,又BC 是定值,所以BE·BF 是定值,即④正确。
所以正确的序号为①③④. 例3 有一容积为1 立方单位的正方体容器ABCD-A 1B 1C 1D 1,在棱AB 、BB 1及对角线B 1C 的中点各有一小孔E 、F 、G ,若此容器可以任意放置,则该容器可装水的最大容积是( )A .21 B .87 C .1211 D .4847 分析 本题很容易认为当水面是过E 、F 、G 三点的截面时容器可装水的容积最大图(1),最大值为8712121211=⋅⋅⋅-=V 立方单位,这是一种错误的解法,错误原因是对题中“容器是可以任意放置”的理解不够,其实,当水平面调整为图(2)△EB 1C 时容器的容积最大,最大容积为1211112121311=⋅⋅⋅⋅-=V ,故选C 。
例4 正四棱锥P ABCD -的底面正方形边长是3,O 是P 在底面上的射影,6, PO Q =是 AC 上的一点,过Q 且与, PA BD 都平行的截面为五边形EFGHL ,求该截面面积的最大值.解:如图,连接, AC BD ,设截面与正四棱锥P ABCD -的底面相交于EL ,AC 与EL 相交于Q 点,由//BD 截面EFGHL 得//LE BD , //AP 截面EFGHL ,得//AP QG ,那么,EL 必定分别与, AB AD 相交于, E L ,否则,截面将是三角形,则//AP EF ,//AP LH ,在正四棱锥P ABCD -中,BD AP ⊥,由//, //, LE BD AP QG GQE ∠是异面直线BD 与PA 所成角,则QG EL ⊥,所以,GFEQ 和GHLQ 是两个全等的直角梯形.设:()03, AE x x AP =<<== 由//AP EF得393EF x-=,故)3EF x =-,而AQ =,由//AP QG得9QG =,于是16x QG ⎫=-⎪⎭,从而:)()221992139292644EFGHL x S x x x x ⎫=⨯-+-=-+=--+⎪⎭ 所以,当2x =时,截面EFGHL 的面积取得最大值9.基本方法介绍①公理法:用平面基本性质中的公理来作平面; ②侧面展开法:将立体图形展开为平面图形进行研究;例5 能否用一个平面去截一个正方体,使得截面为五边形?进一步,截面能否为正五边形呢?解:如图所示,我们可以用一个平面截一个正方体1111ABCD A B C D -,使得截面为一个凸五边形.点I 是1B B 延长线上一点,使得112IB BB =,E 为11A D 的中点,F 为1AA 上的点,使得113AF A F =.则截面1C EFGH 为过直线EF 与1C I (这里1//EF C I )的平面与正方体1111ABCD A B C D -相截所得的凸五边形截面.用一个平面去截一个正方体所得截面不能是一个正五边形.事实上,若截面可以为一个正五边形,则此五边形的五条边分属于此正方体的五个不同的面.我们将正方体的每两个相对的面作为一个抽屉,则上述包含正五边形的边的五个面中,必有两个面为相对的平面,它们是平行的,利用平行平面的性质,可知此五边形中有两条边是平行的.但是正五边形的五条边是彼此不平行的,矛盾.例6 已知一个平面截一个棱长为1的正方体所得的截面是一个六边形(如图所示),证明:此六边形的周长≥证明:如图,我们将正方形的各个面依次展开,从正方形''PQQ P 出发,依次为'''''''''''',,,,,.PP Q Q Q QRR Q R S P R S SR S SPP PSRQ从上述展开图可知截面六边形的周长大于等于'AA ,而'AA ==.一、单选题1.【省市2019-2020学年高二上学期期末数学】在正方体1111ABCD A B C D -中,F 为AD 的中点,E 为棱1D D 上的动点(不包括端点),过点,,B E F 的平面截正方体所得的截面的形状不可能是( ) A .四边形 B .等腰梯形C .五边形D .六边形【答案】D【解析】不妨设正方体的棱长为1,当102DE <≤,截面为四边形BMEF ; 如图特别的,当12DE =时,截面为等腰梯形1BFEC ;如图112DE <<截面为五边形BFENM ,不可能为六边形.如图故选:D2.【2020届省实验中学、八中、二十四中、一中、东北育才学校高三上学期期末】如图圆锥PO ,轴截面P AB 是边长为2的等边三角形,过底面圆心O 作平行于母线P A 的平面,与圆锥侧面的交线是以E 为顶点的抛物线的一部分,则该抛物线的焦点到其顶点E 的距离为( )A .1B .12C .13D .14【答案】D 【解析】过底面圆心O 作平行于母线P A 的平面,与圆锥侧面的交线是以E 为顶点的抛物线的一部分,PA ⊆平面PAB, 平面PAB 与圆锥的侧面交于OE, 所以OE||PA. 因为OA=OB ,所以OE=1=OC, 因为OP ⊥底面ABC,所以OP ⊥OC, 因为OC ⊥OE,OP,OE ⊆平面PAB,OP∩OE=0, 所以OC ⊥平面PAB,所以OC ⊥OB.在平面CED 建立直角坐标系.设抛物线的方程为22(0)y px p =>, 1(1,1),12,2C p p ∴=∴=, 所以该抛物线的焦点到其顶点E 的距离为1.4故选:D3.一个棱长为2的正方体被一个平面截去一部分后,剩余部分的三视图如图,则该截面的面积是( )A B C D【答案】A【解析】由三视图可知几何体是正方体在一个角上截去一个三棱锥, 其截面是等腰三角形ABC ,如下图:由于正方体的棱长为2,所以AC BC AB ===,所以AB 12=ABC S ∆,故选:A .4.如图,在正方体1111ABCD A B C D -中,点E ,F ,G 分别是棱AB ,BC ,1BB 的中点,过E ,F ,G 三点作该正方体的截面,则下列说法错误的是( )A .在平面11BDDB 存在直线与平面EFG 平行 B .在平面11BDD B 存在直线与平面EFG 垂直C .平面1//AB C 平面EFGD .直线1AB 与EF 所成角为45︒ 【答案】D【解析】由线面平行判定定理可得,当O 为BD 的中点时,1B O ∥平面EFG , 由线面垂直判定定理可得,1BD ⊥平面EFG ,选项A ,B 都对.因为1EG AB ∥,1FG B C ∥,所以平面EFG ∥平面1AB C ,选项C 正确, 易得:EFAC ,1AB C ∆为等边三角形,故直线1AB 与AC 所成角为60︒,即直线1AB 与EF 所成角为60︒,故D 不正确, 故选:D.5.【省市2019-2020学年高三下学期1月月考数学】某同学在参加《通用技术》实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为(球心与正方体的中心重合),若其中一个截面圆的周长为4π,则该球的半径是( )A .2B .4C .D .【答案】B【解析】设截面圆半径为r ,球的半径为R ,则球心到某一截面的距离为正方体棱长的一半即截面圆的周长可得42r ππ=,得2r ,故由题意知(222R r =+,即(222216R =+=,所以4R =,故选:B .6.美学四大构件是:史诗、音乐、造型(绘画、建筑等)和数学.素描是学习绘画的必要一步,它包括了明暗素描和结构素描,而学习几何体结构素描是学习素描最重要的一步.某中学2018级某同学在画“切面圆柱体”(用与圆柱底面不平行的平面去截圆柱,底面与截面之间的部分叫做切面圆柱体)的过程中,发现“切面”是一个椭圆,若“切面”所在平面与底面成45︒角,则该椭圆的离心率为( )A .12B .2C .2D .13【答案】B【解析】设圆柱的底面半径为r ,椭圆的长轴为2a ,短轴为2b ,则22b r =,22cos 45222r b a a ︒===,即2b a =,故离心率2c e a ====.故选:B. 7.如图,已知三棱锥V ABC -,点P 是VA 的中点,且2AC =,4VB =,过点P 作一个截面,使截面平行于VB 和AC ,则截面的周长为( )A .12B .10C .8D .6【答案】D 【解析】如图所示,设AB 、BC 、VC 的中点分别为D,E,F ,连接PD,DE,EF,PF. 由题得PD||VB,DE||AC,因为,PD DE ⊆平面DEFP,VB,AC 不在平面DEFP , 所以VB||平面DEFP,AC||平面DEFP, 所以截面DEFP 就是所作的平面.由于11||,||,,22PD VB EF VB PD VB EF VB ===, 所以四边形DEFP 是平行四边形, 因为VB=4,AC=2,所以PD=FE=2,DE=PF=1, 所以截面DEFP 的周长为2+2+1+1=6.故选:D8.【2020届省市高三期末调研测试理科数学试题】已知球O 是正四面体A BCD -的外接球,2BC =,点E 在线段BD 上,且3BD BE =,过点E 作球O 的截面,则所得截面圆面积的最小值是( ) A .89π B .1118πC .512π D .49π 【答案】A【解析】由题,设平面α为过E 的球O 的截面,则当OE ⊥平面α时,截面积最小, 设截面半径为r ,球的半径为R ,则222r R d =-,因为正四面体棱长为a ,设过点A 垂直于平面BCD 的直线交平面BCD 于点M ,则DM =,令AM h =,OM x =,则x h R =-,在Rt AMD 中,222AM DM AD +=,即222h a ⎫+=⎪⎪⎝⎭,则h =,在Rt OMD 中,222DM OM R +=,即222x R ⎫+=⎪⎪⎝⎭,则22213a R R ⎫+-=⎪⎪⎝⎭,解得4R a =,则3412x a a a =-=, 在Rt OED △中,222OE OM EM =+,因为点E 在线段BD 上,3BD BE =,设BC 中点为N ,则2DM MN =, 所以211333EM BN BC a ===,在Rt OED △中,222OE OM EM =+,即222211112372d a a a ⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭,所以22221124729r a a a ⎛⎫=-= ⎪ ⎪⎝⎭,因为2a BC ==, 所以289r =,所以截面面积为289S r ππ==, 故选:A9.【2020届省市高三适应性练习卷数学理科试题】在三棱锥P ABC -中,PA ⊥底面ABC ,,6,8AB AC AB AC ⊥==,D 是线段AC 上一点,且3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上,过点D 作球O 的截面,若所得截面圆的面积的最大值与最小值之差为16π,则球O 的表面积为( ) A .72π B .86πC .112πD .128π【答案】C【解析】将三棱锥P ABC -补成直三棱柱,且三棱锥和该直三棱柱的外接球都是球O , 记三角形ABC 的中心为1O ,设球的半径为R ,2PA x =, 则球心O 到平面ABC 的距离为x ,即1OO x =, 连接1O A ,则15O A =,∴2225R x =+.在ABC 中,取AC 的中点为E ,连接11,O D O E , 则1132O E AB ==,124DE AC ==,所以1O D =.在1Rt OO D 中,OD , 由题意得到当截面与直线OD 垂直时,截面面积最小, 设此时截面圆的半径为r ,则()22222251312r R OD x x =-=+-+=,所以最小截面圆的面积为12π,当截面过球心时,截面面积最大为2R π, 所以21216R π-π=π,228R =, 球的表面积为2112R 4π=π. 故选:C.10.【2020届南开中学高三第五次教学质量检测考试数学文科试题】正三棱锥P ABC -,Q 为BC 中点, PA =,2AB =,过Q 的平面截三棱锥P ABC -的外接球所得截面的面积围为( ) A .13,45ππ⎡⎤⎢⎥⎣⎦B .12,23ππ⎡⎤⎢⎥⎣⎦C .[],2ππD .3,2ππ⎡⎤⎢⎥⎣⎦【答案】D【解析】因为正三棱锥P ABC -,PB PC PA ===2AC BC AB ===,所以222PB PA AB +=,即PB PA ⊥,同理PB PC ⊥,PC PA ⊥, 因此正三棱锥P ABC -可看作正方体的一角,如图,记正方体的体对角线的中点为O ,由正方体结构特征可得,O 点即是正方体的外接球球心,所以点O 也是正三棱锥P ABC -外接球的球心,记外接球半径为R ,则R ==,因为球的最大截面圆为过球心的圆, 所以过Q 的平面截三棱锥P ABC -的外接球所得截面的面积最大为2max 32S R ππ==;又Q 为BC 中点,由正方体结构特征可得122OQ PA ==;由球的结构特征可知,当OQ 垂直于过Q 的截面时,截面圆半径最小为1r ==,所以2min S r ππ==.因此,过Q 的平面截三棱锥P ABC -的外接球所得截面的面积围为3,2ππ⎡⎤⎢⎥⎣⎦.故选:D.11.一个三棱锥的各棱长均相等,其部有一个切球,即球与三梭锥的各面均相切(球在三棱锥的部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面是下列图形中的()A.B.C.D.【答案】C【解析】其空间结构体如下图所示:易知截面是一个非等边的等腰三角形,排除A.D;等腰三角形的底边是正三棱锥的一条,这条棱不可能与切球有交点,所以排除B;截面所得等腰三角形的两条腰正好是正三棱锥两个面的中线,且经过切球在两个面上的切点,所以正确答案是C . 故选:C12.【2020届省部分重点中学高三第二次联考数学试卷理科试题】如图,已知四面体ABCD 的各条棱长均等于4,E ,F 分别是棱AD 、BC 的中点.若用一个与直线EF 垂直,且与四面体的每一个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为( )A .B .4C .D .6【答案】B【解析】将正四面体补成正方体如图,可得EF ⊥平面CHBG ,且正方形边长为由于EF α⊥,故截面为平行四边形MNKL ,且4KL KN +=, 又//KL BC ,//KN AD ,且AD BC ⊥, ∴KN KL ⊥, ∴MNKLSKN KL =⋅242KN KL +⎛⎫≤= ⎪⎝⎭,当且仅当2KL KN ==时取等号,故选:B .13.【2020届省实验中学、八中、二十四中、一中、东北育才学校高三上学期期末】仿照“Dandelin 双球”模型,人们借助圆柱的两个切球完美的证明了平面截圆柱的截面为椭圆面.如图,底面半径为1的圆柱两个切球球心距离为4,现用与两球都相切的平面截圆柱所得到的截面边缘线是一椭圆,则该椭圆的离心率为( )A .12B .3C .2D .2【答案】D【解析】画出图形的轴截面如图所示,则CD 为椭圆的长轴,圆柱的底面直径为椭圆的短轴;依题意4AB =,2CG =,1AE BF ==,则122AO AB == 1sin 2AE AOE AO ∴∠==30AOE ∴∠=︒60GCO ∴∠=︒ 在Rt CDG ∆中有1cos 2CG GCO CD ∠== 4CD ∴=即椭圆中,24a =,22b =2a ∴=,1b =222c a b =-c ∴=c e a ==D14.已知正方体1111ABCD A B C D -的边长为2,边AB 的中点为M ,过M 且垂直1BD 的平面被正方体所截的截面面积为( )A B C .D .【答案】A【解析】如图,连结111,,,AC CB AB BC ,易知11CB BC ⊥,111CB D C ⊥,又1111BC D C C ⋂=,则1CB ⊥平面11BC D ,故11CB BD ⊥,同理可证明CA ⊥平面1BDD ,则1CA BD ⊥,又1CACB C =,故1BD ⊥平面1ACB .取BC 的中点E ,1BB 的中点F ,易知平面//MEF 平面1ACB , 所以1BD ⊥平面MEF ,即MEF 为所求截面.易知MEF 为正三角形,边长ME ==故12MEFS==故选:A.15.在棱长为2的正方体1111ABCD A B C D -中,P ,Q ,R 分别是AB ,AD ,11B C 的中点,设过P ,Q ,R 的截面与面11ADD A ,以及面11ABB A 的交线分别为l ,m ,则l ,m 所成的角为( )A .90︒B .30C .45︒D .60︒【答案】D【解析】因为,在正方体1111ABCD A B C D -中,P ,Q ,R 分别是AB ,AD ,11B C 的中点,取11C D ,1DD ,1BB 的中点分别为G ,F ,E ,连接FG , FQ ,QP ,PE ,ER ,RG ,根据正方体的特征,易知,若连接PG ,EF ,RQ ,则这三条线必相交于正方体的中心,又////GR EF QP ,所以P ,Q ,R ,G ,F ,E 六点必共面,即为过P ,Q ,R 的截面;所以EP 即为直线m ,FQ 即为直线l ;连接1AB ,1AD ,11B D ,因为1//EP AB ,1//FQ AD , 所以11B AD ∠即为异面直线EP 与FQ 所成的角,又因为正方体的各面对角线都相等,所以11AB D 为等边三角形, 因此1160B AD ∠=︒.故选:D.16.在立体几何中,用一个平面去截一个几何体得到的平面图形叫截面,如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点E 、F 分别是棱B 1B 、B 1C 中点,点G 是棱CC 1的中点,则过线段AG 且平行于平面A 1EF 的截面图形为( )A .矩形B .三角形C .正方形D .等腰梯形【答案】D【解析】取BC 的中点H ,如图连接AH 、GH 、1D G 、1AD ,由题意得://GH EF ,1//AH A F ,GH 不在平面1A EF ,EF ⊆平面1A EF ,∴||GH 平面1A EF .AH 不在平面1A EF ,1A F ⊆平面1A EF ,∴||AH 平面1A EF .GHAH H =,,GH AH ⊆平面1AHGD ,∴平面1//AHGD 平面1A EF ,过线段AG 且平行于平面AEF 的截面图形为等腰梯形1AHGD . 故选:D .17.【2020届省吕梁市高三上学期第一次模拟考试数学(理)试题】如图四面体A BCD -中,2,AD BC AD BC ==⊥,截面四边形EFGH 满足//EF BC ;//FG AD ,则下列结论正确的个数为( )①四边形EFGH 的周长为定值 ②四边形EFGH 的面积为定值 ③四边形EFGH 为矩形④四边形EFGH 的面积有最大值1A .0B .1C .2D .3【答案】D【解析】因为//EF BC EF ⊄,平面BCD ,所以//EF 平面BCD ,又平面EFGH 平面BDC GH =,所以//EF GH .同理//FG EH ,所以四边形EFGH 为平行四边形, 又AD BC ⊥,所以四边形EFGH 为矩形.所以③是正确的;由相似三角形的性质得EF AF FC FGBC AC AC AD==,, 所以EF FG AF FCBC AD AC AC+=+,2BC AD ==,所以2EF FG +=, 所以四边形EFGH 的周长为定值4,所以①是正确的;212EFGHEF FG S EF FG ⨯⎛⎫=⨯≤= ⎪⎝⎭,所以四边形EFGH 的面积有最大值1,所以④是正确的.因为①③④正确.故选:D18.【2018年全国普通高等学校招生统一考试理科数学(新课标I 卷)】已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为A B C D【答案】A【解析】首先利用正方体的棱是3组每组有互相平行的4条棱,所以与12条棱所成角相等,只需与从同一个顶点出发的三条棱所成角相等即可,从而判断出面的位置,截正方体所得的截面为一个正六边形,且边长是面的对角线的一半,应用面积公式求得结果. 【解析】根据相互平行的直线与平面所成的角是相等的, 所以在正方体1111ABCD A B C D -中,平面11AB D 与线11111,,AA A B A D 所成的角是相等的,所以平面11AB D 与正方体的每条棱所在的直线所成角都是相等的, 同理平面1C BD 也满足与正方体的每条棱所在的直线所成角都是相等, 要求截面面积最大,则截面的位置为夹在两个面11AB D 与1C BD 中间的,且过棱的中点的正六边形,且边长为2,所以其面积为26(2S ==,故选A. 19.【省江市2019-2020学年高二上学期期末数学(文)试题】已知正三棱锥A BCD -的外接球是球O ,正三棱锥底边3BC =,侧棱AB =E 在线段BD 上,且BE DE =,过点E 作球O 的截面,则所得截面圆面积的取值围是( )A .9,34ππ⎡⎤⎢⎥⎣⎦B .[]2,3ππC .11,44ππ⎡⎤⎢⎥⎣⎦D .9,44ππ⎡⎤⎢⎥⎣⎦【答案】D 【解析】如图,由题,设BCD 的中心为1O ,球O 的半径为R ,连接11,,,O D OD O E OE ,则123sin33O D π=⨯=13AO ==,在1Rt OO D 中,()2223R R =+-,解得2R =,所以111OO AO R =-=, 因为BE DE =,所以32=DE ,在1DEO 中,1O E ==所以OE ==,过点E 作球O 的截面,当截面与OE 垂直时,截面的面积最小,32=,则截面面积为23924ππ⎛⎫⨯= ⎪⎝⎭,当截面过球心时,截面面积最大,最大面积为4π, 故选:D20.【省市2019-2020学年高三第一次教学质量检测数学文科试题】在四面体ABCD 中,3AB BD AD CD ====,4AC BC ==,用平行于AB ,CD 的平面截此四面体,得到截面四边形EFGH ,则四边形EFGH 面积的最大值为( ) A .43B .94C .92D .3【答案】B【解析】设截面分别与棱,,,AD BD BC AC 交于点,,,E F G H .由直线//AB 平面EFGH , 且平面ABC平面EFGH GH =,平面ABD ⋂平面EFGH EF =得//GH AB ,//EF AB ,所以//GH EF ,同理可证//EH FG ,所以四边形EFGH 为平行四边形, 又3AB BD AD CD ====,4AC BC ==, 可证得AB CD ⊥,四边形EFGH 为矩形.设:::BF BD BG BC FG CD x ===,01x <<,则3FG x =,()31HG x =-,于是2199(1)9,0124EFGH S FG HG x x x x ⎛⎫=⋅=-=--+<< ⎪⎝⎭当12x =时,四边形EFGH 的面积有最大值94. 故选:B. 二、填空题21.【省市2019-2020学年高三上学期期末考试数学试题】已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC ,6PA =,AB =2AC =,4BC =,则:(1)球O 的表面积为__________;(2)若D 是BC 的中点,过点D 作球O 的截面,则截面面积的最小值是__________. 【答案】52π 4π【解析】(1)由题,根据勾股定理可得AC AB ⊥,则可将三棱锥P ABC -可放入以,,AP AC AB 为长方体的长,宽,高的长方体中,则体对角线为外接球直径,即2r ==则r =,所以球的表面积为224452r πππ=⨯=;(2)由题,因为Rt ABC ,所以D 为底面ABC 的外接圆圆心,当DO ⊥截面时,截面面积最小,即截面为平面ABC ,则外接圆半径为2,故截面面积为224ππ⨯=故答案为:(1)52π;(2)4π22.【维吾尔自治区乌鲁木齐市2019-2020学年高三第一次诊断性测试数学文试题】 如图,已知正方体1111ABCD A B C D -的棱长为2,E 、F 、G 分别为11,,AB AD B C 的中点,给出下列命题:①异面直线EF 与AG 所成的角的余弦值为6;②过点E 、F 、G 作正方体的截面,所得的截面的面积是 ③1A C ⊥平面EFG④三棱锥C EFG -的体积为1其中正确的命题是_____________(填写所有正确的序号) 【答案】①③④【解析】取11C D 的中点为点H ,连接GH 、AH ,如图1所示,因为//EF GH ,所以AGH ∠就是异面直线EF 与AG 所成的角易知在AGH 中,3,AG AH GH ===,所以2cos 36AGH ∠==,①正确;图1 图2 图3矩形EFGH 即为过点E 、F 、G 所得正方体的截面,如图2所示,易知EF EG ==所以EFGH S ==分别以DA 、DC 、DD 1为x 轴、y 轴、z 轴建立如图3所示直角坐标系,则(2,0,2),(2,1,0),A E(1,0,0),(1,2,2)F G ,1(2,2,2),(1,1,0),(1,1,2)AC FE EG =--==-, 因为110,0AC FE AC EG ⋅=⋅=,所以11,A C EF A C EG ⊥⊥,又EF ⊂平面EFG , EG ⊂平面EFG 且EFEG E =,所以1A C ⊥平面EFG ,故③正确134(111212)22EFCS=-⨯⨯+⨯+⨯=,1113G ECF EFCV SC C -=⋅=,④正确.故答案为:①③④23.如图所示,在长方体1111ABCD A B C D -中,点E 是棱1CC 上的一个动点,若平面1BED 交棱1AA 于点F ,给出下列命题:①四棱锥11B BED F -的体积恒为定值;②对于棱1CC 上任意一点E ,在棱AD 上均有相应的点G ,使得//CG 平面1EBD ;③O 为底面ABCD 对角线AC 和BD 的交点,在棱1DD 上存在点H ,使//OH 平面1EBD ; ④存在唯一的点E ,使得截面四边形1BED F 的周长取得最小值. 其中为真命题的是____________________.(填写所有正确答案的序号)【答案】①③④ 【解析】①111111112B BED F B BED B BFD B BED V V V V ----=+=,又三棱锥11B BED -为三棱锥11E BB D -,则底面11BB D 不变,且因为1//CC 平面11BB D ,故点E 到底面11BB D 的距离即三棱锥11E BB D -底面的高不变,故三棱锥11E BB D -的体积不变,所以四棱锥11B BED F -的体积不变,恒为定值,故①正确;②当点E 在点C 处时,总有CG 与平面1EBD 相交,故②错误; ③由O 为底面ABCD 对角线AC 和BD 的交点,则12DO DB =,设H 为1DD 的中点,则在1D DB 中1//OH D B ,所以//OH 平面1EBD ,故③正确;④四边形1BED F 的周长为()012C BE ED =+,则分析1BE ED +即可,将矩形11BCC B 沿着1CC 展开使得B 在DC 延长线上时,此时B 的位置设为P ,则线段1D P 与1CC 的交点即为截面平行四边形1BED F 的周长取得最小值时唯一点E ,故④正确; 故答案为:①③④24.【2020届省市高三上学期期末数学(文科)试题】在棱长为2的正方体1111ABCD A B C D -中,E 是正方形11BB C C 的中心,M 为11C D 的中点,过1A M 的平面α与直线DE 垂直,则平面α截正方体1111ABCD A B C D -所得的截面面积为______.【答案】【解析】如图,在正方体1111ABCD A B C D -中,记AB 的中点为N ,连接1,,MC CN NA , 则平面1A MCN 即为平面α.证明如下: 由正方体的性质可知,1A MNC ,则1A ,,,M CN N 四点共面,记1CC 的中点为F ,连接DF ,易证DF MC ⊥.连接EF ,则EF MC ⊥, 所以MC ⊥平面DEF ,则DE MC ⊥. 同理可证,DE NC ⊥,NCMC C =,则DE ⊥平面1A MCN ,所以平面1A MCN 即平面α,且四边形1A MCN 即平面α截正方体1111ABCD A B C D -所得的截面. 因为正方体的棱长为2,易知四边形1A MCN 是菱形,其对角线1AC =MN =12S =⨯=故答案为:三、解答题25.【2015年全国普通高等学校招生统一考试文科数学(新课标Ⅱ带解析)】如图,长方体1111ABCD A B C D -中,116,10,8AB BC AA ===,点,E F 分别在1111,A B D C 上,114A E D F ==,过点,E F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由); (2)求平面α把该长方体分成的两部分体积的比值. 【解析】(1)交线围成的正方形EHGF 如图:(2)作垂足为M,则18EM AA ==,,,因为EHGF 是正方形,所以,于是因为长方体被平面α分成两个高为10的直棱柱,其底面积之比为9:7, 所以其体积比值为97(79也正确).。
