大学物理第11章习题课选讲例题
《大学物理》11磁场习题解析共141页文档

25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
《大学物理》11磁场习题解 析
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。Байду номын сангаас—培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
大学物理-第11章小结与习题课

c
d
B 0 nI
电场、磁场中典型结论的比较
电荷均匀分布 长直线 电流均匀分布
E 2 0 r
E0
0 I B 2r
B0
长 直 圆 柱 面
长 直 圆 柱 体
内 外
内 外
E 2 0 r r E 2 0 R 2 E 2 0 r
0 I B 2r 0 Ir B 2R 2 0 I B 2r
o r nI
,
磁场强度H=
nI
.
7.将流过强度为I=1000 A电流的直导线置于匀强磁场 中,且垂直磁力线。若磁感应强度B=1T,磁场作用在 长度为L=1 m的一段导线上的力F为
1000N
.
F BIL
8.质量为m、电量为q的粒子具有动能E,垂直磁力线
方向飞入磁感应强度为B的匀强电场中,当该粒子越出
磁力线闭合、 无自由磁荷 磁场是无源场
1.一运动电荷q,质量m,以初速度 V0 进入均匀磁场 中,若 V0 与磁场的方向夹角为 ,则
A、其动能改变,动量不变. B、其动能和动量都改变. C、其动能不变,动量改变. D、其动能、动量都不变.
[ C
]
2. 有一个半径为 R 的单匝圆线圈,通以电流 I ,若 将该导线弯成 匝数 N = 2 的平面圆线圈,导线长度 不变,并通以同样的电流,则线圈中心的磁感应强 度和线圈的磁矩分别是原来的 (A) 4倍和 1 / 8 , (B) 4倍和 1 / 2 , (C) 2倍和 1 / 4 , (D) 2倍和 1 / 2 。
/4
方法二: 在稳恒磁场中,一个与磁场方向垂直放置的闭 合线圈所受的合力为零。 与直线电流ab所受的力大小相等,方向相反。
F 2BIR
大学物理 磁学习题课

( I 1 I 2 ) ln 2
第11章 恒定电流的磁场
17
MN上电流元I3dx所受磁力:
0 I1
a M
dx N
c I2
d F I 3 B d x I 3 [ 2(r x) 2(2r x) ] d x
r
0 I1
I3 r Or b
r d
x
F I3 [
0
0 I1
2(r x)
0I2
2(2r x)
]d x
0I3
S
B
圆面
Φm
2 B S BR cos
1 B d S B R 2 2
n
60°
R
B
任意曲面
S
S
很多漏掉负号 类似本页二.1(1)磁通量
12
第11章 恒定电流的磁场
P42 一选择1.
H dl 2 I L1
H dl I L2
1
第11章 恒定电流的磁场
16
P44 二1、如图所示,载有电流I1和I2的长直导线ab和cd相互平行,相距为
3r,今有载有电流I3的导线MN = r,水平放置,且其两端MN分别与I1、I2 的距离都是r,ab、cd和MN共面,求导线MN所受的磁力大小和方向.
载流导线MN上任一点处的磁 感强度大小为: I 0 I 2 0 1 I1 B 2( r x ) 2( 2r x )
1
B
•直导线延长线上
a
第11章 恒定电流的磁场
P
6
2.
圆电流轴线上某点的磁场
B
大小:
《大学物理》(下2010.12.9)习题课

第11章光的量子效应及光子理论一、 选择题1. 金属的光电效应的红限依赖于: 【 C 】(A)入射光的频率; (B)入射光的强度;(C)金属的逸出功; (D)入射光的频率和金属的逸出功。
2. 已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是U 0(使电子从金属逸出需做功eU 0),则此单色光的波长λ必须满足: 【 A 】hceU )D (;hceU )C (;eU hc )B (;eU hc)A (0≥≤≥≤λλλλ 3. 关于光电效应有下列说法:(1) 任何波长的可见光照射到任何金属表面都能产生光电效应;(2) 对同一金属如有光电子产生,则入射光的频率不同,光电子的初动能不同; (3) 对同一金属由于入射光的波长不同,单位时间内产生的光电子的数目不同; (4) 对同一金属,若入射光频率不变而强度增加一倍,则饱和光电流也增加一倍。
其中正确的是: 【 D 】(A) (1),(2),(3); (B) (2),(3),(4); (C) (2),(3); (D)(2),(4)二、填空题1. 当波长为300 nm 光照射在某金属表面时,光电子的能量范围从0到.J 100.419-⨯在作上述光电效应实验时遏止电压为V 5.2U a =;此金属的红限频率Hz 104140⨯=ν。
2. 频率为100MHz 的一个光子的能量是J 1063.626-⨯,动量的大小是s N 1021.234⋅⨯-。
3. 如果入射光的波长从400nm 变到300nm ,则从表面发射的光电子的遏止电势增大(增大、减小)V 03.1U =∆。
4. 某一波长的X 光经物质散射后,其散射光中包含波长大于X 光和波长等于X 光的两种成分,其中大于X 光波长的散射成分称为康普顿散射。
三、计算题1. 已知钾的红限波长为558 nm ,求它的逸出功。
如果用波长为400 nm 的入射光照射,试求光电子的最大动能和遏止电压。
由光电方程2m mv 21A h +=ν,逸出功0h A ν=,0chA λ=,eV 23.2A =用波长为400nm 的入射光照射,光电子的最大动能:A h mv 212m -=ν A chE km -=λ,将nm 400=λ和eV 23.2A =代入得到:eV 88.0E km =遏止电压:a 2m eU mv 21=,2m a mv e21U =,V 88.0U a = 2. 从铝中移出一个电子需要4.2 eV 的能量,今有波长为200 nm 的光投射至铝表面。
大学物理课后习题答案(第十一章) 北京邮电大学出版社

习题十一11-1 圆柱形电容器内、外导体截面半径分别为1R 和2R (1R <2R ),中间充满介电常数为ε的电介质.当两极板间的电压随时间的变化k t U =d d 时(k 为常数),求介质内距圆柱轴线为r 处的位移电流密度.解:圆柱形电容器电容12ln 2R R l C πε= 12ln 2R R lU CU q πε== 1212ln ln 22R R r U R R r lU S q D εππε=== ∴ 12ln R R r k t D j ε=∂∂=11-2 试证:平行板电容器的位移电流可写成t U C I d d d =.式中C 为电容器的电容,U 是电容器两极板的电势差.如果不是平板电容器,以上关系还适用吗?解:∵ CU q = S CU D ==0σ ∴ CU DS D ==Φ不是平板电容器时0σ=D 仍成立 ∴ t UC ID d d =还适用.题11-3图11-3 如题11-3图所示,电荷+q 以速度v向O 点运动,+q 到O 点的距离为x ,在O 点处作半径为a 的圆平面,圆平面与v 垂直.求:通过此圆的位移电流.解:如题11-3图所示,当q 离平面x 时,通过圆平面的电位移通量 )1(222a x x q D +-=Φ[此结果见习题8-9(3)] t U C t I D D d d d d ==Φ∴ 23222)(2d d a x v qa tI D D +==Φ 题11-4图11-4 如题11-4图所示,设平行板电容器内各点的交变电场强度E =720sin t π510V ·m -1,正方向规定如图.试求:(1)电容器中的位移电流密度;(2)电容器内距中心联线r =10-2m 的一点P ,当t =0和t =51021-⨯s 时磁场强度的大小及方向(不考虑传导电流产生的磁场).解:(1)t Dj D ∂∂=,E D 0ε= ∴ t t t t E j D ππεπεε50550010cos 10720)10sin 720(⨯=∂∂=∂∂=2m A -⋅ (2)∵ ⎰∑⎰⋅+=⋅)(0d d S D l S j I l H取与极板平行且以中心连线为圆心,半径r 的圆周r l π2=,则D j r r H 22ππ=D j r H 2=0=t 时0505106.3107202πεπε⨯=⨯⨯=r H P 1m A -⋅ 51021-⨯=t s 时,0=P H11-5 半径为R =0.10m 的两块圆板构成平行板电容器,放在真空中.今对电容器匀速充电,使两极板间电场的变化率为t Ed d =1.0×1013 V ·m -1·s -1.求两极板间的位移电流,并计算电容器内离两圆板中心联线r (r <R )处的磁感应强度Br 以及r =R 处的磁感应强度BR .解: (1)t E t D j D ∂∂=∂∂=0ε 8.22≈==R j S j I D D D πA (2)∵ S j I l H S D l d d 0⋅+=⋅⎰∑⎰取平行于极板,以两板中心联线为圆心的圆周r l π2=,则202d d 2r t E r j r H D πεππ==∴t E r H d d 20ε=t E r H B r d d 2000εμμ==当R r =时,600106.5d d 2-⨯==t E R B R εμT *11-6 一导线,截面半径为10-2m ,单位长度的电阻为3×10-3Ω·m -1,载有电流25.1 A .试计算在距导线表面很近一点的以下各量:(1)H 的大小;(2)E 在平行于导线方向上的分量;(3)垂直于导线表面的S 分量.解: (1)∵ ⎰∑=I l H d取与导线同轴的垂直于导线的圆周r l π2=,则I r H =π2 21042⨯==rI H π1m A -⋅(2)由欧姆定律微分形式 E j σ=得 21053.7/1/-⨯====IR RS S I j E σ 1m V -⋅ (3)∵H E S ⨯=,E 沿导线轴线,H 垂直于轴线 ∴S 垂直导线侧面进入导线,大小1.30==EH S 2m W -⋅*11-7 有一圆柱形导体,截面半径为a ,电阻率为ρ,载有电流0I . (1)求在导体内距轴线为r 处某点的E 的大小和方向; (2)该点H 的大小和方向; (3)该点坡印廷矢量S的大小和方向;(4)将(3)的结果与长度为l 、半径为r 的导体内消耗的能量作比较. 解:(1)电流密度S I j 00=由欧姆定律微分形式E j σ=0得2000a I j j E πρρσ===,方向与电流方向一致(2)取以导线轴为圆心,垂直于导线的平面圆周r l π2=,则 由 ⎰⎰=⋅S l S j l H d d 0可得2202a r I r H =π∴202a rI H π=,方向与电流成右螺旋 (3)∵ H E S⨯= ∴ S垂直于导线侧面而进入导线,大小为 42202a r I EH S πρ==可见,电磁波的幅射压强(包括光压)是很微弱的.。
赵近芳大学物理学第五版第十一章课后习题答案

习题1111.1选择题(1)一圆形线圈在均匀磁场中作下列运动时,哪些情况会产生感应电流()(A )沿垂直磁场方向平移;(B )以直径为轴转动,轴跟磁场垂直;(C )沿平行磁场方向平移;(D )以直径为轴转动,轴跟磁场平行。
[答案:B](2)下列哪些矢量场为保守力场()(A )静电场;(B )稳恒磁场;(C )感生电场;(D )变化的磁场。
[答案:A](3)用线圈的自感系数L 来表示载流线圈磁场能量的公式221LI W m=()(A )只适用于无限长密绕线管;(B )只适用于一个匝数很多,且密绕的螺线环;(C )只适用于单匝圆线圈;(D )适用于自感系数L 一定的任意线圈。
[答案:D](4)对于涡旋电场,下列说法不正确的是():(A )涡旋电场对电荷有作用力;(B )涡旋电场由变化的磁场产生;(C )涡旋场由电荷激发;(D )涡旋电场的电力线闭合的。
[答案:C]11.2填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时,圆环将受到。
[答案:磁力](2)产生动生电动势的非静电场力是,产生感生电动势的非静电场力是,激发感生电场的场源是。
[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为l 的金属直导线在垂直于均匀的平面内以角速度ω转动,如果转轴的位置在,这个导线上的电动势最大,数值为;如果转轴的位置在,整个导线上的电动势最小,数值为。
[答案:端点,221l B ω;中点,0]11.3一半径r =10cm 的圆形回路放在B =0.8T的均匀磁场中.回路平面与B垂直.当回路半径以恒定速率trd d =80cm/s 收缩时,求回路中感应电动势的大小.解:回路磁通2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m ΦεV 11.4一对互相垂直的相等的半圆形导线构成回路,半径R =5cm,如题11.4图所示.均匀磁场B =80×10-3T,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α当磁场在5ms内均匀降为零时,求回路中的感应电动势的大小及方向.解:取半圆形cba 法向为i,题11.4图则αΦcos 2π21B R m=同理,半圆形adc 法向为j,则αΦcos 2π22B R m=∵B 与i 夹角和B 与j夹角相等,∴︒=45α则αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV 方向与cbadc 相反,即顺时针方向.题11.5图11.5如题11.5图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -.解:作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ∴0=MeNM ε即MNMeN εε=又∵⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2dcos 0πμπε所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμM 点电势高于N 点电势,即ba ba Iv U U N M -+=-ln 20πμ题11.6图11.6如题11.6所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tId d 的变化率增大,求:(1)任一时刻线圈内所通过的磁通量;(2)线圈中的感应电动势.解:以向外磁通为正则(1)]ln [ln π2d π2d π2000da db a b Il r l r I r l r I ab b a d d m +-+=-=⎰⎰++μμμΦ(2)tI b a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε11.7如题11.7图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题11.7图解:)cos(2π02ϕωΦ+=⋅=t r B S B m∴Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε∴RBf r R I m 22π==ε11.8如题11.8图所示,长直导线通以电流I =5A,在其右方放一长方形线圈,两者共面.线圈长b =0.06m,宽a =0.04m,线圈以速度v =0.03m/s垂直于直线平移远离.求:d =0.05m时线圈中感应电动势的大小和方向.题11.8图解:AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势.DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a I vbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.111(π2-⨯=+-=+=ad d Ibv μεεεV 方向沿顺时针.11.9长度为l 的金属杆ab 以速率v在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角(如题11.9图所示),B的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.解:⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴klvt tm-=-=d d Φε即沿abcd 方向顺时针方向.题11.9图11.10一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如题11.10图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0).解:如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε;题11.10图(a)题11.10图(b)在磁场中时0d d =tΦ,0=ε;出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示.题11.11图11.11导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l磁感应强度B 平行于转轴,如图11.11所示.试求:(1)ab 两端的电势差;(2)b a ,两端哪一点电势高?解:(1)在Ob 上取dr r r +→一小段则⎰==320292d l Ob l B r rB ωωε同理⎰==302181d l Oa l B r rB ωωε∴2261)92181(l B l B Ob aO ab ωωεεε=+-=+=(2)∵0>ab ε即0<-b a U U ∴b 点电势高.题11.12图11.12如题11.12图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向.解:在金属杆上取r d 距左边直导线为r ,则ba b a Iv r r a r Iv l B v b a b a B A AB -+-=-+-=⋅⨯=⎰⎰+-lnd 211(2d )(00πμπμε ∵<AB ε∴实际上感应电动势方向从A B →,即从图中从右向左,∴ba ba Iv U AB -+=ln 0πμ题11.13图11.13磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题11.13图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.解:∵bcab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=--∴tB R acd d ]12π43[22+=ε∵0d d >tB∴0>ac ε即ε从ca →11.14半径为R的直螺线管中,有dtdB>0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题11.14图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量436π(22R R B S B m -=⋅= Φ∴tBR R i d d )436π(22--=ε∵0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题11.14图题11.15图11.15如题11.15图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题11.15图示方向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解:由⎰⎰⋅-=⋅l S tB l Ed d d d 旋知,此时旋E 以O 为中心沿逆时针方向.(1)∵ab 是直径,在ab 上处处旋E与ab 垂直∴⎰=⋅ll 0d 旋∴0=ab ε,有b a U U =(2)同理,0d >⋅=⎰l E cddc旋ε∴0<-c d U U 即dc U U >题11.16图11.16一无限长的直导线和一正方形的线圈如题11.16图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解:设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar r Ia μμΦ∴2ln π2012aI M μΦ==11.17两线圈顺串联后总自感为1.0H,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H.试求:它们之间的互感.解:∵顺串时M L L L 221++=反串联时M L L L 221-+='∴M L L 4='-15.04='-=L L M H题11.18图11.18一矩形截面的螺绕环如题11.18图所示,共有N匝.试求:(1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少?解:如题11.18图示(1)通过横截面的磁通为⎰==baabNIh r h r NI ln π2d π200μμΦ磁链abIh N N lnπ220μΦψ==∴ab h N I L lnπ220μψ==(2)∵221LI W m =∴ab h I N W m lnπ4220μ=11.19一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能.解:在R r <时20π2R I B r μ=∴4222002π82R r I B w m μμ==取r r V d π2d =(∵导线长1=l )则⎰⎰===RR m I R r r I r r w W 00204320π16π4d d 2μμπ。
大学物理第十一章习题解答

第十一章:恒定电流的磁场习题解答1.题号:40941001分值:10分如下图所示,是一段通有电流I 的圆弧形导线,它的半径为R ,对圆心的张角为θ。
求该圆弧形电流所激发的在圆心O 处的磁感强度。
解答及评分标准:在圆弧形电流中取一电流元l Id (1分),则该电流元l Id 在圆心处的磁感强度为:θπμπμd R I RIdl dB 490sin 40020==(2分) 其中θRd dl =则整段电流在圆心处的磁感强度为:θπμθπμθRI d R I dB B 44000===⎰⎰(2分)2.题号:40941002分值:10分一无限长的载流导线中部被弯成圆弧形,如图所示,圆弧形半径为cm R 3=,导线中的电流为A I 2=。
求圆弧形中心O 点的磁感应强度。
解答及评分标准:两根半无限长直电流在O 点的磁感应强度方向同为垂直图面向外,大小相等,以垂直图面向里为正向,叠加后得RI R I B πμπμ242001-=∙-= (3分) 圆弧形导线在O 点产生的磁感应强度方向垂直图面向里,大小为RI R I B 83432002μμ==(3分) 二者叠加后得 T RI R I B B B 500121081.1283-⨯=-=+=πμμ (3分) 方向垂直图面向里。
(1分)3.题号:40941003分值:10分难度系数等级:1一段导线先弯成图(a )所示形状,然后将同样长的导线再弯成图(b )所示形状。
在导线通以电流I 后,求两个图形中P 点的磁感应强度之比。
(a ) (b )解答及评分标准:图中(a )可分解为5段电流。
处于同一直线的两段电流对P 点的磁感应强度为零,其他三段在P 点的磁感应强度方向相同。
长为l 的两段在P 点的磁感应强度为 lI B πμ4201= (2分) 长为2l 的一段在P 点的磁感应强度为 l I B πμ4202=(2分) 所以lI B B B πμ22012=+= (2分) 图(b )中可分解为3段电流。
大学物理课本答案习题 第十一章习题解答

则 在O点产生的 的大小为
而 在O点产生的 的大小为
和 方向相反,大小相等.即
。
直导线 在O点产生的
。
直导线 在O点产生的
,方向垂直纸面向外。
则O点总的磁感强度大小为
方向垂直纸面向外
11-8一载有电流 的长导线弯折成如题图11-8所示的形状,CD为1/4圆弧,半径为R,圆心O在AC,EF的延长线上.求O点处磁场的场强。
原点O处的电流元 在(a,0,0)点产生的 为:
在(0,a,0)点产生的 为:
在(a, 为
11-7用两根彼此平行的长直导线将半径为R的均匀导体圆环联到电源上,如题图11-7所示,b点为切点,求O点的磁感应强度。
解:先看导体圆环,由于 和 并联,设大圆弧有电流 ,小圆弧有电流 ,必有:
任取半径,宽为d的电流环,该电流环共有电流为
该电流环在线圈中心产生的磁感强度大小为
圆心处总磁感强度大小
方向垂直纸面向外。
11-13如题图11-13所示,在顶角为 的圆锥台上密绕以线圈,共N匝,通以电流 ,绕有线圈部分的上下底半径分别为 和 .求圆锥顶O处的磁感应强度的大小.
解:只要将题11-12中的均匀密绕平面线圈沿通过中心的轴垂直上提,便与本题条件相一致,故解题思路也相似。
答:稳恒电场与静电场有相同之处,即是它们都不随时间的变化而变化,基本规律相同,并且都是位场。但稳恒电场由分布不随时间变化的电荷产生,电荷本身却在移动。
正因为建立稳恒电场的电荷分布不随时间变化,因此静电场的两条基本定理,即高斯定理和环路定理仍然适用,所以仍可引入电势的概念。
11-3一根铜导线表面涂以银层,当两端加上电压后,在铜线和银层中,电场强度是否相同?电流密度是否相同?电流强度是否相同?为什么?
赵近芳大学物理学第五版第十一章课后习题答案

习题1111.1选择题(1)一圆形线圈在均匀磁场中作下列运动时,哪些情况会产生感应电流()(A )沿垂直磁场方向平移;(B )以直径为轴转动,轴跟磁场垂直;(C )沿平行磁场方向平移;(D )以直径为轴转动,轴跟磁场平行。
[答案:B](2)下列哪些矢量场为保守力场()(A )静电场;(B )稳恒磁场;(C )感生电场;(D )变化的磁场。
[答案:A](3)用线圈的自感系数L 来表示载流线圈磁场能量的公式221LI W m=()(A )只适用于无限长密绕线管;(B )只适用于一个匝数很多,且密绕的螺线环;(C )只适用于单匝圆线圈;(D )适用于自感系数L 一定的任意线圈。
[答案:D](4)对于涡旋电场,下列说法不正确的是():(A )涡旋电场对电荷有作用力;(B )涡旋电场由变化的磁场产生;(C )涡旋场由电荷激发;(D )涡旋电场的电力线闭合的。
[答案:C]11.2填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时,圆环将受到。
[答案:磁力](2)产生动生电动势的非静电场力是,产生感生电动势的非静电场力是,激发感生电场的场源是。
[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为l 的金属直导线在垂直于均匀的平面内以角速度ω转动,如果转轴的位置在,这个导线上的电动势最大,数值为;如果转轴的位置在,整个导线上的电动势最小,数值为。
[答案:端点,221l B ω;中点,0]11.3一半径r =10cm 的圆形回路放在B =0.8T的均匀磁场中.回路平面与B垂直.当回路半径以恒定速率trd d =80cm/s 收缩时,求回路中感应电动势的大小.解:回路磁通2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m ΦεV 11.4一对互相垂直的相等的半圆形导线构成回路,半径R =5cm,如题11.4图所示.均匀磁场B =80×10-3T,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α当磁场在5ms内均匀降为零时,求回路中的感应电动势的大小及方向.解:取半圆形cba 法向为i,题11.4图则αΦcos 2π21B R m=同理,半圆形adc 法向为j,则αΦcos 2π22B R m=∵B 与i 夹角和B 与j夹角相等,∴︒=45α则αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV 方向与cbadc 相反,即顺时针方向.题11.5图11.5如题11.5图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -.解:作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ∴0=MeNM ε即MNMeN εε=又∵⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2dcos 0πμπε所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμM 点电势高于N 点电势,即ba ba Iv U U N M -+=-ln 20πμ题11.6图11.6如题11.6所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tId d 的变化率增大,求:(1)任一时刻线圈内所通过的磁通量;(2)线圈中的感应电动势.解:以向外磁通为正则(1)]ln [ln π2d π2d π2000da db a b Il r l r I r l r I ab b a d d m +-+=-=⎰⎰++μμμΦ(2)tI b a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε11.7如题11.7图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题11.7图解:)cos(2π02ϕωΦ+=⋅=t r B S B m∴Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε∴RBf r R I m 22π==ε11.8如题11.8图所示,长直导线通以电流I =5A,在其右方放一长方形线圈,两者共面.线圈长b =0.06m,宽a =0.04m,线圈以速度v =0.03m/s垂直于直线平移远离.求:d =0.05m时线圈中感应电动势的大小和方向.题11.8图解:AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势.DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a I vbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.111(π2-⨯=+-=+=ad d Ibv μεεεV 方向沿顺时针.11.9长度为l 的金属杆ab 以速率v在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角(如题11.9图所示),B的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.解:⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴klvt tm-=-=d d Φε即沿abcd 方向顺时针方向.题11.9图11.10一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如题11.10图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0).解:如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε;题11.10图(a)题11.10图(b)在磁场中时0d d =tΦ,0=ε;出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示.题11.11图11.11导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l磁感应强度B 平行于转轴,如图11.11所示.试求:(1)ab 两端的电势差;(2)b a ,两端哪一点电势高?解:(1)在Ob 上取dr r r +→一小段则⎰==320292d l Ob l B r rB ωωε同理⎰==302181d l Oa l B r rB ωωε∴2261)92181(l B l B Ob aO ab ωωεεε=+-=+=(2)∵0>ab ε即0<-b a U U ∴b 点电势高.题11.12图11.12如题11.12图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向.解:在金属杆上取r d 距左边直导线为r ,则ba b a Iv r r a r Iv l B v b a b a B A AB -+-=-+-=⋅⨯=⎰⎰+-lnd 211(2d )(00πμπμε ∵<AB ε∴实际上感应电动势方向从A B →,即从图中从右向左,∴ba ba Iv U AB -+=ln 0πμ题11.13图11.13磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题11.13图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.解:∵bcab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=--∴tB R acd d ]12π43[22+=ε∵0d d >tB∴0>ac ε即ε从ca →11.14半径为R的直螺线管中,有dtdB>0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题11.14图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量436π(22R R B S B m -=⋅= Φ∴tBR R i d d )436π(22--=ε∵0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题11.14图题11.15图11.15如题11.15图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题11.15图示方向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解:由⎰⎰⋅-=⋅l S tB l Ed d d d 旋知,此时旋E 以O 为中心沿逆时针方向.(1)∵ab 是直径,在ab 上处处旋E与ab 垂直∴⎰=⋅ll 0d 旋∴0=ab ε,有b a U U =(2)同理,0d >⋅=⎰l E cddc旋ε∴0<-c d U U 即dc U U >题11.16图11.16一无限长的直导线和一正方形的线圈如题11.16图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解:设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar r Ia μμΦ∴2ln π2012aI M μΦ==11.17两线圈顺串联后总自感为1.0H,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H.试求:它们之间的互感.解:∵顺串时M L L L 221++=反串联时M L L L 221-+='∴M L L 4='-15.04='-=L L M H题11.18图11.18一矩形截面的螺绕环如题11.18图所示,共有N匝.试求:(1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少?解:如题11.18图示(1)通过横截面的磁通为⎰==baabNIh r h r NI ln π2d π200μμΦ磁链abIh N N lnπ220μΦψ==∴ab h N I L lnπ220μψ==(2)∵221LI W m =∴ab h I N W m lnπ4220μ=11.19一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能.解:在R r <时20π2R I B r μ=∴4222002π82R r I B w m μμ==取r r V d π2d =(∵导线长1=l )则⎰⎰===RR m I R r r I r r w W 00204320π16π4d d 2μμπ。
大学物理第11章习题答案解析

第11章 电磁感应11.1 基本要求 12别感应电动势的方向。
34567一些简单情况下的磁场能量。
811.2 基本概念 1W qε=23k E :变化的磁场在其周围所激发的电场。
与静电场不同,感生电场的电场线是闭合的,所以感生电场也称有旋电场。
4变化而产生的感应电动势。
5:有使回路保持原有电流不变的性质,是回路本身的“电磁惯性”的量度。
自感系数L ://m L I N I =ψ=Φ 6L ε:当通过回路的电流发生变化时,在自身回路中所产生的感应电动势。
7M :211212M I I ψψ== 812ε:当线圈2的电流2I 发生变化时,在线圈1中所产生的感应电动势。
9m W :贮存在磁场中的能量。
自感贮存磁能:212m W LI =磁能密度m w :单位体积中贮存的磁场能量22111222m B w μH HB μ===10D d d I dt Φ=s d t∂=∂⎰DS ,位移电流并不表示有真实的电荷在空 间移动。
但是,位移电流的量纲和在激发磁场方面的作用与传导电流是一致的。
11d t∂=∂D j 11.3 基本规律 1(1)楞次定律:感生电流的磁场所产生的磁通量总是反抗回路中原磁通量的改变。
楞 次定律是判断感应电流方向的普适定则。
(2)法拉第电磁感应定律:不论什么原因使通过回路的磁通量(或磁链)发生变化,回路 中均有感应电动势产生,其大小与通过该回路的磁通量(或磁链)随时间的变化成正比,即mi d dtεΦ=-2()BBK AAi εd d ==⨯⎰⎰E l v B l ,若0i ε>,则表示电动势方向由A B →;若0i ε<,则表示电动势方向B A →3m K ls i d Φd εd d dtdt =⋅=-=-⎰⎰BE l S (对于导体回路)BK Ai εd =⎰E l (对于一段导体)4L dIεL dt=- 512212d ΨdIεM dt dt=-=- 6sd ⋅⎰D S =0VdV q ρ=⎰l d ⋅⎰E l = - s d t∂⋅∂⎰BS =0sd ⋅⎰B Sc l sd d t ∂⎛⎫⋅=+⋅ ⎪∂⎝⎭⎰⎰D H l j S11.4 学习指导学习法拉第电磁感应定律要注意,公式中的电动势是整个回路的电动势,式中负号是楞 次定律的要求,用以判断电动势的方向。
大学物理课后答案第十一章

第十一章 机械振动一、基本要求1.掌握简谐振动的基本特征,学会由牛顿定律建立一维简谐振动的微分方程,并判断其是否谐振动。
2. 掌握描述简谐运动的运动方程,理解振动位移,振)cos(0ϕω+=t A x 幅,初位相,位相,圆频率,频率,周期的物理意义。
能根据给出的初始条件求振幅和初位相。
3. 掌握旋转矢量法。
4. 理解同方向、同频率两个简谐振动的合成规律,以及合振动振幅极大和极小的条件。
二、基本内容1. 振动 物体在某一平衡位置附近的往复运动叫做机械振动。
如果物体振动的位置满足,则该物体的运动称为周期性运动。
否则称为非周)()(T t x t x +=期运动。
但是一切复杂的非周期性的运动,都可以分解成许多不同频率的简谐振动(周期性运动)的叠加。
振动不仅限于机械运动中的振动过程,分子热运动,电磁运动,晶体中原子的运动等虽属不同运动形式,各自遵循不同的运动规律,但是就其中的振动过程讲,都具有共同的物理特征。
一个物理量,例如电量、电流、电压等围绕平衡值随时间作周期性(或准周期性)的变化,也是一种振动。
2. 简谐振动 简谐振动是一种周期性的振动过程。
它可以是机械振动中的位移、速度、加速度,也可以是电流、电量、电压等其它物理量。
简谐振动是最简单,最基本的周期性运动,它是组成复杂运动的基本要素,所以简谐运动的研究是本章一个重点。
(1)简谐振动表达式反映了作简谐振动的物体位移随时间)cos(0ϕω+=t A x 的变化遵循余弦规律,这也是简谐振动的定义,即判断一个物体是否作简谐振动的运动学根据。
但是简谐振动表达式更多地用来揭示描述一个简谐运动必须涉及到的物理量、、(或称描述简谐运动的三个参量),显然三个参量A ω0ϕ确定后,任一时刻作简谐振动的物体的位移、速度、加速度都可以由对应地t 得到。
2cos()sin(00πϕωωϕωω++=+-=t A t A v )cos()cos(0202πϕωωϕωω±+=+-=t A t A a (2)简谐运动的动力学特征为:物体受到的力的大小总是与物体对其平衡位置的位移成正比、而方向相反,即,它是判定一个系统的运动过程kx F -=是否作简谐运动的动力学根据,只要受力分析满足动力学特征的,毫无疑问地系统的运动是简谐运动。
大学物理第11章习题课选讲例题

(1) B1 0 , B2 0
I B1
(2)
B1 0 , B2 2
20I
πl
a
I
b
(3)
B1 2
20I
πl
,
B2
0
B2
cd I
(4) B1 2
20I
πl
,
B2
2
20I
πl
例 如图,流出纸面的电流为 2I ,流进纸面的电
流为 I ,则下述各式中哪一个是正确的? ()
每一无限长直线电流在 O 点
的磁感强度 B B1 B2 B3 B4
B 0I 0I
2π 2l 2 2πl
B0 4Bcos45
2R
解:dN = π N2dq
dB =
0I y 2 2(x 2+y 2)3
dN
2
=π(
0 NI x 2+
y y
2
2 )3
2
dq
=π(R2c0oNsI2qR+2cRo2ssi2qn2q )3 2 dq
=
0NI
πR
cos 2q dq
B=
0NI
πR
π
2 0
cos 2q dq
=
0NI 4R
(A)2倍 (B)4倍 (C)1/2倍 (D)1/4倍
例 在均匀磁场中,有两个平面线圈,其面积 A1 =
2A2,通有电流 I1 = 2I2,它们所受到的最大磁力矩之比
M1 / M2等于
(A)1
(B)2
(C)4
(D)1 / 4
例:电流均匀地流过宽度为 b 的无限 长平面导体薄板,电流为 I ,沿板长方向流 动。求:
大学物理课后习题详解(第十一章)中国石油大学
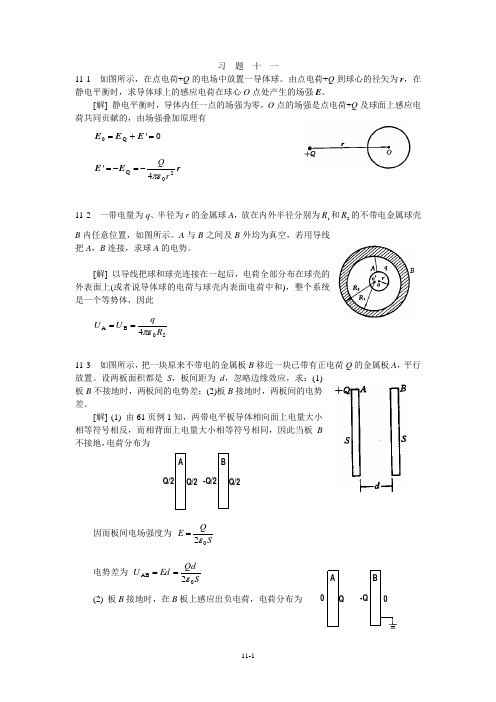
习 题 十 一11-1 如图所示,在点电荷+Q 的电场中放置一导体球。
由点电荷+Q 到球心的径矢为r ,在静电平衡时,求导体球上的感应电荷在球心O 点处产生的场强E 。
[解] 静电平衡时,导体内任一点的场强为零,O 点的场强是点电荷+Q 及球面上感应电荷共同贡献的,由场强叠加原理有0Q 0='+=E E E r E E 20Q 4r Q πε-=-='11-2 一带电量为q 、半径为r 的金属球A ,放在内外半径分别为1R 和2R 的不带电金属球壳B 内任意位置,如图所示。
A 与B 之间及B 外均为真空,若用导线把A ,B 连接,求球A 的电势。
[解] 以导线把球和球壳连接在一起后,电荷全部分布在球壳的外表面上(或者说导体球的电荷与球壳内表面电荷中和),整个系统是一个等势体,因此20B A 4R q U U πε==11-3 如图所示,把一块原来不带电的金属板B 移近一块已带有正电荷Q 的金属板A ,平行放置。
设两板面积都是S ,板间距为d ,忽略边缘效应,求:(1)板B 不接地时,两板间的电势差;(2)板B 接地时,两板间的电势差。
[解] (1) 由61页例1知,两带电平板导体相向面上电量大小相等符号相反,而相背面上电量大小相等符号相同,因此当板B 不接地,电荷分布为因而板间电场强度为 SQ E 02ε=电势差为 SQdEd U 0AB 2ε== (2) 板B 接地时,在B 板上感应出负电荷,电荷分布为B A-Q/2Q/2Q/2Q/2A B -QQ故板间电场强度为 SQ E 0ε=电势差为 SQdEd U 0AB ε==11-4 如图所示,有三块互相平行的导体板,上导体板到中间导体板的距离为5.0cm ,上导体板到下导体板的距离为8.0cm ,外面的两块用导线连接,原来不带电。
中间一块两面上带电,其面电荷密度之和为25m C 103.1-⨯=σ。
求每块板的两个表面的面电荷密度各是多少(忽略边缘效应)?[解] 因忽略边缘效应,可把三个导体板看作无限大平板,由例1知32σσ-= (1) 45σσ-= (2)忽略边缘效应,则导体板可看成无限大的,具有屏蔽性,在相邻导体板之间的电场只由相对于二表面上电荷决定。
大学物理第三版第11章部分习题解答

2
(2) 如果用导线把AB两球连接起来再求以上两 点的电势
第11章部分习题解答
解: (1)
q E 2 4 0 r 1
R1 r R2
r R2
R2
q
R1
U1 q
R2
q 4 0 r
第11章 部分习题解答
第11章部分习题解答
P408题11.3.4 如图所示,两个无限大带电平板,电荷面密度 分别为 ,设P为两板间任意一点.(1)求A板上 的电荷在P点产生的场强 E A ; (2)求B板上的电 荷在P点产生的场强 E B ;(3)求A、B两板上的电 荷在P点产生的场强;(4)如果把B板拿走,A板 上的电荷如何分布?求它在P点产生的场强.
1 Q2 We 2 QU 球壳、 2 8 0 R3
Q 1 1 1 We We1 We 2 ( ) 8 0 R1 R2 R3
2
第11章部分习题解答
(2)
1 Q2 We ' QU 球 壳、 2 8 0 R3
2010.5.25
第11章部分习题解答
解: 因为A、B都是无限大带电平板,所以 (1) (2)
EA 2 0
方向向右
EB 2 0
EP E A EB 0
方向向右
(3)
方向向右
第11章部分习题解答
(4) 如果将B板拿走,A上的电荷将均匀分布在 左右两个面上,每一个面上的电荷面密度为 / 2 ,它们在P点产生的场强大小都是 2 E'A 方向向右 2 0 4 0
第11章部分习题解答
证明: 该电容器是由两个 电容分别为 C1 和 C2 的电容器并联而成 的
大学物理(肖剑荣主编)-习题答案-第11章

个劈尖空气膜,用波长为 564 纳米的单色光垂直照射板面,板上显示出完整的
明暗条纹各 74 条。求金属丝的直径。
解 金属丝与两板之间形成一个劈尖空气膜,其上下表面的反射光相遇而发生干 涉。光程差为 Δ = 2e + λ / 2
由于板上显示出完整的明暗条纹各 74 条,所以该处应为第 74 条明条纹。 由明条纹的条件 2d + λ / 2 = kλ k=74,则 N = d / Δe
能看到第几级明条纹?
解: a + b = 1 mm = 2.0 ´10-3 mm = 2.0 ´10-4 Å 500
由 (a
+
b) sinj
=
kl
知,最多见到的条纹级数 kmax 对应的 j
=
p 2
,
所以有 kmax
=
a+b l
=
2.0 ´104 5900
» 3.39 ,即实际见到的最高级次为 kmax
解得
a = a + b k′ = 1.5 × 10−6 k′ 4
取 k′ = 1 得光栅上狭缝的的最小宽度为1.5 × 10−6 m
(3)由
(a + b)sinϕ = kλ
得
k
=
(
a
+
b) sinϕ λ
当 ϕ=π 2
时,对应 k = k max
k max
=
a+b λ
=
6.0 × 10−6 6000 × 10−10
解 在杨氏双缝干涉实验中,条纹间距 Δx = D λ d
屏幕上 20 条明条纹之间的距离 ΔX = 19Δx = D λ d
ΔX
= 19
大学物理下第11章例题

b
a
.........
c
d
计算环流
b c B dl a Bdl cos 0 b Bdl cos 2
c Bdl cos 0 d Bdl cos
a
d
2
B ab B cd 2 B ab 利用安培环路定理求 B B dl 0 n ab I
大小: B 2( R 2 x 2 )3 2
0 IR 2
x
X
x
结论
方向:
右手螺旋法则
0 IR 2 B 2( R 2 x 2 )3 2
1. x R B ?
B
0 IR 2
2x 3
2. x 0 B ?
载流圆环
B
0 I
2R
圆心角 2
B
I
圆心角
BA
r2
A
I2
l
r3
0 I1 B1 B2 2 d 2
r1
2.0 10 T
BA B1 B2 4.0 10 T
方向
5
5
d d 40cm r2 20cm l 25cm r1 r3 10cm I1 I 2 20 A
如图取微元
d m B dS Bldr
统一积分变量
0 Idl sin B x dB x 4 r 2
sin R r
Idl
I
O
Y
R
r0
d B dB
p dB
0 IR 0 IR dl 2R 3 3 4r 4r 2 0 IR
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱面电流磁场
I
B0
oR + I'
B0
B' 0I ' 0 jdl
B0
0 jdl 2R
2πR 2πR B0 B' 方向如图
例 求无限大均匀通电平面的磁场,已知电流密度如图.
j
L
IB
dI
解:1)对称性分析磁场分布
2)取正方形回路 L 如图,
边长为 l .
例 半径 为 R的带电薄圆盘的电荷面密度
为 , 并以角速度 绕通过盘心垂直于盘面的轴转
动 ,求圆盘中心的磁感强度.
o
R
r
解法一 圆电流的磁场
dI 2π rdr rdr
2π
dr
0,
B 向外
0, B 向内
dB 0dI 0 dr
2r 2
B 0 R dr 0R
20
2
解法二 运动电荷的磁场
(A) 0 I
2R
(B) 0 I
2πR
(C) 0 I 0 I
2R 2πR
(D) 0
R
O
例 如图所示,四条皆垂直于纸面“无限长”载 流直导线,每条中的电流均为 I . 这四条导线被纸面截 得的断面组成了边长为 2a 的正方形的四个顶角,则其 中心点 O 的磁感应强度的大小为
(A) 20 I
πa
(B) 20 I
2πa
2a
(C) 0
(D) 0 I
πa
O
例 图中有两根“无限长” 载流均为 I 的直导线, 有一回路 L,则下述正确的是
(A) B dl 0 ,且环路上任意一点 B 0
L
(B) B dl 0 ,且环路上任意一点 B 0
L
(C) B dl 0 ,且环路上任意一点 B 0
πl
a
I
b
(3)
B1 2
20I
πl
,
B2 0
B2
cd I
(4) B1 2
20I
πl
,
B2
2
20I
πl
例 如图,流出纸面的电流为 2I ,流进纸面的电
流为 I ,则下述各式中哪一个是正确的? ()
(1)
B dl
L1
20I
L2
(2)
B dl
L2
0I
I
(3)
B dl
L3
0I
2I L1 L3
但,是以R1为半径的1/4 圆弧
a
直电流ef与圆弧电流de在 e点相切
求:场点o处的磁感强度
B
解:
场点o处的磁感强度是由五段
特殊形状电流产生的场的叠加,f I
o dc
R1 R2
eI
即
B Bab Bbc Bcd Bde Bef
b
由毕萨拉定律得到各电流的磁感强度分别是 I
Bbc
1 4
B0 B 0I
2π r
度为例B的如均图匀一磁通场有中电,流回路I平的面闭与合磁回感路强放度在磁B感垂应直强.
r 回路由直导线 AB 和半径为 的圆弧导线 BCA 组成 ,
电流为顺时针方向, 求磁场作用于闭合导线的力.
解 F1 I ABBj
y
根据对称性分析
dF2 Idl
C
B
dF2
F2x 0
F2 F2y j
成,使用时,电流 I从一导体流去,从另一导体流回,
设电流都是均匀的分布在导体的横截面上,求:(1)
导体圆柱内(r < a);(2)两导体之间(a < r < b);
(3)导体圆管内(b < r < c)以及(4)电缆外(r > c)
各点处磁感应强度的大小.
解 由 l B dl 0 I 可得
b
BB12 B3
Fx dFx BI 00dy 0
结论 任意平面载 流导线在均匀磁场中所
Fy
dFy
BI
l
0
dx
BIl
受的力 , 与其始点和终 点相同的载流直导线所
F Fy BIlj
受的磁场力相同.
例 半径为 R载有电流 I的2 导体圆环与电流为 I1
的长直导线 放在同一平面内(如图), 直导线与圆心
相距为 d ,且 R < d 两者间绝缘 , 求 作用在圆电流上
F2 dF2y dF2 sinq
I
r
Idl
B
A
q0 o q0 F1
x
y
B
dF2 Idl
C
I
B
q
q0
dq
Idl
r
o
q0 A
x
F1
F2 dF2y dF2 sinq
BIdl sinq
因 dl rdq
F2
BIr
π q0 q0
sinq
dq
F2 BI (2r cosq0 ) j BI AB j
dFy
dF sinq
0 I1I 2
2π
R sinqdq d R cosq
Fx
0 I1I 2 R
2π
2π 0
cosqdq d R cosq
0I1I2 (1
d )
d2 R2
Fy
0 I1I 2 R
2π
2π sinqdq 0 d R cosq
0
. B
y
d
dFy
dF
I1
dFx
dq
q I2dl
圆弧形例载流有导一线半径bc为,按a图,示流方过式稳置恒于电均流匀为外I磁的场1B4
中,则该载流导线所受的安培力大小为多少?
解: Fbc Fbo Foc
Fbo 0
Fbc Foc aIB
c
B
aI
oab
例 有一根流有电流 I 的导线,被折成长度分别 为 a 、b,夹角为120的两段,并置于均匀磁场 B 中, 若导线的长度为b 的一段与B 平行,则 a 、b 两段载
由于 F1 BI AB j
故 F F1 F2 0
例 求 如图不规则的平
面载流导线在均匀磁场中所受 的力,已知 B 和 I.
解 取一段电流元Idl dF Idl B
y
dF q I
Idl
B
P
o
dFx dF sinq BIdl sinq BIdy
L
x
dFy dF cosq BIdl cosq BIdx
0I
2R2
Bde
1 4
0I
2R1
Bef
1 0I 2 2R1
方向:
Bab 0
Bcd 0 a
B
0I
0I
0I
8R1 4R1 8R2
例 无限长载流圆柱体的磁场
I
解 1)对称性分析 2)选取回路
RR
rR
Bdl
l
0I
L
2π rB 0I
B 0I
2π r
r B
0 r R
l
Bd
l
0
π π
2π 2l 2 2πl
B0 4Bcos45
40I
2πl
2 20I
2 πl
例 已知无限长直圆筒,电流密度如图,求筒内 B .
j
B
解:筒内磁感应强度等效于长直密 绕螺线管内磁场
B 0nI
B 0 j 方向向右
例 一根很长的同轴电缆,由一导体圆柱(半径
为a)和一同轴导体圆管(内、外半径分别为 b、c)构
OR
x
I2
Fx
0 I1I 2 R
2π
2π cosqdq 0 d R cosq
0I1I2 (1
d )
d2 R2
Fy
0 I1I 2 R
2π
2π sinqdq 0 d R cosq
0
F Fxi 0I1I2 (1
d )i
d2 R2
.
B
y
d
dFy
dF
I1
dFx
dq
q I2dl
OR
x
I2
(4) 回路 L内的 I 改变,L上各点的B 改变.
例 边长为 l 的正方形线圈 ,分别用图示两种方 式通以电流 I(其中ab 、cd 与正方形共面),在这两
种情况下 ,线圈在其中心产生的磁感强度的大小分别
为: ( )
(1) B1 0 , B2 0
I B1
(2)
B1 0 , B2 2
20I
大柱体的电流在O点的磁感应强度为零, 所以O点的磁场等于小柱体反向电流在O点 所产生的磁场。
d × × × × ×
× ×× × × ×
××
R × ×
×
o× ×
××
××
× ..×o..´×
r× × ×
××
×× × ×
小圆柱体的电流在O´点的磁感应强度为零, 所以O´的磁场等于大圆柱体电流在该点的 磁场。
0Ir / 2πa2 0I / 2πr 0I (c2 r2
)
(r a) (a r b) / 2πr(c2 b
2
)
a c
(b r c)
B4 0
(r c)
例 一质子沿着与磁场垂直的方向运动, 在
某点它的速率为 3.1106 m s1 . 由实验测得这时
质子所受的洛仑兹力为 7.41014 N.求该点的磁
2R
解:dN = πN2dq
dB =
0I y 2 2(x 2+y 2)3
dN
2
=π(
0 NI x 2+
y y
2
)2 3
