极坐标和参数方程
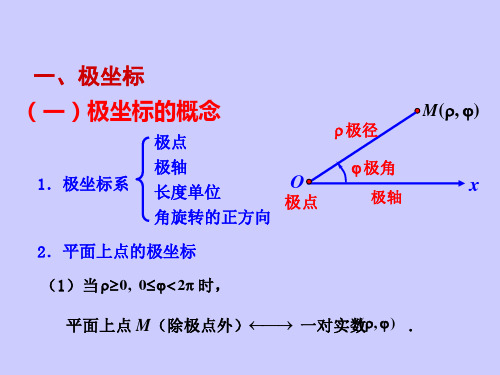
高中数学极坐标与参数方程公式的区别

高中数学极坐标与参数方程公式的区别1. 引言在高中数学课程中,学生常常会遇到极坐标和参数方程,它们是解决几何问题中常用的工具。
尽管它们都能描述曲线的形状,但是极坐标和参数方程在表达方式和使用方法上存在一些区别。
本文将探讨高中数学中极坐标和参数方程公式的区别,以帮助学生更好地理解和应用这两种方法。
2. 极坐标公式极坐标公式是一种将平面直角坐标系中的点转换为极坐标系表示的方法。
每个点由极径 r 和极角θ 表示。
极径 r 表示点到原点的距离,极角θ 表示点与正半轴的夹角。
极坐标公式的一般形式为:(x, y) = (r*cosθ, r*sinθ)其中,x 和 y 分别是点在直角坐标系中的坐标,r 和θ 是点在极坐标系中的坐标。
举个例子,考虑一个点 P 在极坐标系中的表示,其极坐标为(r, θ)。
可以通过极坐标公式将其转换为直角坐标系的表示,即:(x, y) = (r*cosθ, r*sinθ)3. 参数方程公式参数方程公式是一种使用参数变量表示曲线上不同点的方法。
一个曲线可以由两个参数 x(t) 和 y(t) 表示,其中 t 是一个参数变量。
参数方程公式的一般形式为:x = x(t)y = y(t)参数方程公式中的 x(t) 和 y(t) 分别表示曲线上每个点的 x 坐标和 y 坐标。
举个例子,考虑一个曲线 C 在参数方程中的表示,其参数方程为:x = x(t)y = y(t)4. 区别和应用极坐标和参数方程是描述曲线的两种不同方式,它们在表达方式和使用方法上存在一些区别。
4.1 表达方式极坐标使用极径和极角来表示点的位置,将点的坐标转换为极坐标形式。
而参数方程使用参数变量来表示曲线上不同点的位置,通过参数方程的函数表达式来确定曲线上的点。
4.2 描述方式极坐标可以很方便地描述圆、椭圆、螺旋线等具有对称性的曲线。
极坐标描述的曲线方程更简洁,有时可以将复杂的曲线用简单的方程表示出来。
参数方程可以很方便地描述直线、抛物线、双曲线等非对称的曲线。
极坐标和参数方程

极坐标和参数方程
极坐标和参数方程是描述一个图形或者曲线的不同数学描述方法。
极坐标是一种描述平面点位置的坐标系统,以原点为基准,通过一个点到原点的距离(称为极径)和从原点引出到该点的射线与某个参考线(通常为X轴)的夹角(称为极角)来确定一个点的位置。
参数方程是一种描述曲线的数学表示方法,通过一组参数(通常使用常数)来确定曲线上的点的坐标。
参数方程中的参数可以是时间、角度、弧长等。
极坐标和参数方程可以互相转换,即呈现相同的几何形状。
对于一个平面曲线,其极坐标和参数方程的转换公式如下:
极径r = f(t)
极角θ = g(t)
其中,t是参数,f(t)和g(t)是关于t的函数。
通过给定参数t的取值范围,可以确定曲线的一部分或整个形状。
极坐标与参数方程知识讲解

参数方程和极坐标系一、 知识要点一曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即 ⎩⎨⎧==)()(t f y t f x并且对于t 每一个允许值,由方程组所确定的点Mx ,y 都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数.二常见曲线的参数方程如下: 1.过定点x 0,y 0,倾角为α的直线:ααsin cos 00t y y t x x +=+= t 为参数其中参数t 是以定点Px 0,y 0为起点,对应于t 点Mx ,y 为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论.错误!.设A 、B 是直线上任意两点,它们对应的参数分别为t A 和t B ,则AB =A B t t -=B A A B t t t t ⋅--4)(2.错误!.线段AB 的中点所对应的参数值等于2BA t t +. 2.中心在x 0,y 0,半径等于r 的圆:θθsin cos 00r y y r x x +=+= θ为参数3.中心在原点,焦点在x 轴或y 轴上的椭圆:θθsin cos b y a x == θ为参数 或 θθsin cos a y b x ==中心在点x0,y0焦点在平行于x 轴的直线上的椭圆的参数方程为参数)ααα(.sin ,cos 00⎩⎨⎧+=+=b y y a x x 4.中心在原点,焦点在x 轴或y 轴上的双曲线:θθtg sec b y a x == θ为参数 或 θθec a y b x s tg ==5.顶点在原点,焦点在x 轴正半轴上的抛物线:pty pt x 222== t 为参数,p >0直线的参数方程和参数的几何意义过定点Px 0,y 0,倾斜角为α的直线的参数方程是 ⎩⎨⎧+=+=ααsin cos 00t y y t x x t 为参数.极坐标系1、定义:在平面内取一个定点O,叫做极点,引一条射线Ox,叫做极轴,再选一个长度单位和角度的正方向通常取逆时针方向;对于平面内的任意一点M,用ρ表示线段OM 的长度,θ表示从Ox 到OM 的角,ρ叫做点M 的极径,θ叫做点M 的极角,有序数对ρ, θ就叫做点M 的极坐标;这样建立的坐标系叫做极坐标系;2、极坐标有四个要素:①极点;②极轴;③长度单位;④角度单位及它的方向.极坐标与直角坐标都是一对有序实数确定平面上一个点,在极坐标系下,一对有序实数ρ、θ对应惟一点P ρ,θ,但平面内任一个点P 的极坐标不惟一.一个点可以有无数个坐标,这些坐标又有规律可循的,P ρ,θ极点除外的全部坐标为ρ,θ+πk 2或ρ-,θ+π)12(+k ,∈k Z .极点的极径为0,而极角任意取.若对ρ、θ的取值范围加以限制.则除极点外,平面上点的极坐标就惟一了,如限定ρ>0,0≤θ<π2或ρ<0,π-<θ≤π等.极坐标与直角坐标的不同是,直角坐标系中,点与坐标是一一对应的,而极坐标系中,点与坐标是一多对应的.即一个点的极坐标是不惟一的.3、直线相对于极坐标系的几种不同的位置方程的形式分别为: ⑴0ϕθ= ⑵θρcos a = ⑶θρcos a-= ⑷θρsin a =⑸θρsin a-= ⑹)cos(ϕθρ-=a4、圆相对于极坐标系的几种不同的位置方程的形式分别为)0(>a : ⑴a =ρ ⑵θρcos 2a = ⑶θρcos 2a -= ⑷θρsin 2a = ⑸ θρsin 2a -= ⑹)cos(2ϕθρ-=a5、极坐标与直角坐标互化公式:例题参数方程例1.讨论下列问题:1、已知一条直线上两点()111,y x M 、()222,y x M ,以分点Mx ,y 分21M M 所成的比λ为参数,写出参数方程;2、直线⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 211233t 为参数的倾斜角是3、方程⎩⎨⎧+=+-=ααsin 3cos 1t y t x t 为非零常数,α为参数表示的曲线是4、已知椭圆的参数方程是⎩⎨⎧==θθsin 4cos 5y x θ为参数,则椭圆上一点 P 25,32-的离心角可以是 A .3πB .32πC .34πD .35π例2 把弹道曲线的参数方程⎪⎩⎪⎨⎧-⋅=⋅=,21sin ,cos 200gt t v y t v x αα )2()1(化成普通方程. 例3. 将下列数方程化成普通方程.①⎩⎨⎧==t y t x 222,②⎪⎪⎩⎪⎪⎨⎧+=+=221212t t y t x ,③⎪⎪⎩⎪⎪⎨⎧+=+-=2221211t t y t t x ,④⎪⎪⎩⎪⎪⎨⎧-=+=)1()1(t t b y t t a x ,⑤⎩⎨⎧+=+-=11mx y my x .例4. 直线3x -2y +6=0,令y = tx +6t 为参数.求直线的参数方程. 例5.已知圆锥曲线方程是⎩⎨⎧-+-=++=5sin 461cos 532ϕϕt y t x (1) 若t 为参数,ϕ为常数,求该曲线的普通方程,并求出焦点到准线的距离;(2) 若ϕ为参数,t 为常数,求这圆锥曲线的普通方程并求它的离心率; 例6. 在圆x 2+2x +y 2=0上求一点,使它到直线2x +3y -5=0的距离最大. 例7. 在椭圆4x 2+9y 2=36上求一点P ,使它到直线x +2y +18=0的距离最短或最长.例8.已知直线;l :⎩⎨⎧+=--=ty t x 4231与双曲线y-22-x 2=1相交于A 、B 两点,P 点坐标P-1,2;求:1|PA|.|PB|的值; 2弦长|AB|; 弦AB 中点M 与点P 的距离;例9.已知A2,0,点B,C 在圆x 2+y 2=4上移动,且有π32=∠BAC 求ABC ∆重心G 的轨迹方程;例10.已知椭圆183222=+y x 和圆x 2+y-62=5,在椭圆上求一点P 1,在圆上求一点 P 2,使|P 1P 2|达到最大值,并求出此最大值;例11.已知直线l 过定点P-2,0,与抛物线C: x 2+ y-8=0相交于A 、B 两点;1若P 为线段AB 的中点,求直线l 的方程;2若l 绕P 点转动,求AB 的中点M 的方程.例12.椭圆)0(12222>>=+b a by a x 上是否存在点P,使得由P 点向圆x 2+y 2=b 2所引的两条切线互相垂直若存在,求出P 点的坐标;若不存在,说明理由;例题极坐标系例1讨论下列问题:1.在同一极坐标系中与极坐标M -2, 40°表示同一点的极坐标是 A -2, 220° B -2, 140° C 2,-140° D 2,-40°2.已知△ABC 的三个顶点的极坐标分别为A 4,0°, B -4,-120°, C 23+2, 30°,则△ABC 为 ;A 正三角形B 等腰直角三角形C 直角非等腰三角形D 等腰非直角三角形3.在直角坐标系中,已知点M -2,1,以原点O 为极点,x 轴正半轴为极轴建立极坐标系,当极角在-π,π 内时,M 点的极坐标为 A 5,π-argtg -21B -5,argtg -21C -5,π-argtg 21D 5,-π+argtg 21例2..把点)4,3(),6,5(ππ--B A 的极坐标化为直角坐标;例3.把点)0,2(),3,0(),1,3(P N M ---的直角坐标化为极坐标;例4.已知正三角形ABC 中,顶点A 、B 的极坐标分别为)2,3(),0,1(πB A ,试求顶点C 的极坐标;例5.化圆的直角方程x 2+y 2-2ax=0为极坐标方程; 例6.化圆锥曲线的极坐标方程θρcos e i ep-=为直角坐标方程;例7.讨论下列问题:1.在极坐标系里,过点M 4,30°而平行于极轴的直线 的方程是 A θρsin =2 B θρsin =-2 C 2cos =θρ D 2cos -=θρ2.在极坐标系中,已知两点M 14,arcsin 31,M 2-6,-π-arccos -322,则线段M 1M 2的中点极坐标为 A -1,arccos 322 B 1, arcsin 31C -1,arccos -322D 1,-arcsin 313. 已知P 点的极坐标是1,π,则过点P 且垂直于极轴的直线的极坐标方程是 ; A ρ=1 B ρ=cos θ C ρcos θ=-1 D ρcos θ=14. 若ρ>0,则下列极坐标方程中,表示直线的是 ; A θ=3π B cos θ=230≤θ≤π C tg θ=1 D sin θ=10≤θ≤π 5. 若点A -4, 67π与B关于直线θ=3π对称,在ρ>0, -π≤θ<π条件下,B 的极坐标是 ;6. 直线ρcos θ-4π=1与极轴所成的角是 ;7. 直线ρcos θ-α=1与直线ρsin θ-α=1的位置关系是 ;8. 直线y =kx +1 k <0且k ≠-21与曲线ρ2sin θ-ρsin2θ=0的公共点的个数是 ;A 0B 1C 2D 3 例8.讨论下列问题;1. 圆的半径是1,圆心的极坐标是1, 0,则这个圆的极坐标方程是 ; A ρ=cos θ B ρ=sin θ C ρ=2cos θ D ρ=2sin θ2. 极坐标方程分别是ρ=cos θ和ρ=sin θ的两个圆的圆心距是 ; A 2 B 2 C 1 D22 3. 在极坐标系中和圆ρ=4sin θ相切的一条直线方程是 A ρsin θ=2 B ρcos θ=2 C ρsin θ=4 D ρcos θ=4 4.圆ρ=D cos θ-E sin θ与极轴相切的充分必要条件是 AD ·E =0 BD 2+E 2=0 CD =0,E ≠0 DD ≠0,E =05.圆=ρ23sin θ-2cos θ的圆心的极坐标为 ; 6. 若圆的极坐标方程为ρ=6cos θ,则这个圆的面积是 ; 7. 若圆的极坐标方程为ρ=4sin θ,则这个圆的直角坐标方程为 ; 8. 设有半径为4的圆,它在极坐标系内的圆心的极坐标为-4, 0,则这个圆的极坐标方程为 ; 例9.当a 、b 、c 满足什么条件时,直线θθρsin cos 1b a +=与圆θρcos 2c =相切例10.试把极坐标方程cos 62sin 32cos =-+θθρθρm 化为直角坐标方程,并就m 值的变化 讨论曲线的形状;例11.过抛物线y 2=2px 的焦点F 且倾角为θ的弦长|AB|,并证明:||1||1FB FA +为常数学; 例12.设椭圆左、右焦点分别为F 1、F 2,左、右端点分别为A 、A ’,过F1作一条长度等于椭圆短轴弦MN,设MN 的倾角为α.1若椭圆的长、短轴的长分别为2a,2b,求证:;cos 2b a a +=α2若|AA ’|=6,|F 1F 2|=24,求α.例13.求椭圆12222=+by a x的过一个焦点且互相垂直的焦半径为直角边的直角三角形面积的最小值;。
参数方程与极坐标(精华版)

参数方程与极坐标(精华版)y y tsin注意:倾角为的直线,斜率为tan,所以tan=tan,即tcos=tsin,所以cos=sin,即=45,即直线与x轴或y轴夹45角。
Eg:已知直线L过点(1,2)且与x轴夹45角,求直线L的方程。
解:设直线L的参数方程为x=1+tcos45,y=2+tsin45,即x=1+t/2,y=2+t/2,将y=mx+b代入得到m=1,b=3/2,即直线L的方程为y=x+3/2.四、极坐标1、定义:在平面直角坐标系中,点P到原点O的距离r和OP与x轴正半轴的夹角唯一确定点P的位置,称(r,)为点P的极坐标,r为极径,为极角,记作P(r,)。
2、极坐标与直角坐标的转换x=r cos,y=r sinr2=x2+y2,tan=y/x3、常见曲线的极坐标方程1)圆:r=a2)半直线:=0或=3)双曲线:r=a sec或r=a cosec4)椭圆:r=a bcos或r=a sin5)心形线:r=a(1+cos)6)阿基米德螺线:r=a+b7)对数螺线:r=a e b8)伯努利双曲线:r2=a2 sec29)费马螺线:r=2a sin(/2)10)旋轮线:r=a或r=a sin(n)/sin(n为正整数)总结:极坐标的方程形式比较简单,但是不同曲线的极坐标方程需要记忆,转换成直角坐标系方程需要用到三角函数的知识。
P点的有向距离在点P两侧t的符号相反,可以通过直线的参数方程来表示。
其中,t代表有向距离的几何意义。
需要注意的是,t的符号相对于点P,正负在P点两侧,且|PP|=|t|。
直线参数方程可以有多种变式,比如y=y+tsinα和x=x+at,y=y+bt,但此时t的几何意义不是有向距离。
只有当t前面系数的平方和为1时,t的几何意义才是有向距离。
因此,可以将直线参数方程整理为x=x+a2+b2t,XXX,让a2+b2t作为t,这样t的几何意义就是有向距离了。
例如,对于直线x=-1+3t,y=2-4t,可以求其倾斜角。
高等数学课件:极坐标参数方程
例 2.将极坐标方程2 a2cos2 化为直角坐标方程: 解: 2 a2(cos 2sin2), 4 a22(cos2sin2), 4 a2[(cos)2 (sin)2], (x2 y2)2 a2(x2 y2).
(三)极坐标系中曲线的对称性
(2)当 R, R 时,
M(, )
的量法 :逆转为正,顺转为负. O
0
x
的量法 : 0 时,则在角的 终边上取 M 点,使OM ;
0 时,则在角的 终边的反向延长线上取 M 点,
使 OM .
O
0
x
M(, )
M(, )
(, )
O
x
M1(, )
这样,一对实数(, ) 对应唯 一 点 M,
(, 2k) (, (2k
2.
椭圆
x2 a2
y2 b2
1
(ab0)
的参数方程:
xacost
ybsint
,
t[0, 2].
椭圆
(
x
x a2
)2
(
y
y b2
)2
1
(ab0)
的参数方程:
x y
x y
acost bsint
(a
b
0),
t[0, 2].
3.摆线的参数方程:
xa(t sint) y a(1cost )
(
y
)
2 3
1
,
aa
2 22
故普通方程为 x 3 y 3 a 3 .
(二)几种常见曲线的参数方程
1. 圆 x2 y2 a2 的参数方程:
x acost yasint
极坐标与参数方程

选修4-4 极坐标与参数方程一、极坐标1.(1)极坐标系 (2)极坐标2.极坐标与直角坐标的互化 3.简单曲线的极坐标方程二.参数方程 1.概念2.直线、圆、椭圆的参数方程(1)过点M (x 0,y 0),倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数).直线参数方程的标准形式的应用过点M 0(x 0,y 0),倾斜角为α的直线l 的参数方程是⎩⎪⎨⎪⎧x =x 0+t cos α,y =y 0+t sin α.若M 1,M 2是l 上的两点,其对应参数分别为t 1,t 2,则①|M 1M 2|=|t 1-t 2|.②若线段M 1M 2的中点M 所对应的参数为t ,则t =t 1+t 22,中点M 到定点M 0的距离|MM 0|=|t |=⎪⎪⎪⎪t 1+t 22.③若M 0为线段M 1M 2的中点,则t 1+t 2=0. ④|M 0M 1||M 0M 2|=|t 1t 2|.(2)圆心在点M 0(x 0,y 0),半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =x 0+r cos θ,y =y 0+r sin θ(θ为参数).1. (3)椭圆x 2a 2+y 2b 2=1(a >b >0)的参数方程为⎩⎪⎨⎪⎧x =a cos φ,y =b sin φ (φ为参数)一、极坐标方程与直角坐标方程互化及判断曲线类型【例1】化下列极坐标方程为直角坐标方程,并说明它是什么曲线。
(1) 2540ρρ-+=; (2) 53cos 4sin ρθθ=+;(3) 523cos ρθ=-; (4)242ππρθθρ-+=, 其中R ρ∈【解析】(1)方程变形为(1)(4)0ρρ--=,∴1ρ=或4ρ=,即221x y +=或2216x y +=, 故原方程表示圆心在原点半径分别为1和4的两个圆。
(2) 变形得3cos 4sin 5ρθρθ+=,即3450x y +-=,故原方程表示直线3450x y +-=。
极坐标系与参数方程知识点总结

千里之行,始于足下。
极坐标系与参数方程知识点总结
极坐标系与参数方程是描述平面上的点与曲线的两种坐标系统。
1. 极坐标系:
极坐标系由极径(r)和极角(θ)组成,其中极径表示点到原点的距离,极角表示点在极坐标系中的方向。
- 极径:通常用正数表示,表示点到原点的距离。
- 极角:一般用弧度表示,表示点所在的射线与参考射线(通常为 x 轴正半轴)的夹角。
2. 参数方程:
参数方程是一组用参数表示的方程,通过为变量赋予不同的值来表示曲线上的点。
- 参数:参数是代表自变量的符号,可以用任意字母表示。
- 方程组:在参数方程中,通常会有两个或更多的方程,每个方程用参数表示一个坐标分量,用来描述曲线上的点。
极坐标系和参数方程在描述一些特殊曲线时非常有用,例如圆、椭圆、双曲线等。
其中,使用极坐标系描述曲线更加方便,而使用参数方程描述曲线更加灵活。
应用场景:
1. 极坐标系常用于描述圆心在原点的圆形曲线,以及玫瑰线、阿基米德螺线等特殊曲线。
2. 参数方程常用于描述具有特定形状的曲线,如椭圆的参数方程为 x = a * cos(t), y = b * sin(t),其中 t 为参数,a 和 b 分别为椭圆在 x 轴和 y 轴上的半径。
第1页/共2页
锲而不舍,金石可镂。
3. 参数方程也常用于描述轨迹问题,例如描述一个物体在运动过程中的位置随时间而变化的轨迹。
总结:
极坐标系和参数方程是两种用于描述平面上曲线的坐标系统,它们在不同场景下有不同的应用。
熟练掌握这两种坐标系统的表示方法和转换方法,可以更好地理解和描述曲线的性质和特点。
高考文科数学复习专题-极坐标与参数方程

1.曲线的极坐标方程.(1)极坐标系:一般地,在平面上取一个定点O,自点O引一条射线Ox,同时确定一个长度单位和计算角度的正方向(通常取逆时针方向为正方向),这样就建立了一个极坐标系.其中,点O 称为极点,射线Ox称为极轴.(2)极坐标(ρ,θ)的含义:设M是平面上任一点,ρ表示OM的长度,θ表示以射线Ox为始边,射线OM为终边所成的角.那么,有序数对(ρ,θ)称为点M的极坐标.明显,每一个有序实数对(ρ,θ),确定一个点的位置.其中ρ称为点M的极径,θ称为点M的极角.极坐标系和直角坐标系的最大区分在于:在直角坐标系中,平面上的点与有序数对之间的对应关系是一一对应的,而在极坐标系中,对于给定的有序数对(ρ,θ),可以确定平面上的一点,但是平面内的一点的极坐标却不是唯一的.(3)曲线的极坐标方程:一般地,在极坐标系中,假如平面曲线C上的随意一点的极坐标满意方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点都在曲线C上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程.2.直线的极坐标方程.(1)过极点且与极轴成φ0角的直线方程是θ=φ0和θ=π-φ0,如下图所示.(2)与极轴垂直且与极轴交于点(a,0)的直线的极坐标方程是ρcos θ=a,如下图所示.(3)与极轴平行且在x轴的上方,与x轴的距离为a的直线的极坐标方程为ρsin θ=a,如下图所示.3.圆的极坐标方程.(1)以极点为圆心,半径为r的圆的方程为ρ=r,如图1所示.(2)圆心在极轴上且过极点,半径为r的圆的方程为ρ=2rcos_θ,如图2所示.(3)圆心在过极点且与极轴成π2的射线上,过极点且半径为r的圆的方程为ρ2rsin_θ,如图3所示.4.极坐标与直角坐标的互化.若极点在原点且极轴为x 轴的正半轴,则平面内随意一点M 的极坐标M(ρ,θ)化为平面直角坐标M(x ,y)的公式如下:⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ或者ρ=x 2+y 2,tan θ=y x ,其中要结合点所在的象限确定角θ的值.1.曲线的参数方程的定义.在平面直角坐标系中,假如曲线上随意一点的坐标x ,y 都是某个变数t 的函数,即⎩⎪⎨⎪⎧x =f (t ),y =g (t ),并且对于t 的每一个允许值,由方程组所确定的点M(x ,y)都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x ,y 之间关系的变数t 叫做参变数,简称参数.2.常见曲线的参数方程.(1)过定点P(x 0,y 0),倾斜角为α的直线:⎩⎪⎨⎪⎧x =x 0+tcos α,y =y 0+tsin α(t 为参数), 其中参数t 是以定点P(x 0,y 0)为起点,点M(x ,y)为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.依据t 的几何意义,有以下结论:①设A ,B 是直线上随意两点,它们对应的参数分别为t A 和t B ,则|AB|=|t B -t A |=(t B +t A )2-4t A ·t B ;②线段AB 的中点所对应的参数值等于t A +t B2.(2)中心在P(x 0,y 0),半径等于r 的圆:⎩⎪⎨⎪⎧x =x 0+rcos θ,y =y 0+rsin θ(θ为参数) (3)中心在原点,焦点在x 轴(或y 轴)上的椭圆:⎩⎪⎨⎪⎧x =acos θ,y =bsin θ(θ为参数)⎝ ⎛⎭⎪⎫或⎩⎪⎨⎪⎧x =bcos θ,y =asin θ. 中心在点P(x 0,y 0),焦点在平行于x 轴的直线上的椭圆的参数方程为⎩⎪⎨⎪⎧x =x 0+acos α,y =y 0+bsin α(α为参数).(4)中心在原点,焦点在x 轴(或y 轴)上的双曲线:⎩⎪⎨⎪⎧x =asec θ,y =btan θ(θ为参数)⎝ ⎛⎭⎪⎫或⎩⎪⎨⎪⎧x =btan θ,y =asec θ. (5)顶点在原点,焦点在x 轴的正半轴上的抛物线:⎩⎪⎨⎪⎧x =2p ,y =2p(t 为参数,p>0). 注:sec θ=1cos θ.3.参数方程化为一般方程.由参数方程化为一般方程就是要消去参数,消参数时经常采纳代入消元法、加减消元法、乘除消元法、三角代换法,消参数时要留意参数的取值范围对x ,y 的限制.1.已知点A 的极坐标为⎝⎛⎭⎪⎫4,5π3,则点A 的直角坐标是(2,-23).2.把点P 的直角坐标(6,-2)化为极坐标,结果为⎝ ⎛⎭⎪⎫22,-π6.3.曲线的极坐标方程ρ=4sin θ化为直角坐标方程为x 2+(y -2)2=4.4.以极坐标系中的点⎝ ⎛⎭⎪⎫1,π6为圆心、1为半径的圆的极坐标方程是ρ=2cos ⎝⎛⎭⎪⎫θ-π6.5.在平面直角坐标系xOy 中,若直线l :⎩⎪⎨⎪⎧x =t ,y =t -a (t 为参数)过椭圆C :⎩⎪⎨⎪⎧x =3cos θ,y =2sin θ(θ为参数)的右顶点,则常数a 的值为3.解析:由直线l :⎩⎪⎨⎪⎧x =t ,y =t -a ,得y =x -a.由椭圆C :⎩⎪⎨⎪⎧x =3cos θ,y =2sin θ,得x 29=y24=1.所以椭圆C 的右顶点为(3,0).因为直线l 过椭圆的右顶点,所以0=3-a ,即a =3.一、选择题1.在平面直角坐标系xOy 中,点P 的直角坐标为(1,-3).若以原点O 为极点,x 轴正半轴为极轴建立极坐标系,则点P 的极坐标可以是(C )A.⎝ ⎛⎭⎪⎫1,-π3B.⎝ ⎛⎭⎪⎫2,4π3C.⎝ ⎛⎭⎪⎫2,-π3D.⎝⎛⎭⎪⎫2,-4π3 2.若圆的方程为⎩⎪⎨⎪⎧x =2cos θ,y =2sin θ(θ为参数),直线的方程为⎩⎪⎨⎪⎧x =t +1,y =t -1(t 为参数),则直线与圆的位置关系是(B )A .相离B .相交C .相切D .不能确定3.以平面直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线l 的参数方程是⎩⎪⎨⎪⎧x =t +1,y =t -3(t 为参数),圆C 的极坐标方程是ρ=4cosθ,则直线l 被圆C 截得的弦长为(D )A.14 B .214 C. 2 D .2 2解析:由题意可得直线和圆的方程分别为x -y -4=0,x 2+y 2=4x ,所以圆心C(2,0),半径r =2,圆心(2,0)到直线l 的距离d =2,由半径,圆心距,半弦长构成直角三角形,解得弦长为2 2.4.已知动直线l 平分圆C :(x -2)2+(y -1)2=1,则直线l 与圆O :⎩⎪⎨⎪⎧x =3cos θ,y =3sin θ(θ为参数)的位置关系是(A )A .相交B .相切C .相离D .过圆心解析:动直线l 平分圆C :(x -2)2+(y -1)2=1,即圆心(2,1)在直线l 上,又圆O :⎩⎪⎨⎪⎧x =3cos θ,y =3sin θ的一般方程为x 2+y 2=9且22+12<9,故点(2,1)在圆O 内,则直线l 与圆O 的位置关系是相交.二、填空题5.在平面直角坐标系xOy 中,已知曲线C 的参数方程是⎩⎪⎨⎪⎧y =sin θ-2,x =cos θ(θ是参数),若以O 为极点,x 轴的正半轴为极轴,则曲线C 的极坐标方程可写为ρ2+4ρsin_θ+3=0.解析:在平面直角坐标系xOy 中,⎩⎪⎨⎪⎧y =sin θ-2,x =cos θ(θ是参数),∴⎩⎪⎨⎪⎧y +2=sin θ,x =cos θ.依据sin 2θ+cos 2θ=1,可得x 2+(y +2)2=1,即x 2+y 2+4y +3=0.∴曲线C 的极坐标方程为ρ2+4ρsin θ+3=0.6.在平面直角坐标系中圆C 的参数方程为⎩⎪⎨⎪⎧x =2cos θ,y =2+2sin θ(θ为参数),以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系,则圆C 的圆心的极坐标为⎝⎛⎭⎪⎫2,π2.三、解答题7.求极点到直线2ρ=1sin ⎝⎛⎭⎪⎫θ+π4(ρ∈R)的距离.解析:由2ρ=1sin ⎝ ⎛⎭⎪⎫θ+π4⇒ρsin θ+ρcos θ=1⇒x +y =1,故d =|0+0-1|12+12=22. 8.极坐标系中,A 为曲线ρ2+2ρcos θ-3=0上的动点,B 为直线ρcos θ+ρsin θ-7=0上的动点,求|AB|的最小值.9.(2015·大连模拟)曲线C 1的参数方程为⎩⎪⎨⎪⎧x =cos θ,y =sin θ(θ为参数),将曲线C 1上全部点的横坐标伸长为原来的2倍,纵坐标伸长为原来的3倍,得到曲线C 2.以平面直角坐标系xOy 的原点O 为极点,x 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l :ρ(cos θ-2sin θ)=6.(1)求曲线C 2和直线l 的一般方程;(2)P 为曲线C 2上随意一点,求点P 到直线l 的距离的最值.解析:(1)由题意可得C 2的参数方程为⎩⎨⎧x =2cos θ,y =3sin θ(θ为参数),即C 2:x 24+y23=1,直线l :ρ(cos θ-2sin θ)=6化为直角坐标方程为x -2y -6=0.(2)设点P(2cos θ,3sin θ),由点到直线的距离公式得点P 到直线l 的距离为 d =|2cos θ-23sin θ-6|5=⎪⎪⎪⎪⎪⎪6+4⎝ ⎛⎭⎪⎫32sin θ-12cos θ5=⎪⎪⎪⎪⎪⎪6+4sin ⎝⎛⎭⎪⎫θ-π65=55⎣⎢⎡⎦⎥⎤6+4sin ⎝⎛⎭⎪⎫θ-π6. 所以255≤d ≤25,故点P 到直线l 的距离的最大值为25,最小值为255.10.已知在直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =1+4cos θ,y =2+4sin θ(θ为参数),直线l经过定点P(3,5),倾斜角为π3.(1)写出直线l 的参数方程和曲线C 的标准方程.(2)设直线l 与曲线C 相交于A ,B 两点,求|PA|·|PB|的值.解析:(1)由曲线C 的参数方程⎩⎪⎨⎪⎧x =1+4cos θ,y =2+4sin θ(θ为参数),得一般方程为(x -1)2+(y -2)2=16,即x 2+y 2-2x -4y =11=0.直线l 经过定点P(3,5),倾斜角为π3,直线的参数方程为⎩⎪⎨⎪⎧x =3+12t ,y =5+32t (t 是参数).(2)将直线的参数方程代入x 2+y 2-2x -4y -11=0,整理,得t 2+(2+33)t -3=0,设方程的两根分别为t 1,t 2,则t 1t 2=-3,因为直线l 与曲线C 相交于A ,B 两点,所以|PA|·|PB|=|t 1t 2|=3.。
第12讲 极坐标与参数方程

第12讲极坐标与参数方程【知识回顾】1.极坐标(方程)与直角坐标(方程)的相互转化,参数方程与普通方程相互转化,极坐标方程与参数方程相互转化。
方法如下:2.用的参数方程及其应用(1)圆222)()(rbyax=-+-的参数方程可表示为)(.sin,cos为参数θθθ⎩⎨⎧+=+=rbyrax.(2)椭圆的参数方程可表示为(3)已知直线l过),(yxM,倾斜角为α,l与圆锥曲线相交于BA,两点,则求弦长AB的方法如下:将直线l的参数方程)(sincos0为参数ttyytxx⎩⎨⎧+=+=αα代入圆锥曲线的方程,消去yx,得到关于t的一元二次方程,由判别式∆和韦达定理得到21tt+,21t t的值,代入弦长公式21221214)(t tttttAB-+=-=,M到两交点的距离之积为21t tMBMA=•.3.简单参数方程及应用(1)将参数方程化为普通方程的基本途径就是消参,消参过程注意两点:①准确把握参数形式之间的关系;②注意参数取值范围对曲线形状的影响.(2)已知曲线普通方程求参数方程时,(3)一般地,如果题目中涉及圆、椭圆上的动点或求最值范围问题时可考虑用参数方程,设曲线上点的坐标,将问题转化为三角恒等变换问题解决,使解题过程简单明了。
高考题中极坐标与参数方程主要考查简单图形的极坐标方程,极坐标与直角坐标的互化,直线、圆和圆锥曲线的参数方程,参数方程化为直角坐标方程等。
αOyxle MM0)(.sin,cos为参数ϕϕϕ⎩⎨⎧==byax12222=+byax)0(>>ba课堂反馈】1. 在极坐标系中,过点(1, π2)且平行于极轴的直线方程是( )A. ρ=1B. ρsinθ=1C. ρcosθ=1D. ρ=2sinθ2. 点M 的极坐标是(3,π6),则点M 的直角坐标为( )A. (3√32,32)B. (√32,32)C. (32,3√32)D. 以上都不对3. 若点P(2,4)在直线l :{x =1+ty =3−at(t 为参数)上,则a 的值为( ) A. 3 B. 2 C. 1 D. −14. 直线l 的参数方程为{x =1+3t ,y =2+4t(t 为参数),则点(1,0)到直线l 的距离是( ) A. 15B. 25C. 45D. 655. 已知圆的方程为x 2+y 2−2y =0.以原点为极点,x 轴正半轴为极轴建立极坐标系,该圆的极坐标方程为( )A. ρ=−2sinθB. ρ=2sinθC. ρ=−2cosθD. ρ=2cosθ6. 点P(2,0)到直线{x =1+4ty =2+3t,(t 为参数,t ∈R)的距离为( )A. 35B. 45C. 65D. 1157. 已知曲线的参数方程为{x =3t 2+2y =t 2−1(0≤t ≤5),则曲线为( ) A. 线段 B. 双曲线的一支 C. 圆弧 D. 射线8. 直线{x =1+3ty =1+t(t 是参数)上对应t =0,t =1两点间的距离是 ( ) A. 1B. 10C. √10D. 2√29. 曲线θ=2π3与ρ=6sinθ的两个交点之间的距离为( )A. 1B. √3C. 3√3D. 610. 极坐标方程分别是ρ=4cosθ和ρ=4sinθ的两个圆的圆心距是 ( )A. 1B. 2√2C. 2D. √211. 直线{x =1+√3ty =t(t 为参数)与曲线{x =cosθ+1y =sinθ(θ为参数)相交的弦长为( ) A. 1B. 2C. 3D. 412. 若圆的参数方程为为参数),则圆的圆心坐标为( )A. (0,2)B. (0,−2)C. (−2,0)D. (2,0)13. 直线ρ(√3cosθ−sinθ)=2与圆ρ=4sinθ的交点的极坐标为( )A. (2,π6)B. (2,π3)C. (4,π6)D. (4,π3)14. 圆ρ=2sinθ的圆心到直线ρcosθ−2ρsinθ+1=0的距离为( )A. √55B. 2√55C. 3√55D. 4√5515. 曲线{x =−2+5ty =1−2t(t 为参数)与坐标轴的交点是( ) A. (0,25)、(12,0) B. (0,15)、(12,0) C. (0,−4)、(8,0) D. (0,59)、(8,0)16. 已知圆的极坐标方程是ρ=2cosθ,那么该圆的直角坐标方程是( )A. (x −1)2+y 2=1B. x 2+(y −1)2=1C. (x +1)2+y 2=1D. x 2+y 2=2 17. 曲线C :p =2cosθ上任意一点P 到点Q(√2,π4)的最大距离等于( )A. √2B. 2C. √3D. √618. 下列极坐标方程表示圆的是( )A. ρ=1B. θ=π2 C. ρsinθ=1 D. ρ(sinθ+cosθ)=119. 在极坐标系中,曲线ρ2−6ρcosθ−2ρsinθ+6=0与极轴交于A ,B 两点,则A ,B 两点间的距离等于( ) A. √3 B. 2√3 C. 2√15 D. 4 20. 椭圆x 216+y 24=1上的点到直线{x =√2−ty =12t(t 为参数)的最大距离是( ) A. 3 B. √11 C. 2√2 D. √1021. 在直角坐标系xOy 中,圆C 的参数方程{y=sinφx=1+cosφ(φ为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系;(1)设M(x,y)是圆C 上的动点,求m =3x +4y 的取值范围; (2)求圆C 的极坐标方程。
参数方程与极坐标方程的互化

参数方程与极坐标方程的互化引言:数学中常常有需要描述曲线的情况,参数方程和极坐标方程是两种常见的用于描述曲线的方法。
参数方程是将曲线上的点的坐标表示为一个参数的函数形式,而极坐标方程则将曲线上的点的坐标表示为极径和极角的函数形式。
这两种方法在不同的情况下有不同的应用和优势。
本文将介绍参数方程和极坐标方程的基本概念,并探讨它们之间的互化关系。
一、参数方程参数方程是一种用参数的函数形式来表示曲线的方法。
在参数方程中,曲线上的每个点的坐标都是参数的函数,通常用t表示。
比如,一条曲线的参数方程可以表示为x = f(t),y = g(t)。
参数t的取值范围可以是一个区间或者整个实数集。
参数方程的优势在于可以方便地描述复杂的曲线。
通过调整参数t的取值范围和步长,可以精确地控制曲线的形状和密度。
参数方程还可以描述出曲线上的运动轨迹,这在物理学和工程学中有广泛的应用。
二、极坐标方程极坐标方程是一种用极径和极角的函数形式来表示曲线的方法。
在极坐标方程中,曲线上的每个点的坐标都可以表示为(r, θ),其中r 表示极径,θ表示极角。
极径r可以是一个实数,而极角θ通常取值范围是从0到2π。
极坐标方程常常被用来描述圆形、椭圆形和螺旋等特殊曲线。
相比于直角坐标系下的方程,极坐标方程更加简洁和直观。
极坐标方程的优势在于可以方便地描述对称性和旋转对称性,因为极径和极角的改变对应着曲线上点的位置的改变。
三、从参数方程到极坐标方程的互化在一些情况下,参数方程和极坐标方程可以进行互化。
通过改变变量和坐标系的转换,我们可以将参数方程转换为极坐标方程,也可以将极坐标方程转换为参数方程。
1. 将参数方程转换为极坐标方程若已知一条曲线的参数方程为x = f(t),y = g(t),我们可以通过以下步骤将其转换为极坐标方程:(1) 将x和y用极坐标形式表示,即将x和y分别表示为r*cos(θ)和r*sin(θ)的形式;(2) 联立方程,消去t,得到r和θ之间的关系。
专题九:极坐标系与参数方程

专题六极坐标系与参数方程知识梳理1、伸缩变换:设点P(x,y)是平面直角坐标系中的任意一点,在变换,(0):,(0)x x y y λλϕμμ'=>⎧⎨'=>⎩的作用下,点P(x,y)对应到点P′(x′,y′),称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换。
注:当1λ>时,表示横向伸长;当01λ<<时,表示横向压缩。
当1μ>时,表示纵向伸长;当01μ<<时,表示纵向压缩。
这里P(x,y)是变换前的点,P′(x′,y′)是变换后的点。
2、极坐标系:(1)极坐标系的定义:如图,在平面内取一个定点O,自极点O 引一条射线Ox,同时再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系。
其中定义O 称为极点,射线Ox 称为极轴。
(2)极坐标:设M 是平面内的任意一点,ρ表示OM 的长度,θ表示以射线Ox 为始边,以射线OM 为终边所成的角,则有序实数对(,)ρθ称为点M 的极坐标,记为M (,)ρθ.其中ρ称为极径,θ称为极角。
一般地,不作特殊说明,我们认为0ρ≥,θ可以取任意实数。
(3)建立极坐标后,给定ρ和θ,就可以在平面内唯一确定点M;反过来,给定平面任意一点,也可以确定它的极坐标(,)ρθ。
(4)一般地,极坐标(,)ρθ与(,2)()k k Z ρθπ+∈表示同一个点,特别地,极点O 的坐标为(0,)()R θθ∈,和直角坐标不同,平面内一个点的极坐标有无数种表示。
如果规定0ρ>,02θπ≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的,这时点与极坐标是一种一一对应关系。
(5)极坐标系中点的对称:(,)A ρθ3()2:y A ρθπθρπθρπθ⎧⎪⎪=⎨⎪⎪+⎩12关于极轴的对称点:A (,-)关于轴的对称点:A (,-)关于极点的对称点(,)3、极坐标与直角坐标的互化:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的单位长度,设平OAA 2A 1A 3xy····O·xρMθ(,)ρθ面内的任意一点M 的直角坐标和极坐标分别为(x,y)和(,)ρθ,则有:cos sin x y ρθρθ=⎧⎨=⎩,tan ,0yx x ρθ⎧=⎪⎨=≠⎪⎩4、极坐标方程的定义:一般地,在极坐标系中,如果平面曲线C 上任意一点的极坐标中至少有一个满足方程(,)0f ρθ=,并且坐标适合方程(,)0f ρθ=的点都在曲线C 上,那么方程(,)0f ρθ=叫做曲线C 的极坐标方程。
极坐标方程与参数方程的转换

极坐标方程与参数方程的转换在数学中,极坐标方程和参数方程是用于描述平面上的点的两种不同的表示方法。
它们之间存在一种转换关系,可以将一个方程表示形式转换为另一个方程表示形式。
本文将介绍极坐标方程和参数方程的定义,以及它们之间的转换方法。
极坐标方程的定义极坐标是一种描述平面上点位置的坐标系统,它使用径向距离(r)和极角(θ)来表示点的位置。
在极坐标中,点的位置由它与原点的距离和与极轴的夹角来确定。
极坐标方程是描述点在极坐标系统中位置的方程。
极坐标方程的一般形式可以表示为:r = f(θ)其中,r是与极轴的距离,θ是与极轴的夹角,f(θ)是任意给定的函数。
参数方程的定义参数方程是一种用参数表示点的位置的方法。
在参数方程中,点的坐标由一个或多个参数的函数来给出。
参数方程中的参数是自变量,通过改变参数的取值,可以确定点在平面上的位置。
参数方程的一般形式可以表示为:x = f(t) y = g(t)其中,x和y是点的坐标,f(t)和g(t)是与参数t相关的函数。
极坐标方程到参数方程的转换要将极坐标方程转换为参数方程,我们可以使用三角恒等式进行转换。
对于任意给定的θ,点的极坐标坐标可以表示为:r = f(θ)根据三角恒等式,我们有以下关系:x = r * cos(θ) y = r * sin(θ)将极坐标方程中的r用x和y表示,可以得到参数方程的形式:x = f(θ) * cos(θ) y = f(θ) * sin(θ)这样,我们就成功地将极坐标方程转换为参数方程。
参数方程到极坐标方程的转换要将参数方程转换为极坐标方程,我们需要将x和y用r和θ表示。
这可以通过使用反三角函数来实现。
给定参数方程中的x和y,我们可以计算r和θ:r = √(x^2 + y^2) θ = tan^(-1)(y / x)这样,我们就得到了以x和y表示的极坐标方程。
总结极坐标方程和参数方程是描述平面上点位置的两种常用方法。
它们之间存在一种转换关系,可以将一个方程形式转换为另一个方程形式。
参数方程极坐标方程直角坐标方程

参数方程极坐标方程直角坐标方程在数学中,坐标系是用来描述一个对象在空间中的位置关系的重要工具。
常见的坐标系有直角坐标系、极坐标系和参数方程,它们的用途相互独立,但是又有一定的联系。
下面将介绍三者的定义和特点,分析它们的相互转换,探讨它们的应用。
一、直角坐标系直角坐标系是我们最熟悉的一种坐标系,其基本定义是:建立一个以两个相互垂直的坐标轴为基础的平面坐标系,在这个平面上任何一个点都可以用它在 x 和 y 轴上的投影来表示。
直角坐标系的极坐标形式是:$(x,y)$,其中 x 坐标表示点到 y 轴的水平距离,y 坐标表示点到 x 轴的垂直距离。
图1 展示了一个二维平面上的直角坐标系。
二、极坐标系另一种常见的坐标系是极坐标系,它是用来描述圆形和相关曲线的常用坐标系。
极坐标系同样建立在一个平面上,但是坐标点不是由一个点到两个轴的距离来决定,而是以一个点到原点的距离和该点与正 x 轴夹角的大小来确定。
极坐标系通常用$r$ 和 $\theta$ 表示,其中 $r$ 表示极径,也就是点到原点的距离,$\theta$ 表示极角,也就是点到正 x 轴的夹角。
切换到直角坐标系下,极坐标的 x 坐标和 y 坐标表示如下:$$ x = r\cos \theta $$$$ y = r\sin \theta $$图2 展示了一个极坐标系下的点,并给出它在直角坐标系下的坐标 $(x,y)$。
对于一条曲线,若它的极坐标方程是 $r=f(\theta)$,那么这条曲线上的点都可以用它在极坐标系中的坐标 $(r,\theta)$ 来表示。
根据双曲线坐标系下抛物线的方程$y=x^2$,我们可以得到它在极坐标系中的表示形式 $r=\theta^2$。
三、参数方程最后是参数方程,它是一种特殊的函数表达形式,以参数为自变量,将曲线上的点位置表示为几个参数的函数。
一条曲线的参数方程通常可以表示为$(x(t),y(t))$,其中 $t$ 是我们自己规定的参数变量。
极坐标与参数方程

极坐标系与参数方程知识点考纲下载平面直角坐标系中的伸缩变换了解坐标系的作用,了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.极坐标了解极坐标的基本概念,会在极坐标系中用极坐标刻画点的位置,能进行极坐标和直角坐标的互化.能在极坐标系中给出简单图形表示的极坐标方程. 参数方程了解参数方程,了解参数的意义.能选择适当的参数写出直线、圆和椭圆的参数方程.第1课时 坐标系1.坐标系(1)坐标变换设点P (x ,y )是平面直角坐标系中的任意一点,在变换φ:⎩⎪⎨⎪⎧x ′=λ·x (λ>0)y ′=μ·y (μ>0)的作用下, 点P (x ,y )对应到点(λx ,μy )称φ为坐标系中的伸缩变换.(2)极坐标系在平面内取一个定点O ,叫做极点;自极点O 引一条射线Ox ,叫做极轴;再选一个单位长度,一个角度(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.设M 是平面内任意一点,极点O 与点M 的距离|OM |叫做点M 的极径,记为ρ;以极轴Ox 为始 边,射线OM 为终边的角xOM 叫做点M 的极角,记为θ,有序数对(ρ,θ)叫做点M 的极坐标.2. 直角坐标与极坐标的互化把直角坐标系的原点作为极点,x 轴正半轴作为极轴,且在两坐标系中取相同的长度单位. 设M 是平面内的任意一点,它的直角坐标、极坐标分别为(x ,y )和(ρ,θ),则 ⎩⎪⎨⎪⎧x =ρcos θy =ρsin θ,⎩⎪⎨⎪⎧ρ2=x 2+y 2tan θ=yx (x ≠0). 3.直线的极坐标方程(不用)例1,设点P 的极坐标为()11,θρ,直线l 过点P 且与极轴所成角为α,求直线l 的极坐标方程。
解,如图,设M ),(θρ为直线上任意一点,知θρ=∠=xOM OM ,|| 在∆MOP 中,θα-=∠OMP ,)(1θαπ--=∠OPM 由正弦定理得OMPOP OPM OM ∠=∠sin ||sin ||)sin()](sin[11θαρθαπρ-=--⇒)sin()sin(11θαρθαρ-=-⇒,(比直角坐标方程复杂)几个特殊位置的直线的极坐标方程: (1)直线过极点:θ=θ0和θ=π-θ0;(2)直线过点A(a ,0)且垂直于极轴:ρcos_θ=a ;解,在MOA Rt ∆中,a OA MOA OM =⇒=∠θρcos ||cos ||,(即a x =)(3)直线过M (b ,π2)且平行于极轴:ρsin_θ=b . (解,即b y =)4.圆的极坐标方程若圆心为M (ρ0,θ0),半径为r ,则该圆的方程为:(不用)ρ2-2ρ0ρcos(θ-θ0)+ρ20-r 2=0. 几个特殊位置的圆的极坐标方程:例1、在极坐标平面内,已知圆心)0,(a C ,半径为r ,求其极坐标方程。
极坐标与参数方程

极坐标与参数方程1.直角坐标系与极坐标系可以互相转换。
在两个坐标系中取相同的长度单位,将直角坐标系的原点作为极点,x轴正半轴作为极轴。
对于任意点M,其直角坐标为(x,y),极坐标为(ρ,θ),其中ρ表示点M到原点的距离,θ表示点M与极轴的夹角。
它们之间的关系是ρ²=x²+y²,x=ρcosθ,y=ρsinθ,tanθ=y/x(当x≠0时)。
2.直线的极坐标方程为ρsin(θ-α)=d,其中d为直线到极点的距离,α为极轴到直线的角度。
对于特殊位置的直线,如过极点的直线、过点M(a,0)且垂直于极轴的直线、过点M(b,π/2)且平行于极轴的直线,它们的极坐标方程分别为θ=α、ρcosθ=a、ρsinθ=b。
3.圆的极坐标方程为2ρ²-2ρr cos(θ-θ0)+r²=0,其中M(ρ,θ)为圆心,r为半径,θ0为极轴与圆心连线的角度。
对于特殊位置的圆,如圆心位于极点且半径为r的圆,其极坐标方程为ρ=r;圆心位于M(r,0)且半径为r的圆,其极坐标方程为ρ=2rcosθ;圆心位于M(r,π/2)且半径为r的圆,其极坐标方程为ρ=2r sinθ。
4.直线的参数方程为x=x0+t cosα,y=y0+t sinα,其中M(x0,y0)为直线上的一点,α为直线倾斜角,t为参数。
5.圆的参数方程为x=x0+r cosθ,y=y0+r sinθ,其中M(x0,y0)为圆心,r为半径,θ为参数,0≤θ≤2π。
6.椭圆的参数方程为x=a cosθ,y=b sinθ,其中a、b为长轴和短轴的长度;抛物线的参数方程为x=2pt²,y=2pt,其中p 为焦距的一半。
1.给定曲线C的极坐标方程ρ=2cosθ,在以极点为原点、x 轴正半轴为极轴的直角坐标系中,其参数方程为x=2cos(t),y=2sin(t)。
2.给定曲线C的参数方程为x=t²,y=t,在以原点为极点、x轴正半轴为极轴的极坐标系中,其极坐标方程为ρ=tan(θ)。
极坐标与参数方程知识点总结大全

曲线的参数方程和普通方程是曲线方程的不同形式 般地可以通过消去参数而从参数方程得到普通方程. 练习1若直线的参数方程为x = 1 :卜 2t『=2/为参数),则直线的斜率为B .2.下列在曲线x = sin 2 - x (为参数)上的点是( y = COST sin/ 3 1、B .(-;,;)4 2 l x = 2 亠sin 2:3•将参数方程. (V 为参数)化为普通方程为C . (2, -3)D . (1,3)A . y=x-2B . y=x 2C . y=x-2(2 二 x = 3)D . y = x 2(0 乞 y 岂1)注:普通方程化为参数方程,参数方程的形式不一定唯一(由上面练习( 1、3可知))。
应用参数方程解轨迹问题,关键在于适当地设参数,如果选用的参数 不同,那么所求得的曲线的参数方程的形式也不同。
极坐标与参数方程一、参数方程 1. 参数方程的概念般地,在平面直角坐标系 中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函并且对于t 每一个允许值,由方程组所确定的点M (x , y )都在这条曲线上(即曲线上的点在方程上,方程的解都在曲线上) ,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数.相对于参数方程而言,直接给出点的坐标间关系的方程叫做 普通方程. 2. 参数方程和普通方程的互化数,即x = f (t)3.圆的参数方程如图所示,设圆0的半径为,点肋从初始位置•出发,按逆时针方向在圆0上作匀速圆周运动,设極忆加,贝U这就是圆心在原点(),半径为的圆的参数方程,其中0的几何意义是转过的角度(称为旋转角)。
圆心为(□』),半径为的圆的普通方程是(口屏“丿冷 /『:心:(诙细它的参数方程为:力。
4.椭圆的参数方程以坐标原点"为中心,焦点在丄轴上的椭圆的标准方程为[":学&讷参期a沪其参数方程为LJ r=Asm^ ,其中参数卩称为离心与=1(瓯》艮角;焦点在I轴上的椭圆的标准方程是其参数方程为严碍缎覺参飙[y=a^^其中参数爷仍为离心角,通常规定参数爷的范围为爭€ [0,2兀)。
第十章 极坐标和参数方程第二节 参数方程

为了与曲线的参数方程有所区别,我们把表示曲线上点 的坐标之间的直接关系的方程叫做曲线的普通方程.
二、参数方程的作图
在所给曲线的参数方程
x = x t
y
=
y
t
,a t b
中, 先给参数t以某些可能取的值,求出x和y的对应值,这样就
确定了曲线上的点,将这些点连成光滑的曲线,就是参数方程
的图像.
0t
cos
, 纵坐标为0t
sin
1 2
gt
2
,因此我们就以方程组
:
x
0t
cos
y
0 t
sin
1 2
gt 2
,0 t t1
y
v0t sin
T •
v0t
M x, y
•
O
Q
x
v0t cos
图10-17 炮弹运动规律的轨迹
来表示炮弹运动的轨迹方程,其中 g是重力加速度g=9.8m/s2 ,t1
下面我们分别在直角坐标系与极坐标系内建立圆的渐开线 的参数方程.
(1)直角坐标参数方程 如图10-22所示,设基圆的圆心为O, 半径为 r, 绳子全部绕在圆圈上时,端点为 A. 取 O 为原点, 过 OA 的直线为 x 轴,建立直角坐标系.
设M x, y是渐开线上任意一点, BM 是切线,连接 OB,取
0来表示炮弹运动的轨迹方程是比较困难的.但是我们知道, 炮弹
运动的轨迹是由炮弹在各个时刻的位置所决定的.下面就来分析
炮弹在任意位置的坐标x和y分别与时刻t之间的关系.如果不考
虑地心引力,则经过时刻t,炮弹运动到T ,于是OT =0t.但事实上,
炮弹受地心引力的影响,不在点T而在点M .由于点M的横坐标为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
极坐标和参数方程知识点回顾(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即⎩⎨⎧==)()(t f y t f x 并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数. (二)常见曲线的参数方程如下:1.过定点(x 0,y 0),倾角为α的直线:ααsin cos 00t y y t x x +=+= (t 为参数)其中参数t 是以定点P (x 0,y 0)为起点,对应于t 点M (x ,y )为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论.○1.设A 、B 是直线上任意两点,它们对应的参数分别为t A 和t B ,则AB =A B t t -=B A A B t t t t ⋅--4)(2.○2.线段AB 的中点所对应的参数值等于2BA t t +. 2.中心在(x 0,y 0),半径等于r 的圆:θθsin cos 00r y y r x x +=+= (θ为参数)3.中心在原点,焦点在x 轴(或y 轴)上的椭圆:θθsin cos b y a x == (θ为参数) (或 θθsin cos a y b x ==)中心在点(x0,y0)焦点在平行于x 轴的直线上的椭圆的参数方程为参数)ααα(.sin ,cos 00⎩⎨⎧+=+=b y y a x x 4.中心在原点,焦点在x 轴(或y 轴)上的双曲线:θθtg sec b y a x == (θ为参数) (或θθec a y b x s tg ==)5.顶点在原点,焦点在x 轴正半轴上的抛物线:pty pt x 222== (t 为参数,p >0)直线的参数方程和参数的几何意义过定点P (x 0,y 0),倾斜角为α的直线的参数方程是 ⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数). (三)极坐标系1、定义:在平面内取一个定点O ,叫做极点,引一条射线Ox ,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
对于平面内的任意一点M ,用ρ表示线段OM 的长度,θ表示从Ox 到OM 的角,ρ叫做点M 的极径,θ叫做点M 的极角,有序数对(ρ, θ)就叫做点M 的极坐标。
这样建立的坐标系叫做极坐标系。
2、极坐标有四个要素:①极点;②极轴;③长度单位;④角度单位及它的方向.极坐标与直角坐标都是一对有序实数确定平面上一个点,在极坐标系下,一对有序实数ρ、θ对应惟一点P (ρ,θ),但平面内任一个点P 的极坐标不惟一.一个点可以有无数个坐标,这些坐标又有规律可循的,P (ρ,θ)(极点除外)的全部坐标为(ρ,θ+πk 2)或(ρ-,θ+π)12(+k ),(∈k Z ).极点的极径为0,而极角任意取.若对ρ、θ的取值范围加以限制.则除极点外,平面上点的极坐标就惟一了,如限定ρ>0,0≤θ<π2或ρ<0,π-<θ≤π等. 极坐标与直角坐标的不同是,直角坐标系中,点与坐标是一一对应的,而极坐标系中,点与坐标是一多对应的.即一个点的极坐标是不惟一的.3、直线相对于极坐标系的几种不同的位置方程的形式分别为:图1⑴0ϕθ= ⑵θρcos a = ⑶θρcos a-= ⑷θρsin a =⑸θρsin a-= ⑹)cos(ϕθρ-=a4、圆相对于极坐标系的几种不同的位置方程的形式分别为)0(>a : ⑴a =ρ ⑵θρcos 2a = ⑶θρcos 2a -= ⑷θρsin 2a = ⑸ θρsin 2a -= ⑹)cos(2ϕθρ-=aϕθ=θρcos a=θρcos a -=θρsin a=图4θρsin a -=图5)cos(ϕθρ-=a5、极坐标与直角坐标互化公式:[基础训练A 组]一、选择题1.若直线的参数方程为12()23x tt y t=+⎧⎨=-⎩为参数,则直线的斜率为( )x⎩(直极互化 图)θρcos 2a =图2θρsin 2a =图4θρsin 2a-=图5θρcos 2a -=a=ρ图1)cos(2ϕθρ-=a 图6A .23 B .23- C .32 D .32- 2.下列在曲线sin 2()cos sin x y θθθθ=⎧⎨=+⎩为参数上的点是( )A.1(,2B .31(,)42-C. D.(1 3.将参数方程222sin ()sin x y θθθ⎧=+⎪⎨=⎪⎩为参数化为普通方程为( ) A .2y x =- B .2y x =+ C .2(23)y x x =-≤≤ D .2(01)y x y =+≤≤ 4.化极坐标方程2cos 0ρθρ-=为直角坐标方程为( )A .201y y +==2x 或B .1x =C .201y +==2x 或xD .1y = 5.点M的直角坐标是(1-,则点M 的极坐标为( )A .(2,)3πB .(2,)3π-C .2(2,)3πD .(2,2),()3k k Z ππ+∈6.极坐标方程cos 2sin 2ρθθ=表示的曲线为( )A .一条射线和一个圆B .两条直线C .一条直线和一个圆D .一个圆二、填空题1.直线34()45x tt y t =+⎧⎨=-⎩为参数的斜率为______________________。
2.参数方程()2()t tt tx e et y e e --⎧=+⎪⎨=-⎪⎩为参数的普通方程为__________________。
3.已知直线113:()24x tl t y t =+⎧⎨=-⎩为参数与直线2:245l x y -=相交于点B ,又点(1,2)A ,则AB =_______________。
4.直线122()112x t t y t ⎧=-⎪⎪⎨⎪=-+⎪⎩为参数被圆224x y +=截得的弦长为______________。
5.直线cos sin 0x y αα+=的极坐标方程为____________________。
三、解答题1.已知点(,)P x y 是圆222x y y +=上的动点, (1)求2x y +的取值范围;(2)若0x y a ++≥恒成立,求实数a 的取值范围。
2.求直线11:()5x tl t y =+⎧⎪⎨=-⎪⎩为参数和直线2:0l x y --=的交点P 的坐标,及点P与(1,5)Q -的距离。
3.在椭圆2211612x y +=上找一点,使这一点到直线2120x y --=的距离的最小值。
一、选择题1.直线l 的参数方程为()x a tt y b t=+⎧⎨=+⎩为参数,l 上的点1P 对应的参数是1t ,则点1P 与(,)P a b 之间的距离是( )A .1tB .12t C1 D1 2.参数方程为1()2x t t t y ⎧=+⎪⎨⎪=⎩为参数表示的曲线是( )A .一条直线B .两条直线C .一条射线D .两条射线3.直线112()x t t y ⎧=+⎪⎪⎨⎪=-⎪⎩为参数和圆2216x y +=交于,A B 两点,则AB 的中点坐标为( )A .(3,3)- B.( C.3)- D.(3, 4.圆5cos ρθθ=-的圆心坐标是( )A .4(5,)3π--B .(5,)3π-C .(5,)3πD .5(5,)3π- 5.与参数方程为)x t y ⎧=⎪⎨=⎪⎩为参数等价的普通方程为( )A .214y +=2x B .21(01)4y x +=≤≤2x C .21(02)4y y +=≤≤2x D .21(01,02)4y x y +=≤≤≤≤2x 6.直线2()1x tt y t=-+⎧⎨=-⎩为参数被圆22(3)(1)25x y -++=所截得的弦长为( )AB .1404C. D二、填空题1.曲线的参数方程是211()1x t t y t ⎧=-⎪≠⎨⎪=-⎩为参数,t 0,则它的普通方程为__________________。
2.直线3()14x att y t=+⎧⎨=-+⎩为参数过定点_____________。
3.点P(x,y)是椭圆222312x y +=上的一个动点,则2x y +的最大值为___________。
4.曲线的极坐标方程为1tan cos ρθθ=⋅,则曲线的直角坐标方程为________________。
5.设()y tx t =为参数则圆2240x y y +-=的参数方程为__________________________。
三、解答题1.参数方程cos (sin cos )()sin (sin cos )x y θθθθθθθ=+⎧⎨=+⎩为参数表示什么曲线?2.点P 在椭圆221169x y +=上,求点P 到直线3424x y -=的最大距离和最小距离。
3.已知直线l 经过点(1,1)P ,倾斜角6πα=,(1)写出直线l 的参数方程。
(2)设l 与圆422=+y x 相交与两点,A B ,求点P 到,A B 两点的距离之积。
一、选择题1.把方程1xy =化为以t 参数的参数方程是( )A .1212x t y t -⎧=⎪⎨⎪=⎩B .sin 1sin x t y t =⎧⎪⎨=⎪⎩C .cos 1cos x t y t =⎧⎪⎨=⎪⎩D .tan 1tan x t y t =⎧⎪⎨=⎪⎩ 2.曲线25()12x tt y t =-+⎧⎨=-⎩为参数与坐标轴的交点是( )A .21(0,)(,0)52、B .11(0,)(,0)52、C .(0,4)(8,0)-、D .5(0,)(8,0)9、3.直线12()2x tt y t=+⎧⎨=+⎩为参数被圆229x y +=截得的弦长为( )A .125 BCD4.若点(3,)P m 在以点F 为焦点的抛物线24()4x t t y t⎧=⎨=⎩为参数上,则PF 等于( ) A .2 B .3 C .4 D .5 5.极坐标方程cos 20ρθ=表示的曲线为( )A .极点B .极轴C .一条直线D .两条相交直线 6.在极坐标系中与圆4sin ρθ=相切的一条直线的方程为( )A .cos 2ρθ=B .sin 2ρθ=C .4sin()3πρθ=+ D .4sin()3πρθ=-二、填空题1.已知曲线22()2x pt t p y pt ⎧=⎨=⎩为参数,为正常数上的两点,M N 对应的参数分别为12,t t 和,120t t +=且,那么MN =_______________。
2.直线2()3x t y ⎧=-⎪⎨=⎪⎩为参数上与点(2,3)A -_______。
