微积分05-06(1)期中测试试题汇总
交通大学微积分第一学期期中考试试卷及答案
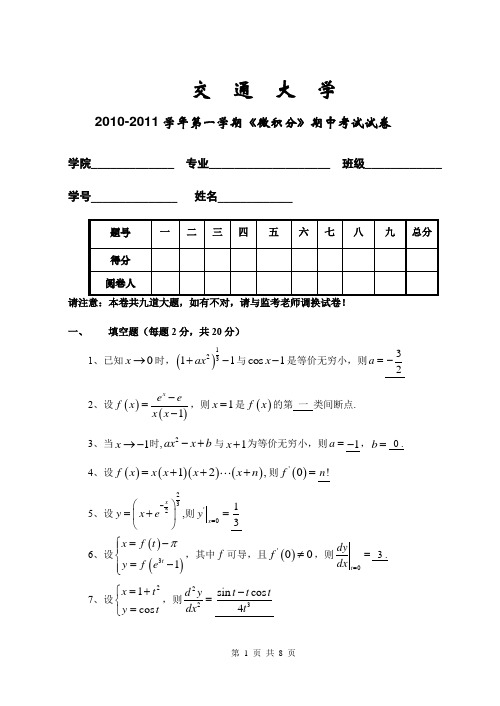
交 通 大 学2010-2011学年第一学期《微积分》期中考试试卷学院_____________ 专业___________________ 班级____________ 学号_______________ 姓名_____________一、填空题(每题2分,共20分)1、已知0x →时,()12311ax+-与cos 1x -是等价无穷小,则a =32-2、设()()1x e ef x x x -=-,则1x =是()f x 的第 一 类间断点.3、当1x →-时,2ax x b -+与1x +为等价无穷小,则a =1-,b = 0 . 4、设()()()()12,f x x x x x n =+++则()'0f =!n5、设232x y x e-⎛⎫=+ ⎪⎝⎭,则'0x y ==136、设()()31tx f t y f e π=-⎧⎪⎨=-⎪⎩,其中f 可导,且()'00f ≠,则0t dy dx == 3 . 7、设21cos x t y t ⎧=+⎨=⎩,则22d y dx =3sin cos 4t t t t -8、设tan y x y =+,则dy =2cot ydx9、()2212x x de e --=)222x x e e -+10、极坐标系下对数螺线r e θ=在点()2,,2r e ππθ⎛⎫= ⎪⎝⎭处的切线的直角坐标方程为2x y e π+=二、单项选择题(每题2分,共30分)1、设()()22,0,,0,2,0,,0,x x x x g x f x x x x x -≤⎧<⎧==⎨⎨+>-≥⎩⎩,则()g f x =⎡⎤⎣⎦ D . (A) 22,0,2,0,x x x x ⎧+<⎨-≥⎩(B )22,0,2,0,x x x x ⎧-<⎨+≥⎩(C )22,0,2,0,x x x x ⎧-<⎨-≥⎩.(D )22,0,2,0,x x x x ⎧+<⎨+≥⎩2、202sinlimtan x x x x→= C . (A) 1,(B )2, (C) 0,(D )不存在.3、当0x →时,tan sin x x -与kx 是同阶无穷小,则k = C . (A)1.(B )2(C )3.(D )4. 4、设()sin 3sin 5x x xf x e eπ=-,则当x π→时, D . (A )()f x 是x π-的等价无穷小, (B )()f x 是x π-的低阶无穷小, (C )()f x 是x π-的高阶无穷小,(D )()f x 是x π-的同阶但非等价的无穷小。
经济数学微积分课程期中模拟考试卷及答案

诚实考试吾心不虚 ,公平竞争方显实力, 考试失败尚有机会 ,考试舞弊前功尽弃。
《经济数学-微积分》课程期中模拟考试卷(A )答案202 ——202 学年第一学期姓名学号班级题号 一二三四五六总分得分一、 单选题(每小题2分,共计10分)1.1=x 是函数xx f -=11arctan)(的 ( C ) A .连续点. B .可去间断点. C .跳跃间断点. D .无穷间断点.2.若1)0(='f ,则=--→hh f f h 3)()0(lim0( B ) A . 0. B . 31. C . 3. D . 31-.3.设⎪⎩⎪⎨⎧=≠--=.1,2;1,1|1|)(2x x x x x f 则在1=x 处函数)(x f ( A )A . 不连续.B . 连续,但不可导.C . 可导,但导函数不连续.D . 可导,且导函数连续.4.设)(x f y =是由方程0ln =+y xy 确定的函数,则=dxdy( C ) A . xy ln -. B . 2y -. C . 12+-xy y . D . xy y 12+-.5.设)(x f 在),(b a 内可导,),(0b a x ∈,若0)(0='x f ,则)(0x f ( D )A . 是极大值.B .是极小值.C . 是拐点的纵坐标.D .可能是极值也可能不是极值.得分二、 填空题(每小题2分,共计10分)1. =+∞→)sin 1sin(lim xx x x x 1 .2. 设xx f 2)(=,则='-'→x f x f x )0()(lim0 2ln 2 . 3. 设xx f 211)(-=,则=)1()10(f !10210⋅- . 4. 设曲线2x y =的切线与曲线3x y =的切线相互垂直,则曲线2x y =上的点的横坐标=x 361- . 5. 函数x y cos =在23,2[ππ上符合罗尔定理结论中的=ξ π .三、计算题(每小题9分,共计54分)1. ])12()12(1531311[lim +⋅-++⋅+⋅∞→n n n .解: )12()12(1531311[lim +⋅-++⋅+⋅∞→n n n211211[21lim ]1211215131311[21lim =+-⋅=+--++-+-⋅=∞→∞→n n n n n .得分 得分2. 已知213)tan )(1ln(lim=-+→x x x x f ,求20)(lim x x f x →.解:由于3ln )(lim 3ln )(lim 3ln tan )(lim 13)tan )(1ln(lim220000x x f x x x f x x x f x x f x x x x x →→→→===-+=,所以3ln 2)(lim2=→x x f x 。
微积分(II)期中考试试题(A卷)

1.设()=+z f ax by ,其中f 可微,则( ). (A )∂∂=∂∂z z x y (B )∂∂=-∂∂z z x y (C )∂∂=∂∂z z a b x y (D )∂∂=∂∂z z b a x y2.定积分⎰--1 12d 1x x 的值是( ).(A )4π (B )2π(C )1 (D )π 3.函数()33ln y x z +=在)(1,1处的全微分=z d ( ). (A )y x d d + (B )()y x d d 2+(C )()y x d d 23+ (D )()y x d d 3+ 4.下列方程是微分方程的是( ). (A )x y x y y d )(d ln -=(B )02tan 3sin =+x x y(C )0232=+-y y (D )533-+=x x y5.下列广义积分发散的是( ). (A )⎰∞+ 1d xx x (B )⎰∞+ 12d x x(C )⎰∞+ 1 2d xx x (D ) 1d x x +∞⎰ 6.设222)ln(yx xx y z --+-=的定义域D 的图形是( ).(A ) (B )(C ) (D )7.(答题区域:1-10行内)求32e x y x z y+=,求 x z∂∂,yz ∂∂, y x z ∂∂∂2.8.(答题区域:11-20行内)设()y x f z xy cos ,e =,其中f 有一阶连续偏导数,求x z ∂∂,yz∂∂.9.(答题区域:21-30行内)设v u z =,y x u 2+=,y x v -=,求xz∂∂,y z ∂∂.三、计算下列各题(本大题共3个小题,每小题7分,共21分)10.求极限21cos 0d e lim2x t xt x ⎰→. 11.求定积分 e2 1ln d x x x ⎰.12.(答题区域:51-60行内)求定积分 8⎰. 添加1. 220|1|d -⎰x x 添加2 设2 0()12 0x x f x x x ⎧≤=⎨+>⎩,,,求2(1)d f x x -⎰.四、解答下列各题(本大题共3个小题,第13小题6分,14、15小题各8分,共22分)13.(答题区域:61-75行内)求微分方程0d )1(d )1(=+--x y y x 的通解.14.求一阶线性微分方程 3)1(12+=+-'x y x y 在初始条件10==x y 下的特解.15. (答题区域:91-105行内)若()f x 在[0,1]上连续,且 122 01()()d 1f x x f t t x=++⎰,求 1()d f x x ⎰及)(x f .五、应用题(本大题共1个小题,共13分)16.(答题区域:106-120行内)设由曲线2x y =与1=y 所围成的平面图形为D ,(1)求D 的面积;(2)求D 绕x 轴旋转而成的旋转体的体积.六、证明题(本大题共1个小题,共5分)17.(答题区域:121-135行内)设)(x f 在],[b a 上连续,证明x x b a f x x f bab ad )(d )(⎰⎰-+=.参考答案一、 单项选择题(本大题共6个小题,每小题3分,共18分)1.D 2.B 3.C 4.A 5.D 6. D二、计算下列各题(本大题共3个小题,每小题7分,共21分)7. 23e 2x xy xz y +=∂∂,)e e (2y y y x y z +=∂∂ y y y y x y x y x z e )1(20)e e (22+=++=∂∂∂ . 8.)(cos e 21y f y f xzxy ⋅'+'=∂∂=21cos e f y f y xy '+',)sin (e 21y x f x f yzxy -'+'=∂∂21sin e f y x f x xy '-'= . ……7分 9.u u vu x zv v ln 1+=∂∂-=⎥⎦⎤⎢⎣⎡+++-+-)2ln(2)2()(y x y x y x y x y x , ……3分)1(ln 21-⋅+⋅=∂∂-u u vu y zv v ⎥⎦⎤⎢⎣⎡+-+-+=-)2ln(2)(2)2()(y x y x y x y x y x . ……7分 10.xx x t x x xt x 2)sin (e lim d e lim22cos 021 cos 0-⋅-=→→⎰ 2e lim2cos0xx →= 2e=. 11. e 2 1ln d x x x ⎰=)31(d ln 3e 1 x x ⎰⎰-=e 1 23d 311e ln 31x x x x ……4分1e 911e ln 3133x x x -= 913e 23+=. 12.令3t x =,t t x d 3d 2=,2080t x ,8⎰=t tt d 132 0 2⎰+ ……4分 =⎪⎪⎭⎫ ⎝⎛++-202)1ln(23t t t ……6分 =3ln 3. ……7分四、解答下列各题13.微分方程0d )1(d )1(=+--x y y x 的通解. 解:分离变量,得x xy y d 11d 11-=+, ……2分两边积分,得C x y ln )1ln()1ln(+--=+,方程的通解为 C y x =+-)1)(1(. ……6分 14.求一阶线性微分方程 3)1(12+=+-'x y x y 在初始条件10==x y 下的特解. 解:12)(+-=x x p ,3)1()(+=x x q . ……2分 方程通解 ⎥⎦⎤⎢⎣⎡+⎰+⎰=⎰+-+--C x x y x x x x d e )1(ed 123d 12 ……3分 []⎰+++=C x x x d )1()1(2 ……5分])1(21[)1(22C x x +++=. ……6分将1|0==x y 代入通解中,得21=C , ……7分所求特解为:]1)1[()1(2122+++=x x y . ……8分15. 若()f x 在[0,1]上连续,且 122 01()()d 1f x x f t t x =++⎰,求 1 0()d f x x ⎰及)(x f .解:设A= 10()d f x x ⎰,则方程化为 2211)(Ax xx f ++=, ……2分 对上式在[0,1]上积分 ,有01)3(arctan 3Ax x A += ,得 8π3=A , 所以, 228π311)(x xx f ++=. ……8分 五、应用题(本大题共1个小题,共13分)16.设由曲线2x y =与1=y 所围成的平面图形为D ,(1)求D 的面积;(2)求D 绕x 轴旋转而成的旋转体的体积.解:(1)面积⎰--=112d )1(x x A ……2分11)31(3--=x x ……4分=34. ……6分 (2)体积x x V d )1(π114⎰--= ……3分11)51(π5--=x x ……5分=5π8. ……7分 六、证明题(本大题共1个小题,共5分)17.设)(x f 在],[b a 上连续,证明x x b a f x x f baad )(d )(b ⎰⎰-+=.证明:设x b a t -+=, ……1分 右⎰-=ab t t f )d )(( ……4分⎰=bat t f d )(=左. ……5分。
微积分试卷及标准答案6套

微积分试题 (A 卷)一. 填空题 (每空2分,共20分)1. 已知,)(lim 1A x f x =+→则对于0>∀ε,总存在δ>0,使得当时,恒有│ƒ(x )─A│< ε。
2. 已知2235lim2=-++∞→n bn an n ,则a = ,b = 。
3. 若当0x x →时,α与β 是等价无穷小量,则=-→ββα0limx x 。
4. 若f (x )在点x = a 处连续,则=→)(lim x f ax 。
5. )ln(arcsin )(x x f =的连续区间是 。
6. 设函数y =ƒ(x )在x 0点可导,则=-+→hx f h x f h )()3(lim000______________。
7. 曲线y = x 2+2x -5上点M 处的切线斜率为6,则点M 的坐标为 。
8. ='⎰))((dx x f x d 。
9. 设总收益函数和总成本函数分别为2224Q Q R -=,52+=Q C ,则当利润最大时产量Q 是 。
二. 单项选择题 (每小题2分,共18分)1. 若数列{x n }在a 的ε 邻域(a -ε,a +ε)内有无穷多个点,则( )。
(A) 数列{x n }必有极限,但不一定等于a (B) 数列{x n }极限存在,且一定等于a(C) 数列{x n }的极限不一定存在 (D) 数列{x n }的极限一定不存在 2. 设11)(-=x arctgx f 则1=x 为函数)(x f 的( )。
(A) 可去间断点 (B) 跳跃间断点 (C) 无穷型间断点(D) 连续点 3. =+-∞→13)11(lim x x x( )。
(A) 1 (B) ∞ (C)2e (D) 3e4. 对需求函数5p eQ -=,需求价格弹性5pE d -=。
当价格=p ( )时,需求量减少的幅度小于价格提高的幅度。
(A) 3 (B) 5 (C) 6 (D) 105. 假设)(),(0)(lim ,0)(lim 0x g x f x g x f x x x x ''==→→;在点0x 的某邻域内(0x 可以除外)存在,又a 是常数,则下列结论正确的是( )。
微积分综合练习题及参考答案1

综合练习题1(函数、极限与连续部分)1.填空题 (1)函数)2ln(1)(-=x x f 的定义域是 . 答案:2>x 且3≠x .(2)函数24)2ln(1)(x x x f -++=的定义域是 .答案:]2,1()1,2(-⋃--(3)函数74)2(2++=+x x x f ,则=)(x f. 答案:3)(2+=x x f(4)若函数⎪⎩⎪⎨⎧≥<+=0,0,13sin )(x k x xx x f 在0=x 处连续,则=k .答案:1=k(5)函数x x x f 2)1(2-=-,则=)(x f .答案:1)(2-=x x f(6)函数1322+--=x x x y 的间断点是 .答案:1-=x(7)=∞→xx x 1sinlim .答案:1(8)若2sin 4sin lim 0=→kxxx ,则=k .答案:2=k2.单项选择题(1)设函数2e e xx y +=-,则该函数是( ).A .奇函数B .偶函数C .非奇非偶函数D .既奇又偶函数 答案:B(2)下列函数中为奇函数是().A .x x sinB .2e e xx +- C .)1ln(2x x ++ D .2x x +答案:C(3)函数)5ln(4+++=x x xy 的定义域为( ).A .5->xB .4-≠xC .5->x 且0≠xD .5->x 且4-≠x 答案:D(4)设1)1(2-=+x x f ,则=)(x f ( ) A .)1(+x x B .2x C .)2(-x x D .)1)(2(-+x x 答案:C(5)当=k ( )时,函数⎩⎨⎧=≠+=0,,2)(x k x e x f x 在0=x 处连续.A .0B .1C .2D .3 答案:D(6)当=k ( )时,函数⎩⎨⎧=≠+=0,,1)(2x k x x x f ,在0=x 处连续.A .0B .1C .2D .1- 答案:B(7)函数233)(2+--=x x x x f 的间断点是( ) A .2,1==x xB .3=xC .3,2,1===x x xD .无间断点 答案:A 3.计算题(1)423lim 222-+-→x x x x .解:4121lim )2)(2()1)(2(lim 423lim22222=+-=+---=-+-→→→x x x x x x x x x x x x (2)329lim 223---→x x x x解:234613lim )1)(3()3)(3(lim 329lim 33223==++=+-+-=---→→→x x x x x x x x x x x x (3)4586lim 224+-+-→x x x x x解:3212lim )1)(4()2)(4(lim 4586lim 44224=--=----=+-+-→→→x x x x x x x x x x x x x综合练习题2(导数与微分部分)1.填空题(1)曲线1)(+=x x f 在)2,1(点的切斜率是 . 答案:21(2)曲线x x f e )(=在)1,0(点的切线方程是 . 答案:1+=x y(3)已知x x x f 3)(3+=,则)3(f '= . 答案:3ln 33)(2x x x f +=')3(f '=27()3ln 1+(4)已知x x f ln )(=,则)(x f ''= . 答案:x x f 1)(=',)(x f ''=21x- (5)若x x x f -=e )(,则='')0(f .答案:x x x x f --+-=''e e 2)(='')0(f 2-2.单项选择题(1)若x x f x cos e )(-=,则)0(f '=( ).A. 2B. 1C. -1D. -2 因)(cos e cos )e ()cos e ()('+'='='---x x x x f x x x)sin (cos e sin e cos e x x x x x x x +-=--=---所以)0(f '1)0sin 0(cos e 0-=+-=- 答案:C(2)设y x =lg2,则d y =( ). A .12d x x B .1d x x ln10 C .ln10x x d D .1d xx 答案:B(3)设)(x f y =是可微函数,则=)2(cos d x f ( ). A .x x f d )2(cos 2' B .x x x f d22sin )2(cos ' C .x x x f d 2sin )2(cos 2' D .x x x f d22sin )2(cos '- 答案:D(4)若3sin )(a x x f +=,其中a 是常数,则='')(x f ( ).A .23cos a x +B .a x 6sin +C .x sin -D .x cos 答案:C3.计算题(1)设xx y 12e =,求y '.解: )1(e e 22121xx x y xx -+=')12(e 1-=x x(2)设x x y 3cos 4sin +=,求y '.解:)sin (cos 34cos 42x x x y -+='x x x 2cos sin 34cos 4-=(3)设xy x 2e 1+=+,求y '. 解:2121(21ex x y x -+='+ (4)设x x x y cos ln +=,求y '.解:)sin (cos 12321x x x y -+=' x x tan 2321-= 综合练习题3(导数应用部分)1.填空题(1)函数y x =-312()的单调增加区间是 . 答案:),1(+∞(2)函数1)(2+=ax x f 在区间),0(∞+内单调增加,则a 应满足 .答案:0>a2.单项选择题(1)函数2)1(+=x y 在区间)2,2(-是( ) A .单调增加 B .单调减少 C .先增后减 D .先减后增 答案:D(2)满足方程0)(='x f 的点一定是函数)(x f y =的( ). A .极值点 B .最值点 C .驻点 D . 间断点 答案:C(3)下列结论中( )不正确. A .)(x f 在0x x =处连续,则一定在0x 处可微.B .)(x f 在0x x =处不连续,则一定在0x 处不可导.C .可导函数的极值点一定发生在其驻点上.D .函数的极值点一定发生在不可导点上. 答案: B(4)下列函数在指定区间(,)-∞+∞上单调增加的是( ). A .x sin B .x e C .2x D .x -3答案:B3.应用题(以几何应用为主)(1)欲做一个底为正方形,容积为108m 3的长方体开口容器,怎样做法用料最省?解:设底边的边长为x m ,高为h m ,容器的表面积为y m 2。
(完整word版)《微积分》各章习题及详细答案

第一单元 函数与极限一、填空题1、已知x xf cos 1)2(sin +=,则=)(cos x f 。
2、=-+→∞)1()34(lim 22x x x x 。
3、0→x 时,x x sin tan -是x 的 阶无穷小。
4、01sin lim 0=→x x k x 成立的k 为 。
5、=-∞→x e x x arctan lim 。
6、⎩⎨⎧≤+>+=0,0,1)(x b x x e x f x 在0=x 处连续,则=b 。
7、=+→xx x 6)13ln(lim0 。
8、设)(x f 的定义域是]1,0[,则)(ln x f 的定义域是__________。
9、函数)2ln(1++=x y 的反函数为_________。
10、设a 是非零常数,则________)(lim =-+∞→xx ax a x 。
11、已知当0→x 时,1)1(312-+ax 与1cos -x 是等价无穷小,则常数________=a 。
12、函数xxx f +=13arcsin )(的定义域是__________。
13、____________22lim22=--++∞→x x n 。
14、设8)2(lim =-+∞→xx ax a x ,则=a ________。
15、)2)(1(lim n n n n n -++++∞→=____________。
二、选择题1、设)(),(x g x f 是],[l l -上的偶函数,)(x h 是],[l l -上的奇函数,则 中所给的函数必为奇函数。
(A))()(x g x f +;(B))()(x h x f +;(C ))]()()[(x h x g x f +;(D ))()()(x h x g x f 。
2、xxx +-=11)(α,31)(x x -=β,则当1→x 时有 。
(A)α是比β高阶的无穷小; (B)α是比β低阶的无穷小; (C )α与β是同阶无穷小; (D )βα~。
微积分试卷及标准答案6套

微积分试题 (A 卷)一. 填空题 (每空2分,共20分)1.已知则对于,总存在δ>0,使得当,)(lim 1A x f x =+→0>∀ε时,恒有│ƒ(x )─A│< ε。
2.已知,则a = ,b =2235lim 2=-++∞→n bn an n 。
3.若当时,α与β 是等价无穷小量,则 。
0x x →=-→ββα0limx x 4.若f (x )在点x = a 处连续,则 。
=→)(lim x f ax 5.的连续区间是 。
)ln(arcsin )(x x f =6.设函数y =ƒ(x )在x 0点可导,则______________。
=-+→hx f h x f h )()3(lim0007.曲线y = x 2+2x -5上点M 处的切线斜率为6,则点M 的坐标为 。
8. 。
='⎰))((dx x f x d 9.设总收益函数和总成本函数分别为,,则当利润最大时产2224Q Q R -=52+=Q C 量是。
Q 二. 单项选择题 (每小题2分,共18分)1.若数列{x n }在a 的ε 邻域(a -ε,a +ε)内有无穷多个点,则()。
(A) 数列{x n }必有极限,但不一定等于a (B) 数列{x n }极限存在,且一定等于a(C) 数列{x n }的极限不一定存在 (D) 数列{x n }的极限一定不存在2.设则为函数的( )。
11)(-=x arctg x f 1=x )(x f(A) 可去间断点(B) 跳跃间断点 (C) 无穷型间断点(D) 连续点3.( )。
=+-∞→13)11(lim x x x(A) 1 (B) ∞(C)(D) 2e 3e4.对需求函数,需求价格弹性。
当价格( )时,5p eQ -=5pE d -==p 需求量减少的幅度小于价格提高的幅度。
(A) 3 (B) 5 (C) 6(D) 105.假设在点的某邻域内(可以除外)存)(),(0)(lim ,0)(lim 0x g x f x g x f x x x x ''==→→得0x 0x 在,又a 是常数,则下列结论正确的是( )。
微积分期中考试试题答案

一,求下列极限: (20分) 1, dtte dt e x t x t x ⎰⎰→0220022)(lim 2, 求极限:dt t f a x x xa a x ⎰-→)(lim ,其中)(x f 连续二,求定积分(30分)1.21⎰ 2.0x xdx e e +∞-+⎰ 3.⎰+20cos sin cos πdx xx x 4.⎰-=++222cos 1cos ππdx x x x 三,求由方程⎰x20 t 2dt +⎰x0 dt t 21+ +xy=0所确定的函数y=y(x)的微分dy 。
(10分) 四,求抛物线23y x =-与直线2y x =及y 轴所围成在第一象限的平面图形的面积A 及该平面图形绕y 轴旋转所成的旋转体的体积V 。
(10分)五,(30分)1)设()f x 在[0,2]a 上连续,证明200()[()(2)]a af x dx f x f a x dx =+-⎰⎰ 2)若f(x)在[0,1]上连续,证明⎰π0)(sin dx x xf =πdx x f ⎰20)(cos π3) 计算20sin 1cos x x dx xπ+⎰1. ()dxte dt e x t x t x ⎰⎰→0220202lim 2220202lim x x x t x xe e dt e ⋅=⎰→20202lim x x t x xe dt e ⎰→= 2222022lim x x xx ex e e +=→2212lim 20=+=→x x 2.dt t f a x x xa a x ⎰-→)(lim)(1)()(lim a af dt t f x xf x a a x =+=⎰→二.1。
210⎰tdt t t t x cos 2cos 2sin 4sin 602⎰=π ⎰=602sin 4πtdt ⎰-=60)2cos 1(2πdt t 602sin 3ππt -=233-=π 2.0x x dx e e +∞-+⎰=dx e e x x 120+=⎰∞+1)(20+=⎰∞+x x e de 0)arctan(∞+=x e 42ππ-=4π= 3.⎰+20cos sin cos πdx x x x ⎰+++-=2cos sin )cos (sin )sin (cos 21πdx x x x x x x ⎰++=20cos sin )cos (sin 21πx x x x d dx ⎰+20121π 4cos sin ln 2120ππ++=x x 4π=4.⎰-=++222cos 1cos ππdx x x x ⎰-+222cos 1ππdx x x +⎰-+222cos 1cos ππdx x x ⎰+=202cos 1sin 2πxx d ⎰-=202sin 2sin 2πx x d x d xx sin )sin 21sin 21(2120-++=⎰π 20sin 2sin 2ln 21πxx -+= 1212ln 21-+=)12ln(2+= 三,解:对原方程⎰x20 t 2dt +⎰x0 dt t 21+ +xy=0两边求微分,得0)(1)2()2(22=+++xy d dx x x d x 有01822=++++xdy ydx dx x dx x 所以所求微分dx xy x x dy +++-=2218四.求抛物线23y x =-与直线2y x =及y 轴所围成在第一象限的平面图形的面积A 及该平面图形绕y 轴旋转所成的旋转体的体积V 。
微积分试卷及答案4套

微积分试卷及答案4套(共14页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2微积分试题 (A 卷)一. 填空题 (每空2分,共20分)1. 已知,)(lim 1A x f x =+→则对于0>∀ε,总存在δ>0,使得当时,恒有│ƒ(x )─A│< ε。
2. 已知2235lim2=-++∞→n bn an n ,则a = ,b = 。
3. 若当0x x →时,与 是等价无穷小量,则=-→ββα0limx x 。
4. 若f (x )在点x = a 处连续,则=→)(lim x f ax 。
5. )ln(arcsin )(x x f =的连续区间是 。
6. 设函数y =ƒ(x )在x 0点可导,则=-+→hx f h x f h )()3(lim000______________。
7. 曲线y = x 2+2x -5上点M 处的切线斜率为6,则点M 的坐标为 。
8. ='⎰))((dx x f x d 。
9. 设总收益函数和总成本函数分别为2224Q Q R -=,52+=Q C ,则当利润最大时产量Q 是 。
二. 单项选择题 (每小题2分,共18分) 1. 若数列{x n }在a 的邻域(a -,a +)内有无穷多个点,则( )。
(A) 数列{x n }必有极限,但不一定等于a (B) 数列{x n }极限存在,且一定等于a(C) 数列{x n }的极限不一定存在 (D) 数列{x n }的极限一定不存在2. 设11)(-=x arctgx f 则1=x 为函数)(x f 的( )。
3(A) 可去间断点 (B) 跳跃间断点 (C) 无穷型间断点 (D) 连续点3. =+-∞→13)11(lim x x x( )。
(A) 1 (B) ∞ (C) 2e (D)3e4. 对需求函数5p eQ -=,需求价格弹性5pE d -=。
微积分试卷及标准答案6套

微积分试题 (A 卷)一. 填空题 (每空2分,共20分)1. 已知,)(lim 1A x f x =+→则对于0>∀ε,总存在δ>0,使得当时,恒有│ƒ(x )─A│< ε。
2. 已知2235lim2=-++∞→n bn an n ,则a = ,b = 。
3. 若当0x x →时,与 是等价无穷小量,则=-→ββα0limx x 。
4. 若f (x )在点x = a 处连续,则=→)(lim x f ax 。
5. )ln(arcsin )(x x f =的连续区间是 。
6. 设函数y =ƒ(x )在x 0点可导,则=-+→hx f h x f h )()3(lim000______________。
7. 曲线y = x 2+2x -5上点M 处的切线斜率为6,则点M 的坐标为 。
8. ='⎰))((dx x f x d 。
9. 设总收益函数和总成本函数分别为2224Q Q R -=,52+=Q C ,则当利润最大时产量Q 是 。
二. 单项选择题 (每小题2分,共18分) 1. 若数列{x n }在a 的邻域(a -,a +)内有无穷多个点,则( )。
(A) 数列{x n }必有极限,但不一定等于a (B) 数列{x n }极限存在,且一定等于a(C) 数列{x n }的极限不一定存在 (D) 数列{x n }的极限一定不存在 2. 设11)(-=x arctgx f 则1=x 为函数)(x f 的( )。
(A) 可去间断点 (B) 跳跃间断点 (C) 无穷型间断点 (D) 连续点 3. =+-∞→13)11(lim x x x( )。
(A) 1 (B) ∞ (C)2e (D) 3e4. 对需求函数5p eQ -=,需求价格弹性5pE d -=。
当价格=p ( )时,需求量减少的幅度小于价格提高的幅度。
(A) 3 (B) 5 (C) 6 (D) 105. 假设)(),(0)(lim ,0)(lim 0x g x f x g x f x x x x ''==→→;在点0x 的某邻域内(0x 可以除外)存在,又a 是常数,则下列结论正确的是( )。
微积分测试题一(极限、连续)答案

微积分测试题(一)极限、连续部分(答案)一、选择题(每小题3分,共21分) 1、 当0x →+时,(A )无穷小量。
A 1sin x xB 1x e C ln x D 1sin x x2、点1x =是函数311()1131x x f x x x x -<⎧⎪==⎨⎪->⎩的(C )。
A 连续点B 第一类非可去间断点C 可去间断点D 第二类间断点 3、函数()f x 在点0x 处有定义是其在0x 处极限存在的(D )。
A 充分非必要条件B 必要非充分条件C 充要条件D 无关条件4、已知极限22lim()0x x ax x→∞++=,则常数a 等于(A )。
A -1B 0C 1D 25、极限201lim cos 1x x e x →--等于(D )。
A ∞B 2C 0D -2 6、设函数11()1x x f x e-=-则(D )。
A x=0,x=1都是()f x 的第一类间断点.B x=0,x=1都是()f x 的第二类间断点C x=0是()f x 的第一类间断点,x=1是()f x )的第二类间断点.D x=0是()f x 的第二类间断点,x=1是()f x 的第一类间断点. . D 【分析】 显然x=0,x=1为间断点,其分类主要考虑左右极限.【详解】 由于函数f(x)在x=0,x=1点处无定义,因此是间断点.且 0lim ()x f x →=∞,所以x=0为第二类间断点;1lim ()0x f x +→=,1lim ()1x f x -→=-,所以x=1为第一类间断点,故应选(D). 【评注】 应特别注意:1lim 1x x x +→=+∞-,1lim 1x xx -→=-∞- 从而+∞=-→+11lim x xx e,.0lim 11=-→-x x x e7已知lim()9xx x a x a→∞+=-,则a =( C ).A.1;B.∞;C.ln 3;D.2ln3.二、填空题(每小题4分,共20分) 1、21lim(1)x x x→∞-2、 当0x →+时,无穷小ln(1)Ax α=+与无穷小sin 3x β=等价,则常数3、 已知函数()f x 在点0x =处连续,且当0x ≠时,函数21()2x f x -=,则函数值(0)f4、 111lim[]1223(1)n n n →∞+++••+5、 若lim ()x f x π→存在,且sin ()2lim ()x xf xf x x ππ→=+-,则lim ()x f x π→三、解答题1、(7分)计算极限 222111lim(1)(1)(1)23n n→∞--- 解:原式=132411111lim()()()lim 223322n n n n n n n n →∞→∞-++•••=•= 2、(6分)计算极限 30tan sin lim x x xx →-解:原式=2322000sin 1sin 1cos 1cos 2lim lim lim cos cos 2x x x x x xx x x x x x x →→→--===3、(7分)计算极限 123lim()21x x x x +→∞++ 解:原式= 11122112221lim(1)lim(1)121211lim(1)lim(1)1122x x x x x x x x x e x x +++→∞→∞+→∞→∞+=+++=+•+=++ 4、(7分)计算极限1x e →-解:原式=201sin 12lim 2x x xx →=5、(7分)设3214lim 1x x ax x x →---++ 具有极限l ,求,a l 的值解:因为1lim(1)0x x →-+=,所以 321lim(4)0x x ax x →---+=,因此 4a = 并将其代入原式321144(1)(1)(4)lim lim 1011x x x x x x x x l x x →-→---++--===++6、(8分)设3()32,()(1)nx x x x c x αβ=-+=-,试确定常数,c n ,使得()()x x αβ解:32221()32(1)(2)(1)(2)3lim ,3,2(1)x x x x x x x x c n c x cα→=-+=-+-+=∴==- 此时,()()x x αβ7、(7分)试确定常数a ,使得函数21sin0()0x x f x xa xx ⎧>⎪=⎨⎪+≤⎩在(,)-∞+∞内连续解:当0x >时,()f x 连续,当0x <时,()f x 连续。
05微积分A(下)期中试题答案

5分
−1 1 −1
所以平面方程为: 2 x
− 3 y − 5 z + 1 = 0. f ( x, y )dy + ∫π dx ∫
2 π cos x
7分
5
I =∫ =∫
π cos x 2 dx 0 0
∫
0
f ( x, y )dy
3分
π cos x 2 dx 0 0
∫
0
f ( x, y )dy + ∫π dx ∫
2
π
0
cos x
− f ( x, y )dy
= ∫ dy ∫
0
1
arccos y
f ( x, y )dx − ∫ dy ∫
−1
0
π
arccos y
f ( x, y )dx
7分
二、1
I = ∫∫∫ ( x + y + z )dxdydz
V
= ∫ dx ∫ dy ∫ ( x + y + z )dz
0 0 0
∫0 ∫0
2 cos θ
ρdρ∫ 2
ρ
2ρ cos θ
ρ 4 sin 2 θdz
6分
2 cos θ
ρ5 sin 2 θ(2ρ cos θ − ρ 2 )dρ
π
π 1 1 = 2 ( − ) ∫ 2 (cos8 θ − cos10 θ)dθ = . 7 8 0 8
六、
8分
V = ∫∫ ( x + y ) dxdy
2x + y − z − 6 2 = 0, 3
2 ), 3
2 =0 7分 3
5分
切平面方程为
2x + y − z + 6
微积分(下)期中考试卷 (含答案)

一、填空题(每题 3 分,共 24 分)
1.已知 A(1, 1, 2) 和 B (2, 2,1) ,则向量 AB 的模=_____________ 11
2.过点 (1, 2,3) 且与平面 x 2 y z 4 0 垂直的直线方程为______
x 1 y 2 z 3 1 2 1
x
2
10 分
解:
x
G
2
y 2 dxdy dx
1 0
1 x
0
y 2 dy
…..5 分 …..10 分
1 . 6
6.计算二重积分
D
x2 dxdy ,其中 D 由 y 2 , y x , xy 1 围成. y2
解:由方程组
2 2 y x xy 1 x2 知 y 1 .于是得 2 dxdy dy 1 2 dx 1 y y y yx D
y ______________ x 2y
6.已知向量 a 4, 3, 4 ,则与它同方向的单位向量为_________ 0 4 3 4 a , , 41 41 41
7 .设函数 f ( x, y ) 2 x 2 ax xy 2 2 y 在点 (1, 1) 取得极值,则常数 a
2 1 0
xy2 x .
解: xy dxdy = dx
2 D 0
1
2 x x
xy dy
2 7 5 x 2 dx 3 3
2.已知 z ln(2 x y ) ,求
解: z 2 x 2 x y 2 z 2 2 xy 2x y
3. 设z
…..5 分 …..10 分
微积分考试题目及答案

微积分考试题目及答案一、选择题1. 下列哪个选项描述了微积分的基本思想?A. 求导运算B. 求积分运算C. 寻找极限D. 都是答案:D2. 求函数f(x) = 2x^3 + 3x^2的导数是多少?A. f'(x) = 4x^2 + 6xB. f'(x) = 6x^2 + 3xC. f'(x) = 6x^2 + 6xD. f'(x) = 4x^2 + 3x答案:A3. 计算积分∫(2x^2 + 3x)dxA. x^3 + 2x^2B. x^3 + 2x + CC. (2/3)x^3 + (3/2)x^2D. (2/3)x^3 + 3x^2答案:C二、填空题4. 函数f(x) = 3x^2 + 2x的导数为_________答案:f'(x) = 6x + 25. 计算积分∫(4x^3 + 5x)dx = __________答案:x^4 + (5/2)x^2 + C6. 函数y = x^2在点x=2处的切线斜率为_________答案:4三、解答题7. 求函数y = x^3 + 2x^2在x=1处的切线方程。
解:首先求函数在x=1处的导数,f'(x) = 3x^2 + 4x。
代入x=1得斜率为7。
又因为该点经过(1,3),故切线方程为y = 7x - 4。
8. 求曲线y = x^3上与x轴围成的面积。
解:首先确定曲线截距为(0,0),解方程得x=0。
利用定积分区间求解:∫[0,1] x^3dx = 1/4。
以上为微积分考试题目及答案,希望对您的学习有所帮助。
感谢阅读!。
微积分测试题一极限连续答案(供参考)

微积分测试题(一)极限、连续部分(答案)一、选择题(每小题3分,共21分) 1、 当0x →+时,(A )无穷小量。
A 1sin x xB 1x e C ln x D 1sin x x2、点1x =是函数311()1131x x f x x x x -<⎧⎪==⎨⎪->⎩的(C )。
A 连续点B 第一类非可去间断点C 可去间断点D 第二类间断点 3、函数()f x 在点0x 处有定义是其在0x 处极限存在的(D )。
A 充分非必要条件B 必要非充分条件C 充要条件D 无关条件4、已知极限22lim()0x x ax x→∞++=,则常数a 等于(A )。
A -1B 0C 1D 25、极限201lim cos 1x x e x →--等于(D )。
A ∞B 2C 0D -2 6、设函数11()1x x f x e-=-则(D )。
A x=0,x=1都是()f x 的第一类间断点.B x=0,x=1都是()f x 的第二类间断点C x=0是()f x 的第一类间断点,x=1是()f x )的第二类间断点.D x=0是()f x 的第二类间断点,x=1是()f x 的第一类间断点. . D 【分析】 显然x=0,x=1为间断点,其分类主要考虑左右极限.【详解】 由于函数f(x)在x=0,x=1点处无定义,因此是间断点.且 0lim ()x f x →=∞,所以x=0为第二类间断点;1lim ()0x f x +→=,1lim ()1x f x -→=-,所以x=1为第一类间断点,故应选(D). 【评注】 应特别注意:1lim 1x x x +→=+∞-,1lim 1x xx -→=-∞- 从而+∞=-→+11lim x xx e,.0lim 11=-→-x x x e7已知lim()9xx x a x a→∞+=-,则a =( C ).A.1;B.∞;C.ln 3;D.2ln3.二、填空题(每小题4分,共20分) 1、21lim(1)x x x→∞-2、 当0x →+时,无穷小ln(1)Ax α=+与无穷小sin 3x β=等价,则常数3、 已知函数()f x 在点0x =处连续,且当0x ≠时,函数21()2x f x -=,则函数值(0)f4、 111lim[]1223(1)n n n →∞+++••+L5、 若lim ()x f x π→存在,且sin ()2lim ()x xf x f x x ππ→=+-,则lim ()x f x π→三、解答题1、(7分)计算极限 222111lim(1)(1)(1)23n n→∞---L 解:原式=132411111lim()()()lim 223322n n n n n n n n →∞→∞-++•••=•=L 2、(6分)计算极限 30tan sin lim x x xx →-解:原式=2322000sin 1sin 1cos 1cos 2lim lim lim cos cos 2x x x x x xx x x x x x x →→→--===3、(7分)计算极限 123lim()21x x x x +→∞++ 解:原式= 11122112221lim(1)lim(1)121211lim(1)lim(1)1122x x x x x x x x x e x x +++→∞→∞+→∞→∞+=+++=+•+=++ 4、(7分)计算极限1x e →-解:原式=201sin 12lim 2x x xx →=5、(7分)设3214lim 1x x ax x x →---++ 具有极限l ,求,a l 的值解:因为1lim(1)0x x →-+=,所以 321lim(4)0x x ax x →---+=,因此 4a = 并将其代入原式321144(1)(1)(4)lim lim 1011x x x x x x x x l x x →-→---++--===++6、(8分)设3()32,()(1)nx x x x c x αβ=-+=-,试确定常数,c n ,使得()()x x αβ:解:32221()32(1)(2)(1)(2)3lim ,3,2(1)x x x x x x x x c n c x cα→=-+=-+-+=∴==-Q 此时,()()x x αβ: 7、(7分)试确定常数a ,使得函数21sin0()0x x f x xa xx ⎧>⎪=⎨⎪+≤⎩在(,)-∞+∞内连续解:当0x >时,()f x 连续,当0x <时,()f x 连续。
微积分试题及答案pdf

微积分试题及答案pdf一、选择题(每题5分,共20分)1. 函数 \( f(x) = x^3 - 6x^2 + 11x - 6 \) 的导数是:A. \( 3x^2 - 12x + 11 \)B. \( 3x^2 - 12x + 6 \)C. \( x^2 - 12x + 11 \)D. \( x^2 - 6x + 11 \)答案:A2. 定积分 \( \int_{0}^{1} x^2 dx \) 的值是:A. \( \frac{1}{3} \)B. \( \frac{1}{2} \)C. \( \frac{1}{4} \)D. \( \frac{1}{6} \)答案:B3. 函数 \( y = \ln(x) \) 的不定积分是:A. \( x\ln(x) + C \)B. \( \frac{x}{\ln(x)} + C \)C. \( x\ln(x) - x + C \)D. \( x + C \)答案:A4. 曲线 \( y = x^2 \) 与直线 \( y = 2x \) 在第一象限的交点坐标是:A. \( (1, 2) \)B. \( (2, 4) \)C. \( (-1, -2) \)D. \( (-2, -4) \)答案:A二、填空题(每题5分,共20分)1. 函数 \( f(x) = \sin(x) \) 的二阶导数是 \( \_\_\_\_\_ \)。
答案:\( -\sin(x) \)2. 曲线 \( y = e^x \) 在 \( x = 0 \) 处的切线斜率是\( \_\_\_\_\_ \)。
答案:13. 函数 \( y = \ln(x) \) 的不定积分是 \( \_\_\_\_\_ \)。
答案:\( x\ln(x) - x + C \)4. 定积分 \( \int_{0}^{1} e^x dx \) 的值是 \( \_\_\_\_\_ \)。
答案:\( e - 1 \)三、解答题(每题10分,共20分)1. 求函数 \( f(x) = x^3 - 3x^2 + 4 \) 在 \( x = 2 \) 处的导数值。
2005-2006-2-微积分B-期中考试卷解答

第3页共5页
2005-2006 学年第二学期微积分期中考试试题与答案
∫∫ ∫∫ ∴ x2dydz = −(x负侧) x2dydz
Σ
x=
D
R2 − x2 − y2
⎡
π
⎤
∫ ∫ =
−⎢⎢ R 2 ⎢⎣
1π 4
R2
−
2 0
dθ
R 0
r
2
rdr
⎥ ⎥
⎥⎦
=
−
π
R4 8
.
13. (8 分)圆锥面 Σ : z = h x 2 + y 2 (0 ≤ z ≤ h),其中a > 0, h > 0. 质量均匀分布,求它重心的位置 a
∫∫ Δu
=
∂ 2u ∂x 2
+
∂2u ∂y 2
+ ∂2u ∂z 2
= 1, 求
Σ
∂udS. ∂n
第4页共5页
2005-2006 学年第二学期微积分期中考试试题与答案
解1: ∵
∂u ∂n
=
(u′x ,u′y ,u′z
) •n0
∫∫ ∫∫ ,u′y ,u′z ) •n 0dS
解:先证必要性,由条件存在一元函数 g(u) 使 z=g(ax+by),
∴ bz′x = bg′ ⋅ a, az′y = ag′ ⋅ b, ⇒ bz′x = az′y , 必要性得证.
再证充分性,先做换元
⎧u
⎨ ⎩
v
= =
ax x
+
by
,
则
bz′x = az′y ⇔ b(zu′ u′x + zv′v′x ) = a(zu′ u′y + zv′v′y ) ⇔ b(zu′ a + zv′ ) = a(zu′ b + 0) ⇔ zv′ = 0 ⇔ z = C(u) ⇔ z = C(ax + by),充分性得证.
高等数学期中考试试卷及答案

高等数学期中考试试卷及答案XXX2005-2006学年第一学期高等数学期中考试试卷一、判断题(每题2分,共10分)1、若数列{x_n}收敛,数列{y_n}发散,则数列{x_n+y_n}发散。
(×)2、limf(x)存在的充分必要条件是limf(x+)和limf(x-)都存在。
(×)3、limx→1 sin(πx/2) = limx→1 πx/2 = π/2.(√)4、limx→∞ sinx/x = 0.(√)5、若f(x)在闭区间[a,b]上有定义,在开区间(a,b)内连续,且f(a)·f(b)<0,则f(x)在(a,b)内有零点。
(√)二、填空题(每题2分,共10分)1、已知f'(3)=2,则lim(h→0) [f(3-h)-f(3)]/h = 2.(答案为2)2、y=π+xn+arctan(x),则y'|x=1 = n+1.(答案为n+1)3、曲线y=e^x在点(0,1)处的切线与连接曲线上两点(0,1),(1,e)的弦平行。
(答案为(1.e^1))4、函数y=ln[arctan(1-x)],则dy/dx = -1/(x^2-2x+2)。
(答案为-1/(x^2-2x+2))5、当x→0时,1-cosx是x的阶一无穷小。
(答案为x^2/2)三、单项选择题(每题2分,共10分)1、数列有界是数列收敛的(必要条件)。
2、f(x)在x=x处有定义是limx→x f(x)存在的(必要条件)。
3、若函数f(x)=(x-1)^2/2(x+1),则limx→1 f(x)≠f(1)。
(以上等式都不成立)4、下列命题中正确的是(无界变量必为无穷大)。
5、lim(n→∞) (1+1/n)^n+1000的值是(e^1000)。
四、计算下列极限(每题6分,共18分)1、lim(x+1-x^-1) = 2.2、lim(x→+∞) [sec(x)-cos(x)]/x = 0.3、lim(x→0) ln(1+x^2)/x = 0.五、计算下列各题(每题6分,共18分)1、y=e^(sin^2x)。
微积分试卷及答案4套

微积分试卷及答案4套微积分试题(A卷)一.填空题(每空2分,共20分)1.已知$\lim\limits_{x\to1^+}f(x)=A$,则对于$\forall\epsilon>0$,总存在$\delta>0$,使得当$x\to1^+$时,恒有$|f(x)-A|<\epsilon$。
2.已知$\lim\limits_{n\to\infty}\dfrac{a_n^2+bn+5}{n^2+3n-2}=2$,则$a=1$,$b=3$。
3.若当$x\to x_0$时,$\alpha$与$\beta$是等价无穷小量,则$\lim\limits_{x\to x_0}\dfrac{\alpha-\beta}{\beta}=0$。
4.若$f(x)$在点$x=a$处连续,则$\lim\limits_{x\toa}f(x)=f(a)$。
5.函数$f(x)=\ln(\arcsin x)$的连续区间是$(0,1]$。
6.设函数$y=f(x)$在$x$点可导,则$\lim\limits_{h\to0}\dfrac{f(x+3h)-f(x)}{h}=3f'(x)$。
7.曲线$y=x^2+2x-5$上点$M$处的切线斜率为6,则点$M$的坐标为$(-1,2)$。
8.$\dfrac{d(xf'(x))}{dx}=xf''(x)+2f'(x)$。
9.设总收益函数和总成本函数分别为$R=24Q-2Q^2$,$C=Q+5$,则当利润最大时产量$Q=6$。
二.单项选择题(每小题2分,共18分)1.若数列$\{x_n\}$在$a$的$\epsilon$邻域$(a-\epsilon,a+\epsilon)$内有无穷多个点,则(B)数列$\{x_n\}$极限存在,且一定等于$a$。
2.设$f(x)=\arctan\dfrac{2}{x-1}$,则$x=1$为函数$f(x)$的(A)可去间断点。
微积分期中考试试卷答案

北 京 交 通 大 学2007 -2008 学年第一学期《微积分》期中考试试卷(考试时间120分钟)班 级 姓 名 学 号一、填空题(每空3分,共30分)1.设()()1,1,0,1,,0,1.1,1.x x f x g x x x ⎧<⎧≤⎪⎪==⎨⎨≥>⎪⎪⎩⎩,则()g f x =⎡⎤⎣⎦ 0 。
2.已知()lim20071abb n n n n →∞=--,则常数a =20062007-,b =12007。
3.当0x →时,sin cos x e x x -+-与n x 是同阶无穷小,则n = 2 。
4.函数()21lim1nn xf x x →∞-=+的间断点为x = -1 。
5.设函数()221,0,cos ,0.x e x f x xa x x x ⎧-<⎪=⎨⎪+≥⎩在(),-∞+∞上连续,则a = 2。
6.设()'0f x 存在,则()()000limx x xf x x f x x x →-=-()()'000f x x f x -。
7.设函数()y y x =由方程()sin 0x y e e xy --=确定,则0x dy ==dx 。
8.已知函数()f x 具有任意阶导数,且()()2'f x f x =⎡⎤⎣⎦,则当2n >时,()()n f x =()1!n n f x +⎡⎤⎣⎦。
9.曲线sin ,cos 2x t y t=⎧⎨=⎩在对应于4t π=的点处的切线方程为20y +-=。
二、计算下列各题 (每题6分,共12分 )1.)()()121cos 211limln 1xx xx-→++解:原式()()2222201221cos 20121cos 0lim 21cos 12lim 21lim 14211.622x xxx x x x x x x x x x x x e e →-→-→-+==+==分分分2.设()11,0,1,0.x x f x x e a x ⎧-≠⎪=-⎨⎪=⎩,求常数a 使()f x 在0x =处连续;并讨论此时()f x 在0x =处是否可导。
