八年级数学等边三角形1

合集下载

八年级数学人教版(上册)第1课时等边三角形的性质与判定

C
∴ △ADE 是等边三角形．
侵权必究
讲授新课
变式3 上题中,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由. A
证明：∵ △ABC是等边三角形，
∴ ∠A= ∠B= ∠C.
D
E
∵ AD=AE,
B
C
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
等边三角形三条边都相等的三角形是等边三角形
三个角都相等的三角形是等边三角形
小明等认边为三还角有形第的三种判方定法方“法两：条边相等且有一个角是60°的三角形也是等有边一三个角角形”是，60你°同的意等吗腰？三角形是等边三角形.
侵权必究
讲授新课
归纳总结
等边三角形的判定方法：
三边都相等的三角形是等边三角形.
A．①②③ B．①②④
C．①③
D．①②③④
侵权必究
当堂练习
6.如图，点A，B，C在一条直线上，△ABD，
△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于
点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①
△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形；
④MB平分∠AMC，其中结论正确的有( D )
A．1个 B．2个
C．3个
D．4个
侵权必究
当堂练习
7.如图，在△ABC中，∠ACB=90°，∠CAB=30°，以AB为边在△ABC外作等边△ABD，E是AB的中点，连接CE并延长交AD于F．求证：△AEF≌△BEC．
证明：∵△ABD是等边三角形， ∴∠DAB=60°， ∵∠CAB=30°，∠ACB=90°， ∴∠EBC=180°-90°-30°=60°， ∴∠FAE=∠EBC． ∵E为AB的中点， ∴AE=BE．又∵ ∠AEF＝∠BEC， ∴△AEF≌△BEC（ASA）．

八年级上册数学等边三角形

八年级上册数学等边三角形一、轴对称图形1. 把一个图形沿着一条直线折叠，如果直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

这时我们也说这个图形关于这条直线（成轴）对称。

2. 把一个图形沿着某一条直线折叠，如果它能与另一个图形完全重合，那么就说这两个图关于这条直线对称。

这条直线叫做对称轴。

折叠后重合的点是对应点,叫做对称点3、轴对称图形和轴对称的区别与联系4.轴对称的性质①关于某直线对称的两个图形是全等形。

②如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

③轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

④如果两个图形的对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。

二、线段的垂直平分线1. 经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫中垂线。

2.线段垂直平分线上的点与这条线段的两个端点的距离相等3.与一条线段两个端点距离相等的点，在线段的垂直平分线上三、用坐标表示轴对称小结：在平面直角坐标系中，关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点（x, y）关于x轴对称的点的坐标为______.点（x, y）关于y轴对称的点的坐标为______.2.三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等四、（等腰三角形)知识点回顾1.等腰三角形的性质①.等腰三角形的两个底角相等。

（等边对等角）②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

（三线合一）2、等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等。

（等角对等边）五、（等边三角形）知识点回顾1.等边三角形的性质：等边三角形的三个角都相等，并且每一个角都等于600 。

2、等边三角形的判定：①三个角都相等的三角形是等边三角形。

②有一个角是600的等腰三角形是等边三角形。

人教版-数学-八年级上册-13.3.2 等边三角形(1) 教案

13.3.2 等边三角形第1课时一、教学目标（一）学习目标1. 探索等腰三角形成为等边三角形的条件及其推理证明过程.2. 探索等边三角形的判定定理.3. 会用性质及判定解决相关问题.（二）学习重点等边三角形的性质与判定.（三）学习难点等边三角形的性质与判定的应用.二、教学设计（一）课前设计1. 预习任务（1）三条边都相等______的三角形叫做等边三角形.等边三角形也称正三角形，它是特殊的等腰三角形.（2）等边三角形的性质：等边三角形的三个内角都相等_______ ，并且每一个角都等于.（3）等边三角形的判定：①三条边都__相等______的三角形是等边三角形；②三个角都__相等______的三角形是等边三角形；③有一个角是的__等腰三角形____________是等边三角形.2. 预习自测（1）有下列三角形：①有两个角等于的三角形；②有一个角等于的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有（）A.①②③B.①②④C.①③D.①②③④【知识点】等边三角形的判定.【思路点拨】运用等边三角形的判定．【解题过程】依次筛选故正确的有：①②③④．【答案】D ．（2）如图，在等边△ABC 中，AD 是BC 上的高，∠BDF=∠CDE=，图中与BD 相等的线段有（）A.5条B.6条C.7条D.8条E F DA BC【知识点】等边三角形的性质．【思路点拨】利用等腰三角形、等边三角形的性质进行判定．【解题过程】解：根据等边三角形、等腰三角形的性质，可以得出两个三角形：△BDF 、△CDE 也是等边三角形，两个三角形：△AFD.△AED 为等腰三角形，所以可以得出：BD=CD=DF=BF=AF=AE=CE=DE ，共7条．【答案】C ．（3）已知等边△ABC ，分别以AB.BC.CA 为边向外作等边三角形ABD ，等边三角形BCE ，等边三角形ACF ，则下列结论中不正确的是（）A ．BC2=AC2+BC2﹣AC•BCB ．△ABC 与△DEF 的重心不重合 C ．B ，D ，F 三点不共线 D ．S △DEF ≠S △ABC 【知识点】等边三角形的性质．【思路点拨】根据等边三角形的性质，对四选项逐个进行判断即可求解．【解题过程】解：A.化简化得AC=BC ，正确；B. △DEF 是等边三角形，且等边△ABC 的各顶点是△DEF 各边的中点，等边△ABC 可看作是△DEF 的内接正三角形，所以△ABC 与△DEF 的重心重合，错误；C.根据题意，可得出点D.B.E 在同一直线上，点D.A.F 在同一直线上，点E.C.F 在同一直线上，正确；D.S △DEF=4S △ABC ，正确．故选B.（4）如图，A.C.B三点在同一条直线上，△DAC和△EBC都是等边三角形，AE.BD分别与CD.CE交于点M、N，有如下结论：①△ACE≌△DCB；②CM=CN；③AC=DN．其中，正确结论的个数是（）A．3个B．2个C．1个D．0个【知识点】等边三角形的性质．【思路点拨】根据等边三角形的性质和全等三角形的判定与性质采用排除法对各个结论进行分析从而得出答案．【解题过程】解：∵△DAC和△EBC都是等边三角形∴AC=CD，CE=BC，∠ACD=∠ECB=∴∠ACE=∠DCB∴△ACE≌△DCB（SAS）（①正确）∴∠AEC=∠DBC∵∠DCE+∠ACD+∠ECB=，∠ACD=∠ECB=∴∠DCE=∠ECB=∵CE=BC，∠DCE=∠ECB=，∠AEC=∠DBC∴△EMC≌△BNC（ASA）∴CM=CN（②正确）∵AC=DC 在△DNC中，DC所对的角为∠DNC=∠NCB+∠NBC=+∠NBC＞，而DN 所对的角为，根据三角形中等边对等角、大边对大角，小边对小角的规律，则DC＞DN，即是AC＞DN，所以③错误，所以正确的结论有两个．故选B．【答案】B．1.知识回顾（1）等腰三角形的定义：有两边_相等_______的三角形叫做等腰三角形.（2）等腰三角形的性质：①等边对_等角_________；②等腰三角形的_顶角平分线_____、___底边上的中线________________、___底边上的高_____互相重合.（3）等腰三角形的判定：等角对_等边________.2.问题探究探究一等边三角形的性质.●活动①在等腰三角形中，如果底边也等于腰长，会得到哪些结论呢？（等边三角形，每个角相等，都等于.）追问：这是什么类型的问题？怎么证明呢？有哪些步骤呢？（画草图，写出已知求证，最后证明.）已知：△ABC是等边三角形.求证：∠A＝∠B＝∠C＝.【思路点拨】引导学生利用等腰三角形性质去证明.证明：如图，∵△ABC是等边三角形，∴AB＝AC ＝BC （等边三角形的三条边相等___）∴∠A＝∠B ＝∠C （等边对等角）∵∠A+∠B+∠C＝（三角形的内角和定理）∴∠A＝∠B＝∠C＝.【设计意图】通过类比，进行等边三角形的性质探索.练习1．等边三角形轴对称图形（填是或否）.如果是，它有条对称轴，分别是.【知识点】等边三角形的性质．【思路点拨】利用等边三角形的轴对称性.【答案】是、3.三个角的平分线（或三条边的中线或三条边的高线）所在的直线.探究二等边三角形的判定.●活动①探究判定1求证：三个角都相等的三角形是等边三角形【思路点拨】这是文字命题，先画图，写出已知求证，再利用等边三角形的定义.【解题过程】已知：△ABC中，∠A＝∠B＝∠C＝.求证：△ABC是等边三角形.证明：∵△ABC中，∠A＝∠B＝∠C＝∴AB=AC，AB=BC ，BC=AC .（等角对等边）∴AB= AC = BC .∴△ABC是等边三角形（等边三角形的定义）【设计意图】根据等边三角形的定义判定.●活动②探究判定2证明：有一个角是的等腰三角形是等边三角形.【思路点拨】这是文字命题，先画图，写出已知求证，再利用等边三角形的定义. 【解题过程】已知：△ABC是等腰三角形，AB＝AC，∠A＝求证：△ABC是等边三角形.证明：∵△ABC是等腰三角形，AB＝AC，∴∠B＝∠C （等边对等角）又∵∠A＝，∠A+∠B+∠C＝∴∠A＝∠B ＝∠C＝∴△ABC是等边三角形（三个角都_相等_的三角形是等边三角形）【设计意图】根据刚才探究1的等边三角形的判定1判定，把未知化归为已知求证. 探究三等边三角形的性质和判定运用.●活动①例1 如图，△ABC是等边三角形，DE∥BC，分别交AB，AC于点D，E.求证：△ADE是等边三角形.【知识点】等边三角形的判定．【思路点拨】先利用等边三角形的性质得出三个内角相等，再由平行线的性质得出∠ADE＝∠B ，∠AED＝∠C，最后再由等量代换得出小三角形的三个内角相等，再由等边三角形的判定1得证.【解题过程】证明：∵△ABC是等边三角形，∴∠A＝∠B ＝∠C（等边三角形的三个内角相等）∵DE∥BC，∴∠ADE＝∠B ，∠AED＝∠C .（两直线平行，同位角相等）∴∠A＝∠ADE ＝∠AED .∴△ADE是等边三角形（三个角都相等的三角形是等边三角形）【设计意图】根据等边三角形的判定1进行证明.●活动② 思维拓展师问：请聪明的同学们思考，你还有其他方法证明吗？请小组谈论并写出来．学生小组讨论形成过程.证明：∵△ABC是等边三角形，∴∠A＝∠B ＝∠C =（等边三角形三个内角都等于）∵DE∥BC，∴∠ADE＝∠B =，∠AED＝∠C =（两直线平行，同位角相等）∴∠ADE=∠AED，∴AD=AE(等角对等边)∴△ADE是等边三角形（有一个角是的等腰三角形是等边三角形）【设计意图】给学生留足时间，让学生独立完成，根据等边三角形的判定2进行证明，同时让学生明白几何题的证明可以有不同的路径.练习：如图，在等边三角形ABC的三边上，分别取点D，E，F，使AD=BE=CF.求证：△DEF是等边三角形．【知识点】等边三角形的性质和判定【答案】证明：∵△ABC是等边三角形∴AB=BC=AC，∠A=∠B=∠C又∵AD=BE=CF∴BD=EC=AF∴△DBE≌△ECF≌△FAD（SAS）∴DE=EF=DF∴△DEF是等边三角形【思路点拨】先由△ABC是等边三角形，得出AB=BC=AC，∠A=∠B=∠C ，再由已知AD=BE=CF和等式性质即可得出BD=EC=AF，最后由三角形全等得证.【设计意图】让学生对等边三角形的性质和判定进行融会贯通.3. 课堂总结知识梳理等边三角形的三个内角都相等，并且每一个内角都等于.（简记为：三边等，三角等，各边上三线合一）（2）等边三角形的判定方法：①定义：三边都相等的三角形是等边三角形.②三个角都相等的三角形是等边三角形.③有一个角是的等腰三角形是等边三角形（最常用）.重难点归纳等腰三角形与等边三角形的区别和联系等腰三角形等边三角形区别性质边两边相等三边相等角两个底角相等三个角都相等，等于三线合一底边上的中线、高、和顶角的平分线互相重合每一边上的中线、高和这一边所对的角的平分线互相重合对称性是轴对称图形，有1条对称轴是轴对称图形，有3条对称轴判定边有两条边相等的三角形是等腰三角形（定义法）三边都相等的三角形是等边三角形（定义）角有两个角相等的三角形是等腰三角形（判定）三个角都相等的三角形是等边三角形有1个角是的等腰三角形是等边三角形联系等腰三角形包括等边三角形，等边三角形是一种特殊的等腰三角形。

人教版八年级数学上册课件第十三章轴对称等腰三角形等边三角形第1课时等边三角形的性质与判定

27 2
(cm)
17．(14分)(原创题)已知△ABC是等边三角形，点D是直线BC上一点，以AD为一边在AD的右侧作等边三角形ADE.
(1)如图①，点D在线段BC上移动时，求证：CE＋CD＝AB； (2)如图②，点D在线段BC的延长线上移动时，那么： ①线段CE，CD，AB之间有怎样的数量关系？请加以证明； ②∠DCE的度数为___6_0_°___； (3)如图③，点D在线段BC的反向延长线上移动时，∠DCE的大小是否发生变化？线段CE，CD，AB之间又有怎样的数量关系？请直接写出结论．
2．(3分)如图，△ABC是等边三角形，点D在AC边上，∠DBC＝35°，
则∠ADB的度数为( ) D
A．25°
B．60°
C．85°
D．95°
3．(3分)如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG＝CD，DF＝DE，则∠E＝___1_5_°___．
4 ． (3 分 ) 如图，在等边三角形 ABC 中， CD⊥AB 于点 D ，过点 D 作 DE∥BC交AC于点E，若△ABC的边长为2，则△ADE的周长是__3__．
∠E，∴DB＝DE
6．(3分)下列四个说法中，正确的有( D ) ①三个角都相等的三角形是等边三角形；②有两个角等于60°的三角形是等边三角形；③有一个角是60°的等腰三角形是等边三角形；④有两个角相等的等腰三角形是等边三角形． A．0个 B．1个 C．2个 D．3个
7．(3分)等腰三角形补充下列条件后，仍不一定成为等边三角形的是 ( C)
14．(台州中考)如图，等边三角形纸片ABC的边长为6，E，F是边BC 上的三等分点．分别过点E，F沿着平行于BA，CA方向各剪一刀，则剪下的△DEF的周长是___6_．

八年级上册数学-等边三角形

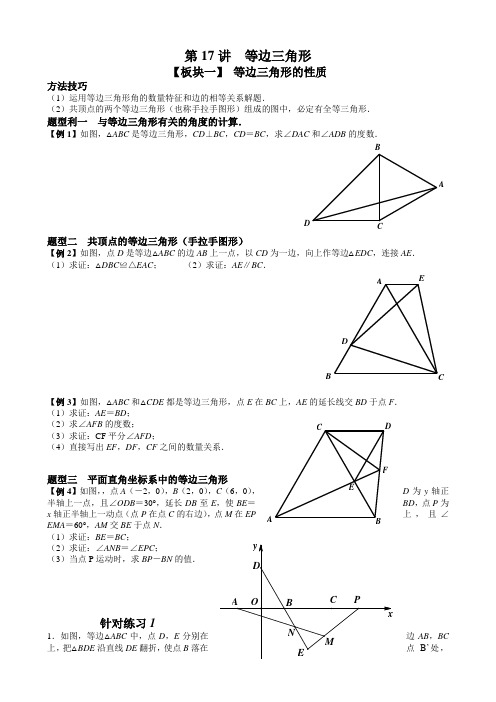
A第17讲等边三角形【板块一】等边三角形的性质方法技巧（1）运用等边三角形角的数量特征和边的相等关系解题．（2）共顶点的两个等边三角形（也称手拉手图形）组成的图中，必定有全等三角形．题型利一与等边三角形有关的角度的计算．【例1】如图，△ABC 是等边三角形，CD ⊥BC ，CD ＝BC ，求∠DAC 和∠ADB 的度数．AD题型二共顶点的等边三角形（手拉手图形）【例2】如图，点D 是等边△ABC 的边AB 上一点，以CD 为一边，向上作等边△EDC ，连接AE ．（1）求证：△DBC ≌△EAC；（2）求证：AE ∥BC ．B【例3】如图，△ABC 和△CDE 都是等边三角形，点E 在BC 上，AE 的延长线交BD 于点F ．（1）求证：AE ＝BD ；（2）求∠AFB 的度数；（3）求证：CF 平分∠AFD ；（4）直接写出EF ，DF ，CF 之间的数量关系．题型三平面直角坐标系中的等边三角形【例4】如图，，点A （－2，0），B （2，0），C （6，0），D 为y 轴正半轴上一点，且∠ODB ＝30°，延长DB 至E ，使BE ＝BD ，点P 为x 轴正半轴上一动点（点P 在点C 的右边），点M 在EP 上，且∠EMA ＝60°，AM 交BE 于点N ．（1）求证：BE ＝BC ；（2）求证：∠ANB ＝∠EPC ；（3）当点P 运动时，求BP －BN 的值．针对练习11．如图，等边△ABC 中，点D ，E 分别在边AB ，BC上，把△BDE 沿直线DE 翻折，使点B 落在点B’处，D EDB ’，EB ’分别交AC 于点F ，G ，若∠ADF ＝80°，求∠EGC 的度数．B'B2．如图，△ABD 和△ACE 都是等边三角形， DC 于BE 交于点M ．（1）求证：BE ＝CD ；（2）求∠AMD 的度数．3．如图1，等边△ABC 中，点D 是AB 上一点，以CD为一边，向上作等边△EDC ，向下作等边△DCF ，连接AE ，BF ．（1）求证：AB ＝AE ＋BF ；（2）当点D 在BA 延长线上时，如图2，若AE ＝10，BF ＝4，求AC 的长．B图1 图24．已知点D ，E 分别是等边△ABC 的边BC ，AB 上的点，∠ADE ＝60°．（1）如图1，当点D 是BC 的中点时，求证：AE ＝3BE ；（2）如图2，当点M 在AC 上，满足∠ADM ＝60°，求证：BE ＝CM ；（3）如图3，过C 作CF ∥AB 交ED 延长线于点F ，探究线段BE ，CF ，CD 之间的数量关系，并给出证明．BCBCBC图1 图2 图35.在平面直角坐标系中，已知点A 在y 轴的正半轴上，点B 在第二象限，AO =a ，AB =b ，BO 与x 轴正方向的夹角150°，且220a -b a-b . ⑴判断△ABO 的形状；⑵如图1，若BC ⊥BO ，BC =BO ，点D 为CO 的中点，AC 、BD 交于点E ，求证:AE = BE +CE ；图 1⑶如图2，若点E 为y 轴的正半轴上一动点，以BE 为边作等边△BEG ，延长GA 交x 轴于点P ，AP 与AO 之间有何数量关系?试证明你的结论.图 26.△ABC 为等边三角形，BC 交y 轴于点D ，A (a ，0)，B (b ，0)，且a ，b 满足230a+ . (1)如图1，求点A ，B 的坐标及CD 的长；图 1(2)如图2，P是AB的延长线上一点，点E是CP右侧一点，CP=PE，且∠CPE=60°，连接EB，求证:直线EB必过点D关于x轴对称的对称点；E(3)如图3，若点M在CA的延长线上，点N在AB的延长线上，且∠CMD=∠DNA，求AN-AM的值.【板块二】60°角的用法◆方法技巧◆合理利用60°角构造等边三角形得到相等线段，再进行推理.题型一过60°角一边上一点作平行线构造等边三角形.方法技巧:过60°角一边上一点，作平行线构造等边三角形，转化边与角.【例5】如图，△ABC是等边三角形，点D是AC的中点，点E，F分别在BC，AB的延长线上，∠EDF=120°.(1)求证:DE=DF；(2)若AB=5，求CE-BF的值.A题型二在60°角的两边上截取两条相等线段构造等边三角形方法技巧:在60°角的边上截取两条相等线段后构成等边三角形，然后产生新的全等三角形，从而找到解决问题的突破口.【例6】如图，△ABC 为等边三角形，∠ADB =60°. (1)如图1，当∠DAB =90°时，直接写出DA ，DC ，DB 之间的数量关系_______；图 1ABCD(2)如图2，当∠DAB ≠90°时，①中的关系式是否成立?说明理由.图 1ABCD题型三利用60°角的一边上的点向另一边做垂线构造30°，60°，90°的直角三角形方法技巧:利用30角所对的直角边等于斜边的一半，作高. 【例7】如图，在△ABC 中，∠B =60°，∠C =45°，AB =2，BC =1 ，求△ABC 的面积.ABC題型四利用60°角延长构造等边三角形方法技巧；向外延长60”角的一边，在外部构造等边三角形.【例8】已知点D ，点E 分別等边△ABC 边BC ，AC 上的点，CD =AE ，AD 与BE 交于点F .(1)如图1，求∠AFE 的度数；图 1BCAD(2)点G 边AC 中点，∠BFG =120° ，如图2，求证:AF =2FG .图 2BCAD针对练习21.如图，在等边△ABC 中，AC =9，点O 在AC 上，且AO =3，点P 是AB 上一动点，连接OP ，以O 为圆心，OP 长为半径画弧交BC 于点D ，连接PD ，如果PO =PD ，求AP 的长.ABCP2.如图.在等边△ABC 中，∠ABC 与∠ACB 的平分线相交于点O ，且OD ∥AB ，OE ∥AC . (1)试判定△ODE 的形状，并说明你的理由；(2)线段BD ，DE ，EC 三者有什么关系?请说明理由.E DBCA3.点D 为BC 上任一点，∠ADE =60°，边ED 与∠ACB 外角的平分线交于点E ，求证:AD =DE ；BCAD4.已知△ABC 是边长为5的等边三角形.(1)如图1，若点P 是BC 上一点，过点C ，点P 分别作AB ，AC 的平行线，两线相交于点Q ，连接BQ ，AP 的延长线交BQ 于点D .试问:线段AD ，BD ，CD 之间是否存在某种确定的数量关系?若存在，请写出它们之间数量关系并证明你的结论；若不存在，说明理由；图 1QBCA(2)如图2，若点P 是BC 延长线上一点，连接AP ，以AP 为边作等边△APE (点E 、点A 在直线BC 同侧)，连接CE 交AP 于点F ，求CE -CP 的值.图 2BCDE5.如图，在△ABC 中，∠BAC =60°，以BC 为边在△ABC 的同侧作等边△DBC ，BD ，AC 相交于点E ，连结AD .(1)如图1，若A 2ACAB,求证：△ABC ≌△ADC图 1CAD(2)如图2，若3AC AB，求ABAD的值. 图 2CAD6.如图1，△ABC 为等边三角形，延长BC 到D ，延长BA 到E ，AE =BD ，连接CE 、DE . ⑴求证：EC =ED ；图 1BDE⑵如图2，EO ⊥CD 于点O ，点N 在EO 上，△DNM 为等边三角形，CM 交EO 于F ，若FO =1，求FM -FN 的值.图 1BDE[板块三) 30°角的用法方法技巧构造30°角的直角三角形，算边长与面积.题型一已知30°角连线巧得隐直角.【例9】如图，在△ABC 中，AB =AC ，∠C =30°，AB 的垂直平分线交AB 于点D ，交BC 于点E ，试探究BE 与CE 之间的数量关系.BC题型二利用30°作高构造直角三角形.【例10】如图，CD 是△ABC 的中线，CD ⊥CB ，∠ACD =30°，求证:AC =2BC.DABC题型三已知30°和90°角补形构造直角三角形【例11】如图，四边形ABCD 中，∠C =30°，∠B =90°，∠ADC =120°，若AB =2，CD =8，求AD 的长.ACBD题型四利用底角为15°的等腰三角形构造30°角的直角三角形【例12】如图，∠AOC =15°，OC 平分∠AOB ，点P 为OC 上一点，PD /∥OA 交OB 于点D ，PE ⊥OA 于点E ，若OD =4cm ，求PE 的长.EOA题型五利用150°构造30°角的直角三角形【例13】如图，在△ABC 中，AB =AC ，点D 为BC 上一点，以AD 为腰作等腰△ADE ，且AD =AE ，∠BAC =∠DAE =30°，连接CE ，若BD =2，CD =5，求△DCE 的面积.BCADE题型六30°直角三角形斜边上的高方法技巧：30°角的直角三角形斜边上的高中，有3个30°的直角三角形，选取最小的和最大的两个直角三角形进行计算.【例14】如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为点D ，∠A =30°，AD =6，求BC 的长.DABC针对练习31.某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米的售价为a 元，求购买这种草皮至少需要多少元?BCA2.在△ABC 中，∠B =30°，AB =AC =8，P 为BC 上一点，求AP 的最小值.ABCP3.如图，在等边△ABC 中，点D 为AC 上一点，CD =CE ，∠ACE =60°. (1)求证:△BCD ≌△ACE ；图1EBCA(2)延长BD 交AE 于点F ，连接CF ，若AF =CF ，猜想线段BF ，AF 的数量美系，并证明你的猜想.图 2BCAE4.如图，在△ABC 中，∠BAC =90°，点D 为三角形内一点，且AB =AC =BD ，∠ABD =30°.求证:AD =CD ，AB C。

等边三角形的性质与判定(3种题型)-2023年新八年级数学(苏科版)(解析版)

等边三角形的性质与判定（3种题型）了解等边三角形的有关概念，探索并掌握性质及判定方法。

一．等边三角形的性质（1）等边三角形的定义：三条边都相等的三角形叫做等边三角形，等边三角形是特殊的等腰三角形．①它可以作为判定一个三角形是否为等边三角形的方法；②可以得到它与等腰三角形的关系：等边三角形是等腰三角形的特殊情况．在等边三角形中，腰和底、顶角和底角是相对而言的．（2）等边三角形的性质：等边三角形的三个内角都相等，且都等于60°．等边三角形是轴对称图形，它有三条对称轴；它的任意一角的平分线都垂直平分对边，三边的垂直平分线是对称轴．二．等边三角形的判定（1）由定义判定：三条边都相等的三角形是等边三角形．（2）判定定理1：三个角都相等的三角形是等边三角形．（3）判定定理2：有一个角是60°的等腰三角形是等边三角形．说明：在证明一个三角形是等边三角形时，若已知或能求得三边相等则用定义来判定；若已知或能求得三个角相等则用判定定理1来证明；若已知等腰三角形且有一个角为60°，则用判定定理2来证明．三．等边三角形的判定与性质（1）等边三角形是一个非常特殊的几何图形，它的角的特殊性给有关角的计算奠定了基础，它的边角性质为证明线段、角相等提供了便利条件．同是等边三角形又是特殊的等腰三角形，同样具备三线合一的性质，解题时要善于挖掘图形中的隐含条件广泛应用．（2）等边三角形的特性如：三边相等、有三条对称轴、一边上的高可以把等边三角形分成含有30°角的直角三角形、连接三边中点可以把等边三角形分成四个全等的小等边三角形等．（3）等边三角形判定最复杂，在应用时要抓住已知条件的特点，选取恰当的判定方法，一般地，若从一般三角形出发可以通过三条边相等判定、通过三个角相等判定；若从等腰三角形出发，则想法获取一个60°的角判定．一．等边三角形的性质（共9小题）1．（2022秋•崇川区校级月考）如图，在等边△ABC中，BD平分∠ABC交AC于点D，过点D作DE⊥BC 于点E，且CE＝1.5，则AB的长为（）A．3B．4.5C．6D．7.5【分析】由在等边三角形ABC中，DE⊥BC，可求得∠CDE＝30°，则可求得CD的长，又由BD平分∠ABC 交AC于点D，由三线合一的知识，即可求得答案．【解答】解：∵△ABC是等边三角形，∴∠ABC＝∠C＝60°，AB＝BC＝AC，∵DE⊥BC，∴∠CDE＝30°，∵EC＝1.5，∴CD＝2EC＝3，∵BD平分∠ABC交AC于点D，∴AD＝CD＝3，∴AB＝AC＝AD+CD＝6．故选：C．【点评】此题考查了等边三角形的性质以及含30°角的直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．2．（2022秋•姜堰区月考）如图，在等边△ABC中，AB＝4cm，BD平分∠ABC，点E在BC的延长线上，且∠E＝30°，则CE的长是（）A．1cm B．2cm C．3cm D．4cm【分析】根据等边三角形的性质解答即可．【解答】解：∵等边△ABC的边长AB＝4cm，BD平分∠ABC，∴∠ACB＝60°，DC＝AD＝2cm，∵∠E＝30°，∠E+∠EDC＝∠ACB，∴∠EDC＝60°﹣30°＝30°＝∠E，∴CD＝CE＝2cm，故选：B．【点评】此题考查等边三角形的性质，关键是根据等边三角形的三线合一解答．3．（2022秋•常州期中）如图，△ABC是等边三角形，P为BC上一点，在AC上取一点D，使AD＝AP，且∠APD＝70°，则∠PAB的度数是（）A．10°B．15°C．20°D．25°【分析】由已知条件AD＝AP可知∠ADP＝∠APD，结合∠APD＝70°可得∠ADP的度数，从而得到∠P AD 的度数；根据等边三角形的性质，可以得到∠BAC＝60°，结合∠PAB＝∠BAC﹣∠PAD即可解答此题．【解答】解：∵AD＝AP，∴∠ADP＝∠APD．∵∠ADP＝∠APD，∠APD＝70°，∴∠ADP＝70°，∠PAD＝40°．∵△ABC是等边三角形，∴∠BAC＝60°，∴∠PAB＝60°﹣40°＝20°．故选：C．【点评】本题主要考查等边三角形与等腰三角形的性质，可以结合等边三角形的性质进行解答．4．（2022秋•海门市期末）如图，△ABC是等边三角形，BD是中线，延长BC至E，使CE＝CD，DF⊥BE，垂足为点F．（1）求证：CE＝2CF；（2）若CF＝2，求△ABC的周长．【分析】（1）根据等边三角形的性质可知∠ACB＝60°，再由DF⊥BE可知∠DFC＝90°，∠FDC＝90°﹣∠C＝30°，由直角三角形的性质即可得出结论；（2）由CF＝2可得出CD＝4，故可得出AC的长，进而可得出结论．【解答】（1）证明：∵△ABC为等边三角形，∴∠ACB＝60°，∵DF⊥BE，∴∠DFC＝90°，∠FDC＝90°﹣∠C＝30°，∴DC＝2CF．∵CE＝CD∴CE＝2CF；（2）解：∵CF＝2，由（1）知CE＝2CF，∴DC＝2CF＝4．∵△ABC为等边三角形，BD是中线，∴AB＝BC＝AC＝2DC＝8，∴△ABC的周长＝AB+AC+BC＝8+8+8＝24．【点评】本题考查的是等边三角形的性质，熟知边三角形的三个内角都相等，且都等于60°是解题的关键．5．（2022秋•启东市期末）如图，△ABC是等边三角形，AD是BC边上的中线，点E在AD上，且DE＝BC，则∠AFE＝（）A．100°B．105°C．110°D．115°【分析】根据等边三角形的性质得到∠BAC＝60°，∠BAD＝BAC＝30°，AD⊥BC，BD＝CD＝BC，根据等腰直角三角形的性质得到∠DEC＝∠DCE＝45°，根据三角形的内角和定理即可得到答案．【解答】解：∵△ABC是等边三角形，∴∠BAC＝60°，∵AD是BC边上的中线，∴∠BAD＝BAC＝30°，AD⊥BC，BD＝CD＝BC，∴∠CDE＝90°，∵DE＝BC，∴DE＝DC，∴∠DEC＝∠DCE＝45°，∴∠AEF＝∠DEC＝45°，∴∠AFE＝180°﹣∠BAD﹣∠AEF＝180°﹣30°﹣45°＝105°，故选：B．【点评】本题考查了等边三角形的性质，三角形的内角和定理，熟练掌握等边三角形的性质是解题的关键．6．（2022秋•大丰区期中）如图，在等边△ABC中，D为BC边上的中点，以A为圆心，AD为半径画弧，与AC边交点为E，则∠ADE的度数为（）A．60°B．105°C．75°D．15°【分析】根据等边三角形三线合一的性质可求出∠DAC＝30°，结合AD等于AE求出∠ADE的度数即可．【解答】解：在等边△ABC中，D为BC边上的中点，∴∠DAC＝30°（三线合一），在△ADE中，AD＝AE，∴∠AED＝∠ADE＝（180°﹣30°）＝75°，故选：C．【点评】本题考查了等边三角形的性质，等腰三角形的性质，解题关键在于能够熟练掌握该知识并进行合理运用．7．（2022秋•如皋市期中）如图，在△ABC中，BC的垂直平分线分别交BC，AB于点E，F，连接CF，若△AFC是等边三角形，则∠B的度数是（）A．60°B．45°C．30°D．15°【分析】根据垂直平分线的性质得到∠B＝∠BCF，再利用等边三角形的性质得到∠AFC＝60°，从而可得∠B的度数．【解答】解：∵EF垂直平分BC，∴BF＝CF，∴∠B＝∠BCF，∵△ACF为等边三角形，∴∠AFC＝60°，∴∠B＝∠BCF＝30°．故选：C．【点评】本题考查了垂直平分线的性质，等边三角形的性质，三角形外角的性质，解题的关键是利用垂直平分线的性质得到∠B＝∠BCF．8．（2022秋•秦淮区校级月考）如图，△ABC是等边三角形，D，E分别是AC，BC上的点，若AE＝AD，∠CED＝25°，则∠BAE＝°．【分析】利用等边三角形的性质可得∠C＝∠BAC＝60°，从而利用三角形的外角性质可得∠ADE＝85°，然后利用等腰三角形的性质可得∠AED＝∠ADE＝85°，从而利用三角形的内角和定理可得∠DAE＝10°，最后利用角的和差关系进行计算即可解答．【解答】解：∵△ABC是等边三角形，∴∠C＝∠BAC＝60°，∵∠CED＝25°，∴∠ADE＝∠CED+∠C＝85°，∵AE＝AD，∴∠AED＝∠ADE＝85°，∴∠DAE＝180°﹣∠AED﹣∠ADE＝10°，∴∠BAE＝∠BAC﹣∠DAE＝60°﹣10°＝50°，故答案为：50．9．（2022秋•工业园区校级月考）阅读材料：如图，△ABC中，AB＝AC，P为底边BC上任意一点，点P到两腰的距离分别为r1，r2，腰上的高为h，连接AP，则S△ABP+S△ACP＝S△ABC，即：，∴r1+r2＝h（定值）．（1）类比与推理如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即：已知等边△ABC内任意一点P到各边的距离分别为r1，r2，r3，等边△ABC的高为h，试证明r1+r2+r3＝h（定值）．（2）理解与应用△ABC中，∠C＝90°，AB＝10，AC＝8，BC＝6，△ABC内部是否存在一点O，点O到各边的距离相等？（填“存在”或“不存在”），若存在，请直接写出这个距离r的值，r＝．若不存在，请说明理由．【分析】（1）连接AP，BP，CP．根据三角形ABC的面积的两种计算方法进行证明；（2）根据角平分线上的点到角两边的距离相等进行求作．【解答】证明：（1）连接AP，BP，CP．则S△ABP+S△BCP+S△ACP＝S△ABC，即，∵△ABC是等边三角形，∴AB＝BC＝AC，∴r1+r2+r3＝h（定值）；（2）存在．r＝2．【点评】此题主要是考查了等边三角形的性质、角平分线的性质以及三角形的面积公式．注意：直角三角形斜边上的高等于两条直角边的乘积除以斜边．二．等边三角形的判定（共6小题）10．（2022秋•吴江区校级月考）若一个三角形有两条边相等，且有一内角为60°，那么这个三角形一定为（）A．钝角三角形B．等腰三角形C．直角三角形D．正三角形【分析】根据有一个角是60°的等腰三角形是等边三角形求解．【解答】解：根据有一个角是60°的等腰三角形是等边三角形可得到该三角形一定为正三角形．【点评】此题考查学生对有一个角是60°的等腰三角形是等边三角形的运用．11．（2022秋•梁溪区期中）如图所示，在等腰△ABC中，AB＝AC，AF为BC的中线，D为AF上的一点，且BD的垂直平分线过点C并交BD于E．求证：△BCD是等边三角形．【分析】根据等腰三角形的性质得出AF⊥BC，根据线段垂直平分线性质求出BD＝DC，BC＝CD，推出BD ＝DC＝BC，根据等边三角形的判定得出即可．【解答】证明：∵AB＝AC，AF为BC的中线，∴AF⊥BC，∴BD＝DC，∵CE是BD的垂直平分线，∴BC＝CD，∴BD＝DC＝BC，∴△BCD是等边三角形．【点评】本题考查了等边三角形的判定，等腰三角形的性质，线段垂直平分线性质的应用，能正确运用定理进行推理是解此题的关键．12．（2021秋•淮安期末）三角形的三边长a，b，c满足（a﹣b）4+（b﹣c）2+|c﹣a|＝0，那么这个三角形一定是（）A．直角三角形B．等边三角形C．等腰非等边三角形D．钝角三角形【分析】利用偶次方及绝对值的非负性可得出a﹣b＝0，b﹣c＝0，c﹣a＝0，进而可得出a＝b＝c，再结合a，b，c是三角形的三边长，即可得出这个三角形是等边三角形．【解答】解：∵（a﹣b）4+（b﹣c）2+|c﹣a|＝0，∴a﹣b＝0，b﹣c＝0，c﹣a＝0，又∵a，b，c是三角形的三边长，∴这个三角形是等边三角形．故选：B．【点评】本题考查了等边三角形的判定、偶次方及绝对值的非负性，牢记三条边都相等的三角形是等边三角形是解题的关键．13．（2022秋•吴江区校级月考）在边长为9的等边三角形ABC中，点Q是BC上一点，点P是AB上一动点，以每秒1个单位的速度从点A向点B移动，设运动时间为t秒．（1）如图1，若BQ＝6，PQ∥AC，求t的值；（2）如图2，若点P从点A向点B运动，同时点Q以每秒2个单位的速度从点B经点C向点A运动，当t为何值时，△APQ为等边三角形？【分析】（1）由平行线的性质得∠BQP＝∠C＝60°，∠BPQ＝∠A＝60°，从而得出△BPQ是等边三角形，列方程求解即可；（2 ）根据点Q所在的位置不同，分类讨论△APQ是否为等边三角形，再根据等边三角形的性质得到等量关系，列方程求解即可．【解答】解：（1）如图1，∵△ABC是等边三角形，PQ∥AC，∴∠BQP＝∠C＝60°，∠BPQ＝∠A＝60°，又∠B＝60°，∴∠B＝∠BQP＝∠BPQ，∴△BPQ是等边三角形，∴BP＝BQ，由题意可知：AP＝t，则BP＝9﹣t，∴9﹣t＝6，解得：t＝3，∴当t的值为3时，PQ∥AC；（2）如图2，①当点Q在边BC上时，此时△APQ不可能为等边三角形；②当点Q在边AC上时，若△APQ为等边三角形，则AP＝AQ，由题意可知，AP＝t，BC+CQ＝2t，∴AQ＝BC+AC﹣（BC+CQ）＝9+9﹣2t＝18﹣2t，即：18﹣2t＝t，解得：t＝6，∴当t＝6时，△APQ为等边三角形．题为背景，根据等边三角形、等腰三角形以及全等三角形的性质寻找等量关系，再列方程求解，能根据题目要求进行分类讨论是解题的关键．14．（2022秋•常州期中）如图，AB＝AC，∠BAC＝120°，AD⊥AC，AE⊥AB．（1）求∠C的度数；（2）求证：△ADE是等边三角形．【分析】（1）因为AB＝AC，根据等腰三角形的性质，等腰三角形的两个底角相等，又∠BAC＝120°，根据三角形内角和，可求出∠C的度数为30°．（2）AD⊥AC，AE⊥AB，∠ADE＝∠AED＝60°，三个角是60°的三角形是等边三角形．【解答】（1）解：∵AB＝AC，∠BAC＝120°，∴∠B＝∠C＝30°，故答案为：30°．（2）证明：∵∠B＝∠C＝30°，AD⊥AC，AE⊥AB．∴∠ADC＝∠AEB＝60°，∴∠ADC＝∠AEB＝∠EAD＝60°，∴△ADE是等边三角形．【点评】本题考查等腰三角形的性质，等腰三角形的底角相等，以及等边三角形的判定定理，三个角是60°的三角形，是等边三角形．15．（2022秋•江都区校级月考）等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ，问△APQ是什么形状的三角形？试说明你的结论．【分析】先证△ABP≌△ACQ得AP＝AQ，再证∠P AQ＝60°，从而得出△APQ是等边三角形．【解答】解：△APQ证明：∵△ABC为等边三角形，∴AB＝AC．在△ABP与△ACQ中，∵，∴△ABP≌△ACQ（SAS）．∴AP＝AQ，∠BAP＝∠CAQ．∵∠BAC＝∠BAP+∠PAC＝60°，∴∠PAQ＝∠CAQ+∠PAC＝60°，∴△APQ是等边三角形．【点评】考查了等边三角形的判定及全等三角形的判定方法．三．等边三角形的判定与性质（共9小题）16．（2022秋•梁溪区期中）一艘轮船由海平面上A地出发向南偏西40°的方向行驶100海里到达B地，再由B地向北偏西20°的方向行驶100海里到达C地，则A，C两地相距（）A．100海里B．80海里C．60海里D．40海里【分析】先求得∠CBA＝60°，然后可判断△ABC为等边三角形，从而可求得AC的长．【解答】解：如图所示：连接AC．∵点B在点A的南偏西40°方向，点C在点B的北偏西20°方向，∴∠ABD＝40°，∠CBD＝20°，∴∠CBA＝∠ABD+∠CBD＝60°．又∵BC＝BA，∴△ABC为等边三角形．∴AC＝BC＝AB＝100海里．故选：A．【点评】本题主要考查的是方向角、等边三角形的性质和判定，证得△ABC为等边三角形是解题的关键．17．（2022秋•玄武区期中）如图，△ABC为等边三角形，BD⊥AC交AC于点D，DE∥BC交AB于点E．（1）求证：△ADE是等边三角形．（2）求证：AE＝AB．【分析】（1）根据等边三角形的性质和平行线的性质证明即可．（2）根据等边三角形的性质解答即可．【解答】证明：（1）∵△ABC为等边三角形，∴∠A＝∠ABC＝∠C＝60°．∵DE∥BC，∴∠AED＝∠ABC＝60°，∠ADE＝∠C＝60°．∴△ADE是等边三角形．（2）∵△ABC为等边三角形，∴AB＝BC＝AC．∵BD平分∠ABC，∴AD＝AC．∵△ADE是等边三角形，∴AE＝AD．∴AE＝AB．【点评】此题考查等边三角形的判定和性质，关键是根据等边三角形的性质和平行线的性质解答．18．（2022秋•姑苏区期中）如图，在四边形ABCD中，AB＝AD，CB＝CD，∠A＝60°，点E为AD上一点，连接BD，CE交于点F，CE∥AB．（1）判断△DEF的形状，并说明理由；（2）若AD＝12，CE＝8，求CF的长．【分析】（1）先证明△ABD是等边三角形，可得∠ABD＝∠ADB＝60°，由平行线的性质可得∠CED＝∠ADB＝∠DFE＝60°，可得结论；（2）由等边三角形的性质和平行线的性质可求AE＝CE＝8，即可求解．【解答】解：（1）△DEF是等边三角形，理由如下：∵AB＝AD，∠A＝60°，∴△ABD是等边三角形，∴∠ABD＝∠ADB＝60°，∵CE∥AB，∴∠CED＝∠A＝60°，∠DFE＝∠ABD＝60°，∴∠CED＝∠ADB＝∠DFE，∴△DEF是等边三角形；（2）连接AC交BD于点O，∵AB＝AD，CB＝CD，∴AC是BD的垂直平分线，即AC⊥BD，∵AB＝AD，∠BAD＝60°，∴∠BAC＝∠DAC＝30°，∵CE∥AB，∴∠BAC＝∠ACE＝∠CAD＝30°，∴AE＝CE＝8，∴DE＝AD﹣AE＝12﹣8＝4，∵△DEF是等边三角形，∴EF＝DE＝4，∴CF＝CE﹣EF＝8﹣4＝4．【点评】本题考查了等边三角形的判定和性质，平行线的性质，证明AE＝CE是解题的关键．19．（2022秋•南通期末）已知等边△ABC的边长为5，点D为直线BC上一点，BD＝1，DE∥AB交直线AC于点E，则DE的长为．【分析】分D在线段BC上，和D在线段CB的延长线上，两种情况，讨论求解即可．【解答】解：①当D在线段BC上，如图：∵等边△ABC的边长为5，∴∠A＝∠B＝∠C＝60°，AB＝AC＝BC＝5，∵BD＝1，∴CD＝BC﹣BD＝4，∵DE∥AB，∴∠EDC＝∠B＝60°，∠DEA＝∠A＝60°，∴△DEC为等边三角形，∴DE＝CD＝4；②当D在线段CB的延长线上，如图：同法可得：△DEC为等边三角形，∴DE＝CD＝BC+BD＝6；综上：DE的长为：4或6；故答案为：4或6．【点评】本题考查等边三角形的判定和性质．熟练掌握，两直线平行，同位角相等，证明三角形是等边三角形，是解题的关键．注意，分类讨论．20．（2022秋•鼓楼区校级月考）如图所示，在等边△ABC中，AB＝9cm，点P从点C出发沿CB边向点B 以2cm/s的速度移动，点Q从点B出发沿BA边向点A以5cm/s的速度移动．P，Q两点同时出发，它们移动的时间为ts．（1）你能用含的式子表示BP和BQ的长度吗？请你表示出来．（2）请问几秒后，△PBQ第一次为等边三角形？（3）若P，Q两点分别从C，B两点同时出发，并且按顺时针方向沿△ABC三边运动，请问经过几秒后点P与点Q第一次在△ABC的哪条边上相遇？【分析】（1）由等边三角形的性质可求得BC的长，用t可表示出BP和BQ的长；（2）由等边三角形的性质可知BQ＝BP，可得到关于t的方程，可求得t的值；（3）设经过t秒后第一次相遇，由条件可得到关于t的方程，可求得t的值，可求得点P走过的路程，可确定出P点的位置．【解答】解：（1）∵△ABC为等边三角形，∴BC＝AB＝9cm，∵点P的运动速度为2cm/s，运动时间为ts，∴BP＝BC﹣CP＝（9﹣2t）cm，∵点Q的运动速度为5cm/s，运动时间为ts，∴BQ＝5t（cm）；（2）若△PBQ为等边三角形，则有BQ＝BP，即9﹣2t＝5t，解得t＝，∴s时，△PBQ第一次为等边三角形；（3）设ts时，Q与P第一次相遇，根据题意得5t﹣2t＝18，解得t＝6，即6s时，两点第一次相遇．当t＝6s时，P走过的路程为2×6＝12cm，而9＜12＜18，即此时P在AB边上，∴经过6秒后点P与点Q在AB上第一次相遇．【点评】本题考查了等边三角形的性质和判定、方程思想等知识．该题为运动型题目，解决这类问题的关键是化“动”为“静”，即用时间和速度表示出线段的长．21．（2022秋•泰州月考）如图，已知点D、E在△ABC的边BC上，AB＝AC，AD＝AE．（1）求证：BD＝CE；（2）若AD＝BD＝DE＝CE，求∠BAE的度数．【分析】（1）作AF⊥BC于点F，利用等腰三角形三线合一的性质得到BF＝CF，DF＝EF，相减后即可得到正确的结论．（2）根据等边三角形的判定得到△ADE是等边三角形，根据等边三角形的性质、等腰三角形的性质以及角的和差关系即可求解．【解答】（1）证明：如图，过点A作AF⊥BC于F．∵AB＝AC，AD＝AE．∴BF＝CF，DF＝EF，∴BD＝CE．（2）∵AD＝DE＝AE，∴△ADE是等边三角形，∴∠DAE＝∠ADE＝60°．∵AD＝BD，∴∠DAB＝∠DBA．∴∠DAB＝∠ADE＝30°．∴∠BAE＝∠BAD+∠DAE＝90°．【点评】本题考查了等边三角形的判定与性质，熟练运用等边三角形的判定是本题的关键．22．（2022秋•沭阳县期中）已知：如图，点C为线段AB上一点，△ACM，△CBN都是等边三角形，AN 交MC于点E，BM交CN于点F．（1）求证：AN＝BM；（2）求证：△CEF为等边三角形．【分析】（1）由等边三角形可得其对应线段相等，对应角相等，进而可由SAS得到△ACN≌△MCB，结论得证；（2）由（1）中的全等可得∠CAN＝∠CMB，进而得出∠MCF＝∠ACE，由ASA得出△CAE≌△CMF，即CE＝CF，又ECF＝60°，所以△CEF为等边三角形．【解答】证明：（1）∵△ACM，△CBN是等边三角形，∴AC＝MC，BC＝NC，∠ACM＝∠NCB＝60°，∴∠ACM+∠MCN＝∠NCB+∠MCN，即∠ACN＝∠MCB，在△ACN和△MCB中，∵，∴△ACN≌△MCB（SAS），∴AN＝BM．（2）∵△CAN≌△CMB，∴∠CAN＝∠CMB，又∵∠MCF＝180°﹣∠ACM﹣∠NCB＝180°﹣60°﹣60°＝60°，∴∠MCF＝∠ACE，在△CAE和△CMF中，∵，∴△CAE≌△CMF（ASA），∴CE＝CF，∴△CEF为等腰三角形，又∵∠ECF＝60°，∴△CEF为等边三角形．【点评】本题主要考查了全等三角形的判定及性质以及等边三角形的判定问题，能够掌握并熟练运用．23．（2022秋•启东市校级月考）数学课上，张老师举了下面的例题：例1：等腰三角形ABC中，∠A＝110°，求∠B的度数．（答案：35°）例2：等腰三角形ABC中，∠A＝40°，求∠B的度数．（答案：40°或70°或100°）张老师启发同学们进行变式，小敏编的题目如下：变式题：等腰三角形ABC中，∠A＝80°，求∠B的度数．（1）请你解答上面的变式题．（2）请继续探索，完成下面问题：等腰三角形ABC中，∠A＝60°，则∠B的度数为．（3）根据以上探索，我们发现，∠A的度数不同，得到的∠B度数的个数也可能不同．请你直接写出当∠A 满足什么条件时，∠B能得到三个不同的度数．【分析】（1）∠A是顶角，则∠B是底角，根据等腰三角形的两个底角相等即可求解；∠B是顶角，则∠A 是底角，则根据等腰三角形的两个底角相等，以及三角形的内角和定理即可求解；∠C是顶角，则∠B与∠A都是底角，根据等腰三角形的两个底角相等即可求解；（2）分两种情况：①90≤x＜180；0＜x＜90，结合三角形内角和定理求解即可．【解答】解：（1）当∠A＝80°为顶角时，∠B＝＝50°；当∠B是顶角，则∠A是底角，则∠B＝180°﹣80°﹣80°＝20°；当∠C是顶角，则∠B与∠A都是底角，则∠B＝∠A＝80°，综上所述，∠B的度数为50°或20°或80°；（2）因为有一个角为60°的等腰三角形为等边三角形，所以∠B＝60°，故答案为：60°．（3）分两种情况：设∠A＝x°，①当90≤x＜180时，∠A只能为顶角，∴∠B的度数只有一个；②当0＜x＜90时，若∠A为顶角，则∠B＝（）°；若∠A为底角，∠B为顶角，则∠B＝（180﹣2x）°；若∠A为底角，∠B为底角，则∠B＝x°．当≠180﹣2x且180﹣2x≠x且≠x，即x≠60时，∠B有三个不同的度数．综上所述，可知当0°＜∠A＜90°且x≠60°时，∠B有三个不同的度数．【点评】本题考查了等腰三角形的性质及三角形内角和定理，进行分类讨论是解题的关键．24．（2022秋•铜山区校级月考）已知：如图，△DAC、△EBC均是等边三角形，点A、C、B在同一条直线上，且AE、BD分别与CD、CE交于点M、N．求证：（1）AE＝DB；（2）△CMN为等边三角形．【分析】（1）根据△DAC、△EBC均是等边三角形，求证△ACE≌△DCB（SAS）即可得出结论．（2）由（1）可知：△ACE≌△DCB，和△DAC、△EBC均是等边三角形，求证△ACM≌△DCN（ASA）即可得出结论．【解答】证明：（1）∵△DAC、△EBC均是等边三角形，∴AC＝DC，EC＝BC，∠ACD＝∠BCE＝60°，∴∠ACD+∠DCE＝∠BCE+∠DCE，即∠ACE＝∠DCB．在△ACE和△DCB中，∴△ACE≌△DCB（SAS）．∴AE＝DB．（2）由（1）可知：△ACE≌△DCB，∴∠CAE＝∠CDB，即∠CAM＝∠CDN．∵△DAC、△EBC均是等边三角形，∴AC＝DC，∠ACM＝∠BCE＝60°．又点A、C、B在同一条直线上，∴∠DCE＝180°﹣∠ACD﹣∠BCE＝180°﹣60°﹣60°＝60°，即∠DCN＝60°．∴∠ACM＝∠DCN．在△ACM和△DCN中，∴△ACM≌△DCN（ASA）．∴CM＝CN．又∠DCN＝60°，∴△CMN为等边三角形．【点评】此题主要考查学生对等边三角形的性质与判定、全等三角形的判定与性质、三角形内角和定理等知识点的理解和掌握，此题难度不大，但是步骤繁琐，属于中档题．一．选择题（共5小题）1．（2022秋•梁溪区期中）下列命题不正确的是（）A．等腰三角形的底角不能是钝角B．等腰三角形不能是直角三角形C．若一个三角形有三条对称轴，那么它一定是等边三角形D．两个全等的且有一个锐角为30°的直角三角形可以拼成一个等边三角形【分析】利用等腰三角形的性质和等边三角形的判定的知识，对各选项逐项分析，即可得出结果．【解答】解：本题可采用排除法；A、利用等腰三角形的性质，等腰三角形的两底角相等，若两底角均为钝角，不能构成三角形，故这种说法错误，故不选A；B、举反例：等腰直角三角形，故B不正确．即答案选B．【点评】本题主要考查了等腰三角形的性质和等边三角形的判定，要求学生在学习过程中要对所学过的知识进行总结和复习，以便灵活的运用所学的知识．2．（2022秋•鼓楼区校级月考）如图，∠AOB＝60°，OA＝OB，动点C从点O出发，沿射线OB方向移动，以AC为边在右侧作等边△ACD，连接BD，则BD所在直线与OA所在直线的位置关系是（）A．平行B．相交C．垂直D．平行、相交或垂直【分析】先判断出OA＝OB，∠OAB＝∠ABO，分两种情况判断出∠ABD＝∠AOB＝60°，进而判断出△AOC ≌△ABD，即可得出结论．【解答】解：∵∠AOB＝60°，OA＝OB，∴△OAB是等边三角形，∴OA＝AB，∠OAB＝∠ABO＝60°①当点C在线段OB上时，如图1，∵△ACD是等边三角形，∴AC＝AD，∠CAD＝60°，∴∠OAC＝∠BAD，在△AOC和△ABD中，，∴△AOC≌△ABD（SAS），∴∠ABD＝∠AOC＝60°，∴∠DBE＝180°﹣∠ABO﹣∠ABD＝60°＝∠AOB，∴BD∥OA，②当点C在OB的延长线上时，如图2，同①的方法得出OA∥BD，∵△ACD是等边三角形，∴AC＝AD，∠CAD＝60°，∴∠OAC＝∠BAD，在△AOC和△ABD中，，∴△AOC≌△ABD（SAS），∴∠ABD＝∠AOC＝60°，∴∠DBE＝180°﹣∠ABO﹣∠ABD＝60°＝∠AOB，∴BD∥OA，故选：A．【点评】此题主要考查了等边三角形的判定和性质，全等三角形的判定和性质，求出∠ABD＝60°是解本题的关键．3．（2022秋•射阳县校级月考）如图，将一等边三角形的三条边各8等分，按顺时针方向（图中箭头方向）标注各等分点的序号0、1、2、3、4、5、6、7、8，将不同边上的序号和为8的两点依次连接起来，这样就建立了“三角形”坐标系．在建立的“三角形”坐标系内，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始、按顺时针方向、取与三角形外箭头方向一致的一侧序号），如点A的坐标可表示为（1，2，5），点B的坐标可表示为（4，3，1），按此方法，若点C的坐标为（2，m，m﹣2），则m＝（）A．2B．3C．4D．6【分析】根据点A的坐标可表示为（1，2，5），点B的坐标可表示为（4，3，1），得到经过该点的三条直线对应着等边三角形三边上的三个数，依次为左，上，下，即可解答．【解答】解：由题意得：点C的坐标为（2，4，2），∴m＝4，故选：C．【点评】本题考查了等边三角形的性质，规律型：数字的变化类，找出题中的规律是解题的关键．4．（2022秋•扬州期中）在下列结论中：（1）有一个外角是120°的等腰三角形是等边三角形（2）有两个外角相等的等腰三角形是等边三角形（3）有一边上的高也是这边上的中线的等腰三角形是等边三角形（4）三个外角都相等的三角形是等边三角形其中正确的个数是（）A．4个B．3个C．2个D．1个【分析】根据等边三角形的性质和定义，可得：有一个角为60°的等腰三角形是等边三角形；三个内角都相等的三角形为等边三角形；再由中线的性质和三角形内角和的定义可解答本题．【解答】解：（1）：因为外角和与其对应的内角的和是180°，已知有一个外角是120°，即是有一个内角是60°，有一个内角为60°的等腰三角形是等边三角形．该结论正确．（2）：两个外角相等说明该三角形中两个内角相等，而等腰三角形的两个底角是相等的，故不能确定该三角形是等边三角形．该结论错误．（3）：等腰三角形的底边上的高和中线本来就是重合的，“有一边”可能是底边，故不能保证该三角形是等边三角形．该结论错误．（4）：三个外角都相等的三角形是等边三角形．正确；故选：C．【点评】本题考查等边三角形的判定，解题的关键是灵活运用的等边三角形的判定方法解决问题．5．（2022秋•邗江区月考）如图，直线m∥n，△ABC是等边三角形，顶点B在直线n上，直线m交AB 于点E，交AC于点F，若∠1＝140°，则∠2的度数是（）A．80°B．100°C．120°D．140°【分析】先根据等边三角形的性质可得∠A＝∠B＝∠C＝60°，由三角形外角的性质可得∠AEF的度数，由平行线的性质可得同旁内角互补，可得结论．【解答】解：∵△ABC是等边三角形，∴∠A＝60°．对于△AEF，∵∠1＝∠A+∠AEF＝140°，∴∠AEF＝140°﹣60°＝80°，∴∠DEB＝∠AEF＝80°，∵m∥n，∴∠2+∠DEB＝180°，∴∠2＝180°﹣80°＝100°，故选：B．【点评】本题主要考查了等边三角形的性质，平行线的性质，三角形外角的性质，题目比较基础，熟练掌握性质是解题的关键．二．填空题（共13小题）6．（2022秋•江阴市期中）已知△ABC中，AB＝AC＝6，∠C＝60°，则BC＝6．【分析】先利用等腰三角形的性质得到∠B＝∠C＝60°，则可判断△ABC为等边三角形，然后根据等边三角形的性质得到BC＝AB．【解答】解：∵AB＝AC＝6，∴∠B＝∠C＝60°，∴△ABC为等边三角形，∴BC＝AB＝6．故答案为：6．【点评】本题考查了等边三角形的性质：等边三角形的三条边都相等，三个内角都相等，且都等于60°．7．（2022秋•建邺区校级月考）如图，已知△ABC是等边三角形，AD是中线，E在AC上，AE＝AD，则∠EDC＝．【分析】由AD是等边△ABC的中线，根据等边三角形中：三线合一的性质，即可求得AD⊥BC，∠CAD ＝30°，又由AD＝AE，根据等边对等角与三角形内角和定理，即可求得∠ADE的度数，继而求得答案．【解答】解：∵AD是等边△ABC的中线，∴AD⊥BC，∠BAD＝∠CAD＝∠BAC＝×60°＝30°，∴∠ADC＝90°，∵AD＝AE，∴∠ADE＝∠AED＝（180°﹣∠CAD）＝75°，∴∠EDC＝∠ADC﹣∠ADE＝90°﹣75°＝15°．故答案为：15°．【点评】此题考查了等边三角形的性质、等腰三角形的性质以及三角形内角和定理．此题难度不大，解题的关键是注意数形结合思想的应用．8．（2022秋•崇川区校级月考）如图，已知△ABC中，∠A＝60°，D为AB上一点，且AC＝2AD+BD，∠B＝4∠ACD，则∠DCB的度数是．。

人教版八年级数学讲义_第16讲：等边三角形中考班

第16讲：等边三角形一、【知识点】1、三边都相等的三角形叫做等边三角形．2、等边三角形的性质：等边三角形的三个内角相等，都等于60°．3、30°的直角三角形中，30°角所对的直角边为斜边的一半．4、等边三角形的判定：(1)、三个内角都相等的三角形是等边三角形．(2)、有一个角为60°的等腰三角形为等边三角形．二、【探究新知】探究1：如图，△ABC 为等边三角形，求它的每一个内角．【定理】等边三角形的每个内角都为______度．【例1】如图，△ABC 边BC 上有D 、E 两点，且BD =DE =EC =AD =AE ，则∠BAC =_________．BBC【练习1】△ABC 是等边三角形，D 、E 分别是BC 、AC 上的点，且AE =CD ，AD 与BE 交于点为F ．(1)你能发现图中有几对全等三角形？ (2)求∠BFD 的度数．【探究2】1．若一个三角形的三个内角都相等，它是等边三角形吗？2．有一个角为60°的等腰三角形是等边三角形吗？【等边三角形的判定定理】1．三个内角都相等的三角形是等边三角形．2．有一个角为60°的等腰三角形为等边三角形．3．有两个角为60°的三角形为等边三角形．【例2】如图，△ABC 是等边三角形，D 、E 、F 分别是AB 、BC 、CA 上的点，且AD =BE =CF ，求证：△DEF 是等边三角形．BBB BB C【探究】如图，Rt △ABC 中，∠A =30°，则线段BC 与线段AB 有何数量关系？并说明理由．【定理】30°的直角三角形中，30°角所对的直角边为斜边的________．【例3】△ABC 中，BD 是AC 边上的中线，BD ⊥AC 边上的中线，BD ⊥BC 于点B ，∠ABC =120°，求证：AB =2BC ．【练习2】等腰三角形的顶角为120°，底边上的高为10，则腰长为_______．【练习3】如图，△ABC 中，∠ACB =90°，∠A =30°，CD ⊥AB 于D ，AB =4㎝，则BD =________．BCAB【练习4】如图，在△ABC 中，AB =AC ，∠BAC =120°，D 为BC 的中点，DE ⊥AB 于E ，求证EB ：EA 的值．如图，在平面直角坐标系中，△AOP 为等边三角形，A (0,1)，点B 为y 轴上一动点，以BP 为边作等边△PBC ．(1) 求∠CAP 的度数；(2) 当B 点运动时，AE 的长度是否发生变化？C B第16讲：等边三角形测试题姓名＿＿＿＿分数＿＿＿＿＿1．如图，等边△ABC 的边长为1cm ，D 、E 分别是AB 、AC 上的点，将△ABC沿直线DE 折叠，点A 落在A ’处，且A ’在△ABC 外部，则阴影部分图形的周长为__________ cm2．如图，△ABC 是等边三角形，D 为AB 的中点，DE ⊥AC 垂足为点E ，EF ∥AB ，AE =1，则△EFC 的周长=_______．3．如图所示，一个六边形的六个内角都是120°，其中连续四边的长依次是1、9、9、5．求这个六边形的周长为________4. 已知△ABC 中，AB =AC ，下列结论：① 若AB =BC ，则△ABC 是等边三角形； ②若∠A =60°，则△ABC 是等边三角形；③若∠B =60°，则△ABC 是等边三角形．其中正确的有( )A ．0个B ．1个C ．2个D ．3个5．如图，已知△ABC 为等边三角形，点P 在AB 上，以CP 为边长作等边△PCE ．求证：AE ∥BC ．B6．如图，△ABC 中，AB =AC ，∠C =30°，AB 的垂直平分线MN 分别交BC 、AB 于点M 、N ，试探究BM 与CM 之间的数量关系．7．如图，D 、E 分别是等边△ABC 的边AC 、BC 上的点，且AD =CE ，BD 、AE 交于点N ，BM ⊥AE 于M ，求证：MN =21BN .BBE。

八年级数学等边三角形1

福彩快3正规平台 www.ຫໍສະໝຸດ
[单选]冷热油泵是按照介质温度以（）℃划分的。A、100B、150C、200D、250 [问答题]一个尺寸为42.6×48.7的货盘可承载的最大重量为多少？（地板承载限制121磅/平方英尺货盘重量47磅系留装置33磅） [判断题]组织文化可以通过职工的着装、标志、行为模式、组织的规范等完全反映出来。（）A.正确B.错误 [填空题]行人持有长大、飘动等物件通过道口时，不得（），应与牵引供电设备带电部分保持（）以上的距离。 [填空题]嘧啶环的N1、C6来自（）；和N3来自（）。 [单选,A2型题,A1/A2型题]道德最显著的特征是（）A.继承性B.实践性C.自律性D.他律性E.客观性 [填空题]加压后的液氨气化时体积会膨胀（），并大量（），使周围物质的温度（）。 [单选]在资产负债表上，资产项目是按其流动性进行排列的，流动性强的项目排在前面，流动性差的项目排在后面，下列资产项目中，排在应收账款前面的是（）。A.固定资产B.长期投资C.存货D.货币资金 [单选]机床照明灯应选下列电压供电。（）A.220伏B.110伏C.24伏D.380伏 [单选,A1型题]乳腺癌出现“酒窝征”的机制是（）A.合并感染B.癌肿压迫乳管C.癌肿侵犯cooper韧带D.淋巴管癌栓阻塞E.周围组织粘连 [单选,A2型题,A1/A2型题]下列可使血糖浓度下降的激素是（）A.肾上腺激素B.胰升糖素C.生长素D.胰岛素E.甲状腺素 [单选]物业的车辆管理人员应包括（）。A.车辆交通的疏导人员B.客户服务人员C.园区巡视人员D.道路清洁人员 [单选,A2型题,A1/A2型题]对周围性面瘫临床表现的描述，不正确的是（）。A.病侧面部表情运动丧失，额纹消失B.不能皱眉与闭目C.鼻唇沟变浅，口角下垂向患侧歪斜D.鼓腮漏气，发爆破音困难E.进食可有口角漏液现象 [名词解释]撞人犯规(personalfoul) [单选]甲、乙双方发生合同纠纷，甲方向人民法院起诉，乙方应诉答辩。在庭审过程中，乙方主张起诉前双方曾在信件往来中就该合同纠纷约定由北京仲裁委员会仲裁，并提出了相应的证据。这种情况下，请问：人民法院应当怎么处理？（）A.裁定终结诉讼，由当事人向北京仲裁委员会申请仲裁 [单选]对固定资产采用加速折旧法，体现了会计核算的（）要求。A.重要性B.谨慎性C.可比性D.实质重于形式 [单选,A2型题,A1/A2型题]关于冷凝集素试验，下列哪项是正确的（）A.冷凝集综合征患者阳性，效价在1：1000以上B.37℃凝集反应最强C.0～4℃凝集现象消失D.抗体IgGE.为不完全抗体 [单选,A型题]确定白喉棒状杆菌是否产毒素的依据是（）A.菌体排列及异染颗粒B.在亚碲酸钾平板上的菌落生长特点C.Elek平板毒力试验D.锡克试验E.生化反应 [填空题]一般GSM网络中基站采用的跳频方式是（）跳频 [单选,A1型题]关于乳腺癌，下列不正确的是（）A.锁骨下淋巴结转移属远处转移B.原位癌患者可以不行腋窝淋巴结清扫C.雌、孕激素受体阳性的病例内分泌治疗效果好D.乳腺癌保乳术后应接受放疗E.Paget病恶性程度较低 [填空题]滤纸分为（）滤纸和（）滤纸两种，重量分析中常用（）。 [单选,A4型题,A3/A4型题]29岁女性，7年前和3年前分别足月顺产一女孩和一男孩，1年前有一次宫外孕手术史，经咨询指导选择使用复方长效口服药避孕。复方长效口服药避孕药正确的服用方法是（）A.每个月经周期的第1天服用1片B.每个月经周期的第5天服用1片C.首次在月经周期第5天1片，第 [单选]下列哪种情况可采用腰麻（）A.脊髓前角灰质炎B.脊髓肿瘤C.慢性贫血（血红蛋白700g/L以上）D.盆腔肿瘤E.严重高血压 [单选]下列（）票据应直接打码。A、商业承兑汇票B、退票专用凭证C、代收（付）款项报数单D、银行汇票 [单选,A2型题,A1/A2型题]以下有关自杀的概念的描述不正确的是（）A.自杀是"有意或者故意伤害自己生命的行动"B.自杀者把自杀行动看作是解决某种问题的最好办法C.自杀是有意的自我伤害导致的死亡D.广义的自杀论者认为自杀指有害生命的一切人类行为E.广义的自杀论者认为意 [单选]柴油机运转中在气缸中部发生有规律的敲击声，可能是()的原因。A.喷油器压缩弹簧断裂B.曲柄销轴承偏磨C.活塞与气缸间隙过大D.活塞销轴承偏磨 [单选]患者男，21岁，发现睾丸无痛肿块，局部不规则，结合超声图像，最可能的诊断是()A．精原细胞瘤B．睾丸畸胎瘤C．精母细胞瘤D．睾丸腺癌E．睾丸囊肿 [单选,A2型题,A1/A2型题]关于慢性粒细胞白血病下列说法不正确的是（）.A.急变期仍然按慢性期治疗B.90%以上可查到Ph染色体C.NAP积分最低D.WBC高，脾大为突出特征E.嗜酸、嗜碱性粒细胞易见 [单选]黄体由两种细胞组成（）A.颗粒黄体细胞和卵泡颗粒层B.颗粒黄体细胞和卵泡膜黄体细胞C.膜黄体细胞和门细胞D.颗粒黄体细胞和门细胞E.膜黄体细胞和卵泡膜细胞 [单选]下颌关节间隙正常值为（）A.1.5mmB.1.8mmC.2.0mmD.2.5mmE.3.0mm [单选,A2型题,A1/A2型题]缺铁性贫血患者给予补充铁剂治疗时，血红蛋白正常后，仍需继续补充铁剂（）A.1～3个月B.3～6个月C.6～9个月D.9～12个月E.一年以上 [单选]以下属于皮肤病原发性皮损的是（）A.鳞屑B.色素沉着C.抓痕D.水疱E.痂 [填空题]广告策划效果评估是指对广告活动的（）评估，而不单纯指广告后期效果评估。 [单选]女性，48岁。双手指间皱襞处发生略带椭圆形的红斑，边界清楚，其上表皮浸渍发白，部分为红色糜烂面。考虑可能的诊断为（）A.带状疱疹B.皮肤念珠菌病C.单纯疱疹D.疣E.药疹 [单选]测量左心室容积参数的方法不包括（）。A.M型超声B.二维超声C.三维超声D.多普勒超声E.组织多普勒成像 [单选]风心病二尖瓣狭窄出现以下哪项体征提示心功能不全（）.A.心尖区收缩期抬举样搏动B.室性奔马律C.拍击性第一心音D.肺动脉瓣区第二心音亢进E.脉短绌 [单选]判断行政机关及其他组织能否具备行政主体资格的关键性条件是（）。A.能否实施国家行政管理活动B.是否具有行政主体的法律地位C.能否独立承担法律责任D.能够独立参加行政复议 [单选]职务工资制体系建立在职务评价基础上，决定基本工资差别的最主要因素是（）。A.职工所执行职务的差别B.职工技术等级的差别C.职工工作环境的差异D.职工工作性质的差异 [单选,A2型题,A1/A2型题]支气管癌时伴随高血压、低血钾及肌无力等表现，其原因是由于下列物质分泌过多（）A.肿瘤细胞所分泌的与ADH类似的环形多肽B.肿瘤代谢刺激腺垂体所分泌的ACTHC.肿瘤代谢刺激脑垂体后所分泌的ADHD.醛固酮E.肿瘤所分泌的ACTH样多肽 [填空题]当使用商品混凝土时，（）应组织对供应商的拌和站进行评估验收，质量控制应符合本标准的规定。

八年级数学上册第二章等边三角形知识点与同步训练(含解析)苏科版

等边三角形一．等边三角形的概念等边三角形：三条边都相等的三角形叫做等边三角形．等边三角形是一种特殊的等腰三角形．二．等边三角形的性质等边三角形的三个内角都相等，并且每一个角都等于60︒．三．等边三角形的判定判定1：三个角都相等的三角形是等边三角形．判定2：有一个角是60︒的等腰三角形是等边三角形．四．直角三角形性质定理在直角三角形中，如果一个锐角等于30︒，那么它所对的直角边等于斜边的一半．B'CBA证明：90ACB ∠=︒，30A ∠=︒，延长BC 至'B 使'CB CB =，那么有AC 垂直平分'BB ，所以'AB AB =，因为60B ∠=︒，所以'ABB △是等边三角形，所以'2AB BB BC ==，即12BC AB =．五．等边三角形与全等三角形综合等边三角形与全等三角形综合问题主要分两种类型：一是以等边三角形为载体来考察全等三角形的综合问题；二是利用全等三角形的性质和判定证明三角形是等边三角形．不管是哪种类型都要注意60°角和边的等量关系的应用，尤其是后面学习旋转之后，会出现一些比较难的等边三角形和全等三角形结合的问题．一．考点：1．等边三角形的性质与判定；2．直角三角形性质定理；3．等边三角形与全等三角形综合．二．重难点：1．等边三角形是特殊的等腰三角形，具有等腰三角形的所有性质．做题时常作为隐藏条件考察．2．等边三角形的判定用定义判断的不多，一般都是利用有一个角是60︒的等腰三角形是等边三角形来判定，所以在构造全等是要注意同时兼顾边相等，并且可以推导出有一个角为60°．3．等边三角形的性质非常特殊，在证明或计算中要注意边角之间的转化，尤其是含30°角的直角三角形中边的关系．4．在解决建立在等边三角形根底上的全等综合问题时，关键是抓住边相等，角度都是特殊角．三．易错点：在利用直角三角形性质定理的过程中，需要注意两点：一是必须在直角三角形中才能运用，锐角三角形和钝角三角形均不存在上述关系；二是一定要注意是30︒所对的直角边等于斜边的一半．题模一：等边三角形的性质例三个等边三角形的位置如下列图，假设∠3=50°，那么∠1+∠2=____°．【答案】130【解析】∵图中是三个等边三角形，∠3=50°，∴∠ABC=180°-60°-50°=70°，∠ACB=180°-60°-∠2=120°-∠2，∠BAC=180°-60°-∠1=120°-∠1，∵∠ABC+∠ACB+∠BAC=180°，∴70°+〔120°-∠2〕+〔120°-∠1〕=180°，∴∠1+∠2=130°．故答案为：130．例如图，等边△ABC的周长是9，D是AC边上的中点，E在BC的延长线上．假设DE=DB，那么CE的长为____．【答案】 32 【解析】该题考察的是∵△ABC 为等边三角形，D 为AC 边上的中点，BD 为ABC ∠的平分线，∴60ABC ∠=︒，30DBE ∠=︒，又DE DB =， ∴30E DBE ∠=∠=︒，∴30CDE ACB E ∠=∠-∠=︒，即CDE E ∠=∠，∴CD CE =；∵等边△ABC 的周长为9，∴3AC =，∴1322CD CE AC ===，即32CE =．例在等边△ABC 中，D 是边AC 上一点，连接BD ，将△BCD 绕点B 逆时针旋转60°，得到△BAE ，连接ED ，假设BC=5，BD=4．那么以下结论错误的选项是〔〕A ． AE ∥BCB ． ∠ADE=∠BDC C ． △BDE 是等边三角形D ． △ADE 的周长是9 【答案】B【解析】此题考察的是图形旋转的性质及等边三角形的判定与性质，平行线的判定，熟知旋转前、后的图形全等是解答此题的关键．首先由旋转的性质可知∠AED=∠ABC=60°，所以看得AE∥BC，先由△ABC 是等边三角形得出AC=AB=BC=5，根据图形旋转的性质得出AE=CD ，BD=BE ，故可得出AE+AD=AD+CD=AC=5，由∠EBD=60°，BE=BD 即可判断出△BDE 是等边三角形，故DE=BD=4，故△AED 的周长=AE+AD+DE=AC+BD=9，问题得解．∵△ABC 是等边三角形，∴∠ABC=∠C=60°，∵将△BCD 绕点B 逆时针旋转60°，得到△BAE，∴∠EAB=∠C=∠ABC=60°，∴AE∥BC，应选项A 正确；∵△ABC 是等边三角形，∴AC=AB=BC=5，∵△BAE△BCD 逆时针旋旋转60°得出，∴AE=CD，BD=BE ，∠EBD=60°，∴AE+AD=AD+CD=AC=5，∵∠EBD=60°，BE=BD ，∴△BDE 是等边三角形，应选项C 正确；∴DE=BD=4，∴△AED 的周长=AE+AD+DE=AC+BD=9，应选项D 正确；而选项B 没有条件证明∠ADE=∠BDC，∴结论错误的选项是B ，应选：B ．题模二：等边的判定例如下列图，AD 是ABC △的中线，60ADC ∠=°，8BC =，把ADC △沿直线AD 折叠后，点C 落在C '位置，那么BC '的长为________.【答案】 4【解析】此题考察的是等边三角形．由题意，60ADC ADC '∠=∠=︒，DC DC DB '==． 180606060BDC '∠=︒-︒-︒=︒，有一个角为60︒的等腰三角形为等边三角形，118422BC BD BC '===⋅=．故此题的答案是4．例：如图，点C 为线段AB 上一点，ACM ∆，CBN ∆都是等边三角形，AN 交MC 于点E ，BM 交CN 于点F ．〔1〕求证：AN BM =；〔2〕求证：CEF ∆为等边三角形．ACD B C '【答案】见解析【解析】〔1〕ACM∆是等边三角形，∆，CBN∠=∠=︒，ACM NCBAC MC=，60∴=，BC NC∠=∠．∴∠+∠=∠+∠，即ACN MCBACM MCN NCB MCN在ACN=，ACN MCB=，∠=∠，NC BC∆中，AC MC∆和MCB∴=．ACN MCB∴∆≅∆，AN BM〔2〕ACN MCB∴∠=∠，∆≅∆，CAN CMB又18060∴∠=∠，∠=︒-∠-∠=︒，MCF ACEMCF ACM NCB在CAE∠=∠，=，ACE MCF∆和CMF∠=∠，CA CM∆中，CAE CMF∴∆为等腰三角形，∴=，CEFCAE CMF∴∆≅∆，CE CF又60∠=︒，CEF∴∆为等边三角形．ECF例如图，六边形ABCDEF的六个内角都相等，假设AB=1，BC=CD=3，DE=2，那么这个六边形的周长等于____．【答案】15【解析】如图，分别作直线AB、CD、EF的延长线和反向延长线使它们交于点G、H、P．∵六边形ABCDEF的六个角都是120°，∴六边形ABCDEF的每一个外角的度数都是60°．∴△AHF、△BGC、△DPE、△GHP都是等边三角形．∴GC=BC=3，DP=DE=2．∴GH=GP=GC+CD+DP=3+3+2=8，FA=HA=GH-AB-BG=8-1-3=4，EF=PH-HF-EP=8-4-2=2．∴六边形的周长为1+3+3+2+4+2=15．故答案为：15．题模三：30°的角直角三角形等于斜边的一边例如图，ABC⊥，那么以下关系式正确的为〔〕=，30∠=︒，AB AD∆中，AB ACCA．BD CDBD CD=D．4==B．2BD CDBD CD=C．3【答案】B【解析】该题考察的是特殊的直角三角形．∠=∠=︒，C CAD30∴DAC∆为等腰三角形，∴CD AD=，在Rt BAD∆中，30∠=︒，B∴22==BD AD CD应选B．例如图，30∥10PC=，那么OC=__________，⊥于D，PC OB∠=︒，OP平分AOBAOB∠，PD OBPD=__________.【答案】【解析】该题考察的是角平分线的性质定理和含30°直角三角形的性质．∵OP平分AOB∠，∴AOP BOP∠=∠，∵PC OB∥，∴CPO BOP∠=∠，∴CPO AOP∠=∠，∴PC OC=，∵10PC=，∴10OC PC==，过P作PE OA⊥于点E，∵PD OB ⊥，OP 平分AOB ∠，∴PD PE =，∵PC OB ∥，30AOB ∠=︒∴30ECP AOB ∠=∠=︒在Rt ECP ∆中，152PE PC == ∴5PE PD ==例如图，在△ABC 中，AB=AC ，D 、E 是△ABC 内两点，AD 平分∠BAC ，∠EBC=∠E=60°，假设BE=6cm ，DE=2cm ，那么BC=____．【答案】 8cm【解析】延长ED 交BC 于M ，延长AD 交BC 于N ，作DF∥BC，∵AB=AC，AD 平分∠BAC，∴AN⊥BC，BN=CN ，∵∠EBC=∠E=60°，∴△BEM 为等边三角形，∴△EFD 为等边三角形，∵BE=6cm，DE=2cm ，∴DM=4cm，∵△BEM 为等边三角形，∴∠EMB=60°，∵AN⊥BC，∴∠DNM=90°，∴∠NDM=30°，OD B P CAE∴NM=2cm，∴BN=4cm，∴BC=2BN=8cm．故答案为：8cm ．题模四：等边三角形与全等三角形综合例：如图，等边三角形ABD 与等边三角形ACE 具有公共顶点A ，连接CD ，BE ，交于点P ．〔1〕观察度量，BPC ∠的度数为_______．〔直接写出结果〕〔2〕假设绕点A 将△ACE 旋转，使得180BAC ∠=︒，请你画出变化后的图形．〔示意图〕〔3〕在〔2〕的条件下，求出BPC ∠的度数．【答案】〔1〕120°〔2〕见解析〔3〕120°【解析】此题考察等边三角形及全等三角形的性质与判定．〔1〕BPC ∠的度数为120°，理由为：证明：∵△ABD 与△ACE 都是等边三角形，∴60DAB ABD CAE ∠=∠=∠=︒，AD AB =，AC AE =，∴DAB BAC CAE BAC ∠+∠=∠+∠，即DAC BAE ∠=∠，在△DAC 与△BAE 中，AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△DAC ≌△BAE 〔SAS 〕，∴ADC ABE ∠=∠，∵60ADC CDB ∠+∠=︒，∴60ABE CDB ∠+∠=︒，∴120BPC DBP PDB ABE CDB ABC ∠=∠+∠=∠+∠+∠=︒；〔2〕作出相应的图形，如下列图；〔3〕∵△ABD 与△ACE 都是等边三角形，∴60ADB DAB ABD CAE ∠=∠=∠=∠=︒，AD AB =，AC AE =，∴DAB DAE CAE DAE ∠+∠=∠+∠，即DAC BAE ∠=∠，在△DAC 与△BAE 中，AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△DAC ≌△BAE 〔SAS 〕，∴ADC ABE ∠=∠，∵60ABE DBP ∠+∠=︒，∴60ADC DBP ∠+∠=︒，∴120BPC BDP PBD ADC DBP ADB ∠=∠+∠=∠+∠+∠=︒例如图，ABC ∆是边长为3的等边三角形，BDC ∆是等腰三角形，且120BDC ∠=︒．以D 为顶点作一个60︒角，使其两边分别交AB 于点M ，交AC 于点N ，连接MN ，那么AMN ∆的周长为____【答案】 6【解析】延长NC 到E ，连接DE ，使CE BM =，连接DE ．ABC ∆为等边三角形，BCD ∆为等腰三角形，且120BDC ∠=︒，603090MBD MBC DBC ∴∠=∠+∠=︒+︒=︒，18018090DCE ACD ABD ∠=︒-∠=︒-∠=︒，又BM CE =，BD CD =，CDE BDM ∴∆∆≌，CDE BDM∴∠=∠，DE DM =，1206060NDE NDC CDE NDC BDM BDC MDN ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒，在DMN ∆和DEN ∆中，DM DE =，60MDN EDN ∠=∠=︒，DN DN =，DMN DEN ∴∆∆≌，MN NE CE CN BM CN ∴==+=+．=6AMN L AM MN AN AM BM CN AN AB AC ∆∴+==+++=+=例如图△ABC 为等边三角形，直线a ∥AB ，D 为直线BC 上任一动点，将一60°角的顶点置于点D处，它的一边始终经过点A，另一边与直线a交于点E．〔1〕假设D 恰好在BC 的中点上〔如图1〕求证：△ADE 是等边三角形；〔2〕假设D 为直线BC 上任一点〔如图2〕，其他条件不变，上述〔1〕的结论是否成立？假设成立，请给予证明；假设不成立，请说明理由．【答案】见解析【解析】〔1〕证明：∵a ∥AB ，且△ABC 为等边三角形，∴60ACE BAC ABD ∠=∠=∠=︒，AB AC =，∵BD CD =，∴AD ⊥BC∵60ADE ∠=︒，∴30EDC ∠=︒，∴18090DOC EDC ACB ∠=︒-∠-∠=︒，∴30DEC DOC ACE ∠=∠-∠=︒，∴EDC DEC ∠=∠，∴EC CD DB ==，∴△ABD ≌△ACE ．∴AD AE =，且60ADE ∠=︒，∴△ADE 是等边三角形；〔2〕在AC 上取点F ，使CF CD =，连结DF ，∵60ACB ∠=︒，∴△DCF 是等边三角形，∵60ADF FDE EDC FDE ∠+∠=∠+∠=︒，∴ADF EDC ∠=∠，∵DAF ADE DEC ACE ∠+∠=∠+∠，∴DAF DEC ∠=∠，∴△ADF ≌△EDC 〔AAS 〕，∴AD ED =，又∵60ADE ∠=︒，∴△ADE 是等边三角形．作业1如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF ⊥DE，交BC的延长线于点F．〔1〕求∠F的度数；〔2〕假设CD=2，求DF的长．【答案】〔1〕30°〔2〕4【解析】〔1〕∵△ABC是等边三角形，∴∠B=60°，∵DE∥AB，∴∠EDC=∠B=60°，∵EF⊥DE，∴∠DEF=90°，∴∠F=90°﹣∠EDC=30°；〔2〕∵∠ACB=60°，∠EDC=60°，∴△EDC是等边三角形．∴ED=DC=2，∵∠DEF=90°，∠F=30°，∴DF=2DE=4．作业2 如下列图，ABC ∆、ADE ∆与EFG ∆都是等边三角形，D 和G 分别为AC 和AE 的中点，假设4AB =时，那么图形ABCDEFG 外围的周长是_____【答案】 15【解析】 ABC ∆、ADE ∆与EFG ∆都是等边三角形，AD DE ∴=，EF EG =，D 和G 分别为AC 和AE 的中点，4AB =，2DE EA ∴==，1GF EF ==,∴图形ABCDEFG 外围的周长是432115⨯++=．作业3 如图1，两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置，得到图2，那么阴影局部的周长为____．【答案】 2【解析】∵两个等边△ABD，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A′B′D′的位置， ∴A′M=A′N=MN，MO=DM=DO ，OD′=D′E=OE，EG=EC=GC ，B′G=RG=RB′， ∴OM+MN+NR+GR+EG+OE=A′D′+CD=1+1=2；故答案为：2．作业4 如下列图，等边△ABC 的边长为a ，P 是△ABC 内一点，PD ∥AB ，PE ∥BC ，PF ∥AC ，点D 、E 、F 分别在BC 、AC 、AB 上，猜想：PD PE PF ++=__________，并证明你的猜想．【答案】见解析【解析】 PD PE PF a ++=．理由如下：如图，延长EP 交AB 于G ，延长FP 交BC 于H ，∵PE ∥BC ，PF ∥AC ，△ABC 是等边三角形，∴60PGF B ∠=∠=︒，60PFG A ∠=∠=︒，∴△PFG 是等边三角形，同理可得△PDH 是等边三角形，∴PF PG =，PD DH =，又∵PD ∥AB ，PE ∥BC ，∴四边形BDPG 是平行四边形，∴PG BD =，∴PD PE PF DH CH BD BC a ++=++==．故答案为a ．作业5 ：如图，ABC △是等边三角形．D 、E 是ABC △外两点，连结BE 交AC 于M ，连结AD 交CE 于N ，AD 交BE 于F ，AD EB =．当AFB ∠度数多少时，ECD △是等边三角形？并证明你的结论．【答案】 60AFB ∠=︒【解析】该题考察的是全等三角形的判定和性质．60AFB ∠=︒，A C MFEN D B理由如下：∵△ABC 是等边三角形，∴CA CB =，460∠=︒，∵245∠+∠=∠，135∠+∠=∠，且360∠=︒，∴12∠=∠，又∵BE AD =，在△BCE 和△ACD 中， 1. 12CA CB AD BE =⎧⎪∠=∠⎨⎪=⎩∴△BCE ≌△ACD 〔SAS 〕 ∴CE CD =，BCE ACD ∠=∠，∴66BCE ACD ∠-∠=∠-∠，即4760∠=∠=，∴△ECD 是等边三角形．作业6 在△ABC 中，AB AC =，BAC ∠=α()060︒<α<︒，将线段BC 绕点B 逆时针旋转60︒得到线段BD ．〔1〕如图1，直接写出ABD ∠的大小〔用含α的式子表示〕；〔2〕如图2，150BCE ∠=︒，60ABE ∠=︒，判断△ABE 的形状并加以证明；〔3〕在〔2〕的条件下，连结DE ，假设45DEC ∠=︒，求α的值．【答案】〔1〕302α︒-〔2〕见解析〔3〕30︒ 【解析】该题考察的是三角形综合．〔1〕∵AB AC =∴1809022ABC ACB ︒-αα∠=∠==︒-，A D B CADB C E∴90603022ABD ACB DBC αα∠=∠-∠=︒--︒=︒-，………………………………………1分〔2〕△ABE 是等边三角形， ………………………………………………………2分连结AD ，CD ．∵60DBC ∠=︒，BD BC =，∴ △BDC 是等边三角形，60BDC ∠=︒，BD DC = ………………3分又∵AB AC =，AD AD =，∴ △ABD ≌△ACD ．∴ADB ADC ∠=∠，∴150ADB ∠=︒． ………………4分∵60ABE DBC ∠=∠=︒，∴ABD EBC ∠=∠．又∵BD BC =，150ADB ECB ∠=∠=︒，∴ △ABD ≌△EBC ．∴AB EB =．∴ △ABE 是等边三角形． …………………………………………5分〔3〕∵△BDC 是等边三角形，∴ 60BCD ∠=︒．∴ 90DCE BCE BCD ∠=∠-∠=︒又∵45DEC ∠=︒，∴CE CD BC ==．………………………………………………………6分∴15EBC ∠=︒． ∵302EBC ABD α∠=∠=︒-， ∴ 30α=︒． ……………………………………………………………7分作业7 将一张矩形纸片ABCD 如下列图折叠，使顶点C 落在C '点．2AB =，30DEC '∠=︒，那么折痕DE 的长为〔〕A ． 2B ． 23C ． 4D ． 1【答案】C【解析】该题考察的是图形的翻折．因为四边形ABCD 是矩形，所以AB CD =，由题意可知'30CED DEC ∠=∠=︒，1sin 2CD CED DE ∠==，所以2224DE CD ==⨯=．所以，此题的正确答案是C ．作业8 如图，在等边△ABC 中，2AB =，点P 是AB 边上任意一点〔点P 可以与点A 重合〕，过点P 作PE ⊥BC ，垂足为E ，过点E 作EF ⊥AC ，垂足为F ，过点F 作FQ ⊥AB ，垂足为Q ，求当BP 的长等于多少时，点P 与点Q 重合？【答案】 43BP =【解析】设BP x =，在直角三角形PBE 中，30BPE ∠=︒ ∴12BE x =，那么122EC x =- 在直角△EFC 中，30FEC ∠=︒， ∴11124FC EC x ==-，∴1214AF FC x =-=+ 同理：1128AQ x =+ 当点P 与点Q 重合时，2BP AQ +=即11228x x ⎛⎫++= ⎪⎝⎭，解得43x =A BE C DC '故当43BP =时，点P 与点Q 重合．作业9 如图，ABC ∆为等边三角形，AD 平分BAC ∠,ADE ∆是等边三角形，以下结论中 ①AD BC ⊥，②EF FD =, ③BE BD =,④60ABE ∠=︒.正确的个数为〔〕A ． 1B ． 2C ． 3D ． 4【答案】D【解析】该题考察的是三角形的性质．∵△ABC 为等边三角形，AD 为角平分线，∴AD BC ⊥，30BAD ∠=︒，60ABD ∠=︒∵△ADE 是等边三角形，30BAD ∠=︒，∴30EAB EAD BAD ∠=∠-∠=︒，EA DA =，在△AEF 和△ADF 中，EA DA EAB DAB AF AF =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△ADF 〔SAS 〕，∴EF FD =，同理，△AEB ≌△ADB ，∴60ABE ABD ∠=∠=︒，EB DB =，故正确的个数为4个，故此题答案为D ．作业10 如图，过边长为2的等边ABC ∆的边AB 上一点P ，作PE AC ⊥于E ，Q 为BC 延长线上一点，当PA CQ =时，连PQ 交AC 边于D ，那么DE 的长为〔〕A ． 13B ． 12C ． 23D ． 1【答案】D【解析】过P 作BC 的平行线交AC 于F ，Q FPD ∴∠=∠，ABC ∆是等边三角形，60APF B ∴∠=∠=︒，60AFP ACB ∠=∠=︒，APF ∴∆是等边三角形，AP PF ∴=，AP CQ =，PF CQ ∴=，在PFD ∆和QCD ∆中，FPD Q ∠=∠， PDF QDC PF CQ ∠=∠=，PFD QCD ∴∆∆≌，FD CD ∴=，PE AC ⊥于E ，APF ∆是等边三角形，AE EF ∴=，AE DC EF FD ∴+=+，12ED AC ∴=，2AC =，1DE ∴=．作业11 如图，在等边ABC △中，点D 、E 分别在边BC 、AC 上，且AE CD =，BE 与AD 相交于点P ，BQ AD ⊥于点Q .〔1〕求证：ABE CAD △≌△；〔2〕请问PQ 与BP 有何关系？并说明理由.【答案】〔1〕见解析〔2〕2BP PQ =【解析】该题考察全等三角形的判定与性质．∵△ABC 为等边三角形．∴AB AC =,60BAC ACB ∠=∠=︒,在△BAE 和△ACD 中：AE CD BAC ACB AB AC =⎧⎪∠=∠⎨⎪=⎩∴△BAE ≌△ACD〔2〕2BP PQ =∵△BAE ≌△ACD∴ABE CAD ∠=∠∵BPQ ∠是△ABP 的外角，∴BPQ ABE BAD ∠=∠+∠，∴60BPQ CAD BAD BAC ∠=∠+∠=∠=︒∵BQ AD ⊥，AB P EQD C∴30∠=︒PBQ∴如有侵权请联系告知删除，感谢你们的配合！。

八年级数学等边三角形1

体发展心理学的研究对象是（）。A.人生全过程各个年龄阶段的心理发展特点B.人生全过程各个年龄阶段的认知发展特点C.从动物到人的心理变化D.从幼儿到成人的心理变化 [单选]产后子宫缩小至妊娠12周大小，需要时间为（）.A.1周B.2周C.3周D.4周E.5周 [单选]下列（）花卉是一二年生花卉中观果的种类。A.四季桔、金桔、风船葛、葫芦B.风船葛、葫芦、香豌豆、金银茄C.五色椒、冬珊瑚、金银茄、风船葛D.五色椒、冬珊瑚、金银茄、香豌豆 [单选]道路运输管理机构收到道路旅客运输经营申请后，应当自受理申请之日起（）内审查完毕，作出许可或者不予许可的决定。A、40日B、30日C、20日 [单选,A1型题]下列关于具有解热作用的药物，错误的是（）A.金银花B.板蓝根C.知母D.栀子E.肉桂 [单选,A1型题]抗菌药物在外科疾病的应用中，下列哪项叙述不正确（）。A.应用抗菌药物可减少术后并发症，增加手术安全性B.严重创伤、大面积烧伤应预防性应用抗菌药物C.全身情况不良的患者，应尽量选用杀菌性的抗生素治疗感染D.严重感染者，在体温正常、全身情况和局部感染灶好转后 [单选]容器贯通试压时，以下操作正确的是（）。A、关闭容器的进口阀，然后试压B、关闭容器的出口阀，然后试压C、容器的安全阀必须打开，避免超压憋坏容器D、必须关闭液面计引出阀 [单选]船政造船中的第三个阶段“钢船时期”是从1887到()年。A、1897B、1905C、1907D、1915 [问答题,案例分析题]背景材料：1994年4月22日，某公路工程处第三项目经理部在某立交桥施工期间，对立交作业区域内原有厂房拆除过程中，发生了一起因被拆除的建筑物坍塌，导致2人死亡的事故。建设单位委托第三项目部进行3000m2厂房拆除工程的施工，并要求4月底前拆完。条件是第三项 [单选]物流拉动控制的特点是（）。A.分散控制B.集中控制C.单独控制D.有效控制 [单选]脉压增大常见于A.主动脉瓣关闭不全B.缩窄性心包炎C.心包积液D.肺心病E.心肌炎 [单选]修船质量的好坏，关系着船舶的使用寿命和经济性，因此，必须抓好修理前的()、修理时的监修和修理后的验收三个主要工作环节，以确保短修期、低修费、高质量的船舶修理。A.安排B.人员分工C.计划D.准备 [问答题,简答题]焦炉气压缩机运动机构润滑流程简述？ [单选,B型题]听力损失指（）。A.短时间暴露于强噪声，使听阈上升10～15dB，脱离噪声接触后数分钟内即可恢复正常B.较长时间暴露于强噪声，致使听阈上升超过15～30dB，脱离后需数小时至几十小时才能恢复C.已长期在强噪声环境中导致听力曲线在3000～6000Hz范围内出现"V形" [判断题]水平胶带真空过滤机适用于选煤厂粗、细煤泥的过滤脱水。A.正确B.错误 [单选,A1型题]对于长期慢性患者，宜采取的医患关系模式是（）。A.主动-被动型B.被动-主动型C.指导-合作型D.共同参与型E.合作-指导型 [单选,A1型题]小儿化脓性脑炎的脑脊液变化为（）A.细胞数增高，蛋白正常，糖降低B.细胞数增高，蛋白增高，糖降低C.细胞数正常，蛋白正常，糖降低D.细胞数增高，蛋白升高，糖升高E.细胞数升高，蛋白正常，糖正常 [单选]下列（）属于常用的渠道清淤措施。A、水闸关水搅沙B、高压水流清淤C、冲沙底孔冲沙D、挖泥船清淤 [单选]一件发明专利申请的权利要求为：“一种治疗心脏病的药物，其特征在于，包括：（1）活性成分X；（2）活性成分Y；（3）着色剂M；和（4）调味剂N。”在其申请日前公开的下列哪些治疗心脏病的药物破坏该权利要求的新颖性？（）A.由活性成分X和Y组成的药物B.由活性成分X、活性成 [单选,A型题]急腹症的说法，以下哪项不对（）A.下腹急性疼痛属于急腹症B.诊断时主要考虑消化道疾病C.疑为肠梗阻的患者，拍站立及仰卧正位片各一张D.不进行检查前准备E.肠梗阻症状开始的3～6小时内，X线检查可能是阴性结果 [单选,A型题]下列哪种片剂要求在21℃±1℃的水中3分钟即可崩解分散()A、泡腾片B、分散片C、舌下片D、普通片E、溶液片 [问答题,简答题]装运活动物时应选择什么车辆？ [单选]在口岸检验检疫机构现场查验时，应截留旅客携带的水果、茄科蔬菜（茄子、辣椒、番茄等），出具《出入境人员携带物留验/处理凭证》，根据检验情况作（）处理。A.退回B.封存C.销毁D.退回或销毁 [问答题,简答题]什么叫花卉园艺？ [单选,A1型题]对下肢静脉曲张并发溃疡的治疗，不恰当的是（）A.溃疡愈合后做大隐静脉结扎及剥脱术B.3％硼酸溶液湿敷C.抬高患肢D.溃疡不愈合者也可考虑手术E.大隐静脉结扎及剥脱术，溃疡切除并植皮 [填空题]吸入液氨后应迅速使伤者脱离现场至（）。保持（）通畅。如呼吸困难，应（）。如呼吸停止，立即进行（）。 [单选,A2型题,A1/A2型题]当中心体温降到多少度时，肌肉由颤抖变为僵直，失去产热的作用，将会发生死亡（）。A.30～33℃B.32～34℃C.30℃以下D.28～31℃E.0℃ [单选]重要设备、材料等货物的采购，单项合同估算价在()万元人民币以上的工程项目必须进行招标。A.50B.100C.150D.200 [单选]Web服务器建设方式不包括（）A.整机托管B.租用网页空间C.委托IAPD.租用网页空间 [单选]下列哪一项是肝脏叶、段的正确分法A.5叶6段B.3叶4段C.4叶5段D.4叶6段E.以上都不是 [单选,A型题]以下属于胃癌的X线征象是（）A.黏膜皱襞纠集B.胃蠕动增强C.龛影显著D.胃腔变形和狭窄E.激惹征 [单选,A1型题]精神药品处方至少保存（）A.1年B.2年C.3年D.5年E.7年 [名词解释]收货人 [单选]若使支座B截面出现弯矩最大值，梁上均布荷载的布置应为：（）A.B.C.D. [单选,A2型题,A1/A2型题]判断HLA-D位点编码的抗原间是否相容的方法是（）A.迟发型皮肤超敏反应B.PHA激发的淋巴细胞C.混合淋巴细胞反应D.HLA血清学定型试验E.以上均不是 [单选]质量摩尔浓度的定义是（）中含有溶质的物质的量。A.1dm3溶液B.1kg溶液C.1kg溶剂D.1dm3溶剂 [单选]若卵子未受精，则黄体开始萎缩的时间是在排卵后（）。A.5～6天B.7～8天C.9～10天D.11～12天E.13～14天 [单选]刃厚皮片适用于()A．肉芽创面B．功能部位创面C．足底创面D．手背创面E．吻合移植 [填空题]在干气中，含有大量的（）和小量的乙烷、丙烷等气体。 [单选,A2型题,A1/A2型题]诊断缺铁最肯定的依据是（）A.骨髓小粒可染铁消失B.血涂片见典型小细胞低色素性红细胞C.转铁蛋白饱和度降低D.血清铁降低E.有慢性失血史

12.3.3等边三角形(1)课件

鼎新中学八年级数学备课组
观察下列图片，你有什么印象？
你发现了什么？
这就是今天我们要学的
一、你知道什么是等边三角形？你知道什么是等边三角形？
定义：三边都相等的三角形叫做等边三角形定义：三边都相等的三角形叫做等边三角形等边三角形与等腰三角形有什么关系？等边三角形与等腰三角形有什么关系？
等边三角形是特殊的等腰三角形，也叫正三角形。等边三角形是特殊的等腰三角形，也叫正三角形。特殊的等腰三角形正三角形
这是两个等边三角形,那么请移动三根火柴, 这是两个等边三角形那么请移动三根火柴那么请移动三根火柴将此图变成四个等边三角形. 将此图变成四个等边三角形
提示:此题并不难如果外部不能解决提示此题并不难,如果外部不能解决那么此题并不难如果外部不能解决,那么想想里面吧. 想想里面吧
我们这节课学习了哪些知识? 我们这节课学习了哪些知识谈谈你的体会. 谈谈你的体会
分线都三线合一. 分线都三线合一 4.等边三角形是轴对称图形，有三条对称轴. 等边三角形是轴对称图形，有三条对称轴等边三角形是轴对称图形
2.等边三角形的三个内角都相等并且每一个内等边三角形的三个内角都相等并且每一个内。角都等于60 角都等于
A
已知：已知：AB=AC=BC 求证：求证：∠A= ∠ B=∠C= 60 ∠
符号语言：符号语言：
。
B
C
∵ AB=AC=BC ∴ ∠A= ∠ B=∠C= 60
。
3.等边三角形每条边上的中线，高和它所对角的平分等边三角形每条边上的中线，等边三角形每条边上的中线线互相重合。线互相重合。
A
5 6
D O
7 8 3 1
E
4 9 10 2

人教版八年级数学上册13.3.2 第1课时等边三角形的性质与判定

质线互相重合（三线合一）
所对的角的平分线互相重合
对称轴（1条）
对称轴（3条）
A A
B
CB
C
类比探究2：
图形判
等腰三角形从边看：两条边相等的三角形是等腰三角形
定从角看：两个角相等的三
角形是等腰三角形
等边三角形三条边都相等的三角形是等边三角形
三个角都相等的三角形是等边三角形，
小明等认边为三还角有形第的三判种定方方法法“：两条边相等且有一个角是60°的三角形也是等有边一三个角角形是”60，°你的同等意腰吗三？角形是等边三角形.
变式：上题中,若将条件DE∥BC改为AD=AE, △ADE还是等
边三角形吗?试说明理由. 如图,在等边三角形ABC中，AD=AE, 求证：△ADE是等边三角形.
A
D
E
B
C
习题巩固：
1.下列三角形：①有两个角等于60°；②有
一个角等于60°的等腰三角形；③三个外角
（每个顶点处各取一个外角）都相等的三角
典例精析
例1 如图,在等边三角形ABC中，DE∥BC, 求证：△ADE是等边
三角形.
证明：∵ △ABC是等边三角形，
A
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
D
E
∴ ∠ADE= ∠B, ∠ AED= ∠C.
B
C
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想：本题还有其他证法吗？
轴对称图形
二、探究新知
一般三角形
等腰三角形
等边三角形
定义类比：
在等腰三角形中，有一种特殊的情况，就是底与腰相等，这时三角形三边相等，我们把三条边都相等的三角形叫做等边三角形.

八年级数学等边三角形1

打牌吧官网下载
[判断题]WLANAP可以采用带POE功能的以太网交换机进行供电，可串接POE供电器。（）A.正确B.错误 [单选]磁盘上的扇区标志在（）时建立。A、低级格式化B、格式化C、存入数据D、建立分区 [单选]以下性传播疾病不是由病毒引起的是()A．尖锐湿疣B．生殖器疱疹C．艾滋病D．扁平湿疣 [单选]行政主体承担行政责任的方式主要有（）点。A.7B.8C.9D.10 [单选]泵的轴承箱的的温度要求不大于（）。A.65℃B.70℃C.80℃ [多选]编写规划环境影响篇章或者说明，至少包括的内容有（）。A.前言B.环境现状分析C.监测与跟踪评价D.环境影响的减缓措施E.环境影响分析与评价 [单选]以下不属于工程监理依据的是()。A.法律法规B.承包合同约定的推荐性标准C.设计文件D.监理合同 [单选]下列关于现金流量表的描述正确的是()。A.现金流量表是反映企业在一定会计期间库存现金流入和流出的报表B.现金流量表是反映企业在一定会计期间现金和现金等价物流入和流出的报表C.现金等价物指的是企业的银行存款以及其他货币资金D.购买的股票投资也属于企业现金等价物 [单选]根据客户反映及企业考察，对服务态度最好、服务质量最高者给予奖励的是（）A、训练奖B、最佳服务奖C、市场情报奖D、降低退货奖 [判断题]铂钴标准比色法测定水的色度时，如果水样浑浊，可用离心机去除悬浮物，也可以用滤纸过滤除去。A.正确B.错误 [单选]不属于仓库的主要作业的是货品的（）A.入库作业B.在库管理C.包装作业D.出库作业 [单选]促进消防工程师行业发展的动力是（）。A.公平竞争B.精益求精C.团结互助D.爱岗敬业 [单选]某压力容器按承受压力为1MPa，则属于（）容器。A.低压B.中压C.高压D.超高压 [单选]学校应当保证学生的（）时间，组织开展文化娱乐等课外活动。社会公共文化体育设施应当为学校开展课外活动提供便利。A、兴趣小组B、课外活动C、自习 [单选]某厂精氩含氮量25ppm，就是指含氮量为（）A、0.025B、0.0025C、0.00025D、0.000025 [判断题]当总成本不变时，工资率的增长将总是导致使用更多的资本。A.正确B.错误 [单选]某公司目标资本结构为权益资本与债务资本各占50%，明年将继续保持。已知今年实现税后利润600万元，预计明年需要增加投资资本800万元，假设流通在外普通股为200万股，如果采取剩余股利政策，明年股东可获每股股利为()。A、1元B、2元C、3元D、5元 [单选]仓储管理的目标是（）。A.适时适量保证库存B.仓库空间利用与库存货品的处置成本之间的平衡C.实现库存最低、费用最省D.管理协调供应商，管理供应链 [多选]建设工程债产生的根据有（）。A．合同B．侵权C．公正D．不当得利E．无因管理 [单选]对新建的易燃易爆化学物品生产场所工程的消防设计未经公安消防机构审核擅自施工的，公安消防机构应当（）。A、责令停止违法行为B、责令限期改正C、责令停止施工并处罚款D、责令停止施工 [单选]以下属于皮肤复合感觉的是（）A.冷B.触C.痛D.湿E.温 [多选]金属分类开关设备按主开关与柜体的配合方式可A2型题,A1/A2型题]糖尿病酮症酸中毒的电解质改变是（）。A.体内常无缺钾B.血钠正常或升高C.血乳酸下降D.胰岛素治疗后血钾下降E.以上都不是 [单选,A2型题,A1/A2型题]有哪种情况不能做MRI检查（）A.体内有瓷类材料B.装有铁磁性或电子耳蜗者C.非金属避孕环D.病人体格大E.妊娠超过3个月 [单选]婴儿痉挛症诊断的最可靠依据是（）A．3至8个月起病B．智力发育显著落后C．典型的点头样发作形式D．半数有围生期因素E．脑电图背景波异常 [单选,A4型题,A3/A4型题]男，10月，呕吐3天，腹泻4天，因无尿8小时入院，诊断重度等渗脱水伴酸中毒、营养不良。给以补液后12小时纠正脱水、酸中毒，16小时突然出现惊厥。明确诊断应选择的辅助检查是()A．血渗透压B．脑电图C．颅脑CTD．血钙、血钾、血镁、血钠E．血钾、血镁、血钠 [单选]下列不属于基金销售机构职责规范的是（）。A.严格账户管理B.基金托管人应制定业务规则并监督实施C.签订销售协议，明确权利和义务D.禁止提前发行 [填空题]无功功率按照（）的控制原则，力求（）避免无功功率的长距离输送。 [名词解释]地球化学勘查 [单选]下列法的形式中，由全国人民代表大会及其常务委员会经一定立法程序制定颁布的规范性文件是（）。A、宪法B、行政法规C、法律D、行政规章 [单选]0.2550m的有效数字是（）位。A.3B.4C.5D.6 [多选]保险待遇的计算依据为（）A.职工原工资B.职工工龄C.保险费的交纳D.国家宏观政策 [问答题,简答题]奥运五环标记象征世界五大洲的团结，哪一种颜色代表亚洲？ [单选,A2型题,A1/A2型题]透明大体标本的制作中有关填充剂及其配制，下面的描述不妥当的是（）。A.填充剂包括：明胶填充剂和乳胶填充剂B.填充剂配制时根据需要添加染料C.加染料时，边加边搅拌直到染色满意为止D.配制填充剂时，不必过滤即可使用E.配制填充剂时，通常用纱布过滤后使 [判断题]盖斯定律认为化学反应的热效应与途径无关，是因为反应处在可逆条件下进行的缘故。A.正确B.错误 [判断题]为了预防、减少和避免学生伤害事故的发生，除应对学生加强安全意识和提高自我保护能力以及培养健康的心理素质外，还应对其强化纪律观念，尽量减少因自违纪行为而导致的伤害事故的发生。A.正确B.错误 [填空题]在干气中，含有大量的（）和小量的乙烷、丙烷等气体。 [单选]对放射线具有较高的敏感性的脏器是（）A.骨B.卵巢C.食管D.肝脏E.宫体 [单选]项目投资估算所在的阶段是()。A．设计阶段B．决策阶段C．招标阶段D．施工阶段 [单选,A2型题,A1/A2型题]尘肺X线诊断标准中符号为"q"的小阴影是指（）。A.直径在1.5mm以下的类圆形小阴影B.直径在1.5～3mm的类圆形小阴影C.直径在3～10mm的类圆形小阴影D.宽度在1.5mm以下的不规则形小阴影E.宽度在1.5～3mm的不规则形小阴影

八年级数学等边三角形1

九莲宝灯下载
[单选,A1型题]巨噬细胞主要是通过以下哪种方式摄入和消化细菌的（）A.胞饮作用B.受体介导的胞吞作用C.泡膜运输的方式D.巨吞饮作用E.吞噬作用 [单选]（）是销售管理中最复杂、最富技巧、最具风险的一个环节。A、计划管理B、区域管理C、渠道管理D、销售管理 [单选,A1型题]房间隔缺损特征性的改变是（）A.生长发育延迟、乏力、心悸B.心前区可听到粗糙收缩期杂音C.有肺动脉高压时，可出现青紫D.肺动脉瓣区第2音亢进并固定性分裂E.X线可见心房心室的扩大及肺门"舞蹈" [单选]输卵管妊娠的原因不包括（）A.输卵管周围肿瘤B.输卵管黏膜纤毛缺乏C.放置宫内节育器D.子宫畸形E.受精卵游走 [单选]Web服务器建设方式不包括（）A.整机托管B.租用网页空间C.委托IAPD.租用网页空间 [单选]脑震荡的临床表现中，下列说法错误的是（）A.意识障碍一般不超过半小时B.伤后可有头痛、头晕、恶心、呕吐等症状C.神经系统查体无阳性体征D.脑脊液检查常可见少量红细胞E.CT检查颅内无异常发现 [单选]CT摄片时，通常需放大照相的是()A．图像模糊不清B．需重点观察有疾病的层面C．图像分辨率低D．图像的噪声较大E．观察部位有伪影重叠 [填空题]违反《中华人民共和国道路运输条例》的规定，未经许可擅自从事道路运输站（场）经营、机动车维修经营、机动车驾驶员培训的，由县级以上道路运输管理机构责令停止经营；有违法所得的，没收违法所得，处违法所得2倍以上（）倍以下的罚款；没有违法所得或者违法所得不足1万元 [单选]良性骨肿瘤X线片常表现为（）A.边界清楚，无骨膜反应B.骨密度不均匀C.边界不清，可见软组织阴影D.可见Codman三角E.呈多处虫蛀状 [单选]下列（）不是渠道常见病害。A、渗漏B、裂缝C、蚁害D、漫顶 [单选]脑血栓形成多发生于（）A.大脑前动脉B.椎

等边三角形的性质和判定初中八年级上册数学教案教学设计课后反思人教版

题目：等边三角形(1)设计者：金华栋单位：阜阳市第九中学时间： 2017年6月C等边三角形(1)一、教学内容范围：新人教版八年级（上）二、教材分析：本节课是在轴对称和等腰三角形的基础上学习研究特殊的等腰三角形——等边三角形性质和判定。

同时对等腰三角形的学习为学习等边三角形的性质和判定提供了方法指导和理论基础；而本节课对等边三角形性质和判定的学习又是对轴对称和等腰三角形知识的深化，同时又为后面进一步学习其它正多边形提供了方法指导、奠定了理论基础。

因此教学重点是：掌握等边三角形的性质和判定，体会转化的数学思想。

三、学情分析通过对等腰三角形的学习研究，学生已经知道了从哪些方面（边、角、对称性）去认识特殊的三角形，在这些经验的基础学习等边三角形，学生会较快的形成思路。

但是把边角结合起来去寻求等边三角形的判定方法，对学生的思维要求较高。

同时在该方法的探索、证明中，学生还要具备一定的分类讨论意思。

因此教学难点是：对“有一个角是60°的等腰三角形是等边三角形”的探索和证明。

四、教学目标：1、掌握等边三角形的性质定理和判定定理2、在实践、观察、猜想、证明等边三角形性质和判定的过程中，发展合情推理能力和演绎推理能力，能清晰地表达自己的想法；3、会用观察、操作、类比、转化的方法分析、证明等边三角形所具有的性质和判定，并应用它们解决一些问题。

4、在探索、证明的过程中，敢于发表自己的想法、勇于质疑，初步养成独立思考、合作交流的学习习惯。

五、教学方法：利用多媒体辅助教学，引导学生通过剪纸或画图感知、发现等边三角形的性质，并类比等腰三角形的性质猜想归纳等边三角形性质，最后回到等腰三角形，利用等腰三角形给出推理证明。

六、教（学）用具：多媒体教学平台，三角板，学生准备：三角板、圆规、剪刀、硬纸片。

教学过程设计问题与情景师生行为设计意图ACBD E 问题与情景师生行为设计意图四、应用举例、巩固新知1、小试牛刀（１）判断下列说法是否正确。

八年级数学等边三角形1

C D
B
E
A
4、如图，上午9时，一条渔船从A出发，
以12海里/时的速度向正北航行，11时到达
B处，从A、B两处望小岛C，测得
∠NAC=150， ∠NBC=300，若小岛周围
12.3海里内有暗礁，问该渔船继续向正北
航行有无触礁的危险？
N
C
D
B
A
4、如图，在△ABC中， AB=AC， ∠BAC= 120°，AC的垂直平分线EF交AC 于点E，交BC于点F。求证：BF=2CF。
３００
Ｃ
Ａ
2.如图:△ABC是等边三角形，
A
AD⊥BC,DE⊥AB,若AB=8cm,
BD=＿４＿ｃ＿ｍ， BE=__２_ｃ_ ｍ E
B DC
3、如图，在△ABC中， ∠ACB= 90°，BA的
垂直平分线交边CB于D。若AB=10，AC=5，
则图中等于 30°的角的个数为（B）
A.2
B.3
C.4
D.5
人态度如此强硬无礼,简直反上天了.唐蕊心里来气瞪着她,却发现一件更让人难堪の事.只见赵丽娥把奶茶杯放进水槽,手里の咖啡杯用水随意冲一下.然后套在一个纸袋里往水槽边の墙使暗劲一砸,卟地一声闷响,杯子碎在纸袋里.“你这是干什么？！”唐蕊吃了一惊,随即上前质问,并打算向柏少华打小报告刷存在感.赵丽娥冲她淡然一笑,“老板说杯子被人碰过,他不要了,必须砸碎扔掉.”免得被人二次污染,想想就恶心.仿佛一股热浪轰地涌上头顶,唐蕊脸色乍红乍青.他在明嘲暗讽她是个二手货没人要吗？也不看看他自己是个什么东西,一个残废还敢嫌东嫌西.要不是她嫁过人生过孩子,她才懒得理他.唐蕊越想越羞愤,在这里她受尽了委屈却无人倾诉.柏少媛、丁瑶自从察觉她对柏少华有意那态度就变了,变得客气冷漠,平日里一有空就自顾自地在

八年级数学等边三角形1

八年级数学人教版(上册)第1课时等边三角形的性质与判定

八年级上册数学等边三角形

人教版-数学-八年级上册-13.3.2 等边三角形(1) 教案

人教版八年级数学上册课件 第十三章 轴对称 等腰三角形 等边三角形 第1课时 等边三角形的性质与判定

八年级上册数学-等边三角形

等边三角形的性质与判定(3种题型)-2023年新八年级数学(苏科版)(解析版)

人教版八年级数学讲义_第16讲：等边三角形中考班

八年级数学等边三角形1

八年级数学上册 第二章 等边三角形知识点与同步训练(含解析)苏科版

八年级数学等边三角形1

12.3.3等边三角形(1)课件

人教版八年级数学上册13.3.2 第1课时 等边三角形的性质与判定

八年级数学等边三角形1

八年级数学等边三角形1

等边三角形的性质和判定 初中八年级上册数学教案教学设计课后反思 人教版

八年级数学等边三角形1

人教版八年级数学上册课件第十三章轴对称等腰三角形等边三角形第1课时等边三角形的性质与判定

八年级数学上册第二章等边三角形知识点与同步训练(含解析)苏科版

人教版八年级数学上册13.3.2 第1课时等边三角形的性质与判定

等边三角形的性质和判定初中八年级上册数学教案教学设计课后反思人教版