对勾函数模型
对勾函数详细分析

对勾函数详细分析对勾函数,又称为Heaviside函数或者单位阶跃函数,是一种常见的数学函数。
它在控制系统、信号处理和电路分析等领域具有广泛的应用。
在数学上,对勾函数可以通过以下方式定义:H(x)=0,x<0H(x)=1/2,x=0H(x)=1,x>0其中,H(x)表示对勾函数,x为自变量。
从定义可以看出,对勾函数在x小于0时取0,在x等于0时取1/2,在x大于0时取1对勾函数在数学上的精确定义可以依赖于Laplace变换或者Fourier 变换等数学工具,用于解决微积分和微分方程等问题。
在实际应用中,对勾函数通常以数学形式存在,用于描述信号的开关行为。
在控制系统中,对勾函数可以表示系统的阶跃响应。
阶跃响应是指当输入信号为一个单位阶跃函数时,系统所产生的响应。
对勾函数可以帮助分析系统的稳定性、零极点和频率响应等性质。
在信号处理中,对勾函数可以用于描述数字信号的采样和量化过程。
当对一个连续信号进行采样时,可以将采样函数表示为对勾函数。
对勾函数在离散时间中具有单位阶跃响应的特性,可以用于分析信号的频谱和滤波等问题。
在电路分析中,对勾函数可以用于描述开关电路的动态响应。
开关电路通常包含开关元件和电容、电感等被控元件。
对勾函数可以帮助确定电路的稳态和暂态响应,并且可以用于分析电路中的信号传输、噪声和功耗等问题。
此外,对勾函数在概率论和统计学中也有应用。
例如,对勾函数可以用于计算累积分布函数(CDF)和概率密度函数(PDF)。
对勾函数可以将离散随机变量转化为连续随机变量,以进行概率计算和数值模拟等工作。
对勾函数具有一些重要的性质。
首先,它是一个连续函数,但不是光滑函数。
它在x=0处的导数不存在,即导数不连续。
其次,对勾函数是一个奇函数,即H(-x)=1-H(x)。
此外,对勾函数是一个分布函数,满足概率的基本性质,即0≤H(x)≤1总结起来,对勾函数是一个常用的数学函数,具有广泛的应用。
它可以表示系统的阶跃响应,在信号处理和电路分析等领域发挥重要作用。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不显现,但考试总喜爱考的函数,因此也要注意它和了解它。
(一)对勾函数的图像对勾函数是一种类似于反比例函数的一样函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x组成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”。
如以下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的转变。
可是,咱们仍然能够看做是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一样地,咱们以为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只只是它的核心和渐进线的位置有所改变算了。
接下来,为了研究方便,咱们规定a>0,b>0。
以后当a<0,b<0时,依照对称就很容易患出结论了。
(二)对勾函数的极点对勾函数性质的研究离不开均值不等式。
利用均值不等式能够取得:当x>0时,。
对勾函数的图像(ab异号)当x<0时,。
即对勾函数的定点坐标:(一) 对勾函数的概念域、值域由(二)取得了对勾函数的极点坐标,从而咱们也就确信了对勾函数的概念域、值域等性质。
(二) 对勾函数的单调性(三) 对勾函数的渐进线由图像咱们不宝贵到:(四) 对勾函数的奇偶性对勾函数在概念域内是奇函数, 利用对勾函数以上性质,在解某些数学题时很简便,下面举例说明: 一、求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,那么22)1(2≥++=x t t t t t y 112+=+= 依照对勾函数t t y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
对勾函数的图象及性质

对勾函数一、定义对勾函数是由两个幂函数相加得到的,对勾函数是一种类似于反比例函数的一般双曲函数,其标准形式为f(x)=ax+(其中ab>0)。
由于函数图像形似两个中心对称的对勾,因此得名“对勾函数”,又被称为“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。
在许多情况下,为了简化分析,常取a=b=1,即函数形式为f(x)=x+。
研究初等函数的一般路径,背景—概念—图象—性质—应用二、图象及性质图像特征:1、对勾函数的图像是分别以y 轴和直线y=ax 为渐近线的两支曲线。
2、图像上任意一点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
3、函数图像整体呈两个“对勾”的形状,且关于原点呈中心对称。
定义域:,即除了x=0外,所有实数都是其定义域内的元素。
值域:。
单调性:函数在(−∞,−1)∪(1,+∞)上单调递增,在(1,0)∪(0,1)上单调递减。
奇偶性:对勾函数是奇函数,即满足f(−x)=−f(x)。
x 122严禁复制三、题型1、基础计算题给定对勾函数表达式,求函数在特定点的值或特定区间的最值。
2.、图像结合题根据对勾函数的图像,判断函数在哪些区间内满足特定条件(如大于某值、小于某值)。
利用图像分析函数与直线、其他曲线的交点情况。
3.、综合应用题求最值问题:利用对勾函数的性质,可以快速求解形如ax+(ab>0)的函数的最值问题。
不等式证明:在不等式证明中,对勾函数的性质也常被用来进行放缩或构造反例。
实际问题建模:在某些经济学问题中,如成本分析、收益最大化等,也可能涉及到对勾函数的应用。
4、参数变化分析:探讨参数a 和b 变化时,对勾函数图像和性质的变化规律。
5、复杂函数组合将对勾函数与其他函数(如二次函数、指数函数等)组合,分析新函数的性质和应用。
四、解题步骤1、对勾函数求最值问题的解题步骤(1)理解函数形式确认函数f(x)=ax+的形式,注意a 和b 都是正数且不相等。
对勾函数讲解与例题解析
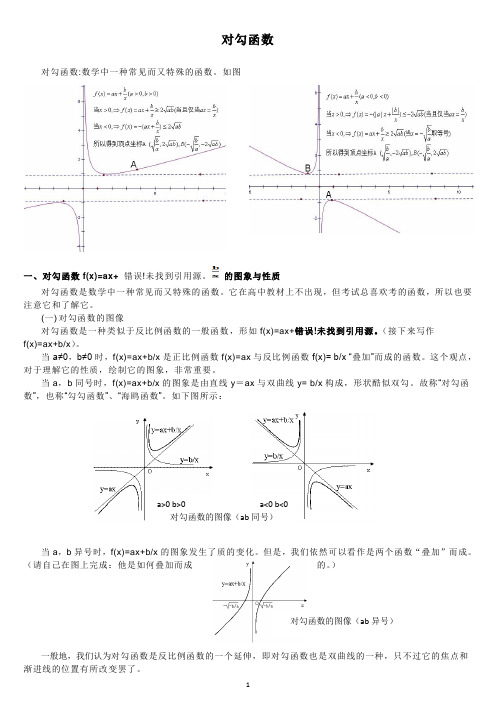
对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
对勾函数模型

第十周 对勾函数模型重点知识梳理1.对勾函数定义对勾函数是指形如:y =ax +b x (ab >0)的一类函数,因其图象形态极像对勾,因此被称为“对勾函数”,又被称为“双勾函数”、“勾函数”、“耐克函数”或“耐克曲线”.2.对勾函数y =ax +b x (a >0,b >0)的性质(1)定义域:(-∞,0)∪(0,+∞).(2)值域:(-∞, ]∪[,+∞).(3)奇偶性:在定义域内为奇函数.(4)单调性:(-∞,-b a ),(b a ,+∞)上是增函数;(-b a ,0),(0,b a )上是减函数. (5)渐近线:y 轴与y=ax(或y=-ax)3.y =ax +b x(a >0,b >0)的单调区间的分界点:±b a. 求分界点方法:令ax =b x ⇒x =±b a . 特殊的,a >0时,y =x +a x的单调区间的分界点:±a .4.对勾函数应用时主要是利用对勾函数单调性求其最值,解题时要先找出对应的单调区间,然后求解.5.利用对勾函数求最值,常常用到如下的重要不等式:若a >0,b >0,则x >0时,ax +b x ≥2ab . 当且仅当ax =b x ,x =b a时取等号. 在应用这个不等式时,要注意使用的前提条件是“一正、二定、三相等”,即加号两边的项ax 和b x 都是正项,且二者乘积为定值,同时ax =b x中等号可取到.若等号取不到,则应根据对勾函数单调性求解.典型例题剖析例1 已知f (x )=x +5x,求f (x )在下列区间的最小值. (1)[1,2]; (2)[3,4]; (3)[-3,-1].【解析】如图,f (x )在 (-∞,-5),(5,+∞)上是增函数,在(-5,0),(0,5)上是减函数.(1)由对勾函数性质可知f (x )在[1,2]上单调递减,∴f (x )min =f (2)=412. (2)因为f (x )在[3,4]上单调递增,所以f (x )min =f (3)=423.(3)因为f (x )在[-3,- 5 ]上单调递增,在(-5,-1]上单调递减,且f (-3)=-423, f (-1)=-6,所以f (x )min =-6.变式训练 已知函数f (x )=x 2+5x 2+4,求f (x )的最小值,并求此时x 的值.【解析】f (x )=x 2+5x 2+4=x 2+4+1x 2+4=x 2+4+1x 2+4令t =x 2+4,则t ≥2,y =t +1t. ∵y =t +1t在[2,+∞)单调递增, ∴当t =2时,y min =2+12=52, 此时,x 2+4=2,x =0.综上,f (x )的最小值为52,此时x 的值为0. 例2 求函数f (x )=x 2-2x -1x +2(0≤x ≤3)的值域. 【解析】令t =x +2,则x =t -2, 2≤t ≤5,y =(t -2)2-2(t -2)-1t=t 2-6t +7t =t +7t-6,2≤t ≤5. ∵y =t +7t-6在[2,7 ]上单调递减,在[7, 5]上单调递增, ∴当t =7时,y min =27-6,且当t =2时,y =2+72-6=-12,当t =5时,y =5+75-6=25,∴y max =25. 综上,f (x )的值域为[27-6,25]. 变式训练 求函数f (x )=x 2-4x +12x -1,x ∈[]2,5的值域. 【解析】f (x )=x 2-4x +12x -1=(x -1)2-2(x -1)+9x -1=x -1+9x -1-2, 令t =x -1,则f (t )=t +9t-2,t ∈[1,4]. 结合y =t +9t的图象与性质, 可知当t ∈[1,3]时,函数单调递减,当t ∈[3,4]时,函数单调递增,又f (1)=8,f (3)=4,f (4)=174, 所以f (x )∈[4,8].例3 某工厂去年的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n 次投入后,每只产品的固定成本为g (n )=kn +1(k >0,k 为常数,n ∈Z 且n ≥0),若产品销售价保持不变,第n 次投入后的年利润为f (n )万元.(1)求k 的值,并求出f (n )的表达式;(2)问从今年算起第几年利润最高?最高利润为多少万元?【解析】(1)由g (n )=k n +1,当n =0时,由题意, 可得k =8,所以f (n )=(100+10n )(10-8n +1)-100n (n ∈Z 且n ≥0).(2)由f (n )=(100+10n )(10-8n +1)-100n =1 000-80(n +1+9n +1) ≤1 000-80×29=520,当且仅当n +1=9n +1,即n =8时取等号, 所以第8年工厂的利润最高,最高为520万元.变式训练 建筑一个容积为800米3,深8米的长方体水池(无盖).池壁,池底造价分别为a 元/米2和2a 元/ 米2.底面一边长为x 米,总造价为y .写出y 与x 的函数式,问底面边长x 为何值时总造价y 最低,是多少?【解析】长方体底面积S =8008=100米2,地面一边长为x 米, 因此另一边长为100x米, 池壁总面积为8·(2x +200x)米2, ∴ 总造价y =100×2a +(2x +200x )·8·a =200a +16a (x +100x)(x >0). ∵函数y =200a +16a (x +100x)在(0,10]上是减函数,在(10,+∞)上是增函数, ∴ 当x =10时,总造价最低,且y min =520a (元).跟踪训练1.下列函数中最小值是4的是( )A .y =x +4xB .y =x +2xC .y =21+x +21-xD .y =x 2+1x 2+1+3,(x ≠0) 2.函数y =x +4x,x ∈(1,3]的值域为( ) A .[133,5) B .[4,5) C .[133,4) D .(4,5)3.函数y =-x +41-x+3,x ∈[)-1,0的值域为____________. 4.y =2x 2+31+x 2的最小值是________. 5.已知x >0,则2+x +4x的最小值是________. 6.函数y =x +3x在区间[1,2]上的最小值为____________. 7.若函数y =x +a x(a >0)在区间(5,+∞)上单调递增,则a ∈________________. 8.建造一个容积为8m 3,深为2 m 的无盖水池,如果池底与池壁的造价每平方米分别是120元和80元,则水池的最低造价为____________元.9.某房地产开发公司计划在一楼区内建造一个长方形公园ABCD ,公园由长方形休闲区A 1B 1C 1D 1和环公园人行道(阴影部分)组成.已知休闲区A 1B 1C 1D 1的面积为4 000 m 2,人行道的宽分别为4 m 和10 m(如图所示).(1)若设休闲区的长和宽的比A 1B 1B 1C 1=x ,求公园ABCD 所占面积S 关于x 的函数解析式; (2)要使公园所占面积最小,休闲区A 1B 1C 1D 1的长和宽应如何设计?10.如图,某单位准备修建一个面积为600平方米的矩形场地(图中ABCD)的围墙,且要求中间用围墙EF隔开,使得ABEF为矩形,EFDC为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为800元每米,设围墙(包括EF)的修建总费用为y元.(1)求出y关于x的函数解析式;(2)当x为何值时,设围墙(包括EF)的的修建总费用y最小?并求出y的最小值.11.已知函数f (x )=x 2+2x +3x(x ∈[2,+∞)). (1)求f (x )的最小值;(2)若f (x )>a 恒成立,求a 的取值范围.12.已知函数f (x )=x +a x,x ∈[1,+∞),a >0. (1) 当a =12时,求函数f (x )的最小值; (2) 若函数f (x )的最小值为4,求实数a .13.为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C (单位:万元)与隔热层厚度x (单位:cm)满足关系:C (x )=k 3x +5(0≤x ≤10,k 为常数),若不建隔热层,每年能源消耗费用为8万元.设f (x )为隔热层建造费用与20年的能源消耗费用之和.(1)求k 的值及f (x )的表达式;(2)隔热层修建多厚时,总费用f (x )达到最小?并求出最小值.参考答案1.C A 选项,由于x 可取负值,显然最小值不是4,排除A ;B 选项,由于x 可取负值,显然最小值也不是4,排除B ;C 选项,由于y =2·2x +22x =2(2x +12x ), 换元,令t =2x ,t >0,则y =2(t +1t)≥4, 当且仅当t =1即x =0时,函数有最小值4,D 选项,由于y =x 2+1x 2+1+3=x 2+1+1x 2+1+2,换元,令t =x 2+1,t >1,则y =t +1t+2,函数在(1,+∞)上单调递增,因此y >4,排除D 选项. 综上,答案为C.2.B 由对勾函数性质可知,当x =4x,即x =2时,表达式有最小值4,又函数在(1,2)上单调递减,在(2,3]上单调递增, f (1)=5,f (3)=3+43=133,所以值域为[4,5),答案为B. 3.[6,7)解析 y =-x +41-x +3=1-x +41-x+2, 换元,令t =1-x ,则x ∈[)-1,0时t ∈(1,2],y =t +4t+2,函数在(1,2]上单调递减, 若t =1,则y =1+41+2=7, 若t =2,则y =2+42+2=6, 故函数值域为[6,7).4.26-2解析 换元,令t =1+x 2,则t ≥1,x 2=t -1,y =2(t -1)+3t =2t +3t-2, 函数在[1,32]上单调递减,在[32,+∞)上单调递增, 所以当t =32时,函数有最小值26-2. 5.6 解析 由对勾函数性质可知,当x =4x,即x =2时,表达式有最小值6. 6.2 3解析 因为y =x +3x在区间[1, 3 ]上单调递减,在[3,2]上单调递增,所以当x =3时函数有最小值2 3.7.(0,5]8.1 760解析 池底面积为82=4 cm 2,设池底宽为x cm ,则长为4x cm ,则水池的造价为4×120+2(4x×2+x ×2)×80=480+1 280x +320x ≥480+2 1 280x×320x =1 760. 9.解析 (1)设休闲区的宽为a 米,则其长为ax 米.由a 2x =4 000,得a =2010x, 则S =(a +8)(ax +20)=a 2x +(8x +20)a +160=4 000+(8x +20)·2010x +160 =8010(2x +5x)+4 160, 即S =8010(2x +5x )+4 160. (2)S =8010(2x +5x )+4 160≥16010·10+4 160=5 760, 当且仅当2x =5x,即x =2.5时取等号,此时a =40, ax =100.所以要使公园所占面积最小,休闲区A 1B 1C 1D 1应设计为长100米,宽40米.10.解析 (1)设AD =t 米,则由题意得xt =600,且t >x ,故t =600x>x ,可得0<x <106, 则y =800(3x +2t )=800(3x +2×600x)=2 400(x +400x), 所以y 关于x 的函数解析式为y =2 400(x +400x)(0<x <106). (2)y =2400(x +400x )≥2 400×2x ·400x=96 000, 当且仅当x =400x,即x =20时等号成立. 故当x 为20米时,y 最小.y 的最小值为96 000元.11.解析 (1)任取x 1,x 2∈[2,+∞),且x 1<x 2,f (x )=x +3x+2. 则f (x 1)-f (x 2)=(x 1-x 2) (1-3x 1x 2), ∵x 1<x 2,∴x 1-x 2<0,又∵x 1≥2,x 2>2,∴x 1x 2>4,1-3x 1x 2>0, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).故f (x )在[2,+∞)上是增函数,∴当x =2时,f (x )有最小值f (2)=112. (2)∵f (x )>a 恒成立,∴只需f (x )min >a .又∵f (x )min =112,∴a <112. 12.解析 (1) a =12时, f (x )=x +12x, x ∈[1,+∞). 令x =12x (x >0),得x =22∉[1,+∞), ∴不能用不等式求最值.设1≤x 1<x 2,则f (x 1)-f (x 2)=(x 1-x 2)+(12x 1-12x 2) =(x 1-x 2)(1-12x 1x 2)<0, ∴函数 f (x ) 在[1,+∞)上是单调递增函数,∴f min (x )=f (1)=32. (2)当0<a <1时,令x =a x,得x =a <1, ∵a ∉[1,+∞) ,∴类似于(1)可知函数f (x )在[1,+∞)上是单调递增函数, ∴f min (x )=f (1)=1+a =4,得a =3,与0<a <1不符(舍);当a ≥1时,a ≥1,∴由不等式知x +a x ≥2a , 当x =a x,即x =a 时, f min (x )=2a =4, 解得a =4.综上所述,函数f (x )的最小值为4时,a =4.13.解析 (1)依题意,当x =0 时,C =8,∴k =40 ,∴C (x )=403x +5, ∴f (x )=6x +20×403x +5=6x +8003x +5(0≤x ≤10). (2)f (x )=2(3x +5)+8003x +5-10, 设3x +5=t ,t ∈[5,35],∴y =2t +800t -10≥22t ·800t-10=70, 当且仅当2t =800t,即t =20时等号成立. 这时x =5 ,因此f (x )的最小值为70.即隔热层修建5 cm 厚时,总费用f (x )达到最小,最小值为70万元.特殊对勾函数f (x )=x + x1 2 3 4 f (x ) 4 3 2 2 2 3 4‘’(1)定义域:(-∞,0)∪(0,+∞).(2)值域:(-∞,-2 ]∪[2,+∞).(3)奇偶性:在定义域内为奇函数.(4)单调性:(-∞,-1),(1,+∞)上↗;(-1,0),(0,1)上↘.(5)分界点(拐点)坐标P(1,2) ; Q(-1,-2)(6)渐近线(7)Y=x和x=0。
对勾函数模型

重点知识梳理1 •对勾函数定义对勾函数是指形如:y= ax+ x(ab>0)的一类函数,因其图象形态极像对勾,因此被称为对入勾函数”又被称为双勾函数” 勾函数” 耐克函数”或耐克曲线”2. 对勾函数y= ax+ b(a>0, b>0)的性质入⑴定义域:(一汽0)U (0 ,+x).(2) 值域:(—X, -2 V????U [2V????+^).(3) 奇偶性:在定义域内为奇函数.⑷单调性:(―X,—、y i),(\脣,+*上是增函数;(―、/a, 0),(0, \/|)上是减函数.⑸渐近线:y轴与y=ax(或y=-ax)b3. y= ax+ b(a>0, b>0)的单调区间的分界点:x求分界点方法:令ax = b x入特殊的,a>0时,y= x+£的单调区间的分界点:土. a.入4. 对勾函数应用时主要是利用对勾函数单调性求其最值,解题时要先找出对应的单调区间,然后求解.5. 利用对勾函数求最值,常常用到如下的重要不等式:b若a>0, b>0,则x>0 时,ax+ b>2 ab.x当且仅当ax二b,x= *时取等号.在应用这个不等式时,要注意使用的前提条件是一正、二定、三相等”即加号两边的项ax和“都是正项,且二者乘积为定值,同时ax= b中等号可取到.若等号取不到,则应根据x x对勾函数单调性求解.典型例题剖析5例1已知f(x) = x ■-,求f(x)在下列区间的最小值.X(1)[1,2]; (2)[3,4]; (3)[- 3,—1].【解析】如图,f(x)在(—X,—5), ( .5,+^上是增函数,在(—,5, 0), (0, .5)上是减函数.(1)由对勾函数性质可知f(x)在[1,2]上单调递减,1 f(x)min 二f(2) = 42.⑵因为f(x)在[3,4]上单调递增,2 所以f(x)min = f(3) = 43.2⑶因为f(x)在[—3,— 5 ]上单调递增,在(—5,—1]上单调递减,且f(—3) = —43, f(—1)= —6,所以f(X)min = — 6.x2+ 5变式训练已知函数f(x) = 7^=,求f(x)的最小值,并求此时x的值.\x + 4【解析】f(x)= x J5 = X +:+ 1= x2+ 4+ 1■収+ 4 彳x2+ 4 彳寸x2+ 4__________ 4 令t=J x2+4,贝U t>2 y= t+-.1••• y= t + ”在[2 ,+x单调递增,t t1 5•••当t = 2 时,y min = 2+ 2= ^,5f(x)的最小值为2,此时x的值为0.x2—2x—1求函数f(x) = + 2 (0叹w 3的值域.X I厶【解析】令t = x+ 2,则x= t —2, 2磴5(t —2)2—2(t —2)—1 y==t —+7 = t+ 7 —6,2 « 5.此时, \/x2+ 4= 2, x= 0. 综上,••• y = t +1-6在[2 , 7 ]上单调递减,在[.7, 5]上单调递增,•••当 t = [ 7时,y min = 2 .J 7 — 6,7 1且当 t = 2 时,y = 2 + 2— 6二一2,7 2 2当 t = 5 时,y = 5 + 5 — 6 = 5,二 y max = 5.2综上,f(x)的值域为[2 7 — 6,耳•=(x — 1)2— 2(x — 1)+ 9 = x — 1+ ®— 2,x — 1 ,9 令 t = x — 1,则 f(t) = t + - — 2, t € [1,4].9 结合y =t + 9的图象与性质,可知当t € [1,3]时,函数单调递减,当t € [3,4]时,函数单调递增,17又 f(1) = 8, f(3) = 4, f ⑷二a ,所以 f(x)€ [4,8].例3某工厂去年的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入 100 万元(科技成本),预计产量年递增10万只,第n 次投入后,每只产品的固定成本为 g(n)=k 寸n +1(k>0, k 为常数,n € Z 且n 》0)若产品销售价保持不变,第n 次投入后的年利润为f(n)万元.(1) 求k 的值,并求出f(n)的表达式;(2) 问从今年算起第几年利润最高?最高利润为多少万元?k 【解析】(1)由g(n) = i --- ,当n = 0时,由题意, 7n + 1可得k = 8,变式训练 求函数f(x) = x 2— 4x + 12,x € [2,5]的值域. 【解析】f(x) = x 2 — 4x + 12x — 18所以 f(n)= (100+ 10n)(10 — ---- ) — 100n(n € Z 且 n 》0.)\/n+ 1⑵由 f(n) = (100+ 10n)(10 — ^n =) — 100n=1 000— 80(pn + 1 + r~7j )< 1 00— 80>2 9= 520,当且仅当n + 1= 9 ,即n = 8时取等号,V V n+1所以第8年工厂的利润最高,最高为520万元.变式训练 建筑一个容积为800米3,深8米的长方体水池 优盖).池壁,池底造价分别为 a 元咪2和2a 元/米2底面一边长为x 米,总造价为y.写出y 与x 的函数式,问底面边长x 为何值时总造价y 最低,是多少?【解析】长方体底面积S =晋二100米2,地面一边长为x 米, 因此另一边长为100米,入池壁总面积为8 (2x +警)米2,入二总造价 y = 100>2a + (2x + 200) 8 ax =200a + 16a(x + ^)(x>0). X•••函数y = 200a + 16a (x +号0)在(0,10]上是减函数,在(10,+ ^上是增函数, 入下列函数中最小值是4的是(4尸X + X2 尸x +xy = 21+x + 21 — x y = x 2+ 計1+ 3, (X M 0)二当x = 10时,总造价最低,且y min = 520a (元).C .42•函数y =x + -, x € (1,3]的值域为( ) XA • [y ,5)c .[等,4) 43•函数 y = — x + — + 3, x € [- 1, 0)的值域为 1 ——4. y = 2x 2 + 3 2的最小值是1 + x45. 已知x>0,则2 + x + -的最小值是 _________ .入36. 函数y =x + 3在区间[1,2]上的最小值为 ___ —7. 若函数y = x + x(a >0)在区间(J5,+上单调递增,则a € _________________________ .入8. 建造一个容积为8m 3,深为2 m 的无盖水池,如果池底与池壁的造价每平方米分别是 120元和80元,则水池的最低造价为 _____________ .9.某房地产开发公司计划在一楼区内建造一个长方形公园 ABCD ,公园由长方形休闲区 A 1B 1C 1D 1和环公园人行道(阴影部分)组成.已知休闲区A 1B 1C 1D 1的面积为4 000 m 2,人行 道的宽分别为4 m 和10 m(如图所示).(1)若设休闲区的长和宽的比琵=x ,求公园ABCD 所占面积S 关于—的函数解析式; (2)要使公园所占面积最小,休闲区 A 1B 1C 1D 1的长和宽应如何设计?10. 如图,某单位准备修建一个面积为 600平方米的矩形场地(图中ABCD)的围墙,且要 求中间用围墙EF 隔开,使得ABEF 为矩形,EFDC 为正方形,设AB =—米,已知围墙(包 括EF)的修建费用均为800元每米,设围墙(包括EF)的修建总费用为y 元.(1)求出y 关于—的函数解析式;⑵当—为何值时,设围墙(包括EF)的的修建总费用y 最小?并求出y 的最小值.—2 + 2—+ 3 11. 已知函数 f(x)= — (x € [2,+x )) (1)求f(x)的最小值;⑵若f(x)>a 恒成立,求a 的取值范围.B . [4,5) D . (4,5)12. 已知函数f(x)= x+ a, x€ [1 , + ^) a>0.入41(1)当a =㊁时,求函数f(x)的最小值;⑵若函数f(x)的最小值为4,求实数a.13 •为了降低能源损耗,某体育馆的外墙需要建造隔热层•体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元•该建筑物每年的能源消耗费用C(单位:万k兀)与隔热层厚度x (单位:cm)满足关系:C(x) = (0叹w 10 k为常数),若不建隔热层,3X十5每年能源消耗费用为8万元•设f(x)为隔热层建造费用与20年的能源消耗费用之和.(1)求k的值及f(x)的表达式;⑵隔热层修建多厚时,总费用f(x)达到最小?并求出最小值.参考答案1. C A选项,由于x可取负值,显然最小值不是4,排除A ;B选项,由于x可取负值,显然最小值也不是4,排除B;2 1C 选项,由于y=2 2x+ 2 = 2(2x+ 歹),一1换兀,令t= 2x,t>0,则y= 2(t+—)当且仅当t= 1即x= 0时,函数有最小值4,D 选项,由于y=x2+ x2+ 1 + 3 = x2+ 1 + x2+ 1 + 2,换兀,令t= x2+ 1,t>1,1则y=t+1 + 2,函数在(1,+^上单调递增,因此y>4,排除D选项.综上,答案为C.42. B由对勾函数性质可知,当x= 4,即x = 2时,表达式有最小值4,又函数在(1,2)上单x4 13调递减,在(2,3]上单调递增,f(1) = 5, f(3) = 3 + 3 =三,所以值域为[4,5),答案为B.3. [6,7)4 4解析y= —x+ + 3= 1 —x+ + 2,1 —x 1 —x4若t= 1,则y= 1 +1 + 2= 7,换元,令t= 1 —x,则x€ [ —1, 0)时t€ (1,2],4y = t + 4+ 2,函数在(1,2]上单调递减,4若t= 2,则y = 2 + 2 + 2 = 6,故函数值域为[6,7).4. 2 6-2解析换元,令t= 1 + x2,则t>1 x2= t- 1,3 3y = 2(t-1)+ t = 2t+ - - 2,函数在[1 , , 3]上单调递减,在[,|,+x上单调递增,所以当t= :j时,函数有最小值2 6 — 2.5. 6解析由对勾函数性质可知,当x=4,即x= 2时,表达式有最小值6.x6. 2 33解析因为y=x+ x在区间[1, 3 ]上单调递减,在[3, 2]上单调递增,所以当x= .3时入函数有最小值2 . 3.7. (0,5]8. 1 760解析池底面积为8= 4 cm2,设池底宽为x cm,则长为4 cm,则水池的造价为4X120+ 2(42 x xX320x = 1 760.9. 解析⑴设休闲区的宽为a米,则其长为ax米.由a2x=4 000,得a= 2°^,则S= (a + 8)(ax+ 20) = a2x+ (8x+ 20)a + 160=4 000+ (8x+ 20) 20 10+ 160=80 10(2 ,x+ 5 ) + 4 160,5(2)S= 80再(2&+玄)+ 4 i60 > i600^i0+ 4 i60= 5 760,当且仅当2 x= 3 4 5,即x= 2.5时取等号,此时a=40,7xax= 100.所以要使公园所占面积最小,休闲区A i B i C i D i应设计为长100米,宽40米.i0.解析(i)设AD= t米,则由题意得xt= 600,且t>x, 故t= 6 7 8 9 10 11x!°>x,可得0<x<i0 6, x则y= 800(3x+ 2t) = 800(3x+ 2^^)x400二2 400(x+ -x0),所以y关于x的函数解析式为y= 2 400(x+ 400)(0<x<i0 6).x(2)y= 2400(x+ 竽 > 2 400 X2x 4;°= 96 000,当且仅当x= 400即x= 20时等号成立.x故当x为20米时,y最小.y的最小值为96 000元.ii .解析(i)任取x i, x2€ [2,+ °°)□ 3且x i<x2,f(x) = x + x + 2.3则f(x i)—f(x2)= (x i —x2) (i—航),T X i<X2,「. x i —X2<0,又••• x i>2 x2>2,3• xix2>4,i—云>0,二f(x i) —f(X2)<0,即f(x1)vf(x2).故f(x)在[2 , + X上是增函数,11•••当x= 2时,f(x)有最小值f(2) = ©.(2) ■/f(x)>a 恒成立,•只需f(x)min>a.E ii ii又••• f(x)min = • a<2.1 112•解析(1) a = 2时,f (x) = x + 2x , x € [1 ,+x ). 令 x = £(x>0),得 x =#[1 ,+G •••不能用不等式求最值.设 1$1<X 2,则 f(X 1)— f(X 2), 1 1二(x1—x2) + (2x 1—2x 2)1二(X 1 — X 2)(1 —融)<0,•函数f(x)在[1 ,+x 上是单调递增函数,3• f min (x) = f(1)=a⑵当 0<a<1 时,令 x = x ,得 x = a<1,入•••、a[1,+ %),•类似于⑴可知函数f(x)在[1,+^上是单调递增函数,• f min (x) = f(1) = 1 + a = 4,得a = 3,与0<a<1不符(舍);当a 》l 时,•由不等式知x + x >2a , X当 x = -,即卩 X = , a 时,f min (x)= 2 , a = 4, X解得a =4.(1)依题意,当 x = 0 时,C = 8,二 k = 40 ,20 >40 800• f(x )= 6x + = 6X + 3X +5(0 x 10) (2)f(x)二 2(3x + 5) + 38+°5—10, 设 3x + 5 = t , t € [5,35],• y = 2t + 800— 10>2 2t 8:0 —10= 70,综上所述, 函数f(x)的最小值为4时,a = 4.40 • C (X) = 3x + 5'13•解析当且仅当2t=-,即t= 20时等号成立.这时x= 5 ,因此f(x)的最小值为70.即隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元. 特殊对勾函数”、 1 f(x) = X+ ??x・・・1413121234・・・f(x)・・・144332222131144・・・(1)定义域:(—X, 0)U (0,+ X).⑵值域:(—X, -2 ] U [2, +X)⑶奇偶性:在定义域内为奇函数. (4) 单调性:(—X,—1), (1 , + X 上/;(—1, 0), (0, 1)上\・⑸分界点(拐点)坐标P(1,2) ; Q(-1,-2)(6)渐近线⑺Y=x和x=0。
对勾函数(目前最全面的版本了吧)
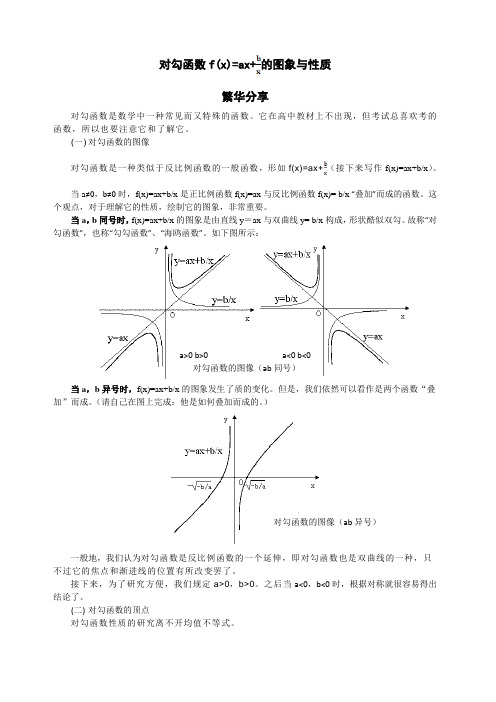
对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,yXOy=ax。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明:1、求函数324222++++=x x x x y 的最小值。
yXOy=ax解:令322++=x x t ,则22)1(2≥++=x ttt t t y 112+=+= 根据对号函数tt y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式能够得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数,二、关于求函数()01>+=x xx y 最小值的解法1. 均值不等式 0>x ,∴21≥+=xx y ,当且仅当x x 1=,即1=x 的时候不等式取到“=”。
∴当1=x 的时候,2min =y 2. ∆法 0112=+-⇒+=yx x xx y 若y 的最小值存有,则042≥-=∆y 必需存有,即2≥y 或2-≤y (舍)找到使2=y 时,存有相对应的x 即可。
数学对勾函数(详细分析“函数”共8张)

性质一
➢ 函数y=ax+b/x的性质 ➢ Ⅰ当a、b均大于零时,性质 : ➢ ⑴定义域:x≠0 ➢ ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,
+∞〕 ⑶奇偶性:奇函数 ➢ ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,
y为减函数 当x﹥根号b/a 时,y为增函 数 当x﹤0时,当- 根号b/a﹤x﹤0时,y 为减函数 当x﹤根号b/a- 时,y为增函 数
第7页,共8页。
图像三
第8页,共8页。
数学对勾函数
第1页,共8页。
简介对Biblioteka 函数:图像,性质,单调性对勾函数是数学中一种常见而又特殊的函数,见图示。 对勾函数是一种类似于反比例函数的一般函数,
又被称为“双勾函数〞、"勾函数"等。也被形象称 为“耐克函数〞
所谓的对勾函数〔双曲线函数〕,是形如 f(x)=ax+b/x的函数。由图像得名。
当x>0时,f(x)=ax+b/x有最小值〔这里为了研究方 便,规定a>0,b>0〕,也就是当x=sqrt(b/a)的时候 〔sqrt表示求二次方根〕
第6页,共8页。
图象二
Ⅰ当a、b均大于零时,性质 : 当a、b>0时,图像分布在第一、三象限两条渐近线的锐角之间局部,由于其对称性,只讨论第一象限中的情形。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 对号函数是双曲线旋转得到的,所以也有渐近线、焦点、顶点等等 对勾函数是数学中一种常见而又特殊的函数,见图示。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 Ⅰ当a、b均大于零时,性质 : ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 当a、b>0时,图像分布在第一、三象限两条渐近线的锐角之间局部,由于其对称性,只讨论第一象限中的情形。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 对号函数永远是奇函数,关于原点呈中心对称 ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,+∞〕 ⑶奇偶性:奇函数 当x>0时,f(x)=ax+b/x有最小值〔这里为了研究方便,规定a>0,b>0〕,也就是当x=sqrt(b/a)的时候〔sqrt表示求二次方根〕 ⑹对称性:图像关于原点对称 利用平均值不等式〔a>0,b>0且ab的值为定值时,a+b≥2√ab〕可知最小值是2倍根号ab,在x=根号下b/a的时候取得,所以在〔0,负根号下b/a〕 上单调递减,在〔根号下b/a,正无穷〕上单调递增
对勾函数讲解与例题解析
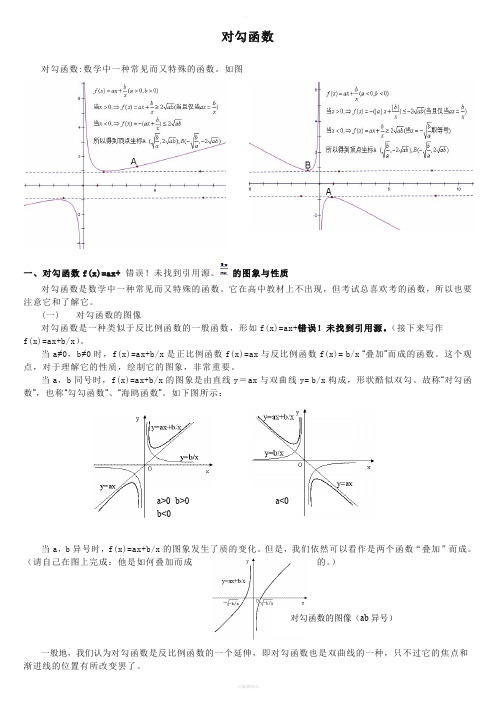
对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x )。
当a ≠0,b ≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数,二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
2017-2018人教版高中数学二轮复习习题:第十周_对勾函数模型

1第十周 对勾函数模型重点知识梳理1.对勾函数定义对勾函数是指形如:y =ax +b x(ab >0)的一类函数,因其图象形态极像对勾,因此被称为“对勾函数”,又被称为“双勾函数”、“勾函数”、“耐克函数”或“耐克曲线”.2.对勾函数y =ax +b x(a >0,b >0)的性质(1)定义域:(-∞,0)∪(0,+∞).(2)值域:(-∞,-2ab ]∪[2ab ,+∞).(3)奇偶性:在定义域内为奇函数.(4)单调性:(-∞,-b a ),(b a,+∞)上是增函数;(-b a ,0),(0,b a )上是减函数. 3.y =ax +b x(a >0,b >0)的单调区间的分界点:±b a . 求分界点方法:令ax =b x ⇒x =±b a. 特殊的,a >0时,y =x +a x 的单调区间的分界点:±a . 4.对勾函数应用时主要是利用对勾函数单调性求其最值,解题时要先找出对应的单调区间,然后求解.25.利用对勾函数求最值,常常用到如下的重要不等式:若a >0,b >0,则x >0时,ax +b x ≥2ab . 当且仅当ax =b x ,x =b a时取等号. 在应用这个不等式时,要注意使用的前提条件是“一正、二定、三相等”,即加号两边的项ax 和b x 都是正项,且二者乘积为定值,同时ax =b x中等号可取到.若等号取不到,则应根据对勾函数单调性求解.典型例题剖析例1 已知f (x )=x +5x,求f (x )在下列区间的最小值. (1)[1,2]; (2)[3,4]; (3)[-3,-1].【解析】如图,f (x )在 (-∞,-5),(5,+∞)上是增函数,在(-5,0),(0,5)上是减函数.(1)由对勾函数性质可知f (x )在[1,2]上单调递减,∴f (x )min =f (2)=412. (2)因为f (x )在[3,4]上单调递增,所以f (x )min =f (3)=423.3(3)因为f (x )在[-3,- 5 ]上单调递增,在(-5,-1]上单调递减,且f (-3)=-423, f (-1)=-6,所以f (x )min =-6.变式训练 已知函数f (x )=x 2+5x 2+4,求f (x )的最小值,并求此时x 的值.【解析】f (x )=x 2+5x 2+4=x 2+4+1x 2+4=x 2+4+1x 2+4令t =x 2+4,则t ≥2,y =t +1t. ∵y =t +1t在[2,+∞)单调递增, ∴当t =2时,y min =2+12=52, 此时,x 2+4=2,x =0.综上,f (x )的最小值为52,此时x 的值为0. 例2 求函数f (x )=x 2-2x -1x +2(0≤x ≤3)的值域. 【解析】令t =x +2,则x =t -2, 2≤t ≤5,y =(t -2)2-2(t -2)-1t=t 2-6t +7t =t +7t-6,2≤t ≤5. ∵y =t +7t-6在[2,7 ]上单调递减,在[7, 5]上单调递增, ∴当t =7时,y min =27-6,且当t =2时,y =2+72-6=-12,4当t =5时,y =5+75-6=25,∴y max =25. 综上,f (x )的值域为[27-6,25]. 变式训练 求函数f (x )=x 2-4x +12x -1,x ∈[]2,5的值域. 【解析】f (x )=x 2-4x +12x -1=(x -1)2-2(x -1)+9x -1=x -1+9x -1-2, 令t =x -1,则f (t )=t +9t-2,t ∈[1,4]. 结合y =t +9t的图象与性质, 可知当t ∈[1,3]时,函数单调递减,当t ∈[3,4]时,函数单调递增,又f (1)=8,f (3)=4,f (4)=174, 所以f (x )∈[4,8].例3 某工厂去年的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n 次投入后,每只产品的固定成本为g (n )=kn +1(k >0,k 为常数,n ∈Z 且n ≥0),若产品销售价保持不变,第n 次投入后的年利润为f (n )万元.(1)求k 的值,并求出f (n )的表达式;(2)问从今年算起第几年利润最高?最高利润为多少万元?【解析】(1)由g (n )=k n +1,当n =0时,由题意, 可得k =8,5所以f (n )=(100+10n )(10-8n +1)-100n (n ∈Z 且n ≥0). (2)由f (n )=(100+10n )(10-8n +1)-100n =1 000-80(n +1+9n +1) ≤1 000-80×29=520,当且仅当n +1=9n +1,即n =8时取等号, 所以第8年工厂的利润最高,最高为520万元.变式训练 建筑一个容积为800米3,深8米的长方体水池(无盖).池壁,池底造价分别为a 元/米2和2a 元/ 米2.底面一边长为x 米,总造价为y .写出y 与x 的函数式,问底面边长x 为何值时总造价y 最低,是多少?【解析】长方体底面积S =8008=100米2,地面一边长为x 米, 因此另一边长为100x米, 池壁总面积为8·(2x +200x)米2, ∴ 总造价y =100×2a +(2x +200x )·8·a =200a +16a (x +100x)(x >0). ∵函数y =200a +16a (x +100x)在(0,10]上是减函数,在(10,+∞)上是增函数, ∴ 当x =10时,总造价最低,且y min =520a (元).跟踪训练1.下列函数中最小值是4的是( )6A .y =x +4xB .y =x +2xC .y =21+x +21-xD .y =x 2+1x 2+1+3,(x ≠0) 2.函数y =x +4x,x ∈(1,3]的值域为( ) A .[133,5) B .[4,5) C .[133,4) D .(4,5)3.函数y =-x +41-x+3,x ∈[)-1,0的值域为____________. 4.y =2x 2+31+x 2的最小值是________. 5.已知x >0,则2+x +4x的最小值是________. 6.函数y =x +3x在区间[1,2]上的最小值为____________. 7.若函数y =x +a x(a >0)在区间(5,+∞)上单调递增,则a ∈________________. 8.建造一个容积为8m 3,深为2 m 的无盖水池,如果池底与池壁的造价每平方米分别是120元和80元,则水池的最低造价为____________元.9.某房地产开发公司计划在一楼区内建造一个长方形公园ABCD ,公园由长方形休闲区A 1B 1C 1D 1和环公园人行道(阴影部分)组成.已知休闲区A 1B 1C 1D 1的面积为4 000 m 2,人行道的宽分别为4 m 和10 m(如图所示).(1)若设休闲区的长和宽的比A 1B 1B 1C 1=x ,求公园ABCD 所占面积S 关于x 的函数解析式;(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽应如何设计?10.如图,某单位准备修建一个面积为600平方米的矩形场地(图中ABCD)的围墙,且要求中间用围墙EF隔开,使得ABEF为矩形,EFDC为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为800元每米,设围墙(包括EF)的修建总费用为y元.(1)求出y关于x的函数解析式;(2)当x为何值时,设围墙(包括EF)的的修建总费用y最小?并求出y的最小值.7811.已知函数f (x )=x 2+2x +3x(x ∈[2,+∞)). (1)求f (x )的最小值;(2)若f (x )>a 恒成立,求a 的取值范围.12.已知函数f (x )=x +a x,x ∈[1,+∞),a >0. (1) 当a =12时,求函数f (x )的最小值; (2) 若函数f (x )的最小值为4,求实数a .13.为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x (单位:cm)满足关系:C(x)=k3x+5(0≤x≤10,k为常数),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.(1)求k的值及f(x)的表达式;(2)隔热层修建多厚时,总费用f(x)达到最小?并求出最小值.910参考答案1.C A 选项,由于x 可取负值,显然最小值不是4,排除A ; B 选项,由于x 可取负值,显然最小值也不是4,排除B ;C 选项,由于y =2·2x +22x =2(2x +12x ), 换元,令t =2x ,t >0,则y =2(t +1t)≥4,11当且仅当t =1即x =0时,函数有最小值4,D 选项,由于y =x 2+1x 2+1+3=x 2+1+1x 2+1+2,换元,令t =x 2+1,t >1, 则y =t +1t+2,函数在(1,+∞)上单调递增,因此y >4,排除D 选项. 综上,答案为C.2.B 由对勾函数性质可知,当x =4x,即x =2时,表达式有最小值4,又函数在(1,2)上单调递减,在(2,3]上单调递增, f (1)=5,f (3)=3+43=133,所以值域为[4,5),答案为B. 3.[6,7)解析 y =-x +41-x +3=1-x +41-x+2, 换元,令t =1-x ,则x ∈[)-1,0时t ∈(1,2],y =t +4t+2,函数在(1,2]上单调递减, 若t =1,则y =1+41+2=7, 若t =2,则y =2+42+2=6, 故函数值域为[6,7).4.26-2解析 换元,令t =1+x 2,则t ≥1,x 2=t -1,y =2(t -1)+3t =2t +3t-2, 函数在[1,32]上单调递减,在[32,+∞)上单调递增, 所以当t =32时,函数有最小值26-2.125.6解析 由对勾函数性质可知,当x =4x,即x =2时,表达式有最小值6. 6.23解析 因为y =x +3x在区间[1, 3 ]上单调递减,在[3,2]上单调递增,所以当x =3时函数有最小值2 3.7.(0,5]8.1 760解析 池底面积为82=4 cm 2,设池底宽为x cm ,则长为4x cm ,则水池的造价为4×120+2(4x ×2+x ×2)×80=480+1 280x +320x ≥480+2 1 280x×320x =1 760. 9.解析 (1)设休闲区的宽为a 米,则其长为ax 米.由a 2x =4 000,得a =2010x, 则S =(a +8)(ax +20)=a 2x +(8x +20)a +160=4 000+(8x +20)·2010x+160 =8010(2x +5x)+4 160, 即S =8010(2x +5x)+4 160. (2)S =8010(2x +5x )+4 160≥16010·10+4 160=5 760, 当且仅当2x =5x,即x =2.5时取等号,此时a =40, ax =100.13所以要使公园所占面积最小,休闲区A 1B 1C 1D 1应设计为长100米,宽40米.10.解析 (1)设AD =t 米,则由题意得xt =600,且t >x ,故t =600x>x ,可得0<x <106, 则y =800(3x +2t )=800(3x +2×600x) =2 400(x +400x), 所以y 关于x 的函数解析式为y =2 400(x +400x)(0<x <106). (2)y =2400(x +400x )≥2 400×2x ·400x=96 000, 当且仅当x =400x,即x =20时等号成立. 故当x 为20米时,y 最小.y 的最小值为96 000元.11.解析 (1)任取x 1,x 2∈[2,+∞),且x 1<x 2,f (x )=x +3x+2. 则f (x 1)-f (x 2)=(x 1-x 2) (1-3x 1x 2), ∵x 1<x 2,∴x 1-x 2<0,又∵x 1≥2,x 2>2,∴x 1x 2>4,1-3x 1x 2>0, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).故f (x )在[2,+∞)上是增函数,∴当x =2时,f (x )有最小值f (2)=112.14(2)∵f (x )>a 恒成立,∴只需f (x )min >a .又∵f (x )min =112,∴a <112. 12.解析 (1) a =12时, f (x )=x +12x, x ∈[1,+∞). 令x =12x (x >0),得x =22∉[1,+∞), ∴不能用不等式求最值.设1≤x 1<x 2,则f (x 1)-f (x 2)=(x 1-x 2)+(12x 1-12x 2) =(x 1-x 2)(1-12x 1x 2)<0, ∴函数 f (x ) 在[1,+∞)上是单调递增函数,∴f min (x )=f (1)=32. (2)当0<a <1时,令x =a x,得x =a <1, ∵a ∉[1,+∞) ,∴类似于(1)可知函数f (x )在[1,+∞)上是单调递增函数, ∴f min (x )=f (1)=1+a =4,得a =3,与0<a <1不符(舍);当a ≥1时,a ≥1,∴由不等式知x +a x≥2a , 当x =a x,即x =a 时, f min (x )=2a =4, 解得a =4.15综上所述,函数f (x )的最小值为4时,a =4.13.解析 (1)依题意,当x =0 时,C =8,∴k =40 ,∴C (x )=403x +5, ∴f (x )=6x +20×403x +5=6x +8003x +5(0≤x ≤10). (2)f (x )=2(3x +5)+8003x +5-10, 设3x +5=t ,t ∈[5,35],∴y =2t +800t -10≥22t ·800t-10=70, 当且仅当2t =800t,即t =20时等号成立. 这时x =5 ,因此f (x )的最小值为70.即隔热层修建5 cm 厚时,总费用f (x )达到最小,最小值为70万元.。
对勾函数模型

第十周 对勾函数模型重点知识梳理1.对勾函数定义对勾函数是指形如:y =ax +b x (ab >0)的一类函数,因其图象形态极像对勾,因此被称为“对勾函数”,又被称为“双勾函数”、“勾函数”、“耐克函数”或“耐克曲线”.2.对勾函数y =ax +b x (a >0,b >0)的性质(1)定义域:(-∞,0)∪(0,+∞).(2)值域:(-∞, ]∪[,+∞).(3)奇偶性:在定义域内为奇函数.(4)单调性:(-∞,-b a ),(b a ,+∞)上是增函数;(-b a ,0),(0,b a )上是减函数. (5)渐近线:y 轴与y=ax(或y=-ax)3.y =ax +b x(a >0,b >0)的单调区间的分界点:±b a. 求分界点方法:令ax =b x ⇒x =±b a . 特殊的,a >0时,y =x +a x的单调区间的分界点:±a .4.对勾函数应用时主要是利用对勾函数单调性求其最值,解题时要先找出对应的单调区间,然后求解.5.利用对勾函数求最值,常常用到如下的重要不等式:若a >0,b >0,则x >0时,ax +b x ≥2ab . 当且仅当ax =b x ,x =b a时取等号. 在应用这个不等式时,要注意使用的前提条件是“一正、二定、三相等”,即加号两边的项ax 和b x 都是正项,且二者乘积为定值,同时ax =b x中等号可取到.若等号取不到,则应根据对勾函数单调性求解.典型例题剖析例1 已知f (x )=x +5x,求f (x )在下列区间的最小值. (1)[1,2]; (2)[3,4]; (3)[-3,-1].【解析】如图,f (x )在 (-∞,-5),(5,+∞)上是增函数,在(-5,0),(0,5)上是减函数.(1)由对勾函数性质可知f (x )在[1,2]上单调递减,∴f (x )min =f (2)=412. (2)因为f (x )在[3,4]上单调递增,所以f (x )min =f (3)=423.(3)因为f (x )在[-3,- 5 ]上单调递增,在(-5,-1]上单调递减,且f (-3)=-423, f (-1)=-6,所以f (x )min =-6.变式训练 已知函数f (x )=x 2+5x 2+4,求f (x )的最小值,并求此时x 的值.【解析】f (x )=x 2+5x 2+4=x 2+4+1x 2+4=x 2+4+1x 2+4令t =x 2+4,则t ≥2,y =t +1t. ∵y =t +1t在[2,+∞)单调递增, ∴当t =2时,y min =2+12=52, 此时,x 2+4=2,x =0.综上,f (x )的最小值为52,此时x 的值为0. 例2 求函数f (x )=x 2-2x -1x +2(0≤x ≤3)的值域. 【解析】令t =x +2,则x =t -2, 2≤t ≤5,y =(t -2)2-2(t -2)-1t=t 2-6t +7t =t +7t-6,2≤t ≤5. ∵y =t +7t-6在[2,7 ]上单调递减,在[7, 5]上单调递增, ∴当t =7时,y min =27-6,且当t =2时,y =2+72-6=-12,当t =5时,y =5+75-6=25,∴y max =25. 综上,f (x )的值域为[27-6,25]. 变式训练 求函数f (x )=x 2-4x +12x -1,x ∈[]2,5的值域. 【解析】f (x )=x 2-4x +12x -1=(x -1)2-2(x -1)+9x -1=x -1+9x -1-2, 令t =x -1,则f (t )=t +9t-2,t ∈[1,4]. 结合y =t +9t的图象与性质, 可知当t ∈[1,3]时,函数单调递减,当t ∈[3,4]时,函数单调递增,又f (1)=8,f (3)=4,f (4)=174, 所以f (x )∈[4,8].例3 某工厂去年的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n 次投入后,每只产品的固定成本为g (n )=kn +1(k >0,k 为常数,n ∈Z 且n ≥0),若产品销售价保持不变,第n 次投入后的年利润为f (n )万元.(1)求k 的值,并求出f (n )的表达式;(2)问从今年算起第几年利润最高?最高利润为多少万元?【解析】(1)由g (n )=k n +1,当n =0时,由题意, 可得k =8,所以f (n )=(100+10n )(10-8n +1)-100n (n ∈Z 且n ≥0).(2)由f (n )=(100+10n )(10-8n +1)-100n =1 000-80(n +1+9n +1) ≤1 000-80×29=520,当且仅当n +1=9n +1,即n =8时取等号, 所以第8年工厂的利润最高,最高为520万元.变式训练 建筑一个容积为800米3,深8米的长方体水池(无盖).池壁,池底造价分别为a 元/米2和2a 元/ 米2.底面一边长为x 米,总造价为y .写出y 与x 的函数式,问底面边长x 为何值时总造价y 最低,是多少?【解析】长方体底面积S =8008=100米2,地面一边长为x 米, 因此另一边长为100x米, 池壁总面积为8·(2x +200x)米2, ∴ 总造价y =100×2a +(2x +200x )·8·a =200a +16a (x +100x)(x >0). ∵函数y =200a +16a (x +100x)在(0,10]上是减函数,在(10,+∞)上是增函数, ∴ 当x =10时,总造价最低,且y min =520a (元).跟踪训练1.下列函数中最小值是4的是( )A .y =x +4xB .y =x +2xC .y =21+x +21-xD .y =x 2+1x 2+1+3,(x ≠0) 2.函数y =x +4x,x ∈(1,3]的值域为( ) A .[133,5) B .[4,5) C .[133,4) D .(4,5)3.函数y =-x +41-x+3,x ∈[)-1,0的值域为____________. 4.y =2x 2+31+x 2的最小值是________. 5.已知x >0,则2+x +4x的最小值是________. 6.函数y =x +3x在区间[1,2]上的最小值为____________. 7.若函数y =x +a x(a >0)在区间(5,+∞)上单调递增,则a ∈________________. 8.建造一个容积为8m 3,深为2 m 的无盖水池,如果池底与池壁的造价每平方米分别是120元和80元,则水池的最低造价为____________元.9.某房地产开发公司计划在一楼区内建造一个长方形公园ABCD ,公园由长方形休闲区A 1B 1C 1D 1和环公园人行道(阴影部分)组成.已知休闲区A 1B 1C 1D 1的面积为4 000 m 2,人行道的宽分别为4 m 和10 m(如图所示).(1)若设休闲区的长和宽的比A 1B 1B 1C 1=x ,求公园ABCD 所占面积S 关于x 的函数解析式; (2)要使公园所占面积最小,休闲区A 1B 1C 1D 1的长和宽应如何设计?10.如图,某单位准备修建一个面积为600平方米的矩形场地(图中ABCD)的围墙,且要求中间用围墙EF隔开,使得ABEF为矩形,EFDC为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为800元每米,设围墙(包括EF)的修建总费用为y元.(1)求出y关于x的函数解析式;(2)当x为何值时,设围墙(包括EF)的的修建总费用y最小?并求出y的最小值.11.已知函数f (x )=x 2+2x +3x(x ∈[2,+∞)). (1)求f (x )的最小值;(2)若f (x )>a 恒成立,求a 的取值范围.12.已知函数f (x )=x +a x,x ∈[1,+∞),a >0. (1) 当a =12时,求函数f (x )的最小值; (2) 若函数f (x )的最小值为4,求实数a .13.为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C (单位:万元)与隔热层厚度x (单位:cm)满足关系:C (x )=k 3x +5(0≤x ≤10,k 为常数),若不建隔热层,每年能源消耗费用为8万元.设f (x )为隔热层建造费用与20年的能源消耗费用之和.(1)求k 的值及f (x )的表达式;(2)隔热层修建多厚时,总费用f (x )达到最小?并求出最小值.参考答案1.C A 选项,由于x 可取负值,显然最小值不是4,排除A ;B 选项,由于x 可取负值,显然最小值也不是4,排除B ;C 选项,由于y =2·2x +22x =2(2x +12x ), 换元,令t =2x ,t >0,则y =2(t +1t)≥4, 当且仅当t =1即x =0时,函数有最小值4,D 选项,由于y =x 2+1x 2+1+3=x 2+1+1x 2+1+2,换元,令t =x 2+1,t >1,则y =t +1t+2,函数在(1,+∞)上单调递增,因此y >4,排除D 选项. 综上,答案为C.2.B 由对勾函数性质可知,当x =4x,即x =2时,表达式有最小值4,又函数在(1,2)上单调递减,在(2,3]上单调递增, f (1)=5,f (3)=3+43=133,所以值域为[4,5),答案为B. 3.[6,7)解析 y =-x +41-x +3=1-x +41-x+2, 换元,令t =1-x ,则x ∈[)-1,0时t ∈(1,2],y =t +4t+2,函数在(1,2]上单调递减, 若t =1,则y =1+41+2=7, 若t =2,则y =2+42+2=6, 故函数值域为[6,7).4.26-2解析 换元,令t =1+x 2,则t ≥1,x 2=t -1,y =2(t -1)+3t =2t +3t-2, 函数在[1,32]上单调递减,在[32,+∞)上单调递增, 所以当t =32时,函数有最小值26-2. 5.6 解析 由对勾函数性质可知,当x =4x,即x =2时,表达式有最小值6. 6.2 3解析 因为y =x +3x在区间[1, 3 ]上单调递减,在[3,2]上单调递增,所以当x =3时函数有最小值2 3.7.(0,5]8.1 760解析 池底面积为82=4 cm 2,设池底宽为x cm ,则长为4x cm ,则水池的造价为4×120+2(4x×2+x ×2)×80=480+1 280x +320x ≥480+2 1 280x×320x =1 760. 9.解析 (1)设休闲区的宽为a 米,则其长为ax 米.由a 2x =4 000,得a =2010x, 则S =(a +8)(ax +20)=a 2x +(8x +20)a +160=4 000+(8x +20)·2010x +160 =8010(2x +5x)+4 160, 即S =8010(2x +5x )+4 160. (2)S =8010(2x +5x )+4 160≥16010·10+4 160=5 760, 当且仅当2x =5x,即x =2.5时取等号,此时a =40, ax =100.所以要使公园所占面积最小,休闲区A 1B 1C 1D 1应设计为长100米,宽40米.10.解析 (1)设AD =t 米,则由题意得xt =600,且t >x ,故t =600x>x ,可得0<x <106, 则y =800(3x +2t )=800(3x +2×600x)=2 400(x +400x), 所以y 关于x 的函数解析式为y =2 400(x +400x)(0<x <106). (2)y =2400(x +400x )≥2 400×2x ·400x=96 000, 当且仅当x =400x,即x =20时等号成立. 故当x 为20米时,y 最小.y 的最小值为96 000元.11.解析 (1)任取x 1,x 2∈[2,+∞),且x 1<x 2,f (x )=x +3x+2. 则f (x 1)-f (x 2)=(x 1-x 2) (1-3x 1x 2), ∵x 1<x 2,∴x 1-x 2<0,又∵x 1≥2,x 2>2,∴x 1x 2>4,1-3x 1x 2>0, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).故f (x )在[2,+∞)上是增函数,∴当x =2时,f (x )有最小值f (2)=112. (2)∵f (x )>a 恒成立,∴只需f (x )min >a .又∵f (x )min =112,∴a <112. 12.解析 (1) a =12时, f (x )=x +12x, x ∈[1,+∞). 令x =12x (x >0),得x =22∉[1,+∞), ∴不能用不等式求最值.设1≤x 1<x 2,则f (x 1)-f (x 2)=(x 1-x 2)+(12x 1-12x 2) =(x 1-x 2)(1-12x 1x 2)<0, ∴函数 f (x ) 在[1,+∞)上是单调递增函数,∴f min (x )=f (1)=32. (2)当0<a <1时,令x =a x,得x =a <1, ∵a ∉[1,+∞) ,∴类似于(1)可知函数f (x )在[1,+∞)上是单调递增函数, ∴f min (x )=f (1)=1+a =4,得a =3,与0<a <1不符(舍);当a ≥1时,a ≥1,∴由不等式知x +a x ≥2a , 当x =a x,即x =a 时, f min (x )=2a =4, 解得a =4.综上所述,函数f (x )的最小值为4时,a =4.13.解析 (1)依题意,当x =0 时,C =8,∴k =40 ,∴C (x )=403x +5, ∴f (x )=6x +20×403x +5=6x +8003x +5(0≤x ≤10). (2)f (x )=2(3x +5)+8003x +5-10, 设3x +5=t ,t ∈[5,35],∴y =2t +800t -10≥22t ·800t-10=70, 当且仅当2t =800t,即t =20时等号成立. 这时x =5 ,因此f (x )的最小值为70.即隔热层修建5 cm 厚时,总费用f (x )达到最小,最小值为70万元.特殊对勾函数f (x )=x + x1 2 3 4 f (x ) 4 3 2 2 2 3 4‘’(1)定义域:(-∞,0)∪(0,+∞).(2)值域:(-∞,-2 ]∪[2,+∞).(3)奇偶性:在定义域内为奇函数.(4)单调性:(-∞,-1),(1,+∞)上↗;(-1,0),(0,1)上↘.(5)分界点(拐点)坐标P(1,2) ; Q(-1,-2)(6)渐近线(7)Y=x和x=0。
对勾函数

对勾函数是一种类似于反比例函数的一般函数。
所谓的对勾函数,是形如f(x)=ax+b/x的函数,是一种教材上没有但考试老喜欢考的函数,所以更加要注意和学习。
一般的函数图像形似两个中心对称的对勾,故名。
当x>0时,f(x)=ax+b/x有最小值(这里为了研究方便,规定a>0,b>0),也就是当x=sqrt(b/a)的时候(sqrt表示求二次方根)。
同时它是奇函数,就可以推导出x<0时的性质。
令k=sqrt(b/a),那么,增区间:{x|x≤-k}∪{x|x≥k};减区间:{x|-k≤x<0}∪{x|0<x≤k}。
由单调区间可见,它的变化趋势是:在y 轴左边,增减,在y轴右边,减增,是两个勾。
对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道,(a-b)2≥0,展开就是a2-2ab+b2≥0,有a2+b2≥2ab,两边同时加上2ab,整理得到(a+b)2≥4ab,同时开根号,就得到了平均值定理的公式:a+b≥2sqrt(ab)。
现在把ax+b/x套用这个公式,得到ax+b/x≥2sqrt(axb/x)=2sqrt(ab),这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
这些知识点也是非常重要的。
其实用导数也可以研究对勾函数的性质。
不过首先要会负指数幂的换算,这也很简单,但要熟练掌握。
举几个例子:1/x=x-1,4/x2=4x-2。
明白了吧,x为分母的时候可以转化成负指数幂。
那么就有f(x)=ax+b/x=ax+bx-1,求导方法一样,求的的导函数为a+(-b)x-2,令f'(x)=0,计算得到b=ax2,结果仍然是x=sqrt(b/a),如果需要的话算出f(x)就行了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十周 对勾函数模型重点知识梳理1.对勾函数定义对勾函数是指形如:y =ax +b x (ab >0)的一类函数,因其图象形态极像对勾,因此被称为“对勾函数”,又被称为“双勾函数”、“勾函数”、“耐克函数”或“耐克曲线”.2.对勾函数y =ax +b x (a >0,b >0)的性质(1)定义域:(-∞,0)∪(0,+∞).(2)值域:(-∞, ]∪[,+∞).(3)奇偶性:在定义域内为奇函数.(4)单调性:(-∞,-b a ),(ba ,+∞)上是增函数;(-ba ,0),(0,b a )上是减函数. (5)渐近线:y 轴与y=ax(或y=-ax)3.y =ax +b x (a >0,b >0)的单调区间的分界点:±b a .求分界点方法:令ax =b x ⇒x =±ba . 特殊的,a >0时,y =x +a x 的单调区间的分界点:±a .4.对勾函数应用时主要是利用对勾函数单调性求其最值,解题时要先找出对应的单调区间,然后求解.5.利用对勾函数求最值,常常用到如下的重要不等式:若a >0,b >0,则x >0时,ax +b x ≥2ab .当且仅当ax =b x ,x =ba 时取等号.在应用这个不等式时,要注意使用的前提条件是“一正、二定、三相等”,即加号两边的项ax 和b x 都是正项,且二者乘积为定值,同时ax =b x 中等号可取到.若等号取不到,则应根据对勾函数单调性求解.典型例题剖析例1 已知f (x )=x +5x ,求f (x )在下列区间的最小值.(1)[1,2]; (2)[3,4]; (3)[-3,-1].【解析】如图,f (x )在 (-∞,-5),(5,+∞)上是增函数,在(-5,0),(0,5)上是减函数.(1)由对勾函数性质可知f (x )在[1,2]上单调递减,∴f (x )min =f (2)=412.(2)因为f (x )在[3,4]上单调递增,所以f (x )min =f (3)=423.(3)因为f (x )在[-3,- 5 ]上单调递增,在(-5,-1]上单调递减,且f (-3)=-423,f (-1)=-6,所以f (x )min =-6.变式训练 已知函数f (x )=x 2+5x 2+4,求f (x )的最小值,并求此时x 的值. 【解析】f (x )=x 2+5x 2+4=x 2+4+1x 2+4=x 2+4+1x 2+4令t =x 2+4,则t ≥2,y =t +1t .∵y =t +1t 在[2,+∞)单调递增,∴当t =2时,y min =2+12=52,此时,x 2+4=2,x =0.综上,f (x )的最小值为52,此时x 的值为0.例2 求函数f (x )=x 2-2x -1x +2(0≤x ≤3)的值域. 【解析】令t =x +2,则x =t -2, 2≤t ≤5,y =(t -2)2-2(t -2)-1t=t 2-6t +7t =t +7t -6,2≤t ≤5.∵y =t +7t -6在[2,7 ]上单调递减,在[7, 5]上单调递增,∴当t =7时,y min =27-6,且当t =2时,y =2+72-6=-12,当t =5时,y =5+75-6=25,∴y max =25.综上,f (x )的值域为[27-6,25].变式训练 求函数f (x )=x 2-4x +12x -1,x ∈[]2,5的值域. 【解析】f (x )=x 2-4x +12x -1=(x -1)2-2(x -1)+9x -1=x -1+9x -1-2, 令t =x -1,则f (t )=t +9t -2,t ∈[1,4].结合y =t +9t 的图象与性质,可知当t ∈[1,3]时,函数单调递减,当t ∈[3,4]时,函数单调递增,又f (1)=8,f (3)=4,f (4)=174,所以f (x )∈[4,8].例3 某工厂去年的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n 次投入后,每只产品的固定成本为g (n )=kn +1(k >0,k 为常数,n ∈Z 且n ≥0),若产品销售价保持不变,第n 次投入后的年利润为f (n )万元.(1)求k 的值,并求出f (n )的表达式;(2)问从今年算起第几年利润最高最高利润为多少万元【解析】(1)由g (n )=kn +1,当n =0时,由题意,可得k =8,所以f (n )=(100+10n )(10-8n +1)-100n (n ∈Z 且n ≥0).(2)由f (n )=(100+10n )(10-8n +1)-100n =1 000-80(n +1+9n +1) ≤1 000-80×29=520,当且仅当n +1=9n +1,即n =8时取等号,所以第8年工厂的利润最高,最高为520万元.变式训练 建筑一个容积为800米3,深8米的长方体水池(无盖).池壁,池底造价分别为a 元/米2和2a 元/ 米2.底面一边长为x 米,总造价为y .写出y 与x 的函数式,问底面边长x 为何值时总造价y 最低,是多少【解析】长方体底面积S =8008=100米2,地面一边长为x 米,因此另一边长为100x 米, 池壁总面积为8·(2x +200x )米2,∴ 总造价y =100×2a +(2x +200x )·8·a=200a +16a (x +100x )(x >0).∵函数y =200a +16a (x +100x )在(0,10]上是减函数,在(10,+∞)上是增函数,∴ 当x =10时,总造价最低,且y min =520a (元).跟踪训练1.下列函数中最小值是4的是( )A .y =x +4xB .y =x +2xC .y =21+x +21-xD .y =x 2+1x 2+1+3,(x ≠0) 2.函数y =x +4x ,x ∈(1,3]的值域为( )A .[133,5)B .[4,5)C .[133,4)D .(4,5)3.函数y =-x +41-x+3,x ∈[)-1,0的值域为____________. 4.y =2x 2+31+x 2的最小值是________. 5.已知x >0,则2+x +4x 的最小值是________.6.函数y =x +3x 在区间[1,2]上的最小值为____________.7.若函数y =x +a x (a >0)在区间(5,+∞)上单调递增,则a ∈________________.8.建造一个容积为8m 3,深为2 m 的无盖水池,如果池底与池壁的造价每平方米分别是120元和80元,则水池的最低造价为____________元.9.某房地产开发公司计划在一楼区内建造一个长方形公园ABCD ,公园由长方形休闲区A 1B 1C 1D 1和环公园人行道(阴影部分)组成.已知休闲区A 1B 1C 1D 1的面积为4 000 m 2,人行道的宽分别为4 m 和10 m(如图所示).(1)若设休闲区的长和宽的比A 1B 1B 1C 1=x ,求公园ABCD 所占面积S 关于x 的函数解析式; (2)要使公园所占面积最小,休闲区A 1B 1C 1D 1的长和宽应如何设计10.如图,某单位准备修建一个面积为600平方米的矩形场地(图中ABCD)的围墙,且要求中间用围墙EF隔开,使得ABEF为矩形,EFDC为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为800元每米,设围墙(包括EF)的修建总费用为y元.(1)求出y关于x的函数解析式;(2)当x为何值时,设围墙(包括EF)的的修建总费用y最小并求出y的最小值.11.已知函数f (x )=x 2+2x +3x(x ∈[2,+∞)). (1)求f (x )的最小值;(2)若f (x )>a 恒成立,求a 的取值范围.12.已知函数f (x )=x +a x ,x ∈[1,+∞),a >0.(1) 当a =12时,求函数f (x )的最小值;(2) 若函数f (x )的最小值为4,求实数a .13.为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C (单位:万元)与隔热层厚度x (单位:cm)满足关系:C (x )=k 3x +5(0≤x ≤10,k 为常数),若不建隔热层,每年能源消耗费用为8万元.设f (x )为隔热层建造费用与20年的能源消耗费用之和.(1)求k 的值及f (x )的表达式;(2)隔热层修建多厚时,总费用f (x )达到最小并求出最小值.参考答案1.C A 选项,由于x 可取负值,显然最小值不是4,排除A ;B 选项,由于x 可取负值,显然最小值也不是4,排除B ;C 选项,由于y =2·2x +22x =2(2x +12x ),换元,令t =2x ,t >0,则y =2(t +1t )≥4,当且仅当t =1即x =0时,函数有最小值4,D 选项,由于y =x 2+1x 2+1+3=x 2+1+1x 2+1+2,换元,令t =x 2+1,t >1, 则y =t +1t +2,函数在(1,+∞)上单调递增,因此y >4,排除D 选项. 综上,答案为C.2.B 由对勾函数性质可知,当x =4x ,即x =2时,表达式有最小值4,又函数在(1,2)上单调递减,在(2,3]上单调递增, f (1)=5,f (3)=3+43=133,所以值域为[4,5),答案为B.3.[6,7)解析 y =-x +41-x +3=1-x +41-x+2, 换元,令t =1-x ,则x ∈[)-1,0时t ∈(1,2],y =t +4t +2,函数在(1,2]上单调递减,若t =1,则y =1+41+2=7,若t =2,则y =2+42+2=6,故函数值域为[6,7).4.26-2解析 换元,令t =1+x 2,则t ≥1,x 2=t -1,y =2(t -1)+3t =2t +3t -2,函数在[1,32]上单调递减,在[32,+∞)上单调递增, 所以当t =32时,函数有最小值26-2. 5.6解析 由对勾函数性质可知,当x =4x ,即x =2时,表达式有最小值6.6.23解析 因为y =x +3x 在区间[1,3 ]上单调递减,在[3,2]上单调递增,所以当x =3时函数有最小值2 3.7.(0,5]8.1 760解析 池底面积为82=4 cm 2,设池底宽为x cm ,则长为4x cm ,则水池的造价为4×120+2(4x ×2+x ×2)×80=480+1 280x +320x ≥480+2 1 280x ×320x =1 760. 9.解析 (1)设休闲区的宽为a 米,则其长为ax 米.由a 2x =4 000,得a =2010x, 则S =(a +8)(ax +20)=a 2x +(8x +20)a +160=4 000+(8x +20)·2010x+160 =8010(2x +5x)+4 160, 即S =8010(2x +5x)+4 160. (2)S =8010(2x +5x )+4 160≥16010·10+4 160=5 760, 当且仅当2x =5x,即x =时取等号,此时a =40, ax =100.所以要使公园所占面积最小,休闲区A 1B 1C 1D 1应设计为长100米,宽40米.10.解析 (1)设AD =t 米,则由题意得xt =600,且t >x ,故t =600x >x ,可得0<x <106,则y =800(3x +2t )=800(3x +2×600x )=2 400(x +400x ),所以y 关于x 的函数解析式为y =2 400(x +400x )(0<x <106).(2)y =2400(x +400x )≥2 400×2x ·400x =96 000, 当且仅当x =400x ,即x =20时等号成立.故当x 为20米时,y 最小.y 的最小值为96 000元.11.解析 (1)任取x 1,x 2∈[2,+∞),且x 1<x 2,f (x )=x +3x +2.则f (x 1)-f (x 2)=(x 1-x 2) (1-3x 1x 2), ∵x 1<x 2,∴x 1-x 2<0,又∵x 1≥2,x 2>2,∴x 1x 2>4,1-3x 1x 2>0, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).故f (x )在[2,+∞)上是增函数,∴当x =2时,f (x )有最小值f (2)=112.(2)∵f (x )>a 恒成立,∴只需f (x )min >a .又∵f (x )min =112,∴a <112.12.解析 (1) a =12时, f (x )=x +12x , x ∈[1,+∞).令x =12x (x >0),得x =22∉[1,+∞),∴不能用不等式求最值.设1≤x 1<x 2,则f (x 1)-f (x 2)=(x 1-x 2)+(12x 1-12x 2) =(x 1-x 2)(1-12x 1x 2)<0, ∴函数 f (x ) 在[1,+∞)上是单调递增函数,∴f min (x )=f (1)=32.(2)当0<a <1时,令x =a x ,得x =a <1,∵a ∉[1,+∞) ,∴类似于(1)可知函数f (x )在[1,+∞)上是单调递增函数, ∴f min (x )=f (1)=1+a =4,得a =3,与0<a <1不符(舍);当a ≥1时,a ≥1,∴由不等式知x +a x ≥2a ,当x =a x ,即x =a 时, f min (x )=2a =4,解得a =4.综上所述,函数f (x )的最小值为4时,a =4.13.解析 (1)依题意,当x =0 时,C =8,∴k =40 ,∴C (x )=403x +5,∴f (x )=6x +20×403x +5=6x +8003x +5(0≤x ≤10). (2)f (x )=2(3x +5)+8003x +5-10, 设3x +5=t ,t ∈[5,35],∴y =2t +800t -10≥22t ·800t -10=70,当且仅当2t =800t ,即t =20时等号成立.这时x =5 ,因此f (x )的最小值为70.即隔热层修建5 cm 厚时,总费用f (x )达到最小,最小值为70万元.特殊对勾函数f (x )=x +x1 2 3 4 f (x ) 4 3 2 2 2 3 4‘’(1)定义域:(-∞,0)∪(0,+∞).(2)值域:(-∞,-2 ]∪[2,+∞).(3)奇偶性:在定义域内为奇函数.(4)单调性:(-∞,-1),(1,+∞)上↗;(-1,0),(0,1)上↘.(5)分界点(拐点)坐标P(1,2) ; Q(-1,-2)(6)渐近线(7)Y=x和x=0。
