2013—2014学年度第一学期期中测试八年级数学检测题

合集下载

2013-2014学年度第一学期初二期中考试数学试卷(含答案)

2013-2014学年度第一学期初二期中考试数学试卷一、选择题：（每题3分，共15分）1．如图所示，图中不是轴对称图形的是 ( ).2．如图，AB 与CD 交于点O ，OA ＝OC ，OD ＝OB ，∠A=50°，∠B＝30°，则∠AOD 的度数为（）. A ．50° B ．30°C ．80°D ．100°3．点M （3，5）关于X 轴对称的点的坐标为（） A 、（－3，－5） B 、（－3，5） C 、（3，－5） D 、（5，－3）4．要测量河两岸相对的两点A 、B 的距离，先在AB 的垂线BF 上取两点C 、D ，使CD ＝BC ，再定出BF 的垂线DE ，使A 、C 、E 在同一条直线上（如图），可以证明，得ED ＝AB ，因此测得ED 的长就是AB 的长．判定△EDC ≌△ABC 的理由是（）A 、“边角边”B 、“角边角”C 、“边边边”D 、“斜边、直角边”5．如图，将△ABC 沿DE 、HG 、EF 翻折，三个顶点均落在点O 处.若1129∠=︒，则2∠的度数为（）（A ）50° （B ）51° （C ）61° （D ）71°第5题二、填空题：（每题4分，共20分）6．等腰三角形的底角是70°，则它的顶角是___________. 7．正方形有条对称轴，正五边形有条对称轴．8．如图，在△ABC 中，BC=5，BC 边上的垂直平分线 DE 交BC 、AB 分别于点D 、E ，△AEC 的周长是11 则△ABC 的周长等于。

O DCBA第2题ACED B第8题9．如图，等边△ABC 的边长为2 cm ，D 、E 分别是AB 、AC 上的点，将△ADE 沿直线DE 折叠，点A 落在点A ' 处，且点A '在△ABC 外部，则阴影部分图形的周长．．为 cm ．10．在直角坐标系中，已知A （-3，3），在x 轴上确定一点P ，使△AOP 为等腰三角形，符合条件的点P 共有_________个。

2013-2014学年八年级数学第一学期期中质量检测试卷 (新人教版第69套)

杭州市高桥初中教学集团2013-2014学年第一学期期中质量检测初二数学试卷新人教版(试卷总分120分考试时间：90分钟)一、仔细选一选（本题有10个小题，每小题3分，共30分）每小题只有一个选项是正确的，不选、多选、错选，均不给分。

注意可以用多种不同的方法来选取正确答案。

1.下列图形中，不一定是轴对称图形的是（）A.线段B.直角C.直角三角形D.等腰三角形2.下列四组线段中，可以构成直角三角形的是（）A. C.4,5,6 D.9,16,253.将一副常规的三角尺按如图方式放置，则图中∠AOB的度数为（）A.75°B.95°C.105°D.120°4、如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形够有（）A.2对B.3对C.4对°D.5对第3题图第4题图第6题图5、下列命题中是假命题的是( )A.两腰相等的两个三角形全等B. 直角三角形三条高相交于直角顶点C. 全等三角形对应边上的高相等D. 顶角和底边对应相等的两个等腰三角形全等6、如图，AD=BC=BA，那么∠1与∠2之间的关系是（）A．∠1=2∠2 B．2∠1+∠2=180° C．∠1+3∠2=180° D．3∠1-∠2=180°7、直角三角形两边长分别是3㎝和4㎝，则斜边上的中线长等于（）㎝A.2B. 2.5C.5D. 2或2.58.如图所示的正方形网格中，网格线的交点称为格点。

已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰直角三角形，则点C的个数是（）A．2 B．4 C．6 D．8第8题图第9题图第10题图9、有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形．再经过一次“生长”后，变成了右图，如果继续“生长”下去，它将变得“枝繁叶茂”．请你算出“生长”了n次后形成的图形中所有正方形的面积和是（）A.nB.n+1C.n2D.(n+1)210、如图：已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB、AC与E、F，给出一下五个结论：①PF=PE；②EF=AP；③2EP2=EF2；④∠E不与A、B重合），上述结论中始终正确的有（）A. 2个B. 3个C.4个D.5个二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案。

2013-2014学年人教版初二上期中考试数学试题含答案

迈陈中学2013-2014学年度八年级上册期中测试数学试卷（满分150分，考试时间90分钟）姓名：班级：座号：成绩：一、选择题：本大题共12小题，每小题4分，满分48分.在每小题给出的四个选项中，只有一项是符合题目要求的。

一、选择题（每小题3分，共30分）1、下面有4个汽车标志图案，其中是轴对称图形的是 ( )① ② ③ ④A 、②③④B 、①②③C 、①②④D 、①②④ 2、如图，已知MB =ND ,∠MBA =∠NDC ，下列条件中不能判定△ABM ≌△CDN 的是（）A ．∠M =∠NB ． AM ∥CNC ．AB = CD D ． AM =CN3、如图，△ABC ≌△CDA ，AB=5，BC=6，AC=7，则AD 的边长是--（）A ．5B ．6C ．7D ．不能确定4、已知等腰三角形的两边长分别为4cm 、8cm ，则该等腰三角形的周长是（）A ．12cmB ．16cmC ．16cm 或20cmD ．20cm5、已知:如图，AC=AE ，∠1=∠2，AB=AD ，若∠D=25°，则∠B的度数为 ( )A 、25°B 、30°C 、15°D 、30°或15°6、画∠AOB 的角平分线的方法步骤是：①以O 为圆心，适当长为半径作弧，交OA 于M 点，交OB 于N 点； ②分别以M 、N 为圆心，大于MN 21的长为半径作弧,两弧在∠AOB 的内部相交于点C ； ③过点C 作射线OC. 射线OC 就是∠AOB 的角平分线。

这样作角平分线的根据是 ( ) A 、SSS B 、SAS C 、 ASA D 、 AAS7、如图所示，已知△ABC 中，∠BAC ＝90°，AB ＝AC ，∠BAD ＝30°，AD ＝AE ，则∠EDC 的度数为（）A 、10°B 、15°C 、20°D 、30°ABDC MNADBC第5题第3题第2题8、在△ABC 内一点P 满足PA=PB=PC ，则点P 一定是△ABC ( )A 、三条角平分线的交点B 、三边垂直平分线的交点C 、三条高的交点D 、三条中线的交点 9、一个多边形的内角和是外角和的2倍，则这个多边形的边数是（） A 、4 B 、5 C 、6 D 、710、如图，点P 为∠AOB 内一点，分别作出点P 关于OA 、OB的对称点1P 、2P ，连接1P ，2P 交OA 于M ，交OB 于N ，若1P 2P ＝6，则△PMN 的周长为（） A 、4 B 、5 C 、6 D 、79．下列图形中：①平行四边形；②有一个角是30°的直角三角形；③长方形；④等腰三角形. 其中是轴对称图形有（）个 A ．1个B ．2个C ．3个D ．4个第10题图第11题图第12题图11．如图，ABC △中，AB AC =，30A ∠=，DE 垂直平分AC ，则B C D ∠的度数为（）Ａ．80 Ｂ．75 Ｃ．65 Ｄ．4512．如图所示，AB = AC ，要说明△ADC ≌△AEB ，需添加的条件不能．．是（） A ．∠B ＝∠CB. AD = AEC ．∠ADC ＝∠AEB D. DC = BE二、填空题：本大题共4小题，每小题4分，共16分）13、如图，在△ABC 中，∠C ＝90°，BD 平分∠ABC ，若CD ＝3cm ，则点D 到AB 的距离为____________cm.ABD ECA BCEDF14、如图把Rt △ABC （∠C=90°）折叠，使A 、B 两点重合，得到折痕ED •，•再沿BE 折叠，C 点恰好与D 点重合，则∠A 等于________度．15、已知点P 到x 轴、y 轴的距离分别是2和3，且点P 关于y 轴对称的点在第四象限，则点P 的坐标是．16、如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，CD 是斜边AB 上的高，若AB ＝8，则BD=__________.三、解答题（本大题共10小题，其中17-18每小题6分，19-22每小题8分，23-25每小题10分，26题12分，共86分。

2013—2014学年度第一学期期中联合调研测八年级数学试卷

•
A.三角形
B.四边形
D.六边形
• C.五边形
• 4.等腰三角形的周长为13cm，其中一边长为3,则该等腰三角形的底边长为( )
•
• C.9
A.7
D.5
B.3
• 5. 如图所示，分别表示△ABC的三边长，则下面不△一定全等的三角形是（）
第5题图
• 6．下列由数字组成的图形中，是轴对称图形的是( )．
• 7．如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个不书上完全一样的三角形，那么这两个三角形完全一样的依据是（） • A. SSS B. SAS • C. AAS D. ASA
• 8．若一个三角形三个内角度数的比为2：7：1，那么这个三角形是 • A．钝角三角形 • B．直角三角形 • C．锐角三角形 • D．等边三角形
A
E B D
F C
• 22.如图，△ABC中，AE是角平分线，且∠B=52°，∠C=78°，求∠AEB的度数
• 23．如图，已知 AC⊥BC,BD⊥AD,AC不BD交于点O，AC=BD， • 求证：BC=AD;
• 24．已知：如图，AB∥CD，AB＝CD．求证： AD∥BC． ∵ AB∥CD ∴ ∠ _____ ＝∠ _____ （），在△ABD和△CDB中， ______ =_____ _____ = _____ _____ =_____ ∴ △ABD≌Δ△CDB （）． ∴ ∠______＝∠______ （）． ∴ AD∥BC．（）．
• 25．△ABC在平面直角坐标系中的位置如图所示 (1)作出△ABC关于y轴对称的三角形△A1B1C1； (2)分别写出点A1 、B1 、C1的坐标和它们关于χ轴对称点A2 、 B2 、C2坐标。

2013～2014学年度第一学期期中质量检测八年级数学试题

2013～2014学年度第一学期期中质量检测八年级数学试题【友情提醒】全卷共三大题，23小题，满分150分，考试时间120分钟。

一、选择题（每小题4分，共40分）1．点A （5-，4）在第象限。

（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2．下列各曲线中，能够表示y 是x 的函数的是（）3．函数y =中自变量x 的取值范围是（） A ．x ≥3- B ．x ≥3-且1x ≠ C ．1x ≠ D ．3x ≠-且1x ≠ 4．下列语句是命题的是（）A ．平分一条线段B ．直角都相等C ．在直线AB 上取一点D ．你喜欢数学吗？5．一个三角形的两边长分别为3和8，则第三边长可能是（）A ．5B ．6C ．3D ．116．点1P （1x ，1y ）、2P （2x ，2y ）是一次函数b kx y +=（0<k ）图象上的两个点，且21x x <，则1y 与2y 的大小关系是（）A ．21y y >B ．21y y =C ．21y y <D ．无法确定 7．一个三角形三个内角的度数之比为2：3：7，这个三角形一定是（）A ．等腰三角形B ．直角三角形C ．锐角三角形D ．钝角三角形8．把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为（）A ．125°B ．120°C ．140°D ．130°9．如图，在棋盘上建立平面直角坐标系，若使“将”位于点（1-，2-），“象”位于点（4，1-），则“炮”位于点（） A ．（2，1-） B ．（1-，2） C ．（2-，1） D ．（2-，2） 10．下列四组点中，可以在同一个正比例函数图象上的一组点是（）A ．（2，3-）、（4-，6）B ．（2-，3）、（4，6）C ．（2-，3-）、（4，6-）D ．（2，3）、（4-，6）二、填空题（每小题5分，共20分）11．在直角坐标系中，把点A （3-，2）先向右平移3个单位，再向下平移2个单位，得到的点的坐标是。

2013-2014学年度上期期中考试八年级数学试题

2013-2014学年度上期期中考试八年级数学试卷一、选择题（3×7=21分）1.给出四个数－1，0，13 ,7 其中无理数是（）A .－1 B.0 C.13 D.72.估计 6 +1的值在（）A.2到3之间B.3到4之间C.4到5之间D.5到6之间 3.下列运算正确的是（）A. 4 =±2B.a 2·a 4=a 8C.(-2a 3)2=4a 6D.a 2+a 2=2a 4 4.下列各式因式分解错误的是（）A.1－9a 2=(1+3a)(1-3a)B.a 2-a+14 =(a －12)2C .－mx+my=－m(x+y)D .－1+14 a 2b 2=(12 ab+1)(12ab －1)5.以下列各组数据为边长能构成直角三角形的有（） ①6，7，8 ②8，15，17 ③7，24，25 ④12，35，37 A.1个 B.2个 C.3个 D.4个6.在一块平地上，张大爷家前9米远处有一棵大树，在一次强风中，这棵大树从离地6米处折断倒下，量得倒下部分的长是10米出门在外的张大爷担心，自己的房子被倒下的大树砸倒，大树倒下时能砸到张大爷的房子吗？（如（6题）图所示）正确选项是（）A.一定不会B.可能会C.一定会D.以上答案都不对 7.如图在矩形ABCD 中，点E 在边AB 上，将矩形ABCD 沿直线DE 折叠，点A 恰好落在边BC 上的F 处，若AB=8，AD=10，则EF 的长为__________A.3B.4C.5D.6 二、填空题（3×9=27分）8.27的立方根是a,16的算术平分根是b ，则b a=__________9.一个长方形面积为81m 2－25n 2，一边长为9m+5n ，则另一边长为__________ 10.若a+b=4,ab=3,则a 2+b 2=____________11.若代数式2a 2+3a+1的值为6，则代数式6a 2+9a+5的值为________12.如图示（单位：mm ）的矩形零件上两孔中心A 和B的距离为_______mm.（12题）（13题）（14题）13.如图所示分别以直角三角形ABC 三边长为直径作半圆，并且斜边AB=4，则面积S 1+S 2=______14.如图示，有一个圆柱它的高等于12cm ，底面半径等于3cm ，在圆柱下底面的A 点，有一只壁虎，它想吃到上底面与A 点相对的B 点处的小虫，则它需要爬行的最短路程为________cm(π=3)15.将4个数a,b,c,d排成两行，两列，两边各画一条竖线段记作a bc d定义a bc d=ad－bc上述记号就叫做二阶行列式若1111x xx x+--+=8，则x=________16.如图所示，在△ABC中，AB=AC=5,BC=6,点M是BC的中点，MN⊥AC于N，则MN=_____三、解答题（3×4=12分）（16题）17.计算（1）20012-2002×2000 （2）1002－992+982－972+…+22－1（3）（－2x2）·(－y)+3xy(1－13x) (4)(2a4+18a3-3a2)÷(-3a2)18.将下列多项式因式分解（4×4=16分）(1).2x3-8x (2) n(m-2)-2（2-m）(3)mn2+6mn+9m (4)(ab+a)+(b+1)19.化简再求值（16分）（1）a(a+b)－(a-b)(a+b)－b2其中a=0.252012 ,b=42012（2）已知x+y=12,xy=20,求x(x+y)(x-y)-x(x+y)2的值。

2013-2014学年八年级数学第一学期期中质量检测试卷 (新人教版第68套)

浙江省杭州市萧山区义蓬学区2013-2014学年第一学期期中质量检测八年级数学试卷请同学们注意：1、本试卷满分为120分，考试时间为 100 分钟；2、答题前，必须在答题卷的密封区内填写班级、学号、姓名；3、所有答案都必须写在答题卷标定的位置上，务必题号对应；4、考试结束后，只需上交答题卷。

一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，注意可以用多种不同的方法来选取正确答案1、如果21∠∠和是内错角，且401=∠，那么 2∠为 ……………………………（）A. 40B.50 C. 140 D.不能确定 2、等腰三角形两边长分别是2和6，则它的周长………………………………………（）A.8B.10C.14D.10或143、作一个角等于已知角用到下面选项的哪个基本事实………………………（） A ．SSS B ．SAS C ．ASA D ．AAS4、如图所示，AB=AC ，要说明△ADC ≌△AEB ，需添加的条件不能是…………………（） A. ∠B=∠C B.AD=AE C. ∠ADC=∠AEB D.DC=BE5、如图，要为一段高为5米，斜长为13米的楼梯铺上红地毯，则红地毯至少要的长度是………………………………………………………………………………………（） A.13米 B.12米 C.5米 D.17米第4题图第5题图第8题图 6、已知a>b,若c 是任意实数，则下列不等式中，总是成立的是………………………（） A ．a+c<b+c B ．a-c>b-c C ．ac<bc D ．ac>bc7、在△ABC 中，∠A ：∠B ：∠C=1：2：3，CD ⊥AB 于D ，AB=a ，则DB 等于…………（） A.2a B.3a C.4aD.以上结果都不对 8、如图，在△ABC 中，∠B=900,ED 是AC 的垂直平分线，交AC 于点D ，交BC 于点E ，已知∠BAE ＝１００，则∠C 的度数为（）A ．60０B ．50０ C.40０ D.30０9、一个三角形的一边长是(x+3)cm ，这边上的高是5cm ，它的面积不大于20cm 2,则………………………………………………………………………………（）第10题图A ．x ＞5B ．-3 ＜ x ≤5C ．x ≥ -3D ．x ≤510、如图，Rt △ABC 中，CF 是斜边AB 上的高，角平分线BD 交CF 于G ，DE ⊥AB 于E ，则下列结论①∠A=∠BCF ，②CD=CG=DE ，③AD=BD ，④BC=BE 中正确的个数是………………………………（）A.4B.3C.2D. 1 二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案 11、等边三角形的对称轴有条．12、如图,在△ABC 中,AB=AC,BAC 的角平分线交BC 于点D,AB=5,BC=6,则AD=（第12题图）（第13题图）（第14题图）（第16题图）13、如图，在△ABC 中，AB=AC=9，∠BAC=1200，AD 是△ABC 的中线，AE 是△ABD 的角平分线，DF ∥AB ，交AE 延长线于点F ，则DF 的长为 .14、如图,点B,D 在射线AM 上, 点C,E 在射线AN 上,且AB=BC=CD=DE,已知∠EDM=840,则∠A= 0.15、已知关于x 的不等式2<(1-a)x 的解集为 ,则a 的取值范围是 .16、如图所示，将长方形ABCD 沿直线EF 对折，使顶点A 与C 重合在一起，折痕EF 分别交CD 、AB 于点F,E 交对角线AC 相交于点O ，已知AB=18cm ，BC=12cm. (1)连结AF ，则AF= cm ；(2)折痕EF= cm.三、全面答一答（本题有7个小题，共66分）解答应写出文字说明，证明过程或推演步骤。

2013-2014学年度八年级数学第一学期期中监测试卷 (新人教版第8套)

北京市朝阳区2013—2014学年度第一学期期中监测八年级数学试卷一、选择题（每小题3分，共24分）1、以下列各组线段为边，不能组成三角形的是( ) A ．1cm ，2cm ，3cm B ．2cm ，3cm ，4cm C ．1cm ，2cm ，2cmD ．2cm ，2cm ，3cm2、下面有4个汽车标志图案，其中是轴对称图形的是( )① ② ③ ④ A.②③④ B.①②③ C.①②④ D.①③④ 3、正多边形的一个外角等于30°，则这个多边形的边数是( ) A ．6 B ．9 C ．12 D ．15 4、下列计算正确的是( )A.2322=-a aB.532)(a a =C.963a a a =⋅D.4222)2(a a = 5、如图E 、B 、F 、C 四点在一条直线上, EB=CF, ∠A=∠D ，再添一个条件仍不能证明ABC ∆≌DEF ∆的是( ) A ．DF ∥AC B ．AB=DE C ．AB ∥DE D ．∠E=∠ABC 6、等腰三角形的一个角是40°，则它的顶角是（） A.40° B.70° C.100° D. 40°或100°7、已知32=n x ，则n n x x 2223)(4)91(⋅的值是（）A.12B.31C.27D.2718、如图，△ABC 中，AB ＝AC ，AD ⊥BC 于D ，DE ⊥AB 于E ，DF ⊥AC 于F ，下列结论：①AD 平分∠BAC ，②DA 平分∠EDF ，③AE ＝AF ，④AD 上的点到AB 、AC 两边距离相等，其中正确的有( ) A ．1个 B ．2个 C ．3个 D ．4个二、填空题（每空3分，共24分）9、计算：322)()3(ab b a ⋅-= 。

第5题图ABFCDFECB A第8题图10、△ABC 中，已知∠B＝40°，∠C 的外角等于100°，则∠A ＝ ° 11、如图：已知∠1=∠2，要根据SAS 判定ABD ACD △≌△，则需要补充的条件为。

2013-2014八年级数学上学期期中考试参考答案

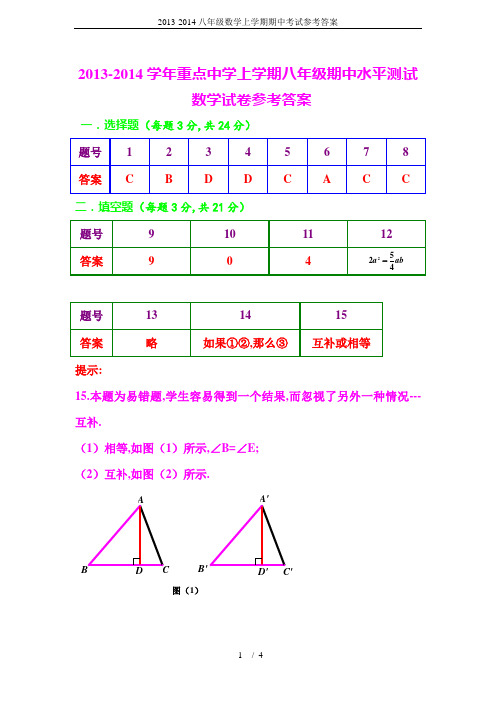
2013-2014学年重点中学上学期八年级期中水平测试数学试卷参考答案一．选择题（每题3分,共24分）二．填空题（每题3分,共21分）提示:15.本题为易错题,学生容易得到一个结果,而忽视了另外一种情况---互补.（1）相等,如图（1）所示,∠B=∠E; （2）互补,如图（2）所示.图（1）B'图（2）题后记:同学们应该对此类题目引起足够的重视,通过加强对此类题目的训练,使自己初步具备分类讨论的思想,从而使自己的思维变得更加严密、严谨!三．解答题（共75分）16.解:（1）原式()()y x y x 23232---=()()1223---=y x y x （2）原式229124y xy x +-= ()232y x -=（3）原式242436223++--+=a a a a a 22623++-=a a a（注意:本题的结果应按字母a 的降幂顺序排列）（4）原式[]()b a b a a b a b -÷---=2)2(2)2(4 a b 24-=17.（1）解: []x xy y y x 224)2(22÷+--()()y x xxy x xxy y y xy x -=÷-=÷+-+-=2122224442222当2,1==y x 时原式232121-=-⨯=（2）()()()()221311714x x x x -++--+()()()1423637748421317124222222+=+-++-++=+-+--++=x x x x x x x x x x x当21-=x 时原式1314221=+⨯-=18.解:()()212=---y x x x()()()()2222222222222222222=-=-=-+-=-+-=-+∴-=-=+-=+--y x xy xy y x xy xyy x xy y x y x y x y x x x19.在平地任找一点O,连OA 、OB,延长AO 至C 使CO=AO,延BO 至D,使DO=BO,则CD=AB,依据是△AOB ≌△COD （SAS ）,图形略. 20.证明:在△ABC 和△BAD 中∵⎪⎩⎪⎨⎧=∠=∠∠=∠BA AB D C 12 ∴△ABC ≌△BAD （AAS ）∴AC=BD. 21.答案不唯一,略. 22.解:（1）∵∠C=90° ∴DC ⊥AC∵AD 平分∠BAC,DE ⊥AB ∴DC=DE在Rt △CDF 和Rt △EDB 中∵⎩⎨⎧==DEDC DB DF ∴Rt △CDF ≌Rt △EDB （HL ）;（2）在△BDE 中,由三角形三边之间的关系得 BE+DE>DB ∵DB=DF ∴BE+DE>DF.23.提示:（1）又因为AB ＝A 1B 1,∠ADB ＝∠A 1D 1B 1＝90°.所以△ADB ≌△A 1D 1B 1,所以∠A ＝∠A 1,又∠C ＝∠C 1,BC ＝B 1C 1,所以△ABC ≌△A 1B 1C 1.（2）由题设和（1）我们可以得到下列结论:若△ABC 、△A 1B 1C 1均为锐角三角形或均为直角三角形或均为钝角三角形,AB ＝A 1B 1,BC ＝B 1C 1,∠C ＝∠C 1,则△ABC ≌△A 1B 1C 1.。

2013-2014年八年级上册数学期中试卷及答案

2013~2014学年第一学期考试八年级数学试卷题号一二三四五六总分得分一、选择题（每题3分，共30分）1、在△ABC 和△DEF 中，AB=DE, ∠B=∠E,如果补充一个条件后不一定能使△ABC ≌△DEF ，则补充的条件是（）A 、BC=EFB 、∠A=∠DC 、AC=DFD 、∠C=∠F 2、下列命题中正确个数为（） ①全等三角形对应边相等；②三个角对应相等的两个三角形全等； ③三边对应相等的两个三角形全等； ④有两边对应相等的两个三角形全等.A ．4个B 、3个C 、2个D 、1个3、已知△ABC ≌△DEF ，∠A=80°，∠E=40°，则∠F 等于（） A 、 80° B 、40° C 、 120° D 、 60°4、已知等腰三角形其中一个内角为70°，那么这个等腰三角形的顶角度数为（）A 、70°B 、70°或55° C、40°或55° D 、70°或40°5、如右图，图中显示的是从镜子中看到背后墙上的电子钟读数，由此你可以推断这时的实际时间是（）A 、10:05B 、20:01C 、20:10D 、10:026、等腰三角形底边上的高为腰的一半，则它的顶角为（） A 、120° B 、90° C 、100° D 、60°7、点P （1，-2）关于x 轴的对称点是P 1，P 1关于y 轴的对称点坐标是P 2，则P 2的坐标为（）A 、（1，-2）B 、(-1，2)C 、(-1，-2)D 、（-2，-1） 8、已知()22x -+=0，求y x 的值（）A 、-1B 、-2C 、1D 、29、如图，DE 是△ABC 中AC 边上的垂直平分线，如果BC=8cm ，AB=10cm ，则△EBC 的周长为（）A 、16 cmB 、18cmC 、26cmD 、28cm10、如图，在△ABC 中，AB=AC ，AD 是BC 边上的高，点E 、F 是AD 的三等分点，若△ABC 的面积为122cm ，则图中阴影部分的面积为（）A 、2cm ²B 、4cm²C 、二、填空题（每题4分，共20分） 11、等腰三角形的对称轴有条. 12、（-0.7）²的平方根是 . 13、若2)(11y x x x +=-+-，则x-y= .14、如图，在△ABC 中，∠C=90°AD 平分∠BAC ，BC=10cm ，BD=6cm ，则点D 到AB 的距离为＿＿ .FED CAE DCBACD第9题图第10题图第14题图15、如图，△ABE ≌△ACD ，∠ADB=105°，∠B=60°则∠BAE= . 三、作图题（6分）16、如图，A 、B 两村在一条小河的同一侧，要在河边建一水厂向两村供水．（1）若要使自来水厂到两村的距离相等，厂址P 应选在哪个位置？（2）若要使自来水厂到两村的输水管用料最省，厂址Q 应选在哪个位置？请将上述两种情况下的自来水厂厂址标出，并保留作图痕迹．四、求下列x 的值（8分）17、 27x ³=-343 18、 (3x-1)²=(-3)²五、解答题（5分）19、已知5+11的小数部分为a ，5－11的小数部分为b ，求 (a+b)2012的值。

2013-2014学年八年级数学第一学期期中学习质量检测试卷 (新人教版第67套)

杭州市萧山区2013-2014学年第一学期期中学习质量检测八年级数学试卷(试卷总分120分考试时间：90分钟)一、仔细选一选（本题有10个小题，每小题3分，共30分）(下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内，注意可以用多种不同的方法来选取正确答案。

) 1.亲爱的同学们，你一定喜欢QQ 吧?以下这四个QQ 表情中哪个不是轴对称图形（）A.第一个B.第二个C.第三个D.第四个2.如图，△ABC 中，延长BC 到点D ，若∠ACD=123°，∠B=45°，则∠A 为（） A.12° B. 88° C.78° D. 68°3.一个三角形三个内角的度数之比为2：3：5，这个三角形一定是（）A. 直角三角形B.等腰三角形C.锐角三角形D.钝角三角形 4、如图，在△ABC 和△DEF 中，已有条件AB=DE ，还需要添加两个条件才能使△ABC ≌△DEF ，不能添加的一组条件是（） A. ∠B=∠E ，BC=EF B. BC=EF ，AC=DF C. ．∠A=∠D ，∠B=∠E D. ∠A=∠D ，BC=EF5、下列几组数中，不能作为直角三角形三边长度的是( ) A.a=6 ,b=8 , c= 10; B. a=1.5 ,b=2 , c=2.5 ; C. a=32 ,b=2 , c=45; D. a= 15,b=8 , c=17 6、如图，这是我国古代一个数学家构造的“勾股圆方图”（见课本第76页），他第一个利用此图证明了“勾股定理”。

这个数学家是（） A.祖冲之 B. 杨辉 C.赵爽 D. 华罗庚7、如图，△ABC 中，AB=AC ，E 为AB 的中点，BD ⊥AC ，若∠DBC=α，则∠BED 为（）A.3αB. 4αC.90°+ αD. 180°-2α8.设M 表示直角三角形，N 表示等腰三角形，P 表示等边三角形，Q表示等腰直第2题图DCBA第7题图EDCBA角三角形，则下列四个图中，能表示它们之间关系的是（）A ．B ．C ．D ．9、如图，在锐角△ABC中，∠BAC=45°，AB=2，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（）A.1B.1.5C.2D. 310、下列命题：（1）斜边和一条直角边对应相等的两个直角三角形全等.（2）若三角形一个外角的平分线平行于第三边，则这个三角形是等腰三角形；（3）三角形的外角必大于任一个内角；（4）若直角三角形斜边上一点（除两个端点外）到直角顶点的距离是斜边的一半，则这个点必是斜边的中点.其中是真命题的有（）A. 1个B. 2个C.3个D.4个二、认真填一填（本题有6个小题，每小题4分，共24分）(要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案。

2013-2014学年鲁教版(五四学制)八年级数学上册期中复习检测题含答案详解

期中检测题（时间：120分钟，满分：120分）一、选择题（每小题3分，共36分）1. 若，都是实数，且则的值为（）A.0B.C.2D.不能确定2. 当=2时，下列分式有意义的是（）A ．B ．C ．D ．3. 小明骑自行车沿公路以km/h的速度行走全程的一半，又以b km/h的速度行走余下的一半路程；小刚骑自行车以km/h的速度行走全程时间的一半，又以b km/h的速度行走另一半时间（≠b），则谁走完全程所用的时间较少？（）A．小明B．小刚C．时间相同D．无法确定4. 某商店销售一种玩具，每件售价92元，可获利15%，求这种玩具的成本价．设这种玩具的成本价为元，依题意列方程正确的是（）A ．=15%B ．=15%C．92-=15%D．=92×15%5. 下列各组数中，成比例的是（）A．-7，-5，14，5B．-6，-8，3，4C．3，5，9，12D．2，3，6，126.“标准对数视力表”对我们来说并不陌生，如图是视力表的一部分，其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形（）A.左上B.左下C.右上D.右下7. 如图，设M、N分别是直角梯形ABCD两腰AD、CB的中点，DE⊥AB于点E，将△ADE沿DE翻折，M与N恰好重合，则AE∶BE 等于（）A．2∶1B．1∶2C．3∶2D．2∶38. 如果三角形的每条边都扩大为原来的5倍，那么三角形的每个角（）A．都扩大为原来的5倍B．都扩大为原来的10倍C．都扩大为原来的25倍D．都与原来的相等第6题图第7题图第9题图9. 如图，等边三角形ABC 的边长为3，点P 为BC 边上一点，且BP =1，点D 为AC 边上一点，若∠APD =60°，则CD 的长为（） A. B. C. D.110. 如图，在平行四边形ABCD 中，E 为AB 的中点，F 为AD 上一点，EF 交AC 于G ，AF =2cm ，DF =4cm ，AG =3cm ，则AC 的长为（）A ．9cmB ．14cmC ．15cmD ．18cm11. 如图，在平行四边形ABCD 中（AB ≠BC ），直线EF 经过其对角线的交点O ，且分别交AD 、BC 于点M 、N ，交BA 、DC 的延长线于点E 、F ，下列结论：①AO =BO ；②OE =OF ； ③△EAM ∽△EBN ；④△EAO ≌△CNO ，其中正确的是（） A ．①② B ．②③ C ．②④ D ．③④12. 如图所示是小孔成像原理的示意图，根据图中所标注的尺寸，这支蜡烛在暗盒中所成的像CD 的长是（）A ．16cm B ．13cm C ．12cm D ．1cm 二、填空题（每小题3分，共24分）13. 已知=1，则分式的值为.14. 某市今年起调整居民用水价格，每立方米水费上涨20%，小方家去年12月份的水费是26元，而今年5月份的水费是50元．已知小方家今年5月份的用水量比去年12月份多8立方米，设去年居民用水价格为元/立方米，则所列方程为.15.张明与李强共同清点一批图书，已知张明清点完200本图书所用的时间与李强清点完300本图书所用的时间相同，且李强平均每分钟比张明多清点10本，则张明平均每分钟清点图书本.16. 现有含盐20%的盐水50千克，在此盐水中再加入千克水后，盐水的浓度（用表示）是.17. 现有四个代数式，分别为2+1、35、、2π，从中取出两个代数式，则可以组成的分式是．（写出一种即可）18. 某车间加工120个零件后，采用了新工艺，工效是原来的1.5倍，这样加工120个零件第10题图第11题图第12题图就少用1小时，采用新工艺前每小时加工多少个零件？若设采用新工艺前每小时加工个零件，则根据题意可列方程为．19. 为了测量校园内一棵不可攀的树的高度，学校数学应用实践小组做了如下的探索：根据光的反射定律，利用一面镜子和皮尺，设计如图所示的测量方案：把镜子放在离树（AB ）8.7m 的点E 处，然后观测者沿着直线BE 后退到点D ，这时恰好在镜子里看到树梢顶点A ，再用皮尺量得DE =2.7m ，观测者目高CD =1.6m ，则树高AB约是．（精确到0.1m ） 20. 如图（1），将一个正六边形各边延长，构成一个正六角星形AFBDCE ，它的面积为1，取△ABC 和△DEF 各边中点，连接成正六角星形A 1F 1B 1D 1C 1E 1，如图（2）中阴影部分；取△A 1B 1C 1和△D 1E 1F 1各边中点，连接成正六角星形A 2F 2B 2D 2C 2E 2，如图（3）中阴影部分；如此下去，则正六角星形A n F n B n D n C n E n 的面积为.三、解答题（共60分）21.（6分）先化简，再求值：，其中满足2--1=0．22.（6分）已知a 、b 、c 为实数，且满足，求的值.23.（8分）已知：如图，是上一点，∥，，分别交于点，∠1=∠2，探索线段之间的关系，并说明理由.24.（8分）小明的数学作业中有一道题为：“如图，E 为平行四边形ABCD 的边BA 延长线上一点，连接EC ，交第20题图第24题图第25题图第23题图第19题图AD 于点F ．若AE =2，EF =1.4，CF =3.5，DF =5，求平行四边形ABCD 的周长．”小明已经探索出△AEF ∽△DCF ，请你继续帮他完成本题．25.（8分）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC 的顶点都在格点上，建立平面直角坐标系．（1）点A 的坐标为，点C 的坐标为.（2）将△ABC 向左平移7个单位，请画出平移后的△A 1B 1C 1．若M 为△ABC 内的一点，其坐标为（，b ），则平移后点M 的对应点M 1的坐标为.（3）以原点O 为位似中心，将△ABC 缩小，使变换后得到的△A 2B 2C 2与△ABC 对应边的比为1∶2．请在网格内画出△A 2B 2C 2，并写出点A 2的坐标：.26.（8分）甲、乙两辆汽车同时分别从A 、B 两城沿同一条高速公路匀速驶向C 城．已知A 、C 两城的距离为360km ，B 、C 两城的距离为320km ，甲车比乙车的速度快10km/h ，结果两辆车同时到达C 城．设乙车的速度为km/h ．（1）根据题意填写下表：行驶的路程（km ）（2）求甲、乙两车的速度．27.（8分）如图是小红设计的钻石形商标，△ABC 是边长为2的等边三角形，四边形ACDE 是等腰梯形，AC ∥ED ，∠EAC =60°，AE =1．（1）证明：△ABE ≌△CBD ；（2）图中存在多对相似三角形，请你找出一对进行证明，并求出其相似比（不添加辅助线，不找全等的相似三角形）；（3）小红发现AM =MN =NC ，请证明此结论；（4）求线段BD 的长．28.（8分）如图，D 是△ABC 的边BC 的中点，过AD 延长线上的点E 作AD 的垂线EF ，E 为第27题图第28题图垂足，EF与AB的延长线相交于点F，点O在AD上，AO=CO，BC∥EF．（1）证明：AB=AC；（2）证明：AO=BO=CO；（3）当AB=5，BC=6时，连接BE，若∠ABE=90°，求AE的长．期中检测题参考答案1.C 解析：要使原式有意义则，则，所以,所以,所以故选C.2.D 解析：A、当=2时，-2=0，无意义；B、当=2时，||-2=0，无意义；C、当=2时，2-3+2=4-6+2=0，无意义；D、当=2时，2-+2=4-2+2=（-1）2+3＞0，有意义．故选D．3.B 解析：设全程为1，小明所用时间是.设小刚走完全程所用时间是小时．根据题意，得+b=1，=．则小刚所用时间是．小明所用时间减去小刚所用时间得＞0，即小明所用时间较多．故选B．4.A 解析：设这种玩具的成本价为元，则=15%．故选A．5.B 解析：因为只有B 中，故选B．6.B 解析：根据位似变换的特点可知：最上面较大的“E”与左下角较小的“E”是位似图形．故选B．7.A 解析：连接MN，设DE与MN交于点F，∵M、N分别是AD、CB上的中点，∴MN∥AB.又∵M是AD的中点，∴MF =AE.又∵翻折后M、N重合，∴MF=NF.又∵梯形ABCD是直角梯形，DE⊥AB，∴FN=EB，∴AE∶BE=2MF∶NF=2∶1，故选A．第7题答图8.D 解析：三角形的每条边都扩大为原来的5倍，则扩大后的三角形与原三角形相似，两个相似的三角形，对应角相等，所以三角形的每个角都与原来的相等，故选D.9.B 解析：∵ ∠APC =∠ABP +∠BAP =60°+∠BAP =∠APD +∠CPD =60°+∠CPD ，∴ ∠BAP =∠CPD ．又∵ ∠ABP =∠PCD =60°，∴ △ABP ∽△PCD ．∴，即．∴ CD =．故选B ．10.C 解析：如图，延长CB 交FE 的延长线于点H .∵ 四边形ABCD 是平行四边形， ∴ BC =AD =AF +FD =6(cm)，BC ∥AD ． ∴ ∠EAF =∠EBH ，∠AFE =∠BHE .又AE =BE ，∴ △AFE ≌△BHE ，∴ BH =AF =2cm ． ∵ BC ∥AD ，∴，即，则CG =12 cm ，则AC =AG +CG =15（cm ）．故选C ．11.B 解析：①平行四边形中邻边垂直，则该平行四边形为矩形，则对角线相等，本题没体现此四边形为矩形，故本题中AC ≠BD ，即AO ≠BO ，故①错误； ②∵ AB ∥CD ，∴ ∠E =∠F .又∵ ∠EOA =∠FOC ，AO =CO ,∴ △AOE ≌△COF ，∴ OE =OF ，故②正确； ③∵ AD ∥BC ，∴ △EAM ∽△EBN ，故③正确；④∵ △AOE ≌△COF ，且△FCO 和△CNO 不相似，故△EAO 和△CNO 不相似，故④错误. 即②③正确．故选B ．12.D 解析：过O 作直线OE ⊥AB ，交CD 于F ，依题意AB ∥CD,∴ OF ⊥CD,∴ OE =12，OF =2.而AB ∥CD 可以得△AOB ∽△COD.∵ OE ，OF 分别是它们的高, ∴，∴∴ CD =1（cm ）．故选D ．13.解析：当=1时，分子2-2-9=-10，分母22-4-13=-15，∴ 原分式=．14.=815.20 解析：设张明平均每分钟清点图书本，则李强平均每分钟清点图书（本，由题意列方程得，解得=20.经检验=20是方程的解．16.解析：因为含的盐有20%×50=10千克.加入千克水后，盐水有（50+）千克．浓度第10题答图．17.解析：可以组成的分式是：，等，答案不唯一,应注意为常数．18.19.5.2 m解析：由题意知∠CED=∠AEB，∠CDE=∠ABE=90°，∴△CED∽△AEB，∴，∴，∴AB≈5.2 m．20.解析：∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点，∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1，且相似比为2∶1.∵正六角星形AFBDCE的面积为1，∴正六角星形A1F1B1D1C1E1的面积为.同理可得，正六角星形A2F2B2D2C2E2的面积为，正六角星形A3F3B3D3C3E3的面积为，…，正六角星形A n F n B n D n C n E n 的面积为．21.解：原式=×=×=.∵2--1=0，∴2=+1，将2=+1代入化简后的式子得：==1．22.解：由题设有()()()⎪⎩⎪⎨⎧=-+-+-≠--,0432,023222cbacb可解得a＝2，3-=b，c＝－2.∴c b b a -+-11＝321321-++＝3232++-＝4. 23.解：. 理由：∵∥∴ ∠∠，又∴.又∵∴ △∽△，∴即.24.分析：根据相似三角形的对应边的比相等求得CD 、AF 的长，即可求得平行四边形的一组邻边，从而求其周长．解：∵ △AEF ∽△DCF ， ∴，即．∴ DC =5，AF =2． ∴ AD =AF +DF =2+5=7．∴ 平行四边形的周长=2（AD +DC ）=2×（5+7）=24． 25.分析：（1）直接根据图形即可写出点A 和C 的坐标；（2）找出三角形平移后各顶点的对应点，然后顺次连接即可，根据平移的规律即可写出点M 平移后的坐标；（3）根据位似变换的要求，找出变换后的对应点，然后顺次连接各点即可，注意有两种情况．解：（1）A 点的坐标为（2，8），C 点的坐标为（6，6）；（2）所画图形如图所示，其中△A 1B 1C 1即为所求，根据平移规律：向左平移7个单位，可知M 1的坐标为（-7，b ）；（3）所画图形如图所示，其中△A 2B 2C 2即为所求，点A 2的坐标为（1，4）或（-1，-4）． 26.分析：（1）设乙车的速度是km/h ，那么甲车的速度是（+10）km/h ，根据时间=可求甲、乙两辆汽车所需时间；（2）路程知道，且同时到达，可以以时间作为等量关系列方程求解．解：（1）由题意可求出甲的速度是（+10）km/h ，甲车所需时间是，乙车所需时间是.（2）依题意得：=，解得=80.经检验：=80是原方程的解，+10=90.第25题答图答：甲车的速度是90千米/时，乙车的速度是80千米/时．27.（1）证明：∵△ABC是等边三角形，∴AB=BC，∠BAC=∠BCA=60°．∵四边形ACDE是等腰梯形，∠EAC=60°，∴AE=CD，∠ACD=∠CAE=60°，∴∠BAC+∠CAE=120°=∠BCA+∠ACD，即∠BAE=∠BCD．在△ABE和△CBD中，AB=BC，∠BAE=∠BCD，AE=CD，∴△ABE≌△CBD．（2）解：如△ABN∽△CDN．（答案不唯一）证明如下：∵∠BAN=60°=∠DCN，∠ANB=∠DNC，∴△ANB∽△CND．∵AB=2，DC=AE=1，∴AB∶DC= 2∶1=2.∴△ANB与△CND的相似比为2.（3）证明：由（2）得AN∶CN= AB∶CD=2，∴CN= AN= AC，同理AM= AC，∴AM=MN=NC．（4）解：作DF⊥BC交BC的延长线于F，∵∠BCD=120°，∴∠DCF=60°．在Rt△CDF中，∵∠DCF=60°，∴∠CDF=30°，∴CF= CD= ，∴DF= ==.在Rt△BDF中，∵BF=BC+CF=2+ = ，DF=，∴BD= =．28.分析：（1）由BC∥EF，AD⊥EF，可证得AD⊥BC，又由D是△ABC的边BC的中点，即可得AD是线段BC的垂直平分线，则可证得AB=AC；（2）由AD是线段BC的垂直平分线，可证得OB=OC，又由AO=CO，则可得AO=BO=CO；（3）首先求得AD的长，又由△ABE∽△ADB，根据相似三角形的对应边成比例，即可求得AE的长．（1）证明：∵D是△ABC的边BC的中点，∴BD=CD.∵BC∥EF，AD⊥EF，∴AD⊥BC，∴AB=AC.（2）证明：∵BD=CD，AD⊥BC，∴BO=CO.∵AO=CO，∴AO=BO=CO.（3）解：∵AB=5，BC=6，AD⊥BC，BD=CD，∴BD=BC=3.∴在Rt△ABD中，AD=4.∵∠ABE=∠ADB=90°，∠BAE=∠DAB，∴△ABE∽△ADB，∴，即，∴AE=．。

2013——2014学年第一学期八年级数学期中试卷

B16925学__________________班____________________姓名___________________考场_______________座：装订线2013—2014学年第一学期八年级数学期中试卷一、选择题（每小题2分，共20分）1．下列几组数据:8, 15, 17；7, 12, 15； 12, 15, 20； 7, 24, 25. 其中能作为直角三角形三边长的有几组( )A.1B.2C.3D.42．如右图字母B 所代表的正方形的面积是 ( ) A.12 B. 13 C.144 D.194 3．81的平方根是（）A.±9B.9C.±3D.34．点P （m ＋3, m ＋1）在x 轴上，则点P 坐标为（） A.（0，－2） B.（ 2，0） C.（ 4，0） D.（0，－4） 5．下列等式不一定成立的是（）A.a a =2B.a a =33C.a a =2)(D.a a =33)(6．一次函数y=ax+b 的图像如图所示，则下面结论中正确的是（） A.a ＞0,b ＞0 B.a ＞0,b ＜0 C.a ＜0,b ＞0 D.a ＜0,b ＜07．在02）（-、22、0、9-、38、0.101001…、2π、722中，无理数的个数是（） A.2 B.3 C.4D.58．下列式子正确的是（）A.16=±4B.±16 =4C.2)4(- =-4 D.±2)4(- =±49．一辆汽车由淮安匀速驶往南京，下列图象中，能大致反映汽车距南京的路程s （千米）和行驶时间t （小时）的关系的是( )10.直角三角形两边长分别是3、4，第三边是（） A.5B.7C.5或7D.无法确定二．填空题（每小题3分，共30分）11．已知弹簧的长度 y （厘米）在一定的限度内是所挂重物质量 x （千克）的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7.2厘米.则y 与x 之间的关系式为 .12．将直线y=-2x+3向下平移2个单位得到的直线的解析式是 .13．点M(a,b)到x 轴的距离是4，到y 轴距离是3，且在第二象限，则点M 的坐标是 . 14．比较大小：3.15．点P （-1，2）关于y 轴对称的点的坐标是 . 16．函数y=-2x+3中，函数y 随x 的增大而 . 17．直线y=2x+4的图像经过点（m ，8），则m ＝ . 18．函数y=-x+3的不经过第象限.19．如图，有两棵树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从一棵树梢飞到另一棵树的树梢，至少飞了米.20．x 是9的平方根，y 是64的立方根，则y x +的值为 . 三、解答题（共70分）21．（4分）在数轴上作出13线段. 22．（4分）画出函数y=32-x +2的图象.23. 计算化简（16分）（1）3612⨯ （2）45 - 1255+ 3（3）)533()352(-+ （4）71+28－70024．解方程（8分）（1）049252=-x （2）8)2(3-=-xs t B O s t A O s t CO s tD OA B C BC A 25．（5分）已知一次函数y=kx+b 的图象经过点（0，1）和（3，-3）,求此一次函数表达式. 26．（5分）如图，正三角形ABC 的边长为 6 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .27．（6分）如图AC 是学校的旗杆,旗杆上的绳子AB 垂到地面还多出1米，如果把绳子的下端B拉开离C 点5米后，发现下端刚好接触地面，请你计算旗杆的高度和绳子的长度.28．（6分）某图书馆开展两种方式的租书业务：一种是使用会员卡，另一种是使用租书卡，使用这两种卡租书，租书金额y （元）与租书时间x （天）之间的关系如下图所示.①分别写出用租书卡和会员卡租书金额y 1、y 2（元）与租书时间x （天）之间的关系式. ②两种租书方式每天的收费是多少元？（x<100） 29．（8分）如图长方体长、宽、高分别为3、2、4，一只蚂蚁从A 点沿长方体的表面爬到B 点，爬行的最短路程是多少？30．（8分）求直线42+-=x y 与x 轴、y 轴的的交点坐标，与x 轴y 轴围成的三角形的面积.B。

11.23--2013-2014年度八年级数学第一学期期中试卷

八年级数学期中试题（ 2013.11）姓名成绩一、选择题（本大题共有9小题，每小题3分，共27分．）1.下列数中，无理数的个数是（）31-2π , 0 ,—. A ． 2 B. 3 C. 4 D. 52. 一个正方形的面积是13,估计它的边长大小在（）A ．2与3之间B ．3与4之间C ．4与5之间D ．5与6之间3. 线段MN 在直角坐标系中的位置如图所示，线段M 1N 1与MN 关于y 轴对称，则点M 的对应的点M 1的坐标为（） A ．(4，2) B ．(－4，2) C ．(4，－2) D ．(－4，－2) 4、已知点P （－3，－3），Q(－3,4)，则直线PQ( )A. 平行于X 轴B.平行于Y 轴C. 既不平行X 轴也不平于Y 轴D.以上都不正确5. 在下列长度的各组线段中，能组成直角三角形的是( )A. 5，6，7B. 1，4，9C. 6，15，17D. 9，12，156.如图是一张直角三角形的纸片，两直角边AC ＝6 cm 、BC ＝8 cm ，现将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则CD 的长为（） A . 4cm B . 254cm C . 5cm D . 74cm 7. 如图，长为cm 8的橡皮筋放置在x 轴上，固定两端A 和B ，然后把中点C 向上拉升cm 3 至D 点，则橡皮筋被拉长了（） A.2cm. B.5cm. C.4cm. D.10cm8.长方形ABCD 中，AB=3，AD=1，AB 在数轴上，若以点A 为圆心，对对角线AC 的长为半径交数轴的正半轴于点M ，则M 表示的数是（）1 C.110- D.59. 下列四个点，在一次函数y=－2x+1的图象上的点是（）A ．（0，1）B ．（2，3）C ．（2，－5）D ．（－1，－3）二、填空题（本大题共有8小题，每小题3分，共24分.）10.16的平方根是第7题 A 第6题 B C D E 第8题2= _______.12. 比较大小：13. 把正比例函数y=2x 图象向上平移3个单位，得到图象解析式是14. 若点P(a,b)在第四象限，则点Q （－b,a ）在第象限；15. 在△ABC 中，∠C=90°， AB ＝2，则2AB +2AC +2BC =_______．16. 点P(m+2,m －1)在y 轴上,则点P 的坐标是17.如图，小正方形边长为1，则△ABC 的面积是_________.三、解答题：（共49分．解答时应写出文字说明、证明过程或演算步骤）18.计算(每题4分，共12分.)（1）48532+- （2+21 （3）2(3(2-19. （6分）在同一直角坐标系中，（1）画出函数32,32,2+=-=-=x y x y x y 的图像,（2）32,32+=-=x y x y 并观察它们的关系.20. 已知点(2，-4)在正比例函数y=kx 的图象上.（9分）⑴求k 的值；⑵若点(-1，m)在直线y=kx 上，试求出m 的值；⑶若(21-，y 1)、B （-2，y 2）、C （1，y 3）都在该直线y=kx 上，试比较y 1、y 2、y 3的大小关系.第17题C BA 21.(6分) 因为974<<，即372<<，所以7的整数部分为2，小数部分为)27(-.(1) 如果29的整数部分为a ，那a = .（2）如果c b +=+33，其中b 是整数，且10<<c ，那么b = , c = .22.(6分) 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．（1）在图1中以格点为顶点画一个面积为5的正方形；（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、5、13．（3）如图3，A 、B 、C 是小正方形的顶点，求∠ABC23．已知：在直角坐标系中，直线2+=x y 与x 轴交于点A ，与y 轴交于点B 。

2013-2014学年第一学期期中八年级数学试卷

2013—2014学年度第一学期期中考试八年级数学一、选择题 (本大题共有8个小题，每小题3分，共24分，在每小题所给出的四个选项中，只有一项符合题目的要求，请将正确选项前的字母代号填在表格里相应位置)题号 1 2 3 4 5 6 7 8 答案1.9的值等于（ ▲ ） A ．3B ．-3C ．±3D ． 32.下面有4个汽车标志图案，其中轴对称图形有 ( ▲ )① ② ③ ④A ．1个B ．2个C ．3个D ．4个3.如图，将△ABC 沿直线DE 折叠后，使得点B 与点A 重合，已知AC=5cm ，△ADC 的周长为17cm ，则BC 的长为（ ▲ ）A ．7cmB ．10cmC ．12cmD ．22cm 4.如图，△ABC 中，D 为AB 中点，E 在AC 上，且BE AC 。

若DE=10，AE=16，则BE 的长度为（ ▲ ）A ．10B ．11C ．12D ．135.用尺规画∠AOB 的角平分线的步骤是：①以O 为圆心，适当长为半径作弧，交OA 于M 点，交OB 于N 点； ②分别以M 、N 为圆心，大于MN 21的长为半径作弧,两弧在∠AOB 的内部相交于点C ； ③过点C 作射线OC, 射线OC 就是∠AOB 的角平分线. 这样作角平分线的根据是 ( ▲ )A ．SSSB ．SASC ．ASAD ． AAS第3题DEBCAABCDE ABCDE F第4题第5题第6题第8题6.如图为八个全等的正六边形紧密排列在同一平面上的情形, 根据图中标示的各点位置，判断与△ACD全等的是（▲）A．△ACF B．△ADE C．△ABC D．△BCF7.P是∠AOB内一点，分别作点P关于直线OA、OB的对称点P１、P２，连接OP１、OP２，则下列结论正确的是（▲）A. OP１⊥OP２B. OP１＝OP２C. OP１⊥OP２且OP１＝OP２D. OP１≠OP２8.已知，如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一条直线上，连接BD、BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2），其中结论正确的是（▲）A．①②③B．①②④C．①③④D．①②③④二、填空题(本大题共有10个小题，每小题3分，共30分，不需写出解答过程，请把答案直接填在横线上)9. 3的平方根是▲．10.如图，在△ABC中，∠C＝90°，AD平分∠ABC，若AD＝5cm，AC＝4cm，则点D到AB的距离为___▲___cm．11.如图，△ABC≌△DEF，请根据图中提供的信息，写出x=▲．12.如图，在△ABC和△DEF中，点B、F、C、E在同一直线上，BF=CE，AC∥DF，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是▲ ．（只需写一个，不添加辅助线）13．若实数x、y满足|4|80x y-+-=，则以x、y的值为边长的等腰三角形的周长为▲．第10题第11题第12题9. 10. 11. 12. 13.14. 15. 16. 17. 18.14.若等腰三角形的一个角为50°，则它的顶角为 ▲ ． 15.如图，AB=AC ，BD=BC ，若∠A=30°，则∠ABD= ▲ °．16.一个正数的两个平方根分别是2a-1和a+4，则a 的值是 ▲ ．17.如图，直线a 经过正方形ABCD 的顶点A ，分别过顶点B 、D 作BF ⊥EF 于F ，DE ⊥EF 于E ，若DE=9，EF=15，则BF= ▲ ．18.如图，△ABC 中，AB=AC ，∠BAC=56°，∠BAC 的平分线与AB 的垂直平分线OD 交于点O ，将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，则∠OEC 度数为 ▲ °．三．解答题（本大项共有10小题，共96分，解答要写出必要的文字说明或计算的过程、步骤）19.（本题8分）已知x 的算术平方根为3，y 的立方根是3-，求x y -的平方根.20. （本题8分）求下列各式中的x .（1）2169x = （2）3(2)8x +=-21. （本题8分）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）和点A 1.利用网格完成下面的作图：（1）画出点B 关于直线AC 的对称点D ；（2）画出一个格点△A 1B 1C 1，并使它的三边长分别是13103、、.DCBA 第15题第17题第18题22. （本题8分）如图，△ABC 中，∠C=90°，AC=9，BC=12，折叠△ABC ，使A ，B 两点重合，折痕分别交BC 、AB 于点D 、E ，求CD 的长．EDBCA23. （本题10分）如图1，在△ABC 中，AB=AC ，点D 是BC 的中点，点E 在AD 上．（1）求证：BE=CE ；（2）如图2，若BE 的延长线交AC 于点F ，且BF ⊥AC ，垂足为F ，∠BAC=45°，请在图中找出一条与BC 相等的线段，并说明理由．FEB CDAEDBCA24. （本题10分）如图，在等腰△ABC 中，∠ABC ＝90°，D 为底边AC 中点，过D 点作DE ⊥DF ，交AB 于E ，交BC 于F ．若AE ＝12，FC ＝5，（1）试说明DE ＝DF ；（2）求EF 长．25. （本题10分）如图,在△ABC 中, D 、E 两点分别在边AC 、AB 上，AB=AC ，BC=BD ，AD=DE=BE ，求∠A 的度数．GF E CBA26. （本题10分）如图1，已知点P 是线段AB 上的动点（P 不与A ，B 重合），分别以AP 、PB 为边向线段AB 的同一侧作等边△APC 和等边△PBD ．连接AD 、BC ，相交于点Q ，AD 交CP 于点E ，BC 交PD 于点F（1）图1中有对全等三角形；（不必证明）（2分）（2）图1中设∠AQC=α，那么α= °；（不必证明）（2分）（3）如图2，若点P 固定，将△PBD 绕点P 按顺时针方向旋转（旋转角小于180°），此时α的大小是否发生变化？请说明理由．（6分）27. （本题12分）已知：如图，△ABC 中，AC=6，BC=8，AB=10，∠BCA 的平分线与AB 边的垂直平分线相交于点D ，DE ⊥AC ，DF ⊥BC ，垂足分别是E 、F ．（1）求证：AE=BF ；（2）求线段DG 的长．E F图1mBA图2P EBCDA28. （本题12分）（1）画图探究：（3分）如图1，若点A 、B 在直线m 同侧，在直线m 上求作一点P ，使AP+BP 的值最小，保留作图痕迹，不写作法；图3DCBA（2）实践运用：（4分）如图2，在等边△ABC 中，AB=2，点E 是AB 的中点，AD 是高，点P 是高AD 上一个动点，求BP+PE 的最小值．（3）拓展延伸（5分）如图3，四边形ABCD 中，∠BAD=125°，∠B=∠D=90°，在BC 、CD 上分别找一点M 、N ，使△AMN 周长最小，并求此时∠MAN 的度数．。