MATLAB绘图
matlab绘图课件

柱状图
总结词
用于比较不同类别数据的数值大小。
详细描述
柱状图是一种常用的数据可视化工具,它通过在垂直或水平方向上绘制一系列的柱子,每个柱子代表一个数据类 别,高度或长度表示该类别的数值大小。柱状图可以清晰地展示不同类别之间的数值差异和比较。
饼图
总结词
用于表示各部分在总体中所占的比例。
VS
详细描述
饼图是一种圆形图表,它将一个完整的圆 分割成若干个扇形,每个扇形代表一个数 据类别,扇形的面积或角度表示该类别的 比例大小。饼图可以清晰地展示各部分在 总体中所占的比例和比较。
动画制作
帧动画
通过在连续的帧上绘制图形或改 变图形属性来创建动画效果。
交互式动画
使用鼠标或键盘控制动画的播放 暂停和停止等操作。
运动轨迹
绘制物体在运动过程中的轨迹, 以展示物体的运动规律和特点。
三维图形
三维曲线
在三维空间中绘制曲线,可以展 示不同变量之间的关系和变化趋
势。
三维曲面
通过绘制三维曲面来展示两个或多 个变量之间的关系和分布情况。
函数调用与执行
在主程序中调用自定义函数,执行绘图操作,实现特定图形的绘 制。
数据导入和导
1 2
数据导入
将外部数据文件(如Excel、CSV等格式)导入 Matlab中,用于后续的绘图分析。
数据处理
对导入的数据进行必要的预处理和清洗,以满足 绘图需求。
3
数据导出
将绘制好的图形和数据导出为特定格式(如PNG 、JPEG、PDF等),方便分享和保存。
三维体图
绘制三维体图来展示数据的空间分 布和密度变化,如云图、等高线图 等。
04
实例分析
绘制正弦函数图像
MATLAB常见绘图问题及解决方法

MATLAB常见绘图问题及解决方法一、引言MATLAB作为一种强大的科学计算和数据可视化工具,广泛应用于各个领域。
在进行数据分析和可视化过程中,经常会遇到一些绘图问题。
本文将针对一些常见的绘图问题进行探讨,并提供相应的解决方法,帮助读者更好地使用MATLAB进行数据可视化。
二、数据处理与准备在进行绘图前,首先需要对数据进行处理和准备。
常见的问题包括数据清洗、数据类型转换以及数据筛选与排序等。
在MATLAB中,可以使用各种功能强大的函数来解决这些问题。
例如,可以使用"readtable"函数读取Excel中的数据,并使用"table2array"函数将表格转换为数组。
此外,还可以使用"sort"函数对数据进行排序,或者使用"unique"函数去除重复值。
三、基本绘图函数的使用MATLAB提供了丰富的基本绘图函数,如"plot"、"bar"、"scatter"等,可以根据需求选择适合的函数进行绘图。
然而,在使用这些函数时,也会遇到一些常见的问题。
1. 如何设置坐标轴范围在绘制图形时,经常需要设置坐标轴的范围,以确保所展示的数据能够完整显示。
可以使用"xlim"和"ylim"函数来设置x轴和y轴的范围。
例如,使用"xlim([0,10])"将x轴范围设置为0到10。
2. 如何设置坐标轴标题为了使图形更加清晰明了,可以为坐标轴添加标题。
可以使用"xlabel"和"ylabel"函数来设置x轴和y轴的标题。
例如,可以使用"xlabel('时间(s)')"来为x轴添加标题。
3. 如何添加图例在绘图时,可能同时展示多条曲线或者多个数据集,此时需要添加图例以区分不同的曲线或数据。
matlab画图

叉号 小正方形
菱形
标记符 ^ v > < p h
方式 向上三角形 向下三角形 向右三角形 向左三角形
五角星 六角星
7/ 38
fplot命令的使用
fplot(function,limits,LineSpec) 在limits指定的范围内绘制function函数的 图形. limits是一个矢量, 指定x轴上的范围[xmin, xmax], 或者x轴和y轴上的范围[xmin xmax ymin ymax]. function必须是M文件函数的名称或句柄, 或者含有变量x的字符串. LineSpec指定属性进行绘图.
meshz: 除了生成网格曲面外,
还在曲面下面加一长方形台柱。
meshz(Z);
colormap([0 0 1]) %设定色图参数
25/ 38
surf: 对网线图的网格块区域着色得到刻画面. surfc: 和meshc类似,在刻面图下方绘上等值线. surfl: 对刻画面中单元颜色进行平滑处理, 得到
27/38
饱和色
[0 0 0] — 黑色 [0 0 1] — 兰色 [0 1 0] — 绿色 [0 1 1] — 浅兰 [1 0 0] — 红色 [1 0 1] — 粉红 [1 1 0] — 黄色 [1 1 1] — 白色
调和色 [0.5 0.5 05] — 灰色 [0.5 0 0] — 暗红色 [1 0.62 0.4] — 铜色 [0.49 1 0.8] — 浅绿 [0.49 1 0.83] —宝石兰
例14. [X,Y]=meshgrid(-2:.2:2,-2:.2:2); Z=X.*exp(-X.^2-Y.^2); mesh(X,Y,Z)
24/38
MATLAB第3讲 MATLAB基本绘图

3.3 基本三维绘图
[X,Y]=meshgrid(-8:0.5:8,-8:0.5,8);
3.3 基本三维绘图
2、格式2:mesh(x,y,z) 功能:x,y,z 为三个矩阵, 以各元素值为三维坐标点绘图, 并连成网格。
3.3 基本三维绘图
例题 7 画一个球体 [xx,yy,zz]=sphere(30);
0
n
3.3 基本三维绘图
形成了33*33网 格矩阵
3.3 基本三维绘图
可以使用meshgrid()函数产生网格坐标:
格式:[X,Y]=meshgrid(x,y) x,y为同维向量,
X的行为x的拷贝,Y的列是y的拷贝,X,Y同维 例如:[xx,yy]=meshgrid([ 1 2 3 4],[1 2 3 4])
3.3 基本三维绘图
3、格式3:plot3(x,y,z,’s’) plot3(x1,y1,z1,’s1’,x2,y2,z2,’s2’) 功能:用于设置绘图颜色和线型 字符串意义同plot。
例如:plot3(x,y,z,’*r’,x,z,y,’:b’)
3.3 基本三维绘图
例题 2
3.3 基本三维绘图
3、hidden on(off) ----隐藏或透视被遮挡的地方
视角变换与三视图
三维图形绘制中的视角定义
z轴
视点
y轴
仰角
方位角
x轴
3.3 基本三维绘图
3. 4 特殊三维绘图 特殊图形库(specgraph)
1、stem3(x,y,z) ----- 三维火柴杆图: 例如:stem3(x,y,z) 2、bar3(z) ------ 三维条形图(同二维) 例如:bar3([1 2 3 2 1]) 3、pie3 (x,p)------ 三维饼图(同二维): 例如:pie3([1 2 3 2 1 1 ],[0 0 1 0 0 0]) 还有其它特殊函数。。。
MATLAB画图——基础篇
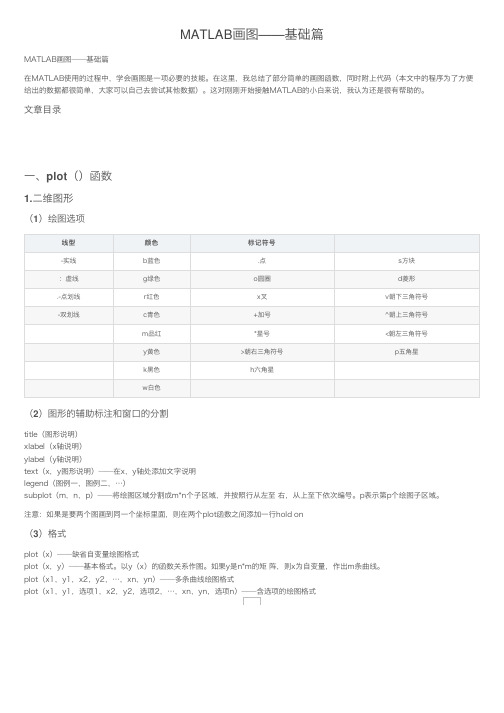
MATLAB画图——基础篇MATLAB画图——基础篇在MATLAB使⽤的过程中,学会画图是⼀项必要的技能。
在这⾥,我总结了部分简单的画图函数,同时附上代码(本⽂中的程序为了⽅便给出的数据都很简单,⼤家可以⾃⼰去尝试其他数据)。
这对刚刚开始接触MATLAB的⼩⽩来说,我认为还是很有帮助的。
⽂章⽬录⼀、plot()函数1.⼆维图形(1)绘图选项线型颜⾊标记符号-实线b蓝⾊.点s⽅块:虚线g绿⾊o圆圈d菱形.-点划线r红⾊x叉v朝下三⾓符号-双划线c青⾊+加号^朝上三⾓符号m品红*星号<朝左三⾓符号y黄⾊>朝右三⾓符号p五⾓星k⿊⾊h六⾓星w⽩⾊(2)图形的辅助标注和窗⼝的分割title(图形说明)xlabel(x轴说明)ylabel(y轴说明)text(x,y图形说明)——在x,y轴处添加⽂字说明legend(图例⼀,图例⼆,…)subplot(m,n,p)——将绘图区域分割成m*n个⼦区域,并按照⾏从左⾄ 右,从上⾄下依次编号。
p表⽰第p个绘图⼦区域。
注意:如果是要两个图画到同⼀个坐标⾥⾯,则在两个plot函数之间添加⼀⾏hold on(3)格式plot(x)——缺省⾃变量绘图格式plot(x,y)——基本格式。
以y(x)的函数关系作图。
如果y是n*m的矩 阵,则x为⾃变量,作出m条曲线。
plot(x1,y1,x2,y2,…,xn,yn)——多条曲线绘图格式plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)——含选项的绘图格式x1=[1 2 3 4 5 6 7 8 9];x2=[2 4 6 8 10 12 14 16 18];y1=[1 4 9 16 25 36 49 64 81];y2=[18 16 14 12 10 8 6 4 2];subplot(4,1,1);plot(x1);title('例⼀');xlabel('⾃变量');ylabel('因变量');subplot(4,1,2);plot(x1,y1);title('例⼆');xlabel('⾃变量');ylabel('因变量');subplot(4,1,3);plot(x1,y1,x2,y2);title('例三');xlabel('⾃变量');ylabel('因变量');subplot(4,1,4);plot(x1,y1,'m+',x2,y2,'c*');title('例四');xlabel('⾃变量');ylabel('因变量');2.三维图形(1)格式plot3(x1,y1,z1,‘选项⼀’,x2,y2,z1,‘选项⼆’,…)x,y,z是长度相同的向量:⼀条曲线x,y,z是维度相同的矩阵:多条曲线(2)⽹格矩阵⽣成函数:meshgrid[X,Y]=meshgrid(x,y)x,y是给定的向量,X,Y是⽹格划分后得到的⽹格矩阵注意,这个函数⽤来⽣成⽹格矩阵,不是直接⽤来画图的,配合mesh使⽤。
MATLAB第三节 绘图

2,0.5],[0,2]上画隐函数 的图. 【例】 在[-2,0.5],[0,2]上画隐函数 e x + sin( xy ) = 0 的图 ezplot('exp(x)+sin(x*y)',[ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])
ezplot(‘x(t) , y(t) ezplot( x(t)’,’y(t) ,[tmin,tmax]) x(t) y(t)’,[tmin,tmax])
上画y=cos x 的图形 的图形. 【例】 在[0,π ]上画 上画
ezplot('sin(x)',[0,pi])
ezplot(‘f(x,y) ,[xmin,xmax,ymin,ymax]) ezplot( f(x,y)’,[xmin,xmax,ymin,ymax]) f(x,y)
note:表示在区间xmin<x<xmax和 ymin<y<ymax绘制隐 函数f(x,y)=0的函数图.
4.2特殊坐标图形 特殊坐标图形
semilogx(x,y)—单对数X semilogx(x,y) 单对数X轴绘图命令 semilogy(x,y)—单对数Y轴绘图命令 semilogy(x,y) 单对数Y
【例】以X轴为对数重新绘制上述曲线; 轴为对数重新绘制上述曲线; x=[0:0.01:2*pi] y=abs(1000*sin(4*x))+1 单对数X semilogx(x,y) %单对数X轴绘图 【例】以Y轴为对数重新绘制上述曲线; 轴为对数重新绘制上述曲线; x=[0:0.01:2*pi] y=abs(1000*sin(4*x))+1 单对数Y semilogy(x,y) %单对数Y轴绘图
第四章___matlab_绘图

例,绘制阶梯曲线 x=0:pi/20:2*pi;y=sin(x);stairs(x,y)
1
0 .8
0 .6
0 .4
0 .2
0
-0 .2
-0 .4
-0 .6
-0 .8
-1
0
1
2
3
4
5
6
7
例:阶梯绘图
h2=[1 1;1 -1];h4=[h2 h2;h2 -h2]; h8=[h4 h4;h4 -h4];t=1:8; subplot(8,1,1);stairs(t,h8(1,:));axis('off') subplot(8,1,2);stairs(t,h8(2,:));axis('off') subplot(8,1,3);stairs(t,h8(3,:));axis('off') subplot(8,1,4);stairs(t,h8(4,:));axis('off') subplot(8,1,5);stairs(t,h8(5,:));axis('off') subplot(8,1,6);stairs(t,h8(6,:));axis('off') subplot(8,1,7);stairs(t,h8(7,:));axis('off') subplot(8,1,8);stairs(t,h8(8,:));axis('off')
1 0.8 0.6 0.4 0.2
0 -0.2 -0.4
y
y1 y2
例 3:y=sin(t);y1=sin(t+0.25);y2=sin(t+0.5); y3=cos(t);y4=cos(t+0.25);y5=cos(t+0.5); plot(t,[y',y1',y2',y3',y4',y5'])
MATLAB实验报告绘图
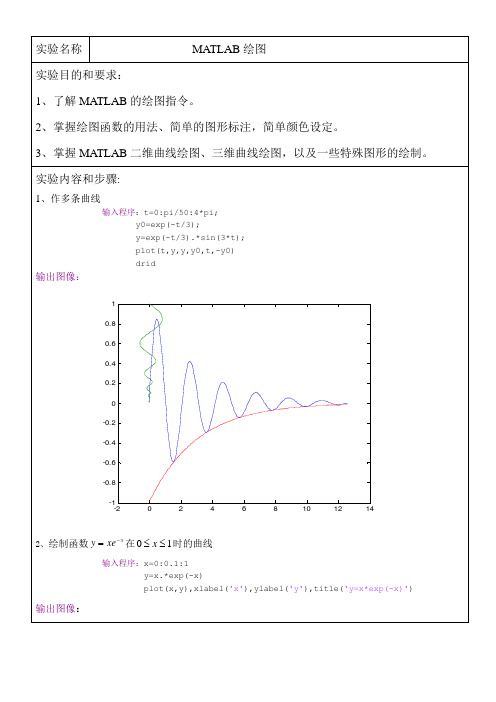
68 54 35;
45 25 12;
48 68 45;
68 54 69];
x=sum(t);
h=pie(x);
textobjs=findobj(h,'type','text');
str1=get(textobjs,{'string'});
val1=get(textobjs,{'extent'});
运行图像
4、采用模型 画一组椭圆
输入程序:th = [0:pi/50:2*pi]';
a = [0.5:.5:4.5];
X = cos(th)*a;
Y = sin(th)*sqrt(25-a.^2);
plot(X,Y),axis('equal'),xlabel('x'), ylabel('y')
title('A set of Ellipses')
oldext=cat(1,val1{:});
names={'商品一;'商品二';'商品三'};
str2=strcat(names,str1);
set(textobjs,{'string'},str2)
val2=get(textobjs,{'extent'});
newext=cat(1,val2{:});
xlable('sin(t)'),ylable('cos(t)'),zlable('t');
gridon;
输出图像
9、用MATLAB绘制饼图
Matlab绘图命令

Matlab绘图命令:1.p lot(x,y):该命令用于描点法作图,给出x的范围,然后利用函数式计算出每一个x对应的y,注意,x间距取得越小,图像会画的越圆滑,这是因为plot描点法作图的原因.如:plot(x,y,’--’)2.f plot(y,[xstart xend]):该命令同样用于绘制图像,但是只需要给出x范围与y关于x的函数式即可,相比于plot 函数更加方便。
3.g rid on可以给图像加上网格4.h old on:用于连续绘图,如果想要在一个坐标系中画出多个图形的话,则需要在每次画完图形之前加入这个命令。
5.l egend(‘y’):在图上标出y曲线线型6.设置图线颜色:plot(x,y,’颜色’)7.a xis ( [xmin xmax ymin ymax] ):设置图像横纵坐标范围例:fplot('cos(x)',[-5 5],'r--'),axis ( [-5 5 -1 1] ),8.s ubplot(m, n, p):用于在一个窗口中绘制多个图像。
例:subplot(1, 2, 1);fplot('sin(x)',[-5 5],'b--');subplot(1, 2, 2);fplot('cos(x)',[-5 5],'r--');9.p lot(thea,r): 绘制极坐标图形,thea 是角变量,r是极轴长度例:a = 2;theta = [0:pi/90:2*pi];r = a*theta;polar(theta,r), title('阿基米德螺线')10.bar(x,y):画直方图11.stem(t,f):绘制针头图,这种图经常用来表示波动情况,或者各值和平均值的偏差,可以一目了然。
例:subplot(1, 2, 1);plot(t,f),xlabel('时间(秒)'),ylabel('弹簧响应');subplot(1, 2, 2);stem(t,f),xlabel('时间(秒)'),ylabel('弹簧响应');12.counter3(x,y,z,n):绘制三维等高图例:[x,y] = meshgrid(-2:0.1:2);z = y.*exp(-x.^2 - y.^2);contour3(x, y, z, 30);surface(x,y,z,'EdgeColor',[.8 .8 .8],'FaceColor','none');grid off;view(-15,20);13.mesh(x,y,z):绘制普通三维图14.surf(x,y,z):绘制颜色渐变三维图15.。
matlab画图大全[资料]
![matlab画图大全[资料]](https://img.taocdn.com/s3/m/0e578e91bdeb19e8b8f67c1cfad6195f312be8c8.png)
matlab绘图大全Matlab绘图系列之高级绘图一、目录1.彗星图二维彗星图三维彗星图2.帧动画3.程序动画4.色图变换5.Voronoi图和三角剖分Voronoi图三角剖分6.四面体7.彩带图彩带图三维流彩带图8.伪彩图9.切片图切片图切片轮廓线图10.轮廓图显示轮廓线显示围裙瀑布效果带光照模式的阴影图11.函数绘图轮廓线、网格图、曲面图、轮廓网格图轮廓曲面图、二维曲线、极坐标曲线图、自定义函数12.三维图形控制视点灯光效果色彩控制二、图形示例1.彗星图二维彗星图t=0:.01:2*pi;x=cos(2*t).*(cos(t).^2);y=sin(2*t).*(sin(t).^2);comet(x,y);title('二维彗星轨迹图')hold onplot(x,y)三维彗星图a=12;b=9;T0=2*pi;%T0是轨道的周期T=5*T0;dt=pi/100;t=[0:dt:T]';f=sqrt(a^2-b^2);%地球与另一焦点的距离th=12.5*pi/180;%未经轨道与x-y平面的倾角E=exp(-t/20);%轨道收缩率x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t));plot3(x,y,z,'g')%画全程轨线hold on,sphere(20);%画地球axis offtitle('卫星返回地球示例')x1=-18*T0;x2=6*T0;y1=-12*T0;y2=12*T0;z1=-6*T0;z2=6*T0;axis([x1 x2 y1 y2 z1 z2])% axis([-15 10 -15 10 -10 10])axis equalcomet3(x,y,z,0.02);%画运动轨线hold off2.帧动画Z=peaks;surf(Z)%绘制网格表面图axis tightset(gca,'nextplot','replacechildren');%设定axis覆盖重画模式title('帧动画播放示例')for j=1:20surf(sin(2*pi*j/20)*Z,Z)%重新绘制网格表面图,这里后面一个Z当成了颜色矩阵F(j)=getframe;%创建帧endmovie(F,20)%播放动画20次3.程序动画t=0:pi/50:10*pii=1;h=plot3(sin(t(i)),cos(t(i)),t(i),'*','erasemode','none');%设定擦除模式grid onaxis([-2 2 -2 2 -1 10*pi])title('程序动画示例')for i=2:length(t)set(h,'xdata',sin(t(i)),'ydata',cos(t(i)),'zdata',t(i));drawnowpause(0.01)end4.色图变换load spineimage(X)colormap coolspinmap(10)5.Voronoi图和三角剖分Voronoi图rand('state',5)x=rand(1,10);y=rand(1,10);subplot(131)voronoi(x,y);%绘制voronoi图形axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(132)[vx,vy]=voronoi(x,y);plot(x,y,'r+',vx,vy,'b-');%应用返回值绘制axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(133)rand('state',5);x=rand(10,2);[v,c]=voronoin(x);%返回值v参数维voronoi顶点矩阵,返回值c 参数为voronoi元胞数组for i=1:length(c)if all(c{i}~=1)patch(v(c{i},1),v(c{i},2),i);%应用色图iendendaxis equalaxis([-0.2 1.6 -0.5 2.5])box on三角剖分[x,y]=meshgrid(1:15,1:15);tri=delaunay(x,y);z=peaks(15);trimesh(tri,x,y,z)6.四面体d=[-1 1];[x,y,z]=meshgrid(d,d,d);%定义一个立方体x=[x(:);0];y=[y(:);0];z=[z(:);0];%[x,y,z]分别为加上中心的立方体顶点X=[x(:) y(:) z(:)];Tes=delaunayn(X);%返回m×n的数组值tetramesh(Tes,X);%绘制四面体图camorbit(20,0);%旋转摄像目标位置7.彩带图彩带图[x,y]=meshgrid(-3:.5:3,-3:.1:3);z=peaks(x,y);ribbon(y,z)三维流彩带图load wind%打开保存的数据lims=[100.64 116.67 17.25 28.75 -0.02 6.86];%定义坐标轴范围[x,y,z,u,v,w]=subvolume(x,y,z,u,v,w,lims);%lims来定义数据子集[sx sy sz]=meshgrid(110,20:5:30,1:5);%定义网格点verts=stream3(x,y,z,u,v,w,sx,sy,sz,.5);%计算彩带顶点cav=curl(x,y,z,u,v,w);%计算卷曲角速度wind_speed=sqrt(u.^2+v.^2+w.^2);%计算流速h=streamribbon(verts,x,y,z,cav,wind_speed,2);%绘制流彩带图view(3)8.伪彩图n=6%定义轮数r=(0:n)'/n;%定义轮的半径theta=pi*(-n:n)/n;%定义轮的扇区角X=r*cos(theta);Y=r*sin(theta);%定义网格顶点C=r*cos(2*theta);%定义色图pcolor(X,Y,C)%绘制伪彩图axis equal tight9.切片图切片图[x,y,z] = meshgrid(-2:.2:2,-2:.25:2,-2:.16:2);v = x.*exp(-x.^2-y.^2-z.^2);xslice = [-1.2,.8,2]; yslice = 2; zslice = [-2,0];slice(x,y,z,v,xslice,yslice,zslice)colormap hsv切片轮廓线图[x y z v]=flow;%打开水流数据h=contourslice(x,y,z,v,[1:9],[],[0],linspace(-8,2,10));%切片轮廓线view([-12 30])10.轮廓图显示轮廓线[x,y,z]=peaks;subplot(1,2,1)meshc(x,y,z);%同时画出网格图与轮廓线title('meshc 网格图与轮廓线')axis([-inf inf -inf inf -inf inf]);subplot(1,2,2)surfc(x,y,z);%同时画出曲面图与轮廓线title('surfc 曲面图与轮廓线')axis([-inf inf -inf inf -inf inf]);显示围裙[x y z]=peaks;meshz(x,y,z);瀑布效果[X,Y,Z]=peaks(30);waterfall(X,Y,Z)带光照模式的阴影图[x,y]=meshgrid(-3:1/8:3);z=peaks(x,y);surfl(x,y,z);shading interp%着色处理colormap(gray);%灰度处理axis([-3 3 -3 3 -8 8])11.函数绘图轮廓线、网格图、曲面图、轮廓网格图%图1绘制轮廓线、网格图、曲面图、轮廓网格图subplot(221)f=['3*(1-x)^2*exp(-(x^2)-(y+1)^2)-10*(x/5-x^3-y^5)*exp(-x^2-y^2)-1/3*exp(-(x+1)^2-y^2)'];%定义双变量x、y的函数式ezcontour(f,[-3,3],49)%x、y为[-3 3],网格为49×49subplot(222)ezmesh('sqrt(x^2+y^2)');subplot(223)ezsurf('real(atan(x+i*y))')%经过滤波,如果相同数据surf绘图没有滤波subplot(224)ezmeshc('y/(1+x^2+y^2)',[-5,5,-2*pi,2*pi])%x、y的数值范围分别为[-5 5]、[-2*pi 2*pi]轮廓曲面图、二维曲线、极坐标曲线图、自定义函数%图2绘制轮廓曲面图、二维曲线、极坐标曲线图、自定义函数figure(2)subplot(221)ezsurfc('sin(u)*sin(v)')subplot(222)ezplot('x^2-y^4');subplot(223)ezpolar('1+cos(t)')subplot(224)fplot('myfun',[-20 20])function Y=myfun(x)Y(:,1)=200*sin(x(:))./x(:);Y(:,2)=x(:).^2;三维曲线图%绘制三维曲线图figure(3)ezplot3('sin(t)','cos(t)','t',[0,6*pi])12.三维图形控制视点View图形旋转subplot(121)surf(peaks);title('旋转前图形');subplot(122)h=surf(peaks);rotate(h,[1 0 1],180)title('旋转后图形');灯光效果%灯光效果(1)camlight(2)light(3)lightangle(4)lighting(5)materialsphere;camlight色彩控制%色彩控制(1)缺省设置colordef、whitebg(2)色图colormap(3)浓淡处理shadingload flujetimage(X)colormap(jet)subplot(131)sphere(16)axis squareshading flattitle('Flat Shading')subplot(132)sphere(16)axis squareshading facetedtitle('Faceted Shading') subplot(133)sphere(16)axis squareshading interptitle('Interpolated Shading')。
第4章 MATLAB 绘图

4.图例标注
菜单Insert---legend 命令legend('string1','string2',...)
4.1.6 一个图形窗口多个子图的绘制
subplot(m,n,i)把图形窗口分为m*n个子图,并在第i个子图 中画图 例 4-11 在同一坐标系中画出两个函数,y=cos2x,y=sinxsin6x 的图形,自变量的范围为0≤ x ≤π,函数y=cos2x用红色星号,函数 y=sinxsin6x用蓝色实线,并加图名、坐标轴、图形、图例标注 解 MATLAB命令为: x=0:pi/50:pi; y1=cos(2*x);y2=sin(x).*sin(6*x); plot(x,y1,'r*',x,y2,'b-'),grid on title(‘曲线y1=cos(2x)曲线y2=sin(x)sin(6x)') xlabel('x轴'),ylabel('y轴') gtext('y1=cos(2x)'),gtext('y2=sin(x)sin(6x)') legend('y1=cos(2x)','y2=sin(x)sin(6x)')
group 8 6 4 2 0 10 30 20
stack
1
2
3
4 stack
5
6
0
1
2
3
4 stack
5
6
8 6 5 4 3 2 1 0 10 20 30 6 4 2 0
其它特殊绘图略(见教科书 )
1
2
3
4
5
6
4.3 三维曲线绘图
matlab绘图教学课件

坐标轴范围
使用xlim和ylim命令控制坐标轴的范围。
坐标轴比例
使用axis命令设置坐标轴的比例,如axis equal确保x轴和y轴比例 一致。
坐标轴标签字体和颜色
使用set命令设置坐标轴标签的字体和颜色等属性。
CHAPTER
02
绘制二维图形
绘制线形图
总结词
展示数据变化趋势
详细描述
线形图用于展示数据随时间或其他变量的变化趋势,通过连接数据点形成线条 ,可以直观地展示数据的走势。
绘制三维柱状图
总结词
三维柱状图是一种展示三维空间中数据分布的图表类型,可以清晰地展示各个数据点在 三个维度上的差异。
详细描述
在Matlab中,可以使用bar3函数绘制三维柱状图。该函数可以接受三个维度的数据, 并按照指定的样式绘制三维柱状图。可以通过调整柱子的颜色、透明度、大小等属性,
来增强三维柱状图的视觉效果。
CHAPTER
05
Matlab绘图应用实例
绘制股票价格走势图
总结词
展示股票价格随时间变化的趋势
详细描述
使用Matlab绘制股票价格走势图,可以清晰地展示股票 价格随时间的变化趋势。通过将股价数据导入Matlab中 ,并使用绘图函数进行绘制,可以方便地观察股票价格 的波动情况。
绘制雷达图
总结词
展示多维数据的综合表现
Matlab绘图教学课件
CONTENTS
目录
• Matlab绘图基础 • 绘制二维图形 • 绘制三维图形 • 图形的高级处理 • Matlab绘图应用实例
CHAPTER
01
Matlab绘图基础
基础绘图函数
01 plot函数:用于绘制二维线图,是最常用 的绘图函数。
第2讲_matlab 绘图

格变化
调用格式: surf(x,y,z) —— 与mesh的调用方式相同 例: [X,Y,Z]=peaks(30) ※peaks为matlab 自动生成的三维测 试图形 surf(X,Y,Z)
surfc(X,Y,Z) — 带等高线的曲面图 [X,Y,Z]=peaks(30);surfc(X,Y,Z)
mesh(X,Y,Z) mesh(Z) —— Z为n×m的矩阵, 默认x=1:n, y=1:m
meshc —— 生成网格线,在xoy面上
生成曲面的等高线图形
meshz —— 生成网格线,在曲面下面 加上一个长方形的台柱
mesh,meshc,meshz的调用方式相 同
例:
x=1:0.1:3; y=1:0.1:4; [X,Y]=meshgrid(x,y); Z=ones(size(X)); mesh(X,Y,Z)
第二讲 matlab 绘图
——matlab语言丰富的图形表 现方法,使得数学计算结果可 以方便地、多样性地实现了可 视化,这是其它语言所不能比 拟的。
一、二维绘图
plot —— 最基本的二维图形指令,绘制线 性图形(描点、连线)
plot的调用格式
plot(x) —— 缺省自变量绘图格式,x为 向量, 以x元素值为纵坐标,以相应元素 下标为横坐标绘图 plot(x,y) —— 基本格式,以y(x)的函数 关系作出直角坐标图。P36
在图形的顶端加注文字作为图名
在当前图形的x轴旁边加注文字 在当前图形的y轴旁边加注文字 在当前图形的z轴旁边加注文字
图形标注 text (x, y, ‘String’) 在(x,y)处加文字‘String’(二维图 形) text (x, y, z, ‘String’) 在(x,y,z)处…(三维图形) gtext (‘String’) 在鼠标指定位置上标注
matlab绘图知识点总结

matlab绘图知识点总结一、Matlab基本绘图函数1. plot函数plot函数是Matlab中最基本的绘图函数之一,用于绘制二维图表。
其基本语法为:plot(x, y)。
其中x是横轴坐标数据,y是纵轴坐标数据。
通过plot函数可以绘制折线图、散点图等。
2. bar函数bar函数用于绘制条形图,其基本语法为:bar(x, y)。
其中x是条形的横轴坐标位置,y是条形的高度。
3. pie函数pie函数用于绘制饼图,其基本语法为:pie(x, labels)。
其中x是用来指定各个扇形区域的大小的矩阵,labels则是用来指定每个扇形区域的标签。
4. hist函数hist函数用于绘制直方图,其基本语法为:hist(x, bins)。
其中x是待绘制的数据,bins则是用来指定直方图的条形数目。
5. scatter函数scatter函数用于绘制散点图,其基本语法为:scatter(x, y)。
其中x和y分别是散点的横轴和纵轴坐标数据。
6. contour函数contour函数用于绘制等高线图,其基本语法为:contour(x, y, z)。
其中x和y分别是网格的横轴和纵轴坐标,z则是用来指定等高线的数值。
二、自定义图形1. 设置标题、标签和图例在Matlab中,可以使用title、xlabel、ylabel和legend等函数分别设置图表的标题、横轴和纵轴标签以及图例。
2. 设置图表样式可以使用line属性、marker属性以及color属性等来设置折线图、散点图等的样式。
3. 修改图表坐标轴可以使用xlim、ylim函数来设置图表的横轴和纵轴范围,并使用xticks和yticks函数来设置坐标刻度。
4. 绘制多个数据集可以使用hold on函数来绘制多个数据集,并使用hold off函数来结束绘制多个图表。
5. 设置图表背景可以使用grid、box、axis equal等函数来设置图表的背景。
三、子图表绘制1. subplot函数subplot函数用于在一个图形窗口中绘制多个子图表,其基本语法为:subplot(m,n,p)。
matlab画图

1.平面作图函数:plot,其基本调用形式:plot(x,y,s)以x作为横坐标,y作为纵坐标.s是图形显示属性的设置选项.例如:x=-pi:pi/10:pi;y=sin(x);plot(x,y,'--rh','linewidth',2,'markeredgecolor','b','markerfacecolor','g')在使用函数plot时,应当注意到当两个输入量同为向量时,向量x与y必须维数相同,而且必须同是行向量或者同是列向量.绘图时,可以制定标记的颜色和大小,也可以用图形属性制定其他线条特征,这些属性包括:linewidth指定线条的粗细.markeredgecolor指定标记的边缘色markerfacecolor指定标记表面的颜色.markersize指定标记的大小.若在一个坐标系中画几个函数,则plot的调用格式如下:plot(x1,y1,s1,x2,y2,s2,……)4.双纵坐标函数plotyy在Matlab中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy函数,它能把具有不同量纲,不同数量级的两个函数绘制在同一个坐标中,有利于图形数据的对比分析。
使用格式为:plotyy(x1,y1,x2,y2)x1,y1对应一条曲线,x2,y2对应另一条曲线。
横坐标的标度相同,纵坐标有两个,左边的对应x1,y1数据对,右边的对应x2,y2。
二.绘制图形的辅助操作绘制完图形以后,可能还需要对图形进行一些辅助操作,以使图形意义更加明确,可读性更强。
1.图形标注在绘制图形时,可以对图形加上一些说明,如图形的名称、坐标轴说明以及图形某一部分的含义等,这些操作称为添加图形标注。
有关图形标注函数的调用格式为:title(’图形名称’)(都放在单引号内)xlabel(’x轴说明’)ylabel(’y轴说明’)text(x,y,’图形说明’)legend(’图例1’,’图例2’,…) P190其中,title、xlabel和ylabel函数分别用于说明图形和坐标轴的名称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绘制二维曲线1.p l o t函数p l o t(x,y)其中x和y为大小相同的向量,分别用于存储x坐标和y坐标数据。
【例】绘制曲线t=0:0.1:8*p i;x=c o s(t)+t.*s i n(t);y=s i n(t)-t.*c o s(t);p l o t(x,y);图形窗口简介(1)当x和y是同维矩阵时,配对的x、y按对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
例如,在同一坐标中绘制3条幅值不同的正弦曲线,命令为x=0:pi/10:2*pi;y=sin(x);plot([x;x;x]',[y;y*2;y*3]')当x是向量,y是有一维与x同维的矩阵时,则绘制出多根曲线,曲线条数等于y矩阵的另一维数,x被作为这些曲线共同的横坐标。
例如,在同一坐标中绘制3条幅值不同的正弦曲线,命令也可以写成:x=0:pi/10:2*pi;y=sin(x);plot(x,[y;y*2;y*3])(2)当plot函数只有一个输入参数时,即plot(y)若y是实型向量,则以该向量元素的下标为横坐标、元素值为纵坐标画出一条连续曲线;若y是复数向量,则分别以向量元素实部和虚部为横、纵坐标绘制一条曲线。
若y是实矩阵,则按列绘制每列元素值相对其下标的曲线,曲线条数等于输入参数矩阵的列数;若y是复数矩阵,则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
(3)当plot函数有多个输入参数,且都为向量时,即plot(x1,y1,x2,y2,…,xn,yn)其中,x1和y1,x2和y2,……,xn和yn分别组成一组向量对,每一组向量对的长度可以不同。
每一向量对可以绘制出一条曲线,这样可以在同一坐标内绘制出多条曲线。
例如,在同一坐标中绘制3条幅值不同的正弦曲线x=0:pi/10:2*pi;y=sin(x);plot(x,y,x,y*2,x,y*3)2.p l o t y y函数绘制出具有不同纵坐标标度的两个图形,可以使用p l o t y y绘图函数。
这种图形有利于图形数据的对比分析。
p l o t y y(x1,y1,x2,y2)其中,x1和y1对应一条曲线,x2和y2对应另一条曲线。
横坐标的标度相同,纵坐标有两个,左纵坐标用于x1、y1数据对,右纵坐标用于x2、y2数据对。
【例】用不同标度在同一坐标内绘制曲线y1=0.2e−0.5x c o s(4 x)和y2=1.5e−0.5x c o s( x)。
x=0:p i/100:2*p i;y1=0.2*e x p(-0.5*x).*c o s(4*p i*x);y2=1.5*e x p(-0.5*x).*c o s(p i*x);p l o t y y(x,y1,x,y2);设置曲线样式M A T L A B提供了一些绘图选项,用于确定所绘曲线的线型、颜色和数据点标记符号。
例如,“b-.”表示蓝色点画线,“r:d”表示红色虚线并用菱形符标记数据点。
当选项省略时,M A T L A B规定,线型一律用实线,颜色将根据曲线的先后顺序依次采用。
表3.1 线型选项选项线型- 实线(默认值): 虚线-- 双画线-. 点画线表3.2 颜色选项选项颜色选项颜色b(blue)蓝色m(magenta)品红色g(green)绿色y(yellow)黄色r(red)红色k(black)黑色c(cyan)青色w(white)白色表3.3 标记符号选项选项标记符号选项标记符号. 点v 朝下三角符号O(字母)圆圈^ 朝上三角符号X(字母)叉号< 朝左三角符号+ 加号> 朝右三角符号* 星号p(pentagram)五角星符s(square)方块符h(hexagram)六角星符d(diamond)菱形符要设置曲线样式可以在plot函数中加绘图选项,其调用格式为plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)【例】在同一坐标内,分别用不同线型和颜色绘制曲线y1 = 0.2e−0.5xcos(4 x) 和 y2 = 1.5e−0.5x cos( x)。
标记两曲线交叉点。
x=linspace(0,2*pi,1000);y1=0.2*exp(-0.5*x).*cos(4*pi*x);y2=1.5*exp(-0.5*x).*cos(pi*x);k=find(abs(y1-y2)<1e-2); %查找y1与y2相等点(近似相等)的下标x1=x(k); %取y1与y2相等点的x坐标y3=0.2*exp(-0.5*x1).*cos(4*pi*x1); %求y1与y2值相等点的y坐标plot(x,y1,x,y2,'k:',x1,y3,'rp');图形标注与坐标控制1.图形标注在绘制图形的同时,可以对图形加上一些说明,如图形名称、坐标轴说明、图形某一部分的含义等,这些操作称为添加图形标注。
有关图形标注函数的调用格式如下。
●t i t l e(图形名称)●x l a b e l(x轴说明)●y l a b e l(y轴说明)●t e x t(x,y,图形说明),g t e x t(图形说明)●l e g e n d(图例1,图例2,……)title和xlabel、ylabel 函数分别用于说明图形和坐标轴的名称。
text函数是在(x,y)坐标处添加图形说明。
添加文本说明也可用gtext命令,执行该命令时,十字坐标光标自动跟随鼠标移动,单击鼠标即可将文本放置在十字光标处,如命令gtext('cos(x)'),即可放置字符串cos(x)。
legend函数用于绘制曲线所用线型、颜色或数据点标记图例。
上述函数中的说明文字,除使用标准的ASCII字符外,还可使用LaTeX(LaTeX是一种十分流行的数学排版软件)格式的控制字符,这样就可以在图形上添加希腊字母、数学符号、公式等内容。
在MATLAB支持的LaTeX字符串中,用\bf、\it、\rm控制字符分别定义黑体、斜体和正体字符,受LaTeX字符串控制部分要加大括号{}括起来。
例如使得“MATLAB”一词黑体显示text(0.3,0.5,'The useful {\bf MATLAB}')得到标注效果sin( t + )text(3,1,'sin({\omega} t+{\beta})')【例】x=linspace(0,2*pi,1000);y=sin(x);plot(x,y,'LineWidth',4);text(1,-0.5,'The useful {\bf MATLAB}');text(3,0.8,'sin({\omega} t+{\beta})');gtext('\leftarrowsin(x)=0.707');【例】在0≤x≤2 区间内,绘制曲线y1 = e−0.5x和y2 = cos(4 x)e−0.5x,并添加图形标注。
x=0:pi/100:2*pi;y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x);plot(x,y1,x,y2)title('x from 0 to 2{\pi}'); %加图形标题xlabel('Variable X'); %加X轴说明ylabel('Variable Y'); %加Y轴说明text(1.5,0.5,'曲线y1=e^{-0.5x}'); %在指定位置添加图形说明text(3,-0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}');legend('y1','y2') %加图例幻灯片172.坐标控制根据要绘制曲线数据的范围选择合适的坐标刻度axis([xmin xmax ymin ymax])系统按照给出的坐标轴的最小值和最大值选择坐标系范围axis函数的其他用法●axis auto:使用默认设置。
●axis equal:纵、横坐标轴采用等长刻度。
●axis square:产生正方形坐标系(默认为矩形)。
●axis on/off:显示/取消坐标轴。
给坐标加网格线用grid命令来控制,grid on/off命令控制是画还是不画网格线。
加边框用box命令来控制。
box on/off命令控制是加还是不加边框线。
【例】绘制曲线及其包络线。
t=(0:pi/100:pi)';y1=sin(t)*[1,-1]; %包络线函数值y2=sin(t).*sin(9*t);plot(t,y1,t,y2)grid on; % grid off %加网格线box on; % box off %加坐标边框axis equal; % axis auto %坐标轴采用等刻度sin sin(9)y t t图形窗口的分割分割后的图形窗口由若干个绘图区组成,每一个绘图区可以建立独立的坐标系并绘制图形。
同一图形窗口中的不同图形称为子图。
s u b p l o t(m,n,p)该函数将当前图形窗口分成m×n个绘图区,区号按行优先编号,且选定第p个区为当前活动区。
在每一个绘图区允许以不同的坐标系单独绘制图形。
【例】在图形窗口中,以子图形式同时绘制多根曲线。
subplot(2,2,[1 3]);fplot('x-cos(x^3)-sin(2*x^2)',[-3,3]);xlabel('(a)');x=-3:0.1:3;subplot(2,2,2);y2 = sin(2.*x.^2);plot(x,y2);xlabel('(b)'); axis([-3 3 -1.2 1.2]);subplot(2,2,4);y3 = cos(x.^3);plot(x,y3);xlabel('(c)'); axis([-3 3 -1.2 1.2]);grid on;图形叠加一般情况下,绘图命令每执行一次就刷新当前图形窗口,图形窗口原有图形将不复存在。
若希望在已存在的图形上再叠加新的图形,可使用图形保持命令h o l d。
h o l d o n/o f f命令控制是保持原有图形还是刷新原有图形。
【例】x=0:p i/100:2*p i;y1=0.2*e x p(-0.5*x).*c o s(4*p i*x);p l o t(x,y1);%h o l d o ny2=1.5*e x p(-0.5*x).*c o s(p i*x);p l o t(x,y2);%h o l d o f f其他坐标系1.对数坐标图形●s e m i l o g x(x1,y1,选项1,x2,y2,选项2,……)●s e m i l o g y(x1,y1,选项1,x2,y2,选项2,……)●l o g l o g(x1,y1,选项1,x2,y2,选项2,……)其中,选项的定义与p l o t函数完全一致,所不同的是坐标轴的选取。
