高考数学大一轮复习第九章平面解析几何12规范答题示范五高考解答题__解析几何真题展示课件理
2019版高考数学大一轮复习人教B版全国通用文档:第九章平面解析几何9.1 Word版含答案

§9.1 直线的方程最新考纲考情考向分析1.在平面直角坐标系中,结合具体图形,确定直线位置的几何要素.2.理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.3.掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、斜截式、截距式、两点式及一般式),了解斜截式与一次函数的关系.以考查直线方程的求法为主,直线的斜率、倾斜角也是考查的重点.题型主要在解答题中与圆、圆锥曲线等知识交汇出现,有时也会在选择、填空题中出现.1.平面直角坐标系中的基本公式 (1)两点的距离公式:已知平面直角坐标系中的两点A (x 1,y 1),B (x 2,y 2),则d (A ,B )=|AB |=(x 2-x 1)2+(y 2-y 1)2. (2)中点公式:已知平面直角坐标系中的两点A (x 1,y 1),B (x 2,y 2),点M (x ,y )是线段AB 的中点,则x =x 1+x 22,y =y 1+y 22.2.直线的倾斜角(1)定义:x 轴正向与直线向上的方向所成的角叫做这条直线的倾斜角,我们规定,与x 轴平行或重合的直线的倾斜角为零度角.(2)倾斜角的范围:[0°,180°). 3.直线的斜率(1)定义:通常,我们把直线y =kx +b 中的系数k 叫做这条直线的斜率,垂直于x 轴的直线,人们常说它的斜率不存在;(2)计算公式:若由A (x 1,y 1),B (x 2,y 2)确定的直线不垂直于x 轴,则k =y 2-y 1x 2-x 1 (x 1≠x 2).若直线的倾斜角为θ⎝⎛⎭⎫θ≠π2,则k =tan_θ. 4.直线方程的五种形式名称 方程 适用范围 点斜式 y -y 0=k (x -x 0) 不含直线x =x 0 斜截式 y =kx +b 不含垂直于x 轴的直线 两点式 y -y 1y 2-y 1=x -x 1x 2-x 1不含直线x =x 1 (x 1≠x 2)和直线y =y 1 (y 1≠y 2)截距式 x a +y b=1 不含垂直于坐标轴和过原点的直线 一般式 Ax +By +C =0(A 2+B 2≠0)平面直角坐标系内的直线都适用题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)根据直线的倾斜角的大小不能确定直线的位置.( √ ) (2)坐标平面内的任何一条直线均有倾斜角与斜率.( × ) (3)直线的倾斜角越大,其斜率就越大.( × ) (4)若直线的斜率为tan α,则其倾斜角为α.( × ) (5)斜率相等的两直线的倾斜角不一定相等.( × )(6)经过任意两个不同的点P 1(x 1,y 1),P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示.( √ ) 题组二 教材改编2.若过点M (-2,m ),N (m,4)的直线的斜率等于1,则m 的值为( ) A .1 B .4 C .1或3 D .1或4答案 A。
2020高考数学大一轮复习第九章平面解析几何12规范答题示范(五)高考解答题——解析几何真题展示课件理

过点P且垂直于OQ的直线l过C的左焦点F.❷
解题思路 ❶看到求点 P 的轨迹方程,想到先设出点的坐标,然后利用已 知条件,采用代入法求轨迹方程. ❷看到过点 P 且垂直于 OQ 的直线 l 过 C 的左焦点 F,想到证 明O→Q⊥P→F.
■标准答案(规范答题 分步得分) (1)设 P(x,y),M(x0,y0), 则 N(x0,0), N→P=(x-x0,y),N→M=(0,y0), 由N→P= 2 N→M,
第九章 平面解析几何
规范答题示范(五) 高考解答题——解析几何
第九章 平面解析几何
真题展示
(12 分)(2017·高考全国卷Ⅱ)设 O 为坐标原点,动点 M 在椭圆 C:
x22+y2=1 上,过点 M 作 x 轴的垂线,垂足为 N,点 P 满足N→P
=
→ 2NM.
(1)求点P的轨迹方程; ❶
(2)设点 Q 在直线 x=-3 上,且O→P·P→Q=1,证明:
7 分 得分点⑤ 8 分 得分点⑥
9 分 得分点⑦
由O→P·P→Q=1 得
-3m-m2+tn-n2=1,
10 分 得分点⑧
又由(1)知 m2+n2=2,
故 3+3m-tn=0.
所以O→Q·P→F=0,
即O→Q⊥P→F,
11 分 得分点⑨
又过点 P 存在唯一直线垂直于 OQ,
所以过点 P 且垂直于 OQ 的直线 l 过 C 的左焦点 F.
得 x0=x,y0= 22y, 因为 M(x0,y0)在椭圆 C 上, 所以x22+y22=1, 因此点 P 的轨迹方程为 x2+y2=2.
1 分 得分点①
3 分 得分点② 5 分 得分点③ 6 分 得分点④
(2)由题意知 F(-1,0), 设 Q(-3,t),P(m,n), 则O→Q=(-3,t), P→F=(-1-m,-n), O→Q·P→F=3+3m-tn, O→P=(m,n), P→Q=(-3-m,t-n),
高考数学一轮复习 第九章 解析几何 第二节 两条直线的位置关系教案 理(含解析)苏教版-苏教版高三全

第二节两条直线的位置关系1.两条直线平行与垂直的判定 (1)两条直线平行:①对于两条不重合的直线l 1,l 2,若其斜率分别为k 1,k 2,则有l 1∥l 2⇔k 1=k 2. ②当直线l 1,l 2不重合且斜率都不存在时,l 1∥l 2. (2)两条直线垂直:①如果两条直线l 1,l 2的斜率存在,设为k 1,k 2,则有l 1⊥l 2⇔k 1·k 2=-1. ②当其中一条直线的斜率不存在,而另一条直线的斜率为0时,l 1⊥l 2. 2.两条直线的交点的求法直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,则l 1与l 2的交点坐标就是方程组⎩⎪⎨⎪⎧A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0的解.3.三种距离公式P 1(x 1,y 1),P 2(x 2,y 2)两点之间的距离|P 1P 2|=x 2-x 12+y 2-y 12点P 0(x 0,y 0)到直线l :Ax +By +C =0的距离 d =|Ax 0+By 0+C |A 2+B 2平行线Ax +By +C 1=0与Ax +By +C 2=0间距离d =|C 1-C 2|A 2+B2[小题体验]1.已知过点A (-2,m )和B (m,4)的直线与直线2x +y -1=0平行,则实数m 的值为________.解析:由k AB =4-mm +2=-2,得m =-8.答案:-82.已知点(a,2)(a >0)到直线l :x -y +3=0的距离为1,则a =________. 解析:由题意知|a -2+3|2=1,所以|a +1|=2,又a >0,所以a =2-1. 答案:2-13.若直线ax +2y -1=0与直线2x -3y -1=0垂直,则a 的值为________.解析:直线ax +2y -1=0的斜率k 1=-a 2,直线2x -3y -1=0的斜率k 2=23,因为两直线垂直,所以-a 2×23=-1,即a =3.答案:31.在判断两条直线的位置关系时,易忽视斜率是否存在,两条直线都有斜率可根据条件进行判断,若无斜率,要单独考虑.2.运用两平行直线间的距离公式时易忽视两方程中的x ,y 的系数分别相等这一条件盲目套用公式导致出错.[小题纠偏]1.已知直线l 1:(t +2)x +(1-t )y =1与l 2:(t -1)x +(2t +3)y +2=0互相垂直,则t 的值为________.解析:①若l 1的斜率不存在,此时t =1,l 1的方程为x =13,l 2的方程为y =-25,显然l 1⊥l 2,符合条件;若l 2的斜率不存在,此时t =-32,易知l 1与l 2不垂直.②当l 1,l 2的斜率都存在时,直线l 1的斜率k 1=-t +21-t ,直线l 2的斜率k 2=-t -12t +3,因为l 1⊥l 2,所以k 1·k 2=-1,即⎝ ⎛⎭⎪⎫-t +21-t ·⎝ ⎛⎭⎪⎫-t -12t +3=-1,所以t =-1.综上可知t =-1或t =1. 答案:-1或12.已知直线3x +4y -3=0与直线6x +my +14=0平行,则它们之间的距离是________. 解析:因为63=m 4≠14-3,所以m =8,直线6x +my +14=0可化为3x +4y +7=0,两平行线之间的距离d =|-3-7|32+42=2. 答案:2考点一 两条直线的位置关系 (基础送分型考点——自主练透)[题组练透]1.(2019·沭阳月考)若直线y =mx +1与直线y =4x -8垂直,则m =________. 解析:由直线y =mx +1与直线y =4x -8垂直, 得m ×4=-1,解得m =-14.答案:-142.(2018·某某模拟)过点(1,0)且与直线x -2y -2=0平行的直线方程是________. 解析:依题意,设所求的直线方程为x -2y +a =0,由于点(1,0)在所求直线上,则1+a =0,即a =-1,则所求的直线方程为x -2y -1=0.答案:x -2y -1=03.(2019·启东调研)已知直线l 1:(a -1)x +y +b =0,l 2:ax +by -4=0,求满足下列条件的a ,b 的值.(1)l 1⊥l 2,且l 1过点(1,1);(2)l 1∥l 2,且l 2在第一象限内与两坐标轴围成的三角形的面积为2. 解:(1)因为l 1⊥l 2,所以a (a -1)+b =0.① 又l 1过点(1,1),所以a +b =0.②由①②,解得⎩⎪⎨⎪⎧a =0,b =0或⎩⎪⎨⎪⎧a =2,b =-2.当a =0,b =0时不合题意,舍去. 所以a =2,b =-2.(2)因为l 1∥l 2,所以a -b (a -1)=0,③由题意,知a >0,b >0,直线l 2与两坐标轴的交点坐标分别为⎝ ⎛⎭⎪⎫4a,0,⎝⎛⎭⎪⎫0,4b .则12×4a ×4b=2,得ab =4,④ 由③④,得a =2,b =2.[谨记通法]1.已知两直线的斜率存在,判断两直线平行垂直的方法 (1)两直线平行⇔两直线的斜率相等且在坐标轴上的截距不等;(2)两直线垂直⇔两直线的斜率之积等于-1.[提醒] 当直线斜率不确定时,要注意斜率不存在的情况. 2.由一般式确定两直线位置关系的方法直线方程l 1:A 1x +B 1y +C 1=0(A 21+B 21≠0)l 2:A 2x +B 2y +C 2=0(A 22+B 22≠0)l 1与l 2垂直的充要条件 A 1A 2+B 1B 2=0 l 1与l 2平行的充分条件 A 1A 2=B 1B 2≠C 1C 2(A 2B 2C 2≠0) l 1与l 2相交的充分条件 A 1A 2≠B 1B 2(A 2B 2≠0) l 1与l 2重合的充分条件A 1A 2=B 1B 2=C 1C 2(A 2B 2C 2≠0) [提醒] 在判断两直线位置关系时,比例式A 1A 2与B 1B 2,C 1C 2的关系容易记住,在解答填空题时,建议多用比例式来解答.考点二 距离问题重点保分型考点——师生共研[典例引领]已知A (4,-3),B (2,-1)和直线l :4x +3y -2=0,在坐标平面内求一点P ,使PA =PB ,且点P 到直线l 的距离为2.解:设点P 的坐标为(a ,b ). 因为A (4,-3),B (2,-1),所以线段AB 的中点M 的坐标为(3,-2). 而AB 的斜率k AB =-3+14-2=-1,所以线段AB 的垂直平分线方程为y +2=x -3,即x -y -5=0. 因为点P (a ,b )在直线x -y -5=0上, 所以a -b -5=0.①又点P (a ,b )到直线l :4x +3y -2=0的距离为2, 所以|4a +3b -2|5=2,即4a +3b -2=±10,②由①②联立可得⎩⎪⎨⎪⎧a =1,b =-4或⎩⎪⎨⎪⎧a =277,b =-87.所以所求点P 的坐标为(1,-4)或⎝⎛⎭⎪⎫277,-87.[由题悟法]距离问题的常见题型及解题策略(1)求两点间的距离.关键是确定两点的坐标,然后代入公式即可,一般用来判断三角形的形状等.(2)解决与点到直线的距离有关的问题.应熟记点到直线的距离公式,若已知点到直线的距离求直线方程,一般考虑待定斜率法,此时必须讨论斜率是否存在.(3)求两条平行线间的距离.要先将直线方程中x ,y 的对应项系数转化成相等的形式,再利用距离公式求解.也可以转化成点到直线的距离问题.[即时应用]1.(2019·阜宁中学检测)在坐标轴上,与点A (1,5),B (2,4)等距离的点的坐标是________.解析:线段AB 的垂直平分线方程为y -92=-1-25-4·⎝ ⎛⎭⎪⎫x -32,令x =0,可得y =3;令y=0,可得x =-3,∴在坐标轴上,与点A (1,5),B (2,4)等距离的点的坐标是(0,3)或(-3,0). 答案:(0,3)或(-3,0)2.(2018·某某中学测试)已知点M 是直线x +3y =2上的一个动点,且点P (3,-1),则PM 的最小值为________.解析:PM 的最小值即为点P (3,-1)到直线x +3y =2的距离, 又d =|3-3-2|1+3=1,故PM 的最小值为1.答案:13.已知直线l 1与l 2:x +y -1=0平行,且l 1与l 2的距离是2,则直线l 1的方程为______________________.解析:因为l 1与l 2:x +y -1=0平行, 所以可设l 1的方程为x +y +b =0(b ≠-1).又因为l 1与l 2的距离是2, 所以|b +1|12+12=2,解得b =1或b =-3,即l 1的方程为x +y +1=0或x +y -3=0. 答案:x +y +1=0或x +y -3=0考点三 对称问题题点多变型考点——多角探明 [锁定考向]对称问题是高考常考内容之一,也是考查学生转化能力的一种常见题型. 常见的命题角度有: (1)点关于点对称; (2)点关于线对称;(3)线关于线对称.[题点全练]角度一:点关于点对称1.(2019·丹阳高级中学检测)点A (2,3)关于点P (0,5)对称的点的坐标为________. 解析:设A (2,3)关于点P (0,5)对称的点的坐标为(x 0,y 0),由中点坐标公式,得2+x 02=0,3+y 02=5,则x 0=-2,y 0=7.∴点A (2,3)关于点P (0,5)对称的点的坐标为(-2,7).答案:(-2,7)角度二:点关于线对称2.(2018·某某模拟)已知△ABC 的两个顶点A (-1,5)和B (0,-1),若∠C 的平分线所在的直线方程为2x -3y +6=0,则BC 边所在的直线方程为______________.解析:设点A 关于直线2x -3y +6=0的对称点为A ′(x ′,y ′),则⎩⎪⎨⎪⎧2×x ′-12-3×y ′+52+6=0,y ′-5x ′+1=-32,即⎩⎪⎨⎪⎧2x ′-3y ′-5=0,3x ′+2y ′-7=0,解得⎩⎪⎨⎪⎧x ′=3113,y ′=-113,即A ′⎝ ⎛⎭⎪⎫3113,-113,由题意知,点A ′在直线BC 上.所以直线BC 的方程为y =-113--13113-0x -1,整理得12x -31y -31=0. 答案:12x -31y -31=0 角度三:线关于线对称3.直线2x -y +3=0关于直线x -y +2=0对称的直线方程是________.解析:设所求直线上任意一点P (x ,y ),则P 关于x -y +2=0的对称点为P ′(x 0,y 0),由⎩⎪⎨⎪⎧x +x 02-y +y 02+2=0,x -x 0=-y -y 0,得⎩⎪⎨⎪⎧x 0=y -2,y 0=x +2,由点P ′(x 0,y 0)在直线2x -y +3=0上, 所以2(y -2)-(x +2)+3=0, 即x -2y +3=0. 答案:x -2y +3=0[通法在握]1.中心对称问题的2个类型及求解方法 (1)点关于点对称:若点M (x 1,y 1)及N (x ,y )关于P (a ,b )对称,则由中点坐标公式得⎩⎪⎨⎪⎧x =2a -x 1,y =2b -y 1进而求解.(2)直线关于点的对称,主要求解方法是:①在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的两点坐标,再由两点式求出直线方程;②求出一个对称点,再利用两对称直线平行,由点斜式得到所求直线方程. 2.轴对称问题的2个类型及求解方法 (1)点关于直线的对称:若两点P 1(x 1,y 1)与P 2(x 2,y 2)关于直线l :Ax +By +C =0对称,由方程组⎩⎪⎨⎪⎧A ⎝ ⎛⎭⎪⎫x 1+x 22+B ⎝ ⎛⎭⎪⎫y 1+y 22+C =0,y 2-y 1x 2-x 1·⎝ ⎛⎭⎪⎫-A B =-1,可得到点P 1关于l 对称的点P 2的坐标(x 2,y 2)(其中B ≠0,x 1≠x 2). (2)直线关于直线的对称:一般转化为点关于直线的对称来解决,有两种情况:一是已知直线与对称轴相交;二是已知直线与对称轴平行.[演练冲关]1.(2019·沭阳期中)已知点A (1,-2)关于直线x +ay -2=0的对称点为B (m,2),则实数a 的值为________.解析:由对称的特点可知,AB 的中点在对称轴上,直线AB 垂直于对称轴,则1+m 2+-2+22a -2=0,2--2m -1·⎝ ⎛⎭⎪⎫-1a =-1,解得m =3,a =2.答案:22.(2018·启东期末)已知直线l 1:2x -y -2=0和直线l 2:x +2y -1=0关于直线l 对称,则直线l 的斜率为________.解析:设P (a ,b )是直线l 上任意一点,则点P 到直线l 1:2x -y -2=0和直线l 2:x +2y -1=0的距离相等, 即|2a -b -2|5=|a +2b -1|5,整理得a -3b -1=0或3a +b -3=0, ∴直线l 的斜率为13或-3.答案:13或-33.已知入射光线经过点M (-3,4),被直线l :x -y +3=0反射,反射光线经过点N (2,6),则反射光线所在直线的方程为________.解析:设点M (-3,4)关于直线l :x -y +3=0的对称点为M ′(a ,b ), 则反射光线所在直线过点M ′,所以⎩⎪⎨⎪⎧b -4a --3·1=-1,-3+a 2-b +42+3=0,解得a =1,b =0.又反射光线经过点N (2,6),所以所求直线的方程为y -06-0=x -12-1,即6x -y -6=0. 答案:6x -y -6=0一抓基础,多练小题做到眼疾手快1.(2019·某某调研)已知点A (1,3)关于直线l 的对称点为B (-5,1),则直线l 的方程为________.解析:∵已知点A (1,3)关于直线l 的对称点为B (-5,1),故直线l 为线段AB 的中垂线.求得AB 的中点为(-2,2),AB 的斜率为1-3-5-1=13,故直线l 的斜率为-3,故直线l 的方程为 y -2=-3(x +2),即3x +y +4=0.答案:3x +y +4=02.(2018·宿迁模拟)过点(1,0)且与直线x -2y -2=0垂直的直线方程是________. 解析:因为直线x -2y -2=0的斜率为12,所以所求直线的斜率ky -0=-2(x -1),即2x +y -2=0.答案:2x +y -2=03.直线y =3x +3关于直线l :x -y -2=0对称的直线方程为________. 解析:取直线y =3x +3上一点A (0,3),设A 关于直线l :x -y -2=0对称的点为A ′(a ,b ),则有⎩⎪⎨⎪⎧b -3a -0·1=-1,a +02-b +32-2=0,解得a =5,b =-2.∴A ′(5,-2).联立⎩⎪⎨⎪⎧y =3x +3,x -y -2=0,解得x =-52,y =-92.令M ⎝ ⎛⎭⎪⎫-52,-92,∵直线y =3x +3关于直线l 对称的直线过A ′,M 两点,∴所求直线方程为y -⎝ ⎛⎭⎪⎫-92-2-⎝ ⎛⎭⎪⎫-92=x -⎝ ⎛⎭⎪⎫-525-⎝ ⎛⎭⎪⎫-52,即x -3y -11=0.答案:x -3y -11=04.(2018·启东中学测试)已知直线l 1的斜率为2,l 1∥l 2,直线l 2过点(-1,1)且与y 轴交于点P ,则点P 的坐标为________.解析:因为l 1∥l 2,且l 1的斜率为2,则直线l 2l 2过点(-1,1),所以直线l 2的方程为y -1=2(x +1),整理得y =2xx =0,得y =3,所以点P 的坐标为(0,3).答案:(0,3)5.若直线2x -y =-10,y =x +1,y =ax -2交于一点,则a 的值为________.解析:解方程组⎩⎪⎨⎪⎧2x -y =-10,y =x +1,可得⎩⎪⎨⎪⎧x =-9,y =-8,所以直线2x -y =-10与y =x +1的交点坐标为(-9,-8), 代入y =ax -2,得-8=a ·(-9)-2, 所以a =23.答案:236.(2019·某某检测)已知直线l 1:mx +2y +4=0与直线l 2:x +(m +1)y -2=0平行,则l 1与l 2间的距离为________.解析:∵直线l 1:mx +2y +4=0与直线l 2:x +(m +1)y -2=0平行,当m =-1时,显然不合题意;当m ≠-1时,有m 1=2m +1≠4-2,解得m =1,∴l 1与l 2间的距离d =|-2-4|1+4=655.答案:655二保高考,全练题型做到高考达标1.已知直线l 1:(m +1)x +2y +2m -2=0,l 2:2x +(m -2)y +2=0,若直线l 1∥l 2,则m =________.解析:由题意知,当m =2时,l 1:3x +2y +2=0,l 2:x +1=0,不合题意;当m ≠2时,若直线l 1∥l 2,则m +12=2m -2≠2m -22,解得m =-2或m =3(舍去). 答案:-22.若直线l 1:x +ay +6=0与l 2:(a -2)x +3y +2a =0平行,则l 1与l 2之间的距离为________.解析:因为l 1∥l 2,所以1a -2=a 3≠62a ,解得a =-1, 所以l 1与l 2的方程分别为l 1:x -y +6=0,l 2:x -y +23=0, 所以l 1与l 2的距离d =⎪⎪⎪⎪⎪⎪6-232=823.答案:823 3.(2019·X 家港模拟)过点P (1,2)作一直线l ,使直线l 与点M (2,3)和点N (4,-5)的距离相等,则直线l 的方程为________________.解析:易知直线l 的斜率存在,∵直线l 过点P (1,2),∴设l 的方程为y -2=k (x -1),即kx -y -k +2=0.又直线l 与点M (2,3)和点N (4,-5)的距离相等, ∴|2k -3-k +2|k 2+1=|4k +5-k +2|k 2+1, 解得k =-4或k =-32, ∴l 的方程为4x +y -6=0或3x +2y -7=0.答案:4x +y -6=0或3x +2y -7=04.若直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,则直线l 2恒过定点________. 解析:由于直线l 1:y =k (x -4)恒过定点(4,0),其关于点(2,1)对称的点为(0,2),又由于直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,所以直线l 2恒过定点(0,2).答案:(0,2)5.已知点P (0,-1),点Q 在直线x -y +1=0上,若直线P Q 垂直于直线x +2y -5=0,则点Q 的坐标是________.解析:设Q(x 0,y 0),因为点Q 在直线x -y +1=0上,所以x 0-y 0+1=0.①又直线x +2y -5=0的斜率k =-12,直线P Q 的斜率k P Q =y 0+1x 0, 所以由直线P Q 垂直于直线x +2y -5=0,得y 0+1x 0·⎝ ⎛⎭⎪⎫-12=-1.② 由①②解得x 0=2,y 0=3,即点Q 的坐标是(2,3).答案:(2,3)6.(2019·某某一模)设m ,n ∈R ,若直线l :mx +ny -1=0与x 轴相交于点A ,与y 轴相交于点B ,且坐标原点O 到直线l 的距离为3,则△AOB 的面积S 的最小值为________.解析:由坐标原点O 到直线l 的距离为3,可得|-1|m 2+n 2=3,化简得m 2+n 2=13. 对直线l :mx +ny -1=0,令x =0,可得y =1n ;令y =0,可得x =1m, 故△AOB 的面积S =12·⎪⎪⎪⎪⎪⎪1m ·1n =12|mn |≥1m 2+n2=3, 当且仅当|m |=|n |=66时,取等号. 故△AOB 的面积S 的最小值为3.答案:37.设m ∈R ,过定点A 的动直线x +my =0和过定点B 的动直线mx -y -m +3=0交于点P (x ,y ),则PA ·PB 的最大值是________.解析:易求定点A (0,0),B (1,3).当P 与A 和B 均不重合时,因为P 为直线x +my =0与mx -y -m +3=0的交点,且易知两直线垂直,则PA ⊥PB ,所以PA 2+PB 2=AB 2=10,所以PA ·PB ≤PA 2+PB 22=5(当且仅当PA =PB =5时,等号成立),当P 与A 或B 重合时,PA ·PB=0,故PA ·PB 的最大值是5.答案:58.将一X 画有直角坐标系的图纸折叠一次,使得点A (0,2)与点B (4,0)重合.若此时点C (7,3)与点D (m ,n )也重合,则m +n 的值是________.解析:由题意知,折痕既是A ,B 的对称轴,也是 C ,D 的对称轴.因为AB 的斜率k AB =0-24-0=-12,AB 的中点为(2,1), 所以图纸的折痕所在的直线方程为y -1=2(x -2),所以k CD =n -3m -7=-12, ① 因为CD 的中点为⎝⎛⎭⎪⎫m +72,n +32, 所以n +32-1=2⎝ ⎛⎭⎪⎫m +72-2. ② 由①②解得m =35,n =315,所以m +n =345. 答案:3459.已知直线l 1:ax +2y +6=0和直线l 2:x +(a -1)y +a 2-1=0.(1)当l 1∥l 2时,求a 的值;(2)当l 1⊥l 2时,求a 的值.解:(1)法一:当a =1时,l 1:x +2y +6=0, l 2:x =0,l 1不平行于l 2;当a =0时,l 1:y =-3,l 2:x -y -1=0,l 1不平行于l 2;当a ≠1且a ≠0时,两直线方程可化为l 1:y =-a 2x -3,l 2:y =11-ax -(a +1), 由l 1∥l 2可得⎩⎪⎨⎪⎧ -a 2=11-a,-3≠-a +1,解得a =-1. 综上可知,a =-1.法二:由l 1∥l 2知⎩⎪⎨⎪⎧ A 1B 2-A 2B 1=0,A 1C 2-A 2C 1≠0, 即⎩⎪⎨⎪⎧ a a -1-1×2=0,a a 2-1-1×6≠0⇒⎩⎪⎨⎪⎧ a 2-a -2=0,a a 2-1≠6⇒a =-1.(2)法一:当a =1时,l 1:x +2y +6=0,l 2:x =0,l 1与l 2不垂直,故a =1不符合;当a ≠1时,l 1:y =-a 2x -3,l 2:y =11-ax -(a +1),由l 1⊥l 2,得⎝ ⎛⎭⎪⎫-a 2·11-a=-1⇒a =23. 法二:因为l 1⊥l 2,所以A 1A 2+B 1B 2=0,即a +2(a -1)=0,得a =23. 10.已知△ABC 的顶点A (5,1),AB 边上的中线CM 所在直线方程为2x -y -5=0,AC 边上的高BH 所在直线方程为x -2y -5=0,求直线BC 的方程.解:依题意知:k AC =-2,A (5,1),所以l AC 的方程为2x +y -11=0,联立⎩⎪⎨⎪⎧ 2x +y -11=0,2x -y -5=0,得C (4,3).设B (x 0,y 0),则AB 的中点M ⎝ ⎛⎭⎪⎫x 0+52,y 0+12, 代入2x -y -5=0,得2x 0-y 0-1=0,联立⎩⎪⎨⎪⎧ 2x 0-y 0-1=0,x 0-2y 0-5=0,得B (-1,-3),所以k BC =65, 所以直线BC 的方程为y -3=65(x -4), 即6x -5y -9=0.三上台阶,自主选做志在冲刺名校1.(2019·江阴检测)直线l 经过点P (2,1),且与两坐标轴围成的三角形的面积为S ,如果符合条件的直线l 能作且只能作三条,则S =________.解析:由已知可得直线l 的斜率一定存在且不为零,设直线l 的方程为y -1=k (x -2),则直线l 与坐标轴的交点为(0,1-2k ),⎝ ⎛⎭⎪⎫2-1k ,0, 则S =12|1-2k |·⎪⎪⎪⎪⎪⎪2-1k =⎪⎪⎪⎪⎪⎪2-12k -2k . 如果符合条件的直线l 能作且只能作三条,则关于k 的方程⎪⎪⎪⎪⎪⎪2-12k -2k =S 只有三个解,即4k 2+2(S -2)k +1=0与4k 2-2(S +2)k +1=0,一个有一解,一个有两解,解得S =4.答案:42.(2018·锡山高级中学检测)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,则直线x sin A +ay +c =0与直线bx -y sin B +sin C =0的位置关系是________.解析:在△ABC 中,由正弦定理a sin A =b sin B ,得b sin B ·sin A ax sin A +ay +c =0的斜率k 1=-sin A a ,bx -y sin B +sin C =0的斜率k 2=b sin B ,因此k 1·k 2=b sin B ·⎝ ⎛⎭⎪⎫-sin A a =-1,所以两条直线垂直.答案:垂直3.已知直线l 经过直线l 1:2x +y -5=0与l 2:x -2y =0的交点.(1)若点A (5,0)到l 的距离为3,求l 的方程;(2)求点A (5,0)到l 的距离的最大值,并求此时l 的方程.解:(1)经过两已知直线交点的直线系方程为(2x +y -5)+λ(x -2y )=0, 即(2+λ)x +(1-2λ)y -5=0,因为点A (5,0)到l 的距离为3,所以|10+5λ-5|2+λ2+1-2λ2=3,即2λ2-5λ+2=0,所以λ=2或λ=12, 所以直线l 的方程为x =2或4x -3y -5=0.(2)如图,由⎩⎪⎨⎪⎧ 2x +y -5=0,x -2y =0,解得交点P (2,1),过P 作任一直线l ,设d 为点A 到l的距离,则d ≤PA (当l ⊥PA 时等号成立).所以d max =PA =5-22+0-12=10.因为k PA =-13,l ⊥PA ,所以k l =3, 所以直线l 的方程为y -1=3(x -2),即3x -y -5=0.。
高考数学一轮复习 第九章 平面解析几何9

高考数学一轮复习 第九章 平面解析几何9.1 直线的方程考试要求 1.理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.2.根据确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式).知识梳理 1.直线的倾斜角(1)定义:当直线l 与x 轴相交时,我们以x 轴为基准,x 轴正向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角.(2)范围:直线的倾斜角α的取值范围为0°≤α<180°. 2.直线的斜率(1)定义:把一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k 表示,即k =tan_α(α≠90°). (2)过两点的直线的斜率公式如果直线经过两点P 1(x 1,y 1),P 2(x 2,y 2)(x 1≠x 2),其斜率k =y 2-y 1x 2-x 1.3.直线方程的五种形式名称 方程 适用范围 点斜式 y -y 0=k (x -x 0) 不含直线x =x 0 斜截式 y =kx +b不含垂直于x 轴的直线 两点式y -y 1y 2-y 1=x -x 1x 2-x 1(x 1≠x 2,y 1≠y 2) 不含直线x =x 1 和直线y =y 1截距式 x a +y b=1 不含垂直于坐标轴和过原点的直线一般式Ax+By+C=0(A2+B2≠0)平面直角坐标系内的直线都适用常用结论直线的斜率k与倾斜角α之间的关系α0°0°<α<90°90°90°<α<180°k 0k>0不存在k<0牢记口诀:1.“斜率变化分两段,90°是分界线;遇到斜率要谨记,存在与否要讨论”.2.“截距”是直线与坐标轴交点的坐标值,它可正,可负,也可以是零,而“距离”是一个非负数.应注意过原点的特殊情况是否满足题意.3.直线Ax+By+C=0(A2+B2≠0)的一个法向量v=(A,B),一个方向向量a=(-B,A).思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)根据直线的倾斜角的大小不能确定直线的位置.(√)(2)若一条直线的倾斜角为α,则此直线的斜率为tan α.(×)(3)斜率相等的两直线的倾斜角不一定相等.(×)(4)截距可以为负值.(√)教材改编题1.若过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为()A.1 B.4C.1或3 D.1或4答案 A解析 由题意得m -4-2-m=1,解得m =1.2.倾斜角为135°,在y 轴上的截距为-1的直线方程是( ) A .x -y +1=0 B .x -y -1=0 C .x +y -1=0 D .x +y +1=0答案 D解析 直线的斜率为k =tan 135°=-1,所以直线方程为y =-x -1,即x +y +1=0. 3.过点P (2,3)且在两坐标轴上截距相等的直线方程为________________. 答案 3x -2y =0或x +y -5=0解析 当截距为0时,直线方程为3x -2y =0; 当截距不为0时, 设直线方程为x a +ya =1,则2a +3a =1,解得a =5. 所以直线方程为x +y -5=0.题型一 直线的倾斜角与斜率例1 (1)直线2x cos α-y -3=0⎝⎛⎭⎫α∈⎣⎡⎦⎤π6,π3的倾斜角的变化范围是( ) A.⎣⎡⎦⎤π6,π3 B.⎣⎡⎦⎤π4,π3 C.⎣⎡⎦⎤π4,π2 D.⎣⎡⎦⎤π4,2π3答案 B解析 直线2x cos α-y -3=0的斜率k =2cos α. 由于α∈⎣⎡⎦⎤π6,π3,所以12≤cos α≤32,因此k =2cos α∈[1,3].设直线的倾斜角为θ,则有tan θ∈[1,3]. 由于θ∈[0,π), 所以θ∈⎣⎡⎦⎤π4,π3,即倾斜角的变化范围是⎣⎡⎦⎤π4,π3.(2)过函数f (x )=13x 3-x 2的图象上一个动点作函数图象的切线,则切线倾斜角的取值范围为( ) A.⎣⎡⎦⎤0,3π4 B.⎣⎡⎭⎫0,π2∪⎣⎡⎭⎫3π4,π C.⎣⎡⎭⎫3π4,π D.⎣⎡⎦⎤π2,3π4答案 B解析 设切线的倾斜角为α,则α∈[0,π), ∵f ′(x )=x 2-2x =(x -1)2-1≥-1, ∴切线的斜率k =tan α≥-1, 则α∈⎣⎡⎭⎫0,π2∪⎣⎡⎭⎫3π4,π. 教师备选1.(2022·安阳模拟)已知点A (1,3),B (-2,-1).若直线l :y =k (x -2)+1与线段AB 相交,则k 的取值范围是( ) A .k ≥12B .k ≤-2C .k ≥12或k ≤-2D .-2≤k ≤12答案 D解析 直线l :y =k (x -2)+1经过定点P (2,1),∵k P A =3-11-2=-2,k PB =-1-1-2-2=12, 又直线l :y =k (x -2)+1与线段AB 相交, ∴-2≤k ≤12.2.若直线l 的斜率为k ,倾斜角为α,且α∈⎣⎡⎭⎫π6,π4∪⎣⎡⎭⎫2π3,π,则k 的取值范围是________. 答案 [-3,0)∪⎣⎡⎭⎫33,1解析 当α∈⎣⎡⎭⎫π6,π4时,k =tan α∈⎣⎡⎭⎫33,1; 当α∈⎣⎡⎭⎫2π3,π时,k =tan α∈[-3,0). 综上得k ∈[-3,0)∪⎣⎡⎭⎫33,1.思维升华 直线倾斜角的范围是[0,π),而这个区间不是正切函数的单调区间,因此根据斜率求倾斜角的范围时,要分⎣⎡⎭⎫0,π2与⎝⎛⎭⎫π2,π两种情况讨论. 跟踪训练1 (1)直线x +(a 2+1)y +1=0的倾斜角的取值范围是( ) A.⎣⎡⎦⎤0,π4 B.⎣⎡⎭⎫3π4,π C.⎣⎡⎦⎤0,π4∪⎝⎛⎭⎫π2,π D.⎣⎡⎭⎫π4,π2∪⎣⎡⎭⎫3π4,π答案 B解析 依题意,直线的斜率k =-1a 2+1∈[-1,0),因此其倾斜角的取值范围是⎣⎡⎭⎫3π4,π. (2)若正方形一条对角线所在直线的斜率为2,则该正方形的两条邻边所在直线的斜率分别为______,______. 答案 13-3解析 如图,在正方形OABC 中,对角线OB 所在直线的斜率为2,建立如图所示的平面直角坐标系.设对角线OB 所在直线的倾斜角为θ,则tan θ=2,由正方形的性质可知,直线OA 的倾斜角为θ-45°,直线OC 的倾斜角为θ+45°,故k OA =tan(θ-45°)=tan θ-tan 45°1+tan θtan 45°=2-11+2=13, k OC =tan(θ+45°)=tan θ+tan 45°1-tan θtan 45°=2+11-2=-3. 题型二 求直线的方程例2 求满足下列条件的直线方程:(1)经过点A (-5,2),且在x 轴上的截距等于在y 轴上截距的2倍; (2)经过点B (3,4),且与两坐标轴围成一个等腰直角三角形. 解 (1)当直线不过原点时, 设所求直线方程为x 2a +ya=1,将(-5,2)代入所设方程,解得a =-12,所以直线方程为x +2y +1=0; 当直线过原点时,设直线方程为y =kx , 则-5k =2,解得k =-25,所以直线方程为y =-25x ,即2x +5y =0.故所求直线方程为2x +5y =0或x +2y +1=0. (2)由题意可知,所求直线的斜率为±1. 又过点(3,4),由点斜式得y -4=±(x -3).所求直线的方程为 x -y +1=0或x +y -7=0.教师备选1.已知A (-1,1),B (3,1),C (1,3),则△ABC 的边BC 上的高所在的直线方程为( ) A .x +y =0 B .x -y +2=0 C .x +y +2=0 D .x -y =0答案 B解析 因为B (3,1),C (1,3),所以k BC =3-11-3=-1,故BC 边上的高所在直线的斜率k =1,又高线经过点A (-1,1),所以其所在的直线方程为x -y +2=0.2.已知点M 是直线l :2x -y -4=0与x 轴的交点,将直线l 绕点M 按逆时针方向旋转45°,得到的直线方程是( ) A .x +y -3=0 B .x -3y -2=0 C .3x -y +6=0 D .3x +y -6=0 答案 D解析 设直线l 的倾斜角为α,则tan α=k =2,直线l 绕点M 按逆时针方向旋转45°,所得直线的斜率k ′=tan ⎝⎛⎭⎫α+π4=2+11-2×1=-3, 又点M (2,0),所以y =-3(x -2),即3x +y -6=0. 思维升华 求直线方程的两种方法(1)直接法:由题意确定出直线方程的适当形式.(2)待定系数法:先由直线满足的条件设出直线方程,方程中含有待定的系数,再由题设条件求出待定系数.跟踪训练2 (1)已知△ABC 的三个顶点坐标为A (1,2),B (3,6),C (5,2),M 为AB 的中点,N 为AC 的中点,则中位线MN 所在直线的方程为( )A .2x +y -12=0B .2x -y -12=0C .2x +y -8=0D .2x -y +8=0答案 C解析 由题知M (2,4),N (3,2),中位线MN 所在直线的方程为y -42-4=x -23-2,整理得2x +y -8=0.(2)过点(2,1)且在x 轴上截距与在y 轴上截距之和为6的直线方程为______________. 答案 x +y -3=0或x +2y -4=0 解析 由题意可设直线方程为x a +yb =1.则⎩⎪⎨⎪⎧a +b =6,2a +1b=1,解得a =b =3或a =4,b =2.故所求直线方程为x +y -3=0或x +2y -4=0.题型三 直线方程的综合应用例3 已知直线l 过点M (2,1),且分别与x 轴的正半轴、y 轴的正半轴交于A ,B 两点,O 为原点,当△AOB 面积最小时,求直线l 的方程. 解 方法一 设直线l 的方程为y -1=k (x -2)(k <0), 则A ⎝⎛⎭⎫2-1k ,0,B (0,1-2k ), S △AOB =12(1-2k )·⎝⎛⎭⎫2-1k =12⎣⎡⎦⎤4+-4k +⎝⎛⎭⎫-1k ≥12×(4+4)=4, 当且仅当-4k =-1k ,即k =-12时,等号成立.故直线l 的方程为y -1=-12(x -2),即x +2y -4=0.方法二 设直线l :x a +yb =1,且a >0,b >0,因为直线l 过点M (2,1), 所以2a +1b =1,则1=2a +1b≥22ab,故ab ≥8, 故S △AOB 的最小值为12×ab =12×8=4,当且仅当2a =1b =12时取等号,此时a =4,b =2,故直线l 的方程为x 4+y2=1,即x +2y -4=0.延伸探究 1.在本例条件下,当|OA |+|OB |取最小值时,求直线l 的方程. 解 由本例方法二知,2a +1b=1,a >0,b >0,所以|OA |+|OB |=a +b =(a +b )·⎝⎛⎭⎫2a +1b =3+a b +2ba≥3+22,当且仅当a =2+2,b =1+2时等号成立,所以当|OA |+|OB |取最小值时,直线l 的方程为x +2y =2+ 2.2.本例中,当|MA |·|MB |取得最小值时,求直线l 的方程. 解 方法一 由本例方法一知A ⎝⎛⎭⎫2k -1k ,0,B (0,1-2k )(k <0).所以|MA |·|MB |=1k 2+1·4+4k 2 =2×1+k 2|k |=2⎣⎡⎦⎤-k +1-k ≥4.当且仅当-k =-1k ,即k =-1时取等号.此时直线l 的方程为x +y -3=0.方法二 由本例方法二知A (a ,0),B (0,b ),a >0,b >0,2a +1b =1.所以|MA |·|MB |=|MA →|·|MB →| =-MA →·MB →=-(a -2,-1)·(-2,b -1) =2(a -2)+b -1=2a +b -5 =(2a +b )⎝⎛⎭⎫2a +1b -5 =2⎝⎛⎭⎫b a +a b ≥4,当且仅当a =b =3时取等号,此时直线l 的方程为x +y -3=0. 教师备选如图所示,为了绿化城市,拟在矩形区域ABCD 内建一个矩形草坪,但△EF A 内部为文物保护区,不能占用,经测量AB =100 m ,BC =80 m ,AE =30 m ,AF =20 m ,应如何设计才能使草坪面积最大?解 如图所示,以A 为坐标原点建立平面直角坐标系,则E (30,0),F (0,20),∴直线EF 的方程为x 30+y20=1.易知当矩形草坪的两邻边在BC ,CD 上,且一个顶点在线段EF 上时,可使草坪面积最大,在线段EF 上取点P (m ,n ),作PQ ⊥BC 于点Q ,PR ⊥CD 于点R , 设矩形PQCR 的面积为S , 则S =|PQ |·|PR |=(100-m )(80-n ), 又m 30+n20=1(0≤m ≤30), ∴n =20-23m ,∴S =(100-m )⎝⎛⎭⎫80-20+23m =-23(m -5)2+18 0503(0≤m ≤30),∴当m =5时,S 有最大值,此时|EP ||PF |=5,∴当矩形草坪的两邻边在BC ,CD 上,一个顶点P 在线段EF 上,且|EP |=5|PF |时,草坪面积最大.思维升华 直线方程综合问题的两大类型及解法(1)与函数相结合的问题:解决这类问题,一般是利用直线方程中x ,y 的关系,将问题转化为关于x (或y )的函数,借助函数的性质解决.(2)与方程、不等式相结合的问题:一般是利用方程、不等式的有关知识来解决. 跟踪训练3 已知直线l :kx -y +1+2k =0(k ∈R ). (1)证明:直线l 过定点;(2)若直线不经过第四象限,求k 的取值范围;(3)若直线l 交x 轴负半轴于A ,交y 轴正半轴于B ,△AOB 的面积为S (O 为坐标原点),求S 的最小值并求此时直线l 的方程. (1)证明 直线l 的方程可化为 k (x +2)+(1-y )=0,令⎩⎪⎨⎪⎧ x +2=0,1-y =0,解得⎩⎪⎨⎪⎧x =-2,y =1.∴无论k 取何值,直线l 总经过定点(-2,1). (2)解 由方程知,当k ≠0时直线在x 轴上的截距为-1+2kk,在y 轴上的截距为1+2k ,要使直线不经过第四象限,则必须有⎩⎪⎨⎪⎧-1+2k k <-2,1+2k >1, 解得k >0;当k =0时,直线为y =1,符合题意,故k 的取值范围是[0,+∞). (3)解 由题意可知k ≠0,再由l 的方程, 得A ⎝⎛⎭⎫-1+2k k ,0,B (0,1+2k ).依题意得⎩⎪⎨⎪⎧-1+2k k <0,1+2k >0, 解得k >0.∵S =12·|OA |·|OB |=12·⎪⎪⎪⎪1+2k k ·|1+2k |=12·1+2k 2k=12⎝⎛⎭⎫4k +1k +4 ≥12×(2×2+4)=4, “=”成立的条件是k >0且4k =1k ,即k =12,∴S min =4,此时直线l 的方程为x -2y +4=0.课时精练1.已知直线l 过点(-2,1),且倾斜角是π2,则直线l 的方程是( )A .x +y +1=0B .y =-12xC .x +2=0D .y -1=0答案 C解析 由于直线l 过点(-2,1),且倾斜角是π2,则直线l 的方程为x =-2,即x +2=0.2.(2022·清远模拟)倾斜角为120°且在y 轴上的截距为-2的直线方程为( ) A .y =-3x +2 B .y =-3x -2 C .y =3x +2 D .y =3x -2答案 B解析 斜率为tan 120°=-3,利用斜截式直接写出方程,即y =-3x -2. 3.直线l 经过点(1,-2),且在两坐标轴上的截距相等,则直线l 的方程为( ) A .x -y -1=0或x -2y =0 B .x +y +1=0或x +2y =0 C .x -y +1=0或2x -y =0 D .x +y +1=0或2x +y =0 答案 D解析 若直线l 过原点, 设直线l 的方程为y =kx , 则k =-2,此时直线l 的方程为y =-2x , 即2x +y =0; 若直线l 不过原点, 设直线l 的方程为x a +ya =1,则1a -2a =1,解得a =-1, 此时直线l 的方程为x +y +1=0.综上所述,直线l的方程为x+y+1=0或2x+y=0.4.若直线y=ax+c经过第一、二、三象限,则有()A.a>0,c>0 B.a>0,c<0C.a<0,c>0 D.a<0,c<0答案 A解析因为直线y=ax+c经过第一、二、三象限,所以直线的斜率a>0,在y轴上的截距c>0. 5.(2022·衡水模拟)1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.有人发现,第三颗小星的姿态与大星相近.为便于研究,如图,以大星的中心点为原点,建立直角坐标系,OO1,OO2,OO3,OO4分别是大星中心点与四颗小星中心点的连接线,α≈16°,则第三颗小星的一条边AB所在直线的倾斜角约为()A.0°B.1°C.2°D.3°答案 C解析∵O,O3都为五角星的中心点,∴OO3平分第三颗小星的一个角,又五角星的内角为36°,可知∠BAO3=18°,过O3作x轴的平行线O3E,如图,则∠OO 3E =α≈16°,∴直线AB 的倾斜角为18°-16°=2°.6.直线l 经过点A (1,2),在x 轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( ) A .-1<k <15B .k >1或k <12C .k >1或k <15D .k >12或k <-1答案 D解析 设直线的斜率为k ,则直线方程为y -2=k (x -1),直线在x 轴上的截距为1-2k ,令-3<1-2k<3,解不等式可得k >12或k <-1.7.直线x -2y +b =0与两坐标轴所围成的三角形的面积不大于1,那么b 的取值范围是( ) A .[-2,2]B .(-∞,-2]∪[2,+∞)C .[-2,0)∪(0,2]D .(-∞,+∞) 答案 C解析 令x =0,得y =b 2,令y =0,得x =-b , 所以所求三角形的面积为12⎪⎪⎪⎪b 2|-b |=14b 2,且b ≠0,14b 2≤1, 所以b 2≤4,所以b 的取值范围是[-2,0)∪(0,2].8.若直线ax +by =ab (a >0,b >0)过点(1,1),则该直线在x 轴与y 轴上的截距之和的最小值为( )A .1B .2C .3D .4 答案 D解析 因为直线ax +by =ab (a >0,b >0), 当x =0时,y =a ,当y =0时,x =b ,所以该直线在x 轴与y 轴上的截距分别为b ,a , 又直线ax +by =ab (a >0,b >0)过点(1,1), 所以a +b =ab ,即1a +1b =1,所以a +b =(a +b )⎝⎛⎭⎫1a +1b =2+b a +a b ≥2+2b a ·ab=4, 当且仅当a =b =2时等号成立.所以直线在x 轴与y 轴上的截距之和的最小值为4.9.过点M (-3,5)且在两坐标轴上的截距互为相反数的直线方程为________________. 答案 5x +3y =0或x -y +8=0解析 ①当直线过原点时,直线方程为y =-53x ,即5x +3y =0;②当直线不过原点时,设直线方程为x a +y-a =1,即x -y =a ,代入点(-3,5),得a =-8,即直线方程为x -y +8=0.综上,直线方程为5x +3y =0或x -y +8=0.10.直线l 过(-1,-1),(2,5)两点,点(1 011,b )在l 上,则b 的值为________. 答案 2 023解析 直线l 的方程为y --15--1=x --12--1,即y +16=x +13,即y =2x +1. 令x =1 011,得y =2 023, ∴b =2 023.11.设直线l 的方程为2x +(k -3)y -2k +6=0(k ≠3),若直线l 的斜率为-1,则k =________;若直线l 在x 轴、y 轴上的截距之和等于0,则k =______. 答案 5 1解析 因为直线l 的斜率存在,所以直线l 的方程可化为y =-2k -3x +2,由题意得-2k -3=-1,解得k =5.直线l 的方程可化为x k -3+y2=1,由题意得k -3+2=0,解得k =1.12.已知点M 是直线l :y =3x +3与x 轴的交点,将直线l 绕点M 旋转30°,则所得到的直线l ′的方程为________________________. 答案 x =-3或y =33(x +3) 解析 在y =3x +3中,令y =0,得x =-3,即M (-3,0).因为直线l 的斜率为3,所以其倾斜角为60°.若直线l 绕点M 逆时针旋转30°,则得到的直线l ′的倾斜角为90°,此时直线l ′的斜率不存在,故其方程为x =-3;若直线l 绕点M 顺时针旋转30°,则得到的直线l ′的倾斜角为30°,此时直线l ′的斜率为tan 30°=33,故其方程为y =33(x +3).13.直线(1-a 2)x +y +1=0的倾斜角的取值范围是( ) A.⎣⎡⎭⎫π4,π2 B.⎣⎡⎭⎫0,3π4 C.⎣⎡⎭⎫0,π2∪⎣⎡⎭⎫3π4,πD.⎣⎡⎦⎤0,π4∪⎝⎛⎦⎤π2,3π4 答案 C解析 直线的斜率k =-(1-a 2)=a 2-1, ∵a 2≥0,∴k =a 2-1≥-1. 倾斜角和斜率的关系如图所示,∴该直线倾斜角的取值范围为⎣⎡⎭⎫0,π2∪⎣⎡⎭⎫3π4,π. 14.已知直线2x -my +1-3m =0,当m 变动时,直线恒过定点( ) A.⎝⎛⎭⎫-12,3 B.⎝⎛⎭⎫12,3 C.⎝⎛⎭⎫12,-3 D.⎝⎛⎭⎫-12,-3 答案 D解析 直线方程可化为2x +1-m (y +3)=0,令⎩⎪⎨⎪⎧2x +1=0,y +3=0,得⎩⎪⎨⎪⎧x =-12,y =-3,∴直线恒过定点⎝⎛⎭⎫-12,-3.15.已知直线x sin α+y cos α+1=0(α∈R ),则下列命题正确的是( ) A .直线的倾斜角是π-αB .无论α如何变化,直线始终过原点C .直线的斜率一定存在D .当直线和两坐标轴都相交时,它和坐标轴围成的三角形的面积不小于1 答案 D解析 根据直线倾斜角的范围为[0,π),而π-α∈R ,所以A 不正确;当x =y =0时,x sin α+y cos α+1=1≠0,所以直线必不过原点,B 不正确;当α=π2时,直线斜率不存在,C 不正确;当直线和两坐标轴都相交时,它和坐标轴围成的三角形的面积为S =12⎪⎪⎪⎪1-sin α·⎪⎪⎪⎪1-cos α=1|sin 2α|≥1,所以D 正确. 16.若ab >0,且A (a ,0),B (0,b ),C (-2,-2)三点共线,则ab 的最小值为________. 答案 16解析 根据A (a ,0),B (0,b )确定直线的方程为x a +yb =1,又因为C (-2,-2)在该直线上, 故-2a +-2b=1, 所以-2(a +b )=ab . 又因为ab >0,故a <0,b <0.根据基本不等式ab =-2(a +b )≥4ab ,从而ab ≤0(舍去)或ab ≥4,故ab ≥16,当且仅当a =b =-4时取等号,即ab 的最小值为16.。
2024年高考数学总复习第九章《平面解析几何》复习试卷及答案解析

2024年高考数学总复习第九章《平面解析几何》复习试卷及答案解析一、选择题1.已知椭圆C:16x2+4y2=1,则下列结论正确的是()A.长轴长为12B.焦距为34C.短轴长为14D.离心率为32答案D解析由椭圆方程16x2+4y2=1化为标准方程可得x2 1 16+y214=1,所以a=12,b=14,c=34,长轴2a=1,焦距2c=32,短轴2b=12,离心率e=ca=32.故选D.2.双曲线x23-y29=1的渐近线方程是()A.y=±3x B.y=±13xC.y=±3x D.y=±33x 答案C解析因为x23-y29=1,所以a=3,b=3,渐近线方程为y=±ba x,即为y=±3x,故选C.3.已知双曲线my2-x2=1(m∈R)与抛物线x2=8y有相同的焦点,则该双曲线的渐近线方程为()A.y=±3x B.y=±3xC.y=±13x D.y=±33x答案A解析∵抛物线x 2=8y 的焦点为(0,2),∴双曲线的一个焦点为(0,2),∴1m +1=4,∴m =13,∴双曲线的渐近线方程为y =±3x ,故选A.4.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)和直线l :x 4+y3=1,若过C 的左焦点和下顶点的直线与l平行,则椭圆C 的离心率为()A.45B.35C.34D.15答案A解析直线l 的斜率为-34,过C 的左焦点和下顶点的直线与l 平行,所以b c =34,又b 2+c 2=a 2+c 2=a 2⇒2516c 2=a 2,所以e =c a =45,故选A.5.(2019·洛阳、许昌质检)若双曲线x 2-y 2b2=1(b >0)的一条渐近线与圆x 2+(y -2)2=1至多有一个交点,则双曲线离心率的取值范围是()A .(1,2]B .[2,+∞)C .(1,3]D .[3,+∞)答案A 解析双曲线x 2-y 2b2=1(b >0)的一条渐近线方程是bx -y =0,由题意圆x 2+(y -2)2=1的圆心(0,2)到bx -y =0的距离不小于1,即2b 2+1≥1,则b 2≤3,那么离心率e ∈(1,2],故选A.6.(2019·河北武邑中学调研)已知直线l :y =k (x +2)(k >0)与抛物线C :y 2=8x 相交于A ,B 两点,F 为C 的焦点,若|FA |=2|FB |,则k 等于()A.13B.23C.23D.223答案D解析=k (x +2),2=8x ,消去y 得k 2x 2+(4k 2-8)x +4k 2=0,Δ=(4k 2-8)2-16k 4>0,又k >0,解得0<k <1,设A (x 1,y 1),B (x 2,y 2),x 1+x 2=8k 2-4,①x 1x 2=4,②根据抛物线定义及|FA |=2|FB |得x 1+2=2(x 2+2),即x 1=2x 2+2,③且x 1>0,x 2>0,由②③解得x 1=4,x 2=1,代入①得k 2=89,∵0<k <1,∴k =223.故选D.7.(2019·唐山模拟)双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±7x ,则E 的离心率为()A .2 B.2147C .22D .23答案C解析由题意,双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±7x ,即ba=7,所以双曲线的离心率为e =ca=a 2+b 2a2=22,故选C.8.(2019·河北衡水中学模拟)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1作圆x 2+y 2=a 2的切线,交双曲线右支于点M ,若∠F 1MF 2=45°,则双曲线的渐近线方程为()A .y =±2xB .y =±3xC .y =±xD .y =±2x答案A解析如图,作OA ⊥F 1M 于点A ,F 2B ⊥F 1M 于点B .因为F 1M 与圆x 2+y 2=a 2相切,∠F 1MF 2=45°,所以|OA |=a ,|F 2B |=|BM |=2a ,|F 2M |=22a ,|F 1B |=2b .又点M 在双曲线上,所以|F 1M |-|F 2M |=2a +2b -22a =2a .整理,得b =2a .所以ba= 2.所以双曲线的渐近线方程为y =±2x .故选A.9.(2019·湖南五市十校联考)在直角坐标系xOy 中,抛物线C :y 2=4x 的焦点为F ,准线为l ,P 为C 上一点,PQ 垂直l 于点Q ,M ,N 分别为PQ ,PF 的中点,直线MN 与x 轴交于点R ,若∠NFR =60°,则|FR |等于()A .2 B.3C .23D .3答案A解析由抛物线C :y 2=4x ,得焦点F (1,0),准线方程为x =-1,因为M ,N 分别为PQ ,PF 的中点,所以MN ∥QF ,所以四边形QMRF 为平行四边形,|FR |=|QM |,又由PQ 垂直l 于点Q ,可知|PQ |=|PF |,因为∠NFR =60°,所以△PQF 为等边三角形,所以FM ⊥PQ ,所以|FR |=2,故选A.10.已知F 1,F 2分别是双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,点M 在E 上,MF 1与x 轴垂直,sin ∠MF 2F 1=13,则E 的离心率为()A.2B.32C.3D .2答案A解析因为MF 1与x 轴垂直,所以|MF 1|=b 2a .又sin ∠MF 2F 1=13,所以|MF 1||MF 2|=13,即|MF 2|=3|MF 1|.由双曲线的定义,得2a =|MF 2|-|MF 1|=2|MF 1|=2b 2a ,所以b 2=a 2,所以c 2=b 2+a 2=2a 2,所以离心率e =ca= 2.11.(2019·湖南长沙长郡中学调研)已知点P (-1,0),设不垂直于x 轴的直线l 与抛物线y 2=2x交于不同的两点A ,B ,若x 轴是∠APB 的角平分线,则直线l 一定过点()B .(1,0)C .(2,0)D .(-2,0)答案B解析根据题意,直线的斜率存在且不等于零,设直线的方程为x =ty +m (t ≠0),与抛物线方程联立,消元得y 2-2ty -2m =0,设A (x 1,y 1),B (x 2,y 2),因为x 轴是∠APB 的角平分线,所以AP ,BP 的斜率互为相反数,所以y 1x 1+1+y 2x 2+1=0,所以2ty 1y 2+(m +1)(y 1+y 2)=0,结合根与系数之间的关系,整理得出2t (-2m )+2tm +2t =0,2t (m -1)=0,因为t ≠0,所以m =1,所以过定点(1,0),故选B.12.(2019·陕西四校联考)已知椭圆和双曲线有共同的焦点F 1,F 2,P 是它们的一个交点,且∠F 1PF 2=2π3,记椭圆和双曲线的离心率分别为e 1,e 2,则3e 21+1e 22等于()A .4B .23C .2D .3答案A解析如图所示,设椭圆的长半轴长为a 1,双曲线的实半轴长为a 2,则根据椭圆及双曲线的定义:|PF 1|+|PF 2|=2a 1,|PF 1|-|PF 2|=2a 2,∴|PF 1|=a 1+a 2,|PF 2|=a 1-a 2,设|F 1F 2|=2c ,∠F 1PF 2=2π3,则在△PF 1F 2中,由余弦定理得4c 2=(a 1+a 2)2+(a 1-a 2)2-2(a 1+a 2)(a 1-a 2)cos2π3,化简得3a 21+a 22=4c 2,该式可变成3e 21+1e 22=4.故选A.二、填空题13.已知双曲线C :x 2-y 2=1,则点(4,0)到C 的渐近线的距离为________.答案22解析双曲线C :x 2-y 2=1的渐近线方程为y =±x ,点(4,0)到C 的渐近线的距离为|±4|2=2 2.14.(2019·新乡模拟)设P 为曲线2x =4+y 2上一点,A (-5,0),B (5,0),若|PB |=2,则|PA |=________.答案4解析由2x =4+y 2,得4x 2=4+y 2(x >0),即x 2-y 24=1(x >0),故P 为双曲线x 2-y 24=1右支上一点,且A ,B 分别为该双曲线的左、右焦点,则|PA |-|PB |=2a =2,|PA |=2+2=4.15.已知抛物线y 2=4x ,圆F :(x -1)2+y 2=1,直线y =k (x -1)(k ≠0)自上而下顺次与上述两曲线交于点A ,B ,C ,D ,则|AB |·|CD |的值是________.答案1解析设A (x 1,y 1),D (x 2,y 2),则|AB |·|CD |=(|AF |-1)(|DF |-1)=(x 1+1-1)(x 2+1-1)=x 1x 2,由y =k (x -1)与y 2=4x 联立方程消y 得k 2x 2-(2k 2+4)x +k 2=0,x 1x 2=1,因此|AB |·|CD |=1.16.(2019·四省联考诊断)在平面上给定相异两点A ,B ,设P 点在同一平面上且满足|PA ||PB |=λ,当λ>0且λ≠1时,P 点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有椭圆x 2a 2+y 2b 2=1(a >b >0),A ,B 为椭圆的长轴端点,C ,D为椭圆的短轴端点,动点P 满足|PA ||PB |=2,△PAB 的面积最大值为163,△PCD 面积的最小值为23,则椭圆的离心率为________.答案32解析依题意A (-a ,0),B (a ,0),设P (x ,y ),依题意得|PA |=2|PB |,(x +a )2+y 2=2(x -a )2+y 2,两边平方化简得-53a +y 2,r =4a3.所以△PAB 的最大面积为12·2a ·43a =163,解得a =2,△PCD 的最小面积为12·2b b ·a 3=23,解得b =1.故椭圆的离心率为e =1-14=32.三、解答题17.(2019·湖南长沙长郡中学调研)在平面直角坐标系xOy 中,已知圆M :(x -3)2+(y -b )2=r 2(r 为正数,b ∈R ).(1)若对任意给定的r ∈(0,+∞),直线l :y =-x +r +4总能把圆M 的周长分成3∶1的两部分,求圆M 的标准方程;(2)已知点A (0,3),B (1,0),且r =103,若线段AB 上存在一点P ,使得过点P 的某条直线与圆M 交于点S ,T (其中|PS |<|PT |),且|PS |=|ST |,求实数b 的取值范围.解(1)根据题意可得,圆心到直线的距离为22r 恒成立,即|3+b -r -4|2=22r ,整理得|b -1-r |=r ,去绝对值符号可得b -1-r =r 或b -1-r =-r ,根据恒成立,可得b =1,所以圆M 的标准方程为(x -3)2+(y -1)2=r 2.(2)根据题意,如果存在满足条件的点,对应的边界值为过圆心的弦,而从另一个角度,即为线段端点值满足条件即可,先考虑点A ,即为|AM |≤3r ,即(0-3)2+(b -3)2≤9×109,解得2≤b ≤4,再考虑点B ,即为|BM |≤3r ,即(1-3)2+b 2≤10,解得-6≤b ≤6,两者取并集,得到b 的取值范围是[-6,4].18.(2019·陕西四校联考)已知抛物线C :y 2=2px 过点A (1,1).(1)求抛物线C的方程;(2)若过点P(3,-1)的直线与抛物线C交于M,N两个不同的点(均与点A不重合).设直线AM,AN的斜率分别为k1,k2,求证:k1·k2为定值.(1)解由题意得2p=1,所以抛物线方程为y2=x.(2)证明设M(x1,y1),N(x2,y2),直线MN的方程为x=t(y+1)+3,代入抛物线方程得y2-ty-t-3=0.所以Δ=(t+2)2+8>0,y1+y2=t,y1y2=-t-3.所以k1·k2=y1-1x1-1·y2-1x2-1=y1-1y21-1·y2-1y22-1=1(y1+1)(y2+1)=1y1y2+y1+y2+1=1-t-3+t+1=-12,所以k1·k2是定值.。
2018版高考数学理人教大一轮复习讲义教师版文档第九章
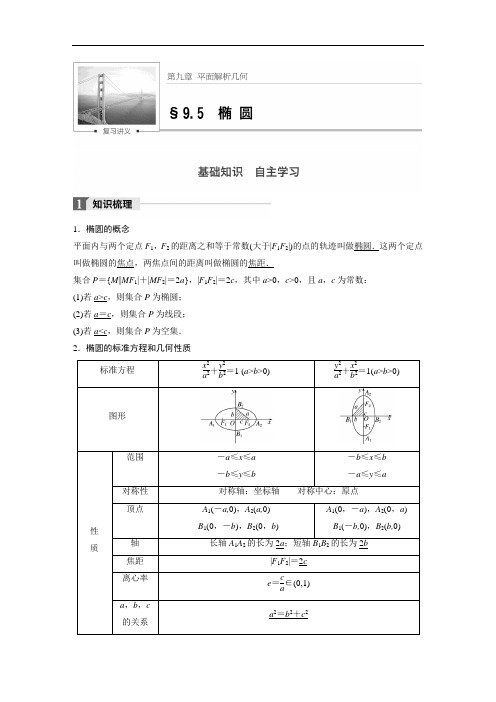
1.椭圆的概念平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数:(1)若a>c,则集合P为椭圆;(2)若a=c,则集合P为线段;(3)若a<c,则集合P为空集.2.椭圆的标准方程和几何性质【知识拓展】点P (x 0,y 0)和椭圆的关系(1)点P (x 0,y 0)在椭圆内⇔x 20a 2+y 20b 2<1.(2)点P (x 0,y 0)在椭圆上⇔x 20a 2+y 20b 2=1.(3)点P (x 0,y 0)在椭圆外⇔x 20a 2+y 20b2>1.【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内与两个定点F 1,F 2的距离之和等于常数的点的轨迹是椭圆.( × )(2)椭圆上一点P 与两焦点F 1,F 2构成△PF 1F 2的周长为2a +2c (其中a 为椭圆的长半轴长,c 为椭圆的半焦距).( √ )(3)椭圆的离心率e 越大,椭圆就越圆.( × )(4)方程mx 2+ny 2=1(m >0,n >0,m ≠n )表示的曲线是椭圆.( √ ) (5)y 2a 2+x 2b 2=1(a ≠b )表示焦点在y 轴上的椭圆.( × ) (6)x 2a 2+y 2b 2=1(a >b >0)与y 2a 2+x 2b2=1(a >b >0)的焦距相等.( √ )1.(教材改编)椭圆x 210-m +y 2m -2=1的焦距为4,则m 等于( )A .4B .8C .4或8D .12 答案 C 解析 由题意知⎩⎪⎨⎪⎧ 10-m >m -2>0,(10-m )-(m -2)=4或⎩⎪⎨⎪⎧m -2>10-m >0,(m -2)-(10-m )=4, 解得m =4或m =8.2.(2015·广东)已知椭圆x 225+y 2m 2=1(m >0)的左焦点为F 1(-4,0),则m 等于( )A .2B .3C .4D .9 答案 B解析 由题意知25-m 2=16,解得m 2=9,又m >0,所以m =3.3.(2016·全国乙卷)直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为( )A.13B.12C.23D.34 答案 B解析 如图,由题意得,|BF |=a ,|OF |=c ,|OB |=b ,|OD |=14×2b =12b .在Rt △FOB 中,|OF |×|OB |=|BF |×|OD |,即cb =a ·12b ,解得a =2c ,故椭圆离心率e =c a =12,故选B.4.如果方程x 2+ky 2=2表示焦点在y 轴上的椭圆,那么实数k 的取值范围是________. 答案 (0,1)解析 将椭圆方程化为x 22+y 22k =1,因为焦点在y 轴上,则2k>2,即k <1,又k >0,所以0<k <1.5.(教材改编)已知点P 是椭圆x 25+y 24=1上y 轴右侧的一点,且以点P 及焦点F 1,F 2为顶点的三角形的面积等于1,则点P 的坐标为__________________. 答案 ⎝⎛⎭⎫152,1或⎝⎛⎭⎫152,-1 解析 设P (x ,y ),由题意知c 2=a 2-b 2=5-4=1,所以c =1,则F 1(-1,0),F 2(1,0),由题意可得点P 到x 轴的距离为1,所以y =±1,把y =±1代入x 25+y 24=1,得x =±152,又x >0,所以x =152,所以P 点坐标为⎝⎛⎭⎫152,1或⎝⎛⎭⎫152,-1.题型一 椭圆的定义及标准方程 命题点1 利用定义求轨迹例1 (2016·济南模拟)如图所示,一圆形纸片的圆心为O ,F 是圆内一定点,M 是圆周上一动点,把纸片折叠使M 与F 重合,然后抹平纸片,折痕为CD ,设CD 与OM 交于点P ,则点P 的轨迹是( )A .椭圆B .双曲线C .抛物线D .圆答案 A解析 由条件知|PM |=|PF |.∴|PO |+|PF |=|PO |+|PM |=|OM |=R >|OF |. ∴P 点的轨迹是以O ,F 为焦点的椭圆. 命题点2 利用待定系数法求椭圆方程例2 (1)已知椭圆以坐标轴为对称轴,且长轴长是短轴长的3倍,并且过点P (3,0),则椭圆的方程为__________________________________________.(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点P 1(6,1),P 2(-3,-2),则椭圆的方程为________________________________. 答案 (1)x 29+y 2=1或y 281+x 29=1(2)x 29+y 23=1 解析 (1)若焦点在x 轴上,设方程为x 2a 2+y 2b 2=1(a >b >0),∵椭圆过P (3,0),∴32a 2+02b 2=1,即a=3,又2a =3×2b ,∴b =1,方程为x 29+y 2=1.若焦点在y 轴上,设方程为y 2a 2+x 2b 2=1(a >b >0).∵椭圆过点P (3,0).∴02a 2+32b 2=1,即b =3.又2a =3×2b ,∴a =9,∴方程为y 281+x 29=1.∴所求椭圆的方程为x 29+y 2=1或y 281+x 29=1.(2)设椭圆方程为mx 2+ny 2=1(m >0,n >0且m ≠n ). ∵椭圆经过点P 1,P 2,∴点P 1,P 2的坐标适合椭圆方程.则⎩⎪⎨⎪⎧6m +n =1, ①3m +2n =1, ②①②两式联立,解得⎩⎨⎧m =19,n =13.∴所求椭圆方程为x 29+y 23=1.命题点3 利用定义解决“焦点三角形”问题例3 已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点,P 为椭圆C 上的一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________. 答案 3解析 设|PF 1|=r 1,|PF 2|=r 2,则⎩⎪⎨⎪⎧r 1+r 2=2a ,r 21+r 22=4c 2, ∴2r 1r 2=(r 1+r 2)2-(r 21+r 22)=4a 2-4c 2=4b 2, 又∵S △PF 1F 2=12r 1r 2=b 2=9,∴b =3. 引申探究1.在例3中增加条件“△PF 1F 2的周长为18”,其他条件不变,求该椭圆的方程. 解 由原题得b 2=a 2-c 2=9, 又2a +2c =18,所以a -c =1,解得a =5, 故椭圆方程为x 225+y 29=1.2.在例3中条件“PF 1→⊥PF 2→”、“△PF 1F 2的面积为9”分别改为“∠F 1PF 2=60°”“S △PF 1F 2=33”,结果如何? 解 |PF 1|+|PF 2|=2a ,又∠F 1PF 2=60°, 所以|PF 1|2+|PF 2|2-2|PF 1||PF 2|cos 60° =|F 1F 2|2,即(|PF 1|+|PF 2|)2-3|PF 1||PF 2|=4c 2, 所以3|PF 1||PF 2|=4a 2-4c 2=4b 2, 所以|PF 1||PF 2|=43b 2,又因为S △PF 1F 2=12|PF 1||PF 2|·sin 60°=12×43b 2×32 =33b 2=33, 所以b =3.思维升华 (1)求椭圆的方程多采用定义法和待定系数法,利用椭圆的定义定形状时,一定要注意常数2a >|F 1F 2|这一条件.(2)求椭圆标准方程的基本方法是待定系数法,具体过程是先定形,再定量,即首先确定焦点所在位置,然后再根据条件建立关于a ,b 的方程组.如果焦点位置不确定,要考虑是否有两解,有时为了解题方便,也可把椭圆方程设为mx 2+ny 2=1(m >0,n >0,m ≠n )的形式. (3)当P 在椭圆上时,与椭圆的两焦点F 1,F 2组成的三角形通常称为“焦点三角形”,利用定义可求其周长;利用定义和余弦定理可求|PF 1|·|PF 2|;通过整体代入可求其面积等.(1)已知两圆C 1:(x -4)2+y 2=169,C 2:(x +4)2+y 2=9,动圆在圆C 1内部且和圆C 1相内切,和圆C 2相外切,则动圆圆心M 的轨迹方程为( ) A.x 264-y 248=1 B.x 248+y 264=1 C.x 248-y 264=1 D.x 264+y 248=1 (2)(2017·大庆质检)设F 1、F 2分别是椭圆x 24+y 2=1的左、右焦点,若椭圆上存在一点P ,使(OP→+OF 2→)·PF 2→=0(O 为坐标原点),则△F 1PF 2的面积是( ) A .4 B .3 C .2 D .1 答案 (1)D (2)D解析 (1)设圆M 的半径为r ,则|MC 1|+|MC 2|=(13-r )+(3+r )=16>8=|C 1C 2|, 所以M 的轨迹是以C 1,C 2为焦点的椭圆, 且 2a =16,2c =8,故所求的轨迹方程为x 264+y 248=1.(2)∵(OP →+OF 2→)·PF 2→=(OP →+F 1O →)·PF 2→=F 1P →·PF 2→=0, ∴PF 1⊥PF 2,∠F 1PF 2=90°. 设|PF 1|=m ,|PF 2|=n ,则m +n =4,m 2+n 2=12,2mn =4, ∴S △F 1PF 2=12mn =1.题型二 椭圆的几何性质例4 (1)已知点F 1,F 2是椭圆x 2+2y 2=2的左,右焦点,点P 是该椭圆上的一个动点,那么|PF 1→+PF 2→|的最小值是( ) A .0 B .1 C .2 D .2 2(2)(2016·全国丙卷)已知O 为坐标原点,F 是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左焦点,A ,B 分别为椭圆C 的左,右顶点.P 为C 上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为( ) A.13 B.12 C.23 D.34 答案 (1)C (2)A解析 (1)设P (x 0,y 0),则PF 1→=(-1-x 0,-y 0), PF 2→=(1-x 0,-y 0),∴PF 1→+PF 2→=(-2x 0,-2y 0), ∴|PF 1→+PF 2→|=4x 20+4y 20=22-2y 20+y 20=2-y 20+2.∵点P 在椭圆上,∴0≤y 20≤1,∴当y 20=1时,|PF 1→+PF 2→|取最小值2.故选C.(2)设M (-c ,m ),则E⎝⎛⎭⎫0,am a -c ,OE 的中点为D ,则D ⎝⎛⎭⎫0,am 2(a -c ),又B ,D ,M 三点共线,所以m 2(a -c )=m a +c,a =3c ,e =13.思维升华 (1)利用椭圆几何性质的注意点及技巧 ①注意椭圆几何性质中的不等关系在求与椭圆有关的一些量的范围,或者最大值、最小值时,经常用到椭圆标准方程中x ,y 的范围,离心率的范围等不等关系. ②利用椭圆几何性质的技巧求解与椭圆几何性质有关的问题时,要结合图形进行分析,当涉及顶点、焦点、长轴、短轴等椭圆的基本量时,要理清它们之间的内在联系. (2)求椭圆的离心率问题的一般思路求椭圆的离心率或其范围时,一般是依据题设得出一个关于a ,b ,c 的等式或不等式,利用a 2=b 2+c 2消去b ,即可求得离心率或离心率的范围.(2016·江苏)如图,在平面直角坐标系xOy 中,F 是椭圆x 2a 2+y 2b2=1(a >b >0)的右焦点,直线y =b2与椭圆交于B ,C 两点,且∠BFC =90°,则该椭圆的离心率是________.答案63解析 联立方程组⎩⎨⎧x 2a 2+y 2b 2=1,y =b2,解得B ,C 两点坐标为B ⎝⎛⎭⎫-32a ,b 2,C ⎝⎛⎭⎫32a ,b 2,又F (c,0),则FB →=⎝⎛⎭⎫-32a -c ,b 2,FC →=⎝⎛⎭⎫3a 2-c ,b 2,又由∠BFC =90°,可得FB →·FC →=0,代入坐标可得 c 2-34a 2+b 24=0,①又因为b 2=a 2-c 2.代入①式可化简为c 2a 2=23,则椭圆离心率为e =c a =23=63. 题型三 直线与椭圆例5 (2016·天津)设椭圆x 2a 2+y 23=1(a >3)的右焦点为F ,右顶点为A .已知1|OF |+1|OA |=3e|F A |,其中O 为原点,e 为椭圆的离心率. (1)求椭圆的方程;(2)设过点A 的直线l 与椭圆交于点B (B 不在x 轴上),垂直于l 的直线与l 交于点M ,与y 轴交于点H .若BF ⊥HF ,且∠MOA ≤∠MAO ,求直线l 的斜率的取值范围. 解 (1)设F (c,0),由1|OF |+1|OA |=3e|F A |,即1c +1a =3c a (a -c ),可得a 2-c 2=3c 2. 又a 2-c 2=b 2=3,所以c 2=1,因此a 2=4. 所以椭圆的方程为x 24+y 23=1.(2)设直线l 的斜率为k (k ≠0), 则直线l 的方程为y =k (x -2).设B (x B ,y B ),由方程组⎩⎪⎨⎪⎧x 24+y 23=1,y =k (x -2)消去y ,整理得(4k 2+3)x 2-16k 2x +16k 2-12=0. 解得x =2或x =8k 2-64k 2+3.由题意得x B =8k 2-64k 2+3,从而y B =-12k4k 2+3.由(1)知,F (1,0),设H (0,y H ),有FH →=(-1,y H ),BF →=⎝ ⎛⎭⎪⎫9-4k24k 2+3,12k 4k 2+3.由BF ⊥HF ,得BF →·FH →=0, 所以4k 2-94k 2+3+12ky H4k 2+3=0,解得y H =9-4k 212k.因此直线MH 的方程为y =-1k x +9-4k212k.设M (x M ,y M ),由方程组⎩⎪⎨⎪⎧y =k (x -2),y =-1k x +9-4k 212k 消去y ,解得x M =20k 2+912(k 2+1).在△MAO 中,∠MOA ≤∠MAO ⇔|MA |≤|MO |,即(x M -2)2+y 2M ≤x 2M +y 2M ,化简,得x M ≥1,即20k 2+912(k 2+1)≥1,解得k ≤-64或k ≥64. 所以直线l 的斜率的取值范围为⎝⎛⎦⎤-∞,-64∪⎣⎡⎭⎫64,+∞. 思维升华 (1)解决直线与椭圆的位置关系的相关问题,其常规思路是先把直线方程与椭圆方程联立,消元、化简,然后应用根与系数的关系建立方程,解决相关问题.涉及弦中点的问题时用“点差法”解决,往往会更简单.(2)设直线与椭圆的交点坐标为A (x 1,y 1),B (x 2,y 2),则|AB |=(1+k 2)[(x 1+x 2)2-4x 1x 2] =(1+1k2)[(y 1+y 2)2-4y 1y 2](k 为直线斜率).提醒:利用公式计算直线被椭圆截得的弦长是在方程有解的情况下进行的,不要忽略判别式.(2016·唐山模拟)已知椭圆x 2a 2+y 2b 2=1(a >b >0)的一个顶点为B (0,4),离心率e =55,直线l 交椭圆于M ,N 两点.(1)若直线l 的方程为y =x -4,求弦|MN |的长;(2)如果△BMN 的重心恰好为椭圆的右焦点F ,求直线l 方程的一般式. 解 (1)由已知得b =4,且c a =55,即c 2a 2=15,∴a 2-b 2a 2=15, 解得a 2=20,∴椭圆方程为x 220+y 216=1.则4x 2+5y 2=80与y =x -4联立, 消去y 得9x 2-40x =0,∴x 1=0,x 2=409,∴所求弦长|MN |=1+12|x 2-x 1| =4029. (2)椭圆右焦点F 的坐标为(2,0),设线段MN 的中点为Q (x 0,y 0), 由三角形重心的性质知 BF →=2FQ →,又B (0,4),∴(2,-4)=2(x 0-2,y 0), 故得x 0=3,y 0=-2, 即Q 的坐标为(3,-2). 设M (x 1,y 1),N (x 2,y 2), 则x 1+x 2=6,y 1+y 2=-4,且x 2120+y 2116=1,x 2220+y 2216=1, 以上两式相减得(x 1+x 2)(x 1-x 2)20+(y 1+y 2)(y 1-y 2)16=0,∴k MN =y 1-y 2x 1-x 2=-45·x 1+x 2y 1+y 2=-45×6-4=65,故直线MN 的方程为y +2=65(x -3),即6x -5y -28=0.8.高考中求椭圆的离心率问题考点分析 离心率是椭圆的重要几何性质,是高考重点考查的一个知识点,这类问题一般有两类:一类是根据一定的条件求椭圆的离心率;另一类是根据一定的条件求离心率的取值范围,无论是哪类问题,其难点都是建立关于a ,b ,c 的关系式(等式或不等式),并且最后要把其中的b 用a ,c 表示,转化为关于离心率e 的关系式,这是化解有关椭圆的离心率问题难点的根本方法.典例1 (2015·福建)已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ,短轴的一个端点为M ,直线l :3x -4y =0交椭圆E 于A ,B 两点.若|AF |+|BF |=4,点M 到直线l 的距离不小于45,则椭圆E 的离心率的取值范围是( ) A.⎝⎛⎦⎤0,32 B.⎝⎛⎦⎤0,34 C.⎣⎡⎭⎫32,1D.⎣⎡⎭⎫34,1解析 左焦点F 0,连接F 0A ,F 0B ,则四边形AFBF 0为平行四边形.∵|AF |+|BF |=4, ∴|AF |+|AF 0|=4, ∴a =2.设M (0,b ),则4b 5≥45,∴1≤b <2.离心率e =ca =c 2a 2= a 2-b 2a 2= 4-b 24∈⎝⎛⎦⎤0,32,故选A. 答案 A典例2 (12分) (2016·浙江)如图,设椭圆x 2a2+y 2=1(a >1).(1)求直线y =kx +1被椭圆截得的线段长(用a ,k 表示);(2)若任意以点A (0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围. 解 (1)设直线y =kx +1被椭圆截得的线段为AM , 由⎩⎪⎨⎪⎧y =kx +1,x 2a 2+y 2=1,得(1+a 2k 2)x 2+2a 2kx =0,[2分] 故x 1=0,x 2=-2a 2k 1+a 2k 2,因此|AM |=1+k 2|x 1-x 2|=2a 2|k |1+a 2k2·1+k 2.[4分] (2)假设圆与椭圆的公共点有4个,由对称性可设y 轴左侧的椭圆上有两个不同的点P ,Q ,满足|AP |=|AQ |.记直线AP ,AQ 的斜率分别为k 1,k 2, 且k 1>0,k 2>0,k 1≠k 2.[5分]由(1)知|AP |=2a 2|k 1|1+k 211+a 2k 21,|AQ |=2a 2|k 2|1+k 221+a 2k 22, 故2a 2|k 1|1+k 211+a 2k 21=2a 2|k 2|1+k 221+a 2k 22,所以(k 21-k 22)[1+k 21+k 22+a 2(2-a 2)k 21k 22]=0.[7分] 由k 1≠k 2,k 1>0,k 2>0得1+k 21+k 22+a 2(2-a 2)k 21k 22=0,因此⎝⎛⎭⎫1k 21+1⎝⎛⎭⎫1k 22+1=1+a 2(a 2-2),① 因为①式关于k 1,k 2的方程有解的充要条件是1+a 2(a 2-2)>1,所以a > 2.因此,任意以点A (0,1)为圆心的圆与椭圆至多有3个公共点的充要条件为1<a ≤2,[10分] 由e =c a =a 2-1a ,得0<e ≤22.所以离心率的取值范围是(0,22].[12分]1.(2016·湖南六校联考)已知椭圆的中心在原点,离心率e =12,且它的一个焦点与抛物线y 2=-4x 的焦点重合,则此椭圆方程为( )A.x 24+y 23=1 B.x 28+y 26=1 C.x 22+y 2=1 D.x 24+y 2=1 答案 A解析 依题意,可设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0),由已知可得抛物线的焦点为(-1,0),所以c =1,又离心率e =c a =12,解得a =2,b 2=a 2-c 2=3,所以椭圆方程为x 24+y 23=1.2.已知椭圆x 29+y 24-k =1的离心率为45,则k 的值为( )A .-21B .21C .-1925或21D.1925或-21 答案 D解析 当9>4-k >0,即4>k >-5时, a =3,c 2=9-(4-k )=5+k , ∴5+k 3=45,解得k =1925. 当9<4-k ,即k <-5时,a =4-k ,c 2=-k -5, ∴-k -54-k =45,解得k =-21,故选D. 3.(2017·青岛月考)已知A 1,A 2分别为椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左,右顶点,P 是椭圆C上异于A 1,A 2的任意一点,若直线P A 1,P A 2的斜率的乘积为-49,则椭圆C 的离心率为( )A.49B.23C.59D.53 答案 D解析 设P (x 0,y 0),则y 0x 0+a ×y 0x 0-a=-49,化简得x 20a 2+y 204a29=1,则b 2a 2=49,e = 1-(b a )2=1-49=53,故选D. 4.2016年1月14日,国防科工局宣布,嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过,正式开始实施.如图所示,假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后,在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c 1和2c 2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a 1和2a 2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①a 1+c 1=a 2+c 2;②a 1-c 1=a 2-c 2;③c 1a 1<c 2a 2;④c 1a 2>a 1c 2.其中正确式子的序号是( )A .①③B .①④C .②③D .②④ 答案 D解析 观察图形可知a 1+c 1>a 2+c 2,即①式不正确;a 1-c 1=a 2-c 2=|PF |,即②式正确;由a 1-c 1=a 2-c 2>0,c 1>c 2>0,知a 1-c 1c 1<a 2-c 2c 2,即a 1c 1<a 2c 2,从而c 1a 2>a 1c 2,c 1a 1>c 2a 2,即④式正确,③式不正确.故选D.5.(2016·贵州七校联考)以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1,则椭圆长轴长的最小值为( ) A .1 B.2C .2 D .2 2 答案 D解析 设a ,b ,c 分别为椭圆的长半轴长,短半轴长,半焦距, 依题意知,当三角形的高为b 时面积最大, 所以12×2cb =1,bc =1,而2a =2b 2+c 2≥22bc =2 2 (当且仅当b =c =1时取等号),故选D.*6.(2016·济南质检)设A 1,A 2为椭圆x 2a 2+y 2b 2=1(a >b >0)的左,右顶点,若在椭圆上存在异于A 1,A 2的点P ,使得PO →·P A 2→=0,其中O 为坐标原点,则椭圆的离心率e 的取值范围是( ) A .(0,12)B .(0,22) C .(12,1)D .(22,1) 答案 D解析 A 1(-a,0),A 2(a,0),设P (x ,y ),则PO →=(-x ,-y ),P A 2→=(a -x ,-y ),∵PO →·P A 2→=0,∴(a -x )(-x )+(-y )(-y )=0, ∴y 2=ax -x 2>0,∴0<x <a . 将y 2=ax -x 2代入x 2a 2+y 2b2=1,整理得(b 2-a 2)x 2+a 3x -a 2b 2=0,其在(0,a )上有解, 令f (x )=(b 2-a 2)x 2+a 3x -a 2b 2, ∵f (0)=-a 2b 2<0,f (a )=0, 如图,Δ=(a 3)2-4(b 2-a 2)·(-a 2b 2) =a 2(a 4-4a 2b 2+4b 4) =a 2(a 2-2b 2)2≥0,∴对称轴满足0<-a 32(b 2-a 2)<a ,即0<a 32(a 2-b 2)<a ,∴a 22c 2<1,∴c 2a 2>12. 又0<c a <1,∴22<ca<1,故选D.7.若椭圆x 2a 2+y 2b 2=1(a >0,b >0)的焦点在x 轴上,过点(2,1)作圆x 2+y 2=4的切线,切点分别为A ,B ,直线AB 恰好经过椭圆的右焦点和上顶点,则椭圆方程为________________. 答案 x 220+y 216=1解析 设切点坐标为(m ,n ), 则n -1m -2·nm=-1, 即m 2+n 2-n -2m =0.∵m 2+n 2=4,∴2m +n -4=0, 即直线AB 的方程为2x +y -4=0.∵直线AB 恰好经过椭圆的右焦点和上顶点, ∴2c -4=0,b -4=0,解得c =2,b =4,∴a 2=b 2+c 2=20, ∴椭圆方程为x 220+y 216=1.8.已知P 为椭圆x 225+y 216=1上的一点,M ,N 分别为圆(x +3)2+y 2=1和圆(x -3)2+y 2=4上的点,则|PM |+|PN |的最小值为________. 答案 7解析 由题意知椭圆的两个焦点F 1,F 2分别是两圆的圆心,且|PF 1|+|PF 2|=10,从而|PM |+|PN |的最小值为|PF 1|+|PF 2|-1-2=7.9.(2017·石家庄质检)椭圆x 24+y 2=1的左,右焦点分别为F 1,F 2,点P 为椭圆上一动点,若∠F 1PF 2为钝角,则点P 的横坐标的取值范围是________________. 答案 (-263,263)解析 设椭圆上一点P 的坐标为(x ,y ), 则F 1P →=(x +3,y ),F 2P →=(x -3,y ). ∵∠F 1PF 2为钝角,∴F 1P →·F 2P →<0, 即x 2-3+y 2<0,①∵y 2=1-x 24,代入①得x 2-3+1-x 24<0,34x 2<2,∴x 2<83. 解得-263<x <263,∴x ∈(-263,263).10.(2016·长沙模拟)已知过椭圆x 2a 2+y 2b 2=1(a >b >0)的左顶点A (-a ,0)作直线l 交y 轴于点P ,交椭圆于点Q ,若△AOP 是等腰三角形,且PQ →=2QA →,则椭圆的离心率为________. 答案255解析 ∵△AOP 是等腰三角形,A (-a,0),∴P (0,a ). 设Q (x 0,y 0),∵PQ →=2QA →, ∴(x 0,y 0-a )=2(-a -x 0,-y 0).∴⎩⎪⎨⎪⎧x 0=-2a -2x 0,y 0-a =-2y 0,解得⎩⎨⎧x 0=-23a ,y 0=a 3,代入椭圆方程化简,可得b 2a 2=15,∴e =1-b 2a 2=255. 11.如图,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ,右顶点,上顶点分别为A ,B ,且|AB |=52|BF |. (1)求椭圆C 的离心率;(2)若斜率为2的直线l 过点(0,2),且l 交椭圆C 于P ,Q 两点,OP ⊥OQ ,求直线l 的方程及椭圆C 的方程.解 (1)由已知|AB |=52|BF |, 即a 2+b 2=52a , 4a 2+4b 2=5a 2,4a 2+4(a 2-c 2)=5a 2, ∴e =c a =32.(2)由(1)知a 2=4b 2,∴椭圆C :x 24b 2+y 2b2=1.设P (x 1,y 1),Q (x 2,y 2),直线l 的方程为y -2=2(x -0),即2x -y +2=0. 由⎩⎪⎨⎪⎧2x -y +2=0,x 24b 2+y 2b 2=1消去y , 得x 2+4(2x +2)2-4b 2=0, 即17x 2+32x +16-4b 2=0.Δ=322+16×17(b 2-4)>0,解得b >21717.x 1+x 2=-3217,x 1x 2=16-4b 217.∵OP ⊥OQ ,∴OP →·OQ →=0,即x 1x 2+y 1y 2=0,x 1x 2+(2x 1+2)(2x 2+2)=0, 5x 1x 2+4(x 1+x 2)+4=0. 从而5(16-4b 2)17-12817+4=0,解得b =1,满足b >21717.∴椭圆C 的方程为x 24+y 2=1.12.(2015·天津)已知椭圆x 2a 2+y 2b 2=1(a >b >0)的上顶点为B ,左焦点为F ,离心率为55.(1)求直线BF 的斜率;(2)设直线BF 与椭圆交于点P (P 异于点B ),过点B 且垂直于BP 的直线与椭圆交于点Q (Q 异于点B ),直线PQ 与y 轴交于点M ,|PM |=λ|MQ |. ①求λ的值;②若|PM |sin ∠BQP =759,求椭圆的方程.解 (1)设F (-c,0).由已知离心率c a =55及a 2=b 2+c 2,可得a =5c ,b =2c ,又因为B (0,b ),F (-c,0),故直线BF 的斜率k =b -00-(-c )=2cc =2.(2)设点P (x P ,y P ),Q (x Q ,y Q ),M (x M ,y M ).①由(1)可得椭圆的方程为x 25c 2+y 24c 2=1,直线BF 的方程为y =2x +2c .将直线方程与椭圆方程联立,消去y ,整理得3x 2+5cx =0,解得x P =-5c3.因为BQ ⊥BP ,所以直线BQ 的方程为y =-12x +2c ,与椭圆方程联立,消去y ,整理得21x 2-40cx =0,解得x Q =40c21.又因为λ=|PM ||MQ |及x M =0,可得λ=|x M -x P ||x Q -x M |=|x P ||x Q |=78.②因为|PM ||MQ |=78,所以|PM ||PM |+|MQ |=77+8=715,即|PQ |=157|PM |. 又因为|PM |sin ∠BQP =759,所以|BP |=|PQ |sin ∠BQP =157|PM |sin ∠BQP =553.又因为y P =2x P +2c =-43c ,所以|BP |=⎝⎛⎭⎫0+5c 32+⎝⎛⎭⎫2c +4c 32=553c ,因此553c =553,得c =1.所以,椭圆方程为x 25+y 24=1.13.(2016·长春调研)已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,右顶点为A ,上顶点为B ,O为坐标原点,M 为椭圆上任意一点.过F ,B ,A 三点的圆的圆心坐标为(p ,q ). (1)当p +q ≤0时,求椭圆的离心率的取值范围;(2)若点D (b +1,0),在(1)的条件下,当椭圆的离心率最小时,(MF →+OD →)·MO →的最小值为72,求椭圆的方程.解 (1)设椭圆半焦距为c .由题意AF ,AB 的中垂线方程分别为x =a -c 2,y -b 2=a b (x -a2),于是圆心坐标为(a -c 2,b 2-ac2b ).所以p +q =a -c 2+b 2-ac2b≤0,整理得ab -bc +b 2-ac ≤0,即(a +b )(b -c )≤0, 所以b ≤c ,于是b 2≤c 2,即a 2=b 2+c 2≤2c 2. 所以e 2=c 2a 2≥12,即22≤e <1.(2)当e =22时,a =2b =2c , 此时椭圆的方程为x 22c 2+y 2c 2=1,设M (x ,y ),则-2c ≤x ≤2c ,所以(MF →+OD →)·MO →=12x 2-x +c 2=12(x -1)2+c 2-12.当c ≥22时,上式的最小值为c 2-12,即c 2-12=72,得c =2; 当0<c <22时,上式的最小值为12(2c )2-2c +c 2, 即12(2c )2-2c +c 2=72, 解得c =2+304,不合题意,舍去. 综上所述,椭圆的方程为x 28+y 24=1.。
高考总复习一轮数学精品课件 第9章 平面解析几何 第2节 两条直线的位置关系

D. 2+1
a=-1+ 2或 a=-1- 2.
∵a>0,∴a=-1+ 2.
(3)直线3x-4y-4=0与直线6x-8y-3=0之间的距离为( C )
1
A.
5
2解析 直线 3x-4y-4=0 即 6x-8y-8=0,显然与另一条直线平行,
则所求距离为
|-8-(-3)|
62 +82
=
(3)点(x,y)关于直线x=a的对称点为(2a-x,y),关于直线y=b的对称点为
(x,2b-y).
(4)点(x,y)关于点(a,b)的对称点为(2a-x,2b-y).
(5)点(x,y)关于直线x+y=k的对称点为(k-y,k-x),关于直线x-y=k的对称点为
(k+y,x-k).
2.三种直线系方程
3.直线外一点与直线上的点的距离的最小值就是点到直线的距离.(
)
题组二 回源教材
4.(人教A版选择性必修第一册2.3.4节练习第1题改编)已知两条平行直线l1:
2 5
2x+y-1=0,l2:2x+y+1=0,则l1与l2之间的距离是__________.
5
解析 利用两平行线间的距离公式得 l1 与 l2 之间的距离 d=
条直线的斜率为0时,l1⊥l2
l1⊥l2⇔__________
k1k2=-1
若 A1,A2,B1,B2,C1,C2 均不为 0,
1
1
1
则 l1 与 l2 重合⇔ = =
2
2
2
l1∥l2⇔__________,且
A1B2-A2B1=0 B1C2-B2C1≠0(或 A1C2-A2C1≠0)
核按钮(新课标)高考数学一轮复习第九章平面解析几何训

第九章 平面解析几何考纲链接1.平面解析几何初步 (1)直线与方程①在平面直角坐标系中,结合具体图形掌握确定直线位置的几何要素.②理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.③能根据两条直线的斜率判定这两条直线平行或垂直.④掌握确定直线的几何要素,掌握直线方程的三种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系.⑤能用解方程组的方法求两相交直线的交点坐标.⑥掌握两点间的距离公式、点到直线的距离公式,会求两平行直线间的距离.(2)圆与方程①掌握确定圆的几何要素,掌握圆的标准方程与一般方程.②能根据给定直线、圆的方程,判断直线与圆的位置关系;能根据给定两个圆的方程判断圆与圆的位置关系.③能用直线和圆的方程解决一些简单的问题. ④初步了解用代数方法处理几何问题的思想. 2.圆锥曲线与方程 (1)掌握椭圆的定义、几何图形、标准方程和简单几何性质(范围、对称性、顶点、离心率).(2)了解双曲线的定义、几何图形和标准方程,知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线).(3)了解抛物线的定义、几何图形和标准方程,知道其简单的几何性质(范围、对称性、顶点、离心率).(4)理解数形结合的思想. (5)了解圆锥曲线的简单应用.§9.1 直线与方程1.平面直角坐标系中的基本公式(1)数轴上A ,B 两点的距离:数轴上点A 的坐标为x 1,点B 的坐标为x 2,则A ,B 两点间的距离|AB |=____________.(2)平面直角坐标系中的基本公式:①两点间的距离公式:在平面直角坐标系中,两点A (x 1,y 1),B (x 2,y 2)之间的距离公式为d (A ,B )=|AB |=_______________________. ②线段的中点坐标公式:若点P 1,P 2的坐标分别为(x 1,y 1),(x 2,y 2),线段P 1P 2的中点M 的坐标为(x ,y ),则⎩⎪⎨⎪⎧x = ,y = . 2.直线的倾斜角与斜率 (1)直线的倾斜角:当直线l 与x 轴相交时,取x 轴作为基准,x 轴____________与直线l 向上方向之间所成的角α叫做直线l 的倾斜角.当直线l 与x 轴________或________时,我们规定它的倾斜角为0°.因此,直线的倾斜角α的取值范围为__________________.(2)斜率:一条直线的倾斜角α的____________叫做这条直线的斜率,常用小写字母k 表示,即k =______(α≠______).当直线平行于x 轴或者与x 轴重合时,k______0;当直线的倾斜角为锐角时,k______0;当直线的倾斜角为钝角时,k______0;倾斜角为______的直线没有斜率.倾斜角不同,直线的斜率也不同.因此,我们可以用斜率表示直线的倾斜程度.(3)经过两点P 1(x 1,y 1),P 2(x 2,y 2)(x 1≠x 2)的直线的斜率公式为k =.3.直线方程的几种形式(1)截距:直线l 与x 轴交点(a ,0)的____________叫做直线l 在x 轴上的截距,直线l 与y 轴交点(0,b )的____________叫做直线l 在y 轴上的截距.注:截距____________距离(填“是”或“不是”).________的特例.(3)过点P 1(x 1,y 1),P 2(x 2,y 2)的直线方程 ①若x 1=x 2,且y 1≠y 2时,直线垂直于x 轴,方程为____________;②若x 1≠x 2,且y 1=y 2时,直线垂直于y 轴,方程为____________;③若x 1=x 2=0,且y 1≠y 2时,直线即为y 轴,方程为____________;④若x 1≠x 2,且y 1=y 2=0,直线即为x 轴,方程为____________.自查自纠: 1.(1)|x 2-x 1|(2)①()x 2-x 12+()y 2-y 12②x 1+x 22 y 1+y 222.(1)正向 平行 重合 0°≤α<180° (2)正切值 tan α 90° = > < 90° (3)y 2-y 1x 2-x 13.(1)横坐标a 纵坐标b 不是 (2)①y -y 0=k (x -x 0) ②y =kx +b③y -y 1y 2-y 1=x -x 1x 2-x 1④x 1≠x 2且y 1≠y 2 ⑤x a +y b=1 ⑥Ax +By +C =0(A ,B 不同时为0)点斜式 两点式(3)①x =x 1 ②y =y 1 ③x =0 ④y =0过点M (-1,m ),N (m +1,4)的直线的斜率等于1,则m 的值为( )A .1 B.12 C .2 D.13解:由4-m m +2=1,得m =1.故选A.直线3x -3y +1=0的倾斜角是( ) A .30° B .60° C .120° D .135°解:直线方程可变形为y =3x +33,tan α=3,∵倾斜角α∈[0°,180°),∴α=60°.故选B.过点(5,2),且在y 轴上的截距是在x 轴上截距2倍的直线方程是( )A .2x +y -12=0B .2x +y -12=0或2x -5y =0 C .x -2y -1=0D .x -2y -1=0或2x -5y =0解:当直线过原点时所求方程为2x -5y =0;当直线不过原点时,可设其截距式为x a +y2a =1,由该直线过点(5,2)即可解得a =6,对应方程为x 6+y12=1,即2x +y -12=0.故选B.已知直线l 过点(0,2),且其倾斜角的余弦值为45,则直线l 的方程为____________.解:∵cos α=45,α∈[0,π),∴sin α=35,k =tan α=34.∴直线l 的方程为y -2=34x ,即3x-4y +8=0.故填3x -4y +8=0.下列四个命题中真命题有______个. ①经过定点P (x 0,y 0)的直线都可以用方程y -y 0=k (x -x 0)表示;②经过任意两点P 1(x 1,y 1),P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示;③不经过原点的直线都可以用方程x a +y b=1表示;④经过定点(0,b )的直线都可以用方程y =kx +b 表示.解:①当k 不存在时,直线方程为x =x 0,不正确;②正确;③当直线与坐标轴垂直时不能用该方程表示,不正确;④k 可能不存在,不正确.故填1.类型一 直线的倾斜角和斜率(1)经过P (0,-1)作直线l ,若直线l 与连接A (1,-2),B (2,1)的线段总有公共点,则直线l 的斜率k 和倾斜角α的取值范围分别为____________,____________.解:如图所示,为使l 与线段AB 总有公共点,则k PA ≤k ≤k PB ,而k PB >0,k PA <0,故k <0时,倾斜角α为钝角;k =0时,α=0;k >0时,α为锐角.又k PA =-2-(-1)1-0=-1,k PB =1-(-1)2-0=1,∴-1≤k ≤1.又当0≤k ≤1时,0≤α≤π4;当-1≤k <0时,3π4≤α<π.故倾斜角α的取值范围为α∈⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫3π4,π. 故填[-1,1];⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫3π4,π.(2)如图所示,直线l 1的倾斜角α1=30°,直线l 1与l 2垂直,则直线l 1的斜率k 1=________,直线l 2的斜率k 2=________.解:由图可知,α2=α1+90°=120°,则直线l 1的斜率k 1=tan α1=tan30°=33,直线l 2的斜率k 2=tan α2=tan120°=-3,故填33;-3.点拨:①直线的倾斜角与斜率均是反映直线倾斜程度的量.倾斜角是从“形”的角度刻画直线的倾斜程度,而斜率是从“数”的角度刻画直线的倾斜程度,两者由公式k =tan α联系.②在使用过两点的直线的斜率公式k =y 2-y 1x 2-x 1时,注意同一直线上选取的点不同,直线的斜率不会因此而发生变化,同时还要注意两点横坐标是否相等,若相等,则直线的倾斜角为90°,斜率不存在,但并不意味着直线的方程也不存在,此时直线的方程可写为x =x 1.③在已知两点坐标,求倾斜角α的值或取值范围时,用tan α=k =y 2-y 1x 2-x 1转化,其中倾斜角α∈[0,π),此时依然要注意斜率不存在的情形,同时注意运用数形结合思想解题.(1)直线x sin α-y +1=0的倾斜角的变化范围是( )A.⎝⎛⎭⎪⎫0,π2 B .(0,π)C.⎣⎢⎡⎦⎥⎤-π4,π4D.⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫34π,π解:直线x sin α-y +1=0的斜率是k =sin α, ∵-1≤sin α≤1,∴-1≤k ≤1,当0≤k ≤1时,倾斜角的范围是⎣⎢⎡⎦⎥⎤0,π4;当-1≤k <0时,倾斜角的范围是⎣⎢⎡⎭⎪⎫34π,π.故选D.(2)已知线段PQ 两端点的坐标分别为P (-1,1)和Q (2,2),若直线l :x +my +m =0与线段PQ 有交点,则实数m 的取值范围是____________.解:如图所示,直线l :x +my +m =0过定点A (0,-1),当m ≠0时,k QA =32,k PA =-2,k l =-1m,∴-1m ≤-2或-1m ≥32,解得0<m ≤12或-23≤m <0;当m =0时,直线l 的方程为x =0,与线段PQ 有交点.∴实数m 的取值范围为⎣⎢⎡⎦⎥⎤-23,12.故填⎣⎢⎡⎦⎥⎤-23,12. 类型二求直线方程 根据所给条件求直线的方程.(1)直线过点(-4,0),倾斜角的正弦值为1010; (2)直线过点(-3,4),且在两坐标轴上的截距相等;(3)直线过点(5,10),且到原点的距离为5. 解:(1)由题意知,直线的斜率存在,设倾斜角为α,则sin α=1010(α∈[0,π)), 从而cos α=±31010,则k =tan α=±13.故所求直线的方程为y =±13(x +4),即x ±3y+4=0.(2)若截距不为0,设直线的方程为x a +y a=1, ∵直线过点(-3,4),∴-3a +4a=1,解得a =1.此时直线方程为x +y -1=0. 若截距为0,设直线方程为y =kx ,代入点(-3,4),有4=-3k ,解得k =-43,此时直线方程为4x+3y =0.综上,所求直线方程为x +y -1=0或4x +3y =0.(3)由题意知,当直线的斜率不存在时符合题意,此时直线方程为x -5=0.当直线斜率存在时,设其方程为y -10=k (x -5),即kx -y +(10-5k )=0.由点到直线的距离公式,得||10-5k 1+k2=5,解得k =34.此时直线方程为3x -4y +25=0. 综上知,所求直线方程为x -5=0或3x -4y +25=0.点拨:本题考查应用直线方程的几种形式求直线方程,难度虽不大,但每小题都有陷阱.(1)给出了倾斜角的正弦值,求正切值时,应注意倾斜角的范围;(2)截距相等包括经过原点的直线,还要注意截距不是距离;(3)应用点斜式求直线方程时,注意点斜式的局限性,它不能表示平面内所有直线.求满足下列条件的所有直线方程:(1)经过点P (4,1),且在两坐标轴上的截距相等;(2)经过点A (-1,-3),倾斜角等于直线y =3x 的倾斜角的2倍.解:(1)根据题意,设直线l 在x ,y 轴上的截距均为a ,若a =0,即l 过点(0,0)和(4,1),∴l 的方程为y =14x ,即x -4y =0.若a ≠0,则设l 的方程为x a +y a=1, ∵l 过点(4,1),∴4a +1a=1,得a =5.∴l 的方程为x +y -5=0.综上可知,直线l 的方程为x -4y =0或x +y-5=0.(2)由已知设直线y =3x 的倾斜角为α,则所求直线的倾斜角为2α.∵tan α=3,∴tan2α=2tan α1-tan 2α=-34. 又直线经过点(-1,-3),因此所求直线方程为y +3=-34(x +1),即3x +4y +15=0.类型三 直线方程的应用(1)已知点A (4,-1),B (8,2)和直线 l :x -y -1=0,动点P (x ,y )在直线l 上,则||PA +||PB 的最小值为__________.解:设点A 1(x 1,y 1)与A (4,-1)关于直线l 对称,P 0为A 1B 与直线l 的交点,∴||P 0A 1=||P 0A ,||PA 1= ||PA .∴||PA +||PB =||PA 1 +||PB ≥||A 1B =||A 1P 0+||P 0B =||P 0A +||P 0B .当P 点运动到P 0点时,||PA +||PB 取到最小值||A 1B .∵点A ,A 1关于直线l 对称,∴由对称的充要条件知,⎩⎪⎨⎪⎧y 1+1x 1-4×1=-1,x 1+42-y 1-12-1=0, 解得⎩⎪⎨⎪⎧x 1=0,y 1=3, 即A 1(0,3).∴(||PA +||PB )min =||A 1B =82+(-1)2=65.故填65.点拨:平面内,两点间连线中直线段最短,这一最基本的公理是解决此类问题的理论基础.求A 关于l 的对称点是关键一步,而点关于直线对称的充要条件又是求对称点的依据.(2)直线l 过点P (1,4),且分别交x 轴的正半轴和y 轴的正半轴于A ,B 两点,O 为坐标原点.①当|OA |+|OB |最小时,求l 的方程; ②若|PA |·|PB |最小,求l 的方程. 解:①依题意,l 的斜率存在,且斜率为负, 设直线l 的斜率为k ,则直线l 的方程为y -4=k (x -1)(k <0).令y =0,可得A ⎝⎛⎭⎪⎫1-4k,0;令x =0,可得B (0,4-k ).|OA |+|OB |=⎝ ⎛⎭⎪⎫1-4k +(4-k )=5-⎝ ⎛⎭⎪⎫k +4k=5+⎝⎛⎭⎪⎫-k +4-k ≥5+4=9. ∴当且仅当-k =4-k且k <0,即k =-2时,|OA |+|OB |取最小值. 这时l 的方程为2x +y -6=0.②|PA |·|PB |=⎝ ⎛⎭⎪⎫4k 2+16·1+k 2=4⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-k +(-k )≥8(k <0), 当且仅当1-k=-k 且k <0,即k =-1时,|PA |·|PB |取最小值. 这时l 的方程为x +y -5=0.点拨:直线方程综合问题的两大类型及解法:(1)与函数相结合的问题,解决这类问题,一般是利用直线方程中的x ,y 的关系,将问题转化为关于x (或y )的函数,借助函数的性质解决;(2)与方程、不等式相结合的问题,一般是利用方程、不等式的有关知识(如方程解的个数、根的存在问题,不等式的性质、基本不等式等)来解决.已知直线l :kx -y +1+2k =0(k ∈R ).(1)证明:直线l 过定点; (2)若直线l 不经过第四象限,求k 的取值范围; (3)若直线l 交x 轴负半轴于点A ,交y 轴正半轴于点B ,△AOB 的面积为S (O 为坐标原点),求S 的最小值并求此时直线l 的方程.解:(1)证明:将直线l 的方程变形得k (x +2)+(1-y )=0,令⎩⎪⎨⎪⎧x +2=0,1-y =0,解得⎩⎪⎨⎪⎧x =-2,y =1, ∴无论k 取何值,直线l 过定点(-2,1). (2)当直线l 的倾斜角θ∈[0°,90°]时,直线l 不经过第四象限,∴k ≥0.(3)由l 的方程,得A ⎝⎛⎭⎪⎫-1+2k k,0,B (0,1+2k ).依题意得⎩⎪⎨⎪⎧-1+2k k <0,1+2k >0,解得k >0. ∵S =12·|OA |·|OB |=12·⎪⎪⎪⎪⎪⎪1+2k k ·|1+2k |=12·(1+2k )2k =12⎝ ⎛⎭⎪⎫4k +1k +4≥12×(2×2+4)=4, 当且仅当4k =1k 且k >0,即k =12时等号成立,∴S min =4,此时直线l 的方程为x -2y +4=0.1.直线的倾斜角和斜率的关系,可借助k =tan α的图象(如图)来解决.这里,α∈[0,π),k 的范围是两个不连续的区间.这说明,每条直线都有倾斜角,但不一定每条直线都存在斜率,故在求直线方程时,若不能确定直线的斜率是否存在,则应对斜率存在或不存在进行分类讨论.2.直线在坐标轴上的截距是直线与坐标轴的交点的坐标,它不是距离,它可正、可负、可为0,在用截距式求直线方程时,不可忽视截距为0的情况.3.在解决直线与坐标轴围成的直角三角形的面积、周长等问题时,应用截距式方程比较简单.4.对于直线方程来说,要注意的是,除“一般式”外,每一种形式的二元一次方程表示的直线都是有限制的,具体可参看本节“考点梳理”栏目.在解决关于直线方程的问题中,要把握限制的条件,在求解时要细心处理,否则容易产生增解或漏解的情形.如利用直线的点斜式、斜截式解题时,要注意防止忽视斜率不存在而出现漏解;利用直线的截距式解题时,要注意防止忽视零截距而造成漏解;利用直线的一般式解题时,要注意防止忽视隐含条件A 2+B 2≠0而出现增解.1.若A -B +C =0,则直线Ax +By +C =0必经过点( )A .(0,1)B .(1,0)C .(1,-1)D .(-1,-1)解:将点(1,-1)代入Ax +By +C =0,得A -B +C =0,∴直线Ax +By +C =0必过点(1,-1).故选C.2.下列命题中,正确的是( ) A .直线的斜率为tan α,则直线的倾斜角是α B .直线的倾斜角为α,则直线的斜率为tan α C .直线的倾斜角越大,则直线的斜率就越大D .直线的倾斜角α∈⎣⎢⎡⎭⎪⎫0,π2∪⎝ ⎛⎭⎪⎫π2,π时,直线的斜率分别在这两个区间上单调递增解:因为直线的斜率k =tan θ,且θ∈[0,π)时,θ才是直线的倾斜角,所以A 不对;因为任一直线的倾斜角α∈[0,π),而当α=π2时,直线的斜率不存在,所以B 不对;当α∈⎝⎛⎭⎪⎫0,π2时,斜率大于0;当α∈⎝ ⎛⎭⎪⎫π2,π时,斜率小于0,C 不对.故选D.3.已知直线的倾斜角为120°,在y 轴上的截距为-2,则此直线的方程为( )A .y =3x +2B .y =-3x +2C .y =-3x -2D .y =3x -2解:∵k =tan120°=-3,且直线在y 轴上的截距为-2,∴由斜截式得y =-3x -2.故选C.4.已知直线l :ax +y -2-a =0在x 轴和y 轴上的截距相等,则实数a 的值是( )A .1B .-1C .-2或-1D .-2或1解:显然a ≠0,由题意得a +2=a +2a,解得a=-2或1.故选D.5.将直线l 沿y 轴的负方向平移a (a >0)个单位,再沿x 轴正方向平移a +1个单位得直线l ′,此时直线l ′与l 重合,则直线l ′的斜率为( )A.aa +1B .-aa +1C.a +1aD .-a +1a解:设直线l 的倾斜角为θ,则根据题意,有tan(π-θ)=-tan θ=a a +1,∴k =tan θ=-aa +1.故选B.6.(2013·北京海淀模拟)已知点A (-1,0),B (cos α,sin α),且||AB =3,则直线AB 的方程为( )A .y =3x +3或y =-3x - 3B .y =33x +33或y =-33x -33C .y =x +1或y =-x -1D .y =2x +2或y =-2x - 2解:∵||AB =(cos α+1)2+sin 2α=2+2cos α=3,∴cos α=12,sin α=±32.当点B 的坐标为⎝ ⎛⎭⎪⎫12,32时,直线AB 的方程为y =33x +33;当点B 的坐标为⎝ ⎛⎭⎪⎫12,-32时,直线AB 的方程为y =-33x -33.故选B. 7.直线l :x sin30°+y cos150°+1=0的斜率是____________.解:由题意得直线l 的斜率k =-sin30°cos150°=tan30°=33,∴直线l 的斜率为33.故填33. 8.若直线l 的斜率为k ,倾斜角为α,而α∈⎣⎢⎡⎦⎥⎤π6,π4∪⎣⎢⎡⎭⎪⎫2π3,π,则k 的取值范围是____________.解:∵k =tan α,α∈⎣⎢⎡⎦⎥⎤π6,π4∪⎣⎢⎡⎭⎪⎫2π3,π,∴-3≤k <0或33≤k ≤1.故填[-3,0)∪⎣⎢⎡⎦⎥⎤33,1. 9.已知直线l 的斜率为16,且和坐标轴围成面积为3的三角形,求直线l 的方程.解:设所求直线l 的方程为x a +yb=1. ∵k =16,∴-b a =16,得a =-6b .又S =12|a |·|b |=3,∴|ab |=6.联立⎩⎨⎧a =-6b ,||ab =6,得⎩⎪⎨⎪⎧a =-6,b =1或⎩⎪⎨⎪⎧a =6,b =-1.∴所求直线方程为:x -6+y 1=1或x 6+y-1=1, 即x -6y +6=0或x -6y -6=0.10.已知△ABC 的三个顶点分别为A (-3,0),B (2,1),C (-2,3),求:(1)BC 边所在直线的方程;(2)BC 边上中线AD 所在直线的方程; (3)BC 边的垂直平分线DE 的方程.解:(1)∵直线BC 经过B (2,1)和C (-2,3)两点,∴由两点式得BC 的方程为y -13-1=x -2-2-2,即x +2y -4=0.(2)易得BC 边的中点D 的坐标为(0,2),∵BC 边的中线AD 过点A (-3,0),D (0,2)两点,∴由截距式得AD 所在直线方程为x -3+y2=1,即2x -3y +6=0.(3)由(1)知,直线BC 的斜率k 1=-12,则直线BC 的垂直平分线DE 的斜率k 2=2. 由(2)知,点D 的坐标为(0,2).由点斜式得直线DE 的方程为y -2=2(x -0), 即2x -y +2=0.11.已知直线l 过点P (3,2),且与x 轴、y 轴的正半轴分别交于A ,B 两点,如图所示,求△ABO 的面积的最小值及此时直线l 的方程.解法一:设直线l 的方程为x a +y b=1(a >0,b >0),将点P (3,2)代入得3a +2b =1≥26ab,得ab ≥24,从而S △AOB =12ab ≥12,当且仅当3a =2b 时等号成立,这时k =-b a =-23,从而所求直线l 的方程为2x +3y -12=0.解法二:依题意知,直线l 的斜率k 存在且k <0, 可设直线l 的方程为y -2=k (x -3)(k <0),则A ⎝⎛⎭⎪⎫3-2k,0,B (0,2-3k ),S △ABO =12(2-3k )⎝ ⎛⎭⎪⎫3-2k=12⎣⎢⎡⎦⎥⎤12+(-9k )+4-k≥12⎣⎢⎡⎦⎥⎤12+2(-9k )·4-k =12×(12+12)=12,当且仅当-9k =4-k ,即k =-23时,等号成立.∴△ABO 的面积的最小值为12,所求直线l 的方程为2x +3y -12=0.已知△ABC 中,顶点A (4,5),点B 在直线l :2x -y +2=0上,点C 在x 轴上,求△ABC 周长的最小值.解:设点A 关于直线l :2x -y +2=0的对称点为A 1(x 1,y 1),点A 关于x 轴的对称点为A 2(x 2,y 2),连接A 1A 2交l于点B ,交x 轴于点C ,则此时△ABC 的周长取最小值,且最小值为||A 1A 2.∵A 1与A 关于直线l :2x -y +2=0对称,∴⎩⎪⎨⎪⎧y 1-5x 1-4×2=-1,2×x 1+42-y 1+52+2=0,解得⎩⎪⎨⎪⎧x 1=0,y 1=7.∴A 1(0,7).易求得A 2(4,-5),∴△ABC 周长的最小值为||A 1A 2=(4-0)2+(-5-7)2=410.§9.2 两条直线的位置关系1.两条直线的位置关系(1)平行:对于两条不重合的直线l 1,l 2,其斜率分别为k 1,k 2,有l 1∥l 2⇔____________,特别地,当直线l 1,l 2的斜率都不存在时,l 1与l 2的关系为____________.(2)垂直:如果两条直线l 1,l 2的斜率都存在,且分别为k 1,k 2,则有l 1⊥l 2⇔____________,特别地,若直线l 1:x =a ,直线l 2:y =b ,则l 1与l 2的关系为____________.2.两条直线的交点坐标一般地,将两条直线的方程联立,得方程组⎩⎪⎨⎪⎧A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0. 若方程组有惟一解,则两条直线__________,此解就是__________;若方程组无解,则两条直线____________,此时两条直线____________.3.距离公式(1)点到直线的距离:点P 0(x 0,y 0)到直线l :Ax +By +C =0的距离d = .(2)两条平行直线间的距离:两条平行直线l 1:Ax +By +C 1=0与l 2:Ax +By +C 2=0(C 1≠C 2)间的距离d =____________________. 4.过两直线交点的直线系方程 若已知直线l 1:A 1x +B 1y +C 1=0与l 2:A 2x +B 2y +C 2=0相交,则方程A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0(其中λ∈R ,这条直线可以是l 1,但不能是l 2)表示过l 1和l 2交点的直线系方程.自查自纠:1.(1)k 1=k 2 l 1∥l 2 (2)k 1k 2=-1 l 1⊥l 2 2.相交 交点的坐标 无公共点 平行3.(1)||Ax 0+By 0+C A 2+B 2(2)||C 1-C 2A 2+B 2直线l 过点(-1,2)且与直线2x -3y +4=0垂直,则l 的方程是( )A .3x +2y -1=0B .3x +2y +7=0C .2x -3y +5=0D .2x -3y +8=0解:由题意知直线l 的斜率是-32,因此直线l的方程为y -2=-32(x +1),即3x +2y -1=0.故选A.(2015·北京海淀区期末)已知直线l 1:x +2y -1=0与直线l 2:mx -y =0平行,则实数m 的值为( )A .-12 B.12C .2D .-2解:∵直线l 1:x +2y -1=0与直线l 2:mx -y=0平行,∴m1=-12≠0,解得m =-12.故选A.(2015·浙江名校联考)已知直线l 1:x +(a -2)y -2=0,l 2:(a -2)x +ay -1=0,则“a =-1”是“l 1⊥l 2”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解:若a =-1,则l 1:x -3y -2=0,l 2:-3x -y -1=0,显然两条直线垂直;若l 1⊥l 2,则(a -2)+a (a -2)=0,解得a =-1或a =2,因此,“a =-1”是“l 1⊥l 2”的充分不必要条件.故选A.(2015·武汉调研)直线x -2y +1=0关于直线x =1对称的直线方程是____________.解:设直线x -2y +1=0关于直线x =1对称的直线为l 2,则l 2的斜率为-12,且过直线x -2y +1=0与x =1的交点(1,1),则l 2的方程为y -1=-12(x -1),即x+2y -3=0.故填 x +2y -3=0. 已知直线l 1与l 2:x +y -1=0平行,且l 1与l 2的距离是2,则直线l 1的方程为____________.解:设l 1的方程为x +y +c =0,则|c +1|2=2,解得c =1或c =-3.∴直线l 1的方程为x +y +1=0或x +y -3=0.故填x +y +1=0或x +y -3=0.类型一 两条直线平行、重合或相交 已知两条直线:l 1:x +my +6=0,l 2:(m -2)x +3y +2m =0,当m 为何值时,l 1与l 2:(1)相交; (2)平行; (3)重合.解:联立两直线方程⎩⎪⎨⎪⎧x +my +6=0,(m -2)x +3y +2m =0.当m =0或m =2时两直线相交;当m ≠0且m ≠2时,此时A 1A 2=1m -2,B 1B 2=m 3,C 1C 2=62m, 当A 1A 2=B 1B 2时,即1m -2=m3,解得m =-1或m =3;当A 1A 2=C 1C 2时,即1m -2=62m,解得m =3. (1)当m ≠-1且m ≠3时,A 1A 2≠B 1B 2,方程组有唯一一组解.∴l 1与l 2相交.(2)当m =-1时,A 1A 2=B 1B 2且A 1A 2≠C 1C 2,方程组无解.∴l 1与l 2平行.(3)当m =3时,A 1A 2=B 1B 2=C 1C 2,方程组有无穷多组解.∴l 1与l 2重合.点拨:由直线的一般式直接判断两条直线是否平行时,可直接应用本题的结论,即:若A 1A 2=B 1B 2≠C 1C 2,则直线A 1x +B 1y +C 1=0与A 2x +B 2y +C 2=0平行,这是一个很实用的结论,但要注意分母不能为零.当实数m 为何值时,三条直线l 1:3x+my -1=0,l 2:3x -2y -5=0,l 3:6x +y -5=0不能围成三角形.解:当m =0时,直线l 1,l 2,l 3可以围成三角形,要使直线l 1,l 2,l 3不能围成三角形,则m ≠0.记l 1,l 2,l 3三条直线的斜率分别为k 1,k 2,k 3,则k 1=-3m ,k 2=32,k 3=-6.若l 1∥l 2,或l 1∥l 3,则k 1=k 2=32,或k 1=k 3=-6,解得m =-2或m =12;若三条直线交于一点,由⎩⎪⎨⎪⎧3x -2y -5=0,6x +y -5=0得⎩⎪⎨⎪⎧x =1,y =-1, l 2与l 3交于点(1,-1),将点(1,-1)代入3x +my -1=0,得m =2.∴当m =±2或12时,l 1,l 2,l 3不能围成三角形.类型二 两条直线垂直(1)已知两条直线l 1:ax -by +4=0和l 2:(a -1)x +y +b =0,若l 1⊥l 2,且l 1过点(-3,-1),求a ,b 的值;(2)已知两直线l 1:x +y sin α-1=0和l 2:2x ·sin α+y +1=0,若l 1⊥l 2,求α的值.解:(1)法一:由已知可得l 2的斜率k 2存在,且k 2=1-a .若k 2=0,则1-a =0,a =1.∵l 1⊥l 2,∴直线l 1的斜率k 1必不存在,即b =0.又∵l 1过点(-3,-1),∴-3a +4=0,得a =43(矛盾). ∴此种情况不存在,∴k 2≠0, ∴k 1,k 2都存在.∵k 2=1-a ,k 1=a b ,l 1⊥l 2,∴k 1k 2=-1,即ab(1-a )=-1.①又∵l 1过点(-3,-1),∴-3a +b +4=0.② 联立①②可得a =2,b =2.法二:∵l 1⊥l 2,∴a (a -1)+(-b )·1=0,即b =a 2-a .①又∵l 1过点(-3,-1), ∴-3a +b +4=0.②联立①②可得⎩⎪⎨⎪⎧a =2,b =2.经验证,符合题意.故a =2,b =2.(2)∵A 1A 2+B 1B 2=0是l 1⊥l 2的充要条件, ∴2sin α+sin α=0,即sin α=0,α=k π,k ∈Z .∴当α=k π,k ∈Z 时,l 1⊥l 2.点拨:判定两直线垂直的方法:(1)判定两直线的斜率是否存在,若存在,可先化成斜截式,若k 1·k 2=-1,则两直线垂直;若一条直线的斜率不存在,另一条直线的斜率为0,则两直线也垂直.(2)直接用以下方法,可避免对斜率是否存在进行讨论.设直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,l 1⊥l 2⇔A 1A 2+B 1B 2=0.(3)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x ,y 的系数不能同时为零这一隐含条件.“m =3”是“直线l 1:2(m +1)x +(m-3)y +7-5m =0与直线l 2:(m -3)x +2y -5=0垂直”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件解:由l 1⊥l 2,得2(m +1)(m -3)+2(m -3)=0,解得m =3或m =-2.∴m =3是l 1⊥l 2的充分不必要条件.故选A.类型三 对称问题已知直线l :2x -3y +1=0,点A (-1,-2).求:(1)点A 关于直线l 的对称点A ′的坐标; (2)直线m :3x -2y -6=0关于直线l 的对称直线m ′的方程;(3)直线l 关于点A (-1,-2)对称的直线l ′的方程.解:(1)设A ′(x ,y ),则有⎩⎪⎨⎪⎧y +2x +1·23=-1,2×x -12-3×y -22+1=0,解得⎩⎪⎨⎪⎧x =-3313,y =413,∴A ′⎝ ⎛⎭⎪⎫-3313,413.(2)在直线m 上取一点,如M (2,0),则M (2,0)关于直线l 的对称点必在m ′上.设对称点为M ′(a ,b ),则⎩⎪⎨⎪⎧2×⎝ ⎛⎭⎪⎫a +22-3×⎝ ⎛⎭⎪⎫b +02+1=0,b -0a -2×23=-1,解得M ′⎝ ⎛⎭⎪⎫613,3013. 设m 与l 的交点为N ,则由⎩⎪⎨⎪⎧2x -3y +1=0,3x -2y -6=0,得N (4,3).又∵m ′经过点N (4,3),∴由两点式得直线m ′的方程为9x -46y +102=0.(3)法一:在l :2x -3y +1=0上任取两点,如P (1,1),N (4,3).则P ,N 关于点A 的对称点P ′,N ′均在直线l ′上.易知P ′(-3,-5),N ′(-6,-7),由两点式可得l ′的方程为2x -3y -9=0.法二:设Q (x ,y )为l ′上任意一点, 则Q (x ,y )关于点A (-1,-2)的对称点为 Q ′(-2-x ,-4-y ),∵Q ′在直线l 上,∴2(-2-x )-3(-4-y )+1=0,即2x -3y -9=0.点拨:(1)关于中心对称问题的处理方法:①若点M (x 1,y 1)及N (x ,y )关于P (a ,b )对称,则由中点坐标公式得⎩⎪⎨⎪⎧x =2a -x 1,y =2b -y 1.②求直线关于点的对称直线的方程,其主要方法是:在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的两点坐标,再由两点式求出直线方程,或者求出一个对称点,再利用两直线平行,由点斜式得到所求直线方程,当然,斜率必须存在.(2)关于轴对称问题的处理方法:①点关于直线的对称.若两点P 1(x 1,y 1)与P 2(x 2,y 2)关于直线l :Ax +By +C =0对称,则线段P 1P 2的中点在l 上,且连接P 1P 2的直线垂直于l ,由方程组⎩⎪⎨⎪⎧A ⎝ ⎛⎭⎪⎫x 1+x 22+B ⎝ ⎛⎭⎪⎫y 1+y 22+C =0,y 2-y 1x 2-x 1·⎝ ⎛⎭⎪⎫-A B =-1,可得到点P 1关于l 对称的点P 2的坐标(x 2,y 2)(其中B ≠0,x 1≠x 2).②直线关于直线的对称.此类问题一般转化为点关于直线的对称问题来解决,有两种情况:一是已知直线与对称轴相交;二是已知直线与对称轴平行.已知三角形的一个顶点A (4,-1),它的两条角平分线所在直线的方程分别为l 1:x -y -1=0和l 2:x -1=0,则BC 边所在直线的方程为____________.解:A 不在这两条角平分线上,因此l 1,l 2是另两个角的角平分线.点A 关于直线l 1的对称点A 1,点A 关于直线l 2的对称点A 2均在边BC 所在直线l 上.设A 1(x 1,y 1),则有 ⎩⎪⎨⎪⎧y 1+1x 1-4×1=-1,x 1+42-y 1-12-1=0,解得⎩⎪⎨⎪⎧x 1=0,y 1=3,∴A 1(0,3).同理设A 2(x 2,y 2),易求得A 2(-2,-1). ∴BC 边所在直线方程为2x -y +3=0. 故填2x -y +3=0.类型四 距离问题(1)已知点P (4,a )到直线4x -3y -1=0的距离不大于3,则a 的取值范围是____________.(2)若两平行直线3x -2y -1=0,6x +ay +c =0之间的距离为21313,则c 的值是____________.解:(1)由题意得,点P 到直线的距离为 |4×4-3×a -1|5=|15-3a |5.又|15-3a |5≤3,即|15-3a |≤15, 解之得0≤a ≤10,∴a 的取值范围是[0,10].故填[0,10].(2)依题意知,63=a -2≠c-1,解得a =-4,c ≠-2,即直线6x +ay +c =0可化为3x -2y +c2=0,又两平行线之间的距离为21313,∴⎪⎪⎪⎪⎪⎪c 2+132+(-2)2=21313,解得c =2或-6. 故填2或-6.点拨:距离的求法:(1)点到直线的距离.可直接利用点到直线的距离公式来求,但要注意此时直线方程必须为一般式.(2)两平行直线间的距离.①利用“化归”法将两条平行线间的距离转化为一条直线上任意一点到另一条直线的距离;②利用两平行线间的距离公式d =|C 1-C 2|A 2+B2.直线l 经过点P (2,-5)且与点A (3,-2)和点B (-1,6)的距离之比为1∶2,求直线l 的方程.解:当直线l 与x 轴垂直时,此时直线l 的方程为x =2,点A 到直线l 的距离为d 1=1,点B 到直线l 的距离为d 2=3,不符合题意,故直线l 的斜率必存在.设直线l 的方程为y +5=k (x -2),即kx -y -2k -5=0,则点A (3,-2)到直线l 的距离d 1=|3k -(-2)-2k -5|k 2+1=|k -3|k 2+1,点B (-1,6)到直线l 的距离d 2=|-k -6-2k -5|k 2+1=|3k +11|k 2+1,∵d 1∶d 2=1∶2,∴|k -3||3k +11|=12,解得k =-1或k =-17.∴所求直线方程为x +y +3=0和17x +y -29=0.类型五 直线系及其应用求证:动直线(m 2+2m +3)x +(1+m -m 2)y +3m 2+1=0(其中m ∈R )恒过定点,并求出定点坐标.证法一:令m =0,则直线方程为3x +y +1=0,①再令m =1时,直线方程为6x +y +4=0,②联立①②,得方程组⎩⎪⎨⎪⎧3x +y +1=0,6x +y +4=0,解得⎩⎪⎨⎪⎧x =-1,y =2. 将点A (-1,2)代入动直线(m 2+2m +3)x +(1+m -m 2)y +3m 2+1=0中,(m 2+2m +3)×(-1)+(1+m -m 2)×2+3m 2+1=(3-1-2)m 2+(-2+2)m +2+1-3=0, 故点A (-1,2)的坐标恒满足动直线方程,所以动直线(m 2+2m +3)x +(1+m -m 2)y +3m 2+1=0恒过定点A .证法二:将动直线方程按m 降幂排列整理得, m 2(x -y +3)+m (2x +y )+3x +y +1=0,① 不论m 为何实数,①式恒为零,∴有⎩⎪⎨⎪⎧x -y +3=0,2x +y =0,3x +y +1=0,解得⎩⎪⎨⎪⎧x =-1,y =2.故动直线恒过点(-1,2).点拨:此题属于数学中恒成立问题,所以证法一是先赋给m 两个特殊值得两条直线,那么这两条直线的交点就是那个定点,但m 只是取两个特殊值,是否m ∈R 时都成立,则要进行代入检验;证法二是将动直线方程按m 的降幂排列,由于∀m ∈R 恒成立,所以得关于x ,y 的方程组,解此方程组便得定点坐标.直线系也称直线束,是具有某一共同性质的直线的集合.常见直线系方程有:(1)过定点(x 1,y 1)的直线系:y -y 1=k (x -x 1)和x =x 1.(2)平行于直线Ax +By +C =0的直线系:Ax +By +λ=0(λ≠C ).(3)垂直于直线Ax +By +C =0的直线系:Bx -Ay +λ=0.(4)过A 1x +B 1y +C 1=0与A 2x +B 2y +C 2=0的交点的直线系:A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0(不包括直线A 2x +B 2y +C 2=0).已知直线l :(a +b )x +(a -b )y +2=0,其中a ,b 满足3a -b +2=0.求证:直线l 恒过一定点.证明:由已知得b =3a +2,则直线l 的方程可化为(4a +2)x -(2a +2)y +2=0,整理得 a (4x -2y )+2x -2y +2=0. 令⎩⎪⎨⎪⎧4x -2y =0,2x -2y +2=0,解得⎩⎪⎨⎪⎧x =1,y =2. ∵点(1,2)恒满足直线l 的方程,∴直线l 恒过定点(1,2).1.当直线的方程中含有字母参数时,不仅要考虑斜率存在与不存在的情况,同时还要注意x ,y 的系数不能同时为零这一隐含条件.2.两条直线的位置关系一般用斜率和截距来判定,但当直线方程用一般式给出且系数中有参数时,往往需要繁琐地讨论.但也可以这样避免:设两直线为A 1x +B 1y +C 1=0和A 2x +B 2y +C 2=0,则两直线垂直的条件为⎝ ⎛⎭⎪⎫-A 1B 1·⎝ ⎛⎭⎪⎫-A 2B 2=-1,由此得A 1A 2+B 1B 2=0,但后者适用性更强,因为当B 1=0或B 2=0时前者不适用但后者适用.3.运用直线系方程,有时会使解题更为简单快捷,常见的直线系方程有:(1)与直线Ax +By +C =0平行的直线系方程是Ax +By +m =0(m ∈R 且m ≠C );(2)与直线Ax +By +C =0垂直的直线系方程是Bx -Ay +m =0(m ∈R );(3)过直线l 1:A 1x +B 1y +C 1=0与l 2:A 2x +B 2y +C 2=0的交点的直线系方程为A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0(λ∈R ),但不包括l 2.4.运用公式d =||C 1-C 2A 2+B 2求两平行直线间的距离时,一定要将两条直线方程中x ,y 的系数化成相等的系数,求两平行直线间的距离也可化归为点到直线的距离,即在一条直线上任取一点(如直线与坐标轴的交点),求该点到另一条直线的距离即为两平行直线间的距离.这一方法体现了化归思想的应用.5.对称主要分为中心对称和轴对称两种,中心对称仅用中点坐标公式即可,轴对称因对称点连线的中垂线就是对称轴,所以根据线段的中点坐标公式和两条直线垂直的条件即可解决.1.过点A (2,3)且垂直于直线2x +y -5=0的直线方程为( )A .x -2y +4=0B .2x +y -7=0C .x -2y +3=0D .x -2y +5=0解:由点斜式得所求直线方程为y -3=12(x -2),即x -2y +4=0.故选A.2.过点(1,0)且与直线x -2y -2=0平行的直线方程是( )A .x -2y -1=0B .x -2y +1=0C .2x +y -2=0D .x +2y -1=0解:设所求直线方程为x -2y +c =0,将(1,0)代入得c =-1.∴所求直线方程为x -2y -1=0.故选A.3.若直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,则直线l 2恒过定点( )A .(0,4)B .(0,2)C .(-2,4)D .(4,-2)解:∵直线l 1与l 2关于点(2,1)对称,且直线l 1过点(4,0),∴直线l 2必过点(4,0)关于点(2,1)的对称点(0,2).故选B.4.(2013·长春调研)已知直线3x +4y -3=0与直线6x +my +14=0平行,则它们之间的距离是( )A .1710B .175C .8D .2 解:由题意得36=4m ≠-314,解得m =8.∴直线6x +my +14=0可化为3x +4y +7=0.∴两平行线间的距离为d =||-3-732+42=2.故选D. 5.已知过点A (-2,m )和点B (m ,4)的直线为l 1,l 2:2x +y -1=0,l 3:x +ny +1=0.若l 1∥l 2,l 2⊥l 3,则实数m +n 的值为( )A .-10B .-2C .0D .8解:∵l 1∥l 2,∴k AB =4-mm +2=-2,解得m =-8.又∵l 2⊥l 3.∴⎝ ⎛⎭⎪⎫-1n ×(-2)=-1,解得n =-2.∴m +n =-10.故选A.6.(2015·洛阳统考)已知点P (x 0,y 0)是直线l :Ax +By +C =0外一点,则方程Ax +By +C +(Ax 0+By 0+C )=0表示( )A .过点P 且与l 垂直的直线B .过点P 且与l 平行的直线C .不过点P 且与l 垂直的直线D .不过点P 且与l 平行的直线解:∵点P (x 0,y 0)不在直线Ax +By +C =0上,∴Ax 0+By 0+C ≠0,∴直线Ax +By +C +(Ax 0+By 0+C )=0不经过点P .又直线Ax +By +C +(Ax 0+By 0+C )=0与直线l :Ax +By +C =0平行.故选D.7.过圆x 2+y 2+2x -4y =0的圆心,且与直线2x +3y =0垂直的直线方程为____________.解:设与直线2x +3y =0垂直的直线方程为3x -2y +m =0,由于其过圆心(-1,2),所以有3×(-1)-2×2+m =0,得m =7,所求直线方程为3x -2y +7=0.故填3x -2y +7=0.8.直线l 过点P (-1,2)且到点A (2,3)和点B (-4,5)的距离相等,则直线l 的方程为____________.解法一:当直线l 的斜率存在时,设直线l 的方程为y -2=k (x +1),即kx -y +k +2=0.由题意知|2k -3+k +2|k 2+1=|-4k -5+k +2|k 2+1,即|3k -1|=|-3k -3|,解得k =-13.∴直线l 的方程为y -2=-13(x +1),即x +3y-5=0.当直线l 的斜率不存在时,直线l 的方程为x =-1,也符合题意.故所求直线l 的方程为x +3y -5=0或x =-1.解法二:当AB ∥l 时,有k =k AB =-13,直线l的方程为y -2=-13(x +1),即x +3y -5=0.当l 过AB 中点时,AB 的中点为(-1,4). ∴直线l 的方程为x =-1.故所求直线l 的方程为x +3y -5=0或x =-1.故填x +3y -5=0或x =-1.9.已知两直线l 1:x +y sin θ-1=0和l 2:2x sin θ+y +1=0,试求θ的值,使得:(1)l 1∥l 2; (2)l 1⊥l 2.解:(1)由12sin θ=sin θ≠-11,得sin θ=±22. 由sin θ=±22,得θ=k π±π4(k ∈Z ). ∴当θ=k π±π4(k ∈Z )时,l 1∥l 2. (2)由2sin θ+sin θ=0,得sin θ=0,θ=k π(k ∈Z ),∴当θ=k π(k ∈Z )时,l 1⊥l 2.10求直线l :x -2y +6=0关于点M (-1,1)对称的直线l ′的方程. 解法一:取l 上的两点A (0,3),B (-6,0),求出它们关于点M 的对称点,A ′(-2,-1), B ′(4,2),再用两点式求出l ′的方程为x -2y =0.解法二:设点P ′(x ′,y ′)为所求直线l ′上的任意一点,则点P ′关于点M 在直线l 上的对称点为P (x ,y ).由⎩⎪⎨⎪⎧-1=x +x ′2,1=y +y ′2得 ⎩⎪⎨⎪⎧x =-2-x ′,y =2-y ′, 代入直线l 的方程得:(-2-x ′)-2(2-y ′)+6=0,得x ′-2y ′=0,即x -2y =0为所求直线l ′的方程.11.设一直线l 经过点(-1,1),此直线被两平行直线l 1:x +2y -1=0和l 2:x +2y -3=0所截得线段的中点在直线x -y -1=0上,求直线l 的方程.解法一:设直线x -y -1=0与l 1,l 2的交点分别为C (x C ,y C ),D (x D ,y D ),则由⎩⎪⎨⎪⎧x +2y -1=0,x -y -1=0解得⎩⎪⎨⎪⎧x C =1,y C=0, ∴C (1,0). 由⎩⎪⎨⎪⎧x +2y -3=0,x -y -1=0解得⎩⎪⎨⎪⎧x D =53,y D =23,∴D ⎝ ⎛⎭⎪⎫53,23.∴CD 的中点为M ⎝ ⎛⎭⎪⎫43,13. 又l 过点(-1,1),由两点式得l 的方程为: y -131-13=x -43-1-43,即2x +7y -5=0. 解法二:∵与l 1,l 2平行且与它们距离相等的直线方程为:x +2y +-1-32=0,即x +2y -2=0,∴由⎩⎪⎨⎪⎧x +2y -2=0,x -y -1=0 得M ⎝ ⎛⎭⎪⎫43,13.(以下同解法一)解法三:过中点且与两直线平行的直线方程为x +2y -2=0,设所求方程为:(x -y -1)+λ(x +2y -2)=0,① ∵(-1,1)在此直线上,∴-1-1-1+λ(-1+2-2)=0,解得λ=-3,代入①得2x +7y -5=0. 解法四:设所求直线与两平行线l 1,l 2的交点为A (x 1,y 1),B (x 2,y 2),则 由⎩⎪⎨⎪⎧x 1+2y 1-1=0,x 2+2y 2-3=0得(x 1+x 2)+2(y 1+y 2)-4=0.①又AB 的中点在直线x -y -1=0上,。
湘教版高考总复习一轮数学精品课件 第九章 平面解析几何 解答题专项五 第2课时 最值与范围问题

(2+1) 2 -1
2
|CD|
−
4 1
(6+1) 2 -3
2
] +[
(2+1) 1 -1
(2+1) 2 -1
−
(6+1) 1 -3 2
]=
(2+1) 1 -1
(8+4) 1 2 -4 2 -(8+4) 1 2 +4 1 2
+
[(2+1) 2 -1][(2+1) 1 -1]
20( 1 - 2 )2
2
+
2 2 -2 1
[(2+1) 2 -1][(2+1) 1 -1]
[(2+1)2 1 2 -(2+1ቤተ መጻሕፍቲ ባይዱ( 1 + 2 )+1]2
2
2
. .......................................................................11 分
11
2 + 12 2 = 12,
(2)由
则
得(12k2+1)x2+12kx-9=0.
-12
-9
x1+x2= 2 ,x1·x2= 2 , ........................................................................6
12 +1
而 yP=-b∈[-5,-3], ..........................................................................................11 分
2023年人教版高考数学总复习第一部分考点指导第九章平面解析几何第五节 第2课时椭圆的几何性质

)
A.m>1
B.m>0
C.0<m<5 且 m≠1 D.m≥1 且 m≠5
【解析】选
D.方法一:由于直线
y=kx+1
恒过点(0,1),所以点(0,1)必在椭圆内或椭圆上,则
1 0<m
≤1 且
m≠5,故 m≥1 且 m≠5.
y=kx+1, 方法二:由
消去 y 整理得(5k2+m)x2+10kx+5(1-m)=0.
【解析】(1)由题意知 e=ac =21 ,2a=4.又 a2=b2+c2,解得 a=2,b= 3 ,所以椭圆方程为x42 +y32 =1. (2)①当两条弦中一条弦所在直线的斜率为 0 时,另一条弦所在直线的斜率不存在,由题意知|AB|+|CD|=7,不满足条件.
②当两弦所在直线的斜率均存在且不为 0 时,设直线 AB 的方程为 y=k(x-1),A(x1,y1),B(x2,y2),则直线 CD 的方程为 y=
第2课时 椭圆的几何性质
第九章 平面解析几何
考点探究·悟法培优
考点探究·悟法培优
考点一 椭圆的几何性质 多维探究
高考考情:椭圆的几何性质是历年高考的重点,其中离心率的求解常出现在小题中,直线与椭圆的交点问题
几乎每年必考,难度较大.
·角度 1 求椭圆的离心率的值(范围) [典例 1](1)已知 F1,F2 是椭圆 C:ax22 +by22 =1(a>b>0)的左、右焦点,A 是 C 的左顶点,点 P 在过 A 且斜
·角度 2 与椭圆有关的范围(最值)问题 [典例 2]已知椭圆ax22 +by22 =1(a>b>0)的右焦点为 F2(3,0),离心率为 e.
(1)若 e=
3 2
,求椭圆的方程;
高考数学一轮复习 第九章 平面解析几何9

高考数学一轮复习 第九章 平面解析几何9.9 圆锥曲线中求值与证明问题题型一 求值问题例1 (12分)(2021·新高考全国Ⅰ)在平面直角坐标系xOy 中,已知点F 1(-17,0),F 2(17,0),点M 满足|MF 1|-|MF 2|=2.记M 的轨迹为C .(1)求C 的方程; [切入点:双曲线定义](2)设点T 在直线x =12上,过T 的两条直线分别交C 于A ,B 两点和P ,Q 两点,且|TA |·|TB |=|TP |·|TQ |,求直线AB 的斜率与直线PQ 的斜率之和. [关键点:利用等式列式]教师备选已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的长轴长是短轴长的2倍,F 是椭圆C 的一个焦点,点M (0,2)且|MF |=10.(1)求椭圆C 的方程;(2)若过点M 的直线l 与椭圆C 交于A ,B 两点,线段AB 的中点为N ,且满足|AM |=|BN |,求l 的方程.解 (1)由题意,可得⎩⎪⎨⎪⎧ a =2b ,c 2+4=10,b 2+c 2=a 2,解得a =22,b =2,故椭圆C 的方程为x 28+y 22=1. (2)根据题意可得,点A 必在点B 的上方,才有|AM |=|BN |.当l 的斜率不存在时,|AM |=2-2,|BN |=2,|AM |≠|BN |,不合题意,故l 的斜率必定存在.设l 的方程为y =kx +2,由⎩⎪⎨⎪⎧ x 28+y 22=1,y =kx +2,得(1+4k 2)x 2+16kx +8=0,Δ=(16k )2-32(1+4k 2)=128k 2-32>0,即k 2>14. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-16k 1+4k 2,x 1x 2=81+4k 2. 设N (x 0,y 0),则x 0=x 1+x 22=-8k 1+4k 2. 由|AM |=|BN |可得,|AB |=|MN |,所以1+k 2|x 1-x 2|=1+k 2|x 0-0|,则x 1+x 22-4x 1x 2=|x 0|, 即424k 2-11+4k 2=⎪⎪⎪⎪8k 1+4k 2, 整理得k 2=12>14, 故k =±22,l 的方程为y =±22x +2. 思维升华 求值问题即是根据条件列出对应的方程,通过解方程求解.跟踪训练1 已知椭圆M :x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1,F 2,且|F 1F 2|=2,P 为椭圆上任意一点,且△PF 1F 2面积的最大值为 3.(1)求椭圆M 的标准方程;(2)设A (4,0),直线y =kx +1与椭圆M 交于C ,D 两点,若直线AC ,AD 均与圆x 2+y 2=r 2(r >0)相切,求k 的值.解 (1)当点P 位于椭圆的上顶点或下顶点时面积最大,即(12PF F S △)max =12·|F 1F 2|·b =3, 解得b =3,又a 2=b 2+c 2,∴c =1,a =2,∴椭圆M 的标准方程为x 24+y 23=1. (2)设C (x 1,y 1),D (x 2,y 2),由⎩⎪⎨⎪⎧ x 24+y 23=1,y =kx +1,得(3+4k 2)x 2+8kx -8=0,Δ>0,∴x 1+x 2=-8k 3+4k 2,x 1x 2=-83+4k 2, ∵直线AC ,AD 都与圆相切,∴k AC +k AD =0,即y 1x 1-4+y 2x 2-4=0, ∴y 1x 2-4y 1+y 2x 1-4y 2x 1-4x 2-4=0, ∴2kx 1x 2+(1-4k )(x 1+x 2)-8=0,即-83+4k 2×2k -(1-4k )8k 3+4k 2-8=0, 即-24k =24,∴k =-1.题型二 证明问题例2 (2021·新高考全国Ⅱ)已知椭圆C 的方程为x 2a 2+y 2b2=1(a >b >0),右焦点为F (2,0),且离心率为63.(1)求椭圆C 的方程;(2)设M ,N 是椭圆C 上的两点,直线MN 与曲线x 2+y 2=b 2(x >0)相切.证明:M ,N ,F 三点共线的充要条件是|MN |= 3. (1)解 由题意得, 椭圆半焦距c =2且e =c a =63, 所以a =3,又b 2=a 2-c 2=1,所以椭圆方程为x 23+y 2=1. (2)证明 由(1)得,曲线为x 2+y 2=1(x >0),当直线MN 的斜率不存在时,直线MN :x =1,不符合题意;当直线MN 的斜率存在时,设M (x 1,y 1),N (x 2,y 2),必要性:若M ,N ,F 三点共线,可设直线MN :y =k (x -2),即kx -y -2k =0,由直线MN 与曲线x 2+y 2=1(x >0)相切可得|2k |k 2+1=1,解得k =±1, 联立⎩⎪⎨⎪⎧ y =±x -2,x 23+y 2=1,可得4x 2-62x +3=0,所以x 1+x 2=322,x 1·x 2=34, 所以|MN |=1+1·x 1+x 22-4x 1·x 2=3,所以必要性成立;充分性:设直线MN :y =kx +b (kb <0),即kx -y +b =0,由直线MN 与曲线x 2+y 2=1(x >0)相切可得|b |k 2+1=1,所以b 2=k 2+1, 联立⎩⎪⎨⎪⎧ y =kx +b ,x 23+y 2=1, 可得(1+3k 2)x 2+6kbx +3b 2-3=0,所以x 1+x 2=-6kb 1+3k 2,x 1·x 2=3b 2-31+3k 2, 所以|MN |=1+k 2·x 1+x 22-4x 1·x 2=1+k 2⎝⎛⎭⎫-6kb 1+3k 22-4·3b 2-31+3k 2 =1+k 2·24k 21+3k 2=3, 化简得3(k 2-1)2=0,所以k =±1,所以⎩⎨⎧ k =1,b =-2或⎩⎨⎧ k =-1,b =2,所以直线MN :y =x -2或y =-x +2,所以直线MN 过点F (2,0),M ,N ,F 三点共线,充分性成立,所以M ,N ,F 三点共线的充要条件是|MN |= 3.高考改编在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F (1,0),离心率为12. (1)求椭圆C 的标准方程;(2)若过点F 的直线l 交C 于A ,B 两点,线段AB 的中点为M ,分别过A ,B 作C 的切线l 1,l 2,且l 1与l 2交于点P ,证明:O ,P ,M 三点共线.(1)解 由⎩⎪⎨⎪⎧ c =1,c a =12,a 2=b 2+c 2,解得⎩⎨⎧a =2,b =3,∴椭圆C 的标准方程为x 24+y 23=1. (2)证明 由题意知直线l 的斜率不为0,设直线l 的方程为x =my +1,A (x 1,y 1),B (x 2,y 2),M (x 0,y 0),P (x 3,y 3),由⎩⎪⎨⎪⎧x =my +1,3x 2+4y 2=12, 整理得3(m 2y 2+2my +1)+4y 2=12,即(3m 2+4)y 2+6my -9=0.∴y 0=y 1+y 22=-3m 3m 2+4, x 0=43m 2+4, ∴k OM =-34m . 直线l 1的方程为x 1x 4+y 1y 3=1,① 直线l 2的方程为x 2x 4+y 2y 3=1,② ②-①⇒y 3(y 2-y 1)=x 4(x 1-x 2) ⇒y x =34·x 1-x 2y 2-y 1=-34m , ∴y 3x 3=-34m =k OP , ∴k OM =k OP ,即O ,P ,M 三点共线.教师备选(2022·湖南师大附中模拟)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,椭圆的短轴顶点到焦点的距离为 6.(1)求该椭圆C 的方程;(2)若直线l 与椭圆C 交于A ,B 两点,且|OA →+OB →|=|OA →-OB →|,求证:直线l 与某个定圆E相切,并求出定圆E 的方程.解 (1)∵椭圆的短轴顶点到焦点的距离为6, ∴b 2+c 2=a =6,∵椭圆的离心率e =c a =22, ∴c =3,∴b 2=a 2-c 2=3,∴椭圆C 的标准方程为x 26+y 23=1. (2)∵|OA →+OB →|=|OA →-OB →|,∴OA →⊥OB →,则OA →·OB →=0,①当直线l 的斜率不存在时,设l :x =t ,代入椭圆方程得,y =±6-t 22, 不妨令A ⎝ ⎛⎭⎪⎫t ,6-t 22,B ⎝⎛⎭⎪⎫t ,-6-t 22, 由OA →·OB →=0得,t 2-3+t 22=0,解得t =±2, 此时l :x =±2,与圆x 2+y 2=2相切;②当直线l 的斜率存在时,设l :y =kx +m ,A (x 1,y 1),B (x 2,y 2),联立⎩⎪⎨⎪⎧x 2+2y 2=6,y =kx +m 得, (1+2k 2)x 2+4kmx +2m 2-6=0,则Δ=16k 2m 2-4(1+2k 2)(2m 2-6)>0,化简得m 2<6k 2+3,①由根与系数的关系得,x 1+x 2=-4km 1+2k 2,x 1x 2=2m 2-61+2k 2, 则y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+km (x 1+x 2)+m 2=m 2-6k 21+2k 2, 由OA →·OB →=0,即x 1x 2+y 1y 2=0可得,2m 2-61+2k 2+m 2-6k 21+2k 2=0, 整理得,m 2=2k 2+2,满足①式, ∴|m |k 2+1=2,即原点到直线l 的距离为2, ∴直线l 与圆x 2+y 2=2相切.综上所述,直线l 与圆E :x 2+y 2=2相切.思维升华 圆锥曲线证明问题的类型及求解策略(1)圆锥曲线中的证明问题,主要有两类:一是证明点、直线、曲线等几何元素中的位置关系,如:某点在某直线上、某直线经过某个点、某两条直线平行或垂直等;二是证明直线与圆锥曲线中的一些数量关系(相等或不等).(2)解决证明问题时,主要根据直线与圆锥曲线的性质、直线与圆锥曲线的位置关系等,通过相关性质的应用、代数式的恒等变形以及必要的数值计算等进行证明. 跟踪训练2 双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的右焦点为F ,以F 点为圆心,a 为半径的圆与C 的渐近线相切.(1)求C 的离心率;(2)已知点A ⎝⎛⎭⎫22a ,0,过F 点的直线与C 的右支交于M ,N 两点,证明:F 点到AM ,AN 的距离相等. (1)解 双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的渐近线方程为bx ±ay =0,令点F (c,0),则c 2=a 2+b 2,因为以F 点为圆心,a 为半径的圆与C 的渐近线相切, 则bc a 2+b 2=a , 整理得b =a ,c =2a ,所以双曲线C 的离心率为e =c a= 2. (2)证明 由(1)知,双曲线C 的方程为2x 2-2y 2=c 2,点A ⎝⎛⎭⎫12c ,0,显然直线MN 不垂直于y轴,设直线MN :x =my +c ,因为直线MN 与双曲线右支交于两点,则直线MN 与双曲线的两条渐近线x ±y =0在y 轴右侧都相交,于是得-1<m <1,由⎩⎪⎨⎪⎧x =my +c ,2x 2-2y 2=c 2消去x 得2(m 2-1)y 2+4cmy +c 2=0, 设M (x 1,y 1),N (x 2,y 2),则y 1+y 2=-2cm m 2-1,y 1y 2=c 22m 2-1, 直线AM 的斜率k AM =y 1x 1-12c =y 1my 1+c -12c =2y 12my 1+c , 同理,直线AN 的斜率k AN =2y 22my 2+c , 于是得k AM +k AN =2y 12my 1+c +2y 22my 2+c=8my 1y 2+2c y 1+y 22my 1+c 2my 2+c=8m ·c 22m 2-1+2c ⎝⎛⎭⎫-2cm m 2-12my 1+c 2my 2+c=0, 因此,直线AM 与AN 的倾斜角互补,则直线AM 与AN 关于x 轴对称,而点F 在x 轴上, 所以点F 到直线AM 与AN 的距离相等.课时精练1.已知抛物线C :y 2=2px (p >0)的准线与x 轴的交点为A (-1,0).(1)求C 的方程;(2)若过点M (2,0)的直线l 与抛物线C 交于P ,Q 两点.求证:1|PM |2+1|QM |2为定值. (1)解 由题意,可得-p 2=-1,即p =2, ∴抛物线C 的方程为y 2=4x .(2)证明 设直线l 的方程为x =my +2,P (x 1,y 1),Q (x 2,y 2),联立⎩⎪⎨⎪⎧x =my +2,y 2=4x , 消去x 得y 2-4my -8=0,则Δ=16(m 2+2)>0,∴y 1+y 2=4m ,y 1y 2=-8,又|PM |=1+m 2|y 1|,|QM |=1+m 2|y 2|.∴1|PM |2+1|QM |2=11+m 2y 21+11+m 2y 22=y 21+y 221+m 2y 21y 22=16m 2+16641+m 2=1+m 241+m2=14. ∴1|PM |2+1|QM |2为定值.2.设椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,上顶点为B .已知椭圆的短轴长为4,离心率为55. (1)求椭圆的方程;(2)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若|ON |=|OF |(O 为原点),且OP ⊥MN ,求直线PB 的斜率.解 (1)设椭圆的半焦距为c ,依题意,2b =4,c a =55, 又a 2=b 2+c 2,可得a =5,b =2,c =1.所以椭圆的方程为x 25+y 24=1. (2)由题意,设P (x P ,y P )(x P ≠0),M (x M ,0).设直线PB 的斜率为k (k ≠0),又B (0,2),则直线PB 的方程为y =kx +2,与椭圆方程联立⎩⎪⎨⎪⎧y =kx +2,x 25+y 24=1,整理得(4+5k 2)x 2+20kx =0,可得x P =-20k 4+5k 2, 代入y =kx +2得y P =8-10k 24+5k 2, 所以直线OP 的斜率y P x P =4-5k 2-10k. 在y =kx +2中,令y =0,得x M =-2k. 由题意得N (0,-1),所以直线MN 的斜率为-k 2. 由OP ⊥MN ,得4-5k 2-10k ·⎝⎛⎭⎫-k 2=-1,化简得k 2=245,从而k =±2305. 所以直线PB 的斜率为2305或-2305.3.(2022·莆田质检)曲线C 上任意一点P 到点F (2,0)的距离与它到直线x =4的距离之比等于22,过点M (4,0)且与x 轴不重合的直线l 与C 交于不同的两点A ,B . (1)求C 的方程;(2)求证:△ABF 内切圆的圆心在定直线上. (1)解 设P (x ,y ),由题意,x -22+y 2|x -4|=22⇒(x -2)2+y 2 =12(x -4)2, 化简得x 28+y 24=1, 即C 的方程为x 28+y 24=1. (2)证明 设直线l :x =my +4,A (x 1,y 1),B (x 2,y 2),将l 代入C 得(m 2+2)y 2+8my +8=0,∴⎩⎨⎧ Δ=64m 2-32m 2+2>0⇒m 2>2,y 1+y 2=-8m m 2+2,y 1·y 2=8m 2+2.设直线AF 与BF 的斜率分别为k 1,k 2,则k 1+k 2=y 1x 1-2+y 2x 2-2=y 1my 1+2+y 2my 2+2 =2my 1y 2+2y 1+y 2my 1+2my 2+2 =2m ·8m 2+2+2⎝⎛⎭⎫-8m m 2+2my 1+2my 2+2=0. ∴k 1=-k 2,则∠BFM =π-∠AFM ,∴直线x =2平分∠AFB ,而三角形内心在∠AFB 的角平分线上, ∴△ABF 内切圆的圆心在定直线x =2上.4.(2022·深圳光明区模拟)已知双曲线C :x 2a2-y 2=1(a >0)的左、右焦点分别为F 1,F 2,E (0,1),过焦点F 2,且斜率为16的直线与C 的两条渐近线分别交于A ,B 两点,且满足AF 1→=2BO →. (1)求C 的方程;(2)过点D ⎝⎛⎭⎫-32,0且斜率不为0的直线l 交C 于M ,N 两点,且|EM |=|EN |,求直线l 的方程. 解 (1)双曲线C 的渐近线方程为y =±1ax , 过F 2(c,0),且斜率为16的直线方程为 y =16(x -c ), 由⎩⎨⎧ y =1a x ,y =16x -c得A ⎝⎛⎭⎫ac a -6,c a -6, 由⎩⎨⎧ y =-1a x ,y =16x -c得B ⎝ ⎛⎭⎪⎫ac a +6,-c a +6, 由于AF 1—→=2BO →,即⎝⎛⎭⎫-c -ac a -6,-c a -6=⎝ ⎛⎭⎪⎫-2ac a +6,2c a +6, 所以-c a -6=2c a +6,解得a =2. 所以双曲线C 的方程为x 24-y 2=1. (2)设l :y =k ⎝⎛⎭⎫x +32(k ≠0), 由⎩⎨⎧ y =k ⎝⎛⎭⎫x +32,x 24-y 2=1,消去y 并化简得(1-4k 2)x 2-12k 2x -9k 2-4=0,Δ=144k 4+4(1-4k 2)(9k 2+4)=16-28k 2>0,k 2<47且k ≠0. 设M (x 1,y 1),N (x 2,y 2),则x 1+x 2=12k 21-4k 2, y 1+y 2=k (x 1+x 2+3)=k ⎝⎛⎭⎫12k 21-4k 2+3 =3k 1-4k 2, 所以M ,N 的中点G 的坐标为⎝ ⎛⎭⎪⎪⎫6k 21-4k 2,32k 1-4k 2, 由于|EM |=|EN |,所以EG ⊥MN ,k EG ·k MN =-1,32k 1-4k 2-16k 21-4k 2-0·k =-1, 化简得8k 2+15k -2=0,(k +2)(8k -1)=0,解得k =-2或k =18, 由于k 2<47且k ≠0, 所以k =18, 所以直线l 的方程为y =18⎝⎛⎭⎫x +32.。
北师版高考总复习一轮数学精品课件 第9章平面解析几何 素能培优(十二)解析几何减少运算量的常用技巧

解
2
(1)由已知得椭圆 C 的焦点在 x 轴上,设椭圆 C 的方程为2
则 A(a,0),B(0,b),F(c,0),c=
a=2b,则 c= 3b.又
2
2 - 2 .由已知得 e2= 2
=
2 -2
2
=
b=1,所以 a=2,c= 3,所以椭圆 C
2 =1(a>b>0),
+ 2 =1(a>b>0)的左焦点
F,交椭圆于 A,B 两点,交 y 轴于点 M,若M=3M,则该椭圆的离心率为( C )
A.
17+ 5
8
C.
17- 5
2
B.
17- 5
4
D.
17+ 5
9
解析 对直线x-2y+2=0,令y=0,解得x=-2,令x=0,解得y=1,
故 F(-2,0),M(0,1),则=(2,1).设 A(x0,y0),则=(-x0,1-y0).
3
,所以 a2=4b2,所以
4
1
1
3
1
S△ABF= |AF||OB|= (a-c)b=1- ,所以 (2b2
2
2
2
2 2
的方程为 4 +y =1.
+
2
3b)b=1-
3
,所以
2
(2)圆 O 的圆心坐标为(0,0),半径 r=1,由直线 l:y=kx+m 与圆 O:x2+y2=1 相切,
得
||
巧用“根与系数的关系”,化繁为简
例3设抛物线C:y2=2px(p>0)的焦点为F,过点P(0,4)的动直线l与抛物线C交
2019版高考数学大一轮复习人教B版全国通用文档:第九章平面解析几何9.2

§9.2 两条直线的位置关系1.两条直线的位置关系已知两条直线的方程为:l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,则(1)l 1与l 2相交的条件是:A 1B 2-A 2B 1≠0或A 1A 2≠B 1B 2(A 2B 2≠0). (2)l 1与l 2平行的条件是:A 1B 2-A 2B 1=0,而B 1C 2-C 1B 2≠0或A 2C 1-A 1C 2≠0;或A 1A 2=B 1B 2≠C 1C 2(A 2B 2C 2≠0).(3)l 1与l 2重合的条件是:A 1=λA 2,B 1=λB 2,C 1=λC 2(λ≠0);或A 1A 2=B 1B 2=C 1C 2(A 2B 2C 2≠0). (4)l 1与l 2垂直的条件是A 1A 2+B 1B 2=0.(5)两条斜率存在且分别为k 1,k 2的直线l 1和l 2垂直的条件是k 1k 2=-1.2.几种距离(1)两点P 1(x 1,y 1),P 2(x 2,y 2)之间的距离|P 1P 2|=(x 2-x 1)2+(y 2-y 1)2.(2)点P 0(x 0,y 0)到直线l :Ax +By +C =0的距离d =|Ax 0+By 0+C |A 2+B 2. (3)两条平行线Ax +By +C 1=0与Ax +By +C 2=0(其中C 1≠C 2)间的距离d =|C 1-C 2|A 2+B 2. 知识拓展1.直线系方程(1)与直线Ax +By +C =0平行的直线系方程是Ax +By +m =0(m ∈R 且m ≠C ).(2)与直线Ax +By +C =0垂直的直线系方程是Bx -Ay +n =0(n ∈R ).2.两直线平行或重合的充要条件直线l 1:A 1x +B 1y +C 1=0与直线l 2:A 2x +B 2y +C 2=0平行或重合的充要条件是A 1B 2-A 2B 1=0.3.两直线垂直的充要条件直线l 1:A 1x +B 1y +C 1=0与直线l 2:A 2x +B 2y +C 2=0垂直的充要条件是A 1A 2+B 1B 2=0.4.过直线l 1:A 1x +B 1y +C 1=0与l 2:A 2x +B 2y +C 2=0的交点的直线系方程为A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0(λ∈R ),但不包括l 2.5.点到直线、两平行线间的距离公式的使用条件(1)求点到直线的距离时,应先化直线方程为一般式.(2)求两平行线之间的距离时,应先将方程化为一般式且x ,y 的系数对应相等.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)当直线l 1和l 2斜率都存在时,一定有k 1=k 2⇒l 1∥l 2.( × )(2)如果两条直线l 1与l 2垂直,则它们的斜率之积一定为-1.( × )(3)已知直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0(A 1,B 1,C 1,A 2,B 2,C 2为常数),若直线l 1⊥l 2,则A 1A 2+B 1B 2=0.( √ )(4)点P (x 0,y 0)到直线y =kx +b 的距离为|kx 0+b |1+k2.( × ) (5)直线外一点与直线上一点的距离的最小值就是点到直线的距离.( √ )(6)若点A ,B 关于直线l :y =kx +b (k ≠0)对称,则直线AB 的斜率等于-1k,且线段AB 的中点在直线l 上.( √ )题组二 教材改编2.已知点(a,2)(a >0)到直线l :x -y +3=0的距离为1,则a 等于( ) A. 2 B .2- 2 C.2-1 D.2+1答案 C解析 由题意得|a -2+3|1+1=1. 解得a =-1+2或a =-1- 2.∵a >0,∴a =-1+ 2.3.已知P (-2,m ),Q (m,4),且直线PQ 垂直于直线x +y +1=0,则m =________. 答案 1解析 由题意知m -4-2-m=1,所以m -4=-2-m , 所以m =1.题组三 易错自纠4.(2017·郑州调研)直线2x +(m +1)y +4=0与直线mx +3y -2=0平行,则m 等于( )A .2B .-3C .2或-3D .-2或-3 答案 C解析 直线2x +(m +1)y +4=0与直线mx +3y -2=0平行,则有2m =m +13≠4-2,故m =2或-3.故选C.5.直线2x +2y +1=0,x +y +2=0之间的距离是______.答案 324 解析 先将2x +2y +1=0化为x +y +12=0, 则两平行线间的距离为d =⎪⎪⎪⎪2-122=324.6.若直线(3a +2)x +(1-4a )y +8=0与(5a -2)x +(a +4)y -7=0垂直,则a =________. 答案 0或1解析 由两直线垂直的充要条件,得(3a +2)(5a -2)+(1-4a )(a +4)=0,解得a =0或a =1.题型一 两条直线的位置关系典例 (2018·青岛模拟)已知两条直线l 1:ax -by +4=0和l 2:(a -1)x +y +b =0,求满足下列条件的a ,b 的值.(1)l 1⊥l 2,且l 1过点(-3,-1);(2)l 1∥l 2,且坐标原点到这两条直线的距离相等.解 (1)由已知可得l 2的斜率存在,且k 2=1-a .若k 2=0,则1-a =0,a =1.∵l 1⊥l 2,直线l 1的斜率k 1必不存在,即b =0.又∵l 1过点(-3,-1),∴-3a +4=0,即a =43(矛盾),∴此种情况不存在, ∴k 2≠0,即k 1,k 2都存在且不为0.∵k 2=1-a ,k 1=a b,l 1⊥l 2, ∴k 1k 2=-1,即a b(1-a )=-1.(*) 又∵l 1过点(-3,-1),∴-3a +b +4=0.(**)由(*)(**)联立,解得a =2,b =2.(2)∵l 2的斜率存在,l 1∥l 2,∴直线l 1的斜率存在,k 1=k 2,即a b=1-a ,① 又∵坐标原点到这两条直线的距离相等,且l 1∥l 2,∴l 1,l 2在y 轴上的截距互为相反数,即4b=b ,② 联立①②,解得⎩⎪⎨⎪⎧ a =2,b =-2或⎩⎪⎨⎪⎧ a =23,b =2.∴a =2,b =-2或a =23,b =2.思维升华 (1)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x ,y 的系数不能同时为零这一隐含条件.(2)在判断两直线平行、垂直时,也可直接利用直线方程的系数间的关系得出结论. 跟踪训练 已知直线l 1:ax +2y +6=0和直线l 2:x +(a -1)y +a 2-1=0.(1)试判断l 1与l 2是否平行;(2)当l 1⊥l 2时,求a 的值.解 (1)方法一 当a =1时,l 1:x +2y +6=0,l 2:x =0,l 1不平行于l 2;当a =0时,l 1:y =-3,l 2:x -y -1=0,l 1不平行于l 2;当a ≠1且a ≠0时,两直线可化为l 1:y =-a 2x -3, l 2:y =11-ax -(a +1), l 1∥l 2⇔⎩⎪⎨⎪⎧ -a 2=11-a ,-3≠-(a +1),解得a =-1, 综上可知,当a =-1时,l 1∥l 2.方法二 由A 1B 2-A 2B 1=0,得a (a -1)-1×2=0,由A 1C 2-A 2C 1≠0,得a (a 2-1)-1×6≠0,∴l 1∥l 2⇔⎩⎪⎨⎪⎧a (a -1)-1×2=0,a (a 2-1)-1×6≠0,⇔⎩⎪⎨⎪⎧a 2-a -2=0,a (a 2-1)≠6,可得a =-1, 故当a =-1时,l 1∥l 2.(2)方法一 当a =1时,l 1:x +2y +6=0,l 2:x =0,l 1与l 2不垂直,故a =1不成立;当a =0时,l 1:y =-3,l 2:x -y -1=0,l 1不垂直于l 2,故a =0不成立;当a ≠1且a ≠0时,l 1:y =-a 2x -3,l 2:y =11-ax -(a +1), 由⎝⎛⎭⎫-a 2·11-a =-1,得a =23. 方法二 由A 1A 2+B 1B 2=0,得a +2(a -1)=0,可得a =23. 题型二 两条直线的交点与距离问题1.已知直线y =kx +2k +1与直线y =-12x +2的交点位于第一象限,则实数k 的取值范围是_____.答案 ⎝⎛⎭⎫-16,12 解析 方法一 由方程组⎩⎪⎨⎪⎧ y =kx +2k +1,y =-12x +2, 解得⎩⎪⎨⎪⎧ x =2-4k 2k +1,y =6k +12k +1.(若2k +1=0,即k =-12,则两直线平行) ∴交点坐标为⎝ ⎛⎭⎪⎫2-4k 2k +1,6k +12k +1. 又∵交点位于第一象限,∴⎩⎪⎨⎪⎧ 2-4k 2k +1>0,6k +12k +1>0,解得-16<k <12. 方法二 如图,已知直线y =-12x +2与x 轴、y 轴分别交于点A (4,0),B (0,2).而直线方程y =kx +2k +1可变形为y -1=k (x +2),表示这是一条过定点P (-2,1),斜率为k 的动直线.∵两直线的交点在第一象限,∴两直线的交点必在线段AB 上(不包括端点),∴动直线的斜率k 需满足k P A <k <k PB .∵k P A =-16,k PB =12. ∴-16<k <12. 2.若直线l 过点P (-1,2)且到点A (2,3)和点B (-4,5)的距离相等,则直线l 的方程为________________________.答案 x +3y -5=0或x =-1解析 方法一 当直线l 的斜率存在时,设直线l 的方程为y -2=k (x +1),即kx -y +k +2=0.由题意知|2k -3+k +2|k 2+1=|-4k -5+k +2|k 2+1, 即|3k -1|=|-3k -3|,∴k =-13. ∴直线l 的方程为y -2=-13(x +1), 即x +3y -5=0.当直线l 的斜率不存在时,直线l 的方程为x =-1,也符合题意.方法二 当AB ∥l 时,有k =k AB =-13, 直线l 的方程为y -2=-13(x +1), 即x +3y -5=0.当l 过AB 的中点时,AB 的中点为(-1,4).∴直线l 的方程为x =-1.故所求直线l 的方程为x +3y -5=0或x =-1.思维升华 (1)求过两直线交点的直线方程的方法先求出两直线的交点坐标,再结合其他条件写出直线方程.(2)利用距离公式应注意:①点P (x 0,y 0)到直线x =a 的距离d =|x 0-a |,到直线y =b 的距离d =|y 0-b |;②两平行线间的距离公式要把两直线方程中x ,y 的系数化为相等.题型三 对称问题命题点1 点关于点中心对称典例 过点P (0,1)作直线l ,使它被直线l 1:2x +y -8=0和l 2:x -3y +10=0截得的线段被点P 平分,则直线l 的方程为________________.答案x+4y-4=0解析设l1与l的交点为A(a,8-2a),则由题意知,点A关于点P的对称点B(-a,2a-6)在l2上,代入l2的方程得-a-3(2a-6)+10=0,解得a=4,即点A(4,0)在直线l上,所以直线l的方程为x+4y-4=0.命题点2点关于直线对称典例如图,已知A(4,0),B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是()A.3 3 B.6C.210 D.2 5答案 C解析直线AB的方程为x+y=4,点P(2,0)关于直线AB的对称点为D(4,2),关于y轴的对称点为C(-2,0),则光线经过的路程为|CD|=62+22=210.命题点3直线关于直线的对称问题典例已知直线l:2x-3y+1=0,求直线m:3x-2y-6=0关于直线l的对称直线m′的方程.解在直线m上任取一点,如M(2,0),则M(2,0)关于直线l的对称点M′必在直线m′上.设对称点M′(a,b),则⎩⎪⎨⎪⎧2×⎝⎛⎭⎫a +22-3×⎝⎛⎭⎫b +02+1=0,b -0a -2×23=-1,解得⎩⎨⎧a =613,b =3013,∴M ′⎝⎛⎭⎫613,3013.设直线m 与直线l 的交点为N ,则由⎩⎪⎨⎪⎧2x -3y +1=0,3x -2y -6=0,得N (4,3). 又∵直线m ′经过点N (4,3),∴由两点式得直线m ′的方程为9x -46y +102=0. 思维升华 解决对称问题的方法(1)中心对称①点P (x ,y )关于Q (a ,b )的对称点P ′(x ′,y ′)满足⎩⎪⎨⎪⎧x ′=2a -x ,y ′=2b -y .②直线关于点的对称可转化为点关于点的对称问题来解决.(2)轴对称①点A (a ,b )关于直线Ax +By +C =0(B ≠0)的对称点A ′(m ,n ),则有⎩⎨⎧n -bm -a ×⎝⎛⎭⎫-A B =-1,A ·a +m 2+B ·b +n 2+C =0.②直线关于直线的对称可转化为点关于直线的对称问题来解决. 跟踪训练 已知直线l :3x -y +3=0,求: (1)点P (4,5)关于l 的对称点;(2)直线x -y -2=0关于直线l 对称的直线方程; (3)直线l 关于(1,2)的对称直线.解 (1)设P (x ,y )关于直线l :3x -y +3=0的对称点为P ′(x ′,y ′),∵k PP ′·k l =-1,即y ′-yx ′-x ×3=-1.①又PP ′的中点在直线3x -y +3=0上, ∴3×x ′+x 2-y ′+y 2+3=0.②由①②得⎩⎨⎧x ′=-4x +3y -95,③y ′=3x +4y +35. ④把x =4,y =5代入③④得x ′=-2,y ′=7, ∴点P (4,5)关于直线l 的对称点P ′的坐标为(-2,7). (2)用③④分别代换x -y -2=0中的x ,y , 得关于l 对称的直线方程为 -4x +3y -95-3x +4y +35-2=0, 化简得7x +y +22=0.(3)在直线l :3x -y +3=0上取点M (0,3), 关于(1,2)的对称点M ′(x ′,y ′),∴x ′+02=1,x ′=2,y ′+32=2,y ′=1,∴M ′(2,1). l 关于(1,2)的对称直线平行于l ,∴k =3,∴对称直线方程为y-1=3×(x-2),即3x-y-5=0.妙用直线系求直线方程一、平行直线系由于两直线平行,它们的斜率相等或它们的斜率都不存在,因此两直线平行时,它们的一次项系数与常数项有必然的联系.典例1求与直线3x+4y+1=0平行且过点(1,2)的直线l的方程.思想方法指导因为所求直线与3x+4y+1=0平行,因此,可设该直线方程为3x+4y+c=0(c≠1).规范解答解由题意,设所求直线方程为3x+4y+c=0(c≠1),又因为直线过点(1,2),所以3×1+4×2+c=0,解得c=-11.因此,所求直线方程为3x+4y-11=0.二、垂直直线系由于直线A1x+B1y+C1=0与A2x+B2y+C2=0垂直的充要条件为A1A2+B1B2=0.因此,当两直线垂直时,它们的一次项系数有必然的联系.可以考虑用直线系方程求解.典例2求经过A(2,1),且与直线2x+y-10=0垂直的直线l的方程.思想方法指导依据两直线垂直的特征设出方程,再由待定系数法求解.规范解答解因为所求直线与直线2x+y-10=0垂直,所以设该直线方程为x-2y+C1=0,又直线过点A(2,1),所以有2-2×1+C 1=0,解得C 1=0, 即所求直线方程为x -2y =0. 三、过直线交点的直线系典例3 (2017·湖南东部十校联考)经过两条直线2x +3y +1=0和x -3y +4=0的交点,并且垂直于直线3x +4y -7=0的直线方程为____________.思想方法指导 可分别求出直线l 1与l 2的交点及直线l 的斜率k ,直接写出方程;也可以根据垂直关系设出所求方程,再把交点坐标代入求解;又可以利用过交点的直线系方程设直线方程,再用待定系数法求解. 答案 4x -3y +9=0解析 方法一 由方程组⎩⎪⎨⎪⎧2x +3y +1=0,x -3y +4=0,解得⎩⎨⎧x =-53,y =79,即交点为⎝⎛⎭⎫-53,79, ∵所求直线与直线3x +4y -7=0垂直, ∴所求直线的斜率为k =43.由点斜式得所求直线方程为y -79=43⎝⎛⎭⎫x +53, 即4x -3y +9=0.方法二 由垂直关系可设所求直线方程为4x -3y +m =0,由方程组⎩⎪⎨⎪⎧2x +3y +1=0,x -3y +4=0,可解得交点为⎝⎛⎭⎫-53,79, 代入4x -3y +m =0,得m =9, 故所求直线方程为4x -3y +9=0.方法三 由题意可设所求直线方程为 (2x +3y +1)+λ(x -3y +4)=0, 即(2+λ)x +(3-3λ)y +1+4λ=0,① 又∵所求直线与直线3x +4y -7=0垂直, ∴3(2+λ)+4(3-3λ)=0,∴λ=2,代入①式得所求直线方程为4x -3y +9=0.1.直线2x +y +m =0和x +2y +n =0的位置关系是( ) A .平行 B .垂直 C .相交但不垂直 D .不能确定答案 C解析 直线2x +y +m =0的斜率k 1=-2,直线x +2y +n =0的斜率k 2=-12,则k 1≠k 2,且k 1k 2≠-1. 故选C.2.(2018·邢台模拟)“a =-1”是“直线ax +3y +3=0和直线x +(a -2)y +1=0平行”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 答案 C解析 由题意得,直线ax +3y +3=0和直线x +(a -2)y +1=0平行的充要条件是⎩⎪⎨⎪⎧a (a -2)=3×1,a ×1≠3×1, 解得a =-1,故选C.3.从点(2,3)射出的光线沿与向量a =(8,4)平行的直线射到y 轴上,则反射光线所在的直线方程为( ) A .x +2y -4=0 B .2x +y -1=0 C .x +6y -16=0 D .6x +y -8=0答案 A解析 由直线与向量a =(8,4)平行知,过点(2,3)的直线的斜率k =12,所以直线的方程为y -3=12(x -2),其与y 轴的交点坐标为(0,2),又点(2,3)关于y 轴的对称点为(-2,3),所以反射光线过点(-2,3)与(0,2),由两点式知A 正确.4.(2017·兰州一模)一只虫子从点O (0,0)出发,先爬行到直线l :x -y +1=0上的P 点,再从P 点出发爬行到点A (1,1),则虫子爬行的最短路程是( ) A. 2 B .2 C .3 D .4 答案 B解析 点O (0,0)关于直线x -y +1=0的对称点为O ′(-1,1),则虫子爬行的最短路程为|O ′A |=(1+1)2+(1-1)2=2.故选B.5.若直线l 1:x +ay +6=0与l 2:(a -2)x +3y +2a =0平行,则l 1与l 2之间的距离为( ) A.423B .4 2 C.823 D .2 2答案 C解析 ∵l 1∥l 2,∴a ≠2且a ≠0, ∴1a -2=a 3≠62a,解得a =-1,∴l 1与l 2的方程分别为l 1:x -y +6=0,l 2:x -y +23=0,∴l 1与l 2的距离d =⎪⎪⎪⎪6-232=823.6.若直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,则直线l 2经过定点 ( ) A .(0,4) B .(0,2) C .(-2,4) D .(4,-2)答案 B解析 直线l 1:y =k (x -4)经过定点(4,0),其关于点(2,1)对称的点为(0,2),又直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,故直线l 2经过定点(0,2).7.若三条直线y =2x ,x +y =3,mx +2y +5=0相交于同一点,则m 的值为________. 答案 -9解析 由⎩⎪⎨⎪⎧ y =2x ,x +y =3,得⎩⎪⎨⎪⎧x =1,y =2.∴点(1,2)满足方程mx +2y +5=0, 即m ×1+2×2+5=0,∴m =-9.8.将一张坐标纸折叠一次,使得点(0,2)与点(4,0)重合,点(7,3)与点(m ,n )重合,则m +n =________. 答案345解析 由题意可知,纸的折痕应是点(0,2)与点(4,0)连线的中垂线,即直线y =2x -3,它也是点(7,3)与点(m ,n )连线的中垂线, 于是⎩⎪⎨⎪⎧3+n 2=2×7+m2-3,n -3m -7=-12, 解得⎩⎨⎧m =35,n =315,故m +n =345.9.(2017·浙江嘉兴一中月考)已知直线l 1:ax +y -6=0与l 2:x +(a -2)y +a -1=0相交于点P ,若l 1⊥l 2,则a =________,此时点P 的坐标为________. 答案 1 (3,3)解析 ∵直线l 1:ax +y -6=0与l 2:x +(a -2)y +a -1=0相交于点P ,且l 1⊥l 2,∴a ×1+1×(a -2)=0,即a =1,联立方程⎩⎪⎨⎪⎧x +y -6=0,x -y =0,易得x =3,y =3,∴P (3,3).10.已知直线l 1:ax +y -1=0,直线l 2:x -y -3=0,若直线l 1的倾斜角为π4,则a =________;若l 1⊥l 2,则a =________;若l 1∥l 2,则两平行直线间的距离为________. 答案 -1 1 2 2解析 若直线l 1的倾斜角为π4,则-a =k =tan π4=1,故a =-1;若l 1⊥l 2,则a ×1+1×(-1)=0,故a =1;若l 1∥l 2,则a =-1,l 1:x -y +1=0,两平行直线间的距离d =|1-(-3)|1+1=2 2.11.已知方程(2+λ)x -(1+λ)y -2(3+2λ)=0与点P (-2,2).(1)证明:对任意的实数λ,该方程都表示直线,且这些直线都经过同一定点,并求出这一定点的坐标;(2)证明:该方程表示的直线与点P 的距离d 小于4 2.(1)解 显然2+λ与-(1+λ)不可能同时为零,故对任意的实数λ,该方程都表示直线. ∵方程可变形为2x -y -6+λ(x -y -4)=0,∴⎩⎪⎨⎪⎧ 2x -y -6=0,x -y -4=0,解得⎩⎪⎨⎪⎧x =2,y =-2,故直线经过的定点为M (2,-2). (2)证明 过P 作直线的垂线段PQ ,由垂线段小于斜线段知|PQ |≤|PM |,当且仅当Q 与M 重合时,|PQ |=|PM |,此时对应的直线方程是y +2=x -2,即x -y -4=0. 但直线系方程唯独不能表示直线x -y -4=0,∴M 与Q 不可能重合,而|PM |=42,∴|PQ |<42,故所证成立.12.已知三条直线:l 1:2x -y +a =0(a >0);l 2:-4x +2y +1=0;l 3:x +y -1=0,且l 1与l 2间的距离是7510.(1)求a 的值;(2)能否找到一点P ,使P 同时满足下列三个条件: ①点P 在第一象限;②点P 到l 1的距离是点P 到l 2的距离的12;③点P 到l 1的距离与点P 到l 3的距离之比是2∶ 5. 若能,求点P 的坐标;若不能,请说明理由.解 (1)直线l 2:2x -y -12=0,所以两条平行直线l 1与l 2间的距离为d =⎪⎪⎪⎪a -⎝⎛⎭⎫-1222+(-1)2=7510,所以⎪⎪⎪⎪a +125=7510,即⎪⎪⎪⎪a +12=72, 又a >0,解得a =3.(2)假设存在点P ,设点P (x 0,y 0). 若点P 满足条件②,则点P 在与l 1,l 2平行的直线l ′:2x -y +c =0上,且|c -3|5=12×⎪⎪⎪⎪c +125,即c =132或116,所以直线l ′的方程为2x 0-y 0+132=0或2x 0-y 0+116=0;若点P 满足条件③,由点到直线的距离公式, 有|2x 0-y 0+3|5=25×|x 0+y 0-1|2, 即|2x 0-y 0+3|=|x 0+y 0-1|, 所以x 0-2y 0+4=0或3x 0+2=0;由于点P 在第一象限,所以3x 0+2=0不可能. 联立方程2x 0-y 0+132=0和x 0-2y 0+4=0,解得⎩⎪⎨⎪⎧x 0=-3,y 0=12(舍去); 联立方程2x 0-y 0+116=0和x 0-2y 0+4=0,解得⎩⎨⎧x 0=19,y 0=3718.所以存在点P ⎝⎛⎭⎫19,3718同时满足三个条件.13.(2017·湖北孝感五校联考)已知直线y =2x 是△ABC 中∠C 的平分线所在的直线,若点A ,B 的坐标分别是(-4,2),(3,1),则点C 的坐标为( ) A .(-2,4) B .(-2,-4) C .(2,4) D .(2,-4)答案 C解析 设A (-4,2)关于直线y =2x 的对称点为(x ,y ),则⎩⎪⎨⎪⎧ y -2x +4×2=-1,y +22=2×-4+x 2, 解得⎩⎪⎨⎪⎧x =4,y =-2, ∴BC 所在直线方程为y -1=-2-14-3(x -3), 即3x +y -10=0.同理可得点B (3,1)关于直线y =2x 的对称点为(-1,3),∴AC 所在直线方程为y -2=3-2-1-(-4)(x +4), 即x -3y +10=0.联立⎩⎪⎨⎪⎧ 3x +y -10=0,x -3y +10=0,解得⎩⎪⎨⎪⎧x =2,y =4, 则C (2,4).故选C.14.(2017·岳阳二模)已知动直线l :ax +by +c -2=0(a >0,c >0)恒过点P (1,m )且Q (4,0)到动直线l 的最大距离为3,则12a +2c的最小值为________. 答案 94解析 因为动直线l :ax +by +c -2=0(a >0,c >0)恒过点P (1,m ),所以a +bm +c -2=0,又Q (4,0)到动直线l 的最大距离为3, 所以(4-1)2+(-m )2=3,解得m =0.所以a +c =2,则12a +2c =12(a +c )·⎝⎛⎭⎫12a +2c =12⎝⎛⎭⎫52+c 2a +2a c ≥12⎝⎛⎭⎫52+2c 2a ·2a c =94, 当且仅当c =2a =43时取等号.15.如图,已知直线l 1∥l 2,点A 是l 1,l 2之间的定点,点A 到l 1,l 2之间的距离分别为3和2,点B 是l 2上的一动点,作AC ⊥AB ,且AC 与l 1交于点C ,则△ABC 的面积的最小值为________.答案 6解析 以A 为坐标原点,平行于l 1的直线为x 轴,建立如图所示的直角坐标系,设 B (a ,-2),C (b,3).∵AC ⊥AB ,∴ab -6=0,ab =6,b =6a. Rt △ABC 的面积S =12a 2+4·b 2+9 =12a 2+4·36a 2+9=1272+9a 2+144a 2 ≥1272+72=6(当且仅当a 2=4时取等号). 16.在平面直角坐标系xOy 中,将直线l 沿x 轴正方向平移3个单位长度,沿y 轴正方向平移5个单位长度,得到直线l 1.再将直线l 1沿x 轴正方向平移1个单位长度,沿y 轴负方向平移2个单位长度,又与直线l 重合.若直线l 与直线l 1关于点(2,3)对称,则直线l 的方程是______________.答案 6x -8y +1=0解析 由题意知直线l 的斜率存在,设直线l 的方程为y =kx +b ,将直线l 沿x 轴正方向平移3个单位长度,沿y 轴正方向平移5个单位长度,得到直线l 1:y =k (x -3)+5+b ,将直线l 1沿x 轴正方向平移1个单位长度,沿y 轴负方向平移2个单位长度,则平移后的直线方程为y =k (x -3-1)+b +5-2,即y =kx +3-4k +b ,∴b =3-4k +b ,解得k =34,∴直线l 的方程为y =34x +b ,直线l 1为y =34x +114+b ,取直线l 上的一点P ⎝⎛⎭⎫m ,b +3m 4,则点P 关于点(2,3)的对称点为⎝⎛⎭⎫4-m ,6-b -3m 4,∴6-b -3m 4=34(4-m )+b +114,解得b =18. ∴直线l 的方程是y =34x +18,即6x -8y +1=0.。
2020版高考数学大一轮复习 第九章 平面解析几何专题探究课五学案 理 新人教B版

专题探究课五高考导航 1.圆锥曲线是平面解析几何的核心部分,也是高考必考知识,主要以一个小题一个大题的形式呈现,难度中等偏上;2.高考中的选择题或填空题主要考查圆锥曲线的基本性质,高考中的解答题,常以求曲线的标准方程、位置关系、定点、定值、最值、范围、探索性问题为主.这些试题的命制有一个共同的特点,就是起点低,但在第(2)问或第(3)问中一般都伴有较为复杂的运算,对考生解决问题的能力要求较高.热点一 定点定值问题(教材VS 高考)定点、定值问题一般涉及曲线过定点、与曲线上的动点有关的定值问题以及与圆锥曲线有关的弦长、面积、横(纵)坐标等的定值问题.圆锥曲线中的最值问题大致可分为两类:一是涉及距离、面积的最值以及与之相关的一些问题;二是求直线或圆锥曲线中几何元素的最值以及这些元素存在最值时求解与之有关的一些问题. 命题角度1 圆锥曲线中定点问题【例1-1】 (满分12分)(2017·全国Ⅰ卷)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0),四点P 1(1,1),P 2(0,1),P 3⎝ ⎛⎭⎪⎫-1,32,P 4⎝ ⎛⎭⎪⎫1,32中恰有三点在椭圆C 上. (1)求C 的方程;(2)设直线l 不经过P 2点且与C 相交于A ,B 两点.若直线P 2A 与直线P 2B 的斜率的和为-1,证明:l 过定点. 教材探源 本题第(1)问源于教材选修2-1P40例1,主要考查利用待定系数法及方程思想求曲线方程. 本题第(2)问源于教材选修2-1P41例3,主要考查利用坐标法研究几何问题,充分考查学生解决综合问题的能力.满分解答 (1)解 由于点P 3,P 4关于y 轴对称,由题设知C 必过P 3,P 4.又由1a 2+1b 2>1a 2+34b2知,椭圆C 不经过点P 1,所以点P 2在椭圆C 上.1分 (得分点1)因此⎩⎪⎨⎪⎧1b 2=1,1a 2+34b 2=1,解得⎩⎪⎨⎪⎧a 2=4,b 2=1.3分 (得分点2)故C 的方程为x 24+y 2=1.5分 (得分点3)(2)证明 设直线P 2A 与直线P 2B 的斜率分别为k 1,k 2. 如果直线l 的斜率不存在,l 垂直于x 轴. 设l :x =m ,A (m ,y A ),B (m ,-y A ),k 1+k 2=y A -1m +-y A -1m =-2m=-1,得m =2,此时l 过椭圆右顶点,不存在两个交点,故不满足. 6分 (得分点4)从而可设l :y =kx +m (m ≠1).将y =kx +m 代入x 24+y 2=1得(4k 2+1)x 2+8kmx +4m 2-4=0.7分 (得分点5)由题设可知Δ=16(4k 2-m 2+1)>0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-8km 4k 2+1,x 1x 2=4m 2-44k 2+1.8分 (得分点6)则k 1+k 2=y 1-1x 1+y 2-1x 2=kx 1+m -1x 1+kx 2+m -1x 2=2kx 1x 2+(m -1)(x 1+x 2)x 1x 2.由题设k 1+k 2=-1,故(2k +1)x 1x 2+(m -1)(x 1+x 2)=0. ∴(2k +1)·4m 2-44k 2+1+(m -1)·-8km4k 2+1=0.10分 (得分点7)解之得m =-2k -1,此时Δ=32(m +1)>0,方程有解, ∴当且仅当m >-1时,Δ>0,11分 (得分点8) ∴直线l 的方程为y =kx -2k -1,即y +1=k (x -2). 当x =2时,y =-1,所以l 过定点(2,-1). 12分 (得分点9)❶得步骤分:抓住得分点的解题步骤,“步步为赢”,在第(1)问中,分析隐含信息,列出方程组,求出方程.在第(2)问中,分类讨论设出直线方程→联立方程→写出根与系数的关系→利用公式化简求解.❷得关键分:(1)列出方程组.(2)直线方程.(3)韦达定理.(4)斜率公式.都是不可少的过程,有则给分,无则没分. ❸得计算分:解题过程中的计算准确是得满分的根本保证,如(得分点3),(得分点5),(得分点7).解答圆锥曲线中的定点问题的一般步骤第一步:研究特殊情形,从问题的特殊情形出发,得到目标关系所要探求的定点. 第二步:探究一般情况.探究一般情形下的目标结论. 第三步:下结论,综合上面两种情况定结论. 命题角度2 圆锥曲线中的定值问题【例1-2】 (2017·唐山一模)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,点Q ⎝ ⎛⎭⎪⎫b ,a b 在椭圆上,O 为坐标原点.(1)求椭圆C 的方程;(2)已知点P ,M ,N 为椭圆C 上的三点,若四边形OPMN 为平行四边形,证明四边形OPMN 的面积S 为定值,并求该定值.(1)解 ∵椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为22,∴e 2=c 2a 2=a 2-b 2a 2=12,得a 2=2b 2,①又点Q ⎝⎛⎭⎪⎫b ,a b在椭圆C 上,∴b 2a 2+a 2b4=1,② 联立①、②得a 2=8,且b 2=4. ∴椭圆C 的方程为x 28+y 24=1.(2)证明 当直线PN 的斜率k 不存在时,PN 方程为x =2或x =-2,从而有|PN |=23, 所以S =12|PN |·|OM |=12×23×22=26;当直线PN 的斜率k 存在时,设直线PN 方程为y =kx +m (m ≠0),P (x 1,y 1),N (x 2,y 2), 将PN 的方程代入椭圆C 的方程, 整理得(1+2k 2)x 2+4kmx +2m 2-8=0, 所以x 1+x 2=-4km 1+2k 2,x 1·x 2=2m 2-81+2k2,y 1+y 2=k (x 1+x 2)+2m =2m1+2k2, 由OM →=OP →+ON →,得M ⎝ ⎛⎭⎪⎫-4km 1+2k 2,2m 1+2k 2. 将M 点坐标代入椭圆C 方程得m 2=1+2k 2. 又点O 到直线PN 的距离为d =|m |1+k2,|PN |=1+k 2|x 1-x 2|,所以S =d ·|PN |=|m |·|x 1-x 2|=1+2k 2·(x 1+x 2)2-4x 1x 2=48k 2+242k 2+1=2 6. 综上,平行四边形OPMN 的面积S 为定值2 6. 探究提高 1.求定值问题常见的方法有两种: (1)从特殊入手,求出定值,再证明这个值与变量无关.(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.2.定值问题求解的基本思路是使用参数表示要解决的问题,然后证明与参数无关,这类问题选择消元的方向是非常关键的.【训练1】 (2017·菏泽调研)已知焦距为22的椭圆C :x 2a 2+y 2b 2=1(a >b >0)的右顶点为A ,直线y =43与椭圆C 交于P ,Q 两点(P 在Q 的左边),Q 在x 轴上的射影为B ,且四边形ABPQ 是平行四边形. (1)求椭圆C 的方程;(2)斜率为k 的直线l 与椭圆C 交于两个不同的点M ,N .若M 是椭圆的左顶点,D 是直线MN 上一点,且DA ⊥AM .点G 是x 轴上异于点M 的点,且以DN 为直径的圆恒过直线AN 和DG 的交点,求证:点G 是定点. (1)解 设坐标原点为O ,∵四边形ABPQ 是平行四边形,∴|AB →|=|PQ →|,∵|PQ →|=2|OB →|,∴|AB →|=2|OB →|,则点B 的横坐标为a 3,∴点Q 的坐标为⎝ ⎛⎭⎪⎫a 3,43,代入椭圆C 的方程得b 2=2,又c 2=2,∴a 2=4,即椭圆C 的方程为x 24+y 22=1.(2)证明 设直线MN 的方程为y =k (x +2),N (x 0,y 0),DA ⊥AM ,∴D (2,4k ).由⎩⎪⎨⎪⎧x 24+y 22=1,y =k (x +2),消去y 得(1+2k 2)x 2+8k 2x +8k 2-4=0, 则-2x 0=8k 2-41+2k 2,即x 0=2-4k 21+2k2,∴y 0=k (x 0+2)=4k 1+2k 2,则N ⎝ ⎛⎭⎪⎫2-4k 21+2k 2,4k 1+2k 2,设G (t ,0),则t ≠-2,若以DN 为直径的圆恒过直线AN 和DG 的交点,则DG ⊥AN ,∴GD →·AN →=0恒成立. ∵GD →=(2-t ,4k ),AN →=⎝ ⎛⎭⎪⎫-8k21+2k 2,4k 1+2k 2,∴GD →·AN →=(2-t )·-8k 21+2k 2+4k ·4k 1+2k 2=0恒成立,即8k 2t1+2k2=0恒成立, ∴t =0,∴点G 是定点(0,0).热点二 圆锥曲线中的范围(最值)问题圆锥曲线中的最值问题大致可分为两类:一是涉及距离、面积的最值以及与之相关的一些问题;二是求直线或圆锥曲线中几何元素的最值以及这些元素存在最值时求解与之有关的一些问题.【例2】 (2018·石家庄质检)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右顶点分别为A ,B ,且长轴长为8,T 为椭圆上一点,直线TA ,TB 的斜率之积为-34.(1)求椭圆C 的方程;(2)设O 为原点,过点M (0,2)的动直线与椭圆C 交于P ,Q 两点,求OP →·OQ →+MP →·MQ →的取值范围. 解 (1)设T (x ,y ),则当x ≠±4时,直线TA 的斜率为k 1=yx +4,直线TB 的斜率为k 2=y x -4.于是由k 1k 2=-34,得y x +4·yx -4=-34,整理得x 216+y 212=1,而点(-4,0)和(4,0)也满足此方程,故椭圆C 的方程为x 216+y212=1. (2)当直线PQ 的斜率存在时,设直线PQ 的方程为y =kx +2,点P ,Q 的坐标分别为(x 1,y 1),(x 2,y 2),直线PQ与椭圆方程联立⎩⎪⎨⎪⎧x 216+y 212=1,y =kx +2消去y 得(4k 2+3)x 2+16kx -32=0,则x 1+x 2=-16k 4k 2+3,x 1x 2=-324k 2+3,从而OP →·OQ →+MP →·MQ →=x 1x 2+y 1y 2+[x 1x 2+(y 1-2)·(y 2-2)]=2(1+k 2)x 1x 2+2k (x 1+x 2)+4=-80k 2-524k 2+3=-20+84k 2+3, ∴-20<OP →·OQ →+MP →·MQ →≤-523,当直线PQ 斜率不存在时,OP →·OQ →+MP →·MQ →的值为-20. 综上所述OP →·OQ →+MP →·MQ →的取值范围为⎣⎢⎡⎦⎥⎤-20,-523. 探究提高 求圆锥曲线中范围、最值的主要方法:(1)几何法:若题目中的条件和结论能明显体现几何特征和意义,则考虑利用图形性质数形结合求解.(2)代数法:若题目中的条件和结论能体现一种明确的函数关系,或者不等关系,或者已知参数与新参数之间的等量关系等,则利用代数法求参数的范围.【训练2】 (2018·合肥质检)设直线l 与抛物线x 2=2y 交于A ,B 两点,与椭圆x 24+y 23=1交于C ,D 两点,直线OA ,OB ,OC ,OD (O 为坐标原点)的斜率分别为k 1,k 2,k 3,k 4.若OA ⊥OB .(1)是否存在实数t ,满足k 1+k 2=t (k 3+k 4),并说明理由; (2)求△OCD 面积的最大值. 解 设直线l 的方程为y =kx +b ,A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),D (x 4,y 4).联立⎩⎪⎨⎪⎧y =kx +b ,x 2=2y ,得x 2-2kx -2b =0,则x 1+x 2=2k ,x 1x 2=-2b ,Δ1=4k 2+8b >0. 因为OA ⊥OB ,所以x 1x 2+y 1y 2=0,得b =2.联立⎩⎪⎨⎪⎧y =kx +2,3x 2+4y 2=12得(3+4k 2)x 2+16kx +4=0, 所以x 3+x 4=-16k 3+4k 2,x 3x 4=43+4k2,由Δ2=192k 2-48>0得k 2>14.(1)存在实数t .因为k 1+k 2=y 1x 1+y 2x 2=k ,k 3+k 4=y 3x 3+y 4x 4=-6k , 所以k 1+k 2k 3+k 4=-16,即t =-16. (2)根据弦长公式|CD |=1+k 2|x 3-x 4|得 |CD |=43·1+k 2·4k 2-13+4k2,根据点O 到直线CD 的距离公式得d =21+k2,所以S △OCD =12|CD |·d =43·4k 2-13+4k 2,设4k 2-1=m >0,则S △OCD =43m m 2+4≤3,所以当m =2,即k =±52时,S △OCD 有最大值 3. 热点三 圆锥曲线中的探索性问题圆锥曲线的探索性问题主要体现在以下几个方面:(1)探索点是否存在;(2)探索曲线是否存在;(3)探索命题是否成立.涉及这类命题的求解主要是研究直线与圆锥曲线的位置关系问题.【例3】 (2018·沈阳调研)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,且过点P ⎝ ⎛⎭⎪⎫1,32,F 为其右焦点. (1)求椭圆C 的方程;(2)设过点A (4,0)的直线l 与椭圆相交于M ,N 两点(点M 在A ,N 两点之间),是否存在直线l 使△AMF 与△MFN 的面积相等?若存在,试求直线l 的方程;若不存在,请说明理由.解 (1)因为c a =12,所以a =2c ,b =3c ,设椭圆方程x 24c 2+y 23c2=1,又点P ⎝ ⎛⎭⎪⎫1,32在椭圆上,所以14c 2+34c 2=1, 解得c 2=1,a 2=4,b 2=3, 所以椭圆方程为x 24+y 23=1.(2)易知直线l 的斜率存在,设l 的方程为y =k (x -4),由⎩⎪⎨⎪⎧y =k (x -4),x 24+y 23=1,消去y 得(3+4k 2)x 2-32k 2x +64k 2-12=0,由题意知Δ=(32k 2)2-4(3+4k 2)(64k 2-12)>0, 解得-12<k <12.设M (x 1,y 1),N (x 2,y 2), 则x 1+x 2=32k23+4k 2,①x 1x 2=64k 2-123+4k2.②因为△AMF 与△MFN 的面积相等, 所以|AM |=|MN |,所以2x 1=x 2+4.③ 由①③消去x 2得x 1=4+16k23+4k2.④将x 2=2x 1-4代入②,得x 1(2x 1-4)=64k 2-123+4k 2.⑤将④代入到⑤式,整理化简得36k 2=5. ∴k =±56,经检验满足题设 故直线l 的方程为y =56(x -4)或y =-56(x -4). 探究提高 1.此类问题一般分为探究条件、探究结论两种.若探究条件,则可先假设条件成立,再验证结论是否成立,成立则存在,不成立则不存在;若探究结论,则应先求出结论的表达式,再针对其表达式进行讨论,往往涉及对参数的讨论.2.求解步骤:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于待定系数的方程组,若方程组有实数解,则元素(点、直线、曲线或参数)存在,否则,元素(点、直线、曲线或参数)不存在. 【训练3】 (2018·衡水联考)在平面直角坐标系xOy 中,过点C (2,0)的直线与抛物线y 2=4x 相交于A ,B 两点,设A (x 1,y 1),B (x 2,y 2).(1)(一题多解)求证:y 1y 2为定值;(2)是否存在平行于y 轴的定直线被以AC 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长;如果不存在,说明理由.(1)证明 法一 当直线AB 垂直于x 轴时,y 1=22,y 2=-2 2.因此y 1y 2=-8(定值). 当直线AB 不垂直于x 轴时, 设直线AB 的方程为y =k (x -2),由⎩⎪⎨⎪⎧y =k (x -2),y 2=4x ,得ky 2-4y -8k =0. ∴y 1y 2=-8.因此有y 1y 2=-8为定值.法二 设直线AB 的方程为my =x -2,由⎩⎪⎨⎪⎧my =x -2,y 2=4x ,得y 2-4my -8=0. ∴y 1y 2=-8.因此有y 1y 2=-8为定值.(2)解 设存在直线l :x =a 满足条件, 则AC 的中点E ⎝⎛⎭⎪⎫x 1+22,y 12,|AC |=(x 1-2)2+y 21. 因此以AC 为直径的圆的半径r =12|AC |=12(x 1-2)2+y 21=12x 21+4, 又点E 到直线x =a 的距离d =⎪⎪⎪⎪⎪⎪x 1+22-a故所截弦长为2r 2-d 2=214(x 21+4)-⎝⎛⎭⎪⎫x 1+22-a 2 =x 21+4-(x 1+2-2a )2=-4(1-a )x 1+8a -4a 2.当1-a =0,即a =1时,弦长为定值2,这时直线方程为x =1.1.在直角坐标系xOy 中,曲线C :y =x 24与直线l :y =kx +a (a >0)交于M ,N 两点,(1)当k =0时,分别求C 在点M 和N 处的切线方程;(2)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM =∠OPN ?说明理由. 解 (1)由题设可得M (2a ,a ),N (-2a ,a ), 或M (-2a ,a ),N (2a ,a ).又y ′=x 2,故y =x 24在x =2a 处的导数值为a ,C 在点(2a ,a )处的切线方程为y -a =a (x -2a ),即ax -y -a =0.y =x 24在x =-2a 处的导数值为-a ,C 在点(-2a ,a )处的切线方程为y -a =-a (x +2a ),即ax +y +a =0.故所求切线方程为ax -y -a =0和ax +y +a =0. (2)存在符合题意的点,证明如下:设P (0,b )为符合题意的点,M (x 1,y 1),N (x 2,y 2),直线PM ,PN 的斜率分别为k 1,k 2. 将y =kx +a 代入C 的方程得x 2-4kx -4a =0. 故x 1+x 2=4k ,x 1x 2=-4a . 从而k 1+k 2=y 1-b x 1+y 2-bx 2 =2kx 1x 2+(a -b )(x 1+x 2)x 1x 2=k (a +b )a. 当b =-a 时,有k 1+k 2=0,则直线PM 的倾斜角与直线PN 的倾斜角互补, 故∠OPM =∠OPN ,所以点P (0,-a )符合题意.2.(2018·东北三省四校联考)已知点A (0,-2),椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,F 是椭圆E 的右焦点,直线AF 的斜率为233,O 为坐标原点.(1)求E 的方程;(2)设过点A 的动直线l 与E 相交于P ,Q 两点,当△OPQ 的面积最大时,求l 的方程. 解 (1)设F (c ,0),由条件知,2c =233,得c = 3.又ca =32,所以a =2,b 2=a 2-c 2=1. 故E 的方程为x 24+y 2=1.(2)当l ⊥x 轴时不合题意,故设l :y =kx -2,P (x 1,y 1),Q (x 2,y 2). 将y =kx -2代入x 24+y 2=1,得(1+4k 2)x 2-16kx +12=0. 当Δ=16(4k 2-3)>0,即k 2>34时,x 1,2=8k ±24k 2-34k 2+1. 从而|PQ |=k 2+1|x 1-x 2|=4k 2+1·4k 2-34k 2+1. 又点O 到直线PQ 的距离d =2k 2+1.所以△OPQ 的面积S △OPQ =12d ·|PQ |=44k 2-34k 2+1. 设4k 2-3=t ,则t >0,S △OPQ =4t t 2+4=4t +4t. 因为t +4t ≥4,当且仅当t =2,即k =±72时等号成立,且满足Δ>0.所以当△OPQ 的面积最大时,l 的方程为y =72x -2或y =-72x -2. 3.(2018·新乡模拟)已知抛物线C :x 2=2py (p >0)的焦点为F ,直线2x -y +2=0交抛物线C 于A ,B 两点,P 是线段AB 的中点,过P 作x 轴的垂线交抛物线C 于点Q .(1)D 是抛物线C 上的动点,点E (-1,3),若直线AB 过焦点F ,求|DF |+|DE |的最小值; (2)是否存在实数p ,使|2QA →+QB →|=|2QA →-QB →|?若存在,求出p 的值;若不存在,说明理由. 解 (1)∵直线2x -y +2=0与y 轴的交点为(0,2), ∴F (0,2),则抛物线C 的方程为x 2=8y ,准线l :y =-2. 设过D 作DG ⊥l 于G ,则|DF |+|DE |=|DG |+|DE |, 当E ,D ,G 三点共线时,|DF |+|DE |取最小值2+3=5. (2)假设存在,抛物线x 2=2py 与直线y =2x +2联立方程组得:x 2-4px -4p =0,设A (x 1,y 1),B (x 2,y 2),Δ=(4p )2+16p =16(p 2+p )>0,则x 1+x 2=4p ,x 1x 2=-4p , ∴Q (2p ,2p ).∵|2QA →+QB →|=|2QA →-QB →|. 则QA →·QB →=0,得(x 1-2p )(x 2-2p )+(y 1-2p )(y 2-2p ) =(x 1-2p )(x 2-2p )+(2x 1+2-2p )(2x 2+2-2p ) =5x 1x 2+(4-6p )(x 1+x 2)+8p 2-8p +4=0,代入得4p 2+3p -1=0,解得p =14或p =-1(舍去). 因此存在实数p =14,且满足Δ>0,使得|2QA →+QB →|=|2QA →-QB →|成立. 4.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,四个顶点构成的菱形的面积是4,圆M :(x +1)2+y 2=r 2(0<r <1).过椭圆C 的上顶点A 作圆M 的两条切线分别与椭圆C 相交于B ,D 两点(不同于点A ),直线AB ,AD 的斜率分别为k 1,k 2.(1)求椭圆C 的方程;(2)当r 变化时,①求k 1·k 2的值;②试问直线BD 是否过某个定点?若是,求出该定点;若不是,请说明理由.解 (1)由题设知,ca =32,12×2a ×2b =4,又a 2-b 2=c 2,解得a =2,b =1. 故所求椭圆C 的方程是x 24+y 2=1. (2)AB :y =k 1x +1,则有|k 1-1|1+k 21=r ,化简得(1-r 2)k 21-2k 1+1-r 2=0. 对于直线AD :y =k 2x +1,同理有(1-r 2)k 22-2k 2+1-r 2=0,于是k 1,k 2是方程(1-r 2)k 2-2k +1-r 2=0的两实根,故k 1·k 2=1.考虑到r →1时,D 是椭圆的下顶点,B 趋近于椭圆的上顶点,故BD 若过定点,则猜想定点在y 轴上. 由⎩⎪⎨⎪⎧y =k 1x +1,x 24+y 2=1,得(4k 21+1)x 2+8k 1x =0, 于是有B ⎝ ⎛⎭⎪⎫-8k 14k 21+1,-4k 21+14k 21+1, D ⎝ ⎛⎭⎪⎫-8k 24k 22+1,-4k 22+14k 22+1. 直线BD 的斜率为k BD =k 1+k 2-3,直线BD 的方程为y --4k 21+14k 21+1=k 1+k 2-3⎝ ⎛⎭⎪⎫x --8k 14k 21+1, 令x =0,得y =-4k 21+14k 21+1+k 1+k 2-3·8k 14k 21+1=20k 21+5-3(4k 21+1)=-53. 故直线BD 过定点⎝ ⎛⎭⎪⎫0,-53. 5.(2018·临沂质检)已知圆x 2+y 2=1过椭圆x 2a 2+y 2b 2=1(a >b >0)的两焦点,与椭圆有且仅有两个公共点,直线l :y =kx +m 与圆x 2+y 2=1相切,与椭圆x 2a 2+y 2b 2=1相交于A ,B 两点.记λ=OA →·OB →,且23≤λ≤34.(1)求椭圆的方程;(2)求k 的取值范围;(3)求△OAB 的面积S 的取值范围.解 (1)由题意知2c =2,所以c =1.因为圆与椭圆有且只有两个公共点,从而b =1,故a =2,所以所求椭圆方程为x 22+y 2=1. (2)因为直线l :y =kx +m 与圆x 2+y 2=1相切,所以原点O 到直线l 的距离为|m |12+k 2=1,即m 2=k 2+1.由⎩⎪⎨⎪⎧y =kx +m ,x 22+y 2=1, 得(1+2k 2)x 2+4kmx +2m 2-2=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-4km 1+2k 2,x 1x 2=2m 2-21+2k 2. λ=OA →·OB →=x 1x 2+y 1y 2=(1+k 2)x 1x 2+km (x 1+x 2)+m 2=k 2+11+2k 2,由23≤λ≤34,得12≤k 2≤1, 即k 的取值范围是⎣⎢⎡⎦⎥⎤-1,-22∪⎣⎢⎡⎦⎥⎤22,1. (3)|AB |2=(x 1-x 2)2+(y 1-y 2)2=(1+k 2)[(x 1+x 2)2-4x 1x 2]=2-2(2k 2+1)2, 由12≤k 2≤1,得62≤|AB |≤43. 设△OAB 的AB 边上的高为d ,则S =12|AB |d =12|AB |, 所以64≤S ≤23. 即△OAB 的面积S 的取值范围是⎣⎢⎡⎦⎥⎤64,23. 6.(2018·大连双基测试)已知椭圆E :x 2a 2+y 2b2=1(a >b >0)的左焦点F 1与抛物线y 2= -4x 的焦点重合,椭圆E 的离心率为22,过点M (m ,0)作斜率存在且不为0的直线l ,交椭圆E 于A ,C 两点,点P ⎝ ⎛⎭⎪⎫54,0,且PA →·PC →为定值. (1)求椭圆E 的方程;(2)求m 的值.解 (1)设F 1(-c ,0),由抛物线y 2=-4x 的焦点坐标(-1,0),且椭圆E 的左焦点F 1与抛物线y 2=-4x 的焦点重合,所以c =1.又椭圆E 的离心率为e =22,得a =2, 于是有b 2=a 2-c 2=1,故椭圆E 的方程为x 22+y 2=1. (2)设直线l 方程为y =k (x -m ),A (x 1,y 1),C (x 2,y 2), 由⎩⎪⎨⎪⎧x 22+y 2=1,y =k (x -m )消y 整理得(1+2k 2)x 2-4mk 2x +2k 2m 2-2=0,x 1+x 2=4mk 21+2k 2,x 1·x 2=2m 2k 2-21+2k2. PA →·PC →=⎝ ⎛⎭⎪⎫x 1-54⎝ ⎛⎭⎪⎫x 2-54+y 1y 2 =⎝ ⎛⎭⎪⎫x 1-54⎝ ⎛⎭⎪⎫x 2-54+k 2(x 1-m )(x 2-m )=(1+k 2)x 1x 2-⎝ ⎛⎭⎪⎫54+mk 2(x 1+x 2)+2516+k 2m 2=(3m 2-5m -2)k 2-21+2k 2+2516. 要使PA →·PC →为定值,则3m 2-5m -2=-4,即3m 2-5m +2=0,解得m =1或23,此时点M (m ,0)在椭圆E 内部,故m 的值为1或23.。
(新课标)高考数学大一轮复习第九章解析几何题组52文

- 4 - / 10
83
88
= 2 ( 5 ) 2- 4× 5=5.
x2 y2 12.(2016 ·福建福州质检 ) 已知 F1, F2 是双曲线 - =1(a>0 , b>0) 的左、右焦点,若双曲
a2 b2 b 线左支上存在一点 P 与点 F2 关于直线 y= ax 对称,则该双曲线的离心率为 ________.
题组层级快练 ( 五十二 )
1.若过抛物线 y= 2x2 的焦点的直线与抛物线交于 A(x 1, y 1) , B(x 2, y2) ,则 x1x2= (
)
A.- 2
1 B.- 2
C.- 4
1 D.- 16
答案 D
解析
由
y=2x 2,得
x2=
1 y.
其焦点坐标为
1 F(0, ) ,取直线
1 y= ,则其与
那么 m的值等于 (
)
3
5
A. 2
B. 2
C. 2
D. 3
答案 解析
A 因为点 A(x 1, y 1) , B(x 2, y 2) 在抛物线 y = 2x2 上,所以 y1= 2x12, y2= 2x22,两式相减,
得 y 1- y2= 2(x 1- x2)(x 1+ x2) ,不妨设 x1<x 2. 因为直线 AB 与直线 y = x + m 互相垂直,所以
e= 5. x2 y2
13.(2016 ·上海静安一模 ) 已知椭圆 C: 2 + 4 = 1,过椭圆 C 上一点 P(1, 2) 作倾斜角互 补的两条直线 PA, PB,分别交椭圆 C于 A, B两点.则直线 AB的斜率为 ________. 答案 2
解析 设 A(x 1 ,y1) , B(x 2, y2 ) ,同时设 PA的方程为 y - 2= k(x - 1) ,代入椭圆方程化简得 (k 2+ 2)x 2-2k(k - 2)x + k2-2 2k- 2= 0,显然 1 和 x1 是这个方程的两解.因此
【精编】高考数学新增分大一轮+第九章平面解析几何9.9

§9.9曲线与方程考情考向分析以考查曲线的轨迹、轨迹方程为主.题型主要以解答题的形式出现,题目为中档题,有时也会在填空题中出现.1.曲线与方程的定义一般地,在直角坐标系中,如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x,y)=0的实数解建立如下的对应关系:那么,这个方程叫做曲线的方程,这条曲线叫做方程的曲线.2.求动点的轨迹方程的基本步骤3.几种常见的求轨迹方程的方法(1)直接法由题设所给(或通过分析图形的几何性质而得出)的动点所满足的几何条件列出等式,再用坐标代替这个等式,化简得曲线的方程,这种方法叫做直接法.(2)定义法利用所学过的圆的定义、椭圆的定义、双曲线的定义、抛物线的定义直接写出所求的动点的轨迹方程,这种方法叫做定义法.这种方法要求题设中有定点与定直线及两定点距离之和或差为定值的条件,或能利用平面几何知识分析得出这些条件. (3)相关点法若动点P (x ,y )随已知曲线上的点Q (x 0,y 0)的变动而变动,且x 0,y 0可用x ,y 表示,则将点Q 的坐标表达式代入已知曲线方程,即得点P 的轨迹方程,这种方法称为相关点法(或代换法). 概念方法微思考1.f (x 0,y 0)=0是点P (x 0,y 0)在曲线f (x ,y )=0上的充要条件吗?提示 是.如果曲线C 的方程是f (x ,y )=0,则曲线C 上的点的坐标满足f (x ,y )=0,以f (x ,y )=0的解为坐标的点也都在曲线C 上,故f (x 0,y 0)=0是点P (x 0,y 0)在曲线f (x ,y )=0上的充要条件.2.曲线的交点与方程组的关系是怎样的? 提示 曲线的交点与方程组的关系(1)两条曲线交点的坐标是两个曲线方程的公共解,即两个曲线方程组成的方程组的实数解; (2)方程组有几组解,两条曲线就有几个交点;方程组无解,两条曲线就没有交点.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)方程x 2+xy =x 的曲线是一个点和一条直线.( × )(2)到两条互相垂直的直线距离相等的点的轨迹方程是x 2=y 2.( × ) (3)y =kx 与x =1ky 表示同一直线.( × )(4)动点的轨迹方程和动点的轨迹是一样的.( × ) 题组二 教材改编2.[P64T10]已知点F ⎝⎛⎭⎫14,0,直线l :x =-14,点B 是l 上的动点,若过点B 垂直于y 轴的直线与线段BF 的垂直平分线交于点M ,则点M 的轨迹方程是________. 答案 y 2=x解析 由已知MF =MB ,根据抛物线的定义知,点M 的轨迹是以点F 为焦点,直线l 为准线的抛物线.3.[P64T9]设圆C 与圆x 2+(y -3)2=1外切,与直线y =0相切,则C 的圆心的轨迹方程为________. 答案 x 2=8y -84.[P64T8]设P 为曲线x 24-y 2=1上一动点,O 为坐标原点,M 为线段OP 的中点,则点M 的轨迹方程是________.答案 x 2-4y 2=1解析 设P (x 0,y 0),M (x ,y ),则x 0=2x ,y 0=2y ,代入x 204-y 20=1, 得x 2-4y 2=1. 题组三 易错自纠5.方程(2x +3y -1)(x -3-1)=0表示的曲线是________. 答案 一条直线和一条射线解析 原方程可化为⎩⎪⎨⎪⎧2x +3y -1=0,x -3≥0或x -3-1=0,即2x +3y -1=0(x ≥3)或x =4,故原方程表示的曲线是一条射线和一条直线.6.到定点(0,7)和到定直线y =-7的距离相等的点的轨迹方程是________. 答案 x 2=28y7.已知M (-2,0),N (2,0),则以MN 为斜边的直角三角形的直角顶点P 的轨迹方程是__________.答案 x 2+y 2=4(x ≠±2)解析 连结OP ,则OP =2,∴P 点的轨迹是去掉M ,N 两点的圆,∴方程为x 2+y 2=4(x ≠±2).题型一 定义法求轨迹方程例1 已知圆M :(x +1)2+y 2=1,圆N :(x -1)2+y 2=9,动圆P 与圆M 外切并且与圆N 内切,圆心P 的轨迹为曲线C ,求C 的方程.解 由已知得圆M 的圆心为M (-1,0),半径r 1=1;圆N 的圆心为N (1,0),半径r 2=3.设圆P 的圆心为P (x ,y ),半径为R .因为圆P 与圆M 外切并且与圆N 内切,所以PM +PN =(R +r 1)+(r 2-R )=r 1+r 2=4>2=MN .由椭圆的定义可知,曲线C 是以M ,N 为左、右焦点,长半轴长为2,短半轴长为3的椭圆(左顶点除外),其方程为x 24+y 23=1(x ≠-2).思维升华 定义法求轨迹方程(1)在利用圆锥曲线的定义求轨迹方程时,若所求的轨迹符合某种圆锥曲线的定义,则根据曲线的方程,写出所求的轨迹方程.(2)利用定义法求轨迹方程时,还要看轨迹是不是完整的曲线,如果不是完整的曲线,则应对其中的变量x 或y 进行限制.跟踪训练1 在△ABC 中,BC =4,△ABC 的内切圆切BC 于D 点,且BD -CD =22,则顶点A 的轨迹方程为______________. 答案 x 22-y 22=1(x >2)解析 以BC 的中点为原点,中垂线为y 轴建立如图所示的坐标系,E ,F 分别为两个切点. 则BE =BD ,CD =CF ,AE =AF .所以AB -AC =22<4,所以点A 的轨迹为以B ,C 为焦点的双曲线的右支(y ≠0),且a =2,c =2,所以b =2, 所以轨迹方程为x 22-y 22=1(x >2).题型二 直接法求轨迹方程例2 已知抛物线C :y 2=2x 的焦点为F ,平行于x 轴的两条直线l 1,l 2分别交C 于A ,B 两点,交C 的准线于P ,Q 两点.(1)若F 在线段AB 上,R 是PQ 的中点,证明:AR ∥FQ ;(2)若△PQF 的面积是△ABF 的面积的两倍,求AB 中点的轨迹方程. (1)证明 由题意知,F ⎝⎛⎭⎫12,0,设l 1:y =a ,l 2:y =b , 则ab ≠0,且A ⎝⎛⎭⎫a 22,a ,B ⎝⎛⎭⎫b 22,b ,P ⎝⎛⎭⎫-12,a ,Q ⎝⎛⎭⎫-12,b ,R ⎝⎛⎭⎫-12,a +b 2. 记过A ,B 两点的直线为l ,则l 的方程为2x -(a +b )y +ab =0. 由于F 在线段AB 上,故1+ab =0. 记AR 的斜率为k 1,FQ 的斜率为k 2, 则k 1=a -b 1+a 2=a -b a 2-ab =1a =-aba =-b =b -0-12-12=k 2.所以AR ∥FQ .(2)解 设过AB 的直线为l , 设l 与x 轴的交点为D (x 1,0), 则S △ABF =12|b -a |·FD =12|b -a |⎪⎪⎪⎪x 1-12,S △PQF =|a -b |2. 由题意可得|b -a |⎪⎪⎪⎪x 1-12=|a -b |2, 所以x 1=1或x 1=0(舍去).设满足条件的AB 的中点为E (x ,y ). 当AB 与x 轴不垂直时,由k AB =k DE 可得2a +b =yx -1(x ≠1).而a +b2=y ,所以y 2=x -1(x ≠1). 当AB 与x 轴垂直时,E 与D 重合, 此时E 点坐标为(1,0),满足方程y 2=x -1. 所以所求轨迹方程为y 2=x -1.思维升华 直接法求曲线方程时最关键的就是把几何条件或等量关系翻译为代数方程,要注意翻译的等价性.通常将步骤简记为建系设点、列式、代换、化简、证明这五个步骤,但最后的证明可以省略,如果给出了直角坐标系则可省去建系这一步,求出曲线的方程后还需注意检验方程的纯粹性和完备性.跟踪训练2 在平面直角坐标系xOy 中,点P (a ,b )为动点,F 1,F 2分别为椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,已知△F 1PF 2为等腰三角形. (1)求椭圆的离心率e ;(2)设直线PF 2与椭圆相交于A ,B 两点,M 是直线PF 2上的点,满足AM →·BM →=-2,求点M 的轨迹方程.解 (1)设F 1(-c,0),F 2(c,0)(c >0). 由题意,可得PF 2=F 1F 2, 即(a -c )2+b 2=2c , 整理得2⎝⎛⎭⎫c a 2+c a -1=0,得c a =-1(舍去)或c a =12,所以e =12. (2)由(1)知a =2c ,b =3c ,可得椭圆方程为3x 2+4y 2=12c 2,直线PF 2的方程为y =3(x -c ).A ,B 两点的坐标满足方程组⎩⎨⎧3x 2+4y 2=12c 2,y =3(x -c ),消去y 并整理,得5x 2-8cx =0. 解得x 1=0,x 2=85c ,代入直线方程得⎩⎨⎧x 1=0,y 1=-3c ,⎩⎨⎧x 2=85c ,y 2=335c .不妨设A ⎝⎛⎭⎫85c ,335c ,B (0,-3c ).设点M 的坐标为(x ,y ),则AM →=⎝⎛⎭⎫x -85c ,y -335c ,BM →=(x ,y +3c ).由y =3(x -c ),得c =x -33y . 于是AM →=⎝⎛⎭⎫8315y -35x ,85y -335x ,BM →=(x ,3x ),由AM →·BM →=-2, 即⎝⎛⎭⎫8315y -35x ·x +⎝⎛⎭⎫85y -335x ·3x =-2. 化简得18x 2-163xy -15=0. 将y =18x 2-15163x 代入c =x -33y ,得c =10x 2+516x>0.所以x >0.因此,点M 的轨迹方程是18x 2-163xy -15=0(x >0). 题型三 相关点法求轨迹方程例3 如图所示,抛物线E :y 2=2px (p >0)与圆O :x 2+y 2=8相交于A ,B 两点,且点A 的横坐标为2.过劣弧AB 上动点P (x 0,y 0)作圆O 的切线交抛物线E 于C ,D 两点,分别以C ,D 为切点作抛物线E 的切线l 1,l 2,l 1与l 2相交于点M .(1)求p 的值;(2)求动点M 的轨迹方程.解 (1)由点A 的横坐标为2,可得点A 的坐标为(2,2), 代入y 2=2px ,解得p =1. (2)由(1)知抛物线E :y 2=2x .设C ⎝⎛⎭⎫y 212,y 1,D ⎝⎛⎭⎫y 222,y 2,y 1≠0,y 2≠0,切线l 1的斜率为k ,则切线l 1:y -y 1=k ⎝⎛⎭⎫x -y 212,代入y 2=2x ,得ky 2-2y +2y 1-ky 21=0,由Δ=0,解得k =1y 1, ∴l 1的方程为y =1y 1x +y 12,同理l 2的方程为y =1y 2x +y 22.联立⎩⎨⎧y =1y 1x +y 12,y =1y 2x +y22,解得⎩⎨⎧x =y 1·y 22,y =y 1+y22.易知CD 的方程为x 0x +y 0y =8,其中x 0,y 0满足x 20+y 20=8,x 0∈[2,22], 由⎩⎪⎨⎪⎧y 2=2x ,x 0x +y 0y =8,得x 0y 2+2y 0y -16=0, ∴y 1,2=-2y 0±4y 20+64x 02x 0,则⎩⎨⎧y 1+y 2=-2y 0x 0,y 1·y 2=-16x,代入⎩⎨⎧x =y 1·y 22,y =y 1+y22,可得M (x ,y )满足⎩⎨⎧x =-8x 0,y =-y0x 0,可得⎩⎨⎧x 0=-8x ,y 0=8yx ,代入x 20+y 20=8,并化简,得x 28-y 2=1,考虑到x 0∈[2,22],知x ∈[-4,-22],∴动点M 的轨迹方程为x 28-y 2=1,x ∈[-4,-22].思维升华 “相关点法”的基本步骤(1)设点:设被动点坐标为(x ,y ),主动点坐标为(x 1,y 1); (2)求关系式:求出两个动点坐标之间的关系式⎩⎪⎨⎪⎧x 1=f (x ,y ),y 1=g (x ,y );(3)代换:将上述关系式代入已知曲线方程,便可得到所求动点的轨迹方程.跟踪训练3 如图,动圆C 1:x 2+y 2=t 2,1<t <3与椭圆C 2:x 29+y 2=1相交于A ,B ,C ,D 四点.点A 1,A 2分别为C 2的左、右顶点,求直线AA 1与直线A 2B 交点M 的轨迹方程.解 由椭圆C 2:x 29+y 2=1,知A 1(-3,0),A 2(3,0).设点A 的坐标为(x 0,y 0),由曲线的对称性, 得B (x 0,-y 0), 设点M 的坐标为(x ,y ),直线AA 1的方程为y =y 0x 0+3(x +3).① 直线A 2B 的方程为y =-y 0x 0-3(x -3).② 由①②相乘得y 2=-y 20x 20-9(x 2-9).③ 又点A (x 0,y 0)在椭圆C 2上,故y 20=1-x 209.④将④代入③得x 29-y 2=1(x <-3,y <0).因此点M 的轨迹方程为x 29-y 2=1(x <-3,y <0).题型四 参数法求轨迹方程例4 (2018·苏州调研)在平面直角坐标系xOy 中,已知两点M (1,-3),N (5,1),若点C 的坐标满足OC →=tOM →+(1-t )ON →(t ∈R ),且点C 的轨迹与抛物线y 2=4x 相交于A ,B 两点. (1)求证:OA ⊥OB ;(2)在x 轴上是否存在一点P (m,0)(m ≠0),使得过点P 任意作一条抛物线y 2=4x 的弦,并以该弦为直径的圆都经过原点?若存在,求出m 的值及圆心的轨迹方程;若不存在,请说明理由. (1)证明 由OC →=tOM →+(1-t )ON →(t ∈R ), 可知点C 的轨迹是直线MN ,∴点C 的轨迹方程为y +31+3=x -15-1,即y =x -4,联立⎩⎪⎨⎪⎧y =x -4,y 2=4x ,得x 2-12x +16=0,设A (x 1,y 1),B (x 2,y 2),则x 1,2=6±25, ∴x 1+x 2=12,x 1x 2=16,∴OA →·OB →=x 1x 2+y 1y 2 =x 1x 2+(x 1-4)(x 2-4) =2x 1x 2-4(x 1+x 2)+16 =2×16-4×12+16=0, ∴OA ⊥OB .(2)解 假设存在这样的点P ,由已知弦所在直线斜率不为0,故设弦所在直线为x =ky +m ,代入y 2=4x ,得y 2-4ky -4m =0, 设弦端点D (x 3,y 3),E (x 4,y 4), 则y 3,4=4k ±16k 2+16m 2=2k ±2k 2+m ,∴y 3+y 4=4k ,y 3y 4=-4m , 由已知OD →⊥OE →,∴x 3x 4+y 3y 4=0,∴y 234×y 244+y 3y 4=m 2-4m =0, 解得m =0(舍去)或m =4, ∴存在点P (4,0)满足条件, 设弦DE 的中点为M (x ,y ), 则x =x 3+x 42,①=ky 3+4+ky 4+42=k (y 3+y 4)+82=2k 2+4, y =y 3+y 42=2k ,②由①②消去k 得y 2=2x -8, 这就是所求圆心的轨迹方程.思维升华 利用参数法求轨迹方程:一是选择合适的参数(可以是单参数,也可以是双参数);二是建立参数方程后消掉参数,消参数的方法有代入消参法、加减消参法、平方消参法等. 跟踪训练4 设椭圆中心为原点O ,一个焦点为F (0,1),长轴和短轴的长度之比为t . (1)求椭圆的方程;(2)设经过原点且斜率为t 的直线与椭圆在y 轴右侧部分的交点为Q ,点P 在该直线上,且OPOQ =t t 2-1,当t 变化时,求点P 的轨迹方程,并说明轨迹是什么图形. 解 (1)设所求椭圆方程为y 2a 2+x 2b2=1(a >b >0).由题意得⎩⎪⎨⎪⎧a 2-b 2=1,a b =t ,解得⎩⎨⎧a 2=t 2t 2-1,b 2=1t 2-1.所以椭圆方程为t 2(t 2-1)x 2+(t 2-1)y 2=t 2. (2)设点P (x ,y ),Q (x 1,y 1),解方程组⎩⎪⎨⎪⎧t 2(t 2-1)x 21+(t 2-1)y 21=t 2,y 1=tx 1,得⎩⎪⎨⎪⎧x 1=12(t 2-1),y 1=t2(t 2-1).由OP OQ =t t 2-1和OP OQ =|x ||x 1|, 得⎩⎨⎧x =t2,y =t22,或⎩⎨⎧x =-t2,y =-t22,其中t >1.消去t ,得点P 的轨迹方程为x 2=22y ⎝⎛⎭⎫x >22和x 2=-22y ⎝⎛⎭⎫x <-22. 其轨迹为抛物线x 2=22y 在直线x =22右侧的部分和抛物线x 2=-22y 在直线x =-22左侧的部分.1.设点A 为圆(x -1)2+y 2=1上的动点,P A 是圆的切线,且P A =1,则点P 的轨迹方程是________________. 答案 (x -1)2+y 2=2 解析 如图,设P (x ,y ),圆心为M (1,0),连结MA ,PM , 则MA ⊥P A ,且MA =1,又∵P A =1,∴PM =MA 2+P A 2=2, 即PM 2=2,∴(x -1)2+y 2=2.2.已知点O (0,0),A (1,2),动点P 满足|OP →+AP →|=2,则P 点的轨迹方程是________________. 答案 4x 2+4y 2-4x -8y +1=0解析 设P 点的坐标为(x ,y ),则OP →=(x ,y ),AP →=(x -1,y -2),OP →+AP →=(2x -1,2y -2).所以(2x -1)2+(2y -2)2=4,整理得4x 2+4y 2-4x -8y +1=0.3.在平面直角坐标系中,已知两点A (3,1),B (-1,3),若点C 满足OC →=λ1OA →+λ2OB →(O 为原点),其中λ1,λ2∈R ,且λ1+λ2=1,则点C 的轨迹方程是________. 答案 x +2y -5=0解析 设C (x ,y ),则OC →=(x ,y ),OA →=(3,1),OB →=(-1,3),∵OC →=λ1OA →+λ2OB →,∴⎩⎪⎨⎪⎧x =3λ1-λ2,y =λ1+3λ2,又λ1+λ2=1,∴化简得x +2y -5=0.4.设过点P (x ,y )的直线分别与x 轴的正半轴和y 轴的正半轴交于A ,B 两点,点Q 与点P 关于y 轴对称,O 为坐标原点.若BP →=2P A →,且OQ →·AB →=1,则点P 的轨迹方程是________________. 答案 32x 2+3y 2=1(x >0,y >0)解析 设A (a,0),B (0,b ),a >0,b >0.由BP →=2P A →,得(x ,y -b )=2(a -x ,-y ),所以⎩⎪⎨⎪⎧x =2(a -x ),y -b =-2y ,即a =32x >0,b =3y >0.由题意得,点Q (-x ,y ),故由OQ →·AB →=1,得(-x ,y )·(-a ,b )=1,即ax +by =1.将a ,b 代入ax +by =1得所求的轨迹方程为32x 2+3y 2=1(x >0,y >0).5.已知A (0,7),B (0,-7),C (12,2),以C 为一个焦点作过A ,B 的椭圆,则椭圆的另一个焦点F 的轨迹方程是______________. 答案 y 2-x 248=1(y ≤-1)解析 由两点间距离公式,可得AC =13,BC =15,AB =14,因为A ,B 都在椭圆上,所以AF +AC =BF +BC ,AF -BF =BC -AC =2<14,故F 的轨迹是以A ,B 为焦点的双曲线的下支.由c =7,a =1⇒b 2=48,F 的轨迹方程是y 2-x 248=1(y ≤-1).6.已知两定点A (-2,0),B (1,0),如果动点P 满足P A =2PB ,则点P 的轨迹所包围的图形的面积为________. 答案 4π解析 设P (x ,y ),由P A =2PB , 得(x +2)2+y 2=2(x -1)2+y 2, ∴3x 2+3y 2-12x =0,即x 2+y 2-4x =0. ∴P 的轨迹为以(2,0)为圆心,2为半径的圆. 即轨迹所包围的图形的面积等于4π.7.直线x a +y2-a =1与x ,y 轴交点连线的中点的轨迹方程是______________.答案 x +y =1(x ≠0且x ≠1)解析 直线x a +y2-a =1与x ,y 轴的交点为A (a,0),B (0,2-a ),设AB 的中点为M (x ,y ),则x =a 2,y =1-a2,消去a ,得x +y =1.因为a ≠0且a ≠2,所以x ≠0且x ≠1.8.已知圆的方程为x 2+y 2=4,若抛物线过点A (-1,0),B (1,0)且以圆的切线为准线,则抛物线的焦点的轨迹方程是______________. 答案 x 24+y 23=1(y ≠0)解析 设抛物线焦点为F ,过A ,B ,O 作准线的垂线AA 1,BB 1,OO 1,垂足分别为A 1,B 1,O 1,则AA 1+BB 1=2OO 1=4,由抛物线定义得AA 1+BB 1=F A +FB ,所以F A +FB =4>2,故F 点的轨迹是以A ,B 为焦点,长轴长为4的椭圆(去掉长轴两端点),其方程为x 24+y 23=1(y ≠0).9.如图,斜线段AB 与平面α所成的角为60°,B 为斜足,平面α上的动点P 满足∠P AB =30°,则点P 的轨迹是________.答案 椭圆解析 可构造如图所示的圆锥.母线与中轴线夹角为30°,然后用平面α去截,使直线AB 与平面α的夹角为60°,则截口为P 的轨迹图形,由圆锥曲线的定义可知,P 的轨迹为椭圆.10.如图,P 是椭圆x 2a 2+y 2b 2=1(a >b >0)上的任意一点,F 1,F 2是它的两个焦点,O 为坐标原点,且OQ →=PF 1→+PF 2→,则动点Q 的轨迹方程是____________.答案 x 24a 2+y 24b2=1解析 由于OQ →=PF 1—→+PF 2—→, 又PF 1—→+PF 2—→=PM →=2PO →=-2OP →, 设Q (x ,y ),则OP →=-12OQ →=⎝⎛⎭⎫-x 2,-y 2, 即P 点坐标为⎝⎛⎭⎫-x 2,-y2,又P 在椭圆上, 则有⎝⎛⎭⎫-x 22a 2+⎝⎛⎭⎫-y 22b 2=1,即x 24a 2+y 24b2=1.11.如图,抛物线关于y 轴对称,它的顶点在坐标原点,点P (2,1),A (x 1,y 1),B (x 2,y 2)均在抛物线上.(1)求抛物线的方程;(2)若∠APB 的平分线垂直于y 轴,求证:直线AB 的斜率为定值. (1)解 由已知可设抛物线的方程为x 2=2py (p >0). 因为点P (2,1)在抛物线上,所以22=2p ×1,解得p =2. 故抛物线的方程为x 2=4y .(2)证明 由题意知k AP +k BP =0,所以y 1-1x 1-2+y 2-1x 2-2=0.所以x 214-1x 1-2+x 224-1x 2-2=0,所以x 1+24+x 2+24=0,所以x 1+x 2=-4.所以k AB =y 1-y 2x 1-x 2=x 214-x 224x 1-x 2=x 1+x 24=-1.所以直线AB 的斜率为定值.12.如图,P 是圆x 2+y 2=4上的动点,点P 在x 轴上的射影是点D ,点M 满足DM →=12DP →.(1)求动点M 的轨迹C 的方程,并说明轨迹是什么图形;(2)过点N (3,0)的直线l 与动点M 的轨迹C 交于不同的两点A ,B ,求以OA ,OB 为邻边的平行四边形OAEB 的顶点E 的轨迹方程. 解 (1)设M (x ,y ),则D (x,0), 由DM →=12DP →知,P (x,2y ),∵点P 在圆x 2+y 2=4上,∴x 2+4y 2=4,故动点M 的轨迹C 的方程为x 24+y 2=1,轨迹C 为椭圆.(2)设E (x ,y ),由题意知l 的斜率存在, 设l :y =k (x -3),代入x 24+y 2=1,得(1+4k 2)x 2-24k 2x +36k 2-4=0,(*) 设A (x 1,y 1),B (x 2,y 2),则x 1,2=24k 2±(-24k 2)2-4(1+4k 2)(36k 2-4)2(1+4k 2),∴x 1+x 2=24k 21+4k 2,∴y 1+y 2=k (x 1-3)+k (x 2-3) =k (x 1+x 2)-6k =24k 31+4k 2-6k =-6k 1+4k 2. ∵四边形OAEB 为平行四边形,∴OE →=OA →+OB →=(x 1+x 2,y 1+y 2)=⎝ ⎛⎭⎪⎫24k 21+4k 2,-6k 1+4k 2, 又OE →=(x ,y ),∴⎩⎪⎨⎪⎧x =24k 21+4k 2,y =-6k 1+4k 2,消去k ,得x 2+4y 2-6x =0,由(*)中Δ=(-24k 2)2-4(1+4k 2)(36k 2-4)>0, 得k 2<15,∴0<x <83.∴顶点E 的轨迹方程为x 2+4y 2-6x =0⎝⎛⎭⎫0<x <83.13.若曲线C 上存在点M ,使M 到平面内两点A (-5,0),B (5,0)距离之差的绝对值为8,则称曲线C 为“好曲线”.以下曲线不是“好曲线”的是________. ①x +y =5; ②x 2+y 2=9; ③x 225+y 29=1; ④x 2=16y .答案 ②解析 ∵M 到平面内两点A (-5,0),B (5,0)距离之差的绝对值为8,∴M 的轨迹是以A (-5,0),B (5,0)为焦点的双曲线,方程为x 216-y 29=1.①中,直线x +y =5过点(5,0),故直线与M 的轨迹有交点,满足题意;②中,x 2+y 2=9的圆心为(0,0),半径为3,与M 的轨迹没有交点,不满足题意; ③中,x 225+y 29=1的右顶点为(5,0),故椭圆x 225+y 29=1与M 的轨迹有交点,满足题意;④中,方程代入x 216-y 29=1,可得y -y 29=1,即y 2-9y +9=0,∴Δ>0,满足题意.14.设点P (x ,y )是曲线a |x |+b |y |=1(a >0,b >0)上的动点,且满足x 2+y 2+2y +1+x 2+y 2-2y +1≤22,则a +2b 的取值范围为________. 答案 [2,+∞)解析 设F 1(0,-1),F 2(0,1),则满足x 2+(y +1)2+x 2+(y -1)2=22的点P 的轨迹是以F 1(0,-1),F 2(0,1)为焦点的椭圆,其方程为x 21+y 22=1.曲线a |x |+b |y |=1(a >0,b >0)为如图所示的菱形ABCD ,C ⎝⎛⎭⎫1a ,0,D ⎝⎛⎭⎫0,1b . 由于x 2+(y +1)2+x 2+(y -1)2≤22, 所以菱形ABCD 在椭圆上或其内部, 所以1a ≤1,1b ≤2,即a ≥1,b ≥22.所以a +2b ≥1+2×22=2.15.已知过点A (-3,0)的直线与x =3相交于点C ,过点B (3,0)的直线与x =-3相交于点D ,若直线CD 与圆x 2+y 2=9相切,则直线AC 与BD 的交点M 的轨迹方程为______________. 答案 x 29+y 294=1(y ≠0)解析 设点M (x ,y ),C (3,m ),D (-3,n ),则直线CD 的方程为(m -n )x -6y +3(m +n )=0,因为直线CD 与圆x 2+y 2=9相切,所以3|m +n |(m -n )2+36=3,所以mn =9,又直线AC 与BD的交点为M ,所以⎩⎪⎨⎪⎧y x +3=y -m x -3,yx -3=y -n x +3,解得⎩⎪⎨⎪⎧m =6y x +3,n =-6yx -3,所以-36y 2x 2-9=9,所以点M 的轨迹方程为x 29+y 294=1(y ≠0).16.曲线C 是平面内与两个定点F 1(-2,0)和F 2(2,0)的距离的积等于常数a 2(a 2>4)的点的轨迹.给出下列三个结论: ①曲线C 过坐标原点; ②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则△F 1PF 2的面积不大于12a 2.其中,所有正确结论的序号是________.答案 ②③解析 因为原点O 到两个定点F 1(-2,0),F 2(2,0)的距离的积是4,又a 2>4,所以曲线C 不过原点,即①错误; 设动点P 在曲线C 上,因为F 1(-2,0),F 2(2,0)关于原点对称,所以PF 1·PF 2=a 2对应的轨迹关于原点对称,即②正确; 因为12F PF S=12PF 1·PF 2sin ∠F 1PF 2≤12PF 1·PF 2=12a 2, 即△F 1PF 2的面积不大于12a 2,即③正确.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 分 得分点①
3 分 得分点② 5 分 得分点③ 6 分 得分点④
(2)由题意知 F(-1,0), 设 Q(-3,t),P(m,n), 则O→Q=(-3,t), P→F=(-1-m,-n), O→Q·P→F=3+3m-tn, O→P=(m,n), P→Q=(-3-m,t-n),
Байду номын сангаас
12 分 得分点⑩
■评分细则 ①设出点的坐标,并求出N→P和N→M得 1 分; ②由N→P= 2N→M,正确求出 x0=x,y0= 22y 得 2 分; ③代入法求出x22+y22=1 得 2 分; ④化简成 x2+y2=2 得 1 分; ⑤求出O→Q和P→F的坐标得 1 分;
⑥正确求出O→Q·P→F的值得 1 分; ⑦正确求出O→P和P→Q的坐标得 1 分; ⑧正确得出-3m-m2+tn-n2=1 得 1 分; ⑨得出O→Q⊥P→F得 1 分; ⑩写出结论得 1 分. ■核心素养 圆锥曲线中的定点、定值问题是高考命题的热点问题,常与向 量巧妙交汇,综合考查考生“数学运算”的核心素养.
过点P且垂直于OQ的直线l过C的左焦点F.❷
解题思路 ❶看到求点 P 的轨迹方程,想到先设出点的坐标,然后利用已 知条件,采用代入法求轨迹方程. ❷看到过点 P 且垂直于 OQ 的直线 l 过 C 的左焦点 F,想到证 明O→Q⊥P→F.
■标准答案(规范答题 分步得分) (1)设 P(x,y),M(x0,y0), 则 N(x0,0), N→P=(x-x0,y),N→M=(0,y0), 由N→P= 2 N→M,
第九章 平面解析几何
规范答题示范(五) 高考解答题——解析几何
第九章 平面解析几何
真题展示
(12 分)(2017·高考全国卷Ⅱ)设 O 为坐标原点,动点 M 在椭圆 C:
x22+y2=1 上,过点 M 作 x 轴的垂线,垂足为 N,点 P 满足N→P
=
→ 2NM.
(1)求点P的轨迹方程; ❶
(2)设点 Q 在直线 x=-3 上,且O→P·P→Q=1,证明:
■解题引领 (1)写全得分步骤:对于解题过程中是得分点的步骤,有则给分, 无则没分,所以对于得分点步骤一定要写全,如第(2)问中求出 -3m-m2+tn-n2=1 就得分. (2)写明得分关键:对于解题过程中的关键点,有则给分,无则 没分,所以在答题时一定要写清得分关键点,如第(2)问一定要 写出O→Q·P→F=0,即O→Q⊥P→F,否则不得分,因此步骤才是关 键的,只有结果不得分.
7 分 得分点⑤ 8 分 得分点⑥
9 分 得分点⑦
由O→P·P→Q=1 得
-3m-m2+tn-n2=1,
10 分 得分点⑧
又由(1)知 m2+n2=2,
故 3+3m-tn=0.
所以O→Q·P→F=0,
即O→Q⊥P→F,
11 分 得分点⑨
又过点 P 存在唯一直线垂直于 OQ,
所以过点 P 且垂直于 OQ 的直线 l 过 C 的左焦点 F.
