最新铁一中小升初数学

合集下载

2023年小升初六年级重点中学某铁一中入学数学真卷

2023年小升初六年级重点中学某铁一中入学数学真卷2023年小升初六年级重点中学某铁一中入学数学真卷一、选择题（每题2分，共40分）1. 下列四个数中，最小的数是____。

A. 0.125B. 0.25C. 0.5D. 0.6252. 两个数的差是8，它们的和是____。

A. 9B. 8C. 4D. 163. 一只铅笔和一本书共重100g，已知这只铅笔重20g，那本书的重量是____。

A. 100gB. 20gC. 80gD. 120g4. 一个数加上30的结果是40，这个数是____。

A. 10B. 20C. 40D. 605. 某数加上72等于121，这个数是____。

A. 49B. 72C. 121D. 1936. 南京市有一架客机，载客总数是140人。

南京站上车的人数是这个数的2/7，这些人数是____。

A. 20B. 35C. 50D. 1007. 三盒铅笔共有75支，第一盒的数目是第二盒的2倍，第三盒的数目是第二盒的3倍。

第一盒铅笔的数目是____。

A. 10B. 15C. 20D. 258. 将单位数换成它的100倍所得的数是____。

A. 十分之一B. 十倍C. 百倍D. 千倍9. 8的2倍是____。

A. 2B. 4C. 8D. 1610. 将100改为1后的数是____。

A. 0.1B. 1C. 10D. 1000二、填空题（每题2分，共20分）11. 5米=____厘米。

12. 1天有____小时。

13. 0.025是百分数，写作____%。

14. 9:15写作___点___分。

15. 1分15秒写作___秒。

16. 人民币的基本单位是____。

17. 119用罗马数字表示为____。

18. 4的2倍是____。

19. 2023减去500等于____。

20. 中国的首都是____。

三、解答题（共40分）21. 用黄铜表示长度，求两个黄铜条的长度和。

第一个黄铜条的长是24cm，第二个黄铜条的长是36cm。

陕西省西安市铁一中学2024--2025学年下学期丘成桐少年班选拔初试数学试题

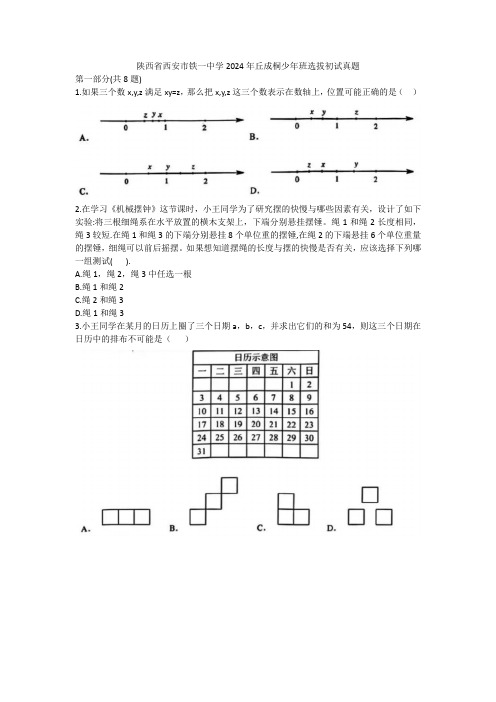
陕西省西安市铁一中学2024年丘成桐少年班选拔初试真题第一部分(共8题)1.如果三个数x,y,z满足xy=z，那么把x,y,z这三个数表示在数轴上，位置可能正确的是（）2.在学习《机械摆钟》这节课时，小王同学为了研究摆的快慢与哪些因素有关，设计了如下实验:将三根细绳系在水平放置的横木支架上，下端分别悬挂摆锤。

绳1和绳2长度相同，绳3较短.在绳1和绳3的下端分别悬挂8个单位重的摆锤,在绳2的下端悬挂6个单位重量的摆锤，细绳可以前后摇摆。

如果想知道摆绳的长度与摆的快慢是否有关，应该选择下列哪一组测试( ).A.绳1，绳2，绳3中任选一根B.绳1和绳2C.绳2和绳3D.绳1和绳33.小王同学在某月的日历上圈了三个日期a，b，c，并求出它们的和为54，则这三个日期在日历中的排布不可能是（）4.如图，在9x9的正方形方格纸中，线段a;b，c，d的端点均在格点上若平移其中两条线段，恰好能使得它们和第三条线段首尾相接组成三角形，则这样组成的不同位置的三角形有( )A.6个B.8个C.12个D.24个5.如图，如图，在一个通道内，有一个长为a米的梯子，底端固定在地面上的C处，当梯子斜靠在左墙上，梯子的顶端距地面的垂直高度为b，∠ACM=75°;当梯子斜靠在右墙上，梯子的顶端距地面的垂直高度为C，∠BCN=45°，则这条通道的宽度是( )米.6.甲、乙、丙、丁四人种菜，甲种了80 棵活了74 棵乙种了100 棵活了95 棵，丙种了120棵活了108棵，丁种了150棵活了138棵，这四人中( )种菜的成活率最高。

A.甲B.乙C.丙D.丁第二部分(共7题)1.如图所示，将一个长方形从上往下等分成三层，第最上层两等分，中间层三等分，最底层四等分，则阴影部分占总面积的________%(精确到十分位)2.如图，将一个圆柱体形状的金属材料，沿着底面直径竖直切成两个工件(损耗不计)，切成的两个工件的表面积之和比原圆柱体的表面积增大了200平方厘米.为了生产需要，给工件的侧面(侧面指不包括上下半圆形底面的其它表面)镀上一层膜，已知镀膜的费用是每平方厘米0.5元，则给这两个工件镀膜的费用是_________元(π取3.14 ).4.已知数A是由0，1，2，3，4，5中的数字组成的整数(每个数字最多只能用一次)，若要使得数A既是8的倍数又要尽可能的大，则此时数被7除的余数是___________。

2023年陕西西安铁一中小升初数学真题卷附参考答案

2023年陕西西安铁一中小升初数学真题B 卷(20221207)一、填空题1.定义一种新运算“*”，其意义是a*b=2a −b ，如果x *(3*2)=4，则x =________.2.如图①，有一张长方形纸片ABCD ，如图②，将它折叠，使AD 边落在AB 边上，折痕为AE ，如图③，再将∠A 折叠，使点A 与点B 重合，折痕为MN.如果图①中的AD=7cm ，图③中的MD=2cm ，那么DB=________cm.3.某校六年级举行语文和数学竞赛，参加竞赛的人数占全年级总人数的20％，参加语文竞赛的人数占竞赛总人数的25，参加数学竞赛的人数占竞赛总人数的56，两项竞赛都参加的有21人，该校六年级共有________名学生.4.如图，现有3×3的方格，每个小方格内均有2～10之间不同的数字，要求方格内每一行、每一列以及每一条对角线上的三个数字之和均相等，图中给出了部分数字，则P 处对应的数字是______.5.某班元旦晚会需要购买甲、乙、丙三种装饰品，若购买甲3件，乙5件，丙1件，共需68元，若购甲4件，乙7件，丙1件共需80元.现在该班需购买甲、乙、丙各一件，共需______元.6.要将50千克浓度为18％的盐水稀释为浓度为15％的盐水，需加入________克的水.7.如果分别从两个体积之和为160cm 3的正方体木块中挖去最大的圆锥做成两个如图所示的工件模具，那么这两个模具的体积之和为________cm 3.(π取3)第4题图4 78P第2题图A图①图②图③B CDCEB(A)8.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为9，宽为7的长方形盒子底部(如图②)，盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分周长和是________.9.如图，△ABC 的面积为18cm 2，BP 平分∠ABC ，AP⊥BP ，则△PBC 的面积为________cm 2.10.某同学求出2021个整数的平均数后，粗心地把这个平均数和原来的2021个数混在一起，成为2022个数，而忘掉哪个是平均数了.如果这2022个数的平均数恰为2022，则原来的2021个数的平均数是________.11.探索实践：如图，用“十字形”分割正方形.分割一次，可以分成4个正方形；分割二次，可以分成7个正方形……用这样的“十字形”连续分割3次，可以分成10个正方形；连续分割45次，可以分成________个正方形.12.甲、乙两人分别在A 、B 两地同时相向而行，于E 处相遇后，甲继续向B 地行走，乙则休息了21分钟，再继续向A 地行走，甲和乙到达B 地和A 地后立即折返，仍在E 处相遇.已知甲每分钟行走60米，乙每分行走80米，则A 和B 两地相距_______米. 13.已知一个半圆工件，未搬动前如上图所示，直径平行于地面放置，搬动时为了保护圆弧部分不受损伤，先将半圆工件作如图所示的无滑动翻转，使它的直径贴地面，再第11题图第13题图l第8题图图①图②第9题图ACBP第7题图将它沿地面向右平移16米.已知半圆工件的直径为4米，则圆心O所经过的路线的长为_______米.(π取3.14)14.A、B、C、D和小红5位同学比赛下象棋，每两人都比赛一盘，到现在为止，A赛了4场，B赛了3场，小红赛了2场，D赛了1场，则C已经比赛了_______场.15.袋子中有5个红球，6个白球，8个黑球，如果要从中摸出一个球，摸到黑球的概为23，则应往袋中再放_______个黑球.二、计算题16.31.8×7.9−12.5×2110+44.3×2.1 17.(114−38)÷(225+214×13)18.113×(57−23)+223×13−113×5719.解方程2(2x−1)3=32x−(x−1)20、解方程x−20.2+x−10.3=10三、解答题21.甲、乙两车从A城出发前往B城，在整个行程中，汽车离开A城的距离y与时刻t 的对应关系如图所示，请问乙出发后，何时甲、乙相距45千米？22.由一个大正方体、四个中正方体、四个小正方体拼成如右图的立体图形，已知大、中、小三个正方体的棱长分别为6厘米、2厘米、1厘米.求这个立体图形的表面积.23.如图，在△ABC 中，AD=12AB ，BE=13BC ，CF=14AC ，如果△ABC 的面积是18，求△DEF的面积.24.甲、乙两人共同接受一批零件的加工任务，两人合作11天可以完成，结果两人合作7天后，乙另有任务，剩下的由甲单独做.如果甲仍按原来的工效，还需7天完成.为了能如期完成任务，甲单独做时采用了新技术，使工效提高了80％，这样不仅如期完成任务，还多做8个零件，问原计划一共要加工多少个零件？25.王师傅生产一批零件，初次检验，不合格产品数与合格产品数之比是1︰19，后来再次检验时，从合格产品中又发现了4个不合格产品，这时产品的合格率是93％，这批零件中不合格产品有多少个？A CFEBD2023年陕西西安铁一中小升初数学真题B 卷(20221207)一、填空题1.定义一种新运算“*”，其意义是a*b=2a −b ，如果x *(3*2)=4，则x =________. 1.解：【定义新运算】x *(3*2)=x *(2×3−2)=x *4=2×x −4=4，解得x =4.2.如图①，有一张长方形纸片ABCD ，如图②，将它折叠，使AD 边落在AB 边上，折痕为AE ，如图③，再将∠A 折叠，使点A 与点B 重合，折痕为MN.如果图①中的AD=7cm ，图③中的MD=2cm ，那么DB=________cm.2.解：【图形折叠】设DB=x cm ，则AB=AD+DB=(7+x )cm ，2BM=AB=(7+x )cm ，即2×(MD+DB)=(7+x )cm ，∴2×(2+ x )=(7+x )，解得x =3cm.3.某校六年级举行语文和数学竞赛，参加竞赛的人数占全年级总人数的20％，参加语文竞赛的人数占竞赛总人数的25，参加数学竞赛的人数占竞赛总人数的56，两项竞赛都参加的有21人，该校六年级共有________名学生.3.解：【容斥原理】设该校六年级共有人数n 人，参加竞赛的人数为0.2n=15n ，参加语文竞赛的人数为15n ×25=225n ，参加数学竞赛的人数为15n ×56=16n ，则有225n+16n −21=15n ，解得n=450名.4.如图，现有3×3的方格，每个小方格内均有2～10之间不同的数字，要求方格内每一行、每一列以及每一条对角线上的三个数字之和均相等，图中给出了部分数字，则P 处对应的数字是______.第4题图4 78P第2题图A图①图②图③B CDCEB(A)4.解：【九宫格】设P 上面的数字为n ，则7下面的数字为n+4，4左侧的数字为11，P 下方的数字为n −3，故有8+7+n=8+n+4+n-3，解得n=6，所以P=11+4+6−(n −3)=12.5.某班元旦晚会需要购买甲、乙、丙三种装饰品，若购买甲3件，乙5件，丙1件，共需68元，若购甲4件，乙7件，丙1件共需80元.现在该班需购买甲、乙、丙各一件，共需______元.5.解：【不定方程】设甲、乙、丙三种装饰品的单价分别为a 、b 、c(元/件)，则有3a+5b+c=68…①，4a+7b+c=80…②，②−①得a+2b=12…③，③×3得3a+6b=36…④，①−④得c −b=32…⑤，③+⑤得a+b+c=44元.6.要将50千克浓度为18％的盐水稀释为浓度为15％的盐水，需加入________克的水. 6.解：【浓度问题】设加入x 克水，则有50×18%=(50+x )×15%，解得x =10克.7.如果分别从两个体积之和为160cm 3的正方体木块中挖去最大的圆锥做成两个如图所示的工件模具，那么这两个模具的体积之和为________cm 3.(π取3)7.解：【圆锥体积】设大正方体的棱长为ncm ，其体积为n 3cm 3，大圆锥的体积为13×π×(n 2)2×n=14n 3cm 3，剩余部分占原大正方体体积的34，同理，小模具的体积也占原小正方体体积的34，故这两个模具的体积之和为160×34=120cm 3.8.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为9，宽为7的长方形盒子底部(如图②)，盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分周长和是________.8.解：【等量代换】设小长方形的长宽分别a 、b ，则阴影部分周长=[a ×2+(7−2b) ×2]+[2b ×2+(7−a)×2]=2a+14−4b+4b+14−2a=28.D 第8题图图①图②第9题图ACBP第7题图9.如图，△ABC 的面积为18cm 2，BP 平分∠ABC ，AP⊥BP ，则△PBC 的面积为________cm 2.9.解：【三线合一与底高模型】延长AP 交BC 于D ，∵BP 平分∠ABC，AP⊥BP，∴AP=DP ，则S △ABP =S △DBP ，S △ACP =S △DCP ，∴S △PBC =S △DBP +S △DCP =12S △ABD +12S △ACD =12S △ABC =9cm 2.10.某同学求出2021个整数的平均数后，粗心地把这个平均数和原来的2021个数混在一起，成为2022个数，而忘掉哪个是平均数了.如果这2022个数的平均数恰为2022，则原来的2021个数的平均数是________.10.解：【平均数问题】设原2021个数的平均数是x ，则有(2021x +x )÷2022=2022，即2022x ÷2022=2022，解得x =2022.11.探索实践：如图，用“十字形”分割正方形.分割一次，可以分成4个正方形；分割二次，可以分成7个正方形……用这样的“十字形”连续分割3次，可以分成10个正方形；连续分割45次，可以分成________个正方形.11.解：【找规律】观察发现，每分割一次，在原来基础上增加3个正方形，即分割0次，有1+3×0=1个；分割1次，有1+3×1=4个；分割2次，有1+3×2=7个；分割n 次，有1+3×n=1个；故连续分割45次，可以分成1+3×45=136个正方形.12.甲、乙两人分别在A 、B 两地同时相向而行，于E 处相遇后，甲继续向B 地行走，乙则休息了21分钟，再继续向A 地行走，甲和乙到达B 地和A 地后立即折返，仍在E 处相遇.已知甲每分钟行走60米，乙每分行走80米，则A 和B 两地相距_______米. 12.解：【行程问题】设A 和B 两地相距x 米，则AE ︰BE=60︰80=3︰4，∴AE=37x ，BE=47x ，∴(47x −60×21+47x )︰( 37x +37x )=3︰4，解得x =2205米.13.已知一个半圆工件，未搬动前如上图所示，直径平行于地面放置，搬动时为了保护圆弧部分不受损伤，先将半圆工件作如图所示的无滑动翻转，使它的直径贴地面，再第11题图第13题图l将它沿地面向右平移16米.已知半圆工件的直径为4米，则圆心O 所经过的路线的长为_______米.(π取3.14)13.解：【动点轨迹及圆弧长】从翻转开始，当直径由平行地面翻转至垂直地面，圆心0的运动轨迹为直径，长为14圆周长，当直径由垂直地面至贴地面，圆心0的运动轨迹为14圆弧，长为14圆周长，故圆心O 所经过的路线的长为14π×4+14π×4+16=2π+16=22.28米.14.A 、B 、C 、D 和小红5位同学比赛下象棋，每两人都比赛一盘，到现在为止，A 赛了4场，B 赛了3场，小红赛了2场，D 赛了1场，则C 已经比赛了_______场. 14.解：【逻辑推理】A 赛了4场，即A 与其他4人均赛了1场；D 赛了1场，即只与A 赛了1场；B 赛了3场，即B 与除D 外其他3人均赛了1场；小红赛了2场，即与A 和B 各赛了1场，故C 与A 赛了1场，与B 赛了1场，共2场.15.袋子中有5个红球，6个白球，8个黑球，如果要从中摸出一个球，摸到黑球的概为23，则应往袋中再放_______个黑球.15.解：【概率问题】设应往袋中再放x 个黑球，(x +8)÷(5+6+8+x )=23，解得x =14个.二、计算题16.31.8×7.9−12.5×2110+44.3×2.1 17.(114−38)÷(225+214×13)16.原式=31.8×7.9−12.5×2.1+44.3×2.1=31.8×7.9+(44.3−12.5)×2.1 =31.8×(7.9+2.1)=31.8×10=318. 17.原式=(108−38)÷(125+94×13)=78÷(125+34)= 78÷(4820+1520)= 78×2063=518.18.113×(57−23)+223×13−113×5719.解方程2(2x−1)3=32x −(x −1)18.原式=113×(57−23)+113×23−113×57=113×(57−23+23−57)= 113×0=0.19.解：4(2x −1)=9x −6x +6 8x −4=3x +6 5x =10x=2.20、解方程x−20.2+x−10.3=1020.解：3(x−2)+2(x−1)=63x−6+2x−2=65x=14x=2.8.三、解答题21.甲、乙两车从A城出发前往B城，在整个行程中，汽车离开A城的距离y与时刻t 的对应关系如图所示，请问乙出发后，何时甲、乙相距45千米？21.解：【S-T图】由图知甲的速度=300÷(10:00−5:00)=60km/h，乙的速度=300÷(9:00−6:00)=100km/h①甲在乙前方：(60−45)÷(100−60)=0.375h=22分30秒，6时+22分30秒=6时22分30秒乙追上甲的时间：60×(6:00−5:00)÷(100−60)=1.5h，即7时30分②乙在甲前方：45÷(100−60)=1.125h=1小时7分30秒，7时30分+1小时7分30秒=8时37分30秒答：乙出发后，6时22分30秒或8时37分30秒时甲、乙相距45千米.22.由一个大正方体、四个中正方体、四个小正方体拼成如右图的立体图形，已知大、中、小三个正方体的棱长分别为6厘米、2厘米、1厘米.求这个立体图形的表面积.22.解：【正方体的表面积】中正方体与大正方体重叠的表面积=2×2×4=16平方厘米小正方体与中正方体重叠的表面积=1×1×4=4平方厘米立体图形的表面积=(6×6+2×2×4+1×1×4)×6−16×2−4×2=336−40=296(平方厘米) 答：这个立体图形的表面积为296平方厘米.或：6×6×6+2×2×4×4+1×1×4×4=296(平方厘米)23.如图，在△ABC 中，AD=12AB ，BE=13BC ，CF=14AC ，如果△ABC 的面积是18，求△DEF的面积.23.解：【底高模型求组合图形面积】连接CD 、BF ∵AD=12AB ，∴S △ACD =S △BCD =12S △ABC =9∵BE=13BC ，∴S △DBE =13S △BCD =3∵CF=14AC ，∴S △ADF =34S △ACD =274，S △BCF =14S △ABC =92，S △CEF =23S △BCF =3故S △DEF =S △ABC −S △DBE −S △ADF −S △CEF =18−3−274−3=214答：△DEF 的面积为214.A CFEBD24.甲、乙两人共同接受一批零件的加工任务，两人合作11天可以完成，结果两人合作7天后，乙另有任务，剩下的由甲单独做.如果甲仍按原来的工效，还需7天完成.为了能如期完成任务，甲单独做时采用了新技术，使工效提高了80％，这样不仅如期完成任务，还多做8个零件，问原计划一共要加工多少个零件？24.解：【工程问题】11−7=4，7−(11−7)=3，故甲工作3天相当于乙工作4天设甲工效为13a ，则乙工效为14a，采用新技术后甲的工效为13a×(1+80%)=35a多完成的工作量：(13a +14a)×7+35a×(11−7) −(13a+14a)×11=115a1 15a =8，解得a=1120，故甲每天做13a=40个，乙每天做14a=30个原计划一共要加工零件：(40+30)×11=770(个)答：原计划一共要加工770个零件.25.王师傅生产一批零件，初次检验，不合格产品数与合格产品数之比是1︰19，后来再次检验时，从合格产品中又发现了4个不合格产品，这时产品的合格率是93％，这批零件中不合格产品有多少个？25.解：【比例与百分数】设这批零件中初次检验有不合格产品有x个，则初次检验有合格产品19x个，依题意有：19x−4=(x+19x)×93%解得x=10故这批零件中不合格产品有10+4=14个答：这批零件中不合格产品有14个.。

2023年西安某铁一中小升初(XK)数学练习题A附详细答案

2023年西安某铁一中小升初(XK)数学练习题A2023.11.02一、填空题1.某班男生与女生的比是5︰4，男生人数比女生人数多________%。

2.某班50人参加考试，其中优秀20人，良好15人，及格11人，不及格4人，如果用扇形统计图把这个班的考试结果表示出来，那么优秀人数的扇形圆心角是________度。

3.观察下列三视图，要摆成如图的情况，最少需要________块正方体。

4.从4点开始，经过________分钟，时针与分针第一次重合。

5.如图，长方形EFGH 的长HE 和宽EF 分别是6cm 和4cm ，四边形ABCD 的面积为2.6平方厘米，那么阴影部分的面积和为________平方厘米。

6.小强前几次考试的数学平均成绩为84分，这次考试要考100分，平均分才能达到88分，则这次是第________次考试。

7.商店运来一批围巾，每条成本价是72元，原来按每条25%的利润标价出售，每天可以售出100条，后来按定价的9折出售，每天的销售量提高至以前的2.5倍。

现在的利润比之前增加了________元。

8.一个圆锥和一个圆柱，底面周长之比为2︰3，体积之比为1︰3，圆锥和圆柱的高之比为________。

9.一个学生用计算题器算题，在最后一步本应该除以10，他却错误的乘10了，因此第4题图从左面看从上面看第5题图A EFGHDBC得出的错误答案是500，正确答案应该是________。

10.定义新运算a*b=a ×b+b ，则(2*3)*1的值是________。

11.字母A 、B 、C 、D 按规律排列：AABBCDAABBCDAABBCD …，第2023个字母是________。

12.两数相除，商4余8，被除数、除数、商、余数四个数的和等于320，则被除数是________。

13.绿化队原计划在120米长的一段路上每隔5米栽一棵树(路的两端也要栽树)，并已经挖好树坑，后改为每隔3米栽一棵树，则重新挖坑时可以少挖________个树坑。

西安铁一中分校小学数学小升初第一次模拟试题带答案(完整版)

西安铁一中分校小学数学小升初第一次模拟试题一.(共8题，共16分)1.数b在数轴上的位置如图所示，则-b是（）。

A.正数B.零C.负数D.非负数2.以下的说法中错误的有（）个。

（1）分针的转速是时针转速的60倍。

（2）用0、1、2、3这四个数字能组成18个不同的四位数。

（3）一个三条边的长度都是整厘米的三角形，其中两条边长度是3厘米和5厘米，那么第三条边的长度有5种可能。

（4）-2℃与10℃相差12℃。

A.4B.3C.2D.13.解比例，并验算。

6.4∶0.8＝x∶1.5，x＝（）A.8B.12C.4.5D.1 04.下面说法中，正确的是（）。

A.读503020时，一个零都不读B.一个不为0的整数，它的倍数一定比它的因数大C.扇形统计图可以清楚地反映各部分数量与总量的关系D.一个圆锥，底面直径和高同时扩大2倍，体积就扩大4倍5.有一种商品，甲店进价比乙店进价便宜10%，甲店按20%的利润定价，乙店按15%的利润定价，甲店的定价比乙店的定价便宜11.2元．则甲店的进价是（）。

A.160元B.124元C.150元D.144元6.一个圆柱形物体，底面周长是12.56厘米，高10厘米．它的表面积是（）。

A.125.6cm2B.150.72cm2C.25.12cm2D.32.21cm27.一条裙子原价430元，现价打九折出售，比原价便宜（）元。

A.430×90%B.430×（1＋90%）C.430×（1－9%）D.430×（1－90%）8.武汉市某日的气温为-2℃～5℃，这一天武汉市的温差是（）。

A.3℃B.-3℃C.7℃D.-7℃二.(共8题，共16分)1.大米的总量一定，吃掉的和剩下的成反比例。

（）2.今年的产量比去年增加了15%,今年的产量就相当于去年的115%。

（）3.如果x与y互为倒数,且x:5=a:y ,那么10a=2。

（）4.圆锥的侧面展开后是一个等腰三角形。