二次函数与线段定值
二次函数——定值问题

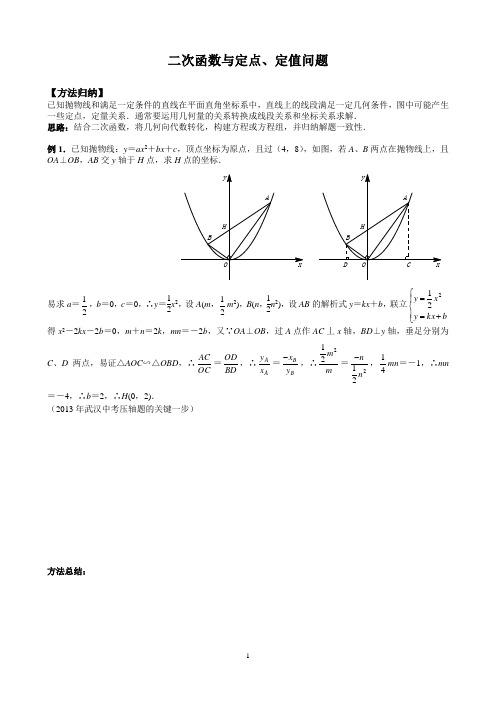
专题九:二次函数之定值问题坐标为定值例题 1 :抛物线y=x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y 轴交于点C.(1)如图1,若OB=2OA=2OC①求抛物线的解析式;②若M 是第一象限抛物线上一点,若cos∠MAC=,求M 点坐标.(2)如图2,直线 E F∥x轴与抛物线相交于E、F两点,P为 E F下方抛物线上一点,且P(m,﹣2).若∠EPF=90°,则 E F所在直线的纵坐标是否为定值,请说明理由.练习1 .如图1,抛物线y=(x﹣m)2的顶点A在x轴正半轴上,交y轴于 B 点,S△OAB=1.1)求抛物线的解析式;(2)如图2,P 是第一象限内抛物线上对称轴右侧一点,过P 的直线L与抛物线有且只有一个公共点,L交抛物线对称轴于C点,连PB交对称轴于 D 点,若∠ BAO=∠ PCD,求证:AC=2AD;(3)如图3,以 A 为顶点作直角,直角边分别与抛物线交于M、N 两点,当直角∠ MAN绕A点旋转时,求证:MN 始终经过一个定点,并求出该定点的坐标.线段之和为定值例题 1 :如图,抛物线 y = x 2 + bx + c 交 x 轴于 A 、 B 两点,其中点 A 坐在抛物线上且满足 ∠PAB= 2∠ACO.求点 P 的 坐标;3)如图②,点 Q 为 x 轴下方抛物线上任意一点,点 D 是抛物线对称轴与 x 轴的交点,直线 AQ 、BQ 分别交抛物线的对称轴于点 M 、N .请问 DM+ DN 是否为定值?如果是,请求出这个定值;如果不是,请说明理由 .2)如图①,连接 AC ,点 P 1)求抛物线的函数表达式;C(0,-3) .练习 1 :抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,且位于x 轴下方.(1)若P(1,﹣3)、B(4,0),①求该抛物线的解析式;②若 D 是抛物线上一点,满足∠ DPO=∠POB,求点D的坐标;(2)如图,在(1)中的抛物线解析式不变的条件下,已知直线PA、PB与y 轴分别交于E、F两点,点P运动时,OE+OF是否为定值?若是,试求出该定值;若不是,请说明理由.面积为定值例题 1 :如图,已知抛物线交x轴于A.B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点 D 为抛物线的顶点.(1)求抛物线的解析式;(2)P 为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P 点坐标;(3)若抛物线上有且仅有三个点M 1、M2、M 3使得△ M1BC、△M2BC、△M3BC 的面积均为定值S,求出定值S及M1、M2、M3 这三个点的坐标.练习 1 . 已知关于x 的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x 轴交于不同的两点A、B,点A的坐标是(1,0)(1)求 c 的值;(2)求 a 的取值范围;(3)该二次函数的图象与直线y=1交于C、D 两点,设A、B、C、D四点构成的四边形的对角线相交于点P,记△ PCD的面积为S1,△ PAB的面积为S2,当0<a<1 时,求证:S1- S2 为常数,并求出该常数。
二次函数-定值问题典型例题

二次函数-定值问题【例1】如图,直线y=kx+b(b>0)与抛物线相交于点A(x1,y1),B(x2,y2)两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且kS+32=0.(1)求b的值;(2)求证:点(y1,y2)在反比例函数的图象上;(3)求证:x1•OB+y2•OA=0.考点:二次函数综合题专题:压轴题.分析:(1)先求出直线y=kx+b与x轴正半轴交点D的坐标及与y轴交点C的坐标,得到△OCD的面积S=﹣,再根据kS+32=0,及b>0即可求出b的值;(2)先由y=kx+8,得x=,再将x=代入y=x2,整理得y2﹣(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线相交于点A(x1,y1),B(x2,y2)两点,知y1,y2是方程y2﹣(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1•y2=64,即点(y1,y2)在反比例函数的图象上;(3)先由勾股定理,得出OA2=+,OB2=+,AB2=(x1﹣x2)2+(y1﹣y2)2,由(2)得y1•y2=64,又易得x1•x2=﹣64,则OA2+OB2=AB2,根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到=,即可证明x1•OB+y2•OA=0.解答:(1)解:∵直线y=kx+b(b>0)与x轴正半轴相交于点D,与y轴相交于点C,∴令x=0,得y=b;令y=0,x=﹣,∴△OCD的面积S=(﹣)•b=﹣.∵kS+32=0,∴k(﹣)+32=0,解得b=±8,∵b>0,∴b=8;(2)证明:由(1)知,直线的解析式为y=kx+8,即x=,将x=代入y=x2,得y=()2,整理,得y2﹣(16+8k2)y+64=0.∵直线y=kx+8与抛物线相交于点A(x1,y1),B(x2,y2)两点,∴y1,y2是方程y2﹣(16+8k2)y+64=0的两个根,∴y1•y2=64,∴点(y1,y2)在反比例函数的图象上;(3)证明:由勾股定理,得OA2=+,OB2=+,AB2=(x1﹣x2)2+(y1﹣y2)2,由(2)得y1•y2=64,同理,将y=kx+8代入y=x2,得kx+8=x2,即x2﹣8kx﹣64=0,∴x1•x2=﹣64,∴AB2=+++﹣2x1•x2﹣2y1•y2=+++,又∵OA2+OB2=+++,∴OA2+OB2=AB2,∴△OAB是直角三角形,∠AOB=90°.如图,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.∵∠AOB=90°,∴∠AOE=90°﹣∠BOF=∠OBF,又∵∠AEO=∠OFB=90°,∴△AEO∽△OFB,∴=,∵OE=﹣x1,BF=y2,∴=,∴x1•OB+y2•OA=0.点评:本题是二次函数的综合题型,其中涉及到的知识点有二次函数、反比例函数图象上点的坐标特征,三角形的面积,一次函数与二次函数的交点,一元二次方程根与系数的关系,勾股定理及其逆定理,相似三角形的判定与性质,综合性较强,难度适中.求出△OCD的面积S是解第(1)问的关键;根据函数与方程的关系,得到y1,y2是方程y2﹣(16+8k2)y+64=0的两个根,进而得出y1•y2=64是解第(2)问的关键;根据函数与方程的关系,一元二次方程根与系数的关系,勾股定理及其逆定理得出∠AOB=90°,是解第(3)问的关键.【例2】如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=x2于点A、B,交抛物线C2:y=x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.【猜想与证明】填表:m 1 2 3由上表猜想:对任意m(m>0)均有= .请证明你的猜想.【探究与应用】(1)利用上面的结论,可得△AOB与△CQD面积比为;(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;【联想与拓展】如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为.考点:二次函数综合题分析:猜想与证明:把P点的纵坐标分别代入C1、C2的解析式就可以AB、CD的值,就可以求出结论,从而发现规律得出对任意m(m>0)将y=m2代入两个二次函数的解析式就可以分别表示出AB与CD的值,从而得出均有=;探究与证明:(1)由条件可以得出△AOB与△CQD高相等,就可以得出面积之比等于底之比而得出结论;(2)分两种情况讨论,当△AOB为等腰直角三角形时,可以求出m的值就可以求出△AOB的面积,从而求出△CQD的面积,就可以求出其差,当△CQD为等腰直角三角形时,可以求出m的值就可以求出△CDQ的面积,进而可以求出结论;联想与拓展:由猜想与证明可以得知A、D的坐标,可以求出F、E的纵坐标,从而可以求出AE、DF的值,由三角形的面积公式分别表示出△MAE与△MDF面积,就可以求出其比值.解答:解:猜想与证明:当m=1时,1=x2,1=x2,∴x=±2,x=±3,∴AB=4,CD=6,∴;当m=2时,4=x2,4=x2,∴x=±4,x=±6,∴AB=8,CD=12,∴;当m=3时,9=x2,9=x2,∴x=±6,x=±9,∴AB=12,CD=18,∴;∴填表为m 1 2 3对任意m(m>0)均有=.理由:将y=m2(m>0)代入y=x2,得x=±2m,∴A(﹣2m,m2),B(2m,m2),∴AB=4m.将y=m2(m>0)代入y=x2,得x=±3m,∴C(﹣3m,m2),D(3m,m2),∴CD=6m.∴,∴对任意m(m>0)均有=;探究与运用:(1)∵O、Q关于直线CD对称,∴PQ=OP.∵CD∥x轴,∴∠DPQ=∠DPO=90°.∴△AOB与△CQD的高相等.∵=,∴AB=CD.∵S△AOB=AB•PO,S△CQD=CD•PQ,∴=,(2)当△AOB为等腰直角三角形时,如图3,∴PO=PB=m2,AB=2OP∴m2=m4,∴4m2=m4,∴m1=0,m2=﹣2,m3=2.∵m>0,∴m=2,∴OP=4,AB=8,∴PD=6,CD=12.∴S△AOB==16∴S△CQD==24,∴S△CQD﹣S△AOB=24﹣16=8.当△CQD是等腰直角三角形时,如图4,∴PQ=PO=PD=m2,CD=2QP∴m2=m4,∴9m2=m4,∴m1=0,m2=﹣3,m3=3.∵m>0,∴m=3,∴OP=6,AB=12,∴PQ=9,CD=18.∴S△AOB==54∴S△CQD==81,∴S△CQD﹣S△AOB=81﹣54=27;联想与拓展由猜想与证明可以得知A(﹣2m,m2),D(3m,m2),∵AE∥y轴,DF∥y轴,∴E点的横坐标为﹣2m,F点的横坐标为3m,∴y=(﹣2m)2,y=(3m)2,∴y=m2,y=m2,∴E(﹣2m,m2),F(3m,m2),∴AE=m2﹣m2=m2,DF=m2﹣m2=m2.S△AEM=×m2•2m=m3,S△DFM=m2•3m=m3.∴=.故答案为:;;.点评:本题考出了对称轴为y轴的抛物线的性质的运用,由特殊到一般的数学思想的运用,等腰直角三角形的性质的运用,三角形的面积公式的运用,轴对称的性质的运用,在解答本题时运用两个抛物线上的点的特征不变建立方程求解是关键.【例3】已知抛物线C1的顶点为P(1,0),且过点(0,).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).[来(1)求抛物线C1的解析式的一般形式;(2)当m=2时,求h的值;(3)若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证:tan∠EDF﹣tan∠ECP=.考点:二次函数综合题.专题:代数几何综合题.分析:(1)设抛物线C2,(a≠0),然后把点(0,)代入求出a的值,再化1的顶点式形式y=a(x﹣1)为一般形式即可;(2)先根据m的值求出直线AB与x轴的距离,从而得到点B、C的纵坐标,然后利用抛物线解析式求出点C的横坐标,再根据关于y轴对称的点的横坐标互为相反数,纵坐标相同求出点A的坐标,然后根据平移的性质设出抛物线C2的解析式,再把点A的坐标代入求出h的值即可;(3)先把直线AB与x轴的距离是m2代入抛物线C1的解析式求出C的坐标,从而求出CE,再表示出点A的坐标,根据抛物线的对称性表示出ED,根据平移的性质设出抛物线C2的解析式,把点A的坐标代入求出h的值,然后表示出EF,最后根据锐角的正切值等于对边比邻边列式整理即可得证.解答:(1)解:设抛物线C1的顶点式形式y=a(x﹣1)2,(a≠0),∵抛物线过点(0,),∴a(0﹣1)2=,解得a=,∴抛物线C1的解析式为y=(x﹣1)2,一般形式为y=x2﹣x+;(2)解:当m=2时,m2=4,∵BC∥x轴,∴点B、C的纵坐标为4,∴(x﹣1)2=4,解得x1=5,x2=﹣3,∴点B(﹣3,4),C(5,4),∵点A、C关于y轴对称,∴点A的坐标为(﹣5,4),设抛物线C2的解析式为y=(x﹣1)2﹣h,则(﹣5﹣1)2﹣h=4,解得h=5;(3)证明:∵直线AB与x轴的距离是m2,∴点B、C的纵坐标为m2,∴(x﹣1)2=m2,解得x1=1+2m,x2=1﹣2m,∴点C的坐标为(1+2m,m2),又∵抛物线C1的对称轴为直线x=1,∴CE=1+2m﹣1=2m,∵点A、C关于y轴对称,∴点A的坐标为(﹣1﹣2m,m2),∴AE=ED=1﹣(﹣1﹣2m)=2+2m,设抛物线C2的解析式为y=(x﹣1)2﹣h,则(﹣1﹣2m﹣1)2﹣h=m2,解得h=2m+1,∴EF=h+m2=m2+2m+1,∴tan∠EDF﹣tan∠ECP=﹣=﹣=﹣=,∴tan∠EDF﹣tan∠ECP=.点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,二次函数图象与结合变换,关于y轴对称的点的坐标特征,抛物线上点的坐标特征,锐角的正切的定义,(3)用m表示出相应的线段是解题的关键,也是本题的难点.【例4】如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.(1)求此抛物线的解析式;(2)求证:AO=AM;(3)探究:①当k=0时,直线y=kx与x轴重合,求出此时的值;②试说明无论k取何值,的值都等于同一个常数.考点:二次函数综合题.3718684专题:代数几何综合题.分析:(1)把点C、D的坐标代入抛物线解析式求出a、c,即可得解;(2)根据抛物线解析式设出点A的坐标,然后求出AO、AM的长,即可得证;(3)①k=0时,求出AM、BN的长,然后代入+计算即可得解;②设点A(x1,x12﹣1),B(x2,x22﹣1),然后表示出+,再联立抛物线与直线解析式,消掉未知数y得到关于x的一元二次方程,利用根与系数的关系表示出x1+x2,x1•2,并求出x12+x22,x12•x22,然后代入进行计算即可得解.解答:(1)解:∵抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1),∴,解得,所以,抛物线的解析式为y=x2﹣1;(2)证明:设点A的坐标为(m,m2﹣1),则AO==m2+1,∵直线l过点E(0,﹣2)且平行于x轴,∴点M的纵坐标为﹣2,∴AM=m2﹣1﹣(﹣2)=m2+1,∴AO=AM;(3)解:①k=0时,直线y=kx与x轴重合,点A、B在x轴上,∴AM=BN=0﹣(﹣2)=2,∴+=+=1;②k取任何值时,设点A(x1,x12﹣1),B(x2,x22﹣1),则+=+==,联立,消掉y得,x2﹣4kx﹣4=0,由根与系数的关系得,x1+x2=4k,x1•x2=﹣4,所以,x12+x22=(x1+x2)2﹣2x1•x2=16k2+8,x12•x22=16,∴+===1,∴无论k取何值,+的值都等于同一个常数1.点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,勾股定理以及点到直线的距离,根与系数的关系,根据抛物线上点的坐标特征设出点A、B的坐标,然后用含有k的式子表示出+是解题的关键,也是本题的难点,计算量较大,要认真仔细.【例5】. 如图,在平面直角坐标系xOy 中,△OAB 的顶点A的坐标为(10,0),顶点B 在第一象限内,且AB=35,sin ∠OAB=55. (1)若点C 是点B 关于x 轴的对称点,求经过O 、C 、A 三点的抛物线的函数表达式;(2)在(1)中,抛物线上是否存在一点P ,使以P 、O 、C 、A 为顶点的四边形为梯形?若存在,求出点P 的坐标;若不存在,请说明理由;(3)若将点O 、点A 分别变换为点Q ( -2k ,0)、点R (5k ,0)(k>1的常数),设过Q 、R 两点,且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ,其顶点为M ,记△QNM 的面积为QMN S ∆,△QNR 的面积QNR S ∆,求QMN S ∆∶QNR S ∆的值.解:(1)如图,过点B 作BD OA ⊥于点D . 在Rt ABD △中,35AB =5sin OAB ∠=5sin 3535BD AB OAB ∴=∠==. 又由勾股定理, 得2222(35)36AD AB BD =-=-=.1064OD OA AD ∴=-=-=.点B 在第一象限内,∴点B 的坐标为(43),.y F P 3BEC D A P 2P 1O∴点B 关于x 轴对称的点C 的坐标为(43)-,. ················ 2分设经过(00)(43)(100)O C A -,,,,,三点的抛物线的函数表达式为2(0)y ax bx a =+≠.由11643810010054a ab a b b ⎧=⎪+=-⎧⎪⇒⎨⎨+=⎩⎪=-⎪⎩,.∴经过O C A ,,三点的抛物线的函数表达式为21584y x x =-. ········· 2分 (2)假设在(1)中的抛物线上存在点P ,使以P O C A ,,,为顶点的四边形为梯形. ①点(43)C -,不是抛物线21584y x =-的顶点, ∴过点C 作直线OA 的平行线与抛物线交于点1P .则直线1CP 的函数表达式为3y =-. 对于21584y x x =-,令34y x =-⇒=或6x =. 1143x y =⎧∴⎨=-⎩,;2263x y =⎧⎨=-⎩,. 而点(43)C -,,1(63)P ∴-,. 在四边形1P AOC 中,1CP OA ∥,显然1CP OA ≠.∴点1(63)P -,是符合要求的点. ······················· 1分 ②若2AP CO ∥.设直线CO 的函数表达式为1y k x =.将点(43)C -,代入,得143k =-.134k ∴=-. ∴直线CO 的函数表达式为34y x =-.于是可设直线2AP 的函数表达式为134y x b =-+. 将点(100)A ,代入,得131004b -⨯+=.1152b ∴=. ∴直线2AP 的函数表达式为31542y x =-+.由223154246001584y x x x y x x ⎧=-+⎪⎪⇒--=⎨⎪=-⎪⎩,即(10)(6)0x x -+=. 11100x y =⎧∴⎨=⎩,;22612x y =-⎧⎨=⎩,; 而点(100)A ,,2(612)P ∴-,. 过点2P 作2P E x ⊥轴于点E ,则212P E =. 在2Rt AP E △中,由勾股定理,得220AP ===.而5CO OB ==.∴在四边形2P OCA 中,2AP CO ∥,但2AP CO ≠.∴点2(612)P -,是符合要求的点.······················· 1分 ③若3OP CA ∥.设直线CA 的函数表达式为22y k x b =+.将点(100)(43)A C -,,,代入,得22222211002435k b k k b b ⎧+==⎧⎪⇒⎨⎨+=-⎩⎪=-⎩,.∴直线CA 的函数表达式为152y x =-. ∴直线3OP 的函数表达式为12y x =.由22121401584y x x x y x x ⎧=⎪⎪⇒-=⎨⎪=-⎪⎩,即(14)0x x -=. 1100x y =⎧∴⎨=⎩,;22147x y =⎧⎨=⎩,.而点(00)O ,,3(147)P ∴,. 过点3P 作3P F x ⊥轴于点F ,则37P F =. 在3Rt OP F △中,由勾股定理,得3OP ===而CA AB ==∴在四边形3P OCA 中,3OP CA ∥,但3OP CA ≠.∴点3(147)P ,是符合要求的点. ······················· 1分 综上可知,在(1)中的抛物线上存在点123(63)(612)(147)P P P --,,,,,, 使以P O C A ,,,为顶点的四边形为梯形. ·················· 1分 (3)由题知,抛物线的开口可能向上,也可能向下.①当抛物线开口向上时,则此抛物线与y 轴的负半轴交于点N . 可设抛物线的函数表达式为(2)(5)(0)y a x k x k a =+->.即22310y ax akx ak =--2234924a x k ak ⎛⎫=-- ⎪⎝⎭.如图,过点M 作MG x ⊥轴于点G .3(20)(50)02Q k R k G k ⎛⎫- ⎪⎝⎭,,,,,,22349(010)24N ak M k ak ⎛⎫-- ⎪⎝⎭,,,,3||2||7||2QO k QR k OG k ∴===,,,22749||||10||24QG k ON ak MG ak ===,,.23117103522QNR S QR ON k ak ak ∴==⨯⨯=△.QNM QNO QMG ONMG S S S S =+-△△△梯形111()222QO ON ON GM OG QG GM =++- 2222114931749210102242224k ak ak ak k k ak ⎛⎫=⨯⨯+⨯+⨯-⨯⨯ ⎪⎝⎭ 3314949212015372884ak ak ⎛⎫=++⨯-⨯= ⎪⎝⎭.3321::(35)3:204QNM QNR S S ak ak ⎛⎫∴== ⎪⎝⎭△△. ················ 2分②当抛物线开口向下时,则此抛物线与y 轴的正半轴交于点N .同理,可得:3:20QNM QNR S S =△△. ····················· 1分 综上可知,:QNM QNR S S △△的值为3:20.【例6】、 如图,在平面直角坐标系xOy 中,一次函数54y x m =+ (m 为常数)的图象与x 轴交于点A(3-,0),与y 轴交于点C .以直线x=1为对称轴的抛物线2y ax bx c =++ (a b c ,, 为常数,且a ≠0)经过A ,C 两点,并与x 轴的正半轴交于点B . (1)求m 的值及抛物线的函数表达式;(2)设E 是y 轴右侧抛物线上一点,过点E 作直线AC 的平行线交x 轴于点F .是否存在这样的点E ,使得以A ,C ,E ,F 为顶点的四边形是平行四边形?若存在,求出点E 的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)若P 是抛物线对称轴上使△ACP 的周长取得最小值的点,过点P 任意作一条与y 轴不平行的直线交抛物线于111M ()x y , ,222M ()x y ,两点,试探究2112P PM M M M ⋅ 是否为定值,并写出探究过程.考点:二次函数综合题。
2020年中考数学压轴解答题10 二次函数与线段关系及最值定值问题(学生版)

备战2020中考数学之解密压轴解答题命题规律专题10 二次函数与线段关系及最值定值问题【类型综述】图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用. 一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【方法揭秘】由勾股定理产生的函数关系,在两种类型的题目中比较常用.类型一,已知“边角边”,至少一边是动态的,求角的对边.如图1,已知点A 的坐标为(3, 4),点B 是x 轴正半轴上的一个动点,设OB =x ,AB =y ,那么我们在直角三角形ABH 中用勾股定理,就可以得到y 关于x 的函数关系式.类型二,图形的翻折.已知矩形OABC 在坐标平面内如图2所示,AB =5,点O 沿直线EF 翻折后,点O 的对应点D 落在AB 边上,设AD =x ,OE =y ,那么在直角三角形AED 中用勾股定理就可以得到y 关于x 的函数关系式.图1 图2【典例分析】【例1】如图①,矩形ABCD 中,2,5,1AB BC BP ===,090MPN ∠=,将MPN ∠绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB (或AD )于点E ,PN 交边AD (或CD )于点F .当PN 旋转至PC 处时,MPN ∠的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D ,此时ABP ∆是否与PCD ∆相似?并说明理由;(2)类比探究:如图③,在旋转过程中,PEPF的值是否为定值?若是,请求出该定值;若不是,请说明理由; (3)拓展延伸:设AE t =时,EPF ∆的面积为S ,试用含t 的代数式表示S ;①在旋转过程中,若1t =时,求对应的EPF ∆的面积; ②在旋转过程中,当EPF ∆的面积为4.2时,求对应的t 的值.【例2】如图1,在矩形ABCD 中,AB =8,AD =10,E 是CD 边上一点,连接AE ,将矩形ABCD 沿AE 折叠,顶点D 恰好落在BC 边上点F 处,延长AE 交BC 的延长线于点G . (1)求线段CE 的长;(2)如图2,M ,N 分别是线段AG ,DG 上的动点(与端点不重合),且∠DMN =∠DAM ,设AM =x ,DN =y . ①写出y 关于x 的函数解析式,并求出y 的最小值;②是否存在这样的点M ,使△DMN 是等腰三角形?若存在,请求出x 的值;若不存在,请说明理由.【例3】抛物线2(0)y ax bx c a =++≠与x 轴交于,A B 两点(点A 在点B 的左侧),与y 轴交于点(0,4)C -.已知(2,0)A -,抛物线的对称轴l 交x 轴于点(1,0)D . (1)求出,,a b c 的值;(2)如图1,连接BC ,点P 是线段BC 下方抛物线上的动点,连接,PB PC .点,M N 分别在y 轴,对称轴l 上,且MN y ⊥轴.连接,AM PN .当PBC ∆的面积最大时,请求出点P 的坐标及此时AM MN NP ++的最小值;(3)如图2,连接AC ,把AOC ∆按照直线y x =对折,对折后的三角形记为A OC ∆'',把A OC ∆''沿着直线BC 的方向平行移动,移动后三角形的记为A O C ∆''''',连接DA '',DC '',在移动过程中,是否存在DA C ∆''''为等腰三角形的情形?若存在,直接写出点C ''的坐标;若不存在,请说明理由.【例4】如图在锐角△ABC 中,BC =6,高AD =4,两动点M 、N 分别在AB 、AC 上滑动(不包含端点),且MN ∥BC,以MN 为边长向下作正方形MPQN,设MN =x,正方形MPQN 与△ABC 公共部分的面积为y . (1)如图(1),当正方形MPQN 的边P 恰好落在BC 边上时,求x 的值;(2)如图(2),当PQ 落△ABC 外部时,求出y 与x 的函数关系式(写出x 的取值范围)并求出x 为何值时y 最大,最大是多少?【例5】如图,抛物线y=12-x2+mx+m(m>0)的顶点为A,交y轴于点C.(1)求出点A的坐标(用含m的式子表示);(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.【例6】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B 点的坐标为(3,0),与y轴交于点C(0,﹣3).(1)求二次函数解析式;(2)若点Q为抛物线上一点,且S△ABQ=12S△ACQ,求点Q的坐标;(3)若直线l:y=mx+n与抛物线有两个交点M,N(M在N的左边),P为抛物线上一动点(不与M,N重合).过P作PH平行于y轴交直线l于点H,若HM HNHP⋅=5,求m的值.【变式训练】1.如图,抛物线y =ax 2+4x +c (a ≠0)与反比例函数y =5x的图象相交于点B ,且点B 的横坐标为5,抛物线与y 轴交于点C (0,6),A 是抛物线的顶点,P 和Q 分别是x 轴和y 轴上的两个动点,则AQ +QP +PB 的最小值为_____.2.如图,在平面直角坐标系中,菱形OABC 的顶点 A 在 x 轴正半轴上,顶点 C 的坐标为(4,3),D 是抛物线 y =﹣x 2+6x 上一点,且在x 轴上方,则△BCD 面积的最大值为__________3.己知抛物线2114y x =+具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x 轴的距离始终相等,如图,点M 的坐标为(3,3),P 是抛物线2114y x =+上一个动点,则△PMF 周长的最小值是__________.4.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =16cm ,AD 为BC 边上的高,动点P 从点A 出发,沿A →D 方向以2/s 的速度向点D 运动,过P 点作PE ∥BC 交AC 于点E ,过E 点作EF ⊥BC 于点F ,设△ABP 的面积为S 1,四边形PDFE 的面积为S 2,则点P 在运动过程中,S 1+S 2的最大值为______.5.在平面直角坐标系中,已知()A 2,4、()P 1,0,B 为y 轴上的动点,以AB 为边构造ABC V ,使点C 在x 轴上,BAC 90.M ∠=o 为BC 的中点,则PM 的最小值为______.6.如图,在平面直角坐标系中,抛物线y=﹣x 2+4x 与x 轴交于点A,点M 是x 轴上方抛物线上一点,过点M 作MP ⊥x 轴于点P,以MP 为对角线作矩形MNPQ,连结NQ,则对角线NQ 的最大值为_________.7.如图,在平面直角坐标系中,过A (-1,0)、B (3,0)两点的抛物线交y 轴于点C,其顶点为点D,设△ACD 的面积为S 1,△ABC 的面积为S 2.小芳经探究发现:S 1︰S 2是一个定值.这个定值为________.8.如图,在平面直角坐标系中,有二次函数23333y x x =--+,顶点为H ,与x 轴交于A 、B 两点(A 在B 左侧),易证点H 、B 关于直线3:33l y x =+对称,且A 在直线l 上.过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连接HN 、NM 、MK ,则HN NM MK ++的最小值为________9.如图,抛物线2(0)y ax bx c a =++≠与直线1y x =+相交于(1,0)A -,(4,)B m 两点,且抛物线经过点(5,0)C(1)求抛物线的解析式.(2)点P 是抛物线上的一个动点(不与点A 点B 重合),过点P 作直线PD x ⊥轴于点D ,交直线AB 于点E .当2PE ED =时,求P 点坐标;(3)如图所示,设抛物线与y 轴交于点F ,在抛物线的第一象限内,是否存在一点Q ,使得四边形OFQC 的面积最大?若存在,请求出点Q 的坐标;若不存在,说明理由.10.如图,在矩形ABCD 中,AB=18,AD=12,点M 是边AB 的中点,连结DM,DM 与AC 交于点G ,点E,F 分别是CD 与DG 上的点,连结EF,(1)求证:CG=2AG .(2)若DE=6,当以E,F,D 为顶点的三角形与△CDG 相似时,求EF 的长.(3)若点E 从点D 出发,以每秒2个单位的速度向点C 运动,点F 从点G 出发,以每秒1个单位的速度向点D 运动.当一个点到达,另一个随即停止运动.在整个运动过程中,求四边形CEFG 的面积的最小值.11.如图①,抛物线y=a(x 2+2x-3)(a≠0)与x 轴交于点A 和点B,与y 轴交于点C,且OC=OB.(1)直接写出点B 的坐标是( , ),并求抛物线的解析式;(2)设点D 是抛物线的顶点,抛物线的对称轴是直线l,连接BD,线段OC 上的点E 关于直线l 的对称点E'恰好在线段BD 上,求点E 的坐标;(3)若点F 为抛物线第二象限图象上的一个动点,连接BF,CF,当△BCF 的面积是△ABC 面积的一半时,求此时点F 的坐标.12.如图,抛物线y =﹣x 2+mx +2与x 轴交于点A ,B ,与y 轴交于点C ,点A 的坐标为(1,0) (1)求抛物线的解析式(2)在抛物线的对称轴l 上找一点P ,使PA +PC 的值最小,求出点P 的坐标 (3)在第二象限内的抛物线上,是否存在点M ,使△MBC 的面积是△ABC 面积的12?若存在,求出点M 的坐标,若不存在,请说明理由.13.如图,抛物线212y x mx n =++交x 轴于A 、B 两点,直线y=kx+b 经过点A,与这条抛物线的对称轴交于点M (1,2),且点M 与抛物线的顶点N 关于x 轴对称.(1)求抛物线的函数关系式;(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;(3)在(2)的条件下,求△AQC面积的最大值.14.如图,抛物线y=﹣12x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.(1)求抛物线的解析式;(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,点A在抛物线y=- x2 + 4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB 的长.(2)点P 为线段AB .上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H,点F 为y 轴上一点,当∆PBE 的面积最大时,求PH + HF + 12FO 的最小值. (3)在(2)中,PH+HF+12方FO 取得最小值时,将∆CFH 绕点C 顺时针旋转60°后得到∆CF'H',过点F'作CF'的垂线与直线AB 交于点Q,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.16.已知,二次函数24y x x c =-+的图像与x 轴的一个交点为O(0,0),点P (m,0)是x 轴正半轴上的一个动点.(1)如图1,求二次函数的图像与x 轴另一个交点的坐标; (2)如图2,过点P 作x 轴的垂线交直线33y x =与点C,交二次函数图像于点D, ①当PD=2PC 时,求m 的值;如图3,已知A (3,-3)在二次函数图像上,连结AP,求12AP OP +的最小值;(3如图4,在第(2)小题的基础上,作直线OD,作点C关于直线OD的对称点C’,当C’落在坐标轴上时,请直接写出m的值.17.如图1,已知抛物线y =ax2+bx +c 经过A(-3,0),B (1,0 ),C (0,3 )三点,其顶点为D,对称轴是直线l , l 与x 轴交于点H .(1)求该抛物线的解析式;(2)若点P 是该抛物线对称轴l 上的一个动点,求∆PBC 周长的最小值;(3)如图2,若 E 是线段AD 上的一个动点(E 与A, D 不重合),过 E 点作平行于y 轴的直线交抛物线于点 F ,交x 轴于点G ,设点 E 的横坐标为m ,四边形AODF 的面积为S 。
中考数学压轴题专题-二次函数与线段最值定值及数量关系问题

专题10二次函数与线段最值定值及数量关系问题图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用.一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【例1】(2021•沈阳)如图,平面直角坐标系中,O是坐标原点,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点B坐标是(3,0).抛物线与y轴交于点C(0,3),点P是抛物线的顶点,连接PC.(1)求抛物线的函数表达式并直接写出顶点P的坐标.(2)直线BC与抛物线对称轴交于点D,点Q为直线BC上一动点.①当△QAB的面积等于△PCD面积的2倍时,求点Q的坐标;②在①的条件下,当点Q在x轴上方时,过点Q作直线l垂直于AQ,直线y=x﹣交直线l于点F,点G在直线y=x﹣上,且AG=AQ时,请直接写出GF的长.【例2】(2021•滨州)如下列图形所示,在平面直角坐标系中,一个三角板的直角顶点与原点O重合,在其绕原点O旋转的过程中,两直角边所在直线分别与抛物线y=x2相交于点A、B(点A在点B的左侧).(1)如图1,若点A、B的横坐标分别为﹣3、,求线段AB中点P的坐标;(2)如图2,若点B的横坐标为4,求线段AB中点P的坐标;(3)如图3,若线段AB中点P的坐标为(x,y),求y关于x的函数解析式;(4)若线段AB中点P的纵坐标为6,求线段AB的长.【例3】(2021•盘锦)如图,抛物线y=﹣x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C,直线y=x﹣2与y轴交于点D,与x轴交于点E,与直线BC交于点F.(1)点F的坐标为;(2)如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q,PM⊥BC于点M,QN⊥BC于点N,若=,求点P的坐标;(3)如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出发,沿射线DE方向以每秒4个单位长度的速度运动,当SE=SG,且tan∠SEG=时,求点G的运动时间t.【例4】(2021•巴中)已知抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C (0,﹣3).(1)求抛物线的表达式;(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当最大时,求点P的坐标及的最大值;(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使△BCD是直角三角形,若存在,请直接写出点D的坐标;若不存在,请说明理由.【例5】(2020•孝感)在平面直角坐标系中,已知抛物线y=ax2+4ax+4a﹣6(a>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.(1)当a=6时,直接写出点A,B,C,D的坐标:A,B,C,D;(2)如图1,直线DC交x轴于点E,若tan∠AED=43,求a的值和CE的长;(3)如图2,在(2)的条件下,若点N为OC的中点,动点P在第三象限的抛物线上,过点P作x 轴的垂线,垂足为Q,交AN于点F;过点F作FH⊥DE,垂足为H.设点P的横坐标为t,记f=FP+FH.①用含t的代数式表示f;②设﹣5<t≤m(m<0),求f的最大值.【例6】(2020•恩施州)如图1,抛物线y=−14x2+bx+c经过点C(6,0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点.(1)求抛物线的解析式;(2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90°,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=−14x2+bx+c只有一个交点时,求点M的坐标.(3)△MPC在(2)的旋转变换下,若PC=2(如图2).①求证:EA=ED.②当点E在(1)所求的抛物线上时,求线段CM的长.【题组一】1.(2021•青山区模拟)已知抛物线y=ax2﹣4ax﹣12a与x轴相交于A,B两点,与y轴交于C点,且OC =OA.设抛物线的顶点为M,对称轴交x轴于点N.(1)求抛物线的解析式;(2)如图1,点E(m,n)为抛物线上的一点,且0<m<6,连接AE,交对称轴于点P.点F为线段BC上一动点,连接EF,当PA=2PE时,求EF+BF的最小值.(3)如图2,过点M作MQ⊥CM,交x轴于点Q,将线段CQ向上平移t个单位长度,使得线段CQ 与抛物线有两个交点,求t的取值范围.2.(2021•赣州模拟)已知抛物线C1:y=x2﹣4x+3m和C2:y=mx2﹣4mx+3m,其中m≠0且m≠1.(1)抛物线C1的对称轴是,抛物线C2的对称轴是;(2)这两条抛物线相交于点E,F(点E在点F的左侧),求E、F两点的坐标(用含m的代数式表示)并直接写出直线EF与x轴的位置关系;(3)设抛物线C1的顶点为M,C2的顶点为N;①当m为何值时,点M与点N关于直线EF对称?②是否存在实数m,使得MN=2EF?若存在,直接写出实数m的值,若不存在,请说明理由.3.(2021•桓台县二模)在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A,B两点,点A,B的坐标分别为(﹣1,0),(3,0),点M为顶点.(1)求抛物线的解析式;(2)过点M作y轴的垂线,垂足为C,过点B作y轴的平行线,交CM于点D,点H为OC上的任一点,将线段HB绕点H逆时针旋转90°到HP.求∠PCD的度数;(3)在(2)的条件下,将点H改为y轴上的一动点,连接OP,BP,求OP+BP的最小值.4.(2021•成都模拟)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)求抛物线的解析式.(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G,H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°,求m的值.【题组二】5.(2021•攸县模拟)材料:对抛物线,定义:点叫做该抛物线的焦点,直线叫做该抛物线的准线,且该抛物线上任意一点到焦点的距离与它到准线的距离相等.运用上述材料解决如下问题:如图所示,已知抛物线C:y=ax2﹣4ax的图象与x轴交于O、A两点,且过点.(1)求抛物线C的解析式和点A的坐标;(2)若将抛物线C的图象先向左平移2个单位,再向上平移1个单位得到抛物线C'的图象.①求抛物线C'的焦点坐标和准线方程.②设M为抛物线C'位于第一象限内图象上的任意一点,MN⊥x轴于点N,求MN+MA的最小值,并求出取得这个最小值时点M的坐标.6.(2021•南沙区一模)已知,抛物线y=mx2+x﹣4m与x轴交于点A(﹣4,0)和点B,与y轴交于点C.点D(n,0)为x轴上一动点,且有﹣4<n<0,过点D作直线l⊥x轴,且与直线AC交于点M,与抛物线交于点N,过点N作NP⊥AC于点P.点E在第三象限内,且有OE=OD.(1)求m的值和直线AC的解析式.(2)若点D在运动过程中,AD+CD取得最小值时,求此时n的值.(3)若△ADM的周长与△MNP的周长的比为5:6时,求AE+CE的最小值.7.(2021•宝安区模拟)(1)已知二次函数经过点A(﹣3,0)、B(1,0)、C(0,3),请求该抛物线解析式;(2)点M为抛物线上第二象限内一动点,BM交y轴于点N,当BM将四边形ABCM的面积分为1:2两部分时,求点M的坐标;(3)点P为对称轴上D点下方一动点,点Q为直线y=x第一象限上的动点,且DP=OQ,求BP+BQ 的最小值并求此时点P的坐标.8.(2021•茶陵县模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是直线BC上方抛物线上的动点.(1)求抛物线的解析式;(2)如图①,连接BC与OP,交于点D,求当的值最大时点P的坐标;(3)如图②,过点P作PD∥AC交x轴于点D,交BC于点E,求BE的最大值及点P的坐标.【题组三】9.(2021•东莞市校级一模)如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.(1)求抛物线的函数解析式;(2)设点P是直线l上的一个动点,当PA+PC的值最小时,求PA+PC长;(3)已知点N(0,﹣1),在y轴上是否存在点Q,使以M、N、Q为顶点的三角形与△BCM相似?若存在,请求出点Q的坐标;若不存在,请说明理由.10.(2021•怀化模拟)如图,已知抛物线y=ax2+bx+3的对称轴是直线x=1,与x轴交于点A、B,与y 轴交于点C,其中点A的坐标是(﹣1,0).(1)直接写出点B的坐标并求出抛物线的解析式;(2)点P是抛物线上的一个动点.①当∠PCB=∠OCB时,求点P的坐标;②当点P在B、C两点之间运动时,连接AP,交BC于点Q,设t=,求当t值最大时点P的坐标.11.(2021•罗湖区三模)如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)直接写出抛物线的解析式:;(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°时,求m的值.12.(2021•南海区二模)如图1,抛物线y=x2+bx+c与x轴交于A、B两点,点A、B分别位于原点左、右两侧,且AO=2BO=4,过A点的直线y=kx+c交y轴于点C.(1)求k、b、c的值;(2)在抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由;(3)如图2,点M为线段AC上一点,连接OM,求AM+OM的最小值.【题组四】13.(2020•西宁二模)如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0,52).(1)求抛物线的解析式;(2)若点M是抛物线的顶点,连接AM,CM,求△AMC的面积;(3)若点P是抛物线上的一个动点,过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x 轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点P的坐标.14.(2020•涡阳县一模)如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式.(2)点P是直线上方的抛物线上的一个动点,求△ABP的面积最大时的P点坐标.(3)若点P是抛物线上的一个动点(不与点A点B重合),过点P作直线PD⊥x轴于点D,交直线AB 于点E.当PE=2ED时,求P点坐标;(4)设抛物线与y轴交于点F,在抛物线的第一象限内,是否存在一点M,使得AM被FC平分?若存在,请求出点M的坐标;若不存在,说明理由.15.(2020•哈尔滨模拟)如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tan C=355OA=3OB.(1)求抛物线的解析式;(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.16.(2020•皇姑区校级一模)如图,在平面直角坐标系中,抛物线y=−12x2+bx+c与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).(1)求抛物线y=−122+bx+c和直线BC的函数表达式;(2)点P是直线BC上方的抛物线上一个动点,当点P到直线BC的距离最大时,求点P的坐标;(3)连接点O与(2)中求出的点P,交直线BC于点D,点N是直线BC上的一个动点,连接ON,作DF⊥ON于点F,点F在线段ON上,当OD=5DF时,请直接写出点N的坐标.【题组五】17.(2020•岳阳二模)如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y 轴相交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)若点E在x轴上,且∠ECB=∠CBD,求点E的坐标.(3)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M.①求线段PM长度的最大值.②在①的条件下,若F为y轴上一动点,求PH+HF的最小值.18.(2020•白云区模拟)如图,抛物线y=x2+bx+c交x轴于点A,B两点,OA=1,与y轴交于点C,连接AC,tan∠OAC=3,抛物线的对称轴与x轴交于点D.(1)求点A,C的坐标;(2)若点P在抛物线上,且满足∠PAB=2∠ACO,求直线PA在与y轴交点的坐标;(3)点Q在抛物线上,且在x轴下方,直线AQ,BQ分别交抛物线的对称轴于点M、N.求证:DM+DN 为定值,并求出这个定值.19.(2020•福安市校级模拟)已知,抛物线y=ax2,其中a>0.(1)如图1,若点A、B是此抛物线上两点,且分属于y轴两侧,连接AB与y轴相交于点C,且∠AOB =90°.求证:CO=1;(2)如图2,若点A是此抛物线上一点,过点A的直线恰好与此抛物线仅有一个交点,且与y轴交于点B,与x轴相交于点C.求证:AC=BC.20.(2020•德城区一模)已知,在以O为原点的直角坐标系中,抛物线的顶点为A(﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.(1)求直线OB以及该抛物线相应的函数表达式;(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB 交于点N,求MN的最大值;(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.【题组六】21.(2020•青山区模拟)如图,在平面直角坐标系xOy中,一次函数y=54x+m(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B(1)求m的值及抛物线的函数表达式;(2)是否存在抛物线上一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若存在,请说明理由;(3)若P是抛物线对称轴上一动点,且使△ACP周长最小,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问1δ212是否为定值,如果是,请求出结果,如果不是请说明理由.(参考公式:在平面直角坐标系中,若A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=(1−2)2+(1−2)2)22.(2020•新都区模拟)已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.(1)如图1,求抛物线的解析式;(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB ﹣TS=23,求点R的坐标.23.(2020•自贡)在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣3,0)、B(1,0),交y 轴于点N,点M为抛物线的顶点,对称轴与x轴交于点C.(1)求抛物线的解析式;(2)如图1,连接AM,点E是线段AM上方抛物线上一动点,EF⊥AM于点F,过点E作EH⊥x轴于点H,交AM于点D.点P是y轴上一动点,当EF取最大值时:①求PD+PC的最小值;②如图2,Q点为y轴上一动点,请直接写出DQ+14OQ的最小值.24.(2020•凉山州)如图,二次函数y=ax2+bx+c的图象过O(0,0)、A(1,0)、B(32,32)三点.(1)求二次函数的解析式;(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.。
14 专题十四、二次函数与定值问题

专题十四、二次函数与定值问题【专题导入】1.若线段AB=x+2,线段PQ=-x+7,则AB+PQ=_____,也即是说,AB与PQ线段和为定值。
2.求证:不论m取什么实数,二次函数y=x2﹣2(m+1)x+m(m+2)的图象与x轴两个交点之间的距离为定值.【方法技巧】所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内变化时,与它有关的某种几何量却始终保持不变(或几何元素间的某种几何性质或位置关系不变)。
平面几何定值一般可分为两类:一类是定量问题(如定长度、定角、定比、平方和或倒数和为定值等);一类是定形问题(如定点、定线、定圆或弧、定方向等),它们有共同的基本特点,即给定条件中一般由固定条件和变动条件两部分组成。
一般来说,二次函数求解几何线段代数式定值问题属于定量问题,方法采用:①参数计算法。
即:在图形运动中,选取其中的变量(如线段长、点坐标)作为参数,将要求的定值用参数表出,然后消去参数即得定值。
②韦达定理法。
当涉及到直线(一次函数图像或x轴)与二次函数交点时,先联立方程消去y之后整理得到一元二次方程,借助韦达定理可得到交点横坐标与参数的关系,可以将要求的定值代数式用交点横坐标的和或积表示,往往会刚好抵消掉参数,则得到定值。
【典例剖析】3.如图,直线y=−32x+6分别交x轴、y轴于A、B两点,抛物线y=−18x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.(1)点A的坐标为_______,点D的坐标为_______;(2)试判断:对于任意一点P,PB+PC的值是否为定值?并说明理由。
4.如图,已知直线y=kx﹣9k(k<0)与抛物线y=x2﹣2x﹣3交于A,B两点,与x轴交于点P.过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,求证:PD•PC为定值.【举一反三】5.(2017•武汉模拟)如图,抛物线y=ax2﹣4ax+3a(a>0)与x轴交于A,B两点,与y轴交于点C.(1)填空:A点坐标是________,B点的坐标是________;(2)当a=1时,如图,将直线BC沿y轴向上平移交抛物线于M,N,交y轴于点P,求证:PM﹣PN是定值.【强化训练】6.已知直线y =kx +2与抛物线y =ax 2(a >0)交于A 、B 两点,AM ⊥y 轴于M ,BN ⊥y 轴于N ,求OM •ON 的值.7.已知关于x 的二次函数y =x 2﹣2mx +m 2+m 的图象与直线y =kx +1.(1)若k =1,求证:无论m 为何值,二次函数图象与直线总有两个不同交点.(2)在(1)条件下,若两图象交于两点A 、B ,试证明AB 的长为定值,并求出这个定值. 8.如图,抛物线C 1:y =ax 2+bx +c 经过A (﹣1,0)、C (0,54)两点,与x 轴正半轴交于点B ,对称轴为直线x =2.(1)求抛物线C 1的函数表达式;(2)设点D (0,2512),若F 是抛物线C 1:y =ax 2+bx +c 的对称轴上使得△ADF 的周长取得最小值的点,过F 任意作一条与y 轴不平行的直线交抛物线C 1于M 1(x 1,y 1)、M 2(x 2,y 2)两点,试探究1M 1F +1M 2F 是否为定值,请说明理由。
二次函数求最值的六种考法(含答案)

二次函数与最值的六种考法-重难点题型【题型1 二次函数中的定轴定区间求最值】【例1】(2021春•瓯海区月考)已知二次函数y=﹣x2+2x+4,关于该函数在﹣2≤x≤2的取值范围内,下列说法正确的是()A.有最大值4,有最小值0B.有最大值0,有最小值﹣4C.有最大值4,有最小值﹣4D.有最大值5,有最小值﹣4【解题思路】根据题目中的函数解析式和二次函数的性质,可以得到该函数的对称轴和开口方向,然后根据﹣2≤x≤2,即可得到相应的最大值和最小值,从而可以解答本题.【解答过程】解:∵二次函数y=﹣x2+2x+4=﹣(x﹣1)2+5,∴该函数的对称轴是直线x=1,函数图象开口向下,∴当﹣2≤x≤2时,x=1时取得最大值5,当x=﹣2时,取得最小值﹣4,故选:D.【变式1-1】(2020秋•龙沙区期中)当﹣1≤x≤3时,二次函数y=x2﹣3x+m最大值为5,则m=.【解题思路】根据题目中的函数解析式和二次函数的性质,可以求得m的值,本题得以解决.【解答过程】解:∵二次函数y=x2﹣3x+m=(x−32)2+m−94,∴该函数开口向上,对称轴为x=3 2,∵当﹣1≤x≤3时,二次函数y=x2﹣3x+m最大值为5,∴当x=﹣1时,该函数取得最大值,此时5=1+3+m,解得m=1,故答案为:1.【变式1-2】(2021•哈尔滨模拟)已知二次函数y=x2﹣4x+3,当自变量满足﹣1≤x≤3时,y的最大值为a,最小值为b,则a﹣b的值为.【解题思路】根据题目中的函数解析式和二次函数的性质,可以得到自变量满足﹣1≤x≤3时,x=﹣1时取得最大值,x=2时取得最小值,然后即可得到a、b的值,从而可以求得a﹣b的值,本题得以解决.【解答过程】解:∵二次函数y=x2﹣4x+3=(x﹣2)2﹣1,∴该函数图象开口向上,对称轴为直线x=2,∵当自变量满足﹣1≤x≤3时,y的最大值为a,最小值为b,∴当x=﹣1时,取得最大值,当x=2时,函数取得最小值,∴a=1+4+3=8,b=﹣1,∴a﹣b=8﹣(﹣1)=8+1=9,故答案为:9.【变式1-3】(2020秋•番禺区校级期中)若函数y=x2﹣6x+5,当2≤x≤6时的最大值是M,最小值是m,则M﹣m=.【解题思路】根据题意画出函数图象,即可由此找到m 和M 的值,从而求出M ﹣m 的值. 【解答过程】解:原式可化为y =(x ﹣3)2﹣4, 可知函数顶点坐标为(3,﹣4), 当y =0时,x 2﹣6x +5=0, 即(x ﹣1)(x ﹣5)=0, 解得x 1=1,x 2=5. 如图:m =﹣4,当x =6时,y =36﹣36+5=5,即M =5. 则M ﹣m =5﹣(﹣4)=9.故答案为9.【题型2 二次函数中的动轴定区间求最值】【例2】(2021•雁塔区校级模拟)已知二次函数y =mx 2+2mx +1(m ≠0)在﹣2≤x ≤2时有最小值﹣2,则m =( ) A .3B .﹣3或38C .3或−38D .﹣3或−38【解题思路】先求出对称轴为x =﹣1,分m >0,m <0两种情况讨论解答即可求得m 的值. 【解答过程】解:∵二次函数y =mx 2+2mx +1=m (x +1)2﹣m +1, ∴对称轴为直线x =﹣1, ①m >0,抛物线开口向上,x =﹣1时,有最小值y =﹣m +1=﹣2, 解得:m =3;②m <0,抛物线开口向下,∵对称轴为直线x =﹣1,在﹣2≤x ≤2时有最小值﹣2, ∴x =2时,有最小值y =4m +4m +1=﹣2,解得:m =−38; 故选:C .【变式2-1】(2021•瓯海区模拟)已知二次函数y =ax 2﹣4ax ﹣1,当x ≤1时,y 随x 的增大而增大,且﹣1≤x ≤6时,y 的最小值为﹣4,则a 的值为( ) A .1B .34C .−35D .−14【解题思路】根据二次函数y =ax 2﹣4ax ﹣1,可以得到该函数的对称轴,再根据当x ≤1时,y 随x 的增大而增大,可以得到a 的正负情况,然后根据﹣1≤x ≤6时,y 的最小值为﹣4,即可得到a 的值. 【解答过程】解:∵二次函数y =ax 2﹣4ax ﹣1=a (x ﹣2)2﹣4a ﹣1, ∴该函数的对称轴是直线x =2, 又∵当x ≤1时,y 随x 的增大而增大, ∴a <0,∵当﹣1≤x ≤6时,y 的最小值为﹣4, ∴x =6时,y =a ×62﹣4a ×6﹣1=﹣4, 解得a =−14, 故选:D .【变式2-2】(2021•章丘区模拟)已知二次函数y =2ax 2+4ax +6a 2+3(其中x 是自变量),当x ≥2时,y 随x 的增大而减小,且﹣2≤x ≤1时,y 的最小值为15,则a 的值为( ) A .1或﹣2B .−√2或√2C .﹣2D .1【解题思路】先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向下a <0,然后由﹣2≤x ≤1时,y 的最小值为15,可得x =1时,y =15,即可求出a . 【解答过程】解:∵二次函数y =2ax 2+4ax +6a 2+3(其中x 是自变量), ∴对称轴是直线x =−4a2×2a=−1, ∵当x ≥2时,y 随x 的增大而减小, ∴a <0,∵﹣2≤x ≤1时,y 的最小值为15, ∴x =1时,y =2a +4a +6a 2+3=15, ∴6a 2+6a ﹣12=0, ∴a 2+a ﹣2=0,∴a =1(不合题意舍去)或a =﹣2. 故选:C .【变式2-3】(2021•滨江区三模)已知二次函数y =12(m ﹣1)x 2+(n ﹣6)x +1(m ≥0,n ≥0),当1≤x ≤2时,y 随x 的增大而减小,则mn 的最大值为( ) A .4B .6C .8D .494【解题思路】由二次函数解析式求出对称轴直线方程,分类讨论抛物线开口向下及开口向上的m ,n 的取值范围,将mn 转化为含一个未知数的整式求最值.【解答过程】解:抛物线y =12(m ﹣1)x 2+(n ﹣6)x +1的对称轴为直线x =6−nm−1, ①当m >1时,抛物线开口向上, ∵1≤x ≤2时,y 随x 的增大而减小, ∴6−n m−1≥2,即2m +n ≤8.解得n ≤8﹣2m , ∴mn ≤m (8﹣2m ),m (8﹣2m )=﹣2(m ﹣2)2+8, ∴mn ≤8.②当0≤m <1时,抛物线开口向下, ∵1≤x ≤2时,y 随x 的增大而减小, ∴6−n m−1≤1,即m +n ≤7,解得m ≤7﹣n , ∴mn ≤n (7﹣n ),n (7﹣n )=﹣(n −72)2+494, ∴mn ≤494, ∵0≤m <1, ∴此情况不存在.综上所述,mn 最大值为8. 故选:C .【题型3 二次函数中的定轴动区间求最值】【例3】(2020秋•马鞍山期末)当a﹣1≤x≤a时,函数y=x2﹣2x+1的最小值为1,则a的值为.【解题思路】利用二次函数图象上点的坐标特征找出当y=1时x的值,结合当a﹣1≤x≤a时函数有最小值1,即可得出关于a的一元一次方程,解之即可得出结论.【解答过程】解:当y=1时,有x2﹣2x+1=1,解得:x1=0,x2=2.∵当a﹣1≤x≤a时,函数有最小值1,∴a﹣1=2或a=0,∴a=3或a=0,故答案为:0或3.【变式3-1】(2021•济南模拟)函数y=﹣x2+4x﹣3,当﹣1≤x≤m时,此函数的最小值为﹣8,最大值为1,则m的取值范围是()A.0≤m<2B.0≤m≤5C.m>5D.2≤m≤5【解题思路】根据题目中的函数解析式和二次函数的性质,可以求得m的取值范围.【解答过程】解:∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,∴该函数图象开口向下,对称轴是直线x=2,顶点坐标为(2,1),∴x=﹣1和x=5对应的函数值相等,∵当﹣1≤x≤m时,此函数的最小值为﹣8,最大值为1,当x=﹣1时,y=﹣8,∴2≤m≤5,故选:D.【变式3-2】(2021•宁波模拟)若二次函数y=ax2﹣x+2的图象经过点(2,﹣1),当t≤x≤2时,y有最大值3,最小值﹣1,则t的取值范围应是()A.﹣6≤t≤2B.t≤﹣2C.﹣6≤t≤﹣2D.﹣2≤t≤2【解题思路】根据二次函数y=ax2﹣x+2的图象经过点(2,﹣1),可以求得a的值,然后即可得到该函数的解析式,再根据二次函数的性质和当t≤x≤2时,y有最大值3,最小值﹣1,即可得到t的取值范围.【解答过程】解:∵二次函数y=ax2﹣x+2的图象经过点(2,﹣1),∴﹣1=a×22﹣2+2,解得a=−1 4,∴y=−14x2﹣x+2=−14(x+2)2+3,∴该函数的图象开口向下,对称轴是直线x=﹣2,当x=﹣2时,该函数取得最大值3,∵当t≤x≤2时,y有最大值3,最小值﹣1,当x=2时,y=﹣1,∴﹣6≤t≤﹣2,故选:C.【变式3-3】(2021•莱芜区二模)已知二次函数y=(x+1)2﹣4,当a≤x≤b且ab<0时,y的最小值为2a,最大值为2b,则a+b的值为()A.2√3B.−72C.√3−2D.0【解题思路】根据a的取值范围分﹣1≤a<0,﹣b﹣2≤a<﹣1,a<﹣b﹣2三种情况讨论,求出满足题目条件的情况即可.【解答过程】解:∵a≤x≤b且ab<0,∴a,b异号,∴a<0,b>0,由二次函数的对称性,b关于对称轴的对称点为﹣b﹣2,若﹣1≤a<0,则(a+1)2﹣4=2a,解得a=−√3(舍),若﹣b﹣2≤a<﹣1,则﹣4=2a,a=﹣2,且(b+1)2﹣3=2b,解得b=√3,∴a+b=√3−2,若a<﹣b﹣2,则2a=﹣4,a=﹣2,2b=(a+1)2﹣4=﹣3,∴b=−32(舍),故选:C.【题型4 二次函数中求线段最值】【例4】(2020春•海淀区校级期末)如图,抛物线y=x2+5x+4与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接AC,点P在线段AC上,过点P作x轴的垂线交抛物线于点Q,则线段PQ长的最大值为.【解题思路】先解方程x2+5x+4=0得A(﹣4,0),再确定C(0,4),则可利用待定系数法求出直线AC的解析式为y=x+4,设P(t,t+4)(﹣4≤t≤0),Q(t,t2+5t+4),所以PQ=t+4﹣(t2+5t+4),然后利用二次函数的性质解决问题.【解答过程】解:当y=0时,x2+5x+4=0,解得x1=﹣4,x2=﹣1,则A(﹣4,0),B(﹣1,0),当x=0时,y=x2+5x+4=4,则C(0,4),设直线AC的解析式为y=kx+b,把A(﹣4,0),C(0,4)代入得{−4k+b=0b=4,解得{k=1b=4,∴直线AC的解析式为y=x+4,设P(t,t+4)(﹣4≤t≤0),则Q(t,t2+5t+4),∴PQ=t+4﹣(t2+5t+4)=﹣t2﹣4t=﹣(t+2)2+4,∴当t=﹣2时,PQ有最大值,最大值为4.故答案为4.【变式4-1】(2020秋•镇平县期末)如图,直线y=−34x+3与x轴交于点C,与y轴交于点B,抛物线y=−38x 2+34x +3经过B ,C 两点,点E 是直线BC 上方抛物线上的一动点,过点E 作y 轴的平行线交直线BC 于点M ,则EM 的最大值为 .【解题思路】设出E 的坐标,表示出M 坐标,进而表示出EM ,化成顶点式即可求得EM 的最大值. 【解答过程】解:∵点E 是直线BC 上方抛物线上的一动点,∴点E 的坐标是(m ,−38m 2+34m +3),点M 的坐标是(m ,−34m +3),∴EM =−38m 2+34m +3﹣(−34m +3)=−38m 2+32m =−38(m 2﹣4m )=−38(m ﹣2)2+32, ∴当m =2时,EM 有最大值为32,故答案为32.【变式4-2】(2021•埇桥区模拟)对称轴为直线x =﹣1的抛物线y =x 2+bx +c ,与x 轴相交于A ,B 两点,其中点A 的坐标为(﹣3,0). (1)求点B 的坐标.(2)点C 是抛物线与y 轴的交点,点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度的最大值.【解题思路】(1)利用二次函数对称性即可得出B 点坐标;(2)首先利用待定系数法求二次函数解析式,进而求出直线AC 的解析式,再利用QD =﹣x ﹣3﹣(x 2+2x ﹣3)进而求出最值.【解答过程】解:(1)∵点A (﹣3,0)与点B 关于直线x =﹣1对称, ∴点B 的坐标为(1,0). (2)∵a =1,∴y =x 2+bx +c .∵抛物线过点(﹣3,0),且对称轴为直线x =﹣1, ∴{9−3b +c =0−b2=−1∴解得:{b =2c =−3,∴y =x 2+2x ﹣3,且点C 的坐标为(0,﹣3). 设直线AC 的解析式为y =mx +n , 则{−3m +n =0n =−3, 解得:{m =−1n =−3,∴y =﹣x ﹣3如图,设点Q 的坐标为(x .y ),﹣3≤x ≤0.则有QD =﹣x ﹣3﹣(x 2+2x ﹣3)=﹣x 2﹣3x =﹣(x +32)2+94∵﹣3≤−32≤0,∴当x =−32时,QD 有最大值94.∴线段QD 长度的最大值为94.【变式4-3】(2020秋•滨海新区期末)如图,在平面直角坐标系中,已知抛物线y =ax 2+bx +52与x 轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C.(Ⅰ)求抛物线的解析式;(Ⅱ)若点M是抛物线的顶点,连接AM,CM,求△ACM的面积;(Ⅲ)若点P是抛物线上的一动点,过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点P的坐标.【解题思路】(Ⅰ)用待定系数法即可求解;(Ⅱ)△AMC的面积=S△MHC+S△MHA=12×MH×OA,即可求解;(Ⅲ)点D在直线AC上,设点D(m,−12m+52),由题意得,四边形OEDF为矩形,故EF=OD,即当线段EF的长度最短时,只需要OD最短即可,进而求解.【解答过程】解:(Ⅰ)令x=0,则y=52,即C(0,52)设抛物线的表达式为y=a(x﹣x1)(x﹣x2)=a(x﹣5)(x+1),将点C的坐标代入上式得:52=a(0﹣5)(0+1),解得a=−1 2,故抛物线的表达式为y=−12(x﹣5)(x+1)=−12x2+2x+52;(Ⅱ)由抛物线的表达式得顶点M(2,92),过点M作MH∥y轴交AC于点H,设直线AC 的表达式为y =kx +t ,则{t =520=5k +t, 解得{k =−12t =52, 故直线AC 的表达式为y =−12x +52,当x =2时,y =32,则MH =92−32=3,则△AMC 的面积=S △MHC +S △MHA =12×MH ×OA =12×3×5=152; (Ⅲ)点D 在直线AC 上,设点D (m ,−12m +52),由题意得,四边形OEDF 为矩形,故EF =OD ,即当线段EF 的长度最短时,只需要OD 最短即可,则EF 2=OD 2=m 2+(−12m +52)2=54m 2−52m +254,∵54>0,故EF 2存在最小值(即EF 最小),此时m =1, 故点D (1,2),∵点P 、D 的纵坐标相同,故2=−12x 2+2x +52,解得x =2±√5,故点P 的坐标为(2+√5,2)或(2−√5,2).【题型5 二次函数中求线段和最值】【例5】(2020秋•安居区期末)如图,在抛物线y =﹣x 2上有A ,B 两点,其横坐标分别为1,2,在y 轴上有一动点C ,当BC +AC 最小时,则点C 的坐标是( )A .(0,0)B .(0,﹣1)C .(0,2)D .(0,﹣2)【解题思路】利用二次函数图象上点的坐标特征可求出点A ,B 的坐标,作点B 关于y 轴的对称点B ′,连接AB ′交y 轴于点C ,此时BC +AC 最小,由点B 的坐标可得出点B ′的坐标,由点A ,B ′的坐标,利用待定系数法可求出直线AB ′的解析式,再利用一次函数图象上点的坐标特征,即可求出点C 的坐标.【解答过程】解:当x =1时,y =﹣12=﹣1,∴点A 的坐标为(1,﹣1);当x =2时,y =﹣22=﹣4,∴点B 的坐标为(2,﹣4).作点B 关于y 轴的对称点B ′,连接AB ′交y 轴于点C ,此时BC +AC 最小,如图所示.∵点B 的坐标为(2,﹣4),∴点B ′的坐标为(﹣2,﹣4).设直线AB ′的解析式为y =kx +b (k ≠0),将A (1,﹣1),B (﹣2,﹣4)代入y =kx +b 得:{k +b =−1−2k +b =−4, 解得:{k =1b =−2, ∴直线AB ′的解析式为y =x ﹣2.当x =0时,y =0﹣2=﹣2,∴点C 的坐标为(0,﹣2),∴当BC +AC 最小时,点C 的坐标是(0,﹣2).故选:D .【变式5-1】(2021•铁岭模拟)如图,已知抛物线y =﹣x 2+px +q 的对称轴为x =﹣3,过其顶点M 的一条直线y =kx +b 与该抛物线的另一个交点为N (﹣1,1).要在坐标轴上找一点P ,使得△PMN 的周长最小,则点P 的坐标为( )A .(0,2)B .(43,0)C .(0,2)或(43,0)D .以上都不正确【解题思路】首先,求得抛物线的解析式,根据抛物线解析式求得M 的坐标;欲使△PMN 的周长最小,MN 的长度一定,所以只需(PM +PN )取最小值即可.然后,过点M 作关于y 轴对称的点M ′,连接M ′N ,M ′N 与y 轴的交点即为所求的点P (如图1);过点M 作关于x 轴对称的点M ′,连接M ′N ,则只需M ′N 与x 轴的交点即为所求的点P (如图2).【解答过程】解:如图,∵抛物线y =﹣x 2+px +q 的对称轴为x =﹣3,点N (﹣1,1)是抛物线上的一点, ∴{−p −2=−31=−1−p +q, 解得{p =−6q =−4. ∴该抛物线的解析式为y =﹣x 2﹣6x ﹣4=﹣(x +3)2+5,∴M (﹣3,5).∵△PMN 的周长=MN +PM +PN ,且MN 是定值,所以只需(PM +PN )最小.如图1,过点M 作关于y 轴对称的点M ′,连接M ′N ,M ′N 与y 轴的交点即为所求的点P .则M ′(3,5).设直线M ′N 的解析式为:y =ax +t (a ≠0),则{5=3a +t 1=−a +t, 解得{a =1t =2, 故该直线的解析式为y =x +2.当x =0时,y =2,即P (0,2).同理,如图2,过点M 作关于x 轴对称的点M ′,连接M ′N ,则只需M ′N 与x 轴的交点即为所求的点P (−43,0).如果点P 在y 轴上,则三角形PMN 的周长=4√2+MN ;如果点P 在x 轴上,则三角形PMN 的周长=2√10+MN ;所以点P 在(0,2)时,三角形PMN 的周长最小.综上所述,符合条件的点P 的坐标是(0,2).故选:A .【变式5-2】(2021•包头)已知抛物线y =x 2﹣2x ﹣3与x 轴交于A ,B 两点(点A 在点B 的左侧)与y 轴交于点C ,点D (4,y )在抛物线上,E 是该抛物线对称轴上一动点,当BE +DE 的值最小时,△ACE 的面积为 .【解题思路】解方程x 2﹣2x ﹣3=0得A (﹣1,0),B (3,0),则抛物线的对称轴为直线x =1,再确定C (0,﹣3),D (4,5),连接AD 交直线x =1于E ,交y 轴于F 点,如图,利用两点之间线段最短可判断此时BE +DE 的值最小,接着利用待定系数法求出直线AD 的解析式为y =x +1,则F (0,1),然后根据三角形面积公式计算.【解答过程】解:当y =0时,x 2﹣2x ﹣3=0,解得x 1=﹣1,x 2=3,则A (﹣1,0),B (3,0), 抛物线的对称轴为直线x =1,当x =0时,y =x 2﹣2x ﹣3=﹣3,则C (0,﹣3),当x =4时,y =x 2﹣2x ﹣3=5,则D (4,5),连接AD 交直线x =1于E ,交y 轴于F 点,如图,∵BE +DE =EA +DE =AD ,∴此时BE +DE 的值最小,设直线AD 的解析式为y =kx +b ,把A (﹣1,0),D (4,5)代入得{−k +b =04k +b =5,解得{k =1b =1, ∴直线AD 的解析式为y =x +1,当x =1时,y =x +1=2,则E (1,2),当x =0时,y =x +1=1,则F (0,1),∴S △ACE =S △ACF +S △ECF =12×4×1+12×4×1=4. 故答案为4.【变式5-3】(2021•涪城区模拟)如图,抛物线y =53x 2−203x +5与x 轴分别交于A 、B 两点(点A 在点B 的左侧),与y 轴交于C ,在其对称轴上有一动点M ,连接MA 、MC 、AC ,则当△MAC 的周长最小时,点M 的坐标是 .【解题思路】点A 关于函数对称轴的对称点为点B ,连接CB 交函数对称轴于点M ,则点M 为所求点,即可求解.【解答过程】解:点A 关于函数对称轴的对称点为点B ,连接CB 交函数对称轴于点M ,则点M 为所求点,理由:连接AC ,由点的对称性知,MA =MB ,△MAC 的周长=AC +MA +MC =AC +MB +MC =CA +BC 为最小,令y =53x 2−203x +5=0,解得x =1或3,令x =0,则y =5,故点A 、B 、C 的坐标分别为(1,0)、(3,0)、(0,5),则函数的对称轴为x =12(1+3)=2,设直线BC 的表达式为y =kx +b ,则{0=3k +b b =5,解得{k =−53b =5, 故直线BC 的表达式为y =−53x +5,当x =2时,y =−53x +5=53,故点M 的坐标为(2,53). 【题型6 二次函数中求面积最值】【例6】(2020秋•盐城期末)如图,抛物线y =x 2+bx +c 与x 轴交于A (﹣1,0),B (3,0)两点,过点A 的直线l 交抛物线于点C (2,m ),点P 是线段AC 上一个动点,过点P 做x 轴的垂线交抛物线于点E .(1)求抛物线的解析式;(2)当P 在何处时,△ACE 面积最大.【解题思路】(1)利用交点式写出抛物线解析式;(2)先利用二次函数解析式确定C (2,﹣3),再利用待定系数法求出直线AC 的解析式为y =﹣x ﹣1,设E (t ,t 2﹣2t ﹣3)(﹣1≤t ≤2),则P (t ,﹣t ﹣1),利用三角形面积公式得到△ACE 的面积=12×(2+1)×PE =32(﹣t 2+t +2),然后根据二次函数的性质解决问题.【解答过程】解:(1)抛物线解析式为y =(x +1)(x ﹣3),即y =x 2﹣2x ﹣3;(2)把C (2,m )代入y =x 2﹣2x ﹣3得m =4﹣4﹣3=﹣3,则C (2,﹣3),设直线AC 的解析式为y =mx +n ,把A (﹣1,0),C (2,﹣3)代入得{−m +n =02m +n =−3,解得{m =−1n =−1, ∴直线AC 的解析式为y =﹣x ﹣1;设E (t ,t 2﹣2t ﹣3)(﹣1≤t ≤2),则P (t ,﹣t ﹣1),∴PE =﹣t ﹣1﹣(t 2﹣2t ﹣3)=﹣t 2+t +2,∴△ACE 的面积=12×(2+1)×PE=32(﹣t 2+t +2)=−32(t −12)2+278,当t =12时,△ACE 的面积有最大值,最大值为278,此时P 点坐标为(12,−32). 【变式6-1】(2021春•金塔县月考)如图,已知抛物线经过A (4,0),B (1,0),C (0,﹣2)三点.(1)求该抛物线的解析式;(2)在直线AC 上方的该抛物线上是否存在一点D ,使得△DCA 的面积最大,若存在,求出点D 的坐标及△DCA 面积的最大值;若不存在,请说明理由.【解题思路】(1)根据题意设出抛物线的交点式,用待定系数法求解即可;(2)根据题意作出相关辅助线,用待定系数法求得直线AC解析式为y=12x﹣2,因为点D在抛物线上,所以可设其坐标为(x,−12x2+52x﹣2),点E在直线AC上则设点E坐标为(x,12x﹣2),由图形可知S△DCA=S△DCE+S△DAE,将相关坐标及线段的长度代入求解,再根据二次函数的性质即可得出△DCA面积的最大值.【解答过程】(1)设该抛物线解析式为y=a(x﹣4)(x﹣1),将点C(0,﹣2)坐标代入解析式得:﹣2=a(0﹣4)(0﹣1),解得a=−1 2,∴y=−12(x﹣4)(x﹣1)=−12x2+52x﹣2,故该抛物线的解析式为:y=−12x2+52x﹣2,(2)如图,设存在点D在抛物线上,连接AD、CD,过点D作DE⊥x轴且与直线AC交于点E,设直线AC表达式为:y=kx+b(k≠0),将A(4,0),C(0,﹣2)代入其表达式得:{0=4k+b−2=b,解得{k=12b=−2,∴直线AC:y=12x﹣2,设点D坐标为(x,−12x2+52x﹣2),则点E坐标为(x,12x﹣2),S△DCA=S△DCE+S△DAE=12×DE×x E+12×DE×(x A﹣x E)=12×DE×x A=12×DE×4=2DE,∵DE=(−12x2+52x﹣2)﹣(12x﹣2)=−12x2+2x,∴S△DCA=2DE=2×(−12x2+2x)=﹣x2+4x=﹣(x﹣2)2+4,∴当x=2时,y=−12x2+52x﹣2═﹣2+5﹣2=1,即点D坐标为(2,1),此时△DCA的面积最大,最大值为4.【变式6-2】(2021春•无为市月考)如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.(1)求抛物线的解析式.(2)若P为直线AB上方的抛物线上一点,且点P的横坐标为m,求四边形BCAP的面积S关于点P横坐标m的函数解析式,并求S的最大值.【解题思路】(1)将点A坐标代入直线解析式可求n的值,可求点B坐标,利用待定系数法可求解;(2)过点P做PE⊥x轴于点E,与直线AB交于点D,求得C的坐标和D的坐标,然后根据S=S△ABC+S △ABP得到S关于m的函数解析式,根据二次函数的性质即可求得结论.【解答过程】解:(1)∵直线y=﹣x+n与x轴交于点A(3,0),∴0=﹣3+n,∴n=3,∴直线解析式为:y=﹣x+3,当x=0时,y=3,∴点B (0,3),∵抛物线y =﹣x 2+bx +c 经过点A ,B ,∴{c =3−9+3b +c =0, ∴{b =2c =3, ∴抛物线的解析式为:y =﹣x 2+2x +3;(2)如图,过点P 做PE ⊥x 轴于点E ,与直线AB 交于点D ,∵点P 的横坐标为m ,∴点P 的坐标为(m ,﹣m 2+2m +3),∵点D 在直线AB 上,∴点D 的坐标为(m ,﹣m +3),∴PD =﹣m 2+2m +3﹣(﹣m +3)=﹣m 2+3m ,在y =﹣x 2+2x +3中.令y =0.则﹣x 2+2x +3=0,解得x 1=﹣1,x 2=3,∴点C 的坐标为(﹣1,0),∴S =S △ABC +S △ABP =12×4×3+12(﹣m 2+3m )×3=−32(m −32)2+758, ∴当m =32时,S 最大,最大值为758.【变式6-3】(2021春•无棣县月考)如图,在平面直角坐标系中,二次函数y =x 2+bx +c 的图象与x 轴交于A 、B 两点,B 点的坐标为(3,0),与y 轴交于点C (0,﹣3),点P 是直线BC 下方抛物线上的一个动点.(1)求二次函数解析式;(2)连接PO ,PC ,并将△POC 沿y 轴对折,得到四边形POP 'C .是否存在点P ,使四边形POP 'C 为菱形?若存在,求出此时点P 的坐标;若不存在,请说明理由;(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.【解题思路】(1)先根据点C坐标求出c=﹣3,再将点B坐标代入二次函数解析式中求出b,即可得出结论;(2)连接PP'交y轴于E,根据菱形的性质判断出点E是OC的中点,进而求出点P的纵坐标,最后代入二次函数解析式中求解,即可得出结论;(3)设出点P的坐标,进而利用梯形的面积+三角形的面积得出S四边形ABPC=−32(m−12)2+398,即可得出结论.【解答过程】解:(1)∵二次函数y=x2+bx+c与y轴的交点C(0,﹣3),∴c=﹣3,∴二次函数的解析式为y=x2+bx﹣3,∵点B(3,0)在二次函数图象上,∴9+3b﹣3=0,∴b=﹣2,∴二次函数的解析式为y=x2﹣2x﹣3;(2)存在,理由:如图1,连接PP'交y轴于E,∵四边形POP'C为菱形,∴PP'⊥OC,OE=CE=12OC,∵点C(0,﹣3),∴OC=3,∴OE=3 2,∴E (0,−32),∴点P 的纵坐标为−32,由(1)知,二次函数的解析式为y =x 2﹣2x ﹣3, ∴x 2﹣2x ﹣3=−32,∴x =2−√102或x =2+√102,∵点P 在直线BC 下方的抛物线上,∴0<x <3,∴点P (2+√102,−32);(3)如图2,过点P 作PF ⊥x 轴于F ,则PF ∥OC , 由(1)知,二次函数的解析式为y =x 2﹣2x ﹣3, 令y =0,则x 2﹣2x ﹣3=0,∴x =﹣1或x =3,∴A (﹣1,0),∴设P (m ,m 2﹣2m ﹣3)(0<m <3),∴F (m ,0),∴S 四边形ABPC =S △AOC +S 梯形OCPF +S △PFB =12OA •OC +12(OC +PF )•OF +12PF •BF =12×1×3+12(3﹣m 2+2m +3)•m +12(﹣m 2+2m +3)•(3﹣m ) =−32(m −32)2+758,∴当m =32时,四边形ABPC 的面积最大,最大值为758,此时,P (32,−154),即点P 运动到点(32,−154)时,四边形ABPC 的面积最大,其最大值为758.。
重难点 二次函数中的线段、周长与面积的最值问题及定值问题(解析版)--2024年中考数学

重难点二次函数中的线段、周长与面积的最值问题及定值问题目录题型01利用二次函数解决单线段的最值问题题型02利用二次函数解决两条线段之和的最值问题题型03利用二次函数解决两条线段之差的最值问题题型04利用二次函数解决三条线段之和的最值问题题型05利用二次函数解决三角形周长的最值问题题型06利用二次函数解决四边形周长的最值问题题型07利用二次函数解决图形面积的最值问题类型一利用割补、拼接法解决面积最值问题类型二利用用铅垂定理巧求斜三角形面积最值问题类型三构建平行线,利用同底等高解决面积最值问题题型08利用二次函数解决定值问题题型01利用二次函数解决单线段的最值问题【解题思路】抛物线中的线段最值问题有三种形式:1.平行于坐标轴的线段的最值问题:常通过线段两端点的坐标差表示线段长的函数关系式,运用二次函数性质求解.求最值时应注意:①当线段平行于y轴时,用上端点的纵坐标减去下端点的纵坐标;②当线段平行于x轴时,用右端点的横坐标减去左端点的横坐标.在确定最值时,函数自变量的取值范围应确定正确.1(2022·辽宁朝阳·统考中考真题)如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,-3),连接BC.(1)求抛物线的解析式及点B 的坐标.(2)如图,点P 为线段BC 上的一个动点(点P 不与点B ,C 重合),过点P 作y 轴的平行线交抛物线于点Q ,求线段PQ 长度的最大值.(3)动点P 以每秒2个单位长度的速度在线段BC 上由点C 向点B 运动,同时动点M 以每秒1个单位长度的速度在线段BO 上由点B 向点O 运动,在平面内是否存在点N ,使得以点P ,M ,B ,N 为顶点的四边形是菱形?若存在,请直接写出符合条件的点N 的坐标;若不存在,请说明理由.【答案】(1)y =x 2+2x -3,(-3,0)(2)94(3)-3,-32或(-2,1)或0,3-32【分析】(1)将A ,C 两点坐标代入抛物线的解析式求得a ,c 的值,进而得出解析式,当y =0时,求出方程的解,进而求得B 点坐标;(2)由B ,C 两点求出BC 的解析式,进而设出点P 和点Q 坐标,表示出PQ 的长,进一步得出结果;(3)要使以点P ,M ,B ,N 为顶点的四边形是菱形,只需△PMB 是等腰三角形,所以分为PM =BM ,PM =PB 和BP =BM ,结合图象,进一步得出结果.【详解】(1)解:把点A (1,0),C (0,-3)代入y =ax 2+2x +c 得:c =-3a +2×1+c =0 ,解得:c =-3a =1 ,∴抛物线解析式为y =x 2+2x -3;令y =0,则x 2+2x -3=0,解得:x 1=1,x 2=-3,∴点B 的坐标为(-3,0);(2)解:设直线BC 的解析式为y =kx +b k ≠0 ,把点B (-3,0),C (0,-3)代入得:b =-3-3k +b =0 ,解得:k =-1b =-3 ,∴直线BC 的解析式为y =-x -3,设点P m ,-m +3 ,则Q m ,m 2+2m -3 ,∴PQ =-m -3 -m 2+2m -3 =-m 2-3m =-m +322+94,∴当m =-32时,PQ 最大,最大值为94;(3)解:存在,根据题意得:PC =2t ,BM =t ,则PB =32-2t ,如图,当BM =PM 时,∵B (-3,0),C (0,-3),∴OB =OC =3,∴∠OCB =∠OBC =45°,延长NP 交y 轴于点D ,∵点P ,M ,B ,N 为顶点的四边形是菱形,∴PN ∥x 轴,BN ∥PM ,即DN ⊥y 轴,∴△CDP 为等腰直角三角形,∴CD =PD =PC ⋅sin ∠OCB =2t ×22=t ,∵BM =PM ,∴∠MPB =∠OBC =45°,∴∠PMO =∠PDO =∠MOD =90°,∴四边形OMPD 是矩形,∴OM =PD =t ,MP ⊥x 轴,∴BN ⊥x 轴,∵BM +OM =OB ,∴t +t =3,解得t =32,∴P -32,-32,∴N -3,-32;如图,当PM =PB 时,作PD ⊥y 轴于D ,连接PN ,∵点P ,M ,B ,N 为顶点的四边形是菱形,∴PN ⊥BM ,NE =PE ,∴BM =2BE ,∴∠OEP =∠DOE =∠ODP =90°,∴四边形PDOE 是矩形,∴OE =PD =t ,∴BE =3-t ,∴t =2(3-t ),解得:t =2,∴P (-2,-1),∴N (-2,1);如图,当PB =MB 时,32-2t =t ,解得:t =6-32,∴PN =BP =BM =6-32,过点P 作PE ⊥x 轴于点E ,∴PE ⊥PM ,∴∠EON =∠OEP =∠EPN =90°,∴四边形OEPN 为矩形,∴PN =OE ,PN ⊥y 轴,∵∠OBC =45°,∴BE =PE =PB ⋅sin ∠OBC =6-32 ×22=32-3,∴OE =OB -BE =3-32-3 =6-32,∴点N 在y 轴上,∴N 0,3-32 ,综上所述,点N 的坐标为-3,-32或(-2,1)或0,3-32 .【点睛】本题考查了二次函数及其图象的性质,用待定系数法求一次函数的解析式,等腰三角形的分类和等腰三角形的性质,菱形的性质等知识,解决问题的关键是正确分类,画出符合条件的图形.2(2021·西藏·统考中考真题)在平面直角坐标系中,抛物线y =-x 2+bx +c 与x 轴交于A ,B 两点.与y 轴交于点C .且点A 的坐标为(-1,0),点C 的坐标为(0,5).(1)求该抛物线的解析式;(2)如图(甲).若点P 是第一象限内抛物线上的一动点.当点P 到直线BC 的距离最大时,求点P 的坐标;(3)图(乙)中,若点M 是抛物线上一点,点N 是抛物线对称轴上一点,是否存在点M 使得以B ,C ,M ,N 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】(1)y =-x 2+4x +5;(2)P 52,354;(3)存在,M 的坐标为:(3,8)或(-3,-16)或(7,-16).【分析】(1)将A 的坐标(-1,0),点C 的坐(0,5)代入y =-x 2+bx +c ,即可得抛物线的解析式为y =-x 2+4x +5;(2)过P 作PD ⊥x 轴于D ,交BC 于Q ,过P 作PH ⊥BC 于H ,由y =-x 2+4x +5可得B (5,0),故OB =OC ,△BOC 是等腰直角三角形,可证明△PHQ 是等腰直角三角形,即知PH =PQ2,当PQ 最大时,PH 最大,设直线BC 解析式为y =kx +5,将B (5,0)代入得直线BC 解析式为y =-x +5,设P (m ,-m 2+4m +5),(0<m <5),则Q (m ,-m +5),PQ =-m -52 2+254,故当m =52时,PH 最大,即点P 到直线BC的距离最大,此时P 52,354 ;(3)抛物线y =-x 2+4x +5对称轴为直线x =2,设M (s ,-s 2+4s +5),N (2,t ),而B (5,0),C (0,5),①以MN 、BC 为对角线,则MN 、BC 的中点重合,可列方程组s +22=5+02-s 2+4s +5+t 2=0+52,即可解得M (3,8),②以MB 、NC 为对角线,则MB 、NC 的中点重合,同理可得s +52=2+02-s 2+4s +4+02=t +52,解得M (-3,-16),③以MC 、NB 为对角线,则MC 、NB 中点重合,则s +02=2+52-s 2+4s +5+52=t +02,解得M (7,-16).【详解】解:(1)将A 的坐标(-1,0),点C 的坐(0,5)代入y =-x 2+bx +c 得:0=-1-b +c 5=c ,解得b =4c =5 ,∴抛物线的解析式为y =-x 2+4x +5;(2)过P 作PD ⊥x 轴于D ,交BC 于Q ,过P 作PH ⊥BC 于H ,如图:在y =-x 2+4x +5中,令y =0得-x 2+4x +5=0,解得x =5或x =-1,∴B (5,0),∴OB =OC ,△BOC 是等腰直角三角形,∴∠CBO =45°,∵PD ⊥x 轴,∴∠BQD =45°=∠PQH ,∴△PHQ 是等腰直角三角形,∴PH =PQ2,∴当PQ 最大时,PH 最大,设直线BC 解析式为y =kx +5,将B (5,0)代入得0=5k +5,∴k =-1,∴直线BC 解析式为y =-x +5,设P (m ,-m 2+4m +5),(0<m <5),则Q (m ,-m +5),∴PQ =(-m 2+4m +5)-(-m +5)=-m 2+5m =-m -52 2+254,∵a =-1<0,∴当m =52时,PQ 最大为254,∴m =52时,PH 最大,即点P 到直线BC 的距离最大,此时P 52,354;(3)存在,理由如下:抛物线y =-x 2+4x +5对称轴为直线x =2,设M (s ,-s 2+4s +5),N (2,t ),而B (5,0),C (0,5),①以MN 、BC 为对角线,则MN 、BC 的中点重合,如图:∴s +22=5+02-s 2+4s +5+t2=0+52,解得s =3t =-3 ,∴M (3,8),②以MB 、NC 为对角线,则MB 、NC 的中点重合,如图:∴s +52=2+02-s 2+4s +4+02=t +52,解得s=-3t =-21 ,∴M (-3,-16),③以MC 、NB 为对角线,则MC 、NB 中点重合,如图:s +02=2+52-s 2+4s +5+52=t +02,解得s =7t =-11 ,∴M (7,-16);综上所述,M 的坐标为:(3,8)或(-3,-16)或(7,-16).【点睛】本题考查二次函数综合应用,涉及待定系数法、函数图象上点坐标的特征、等腰直角三角形、平行四边形等知识,解题的关键是用含字母的代数式表示相关点的坐标和相关线段的长度.3(2021·山东泰安·统考中考真题)二次函数y =ax 2+bx +4(a ≠0)的图象经过点A (-4,0),B (1,0),与y 轴交于点C ,点P 为第二象限内抛物线上一点,连接BP 、AC ,交于点Q ,过点P 作PD ⊥x 轴于点D .(1)求二次函数的表达式;(2)连接BC ,当∠DPB =2∠BCO 时,求直线BP 的表达式;(3)请判断:PQQB是否有最大值,如有请求出有最大值时点P 的坐标,如没有请说明理由.【答案】(1)y =-x 2-3x +4;(2)y =-158x +158;(3)PQ QB有最大值为45,P 点坐标为(-2,6)【分析】(1)将A (-4,0),B (1,0)代入y =ax 2+bx +4(a ≠0)中,列出关于a 、b 的二元一次方程组,求出a 、b 的值即可;(2)设BP 与y 轴交于点E ,根据PD ⎳y 轴可知,∠DPB =∠OEB ,当∠DPB =2∠BCO ,即∠OEB =2∠BCO ,由此推断△OEB 为等腰三角形,设OE =a ,则CE =4-a ,所以BE =4-a ,由勾股定理得BE 2=OE 2+OB 2,解出点E 的坐标,用待定系数法确定出BP 的函数解析式即可;(3)设PD 与AC 交于点N ,过B 作y 轴的平行线与AC 相交于点M .由A 、C 两点坐标可得AC 所在直线表达式,求得M 点坐标,则BM =5,由BM ⎳PN ,可得△PNQ ∽△BMQ ,PQ QB=PN BM =PN5,设P (a 0,-a 20-3a 0+4)(-4<a 0<0),则N (a 0,a 0+4)PQ QB =-a 20-3a 0+4-(a 0+4)5=-a 20-4a 05=-(a 0+2)2+45,根据二次函数性质求解即可.【详解】解:(1)由题意可得:a ⋅(-4)2+b ⋅(-4)+4=0a +b +4=0解得:a =-1b =-3 ,∴二次函数的表达式为y =-x 2-3x +4;(2)设BP 与y 轴交于点E ,∵PD ⎳y 轴,∴∠DPB =∠OEB ,∵∠DPB =2∠BCO ,∴∠OEB =2∠BCO ,∴∠ECB =∠EBC ,∴BE =CE ,设OE =a ,则CE =4-a ,∴BE =4-a ,在Rt △BOE 中,由勾股定理得BE 2=OE 2+OB 2,∴(4-a )2=a 2+12解得a =158,∴E 0,158,设BE 所在直线表达式为y =kx +e (k ≠0)∴k ⋅0+e =158,k ⋅1+e =0.解得k =-158,e =158. ∴直线BP 的表达式为y =-158x +158.(3)设PD 与AC 交于点N .过B 作y 轴的平行线与AC 相交于点M .由A 、C 两点坐标分别为(-4,0),(0,4)可得AC 所在直线表达式为y =x +4∴M 点坐标为(1,5),BM =5由BM ⎳PN ,可得△PNQ ∽△BMQ ,∴PQ QB=PN BM =PN 5设P (a 0,-a 20-3a 0+4)(-4<a 0<0),则N (a 0,a 0+4)∴PQ QB=-a 20-3a 0+4-(a 0+4)5=-a 20-4a 05=-(a 0+2)2+45,∴当a 0=-2时,PQQB 有最大值0.8,此时P 点坐标为(-2,6).【点睛】本题主要考查二次函数以及一次函数解析式的确定,函数图像的性质,相似三角形,勾股定理等知识点,熟练运用待定系数法求函数解析式是解题关键,本题综合性强,涉及知识面广,难度较大,属于中考压轴题.4(2020·辽宁阜新·中考真题)如图,二次函数y =x 2+bx +c 的图象交x 轴于点A -3,0 ,B 1,0 ,交y 轴于点C .点P m ,0 是x 轴上的一动点,PM ⊥x 轴,交直线AC 于点M ,交抛物线于点N .(1)求这个二次函数的表达式;(2)①若点P 仅在线段AO 上运动,如图1.求线段MN 的最大值;②若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M ,N ,C ,Q 为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.【答案】(1)y =x 2+2x -3;(2)①94,②存在,Q 1(0,-32-1),Q 2(0,32-1)【分析】(1)把A (-3,0),B (1,0)代入y =x 2+bx +c 中求出b ,c 的值即可;(2)①由点P m ,0 得M (m ,-m -3),N m ,m 2+2m -3 ,从而得MN =(-m -3)-m 2+2m -3 ,整理,化为顶点式即可得到结论;②分MN =MC 和MC =2MN 两种情况,根据菱形的性质得到关于m 的方程,求解即可.【详解】解:(1)把A (-3,0),B (1,0)代入y =x 2+bx +c 中,得0=9-3b +c ,0=1+x +c .解得b =2,c =-3. ∴y =x 2+2x -3.(2)设直线AC 的表达式为y =kx +b ,把A (-3,0),C (0,-3)代入y =kx +b .得,0=-3k +b ,-3=b . 解这个方程组,得k =-1,b =-3. ∴y =-x -3.∵点P m ,0 是x 轴上的一动点,且PM ⊥x 轴.∴M (m ,-m -3),N m ,m 2+2m -3 . ∴MN =(-m -3)-m 2+2m -3 =-m 2-3m=-m +32 2+94.∵a =-1<0,∴此函数有最大值.又∵点P 在线段OA 上运动,且-3<-32<0∴当m =-32时,MN 有最大值94. ②∵点P m ,0 是x 轴上的一动点,且PM ⊥x 轴.∴M (m ,-m -3),N m ,m 2+2m -3 . ∴MN =(-m -3)-m 2+2m -3 =-m 2-3m(i )当以M ,N ,C ,Q 为顶点的四边形为菱形,则有MN =MC ,如图,∵C (0,-3)∴MC =(m -0)2+(-m -3+3)2=2m 2∴-m 2-3m =2m 2整理得,m 4+6m 3+7m 2=0∵m 2≠0,∴m 2+6m +7=0,解得,m 1=-3+2,m 2=-3-2∴当m =-3+2时,CQ =MN =32-2,∴OQ =-3-(32-2)=-32-1∴Q (0,-32-1);当m =-3-2时,CQ =MN =-32-2,∴OQ =-3-(-32-2)=32-1∴Q (0,32-1);(ii )若MC =2MN ,如图,则有-m 2-3m =22×2m 2整理得,m 2+4m =0解得,m 1=-4,m 2=0(均不符合实际,舍去)综上所述,点Q 的坐标为Q 1(0,-32-1),Q 2(0,32-1)【点睛】本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用线段的和差得出二次函数,又利用了二次函数的性质,解(3)的关键是利用菱形的性质得出关于m 的方程,要分类讨论,以防遗漏.5(2020·天津·中考真题)已知点A (1,0)是抛物线y =ax 2+bx +m (a ,b ,m 为常数,a ≠0,m <0)与x 轴的一个交点.(1)当a =1,m =-3时,求该抛物线的顶点坐标;(2)若抛物线与x 轴的另一个交点为M (m ,0),与y 轴的交点为C ,过点C 作直线l 平行于x 轴,E 是直线l 上的动点,F 是y 轴上的动点,EF =22.①当点E 落在抛物线上(不与点C 重合),且AE =EF 时,求点F 的坐标;②取EF 的中点N ,当m 为何值时,MN 的最小值是22?【答案】(1)抛物线的顶点坐标为(-1,-4);(2)①点F 的坐标为(0,-2-7)或(0,-2+7);②当m 的值为-32或-12时,MN 的最小值是22.【分析】(1)根据a =1,m =-3,则抛物线的解析式为y =x 2+bx -3,再将点A (1,0)代入y =x 2+bx -3,求出b 的值,从而得到抛物线的解析式,进一步可求出抛物线的顶点坐标;(2)①首先用含有m 的代数式表示出抛物线的解析式,求出C (0,m ),点E (m +1,m ).过点A 作AH ⊥l 于点H ,在Rt △EAH 中,利用勾股定理求出AE 的值,再根据AE =EF ,EF =22,可求出m 的值,进一步求出F 的坐标;②首先用含m 的代数式表示出MC 的长,然后分情况讨论MN 什么时候有最值.【详解】解:(1)当a =1,m =-3时,抛物线的解析式为y =x 2+bx -3.∵抛物线经过点A (1,0),∴0=1+b-3.解得b=2.∴抛物线的解析式为y=x2+2x-3.∵y=x2+2x-3=(x+1)2-4,∴抛物线的顶点坐标为(-1,-4).(2)①∵抛物线y=ax2+bx+m经过点A(1,0)和M(m,0),m<0,∴0=a+b+m,0=am2+bm+m,即am+b+1=0.∴a=1,b=-m-1.∴抛物线的解析式为y=x2-(m+1)x+m.根据题意,得点C(0,m),点E(m+1,m).过点A作AH⊥l于点H.由点A(1,0),得点H(1,m).在Rt△EAH中,EH=1-(m+1)=-m,HA=0-m=-m,∴AE=EH2+HA2=-2m.∵AE=EF=22,∴-2m=22.解得m=-2.此时,点E(-1,-2),点C(0,-2),有EC=1.∵点F在y轴上,∴在Rt△EFC中,CF=EF2-EC2=7.∴点F的坐标为(0,-2-7)或(0,-2+7).②由N是EF的中点,得CN=12EF=2.根据题意,点N在以点C为圆心、2为半径的圆上.由点M(m,0),点C(0,m),得MO=-m,CO=-m.∴在Rt△MCO中,MC=MO2+CO2=-2m.当MC≥2,即m≤-1时,满足条件的点N落在线段MC上,MN的最小值为MC-NC=-2m-2=22,解得m=-3 2;当MC<2,-1<m<0时,满足条件的点N落在线段CM的延长线上,MN的最小值为NC-MC=2-(-2m)=22,解得m=-1 2.∴当m的值为-32或-12时,MN的最小值是22.【点睛】本题考查了待定系数法求解析式,抛物线上的点的坐标满足抛物线方程等,解题的关键是学会利用参数解决问题,学会用转化的思想思考问题,属于中考常考题型..6(2023·重庆·统考中考真题)如图,在平面直角坐标系中,抛物线y=14x2+bx+c与x轴交于点A,B,与y轴交于点C,其中B3,0,C0,-3.(1)求该抛物线的表达式;(2)点P 是直线AC 下方抛物线上一动点,过点P 作PD ⊥AC 于点D ,求PD 的最大值及此时点P 的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点E 为点P 的对应点,平移后的抛物线与y 轴交于点F ,Q 为平移后的抛物线的对称轴上任意一点.写出所有使得以QF 为腰的△QEF 是等腰三角形的点Q 的坐标,并把求其中一个点Q 的坐标的过程写出来.【答案】(1)y =14x 2+14x -3(2)PD 取得最大值为45,P -2,-52 (3)Q 点的坐标为92,-1 或92,5 或92,74.【分析】(1)待定系数法求二次函数解析式即可求解;(2)直线AC 的解析式为y =-34x -3,过点P 作PE ⊥x 轴于点E ,交AC 于点Q ,设P t ,14t 2+14t -3 ,则Q t ,-34t -3 ,则PD =45PQ ,进而根据二次函数的性质即可求解;(3)根据平移的性质得出y =14x -92 2-4916,对称轴为直线x =92,点P -2,-52 向右平移5个单位得到E 3,-52 ,F 0,2 ,勾股定理分别表示出EF 2,QE 2,QF 2,进而分类讨论即可求解.【详解】(1)解:将点B 3,0 ,C 0,-3 .代入y =14x 2+bx +c 得,14×32+3b +c =0c =-3解得:b =14c =-3 ,∴抛物线解析式为:y =14x 2+14x -3,(2)∵y =14x 2+14x -3与x 轴交于点A ,B ,当y =0时,14x 2+14x -3=0解得:x 1=-4,x 2=3,∴A -4,0 ,∵C 0,-3 .设直线AC 的解析式为y =kx -3,∴-4k -3=0解得:k =-34∴直线AC 的解析式为y =-34x -3,如图所示,过点P 作PE ⊥x 轴于点E ,交AC 于点Q ,设P t ,14t 2+14t -3 ,则Q t ,-34t -3 ,∴PQ =-34t -3-14t 2+14t -3 =-14t 2-t ,∵∠AQE =∠PQD ,∠AEQ =∠QDP =90°,∴∠OAC =∠QPD ,∵OA =4,OC =3,∴AC =5,∴cos ∠QPD =PD PQ =cos ∠OAC =AO AC=45,∴PD =45PQ =45-14t 2-t =-15t 2-45t =-15t +2 2+45,∴当t =-2时,PD 取得最大值为45,14t 2+14t -3=14×-2 2+14×-2 -3=-52,∴P -2,-52 ;(3)∵抛物线y =14x 2+14x -3=14x +12 2-4916将该抛物线向右平移5个单位,得到y =14x -92 2-4916,对称轴为直线x =92,点P -2,-52 向右平移5个单位得到E 3,-52 ∵平移后的抛物线与y 轴交于点F ,令x =0,则y =14×92 2-4916=2,∴F 0,2 ,∴EF 2=32+2+52 2=1174∵Q 为平移后的抛物线的对称轴上任意一点.则Q 点的横坐标为92,设Q 92,m ,∴QE 2=92-3 2+m +52 2,QF 2=92 2+m -2 2,当QF =EF 时,92 2+m -2 2=1174,解得:m =-1或m =5,当QE =QF 时,92-3 2+m +522=92 2+m -2 2,解得:m =74综上所述,Q 点的坐标为92,-1 或92,5 或92,74.【点睛】本题考查了二次函数综合问题,解直角三角形,待定系数法求解析式,二次函数的平移,线段周长问题,特殊三角形问题,熟练掌握二次函数的性质是解题的关键.题型02利用二次函数解决两条线段之和的最值问题【解题思路】抛物线中的线段最值问题有三种形式:2. 两条线段和的最值问题:解决这类问题最基本的定理就是“两点之间线段最短”,解决这类问题的方法是:作其中一个定点关于已知直线的对称点,连接对称点与另一个定点,它们与已知直线的交点即为所求的点. 其变形问题有三角形周长最小或四边形周长最小等.【常见模型一】(两点在河的异侧):在直线L上找一点M,使PA+PB的值最小.方法:如右图,连接AB,与直线L交于点M,在M处渡河距离最短,最短距离为线段AB的长。
二次函数与线段最值定值问题(八大类型)-2023年中考数学压轴题专项训练(学生版)

二次函数与线段最值定值问题(八大类型)考向分析题型一二次函数与单线段最值问题1.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(-1,0)两点,与.y轴交于点C0,52(1)求抛物线的解析式;(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.题型二二次函数与将军饮马型问题2.如图1,抛物线y=ax2+2x+c与x轴交于A(-4,0),B(1,0)两点,过点B的直线y=kx+23分别与y轴及抛物线交于点C,D.(1)求直线和抛物线的表达式;(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t 秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.题型三二次函数与胡不归型线段最值问题3.已知抛物线y=-1x2+bx+c(b,c为常数)的图象与x轴交于A(1,0),B两点(点A在点B左2侧).与y轴相交于点C,顶点为D.(Ⅰ)当b=2时,求抛物线的顶点坐标;(Ⅱ)若点P是y轴上一点,连接BP,当PB=PC,OP=2时,求b的值;(Ⅲ)若抛物线与x轴另一个交点B的坐标为(4,0),对称轴交x轴于点E,点Q是线段DE上一点,点NQ的最小值.N为线段AB上一点,且AN=2BN,连接NQ,求DQ+54二次函数与三线段和最值问题4.如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c 过A、B两点,且与x轴交于另一点C.(1)求b、c的值;(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR①求证:PG=RQ;②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.二次函数与线段倍分关系最值问题5.抛物线y=-x2+4ax+b(a>0)与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.(1)a=32时,求抛物线的解析式和BC的长;(2)如图a>1时,若AP⊥PC,求a的值;(3)是否存在实数a,使APPN =12若存在,求出a的值,如不存在,请说明理由.题型六二次函数与线段乘积问题6.已知直线y=12x+2分别交x轴、y轴于A、B两点,抛物线y=12x2+mx-2经过点A,和x轴的另一个交点为C.(1)求抛物线的解析式;(2)如图1,点D是抛物线上的动点,且在第三象限,求△ABD面积的最大值;(3)如图2,经过点M(-4,1)的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求OE•OF的值.备注:抛物线顶点坐标公式-b2a,4ac-b24a7.抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上一点,且位于x轴下方.(1)如图1,若P(1,-3),B(4,0).①求该抛物线的解析式;②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时,OE+OFOC是否为定值?若是,试求出该定值;若不是,请说明理由.8.如图,已知抛物线y=ax2+bx+c与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C,且OB=OC.(1)求抛物线的函数表达式;(2)如图1,点D是抛物线顶点,点P(m,n)是在第二象限抛物线上的一点,分别连接BD、BC、BP,若∠CBD=∠ABP,求m的值;(3)如图1,过B、C、O三点的圆上有一点Q,并且点Q在第四象限,连接QO、QB、QC,试猜想线段QO、QB、QC之间的数量关系,并证明你的猜想;(4)如图2,若∠BAC的角平分线交y轴于点G,过点G的直线分别交射线AB、AC于点E、F(不与点A重合),则1AE+1AF的值是否变化?若变化,请说明理由;若不变,请求出它的值.压轴题速练一、解答题1.如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为(5,0),点D的坐标为(1,3).(1)求该二次函数的表达式;(2)试问在该二次函数图象上是否存在点G,使得△ADG的面积是△BDG的面积的35若存在,求出点G的坐标;若不存在,请说明理由.2.在平面直角坐标系中,抛物线y=-x2-4x+c与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为(-5,0).(1)求点C的坐标;(2)如图1,若点P是第二象限内抛物线上一动点,求点P到直线AC距离的最大值;(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.3.如图,已知抛物线y=ax2-32x+c与x轴交于点点A(-4,0),B(1,0),与y轴交于点C.(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在点Q使QB+QC最小?若存在,请求出Q点坐标;若不存在,请说明理由;(3)点P为AC上方抛物线上的动点,过点P作PD⊥AC,垂足为点D,连接PC,当△PCD与△ACO相似时,求点P的坐标.4.如图,抛物线y=-12x2+bx+c过点A3,2,且与直线y=-x+72交于B、C两点,点B的坐标为4,m.(1)求抛物线的解析式;(2)点D为抛物线上位于直线BC上方的一点,过点D作DE⊥x轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求PD+PA的最小值.5.抛物线y=ax2+bx-3(a,b为常数,a≠0)交x轴于A-3,0两点.,B4,0(1)求该抛物线的解析式;(2)点C0,4,D是线段AC上的动点(点D不与点A,C重合).①点D关于x轴的对称点为D ,当点D 在该抛物线上时,求点D的坐标;②E是线段AB上的动点(点E不与点A,B重合),且CD=AE,连接CE,BD,当CE+BD取得最小值时,求点D的坐标.6.如图,在平面直角坐标系中,已知抛物线y =ax 2+bx +2a ≠0 与x 轴交于A -1,0 ,B 3,0 两点,与y 轴交于点C ,连接BC .(1)求该抛物线的解析式;(2)点P 为直线BC 上方的抛物线上一点,过点P 作y 轴的垂线交线段BC 于M ,过点P 作x 轴的垂线交线段BC 于N ,求△PMN 的周长的最大值.(3)若点N 为抛物线对称轴上一点,抛物线上是否存在点M ,使得以B ,C ,M ,N 为顶点的四边形是平行四边形?若存在,请求出所有满足条件的点M 的坐标;若不存在,请说明理由.7.如图,二次函数y=-14x2+12m-1x+m(m是常数,且m>0)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,动点P在对称轴l上,连接AC、BC、PA、PC.(1)求点A、B、C的坐标(用数字或含m的式子表示);(2)当PA+PC的最小值等于45时,求m的值及此时点P的坐标;(3)当m取(2)中的值时,若∠APC=2∠ABC,请直接写出点P的坐标.8.已知抛物线y=x+1(m为常数,m>1)的顶点为P.x-m(1)当m=5时,求该抛物线顶点P的坐标;(2)若该抛物线与x轴交于点A,C(点A在点C左侧),与y轴交于点B.①点Q是该抛物线对称轴上一个动点,当AQ+BQ的最小值为22时,求该抛物线的解析式和点Q 的坐标.②连接BC,与抛物线的对称轴交于点H,过点P作PD⊥BC,垂足为D,若BC=8PD,求该抛物线的解析式.9.已知抛物线y=ax2+bx+c(a、b、c是常数,a>0)的顶点为P,与x轴相交于点A-1,0和点B.(1)若b=-2,c=-3,①求点P的坐标;②直线x=m(m是常数,1<m<3)与抛物线相交于点M,与BP相交于点G,当MG取得最大值时,求点M,G的坐标;(2)若3b=2c,直线x=2与抛物线相交于点N,E是x轴的正半轴上的动点,F是y轴的负半轴上的动点,当PF+FE+EN的最小值为5时,直接写出顶点P的坐标.10.如图,抛物线y=-x2+bx+c交x轴于A、B两点(点A在点B的左侧)坐标分别为-2,0,4,0,交y轴于点C.(1)求出抛物线解析式:5时,请求(2)如图1,过y轴上点D做BC的垂线,交线段BC于点E,交抛物线于点F,当EF=35出点F的坐标;(3)如图2,点H的坐标是0,2在抛物线上,把△PHQ沿HQ翻折,,点Q为x轴上一动点,点P2,8使点P刚好落在x轴上,请直接写出点Q的坐标.11.抛物线y =ax 2+bx +c 与坐标轴交于A -1,0 、B 4,0 、C 0,2 三点.点P 为抛物线上位于BC 上方的一动点.(1)求抛物线的解析式;(2)如图,过点P 作PF ⊥x 轴于点F ,交BC 于点E ,连结CP 、CF .当S ΔPCE =2S ΔCEF 时,求点P 的坐标;(3)过点P 作PG ⊥BC 于点G ,是否存在点P ,使线段PG 、CG 的长度是2倍关系?若存在,求出点P 的坐标;若不存在,请说明理由.12.已知抛物线y=ax2+bx+c经过点A-4,0.、B1,0、C0,4(1)求抛物线解析式和直线AC的解析式;(2)如图(1),若点P是第四象限抛物线上的一点,若S△PAC=20,求点P的坐标;(3)如图(2),点M是直线AC上方抛物线上的一个动点(不与A、C重合),过点M作MH垂直AC于点H,求MH的最大值.13.如图,已知抛物线y=-x2+bx+c与一直线相交于A-1,0两点,与y轴交于点N,其顶,C2,3点为D.(1)求抛物线及直线AC的解析式.(2)设点M3,m,求使MN+MD的值最小时m的值.(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求出点E,F的坐标;若不能,请说明理由.14.已知抛物线y=ax2+bx+c(a≠0)与x轴有且只有一个交点A2,0,且与y轴于交于点B.(1)求a与c的关系式;(2)若a=1时,点P2,1c在抛物线的对称轴上;①若过B点的直线l:y=kx+m(k≠0)与抛物线只有一个交点;证明:直线l平分∠OBP;②设过P点的直线与抛物线交于M,N点,则1PM+1PN是否为定值,若为定值请求出定值,若不是定值请说明理由.15.如图1,抛物线y=ax2+2x+c,交x轴于A、B两点,交y轴于点C,F为抛物线顶点,直线EF垂直于x轴于点E,当y≥0时,-1≤x≤3.(1)求抛物线的表达式;(2)点P是线段BE上的动点(除B、E外),过点P作x轴的垂线交抛物线于点D.①当点P的横坐标为2时,求四边形ACFD的面积;②如图2,直线AD,BD分别与抛物线对称轴交于M、N两点.试问,EM+EN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.16.已知抛物线y=-x2+2kx-k2+4的顶点为H,与y轴交点为A,点P a,b是抛物线上异于点H的一个动点.(1)若抛物线的对称轴为直线x=1,请用含a的式子表示b;(2)若a=1,作直线HP交y轴于点B,当点A在x轴上方且在线段OB上时,直接写出k的取值范围;(3)在(1)的条件下,记抛物线与x轴的右交点为C,OA的中点为D,作直线CD,过点P作PF⊥CD 于点E并交x轴于点F,若a<3,PE=3EF,求a的值.17.已知抛物线y=ax2+bx+c(a≠0)与x轴只有一个公共点A2,0.且经过点3,1(1)求抛物线的函数解析式;(2)直线l:y=-x+m与抛物线y=ax2+bx+c相交于B、C两点(C点在B点的左侧),与对称轴相交于点P,且B、C分布在对称轴的两侧.若B点到抛物线对称轴的距离为n,且CP=t·BP(2≤t≤3).①试探求n与t的数量关系;②求线段BC的最大值,以及当BC取得最大值时对应m的值.18.如图1,二次函数y =ax 2+bx +3的图像与x 轴交于点A -1,0 ,B 3,0 ,与y 轴交于点C .(1)求二次函数的解析式;(2)点P 为抛物线上一动点.①如图2,过点C 作x 轴的平行线与抛物线交于另一点D ,连接BC ,BD .当S △PBC =2S △DBC 时,求点P 的坐标;②如图3,若点P 在直线BC 上方的抛物线上,连接OP 与BC 交于点E ,求PE OE的最大值.19.抛物线y=ax2-4经过A、B两点,且OA=OB,直线EC过点E4,-1,点D是线段,C0,-3OA(不含端点)上的动点,过D作PD⊥x轴交抛物线于点P,连接PC、PE.(1)求抛物线与直线CE的解析式;(2)求证:PC+PD为定值;(3)在第四象限内是否存在一点Q,使得以C、P、E、Q为顶点的平行四边形面积最大,若存在,求出Q点坐标;若不存在,请说明理由.20.如图1.在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A-2,0,,点B4,0与y轴交于点C0,2.(1)求抛物线的解析式;(2)点P是第一象限内的抛物线上一点.过点P作PH⊥x轴于点H,交直线BC于点Q,求PQ+5CQ的最大值,并求出此时点P的坐标;5(3)如图2.将地物线沿射线BC的方向平移5个单位长度.得到新抛物线y1=a1x2+b1x+c1a1≠0,新抛物线与原抛物线交于点G,点M是x轴上一点,点N是新抛物线上一点,若以点C、G、M、N为顶点的四边形是平行四边形时,请直接写出点N的坐标.。
专题3-1 二次函数中的10类定值、定点问题(原卷版)

专题3-1 二次函数中的10类定值、定点问题二次函数背景下的定值与定点问题,解析法类似于高中,但并不超纲!因为解题方法比较特殊,同学们要专门学习和练习,才能在考场上应对自如,这些方法包括联立、转化等,对同学们的代数功底与几何功底都有较高的要求.知识点梳理一、定值问题二、定点问题题型一 面积定值2022·山东淄博·中考真题2023·福建厦门三模题型二 线段长为定值2024届湖北天门市九年级月考2024届福建龙岩市统考期中2020·西藏·中考真题题型二 线段和定值2023广州市二中月考2022·四川巴中·中考真题2024届湖北黄石市·九年级统考2023·四川乐山·统考二模2023·海口华侨中学考模2023·江苏徐州·4月模拟2022·湖南张家界·中考真题题型三 加权线段和定值2023·四川广元·中考真题2020·四川德阳·中考真题题型四 线段乘积为定值2023·四川南充·中考真题2024届·武汉市东湖高新区统考2024届福建省福州屏东中学月考2024届福州市晋安区统考2023·福建福州·校考三模题型五 比值为定值2023年广西钦州市一模2023福建厦门一中模拟2023年福州市屏东中学中考模拟武汉·中考真题题型六 横(纵)坐标定值2023·湖北潜江、天门、仙桃、江汉油田·中考真题2024届湖北潜江市初12校联考题型七 角度为定值2023·成都武侯区西川中学三模四川乐山·统考中考真题题型八 其它定值问题2023·浙江湖州·统考一模2024届福建省南平市统考2023年湖北省武汉市新观察中考四调题型九 结合韦达定理求定点2023年湖北省武汉市外国语学校中考模拟2024届武汉市青山区九年级统考2024届武汉市新洲区12月统考2024届·福建厦门市第九中学期中2023·武汉光谷实验中学中考模拟2023广东省梅州市九年级下期中2024届福州市九校联盟期中2023年湖北省武汉市新观察中考四调题型十 已知定值求定点2024届武汉市洪山区九年级统考2024届湖北省武汉市新洲区九年级上期中2023年广州市天河外国语学校中考三模知识点梳理一、定值问题一般来说,二次函数求解几何线段代数式定值问题属于定量问题,方法采用:1.参数计算法:即在图形运动中,选取其中的变量(如线段长,点坐标)作为参数,将要求的定值用参数表示出,然后消去参数即得定值。
二次函数中线段周长最值及定值问题(八大题型)学生版

二次函数中线段周长最值及定值问题(八大题型)通用的解题思路:一、二次函数中的线段最值问题有三种形式:1.平行于坐标轴的线段的最值问题:常通过线段两端点的坐标差表示线段长的函数关系式,运用二次函数性质求解,求最值时应注意:①当线段平行于y轴时,用上端点的纵坐标减去下端点的纵坐标;②当线段平行于x轴时,用右端点的横坐标减去左端点的横坐标.在确定最值时,函数自变量的取值范围应确定正确。
2.两条线段和的最值问题:解决这类问题最基本的定理就是“两点之间线段最短”,解决这类问题的方法是:作其中一个定点关于已知直线的对称点,连接对称点与另一个定点,它们与已知直线的交点即为所求的点,其变形问题有三角形周长最小或四边形周长最小等.【常见模型一】(两点在河的异侧):在直线L上找一点M,使PA+PB的值最小.方法:如右图,连接AB,与直线L交于点M,在M处渡河距离最短,最短距离为线段AB的长。
【常见模型二】(两点在河的同侧):在直线L上找一点M,使PA+PB的值最小.方法:如右图,作点B关于直线L的对称点B',连接AB',与直线L的交点即为所求的渡河点,最短距离为线段AB'的长。
3. 两条线段差的最值问题:解决这类问题最基本的定理就是“三角形任何两边之差小于第三边”,解决这类问题的方法是:求解时,先根据原理确定线段差取最值时的图形,再根据已知条件求解。
【常见模型一】(两点在同侧):在直线L上求一点P,求|PA-PB|的最大值方法:如右图,延长射线AB,与直线L交于点P,|PA-PB|最大值为AB【常见模型二】(两点在异侧):在直线L上求一点P,求|PA-PB|的最大值。
方法:如右图,作点B关于直线L的对称点B',延长射线AB',与直线L交于点P,|PA-PB|最大值为AB'二、二次函数中的定值问题一般来说,二次函数求解几何线段代数式定值问题属于定量问题,方法采用:1.参数计算法:即在图形运动中,选取其中的变量(如线段长,点坐标)作为参数,将要求的定值用参数表示出,然后消去参数即得定值。
二次函数最值问题及解题技巧(个人整理)

二次函数最值问题及解题技巧(个人整理)一、二次函数线段最值问题1、平行于x轴的线段最值问题1)首先表示出线段两个端点的坐标2)用右侧端点的横坐标减去左侧端点的横坐标3)得到一个线段长关于自变量的二次函数4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值2、平行于y轴的线段最值问题1)首先表示出线段两个端点的坐标2)用上面端点的纵坐标减去下面端点的纵坐标3)得到一个线段长关于自变量的二次函数解析式4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值3、既不平行于x轴,又不平行于y轴的线段最值问题1)以此线段为斜边构造一个直角三角形,并使此直角三角形的两条直角边分别平行于x轴、y轴2)根据线段两个端点的坐标表示出直角顶点坐标3)根据“上减下,右减左”分别表示出两直角边长4)根据勾股定理表示出斜边的平方(即两直角边的平方和)5)得到一个斜边的平方关于自变量的二次函数6)将其化为顶点式,并根据a的正负及自变量的取值规模判断最值7)根据所求得的斜边平方的最值求出斜边的最值即可2、二次函数周长最值问题1、矩形周长最值问题1)一般会给出一点落在抛物线上,从这点向两坐标轴引垂线构成一个矩形,求其周长最值2)可先设此点坐标,点p到x轴、y轴的距离和再乘以2,即为周长3)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值2、利用两点之间线段最短求三角形周长最值1)首先判断图形中那些边是定值,哪些边是变量2)使用二次函数轴对称性及两点之间线段最短找到两条变革的边,并求其和的最小值3)周长最小值即为两条变革的边的和最小值加上不变的边长3、二次函数面积最值问题1、规则图形面积最值问题(这里规则图形指三角形必有一边平行于坐标轴,四边形必有一组对边平行于坐标轴)1)首先表示出所需的边长及高2)使用求面积公式表示出面积3)得到一个面积关于自变量的二次函数4)将其化为顶点式,并根据a的正负及自变量的取值规模判断最值2、不划定规矩图形面积最值问题1)支解。
二次函数中的定值问题

二次函数中的定值问题二次函数定值问题是中考压轴题常考考点,解决二次函数中的定值问题,可以根据特殊位置,特殊点去探求定值是多少,做到心中有数;其次再证明在一般情况下这个结论也成立,在运动变化过程中,应注意分清哪些量是变量,哪些是常量,其中二次函数定值问题常与一次函数结合一起,利用韦达定理解决二次函数中的定值问题是常用的解题思路!例1.抛物线y=ax2﹣6x+c与x轴的交点分别为点A、点B(点A在点B左边),顶点为点D,△ABD为等边三角形.求ac的值例2.如图,已知二次函数y=ax2﹣2ax﹣3a(a>0)与x轴交于A、B两点(A 点在B点左),与y轴交于C点,连接BC,P为对称轴右侧抛物线上的动点,直线PA交y轴于E点,直线PB交y轴于点D,判断的值是否为定值,若是,求出定值,若不是请说明理由.例3.在平面直角坐标系中,抛物线y=﹣x2+(a+1)x﹣a(a>1)交x轴于A、B两点(点A在点B的左边),交y轴于点C.过点B且与抛物线仅有一个交点的直线y=kx+b交y轴于点D,求的值.例4.已知抛物线C1:y=x2﹣1与x轴于A,B两点,与y轴交于点C,点F的坐标为(0,﹣2),直线l分别交线段AF,BF(不含端点)于G,H两点.若直线l与抛物线C1有且只有一个公共点,设点G的横坐标为b,点H的横坐标为a,则a﹣b是定值吗?若是,请求出其定值,若不是,请说明理由.例5.如图,抛物线y=x2﹣2x﹣6与x轴分别相交于A,B两点(点A在点B的左侧),C是AB的中点,平行四边形CDEF的顶点D,E均在抛物线上.点F 在抛物线上,连接DF,求证:直线DF过一定点.解:联立得:,例6.Rt△ABC的三个顶点都在抛物线y=﹣x2+4上,且直角顶点C在该抛物线的顶点处,设直线AB的解析式为y=kx+b,试证明该直线必过一定点.例7.抛物线y=﹣x2+2x+3;与x轴交于点A和点B(点A在原点的左侧),与y 轴交于点C,D为对称轴GT右边抛物线上的任意一点,连接AD,BD分别交GT于M、N两点,试证明MT+NT为定值.例8.如图,抛物线y=﹣x2+3x﹣3;顶点D在x轴上,抛物线与直线l交于A、B两点.∠ADB=90°,求证:直线l经过定点,并求出定点坐标.例10.如图已知抛物线y=x2﹣2x﹣3与x轴交于A(﹣1,0),B(3,0),与y轴交于点C.点N为y轴上一点,AN、BN交抛物线于E、F两点,求•的值.例11.在平面直角坐标系中,已知二次函数y=x2+x+2;的图象经过点A(﹣1,0),B(3,0),与y轴交于点C.直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线AQ,BQ 分别交直线l于点M,N,在点Q的运动过程中,EM+EN的值是否为定值?若是,请求出该定值;若不是,请说明理由.例12.已知y=x2﹣2x﹣3过点A(﹣1,0)和点C(0,﹣3).直线y=kx+k+1与此抛物线交于M、N两点,在抛物线上是否存在定点Q,使得对于任意实数k,都有∠MQN=90°,若存在,求出点Q的坐标,若不存在,请说明理由.例13.如图,抛物线y=x2+x﹣2;与x轴交于A(﹣2,0),B(1,0)两点,与y轴负半轴交于点C.经过定点P作一次函数y=kx+与抛物线交于M,N两点.试探究是否为定值?请说明理由.例14.已知抛物线C1:y=﹣x2+2x+3经过点(2,3),与x轴交于A(﹣1,0)、B两点.平移抛物线C1,使其顶点在y轴上,得到抛物线C2,过定点H(0,2)的直线交抛物线C2于M、N两点,过M、N的直线MR、NR与抛物线C2都只有唯一公共点,求证:R点在定直线上运动.例15.如图,在平面直角坐标系xOy中,直线y=kx﹣3(k≠0)与抛物线y=﹣x2相交于A,B两点(点A在点B的左侧),点B关于y轴的对称点为B'.试探究直线AB'是否经过某一定点.若是,请求出该定点的坐标;若不是,请说明理由.练习1.抛物线y=x2+x﹣2与x轴交于点A、点B(1,0),与y轴交于点C,连接AC,D点为抛物线上第三象限内一动点.过点N(﹣3,0)作y轴的平行线,交AD所在直线于点E,交BD所在直线于点F,在点D的运动过程中,求4NE+NF 的值.2.抛物线与x轴交于点A、B,与y轴交于点C,直线l∥BC,直线l交抛物线于点M、N,直线AM交y轴于点P,直线AN交y轴于点Q,点P、Q的纵坐标为y P,y Q,求证:y P+y Q的值为定值.3.抛物线y=x2﹣2x+1的顶点A在x轴上,与y轴交于点B.P为抛物线对称轴上顶点下方的一点,过点P作直线交抛物线于点E,F,交x轴于点M,求的值.4.抛物线y=x2﹣2x﹣3与x轴交于A、B两点,过点D(0,3)的直线交y=﹣2x于M点,交抛物线于E、F两点,求﹣的值.5.抛物线y=ax2+bx﹣4交x轴于A(﹣2,0),B(4,0)两点交y轴于点C.点P在第四象限的抛物线上,过A,B,P作⊙O1,作PQ⊥x轴于Q,交⊙O于点H,求HQ的值.6.已知抛物线y=x2﹣2x﹣3与x轴正半轴交于点D,M、N为y轴上的两个不同的动点,且OM=ON,射线DM、DN分别与抛物线交于P、Q两点,求的值.7.平面直角坐标系中,已知抛物线y=﹣x2+4x的顶点为A(2,4),且经过坐标原点.若直线y=kx﹣2k+5与抛物线交于M,N两点,点N关于抛物线对称轴的对称点为P,当k<0时,试说明直线MP过一定点Q,并求出点Q的坐标.8.如图,抛物线y=﹣x2+1的顶点C在y轴正半轴上,与x轴交于A、B两点(A 点在B点左边)直线AQ、BP分别交y轴于E、F两点,求OE+OF的值.9.如图,在平面直角坐标系中,抛物线y=x2﹣(m﹣1)x﹣m(其中m>0),交x轴于A、B两点(点A在点B的左侧),交y轴负半轴于点C.平面上一点E(m,2),过点E作任意一条直线交抛物线于P、Q两点,连接AP、AQ,分别交y轴于M、N两点,求证:OM•ON是一个定值.10.已知抛物线y=x2,直线y=kx+2与抛物线交于点E,F,点P是抛物线上的动点,延长PE,PF分别交直线y=﹣2于M,N两点,MN交y轴于Q点,求QM•QN的值.11.如图,过点F(0,2)的直线y=kx+b与抛物线y=x2交于M(x1,y1)和N(x2,y2)两点(M在N的左侧),证明:无论k取何实数,+为定值,并求出该值.12.抛物线y=x2﹣2x﹣3,2,直线y=kx+k+1与抛物线C2交于M、N两点,在抛物线上是否存在定点Q,使得对于任意实数k都有∠MQN=90°?若存在,求点Q的坐标;若不存在,请说明理由.13.抛物线y=﹣x2+2x+3,交x轴于A、B两点,交y轴于点C,F为抛物线顶点,直线EF垂直于x轴于点E,点P是线段BE上的动点(除B、E外),过点P 作x轴的垂线交抛物线于点D.直线AD,BD分别与抛物线对称轴交于M、N 两点.试问,EM+EN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.14.抛物线y=x2﹣1交x轴于A,B两点(A在B的左边).F是原点O关于抛物线顶点的对称点,不平行y轴的直线l分别交线段AF,BF(不含端点)于G,H两点.若直线l与抛物线只有一个公共点,求证:FG+FH的值是定值.15.在平面直角坐标系中,二次函数y=x2﹣x﹣4的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D,交⊙M于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE 的长.16.抛物线y=﹣x2+x+1与x轴交于点A,B.与y轴交于点C.平行于y轴的直线交抛物线于点M,交x轴于点N(2,0).点D是抛物线上A,M之间的一动点,且点D不与A,M重合,连接DB交MN于点E.连接AD并延长交MN于点F.在点D运动过程中,3NE+NF是否为定值?若是,求出这个定值;若不是,请说明理由.17.如图,在平面直角坐标系xOy中,一次函数y=x+,抛物线y=﹣x2+ x+(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B,若P是抛物线对称轴上一动点,且使△ACP周长最小,过点P任意作一条与y 轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问是否为定值,如果是,请求出结果,如果不是请说明理由.18.已知抛物线y=x2﹣2mx+m2﹣2m(m>2),顶点为点M,抛物线与x轴交于A、B点(点A在点B的左侧),与y轴交于点C.若直线CM交x轴于点N,请求的值.。
中考复习压轴题之二次函数压轴之定值问题与定点问题-含详细参考答案

二次函数压轴之定值、定点问题1.如图,抛物线y=x2+bx+c与x轴分别交于A,B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3OA.(1)求该抛物线的函数表达式;(2)如图2,∠BAC的角平分线交y轴于点M,过M点的直线l与射线AB,AC分别于E,F,已知当直线l绕点M旋转时,11AF AE为定值,请直接写出该定值.2.如图,平面直角坐标系中,抛物线y=﹣x2+nx+4过点A(﹣4,0),与y轴交于点N,与x轴正半轴交于点B.直线l过定点A.(1)求抛物线解析式;(2)过点T(t,﹣1)的任意直线EF(不与y轴平行)与抛物线交于点E、F,直线BE、BF分别交y轴于点P、Q,是否存在t的值使得OP与OQ的积为定值?若存在,求t的值,若不存在,请说明理由.3.如图1,已知二次函数y =x 2+bx +c 的图象与x 轴交于点A (﹣1,0)和点B (3,0),与y 轴的负半轴交于点C .(1)求这个函数的解析式;(2)如图2,点T 是抛物线上一点,且点T 与点C 关于抛物线的对称轴对称,过点T 的直线TS 与抛物线有唯一的公共点,直线MN ∥TS 交抛物线于M ,N 两点,连AM 交y 轴正半轴于G ,连AN 交y 轴负半轴于H ,求OH ﹣OG4.如图1,已知抛物线的解析式为21362y x =--,直线y =kx ﹣4k 与x 轴交于M ,与抛物线相交于点A ,B (A 在B 的左侧).(1)当k =1时,直接写出A ,B ,M 三点的横坐标:x A =,x B =,x M =;(2)作AP ⊥x 轴于P ,BQ ⊥x 轴于Q ,当k 变化时,MP •MQ 的值是否发生变化?若变化,求出其变化范围;若不变,求出其值;5.如图,在正方形OABC中,AB=4,点E是线段OA(不含端点)边上一动点,作△ABE 的外接圆交AC于点D.抛物线y=ax2﹣x+c过点O,E.(1)如图1,若抛物线恰好经过点B,求此时点D的坐标;(2)如图2,AC与BE交于点F.请问点E在运动的过程中,CF•AD是定值吗?如果是,请求出这个值,如果不是,请说明理由;6.已知顶点为A的抛物线y=a(x﹣2)2(a≠0)交y轴于点B(0,2),且与直线l交于不同的两点M、N(M、N不与点A重合).(1)求抛物线的解析式;(2)若∠MAN=90°,试说明:直线l必过定点;7.如图,在直角坐标系中有Rt△AOB,O为坐标原点,OB=1,tan∠ABO=3,将此三角形绕原点O顺时针旋转90°,得到Rt△COD,二次函数y=﹣x2+bx+c的图象刚好经过A,B,C三点.(1)求二次函数的解析式及顶点P的坐标;(2)过定点Q(1,3)的直线l:y=kx﹣k+3与二次函数的图象相交于M,N两点.证明:无论k为何值,△PMN恒为直角三角形.8.已知,抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,点P是抛物线上一点.(1)求抛物线的解析式;(2)如图2,当点P位于第二象限时,过P点作直线AP,BP分别交y轴于E,F两点,请问CECF的值是否为定值?若是,请求出此定值;若不是,请说明理由.9.已知点P(0,﹣4)为平面直角坐标系内一点,直线l绕原点O旋转,交经过点(0,﹣2)的抛物线y=14x2+c于M、N两点.(1)请求出该抛物线的解析式;(2)在直线l绕原点O旋转的过程中,请你研究一下(PM+MO)(PN﹣NO)是否定值?若是,请求出这个定值;若不是,请说明理由.10.如图,抛物线C:y=ax2+bx+c(a≠0)的对称轴为直线x=﹣12,且抛物线经过A、B两点,交x轴于另一点C,A(﹣2,0),B(0,2);(1)求抛物线的解析式;(2)在(1)的条件下,设对称轴直线x=﹣12与x轴交于M,点P为抛物线上对称轴左侧一点,直线PM交抛物线于另一点Q,点P关于抛物线对称轴对称点H,直线HQ交抛物线对称轴于G点,在点P运动过程中GM长是否为一定值,若为定值,请求出其值,若不为定值,请求出其变化范围.11.如图,在平面直角坐标系中,已知抛物线的顶点D为(1,﹣1),且经过点B(3,3).(1)求这个抛物线相应的函数表达式;(2)如图1,过点D且平行于x轴的直线l,与直线OB相交于点A,过点B作直线l 的垂线,垂足为C.若点Q是抛物线上BD之间的动点(不与B、D重合),连接DQ并延长交BC于点E.如图2,连接BQ并延长交CD于点F,在点Q运动的过程中,FC(AC+EC)的值是否发生变化?若不变求出该定值,若变化说明理由.12.如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)与坐标轴分别交于点A(﹣3,0),B(1,0)和点C.(1)求出a与c的数量关系式;(2)如图,若抛物线y=-x2-2x+3与直线y=(2k1﹣2)x交于E,F两点,与直线y=(2k2﹣2)x交于M,N两点,且k1k2=﹣1,点P,Q分别是EF、MN的中点,求证:直线PQ必定经过一个定点,并求出该定点坐标.13.已知抛物线y=ax2+bx+5(a≠0)经过点(4,5).(1)若a+b=﹣3,求抛物线y=ax2+bx+5的解析式;(2)在(1)的条件下,经过点A(2,54)的任意直线y=mx+n(m≠0)与(1)中的抛物线交于B,C两点,那么11AB AC的值是定值吗?如果是定值,请求出这个定值,如果不是定值,请说明理由.14.如图1,抛物线C:y=ax2+bx﹣3与x轴的正半轴交于点B,与y轴交于点C,OB=OC,其对称轴为直线x=1.(1)直接写出抛物线C的解析式;(2)如图2,将抛物线C平移得到抛物线C1,使C1的顶点在原点,过点P(t,﹣1)的两条直线PM,PN,它们与y轴不平行,都与抛物线C1只有一个公共点分别为点M和点N,求证:直线MN必过定点.参考答案1.解:(1)OB=OC,C(0,c)则B(-c,0),代入抛物线解析式得c 2-bc+c=0,c-b+1=0,即当x=-1时,y =1-b+c=0,故抛物线过点(-1,0),故A(-1,0),B(3,0),C(0,-3)抛物线的解析式为y =x 2-2x -3(2)过点M 作MG||x 轴交AC 于点G ,作FP||x 轴交AM 于点P ,作CQ||x 轴,易知∆COA~∆CMG ,∆ACQ~∆AGM ,GM CG OA AC =GM AG CQ AC =,GM GM CG AG 1OA CQ AC AC+=+=即得111OA CQ GM+=,而AM 平分∠BAC ,故AC=CQ ,故111OA AC GM +=;同时CG AC GM AE =,AF GM AC CQ=即可得111AE AF GM +=,OA=1,AC=10,故11101AE AF 10+=+2.解:(1)y =-x 2-3x +4(2)存在t 的值使得OP 与OQ 的积为定值,t=-4设E(m ,-m 2-3m+4),F(n,-n 2-3n+4),设BE 的解析式为y =k (x -1),将E 点坐标代入得k =-m -4,同理k =-n -4,则OP=m+4,OQ=-n-4,故OP ∙OQ=(m+4)(-n-4)=-mn-4(m+n)-16,直线CE 的解析式为y =k 1(x-t )-1,与抛物线y =-x 2-3x +4联立得x 2+(k 1+3)x-k 1t -5=0,m+n=-k 1-3,mn =-k 1t -5,OP ∙OQ=k 1t+4k 1+1=4k 1(t+4)+1,当t=-4时,OP ∙OQ 为定值,故当t=-4时,OP ∙OQ=13.解:(1)y =x 2-2x-3(3)易知T(2,-3),设直线TS 的解析式为y=m(x-2)-3,与抛物线y =x 2-2x-3联立得x 2-(m +2)x +2m =0,有两个相等实根,m 2+4m+4-8m=0,故m=2,即TS 解析式为y =2x -7,设MN 的解析式为y =2x+h ,与抛物线联立得x 17+h ,x 27+h 故7+h ,7+h ),N(2-7+h 7+h ),直线AM 解析式为y 1=k 1x+b 1,得b 1737hh +++737hh +++,同理可得773hh ++-,OH-OG=24.解:6,6,4;(2)MP ∙MQ 的值不变.y =21362x -与y =kx -4k 联立得x 2+6kx +9-24k =0,x A +x B =6k ,x A ∙x B =9-24k ,M(4,0),MP ∙MQ=(4-x P )(4-x Q )=16-4(x A +x B )+x A x B =16+24k+9-24k=255.解:(1)易得抛物线的解析式为y =12x 2-x ,圆的直径为BE ,故∠BDE=90°,且∠BED=∠BAD=45°,作MN ⟂OA 交BC 、OA 于点M 、N ,易知∆BDM ≅∆DEN ,设DM=NE=m ,则CM=ON=m ,而OE=2,故m=1,此时D(1,3)(2)不变,CF ∙AD=16,∠DBF=∠BAD=45°,故∆ADB~∆CBF ,故CF ∙AD=AB ∙CB=166.解:(1)y =12(x -2)2(2)设直线MN 的解析式为y=kx+b ,与抛物线联立得x 2-(4+2k )x +4-2b=0,x M +x N =4+2k,x M ∙x N =4-2b ,作ME 、NF 垂直于x 轴,易知∆AME~∆NAF ,AE ME NF AF =,即有AE ∙AF=ME ∙NF ,ME=kx 1+b ,NF=kx 2+b ,AE=2-x 1,AF=x 2-2,(2-x 1)(x 2-2)=(kx 1+b)(kx 2+b),即有4+2(x 1+x 2)-x 1x 2=k 2x 1x 2+kb (x 1+x 2)+b 2,整理得2k+b =0或2k +b -2=0,即当x =2时,y =2,所以直线l 必过定点(2,2)7.解:(1)y =-x 2+2x +3,P(1,4)(2)联立y=kx-k +3和抛物线y =-x 2+2x +3得x 2+(k-2)x-k=0,x 1+x 2=k-2,x 1x 2=-k,过点M 、N 作对称轴的垂线ME 、NF ,tan ∠PME=PE ME =221111114(23)(1)111x x x x x x --++-==---,同理tan ∠PFN=211x -,(1-x)(x2-1)=1,故tan ∠PME=tan ∠FPN,∠PME=∠FPN ,故∠MPN=90°,所以无论k 为何值,∆PMN 恒为直角三角形.8.解:(1)y =-x 2+2x +3(2)CE CF 的值为定值13,设P(t,-t 2+2t+3),直线AP 的解析式为y =(3-t)x +3-t ,直线BP 的解析式为y =(-t-1)x +3t+3,故CE=-t ,CF=-3t ,故CE CF =139.(1)y =2124x -(2)(PM+MO)(PN-ON)为定值,设直线l 的解析式为y=kx ,与抛物线联立得x 2-4kx -8=0,设M(x 1,y 1),N(x 2,y 2)则有x 1x 2=-8,,y 1=kx 1,故PM=|x 1OM=|x 1,同理PN=|x 2,ON=|x 2,故+|x 1)(|x 2-|x 2)=16,故(PM+MO)(PN-ON)为定值16.10.解:(1)y=-x 2-x +2(2)连接MH ,易知AMP=CMH ,设PQ 的解析式为y=kx+b 1,MH 的解析式为y=-kx+b 2,分别代入(-12,0)得b 1=12k ,b 2=12-k ,故PM 的解析式为y=kx+12k ,MH 的解析式为y=-kx-12k 与抛物线联立得x=(1)92k -+±,所以Q((1)92k -++,292k -±),同理可得H(192k -,292k --),易知QH 的解析式为y=-x +992-当x=-12时,y=92,所以G(-12,92),所以点P 运动过程中GM 长为定值9211.解:(1)y =x 2-2x(2)FC(AC+EC)为定值,设Q(m ,m 2-2m ),易得BF 的解析式为y=(m -1)x -3m ,故点F(311m m -+,-1),D(1,-1),DE 的解析式为y=(m-1)x-m ,E(3,2m-3),FC=3-311m m -+=41m +,AC+EC=4+2m-3+1=2m+2,所以FC(AC+EC)=41m +(2m+2)=812.解:(1)c =-3a (2)联立y =-x 2-2x +3与y =(2k 1﹣2)x 得x 2+2k 1x -3=0所以x 1+x 2=-2k 1,y 1+y 2=-4k 12+4k 1,故P(-k 1,-2k 12+2k 1),同理可得Q(-k 2,-2k 22+2k 2),设直线PQ 的解析式为y=kx+b,将P 、Q 两点代入得y =(2k 1+2k 2-2)x -2,所以直线PQ 过定点(0,-2)13.解:(1)y=x 2-4x +5(3)将坐标系向右平移2个单位,向上平移1个单位,此时抛物线的解析式为y=x2,点A(0,14),设B(m,m 2),C(n,n 2),则AB=m 2+14,AC=n 2+14,故11AB AC +=AB AC AB AC +⋅=22221211()()416m n mn m n +++++,同时BC 的解析式y=kx +14,与抛物线联立得x 2-kx -14=0,m+n=k,mn =-14,故11AB AC +=414.解:(1)y =x 2-2x -3(2)平移后的抛物线的解析式为y =x 2,设M(m,m 2),N(n,n 2),直线PM 的解析式设为y=k 1(x-m)+m 2,PN 的解析式为y=k 2(x-n)+n 2,与抛物线联立得x2-k1x+k1m-m2=0,此时∆=0,即有k 1=2m ,PM 的解析式为y=2m(x-m)+m 2=2mx-m 2同理可得PN 的解析式为y=2n(x-n)+n 2=2nx-n 2,可得P(2m n +,mn ),mn =-1,MN 的解析式为y=(m+n)x +1,故MN 过定点(0,1)。
二次函数中的线段最值问题

二次函数中的线段问题例1.如图,已知抛物线y=﹣x2﹣2x+3的对称轴为直线x=﹣1,且抛物线与x轴交于A、B 两点,与y轴交于C点,其中A(1,0),C(0,3).直线BC解析式y=x+3;(1)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(2)在抛物线的对称轴上找一点P使PB﹣PC的值最大,求出P点的坐标变式1.如图,已知抛物线y=﹣2x2﹣4x+6与x轴交于点A(﹣3,0)和点B,与y轴交于点C(0,6).在抛物线的对称轴上是否存在点P使PB﹣PC的值最大?若存在,求出P点的坐标,若不存在,请说明理由;例2.如图,抛物线y=﹣x2+x;过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.当t为何值时,矩形ABCD的周长有最大值?最大值是多少?例3.如图,已知抛物线y=﹣x2+x+4,的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧),与y轴交于C点(0,4).A、B的坐标分别为:(﹣2,0)、(8,0),A、B的坐标分别为:(﹣2,0)、(8,0)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求出M点的坐标.变式1.如图,二次函数y=﹣x2+2x+3,的图象交x轴于A,B两点,交y轴于点D,点B的坐标为(3,0),直线BD解析式为y=﹣x+3,P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限内时,求线段PM长度的最大值.变式2.如图,已知抛物线y=x2﹣2x﹣3经过点A(﹣1,0),B(3,0),C(0,﹣3)三点.直线BC的解析式为y=x﹣3,点P为抛物线在第四象限内的一个动点,过点P作PM⊥直线BC,垂足为M,当PM最大时,请直接写出此时点P的坐标.变式3.抛物线y=x2﹣2x﹣3与x轴交A(﹣1,0)和点B,交y轴于点C,对称轴为直线x=1.如图,若点D为线段BC下方抛物线上一点,过点D作DE⊥x轴于点E,再过点E作EF⊥BC于点F,请求出DE+EF的最大值.变式4.已知顶点为D的抛物线y=﹣x2+2x+3与x轴交于点A,B(点A在点B左边),直线y=n与抛物线分别交于点M,N(点M在点N左边).直线y=n与线段DB交于点P,求PN的最大值;变式5.已知抛物线y =(x ﹣1)2的顶点为(1,0),与y 轴的交点坐标为(0,).R (1,1)是抛物线对称轴l 上的一点.若P 是抛物线上的一个动点,求证:点P 到R 的距离与点P 到直线y =﹣1的距离恒相等;例4.如图,拋物线y=421-2++x x 与坐标轴交于A 、B 、C 三点,对称轴与x 轴交于点P,点E 是x 轴上方抛物线上的动点,过点E 作EN ⊥x 轴于点N.连接AE 交抛物线对称轴于点F,连接BE 并延长交对称轴于点G,试证明PF+PG 的值为定值,并求出该定值.作业1.已知如图,抛物线y=x 2+bx +c 过点A (3,0),B (1,0),交y 轴于点C ,点P 是该抛物线上一动点,点P 从C 点沿抛物线向A 点运动(点P 不与点A 重合),过点P 作PD ∥y 轴交直线AC 于点D .(1)求抛物线的解析式;(2)求点P 在运动的过程中线段PD 长度的最大值;(3)在抛物线对称轴上是否存在点M 使|MA ﹣MC |最大?若存在请求出点M 的坐标,若不存在请说明理由.2.如图,二次函数y =﹣x 2+x +2的图象与x 轴相交于点A (﹣1,0)、B (4,0),与y 轴相交于点C .直线BC 的解析式为y =﹣x +2,点P 为该函数在第一象限内的图象上一点,过点P 作PQ ⊥BC ,垂足为点Q ,连接PC .求线段PQ 的最大值;3.如图,P (m ,n )是抛物线142-=x y 上任意一点,l 是过点(0,﹣2)且与x 轴平行的直线,过点P 作直线PH ⊥l ,垂足为H .(1)填空:当m =0时,OP = ,PH = ;当m =4时,OP = ,PH = ;(2)对任意m ,n ,猜想OP 与PH 的大小关系,并证明你的猜想.4.已知抛物线y =x 2﹣4x+3与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,顶点为 D .点E 为x 轴下方抛物线y =x 2﹣4x+3上一动点,抛物线的对称轴DH 交x 轴于点H ,直线AE 交y 轴于点M ,直线BE 交对称轴DH 于点N ,求MO+NH 的值;。
二次函数与定点定值问题(教师版)
二次函数与定点、定值问题【方法归纳】已知抛物线和满足一定条件的直线在平面直角坐标系中,直线上的线段满足一定几何条件,图中可能产生一些定点,定量关系.通常要运用几何量的关系转换成线段关系和坐标关系求解. 思路:结合二次函数,将几何向代数转化,构建方程或方程组,并归纳解题一致性.例1.已知抛物线:y =ax 2+bx +c ,顶点坐标为原点,且过(4,8),如图,若A 、B 两点在抛物线上,且OA ⊥OB ,AB 交y 轴于H 点,求H 点的坐标.易求a =21,b =0,c =0,∴y =12x 2,设A (m ,21m 2),B (n ,12n 2),设AB 的解析式y =kx +b ,联立⎪⎩⎪⎨⎧+==b kx y xy 221得x 2-2kx -2b =0,m +n =2k ,mn =-2b ,又∵OA ⊥OB ,过A 点作AC 丄x 轴,BD ⊥y 轴,垂足分别为C 、D 两点,易证△AOC ∽△OBD ,∴OC AC =BD OD ,∴A A x y =B B y x -,∴m m221=221n n -,41mn =-1,∴mn=-4,∴b =2,∴H (0,2).(2013年武汉中考压轴题的关键一步)方法总结:_________________________________________________ _________________________________________________ _________________________________________________【练1】抛物线y =21(x -1)2,顶点为M ,直线AB 交抛物线于A 、B 两点,且MA ⊥MB ,求证:直线AB 过定点.设A (x 1,y 1),B (x 2,y 2),易求M (1,0),作AE ⊥x 轴,BF ⊥x 轴,△AEM ∽△BFM ,易得EM AE =FBMF,即111x y -=221y x -,1211)1(21x x --=222)1(211--x x ,∴-21(x 1-1)2=)1(2112-x ,∴-41[x 1x 2-(x 1+x 2)+1]=1,联立⎪⎩⎪⎨⎧+=-=b kx y x y 2)1(21得,21(x -1)2=kx +b ,x 2-2x +1=2kx +2b ,x 2-(2+2k )x +1-2b =0,x 1·x 2=1-2b ,x 1+x 2=2k +2,∴(1-2b )-(2k +2)+1=-4,k +b =2,∴y =kx +b =kx +2-k =k (x -1)+2,∴AB 过定点(1,2).例2.已知抛物线y =41x 2,以M (-2,1)为直角顶点作该抛物线的内接直角三角形MAB (即M ,A ,B 均在抛物线上),求证:直线AB 过定点,并求出该定点坐标.过M 作PQ ∥x 轴,AP ⊥PQ 于P ,BQ ⊥PQ 于Q ,设AB :y =kx +b , 由⎪⎩⎪⎨⎧+==bkx y xy 241得41x 2-kx -b =0,x A +x B =4k ,x A ·x B =-4b , 由△APM ∽△MQB 得AP ·BQ =PM ·MQ ,即(y A -1)(41x B 2-1)=-(x A +2)(x B +2), ∴161(x A -2)(x B -2)=-1,x A ·x B -2(x A +x B )+4=-16, ∴-4b -8k +4=-16,b =5-2k ,∴AB :y =kx +5-2k =k (x -2)+5,过定点(2,5).【练2】(2014武汉中考)如图,已知直线AB :y =kx +2k +4于抛物线y =21x 2交于A 、B 两点. (1)直线AB 总经过一个定点C ,请直接写出点C 坐标; (2)若在抛物线上存在定点D 使∠ADB =90°,求点D 到直线AB 的最大距离.(1)C (-2,4)(2)设A (x 1,21x 12),B (x 2,21x 22),D (m ,21m 2),由⎪⎩⎪⎨⎧++==42212k kx y xy 得x 2-2kx -4k -8=0,x 1+x 2=2k ,x 1·x 2=-4k -8,过D 作EF ∥x 轴,AE ⊥EF 于E ,BF ⊥EF 于F ,由△AED ∽△DFB 得AE ·BF =DE ·DF ,即(21x 12-21m 2)(21x 22-21m 2)=(m -x 1)(x 2-m ),化简x 1x 2+m (x 1+x 2)+m 2=4,∴2k (m -2)+m 2-4=0,当m -2=0,即m =2时,点D 的坐标与k 无关,∴D (2,2),又∵C (-2,4),∴CD =25,作DM ⊥AB 于M ,则DM ≤CD =25,∴当CD ⊥AB 时,点D 到直线AB 的距离最大,最大距离为25.例3.如图,抛物线y =x 2+3顶点为P ,直线l 交抛物线于A 、B 两点,交y 轴于C 点,∠AOC =∠BOC ,求证:直线AB 过定点.设A (m ,m 2+3),B (n ,n 2+3),设直线AB 的解析式为y =kx +b ,⎩⎨⎧+=+=32x y bkx y ,∴kx +b =x 2+3,x 2-kx +3-b =0,∴mn =3-b ,∵∠AOC =∠BOC ,∴tan ∠AOC =tan ∠BOC ,∴32+m m =32+-n n,∴mn 2+3m =-m 2n -3n ,∴mn =-3,∴b =6,∴C (0,6).【练3】抛物线y =x 2-4x +5,对称轴交x 轴于P 点,直线EF 交抛物线于E 、F ,交对称轴于H ,且∠EPH =∠FPH ,求证:EF 恒过定点.E (x 1,y 1),F (x 2,y 2),⎩⎨⎧+-=+=542x x y bkx y ,∴x 2-(4+k )x +5-b =0,x 1+x 2=4+k ,x 1x 2=5-b ,tan ∠EPH =tan ∠FPH ,∴112y x -=222y x -,∴(kx 1+b)(x 2-2)=(kx 2+b )(2-x 1),∴b +2k =2,y =kx +b ,∴直线过(2,2).例4.如图,抛物线y =x 2-1交x 轴于A 、B 两点,直线y =a (a >0)交抛物线于M 、N ,点C 在抛物线上,且∠MCN =90°,点C 到MN 的距离是否为定值?若是,求出这个定值.作CH ⊥MN 于H .则∠MCH =∠CNH ,Rt △MCH ∽Rt △CNH ,CH 2=MH ·HN ,令C (x C ,t ),M (m ,m 2-1),则N (-m ,m 2-1),CH =m 2-1-t ,MH ·HN =(x C -x M )(x N -x C )=-x C 2+m 2,y C =x C 2-1=t ,故x C 2=t +1,-x C 2=-t -1,即MH ·HN =m 2-1-t ,又CH 2=MH ·HN ,∴(m 2-1-t )2=m 2-1-t ,∴m 2-1-t =0(舍去)或m 2-1-t =1,即CH =m 2-1-t =1,点C 到MN 的距离是定值,这个值为1.【练4】(2015永州改)如图,抛物线:y =41(x -1)2,R (1,1)是对称轴l 上一点,点P 为抛物线上一个动点,PM 垂直于直线y =-1于M ,求PRPM的值.设P (t ,41(t -1)2),连PR ,作PM ⊥直线y =-1于点M ,PM =41(t -1)2+1, PR =222]1)1(41[)1(--+-t t =41(t -1)2+1,∴PM =PR ,∴PRPM=1.【课后反馈】1.如图,抛物线y =x 2-1交x 轴正半轴于A (1,0),M 、N 在抛物线上,且MA ⊥NA ,试说明MN 恒过一定点,求此定点的坐标.作MP ⊥x 轴于P ,NQ ⊥x 轴于Q ,设MN :y =mx +n ,由21y mx ny x =+⎧⎪⎨=-⎪⎩得x 2-mx -n -1=0,x M +x N =m ,x M ·x N =-1-n ,tan ∠MAP =PA MP =211M M x x --=-x M -1,tan ∠ANQ =AQ NQ =211N N x x --=11Nx +.由∠MAP =∠ANQ 得-x M -1=11Nx +,即-x M ·x N -(x M +x N )-1=1,1+n -m -1=1,n =m +1,MN :y =mx +m+1=m (x +1)+1,故MN 过定点(-1,1).2.如图,抛物线y =41(x -4)2-4的顶点为P ,M ,N 均在对称轴上,且PM =PN ,延长OM 交抛物线于点A .求证:∠ANM =∠ONM .易求P (4,-4),设A (m ,41m 2-2m ),可求OA :y =(41m -2)x ,点M 在OA 上,x =4时,y =m -8,∴M (4,m -8),故N (4,-m ),tan ∠ONM =N N x y -=4m ,tan ∠ANM =4A A N x y y --=2412()4m m m m ----=41(4)4m m m --=4m ,故∠ANM =∠ONM .3.(2016六初九下2月考T24)已知抛物线y =41x 2+m 与x 轴交于A 、B 两点,与y 轴交于C 点,且OA =2OC ,直线y =kx -2k +4(k ≠0)与抛物线交于D 、E 两点. (1)求m 值及A 点坐标;(2)当k 取何值时,△ADE 的面积最小,并求面积的最小值;(3)若M 、N 为抛物线上两点,其以MN 为直径的圆始终经过A 点,求直线MN 经过的定点P 的坐标.(1)令x =0时,y =m ,∴OC =-m ,令y =0时,x =m -±2,∴OA =m -2, ∵OA =2OC ,∴m -2=2(-m ),m =-1,∴A (2,0);(2)直线y =kx -2k +4过定点(2,4),过点A 作AF ∥y 轴交DE 于F ,∴F (2,4), 设D (x 1,y 1)、E (x 2,y 2),∴S △ADE =21×4×(x 1-x 2)=2(x 1-x 2), 联立⎪⎩⎪⎨⎧-=+-=141422x y k kx y ,整理得41x 2-kx +2k -5=0,∴x 1+x 2=4k ,x 1x 2=8k -15 ∴S △ADE =2212142)(x x x x -+=84)1(2+-k ,当k =1时,S △ADE 有最小值,最小值为16; (3)设M (x 1,y 1)、N (x 2,y 2), ∵∠MAN =90°,过点M 作ME ⊥x 轴于E ,过点N 作NF ⊥x 轴于F ,∴△MEA ∽△AFN ,∴212122y x x y -=-,y 1y 2=(x 2-2)(2-x 1), 即)141)(141(2121--x x )=(x 2-2)(2-x 1),x 1x 2+2(x 1+x 2)+20=0,设直线MN 的解析式为y =kx +b ,联立⎪⎩⎪⎨⎧-=+=1412x y bkx y ,整理得x 2-4kx -4-4b =0, ∴x 1+x 2=4k ,x 1x 2=-4-4b ,∴-4-4b +2×4k +20=0,2k -b =-4, 当x =-2时,-2k +b =4,∴直线MN 必过顶点(-2,4).。
中考数学知识点方法必备07二次函数中定值、定点问题(8类题型)解析版

方法必备07二次函数中定值、定点问题(8类题型)1.(2023•花都区二模)已知,抛物线22(22)2y x m x m m =-+++与x 轴交于A ,B 两点(A 在B 的左侧).(1)当0m =时,求点A ,B 坐标;(2)若直线y x b =-+经过点A ,且与抛物线交于另一点C ,连接AC ,BC ,试判断ABC D 的面积是否发生变化?若不变,请求出ABC D 的面积;若发生变化,请说明理由;(3)当5221m x m --……时,若抛物线在该范围内的最高点为M ,最低点为N ,直线MN 与x 轴交于点D ,且3MDND=,求此时抛物线的解析式.【分析】(1)将0m =代入可得22y x x =-,令0y =,解方程即可求解.(2)令0y =,有22(22)20x m x m m -+++=,解方程得出A 点,B 点坐标,则2AB =,由直线y x b =-+经过点(,0)A m ,可得y x m =-+,联立求解方程组得到C 点坐标,即可求解.(3)求出32m >,由题可知对称轴为1x m =+,则对称轴512x m =+…,求得5122x m =+>…,即抛物线的对称轴在直线2x =的右侧,分情况讨论:①若211m m -+…,2m …,即322m <…时,证明MDH NDG D D ∽,利用相似三角形的性质即可求解;②若2121m m <+<-,即2m >,由||3||M N y y =,得2924153m m -+=,求解即可.【解答】解:(1)当0m =时,22y x x =-,当0y =时,有220x x -=,解得10x =,22x =,A Q 在B 的左侧,\点A 坐标为(0,0),点B 坐标为(2,0).(2)ABC D 的面积不变.对于抛物线22(22)2y x m x m m =-+++,当0y =时,有22(22)20x m x m m -+++=,解得:1x m =,22x m =+.A Q 在B 的左侧,\点A 坐标为(,0)m ,点B 坐标为(2,0)m +,2AB \=,Q 直线y x b =-+经过点(,0)A m ,0m b \=-+,b m \=,y x m \=-+,联立22(22)2y x m y x m x m m =-+ìí=-+++î解得1x m =,21x m =+,Q 点C 在y x m =-+上,当21x m =+时,1C y =-,C \点坐标为(1,1)m +-.11||21122ABC C S AB y D \=´´=´´=,ABC \D 的面积不发生变化,1ABC S D =.(3)5221m x m --Q ……,5221m m \-<-,32m \>.由题可知对称轴为1x m =+,则对称轴512x m =+…,Q522122m m -+-=,即范围5221m x m --……的中点为2x =,\5122x m =+>…,即抛物线的对称轴在直线2x =的右侧.①若211m m -+…,2m …,即322m <…时,Q 抛物线开口向上,当5221m x m --……时,y 随x 的增大而减小,如图,当52x m =-时,取最高点2(52,92415)M m m m --+,当21x m =-时,取最低点2(21,43)N m m m --+,分别过点M ,N 作x 轴的垂线交于点H ,G ,则MDH NDG D D ∽,\3MH MDNG ND ==,即||3||M N y y =,\22|92415|3|43|m m m m -+=-+,解得1m =(舍)或2m =,\当2m =时,抛物线的解析式为268y x x =-+.②若2121m m <+<-,即2m >,\最低点在顶点处取得,(1,1)N m \+-,当52x m =-时,取最高点2(52,92415)M m m m --+,由||3||M N y y =,得2924153m m -+=,解得1222,3m m ==,2m >Q ,1m \与2m 不符合题意,舍去,综上所述,抛物线的解析式为268y x x =-+.【点评】本题考查了二次函数综合,二次函数的图象与性质,相似三角形的性质与判定等知识,熟练掌握二次函数的图象和性质是解题的关键.2.(2023•兴化市一模)已知抛物线2(0)y ax a =>经过第二象限的点A ,过点A 作//AB x 轴交抛物线于点B ,第一象限的点C 为直线AB 上方抛物线上的一个动点.过点C 作CE AB ^于E ,连接AC 、BC .(1)如图1,若点(1,1)A -,1CE =.①求a 的值;②求证:ACE CBE D D ∽.(2)如图2,点D 在线段AB 下方的抛物线上运动(不与A 、B 重合),过点D 作AB 的垂线,分别交AB 、AC 于点F 、G ,连接AD 、BD .若90ADB Ð=°,求DF 的值(用含有a 的代数式表示).(3)在(2)的条件下,连接BG 、DE ,试判断BGF DBE S S D D 的值是否随点D 的变化而变化?如果不变,求出S BGFS DBED D 的值,如果变化,请说明理由.【分析】(1)①待定系数法求a 值,②用两边对应成比例夹角相等判定相似.(2)(3)先设点坐标,依题意代数运算,分别用所设值表示DF 长,BGF D 与DBE D 面积,即可.【解答】(1)①(1,1)A -Q 在抛物线上,2(1)1a \-=,解得:1a =.②B Q 在抛物线上,且//AB x 轴,B \与A 关于2y x =的对称轴y 轴对称.(1,1)B \.1CE =Q ,C \的纵坐标2.令2y =,即:22x =,解得:x =),x =.C \,2),又CE AB ^Q ,E \,1),1AE \=+,1BE =-,\AE CECE BE=,又90AEC CEB Ð=Ð=°Q ,ACE CBE \D D ∽.(2)设:2(,)A n an -,2(,)B n an ,2(,)D m am ,则22DF an am =-.若90ADB Ð=°,则ABD D 为Rt △,根据勾股定理可得:222AD DB AB +=.即:222222222()()()()(2)m n an am an am n m n ++-+-+-=.整理得:221an am a -=,即:1DF a=.(3)依题意设:2(,)A n an -,2(,)B n an ,2(,)C p ap ,2(,)D m am ,2(,)E p an .DG AB ^Q ,CE AB ^,//FG EC \,AFG AEC \D D ∽,\FG AF m n CE AE p n+==+,\22()()()m nFG ap an a m n p n p n+=-=+-+.\22111()()()()()222BGF S BF FG n m a m n p n a p n n m D =××=-×+-=--.2211()()22DBE S BE DF a p n n m D =××=--.\1BGFDBES S D D =.即:BGFDBES S D D 的值不随D 的变化而变化,其值为1.【点评】本题考查了二次函数的性质,相似三角形的判定等知识,先设后求再验证的思路体系,在本题中有充分体现;同时对运算能力要求较高.3.(2023•绵阳)如图,抛物线经过AOD D 的三个顶点,其中O 为原点,(2,4)A ,(6,0)D ,点F 在线段AD 上运动,点G 在直线AD 上方的抛物线上,//GF AO ,GE DO ^于点E ,交AD 于点I ,AH 平分OAD Ð,(2,4)C --,AH CH ^于点H ,连接FH .(1)求抛物线的解析式及AOD D 的面积;(2)当点F 运动至抛物线的对称轴上时,求AFH D 的面积;(3)试探究FGGI的值是否为定值?如果为定值,求出该定值;不为定值,请说明理由.【分析】(1)运用待定系数法可得2132y x x =-+.设点O 到AD 的距离为d ,点A 的纵坐标为A y ,根据三角形面积公式即可求得12AOD S D =;(2)当点F 运动至对称轴上时,点F 的横坐标为3,可得14AF AD =.连接OC 、OH ,由点A 与点C 关于原点O 对称,可得点A 、O 、C 三点共线,且O 为AC 的中点.推出//HO AD ,可得点H 到AD 的距离为d .再根据三角形面积公式即可求得答案;(3)过点A 作AL OD ^于点L ,过点F作FK GE ^于点K.运用勾股定理可得OA ==FIK D 为等腰直角三角形.设FK m =,则KI m=,再运用解直角三角形可求得2GK m =,FG =,即可求得答案.【解答】解:(1)设抛物线的解析式为2(0)y ax bx a =+¹.将(2,4)A ,(6,0)D 代入,得4243660a b a b +=ìí+=î,解得:123a b ì=-ïíï=î,2132y x x \=-+.设点O 到AD 的距离为d ,点A 的纵坐标为A y ,1116412222AOD A S AD d OD y D \=×=×=´´=.(2)221193(3)222y x x x =-+=--+Q ,\抛物线的对称轴为直线3x =.当点F 运动至对称轴上时,点F 的横坐标为3,则321624AF AD -==-,即14AF AD =.如图,连接OC 、OH ,由点(2,4)C -,得点A 与点C 关于原点O 对称,\点A 、O 、C 三点共线,且O 为AC 的中点.AH CH ^Q ,12OH AC OA \==,OAH AHO \Ð=Ð.AH Q 平分CAD Ð,OAH DAH \Ð=Ð,AHO DAH \Ð=Ð,//HO AD \,HO \与AD 间的距离为d ,\点H 到AD 的距离为d .12AFH S AF d D =´´Q ,1122AOD S AD d D =´´=,111111()123224424AFH S AF d AD d AD d D \=´´=´´=´´´=´=.\当点F 运动至抛物线的对称轴上时,AFH D 的面积为3;(3)如图,过点A 作AL OD ^于点L ,过点F 作FK GE ^于点K .由题意得4AL =,2OL =,OA \===.624DL OD OL \=-=-=,在Rt ADL D 中,AL DL =,45ADL \Ð=°,GE DO ^Q ,45FIK \Ð=°,即FIK D 为等腰直角三角形.设FK m =,则KI m =,在Rt AOL D 和Rt GFK D 中,//GF AO Q ,AOL GFK \Ð=Ð,tan tan AOL GFK \Ð=Ð,\AL GKOL FK =,即42GKm=,2GK m \=,23GI GK KI m m m \=+=+=.又sin sin AOL GFK Ð=ÐQ ,\AL GKAO FG =,2m FG =,FG \=,\FG GI ==.\FGGI【点评】本题是二次函数综合题,考查了待定系数法求函数解析式,二次函数的图象和性质,等腰直角三角形的判定和性质,图形的面积计算,相似三角形判定和性质,解直角三角形等,添加辅助线构造直角三角形是解题关键.4.(2023•金东区三模)如图,一次函数(0,0)by x b a b a=-+>>与坐标轴交于A ,B 两点,以A 为顶点的抛物线过点B ,过点B 作y 轴的垂线交该抛物线于另一点D ,以AB ,AD 为边构造ABCD Y ,延长BC 交抛物线于点E .(1)若2a b ==,如图1.①求该抛物线的表达式.②求点E 的坐标.(2)如图2,请问BEAB是否为定值,若是,请求出该定值;若不是,请说明理由.【分析】(1)①将a ,b 的值代入一次函数解析式,可求出点A ,B 的坐标,利用待定系数法可得出结论;②由抛物线的对称性可得点D 的坐标,根据平行四边形的性质可求出点C 的坐标,进而求出直线BE 的表达式,联立直线和抛物线的解析式即可得出结论;(2)根据待定系数法可求出A ,B 的坐标,进而可表达AB 的根据对称性可得出点D 的坐标,根据菱形的性质可得出点C 的坐标,进而求出直线BE 的解析式,联立可求出点E 的坐标,进而求出BE 的长度,求比值即可得出结论.【解答】解:(1)当2a b ==时,一次函数为2y x =-+,令0x =,则2y =;令0y =,则2x =,(2,0)A \,(0,2)B ,\设抛物线的表达式为:2(2)y m x =-,将(0,2)B 代入可得,42m =,解得12m =;\抛物线的解析式为:21(2)2y x =-;②由抛物线的对称性可得,(4,2)D ,由平行四边形的性质可知,(2,4)C ,\直线BE 的解析式为:2y x =+,令21(2)22y x x =-=+,解得0x =(舍)或6x =,(6,8)E \;(2)是定值,理由如下:对于(0,0)by x b a b a=-+>>,令0x =,则y b =;令0y =,则x a =,(,0)A a \,(0,)B b ,\设抛物线的表达式为:2()y m x a =-,AB =将(0,)B b 代入可得,2a m b =,解得2b m a =;\抛物线的解析式为:22()by x a a=-;由抛物线的对称性可得,(2,)D a b ,由平行四边形的性质可知,(,2)C a b ,\直线BE 的解析式为:by x b a=+,令22()b b y x a x b a a=-=+,解得0x =(舍)或3x a =,(3,4)E a b \;BE \==,\3BE AB ==.【点评】本题属于二次函数综合题,主要考查待定系数法求函数解析式,平行四边形的性质,抛物线的对称性,二次函数图象与一次函数图象交点问题等相关知识,表达出点C 的坐标是解题关键.5.(2023•黑龙江一模)已知,抛物线2y ax bx c =++经过(1,0)A -、(3,0)B 、(0,3)C 三点,点P 是抛物线上一点.(1)求抛物线的解析式;(2)当点P 位于第四象限时,连接AC ,BC ,PC ,若PCB ACO Ð=Ð,求直线PC 的解析式;(3)如图2,当点P 位于第二象限时,过P 点作直线AP ,BP 分别交y 轴于E ,F 两点,请问CECF的值是否为定值?若是,请求出此定值;若不是,请说明理由.【分析】(1)将(1,0)A -、(3,0)B 、(0,3)C 代入2y ax bx c =++,即可求解;(2)过点B 作MB CB ^交于点M ,过点M 作MN x ^轴交于点N ,由题意可得1tan 3BMBCM BCÐ==,求出BM =,再由45NBM Ð=°,求出点(2,1)M -,求直线CM 的解析式即为所求;(3)设2(,23)P t t t -++,分别由待定系数法求出直线AP 的解析式,直线BP 的解析式,就能求出CE 和CF 的长,即可求解.【解答】解:(1)将(1,0)A -、(3,0)B 、(0,3)C 代入2y ax bx c =++,\09303a b c a b c c -+=ìï++=íï=î,\123a b c =-ìï=íï=î,223y x x \=-++;(2)过点B 作MB CB ^交于点M ,过点M 作MN x ^轴交于点N ,(1,0)A -Q 、(0,3)C ,(3,0)B ,1OA \=,3OC =,BC =,1tan 3ACO \Ð=,PCB ACO Ð=ÐQ ,1tan 3BMBCM BC\Ð==,BM \=OB OC =Q ,45CBO \Ð=°,45NBM \Ð=°,1MN NB \==,(2,1)M \-,设直线CM 的解析式为y kx b =+,\321b k b =ìí+=-î,\23k b =-ìí=î,\直线PC 的解析式为23y x =-+;(3)CE CF 的值是为定值13.,理由如下:设2(,23)P t t t -++,设直线AP 的解析式为11y k x b =+,\2111123tk b t t k b ì+=-++ïí-+=ïî,\1133k tb t =-ìí=-î,(3)(3)y t x t \=-+-,(0,3)E t \-,CE t \=-,设直线BP 的解析式为22y k x b =+,\222222330k t b t t k b ì+=-++ïí+=ïî,\22133k t b t =--ìí=+î,(1)33y t x t \=--++,(0,33)F t \+,3CF t \=-,\13CE CF =,\CE CF 的值是为定值13.【点评】本题是二次函数的综合题,熟练掌握二次函数的图象及性质,用待定系数法求函数解析式的方法是解题的关键.6.(2023•红桥区三模)已知抛物线22(y ax bx a =++,b 为常数,0)a ¹经过点(1,0)A -,(3,0)B ,与y 轴相交于点C ,其对称轴与x 轴相交于点E .(1)求该抛物线的解析式;(2)连接BC ,在该抛物线上是否存在点P ,使PCB ABC Ð=Ð?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)Q 为x 轴上方抛物线上的动点,过点Q 作直线AQ ,BQ ,分别交抛物线的对称轴于点M ,N ,点Q 在运动过程中,EM EN +的值是否为定值?若是,请求出该定值;若不是,请说明理由.【分析】(1)把A 、B 两点坐标代入22y ax bx =++,求出a ,b 的值即可.(2)点P 的位置要分类讨论,P 在BC 上方时,P 和C 是对称点,已知C 的坐标,可求P .P 在BC 下方时,利用等边对等角,勾股定理求出D 的坐标,求出CD 的表达式,再求直线CD 和抛物线的交点坐标,可得P 的坐标.(3)添加辅助线QF x ^轴,得平行线,找出成比例线段,用坐标表示线段,求出EM EN +的值.【解答】解:(1)抛物线22(y ax bx a =++,b 为常数,0)a ¹经过点(1,0)A -,(3,0)B ,209320a b a b -+=ìí++=î,解得2343a b ì=-ïïíï=ïî.224233y x x \=-++.,(2)224233y x x =-++.\点C 坐标(0,2),①P 点在BC 的上方,PCB ABC Ð=Ð,//PC x \轴,\点C 、P 是一对对称点,对称轴是直线12bx a=-=.P \点坐标为(2,2).②P 在BC 下方,PCB ABC Ð=Ð,DC DB \=,设D 的坐标为(,0)d ,3BD CD d \==-,根据勾股定理得,224(3)d d +=-,56d \=,D \的坐标5(6,0).设直线CD 的表达式为y kx b =+,5062k bb ì=+ïíï=î,解得:1252k b ì=-ïíï=î,1225y x \=-+.当2241222335x x x -++=-+时,解得10x =(不合题意,舍去),2285x =.285x \=,122828625525y =-´+=-.P \的坐标28(5,286)25-.,(3)作QM x ^轴于F .MN x ^Q 轴于E ,//MN QF \,\,AE EM EN EBAF FQ FQ FB ==,\EM EN AE EBFQ AF FB+=+,设Q 点坐标为(,)x y,2AE \=,1AF x =+,2BE =,3BF x =-,224233FQ y x x ==-++.22224((2)1333EM EN x x x x \+=+´-+++-2222()()(23)133x x x x =+´-´--+-222()((3)(1)313x x x x =-+´-++-4(31)3x x =-´--+163=.EM EN \+的值为定值,163EM EN +=.【点评】此题考查了待定系数法,二次函数的性质,等角对等边,勾股定理,比例线段等知识点,以及数形结合的数学思想,难度较大,得分率较低.7.(2023•呼和浩特)探究函数22||4||y x x =-+的图象和性质,探究过程如下:(1)自变量x 的取值范围是全体实数,x 与y 的几组对应值列表如下:x¼52-2-32-1-12-012132252¼y¼52-32m323223252-¼其中,m =2.根据如表数据,在图1所示的平面直角坐标系中,通过描点画出了函数图象的一部分,请画出该函数图象的另一部分.观察图象,写出该函数的一条性质;(2)点F 是函数22||4||y x x =-+图象上的一动点,点(2,0)A ,点(2,0)B -,当3FAB S D =时,请直接写出所有满足条件的点F 的坐标;(3)在图2中,当x 在一切实数范围内时,抛物线224y x x =-+交x 轴于O ,A 两点(点O 在点A 的左边),点P 是点(1,0)Q 关于抛物线顶点的对称点,不平行y 轴的直线l 分别交线段OP ,AP (不含端点)于M ,N 两点.当直线l 与抛物线只有一个公共点时,PM 与PN 的和是否为定值?若是,求出此定值;若不是,请说明理由.【分析】(1)把1x =-代入22||4||y x x =-+即可求得2m =,运用描点法画出22||4||(0)y x x x =-+<部分的图象,观察图象描述性质即可;(2)当0x <时,224y x x =--,当0x …时,224y x x =-+,根据3FAB S D =,可求得点F 的纵坐标,代入解析式解方程即可;(3)利用待定系数法可得:直线OP 的表达式为4y x =①,直线AP 的表达式为48y x =-+②,由直线l 与抛物线只有一个公共点,可得直线l 的表达式为21(4)8y tx t =+-③,联立方程组可求得:1(4)8M x t =--,1(12)8N x t =--,再运用解直角三角形即可求得答案.【解答】解:(1)当1x =-时,22(1)4|1|2y =-´-+´-=,2m \=,函数图象如图所示:由图象可得该函数的性质:该函数关于y 轴对称;当1x <-或01x <…时,y 随x 的增大而增大;当10x -<…或1x …时,y 随x 的增大而减小;故答案为:2;(2)当0x <时,224y x x =--,当0x …时,224y x x =-+,(2,0)A Q ,(2,0)B -,4AB \=,3FAB S D =Q ,\14||32F y ´=,32F y \=±,当32F y =时,若0x <,则23242x x --=,解得:32x =-或12-,若0x …,则23242x x -+=,解得:32x =或12,3(2F \-,32或1(2-,3)2或3(2,3)2或1(2,3)2;当32F y =-时,若0x <,则23242x x --=-,解得:1x =-或1x =-+(舍去),若0x …,则23242x x -+=-,解得:12x =-(舍去)或12x =+,(1F \-+,32-或(1--32-或(1-3)2-或(1+3)2-;综上所述,所有满足条件的点F 的坐标为3(2-,32或1(2-,3)2或3(2,32或1(2,3)2或(1--32-或(1+3)2-;(3)PM 与PN 的和是定值;如图2,连接直线PQ ,Q 抛物线224y x x =-+交x 轴于O ,A 两点,(0,0)O \,(2,0)A ,22242(1)2y x x x =-+=--+Q ,\抛物线224y x x =-+的顶点为(1,2),Q 点P 是点(1,0)Q 关于抛物线顶点(1,2)的对称点,故点P 的坐标为(1,4),由点P 、O 的坐标得,直线OP 的表达式为4y x =①,同理可得,直线AP 的表达式为48y x =-+②,设直线l 的表达式为y tx n =+,联立y tx n =+和224y x x =-+并整理得:22(4)0x t x n +-+=,Q 直线l 与抛物线只有一个公共点,故△2(4)80t n =--=,解得21(4)8n t =-,故直线l 的表达式为21(4)8y tx t =+-③,联立①③并解得1(4)8M x t =--,同理可得,1(12)8N x t =--,Q 射线PO 、PA 关于直线:1PQ x =对称,则APQ OPQ Ð=Ð,设APQ OPQ a Ð=Ð=,则sin sin sin OQ APQ OPQ OP a Ð=Ð====,11)sin sin N M N M x x PM PN x x a a--\+=+=-=【点评】本题主要考查了二次函数的图象与性质,一次函数的图象与性质,抛物线上的点的坐标的特征,一次函数图象上点的坐标的特征,待定系数法确定函数的解析式,抛物线的平移的性质,利用点的坐标表示出相应线段的长度是解题的关键.8.(2023•平遥县一模)综合与探究.如图1,在平面直角坐标系中,已知二次函数224233y x x =-++的图象与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接BC .(1)求A ,B ,C 三点的坐标,并直接写出直线BC 的函数表达式;(2)点P 是二次函数图象上的一个动点,请问是否存在点P 使PCB ABC Ð=Ð?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)如图2,作出该二次函数图象的对称轴直线l ,交x 轴于点D .若点M 是二次函数图象上一动点,且点M 始终位于x 轴上方,作直线AM ,BM ,分别交l 于点E ,F ,在点M 的运动过程中,DE DF +的值是否为定值?若是,请直接写出该定值;若不是,请说明理由.【分析】(1)先根据二次函数的性质求出A ,B ,C 的坐标,再利用待定系数法求一次函数解析式;(2)分两种情况讨论,当点P 在BC 上方时,当点P 在BC 下方时,再利用勾股定理和待定系数法进行求解即可;(3)由(2)得抛物线的对称轴为直线1x =,求出点D 的坐标,设224(,2)33M t t t -++且13t -<<,分别求出直线AM 的解析式和直线BM 的解析式,进而表示出4444,333DE t DF t =-+=+,即可求解.【解答】解:(1)当0y =时,即2242033x x -++=,解得:11x =-,23x =.\图象与x 轴交于点(1,0)A -,(3,0)B ,当0x =时,2y =,\图象与y 轴交于点(0,2)C ,\直线BC 的函数表达式为223BC y x =-+;(2)存在,理由如下:当点P 在BC 上方时,PCB ABC Ð=ÐQ ,//CP AB \,即//CP x 轴,\点P 与点C 关于抛物线的对称轴对称,Q 224233y x x =-++,\抛物线的对称轴为直线43122()3x =-=´-;(0,2)C Q ,(2,2)P \;当点P 在BC 下方时,设CP 交x 轴于点(,0)K m ,则OK m =,3KB m =-.PCB ABC Ð=ÐQ ,3CK BK m \==-.在Rt COK D 中,222OC OK CK +=,2222(3)m m \+=-,解得:56m =,\5(,0)6K ,设直线CK 的解析式为y kx d =+,562k d d ì+=ïíï=î,解得:1252k d ì=-ïíï=î,\直线CK 的解析式为1225y x =-+,联立,得2122524233y x y x x ì=-+ïïíï=-++ïî,解得:1102x y =ìí=î(舍去),2228528625x y ì=ïïíï=-ïî,\28286(,525P -.综上所述,点P 的坐标为(2,2)或28286(,)525-;(3)存在,DE DF +的值为定值163,理由如下:由(2)得抛物线的对称轴为直线1x =,(1,0)D \,设224(,2)33M t t t -++且13t -<<,设直线AM 的解析式为11y k x b =+,将(1,0)A -和点M 的坐标代入得:11211024233k b tk b t t -+ìïí+=-++ïî,解得:11223223k t b t ì=-+ïïíï=-+ïî,\直线AM 的解析式为22(2)233y t x t =-+-+,当1x =时,443y t =-+,\4(1,4)3E t -+,同理,直线BM 的解析式为:22(2233y t x t =--++,当1x =时,4433y t =+,\44(1,33F t +,\4444,333DE t DF t =-+=+,\44416(4)3333DE DF t t +=++-+=,DE DF \+的值是定值,163DE DF +=.【点评】本题考查了二次函数的综合题目,涉及待定系数法求一次函数解析式,二次函数解析式,二次函数的图象和性质,熟练掌握知识点是解题的关键.9.(2023•广元)如图1,在平面直角坐标系中,已知二次函数24y ax bx =++的图象与x 轴交于点(2,0)A -,(4,0)B ,与y 轴交于点C .(1)求抛物线的解析式;(2)已知E 为抛物线上一点,F 为抛物线对称轴l 上一点,以B ,E ,F 为顶点的三角形是等腰直角三角形,且90BFE Ð=°,求出点F 的坐标;(3)如图2,P 为第一象限内抛物线上一点,连接AP 交y 轴于点M ,连接BP 并延长交y 轴于点N ,在点P 运动过程中,12OM ON +是否为定值?若是,求出这个定值;若不是,请说明理由.【分析】(1)待定系数法求解析式即可;(2)求出抛物线的对称轴为直线1x =,设对称轴l 与x 轴交于点G ,过点E 作ED l ^于点D ,证明DFG GBF D @D ,设(1,)F m ,进而得出E 点的坐标,代入抛物线解析式,求得m 的值,当E 点与A 点重合时,可得(1,3)F -或(1,3)F ;(3)设(,)P s t ,直线AP 的解析式为y dx f =+,BP 的解析式为y gx h =+,求得解析式,可得OM ,ON ,即可求解.【解答】解:(1)将点(2,0)A -,(4,0)B ,代入24y ax bx =++得:424016440a b a b -+=ìí++=î,解得:121a b ì=-ïíï=î,\抛物线解析式为2142y x x =-++;(2)Q 点(2,0)A -,(4,0)B ,\抛物线的对称轴为直线2412l x -+==,设直线l 与x 轴交于点G ,过点E 作ED l ^于点D ,当F 在x 轴上方时,如图:Q 以B ,E ,F 为顶点的三角形是等腰直角三角形,且90BFE Ð=°,EF BF \=,90DFE BFG GBF Ð=°-Ð=ÐQ ,90EDF BGF Ð=Ð=°,()DFE GBF AAS \D @D ,GF DE \=,GB FD =,设(1,)F m ,则DE m =,3DG DF FG GB FG m =+=+=+,(1,3)E m m \++,E Q 点在抛物线2142y x x =-++上,\213(1)(1)42m m m +=-++++,解得:3m =-(舍去)或1m =,(1,1)F \;当F 在x 轴下方时,如图:同理可得()DFE GBF AAS D @D ,GF DE =,GB FD =,设(1,)F n ,则(1,3)E n n --,把(1,3)E n n --代入2142y x x =-++得:213(1)(1)42n n n -=--+-+,解得3n =(舍去)或5n =-,(1,5)F \-;当E 点与A 点重合时,如图所示,6AB =Q ,ABF D 是等腰直角三角形,且90BFE Ð=°,\132GF AB ==,此时(1,3)F -,由对称性可得,点(1,3)F ¢也满足条件,综上所述,(1,1)F 或(1,5)-或(1,3)-或(1,3);(3)12OM ON +为定值6,理由如下:设(,)P s t ,直线AP 的解析式为y dx f =+,BP 的解析式为y gx h =+,Q 点(2,0)A -,(4,0)B ,(,)P s t ,\20d f s d f t -+=ìí+=î,40g h s g h t +=ìí+=î,解得:222t d s t f s ì=ïï+íï=ï+î,444t g s t h s ì=ïï-íï=ï-î,\直线AP 的解析式为222t t y x s s =+++,BP 的解析式为444t ty x s s =+--,在222t t y x s s =+++中,令0x =得22ty s =+,\2(0,)2tM s +,在444t t y x s s =+--中,令0x =得44ty s =-,4(0,)4tN s\-,(,)P s t Q 在抛物线上,2114(4)(2)22t s s s s \=-++=--+,21214126(4)(2)6222428(4)(2)t t t s s OM ON s s s s s s --+\+=+´===+--++--+,12OM ON \+为定值6.【点评】本题考查二次函数的综合应用,涉及待定系数法,等腰直角三角形等知识,解题的关键是用含字母的式子表示相关点坐标和相关线段的长度.10.(2023•扬州)在平面直角坐标系xOy 中,已知点A 在y 轴正半轴上.(1)如果四个点(0,0)、(0,2)、(1,1)、(1,1)-中恰有三个点在二次函数2(y ax a =为常数,且0)a ¹的图象上.①a = ;②如图1,已知菱形ABCD 的顶点B 、C 、D 在该二次函数的图象上,且AD y ^轴,求菱形的边长;③如图2,已知正方形ABCD 的顶点B 、D 在该二次函数的图象上,点B 、D 在y 轴的同侧,且点B 在点D 的左侧,设点B 、D 的横坐标分别为m 、n ,试探究n m -是否为定值.如果是,求出这个值;如果不是,请说明理由.(2)已知正方形ABCD 的顶点B 、D 在二次函数2(y ax a =为常数,且0)a >的图象上,点B 在点D 的左侧,设点B 、D 的横坐标分别为m 、n ,直接写出m 、n 满足的等量关系式.【分析】(1)①在2y ax =中,令0x =得0y =,即知(0,2)不在二次函数2(y ax a =为常数,且0)a ¹的图象上,用待定系数法可得1a =;②设BC 交y 轴于E ,设菱形的边长为2t ,可得2(,)B t t -,故AE ==,2(2,)C t t +,代入2y x =得224t t +=,可解得t =③过B 作BF y ^轴于F ,过D 作DE y ^轴于E ,由点B 、D 的横坐标分别为m 、n ,可得BF m =,2OF m =,DE n =,2OE n =,证明()ABF DAE AAS D @D ,有BF AE =,AF DE =,故22m n AF m =--,AF n =,即可得1n m -=;(2)过B 作BF y ^轴于F ,过D 作DE y ^轴于E ,由点B 、D 的横坐标分别为m 、n ,知2(,)B m am ,2(,)D n an ,分三种情况:①当B ,D 在y 轴左侧时,由()ABF DAE AAS D @D ,可得22m am AF an -=--,AF n =-,故1n m a-=;②当B 在y 轴左侧,D 在y 轴右侧时,由()ABF DAE AAS D @D ,有22m am AF an -=+-,AF n =,知0m n +=或1n m a -=;③当B ,D 在y 轴右侧时,22m an AF am =--,AF n =,可得1n m a-=.【解答】解:(1)①在2y ax =中,令0x =得0y =,(0,0)\在二次函数2(y ax a =为常数,且0)a ¹的图象上,(0,2)不在二次函数2(y ax a =为常数,且0)a ¹的图象上,Q 四个点(0,0)、(0,2)、(1,1)、(1,1)-中恰有三个点在二次函数2(y ax a =为常数,且0)a ¹的图象上,\二次函数2(y ax a =为常数,且0)a ¹的图象上的三个点是(0,0),(1,1),(1,1)-,把(1,1)代入2y ax =得:1a =,故答案为:1;②设BC 交y 轴于E ,如图:设菱形的边长为2t ,则2AB BC CD AD t ====,B Q ,C 关于y 轴对称,BE CE t \==,2(,)B t t \-,2OE t \=,AE ==Q ,2OA OE AE t \=+=,2(2,)D t t \+,把2(2,)D t t +代入2y x =得:224t t =,解得t =或0t =(舍去),\③n m -是为定值,理由如下:过B 作BF y ^轴于F ,过D 作DE y ^轴于E ,如图:Q 点B 、D 的横坐标分别为m 、n ,2(,)B m m \,2(,)D n n ,BF m \=,2OF m =,DE n =,2OE n =,Q 四边形ABCD 是正方形,90DAB \Ð=°,AD AB =,90FAB EAD EDA \Ð=°-Ð=Ð,90AFB DEA Ð=Ð=°Q ,()ABF DAE AAS \D @D ,BF AE \=,AF DE =,22m n AF m \=--,AF n =,22m n n m \=--,()()m n n m n m \+=-+,Q 点B 、D 在y 轴的同侧,0m n \+¹,1n m \-=;(2)过B 作BF y ^轴于F ,过D 作DE y ^轴于E ,Q 点B 、D 的横坐标分别为m 、n ,2(,)B m am \,2(,)D n an ,①当B ,D 在y 轴左侧时,如图:BF m \=-,2OF am =,DE n =-,2OE an =,同理可得()ABF DAE AAS D @D ,BF AE \=,AF DE =,22m am AF an \-=--,AF n =-,22m am n an \-=+-,()()m n a n m n m \+=-+,n m a\-=;②当B 在y 轴左侧,D 在y 轴右侧时,如图:BF m \=-,2OF am =,DE n =,2OE an =,同理可得()ABF DAE AAS D @D ,BF AE \=,AF DE =,22m am AF an \-=+-,AF n =,22m am n an \-=+-,()()m n a n m n m \+=+-,0m n \+=或1n m a-=;③当B ,D 在y 轴右侧时,如图:BF m \=,2OF am =,DE n =,2OE an =,同理可得()ABF DAE AAS D @D ,BF AE \=,AF DE =,22m an AF am \=--,AF n =,22m an n am \=--,()()m n a n m n m \+=+-,n m a\-=;综上所述,m 、n 满足的等量关系式为0m n +=或1n m a-=.【点评】本题考查二次函数的应用,涉及待定系数法,三角形全等的判定与性质,解题的关键是分类讨论思想的应用.11.(2023•长汀县模拟)在平面直角坐标系中,抛物线2(0)y ax bx c a =++>经过(2,0)A -,(0,2)B -两点.(1)用含a 的式子表示b ;(2)当2a =时,如图1,点C 是直线AB 下方抛物线上的一个动点,求点C 到直线AB 距离的最大值.(3)当1a =时,如图2,过点1(2P -,2)-的直线交抛物线2(0)y ax bx c a =++>于M ,N .①若//MN x 轴,计算11PM PN+=4 .②若MN 与x 轴不平行,请你探索11PM PN+是否定值?请说明理由.【分析】(1)将(2,0)A -,(0,2)B -代入抛物线解析式,利用待定系数法求解即可;(2)求出抛物线的解析式,进而求出点A ,B 的坐标,可得AOB D 是等腰直角三角形;过点C 作CF x ^轴于F ,交AB 于E ,则ECD D 是等腰直角三角形,设点C 的横坐标为m ,则2(,232)C m m m +-,则(,2)E m m --,可得22(1)2CE m =-++,所以21)CD m ==+,利用二次函数的性质可得结论;(3)①令2y =-,求出x 的值可得出M ,N 的坐标,分别表达PM ,PN 的长度,代入可得结论;②设直线MN 的解析式为22k y kx =+-,1(M x ,1)y ,2(N x ,2)y ,令2222kkx x x +-=+-,整理得2(1)02kx k x +--=,所以121x x k +=-,122k x x =-,分别表达PM ,PN 和MN 的长度,代入可得结论.【解答】解:(1)将(2,0)A -,(0,2)B -代入抛物线2y ax bx c =++,得4202a b c c -+=ìí=-î,21b a \=-;(2)当2a =时,212213b a =-=´-=,2232y x x \=+-,(2,0)A -Q ,(0,2)B -,OA OB \=,AOB \D 是等腰直角三角形,45OAB \Ð=°,如图1,过点C 作CF x ^轴于F ,交AB 于E ,则ECD D 是等腰直角三角形,\直线AB 的解析式为2y x =--,设2(,232)C m m m +-,则(,2)E m m --,2(2)(232)CE m m m \=---+-224m m=--22(1)2m =-++,21)2CD m \==++,0<Q ,20m -<<,\当1m =-时,CD 当1m =-时,2323y =--=-,综上,点C 的坐标为(1,3)--时,CD\点C 到直线AB ;(3)①当1a =时,抛物线的解析式为22y x x =+-,令2y =-,即222x x +-=-,解得0x =或1x =-,(1,2)M \--,(0,2)N -,12PM PN \==,\111141122PM PN +=+=,故答案为:4;②11PM PN+是定值.理由如下:Q 过点1(2P -,2)-的直线交抛物线22y x x =+-于M ,N ,设直线MN 的解析式为22ky kx =+-,1(M x ,1)y ,2(N x ,2)y ,令2222k kx x x +-=+-,整理得2(1)02kx k x +--=,121x x k \+=-,122kx x =-,1122ky kx =+-Q ,2222k y kx =+-,1212()y y k x x \-=-,2221212()()MN x x y y \=-+-2212(1)()k x x =+-221212(1)[()4]k x x x x =++-22(1)[(1)4()]2kk k =+--´-22(1)k =+,21MN k \=+,1(2P -Q ,2)-,======21(1)4k =+14MN =,\11414PM PN MN PM PN PM PN MN ++===×,\11PM PN+是定值.【点评】本题主要考查二次函数与一次函数的综合运用,掌握二次函数图象的性质,函数图象平移的性质,一次函数与二次函数交点的计算方法是解题的关键.12.(2023•宿豫区三模)如图,在平面直角坐标系中,一次函数15544y x =+的图象与x 轴交于点A ,与y 轴交于点C ,对称轴为直线2x =的抛物线22(0)yax bx c a =++¹也经过点A 、点C ,并与x 轴正半轴交于点B .(1)求抛物线22(0)y ax bx c a =++¹的函数表达式;(2)设点25(0,)12E ,点F 在抛物线22(0)y ax bx c a =++¹对称轴上,并使得AEF D 的周长最小,过点F 任意作一条与y 轴不平行的直线交此抛物线于1(P x ,1)y ,2(Q x ,2)y 两点,试探究11FP FQ+的值是否为定值?说明理由;(3)将抛物线22(0)y ax bx c a =++¹适当平移后,得到抛物线23()(1)y a x h h =->,若当1x m <…时,3y x -…恒成立,求m 的最大值.【分析】(1)根据一次函数图象与坐标轴的交点分别解出点A ,C 的坐标,根据抛物线的对称轴解出点C 的坐标,根据待定系数法即可求解抛物线的解析式;(2)根据轴对称求线段的最小值,图形结合分析,计算出点BE 的解析式,再解出点F 的坐标,用点P ,Q 分别表示出直线PQ 的解析式,根据勾股定理分别PQ ,PF ,QF 的值,由此即可求解;(3)根据抛物线的平移确定平移为左右平移,由此确定3y 的二次项系数,画出图形,根据二次函数与直线4y x =-的交点的情况判断34y y >的取值,由此即可求解.【解答】解:(1)一次函数15544y x =+的图象与x 轴交于点A ,与y 轴交于点C ,令0x =,则154y =,令10y =,则1x =-,(1,0)A \-,5(0,4C ,Q 抛物线22(0)y ax bx c a =++¹的对称轴为直线2x =,且抛物线过点(1,0)A -,5(0,)4C ,且抛物线与x 轴正半轴交于点B ,(5,0)B \,设函数表达式为2(1)(5)y a x x =+-,将点5(0,4C 代入解析式得,5(01)(05)4a +-=,解得14a =-,\抛物线的解析式为22115(1)(5)444y x x x x =-+-=-++;(2)11FP FQ+的值是定值,理由如下:AEF D Q 的周长为AE AF EF ++,由AEF D 的周长最小,AE 的长是定值,AF EF \+最小,连接BE 交对称轴于点F ,设BE 所在直线的解析式为BE y mx n =+,且(5,0)B ,25(0,12E ,\502512m n n +=ìïí=ïî,解得,5122512m n ì=-ïïíï=ïî,\直线BE 的解析式为5251212BE y x =-+,Q 点F 在抛物线的对称轴2x =的直线上,\点5(2,)4F ;Q 过点5(2,)4F 任意作一条与y 轴不平行的直线交此抛物线于1(P x ,1)y ,2(Q x ,2)y 两点,如图所示,过点P 作y 的平行线,过点Q 作x 轴的平行线,交于点K ,\设PQ y px q =+,把点5(2,)4F 代入得,\524p q =+,524q p \=-,\直线PQ 的解析为524PQ y px p =+-,令25152444px p x x +-=-++,整理得:2(44)80x p x p ---=,\根据韦达定理得,1244x x p +=-,128x x p =-,Q 点1(P x ,1)y ,2(Q x ,2)y 在直线PQ 上,在Rt PQK D 中,12PK y y =-,12QK x x =-,11524y px p \=+-,22524y px p =+-,1212()y y p x x \-=-,222PQ QK PK \=+221212()()x x y y =-+-2212(1)()p x x =+-221212(1)[()4]p x x x x =++-22(1)[(44)4(8)]p p p =+---2216(1)p =+,24(1)PQ p \=+,同理:PF =,QF =,\11FP FQ FP FQ FP FQ ++=×PQ FP FQ=×=224(1)4(1)p p +=+1=,\11FP FQ+的值是定值.(3)3y x -Q …,设4y x =-,34y y \…,设新的抛物线与直线3y x =-的相交的横坐标分别设为3x ,4x ,如图所示,Q 将抛物线221544y x x =-++适当平移后,得到抛物线23()(1)y a x h h =->,\抛物线是左右平移,则14a =-,231()4y x h \=--,由抛物线221544y x x =-++左右平移得到,观察图象,随着图象向右平移,3x ,4x 的值不断增大,若当1x m <…时,3y x -…恒成立,即231()4y x h x =---…,则m 的最大值在4x 处,\当31x =时,对应的4x 为最大值,21(1)14h \--=-,13h \=,21h =-(舍),231(4)4y x \=--,令21(3)4x x --=-,解得,31x =,49x =,m \的最大值为9.【点评】本题主要考查二次函数与一次函数的综合运用,掌握二次函数图象的性质,函数图象平移的性质,一次函数与二次函数交点的计算方法,数形结合分析是解题的关键.13 .(2023•武侯区校级模拟)如图,抛物线2y x bx c =++与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,若(1,0)A -且3OC OA =.(1)求该抛物线的函数表达式;(2)如图1,点P 是第四象限内抛物线上的一个点且位于对称轴右侧,分别连接BC 、AP 相交于点G ,当12PBG ABG S S D D =时,求点P 的坐标;(3)如图2,在(2)的条件下,AP 交y 轴于点M ,过M 点的直线l 与线段AB ,AC 分别交于E ,F ,当直线l 绕点M 旋转时,m nAE AF+为定值3,请求出m 和n 的值.【分析】(1)用待定系数法求函数的解析式即可;(2)过P 点作//PD y 轴交BC 于点D ,过点A 作//AK y 轴交BC 于点K ,则PD PG AK AG =,由12PBG ABG S S D D =,可得12PD AK =,设2(,23)P t t t --,(13)t <<,分别求出(,3)D t t -,(1,4)K --,根据12PD AK =,建立方程求出t 的值即可求P 点坐标;(3)过M 点作//MH x 轴交AC 于点H ,过点F 作//FT x 轴交AP 于点T ,连接CP ,则////HM FT CP ,根据平行线的性质可得HM CH AO AC =,HM AH CP AC =,HM HF AE AF =,HM AHFT AF=,化简得1HM HM AO CP +=,1HM HM AE FT +=,再由1HM HM AO CP +=,求出23HM =,再由1HM HM AE FT +=,得到1132AE FT +=,根据平行得到FT AFCP AC =,求出5FT AF =,则1132AE AF +=,因为3m n AE AF +=,则112()3AE AF=,即可求2m =,n =.【解答】解:(1)(1,0)A -Q ,1OA \=,3OC OA =Q ,3OC \=,(0,3)C \-,将(1,0)A -、(0,3)C -代入2y x bx c =++,\103b c c -+=ìí=-î,解得23b c =-ìí=-î,\抛物线的解析式为223y x x =--;(2)2223(1)4y x x x =--=--Q ,\抛物线的对称轴为直线1x =,设2(,23)P t t t --,(13)t <<,当0y =时,2230x x --=,解得3x =或1x =-,(3,0)B \,设直线BC 的解析式为3y kx =-,330k \-=,解得1k =,\直线BC 的解析式为3y x =-,过P 点作//PD y 轴交BC 于点D ,过点A 作//AK y 轴交BC 于点K ,//PD AK \,\PD PGAK AG =,Q 12PBG ABG S S D D =,\12PD AK =,(,3)D t t -Q ,(1,4)K --,223(23)3PD t t t t t \=----=-+,4AK =,232t t \-+=,解得1t =(舍)或2t =,(2,3)P \-;(3)过M 点作//MH x 轴交AC 于点H ,过点F 作//FT x 轴交AP 于点T ,连接CP ,(0,3)C -Q ,(2,3)P -,//CP x \轴,////HM FT CP \,\HM CH AO AC =,HM AH CP AC =,HM HF AE AF =,HM AHFT AF =,\1HM HM AO CP +=,1HM HMAE FT+=,设直线AP 的解析式为y k x b ¢¢=+,\023k b k b ¢¢-+=ìí¢¢+=-î,解得11k b ¢=-ìí¢=-î,\直线AP 的解析式为1y x =--,(0,1)M \-,1OA =Q ,3OC =,AC \=,Q1HM HM AO CP+=,112HM HM \+=,23HM \=,Q 1HM HMAE FT +=,\1132AE FT +=,QFT AFCP AC=,FT AF \=,\1132AE AF =,Q3m nAE AF +=,112()3AE AF \+=,\=,n=.m2【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,平行线的性质,灵活的对分式进行变形处理是解题的关键.14.(2023•丹阳市二模)如图,在平面直角坐标系中,二次函数2=++的图象与x轴相交于点A、B,与yy x bx c轴相交于点C,其中B点的坐标为(3,0),点M为抛物线上的一个动点.(1)二次函数图象的对称轴为直线1x=.①求二次函数的表达式;②若点M与点C关于对称轴对称,则点M的坐标是 ;③在②的条件下,连接OM,在OM上任意取一点P,过点P作x轴的平行线,与抛物线对称轴左侧的图象交于点Q,求线段PQ的最大值.+(2)过点M作BC的平行线,交抛物线于点N,设点M、N的横坐标为m、n,在点M运动的过程中,试问m n+的值.的值是否会发生改变?若改变,请说明理由;若不变,请求出m n【分析】(1)①利用对称轴公式求出2b=-,再将点B代入函数解析式确定c的值即可;。
10 二次函数与线段关系及最值定值问题 -备战2020中考数学之解密压轴解答题命题规律

备战2020中考数学之解密压轴解答题命题规律专题10 二次函数与线段关系及最值定值问题【类型综述】图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用. 一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【方法揭秘】由勾股定理产生的函数关系,在两种类型的题目中比较常用.类型一,已知“边角边”,至少一边是动态的,求角的对边.如图1,已知点A 的坐标为(3, 4),点B 是x 轴正半轴上的一个动点,设OB =x ,AB =y ,那么我们在直角三角形ABH 中用勾股定理,就可以得到y 关于x 的函数关系式.类型二,图形的翻折.已知矩形OABC 在坐标平面内如图2所示,AB =5,点O 沿直线EF 翻折后,点O 的对应点D 落在AB 边上,设AD =x ,OE =y ,那么在直角三角形AED 中用勾股定理就可以得到y 关于x 的函数关系式.图1 图2【典例分析】【例1】如图①,矩形ABCD 中,2,5,1AB BC BP ===,090MPN ∠=,将MPN ∠绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB (或AD )于点E ,PN 交边AD (或CD )于点F .当PN 旋转至PC 处时,MPN ∠的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D ,此时ABP ∆是否与PCD ∆相似?并说明理由;(2)类比探究:如图③,在旋转过程中,PEPF的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)拓展延伸:设AE t =时,EPF ∆的面积为S ,试用含t 的代数式表示S ; ①在旋转过程中,若1t =时,求对应的EPF ∆的面积; ②在旋转过程中,当EPF ∆的面积为4.2时,求对应的t 的值.思路点拨(1)根据“两角相等的两个三角形相似”即可得出答案; (2)由EBP PGF ∆∆:得出PE BPPF GF=,又2,1FG AB BP ===为定值,即可得出答案; (3)先设,2AE t BE t ==-结合EPF AEF BEP PFG ABGF S S S S S ∆∆∆∆=---矩形得出245S t t =-+①将t=1代入245S t t =-+中求解即可得出答案;②将s=4.2代入245S t t =-+中求解即可得出答案.满分解答(1)相似理由:∵090BAP BPA ∠+∠=,090CPD BPA ∠+∠=, ∴BAP CPD ∠=∠, 又∵090ABP PCD ∠=∠=, ∴ABP PCD ∆∆:; (2)在旋转过程中PEPF的值为定值, 理由如下:过点F 作FG BC ⊥于点G ,∵BEP GPF ∠=∠,90EBP PGF ∠=∠=,∴EBP PGF ∆∆:,∴PE BPPF GF=, ∵四边形ABCD 为矩形,∴四边形ABGF 为矩形, ∴2,1FG AB BP === ∴12PE PF = 即在旋转过程中,PE PF 的值为定值,12PE PF =; (3)由(2)知:EBP PGF ∆∆:,∴12BE PE PG PF ==, 又∵,2AE t BE t ==-,∴()2242PB t t =-=-,()14252BG AF BP PG t t ==+=+-=-, ∴EPF AEF BEP PFG ABGF S S S S S ∆∆∆∆=---矩形()()()()2111252521224245222t t t t t t t =--⨯--⨯⨯--⨯⨯-=-+即:245S t t =-+;①当1t =时,EPF ∆的面积214152S =-⨯+=, ②当 4.2EPF S ∆=时,∴245 4.2t t -+=解得:1452t =-,2452t =(舍去) ∴当EPF ∆的面积为4.2时,4525t =-; 【点睛】本题考查的是几何综合,难度系数较高,涉及到了相似以及矩形等相关知识点,第三问解题关键在于求出面积与AE的函数关系式.【例2】如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE 折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.(1)求线段CE的长;(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.①写出y关于x的函数解析式,并求出y的最小值;②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.满分解答(1)由翻折可知:AD=AF=10,DE=EF,求出BF,设EC=x,则DE=EF=8﹣x,在Rt△ECF中,利用勾股定理构建方程即可解决问题;(2)①首先求出AG,DG,∠ADM=∠NMG,证明△ADM∽△GMN,可得AD AMMG GN,整理后根据二次函数的最值求解即可.②存在.有两种情形:如图3﹣1中,当MN=MD时.如图3﹣2中,当MN=DN时,分别通过证明三角形相似,利用相似三角形的性质求解即可.思路点拨(1)如图1中,∵四边形ABCD是矩形,∴AD=BC=10,AB=CD=8,∠B=∠BCD=90°,由翻折可知:AD=AF=10,DE=EF,在Rt△ABF中,BF=22AF AB-=6,∴CF=BC﹣BF=10﹣6=4,设CE=x,则DE=EF=8﹣x,在Rt△EFC中,则有:(8﹣x)2=x2+42,∴x=3,即CE=3.(2)①如图2中,,∵AD∥CG,∴AD DE CG CE=,∴1053 CG=,∴CG=6,∴BG=BC+CG=16,在Rt△ABG中,AG2281685+=在Rt△DCG中,DG226810+=,∵AD=DG=10,∴∠DAG=∠AGD,∵∠DMG=∠DMN+∠NMG=∠DAM+∠ADM,∠DMN=∠DAM,∴∠ADM=∠NMG,∴△ADM∽△GMN,∴AD AMMG GN=,1085xyx=--,∴y=110x2﹣455x+10,∴当x=45时,y有最小值,将x=45代入可得,最小值=2;②存在,由①可得∠DMN=∠DGM,∴∠DNM=∠DMG,∴∠DNM≠∠DMN,所以有两种情形:如图3﹣1中,当MN=MD时,∵∠MDN=∠GDM,∠DMN=∠DGM,∴△DMN∽△DGM,∴DM MN DG GM,∵MN=DM,∴DG=GM=10,∴x=AM=85﹣10.如图3﹣2中,当MN=DN时,作MH⊥DG于H.∵MN=DN,∴∠MDN=∠DMN,∵∠DMN =∠DGM , ∴∠MDG =∠MGD , ∴MD =MG , ∵MH ⊥DG , ∴DH =GH =5,∵∠DAG =∠DGA ,∠DAG =∠AGB , ∴∠DGA =∠AGB , 又∵∠MHG =∠ABG =90°, ∴△GHM ∽△GBA , ∴GH MGGB AG =, ∴516=,∴MG =2,∴x =AM =综上所述,满足条件的x 的值为10或2. 【点睛】本题属于四边形综合题,考查了矩形的性质,翻折变换,勾股定理,相似三角形的判定和性质,二次函数的最值,等腰三角形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.【例3】抛物线2(0)y ax bx c a =++≠与x 轴交于,A B 两点(点A 在点B 的左侧),与y 轴交于点(0,4)C -.已知(2,0)A -,抛物线的对称轴l 交x 轴于点(1,0)D . (1)求出,,a b c 的值;(2)如图1,连接BC ,点P 是线段BC 下方抛物线上的动点,连接,PB PC .点,M N 分别在y 轴,对称轴l 上,且MN y ⊥轴.连接,AM PN .当PBC ∆的面积最大时,请求出点P 的坐标及此时AM MN NP++的最小值;(3)如图2,连接AC ,把AOC ∆按照直线y x =对折,对折后的三角形记为A OC ∆'',把A OC ∆''沿着直线BC 的方向平行移动,移动后三角形的记为A O C ∆''''',连接DA '',DC '',在移动过程中,是否存在DA C ∆''''为等腰三角形的情形?若存在,直接写出点C ''的坐标;若不存在,请说明理由.思路点拨(1)由抛物线的对称性可得到(4,0)B ,然后将A 、B 、C 坐标代入抛物线解析式,求出a 、b 、c 的值即可得到抛物线解析式;(2)利用待定系数法求出直线BC 解析式,作//PQ y 轴交BC 于点Q ,设(,4)Q x x -,则21,42P x x x ⎛⎫-- ⎪⎝⎭,表示出PQ 的长度,然后得到△PBC 的面积表达式,根据二次函数最值问题求出P 点坐标,再把A 向左移动1个单位得1(3,0)A -,连接11,A P A N ,易得1+A P MN 即为最小值;(3)由题意可知C ''在直线4y x =+上运动,设(),4''+C m m ,则()4,2''++A m m ,分别讨论:①''''''=A C DC ,②''''''=A C DA ,③''''=D DA C ,建立方程求出m 的值,即可得到C ''的坐标.满分解答(1)由抛物线的对称性知(4,0)B ,把(2,0),(4,0),(0,4)--A B C 代入解析式2y ax bx c =++,得42016404a b c a b c c -+=⎧⎪++=⎨⎪=-⎩解得:1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴抛物线的解析式为2142y x x =--. (2)设BC 直线解析式为为y kx b =+ 将(4,0),(0,4)-B C 代入得,404k b b +=⎧⎨=-⎩,解得14k b =⎧⎨=-⎩ ∴直线BC 的解析式为4y x =-. 作//PQ y 轴交BC 于点Q ,如图,设(,4)Q x x -,则21,42P x x x ⎛⎫-- ⎪⎝⎭,2211(4)4222PQ x x x x x ⎛⎫=----=-+ ⎪⎝⎭. 22214224(2)42PBC CPQ BPQx x S S S x x x ∆∆∆⎛⎫⨯-+ ⎪⎝⎭=+==-+=--+ 当2x =时,PBC S ∆取得最大值,此时,(2,4)P -.把A 向左移动1个单位得1(3,0)A -,连接11,A P A N ,如图111411AM MN NP A N MN NP A N NP MN A P MN ++=++=++≥+=.(3)由题意可知C ''在直线4y x =+上运动, 设(),4''+Cm m ,则()4,2''++A m m ,∴()()22242420''''=+-++--=A m m m m C()()222214261D 7C ''=-++=++m m m m ()()22224122101DA 3''=+-++=++m m m m①当''''''=A C DC 时,22617=20++m m ,解得31522=-±m 此时31551522C ''⎛- ⎝⎭或31551522C ''⎛-++ ⎝⎭;②当''''''=A C DA 时,221013=20++m m ,解得5392=-±m 此时539339,2222C ''⎛⎫--- ⎪ ⎪⎝⎭或539339,2222C ''⎛⎫-++ ⎪ ⎪⎝⎭③当''''=D DA C 时,2221013=2617++++m m m m ,解得1m =,此时(1,5)C '',综上所述C ''的坐标为539339,22C ''⎛⎫--- ⎪ ⎪⎝⎭或539339,22C ''⎛⎫-++ ⎪ ⎪⎝⎭315515,22C ''⎛⎫--- ⎪ ⎪⎝⎭或315515,22C ''⎛⎫-++ ⎪ ⎪⎝⎭或(1,5)C ''. 【点睛】本题考查二次函数的综合问题,涉及待定系数法求函数解析式,面积最值与线段最值问题,等腰三角形存在性问题,是中考常考的压轴题,难度较大,采用数形结合与分类讨论是解题的关键.【例4】如图在锐角△ABC 中,BC =6,高AD =4,两动点M 、N 分别在AB 、AC 上滑动(不包含端点),且MN ∥BC ,以MN 为边长向下作正方形MPQN ,设MN =x ,正方形MPQN 与△ABC 公共部分的面积为y .(1)如图(1),当正方形MPQN 的边P 恰好落在BC 边上时,求x 的值;(2)如图(2),当PQ 落△ABC 外部时,求出y 与x 的函数关系式(写出x 的取值范围)并求出x 为何值时y 最大,最大是多少?思路点拨(1)利用相似三角形的判定和性质列比例式求解;(2)利用相似三角形的判定和性质列比例式求正方形MPQN与△ABC公共部分的长和宽,从而列出函数关系式并求最值.满分解答(1)当PQ恰好落在边BC上时,∵MN∥BC,∴△AMN∽△ABC∴MN AG BC AD=,∵以MN为边长向下作正方形MPQN ∴GD=MN=4即464x x-=,∴x=125.(2)设BC分别交MP,NQ于E,F,则四边形MEFN为矩形.设ME=NF=h,AD交MN于G(如图2)GD=NF=h,AG=4﹣h.∵MN∥BC,∴△AMN∽△ABC.∴MN AGBC AD=,即464x h-=,,∴h=23-x+4.∴y=MN•NF=x(23-x+4)=23-x2+4x(2.4<x<6),配方得:y=23-(x﹣3)2+6.∴当x=3时,y有最大值,最大值是6.【点睛】掌握相似三角形对应高的比等于相似比从而列出比例式是本题的解题关键.【例5】如图,抛物线y=12-x2+mx+m(m>0)的顶点为A,交y轴于点C.(1)求出点A的坐标(用含m的式子表示);(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.思路点拨(1)直接写出顶点式即可得出结论;(2)先将点A坐标代入直线AB的解析式中,得出n=2m+12m2,进而得出直线AB的解析式为y=-x+2m+12m2,再联立抛物线解析式得出方程组,转化成方程,利用根与系数的关系即可得出结论;(3)先求出点A,C关于x轴的对称点,进而得出直线EF解析式,再联立抛物线解析式,过点C作MN ∥x轴,过点E作EM⊥MN于点M,过点F作FN⊥MN,设点E,F坐标,联系抛物线和EF表达式,利用根与系数的关系列出方程求解.满分解答(1)Q 抛物线22222211111(2)()22222y x mx m x mx m m m x m m m =-++=--+++=--++,∴顶点A 的坐标为21(,)2m m m +;(2)由(1)知,顶点A 的坐标为21(,)2m m m +,Q 直线y x n =-+经过点A ,212m m m n ∴+=-+,2122n m m ∴=+,∴直线AB 的解析式为2122y x m m =-++①,设1(A x ,1)y ,2(B x ,2)y ,Q 抛物线2211()22y x m m m =--++②,联立①②得,222111()2222x m m m x m m --++=-++,即:22(1)(2)0x m x m m --+-=, 122(1)x x m ∴+=-,12(2)x x m m =-,AB ∴即:AB 的长是定值,其值为(3)Q 抛物线212y x mx m =-++与y 轴相交于C ,(0,)C m ∴,∴点C 关于x 轴的对称点的坐标为(0,)m -,由(1)知,顶点A 的坐标为21(,)2m m m +,∴点A 关于x 轴的对称点的坐标为21(,)2m m m --, Q 直线EF 是直线AD 关于x 轴的对称点,∴点(0,)m -,21(,)2m m m --在直线EF 上,∴直线EF 的解析式为12y mx m =--③, Q 抛物线212y x mx m =-++④,设E (1x ,1y ),F (2x ,2y ),过点C 作MN ∥x 轴,过点E 作EM ⊥MN 于点M ,过点F 作FN ⊥MN ,如图1, ∵∠ECF=90°, ∴∠ECM+∠FCN=90°, ∠FCN+∠CFN=90°, ∴∠ECM=∠CFN , ∵∠EMC=∠FNC=90°, ∴△EMC ∽△CNF , ∴=EM MCCN FN, 即1122=m y x x m y ---, 化简得:()2121212=m y y m y y x x -++-,联立③④得,2340x mx m --=, 12=3x x m +,124x x m =-,12y y =112mx m ⎛⎫-- ⎪⎝⎭212mx m ⎛⎫-- ⎪⎝⎭=3212m m +,2123=22y y m m +--,∴2232312=422m m m m m m m ⎛⎫---++ ⎪⎝⎭,∴()222m m m +-=0解得:m=1-+m=1-m=0, ∵m>0∴m=1-【点睛】此题是二次函数综合题,主要考查了待定系数法,配方法,根与系数的关系,直角三角形的性质,建立方程组是解本题的关键.【例6】如图,在平面直角坐标系中,二次函数y =x 2+bx +c 的图象与x 轴交于A 、B 两点,A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于点C (0,﹣3).(1)求二次函数解析式;(2)若点Q 为抛物线上一点,且S △ABQ =12S △ACQ ,求点Q 的坐标; (3)若直线l :y =mx +n 与抛物线有两个交点M ,N (M 在N 的左边),P 为抛物线上一动点(不与M ,N 重合).过P 作PH 平行于y 轴交直线l 于点H ,若HM HNHP⋅=5,求m 的值.思路点拨(1)抛物线与y 轴交于点C (0,-3),则c=-3,将点B 的坐标代入抛物线表达式并解得:b=-2,即可求解; (2)分点Q 在x 轴下方、点Q 在x 轴上方两种情况,分别求解即可; (3)MH=21cos RHm α=+t-x 1),同理:NH=(x 2-t 21m +,MH•MN=(m 2+1)(mt+n-t 2+2t+3)=(m 2+1)•PH ,即可求解.满分解答解:(1)抛物线与y 轴交于点C (0,﹣3),则c =﹣3, 将点B 的坐标代入抛物线表达式并解得:b =﹣2,故抛物线的表达式为:y=x2﹣2x﹣3;(2)设:点Q(m,m2﹣2m﹣3),①当点Q在x轴下方时,如图1,S△ACQ=12×4×(﹣m2+2m+3),S△ABQ=S△AOC+S△QOC﹣S△AOQ=32﹣12×3×m﹣12×1×(﹣m2+2m+3)=12m2+12m,则:12×4×(﹣m2+2m+3)=12m2+12m,解得:m=83或﹣1(舍去﹣1),故点P(83,﹣119);②当点Q在x轴上方时,如图2,取AC的中点E(﹣12,﹣32),S△ABQ=12S△ACQ,则点E、B到AQ的距离相等,BE∥AQ,直线BE的表达式中的k值为:37,同理直线BQ的表达式为:y=37x+37,∴2233377y x xy x⎧=--⎪⎨=+⎪⎩,解得:x=247或﹣1(舍去﹣1),故点Q(247,9349);综上,点Q 的坐标为:(83,﹣119)或(247,9349);(3)过点H 作x 轴的平行线RH ,过点M 、N 分别作RH 的垂线交于点R 、S ,设点M 、N 的横坐标分别为x 1,x 2,点P (t ,t 2﹣2t ﹣3),则点H (m ,mt+n ), 则PH =mt+n ﹣t 2+2t+3,联立直线与抛物线的表达式并整理得: x 2﹣(m+2)x ﹣3﹣n =0, 则x 1+x 2=m+2,x 1x 2=﹣3﹣n直线M 、N 的k 值为m ,即tan ∠RHM =m =tanα,则cosα21m +∴MH =21cos RHm α=+(t ﹣x 1),同理:NH =(x 2﹣t 21m + ∴MH•MN =(m 2+1)(mt+n ﹣t 2+2t+3)=(m 2+1)•PH , 而5HM HNHP•=,则m 2+1=5, 解得:m =±2. 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形、图形的面积计算等,解题的关键是掌握二次函数的性质,利用所学的性质进行进行解题,其中(2),要注意数形结合和分类讨论进行求解,避免遗漏.【变式训练】1.如图,抛物线y =ax 2+4x +c (a ≠0)与反比例函数y =5x的图象相交于点B ,且点B 的横坐标为5,抛物线与y 轴交于点C (0,6),A 是抛物线的顶点,P 和Q 分别是x 轴和y 轴上的两个动点,则AQ +QP +PB 的最小值为_____.【答案】170【解析】【分析】根据题意求得B的坐标,然后根据待定系数法求得抛物线的解析式,从而求得顶点A的坐标,求得A关于y轴的对称点A′(-2,10),B点关于x轴的对称点B′为(5,-1),根据两点之间线段最短,即可判断AQ+QP+PB=A′B′是AQ+QP+PB的最小值,利用勾股定理求得即可.【详解】∵点B在反比例函数y=5x的图象,且点B的横坐标为5,∴点B的纵坐标为:y=55=1,∴B(5,1),∵抛物线y=ax2+4x+c(a≠0)与反比例函数y=5x的图象相交于点B,与y轴交于点C(0,6),∴252016a cc++=⎧⎨=⎩,解得16ac=-⎧⎨=⎩,∴抛物线为y=﹣x2+4x+6,∵y=﹣x2+4x+6=﹣(x﹣2)2+10,∴A(2,10),∴A关于y轴的对称点A′(﹣2,10),∵B(5,1),∴B点关于x轴的对称点B′为(5,﹣1),连接A′B′交x轴于P,交y轴于Q,此时AQ+QP+PB的值最小,即AQ+QP+PB=A′B′,A′B′22(52)(110)++--170故AQ +QP +PB 的最小值为170.【点睛】本题考查了反比例函数图象上点的坐标特征,待定系数法求二次函数的解析式,二次函数的性质,轴对称的性质,勾股定理的应用,明确AQ+QP+PB=A′B′是AQ+QP+PB 的最小值是解题的关键.2.如图,在平面直角坐标系中,菱形OABC 的顶点 A 在 x 轴正半轴上,顶点 C 的坐标为(4,3),D 是抛物线 y =﹣x 2+6x 上一点,且在x 轴上方,则△BCD 面积的最大值为__________【答案】15 【解析】试题解析:∵D 是抛物线26y x x =-+上一点,∴设2(,6)D x x x ,-+ ∵顶点C 的坐标为(4,3), 22435OC ,∴+= ∵四边形OABC 是菱形,5,BC OC BC x P ∴==轴,22155(63)(3)1522S BCD x x x V ,∴=⨯⨯-+-=--+502Q ,-<BCD S ∴V 有最大值,最大值为15,故答案为15.3.己知抛物线2114y x =+具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x 轴的距离始终相等,如图,点M 的坐标为(3,3),P 是抛物线2114y x =+上一个动点,则△PMF 周长的最小值是__________.【答案】5 【解析】 【分析】过点M 作ME ⊥x 轴于点E ,ME 与抛物线交于点P′,由点P′在抛物线上可得出P′F=P′E ,结合点到直线之间垂线段最短及MF 为定值,即可得出当点P 运动到点P′时,△PMF 周长取最小值. 【详解】解:过点M 作ME ⊥x 轴于点E ,ME 与抛物线交于点P′,如图所示.∵点P′在抛物线上, ∴P′F=P′E .又∵点到直线之间垂线段最短,22(30)(32)-+-=2,∴当点P 运动到点P′时,△PMF 周长取最小值,最小值为ME+MF=3+2=5. 故答案为5. 【点睛】本题考查了二次函数的性质、二次函数图象上点的坐标特征以及点到直线的距离,根据点到直线之间垂线段最短找出△PMF 周长的取最小值时点P 的位置是解题的关键.4.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =16cm ,AD 为BC 边上的高,动点P 从点A 出发,沿A →D 2cm /s 的速度向点D 运动,过P 点作PE ∥BC 交AC 于点E ,过E 点作EF ⊥BC 于点F ,设△ABP 的面积为S 1,四边形PDFE 的面积为S 2,则点P 在运动过程中,S 1+S 2的最大值为______.【答案】72. 【解析】 【分析】利用三角形的面积公式以及矩形的面积公式,表示出S 1和S 2,然后确定最值即可. 【详解】∵Rt △ABC 中,∠BAC=90°,AB=AC=16cm ,AD 为BC 边上的高, ∴2cm , 又∵2t , 则S 1=12AP•BD=12×2×2t=8t ,22t , ∵PE ∥BC , ∴△APE ∽△ADC , ∴PE AP DC AD=, ∴2t ,∴S 2=PD•PE=(22t )2t ,∴S 1+S 2=8t+(22t )2t=-2(t-6)2+72. ∴S 1+S 2的最大值为72, 故答案为72. 【点睛】本题考查了一元二次方程的应用,以及等腰直角三角形的性质,正确表示出S 1和S 2是关键.5.在平面直角坐标系中,已知()A 2,4、()P 1,0,B 为y 轴上的动点,以AB 为边构造ABC V ,使点C在x 轴上,BAC 90.M ∠=o 为BC 的中点,则PM 的最小值为______.【答案】45【解析】 【分析】如图,作AH ⊥y 轴于H ,CE ⊥AH 于E .则四边形CEHO 是矩形,OH =CE =4,由△AHB ∽△CEA ,得AH BHEC AE=,推出24BH AE=,推出AE =2BH ,设BH =x 则AE =2x ,推出B (0,4﹣x ),C (2+2x ,0),由BM =CM ,推出M (1+x ,42x -),可得PM 222454162455x x x -=+=-+()(),由此即可解决问题. 【详解】如图,作AH ⊥y 轴于H ,CE ⊥AH 于E .则四边形CEHO 是矩形,OH =CE =4.∵∠BAC =∠AHB =∠AEC =90°,∴∠ABH +∠HAB =90°,∠HAB +∠EAC =90°,∴∠ABH =∠EAC ,∴△AHB ∽△CEA ,∴AH BH EC AE =,∴24BHAE=,∴AE =2BH ,设BH =x 则AE =2x ,∴OC =HE =2+2x ,OB =4﹣x ,∴B (0,4﹣x ),C (2+2x ,0). ∵BM =CM ,∴M (1+x ,42x-). ∵P (1,0),∴PM 222454162455x x x -=+=-+()(),∴x 45=时,PM 45. 45. 【点睛】本题考查了相似三角形的判定和性质、两点间距离公式、二次函数的应用等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,学会构建二次函数,利用二次函数的性质解决最值问题,属于中考常考题型.6.如图,在平面直角坐标系中,抛物线y=﹣x 2+4x 与x 轴交于点A ,点M 是x 轴上方抛物线上一点,过点M 作MP ⊥x 轴于点P ,以MP 为对角线作矩形MNPQ ,连结NQ ,则对角线NQ 的最大值为_________.【答案】4 【解析】∵四边形MNPQ 是矩形, ∴NQ=MP ,∴当MP 最大时,NQ 就最大.∵点M 是抛物线24y x x =-+在x 轴上方部分图象上的一点,且MP ⊥x 轴于点P ,∴当点M 是抛物线的顶点时,MP 的值最大.∵224(2)4y x x x =-+=--+,∴抛物线24y x x =-+的顶点坐标为(2,4),∴当点M 的坐标为(2,4)时,MP 最大=4, ∴对角线NQ 的最大值为4.7.如图,在平面直角坐标系中,过A (-1,0)、B (3,0)两点的抛物线交y 轴于点C ,其顶点为点D ,设△ACD 的面积为S 1,△ABC 的面积为S 2.小芳经探究发现:S 1︰S 2是一个定值.这个定值为________.【答案】16【解析】【分析】设二次函数的解析式是y=a (x+1)(x-3),即y=ax²-2ax-3a ,即可求得C 的坐标,表示出的值S 2,然后利用待定系数法求得AD 的解析式,进而求得EO 的值,得到CE 的长,根据三角形面积公式即可求得S 1,进而求解. 【详解】设二次函数的解析式是y=a(x+1)(x−3),即y=ax²−2ax−3a ,AD 与CB 交于点E. 令x=0,解得:y=−3a ,则OC=3a. ∴S2=12 AB ⋅OC= 12×4⋅3a=6a ; ∵D 是抛物线的顶点。
二次函数(定值问题)

二次函数--定值问题解法一:设直线解析式,利用韦达定理进行解题解法二:设点的坐标,利用相似进行解题1、如图,已知抛物线y=ax2﹣2ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.(1)直接写出a的值、点A的坐标及抛物线的对称轴;(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;(3)证明:当直线l绕点D旋转时,+均为定值,并求出该定值.2、如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.(1)求此抛物线的解析式;(2)求证:AO=AM;(3)探究:①当k=0时,直线y=kx与x轴重合,求出此时的值;②试说明无论k取何值,的值都等于同一个常数.3、 如图,在平面直角坐标系xOy 中,一次函数 (为常数)的图象与x 轴交于点A(,0),与y 轴交于点C .以直线x=1为对称轴的抛物线 ( 为常数,且≠0)经过A ,C 两点,并与x 轴的正半轴交于点B .(1)求的值及抛物线的函数表达式;(2)设E 是y 轴右侧抛物线上一点,过点E 作直线AC 的平行线交x 轴于点F .是否存在这样的点E ,使得以A ,C ,E ,F 为顶点的四边形是平行四边形?若存在,求出点E 的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)若P 是抛物线对称轴上使△ACP 的周长取得最小值的点,过点P 任意作一条与y 轴不平行的直线交抛物线于 ,两点,试探究是否为定值,并写出探究过程.54y x m =+m 3-2y ax bx c =++a b c ,,a m 111M ()x y ,222M ()x y ,2112P P M M M M⋅4.如图,已知A B C ∆为直角三角形,90A C B ∠=︒,A C B C=,点A 、C 在x 轴上,点B 坐标为(3,m )(0m >),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B 、D . (1)求点A 的坐标(用m 表示);(2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连结P Q 并延长交B C 于点E ,连结 B Q 并延长交AC 于点F ,试证明:()F C A CE C +为定值.yxQP F EDC BA O5. 如图1所示,在直角坐标系中,O 是坐标原点,点A 在y 轴正半轴上,二次函数y=ax 2+[x/6]+c 的图象F 交x 轴于B 、C 两点,交y 轴于M 点,其中B (-3,0),M (0,-1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、二次函数与线段定值
【探索一】已知抛物线-x²-2x+3与x轴交于点A,B(点A在点B右侧),与y轴交于点c,设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点p,使三角形CMP为等腰三角形,若存在,请求出P点的坐标。
【探索二】抛物线y= -x²-2x+3与x轴交于点A,B(点A在点B右侧),与Y轴相交于点C,点P为抛物线上一动点,若点P到直线Y=X的距离为 ,求P点的坐标。
【探索三】抛物线y= -x²-2x+3与x轴交于点A,B(点A在点B右侧),与Y轴相交于点C,点P为抛物线上一动点,若点P到对称轴和Y的距离相等,求P点的坐标。
【探索四】抛物线y= -x²-2x+3与x轴交于点A,B(点A在点B右侧),与Y轴相交于点C,点P为抛物线上一动点,若点P到对称轴和X轴的距离相等,求P点的坐标。
【探索五】抛物线y= -x²-2x+3与x轴交于点A,B(点A在点B右侧),与Y轴相交于点C,点P为三角形BOC点,且点P到三角形BOC三边所在直线的距离相等,求P点的坐标。
