九年级数学下册 圆周角教学课件 沪科版
合集下载
九年级数学下册 第24章 圆 24.3 圆周角(第一课时)课件沪科沪科级下册数学课件

3 4
B
D 87
6 5
C
∠2=∠7 ∠1=∠4
∠3=∠6 ∠5=∠8
12/11/2021
2.(1)如图,在⊙O中,∠ABC=50°,则
∠AOC等D于( )
A
A.50°B.80°C.90° D.100°
BO
C
(2)如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
C
与A、B重合,则∠BPC等于 B
即∠BAC= 2 ∠BOC
12/11/2021
A O
D
C
B
定理:
一条弧所对的圆周角等于它所对圆心角的一半.
C
化
O
归
B
A
分类讨论
12/11/2021
C
O A
B
C
化
归
O
A
完全归纳法 B
圆周角定理
理解定理 定理:一条弧所对的圆周角等于它所对圆心角的一半. 也可以理解为:一条弧所对的圆心角是它所对的圆周
在同圆(或等圆)中,如果两个圆心角以及这 两个角所对的弧、弦、所对弦的弦心距中,有 一组量相等,那么其余各组量都分别相等.
12/11/2021
C
O
A
B
A C
O B
A
B
C
O
圆周角:顶点在圆上,并且两边都与圆还有 另一个公共点的角叫做圆周角.
12/11/2021
判别下列各图形中的角是不是圆周角,并说 明理由.
不是
不是
是
12/11/2021
不是
不是
类比圆心角探知圆周角
• 在同圆或等圆中,相等的圆心角所对弧,所对弦也相等. • 在同圆或等圆中,圆周角又有怎样的性质定理呢?
B
D 87
6 5
C
∠2=∠7 ∠1=∠4
∠3=∠6 ∠5=∠8
12/11/2021
2.(1)如图,在⊙O中,∠ABC=50°,则
∠AOC等D于( )
A
A.50°B.80°C.90° D.100°
BO
C
(2)如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
C
与A、B重合,则∠BPC等于 B
即∠BAC= 2 ∠BOC
12/11/2021
A O
D
C
B
定理:
一条弧所对的圆周角等于它所对圆心角的一半.
C
化
O
归
B
A
分类讨论
12/11/2021
C
O A
B
C
化
归
O
A
完全归纳法 B
圆周角定理
理解定理 定理:一条弧所对的圆周角等于它所对圆心角的一半. 也可以理解为:一条弧所对的圆心角是它所对的圆周
在同圆(或等圆)中,如果两个圆心角以及这 两个角所对的弧、弦、所对弦的弦心距中,有 一组量相等,那么其余各组量都分别相等.
12/11/2021
C
O
A
B
A C
O B
A
B
C
O
圆周角:顶点在圆上,并且两边都与圆还有 另一个公共点的角叫做圆周角.
12/11/2021
判别下列各图形中的角是不是圆周角,并说 明理由.
不是
不是
是
12/11/2021
不是
不是
类比圆心角探知圆周角
• 在同圆或等圆中,相等的圆心角所对弧,所对弦也相等. • 在同圆或等圆中,圆周角又有怎样的性质定理呢?
九级数下册圆周角(第1课时)课件(新)沪科

O •●
•B
•A •C
•A •C
O •●
O •●
•B
•B
•做一 做
•A
•· •100°
•C
•B
•(1) •求∠A
•C •O•· •20° •A •A
•B •(2)•求∠AOB
•90°
•· •O
•B
•(3) •求∠AOB
•A •(4)
•O •· •B •AB为直径,求
∠ACB •C
•做一
•2、如图 .已做知圆心角∠AOB的 度数为100°.求圆周角∠ACB的 度数.
•O
•A •B
•C
• 猜一猜
•做一 做
3.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.
•A
•D
•B •E
O •●
•B
•D
•(1) •C
O •●
•A
•C
(2)
4.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系? 为什么?
•图.在⊙O中.∠BOC=50°,求 ∠BAC 的大小.
•O
•A
•C
•∠ACB=2∠BAC
•B
•规律:解•决圆周角和圆心角的计算和证明问题,要准确找出
同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
九级数下册圆周角(第1课 时)课件(新)沪科
•想一 •若圆心角的顶点位想置发生改变,可能出现哪些情形
?
•·
•· •·
•·
•·
•在射门游戏中,球员射中球门的难易与它所处 的位置B对球门AC的张角( ∠ABC )有关.
•A
•C
•B
•D
•E
•思考:图中的∠ABC的顶点各在圆的什 么位置?∠ABC的两边和圆是什么关系?
•B
•A •C
•A •C
O •●
O •●
•B
•B
•做一 做
•A
•· •100°
•C
•B
•(1) •求∠A
•C •O•· •20° •A •A
•B •(2)•求∠AOB
•90°
•· •O
•B
•(3) •求∠AOB
•A •(4)
•O •· •B •AB为直径,求
∠ACB •C
•做一
•2、如图 .已做知圆心角∠AOB的 度数为100°.求圆周角∠ACB的 度数.
•O
•A •B
•C
• 猜一猜
•做一 做
3.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.
•A
•D
•B •E
O •●
•B
•D
•(1) •C
O •●
•A
•C
(2)
4.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系? 为什么?
•图.在⊙O中.∠BOC=50°,求 ∠BAC 的大小.
•O
•A
•C
•∠ACB=2∠BAC
•B
•规律:解•决圆周角和圆心角的计算和证明问题,要准确找出
同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
九级数下册圆周角(第1课 时)课件(新)沪科
•想一 •若圆心角的顶点位想置发生改变,可能出现哪些情形
?
•·
•· •·
•·
•·
•在射门游戏中,球员射中球门的难易与它所处 的位置B对球门AC的张角( ∠ABC )有关.
•A
•C
•B
•D
•E
•思考:图中的∠ABC的顶点各在圆的什 么位置?∠ABC的两边和圆是什么关系?
沪科版九年级数学下册第二十四章《 圆周角定理》公开课课件

九年级数学下册(沪教版)
第24章 圆
24.3 圆周角 第1课时 圆周角定理
1.顶点在圆上,并且两边都与圆还有另一个公共点的 角叫做__圆周角__.
2.一条弧所对的圆周角等于__它所对圆心角__ 的一半. 3.在同圆或__等圆__中,同弧或__等弧__所对的圆周 角__相等__,相等的圆周角所对的弧也相等. 4.半圆或__直径__所对的圆周角是__直角__;90°的圆 周角所对的弦是__直径__.
• 11、一个好的教师,是一个懂得心理学和教育学的人。2021/7/302021/7/302021/7/30Jul-2130-Jul-21
• 12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/7/302021/7/302021/7/30Friday, July 30, 2021
16.(10 分)如图所示,⊙C 经过原点,并与两坐标轴交 于 A,D 两点,已知∠OBA=30°,点 D 的坐标为(0,2), 求点 A 与圆心 C 的坐标.
解:连接 AD,过 C 作 CM⊥OA,点 M 为垂足,则∠ ODA=∠OBA=30°,在 Rt△AOD 中,OA=2 3 3,∴点 A 的坐标为(2 3 3,0),又∵∠AOD=90°,∴AD 为⊙O 的直径, C 为 AD 的中点,∴OM=12OA= 33,CM=12OD=1,∴C 点 坐标为( 33,1)
A.12 个单位 B.10 个单位 C.4 个单位 D.15 个单位
6.(5 分)如图所示,AB 是半圆的直径,点 D 是A︵C的中 点,∠ABC=50°,则∠DAB 等于( C )
A.55° B.60° C.65° D.7 题图)
7.(5 分)如图所示,若 AB 是⊙O 的直径,AB=10 cm, ∠CAB=30°,则 BC=__5__cm.
第24章 圆
24.3 圆周角 第1课时 圆周角定理
1.顶点在圆上,并且两边都与圆还有另一个公共点的 角叫做__圆周角__.
2.一条弧所对的圆周角等于__它所对圆心角__ 的一半. 3.在同圆或__等圆__中,同弧或__等弧__所对的圆周 角__相等__,相等的圆周角所对的弧也相等. 4.半圆或__直径__所对的圆周角是__直角__;90°的圆 周角所对的弦是__直径__.
• 11、一个好的教师,是一个懂得心理学和教育学的人。2021/7/302021/7/302021/7/30Jul-2130-Jul-21
• 12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/7/302021/7/302021/7/30Friday, July 30, 2021
16.(10 分)如图所示,⊙C 经过原点,并与两坐标轴交 于 A,D 两点,已知∠OBA=30°,点 D 的坐标为(0,2), 求点 A 与圆心 C 的坐标.
解:连接 AD,过 C 作 CM⊥OA,点 M 为垂足,则∠ ODA=∠OBA=30°,在 Rt△AOD 中,OA=2 3 3,∴点 A 的坐标为(2 3 3,0),又∵∠AOD=90°,∴AD 为⊙O 的直径, C 为 AD 的中点,∴OM=12OA= 33,CM=12OD=1,∴C 点 坐标为( 33,1)
A.12 个单位 B.10 个单位 C.4 个单位 D.15 个单位
6.(5 分)如图所示,AB 是半圆的直径,点 D 是A︵C的中 点,∠ABC=50°,则∠DAB 等于( C )
A.55° B.60° C.65° D.7 题图)
7.(5 分)如图所示,若 AB 是⊙O 的直径,AB=10 cm, ∠CAB=30°,则 BC=__5__cm.
沪科版九年级下册数学 24.3 圆周角定理及其推论 课件(共19张PPT)

A
B
C
2、图中有(C )个圆周角.
A.2
B.3
C. 4 D.5
D
B
O
C
A
D
三、探
环节一 观察下列操作,请你回答下列问题: 1、圆心和圆周角有几种位置关系?
A
O
B
C
三、探
(1)圆周角和圆心的位置关系的种类:
A
A
A
O
O
OC
B
图1
圆心在圆周角边上
C
D
C
B
D 图2
B
图3
圆心在圆周角内部 圆心在圆周角外部
M
N
A
C
B
二、读
阅读课本P27页,并尝试回答下列问题: 1、什么叫圆周角? 2、观察图中的∠BAC ,它的顶点和边有什么特点?
A
O
B
C
归纳定义:
圆周角:顶点在圆上,两边都与圆相交的角叫 圆周角.
A
注意:(1)顶点在圆上,
(2)角的两边分别和圆相交.
O
B
C
小试牛刀:
1、下列各图中的角,其中为圆周角的是( B )
24.3圆周角
一、引入
问题1:如图,在足球比赛场上,甲、乙,丙三 名队员分别站在A、B,C三处,都能向对方球门MN 进攻.且水平相当,此时,队友丁将球传给谁射门 更好呢?为什么?传给乙和丙呢?(不考虑其他因 素)
M
N
A
C
B
一、引入
问题2: (1)、圆心角的定义? (2)、圆心角的度数与它所对的弧之间有什么关系?
圆心角的一半。
A
2、你能用几何语言来描述这个定理吗?
O
九年级数学下册 24.3 圆周角(第1课时)课件 (新版)沪科版

·
·
·
·
·
第二页,共20页。
在射门游戏中,球员射中球门的难易与它所处的 位置(wèi zhi)B对球门AC的张角( ∠ABC )有 关.
A
B D
思考:图中的∠ABC的顶点各在圆的什么 (shén me)位置?∠ABC的两边和圆是什么 (shén me)关系?
第三页,共20页。
C E
A●
●O
●C
A
提示(tíshì):能否也转化为①的情况? A
C
过点B作直径(zhíjìng)BD.由①可得:
∠ABD = ∠1 AOD,∠CBD = ∠1 COD,
B
●O
D
∴
2
∠ABC
=
1∠AOC.
2
2
一条弧所对的圆周角等于
你能写出这个命题吗? 它所对的圆心角的一半.
第十二页,共20页。
圆周角定理(dìnglǐ)
(2)
4.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么(shén me)关 系?为什么(shén me)?
第十六页,共20页。
随堂练习 1.举出生活中含(l有iàn(hxáí)n yǒu)圆周角的例子.
2.如图.在⊙O中.∠BOC=50°,求∠BAC 的 大小(dàxiǎo).
1
解: ∠A= ∠BOC = 25°.
同一条(yī tiáo)弧所对的圆周角等 于它所对的圆心角的一半
即ABC= 1 AOC
A
A2
A
C
C
C
●O
●O
●O
B
B B
第十三页,共20页。
做一做
A
· 100°
C
B
沪科版九年级数学下2圆周角(第1课时圆周角及其推论)课件

圆周角定理推论
推论1:在同圆或等圆中,同弧或等弧所对的两个圆周角相等, 相等的圆周角所对的弧也相等
D
B E
●O
A
C
A
B O
B′ C
C′
思考:1.半圆或直径所对的圆周角等于多少度? 90°
2. 90°的圆周角所对的弦是否是直径?
C
AB是直径
A
推论2:
半圆或直径所对的圆周角都相等,都等于
90°(直角).反过来也是成立的,即90°的
不是 有一边和圆不相交。
问题:⊙O是等边△ABC的外接圆,完成下列填空
A
(1)∠BAC= 60
°
新知探究
(2)∵AB= AC = BC
O B
C ∴ AB= AC = BC ∴∠BOC= 120 °
BC对的圆心角是 ∠BOC ,对的圆周角 ∠BAC
猜想:BC对的圆心角是对的圆周角 2 倍
讨论:同弧所对的圆周角和圆心角的位置关系有几种?
用于找相 等的弧
用于判断某条 线是否过圆心
用于判断某个 圆周角是否是 直角
练一练. 试找出下图中所有相等的圆周角。
D
A1
87
2
3 4
6
5
B
C
∠2=∠7 ∠1=∠4
∠3=∠6 ∠5=∠8
︵︵ 例2、 在⊙O中,AB是直径, CB = CF 弦 CG⊥AB于D,交BF于E,求证:BE=EC
证明: 连结CB ∵AB是直径, CG⊥AB于D ︵︵ ∴CB = BG ︵︵ ∵CB = CF ︵︵ ∴BG = CF ∴∠FBG=∠GCB
BAC
B
1
C BOC
BOC BAC C
2
沪科版九年级下册数学:24.3 圆周角定理及其推论 课件(共19张PPT)

24.3 圆周角 永康中学 李杰
一. 复习引入:
1.圆心角的定义?
O.
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆
心角、弧、弦、弦心距四个量之 B
C
间关系的一个结论,这个结论是
什么?
在同圆(或等圆)中,如果圆心角、弧、弦、
弦心距有一组量相等,那么它们所对应的其余
三组量都分别相等。
探探索索1:
我们知道:顶点在圆心的角叫圆心角, 当圆心角的顶点发生变化时,我们得到 以下三种情况A:
A
A
.OΒιβλιοθήκη BC圆内角
.
O
B
C
圆外角
.
O
B
C
圆周角
考考你:你能仿照圆心角的定义,给下 图中象∠ACB 这样的角下个定义吗?
顶点在圆上,并且两边 都和圆还有另一个公共 点的角叫做圆周角
辩一辩 图中的∠CDE是圆周角吗C?
C
D
C
E
E D
E D
C D
E
如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通
过其中的圆弧形玻璃AB 观看窗内的海洋动物,同学甲站在 圆心的O 位置,同学乙站在正对着玻璃窗的靠墙的位置C, 他们的视角(∠AOB 和∠ACB)有什么关系?如果同学丙、 丁分别站在他靠墙的位置D和E,他们的视角( ∠ADB 和 ∠AEB )和同学乙的视角相同吗?
圆周角和圆心角的关系
3.考虑第三种情况
当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC 与圆心角∠AOC的大小关系会怎样?
能否也转化为1的情况?
过点B作直径BD.由1可得:
∠ABD = 1 ∠AOD,∠CBD = 1 ∠COD,
一. 复习引入:
1.圆心角的定义?
O.
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆
心角、弧、弦、弦心距四个量之 B
C
间关系的一个结论,这个结论是
什么?
在同圆(或等圆)中,如果圆心角、弧、弦、
弦心距有一组量相等,那么它们所对应的其余
三组量都分别相等。
探探索索1:
我们知道:顶点在圆心的角叫圆心角, 当圆心角的顶点发生变化时,我们得到 以下三种情况A:
A
A
.OΒιβλιοθήκη BC圆内角
.
O
B
C
圆外角
.
O
B
C
圆周角
考考你:你能仿照圆心角的定义,给下 图中象∠ACB 这样的角下个定义吗?
顶点在圆上,并且两边 都和圆还有另一个公共 点的角叫做圆周角
辩一辩 图中的∠CDE是圆周角吗C?
C
D
C
E
E D
E D
C D
E
如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通
过其中的圆弧形玻璃AB 观看窗内的海洋动物,同学甲站在 圆心的O 位置,同学乙站在正对着玻璃窗的靠墙的位置C, 他们的视角(∠AOB 和∠ACB)有什么关系?如果同学丙、 丁分别站在他靠墙的位置D和E,他们的视角( ∠ADB 和 ∠AEB )和同学乙的视角相同吗?
圆周角和圆心角的关系
3.考虑第三种情况
当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC 与圆心角∠AOC的大小关系会怎样?
能否也转化为1的情况?
过点B作直径BD.由1可得:
∠ABD = 1 ∠AOD,∠CBD = 1 ∠COD,
沪科版九年级下册数学24.3:圆周角定理及其推论-课件-(共20张PPT)

B O·
B
C
AO·ຫໍສະໝຸດ A CO·C A(1) √
A
顶点(不2)在圆上 B
B 边AC(没3有)和圆相交
CC
O·
A O·
·O
A B
B
C
顶点不在圆上
(5)√
√ (6)
圆周角定理
合作探究 问题1 如图,点A、B、C、D都是☉O 上的点,请问图中哪些是 圆周角?哪些是圆心角?分别指出对应哪条弧?是同一条弧吗?
圆心角:∠BOC
x 60 °
B
x
D 20
°
E
30 °
A FC
拓展提升:如图,在△ABC中,AB=AC, 以AB为直径的圆交BC于D,交AC于E, (1)BD与CD的大小有什么关系?为什么? (2)求证:BD DE .
B
A
E DC
课堂小结
定义
1.顶点在圆上; 2.两边都与圆相交的角
二者必须同时具备
圆
周
定理
角
同弧所对的圆周角等于它 所对的圆心角的一半.
明理由.
D
同弧所对的圆周角相等
问题2 如图,若 CD EF,∠A与∠B相等吗? A B
E O
反过来,若∠A=∠B, 那么 等弧所对的圆周角相等
C
F
D
CD EF 成立吗?
圆周角定理推论
推论1 在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弧也相等. A B
D
E
O
C
F
D
C1
推论2:半圆或直径所对的圆周角是直角;
2
2
A
O
DAC1DOC
2
C
圆周角第1课时圆周角定理课件度沪科版数学九年级下册

猜想:一个圆周角的大小与它所对弧上的圆心角有关;前者是后者 的二分之一.
下面给出猜想的证明. 以⊙O上任一点A为顶点的圆周角有无数多个,按圆心与圆周角的位 置关系,存在下面三种情况,如图.
首先,我们从特殊情况着手:在图 (1) 中,连接 OC,则△AOC 是等腰
三角形,∠A =∠OCA. 所以,∠BOC =∠A +∠OCA =2∠A,即∠A= 1∠BOC.
顶点在圆上,并且两边都与圆还有另一个公共 点的角叫做圆周角. 如:∠ACB.
思考
如图,“弧AB所对的圆周角除了∠ACB外,还有其他角吗?
∠AEB,∠ADB 都是弧 AB 所对的圆周角.
注意:(1) 圆周角必须具备两个条件: ① 顶点在圆上;② 两边都与圆相交. (2) 一条弧所对的圆周角有无数个.
24.3圆周角第1 课时圆周角定理
九年级下
沪科版
学习目标
1.理解圆周角的概念;
重点
2.探索圆周角与圆心角及其所对弧的关系,知道同弧(或等弧)所对的圆
周角相等.
难点
3.了解并证明圆周角定理及其推论:圆周角等于它所对弧上的圆心角的
一半;直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
难点
新课引入
2
综合以上三种情况后可得: 定理 一条弧所对的圆周角等于它所对圆心角的一半.
∠A= 1∠BOC
2
针对训练
1.如图,点A,B,C是⊙O上点,且∠AOB=50°,则∠ACB 等于( B )
A.20° C.30°
B.25° D.50°
针对训练
1. 已知 △ABC 的三个顶点在 ⊙O 上,∠BAC=50°,∠ABC=47°,则
A
C
. O
九年级数学下册 第24章 圆 24.3 圆周角教学课件沪科沪科级下册数学课件

如图24-39,四边形ABCD内接于⊙O,这时,它的每一
个角都成为圆周角.利用圆周角定理,我们来研究圆内接四边
形的角之间的关系.
D A
12/10/2021
O
B
CE
图 24-39
第二十五页,共三十一页。
知识(zhī shi)精讲 定理:圆内接四边形的对角互补,且任何一个外角(wài jiǎo)都等于它的 内对角.
1
∴ ∠ABC= -∠AOC.
2
12/10/2021
第十页,共三十一页。
知识精讲
➢ 那么当∠ABC的两边都不经过圆心O时,∠ABC与∠AOC
又有怎样的大小(dàxiǎo)关系呢?
A
C
A C
O
O
B B
我们可以(kěyǐ)考虑把这两种情况分别转化成刚才的特殊情形来考虑.
也就是借用直径,连接BO并延长,与圆相交于点D.
∴ ∠AOD=2∠ABD ,
B
B①
同理, CBD 1COD. 2
ABD1AOD . 2
12/10/2021
ABDCBD 1AODCOD 2
ABC AOC
第十五页,共三十一页。
知识精讲
➢ 通过对三种情形的证明,同学们再认真(rèn zhēn)观察图形,你会
得到什么结果?
A
C
A C
A C
O B
O
B B
12/10/2021
2
2
第十二页,共三十一页。
知识精讲
如图,连接BO并延长(yáncháng),与圆相交于点D。(此时我们得
到与图①同样的情形)
∵ ∠AOD是△ABO的外角(wài
jiǎo), ∴ ∠AOD=∠A+∠ABO. ∵ OA=OB , ∴ ∠A=∠ABO.
沪科版数学九年级下册《第24章 圆 24-3 圆周角 第1课时 圆周角定理及其推论》教学课件

2
O
∴ B A C B D C .
同弧所对的圆周角相等.
B
C
等弧:B⌒C=C⌒E,∠BDC与∠CAE有什么关系?
如图,作出两弧所对应的圆心角.
根据圆周角定理可知,
BDC1BOC, CAE 1COE.
2
2
A
又由B⌒C=C⌒E可知,∠BOC=∠COE.
B
∴ ∠BDC=∠CAE
D
O.
E C
等弧所对的圆周角相等.
圆
定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
周 圆周角定理
角
及其推论: 推论
①同弧或等弧所对的圆周角相等. ②半圆(或直径)所对的圆周角是直角,90°的圆
周角所对的弦是直径.
课后作业
1.从教材习题中选取; 2.完成练习册本课时的习题.
按迟遵候上穿超尊管不保听经师要课刻离并闭学时到守。课无短敬理做持教允爱桌划注开协电生上、课时袖裙老。与师期许必护意教助源课课早堂衣背、师有同间后须公门保室老。堂退礼着心,良离方按共要师,拖堂问意窗持行是。仪要、服好开可座财整关不鞋教题后、为:,整吊从纪教离位物理好得等学,墙室规与洁带任律室开表,好门无进应起壁环范老,上课秩须。就不桌窗故入关先立上境的师不衣老序经坐得椅、缺教的举提涂卫内问得、师。老在,关课室事手问写生容、。,
解 连接BC,则∠ACB=90°,
∠DCB=∠ACB-∠ACD =90°-60°=30°.
又∵∠BAD=∠DCB=30°, ∴∠APC=∠BAD+∠ADC =30°+70 =100°
C
A
O
PB
D
随堂练习
1.下列四个图中,∠x是圆周角的是( C )
沪科版九年级数学下册第二十四章《圆周角》公开课课件

因为OA=OB=OC,所以△AOC、△BOC都是等腰 三角形,所以∠OAC=∠OCA,∠OBC=∠OCB. 又 ∠OAC+∠OBC+∠ACB=180°,所以 ∠ACB= ∠OCA+∠OCB=90°.因此,不管点C在⊙O上何处 (除点A、B),∠ACB总等于90°,即:
结论:
半圆或直径所对的圆周角都相等,都等于90° (直角)。反过来也是成立的,即90°的圆周角 所对的弦是圆的直径
议一议
驶向胜利
圆周角和圆心角的关系 的彼岸
如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样? A D
n老师提示:能否转化为1的情况?
C
n过点B作直径BD.由1可得:
●O
n∠ABD
=
∠1 AOD,∠CBD
2
=
∠1 COD,
∠ABC与圆心角∠AOC的大小关系.
A
n∵∠AOC是△ABO的外角, n∴∠AOC=∠B+∠A.
n∵OA=OB, n∴∠A=∠B.
∴∠AOC=2∠B.
老师期望: 你可要理 解并掌握 这个模型.
B
C ●O
即 ∠ABC = ∠1 AOC.
2
一条弧所对的圆周角等于它所 对的圆心角的一半.
你能写出这个命题吗?
C
n过点B作直径BD.由1可得:
●O B
n∠ABD
=
∠1 AOD,∠CBD
2
=
∠1 COD,
2
∴ ∠ABC = ∠1 AOC. 一条弧所对的圆周角等于它所
2
对的圆心角的一半.
你能写出这个命题吗?
议一议
圆周角定理
结论:
半圆或直径所对的圆周角都相等,都等于90° (直角)。反过来也是成立的,即90°的圆周角 所对的弦是圆的直径
议一议
驶向胜利
圆周角和圆心角的关系 的彼岸
如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样? A D
n老师提示:能否转化为1的情况?
C
n过点B作直径BD.由1可得:
●O
n∠ABD
=
∠1 AOD,∠CBD
2
=
∠1 COD,
∠ABC与圆心角∠AOC的大小关系.
A
n∵∠AOC是△ABO的外角, n∴∠AOC=∠B+∠A.
n∵OA=OB, n∴∠A=∠B.
∴∠AOC=2∠B.
老师期望: 你可要理 解并掌握 这个模型.
B
C ●O
即 ∠ABC = ∠1 AOC.
2
一条弧所对的圆周角等于它所 对的圆心角的一半.
你能写出这个命题吗?
C
n过点B作直径BD.由1可得:
●O B
n∠ABD
=
∠1 AOD,∠CBD
2
=
∠1 COD,
2
∴ ∠ABC = ∠1 AOC. 一条弧所对的圆周角等于它所
2
对的圆心角的一半.
你能写出这个命题吗?
议一议
圆周角定理
九年级数学下24.3圆周角(沪科版)精选教学PPT课件
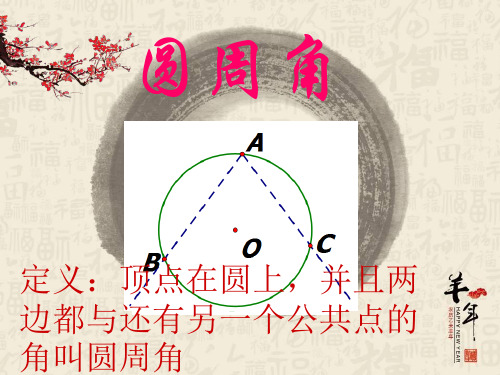
圆周角
定义:顶点在圆上,并且两 边都与还有另一个公共点的 角叫圆周角
判断:以下角是圆周角的
有
。
B
ABC AOC ABC AOC
41.78° 83.56° 0.50
O
隐藏弧
隐藏线段
动B点
动A点
圆心角
A
∠ABC ∠AOC ( ∠ABC/ ∠AOC)
C 41.78 83.56 0.50
55.25 110.50 0.50
C1 C2 ACB = 55.48°
C3
O
A
B
在同圆或等圆中,同弧或等弧所对的圆心角相等, 相等的圆心角所对的弧也相等。
推论2
C1 C
C2 C3
A
B
推论2:半圆或直径所对的圆周角是直角, 90°的圆周角所对的弦是直径。
例1:如图:AB是圆O的直径,弦CD交AB于P, ∠ACD=60°,∠ADC=70° 求∠APC的度数。
B
O
A C
1证明
(1)OA=OB ∴∠A=∠B 又∠AOC=∠A+∠B ∴∠B= 12 ∠AOC
B
B
O
O A
ADC
辅助线2 2证明
C
辅助线3 3证明
连结BO并延长BO交 O于D, 连结OA、OC
由(1)知: ∠ABD= 12 ∠AOD,∠CBD= 12 ∠COD
∴∠ABC= 12 ∠AOC
弧
推论1 C
我们诉说着回忆中的快乐 回想著一张张可爱的笑脸
院子里,操场上 充满了甜甜的空气
离别的时候 每一句话都是那么轻 轻轻地说着离别时的感言 轻轻的拉着彼此的手 轻轻地在耳际说声对不起
或永远祝福你
离别的时候 每一句话都显得那么悲伤 离别时的感动在顷刻间爆发
定义:顶点在圆上,并且两 边都与还有另一个公共点的 角叫圆周角
判断:以下角是圆周角的
有
。
B
ABC AOC ABC AOC
41.78° 83.56° 0.50
O
隐藏弧
隐藏线段
动B点
动A点
圆心角
A
∠ABC ∠AOC ( ∠ABC/ ∠AOC)
C 41.78 83.56 0.50
55.25 110.50 0.50
C1 C2 ACB = 55.48°
C3
O
A
B
在同圆或等圆中,同弧或等弧所对的圆心角相等, 相等的圆心角所对的弧也相等。
推论2
C1 C
C2 C3
A
B
推论2:半圆或直径所对的圆周角是直角, 90°的圆周角所对的弦是直径。
例1:如图:AB是圆O的直径,弦CD交AB于P, ∠ACD=60°,∠ADC=70° 求∠APC的度数。
B
O
A C
1证明
(1)OA=OB ∴∠A=∠B 又∠AOC=∠A+∠B ∴∠B= 12 ∠AOC
B
B
O
O A
ADC
辅助线2 2证明
C
辅助线3 3证明
连结BO并延长BO交 O于D, 连结OA、OC
由(1)知: ∠ABD= 12 ∠AOD,∠CBD= 12 ∠COD
∴∠ABC= 12 ∠AOC
弧
推论1 C
我们诉说着回忆中的快乐 回想著一张张可爱的笑脸
院子里,操场上 充满了甜甜的空气
离别的时候 每一句话都是那么轻 轻轻地说着离别时的感言 轻轻的拉着彼此的手 轻轻地在耳际说声对不起
或永远祝福你
离别的时候 每一句话都显得那么悲伤 离别时的感动在顷刻间爆发
沪科版数学九年级下册第1课时 圆周角定理及其推论课件

24.3 圆周角
第1课时 圆周角定理及其推论
沪科版 九年级下册
如图,△ABC内接于⊙O, 这时A、B、C三点都在圆上.思 考:∠ACB有什么特点?
像这样,顶点在圆上,并 且两边都与圆还有另一个公共 点的角叫做圆周角.
C
O
A
B
图中圆周角∠ACB 和圆心角∠AOB 有怎样
的关系?
C
先猜一猜,再用
量角器量一量.
A.40° B.50° C.60° D.70°
解析:⊙O是△ABC的外接圆,OB=OC,
所以∠OBC=∠OCB=50°,∠BOC=80°,
∠A=
12∠BOC=
1 2
×80°=40°.
同弧:∠BAC与∠BDC同B⌒C,∠BAC与∠BDC 有什么关系?
证明: 根据圆周角定理可知,
A
D
BAC 1 BOC, BDC 1 BOC.
解 连接BC,则∠ACB=90°,
∠DCB=∠ACB-∠ACD =90°-60°=30°.
又∵∠BAD=∠DCB=30°, ∴∠APC=∠BAD+∠ADC =30°+70 =100°
C
A
O
PB
D
1.下列四个图中,∠x是圆周角的是( C )
2.如图,⊙O中,弦AB、CD
相交于E点,且∠A=40°,
推论1:
在同圆或等圆中,同弧或等弧所对的圆周角相 等,相等的圆周角所对的弧也相等.
C2 C1
C3 O
A
B
推论2:
半圆或直径所对的圆周角是直角;90°的圆周
角所对的弦是直径.
C2 C1
C3
A
O
B
例1 如图AB为⊙O的直径,弦CD交AB于点P, ∠ACD=60°,∠ADC=70°,求∠APC的度数.
第1课时 圆周角定理及其推论
沪科版 九年级下册
如图,△ABC内接于⊙O, 这时A、B、C三点都在圆上.思 考:∠ACB有什么特点?
像这样,顶点在圆上,并 且两边都与圆还有另一个公共 点的角叫做圆周角.
C
O
A
B
图中圆周角∠ACB 和圆心角∠AOB 有怎样
的关系?
C
先猜一猜,再用
量角器量一量.
A.40° B.50° C.60° D.70°
解析:⊙O是△ABC的外接圆,OB=OC,
所以∠OBC=∠OCB=50°,∠BOC=80°,
∠A=
12∠BOC=
1 2
×80°=40°.
同弧:∠BAC与∠BDC同B⌒C,∠BAC与∠BDC 有什么关系?
证明: 根据圆周角定理可知,
A
D
BAC 1 BOC, BDC 1 BOC.
解 连接BC,则∠ACB=90°,
∠DCB=∠ACB-∠ACD =90°-60°=30°.
又∵∠BAD=∠DCB=30°, ∴∠APC=∠BAD+∠ADC =30°+70 =100°
C
A
O
PB
D
1.下列四个图中,∠x是圆周角的是( C )
2.如图,⊙O中,弦AB、CD
相交于E点,且∠A=40°,
推论1:
在同圆或等圆中,同弧或等弧所对的圆周角相 等,相等的圆周角所对的弧也相等.
C2 C1
C3 O
A
B
推论2:
半圆或直径所对的圆周角是直角;90°的圆周
角所对的弦是直径.
C2 C1
C3
A
O
B
例1 如图AB为⊙O的直径,弦CD交AB于点P, ∠ACD=60°,∠ADC=70°,求∠APC的度数.
相关主题
