新华师大版八年级数学上册《勾股定理》复习导学案
最新八年级上华东师大版第十四章勾股定理复习教案资料

C O
BD
( 1)底端也将滑动 0.5 米吗?
(2)能否求出 OD的长?
解:根据勾股定理,在 Rt △ OAB中, AB=3m, OA=2.5m, OB2=AB2-OA2= 3 2-2.5 2=2.75 。
2
2
2
22
∴OB≈ 1.658m;在 Rt △ OCD中,OC=OA-AC=2,mCD=AB=3m,OD=CD-OC = 3 -2 =5。∴ OD≈ 2.236m。
名师精编 优秀教案
第十四章 勾股定理
回顾与思考
教学目标
1.知识目标 :掌握直角三角形的边、角之间分别存在着的关系,熟练地运用直角三角形的
勾股定理和其他性质解决实际问题。
2.能力目标 :正确使用勾股定理的逆定理,准确地判断三角形的形状。
3.德育目标 :熟悉勾股定理的历史,进一步了解我国古代数学的伟大成就,激发学生的爱
教学内容
知识 教
能力 学
目 情感
标
第 14 章 勾股定理单元复习
授课班级
1、勾股定理:直角三角形两直角边的平方和等于斜边的平方; 2、如果三角形的三边长 a、b、c 有关系 a2+b2=c 2, 那么这个三角形是直角三角形;
3、勾股定理能解决直角三角形的许多问题, 因此在现实生活和数学中有着广泛
的应用.
BC2
D
所以△ DBC是直角三角形,∠ CDB= 90°
4
12 5
C 13
二、
因此这个零件符合要求。 随堂练习
A 3B
一、判断题。
1 .由于 0.3 , 0.4 , 0.5 不是勾股数,所以以 0.3 ,0.4 , 0.5 为边长的三角形不是直角
三角形()
新华东师大版八年级数学第十四章《勾股定理》导学案

《勾股定理》导学案第一课时一、课堂目标我领悟1.动手探索直角三角形的三边关系,掌握并能运用直角三角形的三边关系解决实际问题。
2.经历用测量计算、数格子等方法探索勾股定理的过程,进一步提高自己的合情推理意识,培养主动探究的思想。
3.培养数形结合的思想,体会数学与现实的紧密联系,感受其价值。
二、重点难点我分析学习重点:掌握勾股定理并能利用它来解决实际问题。
学习难点:探索勾股定理。
三、自主学习我能行(预习与交流)1、知识准备。
回忆:对于直角三角形,我知道哪些知识?AB C2、学生自学课本P48——51,回答问题:(1)勾股定理的成立必须是在哪种三角形中?其余三角形成立吗?(2)勾股定理的具体内容是什么?请结合下图,把勾股定理的具体内容用数学语言和图形结合起来说一说。
A四、探索交流我最棒探究活动一 B C请大家测量你们手中的直角三角形纸片,根据下表填空:(测量的时候都取整数)根据你们的测量与计算,可以做出怎样的猜想?我们猜想:直角三角形三边的关系是探究活动二相传2500年前,古希腊的数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系. 请同学们也观察一下,看看能发现什么?(1)观察每个图形中的三个正方形之间的面积有什么关系?(2)你能把三个正方形的面积与它们的边结合起来,写成一个关系式吗(3)你有什么发现?结论:等腰直角三角形三边的特殊关系:斜边的等于两直角边的。
探究活动三观察课本p49图,填空并交流.问题:正方形P的面积平方厘米正方形Q的面积平方厘米正方形R的面积平方厘米正方形P、 Q、 R的面积之间的关系____________由此我们得到,这个直角三角形ABC的三边长度存在的关系__________ ____ 结论在一般的直角三角形中两直角边的等于斜边的。
探究活动四1、画一画分别以5厘米、12厘米为直角边作出一个直角三角形.2、量一量量出你画的直角三角形的斜边长(取整数)。
【最新】华师大版八年级数学上册14.2 勾股定理的应用学案

新华师大版八年级数学上册14.2 勾股定理的应用学案学习目标:1、能运用勾股定理及直角三角形的判定条件解决实际问题.2、在运用勾股定理解决实际问题的过程中,感受数学的"转化"思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.学习重点:实际问题转化成数学问题再转化为直角三角形中学习难点:"转化"思想的应用学习关键点:在现实情境中建立直角三角形模型,确定好直角三角形之后,再应用勾股定理. 学习过程一、知识回顾1. 在Rt△ABC中,∠C=90°,如果b=15,c=17,求a.2. 问:(1)什么叫勾股定理?(2) 我们以前已学过了中哪几种判断直角三角形的方法?勾股定理的逆定理是:.二、自我测试1. 在直角三角形ABC中,斜边AB=1,则AB222ACBC++的值是()A.2B.4C.6D.82.满足下列条件的三角形中,不是直角三角形的是()A.三个内角比为1∶2∶1B.三边之比为1∶2∶5C.三边之比为3∶2∶5D. 三个内角比为1∶2∶33. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了步路(假设2步为1米),却踩伤了花草.4.已知一根旗杆于离地面12m处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16m,旗杆在断裂之前高多少m?5. 飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米?6. 如图所示,无盖玻璃容器,高18cm ,底面周长为60cm ,在外侧距下底1cm 的点C 处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口1cm 的F 处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,所走的最短路线的长度.三、课后拓展1.已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为( ) A.2 B.102 C.10224或 D.以上都不对2. 直角三角形两直角边长分别为5和12,则它斜边上的高为_______.3.已知三角形ABC 的三边长为c b a ,,满足18,10==+ab b a ,8=c ,则此三角形为 三角形.4.如图所示,在一次夏令营活动中,小明从营地A 点出发,沿北偏东60°方向走了m 3500到达B 点,然后再沿北偏西30°方向走了500m 到达目的地C 点.(1)求A 、C 两点之间的距离.(2)确定目的地C 在营地A 的什么方向.4题图5.如图,某会展中心在会展期间准备将高5m,长13m ,宽2m 的楼道上铺地毯,已知地毯 平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?6.如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?A 1B 1 D 1C 1 2 1 46题图参考答案一、自我测试1.A 提示:根据勾股定理得122=+AC BC ,所以AB 222AC BC ++=1+1=22.C3.4 提示:由勾股定理可得斜边的长为5m ,而3+4-5=2m ,所以他们少走了4步.4. 解:依题意,AB=16m ,AC=12m ,在直角三角形ABC 中,由勾股定理,222222201216=+=+=AC AB BC ,所以BC=20m ,20+12=32(m ),故旗杆在断裂之前有32m 高.5. 解:如图,由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC=30004000500022=-(米), 所以飞机飞行的速度为5403600203=(千米/小时) 6. 解:将曲线沿AB 展开,如图所示,过点C 作CE ⊥AB 于E.在R 90,=∠∆CEF CEF t ,EF=18-1-1=16(cm ),CE=)(3060.21cm =⨯, 由勾股定理,得C F=)(3416302222cm EF CE =+=+三、课后拓展 1.C 提示:当已经给出的两边分别为直角边时,第三边为斜边=;1026222=+当6为斜边时,第三边为直角边=242622=- 2.1360 提示:设斜边的高为x ,根据勾股定理求斜边为1316951222==+ ,再利用面积法得,1360,132112521=⨯⨯=⨯⨯x x 3.直角4.解:(1)过B 点作BE//AD ,如图5∴∠DAB=∠ABE=60°∵30°+∠CBA+∠ABE=180°即△ABC 为直角三角形由已知可得:BC=500m ,AB=m 3500由勾股定理可得:222AB BC AC += 所以)m (1000)3500(500AB BC AC 2222=+=+=(2)在Rt △ABC 中,∵BC=500m ,AC=1000m∴∠CAB=30°∵∠DAB=60°∴∠DAC=30°即点C 在点A 的北偏东30°的方向5. 解:根据勾股定理求得水平长为m 1251322=-,地毯的总长 为12+5=17(m ),地毯的面积为17×2=34()2m ,铺完这个楼道至少需要花为:34×18=612(元)6.分析:蚂蚁由A 点沿长方体的表面爬行到C 1点,有三种方式①沿ABB 1A 1和A 1 B 1C 1D 1②ABB 1A 1和BC C 1 B 1③AA 1 D 1D 和A 1 B 1C 1 D 1把三种方式分别展成平面图行如下:解:①在Rt △ABC 1中 AC 2= AB 2+ BC 2= 42+ 32=25∴AC=25 =5②在Rt △ACC 1中 AC 12= AC 2+ CC 12= 62+ 12=37∴AC 1=37③在Rt △AB 1C 1中AC 12= AB 12+ B 1C 12 = 52+ 22=29① 2 1 B 1A B A 1 D 1 C 1 4 ② 1 2 4 A B B 1 C A 1 C 1 1 A B 1 D 1 D A 1 C 1 ③ 4 2∵25<29<37∴沿图①的方式爬行最短,最短的路线是5.。
初中八年级数学《勾股定理》复习导学案设计

第十七章勾股定理学习目标:1.回顾本章知识,在回顾过程中主动构建起本章知识结构;2.思考勾股定理的发现证明和应用过程,体会出入相补思想、数形结合思想、转化思想在解决数学问题中的作用.学习重点:勾股定理的应用.教学过程:复习勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.一. 基础知识运用第一组练习: 勾股定理的直接应用(一)知两边或一边一角型1.如图,已知在△ABC 中,∠B =90°,一直角边为a,斜边为b,则另一直角边c满足c2 = .【思考】为什么不是c²=a²+b²?2.在Rt△ABC中,∠C=90°,∠A=30°,AC=3.求AB、BC的长。
(二)知一边及另两边关系型如图,已知在△ABC 中,∠B =90°,若BC=4 , AB=x ,AC=8-x,则AB= ,AC= .(三)分类讨论的题型1. 对三角形边的分类.已知一个直角三角形的两条边长是 3 cm和 4 cm,第三条边的长是.注意:这里并没有指明已知的两条边就是直角边,所以4 cm可以是直角边,也可以是斜边,即应分情况讨论.2. 对三角形高的分类.已知:在△ABC中,AB=15 cm,AC=13 cm,高AD=12 cm,求S△ABC.【思考】本组题,利用勾股定理解决了哪些类型题目?注意事项是什么?利用勾股定理能求三角形的边长和高等线段的长度.注意没有图形的题目,先画图,再考虑是否需分类讨论.思考:利用勾股定理解题决实际问题时,基本步骤是什么?第二组练习: 用勾股定理解决简单的实际问题1.在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?()A.一定不会B.可能会C.一定会D.以上答案都不对2. 如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?思考:利用勾股定理解题决实际问题时,基本步骤是什么?二、努力提高:会用勾股定理解决较综合的问题。
【最新】华师大版八年级数学上册14.2勾股定理的应用1导学案

【最新】华师大版八年级数学上册14.2勾股定理的应用1导学案新华师大版八年级数学上册14.2勾股定理的应用1导学案【学习目标】能运用勾股定理及直角三角形的判定条件解决实际问题.【重、难点】在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.【预习指导】一、学前准备1、已知Rt △ABC 中,∠C=90°,若BC=4,AC=2,则AB=_______;若AB=4,BC=则AC=_________.2、一个直角三角形的模具,量得其中两边的长分别为5cm 、3cm ,?则第三边的长是_________.3.要登上8m 高的建筑物,为了安全需要,需使梯子底端离建筑建6m .?问至少需要多长的梯子?二、【教学过程】一.创设情境1.如图,一圆柱体的底面周长为20cm ,高AB为4cm ,BC是上底面的直径.一只蚂蚁从点A 出发,沿着圆柱的侧面爬行到点C ,试求出爬行的最短路程.(精确到0.01cm ).(1)自制一个圆柱,尝试从A 点到C 点沿圆柱侧面画出几条路线,你认为哪条路线最短呢?(2)如图,将圆柱侧面剪开展成一个长方形,从A 点到C 点的最短路程是什么?你画对了吗?(3)蚂蚁从A 点出发,想吃到C 点上的食物,它沿圆柱侧面爬行的最短路程是多少?三、练习1:有一圆柱形油罐,底面周长是12米,高是5米,现从油罐底部A 点环绕油罐建梯子,正好到A 点的正上方B 点,问梯子最短需多少米?2、如图,在长、宽都是3,高是8的长方体纸箱的外部,一只蚂蚁从顶点A 沿纸箱表面爬到顶点B 处,求它所行的最短路线的长。
3. 在一棵树的10 m 高处有两只猴子,其中一只猴子爬下树走到离树20 m 的池塘A 处,另一只爬到树顶后直接跃向池塘的A 处,如果两只猴子所经过的路程相等,试问这棵树有多高学习体会:我们知道勾股定理揭示了直角三角形的三边之间的数量关系,已知直角三角形中的任意两边就可以依据勾股定理求出第三边.从应用勾股定理解决实际问题中,我们进一步认识到把直角三角形中三边关系“a 2+b 2=c 2”看成一个方程,只要依据问题的条件把它转化为我们会解的方程,就把解实际问题转化为解方程.四、例题讲解BA10cm 4cmcmB A例:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如左图的某工厂,问这辆卡车能否通过该工厂的厂门练习:如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设一拖拉机在公路MN上沿PN方向行驶,周围100米以内会受到噪声的影响,那么学校是否会受到噪声的影响?说明理由,若受影响,已知拖拉机的速度为18千米/时,则学校受影响的时间有多长?五、小结由学生分组进行总结,教师请个别组学生在全班总结勾股定理的应用方法六、课堂练习:1.若一个三角形的一个角等于其他两个角的差,那么这个三角形是____________三角形2.在△ABC中,∠A: ∠B: ∠C=1:2:3,则BC:AC:AB=_________3.设直角三角形的三条边长为连续自然数,则这个直角三角形的面积是____________4.甲、乙两人同时从同一地点出发,甲往东走了4km,乙往南走了6km,这时甲、乙两人相距__________km.5.在△ABC中,AB=AC=4cm, ∠A: ∠B=2:5,过点C作△ABC的高CD,与AB交于D点,则CD=_______6.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(取3)是().(A)20cm (B)10cm (C)14cm (D)无法确定7.如果梯子的底端建筑物有5m,15m长的梯子可达到该建筑物的高度大约是()A.13mB.14m C 15m D. 16 m8.如图,一块草坪的形状为四边形ABCD,其中∠B=90°,AB=3m,BC=4m,?CD=?12m,AD=13m.求这块草坪的面积.9、如图所示,在长方形纸片ABCD中,AD=4cm,AB=14cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长。
八年级数学专题:勾股定理中的思想方法(导学案)

专题:勾股定理中的思想方法学习目标 : 理解、掌握勾股定理中的一些解题思想方法,并能较熟练运用这些思想方法解决简单的实际问题.一、复习回忆1.勾股定理勾股定理:直角三角形两条直角边的平方和等于斜边的 . 即:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c ,那么一定有 .2.勾股定理的逆定理如果三角形的三边长a、b、c有关系:a2+b2=,那么这个三角形是直角三角形.利用此定理判定直角三角形的一般步骤:(1)确定最大边;(2)算出最大边的平方与另两边的;(3)比拟最大边的平方与另两边的平方和是否相等,假设相等,则说明这个三角形是三角形.3.勾股数能够成为直角三角形三条边长的三个数,称为勾股数,即满足a2+b2=c2的三个数a、b、c,称为勾股数.[注意] 勾股数都是正整数.4.勾股定理的应用应用勾股定理及其逆定理可解决如下问题:(1) 三角形的任意两边,求第三边长或图形周长、面积的问题;(2)说明线段的平方关系问题;二、典例分析◆类型一数形结合思想例1. 如图,每个小方格都是边长为1的正方形,〔1〕求四边形ABCD的面积;〔2〕求∠ABC的度数.变式训练:如图,网格中每个小正方形的边长都是1,且A,B,C,D都在格点上.〔要求:写出必要的过程〕〔1〕求四边形ABCD的面积;〔2〕求∠ABC的度数.◆类型二分类讨论思想1、直角边和斜边不明时需分类讨论例2.在一个直角三角形中,假设其中两边长分别为5,3,则第三边长的平方为〔〕A.16 B.16或34 C.34 D.不存在变式训练:x,y为正数,且|x-4|+(y-3)2=0,如果以x,y的长为边长作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为〔〕A.5 B.7 C.7或25 D.16或252、锐角和钝角不明时需分类讨论例3.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,求△ABC的面积。
变式训练:等腰三角形的腰长为5,一腰上的高为3,则这个等腰三角形底边长的平方为 .◆类型三方程思想1、利用“连环勾〞列方程例4.如图,在△ABC中,CD⊥AB于D,假设AD∶BD=5∶2,AC=17,BC=10,则BD的长为〔〕A.4 B.5 C.6 D.82、折叠问题中利用勾股定理列方程例5.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC 上与点B′重合,AE为折痕,求BE的长。
华东师大版八年级上册数学学案:第十四章勾股定理复习学案

直角三角形的判定
直角三角形的应用
二、预习自测
1.在△ABC 中,AB=5cm,BC=12cm,要使∠B=90°,则 AC 的长应为
2.等腰三角形的腰长为 10,底边长为 12,则这个等腰三角形的面积为
3.在△ABC 中,AB=c,BC=a,AC=b,∠C=90°,a=2b,c²=125,则 a=
4.校园内有两棵树,相距 12 米,一棵树高 13 米,另一棵树高 8 米 ,一只小鸟从一棵树的 顶端飞到另一 棵树的顶端。请问小鸟至少要飞多少米?
A.3,5,3 B.4,6,7 C.2,3,4 D.6,8,10 2.在△ABC 中,已知 AB=12,AC=9,BC=15,则△ABC 的面积等于( )
A.108 B. 54 C.180 D. 90
3. 如图所示,图中所有三角形是直角三角形,
所有四边形是正方有形, s1 9, s3 144 ,
问题 2:已知三角形的三边,如何判断三角形是直角三角形?
【预习案】
预习自测
一、知识导图
直 角 三 角 形
勾股定理
勾股定理的变形
问题 3:若一直角三角形的斜边长为 2cm,且两直角边比为 3:4,则两直角边长分别为 ______。 二.知识综合应用探究
(一)利用勾股定理解直角三角形 【例 1】在 Rt△ABC 中,∠ACB =90°,AB = 5cm,BC = 3 cm,求 AC 的长பைடு நூலகம்△ABC 的面积.
4
盖盒子中,求细木棒露在盒外面的最短长度是多少?
并说明理由。
E
A
D
F
C B
我的收获: 4/5
5/5
s4 169 ,则 s2 =
.
(二)勾股定理的逆定理的应用
新华师大版八年级数学上册《14.1 勾股定理》学案

新华师大版八年级数学上册《14.1 勾股定理》学案班级: 姓名: 小组: 评价:【学习目标】1、经历勾股定理的探索过程,体会数形结合的思想。
2、理解直角三角形三边的关系,会应用勾股定理解决简单的数学问题。
【学习重点】:应用勾股定理解决简单的数学问题。
【学习难点】:勾股定理的探索过程以及勾股定理的验证。
一、单元导入,明确目标二、新知导学,合作探究预习课本108-112页(5分钟)(1)勾画课本勾股定理;(2)理解直角三角形三边的关系。
自学指导一:探索勾股定理观察下图,如果每一小方格表示1平方厘米,那么可以得到:正方形P 的面积= 平方厘米;正方形Q 的面积= 平方厘米;正方形R 的面积= 平方厘米已知点在已知直线上14.1.1 勾股定理达标测试,当堂反馈1.在Rt △ABC 中,︒=∠90A ,c AB =,a BC =,b AC =(提醒学生注意边的位置)①若24=c ,25=a ,则=b .②若5=b ,12=c ,则=a .③若4:3:=c b ,15=a ,则=b ,=c .2.已知等腰三角形ABC 的腰长为13 cm ,另一边长是10cm ,由顶点作高AD 。
求:(1)高AD 的长; (2)△ABC 的面积。
3、四边形ABCD 中,AD ⊥DC ,AD=8,DC=6,CB=24,AB=26.求四边形ABCD的面积.4、如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?作业14.1 勾股定理第一课时:直角三角形三边的关系班级: 姓名: 小组: 评价:一、填空题1.Rt△ABC中,∠A=90°,如果∠A、∠B、∠C的对边分别是a、b、c,那么a、b、c的关系是错误!未找到引用源。
=_____;2、小强准备用铁丝围成一个直角边分别为7cm和24cm的直角三角形模具,他至少需要购买铁丝___cm;3、张老汉为了知道他家一块直角三角形责任田的斜边长,他量得其他两边的长分别是40米和9米,那么这块地的斜边长是___;二、解答探索题4、马路边一棵高10米的大树被台风拦腰折断,折断处距离地面3米,在大树倒下的一方停着一辆小汽车, 距离大树6.5米,试判断倒下的大树会不会砸到小汽车?为什么?A BC D我们发现,正方形P、 Q、 R的面积之间的关系是.此由,我们得出直角三角形ABC的三边的长度之间存在关系.由上图得出一般直角三角形的三边关系.若∠C=90°,则22c2+a=b勾股定理:直角三角形两直角边的平方和等于斜边的平方几何语言表示为:在△ABC中,∠C= , 则 (a、b 表示两直角边,c表示斜边) 例1: Rt△ABC中,AB=c,BC=a,AC=b,∠B=90°(1)已知a=8,b=10,求c.(2)已知a=5,c=12,求b(注意:“∠B为直角”这个条件。
勾股定理复习导学案

勾股定理复习导学案一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和 ;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 。
2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,无重叠、空隙,面积不改变 ②根据同一种图形的面积不同的表示方法,列等式,推导出定理 常见方法如下:方法一:4E F G H S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可得: 。
方法二:四个直角三角形的面积与小正方形面积的和=大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c=⨯+=+大正方形面积为S= ,所以222a b c +=。
方法三:S梯形= ,2112S 222ADE ABE S S ab c∆∆=+=⋅+梯形,化简得证。
3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是 三角形。
4.勾股定理的应用已知直角三角形的任意两边长,主要求第三边在A B C ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a cb =-5、利用勾股定理作长为的线段 例如:作长为、、的线段。
思路点拨:由勾股定理得,直角边为1的等腰直角三角形,斜边长就等于,直角边为和1的直角三角形斜边长就是,类似地可作。
作法:如图所示6.勾股定理的逆定理①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a cb +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边 7.勾股数:①记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ②用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n为正整数) ,2222,2,m n mn m n -+(,m n >m ,n 为正整数)题型一:直接考查勾股定理例1.在A B C ∆中,90C ∠=︒.⑴ 已知6AC =,8B C =.求AB 的长 ⑵已知17AB =,15A C =,求BC 的长 解:题型二:应用勾股定理建立方程例2.⑴在A B C ∆中,90AC B ∠=︒,5A B =cm ,3B C =cm ,C D AB ⊥于D ,C D =⑵直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为 例3.如图A B C ∆中,90C ∠=︒,12∠=∠, 1.5C D =, 2.5BD =,求A C 的长例4.如图R t A B C ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积BACcba HG F EDCB Abacba ccabcab a bcc baE D CBA21EDCBA题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mABCD E分析:根据题意建立数学模型,如图8A B =m ,2C D =m ,8B C =m ,过点D 作DE AB ⊥,垂足为E ,则6A E =m ,8D E =m 在R t A D E ∆中,由勾股定理得2210AD AE DE=+=题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形 例6.已知三角形的三边长为a ,b ,c ,判定A B C ∆是否为R t ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c =例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状?解:此三角形是直角三角形理由:222()264a b a b ab +=+-= ,且264c =222a b c ∴+= 所以此三角形是直角三角形题型五:勾股定理与勾股定理的逆定理综合应用例8.已知A B C ∆中,13AB =cm ,10B C =cm ,BC 边上的中线12AD =cm ,求证:A B A C = 证明:填空:1.如图1所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm ,正方形A ,B ,C 的面积分别是8cm 2,10cm 2,14cm 2,则正方形D 的面积是 cm 2.2.如图2,在△ABC 中,∠C =90°,BC =60c m ,CA =80c m ,一只蜗牛从C 点出发,以每分钟20c m 的速度沿CA →AB →BC 的路径再回到C 点,需要 分钟的时间.3.已知x 、y 为正数,且|x 2-4|+(y 2-16)2=0,如果以x 、y 的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为 .4.在布置新年联欢会的会场时,小虎准备把同学们做的拉花用上,他搬来了一架高为2.5米的梯子,要想把拉花挂在高2.4米的墙上(设梯子上端要到达或超过挂拉花的高度才能挂上),小虎应把梯子的底端放在距离墙 米处.5.如图3是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两直角边分别为 和 .(注:两直角边长均为整数) 6、如果正方形ABCD 的面积为29,则对角线AC 的长度为( ) 选择:1.下列各组数为勾股数的是( ) A .6,12,13B .3,4,7C .4,7.5,8.5D .8,15,162.要登上某建筑物,靠墙有一架梯子,底端离建筑物5,顶端离地面12,则梯子的长度为( )A .12B .13C .14D .15 3.直角三角形两直角边边长分别为6cm 和8cm ,则连接这两条直角边中点的线段长为( ) A .10cm B .3cm C .4cm D .5cm 4.若将直角三角形的两直角边同时扩大2倍,则斜边扩大为原来的( )A .2倍B .3倍C .4倍D .5倍5.下列说法中, 不正确的是( )A .三个角的度数之比为1∶3∶4的三角形是直角三角形B .三个角的度数之比为3∶4∶5的三角形是直角三角形C .三边长度之比为3∶4∶5的三角形是直角三角形D .三边长度之比为9∶40∶41的三角形是直角三角形6.三角形的三边长满足关系:(a +b )2=c 2+2ab ,则这个三角形是( ) A .钝角三角形B .直角三角形C .锐角三角形D .等边三角形7.某直角三角形的周长为30,且一条直角边为5,则另一直角边为( )A .3B .4C .12D .13解答:四边形ABCD 中已知AB=3,BC=12,CD=13,DA=4, ∠BAD=900,求这个四边形的面积.D CBA勾股定理练习 姓名一.填空题:1. 在Rt △ABC 中,∠C=90°(1)若a=5,b=12,则c=________;(2)b=8,c=17,则S △ABC =________。
勾股定理及逆定理复习导学案
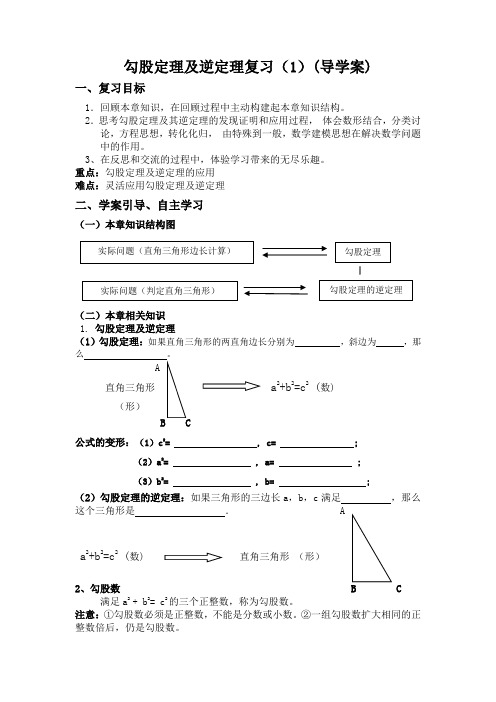
勾股定理及逆定理复习(1)(导学案)一、复习目标1.回顾本章知识,在回顾过程中主动构建起本章知识结构。
2.思考勾股定理及其逆定理的发现证明和应用过程, 体会数形结合,分类讨 论,方程思想,转化化归, 由特殊到一般,数学建模思想在解决数学问题 中的作用。
3、在反思和交流的过程中,体验学习带来的无尽乐趣。
重点:勾股定理及逆定理的应用 难点:灵活应用勾股定理及逆定理二、学案引导、自主学习(一)本章知识结构图(二)本章相关知识 1. 勾股定理及逆定理(1)勾股定理:如果直角三角形的两直角边长分别为 ,斜边为,那么 。
A直角三角形 a 2+b 2=c 2(数) (形)B C公式的变形:(1)c 2= , c= ;(2)a 2= , a= ; (3)b 2= , b= ;(2)勾股定理的逆定理:如果三角形的三边长a ,b ,c 满足 ,那么这个三角形是 . Aa 2+b 2=c 2(数) 直角三角形 (形)2、勾股数 B C满足a 2 + b 2= c 2的三个正整数,称为勾股数。
注意:①勾股数必须是正整数,不能是分数或小数。
②一组勾股数扩大相同的正整数倍后,仍是勾股数。
实际问题(直角三角形边长计算) 勾股定理的逆定理 勾股定理 实际问题(判定直角三角形)3、勾股定理的验证 4.互逆命题和互逆定理5、勾股定理的应用(最短路线、梯子下滑、船在水中航行等)三、合作探究、交流展示考点1:在直角三角形中,已知两边求第三边1、一种盛饮料的圆柱形杯,测得内部底面半径为2.5cm ,高为12cm ,吸管放进杯里,杯口外面至少要露出4.6cm ,问吸管要做 cm .2、已知直角三角形两直角边长分别为5和12, 求斜边上的高.(提示:直角三角形的两条直角边的积等于斜边与其高的积,ab=ch) 考点2:勾股定理与方程联手求线段的长(方程思想)1、如图 ,将一个边长为4、8的长方形纸片ABCD 折叠使C 点与A 点重合,则EB 的长是( ) A 、3 B 、4 C 、5 D 、52、如图,有一片直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,试求CD 的长。
《勾股定理的复习》导学案

《勾股定理的复习》导学案 姓名:学习目标: 掌握两个定理的内容并会用。
教学过程:一、理清知识,初步掌握勾股定理在Rt △ABC 中,∠C=900,则有 2+ 2= 2勾股定理的逆定理: 若 2+ 2= 2,则此三角形是Rt △。
二、运用面积思想,加深理解 二、勾股定理的证明c ca ab bc c aa bb b ac Cabcc aabb (一)(二)(三)证明:∵S 正方形=(从整体看正方形的面积)又∵S 正方形=(从分割组合来表示正方形的面积)∴ =因此,a 2+b 2=c 2图二:(下去后自己证明) 图三: 证明:三、运用定理,尝试成功(一) 直接运用勾股定理求边1.已知:Rt △ABC 中,∠C=90°, 若a=3, b=4, 求c 的值。
解:在Rt △ 中,∠ =90°,由勾股定理得:C= 答:c= 。
检查题:变式练习:1. 在Rt ABC ∆中,90C ∠=︒,其对边为c ,若40,9a b ==,则c =. 2.已知直角三角形的三边长分别为3、4、x ,则x 的值是 ( ) D.无法确定 3、阴影部分是一个正方形,则正方形的面积为 。
4、已知:Rt △ABC 中,∠C=90°,若c-a=2, b=6,求c 的值(二)先构造Rt △,再运用勾股定理 如图,求△ABC 的面积(三)、直接运用勾股定理的逆定理已知在△ABC 中, AC =10cm ,BC =24cm ,AB =26cm ,试说明△ABC 是直角三角形。
证明::∵AC 2+ BC 2= 2+ 2=而AB 2= 2= ∴ 2+ 2= 2 故△ABC 是直角三角形(四)、勾股定理的综合运用 1、四边形ABCD 中,AB=3cm ,AD=4cm ,BC=13cm ,CD=12cm且∠A=90°,∠CBD=550,求∠C 的度数。
解:变式练习:如图,在四边形ABCD 中,∠B=900,AB=BC=4,CD=6,AD=2,求:四边形ABCD 的面积。
勾股定理导学案(精品学案)

课题名称:勾股定理(1)学习目标: 1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
了解我国古代在勾股定理研究方面所取得的成就。
学习目标:经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。
学习重点:勾股定理的内容及证明。
学习难点:勾股定理的证明。
自助探究 1.1、2002年北京召开了被誉为数学界“奥运会”的国际数学家大会, 这就是当时采用的会徽. 你知道这个图案的名字吗?你知道它 的背景吗?你知道为什么会用它作为会徽吗?2、相传2500年前,古希腊的数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系.么?(1) 引导学生观察三个正方形之间的面积的关系;(2) 引导学生把面积的关系转化为边的关系.结论:等腰直角三角形三边的特殊关系:斜边的平方等于两直角边的平方和. 3、等腰直角三角形有上述性质, 其它直角三角形也有这个性质吗?4、猜想:命题1自助提升 1、定理证明(1)赵爽利用弦图证明。
.....显然4个 的面积+中间小正方形的面积=该图案的面积.即4×21× +﹝ ﹞2=c 2,化简后得到 .(2)其他证明方法:教材72页 思考讨论完成2、在Rt △ABC 中,∠C=90,AB=17,BC=8,求AC 的长3、Rt △ABC 和以AB 为边的正方形ABEF ,∠ACB =90°, AC =12,BC =5,则正方形的面积是______.4、(1) 已知Rt △ABC 中,∠C =90°,BC =6,AC =8,求AB .(2) 已知Rt △ABC 中,∠A =90°,AB =5,BC =6,求AC . (3) 已知Rt △ABC 中,∠B =90°,a ,b ,c 分别是∠A ,∠B , ∠C 的对边,c ∶a =3∶4,b =15,求a ,c 及斜边高线h .BC AB5、如图1-1-4,所有的四边形都是正方形,所有的三角 形都是直角三角形,其中最大的正方形的边长为7cm , 则正方形A ,B ,C ,D 的面积之和是多少?自助检测1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )2.斜边长为25 B .三角形的周长为25 C .斜边长为5 D .三角形面积为20 3.一直角三角形的斜边长比一条直角边长多2,另一直角边长为6,则斜边长为( )A .4B .8 C.10 D .124.直角三角形的两直角边的长分别是5和12,则其斜边上的高的长为( ) A .6 B .8 C .1380 D .13605、已知,如图1-1-5,折叠长方形(四个角都是直角,对边相等)的一边AD使点D 落在BC 边的点F 处,已知AB =8cm ,BC =10cm ,求CF CE 小结与反思这节课你学到了一些什么?你想进一步探究的问题是什么? 教学反思§ 勾股定理(2)一、学习目标通过经历和体验,运用勾股定理解决一些实际问题的过程,进一步掌握勾股定理。
新华师大版八年级数学上册导学案:14.1勾股定理

新华师大版八年级数学上册导学案:14.1勾股定理【学习目标】1.理解勾股定理的推导,掌握勾股定理的内容.2.会初步运用勾股定理进行简单的计算和实际运用.【课前导入】1. 计算:132-122= =+2286 =229-152. 如图小方格都是边长为1的正方形,求四边形ABCD 的面积是 。
(你有几种方法计算)【学习探究】一、自主学习:(积极思考,独立完成以下问题;将不能解决的问题标记出来,并写到后面“我的疑惑”处)1.问题1:请观察图中用阴影画出的三个正方形,如果每一小方格表示1cm 2,那么可以得到: =p s cm 2,=Q s cm 2,=R S cm 2我们发现,正方形P 、 Q 、 R 的面积之间的关系是 .由正方形我们得出等腰直角三角形ABC的三边的长度之间存在关系为:这说明,在等腰直角三角形中,三边数量关系(文字表示)是2.问题2:请观察右图,如果每一小方格表示1 cm 2,那么可以得到:=p s cm 2,=Q s cm 2,=R S cm 2(你是怎样得到正方形R 的面积的?与你的小组同学交流)我们发现,正方形P 、 Q 、 R 的面积之间的关系是 .由此,我们得出一般直角三角形ABC的三边的长度之间存在关系 .这说明,在一般直角三角形中,三边数量关系(文字表示)是 归纳:勾股定理:如果直角三角形两条直角边分别为a 、b,斜边为c ,那么 。
ab c几何语言:∵ (已知)∴ (勾股定理) 变一变:22b a c += =b =a我的疑惑:(请将你自主学习中不能解决和有疑惑的问题写在下面,待会提出来与老师同学探究解决)二、质疑探究 (先独立思考,再小组交流讨论,展示小组结果)1.初步尝试,体验勾股定理求下列直角三角形中未知边的长:x=x= x=2.二次尝试,解决生活问题(请仿照111页例题1完成)如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。
接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。
华师大版八年级数学上册 第14章 14.1 勾股定理 导学案(无答案)

§14.1 勾股定理第一课时【学习内容】直角三角形三边的关系(一)【学习目标】1、体验勾股定理的探索过程,掌握勾股定理.2、能利用勾股定理解决实际问题.3、通过观察、操作、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力.【学习重点和难点】1、学习重点:勾股定理的实际运用2、学习难点:探索和验证勾股定理的过程【学习过程】一、知识回顾1、直角三角形的性质:2、三角形三边关系:3、现有四条线段的长度分别为4cm,6cm,8cm,10cm,从中任取三条线段,能组成三角形的个数为().A、1个;B、2个;C、3个;D、4个.二、预习导学1的正方形纸片,沿对角线折叠,你知道折痕有多长吗?小明用一边长为cm①这个问题你是怎样想的?请说出你的想法.1),你能知道斜②若把折叠后的直角三角形纸片放在如图所示的格点图中(每个小正方形边长为cm边的长吗?③观察图形,并填空:cm,⑴正方形P的面积为2cm,正方形Q的面积为2cm.正方形R的面积为2⑵你能发现图中正方形P、Q、R的面积之间有什么关系?从中你发现了什么?活动二:动手做一做其它一般的直角三角形,是否也有类似的性质呢?(你打算用什么方法来研究?共同讨论方法后再确立研究方向)(图中每一小方格表示21cm ) ⑴正方形P 的面积为 2cm , 正方形Q 的面积为 2cm , 正方形R 的面积为 2cm . ⑵正方形P 、Q 、R 的面积之间的关系 是什么?⑶你会用直角三角形的边长表示正方形P 、Q 、R 的面积吗?你能发现直角三角形三边长度之间存在什么关系吗?与你的同伴进行交流.由此我们得到结论是:①勾股定理:对于任意的直角三角形,如果它的两条直角边分别为a 、b ,斜边为c ,那么一定有____________________________________.②用语言怎样叙述?_________________________________________________________. 公式变形:二、预习检测 认真填一填:a 2=c 2-b 2a =c =c 2=a 2 +b 2三、典例剖析例1:在△ABC 中,∠A=90°,BC=a ,AC=b ,AB=c.(1) 若c=10,b=24,求a; (2)若c=9,a=15,求b ;(3)若b=12,a=15,求c.例2:如图14.1.4,将长为5.41米的梯子AC 斜靠在墙上,BC长为2.16米,求梯子上端A 到墙的底边的垂直距离AB.(精确到0.01米)例3:在Rt △ABC 中,∠ACB=90°, ∠A 、∠B 、∠C 的对边分别是a 、b 、c. 若a=6,b=8,求c 的长及斜边上的高.四、分层练习A 组1.在Rt △ABC 中,︒=∠90A ,c AB =,a BC =,b AC = ①若8=c ,10=a ,则=b . ②若5=b ,12=c ,则=a .③若4:3:=c b ,15=a ,则=b ,=c .2.若线段a ,b ,c 能构成直角三角形,则它们的比可为 ( ) A .2:3:4 B .3:4:6 C .5:12:13 D .4:6:73. 如果一个直角三角形的两条直角边长分别为n 2-1、2n(n>0),那么它的斜边长为 ( )A .2nB .n+1C .n 2-lD .n 2+14.若直角三角形的三边长分别是3cm 与5cm ,那么这个三角形的周长是________cm. 5.在直角三角形ABC 中,斜边AB=2,则AB 2+BC 2+CA 2=__________. 6.在等腰三角形ABC 中,AB=AC=13,BC=10,则S △ABC =___________.7、如图,矩形纸片ABCD 中,AD=9cm ,AB=3cm ,将其折叠,使点D 与点B 重合,求折叠后BE 的长为多少?设BE=xcm ,则以下 所列方程正确的是( ). A :(9–x)2+x 2=32B :(9–x)2+32=x 2C :32+x 2=(6–x)2D :(6–x)2+x 2=328、如图,所有的四边形都是正方形,所有的三角形 都是直角三角形,其中最大的正方形边长是cm 7, 则正方形A 、B 、C 、D 的面积和是 2cm .9.如图所示,AC=3cm ,AB=4 cm ,BD=12 cm ,求CD 的长.第二课时【学习内容】直角三角形三边的关系(二) 【学习目标】1、用拼图的方法说明勾股定理的结论正确2、会应用勾股定理解决实际问题【学习重点和难点】1、学习重点:利用勾股定理解决实际问题2、学习难点:构造直角三角形求解 【学习过程】一、知识回顾1. 勾股定理的内容是什么?2.一直角三角形中有两条边的长为1和2,求第三边.二、预习导学剪四个与图14.1.5完全相同的直角三角形,然后将它们拼成以C 边为斜边的正方形.大正方形的面积可以表示为 ,又可以表示为 .对比两种表示方法,看看能不能得到勾股定理的结论.图14.1.5用上面得到的完全相同的四个直角三角形,还可以拼成如图14.1.7所示的图形,与上面的方法类似,也能说明勾股定理是正确的.由下面几种拼图方法,试一试,能否得出222c b a =+的结论.(1) (2) (3) (4) (5)探究点拔:1.将这四个完全相同的直角三角形拼成图(1),(2),(3)中所示的正方形,利用正方形的面积等于各部分面积的和可以得出222c b a =+.2.将两个直角三角形拼成图(4)中的梯形,由梯形面积等于三个直角三角形面积的和可以得到222c b a=+.3.通过剪接的方法构成如图(5)的正方形,可以证得222c b a =+.c b a c b acb a四、典例剖析例1. 如图,为了求出湖两岸的AB 两点之间的距离,一个观测者在点C 设桩,使△ABC 恰好为Rt △,通过测量,得到AC 长160米,BC 长128米,问从A例2 .在一棵树的10米高处有两只猴子,其中一只爬下树走向离树20米的池塘,而另一只爬到树顶后直扑池塘.如果两只猴子经过的距离相等,问这棵树有多高?例3.有一个棱长为1米且封闭的正方形盒子(如图),一只蚂蚁从顶点A 向顶点B 爬行,问这只蚂蚁爬行的最短路程为多少米?五、分层练习1.小雨用竹杆扎了一个长80cm 、宽60cm 的长方形框架,由于四边形容易变形,需要用一根竹杆作斜拉杆将四边形定形,则斜拉杆最长需________cm .2.小杨从学校出发向南走150米,接着向东走了360米到九龙山商场,学校与九龙山商场的距离是 米.3.如图:带阴影部分的半圆的面积是多少?( 取3)B AB A C4.已知,如图在ΔABC 中,AB=BC=CA=2cm ,AD 是边BC 上的高. 求 ①AD 的长; ②ΔABC 的面积.5.在直角ΔABC 中,斜边长为2,周长为2+6,求ΔABC 的面积.6.已知:如图,△ABC 中,AB >AC ,AD 是BC 边上的高. 求证:AB 2-AC 2=BC(BD-DC).7.已知直角三角形两直角边长分别为5和12, 求斜边上的高.8. 如图∠B=90º,AB =16cm ,BC =12cm ,AD =21cm,CD=29cm 求四边形ABCD 的面积.BD CA9.在加工如图的垫模时,请根据图中的尺寸,求垫模中AB间的尺寸.六、学习心得七、课堂作业八、家庭作业第三课时【学习内容】直角三角形的判定【学习目标】1、掌握直角三角形的判定条件,并能进行简单应用2、熟记一些勾股数.能对直角三角形的判别条件进行一些综合应用【学习重点和难点】1、学习重点:直角三角形的判别条件及其应用;它可用边的关系来判断一个三角形是否是直角三角形2、学习难点:直角三角形的判别条件判断一个三角形是否是直角三角形及综合应用直角三角形的知识解题.【学习过程】一、知识回顾问题1:直角三角形有什么性质?(1)有一个角是; (2)两个锐角;(3) 勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么问题2:反之,一个三角形满足什么条件,才能是直角三角形呢?(有一个角是直角;两个锐角互余)问题3:猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系式时,这个三角形才可能是直角三角形呢?二、预习导学1、古代埃及人作直角:古埃及人曾经用下面的方法画直角:用13个等距的结把一根绳子分成等长的12段,然后用桩钉如图那样钉成一个三角形,他们认为其中一个角便是直角. 他们真的能够得到直角三角形吗?你知道这是什么道理吗?2、画图:试画出三边长度分别为如下数据的三角形,看看它们是一些什么形状的三角形:(1)a=3,b=4,c=5; (2)a=4,b=6,c=8; (3)a=6,b=8,c=10. (4)a=2,b=3,c=4以上各组数据为三边所画的三角形是直角三角形的是;以上各组数据为三边所画的三角形不是直角三角形 .3、结合三角形三边长度的平方关系,你能猜一猜三角形的三边长度与三角形的形状有怎样的关系吗?在以上的各组数据中,满足a2 + b2 = c2的是;不满足a2 + b2 = c2的是 .3、归纳:勾股定理的逆定理:如果三角形的三边长a 、b 、c 满足 a 2 + b 2= c 2 , 那么这个三角形是直角三角形.几何语言:∵a 2 + b 2= c 2 ∴ΔABC 为Rt Δ强调:满足较短的两边的平方和等于最长边的平方的三角形是直角三角形 三、典例剖析例1 设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形: (1) 7, 24, 25; (2) 12, 35, 37; (3) 13, 11, 9.注意:①先找最大边②再判断三角形是否满足较短的两边的平方和等于最长边的平方(勾股定理的逆定理)例2、一个零件的形状如下图所示,按照规定这个零件中∠A 和∠DBC 都是直角.量得各边尺寸如图所示,这零件符合要求吗?并说明理由.五、分层练习1.分别以下列四组数为一个三角形的边长:(1)6,8,10; (2)5,12,13; (3)8, 15,17; (4)4,5,6其中能构成直角三角形的有( ).A .4组B .3组C .2组D .1组 2.△ABC 中,b=17,c=8,a=15,则∠ABC=_________.3.若一个三角形的周长123c m,一边长为33c m,其他两边之差为3c m,则这个三角形 是______________________.4.将直角三角形的三边扩大相同的倍数后,得到的三角形是 ( ). A.直角三角形 B.锐角三角形 C.钝角三角形 D.不是直角三角形 5.下列命题中是假命题的是( ).A .△ABC 中,若∠B =∠C -∠A ,则△ABC 是直角三角形. B .△ABC 中,若a 2=(b +c )(b -c ),则△ABC 是直角三角形.C .△ABC 中,若∠A ∶∠B ∶∠C =3∶4∶5则△ABC 是直角三角形.D .△ABC 中,若a ∶b ∶c =5∶4∶3则△ABC 是直角三角形.413D CBA 53 126.在△ABC 中,2:1:1::=c b a ,那么△ABC 是( ).A .等腰三角形B .钝角三角形C .直角三角形D .等腰直角三角形 7.三角形的三边分别为a 2+b 2,2ab ,a 2-b 2(a ,b 都是正整数)则这个三角形是( ). A .直角三角形 B .钝角三角形 C .锐角三角形 D .不能确定8.木工周师傅做一个长方形桌面,测量得到桌面的长为60cm ,宽为32cm ,对角线为68cm ,这个桌面_______ (填”合格”或”不合格”).9.如图,正方形ABCD 中,F 为DC 的中点,E 为BC 上一点, 且BC CE 41=.你能说明∠AFE 是直角吗?六、学习心得七、课堂作业八、家庭作业§14.2 勾股定理的应用第一课时【学习目标】1.能运用勾股定理解决生活中与直角三角形有关的问题;2.能从实际问题中建立数学模型,将实际问题转化为数学问题,同时渗透方程、转化等数学思想. 3.进一步发展有条理思考和有条理表达的能力,体会数学的应用价值【学习重点和难点】 重点:勾股定理的应用难点:将实际问题转化为数学问题 【学习过程】 一、知识回顾(1)在Rt △ABC 中,a=8㎝,b=10㎝,90B ∠=,则第三边长c= . (2)已知△ABC 中,三边长a 、b 、c 为整数,其中a=3㎝,b=4㎝,求第三边c 的长.(3)已知在Rt △ABC 中,两直角边的长为20和15,90BAC ∠=,且BC 边上的高为12,求BD 的长.(4)如图,一块长方形水泥操场,一学生要从A 角走到C 角,至少走 米.二、新知探究问题1. 如图,起重机吊运物体,已知BC=6m,AC=10m,求AB 的长.问题 2. 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?ABC三.例题剖析例1. 如图:一圆柱体的底面周长为20cm ,高AB为4cm ,BC是上底面的直径.一只蚂蚁从点A 出发,沿着圆柱的侧面爬行到点C ,试求出爬行的最短路程.例2.一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门?四、反馈提高A 组1.(1)在Rt △ABC 中,∠C=90°,若BC=4,AC=2,则AB=______;若AB=4,BC=2,则AC=_____; (2)一个直角三角形的模具,量得其中两边的长分别为5cm ,3cm ,则第三边的长是______; (3)甲乙两人同时从同一地出发,甲往东走4km ,乙往南走6km2.如图,圆柱高为8cm ,地面半径为2cm ,一只蚂蚁从点A 爬到点B 处吃食, 要爬行的最短程( 取3)是( )A .20cmB .10cmC .14cmD .无法确定3. 一条河的宽度处处相等,小强想从河的南岸横游到北岸去,由于水流影响,小强上岸地点偏离目标地点200m,他在水中实际游了520m,那么该河的宽度为 ( ) A.440 m B.460 m C.480 m D. 500 m 4.P58 练习1、2题B组1、如图,王大伯家屋后有一块长12m ,宽8m 的矩形空地,他在 以长边BC 为直径的半圆内种菜,他家养的一只羊平时拴A 处的 一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( ). A 、 3 m B 、 5 m C 、6 m D 、7 m2、如图,笔直的公路上A 、B 两点相距25km ,C 、D 为两村庄,DA ⊥AB 于点A ,CB ⊥AB 于点B ,已知DA=15km ,CB=10km ,现在要在公路的AB 段上建一个土特产品收购站E ,使得C 、D 两村到收购站E 的距离相等,则收购站E 应建在离A 点多远处?3.有一圆柱形食品盒,它的高等于16cm,底面直径为20cm, 蚂蚁爬行的速度为2cm/s.⑴如果在盒内下底面的A 处有一只蚂蚁,它想吃到盒内对面中部点B 处的食物,那么它至少需要多少时间? (盒的厚度和蚂蚁的大小忽略不计,结果可含π)⑵如果在盒外下底面的A 处有一只蚂蚁,它想吃到盒内对面中部点B 处的食物,那么它至少需要多少时间? (盒的厚度和蚂蚁的大小忽略不计,结果可含π六.学习收获:七.课堂作业:A D E BC八.课后反思第二课时【学习目标】1、会用勾股定理解决较综合的问题.2、树立数形结合的思想. 【学习重点和难点】重点:勾股定理的综合应用. 难点:勾股定理的综合应用. 【学习过程】 一.预习练习1. 一根32厘米的绳子被折成如图所示的形状钉在P 、Q 两点, PQ=16厘米,且RP ⊥PQ ,则RQ= 厘米.2. 已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求:四边形ABCD 的面积.二.例题剖析1. 如图14.2.5,在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:(1) 从点A 出发画一条线段AB,使它的另一个端点B在格点(即小正方形的顶点)上,且长度为22; (2) 画出所有的以(1)中的AB为边的等腰三角形, 使另一个顶点在格点上,且另两边的长度都是无理数.2.如图,已知CD =6m , AD =8m , ∠ADC =90°, BC =24m , AB=26m .求图中阴影部分的面积.QB三.反馈提高A组1. P60练习1.2题2. 已知,如图,一轮船以16海里/时的速度从港口A 出发向东北方 向航行,另一轮船以12海里/时的速度同时从港口A 出发向东南方 向航行,离开港口2小时后,则两船相距( )海里. A 、25 B 、 30 C 、35 D 、403. 求知中学有一块四边形的空地ABCD ,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m ,BC=12m ,CD=13m ,DA=4m ,若每平方米草皮需要200天,问学校需要投入多少资金买草皮?B组1、 如图,设正方体ABCD-A 1B 1C 1D 1的棱长为1,黑、白两 个甲壳虫同时从A 点出发,以相同的速度分别沿棱向前爬行, 黑甲壳虫爬行的路线是:AA 1⇒A 1D 1⇒D 1C 1⇒C 1C ⇒CB ⇒BA ⇒AA 1⇒A 1D 1…,白甲壳虫爬行的路线是:AB ⇒BB 1⇒B 1C 1⇒ C 1D 1⇒D 1A 1⇒A 1A ⇒AB ⇒BB 1…,那么当黑、白两个甲壳虫各 爬行完第2008条棱分别停止在所到的正方体顶点处时,它们 之间的距离是 .2. 如图所示,折叠矩形的一边AD ,使点D 落在BC 边上的点F 处,已知AB=8cm ,BC=10cm ,求EC 的长.D CBA3.如图,A、B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越森林保护区?为什么?四.学习收获:五.课堂作业:六.课后反思。
2023年华师大版八年级数学上册《勾股定理复习》学案

新华师大版八年级数学上册《勾股定理复习》学案编号:60 执教人:课题课型学生姓名组别学生评价教师评价勾股定理复习复习课一、学习目标二、学习重点正确运用勾股定理及其逆定理。
三、自主预习1.用10分钟的时间,回顾课本,认真研究例题。
2.把自己的疑惑写出来供小组共享,分小组解决。
3.集中解决小组不能解决的问题。
四、合作探究1.利用勾股定理求面积(1)求:(1)阴影部分是正方形;(2)阴影部分是长方形;(3)阴影部分是半圆.(2)如图,以Rt△ABC的三边为直径分别向外作三个半圆,试探索三个半圆的面积之间的关系.2.在直角三角形中,已知两边求第三边。
(1)在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为.(2)(注意分类的思想)已知直角三角形的两边长为3、2,则另一条边长的平方是。
(3)已知直角三角形两直角边长分别为5和12,求斜边上的高。
(提示:直角三角形的两条直角边的积等于斜边与其高的积)。
1 / 32 / 3CPAB C DEAB C DE FBA(4)在数轴上做出表示10 的点?3.构造Rt△,求线段的长(1)如下图1,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,求EB 的长.(2)如下图2,P 为边长为2的正方形ABCD 对角线A C 上一动点,E 为AD 边中点,求EP+DP 最小值。
(3)如下图3,是一个三级台阶,它的每一级的长、宽和高分别为20dm 、3dm 、2dm ,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物,则蚂蚁沿着台阶面爬到B 点最短路程是_____________ dm.图1 图2 图3五、巩固反馈(当堂检测)1.已知直角三角形的两边长为3、2,则另一条边长是________________.2.如图4为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要________________米.5.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时。
2023年华师大版八年级数学上册《勾股定理的应用》导学案

新华师大版八年级数学上册《勾股定理的应用》导学案
学习目标
1. 综合运用勾股定理和逆定理解决实际问题;;
2. 提高综合运用勾股定理和逆定理的能力
学习重点综合运用勾股定理和逆定理解决实际问题;
学习难点:实际问题转化成数学问题再转化为直角三角形中
教学设计:
一. 设置情景(导入新课)
二.自主学习(发现知识)
例:如图,一块地,已知AD=8m,CD=6m,∠D=90°,AB=26m,BC=24m,求这块地的面积.
三. 合作探究(理解知识)
如图,△ABC的三边分别为A C=5,BC=12,AB=13,将△ABC沿AD折叠,使AC•落在AB上,求DC的长.
四. 展示点评(归纳知识)
一只鸭子要从边长分别为16m和6m的长方形水池一角M•游到水池另一边中点N,那么这只鸭子游的最短路程应为多少米?
1、已知等腰△ABC的周长为26,AB=AC,且AB=BC+4,求:
⑴底边BC上的高。
⑵△ABC的面积和一腰上的高。
五.当堂训练(运用知识)
;
已知矩形AB CD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,求DE的长?
如图,铁路上A、B两点相距25km,C、D为两村庄,DA•垂直AB于A,CB垂直AB于B,已知AD=15km,BC=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站建在距A站多少千米处?
六.小结反思(强化知识)
七.课后反思:
:你都学到了些什么?有哪些地方还是让你感到疑惑的?……。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新华师大版八年级数学上册《勾股定理》复习导学案
一、知识要点:
1、勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
也就是说:如果直角三角
形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。
公式的变形:a2 = c2- b2, b2= c2-a2 。
勾股定理在西方叫毕达哥拉斯定理,也叫百牛定理。
它是直角三角形的一条重要性质,揭示的是三边之间的数量关系。
它的主要作用是已知直角三角形的两边求第三边。
勾股定理是一个基本的几何定理,它是用代数思想解决几何问题的最重要的工具之一,是数形结合的纽带之一。
2、勾股定理的逆定理
如果三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。
这个定理叫做勾股定理的逆定理.
该定理在应用时,同学们要注意处理好如下几个要点:
①已知的条件:某三角形的三条边的长度.②满足的条件:最大边的平方=
最小边的平方+中间边的平方.③得到的结论:这个三角形是直角三角形,并且
最大边的对角是直角.
④如果不满足条件,就说明这个三角形不是直角三角形。
3、勾股数
满足a2 + b2= c2的三个正整数,称为勾股数。
注意:①勾股数必须是正整数,不能是分数或小数。
②一组勾股数扩大相同的正整数倍后,仍是勾股数。
4、最短距离问题:
主要运用的依据是。
二、知识结构:三、考点剖析
考点一:利用勾股定理求面积
求:(1)阴影部分是正方形;(2)阴影部分是长方形;(3)阴影部分是半圆.
2. 如图,以Rt△ABC的三边为直径分别向外作三个半圆,试探索三个半圆的面积之间的关系.
考点二:在直角三角形中,已知两边求第三边
例(09年山东滨州)如图2,已知△ABC中,AB=17,AC=10,BC边上的高,AD=8,则边BC的长为()
A.21 B.15 C.6 D.以上答案都不对
【强化训练】:1.在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为.
直角三角形
勾股定理
应用
判定直角三角形的一种方法
2.(易错题、注意分类的思想)已知直角三角形的两边长为3、2,则另一条边长的平方是
3、已知直角三角形两直角边长分别为5和12, 求斜边上的高.(结论:直角三角形的两条
直角边的积等于斜边与其高的积,ab =ch )
考点三:应用勾股定理在等腰三角形中求底边上的高 例、(09年湖南长沙)如图1所示,等腰中,,是底边上的高,
若,求 ①AD 的长;②ΔABC 的面积.
考点四:应用勾股定理解决楼梯上铺地毯问题
例、(09年滨州)某楼梯的侧面视图如图3所示,其中
米,
,
,
因某种活动要求铺设红色地毯,则在AB 段楼梯所铺地毯的长度应为 .
分析:如何利用所学知识,把折线问题转化成直线问题,是问题解决的关键。
仔细观察图形,不难发现,所有台阶的高度之和恰好是直角三角形ABC 的直角边BC 的长度,
所有台阶的宽度之和恰好是直角三角形ABC 的直角边AC 的长度,只需利用勾股定理,求得这两条线段的长即可。
考点五、利用列方程求线段的长(方程思想)
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳
子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
【强化训练】:折叠矩形ABCD 的一边AD,点D 落在BC 边上的点F 处,已知AB=8CM,BC=10CM,
求CF 和EC 。
.
A B
C
A B
C
E
F
D。
