2018年高考数学二轮复习(江苏版)14个填空题专项强化练(一)集合与常用逻辑用语 Word版 含答案
江苏专版2018年高考数学二轮复习14个填空题综合仿真练五

14个填空题综合仿真练(五)1.已知集合U ={1,2,3,4,5},A ={3,4},B ={1,4,5},则A ∪(∁U B )=________. 解析:∵集合U ={1,2,3,4,5},A ={3,4},B ={1,4,5},∴∁U B ={2,3},A ∪(∁U B )={2,3,4}.答案:{2,3,4}2.已知i 为虚数单位,复数z 1=3+y i(y ∈R),z 2=2-i ,且z 1z 2=1+i ,则y =________. 解析:因为z 1z 2=1+i ,所以z 1=(1+i)z 2=(1+i)(2-i)=3+i ,所以y =1. 答案:13.已知倾斜角为α的直线l 的斜率等于双曲线x 2-y 23=1的离心率,则sin ⎝⎛⎭⎪⎫2 019π3-2α=________.解析:因为双曲线的离心率e =2,所以tan α=2,所以sin ⎝⎛⎭⎪⎫2 019π3-2α=sin2α=2sin αcos αsin 2α+cos 2α=2tan α1+tan 2α=45. 答案:454.某中学共有学生2 000人,其中高一年级共有学生650人,高二男生有370人.现在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.则该校高三学生共有________人.解析:设高二女生人数为x 人,所以x2 000=0.19,即x =380,所以高三人数为2 000-650-370-380=600人.答案:6005.已知偶函数f (x )在[0,+∞)上单调递减,且f (3)=0,则不等式f (x 2-2x )>0的解集为________.解析:根据偶函数的性质,可得-3<x 2-2x <3,从而可得-1<x <3,所以不等式的解集为(-1,3).答案:(-1,3)6.阅读如图所示的算法流程图,若输入的n 是30,则输出的变量S 的值是________.解析:根据算法流程图知,当n =30时,n >2,S =30,n =28;当n =28时,n >2,S =58,n =26;……;当n =2时,S =30+28+26+…+2=+2=240,n =0.当n=0时,n <2,输出S =240.答案:2407.已知Ω1是集合{(x ,y )|x 2+y 2≤1}所表示的区域,Ω2是集合{(x ,y )|y ≤|x |}所表示的区域,向区域Ω1内随机的投一个点,则该点落在区域Ω2内的概率为________.解析:如图所示,作出区域Ω1(圆面),Ω2(虚线部分)的图象,根据几何概型的概率计算公式得,该点落在区域Ω2内的概率P =34πr 2πr 2=34.答案:348.数列{a n }满足a 1=2,a 2=1,且a n -1a n +1=a n -1-a na n -a n +1(n ≥2),则使得a n =2a 2 018成立的正整数n =________.解析:显然数列{a n }中通项a n ≠0,由a n -1a n +1=a n -1-a n a n -a n +1可得,a n ·a n -1a n -1-a n =a n ·a n +1a n -a n +1, 两边取倒数可得:1a n -1a n -1=1a n +1-1a n,所以⎩⎨⎧⎭⎬⎫1a n 是等差数列且首项1a 1=12,公差d =1-12=12,所以1a n =12+12(n -1)=n 2,即a n =2n,所以由a n =2a 2 018可得2n =2×22 018,所以n =1 009.答案:1 0099.函数f (x )=sin x +3cos x -a 在区间[0,2π]上恰有三个零点x 1,x 2,x 3,则x 1+x 2+x 3=________.解析:f (x )=sin x +3cos x -a =2sin ⎝⎛⎭⎪⎫x +π3-a ,函数在区间[0,2π]上恰有三个零点x 1,x 2,x 3,则a = 3.令sin ⎝ ⎛⎭⎪⎫x +π3=32,所以x +π3=2k π+π3或x +π3=2k π+π-π3,所以x =2k π或x =2k π+π3,所以x 1=0,x 2=π3,x 3=2π,即x 1+x 2+x 3=7π3. 答案:7π310.已知椭圆C 1:x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2.其中F 2也是抛物线C 2:y 2=4x 的焦点,点M 为C 1与C 2在第一象限的交点,且MF 1=2a -53.则椭圆C 1的方程为________.解析:依题意知F 2(1,0),设M (x 1,y 1),由椭圆的定义可得MF 2=53,由抛物线定义得MF 2=1+x 1=53,即x 1=23,将x 1=23代入抛物线方程得y 1=263,进而由⎝ ⎛⎭⎪⎫232a 2+⎝ ⎛⎭⎪⎫2632b2=1及a2-b 2=1,解得a 2=4,b 2=3,故椭圆C 1的方程为x 24+y 23=1.答案:x 24+y 23=111.在平行四边形ABCD 中,∠A =π3,边AB ,AD 的长分别为2,1,若M ,N 分别是边BC ,CD 上的点,且满足|BM ―→||BC ―→|=|CN ―→||CD ―→|,则AM ―→·AN ―→的最大值为________.解析:以AB 所在直线为x 轴,过点A 作垂直于直线AB 所在的直线为y 轴,建立如图所示的直角坐标系.设|BM ―→||BC ―→|=|CN ―→||CD ―→|=λ(0≤λ≤1),所以|BM ―→|=λ,|CN ―→|=2λ, 所以M ⎝⎛⎭⎪⎫2+λ2,32λ,N ⎝ ⎛⎭⎪⎫52-2λ,32,所以AM ―→·AN ―→=5-4λ+54λ-λ2+34λ=-λ2-2λ+5=-(λ+1)2+6,因为λ∈[0,1],所以AM ―→·AN ―→∈[2,5],所以AM ―→·AN ―→的最大值为5. 答案:512.已知x >0,y >0,且x +y ≤2,则4x +2y +12x +y的最小值为________. 解析:令x +2y =m,2x +y =n (m >0,n >0),则问题转化为m +n ≤6,求4m +1n的最小值,而(m +n )⎝ ⎛⎭⎪⎫4m +1n ≥9,即4m +1n ≥9m +n ≥32,故所求最小值为32. 答案:3213.已知函数f (x )=⎩⎪⎨⎪⎧2x 2+2mx -1,0≤x ≤1,mx +2,x >1,若f (x )在区间[0,+∞)上有且只有2个零点,则实数m 的取值范围是________.解析:法一:由题意得当m ≥0时,函数f (x )=2x 2+2mx -1的对称轴-m2≤0,且f (0)=-1,所以此时f (x )在[0,1]上至多有一个零点,而f (x )=mx +2在(1,+∞)上没有零点.所以m ≥0不符合题意.当m <0时,函数f (x )=2x 2+2mx -1的对称轴-m2>0,且f (0)=-1,所以,此时f (x )在[0,1]上至多有一个零点,而f (x )=mx +2在(1,+∞)上至多有一个零点,若f (x )在[0,+∞)上有且只有2个零点,则要求⎩⎪⎨⎪⎧0<-m2≤1,2+2m -1≥0,m +2>0,解得-12≤m <0.综上,实数m 的取值范围为⎣⎢⎡⎭⎪⎫-12,0. 法二:由题意得x =0不是函数f (x )的零点.当0<x ≤1时,由f (x )=0,得m =12x-x ,此时函数y =12x -x 在(0,1]上单调递减,从而y =12x -x ≥-12,所以,当m ≥-12时,f (x )在(0,1]上有且只有一个零点,当x >1时,由f (x )=0,得m =-2x ,此时函数y =-2x在(1,+∞)上单调递增,从而y =-2x∈(-2,0),所以,当-2<m <0时,f (x )在(1,+∞)上有且只有一个零点,若f (x )在[0,+∞)上有且只有2个零点,则要求⎩⎪⎨⎪⎧m ≥-12,-2<m <0,解得-12≤m <0. 综上,实数m 的取值范围为⎣⎢⎡⎭⎪⎫-12,0. 答案:⎣⎢⎡⎭⎪⎫-12,014.已知函数f (x )=x |x 2-12|的定义域为[0,m ],值域为[0,am 2],则实数a 的取值范围是________.解析:仅考虑函数f (x )在x >0时的情况,可知f (x )=⎩⎨⎧12x -x 3,x <23,x 3-12x ,x ≥2 3.函数f (x )在x =2时,取得极大值16.令x 3-12x =16,解得x =4.作出函数的图象(如图所示).函数f (x )的定义域为[0,m ],值域为[0,am 2],分为以下情况考虑:(1)当0<m <2时,函数的值域为[0,m (12-m 2)],有m (12-m 2)=am 2,所以a =12m-m ,因为0<m <2,所以a >4;(2)当2≤m ≤4时,函数的值域为[0,16],有am 2=16,所以a =16m2,因为2≤m ≤4,所以1≤a ≤4;(3)当m >4时,函数的值域为[0,m (m 2-12)],有m (m 2-12)=am 2,所以a =m -12m,因为m >4,所以a >1,综上所述,实数a 的取值范围是[1,+∞).答案:[1,+∞)。
江苏专版2018年高考数学二轮复习14个填空题综合仿真练七

14个填空题综合仿真练(七)1.已知集合A ={-1,0,1},B =(-∞,0),则A ∩B =________. 解析:A ∩B ={-1,0,1}∩(-∞,0)={-1}. 答案:{-1}2.设z =1+i(i 是虚数单位),则2z+z 2=________.解析:2z +z 2=21+i +(1+i)2=1-i +2i =1+i.答案:1+i3.某路段检测点对200辆汽车的车速进行检测,检测结果表示为频率分布直方图,如图所示,则车速不小于90 km/h 的汽车约有________辆.解析:车速不小于90 km/h 的频率为(0.01+0.02)×10=0.3,车辆数为200×0.3=60. 答案:604.若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的体积为________. 解析:因为半圆面的面积为12πl 2=2π,所以l 2=4,解得l =2,即圆锥的母线为l =2,底面圆的周长2πr =πl =2π,所以圆锥的底面半径r =1,所以圆锥的高h =l 2-r 2=3,所以圆锥的体积为13πr 2h =13×π×3=3π3.答案:3π35.已知A ,B ∈{-3,-1,1,2}且A ≠B ,则直线Ax +By +1=0的斜率小于0的概率为________.解析:所有的基本事件(A ,B )为(-3,-1),(-1,-3),(-3,1),(1,-3),(-3,2),(2,-3),(-1,1),(1,-1),(-1,2),(2,-1),(1,2),(2,1),共12种,其中(-3,-1),(-1,-3),(1,2),(2,1)能使直线Ax +By +1=0的斜率小于0,所以所求的概率为P =412=13.答案:136.如图所示的算法流程图,当输入n 的值为10时,则输出S 的值为________.解析:根据算法流程图执行程序循环结果依次为:当n =1答案:547.若a >0,b >2,且a +b =3,则使得4a +1b -2取得最小值时,实数a =________.解析:∵a >0,b >2,且a +b =3,∴a +b -2=1, ∴⎝ ⎛⎭⎪⎫4a +1b -2[a +(b -2)]=4+1+b -a +ab -2≥5+2b -a·ab -2=9,当且仅当2(b -2)=a 时即取等号.联立⎩⎪⎨⎪⎧b -=a ,a +b =3,解得a =23.答案:238.若双曲线x 2a 2-y 2b2=1(a >0,b >0)的焦点到相应准线的距离等于实轴长,则双曲线的离心率为________.解析:由题意,c -a 2c=2a ,即c 2-2ac -a 2=0,即e 2-2e -1=0,解得e =1±2,又∵e >1,故e =1+ 2.答案:1+ 29.已知函数f (x )=x +2|x |+2,x ∈R ,则f (x 2-2x )<f (3x -4)的解集是________.解析:由题意,f (x )=⎩⎪⎨⎪⎧1,x ≥0,-1-4x -2,x <0,故若要使不等式成立,则有⎩⎪⎨⎪⎧x 2-2x <0,x 2-2x <3x -4,得1<x <2.答案:(1,2)10.记等差数列{a n }的前n 项和为S n ,已知a 1=3,且数列{S n }也为等差数列,则a 11=________.解析:设等差数列{a n }的公差为d (d >0), ∵a 1=3,且数列{S n }为等差数列, ∴2S 2=a 1+S 3, ∴26+d =3+9+3d , 即d 2-12d +36=0,解得d =6, ∴a 11=3+10×6=63. 答案:6311.在平面直角坐标系xOy 中,已知点A (-t,0)(t >0),B (t,0),点C 满足AC ―→·BC ―→=8,且点C 到直线l :3x -4y +24=0的最小距离为95,则实数t 的值是________.解析:设C (x ,y ),则AC ―→·BC ―→=(x +t ,y )·(x -t ,y )=x 2+y 2-t 2=8,所以点C 的轨迹为以原点为圆心, 8+t 2为半径的圆,故圆心到直线的距离d =245=95+8+t 2,解得t =1(负值舍去).答案:112.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若a 2=3b 2+3c 2-23bc sin A ,则C =________.解析:由题意知a 2=3b 2+3c 2-23bc sin A ,① 余弦定理a 2=b 2+c 2-2bc cos A ,②由①-②可得,2b 2+2c 2=23bc sin A -2bc cos A ,化简得,b 2+c 2=3bc sin A -bc cos A ,整理得b 2+c 2=2bc sin ⎝⎛⎭⎪⎫A -π6,∵b 2+c 2≥2bc ,∴sin ⎝ ⎛⎭⎪⎫A -π6=1,∴A =2π3,此时b 2+c 2=2bc ,故得b =c ,即B =C ,∴C =π6.答案:π613.设函数f (x )=⎩⎪⎨⎪⎧3x -1,x <1,2x 2,x ≥1,则满足f (f (a ))=2(f (a ))2的a 的取值范围为________.解析:设t =f (a ),所以f (f (a ))=2(f (a ))2可化为f (t )=2t 2,由函数式得3t -1=2t 2(t <1)或2t 2=2t 2(t ≥1),所以t =12或t ≥1,即f (a )=12或f (a )≥1,所以a =12或a ≥23,因此a 的取值范围为⎩⎨⎧⎭⎬⎫12∪⎣⎢⎡⎭⎪⎫23,+∞. 答案:⎩⎨⎧⎭⎬⎫12∪⎣⎢⎡⎭⎪⎫23,+∞14.已知函数f (x )=a ln x +(x +1)2,若图象上存在两个不同的点A (x 1,y 1),B (x 2,y 2)(x 1>x 2),使得f (x 1)-f (x 2)≤4(x 1-x 2)成立,则实数a 的取值范围为________.解析:由题意可得,f (x )=a ln x +x 2+2x +1,f ′(x )=ax+2(x +1),由题意知,存在x >0,使得f ′(x )≤4成立,即存在x >0,使得a ≤-2x 2+2x 成立,设g (x )=-2x 2+2x=-2⎝ ⎛⎭⎪⎫x -122+12,其最大值为12,因而a ≤12.答案:⎝⎛⎦⎥⎤-∞,12。
精选江苏专用2018版高考数学专题复习专题1集合与常用逻辑用语第5练集合与常用逻辑用语综合练练习理

(江苏专用)2018版高考数学专题复习 专题1 集合与常用逻辑用语第5练 集合与常用逻辑用语综合练练习 理________________.2.(2016·石家庄模拟)定义A ×B ={z |z =xy ,x ∈A 且y ∈B },若A ={x |-1<x <2},B ={-1,2},则A ×B =________________.3.(2016·常州模拟)“c <0”是“实系数一元二次方程x 2+x +c =0有两个异号实根”的________条件.(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”) 4.(2016·徐州二模)给出以下命题:①∀x ∈R ,|x |>x ;②∃α∈R ,sin 3α=3sin α;③∀x ∈R ,x >sin x ;④∃x ∈(0,+∞),(12)x <(13)x.其中正确命题的序号是________.5.(2016·如皋中学阶段练习)已知集合A ={1,2a},B ={a ,b },若A ∩B ={12},则A ∪B =______________.6.(2016·郑州模拟)已知命题p :∀x ∈R,2x <3x ;命题q :∃x 0∈R ,x 30=1-x 20,则下列命题中为真命题的是________________.(填序号) ①p ∧q ;②(綈p )∧q ;③p ∧(綈q );④(綈p )∧(綈q ).7.(2017·广东七校联考)下列有关命题的说法正确的是________. ①命题“若x 2=1,则x =1”的否命题为“若x 2=1,则x ≠1”; ②“x =-1”是“x 2-5x -6=0”的必要不充分条件; ③命题“若x =y ,则sin x =sin y ”的逆否命题为真命题;④命题“∃x ∈R 使得x 2+x +1<0”的否定是“∀x ∈R ,均有x 2+x +1<0”. 8.(2016·苏州模拟)下列命题中正确的个数是________.①命题“若m >-1,则方程x 2+2x -m =0有实根”的逆命题为“若方程x 2+2x -m =0有实根,则m >-1”;②“x ≠1”是“x 2-3x +2≠0”的充分不必要条件;③若p ∧q 为假命题,则p ,q 均为假命题. 9.(2016·镇江模拟)有下列四个命题: ①“若xy =1,则x ,y 互为倒数”的逆命题; ②“面积相等的三角形全等”的否命题;③“若m ≤1,则x 2-2x +m =0有实数解”的逆否命题; ④“若A ∩B =B ,则A ⊆B ”的逆否命题. 其中真命题为________.(填写所有真命题的序号)10.已知i 是虚数单位,a ,b ∈R ,则“a =b =1”是“(a +b i)2=2i”的____________条件.(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)11.设集合A ={x ||x -a |<1,x ∈R },B ={x |1<x <5,x ∈R },若A ∩B =∅,则实数a 的取值范围是__________________.12.已知命题“∃x ∈{x |-1<x <1},使等式x 2-x -m =0成立”是真命题,则实数m 的取值范围是________.13.(2016·成都一诊)已知定义在R 上的奇函数f (x ),当x ≥0时,f (x )=log 3(x +1).若关于x 的不等式f [x 2+a (a +2)]≤f (2ax +2x )的解集为A ,函数f (x )在[-8,8]上的值域为B ,若“x ∈A ”是“x ∈B ”的充分不必要条件,则实数a 的取值范围是________.14.已知f (x )=m (x -2m )(x +m +3),g (x )=2x-2,若满足∀x ∈R ,f (x )<0或g (x )<0,则m 的取值范围是________________. 答案精析1.{x |0≤x ≤1} 2.{x |-2<x <4}3.充要 4.② 5.{-1,1,12} 6.②7.③解析 命题“若x 2=1,则x =1”的否命题为“若x 2≠1,则x ≠1”,①不正确;由x 2-5x -6=0,解得x =-1或6,因此“x =-1”是“x 2-5x -6=0”的充分不必要条件,②不正确;命题“若x =y ,则sin x =sin y ”为真命题,其逆否命题为真命题,③正确;命题“∃x ∈R 使得x 2+x +1<0”的否定是“∀x ∈R ,均有x 2+x +1≥0”,④不正确.综上可得只有③正确. 8.1解析 对于①,命题“若m >-1,则方程x 2+2x -m =0有实根”的逆命题为“若方程x 2+2x -m =0有实根,则m >-1”,故①正确;对于②,由x 2-3x +2=0,解得x =1或x =2,∴“x ≠1”不是“x 2-3x +2≠0”的充分不必要条件,故②错误;对于③,若p ∧q 为假命题,则p ,q 中至少有一个为假命题,故③错误.∴正确命题的个数为1. 9.①②③解析 ①“若xy =1,则x ,y 互为倒数”的逆命题是“若x ,y 互为倒数,则xy =1”,显然是真命题,故①正确;②“面积相等的三角形全等”的否命题是“面积不相等的三角形不全等”,显然是真命题,故②正确;③若x 2-2x +m =0有实数解,则Δ=4-4m ≥0,解得m ≤1,所以“若m ≤1,则x 2-2x +m =0有实数解”是真命题,故其逆否命题是真命题,故③正确;④若A ∩B =B ,则B ⊆A ,故原命题错误,所以其逆否命题错误,故④错误. 10.充分不必要解析 由(a +b i)2=2i ,得⎩⎪⎨⎪⎧a 2-b 2=0,ab =1.∴⎩⎪⎨⎪⎧a =1,b =1或⎩⎪⎨⎪⎧a =-1,b =-1.故“a =b =1”是“(a +b i)2=2i”的充分不必要条件. 11.{a |a ≤0或a ≥6}解析 |x -a |<1⇔-1<x -a <1⇔a -1<x <a +1,又B ={x |1<x <5},A ∩B =∅,故a +1≤1或a -1≥5,即a ≤0或a ≥6. 12.[-14,2)解析 由题意得,方程x 2-x -m =0在(-1,1)上有解,所以m 的取值集合就是函数y =x 2-x 在(-1,1)上的值域. 所以-14≤m <2.13.[-2,0]解析 ∵x ≥0时,奇函数f (x )=log 3(x +1),∴函数f (x )在R 上为增函数, ∴f (x )在[-8,8]上也为增函数, 且f (8)=log 3(8+1)=2,f (-8)=-f (8)=-2,∴B ={x |-2≤x ≤2}.∵f [x 2+a (a +2)]≤f (2ax +2x ),∴x 2+a (a +2)≤2ax +2x ,即x 2-(2a +2)x +a (a +2)≤0,a ≤x ≤a +2,A ={x |a ≤x ≤a +2}.∵“x ∈A ”是“x ∈B ”的充分不必要条件,∴A B ,即⎩⎪⎨⎪⎧a ≥-2,a +2≤2(两等号不能同时取得),∴-2≤a ≤0. 14.(-4,0)解析 f (x )=m (x -2m )(x +m +3)为二次函数. 若∀x ∈R ,f (x )<0或g (x )<0, 则必须有抛物线开口向下,即m <0. 又∵当x ≥1时,g (x )≥0; 当x <1时,g (x )<0. ∴当x ≥1时,f (x )<0.f (x )=0有两根x 1=2m ,x 2=-m -3.当x 1>x 2,即m >-1时, 则x 1<1,即m <12,∴-1<m <0;当x 1<x 2,即m <-1时, 则x 2<1,即m >-4, ∴-4<m <-1; 当x 1=x 2,即m =-1时,x 1=x 2=-2<1.综上可知,m 的取值范围为-4<m <0.。
江苏专版2018年高考数学二轮复习14个填空题专项强化练十空间几何体

14个填空题专项强化练(十) 空间几何体A 组——题型分类练题型一 平面及其基本性质1.若空间中有两条直线,则“这两条直线为异面直线”是“这两条直线没有公共点”的________条件(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”).解析:若两直线为异面直线,则两直线无公共点,反之不一定成立. 答案:充分不必要2.设a ,b ,c 是空间中的三条直线,下面给出四个命题: ①若a ∥b ,b ∥c ,则a ∥c ; ②若a ⊥b ,b ⊥c ,则a ∥c ;③若a 与b 相交,b 与c 相交,则a 与c 相交;④若a ⊂平面α,b ⊂平面β,则a ,b 一定是异面直线. 上述命题中正确的命题是________(写出所有正确命题的序号).解析:由公理4知①正确;当a ⊥b ,b ⊥c 时,a 与c 可以相交、平行或异面,故②错;当a 与b 相交,b 与c 相交时,a 与c 可以相交、平行,也可以异面,故③错;a ⊂α,b ⊂β,并不能说明a 与b “不同在任何一个平面内”,故④错.答案:①题型二 空间中的平行与垂直1.给出下列条件:①l ∥α;②l 与α至少有一个公共点;③l 与α至多有一个公共点.能确定直线l 在平面α外的条件的序号为________.解析:直线l 在平面α外指:l ∥α或直线l 与平面α仅有一个交点. 答案:①③2.如图,在空间四边形ABCD 中,M ∈AB ,N ∈AD ,若AM MB =AN ND,则直线MN 与平面BDC 的位置关系是________.解析:因为AM MB =AN ND,所以MN ∥BD , 又MN ⊄平面BCD ,BD ⊂平面BCD , 所以MN ∥平面BDC . 答案:平行3.已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的序号是________.①若α⊥γ,α⊥β,则γ∥β ②若m ∥n ,m ⊂α,n ⊂β,则α∥β③若m∥n,m⊥α,n⊥β,则α∥β④若m∥n,m∥α,则n∥α解析:垂直于同一个平面的两个平面平行或相交,所以①错误;两个平面内的两条直线平行,这两个平面不一定平行,所以②错误;两个平面同时垂直于两条平行直线,这两个平面平行,所以③正确;两条平行直线中的一条平行于一个平面,另一条不一定平行于该平面,所以④错误.答案:③4.α,β为两个不同的平面,m,n为两条不同的直线,下列命题中正确的是________(写出所有正确命题的序号).①若α∥β,m⊂α,则m∥β;②若m∥α,n⊂α,则m∥n;③若α⊥β,α∩β=n,m⊥n,则m⊥β;④若n⊥α,n⊥β,m⊥α,则m⊥β.解析:在①中,若α∥β,m⊂α,则由面面平行的性质定理得m∥β,故①正确;在②中,若m∥α,n⊂α,则m∥n或m与n异面,故②错误;在③中,若α⊥β,α∩β=n,m⊥n,则m与β相交、平行或m⊂β,故③错误;在④中,若n⊥α,n⊥β,则α∥β.又m⊥α,所以m⊥β,故④正确.答案:①④5.如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.其中正确结论的序号是________.解析:①AE⊂平面PAC,BC⊥AC,BC⊥PA,AC∩PA=A,AC⊂平面PAC,PA⊂平面PAC⇒BC⊥平面PAC⇒AE⊥BC,故①正确;②AE⊥PB,AF⊥PB,AE∩AF=A,AE⊂平面AEF,AF⊂平面AEF⇒PB⊥平面AEF⇒EF⊥PB,故②正确;③若AF⊥BC⇒AF⊥平面PBC,则AF∥AE与已知矛盾,故③错误,由①可知④正确.答案:①②④题型三空间几何体的表面积和体积1.正六棱柱的高为6,底面边长为4,则它的表面积为________.解析:S底=6×34×42=243,S侧=6×4×6=144,所以S表=S侧+2S底=144+483=48(3+3).答案:48(3+3)2.已知正四棱锥的底面边长是2,侧棱长是3,则该正四棱锥的体积为________. 解析:如图,在正四棱锥P ABCD 中,AB =2,PA =3, 设正四棱锥的高为PO ,连结AO ,则AO =12AC = 2.在直角三角形POA 中,PO =PA 2-AO 2=1. 所以V P ABCD =13·S 四边形ABCD ·PO =13×4×1=43.答案:433.若圆锥底面半径为2,高为5,则其侧面积为________.解析:因为圆锥的底面半径为2,高为5,所以母线长为l =4+5=3,所以圆锥的侧面积为πrl =π×2×3=6π.答案:6π4.如图,在三棱柱ABC A 1B 1C 1中,AB 1=BB 1=BA =BC =2,∠B 1BC =90°,D 为AC 的中点,AB ⊥B 1D ,则三棱锥A 1B 1AD 的体积为________.解析:取AB 的中点O ,连结DO ,B 1O ,因为BB 1=AB 1,所以OB 1⊥AB ,又AB ⊥B 1D ,OB 1∩B 1D =B 1,所以AB ⊥平面B 1OD ,因为OD ⊂平面B 1OD ,所以AB ⊥OD ,由已知BC ⊥BB 1,又OD ∥BC ,所以OD ⊥BB 1,因为AB ∩BB 1=B ,所以OD ⊥平面ABB 1A 1,又O ,D 分别为AB ,AC 的中点,BC =2,所以OD =12BC =1,所以VA 1B 1AD =VD B 1AA 1=13×34×4×1=33. 答案:335.如图,已知正方体ABCD A 1B 1C 1D 1的棱长为1,点P 在线段BD 1上,当∠APC 最大时,三棱锥P ABC 的体积为________.解析:连结BD 交AC 于点O ,连结PO ,则∠APC =2∠APO , ∵tan ∠APO =AO PO,∴当PO 最小时,∠APO 最大, 即PO ⊥BD 1时,∠APO 最大.如图,作PE ⊥BD 于点E ,此时PB =13BD 1,∴三棱锥P ABC 的高为点P 到平面ABCD 的距离PE =13,∴三棱锥P ABC 的体积V =13S △ABC·PE =13×12×13=118.答案:118B 组——高考提速练1.如图为正方体表面的一种展开图,则图中的四条线段AB ,CD ,EF ,GH 在原正方体中互为异面的对数为________.解析:平面图形的翻折应注意翻折前后相对位置的变化,则AB ,CD ,EF 和GH 在原正方体中,显然AB 与CD ,EF 与GH ,AB 与GH 都是异面直线,而AB 与EF 相交,CD 与GH 相交,CD 与EF 平行.故互为异面的直线有且只有3对.答案:32.设b ,c 表示两条直线,α,β表示两个平面,现给出下列命题: ①若b ⊂α,c ∥α,则b ∥c ; ②若b ⊂α,b ∥c ,则c ∥α; ③若c ∥α,α⊥β,则c ⊥β; ④若c ∥α,c ⊥β,则α⊥β.其中正确的命题是________.(写出所有正确命题的序号)解析:①b 和c 可能平行或异面,故①错;②可能平行或c ⊂α,故②错;③可能c ⊥β,c ∥β,c ⊂β,故③错;④根据面面垂直判定α⊥β,故④正确.答案:④3.已知高与底面半径相等的圆锥的体积为8π3,其侧面积与高为22的圆柱OO 1的侧面积相等,则圆柱OO 1的体积为________.解析:设圆锥的底面半径为r ,圆柱OO 1的底面半径为R ,因为高与底面半径相等的圆锥的体积为8π3,所以13πr 2·r =8π3,所以r =2.又圆锥的侧面积与高为22的圆柱OO 1的侧面积相等,所以π·r ·2r =2πR ·22,所以R =1,所以圆柱OO 1的体积为πR 2·22=22π.答案:22π4.已知正三棱柱的各条棱长均为a ,圆柱的底面直径和高均为b .若它们的体积相等,则a 3∶b 3的值为________.解析:由题意可得12·a 2·32·a =π⎝ ⎛⎭⎪⎫b 22·b ,即34a 3=14πb 3,则a 3b 3=π3=3π3. 答案:3π35.已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有______个.解析:若α,β换为直线a ,b ,则命题化为“a ∥b ,且a ⊥γ⇒b ⊥γ”,此命题为真命题;若α,γ换为直线a ,b ,则命题化为“a ∥β,且a ⊥b ⇒b ⊥β”,此命题为假命题;若β,γ换为直线a ,b ,则命题化为“a ∥α,且b ⊥α⇒a ⊥b ”,此命题为真命题.答案:26.如图,在正方体ABCD A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上,若EF ∥平面AB 1C ,则线段EF 的长度等于________.解析:因为EF ∥平面AB 1C ,EF ⊂平面ACD ,平面ACD ∩平面AB 1C =AC , 所以EF ∥AC ,又E 为AD 的中点,AB =2, 所以EF =12AC =12×22+22= 2.答案: 27.如图,在圆锥V O 中,O 为底面圆心,半径OA ⊥OB ,且OA =VO =1,则O 到平面VAB 的距离为________.解析:设O 到平面VAB 的距离为h ,由圆锥的几何性质可得VO ⊥平面OAB ,VO ⊥OA ,VO ⊥OB .在Rt △VOA 中,VA =VO 2+AO 2=2,在Rt △VOB中,VB =VO 2+BO 2=2,在Rt △OAB 中,AB =OA 2+OB 2=2,在△VAB 中,S △VAB =12×2×62=32.因为V V AOB =13S △AOB ×VO =16,V V AOB =13S △VAB ×h =16,所以h =33. 答案:338.已知矩形ABCD 的边AB =4,BC =3,若沿对角线AC 折叠,使平面DAC ⊥平面BAC ,则三棱锥D ABC 的体积为________.解析:在平面DAC 内作DO ⊥AC ,垂足为点O ,因为平面DAC ⊥平面BAC ,且平面DAC ∩平面BAC =AC ,所以DO ⊥平面BAC ,因为AB =4,BC =3,所以DO =125,S △ABC =12×3×4=6,所以三棱锥D ABC 的体积为V =13×6×125=245.答案:2459.已知α,β是两个不同的平面,l ,m 是两条不同的直线,l ⊥α,m ⊂β.给出下列命题:①α∥β⇒l ⊥m ;②α⊥β⇒l ∥m ; ③m ∥α⇒l ⊥β;④l ⊥β⇒m ∥α.其中正确的命题是________(填写所有正确命题的序号). 解析:①由l ⊥α,α∥β,得l ⊥β. 又因为m ⊂β,所以l ⊥m ,①正确; ②由l ⊥α,α⊥β,得l ∥β或l ⊂β,又因为m ⊂β,所以l 与m 或异面或平行或相交,②错误;③由l ⊥α,m ∥α,得l ⊥m .因为l 只垂直于β内的一条直线m ,所以不能确定l 是否垂直于β,③错误;④由l ⊥α,l ⊥β,得α∥β.因为m ⊂β,所以m ∥α,④正确. 答案:①④10.已知PD 垂直于正方形ABCD 所在的平面,连结PB ,PC ,PA ,AC ,BD ,则一定互相垂直的平面有________对.解析:如图,由于PD ⊥平面ABCD .故平面PAD ⊥平面ABCD ,平面PDB ⊥平面ABCD ,平面PDC ⊥平面ABCD ,平面PDA ⊥平面PDC ,平面PAC ⊥平面PDB ,平面PAB ⊥平面PAD ,平面PBC ⊥平面PDC ,共7对.答案:711.以一个圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥,若所得的圆锥底面半径等于圆锥的高,则圆锥的侧面积与圆柱的侧面积之比为________.解析:设圆锥的底面半径为 r ,由题意圆锥底面半径等于圆锥的高, 可知圆锥的侧面积为: πr ·2r =2πr 2.圆柱的侧面积为:2πr ·r =2πr 2.所以圆锥的侧面积与圆柱的侧面积之比为: 2πr 2∶2πr 2= 22. 答案:2212.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是________寸.(注:①平地降雨量等于盆中积水的体积除以盆口的面积;②一尺等于十寸)解析:作出圆台的轴截面如图,由题意知,BF =14(单位寸,下同),OC =6,OF =18,OG =9,即G 是OF 中点,所以GE 为梯形的中位线,所以GE =14+62=10,即积水的上底面半径为10.所以盆中积水的体积为13(100π+36π+100π×36π)×9=588π.盆口的面积为142π=196π,所以588π196π=3,即平地降雨量是3寸.答案:313.已知三棱锥P ABC 中,△ABC 为等边三角形,PA =PB =PC ,PA ⊥PB ,点P 到平面ABC 的距离为23,则三棱锥P ABC 的体积为________.解析:法一:因为△ABC 为等边三角形,PA =PB =PC ,所以△PAB ≌△PAC ≌△PBC .因为PA ⊥PB ,所以PA ⊥PC ,PB ⊥PC .设PA =PB =PC =a ,点P 在平面ABC 上的射影为O ,则AB =AC =BC =2a ,AO =63a .又点P 到平面ABC 的距离为23,所以PO =2 3.在Rt △POA 中,PO 2+OA 2=PA 2,即12+23a 2=a 2,解得a =6,所以三棱锥P ABC 的体积为13×34×(62)2×23=36.法二:设PA =PB =PC =a ,因为△ABC 为等边三角形,所以△PAB ≌△PAC ≌△PBC .因为PA ⊥PB ,所以PA ⊥PC ,PB ⊥PC ,以PA ,PB ,PC 为棱作正方体,如图所示,则PA 2+PB 2+PC 2=3a 2,故正方体的体对角线长为3a .又点P 到平面ABC 的距离为23×12×3a =23,解得a =6,所以三棱锥P ABC 的体积为13×12×6×6×6=36.答案:3614.如图,在四棱锥P ABCD 中,PD ⊥平面ABCD ,底面ABCD 为正方形,PD =AD =2,M ,N 均为线段AC 上的点.若∠MBN =30°,则三棱锥M PNB的体积的最小值为________.解析:易知V M PNB =V P MNB=13PD ·S △MNB =13PD ·12MN ·h ,h 为点B 到AC 的距离,又h =12BD =2,所以V M PNB =13×2×12×MN ×2=23MN ,显然当△MNB 为等腰三角形时,MN 取得最小值,此时MN =22tan 15°=42-26,从而可得(V M PNB )min =23×(42-26)=8-433. 答案:8-433。
(新)江苏专版2018年高考数学二轮复习14个填空题专项强化练五三角函数的图象和性质

14个填空题专项强化练(五) 三角函数的图象和性质A 组——题型分类练题型一 三角函数的定义域和值域1.函数y =tan ⎝ ⎛⎭⎪⎫2x -π3的定义域为________. 解析:由2x -π3≠k π+π2(k ∈Z),得x ≠k π2+5π12(k ∈Z),故所求定义域为⎩⎨⎧⎭⎬⎫xx ≠k π2+5π12,k ∈Z .答案:⎩⎨⎧⎭⎬⎫xx ≠k π2+5π12,k ∈Z2.函数y =2sin ⎝⎛⎭⎪⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为________.解析:因为0≤x ≤9,所以-π3≤π6x -π3≤7π6,所以sin ⎝ ⎛⎭⎪⎫π6x -π3∈⎣⎢⎡⎦⎥⎤-32,1.所以y ∈[-3,2],所以y max +y min =2- 3. 答案:2- 33.函数y =2cos 2x +5sin x -4的值域为________. 解析:y =2cos 2x +5sin x -4 =2(1-sin 2x )+5sin x -4 =-2sin 2x +5sin x -2 =-2⎝ ⎛⎭⎪⎫sin x -542+98. 故当sin x =1时,y max =1, 当sin x =-1时,y min =-9,故y =2cos 2x +5sin x -4的值域为[-9,1]. 答案:[-9,1]题型二 三角函数的图象1.将函数y =sin 4x 的图象向左平移π12个单位长度,得到y =sin(4x +φ)⎝ ⎛⎭⎪⎫0<φ<π2的图象,则φ=________.解析:将函数y =sin 4x 的图象向左平移π12个单位长度,得到y =sin ⎣⎢⎡⎦⎥⎤4⎝ ⎛⎭⎪⎫x +π12=sin ⎝⎛⎭⎪⎫4x +π3,所以φ=π3. 答案:π32.已知函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,|φ|<π2的部分图象如图所示,则函数f (x )的解析式为____________________.解析:由题图可知,A =1,函数f (x )的最小正周期T =4⎝ ⎛⎭⎪⎫π3-π12=π,∴ω=2πT=2.又当x =π12时,f (x )取得最大值1,∴1=sin ⎝ ⎛⎭⎪⎫2×π12+φ,∴π6+φ=2k π+π2,k ∈Z , ∴φ=2k π+π3,k ∈Z.又|φ|<π2,∴φ=π3,则函数f (x )的解析式为f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3.答案:f (x )=sin ⎝⎛⎭⎪⎫2x +π33.在同一直角坐标系中,函数y =sin ⎝ ⎛⎭⎪⎫x +π3(x ∈[0,2π])的图象和直线y =12的交点的个数是____________.解析:由sin ⎝ ⎛⎭⎪⎫x +π3=12,解得x +π3=2k π+π6或x +π3=2k π+5π6,k ∈Z ,即x =2k π-π6或x =2k π+π2,k ∈Z ,又因为x ∈[0,2π],所以x =π2或11π6,所以函数y =sin ⎝⎛⎭⎪⎫x +π3 (x ∈[0,2π])的图象和直线y =12 的交点的个数是2. 答案:24.将函数y =5sin ⎝ ⎛⎭⎪⎫2x +π4的图象向左平移φ⎝ ⎛⎭⎪⎫0<φ<π2个单位长度后,所得函数图象关于y 轴对称,则φ=______________.解析:将函数y =5sin ⎝ ⎛⎭⎪⎫2x +π4的图象向左平移φ⎝ ⎛⎭⎪⎫0<φ<π2个单位长度后,所得函数为f (x )=5sin ⎣⎢⎡⎦⎥⎤2x +φ+π4,即f (x )=5sin ⎣⎢⎡⎦⎥⎤2x +⎝⎛⎭⎪⎫2φ+π4.因为所得函数f (x )的图象关于y 轴对称,所以2φ+π4=π2+k π,k ∈Z ,所以φ=π8+k π2,k ∈Z ,因为0<φ<π2,所以φ=π8. 答案:π8题型三 三角函数的性质1.函数y =2sin ⎝ ⎛⎭⎪⎫3x -π3的最小正周期为________. 解析:函数f (x )的最小正周期T =2πω=2π3.答案:2π32.函数y =2sin ⎝⎛⎭⎪⎫2x -π6与y 轴最近的对称轴方程是________. 解析:由2x -π6=k π+π2(k ∈Z),得x =k π2+π3(k ∈Z),因此,当k =-1时,直线x =-π6是与y 轴最近的对称轴.答案:x =-π63.若函数f (x )=2sin(2x +φ)⎝ ⎛⎭⎪⎫0<φ<π2的图象过点(0,3),则函数f (x )在[0,π]上的单调递减区间是____________.解析:由题意可得,2sin(2×0+φ)=3, ∴sin φ=32. 又0<φ<π2,∴φ=π3,∴f (x )=2sin ⎝⎛⎭⎪⎫2x +π3.由2k π+π2≤2x +π3≤2k π+3π2,k ∈Z ,得k π+π12≤x ≤k π+7π12,k ∈Z.∵0≤x ≤π,∴k =0时,π12≤x ≤7π12,∴函数f (x )在[0,π]上的单调递减区间是⎣⎢⎡⎦⎥⎤π12,7π12.答案:⎣⎢⎡⎦⎥⎤π12,7π124.若函数f (x )=sinx +φ3(φ∈[0,2π])是偶函数,则φ=________.解析:若f (x )为偶函数,则f (0)=±1,即sin φ3=±1,所以φ3=k π+π2(k ∈Z).所以φ=3k π+3π2(k ∈Z).因为φ∈[0,2π],所以φ=3π2.答案:3π25.若函数f (x )=4cos ωx sin ⎝⎛⎭⎪⎫ωx -π6+1(ω>0)的最小正周期是π,则函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的最小值是________.解析:由题意知,f (x )=4cos ωx sin ⎝ ⎛⎭⎪⎫ωx -π6+1=23sin ωx cos ωx -2cos 2ωx +1=3sin 2ωx -cos 2ωx =2sin ⎝ ⎛⎭⎪⎫2ωx -π6, 由f (x )的最小正周期是π,且ω>0, 可得2π2ω=π,ω=1,则f (x )=2sin ⎝⎛⎭⎪⎫2x -π6. 又x ∈⎣⎢⎡⎦⎥⎤0,π2,所以2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,故函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的最小值是-1. 答案:-1B 组——高考提速练1.函数y =12sin x -1的定义域是________.解析:由2sin x -1≠0得sin x ≠12,故x ≠π6+2k π(k ∈Z)且x ≠5π6+2k π(k ∈Z),即x ≠(-1)k·π6+k π(k ∈Z).答案:⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠-1k·π6+k π,k ∈Z 2.函数y =sin ⎝⎛⎭⎪⎫x +π6的单调递增区间为________.解析:由2k π-π2≤x +π6≤2k π+π2(k ∈Z),得-2π3+2k π≤x ≤π3+2k π(k ∈Z),所以单调递增区间为⎣⎢⎡⎦⎥⎤-2π3+2k π,π3+2k π(k ∈Z).答案:⎣⎢⎡⎦⎥⎤-2π3+2k π,π3+2k π(k ∈Z)3.函数y =2sin ⎝ ⎛⎭⎪⎫2x +π3-1,x ∈⎣⎢⎡⎦⎥⎤0,π3的值域为________. 解析:∵0≤x ≤π3,∴π3≤2x +π3≤π,∴0≤sin ⎝⎛⎭⎪⎫2x +π3≤1, ∴-1≤2sin ⎝ ⎛⎭⎪⎫2x +π3-1≤1,即值域为[-1,1]. 答案:[-1,1]4.函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω=________.解析:由图象可知,T 2=⎝ ⎛⎭⎪⎫-π3-⎝⎛⎭⎪⎫-2π3=π3,则T =2π3.因为T =2πω=2π3,所以ω=3.答案:35.函数y =tan ⎝ ⎛⎭⎪⎫2x +π4的图象与x 轴的交点坐标是______.解析:由2x +π4=k π(k ∈Z)得,x =k π2-π8(k ∈Z).∴函数y =tan ⎝ ⎛⎭⎪⎫2x +π4的图象与x 轴交点的坐标是⎝ ⎛⎭⎪⎫k π2-π8,0,k ∈Z. 答案:⎝⎛⎭⎪⎫k π2-π8,0,k ∈Z 6.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π3(ω>0),将函数y =f (x )的图象向右平移2π3个单位长度后,所得图象与原函数图象重合,则ω的最小值等于________.解析:将函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π3(ω>0)的图象向右平移2π3个单位长度后,所得函数为y =f ⎝ ⎛⎭⎪⎫x -2π3.因为所得图象与原函数图象重合,所以f (x )=f ⎝⎛⎭⎪⎫x -2π3,所以kT =2π3,k ∈N *,即2k πω=2π3,k ∈N *,所以ω=3k ,k ∈N *,所以ω的最小值等于3. 答案:37.已知函数f (x )=3sin 2ωx -cos 2ωx (其中ω∈(0,1)),若f (x )的图象经过点⎝ ⎛⎭⎪⎫π6,0,则f (x )在区间[0,π]上的单调递增区间为____________.解析:f (x )=3sin 2ωx -cos 2ωx =2sin ⎝ ⎛⎭⎪⎫2ωx -π6,∵f (x )的图象经过点⎝ ⎛⎭⎪⎫π6,0,∴2sin ⎝⎛⎭⎪⎫π3ω-π6=0, ∴π3ω-π6=k π,k ∈Z ,解得ω=3k +12,k ∈Z , ∵ω∈(0,1),∴ω=12,∴f (x )=2sin ⎝⎛⎭⎪⎫x -π6,由-π2+2k π≤x -π6≤π2+2k π,k ∈Z ,得-π3+2k π≤x ≤2π3+2k π,k ∈Z ,∴f (x )在区间[0,π]上的单调递增区间为⎣⎢⎡⎦⎥⎤0,2π3.答案:⎣⎢⎡⎦⎥⎤0,2π38.如果函数y =3cos(2x +φ)的图象关于点⎝⎛⎭⎪⎫4π3,0中心对称,那么|φ|的最小值为________.解析:由题意得3cos ⎝ ⎛⎭⎪⎫2×4π3+φ=3cos ⎝ ⎛⎭⎪⎫2π3+φ=0,所以2π3+φ=k π+π2,k ∈Z ,所以φ=k π-π6,k ∈Z ,取k =0,得|φ|的最小值为π6. 答案:π69.设函数f (x )=sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,0<φ<π2的部分图象如图所示,直线x =π6是它的一条对称轴,则函数f (x )的解析式为______________.解析:由题意可知,T 4=5π12-π6=π4,所以T =2πω=π,所以ω=2,又因为f ⎝ ⎛⎭⎪⎫π6=1,所以sin ⎝ ⎛⎭⎪⎫2×π6+φ=1,所以π3+φ=2k π+π2(k ∈Z),而φ∈⎝ ⎛⎭⎪⎫0,π2, 所以φ=π6,所以f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6.答案:f (x )=sin ⎝⎛⎭⎪⎫2x +π610.已知函数f (x )=2sin(ωx +φ)⎝⎛⎭⎪⎫ω>0,|φ|<π2的最小正周期为π,且它的图象过点⎝ ⎛⎭⎪⎫-π12,-2,则φ的值为________.解析:由题意可得函数f (x )的最小正周期T =2πω=π,解得ω=2.又f ⎝ ⎛⎭⎪⎫-π12=2sin ⎝ ⎛⎭⎪⎫-π6+φ=-2⎝ ⎛⎭⎪⎫|φ|<π2,得φ=-π12.答案:-π1211.函数y =sin(πx +φ)(φ>0)的部分图象如图,设P 是图象的最高点,A ,B 是图象与x 轴的交点,则∠APB =________.解析:由题意知T =2,作PD ⊥x 轴, 垂足为D ,则PD =1,AD =12,BD =32,设α=∠APD ,β=∠BPD ,则tan α=12,tan β=32,∠APB =α+β,故tan ∠APB =12+321-12×32=8.答案:812.已知函数f (x )=sin ⎝⎛⎭⎪⎫2x +π3(0≤x <π),且f (α)=f (β)=12(α≠β),则α+β=________.解析:因为0≤x <π,所以2x +π3∈⎣⎢⎡⎭⎪⎫π3,7π3,由f (x )=12,得2x +π3=5π6或13π6,解得x =π4或11π12,由于f (α)=f (β)=12(α≠β),所以α+β=π4+11π12=7π6.答案:7π613.已知函数f (x )=sin x (x ∈[0,π])和函数g (x )=12tan x 的图象交于A ,B ,C 三点,则△ABC 的面积为________.解析:由题意知,x ≠π2,令sin x =12tan x ,可得sin x =sin x 2cos x ,x ∈⎣⎢⎡⎭⎪⎫0,π2∪⎝ ⎛⎦⎥⎤π2,π,可得sin x =0或cos x =12,则x =0或π或π3,不妨设A (0,0),B (π,0),C ⎝ ⎛⎭⎪⎫π3,32,则△ABC 的面积为12×π×32=3π4. 答案:3π414.已知函数f (x )=sin(2x +φ),其中φ为实数,若f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6对x ∈R 恒成立,且f ⎝ ⎛⎭⎪⎫π2>f (π),则f (x )的单调递增区间是______________. 解析:若f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6对x ∈R 恒成立,则⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6=⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫π3+φ=1, 所以π3+φ=k π+π2,k ∈Z ,φ=k π+π6,k ∈Z.由f ⎝ ⎛⎭⎪⎫π2>f (π), 可知sin(π+φ)>sin(2π+φ), 即sin φ<0,所以φ=2k π+7π6,k ∈Z ,代入f (x )=sin(2x +φ), 得f (x )=sin ⎝⎛⎭⎪⎫2x +7π6, 由2k π-π2≤2x +7π6≤2k π+π2,k ∈Z ,得k π-5π6≤x ≤k π-π3,k ∈Z.答案:⎣⎢⎡⎦⎥⎤k π-5π6,k π-π3(k ∈Z)。
2018年高考数学江苏专版三维二轮专题复习训练:14个填空题综合仿真练(一) Word版含解析

14个填空题综合仿真练(一)1.已知集合A={0,3,4},B={-1,0,2,3},则A∩B=________.解析:因为集合A={0,3,4},B={-1,0,2,3},所以A∩B={0,3}.答案:{0,3}2.已知x>0,若(x-i)2是纯虚数(其中i为虚数单位),则x=________.解析:因为x>0,(x-i)2=x2-1-2x i是纯虚数(其中i为虚数单位),所以x2-1=0且-2x≠0,解得x=1.答案:13.已知函数f(x)=x2-2x-3,则该函数的单调递增区间为________.解析:设t=x2-2x-3,由t≥0,即x2-2x-3≥0,解得x≤-1或x≥3,所以函数f(x)的定义域为(-∞,-1]∪[3,+∞),因为函数t=x2-2x-3的图象的对称轴为x=1,所以函数t=x2-2x-3在(-∞,-1]上单调递减,在[3,+∞)上单调递增,所以函数f(x)的单调递增区间为[3,+∞).答案:[3,+∞)4.从2个白球,2个红球,1个黄球中随机取出2个球,则取出的2球中恰有1个红球的概率是________.解析:将2个白球记为A,B,2个红球记为C,D,1个黄球记为E,则从中任取两个球的所有可能结果为(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E),共10个,恰有1个红球的可能结果为(A,C),(A,D),(B,C),(B,D),(E,C),(E,D)共6个,故所求概率为P=610=3 5.答案:3 55.执行如图所示的伪代码,若输出的y的值为13,则输入的x的值是________.Read xIf x≤2Theny←6xElsey←x+5End IfPrint y解析:若6x=13,则x=136>2,不符合题意;若x+5=13,则x=8>2,符合题意,故x=8.答案:86.一种水稻品种连续5年的平均单位面积产量(单位:t/hm2)分别为:9.4,9.7,9.8,10.3,10.8,则这组样本数据的方差为________.解析:这组数据的平均数为15(9.4+9.7+9.8+10.3+10.8)=10,方差为15[(10-9.4)2+(10-9.7)2+(10-9.8)2+(10-10.3)2+(10-10.8)2]=0.244.答案:0.2447.已知函数f (x )=sin(ωx +φ)(0<ω<2,0<φ<π).若x =-π4为函数f (x )的一个零点,x =π3为函数f (x )图象的一条对称轴,则ω的值为________.解析:函数f (x )的周期T =4×⎝⎛⎭⎫π3+π4=7π3,又T =2πω,所以ω=2π×37π=67. 答案:678.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足cos A 2=255,AB ―→·AC ―→=3,b +c =6,则a =________.解析:∵cos A 2=255,∴cos A =2cos 2A 2-1=35,又由AB ―→·AC ―→=3,得bc cos A =3,∴bc =5,由余弦定理得a 2=b 2+c 2-2bc cos A =(b +c )2-2bc (1+cos A )=36-10×85=20,解得a =2 5.答案:2 59.已知α,β∈(0,π),且tan(α-β)=12,tan β=-15,则tan α的值为________. 解析:tan α=tan[(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β=12-151-12×⎝⎛⎭⎫-15=311. 答案:31110.已知关于x 的一元二次不等式ax 2+bx +c >0的解集为(-1,5),其中a ,b ,c 为常数.则不等式cx 2+bx +a ≤0的解集为________.解析:因为不等式ax 2+bx +c >0的解集为(-1,5),所以a (x +1)(x -5)>0,且a <0,即ax 2-4ax -5a >0,则b =-4a ,c =-5a ,则cx 2+bx +a ≤0即为-5ax 2-4ax +a ≤0,从而5x 2+4x -1≤0,解得-1≤x ≤15. 答案:⎣⎡⎦⎤-1,15 11.已知正数x ,y 满足1x +2y =1,则log 2x +log 2y 的最小值为________.解析:由1x +2y =1,得x =y y -2>0,则log 2x +log 2y =log 2xy =log 2y 2y -2=log 2(y -2+2)2y -2=log 2⎣⎡⎦⎤(y -2)+4y -2+4≥log 28=3,当且仅当(y -2)2=4,即y =4时等号成立,故log 2x +log 2y 的最小值为3.答案:312.在平面直角坐标系xOy 中,已知圆C :x 2+y 2+2x -8=0,直线l :y =k (x -1)(k ∈R)过定点A ,且交圆C 于点B ,D ,过点A 作BC 的平行线交CD 于点E ,则△AEC 的周长为________.解析:易得圆C 的标准方程为(x -1)2+y 2=9,即半径r =3,定点A (-1,0),因为AE ∥BC ,所以EA =ED ,则EC +EA =EC +ED =3,从而△AEC 的周长为5.答案:513.设集合A ={x |x =2n ,n ∈N *},集合B ={x |x =b n ,n ∈N *},满足A ∩B =∅,且A ∪B =N *.若对任意的n ∈N *,b n <b n +1,则b 2 017=________.解析:因为210=1 024<2 017,211=2 048>2 017,所以小于等于2 017的正整数中有10个是集合A 中的元素,所以由集合B 的定义可知b 2 017=2 017+10=2 027.答案:2 02714.已知函数f (x )=kx ,g (x )=2ln x +2e ⎝⎛⎭⎫1e ≤x ≤e 2,若f (x )与g (x )的图象上分别存在点M ,N ,使得M ,N 关于直线y =e 对称,则实数k 的取值范围是________________.解析:设直线y =kx 上的点M (x ,kx ),点M 关于直线y =e 的对称点N (x,2e -kx ),因为点N 在g (x )=2ln x +2e ⎝⎛⎭⎫1e ≤x ≤e 2的图象上,所以2e -kx =2ln x +2e ,所以kx =-2ln x .构造函数y =kx ,y =-2ln x ⎝⎛⎭⎫1e ≤x ≤e 2,画出函数y =-2ln x ⎝⎛⎭⎫1e ≤x ≤e 2的图象如图所示,设曲线y =-2ln x ⎝⎛⎭⎫1e ≤x ≤e 2上的点P (x 0,-2ln x 0),则k OP ≤k ≤k OB (其中B 为端点,P 为切点).因为y ′=-2x ,所以过点P 的切线方程为y +2ln x 0=-2x 0(x -x 0),又该切线经过原点,所以0+2ln x 0=-2x 0(0-x 0),x 0=e ,所以k OP =-2e.又点B ⎝⎛⎭⎫1e ,2,所以k OB =2e ,所以k ∈⎣⎡⎦⎤-2e ,2e . 答案:⎣⎡⎦⎤-2e ,2e。
江苏2018版高考数学复习第一章集合与常用逻辑用语1.1集合及其运算教师用书文苏教版
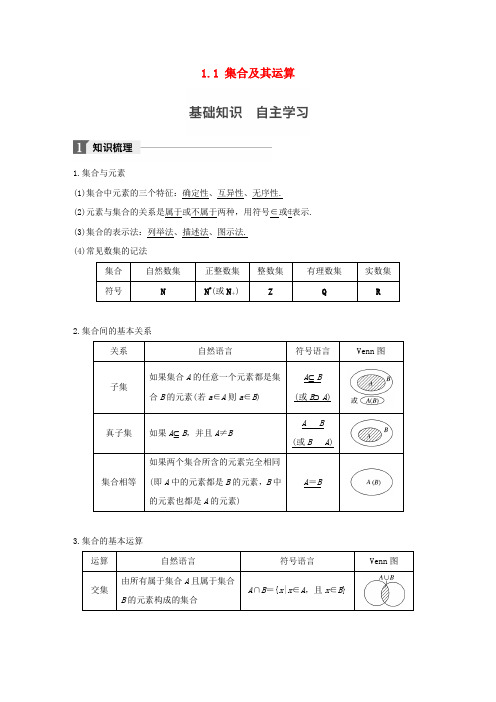
1.1 集合及其运算1.集合与元素(1)集合中元素的三个特征:确定性、互异性、无序性. (2)元素与集合的关系是属于或不属于两种,用符号∈或∉表示. (3)集合的表示法:列举法、描述法、图示法. (4)常见数集的记法2.集合间的基本关系AB (或BA )3.集合的基本运算【知识拓展】1.若有限集A 中有n 个元素,则集合A 的子集个数为2n ,真子集的个数为2n-1. 2.A ⊆B ⇔A ∩B =A ⇔A ∪B =B .3.A ∩∁U A =∅;A ∪∁U A =U ;∁U (∁U A )=A . 【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”) (1)任何一个集合都至少有两个子集.( × )(2){x |y =x 2+1}={y |y =x 2+1}={(x ,y )|y =x 2+1}.( × ) (3)若{x 2,1}={0,1},则x =0,1.( × ) (4){x |x ≤1}={t |t ≤1}.( √ )(5)对于任意两个集合A ,B ,关系(A ∩B )⊆(A ∪B )恒成立.( √ ) (6)若A ∩B =A ∩C ,则B =C .( × )1.(教材改编)设A ={x |x 2-4x -5=0},B ={x |x 2=1},则A ∪B =__________. 答案 {-1,1,5}解析 ∵A ={-1,5},B ={-1,1},∴A ∪B ={-1,1,5}.2.已知集合A ={x |x 2-6x +5≤0},B ={x |y =x -3},则A ∩B =__________. 答案 {x |3≤x ≤5}3.(教材改编)设全集U =R ,A ={x |x <1},B ={x |x ≥m }.若A ∩B =∅,A ∪B =R ,则m =________. 答案 1解析 ∵A ∩B =∅,A ∪B =R ,∴B =∁U A ,故m =1.4.(2016·天津改编)已知集合A ={1,2,3,4},B ={y |y =3x -2,x ∈A },则A ∩B =________.答案 {1,4}解析 因为集合B 中,x ∈A ,所以当x =1时,y =3-2=1; 当x =2时,y =3×2-2=4; 当x =3时,y =3×3-2=7; 当x =4时,y =3×4-2=10; 即B ={1,4,7,10}.又因为A ={1,2,3,4},所以A ∩B ={1,4}.5.(2016·苏州模拟)已知集合A ={1,3,m },B ={3,4},A ∪B ={1,2,3,4},则m =________. 答案 2解析 ∵A ∪B ={1,3,m }∪{3,4}={1,2,3,4}, ∴2∈{1,3,m },∴m =2.题型一 集合的含义例1 (1)已知集合A ={x |x ∈Z ,且32-x∈Z },则集合A 中的元素个数为________. (2)若集合A ={x ∈R |ax 2-3x +2=0}中只有一个元素,则a =________. 答案 (1)4 (2)0或98解析 (1)∵32-x∈Z ,∴2-x 的取值有-3,-1,1,3, 又∵x ∈Z ,∴x 值分别为5,3,1,-1, 故集合A 中的元素个数为4.(2)若a =0,则A =⎩⎨⎧⎭⎬⎫23,符合题意;若a ≠0,则由题意得Δ=9-8a =0,解得a =98.综上,a 的值为0或98.思维升华 (1)用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型是数集、点集还是其他类型的集合;(2)集合中元素的互异性常常容易忽略,求解问题时要特别注意.分类讨论的思想方法常用于解决集合问题.(1)(2016·盐城模拟)已知A ={x |x =3k -1,k ∈Z },则下列表示正确的是________. ①-1∉A②-11∈A ③3k 2-1∈A (k ∈Z )④-34∉A(2)设a ,b ∈R ,集合{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a,b ,则b -a =________.答案 (1)③ (2)2解析 (1)∵k ∈Z ,∴k 2∈Z ,∴3k 2-1∈A . (2)因为{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a,b ,a ≠0,所以a +b =0,得ba=-1, 所以a =-1,b =1,所以b -a =2. 题型二 集合的基本关系例2 (1)设A ,B 是全集I ={1,2,3,4}的子集,A ={1,2},则满足A ⊆B 的B 的个数是________. (2)已知集合A ={x |x 2-2 017x +2 016<0},B ={x |x <a },若A ⊆B ,则实数a 的取值范围是__________________.答案 (1)4 (2)[2 016,+∞)解析 (1)∵{1,2}⊆B ,I ={1,2,3,4},∴满足条件的集合B 有{1,2},{1,2,3},{1,2,4},{1,2,3,4},共4个. (2)由x 2-2 017x +2 016<0,解得1<x <2 016, 故A ={x |1<x <2 016},又B ={x |x <a },A ⊆B ,如图所示,可得a ≥2 016. 引申探究本例(2)中,若将集合B 改为{x |x ≥a },其他条件不变,则实数a 的取值范围是____________. 答案 (-∞,1]解析 A ={x |1<x <2 016},B ={x |x ≥a },A ⊆B ,如图所示,可得a ≤1.思维升华 (1)空集是任何集合的子集,在涉及集合关系时,必须优先考虑空集的情况,否则会造成漏解;(2)已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、Venn 图等来直观解决这类问题.(1)已知集合A ={x ∈R |x 2+x -6=0},B ={x ∈R |ax -1=0},若B ⊆A ,则实数a 的值为____________.(2)(2016·连云港模拟)已知集合A ={x |-2≤x ≤7},B ={x |m +1<x <2m -1},若B ⊆A ,则实数m 的取值范围是____________. 答案 (1)-13或12或0 (2)(-∞,4]解析 (1)由题意知A ={2,-3}. 当a =0时,B =∅,满足B ⊆A ; 当a ≠0时,ax -1=0的解为x =1a,由B ⊆A ,可得1a =-3或1a=2,∴a =-13或a =12.综上,a 的值为-13或12或0.(2)当B =∅时,有m +1≥2m -1,则m ≤2; 当B ≠∅时,若B ⊆A ,如图,则⎩⎪⎨⎪⎧m +1≥-2,2m -1≤7,m +1<2m -1,解得2<m ≤4.综上,m 的取值范围为(-∞,4]. 题型三 集合的基本运算 命题点1 集合的运算例3 (1)(2017·江苏前黄中学月考)设全集U ={n ∈N |1≤n ≤10},A ={1,2,3,5,8},B ={1,3,5,7,9},则(∁U A )∩B =________.(2)设全集U是实数集R,M={x|x<-2或x>2},N={x|1≤x≤3}.如图所示,则阴影部分所表示的集合为________.答案(1){7,9} (2){x|-2≤x<1}解析(1)U={1,2,3,4,5,6,7,8,9,10},画出Venn图,如图所示,阴影部分就是所要求的集合,即(∁U A)∩B={7,9}.(2)阴影部分所表示的集合为∁U(M∪N)=(∁U M)∩(∁U N)={x|-2≤x≤2}∩{x|x<1或x>3}={x|-2≤x<1}.命题点2 利用集合的运算求参数例 4 (1)设集合A={x|-1≤x<2},B={x|x<a},若A∩B≠∅,则a的取值范围是____________.(2)集合A={0,2,a},B={1,a2},若A∪B={0,1,2,4,16},则a的值为________. 答案(1)(-1,+∞)(2)4解析(1)因为A∩B≠∅,所以集合A,B有公共元素,作出数轴,如图所示,易知a>-1.(2)由题意可得{a,a2}={4,16},∴a=4.思维升华(1)一般来讲,集合中的元素若是离散的,则用Venn图表示;集合中的元素若是连续的实数,则用数轴表示,此时要注意端点的情况.(2)运算过程中要注意集合间的特殊关系的使用,灵活使用这些关系,会使运算简化.(1)已知A={x|2a≤x≤a+3},B={x|x>5},若A∩B=∅,则实数a的取值范围为________.(2)已知集合A={x|x2-x-12≤0},B={x|2m-1<x<m+1},且A∩B=B,则实数m的取值范围为________.答案(1)a≤2或a>3 (2)[-1,+∞)解析 (1)要使A ∩B =∅,则⎩⎪⎨⎪⎧2a ≤a +3,a +3≤5,或2a >a +3,∴a ≤2或a >3.(2)由x 2-x -12≤0,得(x +3)(x -4)≤0,即-3≤x ≤4,所以A ={x |-3≤x ≤4}.又A ∩B =B ,所以B ⊆A .①当B =∅时,有m +1≤2m -1,解得m ≥2. ②当B ≠∅时,有⎩⎪⎨⎪⎧-3≤2m -1,m +1≤4,2m -1<m +1,解得-1≤m <2.综上,m 的取值范围为[-1,+∞). 题型四 集合的新定义问题例5 若对任意的x ∈A ,1x ∈A ,则称A 是“伙伴关系集合”,则集合M ={-1,0,12,1,2}的所有非空子集中,具有伙伴关系的集合的个数为________. 答案 7解析 具有伙伴关系的元素组有-1;1;2和12共三组,它们中任一组、两组、三组均可组成非空伙伴关系集合,所以非空伙伴关系集合分别为{1},{-1},{12,2},{-1,1},{-1,12,2},{1,12,2},{-1,1,12,2},共7个.思维升华 解决以集合为背景的新定义问题,要抓住两点(1)紧扣新定义.首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,并能够应用到具体的解题过程之中,这是破解新定义型集合问题难点的关键所在;(2)用好集合的性质.解题时要善于从试题中发现可以使用集合性质的一些因素,在关键之处用好集合的运算与性质.定义一种新的集合运算△:A △B ={x |x ∈A ,且x ∉B }.若集合A ={x |x 2-4x +3<0},B ={x |2≤x ≤4},则按运算△,B △A =____________. 答案 {x |3≤x ≤4}解析 A ={x |1<x <3},B ={x |2≤x ≤4},由题意知B △A ={x |x ∈B ,且x ∉A }={x |3≤x ≤4}.1.集合关系及运算典例 (1)已知集合A ={1,3,m },B ={1,m },A ∪B =A ,则m =____________. (2)设集合A ={0,-4},B ={x |x 2+2(a +1)x +a 2-1=0,x ∈R }.若B ⊆A ,则实数a 的取值范围是________. 错解展示解析 (1)由A ∪B =A 得B ⊆A ,∴m =3或m =m , 故m =3或m =0或m =1. (2)∵B ⊆A ,讨论如下:①当B =A ={0,-4}时,⎩⎪⎨⎪⎧Δ=a +2-a 2-,-a +=-4,a 2-1=0,解得a =1.②当B A 时,由Δ=0得a =-1, 此时B ={0}满足题意,综上,实数a 的取值范围是{1,-1}. 答案 (1)1或3或0 (2){1,-1} 现场纠错解析 (1)A ={1,3,m },B ={1,m },A ∪B =A ,故B ⊆A ,所以m =3或m =m ,即m =3或m =0或m =1,其中m =1不符合题意,所以m =0或m =3. (2)因为A ={0,-4},所以B ⊆A 分以下三种情况:①当B =A 时,B ={0,-4},由此知0和-4是方程x 2+2(a +1)x +a 2-1=0的两个根,由根与系数的关系,得 ⎩⎪⎨⎪⎧Δ=a +2-a 2-,-a +=-4,a 2-1=0,解得a =1; ②当B ≠∅且BA 时,B ={0}或B ={-4},并且Δ=4(a +1)2-4(a 2-1)=0,解得a=-1,此时B={0}满足题意;③当B=∅时,Δ=4(a+1)2-4(a2-1)<0,解得a<-1.综上所述,所求实数a的取值范围是(-∞,-1]∪{1}.答案(1)0或3 (2)(-∞,-1]∪{1}纠错心得(1)集合的元素具有互异性,参数的取值要代入检验.(2)当两个集合之间具有包含关系时,不要忽略空集的情况.1.(2016·江苏苏州暑期检测)已知集合A={0,1},B={-1,0},则A∪B=________.答案{0,-1,1}解析由集合并集的定义可得A∪B={0,-1,1}.2.(2017·扬州月考)已知集合A={x|x2-2x<0},B={0,1,2},则A∩B=__________.答案{1}解析因为A={x|0<x<2},B={0,1,2},所以A∩B={1}.3.(2016·盐城模拟)已知集合A={1,2,3,4,5},B={1,3,5,7,9},C=A∩B,则集合C的子集的个数为________.答案8解析因为A∩B={1,3,5},所以C={1,3,5},故集合C的子集的个数为23=8.4.已知全集U=R,集合A={1,2,3,4,5},B={x∈R|x≥2},则下图中阴影部分所表示的集合为__________.答案{1}解析因为A∩B={2,3,4,5},而图中阴影部分为A去掉A∩B,所以阴影部分所表示的集合为{1}.5.若集合A={(1,2),(3,4)},则集合A的真子集的个数是________.答案 3解析 集合A 中有两个元素,则集合A 的真子集的个数是22-1=3.6.已知集合A ={(x ,y )| x ,y ∈R ,且x 2+y 2=1},B ={(x ,y )|x ,y ∈R ,且y =x },则A ∩B 的元素的个数为_____________________________________________________________. 答案 2解析 集合A 表示圆心在原点的单位圆,集合B 表示直线y =x ,易知直线y =x 和圆x 2+y 2=1相交,且有2个交点,故A ∩B 中有2个元素.7.已知集合A ={x |y =lg(x -x 2)},B ={x |x 2-cx <0,c >0},若A ⊆B ,则实数c 的取值范围是__________. 答案 [1,+∞)解析 由题意知,A ={x |y =lg(x -x 2)}={x |x -x 2>0}=(0,1),B ={x |x 2-cx <0,c >0}=(0,c ).由A ⊆B ,画出数轴,如图所示,得c ≥1.8.(2015·浙江改编)已知集合P ={x |x 2-2x ≥0},Q ={x |1<x ≤2},则(∁R P )∩Q =__________. 答案 {x |1<x <2}解析 ∵P ={x |x ≥2或x ≤0},∁R P ={x |0<x <2}, ∴(∁R P )∩Q ={x |1<x <2}.9.设集合Q ={x |2x 2-5x ≤0,x ∈N },且P ⊆Q ,则满足条件的集合P 的个数是________. 答案 8解析 因为Q ={x |2x 2-5x ≤0,x ∈N }={x |0≤x ≤52,x ∈N }={0,1,2},所以满足P ⊆Q 的集合P 的个数是23=8.10.设集合M =⎩⎨⎧⎭⎬⎫x |m ≤x ≤m +34,N =⎩⎨⎧⎭⎬⎫x |n -13≤x ≤n ,且M ,N 都是集合{x |0≤x ≤1}的子集,如果把b -a 叫做集合{x |a ≤x ≤b }的“长度”,那么集合M ∩N 的“长度”的最小值是________. 答案112解析 由已知,可得⎩⎪⎨⎪⎧m ≥0,m +34≤1,即0≤m ≤14;⎩⎪⎨⎪⎧n -13≥0,n ≤1,即13≤n ≤1,取m 的最小值0,n 的最大值1,可得M =⎣⎢⎡⎦⎥⎤0,34,N =⎣⎢⎡⎦⎥⎤23,1,所以M ∩N =⎣⎢⎡⎦⎥⎤0,34∩⎣⎢⎡⎦⎥⎤23,1=⎣⎢⎡⎦⎥⎤23,34,此时集合M ∩N 的“长度”的最小值为34-23=112. 11.已知集合A ={m +2,2m 2+m },若3∈A ,则m 的值为__________.答案 -32解析 ∵3∈A ,∴m +2=3或2m 2+m =3.当m +2=3,即m =1时,2m 2+m =3,此时集合A 中有重复元素3,不符合集合的互异性,舍去;当2m 2+m =3时,解得m =-32或m =1(舍去), 当m =-32时,m +2=12≠3,符合题意, ∴m =-32. 12.(2016·南通模拟)设全集U =R ,集合A ={x |y =x 2-2x -3},B ={y |y =e x +1},则A ∪B =__________.答案 (-∞,-1]∪(1,+∞)解析 因为A ={x |x ≥3或x ≤-1},B ={y |y >1},所以A ∪B ={x |x >1或x ≤-1}.13.(2016·江苏无锡新区期中)设P 、Q 为两个非空实数集合,定义集合P *Q ={z |z =ab ,a ∈P ,b ∈Q },若P ={-1,0,1},Q ={-2,2},则集合P *Q 中元素的个数是________. 答案 3解析 按P *Q 的定义,P *Q 中元素为2,-2,0,共3个.14.已知集合A ={0,1,2},则集合B ={x -y |x ∈A ,y ∈A }中元素的个数是________. 答案 5解析 当x =0,y =0时,x -y =0;当x =0,y =1时,x -y =-1;当x =0,y =2时,x -y =-2;当x =1,y =0时, x -y =1;当x =1,y =1时,x -y =0;当x =1,y =2时, x -y =-1;当x =2,y =0时,x -y =2;当x=2,y=1时,x-y=1;当x=2,y=2时,x-y=0.根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个.15.已知集合A={x|4≤2x≤16},B=[a,b],若A⊆B,则实数a-b的取值范围是________. 答案(-∞,-2]解析集合A={x|4≤2x≤16}={x|22≤2x≤24}={x|2≤x≤4}=[2,4],因为A⊆B,所以a≤2,b≥4,所以a-b≤2-4=-2,即实数a-b的取值范围是(-∞,-2].。
江苏专版高考数学二轮复习14个填空题专项强化练一集合与常用逻辑用语

14 个填空题专项强化练(一) 集合与常用逻辑用语A组一一题型分类练题型一集合的基本关系1. 已知集合A= { —1,3 , m i},集合 B= {3 , - 2m n 1},若B? A,则实数m^ ___________2 解析:••• B? A,「. m=—2m- 1或—1 = —2m- 1,解得m=—1或m= 0,经检验均满足题意,故m=— 1 或0.答案:— 1 或02. _______________________________________________ 已知集合A= {0,1,2},则A的子集的个数为_______________________________________________ .3解析:集合A中有3个元素,故A的子集个数为2 = 8.答案:83•已知集合A= {123,4,5} , B= {(x, y)| x€ A, y € A, x—y € A},贝U B 中所含元素的个数为________ .解析:由x —y€ A,及A= {1,2,3,4,5},得x>y,当y = 1 时,x 可取2,3,4,5 , 有 4 个;当y = 2时,x可取3,4,5,有3个;当y = 3时,x可取4,5,有2个;当y = 4时,x可取5,有1个.故共有1+2+3+4=10(个).答案:10题型二集合的运算1. ________________________________________________ 已知集合U= {x| x>0}, A= {x| x>2},贝U ?U A=_____________________________________________ .解析:因为集合U= {x| x>0} , A= {x| x >2},所以?U A= {x|0< x<2}.答案:{x|0< x<2}2. _____________________________________________________________________ 已知集合A= {1,2} , B= {a, a2+ 3}.若A n B= {1},则实数a的值为 __________________________ .解析:因为a2+ 3>3,所以由A n B= {1},得a= 1,即实数a的值为1.答案:1223. 设集合A= {( x, y)| y= x + 1, x€ R}, B= {( x, y)| x + y = 1},则满足C? (A n B)的集合C 的个数为________ .y= x+1 ,解析:法一:解方程组 2 2 得x+y=1,(—1,0)},即A n B中有2个元素•因为C?法二:在同一平面直角坐标系中画出直线圆有两个交点,即A n B 中有 2 个元素.因为x= 0,x=—1 ,或所以A n B= {(0,1) ,y= 1 y= 0,(A n B),所以集合C的个数是4.y= x+1 和圆x2+y2= 1 的图象,可知直线和C? (A n B),所以集合C的个数是4.答案:44. _______________________ 已知全集U^ R,集合A= {x|0 w x w 2},B={x|x2—x>0},则图中的阴影部分表示的集合为 .解析:因为B= {x| x —x>0} = {x|x>1 或x<0},所以A U B= R, A Q B={x|1<x w2},所以阴影部分表示的集合为?R(A Q B) = ( —a, 1] U (2 ,+s).答案:(—a, 1] U (2 ,+a)x 25. 已知集合M= x —7>0, x€ R , N= {y|y = 3x + 1, x€ R},则MH N=x —1解析:x x—1所以x>1或x w0,所以M= {x| x>1 或x w 0}.又N={y|y > 1},则MA N= {x| x>1} = (1 ,+a ).答案:(1 ,+a)题型三常用逻辑用语1. ____________________________________________________________ 命题:“若x € R,贝U x2>0”的逆否命题为:" ___________________________________________ .解析:x € R的否定为x?R x2>0的否定为:x2v 0,故原命题的逆否命题为:"若x2 v 0,则x?R'.答案:若x2v 0,则x?R2. ________________________________________________________________ 已知集合A= {1 ,a}, B= {1,2,3},则“ a= 3” 是“ A? B” 的 ______________________________ 条件.(填 "充分不必要”"必要不充分”“充要”"既不充分也不必要”)解析:当a= 3 时,A= {1,3},显然A? B 但A? B 时,a= 2 或 3.故“ a= 3” 是“ A? B” 的充分不必要条件.答案:充分不必要3. ________________________________________________________________________若命题p: 4是偶数,命题q: 5是8的约数.则下列命题中为真的序号是____________________ .①p且q;②p或q;③非p;④非q.解析:命题p为真,命题q为假,故②④为真.答案:②④4. 已知a ,卩表示两个不同的平面,m为平面a内一条直线,则“ a丄卩”是“ ml卩” ______ 件.(填“充分不必要”“必要不充分” “充要”“既不充分也不必要”)解析:由平面与平面垂直的判定定理知如果m为平面a内的一条直线,ml卩,则a 丄卩,反过来则不一定.所以“ a丄卩”是“ ml卩”的必要不充分条件.答案:必要不充分5•若命题“ ? X € R, ax 2 + 4X + a w 0”为假命题,则实数 a 的取值范围是 _________ . 解析:由命题"? x € R , ax 2 + 4x + a <0”为假命题,得“ ? x € R, ax 2 + 4x + a >0”为真 命题.当a w0时,不成立;当 a >0时,由A = 16- 4a 2<0,得a >2.故实数a 的取值范围是 (2 ,+^) •答案:(2 ,+^)B 组——高考提速练1.命题“ ? x >2, x 2>4”的否定是解析:因为全称命题的否定是存在性命题,所以命题“2x >2, x v 4.2答案:? x >2, x v 42.已知集合 M= {0,1,2} , N= {x |x = 2n - 1, n € M },贝U MH N= 解析:由已知条件得 N={ — 1,1,3},所以MT N= {1}. 答案:{1}3 •命题“若一个数是负数,则它的平方是正数”的逆命题是解析:原命题的逆命题是“若一个数的平方是正数,则这个数是负数”. 答案:若一个数的平方是正数,则这个数是负数 4.设m n 为非零向量,则“存在负数入,使得m p Xn ”是“ m- 件.(填“充分不必要”“必要不充分” “充要”“既不充分也不必要”)解析:T m p Xn , • m- n = ^n • n =入 | n |2. •••当 入 <0, n ^0 时,n r n <0.反之,由 m- n = | m i n |cos 〈 m n 〉<0? cos 〈 m n 〉<0? 〈 m n 〉n当〈m n 〉€ —, n 时,m n 不共线.故“存在负数 入,使得m^Xn ”是“ m- n <0”的充分不必要条件. 答案:充分不必要5. _________________________________________________________ 设集合 A = {1,3} ,B = {a + 2,5} , A T B = {3},则 A U B= ________________________________ .解析:由集合 A = {1,3} , B ={a + 2,5} , A T B = {3},可得 a + 2 = 3,则 A U B = {1,3,5} 答案:{1,3,5}6. _________________________________________________________ 已知集合 P = {x | — 1<x <1} , Q= {x |0< x <2},那么 P U Q= _______________________________ .解析:根据集合的并集的定义,得 P U Q= ( — 1,2).答案:(一1,2)7. 已知全集 U = { — 1,2,3 , a },集合 M= { — 1,3}.若?U M = {2,5},贝U 实数 a 的值为? x >2, x 2>4”的否定是:n <0” 的解析:由题意得(?U M U M= { —1,2,3,5} = U,故a= 5.答案:5& 设集合A= {1,2,4} , B= {x|x2—4x + rr^ 0} •若A H B= {1},贝U B= __________ .解析:因为A H B= {1},所以1€ B,所以1是方程x2—4x + m^ 0的根,所以1 — 4 + m2=0, m= 3,方程为x —4x + 3= 0,解得x= 1 或x= 3,所以B= {1,3} •答案:{1,3}9.已知集合A= {( x, y)| x + y = 1}, B= {( x , y)| y= x},贝U A H B中元素的个数为解析:因为A表示圆x2+ y2= 1上的点的集合,B表示直线y= x上的点的集合,直线y =x与圆x2+ y2= 1有两个交点,所以A H B中元素的个数为2.答案:210.已知f(x)是定义在[—2,2]上的奇函数,当x€ (0,2]时,f(x) = 2x—1,函数g(x) =x —2x + m如果对于?X1 € [ —2,2] , ? [ —2,2],使得g(X2)= f(xj,则实数m的取值范围是_________ .解析:当x € (0,2]时,f(x) = 2x—1€ (0,3],因为f(x)是定义在[—2,2]上的奇函数,所以对于? X1€ [ —2,2] , f (xj € [ —3,3].因为对于? X1€ [ —2,2] , ? X2€ [ —2,2],使得g(X2)= f (xj ,所以g(x)在[—2,2]上的值域A [ —3,3].根据函数g(x) = x2—2x+ m= (x—1)2+ m- 1,得A= [m- 1, m^ 8],m-1 w —3,所以解得—5< n W —2 ,m+ 8> 3 ,即实数m的取值范围是[—5 , —2].答案:[—5 , —2]11 •已知集合A= {x|y = lg(4 —x)},集合B={x|x<a},若P “x€ A”是Q:“x€B”的充分不必要条件,则实数a的取值范围是 _________ .解析:由题意得A= {x| x<4},且A B,结合数轴易得a>4.答案:(4 ,+s)212.若y = x + ax+ b, A= {x| y= x} = {a}, M= {( a, b)},贝U M= __________ .2解析:由A= {a}得x + ax+ b= x的两个根为X1 = X2= a,即x + (a—1)x+ b= 0 的两个根X1 = X2= a,得a=3, 1所以X1 + X2= 1 —a = 2a,1 1所以M= 3,9 .1 1答案:3,913•设集合A={a, a2, a s, a。
(江苏专用)2018版高考数学专题复习 专题1 集合与常用逻辑用语 第4练 集合与常用逻辑用语中的易错题练习

(江苏专用)2018版高考数学专题复习 专题1 集合与常用逻辑用语第4练 集合与常用逻辑用语中的易错题练习 理2.已知集合A ={-1,12},B ={x |mx -1=0},若A ∩B =B ,则所有实数m 组成的集合是________.3.已知集合P ={x |x 2≤1},M ={a }.若P ∪M =P ,则a 的取值范围是________.4.(2017·烟台质检)已知命题p :∃x ∈R ,mx 2+2≤0;q :∀x ∈R ,x 2-2mx +1>0.若p ∨q 为假命题,则实数m 的取值范围是________.5.下列四个结论:①命题“若x ≠1,则x 2-3x +2≠0”的逆否命题是“若x 2-3x +2=0,则x =1”;②若p ∧q 为假命题,则p ,q 均为假命题;③若命题p :∃x ∈R ,x 2+2x +3<0,则綈p :∀x ∈R ,x 2+2x +3≥0;④设a ,b 为两个非零向量,则“a ·b =|a |·|b |”是“a 与b 共线”的充要条件.其中正确结论的序号是________.6.满足条件M ⊆{1,2,3,4,5}的集合M 的个数是________.7.设命题p :∀x ∈R ,x 2+1>0,则綈p 为____________________.8.下列命题中,真命题的序号是________.①存在x ∈[0,π2],使sin x +cos x >2; ②存在x ∈(3,+∞),使2x +1≥x 2;③存在x ∈R ,使x 2=x -1;④对任意x ∈(0,π2],均有sin x <x . 9.(2016·江西赣州十二县(市)期中联考)设集合M ={-1,0,1},N ={a ,a 2},若M ∩N =N ,则a =________.10.已知命题p :函数f (x )=2ax 2-x -1(a ≠0)在(0,1)内恰有一个零点;命题q :函数y =x 2-a 在(0,+∞)上是减函数.若p 且綈q 为真命题,则实数a 的取值范围为________.11.已知全集为U =R ,集合M ={x |x +a ≥0},N ={x |log 2(x -1)<1},若M ∩(∁U N )={x |x =1或x ≥3},则a 的值是________.12.(2016·上饶三模)命题p :∃x ∈[-π6,π4],2sin(2x +π6)-m =0,命题q :∃x ∈(0,+∞),x 2-2mx +1<0,若p ∧(綈q )为真命题,则实数m 的取值范围为__________.13.(2016·安阳月考)已知两个命题r (x ):sin x +cos x >m ,s (x ):x 2+mx +1>0.如果对∀x ∈R ,r (x )∧s (x )为假,r (x )∨s (x )为真,那么实数m 的取值范围为________________.14.已知命题p :关于x 的方程a 2x 2+ax -2=0在[-1,1]上有解;命题q :只有一个实数x 满足不等式x 2+2ax +2a ≤0.若命题“p 或q ”是假命题,则a 的取值范围是__________________.答案精析1.4 2.{-1,0,2} 3.[-1,1] 4.[1,+∞) 5.①③ 6.7 7.∃x ∈R ,x 2+1≤08.④解析 ①中,sin x +cos x >2⇒1+sin 2x >2⇒sin 2x >1,命题为假;②中,令f (x )=x 2-2x -1,则当x ∈(3,+∞)时,f (x )∈(2,+∞),即x 2>2x +3,故不存在x ∈(3,+∞),使2x +1≥x 2,命题为假;③中,x 2-x +1=0⇔(x -12)2+34=0,命题为假;④中,sin x <x ⇔x -sin x >0,令f (x )=x -sin x ,求导得f ′(x )=1-cos x ≥0,∴f (x )是增函数,故f (x )>f (0)=0,命题为真,故填④.9.-1解析 因为集合M ={-1,0,1},N ={a ,a 2},M ∩N =N ,又a 2≥0,所以当a 2=0时,a =0,此时N ={0,0},不符合集合元素的互异性,故a ≠0;当a 2=1时,a =±1,a =1时,N ={1,1},不符合集合元素的互异性,故a ≠1,当a =-1时,N ={-1,1},符合题意.故a =-1.10.(1,2]解析 若命题p 为真,则⎩⎪⎨⎪⎧ 1+8a ≥0,f f =-a -<0,得a >1.若命题q 为真,则2-a <0,得a >2,故由p 且綈q 为真命题,得1<a ≤2.11.-1解析 因为x +a ≥0,所以M ={x |x ≥-a }.又log 2(x -1)<1,所以0<x -1<2,所以1<x <3,所以N ={x |1<x <3}.所以∁U N ={x |x ≤1或x ≥3}.又因为M ∩(∁U N )={x |x =1或x ≥3},所以a =-1.12.[-1,1]解析 ∵x ∈[-π6,π4], ∴2x +π6∈[-π6,2π3],∴sin(2x +π6)∈[-12,1], 2sin(2x +π6)∈[-1,2]. ∃x ∈[-π6,π4],2sin(2x +π6)-m =0,即2sin(2x +π6)=m ,∴m ∈[-1,2]. ∃x ∈(0,+∞),x 2-2mx +1<0, 即m >x 2+12x =x 2+12x≥2 x 2·12x=1, 当且仅当x 2=12x,即x =1时,取“=”. ∴綈q 为真命题时,m ∈(-∞,1].∴p ∧(綈q )为真命题时,m ∈[-1,1].13.(-∞,-2]∪[-2,2)解析 ∵sin x +cos x =2sin(x +π4)≥-2,∴当r (x )是真命题时, m <- 2.当s (x )为真命题时,x 2+mx +1>0恒成立,有Δ=m 2-4<0,∴-2<m <2.∵r (x )∧s (x )为假,r (x )∨s (x )为真,∴r (x )与s (x )一真一假,∴当r (x )为真,s (x )为假时,m <-2,同时m ≤-2或m ≥2,即m ≤-2;当r (x )为假,s (x )为真时,m ≥-2,且-2<m <2,即-2≤m <2. 综上,实数m 的取值范围是m ≤-2或-2≤m <2.14.{a |-1<a <0或0<a <1}解析 由a 2x 2+ax -2=0,得(ax +2)(ax -1)=0,显然a ≠0,所以x =-2a 或x =1a. 因为x ∈[-1,1],故|-2a |≤1或|1a|≤1,所以|a |≥1.“只有一个实数x 满足不等式x 2+2ax +2a ≤0”,即抛物线y =x 2+2ax +2a 与x 轴只有一个交点,所以Δ=4a 2-8a =0.所以a =0或a =2.所以命题“p 或q ”为真命题时,|a |≥1或a =0.因为命题“p 或q ”为假命题,所以a的取值范围为{a|-1<a<0或0<a<1}.百度文库是百度发布的供网友在线分享文档的平台。
(江苏专版)2018年高考数学二轮复习14个填空题专项强化练(九)不等式

14个填空题专项强化练(九) 不 等 式A 组——题型分类练题型一 一元二次不等式1.已知函数f (x )=ax 2+bx +c (a ≠0),若不等式f (x )<0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <12或x >3,则f (e x)>0(e 是自然对数的底数)的解集是________.解析:法一:依题意可得f (x )=a ⎝ ⎛⎭⎪⎫x -12(x -3)(a <0),则f (e x)=a ⎝⎛⎭⎪⎫e x -12(e x -3)(a <0),由f (e x)=a ⎝⎛⎭⎪⎫e x -12(e x -3)>0可得12<e x <3,解得-ln 2<x <ln 3.法二:由题知,f (x )>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<x <3, 令12<e x<3,得-ln 2<x <ln 3. 答案:{x |-ln 2<x <ln 3}2.已知函数f (x )=⎩⎪⎨⎪⎧2x-1,x >0,-x 2-4x ,x ≤0,则不等式f (x )>3的解集为________________.解析:当x >0时,2x -1>3,解得x >2,当x ≤0时,-x 2-4x >3,即x 2+4x +3<0,解得-3<x <-1,所以所求不等式的解集为{x |x >2或-3<x <-1}.答案:{x |x >2或-3<x <-1}3.已知函数y =x 2-2x +a 的定义域为R ,值域为[0,+∞),则实数a 的取值集合为________.解析:由定义域为R ,得x 2-2x +a ≥0恒成立.又值域为[0,+∞),则函数y =x 2-2x +a 的图象只能与x 轴有1个交点,所以Δ=4-4a =0,a =1.答案:{1}4.已知函数f (x )=⎩⎪⎨⎪⎧-x +1,x ≥0,-x 2+1,x <0,则关于x 的不等式f (x 2)>f (2-x )的解集是________.解析:由x 2≥0,得f (x 2)=-x 2+1, 所以原不等式可转化为f (2-x )<-x 2+1, 则当2-x ≥0,即x ≤2时,由-(2-x )+1<-x 2+1,得-2<x <1, 所以-2<x <1; 当2-x <0,即x >2时,由-(2-x )2+1<-x 2+1,得x ∈∅.综上得,关于x 的不等式f (x 2)>f (2-x )的解集是{x |-2<x <1}. 答案:{x |-2<x <1} 题型二 基本不等式 1.若x >1,则x +4x -1的最小值为________. 解析:由x >1,得x -1>0,则x +4x -1=x -1+4x -1+1≥4+1=5.当且仅当x -1=4x -1,即x =3时等号成立.故x +4x -1的最小值为5. 答案:52.已知0<x <1,则x (3-3x )取得最大值时x 的值为________. 解析:由0<x <1,故3-3x >0,则x (3-3x )=13×3x (3-3x )≤13×94=34,当且仅当3x =3-3x ,即x =12时等号成立.答案:123.已知正数a ,b 满足1a +9b=ab -5,则ab 的最小值为________.解析:因为正数a ,b 满足1a +9b=ab -5,所以ab -5≥21a ×9b,可化为(ab )2-5ab -6≥0,解得ab ≥6,即ab ≥36,当且仅当1a =9b,即a =2,b =18时取等号.即ab 的最小值为36.答案:364.已知正数x ,y 满足x 2+4y 2+x +2y ≤2-4xy ,则1x +1y的最小值为________.解析:由题意得(x +2y )2+(x +2y )-2≤0,且x >0,y >0,所以0<x +2y ≤1,所以1x +1y=⎝ ⎛⎭⎪⎫1x +1y ·1≥⎝ ⎛⎭⎪⎫1x +1y ·(x +2y )=3+2y x +x y ≥3+22,当且仅当⎩⎪⎨⎪⎧x +2y =1,2y x =xy,即⎩⎪⎨⎪⎧x =2-1,y =1-22时,1x +1y取得最小值3+2 2.答案:3+2 25.已知a >0,b >0,且12a +b +1b +1=1,则a +2b 的最小值是________.解析:a +2b =2a +b +3b +12-32,故a +2b =⎣⎢⎡⎦⎥⎤2a +b 2+3b +12·⎝ ⎛⎭⎪⎫12a +b +1b +1-32=12+32+2a +b 2b +1+3b +122a +b -32≥12+22a +b 2b +1·3b +122a +b =12+3,当且仅当2a +b 2b +1=3b +122a +b ,且12a +b +1b +1=1时取等号. 故a +2b 的最小值为12+ 3.答案:12+ 3题型三 简单的线性规划1.已知实数x ,y 满足⎩⎪⎨⎪⎧x +y -5≤0,2x -y +2≥0,y ≥0,则目标函数z =x -y的最小值为________.解析:根据题意,画出可行域如图所示,易知当目标函数z =x -y 经过点A (1,4)时,取得最小值-3.答案:-32.设不等式⎩⎪⎨⎪⎧x ≥1,x -y ≤0,x +y ≤4,表示的平面区域为M ,若直线l :y =kx -2上存在M 内的点,则实数k 的取值范围是________.解析:作出不等式组所表示的可行域如图中阴影部分所示. 因为直线l :y =kx -2的图象过定点A (0,-2),且斜率为k ,由图知,当直线l 过点B (1,3)时,k取最大值3+21-0=5,当直线l 过点C (2,2)时,k 取最小值2+22-0=2,故实数k 的取值范围是[2,5]. 答案:[2,5]3.已知约束条件⎩⎪⎨⎪⎧x -2y +1≤0,ax -y ≥0,x ≤1表示的平面区域为D ,若区域D 内至少有一个点在函数y =e x的图象上,那么实数a 的取值范围为________.解析:由题意作出约束条件表示的平面区域及函数y =e x的图象,结合函数图象知,当x =1时,y =e ,把点(1,e)代入ax -y ≥0,则a ≥e.故实数a 的取值范围为[e ,+∞).答案:[e ,+∞)B 组——高考提速练1.不等式x +1x<2的解集为______________. 解析:∵x +1x <2,∴x +1x-2<0, 即x +1-2x x =1-xx<0,∴1-xx<0等价于x (x -1)>0,解得x <0或x >1,∴不等式x +1x<2的解集为{x |x <0或x >1}. 答案:{x |x <0或x >1} 2.若实数x ,y 满足⎩⎪⎨⎪⎧2x +y ≤4,x +3y ≤7,x ≥0,y ≥0,则z =3x +2y 的最大值为________.解析:作出不等式组所表示的平面区域如图中阴影部分所示.由z =3x +2y 得y =-32x +12z ,平移直线y =-32x +12z ,由图象可知当直线y =-32x +12z 经过点A 时,直线y =-32x +12z 的截距最大,此时z最大.由⎩⎪⎨⎪⎧2x +y =4,x +3y =7,解得A (1,2),代入目标函数z =3x +2y ,得z =3×1+2×2=7.即目标函数z =3x +2y 的最大值为7. 答案:73.若a ,b 均为大于1的正数,且ab =100,则lg a ·lg b 的最大值为________. 解析:因为a >1,b >1,所以lg a >0,lg b >0. lg a ·lg b ≤lg a +lg b 24=lg ab 24=1.当且仅当a =b =10时取等号, 故lg a ·lg b 的最大值为1. 答案:14.不等式x 2+ax +4<0的解集不是空集,则实数a 的取值范围是________. 解析:因为不等式x 2+ax +4<0的解集不是空集, 所以Δ=a 2-4×4>0,即a 2>16. 所以a >4或a <-4.答案:(-∞,-4)∪(4,+∞)5.若关于x 的不等式ax 2-6x +a 2<0的解集是(1,m ),则m 的值为________. 解析:根据不等式与方程之间的关系知1为方程ax 2-6x +a 2=0的一个根,即a 2+a -6=0,解得a =2或a =-3,当a =2时,不等式ax 2-6x +a 2<0的解集是(1,2),符合要求;当a =-3时,不等式ax 2-6x +a 2<0的解集是(-∞,-3)∪(1,+∞),不符合要求,舍去.故m =2.答案:26.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=1-log 2x ,则不等式f (x )<0的解集是________.解析:法一:当x <0时,f (x )=-f (-x )=log 2(-x )-1,f (x )<0,即log 2(-x )-1<0,得-2<x <0;当x >0时,f (x )=1-log 2x ,f (x )<0,即1-log 2x <0,解得x >2.综上所述,不等式f (x )<0的解集是(-2,0)∪(2,+∞).法二:先作出函数f (x )在x >0时的图象,再根据奇函数f (x )的图象关于原点对称可得f (x )在R 上的图象,结合图象可知,不等式f (x )<0的解集是(-2,0)∪(2,+∞).答案:(-2,0)∪(2,+∞)7.已知点P 是△ABC 内一点(不包括边界),且AP ―→=m AB ―→+n AC ―→,m ,n ∈R ,则(m -2)2+(n -2)2的取值范围是________.解析:因为点P 是△ABC 内一点(不包括边界),且AP ―→=m AB ―→+n AC ―→,所以m ,n 满足条件⎩⎪⎨⎪⎧m >0,n >0,m +n <1,作出不等式组所表示的平面区域如图所示.因为(m -2)2+(n -2)2表示的是区域内的动点(m ,n )到点A (2,2)的距离的平方.因为点A 到直线m +n =1的距离为|2+2-1|2=32,故⎝ ⎛⎭⎪⎫322<(m -2)2+(n -2)2<OA 2,即(m -2)2+(n -2)2的取值范围是⎝ ⎛⎭⎪⎫92,8.答案:⎝ ⎛⎭⎪⎫92,8 8.已知O 为坐标原点,A (1,2),点P 的坐标(x ,y )满足约束条件⎩⎪⎨⎪⎧x +|y |≤1,x ≥0,则z=OA ―→·OP ―→的最大值为________.解析:如图作满足约束条件的可行域,z =OA ―→·OP ―→=x +2y ,显然在B (0,1)处取得最大值,所以z max=2.答案:29.已知正项等比数列{a n }满足:a 7=a 6+2a 5,若存在两项a m ,a n使得 a m a n =4a 1,则1m +4n的最小值为________.解析:设正项等比数列{a n }的公比为q ,由a 7=a 6+2a 5,得q 2-q -2=0,解得q =2(q =-1,舍去)由a m a n =4a 1,即2m+n-22=4,得2m +n -2=24,即m +n =6.故1m +4n =16(m +n )⎝ ⎛⎭⎪⎫1m +4n =56+16⎝ ⎛⎭⎪⎫4m n +n m ≥56+46=32,当且仅当4m n =nm即m =2,n =4时等号成立,即1m +4n 的最小值为32. 答案:3210.已知A ,B ,C 是平面上任意三点,BC =a ,CA =b ,AB =c ,则y =ca +b +b c的最小值是________.解析:y 要取最小值,则a 要最大,而a 的最大值是b +c ,所以y =c a +b +b c ≥c2b +c+b c =12⎝ ⎛⎭⎪⎫b c +12+⎝ ⎛⎭⎪⎫b c +12-12≥ 2-12,当且仅当12⎝ ⎛⎭⎪⎫b c +12=b c +12时取等号,即y 的最小值是2-12. 答案:2-1211.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且a 不是最大边,已知a 2-b 2=2bc sin A ,则tan A -9tan B 的最小值为________.解析:由余弦定理,a 2=b 2+c 2-2bc cos A 及a 2-b 2=2bc sin A ,得c 2-2bc cos A =2bc sinA ,即c -2b cos A =2b sin A ,再由正弦定理,得sin C -2sin B cos A =2sin B sin A , 即sin(A +B )-2sin B cos A =2sin B sin A , 即sin A cos B -cos A sin B =2sin A sin B , 所以tan A -tan B =2tan A tan B . 所以tan B =tan A 2tan A +1,由题意知tan A >0,所以2tan A +1>0, 所以tan A -9tan B =tan A -9tan A2tan A +1=12(2tan A +1)+922tan A +1-5≥2122tan A +1×922tan A +1-5=-2.当且仅当12(2tan A +1)=922tan A +1,即tan A =1时取“=”.故tan A -9tan B 的最小值为-2.答案:-212.已知a ,b 均为正数,且ab -a -2b =0,则a 24-2a +b 2-1b的最小值为________.解析:因为ab -a -2b =0,所以2a +1b=1,因为a ,b 均为正数,所以b >1,所以a 24-2a +b 2-1b =a 24+b 2-1=b 2b -12+b 2-1,令x =b -1>0,所以a 24-2a +b 2-1b =x +12x 2+(x +1)2-1=x 2+1x 2+2x +2x+1=⎝ ⎛⎭⎪⎫x +1x 2+2⎝ ⎛⎭⎪⎫x +1x -1,因为x +1x≥2x ·1x=2,当且仅当x =1时取等号, 所以⎝ ⎛⎭⎪⎫x +1x 2+2⎝ ⎛⎭⎪⎫x +1x -1≥22+2×2-1=7,即a 24-2a +b 2-1b 的最小值为7.答案:713.若关于x 的不等式(ax -1)(ln x +ax )≥0在(0,+∞)上恒成立,则实数a 的取值范围是________.解析:(ax -1)(ln x +ax )≥0⇔⎝ ⎛⎭⎪⎫a -1x ⎝ ⎛⎭⎪⎫a +ln x x ≥0⇔⎩⎪⎨⎪⎧a ≤1x ,a ≤-ln x x 或⎩⎪⎨⎪⎧a ≥1x,a ≥-ln x x .设函数f (x )=1x ,g (x )=-ln xx,在同一平面直角坐标系内画出它们的图象如图所示,由图象可得实数a 的取值范围是⎝ ⎛⎦⎥⎤-∞,-1e ∪{e}.答案:⎝⎛⎦⎥⎤-∞,-1e ∪{e}14.已知a >0,b >0,c >2,且a +b =2,则ac b +c ab -c 2+5c -2的最小值为________. 解析:考虑所求的结构特征,变形为⎝ ⎛⎭⎪⎫a b +1ab -12c +5c -2,先求a b +1ab -12的最小值.a b +1ab -12=a 2+1a 2-a -12=12a +1-a 2+1a 2+1-12=12a +1a 2+1-1-12, 令2a +1=t ,则2a +1a 2+1-1=t ⎝ ⎛⎭⎪⎫t -122+1-1=4t +5t -2-1≤42t ×5t-2-1=5-12, 所以a b +1ab -12≥52, 当且仅当2a +1=52a +1,即a =5-12时等号成立,故ac b +c ab -c 2+5c -2≥5c 2+5c -2=5⎝ ⎛⎭⎪⎫c -22+1c -2+1≥5⎝⎛⎭⎪⎫2c -22×1c -2+1=5+10.当且仅当(c -2)2=2,即c =2+2时等号成立. 答案:5+10。
2018年高考数学江苏专版三维二轮专题复习训练:14个填空题综合仿真练二 含解析 精品

14个填空题综合仿真练(二)1.已知全集U ={1,2,3,4},集合A ={1,4},B ={3,4},则∁U (A ∪B )=_________. 解析:因为A ={1,4},B ={3,4},所以A ∪B ={1,3,4},因为全集U ={1,2,3,4},所以∁U (A ∪B )={2}.答案:{2}2.已知复数z =1-i 2i,其中i 为虚数单位,则复数z 的虚部为________. 解析:z =1-i 2i =i (1-i )2i 2=1+i -2=-12-12i.所以z 的虚部为-12. 答案:-123.某校有足球、篮球、排球三个兴趣小组,共有成员120人,其中足球、篮球、排球的成员分别有40人、60人、20人.现用分层抽样的方法从这三个兴趣小组中抽取24人来调查活动开展情况,则在足球兴趣小组中应抽取________人.解析:设足球兴趣小组中抽取人数为n ,则n 24=40120,所以n =8. 答案:84.如图是一个算法的流程图,则输出的n 的值为________.解析:由题意,n =1,a =1,第1次循环,a =5,n =3,满足a <16,第2次循环,a =17,n =5,不满足a <16,退出循环,输出的n 的值为5.答案:55.从集合{1,2,3,4}中任取两个不同的数,则这两个数的和为3的倍数的概率为__________.解析:从集合{1,2,3,4}中任取两个不同的数,基本事件总数n =6,这两个数的和为3的倍数包含的基本事件有:(1,2),(2,4),共2个,故这两个数的和为3的倍数的概率P =26=13. 答案:136.设x ∈R ,则p :“log 2x <1”是q :“x 2-x -2<0”的__________条件.(填“充分不必要”“必要不充分”“既不充分也不必要”“充要”)解析:由log 2x <1,得0<x <2,由x 2-x -2<0可得-1<x <2,所以p ⇒q ,q ⇒/p ,故p 是q 的充分不必要条件.答案:充分不必要7.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左焦点到渐近线的距离等于实轴长,则双曲线C 的离心率为________.解析:由题意,双曲线C 的左焦点到渐近线的距离d =bc a 2+b 2=b ,则b =2a ,因此双曲线C 的离心率e =c a =1+⎝⎛⎭⎫b a 2= 5. 答案: 58.记公比为正数的等比数列{a n }的前n 项和为S n .若a 1=1,S 4-5S 2=0,则S 5的值为________.解析:由题意q ≠1,设等比数列的公比为q (q ≠1),由a 1=1,S 4-5S 2=0,得1-q 41-q-5(1+q )=0, 化简得1+q 2=5,解得q =±2.∵数列{a n }的各项均为正数,∴q =2.故S 5=1-251-2=31. 答案:319.如图所示,在棱长为4的正方体ABCD -A1B 1C 1D 1中,P 是A 1B 1上一点,且PB 1=14A 1B 1,则多面体P -BB 1C 1C 的体积为________. 解析:因为四棱锥P -BB 1C 1C 的底面积为16,高PB 1=1,所以VP -BB 1C 1C =13×16×1=163. 答案:163 10.已知函数f (x )=sin ⎝⎛⎭⎫2x +π3(0≤x <π),且f (α)=f (β)=13(α≠β),则α+β=__________. 解析:由0≤x <π,知π3≤2x +π3<7π3,因为f (α)=f (β)=13<32,所以⎝⎛⎭⎫2α+π3+⎝⎛⎭⎫2β+π3=2×3π2,所以α+β=7π6. 答案:7π611.已知函数f (x )=⎩⎪⎨⎪⎧x 2-1,x ≥0,-x +1,x <0.若函数y =f (f (x ))-k 有3个不同的零点,则实数k 的取值范围是________.解析:当x <0时,-x >0,故-x +1>0,所以f (-x +1)=x 2-2x +1-1=x 2-2x ,当x ≥0时,f (x )=x 2-1,当0≤x <1时,x 2-1<0,故f (x 2-1)=-x 2+2,当x ≥1时,x 2-1≥0,故f (x 2-1)=x 4-2x 2.故f (f (x ))=⎩⎪⎨⎪⎧ x 2-2x ,x <0,-x 2+2,0≤x <1,x 4-2x 2,x ≥1,作出函数f (f (x ))的图象如图所示,可知当1<k ≤2时,函数y =f (f (x ))-k 有3个不同的零点.答案:(1,2]12.已知△ABC 外接圆O 的半径为2,且AB ―→+AC ―→=2AO ―→,|AB ―→|=|AO ―→|,则CA ―→·CB―→=__________.解析:由AB ―→+AC ―→=2AO ―→,可得OB ―→+OC ―→=0,即BO ―→=OC ―→,所以圆心在BC 中点上,且AB ⊥AC .因为|AB ―→|=|AO ―→|=2,所以∠AOC =2π3,C =π6, 由正弦定理得AC sin 2π3=AO sin π6,故AC =23, 又BC =4,所以CA ―→·CB ―→=|CA ―→|·|CB ―→|·cos C =4×23×32=12. 答案:1213.设a ,b ,c 是三个正实数,且a (a +b +c )=bc ,则a b +c的最大值为__________. 解析:由a (a +b +c )=bc ,得1+b a +c a =b a ·c a ,设x =b a ,y =c a ,则x +y +1=xy ,a b +c=1x +y ,因为x +y +1=xy ≤⎝⎛⎭⎫x +y 22,所以x +y ≥2+22,所以a b +c 的最大值为2-12.答案:2-1214.设a 为实数,记函数f (x )=ax -ax 3⎝⎛⎭⎫x ∈⎣⎡⎦⎤12,1的图象为C .如果任何斜率不小于1的直线与C 都至多有一个公共点,则a 的取值范围是__________.解析:因为任何斜率不小于1的直线与C 都至多有一个公共点,所以f ′(x )≤1在x ∈⎣⎡⎦⎤12,1上恒成立.因为f ′(x )=a -3ax 2,所以3ax 2-a +1≥0在⎣⎡⎦⎤12,1上恒成立. 设g (t )=3at -a +1,t ∈⎣⎡⎦⎤14,1,只需⎩⎪⎨⎪⎧ g ⎝⎛⎭⎫14≥0,g (1)≥0,即⎩⎪⎨⎪⎧ 34a -a +1≥0,3a -a +1≥0,解得-12≤a ≤4. 答案:⎣⎡⎦⎤-12,4。
江苏专版2018年高考数学二轮复习14个填空题专项强化练七平面向量与复数

14个填空题专项强化练(七) 平面向量与复数A 组——题型分类练题型一 平面向量的线性运算1.已知平面上不共线的四点O ,A ,B ,C ,若OA ―→+2OC ―→=3OB ―→,则|BC ―→||AB ―→|的值为________.解析:由OA ―→+2OC ―→=3OB ―→,得OA ―→-OB ―→=2OB ―→-2OC ―→,即BA ―→=2CB ―→,所以|BC ―→||AB ―→|=12. 答案:122.在▱ABCD 中,AB ―→=a ,AD ―→=b ,AN ―→=3NC ―→,M 为BC 的中点,则MN ―→=________(用a ,b 表示).解析:由AN ―→=3NC ―→得AN ―→=34AC ―→=34(a +b ),AM ―→=a +12b ,所以MN ―→=AN ―→-AM ―→=34(a+b )-⎝ ⎛⎭⎪⎫a +12b =-14a +14b .答案:-14a +14b3.已知Rt △ABC 的面积为2,∠C =90°,点P 是Rt △ABC 所在平面内的一点,满足CP ―→=4CB ―→|CB ―→|+9CA ―→|CA ―→|,则PA ―→·PB ―→的最大值是________. 解析:由条件可知|CA ―→|·|CB ―→|=4,CA ―→·CB ―→=0,因为PA ―→=CA ―→-CP ―→=CA ―→-4CB ―→|CB ―→|-9CA ―→|CA ―→|,PB ―→=CB ―→-CP ―→=CB ―→-4CB ―→|CB ―→|-9CA ―→|CA ―→|,故PA ―→·PB ―→=⎝⎛⎭⎪⎪⎫CA ―→-4CB ―→|CB ―→|-9CA ―→|CA ―→|·⎝ ⎛⎭⎪⎪⎫CB ―→-4CB ―→|CB ―→|-9CA ―→|CA ―→|=97-9|CA ―→|-4|CB ―→|≤97-12×2=73,当且仅当9|CA ―→|=4|CB ―→|,即|CA ―→|=43,|CB ―→|=3时等号成立.答案:73题型二 平面向量的坐标表示1.在▱ABCD 中,AC 为一条对角线,AB ―→=(2,4),AC ―→=(1,3),则向量BD ―→的坐标为________.解析:因为BC ―→=AC ―→-AB ―→=(-1,-1), 所以BD ―→=AD ―→-AB ―→=BC ―→-AB ―→=(-3,-5). 答案:(-3,-5)2.已知向量a =(1,2),b =(x,1),u =a +2b ,v =2a -b ,且u ∥v ,则实数x 的值是________.解析:因为u =(1+2x,4),v =(2-x,3),u ∥v , 所以8-4x =3+6x ,所以x =12.答案:123.已知向量a =(1,2),b =(2,-3).若向量c 满足(c +a )∥b ,c ⊥(a +b ),则c =____________.解析:不妨设c =(m ,n ),则a +c =(1+m,2+n ),a +b =(3,-1), 对于(c +a )∥b ,有-3(1+m )=2(2+n ).① 对于c ⊥(a +b ),有3m -n =0.② 联立①②,解得m =-79,n =-73.故c =⎝ ⎛⎭⎪⎫-79,-73.答案:⎝ ⎛⎭⎪⎫-79,-73题型三 平面向量的数量积1.已知向量a =(3,-2),b =(1,0),向量λa +b 与a -2b 垂直,则实数λ的值为________.解析:依题意,λa +b =(3λ+1,-2λ),a -2b =(1,-2),所以(λa +b )·(a -2b )=7λ+1=0,λ=-17.答案:-172.已知非零向量a ,b 满足|a |=|b |=|a +b |,则a 与2a -b 夹角的余弦值为__________. 解析:法一:不妨设|a |=|b |=|a +b |=1,则|a +b |2=a 2+b 2+2a·b =2+2a ·b =1,所以a·b =-12,所以a ·(2a -b )=2a 2-a ·b =52,又因为|a |=1,|2a -b |=a -b2=4a 2-4a·b +b 2=7,所以a 与2a -b 夹角的余弦值为a a -b |a |·|2a -b |=521×7=5714.法二:(特殊化、坐标化)设|a |=|b |=|a +b |=1,则向量a ,b ,a +b 构成以1为边长的正三角形, 故可设a =(1,0),b =⎝ ⎛⎭⎪⎫-12,32,a +b =⎝ ⎛⎭⎪⎫12,32,则a 与2a -b 的夹角的余弦值为a a -b|a |·|2a -b |=,⎝ ⎛⎭⎪⎫52,-3212+02·⎝ ⎛⎭⎪⎫522+⎝ ⎛⎭⎪⎫-322=527=5714. 答案:57143.已知向量AB ―→与AC ―→的夹角为120°,且|AB ―→|=2,|AC ―→|=3.若AP ―→=λAB ―→+AC ―→,且AP ―→⊥BC ―→,则实数λ的值为________.解析:由题意得,AB ―→·AC ―→=-3,由AP ―→·BC ―→=(λAB ―→+AC ―→)·(AC ―→-AB ―→)=0,得λAB ―→·AC ―→-λAB ―→2+AC ―→2-AC ―→·AB ―→=0,即-3λ-4λ+9+3=0,故λ=127.答案:1274.如图,已知△ABC 的边BC 的垂直平分线交AC 于点P ,交BC 于点Q .若|AB ―→|=3,|AC ―→|=5,则(AP ―→+AQ ―→)·(AB ―→-AC ―→)的值为________.解析:由题意知,(AP ―→+AQ ―→)·(AB ―→-AC ―→)=(2AQ ―→+QP ―→)·CB ―→=2AQ ―→·CB ―→=(AB ―→+AC ―→)·(AB ―→-AC ―→)=|AB ―→|2-|AC ―→|2=32-52=-16.答案:-165.在△ABC 中,已知AB =3,C =60°,则CA ―→·CB ―→的最大值为________. 解析:因为AB ―→=CB ―→-CA ―→, 所以AB ―→2=CB ―→2+CA ―→2-2CB ―→·CA―→,所以3=|CB ―→|2+|CA ―→|2-|CB ―→|·|CA ―→|≥2|CB ―→|·|CA ―→|-|CB ―→|·|CA ―→|=|CB―→|·|CA ―→|,即|CB ―→|·|CA ―→|≤3,当且仅当|CA ―→|=|CB ―→|=3时等号成立.所以CA ―→·CB ―→=|CA ―→||CB ―→|cos 60°=12|CA ―→||CB ―→|≤32,所以CA ―→·CB ―→的最大值为32.答案:326.在△ABC 中,AB ⊥AC ,AB =1t ,AC =t ,P 是△ABC 所在平面内一点,若AP ―→=4AB―→|AB ―→|+AC―→|AC ―→|,则△PBC 面积的最小值为________. 解析:由于AB ⊥AC ,故以AB ,AC 所在直线分别为x 轴,y 轴,建立平面直角坐标系(图略),则B ⎝ ⎛⎭⎪⎫1t ,0,C (0,t ),因为AP ―→=4AB ―→|AB ―→|+AC ―→|AC ―→|,所以点P 坐标为(4,1),直线BC 的方程为t 2x +y -t =0,所以点P 到直线BC 的距离为d =|4t 2+1-t |t 4+1,BC =t 4+1t ,所以△PBC 的面积为12×|4t 2+1-t |t 4+1×t 4+1t =12⎪⎪⎪⎪⎪⎪4t +1t -1≥32,当且仅当t =12时取等号. 答案:32题型四 复数1.设复数z =a +b i(a ,b ∈R ,i 为虚数单位).若z =(4+3i)i ,则ab 的值是________. 解析:因为z =a +b i 且z =(4+3i)i ,所以a +b i =4i +3i 2=-3+4i ,所以a =-3,b =4,所以ab =-12.答案:-122.已知复数z 满足z =(1-2i)(3+i),其中i 为虚数单位,则|z |=________. 解析:复数z =(1-2i)(3+i),i 为虚数单位,则|z |=|1-2i||3+i|=12+-2×32+12=5 2.答案:5 23.设复数z 满足z (1+i)=2,其中i 为虚数单位,则z 的虚部为________.解析:由(1+i)z =2,得z =21+i=-+-=-2=1-i.所以z 的虚部为-1.答案:-14.若复数z 满足(2-i)z =1+i ,则复数z 在复平面上对应的点在第________象限. 解析:因为z =1+i2-i =++-+=1+3i 5=15+35i ,所以复数z 在复平面上对应的点在第一象限.答案:一B 组——高考提速练1.复数z =(1+2i)2,其中i 为虚数单位,则z 的实部为________. 解析:因为复数z =(1+2i)2=-3+4i ,所以复数z 的实部为-3. 答案:-32.如图,已知AB ―→=a ,AC ―→=b ,BD ―→=3DC ―→,用a ,b 表示AD ―→,则AD ―→=________.解析:因为CB ―→=AB ―→-AC ―→=a -b ,又BD ―→=3DC ―→,所以CD ―→=14CB ―→=14(a -b ),所以AD ―→=AC ―→+CD ―→=b +14(a -b )=14a +34b .答案:14a +34b3.已知|a |=3,|b |=4,且a 与b 不共线,若向量a +kb 与a -kb 垂直,则k =________. 解析:因为(a +kb )⊥(a -kb ), 所以(a +kb )·(a -kb )=0, 即|a |2-k 2|b |2=0.又因为|a |=3,|b |=4,所以k 2=916,即k =±34.答案:±344.设复数z 1=1-i ,z 2=a +2i ,若z 2z 1的虚部是实部的2倍,则实数a 的值为________. 解析:z 2z 1=a +2i 1-i =a ++-+=a -2++a2,故该复数的实部是a -22,虚部是a +22.由题意,知a +22=2×a -22.解得a =6.答案:65.已知复数z =(1+i)(1+2i),其中i 是虚数单位,则z 的模是________. 解析:法一:复数z =1+2i +i -2=-1+3i , 则|z |=-2+32=10.法二:|z |=|1+i|·|1+2i|=2×5=10. 答案:106.若a ,b 均为单位向量,且a ⊥(a -2b ),则a ,b 的夹角大小为________. 解析:设a ,b 的夹角为θ.因为a ⊥(a -2b ), 所以a ·(a -2b )=a 2-2a·b =0, 所以1-2cos θ=0,所以cos θ=12,而θ∈[0,π],故θ=π3.答案:π37.若复数z 满足z +2z =3+2i ,其中i 为虚数单位,z 为复数z 的共轭复数,则复数z 的模为________.解析:设z =x +y i ,x ,y ∈R ,则z =x -y i ,因为z +2z =3+2i ,所以z +2z =(x +y i)+2(x -y i)=3x -y i =3+2i ,所以x =1,y =-2,所以z =1-2i ,所以复数z 的模为 5.答案: 58.平面向量a ,b 满足|a |=2,|a +b |=4,且向量a 与向量a +b 的夹角为π3,则|b |为________.解析:因为向量a 与向量a +b 的夹角为π3,所以cos π3=a +b a |a +b |·|a |=a 2+a ·b |a +b |·|a |=4+a ·b8,解得a ·b =0,即a ⊥b .所以|a |2+|b |2=|a +b |2, 从而解得|b |=2 3. 答案:2 39.如图,在△ABC 中,AB =AC =3,cos ∠BAC =13,DC ―→=2BD ―→,则AD ―→·BC ―→的值为________.解析:由DC ―→=2BD ―→,得AD ―→=13(AC ―→+2AB ―→).又BC ―→=AC ―→-AB ―→,AB =AC =3,cos∠BAC =13,所以AD ―→·BC ―→ =13(AC ―→+2AB ―→)·(AC ―→-AB ―→)=13×(-9+3)=-2.答案:-210.已知边长为1的正方形ABCD ,CM ―→=2CA ―→+DB ―→,则|CM ―→|=________. 解析:法一:由题意得,CM ―→2=(2CA ―→+DB ―→)2=4CA ―→2+DB ―→2+4CA ―→·DB ―→.又四边形ABCD 是边长为1的正方形,所以CA ―→⊥DB ―→,所以CA ―→·DB ―→=0.又|CA ―→|=2,|DB ―→|=2,所以CM ―→2=4×2+2=10,所以|CM ―→|=10.法二:由题意,作出CM ―→=2CA ―→+DB ―→,如图所示,则|CM ―→|为边长分别为2,22的矩形CFME 的对角线的长,所以|CM ―→|= 22+22=10. 答案:1011.已知AB 为圆O 的直径,M 为圆O 的弦CD 上一动点,AB =8,CD =6,则MA ―→·MB ―→的取值范围是________.解析:因为AB 为圆O 的直径, 所以MA ―→+MB ―→=2MO ―→,① 又MA ―→-MB ―→=BA ―→,②①2-②2,得4MA ―→·MB ―→=4MO ―→2-BA ―→2, 所以MA ―→·MB ―→=MO ―→2-16,因为M 为圆O 的弦CD 上一动点,AB =8,CD =6, 所以根据圆的几何性质知|MO ―→|∈[7,4], 所以MA ―→·MB ―→∈[-9,0]. 答案:[-9,0]12.在△ABC 中,若BC ―→·BA ―→+2AC ―→·AB ―→=CA ―→·CB ―→,则sin A sin C 的值为________.解析:法一:设角A ,B ,C 所对的边分别为a ,b ,c . 由BC ―→·BA ―→+2AC ―→·AB ―→=CA ―→·CB ―→,得ac a 2+c 2-b 22ac +2bc b 2+c 2-a 22bc =ab a 2+b 2-c 22ab,化简可得a =2c .由正弦定理得sin A sin C =ac= 2.法二:建立平面直角坐标系,设A (0,a ),B (b,0),C (c ,0), 所以AC ―→=(c ,-a ),AB ―→=(b ,-a ),BC ―→=(c -b,0), BA ―→=(-b ,a ),CA ―→=(-c ,a ),CB ―→=(b -c,0), 则由BC ―→·BA ―→+2AC ―→·AB ―→=CA ―→·CB ―→, 得b 2+2cb +2a 2-c 2=0,所以b 2-2cb +c 2=(c -b )2=2(a 2+b 2), 所以BC =2AB .由正弦定理得sin A sin C =BCAB = 2.答案: 213.已知平面向量α,β满足|β|=1,且α与β-α的夹角为120°,则|α|的取值范围为________.解析:法一:由|β|=1,且α与β-α的夹角为120°,作向量OA ―→=α,AB ―→=β-α,则OB ―→=β,在△OAB 中,∠OAB =60°,OB =1,则由正弦定理OB sin 60°=OA sin ∠ABO,得OA =233sin ∠ABO ∈⎝⎛⎦⎥⎤0,233,即0<|α|≤233. 法二:设|α|=u ,|β-α|=v ,由|β|2=|α+(β-α)|2=α2+2α·(β-α)+(β-α)2,得v 2-uv +u 2-1=0,再由关于v 的一元二次方程有解,得u 2-4(u 2-1)≥0,又u >0,故0<u ≤233,即0<|α|≤233. 答案:⎝⎛⎦⎥⎤0,23314.在平面直角坐标系xOy 中,设点A (1,0),B (0,1),C (a ,b ),D (c ,d ),若不等式 CD ―→2≥(m -2)OC ―→·OD ―→+m (OC ―→·OB ―→)·(OD ―→·OA ―→)对任意实数a ,b ,c ,d 都成立,则实数m 的最大值是________.解析:原不等式可化为(a -c )2+(b -d )2≥(m -2)·(ac +bd )+mbc ,即a 2+b 2+c 2+d2-m (ac +bd +bc )≥0,整理成关于实数a 的不等式为a 2-mca +b 2+c 2+d 2-mbd -mbc ≥0恒成立,从而Δ1=m 2c 2-4(b 2+c 2+d 2-mbd -mbc )≤0,再整理成关于实数d 的不等式为d 2-mbd +b 2+c 2-mbc -14m 2c 2≥0,从而Δ2=m 2b 2-4⎝ ⎛⎭⎪⎫b 2+c 2-mbc -14m 2c 2≤0,再整理成关于实数b 的不等式为(4-m 2)b 2-4mcb +4c 2-m 2c 2≥0,从而⎩⎪⎨⎪⎧4-m 2>0,Δ3=16m 2c 2--m2c 2-m 2c 2,解得1-5≤m ≤-1+5,所以m 的最大值是5-1.答案:5-1。
2018年高考数学文科江苏专版二轮专题复习与策略课件:专题一 集合与常用逻辑用语 精品

专题限时集训(一) 点击图标进入…
(2)由题意可知 A∩B={1,3,5}, ∴C={1,3,5}, ∴集合 C 的子集共有 23=8 个. (3)由题意可知∁UB={1,5},又 A={1,2}, ∴A∪(∁UB)={1,2,5}.]
【名师点评】 解答集合问题的思路,根据元素的不同属性采用不同的方法 对集合进行化简求解.
1若给定的集合是不等式的解集,用数轴求解; 2若给定的集合是点集,用数形结合法求解; 3若给定的集合是抽象集合或是用列举法表示的集合,用 Venn 图求解.
题型三| 充分条件与必要条件
(1)(2016·镇江期中)实系数一元二次方程 ax2+bx+c=0,则“ac< 0”是“该方程有实数根”的________条件.(选填“充分不必要”“必要不充 分”“充要”或“既不充分也不必要”)
(2)已知命题 p:x2+2x-3>0;命题 q:x>a,且﹁q 的一个充分不必要条件 是﹁p,则 a 的取值范围用区间表示为________.
[1,+∞) [若存在 x0∈R,mx20+2≤0 成立,则 m<0,所以若 p 为假命题, m 的取值范围是[0,+∞);若任意 x∈R,x2-2mx+1>0,则 Δ=4m2-4<0,即 -1<m<1,所以若 q 为假命题,m 的取值范围是(-∞,-1]∪[1,+∞),所以 若“p∨q”为假命题,则实数 m 的取值范围是[1,+∞).]
[解题指导]
一元二次方程 (1) ax2+bx+c=0 ―→ b2-4ac≥0 ―→ b2≥4ac 充―分―不――必―要―条→件
有实根
得出结论 (2) 解出p ―→ 解出﹁p,﹁q 充―分―不――必―要―条→件 得出结论
(1)充分不必要 (2)[1,+∞) [(1)一元二次方程 ax2+bx+c=0 有实根,则 判别式 Δ=b2-4ac≥0,即 b2≥4ac.当 ac<0 时,显然有 b2≥4ac;但 b2≥4ac 未 必推出 ac<0,故“ac<0”是一元二次方程 ax2+bx+c=0 有实根的充分不必要 条件.
最新-江苏省2018届高三数学二轮 专题训练 填空题(54)

江苏省2018届高三数学二轮专题训练:填空题(54)本大题共14小题,请把答案直接填写在答题位置上。
1.已知集合{}11M =-,,11242x N x x +⎧⎫=<<∈⎨⎬⎩⎭Z ,,则M N =__ ▲ .2.复数ii4321+-在复平面上对应的点位于第 __ ▲ 象限. 3.根据表格中的数据,可以判定方程20x e x --=的一个零点所在的区间为))(1,(N k k k ∈+,则k 的值为__ ▲ .4. 若x , y 满足条件4104320,10200x y x y x y x y +≤⎧⎪+≤⎪+⎨≥⎪⎪≥⎩则的最大值等于 ▲ .5.设31sin (), tan(),522πααππβ=<<-=则tan ()βα-的值等于__ ▲ .6.设)(x f 是定义在R 上的奇函数,且当0x >时,32)(-=xx f ,则=-)2(f __▲___.7.在△ABC 中,BC=1,3π=∠B ,当△ABC 的面积等于3时,=C tan __ ▲ .8.若曲线4()f x x x =-在点P 处的切线平行于直线3x -y =0,则点P 的坐标为 ▲ . 9.设)(x f y =是一次函数,1)0(=f ,且)13(),4(),1(f f f 成等比数列,则++)4()2(f f …=+)2(n f _ ▲ .10.函数1)1(log +-=x y a (01)a a >≠且,的图象恒过定点A ,若点A 在一次函数n mx y +=的图象上,其中,0m n >,则12m n+的最小值为__ ▲ . 11.设O 是△ABC 内部一点,且AOC AOB ∆∆-=+与则,2的面积之比为__▲ . 12.若函数)(x f 是定义在(0,+∞)上的增函数,且对一切x>0,y>0满足)()()(y f x f xy f +=,则不等式)4(2)()6(f x f x f <++的解集为__ ▲ .13.第29届奥运会在北京举行.设数列n a =)2(log 1++n n *)(N n ∈,定义使k a a a a ⋅⋅⋅⋅⋅321为整数的实数k 为奥运吉祥数,则在区间[1,2018]内的所有奥运吉祥数之和为____▲____. 14.给出定义:若1122m x m -<≤+(其中m 为整数),则m 叫做离实数x 最近的整数,记作{}x ,即 {}x m =. 在此基础上给出下列关于函数|}{|)(x x x f -=的四个命题: ①函数)(x f y =的定义域是R ,值域是[0,21]; ②函数)(x f y =的图像关于直线2kx =(k ∈Z)对称; ③函数)(x f y =是周期函数,最小正周期是1;④ 函数()y f x =在⎥⎦⎤⎢⎣⎡-21,21上是增函数; 则其中真命题是__ ▲ .1. {}1-2. 三3. 14. 255. 112-6. -17. -8. (1,0)9. )32(+n n 10. 8 11. 1 12. (0,2) 13. 2186 14. ①②③。
2018版高考数学(江苏专用理科)专题复习专题1集合与常用逻辑用语 第3练含解析

q;②p∨q;③p∧(綈q);④(綈p)∨q中,真命题是________.(填序号) 2.命题p的否定是“对所有正数x,x>x+1”,则命题p可写为________________________.3.(2016·肇庆统测)设a,b,c是非零向量,已知命题p:若a·b=0,则a⊥b;命题q:若a∥b,b∥c,则a∥c.则下列命题中假命题是________.(填序号)①p∧q;②p∨q;③(綈p)∨q;④(綈p)∨(綈q).4.已知命题p:x2-2x-3<0,q:1x-2<0,若p∧q为真,则x的取值范围是________.5.下列四个命题:①“∃x∈R,x2-x+1≤0”的否定;②“若x2+x-6≥0,则x>2”的否命题;③在△ABC中,“A>30°”是“sin A>12”的充分不必要条件;④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ(k∈Z)”.其中真命题的序号是________.(填序号)6.(2016·镇江模拟)若命题“∃x∈(1,2),满足不等式x2+mx+4≥0”是假命题,则m的取值范围是__________.7.(2016·泰州一模)已知函数f(x)=x2,g(x)=(12)x-m,若∀x1∈-1,3],∃x2∈0,2],使得f(x1)≥g(x2),则实数m的取值范围是__________.8.(2016·南京模拟)由命题“存在x∈R,使x2+2x+m≤0”是假命题,求得实数m的取值范围是(a,+∞),则实数a的值是________.9.已知命题p:∃x0∈R,使sin x0=52;命题q:∀x∈R,都有x2+x+1>0.给出下列结论:①命题“p∧q”是真命题;②命题“p∧(綈q)”是假命题;③命题“(綈p)∨q”是真命题;④命题“(綈p)∨(綈q)”是假命题.其中正确的命题是________.(填序号)10.(2016·临夏期中)下列结论正确的有________.(填序号)①命题“若p,则q”与命题“若綈q,则綈p”互为逆否命题;②命题p:∀x∈0,1],e x≥1,命题q:∃x∈R,x2+x+1<0,则p∨q为真;③若p∨q为假命题,则p,q均为假命题;④“若am2<bm2,则a<b”的逆命题为真命题.11.(2016·淮安模拟)已知下列命题:①命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1<3x”;②已知p,q为两个命题,若“p∨q”为假命题,则“(綈p)∧(綈q)”为真命题;③“a>2”是“a>5”的充分不必要条件;④“若xy=0,则x=0且y=0”的逆否命题为真命题.其中所有真命题的序号是________.12.(2016·宿迁模拟)已知命题p:∀a∈R,方程ax+4=0有解;命题q:∃m >0,直线x+my-1=0与直线2x+y+3=0平行.给出下列结论,其中正确的有________个.①命题“p∧q”是真命题;②命题“p∧(綈q)”是真命题;③命题“(綈p)∨q”是真命题;④命题“(綈p)∨(綈q)”是真命题.13.(2016·石家庄二模)已知命题p:x2-3x-4≤0,命题q:x2-6x+9-m2≤0,若綈q是綈p的充分不必要条件,则实数m的取值范围是________________.14.设命题p:函数f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式2x2+x >2+ax在x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为__________.答案精析1.②③ 2.∃x ∈(0,+∞),x ≤x +13.④ 4.(-1,2) 5.①② 6.(-∞,-5]7.14,+∞)解析因为∀x1∈-1,3]时,f(x1)∈0,9],即f(x)min=0,若∃x2∈0,2],使得f(x1)≥g(x2),则只要满足g(x)min≤0.而函数g(x)在区间0,2]上是单调减函数,故g(x)min =g(2)=(12)2-m≤0,即m≥14.8.1解析∵“存在x∈R,使x2+2x+m≤0”是假命题,∴“任意x∈R,使x2+2x+m>0”是真命题,∴Δ=4-4m<0,解得m>1,故a的值是1.9.②③解析∵52>1,∴命题p是假命题,又∵x2+x+1=(x+12)2+34≥34>0,∴命题q是真命题,由命题真假的真值表可以判断②③正确.10.①②③解析命题“若p,则q”的逆否命题是“若綈q,则綈p”,所以命题“若p,则q”与命题“若綈q,则綈p”互为逆否命题,故①正确;命题p:∀x∈0,1],e x ≥1,为真命题,命题q:∃x∈R,x2+x+1<0,为假命题,则p∨q为真,故②正确;若p∨q为假命题,则p,q均为假命题,故③正确;“若am2<bm2,则a<b”的逆命题为“若a<b,则am2<bm2”,而当m2=0时,由a<b,得am2=bm2,所以“若am2<bm2,则a<b”的逆命题为假命题,故④不正确.11.②解析命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1≤3x”,故①错;“p ∨q”为假命题说明p假q假,则(綈p)∧(綈q)为真命题,故②正确;a>5⇒a >2,但a>2⇒/a>5,故“a>2”是“a>5”的必要不充分条件,故③错;因为“若xy=0,则x=0或y=0”,所以原命题为假命题,故其逆否命题也为假命题,故④错.12.2解析因为当a=0时,方程ax+4=0无解,所以命题p为假命题;当1-2m=0,即m=12时两条直线平行,所以命题q是真命题.所以綈p为真命题,綈q为假命题,所以①错误,②错误,③正确,④正确.13.{m|m≤-4或m≥4}解析 ∵綈q 是綈p 的充分不必要条件,∴p 是q 的充分不必要条件,∴{x |x 2-3x -4≤0}{x |x 2-6x +9-m 2≤0}, ∴{x |-1≤x ≤4}{x |(x +m -3)(x -m -3)≤0}.当-m +3=m +3,即m =0时,不合题意.当-m +3>m +3,即m <0时,有{x |-1≤x ≤4}{x |m +3≤x ≤-m +3}, 此时⎩⎨⎧ m +3≤-1,-m +3≥4(两等号不能同时取得),解得m ≤-4.当-m +3<m +3,即m >0时,有{x |-1≤x ≤4}{x |-m +3≤x ≤m +3},此时⎩⎨⎧ -m +3≤-1,m +3≥4(两等号不能同时取得),解得,m ≥4.综上,实数m 的取值范围是{m |m ≤-4或m ≥4}.14.1,2]解析 对于命题p :Δ<0且a >0,故a >2;对于命题q :a >2x -2x+1在x ∈(-∞,-1)上恒成立,又函数y =2x -2x +1为增函数,所以2x -2x+1<1,故a ≥1,命题“p ∨q ”为真命题,命题“p ∧q ”为假命题,等价于p ,q 一真一假.故1≤a ≤2.。
2018版高考数学(江苏专用理科)专题复习:专题1集合与常用逻辑用语 第1练 Word版含解析

________.2.已知集合A ={1,2,3,4,5},B ={(x ,y )|x ∈A ,y ∈A ,x <y ,x +y ∈A },则集合B 的子集个数是________.3.(2016·苏州调研)设全集U ={x |x ≥2,x ∈N },集合A ={x |x 2≥5,x ∈N },则∁U A =________.4.(2016·南通、扬州、泰州二调)设集合A ={-1,0,1},B ={a -1,a +1a },A ∩B ={0},则实数a 的值为______.5.设函数f (x )=lg(1-x 2),集合A ={x |y =f (x )},B ={y |y =f (x )},则图中阴影部分表示的集合为____________________________.6.(2016·厦门模拟)设集合A ={(x ,y )|x 24+y 216=1},B ={(x ,y )|y =3x },则A ∩B 的子集的个数是________.7.(2016·苏北四市一模)已知集合A ={2+a ,a },B ={-1,1,3},且A ⊆B ,那么实数a 的值是________.8.(2016·苏州、无锡、常州、镇江三模)已知集合A ={-1,1,3},B ={2,2a -1},A ∩B ={1},那么实数a 的值为________.9.设集合A ={x |x 2+2x -3>0},B ={x |x 2-2ax -1≤0,a >0}.若A ∩B 中恰含有一个整数,则实数a 的取值范围是____________.10.已知集合A ={x |x 2-2x -3>0},B ={x |x 2+ax +b ≤0},若A ∪B =R ,A ∩B ={x |3<x ≤4},则a +b 的值为________.11.(2016·成都模拟)已知集合M ={x |x >x 2},N ={y |y =4x 2,x ∈M },则M ∩N =__________________.12.若集合A ={x |-1<x ≤2},B ={x |(x -a )(x -a +1)≥0},且A ∩B =A ,则实数a 的取值范围是______________________.13.用C (A )表示非空集合A 中的元素个数,定义A *B =⎩⎨⎧C (A )-C (B ),C (A )≥C (B ),C (B )-C (A ),C (A )<C (B ).若A ={1,2},B ={x |(x 2+ax )·(x 2+ax +2)=0},且A *B =1,设实数a 的所有可能取值组成的集合是S ,则C (S )=________.14.设S 是实数集R 的非空子集,若对任意x ,y ∈S ,都有x +y ,x -y ,xy ∈S ,则称S 为封闭集.下列命题:①集合S ={a +b 3|a ,b 为整数}为封闭集;②若S 为封闭集,则一定有0∈S ;③封闭集一定是无限集;④若S 为封闭集,则满足S ⊆T ⊆R 的任意集合T 也是封闭集.其中真命题是________.(写出所有真命题的序号)答案精析1.{1} 2.16 3.{2} 4.15.{x |x ≤-1或0<x <1} 6.47.1解析 因为A ⊆B ,当a =1时,A ={1,3}⊆B .当a =-1,3时不合题意,所以a =1.8.1解析 由题意知1∈B ,所以2a -1=1,解得a =1.9.34,43) 解析 A ={x |x 2+2x -3>0}={x |x >1或x <-3},因为函数y =f (x )=x 2-2ax -1图象的对称轴为直线x =a >0,f (-3)=6a +8>0,根据对称性可知,要使A ∩B 中恰含有一个整数,则这个整数为2,所以有f (2)≤0且f (3)>0,即⎩⎨⎧4-4a -1≤0,9-6a -1>0,所以⎩⎪⎨⎪⎧ a ≥34,a <43,即34≤a <43.10.-7解析 由已知得A ={x |x <-1或x >3},∵A ∪B =R ,A ∩B ={x |3<x ≤4},∴B ={x |-1≤x ≤4},即方程x 2+ax +b =0的两根为x 1=-1,x 2=4.∴a =-3,b =-4,∴a +b =-7.11.{x |12<x <1}解析 对于集合M ,由x >x 2,解得0<x <1,∴M ={x |0<x <1},∵0<x <1,∴1<4x<4,∴12<4x 2<2,∴N ={y |12<y <2},∴M ∩N ={x |12<x <1}.12.(-∞,-1]∪3,+∞)解析 化简B ={x |x ≥a 或x ≤a -1},又A ∩B =A ,所以A ⊆B .由数轴知a ≤-1或a -1≥2,即a ≤-1或a ≥3.所以a 的取值范围是(-∞,-1]∪3,+∞).13.3解析 因为C (A )=2,A *B =1,所以C (B )=1或C (B )=3.由x 2+ax =0,得x 1=0,x 2=-a .关于x 的方程x 2+ax +2=0,当Δ=0,即a =±22时,易知C (B )=3,符合题意;当Δ>0,即a <-22或a >22时,易知0,-a 均不是方程x 2+ax +2=0的根,故C (B )=4,不符合题意;当Δ<0,即-22<a <22时,方程x 2+ax +2=0无实数解,当a =0时,B ={0},C (B )=1,符合题意,当-22<a <0或0<a <22时,C (B )=2,不符合题意.所以S ={0,-22,22}.故C (S )=3.14.①②解析 ①正确,任取x ,y ∈S ,设x =a 1+b 13,y =a 2+b 23(a 1,b 1,a 2,b 2∈Z ),则x +y =(a 1+a 2)+(b 1+b 2)3,其中a 1+a 2∈Z ,b 1+b 2∈Z .即x +y ∈S .同理x -y ∈S ,xy ∈S .②正确,当x =y 时,0∈S .③错误,当S ={0}时,是封闭集,但不是无限集;④错误,设S ={0}⊆T ={0,1},显然T 不是封闭集.因此正确命题为①②.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14个填空题专项强化练(一) 集合与常用逻辑用语A 组——题型分类练题型一 集合的基本关系1.已知集合A ={-1,3,m 2},集合B ={3,-2m -1},若B ⊆A ,则实数m =________. 解析:∵B ⊆A ,∴m 2=-2m -1或-1=-2m -1,解得m =-1或m =0,经检验均满足题意,故m =-1或0.答案:-1或02.已知集合A ={0,1,2},则A 的子集的个数为________. 解析:集合A 中有3个元素,故A 的子集个数为23=8. 答案:83.已知集合A ={1,2,3,4,5},B ={(x ,y )|x ∈A ,y ∈A ,x -y ∈A },则B 中所含元素的个数为________.解析:由x -y ∈A ,及A ={1,2,3,4,5},得x >y , 当y =1时,x 可取2,3,4,5,有4个; 当y =2时,x 可取3,4,5,有3个; 当y =3时,x 可取4,5,有2个; 当y =4时,x 可取5,有1个. 故共有1+2+3+4=10(个). 答案:10题型二 集合的运算1.已知集合U ={x |x >0},A ={x |x ≥2},则∁U A =________. 解析:因为集合U ={x |x >0},A ={x |x ≥2},所以∁U A ={x |0<x <2}. 答案:{x |0<x <2}2.已知集合A ={1,2},B ={a ,a 2+3}.若A ∩B ={1},则实数a 的值为________. 解析:因为a 2+3≥3,所以由A ∩B ={1},得a =1,即实数a 的值为1. 答案:13.设集合A ={(x ,y )|y =x +1,x ∈R},B ={(x ,y )|x 2+y 2=1},则满足C ⊆(A ∩B )的集合C 的个数为________.解析:法一:解方程组⎩⎪⎨⎪⎧y =x +1,x 2+y 2=1,得⎩⎪⎨⎪⎧x =0,y =1或⎩⎪⎨⎪⎧x =-1,y =0,所以A ∩B ={(0,1),(-1,0)},即A ∩B 中有2个元素.因为C ⊆(A ∩B ),所以集合C 的个数是4.法二:在同一平面直角坐标系中画出直线y =x +1和圆x 2+y 2=1的图象,可知直线和圆有两个交点,即A ∩B 中有2个元素.因为C ⊆(A ∩B ),所以集合C 的个数是4.答案:44.已知全集U =R ,集合A ={x |0≤x ≤2},B ={x |x 2-x >0},则图中的阴影部分表示的集合为________.解析:因为B ={x |x 2-x >0}={x |x >1或x <0},所以A ∪B =R ,A ∩B ={x |1<x ≤2},所以阴影部分表示的集合为∁R (A ∩B )=(-∞,1]∪(2,+∞).答案:(-∞,1]∪(2,+∞)5.已知集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪xx -1≥0,x ∈R ,N ={y |y =3x 2+1,x ∈R},则M ∩N =________. 解析:由xx -1≥0,得⎩⎪⎨⎪⎧x ≠1,x x -1 ≥0,所以x >1或x ≤0, 所以M ={x |x >1或x ≤0}. 又N ={y |y ≥1},则M ∩N ={x |x >1}=(1,+∞). 答案:(1,+∞) 题型三 常用逻辑用语1.命题:“若x ∈R ,则x 2≥0”的逆否命题为:“____________________”. 解析:x ∈R 的否定为x ∉R ;x 2≥0的否定为:x 2<0,故原命题的逆否命题为: “若x 2<0,则x ∉R”.答案:若x 2<0,则x ∉R2.已知集合A ={1,a },B ={1,2,3},则“a =3”是“A ⊆B ”的______________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)解析:当a =3时,A ={1,3},显然A ⊆B .但A ⊆B 时,a =2或3.故“a =3”是“A ⊆B ”的充分不必要条件.答案:充分不必要3.若命题p :4是偶数,命题q :5是8的约数.则下列命题中为真的序号是________. ①p 且q ;②p 或q ;③非p ;④非q .解析:命题p 为真,命题q 为假,故②④为真. 答案:②④4.已知α,β表示两个不同的平面,m 为平面α内一条直线,则“α⊥β”是“m ⊥β”________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)解析:由平面与平面垂直的判定定理知如果m 为平面α内的一条直线,m ⊥β,则α⊥β,反过来则不一定.所以“α⊥β”是“m ⊥β”的必要不充分条件.答案:必要不充分5.若命题“∃x ∈R ,ax 2+4x +a ≤0”为假命题,则实数a 的取值范围是________. 解析:由命题“∃x ∈R ,ax 2+4x +a ≤0”为假命题,得“∀x ∈R ,ax 2+4x +a >0”为真命题.当a ≤0时,不成立;当a >0时,由Δ=16-4a 2<0,得a >2.故实数a 的取值范围是(2,+∞).答案:(2,+∞)B 组——高考提速练1.命题“∀x ≥2,x 2≥4”的否定是__________________.解析:因为全称命题的否定是存在性命题,所以命题“∀x ≥2,x 2≥4”的否定是:∃x ≥2,x 2<4.答案:∃x ≥2,x 2<42.已知集合M ={0,1,2},N ={x |x =2n -1,n ∈M },则M ∩N =________. 解析:由已知条件得N ={-1,1,3},所以M ∩N ={1}. 答案:{1}3.命题“若一个数是负数,则它的平方是正数”的逆命题是____________________. 解析:原命题的逆命题是“若一个数的平方是正数,则这个数是负数”. 答案:若一个数的平方是正数,则这个数是负数4.设m ,n 为非零向量,则“存在负数λ,使得m =λn ”是“m ·n <0”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)解析:∵m =λn ,∴m ·n =λn ·n =λ|n |2. ∴当λ<0,n ≠0时,m ·n <0.反之,由m ·n =|m ||n |cos 〈m ,n 〉<0⇔cos 〈m ,n 〉<0⇔〈m ,n 〉∈⎝ ⎛⎦⎥⎤π2,π, 当〈m ,n 〉∈⎝ ⎛⎭⎪⎫π2,π时,m ,n 不共线.故“存在负数λ,使得m =λn ”是“m ·n <0”的充分不必要条件. 答案:充分不必要5.设集合A ={1,3},B ={a +2,5},A ∩B ={3},则A ∪B =________.解析:由集合A ={1,3},B ={a +2,5},A ∩B ={3},可得a +2=3,则A ∪B ={1,3,5}. 答案:{1,3,5}6.已知集合P ={x |-1<x <1},Q ={x |0<x <2},那么P ∪Q =________. 解析:根据集合的并集的定义,得P ∪Q =(-1,2). 答案:(-1,2)7.已知全集U ={-1,2,3,a },集合M ={-1,3}.若∁U M ={2,5},则实数a 的值为________.解析:由题意得(∁U M )∪M ={-1,2,3,5}=U ,故a =5.答案:58.设集合A ={1,2,4},B ={x |x 2-4x +m =0}.若A ∩B ={1},则B =________. 解析:因为A ∩B ={1},所以1∈B ,所以1是方程x 2-4x +m =0的根,所以1-4+m =0,m =3,方程为x 2-4x +3=0,解得x =1或x =3,所以B ={1,3}.答案:{1,3}9.已知集合A ={(x ,y )|x 2+y 2=1},B ={(x ,y )|y =x },则A ∩B 中元素的个数为________.解析:因为A 表示圆x 2+y 2=1上的点的集合,B 表示直线y =x 上的点的集合,直线y =x 与圆x 2+y 2=1有两个交点,所以A ∩B 中元素的个数为2.答案:210.已知f (x )是定义在[-2,2]上的奇函数,当x ∈(0,2]时,f (x )=2x-1,函数g (x )=x 2-2x +m .如果对于∀x 1∈[-2,2],∃x 2∈[-2,2],使得g (x 2)=f (x 1),则实数m 的取值范围是________.解析:当x ∈(0,2]时,f (x )=2x-1∈(0,3], 因为f (x )是定义在[-2,2]上的奇函数, 所以对于∀x 1∈[-2,2],f (x 1)∈[-3,3].因为对于∀x 1∈[-2,2],∃x 2∈[-2,2],使得g (x 2)=f (x 1), 所以g (x )在[-2,2]上的值域A [-3,3]. 根据函数g (x )=x 2-2x +m =(x -1)2+m -1, 得A =[m -1,m +8],所以⎩⎪⎨⎪⎧m -1≤-3,m +8≥3,解得-5≤m ≤-2,即实数m 的取值范围是[-5,-2]. 答案:[-5,-2]11.已知集合A ={x |y =lg(4-x )},集合B ={x |x <a },若P :“x ∈A ”是Q :“x ∈B ”的充分不必要条件,则实数a 的取值范围是________.解析:由题意得A ={x |x <4},且A B ,结合数轴易得a >4. 答案:(4,+∞)12.若y =x 2+ax +b ,A ={x |y =x }={a },M ={(a ,b )},则M =________. 解析:由A ={a }得x 2+ax +b =x 的两个根为x 1=x 2=a , 即x 2+(a -1)x +b =0的两个根x 1=x 2=a , 所以x 1+x 2=1-a =2a ,得a =13,x 1x 2=b =19,所以M =⎩⎨⎧⎭⎬⎫⎝ ⎛⎭⎪⎫13,19.答案:⎩⎨⎧⎭⎬⎫⎝ ⎛⎭⎪⎫13,1913.设集合A ={a 1,a 2,a 3,a 4},若A 的所有三元子集的三个元素之和组成的集合为B ={-1,3,5,8},则集合A =________.解析:在A 的所有三元子集中,每个元素均出现了3次,所以3(a 1+a 2+a 3+a 4)=(-1)+3+5+8=15,故a 1+a 2+a 3+a 4=5,于是集合A 的四个元素分别为5-(-1)=6,5-3=2,5-5=0,5-8=-3,因此,集合A ={-3,0,2,6}.答案:{-3,0,2,6}14.对于函数y =f (x ),x ∈R ,“y =|f (x )|的图象关于y 轴对称”是“y =f (x )是奇函数”的___________条件(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”).解析:若y =f (x )是奇函数,则f (-x )=-f (x ), 所以|f (-x )|=|-f (x )|=|f (x )|,所以y =|f (x )|的图象关于y 轴对称,但若y =|f (x )|的图象关于y 轴对称,如y =f (x )=x 2,而它不是奇函数,故y =|f (x )|的图象关于y 轴对称是y =f (x )是奇函数的必要不充分条件.答案:必要不充分。
