河南省洛阳市2012-2013学年高三年级期末考试文科数学试卷
洛阳市2012-2013学年高三年级统一考试文科综合(三练、历史部分、含答案)word版

洛阳市2012—2013学年高三年级统一考试文科综合试卷(历史部分)第Ⅰ卷(选择题,共48分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考试科目填写在答题卷上。
2.选择题每小题选出答案后,用2B铅笔将答题卷上对应题目答案标号沫黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷上无效。
3.非选择题用0.5毫米黑色墨水签字笔直接写在答题卷上每题对应的答题区域内,答在试题卷上无效。
4.考试结束后,请将答题卷上交。
一、选择题:共12小题,每小题4分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
24.商朝实行内外服制度;内服是指王畿以内地区,即由商王直接控制的地区;外服是商国周围的大小方国,其首领为侯、伯。
商朝内外服之间没有建立隶属关系。
许倬云在《西周史》中认为:“商人与各方国之间,大多有战争及贸易的交往,商以大邑商自居,大约只有商王畿之内的人以此认同。
在王畿之外,未必有一个广泛的共同意识。
”据此判断,西周与商朝政治制度的不同是A.确立了君主专制的政治制度B.形成了“大一统”的政治格局C.实现了国家对土地的实际控制D.加强了中央对地方的控制25.明史记载:“(1425年)夏四月壬寅,帝(明仁宗)闻山东及淮、徐民乏食,有司徵(征)夏税方急,乃御西角门诏大学士杨士奇草诏,免今年夏税及秋粮之半。
士奇言:‘上恩至矣,但须户、工二部预闻。
’帝曰:‘救民之穷当如救焚拯溺,不可迟疑’。
”材料反映明朝A.皇权空前强化B.内阁参:与决策C.内阁统领六部D.六部之位形同虚设26.王夫之认为:“子曰,奢则不孙(通“逊”)。
恶其不孙,非恶其不啬也。
《传》曰,俭,德之共也。
俭以恭己,非俭以守财也。
”材料表明王夫之的消费理念是A.俭奢有度B.崇尚节俭C.量人为出D.自给自足.27.晚清时,一些学者发表了自己对时局的看法。
曾廉认为,“中国一切皆非为制度之不良,而但为人心之败坏而已”。
叶德辉说:“与其言变法,不如言变人。
河南省洛阳市2012-2013下学期高三二练习文科数学试卷及答案

河南省洛阳市2013届高三二练考试数学(文)试题本试卷分第 I 卷(选择题)和第 Ⅱ卷(非选择题)两部分.共 150 分.考试时间 120 分钟。
第I 卷(选择题,共 60 分)注意事项: 1.答卷前,考生务必将自己的姓名、考号填写在答题卷上.2.每小题选出答案后,用铅笔把答题卷上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3.考试结束,将答题卷交回.一、选择超:本题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集2,{|37}{|7100}U Z A x Z x B x Z x x ==∈≤<=∈-+>集合,则()A B =U I ðA .{3,4,5}B .{2,3,4,5}C .{4,5}D .{2,3,4}2.i 是虚数单位,则(1)ii i +的模为A .12B .-12C .12i D . -12i 3.以抛物线28y x =的焦点为圆心,半径为 1 的圆的方程为 A .22430x y x +-+= B .22430x y x ++-=C .228150x y x ++-=D .228150x y x +-+=4.设 a > 0 , b > 0 ,则“221a b +≥ ”是“(a 一1 )( b 一 l )0≤”成立的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件.5.已知双曲线22145x y -=上一点 P 到 F ( 3 ,0)的距离为6 , O 为坐标原点, Q 为 PF 的中点,则|OQ|= A . 1 B . 2C . l 或 5D . 2 或 56 ·如图所示程序框图,如果输出的函数值在区间1,12⎡⎤⎢⎥⎣⎦内, 那么输入实数 X 的取值范围是 A .(],1-∞- B . [-1,0] C .[ 一 1 , 2 ]D .[)0,+∞72,各侧面均为直角三角形, 则它的外接球体积为A 43πB 2πC 3πD .43π 8.已知函数32()f x x bx cx d =+++的图象如图,则函 数2221()33cy og x bx =++的单调递减区间是 A .1(,)2+∞ B .1(,)2-∞C .(-2,3)D .(,2)-∞-9.已知函数()2sin()(0)f x x ωϕω=+>的图象关于直线 3x π=对称,且()012f π=,则ω可取A .4B . 3C .2D .110.已知命题22:,11,:,10,P x R mx q x R x mx ∃∈+≤∀∈++≥若 ()p q ∨⌝为假命题,则实数m的取值范围是 A . ((,0)(2,)-∞+∞U B .[0,2]C .RD .φ11.若 a 是区间[-3,0]上的任意一个数,b 是区间[-2,0] 上的任意一个数,则使原点到直线(1)(1)20a x b y +--+=的距离不大于1的概率是A .1123π- B .1126π- C .5612π- D .7612π-12.动点 P 在正方体A BCD 一 A 1B 1C 1D 1的对角线 BD 1上,过 P 作垂直于平面 BB 1 D 1D 的直线,与正方体表面交于 M , N 两点,设|BP|= x , △ BMN 的面积是 y , 则函数()y f x =的图象大致为第 Ⅱ 卷(非选择题,共 90 分)二、坡空题:本题共 4 个小题,每小题 5 分.共 20 分13.已知,a b r r 满足:1,4,a b a ==r r r ·()1b a -=r r ,则,,a b r r的夹角为 。
河南省洛阳市2013—2014学年高三年级统一考试数学(文科)试题(含答案)(word典藏版)
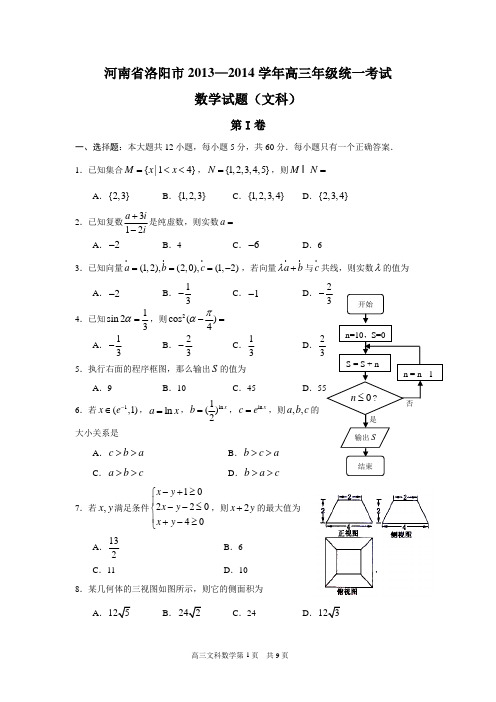
河南省洛阳市2013—2014学年高三年级统一考试数学试题(文科)第I 卷一、选择题:本大题共12小题,每小题5分,共60分.每小题只有一个正确答案. 1.已知集合{|14}M x x =<<,{1,2,3,4,5}N =,则M N =A .{2,3}B .{1,2,3}C .{1,2,3,4}D .{2,3,4}2.已知复数312a ii+-是纯虚数,则实数a = A .2-B .4C .6-D .63.已知向量(1,2),(2,0),(1,2)a b c ===-,若向量a b λ+ 与c 共线,则实数λ的值为A .2-B .13-C .1-D 4.已知1sin 23α=,则2cos (4πα-= A .13-B .23-C .13D 5.执行右面的程序框图,那么输出S 的值为A .9B .10C .45D 6.若1(,1)x e -∈,ln a x =,ln 1()2x b =,ln x c e =,则,,a b c 大小关系是A .c b a >>B .b c a >>C .a b c >>D .b a c >>7.若,x y 满足条件1022040x y x y x y -+≥⎧⎪--≤⎨⎪+-≥⎩,则2x y +的最大值为A .132B .6C .11D .108.某几何体的三视图如图所示,则它的侧面积为A .B .C .24D .9.设等差数列{}n a 的前n 项和n S ,且10a >,3100a a +>,670a a <.则满足0n S >的最大自然数n 的值为A .6B .7C .12D .1310.设函数2()2360f x x x =-+,()()|()|g x f x f x =+,则(1)(2)(20)g g g +++=A .56B .112C .0D .3811.已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ,以12||F F 为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为A .221916x y -= B .22143x y -= C .221169x y -= D .22134x y -= 12.已知函数()cos2f x x π=,3()2|2|4g x x =--,[2,6]x ∈-,则函数()()h x f x =- ()g x 所有零点之和为A .6B .8C .10D .12第II 卷二、填空题:本大题共4小题每小题5分,共20分. 13.设等比数列{}n a 的公比2q =,前n 项和为n S ,则43S a 的值为 . 14.直三棱柱111A B C A B C -的六个顶点都在球O 的球面上.若2AB BC ==,90ABC ∠=,1AA =O 的表面积为 . 15.已知AB 是抛物线24x y =的一条焦点弦,若该弦的中点纵坐标是3,则弦AB 所在的直线方程是 . 16.下列命题:①0x R ∃∈,0023x x >;②若函数()(21)()xf x x x a =+-是奇函数,则实数1a =;③若直线30x y m ++=平分圆22240x y x y ++-=,那么1m =-;④从1,2,3,4,5,6六个数中任取2个数,则取出的两个数是连续自然数的概率是13.其中真命题是 .(填上所有真命题的序号)。
河南省洛阳市2012届高三上学期期中考试(数学文)

河南省洛阳市2011—2012学年高三年级期中考试数 学 试 题(文)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分。
考试时间120分钟。
第I 卷(选择题,共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考场号、座号、考试科目用铅笔涂写在答 题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.考试结束后,将第II 卷答题卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.i 为虚单位,复平面内表示复数3i z i =+的点在 ( ) A .第一象限 B .第二象限C .第三象限D .第四象限 2.函数lg(1)y x =-的定义域为A ,函数3x y =的值域为B ,则A B = ( )A .RB .1(,1)3C .φD .(0,1)3.已知命题,p q 则“p q ∧为真命题”是“p q ∨为真命题”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.设n S 是等差数列{}n a 的前n 项和,若3795,11,a a ==则S = ( )A .36B .72C .108D .144 5.一个几何体的三视图如右图所示,这个几何体的体积为 ( )A .3B .6C .9D .186.正方形ABCD 内接于⊙O ,若在⊙O 内部随机取一个点Q ,则点Q取自正方形ABCD 内部的概率等于 ( )A .13 B .12 C .1π D .2π7.为了得到函数3sin(2)3y x π=-的图象,只需把函数3sin 2y x =的图象 ( )A .向左平移3π个长度单位B .向右平移3π个长度单位C .向左平移6π个长度单位 D .向右平移6π个长度单位 8.已知双曲线22221(,0)xy a b a b -=>的两条渐近线均和圆22:650C x y x +-+=相切,且双曲线的右焦点为⊙O 的圆心,则该双曲线的方程为 ( )A .22154x y -= B .22145x y -= C .22136x y -= D .22163x y -=9.阅读右边的程序框图,运行相应的程序,则输出s 的值为( )A .3B .1C .0D .-110.曲线1x y e =+在点(0,2)处的切线与两条坐标围成的三角形的面积为( ) A .4B .2C .1D .12 11.设函数()f x 对任意x R ∈,都有1(3)()i x f x +=-,且当(3,2)x ∈--时,()5f x x =,则(201.2)f = ( )A .14B .-14C .16D .-16 12.已知函数3()|3|f x x x =-,则关于x 的方程2()()0f x bf x c ++=恰有7个不同实数解的充要条件是( ) A .0240c b c <⎧⎨++=⎩ B .20b c >-⎧⎨=⎩ C .20b c =-⎧⎨=⎩ D .0240c b c >⎧⎨++=⎩第II 卷(非选择题,共90分)二、填空题:本题共4个小题,每小题5分,共20分。
河南省洛阳市2013届高三5月“三练”考试数学(文)试题_Word版含答案

洛阳市2012—2013学年高三年级5月统一考试数学试卷(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.第Ⅰ卷(选择题,共60分)注意事项:1.答卷前,考生务必将自己的姓名、考号填写在答题卷上.2.每小题选出答案后,用铅笔把答题卷上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3.考试结束,将答题卷交回.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x∈R|x+1>0},集合B={x∈R|(x-1)(x+2)<0},则A∩B=A.(-1,1)B.(-2,-1)C.(-∞,-2)D.(1,+∞)2.复数z满足12iz-=2(1)i+,i为虚数单位,则z的实部为A.1 B.12C.-12D.-13.如图所示程序框图,执行该程序后输出的结果是A.126 B.64 C.62 D.304.某三棱锥的三视图如图所示,则该三棱锥外接球的直径为A B C.D.5.直线2x+my=2m-4与直线mx+2y=m-2平行的充要条件是A .m =2B .m =±2C .m =0D .m =-26.已知a r =(2sinx,1),b r =(cosx ,-2),则函数f (x )=a r ·b r+1的一个对称中心是A .(0,0)B .(4π,-1) C .(2π,-1) D .(4π,0)7.椭圆2221x a b2y +=(a >b >0)的左,右焦点分别为F 1,F 2,O 为原点,M 为椭圆上一点,|MO|OF 2|,∠F 1MF 2=120°,则椭圆的离心率为 ABC .12D .348.数列{n a }满足a 1=1,a 2=1,n a =1n a -+2n a -(n ∈N ﹡,n ≥3).从该数列的前15项中随机抽取一项,则它是3的倍数的概率为 A .215 B .15 C .415 D .3109.设变量x ,y 满足不等式组0,0,10.x y x y y ⎧⎪⎨⎪⎩-≤10≤+≤21≤≤则2x +3y 的最大值等于A .20B .45C .50D .5510.直角△ABC 中,∠C =90°,BC =2,AD uuu r =t AB uu u r ,其中1≤t ≤3,则BC uu u r ·DC uuu r的最大值为A .12B .C .3D .11.函数y =2x-2sinx 的图象大致是12.已知函数f (x )=m (x +m )(2x -m -6),g (x )=1()2x -2,命题p :x ∀∈R ,f (x )<0或g (x )<0.命题q :若方程f (x )=0的两根为α,β,则α<1且β>1.如果命题p ∧q 为真命题,则实数m 的取值范嗣是 A .(-8,-2)∪(-1,0) B .(-8,-2)∪(-1,1) C .(-8,-4)∪(-2,0) D .(-8,-4)∪(-1,0)第Ⅱ卷(非选择题,共90分)三、填空题:本题共4小题。
河南省洛阳市2012届高三第二次统一考试(数学文)

洛阳市20 11—2012学年高三年级第二次统一考试数学试卷(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.第Ⅰ卷(选择题,共60分)注意事项:1.答卷前,考生务必将自己的姓名、考号填写在答题卷上.2.每小题选出答案后,用铅笔把答题卷上对应题目的答案标号涂黑.如需改动,用橡 皮擦干净后,再选涂其它答案,不能答在试题卷上. 3.考试结束,将答题卷交回.一、选择题:本题共12个小题。
每小题5分,共60分。
在每小题给出的四个选项中,只有一个是符合题目要求的.1.设i 为虚数单位,复数z 1=1+i ,z 2=2+i ,则复数z 1·z 2在复平面内对应的点所在的象限为A .第一象限B .第二象限C .第三象限D .第四象限 2.设集合M ={x |y =ln (-x 2-x +6),x ∈R},N ={x |1≤x ≤3),则M ∩N = A .[1,2] B .[1,2) C .(2,3] D .[2,3] 3.函数y =cos2x -2cosx 的值域为A .[-1,1]B .[-1,3]C .[-32,3] D .[-32,-1] 4.如图,一个空间几何体的正视图、侧视图都是面积为且有一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为A .B .C .16D .325.设{n a }是等比数列,n S 为{n a }的前n 项和,且105S S =3132, 则52a a = A .-8 B .-18 C .18D .8 6.已知双曲线的中心在坐标原点,两个焦点为F 1,0),F 2,0),点P 是此双曲线上的一点,且1PF ·2PF =0,|1PF |·|2PF |=4,该双曲线的标准方程是A .2143x 2y -=B .2134x 2y -=C .2152x 2y -=D .2125x 2y -=7.执行右侧的程序框图,输出的结果S 的值为 AB.2C .0 D8.曲线y =x 2xe +2x +1在点P (0,1)处的切线与x轴交点的横坐标是A .1B .12 C .-1 D .-129.已知函数f (x )=sin2x +acos2x 的图象的一条对称轴是直线x =12π,则函数g (x )= -asin2x -cos2x 的单调递增区间为A .[2k π-3π,2k π+6π](k ∈Z ) B .[k π-3π,k π+6π](k ∈Z ) C .[2k π+6π,2k π+23π](k ∈Z ) D .[k π+6π,k π+23π](k ∈Z )10.在等差数列{n a }中,其前n 项和为n S ,且S 2011=2011,a 1007=-3,则S 2012= A .-2012 B .-2011 C .2011 D .201211.巳知F 1,F 2是椭圆2221x a b2y +=(a >b >0)的两焦点,以线段F 1F 2为边作正三角形PF 1F 2,若边PF 1的中点在椭圆上,则该椭圆的离心率是 A1 B+1 C .12D12.设函数f (x )的定义域为R ,f (x )=1()1,12x x x x ⎧⎪⎨⎪⎩,0≤≤1,--≤<0.且对任意的x ∈R 都有f (x +1)=f (x -1),若在区间[-1,3]上函数g (x )=f (x )-mx -m 恰有四个不同零点,则实数m 的取值范围是 A .[0,12] B .[0,14) C .(0,12] D .(0,14]第Ⅱ卷(非选择题,共90分)二、填空题:本题共4个小题,每小题5分。
河南省洛阳市示范高中2012届高三下学期联考测试文科数学试题

洛阳市示范高中联考文科数学试题测试数学(文)试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}3,2aM =,{},N a b =,若{}2M N ⋂=,则M N ⋃=( )A .{}0,1,2 B.{}0,1,3 C.{}0,2,3D .{}1,2,32.已知212zi i=-+(z 是z 的共轭复数),则复数z 在复平面内对应的点位于( )A 第一象限B 第二象限C 第三象限D 第四象限3.若3sin 5α=,α是第二象限的角,则2) (4cos =⎪⎭⎫⎝⎛-παABCD4.下列函数中,既是偶函数又在+∞(0,)单调递增的函数是 ( )A 3y x = B1y x =+ C 21y x =-+D2xy -=5.已知等比数列}{na 的公比为正数,且3a ·9a =225a ,2a =1,则1a = ( )A. 21 B 。
22C. 2 D 。
26.已知a ,b 是两条不重合的直线,α,β是两个不重合的平面,下列命题中正确的是( )A.//a b ,//b α,则//a αB. a ,b α⊂,//a β,//b β,则//αβ C 。
a α⊥,//b α,则a b ⊥D 。
当a α⊂,且b α⊄时,若b ∥α,则a ∥b7.函数y =cos2x 的图像可以看作由y =2cos2x +sinxcosx 的图像( )得到.A .向左平移12π个单位长度 B .向右平移12π个单位长度C .向左平移6π单位长度D .向右平移6π单位长度8.已知x 是函数f (x)=2x + 11x-的一个零点。
若1x ∈(1,0x ),2x ∈(0x ,+∞),则A .f (1x )<0,f (2x )<0B . f (1x )<0,f (2x )>0C . f (1x )>0,f (2x )<0D . f (1x )>0,f (2x )>09.若4ln ,3ln 2ln ,46ln 22π=•==c b a ,则a,b,c 的大小关系是 ( ) A a 〉b>c B c>a 〉b C c 〉b 〉a Da>c>b10.已知双曲线22221(0,0)x y a b a b-=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )A 。
