插值计算器(内插)
插值法内插与外插

插值法内插与外插插值法(内插与外插)Interpolation and Extrapolation数学问题探讨当我们在表现资料时,常常会有需要比实际量测点上的值更细密的情况,或者是有需要在范围外预测其值。
比方说天气图的绘制,不论是气压或是雨量,都不可能做到处处都有测量站,又例如我们关心一天之中温度随时间的变化,但是实际上记录气温的动作可能只是每小时一次,则我们要作一个连续的图时,就会用到插值法。
插值法的中心议题是:在我们己具备一组表列数(tabulated value)的情况下,如何得出没被定到之区域的值。
什么样的函数才能被插值,这是数学上讨论的间问题,参见课文p.99第四段。
然而,我们会要用到插值法的场合往往都不知道描述对象背后的函数是什么形式(但相信其有连续的本质),因此我们也只能尽力求真实。
使用插值法所建立的函数,在表列点上一定要重现原本给定的表列值,否则就不是插值法而是函数近似或曲线拟合的间问题了,它们是不一样的。
插值的作法,很直观地来讲,就是,(1)先从表列值来获得函数f(x),再(2)用函数f(x)求出我们所要的任何特定x之f(x)函数值。
然而,比较精密且系统化的数值方法却不是用这两个步骤来进行插值,原因是前述两阶段方法对于插值的精密度并没有控制,效率较差,也比较会有进位误差。
一般在做插值法,是从欲插值点x附近的几个表列点xi开始,建立插值函数f(x),并且也试著网罗更多表列点来插值,看随著项数变多误差会不会变小,如此找出最适合的函数f(x)。
我们会比较希望演算法在从表列值建立插值用函数时,也能提供误差分析以供我们或程式来判断。
毕竟可用的插值函数f(x)并非唯一,而即便是己设定了采用一种方法,如多项式法,也会有该使用多少项才最恰当的问题。
建立插值函数所需之邻近表列值个数,我们称之为插值法的order(阶),较高阶未必保证得到较合理的插值,这点在多项式插值法尤其如此,要小心注意。
详见课文中之例图上两图实线都是原现象背后的真正值,短虚线代表低阶多项式插值结果,长虚线代表高阶多项式插值结果。
内插法计算例子

内插法计算例子随着科技的不断发展,计算机技术的应用越来越广泛,计算方法也在不断地改进和完善。
内插法作为一种常用的计算方法,在工程学科、数学学科和物理学科等领域中得到了广泛的应用。
本文将以内插法计算例子为主题,介绍内插法的定义、原理、分类、应用以及计算实例等内容。
一、内插法的定义和原理内插法(interpolation)是指根据已知数据点的函数值,通过某种方法来推算出未知数据点的函数值的过程。
它的基本思想是在已知数据点之间进行插值,从而得到未知数据点的函数值。
内插法的基本原理是使用已知数据点构造一个函数,然后在这个函数上求解未知数据点的函数值。
内插法的优点是可以精确地计算出未知数据点的函数值,缺点是需要知道足够多的已知数据点。
二、内插法的分类内插法可以分为多种类型,常用的有拉格朗日插值法、牛顿插值法、埃尔米特插值法、三次样条插值法等。
其中,拉格朗日插值法和牛顿插值法是最常用的两种方法。
1.拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法,它的基本思想是通过已知数据点构造一个多项式,并将未知数据点代入这个多项式中求解。
具体来说,拉格朗日插值法的步骤如下:(1)设已知数据点的函数值为f(xi),i=0,1,2,……,n;(2)构造一个n次多项式L(x),满足L(xi)=f(xi),i=0,1,2,……,n;(3)将未知数据点x代入多项式L(x)中,求得f(x)的近似值。
2.牛顿插值法牛顿插值法是一种基于差商的插值方法,它的基本思想是通过已知数据点的差商来构造一个多项式,并将未知数据点代入这个多项式中求解。
具体来说,牛顿插值法的步骤如下:(1)设已知数据点的函数值为f(xi),i=0,1,2,……,n;(2)计算出n个一阶差商f[x0,x1],f[x1,x2],……,f[xn-1,xn]和n-1个二阶差商f[x0,x1,x2],f[x1,x2,x3],……,f[xn-2,xn-1,xn];(3)将差商代入牛顿插值公式中,得到一个n次多项式N(x);(4)将未知数据点x代入多项式N(x)中,求得f(x)的近似值。
炉内传热计算器
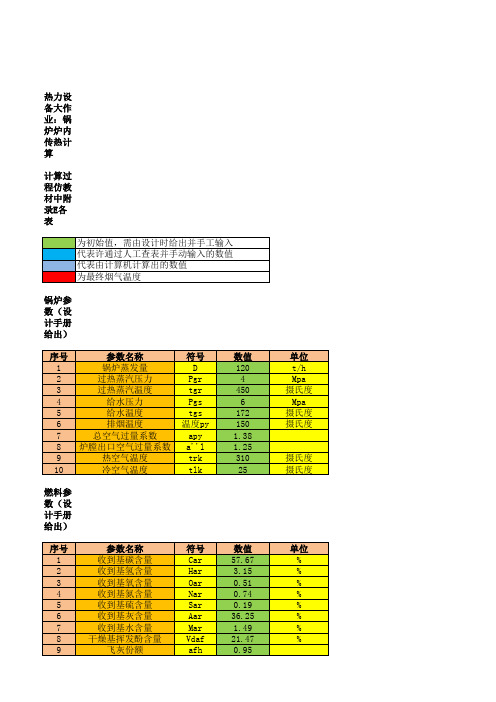
由结果 值与假 设值进 行校 核,并 不断试 算,直 至满足 要求
结果分 析
对烟气 出口温 度影响 较大的 有煤种 的含碳 量,计 算发现 烟气出 口温度 较低, 然后检 查了一 次,发 现没问 题,于 是认为 煤种含 碳量影 响很 大,从 燃烧理 论中亦 可得到 类似的 结论 然后影 响较大 的还有 炉膛的 体积及 面积, 这直接 影响了 有效辐 射层厚 度
折算灰份
符号 V0
V0N2 V0H20 V0RO2 V0g afa Gfa Aar,c
数值 5.9510 4.7072 0.4639 1.0775 6.2486 0.9500 0.3444 17.3023
烟气特 性表 (此表 无需输 入任何 数值)
序号 1 2 3 4 5 6 7 8
参数名称
符号
烟道进口过量空气系数 alfa'
VC
16
水蒸气容积份额
rH2O
17 三原子气体容积份额
rn
18 烟气密度(标准状态) 密度g
19
炉膛压力
p
20
三元子气体分压力
pn
21
pn与s乘积
pns
22
烟气辐射减弱系数
kg
23
飞灰减弱系数
kfa
um kj/kgK
kg/m3 Mpa mMpa m*Mpa m*Mpa-1 m*Mpa-1
24 焦炭粒子辐射减弱系数 kco
序号
参数名称
1 燃料带入热量
2 排烟温度
3 排烟焓
4 冷空气温度
5 理论冷空气焓
符号 Qin 温度ex Iex tca Ica
数值 20951 150.00
1670.80 25.00 278.66
内插法的计算公式

内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
内插法的计算公式

内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
内插法计算公式举例

内插法计算公式举例1。
在指数为正的线性函数y=f(x)|2。
在单调递增区间,当f ( x)>0时|3。
在指数为正的线性函数y=f(x)|4。
两个函数的交点坐标:|5。
若有3个自变量x、 y、 z,则每次自变量取值范围为(0, 1)、(1,0)、(0, 1)或(0, -1)、(1, 0)或(-1, -1)或(-1, 0)3。
f''(x)=f(-x) + x4。
两个函数的交点坐标:|5。
若有3个自变量x、 y、 z,则每次自变量取值范围为(0, 1)、(1, 0)、(0, 1)或(0, -1)、(1,0)或(-1, -1)或(-1, 0)6。
应用中的最后一步:把各个单元格的x值乘以各自的值,加起来,就是总体的平均值,最后将这些数值再求和,即可得到各单元格的结果。
注意事项: 1。
由于在平均分配上采用的是插值计算,因此内插的结果必须保证在内插区域内无其他公式(包括其他函数)的出现,否则容易引起计算错误。
2。
在内插区域内不要设置任何公式。
3。
此方法也适用于包含0值的单元格的情况。
如果包含0值的单元格较多,则可能需要对包含0值的单元格进行筛选,只将公式里没有0的单元格设置成不等于0。
4。
此方法与一般求和方法基本相同。
(以上计算结果适合普通型数据,而实际工作中经常遇到的是条件型数据,因此还需做一下细化处理,并按照其他方法进行数据处理。
) 5。
该法特别适合于合并单元格数据。
6。
该法优势在于运算速度快。
但缺点在于,需要设置较多条件,且只适合处理数值型数据。
(注:包含数值型数据的单元格在统计过程中称为数据点。
) 7。
公式的优势在于利用了线性插值,有效地避免了除法运算中出现的错误。
但是其缺点在于涉及指数运算,有可能会出现极大或极小的数值。
8。
从上面的例子中可以看出,公式所计算出的平均值与真实值之间存在误差,但公式计算的平均值的精确度要远远高于普通方法所计算的平均值的精确度。
,都是关键步骤,都是影响结果准确性的重要步骤。
插值法是如何计算的-插值法的计算原理【2017-2018最新会计实务】

插值法是如何计算的插值法的计算原理【2017-2018最新会计实务】【2017-2018年最新会计实务经验总结,如对您有帮助请打赏!不胜感激!】插值法是计算实际利率的一种方法.是使未来现金流量现值等于债券购入价格的折现率.插值法(或称插插补法、内插法)是财务分析和决策中常用的财务管理方法之一.插值法的原理是根据比例关系建立一个方程,然后,解方程计算得出所要求的数据.假设与A1对应的数据是B1,与A2对应的数据是B2,现在已知与A对应的数据是B,A介于A1和A2之间,则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A 的数值,其中A1、A2、B1、B2、B都是已知数据.验证如下:根据:(A1-A)/(A1-A2)=(B1-B)/(B1-B2)可知:(A1-A)=(B1-B)/(B1-B2)×(A1-A2) A=A1-(B1-B)/(B1-B2)×(A1-A2)=A1+(B1-B)/(B1-B2)×(A2-A1)例如某人向银行存入5000元,在利率为多少时才能保证在未来10年中每年末收到750元?5000/750=6.667 或 750*m=5000 查年金现值表 i=8%,系数为6.710 i=9%,系数为6.418 说明利率在8%-9%之间,设为x%(x%-8%)/(9%-8%)=(6.667-6.71)/(6.418-6.71)计算得出 x=8.147.后语点评:会计学作为一门操作性较强的学科、每一笔会计业务处理和会计方法的选择都离不开基本理论的指导。
为此,要求我们首先要熟悉基本会计准则,正确理解会计核算的一般原则,并在每一会计业务处理时遵循一般原则的要求。
会计学的学习,必须力求总结和应用相关技巧,使之更加便于理解和掌握。
学习时应充分利用知识的关联性,通过分析实质,找出核心要点。
要深入钻研,过细咀嚼,独立思考,切忌囫囵吞枣,人云亦云,随波逐流,粗枝大叶,浅尝辄止。
内插法的计算公式-内插法计算公式

内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
工程监理收费计算器

建筑市政工程(全程监理)121.003 1.004 1.0056100%78总则1.0.1以外其他收费 费用名称:A 9总则1.0.1以外其他收费 费用名称:B 10总则1.0.1以外其他收费 费用名称:C11(调整系数) = (1)×(2)×(3)×(4)600.0015.3819.2219.22监理收费计费额(建安工程费+设备购置费+联合试运转费)分项监理收费(总则:1.0.10)总体协调费 (总则:1.0.11) = (6)+(7)+(8)+(9)+(10)施工监理服务收费= (5+11)×(1±浮动幅度值) * 红色边框单元格内输入动态参数;选择组合框相应参量;点击费用名称查询相关说明(调整系数)(调整系数)(万元)发改价格[2007]670号监理收费基价专业选择复杂程度海拔高程收费基准价其他监理收费(附表二/直线内插值)下浮(20%)海拔高程2001米以下较复杂(Ⅱ级)建筑、人防、市政公用工程全程监理质量.安全监理0%4%5%6%注:计费额 > 1000000万元(100亿元)的,以设计收费计费额乘以1.039%的收费率计算收费基价。
监理收费计费额 = 建筑安装工程费 + 设备及工器具购置费 + 联合试运转费监理收费基准价 = 监理收费基价(基价内插值)×专业调整系数×复杂程度系数 ×高程调整系数其他监理收费 = ∑监理收费基准价 ×其他收费系数监理服务收费 = (收费基准价 + 其他监理收费)×(1 ± 浮动系数)16.5。
内插法的计算公式

内插法的计算公式内插法是一种在数学和金融等领域中经常使用的计算方法。
它能帮助我们在已知的一些数据点之间,估算出未知的数据值。
听起来是不是有点复杂?别担心,咱们一步步来搞清楚它。
比如说,你正在参加一场数学考试,有一道题目是这样的:已知某商品在价格为 10 元时,销量是 50 件;价格为 15 元时,销量是 30 件。
现在想知道价格为12 元时的大概销量。
这时候,内插法就派上用场啦!那内插法的计算公式到底是啥呢?其实就是:假设我们有两个已知点(x1, y1)和(x2, y2),要估算 x 对应的 y 值,那么计算公式就是:y = y1 + (x - x1)×(y2 - y1)/(x2 - x1)咱们拿刚刚那个商品的例子来实际算算。
x1 = 10,y1 = 50;x2 = 15,y2 = 30;x = 12。
先算(y2 - y1)/(x2 - x1),也就是(30 - 50)/(15 - 10)= -4。
然后 y = 50 + (12 - 10)×(-4) = 50 - 8 = 42 件。
这样就估算出价格为 12 元时,销量大概是 42 件。
我还记得之前在给学生们讲内插法的时候,有个小同学一脸困惑地问我:“老师,这内插法到底有啥用啊,感觉好难哦。
”我笑着跟他说:“孩子,你想想看啊,假如你长大了要去买房子,房价可不是一成不变的,但是通过已知的一些房价数据,用内插法就能大概算出你心仪地段在某个价格范围内房子的可能价值,是不是很有用呢?”小同学眨眨眼,好像有点明白了。
内插法在很多领域都有着广泛的应用。
比如在金融领域,计算债券的到期收益率、估计股票的内在价值等;在工程领域,根据实验数据来推测未知条件下的结果;在统计学中,对数据进行插值处理以获得更平滑的曲线。
咱们再举个金融方面的例子。
假设一只债券,当市场利率为5%时,它的价格是 1050 元;当市场利率为 6%时,它的价格是 1000 元。
报价内插法计算公式举例

报价内插法计算公式举例报价内插法是一种常用的数学方法,用于估计或预测某个变量在给定范围内的值。
这种方法通常适用于金融、经济和统计学领域,用于计算证券价格、货币汇率和其他相关变量的值。
在这篇文章中,我们将介绍报价内插法的计算公式,并举例说明其应用。
报价内插法的计算公式是基于线性插值的原理,通过已知的两个点来估计或预测中间某个点的值。
假设我们有两个已知点A和B,它们的横坐标分别为x1和x2,纵坐标分别为y1和y2。
现在我们想要估计或预测在A和B之间某个横坐标为x的点的纵坐标值y。
报价内插法的计算公式如下:y = y1 + (x x1) (y2 y1) / (x2 x1)。
这个公式的含义是,点x对应的纵坐标y等于点A的纵坐标y1加上x与x1的差值乘以点A和点B纵坐标之差与横坐标之差的比值。
这样就可以通过已知的两个点的信息,来估计或预测中间某个点的值。
接下来,我们通过一个具体的例子来说明报价内插法的应用。
假设我们有以下数据:点A,(1, 10)。
点B,(3, 20)。
现在我们想要估计在A和B之间横坐标为2的点的纵坐标值。
根据报价内插法的计算公式,我们可以计算出:y = 10 + (2 1) (20 10) / (3 1)。
= 10 + 1 10 / 2。
= 10 + 5。
= 15。
因此,根据报价内插法的计算公式,我们得出在A和B之间横坐标为2的点的纵坐标值为15。
这个例子说明了报价内插法在实际问题中的应用,通过已知的两个点的信息,我们可以估计出中间某个点的值。
除了线性插值外,报价内插法还可以应用于其他类型的插值,如二次插值、三次插值等。
这些插值方法在实际问题中都有广泛的应用,用于估计或预测某个变量的值。
通过报价内插法,我们可以更准确地分析和预测金融、经济和统计学领域的变量,为决策提供更可靠的依据。
总之,报价内插法是一种常用的数学方法,用于估计或预测某个变量在给定范围内的值。
通过线性插值的原理,我们可以通过已知的两个点的信息,来估计或预测中间某个点的值。
内插法介绍

内插法介绍一、查值法有时,我们做试验的目的是为了确定某些变量之间的函数关系,但是,通过试验往往只能得到函数在某些点上的值。
那末,对于这些点以外的点,其对应的函数值又该怎么取呢?插值法是解决这种问题的方法之一。
内插法实际上是一个数值分析的概念,就是通过有限的点得到一个函数关系,通过这个函数关系求得其余未测点的值,就是插值算法。
一般插值有一次插值,二次和三次。
到四次插值精度已经很高了,千分之一。
一般情况下有两次插值已经足够了。
但是对于一些工程上的问题,一次插值就可以。
设已知某函数()x f 在1+n 各点x 0,x 1,…x n 处的函数为y 0,y 1,…y n 。
我们来确定一个n 次多项式()n n n n n a x a x a x a x ++++=-- 22110ϕ (1-1)使满足()i i n y x =ϕ (i = 0,1,2,…,n ) (1-2)然后,就用多项式()i n x ϕ来近似表示()x f 。
由于这样的近似是在利用x 0,x 1,…x n 各点的已知值求出的,所以只能在这些点的附近才适用。
满足条件(2)式的n 次多项式可以直接写出来:()()()∑∏=≠=--=n i nij ijijn y x x x x x 0,0ϕ (1-3)通常称之为拉格朗日(Lagrange )插值多项式。
例如:当n=1时,()()()()()11001011y x x x x y x x x x x o --+--=ϕ (1-4) 称为线性插值公式。
当n=2时,()()()()()()()()()()()()()2120210121012002010212y x x x x x x x x y x x x x x x x x y x x x x x x x x x ----+----+----=ϕ (1-4)称为抛物线插值公式。
指根据已知的系列数值推算出一个在已知数值之间的数值. 内推法假定数值之间存在某种明确的关系,不是一种精确的推算法。
sinc内插公式

sinc内插公式
(最新版)
目录
1.引言:介绍 sinc 内插公式
2.sinc 内插公式的定义和原理
3.sinc 内插公式的应用
4.结论:总结 sinc 内插公式的特点和优势
正文
sinc 内插公式是一种在离散点上求解内插值的数学公式,广泛应用
于信号处理、图像处理、数值计算等领域。
其独特的计算方式和优秀的插值性能,使其成为内插公式中的一种重要类型。
sinc 内插公式的定义和原理相对简单。
sinc 函数是正弦函数和余弦函数的差值,其取值范围在 [-1,1] 之间。
sinc 内插公式就是利用 sinc 函数在离散点上求解内插值。
其公式表达式为:
y(x) = (sin(πx/h) - sin(π(x-1)/h)) / π
其中,y(x) 表示 x 点的内插值,h 表示采样间隔。
sinc 内插公式的应用主要体现在以下几个方面:
首先,sinc 内插公式在信号处理中的应用十分广泛。
比如在音频处
理中,sinc 内插公式可以用来恢复音频信号中的高频分量,提高音频的
质量。
其次,sinc 内插公式在图像处理中也有广泛的应用。
由于 sinc 内
插公式的插值结果具有较好的平滑性,因此可以用来对图像进行平滑处理,提高图像的视觉效果。
最后,sinc 内插公式在数值计算中也有重要的应用。
比如在求解微
分方程时,sinc 内插公式可以用来进行数值积分,提高数值计算的精度。
