空间插值方法介绍共36页
空间插值方法介绍共38页文档

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
▪
Байду номын сангаас
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
38
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
《空间插值方法简介》PPT课件

表1 样本数据特征值统计
特征值 时期
70年代 80年代 90年代 2000年代
最小值
11.27 11.33 11.77 11.50
最大值
19.53 19.43 19.53 19.80
平均值
17.52 17.51 17.74 17.97
标准差
1.09 1.07 1.03 1.23
变异系数
6.22% 6.11% 5.81% 6.84%
正态分布
检验数据分布 正态QQPlot图
趋势分析
趋势效应分析(Trend Analysis)
为了满足平稳 假设
预测表面 =确定的全局趋势+随机的短程变异
剔除!
趋势分析 ArcGIS软件的地统计分析模块中趋势效应
趋势名称
无
none
常量 const
一阶 first 二阶 second 三阶 third
靠的越近越相似!
反距离加权法
应用条件
研究区域内的采样点分布均匀, 采样点不聚集
假设前提
各已知点对预测点的预测值都有局部性 的影响,其影响随着距离的增加而减小
样点的数量
反距离加权法
各样点的权重
n
公式: Z(s0)=
iZ (si )
i 1
观测值
预测值
注:在预测过程中,权重随着样 点与预测点之间距离的增加而减小。 各样点值对预测点值作用的权重大 小是成比例的,这些权重值的总和 为1。
空间插值常用的两种方法:
确定性插值方法:
地统计方法:
反距离权重(IDW)
3模型分析
不同的方法有其适用的条件
当数据不服从正态分布时,若服从对数正态分布,则选用对数正态克里格; 若不服从简单分布时,选用析取克里格。 当数据存在主导趋势时,选用泛克里格。 当只需了解属性值是否超过某一阈值时,选用指示克里格。 当同一事物的两种属性存在相关关系,且一种属性不易获取时,可选用协同 克里格方法,借助另一属性实现该属性的空间内插。当假设属性值的期望值为 某一已知常数时,选用简单克里格。 当假设属性值的期望值是未知的,选用普通克里格。
空间插值分析课件

26
3.距离反比法
反距离加权法(IDW)的一个改进
? ---按方位取点!
27
空间插值分析
概述 最近邻法 距离反比法 趋势面法 样条法 克里金法 精度评定及方法选择
28
4.趋势面法
趋势面法分析
把实际的地理曲面分解为趋势面和剩余面两部分,具体地 ,趋势面法将样本点的实测点Zi变换分解为两部分,表达 为:
5m-10m的间隔下的半方差图
41
6.克里金法
半变率图的组成
块金值(c0,Nuddget): 当h = 0时
的非零变率,由不可解释的原因
引起 ;
空间自相关部分:C/(c0+c)
基台值(c0+c;sill): 半变率曲线变 平缓时的变率值,表明在某个距 离上样本点不再存在相关性,通 常等于数据集的方差;
缺点
高次多项式在数据区外围产生异常高值或低值; 空间采样选择会影响结果。
32
4.趋势面法
趋势面法的实际应用
1998年全国年平均降水数据
趋势面法插值结果
33
空间插值分析
概述 最近邻法 距离反比法 趋势面法 样条法 克里金法 精度评定及方法选择
34
5.样条法
样条法原理
样条插值的目标就是寻找一
近似插值:插值产生的曲面不通过所有观测点。
当数据存在不确定性时,应该使用近似插值,由于估计值替代 了已知变量值,近似插值可以平滑采样误差。
10
空间插值分析
概述 最近邻法 距离反比法 趋势面法 样条法 克里金法 精度评定及方法选择
11
2.最近邻法
基本原理
最近邻点法由A. H. Thiessen提出,又叫泰森多边形方法。 它采用一种极端的边界内插方法,即只用最近的单个点进
空间插值优秀课件

置在源区上,首先确定两者 面积的交集ats,然后利用 公式计算出目标区各个分区
ats-t区与s相交的面积; σs-s区的面积;
t 的内插值vt .
§6.4 空间插值-区域内插
(2)比重法:根据平滑密度函数的原理,将源区内的统计数 据从各分区内的均匀分布转变为分区内的非均匀分布。
❖ 步骤:
▪ 将原图栅格化,栅格尺寸的大小应保证满足内插精度要求; ▪ 根据原图各分区面积及栅格尺寸,将分区统计数据按比例赋予其中
▪ (1)线性内插
• 使用最靠近内插点的三个已知参考数据点,来确定一个 平面,继而,求出该内插点在平面中的高程值。
▪ (2)双线性多项式内插
• 使用最靠近内插点的四个己知参考数据点组成一个四边 形,确定一个双线性多项式来内插待插点的高程。
§6.4 空间插值-点的内插
16个点
▪ (3)二元样条函数内插
§6.4 空间插值-点的内插
▪ (2)加权平均法
• 是移动拟合法的特例,是在解算待定点 P 的高程时,使 用加权平均值代替误差方程:
• 采样点的权重采用与距离相关的权函数确定;p = 1 / r 2 和
p = (R – r )2 / r 2等。式中,p 是参考点的权,R是圆的半径,r 是待插点到参考点的距离。
§6.4 空间插值
❖Why interpolate?
▪ Visiting every location in a study area to measure the height, magnitude, or concentration of a phenomenon is usually difficult or expensive. Instead, dispersed ample input point locations can be selected, and a predicted value can be assigned to all other locations. Input points can be either randomly, strategically, or regularly spaced points containing height, concentration, or magnitude measurements.
空间插值方法

数据拟合问题就是根据若干参考点上的已知值求出待定点 上(未知点)的研究值。数据拟合问题通常可分为插值问 题和光顺逼近问题。 插值问题的解要求严格经过已知量测点,而光顺逼近问题 的解虽不要求严格经过已知点,但它要求在某种约束条件 下(比如最上 乘意义下 最小曲面能或最小粗糙度意义 下(比如最上二乘意义下、最小曲面能或最小粗糙度意义 下)达到整体逼近效果。
6/21/2010
空间插值方法
第6讲 空间插值方法及 TIN/TEN构建算法
6.1 问题的提出 6.2 空间数据插值方法概述 6.3 几种空间数据插值方法原理
6.1 空间插值问题的提出
6.2 空间数据插值方法概述
GIS在实际应用过程中,很多情况下,比如采样密度不够、 曲线与曲面光滑处理、空间趋势预测、采样结果的可视化 等,必须对空间数据进行插值和拟合,因此空间数据插值 是GIS数据处理的一项重要任务。其主要目的是根据一组 已知的离散数据,按照某种数学关系推求其他未知点和未 知区域的数据的过程。
Delauny三角化方法自提出后并未引起足够多 的重视,到了20世纪80年代才开始研究这个算 法,目前比较有效的算法有:
分治算法 逐点加入法 生长算法 凸壳法
分治算法
分治算法的基本思想是一个递归思想,把点集划分到足够小, 使其易于生成三角网,然后把子集中的三角网合并生成最终 的三角网。 逐点加入法有两个基本步:1.定位,找到包含新加点的三角 形;2.更新,形成新的三角形。 生长法从第一个DT开始,而后由三角形边逐步形成新的DT。 如果二维上的任意一点对应到三维点,可以计算出提升点的 凸壳,除去朝上的凸壳面,剩下的朝下的面就是原始点的DT (这个关系适合于任意n维)。
第六讲 空间插值

每个采样点对插值结果的影响随距离增加而减弱,因 此距目标点近的样点赋予的权重较大。
n
a ttr0 a ttri * w i i1
wi
1 pow er (D isti )n
n
1 pow er(D isti )n
i1
二、空间插值方法
4. 距离反比加权法—参数对插值结果的影响
权重的影响
权重过高,较近点的影响较大,拟合表面更细致(不光 滑);
趋势面分析的一个基本要求就是,所选择的趋势面模型应 该是剩余值最小,而趋势值最大,这样拟合度精确度才能 达到足够的准确性;
在数学上,拟合数学曲面要注意两个问题:一是数学曲面 类型(数学表达式)的确定,二是拟合精度的确定。
二、空间插值方法
5.1 趋势面模型的建立
设地理要素的实际观测数据为Zi(xi,yi)(i=1,2,…,n),
基本内容
空间插值:定义及应用 空间插值方法及特征
泰森多边形( Voronoi )及不规则三角网(TIN) 距离反比加权法(IDW) 地质统计学(Geostatistics)
利用样条曲线优化插值结果 插值精度评估 三参数插值方法(体数据或者动态演化特征)
为何进行插值?
1. 2D离散点转化为连续面,如地表、地层界面 如基于空间离散点,剖面数据和等高线等来构建连续
不足——对权重函数的选择十分敏感;易受数据点集群的 影响,结果常出现一种孤立点数据明显高于周围数据点的 “鸭蛋”分布模式;
全局最大和最小变量值都散布于数据之中。 距离反比很少有预测的特点,内插得到的插值点数据在样
点数据取值范围内。
二、空间插值方法
5. 趋势面分析
实际的地理曲面分解为趋势面和剩余面两部分,前者反应 地理要素的宏观分布规律,属于确定性因素作用的结果; 而后者则对应于微观区域,被认为是随机因素影响的结果。
空间插值IDW(共39张PPT)

定义全局变量: public IMap pMap; public int layerIndex; private double cellsize = 0.013;
private string filepath;
private ITable pTable; private IFeatureLayer pLayer; IFeatureClass m_pFeatureClass;
nA1 += nTemp; nValue += nTemp * ValueList[i]; }
nValue = nValue / nA1; return nValue; }
IDW实现-公共函数2
//获取要素参数 protected void getFeaturesParameters(ref double[] nPointsX, ref double[] nPointsY, ref double[] nValues)
控制反距离加权的参数—搜索半径
1) 搜索半径-固定
对固定型半径,搜索距离一定,所有在该半径内的样点参与 计算。 可预先设定一个阈值,当给定半径内搜索到的点小于该值时 可扩大搜索半径,直到达到该阈值为止。
2) 搜索半径类型-可变
设定参与计算的样点数是固定的,则搜索的半径是可变的。 这样对每个插值点的搜索半径可能都不同,因为要达到规定 的点数所需要搜索的区域是不一样的。
控制反距离加权的参数—障碍设置
可利用一线状和面状数据集来限制样点的搜索。线状 数据集可作为平坦地表的悬崖或脊状障碍物:只有位 于同侧的样点才符合要求。
权重系数和搜索半径的影响图示
Power = 2, search = 150
空间插值PPT课件

第1页/共45页
空间插值
空间插值是用已知点的数值来估算其他点的数值的过程。 在GIS应用中,空间插值主要用于估算出栅格中每个像元的 值。因此,空间插值是将点数据转换成面数据的一种方法。
2
第2页/共45页
控制点
控制点是已知数值的点,它提供了为空间插值建立插值方 法(例如数学方程)的必要数据。
34
第34页/共45页
图15.19 块金、变程、总基台值和基台值。
35
第35页/共45页
普通克里金法(Ordinary Kriging)
假设不存在漂移,普通克里金法重点考虑空间相关的因 素,并用拟合的半变异直接进行插值。
36
第36页/共45页
图15.20 基于指数模型的普通克里 金插值法生成的等雨量线图。
40
第4降水量曲面的标准差 分布图。
41
第41页/共45页
其它克里金法
除了普通克里金和泛克里金外,其它克里金法包括指示性 克里金法、离析克里金法和块克里金法
42
第42页/共45页
空间插值方法的比较
基于相同数据,不同的插值方法将生成不同的插值结果。 同样,用 相同的方法,不同的参数值,将得出不同的预测值。
27
第27页/共45页
区间分组(binning)
半变异云图包含所有的控制点对,使之操作和使用不方便。区 间分组(binning)的过程,是以距离和方向来平均半变异数据。
28
第28页/共45页
图15.15 对图(a)中的1和2 样本按方向进行区间归类的常用方法是径 向扇区(b)。ArcGIS 中的Geostatistical Analyst 则使用如图(c)的格 网像元。
11
第11页/共45页
克里格空间插值法ppt课件

4.高斯模型(Gaussian model) 变程为 。
1.9 理论变异函数模型
图是球状模型、指数模型和高斯模型的比较,可以看出,球状模型的变程最小,指数的模型变程最大,高斯模型的变程介于二者之间。球状模型和指数模型过原点存在切线,高斯模型则没有。
1.9 理论变异函数模型
3.指数模型(Exponential model) 其中,d是控制方程空间范围的距离参数。这里,仅在无穷远处相关性完全消失。变程为3d。指数模型在统计理论中地位重要,它表示了空间随机性的要素,是一阶自回归和马尔可夫过程的半方差函数。作为自相关函数,它们是采样设计有效性的理论基础。
1.4邻域函数的统计函数及其意义
摄影测量得到的正射航片或卫星影象; 卫星或航天飞机的扫描影象; 野外测量采样数据,采样点随机分布或有规律的线性分布(沿剖面线或沿等高线; 数字化的多边形图、等值线图;
1.5 空间插值的数据源
图1 各种不同的采样布置方式
1.6 采样布置方式
1.8 方差变异函数
2)曲线从较低的方差值升高,到一定的间隔值时到达基台值,这一间隔称为变程(range)。在理论函数模型中,变程用a表示。 变程是半方差函数中最重要的参数,它描述了该间隔内样点的空间相关特征。在变程内,样点越接近,两点之间相似性、即空间上的相关性越强。很明显,如果某点与已知点距离大于变程,那么该点数据不能用于数据内插(或外推),因为空间上的自相关性不复存在。 变程的高低取决于观测的尺度,说明了相互作用所影响的范围。不同的属性,其变程值可以变化很大。
1.2.2局部插值方法 分类
1.4邻域函数的统计函数及其意义
众数(majority):邻域中出现频率最高的数值 最大值(max):邻域中最大的数值 最小值(min):邻域中最小的数值 中位数(median):邻域中数值从小到大排列后位于中间的数 平均值(mean):邻域中数值的算术平均 频率最小数(minority):邻域中出现频率最小的数值 范围(range):邻域中数值的范围,最大值与最小值之差 标准差(std):邻域中数值的标准差 和(sum):邻域中数值的和 变异度(varity):邻域中不同数值的个数
空间插值分析课件ppt

篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
3.距离反比法
W = 2, R = 150
W = 2, R = 230
W = 2, R = 600
W = 4, R = 600
不同权重系数(W)和搜索半径(R)的影响
12
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
2.最近邻法
最近邻法的适用性
分布均匀时效果好
分布差异性多大时不适用于最近邻插值?
用于只有少数缺失值时,对缺失值进行填补
数据缺失到什么程度,不能 采用最近邻插值方法?
18
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
3.距离反比法
基本原理
距离反比插值方法最早由 Shepard 提出的,并逐步得到发 展和推广应用。
每个采样对插值结果的影响随距离增加而减弱,因此距离 目标点较近的样点赋予的权重较大。
整个区域的数据都会影响单个插值点,单个数据点变量值 的增加、减少或者删除,都对整个区域有影响。
典型例子:全局趋势面分析
ARCGIS 全局趋势面分析
6
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
1.概述
整体插值和局部插值
8
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
空间插值方法

空间插值方法一、空间插值方法概述空间插值方法是指在给定的有限点数据集合上,通过某种数学模型,对未知位置的数值进行估计或预测的方法。
它广泛应用于地理信息系统、遥感、气象、环境监测等领域中,是一种重要的数据处理和分析手段。
常见的空间插值方法包括:反距离权重法、克里金法、径向基函数插值法等。
二、反距离权重法1. 原理反距离权重法是一种基于距离加权平均的插值方法。
其基本思想是:对于未知点,用已知点到未知点之间的距离作为权重系数,将已知点的观测值按照这些系数进行加权平均,得到未知点的估计值。
该方法假设空间变量在空间上具有连续性,并且与其邻近区域内观测值相关。
2. 步骤(1)确定待插值点和邻近观测点(2)计算待插值点与邻近观测点之间的欧式距离或曼哈顿距离等(3)根据距离计算每个邻近点的权重系数(4)将邻近点的观测值按照权重系数进行加权平均,得到待插值点的估计值3. 优缺点反距离权重法简单易懂,计算速度快,适用于数据密度较小、空间变异性较大的情况。
但其估计结果容易受到邻近点数量和距离的影响,可能出现插值误差较大的情况。
三、克里金法1. 原理克里金法是一种基于统计学原理的空间插值方法。
其基本思想是:通过对已知点之间的空间关系进行建模,利用半方差函数来描述变量在空间上的相关性,并通过最小二乘法求解出半方差函数中未知参数,从而得到未知位置处的预测值。
该方法假设空间变量在空间上具有稳定性,并且与其邻近区域内观测值相关。
2. 步骤(1)确定待插值点和邻近观测点(2)计算待插值点与邻近观测点之间的欧式距离或曼哈顿距离等(3)根据距离和半方差函数计算每个邻近点的权重系数(4)利用最小二乘法求解半方差函数中的未知参数(5)将邻近点的观测值按照权重系数进行加权平均,得到待插值点的估计值3. 优缺点克里金法能够考虑空间变异性和空间相关性,插值结果较为准确,但需要对半方差函数进行拟合,模型复杂度较高,计算量大。
四、径向基函数插值法1. 原理径向基函数插值法是一种基于核函数的空间插值方法。
空间插值方法

空间插值方法1.反距离权重插值:通过与样本点距离大小赋予权重,距离近的样本点被赋予较大的权重,受该样本点的影响越大,同时可以限制插值点的个数、范围,通过幂值来决定样本点对插值点的影响程度,灵活性大,准确性高,但不太适用规则排列的插值点2.克里金插值:克里金插值与IDW插值的区别在于权重的选择,IDW仅仅将距离的倒数作为权重,而克里金考虑到了空间相关性的问题。
它首先将每两个点进行配对,这样就能产生一个自变量为两点之间距离的函数。
使用克里金插值需确定半变异函数的类型、步长、步数。
对于这种方法,原始的输入点可能会发生变化。
在数据点多时,结果更加可靠。
该插值方法对规则排列、较密集的点插值较适用,而离散的插值点则需进行多次调试才可达到较为理想的效果3.自然邻域插值:原理是构建voronoi多边形,也就是泰森多边形。
首先将所有的空间点构建成voronoi多边形,然后将待求点也构建一个voronoi多边形,这样就与圆多边形有很多相交的地方,根据每一块的面积按比例设置权重,这样就能够求得待求点的值了。
该方法不是通过数据模型来进行插值,不需要设置多于的参数,简便但不灵活,不适合离散点进行插值,因为会形成不规则插值边界,但插值结果相对符合实际数值、准确,适合规则排列、较密集的点插值。
4.样条函数插值:这种方法使用样条函数来对空间点进行插值,它有两个基本条件:1.表面必须完全通过样本点2.表面的二阶曲率是最小的。
插值主要受插值类型(Regularized 或Tension)和weight值的影响,一般Regularize 插值结果比Tension插值结果光滑,在Regularized Spline 插值中,weight 值越高生成的表面越光滑,Tension Spline 插值则相反;适合那些空间连续变化且光滑的表面的生成。
该方法虽可生成平滑的插值结果,但其结果会在原有样点值进行数值延伸,产生于实际不符的结果,不建议一般插值使用。
空间插值

§1 插值概论1 插值用已知点来估算其他未知点的过程。
在GIS中,空间插值主要用于栅格数据,估算出栅格中每个单元的值。
空间插值是将点数据转换为面数据的一种方法。
2 需要插值的原因:现有数据不能完全覆盖所要求的区域;现有离散曲面的分辨率、像元大小、方向与要求不符;现有连续曲面的数据模型与要求不一致;3 内插和外推内插:在已观测点的区域内估算未观测点的数据的过程。
外推:在已观测点的区域外估算未观测点的数据的过程.——预测。
4 空间插值基础:控制点控制点分布;控制点密度;控制点的自相关程度§2 内插方法1 全局内插在整个区域用一个数学函数来表达地形曲面。
采用全部控制点计算未知点的数据。
2 局部内插将复杂的地形地貌分解成一系列的局部单元,在这些局部单元内部地形曲面具有单一的结构,由于范围的缩小和曲面形态的简化,用简单曲面就可较好的描述地形曲面。
采用样本控制点计算未知点的数据。
3 内插方法整体内插:趋势面分析;回归模型局部方法:泰森多边形(V oronoi边形,边界内插);反距离权内插;样条函数内插技术;克里金内插方法;密度估算4 趋势面分析的步骤数学曲面函数确定; 内插曲面的复杂程度;计算量;系数求解;最小二乘法;拟合精度分析5 整体内插缺点由于以下缺点,在空间内插中整体内插并不常用:整体内插函数保凸性较差:采样点的增减或移动都需要对多项式的系数作全面调整,从而采样点之间会出现难以控制的振荡现象,致使函数极不稳定,从而导致保凸性较差;多项式系数物理意义不明显解算速度慢且对计算机容量要求较高。
不能提供内插区域的局部地形特征;整体内插函数保凸性较差采样点之间会出现难以控制的振荡现象,致使函数极不稳定6 整体内插优点优点:整个区域上函数的唯一性、能得到全局光滑连续的空间曲面、充分反映宏观地形特征等。
在空间内插中,一般是与局部内插方法配合使用,例如在使用局部内插方法前,利用整体内插去掉不符合总体趋势的宏观地物特征。
空间插值方法

7.空间插值7.1空间插值的概念和理论空间插值常用于将离散点的测量数据转换为连续的数据曲面,以便与其它空间现象的分布模式进行比较,它包括了空间内插和外推两种算法。
空间内插算法是一种通过已知点的数据推求同一区域其它未知点数据的计算方法;空间外推算法则是通过已知区域的数据,推求其它区域数据的方法。
在以下几种情况下必须作空间插值:1)现有的离散曲面的分辨率,象元大小或方向与所要求的不符,需要重新插值。
例如将一个扫描影象(航空像片、遥感影象)从一种分辨率或方向转换到另一种分辨率或方向的影象。
2)现有的连续曲面的数据模型与所需的数据模型不符,需要重新插值。
如将一个连续的曲面从一种空间切分方式变为另一种空间切分方式,从TIN到栅格、栅格到TIN或矢量多边形到栅格。
3)现有的数据不能完全覆盖所要求的区域范围,需要插值。
如将离散的采样点数据内插为连续的数据表面。
空间插值的理论假设是空间位置上越靠近的点,越可能具有相似的特征值;而距离越远的点,其特征值相似的可能性越小。
然而,还有另外一种特殊的插值方法——分类,它不考虑不同类别测量值之间的空间联系,只考虑分类意义上的平均值或中值,为同类地物赋属性值。
它主要用于地质、土壤、植被或土地利用的等值区域图或专题地图的处理,在“景观单元”或图斑内部是均匀和同质的,通常被赋给一个均一的属性值,变化发生在边界上。
7.2空间插值的数据源连续表面空间插值的数据源包括:●摄影测量得到的正射航片或卫星影象;●卫星或航天飞机的扫描影象;●野外测量采样数据,采样点随机分布或有规律的线性分布(沿剖面线或沿等高线);●数字化的多边形图、等值线图;空间插值的数据通常是复杂空间变化有限的采样点的测量数据,这些已知的测量数据称为“硬数据”。
如果采样点数据比较少的情况下,可以根据已知的导致某种空间变化的自然过程或现象的信息机理,辅助进行空间插值,这种已知的信息机理,称为“软信息”。
但通常情况下,由于不清楚这种自然过程机理,往往不得不对该问题的属性在空间的变化作一些假设,例如假设采样点之间的数据变化是平滑变化,并假设服从某种分布概率和统计稳定性关系。
空间插值
当观测点的相互位置越近,其数据的相似性越强;当观测点的相互位置越远,其数 当观测点的相互位置越近,其数据的相似性越强;当观测点的相互位置越远, 越近 相似性越强 越远 据的相似性越低 越低。 据的相似性越低。 加权移动平均法:λ 是采样点i 加权移动平均法:λi是采样点i对应的权值
加权平均内插的结果随使用的函数及其参数、采样点的分布、 加权平均内插的结果随使用的函数及其参数、采样点的分布、窗口的大小等的不 结果随使用的函数及其参数 同而变化。 同而变化。通 对于不规则分布的采样点需要不断地改变 不断地改变窗口的大 常使用的采样点数为6 8 常使用的采样点数为6—8点。对于不规则分布的采样点需要不断地改变窗口的大 形状和方向,以获取一定数量的采样点 一定数量的采样点。 小、形状和方向,以获取一定数量的采样点。
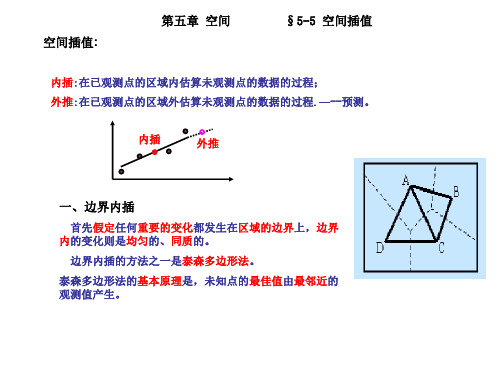
一、边界内插
首先假定任何重要的变化都发生在区域的边界上 首先假定任何重要的变化都发生在区域的边界上,边界 假定任何重要的变化都发生在区域的边界 的变化则是均匀 均匀的 同质的 内的变化则是均匀的、同质的。 泰森多边形法。 边界内插的方法之一是泰森多边形法 边界内插的方法之一是泰森多边形法。 泰森多边形法的基本原理是 未知点的最佳值由最邻近的 泰森多边形法的基本原理是,未知点的最佳值由最邻近的 基本原理 最佳值 观测值产生。 观测值产生。
将内插点周围的16个点的数据带入多项式,可计算出所有的系数。 将内插点周围的16个点的数据带入多项式,可计算出所有的系数。 16个点的数据带入多项式 16个点 16个点
第五章 空间数据的处理 四、移动平均法
§5-5 空间插值
在局部范围(或称窗口)内计算n个数据点的平均值. 在局部范围(或称窗口)内计算n个数据点的平均值.
二维平面的移动平均法也可用相同的公式,但位置X 应被坐标矢量 代替。 坐标矢量X 二维平面的移动平均法也可用相同的公式,但位置Xi应被坐标矢量Xi代替。 的移动平均法也可用相同的公式 窗口的大小对内插的结果有决定性的影响。 窗口的大小对内插的结果有决定性的影响。 对内插的结果有决定性的影响 小窗口将增强近距离数据的影响; 小窗口将增强近距离数据的影响; 将增强近距离数据的影响 小近距离数据的影响。 小近距离数据的影响。 大窗口将增强远距离数据的影响, 大窗口将增强远距离数据的影响,减 将增强远距离数据的影响
空间插值方法介绍共38页

6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
空间插值方法介绍
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— ,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
Thank you
