一种超前进位加法器的新颖BIST架构
超前进位加法器

超前进位加法器超前进位加法器是一种数字电路设备,用于进行二进制数的加法运算。
它通过将多个加法器级联,实现对多位二进制数的加法计算,并且能够在加法过程中实现超前进位,提高计算速度。
超前进位加法器的原理是基于二进制加法的原理。
在二进制加法中,每一位的运算结果可以表示为:两个位的和与进位。
其中,和即为输入位的异或运算结果,进位则是输入位的与运算结果再经过左移一位。
超前进位加法器利用这一原理,通过预测进位产生的结果,以提前得到进位并作用于下一级的运算。
超前进位加法器可以分为两个部分:生成进位部分和传递进位部分。
生成进位部分用于预测进位的产生情况,传递进位部分则是将进位传递给下一级的加法器。
生成进位部分的输入为两个相邻位的和,输出为进位。
传递进位部分的输入为前一级的进位以及生成进位部分的进位,输出为当前位的进位。
为了方便理解,以下以一个四位超前进位加法器为例进行介绍。
这个四位加法器由四个单独的全加器组成,每个全加器负责一个位的运算。
生成进位部分和传递进位部分在全加器中都有相应的电路实现。
首先,生成进位部分。
对于第一位的全加器来说,由于没有前一位的进位,因此直接将两个输入位的和作为输出位的进位。
对于其他位的全加器,需要预测进位的产生。
这个预测的规则是,如果前一位的和为1,则有可能会产生进位。
因此,预测进位部分将前一位输入位的和与该位输入位的和进行与运算,得到预测的进位结果。
接下来,传递进位部分。
对于第一个全加器来说,由于没有前一位的进位,因此直接将生成进位部分的进位作为输出位的进位。
对于其他位的全加器,传递进位部分将前一位的进位与生成进位部分的进位进行或运算,得到当前位的进位。
将多个全加器级联后,就构成了一个超前进位加法器。
通过这种方式,每一位的运算可以并行进行,从而提高了计算速度。
同时,由于提前预测了进位的结果,可以减少了进位的传播延迟,进一步提高了计算效率。
超前进位加法器在数字电路的设计中具有重要的应用价值。
4bits超前加法进位器的全定制设计_微电子卓越班数字集成电路课程设计报告

数字集成电路课程设计题目:4 bits超前加法进位器地全定制设计姓名:席高照学号: 111000833学院:物理与信息工程学院专业:微电子(卓越班)年级: 2010级指导教师:陈群超(签名)2013 年 6 月 3 日目录第1章概述 01.1课程设计目地.......................................... 错误!未定义书签。
1.2课程设计地主要内容.................................... 错误!未定义书签。
1.2.1设计题目.......................................... 错误!未定义书签。
1.2.2设计内容.......................................... 错误!未定义书签。
第2章功能分析及逻辑分析 (2)2.1功能分析 (2)2.2推荐工作条件 (3)2.3电性能 (7)2.4真值表 ................................................ 错误!未定义书签。
2.5表达式 (6)2.6电路图...................................................................... 错误!未定义书签。
第3章电路设计与器件参数设计83.1性能指标: ............................................ 错误!未定义书签。
3.2模块划分 (7)3.2.1输出级电路设计 (7)3.2.2内部反相器 (9)3.2.3内部电路等效 (8)3.2.4输入级电路 (10)3.2.5输出缓冲级电路 (10)3.2.6输入、输出保护电路 (10)3.3本章小结 (10)第4章电路模拟与仿真................................................................................................... 错误!未定义书签。
32超前进位加法器

文档编号:GX_HW_0001文档分类:硬件技术文档访问权限:公开32位超前进位加法器总体设计方案Version 1.1版本信息版本日期描述作者V1.1 2011-10-07 采用超前进位链实现郭新32位超前进位加法器目录目录 (3)1.概述 (4)2.总体描述 (4)2.1.功能描述 (4)2.2.顶层框图 (4)2.3.引脚描述 (4)3.模块划分 (5)3.1 概述(叙述一下划分的几个大的模块) (5)3.2模块A (6)3.2.1功能定义 (6)3.2.2信号描述 (6)3.2.3 详细设计 (6)3.3模块B (7)3.3.1功能定义 (7)3.3.2信号描述 (7)3.3.3 详细设计 (7)3.4模块C (8)3.4.1功能定义 (8)3.4.2信号描述 (8)3.4.3 详细设计 (8)3.5模块D (9)3.5.1功能定义 (9)3.5.2信号描述 (9)3.5.3 详细设计 (9)4.验证方案 (10)5.设计开发环境 (10)6.源代码 (10)6.1顶层模块 (10)6.2模块A (12)6.3模块B (12)6.4模块C (13)6.5模块D (14)6.6测试模块 (15)6.7测试波形 (16)1.概述利用各位数据和最低位进位同时输入,各位之间的进位信号与和就能同时产生,实现超前进位加法器,这种加法器运算速度显著提高,但电路复杂程度也急剧增加。
2.总体描述2.1.功能描述超前进位逻辑从输入中读入进位、传播值和生成值等信息,计算每一位的进位值。
该逻辑产生进位值和加值,加值只是输入的异或。
进位值用4位超前进位块的三级树来计算。
2.2.顶层框图32bit_claa(31:0)b(31:0)cins(31:0)cout图2.1加法器顶层框图2.3.引脚描述表2.1 顶层接口信号描述名称输入/输出功能描述a 输入32位输入b 输入32位输入cin 输入低级进位输入s 输入32位输出cout 输入进位输出3.模块划分(各个模块中不涉及时序,时序分析略去。
超前进位加法器

超前进位加法器超前进位加法器是一种重要的数电电路,广泛应用于计算机和其他电子设备中。
它的作用是在进行多位数相加时,实现进位的自动计算和传递,从而提高计算速度和准确性。
本文将对超前进位加法器进行详细介绍。
超前进位加法器是一种基于逻辑门电路的加法器。
它的设计理念是通过预先检测进位,减少进位的传输延迟,从而加快计算速度。
对于一位加法器来说,传统的进位加法器需要等待当前位的进位计算完成后,才能进行下一位的计算。
而超前进位加法器在当前位计算的同时,预先计算下一位的进位,从而节省了计算时间。
超前进位加法器的基本原理是利用逻辑门的延迟特性实现进位的预先计算。
常见的超前进位加法器包括Ripple Carry Adder(RCA)、Carry Select Adder(CSA)和Carry Lookahead Adder(CLA)。
这些加法器在实现进位预先计算的方式上有所不同,但核心思想都是一样的。
以Ripple Carry Adder为例,它由多个全加器级联而成。
全加器是一种可以同时实现两位相加和进位计算的电路。
Ripple Carry Adder通过将多个全加器级联,实现了对多位数相加的计算。
在每个全加器中,除了计算两位之和外,还需要计算当前位的进位。
传统的Ripple Carry Adder需要等待前一位的进位计算完成后,才能进行下一位的计算,而这就导致了较长的计算时间。
而超前进位加法器则在每个全加器中预先计算下一位的进位。
通过利用逻辑门的传输延迟,将当前位的进位信号传递到下一位,实现了进位的预先计算。
这样,在当前位的计算完成后,下一位的进位已经预先计算好了,从而减少了计算时间。
超前进位加法器在计算速度上有显著的优势。
相比传统的进位加法器,它能够减少计算时间,提高计算效率。
对于大规模的数值计算,超前进位加法器能够显著缩短计算时间,提高计算速度。
这对于例如计算机科学、数据处理和通信等领域的应用非常重要。
除了计算速度的优势,超前进位加法器在准确性上也有一定的优势。
超前进位加法器的设计分解

超前进位加法器的设计分解沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:计算机科学与技术班级:学号:姓名:指导教师:完成日期:2014年01月10日第2章详细设计方案2.1 顶层方案图的设计与实现顶层方案图主要实现一位全加器的逻辑功能,采用原理图设计输入方式完成,超前进位加法器电路的是实现基于XCV200可编程逻辑芯片。
在完成原理图的功能设计后,经过检测调试,把输入/输出信号通过引脚编号安排到XCV200指定的引脚上去,最终实现芯片的引脚锁定。
2.1.1顶层方案的整体设计顶层图形文件主要由2个四位超前进位加法器构成,总共17位输入,9位输出。
顶层图形文件由Xilinx Foundation F3.1软件编辑得到相应的模块,顶层图形的整体设计如下图2.1所示:图 2.1八位超前进位加法器整体设计图2.1.2元器件选择和引脚锁定(1)元器件的选择由于在设计的过程中,硬件设计环境是基于伟福COP2000型计算机组成原理实验仪和XCV200实验板,故采用的目标芯片为Xilinx XCV200可编程逻辑芯片。
(2)引脚锁定在Xilinx Foundation F3.1上面完成软件的设计之后,把顶层图形文件中的输入/输出信号用引脚编号安排到Xilinx XCV200芯片指定的引脚上去,从而实现芯片的设计电路的引脚锁定,各信号及Xilinx XCV200芯片引脚对应关系如下表2.1所示:表 2.1 信号和芯片引脚对应关2.2 功能模块的设计与实现在八位超前进位加法器和四位超前进位加法器的设计中均是采用Schematic 设计输入方式,而在四位超前进位加法器的设计中是由一列的门电路构成,最后在由2个四位超前进位加法器模块构成8位超前进位加法器。
可以扩展开来,16位,32位超前进位加法器原理类似8位的设计原理。
2.2.1 八位超前进位加法器的设计与实现(1)设计描述根据上面在1.1中讲述的四位超前进位加法器的设计原理那样,四位超前进位加法器的实现是建立在进位C1,C2,C3,C4的基础之上的。
超前进位加法器的原理

超前进位加法器的原理
超前进位加法器是一种高速加法器,用来对大量二进制数字进行加法运算。
其名称“超前”即表示它比传统加法器更快,因为它预测了加法运算的进位部分,从而减少了计算量和延迟时间。
超前进位加法器的原理是将待加数分成若干位,然后分别进行加法运算。
其中,除了最底位以外,每位都需要前一位的进位信息。
超前进位加法器利用了这个特点,通过预测进位信息来提高速度。
具体来说,超前进位加法器采用了一种称为“根4”逻辑的结构,通过将输入数字分成四组来实现快速的进位预测。
每组数字包含了一二比特和进位输出。
利用这些信息,超前进位加法器对进位进行预测,从而在每组数字的加法过程中避免了花费时间来等待进位。
这样,整个加法器的速度就得到了显著提升。
除了进位预测外,超前进位加法器还采用了一种高效的逻辑结构来实现快速加法。
其主要思想是将加法运算分为两个阶段:预处理和部分和生成。
在预处理阶段,输入数字被拆分成一组加数和一组补码。
补码被用于加法的后半段,从而使得加法器可以同时处理加法和减法运算。
在部分和生成阶段,各个位的部分和被计算出来,并且可以被累加到最终和中。
总之,超前进位加法器是一种高速加法器,通过巧妙的进位预测和高效的逻辑结构来实现快速加法运算。
由于其高速度和可靠性,超前进位加法器被广泛应用于计算机的中央处理器 (CPU) 和其它高速计算设备中。
数字电路课程设计之超前进位加法器
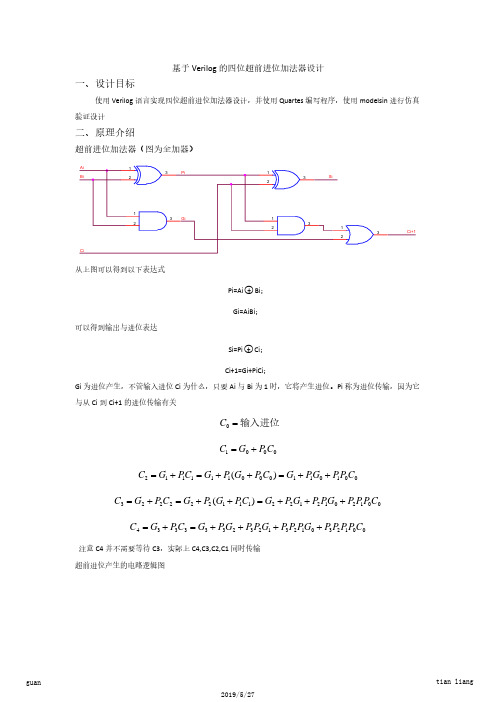
reg
Cin;
wire[3:0] S;
wire
Cout;
carry_look_add CAL (.A(A),.B(B),.Cin(Cin),.Cout(Cout),.S(S)); initial begin
#10 A=4'd0;B=4'd0;Cin=0; #10 A=4'd11;B=4'd1;Cin=0; #10 A=4'd10;B=4'd12;Cin=0; #10 A=4'd11;B=4'd4;Cin=0; #100 $stop; end endmodule
Pi=Ai○+ Bi;
可以得到输出与进位表达
Gi=AiBi;
Si=Pi○+ Ci;
Ci+1=Gi+PiCi; Gi 为进位产生,不管输入进位 Ci 为什么,只要 Ai 与 Bi 为 1 时,它将产生进位。Pi 称为进位传输,因为它 与从 Ci 到 Ci+1 的进位传输有关
C0 = 输入进位
C1 = G0 + P0C0
Half_Add H3(.a(A[2]),.b(B[2]),.s(v6),.c(v5));
Half_Add H4(.a(A[3]),.b(B[3]),.s(v8),.c(v7));
carry_look
CL1(.C0(Cin),.P0(v2),.G0(v1),.P1(v4),.G1(v3),.P2(v6),.G2(v5),.P3(v8),.G3(v7),.C1(o1),.C2(o2),.C3(o3),.C4(Cout));
注意 C4 并不需要等待 C3,实际上 C4,C3,C2,C1 同时传输 超前进位产生的电路逻辑图
4位超前进位加法器设计讲解学习

4位超前进位加法器设计讲解学习4位超前进位加法器设计、、模拟集成电路分析与设计课程设计报告题⽬4位超前进位加法器设计学院(部)电控学院专业电⼦科学与技术班级学⽣姓名学号前⾔20世纪是IC迅速发展的时代。
计算机等信息产业的飞速发展推动了集成电路(Integrated Circuit—IC)产业。
⼤多数超⼤规模集成电路(Very Large Scale IC—VLSI)在⽇常⽣活中有着⼴泛的应⽤。
在这些⼴泛应⽤的运算中,加法器是组成这些运算的基本单元。
在⾼性能微处理器和DSP处理器中,加法器的运算时间⾄关重要。
加法器运算常常处于⾼性能处理器运算部件的关键路径中,特别是在算术逻辑单元中加法器的运算时间对处理器的速度起着决定性的作⽤。
随着微处理器的运算速度越来越快,对快速加法器的需求也越来越⾼。
当今,加法器的设计⾯临两⼤课题,⾸先是如何降低功耗。
随着便携式IC产品例如MP3播放器,⼿机和掌上电脑等的⼴泛使⽤,要求IC⼯程师对现有运算模块的性能作进⼀步改进,尤其是在电路的功耗和尺⼨⽅⾯。
由于现在相应的电池技术难以和微电⼦技术的发展速度匹敌,这使得IC设计师遇到了许多限制因素,⽐如⾼速,⼤吞吐量,⼩尺⼨,低功耗等。
因此,这使得研究低功耗⾼性能加法单元持续升温。
另⼀⽅⾯就是如何提⾼加法器的运算速度。
因为加法运算存在进位问题,使得某⼀位计算结果的得出和所有低于它的位相关。
因此,为了减少进位传输所耗的时间,提⾼计算速度,⼈们设计了多种类型的加法器,如超前进位加法器曼彻斯特加法器、进位旁路加法器、进位选择加法器等。
它们都是利⽤各位之间的状态来预先产⽣⾼位的进位信号,从⽽减少进位从低位向⾼位传递的时间。
本⽂⾸先介绍了的加法器的类型以及其⼯作原理,然后重点分析了超前进位加法器的组成结构、结构参数以及其⼯作原理。
分层设计了加法器的输⼊输出电路,并通过tanner软件进⾏仿真实验,从⽽验证了电路的准确信。
⽬录第⼆章设计过程 (18)2.1 电路设计基础原理 (18)2.2 电路各部分结构设计 (20)异或门的CMOS电路原理图如下: (21)(21)异或门的CMOS波形图如下: (21)(21)两输⼊与门的CMOS电路原理图如下: (22)(22)两输⼊与门的CMOS波形如下: (22)(22)反相器的CMOS电路如下: (23)(23)反相器的CMOS仿真波形如下: (23)(23)四位超前进位加法器进位的逻辑电路图如下: (24)(24)c1,c2,c3,c4的CMOS级电路原理图及仿真 (25)(25)a.c1的原理图 (25)(25)c1的仿真波形 (26)(26)b.c2的原理图 (26)c2的仿真波形 (27)c.c3的原理图 (28)(29)c3的仿真波形 (29)(30)c4的原理图 (30)c3的仿真波形 (31)2.3 主要电路参数的⼿⼯推导 (31)四位超前进位加法器门级电路原理图如下: (34)(34)四位超前进位加法器门级电路分析设定如下: (34)(35)四位超前进位加法器门级电路瞬态分析结果如下: (35)(35)四位超前进位加法器门级电路瞬态分析波形图如下: (35)(36)4.1 ⽤于仿真的电路图如下: (37)四位超前进位加法器门级电路分析设定如下: (38)四位超前进位加法器电路瞬态分析结果如下: (38)(38)四位超前进位加法器门级电路瞬态分析波形图如下: (38)(39)第五章鸣谢及课设总结和体会 (39)参考⽂献 (40)第⼀章设计⽬标1.根据电路原理图,给出电路的CMOS晶体管级电路设计。
超前进位加法器公式

超前进位加法器公式全文共四篇示例,供读者参考第一篇示例:超前进位加法器是一种用来进行超前进位加法的计算器,它在数位计算领域是非常重要和实用的工具。
超前进位加法器的设计原理是利用进位延迟来减少计算时间,提高计算效率。
在本文中,我们将详细介绍超前进位加法器的公式及其工作原理。
超前进位加法器的公式基本上是基于二进制加法的原理进行设计的。
在二进制加法中,当两个位相加时,如果有进位产生,则需要等待进位的延迟时间。
而超前进位加法器通过提前计算进位,可以在加法器的计算周期内完成多个位的相加操作,从而减少计算时间。
超前进位加法器的公式如下:S = A XOR B XOR CinCout = (A AND B) OR ((A XOR B) AND Cin)S是结果位,A和B是待相加的两个位,Cin是前一位相加的进位,Cout是当前位相加产生的进位。
在这个公式中,第一部分计算了没有考虑进位的情况下的结果位S。
通过对A和B进行异或运算,可以得到不考虑进位情况下的结果。
第二部分计算了当前位的进位Cout。
通过A和B的与运算,可以得到进位的生成情况,并且结合前一位的进位Cin,可以得到当前位的进位。
第二篇示例:超前进位加法器是一种用于进行数值加法运算的电子装置,其特点是在进位计算时会提前将进位信号传输到下一位,从而加快计算速度。
它的工作原理是通过预测下一个进位值来提前确定进位的传递路径,从而实现高效的加法运算。
在现代计算机系统中,超前进位加法器被广泛应用于高速运算模块,能够在瞬间完成大规模的数值计算。
超前进位加法器通常由多个加法单元和进位预测单元组成。
加法单元负责实际的加法运算,而进位预测单元则负责提前预测下一个进位值。
在进行加法运算时,进位预测单元会提前计算下一个进位值,并将进位信号传输到下一位。
这种提前传递的方式可以减少计算过程中的等待时间,提高计算效率。
超前进位加法器在数字信号处理、通信系统、图像处理等领域都有着广泛的应用。
超前进位加法器例题

超前进位加法器例题
超前进位加法器是一种用于进行二进制加法的电子逻辑电路。
它可以用于对两个二进制数进行加法运算,并能够处理进位的问题。
下面我将从多个角度来解释超前进位加法器的例题。
首先,让我们考虑一个简单的例题,假设我们要使用超前进位
加法器来计算5(二进制为0101)和3(二进制为0011)的和。
首先,我们从最低位开始相加,得到1+1=10,其中0写在当前位,1进位到下一位。
接着是1+0+1=10,同样地,0写在当前位,1
进位到下一位。
然后是0+1+0=01,这一次没有进位,所以直接写在
当前位。
最后是0+0+0=00,没有进位。
所以最终的结果是1000,即8。
从电路角度来看,超前进位加法器在每一位上都有一个加法器
和一个进位预测器。
加法器用于计算当前位的和,进位预测器用于
预测下一位是否会有进位。
这样,超前进位加法器可以在一次计算
中得到所有位的和,而不需要等待进位的传播。
从数学角度来看,超前进位加法器可以通过预测进位来减少加
法器的延迟,从而提高运算速度。
这种方法在大规模的二进制加法运算中尤其有效,因为它可以减少整体的运算时间。
总的来说,超前进位加法器是一种高效的二进制加法器,它通过预测进位来加速加法运算,并且可以应用于各种计算机和电子设备中。
希望这个例题能帮助你更好地理解超前进位加法器的工作原理和应用。
超前进位加法器

超前进位加法器超前进位加法器是一种在数字电路中常用的电子设备,它具有在加法操作中进位能力更高的特点。
在这篇文章中,我们将探讨超前进位加法器的工作原理、应用场景以及它对现代科技的影响。
首先,让我们了解一下超前进位加法器的工作原理。
超前进位加法器是一种高性能的加法电路,它能够在进行数字加法时更快地产生进位信号。
它通过利用多个位的输入信号和输出信号之间的时序关系来实现进位的超前生成。
通过这种方式,超前进位加法器能够大大提高加法操作的速度和效率。
超前进位加法器的应用场景非常广泛。
它常常被用于高速计算机、图像处理器和通信设备等领域。
在高速计算机中,超前进位加法器可以快速地进行大量的数字运算,从而提高计算机的整体性能。
在图像处理器中,超前进位加法器可以快速地对图像进行处理和分析,提供更高质量的图像处理效果。
在通信设备中,超前进位加法器可以实现高速数据传输和信号处理,提供更快速和可靠的通信服务。
超前进位加法器对现代科技的影响不可忽视。
首先,它极大地提高了数字电路的运算速度和效率。
在过去,传统的进位生成方式虽然能够实现进位的生成,但速度较慢,效率不高。
而超前进位加法器的出现,解决了这个问题,使得数字电路能够更快地进行加法运算。
其次,超前进位加法器的应用为人们的生活带来了便利。
在现代社会中,大量的数字运算都离不开超前进位加法器的支持,例如银行的财务计算、医院的影像处理等。
最后,超前进位加法器的不断创新和发展,也推动了数字电路领域的技术进步。
总结起来,超前进位加法器是一种在数字电路中常用的高性能加法电路。
它通过利用多个位的输入信号和输出信号之间的时序关系,提前生成进位信号,从而大大提高了加法操作的速度和效率。
超前进位加法器的应用场景广泛,它在高速计算机、图像处理器和通信设备等领域发挥着重要作用。
超前进位加法器的出现和应用,不仅极大地提高了数字电路的运算速度和效率,也为人们的生活带来了便利。
随着技术的不断创新和发展,相信超前进位加法器在未来将会有更广泛的应用和更大的影响。
超前进位加法器原理

超前进位加法器原理
超前进位加法器是一种常见的数字电路,用于实现数字加法运算。
它的原理是利用超前进位的概念,通过预先计算进位来加快加法运算的速度。
在传统的加法器中,每一位的进位都是依赖于前一位的计算结果。
这意味着在进行加法运算时,每一位的计算都需要等待前一位的结果才能进行。
而超前进位加法器则通过提前计算进位,使得每一位的计算可以独立进行,从而加快了整个加法运算的速度。
超前进位加法器的原理可以通过以下步骤来说明:
1. 预先计算进位,在进行加法运算之前,先对每一位的进位进行预先计算。
这样可以避免等待前一位的结果,从而加快了计算速度。
2. 并行计算,每一位的计算都可以独立进行,并且不受前一位的影响。
这样可以实现并行计算,从而提高了整个加法运算的效率。
3. 结果输出,最后将每一位的计算结果和预先计算的进位相加,得到最终的加法结果。
超前进位加法器的原理不仅可以应用在数字电路中,也可以应用在计算机系统和通信系统中,用于加快数据处理和传输的速度。
因此,它在现代电子技术中具有重要的应用价值。
总之,超前进位加法器利用预先计算进位的原理,实现了加法运算的高效率和快速性,为数字电路和计算机系统的设计提供了重要的技术支持。
希望通过不断的研究和改进,可以进一步提高超前进位加法器的性能,为数字技术的发展做出更大的贡献。
超前进位加法器原理

超前进位加法器原理超前进位加法器是一种在数字电路中常用的加法器,它可以实现快速、高效地进行数字加法运算。
在本文中,我们将详细介绍超前进位加法器的原理和工作方式。
首先,让我们来了解一下传统的进位加法器。
在传统的进位加法器中,每一位的进位都依赖于前一位的运算结果。
这意味着当我们进行多位数的加法运算时,每一位的计算都需要等待前一位的计算结果,这会导致整体的运算速度变慢。
而超前进位加法器则通过引入预测进位的方式来解决这一问题。
它可以在不等待前一位计算结果的情况下,提前计算出进位的值,从而加快整体的运算速度。
超前进位加法器的原理是基于两个关键的概念,预测进位和进位生成。
预测进位是指在进行加法运算时,提前计算出下一位的进位值。
而进位生成则是指在当前位的计算中,根据当前位的两个加数和上一位的进位值,生成当前位的进位值。
为了更好地理解超前进位加法器的工作原理,让我们来看一个具体的例子。
假设我们要计算两个4位数的加法,1101和1011。
在传统的进位加法器中,我们需要等待前一位的计算结果,而在超前进位加法器中,我们可以提前计算出进位值,从而加快整体的运算速度。
对于上面的例子,我们可以先计算最低位的进位值。
根据预测进位的原理,我们可以提前计算出第二位的进位值为1。
然后,根据进位生成的原理,我们可以计算出最低位的和为0,进位值为1。
接着,我们可以继续计算第二位的和和进位值,依次类推,直到计算出最高位的和和进位值。
通过上面的例子,我们可以看到,超前进位加法器可以在不等待前一位计算结果的情况下,提前计算出进位值,从而加快整体的运算速度。
这种预测进位和进位生成的原理,使得超前进位加法器成为了数字电路中常用的加法器之一。
总之,超前进位加法器通过引入预测进位的方式,提前计算出进位值,从而加快了加法运算的速度。
它的工作原理基于预测进位和进位生成的概念,通过这种方式可以在不等待前一位计算结果的情况下,快速、高效地进行数字加法运算。
超前进位加法器的设计

沈阳航空工业学院课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:计算机科学与技术班级:4401102学号:200403011046姓名:郭丰瑞指导教师:刘泽显完成日期:2006年12月31日沈阳航空工业学院课程设计报告目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (4)2.1顶层方案图的设计与实现 (4)2.1.1创建顶层图形设计文件 (4)2.1.2器件的选择与引脚锁定 (4)2.2功能模块的设计与实现 (6)2.2十六位超前进位加法器的设计 (6)2.3仿真调试 (8)第3章编程下载与硬件测试 (12)3.1编程下载 (12)3.2硬件测试及结果分析 (12)参考文献 (15)附录(程序清单或电路原理图) (16)第1章总体设计方案1.1设计原理十六位超前进位加法器,可以由4个四位超前进位加法器构成。
由第一个四位超前进位加法器的进位输出加进为第二个超前进位加法器的进位输入,依次类推。
超前进位加法器的实现是建立在各位进位的形成条件来实现的。
所以第一位的进位c1=a0*b0+(a0+b0)*c0;第二位的进位c2=a1*b1+(a1+b1)*a0*b0+(a1+b1)(a0+b0)c0第三位的进位c3=a2*b2+(a2+b2)a1*b1+(a1+b1)*(a2+b2)*a0*b0+(a0+b0)(a1+b1)(a2+b2)*c0第四位的进位c4=a3*b3+(a3+b3)*a2*b2+(a3+b3)*(a2+b2)a1*b1+(a3+b3)(a2+b2)(a1+b1)*a0*b0+(a0+b0)(a1+b1)(a2+b2)(a3+b3)*c0 下面我们可以引进传递函数Pi和进位产生函数Gi的概念。
他们定义为:Pi=Ai+BiGi=Ai*BiP1的意义是:当A0和B0中有一个为1时,若有进位输入,则本位向高位传递进位。
4bits超前进位加法器

福州大学至诚学院数字集成电路课程设计报告设计题目:4bits 超前进位加法器全定制设计班级:(1)班专业:微电子学姓名:陈长毅学号:210991804组名:林志龙指导老师:王仁平教师评分:日期:4bits超前进位加法器目录第1章概述.................................................................... - 3 -1.1课程设计目的 (3)1.2课程设计的主要内容 (3)1.2.1设计题目 (3)1.2.2设计要求 ....................................................................1.2.3设计内容 (3)第2章功能分析及逻辑分析...................................................... - 4 -2.1功能分析 (4)2.2推荐工作条件 (4)2.3直流特性....................................................... 错误!未定义书签。
2.4交流(开关)特性 (5)2.5真值表 (6)2.6表达式 (7)2.7电路原理图 (7)2.7.1 4位超前进位加法器镜像实现的电路图2.7.2传输门实现XOR电路第3章功耗估算与延时......................................................... - 10 -3.1电容估算 (10)3.2功耗估算 (11)3.3延时估算 (11)第4章电路原理图设计与仿真................................................... - 12 -4.1原理图和符号图的建立 (12)4.1.1建立新库 (12)4.1.2建立SYMBOL (14)4.2各模块原理图设计与仿真4.2.1反相器的原理图与仿真 (13)4.2.2与门的原理图和仿真......................................... 错误!未定义书签。
超前进位加法器设计(参考资料)

加法器设计(三)超前进位加法器(Verilog)超前进位加法器module add4_head ( a, b, ci, s, pp, gg);input[3:0] a;input[3:0] b;input ci;output[3:0] s;output pp;output gg;wire[3:0] p;wire[3:0] g;wire[2:0] c;assign p[0] = a[0] ^ b[0];assign p[1] = a[1] ^ b[1];assign p[2] = a[2] ^ b[2];assign p[3] = a[3] ^ b[3];assign g[0] = a[0] & b[0];assign g[1] = a[1] & b[1];assign g[2] = a[2] & b[2];assign g[3] = a[3] & b[3];assign c[0] = (p[0] & ci) | g[0];assign c[1] = (p[1] & c[0]) | g[1];assign c[2] = (p[2] & c[1]) | g[2];assign pp = p[3] & p[2] & p[1] & p[0];assign gg = g[3] | (p[3] & (g[2] | p[2] & (g[1] | p[1] & g[0])));assign s[0] = p[0] ^ ci;assign s[1] = p[1] ^ c[0];assign s[2] = p[2] ^ c[1];assign s[3] = p[3] ^ c[2];endmodule首先要明确几个概念:p表示进位否决信号(pass),如果p为0就否决调前一级的进位输入。
否决的意思就是即使前一级有进位,本级也不会向后一级产生进位输出。
一种快速超前进位加法器的优化设计

一种快速超前进位加法器的优化设计
王云贵;杨靓
【期刊名称】《科学技术与工程》
【年(卷),期】2010(010)033
【摘要】加法器是处理器的一个基本功能部件,随着处理器频率的不断提高, 对加法器也提出了更高的要求.超前进位(CLA)是最快的加法器之一.提出了一种新的改善超前进位加法器性能的方法,用DC对4种CLA进行了综合,结果表明与目前已有的CLA相比,提出的CLA速度更快,面积更小,并给出了统计数据.
【总页数】5页(P8262-8266)
【作者】王云贵;杨靓
【作者单位】西安微电子技术研究所,西安,710054;西安微电子技术研究所,西安,710054
【正文语种】中文
【中图分类】TN47
【相关文献】
1.基于方块超前进位的快速进位跳跃加法器 [J], 崔晓平;王成华
2.超前进位加法器的延迟时间公式与优化设计 [J], 王礼平;王观凤
3.超前进位加法器优化设计的结构参数约束 [J], 周大鹏;龙岸文;徐国荣;王礼平
4.超前进位加法器基本单元电路及其组合方案的优化设计 [J], 王礼平;王观凤
5.超前进位加法器的一种优化设计 [J], 黄舒怀;蔡敏
因版权原因,仅展示原文概要,查看原文内容请购买。
杭电计算机组成原理超前进位加法器设计 2

本次试验的超前进位加法器,更好的体现了,我们对于效率地的要求,对于以有些的地方我们可以采取一些手段改进自身的不足,超前进位的思想就是率先计算出我们的需要的进位
的值,然后在处理,解决了不同步的问题,真的很值得我们思考,这种类似的问题
指导教师
评议
成绩评定:指导教师签名:
实验环境
Xilinx ISE Design Suite 13.4
实验内容(算法、程序、步骤和方法)
(1)建立工程;
(2)编写超前进位电路代码;
(3)将全加器模块导入工程中;
(4)编写顶层模块代码;
(5)编写测试代码,进行软件仿真;
(6)生成bit文件并下载入FPGA,进行硬件测试并记录;
(7)得出结论。
O1(P[1],A[1],B[1]),
O2(P[2],A[2],B[2]),
O3(P[3],A[3],B[3]);
MainSection M(Co,G,P,Ci);
Add FA0(A[0],B[0],Ci,F[0]),
FA1(A[1],B[1],Co[1],F[1]),
FA2(A[2],B[2],Co[2],F[2]),
FA3(A[3],B[3],Co[3],F[3]);
Endmodule
4、测试代码:
module test;
// Inputs
reg [3:0] A;
reg [3:0] B;
reg Ci;
// Outputs
wire [3:0] F;
wire [4:1]Co;
// Instantiate the Unit Under Test (UUT)
assign C[2]=G[1]|(P[1]&G[0])|(P[1]&P[0]&Ci);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
件 的可 控性 和可测 性都非常 低 。随着 集成 电路的复 杂 度 日益 加大 , 各 种 内嵌 部 件 设 计 BS 电路 已 为 IT
经 成 为一 种必 要 。高效 的 B S I T提供 了一 系列 的优 点 : 以与 电路 同步 的速度进 行 测试 , 可 可以得到 较高 的故障覆 盖 率 , 等等 。 为逻 辑部件 进 行 B S 设计 在 IT
为逻 辑 电路 设 计 测试 向量 集时 , 根据 具 体 的 问题 应 在 这两 种设计 方法 中进行 折衷 。本 文针 对超前 进位 加法 器提 出 了一 种新 颖 的 B S I T结 构 , 结构 结 合 该 了确定 性 测试 和伪 随机 测 试 的优 点 , 并避 免 了 各 自 的短处 , 结果 不 依赖于 整个 加法器 的规 模 大小 。 其
s nt d t o p tm g ege w at e e or c m tt l l ue
Ke y wor : ds
BI T( uL i efts ) S b i n s L e t ;CLA ;Deemia ets ;P e d rn o ts 1 sg o e tbl y t tr n t e t s u o a d m e t Dein frtsa it i
t k s t ea v n a e fb t e e mi a e t s n s u o a d m e t n l n t st er d s d a t g s A s to a e h d a t g so o h d t r n t e t d p e d r n o t s a d e i a e h i i a v n a e e f a t mi
性 测 试 和 伪 随 机 测 试 的 优 点 , 避 免 了各 自的短 处 。 时 , 提 出 了一 个 测 试 向 量 集 , 充 分 利 用 了 并 同 还 并 C LA 加 法 嚣 内 部 鲒 构 的 规 整 性 , 量 集规 模 较 小 , 于 片 内 集 成 。最 后 , 出 了一 种 计 算 特 征 值 的 向 便 提
时, 部件 测试 向量 集的设 计是 一项重 要的工作 。 ]
一
2 C A 加法器 内部结构 的特 点 L
图 1是 超 前 进 位 / L 加 法 器 的 结 构 框 架 C A) ( 为例子 , 里仅 介绍 8位 C 作 这 LA, 设计 方法 可推 本
W AN G Le,LIY u n, TA N — u a Yiy
( p Elc r n cSc e c n En z e  ̄n De t et o i in e a d g n e g-Nan  ̄ng Un v r iy—Nan i K-Ji n s 1 0 3,P R-Ch n ) i e st ;n a gu2 0 9 ia
新方法 。
关键 词 : 内置 自测 试 {超 前进 住加 法 器; 定性 测 试 ;伪随机 测试 ;可洲性 设计 确
中 图分类 号 : T 7 ; N7 2 TN47 0
文献 标识码 : A
A v l Bu l— n— e f- s c m e f r y- o - e d Add r No e it I - l — - S Te tS he or Ca r — Lo k— Ah a es
ts at r si as n r d c d,whc k sf L u e o h n e n l tu t r e u a i fCLA d es,s h t e tp te n s loito u e ih ma e ul s ft eit ra r cu er g lrt o s y ad r o ta
Abs r e An ef in uL— efts B S t a t: fi e tb i i s e t( I T)s h m ei pe e tdfrc r yto h a ( c tn L c e s r sn e o a r —o k a e d CLA )a d r ,whc d es ih
维普资讯
第 3 2卷第 3期
20 0 2年 6月
微 电 子 学
M ir e e to c c o l c r nis
Vo . 2 № 3 13 .
Ja 02 u 2 0
立章编号 :0 43 6 (0 2 0一 1 50 10 —3 5 2 0 )3O 9— 3
EEAC C : 2 6 J 2 5 5 0 :1 6 B
计 向量集是 很困难 的 。 时 , 以考虑 用伪 随机设 计 此 可
1 引 言
通常, 内嵌 在 大规 模 集 成 电路 中 的常规 逻 辑部
的 方法 , 用这 种 方法 设 计 出来 的 测试 向量 集的 规 但
模 会 随 着 电 路 规 模 的 加 大 呈 几 何 级 数 的新 颖 B S I T架 构
王 乐 ,李 元 ,谈 宜 育 209) 10 3 ( 南京大学 电子科学 与工程 系,江苏 南京
摘
要 : 针 对超 前进位加 法 器( L , 出 了一种 高效 的 BS 架均 。这 种新 的 架构 结合 了确 定 c A)提 IT
