超前进位加法器设计实验实验
设计一个 4 位超前进位加法器(数字逻辑课设)

c[2]=(p[2]&p[1]&p[0]&ci)|(p[2]&p[1]&g[0])|(p[2]&g[1])|g[2],
c[3]=(p[3]&p[2]&p[1]&p[0]&ci)|(p[3]&p[2]&p[1]&g[0])|(p[3]&p[2]&g[1])|(p[3]&g[2])|g[3];
代码如下: add.v
`timescale 1ns/1ps
module add(input [3:0]a,input [3:0]b,input ci,output [3:0]s,output co); //定义所需变量
wire [3:0] p, g; //进位传递函数p,进位产生函数g
wire [3:0] c; //进位函数
设计要求:在这个设计中,你需要使用 Verilog 代码设计一个 4 位的超前进位加法器。这个 4 位超前进位加法器可以完成对两个 4 位二进制数的相加。完成设计后,你还需要设计测试程序(test bench)来验证你的设计。你的测试程序需要考虑到所有可能的输入情况。
设计思路:
因为各进位的产生依赖于低位的进位,所以运算速度较慢。为了提高速度,必须设法使较低位的进位信号越过中间各级直接决定较高位的进位输出,设计Ai和Bi分别表示第i位的被加数和加 数,Ci-1为来自第i-1位全加器的进位,令Pi=Ai^Bi,Gi=Ai&Bi函数表达式为:
Co=PoCo+Go
C1=P1Co+G1
C2=p2C1+G2
4bits超前进位加法器全定制设计实验报告

TPLH
Propagation Delay Time
A1~A4,B1~B4到C4
3
ns
TPHL
3
tT
2.5
tP
2.5
Av Power
4
Layout Area
150*180
2.5真值表
2.6逻辑图
工艺的主要参数(smic18工艺)
参数
参数定义
PMOS数值
NMOS数值
U0
迁移率
8.661m
34m
Vth
-0.4
mA
IOL
Low Level OutputVoltage
8
mA
2.3直流特性
Symbol
Parameter
Test Condition
Value
Units
TA=25°C
Min
Typ
Max
VOH
High Level OutputVoltage
VCC=Min,IOH=Max
VIL=Max,VIH=Min
mA
C0
-0.4
II
InputCurrent @ Max Input Voltage
VCC=Max
VI=7.2V
A,B
0.2
mA
C0
0.1
ICC
Supply Current
VCC=Maxl
Parameter
From (Input )to (Ouput)
Test Condition
(2)点选LM视窗上面的工具列File→New→Library;
(3)会产生New Library画面;
(4)在框内填入库名;
16位超前进位加法器实验报告
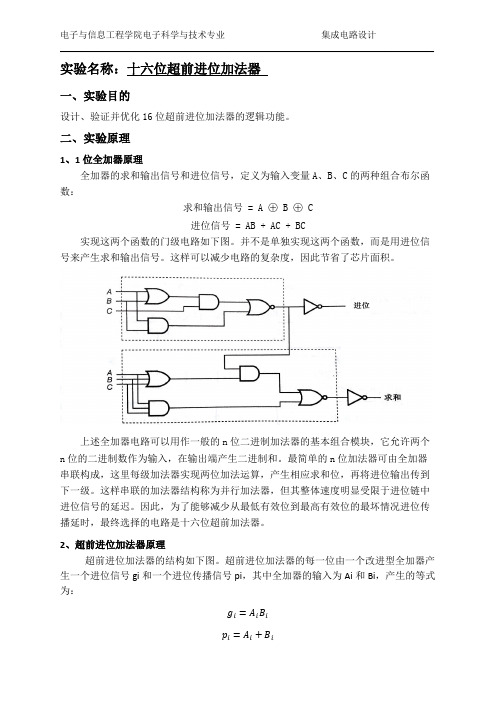
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号 = A ⊕ B ⊕ C进位信号 = AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
四位超前进位加法器

1.课程设计名称四位超前进位加法器2.课程设计内容设计一个四位加法器,要求要有超前进位,减小输出的延迟,采用0.13um工艺设计。
3.课程设计目的训练学生综合运用学过的数字集成电路的基本知识,独立设计相对复杂的数字集成电路的能力。
4.课程设计要求4.1、按设计指导书中要求的格式书写,所有的内容一律打印;4.2、报告内容包括设计过程、仿真的HSPICE网表,软件仿真的结果及分析、延时的手工计算;4.3、要有整体电路原理图,仿真的波形图;4.4、软件仿真必须要有必要的说明;要给出各个输入信号的具体波形和输出信号的测试结果。
4.5、写出对应的HSPICE设计网表,网表仿真结果符合设计要求。
把仿真图形附在报告上。
4.6、设输入端的电容为C,输出端的负载电容为5000C inv,从输入到输出任意找一通inv路,优化通路延时,手工计算确定通路中每个门对应的晶体管的尺寸。
每组三个同学选择不能为同一通路。
此部分的计算参数可采用书中第六章的参数。
4.7、各种器件的具体结构可参考阎石的《数字电子技术基础》一书。
不允许有完全一样的报告,对于报告完全相同者,记为不及格。
5.使用软件软件为HSPICE和COSMOS-SCOPE。
6.课程设计原理由全加器的真值表可得S i和C i的逻辑表达式:定义两个中间变量G i和P i:当A i=B i=1时,G i=1,由C i的表达式可得C i=1,即产生进位,所以G i 称为产生量变。
若P i=1,则A i·B i=0,C i=C i-1,即P i=1时,低位的进位能传送到高位的进位输出端,故P i称为传输变量,这两个变量都与进位信号无关。
将G i和P i代入S i和C i得:进而可得各位进位信号的逻辑表达如下:根据逻辑表达式做出电路图(如图):逻辑功能图中有2输入异或门,2输入与门,3输入与门,4输入与门,2输入或门,3输入或门,4输入或门,其转化成CMOS晶体管图如下:7.课程设计网表*xor 2.subckt xor2 a b c d fmxorpa 1 a vdd vdd pmos l=2 w=8 mxorpb f d 1 vdd pmos l=2 w=8 mxorpc 2 b vdd vdd pmos l=2 w=8 mxorpd f c 2 vdd pmos l=2 w=8 mxorna f a 3 0 nmos l=2 w=4 mxornb 3 b 0 0 nmos l=2 w=4 mxornc f c 4 0 nmos l=2 w=4 mxornd 4 d 0 0 nmos l=2 w=4.ends xor2*and2.subckt and2 a b fmandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4mandna f a 1 0 nmos l=2 w=4 mandnb 1 b 0 0 nmos l=2 w=4.ends and2*and3.subckt and3 a b c fmandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandpc f c vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=6 mandnb 1 b 2 0 nmos l=2 w=6 mandnc 2 c 0 0 nmos l=2 w=6.ends and3*and4.subckt and4 a b c d fmandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandpc f c vdd vdd pmos l=2 w=4 mandpd f d vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=8 mandnb 1 b 2 0 nmos l=2 w=8 mandnc 2 c 3 0 nmos l=2 w=8 mandnd 3 d 0 0 nmos l=2 w=8.ends and4*or2.subckt or2 a b fmorpa 1 a vdd vdd pmos l=2 w=8 morpb f b 1 vdd pmos l=2 w=8 mna f a 0 0 nmos l=2 w=4mnb f b 0 0 nmos l=2 w=4.ends or2*or3.subckt or3 a b c fmorpa 1 a vdd vdd pmos l=2 w=12 morpb 2 b 1 vdd pmos l=2 w=12 morpc f c 2 vdd pmos l=2 w=12 mna f a 0 0 nmos l=2 w=4mnb f b 0 0 nmos l=2 w=4mnc f c 0 0 nmos l=2 w=4.ends or3*or4.subckt or4 a b c d fmorpa 1 a vdd vdd pmos l=2 w=16morpb 2 b 1 vdd pmos l=2 w=16morpc 3 c 2 vdd pmos l=2 w=16morpd f d 3 vdd pmos l=2 w=16mna f a 0 0 nmos l=2 w=4mnb f b 0 0 nmos l=2 w=4mnc f c 0 0 nmos l=2 w=4mnd f d 0 0 nmos l=2 w=4.ends or4*not.subckt not a fmnotpa f a vdd vdd pmos l=2 w=4 mnotna f a 0 0 nmos l=2 w=2.ends not *反相器*or21.subckt or21 a b fxor2 a b 1 or2xnot 1 f not.ends or21 *2输入或门*or31.subckt or31 a b c fxor3 a b c 1 or3xnot 1 f not.ends or31 *3输入或门*or41.subckt or41 a b c d fxor4 a b c d 1 or4xnot 1 f not.ends or41 *4输入或门*xor21.subckt xor21 a b fxm a A5 notxn b B5 notxxor a b A5 B5 f xor2.ends xor21 * 2输入异或门*and21.subckt and21 a b fxand2 a b 1 and2xnot 1 f not.ends and21 *2输入与门*and31.subckt and31 a b c fxand3 a b c 1 and3xnot 1 f not.ends and31 *3输入与门*and41.subckt and41 a b c d fxand4 a b c d 1 and4xnot 1 f not.ends and41 *4输入与门xxor211 a1 b1 p1 xor21xxor212 a2 b2 p2 xor21xxor213 a3 b3 p3 xor21xxor214 a4 b4 p4 xor21xand211 a1 b1 g1 and21xand212 a2 b2 g2 and21xand213 a3 b3 g3 and21xand214 p1 c0 m0 and21xor211 m0 g1 c1 or21 *进位C1xand311 p2 p1 c0 m1 and31xand215 p2 g1 m2 and21xor312 g2 m1 m2 c2 or31 *进位C2 xand411 p3 p2 p1 c0 m3 and41xand313 p3 p2 g1 m4 and31xand216 p3 g2 m5 and21xor412 m3 m4 m5 g3 c3 or41 *进位C3 xxor215 p1 c0 s1 xor21 *输出s1xxor216 p2 c1 s2 xor21 *输出s2xxor217 p3 c2 s3 xor21 *输出s3xxor218 p4 c3 s4 xor21 *输出s4.include "c:\lib\130nm_bulk.l"tt.opt scale=0.05u.global vdd gndvdd vdd 0 1.2va1 a1 0 pulse 1.2 1.2 20n 1f 1f 30n 100nva2 a2 0 pulse 0 0 20n 1f 1f 30n 100nva3 a3 0 pulse 0 0 20n 1f 1f 30n 100nva4 a4 0 pulse 0 0 20n 1f 1f 30n 100nvb1 b1 0 pulse 1.2 1.2 20n 1f 1f 30n 100n vb2 b2 0 pulse 1.2 1.2 20 1f 1f 30n 100nvb3 b3 0 pulse 0 0 20n 1f 1f 30n 100nvb4 b4 0 pulse 1.2 1.2 20n 1f 1f 30n 100nvc0 c0 0 pulse 0 0 4n 1f 1f 0n 100n.tran 1n 100n.plot tran v(s1).plot tran v(s2).plot tran v(s3).plot tran v(s4).end8.结果及分析由波形可知:当输入a1=1,b1=1,前一级进位c0=0时,s1=a1+b1+c0=0,下一级进位c1=1.由波形可知:当输入a2=0,b2=1,前一级进位c1=1时,s2=a2+b2+c1=0,下一级进位c2=1.由波形可知:当输入a3=0,b3=0,前一级进位c2=1时,s3=a3+b3+c2=1,下一级进位c3=0.由波形可知:当输入a4=0,b4=1,前一级进位c3=0时,s4=a4+b4+c2=1。
试验二 超前进位加法器 设计

试验二超前进位加法器设计练习2. 4位超前进位加法器行波进位加法器延时较长,可采用超前进位加法器减少延时,但是由此会造成电路的复杂。
超前进位加法器原理参见《数字集成电路》(周润德第二版)424页。
对以上公式的注解:公式中的C O,K 表示第K 为的进位输出,G K 为第K 位的进位产生,P K 为第K 为的进位传播。
且:K K KK K KG A B P A B ==⊕ A K ,B K 为输入加数的第K 位。
将Co 和S 用G,P 重写为: O ii C G PC S P C =+=⊕由于低位的输出进位是高位的输入进位,所以有上面的(11.15)式源程序://this is a carry lookahead of 4bitmodule clad(ina,inb,ci,co,sum);input[3:0] ina,inb;input ci;output co;output[3:0]sum;wire co0,co1,co2,G0,G1,G2,G3,P0,P1,P2,P3;assignG0=ina[0]&inb[0],P0=ina[0]^inb[0],G1=ina[1]&inb[1],P1=ina[1]^inb[1],G2=ina[2]&inb[2],P2=ina[2]^inb[2],G3=ina[3]&inb[3],P3=ina[3]^inb[3],co0=G0|(P0&ci),co1=G1|(P1&co0),co2=G2|(P2&co1),co=G3|(P3&co2),sum[0]=P0^ci,sum[1]=P1^co0,sum[2]=P2^co1,sum[3]=P3^co2;endmodule测试程序:module clad_test;reg[3:0] ina,inb;reg ci;wire co;wire[3:0]sum;clad CI(.ina(ina),.inb(inb),.ci(ci),.co(co),.sum(sum)); initialbeginina=0;inb=0;ci=0;endalways #5 ina=ina+1'b1;always #80 inb=inb+1'b1;always #1280 ci=~ci;endmodule仿真结果:注:该结果为10进制显示练练手:参考《数字集成电路》(周润德第二版)420-421,设计一个16位的超前进位加法器,基本单元使用4位的加法器,结构自选。
16位超前加法器实验报告

16位超前加法器设计实验一、实验分析:四位超前进位加法器HDL程序:module add4_head ( a, b, ci, s, pp, gg);input[3:0] a;input[3:0] b;input ci;output[3:0] s;output pp;output gg;wire[3:0] p;wire[3:0] g;wire[2:0] c;assign p[0] = a[0] ^ b[0];assign p[1] = a[1] ^ b[1];assign p[2] = a[2] ^ b[2];assign p[3] = a[3] ^ b[3];assign g[0] = a[0] & b[0];assign g[1] = a[1] & b[1];assign g[2] = a[2] & b[2];assign g[3] = a[3] & b[3];assign c[0] = (p[0] & ci) | g[0];assign c[1] = (p[1] & c[0]) | g[1];assign c[2] = (p[2] & c[1]) | g[2];assign pp = p[3] & p[2] & p[1] & p[0];assign gg = g[3] | (p[3] & (g[2] | p[2] & (g[1] | p[1] & g[0])));assign s[0] = p[0] ^ ci;assign s[1] = p[1] ^ c[0];assign s[2] = p[2] ^ c[1];assign s[3] = p[3] ^ c[2];endmodulep表示进位否决信号(pass),如果p为0就否决调前一级的进位输入。
否决的意思就是即使前一级有进位,本级也不会向后一级产生进位输出。
数字电路课程设计之超前进位加法器
reg
Cin;
wire[3:0] S;
wire
Cout;
carry_look_add CAL (.A(A),.B(B),.Cin(Cin),.Cout(Cout),.S(S)); initial begin
#10 A=4'd0;B=4'd0;Cin=0; #10 A=4'd11;B=4'd1;Cin=0; #10 A=4'd10;B=4'd12;Cin=0; #10 A=4'd11;B=4'd4;Cin=0; #100 $stop; end endmodule
Pi=Ai○+ Bi;
可以得到输出与进位表达
Gi=AiBi;
Si=Pi○+ Ci;
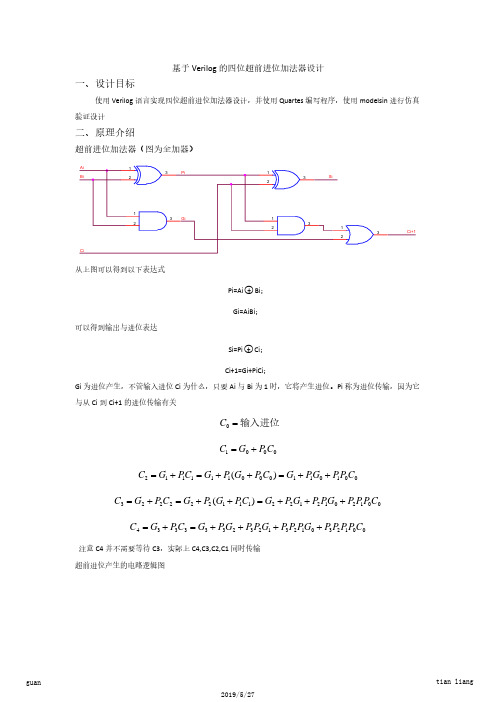
Ci+1=Gi+PiCi; Gi 为进位产生,不管输入进位 Ci 为什么,只要 Ai 与 Bi 为 1 时,它将产生进位。Pi 称为进位传输,因为它 与从 Ci 到 Ci+1 的进位传输有关
C0 = 输入进位
C1 = G0 + P0C0
Half_Add H3(.a(A[2]),.b(B[2]),.s(v6),.c(v5));
Half_Add H4(.a(A[3]),.b(B[3]),.s(v8),.c(v7));
carry_look
CL1(.C0(Cin),.P0(v2),.G0(v1),.P1(v4),.G1(v3),.P2(v6),.G2(v5),.P3(v8),.G3(v7),.C1(o1),.C2(o2),.C3(o3),.C4(Cout));
注意 C4 并不需要等待 C3,实际上 C4,C3,C2,C1 同时传输 超前进位产生的电路逻辑图
数字电路课程设计之超前进位加法器

# MACRO ./mul_run_msim_rtl_verilog.do PAUSED at line 14
通过查阅资料将 Verilog 测试文件
Timsbench 文件没有实例化,修改为
修改后仿真 OK 参考文献: 1.数字设计与 Verilog 实现 M.Morris Mano 著 第五版
Pi=Ai○+ Bi;
可以得到输出与进位表达
Gi=AiBi;
Si=Pi○+ Ci;
Ci+1=Gi+PiCi; Gi 为进位产生,不管输入进位 Ci 为什么,只要 Ai 与 Bi 为 1 时,它将产生进位。Pi 称为进位传输,因为它 与从 Ci 到 Ci+1 的进位传输有关
C0 = 输入进位
C1 = G0 + P0C0
instance name in instantiation of 'carry_look_add'.
#
#
Region: /carry_look_add_tb
# Error loading design
# Error: Error loading design
#
Pausing macro execution
基于 Verilog 的四位超前进位加法器设计
使用 Verilog 语言实现四位超前进位加法器设计,并使用 Quartes 编写程序,使用 modelsin 进行仿真
验证设计
二、原理介绍
超前进位加法器(图为全加器)
Ai
1
3
Pi
Bi
2
1
3
Si
2
1 3 Gi
2
Ci
1
3
计算机组成原理课程设计—超前进位加法器的设计资料

沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:班级:学号:姓名:指导教师:完成日期:沈阳航空航天大学课程设计报告目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (4)2.1顶层方案图的设计与实现 (4)2.1.1创建顶层图形设计文件 (4)2.1.2器件的选择与引脚锁定 (5)2.1.3编译、综合、适配 (7)2.2功能模块的设计与实现 (7)2.2四位超前进位加法器模块的设计与实现 (7)2.3仿真调试 (9)第3章编程下载与硬件测试 (11)3.1编程下载 (11)3.2硬件测试及结果分析 (11)参考文献 (13)附录(程序清单或电路原理图) (14)第1章总体设计方案1.1设计原理八位超前进位加法器,可以由2个四位超前进位加法器构成。
由第一个四位超前进位加法器的进位输出作为第二个超前进位加法器的进位输入即可实现八位超前进位加法器的设计。
超前进位产生电路是根据各位进位的形成条件来实现的。
只要满足下述条件,就可形成进位C1、C2、C3、C4。
所以:第一位的进位C1=X1*Y1+(X1+Y1)*C0第二位的进位C2=X2*Y2+(X2+Y2)*X1*Y1+(X2+Y2)(X1+Y1)C0第三位的进位C3=X3*Y3+(X3+Y3)X2*Y2+(X3+Y3)*(X2+Y2)*X1*Y1+(X3+Y3)(X2+Y2)(X1+Y1)*C0第四位的进位C4=X4*Y4+(X4+Y4)*X3*Y3+(X4+Y4)*(X3+Y3) * X2*Y2+(X4+Y4)(X3+Y3)(X2+Y2)*X1*Y1+(X4+Y4)(X3+Y3)(X2+Y2)(X1+Y1)*C0 下面引入进位传递函数Pi和进位产生函数Gi的概念。
它们定义为:Pi=Xi+YiGi=Xi*YiP1的意义是:当X1和Y1中有一个为1时,若有进位输入,则本位向高位传递此进位。
计组-加法器实验报告

半加器、全加器、串行进位加法器以及超前进位加法器一、实验原理1.一位半加器A和B异或产生和Sum,与产生进位C2.一位全加器将一位半加器集成封装为halfadder元件,使用两个半加器构成一位的全加器3.4位串行进位加法器将一位全加器集成封装为Fulladder元件,使用四个构成串行进位加法器4.超前进位加法器(4位)⑴AddBlock产生并行进位链中的ti(即Cthis)和di(即Cpass),以及本位结果Sum⑵进位链(Cmaker)四位一组并行进位链,假设与或非门的级延迟时间为1.5ty,与非门的延迟时间为1ty,在di和ti产生之后,只需2.5ty就可产生所有全部进位⑶超前进位加法器将以上二者结合起来即可完成,A和B各位作为各个AddBlock的输入,低一位的进位Ci-1作为本位AddBlock的C-1的输入。
各个AddBlock输出的C_this和C_pass作为对应的Cmaker的thisi和passi的输入。
二、实验器材QuartusII仿真软件,实验箱三、实验结果1.串行进位加法器结果2.超前进位加法器结果四、实验结果分析1.实验仿真结果显示串行加法器比超前进位加法器快,部分原因应该是电路结构优化不到位。
另外由于计算的位数比较少,超前进位加法链结构较复杂,所以优势没体现出来,反倒运作的更慢一点。
当位数增加的时候,超前进位加法器会比串行的更快。
2.波形稳定之前出现上下波动,应该与“竞争冒险”出现的情况类似,门的延迟和路径的不同导致了信号变化时到达的时间有先有后,因此在最终结果形成前出现了脉冲尖峰和低谷;另外也可能部分原因由于电路结构优化的不到位所致。
超前进位加法器设计报告解剖

华东交通大学理工学院课程设计报告书所属课程名称EDA课程设计题目超前进位加法器设计分院专业班级学号学生姓名指导教师2013 年7月2日目录第一章设计内容与要求 (3)第二章超前进位加法器设计原理 (3)第三章详细设计流程 (4)3.1.创建工程文件 (4)3.2.程序的编译 (5)3.3.波形的仿真 (7)第四章设计结果分析 (11)第五章源程序代码 (12)第六章心得体会 (14)第七章参考文献 (15)第一章设计内容与要求加法运算是最重要也是最基本的运算,所有的其他基本运算,如减、乘、除运算最终都能归结为加法运算。
但因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于他的位相关。
因此为了减少进位传输所消耗的时间,提高计算速度,人们设计了多种类型的加法器,如跳跃进位加法器、进位选择加法器、超前进位加法器等。
本设计采用的是超前进位加法器。
通过Verilog 设计一个超前8位加法器。
要求在Quartus II软件下,利用Verilog编程完成层次式电路设计,电路中的元件可以用Verilog设计也可以用库元件连线构成再封装。
8位超前进位加法器,借助EDA工具中的综合器,适配器,时序仿真器和编程器等工具进行相应处理。
适配采用Cyclone系列的EP1C6Q240C8。
要求综合出RTL电路,并进行仿真输入波形设计并分析电路输出波形. 试比较并阐述数据类型reg型和wire型的区别。
第二章超前进位加法器设计原理将n个全加器相连可得n位加法器,但是加法时间较长。
解决的方法之一是采用“超前进位产生电路”来同时形成各位进位,从而实现快速加法。
超前进位产生电路是根据各位进位的形成条件来实现的首先对于1位加法器基本位值和与进位输出为1;如果a,b有一个为1,则进位输出等于cin;令G=ab,P=a+b,则有:Cout==ab+(a+b)cin=G+P•cin由此可以G和P来写出4位超前进位链如下(设定四位被加数和加数为A 和B,进位输入Cin,进位输出为cout,进位产生Gi=AiBi,进位传输Pi=Ai+Bi);C0=cin;C1=G0+P0C0=G0+P0•cinC2=G1+P1C1=G1+P1(G0+P0cin)=G1+P1G0+P1P0cinC3=G2+P2C2=G2+P2(G1+P1cin)=G2+P2G1+P2P1G0+P2P1P0cinC4=G3+P3C3=G3+P3(G2+P2C2)=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0cin Cout=c4由超前进位链,各个进位彼此独立产生,将进位级联传播给去掉了,因此,减小了进位产生的延迟时间。
存储器、加法器以及乘法器实验

北京科技大学计算机与通信工程学院实验报告实验名称: 存储器、加法器以及乘法器学生姓名:专业:班级:学号:指导教师:实验成绩:实验地点:实验时间:年月日一、实验目的与实验要求1、实验目的(1)实验一:静态随机存储器实验①掌握静态随机存储器的基本结构。
②掌握静态随机存储器 RAM工作特性及数据的读写方法。
(2)实验二:超前进位加法器设计实验①掌握超前进位加法器的原理及其设计方法。
②熟悉 FPGA 应用设计及 QuartusII 软件的使用。
③理解使用超前进位逻辑设计ALU的方法。
(3)实验三:阵列乘法器设计实验①掌握乘法器的原理及其设计方法。
②熟悉QuartusII 软件的使用及FPGA应用设计。
2、实验要求(1)了解静态随机存储器的工作原理,利用实验箱进行验证性实验,并完成实验箱的写入、读取数据。
(2) 利用QuartusII 软件完成超前进位加法器设计,原理图设计或者程序编程实现其进位加法功能,并且下载到实验箱里完成验证。
(3)用文字描述或者画图方式给出FPGA外围电路接线图,并在QuartusII 软件中完成阵列乘法器的设计,运行观测结果。
二、实验设备(环境)及要求CM3+实验环境、QuartusⅡ8.0环境三、实验内容与步骤1、实验1(1)实验原理本实验所用的静态随机存储器(SRAM)由一片 6116 芯片(2K×8bit)构成(位于 MEM 单元),如图所示。
6116 的容量为 2KB,包含 11 根地址线,即 A10~A0,数据宽度为 8位,除电源和地线外,还有三根控制线:CS (片选线)、OE (读线)、WE (写线),其功能如表3.5 所示,在片选信号有效(CS=0,低电平有效)的前提下,当OE=0 时进行读操作,当WE =0 时进行写操作,本实验平台将CS常接地。
存储器(MEM)最终是要挂接到 CPU 上,所以还需要一个读写控制逻辑,使得 CPU能控制 MEM 的读写,实验中的读写控制逻辑如图所示,图中读信号 RD 和写信号 WR都是高电平有效。
074-王楠-计组实验三(超前进位加法器设计实验)

延安大学计算机学院实验报告专用纸
这个4 x 4阵列乘法器的原理如图1-3-1所示。
FA (全加器)的斜线方向为进位输出,竖线方向为和输出。
图中阵列的最后-行构.成了一个串行进位加法器。
由于FA一级是无需考虑进位的,它的进位被暂时保留下来不往前传递,因此同- -极中任意- -位FA加法器的进位输出与和输出几乎是同时形成的,与“串行移位”相比可大大减少同级间的进位传递延迟,所以送往最后一行串行加法器的输,入延迟仅与FA 的级数(行数)有关,即与乘数位数有关。
本实验用CPLD来设计一个4x4位加法器,且全部采用原理图方式实现。
【5】实验步骤
(1)根据上述阵列乘法器的原理,使用Quartus |I 软件编辑相应的电路原理图并进行编译,其在EPM1270 芯片中对应的引脚如图1-3-2所示,框外文字表示I/O号,框内文字表示该引脚的含义。
(2)关闭实验系统电源,按图1-3-3连接实验电路,图中将用户需要连接的信号用圆圈标明。
(3)实物图如下:
(4)打开实验系统电源,将生成的POF文件下载到EPM1270中去。
(5)以CON单元中的SD10...SD13四个二进制开关为乘数A,SD14.. SD17四个二进制开关为被乘数B,而相乘的结果在CPLD单元的L7...LO八个LED灯显示。
给A和B置不同的数,观察相乘的结果。
【6】实验结果
1、输入:1111 1111
结果:1111111
2、输入:0000 0000
结果:00000000。
16位超前进位加法器实验报告
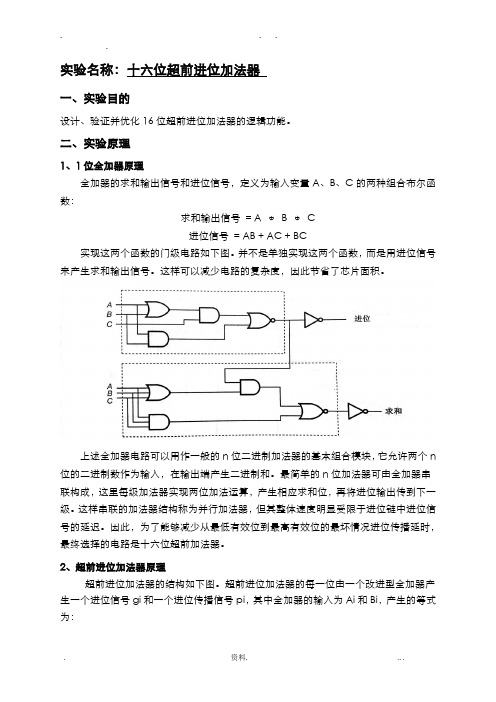
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号= A ⊕B ⊕C进位信号= AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
数字集成电路工程实践64位超前进位加法器

数字集成电路工程实践64位超前进位加法器64位超前进位加法器是一种数字集成电路,可以将两个64位的二进
制数相加,并且正确地处理进位。
64位超前进位加法器通常由多个4位的全加器级联构成。
每个全加
器接收两个输入位和一个进位位,并产生一个和位和一个进位位作为输出。
在64位超前进位加法器中,首先将两个输入数的最低位和进位输入
到第一个全加器。
然后,将每个全加器的和位输出作为下一个全加器的输
入和进位位输入。
最后一个全加器的和位作为输出的结果。
对于进位位的处理,如果两个输入位和进位位中的任意两位有两个以
上为1,则产生进位,否则不产生进位。
每个全加器的进位位输出作为下
一个全加器的进位输入。
64位超前进位加法器可以在一个时钟周期内完成64位二进制数的加
法运算,并且保证了正确地处理进位。
这种数字集成电路在计算机系统中广泛使用,特别是在高性能计算和
数据处理应用中。
它可以进行大规模的数据并行计算,加速数据处理和计
算速度,提高计算机系统的性能。
杭电计组实验2-超前进位加法器设计实验

杭州电子科技大学计算机学院
实验报告
实验项目:实验2-超前进位加法器设计实验
课程名称:计算机组成原理与系统结构课程设计
姓名:学号:同组姓名:学号:
实验位置(机号):
实验日期:指导教师:
#100;
A = 1011;
B = 1101;C0 = 0;
#100;
A = 1010;
B = 0010;C0 = 1;
#100;
A = 0111;
B = 1000;C0= 0;
#100;
A = 0011;
B = 0100;C0 = 1;
#100;
A = 1001;
B = 0001;C0 = 0;
#100;
end
Endmodule
RTL图
二、结果
思考题:
(1)综合得到的电路图,它和想要设计的电路在引脚的输入输出方面是完全相同的,但是相比较内部的RTL图,实验实现的结果是相同的,但是我编写的实验代码并没有调用实验一的全加器设计。
(2)尝试编写8位超前进位加法器设计实验
module add_8 ( input [7:0]a, input [7:0]b, input cin, output [7:0] s, output co );
wire [7:0]c_tmp;
wire [7:0]g;
wire [7:0]p;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《计算机组成原理》实验报告
实验序号:四实验项目名称:超前进位加法器设计实验xx 1xx 姓名xx 专业、班XX
实验地点XX 指导教师xx 实验时间XX
一、实验目的及要求
(1) 掌握超前进位加法器的原理及其设计方法。
(2) 熟悉CPLD 应用设计及EDA 软件的使用。
二、实验设备(环境)及要求
PC 机一台,TD-CM3+或TD-CMX 实验系统一套。
三、实验内容与步骤
(1) 根据上述加法器的逻辑原理使用Quartus II 软件编辑相应的电路原理图并进行编译,其在EPM1270 芯片中对应的引脚如图1-2-7 所示,框外文字表示I/O 号,框内文字表示该引脚的含义(本实验例程见‘安装路径\Cpld\Adder\Adder.qpf’工程)。
(2)关闭实验系统电源,按图1-2-8 连接实验电路,图中将用户需要连接的信号用圆圈标明。
(3) 打开实验系统电源,将生成的POF 文件下载到EPM1270 中去。
(4) 以CON 单元中的SD17…SD10 八个二进制开关为被加数A,SD07…SD00 八个二进制开关为加数B,K7 用来模拟来自低位的进位信号,相加的结果在CPLD 单元的L7…L0 八个LED灯显示,相加后向高位的进位用CPLD 单元的L8 灯显示。
给A 和B 置不同的数,观察相加的结果。
四、实验结果与数据处理
如在SD17...SD10中输入1111 1001,在SD07...SD00中输入1001 1111,在实验箱中可看到用来模拟低位与高位的进位信号K7、L8灯变亮,同时可看到A01...A08与L7...L0上的显示分别为1001与1000。
五、分析与讨论(心得)
这个实验是上个实验的扩展,进一步加深了我对运算器的认识。
现实生活中我们也要学会对已有的知识的一种扩展补充,进一步加深对已有知识的巩固,并探索其更深层次的东西,设计出与众不同的东西来。
这个算法的核心是把8 位加法器分成两个 4 位加法器,先求出低 4 位加法器的各个进位,特别是向高4 位加法器的进位 C 4 。
然后,高4 位加法器把 C 4 作为初始进位,使用低4 位加法器相同的方法来完成计算。
每一个 4 位加法器在计算时,又分成了两个 2
位的加法器。
如此递归。
随着加法器位数的增加,越是高位的进位逻辑电路就会越复杂:
定义
Gi,j=gi+pigi-1+pipi-1gi-2+…+pipi-1…pj+1gj ;Pi,j=pi pi-1…pj+1 pj
则有
Gi,i=gi ;Pi,i=pi ;Gi,j=Gi,k+Pi,kGk-1,j ;Pi,j=Pi,kPk-1,j
Ci+1=Gi,j+Pi,jCj
从而可知四位超前进位加法算法如下:
G1,0=g1+p1g0; P1,0=p1p0
G3,2=g3+p3g2; P3,2=p3p2
G3,0=G3,2+P3,2G1,0; P3,0=P3,2P1,0
C4=G3,0+P3,0C0
八位超前进位加法算法如下:
G1,0=g1+p1g0;P1,0=p1p0
G3,2=g3+p3g2; P3,2=p3p2
G3,0=G3,2+P3,2G1,0; P3,0=P3,2P1,0
G5,4=g5+p5g4; P5,4=p5p4
G7,6=g7+p7g6; P7,6=p7p6
G7,4=G7,6+P7,6G5,4; P7,4=P7,6P5,4
G7,0=G7,4+P7,4G3,0; P7,0=P7,4P3,0
C8=G7,0+P7,0C0
六、教师评语成绩
签名:日期:。
