超前进位加法器设计报告
超前进位加法器

超前进位加法器超前进位加法器是一种重要的数电电路,广泛应用于计算机和其他电子设备中。
它的作用是在进行多位数相加时,实现进位的自动计算和传递,从而提高计算速度和准确性。
本文将对超前进位加法器进行详细介绍。
超前进位加法器是一种基于逻辑门电路的加法器。
它的设计理念是通过预先检测进位,减少进位的传输延迟,从而加快计算速度。
对于一位加法器来说,传统的进位加法器需要等待当前位的进位计算完成后,才能进行下一位的计算。
而超前进位加法器在当前位计算的同时,预先计算下一位的进位,从而节省了计算时间。
超前进位加法器的基本原理是利用逻辑门的延迟特性实现进位的预先计算。
常见的超前进位加法器包括Ripple Carry Adder(RCA)、Carry Select Adder(CSA)和Carry Lookahead Adder(CLA)。
这些加法器在实现进位预先计算的方式上有所不同,但核心思想都是一样的。
以Ripple Carry Adder为例,它由多个全加器级联而成。
全加器是一种可以同时实现两位相加和进位计算的电路。
Ripple Carry Adder通过将多个全加器级联,实现了对多位数相加的计算。
在每个全加器中,除了计算两位之和外,还需要计算当前位的进位。
传统的Ripple Carry Adder需要等待前一位的进位计算完成后,才能进行下一位的计算,而这就导致了较长的计算时间。
而超前进位加法器则在每个全加器中预先计算下一位的进位。
通过利用逻辑门的传输延迟,将当前位的进位信号传递到下一位,实现了进位的预先计算。
这样,在当前位的计算完成后,下一位的进位已经预先计算好了,从而减少了计算时间。
超前进位加法器在计算速度上有显著的优势。
相比传统的进位加法器,它能够减少计算时间,提高计算效率。
对于大规模的数值计算,超前进位加法器能够显著缩短计算时间,提高计算速度。
这对于例如计算机科学、数据处理和通信等领域的应用非常重要。
除了计算速度的优势,超前进位加法器在准确性上也有一定的优势。
设计一个 4 位超前进位加法器(数字逻辑课设)

c[2]=(p[2]&p[1]&p[0]&ci)|(p[2]&p[1]&g[0])|(p[2]&g[1])|g[2],
c[3]=(p[3]&p[2]&p[1]&p[0]&ci)|(p[3]&p[2]&p[1]&g[0])|(p[3]&p[2]&g[1])|(p[3]&g[2])|g[3];
代码如下: add.v
`timescale 1ns/1ps
module add(input [3:0]a,input [3:0]b,input ci,output [3:0]s,output co); //定义所需变量
wire [3:0] p, g; //进位传递函数p,进位产生函数g
wire [3:0] c; //进位函数
设计要求:在这个设计中,你需要使用 Verilog 代码设计一个 4 位的超前进位加法器。这个 4 位超前进位加法器可以完成对两个 4 位二进制数的相加。完成设计后,你还需要设计测试程序(test bench)来验证你的设计。你的测试程序需要考虑到所有可能的输入情况。
设计思路:
因为各进位的产生依赖于低位的进位,所以运算速度较慢。为了提高速度,必须设法使较低位的进位信号越过中间各级直接决定较高位的进位输出,设计Ai和Bi分别表示第i位的被加数和加 数,Ci-1为来自第i-1位全加器的进位,令Pi=Ai^Bi,Gi=Ai&Bi函数表达式为:
Co=PoCo+Go
C1=P1Co+G1
C2=p2C1+G2
超前进位加法器

超前进位加法器超前进位加法器是一种数字电路,用于执行两个二进制数的加法运算。
它具有高速、高效的特点,在计算机领域得到广泛的应用。
超前进位加法器的原理和实现方法值得深入研究和探讨。
本文将详细介绍超前进位加法器的原理、设计和性能优化等方面内容。
1. 引言在计算机科学和工程领域,加法运算是一项基本的操作。
随着计算机性能的要求不断提高,如何在更短的时间内完成加法运算成为了重要的研究方向。
超前进位加法器是一种对加法运算进行优化的方法,可以极大地提高运算速度和效率。
2. 超前进位加法器原理超前进位加法器是一种并行加法器,它利用了信号传输的延迟问题,通过将进位信号从低位传递到高位,实现了高速的运算。
其基本原理是,将两个二进制数按位相加,如果某一位的和等于2,就会产生一个进位信号,进位信号会传递到下一位,直到最高位。
3. 超前进位加法器的设计超前进位加法器的设计分为四个部分:1) 带有进位预测的半加器;2) 带有进位预测的全加器;3) 进位生成和进位传递逻辑电路;4) 加法器的结构和电路实现。
3.1 带有进位预测的半加器半加器是最基本的加法器,可以完成两个二进制位的加法运算,但不能处理进位信号。
为了实现进位预测,我们需要对半加器进行改进。
一种常见的方法是使用XOR门和AND门来实现进位预测功能。
具体的电路设计和逻辑表达式请查阅相关资料。
3.2 带有进位预测的全加器全加器是进一步改进的半加器,可以处理进位信号。
在超前进位加法器的设计中,我们使用带有进位预测的全加器。
全加器的设计和实现方法与半加器类似,但需要增加一个输入端来接收上一位的进位信号,并根据进位预测电路来生成进位信号。
3.3 进位生成和进位传递逻辑电路进位生成和进位传递逻辑电路是超前进位加法器的核心部分。
它们用于计算每一位的进位信号和传递进位信号到下一位。
进位生成电路可以通过AND门实现,进位传递电路可以通过OR 门实现。
具体的电路设计和实现方法请参考相关资料。
试验二 超前进位加法器 设计

试验二超前进位加法器设计练习2. 4位超前进位加法器行波进位加法器延时较长,可采用超前进位加法器减少延时,但是由此会造成电路的复杂。
超前进位加法器原理参见《数字集成电路》(周润德第二版)424页。
对以上公式的注解:公式中的C O,K 表示第K 为的进位输出,G K 为第K 位的进位产生,P K 为第K 为的进位传播。
且:K K KK K KG A B P A B ==⊕ A K ,B K 为输入加数的第K 位。
将Co 和S 用G,P 重写为: O ii C G PC S P C =+=⊕由于低位的输出进位是高位的输入进位,所以有上面的(11.15)式源程序://this is a carry lookahead of 4bitmodule clad(ina,inb,ci,co,sum);input[3:0] ina,inb;input ci;output co;output[3:0]sum;wire co0,co1,co2,G0,G1,G2,G3,P0,P1,P2,P3;assignG0=ina[0]&inb[0],P0=ina[0]^inb[0],G1=ina[1]&inb[1],P1=ina[1]^inb[1],G2=ina[2]&inb[2],P2=ina[2]^inb[2],G3=ina[3]&inb[3],P3=ina[3]^inb[3],co0=G0|(P0&ci),co1=G1|(P1&co0),co2=G2|(P2&co1),co=G3|(P3&co2),sum[0]=P0^ci,sum[1]=P1^co0,sum[2]=P2^co1,sum[3]=P3^co2;endmodule测试程序:module clad_test;reg[3:0] ina,inb;reg ci;wire co;wire[3:0]sum;clad CI(.ina(ina),.inb(inb),.ci(ci),.co(co),.sum(sum)); initialbeginina=0;inb=0;ci=0;endalways #5 ina=ina+1'b1;always #80 inb=inb+1'b1;always #1280 ci=~ci;endmodule仿真结果:注:该结果为10进制显示练练手:参考《数字集成电路》(周润德第二版)420-421,设计一个16位的超前进位加法器,基本单元使用4位的加法器,结构自选。
超前进位加法器的设计分解

超前进位加法器的设计分解沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:计算机科学与技术班级:学号:姓名:指导教师:完成日期:2014年01月10日第2章详细设计方案2.1 顶层方案图的设计与实现顶层方案图主要实现一位全加器的逻辑功能,采用原理图设计输入方式完成,超前进位加法器电路的是实现基于XCV200可编程逻辑芯片。
在完成原理图的功能设计后,经过检测调试,把输入/输出信号通过引脚编号安排到XCV200指定的引脚上去,最终实现芯片的引脚锁定。
2.1.1顶层方案的整体设计顶层图形文件主要由2个四位超前进位加法器构成,总共17位输入,9位输出。
顶层图形文件由Xilinx Foundation F3.1软件编辑得到相应的模块,顶层图形的整体设计如下图2.1所示:图 2.1八位超前进位加法器整体设计图2.1.2元器件选择和引脚锁定(1)元器件的选择由于在设计的过程中,硬件设计环境是基于伟福COP2000型计算机组成原理实验仪和XCV200实验板,故采用的目标芯片为Xilinx XCV200可编程逻辑芯片。
(2)引脚锁定在Xilinx Foundation F3.1上面完成软件的设计之后,把顶层图形文件中的输入/输出信号用引脚编号安排到Xilinx XCV200芯片指定的引脚上去,从而实现芯片的设计电路的引脚锁定,各信号及Xilinx XCV200芯片引脚对应关系如下表2.1所示:表 2.1 信号和芯片引脚对应关2.2 功能模块的设计与实现在八位超前进位加法器和四位超前进位加法器的设计中均是采用Schematic 设计输入方式,而在四位超前进位加法器的设计中是由一列的门电路构成,最后在由2个四位超前进位加法器模块构成8位超前进位加法器。
可以扩展开来,16位,32位超前进位加法器原理类似8位的设计原理。
2.2.1 八位超前进位加法器的设计与实现(1)设计描述根据上面在1.1中讲述的四位超前进位加法器的设计原理那样,四位超前进位加法器的实现是建立在进位C1,C2,C3,C4的基础之上的。
数字集成电路课程设计报告-4bits超前进位加法器

数字集成电路课程设计报告-4bits超前进位加法器福州⼤学⾄诚学院数字集成电路课程设计报告设计题⽬:4bits 超前进位加法器班级:专业:姓名:学号:组名:指导⽼师:教师评分:⽇期:4bits超前进位加法器⽬录第1章概述.................................................................... - 3 -1.1课程设计⽬的 (3)1.2课程设计的主要内容 (3)1.2.1设计题⽬ (3)1.2.2设计内容 (3)第2章功能分析及逻辑分析...................................................... - 3 -2.1功能分析 (3)2.2推荐⼯作条件 (4)2.3电性能 (4)2.4交流(开关)特性 (5)2.5真值表 (6)2.6表达式 (6)2.7电路图 (7)第3章电路设计及器件参数设计.................................................. - 7 -3.1性能指标: (7)3.2模块划分 (7)3.2.1输出级电路设计 (7)3.2.2内部反相器 (8)3.2.3内部电路等效 (8)3.2.4输⼊级电路 (9)3.2.5中间缓冲级电路 (9)3.2.6输出缓冲级电路 (9)3.2.7输⼊、输出保护电路 (10)3.3本章⼩结 (10)第4章功耗估算与延时......................................................... - 10 -4.1电容估算 (10)4.2功耗估算 (11)4.3延时估算 (11)4.4本章⼩结 (12)第5章电路模拟与仿真......................................................... - 12 -5.1电路搭建 (12)5.1.1建⽴新库 (12)5.1.2建⽴SCHEMATIC VIEW (13)5.1.3建⽴SYMBOL (13)5.1.4建⽴总体电路SCHEMATIC VIEW (13)数字集成电路课程设计5.1.5建⽴总体SYMBOL (14)5.1.6测试电路 (14)5.2功能仿真 (15)5.3功耗仿真 (15)5.4仿真结果分析 (16)5.5本章⼩结 (16)第6章版图设计............................................................... - 16 -6.1原理 (16)6.2反相器版图 (17)6.2.1 LAYOUT VIEW的建⽴ (17)6.2.2添加器件 (18)6.2.3互连,实现反相器功能 (18)6.3输⼊级 (19)6.4输出级 (19)6.5输出缓冲 (19)6.6异或门 (20)6.7或⾮门 (20)6.8与门 (20)6.9整体版图 (21)6.10本章⼩结 (21)总体⼼得....................................................................... - 22 -对课程内容的建议................................................... 错误!未定义书签。
数字电路课程设计之超前进位加法器
reg
Cin;
wire[3:0] S;
wire
Cout;
carry_look_add CAL (.A(A),.B(B),.Cin(Cin),.Cout(Cout),.S(S)); initial begin
#10 A=4'd0;B=4'd0;Cin=0; #10 A=4'd11;B=4'd1;Cin=0; #10 A=4'd10;B=4'd12;Cin=0; #10 A=4'd11;B=4'd4;Cin=0; #100 $stop; end endmodule
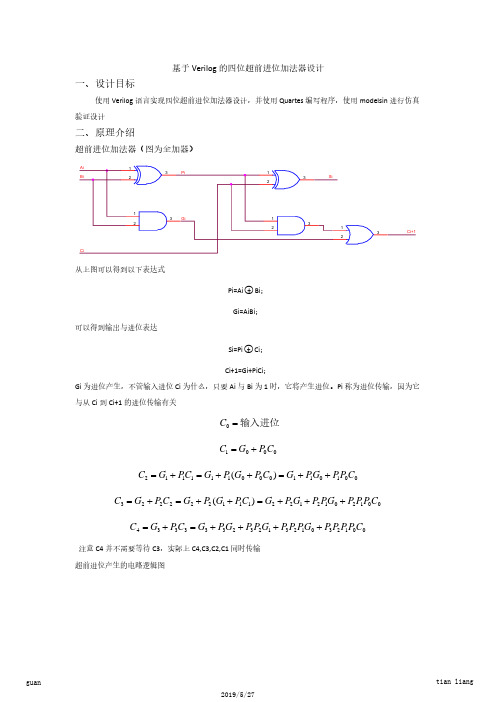
Pi=Ai○+ Bi;
可以得到输出与进位表达
Gi=AiBi;
Si=Pi○+ Ci;
Ci+1=Gi+PiCi; Gi 为进位产生,不管输入进位 Ci 为什么,只要 Ai 与 Bi 为 1 时,它将产生进位。Pi 称为进位传输,因为它 与从 Ci 到 Ci+1 的进位传输有关
C0 = 输入进位
C1 = G0 + P0C0
Half_Add H3(.a(A[2]),.b(B[2]),.s(v6),.c(v5));
Half_Add H4(.a(A[3]),.b(B[3]),.s(v8),.c(v7));
carry_look
CL1(.C0(Cin),.P0(v2),.G0(v1),.P1(v4),.G1(v3),.P2(v6),.G2(v5),.P3(v8),.G3(v7),.C1(o1),.C2(o2),.C3(o3),.C4(Cout));
注意 C4 并不需要等待 C3,实际上 C4,C3,C2,C1 同时传输 超前进位产生的电路逻辑图
超前进位加法器

8位超前进位加法器设计说明书超前进位加法器就是使各位的进位直接由加数和被加数来决定,而不需要依赖低位进位。
即有如下逻辑表达式:1)(-++=i i i i i i C B A B A C当第i 位被加数A i 和加数B i 均为1时,有1=i i B A ,不论低位运算结果如何本位必然有进位输出(1=i C ),所以定义i i i B A G =为进位产生函数。
当A i 和B i 中只有一个为1时,有0=i i B A ,1=+i i B A ,使得1-=i i C C ,所以定义i i i B A P +=为进位传递函数。
将P i 和G i 代入全加器的“和”及“进位”表达式有:1-⊕⊕=i i i i C B A Y从而构成超前进位加法器。
VHDL 示例程序如下:(本程序在MAXPLUSII V9.6上编译通过)--*****8位超前进位加法器*****LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE. STD_LOGIC _ARITH.ALL;USE IEEE. STD_LOGIC _UNSIGNED.ALL;ENTITY ADDER8BIT ISPORT(A, B: IN UNSIGNED(7 downto 0);CI,clk: IN STD_LOGIC;Y_OUT: OUT STD_LOGIC_VECTOR(7 downto 0);CO_OUT: OUT STD_LOGIC);END ADDER8BIT;ARCHITECTURE doing OF ADDER8BIT ISSIGNAL CO,Y: STD_LOGIC_VECTOR(7 downto 0);BEGINY(0)<=A(0) xor B(0) xor CI;CO(0)<=(A(0) and B(0)) or (B(0) and CI) or (A(0) and CI);GEN:for i in 1 to 7 GENERATEY(i)<=A(i) xor B(i) xor CO(i-1); --1-⊕⊕=i i i i C B A YCO(i)<=(CO(i-1) and A(i)) or (CO(i-1) and B(i)) or (A(i) and B(i)); -- 1)(-++=i i i i i i C B A B A Cend GENERATE;process(clk)beginif clk'event and clk='1' thenY_OUT<=Y(7) & Y(6) & Y(5) & Y(4) & Y(3) & Y(2) & Y(1) & Y(0);CO_OUT<=CO(7);end if;end process;END doing;附:仿真时序波形。
超前进位加法器设计(参考资料)

加法器设计(三)超前进位加法器(Verilog)超前进位加法器module add4_head ( a, b, ci, s, pp, gg);input[3:0] a;input[3:0] b;input ci;output[3:0] s;output pp;output gg;wire[3:0] p;wire[3:0] g;wire[2:0] c;assign p[0] = a[0] ^ b[0];assign p[1] = a[1] ^ b[1];assign p[2] = a[2] ^ b[2];assign p[3] = a[3] ^ b[3];assign g[0] = a[0] & b[0];assign g[1] = a[1] & b[1];assign g[2] = a[2] & b[2];assign g[3] = a[3] & b[3];assign c[0] = (p[0] & ci) | g[0];assign c[1] = (p[1] & c[0]) | g[1];assign c[2] = (p[2] & c[1]) | g[2];assign pp = p[3] & p[2] & p[1] & p[0];assign gg = g[3] | (p[3] & (g[2] | p[2] & (g[1] | p[1] & g[0])));assign s[0] = p[0] ^ ci;assign s[1] = p[1] ^ c[0];assign s[2] = p[2] ^ c[1];assign s[3] = p[3] ^ c[2];endmodule首先要明确几个概念:p表示进位否决信号(pass),如果p为0就否决调前一级的进位输入。
否决的意思就是即使前一级有进位,本级也不会向后一级产生进位输出。
超前进位加法器设计报告解剖

华东交通大学理工学院课程设计报告书所属课程名称EDA课程设计题目超前进位加法器设计分院专业班级学号学生姓名指导教师2013 年7月2日目录第一章设计内容与要求 (3)第二章超前进位加法器设计原理 (3)第三章详细设计流程 (4)3.1.创建工程文件 (4)3.2.程序的编译 (5)3.3.波形的仿真 (7)第四章设计结果分析 (11)第五章源程序代码 (12)第六章心得体会 (14)第七章参考文献 (15)第一章设计内容与要求加法运算是最重要也是最基本的运算,所有的其他基本运算,如减、乘、除运算最终都能归结为加法运算。
但因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于他的位相关。
因此为了减少进位传输所消耗的时间,提高计算速度,人们设计了多种类型的加法器,如跳跃进位加法器、进位选择加法器、超前进位加法器等。
本设计采用的是超前进位加法器。
通过Verilog 设计一个超前8位加法器。
要求在Quartus II软件下,利用Verilog编程完成层次式电路设计,电路中的元件可以用Verilog设计也可以用库元件连线构成再封装。
8位超前进位加法器,借助EDA工具中的综合器,适配器,时序仿真器和编程器等工具进行相应处理。
适配采用Cyclone系列的EP1C6Q240C8。
要求综合出RTL电路,并进行仿真输入波形设计并分析电路输出波形. 试比较并阐述数据类型reg型和wire型的区别。
第二章超前进位加法器设计原理将n个全加器相连可得n位加法器,但是加法时间较长。
解决的方法之一是采用“超前进位产生电路”来同时形成各位进位,从而实现快速加法。
超前进位产生电路是根据各位进位的形成条件来实现的首先对于1位加法器基本位值和与进位输出为1;如果a,b有一个为1,则进位输出等于cin;令G=ab,P=a+b,则有:Cout==ab+(a+b)cin=G+P•cin由此可以G和P来写出4位超前进位链如下(设定四位被加数和加数为A 和B,进位输入Cin,进位输出为cout,进位产生Gi=AiBi,进位传输Pi=Ai+Bi);C0=cin;C1=G0+P0C0=G0+P0•cinC2=G1+P1C1=G1+P1(G0+P0cin)=G1+P1G0+P1P0cinC3=G2+P2C2=G2+P2(G1+P1cin)=G2+P2G1+P2P1G0+P2P1P0cinC4=G3+P3C3=G3+P3(G2+P2C2)=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0cin Cout=c4由超前进位链,各个进位彼此独立产生,将进位级联传播给去掉了,因此,减小了进位产生的延迟时间。
16位超前进位加法器实验报告
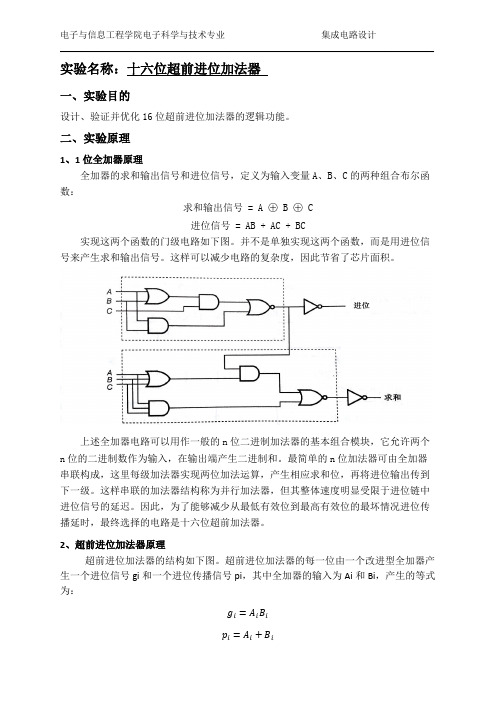
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号 = A ⊕ B ⊕ C进位信号 = AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
074-王楠-计组实验三(超前进位加法器设计实验)

延安大学计算机学院实验报告专用纸
这个4 x 4阵列乘法器的原理如图1-3-1所示。
FA (全加器)的斜线方向为进位输出,竖线方向为和输出。
图中阵列的最后-行构.成了一个串行进位加法器。
由于FA一级是无需考虑进位的,它的进位被暂时保留下来不往前传递,因此同- -极中任意- -位FA加法器的进位输出与和输出几乎是同时形成的,与“串行移位”相比可大大减少同级间的进位传递延迟,所以送往最后一行串行加法器的输,入延迟仅与FA 的级数(行数)有关,即与乘数位数有关。
本实验用CPLD来设计一个4x4位加法器,且全部采用原理图方式实现。
【5】实验步骤
(1)根据上述阵列乘法器的原理,使用Quartus |I 软件编辑相应的电路原理图并进行编译,其在EPM1270 芯片中对应的引脚如图1-3-2所示,框外文字表示I/O号,框内文字表示该引脚的含义。
(2)关闭实验系统电源,按图1-3-3连接实验电路,图中将用户需要连接的信号用圆圈标明。
(3)实物图如下:
(4)打开实验系统电源,将生成的POF文件下载到EPM1270中去。
(5)以CON单元中的SD10...SD13四个二进制开关为乘数A,SD14.. SD17四个二进制开关为被乘数B,而相乘的结果在CPLD单元的L7...LO八个LED灯显示。
给A和B置不同的数,观察相乘的结果。
【6】实验结果
1、输入:1111 1111
结果:1111111
2、输入:0000 0000
结果:00000000。
16位超前进位加法器实验报告
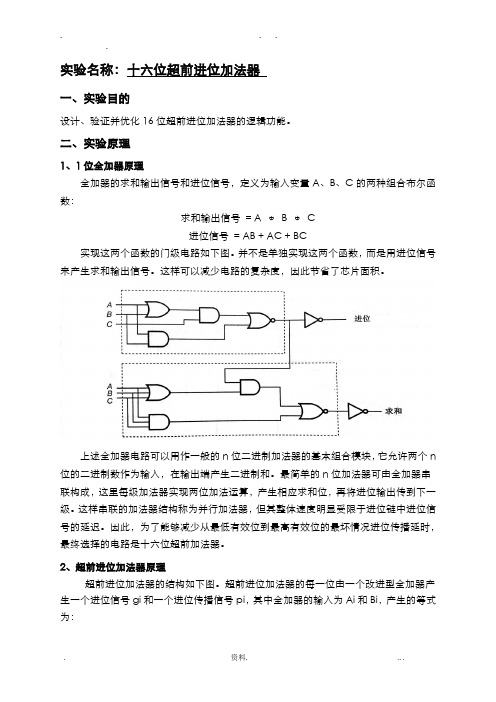
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号= A ⊕B ⊕C进位信号= AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
4位超前进位加法器设计讲解学习

4位超前进位加法器设计、、模拟集成电路分析与设计课程设计报告题目4位超前进位加法器设计学院(部)电控学院专业电子科学与技术班级学生姓名学号前言20世纪是IC迅速发展的时代。
计算机等信息产业的飞速发展推动了集成电路(Integrated Circuit—IC)产业。
大多数超大规模集成电路(Very Large Scale IC—VLSI)在日常生活中有着广泛的应用。
在这些广泛应用的运算中,加法器是组成这些运算的基本单元。
在高性能微处理器和DSP处理器中,加法器的运算时间至关重要。
加法器运算常常处于高性能处理器运算部件的关键路径中,特别是在算术逻辑单元中加法器的运算时间对处理器的速度起着决定性的作用。
随着微处理器的运算速度越来越快,对快速加法器的需求也越来越高。
当今,加法器的设计面临两大课题,首先是如何降低功耗。
随着便携式IC产品例如MP3播放器,手机和掌上电脑等的广泛使用,要求IC工程师对现有运算模块的性能作进一步改进,尤其是在电路的功耗和尺寸方面。
由于现在相应的电池技术难以和微电子技术的发展速度匹敌,这使得IC设计师遇到了许多限制因素,比如高速,大吞吐量,小尺寸,低功耗等。
因此,这使得研究低功耗高性能加法单元持续升温。
另一方面就是如何提高加法器的运算速度。
因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于它的位相关。
因此,为了减少进位传输所耗的时间,提高计算速度,人们设计了多种类型的加法器,如超前进位加法器曼彻斯特加法器、进位旁路加法器、进位选择加法器等。
它们都是利用各位之间的状态来预先产生高位的进位信号,从而减少进位从低位向高位传递的时间。
本文首先介绍了的加法器的类型以及其工作原理,然后重点分析了超前进位加法器的组成结构、结构参数以及其工作原理。
分层设计了加法器的输入输出电路,并通过tanner软件进行仿真实验,从而验证了电路的准确信。
目录第二章设计过程 (18)2.1 电路设计基础原理 (18)2.2 电路各部分结构设计 (20)异或门的CMOS电路原理图如下: (21) (21)异或门的CMOS波形图如下: (21) (21)两输入与门的CMOS电路原理图如下: (22) (22)两输入与门的CMOS波形如下: (22) (22)反相器的CMOS电路如下: (23) (23)反相器的CMOS仿真波形如下: (23) (23)四位超前进位加法器进位的逻辑电路图如下: (24) (24)c1,c2,c3,c4的CMOS级电路原理图及仿真 (25) (25)a.c1的原理图 (25) (25)c1的仿真波形 (26) (26)b.c2的原理图 (26)c2的仿真波形 (27)c.c3的原理图 (28) (29)c3的仿真波形 (29) (30)c4的原理图 (30)c3的仿真波形 (31)2.3 主要电路参数的手工推导 (31)四位超前进位加法器门级电路原理图如下: (34) (34)四位超前进位加法器门级电路分析设定如下: (34) (35)四位超前进位加法器门级电路瞬态分析结果如下: (35) (35)四位超前进位加法器门级电路瞬态分析波形图如下: (35) (36)4.1 用于仿真的电路图如下: (37)四位超前进位加法器门级电路分析设定如下: (38)四位超前进位加法器电路瞬态分析结果如下: (38) (38)四位超前进位加法器门级电路瞬态分析波形图如下: (38) (39)第五章鸣谢及课设总结和体会 (39)参考文献 (40)第一章设计目标1.根据电路原理图,给出电路的CMOS晶体管级电路设计。
杭电计组实验2-超前进位加法器设计实验

杭州电子科技大学计算机学院
实验报告
实验项目:实验2-超前进位加法器设计实验
课程名称:计算机组成原理与系统结构课程设计
姓名:学号:同组姓名:学号:
实验位置(机号):
实验日期:指导教师:
#100;
A = 1011;
B = 1101;C0 = 0;
#100;
A = 1010;
B = 0010;C0 = 1;
#100;
A = 0111;
B = 1000;C0= 0;
#100;
A = 0011;
B = 0100;C0 = 1;
#100;
A = 1001;
B = 0001;C0 = 0;
#100;
end
Endmodule
RTL图
二、结果
思考题:
(1)综合得到的电路图,它和想要设计的电路在引脚的输入输出方面是完全相同的,但是相比较内部的RTL图,实验实现的结果是相同的,但是我编写的实验代码并没有调用实验一的全加器设计。
(2)尝试编写8位超前进位加法器设计实验
module add_8 ( input [7:0]a, input [7:0]b, input cin, output [7:0] s, output co );
wire [7:0]c_tmp;
wire [7:0]g;
wire [7:0]p;。
计算机组成原理课程设计—超前进位加法器的设计资料

课程设计报告
课程设计名称: 计算机组成原理课程设计 课程设计题目: 超前进位加法器的设计
院(系):计算机学院 专 业: 班 级: 学 号: 姓 名: 指导教师: 完成日期:
沈阳航空航天大学课程设计报告
目录
第 1 章 总体设计方案 .................................................................................................. 1
超前进位加法器的进位输出作为第二个超前进位加法器的进位输入即可实现八位
超前进位加法器的设计。
超前进位产生电路是根据各位进位的形成条件来实现的。 只要满足下述条件,
就可形成进位 C1、C2、 C3、C4。所以:
第一位的进位 C1=X1*Y1+(X1+Y1)*C0
第二位的进位 C2=X2*Y2+(X2+Y2)*X1*Y1+(X2+Y2)(X1+Y1)C0
G1 的意义是:当 X1 ,Y1 均为 1 时,不管有无进位输入,本位定会产生向高
位的进位。
将 Pi,Gi 代人 C1~C4 式中,便可得;
C1=G1+P1*C0
式( 1)
C2=G2+P2*G1+P2*P1*C0
式( 2)
C3=G3+P3*G2+P3*P2*G1+P3*P2*P1*C0
式( 3)
1
沈阳航空航天大学课程设计报告
2
沈阳航空航天大学课程设计报告
片中,经硬件测试验证设计的正确性。
1.3 设计环境
·硬件环境:伟福 COP2000型计算机组成原理实验仪、 XCV200 实验板、微 机;
组成原理-超前进位加法器设计

《计算机组成原理》实验报告专业:学号:学生姓名:实验日期:实验二一、实验名称:超前进位加法器设计二、实验目的:1 掌握超前进位加法器的原理及其设计方法。
2 熟悉CPLD 应用设计及EDA 软件的使用。
三、实验设备:PC 机一台,TD-CMA 实验系统一套,排线若干。
四、实验内容:1.了解加法器的工作原理,掌握超前进位产生电路的设计方法.2.正确将电路原理图下载到试验箱中.3.正确通过实验箱连线实现4位二进制数的相加并得到正确结果五、实验原理:加法器是执行二进制加法运算的逻辑部件,也是CPU 运算器的基本逻辑部件(减法可以通过补码相加来实现)。
加法器又分为半加器和全加器(FA),不考虑低位的进位,只考虑两个二进制数相加,得到和以及向高位进位的加法器为半加器,而全加器是在半加器的基础上又考虑了低位过来的进位信号。
表1-2-1 1 位全加器真值表A、B 为2 个1 位的加数,Ci 为来自低位的进位,S 为和,Co 为向高位的进位,根据表1-2-1所示的真值表,可得到全加器的逻辑表达式为:S = ABCi + ABCi + ABCi + ABCiCo = AB+ ACi + BCi根据逻辑表达式,可得到如图1-2-1 所示的逻辑电路图。
有了 1 位全加器,就可以用它来构造多位加法器,加法器根据电路结构的不同,可以分为串行加法器和并行加法器两种。
串行加法器低位全加器产生的进位要依次串行地向高位进位,其电路简单,占用资源较少,但是串行加法器每位和以及向高位的进位的产生都依赖于低位的进位,导致完成加法运算的延迟时间较长,效率并不高。
C0 = 0Ci+1 = AiBi + AiCi + BiCi = AiBi + (Ai + Bi)Ci设gi = AiBipi = Ai + Bi则有:Ci+1 = gi + piCi= gi + pi(gi-1 + pi-1Ci-1)= gi + pi(gi-1 + pi-1(gi-2 + pi-2Ci-2))…= gi + pi (gi-1 + pi-1(gi-2 + pi-2(…(g0 + p0C0)…)))= gi + pigi-1 + pipi-1gi-2 + … + pipi-1…p1g0 + pipi-1…p1p0C0由于gi、pi 只和Ai、Bi 有关,这样Ci+1 就只和Ai、Ai-1、…、A0,Bi、Bi-1、…、B0 及C0有关。
16位超前进位加法器

《VLSI》课程设计报告班级:电子09—1班学号: 0906040107 姓名:李翔一指导教师:张振宇16位超前进位加法器设计目录摘要 (1)1需求分析1.1加法器的发展..................................................................... 错误!未定义书签。
1.2几种串行加法器性能比较 (3)1.2.1串行进位加法器 (3)1.2.1超前进位加法器 (3)2主要内容 (4)2.1设计原理 (7)2.2设计思路 (4)3 设计思想 (5)4 实现方法 (6)4.1顶层方案图的设计与实现 (6).4.1.1顶层方案的整体设计 (6)4.1.2元器件选择和引脚锁定 (7)4.2功能模块的设计与实现 (8)4.2.1设计描述 (8)4.2.2创建RTL代码并得到电路图....................................................... .94.3功能仿真 (11)4.4编程与下载 (12)4.5硬件仿真结果 (12)5小结 (13)参考文献 (13)附录 (14)摘要:加法运算是最重要最基本的运算,所有的其他基本算术运算乘除等都最终可以用加法运算来表示在不同的场合对加法器的要求不同,要的要求速度快有的要求面积小超前进位加法器相比于串行进位加法器是一种快速加法运算器,根据用户的要求追求速度与面积的平衡。
关键词:超前进位加法器串行进位加法器速度面积1需求分析1.1 加法器的发展加法运算是最基本的运算,所有其他基本算术运算都是以加法运算为基础。
但因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于他的位相关,因此,为了减少进位传输所耗的时间提高计算速度人们设计了多种类型的加法器。
如跳跃进位加法器,进位选择加法器,超前进位加法器等他们都是利用各位之间的状态来预先产生高位进位信号从而减少进位从低位到高位的传递时间1.2 几种加法器的性能比较1.2.1串行进位加法器串行进位加法器的每一位加和值都依赖于上一位进位信号,即进位信号是串行的经过加法器的每一位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华东交通大学理工学院课程设计报告书所属课程名称EDA课程设计题目超前进位加法器设计分院专业班级学号学生姓名指导教师2013 年7月2日目录第一章设计内容与要求 (3)第二章超前进位加法器设计原理 (3)第三章详细设计流程 (4)3.1.创建工程文件 (4)3.2.程序的编译 (5)3.3.波形的仿真 (7)第四章设计结果分析 (11)第五章源程序代码 (12)第六章心得体会 (14)第七章参考文献 (15)第一章设计内容与要求加法运算是最重要也是最基本的运算,所有的其他基本运算,如减、乘、除运算最终都能归结为加法运算。
但因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于他的位相关。
因此为了减少进位传输所消耗的时间,提高计算速度,人们设计了多种类型的加法器,如跳跃进位加法器、进位选择加法器、超前进位加法器等。
本设计采用的是超前进位加法器。
通过Verilog 设计一个超前8位加法器。
要求在Quartus II软件下,利用Verilog编程完成层次式电路设计,电路中的元件可以用Verilog设计也可以用库元件连线构成再封装。
8位超前进位加法器,借助EDA工具中的综合器,适配器,时序仿真器和编程器等工具进行相应处理。
适配采用Cyclone系列的EP1C6Q240C8。
要求综合出RTL电路,并进行仿真输入波形设计并分析电路输出波形. 试比较并阐述数据类型reg型和wire型的区别。
第二章超前进位加法器设计原理将n个全加器相连可得n位加法器,但是加法时间较长。
解决的方法之一是采用“超前进位产生电路”来同时形成各位进位,从而实现快速加法。
超前进位产生电路是根据各位进位的形成条件来实现的首先对于1位加法器基本位值和与进位输出为1;如果a,b有一个为1,则进位输出等于cin;令G=ab,P=a+b,则有:Cout==ab+(a+b)cin=G+P•cin由此可以G和P来写出4位超前进位链如下(设定四位被加数和加数为A 和B,进位输入Cin,进位输出为cout,进位产生Gi=AiBi,进位传输Pi=Ai+Bi);C0=cin;C1=G0+P0C0=G0+P0•cinC2=G1+P1C1=G1+P1(G0+P0cin)=G1+P1G0+P1P0cinC3=G2+P2C2=G2+P2(G1+P1cin)=G2+P2G1+P2P1G0+P2P1P0cinC4=G3+P3C3=G3+P3(G2+P2C2)=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0cin Cout=c4由超前进位链,各个进位彼此独立产生,将进位级联传播给去掉了,因此,减小了进位产生的延迟时间。
同样可推导出下面的式子:SUM=A⊕B⊕Cin=(AB)⊕(A+B) ⊕CinU=G⊕P⊕Cin本实验中采用8位超前进位加法器第三章详细设计流程3.1.创建工程文件打开Quartus II 9.1创建一个工程文件adder_ahead选择菜单File中New Project Wizard命令,在如下“工程设置”对话框中单击右侧“…”按钮,找到文件夹D:\atlera\quartus,选中已存盘的add_ahead.vhd的文件。
单击Next,将与工程有关的文件加入此工程。
(1)选择仿真器和综合器类型。
都选默认的None。
(2)选择目标芯片。
(3)工具设置。
这里默认使用QuartusⅡ自含的所有设计工具。
(4)结束设置。
3.2.程序的编译(1).选择菜单“Processing”—“Start Compilation”命令,或者点击运行编译按钮,启动完全编译,这里的完全编译包括分析与综合、适配、装配文件、定时分析、网编文件提取过程。
如果只要进行期中的某一项编译,可以选着“Tools”---“Compiler Tool”命令,或者点击按钮即可出现编译工具选择串口,共包括5个编译工具,分别为分析与综合器、适配器、装配器、定时分析器、网表文件提提取器,单机每个工具前面的小图标可单独启动每一个编译器。
(2)编译完成后,会将有关的编译信息显示在窗口中,可查看其中的相关内容。
还可以查看中和后的电路原理图,选择“Tools”---“Netlist Viewers”---“RTL Viewer”菜单命令,既可观察综合生成的RLT方式的电路原理图,在这里我们可以看到8位超期进位加法器生成的原理图如下:8位超期进位加法器生成的原理图:3.3.波形的仿真仿真时序,对项目进行仿真测试,也可以对项目中的某一个子模块进行仿真,其方法是选择菜单“Assignment”---“Wizard”----“Simulator Set Wizard”命令,在设置过程中指定仿真对象,并指定对象的仿真类型、矢量激励源等。
(1)打开波形编辑器选择菜单“File”---“New”命令,在“New”对话框中选择“Other File”页中的“Vector Wave File”选项,单击“ok”按钮,即出现选择波形按钮;(2)输入信号节点选择菜单“View”---“Utility Windows”---“Node Finder”命令,出现对话框,在“Filter”下拉列表中选择“Pins:all”选项,再次单击“List”按钮,即在下面的“Nodes Found”框中出现本设计项目的所有端口引脚列表,从端口列表中选择所需要的,并逐个拖到波形编辑窗口中(4)编辑输入信号波形点击波形编辑窗口中的全屏显示,使用波形编辑窗口中的各种波形赋值,编辑各输入信号的激励波形。
在仿真的时候需要设置一个合理的区域,选择菜单“Edit”---“End Time”命令,在淡出的“Time”窗口中输入60us.对数据的型号的格式可以选择:Binary(二进制),Hexadecimal(十六进制)、Octal(八进制)、Signed Decimal(有符号十进制),Unsgned Decimal(无符号十进制)。
这里选择的是Binary二进制,便于观察结果。
(5)仿真参数的设置,选择菜单“Assignments”—“Setting”命令,在弹出的对话框选择“Simulator Setting”项下的“Mode”,以选择仿真模式,仿真模式有功能仿真模式和时序仿真模式,这里选择功能仿真。
(6)观察仿真结果选择菜单“Processing”---“Start Simulation”命令,即启动仿真器工作。
仿真完毕后,可以通过输出波形,检验所设计电路的功能是否正确。
8位超前进位的功能输出波形图:第四章设计结果分析输入a 00100110 00100111输入b 001010110 01010111cin 0 1 0 1 sum 01101000 01101001 01101010 01101011 结果中显示是正常的,8位超前进位加法器得到成功的实现8位超前进位器综合后的RTL级原理图第五章源程序代码8位超前进位加法器module add_ahead(sum,cout,a,b,cin);input[7:0] a,b;input cin;output[7:0] sum;output cout;wire[7:0] G,P;wire[7:0 ] C,sum;assign G[0]=a[0]&b[0];assign P[0]=a[0]|b[0];assign C[0]=cin;assign sum[0]=G[0]^P[0]^C[0];assign G[1]=a[1]&b[1];assign P[1]=a[1]|b[1];assign C[1]=G[0]|(P[0]&cin);assign sum[1]= G[1]^P[1]^C[1];assign P[2]=a[2]&b[2];assign C[2]=G[1]|(P[1]&C[1]);assign sum[2]=G[2]^P[2]^C[2];assign G[3]=a[3]&b[3];assign P[3]=a[3]|b[3];assign C[3]=G[2]|(P[2]&C[2]);assign sum[3]=G[3]^P[3]^C[3];assign G[4]=a[4]&b[4]; assign P[4]=a[4]|b[4];assign C[4]=G[3]|(P[3]&C[3]); assign sum[4]=G[2]^P[2]^C[2]; assign G[5]=a[5]&b[5]; assign P[5]=a[5]|b[5];assign C[5]=G[4]|(P[4]&C[4]); assign sum[5]=G[5]^P[5]^C[5]; assign G[6]=a[6]&b[6]; assign P[6]=a[6]|b[6];assign C[6]=G[5]|(P[5]&C[5]); assign sum[6]=G[6]^P[6]^C[6]; assign G[7]=a[7]&b[7]; assign P[7]=a[7]|b[7];assign C[7]=G[6]|(P[6]&C[6]); assign sum[7]=G[7]^P[7]^C[7]; assign cout=G[7]|(P[7]&C[7]); endmodule第六章心得体会本学期学习了EDA技术与Vertlog技术,对EDA技术应用有了一些了解,在如今生活在这个数字化和信息化时代,数字产品的广泛应用越来越多。
EDA技术的使用在我们生活中息息相关,发现了EDA的强大功能。
系统系设计,混合电路设计,综合仿真的设计,数字电路设计,版图设计,PCB 板设计,PLD开发,高速电路设计,模拟电路设计等应用。
这次课设中用到的Quartus Ⅱ软件,在安装过程中遇到不能仿真,后来下载了9.11版本得到解决。
Quartus Ⅱ进行EDA开发包括设计输入,编译,仿真,编程和验证,自己通过设计8位超前加法器对Quartus Ⅱ软件的应用也得到了一定的掌握。
在编译的过程中遇到一些不能编译,通过网上找资料,和同学的讨论得到了一定的了解,通过软件的设置和通过编译错误的提示来更改错误,对设计的原理有了更深的理解。
同时也发现遇到问题不要急着马上就向同学寻求帮助,我们自己可以认真地独立思考,想想问题哪里出错了,这样自己才会有不断地提高。
认识涞源于实践实践是用于检验真理的唯一标准。
这次使用超前进位这样就减少了延时,加快了运行速度。
对于一切的设计我们都要多思考,使用最优的方法到我们实际生活当中去。
这次课设设计,加强了我们自己动手,思考解决问题的能力。
也让我们在学习的道路求知的一段探索道路,是对于我们生活一种充实。
