2006031459黄德荣5位逐级进位和超前进位加法器设计剖析
超前进位加法器

超前进位加法器超前进位加法器是一种数字电路设备,用于进行二进制数的加法运算。
它通过将多个加法器级联,实现对多位二进制数的加法计算,并且能够在加法过程中实现超前进位,提高计算速度。
超前进位加法器的原理是基于二进制加法的原理。
在二进制加法中,每一位的运算结果可以表示为:两个位的和与进位。
其中,和即为输入位的异或运算结果,进位则是输入位的与运算结果再经过左移一位。
超前进位加法器利用这一原理,通过预测进位产生的结果,以提前得到进位并作用于下一级的运算。
超前进位加法器可以分为两个部分:生成进位部分和传递进位部分。
生成进位部分用于预测进位的产生情况,传递进位部分则是将进位传递给下一级的加法器。
生成进位部分的输入为两个相邻位的和,输出为进位。
传递进位部分的输入为前一级的进位以及生成进位部分的进位,输出为当前位的进位。
为了方便理解,以下以一个四位超前进位加法器为例进行介绍。
这个四位加法器由四个单独的全加器组成,每个全加器负责一个位的运算。
生成进位部分和传递进位部分在全加器中都有相应的电路实现。
首先,生成进位部分。
对于第一位的全加器来说,由于没有前一位的进位,因此直接将两个输入位的和作为输出位的进位。
对于其他位的全加器,需要预测进位的产生。
这个预测的规则是,如果前一位的和为1,则有可能会产生进位。
因此,预测进位部分将前一位输入位的和与该位输入位的和进行与运算,得到预测的进位结果。
接下来,传递进位部分。
对于第一个全加器来说,由于没有前一位的进位,因此直接将生成进位部分的进位作为输出位的进位。
对于其他位的全加器,传递进位部分将前一位的进位与生成进位部分的进位进行或运算,得到当前位的进位。
将多个全加器级联后,就构成了一个超前进位加法器。
通过这种方式,每一位的运算可以并行进行,从而提高了计算速度。
同时,由于提前预测了进位的结果,可以减少了进位的传播延迟,进一步提高了计算效率。
超前进位加法器在数字电路的设计中具有重要的应用价值。
数字逻辑 第三章 加法器.ppt

四位二进制并行加法器
三、四位二进制并加法器的外部特性和逻辑符号 1.外部特性
图中,A4、A3、A2、A1 ------- 二进制被加数; B4、B3、 B2、B1 ------- 二进制加数; F4、 F3、 F2、 F1 ------相加产生的和数; C0 --------------------来自低位的进位输入; FC4 -------------------向高位的进位输出。
a3b1
+) 乘积 Z5 a3b2 Z4 a2b2 Z3
a2b1
a1b2 Z2
a1b1
Z1
因为: ☆1位二进制数乘法 法则和逻辑“与”运算法 则相同,“积”项aibj(i =1,2,3;j=1,2)可用 两输入与门实现。 ☆对部分积求和可用 并行加法器实现。 所以:该乘法运算电 路可由6个两输入与门和1 b2 个4位二进制并行加法器构 成。逻辑电路图如右图所 示。
四位二进制并行加法器
实现给定功能的逻辑电路图如下图所示。 1) 输入端A4、A3、A2、 A1输入8421码;
2) 而从另一输入端B4、 B3、B2、B1输入二进 制数0011; 3) 进位输入端C0接上“0”;
4) 可从输出端F4、F3、F2、 F1得到与输入8421码对
应的余3码。
四位二进制并行加法器
Z5 Z4 Z3 Z 2 Z1
F4 F3 F2 F 1 FC4 T 693 C0
0
A4 A3 A2 A1
B4 B 3 B2 B1
&
&
&
&
&
&
b1
a3
a2
a1 0 a 3
a2
a1
FA4
F3 C3
FA3
F2
超前进位加法器的设计

沈阳航空工业学院课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:计算机科学与技术班级:4401102学号:200403011046姓名:郭丰瑞指导教师:刘泽显完成日期:2006年12月31日沈阳航空工业学院课程设计报告目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (4)2.1顶层方案图的设计与实现 (4)2.1.1创建顶层图形设计文件 (4)2.1.2器件的选择与引脚锁定 (4)2.2功能模块的设计与实现 (6)2.2十六位超前进位加法器的设计 (6)2.3仿真调试 (8)第3章编程下载与硬件测试 (12)3.1编程下载 (12)3.2硬件测试及结果分析 (12)参考文献 (15)附录(程序清单或电路原理图) (16)第1章总体设计方案1.1设计原理十六位超前进位加法器,可以由4个四位超前进位加法器构成。
由第一个四位超前进位加法器的进位输出加进为第二个超前进位加法器的进位输入,依次类推。
超前进位加法器的实现是建立在各位进位的形成条件来实现的。
所以第一位的进位c1=a0*b0+(a0+b0)*c0;第二位的进位c2=a1*b1+(a1+b1)*a0*b0+(a1+b1)(a0+b0)c0第三位的进位c3=a2*b2+(a2+b2)a1*b1+(a1+b1)*(a2+b2)*a0*b0+(a0+b0)(a1+b1)(a2+b2)*c0第四位的进位c4=a3*b3+(a3+b3)*a2*b2+(a3+b3)*(a2+b2)a1*b1+(a3+b3)(a2+b2)(a1+b1)*a0*b0+(a0+b0)(a1+b1)(a2+b2)(a3+b3)*c0 下面我们可以引进传递函数Pi和进位产生函数Gi的概念。
他们定义为:Pi=Ai+BiGi=Ai*BiP1的意义是:当A0和B0中有一个为1时,若有进位输入,则本位向高位传递进位。
超前进位加法器原理
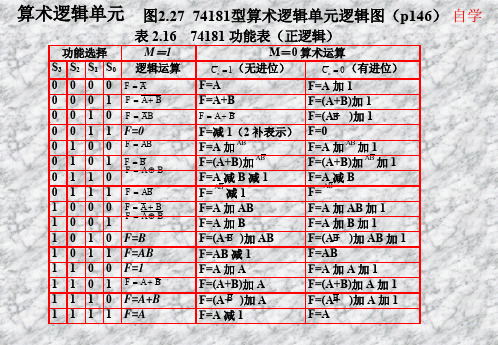
F=A 加 B 加 1
F=(A+B )加 AB
F=(AB+ )加 AB 加 1
F=AB 减 1
F=AB
F=A 加 A
F=A 加 A 加 1
F=(A+B)加 A
F=(A+B)加 A 加 1
F=(A+B )加 A
F=(AB+ )加 A 加 1
F=A 减 1
F=A
P
1
1
&
G
&&
Cnz
1 & &&
Cn y
1 &&
自学
Cnx
1 &
P3 G3
P2 G2
P1 G1
图2.28 74182型超前进位扩展器逻辑图
P0 G0 Cn
C1 Cn PG
Cn PG
Cn PG
74181
Cn Cn4 PG
Cn PG
Cn PG
Cn PG
Cn Cn4 PG
P0 G0 Cn x P1 G1 Cn y P2 G2 Cn z P3G3
自学
累加器
数据输入 AB
组合电路
累加寄存器
求和命令 (时钟)
数据输入 AB
ALU(74181)
控制变量 (S3,S2,S1,S0,M)
累加寄存器
求和命令 (时钟)
数据输出
图2.30累加器结构图
数据输出
图2.31用ALU构成的累加器
Cn
74182
PG
P0 G0 Cn x P1 G1 Cn y P2 G2 Cn z P3G3
Cn
74182
PG
试验二 超前进位加法器 设计

试验二超前进位加法器设计练习2. 4位超前进位加法器行波进位加法器延时较长,可采用超前进位加法器减少延时,但是由此会造成电路的复杂。
超前进位加法器原理参见《数字集成电路》(周润德第二版)424页。
对以上公式的注解:公式中的C O,K 表示第K 为的进位输出,G K 为第K 位的进位产生,P K 为第K 为的进位传播。
且:K K KK K KG A B P A B ==⊕ A K ,B K 为输入加数的第K 位。
将Co 和S 用G,P 重写为: O ii C G PC S P C =+=⊕由于低位的输出进位是高位的输入进位,所以有上面的(11.15)式源程序://this is a carry lookahead of 4bitmodule clad(ina,inb,ci,co,sum);input[3:0] ina,inb;input ci;output co;output[3:0]sum;wire co0,co1,co2,G0,G1,G2,G3,P0,P1,P2,P3;assignG0=ina[0]&inb[0],P0=ina[0]^inb[0],G1=ina[1]&inb[1],P1=ina[1]^inb[1],G2=ina[2]&inb[2],P2=ina[2]^inb[2],G3=ina[3]&inb[3],P3=ina[3]^inb[3],co0=G0|(P0&ci),co1=G1|(P1&co0),co2=G2|(P2&co1),co=G3|(P3&co2),sum[0]=P0^ci,sum[1]=P1^co0,sum[2]=P2^co1,sum[3]=P3^co2;endmodule测试程序:module clad_test;reg[3:0] ina,inb;reg ci;wire co;wire[3:0]sum;clad CI(.ina(ina),.inb(inb),.ci(ci),.co(co),.sum(sum)); initialbeginina=0;inb=0;ci=0;endalways #5 ina=ina+1'b1;always #80 inb=inb+1'b1;always #1280 ci=~ci;endmodule仿真结果:注:该结果为10进制显示练练手:参考《数字集成电路》(周润德第二版)420-421,设计一个16位的超前进位加法器,基本单元使用4位的加法器,结构自选。
先行进位加法器

先⾏进位加法器实验四32位先⾏进位加法器⼀、功能概述串⾏进位加法器延时很⼤,每级的输出结果都要等上⼀级的进位到来才可以求和算出结果,这次实验对普通全加器进⾏改良,改良为先⾏进位加法器。
先⾏进位加法器,各级的进位彼此是独⽴产⽣,只与输⼊数据A,B和C_in有关,将各级间的进位级联传播给去掉了,这样就可以减⼩进位产⽣的延时。
每个等式与只有三级延迟的电路对应,第⼀级延迟对应进位产⽣信号和进位传递信号,后两级延迟对应上⾯的积之和。
通过这种进位⽅式实现的加法器称为超前进位加法器。
因为各个进位是并⾏产⽣的,所以是⼀种并⾏进位加法器。
⼆、实验原理1、设⼆进制加法器第i位为A i,B i,输出为S i,进位输⼊为C i,进位输出为C i+1,则有:S i=A i⊕B i⊕C i(1-1)C i+1 =A i * B i+ A i *C i+ B i*C i =A i * B i+(A i+B i)* C i(1-2)令G i = A i * B i , P i = A i+B i,则C i+1= G i+ P i *C i当A i和B i都为1时,G i = 1,产⽣进位C i+1 = 1当A i和B i有⼀个为1时,P i = 1,传递进位C i+1= C i因此G i定义为进位产⽣信号,P i定义为进位传递信号。
G i的优先级⽐P i⾼,也就是说:当G i = 1时(当然此时也有P i = 1),⽆条件产⽣进位,⽽不管C i是多少;当G i=0⽽P i=1时,进位输出为C i,跟C i之前的逻辑有关。
下⾯推导4位超前进位加法器。
设4位加数和被加数为A 和B,进位输⼊为C in,进位输出为C out,对于第i位的进位产⽣G i = A i·B i ,进位传递P i=A i+B i , i=0,1,2,3。
于是这各级进位输出,递归的展开Ci,有:C0 = C inC1=G0 + P0·C0C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0?C0C3=G2+ P2·C2= G2+ P2·G1+ P2·P1·G0+P2·P1·P0·C0C4=G3+ P3·C3= G3+ P3·G2+ P3·P2·G1+P3·P2·P1·G0 + P3·P2·P1·P0·C0 (1-3)C out=C4由此可以看出,各级的进位彼此独⽴产⽣,只与输⼊数据Ai、Bi和Cin有关。
超前进位加法器的设计分解

超前进位加法器的设计分解沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:计算机科学与技术班级:学号:姓名:指导教师:完成日期:2014年01月10日第2章详细设计方案2.1 顶层方案图的设计与实现顶层方案图主要实现一位全加器的逻辑功能,采用原理图设计输入方式完成,超前进位加法器电路的是实现基于XCV200可编程逻辑芯片。
在完成原理图的功能设计后,经过检测调试,把输入/输出信号通过引脚编号安排到XCV200指定的引脚上去,最终实现芯片的引脚锁定。
2.1.1顶层方案的整体设计顶层图形文件主要由2个四位超前进位加法器构成,总共17位输入,9位输出。
顶层图形文件由Xilinx Foundation F3.1软件编辑得到相应的模块,顶层图形的整体设计如下图2.1所示:图 2.1八位超前进位加法器整体设计图2.1.2元器件选择和引脚锁定(1)元器件的选择由于在设计的过程中,硬件设计环境是基于伟福COP2000型计算机组成原理实验仪和XCV200实验板,故采用的目标芯片为Xilinx XCV200可编程逻辑芯片。
(2)引脚锁定在Xilinx Foundation F3.1上面完成软件的设计之后,把顶层图形文件中的输入/输出信号用引脚编号安排到Xilinx XCV200芯片指定的引脚上去,从而实现芯片的设计电路的引脚锁定,各信号及Xilinx XCV200芯片引脚对应关系如下表2.1所示:表 2.1 信号和芯片引脚对应关2.2 功能模块的设计与实现在八位超前进位加法器和四位超前进位加法器的设计中均是采用Schematic 设计输入方式,而在四位超前进位加法器的设计中是由一列的门电路构成,最后在由2个四位超前进位加法器模块构成8位超前进位加法器。
可以扩展开来,16位,32位超前进位加法器原理类似8位的设计原理。
2.2.1 八位超前进位加法器的设计与实现(1)设计描述根据上面在1.1中讲述的四位超前进位加法器的设计原理那样,四位超前进位加法器的实现是建立在进位C1,C2,C3,C4的基础之上的。
数字集成电路课程设计报告-4bits超前进位加法器

数字集成电路课程设计报告-4bits超前进位加法器福州⼤学⾄诚学院数字集成电路课程设计报告设计题⽬:4bits 超前进位加法器班级:专业:姓名:学号:组名:指导⽼师:教师评分:⽇期:4bits超前进位加法器⽬录第1章概述.................................................................... - 3 -1.1课程设计⽬的 (3)1.2课程设计的主要内容 (3)1.2.1设计题⽬ (3)1.2.2设计内容 (3)第2章功能分析及逻辑分析...................................................... - 3 -2.1功能分析 (3)2.2推荐⼯作条件 (4)2.3电性能 (4)2.4交流(开关)特性 (5)2.5真值表 (6)2.6表达式 (6)2.7电路图 (7)第3章电路设计及器件参数设计.................................................. - 7 -3.1性能指标: (7)3.2模块划分 (7)3.2.1输出级电路设计 (7)3.2.2内部反相器 (8)3.2.3内部电路等效 (8)3.2.4输⼊级电路 (9)3.2.5中间缓冲级电路 (9)3.2.6输出缓冲级电路 (9)3.2.7输⼊、输出保护电路 (10)3.3本章⼩结 (10)第4章功耗估算与延时......................................................... - 10 -4.1电容估算 (10)4.2功耗估算 (11)4.3延时估算 (11)4.4本章⼩结 (12)第5章电路模拟与仿真......................................................... - 12 -5.1电路搭建 (12)5.1.1建⽴新库 (12)5.1.2建⽴SCHEMATIC VIEW (13)5.1.3建⽴SYMBOL (13)5.1.4建⽴总体电路SCHEMATIC VIEW (13)数字集成电路课程设计5.1.5建⽴总体SYMBOL (14)5.1.6测试电路 (14)5.2功能仿真 (15)5.3功耗仿真 (15)5.4仿真结果分析 (16)5.5本章⼩结 (16)第6章版图设计............................................................... - 16 -6.1原理 (16)6.2反相器版图 (17)6.2.1 LAYOUT VIEW的建⽴ (17)6.2.2添加器件 (18)6.2.3互连,实现反相器功能 (18)6.3输⼊级 (19)6.4输出级 (19)6.5输出缓冲 (19)6.6异或门 (20)6.7或⾮门 (20)6.8与门 (20)6.9整体版图 (21)6.10本章⼩结 (21)总体⼼得....................................................................... - 22 -对课程内容的建议................................................... 错误!未定义书签。
数字电路课程设计之超前进位加法器
reg
Cin;
wire[3:0] S;
wire
Cout;
carry_look_add CAL (.A(A),.B(B),.Cin(Cin),.Cout(Cout),.S(S)); initial begin
#10 A=4'd0;B=4'd0;Cin=0; #10 A=4'd11;B=4'd1;Cin=0; #10 A=4'd10;B=4'd12;Cin=0; #10 A=4'd11;B=4'd4;Cin=0; #100 $stop; end endmodule
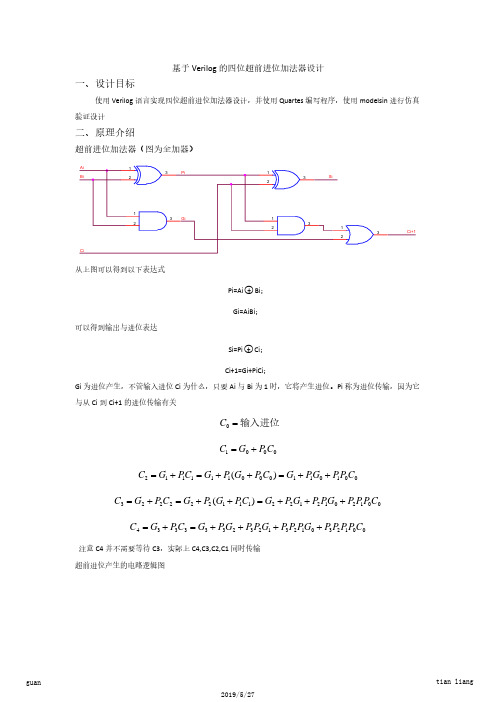
Pi=Ai○+ Bi;
可以得到输出与进位表达
Gi=AiBi;
Si=Pi○+ Ci;
Ci+1=Gi+PiCi; Gi 为进位产生,不管输入进位 Ci 为什么,只要 Ai 与 Bi 为 1 时,它将产生进位。Pi 称为进位传输,因为它 与从 Ci 到 Ci+1 的进位传输有关
C0 = 输入进位
C1 = G0 + P0C0
Half_Add H3(.a(A[2]),.b(B[2]),.s(v6),.c(v5));
Half_Add H4(.a(A[3]),.b(B[3]),.s(v8),.c(v7));
carry_look
CL1(.C0(Cin),.P0(v2),.G0(v1),.P1(v4),.G1(v3),.P2(v6),.G2(v5),.P3(v8),.G3(v7),.C1(o1),.C2(o2),.C3(o3),.C4(Cout));
注意 C4 并不需要等待 C3,实际上 C4,C3,C2,C1 同时传输 超前进位产生的电路逻辑图
超前进位加法器

8位超前进位加法器设计说明书超前进位加法器就是使各位的进位直接由加数和被加数来决定,而不需要依赖低位进位。
即有如下逻辑表达式:1)(-++=i i i i i i C B A B A C当第i 位被加数A i 和加数B i 均为1时,有1=i i B A ,不论低位运算结果如何本位必然有进位输出(1=i C ),所以定义i i i B A G =为进位产生函数。
当A i 和B i 中只有一个为1时,有0=i i B A ,1=+i i B A ,使得1-=i i C C ,所以定义i i i B A P +=为进位传递函数。
将P i 和G i 代入全加器的“和”及“进位”表达式有:1-⊕⊕=i i i i C B A Y从而构成超前进位加法器。
VHDL 示例程序如下:(本程序在MAXPLUSII V9.6上编译通过)--*****8位超前进位加法器*****LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE. STD_LOGIC _ARITH.ALL;USE IEEE. STD_LOGIC _UNSIGNED.ALL;ENTITY ADDER8BIT ISPORT(A, B: IN UNSIGNED(7 downto 0);CI,clk: IN STD_LOGIC;Y_OUT: OUT STD_LOGIC_VECTOR(7 downto 0);CO_OUT: OUT STD_LOGIC);END ADDER8BIT;ARCHITECTURE doing OF ADDER8BIT ISSIGNAL CO,Y: STD_LOGIC_VECTOR(7 downto 0);BEGINY(0)<=A(0) xor B(0) xor CI;CO(0)<=(A(0) and B(0)) or (B(0) and CI) or (A(0) and CI);GEN:for i in 1 to 7 GENERATEY(i)<=A(i) xor B(i) xor CO(i-1); --1-⊕⊕=i i i i C B A YCO(i)<=(CO(i-1) and A(i)) or (CO(i-1) and B(i)) or (A(i) and B(i)); -- 1)(-++=i i i i i i C B A B A Cend GENERATE;process(clk)beginif clk'event and clk='1' thenY_OUT<=Y(7) & Y(6) & Y(5) & Y(4) & Y(3) & Y(2) & Y(1) & Y(0);CO_OUT<=CO(7);end if;end process;END doing;附:仿真时序波形。
数字电路课程设计之超前进位加法器

# MACRO ./mul_run_msim_rtl_verilog.do PAUSED at line 14
通过查阅资料将 Verilog 测试文件
Timsbench 文件没有实例化,修改为
修改后仿真 OK 参考文献: 1.数字设计与 Verilog 实现 M.Morris Mano 著 第五版
Pi=Ai○+ Bi;
可以得到输出与进位表达
Gi=AiBi;
Si=Pi○+ Ci;
Ci+1=Gi+PiCi; Gi 为进位产生,不管输入进位 Ci 为什么,只要 Ai 与 Bi 为 1 时,它将产生进位。Pi 称为进位传输,因为它 与从 Ci 到 Ci+1 的进位传输有关
C0 = 输入进位
C1 = G0 + P0C0
instance name in instantiation of 'carry_look_add'.
#
#
Region: /carry_look_add_tb
# Error loading design
# Error: Error loading design
#
Pausing macro execution
基于 Verilog 的四位超前进位加法器设计
使用 Verilog 语言实现四位超前进位加法器设计,并使用 Quartes 编写程序,使用 modelsin 进行仿真
验证设计
二、原理介绍
超前进位加法器(图为全加器)
Ai
1
3
Pi
Bi
2
1
3
Si
2
1 3 Gi
2
Ci
1
3
超前进位加法器设计报告解剖

华东交通大学理工学院课程设计报告书所属课程名称EDA课程设计题目超前进位加法器设计分院专业班级学号学生姓名指导教师2013 年7月2日目录第一章设计内容与要求 (3)第二章超前进位加法器设计原理 (3)第三章详细设计流程 (4)3.1.创建工程文件 (4)3.2.程序的编译 (5)3.3.波形的仿真 (7)第四章设计结果分析 (11)第五章源程序代码 (12)第六章心得体会 (14)第七章参考文献 (15)第一章设计内容与要求加法运算是最重要也是最基本的运算,所有的其他基本运算,如减、乘、除运算最终都能归结为加法运算。
但因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于他的位相关。
因此为了减少进位传输所消耗的时间,提高计算速度,人们设计了多种类型的加法器,如跳跃进位加法器、进位选择加法器、超前进位加法器等。
本设计采用的是超前进位加法器。
通过Verilog 设计一个超前8位加法器。
要求在Quartus II软件下,利用Verilog编程完成层次式电路设计,电路中的元件可以用Verilog设计也可以用库元件连线构成再封装。
8位超前进位加法器,借助EDA工具中的综合器,适配器,时序仿真器和编程器等工具进行相应处理。
适配采用Cyclone系列的EP1C6Q240C8。
要求综合出RTL电路,并进行仿真输入波形设计并分析电路输出波形. 试比较并阐述数据类型reg型和wire型的区别。
第二章超前进位加法器设计原理将n个全加器相连可得n位加法器,但是加法时间较长。
解决的方法之一是采用“超前进位产生电路”来同时形成各位进位,从而实现快速加法。
超前进位产生电路是根据各位进位的形成条件来实现的首先对于1位加法器基本位值和与进位输出为1;如果a,b有一个为1,则进位输出等于cin;令G=ab,P=a+b,则有:Cout==ab+(a+b)cin=G+P•cin由此可以G和P来写出4位超前进位链如下(设定四位被加数和加数为A 和B,进位输入Cin,进位输出为cout,进位产生Gi=AiBi,进位传输Pi=Ai+Bi);C0=cin;C1=G0+P0C0=G0+P0•cinC2=G1+P1C1=G1+P1(G0+P0cin)=G1+P1G0+P1P0cinC3=G2+P2C2=G2+P2(G1+P1cin)=G2+P2G1+P2P1G0+P2P1P0cinC4=G3+P3C3=G3+P3(G2+P2C2)=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0cin Cout=c4由超前进位链,各个进位彼此独立产生,将进位级联传播给去掉了,因此,减小了进位产生的延迟时间。
超前进位加法器原理

超前进位加法器原理超前进位加法器是一种在数字电路中常用的加法器,它可以实现快速、高效地进行数字加法运算。
在本文中,我们将详细介绍超前进位加法器的原理和工作方式。
首先,让我们来了解一下传统的进位加法器。
在传统的进位加法器中,每一位的进位都依赖于前一位的运算结果。
这意味着当我们进行多位数的加法运算时,每一位的计算都需要等待前一位的计算结果,这会导致整体的运算速度变慢。
而超前进位加法器则通过引入预测进位的方式来解决这一问题。
它可以在不等待前一位计算结果的情况下,提前计算出进位的值,从而加快整体的运算速度。
超前进位加法器的原理是基于两个关键的概念,预测进位和进位生成。
预测进位是指在进行加法运算时,提前计算出下一位的进位值。
而进位生成则是指在当前位的计算中,根据当前位的两个加数和上一位的进位值,生成当前位的进位值。
为了更好地理解超前进位加法器的工作原理,让我们来看一个具体的例子。
假设我们要计算两个4位数的加法,1101和1011。
在传统的进位加法器中,我们需要等待前一位的计算结果,而在超前进位加法器中,我们可以提前计算出进位值,从而加快整体的运算速度。
对于上面的例子,我们可以先计算最低位的进位值。
根据预测进位的原理,我们可以提前计算出第二位的进位值为1。
然后,根据进位生成的原理,我们可以计算出最低位的和为0,进位值为1。
接着,我们可以继续计算第二位的和和进位值,依次类推,直到计算出最高位的和和进位值。
通过上面的例子,我们可以看到,超前进位加法器可以在不等待前一位计算结果的情况下,提前计算出进位值,从而加快整体的运算速度。
这种预测进位和进位生成的原理,使得超前进位加法器成为了数字电路中常用的加法器之一。
总之,超前进位加法器通过引入预测进位的方式,提前计算出进位值,从而加快了加法运算的速度。
它的工作原理基于预测进位和进位生成的概念,通过这种方式可以在不等待前一位计算结果的情况下,快速、高效地进行数字加法运算。
2006031459 黄德荣 5位逐级进位和超前进位加法器设计资料

end Behavioral;
仿真波形
实验结论:
通过实验基本上掌握了 VHDL 的语法,同时对逐级进位和超前进位加法器的 工作原理有了深入的了解。
指导教师批阅意见:
成绩评定:
指导教师签字: 年 月 日
备注:
注:1、报告内的项目或内容设置,可根据实际情况加以调整和补充。
2、教师批改学生实验报告时间应在学生提交实验报告时间后 10 日内。
s: out std_logic_vector(4 downto 0); cout:out std_logic); end adder; architecture Behavioral of adder is signal c:std_logic_vector(4 downto 0); begin c(0)<=cin; s(0)<=a(0) xor b(0) xor c(0); c(1)<=(a(0)and b(0))or (a(0)and c(0))or (b(0)and c(0)); s(1)<=a(1) xor b(1) xor c(1); c(2)<=(a(1)and b(1))or (a(1)and c(1))or (b(1)and c(1)); s(2)<=a(2) xor b(2) xor c(2); c(3)<=(a(2)and b(2))or (a(2)and c(2))or (b(2)and c(2)); s(3)<=a(3) xor b(3) xor c(3); c(4)<=(a(3)and b(3))or (a(3)and c(3))or (b(3)and c(3)); s(4)<=a(4) xor b(4) xor c(4); cout<=(a(4)and b(4))or (a(4)and c(4))or (b(4)and c(4));
性能改进的16位超前进位加法器_李嘉

性能改进的16位超前进位加法器李 嘉,蒋 林(西安邮电学院 陕西西安 710061)摘 要:加法运算是最重要最基本的运算,所有的其他基本算术运算,减、乘、除、模乘运算最终都能归结为加法运算。
在不同的场合使用的加法器对其要求也不同,有的要求速度更快,有的要求面积更小。
基于速度更快的要求,对3种常用加法器从结构与性能上进行比较,给出了综合面积与速度的比较。
进而对超前进位加法器进行了进一步改进,加入了流水线结构设计,大大提高了其速度性能。
关键词:串行进位加法器;超前进位加法器;流水线;逻辑综合中图分类号:T P342+.21 文献标识码:B 文章编号:1004-373X(2007)22-172-03A 16-bit C LA with Improved PerformanceL I Jia,JIA N G L in(Xi an Institute o f P ost and T elecom municat i o ns,Xi an,710061,Chi na)Abstract :T he addition o perat ion is the mo st impo rtant fundamental o per ation,all other o perat ions including subtr action multiplication division and modular mult iplication can be implemented by addition operatio n.A dders using at var ious cases are different since the requirement are different.Some ask for faster,others ask for smaller.T hree co mmon used adder s are com -pared in the st ruct ur al and perfo rmance,based o n the requirement o f faster.T hen so me amelio ratio ns on the CL A are made by adding pipline str ucture to impro ve its perfo rmance fo r w or king faster.Keywords :ripple adder ;car ry loo k -ahead adder;pipeline;log ic sy nthesis收稿日期:2007-04-23加法运算是最重要最基本的运算,所有的其他基本算术运算,减、乘、除、模乘运算最终都能归结为加法运算。
计算机组成原理06-运算方法-加法PPT课件

流水线加法器
• Pipelined Adder:将加法运算拆分成多个阶段,并在每个阶 段之间插入寄存器以存储中间结果。通过流水线技术,可以实 现多个加法运算的并行处理,提高了运算速度。流水线加法器 的缺点是需要额外的硬件资源来存储中间结果,并且可能存在 一些时序问题需要注意。
04
加法运算在计算机系统中的应用
在寄存器间进行加法操作时,通常将一个寄存 器的内容加到另一个寄存器上,或将两个寄存 器的内容相加后存储到第三个寄存器中。
这种加法操作常用Biblioteka 数据处理、地址计算和程 序控制等方面。
内存地址计算中的加法
在计算机系统中,内存用于存储数据和 程序。
内存地址计算是访问内存数据的关键步 在内存地址计算中,加法常用于计算基
溢出误差
运算结果超出计算机所能表示的最大范围而产生的误 差。
精度评估指标与方法
绝对误差
计算结果与真实值之间的绝对差值。
相对误差
绝对误差与真实值之比,用于衡量误差的相对 大小。
有效数字
表示数的精度和可靠性的数字位数,通常用于评估近似数的精度。
提高加法运算精度的策略
采用高精度算法
如Kahan求和算法、成对求和算法等,通过减少误差的累积来提 高加法运算的精度。
详细讲解了加法器的设计过程, 包括全加器、半加器的设计,以 及多位加法器的实现方法。
加法运算的应用
介绍了加法运算在计算机中的应 用,如算术逻辑单元(ALU)中 的加法操作,以及在程序设计和 算法中的应用。
加法运算的发展趋势与挑战
发展趋势
随着计算机技术的不断发展,加法运算的速度和精度将不断提高,同时加法器的设计和实现也将更加优化和高效。
算术逻辑单元(ALU)中的加法
计算机设计与实践——位先行进位加法器学习教案

第2页/共8页
第三页,编辑于星期三:一点 十七分。
module alu_16(gmm,pmm,f16,x16,y16,cii);//16位加法器先行进位加法器
input [16:1]x16;
input [16:1]y16; input cii; output [16:1]f16; output gmm,pmm;
第4页/共8页
第五页,编辑于星期三:一点 十七分。
module jiafaqi_1(x,y,c0,f); //一位加法器模块 input x;
input y; input c0; output f;
assign f=(x^y)^c0; endmodule module cla_4(c,p,g,c0);//4位CLA部件
cla_4 cl_4_1(c,p,g,cii);
assign pmm=p[4]&p[3]&p[2]&p[1]; assign gmm=g[4]|p[4]&g[3]|p[4]&p[3]&g[2]|p[4]&p[3]&p[2]&g[1]; endmodule
第3页/共8页
第四页,编辑于星期三:一点 十七分。
alu_16 alu_16_1(g[1],p[1],f32[16:1],x32[16:1],y32[16:1],ciii); alu_16 alu_16_2(g[2],p[2],f32[32:17],x32[32:17],y32[32:17],c1);
assign c1=g[1]|p[1]&ciii; assign c2=g[2]|p[2]&g[1]|p[2]&p[1]&ciii;
超前进位加法器

超前进位加法器超前进位加法器是一种数字电路,用于执行两个二进制数的加法运算。
它具有高速、高效的特点,在计算机领域得到广泛的应用。
超前进位加法器的原理和实现方法值得深入研究和探讨。
本文将详细介绍超前进位加法器的原理、设计和性能优化等方面内容。
1. 引言在计算机科学和工程领域,加法运算是一项基本的操作。
随着计算机性能的要求不断提高,如何在更短的时间内完成加法运算成为了重要的研究方向。
超前进位加法器是一种对加法运算进行优化的方法,可以极大地提高运算速度和效率。
2. 超前进位加法器原理超前进位加法器是一种并行加法器,它利用了信号传输的延迟问题,通过将进位信号从低位传递到高位,实现了高速的运算。
其基本原理是,将两个二进制数按位相加,如果某一位的和等于2,就会产生一个进位信号,进位信号会传递到下一位,直到最高位。
3. 超前进位加法器的设计超前进位加法器的设计分为四个部分:1) 带有进位预测的半加器;2) 带有进位预测的全加器;3) 进位生成和进位传递逻辑电路;4) 加法器的结构和电路实现。
3.1 带有进位预测的半加器半加器是最基本的加法器,可以完成两个二进制位的加法运算,但不能处理进位信号。
为了实现进位预测,我们需要对半加器进行改进。
一种常见的方法是使用XOR门和AND门来实现进位预测功能。
具体的电路设计和逻辑表达式请查阅相关资料。
3.2 带有进位预测的全加器全加器是进一步改进的半加器,可以处理进位信号。
在超前进位加法器的设计中,我们使用带有进位预测的全加器。
全加器的设计和实现方法与半加器类似,但需要增加一个输入端来接收上一位的进位信号,并根据进位预测电路来生成进位信号。
3.3 进位生成和进位传递逻辑电路进位生成和进位传递逻辑电路是超前进位加法器的核心部分。
它们用于计算每一位的进位信号和传递进位信号到下一位。
进位生成电路可以通过AND门实现,进位传递电路可以通过OR 门实现。
具体的电路设计和实现方法请参考相关资料。
数字逻辑课程设计---全加器的多位加法器电路系统

数字课程设计论文一个全加器的多位加法器电路系统主负责成员:组队成员:所在系:年级专业:指导老师:2011年6 月15日摘要随着科技的日益发展,电子技术领域的发展有了很大的跨越。
加法器在人们的生活中得到了广泛的运用,尤其在计算机方面的内部硬件中更是必不可缺。
我们可以使用多位加法器来实现多位二进制数加法的运算,这样,我们就实现了计算机里面二进制数码的计算的一小部分。
为了能检验这样的效果,我们设计只用一个全加器实现多位二进制数相加的电路系统。
在该设计中,我们主要针对两个四位二进制数相加而出发,该设计采用了双移位寄存器74LS194芯片为整个设计的核心,这样就达到了两个一位二进制数可以实现两个四位二进制数的相加。
该设计的思想是:将74LS283这种四位二进制数超前进位加法器的A3A2A1三个运算输入端都连接到5V的电源,以及B3B2B1三个运算输入端都连接地,这样就可以实现两个一位二进制数的相加。
再借助两个双移位寄存器74LS194分别对74LS283加法器中的A和B两个输入的二进制数(1或0)的移位。
为了解决两个二进制数相加中出现的进位问题,我们在该电路中添加了一个74LS74的触发器来对两个二进制数的进位的保存和输出。
以上的设计思路可以通过加法器、移位寄存器以及触发器来帮助我们实现四位二进制的加法。
最后,我们可以借助5个二极管来显示我们要设计的效果。
整个硬件实物完成后可以通过电路箱进行供电,使用方便;显示的效果相对较小,操作简单。
只要手动控制A和B的输入、点动移位开关以及脉冲开关就可以看到效果。
关键词:74LS283超前进位加法器双移位寄存器74LS19474LS74触发器四位二进制的加目录1、前言 (4)2、测量范围 (4)3、方案设计 (4)3.1 方案设计简图 (4)3.2系统硬件各部分介绍组成 (5)3.2.1.74LS194寄存器介绍 (5)3.2.2. 74LS74触发器介绍 (7)3.2.3.74LS283加法器介绍 (12)4、电路箱上的电路设计 (16)4.1设计思想 (16)4.2原理图设计 (18)5、Multisim软件上的仿真 (19)6、实验及调试 (19)6.1、硬件实物 (19)6.2 硬件实物说明与使用说明 (20)6.2.1硬件实物说明 (20)6.2.2 使用说明 (21)7、操作结果评价 (21)8、结束语 (22)1、前言通过采用移位寄存器对一位二进制数的加法器移位来实现四位二进制数的加法器,它可以帮助我们实现两个四位二进制数的相加。
杭电计组实验2-超前进位加法器设计实验

杭州电子科技大学计算机学院
实验报告
实验项目:实验2-超前进位加法器设计实验
课程名称:计算机组成原理与系统结构课程设计
姓名:学号:同组姓名:学号:
实验位置(机号):
实验日期:指导教师:
#100;
A = 1011;
B = 1101;C0 = 0;
#100;
A = 1010;
B = 0010;C0 = 1;
#100;
A = 0111;
B = 1000;C0= 0;
#100;
A = 0011;
B = 0100;C0 = 1;
#100;
A = 1001;
B = 0001;C0 = 0;
#100;
end
Endmodule
RTL图
二、结果
思考题:
(1)综合得到的电路图,它和想要设计的电路在引脚的输入输出方面是完全相同的,但是相比较内部的RTL图,实验实现的结果是相同的,但是我编写的实验代码并没有调用实验一的全加器设计。
(2)尝试编写8位超前进位加法器设计实验
module add_8 ( input [7:0]a, input [7:0]b, input cin, output [7:0] s, output co );
wire [7:0]c_tmp;
wire [7:0]g;
wire [7:0]p;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s: out std_logic_vector(4 downto 0); cout:out std_logic); end adder; architecture Behavioral of adder is signal c:std_logic_vector(4 downto 0); begin c(0)<=cin; s(0)<=a(0) xor b(0) xor c(0); c(1)<=(a(0)and b(0))or (a(0)and c(0))or (b(0)and c(0)); s(1)<=a(1) xor b(1) xor c(1); c(2)<=(a(1)and b(1))or (a(1)and c(1))or (b(1)and c(1)); s(2)<=a(2) xor b(2) xor c(2); c(3)<=(a(2)and b(2))or (a(2)and c(2))or (b(2)and c(2)); s(3)<=a(3) xor b(3) xor c(3); c(4)<=(a(3)and b(3))or (a(3)and c(3))or (b(3)and c(3)); s(4)<=a(4) xor b(4) xor c(4); cout<=(a(4)and b(4))or (a(4)and c(4))or (b(4)and c(4));
VHDL 代码
--------------------------------------------------------------------------------- Company: -- Engineer: --- Create Date: 02:59:18 10/22/08 -- Design Name: -- Module Name: adder - Behavioral -- Project Name: -- Target Device: -- Tool versions: -- Description: --- Dependencies: --- Revision: -- Revision 0.01 - File Created -- Additional Comments: --------------------------------------------------------------------------------library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.STD_LOGIC_ARITH.ALL; use IEEE.STD_LOGIC_UNSIGNED.ALL; ---- Uncomment the following library declaration if instantiating ---- any Xilinx primitives in this code. --library UNISIM; --use UNISIM.VComponents.all; entity adder is port(a,b:in std_logic_vector(4 downto 0); cin:in std_logic;
深 圳 大 学 实 验 报 告
课程名称:
VHDL 数字电路设计教程
实验项目名称:
5 位逐级进位和超前进位加法器设计
学院:
信息工程学院
专业:
电子信息工程
指导教师:
梁松海
报告人:黄德荣
学号:20006031459 班级:
1班ቤተ መጻሕፍቲ ባይዱ
实验时间:
2008.10.22
实验报告提交时间:
2008.11.5
教务处制
实验目的与要求:
用 XILINX ISE 7.1i 实现逐级进位和超前进位加法器
方法、步骤: 1,逐级进位加法器
对每一位都使用了全加器 FAU,图中 a 和 b 是输入位,cin 是进位输入位。S 是求和 的结果,cout 是进位输出位。C 是进位矢量。图中每个全加器的输出结果都依赖于前一 级产生的进位。由全加器的特性,可以写出如下的逻辑表达式: S=a XOR b XOR cin cout=(a ANDb)OR(aAND cin)OR(b AND cin) 2,超前进位加法器
电路实现是需要两个非常重要的中间信号:generate 和 propagate,分别由 g 和 p 表 示。加法器两个输入位是 a 和 b,则 generate 和 propagate 信号定义如下: g=a AND b p=a XOR b 这两个信号与进位无关,只根据当前的输入计算。 现在两个输入矢量是: a=a(4)a(3)a(2)a(1)a(0) 和 b=b(4)b(3)b(2)b(1)b(0), 那么相应的 generate 矢量为 g=g(4)g(3)g(2)g(1)g(0),相应的 propagate 矢量为 p=p(4)p(3)p(2)p(1)p(0)。 其中: g(j)=a (j) AND b(j) p(j)=a (j)XOR b(j) 同时,进位矢量用 c=c(4)c(3)c(2)c(1)c(0)。进位可由 g 和 p 按照下面的方法计算得 到: c(0) = cin; c(1) = c(0)p(0))+g(0);
c(2) = c(0)p(0)p(1))+g(0)p(1)+g(1); c(3) = c(0)p(0)p(1) p(2)+g(0)p(1)p(2)+(g(1) p(2)+g(2); c(4) = c(0)p(0) p(1) p(2) p(3)+g(0) p(1) p(2) p(3)+g(1) p(2) p(3)+g(2) p(3)+g(3); c(5) =c(0)p(0) p(1) p(2) p(3) p(4)+g(0) p(1) p(2)p(3) p(4)+g(1) p(2) p(3) p(4)+g(2) p(3) p(4)+g(4); 可见超前进位加法器的每个全加器不依赖与前一级进位输出的计算结果,有利于 提高电路执行速度。 实验过程及内容: 1, 逐级进位加法器
