2018年高考数学总复习 11.1 随机事件的概率
(新课标)高考数学总复习-第11章 概率 第1节 随机事件的概率课件 新人教A版

求复杂互斥事件概率的两种方法:一是直接求 解法,将所求事件的概率分解为一些彼此互斥的事 件的概率的和;二是间接法,先求该事件的对立事 件的概率,再由 P(A)=1-P( A )求解.当题目涉及 “至多”“至少”型问题,多考虑间接法.
某超市为了了解顾客的购物量及结算时间等信 息,安排一名员工随机收集了在该超市购物的 100 位 顾客的相关数据,如下表所示.
(2015·陕西高考)随机抽取一个年份,对西安 市该年 4 月份的天气情况进行统计,结果如下:
[典题 3] 某商场有奖销售中,购满 100 元商品得 1 张奖券,多购多得.1 000 张奖券为一个开奖单位, 设特等奖 1 个,一等奖 10 个,二等奖 50 个.设 1 张奖券中特等奖、一等奖、二等奖的事件分别为 A、 B、C,求:
①恰有一个是偶数和恰有一个是奇数;
②至少有一个是奇数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;
④至少有一个是奇数和至少有一个是偶数.
上.①③
对互斥事件要把握住不能同时发生,而对于 对立事件除不能同时发生外,其并事件应为必然 事件.这些也可类比集合进行理解,具体应用时, 可把所有试验结果写出来,看所求事件包含哪几 个试验结果,从而判定所给事件的关系.
大家好
1
第十一章 概 率
第一节 随机事件的概率
考纲要求: 1.了解随机事件发生的不确定性和频率的稳 定性,了解概率的意义以及频率与概率的区别. 2.了解两个互斥事件的概率加法公式.
1.事件的分类
2.频率和概率 (1)在相同的条件 S 下重复 n 次试验,观察某一事
(完整word版)2018年高考数学总复习概率及其计算
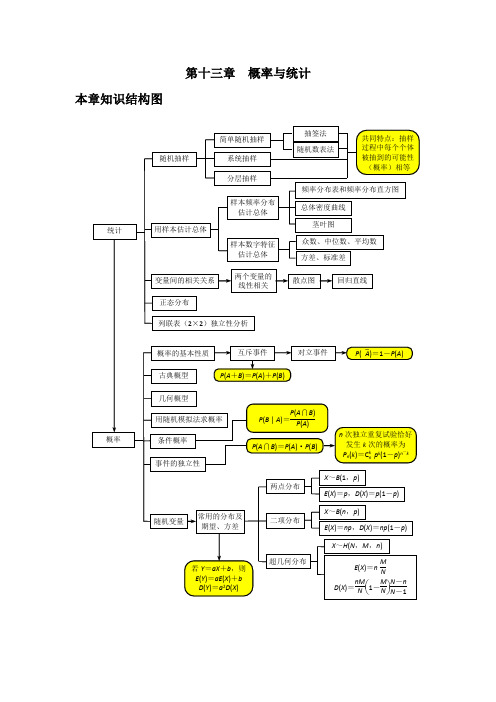
第十三章概率与统计本章知识结构图第一节 概率及其计算考纲解读1.了解随机事件发生的不确定性、频率的稳定性、概率的意义、频率与概率的区别。
2.了解两个互斥事件的概率的加法公式。
3.掌握古典概型及其概率计算公式。
4.了解随机数的意义,能运用模拟方法估计概率。
5.了解几何概型的意义。
命题趋势探究1.本部分为高考必考内容,在选择题、填空题和解答题中都有渗透。
2.命题设置以两种概型的概率计算及运用互斥、对立事件的概率公式为核心内容,题型及分值稳定,难度中等或中等以下。
知识点精讲一、必然事件、不可能事件、随机事件在一定条件下:①必然要发生的事件叫必然事件; ②一定不发生的事件叫不可能事件;③可能发生也可能不发生的事件叫随机事件。
二、概率在相同条件下,做次重复实验,事件A 发生次,测得A 发生的频率为,当很大时,A 发生的频率总是在某个常数附近摆动,随着的增加,摆动幅度越来越小,这时就把这个常数叫做A 的概率,记作。
对于必然事件A ,;对于不可能事件A ,=0.三、基本事件和基本事件空间在一次实验中,不可能再分的事件称为基本事件,所有基本事件组成的集合称为基本事件空间。
四、两个基本概型的概率公式1、古典概型条件:1、基本事件空间含有限个基本事件 2、每个基本事件发生的可能性相同()(A)=()A card P A card =Ω包含基本事件数基本事件总数2、几何概型条件:每个事件都可以看作某几何区域Ω的子集A ,A 的几何度量(长度、面积、体积或时间)记为Aμ.()P A =AμμΩ。
五、互斥事件的概率1、互斥事件在一次实验中不能同时发生的事件称为互斥事件。
事件A 与事件B 互斥,则()()()P A B P A P B =+ 。
2、对立事件事件A,B 互斥,且其中必有一个发生,称事件A,B 对立,记作B A =或A B =。
()()1P A p A =- 。
3、互斥事件与对立事件的联系对立事件必是互斥事件,即“事件A ,B 对立”是”事件A ,B 互斥“的充分不必要条件。
高考数学总复习 第11章 第1节 随机事件的概率 文课件 新人教A版

概率是频率的稳定值,不会随试验次数的变化而变化,
故D错. 答案:B
2.某人打靶,连续射击2次,事件“至少有1次中靶”的 对立事件是( ) B.2次都中靶 D.只有1次中靶
A.至多有1次中靶 C.2次都不中靶
解析:“至少有1次中靶”包括中1次或中2次.
答案:C
3.甲、乙两个下棋,甲获胜的概率是40%,甲不输的概 率为90%,则甲、乙二人下成和棋的概率为( A.60% C.10% B.30% D.50% )
解法二:(利用对立事件求概率) (1)由法一知, 取出 1 球为红球或黑球的对立事件为取出 1 球为白球或绿球,即 A1∪A2 的对立事件为 A3∪A4,所以取 出 1 球为红球或黑球的概率为 P(A1∪A2)=1-P(A3∪A4)=1 2 1 3 -P(A3)-P(A4)=1-12-12=4. (2)因为 A1∪A2∪A3 的对立事件为 A4,所以 1 11 P(A1∪A2∪A3)=1-P(A4)=1-12=12. 12 分 9分
答案:25
1.事件的判断需要对三种事件即不可能事件、必然事 件和随机事件的概念充分理解,特别是随机事件要看它是 否可能发生,并且是在一定条件下的,它不同于判断命题 的真假.
2.对随机事件的理解应包含下面两个方面: (1)随机事件是指一定条件下出现的某种结果,随着条件 的改变其结果也会不同,因此必须强调同一事件必须在相同 的条件下研究.
2分
5 4 1 2 1 则 P(A1)=12,P(A2)=12=3,P(A3)=12=6, 1 P(A4)= , 12 6分
根据题意知,事件 A1、A2、A3、A4 彼此互斥,由互斥事 件的概率公式,得 (1)取出 1 球为红球或黑球的概率为 5 4 3 P(A1∪A2)=P(A1)+P(A2)=12+12=4; (2)取出 1 球为红球或黑球或白球的概率为 P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3) 5 4 2 11 =12+12+12=12. 12 分 9分
2018高考数学复习:随机事件的概率

(2)设 C 表示事件“投保车辆中新司机获赔 4 000 元”,由 已知, 样本车辆中车主为新司机的有 0. 1×1 000=100(辆), 而赔付金额为 4 000 元的车辆中,车主为新司机的有 0.2×120=24(辆),所以样本车辆中新司机车主获赔金额为 24 4000 元的频率为 =0.24,由频率估计概率得 P(C)=0.24. 100 [规律方法] 频率是个不确定的数, 在一定程度上频率可以
A=B __________
若某事件发生 当且仅当事件A ________________, 并事件 发生或事件B发生 ___________________则称此 (和事件) 事件为事件A与事件B的并事件 (或和事件)
A∪B __________ (或A+B)
定义
符号表示
若某事件发生 当且仅当事件A发生 _________ A∩B 交事件 ____________________, 且事件B发生 _ (或 AB (积事件) __________________则称此事件为 _______) 事件A与事件B的交事件(或积事件) 互斥 事件 不可能 若A∩B为__________ 事件,那么称 A∩B=∅ 事件A与事件B互斥 不可能 若A∩B为__________ 事件,A∪B A∩B=∅且 必然事件 为_______________,那么称事件A A∪B=Ω 与事件B互为对立事件
解:(1)由于事件 C“至多订一种报纸”中有可能“只订甲 报纸”, 即事件 A 与事件 C 有可能同时发生, 故A与C不 是互斥事件.
(2) 事件 B“至少订一种报纸”与事件 D“一种报纸也不 订”是不可能同时发生的,故 B 与 D 是互斥事件.由于事 件 B 不发生可导致事件 D 一定发生, 且事件 D 不发生会导 致事件 B 一定发生,故 B 与 D 还是对立事件. (3)事件 B“至少订一种报纸”中有这些可能:“只订甲报 纸”、“只订乙报纸” 、 “订甲、乙两种报纸” ,事件 C“至 多订一种报纸”中有这些可能: “一种报纸也不订”、 “只 订甲报纸”、“只订乙报纸”,由于这两个事件可能同时 发生,故 B 与 C 不是互斥事件. (4)由(3)的分析, 事件 D“一种报纸也不订”是事件 C 的一 种可能,即事件 C 与事件 D 有可能同时发生,故 C 与 D 不是互斥事件.
最新高三教案-高考第一轮复习:2018.1随机事件的概率 精品

第十一章 概率●网络体系总览随机事件的概率互斥事件有一个发生的概率相互独立事件同时发生的概率概率●考点目标定位1.了解等可能性事件的概率的意义,会用排列组合公式计算一些等可能性事件的概率.2.了解互斥事件的意义,会用互斥事件的概率加法公式计算一些事件的概率.3.了解相互独立事件的意义,会用相互独立事件的概率乘法公式计算一些事件的概率,会计算事件在n 次独立重复试验中恰好发生k 次的概率.●复习方略指南概率是新课程中新增加部分的主要内容之一.这一内容是在学习排列、组合等计数知识之后学习的,主要内容为等可能性事件的概率、互斥事件有一个发生的概率及相互独立事件同时发生的概率.这一内容从2000年被列入新课程高考的考试说明.在2000,2001,2018,2003,2004这五年高考中,新课程试卷每年都有一道概率解答题,并且这五年的命题趋势是:从分值上看,从10分提高到17分,从题目的位置看,2000年为第(17)题,2001年为第(18)题,2018年为第(19)题,2003年为第(20)题即题目的位置后移,2004年两题分值增加到17分.从概率在试卷中的分数比与课时比看,在试卷中的分数比(12∶150=1∶12.5)是在数学中课时比(约为11∶330=1∶30)的2.4倍.概率试题体现了考试中心提出的“突出应用能力考查”以及“突出新增加内容的教学价值和应用功能”的指导思想,在命题时,提高了分值,提高了难度,并设置了灵活的题目情境,如普法考试、串联并联系统、计算机上网、产品合格率等,所以在概率复习中要注意全面复习,加强基础,注重应用.11.1 随机事件的概率●知识梳理1.随机事件:在一定条件下可能发生也可能不发生的事件.2.必然事件:在一定条件下必然要发生的事件.3.不可能事件:在一定条件下不可能发生的事件.4.事件A 的概率:在大量重复进行同一试验时,事件A 发生的频率nm总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A 的概率,记作P (A ).由定义可知0≤P (A )≤1,显然必然事件的概率是1,不可能事件的概率是0.5.等可能性事件的概率:一次试验连同其中可能出现的每一个结果称为一个基本事件,通常此试验中的某一事件A 由几个基本事件组成.如果一次试验中可能出现的结果有n 个,即此试验由n 个基本事件组成,而且所有结果出现的可能性都相等,那么每一基本事件的概率都是n 1.如果某个事件A 包含的结果有m 个,那么事件A 的概率P (A )=nm .6.使用公式P (A )=nm计算时,确定m 、n 的数值是关键所在,其计算方法灵活多变,没有固定的模式,可充分利用排列组合知识中的分类计数原理和分步计数原理,必须做到不重复不遗漏.●点击双基1.(2004年全国Ⅰ,文11)从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是A.95B.94C.2111D.2110 解析:基本事件总数为C 39,设抽取3个数,和为偶数为事件A ,则A 事件数包括两类:抽取3个数全为偶数,或抽取3数中2个奇数1个偶数,前者C 34,后者C 14C 25.∴A 中基本事件数为C 34+C 14C 25.∴符合要求的概率为39251434C C C C +=2111. 答案:C2.(2004年重庆,理11)某校高三年级举行的一次演讲比赛共有10位同学参加,其中一班有3位,二班有2位,其他班有5位.若采取抽签的方式确定他们的演讲顺序,则一班的3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为A.101 B.201 C.401 D.1201解析:10位同学总参赛次序A 1010.一班3位同学恰好排在一起,而二班的2位同学没有排在一起的方法数为先将一班3人捆在一起A 33,与另外5人全排列A 66,二班2位同学不排在一起,采用插空法A 27,即A 33A 66A 27.∴所求概率为1010276633AA A A =201. 答案:B3.(2004年江苏,9)将一颗质地均匀的骰子(它是一种各面上分别标有点数1、2、3、4、5、6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是A.2165 B.21625 C.21631 D.21691 解析:质地均匀的骰子先后抛掷3次,共有6×6×6种结果.3次均不出现6点向上的掷法有5×5×5种结果.由于抛掷的每一种结果都是等可能出现的,所以不出现6点向上的概率为666555⨯⨯⨯⨯=216125,由对立事件概率公式,知3次至少出现一次6点向上的概率是1-216125= 21691.答案:D4.一盒中装有20个大小相同的弹子球,其中红球10个,白球6个,黄球4个,一小孩随手拿出4个,求至少有3个红球的概率为________.解析:恰有3个红球的概率P 1=420110310C C C =32380. 有4个红球的概率P 2=420410C C =32314. 至少有3个红球的概率P =P 1+P 2=32394. 答案:323945.在两个袋中各装有分别写着0,1,2,3,4,5的6张卡片.今从每个袋中任取一张卡片,则取出的两张卡片上数字之和恰为7的概率为________.解析:P =1616C C 4⋅=91. 答案:91 ●典例剖析【例1】用数字1,2,3,4,5组成五位数,求其中恰有4个相同数字的概率.解:五位数共有55个等可能的结果.现在求五位数中恰有4个相同数字的结果数:4个相同数字的取法有C 15种,另一个不同数字的取法有C 14种.而这取出的五个数字共可排出C 15个不同的五位数,故恰有4个相同数字的五位数的结果有C 15C 14C 15个,所求概率P =51514155C C C =1254. 答:其中恰恰有4个相同数字的概率是1254. 【例2】 从男女生共36人的班中,选出2名代表,每人当选的机会均等.如果选得同性代表的概率是21,求该班中男女生相差几名? 解:设男生有x 名,则女生有(36-x )人,选出的2名代表是同性的概率为P =2362-362C C C xx +=21, 即3536)1(⨯-x x +3536)35)(36(⨯--x x =21,解得x =15或21.所以男女生相差6人.【例3】把4个不同的球任意投入4个不同的盒子内(每盒装球数不限),计算:(1)无空盒的概率;(2)恰有一个空盒的概率.解:4个球任意投入4个不同的盒子内有44种等可能的结果. (1)其中无空盒的结果有A 44种,所求概率 P =4444A =323. 答:无空盒的概率是323. (2)先求恰有一空盒的结果数:选定一个空盒有C 14种,选两个球放入一盒有C 24A 13种,其余两球放入两盒有A 22种.故恰有一个空盒的结果数为C 14C 24A 13A 22,所求概率P (A )=4221324144A A C C =169. 答:恰有一个空盒的概率是169. 深化拓展把n +1个不同的球投入n 个不同的盒子(n ∈N *).求: (1)无空盒的概率;(2)恰有一空盒的概率. 解:(1)121A C ++n nnn n .(2)111222121311A )A C C C (C +---++⋅⋅+⋅n n n n n n n n.【例4】某人有5把钥匙,一把是房门钥匙,但忘记了开房门的是哪一把.于是,他逐把不重复地试开,问:(1)恰好第三次打开房门锁的概率是多少? (2)三次内打开的概率是多少?(3)如果5把内有2把房门钥匙,那么三次内打开的概率是多少?解:5把钥匙,逐把试开有A 55种等可能的结果. (1)第三次打开房门的结果有A 44种,因此第三次打开房门的概率P (A )=5544A A =51. (2)三次内打开房门的结果有3A 44种,因此,所求概率P (A )=5544A A 3=53. (3)方法一:因5把内有2把房门钥匙,故三次内打不开的结果有A 33A 22种,从而三次内打开的结果有A 55-A 33A 22种,所求概率P (A )=55223355A A A A -=109. 方法二:三次内打开的结果包括:三次内恰有一次打开的结果有C 12A 13A 12A 33种;三次内恰有2次打开的结果有A 23A 33种.因此,三次内打开的结果有C 12A 13A 12A 33+A 23A 33种,所求概率P (A )=55332333121312A A A A A A C +=109. 特别提示1.在上例(1)中,读者如何解释下列两种解法的意义.P (A )=3524A A =51或P (A )=54·43·31= 51. 2.仿照1中,你能解例题中的(2)吗?●闯关训练 夯实基础1.从分别写有A 、B 、C 、D 、E 的5张卡片中,任取2张,这2张上的字母恰好按字母顺序相邻的概率为A.51B.52C.103D.107 解析:P =25C 4=52. 答案:B2.(2004年湖北模拟题)甲、乙二人参加法律知识竞赛,共有12个不同的题目,其中选择题8个,判断题4个.甲、乙二人各依次抽一题,则甲抽到判断题,乙抽到选择题的概率是A.256 B.2521 C.338 D.3325 解析:甲、乙二人依次抽一题有C 112·C 111种方法,而甲抽到判断题,乙抽到选择题的方法有C 14C 18种.∴P =1111121814C C C C =338. 答案:C3.(2004年全国Ⅰ,理11)从数字1、2、3、4、5中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为A.12513 B.12516 C.12518 D.12519解析:从数字1、2、3、4、5中,允许重复地随机抽取3个数字,这三个数字和为9的情况为5、2、2;5、3、1;4、3、2;4、4、1;3、3、3.∴概率为32333332351C A A C ++++=12519. 答案:D4.一次二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇.若任意排列交流次序,则最先和最后交流的论文都为试点学校的概率是________.(结果用分数表示)解析:总的排法有A 88种.最先和最后排试点学校的排法有A 25A 66种.概率为886625A A A ⋅=145. 答案:145 5.甲、乙二人参加普法知识竞答,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙二人依次各抽一题.(1)甲抽到选择题,乙抽到判断题的概率是多少?(2)甲、乙二人中至少有一人抽到选择题的概率是多少? 分析:(1)是等可能性事件,求基本事件总数和A 包含的基本事件数即可.(2)分类或间接法,先求出对立事件的概率.解:(1)基本事件总数甲、乙依次抽一题有C 110C 19种,事件A 包含的基本事件数为C 16C 14,故甲抽到选择题,乙抽到判断题的概率为191101416C C C C =154. (2)A 包含的基本事件总数分三类:甲抽到选择题,乙抽到判断题有C 16C 14;甲抽到选择题,乙也抽到选择题有C 16C 15; 甲抽到判断题,乙抽到选择题有C 14C 16. 共C 16C 14+C 16C 15+C 14C 16.基本事件总数C 110C 19,∴甲、乙二人中至少有一人抽到选择题的概率为19110161415161416C C C C C C C C ++=1513或P (A )=191101314C C C C =152,P (A )=1-P (A )=1513. 6.把编号为1到6的六个小球,平均分到三个不同的盒子内,求: (1)每盒各有一个奇数号球的概率; (2)有一盒全是偶数号球的概率.解:6个球平均分入三盒有C 26C 24C 22种等可能的结果.(1)每盒各有一个奇数号球的结果有A 33A 33种,所求概率P (A )=2224463333C C C A A =52. (2)有一盒全是偶数号球的结果有(C 23C 13)·C 24C 22, 所求概率P (A )=22242622241323C C C C C )C (C ⋅=53. 培养能力7.(2004年全国Ⅱ,18)已知8支球队中有3支弱队,以抽签方式将这8支球队分为A 、B 两组,每组4支.求:(1)A 、B 两组中有一组恰有两支弱队的概率; (2)A 组中至少有两支弱队的概率.(1)解法一:三支弱队在同一组的概率为4815C C +4815C C =71, 故有一组恰有两支弱队的概率为1-71=76. 解法二:有一组恰有两支弱队的概率为 482523C C C +482523C C C =76. (2)解法一:A 组中至少有两支弱队的概率为482523C C C +481533C C C =21. 解法二:A 、B 两组有一组至少有两支弱队的概率为1,由于对A 组和B 组来说,至少有两支弱队的概率是相同的,所以A 组中至少有两支弱队的概率为21. 8.从1,2,…,10这10个数字中有放回地抽取3次,每次抽取一个数字,试求3次抽取中最小数为3的概率.解:有放回地抽取3次共有103个结果,因最小数为3又可分为:恰有一个3,恰有两个3,恰有三个3.故最小数为3的结果有C 13·72+C 23·7+C 33,所求概率P (A )=3332321310C 7C 7C +⋅+⋅=0.169.答:最小数为3的概率为0.169. 探究创新9.有点难度哟!将甲、乙两颗骰子先后各抛一次,a 、b 分别表示抛掷甲、乙两颗骰子所出现的点数. (1)若点P (a ,b )落在不等式组⎪⎩⎪⎨⎧≤+>>4,0,0y x y x 表示的平面区域的事件记为A ,求事件A 的概率;(2)若点P (a ,b )落在直线x +y=m (m 为常数)上,且使此事件的概率最大,求m 的值. 解:(1)基本事件总数为6×6=36.x当a =1时,b =1,2,3; 当a =2时,b =1,2;当a =3时,b =1.共有(1,1),(1,2),(1,3),,∴P (A )=366=61. (2)当m =7时,(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)共有6种,此时P =366= 61最大. ●思悟小结求解等可能性事件A 的概率一般遵循如下步骤:(1)先确定一次试验是什么,此时一次试验的可能性结果有多少,即求出A . (2)再确定所研究的事件A 是什么,事件A 包括结果有多少,即求出m .(3)应用等可能性事件概率公式P =nm计算. ●教师下载中心 教学点睛1.一个随机事件的发生既有随机性(对单次试验),又存在着统计规律(对大量重复试验),这是偶然性和必然性的对立统一.2.随机事件A 的概率P (A )满足0≤P (A )≤1.(3)P (A )=nm既是等可能性事件的概率的定义,又是计算这种概率的基本方法. 拓展题例【例1】 某油漆公司发出10桶油漆,其中白漆5桶,黑漆3桶,红漆2桶.在搬运中所有标签脱落,交货人随意将这些标签重新贴上,问一个定货3桶白漆、2桶黑漆和1桶红漆的顾客,按所定的颜色如数得到定货的概率是多少?解:P (A )=610122335C C C C =72. 答:顾客按所定的颜色得到定货的概率是72. 【例2】 一个口袋里共有2个红球和8个黄球,从中随机地接连取3个球,每次取一个.设{恰有一个红球}=A ,{第三个球是红球}=B .求在下列条件下事件A 、B 的概率.(1)不返回抽样; (2)返回抽样. 解:(1)不返回抽样,P (A )=310281312A A C C =157,P (B )=3102912A A C = 51. (2)返回抽样, P (A )=C 13102(108)2=12548,P (B )=32121010C = 51.。
高中数学11.1概率

第十一章概率与统计一概率【考点阐述】随机事件的概率.等可能性事件的概率.互斥事件有一个发生的概率.相互独立事件同时发生的概率.独立重复试验.【考试要求】(1)了解随机事件的发生存在着规律性和随机事件概率的意义.(2)了解等可能性事件的概率的意义,会用排列组合的基本公式计算一些等可能性事件的概率.(3)了解互斥事件、相互独立事件的意义,会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率.(4)会计算事件在n次独立重复试验中恰好发生κ次的概率.【考题分类】(一)选择题(共8题)1.(福建卷理5)某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是()A.16625B.96625C.192625D.256625【标准答案】B【试题解析】由222444196 (2)55625 P C⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭【高考考点】独立重复实验的判断及计算【易错提醒】容易记成二项展开式的通项,当然这题因为数字的原因不涉及.【学科网备考提示】请考生注意该公式与二项展开式的通项的区别,所以要强化公式的记忆.2.(福建卷文5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是()A.12125B.16125C.48125D.96125【标准答案】C【标准答案】由212334148 (2)55125 P C⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭【高考考点】独立重复实验的判断及计算【易错提醒】容易记成二项展开式的通项.【学科网备考提示】请考生注意该公式与二项展开式的通项的区别,所以要强化公式的记忆.3.(江西卷理11文11)电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为23的概率为()A.1180B.1288C.1360D.1480【标准答案】C.【标准答案】一天显示的时间总共有24601440⨯=种,和为23总共有4种,故所求概率为1360. 4. (辽宁卷理7文7)4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( ) A .13B .12C .23D .34【答案】:C 【解析】:本小题主要考查等可能事件概率求解问题。
高考数学一轮复习 11.1随机事件的概率课件 文 湘教版

3/24/2019
当且仅当事件A 若某事件发生______________ 交事 _________________ 发生且事件B发生 ,则称此 件 (积 事件为事件A与事件B的交事 事件) 件(或积事件)
______ A∩B (或____) AB
不可能 事件,那么 互斥 若A∩B为________ A∩B=∅ 事件 称事件A与事件B互斥 不可能 事件,A∪B 若A∩B为_______ 对立 必然事件 ,那么称事件A 为___________ 事件 与事件B互为对立事件
3/24/2019
A⊇B ,那么称事 相等 若B⊇A且______ _______ A=B 关系 件A与事件B相等 当且仅当 若某事件发生_________ 并事件 ______________________ 事件A发生或事件B发生 , A∪B (和事 则称此事件为事件A与事件 (或_____) A+B 件) B的并事件(或和事件)
3/24/2019
【思探究】 2.互斥事件与对立事件有什么区别与联 系? 提示:在一次试验中,两个互斥的事件有可能都不发 生,也可能有一个发生;而两个对立的事件则必有一
个发生,但不可能同时发生.所以,两个事件互斥,他
们未必对立;反之,两个事件对立,它们一定互斥.也 就是说,两个事件对立是这两个事件互斥的充分而不 必要条件.
3/24/2019
1.在下列六个事件中,随机事件的个数为( ) ①如果a,b都是实数,那么a+b=b+a; ②从分别标有号数 1,2,3,4,5,6,7,8,9,10 的 10 张号签中任取一张,得到 4 号 签; ③没有水分,种子发芽; ④某电话总机在60秒内接到至少10次呼叫; ⑤在101 kPa下,水的温度达到50 ℃时沸腾; ⑥同性电荷,相互排斥. A.2 B.3 C.4 D.5 【解析】 ①⑥是必然事件;③⑤是不可能事件;②④是随机事件. 【答案】 A
2018届高考数学(理)大一轮复习教师用书第十一章第三节随机事件的概率Word版含解析

第三节随机事件的概率突破点(一) 随机事件的频率与概率1.事件的分类2.频率和概率(1)在相同的条件S 下重复n 次试验,观察某一事件A 是否出现,称n 次试验中事件A 出现的次数n A 为事件A 出现的频数,称事件A 出现的比例f n (A )=n An 为事件A 出现的频率.(2)对于给定的随机事件A ,如果随着试验次数的增加,事件A 发生的频率fn (A )稳定在某个常数上,把这个常数记作P (A ),称为事件A 的概率,简称为A 的概率.事件A A 多,它在A 的概率附近摆动幅度越来越小,即概率是频率的稳定值,因此在试验次数足够的情况下,给出不同事件发生的次数,可以利用频率来估计相应事件发生的概率.[典例](2017·湖北七市联考)某电子商务公司随机抽取 1 000名网络购物者进行调查.这1 000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),[0.5,0.6),[0.6,0.7),[0.7,0.8),[0.8,0.9],购物金额的频率分布直方图如下:电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:本节主要包括2个知识点: 1.随机事件的频率与概率;互斥事件与对立事件.(2)以这1 000名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.[解](1)购物者的购物金额x与获得优惠券金额y的频率分布如下表:这1 000名购物者获得优惠券金额的平均数为:50×400+100×300+150×280+200×201 000=96.(2)由获得优惠券金额y与购物金额x的对应关系,由(1)有P(y=150)=P(0.6≤x<0.8)=0.28,P(y=200)=P(0.8≤x≤0.9)=0.02,从而,获得优惠券金额不少于150元的概率为P(y≥150)=P(y=150)+P(y=200)=0.28+0.02=0.3.1.某超市随机选取1 000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.(1)(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率;(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大?解:(1)从统计表可以看出,在这1 000位顾客中有200位顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率可以估计为2001 000=0.2.(2)从统计表可以看出,在这1 000位顾客中有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品,所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为100+2001 000=0.3.(3)与(1)同理,可得:顾客同时购买甲和乙的概率可以估计为2001 000=0.2,顾客同时购买甲和丙的概率可以估计为100+200+3001 000=0.6,顾客同时购买甲和丁的概率可以估计为1001 000=0.1.所以,如果顾客购买了甲,则该顾客同时购买丙的可能性最大.2.如图,A 地到火车站共有两条路径L 1和L 2,现随机抽取100位从A 地到火车站的人进行调查,调查结果如下:(2)分别求通过路径L 1和L 2所用时间落在上表中各时间段内的频率;(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.解:(1)共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44(人), 用频率估计概率,可得所求概率为0.44.(2)选择L 1的有60人,选择L 2的有40人,故由调查结果得所求各频率为(3)记事件A 1,A 2分别表示甲选择L 1和L 2时,在40分钟内赶到火车站;记事件B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站.由(2)知P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,P(A1)>P(A2),故甲应选择L1;P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,P(B2)>P(B1),故乙应选择L2.突破点(二)互斥事件与对立事件1.概率的基本性质(1)概率的取值范围:0≤P(A)≤1.(2)必然事件的概率:P(A)=1.不可能事件的概率:P(A)=0.2.互斥事件和对立事件[例1](1)从1,2,3①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个都是奇数;③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.上述事件中,是对立事件的是()A.①B.②④C.③D.①③(2)设条件甲:“事件A与事件B是对立事件”,结论乙:“概率满足P(A)+P(B)=1”,则甲是乙的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(3)在5张电话卡中,有3张移动卡和2张联通卡,从中任取2张,若事件“2张全是移动卡”的概率是310,那么概率是710的事件是()A.至多有一张移动卡B.恰有一张移动卡C.都不是移动卡D.至少有一张移动卡[解析](1)③中“至少有一个是奇数”即“两个奇数或一奇一偶”,而从1~7中任取两个数根据取到数的奇偶性可认为共有三个事件:“两个都是奇数”、“一奇一偶”、“两个都是偶数”,故“至少有一个是奇数”与“两个都是偶数”是对立事件,易知其余都不是对立事件.(2)若事件A与事件B是对立事件,则A∪B为必然事件,再由概率的加法公式得P(A)+P(B)=1,充分性成立.设掷一枚硬币3次,事件A:“至少出现一次正面”,事件B:“3次出现正面”,则P(A)=78,P(B)=18,满足P(A)+P(B)=1,但A,B不是对立事件,必要性不成立.故甲是乙的充分不必要条件.(3)“至多有一张移动卡”包含“一张移动卡,一张联通卡”,“两张全是联通卡”两个事件,它是“2张全是移动卡”的对立事件,其概率为1-310=710.[答案](1)C(2)A(3)A[方法技巧]事件间的关系的判断方法(1)判断事件间的关系时,可把所有的试验结果写出来,看所求事件包含哪几个试验结果,从而断定所给事件间的关系.(2)对立事件一定是互斥事件,也就是说不互斥的两个事件一定不是对立事件,在确定了两个事件互斥的情况下,就要看这两个事件的和事件是不是必然事件,这是判断两个事件是否为对立事件的基本方法.判断互斥事件、对立事件时,注意事件的发生与否都是对于同一次试验而言的,不能在多次试验中判断.(3)从集合的角度上看:事件A,B对应的基本事件构成了集合A,B,则A,B互斥时,A ∩B =∅;A ,B 对立时,A ∩B =∅且A ∪B =Ω(Ω为全集).两事件互斥是两事件对立的必要不充分条件.互斥事件、对立事件的概率[例2] 某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A ,B ,C ,求:(1)P (A ),P (B ),P (C ); (2)1张奖券的中奖概率;(3)1张奖券不中特等奖且不中一等奖的概率. [解] (1)P (A )=11 000,P (B )=101 000=1100,P (C )=501 000=120. 故事件A ,B ,C 的概率分别为11 000,1100,120.(2)1张奖券中奖包含中特等奖、一等奖、二等奖.设“1张奖券中奖”这个事件为M ,则M =A ∪B ∪C .因为A ,B ,C 两两互斥,所以P (M )=P (A ∪B ∪C )=P (A )+P (B )+P (C ) =1+10+501 000=611 000.故1张奖券的中奖概率为611 000.(3)设“1张奖券不中特等奖且不中一等奖”为事件N ,则事件N 与“1张奖券中特等奖或中一等奖”为对立事件,所以P (N )=1-P (A ∪B )=1-⎝⎛⎭⎫11 000+1100=9891 000. 故1张奖券不中特等奖且不中一等奖的概率为9891 000.[方法技巧]求复杂互斥事件概率的两种方法(1)直接求解法:将所求事件的概率分解为一些彼此互斥的事件的概率的和;(2)间接法:先求该事件的对立事件的概率,再由P (A )=1-P (A )求解.当题目涉及“至多”“至少”型问题时,多考虑间接法.能力练通 抓应用体验的“得”与“失”1.[考点一]把红、黑、蓝、白4张纸牌随机地分发给甲、乙、丙、丁四个人,每人分得1张,事件“甲分得红牌”与事件“乙分得红牌”是( )A .对立事件B .不可能事件C .互斥事件但不是对立事件D .以上答案都不对解析:选C 由互斥事件和对立事件的概念可判断,应选C.2.[考点一]抽查10件产品,设事件A 为“至少有2件次品”,则事件A 的对立事件为( )A .至多有2件次品B .至多有1件次品C .至多有2件正品D .至少有2件正品解析:选B 因为“至少有n 个”的反面是“至多有n -1个”,又因为事件A 为“至少有2件次品”,所以事件A 的对立事件为“至多有1件次品”.3.[考点二]口袋中有100个大小相同的红球、白球、黑球,其中红球45个,从口袋中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为( )A .0.45B .0.67C .0.64D .0.32解析:选D 由题可知,摸出红球的概率为0.45,摸出白球的概率为0.23,故摸出黑球的概率P =1-0.45-0.23=0.32.4.[考点二]围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为17,都是白子的概率是1235.则从中任意取出2粒恰好是同一色的概率是( )A.17B.1235C.1735D .1解析:选C 设“从中取出2粒都是黑子”为事件A ,“从中取出2粒都是白子”为事件B ,“任意取出2粒恰好是同一色”为事件C ,则C =A ∪B ,且事件A 与B 互斥.所以P (C )=P (A )+P (B )=17+1235=1735.即任意取出2粒恰好是同一色的概率为1735.5.[考点二]某超市为了了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.(1)确定x ,y 的值,并估计顾客一次购物的结算时间的平均值;(2)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)解:(1)由已知得25+y +10=55,x +30=45,所以x =15,y =20.该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,顾客一次购物的结算时间的平均值可用样本平均数估计,其估计值为1×15+1.5×30+2×25+2.5×20+3×10100=1.9(分钟).(2)记A 为事件“一位顾客一次购物的结算时间不超过2分钟”,A 1,A 2分别表示事件“该顾客一次购物的结算时间为2.5分钟”,“该顾客一次购物的结算时间为3分钟”,将频率视为概率得P (A 1)=20100=15,P (A 2)=10100=110.则P (A )=1-P (A 1)-P (A 2)=1-15-110=710.故一位顾客一次购物的结算时间不超过2分钟的概率为710.[全国卷5年真题集中演练——明规律] 1.(2016·全国甲卷)某险种的基本保费为a (单位:元),继续购买该保险的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:(1)记A )的估计值; (2)记B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P (B )的估计值;(3)求续保人本年度平均保费的估计值.解:(1)事件A 发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为60+50200=0.55,故P (A )的估计值为0.55.(2)事件B 发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为30+30200=0.3,故P (B )的估计值为0.3.(3)由所给数据得调查的200名续保人的平均保费为0.85a ×0.30+a ×0.25+1.25a ×0.15+1.5a ×0.15+1.75a ×0.10+2a ×0.05=1.192 5a . 因此,续保人本年度平均保费的估计值为1.192 5a .2.(2015·新课标全国卷Ⅱ)某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频数分布表.B 地区用户满意度评分的频数分布表满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).(2)根据用户满意度评分,将用户的满意度分为三个等级:估计哪个地区用户的满意度等级为不满意的概率大?说明理由.解:(1)B地区用户满意度评分的频率分布直方图如图所示.通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值;B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散.(2)A地区用户的满意度等级为不满意的概率大.记C A表示事件:“A地区用户的满意度等级为不满意”;C B表示事件:“B地区用户的满意度等级为不满意”.由直方图得P(C A)的估计值为(0.01+0.02+0.03)×10=0.6,P(C B)的估计值为(0.005+0.02)×10=0.25.所以A地区用户的满意度等级为不满意的概率大.[课时达标检测] 重点保分课时——一练小题夯双基,二练题点过高考[练基础小题——强化运算能力]1.从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )A .“至少有一个黑球”与“都是黑球”B .“至少有一个黑球”与“都是红球”C .“至少有一个黑球”与“至少有一个红球”D .“恰有一个黑球”与“恰有两个黑球”解析:选D A 中的两个事件是包含关系,不是互斥事件;B 中的两个事件是对立事件;C 中的两个事件都包含“一个黑球一个红球”的事件,不是互斥关系;D 中的两个事件是互斥而不对立的关系.2.在一次随机试验中,彼此互斥的事件A ,B ,C ,D 的概率分别为0.2,0.2,0.3,0.3,则下列说法正确的是( )A .A ∪B 与C 是互斥事件,也是对立事件 B .B ∪C 与D 是互斥事件,也是对立事件 C .A ∪C 与B ∪D 是互斥事件,但不是对立事件 D .A 与B ∪C ∪D 是互斥事件,也是对立事件解析:选D 由于A ,B ,C ,D 彼此互斥,且A ∪B ∪C ∪D 是一个必然事件,故其事件的关系可由如图所示的Venn 图表示,由图可知,任何一个事件与其余3个事件的和事件必然是对立事件,任何两个事件的和事件与其余两个事件的和事件也是对立事件.3.甲、乙两人下棋,和棋的概率为12,乙获胜的概率为13,则下列说法正确的是( )A .甲获胜的概率是16B .甲不输的概率是12C .乙输了的概率是23D .乙不输的概率是12解析:选A “甲获胜”是“和棋或乙获胜”的对立事件,所以“甲获胜”的概率是P =1-12-13=16,故A 正确;“乙输了”等于“甲获胜”,其概率为16,故C 不正确;设事件A 为“甲不输”,则A 是“甲胜”、“和棋”这两个互斥事件的并事件,所以P (A )=16+12=23或设事件A 为“甲不输”,则A 是“乙获胜”的对立事件,所以P (A )=1-13=23,故B 不正确;同理,“乙不输”的概率为56,故D 不正确.4.某城市2016年的空气质量状况如下表所示:100<T ≤150时,空气质量为轻微污染,则该城市2016年空气质量达到良或优的概率为________.解析:由题意可知2016年空气质量达到良或优的概率为P =110+16+13=35.答案:355.口袋内装有一些除颜色不同之外其他均相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,若红球有21个,则黑球有________个.解析:摸到黑球的概率为1-0.42-0.28=0.3.设黑球有n 个,则0.4221=0.3n ,故n =15.答案:15[练常考题点——检验高考能力]一、选择题1.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,在正常生产情况下,出现乙级品和丙级品的概率分别是5%和3%,则抽检一个产品是正品(甲级)的概率为( )A .0.95B .0.97C .0.92D .0.08解析:选C 记抽检的产品是甲级品为事件A ,是乙级品为事件B ,是丙级品为事件C ,这三个事件彼此互斥,因而所求概率为P (A )=1-P (B )-P (C )=1-5%-3%=92%=0.92.2.容量为20的样本数据,分组后的频数如下表:A .0.35B .0.45C .0.55D .0.65解析:选B 数据落在[10,40)的概率为2+3+420=920=0.45,故选B.3.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1 534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )A .134石B .169石C .338石D .1 365石解析:选B 这批米内夹谷约为28254×1 534≈169石,故选B.4.从某校高二年级的所有学生中,随机抽取20人,测得他们的身高(单位:cm)分别为:162,153,148,154,165,168,172,171,173,150, 151,152,160,165,164,179,149,158,159,175.根据样本频率分布估计总体分布的原理,在该校高二年级的所有学生中任抽一人,估计该生的身高在155.5 cm ~170.5 cm 之间的概率约为( )A.25B.12C.23D.13解析:选A 从已知数据可以看出,在随机抽取的这20位学生中,身高在155.5 cm ~170.5 cm 之间的学生有8人,频率为25,故可估计在该校高二年级的所有学生中任抽一人,其身高在155.5 cm ~170.5 cm 之间的概率约为25.5.若随机事件A ,B 互斥,A ,B 发生的概率均不等于0,且P (A )=2-a ,P (B )=4a -5,则实数a 的取值范围是( )A.⎝⎛⎭⎫54,2B.⎝⎛⎭⎫54,32 C.⎣⎡⎦⎤54,32D.⎝⎛⎦⎤54,43解析:选D由题意可得⎩⎪⎨⎪⎧0<P (A )<1,0<P (B )<1,P (A )+P (B )≤1,即⎩⎪⎨⎪⎧0<2-a <1,0<4a -5<1,3a -3≤1,解得54<a ≤43.6.做掷一个骰子的试验,事件A 表示“小于5的偶数点出现”,事件B 表示“小于5的点数出现”,则一次试验中,事件A +B -发生的概率为( )A.13B.12C.23D.56解析:选C 由于基本事件总数为6,故P (A )=26=13,P (B )=46=23,从而P (B -)=1-P (B )=1-23=13,又A 与B -互斥,故P (A +B -)=P (A )+P (B -)=13+13=23.故选C.二、填空题7.已知某台纺纱机在1小时内发生0次、1次、2次断头的概率分别是0.8,0.12,0.05,则这台纺纱机在1小时内断头不超过两次的概率和断头超过两次的概率分别为________,________.解析:断头不超过两次的概率P 1=0.8+0.12+0.05=0.97.于是,断头超过两次的概率P 2=1-P 1=1-0.97=0.03.答案:0.97 0.038.2014年6月,一篇关于“键盘侠”的时评引发了大家对“键盘侠”的热议(“键盘侠”一词描述了部分网民在现实生活中胆小怕事、自私自利,却习惯在网络上大放厥词的一种现象).某地新闻栏目对该地区群众对“键盘侠”的认可程度进行调查:在随机抽取的50人中,有14人持认可态度,其余持反对态度,若该地区有9 600人,则可估计该地区对“键盘侠”持反对态度的有________人.解析:在随机抽取的50人中,持反对态度的频率为1-1450=1825,则可估计该地区对“键盘侠”持反对态度的有9 600×1825=6 912(人).答案:6 9129.现有10个数,它们能构成一个以1为首项,-3为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是________.解析:由题意得a n =(-3)n -1,易知前10项中奇数项为正,偶数项为负,所以小于8的项为第一项和偶数项,共6项,即6个数,所以P =610=35. 答案:3510.若A ,B 互为对立事件,其概率分别为P (A )=4x ,P (B )=1y ,则x +y 的最小值为________.解析:由题意,x >0,y >0,4x +1y =1.则x +y =(x +y )·⎝⎛⎭⎫4x +1y =5+⎝⎛⎭⎫4y x +x y ≥9,当且仅当x =2y 时等号成立,故x +y 的最小值为9.答案:9 三、解答题11.某河流上的一座水力发电站,每年六月份的发电量Y (单位:万千瓦时)与该河上游在六月份的降雨量X (单位:毫米)有关.据统计,当X =70时,Y =460;X 每增加10,Y 增加5.已知近20年X的值为140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.(1)完成如下的频率分布表: 近20年六月份降雨量频率分布表(2)率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.解:(1)在所给数据中,降雨量为110毫米的有3个,为160毫米的有7个,为200毫米的有3个.故近20年六月份降雨量频率分布表为(2)由已知可得Y =X2+425,故P (“发电量低于490万千瓦时或超过530万千瓦时”) =P (Y <490或Y >530)=P (X <130或X >210) =P (X =70)+P (X =110)+P (X =220) =120+320+220=310. 故今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率为310.12.某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量 Y (单位:kg)与它的“相近”作物株数X 之间的关系如下表所示:1米.(1)完成下表,并求所种作物的平均年收获量;(2)的概率.解:(1)所种作物的总株数为1+2+3+4+5=15,其中“相近”作物株数为1的作物有2株,“相近”作物株数为2的作物有4株,“相近”作物株数为3的作物有6株,“相近”作物株数为4的作物有3株.列表如下:所种作物的平均年收获量为51×2+48×4+45×6+42×315=102+192+270+12615=69015=46.(2)由(1)知,P(Y=51)=215,P(Y=48)=415.故在所种作物中随机选取一株,它的年收获量至少为48 kg的概率为P(Y≥48)=P(Y=51)+P(Y=48)=215+415=25.。
11.1.1随机事件的概率

从上例可以看出:当抛掷硬币的次数很多时, 出现正面的频率值是稳定的,接近于常数0.5, 在它左右摆动. 例2,表2:某批乒乓球产品质量检查结果表: 抽取球数 优等品数
m
50 45
100 92
200 194 0.97
二,随机事件的概率
1,举例 2,频率的定义 3,概率的定义
例1,掷硬币试验: 将一枚硬币抛掷 5 次,50 次, 掷硬币试验: 500 次, 各做 7 遍, 观察正面出现的次数及频率 观察正面出现的次数及频率. 试验 序号
1 2 3 4 5 6 7
n=5 nH
2 3 1 5 1 2 4
n = 50
导入: 导入:
我们来看下面一些事件: 1,"导体通电时,发热"; 导体通电时,发热" 2,"抛一块石头,下落"; 抛一块石头,下落" 3,"在标准大气压下且温度低于00C时,冰 在标准大气压下且温度低于0 融化" 融化"; 4,"在常温下,焊锡熔化"; 在常温下,焊锡熔化" 5,"某人射击一次,中靶"; 某人射击一次,中靶" 6,"掷一枚硬币,出现正面". 掷一枚硬币,出现正面"
例1,指出下列事件是必然事件,不可能事 指出下列事件是必然事件, 还是随机事件: 件,还是随机事件: (1)"某地1月1日刮西北风"; (1)"某地1 日刮西北风" (2)"当x是实数时,x2≥0"; (2)" 是实数时, ≥0" (3)"手电筒的电池没电,灯泡发亮"; (3)"手电筒的电池没电,灯泡发亮" (4)"一个电影院某天的上座率超过50%". (4)"一个电影院某天的上座率超过50%"
高考数学总复习 11.1随机事件的概率精品课件 文 新人教B版

含有一个元素的子集.包含m个结果的事件A对应于I的含有m
个元素的子集A.于是事件A的概率为P(A)=
(2)必然事件的概率为1;不可能事件的概率为0.
(3)当试验结果出现较多情况时,若把试验结果一一列举 出来显然不现实,这时可借助排列、组合知识来描述,以便准
确、简捷地表述问题.
1.下列说法正确的是 A.某事件发生的频率为P(A)=1.1
2009湖北文10; 相互 独立事件同时发 生的概率,独立 重复试验. 2009北京卷文17 ; 2009湖南卷文17 ; 2009全国Ⅰ卷文 20.
2008湖北14
;
2008全国 Ⅱ19; 2008重庆18 ; 2008江西18 ; 2008四川18. 以考查相互独立 事件为主,以实际问题为 背景,考查独立重复试验 的概率问题.
1 A.32 3 C.32
1 B.64 3 D.64
[解析]
从中有放回的取2次,所有号码共有8×8=64种,
其中和不小于15的有3种,分别是(7,8),(8,7),(8,8),故所求概 率为P= .
[答案] D
3.(山东高考理7)在某地的奥运火炬传递活动中,有编号
为1,2,3,…,18的18名火炬手,若从中任选3人,则选出的火 炬手的编号能组成以3为公差的等差数列的概率为
一、本章知识网络结构
二、最新考纲解读
1.了解随机事件发生的不确定性和频率的稳定性,了解 概率的意义,了解频率与概率的区别.
2.了解互斥事件、对立事件的意义及其运算公式.
3.会用排列、组合的基本公式计算一些等可能事件的概 率.
4.会用互斥事件的概率加法公式计算一些事件的概率.
5.会用相互独立事件的概率乘法公式计算一些事件的概 率.
2018届高考数学一轮复习第十一章概率11.1随机事件的概率课件文北师大版

(2)由互斥与对立的关系及定义知,①不互斥,②对立,③不互斥,④互斥不对
立.
关闭
(1)D (2)④
解析 答案
解题心得判断随机事件之间的关系有两种方法:(1)紧扣事件的分 类,结合互斥事件、对立事件的定义进行分析判断;(2)类比集合进 行判断,把所有试验结果写出来,看所求事件包含哪些试验结果,从 而断定所给事件的关系.若两个事件所含的结果组成的集合的交集 为空集,则这两事件互斥;事件A的对立事件 ������ 所含的结果组成的集 合,是全集中由事件A所含的结果组成的集合的补集.
1.下列结论正确的画“√”,错误的画“×”. (1)事件发生的频率与概率是相同的.( ) (2)随机事件和随机试验是一回事.( ) (3)在大量重复试验中,概率是频率的稳定值.( ) (4)两个事件的和事件是指两个事件至少有一个发生.( (5)若A,B为互斥事件,则P(A)+P(B)=1.( )
)
2.频率与概率 (1)频率:在n次重复次试验中,某一事件A出现的次数与n的比值称 为这n次试验中事件A的频率. (2)概率:在相同的条件下,大量重复进行同一试验时,随机事件A 发生的频率会在某个常数 附近摆动,即随机事件A发生的频率具 有稳定性 .这时我们把这个常数叫随机事件A的概率,记作P(A).概 率的取值范围:0≤P(A)≤1 . (3)频率与概率的关系:频率反映了一个随机事件出现的频繁程度, 频率是随机的,但当试验次数比较大时,频率会在某个常数附近摆 动,这个常数就是概率,所以概率是一个确定的值 .人们用概率 来反映随机事件发生的可能性的大小.
3.互斥事件与对立事件 (1)互斥事件:在一个随机试验中,把一次试验下不能同时 发生 的两个事件A与B称作互斥事件. (2)和事件:给定事件A,B,我们规定A+B为一个事件,事件A+B发生 是指事件A和事件B至少有一个发生 . (3)和事件的概率:在一个随机试验中,如果随机事件A和事件B是 互斥事件,那么有P(A+B)=P(A)+P(B) ;如果随机事件A1,A2,…,An 中任意两个是互斥事件,那么有 P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An). (4)对立事件:在每一次试验中,相互对立的事件A和事件 ������ 不会 同时发生,并且一定有一个发生 .所以有P( ������ )=1-P(A) .
最新-2018届高三数学一轮复习 181 随机事件的概率课件

答案:A
4.从编号为1,2,3,4,5,6,7,8,9,10的10个形状大小相同的球中,任取3个球,则这3个 球编号之和为奇数的概率是________. 解析:解法一:任取3个球有 种结果,编号之和为奇数的结果数为 .
结果,故所求概率为=
解法二:10个球的编号中,恰好有5个奇数和5个偶数,从中任取3个球,3个球 编号之和为奇数与3个球编号之和为偶数的机会是均等的,故所求概率为 答案: .
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)、(6,1)、(6,2)、(6,3)、(6,4)、
(6,5)、(6,6).其中点数和为6的有(1,5)、(2,4)、(3,3)、(4,2)、(5,1)共5
种.由于每个基本事件都是等可能的,所以“所得点数和为6”的概率为
.
变式2:将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所 出现的点数. (1)若点P(a,b)落在不等式组表示的平面区域的事件记为A,求事件A的 概率; (2)若点P(a,b)落在直线x+y=m(m为常数)上,且使此事件的概率最 大,求m的值.
提示:事件的频率与概率有本质上的区别,不可混为一谈.频率是随着试验次
数的改变而改变的,概率却是一个常数,它是频率的科学抽象,不是频率的极
限,只是在大量重复试验中事件出现频率本事件: 一次试验连同其中可能出现的每一个结果 称为一个基本事件. (2)等可能性事件的概率:如果一次试验由n个基本事件组成,而且所有结果出现 的可能性 都相等,那么每一个基本事件的概率都是 果有m个,那么事件A的概率:P(A)= . ,如果某个事件A包含的结
解析:易知①③④正确,②错误.
答案:C
2.在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角 形的概率为( A. B. ) C. D.
2018届高考(新课标)数学(文)大一轮复习课件:第十一章 概率 11-1

【解析】 因为必然事件发生的概率是1,所以该同学的身高超过175 cm的概率为1-0.2-0.5
=0.3,故选B.
【答案】 B
来米1 534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为(
) A.134石 B.169石
C.338石
D.1 365石
28 【解析】 因为样品中米内夹谷的比为254,所以这批米内夹 28 谷为 1 534×254≈169(石).
【答案】 B
4.给出下列三个命题,其中正确的命题有________个. ①有一大批产品,已知次品率为 10%,从中任取 100 件,必 有 10 件是次品; ②做 7 次抛硬币的试验,结果 3 次出现正面,因此正面出现 3 的概率是7; ③随机事件发生的频率就是这个随机事件发生的概率.
3 【解析】 ①错,不一定是 10 件次品;②错,7是频率而非概 率;③错,频率不等于概率,这是两个不同的概念.
(2)随机事件和随机试验是一回事.(
)
) ) )
(3)在大量重复试验中,概率是频率的稳定值.( (4)两个事件的和事件是指两个事件都得发生.(
(5)对立事件一定是互斥事件,互斥事件不一定是对立事件.( (6)两互斥事件的概率和为1.( )
【答案】 (1)× (2)× (3)√ (4)× (5)√ (6)×
A.至多有一张移动卡 B.恰有一张移动卡 C.都不是移动卡 D.至少有一张移动卡
事件都包含“一个黑球一个红球”的事件,不是互斥关系;D中的两个事件是互斥而不对立的关系.
(2)由于A,B,C,D彼此互斥,且A∪B∪C∪D是一个必然事件,故其事件的关系可由如图所示的 韦恩图表示,由图可知,任何一个事件与其余3个事件的和事件必然是对立事件,任何两个事件的和
2018高考数学文人教B版一轮课件:11-1随机事件的概率 精品

概率
-2-
11.1
随机事件的概率
-4知识梳理 双基自测 自测点评
1
2
3
4
1.事件 (1)不可能事件、必然事件、随机事件:在同样的条件下重复进行 试验时,有的结果 始终不会发生 ,它称为不可能事件;有的 结果在每次试验中 一定会发生 ,它称为必然事件;有的结 果 可能发生 ,也 可能不发生 ,它称为随机事件. (2)基本事件、基本事件空间:试验连同它出现的每一个结果称为 一个基本事件,它是试验中不能再分的最 简单 基本事件 随机事件 的 ;所有 构成的 集合 称为 基本事件空间,基本事件空间常用大写希腊字母Ω表示.
-5知识梳理 双基自测 自测点评
1
2
3
4
2.概率与频率 ������ (1)概率定义:在n次重复进行的试验中,事件A发生的频率 当n很 ������ 大时,总是在某个 常数 附近摆动,随着n的增加,摆动幅度越来越 小,这时就把这个 常数 叫做事件A的概率,记作P(A). (2)概率与频率的关系: 概率 可以通过 频率 来“测量”,频率 是 概率 的一个近似值.
-17考点1 考点2 考点3
对点训练1(1)在5张电话卡中,有3张移动卡和2张联通卡,从中任 3 7 取2张,若事件“2张全是移动卡”的概率是 ,则概率是 的事件是 10 10 ( ) A.至多有一张移动卡 B.恰有一张移动卡 C.都不是移动卡 D.至少有一张移动卡 (2)某城市有甲、乙两种报纸供居民订阅,记事件A为“只订甲报 纸”,事件B为“至少订一种报纸”,事件C为“至多订一种报纸”,事件D 为“不订甲报纸”,事件E为“一种报纸也不订”.则下列两个事件是互 斥事件的有 ;是对立事件的有 .(填序号) ①A与C;②B与E;③B与C;④C与E.
高三数学(文)一轮复习课件:11.1随机事件的概率

4/17/2018
2.下列命题:①将一枚硬币抛两次,设事件M:“两次出现正面”, 事件N:“只有一次出现反面”,则事件M与N互为对立事件.②若事 件A与B互为对立事件,则事件A与B为互斥事件.③若事件A与B为 互斥事件,则事件A与B互为对立事件.④若事件A与B互为对立事 件,则事件A∪B为必然事件.其中,真命题是() A.①②④ B.②④ C.③④ D.①②
4/17/2018
1.在下列六个事件中,随机事件的个数为( ) ①如果a,b都是实数,那么a+b=b+a; ②从分别标有号数 1,2,3,4,5,6,7,8,9,10 的 10 张号签中任取一张,得到 4 号 签; ③没有水分,种子发芽; ④某电话总机在60秒内接到至少10次呼叫; ⑤在101 kPa下,水的温度达到50 ℃时沸腾; ⑥同性电荷,相互排斥. A.2 B.3 C.4 D.5 【解析】 ①⑥是必然事件;③⑤是不可能事件;②④是随机事件. 【答案】 A
第十一章
概率
11.1 随机事件的概率 11.2 古典概型 11.3 几何概型
4/17/2018
知识点
考纲下载
1.了解随机事件的不确定性和频率的稳定性,了解概率的 意义,了解频率与概率的区别. 2.理解随机事件的关系与运算. 3.理解两个互斥事件的概率加法公式.. 1.理解古典概型及其概率计算公式.
4/17/2018
4.概率的几个基本性质
0≤P(A)≤1 ; (1)概率的取值范围___________
(2)必然事件的概率P(E)=___ 1 ; (3)不可能事件的概率P(F)=___ 0 ; (4)概率的加法公式 如果事件A与事件B互斥,则P(A∪B)= _____________ P(A)+P(B) . (5)对立事件的概率 若事件A与事件B互为对立事件,则A∪B为 必然事件,P(A∪B)= 1 ,P(A)=__________ 1-P(B) .
高中_11.1.1随机事件的概率(1)

§10.4.1 随机事件的概率 班级 学号 姓名一、 目标要点: (1) 掌握随机事件的概念及随机事件的概率的定义;(2) 掌握等可能事件的概念及等可能事件的概率公式。
二、 要点回忆1. 随机事件的概率〔1〕在一定条件, 叫做必然事件; 叫做不可能事件; 叫做随机事件。
〔2〕一般地,在大量进展同一重复实验时, 总是接近某个常数,在它附近摆动,这时就把这个常数叫做 ,记做)(A P ,)(A P 的范围是 。
2.等可能事件的概率〔1〕一次试验连同 称为一个根本领件。
〔2〕如果一次试验中可能出现的结果有n 个,即此事件由n 个根本领件组成,而且所有结果出现的 ,那么每一个根本领件的概率都是 ,如果某个事件A 包含的结果有m 个,那么事件A 的概率=)(A P 。
三、 目标训练:1.以下语句可能成为事件的是………………………………………………………………〔 〕C.这是一本书吗D.数学测验,某同学两次都是优 ………………………………………………………………〔 〕①连续两次抛一枚硬币,两次都出现正面向上 ②异性电荷,相互吸引 ③在标准大气压下,水在C ︒1结冰A.②B.③C.①D.②③3. 下面的事件是随机事件的有………………………………………………………………〔 〕 x 是实数,那么0<xc bx ax y ++=2或者是二次函数,或者不是二次函数)1,0(≠>=a a a y x 是R 上的增函数4.以下试验是等可能试验的是………………………………………………………………〔〕(1)抛掷一个钢笔套,出现“笔套直立〞与“笔套横放〞两种结果;(2)某人抛掷一枚硬币,出现“正面〞与“反面〞两种结果;(3)某段路上设有两处红绿灯,假设每次红灯,绿灯开启的时间都是相等的,某人骑车经过此路段,出现“遇到两次红灯〞“遇到两次绿灯〞“遇到一次红灯,一次绿灯〞三种结果;A. 0B. 1C. 2D. 35.一枚硬币连续抛掷两次,只有一次出现正面的概率是,连续抛掷三次,有两面出现正面的概率是.6.十个人站成一排,其中甲、乙、丙恰巧都不相邻的概率是. 甲、乙相邻的概率是,甲、乙相邻,但甲、丙不相邻的概率是.7.某小组有成员3人,每人在一个星期中参加一天劳动,如果劳动日期可随机安排,那么三人在不同的三天参加劳动的概率是.(2)这位运发动投篮一次,进球的概率约为多少?9.袋子中有红、白、黄、黑颜色大小一样的四个小球:〔1〕从中任取一球,求取出白球的概率;〔2〕从中任取两球,求取出红球、白球各一个的概率;〔3〕先后各取一球,求分别取出的是红球、白球的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何选择各自的路径.
-21-
考点一
考点二
考点三
解 (1)由已知共调查了100人,其中40分钟内不能赶到火车站的有
12+12+16+4=44人.
故用频率估计相应的概率为
44 100
=0.44.
(2)选择L1的有60人,选择L2的有40人,故由调查结果得频率如下表.
所用时间(分钟) 10~20 20~30 30~40 40~50 50~60
⑤频率是概率的近似值,概率是频率的稳定值.
其中正确的是( B )
A.①②③④
B.①④⑤
C.①②③④⑤ D.②③
解析:由概率的相关定义知①④⑤正确.
知识梳理 考点自测
-10-
4.甲、乙两人下棋,两人下成和棋的概率是12,甲获胜的概率是13, 则甲不输的概率为( A )
A.56
B.25
C.16
D.13
选择 L1 的频率2
0.2
选择 L2 的频率 0
0.1
0.4
0.4
0.1
(3)A1,A2分别表示甲选择L1和L2时,在40分钟内赶到火车站; B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站. 由(2)得P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,P(A1)>P(A2), 故甲应选择L1;P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4 =0.9,P(B2)>P(B1),故乙应选择L2.
事件,A∪B A∩B=⌀,且A∪B=Ω ,则称事件 A 与事件 (Ω 为必然
事件)
知识梳理 考点自测
-7-
4.互斥事件与对立事件的关系 对立事件是互斥事件的特殊情况,而互斥事件未必是对立事件. 5.概率的几个基本性质 (1)概率的取值范围: 0≤P(A)≤1 . (2)必然事件的概率:P(A)= 1 . (3)不可能事件的概率:P(A)= 0 . (4)概率的加法公式:若事件A与事件B互斥,则 P(A∪B)= P(A)+P(B) . (5)对立事件的概率:若事件A与事件B互为对立事件,则A∪B为必 然事件.P(A∪B)= 1 ,P(A)= 1-P(B) .
这个射手射击一次,击中靶心的概率约是 0.90 . 解析:击中靶心的频率依次为0.8,0.95,0.88,0.92,0.89,0.91,易知击 中靶心的频率在0.90附近摆动,故P(A)≈0.90.
-12-
考点一
考点二
考点三
随机事件的关系 例1一枚均匀的正方体玩具的各个面上分别标以数字1,2,3,4,5,6. 将这个玩具向上抛掷1次,设事件A表示向上的一面出现奇数,事件B 表示向上的一面出现的数字不超过3,事件C表示向上的一面出现的 数字不小于4,则 ( D ) A.A与B是互斥而非对立事件 B.A与B是对立事件 C.B与C是互斥而非对立事件 D.B与C是对立事件 解析:根据互斥事件与对立事件的定义作答,A∩B={出现点数1或 3},事件A,B不互斥更不对立;B∩C=⌀,B∪C=Ω (Ω 为必然事件),故事 件B,C是对立事件.
-9-
知识梳理 考点自测
3.下列说法:
①频率反映事件发生的频繁程度,概率反映事件发生的可能性大
小;
②做n次随机试验,事件A发生m次,则事件A发生的频率
������ ������
就是事
件A发生的概率;
③百分率是频率,但不是概率;
④频率是不能脱离n次试验的试验值,而概率是具有确定性的不
依赖于试验次数的理论值;
解析:令 A=“甲、乙下成和棋”,B=“甲获胜”,
∵P(A)=12,P(B)=13,
且 A,B 互斥,
∴甲不输的概率为
P(A∪B)=P(A)+P(B)=12
+
1 3
=
56.
知识梳理 考点自测
-11-
5.某射手在同一条件下进行射击,结果如下:
射击次数
10 20 50 100 200 500
击中靶心次数 8 19 44 92 178 455
出险次数 0 1 2 3 4 ≥5 频 数 60 50 30 30 20 10
考点一
考点二
考点三
-16-
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A) 的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于 基本保费的160%”.求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
-8-
知识梳理 考点自测
1.判断下列结论是否正确,正确的画“√”,错误的画“×”. (1)事件发生的频率与概率是相同的. ( × ) (2)随机事件和随机试验是一回事. ( × )
(3)在大量重复试验中,概率是频率的稳定值. ( √ ) (4)两个事件的和事件是指两个事件至少有一个发生. ( √ )
考点一
考点二
考点三
-14-
对点训练1从装有5个红球和3个白球的口袋内任取3个球,则互斥
而不对立的事件有 ④ .(填序号) ①至少有一个红球,都是红球; ②至少有一个红球,都是白球; ③至少有一个红球,至少有一个白球; ④恰有一个红球,恰有两个红球.
解析:由互斥事件与对立事件的关系及定义知,①不互斥,②对立, ③不互斥,④互斥不对立.
1.从近五年高考试题来看,随 机事件及其概率不单独考
查,往往与统计交汇. 2.高考对该部分内容的考查 主要有两个方面:一是列出 频率分布表,由频率估计概 率;二是考查互斥事件、对立 事件的概率.
知识梳理 考点自测
-3-
1.事件的分类
确定 必然事件
在条件 S 下,一定会发生的事件,叫做相对于条件 S 的必然事件
考点一
考点二
考点三
-17-
解 (1)事件 A 发生当且仅当一年内出险次数小于 2. 由所给数据知,一年内出险次数小于 2 的频率为602+0050=0.55, 故 P(A)的估计值为 0.55. (2)事件 B 发生当且仅当一年内出险次数大于 1 且小于 4.
由所给数据知,一年内出险次数大于 1 且小于 4 的频率为 302+0030=0.3,
-5-
知识梳理 考点自测
3.事件的关系与运算
定义
符号表示
包含 关系
若事件 A 发生 ,则事件 B 一定发生 , 这时称事件 B 包含事件 A(或称事件 A 包 含于事件 B)
B⊇A (或A⊆B)
相等 关系
若 B⊇A,且 A⊇B ,则称事件 A 与事件
B 相等
A=B
并事件 (和事件)
若某事件发生,当且仅当事件A发生或事件, B发生 则称此事件为事件 A 与事件 B 的并事件 A∪B(或A+B) (或和事件)
考点一
考点二
考点三
-13-
思考如何判断随机事件之间的关系? 解题心得判断随机事件之间的关系有两种方法:(1)紧扣事件的分 类,结合互斥事件、对立事件的定义进行分析判断;(2)类比集合进 行判断,把所有试验结果写出来,看所求事件包含哪些试验结果,从 而断定所给事件的关系.由各个事件所含的结果组成的集合彼此的 交集为空集,则事件互斥;事件A的对立事件 ������ 所含的结果组成的集 合,是全集中由事件A所含的结果组成的集合的补集.
考点一
考点二
考点三
-15-
随机事件的频率与概率
例2某险种的基本保费为a(单位:元),继续购买该险种的投保人称 为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 0
12
3
4
≥5
保费
0.85a a 1.25a 1.5a 1.75a 2a
随机调查了该险种的200名续保人在一年内的出险情况,得到如 下统计表:
(5)若A,B为互斥事件,则P(A)+P(B)=1. ( × )
2.设甲:A1,A2是互斥事件;乙:A1,A2是对立事件,则 ( B ) A.甲是乙的充分不必要条件 B.甲是乙的必要不充分条件 C.甲是乙的充要条件 D.甲既不是乙的充分条件,也不是乙的必要条件 解析:互斥事件不一定是对立事件,但对立事件一定是互斥事件.
交事件 (积事件)
若某事件发生当, 且仅当事件A发生且事件,B发生 则称此事件为事件 A 与事件 B 的交事件 A∩B(或AB) (或积事件)
知识梳理 考点自测
-6-
互斥 事件
对立 事件
定义
若 A∩B 为 不可能 与事件 B 互斥 若 A∩B 为 不可能 为 必然事件 B 互为对立事件
符号表示
事件,则称事件 A A∩B=⌀
故 P(B)的估计值为 0.3.
考点一
考点二
考点三
-18-
(3)由所给数据得
保费 0.85a a
1.25a 1.5a 1.75a 2a
频率 0.30 0.25 0.15 0.15 0.10 0.05
调查的200名续保人的平均保费为
0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a ×0.05=1.192 5a.
考点一
考点二
考点三
-23-
解 记“0人排队等候”为事件A,“1人排队等候”为事件B,“2人排队 等候”为事件C,“3人排队等候”为事件D,“4人排队等候”为事件E,“5 人及5人以上排队等候”为事件F,则事件A,B,C,D,E,F彼此互斥.
(1)记“至多2人排队等候”为事件G,则G=A∪B∪C, 所以P(G)=P(A∪B∪C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56. (2)(方法一)记“至少3人排队等候”为事件H,则H=D∪E∪F,所以 P(H)=P(D∪E∪F)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44. (方法二)记“至少3人排队等候”为事件H,则其对立事件为事件G, 所以P(H)=1-P(G)=0.44.
