几何辅助线之角平分线专题
【中考数学必备专题】几何辅助线大揭秘 之角平分线问题(含答案)
【中考数学必备专题】几何辅助线大揭秘之角
平分线问题
一、证明题(共3道,每道40分)
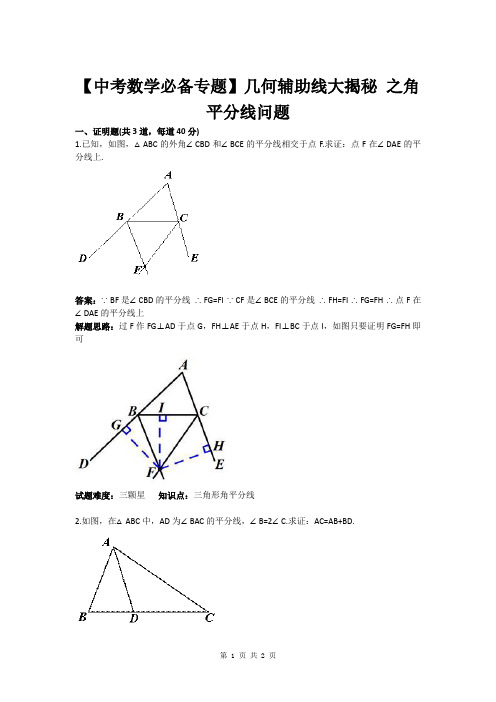
1.已知,如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
答案:∵BF是∠CBD的平分线∴FG=FI ∵CF是∠BCE的平分线∴FH=FI ∴FG=FH ∴点F在∠DAE的平分线上
解题思路:过F作FG⊥AD于点G,FH⊥AE于点H,FI⊥BC于点I,如图只要证明FG=FH即可
试题难度:三颗星知识点:三角形角平分线
2.如图,在△ABC中,AD为∠BAC的平分线,∠B=2∠C.求证:AC=AB+BD.
答案:∵AD是∠BAC的平分线∴∠BAD=∠EAD 在△ABD和△AED中AB=AE ∠BAD=∠EAD AD=AD ∴△ABD≌△AED(SAS)∴BD=ED,∠B=∠AED ∵∠AED=∠B=2∠C ∴∠CDE=∠AED ﹣∠C=∠C ∴DE=CE ∴BD=CE ∵AC=AE+CE ∴AC=AB+BD
解题思路:在AC上截取AE=AB,连接DE,如图只要证明BD=CE即可
试题难度:三颗星知识点:三角形角平分线
3.已知:如图,在△ABC中,BE平分∠ABC,AD⊥BE,垂足为点D.求证:∠BAD=∠DAE+∠C.
答案:∵BE平分∠ABC,AD⊥BE ∴△ABF为等腰三角形(三线合一)∴∠BAD=∠BFD ∵∠BFD 为△ACF的外角∴∠BFD=∠DAE+∠C ∴∠BAD=∠DAE+∠C
解题思路:延长AD与BC交于点F,如图只要证明∠BFD=∠BAD即可
试题难度:三颗星知识点:三角形角平分线。
角平分线四大辅助线模型 总结+习题+解析

角平分线四大辅助线模型角平分线的性质为证明线段或角相等开辟了新的途径,同时也是全等三角形知识的延续,又为后面角平分线的判定定理的学习奠定了基础.涉及到角平分线的考点主要是性质、判定以及四大辅助线模型,在初二上期中、期末考试中都是经常考察的方向。
角平分线性质:角平分线上的点到角两边的距离相等.角平分线判定:到角的两边距离相等的点在角的角平分线上.四大模型1、角平分线+平行线,等腰三角形必出现已知:OC平分∠AOB,CD∥OB交OA于D.则△ODC为等腰三角形,OD=CD.2、角平分线+两垂线,线等全等必出现已知:OC平分∠AOB.辅助线:过点C作CD⊥OA,CE⊥OB.则CD=CE,△ODC ≌△OEC.3、角平分线+一垂线,中点全等必出现已知:OC平分∠AOB,DC垂直OC于点C.辅助线:延长DC交OB于点E.则C是DE的中点,△ODC ≌△OEC.4、角平分线+截长补短线,对称全等必出现已知:OC平分∠AOB,截取OE=OD,连接CD、CE.则△ODC和△OCE关于OC对称,即△ODC ≌△OEC.【核心考点一】角平分线的性质与判定1.(2016•张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上一个动点,若3PA =,则PQ 的最小值为( )A B .2 C .3 D .【分析】首先过点P 作PB OM ⊥于B ,由OP 平分MON ∠,PA ON ⊥,3PA =,根据角平分线的性质,即可求得PB 的值,又由垂线段最短,可求得PQ 的最小值.2.(2016秋•抚宁县期末)如图,在ABC ∆中,AD 是它的角平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ∆∆= )A .3:4B .4:3C .16:9D .9:16【分析】利用角平分线的性质,可得出ABD ∆的边AB 上的高与ACD ∆的AC 上的高相等,估计三角 形的面积公式,即可得出ABD ∆与ACD ∆的面积之比等于对应边之比.3.(2017春•崇仁县校级月考)如图,在ABC ∆中,90ACB ∠=︒,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )。
几何辅助线之角平分线专题

几何辅助线之角平分线专题1、角平分线辅助线四种基本模型已知:AD是∠BOC的角平分线(1)(2)(3)(4)2、补充性质:如图,在△ABC中,AD平分∠BAC,则有AB:AC=BD:DC典型例题例1、已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB.求证:AC+CD=AB例2、已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合,当∠A满足什么条件时,点D恰为AB中点?写出一个你认为适当的条件,并利用此条件证明D为AB中点.例3、如图,AB=2AC,∠BAD=∠DAC,DA=DB ,求证:DC⊥AC。
DEHA BC例4、如图所示,已知AD 是△ABC 的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,F .求证:AD 垂直平分EF .例5、 如图,在△ABC 中,∠A 等于60°,BE 平分∠ABC ,CD 平分∠ACB 求证:DH=EH例6、如图,已知等腰直角三角形ABC 中,∠A =90°,AB =AC ,BD 平分∠ABC ,CE ⊥BD ,垂足为E ,求证: BD =2CE 。
例7、如图,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。
变式练习请你参考上图构造全等三角形的方法,解答下列问题:⑴如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。
请你判断写出FE与FD之间的数量关系;⑵如图,在△ABC中,如果∠ACB不是直角,而⑴中的其他条件不变,请问,你在⑴中所得结论是否依然成立?若成立请证明;若不成立,请说明理由。
课后练习1、已知:如图所示,∠C=2∠B,∠BAD=∠CAD,求证:AB=AC+CD。
2、已知,如图,BN 平分∠ABC,P为BN上一点,且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°。
角平分线三个定理

角平分线三个定理全文共四篇示例,供读者参考第一篇示例:角平分线三个定理是几何学中非常重要的定理之一,它们可以帮助我们更好地理解和运用角平分线的性质。
本文将详细介绍这三个定理的含义和推理过程。
第一个定理是角平分线定理。
所谓角平分线定理指的是:如果一条直线将一个角分成两个大小相等的角,那么这条直线就是这个角的平分线。
换句话说,如果一条直线BD分割一个角ABC,且∠ABD≌∠CBD,则BD就是∠ABC的平分线。
证明这个定理的方法比较简单,可以通过相似三角形或等角相等辅助线的方法进行。
通过这三个定理,我们可以更深入地了解角平分线的性质,进而应用到解决各种与角平分线相关的几何问题中。
熟练掌握和灵活运用这三个定理对于提高我们的几何学水平至关重要。
希望通过本文的介绍,读者们能够更好地理解和掌握角平分线的性质,从而在学习和工作中取得更好的成绩。
愿大家在几何学的道路上不断进步,探索出更多有趣的数学定理和问题!第二篇示例:角平分线三个定理是解析几何中非常重要的定理,对于角平分线的性质进行了深入的研究和总结。
在平面几何中,角平分线是连接一个角的两边中点的线段,将这个角分成两个相等的角。
下面我们来详细介绍一下角平分线的三个定理。
第一个角平分线定理是角平分线定理,它的表述如下:若一条线段从一个角内的顶点引出,又将这个角分成两个相等的小角。
这个定理是解析几何中最基本的定理之一,也是很多其他定理的基础。
通过角平分线定理,我们可以得出许多结论和推论,解决很多关于角平分线的问题。
第二个角平分线定理是角平分线的长度比定理,它的表述如下:如果一条角平分线把一个角分成两个相等的小角,则这条角平分线上的一点到角的两边的距离分别等于这两条边的比值。
这个定理在解决角平分线长度问题时非常有用,能够帮助我们准确计算角平分线的长度。
通过这三个角平分线定理,我们可以更好地理解和运用角平分线的性质,解决各种与角平分线相关的问题。
在解析几何的学习中,掌握这些定理能够提高我们的解题能力和几何思维,帮助我们更好地理解平面几何知识,为进一步学习提供良好的基础。
与角平分线有关的辅助线及结论

与角平分线有关的辅助线及结论打开数学,解开疑惑基础知识点:1.角的平分线分得的两个角相等,角是一个轴对称图形,它的对称轴是角平分线所在的直线;2.角平分线的性质定理:角平分线上的点到这个角的两边的距离相等;3.角平分线性质定理的逆定理:在角的内部,且到角的两边距离相等的点在这个角的角平分线上。
4.三角形的内心:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等,这个交点叫做三角形的内心;5.等腰三角形底边上的高(或中线)平分顶角(三线合一)。
一、根据对称性,截长补短构造全等例题、已知:如图,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB-AC=CD解析:方法一、截长构造全等在线段AB上取点E,使得AC=AE易证△ACD≌△AED再证等腰△EBD即可方法二、补短构造全等延长AC到E,使得CE=CD∴∠E=1/2∠ACD=∠B再证△ABD≌△AED即可二、根据角平分线的性质向角两边作垂线构全等例题、如图,已知AB>AD,∠BAC=∠FAC,CD=BC。
求证:∠ADC+∠B=180°解析:由C点向∠BAF的两边作垂线HL证明Rt△BCN≌Rt△DCM由此得到∠ADC+∠B=180°三、根据等腰三角形三线合一,作角平分线的垂线构造等腰三角形从角的一边上的一点作角平分线的垂线,使之与角的两边相交,则截得一个等腰三角形,垂足为底边上的中点,该角平分线又成为底边上的中线和高,以利用中位线的性质与等腰三角形的三线合一的性质。
(如果题目中有垂直于角平分线的线段,则延长该线段与角的另一边相交)例题、如图,∠BAD=∠DAC,AB>AC,CD⊥AD于D,H是BC 中点。
求证:2DH=(AB-AC)解析:延长CD交AB于点E则可得等腰△ACE进而得到DH为△CBE的中位线问题可证四、以角分线上一点做角的另一边的平行线构造等腰三角形有角平分线时,常过角平分线上的一点作角的一边的平行线,从而构造等腰三角形。
初三几何3角平分线辅助线.基础(2013-2014)教师

B
C
【答案】(利用角平分作对称模型)如图,延长 BD 到 E ,使 DE AD ,在 BC 上截取 BF BA .
∵ 1 2 , BD 为公共边,∴ BAD ≌ BFD , AD FD , ADB FDB .
∵ 1 1 ABC 1 1 180 100 20 ,
2
22
∴ ADB 180 A 1 180 100 20 60 .
B
C
【例4】 如图,在 ABC 中, BAC 60 , AD 是 BAC 的平分线,且 AC AB BD ,求 ABC 的度数.
A
B
D
【答案】解法一(补短):
如图所示,延长 AB 至 E 使 BE BD ,连接 ED 、 EC .
A
由 AC AB BD 知 AE AC ,
而 BAC 60o ,则 AEC 为等边三角形.
结论:① CD CE ② OD OE 2OC cos
D C
③ S四边形DOEC S△ODC S△OCE OC 2 sin cos
难度较大,记得经常复习(庆功独家提供,见几何小秘籍)
O
E
B
中考满分必做题
一、往角两边截取相等的线段
☞考点说明:解读:在角两边截取相等的线段,这也是角平分线常用的辅助线,常用于解决线段和差问题 把两条折线段“拉直”成线段,利用角平分线可以构造全等三角形. 同样地,将长线段拆分成两段,之后再利用三角形全等亦可,此思路也是十分自然的. 需要说明的是,无论采取哪种方法,都体现出关于角平分线“对称”的思想. 常用方法分别称之为“补短法”和“截长法”,它们是证明等量关系时优先考虑的方法.
1
∴ FDB 60 ,故 FDC 60 , EDC 60 .
角平分线的几种辅助线作法与三种模型

一、角平分线的三种“模型”模型一:角平分线+平行线→等腰三角形如图1,过∠AOB平分线OC上的一点P,作PE∥O B,交OA于点E,则EO=EP.AAAEPCECDFEPOBBCOFB图1图2图3例1 如图2,∠ABC,∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.求证:BD+EC=DE.模型二:角平分线+垂线→等腰三角形如图3,过∠AOB平分线OC上的一点P,作EF⊥OC,交OA于点E,交OB于点F,则OE=OF,PE=PF.例2 如图4,BD是∠ABC的平分线,AD⊥BD,垂足为D,求证:∠BAD=∠DAC+∠C.模型三:角平分线+翻折→全等三角形在△ABC中,AD是∠BAC的平分线,沿角平分线AD将△ABD往右边折叠就得到如图5的图形.此时有:△ABD≌△AB/D.此翻折相当于在三角形的一边截取线段等于另一边,或延长一边等于另一边构造出相等的线段.用此方法可解决一些不相等的线段和差类问题.D AE AP/BCDB /BC 图5图6例3 如图6,点P 是△ABC 的外角∠CAD 的平分线上的一点.求证:PB+PC>AB+AC.二、角平分线定理使用中的几种辅助线作法一、已知角平分线,构造三角形1、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。
求证:1()2BE AC AB =- 2、在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E .求证:∠ACE=∠B+∠ECD .二、已知一个点到角的一边的距离,过这个点作另一边的垂线段1、如图所示,∠1=∠2,P 为BN 上的一点,并且PD ⊥BC 于D ,AB +BC=2BD 。
求证:∠BAP +∠BCP=180°。
21F EDCBANPEDCBA ABDCE F图三、已知角平分线和其上面的一点,过这一点作角的两边的垂线段1、如图所示,在△ABC 中,PB 、PC 分别是∠ABC 的外角的平分线,求证:∠1=∠22、2、如图2,AB ∥CD ,E 为AD 上一点,且BE 、CE 分别平分∠ABC 、∠BCD .求证:AE=ED 3、(四(2))四、以角的平分线为对称轴构造对称图形例1如图1,在△ABC 中,AD 平分∠BAC ,∠C=2∠B . 求证:AB=AC+CD .2、例题:如图2,BC >AB ,BD 平分∠ABC ,且∠A+∠C=1800, 求证:AD=DC .五、利用角的平分线构造等腰三角形1、如图,在△ABC 中,AB=AC ,BD 平分 ∠ABC ,DE ⊥BD 于D ,交BC 于点E .求证:CD=21BE .G21PFECBAAG CHDEF图2BB ACDE图1ABDECBA C D E 图。
七(下)几何模型——角平分线
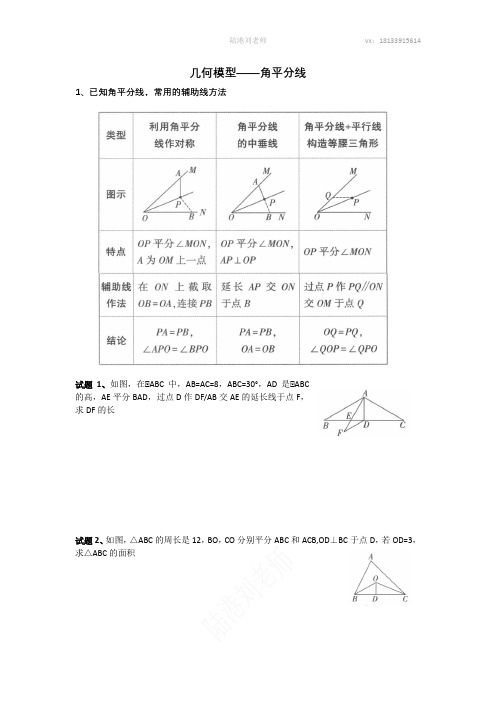
几何模型——角平分线1、已知角平分线,常用的辅助线方法试题1、如图,在△ABC中,AB=AC=8,ABC=30°,AD是△ABC的高,AE平分BAD,过点D作DF/AB交AE的延长线于点F,求DF的长试题2、如图,△ABC的周长是12,BO,CO分别平分ABC和ACB,OD⊥BC于点D,若OD=3,求△ABC的面积2、已知两角平分线,常用双角平分线模型试题3、如图,在四边形ABCD中,∠DAB的平分线与四边形ABCD的外角平分线相交于点P,且∠ADC+∠DCB=210°,求∠P的度数。
试题4、如图,在△ABC中,AD是高,∠BAC、∠ABC的平分线AE,BF相交于点O.(1)若∠ABC=60°,∠C=40°,求∠DAE的度数;(2)若∠C=60°,求∠BOE的度数;(3)若∠ABC=α,∠C=β(a>β),求∠DAE、∠BOE的度数(用含α,B的式子表示)3、已知两角度数关系为1/3时,常用三等分角模型试题5、如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的∠EAC、∠ABC、∠ACF.以下结论:①AD//BC;②∠ACB=2∠ADB;③DB平分∠ADC;④∠ADC=90°-∠ABD.其中正确的结论有()A.0个B.1个C.2个D.3个第5题图第6题图试题6、如图,在△ABC中,∠A=70°,∠ABC的平分线与∠ACD的平分线交于点A1,则∠A1=__________,∠A1AA的平分线与∠A1AA的平分线交于点∠A2,得∠A2,…,∠A2022AA的平分线与∠A2022AA的平分线交于点A2023,则∠A2023=____________.试题7、如图,在等腰△ABC中,AB=AC,BO,CO分别平分∠ABC,∠ACB,若∠ABC+∠ACB=100°,求∠BOC的度数。
角平分线课件PPT

生活中有趣角平分线现象
建筑设计中的应用
在建筑设计中,角平分线常被用来确保建筑物的对称性和平衡感。例如,古希腊的帕特 农神庙就运用了角平分线的原理来设计其立面和柱子。
自然界的角平分线
在自然界中,角平分线的现象也很常见。例如,当阳光照射在树叶上时,树叶的脉络就 会呈现出角平分线的形状,这是因为树叶在生长过程中会自然地沿着角平分线的方向扩
例题2
已知在△ABC中,∠C=90° ,AD是∠BAC的平分线, DE⊥AB于E,F在AC上, BD=DF。求证:CF=EB 。
解析
过点D作DM⊥AC于M。 根据角平分线的性质,可 得DE=DM。在Rt△FCD 和Rt△EBD中,DF=BD, DE=DM。 ∴Rt△FCD≌Rt△EBD(HL )。∴CF=EB。
的两边分别与OA、OB相交于点C、D。求证: PC=PD。
输入 标题
解析
根据角平分线的性质和直角三角形的性质,可以证明 △OPC和△OPD全等,从而得出PC=PD。具体证明过 程略。
例题1
例题2
根据角平分线的性质和勾股定理,可以求出点D到AB 的距离。具体求解过程略。
解析
在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若 BC=32,且BD:CD=9:7,求点D到AB的距离。
04
角平分线在几何变换中应用
旋转对称性质及应用
旋转对称性质
角平分线将一个角分为两个相等的小角,且两个小角关于角平分线对称。当图形 绕角平分线旋转一定角度时,两个小角能够重合,具有旋转对称性。
应用
利用旋转对称性质,可以解决与角平分线相关的角度计算、线段长度等问题。例 如,通过旋转对称性质可以证明两个三角形全等或相似。
建筑设计中角平分线应用
三角形角平分线辅助线的几种做法

三角形角平分线辅助线的几种做法在数学的世界里,三角形就像一个个神秘的小家伙,角平分线更是它们的秘密武器。
嘿,你听说过吗?角平分线可是让三角形变得更有趣的神器。
想象一下,三角形的每个角都是一个小演员,而角平分线就像是导演,把它们的表演完美地分开,让它们各自发挥光彩。
说实话,这个过程就像是把一个美味的披萨切成两半,不仅让每一块都看起来更好看,还能让每个人都吃得开心。
好吧,咱们先聊聊怎么画这个角平分线。
你得有一个三角形。
你可以用铅笔和尺子,或者直接拿出那根神奇的圆规。
把三角形的一个角作为出发点,然后把圆规的尖尖扎在那个角上,转一圈,画一个小圆。
这个小圆像是个神秘的传送门,连接着三角形的两条边。
拿着尺子,把这个小圆和两条边的交点连起来。
哇,看看!这就是你的角平分线!就像魔法一样,瞬间就完成了。
角平分线不只是个小花样。
它还有很多秘密等着你去挖掘。
比如,你知道角平分线有什么特别的性质吗?它能把三角形的两条边分成比例,嘿,这可真是个大新闻!这就意味着,如果你知道了其中一条边的长度,你几乎可以轻松算出另一条边的长度。
就像在玩拼图,拼对了,结果就全对。
这个性质在解决一些复杂问题时,简直就像给你开了一扇窗,让光线照进来。
说到这里,很多小伙伴可能会问,角平分线到底有什么用呢?它在生活中随处可见!比如,建筑师在设计房子的时候,常常会用到角平分线来确保房子的结构均匀美观。
你想啊,谁不想住在一个美得让人拍手叫好的房子里呢?再比如,艺术家在创作的时候,也会用角平分线来找到最佳的构图,让作品更加和谐。
可以说,角平分线就像是生活中的一位默默无闻的英雄,虽然不张扬,但却在每一个重要时刻都能派上用场。
再说说不同的画法吧。
很多时候,老师会教我们用尺子和圆规。
可是,你知道吗?其实用简单的手法也能画出角平分线!比如,只用一个普通的三角板,就能轻松搞定。
把三角板的一个边对准三角形的一个边,另一边对准角的顶点,轻轻一划,嘿,角平分线又出现了!简单得不能再简单了,谁说数学就得复杂呢?此外,还有一种很酷的方式,叫做“分段法”。
初中数学复习几何模型专题讲解3---和角平分线有关的辅助线

初中数学复习几何模型专题讲解专题03 和角平分线有关的辅助线一、单选题1.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE;④BA+BC=2BF.其中正确的是()A.①②③B.①③④C.①②④D.①②③④【答案】D【分析】根据SAS证△ABD≌△EBC,可得∠BCE=∠BDA,结合∠BCD=∠BDC可得①②正确;根据角的和差以及三角形外角的性质可得∠DCE=∠DAE,即AE=EC,由AD=EC,即可得③正确;过E作EG⊥BC于G点,证明Rt△BEG≌Rt△BEF和Rt△CEG≌Rt△AEF,得到BG=BF和AF=CG,利用线段和差即可得到④正确.【详解】解:①∵BD为△ABC的角平分线,∴∠ABD=∠CBD,∴在△ABD和△EBC中,BD BCABD CBD BE BA⎧⎪∠∠⎨⎪⎩===,∴△ABD≌△EBC(SAS),①正确;②∵BD为△ABC的角平分线,BD=BC,BE=BA,∴∠BCD=∠BDC=∠BAE=∠BEA,∵△ABD≌△EBC,∴∠BCE=∠BDA,∴∠BCE+∠BCD=∠BDA+∠BDC=180°,②正确;③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD =∠BEA,∴∠DCE=∠DAE,∴△ACE为等腰三角形,∴AE=EC,∵△ABD≌△EBC,∴AD=EC,∴AD=AE.③正确;④过E作EG⊥BC于G点,∵E是∠ABC的角平分线BD上的点,且EF⊥AB,∴EF=EG(角平分线上的点到角的两边的距离相等),∵在Rt△BEG和Rt△BEF中,BE BE EF EG=⎧⎨=⎩,∴Rt△BEG≌Rt△BEF(HL),∴BG=BF,∵在Rt△CEG和Rt△AFE中,AE CE EF EG=⎧⎨=⎩,∴Rt△CEG≌Rt△AEF(HL),∴AF=CG,∴BA+BC=BF+FA+BG−CG=BF+BG=2BF,④正确.故选D.【点睛】本题考查了全等三角形的判定和全等三角形的对应边、对应角相等的性质,等腰三角形的判定与性质,本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等的性质是解题的关键.2.如图,ABC ∆中,135ACB ∠=︒,CD AB ⊥,垂足为D ,若6AD =,20BD =,则CD 的长为( )A .B .C .72D .4【答案】D【分析】 做,ACD BCD ∆∆分别关于,AC BC 的对称图形,ACE BCF ∆∆延长,AE BF 交于点G ,连接CG ,构造正方形,再根据等量关系用勾股定理计算.【详解】做,ACD BCD ∆∆分别关于,AC BC 的轴对称图形,ACE BCF ∆∆延长,AE BF 交于点G ,连接CG ,如图:∵,ACE BCF ∆∆是,ACD BCD ∆∆的对称三角形∴6,20,AE AD BF BD CE CD CF ======,,,AEC ADC BFC BDC ACE ACD BCF BCD ∠=∠∠=∠=∠∠=∠∵CD AB ⊥∴90ADC BDC AEC BFC ∠=∠=∠=∠=︒又∵135ACB ∠=︒∴135ACE BCF ∠+∠=︒∴36013513590ECF ∠=︒-︒-︒=︒∴四边形CEGF 是正方形设CD CF GF CE GE x =====,在Rt GAB ∆ 中:222AG +BG AB =即:()()22262026x x +++= 解得:124,30x x ==-(舍)∴CD 的长为4.【点睛】本题是一道综合性较强的题目,整体图形的对称构造正方形是解决本题的关键.3.如图,Rt ACB 中,90ACB ︒∠=,ABC 的角平分线AD 、BE 相交于点P ,过P 作PF AD ⊥交BC 的延长线于点F ,交AC 于点H ,则下列结论:①135APB ︒∠=;②PF PA =;③AH BD AB +=;④S 四边形23ABDE S ABP =,其中正确的个数是( )A .4B .3C .2D .1【答案】B【分析】 根据三角形全等的判定和性质以及三角形内角和定理逐一分析判断即可.【详解】解:∵在△ABC 中,∠ACB=90°,∴∠CAB+∠ABC=90°∵AD 、BE 分别平分∠BAC 、∠ABC ,∴∠BAD=12CAB ∠,∠ABE=12ABC ∠ ∴∠BAD+∠ABE=111+=()45222CAB ABC CAB ABC ∠∠∠+∠=︒ ∴∠APB=180°-(∠BAD+∠ABE )=135°,故①正确;∴∠BPD=45°,又∵PF⊥AD,∴∠FPB=90°+45°=135°∴∠APB=∠FPB又∵∠ABP=∠FBPBP=BP∴△ABP≌△FBP(ASA)∴∠BAP=∠BFP,AB=AB,PA=PF,故②正确;在△APH与△FPD中∵∠APH=∠FPD=90°∠PAH=∠BAP=∠BFPPA=PF∴△APH≌△FPD(ASA),∴AH=FD,又∵AB=FB∴AB=FD+BD=AH+BD,故③正确;连接HD,ED,∵△APH ≌△FPD ,△ABP ≌△FBP∴APH FPD S S =,ABP FBP S S =,PH=PD ,∵∠HPD=90°,∴∠HDP=∠DHP=45°=∠BPD∴HD ∥EP ,∴EPH EPD S S =∵ABP BDP AEP EPDABDE S S S S S =+++四边形 ()ABP AEP EPH PBD S S S S =+++ABP APH PBD S S S =++ABP FPD PBD S S S =++ABP FBP S S =+2ABP S =故④错误,∴正确的有①②③,故答案为:B.【点睛】本题考查了三角形全等的判定方法,判定两个三角形全等的方法有:SSS、SAS、AAS、ASA、HL,注意AAA和SAS不能判定两个三角形全等.二、解答题4.如图,ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.(1)求证:BD=CE;(2)若AB=6cm,AC=10cm,求AD的长.【答案】(1)证明见解析;(2)2【分析】=,(1)连接BP、CP,根据线段垂直平分线上的点到两端点的距离相等可得BP CP根据角平分线上的点到角的两边距离相等可得DP EP=,然后利用“HL”证明Rt BDP∆和Rt CEP全等,根据全等三角形对应边相等证明即可;=,(2)利用“HL”证明Rt ADP∆和Rt AEP全等,根据全等三角形对应边相等可得AD AE 再根据AB、AC的长度表示出AD、CE,然后解方程即可.【详解】(1)证明:连接BP、CP,点P在BC的垂直平分线上,BP CP∴=,∠的平分线,AP是DACDP EP,在Rt BDP∆和Rt CEP中,BP CP,DP EPRt BDP Rt CEP(HL),∴=;BD CE(2)解:在Rt ADP∆和Rt AEP中,AP AP,DP EPRt ADP Rt AEP(HL),∴=,AD AE6AB cm =,10AC cm =,610AD AE ,即610AD AD ,解得AD 2cm =.【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,线段垂直平分线上的点到两端点的距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.5.(特例感知)(1)如图(1),ABC ∠是O 的圆周角,BC 为直径,BD 平分ABC ∠交O 于点D ,3CD =,4BD =,求点D 到直线AB 的距离.(类比迁移)(2)如图(2),ABC ∠是O 的圆周角,BC 为O 的弦,BD 平分ABC ∠交O 于点D ,过点D 作DE BC ⊥,垂足为点E ,探索线段AB ,BE ,BC 之间的数量关系,并说明理由.(问题解决)(3)如图(3),四边形ABCD 为O 的内接四边形,90ABC ∠=︒,BD 平分ABC ∠,BD =,6AB =,求ABC 的内心与外心之间的距离.【答案】(1)125;(2)2AB BC BE +=,理由见解析;(3 【分析】 (1)如图①中,作DF AB ⊥于F ,DE BC ⊥于E .理由面积法求出DE ,再利用角平分线的性质定理可得DF DE =解决问题;(2)如图②中,结论:2AB BC BE +=.只要证明()DFA DEC ASA ∆≅∆,推出AF CE =,Rt BDF Rt BDE(HL)∆≅∆,推出AF BE =即可解决问题;(3)如图③,过点D 作DF ⊥BA ,交BA 的延长线于点F ,DE ⊥BC ,交BC 于点E ,连接AC ,作△ABC △ABC 的内切圆,圆心为M ,N 为切点,连接MN ,OM .由(1)(2)可知,四边形BEDF 是正方形,BD 是对角线.由切线长定理可知:610842AN +-==,推出541ON =-=,由面积法可知内切圆半径为2,在Rt OMN ∆中,理由勾股定理即可解决问题;【详解】解:(1)如图①中,作DF AB ⊥于F ,DE BC ⊥于E .图① BD 平分ABC ∠,DF AB ⊥,DE BC ⊥,DF DE ∴=, BC 是直径,90BDC ∴∠=︒,5BC ∴===,1122BC DE BD DC =, 125DE ∴=, 125DF DE =∴=. 故答案为125 (2)如图②中,结论:2AB BC BE +=.图②理由:作DF BA ⊥于F ,连接AD ,DC . BD 平分ABC ∠,DE BC ⊥,DF BA ⊥,DF DE ∴=,90DFB DEB ∠=∠=︒,180ABC ADC ∠+∠=︒,180ABC EDF ∠+∠=︒,ADC EDF ∴∠=∠,FDA CDE ∴∠=∠,90DFA DEC ∠=∠=︒,()DFA DEC ASA ∴∆≅∆,AF CE ∴=,BD BD =,DF DE =,Rt BDF Rt BDE(HL)∴∆≅∆,BF BE ∴=,2AB BC BF AF BE CE BE ∴+=-++=.(3)如图③,过点D 作DF ⊥BA ,交BA 的延长线于点F ,DE ⊥BC ,交BC 于点E ,连接AC ,作△ABC △ABC 的内切圆,圆心为M ,N 为切点,连接MN ,OM .由(1)(2)可知,四边形BEDF 是正方形,BD 是对角线.图③7BD =,∴正方形BEDF 的边长为7,由(2)可知:28BC BE AB =-=,10AC ∴==,由切线长定理可知:610842AN +-==, 541ON ∴=-=,设内切圆的半径为r , 则11111068682222r r r ⨯+⨯⨯+⨯⨯=⨯⨯⨯ 解得2r ,即2MN =,在Rt OMN ∆中,OM ==【点睛】本题属于圆综合题,考查了角平分线的性质定理,全等三角形的判定和性质,勾股定理,解直角三角形,正方形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.6.在平面直角坐标系中,点()5,0A -,()0,5B ,点C 为x 轴正半轴上一动点,过点A 作AD BC ⊥交y 轴于点E .(1)如图①,若点C 的坐标为(3,0),试求点E 的坐标;(2)如图②,若点C 在x 轴正半轴上运动,且5OC <,其它条件不变,连接DO ,求证:OD 平分ADC ∠(3)若点C 在x 轴正半轴上运动,当2OCB DAO ∠=∠时,试探索线段AD 、OC 、DC 的数量关系,并证明.【答案】(1)(0,3);(2)详见解析;(3)AD=OC+CD【分析】(1)先根据AAS判定△AOE≌△BOC,得出OE=OC,再根据点C的坐标为(3,0),得到OC=2=OE,进而得到点E的坐标;(2)先过点O作OM⊥AD于点M,作ON⊥BC于点N,根据△AOE≌△BOC,得到S△AOE=S△BOC,且AE=BC,再根据OM⊥AE,ON⊥BC,得出OM=ON,进而得到OD 平分∠ADC;(3)在DA上截取DP=DC,连接OP,根据三角形内角和定理,求得∠PAO=30°,进而得到∠OCB=60°,根据SAS判定△OPD≌△OCD,得OC=OP,∠OPD=∠OCD=60°,再根据三角形外角性质得PA=PO=OC,故AD=PA+PD=OC+CD.【详解】(1)如图①,∵AD⊥BC,BO⊥AO,∴∠AOE=∠BDE,又∵∠AEO=∠BED,∴∠OAE=∠OBC,∵A(-5,0),B(0,5),∴OA=OB=5,∴△AOE≌△BOC,∴OE=OC,又∵点C的坐标为(3,0),∴OC=3=OE,∴点E的坐标为(0,3);(2)如图②,过点O作OM⊥AD于点M,作ON⊥BC于点N,∵△AOE≌△BOC,∴S△AOE=S△BOC,且AE=BC,∵OM⊥AE,ON⊥BC,∴OM=ON,∴OD平分∠ADC;(3)如所示,在DA上截取DP=DC,连接OP,∵2OCB DAO ∠=∠,∠ADC=90°∴∠PAO+∠OCD=90°,∴∠DAC=903︒=30°,∠DCA=2903⨯︒=60° ∵∠PDO=∠CDO ,OD=OD ,∴△OPD ≌△OCD ,∴OC=OP ,∠OPD=∠OCD=60°,∴∠POA=∠PAO=30°∴PA=PO=OC∴AD=PA+PD=OC+CD即:AD=OC+CD .【点睛】本题属于三角形综合题,主要考查了全等三角形的判定与性质,角平分线的判定定理以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角形的性质进行求解.7.如图,在ABC 中,AB AC =,100A ∠=︒,BD 是ABC ∠的平分线,延长BD 至点E ,DE AD =,试求ECA ∠的度数.【答案】40°【分析】在BC 上截取BF AB =,连接DF ,通过证明()ABD FBD SAS ≌,可得18080DFC A ︒∠=-∠=︒,再通过证明()DCE DCF SAS ≌,即可求得40ECA DCB ∠=∠=︒【详解】解:如图,在BC 上截取BF AB =,连接DF , BD 是ABC ∠的平分线,ABD FBD ∴∠=∠,在ABD △和FBD 中,,,,AB FB ABD FBD BD BD =⎧⎪∠=∠⎨⎪=⎩()ABD FBD SAS ∴△≌△,BFD A ∴∠=∠,AD DF =,∴DE=DF ,18080DFC A ∴∠=︒-∠=︒,又40ABC ACB ∠=∠=︒,60FDC ∴∠=︒,18060EDC ADB ABD A ∠=∠=︒-∠-∠=︒,EDC FDC ∴∠=∠,在DCE 和DCF 中,,,,DE DF EDC FDC DC DC =⎧⎪∠=∠⎨⎪=⎩()DCE DCF SAS ∴△≌△,故40ECA DCB ∠=∠=︒.【点睛】本题考查了全等三角形的问题,掌握全等三角形的性质以及判定定理是解题的关键.8.如图,∠D =∠C =90°,点E 是DC 的中点,AE 平分∠DAB ,∠DEA =28°,求∠ABE 的大小.【答案】28°【分析】过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得DE=CE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC,即可求得∠ABE的度数.【详解】如图,过点E作EF⊥AB于F,∵∠D=∠C=90°,AE平分∠DAB,∴DE=EF,∵E是DC的中点,∴DE=CE,∴CE=EF,又∵∠C=90°,∴点E在∠ABC的平分线上,∴BE平分∠ABC,又∵AD∥BC,∴∠ABC+∠BAD=180°,∴∠AEB=90°,∴∠BEC=90°-∠AED=62°,∴Rt△BCE中,∠CBE=28°,∴∠ABE=28°.【点睛】考查了平行线的性质与判定、角平分线上的点到角的两边距离相等的性质、到角的两边距离相等的点在角的平分线上的性质,解题关键是熟记各性质并作出辅助线.9.如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB﹣BC的理由.【答案】见解析【分析】在AB 上找到F 使得AF =AD ,易证△AEF ≌△AED ,可得AF =AD ,∠AFE =∠D ,根据平行线性质可证∠C =∠BFE ,即可证明△BEC ≌△BEF ,可得BF =BC ,即可解题.【详解】证明:在AB 上找到F 使得AF =AD ,∵AE 平分∠BAD ,∴∠EAD =∠EAF ,∵在△AEF 和△AED 中,AD AFEAD EAF AE AE=⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△AED ,(SAS )∴AF =AD ,∠AFE =∠D ,∵AD ∥BC ,∴∠D +∠C =180°,∵∠AFE +∠BFE =180°∴∠C =∠BFE ,∵BE 平分∠BAD ,∴∠FBE =∠C ,∵在△BEC 和△BEF 中,BFE C FBE CBE BE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BEC ≌△BEF ,(AAS )∴BF =BC ,∵AB =AF +BF ,∴AB =AD +BC ,即AD =AB ﹣BC .【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AEF ≌△AED 和△BEC ≌△BEF 是解题的关键.10.如图,在△ABC 中,AB =AC ,∠ABC =40°,BD 是∠ABC 的平分线,延长BD 至E ,使DE =AD ,求证:∠ECA =40°.【答案】见解析【分析】在BC 上截取BF =AB ,连DF ,根据SAS 可证明△ABD ≌△FBD ,得出DF =DA =DE ,证明△DCE ≌△DCF ,故∠ECA =∠DCB =40°.【详解】证明:在BC 上截取BF =AB ,连DF ,∵BD 是∠ABC 的平分线,∴∠ABD =∠FBD ,在△ABD 和△FBD 中,AB FB ABD FBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△FBD (SAS ),∴DF =DA =DE ,又∵∠ACB =∠ABC =40°,∠DFC =180°﹣∠A =80°,∴∠FDC =60°,∴∠EDC =∠ADB =180°﹣∠ABD ﹣∠A=180°﹣20°﹣100°=60°,在△DCE 和△DCF 中,DF DE FDC EDC DC DC =⎧⎪∠=∠⎨⎪=⎩,∴△DCE ≌△DCF (SAS ),∴∠ECA =∠DCB =40°.【点睛】本题考查了全等三角形的判定与性质,三角形内角和定理,熟练掌握全等三角形的判定与性质是解题的关键.11.已知△ABC 中,AB =AC ,∠A =108°,BD 平分∠ABC ,求证:BC =AC +CD .【答案】见解析【分析】在线段BC 上截取BE =BA ,连接DE .则只需证明CD =CE 即可.结合角度证明∠CDE =∠CED .【详解】证明:在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD 12=∠ABC . 在△ABD 和△EBD 中,BE BA ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBD .(SAS )∴∠BED=∠A=108°,∠ADB=∠EDB.又∵AB=AC,∠A=108°,∠ACB=∠ABC12=⨯(180°﹣108°)=36°,∴∠ABD=∠EBD=18°.∴∠ADB=∠EDB=180°﹣18°﹣108°=54°.∴∠CDE=180°﹣∠ADB﹣∠EDB=180°﹣54°﹣54°=72°.∴∠DEC=180°﹣∠DEB=180°﹣108°=72°.∴∠CDE=∠DEC.∴CD=CE.∴BC=BE+EC=AB+CD.【点睛】本题考查全等三角形的判定和性质,等腰三角形的判定,添加恰当辅助线是本题的关键.12.如图,已知等腰直角三角形ABC中,AB=AC,∠BAC=90°,BF平分∠ABC,CD⊥BD 交BF的延长线于点D,试说明:BF=2CD.【答案】见解析【分析】作BF的中点E,连接AE、AD,根据直角三角形得到性质就可以得出AE=BE=EF,由BD平分∠ABC就可以得出∠ABE=∠DBC=22.5°,从而可以得出∠BAE=∠BAE=∠ACD=22.5°,∠AEF=45°,由∠BAC=90°,∠BDC=90°就可以得出A、B、C、D四点共圆,求出AD=DC,证△ADC≌△AEB推出BE=CD,从而得到结论.【详解】解:取BF的中点E,连接AE,AD,∵∠BAC=90°,∴AE=BE=EF,∴∠ABD=∠BAE,∵CD ⊥BD ,∴A ,B ,C ,D 四点共圆,∴∠DAC =∠DBC ,∵BF 平分∠ABC ,∴∠ABD =∠DBC ,∴∠DAC =∠BAE ,∴∠EAD =90°,∵AB =AC ,∴∠ABC =45°,∴∠ABD =∠DBC =22.5°,∴∠AED =45°,∴AE =AD ,在△ABE 与△ADC 中,ABE DACBAE ACD AE AD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ADC ,∴BE =CD ,∴BF =2CD .【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,四点共圆,直角三角形的性质,角平分线的性质,正确的作出辅助线是解题的关键.13.如图1,点A 是直线MN 上一点,点B 是直线PQ 上一点,且MN//PQ .NAB ∠和ABQ ∠的平分线交于点C .(1)求证:BC AC ⊥;(2)过点C 作直线交MN 于点D (不与点A 重合),交PQ 于点E,①若点D 在点A 的右侧,如图2,求证:AD BE AB +=;②若点D 在点A 的左侧,则线段AD 、BE 、AB 有何数量关系?直接写出结论,不说理由.【答案】(1)见解析;(2)见解析;(3)BE AD AB =+【分析】(1) 由平行线性质可得∠NAB+∠ABQ=180°,再由角平分线定义可得11,22∠=∠∠=∠BAC NAB CBA ABQ ,再利用三角形内角和定理即可得∠C=90°,即可证明BC ⊥AC;(2) ①延长AC 交PQ 点F ,先证明AC=FC,再证明△ACD ≌△FCE,即可得AD+BE=AB; ②方法与①相同.【详解】解:(1)∵MN ∥PQ∴∠NAB+∠ABQ=180°∵AC 平分∠NAB ,BC 平分∠ABQ ∴11,22∠=∠∠=∠BAC NAB CBA ABQ ∴∠BAC+∠ABC=12180⨯︒=90° 在△ABC 中,∵∠BAC+∠ABC+∠C=180°∴∠C=180°- (∠BAC+∠ABC) =180°-90°=90°∴BC ⊥AC;(2)①延长AC 交PQ 于点F∵BC ⊥AC∴∠ACB=∠FCB=90°∵BC 平分∠ABF∴∠ABC=∠FBC∴BC=BC∴△ABC≌△FBC∴AC=CF,AB=BF∵MN∥BQ∴∠DAC=∠EFC∵∠ACD=∠FCE∴△ACD≌△FCE∴AD=EF∴AB=BF=BE+EF=BE+AD 即:AB=AD+BE②线段AD,BE,AB数量关系是:AD+AB=BE 如图3,延长AC交PQ点F,∵MN//PQ .∴∠AFB=∠FAN,∠DAC=∠EFC∵AC平分∠NAB∴∠BAF=∠FAN∴∠BAF=∠AFB∴AB=FB∵BC⊥AC∴C是AF的中点∴AC=FC在△ACD与△FCE中DAC EFC AC FCACD FCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ACD FCE ASA ≅∴AD=EF∵AB=FB=BE-EF∴AD+AB=BE【点睛】本题考查了平行线性质,全等三角形性质判定,等腰三角形性质等,解题关键正确添加辅助线构造全等三角形.14.在平面直角坐标中,等腰Rt △ABC 中,AB=AC ,∠CAB=90°,A (0,a ),B (b ,0).(1)如图1+(a-2)2=0,求△ABO 的面积;(2)如图2,AC与x轴交于D点,BC与y轴交于E点,连接DE,AD=CD,求证:∠ADB=∠CDE;(3)如图3,在(1)的条件下,若以P(0,-6)为直角顶点,PC为腰作等腰Rt△PQC,连接BQ,求证:AP∥BQ.【答案】(1)△ABO的面积=4;(2)证明见解析;(3)证明见解析.【分析】(1)根据绝对值和偶次方的非负性求出a,b,根据三角形的面积公式计算;(2)作AF平分∠BAC交BD于F点,分别证明△ACE≌△BAF,△CED≌△AFD,根据全等三角形的性质证明;(3)过C点作CM⊥y轴于M点,过D点作DN⊥y轴于N点,证明△ACM≌△BAO,根据全等三角形的性质得到CM=AO=2,AM=BO=4,证明四边形ONQB为平行四边形,得到答案.【详解】解:(1)+(a-2)2=0,∴2a-b=0,a-2=0,解得,a=2,b=4,∴A(0,2),B(4,0),∴OA=2,OB=4,∴△ABO 的面积=12×2×4=4;(2)作AF 平分∠BAC 交BD 于F 点,∵AB=AC ,∠CAB=90°,∴∠C=∠ABC=∠DAF=∠BAF=45°,∵∠CAE+∠BAO=∠ABF+∠BAO=90°,∴∠CAE=∠ABF ,在△ACE 和△BAF 中,CAE ABF AC ABACE BAF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACE ≌△BAF (ASA ),∴CE=AF ,在△CED 和△AFD 中,CD AD C DAF CE AF =⎧⎪∠=∠⎨⎪=⎩,∴△CED ≌△AFD (SAS )∴∠CDE=∠ADB ;(3)过C 点作CM ⊥y 轴于M 点,过D 点作DN ⊥y 轴于N 点,则∠AMC=∠BOA=90°,∵∠CAM+∠BAO=∠ABO+∠BAO=90°,∴∠CAM=∠ABO ,在△ACM 和△BAO 中,CAM ABO CMA AOB AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACM ≌△BAO (AAS ),∴CM=AO=2,AM=BO=4,∵A (0,2),P (0,-6),∴AP=8,∴PM=AP-AM=4,在△PCM 和△QPN 中,CPM PQN PMC QNP PC PQ ∠=∠⎧⎪∠=∠⎨⎪=⎩,△PCM ≌△QPN (AAS ),∴NQ=PM=4,∴四边形ONQB 为平行四边形,∴AP ∥BQ .【点睛】本题考查的是全等三角形的判定和性质,非负数的性质,掌握全等三角形的判定定理和性质定理是解题的关键.15.如图,已知 B (-1, 0) , C (1, 0) , A 为 y 轴正半轴上一点, AB = AC ,点 D 为第二象限一动点,E 在 BD 的延长线上, CD 交 AB 于 F ,且∠BDC = ∠BAC . (1)求证: ∠ABD = ∠ACD ;(2)求证:AD 平分∠CDE ;(3)若在D 点运动的过程中,始终有DC =DA +DB ,在此过程中,∠BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC 的度数?【答案】(1)见解析;(2)见解析;(3)∠BAC的度数不变化.∠BAC=60°.【解析】【分析】(1)根据三角形内角和定理等量代换可得结论;(2)作AM⊥CD于点M,作AN⊥BE 于点N,证明△ACM≌△ABN即可;(3)用截长补短法在CD上截取CP=BD,连接AP,证明△ABD≌△ACP,由全等性质可知△ADP是等边三角形,易知∠BAC 的度数. 【详解】(1)∵∠BDC=∠BAC,∠DFB=∠AFC,又∵∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AFC=180°,∴∠ABD=∠ACD;(2)过点A作AM⊥CD于点M,作AN⊥BE于点N.则∠AMC=∠ANB=90°.∵OB=OC,OA⊥BC,∴AB=AC,∵∠ABD=∠ACD,∴△ACM≌△ABN (AAS)∴AM=AN.∴AD平分∠CDE.(到角的两边距离相等的点在角的平分线上);(3)∠BAC的度数不变化.在CD上截取CP=BD,连接AP.∵CD=AD+BD,∴AD=PD.∵AB=AC,∠ABD=∠ACD,BD=CP,∴△ABD≌△ACP.∴AD=AP;∠BAD=∠CAP.∴AD=AP=PD,即△ADP是等边三角形,∴∠DAP=60°.∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°.【点睛】本题考查了三角形的综合,主要考查了三角形内角和定理、全等三角形的证明和性质,等腰等边三角形的性质和判定,采用合适的方法添加辅助线构造全等三角形是解题的关键.16.已知:等腰直角三角形ABC中,∠ACB=90°;AC=BC;∠1=∠3;BE⊥AD。
全等辅助线方法专题——角平分线

全等三角形辅助线方法---角平分线一、知,为行之始1.角平分线的定义2.角平分线的画法3.角平分线的性质定理4.角平分线的判定定理二、行,为知之成1.角平分线辅助线方法一:作垂线(角平分线的性质与判定定理)作法:过角平分线上一点向角两边作垂线,构造全等【例】如图,在四边形ABCD 中,BC>BA ,AD=CD ,BD 平分∠ABC ,求证:∠A+∠C=180°.2.角平分线辅助线方法二:截长(角平分线的对称性)作法:在角的两边截取相等的线段构造全等CDBA【例】如图,四边形ABCD中,AD∥BC,点E在CD上,EA,EB分别平分∠DAB和∠CBA,设AD=x,BC=y 且(x﹣3)2+|y﹣4|=0.求AB的长.3.角平分线辅助线方法三:延长(三线合一)作法:延长垂直于角平分线的线段与角的另一边相交构成等腰三角形【例】如图,在△ABC中,∠C=90°,CA=CB,AD平分∠BAC,BE⊥AD于点E,求证:AD=2BE.三、知行合一1.如图,Rt ABC ∆中,90C ∠=︒,AD 平分BAC ∠,交BC 于点D ,10AB =,15ABD S ∆=,则CD 的长为( ) A .2 B .3 C .4 D .52.如图,在Rt △ABC 中,∠C =90°,∠BAC 的平分线交BC 于点D ,CD =2,BD=3,Q 为AB 上一动点,则DQ 的最小值为( )A .1B .2C .2.5D .33.如图,△ABC 的三条角平分线交于O 点,已知△ABC 的周长为20,OD ⊥AB ,OD=5,则△ABC 的面积=_________.4.如图,已知△ABC 的周长是16,OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D 且OD=2,△ABC 的面积是________________.5.如图,在△ABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,作射线AP交BC于点D.若CD=1,AB=4,则△ABD的面积是_________.6.如图,在△ABC中,以原点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于12MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若AC:AB=3:4,△ACD的面积是21,则△ABD的面积是______.7.如图,四边形ABCD中,CA平分∠BAD,CB=CD,CF⊥AD于F. (1)求证:∠ABC+∠ADC=180°;(2)若AF:CF=3:4,CF=8,求四边形ABCD的面积.8.如图,△ABC 中AP 平分∠CAB ,PD 垂直平分BC 交AP 于P ,PE AE ⊥于E . (1)当28PCB ∠=︒时,BPC ∠的度数是__________;(2)求证:2AC AB AE +=.9.四边形ABCD 中,,AB CD DE ∥平分ADC ∠.(1)如图1,若90ABE ∠=︒,E 是BC 的中点,求证:AE 平分BAD ∠;(2)如图2,若AE 平分BAD ∠,求证:E 是BC 的中点;(3)在(2)的条件下,若8,6AE DE ==,求四边形ABCD 的面积.10.如图1,在ABC △中,BD 平分,ABC CE ∠平分,ACB BD ∠与CE 交于点O .(1)如图1,若60A ∠=︒,①求BOC ∠的度数;②作OF AB ⊥于点F ,求证:2AE AD AF +=;(2)如图2,若490,7A OD OB ∠=︒=,则OE OC的值为____________.图1CDB AF E O图2CD B A O E。
专题06 全等模型-角平分线模型(解析版)

专题06全等模型-角平分线模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各类模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的几类全等模型作相应的总结,需学生反复掌握。
模型1.角平分线垂两边(角平分线+外垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线、CA OA ⊥于点A 时,过点C 作CA OB ⊥.结论:CA CB =、OAC ∆≌OBC ∆.图1图2常见模型1(直角三角形型)条件:如图2,在ABC ∆中,90C ∠=︒,AD 为CAB ∠的角平分线,过点D 作DE AB ⊥.结论:DC DE =、DAC ∆≌DAE ∆.(当ABC ∆是等腰直角三角形时,还有AB AC CD =+.)图3常见模型2(邻等对补型)条件:如图3,OC 是∠COB 的角平分线,AC =BC ,过点C 作CD ⊥O A 、CE ⊥OB 。
结论:①180BOA ACB ∠+∠=︒;②AD BE =;③2OA OB AD =+.例1.(2022·北京·中考真题)如图,在ABC ∆中,AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____.【答案】1【分析】作DF AC ⊥于点F ,由角平分线的性质推出1DF DE ==,再利用三角形面积公式求解即可.【详解】解:如图,作DF AC ⊥于点F ,∵AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,∴1DF DE ==,∴1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1.【点睛】本题考查角平分线的性质,通过作辅助线求出三角形ACD 中AC 边的高是解题的关键.例2.(2022·山东泰安·中考真题)如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =()A .40°B .45°C .50°D .60°【答案】C 【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠FAP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°,∴∠CAF=100°,在Rt△PFA和Rt△PMA中,{PA PA PM PF==,∴Rt△PFA≌Rt△PMA(HL),∴∠FAP=∠PAC=50°.故选C.【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM=PN=PF是解题的关键.例3.(2023·山东·七年级专题练习)如图,∠D=∠C=90°,点E是DC的中点,AE平分∠DAB,∠DEA =28°,求∠ABE的大小.【答案】28°【分析】过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得DE=CE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC,即可求得∠ABE的度数.【详解】如图,过点E作EF⊥AB于F,∵∠D=∠C=90°,AE平分∠DAB,∴DE=EF,∵E是DC的中点,∴DE=CE,∴CE=EF,又∵∠C=90°,∴点E在∠ABC的平分线上,∴BE平分∠ABC,又∵AD∥BC,∴∠ABC+∠BAD=180°,∴∠AEB=90°,(1)填空:角平分线的性质定理:角平分线上的点到.符号语言:∵如图1,OP 为COD ∠上的平分线,且,∴.(2)解答:已知:如图2,60AOB ∠=︒,OP 为AOB ∠的平分线,以点P 为顶点的CPD ∠与角的两边相交于点C 、D ,且120CPD ∠=︒.求证:PC PD =.(3)作图:根据以上种情况,再次寻找其它情况,点P P 为AOB ∠的平分线上的点,请你用尺规作图作PE OA ⊥于E ,作PF OB ⊥于F ,90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒,OP 平分AOB ∠,PE PF ∴=,在四边形EOFP 中,60AOB ∠=︒,90PEO PFO ∠=∠=︒,36060290120EPF ∴∠=︒-︒-⨯︒=︒,120CPD ∠=︒ ,CPD EPF ∴∠=∠,CPD EPD EPF EPD ∴∠-∠=∠-∠,CPE DPF ∴∠=∠,PEC PFD ∴≅ (ASA )PC PD ∴=;(3)证明:如图2,作射线PC ,交OA 于C ,作PCN AOB ∠=∠,反向延长NP ,交OB 于D ,则PC PD =;,(4)解:如图3,当ODP ∠和OCP ∠互补时,PC PD =,理由如下:作PE OA ⊥于E ,作PF OB ⊥于F ,90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒,OP 平分AOB ∠,PE PF ∴=,在四边形EOFP 中,90PEO PFO ∠=∠=︒,360290180EPF AOB ∴∠+∠=︒-⨯︒=︒,180CPD AOB ∠+∠=︒ ,CPD EPF ∴∠=∠,CPD EPD EPF EPD ∴∠-∠=∠-∠,CPE DPF ∴∠=∠,PEC PFD ∴≅ (ASA)PC PD ∴=.【点睛】本题考查全等三角形的判定,角平分线的性质等知识,解决问题的关键是熟练掌握有关基础知识.模型2.角平分线垂中间(角平分线+内垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线,AB OC ⊥,结论:△AOC ≌△BOC ,OAB ∆是等腰三角形、OC 是三线合一等。
专题教材-第2讲:角平分线专题-讲义

角平分线专题1、掌握角平分线的定义、性质及判定定理;2、掌握与角平分线有关的常用辅助线作法,即角平分线的四大基本模型;3、掌握角平分线的常见倒角模型及相关结论。
1、角平分线的四大基本模型;2、角平分线的常见倒角模型及相关结论。
角平分线(1)定义:从一个顶点出发,把一个角分成相等的两个角的射线,叫作这个角的角平分线。
(2)角平分线的性质定理:1如果一条射线是一个角的平分线,那么它把这个角分成两个相等的角。
2在角的平分线上的点到这个角的两边的距离相等。
注意:1在利用角平分线的性质时,“角平分线”和“两个垂直”这两个条件缺一不可。
2角是以其平分线为对称轴的轴对称图形。
(3)角平分线的判定定理:1在角的内部,如果一条射线的端点与角的顶点重合,且把这个角分成两个等角,那么这条射线是这个角的平分线。
2在角的内部,到一个角的两边的距离相等的点在这个角的平分线上。
(4)三角形的三条角平分线交于一点,称作三角形的内心,三角形的内心到三角形三边的距离相等。
类型一:角平分线倒角模型例1.如图所示,把一副三角板(30°,60°,90°和45°,45°,90°)如图(1)放置在平面直角坐标系中,点A在y轴正半轴上,直角边AC与y轴重合,斜边AD与y轴重合,直角边AE交x轴于点F,斜边AB交x轴于点G,O是AC的中点,AC=8.(1)把图(1)中的Rt△AED绕A点顺时针旋转α(0°≤α<90°)得图(2)。
此时△AGH 的面积是10,△AHF的面积是8,分别求F,H,B三点的坐标。
(2)如图(3),设∠AHF的平分线和∠AGH的平分线交于点M,∠EFH的平分线和∠FOC的平分线交于点N,当改变α的大小时,∠N+∠M的值是否会改变?若改变,请说明理由;若不改变,请求出其值.练习1.如图所示,已知点A是y轴上一动点,B是x轴上一动点,点C在线段OB上,连接AC,AC正好是∠OAB的角平分线,∠ABD=∠DBx.问动点A,B在运动的过程中,AC与BD 所在直线得夹角是否发生变化,若变化,请说明理由;若不变,请直接写出具体值.练习2.探究与发现:探究一:我们知道,三角形的一个外角等于它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?已知:如图(1),∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠EDC的数量关系.探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图(2),在△ADC中,DP,CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究三:若将△ADC改为任意四边形ABCD呢?已知:如图(3),在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF,如图(4),请直接写出∠P与∠A+∠B+∠E+∠F的数量关系.本题考查三角形内角和定理,坐标与图形性质,平行线的性质,三角形的面积。
三角形角平分线经典例题讲解

三角形角平分线经典例题讲解今天咱们聊聊三角形的角平分线,这个东西可真有趣。
大家都知道,三角形有三个角,对吧?而角平分线就是把其中一个角分成两个相等的角。
想象一下,一个小朋友在划分他的糖果,想让每一部分都一样,生怕一边多一颗,一边少一颗。
角平分线就是这么一个公正的“糖果分配者”。
说到这,大家有没有想过,三角形的角平分线跟其他线段有什么不同呢?它不仅仅是个直线,它还有许多有趣的性质。
角平分线的定义可不是随便说说的。
它是从一个顶点出发,直达对边,确保两个角完全相等。
想想看,如果你在画图,随便一条线怎么能做到这点呢?得用心!在我们生活中,很多地方都能看到角平分线的影子,想象一下,那些精致的甜品店,做蛋糕时的对称美,都是在追求这种“公平”的理念。
真是妙不可言。
大家知道吗?角平分线还有个酷炫的性质,就是它把对边分成的两部分,有个奇妙的比例关系。
这可不是开玩笑,跟数学中的“比”有关系哦,具体说就是:角平分线把对边分成的两段长度,跟这条线的两条边的长度成比例。
听起来可能有点复杂,咱们举个简单的例子吧。
假设有一个三角形ABC,角A是个大角,咱们把它的角平分线叫做AD。
AD把BC分成了两部分,BD和DC。
这个时候,AD的长度和AB、AC的长度之间就有了某种美丽的平衡。
就像一位和蔼可亲的老师在课堂上把学生分成了两组,确保每组都有足够的成员,让每个孩子都能参与进来。
真是温馨的一幕呢。
角平分线的性质不仅让人觉得公平,还能在一些复杂的问题中帮我们解决难题。
数学题目就像过家家的游戏,难免会有点混乱。
这时,找到角平分线,就好比找到了一根指路明灯,让我们能顺利地走出迷雾。
大家都想过,怎么利用角平分线解决实际问题吗?比如在地理上,角平分线可以帮助我们划分区域,确保每个区域都被合理地利用。
说到这,我就想到了一个经典的应用题。
有一天,小明跟小红在讨论一个三角形的面积,争论得不可开交。
小明说,他觉得从一个顶点画条角平分线,把对边分成两段,面积也分成两个比例,结果小红立刻不服气,开始反驳。
专题、角平分线四种常见辅助线添加方法

角平分线具有两条非常重要的性质:一是对称性;二是角平分线上的点到角两边的距离相等。
对于有角平分线的辅助线的作法,一般有四种:①从角平分线上一点向两边作垂线;②利用角平分线,构造对称图形(如作法是在一侧的长边上截取短边);③做角平分线的垂线,与角两边构造等腰三角形;④过角平分线上的点做边的平行线。
方法一、在证明线段的和差倍分问题中,常用到的方法是延长法或截取法来证明,以此来构造三角形全等,延长短的线段,或在长的线段上截取一部分,使之等于短的线段。
但无论延长,还是截取都要证明线段的相等。
延长要证明延长后的线段与某条线段相等,截取要证明截取后剩下的线段与某条线段相等,进而达到所要证明的目的。
例2中,用到了角平分线,用到了做垂直,利用三线合一证明边相等,利用SAS来证明三角形全等。
此题的证明,也可以在AB上截取AE=AC,先证明△ADE≌△ADC,再利用AB=2AC,得出E 是AB的中点,再利用三线合一证明DE⊥AB,所以DC⊥AC.课后专项练习一,就是利用延长或者截取法,来证明的。
题目不难,非常基础,请同学们,认真仿照例题,认真推敲,加强练习。
方法二、角平分线上的点向角两边做垂线。
通常情况下,出现了直角或是垂直等条件时,一般考虑作垂线;其它情况下考虑构造对称图形。
至于选取哪种方法,要结合题目图形和已知条件。
一般来说,出现角平分线,做双垂直,都是非常通用的方法。
要么过角平线上的点做角两边的垂直,要么做角平分线的垂直交两边,都是必出三角形全等。
方法三,过角平分线上的一点,做角平分线的垂线,必然交于角的两边,构造出等腰三角形。
这个方法,在很多题型中,非常实用。
专项练习三,有两个题,需要自行画图。
只要我们一个专题一个专题的突破,把基础扎实起来,那么初中几何还难吗?初中数学还难吗?方法四、过角平分想上一点,做角的另一边的平行线。
因为角平分线有两角相等,平行线则有内错角相等,则必然出现角相等,得等腰三角形。
角的平分线作辅助线的方法

角的平分线作辅助线的方法角的平分线是指将一个角分成两个相等的角的直线。
在几何学中,角的平分线是一个重要的概念,它可以帮助我们解决一些与角度有关的问题。
本文将介绍一种以角的平分线作为辅助线的方法,以帮助读者更好地理解和运用这一概念。
我们来看一个简单的例子。
假设有一个角ABC,我们想要找到角的平分线。
通过这个例子,我们可以总结出以角的平分线作为辅助线的一般步骤。
首先,选择角的两边上的两个点,记为D和E。
然后,通过点D 和E画出两条直线,分别与角的两边相交,交点分别记为F和G。
最后,连接点F和G,就得到了角的平分线。
当然,要想正确地画出角的平分线,我们还需要一些条件。
首先,角的两边必须在同一平面内。
其次,角的两边不能平行。
如果角的两边平行,那么它们永远不会相交,也就无法画出角的平分线。
此外,角的两边也不能重合,否则平分线就无法确定。
除了以上的基本方法,还有一些特殊情况下的辅助线方法。
例如,当角的两边垂直时,我们可以通过角的顶点引一条垂直平分线,将角分成两个相等的直角。
又如当角的两边相等时,我们可以通过角的顶点引一条垂直平分线,将角分成两个相等的锐角或钝角。
通过角的平分线,我们可以解决一些与角度有关的问题。
例如,我们可以利用角的平分线证明两个角相等。
具体方法是,通过角的平分线将角分成两个相等的角,然后利用两个相等的角的性质,证明原来的两个角相等。
又如我们可以利用角的平分线证明两条直线平行。
具体方法是,假设角的平分线与另一条直线相交于点H,通过证明角AHG和角HGB相等,从而证明直线AB与直线GH平行。
总结起来,角的平分线是一个重要的概念,在几何学中有着广泛的应用。
通过选择角的两边上的两个点,我们可以画出角的平分线,从而解决与角度有关的问题。
在实际应用中,我们还可以根据特殊情况选择不同的辅助线方法。
通过熟练掌握角的平分线的概念和方法,我们可以更好地理解和运用几何学中的相关知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何辅助线之角平分线专题1、角平分线辅助线四种基本模型
已知:AD是∠BOC的角平分线
(1)(2)
(3)(4)
2、补充性质:
如图,在△ABC中,AD平分∠BAC,则有AB:AC=BD:DC
典型例题
例1、已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB.求证:AC+CD=AB
例2、已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合,当∠A满足什么条件时,点D恰为AB中点?写出一个你认为适当的条件,并利用此条件证明D为AB中点.
例3、如图,AB=2AC,∠BAD=∠DAC,DA=DB ,求证:DC⊥AC。
D
E
H
A B
C
例4、如图所示,已知AD 是△ABC 的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,
F .求证:AD 垂直平分EF .
例5、 如图,在△ABC 中,∠A 等于60°,BE 平分∠ABC ,CD 平分∠ACB 求证:DH=EH
例6、如图,已知等腰直角三角形ABC 中,∠A =90°,AB =AC ,BD 平分∠ABC ,CE ⊥BD ,垂足为E ,求证: BD =2CE 。
例7、如图,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。
变式练习
请你参考上图构造全等三角形的方法,解答下列问题:
⑴如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。
请你判断写出FE与FD之间的数量关系;
⑵如图,在△ABC中,如果∠ACB不是直角,而⑴中的其他条件不变,请问,你在⑴中所得结论是否依然成立?若成立请证明;若不成立,请说明理由。
课后练习
1、已知:如图所示,∠C=2∠B,∠BAD=∠CAD,求证:AB=AC+CD。
2、已知,如图,BN 平分∠ABC,P为BN上一点,
且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°。
3、如图,△ABC中,AC=BC,∠BAC的外角平分线交BC的延长线于点D,若∠CAD=2∠ADC,求∠B的度数。
4、如图,D是△ABC一个外角的平分线上一点。
求证:AB+AC<DB+DC。
5、如图所示,AB∥CD,∠B=90°,E是BC的中点。
DE平分∠ADC,求证:AE平分∠DAB。
6、如图所示、在△ABC中,AB=7,BC=24,AC=25。
求内心到边的距离。
7、如图所示,已知在△ABC中,分别以AC、BC为边向外作正△BCE、正△ACD,BD与AE 交于M,求证:(1)AE=BD。
(2)MC平分∠DME。
8、如图所示,AB=CD,△PCD的面积等于△PAB的面积,求证:OP平分∠BOD。
9、如图所示,在△ABC中,∠B=60°,△ABC的角平分线AD、CE交于点O,求证:AE+CD =AC。
10、如图所示,已知在四边形ABCD中,BD>AB,AD=DC,BD平分∠ABC,
求证:∠A+∠C=180°。
11、如图所示,△ABC中,AD是∠A的平分线,E、F分别为AB、AC上的点,且∠EDF+
∠BAF=180°,求证:DE=DF。
12、如图所示,△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AD于点E,交BC
的延长线于点F。
求证:FD2=FB×FC。
