积分学2.1.6
定积分近似计算方法

定积分的近似计算方法摘要 本文主要讨论了一元函数常见的数值积分方法,例如插值型求积公式、龙贝格求积公式、高斯求积公式等近似计算方法,在用这些方法计算定积分时,会产生一些误差,为了减少误差, 可以利用复化求积公式、复化高斯公式等.本文围绕这些方法,系统介绍它们的计算公式以及截断误差,并用例题分析它们产生误差的大小、计算量等.关键词 插值型积分 龙贝格积分 高斯积分 误差分析 近似计算1引言在计算定积分的值()b aI f x dx =⎰时,常常根据微积分学基本定理求出)(x f 的一个原函数)(x F ,再用牛顿-莱布尼茨公式求的积分,()()()baI f x dx F b F a ==-⎰.但在实际应用中,这种方法只限于解决一小部分定积分的求值问题.当函数没有具体表达式,只是一些实验测得数据形成的表格或图形或者是()F x 无法用初等函数表示,例如,2bx ae dx ⎰,2sin ba x dx ⎰等等,这就需要我们用一些近似方法求的积分值.与数值积分一样,把积分区间细分,在每个小区间上,找到简单函数)(x ϕ来近似代替()f x ,且()b a x dx ϕ⎰的值容易求的.这样就把计算复杂的()ba f x dx ⎰转化为求简单的积分值()bax dx ϕ⎰.因此,定积分的近似计算实质上是就是被积函数的近似计算问题.2常见数值方法 2.1牛顿-科茨数值方法牛顿-科茨求积公式是求积节点等距离分布的插值型求积公式.利用插值多项式来构造数值积分公式是最常用、最基本的方法,具体做法是:给定区间[,]a b 上一组节点01...n a x x x b =<<<=,以及节点处函数()(0,1,2,i f x i n =,作()f x 的n 次拉格朗日多项式()()()nn i i i x f x l x ϕ==∑,其中 011011()()()()()()()()()i i n i i i i i i i n x x L x x x x L x x l x x x L x x x x L x x -+-+----=----,将插值公式(1)1()()()()(1)!n n n f f x x x n ξϕω++=++.其中1012()()()()()n n x x x x x x x L x x ω+=----,[,]a b ξ∈,依赖于变量x , 上式积分得(1)1()()()()(1)!n bb bn n aa af f x dx x dx x dx n ξϕω++=++⎰⎰⎰(1)(1)0()()()()(1)!n nb biiin aai f f x l x dx x dx n ξω++==++∑⎰⎰(1)(1)0()()()()(1)!n nbbi i n aai f f x b l x dx x dxn ξω++==++∑⎰⎰若记 (),(0,1,2,bi ia A l x dx i ==⎰….. )n (1)(1)1()[]()(1)!n bn af R f x dxn ξω++=+⎰, (2)则有()()[]nbi i ai f x dx A f x R f ==+∑⎰(3)称式(3)为插值求型公式,其中(0,1,2,i A i =…. )n 与()f x 无关,叫求积系数, i x 为求积节点,[]R f 为求积公式余项,其中求积系数由(1)决定.2.1.1梯形求积公式1梯形公式当插值节点01,x x 分别选取区间端点,a b 时,由式(3)分别求出求积系数10012bb aa x x xb b aA dx dx x x a b ---===--⎰⎰,01102bb aa x x x ab a A dx dx x x b a ---===--⎰⎰.从而的求积公式()[()()]2bab a f x dx f a f b -≈+⎰. (4) 称求积公式(4)为梯形求积公式,简称梯形公式.2梯形公式截断误差: 3*()[](),12b a R f f ξ-''=- *[,]a b ξ∈. (5) 3梯形求积公式的代数精度:1 当()1f x =时,式(5)中 1(1)2bab adx b a x b a -=-=+=-⎰. 精确成立.2.1.2 辛普森求积公式1辛普森求积公式当选取节点为012,,2a bx a x x b +===时,由式(1)求下列求积系数 1200102()()()()2()()6()()2b b a a a b x x b x x x x b a A dx dx a b x x x x a a b +-----===+----⎰⎰,0211002()()()()2()()()3()()22bb aa x x x x x a xb b a A dx dx a b a b x x x x a b -----===++----⎰⎰.0122021()()()()2()()6()()22b b a a a bx a x x x x x b a A dx dx a b a b x x x x a b +-----===++----⎰⎰ .从而求积公式()[()4()()]62bab a a bf x dx f a f f b -+≈++⎰. (6)称式(6)为抛物线积分公式或辛普森积分公式.2抛物线求积公式误差估计定理1.若()f x 在[,]a b 上有四阶连续导数,则抛物线公式(6)的余项为:5(4)**()[](),[,]2880b a R f f a b ξξ--=∈. (7) 3抛物线公式的代数精度为3.易验证,当23()1,,,f x x x x =时,式(6)精确成立,而当4()f x x =时,式(6)不能精确成立.2.1.3 牛顿-科茨公式1牛顿-科茨公式在等距离节点i x a ih =+下,其中(0,1,2b ah i n-==…. )n .作为变量替换x a th =+,那么由求积公式(1),得系数:10(1)(1)(1)()!(1)(1)!ni n t t t i t i t n A h dt i n ---+---==--⎰10(1)(1)...(1)(1)...()(0,1,2,...)!(1)!n nb a t t t i t i t n dt i n n i n -----+---=-⎰ (8)则 ()()n i i A b a C =- (9) 于是差值求积公式为:()0()()()[]nbn i i ai f x dx b a C f x R f ==-+∑⎰(10)称公式(10)为牛顿-科茨求积公式,其中()n iC 称为科茨系数.显然,科茨系数与被积函数()f x 及积分区间[,]a b 无关,它指依赖于n ,且为多项式积分.因此,只要给出n ,就能看出i A ,并写出相应地牛顿-科茨公式.2牛顿-科茨公式的截断误差与代数精度.当1n =与2n =情况分析牛顿-科茨公式的截断误差为(1)()[]()()()(1)!n b b bn aaaf R f f x dx x dx x dxn ξϕω+=-=+⎰⎰⎰牛顿-科茨公式的截断误差还可以写成(2)*1()[]()((2)!n bn a f R f x dx n n ξω++=+⎰为偶数)(1)*1()[]()(1)!n bn a f R f x dx n ξω++=+⎰ (n 为奇数) (11) 其中*[,]a b ξ∈,且不依赖于x ,101()()()...()n n x x x x x x x ω+=---,对()f x 为任何并不超过n 次多项式,均有(1)()0n fx +≡,因而[]0R f ≡,即0()()nbi i ai f x dx A f x ==∑⎰精确成立,也就是说,牛顿-科茨公式的代数精度至少为n ,牛顿-科茨公式在n 为偶数时,至少具有1n +次代数精度,在n 为奇数情况时,至少具有n 次代数精度.2.1.4复化梯形求积公式将区间[,]a b 等分,节点为i x a ih =+ (步长b ah n-=),0,1,2...,i n =)在每个小区间1[,]i i x x -上采用梯形公式(4)得11111()()[(()()]2ii nnbx i i i i ax i i x x f x dx f x dx f x f x ---==-=≈+=∑∑⎰⎰11[()()]2ni i i hf x f x +=+=∑11[()2()()]2n i n i hf a f x f b T -=++=∑ (12)称式(12)为复化梯形公式. 复化梯形公式余项为()2()()()12i n b a R f h f η-''=-(13) 2.1.5复化辛普森求积公式在每个小区间],[1+i i x x 上,辛普森公式(6)得11102()[()4()()]6n bi i ai i hf x dx f x f x f x -++==++∑⎰(14)111012[()4()2((6)]6n n i i i i hf a f x f x f --+===+++∑∑记 )]()(2)(4)([6111021b f x f x f a f hS n i i n i i n +++=∑∑-=-=+ (15)式中,21+i x为],[1+i i x x 的中点,即h x x i i 2121+=+.式(15)称为复化辛普森公式,其余项为∑-=-=-=10)4(4)()2(180)()(n i i n n f h h S f I f R η, 1(,).i i i x x η+∈故 ),(),()2(180)(R )4(4b a f h a b f n ∈--=ηη (16) 为复化辛普森的截断误差. 2.1.6复化科茨求积公式将区间[,]a b n 等分, 4n m =,m 为正整数,在每个子区间444[,]k k x x -上用科茨求积公式得到复化求积公式:412()[7()7()32()45mbk ak hf x dx f a f b f x -≈++∑⎰14241411112()32()14()mmm k k k N k k k f xf x f x C ---===+++=∑∑∑ (17)其中 4b a b a h n m--==, k x a kh =+ 其截断误差为6(6)2()[,](),()945n b a R f C h f a b ηη-=-<. 2.1.7 变步长复化求积方法复化求积公式虽然计算简单,也达到了提高精度的目的,但为了满足精度要求必须顾及误差,利用误差公式往往很困难,因为误差表达式中含有未知函数的导数,而估计各阶导数的最大值不太容易.我们可以采取把积分的区间[,]a b 细分的办法,在计算积分时将步长逐步折半,利用前后两次结果进行误差估计,如此继续,直到相邻两次结果相差不大,取最小的步长算出的结果为积分值,这种方法称为变步长积分法.以复化梯形公式为例,把区间[,]a b 分成n 等分,设复化梯形公式的近似值为n T ,原积分值为I ,由复化梯形公式误差公式(14)知:2"11()()()n b a b a I T f a b N N ηη--=-<<再把区间[,]a b 分成2n 等分,得近似值2n T ,则2222()()()122k b a b a I T f a b nηη--''=-<< 假定()f x ''在[,]a b 上变化不大,既有12()()f f ηη''''≈. 由上式得 .24kkI T I T -≈-于是 222211()()341n n n n n n I T T T T T T ≈+-=+-- (18) 式(18)表明若用2n T 作为I 的近似值,其截断误差约为2()3n n T T - (19)2.2 龙贝格求积公式龙贝格积分法的基本思想是采用复化梯形求积方法不断折半步长过程中,在积分结果中加入时候误差估计值进行补偿,使积分计算的收敛性加速,就可以加工出,,,...n n n S C R 精度较高的积分结果.由式(19), 2n T 的误差大致为23n nT T -,因此,可用这个误差值作为2n T 的一种补偿,加到2n T 上,则可得到积分准确值I ,比2n T 的更好近似值~T .222141()333n n n n nT T T T T T =+-=- 2221(2)21n n T T =-- (20)式(20)左端1n =时 记122121141()333S T T T T T =+-=- 112()()332a b T b a f +=+- [()4()()]62b a a b f a f f b -+=++恰好为[,]a b 上应用辛普生公式(16)的结果.在每个小区间应用辛普生公式:11[()2()()]2n n k k hT f a f x f b -==++∑121()112[()2()()2()]4n n n k k k k hT f a f x f b f x --===+++∑∑代入式(20)的左端得11111[()2()()2()32n nk k k k h f a f x f b f x -==+++--∑∑ 11[()2()()]2n k k h f a f x f b -++∑11111[()4()2()()]62n n k k k k f a f x f x f b -===+-++∑∑n S =从而复化辛普森公式与复化梯形公式公式有以下关系式2441n nn T T S -=- (21)类似也可以推证,在辛普森序列基础上,利用以下关系式22242161151541n n n n n S S C S S -=-=- (22)可以造出收敛速度更快的科茨序列12,...,...n C C C 将此推行下去,在科茨序列基础上,通过243431n nn C C R -=- (23)构造出收敛速度比科茨序列更快的龙贝格序列12,,......n R R R .以上这种通过逐步构造龙贝格序列的积分近似值法就称为龙贝格积分法.2.3高斯求积公式由定理()()()baf x F b F a =-⎰知,插值型求积公式的代数精度与求积节点的个数有关,具有1n +个节点的插值型求积公式至少具有n 次代数精度.不仅如此,代数精度与节点的选取有关,在构造牛顿-科茨求积公式时,为了简化处理过程,限定用等分节点作为求积节点,这样做,虽然公式确实得到简化,但同时也限制了公式的代数精度. 设积分,1,1=-=b a 本段讨论如下求积公式11()()ni i i f x A f x -==∑⎰(24)对任意积分区间[,]a b ,通过变 22ba t ab x ++-= 可以转换到区间]1,1[-上,这时11()()222bab a b a a bf x dx f t dt ---+=+⎰⎰ 此时,求积公式写为0()()222n bii ai b a a b b af x dx A f t =-+-=+∑⎰若一组节点]1,1[.....,10-∈n x x x 使插值型求积公式(24)具有21n +次代数精度,则称此组节点为高斯点,并称相应求积公式(24)为高斯求积公式.2.3.1 高斯求积公式的余项(2)2()[]()()()(22)!n nbb k k aa k f R f f x dx A f x x dx n ηω+==-=+∑⎰⎰ 其中01()()()...(),[,]n x x x x x x x a b ωη=---∈,且不依赖于x .2.3.2 复化高斯求积公式复化高斯求积公式的基本思想是:将积分区间[,]a b 分成n 个等长小区间1[,](1,...)i i t t i m -=,然后在低阶(2n =)高斯求积公式算出近似值,最后将他们相加的积分()baf t dt ⎰的近似值m G ,即11111111()()[]222ii mmbt i i i i i i at i i t t t t t t f t dt f t dt dt -----==-+-==+∑∑⎰⎰⎰1111[()]222m i h ha i h x dx-==+-+∑⎰101[()]222m n j j mi j h hA f a i h x G ==≈+-+≈∑∑ (25)其中mab h -=,j A 与(0,1,2,...,)j t j n =可由书中表中查出. 3 应用3.1插值型积分的应用例1 用牛顿-科茨公式(1,2,4n =)计算积分12211I x =+⎰. 解 1n =时2210112[]0.4512101()2I -≈+=++2n =时22211112[4]0.463725116101()1()42I -≈++=+++4n =时2222111112[7321232]0.46363311390101()1()1()848I =++++≈++++例2 利用复化梯形求积公式计算积分 12211I dx x =+⎰解 设211)(xx f +=,分点个数为n =1,2,4,5时,求出相应积分n T , 111[(()())],21,2(),.n n i i i i i T f a f b f h b a h n n f x f x a ih ih -=⎧=++⎪⎪-⎪==⎨⎪=⎪⎪=+=⎩∑列表如下:n =1的计算结果见表1-1所列 n h0x 1x 0f1f1T10.50.00.51.00.80.45n =2的表格如下 n h0x1x2x0f1f 2f 2T20.250.000.250.501.000.941765 0.800.460294n =4时计算结果如下表 n h 0x1x2x3x4x40.1250.000.1250.250.3750.500f1f2f3f4f4T1.000.98461540.94117650.8767120.800.462813n = 5时计算结果如下 n h0x1x2x3x4x5x50.10.00.10.20.30.40.50f1f2f3f4f5f5T1.00.9900990.96153850.917430.8620690.80.463114例3 利用复化求积公式120x e dx ⎰,问积分区间为多少等分才能得证有5位有效数字?解 由式(14)知322()[],()()1212n b a b a R f h f n f n n--''''=-=- 有1(),(),2x xf x e f x e b a ''==-=,当]21,0[∈x 时,在12|()|f x e ''≤,所以122|[]|96n eR f n≤ 由于120x e dx ⎰的准确值具有一位整数,所以要使近似值具有5位有效数字,n 必须满足4242211048,102196⨯≥⨯≤-e n n e 或 取对数有 19=n .即将区间]21,0[19等分可满足给定的精度要求.例4 利用复化抛物线求积公式计算 120211I dx x =+⎰. 解 设11)(2+=x x f ,取m =1,2, 3时,公式()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++=+=====-=+++=+---=-=+∑∑.)12(,2),(),(),(,,242[31221212221111,1222h i a x ih a x x f f x f f b f f a f f m a b n f f f f h S i i i i i i b a m i m i i b a m当m =1,2,3时结果如下表所示 当m =1时m h(0.0)f )25.0(f )5.0(f2S1 0.25 1.0 0.9411765 0.80 0.463725当m =2时mh(0.0)f(0.125)f (0.025)f (0.35)f )5.0(f4S20.125 1.0 0.9846154 0.9411765 0.8767123 0.80 0.463653当m =3时mh(0.0)f(0.08333)f (0.16667)f (0.35)f(0.33333)f (0.14166667)f )5.0(f4S30.83331.00.99310340.9729730.9411760.90.852070.80.4636例5 用复化梯形公式,辛普森公式和科茨公式计算积分10sin xdx x ⎰的近似值.解按精度要求确定]1,0[分多少等分,即确定步长,要使6441021)1(28801|],[|-⨯≤≤M m S f R n ,只需.4642880102M m ⨯≥令10sin ()cos xf x txdt x==⎰, 则1()0sin ()()(cos )k kk k k d xd fx tx dt dx xdx ==⎰1cos().2k t tx kdt π=+⎰dt ktx t x f k k |)2cos(|max )(|max 10)(π+≤⎰11.1k t d t t≤=+⎰)10(≤≤x (4)1max |()| 5.f x ≤所以只要,9.13831288010264=⨯⨯≥-m 取m =4即可, 当4n =时,在每个子区间上用式(25),或(14),或(17),结果.9460829.0,9460833.0,9456911.0888===C S T3.2 龙贝格积分公式应用例6 用龙贝格算法计算积分1241I dx x=+⎰的近似值,要求误差小于510-. 解 .3,0,14)(2==+=b a x x f 步骤如下:2)1(,4)0()1(==f f 得.3)]1()0([211=+=f f T )2(计算,1.3)]21([21,516)21(12=+==f T T f 由此得 301333334121=-=T T S . (3)算出),(43),41(f f 从而,3013118)]43()41([412124=++=f f T T,14157.334242=-=T T S.30142121516121=-=S S C (4)计算),87(),85(),83(),81(f f f f 从而得到:13899.3)]87()85()83()81([812148=++++=f f f f T T ,,14159.334482=-=T T S,14059.31516242=-=S S C .1458.36364121=-=C C R(5)再计算),1615(),1613(),1611(),169(),167(),165(),163(),161(f f f f f f f f从而得到: 14094.316=T30141598=S ,,14159.3,14159.324==R C 51210||-≤-R R , 所以12043.14159.1dx x ≈+⎰3.3高斯求积公式的应用例7 用两点复化高斯求积公式计算10,x I e dx =⎰要求允许误差.106-=ε解 在本算法中取21=+n 时,,110==A A 其中;,)(mab h e x f x -== =++--=∑=)22(2201j jj b a x a b f A a b G.87189637800.1][21)32121()32121(=++-eem =2时, h =21, ]4121)21([4120202j i j j x i f A G +⨯-=∑∑==.57182571650.1)(41341333413341333413=+++=++--eeee m =3时, h =31. .37182769352.1]631)21([6130203=+⨯-=∑∑==j i j j x i f A G .101027.71||||56323--<⨯≈+-G G G3.4 几种方法的比较分析例8 计算积分211ln 2dx x =⎰,精确到0.001.(1)利用矩形公式计算, 因为对于x x f 1)(=,有320()2f x x''<=<(如果1<x <2),所以按照公式0)2(S =+-dx b a x ba . 0<n R <2112n . 如果取n =10,则我们公式的余项的余数得31010.84101200R -<<⨯,我们还必须加进由于在计算函数值实行四舍五入所产生的误差的界限相差于0.16⨯310-,为了这个目的只要计算1x的值到四位小数精确到0.00005就够了.我们有1232527292132152172192 1.051.151.251.351.551.651.751.851.95x x x x x x x x x =========5128.05405.05714.06061.06897.07407.08.08696.09524.02192172152132927252321=========y y y y y y y y y 和6.928469284.0109284.6=(2) 按照梯形公式作同样的计算,在这种情况下,作公式 210,||6n n R R n<<在这儿也试一试取n =10,虽然此时仅可以证3107.16001||-⨯<<n R ,纵坐标是9.18.17.16.15.14.13.12.11.1987654321=========x x x x x x x x x 5263.05556.05882.06250.06667.07143.07692.08333.09091.0987654321=========y y y y y y y y y和1877.669377.01877.621500101=+)( (3) 用辛普森公式做同样的计算作公式 .0))(()2(180)()4(45<≤≤⨯--=n n R b a f n a b R ξξ 并且n =5时有55104.1||-⨯<R .实行计算到五位数字,精确到0.0000058.16.14.12.14321====x x x x 45636.555556.062500.071429.083333.04321和====y y y y 9.17.15.13.11.12927252321=====x x x x x83820.1352632.058824.066667.076923.090909.029********和=====y y y y y.20.150==x x 50000.150000.060000.150和==y y6931525.083820.345636.550000.1301=++)(. 由此可见,用辛普森公式计算得到的值误差最小,计算量相对一般;而用矩形公式计算得到的值误差较大,计算量也比较大;用梯形公式计算的值误差比用矩形公式得到的值要误差小,计算量也是如此.所以我们计算定积分时用辛普森公式往往得到的值误差小,而对没有要求误差大小的,则可以选择辛普森或者是梯形公式,因为这两种方法计算量相对较小.结 束 语本文只讨论了一些一维数值积分方法及其它们的应用,误差分析等有关内容.其中最常用的方法是插值型积分以及复化方法、龙贝格积分方法和高斯积分方法,并讨论了相关求积方法的代数精度和误差分析,并给出了一些例题,分析各种方法的近似值,得出误差分析最小的近似方法.由于篇幅有限,对于高维数值积分方法本文便不再讨论.参考文献[1] 华东师范大学数学系,数学分析(第一版)[M],北京:高等教育出版社,2001. [2] 李庆阳,关治,白峰杉,数值计算原理(第二版)[M],北京: 清华大学出版社, 2008. [3] 肖筱南,现代数值计算方法(第一版)[M],北京: 北京大学出版社, 1999.[4] 菲赫金格尔茨,微积分学教程(第三版)[M],北京: 高等教育出版社, 2005. [5] 裴礼文,数学分析中的典型问题与方法(第一版)[M] ,北京: 北京大学出版社,2004. [6] 李桂成,计算方法(第三版)[M],北京: 高等教育出版社,2010.[7] Yin Y uezhu ,Yang Zhonglian.Calculating Skillfully the Curve Integral and Surface Integral Type 2 bySymmetry, SCIENCE & TECHNOLOGY INFORMATION ,2008(30)The Approximate Numerical Method of the Definite IntegralAbstract This paper mainly discusses common numerical methods of unary function, such as approximate calculation method of interpolation integral, Lebesgue integral and Gauss integration. With these methods in calculating the integral, it will produce some error. In order to reduce the error, we can use after the formula for product and after the Gauss formula. This paper focus on these methods introducing formula of introduction and truncation errors .In addition they can provide examples to analysis size of the error and computation.Keywords interpolation integral Lebesgue integral Gauss integral error analysis approximate computation。
高等数学大一下知识点

高等数学大一下知识点
高等数学是大一下学期的一门重要课程,主要涵盖了以下几个知识点:
1. 一元函数微积分
1.1 函数的极限与连续性
1.2 导数与微分
1.3 函数的应用
2. 一元函数积分学
2.1 不定积分
2.2 定积分
2.3 微积分基本定理
3. 多元函数微积分
3.1 多元函数的极限与连续性
3.2 偏导数与全微分
3.3 隐函数与参数方程 3.4 多元复合函数求导
4. 多元函数积分学
4.1 二重积分
4.2 三重积分
4.3 曲线与曲面积分
5. 常微分方程
5.1 一阶常微分方程 5.2 高阶常微分方程 5.3 线性常微分方程
6. 线性代数
6.1 线性方程组与矩阵 6.2 矩阵的运算与性质 6.3 行列式与矩阵的逆
6.4 特征值与特征向量
7. 概率与统计
7.1 随机事件与概率
7.2 随机变量与概率分布
7.3 大数定律与中心极限定理
以上是高等数学大一下学期的主要知识点概述。
学习这些知识将为大家打下扎实的数学基础,为以后的学习和应用提供坚实的支持。
希望大家在学习过程中能够切实掌握这些知识,灵活运用于实际问题中,提高数学思维和解决问题的能力。
定积分计算的总结论文

定积分计算的总结论文标题:定积分的计算方法总结摘要:定积分是微积分学中的重要内容,该文通过总结定积分的计算方法,包括基本定积分的计算、利用定积分计算面积和体积、变量替换求解定积分等方面的知识,探讨了定积分在实际问题中的应用,总结了定积分的计算方法,为读者提供了一种关于定积分计算的综合信息。
关键词:定积分;计算方法;面积;体积;变量替换1.引言定积分是微积分学中的重要工具,用于求解一条曲线所围成的面积、计算一些曲面的体积等。
在物理、经济学和工程学等领域,定积分的应用广泛。
本文主要总结并归纳定积分的计算方法,以及定积分在实际问题中的应用。
2.定积分的基本计算方法2.1基本不定积分首先,我们需要了解基本不定积分的常用公式,如幂函数积分、三角函数积分、指数函数积分等。
基本不定积分是求解定积分的基础,需要熟练掌握。
2.2基本定积分的计算基本定积分的计算可以通过牛顿-莱布尼茨公式进行求解,即通过求解不定积分的差来得到定积分的值。
此外,还可以通过分部积分法等方法来简化计算。
3.利用定积分计算面积和体积3.1曲线围成的面积通过定积分的计算方法,可以求解一条曲线所围成的面积。
常见的曲线有直线、抛物线、三角函数曲线等。
通过将曲线用函数表达式表示,并确定积分上下限,可以通过定积分的计算求解面积值。
3.2曲面的体积利用定积分的计算方法,可以计算曲面围成的体积。
例如,通过确定边界曲线的函数表达式,设置积分上下限,可以通过定积分计算出曲面体积的值。
4.变量替换求解定积分变量替换是定积分计算中常用的方法之一,可以将复杂的定积分转化为简单的形式。
通过选择适当的变量替换,使被积函数形式简单化,从而更容易计算定积分。
5.定积分的应用定积分在实际问题中有广泛的应用,如物体质量、质心的计算、平均值的求解、几何问题的解决等。
本文还介绍了一些实际问题,并利用定积分的计算方法得到解答。
6.结论本文总结了定积分的计算方法,包括基本定积分的计算、利用定积分计算面积和体积、变量替换求解定积分等方面的知识。
积分的概念与定积分

积分的概念与定积分引言在数学领域中,积分是一种重要的概念和工具,广泛应用于物理学、经济学、工程学等各个领域。
积分的概念和定积分是数学分析的基础,对于理解和应用微积分的原理和方法具有重要意义。
本教案将系统地介绍积分的概念和定积分的基本性质,帮助学生全面理解和掌握相关知识。
一、积分的概念1.1 微分与积分的关系微分和积分是微积分的两个基本概念,它们之间存在着密切的关系。
通过对函数进行微分,可以得到函数的变化率和导数;而通过对函数进行积分,可以得到函数的面积、体积、平均值等重要信息。
1.2 定积分的引入为了解决曲线下面积的计算问题,人们引入了定积分的概念。
定积分可以看作是将曲线下面的面积划分成无穷多个无穷小的矩形,并将这些矩形的面积相加得到的极限值。
二、定积分的基本性质2.1 定积分的存在性对于连续函数,定积分存在且唯一。
通过引入黎曼和的概念,可以证明定积分的存在性。
2.2 定积分的性质定积分具有线性性、保号性、保序性等基本性质。
线性性表明定积分具有加法和数乘的性质;保号性和保序性则保证了定积分的结果与函数的大小关系一致。
2.3 定积分与不定积分的关系定积分与不定积分是微积分中两个重要的概念。
通过定积分与不定积分的关系,可以将定积分问题转化为不定积分问题,从而更方便地求解。
三、定积分的计算方法3.1 基本积分公式基本积分公式是求解定积分的基础,通过记忆和掌握基本积分公式,可以快速求解一些简单的积分问题。
3.2 曲线的面积计算通过定积分的概念和性质,可以求解曲线下面积的问题。
将曲线分割成无穷多个小矩形,并将这些小矩形的面积相加即可得到曲线下面积的近似值。
3.3 用定积分计算物理量定积分在物理学中有着广泛的应用,可以用来计算物体的质量、重心、转动惯量等重要物理量。
通过将物理问题转化为定积分问题,可以简化计算过程。
四、定积分的应用4.1 定积分在几何学中的应用定积分在几何学中有着重要的应用,可以用来计算曲线的弧长、曲率、曲面的面积等。
不定积分中分部积分法则的教学设计

不定积分中分部积分法则的教学设计【摘要】不定积分中的分部积分法则是微积分中的重要概念之一,能够帮助我们解决复杂的积分问题。
本文从引言、正文和结论三个部分展开,引言部分主要介绍分部积分法则的重要性,正文部分具体阐述了分部积分法则的定义、应用场景、教学设计步骤、示例演练和练习题,通过这些内容可以帮助学生更好地理解和掌握这一概念。
结论部分对分部积分法则的教学设计进行总结,强调了其在学习和应用中的重要性。
通过本文的讲解,读者能够深入了解分部积分法则的相关知识,并在实际的学习和应用中灵活运用。
【关键词】不定积分、分部积分法则、教学设计、重要性、定义、应用场景、步骤、示例演练、练习题、总结1. 引言1.1 分部积分法则的重要性不定积分中的分部积分法则是微积分中的重要概念之一,它在求解复杂函数的不定积分时起着至关重要的作用。
分部积分法则可以将一个复杂的积分问题转化为两个简单的积分问题,从而简化计算过程,提高计算效率。
通过掌握分部积分法则,学生可以更快地解决各种类型的积分问题,提高解题的准确性和速度。
在实际应用中,分部积分法则常常用于求解含有多个函数乘积的不定积分,如多项式函数、三角函数等。
通过适当地选择分部积分法则的顺序,可以有效地将原积分化简为易于计算的形式,进而求得最终的不定积分结果。
深入理解和熟练运用分部积分法则是学习不定积分的重要基础,对于提升学生的数学计算能力和解题技巧具有重要意义。
通过系统学习和实践,学生可以更好地掌握分部积分法则的运用,为进一步深入学习微积分打下坚实的基础。
2. 正文2.1 分部积分法则的定义不定积分中的分部积分法则是求解复杂积分的一种重要方法,它可以将一个复杂的积分问题分解成两个较简单的积分问题来求解。
分部积分法则的定义可以表述为:设u(x)和v(x)是可导函数,那么对于不定积分∫u(x)v'(x)dx,其积分结果为u(x)v(x)-∫u'(x)v(x)dx。
这个公式可以帮助我们将一个乘积形式的积分问题转化为两个更容易求解的积分问题,从而简化求解过程。
微积分第三版答案详解

微积分第三版答案详解微积分是数学中的一门重要学科,以及广泛应用于物理学、工程学、经济学和计算机科学等领域的数学工具。
在学习微积分的过程中,往往会遇到各种难题和复杂的问题。
因此,有一本答案详解书籍是非常必要和有益的,可以帮助学习者更好地理解和掌握微积分的概念和方法。
本文将为您提供一份微积分第三版答案详解。
第一章:函数和极限1.1 函数和数学模型题目1:求函数 f(x) = x^2 - 3x + 2 的零点。
解答:要求函数的零点即求函数在什么时候取零值。
即 f(x) = 0。
解方程得到 x^2 - 3x + 2 = 0。
通过因式分解,可得 (x - 1)(x - 2) = 0,因此 x = 1 或 x = 2。
1.2 极限的概念和性质题目2:计算极限 lim(x->0) (3x^2 - 2x + 1)。
解答:要计算此极限,只需要将 x 替换为 0 得到函数的结果即可。
即将 x 替换为 0 后,函数 f(x) = 3(0)^2 - 2(0) + 1 = 1。
因此,极限 lim(x->0) (3x^2 - 2x + 1) = 1。
第二章:导数和其应用2.1 导数的概念和运算法则题目3:求函数 f(x) = x^3 - 2x^2 + x 的导函数。
解答:使用导数的运算法则,对于 x^n,导函数为 nx^(n-1)。
因此,对于函数 f(x) = x^3 - 2x^2 + x,其导函数为 f'(x) = 3x^2 - 4x + 1。
2.2 平均值定理和导数的应用题目4:计算函数 f(x) = x^3 - 2x^2 + x 在闭区间 [0, 3] 上的极大值和极小值。
解答:首先,计算函数在区间内的导数。
f'(x) = 3x^2 - 4x + 1。
然后,求导函数的零点。
将导函数 f'(x) = 3x^2 - 4x + 1 置零,解方程得到 x = 1 或 x = 1/3。
然后,将极值点带入原函数,计算函数值。
微积分第五版影印版)课后练习题含答案

微积分第五版影印版课后练习题含答案本文提供微积分第五版影印版课后练习题及其答案,方便读者进行练习和自我检验。
前言微积分是高等数学中最基础也是最重要的一门学科,在各个领域中都有广泛的应用。
本文提供微积分第五版影印版的课后练习题及其答案,希望读者通过练习,加深对微积分的理解,提高自己的能力。
课后习题第一章函数与极限1.1 函数的概念与性质1.已知函数f(x)=2x+1,求f(3)。
答案:$f(3)=2 \\times 3 +1=7$。
2.已知函数y=x2+1,求y(2)。
答案:y(2)=22+1=5。
3.已知函数f(x)=x3+3x,求f(−2)。
答案:$f(-2)=(-2)^3+3 \\times (-2)=-8-6=-14$。
…注:为了节约篇幅,本文仅列举几道习题及其答案。
第二章导数与微分2.1 导数的概念1.求函数y=x2在x=1的导数。
答案:y′=2x|x=1=2。
…第三章微分中值定理与导数的应用3.1 中值定理及其应用1.证明函数y=x2在区间[0,1]上满足罗尔定理的条件。
答案:由罗尔定理可得,若f(a)=f(b),且f(x)在[a,b]上连续,f(x)在(a,b)内可导,那么必存在一点 $c\\in(a,b)$,使f′(c)=0。
在本题中,f(0)=0,f(1)=1,f(x)=x2在[0,1]上连续,f(x)在(0,1)内可导,于是满足罗尔定理的条件。
…第四章曲线的性质与应用4.1 曲率1.求函数y=x3在点(1,1)处的曲率半径。
答案:函数y=x3的导函数为y′=3x2,曲率公式为$R=\\frac{[1+(y')^2]^{3/2}}{|y''|}$。
在点(1,1)处,$y'=3\\times1^2=3$,y″=6x|x=1=6。
代入公式得$R=\\frac{[1+3^2]^{3/2}}{|6|}=\\frac{10\\sqrt{10}}{9}$。
…结语本文提供了微积分第五版影印版的课后习题及其答案,希望对读者有所帮助。
大一高等数学积分知识点

大一高等数学积分知识点数学是一门抽象而又广泛应用的学科。
在大一高等数学中,积分是一个重要的概念和工具,被广泛应用于各个领域。
本文将介绍大一高等数学积分的基本概念、常见的积分法和一些常见的积分应用。
一、积分的基本概念积分是微积分的重要内容之一,其概念可以用不定积分和定积分来表达。
不定积分是对一个函数进行积分,得到一族原函数;而定积分是计算函数在一个区间上的总量。
1.1 不定积分不定积分可以看作求导运算的逆运算。
给定一个函数f(x),其不定积分可以表示为∫f(x) dx,其中∫表示积分的符号,f(x)为被积函数,dx表示积分变量。
1.2 定积分定积分用于计算函数在一个给定区间上的总量。
给定一个函数f(x),其在区间[a, b]上的定积分可以表示为∫(a to b) f(x) dx,其中(a to b)表示积分区间。
二、常见的积分法2.1 基本积分法基本积分法是指对常见函数的积分求解方法。
大部分基础函数都有对应的积分公式。
- 幂函数的积分:对于函数x^n,n≠-1,其积分为∫x^n dx = (x^(n+1))/(n+1) + C,其中C为常数。
- 三角函数的积分:对于常见的三角函数,如sin(x),cos(x),tan(x)等,都有相应的积分公式。
- 指数函数和对数函数的积分:对于常见的指数函数和对数函数,如e^x,ln(x),也有特定的积分公式。
2.2 分部积分法分部积分法(乘积法则)是解决积分中乘积形式的函数积分的一种方法。
其公式为∫u dv = uv - ∫v du,其中u和v为函数。
2.3 替换法替换法(换元积分法)是将积分中的变量进行替换,将复杂的积分转化为简单的积分。
常见的替换方法有:- 代入法:通过将一个函数代入为新的变量来进行积分。
- 三角替换法:将与三角函数相关的函数进行替换,以简化积分。
三、常见的积分应用3.1 几何应用积分在几何学中具有广泛的应用,主要用于计算曲线、曲面的长度、面积和体积等。
学生积分表模板

学生积分表模板1. 简介学生积分表是一种记录学生在学校或班级中积累的积分的工具。
通过对学生的表现和成就进行评估,并给予相应的积分,可以激励学生更好地参与学校和班级的各项活动,培养他们的综合素质和能力。
本文将为您提供一个用户友好、易于理解的学生积分表模板,帮助您快速创建一份适用于您所在学校或班级的积分表。
2. 模板结构2.1 学生信息首先,在积分表中需要列出每个学生的基本信息,包括姓名、性别、年级、班级等。
这样可以方便对每个学生进行个性化管理和评估。
示例:姓名性别年级班级张三男三年级1班李四女三年级2班王五男四年级3班2.2 积分项目接下来,在积分表中需要列出各种可以获得积分的项目。
这些项目可以根据学校或班级的实际情况进行调整和扩展,包括学习成绩、参与活动、表现优秀等。
示例:项目积分期末考试成绩100分参加篮球比赛10分帮助清扫教室5分2.3 积分记录最后,在积分表中需要记录每个学生的积分情况。
可以按照时间顺序,每次积分都进行记录,并计算总积分。
示例:姓名性别年级班级总积分张三男三年级1班50李四女三年级2班80王五男四年级3班303. 使用方法使用该学生积分表模板非常简单,只需要按照以下步骤进行操作:1.在第2.1节的表格中填写每个学生的基本信息。
2.在第2.2节的表格中添加各种可以获得积分的项目,以及对应的积分值。
3.在第2.3节的表格中记录每个学生的积分情况,包括每次积分的时间和积分值。
4.根据需要进行调整和扩展,例如添加新的积分项目或者修改学生的基本信息。
4. 注意事项在使用学生积分表模板时,需要注意以下几点:1.积分项目要具有可量化和可评估性,确保公正、公平地给予学生相应的积分。
2.积分记录要及时更新,以便及时了解每个学生的积分情况。
3.激励机制要合理设计,既能够激发学生的参与积极性,又能够培养他们的综合素质和能力。
5. 总结学生积分表是一种有效管理和激励学生参与学校和班级活动的工具。
通过使用本文提供的用户友好、易于理解的模板,您可以快速创建一份适用于您所在学校或班级的积分表。
微积分教学课件第2章导数与微分

微积分
三、 导数的几何意义
y y f(x)
曲线 y f (x)在点 (x0 , y0)的切线斜率为
tan f(x0)
CM
T
若 f(x0)0,曲线过 (x0 , y0)上升;
o x0
nan1
说明:
微积分
对一般幂函数 y x ( 为常数)
(x)x1
(以后将证明)
例如,(
1
x ) (x 2 )
1
x
1 2
2
1 2x
1 x
(x1)
x11
1 x2
(
1
3
) (x 4 )
3
x
7 4
xx
4
微积分
例3. 求函数 f(x)sixn的导数.
解: 令hx,则
f (x) lim f(xh)f(x) lim sin x(h)sixn
u(xh)vu (x()x u)v(ux((x)vxv)2)( (vxxu ())x(x)vh)(x)
故结论成立.
推论h: v(xCvh)v(x)vC2v ( C为常数 )
微积分
例2. 求证 (tax)n se2c x,(c x )s c cx s cc x o . t 证: (tanx)csoinsxx(six)ncocxos s2sxixn(cx o)s
h h
1, 1,
h0 h0
lim f(0h)f(0)不存在 ,即x在x0不可. 导
h 0
h
例6. 设
f
(x0)
存在,
求极限
lim f(x0h)f(x0h).
反常积分的几种计算方法

目录摘要 (1)关键词 (1)Abstract (1)Keywords (1)前言 (1)1反常积分的定义 (1)1.1无穷积分的定义 (1)1.2 瑕积分的定义 (2)2 反常积分的计算方法................................................... (3)2.1利用Newton—Leibniz公式计算反常积分 (3)2.2利用变量替换法计算反常积分 (3)2.3利用分部积分法计算反常积分 (5)2.4利用分段积分自我消去法计算反常积分 (7)2.5利用方程法计算反常积分 (7)2.6利用级数法计算反常积分 (9)2.7利用待定系数法计算反常积分 (10)结束语……………………………………………………………………………………………11参考文献 (11)反常积分的几种计算方法摘要:该文主要对反常积分的计算方法进行归纳、总结.重点描述了在进行计算时各种方法的灵活使用.关键词:反常积分;变量替换;分部积分;级数法;待定系数法Several calculation methods of abnormal integralAbstract: This paper mainly sums up the calculation methods of abnormal integral. This paper emphasizes on describing the flexible use of various methods in the calculation.Keywords: Abnormal integral; Variable substitution; subsection integral; Series method; the method of undetermined coefficient0前言反常积分是微积分学中一类重要的积分,反常积分的计算是学习积分计算中的重难点。
定积分的应用
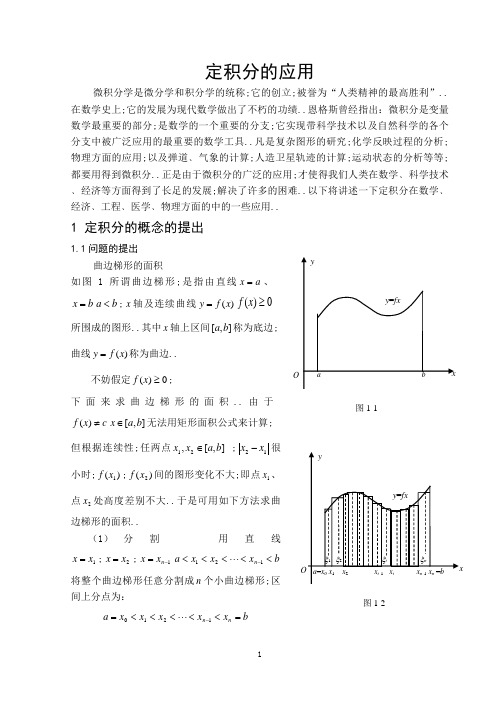
图1-1图1-2定积分的应用微积分学是微分学和积分学的统称;它的创立;被誉为“人类精神的最高胜利”..在数学史上;它的发展为现代数学做出了不朽的功绩..恩格斯曾经指出:微积分是变量数学最重要的部分;是数学的一个重要的分支;它实现带科学技术以及自然科学的各个分支中被广泛应用的最重要的数学工具..凡是复杂图形的研究;化学反映过程的分析;物理方面的应用;以及弹道﹑气象的计算;人造卫星轨迹的计算;运动状态的分析等等;都要用得到微积分..正是由于微积分的广泛的应用;才使得我们人类在数学﹑科学技术﹑经济等方面得到了长足的发展;解决了许多的困难..以下将讲述一下定积分在数学﹑经济﹑工程﹑医学﹑物理方面的中的一些应用..1 定积分的概念的提出1.1问题的提出曲边梯形的面积如图1所谓曲边梯形;是指由直线a x =、b x =b a <;x 轴及连续曲线)(x f y =0)(≥x f 所围成的图形..其中x 轴上区间],[b a 称为底边;曲线)(x f y =称为曲边..不妨假定0)(≥x f ;下面来求曲边梯形的面积..由于c x f ≠)(],[b a x ∈无法用矩形面积公式来计算;但根据连续性;任两点],[,21b a x x ∈ ;12x x -很小时;)(1x f ;)(2x f 间的图形变化不大;即点1x 、点2x 处高度差别不大..于是可用如下方法求曲边梯形的面积..(1) 分割用直线1x x =;2x x =;1-=n x x bx x x a n <<<<<-121 将整个曲边梯形任意分割成n 个小曲边梯形;区间上分点为:b x x x x x a n n =<<<<<=-1210这里取0x a =;n x b =..区间],[b a 被分割成n 个小区间],[1i i x x -;用i x ∆表示小区间],[1i i x x -的长度;i S ∆表示第i 块曲边梯形的面积;),,2,1(n i =;整个曲边梯形的面积S等于n 个小曲边梯形的面积之和;即∑=∆=ni i S S 12近似代替: 对每个小曲边梯形;它的高仍是变化的;但区间长度i x ∆很小时;每个小曲边梯形各点处的高度变化不大;所以用小矩形面积近似代替小曲边梯形的面积;就是;在第i 个小区间],[1i i x x -上任取一点i ξ;用以],[1i i x x -为底;)(i f ξ为高的小矩形面积i i x f ∆)(ξ;近似代替这个小曲边梯形的面积图1-1; 即i i i x f S ∆≈∆)(ξ.3求和 整个曲边梯形面积的近似值为 n 个小矩形面积之和;即n S S S S ∆++∆+∆= 21=∆++∆+∆≈n n x f x f x f )()()(2211ξξξ ini ix f ∆∑=)(1ξ上式由于分割不同;i ξ选取不同是不一样的;即近似值与分割及i ξ选取有关图1-2..4取极限 将分割不断加细;每个小曲边梯形底边长趋于零;它的高度改变量趋于零;曲边梯形的面积与取代它的矩形面积无限接近;从而和式∑=∆ni i i x f 1)(ξ的极限就定义为曲边梯形面积的精确值..令 },,,m ax {21n x x x ∆∆∆= λ;当0→λ时;有∑=→∆=ni i i x f S 1)(lim ξλ上面的例子;最终归结为一个特定的形式和式逼近..在科学技术中还有许多同样的数学问题;解决这类数学问题的思想方法概括说来就是“分割;近似求和;取极限”这是定积分概念的背景..1.2定积分的定义设函数)(x f y =在区间],[b a 上有界;在],[b a 中任意插入若干个分点b x x x x x a n n =<<<<<=-1210把],[b a 分成n 个小区间:],,[10x x ],[,],,[,],,[],,[113221n n i i x x x x x x x x --各个小区间的长度依次为:011x x x -=∆;122x x x -=∆;…; 1--=∆n n n x x x在每个小区间],[1i i x x -上任取一点i ξ)(1i i i x x ≤≤-ξ;作函数值与小区间长度i x ∆的乘积i i x f ∆)(ξ..并作和=S ∑=∆ni i i x f 1)(ξ记},,,m ax {21n x x x ∆∆∆= λ;如果不论对],[b a 怎样分割;也不管在小区间],[1i i x x -上点i ξn i ,,2,1 =怎样取法;只要当0→λ时;和S 总是趋于确定的极限I ;我们称这个极限值为函数)(x f 在区间],[b a 上的定积分简称为积分;记作⎰ba dx x f )(;即⎰badx x f )(==I ∑=→∆ni i i x f 1)(lim ξλ 1其中)(x f 称为被积函数;dx x f )(称为被积表达式;a 称为积分下限;b 称为积分上限;x 称为积分变量;∑=∆ni iixf 1)(ξ称为积分和..(1) 曲边梯形的面积是曲边方程)(x f y =在区间],[b a 上的定积分..即=S ⎰badx x f )()0)((≥x f2定积分在几何学上的应用2.1定积分在平面几何中的应用在初高中我们学习过求圆;三角形;平四边形;梯形等比较规则的图形面积;然而对于不规则的图形就无能为力了;所以再学定积分以前我们只能求一些简单图形的面积;部分稍复杂的图形;可能用有限个简单图形的分割也能求出来;但有很大的局限性;定积分的出现为这些问题;提出了很好的解决条件..一般地;由上、下两条连续曲线y=2f x 与y=1f x 以及两条直线x=a 与x=ba<b 所围成的平面图形;它的面积计算公式为21[()()]baA f x f x dx =-⎰ 1例 求由抛物线2y x =与x-2y-3=0所围成平面图形的面积A 解 该平面图形如图3所示;先求出 直线与抛物线交点P1;-1与Q9;3.用X=1把图形分成左;右两部分;应用公式 (1) 分别求得它们的面积为1110[(-)]24/3,A x x dx xdx =-==⎰⎰921328()23A x x dx -=-=⎰. A=1A +2A =32/3..2.2定积分在立体几何中的应用 2.2.1由截面面积函数求立方体体积设Ω为三维空间中的一立体;它夹在垂直于x 轴的两平面x=a 与 x=b 之间a<b.为了方便起见称Ω为位于a;b 上的立方体..若在任意一点x ∈a;b 处作垂直于x 轴的平面;它截得Ω的截面面积显然是x 的函数;记得Ax;x ∈a;b;并称之为Ω的截面面积函数..则通过定积分的定义;得到由截面面积函数求立方体体积的一般计算公式和旋转体的体积公式V=()ba A x dx ⎰..例 求由椭球面2222221x y z a b c++=所围立体椭球的体积..解 以平面00()x x x a =≤截椭球面;得椭圆它在yoz 平面上的正投影:22222200221(1)(1)y z x x b c aa+=--..所以截面面积函数为Ax=22(1)x bc aπ-;x ∈-a;a.于是求得椭球体积V=224(1)3ba x bc dx abc a ππ-=⎰..显然;当a=b=c=r 时;这就等于球的体积43π3r ..pQ图2-12.2.2旋转曲面的面积设平面光滑曲线C 的方程为y=()f x ;x ∈a;b 不妨设fx>=0.这段曲线绕x 轴旋转一周得到旋转曲面;则面积公式s=2π(baf x ⎰..如果光滑曲线C 由参数方程x=xt;y=yt;t ∈α;β给出;且yt ≥0;那么由弧微分知识推知曲线C 绕x 轴旋转所得旋转曲面的面积为S=2π(y t βα⎰.例 计算圆2x +2y =2R 在1x ;2x ⊂-R;R 上的弧段绕x 轴旋转所得球带的面积.. 解 对曲线在区间1x ;2x 上应用公式3;得到 S=2π21x x ⎰=2πR 21x x -..特别当1x =-R; 2x =R 时;则得球的表面积S 球=4π2R .3定积分在经济学中的应用3.1求经济函数在区间上的增量根据边际成本;边际收入;边际利润以及产量x 的变动区间[,]a b 上的改变量增量就等于它们各自边际在区间[,]a b 上的定积分:()()()ba Rb R a R x dx '-=⎰ 1()()()baC b C a C x dx '-=⎰ 2()()()baL b L a L x dx '-=⎰ 3例 已知某商品边际收入为0.0825x -+万元/t;边际成本为5万元/t;求产量x 从250t 增加到300t 时销售收入()R x ;总成本C ()x ;利润()I x 的改变量增量..解 首先求边际利润()()()0.082550.0820L x R x C x x x '''=-=-+-=-+所以根据式1、式2、式3;依次求出:300250(300)(250)()R R R x dx '-=⎰300250(0.0825)x dx =-+⎰=15300300250250(300)(250)()C C C x dx dx '-==⎰⎰=250万元300300250250(300)(250)()(0.0820)L L L x dx x dx '-==-+⎰⎰=-100万元例 某厂生产某种产品;每日生产的产品的总成本C 的变化率即边际成本是日产量x 的函数xx C 257)(+=';已知固定成本为1000元;求总成本函数y .解 因总成本是边际成本的一个原函数;所以)(x C ⎰+=dx x)257(c x x ++=507已知当0=x 时;1000)0(=C ;代入上式得1000=c ;于是总成本函数为)(x C 1000507++=x x例 某产品销售总收入是销售量x 的函数)(x R ..已知销售总收入对销售量的变化率即边际收入x x R 52300)(-=';求销售量由100增加到400时所得的销售收入. 解 因销售收入是边际收入的一个原函数;按题意;有)300()400(R R -⎰'=400300)(dx x R⎰-=400300)52300(dx x 4003002)51300(x x -=16000=元3.2求经济函数在区间上的平均变化率设某经济函数的变化率为()f t ;则称2121()t t f t dtt t -⎰为该经济函数在时间间隔21[,]t t 内的平均变化率..例 某银行的利息连续计算;利息率是时间t 单位:年的函数:()0.08r t =+求它在开始2年;即时间间隔0;2内的平均利息率..解 由于22()(0.08r t dt dt =+⎰⎰0.160.010.16=+=+所以开始2年的平均利息率为2()0.0820r t dtr ==+-⎰ 0.094≈例 某公司运行t 年所获利润为()L t 元利润的年变化率为()310L t '=⨯/年求利润从第4年初到第8年末;即时间间隔3;8内年平均变化率解 由于3885852333()310210(1)3810L t dt t '=⨯=⨯⋅+=⨯⎰⎰所以从第4年初到第8年末;利润的年平均变化率为853()7.61083L t dt '=⨯-⎰元/年即在这5年内公司平均每年平均获利57.610⨯元..3.3由贴现率求总贴现值在时间区间上的增量设某个项目在t 年时的收入为()f t 万元;年利率为r ;即贴现率是()rt f t e -;则应用定积分计算;该项目在时间区间[,]a b 上总贴现值的增量为()brt af t e ndt -⎰..设某工程总投资在竣工时的贴现值为A 万元;竣工后的年收入预计为a 万元年利率为r ;银行利息连续计算..在进行动态经济分析时;把竣工后收入的总贴现值达到A;即使关系式Trt ae dt A -=⎰成立的时间T 年称为该项工程的投资回收期..例 某工程总投资在竣工时的贴现值为1000万元;竣工后的年收入预计为200万元;年利息率为0.08;求该工程的投资回收期..解 这里1000A =;200a =;0.08r =;则该工程竣工后T 年内收入的总贴现值为0.080.080.0802002002500(1)0.08Tt tT T e dt e e ---==--⎰令 0.082500(1)T e --=1000;即得该工程回收期为110001ln(1)ln 0.60.0825000.08T =--=- =6.39年3.4 利润、产量与开工时数的最佳值的确定例1 某厂生产一种产品;年产量为x 吨时;总费用的变化率即边际费用为)(x f 825.0+=x 单位:百元/吨;这种产品每吨的销售价为3000元;问一年生产多少产品工厂利润最大;并求出年利润的最大值.解 总费用是边际费用的原函数;故=)(x C ⎰+xdx x 0)825.0(x x 8125.02+=而收入函数)(x R x 30=百元;又由)(x L =)(x R =-)(x C 2125.022x x -则 )(x L 'x 25.022-=令 )(x L '0=;得88=x 吨..驻点唯一..此时025.0)88(<-=''L ;由实际问题可知;当88=x 时;)(x L 取得最大值96888125.08822)88(2=⨯-⨯=L 百元.因此;年产量为88吨时工厂获得最大利润96800元..例 2 某工厂生产一种产品;每日总收入的变化率即边际收入是日产量x 的函数x x R 2.030)(-='单位:元/件..该厂生产此种产品的能力为每小时30件;问怎样安排生产才能使这种产品每日的总收入最大 并求出此最大总收入值.解 由题意)(x R ⎰-=xdx x 0)2.030(21.030x x -=;令 02.030)(=-='x x R ;得150=x ;又02.0)(<-=''x R ;因为)(x R 只有唯一的驻点150=x ;由实际问题知;当150=x 时;)(x R 取得最大值22501501.015030)150(2=⨯-⨯=R .因此;每日取得最大总收入的产量为150件;此时2250)150(=R 元.完成150件产品需要的工时为530150=小时;所以;每天生产这种产品5小时;就使每日收入最大;最大值为2250元..3.5 资本存量问题例1 资本存量)(t s s =是时间t 的函数..它的导数等于净投资)(t I ..现知道净投资t t I 3)(=单位:10万元/年..求第一年底到第四年底的资本存量.解 因资本存量s 是净投资的一个原函数;故=-)1()4(s s dt t ⎰41341232t==1410万元所以;第一年底到第四年底的总资本存量为1400000元..例 2 某银行根据前四年存款情况;知该行现金净存量的变化率是时间t 的函数455.14)(t x f =单位:万元/年;计划从第五年起积存现金1000万元..按此变化率需几年时间解 依题意1000⎰+=xdt t 44455.14即 1000]4)4[(9584949-+=x由此;得 49494589000)4(+=+x 解此方程;得9993.94≈+x6≈x .所以;从第五年积存1000万元现金约需6 年.3.6消费者剩余和生产者剩余在自由市场中;生产并销售某一商品的数量可由这一商品的供给与需求曲线描述;它的状态可在如图上直观表现如下:0p 的经济意义是供应者会生产此商品的最低价..1p 是消费者会购买此种商品的最高价..1q 是免费供给此种商品的需求量如卫生纸经市场功能调节后;市场将趋于平衡价*P 和平衡数量*q ;两条曲线在),(**p q 相交..消费者以平衡价格购买了某种商品;他们本来打算出较高的价格购买这种商品;消费者剩余是指消费者因此而省下来的钱的总数..用积分式来表达就是:消费者剩余⎰=*0)(q d dq q Q **q p -=曲边三角形*1p Mp 面积.生产者以平衡价格出售了某种商品;他们本来打算以较低一些的售价售出这些商品;生产者剩余是指生产者因此而获得的额外收入..用积分式表达就是生产者剩余⎰-=***)(q s dq q Q q p =曲边三角形*0p Mp 面积.4定积分在工程中的应用4.1定积分中值定理定积分中值定理作为定积分的一个重要性质;计算河床的平均深度时;应用定积分中值定理知识..此问题主要出现在水利工程专业的《工程水文学》课程中;主要应用于计算河流、湖泊等河床横断面水的平均深度;以此用作河流测流、工程设计或施工的一个依据..只要测量出河面在某处的宽度B;河床的横断面形状和河床的最大深度h ;则可运用定积分中值定理知识计算该处河床的平均深度h ;即⎰-=ba dx x f ab h )(1m. 例 设一河流的河面在某处的宽度为2 b;河流的横断面为一抛物线弓形;河床的最深处在河流的中央;深度为h ;求河床的平均深度-h .分析:首先;选取坐标系使x 轴在水平面上;y 轴正向朝下;且y 轴为抛物线的对称轴..于是;抛物线方程为y=h-22x b h⋅.然后;运用定积分中值定理便可求得河床的平均深度-h . 解:河床的平均深度⎰-=b a dx x f a b h )(1=h 32.4.2定积分的近似计算知识的应用近似求物体的截面积;应用梯形法或抛物线法等定积分的近似计算知识..此问题主要出现在水利工程专业的《灌溉排水技术》课程中;主要应用于近似计算河床、渠道的过水断面面积;进而计算截面流量即渠系测流..由水利学知识可知;单位时间内流过某一截面的流体的体积就叫做通过这个截面的流量;即Q =V/tm 3/s.在水利工程中;流量的计算通常运用公式Q=svm 3/s;即过水断面面积s 与流速v 的乘积..例1有一条宽为24米的大型干渠;正在输水浇灌农田;试利用流速仪并结合梯形法或抛物线法近似求横截面积等高等数学知识进行测流..分析:根据灌溉管理学知识;首先选择测流断面;确定测线..测流断面选择在渠段正直;水流均匀;无漩涡和回流的地方;断面与水流方向垂直;测流断面的测线确定为12条..其次;测定断面..先在渠道两岸拉一条带有尺度的绳索;测出测深线的起点距与断面起点桩的水平距离;测线深度;用木制或竹制的测深杆施测;从渠道一岸到对岸每隔2米测量一次水深;测得数据如下表..根据施测结果绘出测流断面图;如图所示..第三;利用流速仪施测断面流速..例如;利用旋环式流速仪测出该渠道断面平均流速为v=0.60m/s.第四;近似计算渠道过水断面面积和流量... 测线深度施测数据表 单位:m解答:(1) 抛物线法辛卜生公式:A ≈30.67m 2 ; Q=18.40m 3/s. (2) 梯形法:A ≈30.40m 2 ; Q=18.24m 3/s.例 2有一条河流;宽为200米;从河一岸到正对岸每隔20米测量一次水深;测的数据如下表..试分别用梯形法和抛物线法求此河床横截面积的近似值.. 单位:m4.3微元法知识的应用微元法在专业基础课和专业课中应用非常广泛;求解物体所受液体的侧压力;应用微元法知识..此问题主要出现在水利工程专业的《水力学》、《水工建筑物》等课程中;主要应用于计算水闸及输水建筑物如坝下涵管、隧洞、渠道、管道等上的闸门所受水压力的大小;作为设计或校核闸门结构的一个重要依据..水闸是一种低水头水工建筑物;既能挡水;又能泄水;用以调节水位;控制泄流量;多修建于河道、渠系及水库、湖泊岸边;在水利工程中的应用十分广泛..闸门是水闸不可缺少的组成部分;用来调节流量和上、下游水位;宣泄洪水和排放泥沙等..闸门的形式很多;按其结构形式通常分为平面闸门、弧形闸门及自动翻倒闸门等;按其工作条件可分为工作闸门和修理闸门;按其所处的位置不同可分为露顶闸门和潜孔闸门;按其所用的材料可分为钢闸门、钢筋混凝土闸门、钢丝网水泥闸门和木闸门等;按其形状不同又可分为矩形闸门、梯形闸门、圆形闸门和椭圆形闸门等..闸门的主要作用是挡水;承受水压力是其作用荷载之一..运用微元法计算闸门所受水压力时;设受水压力作用的区域与水平面垂直且由曲线y=fx >0;0≤a ≤x ≤bx=a;x=b 及x 轴所组成..x 轴正向朝下;y 轴在水平面上;水的密度为ρ=1000㎏/m 3;则闸门所受的水压力大小为P= ⎰b adx x gxf )(ρN.例 有一个水平放置的无压输水管道;其横断面是直径为6m 的圆;水流正好半满;求此时输水管道一端的竖直闸门上所受的水压力..分析:首先建立合适的直角坐标系;如图所示;则圆的方程为222r y x =+=9. 然后;运用微元法求解即可.. 解答:P=1.76×105N.5定积分在医学的应用如图显示了人的心血管系统..血液流经全身通过静脉进入右心房;然后通过肺动脉泵入肺部补充氧气..之后通过肺静脉流回左心房;再通过主动脉流往全身其它部位;进行血液循环..心输出量就是单位时间一分钟内;心脏泵出的血液量;即血液通过动脉的速率..安静状态下;成年男性每搏输出量为60~80毫升;心率75次/分钟;故心输出量约4.5~6升;女性的心输出量比同体重男性的约低10%..人体的血液一直在周身循环;我图4-2们只能人为定义血液流动的起点和终点;即便这样也很难测定心脏单位时间内泵出的血液总量;所以人们就探索利用辅助材料来测定心输出量..最简单的辅助材料就是染料;即指示剂..具体做法是把指示剂加入到右心房;那么指示剂会和血液一起流经心脏泵入动脉..通过一个插入动脉的探头在一段时间内等间隔测量测出流出心脏的指示剂的浓度;直到指示剂基本消失;即指示剂全部流出心脏..那么剩余的问题就是如何利用测得图5-1 图5-2的浓度计算心输出量呢严格意义;只能测定某一时刻指示剂的浓度;是一系列的离散值;我们假定这些离散值在某一微小的时间段内是不变的;所以当时间段分的越细我们测定的值越接近连续值;这种思想使我们很容易想到积分的概念;所以可建立数学模型解决这个问题..解 令ct 是t 时刻指示剂的浓度..如果把时间段0;t 划分成n 个等长的小时间段t ∆;指示剂流量=ctF t ∆;其中F 为我们测定的心输出量;这样总量即为()()n nc t F t F c t t ∆=∆∑∑;令n →∞时;指示剂总0()TA F c t dt =⎰..那么心输出量F=()TAc t dt⎰.这里的A 为已知量;即投入右心房的指示剂总量;ct 通过测量探头读取..6定积分在物理学的应用6.1变力做功在功的问题中;恒力做功是最简单的;公式为W F S =⋅. “以常代变”;功的微元应该通过恒力做功公式得到的.例 1 一压簧;原长1m ;把它每压缩1cm 时所用的力为0.05N .问在弹性范围内把它由1m 如图6-1压缩到60cm 如图6-2所做的功.图6-1图6-2解令起点为原点;压缩的方向为x 轴的正方向当把弹簧自原点压缩至[]0,0.4之间的任意点x 处时如图6-3图6-3由胡克定律知所承受的弹簧的压力为()0.0550.01F x x x ==在此力的作用下;再继续压缩一点点dx ;即压缩至x dx +处由于dx 很小;这个压缩过程可认为力()F x 不变;即恒力做功 则由恒力做功公式得功的微元dW ()F x dx = 积分得W ()0.40F x dx =⎰0.45xdx =⎰20.4502x =0.4=()J .例2 在原点处有一带电量为q +的点电荷;在它的周围形成了一个电场.现在x a =处有一单位正电荷沿x 轴正方向移至x b =处;求电场力所做的功.又问若把该电荷继续移动;移动至无穷远处;电场力要做多少功. 解点电荷在任意点x 处时所受的电场力为()2qF x kx=k 为常数 电场力做功的微元dW 为点电荷由任意点x 处移动至x dx +处时电场力()F x 所做的功 即()2qdW F x dx kdx x == 则移至x b =处电场力做的功2b a qW k dx x=⎰1bkqax =- 11kq a b ⎛⎫=- ⎪⎝⎭;移至无穷远处电场力做的功2a qW k dx x +∞=⎰kqa=物理学中称此值为电场在x a =处的电位. 例 3 一圆台形水池;深15m ;上下口半径分别为20m 和10m ;如果把其中盛满的水全部抽干;需要做多少功 解水是被“一层层”地抽出去的;在这个过程中;不但每层水的重力在变;提升的高度也在连续地变化图6-4其中抽出任意一层水x 处厚为dx 的扁圆柱体;如图6-4阴影部分所做的功为抽水做功的微元dW即dW dm g x dV g x γ=⋅⋅=⋅⋅⋅22203gx x dx γπ⎛⎫=- ⎪⎝⎭则2152203W gx x dx γπ⎛⎫=- ⎪⎝⎭⎰2152203g x x dx γπ⎛⎫=- ⎪⎝⎭⎰23415801200099g x x x γπ⎛⎫=-+ ⎪⎝⎭20625g γπ=202125000π=()J .6.2求物体质量对于密度均匀的物体的质量l m l γ=⋅或A m A γ=⋅、m V γ=⋅;这时密度是常量;但对于密度不均匀密度是变量的物体的质量就不能直接用上述公式了;而应该用微元法. 例 一半圆形金属丝;其上任意点处的线密度与该点到连接金属丝端点的直径的距离成正比;求金属丝的质量. 解 建立如图6-5坐标系图6-5则()22l x ky R x γ==-()0k >22y R x'=-()()22ds dx dy =+21y dx '=+22R x=-()l dm x ds γ=⋅2222R k R x dx R x=-⋅-kRdx =RR m kRdx -=⎰22kR =.例 1 设有一心脏线1cos r θ=+形的物质薄片;其面密度()2cos A γθθ=+;试求此物质薄片的质量. 解()22111cos 22dA r d d θθθ==+ ()A dm dA γθ=()()212cos 1cos 2d θθθ=++ ()3145cos 2cos 2cos 2d θθθθ=+++ ()230145cos 2cos 2cos 2m d πθθθθ=+++⎰321145sin sin 2sin sin 023πθθθθθ⎛⎫=+++- ⎪⎝⎭ 4π=.例 2 设一立体为曲线211y x=+关于x 轴的旋转体;其上任一点x 的体密度等于其横坐标的绝对值即()x x γ=;试求该立体的质量. 解图6-62211x dV dx x π⎛⎫= ⎪+⎝⎭图6-6中小圆柱体体积 ()x dm x dV γ= 2211x dx x π⎛⎫= ⎪+⎝⎭()221xdx x π=+()221xm dx x π+∞-∞=+⎰()2221xdx x π+∞=+⎰()()22211x d x π+∞-=++⎰2101x π+∞=-+ π=.6.3 液体压力液面下h 深处水平放置的面积为A 的薄板承受的液体压力P 可以由压强乘以面积得到;即P gh A γ=⋅;其中γ为液体密度;压强gh γ是个常量匀压强.现在如若把薄板垂直放置呢 薄板上的压强还是常量吗 还能用上边那个简单的公式吗 例 1 三峡大坝有一上底、下底、高分别为40、20、15米的等腰梯形闸门;闸门垂直放置且上边与水面齐如图6-4;试计算闸门一侧所承受的水压力. 解回顾例3;我们知道抽水做功微元dW 为把x 处一层水抽出所做的功;类似地;侧压力微元dP 为x 处一层水对应的闸门的一个小窄条如图阴影部分所承受的水压力;即dP gxdA γ=2gx ydx γ= 22203gx x dx γ⎛⎫=- ⎪⎝⎭则15022203P gx x dx γ⎛⎫=- ⎪⎝⎭⎰15204403g x x dx γ⎛⎫=- ⎪⎝⎭⎰2315498002009x x ⎛⎫=- ⎪⎝⎭29400000=()N .参考文献1 华东师大数学系.数学分析M.北京:高等教育出版社;2001:130-150.2 朱峰.大学物理M.北京:清华大学出版社;2004:15-80.3曹定华.微积分M.上海:复旦大学出版;2006:13-14.4马敏﹑冯梅.经济应用数学M.苏州:苏州大学出版社;2007:13-20.。
积分应用教案设计

积分应用教案设计积分是高等数学中的一个重要内容,一些实际问题的求解也将用到积分。
如何让学生理解和应用积分,是数学教学中的重要问题。
本文将从教师角度出发,探讨积分应用教案设计的相关问题。
教学目标本节教学内容主要是关于初等函数的积分应用问题,作为高等数学教学内容的一部分,主要包括以下目标:1、引导学生理解积分的定义和基本性质,掌握初等函数的积分计算方法。
2、培养学生应用积分的能力,理解积分在实际问题中的应用。
3、通过实际问题的讲解,使学生感受到数学与现实的联系,提高数学学习的兴趣和积极性。
教学内容1、初等函数的积分计算方法1.1 不定积分的计算方法1.2 定积分的计算方法2、积分的应用2.1 几何应用2.1.1 作图法2.1.2 解析法2.2 物理应用2.2.1 速度与位移的关系2.2.2 加速度与速度的关系2.2.3 粒子的运动轨迹2.3 经济应用2.3.1 利润与成本的关系2.3.2 渐近线与生产问题2.3.3 边际效应与市场经济教学方法1、讲授法在初步介绍不定积分和定积分的概念、计算公式和方法后,以典型例题为主,讲述如何运用所学的知识计算积分,并强化其应用。
2、探究法以具体问题为背景,设置问题,引导学生各自探讨,通过合作、讨论和研究,积极参与到教学中来,具有激发学生学习兴趣的作用。
3、演示法运用多媒体教学,将抽象概念具象化,生动形象地展示出实际运用中的积分计算和解析思路,方便学生理解和掌握。
4、体验法教师利用实际问题,引导学生思考、探究,通过数学的方法实现问题的解决,体验到数学在现实中的重要性和实用性。
教学评价教师可以根据学生的作业、课堂表现和考试结果来对他们的学习情况进行评价。
1、作业评价作业是每次课后巩固知识的重要方式。
教师可通过作业的难度、完成度和答案的正确性来综合评价学生的学习情况。
2、课堂表现评价教师在每堂课的讲解和探究中都会对学生的表现有所观察。
教师可以关注学生的讨论、思考、提问和回答,评价学生在课堂上的表现。
微积分的引入与初步认知

微积分的引入与初步认知微积分作为数学的一个重要分支,是研究变化的学科。
它包括微分学和积分学两个部分,是解决变化问题的有力工具。
在本文中,我们将介绍微积分的引入和初步认知,并探讨其在实际问题中的应用。
1. 微积分的引入微积分的发展历史可以追溯到古代希腊和中国,但其完整的体系建立则要归功于牛顿与莱布尼茨。
他们独立地提出了微积分的基本原理和定义,使得微积分成为现代数学的基础。
微积分的引入主要是为了解决一些难以用传统数学方法解决的问题,如曲线的斜率和曲面的曲率等。
2. 微积分的初步认知2.1 导数导数是微积分中的重要概念之一,表示函数在某一点上的变化率。
对于一个函数f(x),它的导数可以通过求取极限来求解。
导数的应用广泛,例如在物理学中求取速度、加速度等问题时经常用到。
2.2 积分积分是导数的逆运算,用于确定曲线下的面积。
对于一个函数f(x),其积分可以表示为∫f(x)dx,其中积分符号表示对x的连续求和。
积分在概率论、力学、统计学等领域中具有广泛的应用。
3. 微积分在实际问题中的应用微积分在实际问题中具有广泛的应用,下面我们将介绍微积分在几个典型问题中的应用。
3.1 最优化问题最优化问题是指在一定的约束条件下,寻找使得一个函数取得极大值或极小值的自变量。
微积分可以帮助我们解决最优化问题,通过对目标函数求导并找到导数为零的点,我们可以确定这个函数的极值点。
3.2 物理学中的运动问题微积分在物理学中的应用非常广泛,特别是在描述物体的运动和力学问题时。
通过对位置、速度和加速度等物理量进行微分和积分运算,我们可以更好地理解和解释物体的运动规律。
3.3 统计学中的概率问题微积分在统计学中的应用主要体现在求解概率问题上。
通过对概率密度函数进行积分,我们可以计算出变量落在某个区间内的概率。
4. 总结微积分作为数学的重要分支,对于解决变化问题起着关键的作用。
通过引入微积分,我们可以更好地理解和描述曲线、面积以及变化的概念,并将其应用于实际问题中。
高等数学基础教材课后答案解析

高等数学基础教材课后答案解析1. 引言高等数学作为大学中必修的一门学科,旨在培养学生的数学思维能力和解决实际问题的能力。
课后习题是学生巩固所学知识的重要环节,而答案解析则为学生提供了参考。
本文对高等数学基础教材中的部分课后习题答案进行解析,帮助学生更好地理解和掌握相关知识。
2. 函数与极限2.1 习题解析2.1.1 习题1:计算极限$$\lim_{x\to0}\frac{1-\cos x}{x}$$解析:这是一个常见的极限问题,在计算中可以应用泰勒级数展开式来求解。
首先将$\cos x$用它的泰勒级数展开式替代,然后简化表达式,得到最终的极限结果为1。
2.1.2 习题2:求函数$f(x)=\ln(x^2+1)$的倒数函数$f^{-1}(x)$解析:要求函数的倒数函数,需要进行函数的反函数求解。
首先,将$f(x)$表示为$y$,然后交换$x$和$y$,解出$y$,最后将$y$表示为$x$,得到函数$f^{-1}(x)$。
3. 导数与微分3.1 习题解析3.1.1 习题1:求函数$f(x)=\sin^2 x + \cos^2 x$的导数$f'(x)$解析:根据函数的求导法则,对于$\sin^2 x$和$\cos^2 x$来说,其导数都可以通过链式法则求得。
根据求导法则和链式法则,可以得到$f'(x)$的最终结果为0。
3.1.2 习题2:已知曲线$y=x^3-3x^2+1$上的点$A(1, -1)$,求该曲线在点$A$处的切线方程。
解析:要求曲线在指定点处的切线方程,需要计算曲线在该点处的斜率,并利用斜率公式得到切线的方程。
首先,计算点$A$处的斜率,然后利用点斜式得到切线的方程。
4. 微分学应用4.1 习题解析4.1.1 习题1:一座高200米的塔楼,从塔底以角度$30°$向上仰望塔顶,再向上仰望$15°$找不到塔顶。
求塔楼的高度。
解析:根据题意,可以通过建立三角函数的关系式求解该题。
!定积分计算方法总结

摘要定积分是数学分析中的一个基本问题,而计算定积分是最基本最重要的问题.它在许多实际问题有着广泛的应用.下面针对定积分的计算方法做一个比较详细的总结,常见的包括分项积分、分段积分法、换元积分法、分部积分法.但对于不能直接找出原函数的定积分,或者被积函数比较复杂时,往往是比较难求出原函数的,从而无法用牛顿-莱布尼兹公式求解.针对这样的情形,本文总结用欧拉积分求解定积分、留数在定积分上的运用、巧用二重积分求解定积分、反函数求解定积分以及带积分型余项的泰勒公式在定积分上的应用,并列举相应的例子进行说明.关键词: 定积分; 被积函数; 原函数; 牛顿-莱布尼兹公式目录1 引言2 定计算的计算方法2.1 分项积分法······························ (1)2.2 分段积分法······························ (2)2.3 换元积分法 (3)2.4 分部积分法 (5)2.5 欧拉积分在定积分计算中的应用 (9)2.6 留数在定积分计算上的应用 (10)2.7 巧用二重积分求解定积分 (10)2.8 反函数法求解定积分 (10)2.9 带积分型余项的泰勒公式在定积分上的应用 (11)3 总结 (12)浅谈定积分的计算1.引言定积分的计算是微积分学的重要内容,其应用十分广泛,它是包括数学及其其他学科的基础.本文归纳总结了常见的定积分计算方法(如[1-4]),其中包括分项积分法、分段积分法、换元积分法以及分部积分法.另外对于找不出原函数的定积分,或者被积函数十分复杂时,往往是很难求出其原函数,从而无法用牛顿-莱布尼兹公式求解.针对这样的情形,我们有必要在此基础上研究出新的计算方法.对此本文总结了一些另外的方法(如[5-9]),其中包括欧拉积分求解定积分、运用留数计算定积分、巧用二重积分求解定积分、反函数法求解定积分以及带积分型余项的泰勒公式在定积分上的应用,进行了一一列举,并通过例子加以说明.2.定积分的计算方法2.1 分项积分法我们常把一个复杂的函数分解成几个简单的函数之和:,若右端的积分会求,则应用法则1122()()f x k g x k g x =()+,其中,是不全为零的任意常数,就可求1122()()bbba aaf x dx kg x dx k g x dx =⎰⎰⎰()+1k 2k 出积分,这就是分项积分法.()baf x dx ⎰例2-1[1] 计算定积分. 414221(1)dx x x π+⎰解 利用加减一项进行拆项得==414221(1)dx x x π+⎰2241422(1)(1)x x dx x x π+-+⎰41421dx x π⎰-2241222(1)(1)x x dxx x π+-+⎰=+=++.41421dx xπ⎰-41221dx x π⎰412211dx x π+⎰-313x 412π4121xπarctan x412π=.364415arctan 323ππ-+-+例2-2 计算定积分.1⎰解 记J ==1⎰1⎰=+3221x dx ⎰21⎰再将第二项拆开得J=++=++3221x dx ⎰3221(1)x dx -⎰1221(1)x dx -⎰522125x 52212(1)5x -32212(1)3x -=+.52225232.2 分段积分法分段函数的定积分要分段进行计算,这里重要的是搞清楚积分限与分段函数的分界点之间的位置关系,以便对定积分进行正确的分段.被积函数中含有绝对值时,也可以看成分段函数,这是因为正数与负数的绝对值是以不同的方式定义的,0就是其分界点.例2-3[2]计算定积分.221(1)min ,cos 2x x dx ππ-⎧⎫+⎨⎬⎩⎭⎰解 由于为偶函数,在上的分界点为,所以1min ,cos 2x ⎧⎫⎨⎬⎩⎭0,2π⎡⎤⎢⎥⎣⎦3π=+221(1)min ,cos 2x x dx ππ-⎧⎫+⎨⎬⎩⎭⎰221min ,cos 2x x dx ππ-⎧⎫⎨⎬⎩⎭⎰2012min ,cos 2x dx π⎧⎫⎨⎬⎩⎭⎰==.+320312(cos )2dx xdx πππ+⎰⎰23π+例2-4 计算定积分,其中.20(1)f x dx -⎰111,01()xx x x e f x ≥+<+⎧⎪=⎨⎪⎩解 由于函数的分界点为,所以,令后,有()f x 01t x =-==+20(1)f x dx -⎰11()f t dt -⎰0111x dx e -+⎰1011dx x +⎰=+=+011xx e dx e---+⎰10ln(1)x +01ln(1)x e ---+ln 2=.ln(1)e +2.3 换元积分法(变量替换法)换元积分法可以分为两种类型:2.3.1 第一类换元积分法(也被俗称为“凑微分法”)例2-5[3] 计算定积分.21sin tan dxx xπ+⎰解==21sin tan dxx x π+⎰21cos sin (1cos )xdx x x π+⎰22213cos sin 224sin cos 22x x dx x x π-⎰= =2211tan 2tan 22tan 2xx d x π-⎰2111(tan tan 222tan2x xd x π-⎰=2221111ln tan tan 2242x x ππ-=.21111ln tan tan 2424-+-例2-6 计算定积分.解==1()x x -+=1()x x -+= ⎡-⎣=.152.3.2 第二换元积分法常用的变量替换有:①三角替换;②幂函数替换;③指数函数替换④倒替换.下面具体介绍这些方法.① 三角替换例2-7[4] 计算定积分.31240(1)x x dx -⎰解 由于=,故可令,于是31240(1)x x dx -⎰3124201(1)2x dx -⎰2sin x t ===31240(1)x x dx -⎰arcsin1401cos 2tdt ⎰2arcsin11(1cos 2)8t dt +⎰=arcsin101(12cos 28t ++⎰1cos 42t dt +=arcsin1011(32sin 2sin 4)164t t t ++=1(34sin 16t ++2arcsin10sin sin ))t -=2241(3arcsin 4(1216x x x x ++-=.21(3arcsin 5216x x x +-3arcsin116②幂函数替换例2-8 计算定积分.220sin sin cos xdx x xπ+⎰解 作变量代换,得到2x t π=-=,因此220sin sin cos x dx x xπ+⎰220cos sin cos t dt t t π+⎰==220sin sin cos x dx x x π+⎰2222001sin cos ()2sin cos sin cosx t dx dt x x t t ππ+++⎰⎰=20112sin cos dx x x π+⎰201sin()4dx x ππ+⎰3441sin dx x ππ⎰.3441cos )sin x x ππ-+③倒替换例2-9 计算定积分.解=令得1t x====.1-1-6π2.4 分部积分法定理 3-1[5]若,在上连续,则()x μ'()x ν'[],a b 或.bb b a aa uv dx uv u vdx ''=-⎰⎰bbba a a udv uv vdu =-⎰⎰利用分部积分求的解题方法()ba f x dx ⎰(1)首先要将它写成得形式.ba udv ⎰()ba uv dx '⎰或选择,使用分布积分法的常见题型:,u v 表一被积函数的形式所用方法,,()x n P x e α()sin n P x x α()cos n P x xα,其中为次多项式,为常数()n P x n α进行次分部积分,每次均取,n x e α,为,多项式部分sin x αcos x α()v x '为()u x ,,()n P x ln x ()n P x arcsin x α即多项式与对数函数或()n P x arctan x 取为,,,()n P x ()v x 'ln x arcsin x α等为.分部积分一次后被arctan x ()u x反三角函数的乘机积函数的形式发生变化,x e αsin x βx e αcos xβ取=(或),,x e α()v x '()u x sin x β为(或),进行两次分cos x β()u x ()v x '部积分(2)多次应用分部积分法,每分部积分一次得以简化,直至最后求出.(3)用分部积分法有时可导出的方程,然后解出.()ba f x dx ⎰(4)有时用分部积分法可导出递推公式.例2-10[6]计算定积分.2220sin x xdx π⎰解 于,所以21sin (1cos 2)2x x =-==222sin x xdx π⎰2201(1cos 2)2x x dx π-⎰322211sin 264x x d x ππ-⎰连续使用分部积分得=222sin x xdx π⎰32220111(sin 2)sin 2642x x x x xdx ππ-+⎰=3222111(sin 2)cos 2644x x x xd x ππ--⎰=3221111(sin 2cos 2sin 2)6448x x x x x x π--+=.3488ππ+例2-11[7]计算定积分.220sin x x e xdx π⎰解 因为==20sin xe xdx π⎰20sin xxde π⎰20sin xe xπ-20cos xxde π⎰= 所以20(sin cos )xe x x π-20sin x e xdx π-⎰= = 于是2sin xe xdx π⎰1220(sin cos )xe x x π-21(1)2e π+=+20cos xe xdx π⎰cos xe x20π20sin x e xdxπ⎰==201(sin cos )2x e x x π+21(1)2e π-从而=220sin xx e xdx π⎰2201(sin cos )2x x d e x x π⎡⎤-⎢⎥⎣⎦⎰ =2201(sin cos )2x x e x x π-20(sin cos )x xe x x dxπ--⎰=2201(sin cos )2x x e x x π-201(sin cos )2x xd e x x π⎡⎤--⎢⎥⎣⎦⎰201(sin cos )2x xd e x x π⎡⎤++⎢⎥⎣⎦⎰=2201(sin cos )2x x e x x π-21(sin cos )2x xe x x π--201(sin cos )2x e x x dx π+-⎰201(sin cos )2x xe x x π++201(sin cos )2x e x x dx π-+⎰=2201(sin cos )2x x e x x π-20cos xxe xπ+20cos x e xdxπ-⎰=2201(sin cos )2x x e x x π-20cos xxe xπ+-201(sin cos )2x e x x π+=22201(1)sin (1)cos 2x e x x x x π⎡⎤---⎣⎦=.221(1)242e ππ-+例2-12[8] 计算定积分,其中为正整数.sin n x x dx π⎰n 解=(21)2sin k k x x dx ππ+⎰(21)2sin k k x xdxππ+⎰作变量替换得2t x k π=-=(21)2sin k k x xdx ππ+⎰(2)sin t k tdtππ+⎰=0sin 2sin t tdt k tdtπππ+⎰⎰==0cos cos 2cos t ttdt k tππππ-+-⎰(41)k π+=(22)(21)sin k k x x dx ππ++⎰(22)(21)sin k k x xdxππ++-⎰作变量替换得2t x k π=-==-(22)(21)sin k k x xdx ππ++-⎰2(2)sin t k tdt πππ-+⎰22sin 2sin t tdt k tdtπππππ--⎰⎰=222cos cos 2cos t tdttdt k tπππππππ-+⎰=(43)k π+当为偶数时,n =0sin n x x dx π⎰12(21)(22)2(21)0(sin sin )n k k k k k x x dx x xdx ππππ-+++=+∑⎰⎰=[]12(41)(43)n k k k ππ-=+++∑=(1)224222n n n π⎡⎤-⎢⎥=⋅+⎢⎥⎢⎥⎣⎦2n π当为奇数时,n =0sin n x x dx π⎰32(21)(22)2(21)(1)0(sin sin )sin n k k n k k n k x x dx x x dx x x dxππππππ-+++-=++∑⎰⎰⎰=[]321(41)(43)(41)2n k n k k πππ-=-++++⋅+∑=324(21)(21)n k k n ππ-=++-∑=31()()12242(21)22n n n n ππ--⎡⎤⋅⎢⎥-⋅++-⎢⎥⎢⎥⎣⎦=.2nπ2.5 欧拉积分在定积分计算中的应用定义 2-1[4] 形如=的含参变量积分称为函数,或(,)p q B 1110(1)p q x x dx ---⎰Beta 第一类积分。
第二章 泛函极值及变分法(补充内容)

第二章 泛函极值及变分法(补充内容)2.1 变分的基本概念2.1.1 泛函和变分泛函是一种广义的函数,是指对于某一类函数{y (x )}中的每一个函数y (x ),变量J 有一值与之对应,或者说数J 对应于函数y (x )的关系成立,则我们称变量J 是函数y (x )的泛函,记为J [y (x )]。
例1:如果表示两固定端点A (x A ,y A ),B (x B ,y B )间的曲线长度J (图2.1.1),则由微积分相关知识容易得到:dx dx dy J BAx x ⎰+=2)/(1 (2.1.1)显然,对于不同的曲线y (x ),对应于不同的长度J ,即J 是函数y (x )的函数,J =J [y (x )]。
图2.1.1 两点间任一曲线的长度例2:历史上著名的变分问题之一——最速降线问题,如果2.1.2所示。
设在不同铅垂线上的两点P 1与P 2连接成某一曲线,质点P 在重力作用下沿曲线由点P 1自由滑落到点P 2,这里不考虑摩擦作用影响,希望得到质点沿什么样的曲线滑落所需时间最短。
图2.1.2 最速降线问题选取一个表示曲线的函数y (x ),设质点从P 1到P 2沿曲线y =y (x )运动,则其运动速度为:dsv dt ==其中,S 表示曲线的弧长,t 表示时间,于是:dt =设重力加速度为g ,则gy v 2=。
因为P 1和P 2点的横坐标分别为x 1到x 2,那么质点从P 1到P 2所用时间便为:1[()]x x J y x =⎰211/2211[()]2[()()]x x y x dx g y x y x ⎧⎫'+=⎨⎬-⎩⎭⎰(2.1.2)则最速降线问题对应于泛函J [y (x )]取最小值。
回顾函数的微分:对于函数的微分有两种定义: 一种是通常的定义,即函数的增量:),()()()(x x x x A x y x x y y ∆+∆=-∆+=∆ρ (2.1.3) 其中A (x )与∆x 无关,且有∆x →0时ρ(x ,∆x )→0,于是就称函数y (x )是可微的,其线性部分称为函数的微分()()dy A x x y x x '=∆=∆,函数的微分就是函数增量的主部。
微积分概率论线代

微积分概率论线代1. 微积分(Calculus)微积分是数学中的一个重要分支,研究函数的变化和求解各种问题的方法。
它由微分学和积分学组成。
1.1 微分学微分学主要研究函数的变化率和斜率,以及求解极值问题。
微分的概念可以用导数来表示,导数表示函数在某一点上的变化率。
1.1.1 导数定义设函数y=f(x),在x点附近取另一点x+Δx,则函数在这两个点上的纵坐标差为f(x+Δx)−f(x),横坐标差为Δx。
当Δx趋近于0时,纵坐标差与横坐标差之比趋近于一个确定值,这个确定值就是函数f(x)在点x处的导数,记作f’(x)或dy/dx。
1.1.2 常见导数公式•常数函数:(c)’ = 0•幂函数:(x^n)’ = n*x^(n-1)•指数函数:(e^x)’ = e^x•对数函数:(ln(x))’ = 1/x•三角函数:–(sin(x))’ = cos(x)–(cos(x))’ = -sin(x)–(tan(x))’ = sec^2(x)1.2 积分学积分学主要研究函数的面积、曲线长度和求解累计问题。
积分的概念可以用不定积分和定积分来表示。
1.2.1 不定积分对于函数f(x),它的不定积分表示为∫f(x)dx,其中∫表示对x进行求和,f(x)表示函数的被积表达式,dx表示积分变量。
不定积分的结果是一个含有常数C的函数。
1.2.2 定积分对于函数f(x),在区间[a, b]上的定积分表示为∫[a, b]f(x)dx,其中[a, b]表示积分区间。
定积分的结果是一个具体的数值。
1.3 微积分应用微积分在物理、工程、经济学等领域有广泛应用。
例如,在物理学中,微积分用于描述物体运动、力学问题和电磁场等;在经济学中,微积分用于描述供需关系、边际效益和最优化问题等。
2. 概率论(Probability Theory)概率论是研究随机现象及其规律性的数学理论。
它主要包括概率的定义、概率的性质、随机变量和概率分布等内容。
2.1 概率的定义概率是描述事件发生可能性大小的数值。
课程积分方案及细则

课程积分方案及细则1. 背景介绍为了鼓励学生积极参与课程活动,提高学习热情和主动性,学校制定了一套课程积分方案。
该方案旨在通过积分的形式记录学生在课堂和课外活动中的表现,激励学生全面发展和多维度成长。
2. 积分获取方式学生可以通过以下途径获取积分:2.1 课堂表现积分在每节课上,老师将根据学生的表现情况进行评分,评分标准如下:•出勤情况(满分5分):按时到课(2分),迟到(1分),缺席(0分);•课堂参与度(满分5分):积极回答问题,与他人合作,参与课堂讨论等;•作业完成情况(满分10分):按时、正确完成作业;•课堂纪律(满分5分):遵守课堂纪律,不打扰他人。
2.2 课外活动积分学生可以通过参与学校组织和推荐的课外活动获取积分,如参加学术竞赛、社团活动、志愿者服务等。
不同活动的积分将根据活动的重要性和学生的表现情况进行评定,具体规定会在活动通知中说明。
2.3 自主学习积分学生还可以通过自主学习的方式获取积分,如阅读经典文献、参与科研实践、编写学术论文等。
学生需要在自主学习的过程中填写学习笔记,并由学科竞赛指导老师审核后给予相应积分。
3. 积分使用规则学生获取的积分将可以用于以下两个方面:3.1 课程奖励学生可以将积分兑换为一定数额的学术杂志、图书馆借阅券、课外活动优先名额等学术和文化奖励。
不同奖励所需积分数将根据奖励的重要性进行设定,学生可以根据个人需求选择兑换。
3.2 课程抵扣在某些情况下,学生可以使用积分进行课程抵扣。
学生在选修学科时,可以使用一定积分进行课程抵扣,具体抵扣比例和要求将在选课系统中公布和说明。
4. 积分管理及激励机制学校将设立专门的积分管理团队,负责积分的统计、审核和管理。
学生可以在课程网站上查询自己的积分情况,定期进行统计和更新。
为了激励学生积极参与,学校还将对积分排名靠前的学生给予奖励,具体奖励内容将在学年初公布并进行连续跟踪。
5. 计分周期和重置规定积分的计分周期为一个学年,从每年的9月1日开始,到次年的8月31日结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
在[a, b]上可导,且p( x) [ f (t )dt ] f ( x)
a
xa x b来自定理2 (原函数存在定理) 如果f ( x)在[a, b]上连续,则积分上限 函数p( x) f (t )dt为f ( x)在[a, b]上的一个原函数。
a x
【例1】 1.求下列变上限函数的导数。
2.1.6
牛顿—莱布尼兹公式
1、原函数存在定理 2、牛顿—莱布尼兹公式
1、原函数存在定理
设函数f ( x)在区间[a, b]上连续,x为[a, b]上的任意一点,则积分
x
a
f (t )dt存在,将 f (t )dt称为积分上限函数。
a
x
定理1 如果f ( x)在[a, b]上连续,则积分上限函数p( x)= f (t )dt ,
b
a
f ( x)dx F (b) F (a)
公式指出:对于连续函数f ( x),如果求出它的一个原函数F ( x), 那么f ( x)在[a, b]上的定积分就等于F ( x)在区间[a, b]上的改变量 F (b) F (a ),即 f ( x)dx F ( x)
a b b a
= 2x
1 1 x
4
3x
2
1 1 x6
2.
求极限 lim
x 0
x
x
0
( 1 t 2 1 t 2 )dt x
3
。
x d 2 2 2 2 ( 1 t 1 t )dt ( 1 t 1 t ) dt 0 dx 解: lim 0 lim x 0 x 0 x3 (x3)
1 1 1
arctan1 arctan(1)
2
【例5】 求 (2sin x x)dx。
0
解:
0
(2sin x x)dx = 2sin xdx xdx
0 0
= 2 cos x
1 x2
0
1 2 x 2
0
1 2 4 2
【例6】 求 xe dx。
d x 2 (1) sin t dt。 0 dx d x 2 2 解: sin t dt sin t dx 0 d 1 2 (2) ln(1 t )dt。 dx x d 1 d x 2 2 2 解: ln(1 t ) dt ln(1 t ) dt ln(1 x ) dx x dx 1
0
1 1 x2 2 1 x2 解: xe dx e dx e 0 2 0 2
1 x2
1 0
1 1 0 (e e ) (e 1). 2 2
2 sin x tx
d x2 2 (3) 1 t dt。 dx 0 d x2 2 2 2 2 4 解: 1 t d t 1 ( x ) ( x ) 2 x 1 x dx 0
d x3 1 (4) dt。 2 2 x dx 1 t
x3 d x3 1 d b 1 1 解: dt [ 2 dt dt ] 2 b dx x 1 t 2 dx x 1 t 2 1 t2 d x2 1 d x3 1 = dt dt dx b 1 t 2 dx b 1 t 2
1 x2 1 x2 1 x2 1 x2 = lim lim 2 x 0 x 0 3x 3x 2 ( 1 x 2 1 x 2 ) 2 = lim 2 2 x 0 3( 1 x 1 x ) 3 2
2、牛顿—莱布尼兹公式
定理3 如果f ( x)为区间[a, b]上的连续函数,且F ( x)是f ( x)在[a, b] 上的一个原函数,则
F (b) F (a),这样就简化了定
积分的计算。
【例2】 求 xdx。
0
1
1 2 解: xdx x 0 2
1
1 0
1 1 0 2 2
【例3】 求 解:
2
1
1 dx。 x
2
1
1 2 dx = ln x 1 ln 2 ln1 ln 2 x
1
1 【例4】 求 dx。 1 1 x 2 1 解: dx = arctan x 2 1 1 x
