中考易广东省2016中考数学总复习 第一章 数与式 第6课时重点
中考数学总复习资料(基础、简单)

中考数学总复习资料一 ..................................................................................................................................................................................... - 1 -二 ........................................................................................................................................................ 错误!未定义书签。
三 ................................................................................................................................................................................... - 15 -四 ................................................................................................................................................................................... - 26 -五 ........................................................................................................................................................ 错误!未定义书签。
广东中考必备数学总复习:第一章必备数学第一部分第一章第3节

B.
C.
D.
7 39
7. 用棋子摆出如图1-1-3-5所示的一组图形:
按照这种规律摆下去,第n个图形用的棋子个数为
( D )
A. 3n B. 6n C. 3n+6 D. 3n+3 8. 如图1-1-3-6所示的图形都是由同样大小的小圆圈按一定规律 组成的,其中第①个图形中一共有1个空心小圆圈,第②个图形中 一共有6个空心小圆圈,第③个图形中一共有13个空心小圆圈,„, 按此规律排列,则第⑦个图形中空心小圆圈的个数为 ( A )
2. 同底数幂相除:am÷an=am-n(a≠0,m,n为正整数). 3. 幂的乘方:(am)n=amn(m,n为正整数). 4. 积的乘方:(ab)n=anbn(n为正整数). 5. 商的乘方: (a≠0,n为正整数).
6. 平方差公式:(a+b)(a-b)=a2-b2. 7. 完全平方公式:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2.
4. 整式:单项式与多项式统称为整式.
5. 同类项:所含字母相同,并且相同字母的指数也相同的项
叫做同类项.几个常数项也是同类项.
6. 合并同类项:把多项式中的同类项合并成一项,叫做合并 同类项.合并同类项后,所得项的系数是合并前各同类项的系 数的和,且字母连同它的指数不变.
主要公式
1. 同底数幂相乘:am·an=am+n(m,n为正整数).
5. 单项式与多项式相乘:用单项式去乘多项式的每一项,再 把所得的积相加,即m(a+b+c)=ma+mb+mc.
6. 多项式与多项式相乘:先用一个多项式的每一项乘另一个
多项式的每一项,再把所得的积相加.
广东中考数学第一轮复习第一章数与式课时4 整式的运算与因式分解

中考考题精练
解:原式=a2-b2+a2+2ab+b2=2a2+2ab.
当a=-1,b=
1=1.
时,原式=2×(-1)2+2×(-1)× =2-
考点3 因式分解
8. 把式子:-6x2+12x-6因式分解,正确的是 ( A )
A. -6(x-1)2
B. -6(x+1)2
C. -6x(x-2)
D. -6x(x+2)
5. 因式分解:就是把一个多项式化为几个整式的 ____积______的形式. 分解因式要进行到每一个因式都 __不__能__再__分__解___为止. 6. 公因式:一个多项式各项都含有的___公__共_____的因式,叫 做这个多项式各项的___公__因__式___.
7. 提取公因式法:一般地,如果多项式的各项都有公因式, 可以把这个公因式提到括号外面,将多项式写成因式的
9. 把代数式ax2-4ax+4a分解因式,下列结果正确的是( A )
A. a(x-2)2
B. a(x+2)2
C. a(x-4)2
D. a(x+2)(x-2)
10. 把多项式4x2y-4xy2-x3分解因式的结果是 A. 4xy(x-y)-x3 B. -x(x-2y)2 C. x(4xy-4y2-x2) D. -x(-4xy+4y2+x2) 11. 分解因式:ax2-ay2=_a_(__x_+_y_)__(__x_-_y_)_____. 12. 分解因式:4x2-6x=__2_x_(__2_x_-_3_)_________.
广东省中考数学复习 第一部分 知识梳理 第一章 数与式 第2讲 整式与因式分解课件

第一章 数与式
第2讲 整式与因式分解
知识梳理
1. 代数式:用运算符号把数或表示数的字母连接而成 的式子叫做代数式. (1)单项式:只含有数字与字母的积的代数式叫做单项 式. 单独的一个_____数_____或一个___字__母_____也是单 项式. (2)多项式:几个单项式的和叫做多项式. 多项式中 __次__数__最__高____的项的次数,叫做这个多项式的次数. (3)整式:单项式与多项式统称整式.
2. 已知x2+kx+4是一个完全平方式,则k的值是 ____±__4____. 3.分解因式:(1)2a2+4a+2=___2_(_a_+_1_)_2____; (2)x3-2x=____x_(_x_+_2_)_(_x_-__2_)___;(在实数范围内) (3)7(x-1)-x(1-x)=(x-1)(7+x). 4. 某商品的进价为a元,按标价的五折出售,这 时仍可盈利25%,则这种商品的标价是___2_._5_a____ 元. (用含a的式子表示)
易错题汇总
1. 下列运算正确的打“√”,错误的打“×”, 并更正: (1)x2·x3=x6 ( ×) 更正_____x_5 ____; (2)(x3)3=x9 ( √ ) 更正___________; (3)x2+x2=x4 ( × ) 更正__2_x_2______; (4)(x+y)2=x2+y2 ( × ) 更正______x_2+_2__x_y_+_y_2 ____; (5)(- )-2=2a( × ) 更正____a_2_____; (6)(x-2)2=x2-4 ( × ) 更正____x_2-_4_x_+_4____.
【中考易】广东省2016中考数学总复习 第一章 数与式 第6课时 数的开方与二次根式课件

• 13.二次根式的乘法法则:
•
.
• 14.二次根式的除法:
•
(或
).
a • b • 其中a >0;b 0. ab (a 0, b 0)
b b aa
b a ba
x2
2
3
7
考点一:平方根、算术平方根与立方根
• 1.平方根:一个数x的平方等于a,那么x叫做a的平方 根,记作 . a
• 2.算术平方根: 一个正数x的平方等于a,那么x叫 做a的算术平方根,记作 a.
• 0的算术平方根是0.
• 3.立方根:一个数x的立方等于a ,那么叫做的立方根.
记作
3
.
a
考点一:平方根、算术平方根与立方根
考点三:二次根式的性质
• 8.
• 9.
• 10. • 11. •
;2
a a a 0
__a_ a 0 ,
a2 _| a_;|_ _0__ a 0 ,
.
_-_a_
a
0
;
ab _a_•__ba 0,b 0
b
b __a__ a 0, b 0
aபைடு நூலகம்
考点四:二次根式的运算
• 12.二次根式的加减法:一般先把二次根式化为最简二次根式,再把同类二次根式合并.
• 4.填表:
a
3a
0
0
无
3a
考点二:二次根式的有关概念
• 5.二次根式的定义:形如 a(a 0)的式子叫二次根 式. • 6.最简二次根式: • 满足下列两个条件的二次根式,叫做最简二次根式: • (1)被开方数的因数是整数,因式是整式; • (2)被开方数中不含能开得尽方的因数和因式. • 7.同类二次根式:几个二次根式化成最简二次根式 以后,如果被开方数相同,那么这几个二次根式就叫 做同类二次根式.
中考数学重点难点分值题型分布

中考数学重点难点分值题型分布第一章数与式1.1实数考点1:实数的分类与实数的有关概念掌握题型:选择题、填空题; 分值:3分考试内容:1.实数的定义与分类2.实数的大小比较3.数轴4.相反数、倒数、绝对值5.无理数的估算考点2:实数的运算掌握题型:选择题、填空题;分值:3分、4分考试内容:1.平方根与立方根2.实数的混合运算考点3:科学计数法掌握与近似数了解题型:选择题;分值:3分考试内容:1.科学记数法2.近似数1.2代数式考点1:代数式理解——必考点题型:选择题;分值:4分考试内容:1.列代数式表示简单的数量关系2.能解释一些简单代数式的实际意义或几何意义考点2:求代数式的值题型:解答题;分值:6分考试内容:1.代数式的值的概念“了解2.根据问题所提供的资料,求代数式的值1.3整式考点1:整式及其运算灵活运用题型:填空题;分值:3分考试内容:1.整式的有关概念了解2.整数指数幂的意义和基本性质了解3.整式加减乘除法运算的法则4.会进行简单的整式加减乘除法运算考点2:整式乘法公式灵活运用——必考点题型:填空题;分值:3分、4分考试内容:1.完全平方公式、平方差公式的几何背景了解2.平方差公式、完全平方公式3.用平方差公式、完全平方公式进行简单计算考点3:因式分解灵活运用题型:填空题;分值:3分、4分考试内容:1.因式分解的意义及其与整式乘法之间的关系了解2.用提取公因式法、、公式法进行因式分解,会在实数范围内分解因式1.4分式与二次根式考点1:分式的概念与基本性质灵活运用——必考点题型:选择题;分值:3分考试内容:1.分式的概念了解2.确定分式有意义的条件3.确定使分式的值为零的条件4.分式的基本性质5.约分和通分考点2:分式的运算掌握——必考点题型:解答题;分值:6分考试内容:1.分式的加、减、乘、除、乘方运算法则2.简单的分式加减乘除乘方运算,用恰当方法解决与分式有关的问题考点3:二次根式掌握——必考点题型:选择题;分值:3分1.二次根式的概念2.最简二次根式3.二次根式的运算第二章方程组与不等式组2.1整式方程考点1:一元一次方程掌握,灵活运用题型:选择题、解答题;分值:3分、6分、8分考试内容:1.方程是刻画现实世界数量关系的一个数学模型了解2.运用一元一次方程解决简单的实际问题3.方程的解的概念了解4.由方程的解求方程中字母系数的值5.一元一次方程的有关概念了解6.一元一次方程的解法考点2:一元二次方程掌握,灵活运用——必考点题型:选择题、填空题;分值:3分、4分1.一元二次方程的概念了解2.一元二次方程的解法3.用一元二次方程根的判别式判断根的情况4.运用一元二次方程解决简单的实际问题2.2分式方程考点1:分式方程及其解法——必考点题型:选择题、填空题;分值:3分、4分考试内容:1.分式方程的概念2.分式方程的增根3.分式方程的求解4.分式方程的检验考点2:分式方程的应用题型:解答题;分值:10分考试内容:1.利用分式方程解决生活实际问题2.注意分式方程要对方程和实际意义进行双检验2.3方程组考点1:二元一次方程组题型:解答题;分值:7分考试内容:1.二元一次方程组的有关概念了解2.代入消元法、加减消元法的意义3.选择适当的方法解二元一次方程组考点2:二元一次方程组的应用——必考点题型:解答题;分值:9分考试内容:运用二元一次方程组解决简单的实际问题2.4不等式组考点1:不等式和一元一次不等式组题型:选择题、填空题;分值:3分、4分考试内容:1.不等式的意义了解2.根据具体问题中的数量关系列出不等式3.不等式的基本性质4.利用不等式的性质比较两个实数的大小5.一元一次不等式的解集了解6.解不等式组考点2:一元一次不等式组的应用——必考点题型:解答题;分值:8分考试内容:根据具体问题中的数量关系,用一元一次不等式或不等式组解决简单问题第三章变量与函数3.1位置的确定与变量之间的关系考点1:平面直角坐标系题型:选择题、填空题;分值:3分考试内容:1.坐标平面内点的坐标特征的运用2.坐标轴、原点对称的点的坐标的特征考点2:函数及其图象题型:选择题、填空题;分值:3分、8分考试内容:1.求函数自变量的取值范围2.根据条件写出函数关系式3.用描点法画出函数图像考点3:函数的有关应用题型:选择题;分值:3分考试内容:解决与函数有关的应用型问题3.2一次函数考点1:一次函数的概念、图象和性质题型:解答题;分值:3分、10分考试内容:1.对一次函数概念的理解理解2.根据已知条件用待定系数法确定函数解析式3.会画一次函数图象并能根据图象解决相关的问题4.根据自变量的变化判断函数值的增减情况灵活运用5.由函数值的取值范围判断自变量的取值范围,求一次函数图象的交点坐标考点2:一次函数的应用题型:解答题;分值:9分考试内容:与一次函数有关的应用问题灵活运用3.3反比例函数考点1:求反比例函数解析式题型:填空题;分值:4分考试内容:1.对反比例函数的理解2.根据已知条件用待定系数法确定反比例函数解析式考点2:反比例函数的图象和性质题型:解答题;分值:8分考试内容:1.会画反比例函数的增减性;掌握比例系数K的几何意义考点3:反比例函数的应用题型:填空题、解答题;分值:3分、9分考试内容:1.反比例函数与一次函数图象与性质的综合应用2.确定与反比例函数有关的应用型问题3.4二次函数考点1:二次函数的图象和性质题型:选择题、解答题;分值: 3分、3分考试内容:1.用配方法把抛物线的解析式y=ax2+bx+ca≠0化为y=ax-h2+ka≠0的形式2.根据已知条件用待定系数法确定二次函数的解析式3.根据抛物线的位置确定a、b、c的符号,根据公式确定抛物线的顶点和对称轴4.根据自变量的变化判断二次函数值的增减情况5.根据函数图象求一元二次方程的根,由一元二次方程根的情况判断抛物线与x轴的交点;根据图象判断一元二次不等式的解集考点2:二次函数的综合应用题型:解答题;分值:10分、12分考试内容:1.利用二次函数解决简单的实际问题2.与二次函数有关的综合应用第四章图形的认识4.1角、相交线与平行线考点1:角题型:选择题;分值:3分考试内容:1.角的有关概念了解2.角的比较、角的和差计算3.余角、补角考点2:相交线题型:选择题;分值:3分考试内容:1.对顶角2.垂线、点到直线的距离3.作已知直线的垂线4.命题、定理、证明考点3:平行线题型:选择题;分值:3分考试内容:1.平行线的性质2.平行线间的距离3.平行线的判定4.2三角形及其全等考点1:三角形的相关概念题型:选择题;分值:3分考试内容:1.角平分线、中线、高线、中位线以及性质2.画任意三角形的角平分线、中线和高3.三角形的稳定性、三边关系定理、三角形内角和定理考点2:三角形全等题型:填空题、解答题;分值:3分考试内容:1.全等三角形对应边相等、对应角相等2.三角形全等的判定定理:SAS, ASA, AAS, SSS, HL 4.3等腰三角形与直角三角形考点1:等腰三角形题型:选择题;分值:3分考试内容:1.等腰三角形的有关概念、性质和判定2.等边三角形的有关概念、性质和判定考点2:直角三角形题型:选择题;分值:3分考试内容:1.直角三角形的概念、性质和判定2.勾股定理及其逆定理:4.4多边形与平行四边形考点1:多边形题型:选择题;分值:3分考试内容:多边形和正多边形的概念、内角和与外角和公式了解考点2:平行四边形题型:解答题;分值:9分考试内容:1、平行四边形的概念和性质2、平行四边形的判定4.5特殊的平行四边形考点1:矩形题型:选择题、填空题、解答题;分值:3分、8分考试内容:1.矩形的概念、性质2.矩形的判定考点2:菱形题型:选择、解答;分值:3分、10分考试内容:1、菱形的概念、性质2、菱形的判定考点3:正方形题型:选择题、解答题;分值:3分考试内容:1.正方形具有矩形和菱形的性质2.既是矩形又是菱形的四边形是正方形4.6梯形依据考情选用题型:填空题;分值:3分考试内容:1.梯形的概念和性质2.等腰梯形的概念、性质和判定3.直角梯形的概念第五章圆5.1圆的性质及与圆有关的位置关系考点1:圆的有关概念与性质题型:选择题、解答题;分值:3分、4分、9分考试内容:1.垂径定理及其推论的应用2.弧、圆心角、圆周角之间的关系3.圆周角定理及其推论考点2:与圆有关的位置关系题型:选择题、解答题考试内容:1.点和圆的位置关系2.直线和圆的位置关系3.切线的性质和判定5.2与圆有关的计算题型:选择题、填空题、解答题;分值:3分、10分考试内容:1.求圆的周长、弧长及简单组合图形的周长2.求圆的面积、扇形的面积及简单组合图形的面积3.圆柱的侧面积和全面积的计算4.圆锥的侧面积和全面积的计算第六章空间与图形6.1圆形的轴对称、平移与旋转考点1:轴对称的概念及性质题型:选择题;分值:3分考试内容:1.轴对称的概念及性质2.基本图形的对称性及轴对称的应用考点2:图形的平移题型:选择题;分值:3分考试内容:1.平移的概念和性质2.简单图形的平移及平移的应用考点3:图形的旋转题型:选择题;分值:3分考试内容:1.旋转的概念及性质2.基本图形的旋转及旋转的应用6.2图形的相似考点1:相似的有关概念题型:近5年未考考试内容:成比例线段、比例的基本性质、黄金分割考点2:相似三角形的性质与判定题型:填空题;分值:3分考试内容:1.相似的概念及相似的判定2.相似的性质、多边形相似比、周长比与面积比考点3:位似的概念与性质题型:选择题;分值:3分考试内容:1.位似的概念和性质2.利用位似放大或缩小图形,会在坐标系中作位似图形并求出对应的坐标6.3解直角三角形题型:选择题、填空题、解答题;分值:3、6分考点1:锐角三角函数考试内容:1.锐角三角函数的定义及其性质2.特殊角的三角函数值考点2:解直角三角形考试内容:1.解直角三角形的概念2.直角三角形的边角关系3.仰角、俯角、坡度坡比4.用三角函数解决与直角三角形有关的实际问题6.4视图与投影考点1:几何体及其展开图题型:选择题;分值:3分考试内容:基本几何体的展开图考点2:几何体的三视图题型:选择题;分值:3分考试内容:画基本几何体或简单组合体的三视图,根据三视图描述实物考点3:投影题型:近五年未考考试内容:1.中心投影和平行投影2.影子、视点、视角和盲区的概念第七章统计与概率7.1统计考点1:数据的收集题型:选择题;分值:3分考试内容:1.普查和抽样调查2.总体、个体、样本和样本容量3.用样本估计总体的思想考点2:数据的处理题型:选择题;分值:3分考试内容:1.求一组数据的平均数包括加权平均数、众数、中位数、极差与方差2.根据具体问题,选择合适的统计量表示数据的集中程度或离散程度3.根据统计结果做出合理的判断和预测考点3:统计图表题型:解答题;分值:4分、8分考试内容:1.用扇形统计图表示数据2.频数、频率的概念,频数分布的意义和作用3.列频数分布表,画频数分布直方图和频数分布折线图4.利用统计图表解决简单的实际问题7.2概率考点1:事件的分类题型:选择题;分值:3分考试内容:不可能事件、必然事件和随机事件考点2:概率的计算题型:解答题;分值:10分考试内容:1.概率的意义2.运用列举法包括列表、画树状图计算简单事件发生的概率考点3:用频率估计概率题型:填空题;分值:3分考试内容:大量重复试验时,可以用频率估计概率解决一些实际问题。
中考第一轮复习--第一章数与式
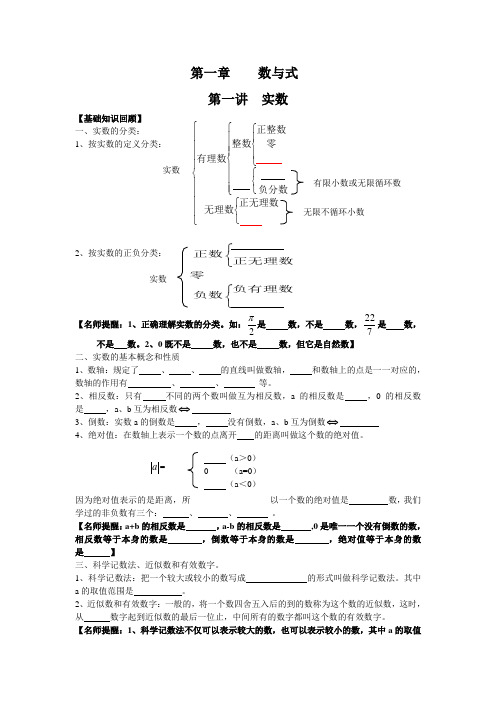
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类: 1、按实数的定义分类: 实数 有限小数或无限循环数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a+b 的相反数是 ,a-b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 (a >0) (a <0) 0 (a=0)范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
初三中考数学数与式

第一部分 中考基础复习第一章 数与式第1讲 实数A 级 基础题1.(2015年广东梅州)12的相反数是( )A .2B .-2 C.12 D .-122.(2015年广东佛山)-3的倒数是( )A .-13 B.13C .3D .-33.(2015年广东广州)四个数-3.14,0,1,2中为负数的是( ) A .-3.14 B .0 C .1 D .24.(2015年内蒙古呼和浩特)以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )A .-3 ℃B .15 ℃C .-10 ℃D .-1 ℃5.(2015年广东汕尾)今年五月份香港举办“保普选反暴力”大联盟大型签名行动,9天共收集超121万个签名,将121万用科学记数法表示为( )A .1.21×106B .12.1×105C .0.121×107D .1.21×1056.(2015年湖南永州)在数轴上表示数-1和2014的两点分别为A 和B ,则A ,B 两点间的距离为( )A .2013B .2014C .2015D .20167.(2015年黑龙江绥化)在实数0,π,227, 2 ,-9中,无理数的个数有( )A .1个B .2个C .3个D .4个 8.(2015年山东威海)已知实数a ,b 在数轴上的位置如图1-1-2,下列结论错误的是( )图1-1-2A.||a <1<||b B .1 <-a <b C .1 < ||a <b D .-b <a <-1 9.(2015年湖北武汉)计算:-10+(+6)=________.10.(2015年吉林长春)比较大小:2__________1.(填“>”“=”或“<”) 11.(2015年江苏镇江)已知一个数的绝对值是4,则这个数是__________. 12.计算:(1)(2015年广东梅州)计算:8+|2 2-3|-⎝⎛⎭⎫13-1-(2015+2)°. (2)(2015年广东佛山)计算:9+20150+(-2)3+2 3×sin60°.B 级 中等题13.(2015年山东青岛)某种计算机完成一次基本运算的时间约为0.000 000 001 s ,将0.000 000 001 s 用科学记数法表示为( )A .0.1×10-8 sB .0.1×10-9 sC .1×10-8 sD .1×10-9 s 14.(2015年山东菏泽)如图1-1-3,四个有理数在数轴上的对应点M ,P ,N ,Q ,若点M ,N 表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )图1-1-3A .点MB .点NC .点PD .点Q 15.(2015年重庆)下列图形都是由几个黑色和白色的正方形按一定规律组成.在图1-1-4中,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,按此规律,图⑩中黑色正方形的个数是( )图1-1-4A .32B .29C .28D .2616.(2015年贵州遵义)按一定规律排列的一列数依次为:45,48,411,414,…,按此规律,这列数中的第10个数与第16个数的积是__________.C 级 拔尖题17.(2015年湖南娄底)下列数据是按一定规律排列的(如图1-1-5),则第7行的第一个数为__________.图1-1-5第2讲 代数式A 级 基础题1.若x =1,y =12,则x 2+4xy +4y 2的值是( )A .2B .4 C.32 D.122.(2015年吉林)购买1个单价为a 元的面包和3瓶单价为b 元的饮料,所需要钱数为( )A .(a +b )元B .3(a +b )元C .(3a +b )元D .(a +3b )元3.(2015年四川自贡)为庆祝抗战胜利70周年,我市某楼盘让利于民,决定将原价为a 元/米2的商品房价降价10%销售,降价后的销售价为( )A .a -10%元/米2B .a ·10%元/米2C .a (1-10%)元/米2D .a (1+10%)元/米24.(2015年福建厦门)某商店举办促销活动,促销的方法是将原价x 元的衣服以⎝⎛⎭⎫45x -10元出售,则下列说法中,能正确表达该商店促销方法的是( )A .原价减去10元后再打8折B .原价打8折后再减去10元C .原价减去10元后再打2折D .原价打2折后再减去10元5.(2015年海南)某企业今年1月份产值为x 万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )A .(1-10%)(1+15%)x 万元B .(1-10%+15%)x 万元C .(x -10%)(x +15%)万元D .(1+10%-15%)x 万元 6.(2015年重庆)如图1-2-4所示的图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第④个图形中小圆圈的个数为( )图1-2-4A .21个B .24个C .27个D .30个7.(2015年湖南株洲)如果手机通话每分钟收费m 元,那么通话a 分钟,收费________元.8.(2014年江苏苏州)若a -2b =3,则9-2a +4b 的值为________. 9.(2015年湖南益阳)如图1-2-5是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n 个图案中有________根小棒.图1-2-510.(2015年四川内江)如图1-2-6是由火柴棒搭成的几何图案,则第n 个图案中有________根火柴棒.(用含n 的代数式表示)图1-2-611.已知a=3,b=|-2|,c=12,求代数式a2+b-4c的值.12.已知a,b互为相反数,c,d互为倒数,m的绝对值是2,求|| a+b2m2+1+4m-3cd的值.B级中等题13.按如图1-2-7所示的程序计算,若开始输入n的值为1,则最后输出的结果是()图1-2-7A.3 B.15 C.42 D.6314.(2015年黑龙江绥化)如图1-2-8,填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a+b+c=________.图1-2-815.(2015年江苏淮安)将连续正整数按如下规律排列(如图1-2-9):图1-2-9若正整数565位于第a 行,第b 列,则a +b =________. 16.(2014年四川达州)《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图1-2-10.图1-2-10由图易得:12+122+123+…+12n =________.C 级 拔尖题17.(2014年安徽)观察下列关于自然数的等式: 32-4×12=5;① 52-4×22=9;② 72-4×32=13;③ ……根据上述规律解决下列问题:(1)完成第四个等式:92-4×________2=________;(2)写出你猜想的第n 个等式(用含n 的式子表示),并验证其正确性.(列代数式)第3讲 整式与分式 第1课时 整式A 级 基础题1.(2015年浙江台州)单项式2a 的系数是( ) A .2 B .2a C .1 D .a2.(2015年广东珠海)计算-3a 2×a 3的结果为( ) A .-3a 5 B .3a 6 C .-3a 6 D .3a 53.(2015年四川巴中)若单项式2x 2y a +b 与-13x a -b y 4是同类项,则a ,b 的值分别为( )A .a =3,b =1B .a =-3,b =1C .a =3,b =-1D .a =-3,b =-1 4.(2015年湖南邵阳)已知a +b =3,ab =2,则a 2+b 2的值为( ) A .3 B .4 C .5 D .65.(2015年广东佛山)若(x +2)(x -1)=x 4+mx +n ,则m +n =( ) A .1 B .-2 C .-1 D .26.(2015年广东深圳)下列说法错误的是( )A .a ·a =a 2B .2a +a =3aC .(a 3)2=a 5D .a 3÷a -1=a 47.(2015年浙江金华)已知a +b =3,a -b =5,则代数式a 2-b 2=________. 8.(2015年广东珠海)填空:x 2+10x +________=(x +________)2. 9.(2015年四川绵阳)计算:a (a 2÷a )-a 2=________.10.(2015年山东菏泽)若x 2+x +m =(x -3)(x +n )对x 恒成立,则n =__________. 11.(2015年广东梅州)已知a +b =-2,求代数式(a -1)2+b (2a +b )+2a 的值.12.(2015年北京)已知2a 2+3a -6=0.求代数式3a ()2a +1-()2a +1()2a -1的值.B 级 中等题13.(2015年山东临沂)观察下列关于x 的单项式,探究其规律: x,3x 2,5x 3,7x 4,9x 5,11x 6,…,按照上述规律,第2015个单项式是( ) A .2015x 2015 B .4029x 2014 C .4029x 2015 D .4031x 201514.(2015年安徽)按一定规律排列的一列数:21,22,23,25,28,213,…,若x,y,z表示这列数中的连续三个数,猜想x,y,z满足的关系式是____________.15.(2014年浙江宁波)一个大正方形和四个全等的小正方形按图1-3-2(1)(2)两种方式摆放,则图(2)的大正方形中未被小正方形覆盖部分的面积是________.(用a,b的代数式表示)图1-3-216.(2015年河北)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:-3x=x2-5x+1(1)求所捂住的二次三项式;(2)若x=6+1,求所捂住的二次三项式的值.C级拔尖题17.利民商店出售一种原价为a的商品,有如下几种方案:(1)先提价10%,再降价10%;(2)先降价10%,再提价10%;(3)先提价20%,再降价20%.问:用这三种方案调价的结果是否一样,最后是不是都恢复了原价?第2课时 因式分解A 级 基础题1.(2014年海南)下列式子从左到右变形是因式分解的是( ) A .a 2+4a -21=a (a +4)-21 B .a 2+4a -21=(a -3)(a +7) C .(a -3)(a +7)=a 2+4a -21 D .a 2+4a -21=(a +2)2-25 2.(2015年湖北武汉)把a 2-2a 分解因式,正确的是( ) A .a (a -2) B .a (a +2) C .a (a 2-2) D .a (2-a ) 3.(2014年辽宁葫芦岛)计算:552-152=( ) A .40 B .1600 C .2400 D .28004.(2015年浙江台州)把多项式2x 2-8分解因式,结果正确的是( ) A .2()x 2-8 B .2()x -22C .2()x +2()x -2D .2x ⎝⎛⎭⎫x -4x 5.(2015年贵州毕节)下列因式分解正确的是( )A .a 4b -6a 3b +9a 2b =a 2b (a 2-6a +9)B .x 2-x +14=⎝⎛⎭⎫x -122 C .x 2-2x +4=(x -2)2 D .4x 2-y 2=(4x +y )(4x -y )6.(2015年广西贺州)把多项式4x 2y -4xy 2-x 3分解因式的结果是( ) A .4xy (x -y )-x 3 B .-x (x -2y )2C .x (4xy -4y 2-x 2)D .-x (-4xy +4y 2+x 2) 7.(2015年山东枣庄)如图1-3-3,边长为a ,b 的矩形的周长为14,面积为10,则a 2b+ab 2的值为( )图1-3-3A .140B .70C .35D .248.(2015年广东梅州)分解因式:m 3-m =________. 9.(2015年广东广州)分解因式:2mx -6my =________. 10.(2015年广东深圳)分解因式:3a 2-3b 2________.11.(2015年山东东营)分解因式:4+12(x -y )+9(x -y )2=________. 12.已知ab =-3,a +b =2.求代数式a 3b +ab 3的值.B 级 中等题13.(2015年湖南衡阳)已知a +b =3,a -b =-1,则a 2-b 2的值为________. 14.(2015年湖北孝感)分解因式:(a -b )2-4b 2__________. 15.(2015年甘肃平凉)分解因式:x 3y -2x 2y +xy =________.16.(2015年湖南株洲)分解因式:x 2()x -2-16()x -2=____________________.C 级 拔尖题17.分解因式:x 2-y 2-3x -3y .第3课时 分式A 级 基础题1.(2015年浙江丽水)分式-11-x可变形为( )A .-1x -1 B.11+x C .-11+x D.1x -12.(2015年浙江金华)要使分式xx +4有意义,则x 的取值应满足( )A .x =-4B .x ≠4C .x >-4D .x ≠-43.(2015年湖南)若分式3-xx +1的值为0,则x 的值为( )A .3或-1B .0C .3D .-14.(2014年内蒙古赤峰)化简a 2b -ab 2b -a的结果正确的是( )A .abB .-abC .a 2-b 2D .b 2-a 25.(2015年山东济南)化简 m 2m -3-9m -3 的结果是( )A .m +3B .m -3 C.m -3m +3 D.m +3m -36.(2015年湖南益阳)下列等式成立的是( ) A.1a +2b =3a +b B.22a +b =1a +b C.ab ab -b 2=a a -b D.a -a +b =-a a +b7.(2015年广东珠海)若分式3x -5有意义,则x 应满足________.8.(2015年江苏镇江)当x =__________时,分式x +1x -2的值为0.9.(2015年吉林)计算:x x -y ·x 2-y 2x=________.10.(2015年贵州六盘水)已知c 4=b 5=a6≠0,则b +c a 的值为________.11.(2015年广东佛山)计算:2x -2-8x 2-4.12.(2015年广东广州)已知A =x 2+2x +1x 2-1-xx -1.(1)化简A ;(2)当x 满足不等式组⎩⎪⎨⎪⎧x -1≥0,x -3<0,且x 为整数时,求A 的值.B 级 中等题 13.(2015年山东临沂)计算:a a +2-4a 2+2a = ______________.14.(2015年湖南邵阳)先化简⎝⎛⎭⎫1x -2-2x ·x 2-2x 2,再从0,1,2中选取一个合适的x 的值代入求值.15.(2015年湖北襄阳)先化简,再求值:⎝ ⎛⎭⎪⎫5x +3yx 2-y 2+2x y 2-x 2÷1x 2y -xy 2,其中x =3+2,y =3- 2.16.(2015年贵州黔东南州)先化简,再求值:m -33m 2-6m ÷⎝⎛⎭⎫m +2-5m -2,其中m 是方程x 2+2x -3=0的根.C 级 拔尖题 17.(2015年广东梅州)若1(2n -1)(2n +1)=a 2n -1+b2n +1,对任意自然数n 都成立,则a=______,b =______;计算:m =11×3+13×5+15×7+…+119×21=________.第4讲 二次根式A 级 基础题1.(2015年重庆)计算3 2-2的值是( )A .2B .3 C. 2 D .2 22.(2015年安徽)计算8×2的结果是( )A.10 B .4 C. 6 D .23.(2015年江苏无锡)函数y =x -4中自变量x 的取值范围是( )A .x >4B .x ≥4C .x ≤4D .x ≠44.(2015年四川凉山州)下列根式中,不能与3合并的是( ) A.13 B.33C.23D.12 5.(2015年江苏淮安)下列式子为最简二次根式的是( )A. 3B. 4C.8D.126.(2015年湖北潜江)下列各式计算正确的是( )A.2+3= 5 B .4 3-3 3=1 C .2 3×3 3=6 3 D.27÷3=37.(2015年湖南衡阳)计算8-2=________.8.(2015年江苏南京)计算5×153的结果是________. 9.(2015年江苏泰州)计算:18-2 12等于________. 10.(2015年湖北荆门)当1<a <2时,代数式()a -22+||1-a 的值是________.11.(2014年广东佛山)计算:8÷2-1+327×[2+(-2)3].12.(2014年湖北荆门)计算:24×13-4×18×(1-2)0.B 级 中等题13.(2014年安徽)设n 为正整数,且n <65<n +1,则n 的值为( )A .5B .6C .7D .814.(2014年山东济宁)如果ab>0,a+b<0,那么下面各式:①ab=ab;②ab·ba=1;③ab÷ab=-b,其中正确的是()A.①②B.②③C.①③D.①②③15.(2015年四川攀枝花)若y=x-3+3-x+2,则x y=________.16.(2014年山东德州)若y=x-4+4-x2-2,则(x+y)y=________.C级拔尖题17.(2015年山西)阅读与计算:阅读以下材料,并完成相应的任务.斐波那契(约1170—1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰好是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用:斐波那契数列中的第n个数可以用15⎝⎛⎭⎪⎫1+52n-⎝⎛⎭⎪⎫1-52n表示.任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.第一章基础题强化提高测试时间:45分钟 满分:100分一、选择题(本大题共6小题,每小题5分,共30分)1.-15的相反数是( )A .15B .-15 C.115 D .-1152.用科学记数法表示316 000 000为( )A .3.16×107B .3.16×108C .31.6×107D .31.6×1063.下列二次根式中的最简二次根式是( ) A.30 B.12 C.8 D.124.下列运算正确的是( )A .a 2+a 3=a 5 B.()-a 32=a 6C .ab 2·3a 2b =3a 2b 2D .-2a 6÷a 2=-2a 35.下列计算正确的是( )A .ab ·ab =2abB .(2a )3=2a 3C .3 a -a =3(a ≥0) D.a ·b =ab (a ≥0,b ≥0)6.下列运算正确的是( )A.2+3= 5 B .3x 2y -x 2y =3C.a 2+b 2a +b=a +b D.()a 2b 3=a 6b 3 二、填空题(本大题共4小题,每小题5分,共20分)7.若分式1x -5有意义,则实数x 的取值范围是________. 8.81的平方根是________.9.若a 2-3b =5,则6b -2a 2+2015=________.10.化简:2(8-2)=________.三、解答题(本大题共5小题,每小题10分,共50分)11.分解因式:m 3n -4mn .12.化简:1x +3+6x 2-9.13.先化简,再求值:(2a +b )(2a -b )+(4ab 3-8a 2b 2)÷4ab ,其中a =-2,b =1.14.计算:|-3|+2sin45°+tan60°-⎝⎛⎭⎫-13-1-12+(π-3)0.15.先化简,再求值:⎝ ⎛⎭⎪⎫a 2-b 2a 2-2ab +b 2+a b -a ÷b 2a 2-ab,其中a ,b 满足a +1+|b -3|=0.第一部分 中考基础复习第一章 数与式第1讲 实数【演练·巩固提升】1.D 2.A 3.A 4.C 5.A 6.C 7.B 8.A9.-4 10.> 11.±412.解:(1)原式=2 2+3-2 2-3-1=-1.(2)原式=3+1-8+2 3×32=-4+3=-1. 13.D 14.C 15.B 16.110017.22 解析:由排列的规律可得,第n -1行结束的时候排了1+2+3+…+n -1=12n (n -1)个数.所以第n 行的第1个数为12n (n -1)+1.所以n =7时,第7行的第1个数为22. 第2讲 代数式【演练·巩固提升】1.B 2.D 3.C 4.B 5.A6.B 7.am 8.3 9.5n +1 10.2n (n +1)11.解:当a =3,b =|-2|=2,c =12时,a 2+b -4c =3+2-2=3. 12.解:根据题意,可知:a +b =0,①cd =1,②|m |=2,即m =±2.③把①②代入原式,可得原式=0+4m -3×1=4m -3.当m =2时,4m -3=2×4-3=5;当m =-2时,4m -3=-2×4-3=-11.所以,原式的值是5或-11.13.C 解析:把n =1代入,得n (n +1)=2<15,把n =2代入,得n (n +1)=6<15,把n =6代入,得n (n +1)=42>15,则最后输出的结果为42.14.110 解析:根据左上角+4=左下角,左上角+3=右上角,右下角的数是左下角与右上角两个数的乘积加上1的和,可得6+4=a,6+3=c ,ac +1=b ,可得a =10,c =9,b =91,所以a +b +c =10+9+91=110.15.147 解析:∵565÷4=141……1,∴正整数565位于第142行,即a =142.∵奇数行的数字在前四列,数字逐渐增加;偶数行的数字在后四列,数字逐渐减小,∴正整数565位于第五列,即b =5.∴a +b =142+5=147.16.2n -12n 解析:取n 天后剩下12n ,所以n 天共取走1-12n ,即12+122+123+…+12n =1-12n=2n -12n . 17.解:(1)4 17(2)第n 个等式为(2n +1)2-4n 2=4n +1.证明如下:左边=(2n +1)2-4n 2=4n 2+4n +1-4n 2=4n +1=右边.∴(2n +1)2-4n 2=4n +1.第3讲 整式与分式第1课时 整式【演练·巩固提升】1.A 2.A 3.A 4.C 5.C 6.C7.15 8.25 5 9.0 10.411.解:原式=a 2-2a +1+2ab +b 2+2a =()a +b 2+1,当a +b =-2时,()a +b 2+1=()-22+1=3.12.解:原式=6a 2+3a -(4a 2-1)=6a 2-4a 2+3a +1=2a 2+3a +1.因为2a 2+3a -6=0,所以2a 2+3a =6,所以原式=7.13.C 解析:先看x 的指数,第一个指数是1,第二个指数是2,第2015个单项式的指数是2015;再看系数,系数是连续的奇数,所以第2015个奇数为4029,所以第2015个单项式为4029x 2015.14.xy =z 解析:∵a m a n =a m +n ,21×22=23,22×23=25,23×25=28,25×28=213,故答案为xy =z .15.ab 解析:设大正方形的边长为x 1,小正方形的边长为x 2,由图①和②列出方程组得⎩⎪⎨⎪⎧ x 1+2x 2=a ,x 1-2x 2=b ,解得⎩⎨⎧ x 1=a +b 2,x 2=a -b 4.图②的大正方形中未被小正方形覆盖部分的面积=⎝⎛⎭⎫a +b 22-4×⎝⎛⎭⎫a -b 42=ab .16.解:(1)设所捂的二次三项式为A ,则A =x 2-5x +1+3x =x 2-2x +1.(2)若x =6+1,则A =()x -12=()6+1-12=6.17.解:方案(1)的调价结果为(1+10%)(1-10%)a =0.99a ;方案(2)的调价结果为(1-10%)(1+10%)a =0.99a ;方案(3)的调价结果为(1+20%)(1-20%)a =0.96a .由此可以得到方案(1)(2)的调价结果是一样的,方案(3)的调价结果与(1)(2)不一样.最后都没有恢复原价. 第2课时 因式分解【演练·巩固提升】1.B 2.A 3.D 4.C 5.B 6.B 7.B8.m ()m +1()m -1 9.2m ()x -3y10.3()a +b ()a -b 11.(3x -3y +2)212.解:∵a +b =2,∴(a +b )2=4.∴a 2+2ab +b 2=4.又∵ab =-3,a 2+2ab +b 2=4,∴a 2+b 2=10.∴a 3b +ab 3=ab (a 2+b 2)=-30.13.-3 14.(a +b )(a -3b ) 15.xy (x -1)216.(x -2)(x -4)(x +4)17.解:原式=(x +y )(x -y )-3(x +y )=(x +y )(x -y -3)第3课时 分式【演练·巩固提升】1.D 2.D 3.C 4.B 5.A 6.C 7.x ≠5 8.-1 9.x +y10.32 解析:由题意,可设a =6k ,b =5k ,c =4k ,则b +c a =5k +4k 6k =32. 11.解:原式=2()x +2-8()x +2()x -2=2()x -2()x +2()x -2=2x +2. 12.解:(1)A =x 2+2x +1x 2-1-x x -1=()x +12()x +1()x -1-x x -1=x +1x -1-x x -1=1x -1. (2)解x -1≥0,得x ≥1.解x -3<0,得x <3.∴⎩⎪⎨⎪⎧x -1≥0,x -3<0的解为1≤x <3. ∵x 为整数,∴x =1,2.当x =1时,分式无意义;当x =2时,A =12-1=1. 13.a -2a 解析:原式=a a +2-4a (a +2)=a 2a (a +2)-4a (a +2)=a 2-4a (a +2)=(a +2)(a -2)a (a +2)=a -2a. 14.解:原式=⎣⎢⎡⎦⎥⎤x x (x -2)-2(x -2)x (x -2)·x (x -2)2=x -2(x -2)x (x -2)·x (x -2)2=x -2x +42=-x +42, 由于x ≠0,且x ≠2,因此只能取x =1.所以当x =1时,原式的值为-x +42=-1+42=32. 15.解:原式=⎝ ⎛⎭⎪⎫5x +3y x 2-y 2-2x x 2-y 2÷1xy (x -y )=3(x +y )(x +y )(x -y )·xy (x -y ) =3xy .把x =3+2,y =3-2代入,可得:原式=3(3+2)(3-2)=3.16.解:原式=m -33m (m -2)÷⎝ ⎛⎭⎪⎫m 2-4m -2-5m -2=m -33m (m -2)·m -2(m +3)(m -3)=13m (m +3). ∵m 是方程x 2+2x -3=0的根,∴m =-3或m =1.当m =-3时,原式无意义;当m =1时,原式=13m (m +3)=13×1×(1+3)=112. 17.12 -12 1021. 解析:∵1()2n -1()2n +1=12()2n -1-12()2n +1 =a 2n -1+b 2n +1, ∴a =12,b =-12. ∴m =11×3+13×5+15×7+…+119×21=⎝⎛⎭⎫12-16+⎝⎛⎭⎫16-110+…+⎝⎛⎭⎫138-142=1021. 第4讲 二次根式【演练·巩固提升】1.D 2.B 3.B 4.C 5.A 6.D 7.2 8.5 9.2 210.1 解析:原式=||a -2+||1-a =2-a +a -1=1.11.解:原式=2 2÷12+3×(2-2 2)=4 2+6-6 2 =6-2 2.12.解:(1)原式=24×13-4×24×1=2 2-2= 2. 13.D 14.B15.9 解析:由题意,得x -3≥0,且3-x ≥0,得x =3,故y =2.∴x y =9. 16.14解析:由题意,得x -4≥0,且4-x ≥0. 解得x ≥4,且x ≤4.所以x =4.所以y =-2.所以(x +y )y =(4-2)-2=14. 17.解:第1个数:当n =1时,15⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1+52n -⎝ ⎛⎭⎪⎫1-52n =15⎣⎢⎡⎦⎥⎤1+52-1-52 =15×5=1. 第2个数:当n =2时,15⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1+52n -⎝ ⎛⎭⎪⎫1-52n =15⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1+522-⎝ ⎛⎭⎪⎫1-522=15⎝ ⎛⎭⎪⎫1+52-1-52⎝ ⎛⎭⎪⎫1+52+1-52 =15×5×1=1. 第一章基础题强化提高测试1.A 2.B 3.A 4.B 5.D 6.D7.x ≠5 8.±3 9.2005 10.211.解:原式=mn ()m 2-4= mn (m +2)(m -2).12.解:原式=x -3(x +3)(x -3)+6(x +3)(x -3)=x -3+6(x +3)(x -3)=x +3(x +3)(x -3)=1x -3. 13.解:原式=4a 2-b 2+b 2-2ab =2a (2a -b ). 当a =-2,b =1时,原式=2×(-2)×[2×(-2)-1]=20.14.解:原式=3+2×22+3-(-3)-2 3+1 =3+1+3+3-2 3+1=5.15.解:原式=⎣⎢⎡⎦⎥⎤(a +b )(a -b )(a -b )2-a a -b ·a (a -b )b 2 =⎝ ⎛⎭⎪⎫a +b a -b -a a -b ·a (a -b )b2=b a -b ·a (a -b )b 2=a b . ∵a +1+|b -3|=0,∴a +1=0,b -3=0.解得a =-1,b = 3.∴原式=-13=-33.。
中考总复习《数与式》教案

中考总复习教案第一章数与式《数与式》是初中数学的基础知识,是中考命题的重要内容之一,年年考查,北京近三年来在新课标中考试题中“数与式”部分的权重:35%左右,分量之中,不容忽视!一、本章知识要点与课时安排(大致安排五课时左右)(一)实数(一课时)(二)整式与因式分解(一至两课时)(三)分式与二次根式(两课时)(四)数式规律的探索(可以揉到前面几讲中去讲,也可以单设一课时)说明:您可以根据自己学生的学习程度,合理安排复习内容.二、课时教案第一课时实数教学目的1.理解有理数的意义,了解无理数等概念。
2.能用数轴上的点表示有理数,掌握相反数的性质,会求实数的绝对值.3。
会用科学记数法表示数。
4.会比较实数的大小,会利用绝对值知识解决简单化简问题.5.掌握有理数的运算法则,并能灵活的运用.教学重点与难点重点:数轴、绝对值等概念及其运用,有理数的运算。
难点:利用绝对值知识解决简单化简问题,实数的大小比较.教学方法:用例习题串知识(复习时要注意知识综合性的复习).教学过程(一)知识梳理1。
2.(二)例习题讲解与练习例1在3.14,1-,0,,cos30°,,,0.2020020002…(数字2后面“0”的个数逐次多一个)这八个数中,哪些是有理数?哪些是无理数?(考查的知识点:有理数、实数等概念.考查层次:易)(最基本的知识,由学生口答,师生共同归纳、小结)【归纳】:(1)整数与分数统称为有理数(强调数字0的特点);无限不循环小数是无理数。
注意:常见的无理数有三类①π,…②,,…,(不是无理数)③0.1010010001…(数字1后面“0”的个数逐次多一个).(2)一个无理数加、减、乘、除一个有理数(0除外)仍是无理数(是无理数).注:此题可以以其它形式出现,如练习题中2或12题等例2(1)已知a—2与2a+1互为相反数,求a的值;(2)若x、y是实数,且满足(x—2)2+=0,求(x+y)2的值.(考查的知识点:相反数的性质、二次根式的性质、非负数等概念.考查层次:易)(这是基础知识,由学生解答,老师总结)【总结】:(1)对于一个具体的数,要会求它的相反数(倒数、绝对值、平方根与算术平方根),对于一个代数式,也要会求它的相反数.解答是要注意从概念中蕴涵的数学关系入手:a、b互为相反数a+b=0;a、b互为倒数a·b=1.(2)非负数概念:例3 (1)若数轴上的点A表示的数为x,点B表示的数为—3,则A与B两点间的距离可表示为________________.(2)实数a、b在数轴上分别对应的点的位置如图所示,请比较a,—b,a-b,a+b的大小(用“<"号连接)___________________.(3)①化简_________;②=__________;③估计与0.5的大小关系是0.5(填“ > "、“="、“〈”) .(答案:(1);(2)a+b〈a〈-b<a—b;(3)①;②;③>)(考查的知识点:数轴、绝对值、比较大小等概念,无理数的估算、有理数的运算法则等。
中考总复习 第一章数与式

多项式的乘方只涉及
(a b) 2 a 2 2ab b 2 , (a b c) 2 a 2 b 2 c 2 2ab 2bc 2ca.
(二)讲解知识要点
| a | | b | (a, b同号) ab | a | | b | (a, b异号) 0(a或b为零)
a 1 a (b 0) b b (5)乘方的相关运算性质 ①乘方的意义 a n aa a
(4)除法法则
n个
1 a n an ②运算性质: a 1(a 0) ;( ) n . ;a n n (a 0, n为正整数 ). a b b
a m a n a m n (m, n是整数) a m a n a mn (a 0, m, n是整数)
多项式乘(除)以单项式, 先把这个多项式的每一项乘(除)以这个单 项式,再把所得的积(商)相加. 多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式 的每一项,再把所得的积相加. 遇到特殊形式的多项式乘法,还可以直接算: ( x a)(x b) x 2 一、知识点 因式分解定义,提取公因式、应用公式法、分组分解法、二次三项 式的因式(十字相乘法) 、因式分解一般步骤。 二、课标要求 理解因式分解的概念, 掌握提取公因式法、 公式法等因式分解方法, 能把简单多项式分解因式。 三、考查重点与常见题型 考查因式分解能力,在中考试题中,因式分解出现的频率很高。重 点考查的分式提取公因式、 应用公式法、 分组分解法及它们的综合运用。 习题类型以填空题为多,也有选择题和解答题。 四、过程 (一)自学并完成下列知识要点: 因式分解知识点 多项式的因式分解,就是把一个多项式化为几个整式的积.分解因 式要进行到每一个因式都不能再分解为止.分解因式的常用方法有: (1)提公因式法 如多项式 am bm cm m(a b c), 其中 m 叫做这个多项式各项的公因式, m 既可以是一个单项式,也可 以是一个多项式. (2)运用公式法,即用
初中数学复习资料大全

初中数学总复习资料㈠数与代数⒈数与式⑴有理数:有限或不限循环性数(无理数:无限不循环小数) ⑵数轴:“三要素” ⑶相反数⑷绝对值:│a │= a(a≥0) │a │=-a(a<0) ⑸倒数 ⑹指数① 零指数:0a =1(a ≠0) ②负整指数: (a ≠0,n 是正整数) ⑺完全平方公式:2222)(b ab a b a +±=± ⑻平方差公式:(a+b )(a-b )=22b a - ⑼幂的运算性质: ①ma ·na =nm a+ ②m a ÷n a =nm a- ③n m a )(=mna④nab )(=n a nb ⑤n nn ba b a =)(⑽科学记数法:na 10⨯(1≤a <10,n 是整数) ⑾算术平方根、平方根、立方根、 ⑿ban d b m c a n d b n m d c b a =++++++⇒≠+++===ΛΛΛΛ:)0(等比性质⒉方程与不等式 ⑴一元二次方程①定义及一般形式:)0(02≠=++a c bx ax ②解法: 1.直接开平方法. 2.配方法 3.公式法:)04(24222,1≥--±-=ac b aac b b x4.因式分解法.③根的判别式:ac b 42-=∆>0,有两个解。
ac b 42-=∆<0,无解。
ac b 42-=∆=0,有1个解。
④维达定理:acx x a b x x =⋅-=+2121,⑤常用等式:2122122212)(x x x x x x -+=+ 212212214)()(x x x x x x -+=- ⑥应用题1.行程问题:相遇问题、追及问题、水中航行:水速船速顺+=v ;水速船速逆-=v2.增长率问题:起始数(1+X)=终止数3.工程问题:工作量=工作效率×工作时间(常把工作量看着单位“1”)。
4.几何问题⑵分式方程(注意检验) 由增根求参数的值: ①将原方程化为整式方程②将增根带入化间后的整式方程,求出参数的值。
广东省中考数学总复习第一部分教材梳理第一章数与式课时5分式课件

考点2 分式的化简求值(高频考点)
1.(2016广东)先化简,再求值:
2. (2015广东)先化简,再求值: 其中
3. (2014广东)先化简,再求值: 其中
解题指导: 本考点在近三年广东中考中均有出现,是中考的高频考点,其 题型一般为解答题,难度中等. 解此类题的关键在于熟练掌握分式的混合运算法则. 熟记以下 要点: (1)分式的混合运算法则:先算乘方,再算乘除,最后算加 减,若有括号,要先算括号里面的; (2)化简分式时,要正确运算,正确通分和约分,如果要变 号,变号要彻底,不要只变部分.
考点巩固训练
考点1 分式有意义或值为零的条件
1. 使分式
A. x≠0 C. x≠1
有意义的x的取值为 B. x≥-2 D. x≠-2
(D)
2. 若分式 A. -1来自的值为零,则x的值为B. 1或-1
(C)
C. 1
D. 1和-1
3. 使分式
A. x≠1
有意义,x应满足的条件是( D )
B. x≠2
C. x≠1或x≠2
2. 分式的基本性质:
(M是不为零的整
式).
3. 约分:把分式的___分__子_____与___分__母_____中的公因式约去,
叫做分式的约分.
4. 通分:利用分式的__基__本__性__质__,使分子和分母同时乘适当 的整式,不改变分式的值,把异分母的分式化成___同__分__母___的 分式,这一过程叫做分式的通分. 5. 最简公分母:一般取各分式分母的所有因式的_最__高__次__幂___ 的_____积_____作为公分母,它叫做最简公分母. 6. 最简分式:一个分式的分子与分母没有___公__因__式___时,这 个分式叫做最简分式.
2016年中考数学基础知识点总结

2016年中考数学基础知识点总结2016年中考数学基础知识点总结一、初中数学基本知识㈠、数与代数A、数与式:1、有理数有理数:①整数→正整数/0/负整数②分数→正分数/负分数数轴:①画一条水平直线,在直线上取一点表示0(原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到数轴。
②任何一个有理数都可以用数轴上的一个点表示。
③如果两个数只有符号不同,那么我们称其中一个数为另外一个数的相反数,也称这两个数互为相反数。
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点距离相等。
④数轴上两个点表示的数,右边的总比左边的大。
正数大于0,负数小于0,正数大于负数。
绝对值:①在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值。
②正数的绝对值是他的本身、负数的绝对值是他的相反数、0的绝对值是0。
两个负数比较大小,绝对值大的反而小。
有理数的运算:加法:①同号相加,取相同的符号,把绝对值相加。
②异号相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
③一个数与0相加不变。
减法:减去一个数,等于加上这个数的相反数。
乘法:①两数相乘,同号得正,异号得负,绝对值相乘。
②任何数与0相乘得0。
③乘积为1的两个有理数互为倒数。
除法:①除以一个数等于乘以一个数的倒数。
②0不能作除数。
乘方:求N个相同因数A的积的运算叫做乘方,乘方的结果叫幂,A叫底数,N叫次数。
混合顺序:先算乘法,再算乘除,最后算加减,有括号要先算括号里的。
2、实数无理数:无限不循环小数叫无理数平方根:①如果一个正数X的平方等于A,那么这个正数X就叫做A的算术平方根。
②如果一个数X的平方等于A,那么这个数X就叫做A的平方根。
③一个正数有2个平方根/0的平方根为0/负数没有平方根。
④求一个数A的平方根运算,叫做开平方,其中A 叫做被开方数。
立方根:①如果一个数X的立方等于A,那么这个数X就叫做A的立方根。
【中考易】广东省2016中考数学总复习 第一章 数与式 第1课时 实数的有关概念课件

O 0.0025 =2.5× .
103
O
O 7.一个近似数,最后一位10数3字是什0.么00位0,2就0精1 确到2哪, 0一1位10.如4:近
似精考数确点0到.四5千01:分,近最后似一位数位,与数也字精可1以确是说在度精千确分到位0.,00就1.说这个近似数
O 例1:(2014•珠海市)- 的相反数是
1.(2015•自贡市) -的1倒数是( ) 2
2.(2014•泉州市)2014的相反数是( )
3.(2015·德州市) 的结果是( )
-1 2
O 4. (2013•梅州市)四个数-1,0, , 1
理数的是( )
2
2中为无
O 5.(2014•内江市)一种微粒的半径是 0.00004米, 这个数据用科学记数法表示为期( )
O 5.绝对值:
a
a ab
ba
O 如:
3.
3
__a__(a 0),
a __0__(a 0),
_a___(a 0).
考点三:科学记数法
O 6.把一个整数或有限小数记成
的形a式,其10中n
为整数1,这|种a记| 1数0法, n叫科学记数法.如:2300 =2.3 .
考点一:实数的概念及分类
有理数
负整数 正分数
无限不循环小数
正分数
正无理数
0
负整数
负实数
负分数
考点二:数轴、相反数、绝对值、倒数
O 3.规定了原点、正方向和单位长度的直线叫数轴,实数与,叫做互为相反数.0的相反数是0; 互为相反数的两个数的和为0.如: 的相反数 是 . 的相反数是 .
()
O 例2:(2015•上海市)下列实数中,是有理数的为 ()
2016中考数学数与运算考点汇总

2016年中考数学数与运算考点汇总考点1:数的整除性以及有关概念(本考点含整数和整除、分解素因数)考核要求:(1)知道数的整除性、奇数和偶数、质数和合数、倍数和因数、公倍数和公因数等的意义;(2)知道能被2或3、5、9整除的正整数的特征;(3)会分解素因数;(4)会求两个正整数的最小公倍数和最大公因数.具体问题讨论涉及的正整数一般不大于100.考点2:分数的有关概念、基本性质和运算考核要求:(1)掌握分数与小数的互化,初步体会转化思想;(2)掌握异分母分数的加减运算以及分数的乘除运算.考点3:比、比例和百分比的有关概念及比例的性质考核要求:(1)理解比、比例、百分比的有关概念;(2)比例的基本性质.对合分比定理、等比定理不作教学要求.考点4:有关比、比例、百分比的简单问题考核要求:(1)考查比、比例的实际应用,结合实际掌握求合格率、出勤率、及格率、盈利率、利率的方法;(2)会解决有关比、比例、百分比的简单问题,了解百分比在经济、生活中的一些基本常识及简单应用.考点5:有理数以及相反数、倒数、绝对值等有关概念,有理数在数轴上的表示考核要求:(1)理解相反数、倒数、绝对值等概念;(2)会用数轴上的点表示有理数.注意:(1)去掉绝对值符号后的正负号的确定,(2)0没有倒数.考点6:平方根、立方根、次方根的概念考核要求:(1)理解平方根、立方根、次方根的概念;(2)理解开方与方根的意义,注意平方根和算术平方根的联系和区别.考点7:实数的概念考核要求:理解实数的有关概念.注意:判断无理数不看形式,要看实质.考点8:数轴上的点与实数的一一对应考核要求:掌握实数与数轴上的点的一一对应关系.解题关键是判断实数的大小.考点9:实数的运算考核要求:(1)掌握实数的加、减、乘、除、乘方、开方等运算的法则、性质(交换律、结合律、分配律、互逆性、数0和数1的特征)、运算顺序,明确有关运算性质的推广和运用;(2)会用计算器进行实数的运算.注意:(1)利用运算定律,力求简便计算和巧算,(2)运算要稳中求快,准确无误.考点10:科学记数法考核要求:(1)理解科学记数法的意义;(2)会用科学记数法表示较大的数.精心整理,仅供学习参考。
初中数学复习资料大全

初中数学总复习资料⒈数与式⑴有理数:有限或不限循环性数(无理数:无限不循环小数) ⑵数轴:“三要素” ⑶相反数⑷绝对值:│a │= a(a≥0) │a │=-a(a<0) ⑸倒数 ⑹指数① 零指数:0a =1(a ≠0) ②负整指数: (a ≠0,n 是正整数) ⑺完全平方公式:2222)(b ab a b a +±=± ⑻平方差公式:(a+b )(a-b )=22b a -⑼幂的运算性质: ①ma ·na =nm a+ ②m a ÷n a =nm a- ③n m a )(=mna④nab )(=n a nb ⑤n nn ba b a =)(⑽科学记数法:na 10⨯(1≤a <10,n 是整数) ⑾算术平方根、平方根、立方根、 ⑿ban d b m c a n d b n m d c b a =++++++⇒≠+++=== :)0(等比性质 ⒉方程与不等式 ⑴一元二次方程①定义及一般形式:)0(02≠=++a c bx ax ②解法: 1.直接开平方法. 2.配方法 3.公式法:)04(24222,1≥--±-=ac b aac b b x4.因式分解法. ③根的判别式:ac b 42-=∆>0,有两个解。
ac b 42-=∆<0,无解。
ac b 42-=∆=0,有1个解。
④维达定理:acx x a b x x =⋅-=+2121,⑤常用等式:2122122212)(x x x x x x -+=+ 212212214)()(x x x x x x -+=- ⑥应用题1.行程问题:相遇问题、追及问题、水中航行:水速船速顺+=v ;水速船速逆-=v2.增长率问题:起始数(1+X)=终止数3.工程问题:工作量=工作效率×工作时间(常把工作量看着单位“1”)。
4.几何问题⑵分式方程(注意检验) 由增根求参数的值: ①将原方程化为整式方程②将增根带入化间后的整式方程,求出参数的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 11.
•
.
考点四:二次根式的运算 • 12.二次根式的加减法:一般先把二次根式 化为最简二次根式,再把同类二次根式合并. • 13.二次根式的乘法法则: a b ab (a 0, b 0) . • • 14.二次根式的除法: b b • (或 b a b a ). a a • 其中a >0;b 0.
3
7
考点一:平方根、算术平方根与立方根
• 1.平方根:一个数x的平方等于a,那么x叫做a的平 方根,记作 a . • 2.算术平方根: 一个正数x的平方等于a,那么x叫 做a的算术平方根,记作 • 0的算术平方根是0. • 3.立方根:一个数x的立方等于a ,那么叫做的立方 平方根、算术平方根与立方根
• 4.填表:
a
0
无
3
a
0
3
a
考点二:二次根式的有关概念
• 5.二次根式的定义:形如 式. • 6.最简二次根式:
a (a 0)
的式子叫二次根
• 满足下列两个条件的二次根式,叫做最简二次根式:
• (1)被开方数的因数是整数,因式是整式; • (2)被开方数中不含能开得尽方的因数和因式. • 7.同类二次根式:几个二次根式化成最简二次根式 以后,如果被开方数相同,那么这几个二次根式就 叫做同类二次根式.
x2
2
考点三:二次根式的性质 • 8. • 9. • 10.
a
2
2
|a| 0 a ___ ___ a 0 ,
-a ___ a 0 ;
a a 0 ; a a 0 , ___
a b a 0, b 0 ; ab ____
