基于BP神经网络的系统建模辨识与预测仿真matlab程序及仿真结果
基于MATLAB的BP神经网络的仿真与实现论文

2012届毕业设计论文基于MatLab的BP神经网络的仿真与实现院、部:计算机与信息科学学院学生姓名:指导教师:职称讲师专业:计算机科学与技术班级:完成时间:2012年5月摘要摘要本文首先说明课题研究的目的和意义,评述课题的国内外研究现状,引出目前存在的问题。
然后分析了神经网络算法的基本原理,给出经典神经网络算法的具体实现方法,总结神经网络算法的特点,并给出神经网络算法的基本流程。
采用Matlab软件编程实现BP神经网络算法。
将神经网络算法应用于函数逼近,样本分类和样本含量估计问题中,并分析相关参数或算法对运行结果的影响。
最后对BP神经网络算法进行了展望。
关键字: 神经网络;BP神经网络;函数逼近;样本分类ABSTRACTABSTRACTFirst, the research purpose and significance of neural network is expounded in this article. Commentary studies current situation at the problem home and abroad. Leads to the existing problems. and then have analyzed algorithmic basal principle of neural networks, Give algorithmic concert of classics neural networks out the realization method. Summing up the characteristics of neural network algorithm. Neural network algorithm is given the basic processes. The arithmetic of BP neural network is realized in Matlab software. The algorithm applies of BP neural networks to the function approximation problem,Sample classification and computes the swatch content. And analysis of relevant parameters on the results of algorithm. Finally, The BP neural network algorithm is Outlook.Key words: Neural network;BP neural network;Function approximation; Sample classfication目录摘要 (I)ABSTRACT........................................................ I I 目录............................................................ I II 前言.. (V)第一章绪论................................................... - 1 -1.1 人工神经网络的研究背景和意义............................ - 1 -1.2 神经网络的发展与研究现状................................ - 2 -1.2.1 神经网络的发展..................................... - 2 -1.2.2 神经网络的现状.................................... - 3 -1.3 神经网络的研究内容和目前存在的问题...................... - 3 -1.3.1 神经网络的研究内容................................. - 3 -1.3.2 神经网络研究目前存在的问题......................... - 3 -1.4 神经网络的应用.......................................... - 4 - 第二章神经网络结构及BP神经网络................................ - 5 -2.1 神经元与网络结构........................................ - 5 -2.1.1 生物神经元......................................... - 5 -2.1.2 人工神经元......................................... - 6 -2.1.3人工神经网络的构成................................. - 6 -2.2 BP神经网络及其原理...................................... - 9 -2.2.1 BP神经网络定义.................................... - 9 -2.2.2 BP神经网络模型及其基本原理........................ - 9 -2.3 BP神经网络的主要功能................................... - 10 -2.4 BP网络的优点以及局限性................................. - 11 - 第三章 BP神经网络在实例中的应用............................... - 13 -3.1 基于MATLAB的BP神经网络工具箱函数..................... - 13 -3.1.1 BP网络创建函数................................... - 14 -3.1.2 神经元上的传递函数................................ - 14 -3.1.3 BP网络学习函数................................... - 15 -3.1.4 BP网络训练函数................................... - 15 -3.2 BP网络在函数逼近中的应用............................... - 15 -3.2.1 问题的提出........................................ - 15 -3.2.2 基于BP神经网络逼近函数........................... - 16 -3.2.3 不同频率下的逼近效果.............................. - 19 -3.2.4 讨论............................................. - 21 -3.3仿真实验................................................ - 21 -3.3.1 BP神经网络MATLAB设计............................ - 21 -3.3.2 各种BP学习算法MATLAB仿真........................ - 23 -3.3.3 各种算法仿真结果比较与分析........................ - 26 -3.3.4 调整初始权值和阈值的仿真.......................... - 27 -3.3.5 其他影响因素仿真.................................. - 29 -3.4 BP网络在样本含量估计中的应用........................... - 30 -3.4.1 问题的提出........................................ - 30 -3.4.2 基于BP神经网络对胆固醇含量估计................... - 31 -3.4.3 不同条件下的输出结果.............................. - 33 -3.4.4 讨论.............................................. - 35 -3.5 BP神经网络在样本分类中的应用........................... - 36 -3.5.1问题的提出........................................ - 36 -3.5.2 基于BP神经网络的样本分类......................... - 36 -3.5.3不同算法条件下的不同测试过程以及输出结果.......... - 38 -3.5.4讨论.............................................. - 42 - 结论........................................................... - 43 - 参考文献 (1)致谢 (2)前言前言BP神经网络是目前人工神经网络模式中最具代表性,应用最广泛的一种模型,具有自学习、自组织、自适应和很强的非线性映射能力,可以以任意精度逼近任意连续函数.近年来,为了解决BP网络收敛速度慢,训练时间长等不足,提出了许多改进算法.然而,在针对实际问题的BP网络建模过程中,选择多少层网络,每层多少个神经元节点,选择何种传递函数等,均无可行的理论指导,只能通过大量的实验计算获得.MATLAB中的神经网络工具箱(Neural NetworkToolbox,简称NNbox),为解决这一问题提供了便利的条件.神经网络工具箱功能十分完善,提供了各种MATLAB函数,包括神经网络的建立、训练和仿真等函数,以及各种改进训练算法函数,用户可以很方便地进行神经网络的设计和仿真,也可以在MATLAB源文件的基础上进行适当修改,形成自己的工具包以满足实际需要。
用matlab编BP神经网络预测程序

求用matlab编BP神经网络预测程序求一用matlab编的程序P=[。
];输入T=[。
];输出% 创建一个新的前向神经网络net_1=newff(minmax(P),[10,1],{'tansig','purelin'},'traingdm')% 当前输入层权值和阈值inputWeights=net_1.IW{1,1}inputbias=net_1.b{1}% 当前网络层权值和阈值layerWeights=net_1.LW{2,1}layerbias=net_1.b{2}% 设置训练参数net_1.trainParam.show = 50;net_1.trainParam.lr = 0.05;net_1.trainParam.mc = 0.9;net_1.trainParam.epochs = 10000;net_1.trainParam.goal = 1e-3;% 调用TRAINGDM 算法训练BP 网络[net_1,tr]=train(net_1,P,T);% 对BP 网络进行仿真A = sim(net_1,P);% 计算仿真误差E = T - A;MSE=mse(E)x=[。
]';%测试sim(net_1,x) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%不可能啊我200928对初学神经网络者的小提示第二步:掌握如下算法:2.最小均方误差,这个原理是下面提到的神经网络学习算法的理论核心,入门者要先看《高等数学》(高等教育出版社,同济大学版)第8章的第十节:“最小二乘法”。
3.在第2步的基础上看Hebb学习算法、SOM和K-近邻算法,上述算法都是在最小均方误差基础上的改进算法,参考书籍是《神经网络原理》(机械工业出版社,Simon Haykin著,中英文都有)、《人工神经网络与模拟进化计算》(清华大学出版社,阎平凡,张长水著)、《模式分类》(机械工业出版社,Richard O. Duda等著,中英文都有)、《神经网络设计》(机械工业出版社,Martin T. Hargan等著,中英文都有)。
用matlab编程实现的基于BP神经网络的预测仿真

0.7753
网络训练过程中的误差记录:
网络实际输出与期望输出的模拟对比:
y(i,j)=1/(1+exp(-net)); %隐含层输出
end
Y(i,:)=[y(i,:),1]; %带阈值隐含层输出
for j=1:outputNums
net=Y(i,:)*W2(:,j); %输出层神经元的输入
legend('T1 is desired output ','O1 is Network real output');
程序运行结果:
网络调整后的权值和阈值:
w1 =
-1.8970 -0.3536 -0.7324 -0.2796 -0.8915 -2.5360
zl(k)=z(k+2); %给样本矩阵ZL赋值
end
HL=(hl-min(min(hl)))/(max(max(hl))-min(min(hl))); %数据归一化
ZL=(zl-min(zl))/(max(zl)-min(zl)); %数据归一化
xlabel('k');ylabel('error');
figure(2);
k=1:H;
plot(k,T1,k,O1,'*'); %期望输出值和BP网络实际输出值
xlabel('k');ylabel('T1andO1');title('BP simulation');
W1(m,n)=W1(m,n)+lc*DW1(m,n)*P(i,m); %隐含层权值阈值的调整
end
基于matlab实现BP神经网络模型仿真

基于BP神经网络模型及改进模型对全国历年车祸次数预测一、背景我国今年来随着经济的发展,汽车需求量不断地增加,所以全国每年的车祸次数也被越来越被关注,本文首先搜集全国历年车祸次数,接着通过这些数据利用BP神经网络模型和改进的径向基函数网络进行预测,最后根据预测结果,分析模型的优劣,从而达到深刻理解BP神经网络和径向基函数网络的原理及应用。
所用到的数据即全国历年车祸次数来自中国汽车工业信息网,网址如下:制作历年全国道路交通事故统计表如下所示:二、问题研究(一)研究方向(1)通过数据利用BP神经网络模型预测历年全国交通事故次数并与实际值进行比较。
(2)分析BP神经网络模型改变训练函数再进行仿真与之前结果进行对比。
(3)从泛化能力和稳定性等方面分析BP神经网络模型的优劣。
(4)利用径向基函数网络模型进行仿真,得到结果与采用BP神经网络模型得到的结果进行比较。
(二)相关知识(1)人工神经网络人工神经网络是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模型。
在工程与学术界也常直接简称为神经网络或类神经网络。
神经网络是一种运算模型,由大量的节点(或称神经元)和之间相互联接构成。
每个节点代表一种特定的输出函数,称为激励函数(activation function)。
每两个节点间的连接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。
网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。
而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
人工神经网络有以下几个特征:(1)非线性关系是自然界的普遍特性。
大脑的智慧就是一种非线性现象。
人工神经元处于激活或抑制二种不同的状态,这种行为在数学上表现为一种非线性网络关系。
具有阈值的神经元构成的网络具有更好的性能,可以提高容错性和存储容量。
(2)非局限性一个通常由多个神经元广泛连接而成。
一个系统的整体行为不仅取决于单个神经元的特征,而且可能主要由单元之间的相互作用、相互连接所决定。
基于MATLAB的BP神经网络实现研究

方法与实验设计
基于MATLAB的BP神经网络实现主要包括以下几个步骤:
1、数据预处理:首先需要对数据进行预处理,包括数据清洗、归一化等操 作。
2、网络设计:根据问题特点选择合适的网络结构,并确定输入层、输出层 和隐藏层的节点数。
3、训练模型:使用MATLAB中的神经网络工具箱进行模型训练。
2、在防止过拟合方面,可以研究更有效的正则化方法和技术,以避免模型 在训练过程中产生过拟合问题。
3、在网络结构设计方面,可以研究更加智能的自适应网络结构设计方法, 以简化人工设计网络的复杂度。
4、可以进一步拓展BP神经网络在其他领域的应用研究,例如自然语言处理、 生物信息学等。
谢谢观看
结论与展望
本次演示研究了基于MATLAB的BP神经网络实现方法,通过实验设计和实验结 果分析,可以得出以下结论:
1、BP神经网络在解决分类、逼近和优化等问题方面具有较好的性能,证实 了其在实际应用中的价值。
2、在超参数调整方面,学习率和迭代次数对模型性能具有重要影响,需要 根据实际问题进行调整。
2、函数逼近:BP神经网络可以用于逼近复杂的非线性函数。例如,在控制 系统、信号处理等领域,可以利用BP神经网络对系统进行建模和预测。
3、优化问题:BP神经网络可以应用于求解各种优化问题。例如,利用BP神 经网络实现函数的最小化、多目标优化等。
然而,目前的研究还存在着一些问题。首先,由于BP神经网络的训练速度较 慢,可能需要进行大量的迭代才能得到较好的结果。其次,BP神经网络的训练过 程中容易出现过拟合问题,这可能导致模型的泛化能力下降。最后,BP神经网络 的性能受到初始参数的影响较大,如何选择合适的参数也是亟待解决的问题。
4、模型评估与优化:通过验证数据集评估模型的性能,并进行参数调整和 优化。
基于MATLAB的BP神经网络建模及系统仿真 (1)

文章编号:1001—9944(2001)01—0034—03基于M AT LAB 的BP 神经网络建模及系统仿真Ξ侯北平,卢 佩(天津轻工业学院自动化系,天津 300222)摘 要:将M A TLAB 中的神经网络工具箱和Si m ulink 有机结合起来,并充分利用它们各自的优势,实现了神经网络控制系统(NN CS )的计算机仿真。
具体仿真实例表明,M A TLAB 是进行人工神经网络计算机仿真的有效工具。
关键词:神经网络;BP 网;M A TLAB ;Si m ulink ;系统仿真中图分类号:T P 391.9 文献标识码:B1 引言控制系统的模拟和仿真是进行科学研究的重要手段。
近年来,几乎所有控制系统的高品质控制均离不开系统仿真研究。
通过仿真研究可以对照比较各种控制方案,优化并确定相关控制参量。
一般来说,对控制系统进行计算机仿真首先应建立系统模型,然后依据模型编制仿真程序,充分利用计算机对其进行动态模拟并显示结果。
对于一个闭环控制系统,我们的控制目标是它的输出曲线是一条从0开始,无限接近于给定值,且超调量极小的上升曲线,这主要是由控制器的输出决定的。
在输入偏差不断变化的情况下,设计什么样的控制器才能达到所需的控制精度和要求呢?在本文中,我们将B P 算法引入控制策略,并建立一个B P 网络模型,利用M A TLAB 中的神经网络工具箱对其进行学习和训练,根据训练出的参量构造一网络控制器,并在Si m u link 环境下组成闭环控制系统,进行系统仿真和动态模拟,观察其品质。
2 BP 网络分析及模型建立B P 网络是目前应用最广泛的神经网络模型。
它的学习规则就是通过反向传播(B P )来调整网络的权值和阈值使网络误差的平方和最小,这是通过在最速下降方向上不断调整网络的权值和阈值来实现的。
B P 网络具有强大的非线性映射能力和泛化功能,任一连续函数或映射均可采用三层网络加以实现。
这样,把它作为控制器就找到了很好的答案。
BP神经网络实验详解(MATLAB实现)

BP神经网络实验详解(MATLAB实现)BP(Back Propagation)神经网络是一种常用的人工神经网络结构,用于解决分类和回归问题。
在本文中,将详细介绍如何使用MATLAB实现BP神经网络的实验。
首先,需要准备一个数据集来训练和测试BP神经网络。
数据集可以是一个CSV文件,每一行代表一个样本,每一列代表一个特征。
一般来说,数据集应该被分成训练集和测试集,用于训练和测试模型的性能。
在MATLAB中,可以使用`csvread`函数来读取CSV文件,并将数据集划分为输入和输出。
假设数据集的前几列是输入特征,最后一列是输出。
可以使用以下代码来实现:```matlabdata = csvread('dataset.csv');input = data(:, 1:end-1);output = data(:, end);```然后,需要创建一个BP神经网络模型。
可以使用MATLAB的`patternnet`函数来创建一个全连接的神经网络模型。
该函数的输入参数为每个隐藏层的神经元数量。
下面的代码创建了一个具有10个隐藏神经元的单隐藏层BP神经网络:```matlabhidden_neurons = 10;net = patternnet(hidden_neurons);```接下来,需要对BP神经网络进行训练。
可以使用`train`函数来训练模型。
该函数的输入参数包括训练集的输入和输出,以及其他可选参数,如最大训练次数和停止条件。
下面的代码展示了如何使用`train`函数来训练模型:```matlabnet = train(net, input_train, output_train);```训练完成后,可以使用训练好的BP神经网络进行预测。
可以使用`net`模型的`sim`函数来进行预测。
下面的代码展示了如何使用`sim`函数预测测试集的输出:```matlaboutput_pred = sim(net, input_test);```最后,可以使用各种性能指标来评估预测的准确性。
基于MATLAB的BP神经网络预测系统的设计

第25卷第4期 计算机应用与软件Vo l 125No .42008年4月 Co m puter Applicati o ns and Soft w are Apr .2008基于MATLAB 的BP 神经网络预测系统的设计李 萍 曾令可 税安泽 金雪莉 刘艳春 王 慧(华南理工大学 广东广州510640)收稿日期:2006-04-25。
李萍,博士,主研领域:材料技术装备及计算机在材料中的应用。
摘 要 利用MAT LAB 设计了BP 神经网络预测系统。
介绍了MATLAB 的BP 神经网络工具箱函数和图形用户界面,详细介绍了BP 神经网络预测系统的设计,并对所设计的预测系统进行了性能评价。
系统具有良好的性能,在很多领域可以发挥较大的作用。
关键词 MATLAB BP 神经网络 预测DESI GN OF FORECAST S YSTEM OF BACK PROPAGATI ON NEURALNET WORK BASED ON MATLABL i Ping Zeng L i n gke ShuiAnze Ji n Xueli Liu Y anchun W ang H u i(S ou t h Ch i na Un i versit y of T e chnolo gy,G uangzhou 510640,G uangd ong,Ch i na )Abstrac t Forecast syste m of Back P ropaga tion neural ne t w ork is developed by MATLAB .The functions i n the too l box o f Back P ropagati on neura l net wo rk and the g raph ica l use r i nter f aces o fMATLAB are i ntroduced .T he desi gn o f forecast system o f Back P ropagati on neura l net wo rk is ana l yzed i n deta i,l and t he perfo r m ance o f the f o recast syste m is ev al uated .T he resu lt i nd i cates tha t the sy stem has good pe rf o r m ance ,and it is use f u l in m any fi e l ds .K eywords MATLAB Back propaga ti on neura l net w ork F orecast0 前 言在系统辨识和预测中,需要建立性能好的、稳定的模型对系统进行准确地辨识和预测。
基于MATLAB的BP人工神经网络设计

基于MATLAB的BP人工神经网络设计目录
一、介绍1
1.1研究背景1
1.2BP神经网络1
二、BP神经网络的设计3
2.1BP神经网络模型原理3
2.2BP神经网络模型参数5
2.3权重偏置矩阵更新方法6
三、MATLAB实现BP神经网络8
3.1MATLAB软件环境8
3.2代码实现8
3.3实验结果10
四、结论及展望12
一、介绍
1.1研究背景
人工神经网络(ANNs)被归类为一种模拟生物神经网络的模型,具有高度学习能力和自适应性,用于解决有关模式识别、拟合曲线、识别图像、辨识声音、推理、预测等问题。
在这些任务中,Backpropagation (BP)神
经网络是应用最广泛的神经网络结构。
BP神经网络是一种反向传播的多
层前馈神经网络,它的结构简单、计算方法有效,可以学习训练集的特征,在测试集上取得较好的精度。
1.2BP神经网络
BP神经网络(或叫反向传播网络,BP网络)是一种多层前馈神经网络,它是由对神经网络训练的单步算法“反向传播算法”δ开发的。
BP神经
网络由输入层、隐层和输出层构成,它将被调节的参数及权值分配给每个
网络层,以调整网络性能的训练过程。
bp神经网络matlab实例(bp神经网络matlab实例)

bp神经网络matlab实例(bp神经网络matlab实例)Case 1 training BP network by momentum gradient descent algorithm.Training samples are defined as follows:Input vector asP =[-1 -2 31-1 15 -3]The target vector is t = [-1 -1 1 1]Solution: the MATLAB program of this example is as follows:Close allClearEcho onCLC% NEWFF - generating a new feedforward neural network% TRAIN -- training BP neural network% SIM -- Simulation of BP neural networkPauseStart by hitting any keyCLCPercent defines training samples% P as input vectorP=[-1, -2, 3, 1; -1, 1, 5, -3];% T is the target vectorT=[-1, -1, 1, 1];Pause;CLC% create a new feedforward neural networkNet=newff (minmax (P), [3,1],{'tansig','purelin'},'traingdm')The current input layer weights and thresholds InputWeights=net.IW{1,1}Inputbias=net.b{1}The current network layer weights and thresholdsLayerWeights=net.LW{2,1}Layerbias=net.b{2}PauseCLC% set training parametersNet.trainParam.show = 50;Net.trainParam.lr = 0.05;Net.trainParam.mc = 0.9;Net.trainParam.epochs = 1000;Net.trainParam.goal = 1e-3;PauseCLC% call TRAINGDM algorithm to train BP network [net, tr]=train (net, P, T);PauseCLCSimulation of BP network by%A = sim (net, P)Calculate the simulation errorE = T - AMSE=mse (E)PauseCLCEcho offExample 2 adopts Bayesian regularization algorithm to improve the generalization ability of BP network. In this case, we used two kinds of training methods, namely L-M algorithm (trainlm) and the Bias regularization algorithm (trainbr), is used to train the BP network, so that it can fit attached to a white noise sine sample data. Among them, the sample data can be generated as follows MATLAB statements:Input vector: P = [-1:0.05:1];Target vector: randn ('seed', 78341223);T = sin (2*pi*P) +0.1*randn (size (P));Solution: the MATLAB program of this example is as follows: Close allClearEcho onCLC% NEWFF - generating a new feedforward neural network% TRAIN -- training BP neural network% SIM -- Simulation of BP neural networkPauseStart by hitting any keyCLC% define training sample vector% P as input vectorP = [-1:0.05:1];% T is the target vectorRandn ('seed', 78341223); T = sin (2*pi*P) +0.1*randn (size (P));Draw the sample data pointsPlot (P, T, +);Echo offHold on;Plot (P, sin (2*pi*P), ':');Draw sine curves without noiseEcho onCLCPauseCLC% create a new feedforward neural networkNet=newff (minmax (P), [20,1], {'tansig','purelin'});PauseCLCEcho offCLCDisp ('1. L-M optimization algorithm TRAINLM'); disp ('2. Bayesian regularization algorithm TRAINBR');Choice=input (\ "please select training algorithm (1,2): ');Figure (GCF);If (choice==1)Echo onCLC% using L-M optimization algorithm TRAINLMNet.trainFcn='trainlm';PauseCLC% set training parametersnet.trainparam.epochs = 500;net.trainparam.goal = 1e-6;NET(.NET);%重新初始化暂停中图分类号“(选择= = 2)回声中图分类号%采用贝叶斯正则化算法trainbr trainfcn = 'trainbr”网;暂停中图分类号%设置训练参数net.trainparam.epochs = 500;randn(“种子”,192736547);NET(.NET);%重新初始化暂停中图分类号结束调用相应算法训练BP网络% [净额],列车=(净额,P,T);暂停中图分类号对BP网络进行仿真%a = sim(NET,p);%计算仿真误差e = a;MSE=MSE(e)暂停中图分类号%绘制匹配结果曲线关闭所有;图(p,a,p,t,+,p,p,p(2),“,”;暂停;中图分类号回音通过采用两种不同的训练算法,我们可以得到如图1和图2所示的两种拟合结果。
(整理)BP神经网络matlab实现和matlab工具箱使用实例.

(整理)BP神经网络matlab实现和matlab工具箱使用实例.BP神经网络matlab实现和matlab工具箱使用实例经过最近一段时间的神经网络学习,终于能初步使用matlab实现BP网络仿真试验。
这里特别感谢研友sistor2004的帖子《自己编的BP算法(工具:matlab)》和研友wangleisxcc的帖子《用C++,Matlab,Fortran实现的BP算法》前者帮助我对BP算法有了更明确的认识,后者让我对matlab下BP函数的使用有了初步了解。
因为他们发的帖子都没有加注释,对我等新手阅读时有一定困难,所以我把sistor2004发的程序稍加修改后加注了详细解释,方便新手阅读。
%严格按照BP网络计算公式来设计的一个matlab程序,对BP网络进行了优化设计%yyy,即在o(k)计算公式时,当网络进入平坦区时(<0.0001)学习率加大,出来后学习率又还原%v(i,j)=v(i,j)+deltv(i,j)+a*dv(i,j); 动量项clear allclcinputNums=3; %输入层节点outputNums=3; %输出层节点hideNums=10; %隐层节点数maxcount=20000; %最大迭代次数samplenum=3; %一个计数器,无意义precision=0.001; %预设精度yyy=1.3; %yyy是帮助网络加速走出平坦区alpha=0.01; %学习率设定值a=0.5; %BP优化算法的一个设定值,对上组训练的调整值按比例修改字串9error=zeros(1,maxcount+1); %error数组初始化;目的是预分配内存空间errorp=zeros(1,samplenum); %同上v=rand(inputNums,hideNums); %3*10;v初始化为一个3*10的随机归一矩阵; v表输入层到隐层的权值deltv=zeros(inputNums,hideNums); %3*10;内存空间预分配dv=zeros(inputNums,hideNums); %3*10;w=rand(hideNums,outputNums); %10*3;同Vdeltw=zeros(hideNums,outputNums);%10*3dw=zeros(hideNums,outputNums); %10*3samplelist=[0.1323,0.323,-0.132;0.321,0.2434,0.456;-0.6546,-0.3242,0.3255]; %3*3;指定输入值3*3(实为3个向量)expectlist=[0.5435,0.422,-0.642;0.1,0.562,0.5675;-0.6464,-0.756,0.11]; %3*3;期望输出值3*3(实为3个向量),有导师的监督学习count=1;while (count<=maxcount) %结束条件1迭代20000次c=1;while (c<=samplenum)for k=1:outputNumsd(k)=expectlist(c,k); %获得期望输出的向量,d(1:3)表示一个期望向量内的值endfor i=1:inputNumsx(i)=samplelist(c,i); %获得输入的向量(数据),x(1:3)表一个训练向量字串4end%Forward();for j=1:hideNumsnet=0.0;for i=1:inputNumsnet=net+x(i)*v(i,j);%输入层到隐层的加权和∑X(i)V(i)endy(j)=1/(1+exp(-net)); %输出层处理f(x)=1/(1+exp(-x))单极性sigmiod函数endfor k=1:outputNumsnet=0.0;for j=1:hideNumsnet=net+y(j)*w(j,k);endif count>=2&&error(count)-error(count+1)<=0.0001o(k)=1/(1+exp(-net)/yyy); %平坦区加大学习率else o(k)=1/(1+exp(-net)); %同上endend%BpError(c)反馈/修改;errortmp=0.0;for k=1:outputNumserrortmp=errortmp+(d(k)-o(k))^2; %第一组训练后的误差计算enderrorp(c)=0.5*errortmp; %误差E=∑(d(k)-o(k))^2 * 1/2%end%Backward();for k=1:outputNumsyitao(k)=(d(k)-o(k))*o(k)*(1-o(k)); %输入层误差偏导字串5endfor j=1:hideNumstem=0.0;for k=1:outputNumstem=tem+yitao(k)*w(j,k); %为了求隐层偏导,而计算的∑endyitay(j)=tem*y(j)*(1-y(j)); %隐层偏导end%调整各层权值for j=1:hideNumsfor k=1:outputNumsdeltw(j,k)=alpha*yitao(k)*y(j); %权值w的调整量deltw(已乘学习率)w(j,k)=w(j,k)+deltw(j,k)+a*dw(j,k);%权值调整,这里的dw=dletw(t-1),实际是对BP算法的一个dw(j,k)=deltw(j,k); %改进措施--增加动量项目的是提高训练速度endendfor i=1:inputNumsfor j=1:hideNumsdeltv(i,j)=alpha*yitay(j)*x(i); %同上deltwv(i,j)=v(i,j)+deltv(i,j)+a*dv(i,j);dv(i,j)=deltv(i,j);endendc=c+1;end%第二个while结束;表示一次BP训练结束double tmp;tmp=0.0; 字串8for i=1:samplenumtmp=tmp+errorp(i)*errorp(i);%误差求和endtmp=tmp/c;error(count)=sqrt(tmp);%误差求均方根,即精度if (error(count)<precision)%另一个结束条件< p="">break;endcount=count+1;%训练次数加1end%第一个while结束error(maxcount+1)=error(maxcount);p=1:count;pp=p/50;plot(pp,error(p),"-"); %显示误差然后下面是研友wangleisxcc的程序基础上,我把初始化网络,训练网络,和网络使用三个稍微集成后的一个新函数bpnet %简单的BP神经网络集成,使用时直接调用bpnet就行%输入的是p-作为训练值的输入% t-也是网络的期望输出结果% ynum-设定隐层点数一般取3~20;% maxnum-如果训练一直达不到期望误差之内,那么BP迭代的次数一般设为5000% ex-期望误差,也就是训练一小于这个误差后结束迭代一般设为0.01% lr-学习率一般设为0.01% pp-使用p-t虚拟蓝好的BP网络来分类计算的向量,也就是嵌入二值水印的大组系数进行训练然后得到二值序列% ww-输出结果% 注明:ynum,maxnum,ex,lr均是一个值;而p,t,pp,ww均可以为向量字串1% 比如p是m*n的n维行向量,t那么为m*k的k维行向量,pp为o*i的i维行向量,ww为o* k的k维行向量%p,t作为网络训练输入,pp作为训练好的网络输入计算,最后的ww作为pp经过训练好的BP训练后的输出function ww=bpnet(p,t,ynum,maxnum,ex,lr,pp)plot(p,t,"+");title("训练向量");xlabel("P");ylabel("t");[w1,b1,w2,b2]=initff(p,ynum,"tansig",t,"purelin"); %初始化含一个隐层的BP网络zhen=25; %每迭代多少次更新显示biglr=1.1; %学习慢时学习率(用于跳出平坦区)litlr=0.7; %学习快时学习率(梯度下降过快时)a=0.7 %动量项a大小(△W(t)=lr*X*ん+a*△W(t-1))tp=[zhen maxnum ex lr biglr litlr a 1.04]; %trainbpx[w1,b1,w2,b2,ep,tr]=trainbpx(w1,b1,"tansig",w2,b2,"purelin", p,t,tp);ww=simuff(pp,w1,b1,"tansig",w2,b2,"purelin"); %ww就是调用结果下面是bpnet使用简例:%bpnet举例,因为BP网络的权值初始化都是随即生成,所以每次运行的状态可能不一样。
基于BP算法的神经网络PID控制器设计及仿真
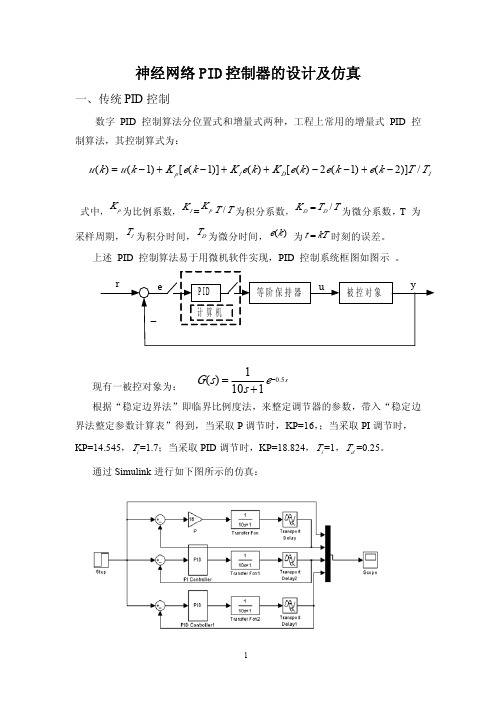
se s s G 5.01101)(−+=()(1)[(1)]()[()2(1)(2)]/p I D Iu k u k K e k K e k K e k e k e k T T =−+−++−−+−神经网络PID 控制器的设计及仿真一、传统PID 控制数字PID 控制算法分位置式和增量式两种,工程上常用的增量式PID 控制算法,其控制算式为:式中,pK 为比例系数,I K =p K /T T为积分系数,/D D K T T =为微分系数,T 为采样周期,IT 为积分时间,DT 为微分时间,()e k 为t kT =时刻的误差。
上述PID 控制算法易于用微机软件实现,PID 控制系统框图如图示。
现有一被控对象为:根据“稳定边界法”即临界比例度法,来整定调节器的参数,带入“稳定边界法整定参数计算表”得到,当采取P 调节时,KP=16,;当采取PI 调节时,KP=14.545,i T =1.7;当采取PID 调节时,KP=18.824,i T =1,d T =0.25。
通过Simulink 进行如下图所示的仿真:仿真结果如下图所示:二、基于BP算法的PID控制基于BP神经网络的PID控制系统结构如下图所示,控制器由两个部分组成:①经典的PID控制器:直接对被控对象进行闭环控制,并且KP,KI,KD三个参数为在线P,I,D整定;②神经网络NN:根据系统的运行状态,调节PID控制器的参数,以期达到某种性能指标的最优化。
即使神经网络的输出层神经元的输出状态对应于PID控制器的三个可调参数KP,KI,KD,通过神经网络的自学习、调整权系数,从而使其稳定P,I,D状态对应于某种最优控制规律下的PID控制器参数。
在这里设计的BP网络采用结构简单的三层BP神经网络,其结构如下图所示,有m个输入节点、Q个隐含层节点、3个输出节点。
输入节点对应所选的系统运行状态量,如系统不同时刻的输入量和输出量等,必要时要进行归一化K K K。
第4章 基于BP的模型优化预测与MATLAB实现

0.3
0.35
0.4
0.45
0.5
图4- 5 系统逼近
图4- 6 PID控制输出
第四章
0.1
MATLAB优化算法案例分析与应用
kp
0.05 0
0
0.05
0.1
0.15
0.2
0.25 time(s)
0.3
0.35
0.4
0.45
0.5
0.1 0.05 0
ki
0
0.05
0.1
0.15
0.2
0.25 time(s)
第四章
MATLAB优化算法案例分析与应用
•4.3 基于BP神经网络的PID参数整定
图4- 2 基于BP神经网络的PID控制结构图
第四章
MATLAB优化算法案例分析与应用
图4- 4 BP_PID算法流程
第四章
epid=[x(1);x(2);x(3)]; % 合并矩阵 I=xi*wi'; for j=1:1:H Oh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j))); %隐藏层 end K=wo*Oh; for l=1:1:Out K(l)=exp(K(l))/(exp(K(l))+exp(-K(l))); end kp(k)=K(1);ki(k)=K(2);kd(k)=K(3); Kpid=[kp(k),ki(k),kd(k)]; %存储 kp,ki,kd三个参数
第四章
MATLAB优化算法案例分析与应用
•4.1 BP神经网络模型及其基本原理
图4- 1 BP神经网络结构
BP神经网络模拟生物神经元信号的传递过程,生物神经元信号的传递是通
BP神经网络实验-Matlab

BP神经网络实验-MatlabBP神经网络是一种常见的人工神经网络模型。
在实际应用中,BP神经网络广泛用于分类、预测、优化等任务中。
本文将介绍如何在Matlab中实现BP神经网络,并通过一个简单的分类问题进行实验验证。
1. 数据准备首先,我们需要准备数据。
本文采用的数据是一个二分类问题,即在一个二维平面中,将数据点分为两类。
为了方便起见,我们可以手动生成一些数据点,或者使用Matlab自带的数据集如“fisheriris”。
2. BP神经网络模型的构建在Matlab中,我们可以使用“newff”函数来构建BP神经网络模型。
该函数可以接受多个参数,包括输入层、隐含层和输出层的节点数量,以及激活函数、学习算法等参数。
以下是构建一个包含1个输入层、1个隐含层和1个输出层的BP神经网络的示例代码:4. BP神经网络模型的测试在训练完成后,我们可以使用BP神经网络模型对测试数据进行分类预测。
在Matlab 中,我们可以使用“sim”函数来预测分类结果。
以下是对测试数据进行分类预测的示例代码:output=round(sim(net,test_data));其中,“output”是分类预测结果;“test_data”是测试数据。
5. 性能评估最后,我们需要对BP神经网络模型的分类性能进行评估。
在Matlab中,我们可以使用“confusionmat”函数来计算分类矩阵,进而计算分类准确率等性能指标。
以下是计算分类准确率的示例代码:[C,order]=confusionmat(test_label,output);accuracy=(C(1,1)+C(2,2))/sum(sum(C));其中,“C”是分类矩阵;“order”是分类标签;“accuracy”是分类准确率。
基于MATLAB的BP神经网络控制器的设计及其实验仿真

摘要虚拟设计是近年来发展起来的一个新的研究领域,智能控制虚拟实验室则是智能控制教学上的一个很好的工具。
鉴于传统实验室需要的设备,资金,场地等问题,利用虚拟实验室进行实验教学能够很大程度上的节约成本,同时用户在计算机前就能完成实验,查看实验结果,也能提高效率,节省时间。
本课题主要是建立可以进行智能控制虚拟实验,其模拟的是天煌教仪生产的“THJ-2型高级过程控制系统实验装置”。
本设计由三个主要部分构成:虚拟实验室的3D造型、智能控制实验仿真、图形用户界面(GUI)。
在具体的实现过程中,利用VRML语言完成虚拟实验室3D模型的建立;通过MATLAB的强大数据处理功能实现了BP神经网络控制实验的仿真和GUI的设计;最后利用MATLAB对系统进行封装,形成独立的可执行程序。
用户可通过封装程序界面打开GUI界面,在GUI界面中进行实验,设置参数,并能够察看系统的仿真曲线,实现虚拟实验的效果。
关键字:虚拟实验室、VRML、BP神经网络、MATLABAbstractVirtual design is developed in new area of research in recent years, Virtual Intelligent Control Laboratory is a good teaching tool of Intelligent Control Education. In view of the need for traditional laboratory equipment, funds, space and other issues, using virtual laboratory for experimental teaching in a large extent the cost savings, while people will be able to be completed the experiment to see results, but also improve efficiency, save time by using computer.The main issue is the establishment of a virtual intelligent control can be simulated laboratory equipment is “THJ-2 advanced process control system experimental” made by Tianhuang company .The design is consists of three main parts: the 3D Virtual Laboratory modeling, the simulation of intelligent control, the graphical user interfaces (GUI).The realization of the specific process, by using of VRML language to complete the virtual 3D model laboratory; through MATLAB's powerful data-processing functions to do a BP neural network control experiment simulation and make GUI design; the final, using MATLAB to let the system package to form an independent executable program. Users can open the GUI interface package interface, the GUI interface in the experiment, set parameters, and be able to see the simulation curve, the effect of virtual experiments.Keywords: Virtual Laboratory, VRML, BP neural network controller, MATLAB目录第1章引言 (1)1.1课题的研究背景及研究目地 (1)1.2虚拟实验室的介绍 (3)1.2.1 虚拟实验室的概念 (3)1.2.2 虚拟设计的技术基础 (3)1.2.3 虚拟设计的特点 (4)1.2.4虚拟设计的优点 (5)1.3课题研究的主要内容 (5)第2章VRML虚拟实验设备设计 (7)2.1 VRML技术基础知识 (7)2.1.1 VRML技术概述 (8)2.1.2 VRML文件组成 (8)2.1.3 VRML节点简介 (8)2.2实验装备简介 (11)2.3虚拟实验室的设计 (11)2.3.1 部分元件设计及程序. (11)2.3.2 由零件组成控制面板的小单元 (14)2.3.3 各控制单元组成完整的控制面板 (16)第3章神经网络理论 (17)3.1神经网络理论概述 (17)3.2 BP神经网络 (18)第4章基于MATLAB的BP神经网络控制器的设计及其实验仿真 (20)4.1基于BP神经网络控制器的设计 (20)4.2 BP-PID控制实验仿真 (23)4.2.1 MATLAB 简介. (23)4.2.2 BP-PID控制实验仿真 (24)4.3图形用户界面(GUI)的设计 (32)4.3.1MATLAB图形用户界面简介. (32)4.3.2图形用户界面实现的功能 (34)4.3.3图形用户界面的实现过程 (34)4.4系统封装 (37)4.4.1 封装目地. (37)4.4.2 MATLAB封装具体过程 (38)第5章结论 (39)参考文献 (40)致谢 (41)附录一VRML设计部分程序 (42)附录二MATLAB设计GUI程序 (46)第一章引言近些年来,迅速发展的计算机硬件技术与不断改进的计算机软件系统相匹配,使得基于大型数据集合的声音和图像的实时动画制作成为可能;人机交互系统的设计不断创新,新颖、实用的输入输出设备不断地进入市场。
用matlab编BP神经网络预测程序加一个优秀程序

求用matlab编BP神经网络预测程序求一用matlab编的程序P=[。
];输入T=[。
];输出% 创建一个新的前向神经网络net_1=newff(minmax(P),[10,1],{'tansig','purelin'},'traingdm')% 当前输入层权值和阈值inputWeights=net_1.IW{1,1}inputbias=net_1.b{1}% 当前网络层权值和阈值layerWeights=net_1.LW{2,1}layerbias=net_1.b{2}% 设置训练参数net_1.trainParam.show = 50;net_1.trainParam.lr = 0.05;net_1.trainParam.mc = 0.9;net_1.trainParam.epochs = 10000;net_1.trainParam.goal = 1e-3;% 调用TRAINGDM 算法训练BP 网络[net_1,tr]=train(net_1,P,T);% 对BP 网络进行仿真A = sim(net_1,P);% 计算仿真误差E = T - A;MSE=mse(E)x=[。
]';%测试sim(net_1,x) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%不可能啊我200928对初学神经网络者的小提示第二步:掌握如下算法:2.最小均方误差,这个原理是下面提到的神经网络学习算法的理论核心,入门者要先看《高等数学》(高等教育出版社,同济大学版)第8章的第十节:“最小二乘法”。
3.在第2步的基础上看Hebb学习算法、SOM和K-近邻算法,上述算法都是在最小均方误差基础上的改进算法,参考书籍是《神经网络原理》(机械工业出版社,Simon Haykin著,中英文都有)、《人工神经网络与模拟进化计算》(清华大学出版社,阎平凡,张长水著)、《模式分类》(机械工业出版社,Richard O. Duda等著,中英文都有)、《神经网络设计》(机械工业出版社,Martin T. Hargan等著,中英文都有)。
基于BP神经网络算法的仿真研究

基于BP神经网络算法的仿真研究BP神经网络算法(Back Propagation Neural Network Algorithm)是一种常用的人工神经网络算法,它具有非常广泛的应用领域,如模式识别、数据挖掘、预测分析等。
本文将基于BP神经网络算法进行仿真研究,重点探讨其在分类问题中的应用。
BP神经网络算法是一种有监督学习的算法,可以通过输入变量进行训练,然后利用已有数据进行预测或分类。
其核心思想是通过反向传播算法来对网络参数进行调整,以达到最小化误差的目标。
BP神经网络是一种多层前馈网络,通常包含输入层、隐层和输出层。
输入层负责接收外部输入,隐层负责进行特征提取和映射,输出层负责产生最终的输出结果。
在训练过程中,通过计算误差和调整权值来不断优化网络的性能。
在本次仿真研究中,我们将以一个真实的案例为例,来说明BP神经网络算法的应用。
假设我们需要对一个银行的客户进行信用评级,以判断其是否有违约的风险。
我们将收集一些已知的客户数据,如年龄、性别、收入、负债情况等作为输入变量;同时,我们还需要针对每位客户进行标记,将其划分为“违约”或“非违约”两个类别。
我们将以80%的数据用作训练集,20%的数据用作测试集。
首先,我们需要对输入数据进行预处理,通常包括数据清洗、特征选择和归一化等步骤。
在本次研究中,我们假设已经完成了这些预处理工作。
接下来,我们构建BP神经网络模型。
假设我们选择了一个包含一个隐层的神经网络,其中隐藏层含有10个神经元。
输入层的节点数与输入变量的数目相同,输出层的节点数为1(即输出一个标记)。
我们将采用sigmoid函数作为激活函数,用于将输入信号转化为输出信号。
在实际训练过程中,我们将采用梯度下降法来更新网络的权值。
每次迭代时,我们计算网络的输出与实际标记之间的误差,并通过反向传播算法来更新网络的参数。
迭代次数与学习率等超参数的选择可以通过实验来确定。
在本次研究中,我们选择迭代100次,并设置学习率为0.01训练完成后,我们将使用测试集来评估模型的性能。
BP神经网络的仿真实验
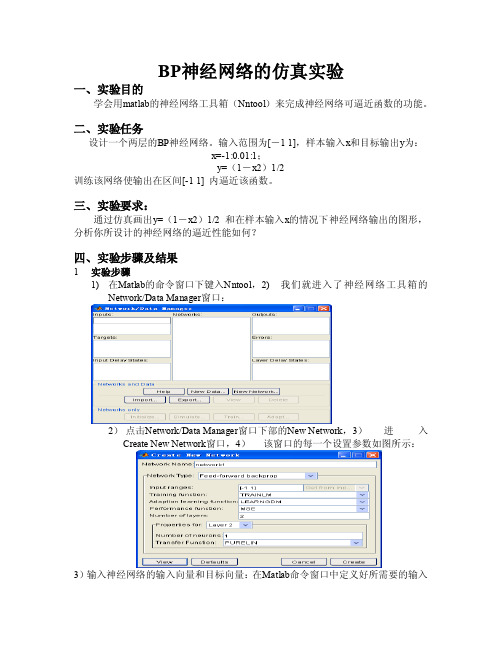
BP神经网络的仿真实验一、实验目的学会用matlab的神经网络工具箱(Nntool)来完成神经网络可逼近函数的功能。
二、实验任务设计一个两层的BP神经网络。
输入范围为[-1 1],样本输入x和目标输出y为:x=-1:0.01:1;y=(1-x2)1/2训练该网络使输出在区间[-1 1] 内逼近该函数。
三、实验要求:通过仿真画出y=(1-x2)1/2 和在样本输入x的情况下神经网络输出的图形,分析你所设计的神经网络的逼近性能如何?四、实验步骤及结果1实验步骤1) 在Matlab的命令窗口下键入Nntool,2) 我们就进入了神经网络工具箱的Network/Data Manager窗口:2)点击Network/Data Manager窗口下部的New Network,3)进入Create New Network窗口,4)该窗口的每一个设置参数如图所示:3)输入神经网络的输入向量和目标向量:在Matlab命令窗口中定义好所需要的输入向量和目标向量,再传送到工具箱中,具体操作为在命令窗口键入以下命令行:>> x=-1:0.01:1;>> y=sqrt(1-x.^2);这样就定义好了输入向量和目标向量。
点击Network/Data Manager窗口下的Import 按钮,进入Import or Load to Network/Data Manager窗口:由于数据来自于工作空间,所以Source项取默认值;如果数据来自于disk,则选择Load from disk file。
在Select a variable中选择想要传送的数据x,再在destination项中键入名字x,同时import as中的选项被激活了,选择其中的Inputs,最后点击Import,这样就完成了输入向量从工作空间向工具箱的传送,在Network/Data Manager窗口下的Inputs列表中出现了新输入的输入向量的名字x;同理可以输入目标向量y。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%BP神经网络用于系统辨识训练预测程序
clear all
clc
%产生随机序列作为系统输入
A=6; x0=1; M=255; f=2; N=60;Q=2*N/3;H=N-Q-1; %初始化
for k=1:N
x2=A*x0; %分别用x2和x0表示xi和xi-1
x1=mod (x2,M); %x2除以M的余数给x1
v1=x1/256; %x1除以256得到小于1的随机数给v1
if v1-0.5>=0
u(:,k)=v1*f-1;%如果随机数v1大于0.5,就乘以系数f减去1,将结 else %果存于U的第k列中
u(:,k)=v1-1; %不满足条件的运算结果存于矩阵U中
end
x0=x1;%xi-1=xi
v0=v1;%vi-1=vi
end
z=zeros(1,N); %输出长度
v=rand(1,N); %随机噪声
for k=3:N
z(k)=1.5*z(k-1)-0.7*z(k-2)+1.1*u(k-1)+0.3*u(k-2)-v(k-1)+0.2*v(k-2); end %理想输出作为观察值
for k=1:N-2
hl(k,:)=[-z(k+1),-z(k),u(k+1),u(k),v(k+1),v(k)];%样本矩阵HL赋值
zl(k)=z(k+2); %给样本矩阵ZL赋值
end
HL=(hl-min(min(hl)))/(max(max(hl))-min(min(hl))); %数据归一化
ZL=(zl-min(zl))/(max(zl)-min(zl)); %数据归一化
p=HL(1:Q,:); %训练样本输入
p1=HL(Q:N-2,:); %测试样本输入
b1=ones(Q,1);b2=ones(H,1); %初始化
P=[p,b1]; %增广训练样本
P1=[p1,b2]; %增广测试样本
T=ZL(1,1:Q)'; %训练样本理想输出
T1=ZL(1,Q:N-2)'; %测试样本理想输出
inputNums=6; %网络输入层节点数
outputNums=1; %网络输出层节点数
hideNums=10; %网络隐层节点数
lc=0.03; %学习率
max_epoch=3000; %最大循环次数
error_goal=0.00001; %期望误差最小值
B1=randn(1,hideNums); %输入层到隐含层的阈值初始化
B2=randn(1,outputNums); %隐含层到输出层的阈值初始化
w1=randn(inputNums,hideNums); %输入层到隐含层的权值初始化
w2=randn(hideNums,outputNums); %隐含层到输出层的权值初始化
W1=[w1;B1]; %输入层到隐含层的增广权矩阵
W2=[w2;B2]; %隐含层到输出层的增广权矩阵error=zeros(1,max_epoch); %训练误差
%训练样本集P对BP神经网络进行训练
for k=1:max_epoch
for i=1:Q %单个样本的输入
for j=1:hideNums
net=P(i,:)*W1(:,j); %隐含层神经元的输入
y(i,j)=1/(1+exp(-net)); %隐含层输出
end
Y(i,:)=[y(i,:),1]; %带阈值隐含层输出
for j=1:outputNums
net=Y(i,:)*W2(:,j); %输出层神经元的输入
O(i,j)=1/(1+exp(-net)); %输出层输出
end
E=T(i)-O(i); %单个样本训练误差
SSE=0.5*E^2; %均方误差
if SSE>=error_goal
for c=1:hideNums
for j=1:outputNums
DW2(c,j)=(T(i,j)-O(i,j))*O(i,j)*(1-O(i,j)); %输出层误差偏导 W2(c,j)=W2(c,j)+lc*DW2(c,j)*Y(i,c); %输出层权值阈值的调整 sumDW1=0;
sumDW1=sumDW1+W2(c,j)*DW2(c,j); %输出层对前一层的误差 end
end
for m=1:inputNums
for n=1:hideNums
DW1(m,n)=Y(i,n)*(1-Y(i,n))*sumDW1; %隐含层误差偏导
W1(m,n)=W1(m,n)+lc*DW1(m,n)*P(i,m); %隐含层权值阈值的调整 end
end
end
end
e=T-O;
error(:,k)=sumsqr(e)/(2*Q); %样本集训练误差
end
w1=W1(1:inputNums,:) %输入层到隐含层的权值
B1=W1(end,:) %输入层到隐含层的阈值
w2=W2(1:hideNums,:) %隐含层到输出层的权值
B2=W2(end,:) %隐含层到输出层的阈值
%测试样本集P1用于BP神经网络预测
for i=1:H
for j=1:hideNums
net=P1(i,:)*W1(:,j); %隐含层的输入
y(i,j)=1/(1+exp(-net)); %隐含层神经元输出
end
Y(i,:)=[y(i,:),1];
for j=1:outputNums
net=Y(i,:)*W2(:,j); %输出层的输入
O1(i,j)=1/(1+exp(-net)); %BP网络实际输出
end
end
figure(1);
k=1:max_epoch;
plot(k,error); %每次训练产生的均方误差
xlabel('k');ylabel('error');
figure(2);
k=1:H;
plot(k,T1,k,O1,'*'); %期望输出值和BP网络实际输出值xlabel('k');ylabel('T1andO1');title('BP simulation');
legend('T1 is desired output ','O1 is Network real output');
程序运行结果:
网络调整后的权值和阈值:
w1 =
-1.8970 -0.3536 -0.7324 -0.2796 -0.8915 -2.5360 -1.4659 -0.8267 1.3088 -2.9194
0.2206 0.3110 -0.4352 1.9239 0.2798 2.2846 2.3745 1.0050 1.9195 1.6357
0.3982 1.2206 -0.3522 0.3303 0.1851 0.4378 0.6983 0.7763 1.0435 1.6692
-0.0396 -0.0303 0.1196 2.5735 1.9985 0.5372 0.7766 0.2509 0.3865 -0.1207
-2.0508 -0.2577 -1.1566 -0.4017 -0.2822 -0.7683 -0.8974 -0.7947 -2.8680 -2.8010
0.5775 0.2247 -1.8290 1.2246 -1.2297 0.4094 -2.0787 -0.0308 1.4659 0.6319
B1 =
-0.0626 1.3940 -0.6442 -2.4781 0.4005 -0.4490 -0.7535 -0.7373 -1.0483 0.6430
w2 =
0.4787
-0.6121
-1.5698
1.1484
-1.3859
2.6040
2.8504
-2.0707
-3.7628
2.8872
B2 =
0.7753
网络训练过程中的误差记录:
网络实际输出与期望输出的模拟对比:。
