2017年高考数学(文科)-几何体与球切、接的问题-专题练习
专题2.7 几何体与球切、接的问题(测)-2017年高考数学(理)二轮复习讲练测(附解析)$769933

专题2.7 几何体与球切、接的问题(测)总分 _______ 时间 _______ 班级 _______ 学号 _______ 得分_______(一) 选择题(12*5=60分)1.【广西梧州市2017届高三上学期摸底联考】若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图1所示,则此几何体的表面积是( )A .(4πB .6π+C .6π+D .(8π+ 【答案】C 【解析】圆柱的侧面积为ππ42121=⨯⨯=S ,半球的表面积为ππ21222=⨯=S ,圆锥的侧面积为ππ2213=⨯⨯=S ,所以几何体的表面积为ππ26321+=++=S S S S ,故选C. 2.【河北省沧州市第一中学2017届高三10月月考】已知四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,其中ABCD 为正方形,PAD ∆为等腰直角三角形,PA PD ==棱锥P ABCD -外接球的表面积为( )A .10πB .4π C. 16π D .8π 【答案】Dππ8242=⨯=S ,应选D.3.【2016届甘肃省天水市一中高三上学期期末考试】利用一个球体毛坯切削后得到一个四棱锥P —ABCD ,其中底面四边形ABCD 是边长为1的正方形,1PA =,且D A BC P A ⊥平面,则球体毛坯体积的最小值应为( )A .3 B C .43πD .2【答案】D4.【2016届河北省邯郸市一中高三下学期研六考试】在菱形ABCD 中,60,A AB =︒=,将ABD 折起到PBD 的位置,若二面角P BD C --的大小为23π,则三棱锥P BCD -的外接球的体积为( )A .43πB C D【答案】C 【解析】取BD 中点E ,连接AE CE ,,则2332AEC AE CE π∠===,,设BCD V 的外接圆的圆心与球心的距离为h ,三棱锥P BCD -的外接球的半径为R ,则22222154()()R h h R =+-+=,∴R h ==∴三棱锥P BCD -的外接球体积为343π⋅=.故选:C . 5.【2016届湖南师大附中高三上学期月考四】若长方体1111D C B A ABCD -中,AB=1,C B 1,D C 1分别与底面ABCD 所成的角为︒45,︒60,则长方体1111D C B A ABCD -的外接球的体积为 ( ) A .677π B .37π C .374π D .67π 【答案】A6.已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的全面积是( )A . 18B .36C . 45D .54【答案】D 【解析】左视图由三视图知:几何体为正三棱柱,∵俯视图是边长为6的正三角形,∴几何体的内切球的半径R=6×33123=⨯, ∴三棱柱的侧棱长为32.∴几何体的表面积35432632366212=⨯⨯+⨯⨯⨯⨯=S ,故选:D . 7.一几何体的三视图如右图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A .4πB .π3C .π2D .π 【答案】B8.设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( ) A.2a π B. 237a π C. 2311a π D. 25a π 【答案】B 【解析】根据题意条件可知三棱柱是棱长都为a 的正三棱柱,上下底面中心连线的中点就是球心,则其外接球的半径为222127)60sin 2()2(a a a R =+=,球的表面积为22371274a a S ππ=⋅=,故选B . 9.【广东省惠州市2017届高三第一次调研】已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2AB =, 2SA SB SC ===,则三棱锥的外接球的球心到平面ABC 的距离是( )A B .1 C D 【答案】A【解析】因为三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2SA SB SC ===,S ∴在面ABC 内的射影为AB 中点H ,SH ∴⊥平面ABC ,SH ∴上任意一点到,,A B C的距离相等.3SH =,1CH =,在面SHC 内作SC 的垂直平分线MO ,则O 为S ABC -的外接球球心.2SC =,1SM ∴=,30OSM ∠=︒,SO OH ∴==O 到平面ABC 的距离,故选A .10.【2016届河北省正定中学高三上学期期末考试】球O 半径为13=R ,球面上有三点A 、B 、C ,312=AB ,12==BC AC ,则四面体OABC 的体积是A .360B .350C .660D .650 【答案】A11.【2016届贵州省贵阳市一中高三第五次月考】如图,已知正三角形ABC 三个顶点都在半径为2的球面上,球心O 到平面ABC 的距离为1,点E 是线段AB 的中点,过点E 作球O 的截面,则截面面积的最小值是( )A .74πB .2πC .94πD .3π【答案】C 【解析】设正ABC △的中心为1O ,连接1O A ,11O O O C ,,∵1O 是正ABC △的中心,A B C ,,三点都在球面上,∴1O O ABC ⊥平面,结合1O C ABC ⊂平面,可得11O O O C ⊥,∵球的半径2R =,球心O 到平面ABC 的距离为1,得11O O =,∴在1Rt O OC △中,1O C 又∵E 为AB 的中点,ABC △是等边三角形,13cos302AE AO =︒=∴,∵过E 作球O 的截面,当截面与OE 垂直时,截面圆的半径最小,此时截面圆的半径32r =,可得截面面积为29ππ4S r ==,故选C . 12.【江西省新余市2016届高三第二次模拟】已知C B A 、、是球O 的球面上三点,2=AB ,32=AC , 60=∠ABC ,且棱锥ABC O -的体积为364,则球O 的表面积为( ) A .π10 B .π24 C .π36 D .π48 【答案】D(二) 填空题(4*5=20分)13.【2016届河北省邯郸一中高三下学期研七】球O 面上四点P 、A 、B 、C 满足:PA 、PB 、PC 两两垂直,3,4,PA PB PC ===,则球O 的表面积等于______.【答案】100π 【解析】空间四个点P A B C 、、、在同一球面上,PA PB PC 、、两两垂直,且3,4,PA PB PC ===,则PA PB PC 、、可看作是长方体的一个顶点发出的三条棱,所以过空间四个点P A B C 、、、的球面即为棱长分别为3,4,PA PB PC ===体的外接球,如下图:10=,所以这个球面的面积21024100S ππ⎛⎫=⎪⎝⎭=.14.【河南省新乡市2017届高三上学期第一次调研】已知一个圆锥内接于球O (圆锥的底面圆周及顶点均在球面上),若球的半径5R =,圆锥的高是底面半径的2倍,则圆锥的体积为__________. 【答案】1283π 【解析】设圆锥底面半径为r ,高为2r .2R r =,解得4r =,所以圆锥的体积为211284833ππ⋅⋅=. 15.【湖北省襄阳市第四中学2017届高三七月第二周周考】已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的表面积为________. 【答案】169π16.【吉林省长春市普通高中2017届高三质量监测(一)】已知三棱锥S ABC -,满足,,SA SB SC 两两垂直,且2SA SB SC ===,Q 是三棱锥S ABC -外接球上一动点,则点Q 到平面ABC 的距离的最大值为 .【答案】3(三) 解答题(共6道小题,共70分)17. 过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ,且两两夹角都为︒60,若球半径为R ,求弦AB 的长度.【答案】3R 【解析】由条件可抓住BCD A -是正四面体,A 、B 、C 、D 为球上四点,则球心在正四面体中心,设a AB =,则截面BCD 与球心的距离R a d -=36,过点B 、C 、D 的截面圆半径a r 33=,所以222)36()33(R a R a --=得R a 362=. 18. 一个倒圆锥形容器,它的轴截面是正三角形,在容器内注入水,并放入一个半径为r 的铁球,这时水面恰好和球面相切.问将球从圆锥内取出后,圆锥内水平面的高是多少?.19. 【改编自浙江高考题】已知球O 的面上四点A 、B 、C 、D ,DA ABC ⊥平面,AB BC ⊥,O 的体积.【答案】92π.【解析】本题用一般方法时,需要找出球心,求出球的半径.而利用长方体模型很快便可找到球的直径,由于DA ABC ⊥平面,AB BC ⊥,联想长方体中的相应线段关系,构造如图所示的长方体,又因为CD 长即为外接球的直径,利用直角三角形解出CD=3.故球O 的体积等于92π.20. 【改编自山东高考题】在等腰梯形ABCD 中,AB=2DC=2,0DAB=60∠,E 为AB 的中点,将ADE ∆与BEC ∆分布沿ED 、EC 向上折起,使A B 、重合于点P ,求三棱锥P-DCE 的外接球的体积..21. 一个正四棱锥的底面边长为2,侧棱长为3,五个顶点都在同一个球面上,求此球的表面积.【答案】9π.【解析】设外接球半径为R ,在△OO 1A 中有()2221+R R -=解得32R =.∴=9S π球.C BA22. 球面上有3个点,其中任意两点的球面距离都等于大圆周长的61,经过3个点的小圆的周长为π4,求这个球的半径.【答案】【解析】设球的半径为R ,小圆的半径为r ,则ππ42=r ,∴2=r .。
2017年高考数学(文科)-几何体与球切、接的问题-专题练习
2017年高考(文科)数学专题练习几何体与球切、接的问题一、练高考1.【2016高考新课标3】在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥, =6AB ,8BC =,13AA =,则V 的最大值是( )A .4πB .9π2C .6πD .32π32.【2016高考山东】一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )A .12π33+B .13+C .13+D .1+ 3.【2016高考新课标1卷】如图.某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3.则它的表面积是( ) A .17π B .18π C .20π D .28π4.【2015高考新课标2】已知,A B 是球O 的球面上两点,90AOB ∠=︒.C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π5.【2014大纲高考】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A .81π4B .16πC .9πD .27π46.【2013年福建卷】已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是__________.二、练模拟1.【广西梧州市2017届高三上学期摸底联考】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的体积为( )A .243π16B .81π16C .81π4D .27π42.【河南省开封市2017届高三上学期10月月考】如图.已知一个八面体的各条棱长均为1.四边形ABCD 为正方形,则下列命题中的假命题是A .不平行的两条棱所在的直线所成的角是60︒或90︒;B .四边形AECF 是正方形;C .点A 到平面BCE 的距离为r =;D .该八面体的顶点在同一个球面上.3.【河南省师范大学附属中学2015届高三12月月考】已知四面体P ABC -中,4PA =,AC =PB BC ==PA ⊥平面PBC ,则四面体P ABC -的外接球体积为( )A .125π6BCD 4.【2016届甘肃河北五市高三第一次联考】体积为4π3的球O 放置在棱长为4的正方体1111ABCD A B C D -上,且与上表面1111A B C D 相切,切点为该表面的中心,则四棱锥O ABCD -的外接球的半径为( )A .103B .3310C .2D .2365.【2016届河北省武邑中学高三上学期期末考试】正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C ABCD 外接球表面积为( )A .7πB .19π CD6.【2016的正六边形的六个顶点都在球O 的球面上,球心O 到正六边形所在平面的距离为O 的体积为V ,球O 的表面积为S ,则V S 的值是( ) A .2 B .1 CD三、练原创1.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )A .3πB .4πC .2πD .5π22.已知四面体P ABC -中.4PA =,AC =PB BC ==PA ⊥平面PBC .则四面体P ABC -的内切球半径与外接球半径的比( )ABCD3.如图,正方体1111ABCD A B C D -A 为球心,2为半径作一个球,则图中球面与正方体的表面积相交所得到的两段弧之和等于( )A .5π6B .2π3C .πD .7π64.三棱锥S ABC -的所有顶点都在球O 的表面上,SA ⊥平面ABC ,AB BC ⊥,又1SA AB BC ===,则球O 的表面积为__________.俯视图正视图 侧视图5.已知三棱锥A BCD -中,2,2AB AC BD CD BC AD =====,直线AD 与底面BCD 所成角为3π,则此时三棱锥外接球的表面积为__________.。
立体几何专题 第2节 与球相关的切、接问题 【教师版】

第二节 与球相关的切、接问题考法(一) 球与柱体的切、接问题[典例] (2017·江苏高考)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________.[解析] 设球O 的半径为R ,因为球O 与圆柱O 1O 2的上、下底面及母线均相切,所以圆柱的底面半径为R 、高为2R ,所以V 1V 2=πR 2·2R 43πR 3=32.[答案] 32考法(二) 球与锥体的切、接问题[典例] (2018·全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D -ABC 体积的最大值为( )A .123B .18 3C .24 3D .54 3[解析] 由等边△ABC 的面积为93,可得34AB 2=93,所以AB =6,所以等边△ABC 的外接圆的半径为r =33AB =2 3.设球的半径为R ,球心到等边△ABC 的外接圆圆心的距离为d ,则d =R 2-r 2=16-12=2.所以三棱锥D -ABC 高的最大值为2+4=6,所以三棱锥D -ABC 体积的最大值为13×93×6=18 3.[答案] B[题组训练]1.(2018·福建第一学期高三期末考试)已知圆柱的高为2,底面半径为3,若该圆柱的两个底面的圆周都在同一个球面上,则这个球的表面积等于( )A .4π B.163πC.323π D .16π解析:选D 如图,由题意知圆柱的中心O 为这个球的球心, 于是,球的半径r =OB =OA 2+AB 2= 12+(3)2=2.故这个球的表面积S =4πr 2=16π.故选D.2.三棱锥P -ABC 中,AB =BC =15,AC =6,PC ⊥平面ABC ,PC =2,则该三棱锥的外接球表面积为________.解析:由题可知,△ABC 中AC 边上的高为15-32=6,球心O 在底面ABC 的投影即为△ABC 的外心D ,设DA =DB =DC =x ,所以x 2=32+(6-x )2,解得x =564,所以R 2=x 2+⎝⎛⎭⎫PC 22=758+1=838(其中R 为三棱锥外接球的半径),所以外接球的表面积S =4πR 2=832π.答案:832π[课时跟踪检测]1.(2019·深圳摸底)过半径为2的球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的体积的比值为( )A.932 B.916 C.38D.316解析:选A 由题意知所得截面为圆,设该圆的半径为r ,则22=12+r 2,所以r 2=3,所以所得截面的面积与球的体积的比值为π×343π×23=932,故选A.2.如图是某一几何体的三视图,则这个几何体的体积为( )A .4B .8C .16D .20解析:选B 由三视图知,此几何体是一个三棱锥,底面为一边长为6,高为2的三角形,三棱锥的高为4,所以体积为V =13×12×6×2×4=8.故选B.3.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A .14斛B .22斛C .36斛D .66斛解析:选B 设米堆的底面半径为r 尺,则π2r =8,所以r =16π,所以米堆的体积为V =14×13π×r 2×5=π12×⎝⎛⎭⎫16π2×5≈3209(立方尺).故堆放的米约有3209÷1.62≈22(斛). 4.(2018·贵阳摸底考试)某实心几何体是用棱长为1 cm 的正方体无缝粘合而成的,其三视图如图所示,则该几何体的体积为( )A .35 cm 3B .40 cm 3C .70 cm 3D .75 cm 3解析:选A 结合题中三视图可得,该几何体是个组合体,该组合体从下到上依次为长、宽、高分别为5 cm,5 cm,1 cm 的长方体,长、宽、高分别为3 cm,3 cm,1 cm 的长方体,棱长为1 cm 的正方体,故该组合体的体积V =5×5×1+3×3×1+1×1×1=35(cm 3).故选A.5.(2019·安徽知名示范高中联考)某几何体的三视图如图所示,则该几何体的体积为( )A .1 B.12 C.13D.14解析:选C 法一:该几何体的直观图为四棱锥S -ABCD ,如图,SD ⊥平面ABCD ,且SD =1,四边形ABCD 是平行四边形,且AB =DC =1,连接BD ,由题意知BD ⊥DC ,BD ⊥AB ,且BD =1,所以S 四边形ABCD =1,所以V S -ABCD =13S 四边形ABCD ·SD =13,故选C. 法二:由三视图易知该几何体为锥体,所以V =13Sh ,其中S 指的是锥体的底面积,即俯视图中四边形的面积,易知S =1,h 指的是锥体的高,从正视图和侧视图易知h =1,所以V =13Sh =13,故选C.6.(2019·重庆调研)某简单组合体的三视图如图所示,则该组合体的体积为( )A.83π3+833B.43π3+833C.43π3+433D.83π3+433解析:选B 由三视图知,该组合体是由一个半圆锥与一个三棱锥组合而成的,其中圆锥的底面半径为2、高为42-22=23,三棱锥的底面是斜边为4、高为2的等腰直角三角形,三棱锥的高为23,所以该组合体的体积V =12×13π×22×23+13×12×4×2×23=43π3+833,故选B.7.(2019·湖北八校联考)已知一几何体的三视图如图所示,它的侧视图与正视图相同,则该几何体的表面积为( )A .16+12πB .32+12πC .24+12πD .32+20π解析:选A 由三视图知,该几何体是一个正四棱柱与半球的组合体,且正四棱柱的高为2,底面对角线长为4,球的半径为2,所以该正四棱柱的底面正方形的边长为22,该几何体的表面积S =12×4π×22+π×22+22×2×4=12π+16,故选A.8.(2019·福州质检)已知正三棱柱ABC -A 1B 1C 1中,底面积为334,一个侧面的周长为63,则正三棱柱ABC -A 1B 1C 1外接球的表面积为( )A .4πB .8πC .16πD .32π解析:选C 如图所示,设底面边长为a ,则底面面积为34a 2=334,所以a = 3.又一个侧面的周长为63,所以AA 1=2 3.设E ,D 分别为上、下底面的中心,连接DE ,设DE 的中点为O ,则点O 即为正三棱柱ABC -A 1B 1C 1的外接球的球心,连接OA 1,A 1E ,则OE =3,A 1E =3×32×23=1.在直角三角形OEA 1中,OA 1=12+(3)2=2,即外接球的半径R =2,所以外接球的表面积S =4πR 2=16π,故选C.9.(2017·天津高考)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为________.解析:由正方体的表面积为18,得正方体的棱长为 3. 设该正方体外接球的半径为R ,则2R =3,R =32,所以这个球的体积为43πR 3=4π3×278=9π2.答案:9π210.某四棱柱的三视图如图所示,则该四棱柱的体积为________.解析:由题意知该四棱柱为直四棱柱,其高为1,底面为上底长为1,下底长为2,高为1的等腰梯形,所以该四棱柱的体积为V =(1+2)×12×1=32. 答案:3211.一个圆锥的表面积为π,它的侧面展开图是圆心角为2π3的扇形,则该圆锥的高为________.解析:设圆锥底面半径是r ,母线长为l ,所以πr 2+πrl =π,即r 2+rl =1,根据圆心角公式2π3=2πrl ,即l =3r ,所以解得r =12,l =32,那么高h =l 2-r 2= 2.答案: 212.(2017·全国卷Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.解析:如图,连接AO ,OB ,∵SC 为球O 的直径, ∴点O 为SC 的中点, ∵SA =AC ,SB =BC , ∴AO ⊥SC ,BO ⊥SC ,∵平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC , ∴AO ⊥平面SCB , 设球O 的半径为R , 则OA =OB =R ,SC =2R . ∴V S -ABC =V A -SBC =13×S △SBC ×AO =13×⎝⎛⎭⎫12×SC ×OB ×AO , 即9=13×⎝⎛⎭⎫12×2R ×R ×R ,解得 R =3, ∴球O 的表面积S =4πR 2=4π×32=36π. 答案:36π13.如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=2,∠A 1B 1C 1=90°,AA 1=4,BB 1=3,CC 1=2,求:(1)该几何体的体积; (2)截面ABC 的面积.解:(1)过C 作平行于A 1B 1C 1的截面A 2B 2C ,交AA 1,BB 1分别于点A 2,B 2.由直三棱柱性质及∠A 1B 1C 1=90°可知B 2C ⊥平面ABB 2A 2,则该几何体的体积V =VA 1B 1C 1-A 2B 2C +VC -ABB 2A 2=12×2×2×2+13×12×(1+2)×2×2=6. (2)在△ABC 中,AB =22+(4-3)2=5, BC =22+(3-2)2=5, AC =(22)2+(4-2)2=2 3.则S △ABC =12×23×(5)2-(3)2= 6.14.如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1)证明:平面AEC ⊥平面BED ;(2)若∠ABC =120°,AE ⊥EC ,三棱锥E -ACD 的体积63,求该三棱锥E -ACD 的侧面积.解:(1)证明:因为四边形ABCD为菱形,所以AC⊥BD.因为BE⊥平面ABCD,AC⊂平面ABCD,所以BE⊥AC.因为BD∩BE=B,BD⊂平面BED,BE⊂平面BED,所以AC⊥平面BED.又AC⊂平面AEC,所以平面AEC⊥平面BED.(2)设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=32x,GB=GD=x2.因为AE⊥EC,所以在Rt△AEC中,可得EG=3 2x.由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=2 2x.由已知得,三棱锥E-ACD的体积V三棱锥E-ACD=13·12AC·GD·BE=624x3=63,故x=2.从而可得AE=EC=ED= 6.所以△EAC的面积为3,△EAD的面积与△ECD的面积均为 5. 故三棱锥E-ACD的侧面积为3+2 5.。
2017年高考数学—立体几何(解答+答案)

2017年高考数学—立体几何(解答+答案)1.(17全国1理18.(12分))如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=o .(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=o ,求二面角A -PB -C 的余弦值.2.(17全国1文18.(12分))如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=o(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=o ,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.如图,四棱锥P ABCD -中,侧面PAD 为等比三角形且垂直于底面ABCD ,o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点. (1)证明:直线//CE 平面PAB(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为o 45 ,求二面角M AB D --的余弦值4.17全国2文18.(12分)如图,四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,12AB BC AD ==,90BAD ABC ∠=∠=o 。
(1) 证明:直线//BC 平面PAD ; (2) 若PCD ∆的面积为27,求四棱锥P ABCD -的体积。
如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形.ABDCBD ??,AB BD =.(1)证明:平面ACD ^平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分.求二面角D AE C --的余弦值.6.(17全国3文19.(12分))如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.DABCE7.(17北京理(16)(本小题14分))如图,在四棱锥P ABCD -中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,//PD 平面,6,4MAC PA PD AB ===(I )求证:M 为PB 的中点; (II )求二面角B PD A --的大小;(III )求直线MC 与平面BDP 所成角的正弦值.8.(17北京文(18)(本小题14分))如图,在三棱锥P ABC -中,,,,2PA AB PA BC AB BC PA AB BC ⊥⊥⊥===,D 为线段AC 的中点,E 为线段PC 上一点.(Ⅰ)求证:PA BD ⊥;(Ⅱ)求证:平面BDE ⊥平面PAC ;(Ⅲ)当//PA 平面BDE 时,求三棱锥E BCD -的体积.9.(17山东理17.)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120︒得到的,G 是»DF的中点. (Ⅰ)设P 是»CE上的一点,且AP BE ⊥,求CBP ∠的大小; (Ⅱ)当3AB =,2AD =,求二面角E AG C --的大小.10.(17山东文(18)(本小题满分12分))由四棱柱1111ABCD A B C D -截去三棱锥111C B CD -后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,1A E ⊥平面ABCD, (Ⅰ)证明:1A O ∥平面11B CD ;(Ⅱ)设M 是OD 的中点,证明:平面1A EM ⊥平面11B CD .11.(17天津理(17)(本小题满分13分))如图,在三棱锥P -ABC 中,PA ⊥底面ABC ,90BAC ∠=︒.点D ,E ,N 分别为棱PA ,P C ,BC 的中点,M 是线段AD 的中点,PA =AC =4,AB =2.(Ⅰ)求证:MN ∥平面BDE ; (Ⅱ)求二面角C -EM -N 的正弦值;(Ⅲ)已知点H 在棱PA 上,且直线NH 与直线BE 所成角的余弦值为7,求线段AH 的长.12.(17天津文(17)(本小题满分13分))如图,在四棱锥P ABCD -中,AD ⊥平面PDC ,AD BC ∥,PD PB ⊥,1AD =,3BC =,4CD =,2PD =.(Ⅰ)求异面直线AP 与BC 所成角的余弦值; (Ⅱ)求证:PD ⊥平面PBC ;(Ⅲ)求直线AB 与平面PBC 所成角的正弦值.如图,已知四棱锥P–ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE与平面PBC所成角的正弦值.14.(17江苏15.(本小题满分14分))-中,AB⊥AD,BC⊥BD,平如图,在三棱锥A BCD面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD。
高考数学复习考点题型专题讲解17 球的切、接、截问题

高考数学复习考点题型专题讲解专题17 球的切、接、截问题1.球的切接问题(1)长方体的外接球①球心:体对角线的交点;②半径:r=a2+b2+c22(a,b,c为长方体的长、宽、高).(2)正方体的外接球、内切球及与各条棱相切的球(a为正方体的棱长)①外接球:球心是正方体中心,半径r=32a,直径等于体对角线长;②内切球:球心是正方体中心,半径r=a2,直径等于正方体棱长;③与各条棱都相切的球:球心是正方体中心,半径r=22a,直径等于面对角线长.(3)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分,a为正四面体的棱长)①外接球:球心是正四面体的中心,半径r=64a;②内切球:球心是正四面体的中心,半径r=612a.2.平面截球平面截球面得圆.截面圆的圆心与球心的连线与截面圆圆面垂直且R2=d2+r2(R为球半径,r为截面圆半径,d为球心到截面圆的距离).类型一外接球问题考向1 墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长.长方体同一顶点的三条棱长分别为a,b,c,外接球半径为R.则(2R)2=a2+b2+c2,即2R=a2+b2+c2.常见的有以下三种类型:例1 已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )A.86πB.46πC.26πD.6π答案 D解析因为点E,F分别为PA,AB的中点,所以EF∥PB.因为∠CEF=90°,所以EF⊥CE,所以PB⊥CE.取AC的中点D,连接BD,PD,易证AC⊥平面BDP,所以PB⊥AC,又AC∩CE=C,AC,CE⊂平面PAC,所以PB⊥平面PAC,所以PB⊥PA,PB⊥PC,因为PA=PB=PC,△ABC为正三角形,所以PA⊥PC,即PA,PB,PC两两垂直,将三棱锥P-ABC放在正方体中如图所示. 因为AB=2,所以该正方体的棱长为2,所以该正方体的体对角线长为6,所以三棱锥P-ABC的外接球的半径R=6 2,所以球O的体积V=43πR3=43π⎝⎛⎭⎪⎫623=6π,故选D.考向2 对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长,如图所示,(2R)2=a2+b2+c2(长方体的长、宽高分别为a,b,c),即R2=18(x2+y2+z2),如图.例2 在三棱锥A -BCD 中,AB =CD =2,AD =BC =3,AC =BD =4,则三棱锥A -BCD 外接球的表面积为________. 答案29π2解析 构造长方体,三个长度为三对面的对角线长,设长方体的长宽高分别为a ,b ,c ,则a 2+b 2=9,b 2+c 2=4,c 2+a 2=16, 所以2(a 2+b 2+c 2)=9+4+16=29, 即a 2+b 2+c 2=4R 2=292, 则外接球的表面积为S =4πR 2=29π2.考向3 汉堡模型汉堡模型是直三棱柱、圆柱的外接球模型,模型如下,由对称性可知,球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2的连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=h2,所以R 2=r 2+h 24.例3(2022·金华调研)在三棱柱ABC -A 1B 1C 1中,AB =BC =AC ,侧棱AA 1⊥底面ABC ,若该三棱柱的所有顶点都在同一个球O 的表面上,且球O 的表面积的最小值为4π,则该三棱柱的侧面积为( ) A.63B.3 3 C.32D.3 答案 B解析 如图,设三棱柱上、下底面中心分别为O 1,O 2,则O 1O 2的中点为O ,设球O 的半径为R ,则OA =R ,设AB =BC =AC =a ,AA 1=h ,则OO 2=12h ,O 2A =23×32AB =33a .在Rt△OO 2A 中,R 2=OA 2=OO 22+O 2A 2=14h 2+13a 2≥2×12h ×33a =33ah , 当且仅当h =233a 时,等号成立,所以S 球=4πR 2≥4π×33ah , 所以43π3ah =4π, 所以ah =3,所以该三棱柱的侧面积为3ah=3 3.考向4 垂面模型垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球;如图所示,由对称性可知球心O的位置是△CBD的外心O1与△AB2D2的外心O2连线的中点,算出小圆O1的半径CO1=r,OO1=h2,则R=r2+h24.例4(2022·广州模拟)已知四棱锥S-ABCD的所有顶点都在球O的球面上,SD⊥平面ABCD,底面ABCD是等腰梯形,AB∥CD且满足AB=2AD=2DC=2,且∠DAB=π3,SC=2,则球O的表面积是( ) A.5π B.4πC.3πD.2π答案 A解析依题意,得AB=2AD=2,∠DAB=π3,由余弦定理可得BD=3,则AD2+DB2=AB2,则∠ADB=π2.又四边形ABCD是等腰梯形,故四边形ABCD的外接圆直径为AB,半径r=AB2=1,设AB的中点为O1,球的半径为R,因为SD ⊥平面ABCD , 所以SD =SC 2-CD 2=1, R 2=12+⎝ ⎛⎭⎪⎫SD 22=54,则S =4πR 2=5π. 考向5 切瓜模型切瓜模型是有一侧面垂直底面的棱锥模型,常见的是两个互相垂直的面都是特殊三角形,在三棱锥A -BCD 中,侧面ABC ⊥底面BCD ,设三棱锥的高为h ,外接球的半径为R ,球心为O ,△BCD 的外心为O 1,O 1到BC 的距离为d ,O 与O 1的距离为m ,△BCD 和△ABC 外接圆的半径分别为r 1,r 2,则⎩⎨⎧R 2=r 21+m 2,R 2=d 2+(h -m )2,解得R ,可得R =r 21+r 22-l 24(l 为两个面的交线段长).例5(2022·济宁模拟)在边长为6的菱形ABCD 中,∠A =π3,现将△ABD 沿BD 折起,当三棱锥A -BCD 的体积最大时,三棱锥A -BCD 的外接球的表面积为________. 答案 60π解析 边长为6的菱形ABCD ,在折叠的过程中, 当平面ABD ⊥平面BCD 时,三棱锥的体积最大; 由于AB =AD =CD =BC =6, ∠C =∠A =π3.所以△ABD 和△CBD 均为正三角形,设△ABD 和△CBD 的外接圆半径为r , 则2r =BDsin C,所以r =2 3.△ABD 和△CBD 的交线段为BD ,且BD =6. 所以三棱锥A -BCD 的外接球的半径R =(23)2+(23)2-624=15.故S 球=4·π(15)2=60π.训练1 (1)(2022·青岛一模)设三棱柱的侧棱垂直于底面,所有棱的长都为1,顶点都在一个球面上,则该球的表面积为( ) A.5π B.π C.113π D.73π (2)在三棱锥P -ABC 中,平面PAB ⊥平面ABC ,平面PAC ⊥平面ABC ,且PA =4,底面△ABC 的外接圆的半径为3,则三棱锥P -ABC 的外接球的表面积为________. 答案 (1)D (2)52π解析 (1)由三棱柱所有棱的长a =1,可知底面为正三角形, 底面三角形的外接圆直径2r =1sin 60°=233,所以r =33, 设外接球的半径为R ,则有R 2=r 2+⎝ ⎛⎭⎪⎫a 22=13+14=712,所以该球的表面积S =4πR 2=73π,故选D.(2)因为平面PAB ⊥平面ABC ,平面PAC ⊥平面ABC , 所以PA ⊥平面ABC .设三棱锥P -ABC 的外接球的半径为R ,结合底面△ABC 的外接圆的半径r =3,可得R 2=⎝ ⎛⎭⎪⎫PA 22+r 2=22+33=13,所以三棱锥P -ABC 的外接球的表面积为S 表=4πR 2=52π. 类型二 内切球问题内切球问题的解法(以三棱锥为例)第一步:先求出四个表面的面积和整个锥体的体积;第二步:设内切球的半径为r ,建立等式V P -ABC =V O -ABC +V O -PAB +V O -PAC +V O -PBC ⇒V P -ABC =13S △ABC ·r +13S △PAB ·r +13S △PAC ·r +13S PBC ·r =13(S △ABC +S △PAB +S △PAC +S △PBC )r ; 第三步:解出r =3V P -ABCS △ABC +S △PAB +S △PAC +S △PBC.例6 (1)(2022·成都石室中学三诊)《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P -ABC 为鳖臑,PA ⊥平面ABC ,PA =BC =4,AB =3,AB ⊥BC ,若三棱锥P -ABC 有一个内切球O ,则球O 的体积为( ) A.9π2B.9π4 C.9π16D.9π (2)在直三棱柱ABC -A 1B 1C 1中,AA 1=AB =6,BC =8,AC =10,则该三棱柱内能放置的最大球的表面积是( ) A.16π B.24π C.36π D.64π答案(1)C (2)A解析(1)设球O的半径为r,则三棱锥P-ABC的体积V=13×12×3×4×4=13×(12×3×4+12×4×3+12×5×4+12×4×5)×r,解得r=34,所以球O的体积V=43πr3=9π16,故选C.(2)由题意,球的半径为底面三角形内切圆的半径r,因为底面三角形的边长分别为6,8,10,所以底面三角形为直角三角形,r=AB+BC-AC2=6+8-102=2.又因为AA1=6,2r=4<6,所以该三棱柱内能放置的最大球半径为2,此时S表面积=4πr2=4π×22=16π.训练 2 已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.答案2 3π解析圆锥内半径最大的球即为圆锥的内切球,设其半径为r.作出圆锥的轴截面PAB,如图所示,则△PAB的内切圆为圆锥的内切球的大圆.在△PAB中,PA=PB=3,D为AB的中点,AB=2,E为切点,则PD=22,△PEO∽△PDB,故PO PB =OE DB ,即22-r 3=r 1,解得r =22, 故内切球的体积为43π⎝ ⎛⎭⎪⎫223=23π.类型三 球的截面问题解决球的截面问题抓住以下几个方面:(1)球心到截面圆的距离;(2)截面圆的半径;(3)直角三角形(球心到截面圆的距离、截面圆的半径、球的半径构成的直角三角形).例7(2022·杭州质检)在正三棱锥P -ABC 中,Q 为BC 中点,PA =2,AB =2,过点Q 的平面截三棱锥P -ABC 的外接球所得截面面积的取值范围为________. 答案⎣⎢⎡⎦⎥⎤π,3π2解析 因为正三棱锥P -ABC 中,PB =PC =PA =2,AC =BC =AB =2,所以PB 2+PA 2=AB 2,即PB ⊥PA , 同理PB ⊥PC ,PC ⊥PA ,因此正三棱锥P -ABC 可看作正方体的一角,如图.记正方体的体对角线的中点为O ,由正方体结构特征可得,点O 即是正方体的外接球球心,所以点O 也是正三棱锥P -ABC 外接球的球心,记外接球半径为R , 则R =122+2+2=62,因为球的最大截面圆为过球心的圆,所以过点Q 的平面截三棱锥P -ABC 的外接球所得截面的面积最大为S max =πR 2=3π2. 又Q 为BC 中点,由正方体结构特征可得OQ =12PA =22;由球的结构特征可知,当OQ 垂直于过点Q 的截面时,截面圆半径最小为r =R 2-OQ 2=1, 所以S min =πr 2=π.因此,过Q 的平面截三棱锥P -ABC 的外接球所得截面面积的取值范围为⎣⎢⎡⎦⎥⎤π,3π2. 训练3 (1)设球O 是棱长为4的正方体的外接球,过该正方体棱的中点作球O 的截面,则最小截面的面积为( ) A.3π B.4π C.5π D.6π(2)(2022·武汉质检)已知棱长为2的正方体ABCD -A 1B 1C 1D 1,球O 与该正方体的各个面相切,则平面ACB 1截此球所得的截面的面积为________. 答案 (1)B (2)2π3解析 (1)当球O 到截面圆心连线与截面圆垂直时,截面圆的面积最小, 由题意,正方体棱的中点与O 的距离为22,球的半径为23, ∴最小截面圆的半径为12-8=2, ∴最小截面面积为π·22=4π.(2)∵正方体ABCD -A 1B 1C 1D 1的棱长为2,球O 与该正方体的各个面相切,则球O 的半径为1,设E ,F ,G 分别为球O 与平面ABCD 、平面BB 1C 1C 、平面AA 1B 1B 的切点, 则等边三角形EFG 为平面ACB 1截此球所得的截面圆的内接三角形, 由已知可得EF =EG =GF =2, ∴平面ACB 1截此球所得的截面圆的半径r =22sin 60°=63,∴截面的面积为π×⎝ ⎛⎭⎪⎫632=2π3.一、基本技能练1.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A.π B.3π4C.π2D.π4 答案 B解析 如图画出圆柱的轴截面ABCD ,O 为球心.球的半径R =OA=1,球心到底面圆的距离为OM =12.∴底面圆半径r =OA 2-OM 2=32故圆柱体积V =π·r 2·h =π·⎝ ⎛⎭⎪⎫322×1=3π4.2.若棱长为23的正方体的顶点都在同一球面上,则该球的表面积为( ) A.12π B.24π C.36π D.144π 答案 C解析 由题意知球的直径2R =(23)2+(23)2+(23)2=6, ∴R =3,∴S 球=4πR 2=36π.故选C.3.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( ) A.3π B.4π C.33π D.6π 答案 A解析 构造棱长为1的正方体,该四面体的外接球也是棱长为1的正方体的外接球, 所以外接球半径R =32, 所以外接球表面积为S =4πR 2=3π.4.已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为( )A.3172B.210C.132D.310 答案 C解析 将直三棱柱补为长方体ABEC -A 1B 1E 1C 1, 则球O 是长方体ABEC -A 1B 1E 1C 1的外接球. ∴体对角线BC 1的长为球O 的直径. 因此2R =32+42+122=13,则R =132.5.(2022·南阳二模)已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的∠BDC =π2,则过A ,B ,C ,D 四点的球的表面积为( )A.3πB.4πC.5πD.6π 答案 C解析 折后的几何体构成以D 为顶点的三棱锥,且三条侧棱互相垂直,可构造长方体,其对角线即为球的直径,三条棱长分别为1,1,3,所以2R =1+1+3=5,球的表面积S =4π⎝ ⎛⎭⎪⎫522=5π.6.(2022·青岛模拟)如图是一个由6个正方形和8个正三角形围成的十四面体,其所有顶点都在球O 的球面上,若十四面体的棱长为1,则球O 的表面积为( )A.2πB.4πC.6πD.8π 答案 B解析 根据图形可知,该十四面体是由一个正方体切去八个角得到的,如图所示,十四面体的外接球球心与正方体的外接球球心相同, 建立空间直角坐标系,∵该十四面体的棱长为1,故正方体的棱长为2, ∴该正方体的外接球球心的坐标为O ⎝ ⎛⎭⎪⎫22,22,22,设十四面体上一顶点为D ,则D ⎝ ⎛⎭⎪⎫2,22,0,所以十四面体的外接球半径R =OD =⎝ ⎛⎭⎪⎫2-222+⎝ ⎛⎭⎪⎫22-222+⎝ ⎛⎭⎪⎫0-222=1,故外接球的表面积为S =4πR 2=4π.故选B.7.四面体ABCD 的四个顶点都在球O 上且AB =AC =BC =BD =CD =4,AD =26,则球O 的表面积为( )A.70π3B.80π3C.30πD.40π答案 B解析如图,取BC的中点M,连接AM,DM,由题意可知,△ABC和△BCD都是边长为4的等边三角形. ∵M为BC的中点,∴AM⊥BC,且AM=DM=23,又∵AD=26,∴AM2+DM2=AD2,∴AM⊥DM,∵BC∩DM=M,BC,DM⊂平面BCD,∴AM⊥平面BCD,∵AM⊂平面ABC,∴平面ABC⊥平面BCD,△ABC与△BCD外接圆半径r=23DM=433,又△ABC与△BCD的交线段BC=4. 所以四面体外接球半径R =⎝ ⎛⎭⎪⎫4332+⎝ ⎛⎭⎪⎫4332-424=2153,四面体ABCD 的外接球的表面积为4π×R 2=803π. 8.已知三棱锥P -ABC 的棱AP ,AB ,AC 两两垂直,且长度都为3,以顶点P 为球心,2为半径作一个球,则球面与三棱锥的表面相交所得到的四段弧长之和等于( ) A.2π3B.5π6C.πD.3π2答案 D解析 如图,∠APC =π4,AP =3,AN =1,∠APN =π6,∠NPM =π12,MN ︵=π12×2=π6,同理GH ︵=π6,HN ︵=π2,GM ︵=2π3,故四段弧长之和为π6+π6+π2+2π3=3π2.9.(多选)(2022·石家庄调研)已知一个正方体的外接球和内切球上各有一个动点M 和N ,若线段MN 长的最小值为3-1,则( ) A.该正方体的外接球的表面积为12π B.该正方体的内切球的体积为π3C.该正方体的棱长为1D.线段MN长的最大值为3+1 答案AD解析设该正方体的棱长为a,则其外接球的半径R=32a,内切球的半径R′=a2,该正方体的外接球与内切球上各有一个动点M,N,由于两球球心相同,可得MN的最小值为3a2-a2=3-1,解得a=2,故C错误;所以外接球的半径R=3,表面积为4π×3=12π,故A正确;内切球的半径R′=1,体积为43π,故B错误;MN的最大值为R+R′=3+1,故D正确.故选AD.10.(多选)设圆锥的顶点为A,BC为圆锥底面圆O的直径,点P为圆O上的一点(异于B,C),若BC=43,三棱锥A-PBC的外接球表面积为64π,则圆锥的体积为( ) A.4π B.8πC.16πD.24π答案BD解析如图,设圆锥AO的外接球球心为M,半径为r,则M在直线AO上,4πr2=64π,解得r=4.由勾股定理得BM2=OM2+OB2,即42=(23)2+OM2,可得OM=2,即OM=|AO-r|=|AO-4|=2,解得AO=6或AO=2.当AO=6时,圆锥AO的体积为V=13π×(23)2×6=24π;当AO=2时,圆锥AO的体积为V=13π×(23)2×2=8π.故选BD.11.在三棱锥A-BCD中,△BCD和△ABD均是边长为1的等边三角形,AC=2,则该三棱锥外接球的表面积为________.答案2π解析取AC的中点O,连接OB,OD,在△ABC中,AB=BC=1,AC=2,所以∠ABC=90°,所以OA=OB=OC=2 2,同理得OD=22,故点O为该三棱锥外接球的球心,所以球O的半径r=22,S球=4πr2=2π.12.如图,已知球O是棱长为3的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为________.答案3π2解析 根据题意知,平面ACD 1是边长为9+9=32的正三角形,且所求截面的面积是该正三角形的内切圆的面积,则由图得,△ACD 1内切圆的半径r =13(32)2-⎝⎛⎭⎪⎫3222=62, 所以平面ACD 1截球O 的截面面积为 S =π×⎝ ⎛⎭⎪⎫622=3π2.二、创新拓展练13.(多选)(2022·华大新高考联考)已知三棱锥S -ABC 中,SA ⊥平面ABC ,SA =AB =BC =2,AC =2,点E ,F 分别是线段AB ,BC 的中点,直线AF ,CE 相交于G ,则过点G 的平面α截三棱锥S -ABC 的外接球O 所得截面面积可以是( ) A.23π B.89π C.π D.32π答案 BCD解析 因为AB 2+BC 2=AC 2,故AB ⊥BC , 故三棱锥S -ABC 的外接球O的半径R =2+2+22=62,取AC 的中点D ,连接BD 必过G , 因为AB =BC =2,故DG =13BD =13,因为OD =22, 故OG 2=⎝ ⎛⎭⎪⎫222+⎝ ⎛⎭⎪⎫132=1118,则过点G 的平面截球O 所得截面圆的最小半径r 2=⎝ ⎛⎭⎪⎫622-1118=89,故截面面积的最小值为89π,最大值为πR 2=32π,故选BCD.14.(多选)(2022·济南模拟)已知三棱锥P -ABC 的四个顶点都在球O 上,AB =BC =AC =1,∠APC =π6,平面PAC ⊥平面ABC ,则( )A.直线OA 与直线BC 垂直B.点P 到平面ABC 的距离的最大值为1+32C.球O 的表面积为13π3D.三棱锥O -ABC 的体积为18答案 ACD解析 设△ABC 外接圆的圆心为O 1,连接OO 1,O 1A . 因为O 为三棱锥P -ABC 外接球的球心, 所以OO 1⊥平面ABC ,所以OO 1⊥BC ,因为AB =BC =AC =1,所以O 1A ⊥BC ,所以BC ⊥平面OO 1A , 所以OA ⊥BC ,故A 选项正确; 设△PAC 外接圆的圆心为O 2,AC 的中点为D ,连接O 2D , 由于AC =1,∠APC =π6,所以圆O 2的半径r 2=12×1sinπ6=1,则易知O 2D =32, 所以点P 到平面ABC 的距离的最大值为1+32(此时P ,O 2,D 三点共线),故B 选项错误;由于AB =BC =AC =1,平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC , 所以圆O 1的半径r 1=12×1sin π3=33, 圆O 2的半径r 2=1,△ABC 与△PAC 的交线段AC =1, 所以三棱锥P -ABC 外接球半径R 2=⎝ ⎛⎭⎪⎫332+12-14=1312.故球O 的表面积S =4π×1312=13π3,故C 选项正确;由于OO 1⊥平面ABC ,且OO 1=O 2D =32,S △ABC =34,所以三棱锥O-ABC的体积为13×OO1×S△ABC=13×32×34=18,故D选项正确,故选ACD.15.(多选)(2022·湖州调研)已知正四面体ABCD的棱长为3,其外接球的球心为O.点E 满足AE→=λAB→(0<λ<1),过点E作平面α平行于AC和BD,设α分别与该正四面体的棱BC,CD,DA相交于点F,G,H,则( )A.四边形EFGH的周长为定值B.当λ=12时,四边形EFGH为正方形C.当λ=13时,平面α截球O所得截面的周长为13π4D.四棱锥A-EFGH的体积的最大值为22 3答案ABD解析将正四面体ABCD放入正方体中.因为正四面体ABCD的棱长为3,所以正方体的棱长为322.如图所示,过点E作平面α平行于AC和BD,平面α与正方体的棱交于M,N,P,Q四点.因为AE→=λAB→,故AH→=λAD→,即有EH=λBD,同理FG=λBD,EF=(1-λ)AC,HG=(1-λ)AC,且EH∥BD,EF∥AC,故四边形EFGH 为平行四边形.因为AC ⊥BD ,故EF ⊥EH ,则四边形EFGH 为矩形.对于A ,四边形EFGH 的周长为2(EF +EH )=2[(1-λ)AC +λBD ]=2[(1-λ)AC +λAC ]=2AC =6,为定值,故A 选项正确;对于B ,当λ=12时,E 为AB 的中点,故EF =EH ,所以四边形EFGH 为正方形,故B 选项正确;对于C ,当λ=13时,球心O 到平面EFGH 的距离即球心到平面MNPQ 的距离,即BC 中点到MF 的距离,经计算为24,球半径为322×32=364,故截面圆的半径为⎝ ⎛⎭⎪⎫3642-⎝ ⎛⎭⎪⎫242=132,所以截面圆的周长为132×2π=13π,故C 选项错误;对于D ,四棱锥A -EFGH 的高为AQ ,所以其体积V =13×322λ×3(1-λ)×3λ=922λ2(1-λ),0<λ<1, 令f (λ)=922λ2(1-λ),则f ′(λ)=922(2λ-3λ2),令f ′(λ)=0得λ=23,故当λ=23时,四棱锥A -EFGH 的体积最大,最大值为922×49×13=223,故D 选项正确,故选ABD.16.(多选)(2022·嘉兴测试)如图,在等腰梯形ABCD 中,AB =2AD =2BC =2CD =4.现将△DAC沿对角线AC所在的直线翻折成△D′AC,记二面角D′-AC-B的大小为α(0<α<π),则( )A.存在α,使得D′A⊥BCB.存在α,使得D′A⊥平面D′BCC.存在α,使得三棱锥D′-ABC的体积为3 3D.存在α=π2,使得三棱锥D′-ABC的外接球的表面积为20π答案ACD解析如图1,取AB的中点E,连接DE交AC于点F.因为AB=2CD,所以CD=EB=AE,所以四边形AECD为菱形,四边形EBCD为菱形,所以△AED,△DEC,△EBC均为等边三角形,所以AC⊥ED,∠DAC=∠BAC=π6,∠ACB=π2,在翻折过程中,如图2,AC⊥D′F,AC⊥FE,所以∠D′FE为二面角D′-AC-B的平面角,所以∠D′FE=α.对于A,当α=π2时,平面D′AC⊥平面ABC.因为BC⊥AC,所以BC⊥平面D′AC.又因为D′A⊂平面D′AC,所以D′A⊥BC,所以存在α,使得D′A⊥BC,故A选项正确;对于B,假设存在α,使得D′A⊥平面D′BC.因为D′C⊂平面D′BC,所以D′A⊥D′C,与∠AD′C=2π3矛盾,故B选项不正确;对于C,由分析可得,D′F=12DE=12AD=1,AC=2AF=2×32×AD=2 3.设D′到平面ABC的距离为d,则V三棱锥D′-ABC=13×S△ABC×d=13×12×AC×BC×d=13×12×23×2×d=33,解得d=1 2,所以sin α=dD′F=12,所以α=π6或5π6,故C选项正确;对于D,当α=π2时,平面D′AC⊥平面ABC,所以BC⊥平面D′AC,D′F⊥平面ABC.如图2所示,因为E,F分别为AB,AC的中点,所以EF∥BC,且EF=12BC=1,所以EF⊥平面D′AC.设△D′AC外接圆圆心为O1,则O1A=O1D′=AD′=2.因为E是Rt△ABC斜边的中点,所以E为Rt△ABC的外心.过O1作平面D′AC的垂线,过点E作平面ABC的垂线,则两垂线的交点O即为三棱锥D′-ABC外接球的球心,显然四边形EFO1O是矩形,所以OO1=EF=1.设三棱锥D′-ABC的外接球半径为R,则在Rt△OO1D′中,R=OD′=O1O2+O1D′2=1+4=5,所以三棱锥D′-ABC的外接球的表面积S=4πR2=20π,故D选项正确.综上所述,故选ACD.17.在菱形ABCD中,AB=23,∠ABC=60°,若将菱形ABCD沿对角线AC折成大小为60°的二面角B-AC-D,则四面体DABC的外接球球O的体积为________.答案5239π27解析如图,设M,N分别为△ABC,△ACD的外心,E为AC的中点,则EN=EM=13BE=1,在平面BDE内过点M作BE的垂线与过点N作DE的垂线交于点O. ∵BE⊥AC,DE⊥AC,BE∩DE=E,∴AC⊥平面BDE.∵OM⊂平面BDE,∴OM⊥AC,∵OM⊥BE,BE∩AC=E,∴OM⊥平面ABC,同理可得ON⊥平面ACD,则O为四面体DABC的外接球的球心,连接OE,∵EM=EN,OE=OE,∠OME=∠ONE=90°,∴△OME≌△ONE,∴∠OEM=30°,∴OE=EMcos 30°=233.∵AC⊥平面BDE,OE⊂平面BDE,∴OE⊥AC,∴OA=OE2+AE2=39 3,即球O的半径R=39 3.故球O的体积V=43πR3=5239π27.18.(2022·湖南三湘名校联考)在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=AA1=4,M 为棱AB的中点,N是棱BC的中点,O是三棱柱外接球的球心,则平面MNB1截球O所得截面的面积为________.答案8π解析如图1,将直三棱柱补形成正方体ABCD-A1B1C1D1,连接BD1,则直三棱柱的外接球也是正方体的外接球,球心O是BD1的中点,半径R=2 3. 连接BD交MN于点E,连接B1E交BD1于点F,过点O作OO1⊥B1E于点O1,连接B1D1,因为MN∥AC,AC⊥平面BB1D1D,所以MN⊥平面BB1D1D,所以OO1⊥MN,所以OO1⊥平面MNB1.如图2,31 / 31 在矩形BB 1D 1D 中,BF FD 1=BE B 1D 1=14, 所以BF OF =23,过点B 作BG ⊥B 1E 于点G , 则BG =BE ·BB 1B 1E =43,BGOO 1=BF OF =23,所以OO 1=2,设截面圆的半径为r , 则r 2=R 2-OO 21=(23)2-22=8,所以截面的面积为8π.。
2017年全国统一高考数学试卷(文科)(新课标ⅱ)(含解析版)

2017 年全国统一高考数学试卷(文科)(新课标Ⅱ)一、选择题:本题共12 小题,每小题5 分,共60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5 分)设集合A={1,2,3},B={2,3,4},则A∪B=()A.{1,2,3,4} B.{1,2,3} C.{2,3,4} D.{1,3,4} 2.(5分)(1+i)(2+i)=()A.1﹣i B.1+3i C.3+i D.3+3i3.(5分)函数f(x)=sin(2x+)的最小正周期为()A.4πB.2πC.πD.4.(5 分)设非零向量,满足|+|=|﹣|则()A.⊥B.||=|| C.∥D.||>||5.(5 分)若a>1,则双曲线﹣y2=1 的离心率的取值范围是()A.(,+∞)B.(,2)C.(1,)D.(1,2)6.(5 分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π7.(5 分)设x,y 满足约束条件,则z=2x+y 的最小值是()A.﹣15 B.﹣9 C.1 D.98.(5 分)函数f(x)=ln(x2﹣2x﹣8)的单调递增区间是()A.(﹣∞,﹣2)B.(﹣∞,﹣1)C.(1,+∞)D.(4,+∞)9.(5 分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2 位优秀,2 位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩10.(5 分)执行如图的程序框图,如果输入的a=﹣1,则输出的S=()A.2 B.3 C.4 D.511.(5 分)从分别写有1,2,3,4,5 的5 张卡片中随机抽取1 张,放回后再随机抽取1 张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为()A.B.C.D.12.(5 分)过抛物线C:y2=4x 的焦点F,且斜率为的直线交C 于点M(M 在x 轴上方),l为C 的准线,点N 在l 上,且MN⊥l,则M 到直线NF 的距离为()A.B.2C.2D.3二、填空题,本题共4 小题,每小题5 分,共20 分13.(5 分)函数f(x)=2cosx+sinx 的最大值为.14.(5 分)已知函数f(x)是定义在R 上的奇函数,当x∈(﹣∞,0)时,f (x)=2x3+x2,则f(2)=.15.(5 分)长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为.16.(5 分)△ABC 的内角A,B,C 的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=.三、解答题:共70 分.解答应写出文字说明,证明过程或演算步骤,第17 至21 题为必考题,每个试题考生都必须作答.第22、23 题为选考题,考生根据要求作答.(一)必考题:共60 分.17.(12 分)已知等差数列{a n}的前n 项和为S n,等比数列{b n}的前n 项和为T n,a1=﹣1,b1=1,a2+b2=2.(1)若a3+b3=5,求{b n}的通项公式;(2)若T3=21,求S3.18.(12 分)如图,四棱锥P﹣ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.(1)证明:直线BC∥平面PAD;(2)若△PCD 面积为2,求四棱锥P﹣ABCD 的体积.19.(12 分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:(1)记A 表示事件“旧养殖法的箱产量低于50kg”,估计A 的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:箱产量<50kg 箱产量≥50kg旧养殖法新养殖法(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.附:P(K2≥K)0.050 0.010 0.001K 3.841 6.635 10.828K2=.20.(12 分)设O 为坐标原点,动点M 在椭圆C:+y2=1 上,过M 作x 轴的垂线,垂足为N,点P 满足= .(1)求点P 的轨迹方程;(2)设点Q 在直线x=﹣3 上,且•=1.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F.21.(12 分)设函数f(x)=(1﹣x2)e x.(1)讨论f(x)的单调性;(2)当x≥0 时,f(x)≤ax+1,求a 的取值范围.选考题:共10 分。
高考必考题—几何体中与球有关的切、接问题(含解析)

几何体中与球有关的切、接问题球的截面的性质(1)球的任何截面是圆面;(2)球心和截面(不过球心)圆心的连线垂直于截面;(3)球心到截面的距离d 与球的半径R 及截面的半径r 的关系为r =R 2-d 2几个与球有关的切、接常用结论(1)正方体的棱长为a ,球的半径为R ,①若球为正方体的外接球,则2R =3a ;②若球为正方体的内切球,则2R =a ;③若球与正方体的各棱相切,则2R =2a .(2)若长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2. (3)正四面体的外接球与内切球的半径之比为3∶1. 一、题型选讲题型一 、几何体的外接球解决多面体的外接球问题,关键是确定球心的位置,方法是先选择多面体中的一面,确定此面外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置.对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置.例1、【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为 A .64π B .48πC .36πD .32π例2、【2020年高考天津】若棱长为 A .12π B .24π C .36πD .144π例3、(2020届山东省潍坊市高三上学期统考)已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,则过A ,B ,C ,D 四点的球的表面积为( )A .3πB .4πC .5πD .6π例4、(2020届山东省日照市高三上期末联考)已知四棱锥P ABCD -的体积是ABCD 是正方形,PAB ∆是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P ABCD -外接球体积为( )A .BCD .例5、(2020届山东省德州市高三上期末)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,AD =ED =P ADE -的外接球的体积为,则阳马P ABCD -的外接球的表面积等于______.题型二、几何体的内切球求解多面体的内切球的问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.例6、【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.例7、(2020届山东省潍坊市高三上期中)如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为__________;若该六面体内有一小球,则小球的最大体积为___________.二、达标训练1、(2020届山东省泰安市高三上期末)已知正三棱锥S ABC -的侧棱长为6,则该正三棱锥外接球的表面积是( ) A .16πB .20πC .32πD .64π2、【2020年高考全国II 卷理数】已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A B .32C .1D 3、【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D4、【2018年高考全国Ⅰ卷理数】设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为A .B .C .D .5、【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 半径的球面与侧面BCC 1B 1的交线长为________.6、(2020届山东省滨州市三校高三上学期联考)已知三棱锥S ABC -,SA ⊥平面ABC ,6ABC π∠=,3SA =,1BC =,直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上,则该球的表面积为________.7、(2020届山东省枣庄、滕州市高三上期末)如图,在三棱锥P -ABC 中,,PA AB ⊥PC BC ⊥,,AB BC ⊥22,AB BC ==PC =,则PA 与平面ABC 所成角的大小为________;三棱锥P -ABC 外接球的表面积是________.8、(2020届山东省烟台市高三上期末)已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC,6PA =,AB =2AC =,4BC =,则:(1)球O 的表面积为__________;(2)若D 是BC 的中点,过点D 作球O 的截面,则截面面积的最小值是__________.9、(2020届山东省滨州市高三上期末)在四面体S ABC -中,2SA SB ==,且SA SB ⊥,BC =,AC=________,该四面体外接球的表面积为________.10、(2020届山东省济宁市高三上期末)下图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形-的外接球的体积为ABCD,现将四边形ABCD沿BD折成直二面角A BD C--,则三棱锥A BCDcm.__________3一、题型选讲题型一 、几何体的外接球解决多面体的外接球问题,关键是确定球心的位置,方法是先选择多面体中的一面,确定此面外接圆的圆心,再过圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点确定球心的准确位置.对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置.例1、【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为 A .64π B .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意, 得24,2r r π=π=∴,ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====, ∴球O 的表面积2464S R ππ==.故选:A.本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.例2、【2020年高考天津】若棱长为 A .12π B .24πC .36πD .144π【答案】C【解析】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R ==,所以,这个球的表面积为2244336S R πππ==⨯=. 故选:C .本题考查正方体的外接球的表面积的求法,求出外接球的半径是本题的解题关键,属于基础题.求多面体的外接球的面积和体积问题,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心. 例3、(2020届山东省潍坊市高三上学期统考)已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,则过A ,B ,C ,D 四点的球的表面积为( )A .3πB .4πC .5πD .6π【答案】C【解析】边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕进行折叠,使折后的2BDC π∠=,构成以D 为顶点的三棱锥,且三条侧棱互相垂直,可构造以其为长宽高的长方体,其对角线即为球的直径,三条棱长分别为1,12R ==2452S ππ==,故选C.例4、(2020届山东省日照市高三上期末联考)已知四棱锥P ABCD -的体积是ABCD 是正方形,PAB ∆是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P ABCD -外接球体积为( )A .BCD .【答案】A【解析】设AB 的中点为Q ,因为PAB ∆是等边三角形,所以PQ AB ⊥,而平面PAB ⊥平面ABCD , 平面PAB ⋂平面ABCD AB =,所以PQ ⊥平面ABCD ,四棱锥P ABCD -的体积是13AB AB PQ =⨯⨯⨯13AB AB AB =⨯⨯,所以边长6AB =,PQ =OH x =,OM x =,()(222222R OA OM AM x==+=+,2222223R OP OH PH x ==+=+,x =2212321R =+=343V R π==球.故选:A.例5、(2020届山东省德州市高三上期末)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,AD =ED =P ADE -的外接球的体积为,则阳马P ABCD -的外接球的表面积等于______.【答案】20π 【解析】四边形ABCD 是正方形,AD CD ∴⊥,即AD CE ⊥,且AD =ED =,所以,ADE ∆的外接圆半径为122AE r ===设鳖臑P ADE -的外接球的半径1R ,则3143R π=,解得12R =.PA ⊥平面ADE ,1R ∴=2PA ==PA ∴=正方形ABCD 的外接圆直径为22r AC ==22r ∴=,PA ⊥平面ABCD ,所以,阳马P ABCD -的外接球半径2R ==因此,阳马P ABCD -的外接球的表面积为22420R ππ=.故答案为:20π. 题型二、几何体的内切球求解多面体的内切球的问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.例6、【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.【解析】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示, 其中2,3BC AB AC ===,且点M 为BC 边上的中点, 设内切圆的圆心为O ,由于AM ==122S =⨯⨯=△ABC 设内切圆半径为r ,则:ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯=解得:2r,其体积:343V r =π=.故答案为:3. 与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.例7、(2020届山东省潍坊市高三上期中)如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为__________;若该六面体内有一小球,则小球的最大体积为___________.【解析】(1)因为16(12S =⨯⨯=. (2)由图形的对称性得,小球的体积要达到最大,即球与六个面都相切时,每个三角形面积是4,六面体体积是正四面体的2倍,所以六面体体积是6. 由于图像的对称性,内部的小球要是体积最大,就是球要和六个面相切,连接球心和五个顶点,把六面体分成了六个三棱锥,设球的半径为R ,所以16()6349R R =⨯⨯⨯⇒=,所以球的体积334433V R ππ===.故答案为:. 二、达标训练1、(2020届山东省泰安市高三上期末)已知正三棱锥S ABC -的侧棱长为6,则该正三棱锥外接球的表面积是( ) A .16π B .20πC .32πD .64π【答案】D【解析】如图所示,因为正三棱锥S ABC -的侧棱长为6,则263AE ==6SE ===, 又由球心O 到四个顶点的距离相等,在直角三角形AOE 中,,6AO R OE SE SO R ==-=-,又由222OA AE OE =+,即222(6)R R =+-,解得4R =, 所以球的表面积为2464S R ππ==, 故选D.2、【2020年高考全国II 卷理数】已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A B .32C .1D 【答案】C【解析】设球O 的半径为R ,则2416R π=π,解得:2R =.设ABC △外接圆半径为r ,边长为a ,ABC △21224a ∴⨯=,解得:3a =,2233r ∴===,∴球心O 到平面ABC 的距离1d ==.故选:C .本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.3、【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D【答案】D 【解析】解法一:,PA PB PC ABC ==△为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CEAC C EF =∴⊥平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分,2R ==即344π33R V R =∴=π==,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,CF ∴=又90CEF ∠=︒,12CE AE PA x ∴===, AEC △中,由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯,作PD AC ⊥于D ,PA PC =,D 为AC 的中点,1cos 2AD EAC PA x ∠==,2243142x x x x+-+∴=,22121222x x x ∴+=∴==,,,PA PB PC ∴=== 又===2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴==R ∴=,34433V R ∴=π==,故选D.本题主要考查学生的空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.4、【2018年高考全国Ⅰ卷理数】设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为 A. B . C.D .【答案】B【解析】如图所示,设点M 为三角形ABC 的重心,E 为AC 中点,当点D 在平面ABC 上的射影为M 时,三棱锥D ABC -的体积最大,此时,4OD OB R ===,2ABC S AB ==△,6AB ∴=,点M 为三角形ABC 的重心,23BM BE ∴==,Rt OBM ∴△中,有2OM ==,426DM OD OM ∴=+=+=,()max 163D ABC V -∴=⨯= B.5、【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 半径的球面与侧面BCC 1B 1的交线长为________.【答案】2. 【解析】如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A B C D -的棱长均为2,所以△111D B C 为等边三角形,所以1D E=111D E B C ⊥,又四棱柱1111ABCD A B C D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BB B C ⊥, 因为1111BB B C B =,所以1D E ⊥侧面11B C CB ,设P 为侧面11B C CB 与球面的交线上的点,则1D E EP ⊥,1D E =,所以||EP ===所以侧面11B C CB 与球面的交线上的点到E ,因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧FG ,因为114B EFC EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得22FG π==.. 6、(2020届山东省滨州市三校高三上学期联考)已知三棱锥S ABC -,SA ⊥平面ABC ,6ABC π∠=,3SA =,1BC =,直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上,则该球的表面积为________. 【答案】13π【解析】如图:SA ⊥平面ABC ,则SBA ∠为直线SB 和平面ABC 所成的角,即3SBA π∠=在Rt SAB ∆中:tan3SA AB π=== 如图,设O 为三棱锥S ABC -外接球的球心,G 为ABC ∆外接圆圆心, 连结,,,,OA OB GA GB OG ,则必有OG ⊥面ABC 在ABC ∆,2222cos 312162AC AB BC AB BC π=+-⋅⋅=+-=, 则1AC = 其外接圆半径122,1sin sin 6AC r r ABC π====∠, 又1322OG SA ==, 所以三棱锥S ABC -外接球半径为R ===该球的表面积为21344134S R πππ==⨯=, 故答案为:13π.7、(2020届山东省枣庄、滕州市高三上期末)如图,在三棱锥P -ABC 中,,PA AB ⊥PC BC ⊥,,AB BC ⊥22,AB BC ==PC =,则PA 与平面ABC 所成角的大小为________;三棱锥P -ABC 外接球的表面积是________.【答案】45︒ 6π【解析】如图,作平行四边形ABCD ,连接PD ,由AB BC ⊥,则平行四边形ABCD 是矩形. 由BC CD ⊥,BC PC ⊥,PCCD C =,∴BC ⊥平面PCD ,而PD ⊂平面PCD ,∴BC PD ⊥,同理可得AB PD ⊥,又AB BC B ⋂=,∴PD ⊥平面ABCD .,PD CD PD AD ⊥⊥,PAD ∠是PA 与平面ABC 所成角.由2,CD AB PC ===1PD =,又1AD BC ==,∴45PAD ∠=︒.∴PA 与平面ABC 所成角是45︒.由,PA AB ⊥PC BC ⊥知PB 的中点到,,,A B C P 的距离相等,PB 是三棱锥P -ABC 外接球的直径.由BC ⊥平面PCD 得BC PC ⊥,PB ===24()62PB S ππ==. 故答案为:45︒;6π.8、(2020届山东省烟台市高三上期末)已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC,6PA =,AB =2AC =,4BC =,则:(1)球O 的表面积为__________;(2)若D 是BC 的中点,过点D 作球O 的截面,则截面面积的最小值是__________. 【答案】52π 4π【解析】(1)由题,根据勾股定理可得AC AB ⊥,则可将三棱锥P ABC -可放入以,,AP AC AB 为长方体的长,宽,高的长方体中,则体对角线为外接球直径,即2r ==则r =,所以球的表面积为224452r πππ=⨯=;(2)由题,因为Rt ABC ,所以D 为底面ABC 的外接圆圆心,当DO ⊥截面时,截面面积最小,即截面为平面ABC ,则外接圆半径为2,故截面面积为224ππ⨯=故答案为:(1)52π;(2)4π9、(2020届山东省滨州市高三上期末)在四面体S ABC -中,2SA SB ==,且SA SB ⊥,BC =,AC =________,该四面体外接球的表面积为________.【答案】68π【解析】因为2SA SB ==,且SA SB ⊥,BC =,AC =AB ==,因此222BC AC AB +=,则AC BC ⊥;取AB 中点为O ,连接OS ,OC ,则OA OB OC OS ====,所以该四面体的外接球的球心为O ,半径为OC=所以该四面体外接球的表面积为248S ππ=⋅=; 又因为SA SB =,所以SO AB ⊥;因为底面三角形ABC 的面积为定值122AC BC ⋅=,SO ,因此,当SO ⊥平面ABC 时,四面体的体积最大,为136ABC V S SO =⋅=.故答案为:(1).6(2). 8π10、(2020届山东省济宁市高三上期末)下图是两个腰长均为10cm 的等腰直角三角形拼成的一个四边形ABCD ,现将四边形ABCD 沿BD 折成直二面角A BD C --,则三棱锥A BCD -的外接球的体积为__________3cm .【答案】 【解析】由题设可将该三棱锥拓展成如图所示的正方体,则该正方体的外接球就是三棱锥的外接球,由于正方体的对角线长为2l R ==即球的半径R =该球的体积343V R π==,应填答案.。
高中数学与球有关的切接问题专项训练(文理科)

与球有关的切接问题专项训练1.已知PC 为球O 的直径,A B ,是球面上两点,且6AB =,4APC BPC π∠=∠=,若球O 的表面积为64π,则棱锥A PBC -的体积为( ).A. 答案:A2.在四面体S ABC -中,AB BC ⊥,AB BC ==2SA SC ==,SB =则该四面体外接球的表面积是( )A. C.24π D.6π答案:D3.已知三棱锥A BCD -中,2AB AC BC ===,BD CD ==点E 为BC 的中点,点A 在平面BCD 内的投影恰好为DE 的中点,则此三棱锥外接球的表面积为_____. 答案:6011π4.已知正四面体ABCD 的四个顶点都在球心为O 的球面上,点P 为棱BC 的中点,BC =过点P 作球O 的截面,则截面面积的最小值为______.答案:18π5.四面体PABC 的四个顶点都在球O 的球面上,8,4,PA BC PB PC AB AC =====,且平面PBC ⊥平面ABC ,则球O 的表面积为( )A.64πB.65πC.66πD.128π答案:B6.已知三棱锥A BCD -中,3AB AC ==,BD CD ==且BD CD ⊥,若点A 在平面BCD 内的投影恰好为点D ,则此三棱锥外接球的表面积为______.答案是:11π7.已知一个高为1的三棱锥,各侧棱长都相等,底面是边长为2的等边三角形,内有一个体积为V 的球,则V 的最大值为( ). A.481π B.427π C.49π D.43π 答案:A8.已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2,2AB SA SB SC ====,则三棱锥的外接球的球心到平面ABC 的距离是( )A.32答案:A9.三棱锥B ACD -的每个顶点都在表面积为16π的球O 的球面上,且AB ⊥平面BCD ,BCD △为等边三角形,2AB BC =,则三棱锥B ACD -的体积为( )32 答案:C10.在三棱锥P ABC -中,,,PA PB PC 两两互相垂直,1,2PA PB PC ===,若三棱锥P ABC -的顶点都在球O 的球面上,则球O 的表面积等于( )A.9πB.16πC.25πD.36π答案:A11.已知90ABC ∠=,PA ⊥平面ABC ,若1PA AB BC ===,则四面体PABC 的外接球(顶点都在球面上)的表面积为______.答案:3π12.设,A B 是球O 的球面上两点,3AOB π∠=,C 是球面上的动点,若四面体O ABC -的体积V 的最大值为4,则此时球的表面积为______. 答案:36π13.已知半径为r 的球O 与正方体1111ABCD A B C D -的各棱都相切,记球O 与正方体1111ABCD A B C D -的各面的交线的总长度为()f r ,则(1)f =______.答案:14.三棱锥D ABC -中,AB CD ==其余四条棱均为2,则三棱锥D ABC -的外接球的表面积为________.答案:7π15.已知三棱锥P ABC -的所有顶点都在表面积为16π的球O 的球面上,AC 为球O 的直径,当三棱锥P ABC -的体积最大时,设二面角P AB C --的大小为θ,则sin θ=( )A .23B .53C .63D .73 答案:C16.四面体ABCD 的四个顶点都在球O 的球面上,2AB AD CD ===,22BD =,BD CD ⊥,平面ABD ⊥平面BCD ,则球O 的体积为( )A .43πB .32π C .42π D .2π 答案:A17.某四棱锥的三视图如图所示,则该四棱锥的外接球的表面积是( )A .4πB .6πC .7πD .12π答案:C18.已知,A B 是球O 球面上的两点,90AOB ∠=,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为________.答案:144π19.三棱锥A BCD -内接于半径为5的球O 中,4AB CD ==,则三棱锥的体积的最大值为( )A .43B .83C .163D .323答案:C20.四棱锥P ABCD -的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P ABCD -的侧面积等于4(12)+,则该外接球的表面积是( )A.4πB.12πC.24πD.36π答案:B21.已知,,P A B C ,是球O 球面上的四点,ABC △是正三角形,三棱锥P ABC -的体积为93,且30APO BPO CPO ∠=∠=∠=,则球O 的表面积为__________. 答案:16π22.已知三棱锥P ABC -的四个顶点均在半径为1的球面上,且满足=0PA PB ⋅,=0PB PC ⋅,=0PC PA ⋅,则三棱锥P ABC -的侧面积的最大值为( )。
专题2.7几何体与球切、接的问题(测)2017年高考二轮复习数学(文)(附解析)

专题2.7 几何体与球切、接的问题(测)总分 _______ 时间 _______ 班级 _______ 学号 _______ 得分_______(一) 选择题(12*5=60分)1.【广西梧州市2017届高三上学期摸底联考】若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图1所示,则此几何体的表面积是( )A .(4π+B .6π+C .6πD .(8π+ 【答案】C 【解析】圆柱的侧面积为ππ42121=⨯⨯=S ,半球的表面积为ππ21222=⨯=S ,圆锥的侧面积为ππ2213=⨯⨯=S ,所以几何体的表面积为ππ26321+=++=S S S S ,故选C. 2.【河北省沧州市第一中学2017届高三10月月考】已知四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,其中ABCD 为正方形,PAD ∆为等腰直角三角形,PA PD ==棱锥P ABCD -外接球的表面积为( )A .10πB .4π C. 16π D .8π 【答案】Dππ8242=⨯=S ,应选D.3.【2016届甘肃省天水市一中高三上学期期末考试】利用一个球体毛坯切削后得到一个四棱锥P —ABCD ,其中底面四边形ABCD 是边长为1的正方形,1PA =,且D A BC P A ⊥平面,则球体毛坯体积的最小值应为( )A B C .43πD 【答案】D4.【2016届河北省邯郸市一中高三下学期研六考试】在菱形ABCD 中,60,A AB =︒=将ABD 折起到PBD 的位置,若二面角P BD C --的大小为23π,则三棱锥P BCD -的外接球的体积为( )A .43π B C D 【答案】C 【解析】取BD 中点E ,连接AE CE ,,则2332AEC AE CE π∠===,,设BCD V 的外接圆的圆心与球心的距离为h ,三棱锥P BCD -的外接球的半径为R ,则22222154()()R h h R =+-+=,∴R h ==∴三棱锥P BCD -的外接球体积为3(6432π⋅=.故选:C . 5.【2016届湖南师大附中高三上学期月考四】若长方体1111D C B A ABCD -中,AB=1,C B 1,D C 1分别与底面ABCD 所成的角为︒45,︒60,则长方体1111D C B A ABCD -的外接球的体积为 ( ) A .677π B .37π C .374π D .67π 【答案】A6.已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的全面积是( )A . 18B .36C . 45D .54【答案】D 【解析】左视图由三视图知:几何体为正三棱柱,∵俯视图是边长为6的正三角形,∴几何体的内切球的半径R=6×33123=⨯, ∴三棱柱的侧棱长为32.∴几何体的表面积35432632366212=⨯⨯+⨯⨯⨯⨯=S ,故选:D . 7.一几何体的三视图如右图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A .4πB .π3C .π2D .π 【答案】B8.设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( ) A.2a π B. 237a π C. 2311a π D. 25a π 【答案】B 【解析】根据题意条件可知三棱柱是棱长都为a 的正三棱柱,上下底面中心连线的中点就是球心,则其外接球的半径为222127)60sin 2()2(a a a R =+=,球的表面积为22371274a a S ππ=⋅=,故选B . 9.【广东省惠州市2017届高三第一次调研】已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2AB =, 2SA SB SC ===,则三棱锥的外接球的球心到平面ABC 的距离是( )A B .1 C D 【答案】A【解析】因为三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2SA SB SC ===,S ∴在面ABC 内的射影为AB 中点H ,SH ∴⊥平面ABC ,SH ∴上任意一点到,,A B C的距离相等.SH = ,1CH =,在面SHC 内作SC 的垂直平分线MO ,则O 为S ABC -的外接球球心.2SC = ,1SM ∴=,30OSM ∠=︒,SO OH ∴==O 到平面ABC 的距离,故选A .10.【2016届河北省正定中学高三上学期期末考试】球O 半径为13=R ,球面上有三点A 、B 、C ,312=AB ,12==BC AC ,则四面体OABC 的体积是A .360B .350C .660D .650 【答案】A11.【2016届贵州省贵阳市一中高三第五次月考】如图,已知正三角形ABC 三个顶点都在半径为2的球面上,球心O 到平面ABC 的距离为1,点E 是线段AB 的中点,过点E 作球O 的截面,则截面面积的最小值是( )A .74πB .2πC .94πD .3π【答案】C 【解析】设正ABC △的中心为1O ,连接1O A ,11O O O C ,,∵1O 是正ABC △的中心,A B C ,,三点都在球面上,∴1O O ABC ⊥平面,结合1O C ABC ⊂平面,可得11O O O C ⊥,∵球的半径2R =,球心O 到平面ABC 的距离为1,得11O O =,∴在1Rt O OC △中,1OC 又∵E 为AB 的中点,ABC △是等边三角形,13cos302AE AO =︒=∴,∵过E 作球O 的截面,当截面与OE 垂直时,截面圆的半径最小,此时截面圆的半径32r =,可得截面面积为29ππ4S r ==,故选C .12.【江西省新余市2016届高三第二次模拟】已知C B A 、、是球O 的球面上三点,2=AB ,32=AC , 60=∠ABC ,且棱锥ABC O -的体积为364,则球O 的表面积为( ) A .π10 B .π24 C .π36 D .π48 【答案】D(二) 填空题(4*5=20分)13.【2016届河北省邯郸一中高三下学期研七】球O 面上四点P 、A 、B 、C 满足:PA 、PB 、PC 两两垂直,3,4,PA PB PC ===O 的表面积等于______.【答案】100π 【解析】空间四个点P A B C 、、、在同一球面上,PA PB PC 、、两两垂直,且3,4,PA PB PC ===PA PB PC 、、可看作是长方体的一个顶点发出的三条棱,所以过空间四个点P A B C 、、、的球面即为棱长分别为3,4,PA PB PC ===体的外接球,如下图:10=,所以这个球面的面积21024100S ππ⎛⎫=⎪⎝⎭=.14.【河南省新乡市2017届高三上学期第一次调研】已知一个圆锥内接于球O (圆锥的底面圆周及顶点均在球面上),若球的半径5R =,圆锥的高是底面半径的2倍,则圆锥的体积为__________. 【答案】1283π15.【湖北省襄阳市第四中学2017届高三七月第二周周考】已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的表面积为________. 【答案】169π 【解析】由下图可知,球心在O 的位置,球的半径为22252514416962444R ⎛⎫=+=+=⎪⎝⎭,故表面积为24169R ππ=.16.【吉林省长春市普通高中2017届高三质量监测(一)】已知三棱锥S ABC -,满足,,SA SB SC 两两垂直,且2SA SB SC ===,Q 是三棱锥S ABC -外接球上一动点,则点Q 到平面ABC 的距离的最大值为 .(三) 解答题(共6道小题,共70分)17. 过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ,且两两夹角都为︒60,若球半径为R ,求弦AB 的长度.R 【解析】由条件可抓住BCD A -是正四面体,A 、B 、C 、D 为球上四点,则球心在正四面体中心,设a AB =,则截面BCD 与球心的距离R a d -=36,过点B 、C 、D 的截面圆半径a r 33=,所以222)36()33(R a R a --=得R a 362=. 18. 一个倒圆锥形容器,它的轴截面是正三角形,在容器内注入水,并放入一个半径为r 的铁球,这时水面恰好和球面相切.问将球从圆锥内取出后,圆锥内水平面的高是多少?.19. 【改编自浙江高考题】已知球O 的面上四点A 、B 、C 、D ,DA ABC ⊥平面,AB BC ⊥,O 的体积.【答案】92π.【解析】本题用一般方法时,需要找出球心,求出球的半径.而利用长方体模型很快便可找到球的直径,由于DA ABC ⊥平面,AB BC ⊥,联想长方体中的相应线段关系,构造如图所示的长方体,又因为CD 长即为外接球的直径,利用直角三角形解出CD=3.故球O 的体积等于92π.20. 【改编自山东高考题】在等腰梯形ABCD 中,AB=2DC=2,0DAB=60∠,E 为AB 的中点,将ADE ∆与BEC ∆分布沿ED 、EC 向上折起,使A B 、重合于点P ,求三棱锥P-DCE 的外接球的体积.. 【解析】如图,因为AE=EB=DC=1,0DAB=CBE=DEA=60∠∠∠,所以AE=EB=BC=DC=DE=CE=1AD =,即三棱锥P-DCE 为正四面体,至此,不难求得三.21. 一个正四棱锥的底面边长为2,侧棱长为3,五个顶点都在同一个球面上,求此球的表面积.【答案】9π.C D C E22. 球面上有3个点,其中任意两点的球面距离都等于大圆周长的61,经过3个点的小圆的周长为π4,求这个球的半径.【答案】【解析】设球的半径为R ,小圆的半径为r ,则ππ42=r ,∴2=r .如图所示,设三点A 、B 、C ,O 为球心,362ππ==∠=∠=∠COA BOC AOB .又∵OB OA =,∴AOB ∆。
专题2.7 几何体与球切、接的问题讲-2017年高考数学文二轮复习讲练测 含解析 精品

纵观近几年高考对于组合体的考查,与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显,要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识学生掌握较为薄弱、认识较为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理. 下面结合近几年高考题对球与几何体的切接问题作深入的探究,以便更好地把握高考命题的趋势和高考的命题思路,力争在这部分内容不失分.从近几年全国高考命题来看,这部分内容以选择题、填空题为主,大题很少见.首先明确定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.1 球与柱体的切接规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题.1.1 球与正方体如图所示,正方体1111ABCD A B C D -,设正方体的棱长为a ,,,,E F H G 为棱的中点,O 为球的球心.常见组合方式有三类:一是球为正方体的内切球,截面图为正方形EFGH 和其内切圆,则2a OJ r ==;二是与正方体各棱相切的球,截面图为正方形EFGH 和其外接圆,则GO R ==;三是球为正方体的外接球,截面图为长方形11ACAC 和其外接圆,则12AO R '==.通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题.(1)正方体的内切球,如图1. 位置关系:正方体的六个面都与一个球都相切,正方体中心与球心重合;=.数据关系:设正方体的棱长为a,球的半径为r,这时有2r a(2)正方体的外接球,如图2. 位置关系:正方体的八个顶点在同一个球面上;正方体中心与球心重合;数据关系:设正方体的棱长为a,球的半径为r,这时有2r=.(3)正方体的棱切球,如图3. 位置关系:正方体的十二条棱与球面相切,正方体中心与球心重合; 数据关系:设正方体的棱长为a ,球的半径为r ,这时有2r =.例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( )A B .1 C .1 D 【答案】D.1.2 球与长方体例 2 自半径为R 的球面上一点M ,引球的三条两两垂直的弦MC MB MA ,,,求222MC MB MA ++的值.【答案】24R .【解析】以MC MB MA ,,为从一个顶点出发的三条棱,将三棱锥ABC M -补成一个长方体,则另外四个顶点必在球面上,故长方体是球的内接长方体,则长方体的对角线长是球的直径. ∴222MC MB MA ++=224)2(R R =.例 3【2016届重庆市巴蜀中学高三上学期一诊】A B C D ,,,四点在半径为225的球面上,且5AC BD ==,AD BC ==,AB CD =,则三棱锥D ABC -的体积是____________. 【答案】20.【解析】根据题意构造长方体,其面上的对角线构成三棱锥D ABC -,如图所示,设长方体的长、宽、高2 球与锥体的切接规则的锥体,如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或者表面积等相关问题.2.1正四面体与球的切接问题(1) 正四面体的内切球,如图4. 位置关系:正四面体的四个面都与一个球相切,正四面体的中心与球心重合;数据关系:设正四面体的棱长为a ,高为h ;球的半径为R ,这时有43R h a ==;(可以利用体积桥证明)(2) 正四面体的外接球,如图5. 位置关系:正四面体的四个顶点都在一个球面上,正四面体的中心与球心重合;数据关系:设正四面体的棱长为a ,高为h ;球的半径为R ,这时有43R h ==;(可用正四面体高h 减去内切球的半径得到)(3) 正四面体的棱切球,如图6. 位置关系:正四面体的六条棱与球面相切,正四面体的中心与球心重合;数据关系:设正四面体的棱长为a ,高为h ;球的半径为R ,这时有4,.R h ===例 4 设正四面体中,第一个球是它的内切球,第二个球是它的外接球,求这两个球的表面积之比及体积之比. 【答案】127依题意得)(31r R S V BCD A +=-, 又S r V V BCD O BCD A ⋅⨯==--3144 r r R 4=+∴即r R 3=.所以914422==R r ππ外接球的表面积内切球的表面积.271343433==R r ππ外接球的体积内切球的体积.点评:正四面体与球的接切问题,可通过线面关系证出,内切球和外接球的两个球心是重合的,为正四面体高的四等分点,即定有内切球的半径h r 41=(h 为正四面体的高),且外接球的半径r R 3=.2.2其它棱锥与球的切接问题球与正棱锥的组合,常见的有两类,一是球为三棱锥的外接球,此时三棱锥的各个顶点在球面上,根据截面图的特点,可以构造直角三角形进行求解.二是球为正棱锥的内切球,例如正三棱锥的内切球,球与正三棱锥四个面相切,球心到四个面的距离相等,都为球半径R .这样求球的半径可转化为球球心到三棱锥面的距离,故可采用等体积法解决,即四个小三棱锥的体积和为正三棱锥的体积.球与一些特殊的棱锥进行组合,一定要抓住棱锥的几何性质,可综合利用截面法、补形法等进行求解.例如,四个面都是直角三角形的三棱锥,可利用直角三角形斜边中点几何特征,巧定球心位置.例5【湖南省长沙市长郡中学2017届高三摸底】已知边长为ABCD 中,60BAD ∠=,沿对角线BD 折成二面角A BD C --为120的四面体ABCD ,则四面体的外接球的表面积为( )A .25πB .26πC .27πD .28π【答案】D图2图1G O EAC ED C BA例6【江西省新余市第一中学2017届高三上学期调研考试(一)】某几何体的正视图和侧视图如图(1)所示, 它的府视图的直观图是'''A B C ,如图(2)所示, 其中0''''2,''A O B O C ===则该几何体的外接球的表面积为 .【答案】1123πEDB A例7【2016届湖南长沙长郡中学高三下学期第六次月考】已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,C S 为球O 的直径,且2SC =,则此棱锥的体积为( )A.6 B.6 C.3 D .2【答案】6.3 球与球相切问题对于球与球的相切组合成复杂的几何体问题,要根据丰富的空间想象力,通过准确确定各个小球的球心的位置,或者巧借截面图等方法,将空间问题转化平面问题求解.例8 已知有半径分别为2、3的球各两个,且这四个球彼此相外切,现有一个球与此四个球都相外切,则此球的半径为 .【答案】6 11【解析】如图:设四个球的球心分别为A、B、C、D,则AD=AC=BD=BC=5,AB=6,CD=4.设AB中点为E、CD中点为F,连结EF.在△ABF中求得,在△EBF中求得EF=由于对称性可得第五个球的球心O在EF上,连结OA、OD.设第五个球的半径为r,则OA=r+3,OD=r+2,于是⇒211+6036=0r r-解得6=11r或6-(舍掉),故答案为611.C例9 把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离.【答案】3622+.4 球与几何体的各条棱相切问题球与几何体的各条棱相切问题,关键要抓住棱与球相切的几何性质,达到明确球心的位置为目的,然后通过构造直角三角形进行转换和求解.如与正四面体各棱都相切的球的半径为相对棱的一半:4r a '=. 例10 把一个皮球放入如图10所示的由8根长均为20 cm 的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为( )A .B .10 cmC .D .30cm【答案】5 球与旋转体切接问题首先画出球及其它旋转体的公共轴截面,然后寻找几何体与几何体几何元素之间的关系. 例11 求球与它的外切圆柱、外切等边圆锥的体积之比.【答案】964∶∶∶∶锥柱球=V V V【解析】如图,等边SAB ∆为圆锥的轴截面,此截面截圆柱得正方形11CDD C ,截球面得球的大圆圆1O .设球的半径R OO =1,则它的外切圆柱的高为R 2,底面半径为R ;R O O OB 330cot 1=︒⋅=, R R OB SO 33360tan =⋅=︒⋅=,∴334R V π=球,3222R R R V ππ=⋅=柱, 3233)3(31R R R V ππ=⋅⋅=锥, ∴964∶∶∶∶锥柱球=V V V .例12在棱长为1的正方体内有两个球相外切且又分别与正方体内切.(1)求两球半径之和;(2)球的半径为多少时,两球体积之和最小.【答案】当433-=R时,V有最小值.∴当433-==rR时,体积之和有最小值.【反思提升】综合上面的五种类型,解决与球的外切问题主要是指球外切多面体与旋转体,解答时首先要找准切点,将问题转化成平面几何问题,应用三角形中的边角关系,建立与球半径,r R的联系,将球的体积之和用r或R表示.如果外切的是多面体,则作截面时主要抓住多面体过球心的对角面来作;把一个多面体的几个顶点放在球面上即为球的内接问题.解决这类问题的关键是抓住内接的特点,即球心到多面体的顶点的距离等于球的半径.发挥好空间想象力,借助于数形结合进行转化,问题即可得解.如果是一些特殊的几何体,如正方体、正四面体等可以借助结论直接求解,此时结论的记忆必须准确.高考题往往与三视图相结合,题目的难易不一,在复习中切忌好高骛远,应重视各种题型的备考演练,重视高考信息的搜集,不断充实题目的类型,升华解题的境界.。
几何体与球切,接的问题(解析版)

2018高考数学二轮复习(文科)几何体与球切、接问题一、选择题(12*5=60分)1.【广西梧州市2017届高三上学期摸底联考】若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图1所示,则此几何体的表面积是( )A .(4π+B .6π+C .6πD .(8π 【答案】C 【解析】圆柱的侧面积为ππ42121=⨯⨯=S ,半球的表面积为ππ21222=⨯=S ,圆锥的侧面积为ππ2213=⨯⨯=S ,所以几何体的表面积为ππ26321+=++=S S S S ,故选C.2.【河北省沧州市第一中学2017届高三10月月考】已知四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,其中ABCD 为正方形,PAD ∆为等腰直角三角形,PA PD ==锥P ABCD -外接球的表面积为( )A .10πB .4π C. 16π D .8π 【答案】Dππ8242=⨯=S ,应选D.3.【2016届甘肃省天水市一中高三上学期期末考试】利用一个球体毛坯切削后得到一个四棱锥P —ABCD ,其中底面四边形ABCD 是边长为1的正方形,1PA =,且D A BC P A ⊥平面,则球体毛坯体积的最小值应为( )A .3 B C .43πD .2【答案】D4.【2016届河北省邯郸市一中高三下学期研六考试】在菱形ABCD 中,60,A AB =︒=将ABD 折起到PBD 的位置,若二面角P BD C --的大小为23π,则三棱锥P BCD -的外接球的体积为( )A .43π B D 【答案】C 【解析】取BD 中点E ,连接AE CE ,,则2332AEC AE CE π∠===,,设BCD V 的外接圆的圆心与球心的距离为h ,三棱锥P BCD -的外接球的半径为R ,则22222154()()R h h R =+-+=,∴22R h ==∴三棱锥P BCD -的外接球体积为3(6432π⋅=.故选:C . 5.【2016届湖南师大附中高三上学期月考四】若长方体1111D C B A ABCD -中,AB=1,C B 1,D C 1分别与底面ABCD 所成的角为︒45,︒60,则长方体1111D C B A ABCD -的外接球的体积为( ) A .677π B .37π C .374π D .67π【答案】A6.已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的全面积是( ) A . 18B .36C . 45D . 54【答案】D 【解析】由三视图知:几何体为正三棱柱,∵俯视图是边长为6的正三角形,∴几何体的内切球的半径R=6×33123=⨯, ∴三棱柱的侧棱长为32. ∴几何体的表面积35432632366212=⨯⨯+⨯⨯⨯⨯=S ,故选:D .7.一几何体的三视图如右图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A .4πB .π3C .π2D .π 【答案】B8.设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为左视图( )A.2a πB. 237a π C. 2311a π D. 25a π 【答案】B 【解析】根据题意条件可知三棱柱是棱长都为a 的正三棱柱,上下底面中心连线的中点就是球心,则其外接球的半径为2202127)60sin 2()2(a a a R =+=, 球的表面积为22371274a a S ππ=⋅=,故选B . 9.【广东省惠州市2017届高三第一次调研】已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2AB =, 2SA SB SC ===,则三棱锥的外接球的球心到平面ABC 的距离是( )A .1 C【答案】A【解析】因为三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2SA SB SC ===,S∴ 在面ABC 内的射影为AB 中点H ,SH ∴⊥平面ABC ,SH ∴上任意一点到,,A B C 的距离相等.S∴ SH 1CH =,在面SHC 内作SC 的垂直平分线MO ,则O 为S ABC -的外接球球心.2SC = ,1SM ∴=,30OSM ∠=︒,SO OH ∴==,即为O 到平面ABC 的距离,故选A .10.【2016届河北省正定中学高三上学期期末考试】球O 半径为13=R ,球面上有三点A 、B 、C ,312=AB ,12==BC AC ,则四面体OABC 的体积是A .360B .350C .660D .650 【答案】A11.【2016届贵州省贵阳市一中高三第五次月考】如图,已知正三角形ABC 三个顶点都在半径为2的球面上,球心O 到平面ABC 的距离为1,点E 是线段AB 的中点,过点E 作球O 的截面,则截面面积的最小值是( )A .74πB .2πC .94πD .3π【答案】C 【解析】设正ABC △的中心为1O ,连接1O A ,11O O O C ,,∵1O 是正ABC △的中心,A B C ,,三点都在球面上,∴1O O ABC ⊥平面,结合1O C ABC ⊂平面,可得11O O O C ⊥,∵球的半径2R =,球心O 到平面ABC 的距离为1,得11O O =,∴在1Rt O OC △中,1OC =又∵E 为AB 的中点,ABC △是等边三角形,13cos302AE AO =︒=∴,∵过E 作球O 的截面,当截面与OE 垂直时,截面圆的半径最小,此时截面圆的半径32r =,可得截面面积为29ππ4S r ==,故选C .12.【江西省新余市2016届高三第二次模拟】已知C B A 、、是球O 的球面上三点,2=AB ,32=AC , 60=∠ABC ,且棱锥ABC O -的体积为364,则球O 的表面积为( ) A .π10 B .π24 C .π36 D .π48 【答案】 D二、填空题(4*5=20分)13.【2016届河北省邯郸一中高三下学期研七】球O 面上四点P 、A 、B 、C 满足:PA 、PB 、PC 两两垂直,3,4,PA PB PC ===O 的表面积等于______.【答案】100π 【解析】空间四个点P A B C 、、、在同一球面上,PA PB PC 、、两两垂直,且3,4,PA PB PC ===则PA PB PC 、、可看作是长方体的一个顶点发出的三条棱,所以过空间四个点P A B C 、、、的球面即为棱长分别为3,4,PA PB PC ===10=,所以这个球面的面积21024100S ππ⎛⎫=⎪⎝⎭=.14.【河南省新乡市2017届高三上学期第一次调研】已知一个圆锥内接于球O (圆锥的底面圆周及顶点均在球面上),若球的半径5R =,圆锥的高是底面半径的2倍,则圆锥的体积为__________. 【答案】1283π15.【湖北省襄阳市第四中学2017届高三七月第二周周考】已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的表面积为________. 【答案】169π 【解析】由下图可知,球心在O 的位置,球的半径为22252514416962444R ⎛⎫=+=+=⎪⎝⎭,故表面积为24169R ππ=.16.【吉林省长春市普通高中2017届高三质量监测(一)】已知三棱锥S ABC -,满足,,SA SB SC 两两垂直,且2SA SB SC ===,Q 是三棱锥S ABC -外接球上一动点,则点Q到平面ABC 的距离的最大值为 .三、解答题(共6道小题,共70分)17. 过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ,且两两夹角都为︒60,若球半径为R ,求弦AB 的长度.【答案】3R 【解析】由条件可抓住BCD A -是正四面体,A 、B 、C 、D 为球上四点,则球心在正四面体中心,设a AB =,则截面BCD 与球心的距离R a d -=36,过点B 、C 、D 的截面圆半径a r 33=,所以222)36()33(R a R a --=得R a 362=.18. 一个倒圆锥形容器,它的轴截面是正三角形,在容器内注入水,并放入一个半径为r 的铁球,这时水面恰好和球面相切.问将球从圆锥内取出后,圆锥内水平面的高是多少?.19. 【改编自浙江高考题】已知球O 的面上四点A 、B 、C 、D ,DA ABC ⊥平面,AB BC ⊥,O 的体积.【答案】92π. 【解析】本题用一般方法时,需要找出球心,求出球的半径.而利用长方体模型很快便可找到球的直径,由于DA ABC ⊥平面,AB BC ⊥,联想长方体中的相应线段关系,构造如图所示的长方体,又因为CD 长即为外接球的直径,利用直角三角形解出CD=3.故球O 的体积等于92π.20. 【改编自山东高考题】在等腰梯形ABCD 中,AB=2DC=2,0DAB=60∠,E 为AB 的中点,将ADE ∆与BEC ∆分布沿ED 、EC 向上折起,使A B 、重合于点P ,求三棱锥P-DCE的外接球的体积.. 【解析】如图,因为AE=EB=DC=1,0DAB=CBE=DEA=60∠∠∠,所以AE=EB=BC=DC=DE=CE=1AD =,即三棱锥P-DCE 为正四面体,至此,不难求得三棱.21. 一个正四棱锥的底面边长为2,侧棱长为3,五个顶点都在同一个球面上,求此球的表面积.【答案】9π.CDCE22. 球面上有3个点,其中任意两点的球面距离都等于大圆周长的61,经过3个点的小圆的周长为π4,求这个球的半径.【答案】【解析】设球的半径为R ,小圆的半径为r ,则ππ42=r ,∴2=r . 如图所示,设三点A 、B 、C ,O 为球心,362ππ==∠=∠=∠COA BOC AOB .又∵OB OA =,∴AOB ∆。
与球有关的切、接问题(有答案)

与球有关的切、接问题1.球的表面积公式:S =4πR 2;球的体积公式V =43πR 3 2.与球有关的切、接问题中常见的组合: (1)正四面体与球:如图,设正四面体的棱长为a ,内切球的半径为r ,外接球的半径为R ,取AB 的中点为D ,连接CD ,SE 为正四面体的高,在截面三角形SDC 内作一个与边SD 和DC 相切,圆心在高SE 上的圆.因为正四面体本身的对称性,内切球和外接球的球心同为O .此时,CO =OS =R ,OE =r ,SE = 23a ,CE =33a ,则有R +r = 23a ,R 2-r 2=|CE |2=a 23,解得R =64a ,r =612a . (2)正方体与球:①正方体的内切球:截面图为正方形EFHG 的内切圆,如图所示.设正方体的棱长为a ,则|OJ |=r =a 2(r 为内切球半径). ②与正方体各棱相切的球:截面图为正方形EFHG 的外接圆,则|GO |=R =22a . ③正方体的外接球:截面图为正方形ACC 1A 1的外接圆,则|A 1O |=R ′=32a . (3)三条侧棱互相垂直的三棱锥的外接球:①如果三棱锥的三条侧棱互相垂直并且相等,则可以补形为一个正方体,正方体的外接球的球心就是三棱锥的外接球的球心.即三棱锥A 1-AB 1D 1的外接球的球心和正方体ABCD -A 1B 1C 1D 1的外接球的球心重合.如图,设AA 1=a ,则R =32a . ②如果三棱锥的三条侧棱互相垂直但不相等,则可以补形为一个长方体,长方体的外接球的球心就是三棱锥的外接球的球心.R 2=a 2+b 2+c 24=l 24(l 为长方体的体对角线长). 角度一:正四面体的内切球1.(2015·长春模拟)若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________.解析:设正四面体棱长为a ,则正四面体表面积为S 1=4·34·a 2=3a 2,其内切球半径为正四面体高的14,即r =14·63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2π6a 2=63π. 角度二:直三棱柱的外接球2.(2015·唐山统考)如图,直三棱柱ABC -A 1B 1C 1的六个顶点都在半径为1的半球面上,AB =AC ,侧面BCC 1B 1是半球底面圆的内接正方形,则侧面ABB 1A 1的面积为( )A .2B .1 C. 2 D.22解析:选C 由题意知,球心在侧面BCC 1B 1的中心O 上,BC 为截面圆的直径,∴∠BAC =90°,△ABC 的外接圆圆心N 是BC 的中点,同理△A 1B 1C 1的外心M 是B 1C 1的中心.设正方形BCC 1B 1的边长为x ,Rt △OMC 1中,OM =x 2,MC 1=x 2,OC 1=R =1(R 为球的半径),∴⎝⎛⎭⎫x 22+⎝⎛⎭⎫x 22=1,即x =2,则AB =AC =1,∴S 矩形ABB 1A 1=2×1= 2.角度三:正方体的外接球3.一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),则该几何体外接球的体积为________.解析:依题意可知,新的几何体的外接球也就是原正方体的外接球,要求的直径就是正方体的体对角线;∴2R =23(R 为球的半径),∴R =3,∴球的体积V =43πR 3=43π. 答案:43π角度四:四棱锥的外接球4.(2014·大纲卷)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π4解析:选A 如图所示,设球半径为R ,底面中心为O ′且球心为O ,∵正四棱锥P -ABCD中AB =2,∴AO ′= 2.∵PO ′=4,∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R=94,∴该球的表面积为4πR 2=4π×⎝⎛⎭⎫942=81π4,故选A. [类题通法]“切”“接”问题的处理规律1.“切”的处理解决与球的内切问题主要是指球内切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.2.“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.[牛刀小试]1.(2015·云南一检)如果一个空间几何体的正视图、侧视图、俯视图都是半径等于5的圆,那么这个空间几何体的表面积等于( )A .100π B.100π3 C .25π D.25π3解析:选A 易知该几何体为球,其半径为5,则表面积为S =4πR 2=100π.2.(2014·陕西高考)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A.32π3 B .4π C .2π D.4π3解析:选D 因为该正四棱柱的外接球的半径是四棱柱体对角线的一半,所以半径r =1212+12+(2)2=1,所以V 球=4π3×13=4π3.故选D. 3.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的底面边长为6时,其高的值为( )A .3 3 B.3 C .2 6 D .2 3解析:选D 设正六棱柱的高为h ,则可得(6)2+h 24=32,解得h =2 3. 4.(2015·山西四校联考)将长、宽分别为4和3的长方形ABCD 沿对角线AC 折起,得到四面体A -BCD ,则四面体A -BCD 的外接球的体积为________.解析:设AC 与BD 相交于O ,折起来后仍然有OA =OB =OC =OD ,∴外接球的半径r =32+422=52,从而体积V =4π3×⎝⎛⎭⎫523=125π6. 5.一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O 的球面上,则该圆锥的体积与球O 的体积的比值为________.解析:设等边三角形的边长为2a ,则V 圆锥=13·πa 2·3a =33πa 3;又R 2=a 2+(3a -R )2,所以R =233a ,故 V 球=4π3·⎝⎛⎭⎫233a 3=323π27a 3,则其体积比为932. [高考全国课标卷真题追踪]1.(15课标1理)已知,A B 是球O 的球面上两点,090AOB ∠=,C 为该球面上的动点,若O ABC -三棱锥体积的最大值为36,则球O 的表面积为( C )(A)36π (B)64π (C)144π (D)256π2.(13课标1理)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为( A )(A )3cm 3500π (B )3cm 3866π (C )3cm 31372π (D )3cm 32048π 3.(12课标理)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( A )(A)26 (B)36 (C)23 (D )224.(12课标文)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为 ( B )(A )6π (B )43π (C )46π (D )63π5.(10新课标理)设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( B )(A) 2a π (B) 273a π (C) 2113a π (D) 25a π 6.(10新课标文)设长方体的长、宽、高分别为2,,a a a ,其顶点都在一个球面上,则该球的表面积为( B )(A )23a π (B )26a π (C )212a π (D )224a π 7.(07新课标文)已知三棱锥S ABC -的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC ,2AC r =,则球的体积与三棱锥体积之比是(D)A.π B.2π C.3π D.4π8.(13新课标2文)已知正四棱锥O ABCD -的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为24π。
【立体几何专题 高考数学复习】第9讲 几何体与球外切与内切的问题-原卷及答案

第9讲 几何体与球知识与方法球作为一个特殊的多面体,与多面体的方正相比,球上点的位置更难想象与刻画.特别是球与多面体的外接与内切问题,很多同学很难想象出来,也很难画出图形,就别提进行具体量的计算了.这一专题,我们就来讨论几何体与球的外接、内切问题,让大家能够抓住外接与内切问题的关键,提升解决问题的能力.典型例题【例1】一直三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此三棱锥的体积为( )A.6B.C.3D.2【例2】在四面体ABCD 中,已知60,3,2ADB BDC CDA AD BD CD ∠∠∠======,则四面体ABCD 的外接球的半径为__________【例3】已知球1O 是正方体ABCD A B C D '-'''的外接球,球2O 是正方体ABCD A B C D '-'''的内切球,球3O 与正方体ABCD A B C D '-'''的各条棱均相切,则三个球的表面积之比为________【例4】 已知正方体 1111ABCD A B C D - 的棱长为 3, P 是正方体表面上一动点, 且 PA =12PA ,则点P 形成的轨迹的长度为_________【例5】一个半径为1的小球在一个内壁棱长为的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是______【例6】把 4 个半径均为 1 的小球装人一个大球内,则此大球半径的最小值为_______【例7】如图, 在四面体 A B C D 中, 截面 A E F 经过四面体的内切球 (与四个面都相切的球)球心O ,且分别与,BC DC 交于点,E F ,如果截面AEF 将四面体分成体积相等的两部分,设四棱锥A BEFD -与三棱锥A EFC -的表面积分别是12,S S ,则必有( )A.12S S <B.12S S >C.12S S =D.12,S S 的大小关系不能确定强化训练1.已知空间四点,,,A B C D 满足,,AB AC AB AD AC AD ⊥⊥⊥,且AB AC ==1,AD Q =是三棱锥A BCD -的外接球上的一个动点,则点Q 到平面BCD 的最大距离是_________2.在四面体P ABCD -中,PA BC PB AC PC AB ======则该四面体的外接球的半径为_______3.已知棱长为6的正方体内有一个棱长为x 的正四面体,且该四面体可以在正方体内任意转动,则x 的最大值为______4.如图,在棱长为2的正方体1111ABCD A B C D -中,点,M N 分别在棱1BB 和CD 上运动,但始终保持MN =设P 为MN 的中点,则点P 的轨迹所形成的图形的长度为_________5.将半径都为1的4个钢球完全装人形状为正四面体的容器里,这个正四面体的高的最小值为( )B.2+C.4+ 6.(1)如图,将三个半径为r 的汤圆(球形)装人半径为6cm 的半球面碗中,三个汤圆的顶端恰与碗口共面,则汤圆的半径r =______cm .(2)已知三个圆柱的侧面两两相切,且它们的轴两两互相垂直.如果每个圆柱底面半径都是1,那么与这三个圆柱的侧面都相切的球的半径的最大值是______7.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,边长为,,a PD a PA PC ===.若在此四棱锥中放人一个球,则球的最大半径是( )A.)1a - C.12a ⎛⎫- ⎪ ⎪⎝⎭ D.a第9讲 几何体与球的外接与内切问题知识与方法球作为一个特殊的多面体,与多面体的方正相比,球上点的位置更难想象与刻画.特别是球与多面体的外接与内切问题,很多同学很难想象出来,也很难画出图形,就别提进行具体量的计算了.这一专题,我们就来讨论几何体与球的外接、内切问题,让大家能够抓住外接与内切问题的关键,提升解决问题的能力.典型例题【例1】一直三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此三棱锥的体积为( )A.6B.6C.3D.2【分析】球心位置已知,只需求出棱锥的高即可.【解析】解法1:因为SC 为球O 的直径,所以O 为SC 的中点,故1SO CO AO BO AB AC BC =======,所以四面体OABC 为正四面体.而2S ABC O ABC V V --=,故要求三棱锥S ABC -的体积,只需计算四面体OABC 的体积.如图(1),设ABC 的中心为H ,则正四面体OABC 的中点O 在底面上的投影为点H ,图(1)而CH =,故OH =所以122233S ABC O ABC ABC V V OH S --==⨯⋅⋅=⨯=.故选A. 【分析】此处注意到四面体OABC 为正四面体,所以可以简化求体积的方式.解法2:如图(2),取OC 的中点M ,连结,AM BM .由OC OA OB ==知,AM OC BM OC ⊥⊥,所以OC ⊥平面ABM .图(2)又12AM BM AB ===,所以4ABM S =.所以1123346S ABC ABM V SC S -=⋅⋅=⨯⨯=.故选A. 【点睛】本题是一个比较简单的球内接多面体的问题.这类问题首先要认识到多面体的每个顶点所在球面上的位置,建立起多面体的空间结构,才能顺利处理该多面体的各类问题.【例2】在四面体ABCD 中,已知60,3,2ADB BDC CDA AD BD CD ∠∠∠======,则四面体ABCD 的外接球的半径为__________【分析】设ABD 的中心为1O ,过点1O 作垂直于底面ABD 的垂线l ,则l 上任意一点到,,A B D ≡点的距离均相等,因此四面体ABCD 的外接球球心O 必在直线l 上.只需在l 上寻找一点O ,使得OC OD =.【解析】解法1:由三余弦定理可得11cos cos cos CDO ADO ADC ∠∠∠⋅=,即1cos 3CDO ∠=. 如图(1),作点C 在1DO 及直线l 上的射影,分别为点H 和点K ,有1,333DH HO CH ===.图(1)设1OO x =,则有CO DO ===解得0x =,即点O 与点1O 重合,点1O 即为四面体ABCD 的外接球球心,【分析】如图(2),设底面ABD 的中心为1O ,延长1DO 交ABD 的外接圆于点E .由四面体ABCD 的对称性可知,球心O 在平面CDE 上.又点,,C D E 均在球上,故CDE 的外接圆即为四面体ABCD 外接球的大圆.解法2:因为ABD 为正三角形,,即DE =图(2)由三余弦定理知cos 3CDE ∠=. 又2CD =,故90DCE ∠=,所以1O 即为CDE 的外心,也即四面体ABCD 的外接球球心.【点睛】求四面体的外接球球心如同三角形外接圆一样,是外接球问题的最根本所在.解决这类问题的关键是㧓住“到四面体四个顶点的距离相等”这一性质找出球心的位置.解法1展现的是四面体外接球球心的通法:先确定某一个面为底面,过底面三角形的外心作该平面的垂线,则球心必定在这条垂线上;然后在垂线上寻找一点使得这一点到底面上一顶点的距离与该点到非底面上的另一顶点的距离相等.通过这样两个步骤就可以求得四面体的外接球球心.而解法2是一类特殊的方法,特别是在具有面对称性质的四面体中,可以先找出球心所在的某个截面,如果在这个球的截面圆上有确定的三个点,那么即便没有【解析】2中的垂直条件,我们也可以通过正弦定理算出这个截面圆的半径,即球的大圆半径,也即球的半径. 很多时候,直观图并不能准确反映多面体及其外接球的位置关系,我们要借助一些截面来更准确地认识和计算.因此截取包含接点或者球心的截面来对外接问题进行刻画和计算,从三维图形中提取二维信息,将三维问题化为二维问题进行计算,是解决此类问题的高效途径.【例3】已知球1O 是正方体ABCD A B C D '-'''的外接球,球2O 是正方体ABCD A B C D '-'''的内切球,球3O 与正方体ABCD A B C D '-'''的各条棱均相切,则三个球的表面积之比为________【分析】图(1)为三个球与正方体位置关系的直观图,显然这个直观图无法让我们认识到几何体之间的准确位置关系,所以我们借助图(2)的平面11AA C C 来解读这个内切与外接的问题.图(1)图(2)【解析】设正方形的棱长为1.球1O 是正方体ABCD A B C D '-'''的外接球,所以在截面11AA C C 上,其截面圆为球1O 的大圆,与长方形11AA C C 接于四个顶点,球2O 是正方体ABCD A B C D '-'''的内切球,所以在截面11AA C C 上,其截面圆为球2O 的大圆,与长方形11AA C C 切于11A C 和AC 的中点,半径为12.球3O 与正方体ABCD A B C D '-'''的各条棱均相切,所以在截面11AA C C 上,其截面圆为球3O 的大圆,与长方形11AA C C 切于1AA 和1CC 的中点,半径为2. 故三个球的表面积之比为3:1:2.【点睛】跟外接球问题一样,内切球问题的解决也依赖于对几何体相互之间位置的准确认识.外接球问题中接点的位置比较明确,而内切球的切点往往不易发现,但却是我们解决内切球问题的关键所在.【例4】 已知正方体 1111ABCD A B C D - 的棱长为 3, P 是正方体表面上一动点, 且 PA =12PA ,则点P 形成的轨迹的长度为_________【分析】本题可利用空间向量坐标法求得点P 的轨迹为球面,再分别求正方体每个面截球面所得的弧,并求弧长的和.【解析】如图,分别以AB 为x 轴、AD 为y 轴、1AA 为z 轴建立空间直角坐标系.设点(),,P x y z ,则2222224(3)x y z x y z ⎡⎤++=++-⎣⎦,整理得222(4)4x y z ++-=,即点P 在以()0,0,4为球心,2为半径的球上.易知点P 在面11ABB A 内的轨迹形成半径为2,且圆心角为3π的圆弧,弧长为23π.同理,点P 在面11ADD A 内的轨迹长度为23π,点P 在面1111A B C D 且圆心角为2π的圆弧,,所以轨迹总长度为43π+. 【点睛】本题关键是求得点,P 的轨迹,然后用平面截球面,利用球心距求弧长,易错点是截面圆的圆心位置.也可由阿波罗尼斯圆的定义知点,P 在面11ABB A 内的轨迹是圆,所以空间中的轨迹是该圆绕着1AA 旋转所得到的球面.【例5】一个半径为1的小球在一个内壁棱长为的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是______【分析】如图(1),小球所能接触到的内壁应为图中阴影部分,其中在内壁PDF 上能接触到的上端点应为PAC 的中心,所以可知小球能接触到的内壁PDF 上的部分为一个正三角形.只需求解该正三角形的大小.如图(2).图(1)图(2)【解析】假设四面体容器为,,,PFDE A B C 分别为,,PD PE PC 的中点.因为一个半径为1的小球的外接正四面体棱长为1÷=故阴影部分正三角形的边长为PDF 边长的12.所以接触不到的内壁PDF 上的三角形的面积为2344⨯⨯=所以接触不到的容器内壁的总面积为【点睛】如果问题改为“求小球永远不可能接触到的容器内壁的体积”,答案也是可求的.其体积为一个四面体挖去内切球,以及六个柱体(其底面为三角形截去弓形).读者不妨一试.【例6】把 4 个半径均为 1 的小球装人一个大球内,则此大球半径的最小值为_______【分析】多球相切问题,要准确把握球心距与半径的关系.【解析】如图,设大球的球心为O ,小球的球心分别为1234,,,O O O O ,则四个小球两两相切,小球的球心距为2.因为大球与小球内切,所以大球球心在四面体1234O O O O 的中心,则大球球心与小球球心的球心距为2切点在大球球心与小球球心的连线上.则大球半径为12+. 【点睛】球与旋转体的内切问题不同于球与多面体的内切,后者需要找出切点,一般是球心゙在平面上的射影,而前者更依赖于解决球心与旋转体的轴(或球心)的距离.【例7】如图, 在四面体 A B C D 中, 截面 A E F 经过四面体的内切球 (与四个面都相切的球)球心O ,且分别与,BC DC 交于点,E F ,如果截面AEF 将四面体分成体积相等的两部分,设四棱锥A BEFD -与三棱锥A EFC -的表面积分别是12,S S ,则必有( )A.12S S <B.12S S >C.12S S =D.12,S S 的大小关系不能确定【分析】有内切球的多面体的体积与表面积之间可以通过内切球半径来联系.【解析】设内切球的半径为r .()()1313A BEFD O ABD O ABE O ADF O BDFEABD ABE ADF BDFE A EFC O AFC O EFC O AECAFC EFC AEC V V V V V r S S S S V V V V r S S S ---------=+++=+++==++=++ 所以ABD ABE ADF BDFE AFC EFC AECS S S S S S S +++=++, 所以ABD ABE ADF BDFE AEF AFC EFC AEC AEF S S S S S S S S S ++++=+++,即12S S =.故选C.【点睛】多面体的内切球问题有一种非常有效的方法,即利用13V rS =表来解决问题往往能取得非常简便的效果,极大地减少计算量.但一定要注意的是,这个算法只在球与多面体的每个面都相切时才能使用.强化训练1.已知空间四点,,,A B C D 满足,,AB AC AB AD AC AD ⊥⊥⊥,且AB AC ==1,AD Q =是三棱锥A BCD -的外接球上的一个动点,则点Q 到平面BCD 的最大距离是_________【解析】由条件知,四面体ABCD 为正方体的一个部分,故可补形为正方体ABEC DGFH -.如图,设正方体中心为O ,则有OB OC OD OA ===,即O 为四面体ABCD 的外接球球心.由正方体的性质可知,点O 到平面BCD所以点Q 到平面BCD +=2.在四面体P ABCD -中,PA BC PB AC PC AB ======则该四面体的外接球的半径为_______【解析】由条件知四面体的对棱长相等,所以该四面体可内接于一长方体,如图所示.该长方体的外接球球心到四面体的四个顶点距离相等,故它也是四面体外接球的球心.设长方体的长、宽、高分别为,,a b c ,其中2222226,8,10a b b c a c +=+=+=,解得2,a b c ===故长方体的体对角线即外接球的直径为.3.已知棱长为6的正方体内有一个棱长为x 的正四面体,且该四面体可以在正方体内任意转动,则x 的最大值为______【答案】【解析】如图,设正四面体PABC 的棱长为,x M 为棱AB 的中点,H 为P 点在底面ABC 上的投影,即为正ABC 的中心,O 为该四面体的外接球的球心,则,,233CM PM x CH x PH x ====. 设正四面体PABC 的外接球半径为R ,内切球半径为r ,即,OP OC R OH r ===.则有2222,31,3R r x R r CH x ⎧+=⎪⎪⎨⎪-==⎪⎩解得,412R x r x ==. 又棱长为6的正方体的内切球半径为3.所以x的最大值为34÷=4.如图,在棱长为2的正方体1111ABCD A B C D -中,点,M N 分别在棱1BB 和CD 上运动,但始终保持MN =设P 为MN 的中点,则点P 的轨迹所形成的图形的长度为_________【答案】4π【解析】如图,连结BN ,有22MN BP ==,所以点P 在以点B 为球心,2为半径的一个球面上.记1111,,,BC AD A D B C 的中点分别为,E F ,,G H .因为P 为MN 的中点,所以P 也在正方形EFGH 内,故点P 的轨迹为球面与正方形EFGH 的交线,为14个圆,其长度为1244l ππ=⨯=.5.将半径都为1的4个钢球完全装人形状为正四面体的容器里,这个正四面体的高的最小值为( )B.2+C.4+ 【答案】C【解析】设小球球心分别为1234,,,O O O O ,则球心距均为2,且四面体1234O O O O 为正四面体,. 下面三个小球的球心到底面的距离为小球半径1.上面的小球球心到四面体容器顶点的距离,可以等同于半径为1的小球球心到其外切四面体顶点的距离,为3.所以答案为13++.6.(1)如图,将三个半径为r 的汤圆(球形)装人半径为6cm 的半球面碗中,三个汤圆的顶端恰与碗口共面,则汤圆的半径r =______cm .【答案】(1)(9;212【解析】(1)设球形碗的球心为点O ,汤圆的球心分别为点123,,O O O ,设123,,O O O 在碗口平面上的射影分别为点123,,H H H .因为球123,,O O O 两两相切,故1223312O O O O O O r ===,点O 应为正123H H H 的中心,所以11,33OH r OO r ===. 又因为球O 与球1O 内切,6r +=,所以92r ==.(2)已知三个圆柱的侧面两两相切,且它们的轴两两互相垂直.如果每个圆柱底面半径都是1,那么与这三个圆柱的侧面都相切的球的半径的最大值是______【解析】如图,各截取长度为2的三个圆柱的部分(111,,AA BC C D 为圆柱的轴),不妨设球心刚好为正方体的中心,而圆柱半径为1,1.7.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,边长为,,a PD a PA PC ===.若在此四棱锥中放人一个球,则球的最大半径是()A.)1a - C.12a ⎛⎫- ⎪ ⎪⎝⎭D.a【答案】C【解析】由已知条件知,PD AD PD CD ⊥⊥,故PD ⊥平面ABCD ,则32133P ABCD a V a a -=⋅=.PAD PCD PAB PBC ABCD S S S S S S =++++表22112222a a a =⋅+⋅+(22a =.所以312P ABCD V r a S -⎛===- ⎝⎭表.。
立体几何中与球相关的接、切、截问题

立体几何中与球相关的接、切、截问题下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!立体几何中的球接、切、截问题解析在立体几何的学习中,我们经常会遇到关于球的接、切、截问题。
高考数学一轮复习第8章立体几何专题研究球与几何体的切接问题练习理

专题研究 球与几何体的切接问题1.(2017·唐山模拟)正三棱锥的高和底面边长都等于6,则其外接球的表面积为( ) A .64π B .32π C .16π D .8π答案 A解析 如图,作PM⊥平面ABC 于点M ,则球心O 在PM 上,PM =6,连接AM ,AO ,则OP =OA =R(R 为外接球半径),在Rt △OAM 中,OM =6-R ,OA =R ,又AB =6,且△ABC 为等边三角形,故AM =2362-32=23,则R 2-(6-R)2=(23)2,则R =4,所以球的表面积S =4πR 2=64π.2.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( ) A .16π B .20π C .24π D .32π答案 C解析 由V =Sh ,得S =4,得正四棱柱底面边长为2.画出球的轴截面可得,该正四棱柱的对角线即为球的直径,所以球的半径为R =1222+22+42= 6.所以球的表面积为S =4πR 2=24π.故选C.3.若一个正方体的体积是8,则这个正方体的内切球的表面积是( ) A .8π B .6π C .4π D .π答案 C解析 设正方体的棱长为a ,则a 3=8.因此内切球直径为2,∴S 表=4πr 2=4π.4.(2017·课标全国Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径长为2的同一个球的球面上,则该圆柱的体积为( ) A .π B.3π4 C.π2 D.π4答案 B解析 根据已知球的半径长是1,圆柱的高是1,如图,所以圆柱的底面半径r =22-122=32,所以圆柱的体积V =πr 2h =π×(32)2×1=34π.故选B. 5.(2018·安徽合肥模拟)已知球的直径SC =6,A ,B 是该球球面上的两点,且AB =SA =SB =3,则三棱锥S -ABC 的体积为( ) 3292C.322D.922答案 D解析 设该球球心为O ,因为球的直径SC =6,A ,B 是该球球面上的两点,且AB =SA =SB =3,所以三棱锥S -OAB 是棱长为3的正四面体,其体积V S -OAB =13×12×3×332×6=924,同理V O -ABC =924,故三棱锥S -ABC的体积V S -ABC =V S -OAB +V O -ABC =922,故选D. 6.已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为( ) A.3172B .210 C.132 D .310答案 C解析 如图,由球心作平面ABC 的垂线,则垂足为BC 的中点M. 又AM =12BC =52,OM =12AA 1=6,所以球O 的半径R =OA =(52)2+62=132. 7.(2018·广东惠州一模)已知一个水平放置的各棱长均为4的三棱锥形容器内有一小球O(质量忽略不计),现从该三棱锥形容器的顶端向内注水,小球慢慢上浮,当注入的水的体积是该三棱锥体积的78时,小球与该三棱锥各侧面均相切(与水面也相切),则小球的表面积等于( ) A.76π B.43π C.23π D.12π 答案 C解析 由题知,没有水的部分的体积是三棱锥形容器的体积的18,三棱锥形容器的体积为13·34·42·63·4=1623,所以没有水的部分的体积为223.设其棱长为a ,则其体积为13×34a 2×63a =223,∴a =2,设小球的半径为r ,则4×13×3×r =223,解得r =66,∴球的表面积为4π×16=23π,故选C.8.如图,ABCD -A 1B 1C 1D 1是棱长为1的正方体,S -ABCD 是高为1的正四棱锥,若点S ,A 1,B 1,C 1,D 1在同一个球面上,则该球的体积为( ) 25π49πC.81π16D.243π128答案 C解析 如图所示,O 为球心,设OG 1=x ,则OB 1=SO =2-x ,同时由正方体的性质可知B 1G 1=22,则在Rt △OB 1G 1中,OB 12=G 1B 12+OG 12,即(2-x)2=x 2+(22)2,解得x =78,所以球的半径R =OB 1=98,所以球的表面积S =4πR 2=81π16,故选C.9.(2018·郑州质检)四棱锥P -ABCD 的五个顶点都在一个球面上,该四棱锥的三视图如图所示,E ,F 分别是棱AB ,CD 的中点,直线EF 被球面所截得的线段长为22,则该球的表面积为( )A .9πB .3πC .22πD .12π答案 D解析 该几何体的直观图如图所示,该几何体可看作由正方体截得,则正方体外接球的直径即为PC.由直线EF 被球面所截得的线段长为22,可知正方形ABCD 对角线AC 的长为22,可得正方形ABCD 的边长a =2,在△PAC 中,PC =22+(22)2=23,球的半径R =3,∴S 表=4πR 2=4π×(3)2=12π.10.(2014·湖南)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A .1B .2C .3D .4答案 B解析 此几何体为一直三棱柱,底面是边长为6,8,10的直角三角形,侧棱为12,故其最大球的半径为底面直角三角形内切圆的半径,故其半径为r =12×(6+8-10)=2,故选B.11.(2017·天津)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为________. 答案 92π解析 设正方体的棱长为a ,则6a 2=18,得a =3,设该正方体外接球的半径为R ,则2R =3a =3,得R =32,所以该球的体积为43πR 3=43π(32)3=92π.12.若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________.答案63π解析 设正四面体的棱长为a , 则正四面体的表面积为S 1=4·34·a 2=3a 2, 其内切球半径为正四面体高的14,即r =14·63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2π6a 2=63π.13.已知一圆柱内接于球O ,且圆柱的底面圆的直径与母线长均为2,则球O 的表面积为________. 答案 8π解析 圆柱的底面圆的直径与母线长均为2,所以球的直径为22+22=8=22,即球半径为2,所以球的表面积为4π×(2)2=8π.14.(2017·衡水中学调研卷)已知正三棱锥P -ABC ,点P ,A ,B ,C 都在半径为3的球面上,若PA ,PB ,PC 两两相互垂直,则球心到截面ABC 的距离为________. 答案33解析 方法一:先在一个正方体中找一个满足条件的正三棱锥,再利用正方体的性质解题.如图,满足题意的正三棱锥P -ABC 可以是正方体的一部分,其外接球的直径是正方体的体对角线,且面ABC 与体对角线的交点是体对角线的一个三等分点,所以球心到平面ABC 的距离等于体对角线长的16,故球心到截面ABC 的距离为16×23=33.方法二:用等体积法:V P -ABC =V A -PBC 求解).15.(2018·四川成都诊断)已知一个多面体的三视图如图所示,其中正视图与侧视图都是直角边长为1的等腰直角三角形,俯视图是边长为1的正方形,若该多面体的顶点都在同一个球面上,则该球的表面积为________.答案 3π解析 由三视图知几何体为四棱锥,且四棱锥的一条侧棱垂直于底面,高等于1,其底面是边长为1的正方形,∴ 四棱锥的外接球即是边长为1的正方体的外接球,∴外接球的直径为3,∴外接球的表面积S =4π×(32)2=3π.16.(2018·河北唐山模拟)已知矩形ABEF 所在的平面与矩形ABCD 所在平面互相垂直,AD =2,AB =3,AF =332,M 为EF 的中点,则多面体M -ABCD 的外接球的表面积为________. 答案 16π解析 记多面体M -ABCD 的外接球的球心为O ,如图,过点O 分别作平面ABCD 和平面ABEF 的垂线,垂足分别为Q ,H ,连接MH 并延长,交AB 于点N ,连接OM ,NQ ,AQ ,设球O 的半径为R ,球心到平面ABCD 的距离为d ,即OQ =d ,∵矩形ABEF 所在的平面与矩形ABCD 所在的平面互相垂直,AF =332,M 为EF 的中点, ∴MN =332,∴AN =NB =32,NQ =1,∴R 2=(4+92)2+d 2=12+(332-d)2, ∴d =32,R 2=4, ∴多面体M -ABCD 的外接球的表面积为4πR 2=16π.1.(2017·课标全国Ⅱ,文)长方体的长,宽,高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为________. 答案 14π解析 依题意得,长方体的体对角线长为32+22+12=14,记长方体的外接球的半径为R ,则有2R =14,R =142,因此球O 的表面积等于4πR 2=14π. 2.(2018·湖南长沙一中模拟)如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三A .8π B.25π2 C .12π D.41π4答案 D解析 根据三视图得出,几何体是正方体中的一个四棱锥O -ABCD ,正方体的棱长为2,A ,D 为所在棱的中点.根据几何体可以判断,球心应该在过A ,D 的平行于正方体底面的中截面上,设球心到平面BCO 的距离为x ,则到AD 的距离为2-x ,所以R 2=x 2+(2)2,R2=12+(2-x)2,解得x =34,R =414,该多面体外接球的表面积为4πR 2=414π,故选D.3.(2014·陕西,理)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( ) A.32π3B .4πC .2π D.4π3答案 D解析 因为该正四棱柱的外接球的半径是四棱柱体对角线的一半,所以半径r =1212+12+(2)2=1,所以V 球=4π3×13=4π3.故选D.4.(2018·洛阳统一考试)如图是某几何体的三视图,则该几何体的外接球的表面积为( )A .200πB .150πC .100πD .50π答案 D解析 由三视图知,该几何体可以由一个长方体截去3个角后得到,该长方体的长、宽、高分别为5、4、3,=50π,故选D.5.(2018·广东清远三中月考)某一简单几何体的三视图如图所示,则该几何体的外接球的表面积是( )A .13πB .16πC .25πD .27π答案 C解析 由三视图可知该几何体是底面为正方形的长方体,底面对角线为4,高为3,设外接球半径为r ,则2r =(22)2+(22)2+32=5,∴r =52,∴长方体外接球的表面积S =4πr 2=25π.6.(2018·福建厦门模拟)已知球O 的半径为R ,A ,B ,C 三点在球O 的球面上,球心O 到平面ABC 的距离为32R ,AB =AC =BC =23,则球O 的表面积为( ) A.163π B .16π C.643π D .64π答案 D解析 因为AB =AC =BC =23,所以△ABC 为正三角形,其外接圆的半径r =232sin60°=2,设△ABC 外接圆的圆心为O 1,则OO 1⊥平面ABC ,所以OA 2=OO 12+r 2,所以R 2=(32R)2+22,解得R 2=16,所以球O 的表面积为4πR 2=64π,故选D.7.(2018·四川广元模拟)如图,边长为2的正方形ABCD 中,点E ,F 分别是AB ,BC 的中点,将△ADE,△EBF ,△FCD 分别沿DE ,EF ,FD 折起,使得A ,B ,C 三点重合于点A ′,若四面体A ′EFD 的四个顶点在同一个球面上,则该球的半径为________.答案62三棱锥的外接球与正四棱柱的外接球是同一个球,易知正四棱柱的外接球的直径为12+12+22= 6.故球的半径为62. 8.(2017·德州模拟)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,该几何体的体积是________;若该几何体的所有顶点在同一球面上,则球的表面积是________.答案 133π解析 由三视图知该几何体是底面为1的正方形,高为1的四棱锥,故体积V =13×1×1×1=13,该几何体与棱长为1的正方体具有相同的外接球,外接球直径为3,该球表面积S =4π×(32)2=3π,正方体、长方体的体对角线即为外接球的直径.。
几何体与球的切、接问题练习题高一用

几何体与球的切、接问题一、直接法:依据几何体的特征找球心的位置,通过解三角形求出半径1、多面体与球(1)正方体棱长为,其外接球直径,内切球直径,棱切球直径(2)正四面体棱长为,高,三球球心为高的四分点。
外接球半径,内切球半径,棱切球半径a 2R =2R a=2R =a h=3R h 4==1R h 4==R =2、直棱柱外接球球心为上、下底面外接圆圆心连线的中点;3、正棱柱(或圆柱)外接球球心为上、下底面中心连线的中点;4、正棱台(或圆台)外接球球心在上、下底面中心连线上;5、正棱锥(或圆锥)外接球球心在几何体的高上,可由勾股定理求R ;6、三棱锥中有公共斜边的直角三角形,则外接球球心为斜边中点,该斜边为直径。
二、补正方体或长方体求外接球半径1、底面为直角三角形的直棱柱;2、同一顶点出发的三条棱两两垂直的三棱锥;3、三节棍体(三条棱两两垂直,且垂足不是同一点的四面体);4、相对棱两两相等的四面体;5、一条侧棱垂直于底面,底面是矩形的四棱锥;6、一条侧棱垂直于底面的椎体补为直棱柱;三、几何的内切球,可通过体积法求半径:四、典型例题1、直三棱柱的各顶点都在同一球面上,若,,,则此球的表面积为2、长方体顶点都在半径为9的球0的球面上,则长方体表面积的最大值是3、球0为正方体的内切球,,分别为棱的中点,则直线被球0截得的线段长为4、正三棱锥中,,为中点,且直线与地面所成角的正切值为外接球的表面积为5、矩形中,,沿将矩形折成一个四面体,则此四面体的外接球体积为,四面体体积最大值为1V S r 3=∙表111ABC A B C -0ABC 120∠=AB 2=1BC CC 1==1111ABCD A B C D -AB 2=E,F 1AD CC 、EF A BCD -BC 2=E BC AE BCD A BCD -ABCD AB 4,BC 3==AC ABCD D ABC -6、在正三棱锥中,是的中点,且,底面边长的外接球的体积为7、四面体满足,,则四面体的外接球表面积为8、已知球的直径,是该球面上的两点,,则三棱锥的体积是9、在封闭的直三棱柱内有一体积为的球,若,AB=6,bc=8,AA 1=3,则的最大值是10、四面体ABCD 中,已知AB=CD=5,,其外接球的表面积为S ABC -M SC AM SB ⊥AB =S ABC -ABCD AB CD ==AC AD BC BD 2====ABCD SC 4=A B 、AB =0ASC BSC 30∠=∠=S ABC -111ABC A B C -V AB BC ⊥V AC BD ==AD BC ==11、体积为的球与正三棱柱的所有面均相切,则该棱柱的体积为 12、已知SC 为球0的直径,A,B 为球面上两点,AB=2,,若棱锥A-SBC,则球0的体积为 13、三棱锥A-BCD 内接于半径为2的球0,BC 过球心0,当三棱锥A-BCD 的体积最大时,三棱锥A-BCD 的表面积为总结:43πASC BSC 4π∠=∠=。
专题15 几何体与球切、接、截的问题(练)【解析版】

第一篇 热点、难点突破篇专题15几何体与球切、接、截的问题(练)【对点演练】一、单选题 1.(2022秋·湖南张家界·高三慈利县第一中学校考阶段练习)如下图是一个正八面体,其每一个面都是正三角形,六个顶点都在球O 的球面上,则球O 与正八面体的体积之比是( )A .πB .4π3C .3π2D .2πAB a ,则R足球赛,比赛于2022年11月21日至12月18日在卡塔尔境内7座城市中的12座球场举行.已知某足球的表面上有四个点A 、B 、C 、P 满足P A =BC =5,PB AC ==PC AB ==则该足球的表面积为( ) A .12π B .8πC .24πD .28π【答案】D【分析】把四面体外接球问题扩展到长方体中,求出长方体外接球半径为R ,进而求出结果. 【详解】因为P A =BC ,PB AC =,PC AB =,所以可以把A ,B ,C ,P 四点放到长方体的则该足球的表面积为四面体A -BCP 外接球的表面积,即为长方体外接球的表面积, 解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”,即如图,一个长方体1111ABCD A B C D -,沿对角面11ABC D 分开(图1),得到两个一模一样的堑堵(图2),将其中一个堑堵11ADD BCC -,沿平面1D BC 分开(图2),得到一个四棱锥1D ABCD -称为阳马(图3),和一个三棱锥11D BCC -称为鳖臑(图4). 若鳖臑的体积为4,且4,3AB BC ==,则阳马1D ABCD -的外接球的表面积为( )A .27πB .29πC .31πD .33π23BAC π∠=.若三棱锥-P ABC 的各顶点都在球O 的球面上,则球O 的表面积为( ) A .4πB .8πC .12πD .20π【分析】利用正弦定理求出底面ABC 的外接圆半径,将三棱锥面外接圆中心作垂线,则垂线的中点即为外接球球心,进而即可求解【详解】在ABC 中,设其外接圆半径为由正弦定理可得2,sin 6AB r π=∠解得ABC 补成三棱柱,如图设三棱锥-P ABC 外接球半径为R ,5.(2022·四川广安·广安二中校考模拟预测)已知在Rt ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且2a =,6A π=.又点A ,B ,C 都在球O 的球面上,且点O 到平面ABC 的O 的体积为______. 【分析】首先求ABC 外接圆的半径,再求球【详解】ABC 中,根据正弦定理所以ABC 外接圆的半径为到平面ABC 的距离为)253=,4π,高为2,上、下底面的圆周在同一球面上,则该圆台外接球的表面积为__________.()2()2长为的正方形,其顶点P到底面ABCD的距离为4.该四棱锥的外接球O的半径为7,若球心O在四棱锥P-ABCD内,则顶点P的轨迹长度为_____________.8.(2022·上海长宁·统考一模)已知1AA 是圆柱的一条母线,AB 是圆柱下底面的直径,C 是圆柱下底面圆周上异于A ,B 的两点,若圆柱的侧面积为4π,则三棱锥1A —ABC 外接球体积的最小值为___________设底面圆半径为r ,圆柱高设为h ,则根据圆柱的侧面积为4π,可得2π4πrh =,解得2rh =.因为ABC 以及2222214ABh r A B ,则224h r ,所以外接球的半径2242hr R.三棱锥—ABC 外接球体积为32244π32hr ,所以要外接球体积最小,只需要224h r 最小即可,又不等式可知2242248r h r rh ,当且仅当12r h ,时成立.故三棱锥外接球体积的最小值为34882ππ323. 故答案为:82π3..(2022秋·江苏南通已知圆台的内切球侧面相切的切点位于圆台高的34______.O 的表面积为______,体积为______.【冲刺提升】一、单选题 1.(2022秋·江苏淮安·高三校考阶段练习)如图,已知三棱柱111ABC A B C 的底面是等腰直角三角形,1AA ⊥底面ABC ,AC =BC =2,14AA =,点D 在上底面111A B C (包括边界)上运动,则三棱锥D -ABC 的外接球表面积的范围为( )A .81π,24π4⎡⎤⎢⎥⎣⎦B .[]9π,24πC .243π,24π16⎡⎤⎢⎥⎣⎦D .243π16⎡⎤⎢⎥⎣⎦因为ABC 为等腰直角三角形,所以ABC 的外接球的截面圆心为,且1AO =1//AA ,所以由球的截面性质可知,(0DE t t =≤OD R ==,所以2814t x =-因为2R =故选:A2.(2022秋·江苏南京·高三南京师大附中校联考阶段练习)四棱锥P ABCD-中,底面ABCD是边长为PAD为正三角形,则其外接球体积最小值为()A B.32 3πC.D.二、多选题3.(2022秋·安徽·高三石室中学校联考阶段练习)已知正四棱台上、下底面的面积分别为2和8,高为()0h h >,则下列结论正确的有( ) A .正四棱台外接球的表面积的最小值为16πB .当(h ∈时,正四棱台外接球球心在正四棱台下底面下方C .正四棱台外接球的半径随h 的增大而增大D .当2h =时,正四棱台存在内切球 1EO B EFB Rt Rt ≌可知O ∠ 2,故可知π2BEC ∠=,,所以1r =,2h =.故D 正确故选:ABD .4.(2022秋·山东潍坊·高三统考阶段练习)截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点处的小棱锥所得的多面体,如图所示,将棱长为3a 的正四面体沿棱的三等分点作平行于底面的截面,得到所有棱长均为a 的截角四面体,则下列说法正确的是( )A 3a B .该截角四面体的体积为312C .该截角四面体的外接球表面积为213π2a D .AEF △外接圆的面积为25π4a【详解】取上下底面的中心为,O O ''',外接球的球心为O ,连接,,,,OC OH CO HO '''如图,.(秋山东高三校联考阶段练习)在棱长为的正方体1111中,点为线段1AD (包含端点)上一动点,则下列选项正确的是( ).A .三棱锥1C BDQ -的体积为定值B .在Q 点运动过程中,存在某个位置使得1AD ⊥平面BQCC .截面三角形BQC 面积的最大值为D .当三棱锥1B B CQ -为正三棱锥时,其内切球半径为66.(2022秋·河北邢台·高三河北南宫中学校考阶段练习)如图,在菱形ABCD 中,π2,,3AB ABC M =∠=为BC 的中点,将ABM 沿直线AM 翻折到1AB M 的位置,连接1B C 和1,B D N 为1B D 的中点,在翻折过程中,则下列结论中正确的是( )A .面1AB M ⊥面1B MCB .线段CN 长度的取值范围为⎡⎣C .直线AM 和CN 所成的角始终为π6D .当三棱锥1B AMD -的体积最大时,点C 在三棱锥1B AMD -外接球的外部B 选项:如图所示,取AD 中点E ,连接EN ,EC ,所以//EC AM ,且EC AM =,又因为,在CEN 中,由余弦,即CN =C 选项:由B 选项得//EN AB ,所以直线AM 和CN 所成角即为与CN 所成角NCE ∠,在AMD 的外接圆内,又AMD 的外接圆在三棱锥1AMD -外接球的内部,故D 选项错误;故选:AC 三、填空题7.(2022秋·江苏·高三校联考阶段练习)已知半径为O 的表面上有A ,B ,C ,D 四点,且满足AD ⊥平面ABC ,BC AB BC =⊥,则四面体D ABC -的体积最大值为_____________;若M 为AD 的中点,当D 到平面MBC 的距离最大时,MBO △的面积为_____________.8.(2022秋·江苏常州·高三统考阶段练习)在正四面体A BCD -中,E 为BC 边的中点,过点E 作该正四面体外接球的截面,记最大的截面面积S ,最小的截面面积为T ,则=T S__________;若记该正四面体内切球和外接球的体积分别为1V 和2V ,则21V V =__________.2面积是___________.【答案】20πAC PC C =,,120APC ∠=所以2O A O P O C '''===,60PO A PO C ''∠=∠=︒.角形的四面体称之为鳖臑.如图,在鳖臑-P ABC 中,PA ⊥平面ABC .已知6AB =,8CB =,10PA AC ==,请写出平面PBC 的直角:_____________;若P ,A ,B ,C 都在球O 的球面上,则球O 的表面积为____________.PAAB A =,,故BC PB ⊥放入长方体中,如图所示:长及对角线BD 的长度均为6,平面ABD ⊥平面CBD ,点M 在AC 上,且2AM MC =,那么ABCD 外接球的半径为______;过点M 作四边形ABCD 外接球的截面.则截面面积最大值与最小值之比为______.【答案】54##1.25 1AE OHCE四、解答题12.(2022秋·安徽·高三校联考阶段练习)如图,长方体1111ABCD A B C D -中,11,2,AB AD AA P ===为棱1DD 的中点.(1)求直线AP 被长方体1111ABCD A B C D -的外接球截得的线段长度;(2)求直线1AC 与平面PAC 所成角的正弦值.()()()()()()10,0,0,1,0,0,0,1,0,0,0,2,0,1,2,0,0,1D A C D C P 设平面PAC 的一个法向量(),,n x y z =因为()()1,1,0,1,0,1AC AP =-=-,00n AC n AP ⎧⋅=⎪⎨⋅=⎪⎩,得,可得()1,1,1n =,又()11,1,2AC =-,设直线1AC 与平面所以()1111,1,1,1,12sin cos ,36AC nAC n AC n θ-⋅====⋅所以直线AC 与平面PAC 所成角的正弦值为。
2017届高三数学第一轮复习专题训练之球的“内切”“外接”问题含答案
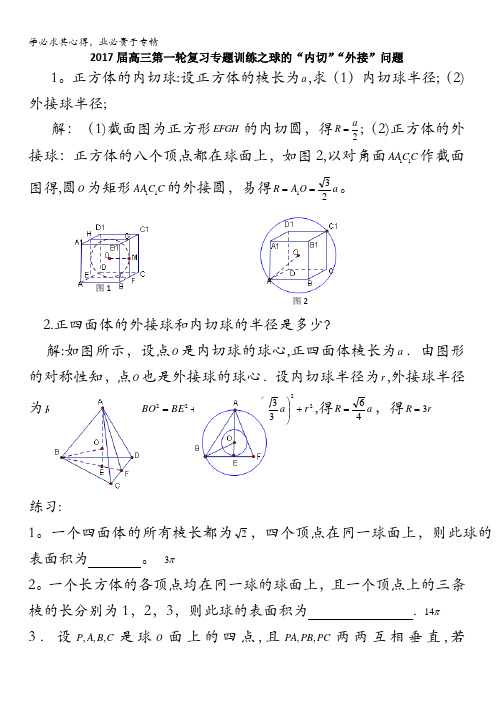
2017届高三第一轮复习专题训练之球的“内切”“外接”问题1。
正方体的内切球:设正方体的棱长为a ,求(1)内切球半径;(2)外接球半径;解:(1)截面图为正方形EFGH 的内切圆,得2a R =;(2)正方体的外接球:正方体的八个顶点都在球面上,如图2,以对角面11AAC C 作截面图得,圆O 为矩形C C AA 11的外接圆,易得a O A R 231==。
2.正四面体的外接球和内切球的半径是多少?解:如图所示,设点O 是内切球的球心,正四面体棱长为a .由图形的对称性知,点O 也是外接球的球心.设内切球半径为r ,外接球半径为R .在BEO Rt ∆中,222EO BE BO +=,即22233r a R +⎪⎪⎭⎫ ⎝⎛=,得a R 46=,得r R 3=练习:1。
一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为 。
3π2。
一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 . 14π 3.设,,,P A B C是球O 面上的四点,且,,PA PB PC两两互相垂直,若图1图2PA PB PC a ===,则球心O 到截面ABC 的距离是。
6a 4.在正三棱锥S ABC -中,侧棱SC SAB ⊥侧面,侧棱2SC =,则此正三棱锥的外接球的表面积为 12π5.半径为R 的球内接一个各棱长都相等的正四棱锥.则四棱锥的体积为 .323R6.正三棱锥的高为3,底面边长为正三棱锥内有一个球与其四个面相切.则球的表面积与体积分别为 .64256;981ππ7.正四棱锥S ABCD -的底面边长和各侧棱长都为点S A B C D 、、、、都在同一球面上,则此球的体积为 . 解: 设正四棱锥的底面中心为1O ,外接球的球心为O ,如图3所示。
∴由球的截面的性质,可得1OO ABCD ⊥平面.又1SOABCD ⊥平面,∴球心O 必在1SO 所在的直线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年高考(文科)数学专题练习
几何体与球切、接的问题
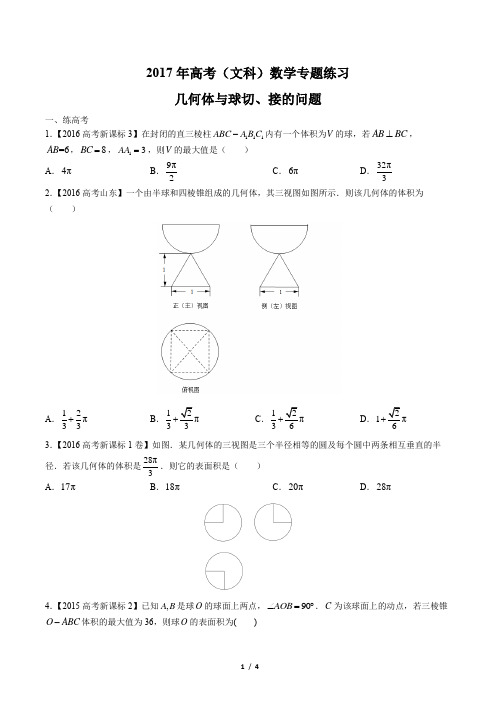
一、练高考
1.【2016高考新课标3】在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥, =6AB ,8BC =,13AA =,则V 的最大值是( )
A .4π
B .9π2
C .6π
D .32π3
2.【2016高考山东】一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )
A .12π33
+ B .13+ C .13+ D .1 3.【2016高考新课标1卷】如图.某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是
28π3.则它的表面积是( ) A .17π B .18π C .20π D .28π
4.【2015高考新课标2】已知,A B 是球O 的球面上两点,90AOB ∠=︒.C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为( )
A .36π
B .64π
C .144π
D .256π
5.【2014大纲高考】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A .81π4
B .16π
C .9π
D .27π4
6.【2013年福建卷】已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是__________.
二、练模拟
1.【广西梧州市2017届高三上学期摸底联考】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的体积为( )
A .243π16
B .81π16
C .81π4
D .27π4
2.【河南省开封市2017届高三上学期10月月考】如图.已知一个八面体的各条棱长均为1.四边形ABCD 为正方形,则下列命题中的假命题是
A .不平行的两条棱所在的直线所成的角是60︒或90︒;
B .四边形AECF 是正方形;
C .点A 到平面BCE 的距离为r ;
D .该八面体的顶点在同一个球面上.
3.【河南省师范大学附属中学2015届高三12月月考】已知四面体P ABC -中,4PA =,AC =
PB BC ==PA ⊥平面PBC ,则四面体P ABC -的外接球体积为( )
A .125π6
B
C
D 4.【2016届甘肃河北五市高三第一次联考】体积为4π3
的球O 放置在棱长为4的正方体1111ABCD A B C D -上,且与上表面1111A B C D 相切,切点为该表面的中心,则四棱锥O ABCD -的外接球的半径为( )
A .103
B .3310
C .2
D .236
5.【2016届河北省武邑中学高三上学期期末考试】正三角形ABC 的边长为2,将它沿高AD 翻折,使点B
与点C ABCD 外接球表面积为( )
A .7π
B .19π
C D
6.【2016
届甘肃省河北五校高三第一次联考】面积为2
的正六边形的六个顶点都在球O 的球面上,球心O 到正六边形所在平面的距离为
O 的体积为V ,球O 的表面积为S ,则V S
的值是( ) A .2
B .1 C
D
三、练原创
1.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
A .3π
B .4π
C .2π
D .5π2
2.已知四面体P ABC -中.4PA =
,AC =
PB BC ==PA ⊥平面PBC .则四面体P ABC -的内切球半径与外接球半径的比( )
A
B
C
D
3.如图,正方体1111ABCD A B C D -
A 为球心,2为半径作一个球,则图中球面与正方体的表面积相交所得到的两段弧之和等于( )
A .5π6
B .2π3
C .π
D .7π6
4.三棱锥S ABC -的所有顶点都在球O 的表面上,SA ⊥平面ABC ,AB BC ⊥,又1SA AB BC ===,则球O 的表面积为__________.
5.已知三棱锥A BCD -中,2,2AB AC BD CD BC AD =====,直线AD 与底面BCD 所成角为3
π,则此时三棱锥外接球的表面积为__________.
俯视图
正视图 侧视图。
