一模考压轴题汇编
2023年北京中考数学一模分类汇编——填空压轴题(学生版)

2023年北京中考数学一模分类汇编——填空压轴题1.(2023•海淀区一模)某陶艺工坊有A和B两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.大中小尺寸数量(个)款式A81525B01020烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品,但烧制较小陶艺品的位置不能替换为烧制较大陶艺品.某批次需要生产10个大尺寸陶艺品,50个中尺寸陶艺品,76个小尺寸陶艺品.(1)烧制这批陶艺品,A款电热窑至少使用次;(2)若A款电热窑每次烧制成本为55元,B款电热窑每次烧制成本为25元,则烧制这批陶艺品成本最低为元.2.(2023•西城区一模)A,B,C三种原料每袋的重量(单位:kg)依次是1,2,3,每袋的价格(单位:万元)依次是3,2,5.现生产某种产品需要A,B,C这三种原料的袋数依次为x1,x2,x3(x1,x2,x3均为正整数),则生产这种产品时需要的这三类原料的总重量W(单位:kg)=(用含x1,x2,x3的代数式表示);为了提升产品的品质,要求W≥13,当x1,x2,x3的值依次是时,这种产品的成本最低.3.(2023•东城区一模)一枚质地均匀的骰子放在棋盘上,骰子的六个面上分别刻有1到6的点数,相对两个面上的点数之和为7.骰子摆放的初始位置如图所示.骰子由初始位置翻滚一次,点数为1的面落在1号格内;再从1号格翻滚一次,点数为5的面落在2号格内;继续这样翻滚……(1)当骰子翻滚到2号格时,朝上一面的点数为;(2)依次翻滚6次到6号格,每次翻滚后骰子朝上一面的点数之和为.4.(2023•朝阳区一模)一个33人的旅游团到一家酒店住宿,酒店的客房只剩下4间一人间和若干间三人间,住宿价格是一人间每晚100元,三人间每晚130元.(说明:男士只能与男士同住,女士只能与女士同住,三人间客房可以不住满,但每间每晚仍需支付130元.)(1)若该旅游团一晚的住宿房费为1530元,则他们租住了间一人间;(2)若该旅游团租住了3间一人间,且共有19名男士,则租住一晚的住宿房费最少为元.5.(2023•丰台区一模)临近端午,某超市准备购进小枣粽、豆沙粽、肉粽共200袋(每袋均为同一品种的粽子),其中小枣粽每袋6个,豆沙粽每袋4个,肉粽每袋2个.为了促销,超市计划将所购粽子组合包装,全部制成A,B两种套装销售.A套装为每袋小枣粽4个,豆沙粽2个;B套装为每袋小枣粽2个,肉粽2个.(1)设购进的小枣粽x袋,豆沙粽y袋,则购进的肉粽的个数为(用含x,y的代数式表示);(2)若肉粽的进货袋数不少于三种粽子进货总袋数的,则豆沙粽最多购进袋.6.(2023•石景山区一模)为落实生态文明建设,推动绿色发展,促进人与自然和谐共生,某公司装修采用同质地的A型、B型环保板材,具体要求如下:板材规格需用量板材要求板材型号A型板材60cm×30cm290块B型板材40cm×30cm180块现只能购得规格为150cm×30cm的符合质地要求的标准板材,一张标准板材尽可能多地裁出A型、B型板材,裁法如下(损耗忽略不计):裁法一裁法二裁法三裁出数量(块)裁法板材型号A型板材210B型板材0a3如表中a的值为;公司需购入标准板材至少张.7.(2023•通州区一模)某学校带领150名学生到农场参加植树劳动,学校同时租用A,B,C三种型号客车去农场,其中A,B,C三种型号客车载客量分别为40人、30人、10人,租金分别为700元、500元、200元.为了节省资金,学校要求每辆车必须满载,并将学生一次性送到农场植树,请你写出一种满足要求的租车方案,满足要求的几种租车方案中,最低租车费用是元.8.(2023•平谷区一模)某货运公司临时接到一个任务,从工厂同时运送A、B两种货物各20箱到展馆,货运公司调派甲货车运送A种货物,乙货车运送B种货物,A种货物每箱80千克,B种货物每箱70千克,因为两种货物包装箱完全一样,装运工人一时疏忽两车虽然所装货物数量正确,但部分货物却装混了.运送途中安检时,两车过地秤,发现甲车比乙车的货物重160千克,则甲、乙两车各有箱货物装错,到达展馆,为了尽快把货物区分开,乙车司机借来了一台最多可以称300千克的秤精选最优称重方案,根据被错装货物出现的所有可能情况,最多需要称次就能把乙车上装错的货物区分出来.9.(2023•门头沟区一模)某校计划租用甲,乙,丙三种型号客车送师生去综合实践基地开展活动.每种型号客车的载客量及租金如下表所示:客车型号甲乙丙每辆客车载客量/人203040每辆客车的租金/元500600900其中租用甲型客车有优惠活动:租用三辆或三辆以上每辆客车的租金打8折.现有280名师生需要前往综合实践基地,要求每种型号的客车至少租1辆,且每辆车都坐满.(1)如果甲,乙,丙三种型号客车的租用数量分别是2,4,3,那么租车的总费用为元;(2)如果租车的总费用最低,那么甲,乙,丙三种型号客车的租用数量可以分别是.10.(2023•房山区一模)为进一步深化“创城创卫”工作,传播健康环保的生活理念,房山区持续推进垃圾分类工作.各乡镇(街道)的党员、志愿者纷纷参与“桶前值守”,在垃圾桶旁监督指导居民对垃圾进行分类.某垃圾值守点有甲、乙、丙、丁四名志愿者,某一天每人可参与值守时间段如下表所示:志愿者可参与值守时间段1可参与值守时间段2甲6:00﹣8:0016:00﹣18:00乙6:30﹣7:3017:00﹣20:00丙8:00﹣11:0018:00﹣19:00丁7:00﹣10:0017:30﹣18:30已知每名志愿者一天至少要参加一个时间段的值守,任意时刻垃圾值守点同时最多需要2名志愿者值守,则该值守点这一天所有参与值守的志愿者的累计值守时间最短为小时,最长为小时(假设志愿者只要参与值守,就一定把相应时间段全部值完)11.(2023•延庆区一模)甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应关系如图所示,下列说法中,①甲、乙两种物质的溶解度均随着温度的升高而增大;②当温度升高至t2℃时,甲的溶解度比乙的溶解度小;③当温度为0℃时,甲、乙的溶解度都小于20g;④当温度为30℃时,甲、乙的溶解度相同.所有正确结论的序号是.12.(2023•顺义区一模)某京郊民宿有二人间、三人间、四人间三种客房供游客住宿,某旅游团有25位女士游客准备同时住这三种客房共8间,如果每间客房都要住满,请写出一种住宿方案;如果二人间、三人间、四人间三种客房的收费标准分别为300元/间、360元/间、400元/间,则最优惠的住宿方案是.13.(2023•大兴区一模)某校需要更换部分体育器材,打算用1800元购买足球和篮球,并且把1800元全部花完.已知每个足球60元,每个篮球120元,根据需要,购买的足球数要超过篮球数,并且足球数不超过篮球数的2倍,写出一种满足条件的购买方案.14.(2023•燕山一模)某工厂用甲、乙两种原料制作A,B,C三种型号的工艺品,三种型号工艺品的重量及所含甲、乙两种原料的重量如下:工艺品型号含甲种原料的重量/kg含乙种原料的重量/kg工艺品的重量/kg A347B325C235现要用甲、乙两种原料共31kg,制作5个工艺品,且每种型号至少制作1个.(1)若31kg原料恰好全部用完,则制作A型工艺品的个数为;(2)若使用甲种原料不超过13kg,同时使用乙种原料最多,则制作方案中A,B,C三种型号工艺品的个数依次为.。
2024年河南省各地市中考数学一模压轴题精选(含解析)

2024年河南省各地市中考数学一模压轴题精选温馨提示:1.本卷共45题,题目均选自2024年河南省各地市一模真题。
2.本卷共分为六部分,解答题留有足够答题空间,试题部分可直接打印出来练习。
3.本卷难度较大,适合基础较好的同学。
第一部分动点问题和函数图象1.(2024·河南省开封市·一模)如图1,在△ABC中,∠B=60°,点D从点B出发,沿BC运动,速度为1cm/s.点P在折线BAC上,且PD⊥BC于点D.点D运动2s时,点P与点A重合.△PBD的面积S(cm2)与运动时间t(s)的函数关系图象如图2所示,E是函数图象的最高点.当S(cm2)取最大值时,PD的长为( )A. 23cmB. (1+3)cmC. (1+23)cmD. (2+23)cm2.(2024·河南省南阳市·一模)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为( )A. 6B. 8C. 10D. 133.(2024·河南省开封市·一模)如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )A. 线段CGB. 线段AGC. 线段AHD. 线段CH4.(2024·河南省南阳市·一模)如图,正方形ABCD的边长为4,动点P从点B出发沿折线BCDA做匀速运动,设点P运动的路程为x,△PAB的面积为y,下列图象能表示y与x之间函数关系的是( )A. B.C. D.5.(2024·河南省洛阳市·一模)正方形ABCD与正方形BEFG按照如图所示的位置摆放,其中点E在AB上,点G、B、C在同一直线上,且AB=4,BE=2,正方形BEFG沿直线BC向右平移得到正方形B′E′F′G′,当点G′与点C重合时停止运动,设平移的距离为x,正方形B′E′F′G′与正方形ABCD的重合部分面积为S,则S与x之间的函数图象可以表示为( )A. B.C. D.6.(2024·河南省驻马店市·一模)如图所示,已知△ABC中,BC=12,BC边上的高ℎ=6,D为BC上一点,EF//BC,交AB于点E,交AC于点F,设点E到边BC的距离为x.则△DEF的面积y关于x的函数图象大致为( )A. B.C. D.7.(2024·河南省漯河市·一模)如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )A. B.C. D.第二部分一次函数与反比例函数8.(2024·河南省南阳市·一模)如图,在平面直角坐标系xOy中,直线l:y=kx+2与x,y轴分别相交于点A,(x>0)的图象相交于点C,已知OA=1,点C的横坐标为2.B,与反比例函数y=mx(1)求k,m的值;(2)平行于y轴的动直线与l和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.(m≠0)的图象相9.(2024·河南省漯河市·一模)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=mx交于点A(1,2),B(a,―1).(1)求反比例函数和一次函数的解析式;<0的解集.(2)请直接写出不等式kx+b―mx(3)若直线y=kx+b(k≠0)与x轴交于点C,x轴上是否存在一点P,使S△APC=4?若存在,请求出点P坐标;若不存在,说明理由.10.(2024·河南省南阳市·一模)如图,在平面直角坐标系中,一次函数y=mx+n与反比例函数y=k的图象x在第一象限内交于A(a,4)和B(4,2)两点,直线AB与x轴相交于点C,连接OA.(1)求一次函数与反比例函数的表达式;(2)当x>0时,请结合函数图象,直接写出关于x的不等式mx+n≥k的解集;x(3)请用无刻度的直尺和圆规过点B作BD//x轴,交OA于点D,(提示:即作一个角∠ABD等于已知角∠ACO,保留作图痕迹,不写作法),并直接写出梯形OCBD的面积.11.(2024·河南省洛阳市·一模)如图,双曲线y=k与直线y=mx+n交于A(6,6),B(a,―1),直线AB交y轴于x点M,交x轴于点N.(1)求双曲线与直线AB的解析式;≥mx+n的解集;(2)直接写出不等式kx(3)请用无刻度的直尺和圆规作出线段ON的垂直平分线(保留作图痕迹,不写作法),交直线AB于点P,交双曲线于点Q.求出点Q的坐标.12.(2024·河南省周口市·一模)如图,在平面直角坐标系中,扇形AOB上的点A(1,3)在反比例函数y=k的图象x上,点B(3,―1)在第四象限,菱形OCDE的顶点D在x轴的负半轴上,顶点E在反比例函数y=k的图象上.x(1)k的值为______;(2)求∠AOB的度数;(3)请直接写出图中阴影部分面积之和.13.(2024·河南省开封市·一模)如图,△ABC的顶点坐标分别为A(0,3),B(1,0),C(2,3),反比例函数y=k(x>0)的图象经过点C.x(1)求k的值.(x>0)的图象上,且BD⊥AC于点E,DE=BE,请说明四边形ABCD是菱形.(2)点D在反比例函数y=kx(3)是否存在除点D外可与A,B,C三点共同组成菱形的点P?若存在,请直接写出点P的坐标;若不存在,请说明理由.第三部分圆与扇形14.(2024·河南省开封市·一模)如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D 两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.若圆半径为2.则阴影部分面积=.15.(2024·河南省南阳市·一模)如图,半径为5的扇形AOB中,∠AOB=90°,C是AB上一点,CD⊥OA,CE⊥OB,垂足分别为D,E,若CD=CE,则图中阴影部分面积为______.16.(2024·河南省开封市·一模)如图,PA是⊙O的切线,A是切点,PB经过圆心O,且与⊙O交于点B,C,若AP=AB=3,则直径BC的长为______.17.(2024·河南省南阳市·一模)如图,已知AB是⊙O的直径,直线DC是⊙O的切线,切点为C,AE⊥DC,垂足为E.连接AC.(1)求证:AC平分∠BAE;(2)若AC=5,tan∠ACE=3,求⊙O的半径.418.(2024·河南省开封市·一模)如图,⊙O的直径AB与其弦CD相交于点E,过点A的切线交CD延长线于点F,且∠AED=∠EAD.(1)求证:AD=FD;(2)若AE=6,sin∠AFE=3,求⊙O半径的长.519.(2024·河南省漯河市·一模)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.(1)求证:BE=EC.(2)填空:①若∠B=30°,AC=23,则DE=______;②当∠B=_____°时,四边形DECO是正方形.20.(2024·河南省驻马店市·一模)阅读与思考九年级学生小刚喜欢看书,他在学习了圆后,在家里突然看到某本数学书上居然还有一个相交弦定理(圆内的两条相交弦,被交点分成的两条线段长的积相等),下面是书上的证明过程,请仔细阅读,并完成相应的任务.圆的两条弦相交,这两条弦被交点分成的两条线段的积相等.已知:如图1,⊙O的两弦AB,CD相交于点P.求证:AP⋅BP=CP⋅DP.证明:如图1,连接AC,BD.∵∠C=∠B,∠A=∠D.∴△APC∽△DPB,(根据)∴AP=@,DP∴AP⋅BP=CP⋅DP,∴两条弦相交,被交点分成的两条线段的积相等.任务:(1)请将上述证明过程补充完整.根据:______;@:______.(2)小刚又看到一道课后习题,如图2,AB是⊙O的弦,P是AB上一点,AB=10cm,PA=4cm,OP=5cm,求⊙O的半径.第四部分全等与相似三角形21.(2024·河南省开封市·一模)已知∠ABC=30°,AB=4,P是BC边上一点,当△ABP是以PA为腰的等腰三角形时,BP的长为______.22.(2024·河南省洛阳市·一模)折纸游戏:小明剪出一个直角三角形的纸片ABC,其中,∠A=60°,AC=1,找出BC的中点M,在AB上找任意一点P,以MP为对称轴折叠△MPB,得到△MPD,点B的对应点为点D,小明发现,当点P的位置不同时,DP与△ABC的三边位置关系也不同,请帮小明解决问题:当DP⊥BC时,AP的长为______.23.(2024·河南省驻马店市·一模)如图,等腰三角形ABC中,AB=AC=5,该三角形的两条高BD与AE交于点F,连接CF,点P为射线AE上一个动点,连接BP,若AD=3,当△ABP与△BFC相似时,AP的长为______.24.(2024·河南省周口市·一模)矩形ABCD中,O为对角线AC的中点,点E从点A出发,沿A→B→C运动到点C,且AB=1,AD=3.当以点A,E,O为顶点的三角形为直角三角形时,AE的长为______.25.(2024·河南省商丘市·一模)如图,在Rt△ABC中,∠ACB=90°,∠ABC=40°,AB=4,斜边AB是半圆O 的直径,点D是半圆上的一个动点,连接CD与AB交于点E,若△BCE是等腰三角形,则∠BOD的度数为______.26.(2024·河南省开封市·一模)如图,在等腰Rt△ABC中,AC=BC=4,∠C=90°,D为边AC的中点,E为边AB上的一个动点,连接DE,将△ABC沿DE折叠,点A的对应点为A′,当A′E⊥AC时,BE的长度为______.27.(2024·河南省漯河市·一模)如图,在△ABC和△ADE中,AB=BC=42,AD=DE=2,∠ABC=∠ADE=90°,连接CE,CD,点O为CE的中点,连接OD.将△ADE绕点A在平面内旋转,当∠CDE=90°时,OD的长为______.28.(2024·河南省南阳市·一模)如图,在Rt△ABC中,∠C=90°,BC<AC.点D,E分别在边AB,BC上,连接DE,将△BDE沿DE折叠,点B的对应点为点B′,若点B′刚好落在边AC上,∠CB′E=30°,CE=3,则BC的长为______.29.(2024·河南省周口市·一模)如图1,在△ABC中,∠BAC=120°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点F,G,H分别为BC,DE,DC的中点.(1)观察猜想图1中,线段GH与FH的数量关系是______,∠GHF的度数为______;(2)探究证明把△ADE绕点A逆时针方向旋转到图2的位置,连接GF,BD,CE,判断△GHF的形状,并说明理;(3)拓展延伸把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出△GHF面积的最大值.30.(2024·河南省开封市·一模)转化是解决数学问题常用的思想方法之一,它可以在数与数、数与形、形与形之间灵话应用.如图1,已知在Rt△ABC中,∠B=90°,BC=4,AB=3.请解答下面的问题:(1)基础巩固:如图1,将△ABC绕点C按顺时针方向旋转60°得到△NMC,连接BM,则BC与BM之间的数量关系是______;(2)拓展探究:如图2,点D,E分别是BC,AC的中点,连接DE,将△CDE绕点C按顺时针方向旋转60°得到△CMN.①求证:△BCM∽△ACN;②用等式表示AC与AN之间的数量关系,并说明理由;(3)问题解决:点D,E分别是BC,AC的中点,连接DE,将△CDE绕点C旋转得到△CMN,请直接写出点A,M,N在同一直线上时BM的长.31.(2024·河南省南阳市·一模)如图,Rt△ABC中,∠ACB=90°,D为AB中点,点E在直线BC上(点E不与点B,C重合),连接DE,过点D作DF⊥DE交直线AC于点F,连接EF.(1)如图1,当点F与点A重合时,请直接写出线段EF与BE的数量关系;(2)如图2,当点F不与点A重合时,请写出线段AF,EF,BE之间的数量关系,并说明理由;(3)若AC=5,BC=3,EC=1,请直接写出线段AF的长.32.(2024·河南省驻马店市·一模)【问题呈现】△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,CB=mCA,CE=mCD,连接AD,BE,探究AD,BE的位置关系.【问题探究】(1)如图1,当m=1时,直接写出AD,BE的位置关系:______.(2)如图2,当m≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当m=3,AB=47,DE=4时,将△CDE绕点C旋转,使A,D,E三点恰好在同一直线上,求BE的长.第五部分特殊四边形33.(2024·河南省南阳市·一模)(1)如图1,在矩形ABCD中,点E,F分别在边DC,BC上,AE⊥DF,垂足为点G.求证:△ADE∽△DCF.【问题解决】(2)如图2,在正方形ABCD中,点E,F分别在边DC,BC上,AE=DF,延长BC到点H,使CH=DE,连接DH.求证:∠ADF=∠H.【类比迁移】(3)如图3,在菱形ABCD中,点E,F分别在边DC,BC上,AE=DF=11,DE=8,∠AED=60°,求CF的长.34.(2024·河南省漯河市·一模)综合与实践数学活动课上,老师让同学们根据下面情境提出问题并解答.问题情境:在▱ABCD中(∠ADC>∠DAB),点P是边AD上一点.将△PDC沿直线PC折叠,点D的对应点为E.数学思考:(1)“兴趣小组”提出的问题是:如图1,若点P与点A重合,过点E作EF//AD,与PC交于点F,连接DF,则四边形AEFD的形状一定是______(选填“菱形”“矩形”或“正方形”);拓展探究:(2)“智慧小组”提出的问题是:如图2,当点P为AD的中点时,延长CE交AB于点F,连接PF.试判断PF与PC 的位置关系,并说明理由;问题解决:(3)“创新小组”在前两个小组的启发下,提出的问题是:若点P是射线DA上一点,当点E恰好落在▱ABCD 的边或边的延长线上时,AP=3,AD=7,CD=10,直接写出BE的长.35.(2024·河南省商丘市·一模)综合与实践课上,老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动.(1)操作判断:如图1,在矩形ABCD中,点E为边AB的中点,沿DE折叠,使点A落在点F处,把纸片展平,延长DF与BC交于点G.请写出线段FG与线段BG的数量关系,并说明理由;(2)迁移思考:如图1,若AB=4,按照(1)中的操作进行折叠和作图,当CG=2时,求AD的值;(3)拓展探索:如图2,四边形ABCD为平行四边形,其中∠A与∠C是对角,点E为边AB的中点,沿DE折叠,使点A落在点F 处,把纸片展平,延长DF与射线BC交于点G.若AD=2,CG=0.5,请直接写出线段DG的值.36.(2024·河南省洛阳市·一模)【问题背景】:如图1,在Rt△ABC中,∠ABC=90°,AB=43,∠BAC=30°,点E是斜边AC的中点,过点E作ED⊥AB交AB于点D.【实验探究】:= (1)数学活动课中,小明同学将图1中的△ADE绕点A按顺时针方向旋转90°,如图2所示,得到结论:①BDCE______;②直线BD与CE所夹锐角的度数为______;(2)若我们继续将△ADE绕点A按顺时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.【拓展延伸】:(3)在以上探究中,当△ADE旋转至D、E、C三点共线时,则△BCD的面积为______.37.(2024·河南省开封市·一模)某数学兴趣小组对具有公共顶点,且其中某个角等于大角一半的几何图形中,边与边之间的数量关系进行了如下探索:初步探索(1)如图1,E,F分别是正方形ABCD的BC边和CD边上的点,并且∠EAF=45°,我们可通过如下方法探索EF 与BE和DF之间的数量关系:因为AD=AB,∠D=∠ABE=90°,所以我们以点A为旋转中心,将△DAF绕点A顺时针旋转90°,使得点D与点B重合,则点F的对应点恰好落在CB的延长线上,记为点F′,由△ADF≌△ABF′且易证△AEF≌△AEF′,从而可知,EF,BE,DF的数量关系是______.探索延伸(2)如图2,E,F是等腰直角△ABD的底边BD上的点,∠EAF=45°,(1)中的结论是否仍然成立?若成立,给出证明;若不成立,写出新的结论,并说明理由.拓展应用(3)如图3,在矩形ABCD中,E是BC边的三等分点,F为CD边上的点,且∠EAF=45°,当AB=4,AD=3时,直接写出DF的长.第六部分二次函数x2+bx+c经过A(―1,0)、B(3,0)两点,与y轴交于点C,38.(2024·河南省周口市·一模)如图,抛物线y=―12点G为抛物线的顶点.(1)求抛物线的解析式及点G的坐标;(2)连接AC,将线段AC向右水平移动m个单位长度,若它与抛物线只有一个交点,求出m的取值范围.39.(2024·河南省开封市·一模)如图,公园的花坛正中间有一个喷灌嘴P,把开关开至最大时,喷出的形状接近于抛物线y=ax2+bx+1,当水柱距地面2m时,距喷嘴的水平距离为4m,水柱落地点距喷嘴的水平距离OA=6m.(1)求水柱所在抛物线的解析式.(2)已知在水柱正下方OA的范围内开有一些鲜花.①若鲜花的高度为1m,求与喷灌嘴的水平距离在多大范围内时,才不会被水柱直接喷到.②开在距喷嘴水平距离为0.4m处的高度为1.3m的鲜花,是否会被水柱直接喷到?判断并说明理由.40.(2024·河南省南阳市·一模)一小球M从斜坡OA上的点O处抛出,球的抛出路线是抛物线的一部分,建立如x刻画.若小球到达最高点的坐标为(4,8).图所示的平面直角坐标系,斜坡可以用一次函数y=12(1)求抛物线的函数解析式(不写自变量x的取值范围);(2)小球在斜坡上的落点A的垂直高度为______米;(3)若要在斜坡OA上的点B处竖直立一个高4米的广告牌,点B的横坐标为2,请判断小球M能否飞过这个广告牌?通过计算说明理由.41.(2024·河南省开封市·一模)跳台滑雪是冬季奥运会的比赛项目之一.如图,运动员通过助滑道后在点A处起跳经空中飞行后落在着陆坡BC上的点P处,他在空中飞行的路线可以看作抛物线的一部分.这里OA表示起跳点A到地面OB的距离,OC表示着陆坡BC的高度,OB表示着陆坡底端B到点O的水平距离.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=―1x2+bx+c.已知OA=70m,OC=60m,落点P的水平距离是40m,竖直高度是30m.16(1)点A的坐标是______,点P的坐标是______;(2)求满足的函数关系式y=―1x2+bx+c;16(3)运动员在空中飞行过程中,当他与着陆坡BC竖直方向上的距离达到最大时,直接写出此时的水平距离.42.(2024·河南省漯河市·一模)掷实心球是某市中考体育考试的选考项目.如图①是一名男生投实心球,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图②所示,掷出时起点处高度m处.为2m,当水平距离为4.5m时,实心球行进至最高点258(1)求y关于x的函数表达式;(2)根据该市2023年中考体育考试评分标准(男生),投掷过程中,实心球从起点到落地点的水平距离大于等于12.4m,此项考试得分为满分17分.按此评分标准,该生在此项考试中是否得满分,请说明理由.43.(2024·河南省南阳市·一模)一名运动员在10m高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面OB的高度y(m)与离起跳点A的水平距离x(m)之间的函数关系如图所示,运动员离起跳点A的水平距离为1m时达到最高点,当运动员离起跳点A的水平距离为3m时离水面的距离为7m.(1)求y关于x的函数表达式;(2)求运动员从起跳点到入水点的水平距离OB的长.44.(2024·河南省洛阳市·一模)一座抛物线型拱桥如图所示,当桥下水面宽度AB为20米时,拱顶点O距离水面的高度为4米.如图,以点O为坐标原点,以桥面所在直线为x轴建立平面直角坐标系.(1)求抛物线的解析式;(2)汛期水位上涨,一艘宽为5米的小船装满物资,露出水面部分的高度为3米(横截面可看作是长为5m,宽为3m的矩形),若它恰好能从这座拱桥下通过,求此时水面的宽度(结果保留根号).45.(2024·河南省商丘市·一模)某校举办“集体跳长绳”体育活动,若在跳长绳的过程中,绳甩到最高处时的形状是抛物线型,示意图如图所示,以ED的中点O为原点建立平面直角坐标系(甲位于x轴的点E处,乙位于x轴的点D处),正在甩绳的甲、乙两名同学握绳的手分别设为A点,B点,且AB的水平距离为4m,绳子甩到最高点C处时,他们握绳的手到地面的距离AE与BD均为1.2m,最高点到地面的垂直距离为2m.(1)求出该抛物线的解析式;(2)如果身高为1.8m的小亮,站在ED之间,且与点E的距离为tm,当绳子甩到最高处时,可以通过他的头顶,请结合函数图象求出t的取值范围;(3)经测定,多人跳长绳且同方向站立时,脚跟之间的距离不小于0.4m才能安全跳绳,小亮与其他4位同学一起跳绳,如果这4位同学与小亮身高相同,通过计算当绳子甩到最高处时,他们是否可以安全跳绳?参考答案1.【答案】B【解析】解:由题意知,点D运动2s时,点P,D的位置如图1所示.此时,在Rt△PBD中,BD=2cm,∠B=60°,PD⊥BC,∴PB=2BD=4(cm),∴PD=PB2―BD2=23(cm).由函数图象得BC=(2+23)×1=(2+23)cm,∴DC=BC―BD=2+23―2=23(cm),∴PD=DC.由题图2点E的位置可知,点P在AC上时,S△PBD有最大值.当2≤t≤2+23时,点P在AC边上,如图2,此时BD=t×1=t(cm),PD=DC=(2+23―t)cm,∴S△PBD=12×BD×PD=12×t×(2+23―t)=―12t2+(1+3)t.∵S△PBD=―12[t―(1+3)]2+2+3,又∵―12<0,∴当t=1+3时,S△PBD的值最大,此时PD=CD=2+23―(1+3)=(1+3)cm.故选:B.先根据点D运动2s时,点P与点A重合.从而求得PD=PB2―BD2=23(cm),再由函数图象求得BC=(2+23)×1=(2+23)cm,从而求得DC=BC―BD=2+23―2=23(cm),得出PD=DC,然后根据由题图2点E的位置可知,点P在AC上时,S△PBD有最大值.所以当2≤t≤2+23时,点P在AC边[t―(1+上,此时BD=t×1=t(cm),PD=DC=(2+23―t)cm,根据三角形面积公式求得S△PBD=―123)]2+2+3,最后根据二次函数的性质求解即可.本题考查动点函数图象,二次函数图象性质,三角形面积.本题属二次函数与几何综合题目.2.【答案】A【解析】解:由图2知,AB+BC=213,∵AB=BC,∴AB=13,∵AB=BC,BD⊥AC,∴AC=2AD,∠ADB=90°,在Rt△ABD中,AD2+BD2=AB2=13①,设点M到AC的距离为ℎ,AD⋅ℎ,∴S△ADM=12∵动点M从A点出发,沿折线AB→BC方向运动,∴当点M运动到点B时,△ADM的面积最大,即ℎ=BD,由图2知,△ADM的面积最大为3,∴1AD⋅BD=3,2∴AD⋅BD=6②,①+2×②得,AD2+BD2+2AD⋅BD=13+2×6=25,∴(AD+BD)2=25,∴AD+BD=5(负值舍去),∴BD=5―AD③,将③代入②得,AD(5―AD)=6,∴AD=3或AD=2,∵AD>BD,∴AD=3,∴AC=2AD=6,故选:A.先根据AB=BC结合图2得出AB=13,进而利用勾股定理得,AD2+BD2=13,再由运动结合△ADM的面AD⋅BD=3,进而建立二元二次方积的变化,得出点M和点B重合时,△ADM的面积最大,其值为3,即12程组求解,即可得出结论.此题主要考查了等腰三角形的性质,三角形的面积公式,判断出AB=13和点M和点B重合时,△ADM的面积为3是解本题的关键.3.【答案】D【解析】解:若线段CG=y,由题意可得,y随x的增大减小,故选项A错误;若线段AG=y,由题意可得,y随x的增大先增大再减小,并且左右对称,故选项B错误;若线段AH=y,由题意可得,y随x的增大先减小再增大,故选项C错误;若线段CH=y,由题意可得,y随x的增大先增大再减小,故选项D正确;故选D.根据选项中的各线段,可以分别得到它们各自随x的变化如何变化,从而可以得到哪个选项是正确的.本题考查动点问题的函数图象,解题的关键是明确题意,利用分类讨论的数学思想解答问题.4.【答案】D【解析】【分析】分段求出函数关系式,再观察图象可得答案.本题考查动点问题的函数图象,解题的关键是分段求出函数关系式.【解答】×4x=2x,当x=4时,y=8;解:当P在BC上,即0<x≤4时,y=12×4×4=8,当P在CD上,即4<x≤8时,y=12×4(12―x)=―2x+24;当P在AD上,即8<x<12时,y=12观察4个选项,符合题意的为D;故选:D.5.【答案】A【解析】【分析】把运动距离分0≤x≤2,2<x≤4和4<x≤6三种情况讨论求解即可本题主要考查了动点问题的函数图象,分析出重叠部分面积的变化情况是解题关键.【解答】解:①当0≤x ≤2时,S 随x 的增大而增大,最大值为4;②当2<x ≤4时,S 随x 的增大而不变,此时S =4;③当4<x ≤6时,S 随x 的增大而减小,最小值为0.故选:A .6.【答案】D【解析】解:过点A 向BC 作AH ⊥BC 于点H ,所以根据相似比可知:EF 12=6―x 6,即EF =2(6―x)所以y =12×2(6―x)x =―x 2+6x.(0<x <6)该函数图象是抛物线的一部分,故选:D .可过点A 向BC 作AH ⊥BC 于点H ,所以根据相似三角形的性质可求出EF ,进而求出函数关系式,由此即可求出答案.此题考查根据几何图形的性质确定函数的图象和函数图象的读图能力.要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件,结合实际意义画出正确的图象.7.【答案】B【解析】解:根据题意BE =CF =t ,CE =8―t ,∵四边形ABCD 为正方形,∴OB =OC ,∠OBC =∠OCD =45°,∵在△OBE 和△OCF 中OB =OC ∠OBE =∠OCF BE =CF,∴△OBE ≌△OCF(SAS),∴S △OBE =S △OCF ,∴S 四边形OECF =S △OBC =14×82=16,∴S =S 四边形OECF ―S △CEF =16―12(8―t)⋅t =12t 2―4t +16=12(t ―4)2+8(0≤t ≤8),∴s(cm 2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t ≤8.故选:B .由点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,得到BE=CF=t,则CE=8―t,再根据正方形的性质得OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE(8―t)⋅t,然后配方得到S= =S△OCF,这样S四边形OECF=S△OBC=16,于是S=S四边形OECF―S△CEF=16―121(t―4)2+8(0≤t≤8),最后利用解析式和二次函数的性质对各选项进行判断.2本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.8.【答案】解:(1)∵OA=1,∴点A的坐标为(―1,0),则―k+2=0,解得:k=2,∴直线l的解析式为y=2x+2,∵点C在直线l上,点C的横坐标为2,∴点C的纵坐标为2×2+2=6,∴点C的坐标为(2,6),∴m=2×6=12;),(2)设点D的坐标为(n,2n+2),则点E的坐标为(n,12n∴DE=|2n+2―12|,n∵OB//DE,∴当OB=DE时,以B,D,E,O为顶点的四边形为平行四边形,∵直线y=2x+2与y轴交于点B,∴OB=2,|=2,∴|2n+2―12n=2时,n1=6,n2=―6(舍去),当2n+2―12n此时,点D的坐标为(6,26+2),=―2时,n1=7―1,n2=―7―1(舍去),当2n+2―12n此时,点D的坐标为(7―1,27),综上所述:以B,D,E,O为顶点的四边形为平行四边形时,点D的坐标为(6,26+2)或(7―1,27).【解析】(1)根据题意求出点A的坐标,进而求出k,再求出点C的坐标,求出m;(2)分2n+2―12n =2、2n+2―12n=―2两种情况,计算即可.本题考查的是反比例函数的图象和性质、平行四边形的性质,灵活运用分情况讨论思想是解题的关键.9.【答案】解:(1)把点A(1,2)代入y=mx 得,2=m1,∴m=2,∴反比例函数的解析式为y=2x;把B(a,―1)代入y=2x得,a=―2,∴B(―2,―1),把点A(1,2),B(―2,―1)代入y=kx+b得k+b=2―2k+b=―1,解得:k=1 b=1,∴一次函数的解析式为y=x+1;(2)当y=0时,0=x+1,解得:x=―1,∴C(―1,0),设P(x,0),∴S△APC=12×|x+1|×2=4,∴x=3或x=―5,∴P(3,0)或(―5,0).【解析】(1)把点A(1,2)代入y=mx得到反比例函数的解析式为y=2x;把点A(1,2),B(―2,―1)代入y=kx+b得到一次函数的解析式为:y=x+1;(2)当y=0时,得到C(―1,0),设P(x,0),根据三角形的面积公式即可得到结论.本题考查了反比例函数与一次函数的交点问题,三角形的面积的计算,待定系数法求函数的解析式,正确的理解题意是解题的关键.10.【答案】解:(1)∵反比例函数图象点B(4,2),∴k=4×2=8,∴反比例函数的表达式为:y=8把A(a,4)代入y=8x得:a=2,∴A(2,4),∵一次函数y=mx+n的图象过点A,点B,∴4m+n=22m+n=4,解得:m=―1 n=6,∴一次函数的表达式为y=―x+6;(2)观察函数图象可得,―x+6≥的解集为:2≤x≤4;(3)用作一个角∠ABD等于已知角∠ACO的方法作出BD,如下图:由一次函数的表达式知,点C(6,0),由点A的坐标得,直线OA的表达式为:y=2x,当y=2时,2y=2x,则x=1,即点D(1,2),则BD=4―1=3,则梯形OCBD的面积=12×(BD+OC)×y B=12×(3+6)×2=9.【解析】(1)利用待定系数法可求解析式;(2)利用数形结合思想可求解;(3)用作一个角∠ABD等于已知角∠ACO的方法作出BD,由梯形OCBD的面积=12×(BD+OC)×y B=12×(3+6)×2=9,即可求解.本题考查的是反比例函数综合运用,涉及到面积的计算、函数作图、解不等式等,有一定的综合性,难度适中.11.【答案】解:(1)将点A的坐标代入反比例函数表达式得:k=6×6=36,则反比例函数表达式为:y=36,将点B的坐标代入上式得:―1=36a,则a=―36,即点B的坐标为:(―36,―1),将A、B的坐标代入一次函数表达式得:―1=―36m+n 6=6m+n,解得:m=16n=5,则直线AB的表达式为:y=16x+5;(2)从函数图象看,不等式kx≥mx+n的解集为:0<x≤6或x≤―36;(3)分别以点O、N为圆心,以大于12NO长度为半径作弧,连接两个弧的交点,即为ON的垂直平分线,令y=16x+5=0,则x=―30,即点N(―30,0),则ON的中垂线为x=―15,当x=―15时,y=36x =―125,即点Q的坐标为:(―15,―125).【解析】(1)用待定系数法即可求解;(2)观察函数图象即可求解;(3)分别以点O、N为圆心,以大于12NO长度为半径作弧,连接两个弧的交点,即为ON的垂直平分线,得到ON 的中垂线为x=―15,即可求解.本题考查了反比例函数综合题,待定系数法求函数的解析式,线段垂直平分线的性质,不等式的解集,熟练掌握待定系数法求函数的解析式是解题的关键.12.【答案】3。
2022年上海初三数学一模(期末)压轴题模拟汇编 第23题精选30道-相似三角形综合问题(解析版)

压轴第23题精选30道-相似三角形综合问题(二)(教师版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,在平面直角坐标系中,一次函数y=2x+8的图象与x轴、y轴分别相交于点B、点A,以线段AB为边作矩形ABCD,且AB=2BC,点C在反比例函数y=kx(x<0)的图象上,则k的值为()A.﹣10B.﹣12C.﹣14D.﹣16【答案】D【分析】过点C作CE⊥x轴于E,证明⊥AOB⊥⊥BEC,可得点C坐标,代入求解即可.【详解】解:⊥当x=0时,y=2x+8=8,⊥A(0,8),⊥OA=8;⊥当y=0时,y=2x+8=0,⊥x=-4,⊥B(-4,0),⊥OB=4;过点C作CE⊥x轴于E,⊥四边形ABCD矩形,⊥⊥ABC=90°,⊥⊥CBE+⊥ABO=90°,⊥BAO+⊥ABO=90°,⊥⊥CBE=⊥BAO.⊥⊥BEC=⊥AOB=90°,⊥⊥AOB⊥⊥BEC,⊥CE BE BC OB OA AB==,⊥AB=2BC,⊥1482CE BE ==, ⊥OE =2,BE =4,⊥C 点坐标为(-8,2),⊥点C 在反比例函数y =k x(x <0)的图象上, ⊥k =-8×2=-16.故选:D .【点睛】本题考查了一次函数与坐标轴的交点、待定系数法求函数教师式、矩形的性质,以及三角形相似的判定与性质,解答此题的关键是正确作出辅助线及数形结合思想的运用.2.如图,在等腰AOB 中,AO AB =,点A 为反比例函数k y x=(其中0x >)图象上的一点,点B 在x 轴正半轴上,过点B 作BC OB ⊥,交反比例函数k y x=的图象于点C ,连接OC 交AB 于点D ,若BCD △的面积为2,则k 的值为( )A .20B .503C .16D .403【答案】A【分析】 过点A 作AF OB ⊥交x 轴于F ,交OC 于点E ,利用等腰三角形性质可得12OF FB OB ==,再由//AF BC ,可得ADE BDC ∆∆∽,2BC EF =,设OF a =,则2=OB a ,可得24AF BC EF ==,3AE EF =,应用相似三角形性质及三角形面积可由BCD ∆的面积为2,求得AOF ∆的面积,应用||k 的几何意义求k .【详解】解:如图,过点A 作AF OB ⊥交x 轴于F ,交OC 于点E ,OA AB =,AF OB ⊥,12OF FB OB ∴==, BC OB ⊥,//AF BC ∴,ADE BDC ∴∆∆∽,12OE EF OF OC BC OB ===, 2BC EF ∴=, 设OF a =,则2=OB a ,(,)k A a a∴,(2,)2k C a a , k AF a ∴=,2k BC a=, 24AF BC EF ∴==,3AE AF EF EF =-=,ADE BDC ∆∆∽, ∴3322DE AE EF DC BC EF ===, ∴29()4ADE BDC S AE S BC ∆∆==, BCD ∆的面积为2,92ADE S ∆∴=, ∴35DE EC =, 12OE OC =, EC OE ∴=, ∴35DE OE =, ∴35ADE AOE S S ∆∆=, 152AOE S ∆∴=, 4433AF EF AE EF ==, ∴43AOF AOE S AF S AE ∆∆==,441510332AOF AOE S S ∆∆∴==⨯=, ∴1102k =, 0k >,20k ∴=.故选:A .【点睛】本题考查了反比例函数图象上点的坐标特征、等腰三角形的性质、三角形面积以及相似三角形的判定与性质,解题的关键是灵活运用等腰三角形的性质和相似三角形的性质. 3.如图,在矩形ABCD 中,AD =10,在BC 边上取一点E ,连接AE 、DE ,使得DE =AD ,H 为AE 中点,连接DH ,在DE 上取一点F ,连接AF ,将⊥AEF 沿着AF 翻折得到⊥AGF ,且GF⊥AD 于M ,连接GD ,若AE =F 到直线DG 的距离为( )A .BCD 【答案】B【分析】 根据三线合一得出DH AE ⊥,根据矩形的性质及同角的余角相等易证ABE DHA △△,然后根据相似三角形的性质即可求得BE 的值,根据勾股定理可求得AB 的值;过点E 作EP AD ⊥于点P ,则四边形ABEP 为矩形,易证DMF DPE △△,再根据相似三角形的性质可设MF =4x ,DM =3x ,DF =5x ,根据折叠的性质可得105GF EF x ==-,AG AE ==103AM AD DM x =-=-,109GM GF MF EF MF x =-=-=-,然后根据勾股定理即可求得x 的值,最后根据面积公式即可得出答案.【详解】解:AD DE =,H 是AE 的中点DH AE ∴⊥四边形ABCD 为矩形90BAE EAD ∴∠+∠=︒,90EAD ADH ∠+∠=︒BAE HDA ∴∠=∠90B AHD ∠=∠=︒ABE DHA ∴△△BE AE HA AD∴= 111022AD AH AE ===⨯=,AE =4BE ∴=8AB ∴==,1046EC BC BE =-=-=过点E 作EP AD ⊥于点P ,则四边形ABEP 为矩形8PE AB ∴==,6PD EC ==GF AD ⊥90DMF DPE ∴∠=∠=︒MDF PDE ∠=∠DMF DPE ∴△△6384DM PD MF PE ∴=== 设MF =4x ,DM =3x ,DF =5x⊥AEF 沿着AF 翻折得到⊥AGF ,105GF EF x ∴==-,AG AE ==103AM AD DM x =-=-,109GM GF MF EF MF x =-=-=-在Rt AMG 中,222AM MG AG +=即()()(222103109x x -+-=解得:2x =(舍去)或23x = 32MD x ∴==,201053GF x =-=,1094MG x =-=GD ∴=设F 到GD 的距离是h ,根据面积公式得S ⊥GFD =1122GF MD GD h ⋅=⋅ 12012232∴⨯⨯=⨯h ∴=故选B .【点睛】本题考查了相似三角形的判定及性质、等腰三角形的性质、勾股定理、折叠的性质、矩形的判定及性质,熟练掌握性质定理及添加合适的辅助线是解题的关键.4.如图,菱形OABC 的顶点C 的坐标为(3,0),D 为AO 上一点,连接BD ,CD ,OB ,CD 与OB 相交于点E ,取EC 的三等分点F (EF >FC ),连接OF 并延长,交BC 于点G ,已知S ⊥BOD :S ⊥BOC =2:3,反比例函数y =k x(k >0)经过D ,G 两点,则k 的值为( )A .25BCD 【答案】A【分析】过点D 、G 分别作x 轴的垂线,垂足分别为M 、N ,设CN =a ,GN =b ,根据相似三角形的性质表示出D 点坐标,根据反比例性质列方程,求出a 、b 值即可.【详解】解:过点D 、G 分别作x 轴的垂线,垂足分别为M 、N ,⊥S ⊥BOD :S ⊥BOC =2:3,⊥OD :BC =2:3,⊥OA ⊥BC ,⊥⊥ODE ⊥⊥BCE ,⊥AOC =⊥GCN , ⊥23DE OD EC BC ==, ⊥OC =BC =3,⊥OD =2,⊥EC 的三等分点为点F (EF >FC ), ⊥14FC DF =, 同理,14GC OD =,CG =12 ⊥⊥AOC =⊥GCN ,⊥DMO =⊥GNC =90°,⊥⊥ODM ⊥⊥CGN , ⊥14GN GC CN DM OD OM ===, 设CN =a ,GN =b ,则OM =4a ,DM =4b ,⊥反比例函数y =k x(k >0)经过D ,G 两点, ⊥4a ×4b =(a +3)b ,解得,15a =,GN =则k 的值为:1(3)5+, 故选:A .【点睛】本题考查了反比例函数的性质、菱形的性质、相似三角形的判定与性质,解题关键是通过设参数,根据相似三角形性质表示点的坐标,依据反比例函数性质列方程.5.如图,正方形ABCD ,点F 在边AB 上,且12AF FB =,CE⊥DF ,垂足为点M ,且交AD 于点E ,AC 与DF 交于点N ,延长CB 至G ,使BG =12BC ,连接CM .有如下结论:⊥AE=BF ;⊥AN;⊥⊥ADF =⊥GMF ;⊥S ⊥ANF =19S ⊥ABC ,上述结论中,正确的是( )A .⊥⊥B .⊥⊥C .⊥⊥⊥D .⊥⊥⊥【答案】C【分析】 ⊥正确.证明⊥ADF ⊥⊥DCE (ASA ),即可判断.⊥正确.利用平行线分线段成比例定理,等腰直角三角形的性质解决问题即可.⊥正确.作GH ⊥CE 于H ,设AF =DE =a ,BF =2a ,则AB =CD =BC =3a ,ECa ,通过计算证明MH =CH 即可解决问题.⊥错误.设⊥ANF的面积为m ,由AF ⊥CD ,推出13AF FN CD DN ==,⊥AFN ⊥⊥CDN ,推出⊥ADN 的面积为3m ,⊥DCN 的面积为9m ,推出⊥ADC 的面积=⊥ABC 的面积=12m ,由此即可判断.【详解】⊥四边形ABCD 是正方形,⊥AD =AB =CD =BC ,⊥CDE =⊥DAF =90°,⊥CE ⊥DF ,⊥⊥DCE +⊥CDF =⊥ADF +⊥CDF =90°,⊥⊥ADF =⊥DCE ,在⊥ADF 与⊥DCE 中,DAF CDE AD CDADF DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ⊥⊥ADF ⊥⊥DCE (ASA ),⊥DE =AF ,⊥AD ﹣DE =BC ﹣AF ,即AE =BF ,故⊥正确;⊥AB ⊥CD ,⊥AF AN CD CN=,⊥AF:FB=1:2,⊥AF:AB=AF:CD=1:3,⊥13 ANCN=,⊥14 ANAC=,⊥AC,⊥AN=4AD;故⊥正确;作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC a,由⊥CMD⊥⊥CDE,可得CM,由⊥GHC⊥⊥CDE,可得CH,⊥CH=MH=12CM,⊥GH⊥CM,⊥GM=GC,⊥⊥GMH=⊥GCH,⊥⊥FMG+⊥GMH=90°,⊥DCE+⊥GCM=90°,⊥⊥FMG=⊥DCE,⊥⊥ADF=⊥DCE,⊥⊥ADF=⊥GMF;故⊥正确,设⊥ANF的面积为m,⊥AF⊥CD,⊥13AF FNCD DN==,⊥AFN⊥⊥CDN,⊥⊥ADN的面积为3m,⊥DCN的面积为9m,⊥⊥ADC的面积=⊥ABC的面积=12m,⊥S⊥ANF:S⊥ABC=1:12,故⊥错误,故选:C.【点睛】本题是一个综合性的题目,综合考查了正方形的性质、相似三角形的判定与性质、三角形全等的判定与性质等知识.6.勾股定理是几何中一个重要定理.著名数学家毕达哥拉斯用如图⊥所示的图形验证了勾股定理,把图⊥放入矩形内得到图⊥,⊥ACB=90°,BC=2AC,E,F,G,H,I都在矩形MNOP的边上,则MNMP的值为()A.911B.910C.45D.34【答案】A【分析】如图所示,延长BA交PM于,J过I作IK AB⊥于,K设BC=2AC=2a,由题意可知,AC=CD=DE=AE=a,BH=HI=CI=BC=2a,由勾股定理可得,AB,可得AB=BG=FG=AF,再利用相似三角形的性质分别用含a的代数式表示,MN MP,即可得到答案.【详解】解:如图所示,延长BA交PM于,J过I作IK AB⊥于,K设BC =2AC =2a ,由题意可知,AC =CD =DE =AE =a ,BH =HI =CI =BC =2a , 由勾股定理可得,AB, ⊥AB =BG =FG =AF,⊥⊥AKI =⊥ACB =90°,⊥CAB =⊥IAK , ⊥⊥AKI ⊥⊥ACB , ⊥AI IK AK AB BC AC==, ⊥IK=2AI AC CI BC BC a AB AB +⨯=⨯=, ⊥MP =MJ +JP =IK +AF,= ⊥AK=AI AC CI AC AC a AB AB +⨯=⨯=, 同理可得:⊥AEJ ⊥⊥BAC , ⊥AJ AE BC BA=, ⊥AJ=AE CB BA ⨯=, 同理可得:⊥ABC ⊥⊥HIN , ⊥BC IN AB IH=,⊥2BC IN IH a AB =⨯==, ⊥MN =MI +IN =AJ +AK +IN=,⊥911MN MP =,故选:A . 【点睛】本题考查的是勾股定理的应用,矩形,正方形的性质,相似三角形的性质与判定,掌握利用相似三角形的性质寻求边与边之间的关系是解题的关键.7.如图,点M 是正方形ABCD 内一点,MBC △是等边三角形,连接AM 、MD 对角线BD 交CM 于点N ,现有以下结论:⊥150AMD ∠=︒;⊥2MA MN MC =⋅;⊥ADM BMC S S =△△,其中正确的结论有( )A .4B .3C .2D .1【答案】C 【分析】⊥根据等边三角形得⊥CMB =60°,再根据等腰三角形的性质得⊥AMB =⊥CMD =75°,最后根据周角的定义即可得出结论;⊥证明⊥MND ⊥⊥MDC ,列比例式即可得出结论;⊥过点M 作MG ⊥AB 于G ,设MG =x ,根据直角三角形30度角的性质和勾股定理分别计算BC 、AG 、BG 的长,根据面积公式计算即可得出结论. 【详解】解:⊥⊥MBC 是等边三角形,⊥⊥MBC =⊥MCB =⊥CMB =60°,BM =BC , ⊥四边形ABCD 是正方形,⊥⊥ABC =⊥BCD =⊥BAD =⊥ADC =90°,AB =BC , ⊥⊥ABM =⊥DCM =30°, ⊥AB =BM ,⊥⊥AMB =⊥BAM =12×(180°−30°)=75°, 同理:⊥CMD =⊥CDM =75°, ⊥⊥AMD =360°−75°−75°−60°=150°; 故⊥正确;⊥四边形ABCD 是正方形, ⊥⊥BDC =45°,⊥⊥MDN =⊥CDM −⊥BDC =75°−45°=30°, ⊥⊥CMD =⊥CMD ,⊥MDN =⊥DCM =30°, ⊥⊥MND ⊥⊥MDC , ⊥MN DMDM MC=, ⊥DM 2=MN •MC ,⊥⊥BAD =⊥ADC ,⊥BAM =⊥CDM , ⊥⊥MAD =⊥MDA , ⊥MA =DM , ⊥MA 2=MN •MC , 故⊥正确;过点M 作MG ⊥AB 于G ,设MG =x ,Rt ⊥BGM 中,⊥GBM =30°, ⊥BM =BC =AB =2x ,BG, ⊥AG =2x,⊥1212ADM BMCAD AGAG BG BC BG S S⋅===⋅故⊥错误. 故选C . 【点睛】本题考查了相似三角形的判定与性质、正方形的性质、等边三角形的性质、等腰三角形的判定与性质,勾股定理、平行线的性质等知识;设出未知数,表示出各边长是解题的关键. 8.如图,在Rt⊥ABC 中,∠BAC=90°,以其三边为边分别向外作正方形,延长EC ,DB 分别交GF ,AH 于点N ,K ,连结KN 交AG 于点M ,若S 1-S 2=2,AC=4,则AB 的长为 ()A .2 BC.D .73【答案】A 【分析】先证ABC ⊥FCN △,根据全等三角形的性质可得AB =FN ;再证⊥BCK ⊥⊥ACB ,根据相似三角形的性质可得214KC BC =;设五边形ACFNM 的面积为S ,可得S 1+S 2=S 正方形ACFG =AC 2=16, S 2+S = S 梯形CFNK ==()2CK NF =+,设AB =x ,BC =y ,可得方程组22216116224x y y x ⎧+=⎪⎨⎛⎫-+= ⎪⎪⎝⎭⎩ ,解方程组即可求解. 【详解】⊥⊥ACB +⊥CAN =90°,⊥FCN +⊥CAN =90°, ⊥⊥ACB =⊥FCN , 在⊥ABC 和⊥FCN 中,90BAC NFC AC CFBCA NCF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩, ⊥ABC ⊥FCN △, ⊥AB =FN ;⊥⊥BAC =⊥KBC =90°, ⊥⊥BCK ⊥⊥ACB , ⊥AC BCBC KC=, ⊥214KC BC =; 设五边形ACFNM 的面积为S ,⊥(S 1+S )-(S 2+S )=2, 设AB =x ,BC =y ,由勾股定理可得,2216x y +=,⊥S 1+S 2=S 正方形ACFG =AC 2=16, S 2+S = S 梯形CFNK =()()()114222CK NF CF CK NF CK NF +⋅=+⨯=+,S 1-S 2=2, ⊥(S 1+S )-(S 2+S )=16-()2CK NF +=16-2124y x ⎛⎫+ ⎪⎝⎭=2,⊥22216116224x y y x ⎧+=⎪⎨⎛⎫-+= ⎪⎪⎝⎭⎩,解得,2x y =⎧⎪⎨=⎪⎩2x y =⎧⎪⎨=-⎪⎩6x y =-⎧⎪⎨=⎪⎩6x y =-⎧⎪⎨=-⎪⎩⊥x 、y 都为正数,⊥2x y =⎧⎪⎨=⎪⎩即AB =2,BC= 故选A . 【点睛】本题考查了正方形的性质、勾股定理、全等三角形的判定与性质及相似三角形的判定与性质,熟练运用相关知识是解决问题的关键.9.如图平面直角坐标系中,矩形ABCD 的顶点B 在x 轴负半轴上,边CD 与x 轴交于点E ,连接,//AE AE y 轴,反比例函数(0)ky x x=>的图象经过点A 及AD 边上一点,4F AF FD =,若,2DA DE OB ==,则k 的值为( )A .11B .12C .15D .16【答案】C根据题意得到ADE ∆和ABE ∆是等腰直角三角形,设AE y =,则1122DM AM EM AE y ====,即可得到(2,)A y y -,进而通过三角形相似对得出F 点的坐标为7(25y -,3)5y ,即可得到73(2)(2)55k y y y y =-=-,解方程即可求得k 的值.【详解】解:作DM AE ⊥于M ,FN AE ⊥于N , 四边形ABCD 是矩形,AD BC ∴=,90ADE BCD ∠=∠=︒, DA DE =,ADE ∴∆是等腰直角三角形,45DAE AED ∴∠=∠=︒,M 是AE 的中点,12DM AM EM AE ∴===,45BAE ∠=︒, //AE y 轴,90AEB ∴∠=︒,ABE ∴∆是等腰直角三角形, BE AE ∴=,设AE y =,则1122DM AM EM AE y ====, 2OB =,2OE y ∴=-, (2,)A y y ∴-, //FN DM , ANF AMD ∴∆∆∽,∴AN NF AFAM DM AD==, 4AF FD =,∴411522AN FN y y ==, 25AN NF y ∴==, 2355EN y y y ∴=-=, 7(25F y ∴-,3)5y ,反比例函数(0)ky k x=>的图象经过点A 、F , 73(2)(2)55k y y y y ∴=-=-,解得5y =或0y =(舍去),(2)15k y y ∴=-=,故选:C .【点睛】本题考查了矩形的性质,等腰直角三角形的性质,三角形相似的判定和性质,反比例函数图象上点的坐标特征,表示出A 、F 的坐标是解题的关键.10.如图所示,G 、E 分别是正方形ABCD 的边AB 、BC 上的点,且AG CE =,AE EF ⊥,AE EF =,现有如下结论:⊥BE DH =;⊥AGE ECF △≌△;⊥45FCD ∠=︒;⊥AGE CHF △∽△.其中,正确的结论有( )A .4个B .3个C .2个D .1个【答案】C 【分析】由⊥BEG =45°知⊥BEA >45°,结合⊥AEF =90°得⊥HEC <45°,据此知 HC <EC ,即可判断⊥;求出⊥GAE +⊥AEG =45°,推出⊥GAE =⊥FEC ,根据 SAS 推出⊥GAE ⊥⊥CEF ,即可判断⊥;求出⊥AGE =⊥ECF =135°,即可判断⊥;求出⊥FEC <45°,根据相似三角形的判定得出⊥GBE 和⊥ECH 不相似,即可判断⊥. 【详解】解:⊥四边形 ABCD 是正方形, ⊥AB =BC =CD ,⊥AG=GE,⊥BG=BE,⊥⊥BEG=45°,⊥⊥BEA>45°,⊥⊥AEF=90°,⊥⊥HEC<45°,⊥HC<EC,⊥CD﹣CH>BC﹣CE,即DH>BE,故⊥错误;⊥BG=BE,⊥B=90°,⊥⊥BGE=⊥BEG=45°,⊥⊥AGE=135°,⊥⊥GAE+⊥AEG=45°,⊥AE⊥EF,⊥⊥AEF=90°,⊥⊥BEG=45°,⊥⊥AEG+⊥FEC=45°,⊥⊥GAE=⊥FEC,在⊥GAE 和⊥CEF 中,⊥AG=CE,⊥GAE=⊥CEF,AE=EF,⊥⊥GAE⊥⊥CEF(SAS)),⊥⊥正确;⊥⊥AGE=⊥ECF=135°,⊥⊥FCD=135°﹣90°=45°,⊥⊥正确;⊥⊥BGE=⊥BEG=45°,⊥AEG+⊥FEC=45°,⊥⊥FEC<45°,∴∠=︒+∠<135︒,FHC FEC90∴∠≠∠FHC AGE,△不相似,⊥AGE和FCH⊥⊥错误;故选C.【点睛】本题考查了正方形的性质,等腰三角形的性质,全等三角形的性质和判定,相似三角形的判定,勾股定理等知识点的综合运用,综合比较强,难度较大.二、填空题11.如图,在Rt⊥ABC 中,⊥ACB =90°,将⊥ABC 沿AB 翻折得⊥ABC′,过点C′作CA 的垂线,交CA 延长线于点F 点D 为边BC′上一点,过点D 作DE⊥BC ,垂足为点E ,连接CD ,交AB 于点M ,若DC 平分⊥EDC′,CE =CF =6,C′F =4,则AM =_____.【分析】延长ED 交FC '的延长线于R ,连接CC '交AB 于J ,过点C 作CT BC ⊥'于T .首先证明四边形ECFR 是正方形,利用全等三角形的性质证明DE DT =,4FC C T '='=,再想办法求出JC ,AJ ,证明JM JC =,可得结论.【详解】解:延长ED 交FC '的延长线于R ,连接CC '交AB 于J ,过点C 作CT BC ⊥'于T .90REC CFR ECF ∴∠=∠=∠=︒,∴四边形ECFR 是矩形,CE CF =,∴四边形ECFR 是正方形,CD 平分EDC ∠',CE DE ⊥,CT EC ⊥',CDE CDT ∴∠=∠,90CED CTD ∠=∠=︒,CD CD =,()CDE CDT AAS ∴∆≅∆,CE CT ∴=.DE DT =,90CTC F ∠'=∠=︒,CF CE CT ==,CC CC '=', Rt ∴⊥CC T Rt '≅⊥()CC F HL ',4FC C T ∴'='=,在Rt CFC '△中,CC ' 由翻折的性质可知,CJ JC ='=ACJ FCC ∠=∠',90CJA F ∠=∠=︒,CJA CFC ∴∆∆'∽,∴CJ AJCF FC =',∴4AJ =,AJ ∴=DCE DCT ∠=∠,C CT C CF ∠'=∠', 45JCM ∴∠=︒,JM CJ ∴=AM JM AJ ∴=+. 【点睛】本题考查翻折变换,正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识,解题的关键是想添加常用辅助线,构造特殊四边形解决问题,学会利用参数构建方程解决问题,属于中考填空题中的压轴题.12.如图,边长为3的等边三角形ABC 中,点M 在直线BC 上,点N 在直线AC 上,且⊥BAM =⊥CBN ,当BM =1时,AN =___.【答案】2或4或92或94【分析】先根据等边三角形的性质可得60,3ABC ACB AB BC AC ∠=∠=︒===,再分⊥点M 在边BC 上,点N 在边AC 上,⊥点M 在边BC 上,点N 在边AC 延长线上,⊥点M 在边CB 延长线上,点N 在边AC 上,⊥点M 在边CB 延长线上,点N 在边AC 延长线上四种情况,然后根据三角形全等的判定定理与性质、相似三角形的判定与性质即可得.【详解】解:ABC 是边长为3的等边三角形,60,3ABC ACB AB BC AC ∴∠=∠=︒===,由题意,分以下四种情况:⊥如图,当点M 在边BC 上,点N 在边AC 上时,在ABM 和BCN △中,BAM CBN AB CB ABM BCN ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ABM BCN ASA ∴≅,1BM CN ∴==,312AN AC CN ∴=-=-=;⊥当点M 在边BC 上,点N 在边AC 延长线上时,如图,过点N 作//ND AB ,交BC 延长线于点D ,60D ABM ∴∠=∠=︒,60DCN ACB ∠=∠=︒,CDN ∴是等边三角形,CN DN CD ∴==,在ABM 和BDN 中,BAM DBN ABM D ∠=∠⎧⎨∠=∠⎩, ABM BDN ~∴,DN BD BC CD BC DN BM AB AB AB ++∴===,即313DN DN +=, 解得32DN =, 32CN ∴=, 39322AN AC CN ∴=+=+=; ⊥当点M 在边CB 延长线上,点N 在边AC 上时,如图,过点N 作//ND AB ,交BC 于点D ,60CDN ABC ACB ∴∠=∠=︒=∠,CDN ∴是等边三角形,CN DN CD ∴==,60CDN ABC ∠=∠=︒,120BDN ABM ∴∠=∠=︒, 在BDN 和ABM 中,DBN BAM BDN ABM ∠=∠⎧⎨∠=∠⎩, BDN ABM ~∴,DN BD BC CD BC DN BM AB AB AB --∴===,即313DN DN -=, 解得34DN =, 34CN ∴=, 39344AN AC CN ∴=-=-=;⊥如图,当点M 在边CB 延长线上,点N 在边AC 延长线上时,60ABC ACB ∠=∠=︒,120ABM BCN ∴∠=∠=︒,在ABM 和BCN △中,BAM CBN AB CB ABM BCN ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ABM BCN ASA ∴≅,1BM CN ∴==,314AN AC CN ∴=+=+=;综上,AN 的值为2或4或92或94, 故答案为:2或4或92或94. 【点睛】本题考查了等边三角形的判定与性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点,正确分四种情况讨论是解题关键.13.如图,在平面直角坐标系中,点A 、B 分别在x 轴、y 轴的正半轴上,且()0,630B OAB ∠=︒,,C 为线段AB 上一点,:1:2BC CA =,若M 为y 轴上一点,且:1:2OM OB =,设直线AM 与直线OC 相交于点N ,则ON 的长为________.或【分析】过点C 作CD ⊥x 轴于D ,证明⊥ACD ⊥⊥ABO ,得到CD AD AC BO AO AB==,求出CD 和AD ,得到点C 坐标,求出直线OC 的教师式,再求出点M 的坐标,分两种情况,联立教师式,求出点N 坐标,利用勾股定理得到ON 的长.【详解】解:过点C 作CD ⊥x 轴于D ,则⊥ADC =⊥AOB =90°,又⊥⊥CAD =⊥BAO ,⊥⊥ACD ⊥⊥ABO , ⊥CD AD AC BO AO AB==, ⊥B (0,6),⊥OB =6,⊥⊥OAB =30°,⊥AB =2OB =12,⊥AO⊥BC :CA =1:2,⊥AC =2812AB ⨯=+, ⊥BC =AB -AC =4,⊥8612CD =, 解得:CD =4,AD=⊥OD =OA -AD=⊥C(4),设直线OC 的教师式为y =kx ,将C 代入,则4=,解得:k = ⊥直线OC的教师式为y =, ⊥OM :OB =1:2,OB =6,⊥OM =3,⊥M 的坐标为(3,0)或(-3,0),当M (3,0)时,记为点M ′,设直线AM ′的教师式为y =ax +b ,则03b b ⎧+=⎪⎨=⎪⎩,解得:3a b ⎧=⎪⎨⎪=⎩⊥直线AM ′的教师式为3y =+, 联立直线AM ′和直线OC的教师式得3y x y ⎧=⎪⎪⎨⎪=+⎪⎩,解得:125x y ⎧=⎪⎪⎨⎪=⎪⎩, ⊥N,125), ⊥ON当M (-3,0)时,同理求得直线AM的教师式为3y =-,联立得3y y ⎧=⎪⎪⎨⎪=-⎪⎩,解得:4x y ⎧=-⎪⎨=-⎪⎩ ⊥N(--4),⊥ON综上:ON或或 【点睛】 本题考查了相似三角形的判定和性质,一次函数与二元一次方程组,勾股定理,有一定难度,解题的关键是根据题意画出图形,分类讨论解决问题.14.如图,在菱形ABCD 中,⊥DAB =60°,AB =3,点E 在边AD 上,且DE =1,点F 为线段AB 上一动点(不与点A 重合),将菱形沿直线EF 折叠,点A的对应点为点A′,当点A′落在菱形的对角线上时,AF 的长为___.【答案】2或5【分析】分两种情况进行讨论:⊥当点A ′在BD 上时,可以证明⊥A ′DE ⊥⊥FBA ′,对应边成比例,可求出AF 的长;⊥当点A ′在AC 上时,可得⊥EAF 是等边三角形,进而可求AF 的长.【详解】解:⊥当点A ′在BD 上时,如图,由折叠可知:⊥EA ′F =⊥DAB =60°,⊥⊥DA ′E +⊥F A ′B =120°,⊥⊥A =60°,AB =AD ,⊥⊥ADB 是等边三角形,⊥⊥DBA =⊥ADB =60°,⊥⊥A ′FB +⊥BA ′F =120°,⊥⊥DA ′E =⊥BF A ′,⊥⊥A ′DE ⊥⊥FBA ′, ⊥DE DA EA A B FB FA ''=='', ⊥AB =AD =DB =3,DE =1,⊥EA ′=EA =AD -DE =2,设F A ′=F A =x ,DA ′=y ,则BA ′=3-y ,BF =3-x , ⊥3123y y x x-==-,解得x =5⊥当点A ′在AC 上时,如图:由折叠可知:EF 垂直平分AA ′,⊥⊥AOF =90°,⊥四边形ABCD 是菱形,⊥DAB =60°,⊥⊥DAC =⊥BAC =30°,⊥⊥AFE =60°,⊥⊥EAF 是等边三角形,⊥AF =AE =AD -DE =2.综上所述:AF =52.故答案为:2或5【点睛】本题考查了翻折变换、等边三角形的判定与性质、菱形的性质,解决本题的关键是掌握菱形的性质.15.如图,正方形ABCD 中,点E 是CD 边上一点,连结BE ,以BE 为对角线作正方形BGEF ,边EF 与正方形ABCD 的对角线BD 相交于点H ,连结AF ,有以下五个结论:⊥ABF DBE ∠=∠;⊥ABF DBE ∽;⊥AF BD ⊥;⊥22BG BH BD =;⊥若:1:3CE DE =,则:17:16BH DH =,你认为其中正确是_____(填写序号)【答案】⊥⊥⊥⊥【分析】⊥四边形BGEF 和四边形ABCD 均为正方形,BD ,BE 是对角线,得⊥ABD =⊥FBE =45°,根据等式的基本性质确定出ABF DBE ∠=∠;⊥倍,得到两边对应成比例,再根据角度的相减得到夹角相等,利用两边成比例且夹角相等的两个三角形相似即可判断;⊥根据两角相等的两个三角形相似得到⊥EBH ⊥⊥DBE ,从而得到比例式,根据BE ,代换即可作出判断;⊥由相似三角形对应角相等得到⊥BAF =⊥BDE =45°,可得出AF 在正方形ABCD 对角线上,根据正方形对角线垂直即可作出判断.⊥设CE =x ,DE =3x ,则BC =CD =4x ,结合BE 2=BH •BD ,求出BH ,DH ,即可判断.【详解】解:⊥⊥四边形BGEF 和四边形ABCD 均为正方形,BD ,BE 是对角线,⊥⊥ABD =⊥FBE =45°,又⊥⊥ABF =45°−⊥DBF ,⊥DBE =45°−⊥DBF ,⊥ABF DBE ∠=∠,⊥选项⊥正确;⊥⊥四边形BGEF 和四边形ABCD 均为正方形,⊥AD =AB ,BF =BE ,⊥BD,,⊥BD BE AB BF== 又⊥ABF DBE ∠=∠,⊥ABF DBE ∽,⊥选项⊥正确;⊥⊥四边形BGEF 和四边形ABCD 均为正方形,BD ,BE 是对角线,⊥⊥BEH =⊥BDE =45°,又⊥⊥EBH =⊥DBE ,⊥⊥EBH ⊥⊥DBE , ⊥BD BE BE BH= ,即BE 2=BH •BD ,又⊥BE ,⊥22BG BH BD =,⊥选项⊥确;⊥由⊥知:ABF DBE ∽,又⊥四边形ABCD 为正方形,BD 为对角线,⊥⊥BAF =⊥BDE =45°,⊥AF 在正方形另外一条对角线上,⊥AF ⊥BD ,⊥⊥正确,⊥⊥:1:3CE DE =,⊥设CE =x ,DE =3x ,则BC =CD =4x ,⊥BE ==,BD =⊥BE 2=BH •BD ,⊥228BE BH x BD ===,⊥DH =BD -BH =x x =, ⊥:17:15BH DH =,故⊥错误,综上所述:⊥⊥⊥⊥正确,故答案是:⊥⊥⊥⊥.【点睛】此题考查了相似三角形的判定与性质,全等三角形的判定与性质,以及正方形的性质,熟练掌握相似三角形的判定和性质是解本题的关键.16.如图,已知Rt AOB ,90∠=︒ABO ,点(15,0)A ,反比例函数(0)k y x x =>经过点B ,交AB 于点C ,若:3:2BC OB =,则k 的值是______.【答案】18【分析】过点B 作BD ⊥x 轴于D ,过点C 作CE ⊥BD 于E ,CF ⊥x 轴于点F ,易证⊥BOD ⊥⊥CBE ,可得32BE EC BC OD BD OB ===,设BE =3a ,EC =3b ,则OD =2a ,BD =2b .易得四边形EDFC 为矩形,则FD =CE =3b ,FC =ED =BD −BE =2b −3a ,得到B (2a ,2b ),C (3b +2a ,2b −3a ).由待定系数法可得:k =2a ×2b =4ab ,k =(3b +2a )(2b −3a ),等量代换可得:4ab =(3b +2a )(2b −3a ),整理得到:b =2a .于是得到BD =4a ,EC =6a ,FC =a ;易证⊥BEC ⊥⊥CF A ,可得12CF BE FA EC ==,求出F A =2a ,从而OA =OD +FD +F A =10a ,由点A (15,0),可得OA =15,a 的值可求,B 点坐标可得,用待定系数法k 值可求.【详解】解:过点B 作BD ⊥x 轴于D ,过点C 作C E ⊥BD 于E ,CF ⊥x 轴于点F ,如图,⊥⊥ABO =90°,⊥⊥OBD +⊥EBC =90°.⊥BD ⊥OD ,⊥⊥OBD +⊥BOD =90°.⊥⊥BOD =⊥EBC .⊥⊥ODB =⊥BEC =90°,⊥⊥BOD ⊥⊥CBE . ⊥32BE EC BC OD BD OB ===, ⊥设BE =3a ,EC =3b ,则OD =2a ,BD =2b . ⊥BD ⊥DF ,CE ⊥BD ,CF ⊥AD ,⊥四边形EDFC 为矩形.⊥FD =CE =3b ,FC =ED =BD −BE =2b −3a . ⊥B (2a ,2b ),C (3b +2a ,2b −3a ). 将B ,C 坐标分别代入教师式(0)k y x x=>中得: k =2a ×2b =4ab ,k =(3b +2a )(2b −3a ). ⊥4ab =(3b +2a )(2b −3a ).整理得到:b =−12a (不合题意,舍去)或b =2a . ⊥BD =4a ,EC =6a ,FC =a .⊥EC ⊥AD ,⊥⊥BCE =⊥A .⊥⊥BEC =⊥CF A =90°,⊥⊥BEC ⊥⊥CF A . ⊥12CF BE FA EC ==, ⊥F A =2CF =2a .⊥点A (15,0),⊥OA =15.⊥OD +FD +F A =15.⊥10a =15.解得:a =32. ⊥OD =3,BD =6.⊥B (3,6).⊥k =3×6=18.故答案为:18.【点睛】本题主要考查了反比例函数图象上点的坐标的特征,三角形相似的判定与性质,矩形的判定与性质,待定系数法确定函数的教师式.利用点的坐标表示出相应线段的长度是解题的关键.17.如图,点A 是边长为2的正方形DEFG 的中心,在ABC 中,90ABC ∠=︒,2AB =,4BC =,//DG BC ,点P 为正方形边上的一动点,在BP 的右侧作90PBH ∠=°且2BH PB =,则AH 的最大值为______.【答案】【分析】连接BD ,连接BG 并延长到D ',且使GD BG '=,易得DPB D HB '△△,由此可得当点P 在DG 上运动时,点H 在过点D '且垂直于BC 的线段D G '' 上运动,且D G ''=-4,仿此,可得点H 在以点C 为中心的边长为4的正方形上运动,可得当点P 与点F 重合时,AH 取得最大值,在Rt ⊥AEF '' 中,利用勾股定理即可求得AH 的长.【详解】如图,当点P 在线段DG 上时,连接BD ,连接BG 并延长到D ',且使GD BG '=⊥BC ⊥DG ,⊥ABC =90°⊥AB ⊥DG⊥四边形DEFG 是正方形,且A 为正方形的中心,AB =DG =2⊥AB 、DG 相互垂直平分⊥BD =BG ,⊥DBG =90°⊥2BD BD '=⊥BH =2PB ⊥2BD BH BD PB'== ⊥⊥DBG =⊥PBH =90°⊥DBP D BH '∠=∠⊥⊥DBP D BH '△△⊥BDG BD H '∠=∠,2D H DP '=⊥⊥BDG =⊥BGD =45°,⊥DGF =90°⊥⊥45FGD '=︒,45BDG BD H '∠=∠=︒⊥FG ⊥D H '⊥DG ⊥FG⊥DG ⊥D H '故当点P 在边DG 上运动时,点H 则在线段D G ''上运动,且2D G ''=DG =4由此可得,当点P 在四边形DEFG 上运动时,点H 在以C 为中心的正方形D E F G ''''上运动,且其边长为4当点P 与点F 重合,点H 与点 F '重合时,AH 最长,此时连接AD ',则AD '=2⊥6AE AD D E ''''=+=在Rt AE F ''中,由勾股定理得:AH AF '===故答案为:【点睛】本题是动点问题,求线段的最大值,它考查了正方形的性质,三角形相似的判定与性质,勾股定理等知识,关键和难点是确定动点H 的运动路径.18.如图1是一种利用镜面反射,放大微小变化的装置.木条BC 上的点P 处安装一平面镜,BC 与刻度尺边MN 的交点为D ,从A 点发出的光束经平面镜P 反射后,在MN 上形成一个光点E .已知,, 6.5AB BC MN BC AB ⊥⊥=,4,8BP PD ==.(1)ED 的长为____________.(2)将木条BC 绕点B 按顺时针方向旋转一定角度得到BC '(如图2),点P 的对应点为P ',BC '与MN 的交点为D′,从A 点发出的光束经平面镜P '反射后,在MN 上的光点为E '.若5DD '=,则EE '的长为____________.【答案】13232【分析】(1)由题意,证明⊥ABP ⊥⊥EDP ,根据相似三角形的性质,即可求出ED 的长度; (2)过A 作AH ⊥BN 交NB 延长线于H ,过E′作E′F ⊥BN 于F ,设E′D =x ,E′D′=5+x ,在Rt ⊥BDN 中,由勾股定理D′B 12=,可证⊥ABH ⊥⊥BD′D ⊥⊥E′D′F ,=6=2.5AH BH ,,6012255,1313x x E F FD ++''==,从A 点发出的光束经平面镜P′反射后,在MN 上形成一个光点E′.⊥AHP′⊥⊥E′FP′,6 6.560+1225591313x x =+-,解得x =1.5. 【详解】解:(1)由题意,⊥,AB BC MN BC ⊥⊥,⊥90ABP EDP ∠=∠=︒,⊥从A 点发出的光束经平面镜P 反射后,在MN 上形成一个光点E .⊥APB EPD ∠=∠,⊥⊥ABP ⊥⊥EDP , ⊥AB BP ED DP =, 即6.548ED =, ⊥13ED =;故答案为:13.(2)过A 作AH ⊥BN 交NB 延长线于H ,过E′作E′F ⊥BN 于F ,设E′D =x ,E′D′=5+x , 在Rt ⊥BDN 中,⊥BD =12,DD′=5,由勾股定理D′B 13=,⊥⊥AHB =⊥ABD =⊥E′FN =⊥BDD′=90°,⊥⊥ABH +⊥DBD′=⊥DBD′+⊥DD′B =FE D ''∠+⊥E′D′F ,⊥⊥ABH =⊥BD′D =⊥E′D′F ,⊥⊥ABH ⊥⊥BD′D ⊥⊥E′D′F , ⊥AB AH BH BD BD DD =='',E D E F FD BD BD DD ''''=='', ⊥6.513125AH BH ==,513125x E F FD ''+==, ⊥=6=2.5AH BH ,,6012255,1313x x E F FD ++''==, ⊥从A 点发出的光束经平面镜P′反射后,在MN 上形成一个光点E′.⊥AP H E P F '''∠=∠,⊥⊥AHP′⊥⊥E′FP′,HP′=HB +BP =2.5+4=6.5,P′D′=BD′-BP′=13-4=9,P′F = P′D′-FD′=9-25513x +,⊥AH P H E F P F '=''即6 6.560+1225591313x x =+-, 解得x =1.5,经检验x =1.5是方程的解,EE′=DE -DE′=13-1.5=11.5=232.故答案为232. 【点睛】本题考查相似三角形性质与判定,勾股定理,光束经平面镜P 性质,掌握相似三角形性质与判定,勾股定理,光束经平面镜P 性质,利用相似三角形的性质构造方程6 6.560+1225591313x x =+-是解题关键. 19.如图,点1B 在直线1:2l y x =上,点1B 的横坐标为2,过点1B 作1B l ⊥,交x 轴于点1A ,以11A B 为边,向右作正方形1121A B B C ,延长21B C 交x 轴于点2A ;以22A B 为边,向右作正方形2232A B B C ,延长32B C 交x 轴于点3A ;以33A B 为边,向右作正方形3343A B B C ,延长的43B C 交x 轴于点4A ;…;按照这个规律进行下去,则第n 个正方形1n n n n A B B C +的边长为________(结果用含正整数n 的代数式表示).132n-⎛⎫⎪⎝⎭【分析】根据题中条件,证明所有的直角三角形都相似且确定相似比,再具体算出前几个正方形的边长,然后再找规律得出第n个正方形的边长.【详解】解:点1B在直线1:2l y x=上,点1B的横坐标为2,∴点1B纵坐标为1.1OB∴=分别过1B,14,,C C⋅⋅⋅作x轴的垂线,分别交于14,,,D D D⋅⋅⋅,下图只显示一条;111111190,B DAC DB B OD A B D∠=∠=︒∠=∠,∴111Rt B DO Rt A DB∽类似证明可得,图上所有直角三角形都相似,有11111211112n nn nC AB D B AC AOD OB C A C A+====⋅⋅⋅=,不妨设第1个至第n个正方形的边长分别用:12,,,nl l l⋅⋅⋅来表示,通过计算得:112OBl==121123322ll l C A=+==,2232233322ll l C A⎛⎫=+== ⎪⎝⎭⋅⋅⋅11113322nnn n n nll l C A----⎛⎫=+= ⎪⎝⎭按照这个规律进行下去,则第n个正方形1n n n nA B B C+132n-⎛⎫⎪⎝⎭,132n-⎛⎫⎪⎝⎭.【点睛】本题考查了三角形相似,解题的关键是:利用条件及三角形相似,先研究好前面几个正方形的边长,再从中去找计算第n个正方形边长的方法与技巧.20.如图,在ABC中,点D是AB边上的一点,且3AD BD=,连接CD并取CD的中点E,连接BE,若45ACD BED∠=∠=︒,且CD=AB的长为__________.【答案】【分析】延长BE交AC于点F,过D点作DG BE G⊥于点,由45ACD BED∠=∠=︒可得此时CEF△为等腰直角三角形,E为CD的中点且CD=CE DE==Rt CEF中,根据勾股定理求得CF,EF长度,由BF DG⊥可得EDG ECF△≌△,即EG EF=,由BF AC⊥,BF DG⊥可得AC DG∥,即BDG BAF△∽△,13BG BDFG AD==∴,求得,4AB BD==∴【详解】如下图,延长BE交AC于点F,过D点作DG BE G⊥于点,⊥45ACD BED∠=∠=︒,=45BED CEF∠=︒∠,⊥90EFC=∠,BF AC⊥,CEF△为等腰Rt CEF.由题意可得E为CD的中点,且CD=⊥CE DE==在等腰Rt CEF中,32CE,3CF EF ==∴,又⊥BF DG ⊥,在ECF EDG △和△中,90CFE DGE CEF DEG CE DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩⊥EDG ECF △≌△(AAS )⊥3EF EG ==,⊥BF AC ⊥,BF DG ⊥,⊥//AC DG , ⊥13BG BD FG AD == 6FG EF EG =+=,⊥2BG =,BD4AB BD ==∴故答案为:【点睛】本题考察了等腰直角三角形的性质,勾股定理求对应边的长度,全等三角形的性质与判定,相似三角形的性质与判定,构造合适的相似三角形,综合运用以上性质是解题的关键.三、解答题21.如图,在平面直角坐标系中,直线4y kx k =+交x 轴于点A ,交y 轴于点B ,且34OB OA =.(1)求直线AB 的教师式;(2)点(),0P t 是x 轴正半轴上一点,连接BP ,将射线PO 沿BP 翻折,与过点B 垂直于BP 的直线交于点C ,过点C 作CD x ⊥轴于点D ,求线段CD 的长;(3)在(2)的条件下,射线BD 交射线CP 于点Q ,若56BCD DCQ S S =△△,求P 点坐标.【答案】(1)334y x =+;(2)6;(3)P ⎫⎪⎪⎝⎭【分析】(1)根据直线4y kx k =+与x 轴,y 轴的交求得A ,继而求得OA ,OB ,再求得点B ,最后根据待定系数法求教师式;(2)根据翻折性质可得BPC BPE ∠=∠,继而易证⊥PBC ⊥⊥PBE (ASA ),可得BC BE =,继而证得OB 是⊥CDE 的中位线,即可求解;(3)作QN ⊥CD 于点N ,作BM ⊥CD 于点M ,设5OD OE BM m ===,6NQ m =, 求得185DN =,根据tan DP NQ DCP CD CN ∠==,求得154m DP =,继而求得CP ,在Rt CDP △中,由勾股定理得:222CD DP CP +=,解得m ,继而即可求解.【详解】(1)令x =0,得4y k =,则(0,4k ),令0y =得40kx k +=,解得:4x =-,则()4,0A -⊥4OA =, ⊥34OB OA = ⊥3OB =,即()0,3B ,⊥043k b b =-+⎧⎨=⎩, 解得:343k b ⎧=⎪⎨⎪=⎩, ⊥直线AB 的教师式334y x =+.(2)由翻折可知BPC BPE ∠=∠,又PB CE ⊥,即⊥PBC =⊥PBE =90°,又BP =BP ,⊥⊥PBC ⊥⊥PBE (ASA ),⊥BC BE =.⊥CD x ⊥轴于点D ,⊥//OB CD ,⊥OB 是⊥CDE 的中位线,⊥26CD OB ==.(3)作QN ⊥CD 于点N ,作BM ⊥CD 于点M ,由56BCD DCQ S S =△△,即151262CD OD CD NQ ⋅=⨯⋅, 5,6OD NQ ∴= ⊥BM ⊥DE ⊥NQ ,12BM DE OD OE ===,DM =OB =3, ⊥⊥BDM ⊥⊥QDN , ⊥DM BM DN NQ=, 设5OD OE BM m ===,6NQ m =, 即356m DN m=, 解得:185DN =, tan DP NQ DCP CD CN ∠==, 6,18665DP m ∴=+ 解得:154m DP =, ⊥15551044m CP PE DP DE m m ==+=+=. 在Rt CDP △中,由勾股定理得:222CD DP CP +=,即2221555644m m ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,解得:m =⊥1535355444OP OD DP m m m =+=+===,⊥P ⎫⎪⎪⎝⎭.【点睛】本题考查一次函数的综合题,涉及到勾股定理,相似三角形的判定及其性质,全等三角形的判定和性质,解题的关键是综合运用所学在求得关键线段和坐标,综合性较强,需认真审题. 22.问题背景:如图1,在矩形ABCD 中,AB =30ABD ∠=︒,点E 是边AB 的中点,过点E 作EF AB ⊥交BD 于点F .实验探究:(1)在一次数学活动中,小王同学将图1中的BEF 绕点B 按逆时针方向旋转90︒,如图2所示,得到结论:⊥AE DF=_____;⊥直线AE 与DF 所夹锐角的度数为______. (2)小王同学继续将BEF 绕点B 按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.拓展延伸:在以上探究中,当BEF 旋转至D 、E 、F 三点共线时,则ADE 的面积为______.【答案】(130°;(2 【分析】(1)通过证明FBD EBA ∆∆∽,可得AE BE DF BF =BDF BAE ∠=∠,即可求解;(2)通过证明ABE DBF ∆∆∽,可得AE BE DF BF =,BDF BAE ∠=∠,即可求解; 拓展延伸:分两种情况讨论,先求出AE ,DG 的长,即可求解.【详解】解:(1)如图1,30ABD ∠=︒,90DAB ∠=︒,EF BA ⊥,cos BE AB ABD BF DB ∴∠===, 如图2,设AB 与DF 交于点O ,AE 与DF 交于点H ,BEF ∆绕点B 按逆时针方向旋转90︒,90DBF ABE ∴∠=∠=︒,FBD EBA ∴∆∆∽,∴AE BE DF BF =,BDF BAE ∠=∠, 又DOB AOF ∠=∠,30DBA AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30,30; (2)结论仍然成立,理由如下:如图3,设AE 与BD 交于点O ,AE 与DF 交于点H ,将BEF ∆绕点B 按逆时针方向旋转,ABE DBF ∴∠=∠,又BE AB BF DB == ABE DBF ∴∆∆∽,∴AE BE DF BF =,BDF BAE ∠=∠, 又DOH AOB ∠=∠,30ABD AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30.拓展延伸:如图4,当点E 在AB 的上方时,过点D 作DG AE ⊥于G ,。
中考物理一模选择压轴汇总(包含答案))

选择压轴题汇总1.(宝山)闭合图2所示电路中电键S ,向右移动滑片P ,保持不变的是A 电流表A 的示数。
B 电压表V 1的示数。
C 电压表V 2示数与电流表A 示数的乘积。
D 电压表V 1示数与电流表A 示数的比值。
2.(宝山)如图3所示,底面积不同的圆柱形容器A 和B 分别盛有质量相等的甲、乙两种液体,此时两液面齐平。
若从两容器中分别抽出部分液体后,两液面仍保持齐平,则此时液体对各自容器底部的压强p A 、p B 和压力F A 、F B 的关系是A p A <pB , F A =F B 。
B p A <p B , F A >F B 。
C p A >p B , F A =F B 。
D p A >p B , F A <F B 。
3.(崇明)如图1所示电路中,电源电压保持不变,当电键由断开到闭合时,下列判断错误的是 A .电流表示数变大B .电压表示数变大C .电压表示数与电流表示数的比值变大D .电压表示数与电流表示数的乘积变大4.(崇明)如图2所示,水平地面上放着两个质地均匀的正方体甲和乙,且甲对地面的压强大于乙.若在两正方体上面各放一个物体,小明认为:若两物体质量相等,正方体甲对地面的压强可能小于乙;小强认为:若两物体体积相等,正方体甲对地面的压强可能小于乙.下列判断正确的是 A .两人的观点均正确 B .两人的观点均不正确C .只有小明的观点正确D .只有小强的观点正确5.(奉贤)如图5所示,电源电压保持不变,故障只发生在R 1或R 2处。
电键S 闭合后,有一个电表的指针没有发生偏转。
移动滑动变阻器的滑片,此时观察到仍然只有一个电表指针的位置在改变,则故障可能是A .变阻器R 1短路B .变阻器R 1断路C .电阻R 2短路D .电阻R 2断路6.(奉贤)装有水的薄壁轻质柱形容器,静止放在水平桌面上,现将A 、B 、C 三个实心物体分别浸没水中(水没有溢出)。
发现放入A 物体时,水对容器底部压强的增加量与容器对桌面压强增加量的比值最小;放入C 物体时,水对容器底部压强的增加量与容器对桌面压强增加量的比值最大,则A 、B 、C 三物体密度满足的条件是A .ρ A >ρB ,ρ A >ρCB .ρA <ρB ,ρA <ρCC .ρA >ρB ,ρA <ρCD .ρA <ρB , ρ A >ρ C图3图2(图1)(图2)7.(虹口)在图2(a )、(b )所示的电路中,电源电压相等且保持不变。
2024届上海初三一模数学各区25题解答压轴题

图11上海市2024届初三一模数学分类汇编—25题解答压轴题【2024届·宝山区·初三一模·第25题】1.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知ABC 中,1AB AC ,D 是边AC 上一点,且BD AD ,过点C 作//CE AB ,并截取CE AD ,射线AE 与BD 的延长线交于点F .(1)求证:2AF DF BF ;(2)设AD x ,DF y ,求y 与x 的函数关系式;(3)如果ADF 是直角三角形,求DF 的长.第25题图2备用图第25题图12.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)已知Rt ABC 中,90ACB ,3AC ,5AB ,点D 是AB 边上的一个动点(不与点A 、B 重合),点F 是边BC 上的一点,且满足CDF A ,过点C 作CE CD 交DF 的延长线于E .(1)如图1,当//CE AB 时,求AD 的长;(2)如图2,联结BE ,设AD x ,BE y ,求y 关于x 的函数解析式并写出定义域;(3)过点C 作射线BE 的垂线,垂足为H ,射线CH 与射线DE 交于点Q ,当CQE 是等腰三角形时,求AD 的长.图122图121 3.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)在直角梯形ABCD 中,//AD BC ,90B ,6AD ,4AB ,BC AD ,ADC 的平分线交边BC 于点E ,点F 在线段DE 上,射线CF 与梯形ABCD 的边相交于点G .(1)如图121 ,当4tan 3BCD 时,求BE 的长;(2)如图122 ,如果点G 在边AD 上,联结BG ,当4DG ,且CGB BAG ∽时,求sin BCD的值;(3)当F 是DE 中点,且1AG 时,求CD 的长.图14①图14②备用图4.(本题满分14分,第(1)小题满分4分,第(2)①小题满分5分,第(2)②小题满分5分)如图14①,在Rt ABC 中,90ACB ,4tan 3ABC,点D 在边BC 的延长线上,联结AD ,点E 在线段AD 上,EBD DAC .(1)求证:DBA DEC ∽;(2)点F 在边CA 的延长线上,DF 与BE 的延长线交于点M (如图14②).①如果2AC AF ,且DEC 是以DC 为腰的等腰三角形,求tan FDC的值;②如果2DE CD,3EM ,:5:3FM DM ,求AF 的长.第25题图(本题满分4分)5.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,O 是Rt ABC 斜边AB 的中点,BH CO 交AC 于D ,垂足为H ,联结OD .(1)求证:2BC AC CD ;(2)如果ODH 与ABC 相似,求其相似比;(3)如果:4:1BH DH ,求ADO 的大小.图11图12备用图6.(本题满分14分,第(1)小题3分,第(2)①小题5分,第(2)②小题6分)如图11,在ABC 和ACD 中,90ACB CAD ,16BC ,15CD ,9DA .(1)求证:B ACD ;(2)已知点M 为边BC 上一点(与点B 不重合),且MAN BAC ,AN 交CD 于点N ,交BC 的延长线于点E .①如图12,设BM x ,CE y ,求y 关于x 的函数关系式,并写出定义域;②当CEN 是等腰三角形时,求BM 的长.第25题图7.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:如图,在ABC 中,AB AC ,CAD ABC ,DC AC ,AD 与边BC 相交于点P .(1)求证:212AB AD BC;(2)如果4sin 5ABC ,求:BP PC 的值;(3)如果BCD 是直角三角形,求ABC 的正切值.第25题图1第25题图2备用图8.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)已知梯形ABCD 中,//AD BC ,2AB ,4AD ,3DC ,7BC .点P 在射线BA 上,点Q 在射线BC 上(点P 、点Q 均不与点B 重合),且PQ BQ ,联结DQ ,设BP x ,DQC 的面积为y .(1)如图1所示,求sin B 的值;(2)如图2所示,点Q 在线段BC 上,求y 关于x 的函数解析式,并写出定义域;(3)当DQC 是等腰三角形时,求BP 的长.第25题图1第25题图2备用图9.(本题满分14分,第(1)小题4分,第(2)①小题5分,第(2)②小题5分)如图,在Rt ABC 中,90ACB ,以AC 、BC 为边在ABC 外部作等边三角形ACE 和等边三角形BCF ,且联结EF .(1)如图1,联结AF 、EB ,求证:ECB ACF ≌;(2)如图2,延长AC 交线段EF 于点M .①当点M 为线段EF 中点时,求ACBC的值;②请用直尺和圆规在直线AB 上方作等边三角形ABD (不要求写作法,保留作图痕迹,并写明结论),当点M 在ABD 的内部时,求ACBC的取值范围.第25题图备用图备用图10.(本题满分14分,第(1)小题5分,第(2)小题5分,第(2)小题4分)如图,已知正方形ABCD 的边长为6,点E 是射线BC 上一点(点E 不与点B 、C 重合),过点A 作AF AE ,交边CD 的延长线于点F ,直线EF 分别交射线AC 、射线AD 于点M 、N .(1)当点E 在边BC 上时,如果15ND AN ,求BAE 的余切值;(2)当点E 在边BC 延长线上时,设线段BE x ,y EN MF ,求y 关于x 的函数解析式,并写出函数定义域;(3)当3CE 时,求EMC 的面积.图1311.(本题满分14分,第(1)小题3分,第(2)小题6分,第(3)小题5分)如图13,在矩形ABCD 中,2AB ,4BC ,E 是边BC 延长线上一点,过点B 作BM DE ,垂足为点M ,联结CM ,设CE a (01a ).(1)求证:DCE BME ∽;(2)CME 的大小是否是一个确定的值?如果是,求出CME 的正切值;如果不是,那么用含字母a的代数式表示CME 的正切值;(3)P 是边AD 上一动点(不与点A 、D 重合),联结PB 、PM .随着点P 位置的变化,在PBM中除BPM 外的两个内角是否会有与CME 相等的角?如果有,请用含字母a 的代数式表示此时线段AP 的长;如果没有,请说明理由.第25题(1)图第25题(2)图第25题(3)图12.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)在ABC 中,90ACB ,6AC ,8BC .点D 、E 分别在边AB 、BC 上,联结ED ,将线段ED ,绕点E 按顺时针方向旋转90 得到线段EF .(1)如图,当点E 与点C 重合,ED AB 时,AF 与ED 相交于点O ,求:AO OF 的值;(2)如果5AB BD (如图),当点A 、E 、F 在一条直线上时,求BE 的长;(3)如图,当DA DB ,2CE 时,联结AF ,求AFE 的正切值.第25题图第25题备用图13.(本题满分14分,第(1)①小题4分,第(1)②小题5分,第(2)小题5分)在ABC 中,AC BC .点D 是射线AC 上一点(不与A 、C 重合),点F 在线段BC 上,直线DF 交直线AB 于点E ,2CD CF CB .(1)如图,如果点D 在AC 的延长线上.①求证:DE BD ;②联结CE ,如果//CE BD ,2CE ,求EF 的长.(2)如果:1:2DF DE ,求:AE EB 的值.第25题图备用图14.(本题满分14分)如图,在Rt ABC 中,90BAC,AB AC ,点D 是边AB 上的动点(点D 不与点B 重合),以CD 为斜边在直线BC 上方作等腰直角三角形DEC .(1)当点D 是边AB 的中点时,求sin DCB 的值;(2)联结AE ,点D 在边AB 上运动的过程中,EAC 的大小是否变化?如果变化,请说明理由;如果不变,请求出EAC 的大小;(3)设DE 与AC 的交点为G ,点P 是边BC 上的一点,且CPD CGD ,如果点P 到直线CD 的距离等于线段GE 的长度,求CDE 的面积.第25题图备用图15.(本题满分14分,第(1)小题4分,第(2)小题10分)如图,已知正方形ABCD ,点P 是边BC 上的一个动点(不与点B 、C 重合),点E 在DP 上,满足AE AB ,延长BE 交CD 于点F .(1)求证:135BED ;(2)联结CE .①当CE BF 时,求BP PC的值;②如果CEF 是以CE 为腰的等腰三角形,求FBC 的正切值.第25题图1备用图备用图16.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知ABC 中,2ABC C ,BG 平分ABC ,8AB ,163AG,点D 、E 分别是边BC 、AC 上的点(点D 不与点B 、C 重合),且ADE ABC ,AD 、BG 相交于点F .(1)求BC 的长;(2)如图1,如果2BF CE ,求:BF GF 的值;(3)如果ADE 是以AD 为腰的等腰三角形,求BD 的长.。
2019-2021年上海各区数学中考一模压轴题分类汇编18题-图形的旋转含详解
专题图形的旋转【知识梳理】【历年真题】1.(2021秋•普陀区期末)如图,在△ABC中,AB=AC=5,BC=4,AD是边BC上的高,将△ABC绕点C旋转,点B落在线段AD上的点E处,点A落在点F处,那么cos∠FAD =.2.(2021秋•静安区期末)如图,正方形ABCD中,将边BC绕着点C旋转,当点B落在边AD的垂直平分线上的点E处时,∠AEC的度数为.3.(2021秋•杨浦区期末)如图,已知在Rt△ABC中,∠C=90°,tan A=512,将△ABC绕点A逆时针旋转90°后得△ADE,点B落在点D处,点C落在点E处,联结BE、CD,作∠CAD的平分线AN,交线段BE于点M,交线段CD于点N,那么AMAN的值为.4.(2021秋•嘉定区期末)如图,在△ABC中,∠C=90°,BC=2,AB=25D在边AC上,CD:AD=1:3,联结BD,点E在线段BD上,如果∠BCE=∠A,那么CE=.5.(2021秋•松江区期末)如图,已知矩形ABCD中,AD=3,AB=5,E是边DC上一点,将△ADE绕点A顺时针旋转得到△AD′E′,使得点D的对应点D'落在AE上,如果D′E′的延长线恰好经过点B,那么DE的长度等于.6、(2021秋•黄浦区期末17)如图,在△ABC中,AB=4,AC=5,将△ABC绕点A旋转,使点B落在AC边上的点D处,点C落在点E处,如果点E恰好在线段BD的延长线上,那么边BC的长等于.7.(2020秋•嘉定区期末)已知在△ABC 中,∠ACB =90°,AB =10,sin A =55(如图),把△ABC 绕着点C 按顺时针方向旋转α°(0<α<360),将点A 、B 的对应点分别记为点A ′,B ′,如果△AA ′C 为直角三角形,那么点A 与点B '的距离为.8.(2020秋•闵行区期末)如图,在Rt △ABC 中,∠ACB =90°,AB =3,tan B =.将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,点C 落在点E 处,射线DE 与边AB 相交于点F ,那么BF =.9.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D 的值为.10.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为.11.(2020秋•宝山区期末)在Rt △ABC 中,∠ACB =90°,AC =BC ,点E 、F 分别是边CA 、CB 的中点,已知点P 在线段EF 上,联结AP ,将线段AP 绕点P 逆时针旋转90°得到线段DP ,如果点P 、D 、C 在同一直线上,那么tan ∠CAP =.12.(2020秋•奉贤区期末)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,CD 是△ABC 的角平分线,将Rt △ABC 绕点A 旋转,如果点C 落在射线CD 上,点B 落在点E 处,联结DE ,那么∠AED 的正切值为.13.(2019秋•奉贤区期末)如图,已知矩形ABCD (AB >BC ),将矩形ABCD 绕点B 顺时针旋转90°,点A 、D 分别落在点E 、F 处,连接DF ,如果点G 是DF 的中点,那么∠BEG 的正切值是.14.(2019秋•浦东新区期末)在Rt △ABC 中,∠C =90°,AC =2,BC =4,点D 、E 分别是边BC 、AB 的中点,将△BDE 绕着点B 旋转,点D 、E 旋转后的对应点分别为点D '、E ',当直线D 'E '经过点A 时,线段CD '的长为.15.(2019秋•长宁、金山区期末)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于.16.(2019秋•松江区期末)如图,矩形ABCD中,AD=1,AB=k,将矩形ABCD绕着点B 顺时针旋转90°得到矩形A′BC′D′,联结AD′,分别交边CD,A′B于E、F,如果AE D′F,那么k=.17.(2019秋•嘉定区期末)在△ABC中,∠ACB=90°,AB=10,cos A=35(如图),把△ABC绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点A'、B'.如果A'B'恰好经过点A,那么点A与点A'的距离为.18.(2019秋•徐汇区期末)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是.19.(2019秋•普陀区期末)如图,在RtΔABC中,∠C=90°,AC=5,sinB=513,点P为边BC上一点,PC=3,将△ABC绕点P旋转得到△A'B'C'(点A,B、C分别与点A'、B'、C'对应).使B'C'∥AB,边A'C'与边AB交于点G,那么A'G 的长等于.专题图形的旋转【历年真题】1.(2021秋•普陀区期末)如图,在△ABC 中,AB =AC =5,BC =4,AD 是边BC 上的高,将△ABC 绕点C 旋转,点B 落在线段AD 上的点E 处,点A 落在点F 处,那么cos ∠FAD =21332-.【考点】旋转的性质;解直角三角形;等腰三角形的性质;勾股定理.【专题】几何综合题;推理能力.【分析】如图,过点F 作FG ⊥AD 于点G ,由旋转可知:CE =BC =4,CF =EF =AB =AC =5,利用三角函数可得∠ECD =60°,进而可得:DE =AF =EF =5,运用勾股定理可得AD ,AE ﹣,由等腰三角形性质可得AG =EG =21332-,再运用三角函数可得cos ∠FAD =AG AF =.【解答】解:如图,过点F 作FG ⊥AD 于点G ,∵将△ABC 绕点C 旋转,点B 落在线段AD 上的点E 处,点A 落在点F 处,∴CE =BC =4,CF =EF =AB =AC =5,∵AB =AC ,AD 是边BC 上的高,∴BD =CD =2,∴cos ∠ECD =2142CD CE ==,∴∠ECD =60°,∴DE =CE •sin ∠ECD =4×sin60°=,∵∠ACF =∠ECD =60°,∴△ACF 是等边三角形,∴AF =EF =5,在Rt △ACD 中,AD ===,∴AE =AD ﹣DE ﹣∵AF =EF ,FG ⊥AD ,∴AG =EG =21332-,∴cos ∠FAD =AG AF ==2-,故答案为:2.【点评】本题考查了旋转的性质,等腰三角形的性质,等边三角形的判定和性质,勾股定理,三角函数定义,解题关键是要熟练运用等腰三角形性质.2.(2021秋•静安区期末)如图,正方形ABCD中,将边BC绕着点C旋转,当点B落在边AD的垂直平分线上的点E处时,∠AEC的度数为45°或135°..【考点】旋转的性质;线段垂直平分线的性质;正方形的性质.【专题】矩形菱形正方形;平移、旋转与对称;推理能力.【分析】分两种情况讨论,由旋转的性质和线段垂直平分线的性质可得△BEC是等边三角形,由等腰三角形的性质可求解.【解答】解:如图,当点E在BC的上方时,连接BE∵MN是AD的垂直平分线,四边形ABCD是正方形,∴MN垂直平分BC,∴BE=EC,∵将边BC绕着点C旋转,∴BC=CE,∴△BEC是等边三角形,∴∠EBC=∠BEC=60°,∴∠ABE=30°,∵AB=BC=BE,∴∠AEB=75°,∴∠AEC=75°+60°=135°;当点E'在BC的下方时,同理可得△BE'C是等边三角形,∴BC=BE',∠BE'C=60°=∠CBE',∴∠ABE'=150°,∵AB=BC=BE',∴∠AE'B=15°,∴∠AE'C=45°,故答案为:45°或135°.【点评】本题考查了旋转的性质,正方形的性质,等边三角形的性质,利用分类讨论思想解决问题是解题的关键.3.(2021秋•杨浦区期末)如图,已知在Rt△ABC中,∠C=90°,tan A=512,将△ABC绕点A逆时针旋转90°后得△ADE,点B落在点D处,点C落在点E处,联结BE、CD,作∠CAD的平分线AN,交线段BE于点M,交线段CD于点N,那么AMAN的值为23.【考点】相似三角形的判定与性质;解直角三角形;旋转的性质.【专题】三角形;等腰三角形与直角三角形;推理能力.【分析】先根据题目条件作出图象,由∠C=90°和tan A=512,设BC=5k,AC=12k,然后由旋转的性质得到AE =AC=12k,ED=BC=5k,AB=AD=13k,以点C为原点、BC和AC所在直线分别为x轴和y轴建立平面直角坐标系,则A(0,12k),B(﹣5k,0),E(12k,12k),D(12k,7k),过点N作NF⊥AC于点F,交BE于点P,NH ⊥AD于点H,得到NF=NH,得到AMCAMDAC12k==AD13kSS△△,然后由高相等的两个三角形的面积之比为底边长之比得到CNDN的值,进而用含有k的式子表示点N的坐标,再求得直线BE的解析式,然后求得点P的坐标得到NP的长,最后通过△MAE∽△MNP得到AMNM的值,即可得到AMAN的值.【解答】方法一:解:由∠C=90°和tan A=512可设BC=5k,AC=12k,∴AB=13k,由旋转得,AE=AC=12k,ED=BC=5k,AB=AD=13k,如图,以点C为原点,BC和AC所在直线分别为x轴和y轴,建立平面直角坐标系,则A(0,12k),B(﹣5k,0),∵旋转角为90°,∴E(12k,12k),D(12k,7k),过点N作NF⊥AC于点F,交BE于点P,作NH⊥AD于点H,∵AN平分∠CAD,∴NF=NH,∴AMCAMDAC12k==AD13kSS△△,又∵△ANC 在边CN 上的高和△AND 在边DN 上的高相等,∴AMC AMD CN 12==DN 13S S △△,∴点N 的坐标为(144k 25,84k 25),设直线BE 的解析式为y =mx +n ,则-5mk+01212n km n k =⎧⎨+=⎩,解得:12m 176017k n ⎧=⎪⎪⎨⎪=⎪⎩,∴直线BE 的解析式为y =1217x +6017k ,当y =8425k 时,1217x +6017k =8425k ,解得:x =﹣625k ,∴P (﹣625k ,8425k ),∴NP =144k 25﹣(﹣625k )=6k ,∵NF ⊥AC ,∠EAC =90°,∴AE ∥NP ,∴△MAE ∽△MNP ,∴126AM AE k MN NP k ===2,∴23AM AN =,方法二:解:由题可知,∠BAC =∠DAE ,∠CAM =∠MAD ,∴∠BAC +∠CAM =∠DAE +∠MAD ,∴∠BAN =∠NAE ,如图,延长AN ,交BC 的延长线于点F ,∵AE ∥BC ,∴∠EAN =∠AFC ,∴∠BAN =∠AFC ,∴BF =BA ,设BC =5,AC =12,AB =13,∴1213AE BF =,∴△AME ∽△FMB ,∴1213AM AE MF BF ==,∴1225AM AF =,延长AD 与BC 的延长线交于点H ,延长ED 与BH 交于点I ,∵DE =5,∴四边形ACIE 为正方形,∴DI =7,延长CD 与AE 延长线交于点G ,易证△EDG ∽△IDC ,∴EG DE CI DI =,即5127EG =,∴EG =607,∴AG =12+607=1447,易知,△ANG ∽△FNC ,∴AN AG NF FC =,∵BF =13,BC =5,∴CF =8,∴14418787AN NF ==,∴1825AN NF =,∵1225AM NF =,∴122183AM AN ==,故答案为:23.【点评】本题考查了旋转的性质、勾股定理、相似三角形的判定与性质、角平分线的性质定理、三角形的面积,解题的关键是通过旋转的性质建立平面直角坐标系.4.(2021秋•嘉定区期末)如图,在△ABC 中,∠C =90°,BC =2,D 在边AC 上,CD :AD =1:3,联结BD ,点E 在线段BD 上,如果∠BCE =∠A ,那么CE =52.【考点】相似三角形的判定与性质;勾股定理.【专题】图形的相似;运算能力.【分析】根据已知∠BCE =∠A ,想到构造这两个角所在的三角形相似,所以过点E 作EF ⊥BC ,垂足为F ,可得△ABC ∽△CEF ,进而可得CF =2EF ,然后设EF 为a ,则CF 为2a ,BF 为2﹣2a ,最后再证明A 字模型相似△BFE ∽△BCD ,从而解答即可.【解答】解:过点E 作EF ⊥BC ,垂足为F ,∵∠ACB =90°,BC =2,25AB =2222(25)24AC AB BC =-=-,∵CD :AD =1:3,∴CD =1,∵∠BCE =∠A ,∠ACB =∠CFE =90°,∴△ABC ∽△CEF ,∴42AC CF BC EF ===2,∴设EF 为a ,则CF 为2a ,BF 为2﹣2a ,∵∠ACB =∠BFE =90°,∠CBD =∠FBE ,∴△BFE ∽△BCD ,∴BF EF BC CD =,∴2221a a -=,∴a =12,∴EF =12,CF =1,∴CE 22215()122EF CF +=+=,故答案为:52.【点评】本题考查了相似三角形的判定与性质,勾股定理,熟练掌握A 字模型相似是解题的关键.5.(2021秋•松江区期末)如图,已知矩形ABCD 中,AD =3,AB =5,E 是边DC 上一点,将△ADE 绕点A 顺时针旋转得到△AD ′E ′,使得点D 的对应点D '落在AE 上,如果D ′E ′的延长线恰好经过点B ,那么DE 的长度等于94.【考点】旋转的性质;矩形的性质.【专题】平移、旋转与对称;推理能力.【分析】如图,连接BE 、BE ′,根据矩形的性质和旋转变换的性质可得:AD ′=AD =3,∠AD ′E =∠D =90°,利用勾股定理可得BD ′=4,再运用面积法可得:AB •AD =AE •BD ′,求出AE =,再运用勾股定理即可求得答案.【解答】解:如图,连接BE 、BE ′,∵矩形ABCD 中,AD =3,AB =5,∴∠D =90°,由旋转知,△AD ′E ′≌△ADE ,∴AD′=AD=3,∠AD′E=∠D=90°,∵D′E′的延长线恰好经过点B,∴∠AD′B=90°,在Rt△ABD′中,BD4==,∵AB•AD=AE•BD′,∴AE='5315 44AB AD BD⨯==,在Rt△ADE中,DE94 =,方法二:∵△ADE∽△BDA,∴'' DE AD AD BD=∴334DE=∴DE=94故答案为:9 4.【点评】本题考查了矩形的性质,旋转变换的性质,勾股定理,三角形面积等,解题关键是运用面积法求得AE.6、(2021秋•黄浦区期末17)如图,在△ABC中,AB=4,AC=5,将△ABC绕点A旋转,使点B落在AC边上的点D处,点C落在点E处,如果点E恰好在线段BD的延长线上,那么边BC【考点】旋转的性质;相似三角形的判定.【专题】平移、旋转与对称;推理能力.【分析】如图所示,连接CE,由旋转的性质可得:AD=AB=4,BC=DE,∠BCD=∠DEA,AE=AC=5,则CD=AC-AD=1,然后证明△BDC∽△ADE,得到BC DCAE DE=,即15BCBC=,则BC2=5,由此即可得到答案.【解答】解:如图所示,连接CE,由旋转的性质可得:AD=AB=4,BC=DE,∠BCD=∠DEA,AE=AC=5,∴CD=AC-AD=1又∵∠BDC=∠ADE∴△BDC∽△ADE,∴BC DCAE DE=,即15BCBC=,∴BC2=5,∴BC (负值已经舍去),【点评】本题主要考查了旋转的性质,相似三角形的性质与判定,熟知相似三角形的性质与判定条件是解题的关键.7.(2020秋•嘉定区期末)已知在△ABC中,∠ACB=90°,AB=10,sin A=55(如图),把△ABC绕着点C按顺时针方向旋转α°(0<α<360),将点A、B的对应点分别记为点A′,B′,如果△AA′C为直角三角形,那么点A与点B'的距离为【考点】旋转的性质;解直角三角形.【专题】分类讨论;平移、旋转与对称;几何直观.【分析】根据△AA′C为直角三角形,分两种情况:①当点B'在线段AC上时,△AA′C为直角三角形;②当点B'在线段AC的延长线上时,△AA′C为直角三角形,依据线段的和差关系进行计算即可得到点A与点B'的距离.【解答】解:分两种情况:①当点B'在线段AC上时,△AA′C为直角三角形,∵∠ACB=90°,AB=10,sin A=5 5,∴BC=AB×5=10×5=∴B'C=AC=,∴AB'=AC﹣B'C=②当点B'在线段AC的延长线上时,△AA′C为直角三角形,同理可得,B'C=AC=,∴AB'=AC+B'C=综上所述,点A与点B'的距离为故答案为:【点评】本题考查了旋转的性质,勾股定理,锐角三角函数的应用,运用分类思想是本题的关键.8.(2020秋•闵行区期末)如图,在Rt△ABC中,∠ACB=90°,AB=3,tan B=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF=3【考点】旋转的性质;解直角三角形.【专题】平移、旋转与对称;解直角三角形及其应用;运算能力;推理能力.【分析】过点F作FG⊥AC于点G,由旋转的性质得出∠B=∠D,得出tan∠B=tan∠D=12FGGD=,由平行线的性质得出∠B=∠AFG,设AG=x,则FG=2x,则2132xx=+,求出AG=1,则可得出答案.【解答】解:如图,过点F作FG⊥AC于点G,∵将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,∴∠B =∠D ,∴tan ∠B =tan ∠D =12FG GD =,∵∠ACB =∠FGA =90°,∴BC ∥FG ,∴∠B =∠AFG ,∴tan ∠B =tan ∠AFG =12AG FG =,设AG =x ,则FG =2x ,∴2132x x =+,解得x =1,∴AG =1,FG =2,∴AF 225FG AG +=∴BF =AB ﹣AF =35.故答案为:35【点评】本题考查了旋转的性质,直角三角形的性质,锐角三角函数的定义,勾股定理,熟练掌握旋转的性质是解题的关键.9.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D 的值为3135.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;几何直观.【分析】过C 作CE ⊥AB 于E ,根据勾股定理和正切的定义得到AC =213,BC =313,根据三角形面积得到CE =6,再根据旋转的性质和相似三角形的判定与性质即可求解.【解答】解:过C 作CE ⊥AB 于E ,∵tan B =23,∴23AC BC =,设AC =2x ,则BC =3x ,在Rt △ABC 中,AB=13,解得x=AC =,BC =,S △ABC =12AC •BC =12AB •CE ,即12××312×13×CE ,解得CE =6,∵tan B =CE EB =23,∴EB =9,∵将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',∴∠B =∠B ′,AC =AC ′,∵CE ⊥AB ,∴AE ′=AE =AB ﹣BE =13﹣9=4,∴A ′B =AB ﹣A ′E =9﹣4=5,∵∠A ′DB =∠CDB ′,∴△A ′DB ∽△B ′DC ,∴'CD A D =''CB A B ='CB A B..【点评】本题考查了勾股定理,解直角三角形,旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.10.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为622.【考点】旋转的性质;平行线的性质.【专题】平移、旋转与对称;推理能力.【分析】由旋转的性质和等腰三角形的性质可求∠B1AB=30°,由直角三角形的性质可求DB1=DE,DB=﹣DE,即可求解.【解答】解:如图,过点D作DE⊥AB1于E,∵∠B=45°,∠C=60°,∴∠CAB=75°,∵BB1∥AC,∴∠CAB=∠ABB1=75°,∵将△ABC绕点A旋转,∴AB=AB1,∠AB1C1=∠ABC=45°,∴∠AB1B=∠ABB1=75°,∴∠B1AB=30°,又∵DE⊥AB1,∠AB1C1=45°,∴AD=2DE,AE=DE,DE=B1E,∴AB1DE+DE=AB,DB1DE,∴DB=AB﹣ADDE﹣DE,∴1BDB D622=,故答案为:622.【点评】本题考查了旋转的性质,等腰三角形的性质,直角三角形的性质,灵活运用这些性质进行推理是本题的关键.11.(2020秋•宝山区期末)在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是边CA、CB的中点,已知点P在线段EF上,联结AP,将线段AP绕点P逆时针旋转90°得到线段DP,如果点P、D、C在同一直线上,那么tan∠CAP﹣1.【考点】旋转的性质;解直角三角形;等腰直角三角形;三角形中位线定理.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;解直角三角形及其应用;推理能力.【分析】分两种情形:①当点D在线段PC上时,延长AD交BC的延长线于H.证明AD=DC即可解决问题.②当点P在线段CD上时,同法可证:DA=DC解决问题.【解答】解:如图1,当点D在线段PC上时,延长AD交BC的延长线于H.∵CE=EA,CF=FB,∴EF∥AB,∴∠EFC=∠ABC=45°,∵∠PAO=45°,∴∠PAO=∠OFH,∵∠POA=∠FOH,∴∠H=∠APO,∵∠APC=90°,EA=EC,∴PE=EA=EC,∴∠EPA=∠EAP=∠BAH,∴∠H=∠BAH,∴BH=BA,∵∠ADP=∠BDC=45°,∴∠ADB=90°,∴BD⊥AH,∴∠DBA=∠DBC=22.5°,∵∠ADB=∠ACB=90°,∴A,D,C,B四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,则DC=AD=a,AP=PD =22a,∴PC=a +22a,∴tan∠CAP=22122a aCPAP+==;如图2中,当点P在线段CD上时,同法可证:DA=DC,设AD=a,则CD=AD=a,PD =2 2 a,∴PC=a ﹣22 a,∴tan∠CAP=22122a aCPAP+==,∵点P在线段EF上,∴情形1,不满足条件,情形2满足条件,﹣1.【点评】本题考查了旋转变换,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.12.(2020秋•奉贤区期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD是△ABC的角平分线,将Rt△ABC绕点A旋转,如果点C落在射线CD上,点B落在点E处,联结DE,那么∠AED的正切值为3 7.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】设点C落在射线CD上的点C'处,由勾股定理可求AB=5,由旋转的性质可得∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',由平行线分线段成比例可求AD的长,即可求解.【解答】解:如图,设点C落在射线CD上的点C'处,∵∠ACB=90°,AC=3,BC=4,∴AB=5,∵CD是△ABC的角平分线,∴∠ACD=∠DCB=45°,∵将Rt△ABC绕点A旋转,∴∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',∴∠CAC'=90°=∠EAB,∴AC'∥BC,∴'34AD ACDB BC==,∴AD=157,∴tan∠AED=37 ADAE=,故答案为:3 7.【点评】本题考查了旋转的性质,勾股定理,锐角三角函数,平行线的性质等知识,灵活运用这些性质解决问题是本题的关键.13.(2019秋•奉贤区期末)如图,已知矩形ABCD(AB>BC),将矩形ABCD绕点B顺时针旋转90°,点A、D分别落在点E、F处,连接DF,如果点G是DF的中点,那么∠BEG的正切值是1.【考点】旋转的性质;矩形的性质.【专题】平移、旋转与对称;应用意识.【分析】连接BD,BF,EG.利用四点共圆证明∠BEG=∠BFD=45°即可.【解答】解:连接BD,BF,EG.由题意:BD=BF,∠DBF=90°,∵DG=GF,∴BG⊥DF,∴∠BGF=∠BEF=90°,∴B,G,E,F四点共圆,∠BEG=∠BFD=45°,∴∠BEG的正切值是1.故答案为1.【点评】本题考查旋转变换,等腰直角三角形的判定和性质,四点共圆,锐角三角函数等知识,解题的关键是学会添加常用辅助线解决问题,属于中考常考题型.14.(2019秋•浦东新区期末)在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D'、E',当直线D'E'经过点A时,线段CD'的长为【考点】三角形综合题.【专题】图形的全等;等腰三角形与直角三角形;矩形菱形正方形;图形的相似;推理能力.【分析】分两种情况:①点A在E'D'的延长线上时;②点A在线段D'E'的延长线上时;然后分类讨论,求出线段BD的长各是多少即可.【解答】解:如图1,当点A 在E 'D '的延长线上时,∵∠C =90°,AC =2,BC =4,∴AB ==2,∵点D 、E 分别是边BC 、AB 的中点,∴DE ∥AC ,DE =12AC =1,BD =12BC =2,∴∠EDB =∠ACB =90°,∵将△BDE 绕着点B 旋转,∴∠BD 'E '=∠BDE =90°,D 'E '=DE =1,BD =BD '=2,∵在Rt △ABC 和Rt △BAD '中,D 'B =AC =2,AB =BA ,∴Rt △ABC ≌Rt △BAD '(HL ),∴AD '=BC ,且AC =D 'B ,∴四边形ACBD '是平行四边形,且∠ACB =90°,∴四边形ACBD '是矩形,∴CD '=AB =如图2,当点A 在线段D 'E '的延长线上时,∵∠AD 'B =90°,∴AD '==4,∴AE '=AD '﹣D 'E '=3,∵将△BDE 绕着点B 旋转,∴∠ABC =∠E 'BD ',∵'12BE AB ==BD BC ,∴△ABE '∽△CBD ',∴''AE AB CD BC=,∴'3254CD =,∴CD '故答案为:.【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,矩形的判定和性质,勾股定理等知识,解题的关键是理解题意,正确寻找相似三角形解决问题,属于中考常考题型.15.(2019秋•长宁、金山区期末)如图,在Rt △ABC 中,∠ABC =90°,AB =2,BC =4点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于5.【考点】旋转的性质;相似三角形的判定与性质.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,延长AB'交BC于E,过点B'作B'D⊥AB于点D,由勾股定理可求AC的长,由旋转的性质可求AP=AM,∠PAB=∠CAE,AB=AB'=2,通过证明△ABP∽△CBA,可得∠PAB=∠C,可得CE=AE,由勾股定理可求CE,BE的长,由相似三角形的性质可求B'D,BD的长,即可求解.【解答】解:如图,延长AB'交BC于E,过点B'作B'D⊥AB于点D,∵∠ABC=90°,AB=2,BC=4,∴AC==∵点M是AC中点,∴AM∵将△ABP绕着点A旋转,使得点P与边AC的中点M重合,∴AP=AM,∠PAB=∠CAE,AB=AB'=2,∵AP2=AB2+PB2,∴PB=1,∵BAPB=2=BCAB,且∠ABP=∠ABC=90°,∴△ABP∽△CBA,∴∠PAB=∠C,∴∠C=∠CAE,∴CE=AE,∵AE2=AB2+BE2,∴CE2=4+(4﹣CE)2,∴CE=AE=52,∴BE=32,∵B'D∥BC,∴△AB'D∽△AEB,∴''AB AD B DAE AB BE==,∴'253222AD B D==,∴AD=85,B'D=65,∴BD=25,∴BB'=2105,故答案为:2105.【点评】本题考查了旋转的性质,相似三角形的判定和性质,等腰三角形的性质,勾股定理等知识,求出CE 的长是本题的关键.16.(2019秋•松江区期末)如图,矩形ABCD 中,AD =1,AB =k ,将矩形ABCD 绕着点B顺时针旋转90°得到矩形A ′BC ′D ′,联结AD ′,分别交边CD ,A ′B 于E 、F ,如果AED ′F ,那么k【考点】旋转的性质;相似三角形的判定与性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】由矩形的性质和旋转的性质可求AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,通过证明△ADE ∽△FA 'D ',可得''''AD DE AE A F A D D F ==,可求DE ,A 'F 的长,通过证明△A 'D 'F ∽△CEF ,由相似三角形的性质可求解.【解答】解:∵将矩形ABCD 绕着点B 顺时针旋转90°得到矩形A ′BC ′D ′,∴AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,∴A 'D '∥BA ∥CD∴∠A 'D 'F =∠FEC =∠DEA ,且∠D =∠A '=90°,∴△ADE ∽△FA 'D ',∴''''AD DE AE A F A D D F==,且AED ′F ,∴DEA 'D ',A 'FAD=2,∵∠A '=∠DCF =90°,∠A 'FD '=∠EFC ,∴△A 'D 'F ∽△CEF ,∴'''EC FC A D A F =,∴''21222k k A D ---=∴k+1,+1.【点评】本题考查了旋转的性质,矩形的性质,相似三角形的判定和性质,利用相似三角形的性质求DE ,A 'F 的长是本题的关键.17.(2019秋•嘉定区期末)在△ABC中,∠ACB=90°,AB=10,cos A=35(如图),把△ABC绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点A'、B'.如果A'B'恰好经过点A,那么点A与点A'的距离为36 5.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】如图,过点C作CE⊥A'B',由锐角三角函数可求AC=6,由旋转的性质可得AC=A'C=6,∠A'=∠BAC,即可求A'E的长,由等腰三角形的性质可求AA'的长.【解答】解:如图,过点C作CE⊥A'B',∵在△ABC中,∠ACB=90°,AB=10,cos∠BAC=35,∴AC=6,∵把△ABC绕着点C按照顺时针的方向旋转,∴AC=A'C=6,∠A'=∠BAC,∵cos∠A'=cos∠BAC==35,∴A'E=185,∵AC=A'C,CE⊥A'B',∴AA'=2A'E=36 5,故答案我:36 5.【点评】本题考查了旋转的性质,等腰三角形的性质,锐角三角函数的应用,求出A'E的长是本题的关键.18.(2019秋•徐汇区期末)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是25 8.【考点】旋转的性质;相似三角形的性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC ,由勾股定理可求AC =5,由面积法可求BF =125,由勾股定理可求AF =95,由旋转的性质可得AB =BA ',∠BAD =∠BA 'D '=90°,可求CA '=75,由等腰三角形的性质可求HC 的长,通过证明△EHC ∽△ABC ,可得EC BC HC AC =,可求EC 的长,即可求解.【解答】解:如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC,∵AB =3,AD =4,∠ABC =90°,∴AC ===5,∵S △ABC =12AB ×BC =12AC ×BF ,∴3×4=5BF ,∴BF =125∴AF 22144925AB BF -=-95,∵将矩形ABCD 绕着点B 顺时针旋转后得到矩形A 'BC 'D ',∴AB =BA ',∠BAD =∠BA 'D '=90°,且BF ⊥AC ,∴∠BAC =∠BA 'A ,AF =A 'F =95,∠BA 'A +∠EA 'C =90°,∴A 'C =AC ﹣AA '=75,∵∠BA 'A +∠EA 'C =90°,∠BAA '+∠ACB =90°,∴∠ACB =∠EA 'C ,∴A 'E =EC ,且EH ⊥AC ,∴A 'H =HC =12A 'C =710,∵∠ACB =∠ECH ,∠ABC =∠EHC =90°,∴△EHC ∽△ABC ,∴BC HC AC EC =∴74105EC =∴EC =78,∴BE =BC ﹣EC =4﹣78=258,故答案为:258.【点评】本题考查了旋转的性质,矩形的性质,勾股定理,等腰三角形的性质,相似三角形的判定和性质,求出HC 的长是本题的关键.19.(2019秋•普陀区期末)如图,在RtΔABC 中,∠C=90°,AC=5,sinB=513,点P 为边BC 上一点,PC=3,将△ABC 绕点P 旋转得到△A'B'C'(点A ,B 、C 分别与点A'、B'、C'对应).使B'C'∥AB ,边A'C'与边AB 交于点G ,那么A'G 的长等于2013.【考点】旋转的性质;解直角三角形;平行线的判定,图形的旋转【专题】矩形菱形正方形;平移,旋转与对称;解直角一角形及其应用;应用意识。
2024年湖南省各地市中考数学一模压轴题精选(含解析)

2024年湖南省各地市中考数学一模压轴题精选温馨提示:1.本卷共50题,题目均选自2024年湖南省各地市一模试题。
2.本卷分为几何和代数两部分,解答题留有足够答题空间,试题部分可直接打印出来练习。
3.本卷难度较大,适合基础较好的同学。
第一部分代数部分1.(2024·湖南省衡阳市珠晖区·一模)已知三角形的两条边分别是3和8,第三边是方程x2−13x+42=0的根,则这个三角形的周长为( )A. 17或18B. 17C. 18D. 不能确定2.(2024·湖南省长沙市长沙县·一模)对于二次函数y=x2−12x+42,有以下结论:①当x>5时,y随x的增大而增大;②当x=6时,y有最小值6:③图象与x轴有两个交点;④图象是由抛物线y=x2向左平移6个单位长度,再向上平移6个单位长度得到的.其中结论错误的有( )A. ①②③B. ①③④C. ②③④D. ①②③④3.(2024·湖南省益阳市·一模)在日常生活中如取款、上网等都需要密码,有一种用“因式分解”法产生的密码记忆方便.原理是:如对于多项式x4−y4,因式分解的结果是(x−y)(x+y)(x2+y2),若取x=9,y=9,则各个因式的值是:x−y=0,x+y=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式x3−xy2,取x=50,y=20,用上述方法产生的密码不可能是( )A. 503070B. 507030C. 307040D. 7030504.(2024·湖南省常德市·一模)将抛物线y=−x2+2x+3中x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分不变,得到的新图象与直线y=x+m有4个交点,则m的取值范围是( )A. m≤−5B. −214≤m<−5 C. −214<m<−3 D. m≥−35.(2024·湖南省株洲二中·一模)若一个点的坐标满足(k,2k),我们将这样的点定义为“倍值点”.若关于x的二次函数y=(t+1)x2+(t+2)x+s(s,t为常数,t≠−1)总有两个不同的倍值点,则s的取值范围是( )A. s<−1B. s<0C. 0<s<1D. −1<s<06.(2024·湖南省株洲市石峰区·一模)如图,一次函数y 1=k 1x +b 的图象与反比例函数y 2=k2x (k 2>0)的图象交于点A(4,n)与点B(−1,−4).连接BO 并延长交反比例函数于另一点C ,过点C 作y 轴的平行线交直线AB 于点D ,连接OD ,则CD 的长为( )A. 3B. 6C. 8D. 107.(2024·湖南省益阳市大通湖区·一模)如图所示,已知二次函数y =ax 2+bx +c 的图象与x 轴交于A ,B 两点,与y 轴交于点C ,OA =OC ,对称轴为直线x =1,则下列结论:①abc <0;②a +12b +14c =0;③ac −b +1=0;④2+c 是关于x 的一元二次方程ax 2+bx +c =0的一个根.其中正确的有( )A. 1个B. 2个C. 3个D. 4个8.(2024·湖南省益阳市大通湖区·一模)如图,二次函数y =ax 2+bx +c 的图象经过点(3,0),对称轴为直线x =1,下列结论:①abc >0;②9a −3b +c =0;③3b +2c =0;④若A(a +1,y 1),B(a +2,y 2)两点在该二次函数的图象上,则y 1−y 2<0.其中正确的有( )A. 1个B. 2个C. 3个D. 4个9.(2024·湖南省张家界市桑植县·一模)已知二次函数y =ax 2−2ax +c(a ≠0)的图象与x 轴的一个交点为(−2,0),则关于x 的一元二次方程ax 2−2ax +c =0的两根之积是______.10.(2024·湖南省株洲市石峰区·一模)反比例函数y =−6x 的图象与直线y =kx(k <0)相交于A(x 1,y 1),B(x 2,y 2)两点,则x 1y 2+x 2y 1的值是______.11.(2024·湖南省常德市·一模)已知a ,b ,c 满足a −2b =c ,b +c =−4a ,则二次函数y =ax 2+bx +c(a ≠0)的图象的对称轴为直线______.12.(2024·湖南省益阳市大通湖区·一模)如图,△OAC 和△BAD 都是等腰直角三角形,∠ACO =∠ADB =90°,反比例函数y =6x 在第一象限的图象经过点B ,则OA 2−AB 2=______.13.(2024·湖南省长沙市长沙县·一模)如图,已知一次函数y =kx +b 的图象经过点P(4,6),与反比例函数y =2x的图象在第一象限交于点Q(m,n).若一次函数y 的值随x 值的增大而增大,则m 的取值范围是______.14.(2024·湖南省株洲市石峰区·一模)如图,直线y =13x +4与反比例函数y =k x(x >0)的图象交于点A ,与y 轴正半轴交于点B ,过点A 作x 轴的垂线,垂足为点C ,已知OB :OC =4:3,则k 的值为______.15.(2024·湖南省株洲市石峰区·一模)已知直线l:y=kx+b(k≠0)与双曲线y=−1x交于点A(m1,n1),B(m2, n2).(1)若m1+m2=0,则n1+n2=______;(2)若m1+m2>0时,n1+n2>0,则k______0,b______0(填“>”“=”或“<”).16.(2024·湖南省张家界市桑植县·一模)已知关于x的一元二次方程x2−(2m−1)x−3m2+m=0.(1)求证:无论m为何值,方程总有实数根;(2)若x1,x2是方程的两个实数根,且x2x1+x1x2=−52,求m的值.17.(2024·湖南省张家界市桑植县·一模)某校运动会需购买A,B两种奖品,若购买A种奖品2件和B种奖品1件,共需35元;若购买A种奖品1件和B种奖品2件,共需40元.(1)求A、B两种奖品的单价各是多少元?(2)学校计划购买A,B两种奖品共100件,购买费用不超过1135元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.(x>0)经过点B交CD于点E,延长OB至点C.使OB=BC,过点C作CD//BA交x轴于点D,反比例函数y1=k1x(x>0)经过点C.反比例函数y2=k2x(1)求反比例函数y1,y2的解析式;(2)连接BE,BD,计算△BED的面积.(k>0)的图象交于点A(1,m),19.(2024·湖南省衡阳市珠晖区·一模)如图,直线y=2x+6与反比例函数y=kx与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.(1)求m的值和反比例函数的解析式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?(k>0,x>0)的图象经过点D,上,OA=4,OC=2,点D是BC边上的动点(不与B,C重合),反比例函数y=kx且与AB交于点E,连接OD,OE,DE.(1)若点D的横坐标为1.①求k的值;②点P在x轴上,当△ODE的面积等于△ODP的面积时,试求点P的坐标;(2)延长ED交y轴于点F,连接AC,判断四边形AEFC的形状,并说明理由.x+c的图象与x轴交于点A(3,0),与y轴交于点B(0,−21.(2024·湖南省常德市·一模)如图,二次函数y=ax2−432).(1)求二次函数的解析式;(2)若点P为抛物线上一动点(直线AB上方),且S△PBA=4,求点P的坐标.22.(2024·湖南省益阳市大通湖区·一模)如图,已知抛物线y=ax2+bx+3与x轴交于A(−1,0)、B(3,0)两点,与y轴交于点C,连接BC.(1)求抛物线的解析式;(2)若点P为线段BC上的一动点(不与B、C重合),PM//y轴,且PM交抛物线于点M,交x轴于点N,当△BCM 的面积最大时,求点P的坐标.23.(2024·湖南省永州市祁阳市·一模)已知:抛物线C1:y=ax2+bx+c(a>0).(1)若顶点坐标为(1,1),求b和c的值(用含a的代数式表示);(2)当c<0时,求函数y=−2024|ax2+bx+c|−1的最大值;(3)若不论m为任何实数,直线y=m(x−1)−m2与抛物线C1有且只有一个公共点,求a,b,c的值;此时,若4k≤x≤k+1时,抛物线的最小值为k,求k的值.x2+bx+c与x轴交于A,24.(2024·湖南省长沙市长沙县·一模)如图,在平面直角坐标系中,已知抛物线y=12B两点,与y轴交于C点,且OB=OC=2OA.(1)求该抛物线的解析式;(2)抛物线上是否存在点M,使∠ABC=∠BCM,如果存在,求点M的坐标,如果不存在,说明理由;(3)若点D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A,B,D的圆与DF交于点E,连接AE,BE,求△ABE的面积.25.(2024·湖南省株洲二中·一模)如图所示,抛物线y=x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,−3),其对称轴x=1与x轴相交于点D,点M为抛物线的顶点.(1)求抛物线的表达式.(2)若直线CM交x轴于点E,求证:BC=EC.(3)若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与△ABC相似.若存在,求出点P的坐标;若不存在,请说明理由.26.(2024·湖南省长沙市望城区·一模)如图,二次函数y=x2+bx+c的对称轴是直线x=1,图象与x轴相交于点A(−1,0)和点B,交y轴于点C.(1)求此二次函数的解析式;(2)点P是对称轴上一点,当△BOC∽△APB时,求点P的坐标(请在图1中探索);(3)二次函数图象上是否存在点M,使△ABC的面积S1与△ABM的面积S2相等?若存在,请求出所有满足条件的点M的坐标;若不存在,请说明理由(请在图2中探索).27.(2024·湖南省长沙市望城区·一模)定义:在平面直角坐标系xOy 中,当点N 在图形M 的内部,或在图形M 上,且点N 的横坐标和纵坐标相等时,则称点N 为图形M 的“梦之点”.(1)如图①,矩形ABCD 的顶点坐标分别是A(−1,2),B(−1,−1),C(3,−1),D(3,2),在点N 1(1,1),N 2(2,2),N 3(3,3)中,是矩形ABCD “梦之点”的是______;(2)如图②,已知点A ,B 是抛物线y =−12x 2+x +92上的“梦之点”,点C 是抛物线的顶点.连接AC ,AB ,BC ,判断△ABC 的形状并说明理由.(3)在(2)的条件下,点P 为抛物线上一点,点Q 为平面内一点,是否存在点P 、Q ,使得以AB 为对角线,以A 、B 、P 、Q 为顶点的四边形是菱形?若存在,求出P 点坐标;若不存在,请说明理由.28.(2024·湖南省怀化市·一模)如图1,在平面直角坐标系中,抛物线y=−x2+bx+c与x轴交于A,B两点(点A 在点B的左侧),与y轴交于点C,OB=OC=5,顶点为D,对称轴交x轴于点E.(1)求抛物线的解析式、对称轴及顶点D的坐标;(2)如图2,点Q为抛物线对称轴上一动点,当Q在什么位置时QA+QC最小,求出Q点的坐标,并求出此时△QAC的周长;(3)如图3,在对称轴左侧的抛物线上有一点M,在对称轴右侧的抛物线上有一点N,满足∠MDN=90°.求证:直线MN恒过定点,并求出定点坐标.29.(2024·湖南省益阳市大通湖区·一模)已知抛物线y=a(x+2)(x−4)(a为常数,且a<0)与x轴交于A,B两点x+b与抛物线的另一交点为点D,与y轴的交点为(点A在点B的右侧),与y轴交于点C,经过点B的直线y=12点E.(1)如图1,若点D的横坐标为3,试求抛物线的函数表达式;(2)如图2,若DE=BE,试确定a的值;(3)如图3,在(1)的情形下,连接AC,BC,点P为抛物线在第一象限内的点,连接BP交AC于点Q,当S△APQ−S△BCQ取最大值时,试求点P的坐标.第二部分几何部分30.(2024·山东省济南市·一模)如图,AB为⊙O的直径,C为⊙O上一点,过点C作CD⊥AB交⊙O于点D,交AB于点E,连接AC,BD,过点C作CF⊥BD于点F,交AB于点G,若CD=8,OG=1,则⊙O的半径为( ) A. 4B. 133C. 265D. 631.(2023·湖南省益阳市大通湖区·一模)如图,⊙O是等边△ABC的外接圆,点D是弧AC上一动点(不与A,C 重合),下列结论:①∠ADB=∠BDC;②DA=DC;③当DB最长时,DB=2DC;④DA+DC=DB,其中一定正确的结论有( )A. 1个B. 2个C. 3个D. 4个32.(2024·湖南省常德市·一模)如图,AC与⊙O相切于点C,线段AO交⊙O于点B.过点B作BD//AC交⊙O 于点D,连接CD,OC,且OC交DB于点E.若∠CDB=30°,DB=23cm.则图中阴影部分的面积为______.33.(2024·湖南省益阳市大通湖区·一模)如图,正方形ABCD的边长为16,线段CE绕着点C逆时针方向旋转,AM,当线段FM的长最小时,且CE=6,连接BE,以BE为边作正方形BEFG,M为AB边上的点,且BM=13tan∠ECB=______.34.(2024·湖南省永州市祁阳市·一模)如图,在矩形ABCD中,连接BD,分别以B,D为圆心,大于1BD的长为2半径画弧,两弧交于P,Q两点,作直线PQ,分别与AD,BC交于点M,N,连接BM,DN.若AD=6,AB=3.则四边形MBND的周长为______.35.(2024·湖南省长沙市望城区·一模)如图,在△ABC中,∠ACB=90°,AC=BC=3,以BC为直径作半圆O,过点A作半圆O的切线,切点为D,过点D作DE//BC交BC于点E,则DE=______.36.(2024·四川省内江市·一模)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=7,F为DE的中点,若△CEF的周长为32,则OF的长为______.37.(2024·湖南省衡阳市珠晖区·一模)如图,在△ABC中,AC=BC,∠ACB=90°,以点A为圆心,AB长为半的值为______.径画弧,交AC延长线于点D,过点C作CE//AB,交BD于点E,连接BE,则CEBE38.(2024·衡阳市珠晖区·一模)如图,点D在以AB为直径的⊙O上,AD平分∠BAC,DC⊥AC,过点B作⊙O的切线交AD的延长线于点E.(1)求证:直线CD是⊙O的切线.(2)求证:CD⋅BE=AD⋅DE.39.(2024·湖南省怀化市·一模)如图,在圆内接四边形ABCD中,AB=BC,AD=CD,四边形ABCD的对角线AC,BD交于点E.(1)求∠BCD的度数;(2)过点C作CF//AD交AB的延长线于点F,若∠ABC=120°,求证:CF是圆的切线.40.(2024·湖南省永州市祁阳市·一模)如图,以AB为直径的⊙O上有两点E,F,E是BF弧的中点,过点E作直线CD⊥AF交AF的延长线于点D,交AB的延长线于点C,过C作CM平分∠ACD交AE于点M,交BE于点N.(1)求证:CD是⊙O的切线;(2)求证:EM=EN;(3)如果N是CM的中点,且AB=75,求EN的长.41.(2024·湖南省常德市·一模)如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作⊙A,交AB 于点D,交CA延长线于点E,BF是⊙A的切线,连接EF,DF.(1)求证:EF//AB;(2)若⊙A的半径为2,当四边形ADFE为菱形时,求BF的长.42.(2024·湖南省长沙市望城区·一模)如图,AB为⊙O的直径,C为⊙O上一点,连接CB,过C作CD⊥AB于点D,过C作∠DCE,使∠DCE=2∠BCD,其中CE交AB的延长线于点E.(1)求证:CE是⊙O的切线;(2)如图2,点F是⊙O上一点,且满足∠FCE=2∠ABC,连接AF并延长交EC的延长线于点G.①试探究线段CF与CD之间满足的数量关系;②若CD=4,tan∠BCE=1,求线段AF的长.243.(2024·湖南省株洲二中·一模)如图,已知AB是⊙O的直径,直线DC是⊙O的切线,切点为C,AE⊥DC,垂足为E.连接AC.(1)求证:AC平分∠BAE;(2)若AC=5,tan∠ACE=3,求⊙O的半径.444.(2024·湖南省长沙市长沙县·一模)定义:对角线互相垂直的圆内接四边形叫做圆的“奇妙四边形”.(1)若▱ABCD是圆的“奇妙四边形”,则▱ABCD是______(填序号);①矩形;②菱形;③正方形(2)如图1,已知⊙O的半径为R,四边形ABCD是⊙O的“奇妙四边形”.求证:AB2+CD2=4R2;(3)如图2,四边形ABCD是“奇妙四边形”,P为圆内一点,∠APD=∠BPC=90°,∠ADP=∠PBC,BD=4,且AB=3DC,当DC的长度最小时,求APDP的值.45.(2024·湖南省张家界市桑植县·一模)如图,⊙O的直径AB垂直于弦CD于点E,AB=10,CD=6,点P是CD延长线上异于点D的一个动点,连结AP交⊙O于点Q,连结CQ交AB于点F,则点F的位置随着点P位置的改变而改变.(1)如图1,当DP=4时,求tan∠P的值;(2)如图2,连结AC,DQ,在点P运动过程中,设DP=x,S△QACS△QDC=y.①求证:∠ACQ=∠CPA;②求y与x之间的函数关系式.46.(2024·湖南省长沙市望城区·一模)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M是线段DC延长线上的一点,连结MA交⊙O于点F,连结DF交AB于点G,连结AD,BD,CF.(1)求证:△MAD∽△DAF.(2)若AD=25BE,求tan∠AFD的值.(3)在(2)的条件下,设tan∠M=x,AG=y.GB①求y关于x的函数表达式;②若E为BG的中点,求S△CFD的值.S△AFD47.(2024·湖南省益阳市大通湖区·一模)已知:如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.(1)求证:四边形ABGE是菱形;(2)若∠ABC=60°,AB=4,AD=5,求CF的长.48.(2024·湖南省长沙市长沙县·一模)如图1,在矩形ABCD中,已知AB=3,BC=4,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.点B与点B′关于直线AF对称,延长AB′交CD于点M,连接B′E.(1)求证:AM=FM;(2)如图2,若点B′恰好落在对角线AC上,求tan∠F的值;(3)若BECE =53,求线段AM的长.49.(2024·湖南省常德市·一模)已知Rt△ABC,∠ACB=90°,∠BAC=30°,D是AC边上一点,过点D作DE⊥AB于点E,连接BD,F是BD中点,连接EF,CF.(1)如图①,线段EF,CF之间的数量关系为______,∠EFC的度数为______;(2)如图②,将△AED绕点A按顺时针方向旋转α(0°<α<30°),请判断线段EF,CF之间的数量关系及∠EFC 的度数,并说明理由;(3)在△AED绕点A旋转的过程中,当点D落到直线AB边上时,连接BE,若BC=3,AD=2,请直接写出BE 的长度.50.(2024·湖南省怀化市·一模)已知正方形ABCD和正方形EFGH按图1所示叠放在一起,其中AB=4,EF=2,点O为AB和EF的中点.(1)图2中正方形EFUV为图1中正方形EFGH关于直线AB的轴对称图形,求点D和点U的连结线段DU的长度;(2)将图1中的正方形EFGH绕点O旋转,如图3所示,求运动过程中点D和点G之间距离的最大值和最小值.参考答案1.【答案】A【解析】解:∵三角形的两条边分别是3和8,设第三边为a,∴8−3<a<6+3,即5<a<11,解方程x2−13x+42=0,得:x1=6,x2=7,∴该方程的两个根都在a的取值范围内,∴当x=6时,该三角形的周长为:3+8+6=17,当x=7时,该三角形的周长为:3+8+7=18.故选:A.首先设第三边为a,根据三角形三边之间的关系得5<a<11,再解方程x2−13x+42=0,得:x1=6,x2=7,由此可得出该三角形的周长.此题主要考查了三角形三边之间的关系,解一元二次方程,三角形的周长等,理解三角形三边之间的关系,熟练掌握解一元二次方程是解决问题的关键.2.【答案】B【解析】解:∵二次函数y=x2−12x+42=(x−6)2+6,∴该函数的对称轴为直线x=6,函数图象开口向上,当5<x<6时,y随x的增大而减小,当x>6时,y随x的增大而增大,故①符合题意;当x=6时,y有最小值6,故②不符合题意;当y=0时,无实数根,即图象与x轴无交点,故③符合题意;图象是由抛物线y=x2向右平移6个单位长度,再向上平移6个单位长度得到的,故④符合题意;故选:B.将题目中的函数解析式化为顶点式,然后根据二次函数的性质,可以判断各个小题中的结论是否正确,从而可以解答本题.本题考查抛物线与x轴的交点,二次函数的性质、二次函数图象与几何变换,解答本题的关键是明确题意,利用二次函数的性质解答.3.【答案】C【解析】解:∵x3−xy2=x(x2−y2)=x(x+y)(x−y),∵x=50,y=20,则各个因式的值为x=50,x+y=70,x−y=30,∴产生的密码不可能是307040,故选:C.先提公因式x,然后根据平方差公式因式分解,进而代入字母的值即可求解.本题主要考查提公因式法分解因式、平方差公式分解因式,熟记公式结构是解题的关键.4.【答案】C【解析】解:令y=0,则−x2+2x+3=0,解得x1=−1,x2=3,∴抛物线与x轴的交点为(−1,0)、(3,0),∵将抛物线y=−x2+2x+3中x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分不变,∴新图象中当−1≤x≤3时,解析式为y=x2−2x−3,如图,当直线y=x+m.经过(3,0)时,此时直线y=x+m与新函数图象有3个交点,把(3,0)代入直线y=x+m,解得m=−3,直线y=x+m再向下平移时,有4个交点;当y=x2−2x−3与直线y=x+m有一个交点时,此时直线y=x+m与新函数图象有3个交点,联立方程组{y=x+my=x2−2x−3,整理得x2−3x−3−m=0,∴Δ=b2−4ac=21+4m=0,,解得m=−214<m<−3.综上所述,新图象与直线y=x+m有4个交点时,m的取值范围是−214故选:C.先求出抛物线y=−x2+2x+3与x轴的交点坐标,再根据抛物线y=−x2+2x+3中x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分不变,得到的新图象的解析式为y=x2−2x−3(−1≤x≤3),画出图象,结合图象求出满足题意的m的取值范围.本题考查了二次函数图象与几何变换,二次函数图形上点的坐标特征,正确的理解题意是解题的关键.5.【答案】D【解析】解:将(k,2k)代入二次函数,得2k=(t+1)k2+(t+2)k+s,整理得(t+1)k2+tk+s=0.∵(t+1)k2+tk+s=0是关于k的二次方程,总有两个不同的实根,∴Δ=t2−4s(t+1)>0.令f(t)=t2−4s(t+1)=t2−4st−4s∵f(t)>0,∴Δ=(4s)2+16s=16s2+16s<0,即Δ=s(s+1)<0,解得−1<s<0.故选:D.根据根与系数的关系解答即可.本题主要考查二次函数图象上点的坐标特征.根与系数的关系是二次函数部分非常重要的关系式,这里进行了反复运用,一定要牢牢掌握并灵活运用.6.【答案】B(k2>0)的图象交于点A(4,n)与点B(−1,−4),【解析】解:∵反比例函数y2=k2x∴k2=4n=−1×(−4),∴k2=4,n=1,∴A(4,1),把A、B的坐标代入y1=k1x+b得{4k1+b=1−k1+b=−4,解得{k1=1b=−3,∴直线AB为y=x−3,∵B(−1,−4),∴C(1,4),∵CD//y轴,∴D(1,−2),∴CD=4+2=6,故选:B.利用待定系数法求得反比例函数的解析式即可求得点A的坐标,进一步求得直线AB的解析式,利用反比例函数的中心对称性求得C 的坐标,即可求得D 点的坐标,从而求得CD 的长度.本题是反比例函数与一次函数的交点问题,考查了待定系数法求函数的解析式,反比例函数图象上点的坐标特征,反比例函数的对称性,求得直线AB 的解析式以及C 点的坐标是解题的关键.7.【答案】C【解析】解:∵抛物线开口向下,∴a <0,∵抛物线的对称轴为直线x =−b 2a=1,∴b =−2a >0,∵抛物线与y 轴的交点在x 轴上方,∴c >0,∴abc <0,所以①正确;∵点A 到直线x =1的距离大于1,∴点B 到直线x =1的距离大于1,即点B 在(2,0)的右侧,∴当x =2时,y >0,即4a +2b +c >0,∴a +12b +14c >0,所以②错误;∵C (0,c ),OA =OC ,∴A (−c ,0),∴ac 2−bc +c =0,即ac −b +1=0,所以③正确;∵点A 与点B 关于直线x =1对称,∴B (2+c ,0),∴2+c 是关于x 的一元二次方程ax 2+bx +c =0的一个根,所以④正确.故选:C .利用抛物线开口方向得到a <0,利用对称轴方程得到b =−2a >0,利用抛物线与y 轴的交点位置得到c >0,则可对①进行判断;利用对称性可判断点B 在(2,0)的右侧,则当x =2时,4a +2b +c >0,则可对②进行判断;利用C (0,c ),OA =OC 得到A (−c ,0),把A (−c ,0)代入抛物线解析式可对③进行判断;利用抛物线的对称性得到B (2+c ,0),则根据抛物线与x 轴的交点问题可对④进行判断.本题考查了二次函数图象与系数的关系:二次项系数a 决定抛物线的开口方向和大小.当a >0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时,对称轴在y轴左;当a与b异号时,对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由判别式确定:△=b2−4ac>0时,抛物线与x轴有2个交点;△=b2−4ac=0时,抛物线与x轴有1个交点;△=b2−4ac<0时,抛物线与x轴没有交点.8.【答案】B【解析】解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x=1,∴−b=1,2a∴b=−2a<0,∵抛物线与y轴的交点在y轴的负半轴,∴c<0,∴abc>0,所以①正确;∵抛物线与x轴的一个交点坐标为(3,0),对称轴为直线x=1,∴抛物线与x轴的一个交点坐标为(−1,0),∴当x=−3时,y>0,∴9a−3b+c>0,所以②错误;∵x=−1时,y=0,∴a−b+c=0,而b=−2a,∴a+2a+c=0,即c=−3a,∴3b+2c=−6a−6a=−12a<0,所以③错误;∵a>0,∴A(a+1,y1),B(a+2,y2)两点在对称轴的右侧,而a+1<a+2,∴y1<y2,即y1−y2<0,所以④正确.故选:B.利用抛物线开口方向得到a>0,利用对称轴方程得到b=−2a<0,利用抛物线与y轴的交点在y轴的负半轴得到c<0,则可对①进行判断;根据抛物线的对称性得到抛物线与x轴的一个交点坐标为(−1,0),则当x=−3时,y>0,所以9a−3b+c>0,从而可对②进行判断;由于x=−1时,y=0,则a−b+c=0,利用b=−2a得到c=−3a,所以3b+2c=−12a<0,则可对③进行判断;由于a>0,所以A(a+1,y1),B(a+2,y2)两点在对称轴的右侧,然后根据二次函数的性质可对④进行判断.本题考查了二次函数与不等式(组):利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,从而比较两函数值的大小确定不等式的解集.也考查了二次函数的性质.9.【答案】−8=1,【解析】解:∵二次函数y=ax2−2ax+c的对称轴为直线x=−−2a2a二次函数的图象与x轴的一个交点为(−2,0),∴二次函数的图象与x轴的另一个交点为(4,0),∴关于x的一元二次方程ax2−2ax+c=0的两根为x1=−2,x2=4,∴关于x的一元二次方程ax2−2ax+c=0的两根之积为−8.故答案为:−8.先利用抛物线的对称轴方程得到二次函数y=ax2−2ax+c的对称轴为直线x=1,则利用抛物线的对称性得到二次函数的图象与x轴的另一个交点为(4,0),然后根据抛物线与x轴的交点问题得到关于x的一元二次方程ax2−2ax+c=0的两根为x1=−2,x2=4,从而得到关于x的一元二次方程ax2−2ax+c=0的两根之积.本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.10.【答案】12【解析】解:∵A(x1,y1),B(x2,y2)两点关于原点对称,∴x1=−x2,y1=−y2,把A(x1,y1)代入反比例函数解析式得:x1⋅y1=−6,∴x1y2+x2y1=−x1y1−x2y2=6+6=12.故答案为:12.根据反比例函数图象上点的坐标特征解答即可.本题考查了反比例函数图象上点的坐标特征,熟练掌握得到坐标特征是关键.11.【答案】x=−52【解析】解:由题意,∵a−2b=c,b+c=−4a,∴c=−4a−b=a−2b.∴5a=b.∴二次函数y=ax2+bx+c(a≠0)的图象的对称轴为直线x=−b2a =−5a2a=−52.故答案为:x=−52.依据题意,由a−2b=c,b+c=−4a,从而可得c=−4a−b=a−2b,进而可得5a=b,再结合抛物线的对称轴是直线x=−b2a进行计算可以得解.本题主要考查了二次函数的图象与性质,解题时要熟练掌握二次函数的对称轴为直线x=−b2a是关键.12.【答案】12【解析】解:设OC=a,BD=b,则点A的坐标为(a,a),点B的坐标为(a+b,a−b).∵反比例函数y=6x在第一象限的图象经过点B,∴(a+b)(a−b)=6,即a2−b2=6,∴OA2−AB2=2a2−2b2=2(a2−b2)=12.故答案为:12.设OC=a,BD=b,则点A的坐标为(a,a),点B的坐标为(a+b,a−b),利用反比例函数图象上点的坐标特征可得出a2−b2=6,再由勾股定理可得出OA2−AB2=2a2−2b2=12,此题得解.本题考查了反比例函数图象上点的坐标特征、等腰直角三角形以及勾股定理,利用反比例函数图象上点的坐标特征找出a2−b2=6是解题的关键.13.【答案】13<m<6【解析】解:过点P作PA//x轴,交双曲线于点A,过点P作PB//y轴,交双曲线于点B,如图,∵P(4,6),反比例函数y=2x,∴A (13,6),B (4,12).∵一次函数y 的值随x 值的增大而增大,∴点Q (m ,n )在A ,B 之间,∴13<m <6.故答案为:13<m <6.过点P 分别作x 轴,y 轴的平行线,与双曲线分别交于点A ,B ,利用解析式分别求得A ,B 坐标,依据题意确定点Q 的移动范围,从而得出结论.本题主要考查了反比例函数与一次函数图象的交点问题,待定系数法,反比例函数的性质,一次函数的性质,一次函数图象上点的坐标的特征,确定点Q 的移动范围是解题的关键.14.【答案】15【解析】解:∵直线y =13x +4与反比例函数y =k x (x >0)的图象交于点A ,与y 轴正半轴交于点B ,∴B (0,4),∵OB :OC =4:3,∴OC =3,即C (3,0),当x =3时,y =13x +4=5,∴A (3,5),∵点A 在反比例函数图象上,∴k =3×5=15.故答案为:15.根据反比例函数图象上点的坐标特征进行解答即可.本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是关键.15.【答案】0 < >【解析】解:(1)由m 1+m 2=0可知,m 1=−m 2,点A (m 1,n 1),B (m 2,n 2)在反比例函数图象上,∴n 1=1m 1=−1−m 2=1m 2,n 2=−1m 2,∴n 1+n 2=0,故答案为:0.(2)∵反比例函数图象在第二、四象限,且m 1+m 2>0时,n 1+n 2>0,∴点A (m 1,n 1),B (m 2,n 2)在不同的象限,设A(m1,n1)在第二象限,B(m2,n2)在第四象限,则m1<0,n1>0,n2<0,且丨m2丨>丨m1丨,丨n1丨>丨n2丨,∴直线y=kx+b(k≠0)经过第一、二、四象限,∴k<0,b>0.故答案为:<;>.(1)根据题意可知m1=−m2,将点A、B坐标代入反比例函数解析式即可得到结果;(2)根据题意得到点A(m1,n1),B(m2,n2)在不同的象限,设A(m1,n1)在第二象限,B(m2,n2)在第四象限,则m1<0,n1>0,n2<0,且丨m2丨>丨m1丨,丨n1丨>丨n2丨,则直线y=kx+b(k≠0)经过第一、二、四象限,据此得到结果.本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式.16.【答案】(1)证明:∵Δ=[−(2m−1)]2−4×1×(−3m2+m)=4m2−4m+1+12m2−4m=16m2−8m+1=(4m−1)2≥0,∴方程总有实数根;(2)解:由题意知,x1+x2=2m−1,x1x2=−3m2+m,∵x2x1+x1x2=x21+x22x1x2=(x1+x2)2x1x2−2=−52,∴(2m−1)2−3m2+m −2=−52,整理得5m2−7m+2=0,解得m=1或m=25.【解析】(1)由判别式Δ=(4m−1)2≥0,可得答案;(2)根据根与系数的关系知x1+x2=2m−1,x1x2=−3m2+m,由x2x1+x1x2=−52进行变形直接代入得到5m2−7m+2=0,求解可得.本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=−ba,x1x2=ca.也考查了根的判别式.17.【答案】解:(1)设A种奖品的单价为a元,B种奖品的单价为b元,由题意可得:{2a+b=35a+2b=40,解得{a=10b=15,答:A 种奖品的单价为10元,B 种奖品的单价为15元;(2)由题意可得,W =10m +15(100−m )=−5m +1500,∴W 随m 的增大而减小,∵购买费用不超过1135元,且A 种奖品的数量不大于B 种奖品数量的3倍,∴{−5m +1500≤1135m ≤3(100−m ),解得73≤m ≤75,∴当m =75时,W 取得最小值,此时W =1125,答:W (元)与m (件)之间的函数关系式是W =−5m +1500(73≤m ≤75),最少费用W 的值为1125. 【解析】(1)根据题意可以写出相应的二元一次方程组,然后求解即可;(2)根据题意和题目中的数据,可以写出W (元)与m (件)之间的函数关系式.本题考查二元一次方程组的应用、一次函数的应用、一元一次不等式组的应用,解答本题的关键是明确题意,列出相应的方程和不等式组,写出相应的函数解析式,利用一次函数的性质求最值.18.【答案】解:(1)过点B 作BF ⊥OA ,垂足为F ,如图:∵等边△AOB 的边长为2,∴OF =AF =1,BF = 3,∴B (1, 3),∵OB =BC ,∴C (2,2 3),把点B (1, 3),C (2,2 3)分别代入y 1=k 1x(x >0)和y 2=k 2x(x >0)得: 3=k 11,2 3=k 22,解得k 1= 3,k 2=4 3;∴y 1=3x ,y 2=43x;(2)连接AE ,如图:。
2019-2021年上海各区一模压轴题分类汇编18题-定义新图形及其他题型

2019-2021年上海各区一模压轴题分类汇编18题-定义新图形及其他题型专题定义新图形及其他题型【知识梳理】根据题目中给的知识点,结合所学函数及图形知识解答【历年真题】1.(2021秋•浦东新区期末)如图,a∥b∥c,直线a与直线b之间的距离为3,直线c与直线b之间的距离为23,等边△ABC的三个顶点分别在直线a、直线b、直线c上,则等边三角形的边长是.2.(2021秋•宝山区期末)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征三角形”.已知y=x2+bx(b>0)的“特征三角形”是等腰直角三角形,那么b的值为.3.(2021秋•青浦区期末)如图,一次函数y=ax+b(a<0,b>0)的图象与x 轴,y轴分别相交于点A,点B,将它绕点O逆时针旋转90°后,与x轴相交于点C,我们将图象过点A,B,C的二次函数叫做与这个一次函数关联的二次函数.如果一次函数y=﹣kx+k(k>0)的关联二次函数是y=mx2+2mx+c(m≠0),那么这个一次函数的解析式为.4. (2021秋•青浦区期末)若抛物线y1=ax2+b1x+c1的顶点为A,抛物线y2=ax2+b1x+c1的顶点为B,且满足顶点A在抛物线y2上,顶点B在抛物线y1上,则称抛物线y1与抛物线y2互为“关联抛物线”已知顶点为M的抛物线y=(x-2)2+3与顶点为N的抛物线互为“关联抛物线”,直线MN与x轴正半轴交于点D,如果3tan MDO=4∠,那么顶点为N的抛物线的表达式为5.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=ACAD=CD=32,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于.6.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=.7.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D 是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为.8.(2020秋•徐汇区期末)如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=45,ED=5,如果△ECD的面积是6,那么BC的长是.9.(2020秋•金山区期末)已知在Rt△ABC中,∠C=90°,BC=1,AC=2,以点C为直角顶点的Rt△DCE的顶点D在BA的延长线上,DE交CA的延长线于点G,若tan∠CED=12,CE=GE,那么BD的长等于.10.(2020秋•黄浦区期末)已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为.11.(2019秋•黄浦区期末)如图,在△ABC中,AB=AC,点D、E在边BC上,∠DAE=∠B=30°,且AD3=AE2,那么DEBC的值是.12.(2019秋•宝山区期末)如图,点A在直线34y x上,如果把抛物线y=x²沿OA方向平移5个单位,那么平移后的抛物线的表达式为_ _.。
初中数学:2024年江苏省各地市中考数学一模压轴题精选

2024年江苏省各地市中考数学一模压轴题精选第一部分代数部分1.(2024·江苏省南通市·一模)已知实数a,b满足4a2+√ 7b=n,b2+2√ 7a=n,b≠2a,其中n为自然数,则n的最小值是( )A.4B.5C.6D.72.(2024·江苏省无锡市·一模)已知x、y、z满足等式x5+y20=z4,则下列结论不正确的是( )A.若x=y,则x=zB.若z=4x,则y=4xC.若x<z,则y<zD.若x<y,则x<z3.(2024·江苏省南京市·一模)若A(−4,m−2),B(−2,m),C(2,m)三点在同一函数图像上,则该函数图像可能是( )A. B. C. D.4.(2024·江苏省盐城市·一模)在平面直角坐标系中,M(x1,y1)、N(x2,y2)为抛物线y=ax2+bx+c(a>0)上任意两点,其中x1<x2,设抛物线的对称轴为x=t,若对于x1+x2>4,都有y1<y2,则t的取值范围是( ) A.t<1 B.t≤1 C.t<2 D.t≤25.(2024·江苏省扬州市·一模)对于函数y=x2+1x的图像和性质,下列说法正确的有:①图像与x轴的交点坐标为(−1,0);②图像与y轴没有交点;③图像不经过第四象限;④当x>0时,y随着x的增大而增大.( ) A.①② B.①②③ C.①②③④ D.①②④6.(2024·江苏省泰州市·一模)已知二次函数y =(x −m )2−1(m 为常数),如果当自变量x 分别取−3,−1,1时,所对应的y 值只有一个小于0,则m 的值可能是( )A.−2B.−1C.0D.27.(2024·江苏省无锡市·一模)已知二次函数y =ax 2+bx +c(a <0)图象的对称轴为直线x =t ,该二次函数图象上存在两点A(x 1,y 1),B(x 2,y 2),若对于1<x 1<2<x 2<3,始终有y 1<y 2,则t 的取值范围是( )A.t ≥3B.t ≥52C.t ≥2D.c <18.(2024·江苏省南通市·一模)定义:在平面直角坐标系xOy 中,若经过x 轴上一点P 的直线l 与双曲线m 相交于M ,N 两点(点M 在点N 的左侧),则把PN PM 的值称为直线l 和双曲线m 的“适配比”.已知经过点P(−3,0)的直线y =x +b 与双曲线y =k x(k <0)的“适配比”不大于2,则k 的取值范围为( ) A.−2≤k <−1 B.−94<k ≤−2 C.−52<k ≤−2 D.−94≤k ≤−2 9.(2024·江苏省连云港市·一模)如图,在平面直角坐标系xOy 中,点A(x 1,y 1),点B(x 2,y 2)在双曲线y =3x上,且0<x 1<x 2,分别过点A ,点B 作x 轴的平行线,与双曲线y =6x 分别交于点C ,点D.若△AOB 的面积为94,则AC BD 的值为( ) A. 23B. √ 32C. 12D. √ 3310.(2024·江苏省苏州市·一模)如图①,点A ,B 是⊙O 上两定点,圆上一动点P 从圆上一定点B 出发,沿逆时针方向匀速运动到点A ,运动时间是x (s ),线段AP 的长度是y (cm ).图②是y 随x 变化的关系图象,则图中m 的值是( )A. 92B.4√ 2C. 143D.511.(2024·江苏省无锡市·一模)在平面直角坐标系中,已知点A(−1,2),点B(−2,0),点C(2,0),将△ABC 绕点B 顺时针旋转某个角度后,点A 落在y 轴的负半轴上,此时点C 恰好落在反比例函数y =k x (k 为常数,且k ≠0)的图象上,则k 的值为______. 12.(2024·江苏省泰州市·一模)一次函数y = kx + 2 − k 的图像经过点A (m, 3)和点B (n, 1),若km < 0,则n 的取值范围为 .13.(2024·江苏省扬州市·一模)若关于x 的方程x 2 − (m + 3)x + m + 6 = 0的两根x 1,x 2满足1 < x 1 ≤ 2 < x 2,则二次函数y = x 2 − (m + 3)x + m + 6的顶点纵坐标的最大值是_____.14.(2024·江苏省无锡市·一模)已知某二次函数的图象开口向上,与x 轴的交点坐标为(−2,0)和(6,0),点P (m + 4, n 1)和点Q (3m − 2, n 2)都在函数图象上,若n 1 < n 2,则m 的取值范围为_____.15.(2024·江苏省连云港市·一模)在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标[2,0],对称轴为直线x=1,其部分图象如图所示,下列结论:①抛物线过原点;②a−b+c<0;③2a+ b+c=0;④抛物线的顶点坐标为(1,b2);⑤当x<1时,y随x的增大而增大.其中结论正确的是______.16.(2024·江苏省盐城市·一模)如图,点A在反比例函数y=1x(x>0)的图像上,点B在反比例函数y=−4x (x<0)的图像上,OA⊥OB,连结AB交y=1x(x>0)的图像于点C,若C是AB的中点,则▵AOB的面积是___.17.(2024·江苏省徐州市·一模)如图,在平面直角坐标系中,点A(4,3)、B(5,2),点C在x轴上运动,点D在直线y=x上运动,则四边形ABCD周长的最小值是_______.18.(2024·江苏省苏州市·一模)如图,在平面直角坐标系中,将直线y=−3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数y=k(x>0)的图象x经过点C,则k的值为.19.(2024·江苏省南通市·一模)定义:若一个函数的图象上存在横、纵坐标之和为零的点,则称该点为这个函数图像的“平衡点”.例如,点(−1,1)是函数y=x+2的图像的“平衡点”.,③y=−x2+2x+1,④y=x2+x+7的图象上,存在“平衡点”的(1)在函数①y=−x+3,②y=3x函数是________;(填序号)(x>0)与y=2x+b的图象的“平衡点”分别为点A、B,过点A作AC⊥y轴,垂足为C.当(2)设函数y=−4x▵ABC为等腰三角形时,求b的值;(3)若将函数y=x2+2x的图像绕y轴上一点M旋转180∘,M在(0,−1)下方,旋转后的图象上恰有1个“平衡点”时,求M的坐标.20.(2024·江苏省徐州市·一模)若关于x的函数y,当t−1≤x≤t+1时,函数y的最大值为M,最小值为N,,我们不妨把函数h称之为函数y的“合体函数”.令函数h=M−N2(1)①若函数y=−2024x,当t=1时,则函数y的“合体函数”h=;②若函数y=kx+5(k≠0,k为常数),求函数y的“合体函数”h的表达式;(x≥2),求函数y的“合体函数”h的最大值.(2)若函数y=1x21.(2024·江苏省南京市·一模)已知二次函数y=ax+bx+2(a<0).(1)求证:该函数的图像与x轴总有两个公共点;(2)若该函数图像与x轴的两个交点坐标分别为(x,0),(x,0),且x=−2x,求证a+b=0;(3)若A(k,y1),B(6,y2),C(k+4,y1)都在该二次函数的图像上,且2<y2<y1,结合函数的图像,直接写出k 的取值范围.22.(2024·江苏省无锡市·一模)在平面直角坐标系中,二次函数y=mx2+mx−6m的图象与x轴交于A、B(A在B左侧),与y轴交于C,一次函数y=2x+n的图象经过A、C两点.(1)分别求出m、n的值;(2)在二次函数图象上是否存在点P,且P满足∠POC+∠BCO=45∘若存在,请求出点P的坐标;若不存在,请说明理由.23.(2024·江苏省无锡市·一模)在平面直角坐标系中,二次函数y=mx2−3mx−10m(m为常数,且m<0)的图象与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.过点D(1,0)且平行于y轴的直线l交该二次函数图象于点E,交线段BC于点F.(1)求点A和点B的坐标;(2)求证:∠ECF=2∠DBF;(3)若点B关于CE的对称点B′恰好落在直线l上,求此时二次函数的表达式.24.(2024·江苏省盐城市·一模)我们约定:若关于x的二次函数y1=ax2+bx+c与y2=cx2−bx+a,则称函数y1与函数y2互为“共赢”函数.根据该约定,解答下列问题:(1)若关于x的二次函数y1=−3x2+kx+2与y2=mx2+x+n互为“共赢”函数,则k=;m=;n=.(2)对于任意非零实数r、s,点P(r,t)与点Q(s,t)(r≠s)始终在关于x的函数y1=x2+2rx+s的图像上运动,函数y2与y1互为“共赢”函数.①求函数y2的图像的对称轴;②函数y2的图像与直线y=−x+1交于A、B两点,且AB长为√ 2,求y2的函数表达式;3(3)在同一平面直角坐标系中,若关于x的二次函数y1=ax2+bx+c与它的“共赢”函数y2的图像顶点分别为点A、点B.若函数y1,y2的图像交于不同两点C,D,且四边形ACBD为菱形,∠CAD=60∘,请求出该菱形面积的取值范围.25.(2024·江苏省泰州市·一模)如图所示,在平面直角坐标系xOy中,点A(0,k)是y轴正半轴上一点,点B是反比例函数y=k图像上的一个动点,连接AB,以AB为一边作正方形ABCD,使点D在第一象限.设点B的横坐标x为m(m<0).(1)若k=2,m=−3,求点B和点D的坐标;2(2)若k=2,点D落在反比例函数图像上,求m的值;(3)若点D落在反比例函数图像上,设点D的横坐标为n(n>0),试判断m+n是否为定值?并说明理由.26.(2024·江苏省苏州市·一模)如图1,在平面直角坐标系中,直线y=−5x+5与x轴,y轴分别交于A、C两点,抛物线y=x2+bx+c经过A、C两点,与x轴的另一交点为B.(1)求抛物线解析式;,求此(2)若点M为x轴下方抛物线上一动点,当点M运动到某一位置时,▵ABM的面积等于▵ABC面积的35时点M的坐标;(3)如图2,以B为圆心,2为半径的⊙B与x轴交于E、F两点(F在E右侧),若P点是⊙B上一动点,连接PA,以PA为腰作等腰Rt△PAD,使∠PAD=90∘(P、A、D三点为逆时针顺序),连接FD.求FD长度的取值范围.27.(2024·江苏省连云港市·一模)如图,已知抛物线y=−1x2+bx+c与x轴交于A、B(4,0)两点,与y轴交于2点C(0,2).点P为第一象限抛物线上的点,连接CA,CB,PB,PC.(1)直接写出结果:b=______;c=______;点A的坐标为______;tan∠ABC=______;(2)如图1,当∠PCB=2∠OCA时,求点P的坐标;(3)如图2,点D在y轴负半轴上,OD=OB,点Q为抛物线上一点,∠QBD=90°.点E,F分别为△BDQ的边DQ,DB上的动点,且QE=DF,求BE+QF的最小值.28.(2024·江苏省泰州市·一模)综合与实践 【研究素材】二次函数:y =x −1的图像与y 轴交于点C ,与x 轴分别交于A ,B 两点.小亮对素材进行了深入的研究,提出研究思路,并布置了相关任务,请你根据小亮的研究完成下列任务.(为了方便研究,规定点A 在点B 的右边)【探究1】确定【素材】中∠ACB 的度数【任务1】证明∶∠ACB =90∘;【探究2】改变相交的对象研究若二次函数y =x 2−1的图像与y 轴交于点C ,与一次函数y =x +n 的图像分别交于A ,B 两点.【任务2】若“∠ACB =90°”成立,求n 的值; 【探究3】改变表达式的系数研究 若二次函数.y =ax +c(a >0,c <0)的的图像与y轴交于点C ,与一次函数y =kx +n (k ≠0)的图像分别交于A ,B 两点. 【任务3】若“∠ACB =90∘”成立,当ac =−2时,求n 与c 之间的关系式;【任务4】当n =0时,若直线BC 与x 轴交于点D ,连结AD 交y 轴于点E ,试比较S ▵AOE 与S ▵DOE 的大小,并说明理由.29.(2024·江苏省南通市·一模)在二次函数y=x2的图象上分别取三个点P,A,B,其中,点P(p,−p)在第二象限内,A,B两点横坐标分别为a,b,且满足a≤p≤b.(1)求p的值;(2)记a≤x≤b时二次函数y=x2的最大值为y1,最小值为y2.若b−a=3,求y1−y2的取值范围;(3)连接PA,PB,AB.当PA⊥PB时,作PH⊥AB,垂足为点H,PH是否存在最大值?若存在,求PH的最大值;若不存在,请说明理由.30.(2024·江苏省扬州市·一模)跳台滑雪是冬季奥运会的比赛项目之一.如图,运动员通过助滑道后在点A处起跳,经空中飞行后落在着陆坡BC上的点P处,他在空中飞行的路线可以看作抛物线的一部分.这里OA表示起跳点A到地面OB的距离,OC表示着陆坡BC的高度,OB表示着陆坡底端B到点O的水平距离.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员到地面OB的竖直距离y(单位:m)与他在水平方向上x2+bx+c.已知OA=70m,OC=60m,落点P到OC的水移动的距离x(单位:m)近似满足函数关系y=−112平距离是30m,到地面OB的竖直高度是37.5m.(1)求y与x的函数表达式;(2)进一步研究发现,运动员在空中飞行过程中,其水平方向移动的距离x(m)与飞行时间t(s)具备一次函数关系,当运动员在起跳点腾空时,t=0,x=0;当他在点P着陆时,飞行时间为5s;①求x与t的函数表达式;②当运动员与着陆坡BC在竖直方向上的距离达到最大时,求出此时他飞行时间t的值.第二部分几何部分31.(2024·江苏省南通市·一模)如图,P为正方形ABCD内一点,∠APD=∠ADP=75∘,延长DP交BC于点E.若EP=√ 2,则正方形的边长为( )A.√ 6B.2√ 2C.√ 2+1D.√ 3+132.(2024·江苏省无锡市·一模)如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条平行线中相邻两条之间的距离依次为a、b、c.若32a+b=1,当a变化时,正方形ABCD面积的最小值为( )A. 45B. 34C. 89D. 1233.(2024·江苏省苏州市·一模)如图,正方形ABCD 的面积为3,点E 在边CD 上,且CE = 1,∠ABE 的平分线交AD 于点F ,点M ,N 分别是BE ,BF 的中点,则MN 的长为( )A. √ 62B. √ 32C.2−√ 3D. √ 6−√ 2234.(2024·江苏省南京市·一模)如图,在边长为2的正方形ABCD 中,E 是AD 边上一点,将▵ABE 沿BE 翻折,得到▵A ′BE.若▵A′BC 为等边三角形,则AE 的长为( )A.4−2√ 3B.√ 3−1C.6−3√ 3D.4√ 3−635.(2024·江苏省徐州市·一模)如图,已知矩形ABCD 的边AB =√ 3,BC =3,E 为边CD 上一点.将▵BCE 沿BE 所在的直线翻折,点C 恰好落在AD 边上的点F 处,过点F 作FM ⊥BE ,垂足为点M ,取AF 的中点N ,连接MN ,则MN 的长为( )A.3B.√ 2C.√ 6−1D.√ 336.(2024·江苏省无锡市·一模)如图,Rt ▵ABC 中,∠C =90∘,∠A =30∘,AC =9,D 为AB 中点,以DB 为对角线长作边长为3的菱形DFBE ,现将菱形DFBE 绕点D 顺时针旋转一周,旋转过程中当BF 所在直线经过点A 时,点A 到菱形对角线交点O 之间的距离为( )A. 43√21B. 32√3C. 43√21或32√3D. 32√21或32√337.(2024·江苏省泰州市·一模)用四个全等的直角三角形围成一个如图1大正方形,中间是一个小正方形,这个图形是我国三国时期赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,现用如图2的两种直角三角形各两个围成一个如图3的四边形ABCD ,若知道图3中阴影部分的面积,则一定能求出图3中( )A.四边形ABCD 的面积B.四边形EFGH 的面积C.▵ADH 的面积D.▵CDG 的面积38.(2024·江苏省无锡市·一模)如图,四边形ABCD 是边长为4的菱形,∠A =60∘,将▵ABD 沿着对角线BD 平移到▵A′B′D′,在移动过程中,A′B′与AD 交于点E ,连接D′E 、CE 、CD′.则下列结论:①A′E =BB′;②当D′E ⊥CE 时,∠A′D′E −∠CEB′=30∘;③当∠ED′C =60∘时,BB′的长为√ 5;④▵CED′的面积最大值为5√ 3.其中正确的为( )A.①③B.②③C.①②③D.①②④39.(2024·江苏省泰州市·一模)在▵ABC 中,∠C =90∘,∠B =60∘,D 为边AC 上的一点,若线段AB 上存在两个点到D 的距离等于12BC,则AD AB 的取值范围为 .40.(2024·江苏省苏州市·一模)如图,在平行四边形ABCD 中,AD =5,AB =6√ 2,∠D 是锐角,CE ⊥AD 于点E ,F 是CD 的中点,连接BF ,EF.若∠EFB =90∘,则CE 的长为 .41.(2024·江苏省连云港市·一模)如图,直线y=−3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,第一象限内作正方形ABCD,点C落在双曲线y=kx(k≠0)上的点D1处,则a=.使点D恰好落在双曲线y=kx42.(2024·江苏省泰州市·一模)如图,将▱ABCD沿AD翻折得四边形AEFD,AB=6,BC=12,M、N分别是AB、DF的中点,则MN长的范围是.43.(2024·江苏省南通市·一模)如图,点A,B在反比例函数y=k(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂x足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是.44.(2024·江苏省泰州市·一模)如图,在矩形ABCD中,AB=6,AD=12,E是线段AD上一动点,以E为直角顶点在EB的右侧作等腰三角形EBF,连接DF,设DF=t,当t为整数时,点F位置有个.45.(2024·江苏省无锡市·一模)如图,▱ABCD中,∠A=45∘,AB=3,AD=4,点E为AD上一点(端点除外),连接BE、CE,点A关于BE的对称点记为A′,当点A′恰好落在线段EC上时,此时EC=_____,AE=_____.46.(2024·江苏省南京市·一模)如图,将矩形ABCD绕点A旋转,使点B的对应点B′恰好落在BD上.若AB=5,BC=12,连接DD′,则DD′的长为__________.47.(2024·江苏省无锡市·一模)如图,Rt▵ABC中,∠ACB=90∘,tanA=2,AC=√ 5,以BC为直径作圆,圆心为O,过圆上一点D作直线AB的垂线,垂足为E,则AE+DE的最大值是________.48.(2024·江苏省南通市·一模)如图,在四边形ABCD中,AC⊥BD,AC+BD=10,点M和点N分别是BD和AC的中点,BA和CD的延长线交于点P,则▵PMN面积的最大值等于.49.(2024·江苏省无锡市·一模)如图,在矩形ABCD中,AB=3,将边AD翻折到AE,使点D的对应点E在边BC上;再将边DA翻折到DF,点A的对应点为F,连接DE、FA、FE.(1)若AD=5,则CE的长为______;(2)若点F为△ABE的内心,则AD的长为______.50.(2024·江苏省南通市·一模)如图1,P是正方形ABCD边BC上一点,线段AE与AD关于直线AP对称,连接EB 并延长交直线AP于点F,连接CF.(1)补全图形,求∠AFE的大小;(2)用等式表示线段CF,BE之间的数量关系,并证明;(3)连接CE,G是CE的中点,AB=2,若点P从点B运动到点C,直接写出DG的最大值.51.(2024·江苏省无锡市·一模)矩形ABCD中,AB=1,AD=2,点M是AD中点,点N从点B出发,沿BC边运动至点C停止,四边形MNB′A′与四边形MNBA关于直线MN对称,设BN=x,四边形MNB′A′与矩形ABCD重叠部分的面积记为S.(1)当点M、A′、C三点共线时,求x;(2)求S关于x的函数表达式.52.(2024·江苏省苏州市·一模)我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形.(1)如图1,▵ABC是等边三角形,在BC上任取一点D(B、C除外),连接AD,我们把▵ABD绕点A逆时针旋转60∘,则AB与AC重合,点D的对应点E.请根据给出的定义判断,四边形ADCE(选择是或不是)等补四边形.=8,求BD的长.(2)如图2,等补四边形ABCD中,AB=BC,∠ABC=∠ADC=90∘,若S四边形ABCD(3)如图3,四边形ABCD中,AB=BC,∠A+∠C=180∘,BD=4,求四边形ABCD面积的最大值.53.(2024·江苏省南京市·一模)几何问题中需建构模型去研究图形中元素之间的关系…在▵ABC中,P是BC上一点,点E在直线BC的上方,连接AP,EP,EC,探究下列问题:【认识模型】(1)如图①,▵APB∽▵CPE,①连接BE,求证:△PEB∽△PCA;②∠BEC与∠BAC满足的数量关系为____;【运用模型】(2)已知∠BAC=90∘,D是AB的中点,且▵APD∽▵CPE,①如图②,若P是BC的中点,连接DE,求证:DE//BC;②若∠B=30∘,BC=4,当点P在BC上运动时,点E的位置随点P的位置的变化而变化,直接写出AE的长的最小值.54.(2024·江苏省无锡市·一模)如图,等边▵ABC中,AB=4cm,点E在AB上,从A向B运动,运动速度为1cm/s;点F在BC上,从B向C运动,运动速度是v,两点同时出发,设运动时间为t(s),当一点到达终点时,另一点停止运动.连接CE、AF,交点为G.(1)若v=1cm/s,求∠FGC的度数;(2)在(1)的条件下,取AB中点P,N为BC上一动点,连接PN、GN,则PN+GN的最小值为______;(3)若v=0.5cm/s,求t为何值时,EC+2AF的值最小,并求出最小值是多少?55.(2024·江苏省盐城市·一模)综合与探究【特例感知】(1)如图1,E是正方形ABCD外一点,将线段AE绕点A顺时针旋转90∘得到AF,连接DE、BF.求证:DE=BF;【类比迁移】(2)如图2,在菱形ABCD中,AB=6,∠B=60∘,P是AB的中点,将线段PA、PD分别绕点P顺时针旋转90∘得到PE、PF,PF交BC于点G,连接CE、CF,求四边形CEGF的面积;【拓展提升】(3)如图3,在平行四边形ABCD中,AB=12,AD=10,∠B为锐角且满足sinB=4.P是射线BA上一动点,点5C、D同时绕点P顺时针旋转90∘得到点C′、D′,当△BC′D′为直角三角形时,直接写出BP的长.56.(2024·江苏省泰州市·一模)【定义呈现】有两个内角分别是它们对角的两倍的四边形叫做倍对角四边形,其中,这两个内角称为倍角.例如:如图1,在四边形ABCD中,∠A=2∠C,∠D=2∠B,那么我们就叫这个四边形是倍对角四边形,其中∠A,∠D称为倍角.【定义理解】如图1,四边形ABCD是倍对角四边形,且∠A,∠D是倍角.求∠B+∠C的度数;【拓展提升】如图2,四边形BDEC是倍对角四边形,且∠DEC,∠BDE是倍角,延长BD、CE交于点A.在BC下方作等边三角形▵BCF,延长FC、DE交于点G.若AB=AC,BC=2,FG=kAB,四边形BDEC的周长记为l.(1)用k的代数式表示l;(2)如图3,把题中的“AB=AC”条件舍去,其它条件不变.①求证:CE=EG;②探究l是否为定值.如果是定值,求这个定值,如果不是,请说明理由.k+157.(2024·江苏省扬州市·一模)如图①∼⑧是课本上的折纸活动.【重温旧知】上述活动,有的是为了折出特殊图形,如图①、③和⑧;有的是为了发现或证明定理,如图④和⑦;有的是计算角度,如图②;有的是计算长度,如图⑤和⑥.(1)图③中的▵ABC的形状是______;图④的活动发现了定理“____________”(注:填写定理完整的表述);图⑤中的BF的长是_______;【继续探索】(2)如图,将一个边长为4的正方形纸片ABCD折叠,使点A落在边BC上的点E处,点E不与B、C重合,MN为折痕.折叠后的梯形MNFE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.58.(2024·江苏省连云港市·一模)【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出BDCE的值.【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且ABBC =ADDE=34.连接BD,CE.(1)求BDCE的值;(2)延长CE交BD于点F,交AB于点G.求sin∠BFC的值.59.(2024·江苏省泰州市·一模)已知,点P是边长为a(a为常数)的正方形ABCD内部一动点,PE⊥AB于E,PF⊥BC于F,连结PD,EF,DE,DF,记▵PDE,▵PDF,▵PEF的面积分别为S1,S2,S3,令PE=x,PF=y.(1)如图1,点P在对角线AC上.①求S1+S2(用含a、x的代数式表示)②是否存在实数k,使S1+S2+kS3的值与P点在AC上的位置无关.若存在,请求出k的值;若不存在,请说明理由;(2)若xy =12,当点P在▵ABC内部(不含边界)时(如图2).①求x的取值范围;②试说明:S1+S2的值随着x的增大而增大.60.(2024·江苏省泰州市·一模)已知:在矩形ABCD中,AB=4,AD=8,点G是边AD的中点,连接BG.以点A为圆心、2为半径作⊙A,点E是⊙A上的一个动点,连接AE、BE.将线段EB绕点E逆时针旋转90∘得到线段EF,连接BF、GF、DF.知识回顾(1)如图1,当点E在直线AB的左侧时,试证明▵ABE∽▵GBF,并求出GF的长.(2)初步探索直接写出DF的最小值是,最大值是.(3)操作并思考如图2,当点E落在边AD上时,试猜想BG和DF有怎样的位置关系,并说明理由;(4)若点E到G、F之间的距离相等,请根据图1、图3两种情况,求DF的长.。
上海各区初三中考一模压轴题(学生版)
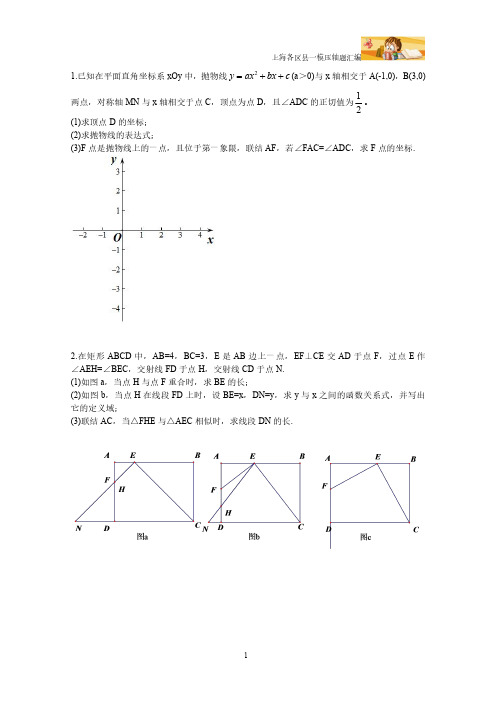
1.已知在平面直角坐标系xOy 中,抛物线c bx ax y ++=2(a >0)与x 轴相交于A(-1,0),B(3,0)两点,对称轴MN 与x 轴相交于点C ,顶点为点D ,且∠ADC 的正切值为21。
(1)求顶点D 的坐标;(2)求抛物线的表达式;(3)F 点是抛物线上的一点,且位于第一象限,联结AF ,若∠FAC=∠ADC ,求F 点的坐标.2.在矩形ABCD 中,AB=4,BC=3,E 是AB 边上一点,EF ⊥CE 交AD 于点F ,过点E 作∠AEH=∠BEC ,交射线FD 于点H ,交射线CD 于点N.(1)如图a ,当点H 与点F 重合时,求BE 的长;(2)如图b ,当点H 在线段FD 上时,设BE=x ,DN=y ,求y 与x 之间的函数关系式,并写出它的定义域;(3)联结AC ,当△FHE 与△AEC 相似时,求线段DN 的长.3.如图,△AOB 的顶点A 、B 在二次函数23312++-=bx x y 的图像上,又点A 、B 分别在y 轴和x 轴上,tan ∠ABO=1.⑴求此二次函数的解析式;(4分)⑵过点A 作AC ∥BO 交上述函数图象于点C ,点P 在上述函数图象上,当△POC 与△ABO 相似时,求点P 得坐标.(8分)4.如图a ,在Rt △ABC 中,∠ACB=90°,CE 是斜边AB 上的中线,AB=10,tanA=34,点P 是CE 延长线上的一动点,过点P 作PQ ⊥CB ,交CB 延长线于点Q ,设EP=x ,BQ=y.⑴求y 关于x 的函数关系式及定义域;(4分)⑵联结PB ,当PB 平分∠CPQ 时,求PE 的长;(4分)⑶过点B 作BF ⊥AB 交PQ 于F ,当△BEF 和△QBF 相似时,求x 的值.(6分)5.如图,梯形OABC ,BC ∥OA ,边OA 在x 轴正半轴上,边OC 在y 轴正半轴上,点B (3,4),AB=5.(1)求∠BAO 的正切值;(2)如果二次函数c bx x y ++=294的图像经过O 、A 两点,求这个二次函数的解析式并求图像顶点M 的坐标;(3)点Q 在x 轴上,以点Q 、点O 及(2)中的点M 位顶点的三角形与△ABO 相似,求点Q的坐标.6.把两块边长为4的等边三角板ABC 和DEF 先如图a 放置,使三角板DEF 的顶点D 与三角板ABC 的AC 边的中点重合,DF 经过点B ,射线DE 与射线AB 相交于点M ,接着把三角形版ABC 固定不动,将三角形板DEF 由图11-1所示的位置绕点D 按逆时针方向旋转,设旋转角为α.其中0°<α<90°,射线DF 与线段BC 相交于点N (如图b 所示).(1)当0°<α<60°时,求AM·CN 的值.(2)当0°<α<60°时,设AM=x ,两块三角形板重叠部分的面积为y ,求y 与x 的函数解析式并求定义域.(3)当BM=2时,求两块三角形板重叠部分的面积.7.如图,已知点A (1,0)、B (3,0)、C (0,1).(1)若二次函数图像经过点A 、C 和点D (2,31)三点,求这个二次函数的解析式.(2)求∠ACB 的正切值(3)若点E 在线段BC 上,且△ABE 与△ABC 相似,求出点E 的坐标.8.已知:如图,在Rt△ABC中,∠ACB=90°,点P是边AB上的一个动点,联结CP,过点B 作BD⊥CP,垂足为点D.(1)如图1,当CP经过△ABC的重心时,求证:△BCD∽△ABC.(2)如图2,若BC=2厘米,cotA=2,点P从点A向点B运动(不与A、B重合),点P的速度是5厘米/秒.设点P运动的时间为t秒,△BCD的面积为S平方厘米,求出S关于t的函数解析式,并写出它的定义域.(3)在第(2)小题的条件下,如果△PBC是以CP为腰的等腰三角形,求△BCD的面积.9.如图1,已知等边△ABC 的边长为6,点D 是边BC 上的一个动点,折叠△ABC ,使得点A 恰好与边BC 上的点D 重合,折痕为EF (点E 、F 分别在边AB 、AC 上).(1)当AE :AF=5:4时,求BD 的长;(2)当ED ⊥BC 时,求EFEB的值;(3)当以B 、E 、D 为顶点的三角形与△DEF 相似时,求BE 的长.10如图,在矩形ABCD 中,AB=4,AD=6,点P 是射线DA 上的一个动点,将三角板的直角顶点重合于点P ,三角板两直角边中的一边始终经过点C ,另一直角边交射线BA 于点E.(1)判断△EAP 与△PDC 一定相似吗?请证明你的结论;(2)设PD=x ,AE=y ,求y 与x 的函数关系式,并写出它的定义域;(3)是否存在这样的点P ,使△EAP 周长等于△PDC 的周长的2倍?若存在,请求出PD 的长;若不存在,请简要说明理由。
2023年上海各区数学中考一模压轴题分类汇编

2023年上海各区数学中考一模压轴题分类汇
编
一、整数与有理数
1. 下列说法中与负数有理数有关的是()
A.偶数是自然数,也是有理数
B.奇数是整数,也是有理数
C.零是整数,也是有理数
D.所有的整数都是有理数
2. 结果为有理数的是()
A.3-3√2
B.√2+√3
C.√5-2√5
D.1+2√3
二、代数式与方程
3. 如果代数式3x-7的值在3和6之间,则x的范围是()
A.3<x<6
B.3≤x≤6
C.3≤x<6
D.3<x≤6
4. 已知代数式2x-a的值在-5和3之间,则实数a的范围是()
A.-8≤a≤1
B.-1≤a≤8
C.-8<a≤1
D.-1<a≤8
三、图形与几何
5. 在坐标平面直角坐标系中,若点P的坐标是(3,-4),则点P 所在的象限是()
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6. 平面内的点集合最可能是()
四、函数与不等式
7. 在函数图象上,若x增大时y不断减小,则该函数是()
A.单调递增函数
B.单调递减函数
8. 若|2x-5|<7,则x的取值范围是()
A.-1<x<6
B.-6<x<1
C.1<x<6
D.-1≤x≤6
以上就是2023年上海各区数学中考一模压轴题的分类汇编,希望同学们认真复习,提前了解考点,为考试做好充分准备。
祝各位同学顺利通过考试!。
浙江省温州市中考一模数学解答压轴题汇编(答案版)

9、2023年浙江省温州市中考一模数学解答压轴题汇编1.【答案】(1)见解析过程;(2)2.【解答】(1)证明:∵E,F分别是AC,AB的中点,∴FE∥BD,BC=2FE,∵∠FCE=∠CED,∴DE∥CF,∴四边形EFCD是平行四边形,∴OD=OF;(2)解:∵AD⊥BC,∴∠ADB=90°.又∵F是AB的中点,∴AB=2FD=4FO=10,∵tan B=,∴DB=6,DA=8,∵四边形CDEF是平行四边形,∴CD=FE,即BC=2CD,∴CD=2,∴AC===2.2.【答案】(1)甲车间每天能生成1200个,乙车间每天能生成600个;(2)甲、乙每个车间各被抽走了3人;(3)甲车间安排4天,乙车间安排29天,公司在完成该任务时支付的总工资最少,最少需要58840元.【解答】解:(1)设乙车间每天能生成x个旅行包,则甲车间每天能生成2x个旅行包,由题意得:,解得x=600,经检验,x=600是原方程的解,也符合题意,∴2x=1200,∴甲车间每天能生成1200个,乙车间每天能生成600个;(2)由题意知:甲车间共有1200÷60=20(人),乙车间共有600÷40=15(人),设甲乙车间各被抽走a人,根据题意得:(20﹣a)×60×(1+20%)+(15﹣a)×40×(1+20%)=1200+600,解得a=3,∴甲、乙每个车间各被抽走了3人;(3)设甲车间工作m天,乙车间工作n天,根据题意得:60×(1+20%)×(20﹣3)m+40×(1+20%)×(15﹣3)n=21600,整理得:17m+8n=300,∴m=﹣n+,设总费用为W元,则W=3400m+1560n=3400×(﹣n+)+1560n=﹣40n+60000,∵﹣40<0,∴W随n的增大而减少,∵17m+8n=300,∴m为4的倍数,即m最小为4,∴n最大值为29,∴当n=29时,总费用W最小值为﹣40×29+60000=58840(元),∴甲车间安排4天,乙车间安排29天,公司在完成该任务时支付的总工资最少,最少需要58840元.3.【答案】(1)见解析;(2)DE=PF,理由见解析;(3)①4;②AQ的长是或6.【解答】(1)证明:如图1,∵点E在△ABP的外接圆上,∴∠AEP+∠A=180°,∴∠AEP=90°,∴∠EAP+∠EPA=90°.∵,∴∠EAP=∠EPA=45°,∴△PAE是等腰直角三角形;(2)解:DE=PF,理由:如图2,延长FE交AD于点H,∵EF⊥BC,BC∥AD,∴EH⊥AD,即∠AHE=∠EFP=90°,∴∠EAH+∠AEH=90°,∵∠AEP=90°,∴∠PEF+∠AEH=90°,∴∠EAH=∠PEF,又∵△PAE是等腰直角三角形,∴EA=EP,∴△EAH≌△PEF(AAS),∴AH=EF,EH=PF,∵AD=DC=HF,∴AH+HD=EF+HE,∴HD=HE=PF,∴;(3)解:①由(2)知.∵DE=2,∴PF=.∵P是BC的中点,∴,②∵,∴∠EAD<∠EDA=45°=∠PAE,∴存在∠PAQ=∠EDA或∠PAQ=∠EAD,当∠PAQ=∠EDA时,如图3,∠PAQ=45°=∠PAE,∴=,∵∠B=90度,∴AP是圆的直径,∴,∴;当∠PAQ=∠EAD时,如图4,连结PQ;∵AP是圆的直径,∴∠AQP=90°=∠AHE,∴△APQ∽△AEH,∴,∴,综上所述,AQ的长是或6.4.【答案】(1)证明过程见解答;(2)4+4.【解答】(1)证明:∵D,E分别是AB,AC的中点,∴DE∥BC,DE=BC,∵DF=DE=EF,∴EF∥BC,EF=BC,∴四边形BCEF是平行四边形;(2)解:设BG与FC交于点H,∵G是CE的中点,∴EC=2EG=2CG,∵四边形BCEF是平行四边形,∴FB=EC,EF=BC,FB∥EC,设EG=CG=x,则FB=EC=2x,∵FB∥EC,∴△FBH∽△CGH,∴===,∵FH+HC=CF=6,∴FH=4,HC=2,∵tan∠BCG==3,∴BG=3CG=3x,∵BH=2GH,BG=BH+GH,∴BH=2x,GH=x,∴GH=CG=x,∵BG⊥CE,∴△GHC是等腰直角三角形,∴GH=CG=x=HC=,∴FB=EC=2x=2,在Rt△BCG中,根据勾股定理得:BC===x=2,∴平行四边形BCEF的周长=2(BC+FB)=2(2+2)=4+4.5.【答案】(1)y关于x的函数表达式:y=x;(2)正午时1号楼的影子不落在2号楼的墙上;(3)21,8,168等.【解答】解:(1)由表得,BC=AB=x,∵sin g∠BCD==,∴BH=BC,∴y=x=x;(2)如图所示:延长影子,得到▱GLMN,LP交GN于点Q,∴sin∠LQG=sin∠MLQ=sinα=,∴tan∠LGQ=,∴LQ=15=,∵LP=12,∴正午时1号楼的影子不落在2号楼的墙上;(3)见下表:方案设计1每幢楼层数n的值层数总和218168方案设计2每幢楼层数n的值层数总和228176故答案为:21,8,168等.6.【答案】(1)CH=3+x,FH=(3+x);(2)x的值为5或或;拓展:4﹣3.【解答】解:(1)过点C作CH⊥DF于点H,CG⊥AB于点G,如图,设BD=x,∵AC=BC=5,AB=6,CG⊥AB,∴AG=BG=AB=3,∴CG==4,∴GD=3+x.∵CG⊥AB,FD⊥AB,CH⊥DF,∴四边形CGDH为矩形,∴CH=GD=3+x,DH=CG=4.∵四边形CBDF为圆的内接四边形,∴∠CBA=∠CFD.∵∠CGB=∠CHF=90°,∴△CGB∽△CHF,∴,∴,∴FH=(3+x),CF=(3+x).∴用x的代数式分别表示CH=3+x,FH=(3+x);(2)当△CDF为等腰三角形时,①当CF=CD时,∵CH⊥DF,∴FH=DH,由(1)得:(3+x)=4,∴x=.②当CF=FD时,∵FH=(3+x),DH=4,∴FD=(3+x)+4,∴(3+x)+4=(3+x).解得:x=5.③当DF=CD时,∵CD2=CH2+DH2=(3+x)2+42,∴,解得:x=或x=﹣3(不合题意,舍去),∴x=.综上,当△CDF为等腰三角形时,x的值为5或或.拓展:作出点A关于CD的对称点A′,连接A′C,A′F,A′D,如图,由对称的性质可得:CA=CA′,∠CDA=∠CDA′.∵A'恰为的中点,∴∠CDA′=∠FDA′,∴∠CDA′=∠FDA′=∠CDA,∵DE⊥AD,∴∠ADE=90°,∴∠CDA′=∠FDA′=∠CDA=30°.点C作CG⊥AB于点G,∵AC=BC=5,AB=6,CG⊥AB,∴AG=BG=AB=3,∴CG==4,在Rt△CGD中,∵tan∠CDA=,∴,∴BD=4﹣3.7.【答案】(1)证明过程见解答;(2)3.【解答】(1)证明:在矩形ABCD中,AB∥CD,∵点E,O分别为BC,BD的中点,∴OE∥CD∥AB,即OF∥AB,又∵AF∥BD,∴四边形ABOF为平行四边形;(2)解:连结OC,由(1)得,四边形ABOF为平行四边形,∴AB=OF=CD,AB∥OF∥CD,∴∠OFG=∠DCG,在△OFG和△DCG中,,∴△OFG≌△DCG(AAS),∴OG=DG,∵CF⊥BD,∴CO=CD,∵OC为Rt△BCD斜边BD上的中线,∴OC=OD,即△OCD为等边三角形.∴OD=CD=AB=6,∴.8.【答案】任务1:h关于x的函数关系式为h=0.72x2;任务2:计时器的计时时长为min;任务3:方案一,“漏水壶”水位高度为128mm,计时器计时时长15min;方案二,“漏水壶”水位高度为200mm,计时器计时时长12min.【解答】解:任务1:把x=10,h=72和x=20,h=288分别代入h=ax2+c,得,解得所以h关于x的函数关系式为h=0.72x2;任务2:当h=98时,98=0.72x2,解得x=或x=﹣(舍去),∴T===(min),∴计时器的计时时长为min;任务3:由112.5≤h≤220.5,得12.5≤x≤17.5,∵,∴.∵h和T都是整数,∴T=12,13,14,15,16,当T=12时,,h=200;当T=13时,x=,h=0.72×≈170.41;T=14时,x==,h=0.72×≈146.94;当T=15时,,h=128;所以符合要求的方案有两种,方案一,“漏水壶”水位高度为128mm,计时器计时时长15min;方案二,“漏水壶”水位高度为200mm,计时器计时时长12min.9.【答案】(1)见解析;(2);(3)①1或;②.【解答】(1)证明:∵AB为直径,∴∠AEB=90°.∵∠BAD=60°,∴.∵AB=AD,AB∥CD,∴.∴AE=DE.∴∠EAF=∠D,∠EFA=∠DGE.∴△AFE≌△DGE(AAS).∴AF=DG;(2)解:连结OE,∵FG为⊙O的切线,∴∠OEF=90°.∵∠BAD=60°,OA=OE,∴△AOE为等边三角形,∴∠OEA=60°,∠AEF=30°,∴∠F=∠EAB﹣∠AEF=30°.∵AB=4,∴AE=AF=2,.由(1)得△AFE≌△DGE,∴EF=EG,∴.∵当点P从点G运动至点F,点Q恰好从点A运动至点B,∴,∴,∴.(3)解:①当PQ∥AE时,∠AEF=∠QPF=∠F,∴FQ=QP.又∵∠F=30°,∴,∴.∴x=1.如图当PQ∥BE时,∠PQF=∠EBF=∠F,∴FP=QP.又∵∠F=30°,∴,∴.∴.综上所述:x的值为1或.②过点Q作△BQM的高线QN交EB于点N,∵BE=EF=EG,∴∠F=∠EBF,∠EGB=∠EBG,∴∠FBG=90°.∵∠F=30°,∴∠BGF=60°,∴△BEG为等边三角形,∴∠PEM=∠GBM=60°,∵∠EPM=∠MGB,∴△EPM∽△BGM,∴,∴,∴,则.在Rt△BQN中,∵∠QBN=30°,BQ=4﹣x,∴.∴.10.【答案】任务一:抛物线解析式为y=x2;任务二:这样的抛物线图案每边最多可以摆放6个;任务三:方案1:较大的抛物线段1条,较小的抛物线4条;方案2:较大的抛物线段2条,较小的抛物线4条;方案3:较大的抛物线段3条,较小的抛物线2条.【解答】解:任务一:由题意得:AB=200÷5=40(m),点B的坐标为(20,0.8),设抛物线解析式为y=ax2,将B点坐标代入解析式得:0.8=400a,解得a=,∴抛物线解析式为y=x2;任务二:h=0.7时,点D的纵坐标为:(1.6﹣0.7)÷2=0.45,当y=0.45时,代入y=x2,得0.45=x2,解得x1=﹣15,x2=15,∴CD=30,200÷30=6,∴这样的抛物线图案每边最多可以摆放6个;任务三:设较大的抛物线可以摆放m条,较小的抛物线n条,由以上条件可知:AB=40,CD=30,40m+30n≤200(m,n为正整数,且m≤5),①m=1,n=5(不能对称摆放,舍去),②m=1,n=4(中间摆1个较大的,左右摆2个较小的,两边各余20米,符合题意),③m=2,n=4(中间摆2个较大的,左右摆2个较小的,两边各余20米,符合题意),④m=3,n=2(中间摆3个较大的,左右摆1个较小的,两边各余10米,符合题意).⑤m=4,n=1(不对称摆放,舍去),综上所述,方案1:较大的抛物线段1条,较小的抛物线4条;方案2:较大的抛物线段1条,较小的抛物线4条;方案3:较大的抛物线段3条,较小的抛物线2条.11.【答案】(1)证明见解析;(2)①1;②满足条件的BC的长为或;(3).【解答】(1)证明:∵BE为直径,∴∠BAE=∠BGE=90°.在Rt△ABE和Rt△GBE中,,∴Rt△ABE和Rt△GBE(HL);(2)解:①∵EF与⊙O相切,∴BE⊥EF,∴∠BEF=90°,∴∠AEB+∠DEF=90°.∵四边形ABCD为矩形,∴∠BAE=90°,∴∠ABE+∠AEB=90°,∴∠ABE=∠DEF,∵∠BAE=∠D=90°,∴△ABE∽△DEF,∴.在Rt△BEF中,∵tan∠EBF=,∴,∴DE=AB=2=1;②若△ABG是以AG为腰的等腰三角形,Ⅰ.当GA=GB时,∵GA=GB,∴∠GAB=∠GBA,∵∠DAB=∠CBA=90°,∴∠EAG=∠FBC.∵∠EAG=∠EBG,∴∠EBG=∠FBC.在△BEF和△BCF中,,∴△BEF≌△BCF(AAS),∴BE=BC.设BC=x,则AD=BC=x,∴AE=AD﹣DE=x﹣1,∵AB2+AE2=BE2,∴22+(x﹣1)2=x2,解得:x=,∴BC=;Ⅱ.当GA=AB=2时,∵GA=AB,∴∠ABG=∠AGB.∵∠AEB=∠AGB.∴∠AEB=∠ABG.∵∠AEB+∠ABE=90°,∠ABG+∠FBC=90°,∴∠ABE=∠FBC,∵∠BAE=∠C=90°,∴△BAE∽△BCF,∴.由(2)知:,∴,∴,∴BC=.综上,若△ABG是以AG为腰的等腰三角形,满足条件的BC的长为或;(3)解:∵BE为圆的直径,∴∠EGF=90°.在Rt△EGF和Rt△EDF中,,∴Rt△EGF≌Rt△EDF(HL),∴∠DEF=∠GEF,DF=FG.∵∠AEG+∠GEF=90°,∠DEF+∠AEB=90°,∴∠AEB=∠GEB.在Rt△EAB和Rt△EGB中,,∴Rt△EAB≌Rt△EGB(AAS),∴AB=BG,AE=EG,∴AE=EG=DE,∴BE⊥AC.∵BE⊥EF,∴EF∥AC.∴EF为△DAC的中位线,∴DF=FC,∴DF=FC=FG.设DF=FC=FG=a,则AB=CD=BG=2a,∴BF=BG+GF=3a.取BF的中点H,连接EH,如图,则EH为梯形ABFD的中位线,∴EF=a.∵EF∥AC,∴∠FGC=∠EFH.∵EH∥CD,∴∠CFG=∠EHF,∴△CFG∽△EHF,∴.12.【答案】(1)见解析;(2)4.【解答】(1)证明:如图,连接OE,∵EF是⊙O切线,∴OE⊥EF,∵OE=OA,∴∠OEA=∠OAE,∵BD=AD,∴∠B=∠OAE,∴∠B=∠OEA,∴OE∥BC,∴EF⊥BC.(2)解:如图,连接OE,∵OE∥BC,∴,即AE=BE,∵AD是⊙O直径,∴AC⊥BC,∵EF⊥BC,∴EF∥AC,∴,即BF=CF,∴AC=2EF(三角形的中位线定理),∵CD=5,,∴设EF=2x,则CF=BF=3x,AC=4x,∴AD=BD=BF+CF﹣CD=6x﹣5,在Rt△ACD中,AC2+CD2=AD2,即(4x)2+52=(6x﹣5)2,解得x=3或x=0(不符合题意,舍去),则DF=CF﹣CD=3x﹣5=3×3﹣5=4.13.【答案】(1)笔记本的单价为5元,钢笔的单价为10元;(2)可购买钢笔30支,笔记本20本;或购买钢笔25支,笔记本30本;或购买钢笔20支,笔记本40本.(3)文具店赠送5张兑换券,其中3张兑换钢笔,2张兑换笔记本.(答案不唯一)【解答】解:任务1:设笔记本的单价为x元,根据题意,得,解得x=5,经检验,x=5是原方程的根,这时2x=10.∴笔记本的单价为5元,钢笔的单价为10元;任务2:设购买钢笔为a支,笔记本为b本,根据题意,得10a+5b=400,化简得,由题意,a≥20,b≥20,且b是10的倍数,∴或或,∴可购买钢笔30支,笔记本20本;或购买钢笔25支,笔记本30本;或购买钢笔20支,笔记本40本.任务3:当原有钢笔30支,笔记本20本时,设有y张兑换券兑换钢笔,根据题意,得30+10y=20+20(m﹣y),整理得,∵1<m<10,且m,y均为正整数,∴经尝试检验得,∴文具店赠送5张兑换券,其中3张兑换钢笔,2张兑换笔记本.(答案不唯一)14.【答案】(1);(2)或2;(3)①,②.【解答】解:(1)在矩形ABCD中,CD=AB=4.∵∠ACB=30°,AB=4,∴AC=2AB=8.∵AP=y,∴CP=8﹣y.∵,∴.∴.(2)(ⅰ)当PQ⊥AC时,∵DQ=x,AP=y,∴CQ=4﹣x,CP=8﹣Y.∵,∴,解得,即.(ⅱ)当QE⊥AC时,延长EQ交AC于点H.∵AD∥BC,∴∠CAD=∠ACB=30°,∠ACD=60°.∵AP=PE,∴∠EPA=2∠EAC=60°,∴△KPC是等边三角形.∴,∴.在Rt△DEK中,,在Rt△DEQ中,,∴,即,解得x=2,即DQ=2.(ⅲ)∵∠AEP=∠CAD=30°,∴∠APE=120°,综上,DQ的值为或2;∴PE不可能垂直于AC.(3)当x=4时,,即,∴.①在平行四边形PQFG中,DG∥PQ,∴,即=,解得x=2,∴CQ=4﹣2=2,PF=FC﹣CP=.过点Q作QH⊥PC,则.=2S△FQP=PF•QH=.∴S平行四边形PQFG②.提示:当点G落在AB边上时,∵FG∥QP,∴∠GFP=∠QPF,∴∠AFG=∠QPC.∵AB∥CD,∴∠BAC=∠DCA.∵FG=PQ,∴△AFG≌△CQP(AAS).∴AF=CP,即,解得.当点G落在BC边上时,作QN∥AD交AC于点N,作NM⊥AD于点M,则MN=DQ=x,QN∥BC,∴AN=2x,NF=.∠QNF=∠BCP,∵四边形PQFG是平行四边形,∴QF=PG,∠QFP=∠GPF,∴∠QFN=∠GPC,∴△QNF≌△GCP(AAS),∴NF=CP,即,解得,∴.15.【答案】(1)见解析;(2)8.【解答】(1)证明:∵AB=AE,∴∠ABE=∠AEB,同理,∠DEC=∠DCE,∵AE∥CD,∴∠AEB=∠DCE,∴∠ABE=∠DEC,∴AB∥DE,∴∠BAF=∠AED,∵∠ABF=∠DAE,∴△ABF≌△EAD(ASA),∴AF=CD,∴四边形ADCF是平行四边形;(2)解:如图,作AG⊥BC于点G,FH⊥BC于点H,则EG=BG,在平行四边形ADCF中,AD=CF=5,∵△ABF≌△EAD,∴BF=AD=CF=5,∴BH=CH,∵EF=2AF,AG∥FH,∴,∴EH=2GH,设GH=x,则EH=2x,EG=BG=3x,∴BH=CH=4x,∵,∴,∴FH=3x,∴,∴5x=5,即x=1,∴BC=8x=8.16.【答案】任务2:见解析;任务2:能完成改造,理由见解析;任务3:1.6米.【解答】解:(1)如图,以O为原点,建立如图1所示的坐标系,∴A(0,1),C(6,3.4),∴设抛物线解析式为y=ax2+bx+1,∵OF=DF=BD=2,DE=BC,∴抛物线的对称轴为直线,∴y=ax2﹣10ax+1,将C(6,3.4)代入解析式得,,∴.(2)如图,建立与(1)相同的坐标系,∵CC'=1,∴C'为(6,4.4),∵改造后对称轴不变,设改造后抛物线解析式为y=ax2﹣10ax+1,将C'(6,4.4)代入解析式得,∴,∴G为,G'为,∴,∴共需改造经费,∴能完成改造.图2(3)如图2,设改造后抛物线解析式为y=ax2﹣10ax+1,则G'为(2,﹣16a+1),E'为(4,﹣24a+1),∴,由题意可列不等式,(﹣40a﹣4)×200×60≤32000,解得,∵CC'=EE'=﹣24a+1﹣3.4,∴时,CC'的值最大,为1.6米.17.【答案】(1)见解析;(2)24;(3)①或或;②.【解答】(1)证明:在矩形OABC中,AD=CD,∠AOC=90°,∵AE=CE,AD=CD∴DE是AC的垂直平分线,即ED⊥AC,∴∠AOC=∠ADE=90°,又∵∠OAC=∠DAE,∴△ADE∽△AOC.(2)解:如图,连结OF,∵CE切半圆于点F,则∠OFC=90°,∵OC=15,OA=5,∴,∴,由△ADE∽△AOC,得,∴AE=CE=25,OE=20,=,即:OF==12,∴S△COE∴半圆O的直径为24.(3)解:①∵,EF=16,EM=8,,∵P,Q同时出发且同时到达终点,∴,∴设CP=3x,MQ=8x,EP=25﹣3x,EQ=8+8x,情况1:PQ∥BD,如图,作PR⊥MN于点R,∴tan∠RQP=tan∠AOB=tan∠OAC=3,∴PR=3QR,∴PR=EP•sin∠OEC=,ER=EP•cos∠OEC=,∴,∴,解得,∴.情况2:PQ∥AD,如图,此时EP=EQ,则25﹣3x=8+8x,∴,∴.情况3:PQ∥AB,如图,此时PQ⊥MN,则EP•cos∠OEC=EQ,∴,解得,∴,综上所述MQ的长为或或.②如图,若F'落在半圆O上,由圆的对称性可知,PQ必经过点O,即点Q与点O重合,此时MQ=12,,可得,∴,.∴.18.【答案】(1)证明见解析;(2)8.【解答】(1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD,∵AF=DF,∴∠CAD=∠ADF,∴∠BAD=∠ADF,∵点G是AD的中点,∴AG=DG,在△ABG和△DEG中,,∴△ABG≌△DEG(ASA),∴BG=EG,又∵AG=DG,∴四边形ABDE是平行四边形;(2)解:由(1)可知,四边形ABDE是平行四边形,∴AE∥BC,AB∥DE,∴∠CDF=∠ABC,∴sin∠CDF==,设CF=2x,则AF=DF=3x,∵∠C=90°,∴CD===x,∵AE∥BC,∴△CDF∽△AEF,∴===,即=,解得:x=4,∴CF=2x=8,即CF的长为8.19.【答案】【任务1】BC=,CD=2;【任务2】;【任务3】m.【解答】解:【任务1】如图,由题意得,∠CDB=∠EAM,∠CDA=∠DAM,∴tan∠CDB=,∴tan,设BC=x,则CD=3x,AC=4x,∴AB=4x﹣x=3x=2,∴x=,∴BC=x=,CD=3x=2;【任务2】如图,取BD的中点O,连接OF交CD于点E,则OF⊥CD,CE=DE=1,∵∠BCD=90°,∴BD为直径,∴点O为圆心,∴OE是△BCD的中位线,∴OE=,∴OF=OD=,∴弧CD的弓高EF=OF﹣OE=;【任务3】如图,连接BD'交CD于点G,作D'H⊥CD于点H,由题意得,此时BD'与太阳光线平行,则∠D'GH=∠CGB=γ,∴tan∠GD'H=tan∠CGB=tanγ=,∴CG=,∴点G为CD的中点,∵∠BGC=∠DGD',∠CBD'=∠CDD',∴△CBG∽△D'DG,∴,∴,∴D'G=,∴D'H=D'G=,∴点D′到CD的距离为m,即遮阳篷点D上升高度的最小值为m.20.【答案】(1)2;2;(2)①y=x﹣1;②满足条件x的值为或;(3).【解答】解:(1)∵半圆O切AC于点D,切BC于点E,∴OD⊥AC,OE⊥BC,∴∠ODC=∠OEC=∠DCE=90°,∴四边形OECD为矩形,∵OD=OE,∴矩形OECD为正方形,∴OD=CD=CE=OE,∴OD∥BC,OE∥AC,∴∠AOD=∠B,∴△AOD∽△ABC,∴,∴OD=2AD,∴CD=2AD,∴CD+AD=AC=3,∴2AD+AD=3∴AD=1,∴BD=2,∴OD=2,∴AO==,∵AB==3,∴BO=AB﹣AO=2.(2)①∵OP=x,∴BP=BO﹣OP=2﹣x,∵EQ=y,∴BQ=BC﹣CE﹣EQ=6﹣2﹣y=4﹣y,∵cos∠B==,∵PQ⊥AB,∴=cos∠B=,∴,∴y=x﹣1;②当∠FQP为90°时,如图,PQ=tan∠B•BP=•BP=•(2﹣x)=﹣x,∵FQ⊥PQ,AB⊥PQ,∴FQ∥AB,∴∠FQE=∠B,∵∠FEQ=90°,∴FQ==,∵FQ=PQ,∴﹣x=,∴x=,如图,当∠PFQ=90°时,过F点作FM⊥OP交OP于M点,∵FQ=FP,∠PFQ=90°,∴FQ=FP=PQ,∠FPQ=∠FQP=45°,∴∠FPM=45°,∴FM=PM=FP=PQ=(﹣x)=x,∴OM=OP﹣PM=OP﹣PQ=x﹣(﹣x)=,∵FM⊥OB,∴∠FOM+∠OFM=90°,∵OE⊥BC,∴∠FOM+∠B=90°,∴∠OFM=∠B.∴tan∠OFM=tan∠B=.∵tan∠OFM=,∴,解:x=.综上,满足条件x的值为或;(3)过点G作GH⊥BC于点H,GN⊥OE于点N,连接OG,如图,∵OE⊥BC,GH⊥BC,GN⊥OE,∴四边形HGNE为矩形,∴GH=EN,HE=GN.∵GH⊥BC,∴∠QGH+∠GQH=90°,∵QP⊥AB,∴∠B+∠GQH=90°,∴∠QGH=∠B,∴tan∠QGH=tan∠B=.∵tan∠QGH=,∴,设QH=a,则GH=2a,QG=a.∴EN=GH=2a,∴ON=OE﹣EN=2﹣2a.∵G为的中点,∴∠GOE=∠GOD=∠DOE=45°,∴△OGN为等腰直角三角形,∴ON=OG,∴2﹣2a=2,∴a=,∴QG=a=.。
2022年上海初三数学一模(期末)压轴题模拟汇编 压轴题精选30道-锐角的三角比综合问题(解析版)

压轴题精选30道-锐角的三角比综合问题(教师版) 学校:___________姓名:___________班级:___________考号:___________一、单选题1.(2021·黑龙江龙沙·二模)如图,在△ABC 中,AC =2,△CAB =45°,AD 为△CAB 的角平分线,若点E 、F 分别是AD 和AC 上的动点,则CE+EF 的最小值为( )A.1B C .2 D .3【答案】B【分析】过点C 作CG AB ⊥,交AD 于点E ,过点E 作EF AC ⊥,利用等腰直角三角形的性质即可求解.【详解】解:过点C 作CG AB ⊥,交AD 于点E ,过点E 作EF AC ⊥,△AD 为△CAB 的角平分线,△EF EG =,△CE +EF 的最小值即为CE +EG 的最小值,当CG AB ⊥时,CE +EG 的值最小,△AC =2,△CAB =45°,△CG == 故答案为:B .【点睛】本题考查角平分线的性质,垂线段最短,等腰直角三角形的性质等内容,掌握上述性质定理是解题的关键.2.(2021·四川南充·中考真题)如图,在矩形ABCD 中,15AB =,20BC =,把边AB 沿对角线BD 平移,点'A ,'B 分别对应点A ,B .给出下列结论:△顺次连接点'A ,'B ,C ,D 的图形是平行四边形;△点C 到它关于直线'AA 的对称点的距离为48;△''A C B C -的最大值为15;△''A C B C +的最小值为 )A .1个B .2个C .3个D .4个【答案】D【分析】 根据平移的性质和平行四边形的判定方法判断△,再利用等积法得出点C 到BD 的距离,从而对△做出判断,再根据三角形的三边关系判断△,如图,作D 关于AA '的对称点D ,DD '交AA '于,M 连接BD ',过D 作D N BC '⊥于,N 分别交,AM BD 于,,K H 证明D C ' 是最小值时的位置,再利用勾股定理求解D C ',对△做出判断.【详解】解:由平移的性质可得AB //A B ''且AB =A B ''△四边形ABCD 为矩形△AB //CD ,AB =CD =15△A B ''//CD 且A B ''=CD△四边形A B ''CD 为平行四边形,故△正确在矩形ABCD 中,BD过A 作AM △BD ,CN △BD ,则AM =CN△S △ABD =12AB ·CD =12 BD ·AM△AM =CN =152025⨯=12 △点C 到AA '的距离为24△点C 到它关于直线AA '的对称点的距离为48△故△正确△A C B C A B ''''-≤△当,,A B C ''在一条直线时A C B C ''-最大,此时B '与D 重合△A C B C ''-的最大值=A B ''=15△故△正确,如图,作D 关于AA '的对称点D ,DD '交AA '于,M 连接BD ',过D 作D N BC '⊥于,N 分别交,AM BD 于,,K H则////,15,AB A B KH AB KH ''== KM 为D HD '的中位线, BD DD '⊥,15,D K HK '∴==由A B CD ''可得B C A D ''=,,B C A D A D ''''∴==,A C B C A C A D D C ''''''∴+=+= 此时最小,由△同理可得:12,DM D M '==153tan =,204DC HN DBC BC BN∠=== 设3,HN x = 则4,BN x =由勾股定理可得:22222,DD BD BD BN D N '''+==+()()222225243034,x x ∴+=++整理得:2251803010,x x +-= ()()575430,x x ∴-+= 解得:12743,55x x ==-(负根舍去), 72171204,,55NC x D N '∴=-==D C '∴== △故△正确故选D .【点睛】本题主要考查了平行四边形的判定,矩形的性质以及平移的性质,锐角三角函数的应用等知识点,熟练掌握相关的知识是解题的关键.3.(2021·黑龙江鹤岗·模拟预测)如图,在正方形ABCD 中,对角线AC 与BD 相交于点O ,点E 在BC 的延长线上,连接DE ,点F 是DE 的中点,连接OF 交CD 于点G ,连接CF ,若4CE =,6OF =.则下列结论:△2GF =;△OD =;△1tan 2CDE ∠=;△90ODF OCF ∠=∠=︒;△点D 到CF .其中正确的结论是( )A .△△△△B .△△△△C .△△△△D .△△△△【答案】C【分析】由题意易得,,45,90BC CD BO OD OA OC BDC BCD DCE ====∠=︒∠=∠=︒,△由三角形中位线可进行判断;△由△DOC 是等腰直角三角形可进行判断;△根据三角函数可进行求解;△根据题意可直接进行求解;△过点D 作DH △CF ,交CF 的延长线于点H ,然后根据三角函数可进行求解.【详解】解:△四边形ABCD 是正方形,△,,45,90BC CD BO OD OA OC BDC BCD DCE ====∠=︒∠=∠=︒,AC BD ⊥,△点F 是DE 的中点, △1,//2OF BE OF BE =, △6OF =,4CE =,△12BE =,则8CD BC ==,△OF △BE ,△△DGF △△DCE , △12DG GF CD CE ==, △2GF =,故△正确;△点G 是CD 的中点,△OG △CD ,△△ODC =45°,△△DOC 是等腰直角三角形,△OD =,故△正确;△CE =4,CD =8,△DCE =90°, △1tan 2CE CDE CD ∠==,故△正确; △1tan 12CDE ∠=≠, △45CDE ∠≠︒,△90ODF ∠≠︒,故△错误;过点D 作DH △CF ,交CF 的延长线于点H ,如图所示:△点F 是CD 的中点,△CF =DF ,△△CDE =△DCF , △1tan tan 2CDE DCF ∠=∠=, 设DH x =,则2CH x =,在Rt △DHC 中,22464x x +=,解得:x =△DH =△正确; △正确的结论是△△△△;故选C .【点睛】本题主要考查正方形的性质、相似三角形的性质与判定及三角函数,熟练掌握正方形的性质、相似三角形的性质与判定及三角函数是解题的关键.4.(2021·四川·广安中学九年级开学考试)如图,在正方形ABCD 中,4AB =,E 为对角线AC 上与A ,C 不重合的一个动点,过点E 作EF AB ⊥于点F ,EG BC ⊥于点G ,连接,DE FG .下列结论:△DE FG =;△DE FG ;△BFG ADE ∠=∠;△FG 的最小值为3.其中正确结论的个数有( )A .1个B .2个C .3个D .4个【答案】C【分析】 延长DE ,交FG 于点N ,交AB 于点M ,连接BE ,交FG 于点O ,先根据正方形的性质、三角形全等的判定定理与性质得出DE BE =,再根据矩形的判定与性质可得BE FG =,由此可判断△;先根据三角形全等的性质可得ABE ADE ∠=∠,再根据矩形的性质可得OB OF =,然后根据等腰三角形的性质可得BFG ABE ∠=∠,由此可判断△;根据直角三角形的性质可得90ADE AMD ∠+∠=︒,从而可得90BFG AMD ∠+∠=︒,由此可判断△;先根据垂线段最短可得当DE AC ⊥时,DE 取得最小值,再解直角三角形可得DE 的最小值,从而可得FG 的最小值,由此可判断△.【详解】解:如图,延长DE ,交FG 于点N ,交AB 于点M ,连接BE ,交FG 于点O ,四边形ABCD 是正方形,4AB =,4,90,45AD AB ABC BAD BAE DAE ∴==∠=∠=︒∠=∠=︒,在ABE △和ADE 中,AB AD BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩,()ABE ADE SAS ∴≅,,BE DE ABE ADE ∴=∠=∠,90,,ABC EF AB EG BC ∠=︒⊥⊥,∴四边形BFEG 是矩形,,BE FG OB OF ∴==,DE FG ∴=,即结论△正确;OB OF =,BFG ABE ∴∠=∠,BFG ADE ∴∠=∠,即结论△正确;90BAD ∠=︒,90ADE AMD ∴∠+∠=︒,90BFG AMD ∴∠+∠=︒,90FNM ∴∠=︒,即DE FG ,结论△正确;由垂线段最短可知,当DE AC ⊥时,DE 取得最小值,此时在Rt ADE △中,sin 4DE AD DAE =⋅∠== 又DE FG =,FG ∴的最小值与DE 的最小值相等,即为△错误;综上,正确的结论为△△△,共有3个,故选:C .【点睛】本题考查了正方形的性质、三角形全等的判定定理与性质、解直角三角形等知识点,通过作辅助线,构造全等三角形和直角三角形是解题关键.5.(2021·黑龙江·二模)如图,四边形ABCD 中,BC//AD ,60,24A D AD BC ∠=∠=︒==,动点P 从点A 以每秒1个单位长度的速度向点D 运动,动点Q 也同时从点A 沿A B C D →→→的路线以每秒2个单位长度的速度向点D 运动,当点Q 到达点D 时,点P 也随之停止运动,设点P 运动的时间为t (单位:秒),DPQ 的面积为S ,当S =t 的值为( )A .2或2B .3或2C .3D .2【答案】D【分析】 分△点Q 在AB 边上,△点Q 在BC 边上,△点Q 在CD 边上三种情况进行讨论即可【详解】解:过点C 作CE △AD 于E 、点B 作BF △AD 于F ,△BC //AD ,△得到矩形AEFB 及直角△ABF ,△DCE .△60A CDA ∠=∠=︒,△△ABF △△DCE , △1()2DE AF AD BC ==-,AB =CD ; △24AD BC ==,△DE =AF =1,△=1cos60=2AB CD =÷△如图△,当点Q 在AB 边上运动时,01t ≤≤,作QE AD ⊥于点E .211(4)22S DP QE t =⋅=-=+.当S =2t =+2t = △如图△,当点Q 在BC 边上运动时,12t <≤,作BF AD ⊥于点F .11(4)22S DP BF t =⋅=-+当S =3t =(舍); △如图△,当点Q 在CD 边上运动时,23t <≤,作QH AD ⊥于点H .211(4))22S DP QH t t =⋅=--=+当S =t =t = 故选D .【点睛】此题主要考查了四边形的动点问题,以及解一元二次方程,关键是注意分类讨论,不要漏解.6.(2021·浙江龙湾·二模)如图,六边形AEBCFD 是中心对称图形.点M ,N 在面积为8的正方形ABCD 的对角线上.若1BM DN ==,点E ,M 关于AB 对称,则四边形AGCH 的面积为( )A .275B .325C .9215D .9415【答案】B【分析】连AC 交B D 于O ,过M 作MK △BC 于K ,连结ME 交BA 于L ,FN 交CD 于R ,由正方形ABCD 面积为8,可求AD,BD =4,M 、E 关于AB 对称,可得EB =MB =1,可证△BEA △△BMC (SAS ),由三角函数BK =MK,KCMC四边形AGCH 为矩形,再证△MOC △△ACG,可求AG =,CG 【详解】解:连AC 交B D 于O ,过M 作MK △BC 于K ,连结ME 交BA 于L ,FN 交CD 于R , △正方形ABCD 面积为8,△AD 2=8,AD△BD 为正方形对角线,△BD4,△M 、E 关于AB 对称,△EL =LM ,EB =MB =1,△EBA =△MBA =45°=△MBC ,在△BEA 和△BMC 中,BE BM EBA MBC BA BC =⎧⎪∠=∠⎨⎪=⎩,△△BEA △△BMC (SAS ),△AE =MC ,△EAB =△MCB ,△BM =1,△BK =MK△KC =BC -BK△MC =△六边形AEBCFD 是中心对称图形. △△AND △△CMB ,△AEB △△CFD , △△AND △△CMB △△AEB △△CFD , 设CG 交AB 于W ,△△GAW =△BCW ,△AWG =△CWB , △△AGW =△CBW =90°,△同理可证AH △CF ,△AHC =90°, △△BCM =△DCF ,△△GCH =△DCH +△GCD =△BCG +△GCD =△BCD =90°, △△AGC =△GCH =△AHC =90°, △四边形AGCH 为矩形, △AC △BD ,△△MOC =△AGC =90°, △△MCO =△ACG , △△MOC △△AGC ,△=MO MC OC AG AC CG =即12AG CG,△AG =,CG△S 矩形AGCH =AG ·GC 325, 故选择B .【点睛】本题考查正方形性质,中心对称图形性质,轴对称性质,三角形全等判定与性质,锐角三角函数应用,勾股定理应用,三角形相似判定与性质,矩形判定与性质,掌握正方形性质,中心对称图形性质,轴对称性质,三角形全等判定与性质,锐角三角函数应用,勾股定理应用,三角形相似判定与性质,矩形判定与性质.7.(2021·山东东营·二模)如图,在正方形ABCD 中,连接AC ,以点A 为圆心,适当长为半径画弧,交AB 、AC 于点M ,N ,分别以M ,N 为圆心,大于MN 长的一半为半径画弧,两弧交于点H ,连结AH 并延长交BC 于点E ,再分别以A 、E 为圆心,以大于AE 长的一半为半径画弧,两弧交于点P ,Q ,作直线PQ ,分别交CD ,AC ,AB 于点F ,G ,L ,交CB 的延长线于点K ,连接GE ,下列结论:△22.5LKB ∠=︒;△//GE AB ; △tan KBCGF LB∠=; △CGECABS :S1:4=.其中正确的是( )A .△△△B .△△△C .△△△D .△△△【答案】A 【分析】△在△AOL 和△BLK 中,根据三角形内角和定理,如图两个角对应相等,则第三个角△LKB =△BAC =22.5°;△根据线段中垂线定理证明△AEG =△EAG =22.5°=△BAE ,可得EG △AB ;△根据等量代换可得:△CGF =△BLK ,可作判断;△连接EL ,证明四边形ALEG 是菱形,根据EL >BL ,及相似三角形的性质可作判断. 【详解】解:△△四边形ABCD 是正方形,△△BAC=12△BAD=45°,由作图可知:AE平分△BAC,△△BAE=△CAE=22.5°,△PQ是AE的中垂线,△AE△PQ,△△AOL=90°,△△AOL=△LBK=90°,△ALO=△KLB,△△LKB=△BAE=22.5°;故△正确;△△OG是AE的中垂线,△AG=EG,△△AEG=△EAG=22.5°=△BAE,△EG△AB,故△正确;△△△LAO=△GAO,△AOL=△AOG=90°,△△ALO=△AGO,△△CGF=△AGO,△BLK=△ALO,△△CGF=△BLK,在Rt△BKL中,tan△CGF=tan△BLK=BK BL,故△正确;△连接EL,△AL=AG=EG,EG△AB,△四边形ALEG是菱形,△AL=EL=EG>BL,△12 EGAB,△EG△AB,△△CEG△△CBA,△21()4CEG CBA S EG S AB ∆∆=≠, 故△不正确;本题正确的是:△△△, 故选:A . 【点睛】本题考查了基本作图:角平分线和线段的垂直平分线,三角形相似的性质和判定,菱形的性质和判定,三角函数,正方形的性质,熟练掌握基本作图是关键,在正方形中由于性质比较多,要熟记各个性质并能运用;是中考常考的选择题的压轴题.8.(2021·山东历下·三模)如图1,在Rt△ABC 中,△A =90°,BC =10cm ,点P ,点Q 同时从点B 出发,点P 以2cm/s 的速度沿B→A→C 运动,终点为C ,点Q 出发t 秒时,△BPQ 的面积为ycm 2,已知y 与t 的函数关系的图象如图2(曲线OM 和MN 均为抛物线的一部分),给出以下结论:△AC =6cm ;△曲线MN 的教师式为y =﹣45t 2+285t (4≤t≤7);△线段PQ;△若△PQC 与△ABC 相似,则t =407秒,其中正确的说法是( )A .△△△B .△△△C .△△△D .△△△【答案】A 【分析】△根据图2可知:P 走完AB 用了4秒,得248AB cm =⨯=,利用勾股定理得AC 的长;△当P 在AC 上时,47t ≤≤,利用同角的三角函数表示高PD 的长,利用三角形面积公式可得y 与t 的关系式;△当P 与A 重合时,PQ 最大,如图4,此时4t =,求出PQ 的长;△当P 在AC 上时,PQC ∆与ABC ∆,列比例式可得t 的值.【详解】解:△由图2可知:4t =时,485y =, 248AB cm ∴=⨯=,90A ∠=︒,BC 10cm =,6AC cm ∴=,故△正确;△当P 在AC 上时,如图3,过P 作PD BC ⊥于D ,此时:6872+=, △47t ≤≤,由题意得:2AB AP t +=,BQ t =,142PC t ∴=-,sin PD ABC PC BC∠==, ∴84142105PD t ==-, 4(142)5t PD -∴=, 2114(142)42822555BPQ t y S BQ PD t t t ∆-∴====-+,故△正确; △当P 与A 重合时,PQ 最大,如图4,此时4t =,4BQ ∴=,过Q 作GH AB ⊥于H ,sin QH AC B BQ BC∠==, ∴6410QH =, 125QH ∴=, 同理:165BH =,1624855AH ∴=-=,PQ ∴==∴线段PQ △不正确; △若PQC ∆与ABC ∆相似,点P 只有在线段AC 上, 分两种情况:142PC t =-,10QC t =-,)i 当CPQ CBA ∆∆∽,如图5,则PC CQCB AC=,∴14210106t t--=, 解得8t 不合题意.)ii 当PQC ABC ∆∆∽时,如图6,∴PC QC AC BC=, ∴14210610t t--=, 407t =; ∴若PQC ∆与ABC ∆相似,则407t =秒,故△正确; 其中正确的有:△△△, 故选:A .【点睛】本题是动点问题的图象问题,此类问题比较复杂,考查了二次函数的关系式、三角形相似的性质和判定、勾股定理、三角函数,解题的关键是学会读懂函数图象信息,并构建直角三角形,利用三角形相似或三角函数列方程解决问题.9.(2021·广东深圳·中考真题)在正方形ABCD 中,2AB =,点E 是BC 边的中点,连接DE ,延长EC 至点F ,使得EF DE =,过点F 作FG DE ⊥,分别交CD 、AB 于N 、G 两点,连接CM 、EG 、EN ,下列正确的是:△1tan 2GFB ∠=;△MN NC =;△12CM EG =;△GBEM S =四边形 )A .4B .3C .2D .1【答案】B 【分析】解:△中由FG DE ⊥即可得到GFB EDC ∠=∠,再由正切等于对边比邻边即可求解; △中先证明DEC FEM △≌△得到EM=EC ,DM=FC ,再证明DMN FCN △≌△即可求解;△中先证明GE //CM ,得到CM CF EG EF ==即可求解;△中由1tan tan 2GB F EDC BF ∠=∠==得到12GB BF ==再由2GBE GBEM S S △四边形=即可求解. 【详解】解:△△FG DE ⊥,△△DMF =90°=△NCF ,且对顶角△MND =△CNF , △△GFB =△EDC ,△ABCD 为正方形,E 是BC 的中点, △BC =CD ,△1tan tan 2EC GFB EDC CD ∠=∠==,△正确; △由△知MDN CFN ∠=∠,又=90ECD EMF ∠=∠,已知EF ED =,△DEC FEM △≌△(SAS ), △EM EC =, △DM FC =,△MDN CFN ∠=∠,MND CNF ∠=∠,DM FC =, △DMN FCN △≌△(AAS ), △MN NC =,故△正确; △△BE EC =,ME EC =, △BE =ME ,且△B =△GME =90°,GE 为Rt GBE 和Rt GME 的公共边, △Rt GBE Rt GME △≌△(HL ), △BEG MEG ∠=∠, △ME EC =, △EMC ECM ∠=∠,由三角形外角定理可知:EMC ECM BED BEG MEG ∠+∠=∠=∠+∠, △GEB MCE ∠=∠, △//MC GE , △CM CFEG EF=,△EF DE =,1CF EF EC =-=,△CM CF EG EF ===△错误;△由上述可知:1BE EC ==,1CF ,△1BF =, △1tan tan 2GB F EDC BF ∠=∠==,△12GB BF ==△1222GBE GBEM S S BE BG ==⋅⋅⋅=△四边形△正确.故选B . 【点睛】本题考查正方形的性质,全等三角形的判定和性质,平行线分线段成比例定理,三角函数等知识,解题的关键是灵活运用所学知识解决问题.10.(2021·四川达州·中考真题)在平面直角坐标系中,等边AOB ∆如图放置,点A 的坐标为()1,0,每一次将AOB ∆绕着点О逆时针方向旋转60︒,同时每边扩大为原来的2倍,第一次旋转后得到11A OB ∆,第二次旋转后得到22A OB ∆,…,依次类推,则点2021A 的坐标为( )A .()202020202,2-B .()202120212,2C .()202020202,2D .()201120212,2-【答案】C 【分析】由题意,点A 每6次绕原点循环一周,利用每边扩大为原来的2倍即可解决问题. 【详解】解:由题意,点A 每6次绕原点循环一周,20216371......5÷=,2021A ∴点在第四象限,202120212OA =,202160xOA ∠=︒ ,∴点2020A 的横坐标为20212020122=2⨯,纵坐标为20212020=22,()2020202020212,2A ∴,故选:C . 【点睛】本题考查坐标与图形变化-旋转,规律型问题,解题的关键是理解题意,学会探究规律的方法,属于中考常考题型.二、填空题 11.(2021·全国·九年级专题练习)将矩形ABCD 按如图所示的方式折叠,BE 、EG 、FG 为折痕,若顶点A 、C 、D 都落在点O 处,且点B 、O 、G 在同一条直线上,同时点E 、O 、F 在另一条直线上.(1)EGBE的值为________.(2)若BEGF 的面积为________.【分析】(1)由折叠可得,E ,G 分别为AD ,CD 的中点,证明△BEG =90°,将EGBE 转化为AE AB,设CD =2a ,AD =2b ,在Rt △BCG 中,CG 2+BC 2=BG 2,可得a 2+(2b )2=(3a )2,则b a ,进而得出EGBE的值; (2)在△BCG 中,由勾股定理得出a 2+42=(3a )2,解得a ,证明△EDG △△GCF ,得出比例线段ED DGCG CF=,求出CF .则可求出EF .由四边形面积公式可求出答案. 【详解】解:(1)△四边形ABCD 是矩形, △△A =△D =△C =90°,AB =CD ,AD =BC , 由折叠的性质得:AE =OE =DE ,CG =OG =DG , △ABE =△OBE ,△AEB =△OEB ,△DEG =△OEG ,△△BEG =180°÷2=90°,且E ,G 分别为AD ,CD 的中点, △tan △OBE =EGBE =tan △ABE =AE AB, 设CD =2a ,AD =2b ,则AB =2a =OB ,DG =OG =CG =a ,BG =3a ,BC =AD =2b , 在Rt △BCG 中,CG 2+BC 2=BG 2, 即a 2+(2b )2=(3a )2, △b 2=2a 2,△b ,△ba=△11212222AD bEG AE b BE AB AB a a ⨯====⨯=(2)由(1)得:AB =2a =OB ,DG =OG =CG =a ,BG =3a ,BC =AD=△△C =90°,△Rt △BCG 中,CG 2+BC 2=BG 2,△a 2+(2=(3a )2,△a =2或-2(舍),△DG =CG =2,△BG =OB +OG =4+2=6,由折叠可得△EGD =△EGO ,△OGF =△FGC ,△△EGF =90°,△△EGD +△FGC =90°,△△EGD +△DEG =90°,△△FGC =△DEG ,△△EDG =△GCF =90°,△△EDG △△GCF , △ED DG CG CF =,2CF=, △CF,△FO△EF=△点B ,O ,G 在同一条直线上,△EF △BG ,△S 四边形EBFG =12×BG ×EF=162⨯⨯,. 【点睛】本题考查了折叠的性质,相似三角形的判定与性质,直角三角形的性质,勾股定理等知识,熟练掌握折叠的性质是解题的关键.12.(2021·浙江鹿城·二模)矩形ABCD 的面积记为1S 、正方形DEFG 的面积记为2S 、正方形FHMN 的面积记为3S ,它们的位置如图所示,点C 在FH 上,FG 交CD 于点P ,延长DE 交AB 于点K ,26AD AK ==,点B ,C ,M 在同一直线上,则23S S =_______;若123S S S +=,射线EP 交HM 于点Q ,则QM 的长为__________.【答案】14【分析】先推出△ADK =△GDP ,可得12AK PG AD DG ==,再证明DPG CPF ≌,然后证明12CH DE HM CE ==,HF =2CF =2DG , 进而即可得23S S 的值;设DE =x ,则EC = FH =HM =2x ,DC ==,列出方程,求出x 的值,再证明12QH AK EH AD ==,进而即可得到QM 的长. 【详解】 解:△在矩形ABCD 、正方形DEFG 中,△ADC =△EDG =90°,△△ADK =△GDP , △tan△ADK =tan△GDP ,即:12AK PG AD DG ==, △GP =1122DG FG =, △GP=FP ,△△DGP =△CFP =90°,△DPG =△CPF ,△DPG CPF ≌,△DG =CF ,△DE =DG =EF =CF ,即EC =2DE ,△点B,C ,M 在同一直线上,△△DCM =90°,△△DCE +△MCH =△MCH +△CMH ,△△DCE =△CMH ,即:tan△DCE =tan△CMH , △12CH DE HM CE ==, △HM =HF =2CH ,△CF =CH ,△HF =2CF =2DG , △222314S DG S FH ==. 设DE =x ,则EC = FH =HM =2x ,DC =,△123S S S +=,+x 2=4 x 2,解得:x x =0(舍去),△EH =x +2x =3x△PF 垂直平分EC ,△PE =PC ,△△PEC =△PCE =△PDG =△ADK , △tan△PEC =tan△ADK ,即:12QH AK EH AD ==, △QH =12△Q M =HM-QH故答案是:14 【点睛】本题主要考查正方形的性质,锐角三角函数的定义,全等三角形的判定和性质,勾股定理,通过锐角三角函数的定义,推出小正方形边长是大正方形边长的一半,是解题的关键. 13.(2021·浙江婺城·二模)有一种双层长方体垃圾桶AB =70cm ,BC =25cm ,CF =30cm ,侧面如图1所示,隔板EG 等分上下两层,下方内桶BCHG 绕底部轴(CF )旋转开,若点H 恰好能卡在原来点G 的位置,则内桶边CH 的长度应设计为___;现将CH 调整为25cm ,打开最大角度时,点H 卡在隔板上,如图2所示,则可完全放入下方桶内的球体的直径不大于____.【答案】 21【分析】△ 由题意,EG 等分上下两层,BH BG =,勾股定理直接求解即可△过点G '作G I BH '⊥于点I ,交BG 于点J ,过点J 作JK BG '⊥于点K ,分别通过勾股定理和三角函数求出,,JK JB 继而求出sin JBK ∠,过点H 作HL ⊥BG '于点L ,交BG 于点N ,过G 作GM HL ⊥于点M ,通过证明JBK GHM ∠=∠,继而用勾股定理和锐角三角函数解直角三角形,求出ML ,即为球的直径大小【详解】△点H 恰好能卡在原G 点的位置1352BH BG AB ∴=== 25BC =CH ∴=故答案为:△如图:根据旋转,25BC BC '==,25C H CH '==,BH ∴=5GH ∴C H C B ''=45C BH '∴∠=︒45HBG '∴∠=︒过点G '作G I BH '⊥于点I ,交BG 于点J过点J 作JK BG '⊥于点K ,BI G I '===51tan 357HG HBG BG ∠===1tan 7IJ HBG BI ∴=∠⨯==G J IG IJ ''∴=-==1122BJG S JG BI BG JK '''=⨯=⨯△21535JG BI JK BG '⨯∴==='25BJ BI === 153sin 255JK JBK JB ∴∠=== 过点H 作HL ⊥BG '于点L ,交BG 于点N ,过G 作GM HL ⊥于点M90JBK BNL HNG GHM ∠+∠=∠+∠=︒又HNG BNL ∠=JBK GHM ∴∠=∠3sin 5GHM ∴∠=,4cos 5GHM ∠= 4cos 545HM GH GHM ∴=⋅∠=⨯= 25421ML HL HM ∴=-=-=∴球体的直径不大于21cm故答案为21.【点睛】本题考查了解直角三角形,锐角三角函数的实际应用,正确的添加辅助线是解题的关键.14.(2021·黑龙江牡丹江·中考真题)如图,矩形ABCD 中,AD ,点E 在BC 边上,且AE=AD ,DF△AE 于点F ,连接DE ,BF ,BF 的延长线交DE 于点O ,交CD 于点G .以下结论:△AF=DC ,△OF :BF=CE :CG ,△S △BCG △DFG ,△图形中相似三角形有6对,则正确结论的序号是____.【答案】△△【分析】通过证明△ABE 和△ADF 是等腰直角三角形,结合已知条件,可判断△正确;通过证明△DCE △△BCG ,得到2CE CG =△ABF △△ADE ,得到2BF DE =,再通过相似和三角形的外角性质,得到OE =12DE ,进而证得OF CE BF CG=,可判断△正确;证明△BEF △△FDG ,连接CF 后,可知BCF BEF S △△,结合图象,即可判断△不正确;通过图形中相似三角形超过6对,可判断△不正确,问题即可得解.【详解】△AE =AD ,AD =AB ,△AE .在Rt△ABE 中,△ABE =90°,cos△BAE =AB AE,△cos△BAE =2AB AE = △△BAE =45°,即△ABE 是等腰直角三角形.△在矩形ABCD 中,△BAD =90°,△△DAF =45°.△DF △AE ,△△ADF=45°,即△ADF 是等腰直角三角形.△AD .△AF =AB .△在矩形ABCD 中,AB =CD ,△AF =CD .故△正确;又△AF =AB ,△BAE =45°,△△ABF =67.5°.△△CBG =22.5°.又△AE =AD ,△DAE =45°,△△ADE =67.5°.△△CDE =22.5°.△△CBG =△CDE .△△C=△C ,△△DCE △△BCG . △CE DC CG BC=.△在矩形ABCD 中,BC =AD ,△CE CG = 在△ABF 和△ADE 中.△BAF =△DAE =45°,AF =AB ,AE =AD ,△△ABF △△ADE .△BF AB DE AD == 在△ABF 和△OEF 中,△OEF =△ADE =67.5°=△ABF ,△△AFB =△OFE ,△AFB =△ABF ,△△ABF △△OEF ,△OEF=△OFE .△OE =OF ,△EOF =45°.又△△EOF =△DFO +△ODF =45°,△ODF =△ADE -△ADF =22.5°,△△ODF =△DFO .△OF =OD .△OE =OF =OD 12=DE .△12OF DE CE BF BF CG=⋅== .故△正确; 在△BEF 和△FDG 中, BE =FD ,△EBF =△DFG ,△BEF =△FDG=△ADC -△ADF =45°, △△BEF △△FDG .连接CF .又△ BC =AD ,△BCF BEF DFG BCG S S =△△△△< .故△不正确;△△ABF △△ADE ,△ABF △△OEF ,△△ADE △△OEF .在△BEF 和△BOE 中, △BEF =△BOE =45°,△EBF =△OBE ,△△BEF △△BOE .在△BOE 和△DOG 中, △ODG =△OBE ,△BOE =△DOG ,△△BOE △△DOG .△△BEF △△DOG .又△△DCE △△BCG ,△图形中相似三角形超过6对,故△不正确.综上,正确的结论是△△.故答案为:△△.【点睛】本题主要考查了矩形的性质、等腰三角形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质,涉及了特殊角的三角函数值、三角形的外角性质、举反例等,是一道综合题.相似和全等是证明边的比例关系中最常用的方法.15.(2021·重庆实验外国语学校二模)如图,在菱形ABCD 中,△BAD =120°,2BC =+将菱形纸片翻折,使点B落在CD边上的点P处,折痕为MN,点M、N分别在边BC、AB 上,若PN△AB,则点N到边MP的距离为________.【分析】过点P作PE△BC于E,作MF△AB于F,作NH△BM于H,根据菱形的性质和翻折的性质,求点N到边MP的距离等于求点N到BM的距离NH,在Rt△NBH中求出NH即可.【详解】解:如图,过点P作PE△BC于E,过点M作MF△AB于F,过点N作NH△BM于H,NG△MP,△四边形ABCD为菱形,AB△CD,AD△BC,△BAD=120°,△△ABC=△DCE=60°,又PE△BC,△△CPE=30°,△PC=2CE,PE,△翻折,△△NBM△△NPM,△NH=NG,△BNM=△PNM,BM=MP,△B=△NPM=60°,△NP△BA,△△BNP=90°,△△BNM=△PNM=45°,△△B+△BNP+△NPM+△BMP=360°,△△BMP=150°,△△PME=30°,△MP=2PE=,ME=3CE,△BM=PM=,MC=2CE,△BC=2+2CE+,△CE=1,△MB=△MF=MB×sin B==3,BF=MB×cos B=△△FNM=45°,FM△FN,△FN=MF=3,△BN=BF+FN3,△NH=BN×sin B=(3×sin60°△NG【点睛】此题主要考查四边形的综合性质求解,解题的关键是根据题意作出辅助线,利用菱形与三角函数的性质求解.16.(2021·山东庆云·九年级期末)如图,在Rt△ABC中,△ABC=90°,BC=3,D为斜边AC的中点,连接BD,点F是BC边上的动点(不与点B、C重合),过点B作BE△BD交DF延长线交于点E,连接CE,下列结论:△若BF=CF,则CE2+AD2=DE2;△若△BDE=△BAC,AB=4,则CE=158;△△ABD和△CBE一定相似;△若△A=30°,△BCE=90°,则DE_____.(填写所有正确结论的序号)【答案】△△△.【分析】△由直角三角形斜边上的中线等于斜边的一半,得AD=BD,由BF=CF,BD=CD得DE 是BC的垂直平分线,得BE=CE,再由勾股定理便可得结论,由此判断结论的正误;△证明△ABC△△DBE,求得BE,再证明DE△AB,得DE垂直平分BC,得CE=BE,便可判断结论的正误;△证明△ABD=△CBE,再证明BE与BC或BC与BE两边的比不一定等于AB与BD的比,便可判断结论正误;△先求出AC,进而得BD,再在Rt△BCE中,求得BE,进而由勾股定理求得结果,便可判断正误.【详解】解:△△△ABC=90°,D为斜边AC的中点,△AD=BD=CD,△BF=CF,△DE△BC,△BE=CE,△BE△BD,△BD2+BE2=DE2,△CE2+AD2=DE2,故△正确;△△AB=4,BC=3,△AC5,△52BD AD CD,△△A=△BDE,△ABC=△DBE=90°,△△ABC△△DBE,△AB BCDB BE,即4352BE=.△BE=158,△AD=BD,△△A=△ABD,△△A=△BDE,△△ABD=△BDE,△DE△AB,△DE△BC,△BD=CD,△DE 垂直平分BC ,△BE =CE ,△CE =158, 故△正确;△△△ABD 一定是等腰三角形,而△CBE 不一定是等腰三角形,△△ABD 和△CBE 不一定相似,故△错误;△△△A =30°,BC =3,△△A =△ABD =△CBE =30°,AC =2BC =6,△BD =132AC =, △BC =3,△BCE =90°,△BE =cos30BC ︒=△DE ==故△正确;故答案为:△△△.【点睛】本题是三角形的一个综合题,主要考查了勾股定理,相似三角形的性质与判定,解直角三角形,直角三角形的性质,线段垂直平分线的判定与性质,考试的内容多,难度较大,关键是综合应用以上性质灵活解题.17.(2021·辽宁锦州·中考真题)如图,△MON =30°,点A 1在射线OM 上,过点A 1作A 1B 1△OM 交射线ON 于点B 1,将△A 1OB 1沿A 1B 1折叠得到△A 1A 2B 1,点A 2落在射线OM 上;过点A 2作A 2B 2△OM 交射线ON 于点B 2,将△A 2OB 2沿A 2B 2折叠得到△A 2A 3B 2,点A 2落在射线OM 上;…按此作法进行下去,在△MON 内部作射线OH ,分别与A 1B 1,A 2B 2,A 3B 3,…,A n B n 交于点P 1,P 2,P 3,…P n ,又分别与A 2B 1,A 3B 2,A 4B 3,…,A n +1B n ,交于点Q 1,Q 2,Q 3,…,Q n .若点P 1为线段A 1B 1的中点,OA 1A n P n Q n A n +1的面积为___________________(用含有n 的式子表示).【分析】先证明△OA 1P 1△△OA 2P 2,△OP 1B 1△△OP 2B 2,又点P 1为线段A 1B 1的中点,从而可得P 2为线段A 2B 2的中点,同理可证P 3、P 4、P n 依次为线段A 3B 3、A 4B 4、△A n B n 的中点.结合相似三角形的性质可得△P 1B 1Q 1的P 1B 1上的高与△P 2A 2O 1的A 2P 2上的高之比为1△2,所以△P 1B 1Q 1的P 1B 1上的高为1213A A ,同理可得△P 2B 2Q 2的P 2B 2上的高为2313A A △,从而1121PQ A A S 四边形=112AB A S ∆﹣111P B Q S ∆,以此类推来求2232P Q A A S 四边形,从而找到四边形P An nQnAn S 的面积规律. 【详解】解:由折叠可知,OA 1=A 1A 2由题意得:A 1B 1//A 2B 2,△△OA 1P 1△△OA 2P 2,△OP 1B 1△△OP 2B 2, △111222A P OA A P OA ==12OP OP =1122P B P B= 12,又△点P 1为线段A 1B 1的中点,△A 1P 1=P 1B 1,△A 2P 2=P 2B 2,则点P 2为线段A 2B 2的中点,同理可证,P 3、P 4、△P n 依次为线段A 3B 3、A 4B 4、△A n B n 的中点.△A 1B 1//A 2B 2,△△P 1B 1Q 1△△P 2A 2O 1, △1122P B P A =1122A P P A =12, 则△P 1B 1Q 1的P 1B 1上的高与△P 2A 2O 1的A 2P 2上的高之比为1△2,△△P 1B 1Q 1的P 1B 1上的高为1213A A ,同理可得△P2B 2Q 2的P 2B 2上的高为2313A A , ,由折叠可知A 2A 3=A 3A 4=△△MON =30°,△A 1B 1=tan30°×OA 1=1,△A 2B 2=2,A 3B 3=4, ,△1121PQ A A S 四边形=112A B A S ∆﹣111P B Q S ∆ =121112A A A B ⋅﹣11121123A P A A ⋅=1111222-⨯ 同理,2232P Q A A S 四边形=223A B A S ∆﹣222P B Q S ∆ =232212A A A B ⋅﹣22231123A P A A ⋅=11121223⨯-⨯⨯⨯1n n n n A P Q A S +四边形=1n n n A B A S +∆﹣n n nP B Q S ∆=1111212222223n n n n ----⨯-⨯⨯⨯22122(2)3n n n ----【点睛】本题考查了规律型:图形的变化类,相似三角形的判定与性质,折叠的性质,锐角三角函数等知识,解决本题的关键在根据图形的变化找到规律.18.(2021·黑龙江·哈尔滨工业大学附属中学校一模)如图,在菱形ABCD 中,点F 是CD 的中点,BF 与AC 交于点E ,点N 在FB 上,CN 与AB 交于点M ,若tan FBC ∠=32AM DF =,BM =AE =__________.【分析】如图1中:过点F作FP△BC交BC的延长线于P.由tan FBC∠PFPB,可以假设PF,PB=5k,在Rt△PFC中,根据CF2=PF2+PC2,构建方程求出k,再证明△FCP=60°即可解决问题;【详解】解:如图1中:过点F作FP△BC交BC的延长线于P.△四边形ABCD是菱形,△AB=BC=CD,AB△CD,△点F是CD的中点,△DF=CF=12CD=12AB,△3AM=2DF,△设DF=3a,AM=2a,△CD=AB=6a,△BM=AB−AM=4a,△BM=4a.△a△CF BC△tan FBC∠=PF PB,△可以假设PF ,PB =5k ,在Rt △PFC 中,△CF 2=PF 2+PC 2,△2)2+(5k 2, 整理得:282k 2−600k +3×225=0,解得k ,△PF PC =5k△tan△FCP =PF PC △△PCF =60°,△AB △CD ,△△ABC =△FCP =60°,△四边形ABCD 是菱形,△AB =BC ,△△ABC 是等边三角形,△BC △CF △AB ,△△FCE △△BAE , △12CF CE AB AE ==,△AE =23【点睛】本题考查相似三角形综合题,菱形的性质、解直角三角形、勾股定理、锐角三角函数等知识,解题的关键是学会利用参数构建方程解决问题,属于中考填空题中的压轴题.19.(2021·湖南长沙·九年级期中)如图,在正方形ABCD 中,2AB =.G 为对角线BD 的延长线上一点,E 为线段CD 的中点,BF AE ⊥,连接OF .已知15DAG ∠=︒,下列说法正确的是______.(将正确答案的序号填写下来)△AG BD =;△BF =△13OP OA =;△13POF S =△;△若E 点为线段CD 上一动点,当AE EC CQ =+时,4AQ =.【答案】△△△【分析】根据正方形的性质与解直角三角形的方法逐个解题求解.△根据15DAG ∠=︒可得含60︒角的直角三角形AOG ,求出2AG AO =.△由90DAE BAF ∠+∠=︒,90BAF ABF ∠+∠=︒得BAF DAE ∠=∠,1tan tan 2DE AF BAF DAE AD BF ∠=∠===,通过解直角三角形求出BF 长度. △将:OP OA 转化为:OP OD ,通过ADP QBP ∆∆∽求解.△先通过:1:3OP OD =求出三角形OAP 的面积,再通过PF 与AP 的比值求出三角形POF 的面积.△设ED x =,2EC x =-,通过相似三角形与勾股定理求出x 的值从而求出AQ .【详解】解:△15DAG ∠=︒,60GAO DAG DAO ∴∠=∠+∠=︒,30G ∴∠=︒,2AG AO =,2BD AO =,AG BD ∴=,∴△正确,符合题意.△E 为CD 中点,12DE CD ∴=, 90DAE BAF ∠+∠=︒,90BAF ABF ∠+∠=︒,BAF DAE ∴∠=∠,1tan tan 2DE AF BAF DAE AD BF ∴∠=∠===, 2BF AF ∴=,在Rt ABF 中,由勾股定理得:2AB ===,AF ∴=2BF AF = ∴△错误,不符合题意.△E 为CD 中点,//EC AB ,EC ∴为ABQ ∆的中位线,C 为BQ 中点,22BQ BC AD ∴==,//AD BQ ,ADP QBP ∴∆∆∽, ∴12DP AD BP QB ==, ∴12DP BD DP =-, 13DP BD ∴=,111236OP OD DP BD BD BD =-=-=, ∴116132OD OP OP OA OD OD ===, ∴△正确,符合题意.△2AB =,24BQ AB ==,AQ ∴=12AP AD PQ BQ ==,13AP AQ ∴=∴35AF AP =, ∴32155FP AP =-=, 即25POF AOP S S ∆∆=,13OP OA =, 11113343AOP AOD ABCD S S S ∆∆∴==⨯=正方形, 22515POF AOP S S ∆∆∴==, ∴△错误,不符合题意.△设ED x =,2EC x =-,则DE ADEC CQ =, 即22x x CQ =-,42x CQ x -∴=, 24242x x AE EC CQ x x x--∴=+=-+=, 在Rt ADE △中,由勾股定理得:AE∴24x x-解得x =或x =).AE ∴ //AD BQ , DAE BQA ∴∠=∠,1sin sin 2DE DAE BQA AE ∴∠=∠==, 24AQ AB ∴==,∴△正确,符合题意.故答案为:△△△.【点睛】本题考查正方形与三角形的综合问题,解题关键是熟练掌握正方形的性质与解直角三角形的方法.20.(2021·广东龙岗·九年级期末)如图,已知在菱形ABCD ,BC=9,△ABC=60°,点E 在BC 上,且BE=6,将ΔABE 沿AE 折叠得到ΔAB′E ,其中B′E 交CD 于点F ,则CF=____________.【答案】95【分析】过点A 作AG △BC 交BC 于G ,取HG 使HG =GE ,过H 作HM △AE 于H ,过F 作FN △BC 交BC 延长线于N ,通过直角三角形求出BG 、AE ,由三角形的面积求得HM ,再通过折叠求出CF .【详解】解:过点A 作AG △BC 交BC 于G ,取HG 使HG =GE ,过H 作HM △AE 于H ,过F 作FN △BC 交BC 延长线于N ,△四边形ABCD 是菱形,△AB =BC =9,在Rt △ABG 中,△B =60°,△sinB =sin 60°=AG AB =,△AG △cosB =cos 60°=12BG AB =, △BG =12AB =92, △BE =6,△HE =2GE =2(BE -BG )=2×(962-)=3, 在Rt △AGE 中,AE = △S △AHE =12×HE ×AG =12×AE ×HM ,△1212HM ,解得,HM , △HG =GE ,AG △HE ,△△AHE 是等腰三角形,△AH =AE ,△AHE =△HEA ,在Rt △AHM 中,AM, △AB △CD ,△△FCN =△B =60°,△FN CN =tan △折叠,△△AEB ′=△HEA ,在△AHE 中,△△HAE =180°-△HEA -△AHE =180°-2△HEA ,又△FEN =180°-△HEA -△AEB ′=180°-2△HEA ,△△HAE =△FEN,设CN =x ,FN ,△tan △FEC =tan △HAM =FN HM EN AM=,==, △910x =, △CN=910, FN, △CF 95=. 故答案为:95. 【点睛】本题考查了翻折求线段,综合利用了等腰三角形和直角三角形等性质以及三角函数关系求线段,综合难度较高.三、解答题21.(2021·山东·日照市新营中学三模)(1)如图1,在正方形ABCD 中,E 是AB 上一点,点F 是AD 延长线上一点,且DF=BE ,求证:CE=CF .(2)如图2,在正方形ABCD 中,E 是AB 上一点,G 是AD 上一点,如果45GCE ∠=︒,请你利用(1)的结论证明:GE=BE+GD .(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在四边形ABCD 中,AD //BC (BC>AD ),90B ∠=︒,AB=BC=2AD ,E 是AB 上一点,且45DCE ∠=︒,求sin DEC ∠的值.【答案】(1)证明见教师;(2)证明见教师;(3【分析】 (1)利用正方形的性质证明△CBE △△CDF ,从而可得结论;(2)延长AD 至F ,使DF =BE .连接CF ,利用(1)的结论,再证明△ECG △△FCG ,从而可得结论;(3)如图,延长,AD 过C 作CM AD ⊥于,M 在AM 的延长线上截取,MQ BE = 先证明四边形ABCM 是正方形,结合(1)(2)可得:,,CBE CMQ CDE CDQ ≌≌ 设,,BE x AB a == 再利用勾股定理可得:3,a x = 从而可得答案.【详解】证明(1)解:(1)在正方形ABCD 中,,90,CB CD B ADC =∠=∠=︒90,CDF ∴∠=︒90CB CD B CDF BE DF =⎧⎪∴∠=∠=︒⎨⎪=⎩△△CBE △△CDF ,△CE =CF ;(2)如图, 延长AD 至F ,使DF =BE .连接CF ,由(1)知△CBE △△CDF ,。
中考数学一模汇编创型压轴题试题

2021年中考一模汇编制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日创新压轴题【专题汇编导引】2021年各区一模最后一道题都使用了创新型压轴题,引进了“等角点〞、“园的相邻点、相邻线〞、“相邻函数〞、“圆的限距点〞、“点到直线的疏距〞、“等距圆〞、“阳光点〞和“阴影点〞等一系列新概念,这几乎是继动点问题作为压轴题被更换后的最大规模类型压轴题。
亲爱的同学,假如你真正搞明白上面这些概念的数学含义,真正做到可以应用,创新型压轴题也就不难了。
预祝你中考获得好成绩!【各区中考题专题汇编】1. 【2021一模,第29题】在平面直角坐标系xOy 中,A 〔t ,0〕,B 〔3t,0〕,对于线段AB 和x 轴上方的点P 给出如下定义:当∠APB=60°时,称点P 为AB 的“等角点〞.〔1〕假设32t,在点302C ⎛⎫ ⎪⎝⎭,,D ⎫⎪⎪⎭,32E ⎛⎫⎪ ⎪⎝⎭中,线段AB 的“等角点〞是;〔2〕直线MN 分别交x 轴、y 轴于点M 、N ,点M 的坐标是〔6,0〕,∠OMN=30°.①线段AB 的“等角点〞P 在直线MN 上,且∠ABP =90°,求点P 的坐标; ②在①的条件下,过点B 作BQ ⊥PA ,交MN 于点Q ,求∠AQB 的度数;③假设线段AB 的所有“等角点〞都在△MON 内部,那么t 的取值范围是.2. 【2021东城一模,第29题】对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:假设存在过点P 的直线l 交⊙C 于异于点P 的A ,B 两点,在P ,A ,B 三点中,位于中间的点恰为以另外两点为端点的线段的中点时,那么称点P 为⊙C 的相邻点,直线l 为⊙C 关于点P 的相邻线.〔1〕当⊙O 的半径为1时, ○1分别判断在点D 〔21,14〕,E 〔0,3〕,F 〔4,0〕中,是⊙O 的相邻点 有__________;○2请从○1中之答案中,任选一个相邻点,在图1中做出⊙O 关于它的一条相邻线,并说明你的作图过程.○3点P 在直线3y x =-+上,假设点P 为⊙O 的相邻点,求点P 横坐标的取值范围; 〔2〕⊙C 的圆心在x 轴上,半径为1,直线3233y x =+与x 轴,y 轴分别交于点M ,N ,假设线段..MN 上存在⊙C 的相邻点P ,直接写出圆心C 的横坐标的取值范围.xy12345–1–112345678O图1 备用图1备用图23. 【2021丰台一模,第29题】如图,点P(x, y1)与Q(x, y2)分别是两个函数图象C1与C2上的任一点. 当a≤x≤b时,有-1≤y1- y2≤1成立,那么称这两个函数在a≤x≤b 上是“相邻函数〞,否那么称它们在a≤x≤b上是“非相邻函数〞. 例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x- 1图象上的任一点,当-3≤x≤ -1时,y1- y2=(3x+1) - (2x- 1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤ -1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1- y2≤1成立,因此这两个函数在-3≤x≤ -1上是“相邻函数〞.yC2Q〔1〕判断函数y =3x +2与y =2x +1在-2≤ x ≤ 0上是否为“相邻函数〞,并说明理由; 〔2〕假设函数y =x 2- x 与y =x - a 在0 ≤ x ≤ 2上是“相邻函数〞,求a 的取值范围; 〔3〕假设函数y =xa与y =-2x + 4在1 ≤x ≤ 2上是“相邻函数〞,直接写出a 的最大值与最小值.4. 【2021海淀一模,第29题】在平面直角体系xOy 中,⊙C 的半径为r ,P 是与圆心C 不重合的点,点P 关于⊙C 的限距点的定义如下:假设P '为直线PC 与⊙C 的一个交点,满足2r PP r '≤≤,那么称P '为点P 关于⊙C 的限距点,下列图为点P 及其关于⊙C 的限距点P '的示意图。
2023北京高三一模数学汇编:压轴填空(第15题)

2023北京高三一模数学汇编 压轴填空(第15题)1.(2023·北京西城·统考一模)如图,在棱长为2的正方体1111ABCD A B C D −中,点M ,N 分别在线段1AD 和11B C 上.给出下列四个结论: ①MN 的最小值为2; ②四面体NMBC 的体积为43; ③有且仅有一条直线MN 与1AD 垂直; ④存在点M ,N ,使MBN △为等边三角形. 其中所有正确结论的序号是____.2.(2023·北京东城·统考一模)已知函数()()πsin 0,0π2f x x λϕλϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图1所示,A 、B 分别为图象的最高点和最低点,过A 作x 轴的垂线,交x 轴于A ',点C 为该部分图象与x 轴的交点.将绘有该图象的纸片沿x 轴折成直二面角,如图2所示,此时10AB ,则λ=______.给出下列四个结论: ①π3ϕ=; ②图2中,5AB AC ⋅=;③图2中,过线段AB 的中点且与AB 垂直的平面与x 轴交于点C ;④图2中,S 是A BC '及其内部的点构成的集合.设集合{}2T Q S AQ =∈≤,则T 表示的区域的面积大于π4.其中所有正确结论的序号是______.3.(2023·北京朝阳·统考一模)某军区红、蓝两方进行战斗演习,假设双方兵力(战斗单位数)随时间的变化遵循兰彻斯特模型:()))()))0000cosh sinh cosh sinh x t X y t Y ⎧=⎪⎪⎨⎪=⎪⎩,其中正实数0X ,0Y 分别为红、蓝两方初始兵力,t 为战斗时间;()x t ,()y t 分别为红、蓝两方t 时刻的兵力;正实数a ,b 分别为红方对蓝方、蓝方对红方的战斗效果系数;e e cosh 2x xx −+=和e e sinh 2x x x −−=分别为双曲余弦函数和双曲正弦函数.规定当红、蓝两方任何一方兵力为0时战斗演习结束,另一方获得战斗演习胜利,并记战斗持续时长为T .给出下列四个结论:①若00X Y >且a b =,则()()()0x t y t t T >≤≤; ②若00X Y >且a b =,则1T a =③若00X bY a>,则红方获得战斗演习胜利;④若00X Y 其中所有正确结论的序号是________.4.(2023·北京石景山·统考一模)项数为(),2k k k *∈≥N 的有限数列{}n a 的各项均不小于1−的整数,满足123123122220k k k k k a a a a a −−−−⋅+⋅+⋅+⋅⋅⋅+⋅+=,其中10a ≠.给出下列四个结论:①若2k =,则22a =;②若3k =,则满足条件的数列{}n a 有4个; ③存在11a =的数列{}n a ;④所有满足条件的数列{}n a 中,首项相同. 其中所有正确结论的序号是_________.5.(2023·北京房山·统考一模)设函数2ln ,0,()41,0.x x f x x x x ⎧>=⎨++≤⎩给出下列四个结论:①函数()f x 的值域是R ;②1a ∀>,方程()f x a =恰有3个实数根;③0x +∃∈R ,使得()()000f x f x −−=;④若实数1234x x x x <<<,且()()()()1234f x f x f x f x ===.则()()1234x x x x +−的最大值为44e e−.其中所有正确结论的序号是__________.6.(2023·北京顺义·统考一模)如果函数()f x 满足对任意s ,(0,)t ∈+∞,有()()()f s t f s f t +<+,则称()f x 为优函数.给出下列四个结论:①()ln(1)(0)g x x x =+>为优函数;②若()f x 为优函数,则(2023)2023(1)f f <; ③若()f x 为优函数,则()f x 在(0,)+∞上单调递增; ④若()()f x F x x=在(0,)+∞上单调递减,则()f x 为优函数. 其中,所有正确结论的序号是______________.7.(2023·北京平谷·统考一模)如图,矩形ABCD 中,22AD AB ==,M 为BC 的中点,将ABM 沿直线AM 翻折,构成四棱锥B AMCD −1,N 为1B D 的中点,则在翻折过程中, ①对于任意一个位置总有CN ∥平面1AB M ; ②存在某个位置,使得1CN AB ⊥; ③存在某个位置,使得1AD MB ⊥;④四棱锥B AMCD −1.上面说法中所有正确的序号是____________.8.(2023·北京海淀·统考一模)在ABC 中,902ACB AC BC ∠=︒==,,D 是边AC 的中点,E 是边AB 上的动点(不与A ,B 重合),过点作AC 的平行线交BC 于点F ,将BEF △沿EF 折起,点B 折起后的位置记为点P ,得到四棱锥P ACFE −.如图所示.给出下列四个结论: ①//AC 平面PEF ;②PEC 不可能为等腰三角形; ③存在点E ,P ,使得PD AE ⊥;④当四棱锥P ACFE −的体积最大时,AE = 其中所有正确结论的序号是_________.9.(2023·北京丰台·统考一模)三等分角是“古希腊三大几何问题”之一,目前尺规作图仍不能解决这个问题.古希腊数学家Pappus (约300~350前后)借助圆弧和双曲线给出了一种三等分角的方法:如图,以角的顶点C 为圆心作圆交角的两边于A ,B 两点;取线段AB 的三等分点O ,D ;以B 为焦点,A ,D 为顶点作双曲线H .双曲线H 与弧AB 的交点记为E ,连接CE ,则13BCE ACB ∠∠=.①双曲线H 的离心率为________;②若π2ACB ∠=,||AC =CE 交AB 于点P ,则||OP =________.参考答案1.①②④【分析】对于①,利用直线之间的距离即可求解;对于②,以M 为顶点,NBC 为底面即可求解;对于③,利用直线的垂直关系即可判断;对于④,利用空间坐标即可求解.【详解】对于①,由于M 在1AD 上运动,N 在11B C 上运动,所以MN 的最小值就是两条直线之间距离11D C ,而112D C =,所以MN 的最小值为2;对于②,111233M BNC BNC BNC V SD C S −=⋅⋅=⋅,而12222BNCS=⨯⨯=,所以四面体NMBC 的体积为43; 对于③,由题意可知,当M 与1D 重合,N 与1C 重合时, 111D C AD ⊥,又根据正方体性质可知,111AD A B CD ⊥,所以当M 为1AD 中点,N 与1B 重合时,此时1MN AD ⊥,故与1AD 垂直的MN 不唯一,③错误;对于④,当MBN △为等边三角形时,BM BN =,则此时1AM B N =.所以只需要BM 与BN 的夹角能等于π3即可.以D 为原点,DA 、DC 、1DD 分别为x 轴、y 轴、z 轴建立空间直角坐标系,如下图,设1AM B N n ==,则由题意可得2M ⎛⎝,()2,2,0B ,()2,2,2N n −,则可得BM ⎛=− ⎝,(),0,2BN n =−,则12cos 2nBM BN MBN BMBN ⋅∠===⋅,整理可得2120n n⎫−+=⎪⎪⎝⎭,该方程看成关于n 的二次函数,44140⎫∆=−⨯⨯=>⎪⎪⎝⎭,所以存在n 使得MBN △为等边三角形. 故答案为:①②④ 2. ②③【分析】在图2中,以点O 为坐标原点,OC 、A A '的方向分别为y '、z '轴的正方向建立空间直角坐标系O x y z '''−,根据已知条件求出λ的值,结合ϕ的取值范围求出ϕ的值,可判断①;利用空间向量数量积的坐标运算可判断②;求出线段AB 的中点M 的坐标,计算CM AB ⋅,可判断③;求出cos BA C '∠,结合扇形的面积公式可判断④.【详解】函数()f x 的最小正周期为2π4π2T ==, 在图2中,以点O 为坐标原点,OC 、A A '的方向分别为y '、z '轴的正方向建立如下图所示的空间直角坐标系O x y z '''−,设点()0,,0A t ',则点()0,,A t λ、(),2,0B t λ+,AB ===,因为0λ>,解得λ=所以,()π2x f x ϕ⎛⎫+⎪⎝⎭,则()0f ϕ==1sin 2ϕ=,又因为函数()f x 在0x =附近单调递减,且0πϕ<<,所以,5π6ϕ=,①错; 因为()π5π26t f t ⎛⎫+= ⎪⎝⎭π5πsin 126t ⎛⎫+= ⎪⎝⎭,又因为点A 是函数()f x 的图象在y 轴左侧距离y 轴最近的最高点,则π5ππ262t +=,可得23t =−,所以,()π5π26x f x ⎛⎫+ ⎪⎝⎭,因为点C 是函数()f x 在y 轴右侧的第一个对称中心,所以,π5ππ26C x +=,可得13C x =,翻折后,则有20,3A ⎛− ⎝、4,03B ⎫⎪⎭、10,,03C ⎛⎫ ⎪⎝⎭、20,,03A ⎛⎫'− ⎪⎝⎭,所以,(3,2,AB =,(0,1,AC =,所以,在图2中,(20215AB AC ⋅=+⨯+=,②对;在图2中,线段AB的中点为13M ⎝⎭,因为322CM ⎛=⎝⎭,则(3002AB CM ⋅==,即CM AB ⊥,③对; 在图2中,设点(),,0Q x y ,2AQ =≤,可得22213x y ⎛⎫++≤ ⎪⎝⎭,()0,1,0A C '=,()3,2,0A B '=,2cos 721A C A B BA C A C A B ''⋅'∠===>⨯''⋅,易知BA C '∠为锐角,则π04BA C '<∠<, 所以,区域T 是坐标平面x Oy ''内以点A '为圆心,半径为1A C '=,且圆心角为BA C '∠的扇形及其内部, 故区域T 的面积21ππ1248T S <⨯⨯=,④错..【点睛】关键点点睛:本题考查翻折问题,解题的关键在于建立空间直角坐标系,通过空间向量法来求解相应问题. 3.①②④【分析】对于①根据已知条件利用作差法比较大小即可得出()()()000eatx t y t X Y −−=>,所以①正确;对于②,利用①中结论可得蓝方兵力先为0,即000e e e e 22at at at atY X −−+−=−解得1T a =对于③和④,若要红方获得战斗演习胜利,分别解出红、蓝两方兵力为0时所用时间1t 、2t ,比较大小即可知③错误,④正确.【详解】对于①,若00X Y >且a b =,则()()()()()()0000cosh sinh cosh sinh x t X at Y at y t Y at X at ⎧=−⎪⎨=−⎪⎩,即()()0000e e e e 22e e e e 22at at at atat at at atx t X Y y t Y X−−−−⎧+−=−⎪⎪⎨+−⎪=−⎪⎩,所以()()()00e atx t y t X Y −=−, 由00X Y >可得()()()000e atx t y t X Y −−=>,即①正确;对于②,当a b =时根据①中的结论可知()()x t y t >,所以蓝方兵力先为0,即()00e e e e 220at at at at y Y X t −−+−==−,化简可得()()0000e e at atX Y X Y −−=+,即20000eatX Y X Y +=−,两边同时取对数可得0000ln 2X Y at X Y ⎛⎫+= ⎪−⎝⎭,即00001l1ln 2X Y t X a Y a ⎛⎫+== ⎪⎝−⎭1T a= 所以②正确;对于③,若红方获得战斗演习胜利,则红方可战斗时间大于蓝方即可, 设红方兵力为0时所用时间为1t ,蓝方兵力为0时所用时间为2t ,即()))100coshsinh 0x t X ==,可得e=同理可得e0=,解得022X bY a>又因为,,,Y a bX都为正实数,所以可得0XY>所以可得③错误,④正确.故答案为:①②④.4.①②④【分析】根据有限数列{}n a的性质1na≥−,*N,Znn a∈∈,及满足123123122220k k kk ka a a a a−−−−⋅+⋅+⋅+⋅⋅⋅+⋅+=,其中1a≠,利用不等式放缩,结合等比数列求和可得1111112ka−⎛⎫−≤≤−<⎪⎝⎭,即可确定1a的值,从而可判断①③④的正误,若3k=,得123420a a a++=,结合1a,求得23,a a的关系,根据不等式求得2a的范围,一一列举得数列{}n a,即可判断②.【详解】由于有限数列{}n a的各项均不小于1−的整数,所以1na≥−,*N,Znn a∈∈,又因为123123122220k k kk ka a a a a−−−−⋅+⋅+⋅+⋅⋅⋅+⋅+=,所以()()123231112312222222121k k k k k kk ka a a a a−−−−−−−⋅=−⋅+⋅++⋅+≤++++=−所以1111112ka−⎛⎫−≤≤−<⎪⎝⎭,且10a≠,1a为整数,所以11a=−,故③不正确,④正确;当2k=时,得1220a a+=,所以11a=−,则22a=,故①正确;当3k=时,得123420a a a++=,因为11a=−,所以2324a a+=,则23245a a=−≤,所以2512a−≤≤,2a为整数,则2a的可能取值为1,012−,,,对应的3a的取值为6,4,2,0,故数列{}n a可能为1,1,6−−;1,0,4−;1,1,2−;1,2,0−,共4个,故②正确.故答案为:①②④.【点睛】思路点睛:项数为(),2k k k*∈≥N的有限数列{}n a的性质入手1na≥−,*N,Znn a∈∈从各项1na≥−,结合不等式放缩,确定1a的范围,从而得1a的值,逐项验证即可.5.②③④【分析】画出函数图象,结合图象对四个结论依次分析,即可求解结论.【详解】因为函数2ln,0,()41,0.x xf xx x x⎧>=⎨++≤⎩,其图象如下图所示:对于①,由图可知,函数()f x 的值域不是R ,故①不正确;对于②,由图可知,1a ∀>,方程()f x a =恰有3个实数根,故②正确;对于③,当0x +∃∈R 时,使得有00()()f x f x −=成立,即24+1=−y x x 与ln y x =有交点,这显然成立,故③正确;对于④,不妨设互不相等的实数1234,,,x x x x 满足1234x x x x <<<,当满足()()()()1234f x f x f x f x ===时, 由图可知1222+=−x x ,即124x x +=−, 34ln ln x x =,即34341ln ln ,x x x x −==, 所以()124444114x x x x x x ⎛⎫⎛⎫+−=−− ⎪ ⎪⎝⎭⎝⎭,由图可知,(]41,e x ∈,而1y x x =−在(]1,e x ∈上单调递减,所以4411e,0e x x ⎡⎫−∈−⎪⎢⎣⎭,所以()12343411440,4e e x x x x x x ⎛⎫⎛⎫⎛⎤+−=−−∈− ⎪ ⎪ ⎥⎝⎦⎝⎭⎝⎭,则()()1234x x x x +−的最大值为44e e−,故④正确. 故答案为:②③④. 6.①②④【分析】①计算出()()()ln 1ln101st g s g t g s t s t ⎛⎫+−+=+>= ⎪++⎝⎭,故()()()g s g t g s t +>+,得到①正确;②赋值法得到()()212f f >,()()313f f >,依次类推得到(2023)2023(1)f f <; ③举出反例; ④由()()f x F x x=在(0,)+∞上单调递减,得到()()()(),f s t f s f s t f t s t s s t t ++<<++,整理变形后相加得到()()()()()s t f s t s t f s f t ++<++⎡⎤⎣⎦,即()()()f s t f s f t +<+,④正确.【详解】因为(),0,s t ∈+∞,所以()()()()()()()()11ln 1ln 1ln 1ln 1s t g s g t g s t s t s t s t+++−+=+++−++=++1lnln 1ln1011s t st st s t s t +++⎛⎫==+>= ⎪++++⎝⎭,故()()()g s g t g s t +>+,故()ln(1)(0)g x x x =+>是优函数,①正确; 因为()f x 为优函数,故()()()1111f f f +>+,即()()212f f >,()()()()21213f f f f +>+=,故()()313f f >,同理可得()()414f f >,……,()()202312023f f >,②正确;例如()2,0f x x x =−>,满足()222()()()20f s t f s f t s t s t st +−−=−+++=−<,即()()()f s t f s f t +<+,为优函数,但()2f x x =−在()0,x ∈+∞上单调递减,故③错误; 若()()f x F x x=在(0,)+∞上单调递减, 任取(),0,s t ∈+∞,,s t s s t t +>+>, 则()()()(),F s t F s F s t F t +<+<,即()()()(),f s t f s f s t f t s t s s t t++<<++, 变形为()()()()()(),sf s t s t f s tf s t s t f t +<++<+, 两式相加得:()()()()()s t f s t s t f s f t ++<++⎡⎤⎣⎦, 因为0s t +>,所以()()()f s t f s f t +<+, 则()f x 为优函数,④正确. 故答案为:①②④【点睛】函数新定义问题的方法和技巧:(1)可通过举例子的方式,将抽象的定义转化为具体的简单的应用,从而加深对信息的理解; (2)可用自己的语言转述新信息所表达的内容,如果能清晰描述,那么说明对此信息理解的较为透彻; (3)发现新信息与所学知识的联系,并从描述中体会信息的本质特征与规律;(4)如果新信息是课本知识的推广,则要关注此信息与课本中概念的不同之处,以及什么情况下可以使用书上的概念. 7.①④【分析】证明EM ∥NC ,结合线面平行判定判断①;由EM ∥NC 结合1AB 与EM 不垂直,判断②;由线面垂直的判定得出点1B 与点F 重合,从而判断③;取AM 的中点为G ,连接1B G ,当1B G ⊥平面AMCD 时,四棱锥B AMCD −1的体积最大,从而判断④.【详解】分别取1,AB AD 的中点为,E F ,连接1,,,EN EM B F FM . 因为11,AB B D 的中点分别为,E N ,所以EN ∥AD ∥MC ,且12EN AD MC ==.即四边形ENCM 为平行四边形,故EM ∥NC ,由线面平行的判定可知对于任意一个位置总有CN ∥平面1AB M ,故①正确;因为190AB M ∠=︒,所以1AB 与EM 不垂直,由EM ∥NC 可知,1AB 与NC 不垂直,故②错误; 由题意11AB B M ⊥,若1AD MB ⊥,则由线面垂直的判定可得1MB ⊥平面1AB D .则11MB B D ⊥,因为AM MD =,所以1AMB △与1MB D △全等,则111AB B D ==,此时点1B 与点F 重合,不能形成四棱锥B AMCD −1,故③错误;取AM 的中点为G ,连接1B G ,1B G =,当1B G ⊥平面AMCD 时,四棱锥B AMCD −1的体积最大,最大值为11(12)132+⨯⨯,故④正确; 故答案为:①④8.①③【分析】根据线面平行的判断定理,判断①;证明PFC EFC ≅,即可判断②;利用垂直关系转化,结合反证法,即可判断③;表示四棱锥的体积后,利用导数计算最值,即可判断④.【详解】①因为//AC EF ,EF ⊂平面PEF ,AC ⊄平面PEF ,所以//AC 平面PEF ,故①正确;②因为ABC 是等腰直角三角形,所以PEF 也是等腰直角三角形,则EF PF =,因为AC BC ⊥,//EF AC ,所以EF BC ⊥,且⊥EF PF当90PFC ∠=时,PFC EFC ≅,所以EC PC =,此时PEC 是等腰三角形,故②错误;③因为EF BC ⊥,且⊥EF PF ,BC PF F =,且BC ⊂平面PCF ,PF ⊂平面PCF ,所以EF ⊥平面PCF ,EF ⊂平面ABC ,所以平面ABC ⊥平面PEF ,且平面ABC ⋂平面PEF BC =,如图,过点P 作PM BC ⊥,连结DM ,则PM ⊥平面ABC ,AE ⊂平面ABC ,所以PM AE ⊥,若PD AE ⊥,PD PM P ⋂=,PD ⊂平面PDM ,PM ⊂平面PDM ,所以⊥AE 平面PDM ,DM ⊂平面PDM ,所以AE DM ⊥,如图,2AC =,延长MD ,交AB 于点N ,则DCM △和AND △都是等腰直角三角形,则1CM =,点N 到直线AC 的距离等于12,这样在翻折过程中,若能构成四棱锥,则BF FM >,设FC x =,则21x x −>+,则102x <<, 则存在点E ,P ,使得PD AE ⊥,故③正确;④当底面ACFE 的面积一定时,平面平面ABC ⊥平面PEF 时,即PF ⊥平面ABC 时,四棱锥P ACFE −的体积最大,设FC x =,2EF BF PF x ===−,02x <<()()1122232P ACFE V x x x −=⨯⨯−+⋅⋅− 321463x x x =−+ ()22141231280236V x x x x '=−+=−+=得2x =2x =−,当0,2x ⎛∈ ⎝⎭,0V '>,函数单调递增,当2x ⎛⎫∈ ⎪ ⎪⎝⎭,0V '<,函数单调递减,所以当2x =3AE =,故④错误;故答案为:①③【点睛】思路点睛:本题考查几何体的线线,线面位置关系,以及动点问题,和导数相联系的最值问题,本题的关键是第三问,需在变化过程中找到位置关系,建立不等式,即可判断.9. 27−【分析】①根据图形关系确定2c a =即可求解;利用面积之比1sin 21sin 2ACPBCP AC CP ACP AP S S BP BC CP BCP ⋅∠==⋅∠△△,进而可求出3BP =,再根据OP OB BP =−求解. 【详解】①由题可得,,OA a OB c ==所以2c a =,所以双曲线H 的离心率为2c a =; ②,因为π2ACB ∠=,且AC BC ==,所以6AB , 又因为13BCE ACB ∠∠=,所以ππ,,36ACP BCP ∠=∠=所以1sin 2211sin 22ACPBCP AC CP ACP AP S S BP BC CP BCP ⋅∠===⋅∠△△,所以AP =,因为1)6AB AP BP BP =+==,解得3BP =,所以7OP OB BP =−=−故答案为:2; 7−。
2020-2021年广州市一模考压轴题汇编专练2含解析

2020-2021年广州市一模考压轴题汇编专练2一.选择题(共10小题)【几何】1.(2021•天河区一模)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连接OG.问:OG的长是多少?大臣给出的正确答案应是()A.r B.(1+)r C.(1+)r D.r2.(2021•越秀广大附一模)如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N 分别在边AB,CD上,CN=1cm.现将四边形BCNM沿MN折叠,使点B,C分别落在点B′,C′上.在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为()cm.A.﹣B.C.D.3.(2021•荔湾西关外国语一模)如图,在扇形OAB中,∠AOB=105°,OA=6,点C在半径OB上,沿AC折叠,圆心O落在上,则图中阴影部分的面积是()A.12π﹣6B.9π﹣9C.D.4.(2021•荔湾西关外国语一模)如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为()A.B.C.D.5.(2021•增城区一模)如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F 为EC上一个动点,点P为DF的中点,连接PB,当PB的最小值为3时,则AD的值为()A.2B.3C.4D.6【函数】6.(2021•荔湾西关外国语一模)如图,Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,点P从点A出发,以1cm/s的速度沿A→C向点C运动,同时点Q从点A出发,以2cm/s 的速度沿A→B→C向点C运动,直到它们都到达点C为止.若△APQ的面积为S(cm2),点P的运动时间为t(s),则S与t的函数图象是()A.B.C.D.7.(2021•白云区一模)设函数y1=,y2=﹣(k>0),当2≤x≤3时,函数的y1最大值是a,函数y2的最小值是a﹣4,则ak=()A.4B.6C.8D.108.(2021•黄埔区一模)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于点A(3,0)、点B(﹣1,0).下列结论:①abc>0;②b﹣2a>0;③8a+c<0;④a+b>n (an+b)(n≠1).正确的有()A.4个B.3个C.2个D.1个9.(2021•越秀广大附一模)如图,抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,则抛物线y=cx2+bx+a的图象大致为()A.B.C. D.10.(2021•龙岗区模拟)二次函数y=ax2+bx+c的图象如图所示,反比例函数y=与正比例函数y=(2a+c)x在同一坐标系内的大致图象是()A.B.C.D.二.填空题(共7小题)【几何】1.(2021•荔湾西关外国语一模)如图,在菱形ABCD中,∠DAB=60°,AB=3,点E在边AD上,且DE=1,点F为线段AB上一动点(不与点A重合),将菱形沿直线EF折叠,点A的对应点为点A′,当点A′落在菱形的对角线上时,AF的长为.2.(2021•白云区一模)如图,在平面直角坐标系中,有一个Rt△OAB,∠ABO=90°,∠AOB=30°,直角边OB在y轴正半轴上,点A在第一象限,且OA=1,将Rt△OBA绕原点O逆时针旋转30°,同时把各边长扩大为原来的2倍(即OA1=2OA),得到Rt△OA1B1,同理,将Rt△OA1B1绕原点O逆时针旋转30°,同时把各边长扩大为原来的2倍,得到Rt△OA2B2,…,依此规律,得到Rt△OA2021B2021,则点B2021的纵坐标为.3.(2021•增城区一模)如图.在矩形纸片ABCD中,AB=4,AD=6,点E是AB的中点,点F是边AD上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则线段A′C的最小值是.4.(2021•黄浦区一模)如图,⊙O的直径CD为6cm,OA,OB都是⊙O的半径,∠AOD=2∠AOB=60°,点P在直径CD上移动,则AP+BP的最小值为.5.(2021•越秀广大附一模)如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上一动点,若OB=1,则阴影部分周长的最小值为.6.(2021•天河区一模)如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,则下列结论正确的是.(1)DC=3OG;(2)OG=BC;(3)△OGE是等边三角形;(4)S△AOE=.【函数】7.(2021•增城区一模)抛物线y=mx2+(1﹣4m)x+1﹣5m一定经过非坐标轴上的一点P,则点P的坐标为.三.解答题(共23小题)【应用】1.(2021•荔湾西关外国语一模)农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:销售价格x(元/千克)3035404550日销售量p(千克)6004503001500(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p 与x之间的函数表达式;(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)2.(2021•增城区一模)某种型号油电混合动力汽车,从A地到B地,只用燃油行驶,需用燃油76元;从A地到B地,只用电行驶,需用电26元,已知每行驶1千米,只用燃油的费用比只用电的费用多0.5元.(1)若只用电行驶,每行驶1千米的费用是多少元?(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少需用电行驶多少千米?【反比例函数与一次函数】3.(2021•荔湾西关外国语一模)如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数y=(k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.(1)当m=1时,求一次函数的解析式;(2)若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,求反比例函数的解析式.4.(2021•白云区一模)一次函数y=kx+b与反比例函数y=的图象都经过点(2,﹣1).(1)求b的值;(2)点(2a,y1),(a,y2),(3a,y3),a≠0,都在反比例函数图象上,根据图象比较y1,y2,y3的大小.5.(2021•增城区一模)已知反比例函数y=和一次函数y=﹣x+a﹣1(a为常数).(1)当a=5时,求反比例函数与一次函数的交点坐标;(2)是否存在实数a,使反比例函数与一次函数有且只有一个交点,如果存在,求出实数a,如果不存在,说明理由.6.(2021•黄浦区一模)如图,平行四边形OABC的顶点A在x轴的正半轴上,顶点B的坐标为(,3),点D在边AB上,已知三角形ODC的面积是,反比例函数y=(k >0,x>0)的图象经过C、D两点.(1)求点C的坐标;(2)求点D的横坐标.7.(2021•天河区一模)如图,四边形ABCO是平行四边形,OA=2,AB=6,点A在第一象限,点C在x轴的负半轴上,将▱ABCO绕点A逆时针旋转得到▱ADEF.点D在反比例函数y=的图象上,且AD经过点O,点F恰好落在x轴的正半轴上.(1)求点A的坐标;(2)求k的值.【二次函数】8.(2021•荔湾西关外国语一模)已知抛物线G:y=x2﹣2mx与直线l:y=3x+b相交于A,B两点(点A的横坐标小于点B的横坐标).(1)求抛物线y=x2﹣2mx顶点的坐标(用含m的式子表示);(2)已知点C(﹣2,1),若直线l经过抛物线G的顶点,求△ABC面积的最小值;(3)若平移直线l,可以使A,B两点都落在x轴的下方,求实数m的取值范围.9.(2021•白云区一模)抛物线G:y=x2﹣2ax﹣a+3(a为常数)的顶点为A.(1)用a表示点A的坐标;(2)经过探究发现,随着a的变化,点A始终在某一抛物线H上,若将抛物线G向右平移t(t>0)个单位后,所得抛物线顶点B仍在抛物线H上;①平移距离t是a的函数吗?如果是,求出函数解析式,并写出a的取值范围;如果不是,请说明理由;②若y=x2﹣2ax﹣a+3在x≥﹣4时,都有y随x的增大而增大,设抛物线H的顶点为C,借助图象,求直线AC与x轴交点的横坐标的最小值.10.(2021•增城区一模)已知抛物线y=﹣x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.(1)求抛物线的函数表达式和顶点B的坐标;(2)如图1,抛物线与y轴交于点C,连接AC,过A作AD⊥x轴于点D,E是线段AC 上的动点(点E不与A,C两点重合);(i)若直线BE将四边形ACOD分成面积比为1:3的两部分,求点E的坐标;(ii)如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在y轴上的同时点F恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.11.(2021•黄浦区一模)如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.(1)求抛物线的二次函数解析式:(2)若点P在抛物线上,点Q在x轴上,当以点B、C、P、Q为顶点的四边形是平行四边形时,求点P的坐标;(3)如图2,点H是直线BC下方抛物线上的动点,连接BH,CH.当△BCH的面积最大时,求点H的坐标.12.(2021•越秀广大附一模)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+与x轴正半轴交于点A,且点A的坐标为(3,0),过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作PQ⊥l于点Q;M是直线l上的一点,其纵坐标为﹣m+,以PQ,QM为边作矩形PQMN.(1)求b的值.(2)当点Q与点M重合时,求m的值.(3)当矩形PQMN是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)抛物线在矩形PQMN内的部分称为被扫描部分.请问该抛物线是否全部被扫描?若是,请说明理由,若否,直接写出抛物线被扫描部分自变量的取值范围.13.(2021•天河区一模)已知抛物线y=mx2﹣2mx+3(m<0)与x轴交于A,B两点(点A 在点B的左侧),与y轴交于点C,且OB=3OA.(1)求抛物线的解析式;(2)若M,N是第一象限的抛物线上不同的两点,且△BCN的面积恒小于△BCM的面积,求点M的坐标;(3)若D为抛物线的顶点,P为第二象限的抛物线上的一点,连接BP,DP,分别交y 轴于E,F,若EF=OC,求点P的坐标.【几何】14.(2021•增城区一模)如图,已知△ABC.(1)尺规作图:先作∠ABC的平分线BD交AC于点D,再作线段BD的垂直平分线,分别交BC、AB于点E、F.(不写作法,保留作图痕迹)(2)连接DE、DF,若AB=3,BC=2,求四边形BEDF的边长.15.(2021•黄浦区一模)如图1所示,点C把线段AB分成AC与CB,若,则称线段AB被点C黄金分割(golden sec tion),点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.(1)根据上述定义求黄金比;(2)在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段AB的垂直平分线,得线段AB的中点M;②过点B作AB垂线l;③以点B为圆心,以BM为半径作圆交l于N;④连接AN、BN,以N为圆心,以NB为半径作圆交AN于P;⑤以点A为圆心,以AP为半径作圆交AB于C.(3)证明你按以上步骤作出的C点就是线段AB的黄金分割点.16.(2021•增城区一模)如图,已知Rt△ABC,∠ABC=90°,AB为⊙O的直径,斜边AC 交⊙O于点E,AC平分∠DAB,ED⊥AD于点D,DE的延长线与BC交于点F.(1)求证:DE是⊙O切线;(2)求证:CF=BF;(3)若AD:AB=3:4,DE=,求EF的长.17.(2021•荔湾西关外国语一模)如图,半径为4的⊙O中,弦AB的长度为4,点C 是劣弧上的一个动点,点D是弦AC的中点,点E是弦BC的中点,连接DE、OD、OE.(1)求∠AOB的度数;(2)当点C沿着劣弧从点A开始,逆时针运动到点B时,求△ODE的外心P所经过的路径的长度;(3)分别记△ODE,△CDE的面积为S1,S2,当S12﹣S22=21时,求弦AC的长度.18.(2021•白云区一模)如图,⊙O是四边形ABCD的外接圆,AC是⊙O的直径,BE⊥DC,交DC的延长线于点E,CB平分∠ACE.(1)求证:BE是⊙O的切线.(2)若=2,CE=1,求点B到AD的距离.19.(2021•白云区一模)不在射线DA上的点P是边长为2的正方形ABCD外一点(P在AB左侧),且满足∠APB=45°,以AP,AD为邻边作▱APQD.(1)如图,若点P在射线CB上,请用尺规补全图形;(2)若点P不在射线CB上,求∠P AQ的度数;(3)设AQ与PD交点为O,当△APO的面积最大时,求tan∠ADO的值.20.(2021•黄浦区一模)如图1,正方形ABCD的对角线相交于点O,延长OD到点G,延长OC到点E,使OG=2OD,OE=2OC,以OG,OE为邻边作正方形OEFG,连接AG,DE.(1)探究AG与DE的位置关系与数量关系,并证明;(2)固定正方形ABCD,以点O为旋转中心,将图1中的方形OEFG逆时针转n°(0<n<180)得到正方形OE1F1G1,如图2.①在旋转过程中,当∠OAG1=90°时,求n的值;②在旋转过程中,设点E1到直线AG1的距离为d,着正方形ABCD的边长为1,请直接写出d的最大值与最小值,不必说明理由.21.(2021•越秀广大附一模)△ABC为等边三角形,AB=8,AD⊥BC于点D,E为线段AD 上一点,AE=2.以AE为边在直线AD右侧构造等边三角形AEF,连接CE,N为CE 的中点.(1)如图1,EF与AC交于点G,连接NG,求线段NG的长;(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接DN,MN.当30°<α<120°时,猜想∠DNM的大小是否为定值,并证明你的结论;(3)连接BN,在△AEF绕点A逆时针旋转过程中,求线段BN的取值范围.22.(2021•天河区一模)如图,△ABC中,∠BAC≥120°,AB=AC,点A关于直线BC的对称点为点D,连接BD,CD.(1)求证:四边形ABDC是菱形;(2)延长CA到E,使得AB=BE.求证:BC2﹣AC•CE=AC2;(3)在(2)小题条件下,可知E,B,D,C四点在同一个圆上,设其半径为a(定值),若BC=kAB,问k取何值时,BE•CE的值最大?2020-2021年广州市一模考压轴题汇编专练2一.选择题(共10小题)【几何】1.(2021•天河区一模)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连接OG.问:OG的长是多少?大臣给出的正确答案应是()A.r B.(1+)r C.(1+)r D.r 【分析】如图连接CD,AC,DG,AG.在直角三角形即可解决问题;【解答】解:如图连接CD,AC,DG,AG.∵AD是⊙O直径,∴∠ACD=90°,在Rt△ACD中,AD=2r,∠DAC=30°,∴AC=r,∵DG=AG=CA,OD=OA,∴OG⊥AD,∴∠GOA=90°,∴OG===r,故选:D.【点评】本题考查作图﹣复杂作图,正多边形与圆的关系,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.2.(2021•越秀广大附一模)如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N 分别在边AB,CD上,CN=1cm.现将四边形BCNM沿MN折叠,使点B,C分别落在点B′,C′上.在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为()cm.A.﹣B.C.D.【分析】探究点E的运动轨迹,寻找特殊位置解决问题即可.【解答】解:如图1中,∵四边形ABCD是矩形,∴AB∥CD,∴∠1=∠3,由翻折的性质可知:∠1=∠2,BM=MB′,∴∠2=∠3,∴MB′=NB′,∵NB′===(cm),∴BM=NB′=(cm).如图2中,当点M与A重合时,AE=EN,设AE=EN=xcm,在Rt△ADE中,则有x2=22+(4﹣x)2,解得x=,∴DE=4﹣=(cm),如图3中,当点M运动到MB′⊥AB时,DE′的值最大,DE′=5﹣1﹣2=2(cm),如图4中,当点M运动到点B′落在CD时,DB′(即DE″)=5﹣1﹣=(4﹣)(cm),∴点E的运动轨迹E→E′→E″,运动路径=EE′+E′B′=2﹣+2﹣(4﹣)=(﹣)(cm).故选:A.【点评】本题考查翻折变换,矩形的性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考填空题中的压轴题.3.(2021•荔湾西关外国语一模)如图,在扇形OAB中,∠AOB=105°,OA=6,点C在半径OB上,沿AC折叠,圆心O落在上,则图中阴影部分的面积是()A.12π﹣6B.9π﹣9C.D.【分析】连接AO'、OO',根据折叠性质可知△AOO'是等边三角形,然后再求出S扇形AOO'、S扇形AOB、S△COO',即可求解.【解答】解:如图,连接AO'、OO'交AC于点D,由折叠的性质可得,AC⊥OO',OD=O'D,AO=AO'=OO',∴△AO O'是等边三角形,∴∠AO O'=60°,∵∠AOB=105°,∴∠COD=45°.∵OA=6,AC⊥OO',OD=O'D,∴CD=OD=OO'=OA=3,∴,,,∴.故选:C.【点评】本题是扇形面积的综合练习题,考查了折叠的性质,以及扇形面积的公式,灵活运用即可.4.(2021•荔湾西关外国语一模)如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为()A.B.C.D.【分析】设⊙O的半径是R,PE=PF=x,BQ=y,连接OD,OG,OF,OE,得出正方形CDOE和OGQF,推出OD=CD=CE=OE=GQ=QF=R,求出y=2R,x=R,根据锐角三角函数值求出即可.【解答】解:设⊙O的半径是R,PE=PF=x,BQ=y,连接OD,OG,OF,OE,∵⊙O内切于Rt△ABC,∴∠ODC=∠OEC=90°=∠C,AD=AG,∵OD=OE,∴四边形CDOE是正方形,∴OD=CD=CE=OE=R,同理OG=GQ=FQ=OF=R,则PQ=CP,AC=AQ,∵PQ⊥AB,∠C=90°,∴∠C=∠PQB=90°,∵∠B=∠B,∴△BQP∽△BCA,∴==,∴BC=2BQ=2y,根据BG=BE得:y+R=2y﹣R,解得:y=2R,在Rt△PQB中,由勾股定理得:PQ2+BQ2=BP2,即(2R)2+(R+x)2=(4R﹣R﹣x)2,解得:x=R,即PQ=R+R=R,BQ=2R,tan B===.故选:C.【点评】本题考查了正方形的性质和判定,切线的性质,勾股定理,相似三角形的性质和判定,切线长定理等知识点的应用,主要考查学生的推理和计算能力,难度偏大.5.(2021•增城区一模)如图,矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F 为EC上一个动点,点P为DF的中点,连接PB,当PB的最小值为3时,则AD的值为()A.2B.3C.4D.6【分析】根据中位线定理可得出点P的运动轨迹是线段P1P2,再根据垂线段最短可得当BP⊥P1P2时,PB取得最小值;由矩形的性质以及已知的数据即可知BP1⊥P1P2,故BP 的最小值为为BP1的长,由勾股定理求解即可.【解答】解:如图,当点F与点C重合时,点P在P1处,CP1=DP1,当点F与点E重合时,点P在P2处,EP2=DP2,∴P1P2∥CE且P1P2=CE..且当点F在EC上除点C、E的位置处时,有DP=FP.由中位线定理可知:P1P∥CE且P1P=CF,∴点P的运动轨迹是线段P1P2,.∴当BP⊥P1P2时,PB取得最小值.∵矩形ABCD中,AB:AD=2:1,设AB=2t,则AD=t,∵E为AB的中点,∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=t,∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.∴∠DP2P1=90°.∴∠DP1P2=45°.∴∠P2P1B=90°,即BP1⊥P1P2,∴BP的最小值为BP1的长.在等腰直角△BCP1中,CP1=BC=t,∴BP1=t=3,∴t=3.故选:B.【点评】本题考查轨迹问题、矩形的性质等知识,解题的关键是学会利用特殊位置解决问题,有难度.【函数】6.(2021•荔湾西关外国语一模)如图,Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,点P从点A出发,以1cm/s的速度沿A→C向点C运动,同时点Q从点A出发,以2cm/s 的速度沿A→B→C向点C运动,直到它们都到达点C为止.若△APQ的面积为S(cm2),点P的运动时间为t(s),则S与t的函数图象是()A.B.C.D.【分析】分两种情况讨论:当0≤t≤2时,过Q作QD⊥AC交AC于点D,S△APQ=×AP×QD;当2<t≤4时,S△APQ=S△ABC﹣S△CPQ﹣S△ABQ.【解答】解:①当0≤t≤2时,点Q在AB上,∴AQ=2t,AP=t,过Q作QD⊥AC交AC于点D,∵Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,∴BC=3cm,∴=,∴QD=t,S△APQ=×AP×QD=×t×t=t2,②当2<t≤4时,点Q在BC上,S△APQ=S△ABC﹣S△CPQ﹣S△ABQ=×3×4﹣×(4﹣t)×(8﹣2t)﹣×4×(2t﹣5)=﹣t2+4t=﹣(t﹣2)2+4,综上所述,正确的图象是C.故选:C.【点评】本题考查动点运动,三角形面积.B点是Q点运动的分界点,将运动过程分两种情况进行讨论是解题的关键.7.(2021•白云区一模)设函数y1=,y2=﹣(k>0),当2≤x≤3时,函数的y1最大值是a,函数y2的最小值是a﹣4,则ak=()A.4B.6C.8D.10【分析】首先根据k与x的取值分析函数y1,y2增减性,根据增减性确定最值,进而求解.【解答】解:∵k>0,2≤x≤3,∴y1随x的增大而减小,y2随x的增大而增大,∴当x=2时,y1取最大值,最大值为=a①;当x=2时,y2取最小值,最小值为﹣=a﹣4②;由①②得a=2,k=4,∴ak=8,故选:C.【点评】本题考查了反比例函数的性质,关键是能根据反比例函数的增减性确定最值,进而求解.8.(2021•黄埔区一模)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于点A(3,0)、点B(﹣1,0).下列结论:①abc>0;②b﹣2a>0;③8a+c<0;④a+b>n (an+b)(n≠1).正确的有()A.4个B.3个C.2个D.1个【分析】根据抛物线开口向下判断出a<0,再根据顶点横坐标用a表示出b,根据与y 轴的交点求出c的取值范围,然后判断出①错误,根据对称轴是直线x=1,可以判断出②正确,根据b=﹣2a,对称轴为x=1,点A(3,0),故9a+3b+c=0,即可判断③正确;根据顶点坐标即可判断出④正确,进而可得结论.【解答】解:∵抛物线开口向下,∴a<0,∵顶点坐标(1,n),∴对称轴为直线x=1,∴﹣=1,∴b=﹣2a>0,∵与y轴的交点在正半轴上,∴c>0,∴abc<0,故①错误;∵﹣=1,∴b+2a=0,得b=﹣2a,所以b﹣2a=﹣2a﹣2a=﹣4a,a<0,所以﹣4a>0,故②正确;∵点A(3,0),∴9a+3b+c=0,∵b=﹣2a,∴3a+c=0,∵a<0,8a+c<0,故③正确;∵顶点坐标的横坐标为1,∴当x=1时,函数有最大值,∴a+b+c≥an2+bn+c,∴a+b≥an2+bn=n(an+b),故④正确,综上所述,结论正确的是②③④共3个.故选:B.【点评】本题考查了抛物线与x轴的交点,二次函数的性质,主要利用了二次函数的开口方向,对称轴,最值问题,以及二次函数图象上点的坐标特征,关键在于根据顶点横坐标表示出a、b的关系.7.(2021•越秀广大附一模)如图,抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,则抛物线y=cx2+bx+a的图象大致为()A.B.C.D.【分析】根据题意得到a﹣b+c=0,a>0,b<0,c=﹣1,即可得到抛物线y=cx2+bx+a 的开口向下,对称轴直线x=﹣<0,交y轴正半轴,经过点(﹣1,0),据此即可判断.【解答】解:∵抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,∴开口向上,对称轴在y轴的右侧,∴a﹣b+c=0,a>0,b<0,c=﹣1,∴抛物线y=cx2+bx+a的开口向下,对称轴直线x=﹣<0,交y轴正半轴,当x=﹣1时,y=c﹣b+a=0,∴抛物线y=cx2+bx+a经过点(﹣1,0),故选:B.【点评】本题考查了二次函数的图象与性质,二次函数图象上点的坐标特征,判断出a、b、c以及a﹣b+c的符号是解题的关键.9.(2021•龙岗区模拟)二次函数y=ax2+bx+c的图象如图所示,反比例函数y=与正比例函数y=(2a+c)x在同一坐标系内的大致图象是()A.B.C.D.【分析】首先根据二次函数图象的开口方向确定a<0,再根据对称轴在y轴右,可确定a与b异号,然后再根据对称轴可以确定2ac+<>0,再根据反比例函数的性质和正比例函数的性质确定出两个函数图象所在象限,进而得到答案.【解答】解:∵抛物线开口向下,∴a<0,∵﹣=,∴b=﹣a>0,∵当x=﹣1时,y<0,∴当x=2时,y<0,∴4a+2b+c<0,∴2a+c<0,∴反比例函数y=在二四象限,正比例函数y=(2a+c)x的图象经过原点,且在二四象限,故选:B.【点评】此题主要考查了二次函数图象与系数的关系,以及正比例函数与反比例函数的性质,关键是正确判断出a、b、c的符号.二.填空题(共7小题)【几何】11.(2021•荔湾西关外国语一模)如图,在菱形ABCD中,∠DAB=60°,AB=3,点E在边AD上,且DE=1,点F为线段AB上一动点(不与点A重合),将菱形沿直线EF折叠,点A的对应点为点A′,当点A′落在菱形的对角线上时,AF的长为2或5﹣.【分析】分两种情况进行讨论:①当点A′在BD上时,可以证明△A′DE∽△FBA′,对应边成比例,可求出AF的长;②当点A′在AC上时,可得△EAF是等边三角形,进而可求AF的长.【解答】解:①当点A′在BD上时,如图,由折叠可知:∠EA′F=∠DAB=60°,∴∠DA′E+∠F A′B=120°,∵∠A=60°,AB=AD,∴△ADB是等边三角形,∴∠DBA=∠ADB=60°,∴∠A′FB+∠BA′F=120°,∴∠DA′E=∠BF A′,∴△A′DE∽△FBA′,∴==,∵AB=AD=DB=3,DE=1,∴EA′=EA=AD﹣DE=2,设F A′=F A=x,DA′=y,则BA′=3﹣y,BF=3﹣x,∴==,解得x=5﹣;②当点A′在AC上时,如图:由折叠可知:EF垂直平分AA′,∴∠AOF=90°,∵四边形ABCD是菱形,∠DAB=60°,∴∠DAC=∠BAC=30°,∴∠AFE=60°,∴△EAF是等边三角形,∴AF=AE=AD﹣DE=2.综上所述:AF=5﹣或2.故答案为:2或5﹣.【点评】本题考查了翻折变换、等边三角形的判定与性质、菱形的性质,解决本题的关键是掌握菱形的性质.12.(2021•白云区一模)如图,在平面直角坐标系中,有一个Rt△OAB,∠ABO=90°,∠AOB=30°,直角边OB在y轴正半轴上,点A在第一象限,且OA=1,将Rt△OBA 绕原点O逆时针旋转30°,同时把各边长扩大为原来的2倍(即OA1=2OA),得到Rt △OA1B1,同理,将Rt△OA1B1绕原点O逆时针旋转30°,同时把各边长扩大为原来的2倍,得到Rt△OA2B2,…,依此规律,得到Rt△OA2021B2021,则点B2021的纵坐标为﹣3×22019.【分析】根据余弦的定义求出OB,根据题意求出OB n,根据题意找出规律,根据规律解答即可.【解答】解:在Rt△AOB中,∠AOB=30°,OA=1,∴OB=OA•cos∠AOB=,由题意得,OB1=2OB=×2,OB2=2OB1=×22,……OB n=2OB1=×2n=×2n﹣1,∵2021÷12=168……5,∴点B2021的纵坐标为:﹣×22020×cos30°=﹣×22020×=﹣3×22019,故答案为:﹣3×22019.【点评】本题考查的是位似变换的性质、图形的变化规律、锐角三角函数的定义,正确得到图形的变化规律是解题的关键.13.(2021•增城区一模)如图.在矩形纸片ABCD中,AB=4,AD=6,点E是AB的中点,点F是边AD上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则线段A′C的最小值是2﹣2.【分析】以点E为圆心,AE长度为半径作圆,连接CE,当点A在线段CE上时,A'C的长取最小值,根据折叠的性质可知A'E=2,在Rt△BCE中利用勾股定理可求出CE的长度,用CE﹣A'E即可求出结论.【解答】解:如图,以点E为圆心,AE长度为半径作圆,连接CE,当点A在线段CE 上时,A'C的长取最小值,由折叠可知,A′E=AE=BE=AB=2,在Rt△BCE中,由勾股定理可得,CE===2,∴A′C的最小值=CE﹣A'E=2﹣2,故答案为:2﹣2.【点评】本题考查了翻折变换、矩形的性质以及勾股定理,利用作圆,找出A′C取最小值时点A′的位置是解题的关键.15.(2021•黄浦区一模)如图,⊙O的直径CD为6cm,OA,OB都是⊙O的半径,∠AOD =2∠AOB=60°,点P在直径CD上移动,则AP+BP的最小值为3cm.【分析】作点A关于CD的对称点A′,连接A′B就是最小值(P此时为A′B与CD 的交点),根据垂径定理及圆周角定理可得∠DOA′=∠AOD=60°,最后由勾股定理可得答案.【解答】解:作点A关于CD的对称点A′,连接A′B就是最小值(P此时为A′B与CD的交点),∵|OA|=|OB|=|OA′|=|CD|=3cm且∠AOD=2∠AOB=60°,∴∠AOB=∠BOD=30°,∵A关于CD的对称点A′,∴∠DOA′=∠AOD=60°,∴∠BOA′=∠BOD+∠DOA′=90°,∴△BOA′为等腰直角三角形,∴AP+BP的最小值为:|A′B|==3cm.故答案为:3cm.【点评】此题考查的是圆的性质,掌握圆满周角定理、垂径定理是解决此题关键.16.(2021•越秀广大附一模)如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上一动点,若OB=1,则阴影部分周长的最小值为+.【分析】利用轴对称的性质,得出当点E移动到点E′时,阴影部分的周长最小,此时的最小值为弧CD的长与CD′的长度和,分别进行计算即可.【解答】解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,此时E′C+E′D最小,即:E′C+E′D=CD′,由题意得,∠COD=∠DOB=∠BOD′=30°,∴∠COD′=90°,∴CD′===,的长l==,∴阴影部分周长的最小值为+.故答案为:+.【点评】本题考查与圆有关的计算,掌握轴对称的性质,弧长的计算方法是正确计算的前提,理解轴对称解决路程最短问题是关键.17.(2021•天河区一模)如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,则下列结论正确的是(1)(3)(4).(1)DC=3OG;(2)OG=BC;(3)△OGE是等边三角形;(4)S△AOE=.【分析】根据直角三角形斜边上的中线等于斜边的一半可得OG=AG=GE=AE,再根据等边对等角可得∠OAG=30°,根据直角三角形两锐角互余求出∠GOE=60°,从而判断出△OGE是等边三角形,判断出(3)正确;设AE=2a,根据等边三角形的性质表示出OE,利用勾股定理列式求出AO,从而得到AC,再求出BC,然后利用勾股定理列式求出AB=3a,从而判断出(1)正确,(2)错误;再根据三角形的面积和矩形的面积列式求出判断出(4)正确.【解答】解:∵EF⊥AC,点G是AE中点,∴OG=AG=GE=AE,∵∠AOG=30°,∴∠OAG=∠AOG=30°,∠GOE=90°﹣∠AOG=90°﹣30°=60°,∴△OGE是等边三角形,故(3)正确;设AE=2a,则OE=OG=a,由勾股定理得,AO===a,∵O为AC中点,∴AC=2AO=2a,∴BC=AC=×2a=a,在Rt△ABC中,由勾股定理得,AB==3a,∵四边形ABCD是矩形,∴CD=AB=3a,∴DC=3OG,故(1)正确;∵OG=a,BC=a,∴OG≠BC,故(2)错误;∵S△AOE=a•a=a2,S ABCD=3a•a=3a2,∴S△AOE=S ABCD,故(4)正确;综上所述,结论正确的是(1)(3)(4).故答案为:(1)(3)(4).【点评】本题考查了矩形的性质,直角三角形斜边上的中线的性质,等边三角形的判定与性质的运用,设出AE、OG,然后用a表示出相关的边更容易理解.【函数】14.(2021•增城区一模)抛物线y=mx2+(1﹣4m)x+1﹣5m一定经过非坐标轴上的一点P,则点P的坐标为(5,6).【分析】经过定点,即坐标中不含参数m,对解析式进行变形,可得y=(x2﹣4x﹣5)m+x+1,令m的系数为0,即可求出.【解答】解:y=mx2+(1﹣4m)x+1﹣5m=(x2﹣4x﹣5)m+x+1,令x2﹣4x﹣5=0,解得x=﹣1或x=5,当x=﹣1时,y=0;当x=5时,y=6;∴非坐标轴上的点P的坐标为(5,6).故答案为:(5,6).【点评】本题主要考查二次函数过定点问题,把解析式进行合适的变形是解题关键.三.解答题(共23小题)【应用】19.(2021•荔湾西关外国语一模)农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:销售价格x(元/千克)3035404550日销售量p(千克)6004503001500(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p 与x之间的函数表达式;(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)【分析】(1)首先根据表中的数据,可猜想y与x是一次函数关系,任选两点求表达式,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一模考压轴题汇编1、已知:如图5,在△ABC 中,AB =AC ,D 是边BC 延长线上一点,E 是边AC 上一点,如果∠EBC =∠D ,BC =4,cos ∠ABC =31. (1)求证:BDBCAB CE =; (2)如果S 1、S 2分别表示△BCE 、△ABD 的面积,求:21S S ⋅的值;(3)当∠AEB=∠ACD 时,求△ACD 的面积.(2008市调研25)2、已知:如图一,点D 是等腰直角三角形ABC 的斜边AB 上的一个动点(不与A 、B 重合),过点D 作DE ⊥AB 交边AC 于点F ,连结BE .∠E =30°,AB =4. 设DE 的长度为x,四边形DBCF 的面积为y . (1)求y 与x 之间的函数关系式,并指出它的定义域; (2)连结BF ,①当△BDF 与△DBE 相似时,求 出x 的值;②是否存在x 的值,使得△BCF 与△DBE 相似?若存在,求出x 的值;若不存在,请说明理由. (2008普陀25)ABCDE图5(图二)B CDA EF3、如图,直线221+-=x y 交x 轴、y 轴于A 、B 两点,抛物线c bx x y ++=221经过A 、B 两点,且与x 轴另有交点C .(1) 试求AOB ∆的面积; (2) 试求抛物线的解析式;(3) 试问:AOB ∆与BOC ∆是否相似?并说明理由. (2008黄浦25)4、如图六,在正方形ABCD 中,点F 是边BC 上一点 (点F 与点B 、点C 均不重合),AE ⊥AF ,AE 交CD 的延长线于点E ,连结EF 交AD 于点G .(1)求证:BF ·FC =DG ·EC ;(2)设正方形ABCD 的边长为1,是否存在这样 的点F ,使得AF =FG ?若存在,求出这时BF 的长; 若不存在,请说明理由.(2008宝山24)(图六)G A DCB FE5、已知:如图七,在Rt △ABC 中,∠C =90°,BC =6,AC =8.点P 是边AB 的中点,以P 为顶点,作 ∠MPN =∠A ,∠MPN 的两边分别与边AC 交于点M 、N .(1)当△MPN 是直角三角形时,求CM 的长度; (2)当∠MPN 绕点P 转动时,下列式子:(甲)CM ·AN ,(乙)CN ·AM 的值是否保持不变?若保持不变,试求出这个不变的值,并证明你的结论;(3)连接BM ,是否存在这样的点M ,使得△BMP 与△ANP 相似?若存在,请求出这时CM 的长;若不存在,请说明理由.(2008宝山25)6、阅读材料:我们把形如:x +x 1=m +m1(其中x 是未知数,m 是常数)的方程称为两边互为倒数关系的方程.它的两个解也互为倒数,即x 1=m ,x 2=m1.利用上述结论解方程:2x +121 x =531.(2008长宁24)(图七)BC PA NM7、已知:如图一,在梯形ABCD 中,AB ∥CD ,且 AB =2CD ,点E 、F 分别是AB 、BC 的中点,EF 与 BD 相交于点M .(1)求证:△EDM ∽△FBM ;(2)若DB =6,求BM . (2008虹口24)8、已知:如图一,在矩形ABCD 中,AB =3,BC =3,在BC 边上取两点E 、F (点E 在点F 的左边),以EF 为边作等边△PEF ,使顶点P 在AD 上,PE 、PF 分别交AC 于点G 、H ,(1)求△PEF 的边长; (2)求证:GHPG =GC EG ;(3)若△PEF 的边EF 在线段BC 上移动.试猜想: PH 与BE 有何数量关系?并证明你猜想的结论.(2008虹口25)(图四)BC DAEF M(图三)B CA DFPEGH9、已知:如图九,∠ACB =90°,DF ⊥AB 于点F ,sinB =54,S △DCE =41S △BFE ,且CE =5,求:(1)BC 的长;(2)S △CEF .(2008南汇24)10、如图十,点A 的坐标为(0,5),点B 在第一象限,△AOB 为等边三角形,点C 在x 轴正半轴上.(1)以AC 为边,在第一象限作等边△ACE (保 留作图痕迹,不写作法和证明); (2)设AC 与OB 的交点为点D ,CE 与AB 的延长线交于点F ,求证:△ADB ∽△AF C ;(3)连结BE ,试猜想∠ABE 的度数,并证明你的猜想; (4)若点E 的坐标为(s ,t ),当点C 在x 正半轴运动时,求s 、t 的关系式. (2008南汇25)(图十)(图九)BADEFC11、如图八,直线y =x +5与x 轴、y 轴交于A 、 B 两点,抛物线y =ax 2+bx +c 经过点A 、B ,且与x轴的另一个交点为C (1,0). (1)求该抛物线的解析式及顶点坐标;(2)点P 是抛物线y =ax 2+bx +c 上的一动点, 点P 在运动过程中,射线OP (O 是坐标原点)能否 经过△ABC 的重心?如能,请指出点P 的位置;如 不能,请说明理由.(2008青浦24)12、已知:如图九,在梯形ABCD 中,AD ∥BC ,AP ⊥BC ,垂足为点P ,AB =CD =2,BC =5,∠B =60°,(1)求AD 的长;(2)若把三角尺60°的顶点与点P 重合,使三角尺绕点P 旋转,该60°角的两边PE 与PF (看作射线)分别与边AD 交于点E (点E 不与点A 、点D 重合),与射线DC 交于点F(点F 不与点C 重合),如设AE 为x ,CF 为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围;(3)在第(2)小题的条件下,三角尺绕点P 旋转 过程中,△PED 与△PDF 这两个三角形中,哪一个三角 形可能成为等腰三角形?如有可能,请指出是哪一个三 角形,并求出AE 的长;如不能,请说明理由.(2008青浦25)(图八)(图九)B A DC P第24题图13、如图,在平面直角坐标系中,点O 为坐标原点,已知点A 的坐标为(2,2),点B 、C 在y 轴上,BC =8,AB=AC ,直线AB 与x 轴相交于点D , (1) 求C 、D 的坐标;(2)求经过A 、C 、D 三点的二次函数解析式; (3)求∠CAD 的正弦。
(2010年奉贤24)14、如图9,在平面直角坐标系中,矩形OABC 的顶点A (3,0),C (0,1).将矩形OABC 绕原点逆时针旋转90°,得到矩形C B A O '''.设直线B B '与x 轴交于点M 、与y 轴交于点N ,抛物线2y ax bx c =++的图像经过点C '、M 、N .解答下列问题:(1)求出该抛物线所表示的函数解析式; (2)将△MON 沿直线B B '翻折,点O 落在点P 处,请你判断点P 是否在该抛物线上,并请说明理由;(3)将该抛物线进行一次平移(沿上下或左右方向),使它恰好经过原点O ,求出所有符合要求的新抛物线的解析式.(2010年虹口24)15、在平面直角坐标系中,已知点A (4,0),点B (0,3). 点P 从点A 出发,以每 秒1个单位的速度向右平移,点Q 从点B 出发,以每秒2个单位的速度向右平移,又P 、Q 两点同时出发.(1) 联结AQ ,当△ABQ 是直角三角形时,求点Q 的坐标;(2) 当P 、Q 运动到某个位置时,如果沿着直线AQ 翻折,点P 恰好落在线段AB 上,求这时∠AQP 的度数;(3) 过点A 作AC ⊥AB ,AC 交射线PQ 于点C ,联结BC ,D 是BC 的中点. 在点P 、Q 的运动过程中,是否存在某时刻,使得以A 、C 、Q 、D 为顶点的四边形是平行四边形,若存在,试求出这时ABC cot 的值;若不存在,试说明理由。
(2010年宝山25)16、如图10,已知//AM BN ,90A B ∠=∠=︒,4AB =,点D 是射线AM 上的一个动点(点D 与点A 不重合),点E 是线段AB 上的一个动点(点E 与点A 、B 不重合),联结DE ,过点E 作DE 的垂线,交射线BN 于点C ,联结DC .设AE x =,BC y =.(1)当1AD =时,求y 关于x 的函数关系式,并写出它的定义域;(2)在(1)的条件下,取线段DC 的中点F ,联结EF ,若 2.5EF =,求AE 的长;(3)如果动点D 、E 在运动时,始终满足条件A D D E AB +=,那么请探究:BCE ∆的周长是否随着动点D 、E 的运动而发生变化?请说明理由.(2010年虹口25)BMN备用图图10ABCDA 17、已知二次函数k x k x y -++-=)1(2的图像经过一次函数4+-=x y 的图像与x 轴的交点A .(如图)(1)求二次函数的解析式;(2)求一次函数与二次函数图像的另一个交点B 的坐标;(3)若二次函数图像与y 轴交于点D ,平行于y 轴的直线l 将四边形ABCD 的面积分成1∶2的两部分,则直线l 截四边形ABCD 所得的线段的长是多少?(直接写出结果)(2010年黄浦24)18、在梯形ABCD 中,AD ∥BC ,︒=∠===90,2,1A BC AB AD .(如图1)(1)试求C ∠的度数;(2)若E 、F 分别为边AD 、CD 上的两个动点(不与端点A 、D 、C 重合),且始终保持︒=∠45EBF ,BD 与EF 交于点P .(如图2)①求证:BDE ∆∽BCF ∆;②试判断BEF ∆的形状(从边、角两个方面考虑),并加以说明;③设y DP x AE ==,,试求y 关于x 的函数解析式,并写出定义域. (2010年黄浦25)(图1)BC D P E F A P G A D E F 第25题19、已知△ABC 为等边三角形,AB =6,P 是AB 上的一个动点(与A 、B 不重合),过点P 作AB 的垂线与BC 相交于点D ,以 点D 为正方形的一个顶点,在△ABC 内作正方形DEFG ,其中D 、E 在BC 上,F 在AC 上,(1)设BP 的长为x ,正方形DEFG 的边长为y ,写出y 关于x 的函数解析式及定义域;(2)当BP =2时,求CF 的长;(3)△GDP 是否可能成为直角三角形?若能,求出BP 的长;若不能,请说明理由. (2010年普陀25)。
