有理数的混合运算习题
有理数的混合运算练习题(含答案)(大综合17套)

有理数的混合运算练习题(含答案)(大综合17套)有理数混合运算练习题及答案 第1套同步练习(满分100分)1.计算题:(10′×5=50′)(1)3.28-4.76+121-43;(2)2.75-261-343+132;(3)42÷(-121)-143÷(-0.125);(4)(-48) ÷82-(-25) ÷(-6)2; (5)-52+(1276185+-)×(-2.4).2.计算题:(10′×5=50′)(1)-23÷153×(-131)2÷(132)2;(2)-14-(2-0.5)×31×[(21)2-(21)3];(3)-121×[1-3×(-32)2]-( 41)2×(-2)3÷(-43)3(4)(0.12+0.32) ÷101[-22+(-3)2-321×78];(5)-6.24×32+31.2×(-2)3+(-0.51) ×624.【素质优化训练】1.填空题:(1)如是0,0>>cbb a ,那么ac 0;如果0,0<<cbb a ,那么ac 0;(2)若042=-++++c c b a ,则abc=; -a 2b 2c 2=;(3)已知a ,b 互为相反数,c ,d 互为倒数,x 的绝对值等于2,那么x 2-(a+b)+cdx=.2.计算:(1)-32-;)3(18)52()5(223--÷--⨯-(2){1+[3)43(41--]×(-2)4}÷(-5.043101--);(3)5-3×{-2+4×[-3×(-2)2-(-4) ÷(-1)3]-7}.【生活实际运用】甲用1000元人民币购买了一手股票,随即他将这手股票转卖给乙,获利10%,而后乙又将这手股票反卖给甲,但乙损失了10%.最后甲按乙卖给甲的价格的九折将这手股票卖给了乙,在上述股票交易中( )A .甲刚好亏盈平衡;B .甲盈利1元;C .甲盈利9元;D .甲亏本1.1元.参考答案【同步达纲练习】1.(1)-0.73 (2)-121; (3)-14; (4)-181; (5)-2.9 2.(1)-351 (2)-1161; (3)- 5437; (4)1; (5)-624.【素质优化训练】1.(1)>,>; (2)24,-576; (3)2或6.[提示:∵x =2 ∴x 2=4,x=±2].2.(1)-31; (2)-8;2719(3)224【生活实际运用】 B有理数的四则混合运算练习 第2套◆warmup知识点 有理数的混合运算(一)1.计算:(1)(-8)×5-40=_____;(2)(-1.2)÷(-13)-(-2)=______. 2.计算:(1)-4÷4×14=_____;(2)-212÷114×(-4)=______. 3.当||a a=1,则a____0;若||a a =-1,则a______0.4.(教材变式题)若a<b<0,那么下列式子成立的是( ) A .1a <1b B .ab<1 C .a b <1 D .ab>15.下列各数互为倒数的是()A.-0.13和-13100B.-525和-275C.-111和-11 D.-414和4116.(体验探究题)完成下列计算过程:(-25)÷113-(-112+15)解:原式=(-25)÷43-(-1-12+15)=(-25)×()+1+12-15=____+1+52 10 -=_______.◆Exersising7.(1)若-1<a<0,则a______1a;(2)当a>1,则a_______1a;(3)若0<a≤1,则a______1a.8.a,b互为相反数,c,d互为倒数,m的绝对值为2,则||4a bm++2m2-3cd值是()A.1 B.5 C.11 D.与a,b,c,d值无关9.下列运算正确的个数为()(1)(+34)+(-434)+(-6)=-10 (2)(-56)+1+(-16)=0(3)0.25+(-0.75)+(-314)+34=-3(4)1+(-3)+5+(-7)+9+(-1)=4A.3个 B.4个 C.2个 D.1个10.a,b为有理数,在数轴上的位置如右上图所示,则()A.1a>1b>1 B.1a>1>-1bC.1>-1a>1bD.1>1a>1b11.计算:(1)-20÷5×14+5×(-3)÷15 (2)-3[-5+(1-0.2÷35)÷(-2)]-1ob a(3)[124÷(-114)]×(-56)÷(-316)-0.25÷14◆Updating 12.(经典题)对1,2,3,4可作运算(1+2+3)×4=24,现有有理数3,4,-6,10,请运用加,减,乘,除法则写出三种不同的计算算式,使其结果为24. (1)____________ (2)____________ (3)____________ 答案: 课堂测控1.(1)-80 (2)535 2.(1)-14(2)8 3.>,< 4.D 5.C 6.34,-310,1[总结反思]先乘除,后加减,有括号先算括号内的.课后测控 7.(1)> (2)> (3)≤ 8.B 9.B 10.B11.解:(1)原式=-20×15×14+5×(-3)×115=-1-1=-2 (2)原式=124×(-45)×(-56)×(-619)-14÷14=124×(-419)-1=-1114-1=-11114(3)原式=-3[-5+(1-15×53)÷(-2)]=-3[-5+23×(-12)]=-3[-5-13]=15+1=16[解题技巧]除法转化为乘法,先乘除,后加减,有括号先算括号内的. 拓展测控 12.解:(1)4-(-6)÷3×10 (2)(10-6+4)×3 (3)(10-4)×3-(-6)[解题思路]运用加,减,乘除四种运算拼凑得24点.有理数的混合运算习题 第3套一.选择题1. 计算3(25)-⨯=( )A.1000B.-1000C.30D.-302. 计算2223(23)-⨯--⨯=( )A.0B.-54C.-72D.-183. 计算11(5)()555⨯-÷-⨯=A.1B.25C.-5D.354. 下列式子中正确的是( )A.4232(2)(2)-<-<- B. 342(2)2(2)-<-<- C. 4322(2)(2)-<-<-D. 234(2)(3)2-<-<-5. 422(2)-÷-的结果是( )A.4B.-4C.2D.-26. 如果210,(3)0a b -=+=,那么1ba+的值是( ) A.-2 B.-3C.-4D.4二.填空题1.有理数的运算顺序是先算 ,再算 ,最算 ;如果有括号,那么先算 。
有理数混合运算习题(含答案)300道
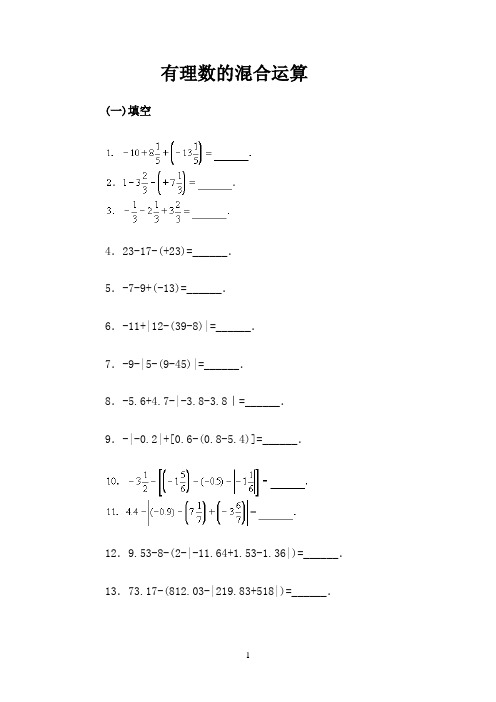
有理数的混合运算(一)填空4.23-17-(+23)=______.5.-7-9+(-13)=______.6.-11+|12-(39-8)|=______.7.-9-|5-(9-45)|=______.8.-5.6+4.7-|-3.8-3.8|=______.9.-|-0.2|+[0.6-(0.8-5.4)]=______.12.9.53-8-(2-|-11.64+1.53-1.36|)=______.13.73.17-(812.03-|219.83+518|)=______.36.38×(-7)+5[(-2)3(-32)-(-22)]-38×339÷(-3)38=______.48.(-2)×{(-3)×[(-5)+2×(0.3-0.3)÷83-3]+4}=______.112.413-74-(-5+26).116.-84-(16-3)+7.118.-0.182+3.105-(0.318-6.065).119.-2.9+[1.7-(7+3.7-2.1)].121.34.23-[194.6-(5.77-5.4)].125.23.6+[3.9-(17.8-4.8+15.4)].134.(-3)2÷2.5.135.(-2.52)×(-4).136.(-32)÷(-2)2.173.(-1)2×5+(-1)×52-12×5+(-1×5)2.174.(-2)(-3)(-36)+(-1)20×63.178.(-32)÷(3×2)×(-3-2).180.3×(-2)2+(-2×3)2+(-2+3)2.188.2+42×(-8)×16÷32.190.[5.78+3.51-(0.7)2]÷(0.2)3×11.191.(1.25)4÷(0.125)4×0.0036-(0.6)2.194.(-42×26+132×2)÷(-3)7×(-3)5.195.(3-9)4×23×(-0.125)2.201.741×[(-30)2-(-402)]3÷(1250)2.211.[(-5)3+3.4×2-2×4+53]2.213.(24-5.1×3-3×5+33)2.234.(-5)×(-3)×(-4)2+(-2)3×(-8)×(-3)-(-12)×3÷24.240.-18-23×[(-4)3÷(-43)+0.2×8+(-3)2÷(-32)].(四)用符号“>”,“<”,“≥”,“≤”,“=”之一填空241.当两个数和的绝对值______这两个数差的绝对值时,这两个数同号.242.一个正数与一个负数差的绝对值______这两个数绝对值的和.243.一个正数与一个负数和的绝对值______这两个数绝对值的差.244.一个正数与一个负数差的绝对值______这两个数绝对值的差.245.一个正数与一个负数和的绝对值______这两个数绝对值的和.246.当两个数和的绝对值______这两个数差的绝对值时,这两个数异号.247.当两数和的绝对值______这两个数差的绝对值时,这两个数至少有一个是零.248.当两数和的绝对值______这两个数的绝对值之和时,这两个数可以是任意的有理数.249.当两数差的绝对值______这两个数的绝对值之和时,这两个数可以是任意的有理数.250.当两个数和的绝对值______这两个数绝对值的差时,这两个数可以是任意的有理数.251.当两个数差的绝对值______这两个数绝对值的差时,这两个数可以是任意的有理数.252.欲使两个数的绝对值的和等于这两个数的和的绝对值,这两个数必须是怎样的数?253.欲使两个数和的绝对值不小于这两个数的差的绝对值,这两个数必须是怎样的数?254.欲使两数和的绝对值不大于这两数差的绝对值,这两个数必须是怎样的数?255.欲使两数和的绝对值不小于这两个数的绝对值的和,这两个数必须是怎样的数?256.一个盛有水的圆柱形水桶,其底面半径为1.6分米①.现将一个半径为1.2分米的铁球沉没在桶内水面下,问桶内水面升高多少分米?(列综合算式计算,球的体积公式为,其中V表示体积,R表示球的半径)257.一个盛有水的长方体状容器,它的底面是边长为2.4分米的正方形,现将一个半径是1.2分米的铁球放在容器内,正好铁球体积的1/3在水面下,问放入铁球后,水面升高了多少分米?(列综合算式计算,球的体积公式为V表示体积,R表示球的半径,π取3.14。
有理数的混合运算练习题(含答案)(大综合17套)

【素质优化训练】
1.(1)>,>; (2)24,-576; (3)2 或 6.[提示:∵ x =2 ∴x2=4,x=±2]. 2.(1)-31; (2)-8 19 ; 27
【生活实际运用】 B
(3)224
有理数的四则混合运算练习 第 2 套
◆warmup
知识点 有理数的混合运算(一)
1.计算:(1)(-8)×5-40=_____;(2)(-1.2)÷(- 1 )-(-2)=______. 3
有理数的混合运算练习题(含答案)(大综合 17 套)
有理数混合运算练习题及答案 第 1 套
同步练习(满分 100 分) 1.计算题:(10′×5=50′)
(1)3.28-4.76+1 1 - 3 ; 24
(2)2.75-2 1 -3 3 +1 2 ; 64 3
(3)42÷(-1 1 )-1 3 ÷(-0.125); 24
53
25
=(- 2 )×( )+1+ 1 - 1
5
25
=____+1+ 5 2 10
=_______.
◆Exersising
7.(1)若-1<a<0,则 a______ 1 ; (2)当 a>1,则 a_______ 1 ;
a
a
(3)若 0<a≤1,则 a______ 1 . a
8.a,b 互为相反数,c,d 互为倒数,m 的绝对值为 2,则 | a b | +2m2-3cd 值是( )
(3)-1 1 ×[1-3×(- 2 )2]-( 1 )2×(-2)3÷(- 3 )3
2
34
4
(4)(0.12+0.32) ÷ 1 [-22+(-3)2-3 1 × 8 ];
有理数的混合运算练习题

有理数的混合运算练习题练习题一:四则运算1. 将有理数4和-5.6相加,并化简结果。
2. 计算式子:(3.2 - 1.5) × (-2.3) ÷ 0.2,并将结果化为最简分数形式。
3. 某物体原价为120元,经过折扣后降价了30%,求降价后的价格。
4. 小明现在身高1.5米,长大后每年增长0.05米,那么10年后他的身高将是多少米?5. 一辆汽车以每小时60公里的速度行驶了4小时,然后以每小时45公里的速度行驶了2小时,求这段路程的平均速度。
练习题二:比较运算1. 比较-5.6和-4.9的大小,写出结论。
2. 比较-2/3和-0.7的大小,写出结论。
3. 比较-0.2和1/5的大小,写出结论。
4. 某学生的数学成绩是89.5分,某学生的语文成绩是88.2分,谁的成绩更高?5. 某超市的西瓜每斤售价3.5元,某超市的苹果每斤售价3.8元,哪个水果更贵?练习题三:综合运算1. 计算式子:-8 + 2 × (-5) - 3 × (-4) ÷ 2,并将结果化为最简分数形式。
2. 某书店原价书本打折后降价了25%,折后的价格是48元,求原价是多少元。
3. 一个正方形的边长是1/4米,求它的面积。
4. 某地每天的最高气温比前一天的最高气温高5摄氏度,今天气温是26摄氏度,求昨天的最高气温。
5. 某电商平台中,一件商品的原价是180元,限时促销降价45元,再使用优惠券减免了30元,求最终的价格。
练习题四:应用题1. 若横线上的数表示某地的气温(单位:摄氏度),请将下列气温表示在数轴上:-5°C、0°C、3.5°C、-1.8°C、7°C。
并指出数轴上哪个点代表的气温最高,哪个点代表的气温最低。
2. 某手机品牌的生产商在某个城市开设了15家专卖店,每家专卖店每个月的销售额平均为11.8万元。
如果每年的销售额均保持稳定,那么这个手机品牌在该城市的年销售额是多少万元?3. 某电动车从A地出发,按常规速度行驶了2小时后,由于道路拥堵,它以减速的速度行驶了3小时,总共行驶了70千米。
有理数的加减乘除混合运算100道

有理数的加减乘除混合运算100道以下是一篇关于有理数加减乘除混合运算的文章。
有理数的加减乘除混合运算100道在数学中,有理数是指可以表示为两个整数的比值的数字,包括整数、分数和小数。
有理数的运算是数学中的基础内容,掌握有理数的加减乘除混合运算是进行更高级别数学运算的前提。
本文将提供100道有理数的加减乘除混合运算题目,以帮助读者巩固相关知识。
1. 1/2 + 3/4 - 5/8答案:3/82. 12/5 - 3/4 × 2/3答案:33/103. -1.5 × 2/3 ÷ 0.5答案:-94. 5/6 + (-2/3) - (-2/3)答案:5/65. -4 + (-3) × 2/5答案:-22/56. 1/4 ÷ 2/3 × 1.5答案:3/8答案:8/38. -7/8 + (-1/4) + 1/2答案:-1/89. 3.5 × (-2) - 1/3 × (-4/5)答案:7/610. -2/5 ÷ (3/4 - 5/6)答案:10/911. 1/3 + (-0.25) + 0.4 - (-1/5)答案:1.8512. 3/4 - (1/2 + 1/8)答案:13/3213. -6 × (-0.25) ÷ (-1/3)答案:414. 2.5 - (-1/4) + (-3/8)答案:2.7515. (-4) ÷ (-0.25) × (1/2)答案:32答案:3/217. 5/6 × (-1/4 - 3/5)答案:-17/6018. 0.4 ÷ 0.2 + 1/5答案:7/519. (-3/4) + (-1/2) - 0.25答案:-7/420. -0.6 × 0.3 ÷ (-0.5)答案:0.3621. (-2/3) - 1/4 + 0.2 - (-1/5)答案:-13/6022. -1.25 - (1.5 - 1/3)答案:-0.416723. 1/2 + 3/4 + (-5/8)答案:7/824. 12/5 - (3/4 × 2/3)答案:3/10答案:-326. 5/6 + (-2/3) - (-2/3)答案:5/627. -4 + ((-3) × 2/5)答案:-22/528. (1/4 ÷ 2/3) × 1.5答案:3/829. 2/3 - 1.5 ÷ (-2/5)答案:8/330. -7/8 + (-1/4) + 1/2答案:-1/8⋮经过以上30道题目的训练,相信读者对有理数的加减乘除混合运算已经有了更深入的理解。
7年级有理数混合运算100题

7年级有理数混合运算100题一、练习题(前20题)1. (-2)+3-(-5)2. 4 - (-2)×(-3)3. (-3)×(-4)+(-2)^24. 12÷(-3)+(-4)×(-2)5. (-2)^3 - (-3)^26. -5 + 2×(-3)^27. (-1)^2023+(-2)^2×38. 3×(-2)+4÷(-(1)/(2))9. [(-3)+(-4)]×(-5)10. (-2)^2 - 2×(-3)11. (-4)×(-(1)/(2))-(-3)^212. 2×(-3)+(-4)^2÷(-2)13. (-3)^3÷(-9)-(-2)14. (-2)^4 - 3×(-1)^315. (-5)×(-(1)/(5))+(-6)16. 4 - (-3)^2÷(-1)17. (-2)^3×(-(1)/(2))+(-3)^218. (-1)^5+(-3)×[(-4)^2 - 2]19. (-2)^2×(-3)+4×(-1)^320. (-3)×(-2)^2 - (-1)^4二、解析。
1. (-2)+3-(-5)- 解析:根据有理数的减法法则,减去一个数等于加上它的相反数。
所以-(-5)= + 5。
则原式=(-2)+3 + 5=1 + 5 = 6。
2. 4-(-2)×(-3)- 解析:先计算乘法,(-2)×(-3)=6,再计算减法,4 - 6=-2。
3. (-3)×(-4)+(-2)^2- 解析:先算乘方,(-2)^2 = 4,再算乘法(-3)×(-4)=12,最后算加法12 + 4 = 16。
4. 12÷(-3)+(-4)×(-2)- 解析:先算除法12÷(-3)=-4,再算乘法(-4)×(-2)=8,最后算加法-4+8 = 4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理数的混合运算典型例题
例1? 计算:.
分析:此算式以加、减分段, 应分为三段: , , .这三段可以同时进行计算,先算乘方,再算乘除.式中-化为参加计算较为方便.
解:原式
说明:做有理数混合运算时,如果算式中不含有中括号、大括号,那么计算时一般用“加”、“减”号分段,使每段只含二、三级运算,这样各段可同时进行计算,有利于提高计算的速度和正确率.
例2 计算:.分析:运算顺序是:第一步计算和;第二步做乘法;第三步做乘方运算;第四步做除法.
解:原式
说明:由此例题可以看出,括号在确定运算顺序上的作用,所以计算题也需认真审题.
例3 计算:
分析:要求、、的值,用笔算在短时间内是不可能的,必须另辟途径.观察题目发现,,,逆用乘法分配律,前三项可以凑成含有0的乘法运算,此题即可求出.解:原式
说明:“0”乘以任何数等于0.因为运用这一结论必能简化数的计算,所以运算中,能够凑成含“0”因数时,一般都凑成含有0的因数进行计算.当算式中的数字很大或很繁杂时,要注意使用这种“凑0法”.
例4 计算分析:是的倒数,应当先把它化成分数后再求倒数;右边两项含绝对值号,应当先计算出绝对值的算式的结果再求绝对值.
解:原式
说明:对于有理数的混合运算,一定要按运算顺序进行运算,注意不要跳步,每一步的运算结果都应在算式中体现出来,此题(1)要注意区别小括号与绝对值的运算;(2)要熟练掌握乘方运算,注意3,,(-2)3,-32在意义上的不同.
例5 计算:.
分析:含有括号的混合运算,一般按小、中、大括号的顺序进行运算,括号里面仍然是先进行第三级运算,再进行第二级运算,最后进行第一级运算.
解:原式
例6? 计算
解法一:原式
解法二:原式
说明:加减混合运算时,带分数可以化为假分数,也可把带分数的整数部分与分数部分分别加减,这是因为带分数是一个整数和一个分数的和.
例如:
有理数的混合运算习题精选
一、选择题
1.若,,则有(? ) .A. B. C. ? D.
2.已知,当时,,当时,的值是(? ) .
A. B.44C.28? D.17
3.如果,那么的值为(? ) .A.0B.4C.-4D.2
4.代数式取最小值时,值为(? ) .A. ? B. C. D.无法确定
5.六个整数的积,互不相等,则
( ) .A.0?B.4C.6D.8
6.计算所得结果为(? ) .A.2B. C. D.
二、填空题
1.有理数混合运算的顺序是__________________________.
2.已知为有理数,则 _________0, _________0, _______0.(填“>”、“<”或“≥”=)
3.平方得16的有理数是_________,_________的立方等于-8.
4. __________.
5.一个负数减去它的相反数后,再除以这个负数的绝对值,所得商为__________.
三、判断题
1.若为任意有理数,则 .(? ) 3..(? ) 2..(? ) 4..()
5..(? )
四、解答题1.计算下列各题:
(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8).
2.若有理数、、满足等式,试求的值.3.当,时,求代数式的值.
4.已知如图2-11-1,横行和竖列的和相等,试求的值.
5.求的值.
6.计算.
计算:
有理数的混合运算参考答案:
一、1.C? 2.C? 3.C? 4.B 5.A? 6.B?
二、1.略;2.≥,>,<;3.,;4.1;5..
三、1.× 2.×3.√4.×5.√
四、1.(1)(2)(3)(4)(5)30(6)(7)(8);2.∵,,∴;
3. ;
4.,, ;
5.设,则, ;
6.原式 .
原式=3×31998-5×31998+2×3×31997-1999
=3×31998-5×31998+2×31998-1999
=(3-5+2)×31998-1999
=0×31998-1999
=-1999。
