春学期八年级数学下册第9章中心对称图形_平行四边形本章中考演练练习(苏科版)
苏科版八年级数学下册 第九章 中心对称图形-----平行四边形 练习(包含答案)

第九章中心对称图形-----平行四边形一、单选题1.如图,把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C,△A=30°,△1=70°,则旋转角θ可能等于()A.40°B.50°C.70°D.100°2.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是()A.点A B.点B C.点C D.点D3.剪纸艺术是中国传统的民间工艺.下列剪纸的图案中,属于中心对称图形的是()A.B.C.D.4.如图,平行四边形ABCD中,AE平分△DAB,△B=100°,则△DEA等于()A .100°B .80°C .60°D .40°5.如图,在平行四边形ABCD 中,CE 平分BCD ∠与AB 交于点E ,DF 平分ADC ∠与AB 交于点F ,若8AD =,3EF =,则CD 长为( )A .8B .10C .13D .166.如图,在平面直角坐标系xOy 中,若菱形ABCD 的顶点A ,B 的坐标分别为(﹣3,0),(2,0),点D 在y 轴上,则点C 的坐标是( )A .(4,5)B .(5,4)C .(4,4)D .(5,3) 7.矩形ABCD 中AB=10,BC=8,E 为AD 边上一点,沿CE 将△CDE 对折,点D 正好落在AB 边上的F 点.则AE 的长是( )A .3B .4C .5D .68.下列说法正确的是( )A .三条边相等的四边形是菱形B .对角线相等的平行四边形是矩形C .对角线互相垂直且相等的四边形是正方形D .一组对边平行,另一组对边相等的四边形是平行四边形9.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:△AB=BC ,△△ABC=90°,△AC=BD ,△AC△BD 中选两个作为补充条件,使△ABCD 为正方形(如图),现有下列四种选法,你认为其中错误的是( )A .△△B .△△C .△△D .△△10.如图,在菱形ABCD 中,2AB =,120ABC ∠=︒,点P ,E ,F 分别是线段AC ,AB ,BC 上的任意一点,则PE PF +的最小值是( )A .1BC .2D .1+二、填空题11.已知点P 1(a ,3)与P 2(-4,b )关于原点对称,则ab =_____.12.如图,在平行四边形ABCD 中,AD BD =,BE AD ⊥于点E ,若20DBE ∠=︒,则ABC ∠的度数是__________.13.如图,平行四边形ABCD 的周长为20cm ,对角线交于点O ,点E 是边AB 的中点,已知6AB cm =,则OE =______cm .14.如图,菱形ABCD 和菱形BEFG 的边长分别是5和2,△A =60°,连结DF ,则DF 的长为_____.三、解答题15.如图,在ABC V 中,点E ,F 分别为边AB ,AC 的中点,延长EF 到点G 使FG EF =. 求证:四边形EGCB 是平行四边形.16.如图,矩形ABCD 中,点E 是BC 上一点,AE AD =, DF AE ⊥于F ,连接DE .(1)求证:DF DC =;(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于线段AF 的长.17.如图,在菱形ABCD 中,AB=4cm ,△BAD=60°.动点E 、F 分别从点B 、D 同时出发,以1cm/s 的速度向点A 、C 运动,连接AF 、CE ,取AF 、CE 的中点G 、H ,连接GE 、FH .设运动的时间为ts (0<t <4).(1)求证:AF△CE ;(2)当t 为何值时,四边形EHFG 为菱形;(3)试探究:是否存在某个时刻t ,使四边形EHFG 为矩形,若存在,求出t 的值,若不存在,请说明理由.18.如图,点 O 是等边△ABC 内一点,△AOB =105°,△BOC 等于α,将△BOC 绕点 C 按顺时针方向旋转60°得△ADC,连接OD.(1)求证:△COD 是等边三角形.(2)求△OAD 的度数.(3)探究:当α为多少度时,△AOD 是等腰三角形?19.如图,已知点E,F,M,N分别是正方形ABCD四条边上的点,并且===.AE BF CM DN(1)求证:四边形EFMN是正方形;AB=,当点E在什么位置时,四边形EFMN的周长最小?并求四边形EFMN (2)若4周长的最小值.答案1.A2.B3.D4.D5.C6.B7.A8.B9.B10.B11.﹣1212.125°13.21415.解:△E,F分别为AB,AC的中点,△EF是△ABC的中位线,△12EF BC∥.△EF FG =,△EG BC =.△EG BC =∥△四边形EGCB 是平行四边形.16.(1)证明:△四边形ABCD 是矩形,BCD 90AD BC ∴∠=︒∥,,DC BC ADE DEC ∴⊥∠=∠,,AE AD =Q ,ADE AED ∴∠=∠,DEC AED ∴∠=∠,DF AE ⊥Q ,△△DFE=90°,在△DFE 和△DCE 中DFE=BCD DE=DE DEC AED ∠∠⎧⎪∠=∠⎨⎪⎩△△DFE△△DCE (AAS ),DF DC ∴=;(2)由题知,AE -EF=AF ,△AE=AD=BC ,△AD -EF=AF ,BC -EF=AF ,△△DFE△△DCE ,△EF=CE ,△AE -CE=AF ,综上,使每对中较长线段与较短线段长度的差等于线段AF 的长, 则AE 与EF ;AD 与EF ; BC 与EF ;AE 与CE ;(写出四对即可). 17.(1)证明:△动点E 、F 同时运动且速度相等,△DF=BE ,△四边形ABCD 是菱形,△△B=△D ,AD=BC ,AB△DC ,在△ADF 与△CBE 中,,DF BE B D AD BC =⎧⎪∠=∠⎨⎪=⎩△△ADF△△CBE ,△△DFA=△BEC ,△AB△DC ,△△DFA=△FAB ,△△FAB=△BEC ,△AF△CE ;(2)过D 作DM△AB 于M ,连接GH ,EF ,△DF=BE=t,△AF△CE,AB△CD,△四边形AECF是平行四边形,△G、H是AF、CE的中点,△GH△AB,△四边形EGFH是菱形,△GH△EF,△EF△AB,△FEM=90°,△DM△AB,△DM△EF,△四边形DMEF是矩形,△ME=DF=t,△AD=4,△DAB=60°,DM△AB,△122AM AD,==△BE=4﹣2﹣t=t,△t=1,(3)不存在,假设存在某个时刻t,使四边形EHFG为矩形,△四边形EHFG为矩形,△EF=GH ,△EF 2=GH 2,即()(()222224t t -+=-,解得t=0,0<t <4, △与原题设矛盾,△不存在某个时刻t ,使四边形EHFG 为矩形.18.(1)△△BOC 旋转 60°得到△ADC ,△△BCO △△ACD ,△OC =CD ,且△OCD =60°,则△OCD 是等边三角形;(2)△△ABC 为等边三角形,△△BAO +△OAC =60°,△ABO +△OBC =60°. △△AOB =105°,△△BAO +△ABO =75°,△△OAC +△OBC =120°﹣105°=45°. △△BOC 旋转 60°得到△ADC ,△△BCO △△ACD ,△△DAC =△OBC ,△△OAD =△OAC +△CAD =45°.(3)若△AOD 是等腰三角形 .△由(1)知△OCD 是等边三角形,△△COD =60°.由(2)知△OAD =45°, 分三种情况讨论:△当 OA =OD 时,△AOD =90°,△α=360°﹣105°﹣60°﹣90°=105°;△当 OA =AD 时,△AOD =67.5°,△α=360°﹣105°﹣60°﹣67.5°=127.5°; △当 AD =OD 时,△AOD =45°,△α=360°﹣105°﹣60°﹣45°=150°.综上所述:当α=105°,127.5°或 150°时,△AOD 是等腰三角形 .19.解:(1)证明:△四边形ABCD 是正方形,△AB BC CD DA ===,△AE BF CM DN ===,△BE CF DM NA ===,又90A B C D ∠=∠=∠=∠=︒,△BEF CFM DMN ANE ≌≌≌△△△△,△EF FM MN NE ===,△四边形EFMN 是菱形.△AEN BFE ∠=∠,且90BEF BFE ∠+∠=︒ △90BEF AEN ∠+∠=︒,△90FEN ∠=︒.△菱形EFMN 是正方形;(2)通过观察可知:当点E 是AD 边的中点时,四边形EFMN 的周长最小. △当点E 是AD 边的中点时,EFB △是等腰直角三角形,△114222BE BF AB ===⨯=,△由2228EF BE BF =+=,得:EF =EFMN 是正方形,△四边形EFMN 周长的最小值为4=。
(精练)苏科版八年级下册数学第9章 中心对称图形——平行四边形含答案

苏科版八年级下册数学第9章中心对称图形——平行四边形含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为()A.34B.32C.22D.202、下列说法中错误的是()A.两条对角线互相平分的四边形是平行四边形B.两条对角线相等的四边形是矩形C.两条对角线互相垂直的矩形是正方形D.两条对角线相等的菱形是正方形3、下列命题:①两条对角线互相平分且相等的四边形是菱形;②对角线相等的四边形是矩形;③菱形的每一条对角线平分一组对角;④顺次连接四边形各边中点所得到的四边形是平行四边形;⑤平行四边形对角线相等.其中正确的命题为( )A.1B.2C.3D.44、如图所示,矩形ABCD中,AE平分交BC于E,,则下面的结论:① 是等边三角形;② ;③ ;④ ,其中正确结论有()A.1个B.2个C.3个D.4个5、如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于()A. B. C. D.6、如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有()次平行于AB?A.1B.2C.3D.47、如图,在四边形中,,要使四边形是平行四边形,下列可添加的条件不正确的是()A. B. C. D.8、下列图形中,是轴对称图形,不是中心对称图形的是()A. B. C. D.9、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF 的中点,那么CH的长是().A. B.2 C. D.10、下列汽车标志的图形中,是中心对称图形的是()A. B. C. D.11、如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB’C’(点B的对应点是点B’,点C的对应点是点C’),连接CC’.若∠CC’B’=32°,则∠B的大小是( )A.32°B.64°C.77°D.87°12、菱形具有而矩形不具有的性质是()A.对边相等B.对角线互相平分C.对角线互相垂直D.对角线相等13、如图,在矩形ABCD中,E , F分别是AD , BC中点,连接AF , BE ,CE , DF分别交于点M , N ,四边形EMFN是().A.正方形B.菱形C.矩形D.无法确定14、正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M,N,则MN的长为( )A. B. ﹣1 C. D.15、如图,矩形ABCD中,,,且BE与DF之间的距离为3,则AE的长是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,在正方形ABCD中,AD=1.将△ABD绕点B顺时针旋转45°得到△A′BD′,此时AD与CD交于点E,则DE的长度为________17、如图,直线AB与CD分别与⊙O 相切于B、D两点,且AB⊥CD,垂足为P,连接BD.若BD=4,则阴影部分的面积为________.18、在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距________cm.19、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C 旋转得到△EDC,使点D在AB边上,斜边DE交AC边于点F,则图中△CDF的周长为________.20、如图,在平面直角坐标系中,菱形的顶点A与D在函数()的图象上,轴,垂足为C,,点B的坐标为,则k的值为________.21、正方形的对角线长为2,则对角线的交点到各边的距离是________.22、用反证法证明命题“三角形中至少有一个内角大于或等于60°,第一步应假设________23、如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件________.24、在菱形ABCD中,∠A=60°,AB=4 ,点P在对角线AC上,且PB=PD=4,则∠PDC的度数为________.25、在矩形ABCD.对角线AC、BD交于点O,AB=1,∠AOB=60°,则AD=________.三、解答题(共5题,共计25分)26、如图,在每个小正方形的边长为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上。
苏科版八年级下册数学第9章 中心对称图形——平行四边形 含答案(精炼题)

苏科版八年级下册数学第9章中心对称图形——平行四边形含答案一、单选题(共15题,共计45分)1、在下列四个图形中,是中心对称图形的是()A. B. C. D.2、如图,将△ABC绕点A按顺时针方向旋转60°后得到△ADE,连接BD。
若AB=8,则图中阴影部分的面积为()A.16B.16C.32D.323、下列标志图中,既是轴对称图形,又是中心对称图形的是()A. B. C. D.4、如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为()A.12B.13C.14D.155、如图,在正方形ABCD中,E,F分别是AB,CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是()A.y=3 x 2B.y=4 x 2C.y=8x 2D.y=9x 26、下列图形既可看成轴对称图形又可看成中心对称图形的是()A. B. C. D.7、如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D 1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015,到BC的距离记为h2015.若h 1=1,则h2015的值为()A. B. C.1- D.2-8、如图,AC是平行四边形ABCD的对角线,当它满足以下:①∠1=∠2;②∠2=∠3;③∠B=∠3;④∠1=∠3中某一条件时,平行四边形ABCD是菱形,这个条件是()A.①或②B.②或③C.③或④D.①或④9、如图,图①是一个对角线长分别是6和8的菱形,将其沿对角线剪成四个全等的三角形,把这四个三角形无重叠地拼成如图②所示的大正方形,则图②中小正方形的面积为()A.1B.2C.4D.610、已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC=BD时,它是正方形C.当∠ABC=90°时,它是矩形 D.当AC⊥BD时,它是菱形11、下列说法中错误的有()个.⑴平行四边形对角线互相平分且相等;⑵对角线相等的平行四边形是矩形;⑶菱形的四条边相等,四个角也相等;⑷对角线互相垂直的矩形是正方形;⑸顺次连接四边形各边中点所得到的四边形是平行四边形.A.1B.2C.3D.412、如图,在Rt△ABC中,∠BCA=90°,∠BAC=30°,BC=2,将Rt△ABC绕A 点顺时针旋转90°得到Rt△ADE,则BC扫过的面积为()A. B.(2﹣)π C. π D.π13、下列说法中正确的个数为()①如果三角形的三边长a,b,c满足,那么这个三角形是直角三角形;②对角线相等的平行四边形是菱形;③如果一个一元二次方程有实数根,那么;④三个角相等的四边形是矩形.A.1个B.2个C.3个D.4个14、如图,一块等腰直角的三角板,在水平桌面上绕点按顺时针方向旋转到的位置,使三点共线,那么旋转角度的大小为( )A. B. C. D.15、如图(1)中,△和△都是等腰直角三角形,∠和∠都是直角,点在上,△绕着点经过逆时针旋转后能够与△重合,再将图(1)作为“基本图形”绕着点经过逆时针旋转得到图(2).两次旋转的角度分别为()A.45°,90°B.90°,45°C.60°,30°D.30°,60°二、填空题(共10题,共计30分)16、菱形ABCD的边长为5,对角线交于O点,且AO、BO的长分别是关于x的方程的两个根,则m的值为________17、如图,阴影部分是一个正方形,此正方形的面积为________。
苏科版八年级数学下册第9章 中心对称图形-平行四边形 单元测试卷(含答案)

苏科版八年级数学下册第9章 中心对称图形-平行四边形 单元测试卷一、单选题1.下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )A .B .C .D .2.下列结论中,正确的是( )A .四边相等的四边形是正方形B .对角线相等的菱形是正方形C .正方形两条对角线相等,但不互相垂直平分D .矩形、菱形、正方形都具有“对角线相等”的性质3.如图,在四边形ABCD 中,P 是对角线BD 的中点,E 、F 分别是AB 、CD 的中点,AD BC =,136EPF ∠=︒,则EFP ∠的度数是( )A .68︒B .34︒C .22︒D .44︒4.如图,在矩形ABCD 中,AB =8,AD =6,过点D 作直线m∥AC ,点E 、F 是直线m 上两个动点,在运动过程中EF∥AC 且EF =AC ,四边形ACFE 的面积是( )A .48B .40C .24D .305.如图,四边形ABCD 中,90DAB CBA ∠=∠=︒,将CD 绕点D 逆时针旋转90︒至DE ,连接AE ,若6AD =,10BC =,则ADE ∆的面积是( )A .272B .12C .9D .86.菱形ABCD 中,对角线AC 、BD 相交于点O ,H 为AD 边中点,菱形ABCD 的周长为28,则OH 的长等于( ) A .3.5 B .4 C .7 D .147.如图,在正方形ABCD 中,点M 、N 为边BC 和CD 上的动点(不含端点),45MAN ∠=︒.下列三个结论:∥当MN =时,则22.5BAM ∠=︒;∥290AMN MNC ∠-∠=︒;∥MNC ∆的周长不变,其中正确结论的个数是( )A .0B .1C .2D .38.如图,在∥ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE∥AB 于 E ,PF∥AC 于 F ,M 为 EF 中点,则 AM 的最小值为( )A .1B .1.3C .1.2D .1.59.如图,在菱形ABCD 中,AC 与BD 相交于点O ,AB =4,BD =E 为AB 的中点,点P 为线段AC 上的动点,则EP+BP 的最小值为( )A .4B .C .D .810.如图,在∥ABC中,∥ACB=90o,∥B=30o,AC=1,AB=2,AC在直线l上,将∥ABC绕点A顺时针转到位置∥可得到点P1,此时AP1=2;将位置∥的三角形绕点P1顺时针旋转到位置∥,可得到点P2,此时AP2=2+∥的三角形绕点P2顺时针旋转到位置∥,可得到点P3,此时AP3,按此顺序继续旋转,得到点P2016,则AP2016=( )A.B.C.D.二、填空题11.如图,在∥ABC中,∥BAC=65°,将∥ABC绕点A逆时针旋转,得到∥AB'C',连接C'C.若C'C∥AB,则∥BAB'=_____°.12.如图,矩形ABCD的对角线AC和BD相交于点O,直线EF经过点O,交BC于点E,AD于点F,若AB=5cm,AC=13 cm,则阴影部分的面积为_________.13.在菱形ABCD中,对角线AC=2,BD=4,则菱形ABCD的周长是________.14.如图.将长方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∥EBF的大小为_____ .15.如图,在∥ABC中,∥ACB=90°,AC=BC=4,O是BC的中点,P是射线AO上的一个动点,则当∥BPC=90°时,AP的长为______.16.已知,点(,1)A a 和点(3,)B b 关于原点O 对称,则+a b 的值为__________.17.如图,∥ABC 中,AB=AC ,BE∥AC ,D 为AB 中点,若DE=5,BE=8.则EC=______.18.如图,在∥ABC 中,CD∥AB 于点D ,BE∥AC 于点E ,F 为BC 的中点,DE =5,BC =8,则∥DEF 的周长是______.19.如图,在ABC V 中,3AB =,4AC =,5BC =,P 为边BC 上一动点,PE AB ⊥于E ,PF AC ⊥于F ,M 为EF 的中点,则AM 的最小值为________.20.如图,在一张矩形纸片ABCD 中,AB=4,BC=8,点E ,F 分别在AD ,BC 上,将纸片ABCD 沿直线EF 折叠,点C 落在AD 上的一点H 处,点D 落在点G 处,有以下四个结论:∥四边形CFHE是菱形;∥EC平分∥DCH;∥线段BF的取值范围为3≤BF≤4;∥当点H与点A重合时,以上结论中,你认为正确的有.(填序号)三、解答题21.已知如图,O为平行四边形ABCD的对角线AC的中点,EF经过点O,且与AB交于E,与CD 交于F.求证:四边形AECF是平行四边形.22.如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.23.如图,在边长为1的正方形网格中,∥ABC 的顶点均在格点上.(1)画出∥ABC 绕点O 顺时针旋转90°后的∥A′B′C′.(2)求点B 绕点O 旋转到点B′的路径长(结果保留π).24.如图,在ABCD Y 中,对角线BD 平分ABC ∠,过点A 作AE BD P ,交CD 的延长线于点E ,过点E 作EF BC ⊥,交BC 延长线于点F .(1)求证:四边形ABCD 是菱形;(2)若452ABC BC ∠︒=,=,求EF 的长.25.如图,矩形ABCD 的对角线AC ,BD 交于点O ,且DE AC P ,CE BD P .求证:四边形OCED 是菱形.26.如图,在∥ABCD 中,E ,F 分别是AD ,BC 上的点,且DE=BF ,AC∥EF .求证:四边形AECF 是菱形.27.如图,在ABCD Y 中,AE BC ⊥于点E 点,延长BC 至F 点使=CF BE ,连接AF ,DE ,DF .(1)求证:四边形AEFD 是矩形;(2)若6AB =,8DE =,10BF =,求AE 的长.28.如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).(1)∥PBD的度数为,点D的坐标为(用t表示);(2)当t为何值时,∥PBE为等腰三角形?29.在∥ABCD中,∥BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明CE=CF;(2)若∥ABC=90°,G是EF的中点(如图2),直接写出∥BDG的度数;(3)若∥ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∥BDG的度数.30.如图,∥ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE∥AB于E,连接PQ交AB于D.(∥)若设AP=x,则PC=,QC=;(用含x的代数式表示)(∥)当∥BQD=30°时,求AP的长;(∥)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.苏科版八年级数学下册第9章中心对称图形-平行四边形单元测试卷(含答案)一、填空题1.C 2.B 3.C 4.A 5.B6.A 7.D 8.C 9.C 10.B二、填空题11.50 12.15cm2 13.14.45° 15.±216.4-17.4 18.13 19.1.2 20.∥∥∥三、解答题21.证明见解析.【分析】求证四边形AECF是平行四边形,只要求证OE=OF,根据对角线互相平分的四边形是平行四边形即可求证,依据∥AOE∥∥COF即可证明OE=OF.【详解】证明:∥平行四边形ABCD中AB∥CD,∥∥OAE=∥OCF,又∥OA=OC,∥COF=∥AOE,∥∥AOE∥∥COF(ASA),∥OE=OF,又∥OA=OC∥四边形AECF是平行四边形.22.证明见解析.根据平行四边形的判定推出四边形OBEC 是平行四边形,根据菱形性质求出∥AOB=90°,根据矩形的判定推出即可.【详解】∥BE∥AC ,CE∥DB ,∥四边形OBEC 是平行四边形,又∥四边形ABCD 是菱形,且AC 、BD 是对角线,∥AC∥BD ,∥∥BOC =90°,∥平行四边形OBEC 是矩形.23.(1)画图见解析;(2)点B 绕点O 旋转到点B′. 【分析】(1)利用网格特点和旋转的性质画出点A 、B 、C 的对应点A′、B′、C′,从而得到∥A′B′C′;(2)先计算出OB 的长,然后根据弧长公式计算点B 绕点O 旋转到点B′的路径长.【详解】(1)如图,∥A′B′C′为所作;(2)OB =,点B 绕点O 旋转到点B′的路径长=90180π⨯⨯π.24.(1)见解析;(2)(1)证明ADB ABD ∠∠=,得出AB AD =,即可得出结论;(2)由菱形的性质得出2AB CD BC ===,证明四边形ABDE 是平行四边形,45ECF ABC ∠∠︒==,得出24AB DE CE CD DE +==,==,在Rt CEF △中,由等腰直角三角形的性质和勾股定理即可求出EF 的长.【详解】(1)证明:∥四边形ABCD 是平行四边形,AD BC AB CD AB CD ∴P P ,=,,ADB CBD ∴∠∠=,, ∥BD 平分ABC ∠,ABD CBD ∴∠∠=,, ADB ABD ∴∠∠=,, AB AD ∴=,, ABCD ∴Y 是菱形;(2)解:∥四边形ABCD 是菱形,2AB CD BC ∴===,AB CD AE BD Q P P ,,∥四边形ABDE 是平行四边形,45ECF ABC ∠∠︒==,2AB DE ∴==,4CE CD DE ∴+==,45EF BC ECF ⊥∠︒Q ,=,CEF ∴V 是等腰直角三角形,2EF CF ∴=== 25.见解析【分析】首先根据两对边互相平行的四边形是平行四边形证明四边形OCED 是平行四边形,再根据矩形的性质可得OC=OD ,即可利用一组邻边相等的平行四边形是菱形判定出结论.【详解】证明:∥DE AC P ,CE BD P ,∥四边形OCED 是平行四边形,∥四边形ABCD 是矩形,∥AC BD =,OA OC =,OB OD =,∥OC OD =,∥四边形OCED 是菱形.26.见解析.【分析】根据对角线互相垂直的平行四边形是菱形即可证明【详解】证明:Q 四边形ABCD 是平行四边形,AD BC ∴=,//AD BC ,DE BF =Q ,AE CF ∴=,//AE CF Q ,∴四边形AECF 是平行四边形,AC EF ⊥Q ,∴四边形AECF 是菱形.27.(1)见解析;(2)245【解析】试题分析:(1)先证明四边形AEFD 是平行四边形,再证明∥AEF=90°即可.(2)证明∥ABF 是直角三角形,由三角形的面积即可得出AE 的长.试题解析:(1)证明:∥CF=BE ,∥CF+EC=BE+EC .即 EF=BC .∥在∥ABCD 中,AD∥BC 且AD=BC ,∥AD∥EF 且AD=EF .∥四边形AEFD是平行四边形.∥AE∥BC,∥∥AEF=90°.∥四边形AEFD是矩形;(2)∥四边形AEFD是矩形,DE=8,∥AF=DE=8.∥AB=6,BF=10,∥AB2+AF2=62+82=100=BF2.∥∥BAF=90°.∥AE∥BF,∥∥ABF的面积=12AB•AF=12BF•AE.∥AE=•6824105 AB AFBF⨯==.28.(1)45°(t,t);(2)t=4秒或(-4)秒【分析】(1)易证∥BAP∥∥PQD,从而得到DQ=AP=t,从而可以求出∥PBD的度数和点D的坐标.(2)由于∥EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.由于∥PBE底边不定,故分三种情况讨论,借助于三角形全等及勾股定理进行求解,然后结合条件进行取舍,最终确定符合要求的t值.【详解】(1)如图1,由题可得:AP=OQ=1×t=t(秒)∥AO=PQ .∥四边形OABC 是正方形,∥AO=AB=BC=OC ,∥BAO=∥AOC=∥OCB=∥ABC=90°.∥DP∥BP ,∥∥BPD=90°.∥∥BPA=90°-∥DPQ=∥PDQ .∥AO=PQ ,AO=AB ,∥AB=PQ .在∥BAP 和∥PQD 中,BAP PQD BPA PDQ AB PQ ∠∠∠∠⎧⎪⎨⎪⎩===∥∥BAP∥∥PQD (AAS ).∥AP=QD ,BP=PD .∥∥BPD=90°,BP=PD ,∥∥PBD=∥PDB=45°.∥AP=t ,∥DQ=t .∥点D 坐标为(t ,t ).故答案为:45°,(t ,t ).(2)∥若PB=PE ,则t=0(舍去),∥若EB=EP ,则∥PBE=∥BPE=45°.∥∥BEP=90°.∥∥PEO=90°-∥BEC=∥EBC .在∥POE 和∥ECB 中,PEO EBC POE ECB EP BE ∠∠∠∠⎧⎪⎨⎪⎩===∥∥POE∥∥ECB (AAS ).∥OE=CB=OC .∥点E 与点C 重合(EC=0).∥点P 与点O 重合(PO=0).∥点B (-4,4),∥AO=CO=4.此时t=AP=AO=4.∥若BP=BE ,在Rt∥BAP 和Rt∥BCE 中,BA BC BP BE ⎧⎨⎩== ∥Rt∥BAP∥Rt∥BCE (HL ).∥AP=CE .∥AP=t ,∥CE=t .∥PO=EO=4-t .∥∥POE=90°,4-t ).延长OA 到点F ,使得AF=CE ,连接BF ,如图2所示.在∥FAB 和∥ECB 中,90AB CB BAF BCE AF CE ⎧⎪⎨⎪∠∠⎩︒====∥∥FAB∥∥ECB .∥FB=EB ,∥FBA=∥EBC .∥∥EBP=45°,∥ABC=90°,∥∥ABP+∥EBC=45°.∥∥FBP=∥FBA+∥ABP=∥EBC+∥ABP=45°.∥∥FBP=∥EBP .在∥FBP 和∥EBP 中,BF BE FBP EBP BP BP ⎪∠⎪⎩∠⎧⎨===∥∥FBP∥∥EBP (SAS ).∥FP=EP .∥EP=FP=FA+AP=CE+AP .∥EP=t+t=2t .(4-t )=2t .解得:-4∥当t 为4秒或(-4)秒时,∥PBE 为等腰三角形.29.(1)见解析;(2)45°;(3)见解析.【分析】(1)根据AF 平分∥BAD ,可得∥BAF=∥DAF ,利用四边形ABCD 是平行四边形,求证∥CEF=∥F 即可;(2)根据∥ABC=90°,G 是EF 的中点可直接求得;(3)分别连接GB 、GC ,求证四边形CEGF 是平行四边形,再求证∥ECG 是等边三角形,由AD∥BC 及AF 平分∥BAD 可得∥BAE=∥AEB ,求证∥BEG∥∥DCG ,然后即可求得答案.【详解】(1)证明:如图1,∥AF 平分∥BAD ,∥∥BAF=∥DAF ,∥四边形ABCD 是平行四边形,∥AD∥BC ,AB∥CD ,∥∥DAF=∥CEF ,∥BAF=∥F ,∥∥CEF=∥F .∥CE=CF .(2)解:连接GC 、BG ,∥四边形ABCD 为平行四边形,∥ABC=90°,∥四边形ABCD 为矩形,∥AF 平分∥BAD ,∥∥DAF=∥BAF=45°,∥∥DCB=90°,DF∥AB ,∥∥DFA=45°,∥ECF=90°∥∥ECF 为等腰直角三角形,∥G 为EF 中点,∥EG=CG=FG ,CG∥EF ,∥∥ABE 为等腰直角三角形,AB=DC ,∥BE=DC ,∥∥CEF=∥GCF=45°,∥∥BEG=∥DCG=135°在∥BEG 与∥DCG 中,∥EG CG BEG DCG BE DC =⎧⎪∠=∠⎨⎪=⎩,∥∥BEG∥∥DCG ,∥BG=DG ,∥CG∥EF ,∥∥DGC+∥DGA=90°,又∥∥DGC=∥BGA ,∥∥BGA+∥DGA=90°,∥∥DGB为等腰直角三角形,∥∥BDG=45°.(3)解:延长AB、FG交于H,连接HD.∥AD∥GF,AB∥DF,∥四边形AHFD为平行四边形∥∥ABC=120°,AF平分∥BAD∥∥DAF=30°,∥ADC=120°,∥DFA=30°∥∥DAF为等腰三角形∥AD=DF,∥CE=CF,∥平行四边形AHFD为菱形∥∥ADH,∥DHF为全等的等边三角形∥DH=DF,∥BHD=∥GFD=60°∥FG=CE,CE=CF,CF=BH,∥BH=GF在∥BHD与∥GFD中,∥DH DFBHD GFD BH GF=⎧⎪∠=∠⎨⎪=⎩,∥∥BHD∥∥GFD,∥∥BDH=∥GDF∥∥BDG=∥BDH+∥HDG=∥GDF+∥HDG=60°.30.(∥)6﹣x,6+x;(∥)2;(∥)线段DE的长度不会改变.DE=3【分析】(1)根据等边三角形的性质可知AB=BC=AC=6,然后根据题意解答即可;(2)在(1)的基础上,再利用直角三角形30°所对的边等于斜边的一半进行解答即可.(3) 作QF∥AB,交直线AB的延长线于点F,连接QE,PF;根据题意和等边三角形的性质证明∥APE∥∥BQF(AAS),进一步说明四边形PEQF是平行四边形,最后说明DE=AB,即可说明DE的长度不变.【详解】解:(∥)∥∥ABC是边长为6的等边三角形,∥AB =BC =AC =6,设AP =x ,则PC =6﹣x ,QB =x ,∥QC =QB +BC =6+x ,故答案为:6﹣x ,6+x ;(∥)∥在Rt∥QCP 中,∥BQD =30°,∥PC =12QC ,即6﹣x =12(6+x ),解得x =2, ∥AP =2;(∥)当点P 、Q 运动时,线段DE 的长度不会改变.理由如下:作QF ∥AB ,交直线AB 的延长线于点F ,连接QE ,PF , 又∥PE ∥AB 于E ,∥∥DFQ =∥AEP =90°,∥点P 、Q 速度相同,∥AP =BQ ,∥∥ABC 是等边三角形,∥∥A =∥ABC =∥FBQ =60°,在∥APE 和∥BQF 中,∥∥AEP =∥BFQ =90°,∥∥APE =∥BQF ,∥在∥APE 和∥BQF 中,AEP BFQ A FBQ AP BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩,∥∥APE∥∥BQF(AAS),∥AE=BF,PE=QF且PE∥QF,∥四边形PEQF是平行四边形,∥DE=12 EF,∥EB+AE=BE+BF=AB,∥DE=12 AB,又∥等边∥ABC的边长为6,∥DE=3,∥当点P、Q运动时,线段DE的长度不会改变.。
苏科版八年级数学下册第9章 中心对称图形-平行四边形单元测试卷(含答案)

苏科版八年级数学下册第9章中心对称图形-平行四边形单元测试卷(含答案)一、选择题1.下列图案中,是中心对称图形但不是轴对称图形的是()图12.四边形ABCD的对角线AC与BD相交于点O,下列四组条件中,一定能判定四边形ABCD 为平行四边形的是()A.AD∥BCB.OA=OC,OB=ODC.AD∥BC,AB=DCD.AC⊥BD3.下列结论中,矩形具有而菱形不一定具有的性质是()A.内角和为360°B.对角线互相平分C.对角线相等D.对角线互相垂直4.如图2,在▱ABCD中,M,N是BD上的两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,则这个条件可以是()图2A.OM=ACB.MB=MOC.BD⊥ACD.∠AMB=∠CND5.如图3,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.有下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()图3A.1B.2C.3D.46.如图4,E是正方形ABCD的边CD上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为20,DE=2,则AE2的值为()图4A.16B.50C.36D.24二、填空题7.如图5,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α=°.图5 图68.如图6,▱ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么▱ABCD的周长是.9.如图7,在矩形ABCD中,AC=8,对角线AC与BD相交于点O,AE⊥BD,垂足为E,且AE平分∠BAC,则AB的长为.图710.如图8,连接四边形ABCD各边中点,得到四边形EFGH,只要添加条件,就能保证四边形EFGH是菱形.图811.如图9,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥AD于点E,交BC 于点F,则EF的长为.图912.如图10,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是.图10三、解答题13.(8分)如图11,在△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.(1)求证:EF=BC;(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.图1114.(10分)如图12,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,求MN的长度.图1215.(12分)如图13,在正方形ABCD中,P是对角线AC上的一点,连接BP,DP,延长BC到点E,使PE=PB.求证:∠PDC=∠PEC.图1316.(12分)已知:如图14,在▱ABCD中,对角线AC与BD相交于点E,G为AD的中点,连接CG 并延长交BA的延长线于点F,连接FD.(1)求证:AB=AF;(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.图1417.(14分)如图15(a),在矩形纸片ABCD中,AB=3 cm,AD=5 cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.(1)求证:四边形BFEP为菱形.(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.①当点Q与点C重合时,如图(b),求菱形BFEP的边长;②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.图15答案1. C2. B3. C4. A5. A6. D7. 908. 169.410.AC=BD11.12. 1013.解:(1)证明:由旋转的性质可知AC=AF.又知∠CAF=∠BAE, 则∠EAF=∠BAC.在△ABC与△AEF中,∴△ABC≌△AEF(SAS),∴EF=BC.(2)∵AB=AE,∠ABC=65°,∴∠BAE=180°-65°×2=50°,∴∠FAG=∠BAE=50°.∵△ABC≌△AEF,∴∠F=∠C=28°,∴∠FGC=∠FAG+∠F=50°+28°=78°.14.解:∵BN平分∠ABC,BN⊥AE,∴∠NBA=∠NBE,∠BNA=∠BNE.在△BNA和△BNE中,∴△BNA≌△BNE,∴BA=BE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴N是AE中点,M是AD中点(三线合一),∴MN是△ADE的中位线.∵BE+CD=AB+AC=19-BC=19-7=12,∴DE=BE+CD-BC=5,∴MN=DE=.15.证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP.在△BCP和△DCP中,∴△BCP≌△DCP(SAS),∴∠PBC=∠PDC.∵PB=PE,∴∠PBC=∠PEC,∴∠PDC=∠PEC.16.解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠AFC=∠DCG.∵GA=GD,∠AGF=∠CGD,∴△AGF≌△DGC(AAS),∴AF=CD,∴AB=AF.(2)结论:四边形ACDF是矩形.证明:∵AF=CD,AF∥CD,∴四边形ACDF是平行四边形.∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=120°,∴∠FAG=60°.∵AB=AG=AF,∴△AFG是等边三角形,∴AG=GF.∵△AGF≌△DGC,∴FG=CG.又∵AG=GD,∴AD=CF,∴四边形ACDF是矩形.17.解:(1)证明:∵折叠纸片使点B落在边AD上的点E处,折痕为PQ, ∴点B与点E关于PQ对称,∴PB=PE,BF=EF,∠BPF=∠EPF.又∵EF∥AB,∴∠BPF=∠EFP,∴∠EPF=∠EFP,∴PE=EF,∴PB=BF=EF=PE,∴四边形BFEP为菱形.(2)①∵四边形ABCD是矩形,∴BC=AD=5 cm,CD=AB=3 cm,∠A=∠D=90°.∵点B与点E关于PQ对称,∴CE=BC=5 cm.在Rt△CDE中,DE==4 cm,∴AE=AD-DE=5-4=1(cm).在Rt△APE中,AE=1 cm,AP=3-PB=3-EP,∴EP2=12+(3-EP)2,解得EP=cm, ∴菱形BFEP的边长为cm.②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1 cm;当点P与点A重合时,如图所示:点E离点A最远,此时四边形ABQE为正方形,AE=AB=3 cm.∵3-1=2(cm),∴点E在边AD上移动的最大距离为2 cm.。
八年级数学下册《第九章 中心对称图形-平行四边形》练习题与答案(苏科版)

八年级数学下册《第九章中心对称图形-平行四边形》练习题与答案(苏科版)一、选择题1.下列交通标志中,是中心对称图形的是( )2.在下列几何图形中:(1)两条互相平分的线段;(2)两条互相垂直的直线;(3)两个有公共顶点的角;(4)两个有一条公共边的正方形.其中是中心对称图形的有( )A.1个B.2个C.3个D.4个3.下列四个图案是小明家在瓷砖厂选购的四种地砖图案,其中既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的是()4.如图,平行四边形ABCD中,∠ABC的角平分线交边CD于点E,∠A=130°,则∠BEC的度数是( )A.20°B.25°C.30°D.50°5.如图,在△ABC中,E,D,F分别是AB,BC,CA的中点,AB=6,AC=4,则四边形AEDF的周长是( )A.10B.12C.14D.166.下列三个命题中,是真命题的有( )①对角线相等的四边形是矩形;②三个角是直角的四边形是矩形;③有一个角是直角的平行四边形是矩形.A.3个B.2个C.1个D.0个7.用矩形纸片折出直角的平分线,下列折法正确的是( )A. B. C. D.8.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )A.3B.4C.5D.69.如图,将一正方形纸片沿图(1)、(2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )A. B. C. D.10.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )A.45°B.30°C.60°D.55°11.如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB 边上一动点,以PA,PC为边作▱PAQC,则对角线PQ长度的最小值为( )A.6B.8C.2 2D.4 212.如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB 的最小值是( )A.2B.4C. 2D.2 2二、填空题13.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是______.14.在四边形ABCD中,BD是对角线,∠ABD=∠CDB,要使四边形ABCD是平行四边形只须添加一个条件,这个条件可以是(只需写出一种情况).15.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=120°,则∠AOE=.16.如图,在平行四边形ABCD中,点E在边AD上,使BF=BE,连接EC并延长至点G,连接FG,点H为FG 的中点,AF.若∠BAE=70°,∠DCE=20°.17.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为____.18.如图,点P的坐标为(2,2),点A,B分别在x轴,y轴的正半轴上运动,且∠APB=90°.下列结论:①PA=PB;②当OA=OB时四边形OAPB是正方形;③四边形OAPB的面积和周长都是定值;④连接OP,AB,则AB>OP.其中正确的结论是.(把你认为正确结论的序号都填上)三、作图题19.如图所示,△ABC在边长为1cm的小正方形组成的网格中.(1)将△ABC沿y轴正方向向上平移5个单位长度后,得到△A1B1C1,请作出△A1B1C1,并求出A1B1的长度;(2)再将△A1B1C1绕坐标原点O顺时针旋转180°,得到△A2B2C2请作出△A2B2C2,并直接写出点B2的坐标.四、解答题20.如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.(1)求证:四边形EFPQ是平行四边形;(2)请直接写出BG与GE的数量关系:.(不要求证明)21.如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.22.如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.求证:(1)△ABF≌△DEA;(2)DF是∠EDC的平分线.23.如图,在正方形ABCD中,BC=2,E是对角线BD上的一点,且BE=AB.求△EBC的面积.24.如图,在▱ABCD中,BD是对角线,∠ADB=90°,E、F分别为边AB、CD的中点.(1)求证:四边形DEBF是菱形;(2)若BE=4,∠DEB=120°,点M为BF的中点,当点P在BD边上运动时,则PF+PM的最小值为,并在图上标出此时点P的位置.25.如图1,在矩形纸片ABCD中,AB=12 cm,AD=20 cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形BFEP为菱形;(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动;①当点Q与点C重合时(如图2),求菱形BFEP的边长;②若限定P,Q分别在边BA,BC上移动,求出点E在边AD上移动的最大距离.图1 图2参考答案1.D2.C3.C4.B.5.A6.B.7.D.8.B9.D.10.A11.D12.D.13.答案为:4.14.答案为:AB=CD或AD∥BC15.答案为:60°.16.答案为:50°.17.答案为:12.18.答案为:①②.19.解:(1)如图所示,△A1B1C1即为所求,A1B1=32(cm).(2)如图,△A2B2C2即为所求,B2(4,﹣4).20.证明:(1)∵BE,CF是△ABC的中线∴EF是△ABC的中位线∴EF∥BC且EF=0.5BC.∵P,Q分别是BG,CG的中点∴PQ是△BCG的中位线∴PQ∥BC且PQ=0.5BC,∴EF∥PQ且EF=PQ.∴四边形EFPQ是平行四边形.(2)BG=2GE.21.证明:∵BE∥AC,CE∥DB∴四边形OBEC是平行四边形又∵四边形ABCD是菱形∴AC⊥BD∴∠AOB=90°∴平行四边形OBEC是矩形.22.证明:(1)∵四边形ABCD是矩形∴∠B=90°,AD=BC,AD∥BC∴∠DAE=∠AFB∵DE⊥AF∴∠DEA=∠B=90°∵AF=BC∴AF=AD在△DEA和△ABF中∵∴△DEA≌△ABF(AAS);(2)证明:∵由(1)知△ABF≌△DEA ∴DE=AB∵四边形ABCD是矩形∴∠C=90°,DC=AB∴DC=DE.∵∠C=∠DEF=90°∴在Rt△DEF和Rt△DCF中∴Rt △DEF ≌Rt △DCF(HL)∴∠EDF =∠CDF∴DF 是∠EDC 的平分线.23.解:作EF ⊥BC 于F ,如图所示:则∠EFB =90°∵四边形ABCD 是正方形∴AB =BC =2,∠DAB =∠ABC =90°∴∠ABD =∠DBC =12∠ABC =45°∴△BEF 是等腰直角三角形∴EF =BF∵BE =AB∴BE =BC =2∴EF =BF =22BE = 2∴△EBC 的面积=12BC •EF =12×2×2=2.24.证明:(1)∵平行四边形ABCD 中,AD ∥BC∴∠DBC =∠ADB =90°.∵△ABD 中,∠ADB =90°,E 时AB 的中点∴DE =12AB =AE =BE.同理,BF =DF∵平行四边形ABCD 中,AB =CD∴DE =BE =BF =DF∴四边形DEBF 是菱形;(2)解:连接BF∵菱形DEBF 中,∠DEB =120°∴∠EF =60°∴△BEF 是等边三角形∵M 是BF 的中点∴EM ⊥BF.则EM =2 3. 即PF +PM 的最小值是2 3.25. (1)证明:∵折叠纸片使B 点落在边AD 上的E 处,折痕为PQ ∴点B 与点E 关于PQ 对称∴PB =PE ,BF =EF ,∠BPF =∠EPF.又∵EF ∥AB∴∠BPF =∠EFP ,∴∠EPF =∠EFP∴EP =EF ,∴BP =BF =EF =EP∴四边形BFEP 为菱形.(2)解:①∵四边形ABCD 是矩形∴BC =AD =20,CD =AB =12,∠A =∠D =90°.∵点B 与点E 关于PQ 对称∴CE =BC =20.在Rt △CDE 中,DE =CE 2-CD 2=16∴AE =AD -DE =20-16=4.在Rt △APE 中,AE =4,AP =12-PB =12-PE∴EP 2=42+(12-EP)2.解得EP =203∴菱形BFEP 的边长为203cm. ②当点Q 与点C 重合时,点E 离点A 最近,由①知,此时AE =4. 当点P 与点A 重合时,如图点E 离点A 最远,此时四边形ABQE 为正方形,AE =AB =12 ∴点E 在边AD 上移动的最大距离为8 cm.。
苏科版八年级下册数学第9章《中心对称图形—平行四边形》单元综合练习(有答案)

八年级数学第9章《中心对称图形—平行四边形》单元综合练习一、选择题:1、如图,在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是()A.45°B.55°C.65°D.75°2、如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论中不成立的是( ) A.OC=OC′ B.OA=OA′C.BC=B′C′D.∠ABC=∠A′C′B′3、把图形绕点A按逆时针方向旋转70°后所得的图形与原图作比较,保持不变的是()A.位置与大小B.形状与大小C.位置与形状D.位置、形状及大小4、如图,D,E分别是△ABC的边AB,AC的中点.如果△ADE的周长是6,则△ABC的周长是( )A.6 B.12 C.18 D.245、已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是()A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC6、平面直角坐标系中,已知□ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )A.(-2,1) B.(-2,-1) C.(-1,—2) D.(-1,2)7、如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是()A.20 B.24 C.40 D.488、在梯形ABCD中,AB∥CD,DC:AB=1:2,E、F分别是两腰BC、AD的中点,则EF:AB等于()A.1:4 B.1:3 C.1:2 D.3:49、如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是()A.AD=BD B.AE=AC C.ED+EB=DB D.AE+CB=AB10、矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF 的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=()A.1 B.C.D.11、如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的是()A.①②③B. ②③C. ①②D. ①③12、如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为()A.(﹣,)B.(﹣,)C.(﹣,)D.(﹣,)二、填空题:13、在平面直角坐标系中,点P(3,-2)关于原点O成中心对称的点的坐标是________.14、如图,△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是.15、如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是.16、如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是。
2020年春苏科版八年级数学下册第九章中心对称图形-平行四边形单元测试含答案

第九章中心对称图形-平行四边形单元测试一、单选题1.下列手机手势解锁图案中,是中心对称图形的是()A.B.C.D.2.在下列命题中,属于真命题的是()A.两条对角线相等的四边形是矩形 B.两条对角线互相垂直的四边形是菱形C.两条对角线互相平分的四边形是平行四边形D.两条对角线互相垂直且相等的四边形是正方形3.顺次连结矩形各边的中点所得的四边形是()A.正方形B.菱形C.矩形D.平行四边形4.正方形具有而菱形不一定具有的性质是 ( )A.对角线相等B.对角线互相垂直平分C.四条边相等D.对角线平分一组对角5.如图,菱形ABCD中,对角线AC、BD交于点O,E为边AD中点,菱形ABCD的周长为28,则OE 的长等于()A.3.5 B.4 C.7 D.146.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A 在边B′C上,则∠B′的大小为( )A.42° B.48° C.52°D.58°7.如图,△ABC中,D是AB的中点,DE∥BC,连接BE.若AE=6,DE=5,∠BEC=90°,则△BCE的周长是()A.12 B.24 C.36 D.488.如图,下列条件不能判定四边形ABCD是矩形的是()A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥ADC.AO=BO,CO=DO D.AO=BO=CO=DO9.如图,O是菱形ABCD的对角线的交点,E、F分别是OA、OC的中点,下列结论:①四边形BFDE是菱形;②S四边形ABCD=EF×BD;③∠ADE=∠EDO;④△DEF是轴对称图形.其中正确的结论有()A.1个B.2个C.3个D.4个10.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()12cmA.24cm C.23cm B.26cm D.2二、填空题11.如图,在菱形ABCD中,E,F分别是AD,DC的中点,若BD=4,EF=3,则菱形ABCD的周长为__.12.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2.5,则AC的长为.13.如图,将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=_________.14.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为_______度.15.如图,P是正方形ABCD内一点,且PA=PD,PB=PC.若∠PBC=60°,则∠PAD=_____.16.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE=_______.P绕原点O顺时针旋转90︒得到点P',则P'的坐标为______. 17.如图,在平面直角坐标系中,将点(2,3)18.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为______.三、解答题19.如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.20.如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE(1)求证:△BEC≌△DFA;(2)求证:四边形AECF是平行四边形.21.小宇将两张长为8宽为2的矩形条交叉如图①,发现重叠部分可能是一个菱形.(1)请你帮助小宇证明四边形ABCD是菱形.(2)小宇又发现:如图②时,菱形ABCD的周长最小,等于;(3)如图③时菱形ABCD的周长最大,求此时菱形ABCD的周长.22.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B ﹣C﹣D回到点A,设点P运动的时间为t秒.(1)当t=3秒时,求△ABP的面积;(2)当t为何值时,点P与点A的距离为5cm?(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边.23.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.24.如图,E为正方形ABCD内一点,且EBC是等边三角形,求∠EAD的度数.25.已知:如图,90ABC ADC ∠=∠=o ,M ,N 分别是AC ,BD 的中点.求证:MN BD ⊥.26.如图,在平面直角坐标系中,A 、B 坐标分别为A (0,a )、B (b ,a ),且a ,b 满足:(a-3)2+b 5-=0,现同时将点A 、B 分别向下平移3个单位,再向左平移1个单位,分别得到点A 、B 的对应点C 、D ,连接AC 、BD 、AB .(1)求点C 、D 的坐标及四边形ABDC 的面积S 四边形ABDC ;(2)在y 轴上是否存在点M ,连接MC 、MD ,使S △MCD =四边形ABDC ?若存在这样的点,求出点M 的坐标;若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PA 、PO ,当点P 在BD 上移动时(不与B 、D 重合),BAP DOP APO∠∠∠+的值是否发生变化,并说明理由.参考答案1.B2.C3.B4.A5.A6.A7.B8.C9.C10.C11.413. 12.5. 13.. 14.15 15.15° 16.1201317.(3,2)- 18.12. 19.略20.(1)证明略,(2)证明略21.(1)略;(2)8;(3)1722.(1)4;(2)当72t =秒或152t =时,AP=5cm ;(3)t=133. 23.解:(1)证明:∵点O 为AB 的中点,连接DO 并延长到点E ,使OE=OD , ∴四边形AEBD 是平行四边形.∵AB=AC ,AD 是△ABC 的角平分线,∴AD ⊥BC .∴∠ADB=90°.∴平行四边形AEBD 是矩形.(2)当∠BAC=90°时,矩形AEBD 是正方形.理由如下:∵∠BAC=90°,AB=AC ,AD 是△ABC 的角平分线,∴AD=BD=CD .∵由(1)得四边形AEBD 是矩形,∴矩形AEBD 是正方形.24.15°25.略.26.(1)S 四边形ABDC =15;(2)存在点M (0,6)或(0,-6),使S △MCD =S 四边形ABDC ,见解析;(3)不变,略.。
春八年级数学下册 第9章 中心对称图形—平行四边形本章中考演练练习 (新版)苏科版-(新版)苏科版初
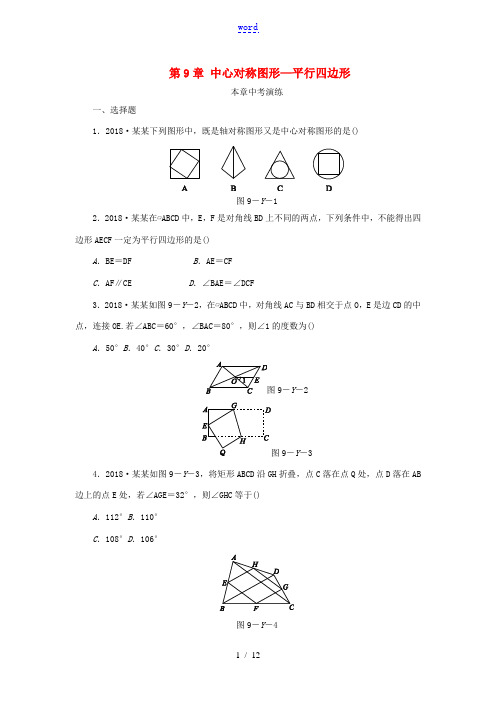
第9章中心对称图形—平行四边形本章中考演练一、选择题1.2018·某某下列图形中,既是轴对称图形又是中心对称图形的是()图9-Y-12.2018·某某在▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是()A.BE=DF B.AE=CFC.AF∥CE D.∠BAE=∠DCF3.2018·某某如图9-Y-2,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为()A.50°B.40°C.30°D.20°9-Y-29-Y-34.2018·某某如图9-Y-3,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB 边上的点E处,若∠AGE=32°,则∠GHC等于()A.112°B.110°C.108°D.106°图9-Y-45.2018·某某如图9-Y-4,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1 B.2 C.3 D.4图9-Y-56.2018·某某如图9-Y-5,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E 在同一条直线上,∠ACB=20°,则∠ADC的度数是()A.55° B.60°C.65° D.70°二、填空题7.2018·某某如图9-Y-6,▱ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么▱ABCD的周长是________.图9-Y-69-Y-78.2018·某某如图9-Y-7,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是________.9.2018·株洲如图9-Y-8,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q 分别为AO,AD的中点,则PQ的长为________.9-Y-89-Y-910.2018·某某如图9-Y-9,四边形OABC是矩形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形OABC沿OB折叠,点C落在点D处,则点D的坐标为________.图9-Y-1011.2018·某某如图9-Y-10,已知正方形ABCD的边长为5,点E,F分别在AD,DC 上,AE=DF=2,BE与AF相交于点G,H为BF的中点,连接GH,则GH的长为________.三、解答题12.2018·某某已知:如图9-Y-11,▱ABCD的对角线AC,BD相交于点O,过点O的直线分别与AD,BC相交于点E,F.求证:AE=CF.图9-Y-1113.2018·枣庄如图9-Y-12,在4×4的方格纸中,△ABC的三个顶点都在格点上.(1)在图①中,画出一个与△ABC成中心对称的格点三角形;(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;(3)在图③中,画出△ABC绕点C按顺时针方向旋转90°后的三角形.图9-Y-1214.2018·某某如图9-Y-13,在▱ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:CF=AB;(2)连接BD,BF,当∠BCD=90°时,求证:BD=BF.图9-Y-1315.2018·某某已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:(1)构造一个真命题,画图并给出证明;(2)构造一个假命题,举反例加以说明.16.2018·某某如图9-Y-14,在△ABC中,D是AB上一点,DE⊥AC于点E,F是AD 的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.(1)求证:△ECG≌△GHD;(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;(3)若∠B=30°,判断四边形AEGF是不是菱形,并说明理由.图9-Y-14详解详析本章中考演练1.[解析] DA.不是轴对称图形,是中心对称图形;B.是轴对称图形,不是中心对称图形;C.是轴对称图形,不是中心对称图形;D.是轴对称图形,也是中心对称图形.故选D.2.[解析] B如图,连接AC,与BD相交于点O,在▱ABCD中,OA=OC,OB=OD,要使四边形AECF为平行四边形,只需证明得到OE=OF即可.A.若BE=DF,则OB-BE=OD-DF,即OE=OF,故本选项不符合题意;B.若AE=CF,则无法证得OE=OF,故本选项符合题意;C.若AF∥CE,则能够利用“角边角”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;D .若∠BAE =∠DCF ,则能够利用“角边角”证明△ABE 和△CDF 全等,从而得到DF =BE ,然后同A 选项,故本选项不符合题意.故选B .3.[解析] B ∵∠ABC =60°,∠BAC =80°, ∴∠BCA =180°-60°-80°=40°.∵对角线AC 与BD 相交于点O ,E 是边CD 的中点, ∴EO 是△DBC 的中位线, ∴EO ∥BC ,∴∠1=∠BCA =40°. 故选B .4.[解析] D 根据折叠前后对应角相等可知∠DGH =∠EGH.∵∠AGE =32°,∴∠EGH =12×(180°-32°)=74°.∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠GHC =∠AGH =∠EGH +∠AGE =106°.故选D .5.[解析] A 因为一般四边形的中点四边形是平行四边形,所以当对角线AC =BD 时,中点四边形是菱形,当对角线AC ⊥BD 时,中点四边形是矩形,当对角线AC =BD ,且AC ⊥BD 时,中点四边形是正方形,故说法④正确,故选A .6.[解析] C ∵将△ABC 绕点C 顺时针旋转90°得到△EDC. ∴∠DCE =∠ACB =20°,∠BCD =∠ACE =90°,AC =CE , ∴∠ACD =90°-20°=70°. ∵点A ,D ,E 在同一条直线上, ∴∠ADC +∠EDC =180°. 又∵∠EDC +∠E +∠DCE =180°, ∴∠ADC =∠E +20°. ∵∠ACE =90°,AC =CE ,∴∠DAC +∠E =90°,∠E =∠DAC =45°. 在△ADC 中,∠ADC +∠DAC +∠ACD =180°,即45°+70°+∠ADC =180°, 解得∠ADC =65°,故选C . 7.[答案] 16[解析] ∵四边形ABCD 是平行四边形, ∴OA =OC.又∵OM ⊥AC ,∴AM =MC. ∴△CDM 的周长=AD +CD =8, ∴平行四边形ABCD 的周长是2×8=16. 8.[答案] (-5,4)[解析] ∵菱形ABCD 的顶点A ,B 的坐标分别为(3,0),(-2,0),点D 在y 轴上, ∴AB =5,∴AD =5,∴由勾股定理知:OD =AD 2-OA 2=52-32=4, ∴点C 的坐标是(-5,4). 故答案为(-5,4). 9.[答案[解析] ∵四边形ABCD 是矩形, ∴BD =AC =10,BO =DO =12BD ,∴DO =12BD =5.∵P ,Q 分别是AO ,AD 的中点, ∴PQ 是△AOD 的中位线, ∴PQ =12DO =2.5.故答案为2.5.10.[答案] (165,-125)[解析] 由折叠得∠CBO =∠DBO. 在矩形ABCO 中,BC ∥OA , ∴∠CBO =∠BOA ,∴∠DBO =∠BOA , ∴BE =OE.在△ODE 和△BAE 中,⎩⎪⎨⎪⎧∠ODE =∠BAE =90°,∠OED =∠BEA ,OE =BE ,∴△ODE ≌△BAE(AAS ), ∴AE =DE.设DE =AE =x ,则有OE =BE =8-x.在Rt △ODE 中,根据勾股定理,得42+x 2=(8-x)2, 解得x =3,即DE =3,OE =5. 过点D 作DF ⊥OA 于点F ,∵S △OED =12OD ·DE =12OE ·DF ,∴DF =125,OF =42-(125)2=165,则D(165,-125).11.[答案]342[解析] ∵四边形ABCD 是正方形,∴AB =AD =BC =CD =5,∠BAD =∠D =∠C =90°.又∵AE =DF ,∴△ABE ≌△DAF ,∴∠DAF =∠ABE ,∴∠ABE +∠BAG =90°,∴∠BGF =∠BGA =90°.在Rt △BCF 中,BC =5,CF =3,∴BF =52+32=34.在Rt △BGF 中,∵H 为BF 的中点,∴GH =12BF =342.12.证明:∵▱ABCD 的对角线AC ,BD 交于点O , ∴AO =CO ,AD ∥BC , ∴∠EAC =∠FCO.在△AOE 和△COF 中,⎩⎪⎨⎪⎧∠EAO =∠FCO ,AO =CO ,∠AOE =∠COF ,∴△AOE ≌△COF , ∴AE =CF.13.解:(1)答案不唯一,如图①所示,△DCE 即为所作.(2)答案不唯一,如图②所示,△ACD 即为所作.(3)如图③所示,△ECD 即为所作.14.证明:(1)∵四边形ABCD 是平行四边形, ∴AB ∥DF , ∴∠BAE =∠CFE.又∵BE =CE ,∠AEB =∠FEC , ∴△AEB ≌△FEC ,∴CF =AB. (2)如图,连接AC.∵四边形ABCD是平行四边形,∠BCD=90°,∴四边形ABCD是矩形,∴BD=AC.∵AB=CF,AB∥CF,∴四边形ACFB是平行四边形,∴BF=AC,∴BD=BF.15.解:(1)答案不唯一,如以①④为条件构成真命题:在四边形ABCD中,OA=OC,AD ∥BC,则四边形ABCD是平行四边形.证明如下:如图,∵AD∥BC,∴∠DAC=∠BCA,∠ADB=∠DBC.又∵OA=OC,∴△AOD≌△COB,∴AD=BC,∴四边形ABCD为平行四边形.(2)答案不唯一,如以②④为条件构成假命题:在四边形ABCD中,AB=CD,AD∥BC,则四边形ABCD是平行四边形.理由如下:如图,在四边形ABCD中,满足AB=CD,AD∥BC,四边形ABCD是等腰梯形,不是平行四边形.16.解:(1)证明:∵AF=FG,∴∠FAG=∠FGA.∵AG平分∠CAB,∴∠CAG =∠FAG ,∴∠CAG =∠FGA ,∴AC ∥FG. ∵DE ⊥AC ,∴FG ⊥DE.又∵FG ⊥BC ,∴DE ∥BC , ∴AC ⊥BC ,∠CGE =∠GED , ∴∠C =∠DHG =90°.∵F 是AD 的中点,FG ∥AE , ∴H 是DE 的中点,∴FG 是线段DE 的垂直平分线, ∴GE =GD ,∴∠GDE =∠GED ,∴∠CGE =∠GDE ,∴△ECG ≌△GHD.(2)证明:过点G 作GP ⊥AB 于点P , ∴GC =GP ,而AG =AG , ∴Rt △CAG ≌Rt △PAG ,∴AC =AP.由(1)可得EG =DG ,∴Rt △ECG ≌Rt △DPG ,∴EC =PD ,∴AD =AP +PD =AC +EC.(3)四边形AEGF 是菱形.理由:∵∠B =30°,DE ∥BC , ∴∠ADE =30°,∴AE =12AD.而F 是AD 的中点,∴AE=AF=FG.又由(1)得AE∥FG,∴四边形AEGF是平行四边形.又∵AE=AF,∴四边形AEGF是菱形.。
苏科版八年级数学下册第九章 中心对称图形------平行四边形练习(含答案)
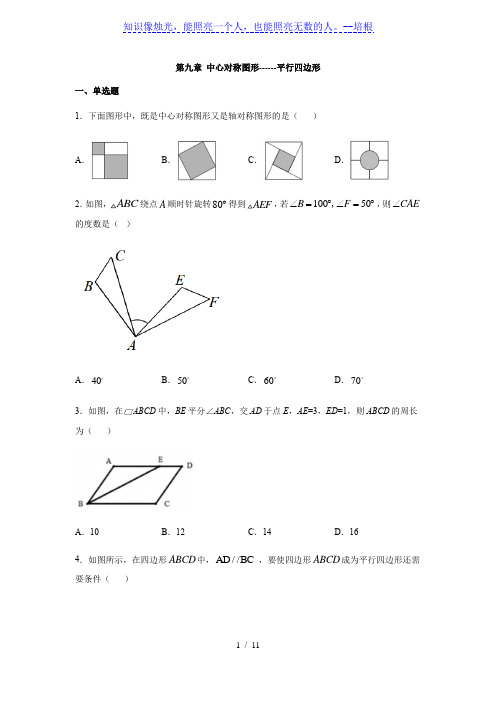
第九章 中心对称图形------平行四边形一、单选题1.下面图形中,既是中心对称图形又是轴对称图形的是( )A .B .C .D . 2.如图,ABC 绕点A 顺时针旋转80︒得到AEF ,若10050B F ∠=︒∠=︒,,则CAE ∠的度数是( )A .40B .50C .60D .70 3.如图,在ABCD 中,BE 平分∠ABC ,交AD 于点E ,AE =3,ED =1,则ABCD 的周长为( )A .10B .12C .14D .164.如图所示,在四边形ABCD 中,AD //BC ,要使四边形ABCD 成为平行四边形还需要条件( )A .AB DC = B .D B ∠=∠ C .AB AD = D .12∠=∠ 5.将矩形ABCD 沿AE 折叠,得到如图所示的图形,已知60CED ∠='︒,则BAD '∠的大小是( )A .30B .45︒C .50︒D .60︒6.下列命题正确的是( )A .有一组对边平行的四边形是平行四边形B .对角线相等的四边形是矩形C .一组邻边相等且对角线垂直的四边形是菱形D .四边相等且有一个直角的四边形是正方形7.如图,四边形ABCD 是菱形,8AC =,6DB =,DH AB ⊥于点H .则DH =()A .6B .245 C .485 D .58.如图,已知ABCD 中,,M N 分别是 AD CD 、上的点,,E F 分别是 BM MN 、的中点, 当M 在 AD 上从A 向D 移动而N 不动时,那么下列结论成立的是( )A .线段 EF 的长逐渐增大B .线段 EF 的长逐渐减小C .线段 EF 的长不改变D .线段 EF 的长不能确定9.如图,在正方形ABCD 中,AB=6,E 为AD 的中点,P 为对角线BD 上的一个动点,则AP EP +最小值的是( )A .6B .C .D . 10.如图,矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB ,CD 交于点E ,F ,连结BF ,交AC 于点M ,连结DE ,BO .若60BOC ∠=︒,FO FC =,则下列结论:①AE CF =;②BF 垂直平分线段OC ;③EOB CMB ∆∆≌;④四边形是BFDE 菱形.其中正确结论的个数是( )A .1个B .2个C .3个D .4个二、填空题11.已知()213A a +,,()533B b --,关于原点对称,则a b +=__________. 12.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是_____.13.如图,在ABC ∆中,90ACB ∠=︒,3AC =,4BC =,CD 为ABC ∆的中线,则ACD ∆的面积为________.14.如图,在正方形ABCD 中,点E 在对角线AC 上,EF ⊥AB 于点F ,EG ⊥BC 于点G ,连接DE ,若AB =10,AE =,则ED 的长度为__.三、解答题15.如图,△ABC 的顶点坐标分别为A (0,1)、B (3,3)、C (1,3).(1) 画出△ABC关于点O的中心对称图形△A1B1C1(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______. 16.已知,如图,在平行四边形ABCD中,延长AB到点E,延长CD到点F,使得BE=DF,连接EF,分别交BC,AD于点M,N,连接AM,CN.(1)求证:△BEM≌△DFN;(2)求证:四边形AMCN是平行四边形.17.如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.(1)求证:四边形AODE是矩形.(2)若AB=5,BD=8,求矩形AODE的周长.18.如图1,在正方形ABCD中,点E,F分别在AB,BC上,且AE=BF,(1)试探索线段AF,DE的数量关系,写出你的结论并说明理由;(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,则四边形HIJK是什么特殊四边形.请在图2中补全图形,并说明理由.知识像烛光,能照亮一个人,也能照亮无数的人。
2022春八年级数学下册第9章中心对称图形__平行四边形达标检测卷新版苏科版(含答案)

八年级数学下册新版苏科版:第9章达标检测卷一、选择题(每题3分,共24分)1.下列图形中,是中心对称图形,但不是轴对称图形的是( )A B C D2.对角线互相垂直平分的四边形是( )A.平行四边形、菱形B.矩形、菱形C.矩形、正方形D.菱形、正方形3.用两块边长为a的等边三角形纸片拼成的四边形是( )A.等腰梯形B.菱形 C.矩形 D.正方形4.下列图形:①等腰三角形;②平行四边形;③矩形;④菱形;⑤正方形.用两个全等但不是等腰的直角三角形,一定能拼成的是( )A.①②③B.②③④C.①③⑤D.①②③④⑤5.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角有( )A.4个B.3个C.2个D.1个6.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC.以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )A.3-1B.3- 5C.5+1D.5-17.如图,在正方形ABCD 中,AB =4,E 为对角线AC 上与A ,C 不重合的一个动点,过点E作EF ⊥AB 于点F ,EG ⊥BC 于点G ,连接DE ,FG ,下列结论:①DE =FG ;②DE ⊥FG ;③∠BFG =∠ADE ;④FG 的最小值为3,其中正确结论的个数有( ) A .1个 B .2个 C .3个 D .4个8.如图,矩形ABCD 的面积为20 cm 2,对角线交于点O ;以AB 、AO 为邻边作平行四边形AOC 1B ,对角线交于点O 1;以AB 、AO 1为邻边作平行四边形AO 1C 2B ,对角线交于点O 2;…,依此类推,则平行四边形AO 4C 5B 的面积为( ) A .54 cm 2B .58 cm 2C .516 cm 2D .532cm 2二、填空题(每题2分,共20分)9.如图,在平行四边形ABCD 中,AE =CG ,DH =BF ,则四边形EFGH 是________.10.如图,两个完全相同的三角尺ABC 和DEF 在直线l 上滑动,要使四边形CBFE 为菱形,还需添加的一个条件是________.(填一个即可)11.如图,在矩形ABCD 中,DE 平分∠ADC 交BC 于点E ,EF ⊥AD 交AD 于点F ,连接AE ,若EF =3,AE =5,则AD =________.12.如图,在矩形ABCD中,AE⊥BD.若∠DAE∶∠BAE=3 ∶1,则∠EAO=________.13.如图,四边形ABCD是菱形,对角线AC=8 cm,BD=6 cm,DH⊥AB于点H,则DH=________.14.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是______________________________________________________.15.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF 的长为________.16.如图,菱形ABCD中,∠B=60°,AB= 4,则以AC为边长的正方形ACEF的周长为________.17.如图,在矩形ABCD中,E,F分别为BC,DA的中点,以CD为斜边作Rt△GCD,GD=GC,连接GE,GF.若BC=2GC,则∠EGF=________.18.如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=________.三、解答题(19~21题每题6分,22~23题每题7分,24~26题每题8分,共56分) 19.如图,在▱ABCD中,直线EF∥BD,并且与CD、CB的延长线分别交于点E、F,交AD于点M,交AB于点N.求证:EN=FM.20.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.21.如图,在四边形ABCD中,AD∥BC,AD≠BC,∠B=90°,AG∥CD交BC于点G,点E、F 分别为AG、CD的中点,连接DE、FG.(1)求证:四边形DEGF是平行四边形;(2)当点G是BC的中点时,求证:四边形DEGF是菱形.22.如图,已知在菱形ABCD中,∠B=72°,请设计三种不同的方法,将菱形ABCD分割成四个三角形,使每个三角形都是等腰三角形.(要求画出分割线段,标出所得的三角形内角的度数.注:只要有一条分割线段位置不同,就认为是两种不同的方法)23.如图,在▱ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA、DC的延长线分别交于点E、F.(1)求证:AE=CF;(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.24.已知四边形ABCD为矩形,E是AB延长线上的一点.(1)若AC=EC,如图1,求证:四边形BECD为平行四边形;(2)若AB=AD,点F是AB上的点,AF=BE,EG⊥AC于点G,如图2,求证:△DGF是等腰直角三角形.25.如图,在▱ABCD中,AB⊥AC,AB=1,BC=5,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转(不超过180°)分别交BC、AD于点E、F.(1)试说明在旋转过程中,AF与CE总保持相等;(2)证明:当旋转角为90°时,四边形ABEF是平行四边形;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,求出此时AC绕点O顺时针旋转的角度.26.已知,矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.①求证四边形AFCE为菱形;②求AF的长.(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周后停止.即点P沿A→F→B→A运动,点Q沿C→D→E→C运动.在运动过程中,①已知点P的速度为每秒5 cm,点Q的速度为每秒4 cm,运动时间为t s,当以A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.②若点P、Q的运动路程分别为a cm、b cm(ab≠0),已知以A、C、P、Q四点为顶点的四边形是平行四边形,直接写出a与b满足的数量关系式.答案一、1.B 2.D 3.B 4.A 5.B6.D 7.C 8.B 二、9.平行四边形 10.BE ⊥CF (答案不唯一) 11.7 12.45° 13.4.8 cm 14.对角线互相垂直的四边形15.1.5 16.16 17.45° 18.135° 三、19.证明:∵在▱ABCD 中,AB ∥CD ,AD ∥BC ,EF ∥BD ,∴四边形BNED 和四边形FBDM 为平行四边形, ∴FM =BD ,EN =BD ,∴EN =FM . 20.证明:∵DE ⊥BC ,DF ⊥AC ,∴∠CFD =∠CED =90°, 又∵∠ACB =90°, ∴四边形CFDE 是矩形.又∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC , ∴DF =DE ,∴矩形CFDE 是正方形. 21.证明:(1)∵AD ∥BC ,AG ∥CD ,∴四边形AGCD 为平行四边形, ∴AG =CD .又∵点E 、F 分别为AG 、CD 的中点, ∴EG =12AG =12DC =DF ,∴四边形DEGF 是平行四边形. (2)连接DG . ∵G 是BC 的中点, ∴BG =CG ,由(1)易得AD =CG ,∴AD =BG . 又∵AD ∥BC ,∴四边形ABGD 是平行四边形,∴AB ∥DG ,∴∠DGC =∠B =90°, ∴GF =12CD =DF ,∴平行四边形DEGF 是菱形.22.解:方法多样,提供几例仅供参考,如图.23.(1)证明:∵四边形ABCD 是平行四边形,∴OA =OC ,BE ∥DF ,∴∠AEO =∠CFO . 在△AOE 和△COF 中, ⎩⎪⎨⎪⎧∠AEO =∠CFO ,∠AOE =∠COF ,OA =OC ,∴△AOE ≌△COF (AAS),∴AE =CF .(2)解:当EF ⊥BD 时,四边形BFDE 是菱形,理由如下: ∵四边形ABCD 是平行四边形, ∴OB =OD . ∵△AOE ≌△COF , ∴OE =OF ,∴四边形BFDE 是平行四边形, ∵EF ⊥BD ,∴四边形BFDE 是菱形.24.证明:(1)∵四边形ABCD 为矩形,∴AB ∥CD ,AB =CD ,CB ⊥AB . 又∵AC =EC , ∴AB =BE , ∴BE =CD ,(2)∵AB =AD , ∴矩形ABCD 是正方形, ∵EG ⊥AC ,∴∠E =90°-45°=45°=∠GAD , ∴GE =GA . ∵AF =BE , ∴AB =FE , ∴FE =AD .在△EGF 和△AGD 中,⎩⎪⎨⎪⎧GE =GA ,∠E =∠GAD ,EF =AD ,∴△EGF ≌△AGD (SAS), ∴GF =GD ,∠DGA =∠FGE ,∴∠DGF =∠DGA +∠AGF =∠FGE +∠AGF =∠AGE =90°, ∴△DGF 是等腰直角三角形.25.(1)解:在▱ABCD 中,AD ∥BC ,OA =OC ,∴∠1=∠2. 在△AOF 和△COE 中,∠1=∠2,OA =OC ,∠3=∠4, ∴△AOF ≌△COE (ASA), ∴AF =CE .(2)证明:此时∠AOF =90°. ∵AB ⊥AC , ∴∠BAO =90°, ∴∠BAO =∠AOF =90°, ∴BA ∥EF .∵四边形ABCD 是平行四边形, ∴AD ∥BC ,即AF ∥BE .(3)解:可能.∵AF =CE ,AD ∥BC ,AD =BC , ∴FD ∥BE ,DF =BE ,∴四边形BEDF 是平行四边形. ∴当EF ⊥BD 时,▱BEDF 是菱形. ∵∠BAC =90°,∴BC 2=AB 2+AC 2. ∵AB =1,BC =5, ∴AC =BC 2-AB 2=2.∵四边形ABCD 是平行四边形. ∴OA =12AC =12×2=1.∵在△AOB 中,AB =AO =1, ∠BAO =90°, ∴∠BOA =45°.∵EF ⊥BD , ∴∠BOF =90°.∴∠3=∠BOF -∠BOA =90°-45°=45°, 即旋转角为45°.26.(1)①证明:∵在矩形ABCD 中,AD ∥BC ,∴∠EAO =∠FCO ,∵EF 垂直平分AC .∴AO =CO ,又∵∠AOE =∠COF , ∴△AOE ≌△COF (ASA), ∴AE =CF ,又∵AE ∥CF , ∴四边形AFCE 为平行四边形. 又∵EF ⊥AC ,∴平行四边形AFCE 为菱形. ②解:由①知AF =CF .设AF =x cm ,则CF =x cm ,BF =BC -CF =(8-x )cm ,在Rt △ABF 中,AB 2+BF 2=AF 2,∴42+(8-x )2=x 2,解得x =5.11 ∴AF =5cm.(2)①解:情况一:当P 在AF 上,Q 在CD 上时,四边形APCQ 显然不可能是平行四边形. 情况二:当P 在BF 上,Q 在ED 上时,则当BP =DQ 时,四边形APCQ 为平行四边形,即8-5t =4t -4, t =43.情况三:当P 在AB 上,Q 在ED 上时,四边形APCQ 显然不可能为平行四边形; 情况四:当P 在AB 上,Q 在EC 上时,四边形APCQ 显然不可能为平行四边形. ∴当t =43时,四边形APCQ 为平行四边形.②解:a +b =12.。
八年级数学下《第9章中心对称图形―平行四边形9.3-9.4》同步练习(苏科版带答案)

适用精选文件资料分享八年级数学下《第9 章中心对称图形―平行四边形9.3-9.4 》同步练习(苏科版带答案)第 9 章《中心对称图形―平行四边形》9.3 ~9.41.如图,的对角线交于点,已知, ,,则的周长为( ). A. 13B.17C.20D.26(第1题)(第2题)2.如图,在中,,按以下步骤作图 : 以点为圆心,小于的长为半径画弧,分别交于点 ; 再分别以点为圆心,大于的长为半径画弧,两弧交于点; 作射线交于点,则以下结论中不可以由条件推理得出的是 ( ). A. 均分 B. C. D.3.平行四边形的对角线必定拥有的性质是 ( ). A. 相等 B. 相互均分C.相互垂直D. 相互垂直且相等 4. 如图,在中,均分,则的周长是 .5. 如图,在中,的均分线交边于点 , 的均分线交于点,交于点 , 请说明的原因. 6.如图,在中,点分别在边和上,且 . 求证 : (1)≌ ; (2) . 7.把边长为 3 cm、5 cm、7 cm的两个全等三角形拼成四边形,一共能拼成种不一样的四边形,此中有个平行四边形 . 8. 如图,在中, , 为中点,连结 , 过点作于点,在的延伸线上取一点 , 使 . 求证 : 四边形是平行四边形 . 9. 已知 : 如图,梯形中,,点是的中点,的延伸线与的延伸线订交于点 .(1)说明和全等的原因 ; (2) 连结,判断四边形的形状,并证明你的结论 .10. 如图,在中,的垂直均分线交于点,则的周长是 ( ). A. 7B. 10C. 11D. 12(第 10 题) ( 第 11题) 11. 如图, 的对角线与相交于点. ,若,,则的长是().A.8B.9C.10D.1112.已知: 如图,在中,点在上,且 . 求证 : 四边形是平行四边形 .13.如图,在中,都是等边三角形 . 试说明是等边三角形 . 14. 如图,在中,的平行线交的延伸线于点,交的延伸线于点,交于点 . (1) 请指出图中平行四边形的个数,并说明原因 ; (2) 与相等吗?为何 ?15.如图,在矩形中,. 过对角线交点作交于点,则的长是 ( ).A.1.6B.2.5C.3D.3.4(第15题)(第16题)16.如图,矩形的极点分别在直线上,且,. 则的度数为 ( ). A. 30° B. 45°C. 60 °D. 75 ° 17.如图,矩形的对角线与订交于点, . ,,则四边形的面积( ). A. B. 4 C. D. 8 18.如图,将矩形以点为旋转中心,逆时针旋转90°获得矩形,试说明是等腰直角三角形.19.如图,在矩形中,点是上一点, , 于点,连结 . 求证 : .20.如图,矩形的对角线订交于点,过点作的垂线与的均分线订交于点 . 求证: .21.如图,在矩形中,分别是边上的点,且 , . 求证 : 均分 .22.如图,为内部一点,两点分别在上,且四边形为矩形,直线交于点.若,, ,则的面积为23.如图,菱形的对角线订交于点,且 , . 求证 : 四边形是矩形 . (第35 题)24.如图,点在矩形的对角线上,且不与点重合,过点分别作边的平行线,交两组对边于点和 . (1) 求证 : ≌ ; (2) 证明四边形和四边形都是矩形,并直接写出它们面积之间的关系 . ( 第 36 题)25.如图,在中, , 为斜边的中点 (1) 依据要求画出图形 ; ①连结,并延伸到点,使 ; ②连结 . (2) 四边形是什么四边形 ?说明你判断的原因 ; (3) 与有如何的数目关系 ?这个结论对全部的直角三角形都建立吗 ?26.如图,在中,,若将绕点顺时针旋转180°获得 . (1) 试猜想与有何关系 ?说明原因 ; (2) 若的面积为 3 cm2,求四边形的面积; (3) 当为多少度时,四边形为矩形 ?说明原因 .27.如图,在中,均分 . 四边形是平行四边形,交于点,连结 .求证 : 四边形是矩形 .参照答案 1.B2D3.B4.205.,又 .同理 .又.6.(1)四边形是平行四边形 .. 在和中,≌.(2)由(1)知, ≌,.7.63 8. 点为的斜边中点, .又 ,四边形是平行四边形 . 9. (1)又 , ≌ . (2) 平行四边形,证明以下:由(1)可得 .又, 四边形是平行四边形 . 10. B 11. C 12.如图,连结,设与交于点 .四边形是平行四边形 ,四边形是平行四边形 . 13. 在中,、是等边三角形,..≌..同理可证≌ ,是等边三角形 .14.(1) 、、,共 3 个,原因略 .(2), 原因以下:四边形是平行四边形 . .同理 . 15. D 16. C 17. A 18.由旋转可知: . 是等腰直角三角形,19. 由≌,可证得 . 20.过点作于点,因为 ..在和中,.四边形是矩形,均分 ,, 即. 21. 提示:易证≌. . 又, . 又,即平分.22.B23.四边形为菱形,又四边形为平行四边形 . 四边形是矩形 . 24. (1)四边形为矩形,在和中,≌ . (2)四边形为矩形, .又四边形和四边形都是矩形 .在中,, 在中,,. 25.(1) 如图 : (2)是矩形,原因以下:四边形是平行四边形 . 是矩形. (3) 都建立 . 26.(1) 由旋转可知:≌ . 即与的关系为与平行且相等 . (2)≌ , .又 . 同理 . . (cm2) (3)当时,四边形为矩形 . 四边形为平行四边形 . 当时,为等边三角形 . . 四边形为矩形,即当时,四边形为矩形 . 27. 均分,四边形是平行四边形,四边形是平行四边形 . . 是矩形 .。
2019年春八年级数学下册第9章中心对称图形—平行四边形本章中考演练练习(新版)苏科版
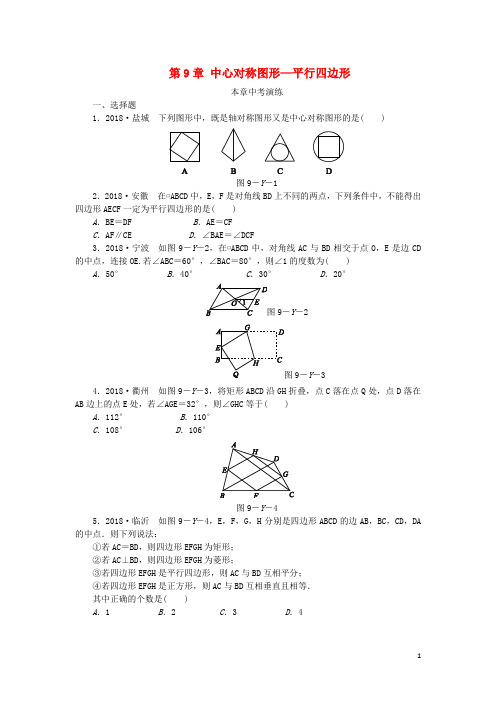
第9章中心对称图形—平行四边形本章中考演练一、选择题1.2018·盐城下列图形中,既是轴对称图形又是中心对称图形的是( )图9-Y-12.2018·安徽在▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )A.BE=DF B.AE=CFC.AF∥CE D.∠BAE=∠DCF3.2018·宁波如图9-Y-2,在▱ABCD中,对角线AC与BD相交于点O,E是边CD 的中点,连接OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( ) A.50°B.40°C.30°D.20°9-Y-29-Y-34.2018·衢州如图9-Y-3,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )A.112°B.110°C.108°D.106°图9-Y-45.2018·临沂如图9-Y-4,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA 的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是( )A.1 B.2 C.3 D.4图9-Y-56.2018·金华如图9-Y-5,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )A.55° B.60°C.65° D.70°二、填空题7.2018·衡阳如图9-Y-6,▱ABCD的对角线相交于点O,且AD≠CD,过点O作OM ⊥AC,交AD于点M.如果△CDM的周长为8,那么▱ABCD的周长是________.9-Y-69-Y-78.2018·广州如图9-Y-7,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是________.9.2018·株洲如图9-Y-8,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长为________.9-Y-89-Y-910.2018·扬州如图9-Y-9,四边形OABC是矩形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形OABC沿OB折叠,点C落在点D处,则点D的坐标为________.图9-Y-1011.2018·青岛如图9-Y-10,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,H为BF的中点,连接GH,则GH的长为________.三、解答题12.2018·淮安已知:如图9-Y-11,▱ABCD的对角线AC,BD相交于点O,过点O 的直线分别与AD,BC相交于点E,F.求证:AE=CF.图9-Y-1113.2018·枣庄如图9-Y-12,在4×4的方格纸中,△ABC的三个顶点都在格点上.(1)在图①中,画出一个与△ABC成中心对称的格点三角形;(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;(3)在图③中,画出△ABC绕点C按顺时针方向旋转90°后的三角形.图9-Y-1214.2018·南通如图9-Y-13,在▱ABCD中,E是BC的中点,连接AE并延长交DC 的延长线于点F.(1)求证:CF=AB;(2)连接BD,BF,当∠BCD=90°时,求证:BD=BF.图9-Y-1315.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:(1)构造一个真命题,画图并给出证明;(2)构造一个假命题,举反例加以说明.16.2018·泰安如图9-Y-14,在△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.(1)求证:△ECG≌△GHD;(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;(3)若∠B=30°,判断四边形AEGF是不是菱形,并说明理由.图9-Y-14详解详析 本章中考演练1.[解析] D A .不是轴对称图形,是中心对称图形;B .是轴对称图形,不是中心对称图形;C .是轴对称图形,不是中心对称图形;D .是轴对称图形,也是中心对称图形.故选D .2.[解析] B 如图,连接AC ,与BD 相交于点O ,在▱ABCD 中,OA =OC ,OB =OD ,要使四边形AECF 为平行四边形,只需证明得到OE =OF 即可.A .若BE =DF ,则OB -BE =OD -DF ,即OE =OF ,故本选项不符合题意; B .若AE =CF ,则无法证得OE =OF ,故本选项符合题意;C .若AF ∥CE ,则能够利用“角边角”证明△AOF 和△COE 全等,从而得到OE =OF ,故本选项不符合题意;D .若∠BAE =∠DCF ,则能够利用“角边角”证明△ABE 和△CDF 全等,从而得到DF =BE ,然后同A 选项,故本选项不符合题意.故选B .3.[解析] B ∵∠ABC =60°,∠BAC =80°, ∴∠BCA =180°-60°-80°=40°.∵对角线AC 与BD 相交于点O ,E 是边CD 的中点, ∴EO 是△DBC 的中位线,∴EO ∥BC ,∴∠1=∠BCA =40°. 故选B .4.[解析] D 根据折叠前后对应角相等可知∠DGH =∠EGH.∵∠AGE =32°,∴∠EGH =12×(180°-32°)=74°.∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠GHC =∠AGH =∠EGH +∠AGE =106°.故选D .5.[解析] A 因为一般四边形的中点四边形是平行四边形,所以当对角线AC =BD 时,中点四边形是菱形,当对角线AC ⊥BD 时,中点四边形是矩形,当对角线AC =BD ,且AC ⊥BD 时,中点四边形是正方形,故说法④正确,故选A .6.[解析] C ∵将△ABC 绕点C 顺时针旋转90°得到△EDC. ∴∠DCE =∠ACB =20°,∠BCD =∠ACE =90°,AC =CE , ∴∠ACD =90°-20°=70°. ∵点A ,D ,E 在同一条直线上, ∴∠ADC +∠EDC =180°.又∵∠EDC +∠E +∠DCE =180°, ∴∠ADC =∠E +20°. ∵∠ACE =90°,AC =CE ,∴∠DAC +∠E =90°,∠E =∠DAC =45°. 在△ADC 中,∠ADC +∠DAC +∠ACD =180°, 即45°+70°+∠ADC =180°,解得∠ADC =65°,故选C . 7.[答案] 16[解析] ∵四边形ABCD 是平行四边形, ∴OA =OC.又∵OM ⊥AC ,∴AM =MC.∴△CDM 的周长=AD +CD =8,∴平行四边形ABCD 的周长是2×8=16. 8.[答案] (-5,4)[解析] ∵菱形ABCD 的顶点A ,B 的坐标分别为(3,0),(-2,0),点D 在y 轴上, ∴AB =5,∴AD =5,∴由勾股定理知:OD =AD 2-OA 2=52-32=4, ∴点C 的坐标是(-5,4). 故答案为(-5,4). 9.[答案] 2.5[解析] ∵四边形ABCD 是矩形, ∴BD =AC =10,BO =DO =12BD ,∴DO =12BD =5.∵P ,Q 分别是AO ,AD 的中点, ∴PQ 是△AOD 的中位线, ∴PQ =12DO =2.5.故答案为2.5.10.[答案] (165,-125)[解析] 由折叠得∠CBO =∠DBO.在矩形ABCO 中,BC ∥OA , ∴∠CBO =∠BOA , ∴∠DBO =∠BOA , ∴BE =OE.在△ODE 和△BAE 中,⎩⎪⎨⎪⎧∠ODE =∠BAE =90°,∠OED =∠BEA ,OE =BE ,∴△ODE ≌△BAE(AAS ),∴AE =DE.设DE =AE =x ,则有OE =BE =8-x.在Rt △ODE 中,根据勾股定理,得42+x 2=(8-x)2, 解得x =3,即DE =3,OE =5. 过点D 作DF ⊥OA 于点F ,∵S △OED =12OD ·DE =12OE ·DF ,∴DF =125,OF =42-(125)2=165,则D(165,-125).11.[答案]342[解析] ∵四边形ABCD 是正方形,∴AB =AD =BC =CD =5,∠BAD =∠D =∠C =90°.又∵AE =DF ,∴△ABE ≌△DAF ,∴∠DAF =∠ABE ,∴∠ABE +∠BAG =90°,∴∠BGF =∠BGA =90°.在Rt △BCF 中,BC =5,CF =3,∴BF =52+32=34.在Rt △BGF 中,∵H 为BF 的中点,∴GH =12BF =342.12.证明:∵▱ABCD 的对角线AC ,BD 交于点O , ∴AO =CO ,AD ∥BC , ∴∠EAC =∠FCO.在△AOE 和△COF 中,⎩⎪⎨⎪⎧∠EAO =∠FCO ,AO =CO ,∠AOE =∠COF ,∴△AOE ≌△COF ,∴AE =CF.13.解:(1)答案不唯一,如图①所示,△DCE 即为所作.(2)答案不唯一,如图②所示,△ACD 即为所作.(3)如图③所示,△ECD 即为所作.14.证明:(1)∵四边形ABCD是平行四边形,∴AB∥DF,∴∠BAE=∠CFE.又∵BE=CE,∠AEB=∠FEC,∴△AEB≌△FEC,∴CF=AB.(2)如图,连接AC.∵四边形ABCD是平行四边形,∠BCD=90°,∴四边形ABCD是矩形,∴BD=AC.∵AB=CF,AB∥CF,∴四边形ACFB是平行四边形,∴BF=AC,∴BD=BF.15.解:(1)答案不唯一,如以①④为条件构成真命题:在四边形ABCD中,OA=OC,AD ∥BC,则四边形ABCD是平行四边形.证明如下:如图,∵AD∥BC,∴∠DAC=∠BCA,∠ADB=∠DBC.又∵OA=OC,∴△AOD≌△COB,∴AD=BC,∴四边形ABCD为平行四边形.(2)ABCD中,AB=CD,AD∥BC,则四边形ABCD是平行四边形.理由如下:如图,在四边形ABCD中,满足AB=CD,AD∥BC,四边形ABCD是等腰梯形,不是平行四边形.16.解:(1)证明:∵AF=FG,∴∠FAG=∠FGA.∵AG平分∠CAB,∴∠CAG =∠FAG ,∴∠CAG =∠FGA ,∴AC ∥FG. ∵DE ⊥AC ,∴FG ⊥DE. 又∵FG ⊥BC ,∴DE ∥BC , ∴AC ⊥BC ,∠CGE =∠GED , ∴∠C =∠DHG =90°.∵F 是AD 的中点,FG ∥AE , ∴H 是DE 的中点,∴FG 是线段DE 的垂直平分线, ∴GE =GD ,∴∠GDE =∠GED , ∴∠CGE =∠GDE , ∴△ECG ≌△GHD.(2)证明:过点G 作GP ⊥AB 于点P , ∴GC =GP ,而AG =AG , ∴Rt △CAG ≌Rt △PAG , ∴AC =AP.由(1)可得EG =DG , ∴Rt △ECG ≌Rt △DPG , ∴EC =PD ,∴AD =AP +PD =AC +EC. (3)四边形AEGF 是菱形.理由:∵∠B =30°,DE ∥BC , ∴∠ADE =30°, ∴AE =12AD.而F 是AD 的中点, ∴AE =AF =FG.又由(1)得AE ∥FG ,∴四边形AEGF 是平行四边形. 又∵AE =AF ,∴四边形AEGF 是菱形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章中心对称图形—平行四边形本章中考演练一、选择题1.2018·盐城下列图形中,既是轴对称图形又是中心对称图形的是( )图9-Y-12.2018·安徽在▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )A.BE=DF B.AE=CFC.AF∥CE D.∠BAE=∠DCF3.2018·宁波如图9-Y-2,在▱ABCD中,对角线AC与BD相交于点O,E是边CD 的中点,连接OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( ) A.50°B.40°C.30°D.20°9-Y-29-Y-34.2018·衢州如图9-Y-3,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )A.112°B.110°C.108°D.106°图9-Y-45.2018·临沂如图9-Y-4,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA 的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是( )A.1 B.2 C.3 D.4图9-Y-56.2018·金华如图9-Y-5,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )A.55° B.60°C.65° D.70°二、填空题7.2018·衡阳如图9-Y-6,▱ABCD的对角线相交于点O,且AD≠CD,过点O作OM ⊥AC,交AD于点M.如果△CDM的周长为8,那么▱ABCD的周长是________.9-Y-69-Y-78.2018·广州如图9-Y-7,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是________.9.2018·株洲如图9-Y-8,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长为________.9-Y-89-Y-910.2018·扬州如图9-Y-9,四边形OABC是矩形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形OABC沿OB折叠,点C落在点D处,则点D的坐标为________.图9-Y-1011.2018·青岛如图9-Y-10,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,H为BF的中点,连接GH,则GH的长为________.三、解答题12.2018·淮安已知:如图9-Y-11,▱ABCD的对角线AC,BD相交于点O,过点O 的直线分别与AD,BC相交于点E,F.求证:AE=CF.图9-Y-1113.2018·枣庄如图9-Y-12,在4×4的方格纸中,△ABC的三个顶点都在格点上.(1)在图①中,画出一个与△ABC成中心对称的格点三角形;(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;(3)在图③中,画出△ABC绕点C按顺时针方向旋转90°后的三角形.图9-Y-1214.2018·南通如图9-Y-13,在▱ABCD中,E是BC的中点,连接AE并延长交DC 的延长线于点F.(1)求证:CF=AB;(2)连接BD,BF,当∠BCD=90°时,求证:BD=BF.图9-Y-1315.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:(1)构造一个真命题,画图并给出证明;(2)构造一个假命题,举反例加以说明.16.2018·泰安如图9-Y-14,在△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.(1)求证:△ECG≌△GHD;(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;(3)若∠B=30°,判断四边形AEGF是不是菱形,并说明理由.图9-Y-14详解详析 本章中考演练1.[解析] D A .不是轴对称图形,是中心对称图形;B .是轴对称图形,不是中心对称图形;C .是轴对称图形,不是中心对称图形;D .是轴对称图形,也是中心对称图形.故选D .2.[解析] B 如图,连接AC ,与BD 相交于点O ,在▱ABCD 中,OA =OC ,OB =OD ,要使四边形AECF 为平行四边形,只需证明得到OE =OF 即可.A .若BE =DF ,则OB -BE =OD -DF ,即OE =OF ,故本选项不符合题意; B .若AE =CF ,则无法证得OE =OF ,故本选项符合题意;C .若AF ∥CE ,则能够利用“角边角”证明△AOF 和△COE 全等,从而得到OE =OF ,故本选项不符合题意;D .若∠BAE =∠DCF ,则能够利用“角边角”证明△ABE 和△CDF 全等,从而得到DF =BE ,然后同A 选项,故本选项不符合题意.故选B .3.[解析] B ∵∠ABC =60°,∠BAC =80°, ∴∠BCA =180°-60°-80°=40°.∵对角线AC 与BD 相交于点O ,E 是边CD 的中点, ∴EO 是△DBC 的中位线,∴EO ∥BC ,∴∠1=∠BCA =40°. 故选B .4.[解析] D 根据折叠前后对应角相等可知∠DGH =∠EGH.∵∠AGE =32°,∴∠EGH =12×(180°-32°)=74°.∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠GHC =∠AGH =∠EGH +∠AGE =106°.故选D .5.[解析] A 因为一般四边形的中点四边形是平行四边形,所以当对角线AC =BD 时,中点四边形是菱形,当对角线AC ⊥BD 时,中点四边形是矩形,当对角线AC =BD ,且AC ⊥BD 时,中点四边形是正方形,故说法④正确,故选A .6.[解析] C ∵将△ABC 绕点C 顺时针旋转90°得到△EDC. ∴∠DCE =∠ACB =20°,∠BCD =∠ACE =90°,AC =CE , ∴∠ACD =90°-20°=70°. ∵点A ,D ,E 在同一条直线上, ∴∠ADC +∠EDC =180°.又∵∠EDC +∠E +∠DCE =180°, ∴∠ADC =∠E +20°. ∵∠ACE =90°,AC =CE ,∴∠DAC +∠E =90°,∠E =∠DAC =45°. 在△ADC 中,∠ADC +∠DAC +∠ACD =180°, 即45°+70°+∠ADC =180°,解得∠ADC =65°,故选C . 7.[答案] 16[解析] ∵四边形ABCD 是平行四边形, ∴OA =OC.又∵OM ⊥AC ,∴AM =MC.∴△CDM 的周长=AD +CD =8,∴平行四边形ABCD 的周长是2×8=16. 8.[答案] (-5,4)[解析] ∵菱形ABCD 的顶点A ,B 的坐标分别为(3,0),(-2,0),点D 在y 轴上, ∴AB =5,∴AD =5,∴由勾股定理知:OD =AD 2-OA 2=52-32=4, ∴点C 的坐标是(-5,4). 故答案为(-5,4). 9.[答案] 2.5[解析] ∵四边形ABCD 是矩形, ∴BD =AC =10,BO =DO =12BD ,∴DO =12BD =5.∵P ,Q 分别是AO ,AD 的中点, ∴PQ 是△AOD 的中位线, ∴PQ =12DO =2.5.故答案为2.5.10.[答案] (165,-125)[解析] 由折叠得∠CBO =∠DBO.在矩形ABCO 中,BC ∥OA , ∴∠CBO =∠BOA , ∴∠DBO =∠BOA , ∴BE =OE.在△ODE 和△BAE 中,⎩⎪⎨⎪⎧∠ODE =∠BAE =90°,∠OED =∠BEA ,OE =BE ,∴△ODE ≌△BAE(AAS ),∴AE =DE.设DE =AE =x ,则有OE =BE =8-x.在Rt △ODE 中,根据勾股定理,得42+x 2=(8-x)2, 解得x =3,即DE =3,OE =5. 过点D 作DF ⊥OA 于点F ,∵S △OED =12OD ·DE =12OE ·DF ,∴DF =125,OF =42-(125)2=165,则D(165,-125).11.[答案]342[解析] ∵四边形ABCD 是正方形,∴AB =AD =BC =CD =5,∠BAD =∠D =∠C =90°.又∵AE =DF ,∴△ABE ≌△DAF ,∴∠DAF =∠ABE ,∴∠ABE +∠BAG =90°,∴∠BGF =∠BGA =90°.在Rt △BCF 中,BC =5,CF =3,∴BF =52+32=34.在Rt △BGF 中,∵H 为BF 的中点,∴GH =12BF =342.12.证明:∵▱ABCD 的对角线AC ,BD 交于点O , ∴AO =CO ,AD ∥BC , ∴∠EAC =∠FCO.在△AOE 和△COF 中,⎩⎪⎨⎪⎧∠EAO =∠FCO ,AO =CO ,∠AOE =∠COF ,∴△AOE ≌△COF ,∴AE =CF.13.解:(1)答案不唯一,如图①所示,△DCE 即为所作.(2)答案不唯一,如图②所示,△ACD 即为所作.(3)如图③所示,△ECD 即为所作.14.证明:(1)∵四边形ABCD是平行四边形,∴AB∥DF,∴∠BAE=∠CFE.又∵BE=CE,∠AEB=∠FEC,∴△AEB≌△FEC,∴CF=AB.(2)如图,连接AC.∵四边形ABCD是平行四边形,∠BCD=90°,∴四边形ABCD是矩形,∴BD=AC.∵AB=CF,AB∥CF,∴四边形ACFB是平行四边形,∴BF=AC,∴BD=BF.15.解:(1)答案不唯一,如以①④为条件构成真命题:在四边形ABCD中,OA=OC,AD ∥BC,则四边形ABCD是平行四边形.证明如下:如图,∵AD∥BC,∴∠DAC=∠BCA,∠ADB=∠DBC.又∵OA=OC,∴△AOD≌△COB,∴AD=BC,∴四边形ABCD为平行四边形.(2)答案不唯一,如以②④为条件构成假命题:在四边形ABCD中,AB=CD,AD∥BC,则四边形ABCD是平行四边形.理由如下:如图,在四边形ABCD中,满足AB=CD,AD∥BC,四边形ABCD是等腰梯形,不是平行四边形.16.解:(1)证明:∵AF=FG,∴∠FAG=∠FGA.∵AG平分∠CAB,∴∠CAG =∠FAG ,∴∠CAG =∠FGA ,∴AC ∥FG. ∵DE ⊥AC ,∴FG ⊥DE. 又∵FG ⊥BC ,∴DE ∥BC , ∴AC ⊥BC ,∠CGE =∠GED , ∴∠C =∠DHG =90°.∵F 是AD 的中点,FG ∥AE , ∴H 是DE 的中点,∴FG 是线段DE 的垂直平分线, ∴GE =GD ,∴∠GDE =∠GED , ∴∠CGE =∠GDE , ∴△ECG ≌△GHD.(2)证明:过点G 作GP ⊥AB 于点P , ∴GC =GP ,而AG =AG , ∴Rt △CAG ≌Rt △PAG , ∴AC =AP.由(1)可得EG =DG , ∴Rt △ECG ≌Rt △DPG , ∴EC =PD ,∴AD =AP +PD =AC +EC. (3)四边形AEGF 是菱形.理由:∵∠B =30°,DE ∥BC , ∴∠ADE =30°, ∴AE =12AD.而F 是AD 的中点, ∴AE =AF =FG.又由(1)得AE ∥FG ,∴四边形AEGF 是平行四边形. 又∵AE =AF ,∴四边形AEGF 是菱形.。
