上海市虹口区2010年中考数学第二次模拟试卷及答案
2010年上海市中考数学二模卷及答案

中考数学一.选择题(本大题共10个小题,每小题4分,共40分)1.-2的相反数是 ( ) (A )1/2 (B )-1/2 (C )-2 (D )22.如果t>0,那么a+t 与a 的大小关系是 ( )(A )a+t >a (B )a+t <a (C )a+t ≥a (D )不能确定 3.若∠A =34°,则∠A 的余角的度数为 ( )(A )54° (B )56° (C )146° (D )66° 4.下列交通标志图中,属于轴对称图形的是 ( )5.△ABC 中,∠C =90°,BC =5,AB =13,则sin A 的值是 ( )(A )135 (B )1312 (C )125 (D )5126.如果两圆的半径长分别为2cm 和5cm ,圆心距为8cm ,那么这两个圆的位置关系是( )(A )内切 (B )外切 (C )相交 (D )外离7.下列调查,比较容易用普查方式的是 ( ) (A )了解嘉兴市居民年人均收入 (B )了解嘉兴市初中生体育中考的成绩 (C )了解嘉兴市中小学生的近视率 (D )了解某一天离开嘉兴市的人口流量8.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( ) (A )小明的影子比小强的影子长 (B )小明的影长比小强的影子短 (C )小明的影子和小强的影子一样长 (D )无法判断谁的影子长9.图1所示的电路的总电阻为10Ω,若R 1=2R 2,则R 1,R 2( )(A)R 1=30Ω,R 2=15Ω (B )R 1=203Ω,R 2=103Ω(C )R 1=15Ω,R 2=30Ω (D )R 1=103Ω,R 2=203Ω10.若用(1)、(2)、(3)、(4)四幅图象分别表示变量之间的关系, ( )(1) (2) (3) (4) 请按图象所给顺序,将下面的(a )、(b )、(c )、(d )对应排序 (a )小车从光滑的斜面上滑下(小车的速度与时间的关系)(b )一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物的重量的关系) (c )运动员推出去的铅球(铅球的高度与时间的关系)(d )小杨从A 到B 后,停留一段时间,然后按原速度返回(路程与时间的关系)正确的顺序是 ( ). A.(c )(d )(b )(a ) B.(a )(b )(c )(d ) C.(b )(c )(a )(d ) D.(d )(a )(c )(b )图1二.填空题(每小题5分,共30分)11.函数y=3-x 中自变量x 的取值范围是 。
2010上海各区中考二模数学压轴25题解析

2010上海各区二模数学压轴25题解析1、(松江)解:1(1)∵90=Ð=ÐFEB DEC ,∴BEC DEF Ð=Ð…………11分∵90=Ð+Ð=Ð+ÐDCP BCE DCP EDF ,…………………………,…………………………11分∴BCE EDF Ð=Ð,∴△DEF ∽△CEB ……………………………………………………………………11分(2)∵PDC Rt D 中,CP DE ^,∴90=Ð=ÐCED CDP ∴△DEC ∽△PDC ,∴DC PDECDE=………………………………………………………………………………11分∵△DEF ∽△CEB ,∴DCDF CBDF ECDE ==……………………………………………………………………11分∴DCDF DCPD =,∴DF PD =………………………………………………………………………………………………11分∵AP =x ,DF =y ,∴,1x PD -=∴x y -=1…………………………………………………………11分)10(<<x ……………………………………………………………………………………………………………………………………11分(3)∵△DEF ∽△CEB ,∴22CBDF S S CEBDEF =D D (1)……………………………………………………11分∵CFDF S S CEFDEF =D D (2),∴(1)¸(2)得2CBCF DF S S CEBcEF ×=D D …………………………11分又∵EFC BECS SD D =4,∴412=×=D D CB CFDF S S CEBcEF …………………………………………………………11分当P 点在边DA 上时,有411)1(=×-xx ,解得21=x ………………………………………………………………………………………………22分当P 点在边DA 的延长线上时,411)1(=×+xx ,解得212-=x …………………………………………………………………………………………11分2、(浦东)解:(1)在矩形ABCD 中,中,∵AD ∥BC ,∴∠APB =∠DAP .又由题意,得∠QAD =∠DAP ,∴∠APB =∠QAD .∵∠B =∠ADQ =90°,∴△ADQ ∽△PBA .………………………………(1分)∴BPAD ABDQ =,即443+=x y .∴412+=x y .………………………………………………………………(1分)定义域为0>x .……………………………………………………………(1分)(2)不发生变化.…………………………………………………………………(1分) 证明如下:证明如下:∵∠QAD =∠DAP ,∠ADE =∠ADQ =90°,AD =AD , ∴△ADE ≌△ADQ .∴DE =DQ =y .………………………………………………………………(1分)∴124124482121=+++=×+×=+=D D x x x PC QE AD QE S S S PQE AQE .…(3分)(3)过点Q 作QF ⊥AP 于点F .∵以4为半径的⊙Q 与直线AP 相切,∴QF =4.…………………………(1分) ∵12=S ,∴AP =6.………………………………………………………(1分)分) 在Rt △ABP 中,中,∵AB =3,∴∠BPA =30°.…………………………………………………(1分) ∴∠PAQ =60°.°. ∴AQ =338.………………………………………………………………(1分)分)设⊙A 的半径为r .∵⊙A 与⊙Q 相切,∴⊙A 与⊙Q 外切或内切.外切或内切.(i )当⊙A 与⊙Q 外切时,AQ =r +4,即338=r +4.∴r =4338-.………………………………………………………………(1分)(ii )当⊙A 与⊙Q 内切时,AQ =r -4,即338=r -4.∴r =4338+.………………………………………………………………(1分)综上所述,⊙A 的半径为4338-或4338+.3、(长宁)(1)由题意知由题意知 ∠COB = 90°B(8,0) OB=8 在Rt △OBC 中tan ∠ABC = 21OBOC = OC= O B ×tan tan∠∠ABC = 8ABC = 8××21=4 =4 ∴∴C(0,4) …1分 8OC AB 21S ABC =×=D ∴AB = 4 A(4,0)………………………1分 把A 、B 、C 三点的坐标带入)0(2>++=a c bx ax y 得 ïîïíì==++=++408640416c c b a c b a解得解得ïîïíì=-==42381c b a ……………………………………….2分 所以抛物线的解析式为423812+-=x x y 。
2010年上海数学各区二模试卷填空选择部分答案

2010年上海各区二模试卷答案填空选择部分 奉贤区:一 、选择题:(本大题共8题,满分24分)1.D ; 2.B ; 3.A ; 4.B ; 5.D ; 6.D ; 二、填空题:(本大题共12题,满分48分)7.2±; 8.)2)(22-+m m (1; 9.4; 10.0=x ; 11.3-; 12.1=y ; 13.201; 14.面ABFE 和面DCGH ; 15.1︰4; 16.21; 17.6; 18.10或310; 虹口区:一、选择题:(本大题共6题,满分24分)1.C ; 2.C ; 3.D ; 4.B ; 5.D ;6.D . 二、填空题:(本大题共12题,满分48分)7.21x - ; 8.1; 9.2x =-; 10.1x ≠;11.增大; 12.(1,2)--; 13.23200(1)2500x -=; 14.13; 15.70°; 16.1:2; 17.24; 18.25或23.黄浦区:一、选择题1、D ;2、B ;3、D ;4、C ;5、B ;6、A .二、填空题7、1-x ; 8、x ≤-1<2; 9、()()11-+++y x y x ; 10、2±;11、21; 12、()7,2-; 13、0,12; 14、2-; 15、132; 16、3232+; 17、6; 18、0.8.金山区:一.选择题:(本大题共6题,满分24分)1. B ; 2.B ; 3.C ; 4.A ; 5.C ; 6.D . 二.填空题:(本大题共12题,满分48分)7.()2x x -; 8.3a =-; 9.略; 10.1x ≠; 11.6a b -;12.18; 13.8; 14.110°; 15.1∶16;16. 17.略; 18.1。
静安区:一、选择题:(本大题共6题,每题4分,满分24分) 1.C ; 2.B ; 3.D ; 4.D ; 5.A ; 6.A . 二.填空题:(本大题共12题,满分48分) 7.2; 8.253+; 9.2=x ; 10.43,43-=-=-y x y x ; 11.32≤a ; 12.x y 45=; 13.94; 14.BF ; 15.163; 16.2--; 17.31; 18.37π. 卢湾区:一、选择题(本大题共6题,每题4分,满分24分)1. C ; 2. A ; 3.B ; 4.D ; 5.B ; 6.C .二、填空题(本大题共12题,每题4分,满分48分)7. 2-; 8.9.49; 10.22(1)x -;11. 321y y-=;12. 4; 13.24y x =--; 14.232y x =-+;15.13a b + ; 16; 17.15 ; 18. 15或105.闵行区:一、选择题:(共6题,每题4分,满分24分) 1.B ; 2.C ; 3.D ; 4.A ; 5.B ; 6.C .二、填空题:(共12题,每题4分,满分48分) 7.69a ; 8.32x >; 9.x = 4; 10.2; 11.-2; 12.-5; 13.下降; 14.13;15.b a -; 16.24; 17.AD = BC 或AB // CD 或∠A =∠C 等,正确即可;18.3.浦东新区:一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.D ; 3.C ; 4.C ; 5.A ; 6.D .二、填空题:(本大题共12题,每题4分,满分48分)7.4; 8.()()222+-x x ; 9.1-=x ; 10.12-; 11.41≤m ; 12.23-; 13.30 %; 14.a m -2; 15.33 ; 16.6; 17.4; 18.(2-,6).普陀区:1.(A) ; 2.(B) ; 3.(C); 4.(D) ; 5.(C) ; 6.(B) .二、填空题:(本大题共12题,每题4分,满分48分)7. 45a ; 8. 34.310-⨯; 9. 1; 10. 25x -<<; 11. c =0; 12. ;13.2x ≠; 14.23y x =+; 15. 30; 16.AB =CD 等; 17.5 ; 18. 9.青浦区:一、选择题:(本大题共6题,每题4分,满分24分) 1.(B );2.(C );3.(D );4.(C );5.(B );6.(B ). 二、填空题:(本大题共12题,每题4分,满分48分)7.2-π;8.2≤x ;9.1->x ;10.2=x ;11.)1)(2(-+a a a ;12.1<k 且0≠k ; 13.二;14.21;15.4.2:1;16.-3;17.10;18. 65或25. 松江区:一、选择题1、D ;2、C ;3、B ;4、D ;5、A ;6、A 二、填空题7、1-; 8、3≥x ; 9、)1)(1(-+x x x ; 10、5=x ; 11、x y 2-=; 12、a 64.0; 13、51; 14、5; 15、8; 16、4; 17、3132+; 18、52 徐汇区:一、选择题1.B; 2.C; 3.D; 4.C ; 5.A; 6.B . 二、填空题7.)2)(2(-+a a a ; 8.4=x ; 9.9<a ; 10.)3,1(; 11.①③④;12.15)1(5.122=+x ; 13.43; 14.)(21→→-a b ; 15.161; 16.623π-;17.216; 18.5144。
2010年上海市虹口区中考数学二模卷及答案

中考数学模拟练习卷一、选择题:(本大题共6题,每题4分,满分24分)1.小杰于3月26日20:00,在“百度”搜索引擎中输入“上海世博会”,能搜索到与之相关的网页约23 800 000个,将这个数字用科学记数法表示为 A.2.38×105 ; B.2.38×106; C.2.38×107; D.2.38×108. 2. 下列运算中,正确的是A.326()xy xy = ; B.3412x x x ⋅= ; C.235()x x x -=; D.()32626x x -=-.3. 把不等式组2020x x +>⎧⎨-≤⎩的解集表示在数轴上,正确的是4. 在一次射击测试中,甲、乙、丙、丁的平均环数相同,而方差分别为8.7、6.5、9.1、7.7,则这四人中,射击成绩最稳定的是A .甲;B .乙;C .丙;D .丁. 5.在下列关于向量的等式中,正确的是[来源:学§科§网Z §X §X §K]A.AB BC CA =+; B.AB BC CA =-; C.AB CA BC =-; D.0AB BC CA ++=. 6. 下列命题中不是真命题的是A .两组对边分别相等的四边形是平行四边形;B .对角线相等的平行四边形是矩形;C .一组邻边相等的平行四边形是菱形;D .一组对边平行的四边形是梯形. 二、填空题:(本大题共12题,每题4分,满分48分) 7. 计算:(1)(1)x x +-= ▲ .8. 如果关于x 的方程220x x m -+=有两个相等的实数根,那么m 的值是 ▲ . 9. 1=的根是 ▲ .10. 在函数11y x =-中,自变量x 的取值范围是 ▲ . 11. 已知一次函数21y x =+,则函数值y 随自变量x 的增大而 ▲ .(填“增大”或“减小”).12. 二次函数221y x x =+-的图像的顶点坐标是 ▲ .13. 某种品牌的手机经过四、五月份连续两次降价,每部售价由3200元降到了2500元.如果每个月降价的百分率相同,并设该百分率为x ,那么根据题意列出关于x 的方程是 ▲ .14. 布袋里有2个红球、3个黄球、4个白球,它们除颜色外其他都相同.从布袋里任意摸出A B C D图3一个球恰好是黄球的概率是 ▲ .15. 如图1,直线a ∥b ,直线c 与a 、b 相交,若170∠=︒,则2∠的度数是 ▲ . 16. 如果两个相似三角形的面积比是1:4,那么它们对应的角平分线比是 ▲ . 17. 如图2,把矩形纸条ABCD 沿EF 、GH 同时折叠,B 、C 两点恰好落在AD 边的P 点处,若90FPH =∠,8PF =,6PH =,则矩形ABCD 的边BC 长为 ▲ .18. 已知平行四边形ABCD 中,点E 是BC 的中点,在直线BA 上截取2BF AF =,EF 交BD 于点G ,则GBGD= ▲ . 三、解答题(本大题共7题,满分78分)[来源:学*科*网] 19.(本题满分10分)先化简,再求值:22121126x x x x x ++⎛⎫-÷ ⎪+--⎝⎭,其中3x =-. 20.(本题满分10分) 解方程:211()60x x x x+++-=.21.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)如图3,在菱形ABCD 中,120ADC ∠=︒,过点C 作CE AC ⊥且与AB 的延长线交于点E . (1)求证:四边形AECD 是等腰梯形; (2)若4AD =,求梯形AECD 的面积.图2 a b c 图1分,第(4)小题满分2分)下表1是三峡水库2009年1-12月平均水位情况.小杰根据表1中的数据,在平面直角坐标系中以月份(月)为横坐标、月平均水位(米)为纵坐标描出了部分点(如图4),并绘制了不完整的频数分布直方图(如图5).请根据表1与图4、5中提供的信息,回答下列问题:(1)根据表1,补全图4、图5;(2)根据图4,可知平均水位相比其上个月平均水位上升最大的月份是 ▲ 月; (3)在2009年三峡水库1—12月各月的平均水位中,众数是 ▲ 米,中位数是▲ 米;(4)观察图4中1-4月这些点的发展趋势,猜想1-4月y 与x 之间可以存在怎样的函数关系,请你用所学过的函数知识直接写出该函数关系式(不要求写定义域).[图4图5(每组仅含最小值,不含最大值)分)如图6-8中,点E 、D 分别是正三角形ABC 、正四边形ABCM 、正五边形ABCMN 中以C 点为顶点的一边延长线和另一边反向延长线上的点,且BE CD =,DB 延长线交AE 于点F .(1)求图6中AFB ∠度数,并证明2CD BD EF =⋅;(2)图7中AFB ∠的度数为 ▲ ,图8中AFB ∠度数为 ▲ ,在图7、图8中,(1)中的等式 ▲ ;(填“成立”或“不成立”,不必证明)(3)若将条件“正三角形、正四边形、正五边形”改为“正n 边形”,其它条件不变,则AFB ∠度数为 ▲ .(可用含n 的代数式表示,不必证明)图6C B E AF分)已知等腰OAB ∆在平面直角坐标系中的位置如图9,点A坐标为2),点B 坐标为(4,0).(1)若将OAB ∆沿x 轴向左平移m 个单位,此时点A恰好落在反比例函数y =的图像上,求m 的值;(2)若将OAB ∆绕点O 顺时针旋转30︒,点B 恰好落在反比例函数ky x=的图像上,求k 的值;(3)若将OAB ∆绕点O 顺时针旋转α度(0<α<180)到OA B ''∆位置,当点A '、B '恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点A '、B '且以y 轴为对称轴的抛物线解析式.分)如图10,在直角梯形ABCD 中,//AD BC ,90C ∠=︒,,12=BC 18=AD ,10=AB .动点P 、Q 分别从点D 、B 同时出发,动点P 沿射线DA 的方向以每秒2个单位长的速度运动,动点Q 在线段BC 上以每秒1个单位长的速度向点C 运动,当点Q 运动到点C 时,点P 随之停止运动.设运动的时间为t (秒).(1)当点P 在线段DA 上运动时,联结BD ,若ABP ∠=ADB ∠,求t 的值; (2)当点P 在线段DA 上运动时,若以BQ 为直径的圆与以AP 为直径的圆外切,求t 的值;(3)设射线PQ 与射线AB 相交于点E ,AEP ∆能否为等腰三角形?如果能,请直接写出t 的值;如果不能,请说明理由.CDBAQP图10CDBA 备用图1CDBA备用图2一、选择题:(本大题共6题,满分24分)1.C ; 2.C ; 3.D ; 4.B ; 5.D ;6.D . 二、填空题:(本大题共12题,满分48分)7.21x - ; 8.1; 9.2x =-; 10.1x ≠;11.增大; 12.(1,2)--; 13.23200(1)2500x -=; 14.13; 15.70°; 16.1:2; 17.24; 18.25或23.三、解答题:(本大题共7题,满分78分)19. 解:原式221(1)2(2)(3)x x x x x +-+=÷++- ······················································ (3分)21(2)(3)2(1)x x x x x ++-=++ ···························································· (2分) 31x x -=+. ············································································· (2分) 当3x =-时,原式33331--==-+.···················································· (3分) 20.解:设1x y x+=,则原方程可化为:260y y +-= ………………………………………………… (2分)解得:13y =-,22y = ………………………………………………………… (2分)当13y =-时,13x x +=-,解得14x =- …………………………………… (2分) 当22y =时,12x x +=,解得1x = ……………………………………………(2分) 经检验,114x =-,21x =都是原方程的根,所以原方程的根是114x =-,21x =……………………………………………………………………………………… (2分)21.解:(1)∵四边形ABCD 是菱形∴//DC AB ,即://DC AE ………………………………………………… (1分) 又AE AB DC >=∴四边形AECD 是梯形. …………………………………………………… (2分) ∴180********DAE ADC ∠=︒-∠=︒-︒=︒…………………………… (1分) ∵四边形ABCD 是菱形∴1302CAE DAB ∠=∠=︒ 又AC CE ⊥, ∴60E ∠=︒…………………………………………(1分)∴DAE E ∠=∠………………………………………………………………… (1分) ∴四边形AECD 是等腰梯形.图6(每组仅含最小值,不含最大值)图5 (2)过点D 作DH AE ⊥于H ,则:sin 4sin 60DH AD DAH =⋅∠=︒=…………………………………(2分)∴1(48)2AECD S =⨯+⨯=梯形 (2分) 22.(1)[来源………………………………………………………… (3分)(2)10………………………………………………………………………………… (2分) (3)169 161.5 …………………………………………………………… (1分,2分)(4)3172y x =-+ ………………………………………………………………… (2分) 23.解:(1)在等边三角形ABC 中,AB=BC ,∠ABC=∠ACB =60°∴∠ABE=∠BCD =120° 又∵BE CD =∴△ABE ≌△BCD …………………………………………………………… (2分) ∴∠E=∠D又∵∠FBE=∠CBD∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°…………………………… (2分) 由∠FBE=∠CBD ,∠E=∠D 得:△FBE ∽△CBD …………………………… (2分)∴CD BDEF EB =又BE CD =∴2CD BD EF =⋅……………………………………………………………… (1分) (2)90°, 108°,成立………………………………………………………… (3分)(3)0(2)180n n-⋅ ………………………………………………………… (2分)24. (1)设点A 平移后落在反比例函数y x=-图像上的点记为:1(,)A a b , ∵2)A , ∴b =2……………………………………………………………(1分)代入y =求得a =(2分)∴(m ==………………………………………………………(2分) (2) 将点B 恰好落在反比例函数ky x=图像上的点记为1B ,可求得:1B 2)- ……………………………………………………………(2分)∴(2)k =-=-…………………………………………………………(2分)(3)2114y x =+-…………………………………………………………(3分) 25. 解:(1)可求得:t DP 2=,t AP 218-=,……………………………………(1分)∵ABP ∠=ADB ∠,A A ∠=∠∴ABP ∆∽ADB ∆,…………………………………………………………(1分)∴ABAPAD AB =, ………………………………………………………………(1分) 即2AB AD AP =⋅,∴)218(18102t -⨯=, ……………………………(1分)解得:569t =. ∵5699< ∴569t =.…………………………………………………(1分) (2)过点B 作AD BH ⊥,垂足为H ,得8=BH ,………………………………(1分)记BQ 中点为1O 、AP 中点为2O ,联结21O O ,过点1O 作AD I O ⊥1,垂足为I ,则81==BH I O ,21t BO =,2121t CO -=,t t AO -=-=922182,t DO +=92,323)212()9(2-=--+=∴tt t I O ,…………………………………………………(1分)当29)9(22121tt t AO BO O O -=-+=+=时………………………………………(1分)以BQ 为直径的圆与以AP 为直径的圆外切,在21IO O Rt ∆中,2221221I O I O O O +=,即222)323(8)29(-+=-tt ,………………………………………………(1分)整理得:42=t ,0>t ,2=∴t ;…………………………………………………(1分) (3)能,t 的值可以是929=t 或38=t 或2=t 或328=t .……………………………(4分)。
虹口区2010学年度第一学期初三年级数学(含答案).

虹口区2010学年度第一学期初三年级数学学科期中教学质量监控试题(满分150分,考试时间100分钟)2010.11考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.在ABC ∆中,90C ∠=︒,3AC =,4=CB ,则tan A 的值为 A .45 B .35 C .43 D .342.已知两个相似三角形的相似比为1:4,则它们的面积比为A .1:4B .4:1C .1:2D .1:163.已知53=b a ,下列说法中,错误的是 A .58=+b b a B .25a b b --= C . 11a a b b +=+ D . 53b a =4.已知ABC ∆中,D 、E 分别是边BC 、AC 上的点,下列各式中,不能判断DE ∥AB 的是A .AE BD EC DC = B .AE BD AC BC = C .AC EC BC DC = D .DE CEAB AC=5.已知点C 是线段AB 的中点,下列结论中,正确的是A .21=B . 21= C .0=+BC AC D .0=+CB AC6. 手工制作课上,小丽利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心的直角三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是A .B .C .D .第6题图二、填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】7.已知线段2a =厘米,8c =厘米,则线段a 和c 的比例中项b 是 ▲ 厘米.8.已知点P 是线段AB 的黄金分割点,4AB =厘米,则较长线段AP 的长是 ▲ 厘米. 9.已知a 与单位向量e 的方向相反,且长度为2,那么用e 表示a = ▲ . 10.计算:12()3()3a b a b --+= ▲ .11.如果2a b c +=,2a b c -=,那么用b 表示a = ▲ .12. 已知ABC ∆∽111A B C ∆,顶点A 、B 、C 分别与1A 、1B 、1C 对应,11:3:5AB A B =,BE 、11B E 分别是它们的对应中线,则11:BE B E = ▲ _. 13.如图,在平面直角坐标系内有一点(512)P ,,那么OP 与x 轴正半轴的夹角α的余弦值__ ▲ .14.如图,已知AD 为ABC ∆的角平分线,//DE AB ,如果32=EC AE ,那么AE AB= ▲ .15.如图,在平行四边形ABCD 中,点E 在边BC 上,2EC BE =,联结AE 交BD 于点F ,若BFE ∆的面积为2,则AFD ∆的面积为 ▲ _.16. 如图,已知AB BD ⊥,ED BD ⊥,C 是线段BD 的中点,且AC CE ⊥,1ED =,4BD =,那么AB = ▲ . 17.已知菱形ABCD 的边长为6,对角线AC 与BD 相交于点O ,OE ⊥AB ,垂足为点E ,AC =4,那么sin AOE ∠= ▲ .18.如图,用形状相同、大小不等的3块直角三角形木板,恰好能拼成如图所示的四边形ABCD ,如果2AE =,3CE BE =,那么这个四边形的面积是__ ▲ .第18题图 ABCDE第14题图第15题图第17题图 第13题图第16题图三、解答题:(本大题共7题,满分78分) 【请将解题过程写在答题纸的相应位置】 19.(本题满分10分)已知:234a b c==,且27a b c ++=,求a 、b 、c 的值.20.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)如图,已知////AD BE CF ,它们依次交直线l 1、l 2于点A 、B 、C 和点D 、E 、F . (1)如果6AB =,8BC =,21DF =,求DE 的长;(2)如果:2:5DE DF =,9AD =,14CF =,求BE 的长.21.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)如图,在ABC ∆和ADE ∆中,BAD CAE ∠=∠,ABC ADE ∠=∠. (1) 求证:ABC ∆∽ADE ∆; (2) 判断ABD ∆与ACE ∆是否相似?并证明.22.(本题满分10分)在ABC ∆中,边BC 、AC 上的中线AE 、BD 相交于点G ,过点G 作//MN BC ,已知BD a =,AC b =,试用a 和b 表示BC 、MN .ABCD M N GABC D E 第20题图F 1l 2l 第22题图A BC D E 第21题图23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,点P 是菱形ABCD 的对角线BD 上一点,联结CP 并延长,交AD 于点E ,交BA 的延长线于点F .(1)求证:2PC PE PF =⋅;(2)若菱形边长为8,2PE =,6EF =,求FB24.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,在平行四边形ABCD 中,E 为BC 边上一点,且AEDB ∠=∠,在DE 上取一点F ,使AF AE =.(1)请直接写出图中所有相似的三角形(不必证明); (2)若AE =3BC BE =,求DE DF ⋅的值. (可以直接使用第(1)小题结论).25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图,在Rt ABC ∆中,90C ∠=︒,6AC BC ==,点D 为AC 中点,点E 为边AB 上一动点,点F 为射线BC 上一动点,且90FDE ∠=︒.(1)当//DF AB 时,联结EF ,求DEF ∠的余切值;(2)当点F 在线段BC 上时,设AE x =,BF y =,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结CE ,若C DE ∆为等腰三角形,求BF 的长.第24题图 第23题图虹口区2010学年度第一学期初三年级数学学科期中教学质量监控试题答案要点与评分标准说明:1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;2.第一、二大题若无特别说明,每题评分只有满分或零分;3.第三大题中各题右端所注分数,表示考生正确做对这一步应得分数;4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半; 5.评分时,给分或扣分均以1分为基本单位.一、选择题:(本大题共6题,每题4分,满分24分) 1. C 2. D 3. C 4. D 5. B 6. D二、填空题:(本大题共12题,每题4分,满分48分)7. 4 8. (2) 9. 2e - 10. 3a b --11. b 12. 3:5 13. 513 14. 3515. 18 16. 4 17. 1318.三、解答题:(本大题共7题,满分78分)19.解:设k cb a ===432 ,则 k a 2=,k b 3=,k c 4=………………………………………………………(3分)∵27=++c b a∴27432=++k k k ………………………………………………………………(2分) ∴3=k ………………………………………………………………………………(2分) ∴6=a ,9=b ,12=c …………………………………………………………(3分)20.解:(1)∵AD ∥BE ∥CF∴ACABDF DE =…………………………………………………………………………(2分) ∵21,8,6===DF BC AB ∴86621+=DE ………………………………………………………………………(1分)∴9=DE ……………………………………………………………………………(2分) (2)过点D 作DG ∥AC ,交BE 于点H ,交CF 于点G则9CG BH AD ===………………………………………………………………(1分) ∴5914=-=GF …………………………………………………………………(1分)∵HE ∥GF ∴DFDEGF HE =………………………………………………(1分) ∵5:2:=DF DE ,5=GF ∴525=HE∴2=HE ……………………………………………………………………………(1分) ∴1129=+=BE …………………………………………………………………(1分)21.(1)证明:∵BAD CAE ∠=∠∴BAC DAE ∠=∠…………………………………………………………………(2分) ∵ABC ADE ∠=∠∴△ABC ∽△ADE ………………………………………………………………(2分) (2)△ABD ∽△ACE ……………………………………………………………………(2分)证明:由(1)知△ABC ∽△ADE∴AB AC AD AE =即AB ADAC AE =…………………………………………………………(2分) ∵BAD CAE ∠=∠∴△ABD ∽△ACE …………………………………………………………………(2分)22.解:∵AC DC 21=∴1122DC AC b ==………………………………………………………………(2分)∴12BC BD DC a b =+=+ ……………………………………………………(2分)∵中线AE 、BD 相交于点G 即点G 为△ABC 的重心 ∴23AG AE = …………………………………………………………………………(2分) ∵MN ∥BC∴23MN AN AG BC AC AE === ∴23MN BC =………………………………………………………………………(2分)∴22121()33233MN BC a b a b ==+=+…………………………………………(2分)23.(1)证明:法1:∵四边形ABCD 是菱形∴DC DA =,ADP CDP ∠=∠,DC ∥AB又∵DP 是公共边 ∴△DAP ≌△DCP∴PA PC = ,DAP DCP ∠=∠………………………………………………(2分) 由DC ∥FA 得,F DCP ∠=∠∴F DAP ∠=∠ 又∵EPA APF ∠=∠∴AEP ∆∽FAP ∆…………………………………………………………………(2分)∴2PA PE PF =⋅∴2PC PE PF =⋅ ……………………………………………………………………(2分)法2:∵四边形ABCD 是菱形∴DC ∥AB ,AD ∥BC ……………………………………………………………(1分)∴PC DP PF PB =,DP PEPB PC =…………………………………………………………(4分) ∴PC PE PF PC= ∴2PC PE PF =⋅……………………………………………………………………(1分) (2)解:∵2PE =,6EF = ∴8PF =∵2PC PE PF =⋅ ∴216PC = ∴4PC =………………………………(2分) ∵DC ∥FB∴FB PFDC PC=…………………………………………………………………………(2分) 又8DC = ∴884FB =∴16FB =……………………………………………………………………………(2分)24.(1)△ABE ∽△DEA ,△AFD ∽△DCE ………………………………(3分, 3分)(2)∵3BC BE = ∴设BE x =,则3BC x =,∴3AD x =,2EC x =由△ABE ∽△DEA ,得:AE BEAD AE=∵AE ==2分) ∴2x =…………………………………………………………………………………(1分)又由△AFD ∽△DCE 得2326DE DF AD EC x x x ⋅=⋅=⋅= …………………(2分) ∴24DE DF ⋅=………………………………………………………………………(1分)25.解:(1)∴6AC BC ==,∠90=ACB °∴26=AB ∵DF ∥AB ,AC CD 21=∴2321==AB DF …………………………………………………………………(1分)∴223=DE …………………………………………………………………………(1分)在Rt DEF ∆中,1cot 2DE DEF DF ∠===…………………………………(2分) (2)过点E 作EH AC ⊥于点H可求得x HA HE 22==……………………(1分) ∴x HD 223-= 又可证HDE ∆∽CFD ∆ ∴DCHECF HD =…………………………………………………………………………(1分) ∴3226223x y x =--∴929+-=xy x <≤……………………………………………(2分,1分) (3)∵32321>=≥AB CE ,3=CD ∴CD CE > ∴若DCE ∆为等腰三角形,只有DE DC =或EC ED =两种可能.…………(1分) ① 当DE DC =时,点F 在边BC 上,过点D 作DG ⊥AE 于点G (如图①)可得:232==AG AE ,第25题图第25题图B即点E 在AB 中点∴此时F 与C 重合 ∴6=BF ……………………(2分) ② 当EC ED =时,点F 在BC 的延长线上, 过点E 作EM ⊥CD 于点M (如图②) 可证: △DFC ∽△DEM∴CF CDDM EM =∴233323+=CF ∴1=CF ∴7=BF ……………………………(2分) 综上所述,BF 为6或7.C DABFE第25题图②M。
2010年虹口区数学二模卷

2010虹口区高三数学二模试卷一、填空题(每小题4分,满分56分) 1.若1zii 211+-=0,则复数z = .2.直线1l :01=++my x 与直线2l :12-=x y 垂直,则=m . 3.若函数()x f 的反函数是()x f1-=()1log 2-x ,则=⎪⎭⎫⎝⎛21f . 4.若向量a ,b1=2=,且a 与b 夹角为π32= .5.以双曲线14522=+-yx的顶点为焦点,焦点为顶点的椭圆方程是 .6.函数x x y 2sin 3sin 22-=的最大值是 .7.本题流程图运行后,所得i 值的输出结果是 .8.62⎪⎪⎭⎫ ⎝⎛-x x 展开式中常数项为 .9.函数()x f =()()a bx a x 2+-(常数a ,b ∈R )是偶函数,且它的值域为[)+∞-,10,则该函数的解析式()x f = .10.一组数据为x ,y ,10,11,9,这组数据平均数为10,则方差的最小值为 . 11.当210≤≤x 时,不等式kx x ≥πsin 恒成立.则实数k 的取值范围是 .12.(理)函数2sin cos 189y x x ππ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭的最小值= . (文)变量x ,y 满足约束条件:⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x ,则目标函数y x z +=5的最小值为 .13.从集合{}4,3,2,1的所有非空..子集中,等可能地取出一个.(理)记所取出的非空子集中元素的个数为ξ,则ξ的数学期望= . (文)取出的非空子集中所有元素之和恰为6的概率= .14.如对自然数n 作竖式加法()()21++++n n n 均不产生进位现象,则称n 为“可连数”.例如:32是“可连数”,因32+33+34不产生进位现象,而23不是可连数,因23+24+25产生进位现象,那么小于100的“可连数”共有 个.二、选择题(每小题4分,满分16分)15.已知:过球面上A,B,C 三点的截面和球心的距离是球半径的31,且22=AB , 0=⋅BC AC ,则球的表面积是( )(A )π81 (B )π9 (C )π481 (D )π4916.已知:()x f y =是最小正周期为2的函数,当[]1,1-∈x 时,()2x x f =,则函数()x f y =()R x ∈图像与x y5log=图像的交点的个数是( )(A )8 (B )9 (C )10 (D )1217.圆01222=--+y y x 关于直线032=--y x 对称的圆方程是( )(A )()()213222=++-y x (B )()()23222=++-y x(C )()()213222=-++y x (D )()()23222=-++y x18.如果n S n +++= 21 ()*∈N n ,1113322-⨯⨯-⨯-=n n n S S S S S S T ()*∈≥N n n ,2,则下列各数中与2010T 最接近的数是( )(A )2.9 (B )3.0 (C )3.1 (D )3.2三、解答题(满分78分) 19.(本题14分)如图,四棱锥ABCD P -中,底面ABCD 是矩形,PA ⊥平面ABCD ,PA=AB=1,BC=2,E 为PD 的中点 (1)求异面直线PA 与CE 所成角的大小; (2)(理)求二面角E-AC-D 的大小。
虹口区2010年初三数学分层练习2(B卷)答案

第 1 页 共 3 页虹口区2009学年度第二学期初三数学分层练习2(B 卷)参考答案与评分建议一.选择题:(本大题共6题,每题4分,满分24分) 1.C 2.A 3.B 4.A 5.C6.D二.填空题:(本大题共12题,每题4分,满分48分) 7.72 8.19.甲10.13 1112.相离1314.内切 15.B 在A 外16.35OP ≤≤ 17.4 18.132或12三.解答题:(19~22每题10分,23,24每题12分,25题14分,共78分)19.解:⑴20…………………………………………………………………………………3分 ⑵7040……………………………………………………………………………………3分⑶60%……………………………………………………………………………………4分20.解:联结AC ,作AC 中垂线,交CD 延长线于O ,则O 即为弓形所确定圆的圆心。
………………………………………………………………………………………1分 联结AO ,设半径为r ,则OA OC r ==,2OD OC CD r =-=-……………1分又OD AB ⊥∴OD 平分AB 即118422AD AB ==⨯=…………………2分 在Rt AOD 中,222OA AD OD =+∴()22242r r =+-………………3分解得 5r =…………………………………………………………………………2分答:这个弓形所确定圆的半径为5米…………………………………………………1分21.解:联结OD ,作OH CD ⊥于H 。
…………………………………………………1分 ∵1,5AE BE == ∴直径156AB =+=,半径1632OD =⨯=……………………1分 又 3OA OD ==∴312OE OA AE =-=-=………………………………………2分在Rt OHE 中,90OHE ∠=,45OEH AEC ∠=∠=∴sin 2sin 452OH OE OEH =⋅∠===2分 在Rt OHD 中,90OHD ∠=,HD ===…………………2分又 OH CD ⊥∴2CD HD ==2分第 2 页 共 3 页22.解:⑴6天………………………………………………………………………………1分 12天………………………………………………………………………………1分 ⑵略…………………………………………………………………………………2分,2分 ⑶()52412101000240000⨯+⨯⨯=…………………………………………………3分 答:最少要发放高温补贴共24万元……………………………………………………1分23.证明:作1OH AD ⊥于1H ,2OH BC ⊥于2H ,……………………………………2分则1OH ,2OH 分别为弦AD ,BC 的弦心距。
2024年上海市虹口区中考二模数学试题(解析版)

虹口区2023学年度初三年级第二次学生学习能力诊断练习数学 练习卷(满分150分,考试时间100分钟)注意:1.本练习卷含三个大题,共25题.答题时,请务必按答题要求在答题纸规定的位置上作答,在草稿纸、本练习卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]1. 下列各数中,无理数是( )A. B. 3.14159 C. D. 【答案】C【解析】【分析】本题主要考查的是对无理数定义的应用,熟练掌握理解无理数的定义是解此题的关键.根据无理数的定义(无理数是指无限不循环小数)判断即可.【详解】解:A、是分数,不是无理数,故本选项错误;B 、3.14159是小数,不是无理数,故本选项错误;C 是无理数,故本选项正确;D 、是循环小数,不是无理数,故本选项错误;故选C .2. 关于一元二次方程无实数根,则实数的取值范围是( )A. B. C. D. 【答案】D【解析】【分析】根据一元二次方程判别式与根情况的关系,列代数式求解即可.【详解】解:一元二次方程无实数根,的211 1.22111.2x 220x x m -+=m 1m <1m £m 1≥1m >220x x m -+=则判别式解得,故选:D .【点睛】此题考查了一元二次方程判别式与根情况的关系,解题的关键是掌握相关基础知识,一元二次方程的判别式,当时有两个不相等的实数根,当时,有两个相等的实数根,当时,无实数根.3. 已知二次函数,如果函数值随自变量的增大而减小,那么的取值范围是( )A. B. C. D. 【答案】A【解析】【分析】本题考查二次函数的性质,熟练掌握二次函数的增减性是解题关键.根据二次函数,可得函数图象开口向下,对称轴为,函数值随自变量的增大而减小,则,得以解答.【详解】解:二次函数,,函数图象开口向下,对称轴为,时,函数值随自变量的增大而减小,故选:A .4. 下列事件中,必然事件是( )A. 随机购买一张电影票,座位号恰好是偶数B. 抛掷一枚质地均匀的硬币,落地后反面朝上C. 在只装有2个黄球和3个白球的盒子中,摸出一个球是红球D. 在平面内画一个三角形,该三角形的内角和等于【答案】D【解析】【分析】本题考查是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断.的()224240b ac m ∆=-=--<1m >()200ax bx c a ++=≠24b ac ∆=-0∆>Δ0=Δ0<()24y x =--y x x 4x ≥4x ≤4x ≥-4x ≤-()24y x =--()24y x =--4x =y x 4x ≥()24y x =--10-< ∴()24y x =--4x =∴4x ≥y x 180︒【详解】解:A 、随机购买一张电影票,座位号是偶数,是随机事件;B 、抛掷一枚质地均匀的硬币,反面朝下,是随机事件;C 、在只装有2个黄球和3个白球的盒子中,摸出一个球是红球,是不可能事件;D 、在平面内画一个三角形,该三角形的内角和等于,是必然事件;故选D .5. 如图,在正方形中,点、分别在边和上,,,如果,那么的面积为( )A. 6B. 8C. 10D. 12【答案】B【解析】【分析】本题主要考查了正方形的性质,平行四边形的性质与判定,先根据正方形的性质得到,进而证明四边形是平行四边形,得到,则,最后根据三角形面积计算公式求解即可.【详解】解:∵四边形是正方形,∴,∵,∴四边形是平行四边形,∴,∴,∴,故选:B .6. 在中,,.如果以顶点为圆心,为半径作,那么与边所在直线的公共点的个数是( )A. 3个B. 2个C. 1个D. 0个.180︒ABCD E F BC AD 2BE =6AF =AE CF ABE 90AD BC AB CD ABE =∠=︒∥,,AECF 6AF CE ==8AB BC BE CE ==+=ABCD 90AD BC AB CD ABE =∠=︒∥,,AE CF AECF 6AF CE ==8AB BC BE CE ==+=1128822ABE S AB BE =⋅=⨯⨯=△ABCD Y 5BC =20ABCD S = C BC C C AD【答案】B【解析】【分析】本题考查了平行四边形的面积,直线与圆的位置关系d 、r 法则,熟练掌握法则是解题的关键.根据面积公式计算点C 到的距离d ,比较d 与半径的大小判断即可.【详解】解:如图,∵在平行四边形中,,,设点C 到的距离为d ,∴点C 到的距离,∴直线与圆C 相交,即有2个交点,故选:B .二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置]7.=___.【答案】﹣2【解析】【分析】根据立方根的定义,求数a 的立方根,也就是求一个数x ,使得x 3=a ,则x 就是a 的立方根.【详解】∵(-2)3=-8,,故答案为:-28. 分解因式:_______.【答案】【解析】【分析】根据平方差公式因式分解即可求解.【详解】解:AD BC ABCD 5BC =20ABCD S = AD AD 2054d =÷= 45BC<=AD 2-229a b -=()()33a b a b +-229a b -=()()33a b a b +-故答案为:.【点睛】本题考查了因式分解,熟练掌握因式分解的方法是解题的关键.9. 解不等式:,的解集为________.【答案】【解析】【分析】本题主要考查的是解一元一次不等式;按照去括号、移项、合并同类项、系数化为1的步骤解一元一次不等式即可求解.【详解】解:去括号,移项,合并同类项,化系数为1,故答案为:.10. 函数的定义域是 【答案】>【解析】【分析】定义域是指该函数的自变量的取值范围,根据二次根号下被开方数≥0;分式中分母不为0;即可解答.【详解】定义域是指该函数的自变量的取值范围,二次根号下被开方数≥0;分式中分母不为0;∴∴故答案为11. 将抛物线先向右平移3个单位,再向下平移4个单位后,所得到的新抛物线的表达式为________.【答案】【解析】【分析】本题主要考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并()()33a b a b +-()5232x x +≤+2x ≤()5232x x +≤+5263+≤+x x5362x x -≤-24x ≤2x ≤2x≤y =10x +>1x >-1x >-()221y x =-+()253y x =--用规律求函数解析式.根据平移规律“左加右减,上加下减”写出新抛物线解析式.【详解】解:抛物线先向右平移3个单位,再向下平移4个单位后,所得到的新抛物线的表达式为,即.故答案为:.12. 在一个不透明袋子中,装有2个红球和一些白球,这些球除颜色外其他都一样,如果从袋中随机摸出一个球是红球的概率为,那么白球的个数是________.【答案】6【解析】【分析】本题考查了概率的定义.解题的关键与难点在于理解概率的定义,求出球的总数.随机摸出一个球是红球的概率是,可以得到球的总个数,进而得出白球的个数.【详解】解:设红、白球总共n 个,记摸出一个球是红球为事件A ,,白球有个故答案为:.13. 某校为了解该校1200名学生参加家务劳动的情况,随机抽取40名学生,调查了他们的周家务劳动时间并制作成频数分布直方图,那么估计该校周家务劳动时间不少于2小时的学生大约有________名.【答案】780【解析】【分析】本题主要考查了用样本估计总体,根据条形统计图获取信息是解题的关键.根据条形统计图直接得出家务劳动时间不少于2小时的学生有26名,进而估计该校1200名学生参加家务劳动时间不少于2小时的学生人数即可求解.()221y x =-+()22314y x =--+-()253y x =--()253y x =--0.2520.25n=()20.25P A n==8n ∴=∴826-=6【详解】解:由题意得:被调查的40人中,家务劳动时间不少于2小时的学生有26名,该校周家务劳动时间不少于2小时的学生大约有(名),故答案为:780.14. 一根蜡烛长30厘米,点燃后匀速燃烧,经过50分钟其长度恰为原长的一半.在燃烧的过程中,如果设蜡烛的长为(厘米),燃烧的时间为(分钟),那么关于的函数解析式为________(不写定义域).【答案】【解析】【分析】本题主要考查由实际问题列一次函数的解析式,解题的关键是理解题意.根据题意先求出蜡烛燃烧的速度为(厘米/分),即可直接进行求解.【详解】解:由题意可得:蜡烛长30厘米,经过50分钟其长度恰为原长的一半,经过50分钟蜡烛燃烧的长度为15厘米,蜡烛燃烧的速度为(厘米/分),蜡烛的长为蜡烛燃烧前长度减去燃烧的长度,,故答案为:.15. 如图,正六边形螺帽的边长是,那么这个扳手的开口的值是______.【答案】【解析】【分析】本题考查解直角三角形,等腰三角形的性质,含角的直角三角形的性质.由螺帽是正六边形,可得是含角的直角三角形,再根据即可求出和.【详解】解:如图,连接,则,过点作于∴26120078040⨯=y t y t 300.3y t=-15500.3÷=∴∴15500.3÷=300.3y t \=-300.3y t =-4cm a 30︒ACD 30︒4AC =AD AB AB a AB =C CD AB ⊥D螺帽是正六边形,,.故答案为:16. 如图,在梯形中,,,点、分别是边、的中点,连接,设,,那么用向量、表示向量________.【答案】【解析】【分析】本题考查了平面向量的问题,熟练掌握三角形法则是解题的关键,根据梯形的中位线定理及向量的三角形法则解答即可.【详解】解:,,,,, 120ACB ∴∠=︒CD AB ⊥AC BC=1120602ACD ∴∠=⨯︒=︒AD BD =4AC = 4AD AC ∴===22a AB AD ∴===⨯=ABCD AD BC ∥2BC AD =E F AB CD AC AB a =AC b = a b EF = 3344a b -+ AB a = AC b =BC BA AC a b \=+=-+ ,2AD BC BC AD = ∥111222AD BC a b \==-+,点、分别是边、的中点,,,,故答案为:.17. 如图,在中,,,.点在边上,,以点为圆心,为半径作.点在边上,以点为圆心,为半径作.如果和外切,那么的长为________.【答案】##【解析】【分析】本题考查的是圆和圆的位置关系、解直角三角形的知识,作于点H ,连接,先求出,设,在中,根据勾股定理列方程即可解决.【详解】解:作于点H ,连接,,,,在中,,11112222DC DA AC AD AC a b b a b \=+=-+=-+=+ E F AB CD 111222EA BA AB a \==-=- 111244DF DC a b \==+ 11111332224444EF EA AD DF a a b a b a b æöæöç÷ç÷\=++=-+-+++=-+ç÷ç÷èøèø3344a b -+ ABCD Y 7AB =8BC =4sin 5B =P AB 2AP =P AP P Q BC Q CQ Q P Q CQ 37149214PH BC ⊥PQ 43PH BH ==,CQ a =Rt QPH △PH BC ⊥PQ 7AB = 2AP =725BP \=-=Rt BPH 4sin 5B =,,设,和外切,半径为2,,在中,,,解得:,故答案为:.18. 如图,在扇形中,,,点在半径上,将沿着翻折,点的对称点恰好落在弧上,再将弧沿着翻折至弧(点是点A 的对称点),那么的长为________.【答案】##【解析】【分析】本题考查翻折性质,圆的基本性质,等边三角形判定与性质、勾股定理的应用,连接,由翻折得,证出是等边三角形,设,在中,根据勾股定理列方程并解出进而求出结论.【详解】解:连接,455PH \=43PH BH \==,CQ a =P Qe Q P 2PQ a \=+Rt QPH △4,835PH HQ a a ==--=-()()222452a a ∴+-=+3714a =3714AOB 105AOB ∠=︒8OA =C OA BOC BC O D AB AD CD 1A D 1A 1OA 8-8-+OD 1105OB BD AC A C BOC BDC ==∠=∠=︒,,OBD AC a =Rt COD AC OD由翻折得:,,,是等边三角形,,,设,则,在中,,,解得:(舍去),,故答案为:.三、解答题:(本大题共7题,满分78分)19.先化简,再求值:,其中.【答案】【解析】【分析】本题主要考查分式的化简求值,分母有理化,掌握分式的基本性质与运算法则是解题的关键,注意化简过程中能因式分解要先因式分解.先算括号内的减法,把除法变成乘法,算乘法,最后代入求值即可.【详解】解:1105OB BD AC A C BOC BDC ==∠=∠=︒,,OC CD =OB OD = OBD ∴△60OBD ∴∠=︒3601051056090OCD \Ð=°-°-°-°=°AC a =1882OC a CD A O a =-==-,Rt COD 8OC CD a ==-()()222888a a ∴-+-=12888a a =-=+>(128288OA OA AC ∴=-=--=8-22214133m m m m m -+⎛⎫÷- ⎪++⎝⎭m 1m m -22214133m m m m m -+⎛⎫÷- ⎪++⎝⎭()()2134333m m m m m m -+⎛⎫=÷- ⎪+++⎝⎭;当.20. 解方程组:【答案】【解析】【分析】将第二个方程进行因式分解得到,然后令因式和因式分别为0即可求解.【详解】解:由题意可知: 对方程②进行因式分解得:即或∴原方程组化为 或 解得或故原方程组的解为:或.【点睛】本题考查了因式分解的方法及二元方程组,熟练掌握常见的二元一次方程组的解法是解决此类题的关键.21. 如图,一次函数图像在反比例函数图像相交于点和点,与轴交于点.点在反比例函数图像上,过点作轴的垂线交一次函数图像于点.()()21133m m m m m --=÷++()()21331m m m m m -+=⨯+-1m m-=m =1m m -222-620x y x xy y =⎧⎨--=⎩121242,22x x y y ==⎧⎧⎨⎨==-⎩⎩()(2)0+-=x y x y 2x y -x y +222-620x y x xy y =⎧⎨--=⎩①②()(2)0+-=x y x y 20x y -=0x y +=2620x y x y -=⎧⎨-=⎩260x y x y -=⎧⎨+=⎩1142x y =⎧⎨=⎩2222x y =⎧⎨=-⎩1142x y =⎧⎨=⎩2222x y =⎧⎨=-⎩(),2A m ()2,4B -y C ()1,D n -D x E(1)求反比例函数和一次函数的解析式;(2)求面积.【答案】(1)反比例函数为,一次函数解析式 (2)【解析】【分析】此题考查了反比例函数综合题,涉及的知识有:待定系数法确定反比例函数和一次函数解析式,三角形面积.()利用待定系数法求解即可;()先分别求出、、的坐标,进而利用三角形面积公式解答即可.【小问1详解】解:设反比例函数为,把点代入得,,∴反比例函数为,把点,点代入,得,,∴,,∴点,点,设一次函数解析式,的CDE 8y x=-2y x =--9212C D E k y x=()2,4B -k y x=428k =-⨯=-8y x=-(),2A m ()1,D n -8y x =-82m =-881n =-=-4m =-8n =()4,2A -()1,8D -y cx d =+把点,点代入得,解得,∴一次函数解析式;【小问2详解】∵一次函数解析式,∴把点代入,得,∴,∴点,∵轴,∴点横坐标为,把代入得,∴∴,∴22. 根据以下素材,完成探索任务.探究斜坡上两车之间距离素材1图①是某高架入口的横断面示意图.高架路面用表示,地面用表示,斜坡用表示.已知,高架路面离地面的距离为25米,斜坡长为65米.素如图②,矩形为一辆大巴车的侧面示意图,长为10米,长为的()4,2A -()2,4B -4224c d c d-=+⎧⎨=-+⎩12c d =-⎧⎨=-⎩2y x =--2y x =--()0,2C -,()1,D n -8y x =-881n =-=-8n =()1,8D -DE x ⊥E 1-1x =-2y x =--121y =-=-()1,1E --,189DE =+=119191222CDE S DE =⋅=⨯⨯= .BM AN AB BM AN ∥BM BH AB ECKG CK EC 3.5材2米.如图③,该大巴车遇堵车后停在素材1中的斜坡上,矩形的顶点与点重合,点与指示路牌底端点之间的距离为米,且.小张驾驶一辆小轿车跟随大巴车行驶,小张的眼睛到斜坡的距离为1米.任务一如图①,求斜坡的坡比.问题解决任务二如图③,当小张正好可以看到整个指示路牌(即、、在同一条直线上)时,试求小张距大巴车尾的距离.【答案】任务一:斜坡的坡比;任务二:米【解析】【分析】本题考查的是解直角三角形坡度坡角问题及相似三角形判定与性质,矩形判定与性质,任务一:根据勾股定理求出第三边进而求出坡度;任务二:作交延长线于点O ,作于点Q ,交于点R ,通过解直角三角形结合矩形判定与性质求出相关线段长度,再证明,根据性质求出结论即可.【详解】解:任务一:如图①,由题意得:在中,25米,斜坡长为65米,(米),斜坡的坡比;任务二:如图③,作交延长线于点O ,作于点Q ,交于点R ,为ECKG K B B P BP 6.5BP BM ⊥FD AB P E F EC CD AB 1:2.4i =12.5PO DB ⊥DB FQ PO ^CE FER FPQ ∽Rt ABH △BH AB 60AH \=∴AB 251:2.460BH i AH ===PO DB ⊥DB FQ PO ^CE则四边形为矩形,四边形为矩形,米,米,,为米,,解得:米,米,米,米,,,,,,解得:,经检验,是原方程的解,米.23. 如图,在中,,延长至点,使得,过点、分别作,,与相交于点,连接.CRQO FDCR,1RQ CO FR DC FD CR OQ\=====,3.51 2.5ER\=-=,90ABH PBO O HÐ=ÐÐ=Ð=°BP 6.525cos cos6.565BOPBO ABH\Ð==Ð=2.5BO=6PO\==615PQ∴=-=10 2.512.5RQ CO==+=,EC AB PQ AB^^ER PQ\∥FER FPQ\∽ER FRPQ FQ\=2.5512.5FRFR\=+12.5FR=12.5FR=12.5CD FR\==Rt ABC△90C∠=︒CB D DB CB=A DAE BC∥DE BA∥AE DE E BE(1)求证:;(2)连接交于点,连接交于点.如果,求证:.【答案】(1)证明见解析(2)证明见解析【解析】【分析】本题考查平行四边形的判定与性质,矩形的判定与性质,勾股定理等,解题的关键是掌握平行四边形和矩形的判定方法.(1)先证四边形是平行四边形,得出从而证出四边形是矩形,即可证明结论;(2)设,算出,证明,求出 ,进而证出结论;【小问1详解】证明:,,四边形是平行四边形,,,,又,点D 在的延长线上,,四边形是平行四边形,又,四边形是矩形,;【小问2详解】解:如图,BE CD ⊥AD BE F CE AD G FBA ADB ∠=∠AG AB =AEDB AE CB =AEBC EF BF a ==AE =AEG DCG V ∽△AGAB = AE BD DE BA ∥∴AEDB ∴AE BD = BD CB =∴AE CB = AE BD CB ∴AE CB ∥∴AEBC 90C ∠=︒∴AEBC ∴BE CD ⊥四边形是平行四边形,,设,,,,,,,,,,,在中,,,,在中,,AEDB ,EF BF AF DF \==EF BF a ==FBA ADB Ð=Ð tan tan FBA ADB \Ð=ÐAE BF BE BD\=AE BD = 222AE a \=AE ∴=BD BC AE \==AE CD AEG DCG \ ∽12AE AG CD DG \==Rt DBF △DF ==AD \=AG \=Rt ABC △AB ==.24. 新定义:已知抛物线(其中),我们把抛物线称为的“轮换抛物线”.例如:抛物线的“轮换抛物线”为.已知抛物线:的“轮换抛物线”为,抛物线、与轴分别交于点、,点在点的上方,抛物线的顶点为.(1)如果点的坐标为,求抛物线的表达式;(2)设抛物线的对称轴与直线相交于点,如果四边形为平行四边形,求点的坐标;(3)已知点在抛物线上,点坐标为,当时,求的值.【答案】(1) (2) (3)或【解析】【分析】本题考查的是二次函数综合题,重点考查二次函数的性质、平行四边形性质及相似三角形性质,(1)将点代入表达式,求出m 的值,根据“轮换抛物线”定义写出即可;AG AB \=AG AB \=2y ax bx c =++0abc ≠2y cx ax b =++2y ax bx c =++2231y x x =++223y x x =++1C ()2445y mx m x m =+-+2C 1C 2C y E F E F 2C P E ()0,12C 2C 38y x =+Q PQEF E ()4,M n -2C N 12,72⎛⎫-- ⎪⎝⎭PMN PEF △∽△m 241y x x =+-20,3E ⎛⎫- ⎪⎝⎭1m =-1732()0,1E(2)根据轮换抛物线定义得出抛物线表达式及点E 、F 坐标,并求出P 、Q 坐标,根据平行四边形性质得出列方程并解出m 值,进而解决问题;(3)先求,结合求出的点P 、E 、F 坐标得出及,根据相似三角形性质得出关于m 的方程,解方程即可解决.【小问1详解】解:抛物线:与轴交于点坐标为,当,代入,得,,抛物线表达式为,抛物线的“轮换抛物线”为表达式为;【小问2详解】解:抛物线:,当时,,即与y 轴交点为,抛物线:的“轮换抛物线”为,抛物线表达式为,同理抛物线与y 轴交点为,抛物线对称轴为直线,当时,,抛物线的顶点坐标为,当时,,抛物线的对称轴与直线交点,点在点的上方,,解得:,2C PQ EF =()4,45M m --2PN 2PF 1C ()2445y mx m x m =+-+y E ()0,10x =1y =1m =451m \-=-∴1C 241y x x =-+∴1C 2C 241y x x =+-1C ()2445y mx m x m =+-+0x =y m =()0,E m 1C ()2445y mx m x m =+-+2C ∴2C ()2445y mx mx m =++-2C ()0,45F m -2C 422m x m=-=-2x =-5y =-∴2C ()25P --,2x =-382y x =+=∴2C 38y x =+()2,2Q - E F 45m m \>-53m <,四边形为平行四边形,,即,解得:,;【小问3详解】解:点在抛物线上,当时,,即,点坐标为,,,,,,,,,,解得:.25. 在梯形中,,点在射线上,点在射线上,连接、相交于点,.()4553EF m m m \=--=- PQEF PQ EF \=()2553m --=-23m =-20,3E ⎛⎫∴- ⎪⎝⎭ ()4,M n -2C 4x =-()244545y mx mx m m =++-=-()4,45M m -- N 12,72⎛⎫-- ⎪⎝⎭()25P --,()0,E m ()0,45F m -()222125225724PN æöç÷\=-++-+=ç÷èø()()22222455416PF m m =-+-+=+()115325322PEF P S EF x m m =×=-´=- ()111557242222PMN M P S PN x x æöç÷=×-=´-+´-+=ç÷èø PMN PEF ∽222PEF PMN S PF PF S PN PN æöç÷\==ç÷èø 25341652524m m -+\=12171,32m m =-=ABCD AD BC ∥E DA F AB CE DF P EPF ABC ∠=∠(1)如图①,如果,点、分别在边、上.求证:;(2)如图②,如果,,,.在射线的下方,以为直径作半圆,半圆与的另一个交点为点.设与弧的交点为.①当时,求和的长;②当点为弧的中点时,求的长.【答案】(1)见解析(2)①;;②【解析】【分析】(1)根据等腰梯形的性质可得,,,根据三角形的外角性质得出,进而可得,即可证明,根据相似三角形的性质,即可求解;(2)①同(1)证明,如图所示,过点作于点,连接,得出,,解直角三角形,分别求得,,进而根据相似三角形的性质求得的长;②根据题意画出图形,根据垂径定理得出,根据题意可设,,则,得出,设,则,则,在中,得出,根据得出,即可求解.【小问1详解】证明:∵梯形中,,,∴,,,又∵,∴AB CD =E F ADAB AF DF DE CE =AD CD ⊥5AB =10BC =3cos 5ABC ∠=DA DE O O CE G DF EG Q 6DE =EG AF Q EG AF EG =215AF =15B DCB DCE BCE ∠=∠=∠+∠A EDC ∠=∠DEC BCE ∠=∠FPE CED EDP ∠=∠+∠ADF DCE ∠=∠ADF DCE ∽ADF PDE ∽A AM BC ⊥M DG cos DEC ∠=sin DEC ∠=EG EP AF OQ EQ ⊥EPF ABC α∠=∠=ODQ OQD β∠=∠=90αβ+=︒43tan tan 34αβ==12FR a =9AR a =15AF a =Rt DFR 16DR a =1697AD DR AR a a a =-=-=1a =ABCD AD BC ∥AB CD =B DCB DCE BCE ∠=∠=∠+∠A EDC ∠=∠DEC BCE ∠=∠FPE CED EDP ∠=∠+∠EPF ABC∠=∠ADF DCE∠=∠∴,∴;【小问2详解】解:∵,∵,则∴∴∵∴又∵∴,如图所示,过点作于点,连接,∵,∴,则,,∵∴∵∴又∵∴,在中,∴∴,ADF DCE ∽AF DF DE CE=EPF ABC ∠=∠DPC EPF∠=∠180FPC DPC ∠+∠=︒180FPC B ∠+∠=︒180ECB PFB ∠+∠=︒ECB AFD∠=∠AD BC∥ECB DEC∠=∠EDP FDA∠=∠ADF PDE ∽A AM BC ⊥M DG 5AB =3cos 5ABC ∠=3BM =4AM =4sin 5AM ABC AB ∠==,AD BC AD CD⊥∥4CD AM==10BC =1037AD MC BC BM ==-=-=6DE =1AE=Rt EDC 6,4ED CD ==EC ===cos DE DEC EC ∠===sin DC DEC EC ∠===∵为直径∴∴,∴,∵∴∴②过点作于点,∵∴∵∴设,,则ED 90DGE ∠=︒cos 6EG ED DEC =⨯∠==sin 6DG ED DEC =∠==sin sin DG DG PD DPG ABC ====∠∠3cos 5PG PD DPG =∠==EP EG PG =-=ADF PDE∽AF AD PE PD=215D A PE AF PD ⋅===F FR AD ⊥R EQGQ =OQ EQ⊥OQ OD=ODQ OQD∠=∠EPF ABC α∠=∠=ODQ OQD β∠=∠=90αβ+=︒∵,则设,则∴∵∴设,则,∴,在中,∴又∵∴∴【点睛】本题考查了解直角三角形,等腰梯形的性质,相似三角形的性质与判定,垂径定理,熟练掌握以上知识是解题的关键.3cos os cos 5DPG EPF ABC ∠=∠=∠=35PG PD =3,5PG k PD k ==4GD k =43tan tan 34αβ==AD BC∥RAF α∠=12FR a =9AR a =15AF a =Rt DFR 3tan 4RF DR β==16DR a=1697AD DR AR a a a =-=-=7=1a =15AF =。
虹口区2010年初三数学分层练习2(A卷)

虹口区2009学年度第二学期初三数学分层练习2(A 卷)(考试时间:100分钟, 满分150分)2010.3考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一.选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填写在答题纸的相应位置上】1.O 中,弦AB 长为6厘米,圆心O 到AB 的距离为4厘米,则O 的半径长为 A .3厘米; B .4厘米; C .5厘米; D .6厘米. 2.下列命题中,正确的是A .直径是圆内最长的弦;B .三点确定一个圆;C .平分弦的直径垂直于弦;D .如果弦相等,那么弦所对的弧相等. 3.正多边形的中心角与这个正多边形的一个内角的关系是A .互余;B .互补;C . 相等;D .不确定.4.为了了解某区3万名学生参加中考的情况,有关部门从中抽取了600名学生的成绩进行统计分析,这个问题中表达正确的是 A .样本容量是600; B .每个考生是个体; C .3万名考生是总体; D .600名考生是总体的一个样本. 5.依据某校九年级一班体育毕业考试中全班所有学生成绩制成的频数分布直方图,则成绩在21.5~24.5这一分数段的频数和频率分别是 A .4,0.1; B .10,0.1 ;C .10,0.2;D .20,0.2.6.下列调查方式,适合的是A .要了解一批灯泡的寿命,采用普查方式;B 采用普查方式;C .要保证“神舟六号”载人飞船成功发射, 对重要零部件的检查采用抽样调查方式;D .要了解人们对环境的保护意识,采用抽样调查方式. 二.填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置】7.一次考试中,7名学生成绩如下(单位:分):36,92,45,68,72,95,86,则这组数据的中位数是 ▲ . 8.一组数据14x =,25x =,36x =,47x =,51x =,他们出现的次数依次是2,3,2,1,4,则这组数据的众数是 ▲ .27.524.521.518.5第5题图 学校_______________________班级_____________姓名___________________学号___________……………………………………………………………………………………………………………………………………………………………9.已知甲、乙两组数据的平均数相同,若甲组数据的方差为0.155,乙组数据的方差为0.105,则数据波动较大的为 ▲ 组.(填“甲”或“乙”) 10.把50个数据分成4组,第一组频率为0.3,第二组频率为0.24,第三组频率为0.2,那么第四组共有 ▲ 个数据.11.数据12,10,9,8,11的标准差是 ▲ .12.已知O 半径为6.5厘米,圆心O 到直线l 的距离为9厘米,则直线l 和O 的位置关系为 ▲ .13.正三角形的外接圆半径为R ,则正三角形的边长为 ▲ .14.已知1O 的半径为3厘米,2O 的半径为4厘米,两圆的圆心距12O O 为1厘米,则这两圆的位置关系是 ▲ . 15.在数轴上,点A 所表示的实数为3,点B 所表示的实数为a ,A 的半径为2,当5a >时,则点B 与A 的位置关系是 ▲ .16.已知O 半径为5,弦8AB =,P 是弦AB 上任意一点,则OP 长的取值范围是 ▲ .17.相交两圆的公共弦长为6,两圆半径分别为5,6,则这两圆的圆心距为 ▲ .18.ABC 为O 的内接三角形,且 AB AC =,已知O 的直径为10,8BC =,则ABC 的BC 边上的高为 ▲ . 三.解答题:(本大题共7题,满分78分)19.(本题满分10分,第⑴题3分,第⑵题3分,第⑶题4分)随着网络的普及,越来越多的人喜欢网上购物.某公司对某个网站2005到2009网上商店的数量和购物顾客人次进行调查,根据调查,将五年来该网站网上商店的数量和每个网上商店年平均购物顾客人次分别制成了折线统计图(如图1)和条形统计图(如图2),请你根据统计图提供的信息完成下列填空:⑴2005年该网站共有网上商店 ▲ 个;⑵2009年该网站网上购物顾客共有 ▲ 万人次; ⑶对于该网站网上商店的数量,如果20072008-年的年增长率与20082009-年的年增长率相同,那么该年增长率是 ▲ .20.(本题满分10分)如图,弓形是一条隧道的横截面,弦8AB =米,弓形高2CD =米,求这个弓形所确定的圆的半径. 21.(本题满分10分)如图,已知O 的直径AB 与CD 相交于点E ,1AE =,5BE =,45AEC ∠= ,求CD 的长;22.(本题满分10分,第⑴题2分,第⑵题4分,第⑶题4下图是某市2009年夏季连续60天日最高气温统计图的一部分.根据下图提供的信息,回答下列问题:⑴若日最高气温为40C 及其以上的天数是日最高气温为30C~35C的天数的2倍,那么日最高气温为30C~35C的天数有 ▲ 天,日最高气温为40C及其以上的天数有 ▲ 天;⑵补全该条形统计图;(补在答题纸上)⑶《某市高温天气劳动保护办法》规定,劳动者在37C及其以上的高温天气下工作,除用人单位全额支付工资外,还应享受高温补贴,具体补贴标准如下表:某建筑企业2009年有职工人,在2009年夏季这连续统计日最高气温的天里,试求该企业最少要发放高温补贴共多少元?D CB A 第20题图23.(本题满分12分)如图,在O 中,弦AD 、BC 相交于点E , 且AB CD =,求证:OE 平分AEC ∠;24.(本题满分12分,第⑴题4分,第⑵题4分,第⑶题4分)某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后,做出统计图,甲同学计算前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频率比为4:17:15,结合统计图回答下列问题:⑴这次共抽调了多少人? ⑵若跳绳次数不小于130次为 优秀,则这次测试成绩优秀率为多少?⑶这次跳绳测试成绩的中位数落在哪一组?25.(本题满分14分,第⑴题4分,第⑵题6分,第⑶题4分)如图,已知在等腰直角ABC 中,90C ∠=,2AC =,M 是AC 上一点,过点M 的直线交CB 的延长线于N ,交边AB 于点P ,且AM BN =, ⑴求证:MP NP =;⑵设AM x =,四边形MCBP 的面积为y ,求y 与x 的函数解析式,并写出函数的定义域; ⑶试探索:以线段CM 为直径的圆能否与边AB 相切?如果能够相切,请求出x 的值;若不能相切,请说明理由.M PNBCA15014013012011010090(每组含最小值,不含最大值)第23题图第24题图。
二模25题
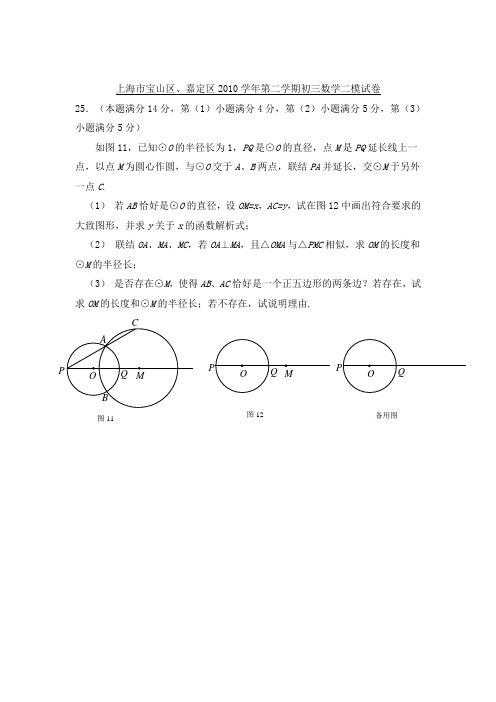
上海市宝山区、嘉定区2010学年第二学期初三数学二模试卷25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知⊙O 的半径长为1,PQ 是⊙O 的直径,点M 是PQ 延长线上一点,以点M 为圆心作圆,与⊙O 交于A 、B 两点,联结PA 并延长,交⊙M 于另外一点C .(1) 若AB 恰好是⊙O 的直径,设OM=x ,AC=y ,试在图12中画出符合要求的大致图形,并求y 关于x 的函数解析式;(2) 联结OA 、MA 、MC ,若OA ⊥MA ,且△OMA 与△PMC 相似,求OM 的长度和⊙M 的半径长;(3) 是否存在⊙M ,使得AB 、AC 恰好是一个正五边形的两条边?若存在,试求OM 的长度和⊙M 的半径长;若不存在,试说明理由.图12 Q POM备用图QPOA B 图11C Q P O M2010学年第二学期奉贤区调研测试2011. 0425.(本题满分14分,第(1)、(2)小题每小题满分5分,第(3)小题满分4分)已知,在边长为6的正方形ABCD 的两侧如图作正方形BEFG 、正方形DMNK ,恰好使得N 、A 、F 三点在一直线上,联结MF 交线段AD 于点P ,联结NP ,设正方形BEFG 的边长为x ,正方形DMNK 的边长为y ,(1)求y 关于x 的函数关系式及自变量x 的取值范围; (2)当△NPF 的面积为32时,求x 的值;(3)以P 为圆心,AP 为半径的圆能否与以G 为圆心,GF 为半径的圆相切,若能请求x 的值,若不能,请说明理由。
A B CD E FG M N K P 第25题图上海市虹口区2010学年第二学期初三数学二模试卷25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,在Rt△ABC 中,∠BAC = 90°,AB =3,AC =4,AD 是BC 边上的高,点E 、F 分别是AB 边和AC 边上的动点,且∠EDF = 90°. (1)求DE ︰DF 的值;(2)联结EF ,设点B 与点E 间的距离为x ,△DEF 的面积为y ,求y 关于x 的函数解析式,并写出x 的取值范围;(3)设直线DF 与直线AB 相交于点G ,△EFG 能否成为等腰三角形?若能,请直接写出线段BE 的长;若不能,请说明理由.第25题图BCD EFA 备用图1BCD备用图2BCDAA上海市黄浦区2010学年第二学期初三数学二模试卷25.(本题14分)如图11,在△ABC 中,A C B ∠=︒90,2AC BC ==,M 是边A C的中点,C H B M ⊥于H .(1)试求sin M C H ∠的值; (2)求证:A B M C A H ∠=∠;(3)若D 是边AB 上的点,且使△AH D 为等腰三角形,请直接写出A D 的长为________.MABCD H (图11)上海市金山区2010学年第二学期初三数学二模试卷25.(本题满分14分)如图,正方形ABCD 的边长是4,M 是AD 的中点.动点E 在线段AB 上运动.连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连接EG 、FG . (1)求证:GEF ∆是等腰三角形;(2)设x AE =时,EGF ∆的面积为y .求y 关于x 的函数关系式,并写出自变量x 的取值范围;(3)在点E 运动过程中GEF ∆是否可以成为等边三角形?请说明理由.错误!未指定书签。
虹口区初中二模数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √-4B. √9C. √16D. √252. 已知x²=1,那么x的值为()A. 1B. -1C. 1或-1D. 03. 下列函数中,是反比例函数的是()A. y=2x+3B. y=3/xC. y=x²D. y=2x4. 在直角坐标系中,点A(2,3)关于x轴的对称点是()A. A(2,-3)B. A(-2,3)C. A(-2,-3)D. A(2,6)5. 已知等腰三角形底边长为6cm,腰长为8cm,那么这个三角形的周长是()A. 20cmB. 24cmC. 26cmD. 28cm6. 下列各式中,正确的是()A. (a+b)²=a²+2ab+b²B. (a-b)²=a²-2ab+b²C. (a+b)²=a²-2ab+b²D. (a-b)²=a²+2ab-b²7. 下列各数中,无理数是()A. √2B. √4C. √9D. √168. 已知x=√3,那么x²的值为()A. 3B. √3C. 1D. 09. 下列函数中,是正比例函数的是()A. y=2x+3B. y=3/xC. y=x²D. y=2x10. 在平面直角坐标系中,点P(-3,2)关于原点的对称点是()A. P(3,-2)B. P(-3,-2)C. P(3,2)D. P(-3,2)二、填空题(每题3分,共30分)11. 已知x=√3,那么x²+2x+1的值为______。
12. 下列函数中,y=kx+b(k≠0)是反比例函数的条件是______。
13. 在直角三角形ABC中,∠C=90°,AB=10cm,BC=6cm,那么AC的长度是______cm。
14. 已知等差数列{an}中,a1=3,公差d=2,那么第10项an的值为______。
2010上海中考二模真题综合复习二

中考二模真题综合复习二(2010上海中考)嘉定,虹口,长宁,杨浦,普陀,卢湾【填空选择】1.如果直线上一点与一个圆的圆心的距离等于这个圆的半径,那么这条直线与这个圆的位置关系是( )(A )相交; (B )相切; (C )相交或相切; (D )以上都不正确. 2. 已知P 是△ABC 内一点,联结PA 、PB 、PC ,把△ABC 的面积三等分,则P 点一定是( ) A. △ABC 的三边的中垂线的交点 B. △ABC 的三条内角平分线的交点 C. △ABC 的三条高的交点 D. △ABC 的三条中线的交点3.一个面积为20的矩形,若长与宽分别为y x ,,则y 与x 之间的关系用图像可表示为……………………………………………………………( )4.如图1,在矩形ABCD 中,1=AB ,2=AD ,点E 在边DC 上,联结AE ,将△AED 沿折痕AE 翻折,使点D 落在边BC 上的1D 处,那么=∠EAD 度.5. 如图2,把矩形纸条A B C D 沿EF 、G H 同时折叠,B 、C 两点恰好落在A D 边的P 点处,若90FPH = ∠,8P F =,6PH =,则矩形A B C D 的边B C 长为 .6. 已知平行四边形A B C D 中,点E 是B C 的中点,在直线B A 上截取2B F A F =,EF 交BD 于点G ,则G B G D= .7. 一人群中,如果有一人患流感,经过两轮传染后共有121人患了流感,设每轮传染中平均一个人传染x 人,则列出关于x 的方程是 。
8. 如图,已知O 是△ABC 内一点,AO AD 41=,BO BE 41=,CO C 41=F .设a AB =,b BC =,则用向量b a ,表示F D = 。
A .B .C .D .yx Oyx O yx O yxO ABCD E1D图1E PGHF BA CD 图2MBAD C第9题FBAOE DC第8题9. 在R t △ABC 中,∠A<∠B,CM 是斜边AB 上的中线,将△ACM 沿直线CM 翻折,点A 落在D 处,若CD 恰好与AB 垂直,则∠A = 度。
2010上海中考二模数学压轴题精选
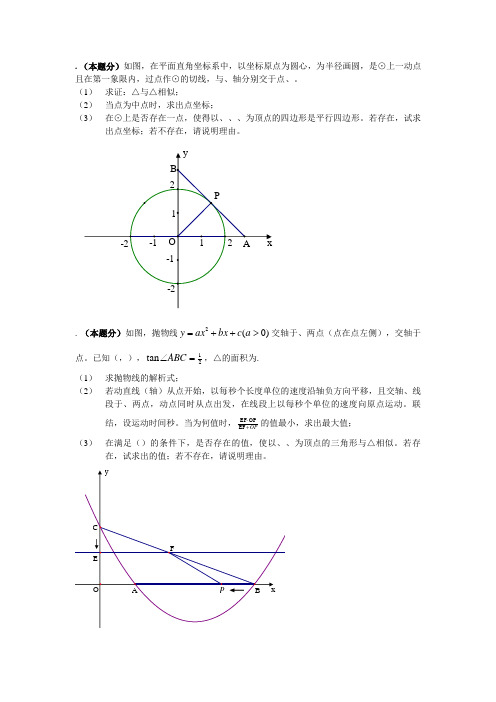
. (本题分)如图,在平面直角坐标系中,以坐标原点为圆心,为半径画圆,是⊙上一动点且在第一象限内,过点作⊙的切线,与、轴分别交于点、。
(1) 求证:△与△相似;(2) 当点为中点时,求出点坐标;(3) 在⊙上是否存在一点,使得以、、、为顶点的四边形是平行四边形。
若存在,试求出点坐标;若不存在,请说明理由。
Py xB A O 2121-1-1. (本题分)如图,抛物线)0(2>++=a c bx ax y 交轴于、两点(点在点左侧),交轴于点。
已知(,),21tan =∠ABC ,△的面积为.(1) 求抛物线的解析式;(2) 若动直线(轴)从点开始,以每秒个长度单位的速度沿轴负方向平移,且交轴、线段于、两点,动点同时从点出发,在线段上以每秒个单位的速度向原点运动。
联结,设运动时间秒。
当为何值时,OP +⋅EF OPEF 的值最小,求出最大值;(3) 在满足()的条件下,是否存在的值,使以、、为顶点的三角形与△相似。
若存在,试求出的值;若不存在,请说明理由。
y.(本题满分分,每小题各分)已知,矩形在平面直角坐标系中位置如图所示,的坐标)0,4(,的坐标)20(-,,直线x y 32-=与边相交于点,()求点的坐标;()抛物线c bx ax y ++=2()在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点 若不存在,请说明理由。
第题图x 32.(本题满分分,第()小题分,第()小题分,第()小题分)已知:在Rt ABC △中,∠°,,,过点A 作直线⊥,点是直线上的一个动点, ()如图,如果点是射线上的一个动点(不与点重合),联结交于点.若为x ,为y ,求关于的函数解析式,并写出它的定义域;() 在射线上是否存在一点,使以点、、组成的三角形与△相似,若存在求的长,若不存在,请说明理由;()如图,过点作⊥,垂足为D ,以点为圆心,若以为半径的⊙与以为半径的⊙相切,求⊙的半径.. (本题分)已知点是函数x y 21=(>)图像上一点,⊥轴于点,交函数xy 1=(>)图第题图像于点, ⊥轴于点,交函数xy 1(>)图像于点.(点、不重合) ()当点的横坐标为时,求△的面积; ()证明:‖;(如图)()试问:△能否为直角三角形?若能,请求出此时点的坐标;若不能,请说明理由.、(本题分)如图,一把“型”尺(图),其中⊥,将这把“型”尺放置于矩形中(其中),使边始终经过点,且保持,“型”尺在绕点转动的过程中,直线交边、于、两点.(图)()试问线段与的长度关系如何?并说明理由;()当△是等腰直角三角形时,求线段的长;()设,试求关于的函数解析式,并写出函数定义域.(图) (图).(本题满分分,每小题满分各分)在直角坐标平面内,O为原点,二次函数2y x bx c=-++的图像经过(,)和点(,),顶点为。
虹口区中考二模数学试卷

一、选择题(本大题共10小题,每小题3分,共30分)1. 下列各数中,不是有理数的是()A. 3.14B. √9C. -2D. √22. 若a=3,b=-2,则下列等式中不成立的是()A. a+b=1B. a-b=5C. a×b=-6D. a÷b=-1.53. 已知函数f(x)=2x+1,若f(2)=7,则f(x)的图象是()A.B.C.D.4. 在直角坐标系中,点A(2,3)关于y轴的对称点是()A.(-2,3)B.(2,-3)C.(-2,-3)D.(2,3)5. 下列各式中,正确的是()A. a²+b²=c²B. (a+b)²=a²+2ab+b²C. (a-b)²=a²-2ab+b²D. (a+b)³=a³+3a²b+3ab²+b³6. 已知等差数列{an}的前三项分别为2,5,8,则该数列的通项公式为()A. an=3n-1B. an=3n+1C. an=3nD. an=3n²7. 在△ABC中,∠A=60°,∠B=45°,则∠C的度数为()A. 45°B. 60°C. 75°D. 90°8. 若a,b,c是△ABC的三边,且满足a²+b²=c²,则△ABC是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 钝角三角形9. 已知二次函数y=ax²+bx+c的图象开口向上,且顶点坐标为(-1,2),则下列结论正确的是()A. a>0,b<0,c>0B. a>0,b>0,c<0C. a<0,b<0,c>0D. a<0,b>0,c<010. 下列关于函数y=2x-1的描述正确的是()A. 图象是一条斜率为2的直线B. 图象是一条斜率为-1的直线C. 图象是一条斜率为2的平行线D. 图象是一条斜率为-1的平行线二、填空题(本大题共10小题,每小题3分,共30分)11. 若a=2,b=-3,则a²+b²的值为______。
虹口二模初三数学试卷答案

一、选择题(每题4分,共20分)1. 已知函数f(x) = x^2 - 4x + 3,那么f(2)的值为:A. -1B. 0C. 3D. 5答案:B解析:将x=2代入函数f(x)中,得到f(2) = 2^2 - 42 + 3 = 4 - 8 + 3 = -1。
2. 在直角坐标系中,点A(2,3)关于x轴的对称点B的坐标为:A. (2,-3)B. (-2,3)C. (2,3)D. (-2,-3)答案:A解析:点A关于x轴对称,意味着横坐标不变,纵坐标取相反数,所以B的坐标为(2,-3)。
3. 下列方程中,只有一个解的是:A. x + 2 = 0B. x^2 - 4 = 0C. x^2 + 2x + 1 = 0D. x^2 - 4x + 3 =答案:B解析:方程x^2 - 4 = 0可以分解为(x+2)(x-2)=0,所以x有两个解x=-2和x=2。
其他选项至少有两个解。
4. 一个等腰三角形的底边长为8cm,腰长为10cm,那么这个三角形的面积为:A. 40cm^2B. 48cm^2C. 50cm^2D. 64cm^2答案:B解析:作高AD,则AD垂直于BC,且BD=DC=4cm,所以三角形ABD和三角形ACD是两个等腰直角三角形。
由勾股定理得到AD=√(10^2-4^2)=√(100-16)=√84=2√21cm。
所以三角形ABC的面积为1/2BCAD=1/282√21=8√21cm^2≈48cm^2。
5. 已知函数f(x) = kx + b,若f(1) = 3,f(2) = 5,那么k和b的值为:A. k=1, b=2B. k=1, b=3C. k=2, b=1D. k=2, b=3答案:B解析:根据题意,列出方程组:k + b = 32k + b = 5解得k=1,b=2,所以答案为B。
二、填空题(每题5分,共20分)6. 若a+b=5,a-b=1,则a^2+b^2的值为______。
答案:26解析:将a+b=5和a-b=1相加,得到2a=6,所以a=3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
虹口区2010年中考数学模拟练习卷(满分150分,考试时间100分钟)2010.4考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]1.小杰于3月26日20:00,在“百度”搜索引擎中输入“上海世博会”,能搜索到与之相关的网页约23 800 000个,将这个数字用科学记数法表示为 A.2.38×105 ; B.2.38×106; C.2.38×107; D.2.38×108. 2. 下列运算中,正确的是A.326()xy xy = ; B.3412x x x ⋅= ; C.235()x x x -=; D.()32626xx -=-.3. 把不等式组2020x x +>⎧⎨-≤⎩的解集表示在数轴上,正确的是4. 在一次射击测试中,甲、乙、丙、丁的平均环数相同,而方差分别为8.7、6.5、9.1、7.7,则这四人中,射击成绩最稳定的是A .甲;B .乙;C .丙;D .丁. 5.在下列关于向量的等式中,正确的是[来源:学§科§网Z §X §X §K]A.AB BC CA =+ ; B.AB BC CA =-; C.AB CA BC =- ; D.0AB BC CA ++= .6. 下列命题中不是真命题的是A .两组对边分别相等的四边形是平行四边形;B .对角线相等的平行四边形是矩形;C .一组邻边相等的平行四边形是菱形;D .一组对边平行的四边形是梯形. 二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置] 7. 计算:(1)(1)x x +-= ▲ .A B C D图38. 如果关于x 的方程220x x m -+=有两个相等的实数根,那么m 的值是 ▲. 9. 1=的根是 ▲ .10. 在函数11y x =-中,自变量x 的取值范围是 ▲ . 11. 已知一次函数21y x =+,则函数值y 随自变量x 的增大而 ▲ .(填“增大”或“减小”).12. 二次函数221y x x =+-的图像的顶点坐标是 ▲ .13. 某种品牌的手机经过四、五月份连续两次降价,每部售价由3200元降到了2500元.如果每个月降价的百分率相同,并设该百分率为x ,那么根据题意列出关于x 的方程是 ▲ .14. 布袋里有2个红球、3个黄球、4个白球,它们除颜色外其他都相同.从布袋里任意摸出一个球恰好是黄球的概率是 ▲ . 15. 如图1,直线a ∥b ,直线c 与a 、b 相交,若170∠=︒,则2∠的度数是 ▲ . 16. 如果两个相似三角形的面积比是1:4,那么它们对应的角平分线比是 ▲ . 17. 如图2,把矩形纸条ABCD 沿EF 、GH 同时折叠,B 、C 两点恰好落在AD 边的P 点处,若90FPH = ∠,8PF =,6PH =,则矩形ABCD 的边BC 长为 ▲ .18. 已知平行四边形ABCD 中,点E 是BC 的中点,在直线BA 上截取2BF AF =,EF 交BD 于点G ,则GBGD= ▲ .三、解答题(本大题共7题,满分78分)[来源:学*科*网] 19.(本题满分10分)先化简,再求值:22121126x x x x x ++⎛⎫-÷ ⎪+--⎝⎭,其中3x =-.20.(本题满分10分) 解方程:211()60x x x x+++-=.21.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)如图3,在菱形ABCD 中,120ADC ∠=︒,过点C 作CE AC ⊥且与AB 的延长线交于点E . (1)求证:四边形AECD 是等腰梯形; (2)若4AD =,求梯形AECD的面积.图2 a b c 图122.(本题满分10分,第(1)小题满分3分,第(2)小题满分2分,第(3)小题满分3分,第(4)小题满分2分)下表1是三峡水库2009年1-12月平均水位情况.小杰根据表1中的数据,在平面直角坐标系中以月份(月)为横坐标、月平均水位(米)为纵坐标描出了部分点(如图4),并绘制了不完整的频数分布直方图(如图5).请根据表1与图4、5中提供的信息,回答下列问题:(1)根据表1,补全图4、图5;(2)根据图4,可知平均水位相比其上个月平均水位上升最大的月份是▲月;(3)在2009年三峡水库1—12月各月的平均水位中,众数是▲米,中位数是▲米;(4)观察图4中1-4月这些点的发展趋势,猜想1-4月y与x之间可以存在怎样的函数关系,请你用所学过的函数知识直接写出该函数关系式(不要求写定义域).[23.(本题满分12分,第(1)小题满分7分,第(2)小题满分3分,第(3)小题满分2分)如图6-8中,点E、D分别是正三角形ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE CD=,DB延长线交AE于点F.(1)求图6中AFB∠度数,并证明2CD BD EF=⋅;(2)图7中AFB∠的度数为▲,图8中AFB∠度数为▲,在图7、图8中,(1)中的等式▲;(填“成立”或“不成立”,不必证明)(3)若将条件“正三角形、正四边形、正五边形”改为“正n边形”,其它条件不变,则AFB∠度数为▲.(可用含n的代数式表示,不必证明)图4图5(每组仅含最小值,不含最大值)CAF24.(本题满分12分,第(1)小题满分5分,第(2)小题满分4分,第(3)小题满分3分)已知等腰OAB ∆在平面直角坐标系中的位置如图9,点A坐标为,点B 坐标为(4,0).(1)若将OAB ∆沿x 轴向左平移m 个单位,此时点A恰好落在反比例函数y =的图像上,求m 的值;(2)若将OAB ∆绕点O 顺时针旋转30︒,点B 恰好落在反比例函数ky x=的图像上,求k 的值;(3)若将OAB ∆绕点O 顺时针旋转α度(0<α<180)到OA B ''∆位置,当点A '、B '恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点A '、B '且以y 轴为对称轴的抛物线解析式.25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)如图10,在直角梯形ABCD 中,//AD BC ,90C ∠=︒,,12=BC 18=AD ,10=AB .动点P 、Q 分别从点D 、B 同时出发,动点P 沿射线DA 的方向以每秒2个单位长的速度运动,动点Q 在线段BC 上以每秒1个单位长的速度向点C 运动,当点Q 运动到点C 时,点P 随之停止运动.设运动的时间为t (秒).(1)当点P 在线段DA 上运动时,联结BD ,若ABP ∠=ADB ∠,求t 的值; (2)当点P 在线段DA 上运动时,若以BQ 为直径的圆与以AP 为直径的圆外切,求t 的值;(3)设射线PQ 与射线AB 相交于点E ,AEP ∆能否为等腰三角形?如果能,请直接写出t 的值;如果不能,请说明理由.CDBAQP图10CDBA 备用图1CDBA备用图22010年虹口区中考数学模拟练习卷答案要点与评分标准说明:1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;2.第一、二大题若无特别说明,每题评分只有满分或零分;3.第三大题中各题右端所注分数,表示考生正确做对这一步应得分数;4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半; 5.评分时,给分或扣分均以1分为基本单位.一、选择题:(本大题共6题,满分24分)1.C ; 2.C ; 3.D ; 4.B ; 5.D ;6.D . 二、填空题:(本大题共12题,满分48分)7.21x - ; 8.1; 9.2x =-; 10.1x ≠;11.增大; 12.(1,2)--; 13.23200(1)2500x -=; 14.13; 15.70°; 16.1:2; 17.24; 18.25或23.三、解答题:(本大题共7题,满分78分)19. 解:原式221(1)2(2)(3)x x x x x +-+=÷++- ···································································· (3分) 21(2)(3)2(1)x x x x x ++-=++ ············································································ (2分) 31x x -=+. ································································································· (2分) 当3x =-时,原式33331--==-+. ································································· (3分) 20.解:设1x y x+=,则原方程可化为: 260y y +-= ………………………………………………… (2分)解得:13y =-,22y = ………………………………………………………… (2分) 当13y =-时,13x x +=-,解得14x =- …………………………………… (2分)图6(每组仅含最小值,不含最大值)图5 当22y =时,12x x +=,解得1x = …………………………………………… (2分) 经检验,114x =-,21x =都是原方程的根,所以原方程的根是114x =-,21x =……………………………………………………………………………………… (2分)21.解:(1)∵四边形ABCD 是菱形∴//DC AB ,即://DC AE ………………………………………………… (1分) 又AE AB DC >=∴四边形AECD 是梯形. …………………………………………………… (2分) ∴180********DAE ADC ∠=︒-∠=︒-︒=︒…………………………… (1分) ∵四边形ABCD 是菱形∴1302CAE DAB ∠=∠=︒ 又AC CE ⊥, ∴60E ∠=︒……………………………………………… (1分)∴DAEE ∠=∠………………………………………………………………… (1分) ∴四边形AECD 是等腰梯形.(2)过点D 作DH AE ⊥于H ,则:sin 4sin60DH AD DAH =⋅∠=︒=…………………………………(2分)∴1(48)2AECD S =⨯+⨯=梯形 (2分)22.(1)[来源………………………………………………………… (3分)(2)10………………………………………………………………………………… (2分) (3)169 161.5 …………………………………………………………… (1分,2分)(4)3172y x =-+ ………………………………………………………………… (2分)23.解:(1)在等边三角形ABC 中,AB=BC ,∠ABC=∠ACB =60°∴∠ABE=∠BCD =120°又∵BE CD =∴△ABE ≌△BCD …………………………………………………………… (2分) ∴∠E=∠D又∵∠FBE=∠CBD∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°…………………………… (2分) 由∠FBE=∠CBD ,∠E=∠D 得:△FBE ∽△CBD …………………………… (2分)∴CD BDEF EB = 又BE CD =∴2CD BD EF =⋅……………………………………………………………… (1分) (2)90° , 108°,成立………………………………………………………… (3分)(3)0(2)180n n-⋅ ………………………………………………………… (2分)24. (1)设点A 平移后落在反比例函数y x=-1(,)A a b ,∵A , ∴b =2……………………………………………………………(1分)代入y x=-求得a =(2分)∴(m ==………………………………………………………(2分) (2) 将点B 恰好落在反比例函数ky x=图像上的点记为1B ,可求得:1B 2)- ……………………………………………………………(2分)∴(2)k =-=-(2分)(3)21y x =+-(3分)25. 解:(1)可求得:t DP 2=,t AP 218-=,……………………………………(1分)∵ABP ∠=ADB ∠,A A ∠=∠∴ABP ∆∽ADB ∆,…………………………………………………………(1分)∴ABAPAD AB =, ………………………………………………………………(1分) 即2AB AD AP =⋅,∴)218(18102t -⨯=, ……………………………(1分)解得:569t =.∵5699< ∴569t =.…………………………………………………(1分) (2)过点B 作AD BH ⊥,垂足为H ,得8=BH ,………………………………(1分)记BQ 中点为1O 、AP 中点为2O ,联结21O O ,过点1O 作AD I O ⊥1,垂足为I ,则81==BH I O ,21t BO =,2121t CO -=,t tAO -=-=922182,t DO +=92,323)212()9(2-=--+=∴tt t I O ,…………………………………………………(1分)当29)9(22121tt t AO BO O O -=-+=+=时………………………………………(1分) 以BQ 为直径的圆与以AP 为直径的圆外切,在21IO O Rt ∆中,2221221I O I O O O +=,即222)323(8)29(-+=-tt ,………………………………………………(1分)整理得:42=t ,0>t ,2=∴t ;…………………………………………………(1分)(3)能,t 的值可以是929=t 或38=t 或2=t 或328=t .……………………………(4分)。
