三角形问题学生做
专题17 等腰(等边)三角形问题(学生版)

备考2024中考二轮数学《高频考点冲刺》(全国通用)专题17 等腰(等边)三角形问题考点扫描☆聚焦中考等腰(等边)三角形问题近几年各地中考主要以填空题或选择题考查,也有解答题出现,难度系数小,较简单,属于低档题;考查的知识点主要有:等腰三角形的性质与判定、等边三角形的性质与判定、线段的垂直平分线的性质;考查热点主要有:等腰三角形性质与判定、等边三角形性质与判定、线段垂直平分线的性质.考点剖析☆典型例题(2023•宿迁)若等腰三角形有一个内角为110°,则这个等腰三角形的底角是()A.70°B.45°C.35°D.50°2020•青海)已知a,b,c为△ABC的三边长.b,c满足(b﹣2)2+|c﹣3|=0,且a为方程|x ﹣4|=2的解,则△ABC的形状为三角形.2023•益阳)如图,AB∥CD,直线MN与AB,CD分别交于点E,F,CD上有一点G且GE =GF,∠1=122°,求∠2的度数.例4(2023•绵阳)如图,在等边△ABC中,BD是AC边上的中线,延长BC至点E,使CE=CD,若DE=,则AB=()A.B.6C.8D.例5(2021•宁夏)如图,在▱ABCD中,AD=4,对角线BD=8,分别以点A、B为圆心,以大于AB 的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,则GA的长是()A.2B.3C.4D.5考点过关☆专项突破类型一等腰三角形的性质与判定1.(2023•南京)若一个等腰三角形的腰长为3,则它的周长可能是()A.5B.10C.15D.202.(2023•眉山)如图,△ABC中,AB=AC,∠A=40°,则∠ACD的度数为()A.70°B.100°C.110°D.140°3.(2023•内蒙古)如图,直线a∥b,直线l与直线a,b分别相交于点A,B,点C在直线b上,且CA=CB.若∠1=32°,则∠2的度数为()A.32°B.58°C.74°D.75°4.(2023•菏泽)△ABC的三边长a,b,c满足(a﹣b)2++|c﹣3|=0,则△ABC是()A.等腰三角形B.直角三角形C.锐角三角形D.等腰直角三角形5.(2022•宁波)如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE中点.若AE=AD,DF=2,则BD的长为()A.2B.3C.2D.46.(2023•重庆)如图,在△ABC中,AB=AC,AD是BC边的中线,若AB=5,BC=6,则AD的长度为.7.(2023•西宁)在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADB的度数是.8.(2023•山西)如图,在四边形ABCD中,∠BCD=90°,对角线AC,BD相交于点O.若AB=AC=5,BC=6,∠ADB=2∠CBD,则AD的长为.9.(2022•温州)如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.(1)求证:∠EBD=∠EDB.(2)当AB=AC时,请判断CD与ED的大小关系,并说明理由.10.(2023•烟台)如图,点C为线段AB上一点,分别以AC,BC为等腰三角形的底边,在AB的同侧作等腰△ACD和等腰△BCE,且∠A=∠CBE.在线段EC上取一点F,使EF=AD,连接BF,DE.(1)如图1,求证:DE=BF;(2)如图2,若AD=2,BF的延长线恰好经过DE的中点G,求BE的长.类型二等边三角形的性质与判定1.(2023•金昌)如图,BD是等边△ABC的边AC上的高,以点D为圆心,DB长为半径作弧交BC 的延长线于点E,则∠DEC=()A.20°B.25°C.30°D.35°2.(2022•绵阳)下列关于等边三角形的描述不正确的是()A.是轴对称图形B.对称轴的交点是其重心C.是中心对称图形D.绕重心顺时针旋转120°能与自身重合3.(2022•鞍山)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠2=40°,则∠1的度数为()A.80°B.70°C.60°D.50°4.(2023•滨州)已知点P是等边△ABC的边BC上的一点,若∠APC=104°,则在以线段AP,BP,CP为边的三角形中,最小内角的大小为()A.14°B.16°C.24°D.26°5.(2019•铜仁市)如图,四边形ABCD为菱形,AB=2,∠DAB=60°,点E、F分别在边DC、BC上,且CE=CD,CF=CB,则S△CEF=()A.B.C.D.6.(2022•张家界)如图,点O是等边三角形ABC内一点,OA=2,OB=1,OC=,则△AOB 与△BOC的面积之和为()A.B.C.D.7.(2020•台州)如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是.8.(2023•雅安)如图,四边形ABCD中,AB=AD,BC=DC,∠C=60°,AE∥CD交BC于点E,BC=8,AE=6,则AB的长为.9.(2023•凉山州)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是.10.(2023•武汉)如图,DE平分等边△ABC的面积,折叠△BDE得到△FDE,AC分别与DF,EF 相交于G,H两点.若DG=m,EH=n,用含m,n的式子表示GH的长是.类型三线段垂直平分线的性质1.(2023•青海)如图,在△ABC中,DE是BC的垂直平分线.若AB=5,AC=8,则△ABD的周长是.2.(2023•丽水)如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是.3.(2022•青海)如图,在Rt△ABC中,∠ABC=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E,∠BAE=10°,则∠C的度数是.4.(2021•淮安)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是()A.2B.4C.6D.85.(2022•宜昌)如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为()A.25B.22C.19D.186.(2022•湖北)如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC 的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:①四边形AECF是菱形;②∠AFB=2∠ACB;③AC•EF=CF•CD;④若AF平分∠BAC,则CF=2BF.其中正确结论的个数是()A.4B.3C.2D.17.(2021•河北)如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是()A.0B.5C.6D.78.(2021•长沙)如图,在△ABC中,AD⊥BC,垂足为D,BD=CD,延长BC至E,使得CE=CA,连接AE.(1)求证:∠B=∠ACB;(2)若AB=5,AD=4,求△ABE的周长和面积.。
专题25 费马点、布洛卡点、拿破仑三角形问题(学生版)

专题25 费马点、布洛卡点、拿破仑三角形问题一.选择题(共4小题)1.(2021春•顺德区期末)点P 为ABC ∆所在平面内一点,当PA PB PC ++取到最小值时,则称该点为ABC ∆的“费马点”.当ABC ∆的三个内角均小于120︒时,费马点满足如下特征:120APB BPC CPA ∠=∠=∠=︒.如图,在ABC ∆中,AB AC ==BC 点到A ,B ,C 三点的距离之和为( )A .4B .2C .2-D .2+2.(2020秋•新华区校级期末)“费马点”是指位于三角形内且到三角形三个顶点距离之和最小的点,当三角形三个内角均小于120︒时,“费马点”与三个顶点的连线正好三等分“费马点”所在的周角,即该点所对的三角形三边的张角相等均为120︒,根据以上性质,函数()f x =的最小值为( )A .2BC .2-D .2+3.(2020秋•安徽月考)17世纪法国数学家费马曾提出这样一个问题:怎样在一个三角形中求一点,使它到每个顶点的距离之和最小?现已证明:在ABC ∆中,若三个内角均小于120︒,当点P 满足120APB APC BPC ∠=∠=∠=︒时,则点P 到三角形三个顶点的距离之和最小,点P 被人们称为费马点.根据以上性质,已知a 为平面内任意一个向量,b 和c 是平面内两个互相垂直的单位向量,则||||||a b a b a c -+++-的最小值是( )A .2B .2C 1-D 1+4.(2014春•鹿城区校级期末)设点F 为锐角ABC ∆的“费马点”,即F 是在ABC ∆内满足120AFB BFC CFA ∠=∠=∠=︒的点.若||3FA =,|4FB =,||5FC =,且实数x ,y 满足AF xAB y AC =+,则(x y= ) A .54 B .2516 C .32 D .94二.填空题(共15小题)5.(2021•泰安模拟)在一个三角形ABC 中到三个顶点距离之和最小的点叫做这个三角形的费马点,经证明它也满足120APB BPC CPA ∠=∠=∠=︒,因此费马点也称为三角形的等角中心如图,在ABC ∆外作等边ACD ∆,再作ACD ∆的外接圆,则外接圆与线段BD 的交点P 即为费马点.若1AB =,2BC =,90CAB ∠=︒,则PA PB PC ++= .6.(2021•深圳模拟)著名的费马问题是法国数学家皮埃尔⋅德费马(16011665)-于1643年提出的平面几何极值问题:“已知一个三角形,求作一点,使其与此三角形的三个顶点的距离之和最小.”费马问题中的所求点称为费马点,已知对于每个给定的三角形,都存在唯一的费马点,当ABC ∆的三个内角均小于120︒时,则使得120APB BPC CPA ∠=∠=∠=︒的点P 即为费马点.已知点P 为ABC ∆的费马点,且AC BC ⊥,若||||||PA PB PC λ+=,则实数λ的最小值为 .7.(2021•江西模拟)费马点是指位于三角形内且到三角形三个顶点距离之和最小的点.当三角形三个内角都小于23π时,费马点与三角形三个顶点的连线构成的三个角都为23π.已知点P 为ABC ∆的费马点,角A ,B ,C 的对边分别为a ,b ,c ,若cos 2sin()cos 6A C B π=-,且22()6b a c =-+,则PA PB PB PC PA PC ⋅+⋅+⋅的值为 .8.(2020秋•全国月考)费马点是指到三角形三个顶点距离之和最小的点,当三角形三个内角均小于120︒时,费马点在三角形内,且费马点与三个顶点连线正好三等分费马点所在的周角,即该点对三角形三边的张角相等,均为120︒.已知ABC ∆的三个内角均小于120︒,P 为ABC ∆的费马点,且3PA PB PC ++=,则ABC ∆面积的最大值为 .9.(2020•江西模拟)我们把三角形三个顶点距离之和最小的点称为费马点,若三角形内角均小于120︒,则该三角形的费马点与三角形三边的张角均为120︒.已知三角形ABC 中内角A ,B ,C 所对的边分别是a ,b ,c .若||a b -=,60C =︒,若三角形ABC 的费马点为O ,则OA OB OB OC OC OA ++= .10.(2018秋•上虞区期末)费马点是指三角形内到三角形三个顶点距离之和最小的点,当三角形三个内角均小于120︒时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为120︒.根据以上性质,已知(1,0)A -,(1,0)B ,(0,2)C ,P 为ABC ∆内一点,记()||||||f P PA PB PC =++,则()f P 的最小值为 ,此时sin PBC ∠= .11.(2019•凉山州模拟)点M 是ABC ∆内部或边界上的点,若M 到ABC ∆三个顶点距离之和最小,则称点M 是ABC ∆的费马点(该问题是十七世纪法国数学家费马提出).若(0,2)A ,(1,0)B -,(1,0)C 时,点0M 是ABC ∆的费马点,且已知0M 在y 轴上,则000||||||AM BM CM ++的大小等于 .12.(2018秋•荆州区校级期中)以三角形边BC ,CA ,AB 为边向形外作正三角形BCA ',CAB ',ABC ',则AA ',BB ',CC '三线共点,该点称为ABC ∆的正等角中心.当ABC ∆的每个内角都小于120︒时,正等角中心点P 满足以下性质:(1)120APB APC BPC ∠=∠=∠=︒;(2)正等角中心是到该三角形三个顶点距离之和最小的点(也即费马点).由以上性质得的最小值为 .13.(2019春•石家庄期末)费马点是指三角形内到三角形三个顶点距离之和最小的点.当三角形三个内角均小于120︒时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为120︒.根据以上性质,函数()f x =的最小值为 .14.(2021春•湖北期末)拿破仑定理是法国著名军事家拿破仑⋅波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边,向外构造三个等边三角形,则这三个等边三角形的外接圆圆心恰为另一个等边三角形(此等边三角形称为拿破仑三角形)的顶点.”已知ABC ∆内BC ,AC ,AB 为边向外作三个等边三角形,其外接圆圆心依次记为A ',B ',C '.若30ACB ∠=︒,则△A B C '''的面积最大值为 .15.(2021春•润州区校级期中)拿破仑定理是法国著名军事家拿破仑⋅波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边,向外构造三个等边三角形,则这三个等边三角形的外接圆圆心恰为另一个等边三角形(此等边三角形称为拿破仑三角形)的顶点.”已知ABC ∆内接于单位圆,以BC ,AC ,AB 为边向外作三个等边三角形,其外接圆圆心依次记为A ',B ',C '.若90ACB ∠=︒,则△A B C '''的面积最大值为 .16.(2021•泉州二模)拿破仑定理:“以任意三角形的三条边为边,向外构造三个正三角形,则这三个正三角形的中心恰为另一个正三角形的顶点.”利用该定理可为任意形状的市区科学地确定新的发展中心区位置,合理组织人流、物流,使城市土地的利用率,建筑的使用效率达到最佳,因而在城市建设规划中具有很好的应用价值.如图,设ABC ∆代表旧城区,新的城市发展中心1O ,2O ,3O 分别为正ACD ∆,正ABE ∆,正BCF ∆的中心.现已知2AB =,30ACB ∠=︒,△123O O O ABC 的面积为 .17.(2021•浔阳区校级模拟)法国著名的军事家拿破仑.波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”.在三角形ABC 中,角60A =︒,以AB 、BC 、AC 为边向外作三个等边三角形,其外接圆圆心依次为1O 、2O 、3O ,若三角形123O O O 角形ABC 的周长最小值为 .18.(2021•淮安模拟)拿破仑定理是法国著名的军事家拿破仑⋅波拿马最早提出的一个几何定理:“以任意三角形的三条边为边,向外构造三个等边三角形,则这三个三角形的外接圆圆心恰为另一个等边三个角形的顶点”.在ABC ∆中,120A ∠=︒,以AB ,BC ,AC 为边向外作三个等边三角形,其外接圆圆心依次为1O ,2O ,3O ,若△123O O O ABC ∆的周长的取值范围为 .19.(2021•江苏模拟)法国著名的军事家拿破仑.波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”.在三角形ABC 中,角60A =︒,以AB 、BC 、AC 为边向外作三个等边三角形,其外接圆圆心依次为1O 、2O 、3O ,若三角形123O O O ,则三角形ABC 的周长最小值为 .三.解答题(共3小题)20.(2021春•台江区校级期中)法国数学家费马被称为业余数学之王,很多数学定理以他的名字命名.对ABC ∆而言,若其内部的点P 满足120APB BPC CPA ∠=∠=∠=︒,则称P 为ABC ∆的费马点.如图所示,在ABC ∆中,已知45BAC ∠=︒,设P 为ABC ∆的费马点,且满足45PBA ∠=︒,2PA =.(1)求PAC ∆的面积;(2)求PB 的长度.21.如图,在ABC∆中,90ABC∠=︒,AB,1BC=,P为ABC∆内一点,90BPC∠=︒.(1)若12PB=,求PA;(2)若150APB∠=︒,求tan PBA∠.22.在ABC∆内存在一点O,满足BAO CAO CBO ACO∠=∠=∠=∠,求证:ABC∆的三边构成等比数列.。
中考数学专题复习 专题20 相似三角形问题(学生版)

中考专题20 相似三角形问题一、比例1.成比例线段(简称比例线段):对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即dcb a =(或a :b=c :d),那么,这四条线段叫做成比例线段,简称比例线段。
如果作为比例内项的是两条相同的线段,即cbb a =或a :b=b :c ,那么线段b 叫做线段a ,c 的比例中项。
2.黄金分割:用一点P 将一条线段AB 分割成大小两条线段,若小段与大段的长度之比等于大段与全长之比,则可得出这一比值等于0·618…。
这种分割称为黄金分割,分割点P 叫做线段AB 的黄金分割点,较长线段叫做较短线段与全线段的比例中项。
3.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
4.两条直线被一组平行线所截,所得的对应线段成比例。
5.平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
二、相似、相似三角形及其基本的理论1. 相似:相同形状的图形叫相似图形。
相似图形强调图形形状相同,与它们的位置、大小无关。
2.相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形。
相似多边形对应边的比叫做相似比。
3.三角形相似的判定方法(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其他两边(或两边延长线)相交,构成的三角形与原三角形相似。
(3)两个三角形相似的判定定理判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似。
中考复习函数专题28 二次函数中的三角形问题(学生版)

专题28 二次函数中的三角形问题知识对接考点一、二次函数中的三角形问题考点分析:二次函数与三角形的综合解答题一般涉及到这样几个方面:1.三角形面积最值问题2.特殊三角形的存在问题包括等腰等边和直角三角形。
这类题目一般出现在压轴题最后两道上,对知识的综合运用要求比较高。
考点二、解决此类题目的基本步骤与思路1.抓住目标三角形,根据动点设点坐标2.根据所设未知数去表示三角形的底和高,一般常用割补法去求解三角形的面积从而得出面积的关系式3. 根据二次函数性质求出最大值.4.特殊三角形问题首先要画出三角形的大概形状,分类讨论的去研究。
例如等腰三角形要弄清楚以哪两条边为要,直角三角形需要搞清楚哪个角作为直角都需要我们去分类讨论。
要点补充:1.简单的直角三角形可以直接利用底乘高进行面积的表示2.复杂的利用“补”的方法构造矩形或者大三角形,整体减去部分的思想3.利用“割”的方法时,一般选用横割或者竖割,也就是做坐标轴的垂线。
4.利用点坐标表示线段长度时注意要用大的减去小的。
5.围绕不同的直角进行分类讨论,注意检验答案是否符合要求。
6.在勾股定理计算复杂的情况下,灵活的构造K字形相似去处理。
要点补充:一、单选题1.如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s (阴影部分),则s与t的大致图象为()A .B .C .D .2.定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线l :13y x b =+经过点10,4M ⎛⎫ ⎪⎝⎭一组抛物线的顶点()111B y ,,()222,B y ,()333,B y ,…(),n n B n y (n 为正整数),依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:()11,0A x ,()22,0A x ,()33,0A x ,…()11,0n n A x ++(n 为正整数).若()101x d d =<<,当d 为( )时,这组抛物线中存在美丽抛物线A .512或712B .512或1112C .712或1112D .7123.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O 为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB 的两个交点之间的距离为形的三个顶点,则满足上述条件且对称轴平行于y 轴的抛物线条数是A .16B .15C .14D .134.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,A,B,C的横坐标x A,x B,x C满足x A<x C<x B,那么符合上述条件的抛物线条数是()A.7B.8C.14D.165.如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图△);固定△ADC,把△ABC沿AD方向平移(如图△),当两个三角形重叠部分的面积最大时,移动的距离AA′等于()A.1B.1.5C.2D.0.8或1.26.如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是()A.B.C.D.7.如图,正三角形ABC和正三角形ECD的边BC,CD在同一条直线上,将ABC向右平移,直到点B 与点D 重合为止,设点B 平移的距离为x ,=2BC ,4CD =.两个三角形重合部分的面积为Y ,现有一个正方形FGHI 的面积为S ,已知sin 60Y S=︒,则S 关于x 的函数图像大致为( )A .B .C .D .8.以下说法正确的是( )A .三角形的外心到三角形三边的距离相等B .顺次连接对角线相等的四边形各边中点所得的四边形是菱形C .分式方程11222x x x -=---的解为x =2 D .将抛物线y =2x 2-2向右平移1个单位后得到的抛物线是y =2x 2-39.二次函数2(1)22y m x mx m =+-+-的图象与x 轴有两个交点()1,0x 和()2,0x ,下列说法:△该函数图象过点(1,1)-;△当0m =时,二次函数与坐标轴的交点所围成的三角形面积是△若该函数的图象开口向下,则m 的取值范围为21m -<<-;△当0m >,且21x --时,y 的最大值为(92)m +.正确的是( )A .△△△B .△△△C .△△△D .△△△△ 10.以下四个命题:△如果三角形的三个内角的度数比是3:4:5,那么这个三角形是直角三角形;△在实数-7.54-π,)2中,有4个有理数,2个无理数;△的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为43; △二次函数221y ax ax =-+,自变量的两个值x 1,x 2对应的函数值分别为y 1,y 2,若|x 1-1|>|x 2-1|,则a (y 1-y 2)>0.其中正确的命题的个数为( )A .1个B .2个C .3个D .4个二、填空题11.定义[a ,b ,c ]为二次函数y =ax 2+bx +c (a ≠0)的特征数,下面给出特征数为[2m ,1-m ,-1-m ]的函数的一些结论:△当m ≠0时,点(1,0)一定在函数的图象上;△当m >0时,函数图象截x 轴所得的线段长度大于32;△当m <0时,函数在14x >时,y 随x 的增大而减小;△当m >0,若抛物线的顶点与抛物线与x 轴两交点组成的三角形为等腰直角三角形,则13m =,正确的结论是________.(填写序号)12.如图,在第一象限内作与x 轴的夹角为30°的射线OC ,在射线OC 上取点A ,过点A作AH △x 轴于点H ,在抛物线y =x 2(x >0)上取一点P ,在y 轴上取一点Q ,使得以P ,O ,Q 为顶点的三角形与△AOH 全等,则符合条件的点A 有____个.13.如图,直线l :1134y x =+经过点M(0,14),一组抛物线的顶点B 1(1,y 1),B 2(2,y 2),B 3(3,y 3)…B n (n ,y n )(n 为正整数)依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:A 1(x 1,0),A 2(x 2,0),A 3(x 3,0)…,A n+1(x n+1,0)(n 为正整数),设x 1=d (0<d <1)若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则我们把这种抛物线就称为:“美丽抛物线”.则当d (0<d <1)的大小变化时美丽抛物线相应的d 的值是__.14.如图,抛物线与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点()0,3C ,设抛物线的顶点为D .坐标轴上有一动点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似.则点P 的坐标______.。
解三角形(中线问题)(学生版)
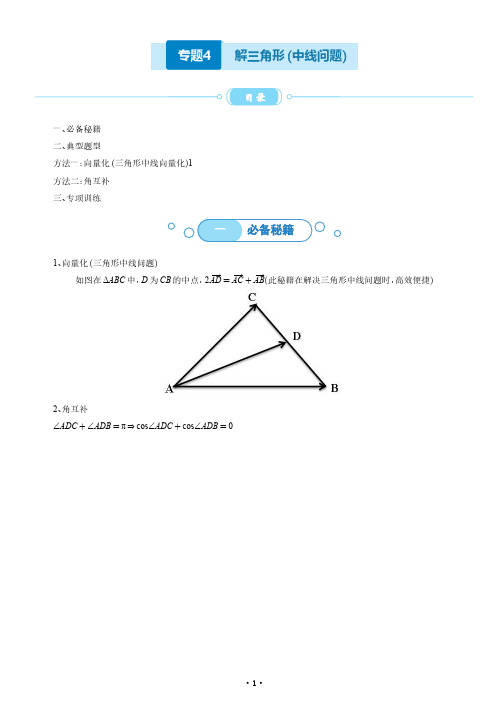
专题4解三角形(中线问题)目录一、必备秘籍二、典型题型方法一:向量化(三角形中线向量化)1方法二:角互补三、专项训练一必备秘籍1、向量化(三角形中线问题)如图在ΔABC 中,D 为CB 的中点,2AD =AC +AB (此秘籍在解决三角形中线问题时,高效便捷)2、角互补∠ADC +∠ADB =π⇒cos ∠ADC +cos ∠ADB =0二典型题型方法一:向量化1(2023·四川泸州·校考三模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,a 2sin C +3a cos C =3b ,A =60°.(1)求a 的值;(2)若BA ⋅AC =-12,求BC 边上中线AT 的长.2(2023·四川宜宾·统考模拟预测)△ABC 的内角A ,B ,C 所对边分别为a ,b ,c ,已知c sin C sin A -c =b sin B sin A -a ,b =2.(1)若a =2c ,求△ABC 的周长;(2)若AC 边的中点为D ,求中线BD 的最大值.3(2023·安徽安庆·安庆市第二中学校考模拟预测)已知函数f x =sin 2x +π3 -cos 2x +π6 +31-2sin 2x .(1)求f x 的单调递增区间;(2)记a ,b ,c 分别为△ABC 内角A ,B ,C 的对边,且f A 2=3,BC 的中线AD =3,求△ABC 面积的最大值.方法二:角互补1(2023·全国·高三专题练习)在①sin Asin B +sin Bsin A+1=c2ab;②(a+2b)cos C+c cos A=0;③3a sinA+B2=c sin A,这三个条作中任选一个,补充在下面的横线上,并解答.在△ABC中,角A,B,C所对的边分别为a,b,c,且.(1)求角C的大小;(2)若c=4,求AB的中线CD长度的最小值.2(2023·全国·高三专题练习)在△ABC中,内角A,B,C的对边分别为a,b,c,且3a cos C-b=c sin A.(1)求角A;(2)若AD为BC边上中线,AD=1292,AB=5,求△ABC的面积.3(2023·全国·高三专题练习)已知函数f x =32sin x2cos x2-12cos2x2.(1)求函数f x 的单调递增区间;(2)在△ABC中,a,b,c分别是角A,B,C的对边,f A =0,a=3,若D为BC上一点,且满足,求△ABC的面积S.请从①3sin B=b cos C;②AD为△ABC的中线,且AD=72;③AD为△ABC的角平分线,且AD=233.这三个条件中任意选一个补充到横线处并作答.(注:如果选择多个条件分别解答,按第一个解答计分)三专项训练1.(2023·全国·高三专题练习)在等腰△ABC 中,AB =AC ,若AC 边上的中线BD 的长为3,则△ABC 的面积的最大值是()A.6B.12C.18D.242.(2023·安徽·合肥一中校联考模拟预测)记△ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,已知sin π2+B=2c -b 2a.(1)求A ;(2)若b +c =3,求BC 边中线AM 的取值范围.3.(2023·湖北·荆门市龙泉中学校联考二模)已知在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,C =π3.(1)若BC 边上的高等于33a ,求cos A ;(2)若CA ⋅CB =2,求AB 边上的中线CD 长度的最小值.。
专题 三角形中的重要模型-等积模型(学生版)
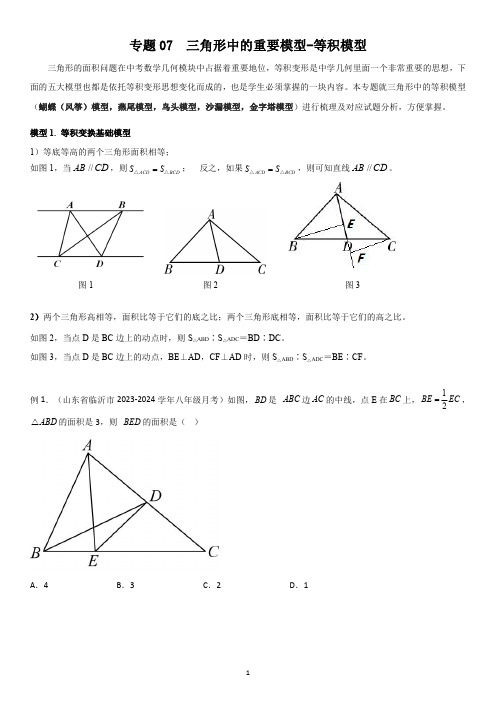
专题07三角形中的重要模型-等积模型三角形的面积问题在中考数学几何模块中占据着重要地位,等积变形是中学几何里面一个非常重要的思想,下面的五大模型也都是依托等积变形思想变化而成的,也是学生必须掌握的一块内容。
本专题就三角形中的等积模型(蝴蝶(风筝)模型,燕尾模型,鸟头模型,沙漏模型,金字塔模型)进行梳理及对应试题分析,方便掌握。
模型1.等积变换基础模型1)等底等高的两个三角形面积相等;如图1,当AB //CD ,则ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB //CD 。
图1图2图32)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如图2,当点D 是BC 边上的动点时,则S △ABD ∶S △ADC =BD ∶DC 。
如图3,当点D 是BC 边上的动点,BE ⊥AD ,CF ⊥AD 时,则S △ABD ∶S △ADC =BE ∶CF 。
A .4B .3C .2的边,则阴影部分的面积是(A.9B.12八年级统考期中)基本性质:三角形中线等分三角形的面积.=,连接DA.若(1)如图2,延长ABC的边BC到点D,使CD BC的代数式表示);=(2)如图3,延长ABC的边BC到点D,延长边CA到点E,使CD BC则2S=(用含a的代数式表示);=,连接FD,FE,得到(3)在图3的基础上延长AB到点F,使BF AB上,当点模型2.蝴蝶(风筝)模型蝴蝶模型(定理)提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
蝴蝶定理:任意四边形中的比例关系如图1,结论:①1243::S S S S =或1324S S S S ⨯=⨯;②()()1243::AO OC S S S S =++。
梯形蝴蝶定理:梯形中比例关系如图2,结论:①2213::S S a b =;②221324::::::S S S S a b ab ab =;③梯形S 的对应份数为()2a b +。
五类解三角形题型--新高考数学大题秒杀技巧(学生版)

五类解三角形题型解三角形问题一般分为五类:类型1:三角形面积最值问题;类型2:三角形周长定值及最值;类型3:三角形涉及中线长问题;类型4:三角形涉及角平分线问题;类型5:三角形涉及长度最值问题。
类型1:面积最值问题技巧:正规方法:面积公式+基本不等式①S=12ab sin Ca2+b2−c2=2ab cos C⇒a2+b2=2ab cos C+c2≥2ab⇒ab≤c221−cos C②S=12ac sin Ba2+c2−b2=2ac cos B⇒a2+c2=2ac cos B+b2≥2ac⇒ac≤b221−cos B③S=12bc sin Ab2+c2−a2=2bc cos A⇒b2+c2=2bc cos A+a2≥2bc⇒bc≤a221−cos A秒杀方法:在ΔABC中,已知B=θ,AC=x则:SΔABC max=AB+BC2max8⋅sin B其中AB+BCmax=2R⋅m2+n2+2mn cosθm,n分别是BA、BC的系数2R=x sinθ面积最值问题专项练习1△ABC的内角A,B,C的对边分别为a,b,c,c=2a cos C-b,c2+a2=b2+3ac,b=2.(1)求A;(2)若M,N在线段BC上且和B,C都不重合,∠MAN=π3,求△AMN面积的取值范围.2已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若3c sin B =a -b cos C .(1)求B ;(2)若DC =AD ,BD =2,求△ABC 的面积的最大值.3在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =2b -c sin B +c 2sin C -sin B .(1)求A ;(2)点D 在边BC 上,且BD =3DC ,AD =4,求△ABC 面积的最大值.4△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知c =2a cos C -b ,c 2+a 2=b 2+3ac ,b =2.(1)求A ;(2)若M 是直线BC 外一点,∠BMC =π3,求△BMC 面积的最大值.5在△ABC 中,角A ,B ,C 对边分别为a ,b ,c ,(sin A +sin B )(a -b )=c (sin C -sin B ),D 为BC 边上一点,AD 平分∠BAC ,AD =2.(1)求角A ;(2)求△ABC 面积的最小值.6在①m =2a -c ,b ,n =cos C ,cos B ,m ⎳n ;②b sin A =a cos B -π6;③a +b a -b =a -c c 三个条件中任选一个,补充在下面的问题中,并解决该问题.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,且满足.注:如果选择多个条件分别解答,按第一个解答计分.(1)求角B ;(2)若b =2,求△ABC 面积的最大值.类型2:三角形周长定值及最值类型一:已知一角与两边乘积模型第一步:求两边乘积第二步:利用余弦定理求出两边之和类型二:已知一角与三角等量模型第一步:求三角各自的大小第二步:利用正弦定理求出三边的长度最值步骤如下:第一步:先表示出周长l =a +b +c第二步:利用正弦定理a =2R sin A ,b =2R sin B ,c =2R sin C 将边化为角第三步:多角化一角+辅助角公式,转化为三角函数求最值周长定值及最值问题专项练习7在锐角三角形△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,CD 为CA 在CB 方向上的投影向量,且满足2c sin B =5CD .(1)求cos C 的值;(2)若b =3,a =3c cos B ,求△ABC 的周长.8如图,在梯形ABCD 中,AB ⎳CD ,∠D =60°.(1)若AC =3,求△ACD 周长的最大值;(2)若CD =2AB ,∠BCD =75°,求tan ∠DAC 的值.9已知△ABC的面积为S,角A,B,C所对的边为a,b,c.点O为△ABC的内心,b=23且S=3 4(a2+c2-b2).(1)求B的大小;(2)求△AOC的周长的取值范围.10在锐角△ABC中,角A,B,C所对应的边分别为a,b,c,已知sin A-sin B3a-c=sin Ca+b.(1)求角B的值;(2)若a=2,求△ABC的周长的取值范围.11在△ABC中,角A,B,C的对边分别是a,b,c,a-ca+c+b b-a=0.(1)求C;(2)若c=3,△ABC的面积是32,求△ABC的周长.类型3:三角形涉及中线长问题①中线长定理:(两次余弦定理推导可得)+(一次大三角形一次中线所在三角形+同余弦值)如:在ΔABC与ΔABD同用cos B求ADAB2+AC2=AD2+CD22②中线长常用方法cos∠ADB+cos∠ADC=0③已知AB+AC,求AD的范围∵AB+AC为定值,故满足椭圆的第一定义∴半短轴≤AD<半长轴三角形涉及中线长问题专项练习12在△ABC中,角A,B,C的对边分别为a,b,c,且b=7,c=5.(1)若sin B=78,求cos C的值;(2)若BC边上的中线长为21,求a的值.13在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a=2,b=5,c=1.(1)求sin A,sin B,sin C中的最大值;(2)求AC边上的中线长.14在△ABC中,角A,B,C所对的边分别为a,b,c,且满足3b sin A=a cos B+a.(1)求角B的值;(2)若c=8,△ABC的面积为203,求BC边上中线AD的长.15如图,在△ABC中,内角A、B、C的对边分别为a、b、c.已知b=3,c=6,sin2C=sin B,且AD 为BC边上的中线,AE为∠BAC的角平分线.(1)求cos C及线段BC的长;(2)求△ADE的面积.16在△ABC中,∠A=2π3,AC=23,点D在AB上,CD=32.(1)若CD为中线,求△ABC的面积;(2)若CD平分∠ACB,求BC的长.17在①3b=a sin C+3cos C;②a sin C=c sin B+C2;③a cos C+12c=b,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.在△ABC中,内角A,B,C的对边分别为a,b,c.已知.(1)求角A;(2)若b=1,c=3,求BC边上的中线AD的长.注:若选择多个条件分别进行解答,则按第一个解答进行计分.类型4:三角形涉及角平分线问题张角定理如图,在ΔABC中,D为BC边上一点,连接AD,设AD=l,∠BAD=α,∠CAD=β则一定有sinα+βl=sinαb+sinβc三角形涉及角平分线问题专项练习18设a,b,c分别是△ABC的内角A,B,C的对边,sin B-sin Cb=a-csin A+sin C.(1)求角A的大小;(2)从下面两个问题中任选一个作答,两个都作答则按第一个记分.①设角A的角平分线交BC边于点D,且AD=1,求△ABC面积的最小值.②设点D为BC边上的中点,且AD=1,求△ABC面积的最大值.19在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且c sin B+33b cos A+B=33b.(1)求角C的大小;(2)若c=3,角A与角B的内角平分线相交于点D,求△ABD面积的取值范围.20已知△ABC的三个内角A,B,C的对边分别为a,b,c满足b cos C+c cos Bsin B+3b cos A= 0.(1)求A;(2)若c=2,a=23,角B的角平分线交边AC于点D,求BD的长.21已知△ABC的内角A,B,C的对应边分别为a,b,c,且有3cos A c cos B+b cos C+a sin A=0.(1)求A;(2)设AD是△ABC的内角平分线,边b,c的长度是方程x2-6x+4=0的两根,求线段AD的长度.22在①b sin B+c sin C=233b sin C+asin A;②cos2C+sin B sin C=sin2B+cos2A;③2b=2a cos C+c这三个条件中任选一个,补充在下面的问题中并作答.在△ABC中,内角A,B,C的对边分别为a,b,c,已知△ABC外接圆的半径为1,且.(1)求角A;(2)若AC=2,AD是△ABC的内角平分线,求AD的长度.注:如果选择多个条件分别解答,按第一个解答计分.类型5:三角形涉及长度最值问题秒杀:解三角形中最值或范围问题,通常涉及与边长常用处理思路:①余弦定理结合基本不等式构造不等关系求出答案;②采用正弦定理边化角,利用三角函数的范围求出最值或范围,如果三角形为锐角三角形,或其他的限制,通常采用这种方法;③巧妙利用三角换元,实现边化角,进而转化为正弦或余弦函数求出最值三角形涉及长度最值问题专项练习23设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知△ABC 的面积为34c 2-a 2-b 2 .(1)求C ;(2)延长BC 至D ,使BD =3BC ,若b =2,求AD AB 的最小值.24在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a 2-b 2=ac cos B -12bc(1)求A ;(2)若a =6,2BD =DC ,求线段AD 长的最大值.25锐角△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,已知sin C =2cos A sin B +π3 .(1)求A ;(2)若b +c =6,求BC 边上的高AD 长的最大值.26在△ABC中,角A,B,C的对边分别是a,b,c,a sin B+C=b-csin B+c sin C.(1)求A;(2)若D在BC上,a=2,且AD⊥BC,求AD的最大值.27记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为312b2.(1)若A=π6,求sin B sin C;(2)求a2+c2ac的最大值.。
解三角形的最值和范围问题 (学生版)-高中数学

解三角形的最值和范围问题【新高考专用】【题型1三角形、四边形面积的最值或范围问题】【题型2三角形边长的最值或范围问题】【题型3三角形周长的最值或范围问题】【题型4三角形的角(角的三角函数值)的最值或范围问题】【题型5利用基本不等式求最值(范围)】【题型6转化为三角函数求最值(范围)】【题型7转化为其他函数求最值(范围)】【题型8“坐标法”求最值(范围)】【题型9与平面向量有关的最值(范围)问题】1、解三角形的最值和范围问题解三角形中的最值或范围问题,通常涉及与边长、周长有关的范围问题,与面积有关的范围问题,或与角度有关的范围问题,一直是高考的热点与重点,有时也会与三角函数、平面向量等知识综合考查,主要是利用三角函数、正余弦定理、三角形面积公式、基本不等式等工具研究三角形问题,解决此类问题的关键是建立起角与边的数量关系.【知识点1三角形中的最值和范围问题】1.三角形中的最值(范围)问题的常见解题方法:(1)利用正、余弦定理结合三角形中的不等关系求最值(范围);(2)利用基本不等式求最值(范围);(3)转化为三角函数求最值(范围);(4)转化为其他函数求最值(范围);(5)坐标法求最值(范围).2.三角形中的最值(范围)问题的解题策略:(1)正、余弦定理是求解三角形的边长、周长或面积的最值(范围)问题的核心,要牢牢掌握并灵活运用.解题时要结合正弦定理和余弦定理实现边角互化,再结合角的范围、辅助角公式、基本不等式等研究其最值(范围).(2)转化为三角函数求最值(范围)问题的解题策略三角形中最值(范围)问题,如果三角形为锐角三角形,或其他的限制,一般采用正弦定理边化角,利用三角函数的范围求出最值或范围.(3)坐标法求最值(范围)求最值(范围)问题的解题策略“坐标法”也是解决三角形最值问题的一种重要方法.解题时,要充分利用题设条件中所提供的特殊边角关系,建立合适的直角坐标系,正确求出关键点的坐标,将所要求的目标式表示出来并合理化简,再结合三角函数、基本不等式等知识求其最值.【题型1三角形、四边形面积的最值或范围问题】1.(2024·河北石家庄·三模)在△ABC中,角A、B、C所对的边分别为a、b、c,c=4,ab=9.(1)若sin C=23,求sin A⋅sin B的值;(2)求△ABC面积的最大值.2.(2024·全国·模拟预测)记锐角三角形ABC的内角A,B,C的对边分别为a,b,c,已知b cos A=3-a cos B,2a sin C=3.(1)求A.(2)求△ABC面积的取值范围.3.(2024·辽宁·模拟预测)如图,在平面内,四边形ABCD满足B,D点在AC的两侧,AB=1,BC=2,△ACD为正三角形,设∠ABC=α.(1)当α=π3时,求AC;(2)当α变化时,求四边形ABCD面积的最大值.4.(2024·上海·三模)已知△ABC的内角A,B,C的对边分别为a,b,c,且3a=2c sin A.(1)求sin C的值;(2)若c=3,求△ABC面积S的最大值.【题型2三角形边长的最值或范围问题】1.(2024·四川·三模)在△ABC中,内角A,B,C的对边分别为a,b,c,且满足2c sin B cos A=b sin A cos B+cos A sin B.(1)求A;(2)若△ABC的面积为163,D为AC的中点,求BD的最小值.2.(2024·江西·模拟预测)在△ABC中,角A,B,C所对的边分别记为a,b,c,且tan A=cos B-sin Ccos C+sin B.(1)若B=π6,求C的大小.(2)若a=2,求b+c的取值范围.3.(2024·广东广州·三模)在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且c=b sin A2+a cos B.(1)求A;(2)若D是边BC上一点(不包括端点),且∠ABD=∠BAD,求CDBD的取值范围.4.(2024·江西鹰潭·二模)△ABC的内角A,B,C的对边分别为a,b,c,满足1-sin Acos A =sin B cos B.(1)求证:A+2B=π2;(2)求a2+b2c2的最小值.【题型3三角形周长的最值或范围问题】1.(2024·安徽淮北·二模)记△ABC的内角A,B,C的对边分别为a,b,c,已知c-b=2c sin2A2(1)试判断△ABC的形状;(2)若c=1,求△ABC周长的最大值.2.(2024·四川绵阳·模拟预测)已知在△ABC中,D为BC边的中点,且AD=5.(1)若△ABC的面积为2,cos∠ADC=55,求B;(2)若AB2+AC2=18,求△ABC的周长的最大值.3.(2024·云南曲靖·二模)在△ABC中,角A,B,C的对边分别为a,b,c,且a cos C+3c sin A=b+c.(1)求角B的取值范围;(2)已知△ABC内切圆的半径等于32,求△ABC周长的取值范围.=2b.4.(2024·湖南常德·一模)已知△ABC的内角A,B,C的对边分别是a,b,c,且acos C(1)判断△ABC的形状;(2)若△ABC的外接圆半径为2,求△ABC周长的最大值.【题型4三角形的角(角的三角函数值)的最值或范围问题】1.(2024·内蒙古呼和浩特·一模)记△ABC的内角A,B,C的对边分别为a,b,c.若a=3,b=2,则B+C的取值范围是()A.2π3,5π6B.2π3,πC.5π6,πD.π2,5π62.(2024·内蒙古呼和浩特·二模)在△ABC中,角A、B、C的对边分别为a、b、c,若1b2+54a2=c2a2b2,则tan A-1tan C的最小值为()A.13B.23C.29D.193.(2024·陕西宝鸡·二模)△ABC中,D为BC边的中点,AD=1.(1)若△ABC的面积为23,且∠ADC=2π3,求sin C的值;(2)若BC=4,求cos∠BAC的取值范围.4.(2024·北京石景山·一模)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且2b sin A-3a=0.(1)求角B的大小;(2)求cos A+cos C的取值范围.【题型5利用基本不等式求最值(范围)】1.(2024·山西太原·三模)已知△ABC中,A=120°,D是BC的中点,且AD=1,则△ABC面积的最大值()A.3B.23C.1D.22.(2024·黑龙江哈尔滨·三模)已知△ABC的内角A,B,C的对边分别为a,b,c,且a=3,BC边上中线AD长为1,则bc最大值为()A.74B.72C.3D.233.(2024·安徽合肥·二模)记△ABC的内角A,B,C的对边分别为a,b,c,已知c=2,1tan A +1tan B+1tan A tan B=1.则△ABC面积的最大值为()A.1+2B.1+3C.22D.234.(2024·浙江台州·二模)在△ABC中,角A,B,C所对的边分别为a,b,c,若a cos C=2c cos A,则bca2的最大值为()A.3B.32C.32D.3【题型6转化为三角函数求最值(范围)】1.(2024·辽宁沈阳·模拟预测)在△ABC中,内角A,B,C所对的边分别为a,b,c,且sin2C-sin C sin Bcos2B-cos2A=1.(1)求角A的大小;(2)若△ABC为锐角三角形,点F为△ABC的垂心,AF=6,求CF+BF的取值范围.2.(2024·辽宁·模拟预测)已知△ABC的内角A,B,C的对边分别为a,b,c,c-3bsin C= a-bsin A+sin B.(1)求A;(2)若△ABC为锐角三角形,且b=6,求△ABC的周长l的取值范围.3.(2024·河北衡水·一模)在△ABC中,内角A,B,C所对的边分别是a,b,c,三角形面积为S,若D为AC边上一点,满足AB⊥BD,BD=2,且a2=-233S+ab cos C.(1)求角B;(2)求2AD +1CD的取值范围.4.(2024·福建漳州·模拟预测)如图,在四边形ABCD中,∠DAB=π2,B=π6,且△ABC的外接圆半径为4.(1)若BC=42,AD=22,求△ACD的面积;(2)若D=2π3,求BC-AD的最大值.【题型7转化为其他函数求最值(范围)】1.(2024·四川成都·模拟预测)设锐角△ABC 的三个内角A ,B ,C 的对边分别为a ,b ,c ,且c =2,B =2C ,则a +b 的取值范围为()A.2,10B.2+22,10C.2+22,4+23D.4+23,102.(2024·全国·模拟预测)已知△ABC 是锐角三角形,内角A ,B ,C 所对应的边分别为a ,b ,c .若a 2-b 2=bc ,则b a +c的取值范围是()A.33,22B.2-3,1C.2-3,2-1D.2+1,3+23.(2023·全国·模拟预测)已知△ABC 为锐角三角形,其内角A ,B ,C 所对的边分别为a ,b ,c ,cos B =cos2A .(1)求ba的取值范围;(2)若a =1,求△ABC 周长的取值范围.4.(2024·全国·模拟预测)已知△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,S △ABC =b 2-c 2+164⋅tan C .(1)求a 的值;(2)若D 为线段BC 上一点且满足BD =1,DA 平分∠BAC ,求△ABC 的面积的取值范围.【题型8“坐标法”求最值(范围)】1.(23-24高一下·四川宜宾·期末)如图,在平面四边形ABCD 中,AB ⊥BC ,∠BCD =60°,∠ADC =150°,BE =3EC ,CD =233,BE =3,若点F 为边AD 上的动点,则EF ⋅BF 的最小值为()A.1B.1516C.3132D.22.(2023·安徽马鞍山·模拟预测)已知平行四边形ABCD 中,∠ADC =60°,E ,F 分别为边AB ,BC 的中点,若DE ⋅DF=13,则四边形ABCD 面积的最大值为()A.2B.23C.4D.433.(2023·全国·模拟预测)在等腰△ABC 中,角A ,B ,C 所对应的边为a ,b ,c ,B =C =π6,a =23,P 是△ABC 外接圆上一点,则P A ⋅PB +PB ⋅PC +PC ⋅P A的取值范围是()A.-3,23B.-1,33C.-2,30D.-4,204.(2024·江西南昌·三模)如图,在扇形OAB 中,半径OA =4,∠AOB =90°,C 在半径OB 上,D 在半径OA 上,E 是扇形弧上的动点(不包含端点),则平行四边形BCDE 的周长的取值范围是()A.8,12B.82,12C.8,82D.4,82【题型9与平面向量有关的最值(范围)问题】1.(2023·河南开封·三模)已知e 1 、e 2 为单位向量,e 1 -e 2 =3,非零向量a 满足a-2e 2 =1,则e 1 -a 的最小值为()A.7B.7-1C.3D.3-12.(23-24高三上·北京通州·期末)在菱形ABCD 中,AB =2,∠BAD =60°,E 是BC 的中点,F 是CD 上一点(不与C ,D 重合),DE 与AF 交于G ,则AG ⋅DG的取值范围是()A.0,23B.0,43C.0,2D.0,33.(2024·福建泉州·模拟预测)已知平行四边形ABCD 中,AB =2,BC =4,B =2π3,若以C 为圆心的圆与对角线BD 相切,P 是圆C 上的一点,则BD ⋅CP -CB的最小值是()A.8-23B.4+23C.12-43D.6+234.(2023·福建厦门·二模)在△AOB 中,已知OB =2,AB=1,∠AOB =45°,若OP =λOA +μOB,且λ+2μ=2,μ∈0,1 ,则OA 在OP 上的投影向量为me (e为与OP 同向的单位向量),则m 的取值范围是()A.-22,1B.22,1C.-22,1D.22,1一、单选题1.(2024·江苏连云港·模拟预测)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若a =1,b cos A =1+cos B ,则边b 的取值范围为()A.0,1B.1,2C.0,2D.2,32.(2024·安徽合肥·模拟预测)已知△ABC 角A 、B 、C 的对边分别为a 、b 、c 满足2b a -c =sin A +sin Csin B ,则角B 的最大值为()A.π6B.π4C.π3D.2π33.(2024·广东东莞·模拟预测)已知在同一平面内的三个点A ,B ,C 满足AB =2,CA CA -CBCB≥1,则AC +BC的取值范围是()A.0,1 B.0,2 C.0,3 D.0,234.(2024·河南·三模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a cos A+b cos B =3ccos C ,则tan A +tan C 的最小值是()A.43B.83C.23D.45.(2024·河南·模拟预测)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,满足b 3+c 3b +c=a 2.若a =23,则b 2+c 2的取值范围为()A.12,24B.20,24C.12,24D.20,246.(2024·江西·二模)在△ABC 中,若sin A =2cos B cos C ,则cos 2B +cos 2C 的取值范围为()A.1,65B.1,2+12C.65,2D.2+12,2 7.(2024·全国·二模)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,2a cos A =b cos C +c cos B ,且a =4sin A ,则△ABC 周长的最大值为()A.42B.62C.43D.638.(2024·陕西咸阳·三模)为了进一步提升城市形象,满足群众就近健身和休闲的需求,2023年某市政府在市区多地规划建设了“口袋公园”.如图,在扇形“口袋公园”OPQ 中,准备修一条三角形健身步道OAB ,已知扇形的半径OP =3,圆心角∠POQ =π3,A 是扇形弧上的动点,B 是半径OQ 上的动点,AB ⎳OP ,则△OAB 面积的最大值为()A.334B.34C.335D.35二、多选题9.(2024·江苏南京·二模)已知△ABC 内角A ,B ,C 的对边分别为a ,b ,c ,O 为△ABC 的重心,cos A =15,AO =2,则()A.AO =13AB +13ACB.AB ⋅AC ≤3C.△ABC 的面积的最大值为36D.a 的最小值为2510.(2024·湖南·二模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且c =b 2cos A +1 ,则下列结论正确的有()A.A =2BB.若a =3b ,则△ABC 为直角三角形C.若△ABC 为锐角三角形,1tan B -1tan A 的最小值为1D.若△ABC 为锐角三角形,则c a 的取值范围为22,23311.(2024·河北邯郸·三模)已知△ABC 的三个内角A ,B ,C 的对边分别是a ,b ,c ,面积为34a 2+c 2-b 2,则下列说法正确的是()A.cos A cos C 的取值范围是-12,14B.若D 为边AC 的中点,且BD =1,则△ABC 的面积的最大值为33C.若△ABC 是锐角三角形,则a c 的取值范围是12,2 D.若角B 的平分线BE 与边AC 相交于点E ,且BE =3,则a +4c 的最小值为10三、填空题12.(2024·北京·三模)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且a +c =2b ,则角B 的取值范围为0,π3 .13.(2024·陕西安康·模拟预测)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若b =2,2a cos C=2cos B +c cos C ,则2a +c 的最大值为4213.14.(2024·江苏盐城·一模)在△ABC 中,已知AB =2,BC =3,点P 在△ABC 内,且满足CP =2,∠APC +∠ABC =π,则四边形ABCP 面积的最大值为.四、解答题15.(2024·山东菏泽·模拟预测)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知AB ⋅AC -BA ⋅BC =λAB 2(1)若λ=1,判断△ABC 的形状;(2)若λ=12,求tan B -A 的最大值.16.(2024·江苏盐城·模拟预测)在△ABC 中,已知角A ,B ,C 所对的边分别为a ,b ,c ,a sin 2B 2+b sin 2A 2=3ab2a +b +c.(1)求角C 的大小;(2)若△ABC 为锐角三角形,求a +bc的取值范围.17.(2024·重庆渝中·模拟预测)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且满足3ca-sin B =tan A ⋅cos B .(1)求角A 的大小;(2)若△ABC 为锐角三角形且a =26,求△ABC 面积的取值范围.18.(2024·四川南充·模拟预测)在△ABC中,sin Csin A+sin B =sin A-sin B sin B+sin C.(1)求A;(2)若BC=3,求△ABC周长的最大值.19.(2024·陕西商洛·模拟预测)在锐角△ABC中.内角A,B,C所对的边分别是a,b,c,已知a-2c cos B=c.(1)求证:B=2C;(2)求sin B+23cos2C的取值范围.。
数学教案图形分类:三角形教学中的常见问题及解决方法

数学教案图形分类:三角形教学中的常见问题及解决方法三角形教学中的常见问题及解决方法在学习数学时,我们经常会涉及到图形分类的问题。
图形分类的重要性在于,它不仅可以帮助我们更好地理解各类图形的性质和特点,还可以帮助我们更好地应用数学知识解决实际问题。
在图形分类中,三角形是一个常见的图形。
在三角形的教学中,会遇到许多的问题。
本文将从常见问题入手,探讨三角形教学中的解决方法。
常见问题一:学生对三角形的基本概念不理解在三角形的教学中,常见的基本概念有三角形的定义、三角形的分类、三角形的性质等等。
但是,对于初学者来说,这些概念能会比较抽象,导致学生无法理解。
解决这个问题的方法是,要引导学生从具体的例子中去理解和抽象出三角形的基本概念。
例如,可以让学生观察各种实际的三角形,然后引导他们找到这些三角形的共同性质,从而理解三角形的定义。
此外,还可以通过将三角形分类成等边三角形、等腰三角形及普通三角形等,让学生更深入地认识三角形的特点。
常见问题二:学生对三角形的性质掌握不够深入在三角形的教学中,学生需要掌握很多关于三角形的性质,如角平分线的性质、中线的性质、高的性质等等。
而掌握这些性质,需要学生具备一定的抽象思维和逻辑能力。
尽管这些性质看似单纯,但是它们在求解三角形的各种问题时十分关键。
为了让学生更深入了解三角形的性质,我们可以引导学生通过多方面的思维训练,如:画图加深理解,让学生练习构造各种类型的三角形,并以此来认识各种三角形的性质;同时,还可以通过问题解决的方式来让学生更好地掌握三角形的性质。
常见问题三:学生对三角形的应用能力不足在三角形的教学中,学生不仅要掌握三角形的基本概念和性质,还要学会如何应用这些概念和性质来解决实际问题。
对于初学者来说,这可能是最难的部分,因为它需要学生熟练掌握角形的各种性质,并能把它们应用到实际场景中去。
为了提高学生的应用能力,我们可以通过实例教学的方式来进行针对性的教学,让学生在学习时感受到实际应用的实用性。
决胜2021年中考数学压轴题全揭秘精品 专题10 三角形问题(学生版)

决胜2021中考数学压轴题全揭秘精品专题10 三角形问题【考点1】三角形基础知识【例1】1.(2020·湛江)如图,在ABC 中,30A ∠=︒,=50∠︒B ,CD 平分ACB ∠,则ADC ∠的度数是( )A .80︒B .90︒C .100︒D .110︒【变式1-1】(2020·浙江绍兴·中考真题)长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A .4B .5C .6D .7【变式1-2】(2020·甘肃天水·)一个三角形的两边长分别为2和5,第三边长是方程28120x x -+=的根,则该三角形的周长为_______.【考点2】全等三角形的判定与性质的应用【例2】(2020·辽宁鞍山·中考真题)如图,在四边形ABCD 中,90B D ∠=∠=︒,点E ,F 分别在AB ,AD 上,AE AF =,CE CF =,求证:CB CD =.【变式2-1】(2020·山东东营·中考真题)如图1,在等腰三角形ABC 中,120,,A AB AC ∠==点D E 、分别在边AB AC 、上,,AD AE =连接,BE 点M N P 、、分别为DE BE BC 、、的中点.(1)观察猜想图1中,线段NM NP 、的数量关系是____,MNP ∠的大小为_____;(2)探究证明把ADE 绕点A 顺时针方向旋转到如图2所示的位置,连接,MP BD CE 、、判断MNP △的形状,并说明理由;(3)拓展延伸把ADE 绕点A 在平面内自由旋转,若1,3AD AB ==,请求出MNP △面积的最大值.【变式2-2】(2020·山东烟台·中考真题)如图,在等边三角形ABC 中,点E 是边AC 上一定点,点D 是直线BC 上一动点,以DE 为一边作等边三角形DEF ,连接CF .(问题解决)(1)如图1,若点D 在边BC 上,求证:CE+CF =CD ;(类比探究)(2)如图2,若点D 在边BC 的延长线上,请探究线段CE ,CF 与CD 之间存在怎样的数量关系?并说明理由.【考点3】等腰三角形与等边三角形的判定与性质的应用【例3】(2020·内蒙古鄂尔多斯·中考真题)(1)(操作发现)如图1,在边长为1个单位长度的小正方形组成的网格中,ABC的三个顶点均在格点上.①请按要求画图:将ABC绕点A顺时针方向旋转90°,点B的对应点为点B',点C的对应点为点C'.连接BB';∠AB B=°.②在①中所画图形中,'(2)(问题解决)如图2,在Rt ABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.(3)(拓展延伸)如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k 为常数),求BD的长(用含k的式子表示).【变式3-1】(2020·四川凉山·中考真题)如图,点P、Q分别是等边ABC∆边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.(1)如图1,连接AQ 、CP 求证:ABQ CAP ∆≅∆(2)如图1,当点P 、Q 分别在AB 、BC 边上运动时,AQ 、CP 相交于点M ,QMC ∠的大小是否变化?若变化,请说明理由;若不变,求出它的度数(3)如图2,当点P 、Q 在AB 、BC 的延长线上运动时,直线AQ 、CP 相交于M ,QMC ∠的大小是否变化?若变化,请说明理由;若不变,求出它的度数.【变式3-2】(2020·吉林中考真题)如图,ABC 是等边三角形,4AB cm =,动点P 从点A 出发,以2/cm s 的速度沿AB 向点B 匀速运动,过点P 作PQ AB ⊥,交折线AC CB -于点Q ,以PQ 为边作等边三角形PQD ,使点A ,D 在PQ 异侧.设点P 的运动时间为()x s ()02x <<,PQD △与ABC 重叠部分图形的面积为y ()2cm .(1)AP 的长为______cm (用含x 的代数式表示).(2)当点D 落在边BC 上时,求x 的值.(3)求y 关于x 的函数解析式,并写出自变量x 的取值范围.【考点4】直角三角形的性质【例4】(2020·云南中考真题)如图,四边形ABCD 是菱形,点H 为对角线AC 的中点,点E 在AB 的延长线上,CE AB ⊥,垂足为E ,点F 在AD 的延长线上,CF AD ⊥,垂足为F .(1)若60BAD ∠=︒,求证:四边形CEHF 是菱形;(2)若4CE =,ACE △的面积为16,求菱形ABCD 的面积.【变式4-1】(2019·黑龙江中考真题)一张直角三角形纸片ABC ,90ACB ∠=,10AB =,6AC =,点D 为BC 边上的任一点,沿过点D 的直线折叠,使直角顶点C 落在斜边AB 上的点E 处,当BDE ∆是直角三角形时,则CD 的长为_____.【变式4-2】(2020·海南中考真题)如图,在Rt ABC 中,90,30,1,C ABC AC cm ∠=︒∠=︒=将Rt ABC 绕点A 逆时针旋转得到Rt AB C ''△,使点C '落在AB 边上,连接BB ',则BB '的长度是( )A .1cmB .2cmC .3cmD .23cm【考点5】相似三角形的判定与性质的应用【例5】(2020·上海中考真题)已知:如图,在菱形ABCD 中,点E 、F 分别在边AB 、AD 上,BE =DF ,CE 的延长线交DA 的延长线于点G ,CF 的延长线交BA 的延长线于点H .(1)求证:△BEC ∽△BCH ;(2)如果BE 2=AB •AE ,求证:AG =DF .【变式5-1】(2020·山东济南·中考真题)在等腰△ABC 中,AC =BC ,ADE 是直角三角形,∠DAE =90°,∠ADE =12∠ACB ,连接BD ,BE ,点F 是BD 的中点,连接CF . (1)当∠CAB =45°时.①如图1,当顶点D 在边AC 上时,请直接写出∠EAB 与∠CBA 的数量关系是 .线段BE 与线段CF 的数量关系是 ;②如图2,当顶点D 在边AB 上时,(1)中线段BE 与线段CF 的数量关系是否仍然成立?若成立,请给予证明,若不成立,请说明理由;学生经过讨论,探究出以下解决问题的思路,仅供大家参考:思路一:作等腰△ABC 底边上的高CM ,并取BE 的中点N ,再利用三角形全等或相似有关知识来解决问题; 思路二:取DE 的中点G ,连接AG ,CG ,并把CAG 绕点C 逆时针旋转90°,再利用旋转性质、三角形全等或相似有关知识来解快问题.(2)当∠CAB =30°时,如图3,当顶点D 在边AC 上时,写出线段BE 与线段CF 的数量关系,并说明理由.【变式5-2】(2020·湖南益阳·中考真题)定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形,根据以上定义,解决下列问题:(1)如图1,正方形ABCD 中,E 是CD 上的点,将BCE ∆绕B 点旋转,使BC 与BA 重合,此时点E 的对应点F 在DA 的延长线上,则四边形BEDF 为“直等补”四边形,为什么?(2)如图2,已知四边形ABCD 是“直等补”四边形,5AB BC ==,1CD =,AD AB >,点B 到直线AD 的距离为BE .①求BE 的长.②若M 、N 分别是AB 、AD 边上的动点,求MNC ∆周长的最小值.【考点6】锐角三角函数及其应用【例6】(2020·山东日照·中考真题)阅读理解:如图1,Rt △ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,∠C =90°,其外接圆半径为R .根据锐角三角函数的定义:sin A =a c ,sin B =b c ,可得sin a A =sin b B =c =2R ,即:sin a A =sin b B =sin c C =2R ,(规定sin90°=1).探究活动:如图2,在锐角△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,其外接圆半径为R ,那么:sin a Asin b B sin c C(用>、=或<连接),并说明理由. 事实上,以上结论适用于任意三角形.初步应用:在△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,∠A =60°,∠B =45°,a =8,求b . 综合应用:如图3,在某次数学活动中,小凤同学测量一古塔CD 的高度,在A 处用测角仪测得塔顶C 的仰角为15°,又沿古塔的方向前行了100m 到达B 处,此时A ,B ,D 三点在一条直线上,在B 处测得塔顶C 的仰角为45°,求古塔CD 的高度(结果保留小数点后一位).3,sin15°=624) 【变式6-1】(2020·湖北荆门·中考真题)如图,海岛B 在海岛A 的北偏东30方向,且与海岛A 相距20海里,一艘渔船从海岛B 出发,以5海里/时的速度沿北偏东75︒方向航行,同时一艘快艇从海岛A 出发,向正东方向航行.2小时后,快艇到达C 处,此时渔船恰好到达快艇正北方向的E 处.(1)求ABE ∠的度数;(2)求快艇的速度及C ,E 之间的距离.(参考数据:sin150.26,cos150.97,tan150.27,3 1.73︒︒︒≈≈≈≈)【变式6-2】(2020·山东淄博·中考真题)如图,著名旅游景区B 位于大山深处,原来到此旅游需要绕行C 地,沿折线A→C→B 方可到达.当地政府为了增强景区的吸引力,发展壮大旅游经济,修建了一条从A 地到景区B 的笔直公路.请结合∠A =45°,∠B =30°,BC =100千米,2≈1.4,3≈1.7等数据信息,解答下列问题:(1)公路修建后,从A 地到景区B 旅游可以少走多少千米?(2)为迎接旅游旺季的到来,修建公路时,施工队使用了新的施工技术,实际工作时每天的工效比原计划增加25%,结果提前50天完成了施工任务.求施工队原计划每天修建多少千米?1.(2020·广西玉林·中考真题)如图是A ,B ,C 三岛的平面图,C 岛在A 岛的北偏东35度方向,B 岛在A 岛的北偏东80度方向,C 岛在B 岛的北偏西55度方向,则A ,B ,C 三岛组成一个( )A .等腰直角三角形B .等腰三角形C .直角三角形D .等边三角形2.(2020·湖北荆门·中考真题)ABC 中,,120,23AB AC BAC BC =∠=︒=,D 为BC 的中点,14AE AB =,则EBD △的面积为( )A .334B .338C .34D .383.(2020·山东济南·中考真题)如图,在ABC 中,AB =AC ,分别以点A 、B 为圆心,以适当的长为半径作弧,两弧分别交于E ,F ,作直线EF ,D 为BC 的中点,M 为直线EF 上任意一点.若BC =4,ABC 面积为10,则BM +MD 长度的最小值为( )A .52B .3C .4D .54.(2020·宁夏中考真题)如图摆放的一副学生用直角三角板,3045F C ∠=∠=,,AB 与DE 相交于点G ,当//EF BC 时,EGB ∠的度数是( )A .135°B .120°C .115°D .105°5.(2020·山东枣庄·中考真题)如图,平面直角坐标系中,点B 在第一象限,点A 在x 轴的正半轴上,30AOB B ∠=∠=︒,2OA =,将AOB ∆绕点O 逆时针旋转90︒,点B 的对应点B '的坐标是( )A .()1,23-+B .()3,3-C .()3,23-+D .()3,3- 6.(2020·四川内江·中考真题)如图,矩形ABCD 中,BD 为对角线,将矩形ABCD 沿BE 、BF 所在直线折叠,使点A 落在BD 上的点M 处,点C 落在BD 上的点N 处,连结EF .已知34AB BC ==,,则EF 的长为( )A .3B .5C .5136D .137.(2020·江苏南通·中考真题)如图,在△ABC 中,AB =2,∠ABC =60°,∠ACB =45°,D 是BC 的中点,直线l 经过点D ,AE ⊥l ,BF ⊥l ,垂足分别为E ,F ,则AE +BF 的最大值为( )A .6B .22C .23D .328.(2020·四川绵阳·中考真题)如图,在四边形ABCD 中,∠A =∠C =90°,DF ∥BC ,∠ABC 的平分线BE 交DF 于点G ,GH ⊥DF ,点E 恰好为DH 的中点,若AE =3,CD =2,则GH =( )A .1B .2C .3D .49.(2020·四川绵阳·中考真题)在螳螂的示意图中,AB ∥DE ,△ABC 是等腰三角形,∠ABC =124°,∠CDE =72°,则∠ACD =( )A .16°B .28°C .44°D .45°10.(2020·湖北中考真题)如图,D 是等边三角形ABC 外一点.若8,6BD CD ==,连接AD ,则AD 的最大值与最小值的差为_____.11.(2020·湖北黄石·中考真题)匈牙利著名数学家爱尔特希(P. Erdos ,1913-1996)曾提出:在平面内有n 个点,其中每三个点都能构成等腰三角形,人们将具有这样性质的n 个点构成的点集称为爱尔特希点集.如图,是由五个点A 、B 、C 、D 、O 构成的爱尔特希点集(它们为正五边形的任意四个顶点及正五边形的中心构成),则ADO ∠的度数是_____.12.(2020·辽宁营口·中考真题)如图,∠MON =60°,点A 1在射线ON 上,且OA 1=1,过点A 1作A 1B 1⊥ON 交射线OM 于点B 1,在射线ON 上截取A 1A 2,使得A 1A 2=A 1B 1;过点A 2作A 2B 2⊥ON 交射线OM 于点B 2,在射线ON 上截取A 2A 3,使得A 2A 3=A 2B 2;…;按照此规律进行下去,则A 2020B 2020长为_____.13.(2020·广东深圳·中考真题)如图,已知四边形ABCD ,AC 与BD 相交于点O ,∠ABC =∠DAC =90°,14tan ,23BO ACB OD ∠==,则ABDCBD S S =___.14.(2020·四川宜宾·中考真题)在直角三角形ABC 中,90,ACB D ︒∠=是AB 的中点,BE 平分ABC ∠交AC 于点E 连接CD 交BE 于点O ,若8,6AC BC ==,则OE 的长是________.15.(2020·贵州黔南·中考真题)如图所示,在四边形ABCD 中,90B ∠=︒,2AB =,8CD =.连接AC ,AC CD ⊥,若1sin 3ACB ∠=,则AD 长度是_________.16.(2020·江苏常州·中考真题)如图,点C 在线段AB 上,且2AC BC =,分别以AC 、BC 为边在线段AB 的同侧作正方形ACDE 、BCFG ,连接EC 、EG ,则tan CEG ∠=_________.17.(2020·山东济宁·中考真题)如图,在△ABC 中,AB=AC ,点P 在BC 上.(1)求作:△PCD ,使点D 在AC 上,且△PCD ∽△ABP ;(要求:尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若∠APC=2∠ABC ,求证:PD//AB .18.(2020·广西河池·中考真题)(1)如图(1),已知CE 与AB 交于点E ,AC =BC ,∠1=∠2.求证:△ACE ≌△BCE .(2)如图(2),已知CD 的延长线与AB 交于点E ,AD =BC ,∠3=∠4.探究AE 与BE 的数量关系,并说明理由.19.(2020·山东菏泽·中考真题)如图1,四边形ABCD 的对角线AC ,BD 相交于点O ,OA OC =,OB OD CD =+.图1 图2(1)过点A 作//AE DC 交BD 于点E ,求证:AE BE =;(2)如图2,将ABD △沿AB 翻折得到ABD '△.①求证://BD CD ';②若//AD BC ',求证:22CD OD BD =⋅.20.(2020·贵州黔东南·中考真题)如图1,△ABC 和△DCE 都是等边三角形.探究发现(1)△BCD 与△ACE 是否全等?若全等,加以证明;若不全等,请说明理由.拓展运用(2)若B 、C 、E 三点不在一条直线上,∠ADC =30°,AD =3,CD =2,求BD 的长.(3)若B 、C 、E 三点在一条直线上(如图2),且△ABC 和△DCE 的边长分别为1和2,求△ACD 的面积及AD 的长.21.(2020·辽宁沈阳·中考真题)如图,在矩形ABCD 中,对角线AC 的垂直平分线分别与边AB 和边CD 的延长线交于点M ,N ,与边AD 交于点E ,垂足为点O .(1)求证:AOM CON △△≌;(2)若3AB =,6AD =,请直接写出AE 的长为__________.22.(2020·四川眉山·中考真题)如图,ABC 和CDE △都是等边三角形,点B 、C 、E 三点在同一直线上,连接BD ,AD ,BD 交AC 于点F .(1)若2AD DF DB =⋅,求证:AD BF =;(2)若90BAD ∠=︒,6BE =.①求tan DBE ∠的值;②求DF 的长.23.(2020·湖南郴州·中考真题)如图1,在等腰直角三角形ADC 中,90,4ADC AD ∠==.点E 是AD 的中点,以DE 为边作正方形DEFG ,连接,AG CE .将正方形DEFG 绕点D 顺时针旋转,旋转角为(090)αα<<.(1)如图2,在旋转过程中,①判断AGD ∆与CED ∆是否全等,并说明理由;②当CE CD =时,AG 与EF 交于点H ,求GH 的长.(2)如图3,延长CE 交直线AG 于点P .①求证:AG CP⊥;②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.24.(2020·黑龙江朝鲜族学校中考真题)∆ABC中,点D在直线AB上.点E在平面内,点F在BC的延长线上,∠E=∠BDC,AE=CD,∠EAB+∠DCF=180º.(1)如图①,求证AD+BC=BE;(2)如图②、图③,请分别写出线段AD,BC,BE之间的数量关系,不需要证明;(3)若BE⊥BC,tan∠BCD=34,CD=10,则AD=______.25.(2020·湖南娄底·中考真题)如实景图,由华菱涟钢集团捐建的早元街人行天桥于2019年12月18日动工,2020年2月28日竣工,彰显了国企的担当精神,展现了高效的“娄底速度”.该桥的引桥两端各由2个斜面和一个水平面构成,如示意图所示:引桥一侧的桥墩顶端E点距地面5m,从E点处测得D点俯角为30°,斜面ED长为4m,水平面DC长为2m,斜面BC的坡度为1∶4,求处于同一水平面上引桥底部AB的长.(结果精确到0.1m,2 1.41,3 1.73≈≈).26.(2020·湖北随州·中考真题)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1)后人称之为“赵爽弦图”,流传至今.(1)①请叙述勾股定理;②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)(2)①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足123S S S +=的有_______个;②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为1S ,2S ,直角三角形面积为3S ,请判断1S ,2S ,3S 的关系并证明;(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M 的边长为定值m ,四个小正方形A ,B ,C ,D 的边长分别为a ,b ,c ,d ,已知123α∠=∠=∠=∠,则当α∠变化时,回答下列问题:(结果可用含m 的式子表示)①2222a b c d +++=_______;②b 与c 的关系为_______,a 与d 的关系为_______.。
二次函数中的菱形、三角形存在性问题 学生版

二次函数中的菱形、三角形存在性问题学生版简介这个文档将讨论二次函数中的菱形和三角形的存在性问题。
我们将探讨在何种情况下,二次函数图像可能呈现出菱形或三角形的形状。
菱形存在性问题当二次函数的方程为 $ax^2+bx+c=0$ 时,可以通过求解方程得到二次函数的根。
如果方程有两个不同的实根,我们可以预期函数图像将呈现出一个开口向下的U形。
然而,当方程有两个相同的实根时,即存在两个相同的解 $x_1=x_2$,函数图像将呈现出一个菱形的形状。
菱形形状的二次函数图像的特点是,函数在两个实根处的斜率为0。
这意味着函数图像在这两个点上的变化趋势为平行于x轴。
在这种情况下,函数图像没有顶点,而是一个平缓的平行四边形形状。
三角形存在性问题当二次函数的方程为 $ax^2+bx+c=0$ 时,如果方程有两个不同的虚根,即解为复数,我们可以预期函数图像将呈现出一个开口向上的U形。
然而,当方程有一个实根和一个虚根时,即存在一个复根和一个实根,函数图像将呈现出一个三角形的形状。
三角形形状的二次函数图像的特点是,函数在实根处的斜率不为0。
这意味着函数图像在这个实根点上的变化趋势不平行于x轴。
在这种情况下,函数图像有一个顶点,且图像从这个顶点开始呈现出一个向上开口的三角形形状。
总结在二次函数中,存在着菱形和三角形的图像形状。
当方程有两个相同的实根时,函数图像将呈现出一个菱形的形状;当方程有一个实根和一个虚根时,函数图像将呈现出一个三角形的形状。
这些特殊的图像形状提供了二次函数的一种变化和特性,我们可以通过观察方程的根来探索图像的形状。
希望这份文档能帮助你了解二次函数中的菱形和三角形存在性问题。
如果你有进一步的问题或需要详细的解释,请随时向老师或同学寻求帮助。
专题15 三角形边角问题(学生版)

备考2024中考二轮数学《高频考点冲刺》(全国通用)专题15 三角形边角问题考点扫描☆聚焦中考三角形边角问题,近几年各地中考主要以选择题、填空题的形式考查,难度不大;考查的知识点主要有三角形三边关系、三角形中的主要线段、三角形内角和和三角形外角性质等;考查的热点有三角形三边关系、三角形内角和定理等。
考点剖析☆典型例题(2023•福建)若某三角形的三边长分别为3,4,m,则m的值可以是()A.1B.5C.7D.92022•杭州)如图,CD⊥AB于点D,已知∠ABC是钝角,则()A.线段CD是△ABC的AC边上的高线B.线段CD是△ABC的AB边上的高线C.线段AD是△ABC的BC边上的高线D.线段AD是△ABC的AC边上的高线2023•十堰)一副三角板按如图所示放置,点A在DE上,点F在BC上,若∠EAB=35°,则∠DFC=.2021•辽宁)一副三角板如图所示摆放,若∠1=80°,则∠2的度数是()A.80°B.95°C.100°D.110°考点过关☆专项突破类型一三角形三边关系1.(2023•长沙)下列长度的三条线段,能组成三角形的是()A.1,3,4B.2,2,7C.4,5,7D.3,3,6 2.(2023•盐城)下列每组数分别表示3根小木棒的长度(单位:cm),其中能搭成一个三角形的是()A.5,7,12B.7,7,15C.6,9,16D.6,8,12 3.(2023•金华)在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是()A.1cm B.2cm C.13cm D.14cm4.(2022•西藏)如图,数轴上A,B两点到原点的距离是三角形两边的长,则该三角形第三边长可能是()A.﹣5B.4C.7D.85.(2023•徐州)若一个三角形的边长均为整数,且两边长分别为3和5,则第三边的长可以为(写出一个即可).类型二三角形的角平分线、中线和高1.(2022•陕西)如图,AD是△ABC的中线,AB=4,AC=3.若△ACD的周长为8,则△ABD的周长为.2.(2018•贵阳)如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是()A.线段DE B.线段BE C.线段EF D.线段FG 3.(2022•玉林)请你量一量如图△ABC中BC边上的高的长度,下列最接近的是()A.0.5cm B.0.7cm C.1.5cm D.2cm4.(2022•常州)如图,在△ABC中,E是中线AD的中点.若△AEC的面积是1,则△ABD的面积是.类型三三角形内角和定理1.(2023•聊城)如图,分别过△ABC的顶点A,B作AD∥BE.若∠CAD=25°,∠EBC=80°,则∠ACB的度数为()A.65°B.75°C.85°D.95°2.(2021•宿迁)如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE ∥AB,交BC于点E,则∠BDE的度数是()A.30°B.40°C.50°D.60°3.(2021•陕西)如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为()A.60°B.70°C.75°D.85°4.(2023•株洲)《周礼•考工记》中记载有:“…半矩谓之宣(xuān),一宣有半谓之欘(zhú)…”.意思是:“…直角的一半的角叫做宣,一宣半的角叫做欘…”即:1宣=矩,1欘=1宣(其中,1矩=90°).问题:图(1)为中国古代一种强弩图,图(2)为这种强弩图的部分组件的示意图,若∠A=1矩,∠B=1欘,则∠C=度.5.(2023•徐州)如图,在△ABC中,若DE∥BC,FG∥AC,∠BDE=120°,∠DFG=115°,则∠C=°.6.(2023•遂宁)若三角形三个内角的比为1:2:3,则这个三角形是直角三角形.7.(2022•哈尔滨)在△ABC中,AD为边BC上的高,∠ABC=30°,∠CAD=20°,则∠BAC是80或40度.24.(2022•北京)下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.三角形内角和定理:三角形三个内角的和等于180°.已知:如图,△ABC,求证:∠A+∠B+∠C=180°.方法一证明:如图,过点A 作DE ∥BC . 方法二 证明:如图,过点C 作CD ∥AB .类型四 三角形的外角性质 1.(2021•盐城)将一副三角板按如图方式重叠,则∠1的度数为( )A .45°B .60°C .75°D .105°2.(2021•河北)定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD 是△ABC 的外角.求证:∠ACD =∠A +∠B .证法1:如图,∵∠A +∠B +∠ACB =180°(三角形内角和定理),又∵∠ACD +∠ACB =180°(平角定义),∴∠ACD +∠ACB =∠A +∠B +∠ACB (等量代换).∴∠ACD =∠A +∠B (等式性质).证法2:如图,∵∠A =76°,∠B =59°,且∠ACD =135°(量角器测量所得)又∵135°=76°+59°(计算所得)∴∠ACD =∠A +∠B (等量代换).下列说法正确的是( )A .证法1还需证明其他形状的三角形,该定理的证明才完整B .证法1用严谨的推理证明了该定理C.证法2用特殊到一般法证明了该定理D.证法2只要测量够一百个三角形进行验证,就能证明该定理3.(2021•毕节市)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为()A.70°B.75°C.80°D.85°4.(2021•河池)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的大小是()A.90°B.80°C.60°D.40°5.(2021•河北)如图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E 保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应(填“增加”或“减少”)度.6.(2020•湖北)将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B =∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是()A.15°B.20°C.25°D.30°。
二次函数中的矩形、三角形存在性问题 学生版

二次函数中的矩形、三角形存在性问题学生版二次函数是一种常见的数学函数形式,常被用于描述抛物线。
在二次函数图像中,矩形和三角形是两种常见的图形形状。
本文将探讨在二次函数中矩形和三角形的存在性问题。
矩形的存在性问题对于二次函数图像而言,矩形的存在性问题是指是否存在能与二次函数图像完全匹配的矩形。
换句话说,是否存在一条水平线段与二次函数的图像上的一段相邻的线段平行,并且与二次函数的图像上的另一段相邻的线段平行。
我们将以一元二次函数的标准形式为例进行讨论:$$f(x) = ax^2 + bx + c$$其中,$a$、$b$和$c$为常数,且$a$不等于零。
通过观察二次函数的图像,我们可以发现,矩形的存在性问题取决于二次函数的开口方向和形状。
当二次函数图像开口向上或向下,并且形状不对称时,很难找到能与图像完全匹配的矩形。
因此,可以得出结论,在一般情况下,不存在与二次函数图像完全匹配的矩形。
三角形的存在性问题类似于矩形的存在性问题,对于二次函数图像而言,三角形的存在性问题是指是否存在能与二次函数图像完全匹配的三角形。
换句话说,是否存在一条与二次函数的图像上的一段相邻的线段平行,并且与二次函数的图像上的另一段相邻的线段倾斜相交。
同样,我们以一元二次函数的标准形式进行讨论。
通过观察二次函数的图像,我们可以发现,三角形的存在性问题也取决于二次函数的开口方向和形状。
当二次函数图像开口向上或向下,并且形状对称时,能找到与图像完全匹配的三角形。
具体而言,只有当二次函数的开口方向、形状以及三角形的位置和大小相互配合时,才可能存在与二次函数图像完全匹配的三角形。
综上所述,在二次函数中,一般情况下不存在完全匹配的矩形,而存在完全匹配的三角形的可能性取决于二次函数的开口方向、形状以及三角形的位置和大小。
以上是关于二次函数中矩形、三角形存在性问题的讨论。
希望对学生们理解和掌握二次函数的图像有所帮助。
*注意:本文所讨论的是一般情况下的情况,对于特殊情况可能存在例外。
解三角形中的结构不良问题 学生版

解三角形中的结构不良问题知识点梳理一、“结构不良问题”的解题策略(1)题目所给的三个可选择的条件是平行的,无论选择哪个条件,都可解答题目;(2)在选择的三个条件中,并没有哪个条件让解答过程比较繁杂,只要推理严谨、过程规范,都会得满分,但计算要细心、准确,避免出现低级错误导致失分.二、“正弦定理”与“余弦定理”的选用策略在解有关三角形的题目时,要有意识地考虑用哪个定理更合适,或是两个定理都要用,要抓住能够利用某个定理的信息.(1)如果式子中含有角的余弦或边的二次式时,要考虑用余弦定理;(2)如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;(3)以上特征都不明显时,则要考虑两个定理都有可能用到.三、“边化角”或“角化边”的变换策略(1)若式子中含有正弦的齐次式,优先考虑正弦定理“角化边”;(2)若式子中含有a、b、c的齐次式,优先考虑正弦定理“边化角”;(3)若式子中含有余弦的齐次式,优先考虑余弦定理“角化边”;(4)代数式变形或者三角恒等变换前置;(5)含有面积公式的问题,要考虑结合余弦定理求解;(6)同时出现两个自由角(或三个自由角)时,要用到三角形的内角和定理.题型精讲精练1在△ABC中,角A,B,C所对的边分别为a,b,c,且满足2b cos C=2a-c(1)求角B;(2)在①△ABC的外接圆的面积为16π3,②△ABC的周长为12,③b=4,这三个条件中任选一个,求△ABC的面积的最大值.注:如果选择多个条件分别解答,按第一个解答计分.一、解答题1(2023·北京·统考高考真题)设函数f(x)=sinωx cosφ+cosωx sinφω>0,|φ|<π2.(1)若f(0)=-32,求φ的值.(2)已知f(x)在区间-π3,2π3上单调递增,f2π3=1,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数f(x)存在,求ω,φ的值.条件①:fπ3=2;条件②:f-π3=-1;条件③:f(x)在区间-π2,-π3上单调递减.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.2(2021·北京·统考高考真题)在△ABC中,c=2b cos B,C=2π3.(1)求∠B;(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,使△ABC存在且唯一确定,求BC边上中线的长.条件①:c=2b;条件②:△ABC的周长为4+23;条件③:△ABC的面积为33 4;一、解答题3(2023·四川·校联考模拟预测)已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .在下列三个条件①m =sin A ,-32,n =2cos2A ,2cos A ,且m ⎳n ;②a sin B =3b cos A ;③cos 2B +cos 2C =cos 2A +1-sin B sin C 中任选一个,回答下列问题.(1)求A ;(2)若a =2,求△ABC 面积的最大值.4(2023·北京东城·统考模拟预测)已知函数f x =23sin ωx cos ωx -2sin 2ωx +10<ω<2 .在下面两个条件中选择其中一个,完成下面两个问题:条件①:在f x 图象上相邻的两个对称中心的距离为π2;条件②:f x 的一条对称轴为x =π6.(1)求ω;(2)将f x 的图象向右平移π3个单位(纵坐标不变),得到函数g x 的图象,求函数g x 在-π3,π3上的值域.5(2023·全国·模拟预测)在①b sin C +3c cos B =3a ,②sin B +π6 =a +b 2c,③a sin C +π3 =c A sin 这三个条件中任选一个,补充在下面的问题中,并解答问题.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且.(1)求角C ;(2)若△ABC 外接圆的面积为4π,求△ABC 面积的最大值.注:如果选择多个条件分别解答,按第一个解答计分.6(2023·宁夏石嘴山·平罗中学校考模拟预测)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,sin B =13,且.(1)求△ABC 的面积;(2)若sin A sin C =23,求b .在①a 2-b 2+c 2=2,②AB ⋅BC=-1这两个条件中任选一个,补充在横线中,并解答.注:如果选择多个条件分别解答,按第一个解答计分.7(2023·云南昆明·昆明一中校考模拟预测)△ABC的内角A,B,C所对边分别为a,b,c,点O为△ABC的内心,记△OBC,△OAC,△OAB的面积分别为S1,S2,S3,已知S21+S23-S1S3=S22,AB=2.(1)若△ABC为锐角三角形,求AC的取值范围;(2)在①4sin B sin A+cos2A=1;②1-2cos Asin A +1-2cos Bsin B=0;③a cos C+c cos A=1中选一个作为条件,判断△ABC是否存在,若存在,求出△ABC的面积,若不存在,说明理由.(注:如果选择多个条件分别解答,按第一个解答计分.)8(2023·四川成都·四川省成都列五中学校考模拟预测)在△ABC中,内角A,B,C所对的边分别为a, b,c,且a-c cos B=33b sin C.(1)求角C的大小;(2)若c=23,且,求△ABC的周长.请在下列三个条件中,选择其中的一个条件补充到上面的横线中,并完成作答.①sin A sin B=112;②△ABC的面积为33;③CA⋅BC=-23.注:如果选择多个条件分别解答,那么按第一解答计分.9(2023·河北·统考模拟预测)在△ABC中,内角A,B,C对应的边为a,b,c,△ABC的面积为S,若a cos B+b cos A=2a.(1)当B=π3时,求A;(2)若角B为△ABC的最大内角.从下面①②③中选取两个作为条件,证明另外一个成立,①a2+c2+ac=b2;②b=7;③S=3 2.注:若选择不同的组合分别解答,则按第一个解答计分.10(2023·云南曲靖·统考模拟预测)在①a sin A+C=b cos A-π6;②1+2cos C cos B=cos C-B-cos C+B;③2tan Btan A+tan B=bc这三个条件中选择一个补充在下面问题中的横线上,然后求解.问题:在△ABC中,内角A,B,C的对边分别为a,b,c,且b+c=23,a=6,.(说明:只需选择一个条件填入求解,如果三个都选择并求解的,只按选择的第一种情形评分)(1)求角A的大小;(2)求△ABC内切圆的半径.11(2023·宁夏中卫·统考二模)在①tan A+tan B+3=3tan A tan B;②(c+a-b)(sin C-sin A +sin B)=a sin B;③3c sin B=b(cos C+1);这三个条件中任选一个,补充在下面的问题中,并进行解答.问题:在△ABC 中,内角A,B,C的对边分别为a,b,c,且.(1)求角C;(2)若△ABC的内切圆半径为32,b=4,求a-c.12(2023·重庆·统考模拟预测)如图所示,已知圆O是△ABC的外接圆,圆O的直径BD=2.设BC =a,AC=b,AB=c,在下面给出条件中选一个条件解答后面的问题,①tan C⋅b-3c sin A+3c⋅cos A=0;②2cos C+cos A=2sin C-sin A⋅tan A;③△ABC的面积为34a2+c2-b2.选择条件.(1)求b的值;(2)求△ACD的周长的取值范围.13(2023·湖南益阳·统考模拟预测)△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,从下列三个条件中任选一个作为已知条件,并解答问题.①c sin B +C 2=a sin C ;②a sin C1-cos A=3c ;③△ABC 的面积为34b 2+c 2-a 2 .(1)求角A 的大小;(2)求sin B sin C 的取值范围.注:如果选择多个条件分别解答,按第一个解答计分.14(2023·宁夏石嘴山·平罗中学校考模拟预测)在①m =2a -c ,b ,n =cos C ,cos B ,m ⎳n;②b sin A =a cos B -π6;③a +b a -b =a -c c 三个条件中任选一个,补充在下面的问题中,并解决该问题.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,且满足.注:如果选择多个条件分别解答,按第一个解答计分.(1)求角B ;(2)若b =2,求△ABC 面积的最大值.15(2023·山西吕梁·统考三模)在①3ab sin C =4AB ⋅AC;②a 3sin B +4cos B =4c ,这两个条件中任选一个,补充在下面问题中,并加以解答.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,.(1)求sin A 的值;(2)若△ABC 的面积为2,a =4,求△ABC 的周长.注:如选择多个条件分别解答,按第一个解答计分.16(2023·全国·模拟预测)从①2sin B =2sin A cos C +sin C ,②4S sin A =ab sin C tan A (S 为△ABC 的面积),③b cos A +a cos B +2a cos C =2b 这三个条件中任选一个,补充在下面横线上,并加以解答.在△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,且.(1)求角A 的大小;(2)若4sin B =b sin A ,求b +c 的取值范围.注:如果选择多个条件分别解答,按第一个解答计分.17(2023·河北邯郸·统考二模)已知条件:①2a=b+2c cos B;②2a sin A cos B+b sin2A= 23a cos C;③3sin C=3-2cos2C2.从三个条件中任选一个,补充在下面的问题中,并解答.问题:在△ABC中,角A,B,C所对的边分别为a,b,c,满足:.(1)求角C的大小;(2)若c=23,∠ABC与∠BAC的平分线交于点I,求△ABI周长的最大值.注:如果选择多个条件分别作答,按第一个解答计分18(2023·海南·海口市琼山华侨中学校联考模拟预测)在①8cos x cos x+π3;②-4sin2x-43sin x ⋅cos x+4;③8cos2x-4sin2x+π6-2这三个条件中任选一个,补充在下面问题中并解答.问题:已知函数f(x)=.(1)求函数f(x)的最小正周期及单调递减区间;(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,S为△ABC的面积.若f(x)在x=A处有最小值-a,求△ABC面积的最大值.注:如果选择多个条件分别解答,按第一个解答计分.19(2023·江苏·校联考模拟预测)在①a cos A+C2=b sin A,②sin2B1+cos2B+1-cos Bsin B=0这两个条件中任选一个,补充在下面问题中,并完成解答.在△ABC中,内角A,B,C所对应的边分别为a,b,c,且满足.(1)求B;(2)若b=7,c=3,D为AC边上的一点,且∠DBC=∠DCB,求BD.20(2023·海南·统考模拟预测)在①cos A+3π2tan C+cos A=12;②4cos2B-cos2C=3这两个条件中任选一个,补充在下面问题中并解答.问题:已知△ABC中,点M在线段BC上,且∠BAM=∠CAM,,AC=2,BM=2.(1)求BMCM的值;(2)求AM的值.注:如果选择多个条件分别解答,按第一个解答计分.·11·。
针对三角形错题后学生改正,教师给出的评语

针对三角形错题后学生改正,教师给出
的评语
一篇针对三角形错题后学生改正,教师给出的评语的材料。
如果学生在做三角形题目时出现了错误,教师可以给出一些评语来帮助学生改正错误。
下面是一些教师可能会给出的评语:
1."你的解题过程有一些问题,你需要仔细检查你
的步骤是否正确。
"
这句话的意思是,学生在做题过程中有一些问题,需要仔细检查自己的步骤是否正确。
教师可能会提供一些指导,帮助学生找到问题所在,并改正错误。
2."你需要更多的练习,这样才能掌握做题的技巧。
"
这句话的意思是,学生需要更多的练习,才能掌握做题的技巧。
教师可能会提供一些练习材料,帮助学生提高自己的能力。
3."你可以和同桌或者朋友一起做题,这样可以帮
助你更好地理解题目。
"
这句话的意思是,学生可以和同桌或者朋友一起做题,这样可以帮助他们更好地理解题目。
教师可能会提供一些合作学习的机会,帮助学生回顾一下自己在学习三角形的过程
中所学的知识。
微专题 妙用奔驰定理解决三角形面积比问题(学生版)

妙用奔驰定理解决三角形面积比问题【题型归纳目录】题型一:直接使用奔驰定理题型二:三角形面积比问题【方法技巧与总结】奔驰定理---解决面积比例问题重心定理:三角形三条中线的交点.已知△ABC 的顶点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),则△ABC 的重心坐标为G x 1+x 2+x 33,y 1+y 2+y 33.注意:(1)在△ABC 中,若O 为重心,则OA +OB +OC =0.(2)三角形的重心分中线两段线段长度比为2:1,且分的三个三角形面积相等.重心的向量表示:.奔驰定理:S A ⋅OA +S B ⋅OB +S C ⋅OC =0,则△AOB 、△AOC 、△BOC 的面积之比等于λ3:λ2:λ1奔驰定理证明:如图,令λ1OA =OA 1 ,λ2OB =OB 1 ,λ3OC =OC 1 ,即满足OA 1+OB 1+OC1=0S △AOB S △A 1OB 1=1λ1λ2,S △AOC S △A 1OC 1=1λ1λ3,S △BOC S △B 1OC 1=1λ2λ3,故S △AOB :S △AOC :S △BOC =λ3:λ2:λ1.(3)P 为ΔABC 内一点,a ×PA +b ×PB +c ×PC =0 ,则S ΔPBC :S ΔPAC :S ΔPAB =a :b :c .重要结论:S ΔPBC S ΔABC =a a +b +c ,S ΔPAC S ΔABC =b a +b +c ,S ΔPAB S ΔABC =c a +b +c.结论1:对于ΔABC 内的任意一点P , 若ΔPBC 、ΔPCA 、ΔPAB 的面积分别为S A 、S B 、S C ,则:S A ⋅PA +S B ⋅PB+S C ⋅PC =0 .即三角形内共点向量的线性加权和为零,权系数分别为向量所对的三角形的面积.结论2:对于ΔABC 平面内的任意一点P ,若点P 在ΔABC 的外部,并且在∠BAC 的内部或其对顶角的内部所在区域时,则有-S ΔPBC ⋅PA +S ΔPAC ⋅PB+S PAB ⋅PC =0 .结论3:对于ΔABC 内的任意一点P , 若λ1PA +λ2PB+λ3PC =0 ,则ΔPBC 、ΔPCA 、ΔPAB 的面积之比为λ1:λ2:λ3.即若三角形内共点向量的线性加权和为零,则各向量所对的三角形面积之比等于权系数之比.结论4:对于ΔABC 所在平面内不在三角形边上的任一点P ,λ1PA +λ2PB+λ3PC =0 ,则ΔPBC 、ΔPCA 、ΔPAB 的面积分别为λ1: λ2: λ3 .即若三角形平面内共点向量的线性加权和为零,则各向量所对应的三角形面积之比等于权系数的绝对值之比.各向量所对应的三角形是指另外两个向量所在的三角形.【典型例题】题型一:直接使用奔驰定理例1.(2023春·河南安阳·高一统考期末)已知O 是△ABC 内的一点,若△BOC ,△AOC ,△AOB 的面积分别记为S 1,S 2,S 3,则S 1⋅OA +S 2⋅OB +S 3⋅OC =0.这个定理对应的图形与“奔驰”轿车的log o 很相似,故形象地称其为“奔驰定理”.如图,已知O 是△ABC 的垂心,且OA +2OB +3OC =0,则tan ∠BAC :tan ∠ABC :tan ∠ACB =( )A.1:2:3B.1:2:4C.2:3:4D.2:3:6例2.(多选题)(2023·高一单元测试)如图,P 为△ABC 内任意一点,角A ,B ,C 的对边分别为a ,b ,c ,则总有优美等式S △PBC ⋅PA +S △PAC ⋅PB+S △PAB ⋅PC =0 成立,此结论称为三角形中的奔驰定理.由此判断以下命题中,正确的有( )A.若P 是△ABC 的重心,则有PA +PB +PC =0B.若a ⋅PA +b ⋅PB+c ⋅PC =0 ,则P 是△ABC 的内心C.若AP =15AB +25AC ,则S △PBC :S △PAC :S △PAB =2:2:1D.若P 是△ABC 的外心,且A =π4,则PA +sin ∠APC ⋅PB +sin 3π2-∠APC ⋅PC =0例3.(多选题)(2023秋·河南洛阳·高一宜阳县第一高级中学校考阶段练习)点P 是△ABC 所在平面内一点,且AP =xAB +yAC,下列说法正确的是( )A.若x =y =12,则点P 是边BC 的中点B.若点P 是边BC 靠近B 点的三等分点,则x =13,y =23C.若点P 在BC 边的中线上且x +y =12,则点P 是△ABC 的重心D.若x +y =2,则△PBC 与△ABC 的面积相等例4.(多选题)(2023·全国·高三专题练习)“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车,(Mercedesbenz )的log o 很相似,故形象地称其为“奔驰定理”,奔驰定理:已知O 是△ABC 内一点,△BOC ,△AOC ,△AOB 的面积分别为S A ,S B ,S C ,且S A ⋅OA+S B ⋅OB +S C ⋅OC =0.设O 是锐角△ABC 内的一点,∠BAC ,∠ABC ,∠ACB 分别是的△ABC 三个内角,以下命题正确的有( )A.若OA +2OB +3OC =0 ,则S A :S B :S C =1:2:3B.若OA =OB =2,∠AOB =5π6,2OA +3OB +4OC =0 ,则S △ABC =92C.若O 为△ABC 的内心,3OA +4OB +5OC =0 ,则∠C =π2D.若O 为△ABC 的垂心,3OA +4OB +5OC =0 ,则cos ∠AOB =-66例5.(多选题)(2023秋·河南洛阳·高一宜阳县第一高级中学校考阶段练习)已知点O 为△ABC 所在平面内一点,且2OA +3OB +4OC =0则下列选项正确的有( )A.AO =13AB +49ACB.直线AO 过BC 边的中点C.S △AOB :S △BOC =2:1D.若|OA |=|OB |=|OC |=1,则OC ⋅AB =-316例6.(多选题)(2023春·湖南永州·高一永州市第一中学校考期中)已知点O 为△ABC 所在平面内一点,2OA +3OB +4OC =0 ,则下列选项正确的是( )A.AO =13AB +49ACB.直线AO 必过BC 边的中点C.S △ABC :S △AOC =3:1D.若|OB |=|OC |=|OA |=1,则cos <OA ,OB >=14例7.(2023春·江苏徐州·高一徐州市第三十六中学(江苏师范大学附属中学)校考阶段练习)定理:如图,已知P 为△ABC 内一点,则有S △PBC ⋅PA +S △PAC ⋅PB+S △PAB ⋅PC =0 .由于这个定理对应的图象和奔驰车的标志很相似,我们把它称为“奔驰定理”.这个定理对于利用平面向量解决平面几何问题,尤其是解决跟三角形的面积和“四心”相关的问题,有着决定性的基石作用.已知点O 在△ABC 内部,有以下四个推论:①若O 为△ABC 的重心,则OA +OB +OC =0;②若O 为△ABC 的外心,则sin2A ⋅OA +sin2B ⋅OB +sin2C ⋅OC =0;③若O 为△ABC 的内心,则a ⋅OA +b ⋅OB +c ⋅OC =0;备注:若O 为△ABC 的内心,则sin A ⋅OA+sin B ⋅OB +sin C ⋅OC =0也对.④若O 为△ABC 的垂心,则tan A ⋅OA +tan B ⋅OB +tan C ⋅OC =0.试用“奔驰定理”或其它方法解决下列问题.(1)点P 在△ABC 内部,满足PA +2PB+3PC =0 ,求S △ABC :S △APC 的值;(2)点O 为△ABC 内一点,若S △AOB :S △BOC :S △AOC =4:3:2,设AO =λAB +μAC,求实数λ和μ的值;(3)用“奔驰定理”证明推论②.题型二:三角形面积比问题例8.(多选题)(2023·高一课时练习)若点O 为△ABC 所在平面内一点,AO =13AB +49AC ,则下列选项正确的是( )A.直线AO 必过BC 边的中点B.S △AOC :S △ABC =1:3C.若△ABC 的面积为9,则△AOB 的面积是4D.2OA +3OB +4OC =0例9.(多选题)(2023春·江苏南京·高二金陵中学校考阶段练习)已知点O 为△ABC 所在平面内一点,且AO +2OB +3OC =0 ,则下列选项正确的是( )A.AO =12AB +34ACB.直线AO 必过BC 边的中点C.S △AOB :S △AOC =3:2D.若OB =OC =1,且OB ⊥OC,则OA =13例10.(2023·江苏泰州·高三阶段练习)已知点O 为△ABC 内一点,且OA +2OB +3OC =0,则△AOB,△AOC ,△BOC 的面积之比等于_______.例11.(2023秋·江苏泰州·高三阶段练习)已知点O 为△ABC 内一点,且OA +2OB +3OC =0 ,则△AOB ,△AOC ,△BOC 的面积之比等于_________.例12.(2023·河南南阳·统考三模)已知O 为△ABC 内一点,且OA +2OB +3OC =0 ,则△AOB ,△AOC ,△BOC 的面积之比为________.例13.(2023·全国·高三专题练习)奔驰定理:已知O 是△ABC 内的一点,△BOC ,△AOC ,△AOB 的面积分别为S A ,S B ,S C ,则S A ⋅OA +S B ⋅OB +S C ⋅OC =0.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车的log o 很相似,故形象地称其为“奔驰定理”.设O 为三角形ABC 内一点,且满足:OA +2OB +3OC =3AB +2BC +CA ,则S△AOB S △ABC=( )A.25B.12C.16D.13【同步练习】一、单选题1.(2023·全国·高三专题练习)已知P 为△ABC 内任意一点,若满足x PA +y PB +z PC =0x ,y ,z >0 ,则称P 为△ABC 的一个“优美点”.则下列结论中正确的有( )①若x =y =z =1,则点P 为△ABC 的重心;②若x =1,y =2,z =3,则S △PBC =16S △ABC;③若PA ⋅PB =PB ⋅PC =PA ⋅PC ,则点P 为△ABC 的垂心;④若x =1,y =3,z =1且D 为AC 边中点,则BP =25BD.A.1个B.2个C.3个D.4个2.(2023秋·河南安阳·高三阶段练习)P 是△ABC 所在平面上一点,满足PA +PB +PC =2AB,若S △ABC =12,则△PAB 的面积为( )A.4B.6C.8D.163.(2023·全国·高三专题练习)P 是△ABC 所在平面上的一点,满足PA +PB +PC =2AB ,若S △ABC =6,则△PAB 的面积为( ).A.2B.3C.4D.84.(2023春·安徽黄山·高一统考期末)已知O 是△ABC 所在平面内的一点,∠A ,∠B ,∠C 所对的边分别为a =3,b =2,c =4,若aOA +bOB +cOC =0,过O 作直线l 分别交AB 、AC (不与端点重合)于P 、Q ,若AP =λAB ,AQ =μAC ,若△PAO 与△QAO 的面积之比为32,则λμ=( )A.56B.13C.43D.345.(2023·全国·高三专题练习)已知点P 为ABC 内一点,PA +2PB+3PC =0 ,则△APB ,△APC ,△BPC 的面积之比为( )A.9:4:1B.1:4:9C.1:2:3D.3:2:16.(2023秋·河北邯郸·高三校联考阶段练习)已知点M 是△ABC 所在平面内一点,若AM =12AB +13AC ,则△ABM 与△BCM 的面积之比为( )A.83B.52C.2D.437.(2023春·陕西延安·高一校考阶段练习)已知M 是ΔABC 所在平面内一点,且满足2AM =14AB+34AC ,则ΔA MB 与ΔABC 的面积之比为A.1:4B.3:4C.3:8D.1:88.(2023秋·江西宜春·高三江西省丰城中学校考阶段练习)记△ABC 所在平面内一点为P ,满足xAB+yAC =AP ,其中x 2+y 2=1,则S △ABP S △ABC的取值范围为( )A.[2-1,+∞)B.(0,2-1]C.(0,1]D.[2+1,+∞)【答案】C【解析】过C 点作AB 的垂线,垂足为D ,则AC =AD +DC ,AP =xAB +y (AD +DC ),而AB 与AD 共线,易得S △ABP S △ABC=12|AB |⋅|y |⋅|DC |12|AB |⋅|DC |=|y |,而x 2+y 2=1,y ≠0,故S△ABP S △ABC ∈(0,1],故选:C9.(2023秋·江西景德镇·高二校联考期末)已知点P 为ΔABC 内一点,且满足AP =12AB +13AC ,则SΔABC S ΔABP=A.2 B.3C.4D.5二、多选题10.(2023秋·辽宁大连·高一统考期末)已知点P 为△ABC 所在平面内一点,且PA +2PB +3PC =0 ,若E 为AC 的中点,F 为BC 的中点,则下列结论正确的是( )A.向量PA 与PC可能平行B.点P 在线段EF 上C.PE :PF=2:1D.S △PAB :S △PAC :S △PBC =1:2:3三、填空题11.(2023·全国·高三专题练习)如图,P 为△ABC 内任意一点,角A ,B ,C 的对边分别为a ,b ,c .总有优美等式S △PBC PA +S △PAC PB+S △PAB PC =0 成立,因该图形酷似奔驰汽车车标,故又称为奔驰定理.现有以下命题:①若P 是△ABC 的重心,则有PA +PB +PC =0 ;②若aPA +bPB+cPC =0 成立,则P 是△ABC 的内心;③若AP =25AB +15AC ,则S △ABP :S △ABC =2:5;④若P 是△ABC 的外心,A =π4,PA=mPB +nPC ,则m +n ∈-2,1 .则正确的命题有___________.12.(2023·全国·高一专题练习)设P 为ΔABC 所在平面上一点,且满足3PA +4PC=mAB (m >0).若ΔABP 的面积为8,则ΔABC 的面积为__________.13.(2023春·河南濮阳·高一统考期中)P 是△ABC 所在平面上的一点,满足PA +PB +PC =2AB ,若S △PAB =4,则△ABC 的面积为___________.14.(2023·湖北·高三竞赛)已知P 是ΔABC 所在平面上一点,满足PA +PB +2PC =3AB .则ΔABP 与ΔABC 的面积之比为_______.15.(2023·全国·高三竞赛)设P 是△ABC 所在平面内一点,满足PA +PB +PC =3AB ,若△PAC 的面积为1,则△PAB 的面积为__________.16.(2023·全国·高三专题练习)已知点P 为△ABC 内一点,2PA +3PB +5PC =0 ,则△APB ,△APC ,△BPC 的面积之比为______.17.(2023·上海·高三专题练习)已知ΔABC 的面积为360,点P 是三角形所在平面内一点,且AP =14AB +14AC,则ΔPAB 的面积为__.四、解答题18.(2023春·山东济南·高一统考期末)在△ABC 中,点P 为△ABC 内一点.(1)若点P 为△ABC 的重心,用AB ,AC 表示AP;(2)记△PBC ,△PAC ,△PAB 的面积分别为S A ,S B ,S C ,求证:S A PA +S B PB+S C PC =0;(3)若点P 为△ABC 的垂心,且PA +2PB+3PC =0,求cos ∠APB .19.(2023春·河北保定·高二河北省曲阳县第一高级中学校考阶段练习)已知点P 为△ABC 内一点2PA +3PB +5PC =0 ,若F 为AC 中点,G 为BC 中点,|PF||PG |=___________.△APB,△APC ,△BPC 的面积之比为_____________.。
中考专题:三角形探究操作问题(学生版)

三角形探究操作问题1.(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.AB、AD、DC之间的等量关系为;(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE 是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.2.请认真阅读下面的数学小探究系列,完成所提出的问题:(1)探究1,如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=3,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D做BC边上的高DE,则DE与BC的数量关系是,△BCD的面积为;(2)探究2,如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由;(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.(1)当点E在线段BD上移动时,如图1所示,求证:AE=EF;(2)当点E在直线BD上移动时,如图2,线段AE与EF又有怎样的数量关系?(3)当点E在直线BD上移动时,如图3,线段AE与EF又有怎样的数量关系?请直接写出你的猜想,不用证明.(1)当点E在线段BD上移动时,如图(1)所示,求证:BC﹣DE=DF.(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段BC、DE与DF又有怎样的数量关系?请直接写出你的猜想,不需证明.5.如图1,将两个等腰直角三角形纸片ABC和DEC的顶点C重合放置,点D和E分别在边AC和BC上,其中∠C=90°,AC=BC,DC=EC.(1)操作发现:如图2,固定△ABC,使△DEC绕点C顺时针旋转45°,点D恰好落在AB边上,填空:①线段DE与AC的位置关系是;②设△BDC面积为S1,△AEC的面积为S2,则S1与S2的数量关系是.(2)猜想论证:当△DEC绕点C继续旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,AC边上的高DM,EN,请你证明小明的猜想.(3)拓展探究:已知∠ABC=60°,点D是∠ABC平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4),若在射线BA =S△BDE,请直接写出相应的线段BF的长.上存在点F,使S△DCF6.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现如图2,固定△ABC,使△DEC绕点C顺时针旋转,当点D恰好落在AB边上时,①线段DE与AC的位置关系是;②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是;并证明你的结论.(2)猜想论证①当△DEC绕点C旋转到图3所示的位置时,猜想(1)中S1与S2的数量关系是否仍然成立,并证明你的猜想.②已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4),若在射线BA=S△BDE,请直接写出相应的BF的长.上存在点F,使S△DCF7.问题情境:数学活动课上,老师出示了一个问题:如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,转动△DEF使DF⊥AB交AC于点G,DE交BC于点H.求两三角形重叠部分(四边形DHCG)的面积.(1)独立思考:请解答老师提出的问题.(2)合作交流:将△DEF绕点D继续旋转,如图(2),使DF经过点C,DE交BC于点H,你能求出两三角形重叠部分(△DHC)的面积,请写出解答过程.(3)拓展探究:边EF在绕点D旋转的过程中扫过了一个(注:填图形名称),该图形的面积为.。
三角形的内角重难点题型(学生版)

三角形的内角-重难点题型【北师大版】【题型1 三角形的内角和定理】【例1】(2021春•玄武区校级月考)在△ABC中,(1)若∠A:∠B:∠C=4:5:6,则∠C=度.(2)若∠A=12∠B=13∠C,则∠B=度.【变式1-1】(2020秋•下城区期末)在△ABC中,∠A是钝角,∠B=30°,设∠C的度数是α,则α的取值范围是.【变式1-2】(2021春•靖江市月考)如图,线段AD和BC相交于点O,若∠A=70°,∠C=85°,则∠B﹣∠D=.【变式1-3】(2020秋•洪山区期中)如图所示的折线图形中,α+β=.【题型2 三角形的内角和定理的应用(含三角板)】【例2】(2020春•江都区期末)将一副三角板如图放置,则图中的∠1=°.【变式2-1】(2020秋•光明区期末)将两块分别含有30°和45°角的直角三角板按如图所示叠放,若∠1=∠2,则∠3=°.【变式2-2】(2020秋•涪城区校级期末)一副三角板如图方式摆放,BM平分∠ABD,DM 平分∠BDC,则∠BMD的度数为()A.102°B.107.5°C.112.5°D.115°【变式2-3】(2020春•盐都区期中)如图,将一块直角三角板DEF放置在锐角三角形ABC 上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=45°,则∠ABD+∠ACD的值为()A.40°B.45°C.50°D.55°【题型3 三角形的内角和定理的应用(含高线、角平分线)】【例3】(2020秋•呼和浩特期末)如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=45°,∠C=73°,则∠DAE的度数是()A.14°B.24°C.19°D.9°【变式3-1】(2021春•碑林区校级期中)如图,AD,AE为△ABC的高线,角平分线,DF ⊥AE于点F.当∠DAC=21°,∠B=25°时,∠DAF的度数为()A.21°B.22°C.25°D.30°【变式3-2】(2020秋•蚌埠期末)如图,在△ABC中,AD是△ABC的角平分线,DE⊥AC,若∠B=40°,∠C=60°,则∠ADE的度数为()A.30°B.40°C.50°D.60°【变式3-3】(2020秋•夏津县期末)如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是()A.59°B.60°C.56°D.22°【题型4 三角形的内角和定理的应用(含平行线)】【例4】(2020秋•兴化市期末)如图,在△ABC中,BD平分∠ABC交AC于点D,EF∥BC交BD于点G,若∠BEG=130°,则∠DGF=°.【变式4-1】(2021春•姑苏区期中)如图,△EFG的三个顶点E,G和F分别在平行线AB,CD上,FH平分∠EFG,交线段EG于点H,若∠AEF=36°,∠BEG=57°,则∠EHF 的大小为.【变式4-2】(2021春•周村区月考)如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是()A.45°B.50°C.55°D.80°【变式4-3】(2021春•东城区校级期中)如图,在△ABC中,∠ABC的角平分线交AC于点E,过点E作DF∥BC,交AB于点D,且EC平分∠BEF.(1)若∠ADE=50°,求∠BEC的度数;(2)若∠ADE=α,则∠AED=(含α的代数式表示).【题型5 三角形的内角和定理的应用(含折叠)】【例5】(2021春•江都区校级期末)如图△ABC中,将边BC沿虚线翻折,若∠1+∠2=110°,则∠A的度数是度.【变式5-1】(2020春•杨浦区期中)如图,在△ABC中,∠B=40°,∠C=30°,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,联结DE,如果DE∥AB,那么∠CAD的度数是度.【变式5-2】(2020秋•灵山县期中)如图,△ABC中,∠A=40°,将△ABC沿DE折叠,点A落在F处,则∠FDB+∠FEC的度数为()A.140°B.120°C.70°D.80°【变式5-3】(2020秋•芜湖期中)如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为()A.27°B.59°C.69°D.79°【题型6 三角形的内角和定理的应用(新定义)】【例6】(2020秋•海淀区校级月考)定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为30°,那么这个“特征角”α的度数为.【变式6-1】(2020春•成都期末)三角形中,如果有一个内角是另外一个内角的3倍,我们把这个三角形叫做“三倍角三角形”.在一个“三倍角三角形”中有一个内角为60°,则另外两个角分别为.【变式6-2】(2021春•邗江区月考)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB ⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).当△ABC为“灵动三角形”时,则∠OAC的度数为.【变式6-3】(2020秋•南海区校级期末)阅读理解:如果三角形满足一个角α是另一个角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”.解答问题:(1)一个角为60°的直角三角形(填“是”或“不是”)“智慧三角形”,若是,“智慧角”是.(2)已知一个“智慧三角形”的“智慧角”为108°,求这个“智慧三角形”各个角的度数.【题型7 直角三角形的性质】【例7】(2021春•九龙坡区校级期中)如图,在△ABC中,AB⊥AC,过点A作AD⊥BC 交BC于点D,若∠B=36°,则∠DAC的度数为()A.36°B.46°C.54°D.64°【变式7-1】(2021春•青羊区校级期中)如图,将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)的直角顶点重合并如图叠放,当∠DEB=m°,则∠AOC=()A.30°B.(m﹣15)°C.(m+15)°D.m°【变式7-2】(2020秋•德城区校级月考)如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠EDF.【变式7-3】(2020春•沭阳县期末)已知:如图,在△ABC中,∠ACB=90°,CD是高,AE是△ABC内部的一条线段,AE交CD于点F,交CB于点E,且∠CFE=∠CEF.求证:AE平分∠CAB.【题型8 直角三角形的判定】【例8】(2020春•历下区期中)在下列条件:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=2∠C;④∠A=12∠B=13∠C;⑤∠A=∠B=12∠C中,能确定△ABC为直角三角形的条件有()A.5个B.4个C.3个D.2个【变式8-1】(2020秋•盐湖区期中)如图,在由25个边长为1的小正方形拼成的网格中以AB为边画Rt△ABC,使点C在格点上,满足这样条件的点C共()个.A.5B.6C.7D.8【变式8-2】(2020秋•九龙坡区校级月考)如图所示,在△ABC中,AD是BC边上的高,点E是AB上一点,CE交AD于点M,且∠DCM=∠MAE,求证:△ACE是直角三角形.【变式8-3】(2020秋•潮安区期末)如图,AB、ED分别垂直于BD,点B、D是垂足,且∠ACB=∠CED.求证△ACE是直角三角形.。
专题 反比例函数中的三角形存在性问题(学生版)

专题6.3反比例函数中三角形存在性问题【例题精讲】【例1】如图,一次函数11y x=--的图象与x轴交于点A,与y轴交于点B,与反比例函数2kyx=的图象的一个交点为(2,)M m-,另一个交点为N.(1)求反比例函数的解析式;(2)求点B到直线OM的距离;(3)在x轴上是否存在点P,使得PMN∆为等腰三角形,若存在,直接写出点P的坐标,若不存在,请说明理由.【例2】如图,直线y mx=与双曲线kyx=相交于A,B两点,A点的坐标为(1,2).(1)求直线和双曲线的函数表达式;(2)在x轴正半轴上是否存在点C,使ABC∆为直角三角形,若存在,请求出点C的坐标;若不存在,请说明理由.【例3】如图,在平面直角坐标系中,点B,D分别在反比例函数6(0)y xx=-<和(0,0)ky k xx=>>的图象上,AB x⊥轴于点A,DC x⊥轴于点C,O是线段AC的中点,3AB=,2DC=.(1)求反比例函数kyx=的表达式.(2)连接BD,OB,OD,求ODB∆的面积.(3)P是线段AB上的一个动点,Q是线段OB上的一个动点,试探究是否存在点P,使得APQ∆是等腰直角三角形?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.【题组训练】1.如图,直线:33AD y x =+与坐标轴交于A 、D 两点,以AD 为边在AD 右侧作正方形ABCD ,过C 作CG y ⊥轴于G 点,过点C 的反比例函数(0)k y k x =≠与直线AD 交于E 、F 两点.(1)求反比例函数k y x=表达式;(2)根据图象,求出不等式033k x x <+<的解集;(3)在x 上是否存在一点Q 使CBQ ∆为等腰三角形,若存在,求出Q 点坐标,若不存在,请说明理由.2.如图,平行四边形ABCD 的面积为12,//AB y 轴,AB ,CD 与x 轴分别交于点M ,N ,对角线AC ,BD 的交点为坐标原点,点A 的坐标为(2,1)-,反比例函数k y x=的图象经过点B ,D .(1)求反比例函数的解析式;(2)点P 为y 轴上的点,连接AP ,若AOP ∆为等腰三角形,求满足条件的点P 的坐标.3.如图,一次函数11(0)y k x b k =+≠与反比例函数22(0)k y k x=≠的图象交于点(2,3)A ,(,1)B a -,设直线AB 交x 轴于点C .(1)求反比例函数和一次函数的表达式;(2)若点P 是反比例函数图象上的一点,且POC ∆是以OC 为底边的等腰三角形,求P 点的坐标.4.已知点(3,2)A 、点(,)B m n 在反比例函数(0)k y x x=>图象上,点C 是x 轴上的一个动点.(1)求k 的值;(2)若1m =,(1,0)C -,试判断ABC ∆的形状,并说明理由;(3)若点C 在x 轴正半轴上,当ABC ∆为等腰直角三角形时,求出点C 的坐标.5.如图,正比例函数y kx =的图象与反比例函数m yx=的图象交于点(A a ,2)(0)a a >和点B ,且OA =,点C 是x 轴正半轴上一点,过点C 作x 轴的垂线,与正比例函数图象交于点P ,与反比例函数图象交于点Q .(1)求正比例函数与反比例函数的表达式;(2)当点Q 是PC 的中点时,求C 点的坐标;(3)是否存在点C ,使ABC ∆是直角三角形,若存在,求出此时点C 的坐标,若不存在,说明理由.6.如图,在平面直角坐标系xOy 中,一次函数1y x =+的图象与反比例函数(0)k y k x=≠的图象交于A ,B 两点,直线AB 与x 轴交于点C ,点B 的坐标为(2,)n -,点A 的坐标为(,2)m .(1)求反比例函数的解析式;(2)求AOB ∆的面积;(3)在x 轴上是否存在一点P ,使AOP ∆是等腰三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系xOy 中,矩形OABC 的顶点A ,C 分别在x 轴,y 轴上,D 是BC 的中点,过点D 的反比例函数(0)k y x x =>的图象交AB 于点E ,连接DE .若5OD =,3cos 5COD ∠=.(1)求反比例函数的解析式;(2)若点P 在x 轴上,且以P ,A ,E 为顶点的三角形是等腰直角三角形,请直接写出P 点坐标.8.如图,一次函数11y k x b =+经过点(0,4)A ,(4,0)B ,与反比例函数22(0)k y x x=>的图象交于点(1,)C n ,D 两点.(1)求反比例函数和一次函数的解析式;(2)结合函数图象,直接写出当210k k x b x <+ 时x 的取值范围;(3)点P 在x 轴上,是否存在PCD ∆是以CD 为腰的等腰三角形,若存在,请直接写出点P 的坐标;若不存在,说明理由.9.如图,一次函数114y k x =+与反比例函数22k y x=的图象交于点(2,)A m 和(6,2)B --,与y 轴交于点C .(1)求一次函数与反比例函数的表达式;(2)过点A 作AD x ⊥轴于点D ,点P 是反比例函数在第一象限的图象上一点,设直线OP 与线段AD 交于点E ,当:5:1ODE ODAC S S ∆=四边形时,求点P 的坐标;(3)在(2)的条件下,点M 是直线OP 上的一个动点,当MBC ∆是以BC 为斜边的直角三角形时,求点M 的坐标.10.已知一次函数y kx b =+与反比例函数m y x=的图象交于(4,3)A -、(2,)B n 两点.(1)求一次函数和反比例函数的表达式;(2)求AOB ∆的面积;(3)点P 在x 轴上,当PAO ∆为等腰三角形时,直接写出点P 的坐标.11.【模型建立】(1)如图一,在ABC ∆中,90ACB ∠=︒,CB CA =,直线ED 经过点C ,过点A 作AD ED ⊥于D ,过点B 作BE ED ⊥于E .求证:AD CE =.【模型应用】(2)如图二,直线14:43l y x =+与坐标轴交于点A 、B ,将直线1l 绕点B 顺时针旋转45︒得到直线2l ,求直线2l 的函数表达式;【拓展探究】(3)如图三,一次函数483y x =+的图象与坐标轴分别相交于点A 、B ,点C 在反比例函数(0)k y x x=<的图象上,若ABC ∆为等腰直角三角形,请直接写出k 的所有可能的值.12.如图,一次函数5y x =-+与反比例函数4(0)y x x=≠的图象交于点A ,B .(1)求点A ,B 的坐标;(2)观察图象写出不等式45x x -+>的解集;(3)若位于第三象限的点M 在反比例函数4(0)y x x=≠的图象上,且MAB ∆是以AB 为底的等腰三角形,请直接写出点M 的坐标和MAB ∆的面积.13.如图:AOB ∆为等腰直角三角形,斜边OB 在x 轴上,一次函数34y x =-的图象经过点A ,交y 轴于点C ,反比例函数(0)k y x x=>的图象也经过点A .(1)求反比例函数的解析式;(2)过O 点作OD AC ⊥于D 点,求22CD AD -值;(3)若点P 是x 轴上的动点,点Q 在反比例函数的图象上使得PAQ ∆为等腰直角三角形?直接写出所有符合条件的点Q 的坐标.14.如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA ,OC 分别在x 轴和y 轴上,顶点B 的坐标为(4,2),反比例函数(0)k y x x=>的图象经过对角线OB 的中点E ,与矩形的边BC ,BA 分别交于点F ,G ,设直线FG 的函数表达式为y ax b =+.(1)求k ,a ,b 的值;(2)利用图象,直接写出当k ax b x+ 时x 的取值范围;(3)若点P 在矩形的边OA 上,且PFG ∆为等腰三角形,求点P 的坐标.15.如图,在平面直角坐标系中,将一块等腰直角三角板ABC 放在第二象限,斜靠在两坐标轴上,点C 坐标为(1,0)-,点A 的坐标为(0,2),一次函数y kx b =+的图象经过点B ,C ,反比例函数m y x=图象也经过点B .(1)求反比例函数的关系式;(2)直接写出当0x <时,0m kx b x+-<的解集.(3)若P 是y 轴正半轴一点,当ACP ∆是等腰三角形时,求出点P 的坐标.16.如图,一次函数11(0)y k x b k =+≠与反比例函数22(0)k y k x=≠的图象交于点(2,3)A ,(,1)B a -,设直线AB 交x 轴于点C .(1)求反比例函数和一次函数的解析式.(2)直接写出21k k x b x+<的解集.(3)若点P 是反比例函数图象上的一点,且POC ∆是以OC 为底边的等腰三角形,求P 点的坐标.17.如图,在平面直角坐标系中,O 为坐标原点,ABO ∆的边AB 垂直于x 轴,垂足为点B ,反比例函数(0)k y x x=>的图象经过AO 的中点C ,交AB 于点D ,且3AD =.(1)若点D 的坐标为(4,)n .①求反比例函数k y x =的表达式;②求经过C ,D 两点的直线所对应的函数解析式;(2)在(1)的条件下,设点E 是x 轴上的点,使CDE ∆为以CD 为直角边的直角三角形,求E 点的坐标.18.如图,一次函数3y x =-+的图象与反比例函数(0)k y k x=≠在第一象限的图象交于(1,)A a 和B 两点,与x 轴交于点C .(1)求反比例函数的解析式;(2)若点P 在x 轴上,且APC ∆的面积为5,求点P 的坐标;(3)若点P 在y 轴上,是否存在点P ,使ABP ∆是以AB 为一直角边的直角三角形?若存在,求出所有符合条件的P 点坐标;若不存在,请说明理由.19.如图,一次函数22y x =--的图象分别交x 轴、y 轴于点B 、A ,与反比例函数(0)m y m x=≠的图象在第二象限交于点M ,OBM ∆的面积是1.(1)求反比例函数的解析式;(2)若x 轴上的点P 与点A ,M 是以AM 为直角边的直角三角形的三个顶点,求点P 的坐标.20.如图,在平面直角坐标系xOy 中,矩形OABC 的顶点A 在x 轴上,顶点C 在y 轴上,D 是BC 的中点,过点D 的反比例函数图象交AB 于E 点,连接DE .若5OD =,4tan 3COD ∠=.(1)求过点D 的反比例函数的解析式;(2)求DBE ∆的面积;(3)x 轴上是否存在点P 使OPD ∆为直角三角形?若存在,请直接写出P 点的坐标;若不存在,请说明理由.21.如图,直线43y x =与双曲线(0)k y k x =≠交于A ,B 两点,点A 的坐标为(,4)m -,点C 是双曲线第一象限分支上的一点,连接BC 并延长交x 轴于点D ,且BC CD =.(1)求k 的值并直接写出点B 的坐标;(2)点G 是y 轴上的动点,连接GB ,GC ,求GB GC +的最小值;(3)P 是x 轴上的一点,当PAB ∆为直角三角形时,请求出符合条件的所有P 点的坐标.22.已知一次函数y kx b =+的图象与反比例函数m y x=的图象交于点A ,与x 轴交于点(5,0)B ,若OB AB =,且152OAB S ∆=.(1)求反比例函数与一次函数的表达式;(2)若点P 为x 轴上一点,ABP ∆是等腰三角形,直接写出点P 的坐标.(3)若点Q 为x 轴上一点,ACQ ∆是直角三角形,直接写出点Q 的坐标.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tanB 2c 在△ABC 中,角 A,B,C 所对的边分别为 a,b,c,且 +1= . tanA a (1)求 B; π 1 (2)若 cos(C+ )= ,求 sinA 的值. 6 3 tanB 2c sinBcosA 2sinC 解: (1)由 +1= 及正弦定理, 得 +1= , ……………………………………… tanA a cosBsinA sinA 2分
是函数 f ( x ) 的最小值;④ 其中真命题有( A. ①②③④ )
m 3 . n 3
B.②③ C. ①②④ D.②④
4. 函数 y=sin2x+acos2x 的图象左移 π 个单位后所得函数的图象关于直线 x 则 a=( )
8
对称,
A. 1
B.
3
C. -1
D. - 3
9.若函数 f ( x ) sin( x 则 的最小正值是 ( A.
(第 16 题图) D O y B A
C
x
π π π 2 所以 x2=cos(α+ )=cosαcos -sinαsin =- . 4 4 4 10 6分
…………………………………
3 4 3 4 → 3 4 2 解法二:因为 x1= ,y1>0,所以 y1= 1-x1 = .A( , ),则OA=( , ),…………2 5 5 5 5 5 5
3 2
(2)设 g ( x) 6mf ( x) 1 ,若 g ( x) 的值域为 (1, ] ,求实数 m 的值. 在斜三角形 ABC 中,角 A,B,C 的对边分别为 a,b,c.
(1)若 2sin A cos C sin B ,求 a 的值; c (2)若 sin(2 A B) 3sin B ,求 tan A 的值. tan C 解: (1)由正弦定理,得 sin A a . sin B b 从而 2sin A cos C sin B 可化为 2a cos C b .……………………………3 分
2 2 2 由余弦定理,得 2a a b c b . 2ab
整理得 a c ,即 a 1 . …………………………………………………………7 c 分 (2)在斜三角形 ABC 中, A B C , 所以 sin(2 A B) 3sin B 可化为 sin A C 3sin A C , 即 sin A C 3sin A C .…………………………………………10 分 故 sin A cos C cos A sin C 3(sin A cos C cos A sin C ) . 整理,得 4sin A cos C 2 cos A sin C , …………………………………12 分 因为△ABC 是斜三角形,所以 sinAcosAcosC 0 , 所以 tan A 1 .…………………………………………………………14 分 tan C 2 在平面直角坐标系 xOy 中,角 α 的顶点是坐标原点,始边为 x 轴的正半轴,终边与单 位圆 O 交 π π π 于点 A(x1 , y1 ), α∈( , ). 将角 α 终边绕原点按逆时针方向旋转 , 交单位圆于点 B(x2, 4 2 4 y2). 3 (1)若 x1= ,求 x2; 5 (2)过 A,B 作 x 轴的垂线,垂足分别为 C,D,记△AOC 及 4 △BOD 的面积分别为 S1,S2,且 S1= S2,求 tanα 的值. 3 3 4 2 16.解: (1)解法一:因为 x1= ,y1>0,所以 y1= 1-x1 = . 5 5 4 3 所以 sinα= ,cosα= . 5 5 ………………………2 分
3
) 的图像向右平移
)
个单位后与原函数的图像关于 x 轴对称, 3
1 2
B.1
C. 2
D.3
10.若函数 f ( x) sin( x) 3 sin( 小值是
,则 f ( x) 的单调递增区间是 2
5 x) ,且 f () 2, f( ) 0 , 的最 2
6
4
C.
3
D.
AP m AB 1 mAC ,则 AP AD 的值为______
在△ABC 中,BC= 2 ,AC=1,以 AB 为边作等腰直角三角形 ABD(B 为直角顶点,C、D 两点 在直线 AB 的两侧) .当 C 变化时,线段 CD 长的最大值为 ▲ . 【答案】3
1 所以 cos B , B .………………………6 分 2 3
(Ⅱ)当△ABC 的外接圆面积为π 时,则 R=1, 所以直径 2R=2, b=2RsinB= 3 ,……………………8 分 由余弦定理,b =a +c -2accosB 得 3=a +c -ac≥ac,当且仅当 a=c 时取到等号。 所以得到 ac≤3,………………………10 分 则 sABC
………………………
3 4 4 因此 A( , ), 所以 tanα= . ……… 5 5 3
……………4
…………………6
分 1 1 (2)S1= sinαcosα=- sin2α. 2 4 8分 π π π π 3π 因为 α∈( , ),所以 α+ ∈( , ). 4 2 4 2 4 1 π π 1 π 1 所以 S2=- sin(α+ )cos(α+ )=- sin(2α+ )=- cos2α.…………………………… 2 4 4 4 2 4 10 分 4 4 4 因为 S1= S2, 所以 sin2α=- cos2α, 即 tan2α=- . 3 3 3 12 分 2tanα 4 1 π π 所以 =- , 解得 tanα=2 或 tanα=- . 因为 α∈( , ), 所以 tanα=2. ……… 3 2 4 2 1-tan2α 14 分 ………………………………… …………………………………………
π 37. 如图,在△ABC 中,已知 B= ,AC=4 3,D 为 BC 边上一点.若 3 AB=AD,则△ADC 的周长的最大值为________.
如图,C,D 两点在△PAB 的边 AB 上,AC=BD,若角 CPD=90°,且 PA^2+PB^2=10,则 2AB+CD 的最大值是
6.在 ABC 中,已知 a b c cos B c cos A ,则 ABC 为 10
8. 已知函数 f ( x) m sin x n cos x , 且 f ( ) 是它的最大值, (其中 m、 n 为常数且 mn 0 )
6
给出下列命题: ① f (x
3
②函数 f ( x ) 的图象关于点 ( ) 是偶函数;
3 8 ) ③ f ( , 0) 对称; 2 3
2 2 2 2 2
1 3 3 3 3 .…………………12 分 ac sin B , 即ABC的面积的最大值为 2 4 4
已知 ABC 中, AC 1, ABC (1)求 f ( x ) 解析式并标出其定义域;
2 , BAC x ,记 f ( x) AB BC . 3
在锐角三角形 ABC 中,角 A,B,C 的对边分别为 a,b,c,已知
c cos( A) c 2b sin( C ) 2
(I)求角 A 的大小; (Ⅱ)求函数 y 2cos B sin(
2
6
2 B) 的值域.
17. 解: (Ⅰ) :由已知 b cos B是a cos C和c cos A的等差中项 得 2bcosB=acosC+ccosA…………………………2 分 代入 a=2RsinA,b=2RsinB,c=2RsinC,化简得 2sinBcosB=sinAcosC+cosAsinC,………………………4 分 所以 2sinBcosB=sin(A+C)=sinB ,在三角形 ABC 中,sinB 0,
12.设△ ABC 的内角 A, B, C 的所对的边 a, b, c 成等比数列,则 (Asin A
)
5 1 2
(C)
5 1 5 1 , 2 2
(D)
5 1 , 2
………………………………………10 分 sinA = sin(B + C) = sin(C + π π ) = sin[(C + ) + 3 6
………………………………………12 分 π π π π =sin(C+ )cos +cos(C+ )sin 6 6 6 6 =
2 6+1 . 6
………………………………………14 分
sinBcosA+cosBsinA 2sinC sin(A+B) 2sinC sinC 2sinC 所以 = ,即 = ,则 = . cosBsinA sinA cosBsinA sinA cosBsinA sinA 因为在△ABC 中,sinA≠0,sinC≠0, 所 1 . 2 π 因为 B∈(0, π), 所以 B= . 3 7分 2π π π 5π (2)因为 0<C< ,所以 <C+ < . 3 6 6 6 因 2 2 . 3 所 以 π ] 6 为 cos(C + π 6 ) = 1 3 , 所 以 sin(C + π 6 ) = 以 cosB ………………………………………5 分 ……………………………………… =
( )
n is A n i b s B n is c C 3s n i a B 11.在 ABC 中, 角 A, B, C 所对的边长分别为 a, b, c. 若a
. 则
角 C 等于( A.
) B.
5 6 2 12. 在 ABC 中 , AD BC 0 , AB 5, BC 10, BD DC , 点 P 满 足 3
三角形.
在 △ ABC 中,角 A 、 B 、 C 所对的边分别为 a 、 b 、 c ,已知 sin A sin C p sin B ( pR) ,且 ac (1)当 p
