激光原理及应用[陈家璧主编][习题解答]
陈家璧版光学信息技术原理及应用习题解答(7-8章)

陈家璧版光学信息技术原理及应用习题解答(7-8章)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第七章 习题解答1. 某种光盘的记录范围为内径80mm,外径180mm 的环形区域,记录轨道的间距为2um.假设各轨道记录位的线密度均相同记录微斑的尺寸为um,试估算其单面记录容量. (注: 内、外径均指直径)解: 记录轨道数为 25000002.0280180=⨯-=N单面记录容量按位计算为 ∑=⨯≈⨯+=Nn n M 110107.10006.0)002.040(2π bits = 17 Gb.按字节数计算的存储容量为 2.1GB.2. 证明布拉格条件式(7-1)等效于(7-17)式中位相失配= 0的情形, 因而(7-18)式描述了体光栅读出不满足布拉格条件时的位相失配。
证明: 将体光栅读出满足布拉格条件时的照明光波长(介质内) 和入射角 (照明光束与峰值条纹面间夹角)分别记为0和θ0, 则根据布拉格条件式(7-1)有: 2sin θ0= 0 其中为峰值条纹面间距.对于任意波长λa (空气中) 和入射角θr (介质内), 由(7-17)式, 位相失配 δ 定义为:24)cos(n K K ar πλθφδ--=其中n 0为介质的平均折射率, K = 2π/Λ为光栅矢量K 的大小,φ为光栅矢量倾斜角,其值为 22πθθφ++=sr ,θr 为再现光束与系统光轴夹角 (参见图7-9).当 δ = 0 时,有2422cos n K K a r s r πλθπθθ=⎪⎭⎫ ⎝⎛-++ 即:Λ=Λ=⎪⎭⎫ ⎝⎛-2422sin 0λππλθθn s rλ为介质中的波长. 由于角度2sr θθ-恰为照明光与峰值条纹面的夹角θ, ∑ ©亦即布拉格条件2Λ sin θ = λ.当读出光偏离布拉格角θo 和布拉格波长λo 的偏移量分别为∆θ和∆λ时,有[]0200200002044sin )sin(cos )cos( 4)()(cos n K n K K K n K K πλπλθθφθθφπλλθθφδ∆--∆--∆-=∆+-∆+-=利用布拉格条件式(7-17), 以及∆θ和∆λ很小时的近似关系 cos ∆θ≈1 和 sin ∆θ≈∆θ, 立即可得:δ =∆θK sin(φ-θ0) - ∆λK 2/4πn 0 即(7-18)式 原题得证。
陈家璧版-光学信息技术原理及应用习题解答(4-7章)

第四章习题4.1若光波的波长宽度为λΔ,频率宽度为νΔ,试证明:λλννΔΔ=。
设光波波长为nm 8632=.λ,nm 8-10⨯2=λΔ,试计算它的频宽νΔ。
若把光谱分布看成是矩形线型,那么相干长度?=c l 证明:参阅苏显渝,李继陶《信息光学》P349,第4.1题答案。
421.510c λνλ∆∆==⨯赫,32010()c c cl ct m ν===⨯∆4.2设迈克尔逊干涉仪所用的光源为nm 0589=1.λ,nm 6589=.2λ的钠双线,每一谱线的宽度为nm 010.。
(1)试求光场的复自相干度的模。
(2)当移动一臂时,可见到的条纹总数大约为多少?(3)可见度有几个变化周期?每个周期有多少条纹?答:参阅苏显渝,李继陶《信息光学》P349,第4.2题答案。
假设每一根谱线的线型为矩形,光源的归一化功率谱为()^1212rect rect νννννδνδνδν⎡--⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦G (1)光场的复相干度为^1()()exp(2)1sin ()exp(2)[1exp(2)]2r j d c j j τνπντνδντπντπντ∞==+∆⎰G 式中12ννν-=∆,复相干度的模为ντπδνττ∆=cos )(sin )(c r 由于νδν∆ ,故第一个因子是τ的慢变化非周期函数,第二个因子是τ的快变化周期函数。
相干时间由第一个因子决定,它的第一个零点出现在δντ1=c 的地方,c τ为相干时间,故相干长度δλλδλλδντ22≈===cc l c c 。
(2)可见到的条纹总数589301.05893====δλλλcl N (3)复相干度的模中第二个因子的变化周期ντ∆=1,故可见度的变化周期数601.06==∆=∆==δλλδννττc n 每个周期内的条纹数9826058930===n N 4.3假定气体激光器以N 个等强度的纵模振荡,其归一化功率谱密度可表示为()()()()∑21-21--=+-1=N N n n NνννδνΔgˆ式中,νΔ是纵模间隔,ν为中心频率并假定N 为奇数。
激光原理与应用答案(陈家壁主编)

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
激光原理及应用_陈家璧_第一章

4
1.1.1 光波
(3)平面波的复数表示法 光强 线偏振的单色平面波的复数表示:
~ :模量U 代表振幅在空间的分布,辐角(-kz)代表位相在空间的分布 复振幅U 0 ~ ~ U U0 exp ikz U U expit
光强:光强与光矢量大小的平方成正比,即 I U T 1 2 U0 1 2 2 1 T 2 2 I T U dt 1 U 0 cos (t kz)dt T 2 T T 2
( Em En ) kT
gi
ni gi eEi
kT
2. 分别处于Em和En能级上的原子数nm和nn必然满足下一关系
nm g m e nn g n
3. 为简单起见,假定 g m g n nm nn 1 E Em En kT , 讨论:1) nm nn 0 E Em En kT , 2) 3)T>0且EmEn ,nm<nn
分析: (a)z一定时,则U代表场矢量在该点作 时间上的周期振动
图(1-1)电磁波的传播
(b)t一定时,则U代表场矢量随位置的不同作空间的周期变化
(c)z、t同时变化时,则U代表一个行波方程,代表两个不同时刻空 间各点的振动状态。从下式可看出,光波具有时间周期性和空间周期性。 时间周期为T,空间周期为;时间频率为1/T,空间频率为1/ z 2 t 2 z U U 0 cos t U 0 cos c T 简谐波是具有单一频率的单色波,但通常原子发光的时间约为10-8 s, 形成的波列长度约等于3m,因此它的波列长度有限即必然有一 定的频率宽度。
陈家璧版-光学信息技术原理及应用习题解答(4-7章)

第四章习题4.1 若光波的波长宽度为λΔ,频率宽度为νΔ,试证明:λλννΔΔ=。
设光波波长为nm 8632=.λ,nm 8-10⨯2=λΔ,试计算它的频宽νΔ。
若把光谱分布看成是矩形线型,那么相干长度?=c l证明:参阅苏显渝,李继陶《信息光学》P349,第4.1题答案。
421.510c λνλ∆∆==⨯赫,32010()c c cl ct m ν===⨯∆ 4.2 设迈克尔逊干涉仪所用的光源为nm 0589=1.λ,nm 6589=.2λ的钠双线,每一谱线的宽度为nm 010.。
(1)试求光场的复自相干度的模。
(2)当移动一臂时,可见到的条纹总数大约为多少?(3)可见度有几个变化周期?每个周期有多少条纹?答:参阅苏显渝,李继陶《信息光学》P349,第4.2题答案。
假设每一根谱线的线型为矩形,光源的归一化功率谱为 (1)光场的复相干度为式中12ννν-=∆,复相干度的模为 由于νδν∆,故第一个因子是τ的慢变化非周期函数,第二个因子是τ的快变化周期函数。
相干时间由第一个因子决定,它的第一个零点出现在ντ1=c 的地方,c τ为相干时间,故相干长度δλλδλλδντ22≈===cc l c c 。
(2)可见到的条纹总数589301.05893====δλλλcl N (3)复相干度的模中第二个因子的变化周期ντ∆=1,故可见度的变化周期数601.06==∆=∆==δλλδννττc n 每个周期内的条纹数9826058930===n N 4.3假定气体激光器以N 个等强度的纵模振荡,其归一化功率谱密度可表示为 式中,νΔ是纵模间隔,ν为中心频率并假定N 为奇数。
(1)证明复自相干度的模为 (2)若3=N ,且ντΔ10≤≤,画出()τγ与ντΔ的关系曲线。
答:参阅《统计光学(基本概念个习题)》P131。
证明(1),复相干度)(τγ与归一化功率谱密度即光源的光谱特性间具有下列关系: 将(4.3.1)式带入得到其中()∑-=∆+∆∆--=2)1(022/)1(2211N n j N j nj e e eντπντπντπ 因而(){[]()[][][][]})2e xp ()2e xp (2/2/)1(2e xp 2/)1(2e xp 2/12e xp 2/)1(2e xp)2e xp (1ντπντπντπντπντπντπτνπτγ∆--∆-+∆--+∆--∆-+-∆-=j j N j N j N j N j j N=ντπντπντπτνπ∆-+∆--∆-2cos 12/)1(2cos 2/)1(2cos 12N N eN j =ντπντπτνπ∆∆-sin sin 12N e N j 复相干度的包络则为 (2),当N=3时,其ντγ∆-曲线如图1所示。
《激光原理及应用》陈家璧第二版 - 第七章

图7-2 等离子云变化的过程
7.2.1 激光淬火技术的原理与应用
1.激光淬火技术,又称激光相变硬化,它利用聚焦后的激光束照射到钢铁材料表 面,使其温度迅速升到相变点以上。当激光移开后,由于仍处于低温的内层材料 的快速导热作用,使表层快速冷却到马氏体相变点以下,获得淬硬层。 2.图7-3 为一台柔性激光加工系统的示意图。它通过五维运动的工作头把激光照 射到被加工的表面,在计算机控制下直接扫描被加工表面完成激光淬火 3. 激光淬火可以使工件表层0.1到1.0mm范围内的组 织结构和性能发生明显变化。图7-4所示为45钢表 面激光淬火区横截面金相组织图
图7-5该淬火区显微硬度沿深度方向的分布曲线图
图7-6 基材含碳量与激光淬火层显微 Nhomakorabea度的关系
7.2.1 激光淬火技术的原理与应用
5.依据激光器的特点不同,激光淬火可分为CO2激光淬火和因素YAG激光淬火。 但两者中影响淬硬性能的主要基本相同 2) 激光工艺参数:激光淬火层的宽度主要决定于光斑直径;淬硬层深度由激光功 率、光斑直径和扫描速度共同决定;描述激光淬火的另一个重要工艺参数为功率 密度,即单位面积注入工件表面的激光功率。为了使材料表面不熔化,激光淬火 的功率密度通常低于104W/cm2,一般为1000-6000W/cm2。 3)表面预处理状态:一是表面组织淮备,即通过调质处理等手段使钢铁材料表面 具有较细的表面组织,以便保证激光淬火时组织与性能的均匀、稳定。如图7-7 为原始组织及扫描速度对激光淬硬层深度的影响;二是表面“黑化”处理,以便 提高钢铁表面对激光束的吸收率。
(2) 材料的加热 设入射激光束的光功率密度为qi,材料表面吸收的光功率密度为q0 ,则有 q0 Aqi qi 1 R az 激光从表面入射到材料内部深度为处的光强 qz q0 e 一般将激光在材料内的穿透深度定义为光强降至I0/e时的深度,因而穿透深 度为1/a
激光原理及应用1-6章部分课后答案

激光原理及应用部分课后答案1-4为使He-Ne 激光器的相干长度达到1KM ,它的单色性0λλ∆应是多少?2-2当每个模式内的平均光子数(光子简并数)大于1时,以受激辐射为主。
2-3如果激光器和微波激射器分别在um 10=λm 500n =λ和z 3000MH =ν输出1W 连续功率,问美秒从激光上能级向下能级跃迁的粒子数是多少?2-4当一对激光能级为E2和E1(f1=f2),相应的频率为v (波长为λ),能级上的粒子数密度分别为n2和n1,q 求:(1)当v=3000MHZ ,T=3000K 时,n2/n1=?(2)当λ=1um ,T=3000K 时,n2/n1=?(3)当λ=1um ,n2/n1=0时,温度T=?解:2-5激发态的原子从能级E2跃迁到E1时,释放出λ=5um的光子,求这个两个能级的能量差。
若能级E1和E2上的原子数分别为N1和N2,试计算室温T=300K的N2/N值。
2-7如果工作物质的某一跃迁是波长为100nm的远紫外光,自发辐射跃迁概率1621s10-=A,试问:(1)改跃迁的受激辐射爱因斯坦系数B21是多少?(2)为使受激辐射跃迁概率比自发辐射跃迁概率大三倍,腔内的单色能量密度νρ应为多少?2-9某一物质受光照射,沿物质传播1mm的距离时被吸收了1%,如果该物质的厚度是0.1m,那么入射光中有百分之几能通过该物质?并计算该物质的吸收系数α。
2-10激光在0.2m 长的增益介质中往复运动过程中,其增强了30%。
求该介质的小信号增益系数0G 。
假设激光在往复运动中没有损耗。
3-2CO2激光器的腔长L=100cm,反射镜直径D=1.5cm,两镜的光强反射系数分别为r1=0.985,r2=0.8.求由衍射损耗及输出损耗所分别引起的δ,τ。
3-4,分别按下图中的往返顺序,推导近轴光线往返一周的光学变换矩阵⎪⎪⎭⎫ ⎝⎛D C B A ,并证明这两种情况下的)(D A +21相等。
激光原理与应用课后题答案 陈家壁版

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h qn 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kT n n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kTh e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
陈家璧版-光学信息技术原理及应用习题解答(9-11章)

第九章习题解答9-1. 用白光再现彩虹全息时,如果彩虹全息有实狭缝象,在狭缝实象处观察全息图,人眼将能观察到单色的全息象,试分析人眼在狭缝前后位置时的全息象的颜色分布情况。
如彩虹全息再现的是虚狭缝,再分析人眼观察到的全息象情况。
答:在图示的情况下,物的两个端点为A 和B 点,它们被全息记录在一条线区域上,当白光再现时,这一区域的衍射光是色散的,长波长的衍射角较大,而短波长的衍射较小,。
按图示的光路结构, A 点的长波长沿AM 方向衍射,短波长沿AN 方向衍射,B 点的长波长沿BN 方向衍射,短波长沿BM 方向衍射。
假设沿AP 和BP 方向衍射的波长相同,那么人眼在P 处观察将看到单色象,当眼睛靠近全息图时,将看到象的上方偏蓝,而下方偏红,反之则相反。
对于虚狭缝的情况,如上图所示,P 点是某一衍射波长的虚狭缝,A 和B 两点是两线全息图,象上的两点与它们对应,AM 是线全息图A 最短波长的衍射方向,BM 是线全息图B 的最长波长衍射方向。
显然,眼睛在M 点观察,将能看到A 、B 之间的所有象点,但它们的颜色呈光谱色分布,在图示情况下,上部是紫色,下部是红色。
眼睛观察到的象的范围由眼睛离全息图的距离决定,离得越远,观察到的范围越大。
9-2. 用白光点光源再现彩虹全息时,人眼将能观察到由光谱色组成的单色象。
如果用白光线光源作为再现光源,线光源的扩展方向与狭缝方向垂直,这时观察到的是消色差的黑白象,试解释其原因。
答:线光源可以看成由无数个点光源组成,每一个点光源都按光谱色排列形成一组彩色狭缝,线光源上不同点形成的狭缝的位置各不相同,它们在与狭缝垂直的方向上平移。
这无数个狭缝相互迭合在一起,使人眼在该处观察时,无数个不同波长的再现象重合在一起,这也就形成了消色差的黑白象。
9-3. 在一步法彩虹全息记录光路中,物的大小为10cm ,人双眼的瞳孔间距为6.5cm ,透镜的孔径为20cm ,对物体1:1成像,如狭缝距全息图30cm ,要求人双眼能同时看见完整的象,试计算成像透镜的焦比。
《激光原理及应用》陈家璧第二版 - 第七章

图7-9 激光熔凝处理后横截面组织示意图
图7-10 T10钢激光熔凝层显微硬度沿淬硬层深度的分布
7.2.3 激光熔覆技术
1.激光熔覆(Laser Cladding)技术亦称激光包覆、激光涂覆、激光熔敷,是一种新 的表面改性技术。它通过在基材表面添加熔覆材料,利用高功率密度的激光束使 之与基材表面一起熔凝的方法,在基材表面形成与其为冶金结合的添料熔覆层, 以改善其表面性能的工艺。 2.激光熔覆技术具有如下优点 3.激光熔覆工艺依据材料的添加方式不同,分为预置涂层法和同步送料法。 4.同步送料法指在激光束照射基材的同时,将待熔覆的材料送入激光熔池,经 熔融、冷凝后形成熔覆层的工艺过程。激光熔覆材料包括金属、陶瓷或者金属 陶瓷,材料的形式可以是粉末、丝材或者板材,工艺过程如图7-11所示。 。
T 0,0,
(2) 材料的熔化与汽化
AqS 0r 23 2 t
激光功率密度过高,材料在表面汽化,不在深层熔化;激光功率密度过低, 则能量会扩散到较大的体积内,使焦点处熔化的深度很小
7.1 激光热加工原理
(4) 激光等离子体屏蔽现象 激光作用于靶表面,引发蒸汽,蒸汽继续吸收激光能量,使温度升高,最后 在靶表面产生高温高密度的等离子体。等离子体迅速向外膨胀,在此过程中继 续吸收入射激光,阻止激光到达靶面,切断了激光与靶的能量耦合。 如图7-2所示,为等离子云变化的过程
7.3.1 激光打孔
2. 激光打孔的激光束几何参数和总能量与孔的深度和孔径之间的关系进行估算。 如图7-14的激光打孔原理简图 如果在t时刻孔的底面半径为r(t),孔深为h(t),则 有
r t r0 tg ht
考虑材料从孔底蒸发,而熔化的液体从孔壁流走,t 时刻的能量守衡方程为
《激光原理及应用》陈家璧第二版 - 第七章

图7-15 激光切割头的结构示意图
※ 氧助熔化切割: 金属被激光迅速加热至燃点以上,与氧发生剧烈的氧化反应(即燃 烧),放出大量的热,又加热下一层金属,金属被继续氧化,并借助气体压力将氧 化物从切缝中吹掉。
7.3.2 激光切割
4. 激光切割的工艺参数及其规律 ※ 激光功率: 激光切割时所需功率的大小,是由材料性质和切割机理决定的。 ※ 切割速度: 在一定功率条件下,板厚越大,切割速度越小。切割速度对切口表 面粗糙度也有较大影响。 ※ 气体的压力:在功率和切割材料板厚一定时,有一最佳切割气体流量,这时切 割速度最快。随着激光功率的增加,切割气体的最佳流量是增大的。 ※ 光束在质量、透镜焦距和离焦量:激光器输出光束的模式为基横模时对激光切 割最为有利。光斑大小与聚焦透镜的焦距成正比。短焦距的透镜虽然可以得到较 小光斑,但焦深很小。离焦量对切割速度和切割深度影响较大,切割过程中必须 保持不变,一般离焦量选用负值,即焦点位置置于切割板面下面某一点。 ※ 喷嘴:喷嘴是影响激光切割质量和效率的—个重要部件。激光切割一般采用 同轴(气流与光轴同心)喷嘴,喷嘴出口直径大小应依据板厚加以选择。另外,喷 嘴到工件表面的距离对切割质量也有较大影响,为了保证切割过程稳定,这个距 离必须保持不变。
图7-9 激光熔凝处理后横截面组织示意图
图7-10 T10钢激光熔凝层显微硬度沿淬硬层深度的分布
7.2.3 激光熔覆技术
1.激光熔覆(Laser Cladding)技术亦称激光包覆、激光涂覆、激光熔敷,是一种新 的表面改性技术。它通过在基材表面添加熔覆材料,利用高功率密度的激光束使 之与基材表面一起熔凝的方法,在基材表面形成与其为冶金结合的添料熔覆层, 以改善其表面性能的工艺。 2.激光熔覆技术具有如下优点 3.激光熔覆工艺依据材料的添加方式不同,分为预置涂层法和同步送料法。 4.同步送料法指在激光束照射基材的同时,将待熔覆的材料送入激光熔池,经 熔融、冷凝后形成熔覆层的工艺过程。激光熔覆材料包括金属、陶瓷或者金属 陶瓷,材料的形式可以是粉末、丝材或者板材,工艺过程如图7-11所示。 激光熔覆技术
[激光原理及应用(第4版)][陈家璧, (13)[6页]
![[激光原理及应用(第4版)][陈家璧, (13)[6页]](https://img.taocdn.com/s3/m/2f65d28871fe910ef12df81d.png)
s
2
s
3.在共焦腔中心(z=0)的截面内的光斑有极小值,称为高斯光束的束腰半径
0
1 1 s 2 2
L
上一页 回首页 下一页 回末页 回目录
3.3.1 高斯光束的振幅和强度分布
第 三 章 激 光 器 的 输 出 特 性
§
3 3 高 斯 光 束 传 播 特 性 .
图(3-8) 基模光斑半径随z按双曲线规律的变化
3.3.1 高斯光束的振幅和强度分布
第 三 章 激 光 器 的 输 出 特 性
§
3 3 高 斯 光 束 传 播 特 性 .
1. 基横模TEM00的场振幅U00和强度I00分布分别为:
2 x2 y 2 U 00 exp 1 2 2 s
I 00 U 00
上一页 回首页 下一页 回末页 回目录
3.3.4 高斯光束的高亮度
第 三 章 激 光 器 的 输 出 特 性
§
3 3 高 斯 光 束 传 播 特 性 .
1. 亮度B:单位面积的发光面在其法线方向上单位立体角范围内输出去的辐射功率。 I B SΩ
2 ( z ) z z
2.由波动光学知道,在单色平行光照明下,一个半径为 r 的圆孔夫琅和费衍射角 (主极大至第一极小值之间的夹角) 0.61 r 。与上式相比较可知.高斯光束 半角远场发散角在数值上等于以腰斑0 为半径的光束的衍射角,即它已达到了衍 射极限。 3.共焦腔基模光束的理论发散角具有毫弧度的数量缀,它的方向性相当好。 4.由于高阶模的发散角是随着模的阶次的增大而增大,所以多模振荡时,光束的 方向性要比单基模振荡差。
上一页 回首页 下一页 回末页 回目录
3.3.2 高斯光束的相位分布
《激光原理及应用》习题参考答案仅供大家学习参考用

《激光原理及应用》习题参考答案思考练习题11•解答:设每秒从上能级跃迁到下能级的粒子数为n 。
单个光子的能量:g = h v = he / Z 连续功率:p 二n ; 则,n = p/ ;a.对发射■ = 0.5000的光:p 1 0.5000 10-6 n — —he 6.63 10 ⑶ 3.0 108-2.514 1018(个)b.对发射、• = 3000 MHz 的光_________ 16.63 10 "4 3000 106= 5.028 1023(个)E 2 a 匹Tn 1hv些=小-1n 1hc 3T6.26 103(K)'■ ln 匹3.解答:(1) 由玻耳兹曼定律可得_E 2 -E 1e '丁 , m/g20且4g 1 =g 2, m • n 2 =10代入上式可得: n 2 :30 (个)(2 )由 (a ), (b ) ,(c)式可得:2.解答:E 2 - E<| = h..(a).(b) (1 )由 ■■■. = c/ ■ .......(a ), (b )式可得:.(c)n 2 /g 2(2) p =108 n 2(E 2 -EJ =5.028 10-(W) 4•解答:(1)由教材(1-43)式可得e kT —1因此:fT ' =2.82kh ,hc同样可求得: 一丄 =4.96九m kT故' m - m = 0.568c8h1 3 A-2000J s/m 3 -3.860 10, J s/m 3 (0.6328 10冷3 5.0 10*8- 6.63 10 ^4= 7.592 10 5•解答:(1)红宝石半径 r = 0.4cm ,长L -8cm ,铬离子浓度匸=2 1018cm‘,发射波长• =0.6943 10 “m ,巨脉冲宽度 -T = 10 ns 则输出最大能量2 ,、he18E - (:r L) 2 1034826.63 1030 108二 0.42 86(J)二 2.304(J)0.6943 10」脉冲的平均功率:P =E /.「23041010"2.304 叫) (2)自发辐射功率 _ hcN 2heP (兀r 2L)Q 自皿z-X663计 3° IO 8 *1。
陈家璧版 光学信息技术原理及应用习题解答(5-6章)

第五章习题解答5.1两束夹角为 θ = 450的平面波在记录平面上产生干涉,已知光波波长为632.8nm ,求对称情况下(两平面波的入射角相等)该平面上记录的全息光栅的空间频率。
答案:已知:θ = 450,λ= 632.8nm求:全息光栅空间频率f x解:根据平面波相干原理,干涉条纹的空间分布满足关系式 2 d sin (θ/2)= λ其中d 是干涉条纹间隔。
由于两平面波相对于全息干板是对称入射的,故记录在干板上的全息光栅空间频率为f x = (1/d )= (1/λ)·2 sin (θ/2)= 1209.5 l /mm 答:全息光栅的空间频率为1209.5 l /mm 。
5.2 如图5.33所示,点光源A (0,-40,-150)和B (0,30,-100)发出的球面波在记录平面上产生干涉:xz图5.33 (5.2题图)(1)写出两个球面波在记录平面上复振幅分布的表达式;解答:设:点源A 、B 发出的球面波在记录平面上的复振幅分布分别为U A 和U B , 则有 ()[{]}22--22)()()/(e x p e x p A A A A A A y y x x z jk jkz a U +=()[{]}22--22)()()/(e x p e x p B B B B B B y y x x z jk jkz a U +=其中: x A = x B = 0, y A = -40, z A = -150, y B = 30, z B = -100; a A 、a B 分别是球面波的振幅;k 为波数。
(2)写出干涉条纹强度分布的表达式;I = |U A +U B |2 = U A ·U A * + U B ·U B * +U A *·U B + U A ·U B *[{]{[]}}[{]{[]}}--2---2-4--2--2--442222222222)()()/()()()/(exp )exp()()()/()()()/(exp )exp(B B B A A A B A BA B B B A A A B ABA BA y y x x z jk y y x x z jk jkz jkz a a y y x x z jk y y x x z jk jkz jkz a a a a ++•+++++•++=(3)设全息干板的尺寸为100 × 100 mm 2,λ = 632.8nm ,求全息图上最高和最低空间频率;说明这对记录介质的分辨率有何要求?解答:设全息干板对于坐标轴是对称的,设点源A 与点源B 到达干板的光线的最大和最小夹角分别为θmax和θmin,A 、B 发出的到达干板两个边缘的光线与干板的夹角分别为θA 、θB 、θA ’和θB ’,如图所示,它们的关系为θA = tg-1[z A /(-y A - 50)] ,θB = tg-1[z B /(-y B - 50)]θA ’= tg -1[z A /(y A - 50)] ,θ B ’= tg -1[z B /(y B - 50)]θmax =θ A -θB, θmin =θ B ’-θA ’根据全息光栅记录原理,全息图上所记录的 最高空间频率 f max = (2/λ)sin (θmax /2)·cos α 1 最低空间频率 f min = (2/λ)sin (θmin /2)·cos α2其中α角表示全息干板相对于对称记录情况的偏离角,由几何关系可知 cos α 1 = sin (θA+θB )/2 , cos α 2 = sin (θA ’+θB ’)/2将数据代入公式得 f max = 882 l /mm ,f min = 503 l /mm答:全息图的空间频率最高为882 l /mm ,最低为503 l /mm ,要求记录介质的分辨率不得低于900 l /mm 。
激光原理及应用的答案

激光原理及应用的答案1. 激光原理激光是指通过激活原子、分子或离子的能级从而形成一种具有高强度、高单色性和高相干性的电磁辐射的过程。
激光的产生基于以下几个原理:•受激辐射:当一个物质中某个能级的粒子被外界的激发所占据时,如果有一个辐射场作用于这些粒子,它们就可能跳到较低能级,从而向辐射场辐射出一个与外界辐射场的频率和相位相同的光子,这就是受激辐射。
•斯托克斯辐射:当一个粒子从一个高能级跃迁到一个低能级,同时放出一个光子,这个过程称为斯托克斯辐射。
斯托克斯辐射是激光产生过程中的重要原理之一。
•光增强:通过将一系列粒子激发到一个高能级,然后通过受激辐射放出一束光,然后再将该光束通过增强反射和光放大等技术放大,从而形成一束高强度的激光。
2. 激光的应用激光作为一种特殊的光源,具有许多重要的应用。
下面列举了一些主要的激光应用:•激光切割和焊接:激光切割和焊接技术广泛应用于金属加工、电子制造和汽车制造等领域。
激光切割和焊接具有高精度、高效率和无污染等优点,在工业生产中发挥着重要作用。
•激光医学:激光在医学领域有广泛的应用,如激光手术、激光治疗、激光诊断等。
激光手术使用高能激光在手术过程中进行切割、蒸发、烧灼等操作,具有创伤小、恢复快的优点。
激光治疗可以用于肿瘤治疗、皮肤美容等方面。
激光诊断可以用于眼科、皮肤病等疾病的检测和治疗。
•激光测距和测速:激光测距和测速技术被广泛应用于工程建设、地质勘探、安防监控等领域。
利用激光的高单色性和高相干性,可以实现精准的距离和速度测量。
•激光通信:激光通信技术是一种高速、大容量的无线通信技术。
激光通信利用激光器将信息通过光波传输,具有传输速度快、抗干扰能力强的优点,可以用于远距离的通信。
•激光显示:激光显示技术是一种新型的显示技术,具有高亮度、高对比度和高颜色纯度等特点。
激光显示可以用于电视、电影院、虚拟现实等领域,提供更好的显示效果和观看体验。
3. 激光的发展和前景激光技术的发展正在不断推动人类科技的进步。
第八章陈家璧版_光学信息技术原理及应用习题解答
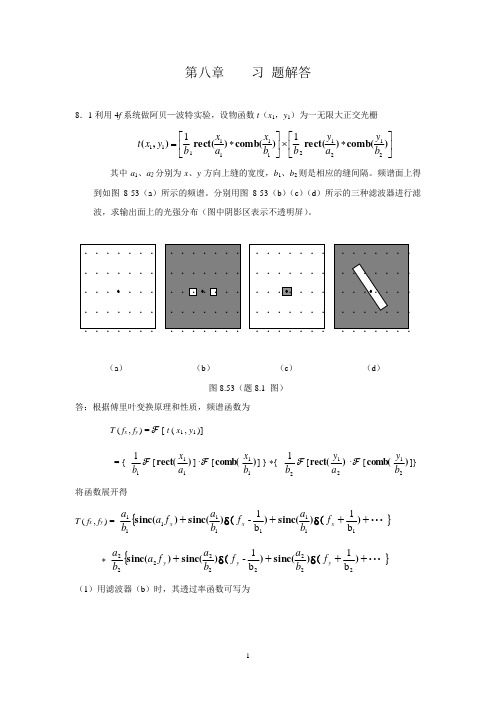
第八章 习 题解答8.1利用4f 系统做阿贝—波特实验,设物函数t (x 1,y 1)为一无限大正交光栅 ⎥⎦⎤⎢⎣⎡*⨯⎥⎦⎤⎢⎣⎡*=)comb(rect()comb()rect(),(21212111111111b y a y b b x a x b y x t其中a 1、a 2分别为x 、y 方向上缝的宽度,b 1、b 2则是相应的缝间隔。
频谱面上得到如图8-53(a )所示的频谱。
分别用图8-53(b )(c )(d )所示的三种滤波器进行滤波,求输出面上的光强分布(图中阴影区表示不透明屏)。
(a ) (b ) (c ) (d )图8.53(题8.1 图)答:根据傅里叶变换原理和性质,频谱函数为 T ( f x , f y ) = ℱ [ t ( x 1 , y 1 )] = { 11b ℱ [)re ct(11a x ]·ℱ [)comb(11b x ] } *{21b ℱ [)rect(21a y ·ℱ [)comb(21b y ]} 将函数展开得 T ( f x , f y ) ={}•••++++)δ()sinc()δ()sinc()sinc(111111111b 1b 1-x x x f b a f b a f a b a *{}•••++++)δ()sinc()δ(sinc()sinc(222222222b 1b 1-y y y f b a f b a f a b a (1) 用滤波器(b )时,其透过率函数可写为1111/0(,)01/x y x y x y f b f F f f f b f =±=⎧=⎨≠=⎩任何值滤波后的光振幅函数为 T ·F =[])δ()δ()sinc(111111b 1b 1-++x x f f b a b a 输出平面光振幅函数为 t ’(x 3,y 3)= ℱ -1[ T ·F ] =)]}(exp[)](){exp[sinc(13131111b 2-b 2x j x j b ab a ππ+ =)(cos )sinc(131111b 22x b ab a π• 输出强度分布为I (x 3,y 3)= )(cos )(sinc 1321122121b 24x b a b a π• = )cos()(sinc 131122121b 42x b a b a π• - C 其中C 是一个常数,输出平面上得到的是频率增加一倍的余弦光栅。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
设红宝石直径0.8cm ,长8cm ,铬离子浓度为2×1018cm -3,巨脉冲宽度为10ns 。
求:(1)输出0.6943μm 激光的最大能量和脉冲平均功率;(2)如上能级的寿命τ=10-2s ,问自发辐射功率为多少瓦? 答:(1)最大能量J ch d r h N W 3.2106943.01031063.61010208.0004.0683461822=⨯⨯⋅⨯⋅⨯⨯⋅⋅⨯=⋅⋅⋅⋅=⋅=--πλρπν脉冲平均功率=瓦8961030.21010103.2⨯=⨯⨯=--t W (2)瓦自自自145113.2112002021=⎪⎭⎫⎝⎛-⨯==⎪⎭⎫⎝⎛-==⎰-e h N P e n dt e n N t A τνττ6.试证单色能量密度公式,用波长λ来表示应为5811hc kThc eλλπρλ=-证明:11811852322-⨯=⋅-⨯=⋅=⋅==kTh kT h e hc c e h c c dVd dw dVd dw νννλλπλλπλρλνλρ 7. 试证明,黑体辐射能量密度()ρν为极大值的频率m ν由关系112.82m T kh ν--=给出,并求出辐射能量密度为极大值的波长m λ与m ν的关系。
答:(1)由 33811hv kTh c eνπνρ=-可得:0))1(113(82323=⋅⋅--⋅+-=∂∂kT he e e c h kT h kT h kT h ννννννπνρ 令kTh x ν=,则上式可简化为:xx xe e =-)1(3解上面的方程可得:82.2≈x 即:1182.282.2--=⇒≈kh T kTh m mνν (2)辐射能量密度为极大值的波长m λ与m ν的关系仍为mm c λν=8.由归一化条化证明(1-65a)式中的比例常数1A τ=证明: 2202)2/1()(4)(τννπν+-=Af N ,由归一化条件且0ν是极大的正数可得: ⇒=+-⎰∞1)2/1()(402202ντννπd A ⇒=+-⎰∞1)2/1()(4202202ντννπνd A⇒='+'⎰∞1)41(120222νπτνπd A τπτνπτπ11]'4[4202=⇒=⋅⋅∞A arctg A9.试证明:自发辐射的平均寿命211A =τ,21A 为自发辐射系数。
证明:自发辐射时在上能级上的粒子数按(1-26)式变化:t A e n t n 21202)(-=自发辐射的平均寿命可定义为()dt t n n ⎰∞=2201τ式中()dt t n 2为t 时刻跃迁的原子已在上能级上停留时间间隔dt 产生的总时间,因此上述广义积分为所有原子在激发态能级停留总时间,再按照激发态能级上原子总数平均,就得到自发辐射的平均寿命。
将(1-26)式代入积分即可得出 21121A dt e t A ==⎰∞-τ10.光的多普勒效应中,若光源相对接收器的速度为c υ<<,证明接收器接收到的频率01/1/ccυννυ+=-,在一级近似下为:0(1)c υνν≈+证明:0022021220)1()211)(1()1)(1(11υυυυυυυυυυυν⋅+≈⋅⋅++≈⋅-+=⋅-+=-c c c cc c c 即证11.静止氖原子的3S 2→2P 4谱线的中心波长为0.6328μm ,设氖原子分别以±0.1c ,±0.5c 的速度向着接收器运动,问接收到的频率各为多少? 答:Hz cc cc 146801.010241.5106328.01039.01.19.01.111⨯=⨯⨯⋅=⋅=-+=-+λυυνν 同理可求:Hz c 141.010288.4⨯=-ν;Hz c 145.010211.8⨯=+ν;Hz c 145.010737.2⨯=-ν12.设氖原子静止时发出0.6328μm 红光的中心频率为4.74×1014Hz ,室温下氖原子的平均速率设为560m/s 。
求此时接收器接收频率与中心频率相差若干? 答:Hzc 81460680010848.81074.4108667.1)108667.11()1035601()1(⨯=⨯⨯⨯=∆⇒⨯+=⨯+=+=--νννυνν13.(1) 一质地均匀的材料对光的吸收为0.01mm -1、光通过10cm 长的该材料后,出射光强为入射光强的百分之几? (2) —光束通过长度为1m 的均匀激活的工作物质,如果出射光强是入射光强的两倍,试求该物质的增益系数。
答;(1)368.01)0()()0()(10001.0===⇒=⋅--ee I z I eI z I Az(2)11693.02ln 2)0()()0()(-⋅==⇒==⇒=m G e I z I e I z I G Gz思考练习题21. 利用下列数据,估算红宝石的光增益系数n 2-n 1=5⨯1018cm -3,1/f (ν)=2×1011 s -1,t 自发=211A -≈3⨯10-3s ,λ=0.6943μm ,μ=l.5,g 1=g 2。
答:)(8)(8)(8)()(222133321333212121νπμλννμνπμννπμννμνf A n f h c h c A n G c h B A f h c nB G ⋅⋅∆=⋅⋅∆=⇒⎪⎪⎭⎪⎪⎬⎫=∆=11122431871.010215.18)106943.0(1031105)(---=⨯⨯⨯⋅⨯⋅⨯=cm G πν 2. He-Ne 激光器中,Ne 原子数密度n 0=n 1+n 2=l012 cm -3,1/f (ν)=15×109 s -1,λ=0.6328μm ,t 自发=211A -=10-17s ,g 3=3,g 2=5,11μ≈,又知E 2、E 1能级数密度之比为4,求此介质的增益系数G 值。
答:11112211211112312210103141081021410⨯=-=∆⇒⎪⎩⎪⎨⎧⨯=⨯=⇒⎭⎬⎫=+=-n g g n n n n E E cm n n n 比能级数密度之比为和 332121333332121888νπνπνπμh c A B c h c h B A =⇒== 192617112212172.0105.118)106328.0(1010314)(8)()(--=⨯⨯⨯⨯⨯=∆=∆=cmf A n f h c nB G πνπλννμν3. (a)要制作一个腔长L =60cm 的对称稳定腔,反射镜的曲率半径取值范围如何?(b)稳定腔的一块反射镜的曲率半径R 1=4L ,求另一面镜的曲率半径取值范围。
答:(a )R R R ==21;cm R RLR L 301)1)(1(0≥⇒≤--≤ (b )L R L R R LR L R L 31)1(4301)1)(1(022221-≤≥⇒≤-⋅≤⇒≤--≤或 4. 稳定谐振腔的两块反射镜,其曲率半径分别为R 1=40cm ,R 2=100cm ,求腔长L 的取值范围。
答:cm L cm L L L R L R L 1401004001)1001)(401(01)1)(1(021≤≤≤≤⇒≤--≤⇒≤--≤或5. 试证非均匀增宽型介质中心频率处的小讯号增益系数的表达式(2-28)。
证明:2102100021000210002100)ln2( 2)()2ln (2)()( )()( )(πννμνπννννμνννμνh c B n G f f h c B n G f h cB n G D D DD D D D D ∆∆=⇒⎪⎪⎭⎪⎪⎬⎫∆=∆=⇒∆= 即证。
6. 推导均匀增宽型介质,在光强I ,频率为ν的光波作用下,增益系数的表达式(2-19)。
证明:220022000)2)(1()()(])2()[()()(1 )()(ννννννννννν∆++-∆+-=+=s s I I G f f I I G G 而:())()(2)2()(12)()()(2)()( )()( )(0022000000002100002100ννπνννπννννννπνννμνννμνG G f f G f f h c B n G f h cB n G ∆∆+-∆==⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫∆=∆=∆≈依据上面两式可得:220002)2)(1()()()2()(νννννν∆++-∆=s I I G G ;即证。
