2019年云南省曲靖市沾益区大坡乡中考第二次模拟含答案解析
云南省曲靖市2019-2020学年中考语文二模试卷含解析

云南省曲靖市2019-2020学年中考语文二模试卷一、选择题1.下列句子语言表达得体的一项是()A.班长路上偶遇英语老师后,上前说:“张老师,我们全班同学都很赏识您的教学方法。
”B.班长对同学们说:“让我们用热烈的掌声,欢迎李华同学荣幸地加入我们班级。
”C.提起老张,老李对小张说:“令尊当年和我是同事,他做人堂堂正正,我很敬重他。
”D.“礼轻情意重。
”小妮将画作《花开富贵》送给闺蜜,“这是我亲手画的,还望你海涵。
”【答案】C【解析】【详解】C项句子语言表达得体。
A项:敬谦误用,“赏识”是敬辞,认识到别人的才能或作品等的价值而给予重视或赞扬。
多半用于前辈对后代、领导对下属、大师对学生,此处不合语境。
B项:“荣幸”是谦辞,用于句中不得体。
D项:“海涵”多用于请人原谅时的敬辞,用于句中不得体。
2.下列加点词解释有误的一项是()A.家贫,无从致.书以观(得到)B.大王加惠.,以小易大,甚善(聪明)C.旦日..,客从外来(第二天)D.不求闻达..于诸侯(有名望,显贵)【答案】B【解析】【详解】试题分析:B.“大王加惠”中的“惠”是“恩惠”。
不是“聪明”的意思。
故答案为B。
二、名句名篇默写3.古诗文名句默写。
桃李不言,__________。
(司马迁《史记》)衣带渐宽终不悔,__________。
(柳永《凤栖梧》)__________,潭影空人心。
(常建《题破山寺后禅院》)一水护田将绿绕,__________。
(王安石《书湖阴先生壁》)__________,沉鳞竞跃。
(陶弘景《与谢中书书》)青山有幸埋忠骨,__________。
(《对联六副》)__________,__________,国恒亡。
(《孟子》)李贺《雁门太守行》一诗,从听觉和视觉两方面,把激战中的边塞风光写得很壮美的颌联是:“__________,__________。
”【答案】(1)下自成蹊(2)为伊消得人憔悴(3)山光悦鸟性(4)两山排闼送青来(5)夕日欲颓(6)白铁无辜铸佞臣(7)入则无法家拂士出则无敌国外患者(8)角声满天秋色里塞上燕脂凝夜紫【解析】【详解】试题分析:默写题作答时,一是要透彻理解诗文的内容;二是要认真审题,找出符合题意的诗文句子;三是答题内容要准确,做到不添字、不漏字、不写错字。
云南省曲靖市2019-2020学年中考第二次大联考语文试卷含解析

云南省曲靖市2019-2020学年中考第二次大联考语文试卷一、选择题1.下列各句中,表达得体的一句是()A.获悉贵公司明天开业,甚喜,届时定拨冗..出席庆典,特此告知。
B.拙作《皋城名人汇编》新成,惶恐以赠,尚祈雅正..,不吝赐教。
C.家慈..大人今年高寿? 身体是否安康? 久在他乡甚为牵挂,适逢明日回乡,我一定登门看望。
D.明天小女周岁,为答谢您的祝贺,特于府上..备下薄酒,恭请光临。
【答案】B【解析】【详解】此题考查学生的语言表达能力。
A项,“拨冗”是具有文言色彩的客套话,意思是“请对方推开繁忙的工作,抽出时间来做某件事情”,用在这里不得体;B项“拙作”是谦词,用于形容自己的作品。
“雅正”敬辞,把自己的诗文书画送人时,表示请对方指教(套语)。
“赐教”,敬辞,表示请求对方给予指教。
三个词语使用都正确;C项“家慈”是对别人称自己的母亲,应改为“令堂”;D项“府上”是对别人的家的尊称,应改为“寒舍”。
故选B。
2.下列各组词语中,加点字的注音全部正确的一项是 ( )A.地窖.(gào)确凿.(záo)挑衅.(xìn)忍俊不禁.(jìn)B.枯涸.(hé)殒.落(yǔn) 锃.亮(zèng)猝.然而逝(cù)C.滑稽.(jì)羼.水(chàn)恻.隐(cè) 锲.而不舍(qiè)D.骸.骨(hái)胚.芽(pēi)匀称.(chèng)怒不可遏.(è)【答案】B【解析】【详解】A. 地窖.(jiào)忍俊不禁.(jīn)。
C. 滑稽.(jī)。
D.匀称.(chèn)。
二、名句名篇默写3.古诗文默写填空①_______________________,松柏有本性!(刘桢《赠从弟》)②锦江春色来天地,__________________________________。
云南省曲靖市2019-2020学年中考第二次适应性考试物理试题含解析

云南省曲靖市2019-2020学年中考第二次适应性考试物理试题一、单选题(本大题共10小题,共30分)1.下列光现象中,由于光的反射而形成的是A.深水看上去变“浅”了B.水中“断笔”C.水中“倒影”D.物体看上去变“大”了C【解析】【分析】【详解】A.水看起来很浅,是由于光线通过水、空气进入人的眼睛时,光线的传播方向发生改变而形成的现象,属于光的折射现象,故A不符合题意;B.水中的“断笔”是由于光从水中通过空气进入人的眼睛时,光线的传播方向发生改变而形成的虚像,属于光的折射现象,故B不符合题意;C.平静的水面相当于平面镜,水中的倒影是平面镜成像现象,属于光的反射,故C符合题意;D.凸透镜成像是根据光的折射原理制成的,而放大镜是凸透镜的一种应用,因此通过放大镜看到放大的物体,属于光的折射现象,故D不符合题意。
故选C。
2.下列关于声现象的说法正确的是A.声音在空气中传播的最快B.“声纹门锁”是依据声音的音调来识别的C.声呐是利用超声波传递信息的D.城市街头设置的噪声检测仪能减弱噪声C【解析】【详解】A .声音在气体中的传播速度小于在液体、固体中的速度,故A 错误;B .声音的三要素是音调、响度和音色,我们能区分不同人的声音是依据音色来辨别的,声纹锁辨别声音的依据是音色,故B 错误;C .声波能传递信息和能量,轮船上的“声呐”是利用超声波能传递信息来探索海底世界的,故C 正确;D .在街头设置噪声检测仪只能用来检测声音强弱等级,不能减弱噪声,故D 错误。
3.底面积为100cm 2的平底圆柱形容器内装有适量的水,放置于水平桌面上.现将体积为500cm 3,重为3N 的木块A 轻放入容器内的水中,静止时如图甲,若将一重为6N 的物体B 用细绳系于A 的下方,使其恰好浸没在水中,如图乙 (水未溢出),不计绳重及其体积.则下列说法正确的是A .物体B 的体积为900cm 3B .物体B 的密度为1.2×103kg/m 3C .从甲到乙,容器对桌面的压强增加600PaD .绳子受到的拉力为4NC【解析】【详解】A. 乙图中,将A 、B 两物体看为一个整体,它们刚好浸没处于静止,则它们受到的浮力等于它们的总重力,即F 浮=G 总=1N+6N=9N .则它们排开水的中体积为V 排总=F g ρ浮水=339N 110kg/m 10N/kg⨯⨯=9×10-4m 1=900cm 1,所以物体B 的体积为V B = V 排总-V 木=900cm 1-500cm 1=400cm 1.故A 错误.B. 物体B 的质量为m B =B G g =6N 10N/kg=0.6kg ,则物体B 的密度为ρB =B B m V =-630.6kg 40010m⨯=1.5×101kg/m 1.故B 错误. C. 从甲到乙,容器对桌面的压力大小增加B 物体的重力,即压力增加了6N .则容器对桌面的压强增加量为△p=FS∆=-426N10010m⨯=600Pa.故C正确.D. 乙图中B物体排开水的体积等于其自身体积,则B物体受到的浮力为F浮B=ρ水gVB=1×101kg/m1×10N/kg×400×10-6m1=4N.因物体B此时静止,受平衡力,其重力等于绳子的拉力加其受到的浮力.则绳子受到的拉力为F=G B- F浮B=6N-4N=2N.故D错误.4.下图为“测滑轮组机械效率”的实验.在弹簧测力计拉力作用下,重6N的物体2s内匀速上升0.1m,弹簧测力计示数如图示(不计绳重与摩擦).下列说法错误的是()A.弹簧测力计的拉力是2.4NB.物体上升的速度为0.05m/sC.弹簧测力计拉力的功率为0.12WD.滑轮组的机械效率约83.3%C【解析】分析:由图可知使用滑轮组承担物重的绳子股数n,拉力端移动的距离,利用求拉力做的总功,再利用求功率;已知物体的重力和上升高度,利用求有用功,滑轮组的机械效率等于有用功与总功之比。
初中数学曲靖市沾益区大坡乡中考模拟第二次模拟数学考试卷含答案.docx

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:的相反数是()A、-2B、2C、D、试题2:下列运算正确的是()A、 B、C、 D、试题3:如图是几何体的三视图,则这个几何体是()A、圆锥B、正方体D、球试题4:用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.(SAS) B.(SSS)C.(ASA) D.(AAS)试题5:将一副三角板如图放置,使点A在DE上,BC∥DE,∠C=45°,∠D=30°,则∠ABD的度数为()A. 10°B. 15°C. 20°D. 25°试题6:关于的一元二次方程的根的情况()A.无实数根 B.有两个相等的实数根C.有两个不相等的实数根D.无法确定试题7:如图,⊙O的半径为5,弦AB=8, M是弦AB上的动点,则OM不可能为()A. 2B. 3C. 4D. 5已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有()A.0个 B.1个 C.2个 D.3个试题9:为了方便市民出行,提倡低碳交通,近几年某市大力发展公共自行车系统,根据规划,全市公共自行车总量明年将达62000辆,用科学记数法表示62000是_____.试题10:一个正多边形的内角和大于等于540度而小于1000度,则这个正多边形的每一个内角可以是度。
(填出一个即可)试题11:在Rt△ABC中,∠C=90°,∠A=30°,BC=3,则AC的长为_____.(结果保留根号)试题12:若点P(m,-2)与点Q(3,n)关于原点对称,则(m+n)2018 =__________.试题13:如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2,则阴影部分的面积为_____.试题14:、下面是用棋子摆成的“上”字:第一个“上”字第二个“上”字第三个“上”字如果按照以上规律继续摆下去,那么通过观察,可以发现:第n个“上”字需用________枚棋子.试题15:计算: +()﹣1﹣|﹣2|﹣(2﹣)0.试题16:先化简再求值:,其中.试题17:如图,已知△ABC,按如下步骤作图:①分别以A,C为圆心,大于AC的长为半径画弧,两弧交于P,Q两点;②作直线PQ,分别交AB,AC于点E,D,连接CE;③过C作CF∥AB交PQ于点F,连接AF.(1)求证:△AED≌△CFD;(2)求证:四边形AECF是菱形.试题18:经过建设者三年多艰苦努力地施工,贯通我市A、B两地又一条高速公路全线通车.已知原来A地到B地普通公路长150km,高速公路路程缩短了30km,如果一辆小车从A地到B地走高速公路的平均速度可以提高到原来的1.5倍,需要的时间可以比原来少用1小时.求小车走普通公路的平均速度是多少?试题19:如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC 为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.(1)求两建筑物两底部之间的水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).试题20:我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
2019年云南省曲靖市中考历史二模试卷(解析版)

2019年云南省曲靖市中考历史二模试卷一、选择题(本大题共25小题,每小题2分,共50分.在每小题给出的四个选项中,只有一项是最符合题目要求的)1.(2分)孔子是一位伟大的思想家,针对他所处时代的社会问题,主张()A.以“德”治国B.无为而治C.君主集权D.“兼爱”和“非攻”2.(2分)公元5世纪末,北魏孝文帝迁都洛阳,推行一系列移风易俗的措施。
其作用是()A.实现了南北方的统B.促进了北方民族交融C.确立了三国鼎立局面D.加快了江南地区开发3.(2分)电影《荡寇风云》主题歌词:“上报天子兮,下救黔首。
杀尽倭奴兮,觅个封侯!”与歌词相关的历史事件是()A.武王伐纣B.国人暴动C.葵丘会盟D.戚继光抗倭4.(2分)1839年,湖广总督上书道光帝:“窃臣等钦遵谕旨,将夷船缴到烟土二万余箱,在粵销毁。
时任湖广总督的人是()A.关天培B.林则徐C.奕诉D.邓世昌5.(2分)“有田同耕,有饭同食。
有衣同穿,有钱同使,无处不均匀,无人不饱暖”的理想社会方案出自()A.《四洲志》B.《海国图志》C.《天朝田亩制度》D.《资政新篇》6.(2分)有人说:“办洋务的难处,在于外国人的不讲道理,中国人的不明时势,只有徐图自强,才能扭转形势”洋务派“徐图自强”的措施是()①学习西方先进技术②仿效西方政治制度③创办近代民用工业④兴办近代军事工业A.①②③B.①③④C.①②④D.②③④7.(2分)近代的许多报刊杂志在传播新思想和新知识方面发挥了重要的作用。
下图所示的刊物,高举“民主”、“科学”大旗的是()A.B.C.D.8.(2分)有人说:1901年,中国陷入无尽的黑暗中;1911年,一道闪电划过,却黑暗旧;1921年,中国终于迎来了曙光。
与“中国终于迎来了曙光”相关的重大历史事件是()A.义和团运动B.辛亥革命C.五四运动D.中共一大的召开9.(2分)“国民痛苦,水深火热;土匪军阀,为虎作伥;帝国主义,以枭以张。
本军兴师,救国救民;总理遗命,炳若晨星。
云南省曲靖市2019年中考数学模拟试卷(2)含答案解析+【精选五套中考模拟卷】

云南省曲靖市2019年中考数学模拟试卷(2)含答案解析一、选择题:每小题3分,共24分.1.﹣3的绝对值是()A.3B.C.D.2.如图,该几何体的俯视图是()A.B.C.D.3.下列运算正确的是()A.B.23=6 C.(x+y)2=x2+y2D.4.甲安装队为A小区安装56台热水器,乙安装队为B小区安装60台热水器,两队同时开工且恰好同时完成,甲队比乙队每天多安装2台,设乙队每天安装x台,根据题意,下面所列方程中正确的是()A.B.C.D.5.如图,AB∥DE,∠D=130°,∠C=70°,则∠B的度数为()A.50° B.20° C.70° D.55°6.甲乙两同学在7次体育测试中成绩如折线图,下列说法正确的是()A.甲同学7次测试成绩的众数为20和30,中位数为30B.乙同学7次测试成绩的中位数为30,7次测试成绩中甲同学成绩较稳定C.甲同学7次测试成绩的众数为20,中位数为30D.乙同学7次测试成绩的众数为10和30,7次测试成绩中乙同学成绩较稳定7.若在平面直角坐标系内A(m﹣1,6),B(﹣2,n)两点关于原点对称,则m+n的值为()A.9 B.﹣3 C.3 D.58.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,AO=OM,下列说法错误的是()A.AE=AF B.AM⊥EF C.DF=FC D.AF=FM二、填空题:每小题3分,共24分.9.某市人口数约为790万人,这个数用科学记数法表示为人.10.若代数式有意义,则x的取值范围是.11.三角形两边长分别为3和6,第三边是方程x2﹣6x+8=0的解,则此三角形周长是.12.如图,在⊙O中,直径CD交弦AB于点H,∠OBH=20°,∠C的度数为.13.分别以线段AB的两端点A、B为圆心,大于AB为半径画弧,两弧交于点C,过C作CH⊥AB,若AC=6,sinA=,则AB的长为.14.从写有﹣5,0,3,6四个数字中的卡片中(卡片除数字外,形状大小均相同)随机抽取一张,将上面的数字记为x,放回后再随机抽取一张,将上面的数字记为y,则组成的点(x,y)在第四象限的概率为.15.直线y=3x+2与双曲线y=交于点A(1,y),则k= .16.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第36次运动后,动点P的坐标是.三、解答题:共72分.17.计算:(﹣1)2019﹣+()0﹣|﹣3|.18.先化简,再求值:(x﹣1)÷(1﹣),其中x2+3x+2=0.19.某玩具厂共有300名生产工人,每个工人每天可生产玩具车架20个或车轮40个,如果1个车架与4个车轮配成一套,那么每天安排多少名工人生产车架,多少名工人生产车轮,才能使每天生产出来的产品刚好配套?20.为了解初中生的健康状况,相关部分随机抽取了某校的部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分,请根据图表信息回答下列问题:组别测试成绩百分比A 优秀10%B 良好 aC 及格30%D 不及格 b(1)表中a= ,b= ,本次共抽取了多少名学生进行测试?(2)扇形图中区域B所对应的扇形圆心角的度数为;(3)若该校有2000名学生,请估计成绩为优秀或良好的学生人数.21.如图,在矩形ABCD中,点E、F分别在AB、CD上,且CF=AE.(1)求证:四边形BFDE为平行四边形;(2)若BD平分∠ABF,试判断四边形BFDE的形状,并证明你的结论.22.如图,有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个不同的算式,将这四张卡片背面向上洗匀.(1)求从这四张卡片中随机抽取一张,其计算结果正确的概率;(2)从这四张卡片中随机抽取两张,用列举法求这两张卡片算式计算结果均正确的概率.23.如图,BC为⊙O的直径,DE为⊙O的切线,CA与弦BE的延长线交于点A,D为AC的中点.(1)求证:AC为⊙O的切线;(2)若DE=3,tanB=,求⊙O的半径.24.(12分)如图,抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(﹣3,0)两点,与y轴交于点C、D为抛物线的顶点.(1)求抛物线的解析式与顶点D的坐标;(2)若抛物线上有一点M,且S△ABM=6,求M的坐标;(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角线与△BCD相似?若存在,请求出符合条件的点P;若不存在,请说明理由.参考答案与试题解析一、选择题:每小题3分,共24分.1.﹣3的绝对值是( )A .3B .C .D .【考点】绝对值.【分析】根据绝对值的定义直接计算即可解答.【解答】解:﹣3的绝对值是3.故选:A .【点评】本题主要考查绝对值的性质.绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.如图,该几何体的俯视图是( )A .B .C .D .【考点】简单几何体的三视图.【分析】可根据几何体的特点,得出俯视图的形状.【解答】解:如图所示可得其俯视图为:.故选:C .【点评】此题主要考查了几何体的三种视图,掌握定义是关键.俯视图是从物体上面看,所得到的图形.3.下列运算正确的是( )A .B .23=6C .(x+y )2=x 2+y 2D . 【考点】二次根式的乘除法;有理数的乘方;算术平方根;完全平方公式.【分析】根据二次根式的乘法计算公式、乘方、完全平方公式和开方分别进行计算即可.【解答】解:A 、=,a ≥0,b ≥0,故此选项错误;B 、23=8,顾此选项错误;C 、(x+y )2=x 2+y 2+2xy ,故此选项错误;D、==2,故此选项正确;故选:D.【点评】此题主要考查了二次根式的乘法计算公式、乘方、完全平方公式和开方,关键是掌握各计算公式.4.甲安装队为A小区安装56台热水器,乙安装队为B小区安装60台热水器,两队同时开工且恰好同时完成,甲队比乙队每天多安装2台,设乙队每天安装x台,根据题意,下面所列方程中正确的是()A.B.C.D.【考点】由实际问题抽象出分式方程.【分析】根据题意可以列出相应的分式方程,本题得以解决.【解答】解:由题意可得,,故选D.【点评】本题考查由实际问题抽象出分式方程,解题的关键是明确题意,列出相应的分式方程.5.如图,AB∥DE,∠D=130°,∠C=70°,则∠B的度数为()A.50° B.20° C.70° D.55°【考点】平行线的性质.【分析】过C作CP∥AB,利用平行线的性质可得到∠BCD和∠B、∠D之间的关系,可求得答案.【解答】解:如图,过C作CP∥AB,∵AB∥DE,∴CP∥DE,∴∠1=180°﹣∠D=50°,∴∠2=70°﹣50°=20°,∴∠B=∠2=20°,故选B.【点评】本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补.6.甲乙两同学在7次体育测试中成绩如折线图,下列说法正确的是()A.甲同学7次测试成绩的众数为20和30,中位数为30B.乙同学7次测试成绩的中位数为30,7次测试成绩中甲同学成绩较稳定C.甲同学7次测试成绩的众数为20,中位数为30D.乙同学7次测试成绩的众数为10和30,7次测试成绩中乙同学成绩较稳定【考点】折线统计图;中位数;众数;方差.【分析】根据折线统计图,可得甲七次的成绩,乙七次的成绩,根据众数、中位数,可得答案.【解答】解:由折线统计图,得甲的成绩为20,30,20,30,22,40,30;乙的成绩为40,10,30,20,10,30,10,A、甲同学7次测试成绩的众数为20和30,中位数为30,故A正确;B、乙同学7次测试成绩的中位数为20,7次测试成绩中甲同学成绩较稳定,故B错误;C、甲同学7次测试成绩的众数为20和30,中位数为30,故C错误;D、乙同学7次测试成绩的众数为10,7次测试成绩中甲同学成绩较稳定,故D错误;故选:A.【点评】本题考查了折线统计图,利用折线统计图获得有效信息是解题关键,又利用了众数、中位数的定义.7.若在平面直角坐标系内A(m﹣1,6),B(﹣2,n)两点关于原点对称,则m+n的值为()A.9 B.﹣3 C.3 D.5【考点】关于原点对称的点的坐标.【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数列方程求出m、n的值,然后相加计算即可得解.【解答】解:∵A(m﹣1,6),B(﹣2,n)两点关于原点对称,∴,解得,所以,m+n=3+(﹣6)=﹣3.【点评】本题考查了关于原点对称的点的坐标,熟记关于原点对称的点的横坐标与纵坐标都互为相反数是解题的关键.8.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,AO=OM,下列说法错误的是()A.AE=AF B.AM⊥EF C.DF=FC D.AF=FM【考点】正方形的性质.【分析】根据正方形的性质可得AB=AD,∠B=∠D=90°,然后利用“HL”证明Rt△ABE和Rt△ADF全等,求出CE=CF,然后利用“边边边”证明△AEC和△AFC全等,根据全等三角形对应角相等可得∠EAC=∠FAC,再根据等腰三角形三线合一的性质可得AC垂直平分EF,根据线段垂直平分线上的点到两端点的距离相等可得EM=FM,再判断出EF垂直平分AM,根据线段垂直平分线上的点到两端点的距离相等可得AE=EM,然后根据四条边都相等的四边形是菱形,继而证得AM⊥EF.【解答】解:在正方形ABCD中,AB=AD,∠B=∠D=90°,在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF;∵BC=CD,BE=DF,∴BC﹣BE=CD﹣CF,即CE=CF,在△AEC和△AFC中,,∴△AEC≌△AFC(SSS),∴∠EAC=∠FAC,又∵AE=AF,∴AC垂直平分EF,∴EM=FM,∴EF垂直平分AM,∴AE=EM,∴AE=EM=FM=AF,故A、D正确;∴四边形AEMF是菱形,∴AM⊥EF;故B正确.故选C.【点评】此题考查了正方形的性质,全等三角形的判定与性质以及菱形的判定与性质.注意证得四边形AEMF是菱形是解此题的关键.二、填空题:每小题3分,共24分.9.某市人口数约为790万人,这个数用科学记数法表示为7.9×106人.【考点】科学记数法—表示较大的数.【专题】推理填空题.【分析】用科学记数法表示较大的数时,一般形式为a×10﹣n,其中1≤|a|<10,n为整数,据此判断即可.【解答】解:790万=7.9×106.故答案为:7.9×106.【点评】此题主要考查了用科学记数法表示较大的数,一般形式为a×10﹣n,其中1≤|a|<10,确定a与n的值是解题的关键.10.若代数式有意义,则x的取值范围是x≥﹣1且x≠5 .【考点】二次根式有意义的条件.【分析】根据二次根式有意义的条件、分式有意义的条件列出不等式,解不等式即可.【解答】解:由题意得,x+1≥0,x﹣5≠0,解答,x≥﹣1且x≠5,故答案为:x≥﹣1且x≠5.【点评】本题考查的是二次根式有意义的条件、分式有意义的条件,掌握二次根式中的被开方数必须是非负数、分式分母不为0是解题的关键.11.三角形两边长分别为3和6,第三边是方程x2﹣6x+8=0的解,则此三角形周长是13 .【考点】解一元二次方程-因式分解法;三角形三边关系.【专题】计算题;分类讨论.【分析】求出方程的解,有两种情况:x=2时,看看是否符合三角形三边关系定理;x=4时,看看是否符合三角形三边关系定理;求出即可.【解答】解:x2﹣6x+8=0,(x﹣2)(x﹣4)=0,x﹣2=0,x﹣4=0,x1=2,x2=4,当x=2时,2+3<6,不符合三角形的三边关系定理,所以x=2舍去,当x=4时,符合三角形的三边关系定理,三角形的周长是3+6+4=13,故答案为:13.【点评】本题考查了三角形的三边关系定理和解一元二次方程等知识点,关键是确定第三边的大小,三角形的两边之和大于第三边,分类讨论思想的运用,题型较好,难度适中.12.如图,在⊙O中,直径CD交弦AB于点H,∠OBH=20°,∠C的度数为35°.【考点】圆周角定理.【分析】由“等弧所对的圆周角是所对的圆心角的一半”推知∠DOB=2∠C;则在直角△BOE中,利用“直角三角形的两个锐角互余”的性质解题.【解答】解:∵在⊙O中,直径CD垂直于弦AB,∴=,∴∠C=∠BOH=(90°﹣20°)=35°.故答案为35°.【点评】本题考查了圆周角定理、垂径定理.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.13.分别以线段AB的两端点A、B为圆心,大于AB为半径画弧,两弧交于点C,过C作CH⊥AB,若AC=6,sinA=,则AB的长为8.【考点】解直角三角形.【专题】计算题;解直角三角形及其应用.【分析】由作图得到AC=BC,再利用三线合一得到H为AB中点,在直角三角形AHC中,利用锐角三角函数定义求出CH的长,再利用勾股定理求出AH的长,进而确定出AB的长即可.【解答】解:根据题意得:AC=BC,CH⊥AB,∴AH=BH=AB,在Rt△AHC中,CH=AC•sinA=6×=2,∴AH==4,则AB=2AH=8,故答案为:8【点评】此题考查了解直角三角形,熟练掌握锐角三角函数定义是解本题的关键.14.从写有﹣5,0,3,6四个数字中的卡片中(卡片除数字外,形状大小均相同)随机抽取一张,将上面的数字记为x,放回后再随机抽取一张,将上面的数字记为y,则组成的点(x,y)在第四象限的概率为.【考点】列表法与树状图法;点的坐标.【分析】根据题意可以写出所有的可能性,从而可以得到在第四象限的概率,本题得以解决.【解答】解:由题意可得,所有的可能性是:(﹣5,﹣5)、(﹣5,0)、(﹣5,3)、(﹣5,6)、(0,﹣5)、(0,0)、(0,3)、(0,6)、(3,﹣5)、(3,0)、(3,3)、(3,6)、(6,﹣5)、(6,0)、(6,3)、(6,6),在第四象限的点是:(3,﹣5)、(6,﹣5),故组成的点(x,y)在第四象限的概率为:,故答案为:.【点评】本题考查列表法与树状图法、点的坐标,解题的关键是写出所有的可能性,明确第四象限点的坐标的特点.15.直线y=3x+2与双曲线y=交于点A(1,y),则k= 5 .【考点】反比例函数与一次函数的交点问题.【分析】先把点A代入直线y=3x+2求出y的值,得出A点坐标,再代入双曲线y=求出k的值即可.【解答】解:∵线y=3x+2与双曲线y=交于点A(1,y),∴把x=1代入直线y=3x+2得,y=3+2=5,∴A(1,5),∴k=xy=1×5=5.故答案为:5.【点评】本题考查的是反比例函数与一次函数的交点问题,熟知两个函数交点的坐标适合函数的解析式是解答此题的关键.16.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第36次运动后,动点P的坐标是(72,0).【考点】规律型:点的坐标.【分析】根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数的2倍,纵坐标为2,0,1,0,每4次一轮这一规律,进而求出即可.【解答】解:根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),∴第4次运动到点(8,0),第5次接着运动到点(10,2),…,∴横坐标为运动次数的2倍,经过第36次运动后,动点P的横坐标为72,纵坐标为2,0,1,0,每4次一轮,∴经过第36次运动后,动点P的纵坐标为:36÷4=9,故纵坐标为0,∴经过第36次运动后,动点P的坐标是:(72,0),故答案为:(72,0).【点评】此题主要考查了点的坐标规律,培养学生观察和归纳能力,从所给的数据和图形中寻求规律进行解题是解答本题的关键.三、解答题:共72分.17.计算:(﹣1)2019﹣+()0﹣|﹣3|.【考点】实数的运算;零指数幂.【分析】本题涉及乘方、立方根、零指数幂、绝对值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:(﹣1)2019﹣+()0﹣|﹣3|=1+3+1﹣3=2.【点评】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握乘方、立方根、零指数幂、绝对值等考点的运算.18.先化简,再求值:(x﹣1)÷(1﹣),其中x2+3x+2=0.【考点】分式的化简求值.【专题】计算题;分式.【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出方程的解得到x的值,代入计算即可求出值.【解答】解:原式=(x﹣1)÷=(x﹣1)•=x+1,由x2+3x+2=0,即(x+1)(x+2)=0,解得:x=﹣1(舍去)或x=﹣2,当x=﹣2时,原式=﹣2+1=﹣1.【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.19.某玩具厂共有300名生产工人,每个工人每天可生产玩具车架20个或车轮40个,如果1个车架与4个车轮配成一套,那么每天安排多少名工人生产车架,多少名工人生产车轮,才能使每天生产出来的产品刚好配套?【考点】二元一次方程组的应用.【分析】设每天安排多x名工人生产车架,y名工人生产车轮,根据共有300名工人及1个车架与4个车轮配成一套,可得出方程组,解出即可得出答案.【解答】解:设每天安排多x名工人生产车架,y名工人生产车轮,由题意得,,解得:,答:每天安排多100名工人生产车架,200名工人生产车轮,才能使每天生产出来的产品刚好配套.【点评】本题考查了二元一次方程组的应用,解答本题的关键是仔细审题,设出未知数,注意得出结果后要结合实际解答.20.为了解初中生的健康状况,相关部分随机抽取了某校的部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分,请根据图表信息回答下列问题:组别测试成绩百分比A 优秀10%B 良好 aC 及格30%D 不及格 b(1)表中a= 45% ,b= 15% ,本次共抽取了多少名学生进行测试?(2)扇形图中区域B所对应的扇形圆心角的度数为162°;(3)若该校有2000名学生,请估计成绩为优秀或良好的学生人数.【考点】条形统计图;用样本估计总体;统计表;扇形统计图.【分析】(1)根据A组人数及其百分比可求得抽查学生人数,继而用B组人数除以总人数可得B组所占百分比,最后用1减去A、B、C三组百分比可得D组所占百分比;(2)用360°乘以B组占被调查人数的百分比即可得;(3)用总人数2000乘以A、B两组百分比之和即可得.【解答】解:(1)本次共抽取学生=200(人),a=×100%=45%,b=1﹣10%﹣45%﹣30%=15%,故答案为:45%,15%;(2)扇形图中区域B所对应的扇形圆心角的度数为360°×45%=162°,故答案为:162°;(3)2000×(10%+45%)=1100(名),答:估计成绩为优秀或良好的学生人数有1100名.【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大21.如图,在矩形ABCD中,点E、F分别在AB、CD上,且CF=AE.(1)求证:四边形BFDE为平行四边形;(2)若BD平分∠ABF,试判断四边形BFDE的形状,并证明你的结论.【考点】矩形的性质;平行四边形的判定与性质.【分析】(1)在▱ABCD中,根据平行四边形的性质AB=CD,AB∥CD,又由于AE=CF,则BE=CF,根据平行四边形的判定可证四边形EBFD是平行四边形.(2)证出DF=BF,即可得出结论.【解答】解:∵在矩形ABCD中,AB=CD,AB∥CD.又∵AE=CF,∴BE=DF.∴四边形BFDE为平行四边形.(2)解:四边形BFDE是菱形;理由如下:∵BD平分∠ABF,AB∥CD,∴∠ABD=∠FBD,∠ABD=∠CDF,∴∠FBD=∠CDF,∴DF=BF,∴四边形BFDE是菱形.【点评】本题考查了平行四边形的判定与性质、菱形的判定;熟练掌握性质定理和判定定理是解题的关键.22.如图,有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个不同的算式,将这四张卡片背面向上洗匀.(1)求从这四张卡片中随机抽取一张,其计算结果正确的概率;(2)从这四张卡片中随机抽取两张,用列举法求这两张卡片算式计算结果均正确的概率.【考点】列表法与树状图法;概率公式.【分析】(1)根据题意可以知道四张卡片中有几张计算正确,有几张计算错误,从而可以得到从这四张卡片中随机抽取一张,计算结果正确的概率;(2)根据题意可以画出树状图,从而可以解答本题.A、C、D计算正确,C计算错误,故从这四张卡片中随机抽取一张,其计算结果正确的概率是;(2)由题意可得,共有12种等可能的结果,其中正确的有:(A,B),(A,D),(B,A),(B,D),(D,A),(D,B),故这两张卡片算式计算结果均正确的概率是:,即这两张卡片算式计算结果均正确的概率是.【点评】本题考查列表法与树状图法、概率公式,解题的关键是明确题意,找出所求问题需要的条件.23.如图,BC为⊙O的直径,DE为⊙O的切线,CA与弦BE的延长线交于点A,D为AC的中点.(1)求证:AC为⊙O的切线;(2)若DE=3,tanB=,求⊙O的半径.【考点】切线的判定与性质;解直角三角形.【分析】(1)连接OE,CE,根据切线的性质得到OE⊥DE,由BC为⊙O的直径,得到∠BEC=90°,根据等腰三角形的性质得到∠1=∠2,∠3=∠4,由余角的性质得到∠ACB=90°,即可得到结论;(2)根据直角三角形的性质即可得到结论.【解答】解:(1)证明:连接OE,CE,∵DE为⊙O的切线,∴OE⊥DE,∵BC为⊙O的直径,∴∠BEC=90°,∵D为AC的中点,∴AD=DE,∴∠1=∠2,∵OE=OB,∴∠3=∠4,∵∠2+∠3=90°,∴∠1+∠4=90°,∴∠ACB=90°,∴BC⊥AC,∴AC为⊙O的切线;(2)∵DE=3,∴AC=6,∴BC==6=18.【点评】本题考查了切线的判定和性质,解直角三角形,直角三角形的性质,熟练掌握切线的判定和性质是解题的关键.24.如图,抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(﹣3,0)两点,与y轴交于点C、D为抛物线的顶点.(1)求抛物线的解析式与顶点D的坐标;(2)若抛物线上有一点M,且S△ABM=6,求M的坐标;(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角线与△BCD相似?若存在,请求出符合条件的点P;若不存在,请说明理由.【考点】二次函数综合题.【分析】(1)用待定系数法求出抛物线解析式;(2)设出点M的坐标,用S△ABM=6,建立方程求解即可;【解答】解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(﹣3,0),∴,∴,∴抛物线解析式为y=﹣x2﹣2x+3,∴抛物线顶点坐标为D(﹣1,4),(2)设M(m,n),∴n=﹣m2﹣2m+3∵S△ABM=6,∴AB×|n|=6,∴×4×|n|=6,∴n=±3,①当n=3时,则﹣m2﹣2m+3=3,∴m=0或m=﹣2,∴M(0,3)或(﹣2,3)②当n=﹣3时,则﹣m2﹣2m+3=﹣3∴m=﹣1+或m=﹣1﹣,∴M(﹣1+,﹣3)或(﹣1﹣,﹣3),∴满足条件的M点坐标为(0,3)或(﹣2,3)或(﹣1+,﹣3)或(﹣1﹣,﹣3),(3)存在,如图,∵A(1,0),B(﹣3,0),C(0,3),D(﹣1,4),∴OA=1,OC=3,∴∵B(﹣3,0),C(0,3),D(﹣1,4),∴BC2=(﹣3)2+32=18,BD2=(﹣1+3)2+42=20,CD2=(﹣1)2+(4﹣3)2=2,∴△BCD是直角三角形,∴,∴,∵∠AOC=∠BCD=90°,∴Rt△AOC∽Rt△DCB,理由:①∵Rt△AOC∽Rt△DCB,∴点P与点O重合,∴P(0,0),②过点A作AP'⊥AC,交y轴于点P',∴∠P'AC=∠AOC=90°∵∠ACO=∠P'CA,∴Rt△AOC∽Rt△P'AC,∴Rt△AOC∽Rt△DCB∽Rt△P'AC,∴OP'×OC=OA2,∵OA=1,OC=3,∴OP'=,∴P'(0,﹣),③过点C作CP''⊥AC,交x负半轴于点P'',∴∠ACP''=90°,∴∠ACP''=∠BCD=90°∵∠OAC=∠CAP'',∴Rt△AOC∽Rt△ACP''∴Rt△AOC∽Rt△DCB∽Rt△ACP'',∴OC2=OA×OP'',∵OA=1,OC=3,∴OP''=9,∴P''(﹣9,0),∴存在符号条件的点P它的坐标为(0,0),(0,﹣),(﹣9,0).【点评】此题是二次函数综合题,主要考查了待定系数法,三角形的面积公式,相似三角形的性质和判定,解本题的关键是判断出Rt△AOC∽Rt△DCB.中考数学模拟试卷一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡...相应位置....上)1. 下列各数中,属于无理数的是A.0.010010001B.3C.3.14D.-122.下面调查中,适合采用普查的是A.调查全国中学生心理健康现状. B.调查你所在的班级同学的身高情况.C.调查50枚导弹的杀伤半径. D.调查扬州电视台《今日生活》收视率.3. 下列各式计算正确的是A.23523a a a+= B.235()a a= C.623a a a÷= D.235a a a⋅=4. 下列函数中,自变量的取值范围是3x>的是A.3y x=- B.13yx=-C.3y x=- D.13yx=-5.如图,下列选项中不是..正六棱柱三视图的是A B C D6.用直尺和圆规作一个角等于已知角的作法如图,能得出A O B AOB'''∠=∠的依据是A.(SAS) B.(SSS) C.(AAS)D.(A SA)7. 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为A.2 B. 4 C.22 D.28.一种包装盒的设计方法如图所示,ABCD是边长为80cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒,设BE=CF=x cm,要使包装盒的侧面积最大,则x应取().A.30cm B.25cm C.20cm D.15cm(第4题)ABPO(第7题)(第6题)OA D二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相....应位置...上) 9. 我国南海资源丰富,其面积约为3 500 000平方千米,相当于我国渤海、黄海和东海总面积的3倍.其中3 500 000用科学记数法表示为 ▲ .10. 正方形的面积为18,则该正方形的边长为 ▲ . 11. 分解因式:244a b ab b -+= ▲ . 12. 若双曲线42k y x -=与直线12y x =无交点,则k 的取值范围是 ▲ . 13. 口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 ▲ .14.一个矩形的周长为16,面积为14,则该矩形的对角线长为 ▲ . 15.如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则sin∠ABC= ▲ .16. 如图,在□ABCD 中, E ,F 是对角线BD 上的两点,要使四边形AFCE 是平行四边形,则需添加的一个条件可以是 ▲ .(只添加一个条件)17. 如图,正五边形ABCDE 的边长为2,分别以点C 、D 为圆心,CD 长为半径画弧,两弧交于点F ,则弧BF 的长为 ▲ .(结果保留π)18. 如图,△ABC 三个顶点分别在反比例函数y = 1 x ,y = k x的图像上,若∠C =90°,AC ∥y 轴,BC ∥x 轴,S △ABC =8,则k 的值为 ▲ .三、解答题(本大题共有10小题,共96分.请在答题卡指定区域.......内作答,解答时应写出必要的文字说明、证明过程或演算步骤) 19.(本题满分8分)(1)计算:12︒-30tan 32)21(--; (2)解方程:2410x x --=.20.(本题满分8分)先化简再求值:232(1)121x x x x x ---÷--+,其中x 是不等式组3(2)2,4251x x x x --≥⎧⎨-<-⎩的一个整数解. C BA(第14题)AB CD FE(第16题)(第18题)yy = 1 xy =k xxOABCE(第17题)BCDF A21.(本题满分8分)中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:请你根据图中的信息,解答下列问题:(1)写出扇形图中a ▲ %,并补全条形图;(2)在这次抽测中,测试成绩的众数和中位数分别是 ▲ 个、 ▲ 个;(3)该区体育中考选报引体向上的男生共1800人,如果引体向上达6个以上(含6个)得满分,请你估计该区选报引体向上的男生能获得满分的有多少人?22.(本题满分8分)4张奖券中有2张是有奖的,甲、乙先后各抽一张. (1)甲中奖的概率是 ▲ ;(2)试用树状图或列表法求甲、乙都中奖的概率.23.(本题满分10分)如图,在□ABCD 中,点E 、F 、G 、H 分别在边AB 、BC 、CD 、DA 上,AE =CG ,AH =CF .(1)求证:△AEH ≌△CGF ;(2)若EG 平分∠HEF ,求证:四边形EFGH 是菱形.24.(本题满分10分)扬州市某土特产商店购进960盒绿叶牌牛皮糖,由于进入旅游旺季,实际每天销售的盒数比原计划每天多20%,结果提前2天卖完.请你根据以上信息,提出一个用分式方程....解决的问题,并写出解答过程.25.(本题满分10分)同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y (cm )与燃烧时间x (min )的关系如图A BCDHEGF。
云南省曲靖市2019-2020学年中考数学模拟试题(2)含解析

云南省曲靖市2019-2020学年中考数学模拟试题(2)一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列计算正确的是( )A.2x﹣x=1 B.x2•x3=x6C.(m﹣n)2=m2﹣n2D.(﹣xy3)2=x2y62.下列叙述,错误的是( )A.对角线互相垂直且相等的平行四边形是正方形B.对角线互相垂直平分的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线相等的四边形是矩形3.下列运算正确的是()A.(a2)5=a7B.(x﹣1)2=x2﹣1C.3a2b﹣3ab2=3 D.a2•a4=a64.如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为()A.1:2 B.1:3 C.1:4 D.1:15.小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是().A.众数是6吨B.平均数是5吨C.中位数是5吨D.方差是6.“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.M N S T四位同学的单词记忆效率y与复习的单词个数x的情况,则这四位右图描述了某次单词复习中,,,A .MB .NC .SD .T7.如图,将△ABC 绕点A 逆时针旋转一定角度,得到△ADE ,若∠CAE=65°,∠E=70°,且AD ⊥BC ,∠BAC 的度数为( ).A .60 °B .75°C .85°D .90°8.在2014年5月崇左市教育局举行的“经典诗朗诵”演讲比赛中,有11名学生参加决赛,他们决赛的成绩各不相同,其中的一名学生想知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的( ) A .众数B .中位数C .平均数D .方差9.据《关于“十三五”期间全面深入推进教育信息化工作的指导意见》显示,全国6000万名师生已通过“网络学习空间”探索网络条件下的新型教学、学习与教研模式,教育公共服务平台基本覆盖全国学生、教职工等信息基础数据库,实施全国中小学教师信息技术应用能力提升工程.则数字6000万用科学记数法表示为( ) A .6×105B .6×106C .6×107D .6×10810.如图,若AB ∥CD ,则α、β、γ之间的关系为( )A .α+β+γ=360°B .α﹣β+γ=180°C .α+β﹣γ=180°D .α+β+γ=180°11.使用家用燃气灶烧开同一壶水所需的燃气量y (单位:3m )与旋钮的旋转角度x (单位:度)(090x <≤o o )近似满足函数关系y=ax 2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角A.18o B.36o C.41o D.58o12.如图,某计算机中有、、三个按键,以下是这三个按键的功能.(1).:将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下后会变成1.(2).:将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下后会变成0.2.(3).:将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下后会变成3.若荧幕显示的数为100时,小刘第一下按,第二下按,第三下按,之后以、、的顺序轮流按,则当他按了第100下后荧幕显示的数是多少()A.0.01 B.0.1 C.10 D.100二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,直线y1=kx+n(k≠0)与抛物线y2=ax2+bx+c(a≠0)分别交于A(﹣1,0),B(2,﹣3)两点,那么当y1>y2时,x的取值范围是_____.14.若从-3,-1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组21x y bax y-=⎧⎨+=⎩有整数解,且点(a,b)落在双曲线3yx=-上的概率是_________.15.已知菱形的周长为10cm,一条对角线长为6cm,则这个菱形的面积是_____cm1.17.如图,直线y=x+2与反比例函数y=kx的图象在第一象限交于点P.若OP=10,则k的值为________.18.计算:﹣22÷(﹣14)=_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图1,△ABC中,AB=AC=6,BC=4,点D、E分别在边AB、AC上,且AD=AE=1,连接DE、CD,点M、N、P分别是线段DE、BC、CD的中点,连接MP、PN、MN.(1)求证:△PMN是等腰三角形;(2)将△ADE绕点A逆时针旋转,①如图2,当点D、E分别在边AC两侧时,求证:△PMN是等腰三角形;②当△ADE绕点A逆时针旋转到第一次点D、E、C在一条直线上时,请直接写出此时BD的长.20.(6分)如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过»BD上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.(1)求证:∠G=∠CEF;(2)求证:EG是⊙O的切线;(3)延长AB交GE的延长线于点M,若tanG =34,3EM的值.21.(6分)如图,在平面直角坐标系中,矩形DOBC 的顶点O 与坐标原点重合,B 、D 分别在坐标轴上,点C 的坐标为(6,4),反比例函数y=1k x(x >0)的图象经过线段OC 的中点A ,交DC 于点E ,交BC 于点F .(1)求反比例函数的解析式; (2)求△OEF 的面积;(3)设直线EF 的解析式为y=k 2x+b ,请结合图象直接写出不等式k 2x+b >1k x的解集.22.(8分)如图,已知点D 在反比例函数y=mx的图象上,过点D 作x 轴的平行线交y 轴于点B (0,3).过点A (5,0)的直线y=kx+b 与y 轴于点C ,且BD=OC ,tan ∠OAC=25.(1)求反比例函数y=mx和直线y=kx+b 的解析式;(2)连接CD ,试判断线段AC 与线段CD 的关系,并说明理由;(3)点E 为x 轴上点A 右侧的一点,且AE=OC ,连接BE 交直线CA 与点M ,求∠BMC 的度数.23.(8分)如图,一次函数y=k 1x+b(k 1≠0)与反比例函数22 ( 0 )k y k x=≠的图象交于点A(-1,2),B(m ,(2)在x 轴上是否存在点P(n ,0),使△ABP 为等腰三角形,请你直接写出P 点的坐标.24.(10分)将二次函数2241y x x =+-的解析式化为2()y a x m k =++的形式,并指出该函数图象的开口方向、顶点坐标和对称轴.25.(10分)如图,已知□ABCD 的面积为S ,点P 、Q 时是▱ABCD 对角线BD 的三等分点,延长AQ 、AP ,分别交BC ,CD 于点E ,F ,连结EF 。
云南省曲靖市2019-2020学年中考第二次质量检测语文试题含解析

云南省曲靖市2019-2020学年中考第二次质量检测语文试题一、选择题1.对下面这首诗理解有误的一项是()酬乐天扬州初逢席上见赠刘禹锡巴山楚水凄凉地,二十三年弃置身。
怀旧空吟闻笛赋,到乡翻似烂柯人。
沉舟侧畔千帆过,病树前头万木春。
今日听君歌一曲,暂凭杯酒长精神。
A.首联通过“凄凉地”和“弃置身”,对自己被贬谪、遭弃置的境遇,表达了心酸和愧疚之情。
B.颔联运用了两个典故,表达了对故友的怀念,对岁月流逝,人事变迁的感叹。
C.颈联一洗伤感低沉情调,尽显慷慨激昂气概,新生事物必然要发展起来,前景无限美好。
D.尾联点明酬赠题意,既是对友人关怀的感谢,也是和友人的共勉,表现诗人坚定的意志和乐观的精神。
【答案】A【解析】【详解】A项有误。
词语“凄凉地”“弃置身”写出了作者被贬谪、遭弃置的境遇,暗含诗人长期谪居的痛苦和抑制已久的愤激心情。
2.下列加点成语使用恰当..的一项是()A.虽然我只是芸芸众生....,但我仍固执地希望我的生命能开出光艳的花来,而不愿成为像蚂蚁一般的虫豸。
B.暑假要不要外出旅游,妈妈的态度莫衷一是....,最后也没告诉大家她的决定。
C.这种草药能治疗高血压,对人体又没有任何副作用,我们屡试不爽....,你还有什么怀疑的?D.某些管理机构缺乏“大数据思维”,以邻为壑....,不与相关机构共享信息资源,公共数据中心的建设将有助于改变这种状况。
【答案】C【解析】【详解】A芸芸众生:原指世间的一切生灵。
后多指大群无知无识的人。
“我”是一个人,自然不能说是“芸芸众生”。
B莫衷一是:指不能决定哪个是对的。
形容意见分歧,没有一致的看法。
使用时,主语不能是某一个人。
D以邻为壑:拿邻国当作大水坑,把本国的洪水排泄到那里去。
比喻只图自己一方的利益,把困难或祸害转嫁给别人。
使用语境明显错误。
二、名句名篇默写3.根据课文默写古诗文。
⑴_________________?烟波江上使人愁。
(崔颢《黄鹤楼》)⑵造化钟神秀,阴阳割昏晓。
云南省曲靖市2019-2020学年中考语文二模试卷含解析

云南省曲靖市2019-2020学年中考语文二模试卷一、选择题1.下列句子语言表达得体的一项是()A.班长路上偶遇英语老师后,上前说:“张老师,我们全班同学都很赏识您的教学方法。
”B.班长对同学们说:“让我们用热烈的掌声,欢迎李华同学荣幸地加入我们班级。
”C.提起老张,老李对小张说:“令尊当年和我是同事,他做人堂堂正正,我很敬重他。
”D.“礼轻情意重。
”小妮将画作《花开富贵》送给闺蜜,“这是我亲手画的,还望你海涵。
”【答案】C【解析】【详解】C项句子语言表达得体。
A项:敬谦误用,“赏识”是敬辞,认识到别人的才能或作品等的价值而给予重视或赞扬。
多半用于前辈对后代、领导对下属、大师对学生,此处不合语境。
B项:“荣幸”是谦辞,用于句中不得体。
D项:“海涵”多用于请人原谅时的敬辞,用于句中不得体。
2.下列加点词解释有误的一项是()A.家贫,无从致.书以观(得到)B.大王加惠.,以小易大,甚善(聪明)C.旦日..,客从外来(第二天)D.不求闻达..于诸侯(有名望,显贵)【答案】B【解析】【详解】试题分析:B.“大王加惠”中的“惠”是“恩惠”。
不是“聪明”的意思。
故答案为B。
二、名句名篇默写3.古诗文名句默写。
桃李不言,__________。
(司马迁《史记》)衣带渐宽终不悔,__________。
(柳永《凤栖梧》)__________,潭影空人心。
(常建《题破山寺后禅院》)一水护田将绿绕,__________。
(王安石《书湖阴先生壁》)__________,沉鳞竞跃。
(陶弘景《与谢中书书》)青山有幸埋忠骨,__________。
(《对联六副》)__________,__________,国恒亡。
(《孟子》)李贺《雁门太守行》一诗,从听觉和视觉两方面,把激战中的边塞风光写得很壮美的颌联是:“__________,__________。
”【答案】(1)下自成蹊(2)为伊消得人憔悴(3)山光悦鸟性(4)两山排闼送青来(5)夕日欲颓(6)白铁无辜铸佞臣(7)入则无法家拂士出则无敌国外患者(8)角声满天秋色里塞上燕脂凝夜紫【解析】【详解】试题分析:默写题作答时,一是要透彻理解诗文的内容;二是要认真审题,找出符合题意的诗文句子;三是答题内容要准确,做到不添字、不漏字、不写错字。
云南省曲靖市2019-2020学年第二次中考模拟考试地理试卷含解析

云南省曲靖市2019-2020学年第二次中考模拟考试地理试卷一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.区域位置对自然环境影响深远,进而影响人们的生产和生活,据图回答下面小题。
1.对该区域位置的描述不正确的是( )A.深居内陆B.位于北温带中部C.海陆兼备D.位于中纬度地区2.根据地理位置,我们可以推测该区域( )A.气候比较干旱B.地势四周高中部低C.河流均为外流河D.植被四季茂密常青【答案】1.C2.A【解析】【分析】1.读图可知,该地区位于亚洲中部,位于北温带中部中纬度地区。
深居内陆,距海远,故海陆兼备是错误的。
所以不正确的是C。
2.根据深居内陆,距海远,位于中纬度的位置可以推断出,该地区受海洋的影响小,降水稀少,气候比较干旱。
所以选A。
2.下列地点中,位于“北半球”“中纬度”“西半球”的是()A.30°W,40°N B.15°W,40°N C.30°W,29°N D.170°W,40°S【答案】A【解析】【详解】由题目可知,以上四个点中,“30°W,40°N”位于西半球、北半球和中纬度;“15°W,40°N”位于东半球、北半球和中纬度;“30°W,29°N”位于西半球、北半球和低纬度;“170°W,40°S”位于西半球、南半球和中纬度,故选A。
3.大兴安岭——太行山——巫山——雪峰山一线是我国()A.地势第二、三级阶梯的分界线B.湿润区和半湿润区的分界线C.季风区和非季风区的分界线D.人口稀疏区与人口稠密区的分界线【答案】A【解析】【分析】【详解】大兴安岭---太行山---巫山---雪峰山是地势第二、三级阶梯的分界线;秦岭—淮河是湿润区和半湿润区的分界线;季风区和非季风区的分界线是大兴安岭—阴山山脉—贺兰山——巴颜喀拉山脉——冈底斯山脉。
云南省曲靖市2019年高中毕业生(第二次)复习统一检测(文数)(含答案)

第1页曲靖市2019年高中毕业生(第二次)复习统一检测文科数学参考答案一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.D 提示:{}1≠∈=x R x x A 且,⎭⎫⎩⎨⎧≥=21x x B ,则()+∞⎪⎭⎫⎢⎣⎡=,11,21 B A .2.B 提示:i i z -=+=225.3.C2=3=52cos 2440=-=-θ,21cos -=θ,又[]πθ,0∈,所以32πθ=.4.C 提示:x x x f 2)(2-=是偶函数,0≥x 时,x x x f 2)(2-=,由二次函数的图像特征即得选项C 符合.5.A 提示:由题意,22-=-p ,4=p ,x y C 8:2=,)0,2(F ,直线AF 的方程为0643=-+y x ,则原点到直线AF 的距离为56=d ,也就是所求的圆的半径.6.A 提示:由231,21,2a a a 成等差数列,可得q a a q a 11212+=,∴022=--q q ,而0>q ,∴2=q .14a =,∴422162==-+n m ,∴6=+n m ,∴3)82210(61)8210(6182)((6182=⋅+≥++=++=+nm m n n m m n n m n m n m ,当且仅当n m m n 82=即4,2==n m 时,等号成立.第2页7.B提示:若输入的[]1,0∈m ,则输出的[]34-,-∈n ;若输入的[)0,1-∈m ,则输出的(]2,2-∈n ,即输出的[](]2,234-∈ -,-n ,由几何概型的概率公式得事件“输出的[]1,1-∈n ”发生的概率为52412=+=P .8.D提示:根据抽样是间隔相同,且样本间无明显差异,故①应是系统抽样,即①为假命题;“b a >”成立的必要而不充分条件是“b a >+1”即为“b a >+1”是“b a >”的必要而不充分条件,因为由b a >可得b a >+1是成立的,而由b a >+1不能得到b a >成立,故②为真命题;样本数据201921,,,x x x 的标准差为3=s ,则方差为92=s ,于是14,,14,14201921+++x x x 的方差为144916422=⨯=⋅s ,故③为假命题;向量的数量积满足交换律,故④为真命题.∴正确的结论是②④.9.D提示:由三视图可知,其对应的几何体是棱长为2的正方体中挖掉一个底面直径为2,高也为2的圆锥,其体积为正方体的体积与圆锥的体积之差,823==正方体V ,22112ππV =⋅⋅⋅=圆锥,故几何体体积为28π-,即是不规则几何体的体积.10.C 提示:)2sin(2)(πx ωx f -=.由πx <<0得,22πωππx ωπ-<-<-,根据正弦函数图像知,当)(x f 在区间()π,0内无极值点时,2323ππωππ≤-<-且0>ω,解得1250≤<ω.11.A提示:由题意,1622=+b a ,设点())0,0(,0000>>y x y x P ,则⎪⎪⎩⎪⎪⎨⎧=+=⋅⋅1925638120200y x y ,解得⎪⎪⎩⎪⎪⎨⎧==463410500y x ,即)463,4105(P ,代入双曲线1C 的方程,并将2216a b -=代入,化得02503524=+-a a ,则0)25)(10(22=--a a ,又40=<<c a ,解得10=a ,所以双曲线1C 的离心率为5102104==a c .第3页12.B提示:当0>x 时,由0)()(2'>+x xf x f 得,0)]([)()(2'2'2>=+x f x x f x x xf ,令)()(2x f x x g =,则)(x g 在()()+∞∞-,00, 上也为偶函数,且当0>x 时,0)('>x g 总成立,)(x g 在区间),0(+∞上是增函数.4)(2<x f x 可化为)2()(g x g <,则2<x ,又()()+∞∞-∈,00, x ,解得)2,0()0,2( -∈x .二、填空题:本题共4小题,每小题5分,共20分.13.5提示:画出可行域,易知当⎩⎨⎧=-+=-,03,02y x y x 即⎩⎨⎧==21y x 时目标函数541max =+=z .14.2π提示:平移后的函数的解析式为)2sin(2(2sin πϕϕπ-+=⎥⎦⎤⎢⎣⎡+-=x x y ,其图像与函数sin(23y x π=-的图像重合,故Z k k ∈-=-,32πππϕ,即Z k k ∈+=,322ππϕ,因为πφ<<0,所以32πϕ=(此时0=k ).15.π64提示:取BD 的中点E ,连接AE ,CE ,取CE 的三等分点为O ,使得CO =2OE ,则O 为等边△BCD 的中心.由于平面ABD ⊥平面BCD ,且交线为BD ,CE ⊥BD ,所以平面ACE ⊥平面ABD .而48222==+BD AD AB ,所以△ABD 为等腰直角三角形,且E 为△ABD 的外心,所以OA =OB =OD .又OB =OC =OD ,所以O 为四面体ABCD 外接球的球心,其半径4342332=⋅⋅=r .故四面体ABCD 外接球的表面积为ππS 64442=⋅=.16.1提示:由1()1n n n n a a a +-=+得111)1(111+-=+=-++n n n n n a n a n n ,于是n a n a n 1111-=-,则*∈-=N n n a n ,12,11211211+-=++=++n n n n a n ,单调递增,所以23112min 1=⎪⎭⎫ ⎝⎛+≤-+n a at n ,45)45(max =≤t a ,所以整数a 的最大值为1.第4页三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17—21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(本小题满分12分)解:(1)依题意,由正弦定理得:CA B c a b C B sin sin 2sin 2cos cos -=-=于是:CB C B B A cos sin sin cos cos sin 2=-即:()AC B C B C B B A sin sin sin cos cos sin cos sin 2=+=+=又()0sin ,,0>∈A A π,所以21cos =B ,又()π,0∈B ,所以3πB =;……………6分(2)由余弦定理:()212212222cos 22222=-=--+=-+=ac ac ac b ac c a ac b c a B 解得4=ac ,又因为3πB =,所以23sin =B ,所以3341sin 1=⨯⨯==∆B ac S ABC .……………………………………………12分18.(本小题满分12分)解:(1)记六组依次为1,2,3,4,5,6,从这六组数据中随机选取4组数据后,剩余的2组数据所有可能的情况为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15种,其中2组数据都是20日,即都取自第2,4,6组的情况有3种.根据古典概型概率公式,剩余的2组数据都是20日的概率为:51153==P ;………4分(2)①由所选数据得1148121311=+++=x ,24416262925=+++=y ,由参考公式得718114812131124114168261229132511ˆ22222=⨯-+++⨯⨯-⨯+⨯+⨯+⨯=b ,则7301171824ˆˆ-=⨯-=-=x b y a .所以y 关于x 的线性回归方程为730718ˆ-=x y .……………………………………10分②当7=x 时,14796ˆ≈=y ,所以昼夜温差为7C 时,当日就诊人数约为14人.………………………………12分19.(本小题满分12分)(1)证明:连结BD ,设BD 交AC 于O ,连结OM .在菱形ABCD 中,OD AC ⊥,∵PA ⊥平面ABCD ,OD ⊂平面ABCD ,∴OD PA ⊥,又PA AC A = ,PA ,AC ⊂平面PAC ,∴OD ⊥平面PAC ,∵O ,M 分别是AC ,PC 的中点,∴PA OM //,12OM PA =,又PA DE //,12DE PA =,∴DE OM //,且OM DE =,∴四边形OMED 是平行四边形,则EM OD //,∴EM ⊥平面PAC .……………………………………………………………………5分(2)解:由(1)中证明知,EM ⊥平面PAC ,EM 就是三棱锥PAC E -的高,由222PA AB BF DE ====及ABCD 是菱形,60ABC ∠=︒得,32,2==BD AC ,则3==OD EM ,2222121Δ=⋅⋅=⋅⋅=PA AC S PAC ,所以332323131Δ=⋅⋅=⋅⋅=-EM S V PAC PAC E 三棱锥,……………………………9分ACE Δ中,5,2===CE AE AC ,21)5(2212Δ=-⋅⋅=ACE S .设点P 到ACE 平面的距离为d ,即三棱锥ACE P -的高,则由ACE P PAC E V V --=三棱锥三棱锥得,332231=⋅⋅d ,解得3=d ,所以点P 到ACE 平面的距离为3.…………………………………………………12分20.(本小题满分12分)解:(1)由2212122222=+-+++++x y x x y x 可化得22)1()1(2222=+-+++y x y x ,设)0,1(F ,)0,1('-F ,则等式即为22'=+PF PF ,且222'<=FF ,所以曲线C 是椭圆,焦点为',F F (在x 轴上),长半轴长2=a ,半焦距1=c ,短半轴长122=-=c a b ,所以曲线C 的方程为2212x y +=.…………………………………………………5分(2)联立直线l 与曲线C 的方程:⎪⎩⎪⎨⎧=++=1222y x m kx y ,消y 整理得0224)12(222=-+++m kmx x k ,∵直线l 与曲线C 交于不同两点A ,B ,∴08816)22)(12(416Δ222222>+-=-+-=m k m k m k ,得2212m k >+,设l 与C 的交点11(,)A x y ,22(,)B x y ,则124221+-=+k km x x ,12222221+-=k m x x .…………………………………………9分由题意,∴,由120k k +=得0=+m k ,且满足2212m k >+,则)1(:-=x k y l ,所以直线l 经过定点)0,1(.………………………………………………………12分21.(本小题满分12分)解:(1)0,))(1(1)('>++=+++=x a x x a x a x f ,当0≥a 时,0)('>x f ,函数)(x f 在区间),0(+∞上是增函数;当0<a 时,令0)('>x f ,解得a x ->,则函数)(x f 在区间),0(a -上是减函数,在区间),(+∞-a 上是增函数.综上得:当0≥a 时,函数)(x f 的单调递增区间是),0(+∞,无单调递减区间;当0<a 时,函数)(x f 的单调递减区间是),0(a -,单调递增区间是),(+∞-a .……4分证明:(2)由题意x x x a x g 2ln 2)(2-+=,x a x x x x a x g 222222)(2'+-=-+=,因为)(x g 有两个相异极值点21,x x ,(21x x <)所以21,x x 是方程02=+-a x x 的两个实根,140,0,a a ∆=->⎧⎨>⎩解得104a <<,……6分12121212121212122(2)()40(2)(2)y y kx m kx m k k kx x m k x x m x x +++=+=+----+-+-==--12)(44124)2(122224))(2(222222121++-=-+⋅--+-⋅=-+-+k m k m k km k m k m k m x x k m x kx12121,,x x x x a +=⎧⎨=⎩其中104a <<.故令12ln 2)(--=a a a a h ,其中104a <<.故0ln 2)('<=a a h ,)(a h 在1(0,)4上单调递减,232ln )41()(--=>h a h ,即232ln )()(21-->+x g x g ,所以0232ln )()(21>+++x g x g .……………………………………………………12分(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.(本小题满分10分)【选修4—4:坐标系与参数方程】解:(1)由)(2为参数t t y t x ⎩⎨⎧=+=消去参数t ,即得直线1C 的普通方程为20x y --=,……………………………………………2分将θρy θρx sin ,cos ==代入9sin 9cos 2222=+θρθρ,得9922=+y x ,即椭圆2C 的直角坐标方程为1922=+y x ……………………………………………5分(2)由(1)知直线1C :20x y --=与x 轴的交点E 的坐标为()2,0,直线1C 的标准参数方程为:)(22222为参数m m y m x ⎪⎪⎩⎪⎪⎨⎧=+=,………………………………………………7分代入1922=+y x ,化得052252=-+m m ,设点A ,B 对应的参数值分别为21,m m ,则1,5222121-=-=+m m m m ,且21,m m 异号,所以5364)(212212121=-+=-=+=+m m m m m m m m EB EA ……………10分12ln 2)(22)()ln(22ln 22ln 2)()(2121221212222121121--=+--++=-++-+=+a a a x x x x x x x x a x x x a x x x a x g x g ………………9分23.(本小题满分10分)【选修4—5:不等式选讲】解:(1)()23f x x ≥+即23x a x +≥+,平方整理得,()22312290x a x a +-+-≤,由题意知3,1--是二次方程()22312290x a x a +-+-=的两实根,所以21224933a a -⎧=-⎪⎪-⎨-⎪=⎪⎩,解得0a =.…………………………………………………5分(2)()()()2f x x a x a x a a +-≥+--=,因为对任意x R ∈,()22f x x a a a +-≥-恒成立,所以222a a a ≥-.当0a ≥时,222a a a ≥-,解得04a ≤≤;当0a <时,222a a a -≥-,此时满足条件的a 不存在,综上可得,实数a 的取值范围是[]0,4.…………………………………………10分。
云南省曲靖市2019-2020学年第二次中考模拟考试语文试卷含解析

云南省曲靖市2019-2020学年第二次中考模拟考试语文试卷一、选择题1.下列句子中标点符号使用合乎规范的一项是()A.过了十多天,我碰见老王同院的老李。
我问:“老王怎么了,好些没有?”B.做了再说,做了不说,这仅是闻一多先生的一个方面——作为学者的方面。
C.叶圣陶,原名叶绍钧,字圣陶,现代作家、编辑家、教育家,被誉为“优秀的语言艺术家。
”D.我们的校刊“芳草地”里面开辟了《教师寄语》、《校园动态》、《习作选登》、《时事之窗》……等多个栏目。
【答案】B【解析】【详解】A引号里面属于连续问,其中的逗号应为问号。
C引号里面的内容是句子的一部分,句号应在引号外。
D 校刊用书名号,栏目名称用引号,引号或书名号之间不用顿号,省略号与“等”不能同时使用。
2.下列各项中分析有误的一项是()学业重要,分秒必争。
然而,我想说:何不留点时间来“浪费”?(甲)因为“浪费”,你会发现生活原来那么美好。
就拿我来讲吧,只要..一有空,我就.一定会去打篮球①,我有心模仿姚明的动作,让球在众人瞩目中划出漂亮的弧线。
尽管姿势很酷,进球却总与我无练。
(乙)打篮球,不但有助于磨炼意志,而且能增强了我的体质。
把时间留一点“浪费”在自己喜欢的事情上,真好!留点时间来“浪费”。
②但是,这又有什么关系呢!有张有弛,生活才能更快乐。
A.第①处的标点使用有误,应将“,”改为“。
”B.第②句的位置不当,应该放在(乙)处。
C.划线句“打篮球,不但有助于磨炼意志,而且能增强了我的体质。
”这个句子有语病。
D.语段中加点的一对关联词“只要…就…”是递进关系复句。
【答案】D【解析】【详解】D.语段中加点的一对关联词“只要…就…”是条件复句。
二、名句名篇默写3.请根据提示的语境内容,填写出相应的古诗文名句。
①鬓微霜,又何妨!__________,___________?(《江城子•密州出猎》)②臣本布衣,躬耕于南阳,__________,___________。
云南省曲靖市2019-2020学年中考数学二月模拟试卷含解析

云南省曲靖市2019-2020学年中考数学二月模拟试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知方程组2728x y x y +=⎧⎨+=⎩,那么x+y 的值( )A .-1B .1C .0D .52.如图1,点P 从矩形ABCD 的顶点A 出发,沿以的速度匀速运动到点C ,图2是点P 运动时,APD ∆的面积2()y cm 随运动时间()x s 变化而变化的函数关系图象,则矩形ABCD 的面积为( )A .36B .C .32D .3.在平面直角坐标系中,把直线y =x 向左平移一个单位长度后,所得直线的解析式为( ) A .y =x +1 B .y =x -1 C .y =x D .y =x -24.据资料显示,地球的海洋面积约为360000000平方千米,请用科学记数法表示地球海洋面积面积约为多少平方千米( ) A .73610⨯B .83.610⨯C .90.3610⨯D .93.610⨯5.如图,直线 AB 与▱ MNPQ 的四边所在直线分别交于 A 、B 、C 、D ,则图中的相似三角形有( )A .4 对B .5 对C .6 对D .7 对 6.已知反比例函数y=kx的图象在一、三象限,那么直线y=kx ﹣k 不经过第( )象限. A .一B .二C .三D .四7.如图1是一座立交桥的示意图(道路宽度忽略不计),A 为人口,F ,G 为出口,其中直行道为AB ,CG ,EF ,且AB =CG =EF ;弯道为以点O 为圆心的一段弧,且»BC ,»CD,»DE 所对的圆心角均为90°.甲、乙两车由A 口同时驶入立交桥,均以10m/s 的速度行驶,从不同出口驶出,其间两车到点O 的距离y (m )与时间x (s )的对应关系如图2所示.结合题目信息,下列说法错误的是( )A.甲车在立交桥上共行驶8s B.从F口出比从G口出多行驶40m C.甲车从F口出,乙车从G口出D.立交桥总长为150m8.如图,△ABC为等腰直角三角形,∠C=90°,点P为△ABC外一点,CP=2,BP=3,AP的最大值是()A.2+3 B.4 C.5 D.329.观察下列图形,则第n个图形中三角形的个数是()A.2n+2 B.4n+4 C.4n﹣4 D.4n10.用教材中的计算器依次按键如下,显示的结果在数轴上对应点的位置介于()之间.A.B与C B.C与D C.E与F D.A与B11.抛物线y=mx2﹣8x﹣8和x轴有交点,则m的取值范围是()A.m>﹣2 B.m≥﹣2 C.m≥﹣2且m≠0D.m>﹣2且m≠012.下列运算结果正确的是()A.x2+2x2=3x4B.(﹣2x2)3=8x6C.x2•(﹣x3)=﹣x5D.2x2÷x2=x二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数kyx(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为▲ .14.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为_____.15.在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)16.廊桥是我国古老的文化遗产如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是______米精确到1米17.如果两圆的半径之比为32:,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d的取值范围是__________.18.如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,已知AD=2,DB=4,DE=1,则BC=_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A ,B ,C ,D 四个等级.请根据两幅统计图中的信息回答下列问题: (1)本次抽样调查共抽取了多少名学生?(2)求测试结果为C 等级的学生数,并补全条形图;(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D 等级的学生有多少名?(4)若从体能为A 等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.20.(6分)如图,若要在宽AD 为20米的城南大道两边安装路灯,路灯的灯臂BC 长2米,且与灯柱AB 成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO 与灯臂BC 垂直,当灯罩的轴线CO 通过公路路面的中心线时照明效果最好.此时,路灯的灯柱AB 的高应该设计为多少米.(结果保留根号)21.(6分)在平面直角坐标系中,点A (1,0),B (0,2),将直线AB 平移与双曲线(0)k y x x=>在第一象限的图象交于C 、D 两点.(1)如图1,将AOB ∆绕O 逆时针旋转90︒得(EOF E ∆与A 对应,F 与B 对应),在图1中画出旋转后的图形并直接写出E 、F 坐标; (2)若2CD AB =,①如图2,当135OAC ∠=︒时,求k 的值;②如图3,作CM x ⊥轴于点M ,DN y ⊥轴于点N ,直线MN 与双曲线ky x=有唯一公共点时,k 的值为 .22.(8分)如图,一次函数y=﹣x+的图象与反比例函数y=(k >0)的图象交于A ,B 两点,过A 点作x 轴的垂线,垂足为M ,△AOM 面积为1. (1)求反比例函数的解析式;(2)在y 轴上求一点P ,使PA+PB 的值最小,并求出其最小值和P 点坐标.23.(8分)解不等式组:10241x x x +>⎧⎨+≥-⎩,并把解集在数轴上表示出来。
云南省曲靖市2019-2020学年中考第二次适应性考试数学试题含解析

云南省曲靖市2019-2020学年中考第二次适应性考试数学试题一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.如果关于x的分式方程1311 a x xx--=++有负分数解,且关于x 的不等式组2()4,3412a x xxx-≥--⎧⎪⎨+<+⎪⎩的解集为x<-2,那么符合条件的所有整数a的积是()A.-3 B.0 C.3 D.92.若α,β是一元二次方程3x2+2x-9=0的两根,则+βααβ的值是().A.427B.-427C.-5827D .58273.如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是A.B.C.D.4.如图,若AB∥CD,CD∥EF,那么∠BCE=( )A.∠1+∠2 B.∠2-∠1C.180°-∠1+∠2 D.180°-∠2+∠15.反比例函数y=的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是()A.t<B.t>C.t≤D.t≥6.若一次函数y=(2m﹣3)x﹣1+m的图象不经过第三象限,则m的取值范图是()A.1<m<32B.1≤m<32C.1<m≤32D.1≤m≤327.如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有()A.2个B.3个C.4个D.5个8.如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为()A.(1345,0)B.(1345.5,32)C.(1345,32)D.(1345.5,0)9.如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,⊙A的半径为3,那么下列说法正确的是()A.点B、点C都在⊙A内B.点C在⊙A内,点B在⊙A外C.点B在⊙A内,点C在⊙A外D.点B、点C都在⊙A外10.不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是()A.摸出的是3个白球B.摸出的是3个黑球C.摸出的是2个白球、1个黑球D.摸出的是2个黑球、1个白球11.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是()A.①②B.②③C.①③D.②④12.下列4个数:9,227,π,(3)0,其中无理数是()A.9B.227C.πD.(3)0二、填空题:(本大题共6个小题,每小题4分,共24分.)13.因式分解:3x2-6xy+3y2=______.14.如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD 相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为__________.15.为了了解贯彻执行国家提倡的“阳光体育运动”的实施情况,将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图,根据统计图提供的数据,该班50名同学一周参加体育锻炼时间的中位数与众数之和为_____.16.分解因式:4a2-4a+1=______.17.对甲、乙两台机床生产的零件进行抽样测量,其平均数、方差计算结果如下:机床甲:x甲=10,2S甲=0.02;机床乙:x乙=10,2S乙=0.06,由此可知:________(填甲或乙)机床性能好.18.如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=kx的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.该项绿化工程原计划每天完成多少米2?该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?20.(6分)甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y (米)与登山时间x (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:(1)甲登山上升的速度是每分钟 米,乙在A 地时距地面的高度b 为 米;(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y (米)与登山时间x (分)之间的函数关系式.(3)登山多长时间时,甲、乙两人距地面的高度差为50米?21.(6分)如图,在ABC ∆中,D 是BC 的中点,过点D 的直线GF 交AC 于点F ,交AC 的平行线BG 于点G ,ED DF ⊥交AB 于点E ,连接EG 、EF .求证:BG CF =;请你判断BE CF +与EF 的大小关系,并说明理由.22.(8分)计算:﹣16+(﹣12)﹣2﹣32|+2tan60° 23.(8分)如图,△ABC 内接于⊙O ,过点C 作BC 的垂线交⊙O 于D ,点E 在BC 的延长线上,且∠DEC =∠BAC .求证:DE 是⊙O 的切线;若AC ∥DE ,当AB =8,CE =2时,求⊙O 直径的长.24.(10分)如图,大楼AB的高为16m,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为60°,在楼顶B处测得塔顶D处的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高.(3=1.73,结果保留一位小数.)25.(10分)某汽车制造公司计划生产A、B两种新型汽车共40辆投放到市场销售.已知A型汽车每辆成本34万元,售价39万元;B型汽车每辆成本42万元,售价50万元.若该公司对此项计划的投资不低于1536万元,不高于1552万元.请解答下列问题:(1)该公司有哪几种生产方案?(2)该公司按照哪种方案生产汽车,才能在这批汽车全部售出后,所获利润最大,最大利润是多少?(3)在(2)的情况下,公司决定拿出利润的2.5%全部用于生产甲乙两种钢板(两种都生产),甲钢板每吨5000元,乙钢板每吨6000元,共有多少种生产方案?(直接写出答案)26.(12分)从2017年1月1日起,我国驾驶证考试正式实施新的驾考培训模式,新规定C2驾驶证的培训学时为40学时,驾校的学费标准分不同时段,普通时段a元/学时,高峰时段和节假日时段都为b元/学时.(1)小明和小华都在此驾校参加C2驾驶证的培训,下表是小明和小华的培训结算表(培训学时均为40),请你根据提供的信息,计算出a,b的值.学员培训时段培训学时培训总费用小明普通时段206000元高峰时段 5节假日时段15小华普通时段305400元高峰时段 2节假日时段8(2)小陈报名参加了C2驾驶证的培训,并且计划学够全部基本学时,但为了不耽误工作,普通时段的培训学时不会超过其他两个时段总学时的12,若小陈普通时段培训了x学时,培训总费用为y元①求y与x之间的函数关系式,并确定自变量x的取值范围;②小陈如何选择培训时段,才能使得本次培训的总费用最低?27.(12分)“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为度;请补全条形统计图;若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.D【解析】解:2()43412a x x x x ①②-≥--⎧⎪⎨+<+⎪⎩,由①得:x≤2a+4,由②得:x <﹣2,由不等式组的解集为x <﹣2,得到2a+4≥﹣2,即a≥﹣3,分式方程去分母得:a ﹣3x ﹣3=1﹣x ,把a=﹣3代入整式方程得:﹣3x ﹣6=1﹣x ,即72x =-,符合题意;把a=﹣2代入整式方程得:﹣3x ﹣5=1﹣x ,即x=﹣3,不合题意;把a=﹣1代入整式方程得:﹣3x ﹣4=1﹣x ,即52x =-,符合题意; 把a=0代入整式方程得:﹣3x ﹣3=1﹣x ,即x=﹣2,不合题意;把a=1代入整式方程得:﹣3x ﹣2=1﹣x ,即32x =-,符合题意; 把a=2代入整式方程得:﹣3x ﹣1=1﹣x ,即x=1,不合题意;把a=3代入整式方程得:﹣3x=1﹣x ,即12x =-,符合题意; 把a=4代入整式方程得:﹣3x+1=1﹣x ,即x=0,不合题意,∴符合条件的整数a 取值为﹣3;﹣1;1;3,之积为1.故选D .2.C【解析】分析:根据根与系数的关系可得出α+β=-23、αβ=-3,将其代入+βααβ=()22αβαβαβ+-中即可求出结论. 详解:∵α、β是一元二次方程3x 2+2x-9=0的两根,∴α+β=-23,αβ=-3, ∴+βααβ=22βααβ+=()22αβαβαβ+-=()22()23583327--⨯-=--. 故选C .点睛:本题考查了根与系数的关系,牢记两根之和等于-b a 、两根之积等于c a是解题的关键. 3.B【解析】【分析】根据网格的特点求出三角形的三边,再根据相似三角形的判定定理即可求解.【详解】已知给出的三角形的各边AB 、CB 、AC、2、只有选项B 的各边为1B .此题主要考查相似三角形的判定,解题的关键是熟知相似三角形的判定定理.4.D【解析】【分析】先根据AB∥CD得出∠BCD=∠1,再由CD∥EF得出∠DCE=180°-∠2,再把两式相加即可得出结论.【详解】解:∵AB∥CD,∴∠BCD=∠1,∵CD∥EF,∴∠DCE=180°-∠2,∴∠BCE=∠BCD+∠DCE=180°-∠2+∠1.故选:D.【点睛】本题考查的是平行线的判定,用到的知识点为:两直线平行,内错角相等,同旁内角互补.5.B【解析】【分析】将一次函数解析式代入到反比例函数解析式中,整理得出x2﹣2x+1﹣6t=0,又因两函数图象有两个交点,且两交点横坐标的积为负数,根据根的判别式以及根与系数的关系可求解.【详解】由题意可得:﹣x+2=,所以x2﹣2x+1﹣6t=0,∵两函数图象有两个交点,且两交点横坐标的积为负数,∴解不等式组,得t>.故选:B.点睛:此题主要考查了反比例函数与一次函数的交点问题,关键是利用两个函数的解析式构成方程,再利用一元二次方程的根与系数的关系求解.6.B【分析】根据一次函数的性质,根据不等式组即可解决问题;【详解】∵一次函数y=(2m-3)x-1+m的图象不经过第三象限,∴230 10 mm<-⎧⎨-+≥⎩,解得1≤m<32.故选:B.【点睛】本题考查一次函数的图象与系数的关系等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.7.C【解析】【分析】分为三种情况:①AP=OP,②AP=OA,③OA=OP,分别画出即可.【详解】如图,分OP=AP(1点),OA=AP(1点),OA=OP(2点)三种情况讨论.∴以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有4个.故选C.【点睛】本题考查了等腰三角形的判定和坐标与图形的性质,主要考查学生的动手操作能力和理解能力,注意不要漏解.8.B【解析】连接AC,如图所示.∵四边形OABC是菱形,∴OA=AB=BC=OC.∵∠ABC=60°,∴△ABC是等边三角形.∴AC=AB.∴AC=OA.∵OA=1,∴AC=1.画出第5次、第6次、第7次翻转后的图形,如图所示.由图可知:每翻转6次,图形向右平移2.∵3=336×6+1,∴点B1向右平移1322(即336×2)到点B3.∵B1的坐标为(1.5,3),∴B3的坐标为(1.5+1322,3),故选B.点睛:本题是规律题,能正确地寻找规律“每翻转6次,图形向右平移2”是解题的关键.9.D【解析】【分析】先求出AB的长,再求出AC的长,由B、C到A的距离及圆半径的长的关系判断B、C与圆的关系. 【详解】由题意可求出∠A=30°,∴AB=2BC=4, 由勾股定理得22AB BC-3Q3>3,∴点B、点C都在⊙A外.故答案选D.【点睛】本题考查的知识点是点与圆的位置关系,解题的关键是熟练的掌握点与圆的位置关系.10.A【解析】由题意可知,不透明的袋子中总共有2个白球,从袋子中一次摸出3个球都是白球是不可能事件,故选B.11.B【解析】【详解】A、∵四边形ABCD是平行四边形,当①AB=BC时,平行四边形ABCD是菱形,当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;B、∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当AC=BD时,这是矩形的性质,无法得出四边形ABCD 是正方形,故此选项错误,符合题意;C、∵四边形ABCD是平行四边形,当①AB=BC时,平行四边形ABCD是菱形,当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;D、∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.故选C.12.C【解析】9=3,227是无限循环小数,π是无限不循环小数,()031=,所以π是无理数,故选C.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.3(x﹣y)1【解析】试题分析:原式提取3,再利用完全平方公式分解即可,得到3x1﹣6xy+3y1=3(x1﹣1xy+y1)=3(x﹣y)1.考点:提公因式法与公式法的综合运用14.4.1【解析】解:如图所示:∵四边形ABCD是矩形,∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=1,根据题意得:△ABP≌△EBP,∴EP=AP,∠E=∠A=90°,BE=AB=1,在△ODP和△OEG中,,∴△ODP≌△OEG(ASA),∴OP=OG,PD=GE,设AP=EP=x ,则PD=GE=6﹣x ,DG=x ,∴CG=1﹣x ,BG=1﹣(6﹣x )=2+x ,根据勾股定理得:BC 2+CG 2=BG 2,即62+(1﹣x )2=(x+2)2,解得:x=4.1,∴AP=4.1;故答案为4.1.15.17【解析】∵8是出现次数最多的,∴众数是8,∵这组数据从小到大的顺序排列,处于中间位置的两个数都是9,∴中位数是9,所以中位数与众数之和为8+9=17.故答案为17小时.16.2(21)a -【解析】【分析】根据完全平方公式的特点:两项平方项的符号相同,另一项是两底数积的2倍,本题可用完全平方公式分解因式.【详解】解:22441(21)a a a -+=-.故答案为2(21)a -.【点睛】本题考查用完全平方公式法进行因式分解,能用完全平方公式法进行因式分解的式子的特点需熟练掌握.17.甲.【解析】试题分析:根据方差的意义可知,方差越小,稳定性越好,由此即可求出答案.试题解析:因为甲的方差小于乙的方差,甲的稳定性好,所以甲机床的性能好.考点:1.方差;2.算术平均数.18.﹣1【解析】【详解】∵OD=2AD,∴23 ODOA=,∵∠ABO=90°,DC⊥OB,∴AB∥DC,∴△DCO∽△ABO,∴23 DC OC ODAB OB OA===,∴22439 ODCOABSS⎛⎫==⎪⎝⎭VV,∵S四边形ABCD=10,∴S△ODC=8,∴OC×CD=8,OC×CD=1,∴k=﹣1,故答案为﹣1.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(1)2000;(2)2米【解析】【分析】(1)设未知数,根据题目中的的量关系列出方程;(2)可以通过平移,也可以通过面积法,列出方程【详解】解:(1)设该项绿化工程原计划每天完成x米2,根据题意得:4600022000x-﹣46000220001.5x-= 4解得:x=2000,经检验,x=2000是原方程的解;答:该绿化项目原计划每天完成2000平方米;(2)设人行道的宽度为x米,根据题意得,(20﹣3x)(8﹣2x)=56解得:x=2或x=263(不合题意,舍去).答:人行道的宽为2米.20.(1)10;1;(2)15(02)3030(211)x xyx x⎧=⎨-⎩剟剟;(3)4分钟、9分钟或3分钟.【解析】【分析】(1)根据速度=高度÷时间即可算出甲登山上升的速度;根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;(3)当乙未到终点时,找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程,解之即可求出x值;当乙到达终点时,用终点的高度-甲登山全程中y关于x的函数关系式=50,即可得出关于x的一元一次方程,解之可求出x值.综上即可得出结论.【详解】(1)(10-100)÷20=10(米/分钟),b=3÷1×2=1.故答案为:10;1.(2)当0≤x≤2时,y=3x;当x≥2时,y=1+10×3(x-2)=1x-1.当y=1x-1=10时,x=2.∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为15(02)3030(211)x xyx x⎧=⎨-⎩剟剟.(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).当10x+100-(1x-1)=50时,解得:x=4;当1x-1-(10x+100)=50时,解得:x=9;当10-(10x+100)=50时,解得:x=3.答:登山4分钟、9分钟或3分钟时,甲、乙两人距地面的高度差为50米.【点睛】本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系列式计算;(2)根据高度=初始高度+速度×时间找出y关于x的函数关系式;(3)将两函数关系式做差找出关于x的一元一次方程.21.(1)证明见解析;(2)证明见解析.【解析】(1)利用平行线的性质和中点的定义得到,BGD CFD BD CD ∠=∠= ,进而得到三角形全等,从而求证结论;(2)利用中垂线的性质和三角形的三边关系进行判断即可.【详解】证明:(1)∵BG ∥AC∴BGD CFD ∠=∠∵D 是BC 的中点∴BD CD =又∵BDG CDF ∠=∠∴△BDG ≌△CDF∴BG CF =(2)由(1)中△BDG ≌△CDF∴GD=FD,BG=CF又∵ED DF ⊥∴ED 垂直平分DF∴EG=EF∵在△BEG 中,BE+BG>GE,∴BE CF +>EF【点睛】本题考查平行线性质的应用、全等三角形的判定和性质的应用及三角形三边关系,熟练掌握相关知识点是解题关键.22.【解析】【分析】先根据乘方、负指数幂、绝对值、特殊角的三角函数值分别进行计算,然后根据实数的运算法则求得计算结果.【详解】﹣16+(﹣12)﹣2﹣﹣2|+2tan60°=﹣1+4﹣(2,=﹣1+4﹣本题主要考查了实数的综合运算能力,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、二次根式、绝对值等考点的运算法则.23.(1)见解析;(2)⊙O直径的长是45.【解析】【分析】(1)先判断出BD是圆O的直径,再判断出BD⊥DE,即可得出结论;(2)先判断出AC⊥BD,进而求出BC=AB=8,进而判断出△BDC∽△BED,求出BD,即可得出结论.【详解】证明:(1)连接BD,交AC于F,∵DC⊥BE,∴∠BCD=∠DCE=90°,∴BD是⊙O的直径,∴∠DEC+∠CDE=90°,∵∠DEC=∠BAC,∴∠BAC+∠CDE=90°,∵弧BC=弧BC,∴∠BAC=∠BDC,∴∠BDC+∠CDE=90°,∴BD⊥DE,∴DE是⊙O切线;解:(2)∵AC∥DE,BD⊥DE,∴BD⊥AC.∵BD是⊙O直径,∴AF=CF,∴AB=BC=8,∵BD⊥DE,DC⊥BE,∴∠BCD =∠BDE =90°,∠DBC =∠EBD ,∴△BDC ∽△BED , ∴BD BE =BC BD , ∴BD 2=BC•BE =8×10=80,∴BD =45.即⊙O 直径的长是45.【点睛】此题主要考查圆周角定理,垂径定理,相似三角形的判定和性质,切线的判定和性质,第二问中求出BC=8是解本题的关键.24.塔CD 的高度为37.9米【解析】试题分析:首先分析图形,根据题意构造直角三角形.本题涉及两个直角三角形,即Rt △BED 和Rt △DAC ,利用已知角的正切分别计算,可得到一个关于AC 的方程,从而求出DC .试题解析:作BE ⊥CD 于E .可得Rt △BED 和矩形ACEB .则有CE=AB=16,AC=BE .在Rt △BED 中,∠DBE=45°,DE=BE=AC .在Rt △DAC 中,∠DAC=60°,DC=ACtan60°=3AC . ∵16+DE=DC ,∴16+AC=3AC ,解得:AC=83+8=DE .所以塔CD 的高度为(83+24)米≈37.9米,答:塔CD 的高度为37.9米.25.(1)共有三种方案,分别为①A 型号16辆时, B 型号24辆;②A 型号17辆时,B 型号23辆;③A 型号18辆时,B 型号22辆;(2)当16x =时,272W =最大万元;(3)A 型号4辆,B 型号8辆; A 型号10辆,B 型号 3辆两种方案【解析】【分析】(1)设A 型号的轿车为x 辆,可根据题意列出不等式组,根据问题的实际意义推出整数值; (2)根据“利润=售价-成本”列出一次函数的解析式解答;(3)根据(2)中方案设计计算.【详解】(1)设生产A 型号x 辆,则B 型号(40-x )辆1536≤34x+42(40-x)≤1552解得1618x ≤≤,x 可以取值16,17,18共有三种方案,分别为A 型号16辆时,B 型号24辆A 型号17辆时,B 型号23辆A 型号18辆时,B 型号22辆(2)设总利润W 万元则W=()5840x x +-=3320x -+30k =-<Q∴w 随x 的增大而减小当16x =时,272W =最大万元(3)A 型号4辆,B 型号8辆; A 型号10辆,B 型号 3辆两种方案【点睛】本题主要考查了一次函数的应用,以及一元一次不等式组的应用,此题是典型的数学建模问题,要先将实际问题转化为不等式组解应用题.26.(1)120,180;(2)①y=-60x+7200,0≤x≤403;②x=403时,y 有最小值,此时y 最小=-60×403+7200=6400(元).【解析】【分析】(1)根据小明和小华的培训结算表列出关于a 、b 的二元一次方程组,解方程即可求解;(2)①根据培训总费用=普通时段培训费用+高峰时段和节假日时段培训费用列出y 与x 之间的函数关系式,进而确定自变量x 的取值范围;②根据一次函数的性质结合自变量的取值范围即可求解.【详解】(1)由题意,得{20a 20b 600030a 10b 5400+=+=, 解得{a 120b 180==,故a ,b 的值分别是120,180;(2)①由题意,得y=120x+180(40-x ),化简得y=-60x+7200, ∵普通时段的培训学时不会超过其他两个时段总学时的12, ∴x≤12(40-x ), 解得x≤403, 又x≥0,∴0≤x≤403; ②∵y=-60x+7200,k=-60<0,∴y 随x 的增大而减小,∴x 取最大值时,y 有最小值,∵0≤x≤403; ∴x=403时,y 有最小值,此时y 最小=-60×403+7200=6400(元). 【点睛】本题考查了一次函数的应用,二元一次方程组的应用,理解题意得出数量关系是解题的关键. 27. (1) 60,90;(2)见解析;(3) 300人【解析】【分析】(1)由了解很少的有30人,占50%,可求得接受问卷调查的学生数,继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角;(2)由(1)可求得了解的人数,继而补全条形统计图;(3)利用样本估计总体的方法,即可求得答案.【详解】解:(1)∵了解很少的有30人,占50%,∴接受问卷调查的学生共有:30÷50%=60(人);∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:1560×360°=90°;故答案为60,90;(2)60﹣15﹣30﹣10=5;补全条形统计图得:(3)根据题意得:900×15560=300(人), 则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人.【点睛】本题考查了条形统计图与扇形统计图,解题的关键是熟练的掌握条形统计图与扇形统计图的相关知识点.。
云南省曲靖市2019-2020学年中考数学第二次调研试卷含解析

云南省曲靖市2019-2020学年中考数学第二次调研试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.对于一组统计数据1,1,6,5,1.下列说法错误的是( ) A .众数是1B .平均数是4C .方差是1.6D .中位数是62.下列所给函数中,y 随x 的增大而减小的是( ) A .y=﹣x ﹣1 B .y=2x 2(x≥0) C .2y x=D .y=x+13.已知a m =2,a n =3,则a 3m+2n 的值是( ) A .24B .36C .72D .64.若2(3)3b b -=-,则( ) A .3b >B .3b <C .3b ≥D .3b ≤5.如图所示的四张扑克牌背面完全相同,洗匀后背面朝上,则从中任意翻开一张,牌面数字是 3 的倍数的概率为( )A .14B .13C .12D .346.钟鼎文是我国古代的一种文字,是铸刻在殷周青铜器上的铭文,下列钟鼎文中,不是轴对称图形的是( )A .B .C .D .7.2016的相反数是( ) A .12016-B .12016C .2016-D .20168.如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC ,BN ⊥AN 于点N ,且AB=10,BC=15,MN=3,则AC 的长是( )A .12B .14C .16D .189.一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是()A.12B.14C.16D.11210.如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC 的度数是()A.85°B.105°C.125°D.160°11.已知矩形ABCD中,AB=3,BC=4,E为BC的中点,以点B为圆心,BA的长为半径画圆,交BC 于点F,再以点C为圆心,CE的长为半径画圆,交CD于点G,则S1-S2=()A.6 B.1364π+C.12﹣94πD.12﹣134π12.小王抛一枚质地均匀的硬币,连续抛4次,硬币均正面朝上落地,如果他再抛第5次,那么硬币正面朝上的概率为( )A.1 B.12C.14D.15二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,四边形ABCD中,∠D=∠B=90°,AB=BC,CD=4,AC=8,设Q、R分别是AB、AD上的动点,则△CQR 的周长的最小值为_________ .14.如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为_____.15.七巧板是我国祖先创造的一种智力玩具,它来源于勾股法,如图①整幅七巧板是由正方形ABCD 分割成七小块(其中:五块等腰直角三角形、一块正方形和一块平行四边形)组成,如图②是由七巧板拼成的一个梯形,若正方形ABCD 的边长为12cm ,则梯形MNGH 的周长是 cm (结果保留根号).16.如图,已知抛物线和x 轴交于两点A 、B ,和y 轴交于点C ,已知A 、B 两点的横坐标分别为﹣1,4,△ABC 是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为_____.17.如图,把一个面积为1的正方形分成两个面积为12的长方形,再把其中一个面积为12的长方形分成两个面积为14的正方形,再把其中一个面积为14的正方形分成两个面积为18的长方形,如此进行下去……,试用图形揭示的规律计算:111111248163264+++++11128256++=__________.18.分式方程32xx 2--+22x-=1的解为________. 三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤. 19.(6分)庞亮和李强相约周六去登山,庞亮从北坡山脚C 处出发,以24米/分钟的速度攀登,同时,李强从南坡山脚B 处出发.如图,已知小山北坡的坡度,山坡长为240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A ?(将山路AB 、AC 看成线段,结果保留根号)20.(6分)一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.甲,乙两公司单独完成此项工程,各需多少天?若让一个公司单独完成这项工程,哪个公司的施工费较少?21.(6分)综合与实践﹣猜想、证明与拓广问题情境:数学课上同学们探究正方形边上的动点引发的有关问题,如图1,正方形ABCD中,点E是BC边上的一点,点D关于直线AE的对称点为点F,直线DF交AB于点H,直线FB与直线AE交于点G,连接DG,CG.猜想证明(1)当图1中的点E与点B重合时得到图2,此时点G也与点B重合,点H与点A重合.同学们发现线段GF与GD有确定的数量关系和位置关系,其结论为:;(2)希望小组的同学发现,图1中的点E在边BC上运动时,(1)中结论始终成立,为证明这两个结论,同学们展开了讨论:小敏:根据轴对称的性质,很容易得到“GF与GD的数量关系”…小丽:连接AF,图中出现新的等腰三角形,如△AFB,…小凯:不妨设图中不断变化的角∠BAF的度数为n,并设法用n表示图中的一些角,可证明结论.请你参考同学们的思路,完成证明;(3)创新小组的同学在图1中,发现线段CG∥DF,请你说明理由;联系拓广:(4)如图3若将题中的“正方形ABCD”变为“菱形ABCD“,∠ABC=α,其余条件不变,请探究∠DFG 的度数,并直接写出结果(用含α的式子表示).22.(8分)地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识,提高学生生态环境保护意识,举办了“我参与,我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:初一:76 88 93 65 78 94 89 68 95 5089 88 89 89 77 94 87 88 92 91初二:74 97 96 89 98 74 69 76 72 7899 72 97 76 99 74 99 73 98 74(1)根据上面的数据,将下列表格补充完整;整理、描述数据:成绩x人数班级5059x≤≤6069x≤≤7079x≤≤8089x≤≤90100x≤≤初一 1 2 3 6初二0 1 10 1 8(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下为不合格)分析数据:年级平均数中位数众数初一84 88.5初二84.2 74(2)得出结论:你认为哪个年级掌握生态环保知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性). 23.(8分)如图,AD是△ABC的中线,过点C作直线CF∥AD.(问题)如图①,过点D作直线DG∥AB交直线CF于点E,连结AE,求证:AB=DE.(探究)如图②,在线段AD上任取一点P,过点P作直线PG∥AB交直线CF于点E,连结AE、BP,探究四边形ABPE是哪类特殊四边形并加以证明.(应用)在探究的条件下,设PE交AC于点M.若点P是AD的中点,且△APM的面积为1,直接写出四边形ABPE的面积.24.(10分)瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目.某公司生产了一种纪念花灯,每件纪念花灯制造成本为18元.设销售单价x(元),每日销售量y(件)每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:(元)19 20 21 30(件)62 60 58 40(1)根据表中数据的规律,分别写出毎日销售量y(件),每日的利润w(元)关于销售单价x(元)之间的函数表达式.(利润=(销售单价﹣成本单价)×销售件数).当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?根据物价局规定,这种纪念品的销售单价不得高于32元,如果公司要获得每日不低于350元的利润,那么制造这种纪念花灯每日的最低制造成本需要多少元?25.(10分)(1)(问题发现)小明遇到这样一个问题:如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.(1)小明发现,过点D作DF//AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系:;(2)(类比探究)如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件不变),试猜想AD与DE之间的数量关系,并证明你的结论.(3)(拓展应用)当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,请直接写出△ABC与△ADE的面积之比.26.(12分)如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(32,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.27.(12分)先化简(31a+-a+1)÷2441a aa-++,并从0,-1,2中选一个合适的数作为a的值代入求值.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.D【解析】【分析】根据中位数、众数、方差等的概念计算即可得解.【详解】A、这组数据中1都出现了1次,出现的次数最多,所以这组数据的众数为1,此选项正确;B、由平均数公式求得这组数据的平均数为4,故此选项正确;C、S2=15[(1﹣4)2+(1﹣4)2+(6﹣4)2+(5﹣4)2+(1﹣4)2]=1.6,故此选项正确;D、将这组数据按从大到校的顺序排列,第1个数是1,故中位数为1,故此选项错误;故选D.考点:1.众数;2.平均数;1.方差;4.中位数.2.A【解析】【分析】根据二次函数的性质、一次函数的性质及反比例函数的性质判断出函数符合y随x的增大而减小的选项.【详解】解:A.此函数为一次函数,y随x的增大而减小,正确;B.此函数为二次函数,当x<0时,y随x的增大而减小,错误;C.此函数为反比例函数,在每个象限,y随x的增大而减小,错误;D.此函数为一次函数,y随x的增大而增大,错误.故选A.【点睛】本题考查了二次函数、一次函数、反比例函数的性质,掌握函数的增减性是解决问题的关键.3.C【解析】试题解析:∵a m=2,a n=3,∴a 3m+2n =a 3m •a 2n =(a m )3•(a n )2 =23×32 =8×9 =1. 故选C. 4.D 【解析】 【分析】等式左边为非负数,说明右边3b 0-≥,由此可得b 的取值范围. 【详解】解:3b =-Q,3b 0∴-≥,解得b 3.≤故选D . 【点睛】()0a 0≥≥()a a 0=≥.5.C 【解析】 【分析】根据题意确定所有情况的数目,再确定符合条件的数目,根据概率的计算公式即可. 【详解】解:由题意可知,共有4种情况,其中是 3 的倍数的有6和9, ∴是 3 的倍数的概率2142=, 故答案为:C . 【点睛】本题考查了概率的计算,解题的关键是熟知概率的计算公式. 6.A 【解析】根据轴对称图形的概念求解.解:根据轴对称图形的概念可知:B ,C ,D 是轴对称图形,A 不是轴对称图形, 故选A .“点睛”本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.7.C【解析】根据相反数的定义“只有符号不同的两个数互为相反数”可知:2016的相反数是-2016.故选C.8.C【解析】延长线段BN交AC于E.∵AN平分∠BAC,∴∠BAN=∠EAN.在△ABN与△AEN中,∵∠BAN=∠EAN,AN=AN,∠ANB=∠ANE=90∘,∴△ABN≌△AEN(ASA),∴AE=AB=10,BN=NE.又∵M是△ABC的边BC的中点,∴CE=2MN=2×3=6,∴AC=AE+CE=10+6=16.故选C.9.C【解析】【分析】画树状图求出共有12种等可能结果,符合题意得有2种,从而求解.【详解】解:画树状图得:∵共有12种等可能的结果,两次都摸到白球的有2种情况,∴两次都摸到白球的概率是:21 126.故答案为C.【点睛】本题考查画树状图求概率,掌握树状图的画法准确求出所有的等可能结果及符合题意的结果是本题的解题关键.10.C【解析】【分析】首先求得AB与正东方向的夹角的度数,即可求解.【详解】根据题意得:∠BAC=(90°﹣70°)+15°+90°=125°,故选:C.【点睛】本题考查了方向角,正确理解方向角的定义是关键.11.D【解析】【分析】根据题意可得到CE=2,然后根据S1﹣S2 =S矩形ABCD-S扇形ABF-S扇形GCE,即可得到答案【详解】解:∵BC=4,E为BC的中点,∴CE=2,∴S1﹣S2=3×4﹣229039021312 3603604πππ⨯⨯-=-g g,故选D.【点睛】此题考查扇形面积的计算,矩形的性质及面积的计算. 12.B【解析】【分析】直接利用概率的意义分析得出答案.【详解】解:因为一枚质地均匀的硬币只有正反两面,所以不管抛多少次,硬币正面朝上的概率都是12,故选B.【点睛】此题主要考查了概率的意义,明确概率的意义是解答的关键.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.4【解析】【分析】作C关于AB的对称点G,关于AD的对称点F,可得三角形CQR的周长=CQ+QR+CR=GQ+QR +RF≥GF.根据圆周角定理可得∠CDB=∠CAB=45°,∠CBD=∠CAD=30°,由于GF=2BD,在三角形CBD中,作CH⊥BD于H,可求BD的长,从而求出△CQR的周长的最小值.【详解】解:作C关于AB的对称点G,关于AD的对称点F,则三角形CQR的周长=CQ+QR+CR=GQ+QR +RF=GF,在Rt△ADC中,∵sin∠DAC=12 CDAC=,∴∠DAC=30°,∵BA=BC,∠ABC=90°,∴∠BAC=∠BCA=45°,∵∠ADC=∠ABC=90°,∴A,B,C,D四点共圆,∴∠CDB=∠CAB=45°,∠CBD=∠CAD=30°在三角形CBD中,作CH⊥BD于H,BD=DH+BH=4×cos45°+42cos30°=2226∵CD=DF,CB=BG,∴GF=2BD=4246,△CQR的周长的最小值为426.【点睛】本题考查了轴对称问题,关键是根据轴对称的性质和两点之间线段最短解答.14.25【解析】试题解析:由题意»10DB CD BC=+=»11·1052522ABD S BD AB =⨯=⨯⨯=扇形15.【解析】【分析】仔细观察梯形从而发现其各边与原正方形各边之间的关系,则不难求得梯形的周长.【详解】解:观察图形得MH=GN=AD=12,HG=12AC , AD=DC=12,,.梯形MNGH 的周长.故答案为.【点睛】此题主要考查学生对等腰梯形的性质及正方形的性质的运用及观察分析图形的能力.16.(32 ,258) 【解析】【分析】连接AC ,根据题意易证△AOC ∽△COB ,则AO OC OC OB=,求得OC=2,即点C 的坐标为(0,2),可设抛物线解析式为y=a (x+1)(x ﹣4),然后将C 点坐标代入求解,最后将解析式化为顶点式即可.【详解】解:连接AC ,∵A 、B 两点的横坐标分别为﹣1,4,∴OA=1,OB=4,∵∠ACB=90°,∴∠CAB+∠ABC=90°,∵CO ⊥AB ,∴∠ABC+∠BCO=90°,∴∠CAB=∠BCO ,又∵∠AOC=∠BOC=90°,∴△AOC ∽△COB ,∴AO OC OC OB =, 即1OC =4OC , 解得OC=2,∴点C 的坐标为(0,2),∵A 、B 两点的横坐标分别为﹣1,4,∴设抛物线解析式为y=a (x+1)(x ﹣4),把点C 的坐标代入得,a (0+1)(0﹣4)=2,解得a=﹣12, ∴y=﹣12(x+1)(x ﹣4)=﹣12(x 2﹣3x ﹣4)=﹣12(x ﹣32)2+258, ∴此抛物线顶点的坐标为(32 ,258). 故答案为:(32 ,258).【点睛】本题主要考查相似三角形的判定与性质,抛物线的顶点式,解此题的关键在于熟练掌握其知识点,利用相似三角形的性质求得关键点的坐标.17.8112- 【解析】【分析】结合图形发现计算方法:11111=1-+=1-22244; ,即计算其面积和的时候,只需让总面积减去剩下的面积. 【详解】 解:原式=12551-=256256=8112- 故答案为:8112- 【点睛】此题注意结合图形的面积找到计算的方法:其中的面积和等于总面积减去剩下的面积.18.x 1=【解析】【分析】根据解分式方程的步骤,即可解答.【详解】方程两边都乘以x 2-,得:32x 2x 2--=-,解得:x 1=,检验:当x 1=时,x 21210-=-=-≠,所以分式方程的解为x 1=,故答案为x 1=.【点睛】考查了解分式方程,()1解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解().2解分式方程一定注意要验根.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.李强以122米/分钟的速度攀登才能和庞亮同时到达山顶A【解析】过点A 作AD ⊥BC 于点D ,在Rt △ADC 中,由得tanC=∴∠C=30°∴AD=AC=×240=120(米)在Rt △ABD 中,∠B=45°∴AB =AD =120(米) 120÷(240÷24)=120÷10=12(米/分钟) 答:李强以12米/分钟的速度攀登才能和庞亮同时到达山顶A20.解:(1)设甲公司单独完成此项工程需x 天,则乙公司单独完成此项工程需1.5x 天.根据题意,得111x 1.5x 12+=, 解得x=1.经检验,x=1是方程的解且符合题意.1.5 x=2.∴甲,乙两公司单独完成此项工程,各需1天,2天.(2)设甲公司每天的施工费为y 元,则乙公司每天的施工费为(y ﹣1500)元,根据题意得12(y+y ﹣1500)=10100解得y=5000,甲公司单独完成此项工程所需的施工费:1×5000=100000(元);乙公司单独完成此项工程所需的施工费:2×(5000﹣1500)=105000(元);∴让一个公司单独完成这项工程,甲公司的施工费较少.【解析】(1)设甲公司单独完成此项工程需x 天,则乙工程公司单独完成需1.5x 天,根据合作12天完成列出方程求解即可.(2)分别求得两个公司施工所需费用后比较即可得到结论.21. (1) GF=GD ,GF ⊥GD;(2)见解析;(3)见解析;(4) 90°﹣2 . 【解析】【分析】(1)根据四边形ABCD 是正方形可得∠ABD=∠ADB=45°,∠BAD=90°,点D 关于直线AE 的对称点为点F ,即可证明出∠DBF=90°,故GF ⊥GD ,再根据∠F=∠ADB ,即可证明GF=GD ;(2)连接AF ,证明∠AFG=∠ADG ,再根据四边形ABCD 是正方形,得出AB=AD ,∠BAD=90°,设∠BAF=n ,∠FAD=90°+n ,可得出∠FGD=360°﹣∠FAD ﹣∠AFG ﹣∠ADG=360°﹣(90°+n )﹣(180°﹣n )=90°,故GF ⊥GD ;(3)连接BD ,由(2)知,FG=DG ,FG ⊥DG ,再分别求出∠GFD 与∠DBC 的角度,再根据三角函数的性质可证明出△BDF ∽△CDG ,故∠DGC=∠FDG ,则CG ∥DF ;(4)连接AF ,BD ,根据题意可证得∠DAM=90°﹣∠2=90°﹣∠1,∠DAF=2∠DAM=180°﹣2∠1,再根据菱形的性质可得∠ADB=∠ABD=12α,故∠AFB+∠DBF+∠ADB+∠DAF=(∠DFG+∠1)+(∠DFG+∠1+12α)+12α+(180°﹣2∠1)=360°,2∠DFG+2∠1+α﹣2∠1=180°,即可求出∠DFG . 【详解】解:(1)GF=GD ,GF ⊥GD ,理由:∵四边形ABCD 是正方形,∴∠ABD=∠ADB=45°,∠BAD=90°,∵点D 关于直线AE 的对称点为点F ,∠BAD=∠BAF=90°,∴∠F=∠ADB=45°,∠ABF=∠ABD=45°,∴∠DBF=90°,∴GF ⊥GD ,∵∠BAD=∠BAF=90°,∴点F ,A ,D 在同一条线上,∵∠F=∠ADB ,∴GF=GD,故答案为GF=GD,GF⊥GD;(2)连接AF,∵点D关于直线AE的对称点为点F,∴直线AE是线段DF的垂直平分线,∴AF=AD,GF=GD,∴∠1=∠2,∠3=∠FDG,∴∠1+∠3=∠2+∠FDG,∴∠AFG=∠ADG,∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,设∠BAF=n,∴∠FAD=90°+n,∵AF=AD=AB,∴∠FAD=∠ABF,∴∠AFB+∠ABF=180°﹣n,∴∠AFB+∠ADG=180°﹣n,∴∠FGD=360°﹣∠FAD﹣∠AFG﹣∠ADG=360°﹣(90°+n)﹣(180°﹣n)=90°,∴GF⊥DG,(3)如图2,连接BD,由(2)知,FG=DG,FG⊥DG,∴∠GFD=∠GD F=12(180°﹣∠FGD)=45°,∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∴∠BDC=∠DBC=12(180°﹣∠BCD)=45°,∴∠FDG=∠BDC,∴∠FDG﹣∠BDG=∠BDC﹣∠BDG,∴∠FDB=∠GDC,在Rt△BDC中,sin∠DFG=DGDF=sin45°=22,在Rt△BDC中,sin∠DBC=DCDB=sin45°=22,∴DG DC DF DB=,∴DG DF DC DB=,∴△BDF ∽△CDG ,∵∠FDB=∠GDC ,∴∠DGC=∠DFG=45°,∴∠DGC=∠FDG ,∴CG ∥DF ;(4)90°﹣2α,理由:如图3,连接AF ,BD , ∵点D 与点F 关于AE 对称,∴AE 是线段DF 的垂直平分线,∴AD=AF ,∠1=∠2,∠AMD=90°,∠DAM=∠FAM ,∴∠DAM=90°﹣∠2=90°﹣∠1,∴∠DAF=2∠DAM=180°﹣2∠1,∵四边形ABCD 是菱形,∴AB=AD ,∴∠AFB=∠ABF=∠DFG+∠1,∵BD 是菱形的对角线,∴∠ADB=∠ABD=12α, 在四边形ADBF 中,∠AFB+∠DBF+∠ADB+∠DAF=(∠DFG+∠1)+(∠DFG+∠1+12α)+α+(180°﹣2∠1)=360°∴2∠DFG+2∠1+α﹣2∠1=180°,∴∠DFG=90°﹣2α.【点睛】本题考查了正方形、菱形、相似三角形的性质,解题的根据是熟练的掌握正方形、菱形、相似三角形的性质.22.(1)1,2,19;(2)初一年级掌握生态环保知识水平较好.【解析】【分析】(1)根据初一、初二同学的测试成绩以及众数与中位数的定义即可完成表格;(2)根据平均数、众数、中位数的统计意义回答.【详解】(1)补全表格如下:整理、描述数据:初一成绩x满足10≤x≤19的有:11 19 19 11 19 19 17 11,共1个.故答案为:1.分析数据:在76 11 93 65 71 94 19 61 95 50 19 11 19 19 2 94 17 11 92 91中,19出现的次数最多,故众数为19;把初二的抽查成绩从小到大排列为:69 72 72 73 74 74 74 74 76 76 71 19 96 97 97 91 91 99 99 99,第10个数为76,第11个数为71,故中位数为:(76+71)÷2=2.故答案为:19,2.(2)初一年级掌握生态环保知识水平较好.因为两个年级的平均数相差不大,但是初一年级同学的中位数是11.5,众数是19,初二年级同学的中位数是2,众数是74,即初一年级同学的中位数与众数明显高于初二年级同学的成绩,所以初一年级掌握生态环保知识水平较好.【点睛】本题考查了频数(率)分布表,众数、中位数以及平均数.掌握众数、中位数以及平均数的定义是解题的关键.23.【问题】:详见解析;【探究】:四边形ABPE是平行四边形,理由详见解析;【应用】:8.【解析】【分析】(1)先根据平行线的性质和等量代换得出∠1=∠3,再利用中线性质得到BD =DC ,证明△ABD ≌△EDC ,从而证明AB =DE (2)方法一:过点D 作DN ∥PE 交直线CF 于点N ,由平行线性质得出四边形PDNE 是平行四边形,从而得到四边形ABPE 是平行四边形.方法二: 延长BP 交直线CF 于点N ,根据平行线的性质结合等量代换证明△ABP ≌△EPN ,从而证明四边形ABPE 是平行四边形(3)延长BP 交CF 于H ,根据平行四边形的性质结合三角形的面积公式求解即可.【详解】证明:如图①12,42313DG ABB CF AD∴∠=∠∠=∠∴∠=∠∴∠=∠Q Q ‖‖AD Q 是ABC V 的中线,BD DC ∴=,ABD EDC V V ≌,∴ AB DE ∴=.(或证明四边形ABDE 是平行四边形,从而得到AB DE =.)【探究】四边形ABPE 是平行四边形.方法一:如图②,证明:过点D 作DN PE P 交直线CF 于点N ,CF AD Q P ,∴四边形PDNE 是平行四边形,PE DN ∴=,∵由问题结论可得 AB DN =,PE AB =,∴ ∴四边形ABPE 是平行四边形. 方法二:如图③,证明:延长BP 交直线CF 于点N , PG AB Q P ,1254=,=,∠∠∠∠∴ CF AD Q P ,23∠∠∴=,13∠∠∴=,∵AD 是ABC V 的中线,CF AD P ,BP PN ∴=,ABP EPN V V ≌,∴ AB PE ∴=,∴四边形ABPE 是平行四边形.【应用】如图④,延长BP 交CF 于H .由上面可知,四边形ABPE 是平行四边形, AE BH ∴P ,PA EH ∴P ,∴四边形APHE是平行四边形,PA EH∴=,BD DC DP CHQ P=,,BP PH∴=,CH2PD∴=,AP PDQ=,EC3PA∴=,PA ECQ P,PM PA1EM EC3∴==,S AEM3S APM3∴V V==,S ABP S APE4∴V V==,S ABPE8∴平行四边形=.【点睛】此题重点考查学生对平行线性质,平行四边形性质的综合应用能力,熟练掌握平行线的性质是解题的关键. 24.(1)y=﹣2x+100,w=﹣2x2+136x﹣1800;(2)当销售单价为34元时,每日能获得最大利润,最大利润是1元;(3)制造这种纪念花灯每日的最低制造成本需要648元.【解析】【分析】(1)观察表中数据,发现y与x之间存在一次函数关系,设y=kx+b.列方程组得到y关于x的函数表达式y=﹣2x+100,根据题意得到w=﹣2x2+136x﹣1800;(2)把w=﹣2x2+136x﹣1800配方得到w=﹣2(x﹣34)2+1.根据二次函数的性质即可得到结论;(3)根据题意列方程即可得到即可.【详解】解:(1)观察表中数据,发现y与x之间存在一次函数关系,设y=kx+b.则62196020k bk b=+⎧⎨=+⎩,解得k2b100=-⎧⎨=⎩,∴y=﹣2x+100,∴y关于x的函数表达式y=﹣2x+100,∴w=(x﹣18)•y=(x﹣18)(﹣2x+100)∴w=﹣2x2+136x﹣1800;(2)∵w=﹣2x2+136x﹣1800=﹣2(x﹣34)2+1.∴当销售单价为34元时,∴每日能获得最大利润1元;(3)当w=350时,350=﹣2x2+136x﹣1800,解得x=25或43,由题意可得25≤x≤32,则当x=32时,18(﹣2x+100)=648,∴制造这种纪念花灯每日的最低制造成本需要648元.【点睛】此题主要考查了二次函数的应用,根据已知得出函数关系式.25.(1)AD=DE;(2)AD=DE,证明见解析;(3)13.【解析】试题分析:本题难度中等.主要考查学生对探究例子中的信息进行归纳总结.并能够结合三角形的性质是解题关键.试题解析:(10分)(1)AD=DE.(2)AD=DE.证明:如图2,过点D作DF//AC,交AC于点F,∵△ABC是等边三角形,∴AB=BC,∠B=∠ACB=∠ABC=60°.又∵DF//AC,∴∠BDF=∠BFD=60°∴△BDF是等边三角形,BF=BD,∠BFD=60°,∴AF=CD,∠AFD=120°.∵EC是外角的平分线,∠DCE=120°=∠AFD.∵∠ADC是△ABD的外角,∴∠ADC=∠B+∠FAD=60°+∠FAD.∵∠ADC=∠ADE+∠EDC=60°+∠EDC,∴∠FAD=∠EDC.∴△AFD≌△DCE(ASA),∴AD=DE;(3)13.考点:1.等边三角形探究题;2.全等三角形的判定与性质;3.等边三角形的判定与性质. 26.(1)y=2x 2﹣3x ;(2)C (1,﹣1);(3)(4564,316)或(﹣316,4564). 【解析】【分析】(1)由直线解析式可求得B 点坐标,由A 、B 坐标,利用待定系数法可求得抛物线的表达式;(2)过C 作CD ∥y 轴,交x 轴于点E ,交OB 于点D ,过B 作BF ⊥CD 于点F ,可设出C 点坐标,利用C 点坐标可表示出CD 的长,从而可表示出△BOC 的面积,由条件可得到关于C 点坐标的方程,可求得C 点坐标;(3)设MB 交y 轴于点N ,则可证得△ABO ≌△NBO ,可求得N 点坐标,可求得直线BN 的解析式,联立直线BM 与抛物线解析式可求得M 点坐标,过M 作MG ⊥y 轴于点G ,由B 、C 的坐标可求得OB 和OC 的长,由相似三角形的性质可求得OM OP 的值,当点P 在第一象限内时,过P 作PH ⊥x 轴于点H ,由条件可证得△MOG ∽△POH ,由OM MG OG OP PH OH==的值,可求得PH 和OH ,可求得P 点坐标;当P 点在第三象限时,同理可求得P 点坐标.【详解】(1)∵B (2,t )在直线y=x 上,∴t=2,∴B (2,2),把A 、B 两点坐标代入抛物线解析式可得:42293042a b a b +=⎧⎪⎨+=⎪⎩,解得:23a b =⎧⎨=-⎩, ∴抛物线解析式为223y x x =-;(2)如图1,过C 作CD ∥y 轴,交x 轴于点E ,交OB 于点D ,过B 作BF ⊥CD 于点F ,∵点C 是抛物线上第四象限的点,∴可设C (t ,2t 2﹣3t ),则E (t ,0),D (t ,t ),∴OE=t ,BF=2﹣t ,CD=t ﹣(2t 2﹣3t )=﹣2t 2+4t ,∴S △OBC =S △CDO +S △CDB =12CD•OE+12CD•BF=12(﹣2t 2+4t )(t+2﹣t )=﹣2t 2+4t , ∵△OBC 的面积为2,∴﹣2t 2+4t=2,解得t 1=t 2=1,∴C (1,﹣1);(3)存在.设MB 交y 轴于点N ,如图2,∵B (2,2),∴∠AOB=∠NOB=45°,在△AOB 和△NOB 中,∵∠AOB=∠NOB ,OB=OB ,∠ABO=∠NBO ,∴△AOB ≌△NOB (ASA ),∴ON=OA=32, ∴N (0,32), ∴可设直线BN 解析式为y=kx+32,把B 点坐标代入可得2=2k+32,解得k=14, ∴直线BN 的解析式为1342y x =+,联立直线BN 和抛物线解析式可得:2134223y x y x x ⎧=+⎪⎨⎪=-⎩,解得:22x y =⎧⎨=⎩或384532x y ⎧=-⎪⎪⎨⎪=⎪⎩, ∴M (38-,4532), ∵C (1,﹣1),∴∠COA=∠AOB=45°,且B (2,2),∴OB=222,∵△POC ∽△MOB , ∴2OM OB OP OC==,∠POC=∠BOM ,当点P 在第一象限时,如图3,过M 作MG ⊥y 轴于点G ,过P 作PH ⊥x 轴于点H ,如图3∵∠COA=∠BOG=45°,∴∠MOG=∠POH ,且∠PHO=∠MGO ,∴△MOG ∽△POH , ∴2OM MG OG OP PH OH === ∵M (38-,4532), ∴MG=38,OG=4532, ∴PH=12MG=316,OH=12OG=4564, ∴P (4564,316); 当点P 在第三象限时,如图4,过M 作MG ⊥y 轴于点G ,过P 作PH ⊥y 轴于点H ,同理可求得PH=12MG=316,OH=12OG=4564, ∴P (﹣316,4564); 综上可知:存在满足条件的点P ,其坐标为(4564,316)或(﹣316,4564).【点睛】本题为二次函数的综合应用,涉及待定系数法、三角形的面积、二次函数的性质、全等三角形的判定和性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中用C 点坐标表示出△BOC 的面积是解题的关键,在(3)中确定出点P 的位置,构造相似三角形是解题的关键,注意分两种情况.27.1.【解析】试题分析:首先把括号的分式通分化简,后面的分式的分子分解因式,然后约分化简,接着计算分式的乘法,最后代入数值计算即可求解.试题解析:原式=223111(2)a aa a-++⨯+-=2(2)(2)11(2)a a aa a-+-+⨯+-=22aa+--;当a=0时,原式=1.考点:分式的化简求值.。
云南省曲靖市2019-2020学年中考第二次模拟数学试题含解析
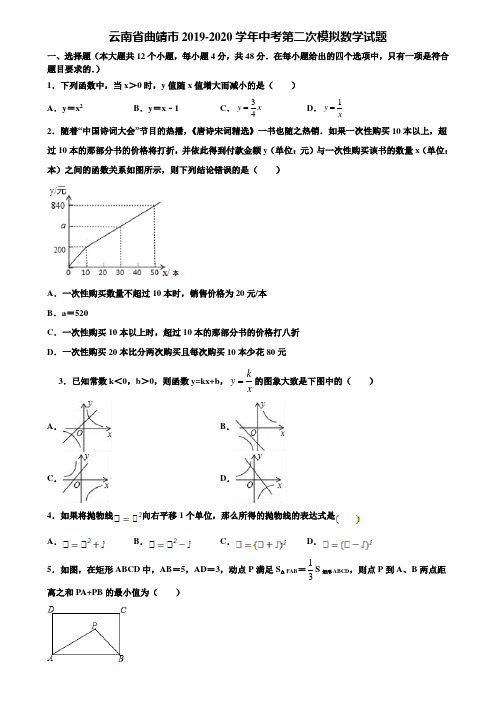
云南省曲靖市2019-2020学年中考第二次模拟数学试题一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列函数中,当x>0时,y值随x值增大而减小的是()A.y=x2B.y=x﹣1 C.34y x=D.1yx=2.随着“中国诗词大会”节目的热播,《唐诗宋词精选》一书也随之热销.如果一次性购买10本以上,超过10本的那部分书的价格将打折,并依此得到付款金额y(单位:元)与一次性购买该书的数量x(单位:本)之间的函数关系如图所示,则下列结论错误的是()A.一次性购买数量不超过10本时,销售价格为20元/本B.a=520C.一次性购买10本以上时,超过10本的那部分书的价格打八折D.一次性购买20本比分两次购买且每次购买10本少花80元3.已知常数k<0,b>0,则函数y=kx+b,kyx=的图象大致是下图中的()A.B.C.D.4.如果将抛物线向右平移1个单位,那么所得的抛物线的表达式是A.B.C.D.5.如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=13S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为()A .29B .34C .52D .416.如图,AB 是⊙O 的弦,半径OC ⊥AB 于D ,若CD=2,⊙O 的半径为5,那么AB 的长为( )A .3B .4C .6D .87.如图,在ABC ∆中,,4,AB AC BC ==面积是16,AC 的垂直平分线EF 分别交,AC AB 边于,E F 点,若点D 为BC 边的中点,点M 为线段EF 上一动点,则CDM ∆周长的最小值为( )A .6B .8C .10D .128.如图,△ABC 中,AD ⊥BC ,AB=AC ,∠BAD=30°,且AD=AE ,则∠EDC 等于( )A .10°B .12.5°C .15°D .20°9.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为 2s 0.51=甲,2s 0.62=乙,2s 0.48=丙,2s 0.45=丁,则四人中成绩最稳定的是( )A .甲B .乙C .丙D .丁10.下列各式:①33②177;2682;2432;其中错误的有( ).A .3个B .2个C .1个D .0个11.抛物线223y x +=(﹣)的顶点坐标是( ) A .(2,3)B .(-2,3)C .(2,-3)D .(-2,-3)12.如图,分别以等边三角形ABC 的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为( )A .3π+B .3π-C .23π-D .223π-二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,△ABC 的两条高AD ,BE 相交于点F ,请添加一个条件,使得△ADC ≌△BEC (不添加其他字母及辅助线),你添加的条件是_____.14.把一张长方形纸条按如图所示折叠后,若∠AOB′=70°,则∠B′OG =_____.15.方程x+1=25x +的解是_____.16.如图是利用直尺和三角板过已知直线l 外一点P 作直线l 的平行线的方法,其理由是__________.17.如图所示,D 、E 之间要挖建一条直线隧道,为计算隧道长度,工程人员在线段AD 和AE 上选择了测量点B ,C ,已知测得AD =100,AE =200,AB =40,AC =20,BC =30,则通过计算可得DE 长为_____.18.如图,点A 在反比例函数y=3x(x >0)上,以OA 为边作正方形OABC ,边AB 交y 轴于点P ,若PA:PB=1:2,则正方形OABC的面积=_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)(问题发现)(1)如图(1)四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为;(拓展探究)(2)如图(2)在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD 和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN 的形状,并说明理由;(解决问题)(3)如图(3)在正方形ABCD中,AB=22,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.20.(6分)解不等式组:12231 xx x-⎧⎨+≥-⎩<.21.(6分)计算:|﹣2|++(2017﹣π)0﹣4cos45°22.(8分)据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:(1)接受问卷调查的学生共有___名,扇形统计图中“基本了解”部分所对应扇形的圆心角为___;请补全条形统计图;(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数;(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.23.(8分)甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y (米)与登山时间x (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:(1)甲登山上升的速度是每分钟 米,乙在A 地时距地面的高度b 为 米;(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y (米)与登山时间x (分)之间的函数关系式.(3)登山多长时间时,甲、乙两人距地面的高度差为50米?24.(10分)在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A 、B 、C ,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果,并求甲、乙抽中同一篇文章的概率.25.(10分)有A ,B 两个黑布袋,A 布袋中有两个完全相同的小球,分别标有数字1和1.B 布袋中有三个完全相同的小球,分别标有数字﹣1,﹣1和﹣2.小明从A 布袋中随机取出一个小球,记录其标有的数字为x ,再从B 布袋中随机取出一个小球,记录其标有的数字为y ,这样就确定点Q 的一个坐标为(x ,y ).(1)用列表或画树状图的方法写出点Q 的所有可能坐标; (1)求点Q 落在直线y=﹣x ﹣1上的概率.26.(12分)如果一条抛物线()2=++0y ax bx c a ≠与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.(1)“抛物线三角形”一定是 三角形;(2)若抛物线()2=-+>0y x bx b 的“抛物线三角形”是等腰直角三角形,求b 的值;(3)如图,△OAB 是抛物线()2=-+''>0y x bx b 的“抛物线三角形”,是否存在以原点O 为对称中心的矩形ABCD ?若存在,求出过O C D 、、三点的抛物线的表达式;若不存在,说明理由.27.(12分)如图1,在△ABC 中,点P 为边AB 所在直线上一点,连结CP ,M 为线段CP 的中点,若满足∠ACP =∠MBA ,则称点P 为△ABC 的“好点”.(1)如图2,当∠ABC =90°时,命题“线段AB 上不存在“好点”为 (填“真”或“假”)命题,并说明理由; (2)如图3,P 是△ABC 的BA 延长线的一个“好点”,若PC =4,PB =5,求AP 的值;(3)如图4,在Rt △ABC 中,∠CAB =90°,点P 是△ABC 的“好点”,若AC =4,AB =5,求AP 的值.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.DA、、∵y=x2,∴对称轴x=0,当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x 的增大而减小,故此选项错误B、k>0,y随x增大而增大,故此选项错误C、B、k>0,y随x增大而增大,故此选项错误D、y=1x(x>0),反比例函数,k>0,故在第一象限内y随x的增大而减小,故此选项正确2.D【解析】【分析】A、根据单价=总价÷数量,即可求出一次性购买数量不超过10本时,销售单价,A选项正确;C、根据单价=总价÷数量结合前10本花费200元即可求出超过10本的那部分书的单价,用其÷前十本的单价即可得出C正确;B、根据总价=200+超过10本的那部分书的数量×16即可求出a值,B正确;D,求出一次性购买20本书的总价,将其与400相减即可得出D错误.此题得解.【详解】解:A、∵200÷10=20(元/本),∴一次性购买数量不超过10本时,销售价格为20元/本,A选项正确;C、∵(840﹣200)÷(50﹣10)=16(元/本),16÷20=0.8,∴一次性购买10本以上时,超过10本的那部分书的价格打八折,C选项正确;B、∵200+16×(30﹣10)=520(元),∴a=520,B选项正确;D、∵200×2﹣200﹣16×(20﹣10)=40(元),∴一次性购买20本比分两次购买且每次购买10本少花40元,D选项错误.故选D.【点睛】考查了一次函数的应用,根据一次函数图象结合数量关系逐一分析四个选项的正误是解题的关键.3.D【解析】【分析】当k<0,b>0时,直线经过一、二、四象限,双曲线在二、四象限,由此确定正确的选项.【详解】解:∵当k<0,b>0时,直线与y轴交于正半轴,且y随x的增大而减小,∴直线经过一、二、四象限,双曲线在二、四象限.故选D.本题考查了一次函数、反比例函数的图象与性质.关键是明确系数与图象的位置的联系. 4.D 【解析】 【分析】本题主要考查二次函数的解析式 【详解】解:根据二次函数的解析式形式可得,设顶点坐标为(h,k),则二次函数的解析式为.由原抛物线解析式可得a=1,且原抛物线的顶点坐标为(0,0),向右平移1个单位后的顶点坐标为(1,0),故平移后的解析式为.故选D. 【点睛】本题主要考查二次函数的顶点式,根据顶点的平移可得到二次函数平移后的解析式. 5.D 【解析】解:设△ABP 中AB 边上的高是h .∵S △PAB =13S 矩形ABCD ,∴12 AB•h=13AB•AD ,∴h=23AD=2,∴动点P 在与AB 平行且与AB 的距离是2的直线l 上,如图,作A 关于直线l 的对称点E ,连接AE ,连接BE ,则BE 就是所求的最短距离.在Rt △ABE 中,∵AB=5,AE=2+2=4,∴BE=22AB AE + =2254+=41,即PA+PB 的最小值为41.故选D .6.D 【解析】 【分析】连接OA ,构建直角三角形AOD ;利用垂径定理求得AB=2AD ;然后在直角三角形AOD 中由勾股定理求得AD 的长度,从而求得AB=2AD=1. 【详解】 连接OA .∵⊙O的半径为5,CD=2,∵OD=5-2=3,即OD=3;又∵AB是⊙O的弦,OC⊥AB,∴AD=12 AB;在直角三角形ODC中,根据勾股定理,得22OA OD-=4,∴AB=1.故选D.【点睛】本题考查了垂径定理、勾股定理.解答该题的关键是通过作辅助线OA构建直角三角形,在直角三角形中利用勾股定理求相关线段的长度.7.C【解析】【分析】连接AD,AM,由于△ABC是等腰三角形,点D是BC的中点,故AD BC⊥,在根据三角形的面积公式求出AD的长,再根据EF是线段AC的垂直平分线可知,点A关于直线EF的对称点为点C,MA MC=,推出MC DM MA DM AD+=+≥,故AD的长为BM+MD的最小值,由此即可得出结论.【详解】连接AD,MA∵△ABC是等腰三角形,点D是BC边上的中点∴AD BC⊥∴1141622S ABC BC AD AD==⨯⨯=g△解得8AD=∵EF是线段AC的垂直平分线∴点A关于直线EF的对称点为点C ∴MA MC=∵AD AM MD≤+∴AD的长为BM+MD的最小值∴△CDM 的周长最短()CM MD CD =++12AD BC =+1842=+⨯10=故选:C .【点睛】本题考查了三角形线段长度的问题,掌握等腰三角形的性质、三角形的面积公式、垂直平分线的性质是解题的关键. 8.C 【解析】试题分析:根据三角形的三线合一可求得∠DAC 及∠ADE 的度数,根据∠EDC=90°-∠ADE 即可得到答案.∵△ABC 中,AD ⊥BC ,AB=AC ,∠BAD=30°, ∴∠DAC=∠BAD=30°, ∵AD=AE (已知), ∴∠ADE=75°∴∠EDC=90°-∠ADE=15°. 故选C .考点:本题主要考查了等腰三角形的性质,三角形内角和定理点评:解答本题的关键是掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合. 9.D 【解析】 【分析】根据方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好可得答案. 【详解】∵0.45<0.51<0.62,∴丁成绩最稳定,故选D.【点睛】此题主要考查了方差,关键是掌握方差越小,稳定性越大.10.A【解析】33+3=63,错误,无法计算;②177=1,错误;③2+6=8=22,错误,不能计算;④243=22,正确.故选A.11.A【解析】【分析】已知解析式为顶点式,可直接根据顶点式的坐标特点,求顶点坐标.【详解】解:y=(x-2)2+3是抛物线的顶点式方程,根据顶点式的坐标特点可知,顶点坐标为(2,3).故选A.【点睛】此题主要考查了二次函数的性质,关键是熟记:顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.12.D【解析】【分析】莱洛三角形的面积是由三块相同的扇形叠加而成,其面积=三块扇形的面积相加,再减去两个等边三角形的面积,分别求出即可.【详解】过A作AD⊥BC于D,∵△ABC是等边三角形,∴AB=AC=BC=2,∠BAC=∠ABC=∠ACB=60°,∵AD⊥BC,∴BD=CD=1,AD=3BD=3,∴△ABC的面积为12BC•AD=1232⨯⨯=3,S扇形BAC=2602360π⨯=23π,∴莱洛三角形的面积S=3×23π﹣2×3=2π﹣23,故选D.【点睛】本题考查了等边三角形的性质和扇形的面积计算,能根据图形得出莱洛三角形的面积=三块扇形的面积相加、再减去两个等边三角形的面积是解此题的关键.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.AC=BC.【解析】分析:添加AC=BC,根据三角形高的定义可得∠ADC=∠BEC=90°,再证明∠EBC=∠DAC,然后再添加AC=BC可利用AAS判定△ADC≌△BEC.详解:添加AC=BC,∵△ABC的两条高AD,BE,∴∠ADC=∠BEC=90°,∴∠DAC+∠C=90°,∠EBC+∠C=90°,∴∠EBC=∠DAC,在△ADC和△BEC中,∴△ADC≌△BEC(AAS),故答案为:AC=BC.点睛:此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.14.55°【解析】【分析】由翻折性质得,∠BOG=∠B′OG,根据邻补角定义可得. 【详解】解:由翻折性质得,∠BOG=∠B′OG,∵∠AOB′+∠BOG+∠B′OG=180°,∴∠B′OG=12(180°﹣∠AOB′)=12(180°﹣70°)=55°.故答案为55°.【点睛】考核知识点:补角,折叠.15.x=1【解析】【分析】无理方程两边平方转化为整式方程,求出整式方程的解得到x的值,经检验即可得到无理方程的解.【详解】两边平方得:(x+1)1=1x+5,即x1=4,开方得:x=1或x=-1,经检验x=-1是增根,无理方程的解为x=1.故答案为x=116.同位角相等,两直线平行.【解析】试题解析:利用三角板中两个60°相等,可判定平行考点:平行线的判定17.1.【解析】【分析】先根据相似三角形的判定得出△ABC∽△AED,再利用相似三角形的性质解答即可.【详解】∵401201,20051005 AB ACAE AD====,∴AB AC AE AD=,又∵∠A=∠A,∴△ABC∽△AED,∴15 BC ABDE AE==,∵BC=30,∴DE=1,故答案为1.【点睛】考查相似三角形的判定与性质,掌握相似三角形的判定定理是解题的关键.18.1.【解析】【分析】根据题意作出合适的辅助线,然后根据正方形的性质和反比例函数的性质,相似三角形的判定和性质、勾股定理可以求得AB的长.【详解】解:由题意可得:OA=AB,设AP=a,则BP=2a,OA=3a,设点A的坐标为(m,3m),作AE⊥x轴于点E.∵∠PAO=∠OEA=90°,∠POA+∠AOE=90°,∠AOE+∠OAE=90°,∴∠POA=∠OAE,∴△POA∽△OAE,∴APAO=OEEA,即3aa=3mm,解得:m=1或m=﹣1(舍去),∴点A的坐标为(1,3),∴OA=10,∴正方形OABC的面积=OA2=1.故答案为1.【点睛】本题考查了反比例函数图象点的坐标特征、正方形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(1)AC垂直平分BD;(2)四边形FMAN是矩形,理由见解析;(3)316﹣3【解析】【分析】(1)依据点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,即可得出AC垂直平分BD;(2)根据Rt△ABC中,点F为斜边BC的中点,可得AF=CF=BF,再根据等腰三角形ABD 和等腰三角形ACE,即可得到AD=DB,AE=CE,进而得出∠AMF=∠MAN=∠ANF=90°,即可判定四边形AMFN 是矩形;(3)分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,②以点A为旋转中心将正方形ABCD顺时针旋转60°,分别依据旋转的性质以及勾股定理,即可得到结论.【详解】(1)∵AB=AD,CB=CD,∴点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,∴AC垂直平分BD,故答案为AC垂直平分BD;(2)四边形FMAN是矩形.理由:如图2,连接AF,∵Rt△ABC中,点F为斜边BC的中点,∴AF=CF=BF,又∵等腰三角形ABD 和等腰三角形ACE,∴AD=DB,AE=CE,∴由(1)可得,DF⊥AB,EF⊥AC,又∵∠BAC=90°,∴∠AMF=∠MAN=∠ANF=90°,∴四边形AMFN是矩形;(3)BD′的平方为16+83或16﹣83.分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,如图所示:过D'作D'E⊥AB,交BA的延长线于E,由旋转可得,∠DAD'=60°,∴∠EAD'=30°,∵AB=22=AD', ∴D'E=12AD'=2,AE=6, ∴BE=22+6,∴Rt △BD'E 中,BD'2=D'E 2+BE 2=(2)2+(22+6)2=16+83 ②以点A 为旋转中心将正方形ABCD 顺时针旋转60°, 如图所示:过B 作BF ⊥AD'于F ,旋转可得,∠DAD'=60°, ∴∠BAD'=30°, ∵AB=22=AD', ∴BF=12AB=2,AF=6,∴26,∴Rt △BD'F 中,BD'2=BF 2+D'F 2=2)2+(26)2=16﹣3综上所述,BD′平方的长度为316﹣3. 【点睛】本题属于四边形综合题,主要考查了正方形的性质,矩形的判定,旋转的性质,线段垂直平分线的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构造直角三角形,依据勾股定理进行计算求解.解题时注意:有三个角是直角的四边形是矩形. 20.﹣4≤x <1 【解析】 【分析】 先求出各不等式的 【详解】12231x x x -⎧⎨+≥-⎩< 解不等式x ﹣1<2,得:x <1, 解不等式2x+1≥x ﹣1,得:x≥﹣4,则不等式组的解集为﹣4≤x <1. 【点睛】考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 21.1. 【解析】 【分析】直接利用零指数幂的性质以及特殊角的三角函数值和绝对值的性质分别化简得出答案. 【详解】 解:原式=2+2+1﹣4×=2+2+1﹣2=1.【点睛】此题主要考查了实数运算,正确化简各数是解题关键. 22.(1)60;90°;统计图详见解析;(2)300;(3). 【解析】试题分析:(1)由“了解很少”的人数除以占的百分比得出学生总数,求出“基本了解”的学生占的百分比,乘以360得到结果,补全条形统计图即可;(2)求出“了解”和“基本了解”程度的百分比之和,乘以900即可得到结果; (3)列表得出所有等可能的情况数,找出两人打平的情况数,即可求出所求的概率. 试题解析:(1)根据题意得:30÷50%=60(名),“了解”人数为60﹣(15+30+10)=5(名), “基本了解”占的百分比为1560×100%=25%,占的角度为25%×360°=90°, 补全条形统计图如图所示:(2)根据题意得:900×15560=300(人), 则估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数(3)列表如下:剪石布剪(剪,剪)(石,剪)(布,剪)石(剪,石)(石,石)(布,石)布(剪,布)(石,布)(布,布)所有等可能的情况有9种,其中两人打平的情况有3种,则P=39=13.考点:1、条形统计图,2、扇形统计图,3、列表法与树状图法23.(1)10;1;(2)15(02)3030(211)x xyx x⎧=⎨-⎩剟剟;(3)4分钟、9分钟或3分钟.【解析】【分析】(1)根据速度=高度÷时间即可算出甲登山上升的速度;根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;(3)当乙未到终点时,找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程,解之即可求出x值;当乙到达终点时,用终点的高度-甲登山全程中y关于x的函数关系式=50,即可得出关于x的一元一次方程,解之可求出x值.综上即可得出结论.【详解】(1)(10-100)÷20=10(米/分钟),b=3÷1×2=1.故答案为:10;1.(2)当0≤x≤2时,y=3x;当x≥2时,y=1+10×3(x-2)=1x-1.当y=1x-1=10时,x=2.∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为15(02)3030(211)x xyx x⎧=⎨-⎩剟剟.(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).当10x+100-(1x-1)=50时,解得:x=4;当1x-1-(10x+100)=50时,解得:x=9;当10-(10x+100)=50时,解得:x=3.答:登山4分钟、9分钟或3分钟时,甲、乙两人距地面的高度差为50米.本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系列式计算;(2)根据高度=初始高度+速度×时间找出y关于x的函数关系式;(3)将两函数关系式做差找出关于x的一元一次方程.24.13.【解析】试题分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙抽中同一篇文章,再利用概率公式求解即可求得答案.试题解析:解:如图:所有可能的结果有9种,甲、乙抽中同一篇文章的情况有3种,概率为39=13.点睛:本题主要考查了用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.25.(1)见解析;(1)1 3【解析】试题分析:先用列表法写出点Q的所有可能坐标,再根据概率公式求解即可. (1)由题意得1 1-1 (1,-1)(1,-1)-1 (1,-1)(1,-1)-2 (1,-2)(1,-2)(1)共有6种等可能情况,符合条件的有1种P(点Q在直线y=−x−1上)=1 3 .考点:概率公式点评:解题的关键是熟练掌握概率公式:概率=所求情况数与总情况数的比值.26.(1)等腰(2)=2b (3)存在, 2=y x【解析】解:(1)等腰(2)∵抛物线()2=-+>0y x bx b 的“抛物线三角形”是等腰直角三角形,∴该抛物线的顶点224b b ⎛⎫ ⎪⎝⎭,满足2=24b b ()>0b .∴=2b . (3)存在.如图,作△OCD 与△OAB 关于原点O 中心对称,则四边形ABCD 为平行四边形.当=OA OB 时,平行四边形ABCD 为矩形. 又∵=AO AB ,∴△OAB 为等边三角形. 作AE OB ⊥,垂足为E .∴=AE .∴()2'''>042b b b .∴b∴)A,()B .∴()C ,()D . 设过点O C D 、、三点的抛物线2=+y mx nx ,则12-23=03-3=-3.m n m n ⎧⎪⎨⎪⎩, 解之,得=1=2 3.m n ⎧⎪⎨⎪⎩, ∴所求抛物线的表达式为2=+23y x x . 27.(1)真;(2)85;(3)2AP =或8AP =或415AP =-. 【解析】【分析】(1)先根据直角三角形斜边的中线等于斜边的一半可知MP=MB ,从而∠MPB=∠MBP ,然后根据三角形外角的性质说明即可;(2)先证明△PAC ∽△PMB ,然后根据相似三角形的性质求解即可;(3)分三种情况求解:P 为线段AB 上的“好点”, P 为线段AB 延长线上的“好点”, P 为线段BA 延长线上的“好点”.【详解】(1)真 .理由如下:如图,当∠ABC=90°时,M 为PC 中点,BM=PM ,则∠MPB=∠MBP>∠ACP ,所以在线段AB 上不存在“好点”;(2)∵P 为BA 延长线上一个“好点”;∴∠ACP=∠MBP ;∴△PAC ∽△PMB ;∴PM PA PB PC=即PM PC PA PB ⋅=⋅; ∵M 为PC 中点,∴MP=2;∴245PA ⨯=;∴85PA =. (3)第一种情况,P 为线段AB 上的“好点”,则∠ACP=∠MBA ,找AP 中点D ,连结MD ;∵M 为CP 中点;∴MD 为△CPA 中位线;∴MD=2,MD//CA ;∴∠DMP=∠ACP=∠MBA;∴△DMP∽△DBM;∴DM2=DP·DB即4= DP·(5-DP);解得DP=1,DP=4(不在AB边上,舍去;)∴AP=2第二种情况(1),P为线段AB延长线上的“好点”,则∠ACP=∠MBA,找AP中点D,此时,D在线段AB上,如图,连结MD;∵M为CP中点;∴MD为△CPA中位线;∴MD=2,MD//CA;∴∠DMP=∠ACP=∠MBA;∴△DMP∽△DBM∴DM2=DP·DB即4= DP·(5-DA)= DP·(5-DP);解得DP=1(不在AB延长线上,舍去),DP=4∴AP=8;第二种情况(2),P为线段AB延长线上的“好点”,找AP中点D,此时,D在AB延长线上,如图,连结MD;此时,∠MBA>∠MDB>∠DMP=∠ACP,则这种情况不存在,舍去;第三种情况,P 为线段BA 延长线上的“好点”,则∠ACP=∠MBA ,∴△PAC ∽△PMB ;∴90PMB PAC ∠=∠=︒∴BM 垂直平分PC 则41 ; ∴415AP =∴综上所述,2AP =或8AP =或415AP =; 【点睛】本题考查了信息迁移,三角形外角的性质,直角三角形斜边的中线等于斜边的一半,相似三角形的判定与性质及分类讨论的数学思想,理解“好点”的定义并能进行分类讨论是解答本题的关键.。
云南省曲靖市2019-2020学年第二次中考模拟考试物理试卷含解析

云南省曲靖市2019-2020学年第二次中考模拟考试物理试卷一、单选题(本大题共10小题,共30分)1.生活中经常要对一些物理量进行估测,以下估测值中,最符合实际的是A.一辆电动自行车的重力约为30NB.一个普通矿泉水瓶的容积约为500LC.家用电风扇正常工作的电流约0.5AD.一张考试卷厚度大约为70mmC【解析】【分析】【详解】A.一辆电动自行车的重力约为300N,故A不符合实际;B.一个普通矿泉水瓶的容积约为500mL,故B不符合实际;C.家用电风扇电功率约为100W,家庭电路的电压为220V,所以通过的电流I=100220P WU V≈0. 5A. 故C符合实际;D.一张考试卷厚度大约为70μm,故D不符合实际;2.在2016年举重世锦赛上,中国选手张湘祥在男子举重62kg级的决赛中获得金牌,挺举成绩是176kg,其中举起杠铃大约用了3s钟,杠铃在头顶停止3s不动,如图所示.若他毎只脚与地面的接触面积大约200cm2,则下列说法中错误的是A.张湘祥手上涂有镁粉可以增大摩擦B.地面对张湘祥的支持力与张湘祥的重力是一对平衡力C.张湘祥举起杠铃时对杠铃做功大约3200JD.张湘祥举着杠铃不动时对地面的压强大约是6×104PaB【解析】【详解】A.张湘祥手上涂有镁粉是通过增大接触面粗糙程度的方法增大摩擦,故A正确;B.地面对张湘祥的支持力的大小大于张湘祥的重力大小,所以不是一对平衡力,故B错误,符合题意;C.由题知道杠铃的重力是:G=mg=176kg×10N/kg=1760N,举起的高度大约是2m,所以对杠铃做的功大约是:W=Gh=1760N×2m=3520J,与3200J较为接近,可认为近似相等,故C正确;D.张湘祥举着杠铃不动时对地面的压力等于人和杠铃的总重力,即F=G总=m总g=(62kg+176kg)×10N/kg=2380N,此时对地面的压强是:p=F/S=G总/S=2380N/2×200×10−4m2=5.95×104 Pa,近似为6×104 Pa,故D正确.3.如图是一同学正在体育课中进行铅球投掷训练,若忽略铅球的体积和空气阻力,下列有关铅球的说法正确的是A.上升时,机械能不变、重力势能增加B.上升到最髙点时,动能为零,重力势能最大C.下落时,动能不变,重力势能减小D.整个过程中铅球受到平衡力的作用A【解析】【详解】A.实心球在上升过程中,因为质量不变、速度减小、高度增大,所以实心球的动能减小,重力势能增加,动能转化为重力势能;不考虑空气阻力,机械能总量不变,故A正确;B.上升到最髙点时,重力势能最大,但实心球仍有水平方向的速度,因此动能不为零,故B错误;C.下落时,重力势能转化为动能,动能增加,重力势能减小,故C错误;D.整个过程中铅球只受重力作用,铅球的运动状态不断发生改变,故铅球受到非平衡力的作用,故D错误;4.如图所示的电路中,电源两端电压保持不变.闭合开关S,将滑动变阻器的滑片P向右滑动,下列判断正确的是A.滑动变阻器接入电路中的电阻变小B.电路中的总电阻变小C.电流表的示数变小D.电压表的示数变小C【解析】【详解】由电路图可知,R1与R2串联,电压表测R1两端的电压,电流表测电路中的电流,将滑动变阻器的滑片P向右滑动,变阻器接入电路中电阻丝的长度变长,接入电路中的电阻变大,故A错误;因串联电路中总电阻等于各分电阻之和,所以,电路中的总电阻变大,故B错误;由IUR=可知,电路中的电流变小,即电流表的示数变小,故C正确;由U=IR可知,R2两端的电压变小,R1两端的电压变大即电压表的示数变大,故D错误.5.如图所示的电路中,闭合开关S后,下列说法正确的是A.开关 S 只能控制灯泡 L1B.灯泡 L1和 L2并联在电路中C.电流表可以测量灯泡L1的电流D.电压表测量灯泡 L1两端的电压C【解析】【分析】串联电路电流只有一条路径,各处电路相等,用电器不能独立工作;并联电路:电流有两条或两条以上路径,各用电器可以独立工作,各支路电压相等.电流表与被测电路串联,电压表与被测电路并联.由此分析判断.【详解】由图可知,电流从电源正极流出通过电流表和L1、开关和L2回到电源负极,所以灯泡L1和L2串联,开关S 控制灯泡L1和L2电流表测电路中的电流,电压表测L1两端电压.故ABD错误,C正确.故选C.6.如图所示,水平桌面上有两个完全相同的溢水杯甲和乙、杯中装满了水,将两个体积相同、材料不同的实心小球A和B分别放入溢水杯中。
云南省曲靖市2019-2020学年中考语文二模考试卷含解析

云南省曲靖市2019-2020学年中考语文二模考试卷一、选择题1.下列句子组成语段顺序排列正确的一项是()①而当地球穿过这条尘埃带时,这些流星体便会落入地球的怀抱中。
②人们不禁要问,这些陨石是从哪里来的?③受到其他天体引力的影响,它们会慢慢扩散开来,在彗星轨道上形成一条尘埃带。
④当然这也可能是彗星靠近太阳时抛洒出的流星体。
⑤它们大部分可能来自位于火星与木星之间的小行星带,受到火星、木星的影响,它们自身的轨道渐渐产生偏离,以致闯入地球。
A.②④③①⑤B.②⑤④③①C.④③⑤②①D.④⑤①③②【答案】B【解析】这是一段说明文的材料,解答的时候,先研读材料,抓住中心,从而确定首句。
第二步,理清思路。
说明文,往往把事理句放在前面,把材料句放在后面。
第三步,抓住标志。
抓住语言标志,如呼应的关联词语、暗示性词语,有指代意义的词语等。
完成排序后再通读一遍看是否流畅。
通过阅读材料得知,给文段是讲“陨石从何而来”,确定首句是②;接着说陨石的来源,再根据“大部分”和“当然也可能”确定第二句是⑤,第三句是④;③中“在彗星轨道上”紧承上句,确定第四句是③;最后流星落到地球形成陨石,确定第五句是①。
该文段的排列顺序是②⑤④③①。
故选B。
2.下列表述不正确的一项是()A.《史记》是一部纪传体史书,作者司马迁,西汉史学家。
B.《我的叔叔于勒》中的克拉丽丝,《范进中举》中的胡屠户,都和契诃夫笔下的奥楚蔑洛夫一样具有“变色龙”的特点。
C.茅盾的《白杨礼赞》和高尔基的《海燕》都运用了象征手法。
D.古人称人七十岁为耄耋,八九十岁为古稀,一百岁为期颐。
【答案】D【解析】【详解】“古稀”指七十岁,“耄耋”指八九十岁,“期颐”指百岁。
故选D。
二、名句名篇默写3.根据课文默写古诗文。
求之不得,__________。
悠哉悠哉,__________。
(《诗经·关雎》)__________。
鬓微霜,又何妨!(苏轼《江城子·密州出猎》)__________,天与云与山与水,上下一白。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年沾益区大坡乡中考模拟考试(第二次)数 学 试 题 卷(满分120分,考试用时120分钟)班级 姓名一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题4分,满分32分)1、21-的相反数是( )A 、-2B 、2C 、21D 、21-2、下列运算正确的是( )A 、1052a a a =⋅B 、a a a 236=÷C 、222)(b a b a +=+D 、55245=-3、如图是几何体的三视图,则这个几何体是( )A 、圆锥B 、正方体C 、圆柱D 、球4.用直尺和圆规作一个角等于已知角,如图,能得出∠A ′O ′B ′=∠AOB 的依据是( )A .(SAS )B . (SSS )C . (ASA )D . (AAS )5. 将一副三角板如图放置,使点A 在DE 上,BC ∥DE ,∠C=45°,∠D=30°,则∠ABD 的度数为( )A. 10°B. 15°C. 20°D. 25°6. 关于x 的一元二次方程0132=-+x x 的根的情况( ) A.无实数根 B .有两个相等的实数根 C.有两个不相等的实数根 D .无法确定7. 如图,⊙O 的半径为5,弦AB=8, M 是弦AB 上的动点,则OM 不可能为( )A. 2B. 3C. 4D. 58.已知二次函数y=ax 2+bx+c 的图象如图所示,它与x 轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc <0;③b 2﹣4ac >0;④8a+c >0.其中正确的有( )A .0个B .1个C .2个D .3个第7题图 第8题图 第13题图 二、填空题(本大题共7个小题,每小题3分,共21分)9. 为了方便市民出行,提倡低碳交通,近几年某市大力发展公共自行车系统,根据规划,全市公共自行车总量明年将达62000辆,用科学记数法表示62000是_____. 10.一个正多边形的内角和大于等于540度而小于1000度,则这个正多边形的每一个内角可以是 度。
(填出一个即可)11. 在Rt △ABC 中,∠C=90°,∠A=30°,BC=3,则AC 的长为_____.(结果保留根号)12. 若点P (m ,-2)与点Q (3,n )关于原点对称,则(m +n )2018=__________.13. 如图,AB 是⊙O 的直径,CD ⊥AB ,∠ABD=60°,CD=2,则阴影部分的面积为_____.14、下面是用棋子摆成的“上”字:第一个“上”字第二个“上”字第三个“上”字如果按照以上规律继续摆下去,那么通过观察,可以发现:第n个“上”字需用________枚棋子.三、解答题(本大题共9个小题,满分75分)15.(6分)计算: +()﹣1﹣|﹣2|﹣(2﹣)0.16.(6分)先化简再求值:,其中.17.(8分)如图,已知△ABC,按如下步骤作图:①分别以A,C 为圆心,大于AC的长为半径画弧,两弧交于P,Q两点;②作直线PQ,分别交AB,AC于点E,D,连接CE;③过C作CF∥AB交PQ于点F,连接AF.(1)求证:△AED≌△CFD;(2)求证:四边形AECF是菱形.18.(6分)经过建设者三年多艰苦努力地施工,贯通我市A、B两地又一条高速公路全线通车.已知原来A地到B地普通公路长150km,高速公路路程缩短了30km,如果一辆小车从A地到B地走高速公路的平均速度可以提高到原来的1.5倍,需要的时间可以比原来少用1小时.求小车走普通公路的平均速度是多少?19. (8分)如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.(1)求两建筑物两底部之间的水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).20. (8分)我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
组别投进个数人数A 80<≤x10B 168<≤x15C 2416<≤x30D 3224<≤x mE 4032<≤x n根据以上信息完成下列问题。
①本次抽取的学生人数为多少?②统计表中的m=__________。
③扇形统计图中E组所占的百分比;④补全频数分布直方图。
⑤扇形统计图中“C组”所对应的圆心角的度数。
⑥本次比赛中投篮个数的中位数落在哪一组。
⑦已知该校共有900名学生,如投进个数少于24个定为不合格,请你估计该校本次投篮比赛不合格的学生人数。
21. (7分)某商场,为了吸引顾客,在“五一劳动节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.球两红一红一白两白礼金券(元)18 24 18(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼金券,请你帮助分析选择哪种方案较为实惠.22.(9分)如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.(1)求证:∠DAC=∠DCE;(2)若AE=ED=2,求⊙O的半径。
23、(12分)如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A,O,B三点,连接OA,OB,AB,线段AB交y轴于点C.已知实数m,n(m<n)是方程0322=--xx的两根.(1)求抛物线的解析式.(2)若P为线段OB上的一个动点(不与点O,B重合),直线PC与抛物线交于D,E两点(点D在y轴右侧),连接OD,BD.①当△OPC为等腰三角形时,求点P的坐标;②求△BOD面积的最大值,并写出此时点D的坐标.第二次检测参考答案一、选择题(共8个小题,每小题只有一个正确选项,每小题4分,满分32分)题号 1 2 3 4 5 6 7 8 答案CDABBCAD二、填空题(共6个小题,每小题3分,共18分)9、1042.6⨯_. 10、108或120或7900. 11、 29.12、 1 .13、 π32. 14、 2n 4+ 。
三、解答题(本大题共9个小题,满分70分)15题解:原式=2+2-2-1 …………(4分) =1 …………(6分)16题解:原式=1121)1)(1()2(2++--÷-+-x x x x x x x…………(2分) =11)2(1)1)(1()2(-=-+⋅-+-x x x x x x x x …………(4分)当13+=x 时,原式=3311=+x …………(6分) 17题证明:(1)由作图知:PQ 为线段AC 的垂直平分线, …………(1分) ∴AE =CE ,AD =CD , ∵CF ∥AB∴∠EAC =∠FCA ,∠CFD =∠AED , …………(3分) 在△AED 与△CFD 中,,∴△AED ≌△CFD ; …………(5分) (2)∵△AED ≌△CFD , ∴AE =CF ,∵EF 为线段AC 的垂直平分线, ∴EC =EA ,FC =FA , ∴EC =EA =FC =FA ,∴四边形AECF 为菱形. …………(8分)18题:设小车走普通公路的平均速度是x 千米/时,得 …………(1分) 15.130150150+-=xx …………(3分)解得x=70 …………(4分)经检验:x=70是原方程的解,且符合题意 …………(5分)答:小车走普通公路的平均速度是70千米/时。
…………(6分)19题解:(1)根据题意得BD ∥AE ,∴∠ADB =∠EAD =45° …………(1分)∵∠ABD =90°,∴∠BAD =∠ADB =45° …………(2分) ∴BD =AD =60(米) …………(3分) ∴两建筑物两底部之间的水平距离BD 的长度为60米 ………(4分) (2)延长AE 、DC 交于点F ,根据题意可知四边形ABDF 是正方形………(5分) ∴AF =BD =DF =60在Rt △AFC 中,∠FAC =30°,由tan ∠CAF =CFAF,得CF =AF tan ∠CAF =60tan30°=60×33=203.…………(6分) 又∵DF =60,∴CD =60-203.答:建筑物CD 的高度为(60-203)米. …………(8分) 20题解:①学生人数为 100 , ②统计表中的m= 25 , ③扇形统计图中E 组所占的百分比是 20% , ④D 组人数为25,E 组人数为20⑤“C 组”所对应的圆心角的度数是 108 度, ⑥本次比赛中投篮个数的中位数落在 C 组,⑦495%)30%15%10(900=++⨯人答:该校本次投篮比赛不合格的学生人数495人。
21题解:(1)树状图为:∴一共有6种情况,摇出一红一白的情况共有4种,…………(2分)∴摇出一红一白的概率=;…………(5分)(2)∵两红的概率P=,两白的概率P=,一红一白的概率P=,∴摇奖的平均收益是:×18+×24+×18=22,…………(6分)∵22>20,∴选择摇奖.…………(7分)22题解:证明:(1)AD是⊙O的切线,∴∠DAB=90°,即∠DAC+∠CAB=90°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°,∴∠DAC=∠B,…………(2分)∵OC=OB,∴∠B=∠OCB=∠DAC,又∵∠DCE=∠OCB,∴∠DAC=∠DCE;…………(4分)(2)解:∵∠DAC=∠DCE, ∠D=∠D∴△DCE∽△DAC∴DADCDCDE=即42DCDC=∴DC=22…………(6分)设⊙O的半径为x,则OA=OC=x在Rt△OAD中,由勾股定理,得4)22222=-+xx(解得x =2…………(8分)答:⊙O的半径为2。
…………(9分)23题解:(1)解方程x2-2x-3=0,得x1=3,x2=-1. ∵m<n,∴m=-1,n=3.∴A(-1,-1),B(3,-3).…………(2分)∵抛物线过原点,∴可设抛物线的解析式为y=ax2+bx,得⎩⎨⎧-=+-=-3391baba解得⎪⎩⎪⎨⎧=-=2121ab∴抛物线的解析式为y=-12x2+12x. …………(4分)(2)①设直线AB的解析式为y=kx+b,根据题意,得⎩⎨⎧-=+-=+-331bkbk解得⎪⎩⎪⎨⎧-=-=2321bk∴直线AB的解析式为y=-12x-32,…………(5分)∴C(0,-32).又∵直线OB的解析式为y=-x,故设P(x,-x).…………………(6分)∵△OPC为等腰三角形,则Ⅰ)当OC=OP时,x2+(-x)2=9 4,解得x1=3 24,x2=-3 24(舍去),∴P1(3 24,-3 24).(Ⅱ)当PO=PC时,x2+(-x)2=x2+(x-32)2,解得x=3 4,∴P2(34,-34).(Ⅲ)当OC=PC时,x2+(x-32)2=94,解得x1=32,x2=0(舍去),∴P3(32,-32).综上所述,点P的坐标为(3 24,-3 24)或(34,-34)或(32,-32).……(9分)②设D(x,y)(x>0).分别过点D,B作DG⊥y轴于点G,BF⊥y轴于点F,则G(0,y),F(0,-3),∴S△BOD =S Rt△ODG+S梯形DGFB-S Rt△OBF=12x×(-y)+12(x+3)×(3+y)-12×3×3=-12xy+32x+12xy+92+32y-92=32y+32x.又∵y=-12x2+12x,∴S△BOD=-34x2+94x=-34(x-32)2+2716. …………(11分)∵0<x<3,∴当x=32时,S△BOD的最大值为2716,此时D(32,-38).…………(12分)。
