相交线平行线培优-
第五章相交线与平行线单元试卷(培优篇)(Word版 含解析)

解:∵A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n,
根据平行线之间的距离相等可得:△ABC与△PBC是同底等高的三角形,
故△ABC的面积等于△PBC的面积.
故选D.
【点睛】
本题考查平行线之间的距离;三角形的面积.
2.A
解析:A
【分析】
根据两直线平行,内错角相等、同旁内角互补逐一判断可得.
(1)求a、b的值;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图,两灯同时转动,在灯A射线到达AN之前,若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC()
∴∠C=∠CEF.()
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C=(等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究
如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°﹣∠BEC.
27.如图1.已知直线 .点 为 , 内部的一个动点,连接 , ,作 的平分线交直线 于点 ,作 的平分线交直线 于点 , 和 交于点 .
(1)若 ,猜想 和 的位置关系,并证明;
(2)如图2,在(1)的基础上连接 ,则在点 的运动过程中,当满足 且 时,求 的度数.
28.如图1,直线 与直线 交于点 , .小明将一个含 的直角三角板 如图1所示放置,使顶点 落在直线 上,过点 作直线 交直线 于点 (点 在 左侧).
(完整版)初一数学下册相交线与平行线试题(带答案) (一)培优试卷
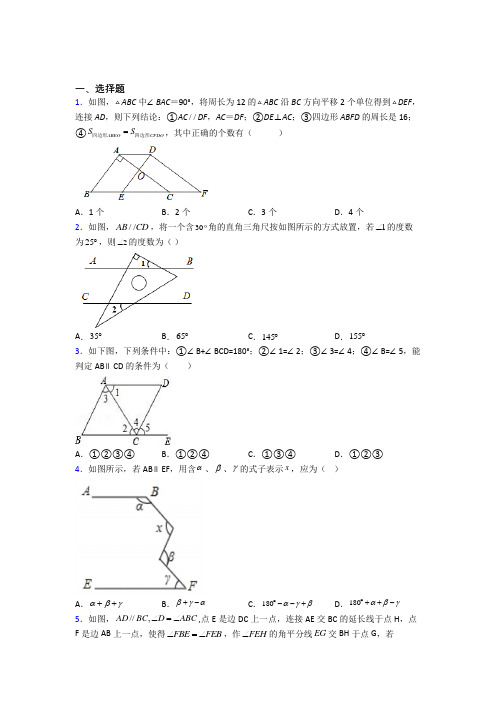
一、选择题1.如图,ABC 中∠BAC =90°,将周长为12的ABC 沿BC 方向平移2个单位得到DEF ,连接AD ,则下列结论:①AC //DF ,AC =DF ;②DE ⊥AC ;③四边形 ABFD 的周长是16;④ABEO CFDO S S =四边形四边形,其中正确的个数有( )A .1个B .2个C .3个D .4个2.如图,//AB CD ,将一个含30角的直角三角尺按如图所示的方式放置,若1∠的度数为25︒,则2∠的度数为( )A .35︒B .65︒C .145︒D .155︒3.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB ∥CD 的条件为( )A .①②③④B .①②④C .①③④D .①②③ 4.如图所示,若AB ∥EF ,用含α、β、γ的式子表示x ,应为( )A .αβγ++B .βγα+-C .180αγβ︒--+D .180αβγ︒++- 5.如图,//,AD BC D ABC ∠=∠,点E 是边DC 上一点,连接AE 交BC 的延长线于点H ,点F 是边AB 上一点,使得FBE FEB ∠=∠,作FEH ∠的角平分线EG 交BH 于点G ,若100DEH ︒∠=,则BEG ∠的度数是( )A .30︒B .40︒C .50︒D .60︒6.如图,//AB CD ,PF CD ⊥于F ,40AEP ∠=︒,则EPF ∠的度数是( )A .120︒B .130︒C .140︒D .150︒7.如图,已知直线AB ,CD 被直线AC 所截,AB ∥CD ,E 是平面内CD 上方的一点(点E 不在直线AB ,CD ,AC 上),设∠BAE =α,∠DCE =β.下列各式:①α+β,②α﹣β,③β﹣α,④180°﹣α﹣β,⑤360°﹣α﹣β中,∠AEC 的度数可能是( )A .①②③B .①②④⑤C .①②③⑤D .①②③④⑤ 8.如图,从①12∠=∠,②C D ∠=∠,③//DF AC 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )A .0B .1C .2D .39.如图,直线a ,b 被直线c ,d 所截,若12∠=∠,3125∠=︒,则4∠的度数是( )A .65︒B .60︒C .55︒D .75︒ 10.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )A .50°、130°B .都是10°C .50°、130°或10°、10°D .以上都不对 二、填空题11.如图,已知//AB CD ,CE 、BE 的交点为E ,现作如下操作:第一次操作,分别作ABE ∠和DCE ∠的平分线,交点为1E ,第二次操作,分别作1ABE ∠和1DCE ∠的平分线,交点为2E ,第三次操作,分别作2ABE ∠和2DCE ∠的平分线,交点为3E ,…,第n 次操作,分别作1n ABE -∠和1n DCE -∠的平分线,交点为n E .若BEC α∠=,则n E ∠的度数是__________.12.如图,已知AB ∥CD ,点E ,F 分别在直线AB ,CD 上点P 在AB ,CD 之间且在EF 的左侧.若将射线EA 沿EP 折叠,射线FC 沿FP 折叠,折叠后的两条射线互相垂直,则∠EPF 的度数为 _____.13.如图,在平面内,两条直线1l ,2l 相交于点O ,对于平面内任意一点M ,若p ,q 分别是点M 到直线1l ,2l 的距离,则称(,)p q 为点M 的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有________个.14.某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ ∥MN . 如图所示,灯A 射线从AM 开始顺时针旋转至AN 便立即回转,灯B 射线从BP 开始顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯A 转动的速度是每秒2度,灯B 转动的速度是每秒1度. 若灯B 射线先转动30秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动_________秒,两灯的光束互相平行.15.如图,AB ∥CD ,点P 为CD 上一点,∠EBA 、∠EPC 的角平分线于点F ,已知∠F =40°,则∠E =_____度.16.如图,已知∠A =(60﹣x )°,∠ADC =(120+x )°,∠CDB =∠CBD ,BE 平分∠CBF ,若∠DBE =59°,则∠DFB =___.17.如图,已知//AB CD ,BF 平分ABE ∠,//BF DE ,且40D ∠=︒,则BED ∠的度数为______.18.如图,//AB DE ,AD AB ⊥,AE 平分BAC ∠交BC 于点F .如果24CAD ∠=︒,则=E ∠__︒.19.如图,在长方形ABCD 中,4AB =,6BC =,将长方形ABCD 沿着BC 方向平移得到长方形A B C D ''''.若ABB A ''是正方形,则四边形ABC D ''的周长是______.20.如图,直线//MN PQ ,MN 与直线AB ,AC 分别交于D ,E ,PQ 与直线AB ,AC 分别交于F ,G ,若75C ∠=︒,26BGF ∠=︒,则AEN ∠=_________度.三、解答题21.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若1∠与2∠都是锐角,请写出C ∠与1∠,2∠之间的数量关系并说明理由; (2)把直角三角形ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有BDF GDF ∠=∠,求AEN CDG∠∠的值; (3)如图3,若点D 是MN 下方一点,BC 平分PBD ∠, AM 平分CAD ∠,已知25PBC ∠=︒,求ACB ADB ∠+∠的度数.22.如图,//MN PQ ,直线AD 与MN 、PQ 分别交于点A 、D ,点B 在直线PQ 上,过点B 作BG AD ⊥,垂足为点G .(1)如图1,求证:90MAG PBG ∠+∠=︒;(2)若点C 在线段AD 上(不与A 、D 、G 重合),连接BC ,MAG ∠和PBC ∠的平分线交于点H 请在图2中补全图形,猜想并证明CBG ∠与AHB ∠的数量关系;23.已知,如图:射线PE 分别与直线AB 、CD 相交于E 、F 两点,PFD ∠的角平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设PFM α∠=︒,EMF β∠=︒且()2350αβα-+-=.(1)α=________,β=________;直线AB 与CD 的位置关系是______;(2)如图,若点G 是射线MA 上任意一点,且MGH PNF ∠=∠,试找出FMN ∠与GHF ∠之间存在一个什么确定的数量关系?并证明你的结论.(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图)分别与AB 、CD 相交于点1M 和点1N 时,作1PM B ∠的角平分线1M Q 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q∠∠的值变不变?若不变,请求出其值;若变化,请说明理由.24.如图1,点E 在直线AB 、DC 之间,且180DEB ABE CDE ∠+∠-∠=︒.(1)求证://AB DC ;(2)若点F 是直线BA 上的一点,且BEF BFE ∠=∠,EG 平分DEB ∠交直线AB 于点G ,若20D ∠=︒,求FEG ∠的度数;(3)如图3,点N 是直线AB 、DC 外一点,且满足14CDM CDE ∠=∠,14ABN ABE ∠=∠,ND 与BE 交于点M .已知()012CDM αα∠=︒<<︒,且//BN DE ,则NMB ∠的度数为______(请直接写出答案,用含α的式子表示).25.如图,已知直线12//l l ,点A B 、在直线1l 上,点C D 、在直线2l 上,点C 在点D 的右侧,()80,2,ADC ABC n BE ∠=︒∠=︒平分,ABC DE ∠平分ADC ∠,直线BE DE 、交于点E .(1)若20n =时,则BED ∠=___________;(2)试求出BED ∠的度数(用含n 的代数式表示);(3)将线段BC 向右平行移动,其他条件不变,请画出相应图形,并直接写出BED ∠的度数.(用含n 的代数式表示)【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据平移的性质逐一判定即可.【详解】解:∵将ABC 沿BC 向右平移2个单位得到DEF ,∴AC //DF ,AC =DF ,AB =DE ,BC =EF ,AD =BE =CF =2,∠BAC =∠EDF =90°, ∴ED ⊥DF ,四边形ABFD 的周长=AB +BC +CF +DF +AD =12+2+2=16.∵S △ABC =S △DEF ,∴S △ABC ﹣S △OEC =S △DEF ﹣S △OEC ,∴S 四边形ABEO =S 四边形CFDO ,即结论正确的有4个.故选:D.【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了平移的距离以及图形的面积.2.A解析:A【分析】过三角板60°角的顶点作直线EF∥AB,则EF∥CD,利用平行线的性质,得到∠3+∠4=∠1+∠2=60°,代入计算即可.【详解】如图,过三角板60°角的顶点作直线EF∥AB,∵AB∥CD,∴EF∥CD,∴∠3=∠1,∠4=∠2,∵∠3+∠4=60°,∴∠1+∠2=60°,∵∠1=25°,∴∠2=35°,故选A.【点睛】本题考查了平行线的辅助线构造,平行线的判定与性质,三角板的意义,熟练掌握平行线的判定与性质是解题的关键.3.C解析:C【详解】解:①∵∠B+∠BCD=180°,∴AB∥CD;②∵∠1=∠2,∴AD∥BC;③∵∠3=∠4,∴AB∥CD;④∵∠B=∠5,∴AB∥CD;∴能得到AB∥CD的条件是①③④.故选C.【点睛】此题主要考查了平行线的判定,解题关键是合理利用平行线的判定,确定同位角、内错角、同旁内角. 平行线的判定:同旁内角互补,两直线平行;内错角相等,两直线平行;同位角相等,两直线平行.4.C解析:C【分析】过C作CD∥AB,过M作MN∥EF,推出AB∥CD∥MN∥EF,根据平行线的性质得出α+∠BCD=180°,∠DCM=∠CMN,∠NMF=γ,求出∠BCD=180°-α,∠DCM=∠CMN=β-γ,即可得出答案.【详解】过C作CD∥AB,过M作MN∥EF,∵AB∥EF,∴AB∥CD∥MN∥EF,∴α+∠BCD=180°,∠DCM=∠CMN,∠NMF=γ,∴∠BCD=180°-α,∠DCM=∠CMN=β-γ,∴x=∠BCD+∠DCM=180αγβ︒--+,故选:C.【点睛】本题考查了平行线的性质的应用,主要考查了学生的推理能力.5.B解析:B【分析】AD∥BC,∠D=∠ABC,则AB∥CD,则∠AEF=180°-∠AED-∠BEG=180°-2β,在△AEF中,100°+2α+180°-2β=180°,故β-α=40°,即可求解.【详解】解:设FBE=∠FEB=α,则∠AFE=2α,∠FEH的角平分线为EG,设∠GEH=∠GEF=β,AD∥BC,∴∠ABC+∠BAD=180°,而∠D=∠ABC,∴∠D+∠BAD=180°,∴AB∥CD,∠DEH=100°,则∠CEH=∠FAE=80°,∠AEF=180°-∠FEG-∠BEG=180°-2β,在△AEF中,在△AEF中,80°+2α+180-2β=180°故β-α=40°,而∠BEG=∠FEG-∠FEB=β-α=40°,故选:B.【点睛】此题考查平行线的性质,解题关键是落脚于△AEF内角和为180°,即100°+2α+180°-2β=180°,题目难度较大.6.B解析:B【分析】过点P作MN∥AB,结合垂直的定义和平行线的性质求∠EPF的度数.【详解】解:如图,过点P作MN∥AB,∵∠AEP=40°,∴∠EPN=∠AEP=40°∵AB∥CD,PF⊥CD于F,∴PF⊥MN,∴∠NPF=90∴∠EPF=∠EPN+∠NPF=40°+90°=130°故答案为B【点睛】本题考查了平行线的判定定理和性质,作出辅助线构造平行线是解答本题的关键.7.C解析:C【分析】根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.【详解】解:(1)如图1,由AB∥CD,可得∠AOC=∠DCE1=β,∵∠AOC=∠BAE1+∠AE1C,∴∠AE1C=β﹣α.(2)如图2,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,∴∠AE2C=α+β.(3)如图3,由AB∥CD,可得∠BOE3=∠DCE3=β,∵∠BAE3=∠BOE3+∠AE3C,∴∠AE3C=α﹣β.(4)如图4,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,∴∠AE4C=360°﹣α﹣β.综上所述,∠AEC的度数可能是β﹣α,α+β,α﹣β,360°﹣α﹣β.故选:C.【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.8.D解析:D【分析】分别任选其中两个条件作为已知,然后结合平行线的判定与性质,证明剩余一个条件是否成立即可.【详解】解:如图所示:(1)当①∠1=∠2,则∠3=∠2,故DB∥EC,则∠D=∠4;当②∠C=∠D,故∠4=∠C,则DF∥AC,可得:∠A=∠F,即①②可证得③;(2)当①∠1=∠2,则∠3=∠2,故DB∥EC,则∠D=∠4,当③∠A=∠F,故DF∥AC,则∠4=∠C,故可得:∠C=∠D,即①③可证得②;(3)当③∠A=∠F,故DF∥AC,则∠4=∠C,当②∠C=∠D,则∠4=∠D,故DB∥EC,则∠2=∠3,可得:∠1=∠2,即②③可证得①.故正确的有3个.故选:D.【点睛】本题主要考查了平行线的判定和性质,正确掌握并熟练运用平行线的判定与性质是解题关键.9.C解析:C【分析】首先证明a∥b,推出∠4=∠5,求出∠5即可.【详解】解:∵∠1=∠2,∴a∥b,∴∠4=∠5,∵∠5=180°﹣∠3=55°,∴∠4=55°,故选:C.【点睛】本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型.10.C解析:C【分析】首先由两个角的两边分别平行,可得这两个角相等或互补.然后设其中一角为x°,由其中一个角比另一个角的3倍少20°,然后分别从两个角相等与互补去分析,即可求得答案,注意别漏解.【详解】解:∵两个角的两边分别平行,∴这两个角相等或互补.设其中一角为x°,若这两个角相等,则x=3x﹣20,解得:x=10,∴这两个角的度数是10°和10°;若这两个角互补,则180﹣x=3x﹣20,解得:x=50,∴这两个角的度数是50°和130°.∴这两个角的度数是50°、130°或10°、10°.故选:C.【点睛】此题考查了平行线的性质与一元一次方程的解法.此题难度适中,解题的关键是掌握如果两个角的两边分别平行,则这两个角相等或互补,注意方程思想的应用.二、填空题11.【分析】先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;根据∠ABE和∠DCE的平分线交点为E1,解析:12n α⎛⎫⎪⎝⎭【分析】先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;根据∠ABE和∠DCE的平分线交点为E1,则可得出∠CE1B=∠ABE1+∠DCE1=12∠ABE+12∠DCE=12∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=12∠ABE1+12∠DCE1=12∠CE1B=14∠BEC;根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C=18∠BEC;…据此得到规律∠E n=n12∠BEC,最后求得度数.【详解】如图1,过E作EF∥AB.∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2.∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE;如图2:∵∠ABE 和∠DCE 的平分线交点为E 1,∴∠CE 1B =∠ABE 1+∠DCE 1=12∠ABE +12∠DCE =12∠BEC .∵∠ABE 1和∠DCE 1的平分线交点为E 2,∴∠BE 2C =∠ABE 2+∠DCE 2=12∠ABE 1+12∠DCE 1=12∠CE 1B =14∠BEC ; ∵∠ABE 2和∠DCE 2的平分线,交点为E 3,∴∠BE 3C =∠ABE 3+∠DCE 3=12∠ABE 2+12∠DCE 2=12∠CE 2B =18∠BEC ; …以此类推,∠E n =n12∠BEC , ∵BEC α∠=, ∴n E ∠的度数是12n⎛⎫ ⎪⎝⎭α. 故答案为:12n ⎛⎫ ⎪⎝⎭α. 【点睛】本题考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线. 12.45°或135°【分析】根据题意画出图形,然后利用平行线的性质得出∠EMF 与∠AEM 和∠CFM 的关系,然后可得答案.【详解】解:如图1,过作,,,,,,,同理可得,由折叠可解析:45°或135°【分析】根据题意画出图形,然后利用平行线的性质得出∠EMF 与∠AEM 和∠CFM 的关系,然后可得答案.【详解】解:如图1,过M 作//MN AB ,//AB CD ,////AB CD NM ∴,AEM EMN ∴∠=∠,NMF MFC ∠=∠,90EMF ∠=︒,90AEM CFM ∴∠+∠=︒,同理可得P AEP CFP ∠=∠+∠, 由折叠可得:12AEP PEM AEM ∠=∠=∠,12PFC PFM CFM ∠=∠=∠, 1()452P AEM CFM ∴∠=∠+∠=︒, 如图2,过M 作//MN AB ,//AB CD ,////AB CD NM ∴,180AEM EMN ∴∠+∠=︒,180NMF MFC ∠+∠=︒,360AEM EMF CFM ∴∠+∠+∠=︒,90EMF ∠=︒,36090270AEM CFM ∴∠+∠=︒-︒=︒, 由折叠可得:12AEP PEM AEM ∠=∠=∠,12PFC PFM CFM ∠=∠=∠, 12701352P ∴∠=︒⨯=︒, 综上所述:EPF ∠的度数为45︒或135︒,故答案为:45°或135°.【点睛】本题主要考查了平行线的性质,关键是正确画出图形,分两种情况分别计算出∠EPF 的度数.13.4【分析】到的距离是2的点,在与平行且与的距离是2的两条直线上;同理,点在与的距离是1的点,在与平行,且到的距离是1的两直线上,四条直线的距离有四个交点.因而满足条件的点有四个.【详解】解:解析:4【分析】到1l 的距离是2的点,在与1l 平行且与1l 的距离是2的两条直线上;同理,点M 在与2l 的距离是1的点,在与2l 平行,且到2l 的距离是1的两直线上,四条直线的距离有四个交点.因而满足条件的点有四个.【详解】解:到1l 的距离是2的点,在与1l 平行且与1l 的距离是2的两条直线上;到2l 的距离是1的点,在与2l 平行且与2l 的距离是1的两条直线上;以上四条直线有四个交点,故“距离坐标”是(2,1)的点共有4个.故答案为:4.【点睛】本题主要考查了到直线的距离等于定长的点的集合.14.30或110【分析】分两种情况讨论:两束光平行;两束光重合之后(在灯B射线到达BQ之前)平行,然后利用平行线的性质求解即可.【详解】解:设灯转动t秒,两灯的光束互相平行,即AC∥BD,①当解析:30或110【分析】分两种情况讨论:两束光平行;两束光重合之后(在灯B射线到达BQ之前)平行,然后利用平行线的性质求解即可.【详解】解:设灯转动t秒,两灯的光束互相平行,即AC∥BD,①当0<t≤90时,如图1所示:∵PQ∥MN,则∠PBD=∠BDA,∵AC∥BD,则∠CAM=∠BDA,∴∠PBD=∠CAM有题意可知:2t=30+t解得:t=30,②当90<t<150时,如图2所示:∵PQ∥MN,则∠PBD+∠BDA=180°,∵AC∥BD,则∠CAN=∠BDA,∴∠PBD+∠CAN=180°,∴30+t+(2t-180)=180解得:t=110综上所述,当t=30秒或t=110秒时,两灯的光束互相平行.故答案为:30或110【点睛】本题主要考查补角、角的运算、平行线的性质的应用,解题的关键是熟练掌握平行线的性质,注意分两种情况谈论.15.80【详解】如图,根据角平分线的性质和平行线的性质,可知∠FMA=∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE=2∠FMA,即∠E=2∠F=2×40°=80°.故答案为80.解析:80【详解】如图,根据角平分线的性质和平行线的性质,可知∠FMA=12∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE=2∠FMA,即∠E=2∠F=2×40°=80°.故答案为80.16.【分析】根据题意可得,设,分别表示出,进而根据平行线的性质可得∠DFB.【详解】∠A=(60﹣x)°,∠ADC=(120+x)°,,,,,,BE 平分∠CBF ,,设,∠DB解析:62︒【分析】根据题意可得//AB CD ,设EBF EBC α∠=∠=,分别表示出,ABD DBF ∠∠,进而根据平行线的性质可得∠DFB .【详解】∠A =(60﹣x )°,∠ADC =(120+x )°,180A ADC ∴∠+∠=︒,//AB CD ∴,CDB ABD ∴∠=∠,CDB CBD ∠=∠,ABD CBD ∴∠=∠,BE 平分∠CBF ,EBF EBC ∴∠=∠,设EBF EBC α∠=∠=,∠DBE =59°,∴59DBF α∠=︒-,59ABD DBC α∴∠=∠=︒+,5959118ABF ABD DBF αα∴∠=∠+∠=︒++︒-=︒,//AB CD ,180********DFB ABF ∴∠=︒-∠=︒-︒=︒.故答案为:62︒.【点睛】本题考查了平行线的判定与性质,角平分线的定义,证明//AB CD 是解题的关键. 17.140°【分析】延长DE 交AB 的延长线于G ,根据两直线平行,内错角相等可得∠D =∠AGD ,再根据两直线平行,同位角相等可得∠AGD =∠ABF ,然后根据角平分线的定义得∠EBF =∠ABF ,再根据平解析:140°【分析】延长DE 交AB 的延长线于G ,根据两直线平行,内错角相等可得∠D =∠AGD ,再根据两直线平行,同位角相等可得∠AGD =∠ABF ,然后根据角平分线的定义得∠EBF =∠ABF ,再根据平行线的性质解答.【详解】解:如图,延长DE 交AB 的延长线于G ,∵//AB CD ,∴∠D =∠AGD =40°,∵BF //DE ,∴∠AGD =∠ABF =40°,∵BF 平分∠ABE ,∴∠EBF =∠ABF =40°,∵BF //DE ,∴∠BED =180°﹣∠EBF =140°.故答案为:140°.【点睛】本题考查了平行线的性质,角平分线的定义,熟记性质并作辅助线是解题的关键. 18.33【分析】根据求出∠C=90°,再求出∠BAD=66°,根据角平分线性质得∠DAE=33°,由三角形的外角性质得∠ADE=114°,最后由三角形内角和定理可得结论.【详解】解:∵,,∴∠解析:33【分析】根据//AB DE 求出∠C=90°,再求出∠BAD=66°,根据角平分线性质得∠DAE=33°,由三角形的外角性质得∠ADE=114°,最后由三角形内角和定理可得结论.【详解】解:∵//AB DE ,AD AB ⊥,∴∠180BAD D ∠+∠=︒,且90BAD ∠=︒∴90D ∠=︒∵∠CAD =24°∴∠BAC =90°-∠CAD =90°-24°=66°,∵AE 是∠BAC 的平分线∴∠EAB =11663322BAC ∠=⨯︒=︒ ∵//AB DE ,∴33E EAB ∠=∠=︒故答案为:33【点睛】此题主要考查了平行线的性质,角平分线的定义,准确识图,灵活运用相关知识是解题的关键.19.28【分析】根据平移的性质求出,再由长方形的周长公式求解即可.【详解】解:由题意可知,四边形是正方形,∴,,又∵长方形由长方形平移得到,∴∵∴四边形的周长为:故答案为:28【点解析:28【分析】根据平移的性质求出10BC '=,再由长方形的周长公式求解即可.【详解】解:由题意可知,四边形ABB A ''是正方形,∴4BB AB '==,642B C BC '==-=,又∵长方形A B C D ''''由长方形ABCD 平移得到,∴6B C BC ''==∵4610BC BB B C ''''=+=+=∴四边形ABC D '的周长为:(104)228+⨯=故答案为:28【点睛】此题主要考查了平移的性质,求出10BC '=是解答此题的关键.20.131【分析】过点C 作CH ∥MN ,根据平行线的性质求出∠NEC 即可.【详解】解:过点C 作CH ∥MN ,∵,∴CH ∥PQ ,∴,∵,∴,∵CH ∥MN ,∴,∴故答案为:131.解析:131【分析】过点C 作CH ∥MN ,根据平行线的性质求出∠NEC 即可.【详解】解:过点C 作CH ∥MN ,∵//MN PQ ,∴CH ∥PQ ,∴26HCB BGF ∠=∠=︒,∵75ACB ∠=︒,∴49ACH ∠=︒,∵CH ∥MN ,∴49CEN ACH ∠=∠=︒,∴131180CEN AEN ∠︒∠==︒-故答案为:131.【点睛】本题考查了平行线的性质与判定,解题关键是恰当作平行线,根据平行线的性质进行推理计算.三、解答题21.(1)见解析;(2)12;(3)75°【分析】(1)根据平行线的性质、余角和补角的性质即可求解.(2)根据平行线的性质、对顶角的性质和平角的定义解答即可.(3)根据平行线的性质和角平分线的定义以及三角形内角和解答即可.【详解】解:(1)∠C=∠1+∠2,证明:过C作l∥MN,如下图所示,∵l∥MN,∴∠4=∠2(两直线平行,内错角相等),∵l∥MN,PQ∥MN,∴l∥PQ,∴∠3=∠1(两直线平行,内错角相等),∴∠3+∠4=∠1+∠2,∴∠C=∠1+∠2;(2)∵∠BDF=∠GDF,∵∠BDF=∠PDC,∴∠GDF=∠PDC,∵∠PDC+∠CDG+∠GDF=180°,∴∠CDG+2∠PDC=180°,∴∠PDC=90°-12∠CDG,由(1)可得,∠PDC+∠CEM=∠C=90°,∴∠AEN=∠CEM,∴190(90)90122CDGAEN CEM PDCCDG CDG CDG CDG︒-︒-∠∠∠︒-∠====∠∠∠∠,(3)设BD交MN于J.∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°,∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,∵PQ∥MN,∴∠BJA=∠PBD=50°,∴∠ADB=∠AJB-∠JAD=50°-∠JAD=50°-∠CAM,由(1)可得,∠ACB=∠PBC+∠CAM,∴∠ACB+∠ADB=∠PBC+∠CAM+50°-∠CAM=25°+50°=75°.【点睛】本题考查了平行线的性质、余角和补角的性质,解题的关键是根据平行找出角度之间的关系.22.(1)证明见解析;(2)补图见解析;当点C 在AG 上时,290AHB CBG ∠-∠=︒;当点C 在DG 上时,290AHB CBG ∠+∠=︒.【分析】(1)过点G 作//GE MN ,根据平行线的性质即可求解;(2)分两种情况:当点C 在AG 上,当点C 在DG 上,再过点H 作//HF MN 即可求解.【详解】(1)证明:如图,过点G 作//GE MN ,∴MAG AGE ∠=∠,∵//MN PQ ,∴//GE PQ .∴PBG BGE ∠=∠.∵BG AD ⊥,∴90AGB ∠=︒,∴90MAG PBG AGE BGE AGB ∠+∠=∠+∠=∠=︒.(2)补全图形如图2、图3,猜想:290AHB CBG ∠-∠=︒或290AHB CBG ∠+∠=︒.证明:过点H 作//HF MN .∴1AHF ∠=∠.∵//MN PQ ,∴//HF PQ∴2BHF ∠=∠,∴12AHB AHF BHF ∠=∠+∠=∠+∠.∵AH 平分MAG ∠,∴21MAG ∠=∠.如图3,当点C 在AG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠+∠=∠,∵//MN PQ ,∴MAG GDB ∠=∠,2212290AHB MAG PBG CBGGDB PBG CBG CBG∴∠=∠+∠=∠+∠+∠=∠+∠+∠=︒+∠即290AHB CBG ∠-∠=︒.如图2,当点C 在DG 上时,∵BH 平分PBC ∠,∴22PBC PBG CBG ∠=∠-∠=∠.∴2212290AHB MAG PBG CBG CBG ∠=∠+∠=∠+∠-∠=︒-∠.即290AHB CBG ∠+∠=︒.【点睛】本题考查了平行线的基本性质、角平分线的基本性质及角的运算,解题的关键是准确作出平行线,找出角与角之间的数量关系.23.(1)35,35,平行;(2)∠FMN +∠GHF =180°,证明见解析;(3)不变,2【分析】(1)根据(α-35)2+|β-α|=0,即可计算α和β的值,再根据内错角相等可证AB ∥CD ; (2)先根据内错角相等证GH ∥PN ,再根据同旁内角互补和等量代换得出∠FMN +∠GHF =180°;(3)作∠PEM 1的平分线交M 1Q 的延长线于R ,先根据同位角相等证ER ∥FQ ,得∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y ,得出∠EPM 1=2∠R ,即可得1FPN Q∠∠=2. 【详解】解:(1)∵(α-35)2+|β-α|=0,∴α=β=35,∴∠PFM =∠MFN =35°,∠EMF =35°,∴∠EMF =∠MFN ,∴AB ∥CD ;(2)∠FMN +∠GHF =180°;理由:由(1)得AB ∥CD ,∴∠MNF =∠PME ,∵∠MGH =∠MNF ,∴∠PME =∠MGH ,∴GH ∥PN ,∴∠GHM =∠FMN ,∵∠GHF +∠GHM =180°,∴∠FMN +∠GHF =180°;(3)1FPN Q∠∠的值不变,为2, 理由:如图3中,作∠PEM 1的平分线交M 1Q 的延长线于R ,∵AB ∥CD ,∴∠PEM 1=∠PFN ,∵∠PER =12∠PEM 1,∠PFQ =12∠PFN ,∴∠PER =∠PFQ ,∴ER ∥FQ ,∴∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y ,则有:122y x Ry x EPM ⎧⎨⎩=+∠=+∠, 可得∠EPM 1=2∠R ,∴∠EPM 1=2∠FQM 1,∴11EPM FQM ∠∠=1FPN Q∠∠=2. 【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.24.(1)见解析;(2)10°;(3)18015α︒-【分析】(1)过点E 作EF ∥CD ,根据平行线的性质,两直线平行,内错角相等,得出,CDE DEF ∠=∠结合已知条件180DEB ABE CDE ∠+∠-∠=︒,得出180,FEB ABE ∠+∠=︒即可证明;(2)过点E 作HE ∥CD ,设,,GEF x FEB EFB y ∠=∠=∠= 由(1)得AB ∥CD ,则AB ∥CD ∥HE ,由平行线的性质,得出20,DEF D EFB y ∠=∠+∠=︒+再由EG 平分DEB ∠,得出,DEG GEB GEF FEB x y ∠=∠=∠+∠=+则2DEF DEG GEF x y ∠=∠+∠=+,则可列出关于x 和y 的方程,即可求得x ,即GEF ∠的度数;(3)过点N 作NP ∥CD ,过点M 作QM ∥CD ,由(1)得AB ∥CD ,则NP ∥CD ∥AB ∥QM ,根据14CDM CDE ∠=∠和CDM α∠=,得出3,MDE α∠=根据CD ∥PN ∥QM ,DE ∥NB ,得出,PND CDM DMQ α∠=∠=∠=3,EDM BNM α∠=∠=即4,BNP α∠=根据NP ∥AB ,得出4,PNB ABN α∠=∠=再由14ABN ABE ∠=∠,得出16,ABM α∠=由AB ∥QM ,得出18016,QMB α∠=︒-因为NMB NMQ QMB ∠=∠+∠,代入α的式子即可求出BMN ∠.【详解】(1)过点E 作EF ∥CD ,如图,∵EF ∥CD ,∴,CDE DEF ∠=∠∴,DEB CDE DEB DEF FEB ∠-∠=∠-∠=∠∵180DEB ABE CDE ∠+∠-∠=︒,∴180,FEB ABE ∠+∠=︒∴EF ∥AB ,∴CD ∥AB ;(2)过点E 作HE ∥CD ,如图,设,,GEF x FEB EFB y ∠=∠=∠=由(1)得AB ∥CD ,则AB ∥CD ∥HE ,∴20,,D DEH HEF EFB y ∠=∠=︒∠=∠=∴20,DEF DEH HEF D EFB y ∠=∠+∠=∠+∠=︒+又∵EG 平分DEB ∠,∴,DEG GEB GEF FEB x y ∠=∠=∠+∠=+∴2,DEF DEG GEF x y x x y ∠=∠+∠=++=+即220,x y y +=︒+解得:10,x =︒即10GEF ∠=︒;(3)过点N 作NP ∥CD ,过点M 作QM ∥CD ,如图,由(1)得AB ∥CD ,则NP ∥CD ∥AB ∥QM ,∵NP ∥CD ,CD ∥QM ,,CDM α∠=∴PND CDM DMQ α∠=∠=∠=,又∵14CDM CDE ∠=∠, ∴33,MDE CDM α∠=∠=∵//BN DE ,∴3,MDE BNM α∠=∠=∴34,PNB PND BNM ααα∠=∠+∠=+=又∵PN ∥AB ,∴4,PNB NBA α∠=∠= ∵14ABN ABE ∠=∠, ∴44416,ABM ABN αα∠=∠=⨯=又∵AB ∥QM ,∴180,ABM QMB ∠+∠=︒∴18018016,QMB ABM α∠=︒-∠=︒-∴1801618015NMB NMQ QMB ααα∠=∠+∠=+︒-=-.【点睛】本题考查平行线的性质,角平分线的定义,解决问题的关键是作平行线构造相等的角,利用两直线平行,内错角相等,同位角相等来计算和推导角之间的关系.25.(1)60°;(2)n °+40°;(3)n °+40°或n °-40°或220°-n °【分析】(1)过点E 作EF ∥AB ,然后根据两直线平行内错角相等,即可求∠BED 的度数; (2)同(1)中方法求解即可;(3)分当点B 在点A 左侧和当点B 在点A 右侧,再分三种情况,讨论,分别过点E 作EF ∥AB ,由角平分线的定义,平行线的性质,以及角的和差计算即可.【详解】解:(1)当n =20时,∠ABC =40°,过E 作EF ∥AB ,则EF ∥CD ,∴∠BEF =∠ABE ,∠DEF =∠CDE ,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠BEF =∠ABE =20°,∠DEF =∠CDE =40°,∴∠BED =∠BEF +∠DEF =60°;(2)同(1)可知:∠BEF=∠ABE=n°,∠DEF=∠CDE=40°,∴∠BED=∠BEF+∠DEF=n°+40°;(3)当点B在点A左侧时,由(2)可知:∠BED=n°+40°;当点B在点A右侧时,如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=2n°,∠ADC=80°,∴∠ABE=12∠ABC=n°,∠CDG=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=∠ABE=n°,∠CDG=∠DEF=40°,∴∠BED=∠BEF-∠DEF=n°-40°;如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=2n°,∠ADC=80°,∴∠ABE=12∠ABC=n°,∠CDG=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=180°-∠ABE=180°-n°,∠CDE=∠DEF=40°,∴∠BED=∠BEF+∠DEF=180°-n°+40°=220°-n°;如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,∴∠ABG=12∠ABC=n°,∠CDE=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=∠ABG=n°,∠CDE=∠DEF=40°,∴∠BED=∠BEF-∠DEF=n°-40°;综上所述,∠BED的度数为n°+40°或n°-40°或220°-n°.【点睛】此题考查了平行线的判定与性质,以及角平分线的定义,正确应用平行线的性质得出各角之间关系是解题关键.。
平行线相交线 培优

第5题 A FE C B D 第6题 E D CB A γβα平行线相交线培优1.如图, l 1∥l 2,∠1 = 105°,∠2 = 140°,则∠α = .2.如图2,是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2= 度.3.如图3,a b ∥,M N ,分别在a b ,上,P 为两平行线间一点,那么123∠+∠+∠=4.用等腰直角三角板画45AOB =∠,并将三角板沿OB 方向平移到如图4所示的虚线处后绕点M 逆时针方向旋转22,则三角板的斜边与射线OA 的夹角α为______.5.如图,将一副三角板如图放置,使点A 在DE 上,BC//DE ,则AFC 的度数为________第4题 6. 如图所示,已知AB//CD ,则α、β、γ之间的等量关系为_______________7.如图7,把长方形纸片沿EF 折叠,使D ,C 分别落在D ',C '的位置,若65EFB =∠,则AED '∠等于( )A.50 B.BA CD EF G MNC.60 D.658.如图,把长方形纸片ABCD 沿EF 折叠,若∠EFG=50º, (1)找出图中也是50º的角;(2)说明∠FGM=2∠EFG=100º的理由.ab MP N 12 3第1题第2题 第3题 BA CD EF G MN12O M B A 22 α9.如图,AB//CD ,试解决下列问题:⑴∠1+∠2=___ __;⑵∠1+∠2+∠3=___ __; ⑶试探究∠1+∠2+∠3+∠4+…+∠n = .10.已知:如图,AB ∥CD ,求证:∠B+∠D+∠F=∠E+∠G11.如图,直线AC ∥BD ,连结AB ,直线AC 、BD 及线段AB 把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P 落在某个部分时,连结PA 、PB ,构成∠PAC 、∠APB 、∠PBD 三个角.(提示:有公共端点的两条重合的射线所组成的角是0°) (1)当动点P 落在第①部分时,求证:∠APB =∠PAC +∠PBD ;(2)当动点P 落在第②部分时,∠APB =∠PAC +∠PBD 是否成立(直接回答成立或不成立)?(3)当动点P 落在第③部分时,全面探究∠PAC 、∠APB 、∠PBD 之间的关系,并写出动点P 的具体位置和相应的结论.选择其中一种结论加以证明.12.如图,四个矩形的长均为a ,宽均为b 。
人教版七年级下册数学《命题、定理、证明》相交线与平行线培优说课教学复习课件

题设是已知事项,结论是由已知事项推出的事项.
许多数学命题常可以写成 “如果……,那么……”的形式 .“ 如果”后面连接的部分是题设,“那么”后面连接的部分就 是结论.
例题
下列语句是命题吗?如果是,请将它们改写成 “ 如果……,
那么……” 的形式 . (1)两条直线被第三条直线所截,同旁内角互补;
B
3.下列句子哪些是命题?是命题的,指出是真命题还
是假命题?
(1)一条狗有四只脚;是
(2)内错角相等; 是 (3)画一条直线; 否 (4)四边形是正方形;是
真命题 假命题
假命题
(5)你的黑板报做完了吗?否
(6)内错角相等,两直线平行; 是 真命题
(7)平行于同一直线的两直线平行; 是 (8)过点P画线段MN的垂线; 否 (9)x<3. 否
1、基本事实 数学中有些命题的正确性是人们在长期实践中总结出 来的,并把它们作为判断其他命题真假的原始依据, 这样的真命题叫做基本事实.
直线的基本事实: 两点确定一条直线. 线段的基本事实: 两点间线段最短. 平行线的基本事实:经过直线外的一点有且仅有一条直线
与已知直线平行.
2、定理的概念 有些命题是基本事实,还有些命题它们的正确性是经 过推理证实的,这样得到的真命题叫做定理.定理也 可以作为继续推理的依据.
是假命题 ,可以举出如下反例:
A
如图,OC是∠AOB的平分线, ∠1=∠2,但它们不是对顶角. O
))12
C
B
确定一个命题是假命题的方法:
只要举出一个例子(反例):它符合命题
的题设,但不满足结论即可.
随堂训练
1.下列命题是假命题的是( A ) A.同位角相等 B.对顶角相等 C.钝角三角形有两个锐角 D.两直线平行,内错角相等
相交线与平行线(培优)-教师版

七年级下册数学培优——相交线与平行线例1.平面上n 条直线两两相交且无3条或3条以上直线共点,有多少个不同交点 解:2条直线产生1个交点,第3条直线与前面2条均相交,增加2个交点,这时平面上3条直线共有1+2=3个交点; 第4条直线与前面3条均相交,增加3个交点,这时平面上4条直线共有1+2+3=6个交点; …则 n 条直线共有交点个数:1+2+3+…+ (n-1)=21n(n-1) 评注:此题是平面上n 条直线交点个数最多的情形,需要仔细观察,由简及繁,深入思考,从中发现规律。
例2.6个不同的点,其中只有3点在同一条直线上,2点确定一条直线,问能确定多少条直线 解:6条不同的直线最多确定:5+4+3+2+1=15条直线,除去共线的3点中重合多算的2条直线,即能确定的直线为15-2=13条。
另法:3点所在的直线外的3点间最多能确定3条直线,这3点与直线上的3点最多有3×3=9条直线,加上3点所在的直线共有:3+9+1=13条评注:一般地,平面上n 个点最多可确定直线的条数为:1+2+3+…+(n-1)=21n(n-1) 例3.10条直线两两相交,最多将平面分成多少块不同的区域解:2条直线最多将平面分成2+2=4个不同区域;3条直线中的第3条直线与另两条直线相交,最多有两个交点,此直线被这两点分成3段,每一段将它所在的区域一分为二,则区域增加3个,即最多分成2+2+3=7个不同区域; 同理:4条直线最多分成2+2+3+4=11个不同区域;…∴ 10条直线最多分成2+2+3+4+5+6+7+8+9+10=56个不同区域 推广:n 条直线两两相交,最多将平面分成2+2+3+4+…+n=1+21n(n+1)=21(n 2+n+2)块不同的区域 思考:平面内n 个圆两两相交,最多将平面分成多少块不同的区域例4、两条直线相交于一点,所形成的的角中有2对对顶角,4对邻补角,那么,三条直线相交于一点时,有多少对对顶角,多少对邻补角四条直线相交于一点时,有多少对对顶角,多少对邻补角n 条直线相交于一点时,有多少对对顶角,多少对邻补角)条A .6B . 7C .8D .9解析: 5个点中任取2点,可以作4+3+2+1=10条直线,在一直线上的3个点中任取2点,可作2+1=3条,共可作10-3+1=8(条)故选C例6.平面上三条直线相互间的交点个数是 ( ) A .3 B .1或3 C .1或2或3 D .不一定是1,2,3 解析:平面上3条直线可能平行或重合。
《第5章相交线与平行线》期末复习培优训练(附答案) 2020-2021学年七年级数学人教版下册

2021年人教版七年级数学下册《第5章相交线与平行线》期末复习培优训练(附答案)1.一辆汽车在笔直的公路上行驶,在两次转弯后,前进的方向仍与原来相同,那么这两次转弯的角度可以是()A.先右转45°,再左转45°B.先左转45°,再右转135°C.先左转45°,再左转45°D.先右转45°,再右转135°2.两个角的一组对应边同向平行,另一组对应边反向平行,且这两个角的度数比是5:31,则两个角的度数是()A.150°30°B.140°40°C.25°155°D.135°45°3.如图所示,将一张长方形纸片ABCD沿着直线EF折叠,A、B两点分别落在A′、B′处,若∠AEA′=70°,则∠BFE的角度为()A.40°B.35°C.45°D.30°4.如图,AB∥DE,BC⊥CD,则以下说法中正确的是()A.α,β的角度数之和为定值B.α,β的角度数之积为定值C.β随α增大而增大D.β随α增大而减小5.如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF∥HC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①AD∥BC;②GK平分∠AGC;③∠E+∠EAG+∠HCK=180°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有()A.4个B.3个C.2个D.1个6.某学生上学路线如图所示,他总共拐了三次弯,最后行车路线与开始的路线相互平行,已知第一次转过的角度,第三次转过的角度,则第二次拐弯角(∠1)的度数是()A.55°B.70°C.80°D.90°7.如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.从C村到D村的公路平行于从A村到B村的公路,则C,D两村与B,C两村公路之间夹角的度数为()A.100°B.80°C.75°D.50°8.如图所示,∠1=∠2=∠3=55°,则∠4的补角的度数为()A.55°B.75°C.105°D.125°9.如图,AB∥DC,∠ABD=30°,∠ADB=85°,求∠ADC和∠A的角度.10.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.11.如图,AB∥DF,DE∥BC,∠1=65°,求∠2、∠3的度数.12.如图,AB∥CD,∠1=50°,∠2=110°,求∠3的度数.13.如图,CD平分∠ACB,DE∥BC,∠AED=46°,求∠CDE的度数.14.如图,AC∥ED,AB∥FD,∠A=64°,求∠EDF的度数.15.如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上.若∠2=50°,求∠1的大小.16.如图,∠B、∠D的两边分别平行.(1)在图①中,∠B与∠D的数量关系是什么?为什么?(2)在图②中,∠B与∠D的数量关系是什么?为什么?(3)由(1)(2)可得结论;(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少30°,求这两个角的度数.17.直线AB∥CD,E、F分别是直线AB、CD上的点.(1)如图1,若G是在直线AB和直线CD内部,在EF的右侧一点,证明:∠G=∠GEB+∠GFD.(2)如图2,EF⊥AB,射线EI从射线EB位置出发,绕着点E以10度/秒的角速度顺时针旋转.射线FH从射线FD位置出发,绕着点F以15度/秒的角速度逆时针旋转.两条射线同时出发,当射线FH转完一周的时候两射线同时停止.请问在保证射线FH和射线EI有交点G的前提下,过几秒钟时,∠EGF=50°?18.如图,已知AM∥BN.C为直线BN上一点,且∠MAC=70°,∠ABC=80°.点P从A出发,沿AM方向运动,∠P AC与∠PBC的角平分线相交于点D.探究一:①当∠ABP=20°时,求角ADB的度数;聪明的小华看到这一问题,采用了如下解题方法:如图2,过点D作DE∥AM,于是,他很快就得到了正确答案,即∠ADB=.探究二:设∠ABP=α,∠ADB=β,试探究:①若β不小于α,求α的取值范围;②若点P运动的过程中,是否会出现α与β互补的情况?若会,请求出α与β的值;若不会,请说明理由.19.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°).(1)若∠DCE=40°,则∠ACB的度数为;(2)如图1,∠ACE=∠;若点E在AC的上方,设∠ACB=α(90°<α<180°),则∠DCE的度数为.(用含α的式子表示)(3)当∠ACE<180°且点E在直线AC的上方时,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两个三角尺的顶点C重合①当BE∥AC(如图2)时,直接写出∠ACE的度数是度.②当BC∥DA时,直接写出∠ACE的度数是度.(4)在(3)的条件下,当∠ACE<180°且点E在直线AC的上方,(3)中的两种情况除外,这两块三角板是否还存在一组边互相平行,若存在请直接写出此时∠ACE所有可能的角度数值为度,若不能请说明理由.20.(1)如图1,AB∥CD,点P在AB、CD外部,若∠B=60°,∠D=30°,则∠BPD =°;(2)如图2,AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;(3)在图2中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图3,若∠BPD=86°,∠BMD=40°,求∠B+∠D的度数.参考答案1.解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于方向仍与原来相同,所以平行前进,可以得到∠1=∠2.故选:A.2.解:如图,BC∥ED,AB∥EF,∠B:∠E=5:31,∴∠B=∠1,∠1+∠E=180°,∴∠B+∠E=180°,∵∠B:∠E=5:31,设∠B=5x,∠E=31x,∴5x+31x=180°,解得:x=5,∴∠B=25°,∠E=155°,故选:C.3.解:由平行线的性质得,∠AEA'=∠1=70°,∵AD∥BC,∴∠1=∠BFB'=70°,由折叠性质得,∠BFE=∠EFB'=∠BFB'=35°,故选:B.4.解:过C点作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠α=∠BCF,∠β+∠DCF=180°,∵BC⊥CD,∴∠BCF+∠DCF=90°,∴∠α+180°﹣∠β=90°,∴∠β﹣∠α=90°,∴β随α增大而增大,故选:C.5.解:∵∠EAD=∠D,∠B=∠D,∴∠EAD=∠B,∴AD∥BC,故①正确;∴∠AGK=∠CKG,∵∠CKG=∠CGK,∴∠AGK=∠CGK,∴GK平分∠AGC;故②正确;延长EF交AD于P,延长CH交AD于Q,∵EF∥CH,∴∠EPQ=∠CQP,∵∠EPQ=∠E+∠EAG,∴∠CQG=∠E+∠EAG,∵AD∥BC,∴∠HCK+∠CQG=180°,∴∠E+∠EAG+∠HCK=180°;故③正确;∵∠FGA的余角比∠DGH大16°,∴90°﹣∠FGA﹣∠DGH=16°,∵∠FGA=∠DGH,∴90°﹣2∠FGA=16°,∴∠FGA=∠DGH=37°,设∠AGM=α,∠MGK=β,∴∠AGK=α+β,∵GK平分∠AGC,∴∠CGK=∠AGK=α+β,∵GM平分∠FGC,∴∠FGM=∠CGM,∴∠FGA+∠AGM=∠MGK+∠CGK,∴37°+α=β+α+β,∴β=18.5°,∴∠MGK=18.5°,故④错误,故选:B.6.解:如图,延长ED交BF于C,∵BA∥DE,∴∠BCD=∠B=120°,∠FCD=60°,又∵∠FDE是△CDF的外角,∴∠1=∠FDE﹣∠DCF=150°﹣60°=90°,故选:D.7.解:由题意可得:AN∥FB,DC∥BE,∴∠NAB=∠FBE=75°,∵∠CBF=25°,∴∠CBE=100°,则∠DCB=180°﹣100°=80°.故选:B.8.解:∵∠1=∠2,∠2=∠5,∴∠1=∠5,∴a∥b,∴∠3=∠6=55°,∴∠4的补角的度数为55°,故选:A.9.解:∵AB∥DC,∠ABD=30°,∴∠BDC=∠ABD=30°,∵∠ADB=85°,∴∠ADC=∠ADB+∠BDC=115°,∠A=180°﹣(∠ADB+∠ABD)=65°.10.解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°,又∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°,∴∠DCF=50°,∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.11.解:∵DE∥BC∴∠1=∠2=65°∵AB∥DF∴∠2+∠3=180°,∴∠3=180°﹣65°=115°.故答案为∠2=65°,∠3=115°.12.解:如图,过点E作EF∥AB,∵AB∥CD,∴AB∥EF∥CD,∴∠4=∠1,∠3+∠4=∠2,∴∠3=∠2﹣∠1=110°﹣50°=60°.13.解:∵DE∥BC,∠AED=46°,∴∠ACB=∠AED=46°,∵CD平分∠ACB,∴∠BCD=∠ACB=23°,∵DE∥BC,∴∠CDE=∠BCD=23°.14.解:∵AC∥ED,∴∠BED=∠A=64°,∵AB∥FD,∴∠EDF=∠BED=64°.15.解:∵AC∥DF,∴∠2=∠F,∵AB∥EF,∴∠1=∠F,∴∠1=∠2=50°16.解:(1)∠B=∠D.理由:∵AB∥CD,BE∥DF,∴∠B=∠1,∠1=∠D,∴∠B=∠D.(2)∠B+∠D=180°,理由:∵AB∥CD,BE∥DF,∴∠B=∠1,∠1+∠D=180°,∴∠B+∠D=180°.(3)由(1)(2)可得结论:若两个角的两边两两互相平行,则这两个角相等或互补.故答案为:若两个角的两边两两互相平行,则这两个角相等或互补.(4)设一个角为x°,则另一个角的(2x﹣30)°,若相等:x=2x﹣30,解得:x=30,则这两角分别为:30°,30°;若互补,则x+2x﹣30=180,解得:x=70,则这两角分别为:70°,110°;答:这两个角的度数分别为:30°,30°或70°,110°.17.解:(1)如图1,过G作GH∥AB,∵AB∥CD,∴GH∥AB∥CD,∴∠BEG=∠HGE,∠DFG=∠HGF,∴∠EGF=∠HGE+∠HGF=∠BEG+∠DFG;(2)设过t秒钟时,∠EGF=50°,由题可得∠BEG=10t°,∠DFG=15t°,如图2,当点G在EF右侧时,由(1)可得,∠EGF=∠BEG+∠DFG,即50°=10t°+15t°,解得t=2;如图3,当点G在EF的左侧时,过G作PG∥AB,∵AB∥CD,∴GP∥AB∥CD,∴∠AEG=∠PGE,∠CFG=∠PGF,∴∠EGF=∠PGE﹣∠PGF=∠AEG﹣∠CFG,又∵∠AEG=180°﹣10t°,∠CFG=15t°﹣180°,∴50°=(180°﹣10t°)﹣(15t°﹣180°),解得t=12.4,综上所述,过2秒或12.4秒时,∠EGF=50°.18.解:探究一:①如图2,∵AM∥BN,DE∥AM,∴BN∥DE,∴∠1=∠2,∠3=∠4,∵∠P AC与∠PBC的角平分线相交于点D,∴=35°,∠3=∠PBC=(80°﹣20°)=30°,∴∠ADB=∠2+∠4=∠1+∠3=65°,故答案为:65°;探究二:①如图2,∵AM∥BN,DE∥AM,∴BN∥DE,∴∠1=∠2,∠3=∠4,∵∠P AC与∠PBC的角平分线相交于点D,∴=35°,∠3=∠PBC=(80°﹣α)=40°﹣,∴∠ADB=∠2+∠4=∠1+∠3=75°﹣=β,∵β≥α,∴75°﹣≥α,∴0<α≤50,∴α的取值范围是:0<α≤50.②不会,理由:∵75°﹣=β,假设α+β=180°,则75°﹣+α=180°,解答α=210°>180°,∴不会出现α与β互补的情况.19.解:(1)由互余∠ACE=90°﹣∠DCE=90°﹣40°=50°,由角的和差得∠ACB=∠ACE+∠BCE=50°+90°=140°,故答案为:140°;(2)∵∠ACE+∠DCE=90°,∠DCB+∠DCE=90°,∴∠ACE=∠DCB;∴∠ACE=∠ACB﹣∠ECB=α﹣90°,∴∠DCE=90°﹣∠ACE=90°﹣(α﹣90°)=180°﹣α,故答案为:DCB,180°﹣α;(3)①当BE∥AC时,∵BE∥AC,∴∠ACE=∠E=45°;②当BC∥DA时,∵BC∥DA,∴∠BCD=∠D=30°,∴∠ACB=90°+30°=120°,∴∠ACE=∠ACB﹣∠BCE=120°﹣90°=30°.故答案为:①45;②30;(4)①当AD∥CE时,∵AD∥CE,∴∠DCE=∠D=30°,∴∠ACE=90°+30°=120°;②当BE∥CD时,∴∠ACE=90°+45°=135°;③当BE∥AD时,过点C作CF∥AD,∵BE∥AD,CF∥AD,∴BE∥AD∥CF,∴∠ECF=∠E=45°,∠DCF=∠D=30°,∴∠DCE=30°+45°=75°∴∠ACE=90°+75°=165°.故答案为:120或135或165.20.解:(1)如图1,∵AB∥CD,∠B=60°,∴∠BOD=∠B=60°,∴∠BPD=∠BOD﹣∠D=60°﹣30°=30°.故答案为:30°;(2)∠BPD=∠B+∠D.如图2,过点P作PE∥AB,∵AB∥CD,∴AB∥PE∥CD,∴∠1=∠B,∠2=∠D,∴∠BPD=∠1+∠2=∠B+∠D;(3)延长BP交CD于点E,∵∠1=∠BMD+∠B,∠BPD=∠1+∠D,∴∠BPD=∠BMD+∠B+∠D,∵∠BPD=86°,∠BMD=40°,∴∠B+∠D=∠BPD﹣∠BMD=86°﹣40°=46°。
七年级数学下册第五章《相交线与平行线》经典习题(课后培优)

一、选择题1.下列命题中是真命题的有()①两个角的和等于平角时,这两个角互为邻补角;②过一点有且只有一条直线与已知直线平行;③两条平行线被第三条直线所截,所得的一对内错角的角平分线互相平行;④图形B由图形A平移得到,则图形B与图形A中的对应点所连线段平行(或在同一条直线上)且相等;A.1个B.2个C.3个D.4个B解析:B【分析】根据补角和邻补角的定义可判断①,根据平行公理可判断②,根据平行线的性质和判定可判断③,根据平移的性质可判断④,进而可得答案.【详解】解:两个角的和等于平角时,这两个角互为补角,故命题①是假命题;过直线外一点有且只有一条直线与已知直线平行,故命题②是假命题;两条平行线被第三条直线所截,所得的一对内错角的角平分线互相平行,故命题③是真命题;图形B由图形A平移得到,则图形B与图形A中的对应点所连线段平行(或在同一条直线上)且相等,故命题④是真命题.综上,真命题有2个.故选:B.【点睛】本题考查了真假命题、平行线的判定和性质以及平移的性质等知识,属于基础题型,熟练掌握上述知识是解题的关键.2.下列语句是命题的是()A.平分一条线段B.直角都相等C.在直线AB上取一点D.你喜欢数学吗?B解析:B【分析】根据命题的定义分别进行判断.【详解】A.平分一条线段,为描述性语言,不是命题;B.直角都相等,是命题;C.在直线AB上取一点,为描述性语言,不是命题;D.你喜欢数学吗?是疑问句,不是命题.故选:B.【点睛】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.3.下列命题:①同位角相等;②过一点有且只有一条直线与已知直线平行; ③过一点有且只有一条直线与已知直线垂直; ④如果同一平面内的三条直线只有两个交点,那么这三条直线中必有两条直线互相平行.其中假命题的个数是( )A .1个B .2个C .3个D .4个A解析:A【分析】根据平行线的性质、八个基本事实、平行线的判定等知识分别判断即可.【详解】解:同位角不一定相等,①是假命题;过直线外一点有且只有一条直线与已知直线平行,②是假命题;在同一平面内,过一点有且只有一条直线与已知直线垂直,③是假命题;如果同一平面内的三条直线只有两个交点,那么这三条直线中必有两条直线互相平行,④是真命题,故选:A .【点睛】本题考查了命题与定理、平行线的判定与性质、八个基本事实,熟记八个基本事实,会判断命题的真假是解答的关键.4.如图,直线a ,b 被直线c 所截,则1∠与2∠是( )A .同位角B .内错角C .同旁内角D .对顶角A 解析:A【分析】 根据同位角的定义求解.【详解】解:直线a ,b 被直线c 所截,∠1与∠2是同位角.故选:A .【点睛】本题考查了同位角、内错角、同位角:三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.5.如图,//AB EF ,90C ∠=︒,则α∠,β∠,γ∠之间的关系是( )A .βαγ∠=∠+∠B .180αβγ∠+∠+∠=︒C .90αβγ∠+∠-∠=︒D .90βγα∠+∠-∠=︒C解析:C【分析】分别过C 、D 作AB 的平行线CM 和DN ,由平行线的性质可得到∠α+∠β=∠C+∠γ,可求得答案.【详解】如图,分别过C 、D 作AB 的平行线CM 和DN ,∵AB//EF ,∴AB//CM //DN //EF ,∴αBCM ∠∠=,MCD NDC ∠∠=,NDE γ∠∠=,∴αβBCM CDN NDE BCM MCD γ∠∠∠∠∠∠∠∠+=++=++, 又∵BC CD ⊥,∴BCD 90∠=,∴αβ90γ∠∠∠+=+,即αβγ90∠∠∠+-=,故选C .【点睛】本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a//b ,b//c ⇒a//c .6.如图,下列条件:13241804523623∠=∠∠+∠=∠=∠∠=∠∠=∠+∠①,②,③,④,⑤中能判断直线12l l 的有( )A.5个B.4个C.3个D.2个B 解析:B【分析】根据平行线的判定定理对各小题进行逐一判断即可.【详解】解:①∵∠1=∠3,∴l1∥l2,故本小题正确;②∵∠2+∠4=180°,∴l1∥l2,故本小题正确;③∵∠4=∠5,∴l1∥l2,故本小题正确;④∠2=∠3不能判定l1∥l2,故本小题错误;⑤∵∠6=∠2+∠3,∴l1∥l2,故本小题正确.故选B.【点睛】本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.7.(2017•十堰)如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=()A.40°B.50°C.60°D.70°B 解析:B【解析】试题分析:由AB∥DE,∠CDE=40°,∴∠B=∠CDE=40°,又∵FG⊥BC,∴∠FGB=90°﹣∠B=50°,故选B.考点:平行线的性质8.如图,直线a,b被直线c所截,且a//b,若∠1=55°,则∠2等于()A .35°B .45°C .55°D .125°C解析:C【解析】 试题分析:根据图示可得:∠1和∠2是同位角,根据两直线平行,同位角相等可得:∠2=∠1=55°.考点:平行线的性质9.如图,已知AB CD ∕∕,AF 交CD 于点E ,且,40BE AF BED ⊥∠=︒,则A ∠的度数是( )A .40︒B .50︒C .80︒D .90︒B解析:B【分析】 直接利用垂线的定义结合平行线的性质得出答案.【详解】解:∵,40BE AF BED ⊥∠=︒,∴50FED ∠=︒,∵AB CD ∕∕,∴50A FED ∠=∠=︒.故选B .【点睛】此题主要考查了平行线的性质以及垂线的定义,正确得出FED ∠的度数是解题关键. 10.如图,将△ABE 向右平移50px 得到△DCF ,如果△ABE 的周长是400px(1px=0.04cm ),那么四边形ABFD 的周长是( )A .16cmB .18cmC .20cmD .21cm C解析:C【分析】根据平移的性质可得DF=AE,然后判断出四边形ABFD的周长=△ABE的周长+AD+EF,然后代入数据计算即可得解.注意:1px = 0.04cm .【详解】∵1px = 0.04cm,∴50px=2cm,400px=16cm,∵△ABE向右平移2cm得到△DCF,∴DF=AE,∴四边形ABFD的周长=AB+BE+DF+AD+EF=AB+BE+AE+AD+EF=△ABE的周长+AD+EF.∵平移距离为2cm,∴AD=EF=2cm,∵△ABE的周长是16cm,∴四边形ABFD的周长=16+2+2=20cm.故选:C.【点睛】本题考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.二、填空题11.高兴同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP=_____°.64【分析】由长方形直尺可得MP//OB再根据作图过程可知OP平分∠AOB进而可得∠AMP的度数【详解】解:∵OP平分∠AOB∴∠MOB=2∠BOP=64°由长方形直尺可知:MP//OB∴∠AMP=解析:64【分析】由长方形直尺可得MP//OB,再根据作图过程可知OP平分∠AOB,进而可得∠AMP的度数.【详解】解:∵OP 平分∠AOB ,∴∠MOB =2∠BOP =64°,由长方形直尺可知:MP //OB ,∴∠AMP =∠MOB =64°,故答案为:64.【点睛】此题主要考查了基本作图,关键是掌握角平分线的作法.12.已知A ∠与B (A ∠,B 都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且227A B ∠-∠=︒,则A ∠的度数为_________.或【分析】分两种情况:①如图1作EF ∥BD 由BD ∥AC 推出EF ∥AC 得到∠B=∠BEF ∠A=∠AEF 根据∠A+∠B=求出∠A=;②如图2作EF ∥BD 由BD ∥AC 推出EF ∥AC 得到∠B+∠BEF=∠A 解析:39︒或99︒.【分析】分两种情况:①如图1,作EF ∥BD ,由BD ∥AC 推出EF ∥AC ,得到∠B=∠BEF ,∠A=∠AEF ,根据∠A+∠B=90︒,227A B ∠-∠=︒,求出∠A=39︒;②如图2,作EF ∥BD ,由BD ∥AC 推出EF ∥AC ,得到∠B+∠BEF=180︒,∠A+∠AEF=180︒,根据∵∠AEB=∠AEF+∠BEF=90︒,227A B ∠-∠=︒,计算得出答案.【详解】分两种情况:①如图1,作EF ∥BD ,∴∠B=∠BEF ,∵EF ∥BD ,BD ∥AC ,∴EF ∥AC ,∴∠A=∠AEF ,∴∠A+∠B=∠AEF+∠BEF=90︒,∵227A B ∠-∠=︒,∴∠A=39︒;②如图2,作EF ∥BD ,∴∠B+∠BEF=180︒,∵EF ∥BD ,BD ∥AC ,∴EF ∥AC ,∴∠A+∠AEF=180︒,∴∠A+∠AEB+∠B=360︒,∵∠AEB=∠AEF+∠BEF=90︒,∴∠A+∠B=270︒,∵227A B ∠-∠=︒,∴∠A=99︒;故答案为:39︒或99︒..【点睛】此题考查平行线的性质,平行公理的推论,根据题意作出图形,引出恰当的辅助线解决问题是解题的关键.13.如图,在△ABC 中,AB =4,BC =6,∠B =60°,将△ABC 沿射线BC 的方向平移2个单位后,得到A B C ''',连接A C ',则A B C ''的周长为________.12【分析】根据平移的性质得则可计算则可判断为等边三角形继而可求得的周长【详解】平移两个单位得到的又是等边三角形的周长为故答案为:12【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动会解析:12【分析】根据平移的性质得2BB '=,4A B AB ''==,=60A B C B ∠''∠=︒,则可计算624B C BC BB '=-'=-=,则4A B B C ''='=,可判断A B C ''△为等边三角形,继而可求得A B C ''△的周长.【详解】 ABC 平移两个单位得到的A B C ''',2BB ∴'=,AB A B ='',4AB =,6BC =,4A B AB ∴''==,624B C BC BB '=-'=-=,4A B B C ∴''='=,又60B ∠=︒,60A B C ∴∠''=︒,A B C ∴''是等边三角形,A B C ∴''的周长为4312⨯=.故答案为:12.【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.14.如图,//,//,62AC ED AB FD A ∠=︒,则EDF ∠度数为___________.62°【分析】首先根据两直线平行同位角相等求出∠DEB 的度数再根据两直线平行内错角相等求出∠EDF 的度数【详解】解:∵AC//DE ∠A=62°∴∠DEB=∠A=62°(两直线平行同位角相等)∵DF/解析:62°【分析】首先根据两直线平行,同位角相等求出∠DEB 的度数,再根据两直线平行,内错角相等求出∠EDF 的度数.【详解】解:∵AC//DE ,∠A=62°,∴∠DEB=∠A=62°(两直线平行,同位角相等),∵DF//AB ,∴∠EDF=∠DEB=62°(两直线平行,内错角相等).故答案为:62°.【点睛】本题考查了平行线的性质,解决本题的关键是熟记平行线的性质.平行线的性质:①两直线平行同位角相等,②两直线平行内错角相等,③两直线平行同旁内角互补. 15.“等腰三角形的两条边相等”的逆命题是________________.(填真命题或假命题)真命题【分析】交换命题的题设和结论即可得到该命题的逆命题根据等腰三角形的定义判断即可【详解】等腰三角形的两条边相等的逆命题是:两条边相等的三角形是等腰三角形;它是真命题故答案为:真命题【点睛】本题考 解析:真命题【分析】交换命题的题设和结论即可得到该命题的逆命题,根据等腰三角形的定义判断即可.【详解】“等腰三角形的两条边相等”的逆命题是:两条边相等的三角形是等腰三角形;它是真命题,故答案为:真命题.【点睛】本题考查了命题的真假判断、逆命题的概念,掌握等腰三角形的定义是解题的关键. 16.如图,请你添加一个条件....使得AD ∥BC ,所添的条件是__________.∠EAD=∠B或∠DAC=∠C【解析】当∠EAD=∠B时根据同位角相等两直线平行可得AD//BC;当∠DAC=∠C时根据内错角相等两直线平行可得AD//BC;当∠DAB+∠B=180°时根据同旁内角解析:∠EAD=∠B或∠DAC=∠C【解析】当∠EAD=∠B时,根据“同位角相等,两直线平行”可得AD//BC;当∠DAC=∠C时,根据“内错角相等,两直线平行”可得AD//BC;当∠DAB+∠B=180°时,根据“同旁内角互补,两直线平行”可得AD//BC,故答案是:∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°(答案不唯一).17.如图,点A、B为定点,直线l∥AB,P是直线l上一动点,对于下列各值:①线段AB的长;②△PAB的周长;③△PAB的面积;④∠APB的度数,其中不会随点P的移动而变化的是(填写所有正确结论的序号)______________.①③【分析】求出AB长为定值P到AB的距离为定值再根据三角形的面积公式进行计算即可;根据运动得出PA+PB不断发生变化∠APB的大小不断发生变化【详解】解:∵AB为定点∴AB长为定值∴①正确;∵点A解析:①③【分析】求出AB长为定值,P到AB的距离为定值,再根据三角形的面积公式进行计算即可;根据运动得出PA+PB不断发生变化、∠APB的大小不断发生变化.【详解】解:∵A、B为定点,∴AB长为定值,∴①正确;∵点A,B为定点,直线l∥AB,∴P到AB的距离为定值,故△APB的面积不变,∴③正确;当P点移动时,PA+PB的长发生变化,∴△PAB的周长发生变化,∴②错误;当P点移动时,∠APB发生变化,∴④错误;故选A.【点睛】本题考查了平行线的性质,等底等高的三角形的面积相等,平行线间的距离的运用,熟记定理是解题的关键.18.把命题“等角的余角相等”改写成“如果…,那么…”的形式为______.如果两个角相等那么这两个角的余角相等【分析】把命题的题设写在如果的后面把命题的结论部分写在那么的后面即可【详解】解:命题等角的余角相等写成如果…那么…的形式为:如果两个角是相等角的余角那么这两个角相解析:如果两个角相等,那么这两个角的余角相等【分析】把命题的题设写在如果的后面,把命题的结论部分写在那么的后面即可.【详解】解:命题“等角的余角相等”写成“如果…,那么….”的形式为:如果两个角是相等角的余角,那么这两个角相等.故答案为:如果两个角是相等角的余角,那么这两个角相等.【点睛】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.19.如图,AD∥BC,∠D=100°,CA平分∠BCD,则∠DAC=________度.40°【分析】本题主要利用两直线平行同旁内角互补两直线平行内错角相等以及角平分线的定义进行做题【详解】∵AD∥BC∴∠BCD=180°-∠D=80°又∵CA平分∠BCD∴∠ACB=∠BCD=40°∴解析:40°【分析】本题主要利用两直线平行,同旁内角互补、两直线平行,内错角相等以及角平分线的定义进行做题.【详解】∵AD∥BC,∴∠BCD=180°-∠D=80°,又∵CA平分∠BCD,∠BCD=40°,∴∠ACB=12∴∠DAC=∠ACB=40°.【点睛】本题重点考查了平行线的性质及角平分线的定义,是一道较为简单的题目.20.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,AB=10,DH=4,平移距离为8,则阴影部分的面积是_______________.64【分析】根据平移变化只改变图形的位置不改变图形的形状可得出两个三角形大小一样阴影部分面积等于梯形ABEH的面积;DE=AB根据线段的和差关系可求出HE的长度再根据梯形的面积公式即可得答案【详解】解析:64【分析】根据平移变化只改变图形的位置,不改变图形的形状,可得出两个三角形大小一样,阴影部分面积等于梯形ABEH的面积;DE=AB,根据线段的和差关系可求出HE的长度,再根据梯形的面积公式即可得答案.【详解】∵两个三角形大小一样,∴S△ABC=S△DEF,∴S△ABC-S△HEC=S△DEF-S△HEC,∴S阴影=S梯形ABEH,∵其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,AB=10,∴DE=AB=10,∵DH=4,∴HE=DE-DH=6,∵平移距离是8,∴BE=8,∴S阴影=S梯形ABEH=12(HE+AB)·BE=12×(10+6)×8=64,故答案为:64【点睛】本题主要考查了平移的性质,通过观察图形把阴影部分的面积转化为熟知图形的面积是关键的一步.三、解答题21.利用网格画图,每个小正方形边长均为1(1)过点C 画AB 的平行线CD ;(2)仅用直尺,过点C 画AB 的垂线,垂足为E ;(3)连接CA 、CB ,在线段CA 、CB 、CE 中,线段______最短,理由___________. (4)直接写出△ABC 的面积为 _________.解析:(1)见详解;(2)见详解;(3)CE ,垂线段最短;(4)8.【分析】(1)取点D 作直线CD 即可;(2)取点F 作直线CF 交AB 与E 即可;(3)根据垂线段最短即可解决问题;(4)用割补法,大长方形的面积减去三个小三角形的面积即可;【详解】 解:(1)直线CD 即为所求;(2)直线CE 即为所求;(3)在线段CA 、CB 、CE 中,线段CE 最短,理由:垂线段最短;故答案为CE ,垂线段最短;(4) S △ABC =18﹣12×1×5﹣12×1×3﹣12×2×6=8, ∴△ABC 的面积为8.【点睛】本题主要考查垂线、平行线及其做图,注意作图的准确性.22.如图,已知AC BC ⊥,CD AB ⊥,DE AC ⊥,1∠与2∠互补,判断HF 与AB 是否垂直,并说明理由(填空).解:垂直,理由如下:∵DE AC ⊥,AC BC ⊥,∴90AED ACB ==︒∠∠(垂直的意义)∴//DE BC (_____)∴1DCB ∠=∠(_____)∵1∠与2∠互补(已知)∴DCB ∠与2∠互补∴_________//________(_____)∴BFH CDB ∠=∠(_____)∵CD AB ⊥∴90CDB ∠=︒∴90HFB ︒∠=∴HF AB ⊥.解析:同位角相等,两直线平行;两直线平行,内错角相等;CD ;FH ;同旁内角互补,两直线平行;两直线平行,同位角相等.【分析】根据平行线的性质及平行线的判定解答.【详解】解:垂直,理由如下:∵DE AC ⊥,AC BC ⊥,∴90AED ACB ==︒∠∠(垂直的意义)∴//DE BC (同位角相等,两直线平行)∴1DCB ∠=∠(两直线平行,内错角相等)∵1∠与2∠互补(已知)∴DCB ∠与2∠互补∴CD //FH (同旁内角互补,两直线平行)∴BFH CDB ∠=∠(两直线平行,同位角相等)∵CD AB ⊥∴90CDB ∠=︒∴90HFB ︒∠=∴HF AB ⊥.故答案为:同位角相等,两直线平行;两直线平行,内错角相等;CD ;FH ;同旁内角互补,两直线平行;两直线平行,同位角相等.【点睛】此题考查平行线的判定及性质定理,熟记定理并熟练应用解决问题是解题的关键. 23.如图,已知:∠DGA=∠FHC ,∠A=∠F .求证:DF ∥AC .(注:证明时要求写出每一步的依据)解析:见解析.【分析】先根据∠DGA=∠EGC 证出AE ∥BF ,再根据平行证明出∠F=∠FBC 即可求证出结论.【详解】证明:∵∠DGA=∠EGC(对顶角相等)又∵∠DGA=∠FHC (已知)∴∠EGC=∠FHC (等量代换)∴AE ∥BF (同位角相等,两直线平行)∴∠A=∠FBC (两直线平行,同位角相等)又∵∠A=∠F (已知)∴∠F=∠FBC (等量代换)∴DF ∥AC (内错角相等,两直线平行).【点睛】此题考查平行线的判定与性质:同位角相等,两直线平行;两直线平行,同位角相等;内错角相等,两直线平行.24.如图,有三个论断:①12∠=∠;②B C ∠=∠;③A D ∠=∠,请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.解析:答案见解析【分析】先从①②③中任选两个作为条件,另一个作为结论构成一个命题,然后根据平行线的判定和性质及对顶角相等进行证明即可.【详解】已知:12∠=∠,B C ∠=∠求证:A D ∠=∠证明:如图:13∠=∠ 又12∠=∠32∴∠=∠//EC BF ∴AEC B ∴∠=∠又B C ∠=∠AEC C ∴∠=∠//AB CD ∴A D ∴∠=∠.【点睛】本题主要考查了平行线的判定与性质以及命题与定理的证明问题,证明的一般步骤包括写出已知、求证、画出图形和证明.25.如图,在△ABC 中,CD ⊥AB ,垂足为D ,点E 在BC 上,EF ⊥AB ,垂足为F . (1)CD 与EF 平行吗?为什么?(2)如果∠1=∠2,且∠3=115°,∠A=30°,求∠B 的度数.解析:(1)CD与EF平行.理由见解析;(2)∠B=35°【分析】(1)先根据垂直的定义得到∠CDB=∠EFB=90°,然后根据同位角相等,两直线平行可判断EF∥CD;(2)由EF∥CD,根据平行线的性质得∠2=∠BCD,而∠1=∠2,所以∠1=∠BCD,根据内错角相等,两直线平行得到DG∥BC,所以∠ACB=∠3=115°,根据三角形的内角和即可得到结论.【详解】(1)CD与EF平行.理由如下:∵CD⊥AB,EF⊥AB,∴∠CDB=∠EFB=90°,∴EF∥CD;(2)∵EF∥CD,∴∠2=∠BCD,∵∠1=∠2,∴∠1=∠BCD,∴DG∥BC,∴∠ACB=∠3=115°,∵∠A=30°,∴∠B=35°.【点评】本题考查了平行线的判定与性质,注意:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等.26.平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′.解析:见解析【分析】先分别确定A、B、C平移后的对应点A′、B′、C′,然后再顺次连接即可.【详解】解:如图:连接AA′,在AA′在一条直线上CC′=AA′,得到C′;再作BB′∥AA′且BB′=AA′,最后顺次连接得到△A′B′C′即为所求三角形.【点睛】本题主要考查了平移作图,根据题意确定A、B、C平移后的对应点A′、B′、C′是解答本题的关键.27.如图,已知直线l1//l2,l3、和l1、l2分别交于点A、B、C、D,点P在直线l3或上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明;(4)若点P在线段DC延长线上运动时,请直接写出∠1、∠2、∠3之间的关系.解析:(1)证明见详解;(2)∠3=∠2﹣∠1;(3)∠3=360°﹣∠1﹣∠2,证明见详解;(4)∠3=360°﹣∠1﹣∠2.【分析】此题四个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,即可得出∠1、∠2、∠3的数量关系.【详解】解:(1)如图(1)证明:过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠EPF=∠QPE+∠QPF,∴∠EPF=∠1+∠2.(2)∠3=∠2﹣∠1;证明:如图2,过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠EPF=∠QPF﹣∠QPE,∴∠EPF=∠2﹣∠1.(3)∠3=360°﹣∠1﹣∠2.证明:如图(3),过P作PQ∥l1∥l2;∴∠EPQ+∠1=180°,∠FPQ+∠2=180°,∵∠EPF=∠EPQ+∠FPQ;∴∠EPQ +∠FPQ +∠1+∠2=360°,即∠EPF=360°﹣∠1﹣∠2;(4)点P在线段DC延长线上运动时,∠3=∠1﹣∠2.证明:如图(4),过P作PQ∥l1∥l2;∴∠1=∠QPE、∠2=∠QPF;∵∠QPE﹣∠QPF=∠EPF;∴∠3=∠1﹣∠2.【点睛】此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键. 28.如图1所示的是北斗七星的位置图,图2将北斗七星分别标为A ,B ,C ,D ,E ,F ,G ,并顺次首尾连接,若AF 恰好经过点G ,且//AF DE ,105D E ∠=∠=︒.(1)求F ∠的度数.(2)连接AD ,当ADE ∠与CGF ∠满足怎样的数量关系时,//BC AD ,并说明理由.解析:(1)75°;(2)当∠ADE+∠CGF=180°时,BC ∥AD .【分析】(1)根据平行线的性质解答即可;(2)根据平行线的判定和性质解答即可.【详解】解:(1)∵AF ∥DE ,∴∠F+∠E=180°,∵105E ∠=︒∴∠F=180°-105°=75°;(2)如图,当∠ADE+∠CGF=180°时,BC ∥AD ,∵AF∥DE,∴∠GAD+∠ADE=180°,∠ADE+∠CGF=180°,∴∠GAD=∠CGF,∴BC∥AD.【点睛】此题考查平行线的判定和性质,关键是根据平行线的判定和性质解答.。
相交线与平行线培优专题一

l 3l 2l 1O相交线与平行线一、知识要点1、平面内两条直线的位置关系:相交或平行。
(1)相交线:如果两条直线有一个公共点,则称为两相交直线; (2)平行线:如果两条直线没有公共点,则称为平行直线。
2、两条直线的垂直:如果两条直线相交所成的角为直角,则称这两条直线互相垂直。
3、两条直线垂直的两个重要结论:(1)过一点有且只有一条直线与已知直线垂直;(2)直线外一点与直线上各点连结的所有线段中,垂线段最短。
4、平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
5、两条直线平行的判定: (1)两直线没有公共点; (2)同时与第三条直线平行;(3)被第三条直线所截,同位角相等; (4)被第三条直线所截,内错角相等; (5)被第三条直线所截,同旁内角互补; (6)垂直于同一直线。
6、两平行直线被第三直线所截,有: (1)同位角相等;(2)内错角相等; (3)同旁内角互补。
例1、三条直线相交于一点,共可组成几对对顶角?若三条直线两两相交,但未必相交于一点呢?一般地,n(n 2)条直线两两相交,共可组成几对对顶角?例2、10条直线两两相交,最多将平面分成多少块不同的区域?例3、如图,平行直线EF 、MN 被相交直线AB 、CD 所截,请问图中有多少对同旁内角?其中互补的有多少对?例4、有10条公路(假设公路是笔直的,并且可以无限延伸),无任何三条公路交于同一个岔口,现有31名交警,刚好满足每个岔口有且只有一名交警执勤,请你画出公路示意图.例5、设a,b,c为锐角三角形 ABC的边长,而为对应边上的三条高线长,求证:h a+,h b+,h c<a+b+c例6、如图,直线a∥b,直线 AB交 a与 b于 A,B,CA平分∠1,CB平分∠ 2,求证:∠C=90°例7、如图1,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化?若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?例8、如图(1),∠ABC=120o,∠BCD=85o, ED,求∠CDE的度数。
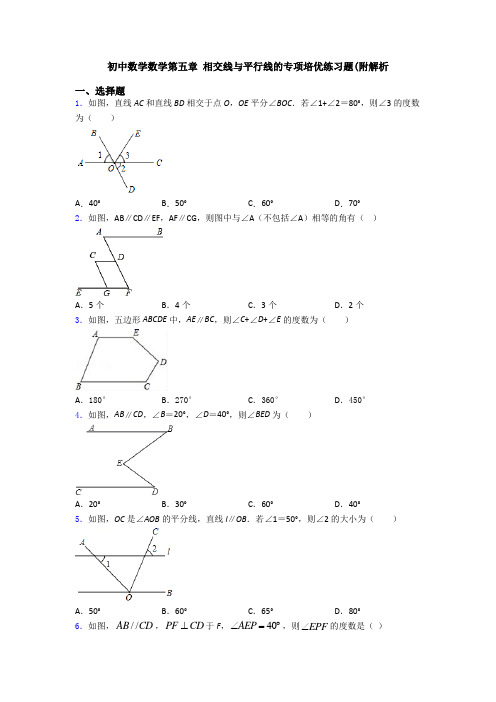
初中数学数学第五章 相交线与平行线的专项培优练习题(附解析
初中数学数学第五章 相交线与平行线的专项培优练习题(附解析一、选择题1.如图,直线AC 和直线BD 相交于点O ,OE 平分∠BOC .若∠1+∠2=80°,则∠3的度数为( )A .40°B .50°C .60°D .70°2.如图,AB ∥CD ∥EF ,AF ∥CG ,则图中与∠A (不包括∠A )相等的角有( )A .5个B .4个C .3个D .2个3.如图,五边形ABCDE 中,AE ∥BC ,则∠C +∠D +∠E 的度数为( )A .180°B .270°C .360°D .450°4.如图,AB ∥CD ,∠B =20°,∠D =40°,则∠BED 为( )A .20°B .30°C .60°D .40°5.如图,OC 是∠AOB 的平分线,直线l ∥OB .若∠1=50°,则∠2的大小为()A .50°B .60°C .65°D .80°6.如图,//AB CD ,PF CD ⊥于F ,40AEP ∠=︒,则EPF ∠的度数是( )A .120︒B .130︒C .140︒D .150︒7.如图,∠1=70°,直线a 平移后得到直线b ,则∠2-∠3( )A .70°B .180°C .110°D .80°8.如图,已知AB ∥CD, EF ∥CD ,则下列结论中一定正确的是( )A .∠BCD= ∠DCE;B .∠ABC+∠BCE+∠CEF=360︒;C .∠BCE+∠DCE=∠ABC+∠BCD;D .∠ABC+∠BCE -∠CEF=180︒.9.下列命题:①同位角相等;②过一点有且只有一条直线与已知直线平行; ③过一点有且只有一条直线与已知直线垂直; ④如果同一平面内的三条直线只有两个交点,那么这三条直线中必有两条直线互相平行.其中假命题的个数是( )A .1个B .2个C .3个D .4个10.如图,//AB EF ,90C ∠=︒,则α∠,β∠,γ∠之间的关系是( )A .βαγ∠=∠+∠B .180αβγ∠+∠+∠=︒C .90αβγ∠+∠-∠=︒D .90βγα∠+∠-∠=︒二、填空题11.如图,已知AB 、CD 相交于点O,OE ⊥AB 于O ,∠EOC=28°,则∠AOD=_____度;12.如图,//AB CD ,GF 与AB 相交于点H ,与CD 于F ,FE 平分HFD ∠,若50EHF ∠=︒,则HFE ∠的度数为______.13.已知直线AB ∥CD ,点P 、Q 分别在AB 、CD 上,如图所示,射线PB 按顺时针方向以每秒4°的速度旋转至PA 便立即回转,并不断往返旋转;射线QC 按顺时针方向每秒1°旋转至QD 停止,此时射线PB 也停止旋转.(1)若射线PB 、QC 同时开始旋转,当旋转时间30秒时,PB'与QC'的位置关系为_____; (2)若射线QC 先转45秒,射线PB 才开始转动,当射线PB 旋转的时间为_____秒时,PB′∥QC′.14.如图,已知AB ∥CD ,CE 、BE 的交点为E ,现作如下操作:第一次操作,分别作∠ABE 和∠DCE 的平分线,交点为E 1,第二次操作,分别作∠ABE 1和∠DCE 1的平分线,交点为E 2,第三次操作,分别作∠ABE 2和∠DCE 2的平分线,交点为E 3,…,第n 次操作,分别作∠ABE n ﹣1和∠DCE n ﹣1的平分线,交点为E n .若∠E n =1度,那∠BEC 等于________度15.设a 、b 、c 为平面上三条不同直线,(1)若//,//a b b c ,则a 与c 的位置关系是_________;(2)若,a b b c ⊥⊥,则a 与c 的位置关系是_________;a b,bc ,则a与c的位置关系是________.(3)若//16.如图,请你添加一个条件....使得AD∥BC,所添的条件是__________.17.如图,AC⊥AB,AC⊥CD,垂足分别是点A、C,如果∠CDB=130°,那么直线AB与BD 的夹角是________度.18.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOD=120°,则∠BOD=__________°.19.如图,AC∥BD,AE平分∠BAC交BD于点E,若∠1=62°,则∠2=______.20.如图,直角△ABC中,AC=3,BC=4,AB=5,则内部五个小直角三角形的周长为_____.三、解答题21.如图1,D是△ABC延长线上的一点,CE//AB.(1)求证:∠ACD=∠A+∠B;(2)如图2,过点A作BC的平行线交CE于点H,CF平分∠ECD,FA平分∠HAD,若∠BAD=70°,求∠F的度数.(3)如图3,AH//BD,G为CD上一点,Q为AC上一点,GR平分∠QGD交AH于R,QN 平分∠AQG交AH于N,QM//GR,猜想∠MQN与∠ACB的关系,说明理由.22.如图1,//,AB CD 直线MN 分别交AB CD 、于点,E F BEF ∠、与EFD ∠的角平分线交于点P EP ,与CD 交于点G GH EG ⊥,交MN 于H .(1)求证:// ;PF GH (2)如图2,连接PH K ,为GH 上一动点,PHK HPK PO ∠=∠,平分EPK ∠交MN 于,Q 则HPQ ∠的大小是否发生变化?若不变,求出其值;若改变,请说明理由.23.如图,已知C 为两条相互平行的直线AB ,ED 之间一点,ABC ∠和CDE ∠的角平分线相交于F ,180FDC ABC ∠+∠=︒.(1)求证://AD BC ;(2)连结CF ,当//CF AB ,且32CFB DCF ∠=∠时,求BCD ∠的度数;(3)若DCF CFB ∠=∠时,将线段BC 沿直线AB 方向平移,记平移后的线段为PQ (B ,C 分别对应P ,Q ,当20PQD QDC ∠-∠=︒时,请直接写出DQP ∠的度数______.24.如图1.已知直线AB ED .点C 为AB ,ED 内部的一个动点,连接CB ,CD ,作ABC ∠的平分线交直线ED 于点E ,作CDE ∠的平分线交直线BA 于点A ,BE 和DA 交于点F .(1)若180FDC ABC ∠+∠=︒,猜想AD 和BC 的位置关系,并证明;(2)如图2,在(1)的基础上连接CF ,则在点C 的运动过程中,当满足CF AB ∥且32CFB DCF ∠=∠时,求BCD ∠的度数. 25.问题情境(1)如图①,已知360B E D ∠+∠+∠=︒,试探究直线AB 与CD 有怎样的位置关系?并说明理由.小明给出下面正确的解法:直线AB 与CD 的位置关系是//AB CD .理由如下:过点E 作//EF AB (如图②所示)所以180B BEF ∠+∠=︒(依据1)因为360B BED D ∠+∠+∠=︒(已知)所以360B BEF FED D ∠+∠+∠+∠=︒所以180FED D ∠+∠=︒所以//EF CD (依据2)因为//EF AB所以//AB CD (依据3)交流反思上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?“依据1”:________________________________;“依据2”:________________________________;“依据3”:________________________________.类比探究(2)如图,当B 、E ∠、F ∠、D ∠满足条件________时,有//AB CD .拓展延伸(3)如图,当B 、E ∠、F ∠、D ∠满足条件_________时,有//AB CD .26.如图,如图1,在平面直角坐标系中,已知点A (﹣4,﹣1)、B (﹣2,1),将线段AB 平移至线段CD ,使点A 的对应点C 在x 轴的正半轴上,点D 在第一象限. (1)若点C 的坐标(k ,0),求点D 的坐标(用含k 的式子表示);(2)连接BD 、BC ,若三角形BCD 的面积为5,求k 的值;(3)如图2,分别作∠ABC 和∠ADC 的平分线,它们交于点P ,请写出∠A 、和∠P 和∠BCD 之间的一个等量关系,并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据对顶角和邻补角的定义即可得到∠BOC的度数,再根据角平分线即可得出∠3的度数.【详解】解:∵∠1=∠2,∠1+∠2=80°,∴∠1=∠2=40°,∴∠BOC=140°,又∵OE平分∠BOC,∴∠3=70°.故选:D.【点睛】本题考查了邻补角、对顶角、角平分线的应用,解题时注意运用:对顶角相等,邻补角互补,即和为180°.2.B解析:B【分析】由平行线的性质,可知与∠A相等的角有∠ADC、∠AFE、∠EGC、∠GCD.【详解】∵AB∥CD,∴∠A=∠ADC;∵AB∥EF,∴∠A=∠AFE;∵AF∥CG,∴∠EGC=∠AFE=∠A;∵CD∥EF,∴∠EGC=∠DCG=∠A;所以与∠A相等的角有∠ADC、∠AFE、∠EGC、∠GCD四个,故选B.3.C解析:C【分析】首先过点D作DF∥AE,交AB于点F,由AE∥BC,可证得AE∥DF∥BC,然后由两直线平行,同旁内角互补,证得∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,继而证得结论.【详解】过点D作DF∥AE,交AB于点F,∵AE∥BC,∴AE∥DF∥BC,∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,∴∠C+∠CDE+∠E=360°,故选C.【点睛】本题考查了平行线的性质,解题时掌握辅助线的作法,注意数形结合思想的应用.4.C解析:C【分析】过点E作EF∥AB,得∠B=∠BEF=20°,结合AB∥CD知EF∥CD,据此得∠D=∠DEF=40°,根据∠BED=∠BEF+∠DEF可得答案.【详解】解:如图,过点E作EF∥AB,∴∠B=∠BEF=20°,∵AB∥CD,∴EF∥CD,∴∠D=∠DEF=40°,则∠BED=∠BEF+∠DEF=20°+40°=60°,故答案为:60°.【点睛】本题考查平行线的性质,解题关键是掌握两直线平行内错角相等的性质和平行与平面内同一直线的两直线平行的性质.5.C解析:C【分析】根据平行线的性质可求∠AOB,再根据角平分线的定义求得∠BOC,再根据平行线的性质可求∠2.【详解】∵l∥OB,∴∠AOB+∠1=180°∴∠AOB=180°﹣∠1=130°,∵OC是∠AOB的平分线,∴∠BOC=65°,∴∠2=∠BOC=65°.故选:C.【点睛】考查了角平分线,平行线的性质,关键是熟悉两直线平行,同位角相等;两直线平行,同旁内角互补的知识点.6.B解析:B【分析】过点P作MN∥AB,结合垂直的定义和平行线的性质求∠EPF的度数.【详解】解:如图,过点P作MN∥AB,∵∠AEP=40°,∴∠EPN=∠AEP=40°∵AB∥CD,PF⊥CD于F,∴PF⊥MN,∴∠NPF=90∴∠EPF=∠EPN+∠NPF=40°+90°=130°故答案为B【点睛】本题考查了平行线的判定定理和性质,作出辅助线构造平行线是解答本题的关键.7.C解析:C【解析】【分析】作AB∥a,先证AB∥a∥b,由平行线性质得∠2=180°-∠1+∠3,变形可得结果.【详解】作AB∥a,由直线a平移后得到直线b,所以,AB∥a∥b所以,∠2=180°-∠1+∠3,所以,∠2-∠3=180°-∠1=180°-70°=110°.故选:C【点睛】本题考核知识点:平行线性质.解题关键点:熟记平行线性质.8.D解析:D【解析】分析:根据平行线的性质,找出图形中的同旁内角、内错角即可判断.详解:延长DC到H∵AB∥CD,EF∥CD∴∠ABC+∠BCH=180°∠ABC=∠BCD∠CE+∠DCE=180°∠ECH=∠FEC∴∠ABC+∠BCE+∠CEF=180°+∠FEC∠ABC+∠BCE -∠CEF=∠ABC+∠BCH+∠ECH-∠CEF=180°.故选D.点睛:此题主要考查了平行线的性质,关键是熟记平行线的性质:两直线平行,内错角相等,同旁内角互补,同位角相等.9.A解析:A【分析】根据平行线的性质、八个基本事实、平行线的判定等知识分别判断即可.【详解】解:同位角不一定相等,①是假命题;过直线外一点有且只有一条直线与已知直线平行,②是假命题;在同一平面内,过一点有且只有一条直线与已知直线垂直,③是假命题;如果同一平面内的三条直线只有两个交点,那么这三条直线中必有两条直线互相平行,④是真命题,故选:A .【点睛】本题考查了命题与定理、平行线的判定与性质、八个基本事实,熟记八个基本事实,会判断命题的真假是解答的关键.10.C解析:C【分析】分别过C 、D 作AB 的平行线CM 和DN ,由平行线的性质可得到∠α+∠β=∠C+∠γ,可求得答案.【详解】如图,分别过C 、D 作AB 的平行线CM 和DN ,∵AB//EF ,∴AB//CM //DN //EF ,∴αBCM ∠∠=,MCD NDC ∠∠=,NDE γ∠∠=,∴αβBCM CDN NDE BCM MCD γ∠∠∠∠∠∠∠∠+=++=++,又∵BC CD ⊥,∴BCD 90∠=,∴αβ90γ∠∠∠+=+,即αβγ90∠∠∠+-=,故选C .【点睛】本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a//b ,b//c ⇒a//c .二、填空题11.62【详解】∵,,∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.解析:62【详解】∵OE AB ⊥,28EOC ∠=,∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.12.65°【分析】由AB//CD 可得∠HFD=130︒,再由FE 平分∠HFD 可求出∠HFE .【详解】∵∴∠EHF+∠HFD=180°∵∴∠HFD=130°∵平分,∴∠HFE=∠HFD=解析:65°【分析】由AB//CD 可得∠HFD=130︒,再由FE 平分∠HFD 可求出∠HFE .【详解】∵//AB CD∴∠EHF+∠HFD=180°∵50EHF ∠=︒∴∠HFD=130°∵FE 平分HFD ∠,∴∠HFE=12∠HFD=1130652⨯︒=︒ 故答案为:65°.【点睛】此题主要考查了平行线的性质以及角平分线的定义,熟练掌握平行线的性质以及角平分线的定义是解题的关键.13.PB′⊥QC′ 15秒或63秒或135秒.【分析】(1)求出旋转30秒时,∠BPB′和∠CQC′的度数,过E 作EF∥AB,根据平行线的性质求得∠PEF 和∠QEF 的度数,进而得结论;解析:PB′⊥QC′ 15秒或63秒或135秒.【分析】(1)求出旋转30秒时,∠BPB′和∠CQC′的度数,过E作EF∥AB,根据平行线的性质求得∠PEF和∠QEF的度数,进而得结论;(2)分三种情况:①当0s<t≤45时,②当45s<t≤67.5s时,③当67.5s<t<135s时,根据平行线的性质,得出角的关系,列出t的方程便可求得旋转时间.【详解】(1)如图1,当旋转时间30秒时,由已知得∠BPB′=4°×30=120°,∠CQC′=30°,过E作EF∥AB,则EF∥CD,∴∠PEF=180°﹣∠BPB′=60°,∠QEF=∠CQC′=30°,∴∠PEQ=90°,∴PB′⊥QC′,故答案为:PB′⊥QC′;(2)①当0s<t≤45时,如图2,则∠BPB′=4t°,∠CQC′=45°+t°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠PEC=∠CQC′,即4t=45+t,解得,t=15(s);②当45s<t≤67.5s时,如图3,则∠APB′=4t﹣180°,∠CQC'=t+45°,∵AB∥CD,PB′∥QC′,∴∠APB′=∠PED=180°﹣∠CQC′,即4t﹣180=180﹣(45+t),解得,t=63(s);③当67.5s<t<135s时,如图4,则∠BPB′=4t﹣360°,∠CQC′=t+45°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠PEC=∠CQC′,即4t﹣360=t+45,解得,t=135(s);综上,当射线PB旋转的时间为15秒或63秒或135秒时,PB′∥QC′.故答案为:15秒或63秒或135秒.【点睛】本题主要考查了平行线的性质,第(1)题关键是作平行线,第(2)题关键是分情况讨论,运用方程思想解决几何问题.14.2n .【解析】如图①,过E作EF∥AB,∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE;如图②,∵∠ABE和∠解析:2n .【解析】如图①,过E作EF∥AB,∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE;如图②,∵∠ABE和∠DCE的平分线交点为E1,∴∠CE1B=∠ABE1+∠DCE1=12∠ABE+12∠DCE=12∠BEC.∵∠ABE1和∠DCE1的平分线交点为E2,∴∠BE2C=∠ABE2+∠DCE2=12∠ABE1+12∠DCE1=12∠CE1B=14∠BEC;如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,∴∠BE3C=∠ABE3+∠DCE3=12∠ABE2+12∠DCE2=12∠CE2B=18∠BEC;…以此类推,∠E n=12n∠BEC.∴当∠E n=1度时,∠BEC等于2n度.故答案为2n .点睛:本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.15.平行平行垂直【解析】根据平行公理的推论,可由,得出a∥c;根据垂直的性质以及平行线的判定,可由,得到a∥c;根据,,得到a⊥c.故答案为平行,平行,垂直.点睛:由平解析:平行平行垂直【解析】根据平行公理的推论,可由//,//a b b c ,得出a ∥c ;根据垂直的性质以及平行线的判定,可由,a b b c ⊥⊥,得到a∥c;根据//a b ,b c ⊥,得到a⊥c.故答案为平行,平行,垂直.点睛:由平行于同一条直线的两条直线互相平行,可求解(1),因为在同一平面内,垂直于同一条直线的两条直线互相平行,可求解(2),再根据平行线的性质可求解(3).16.∠EAD=∠B 或∠DAC=∠C【解析】当∠EAD=∠B 时,根据“同位角相等,两直线平行”可得AD//BC ;当∠DAC=∠C 时,根据“内错角相等,两直线平行”可得AD//BC ;当∠DAB+∠B解析:∠EAD =∠B 或∠DAC =∠C【解析】当∠EAD =∠B 时,根据“同位角相等,两直线平行”可得AD//BC ;当∠DAC =∠C 时,根据“内错角相等,两直线平行”可得AD//BC ;当∠DAB+∠B=180°时,根据“同旁内角互补,两直线平行”可得AD//BC ,故答案是:∠EAD =∠B 或∠DAC =∠C 或∠DAB+∠B=180°(答案不唯一).17.50【分析】先根据平行线的判定可得,再根据平行线的性质、两直线的夹角的定义即可得.【详解】∵,,∴,∵,∴,∴直线AB 与BD 的夹角是50度,故答案为:50.【点睛】本题考查了平解析:50【分析】先根据平行线的判定可得//AB CD ,再根据平行线的性质、两直线的夹角的定义即可得.【详解】∵AC AB ⊥,AC CD ⊥,∴//AB CD ,∵130CDB ∠=︒,∴18050ABD CDB ∠=︒-∠=︒,∴直线AB 与BD 的夹角是50度,故答案为:50.【点睛】本题考查了平行线的判定与性质、两直线的夹角的定义,熟练掌握平行线的判定与性质是解题关键.18.30°【分析】先利用补角的定义求出∠EOC=60°,再根据角平分线的性质计算.【详解】解:∵∠EOD=120°,∴∠EOC=60°(邻补角定义).∵OA 平分∠EOC,∴∠AOC=∠EOC=解析:30°【分析】先利用补角的定义求出∠EOC=60°,再根据角平分线的性质计算.【详解】解:∵∠EOD=120°,∴∠EOC=60°(邻补角定义).∵OA 平分∠EOC ,∴∠AOC=12∠EOC=30°(角平分线定义), ∴∠BOD=30°(对顶角相等).故答案为:30.【点睛】本题考查由角平分线的定义,结合补角的性质,易求该角的度数.19.121°【分析】由AC∥BD,根据两直线平行,同位角相等,即可求得∠B 的度数;由邻补角的定义,求得∠BAC 的度数;又由AE 平分∠BAC 交BD 于点E ,即可求得∠BAE 的度数,根据三角形外角的性质即解析:121°【分析】由AC ∥BD ,根据两直线平行,同位角相等,即可求得∠B 的度数;由邻补角的定义,求得∠BAC 的度数;又由AE 平分∠BAC 交BD 于点E ,即可求得∠BAE 的度数,根据三角形外角的性质即可求得∠2的度数.【详解】∵AC ∥BD ,∴∠B=∠1=64°,∴∠BAC=180°-∠1=180°-62°=118°,∵AE 平分∠BAC 交BD 于点E ,∴∠BAE=12∠BAC=59°, ∴∠2=∠BAE+∠B=62°+59°=121°.故答案为121°.【点睛】此题考查了平行线的性质,角平分线的定义,邻补角的定义以及三角形外角的性质.题目难度不大,注意数形结合思想的应用.20.12【解析】分析:由图形可知,内部小三角形直角边是大三角形直角边平移得到的,故内部五个小直角三角形的周长为大直角三角形的周长.详解:由图形可以看出:内部小三角形直角边是大三角形直角边平移得到的 解析:12【解析】分析:由图形可知,内部小三角形直角边是大三角形直角边平移得到的,故内部五个小直角三角形的周长为大直角三角形的周长.详解:由图形可以看出:内部小三角形直角边是大三角形直角边平移得到的, 故内部五个小直角三角形的周长为AC+BC+AB=12.故答案为12.点睛:本题主要考查了平移的性质,需要注意的是:平移前后图形的大小、形状都不改变.三、解答题21.(1)证明见解析;(2)∠F=55°;(3)∠MQN =12∠ACB ;理由见解析. 【分析】(1)首先根据平行线的性质得出∠ACE =∠A ,∠ECD =∠B ,然后通过等量代换即可得出答案;(2)首先根据角平分线的定义得出∠FCD =12∠ECD ,∠HAF =12∠HAD ,进而得出∠F =12(∠HAD+∠ECD ),然后根据平行线的性质得出∠HAD+∠ECD 的度数,进而可得出答案;(3)根据平行线的性质及角平分线的定义得出12QGR QGD ∠=∠,12NQG AQG ∠=∠,180MQG QGR ∠+∠=︒ ,再通过等量代换即可得出∠MQN =12∠ACB . 【详解】解:(1)∵CE //AB ,∴∠ACE =∠A ,∠ECD =∠B ,∵∠ACD =∠ACE+∠ECD ,∴∠ACD =∠A+∠B ;(2)∵CF 平分∠ECD ,FA 平分∠HAD ,∴∠FCD =12∠ECD ,∠HAF =12∠HAD , ∴∠F =12∠HAD+12∠ECD =12(∠HAD+∠ECD ), ∵CH //AB ,∴∠ECD =∠B ,∵AH //BC ,∴∠B+∠HAB =180°,∵∠BAD =70°,110B HAD ∴∠+∠=︒,∴∠F =12(∠B+∠HAD )=55°; (3)∠MQN =12∠ACB ,理由如下: GR 平分QGD ∠,12QGR QGD ∴∠=∠. GN 平分AQG ∠,12NQG AQG ∴∠=∠. //QM GR ,180MQG QGR ∴∠+∠=︒ .∴∠MQN =∠MQG ﹣∠NQG=180°﹣∠QGR ﹣∠NQG=180°﹣12(∠AQG+∠QGD ) =180°﹣12(180°﹣∠CQG+180°﹣∠QGC ) =12(∠CQG+∠QGC ) =12∠ACB .【点睛】本题主要考查平行线的性质和角平分线的定义,掌握平行线的性质和角平分线的定义是解题的关键.22.(1)详见解析;(2)HPQ ∠的大小不发生变化,一直是45︒.【分析】(1)利用平行线的性质推知180BEF EFD ∠+∠=︒;然后根据角平分线的性质、三角形内角和定理证得90EPF ∠=︒,即EG PF ⊥,故结合已知条件GH EG ⊥,易证//PF GH ;(2)利用三角形外角定理、三角形内角和定理求得49039022∠=︒-∠=︒-∠;然后由邻补角的定义、角平分线的定义推知14522QPK EPK ∠=∠=︒+∠;最后根据图形中的角与角间的和差关系求得HPQ ∠的大小不变,是定值45︒.【详解】解:(1)证明:如图1,//AB CD ,180BEF EFD ∴∠+∠=︒.又BEF ∠与EFD ∠的角平分线交于点P ,1()902FEP EFP BEF EFD ∴∠+∠=∠+∠=︒, 90EPF ∴∠=︒,即EG PF ⊥.GH EG ⊥,//PF GH ∴;(2)HPQ ∠的大小不发生变化,理由如下:如图2,12∠=∠, 322∠=∠∴. 又GH EG ⊥,49039022∠=︒-∠=︒-∠∴.18049022EPK ∠=︒-∠=︒+∠∴.PQ ∵平分EPK ∠,14522QPK EPK ∴∠=∠=︒+∠. ∴245HPQ QPK ∠=∠-∠=︒,∴HPQ ∠的大小不发生变化,一直是45︒.【点睛】本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④//a b ,////b c a c ⇒.23.(1)证明见解析;(2)∠BCD =108°;(3)70°【分析】(1)根据两直线平行,内错角相等得出∠EDF =∠DAB ,由角平线的定义得出∠EDF =∠FDC ,最后根据同旁内角互补,两直线平行进行求证;(2)设∠DCF =x ,则∠CFB =1.5x ,由两直线平行,内错角相等得出∠ABF =1.5x ,由角平分线的定义得出∠ABC =3x ,最后利用两直线平行,同旁内角互补得出关于x 的方程,求解即可;(3)画出图形,根据两直线平行,同旁内角互补得出∠CDF =∠CBF ,由角平分线的定义与已知条件可求出∠ABC 与∠FDC ,由平移的性质与平行公理的推论得出AD ∥PQ ,最后根据两直线平行,同旁内角互补列式求解.【详解】解:(1)证明:∵AB ∥DE ,∴∠EDF =∠DAB ,∵DF 平分∠EDC ,∴∠EDF =∠FDC ,∴∠FDC =∠DAB ,∵∠FDC+∠ABC=180°,∴∠DAB+∠ABC=180°,∴AD∥BC;(2)∵32CFB DCF∠=∠,设∠DCF=x,则∠CFB=1.5x,∵CF∥AB,∴∠ABF=∠CFB=1.5x,∵BE平分∠ABC,∴∠ABC=2∠ABF=3x,∵AD∥BC,∴∠FDC+∠BCD=180°,∵∠FDC+∠ABC=180°,∴∠BCD=∠ABC=3x,∴∠BCF=2x,∵CF∥AB,∴∠ABC+∠BCF=180°,∴3x+2x=180°,∴x=36°,∴∠BCD=3×36°=108°;(3)如图,∵∠DCF=∠CFB,∴BF∥CD,∴∠CDF +∠BFD=180°,∵AD∥BC,∴∠CBF +∠BFD=180°,∴∠CDF=∠CBF,∵AD,BE分别平分∠ABC,∠CDE,∴∠ABC=2∠CBF,∠CDE=2∠FDC,∴∠ABC=∠CDE=2∠FDC,∵∠FDC+∠ABC=180°,∴∠ABC=120°,∠FDC=60°,∵线段BC沿直线AB方向平移得到线段PQ,∴BC∥PQ,∵AD∥BC,∴AD∥PQ,∵∠PQD﹣∠QDC=20°,∴∠QDC=∠PQD﹣20°,∴∠FDC+∠QDC +∠PQD=60°+∠PQD﹣20°+∠PQD=180°,∴∠PQD=70°,即∠DQP=70°.故答案为:70°.【点睛】本题考查平行线的判定与性质,平行公理的推论,角平分线的定义,平移的性质,熟练运用平行线的判定与性质是解题的关键.24.(1)AD BC ∥,见解析;(2)108°【分析】(1)//AD BC ,根据角平分线的性质可知EDF FDC ∠=∠,又因为//AB ED ,因此EDF DAB ∠=∠,推出FDC DAB ∠=∠,再结合已知条件即可得出结论;(2)设DCF x ,则32CFB x ∠=,根据平行线的的性质有32ABF CFB x ∠=∠=,再根据角平分线性质可得23ABC ABF x ∠=∠=,又因为//AD BC ,推出3BCD ABC x ∠=∠=,2BCF x ∠=,由//CF AB 得180ABC BCF ∠+∠=︒,从而可解得x 的值,即可得出答案.【详解】解:(1)//AD BC .证明如下:∵//AB ED ,∴EDF DAB ∠=∠,∵DF 平分EDC ∠,∴EDF FDC ∠=∠,∴FDC DAB ∠=∠,∵180FDC ABC ∠+∠=︒,∴180DAB ABC ∠+∠=︒,∴//AD BC .(2)∵32CFB DCF ∠=∠, ∴设DCF x ,则32CFB x ∠=, ∵//CF AB , ∴32ABF CFB x ∠=∠=, ∵BE 平分ABC ∠,∴23ABC ABF x ∠=∠=,由(1)得//AD BC ,∴180FDC BCD ∠+∠=︒,∵180FDC ABC ∠+∠=︒,∴3BCD ABC x ∠=∠=,∴2BCF x ∠=,∵//CF AB ,∴180ABC BCF ∠+∠=︒,即32180x x +=︒,解得36x =︒,∴3108BCD x ∠==︒.【点睛】本题考查的主要知识点是平行线的判定及性质以及角平分线的性质,根据图形找准角与角之间的关系 是解此题的关键.25.(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)∠B +∠E +∠F +∠D =540°;(3)∠B +∠E +∠D -∠F =180°.【分析】(1)根据平行线的性质和判定,平行公理的推论回答即可;(2)过点E 、F 分别作GE ∥HF ∥CD ,根据两直线平行,同旁内角互补及已知条件求得同旁内角∠ABE +∠BEG =180°,得到AB ∥GE ,再根据平行线的传递性来证得AB ∥CD ; (3)过点E 、F 分别作ME ∥FN ∥CD ,根据两直线平行,内错角相等及已知条件求得同旁内角∠B +∠BEM =180°,得到AB ∥ME ,再根据平行线的传递性来证得AB ∥CD .【详解】解:(1)由题意可知:“依据1”:两直线平行,同旁内角互补;“依据2”: 同旁内角互补,两直线平行;“依据3”: 如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)当∠B 、∠E 、∠F 、∠D 满足条件∠B +∠E +∠F +∠D =540°时,有AB ∥CD . 理由:如图,过点E 、F 分别作GE ∥HF ∥CD ,则∠GEF +∠EFH =180°,∠HFD +∠CDF =180°,∴∠GEF +∠EFD +∠FDC =360°;又∵∠B +∠BEF +∠EFD +∠D =540°,∴∠ABE +∠BEG =180°,∴AB ∥GE ,∴AB ∥CD ;(3)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠D-∠F=180°时,有AB∥CD.如图,过点E、F分别作ME∥FN∥CD,则∠MEF=EFN,∠D=∠DFN,∵∠B+∠BEF+∠D-∠EFD=180°,∴∠B+∠BEM+∠MEF+∠D-∠EFN-∠DFN=180°,∴∠B+∠BEM=180°,∴AB∥ME,∴AB∥CD.【点睛】本题考查平行线的判定和性质的综合应用,作出合适的辅助线,灵活运用平行线的性质定理和判定定理是解题的关键.26.(1)D(k+2,2);(2)k=2;(3)∠BPD=12∠BCD+12∠A,理由详见解析【分析】(1)由平移的性质可得出答案;(2)过点B作BE⊥x轴于点E,过点D作DF⊥x轴于点F,由四边形BEFD的面积可得出答案;(3)过点P作PE∥AB得出∠PBA=∠EPB,由平移的性质得出AB∥CD,由平行线的性质得出PE∥CD,则∠EPD=∠PDC,得出∠BPD=∠PBA+∠PDC,由角平分线的性质得出∠PBA=12∠ABC,∠PDC=12∠ADC,即可得出结论.【详解】解:(1)∵点A(﹣4,﹣1)、B(﹣2,1),C(k,0),将线段AB平移至线段CD,∴点B向上平移一个单位,向右平移(k+4)个单位到点D,∴D(k+2,2);(2)如图1,过点B作BE⊥x轴于点E,过点D作DF⊥x轴于点F,∵A(﹣4,﹣1)、B(﹣2,1),C(k,0),D(k+2,2),∴BE=1,CE=k+2,DF=2,EF=k+4,CF=2,∵S四边形BEFD=S△BEC+S△DCF+S△BCD,∴1(12)(k4)2⨯+⨯+=111(k2)22522⨯⨯++⨯⨯+,解得:k=2.(3)∠BPD=12∠BCD+12∠A;理由如下:过点P作PE∥AB,如图2所示:∴∠PBA=∠EPB,∵线段AB平移至线段CD,∴AB∥CD,∴PE∥CD,∠ADC=∠A,∠ABC=∠BCD,∴∠EPD=∠PDC,∴∠BPD=∠PBA+∠PDC,∵BP平分∠ABC,DP平分∠ADC,∴∠PBA=12∠ABC,∠PDC=12∠ADC,∴∠BPD=12∠ABC+12∠ADC=12∠BCD+12∠A.【点睛】本题考查了平移的综合问题,掌握平移的性质、平行线的性质、角平分线的性质是解题的关键.。
七年级数学相交线与平行线 培优复习附详细答案word版本

七年级数学:相交线与平行线培优复习 )案答细详附(精品文档七年级数学:相交线与平行线培优复习例题精讲例1.如图(1),直线a与b平行,∠1=(3x+70)°,∠2=(5x+22)°,的度数。
求∠3la3,a∥b解:∵4b2(两直线平行,内错角相等)4∴∠3=∠) 平角的定义4=180°(∵∠1+∠3=∠2+∠) 等式性质∠1=∠2 (∴x=24 3x+70=5x+22解得则=142°即∠1 图(1)38°=3180°-∠1=∴∠评注:建立角度之间的关系,即建立方程(组),是几何计算常用的方法。
D ∠B+∠BED+,EG平分∠BEF,∠∥例2.已知:如图(2),AB∥EFCD°,=192 的度数。
°,求∠GEF∠B-∠D=24 AB CD∥∥EF解:∵AB GE∠BEF,∠DEF=∠D(两直线平行,内错角相等)∴∠B=FCD D =192∠°(已知)∵∠B+∠BED+ °DEF+∠D=192∠即∠B+∠BEF+ °(等量代换))B+∠D=192(∠∴2°(等式性质)∠则∠B+D=96收集于网络,如有侵权请联系管理员删除.精品文档∵∠B-∠D=24°(已知)图(2)∴∠B=60°(等式性质)即∠BEF=60°(等量代换)∵EG平分∠BEF(已知)1∠BEF=30°(角平分线定义)∴∠GEF=2DEB的度数。
),已知AB∥CD,且∠B=40°,∠D=70°,求∠例3.如图(3DCAB EF∥解:过E作(已知)AB∥CD∵ABFE∴EF∥CD(平行公理)∴°(两直线平行,内错角相等)DEF=∠∠D=70∠BEF=∠B=40°BEF -∠DEB=∵∠∠DEF -∠D∠B=30°∠∴DEB =评注:证明或解有关直线平行的问题时,如果不构成“三线八角”,则应添出辅3)图(助线。
相交线平行线培优-

初一下数学寒假培优训练一(余角、补角以及三线八角、平行线的判定)一、考点讲解:1.余角:如果两个角的和是直角,那么称这两个角互为余角. 2.补角:如果两个角的和是平角,那.么称这两个角互为补角.3.对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角. 4.互为余角的有关性质:① ∠1+∠ 2=90°,则∠1、∠2互余.反过来,若∠1,∠2互余.则∠1+∠2=90○.②同角或等角的余角相等,如果∠l 十∠2=90○ ,∠1+∠ 3= 90○,则∠ 2= ∠ 3.5.互为补角的有关性质:①若∠A +∠B=180○则∠A 、∠B 互补,反过来,若∠A 、∠B 互补,则∠A+∠B =180○.②同角或等角的补角相等.如果∠A + ∠C=18 0○,∠A+∠B=18 0°,则∠B=∠C . 6.对顶角的性质:对顶角相等.项目定义性质图形互余角两个角和等于︒90(直角)︒=∠+∠9021同角或等角的余角相等互补角两个角和等于︒180(平角)︒=∠+∠18021同角或等角的补角相等对顶角两直线相交而成的一个角两边分别是另一角两边反向延长线对顶角相等21∠=∠三、经典例题题剖析:例1.已知一个角的余角比它的补角的135还少︒4,求这个角。
例2.如图所示,AOB 是一条直线,︒=∠︒=∠90,90DOE AOC ,问图中互余的角有哪几对?哪些角是相等的?例3.如图l -2-1,直线AB ,CD 相交于点O ,OE ⊥AB 于点O ,OF 平分∠AOE ,∠ 1=15○30’,则下列结论中不正确的是( )A .∠2 =45○B .∠1=∠3C .∠AOD 与∠1互为补角 D .∠1的余角等于75○30′ 解:D 点拨:此题考查了互为余角,互为补角和对顶角之间的综合运用知识. 四、巩固练习:1._______的余角相等,_______的补角相等.2.∠1和∠2互余,∠2和∠3互补,∠1=63○,∠3=__3.下列说法中正确的是( )A .两个互补的角中必有一个是钝角 B .一个角的补角一定比这个角大 C .互补的两个角中至少有一个角大于或等于直角 D .相等的角一定互余4.轮船航行到C 处测得小岛A 的方向为北偏东32○,那么从A 处观测到C 处的方向为( )A .南偏西32○B .东偏南32○C .南偏西58○D .东偏南58○121 212 ABEOCD12 3 45.若∠l=2∠2,且∠1+∠2=90○则∠1=___,∠2=___.6.一个角的余角比它的补角的九分之二多1°,求这个角的度数.7.∠1和∠2互余,∠2和∠3互补,∠3=153○,∠l=_8.如果一个角的补角是150○,那么这个角的余角是_________ 9.一个角的余角( )A 、一定是钝角B 、一定是锐角C 、可能是锐角,也可能是钝角D 、以上答案都不对 10.若两个角互补,则( ) A 、这两个都是锐角 B 、这两个角都是钝角 C 、这两个角一个是锐角,一个是钝角 D 、以上结论都不对11.一个角等于它的余角的2倍,那么这个角等于它补角的( ) A 、2倍B 、21倍 C 、5倍 D 、51倍 12.下列说法中正确的是( ) A 、相等的角是对顶角B 、不是对顶角的角不相等C 、对顶角必相等D 、有公共顶点的角是对顶角13.三条直线相交于一点,所成对顶角有( ) A 、3对B 、4对C 、5对D 、6对14.下列说法正确的是( ) A 、不相等的角一定不是对顶角 B 、互补的两个角是邻补角C 、两条直线相交所成的角是对顶角D 、互补且有一条公共边的两个角是邻补角15.如图所示,AOE 是一条直线,︒=∠=∠90COD AOB ,则 (1)如果,301︒=∠那么=∠2 ,3∠= 。
完整版人教版七年级下册相交线与平行线培优50题含答案

人教版七年级下册相交线与平行线培优50题一.选择题(共20小题)1.如图:直线AB∥CD,直线EF分别与直线AB、CD相交于点G,H,若∠1=105°,则∠2的度数为()A.45°B.55°C.65°D.75°2.如图,直线AB∥CD,EG平分∠AEF,EH⊥EG,且平移EH恰好到GF,则下列结论:①EH 平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°.其中正确的结论个数是()A.1个B.2个C.3个D.4个3.如图,在△ABC中,已知∠1+∠2=180°,∠3=∠B=72°,∠AED=58°,则∠C=()A.32°B.58°C.72°D.108°4.将一副三角尺按如图的方式摆放,则∠α的度数是()第1页(共53页)105°°D.B.60°C.75A.45°,=4G,BG于点AC的方向平移到△DEF的位置,E交BC5.如图,将直角△ABC沿斜边;平移的距离是4②△ABC,下列结论:①∠A=∠BED;EF=10,△BEG的面积为4),正确的有(④CF;四边形GCFE的面积为16③BE=①②③④D.①②③C.①③④BA.②③.)b,c应满足的条件是(c为同一平面内不同的三条直线,要使a∥b,则a,,6.若ab,∥cc,b∥c D.a∥bc B c.a∥c,b⊥C.a ⊥c,ba A.⊥b,⊥)=(55°,则∠B+∠CAB7.如图,∥DE,∠E=45°°35D.B125°.55°C..A B、,按如图所示方式放置,其中°角的直角三角板ABCA.已知直线8m∥n,将一块含30)=35°,则∠2的度数是(上,若∠两点分别落在直线m、n1°55.D25C°.B°.A3530.°页)53页(共2第9.已知直线l∥l,∠1和∠2互余,∠4=149°,则∠3的度数()21A.121°B.120°C.59°D.149°10.将一副三角板按如图的所示放置,下列结论中不正确的是()A.若∠2=30°,则有AC∥DEB.∠BAE+∠CAD=180°C.若BC∥AD,则有∠2=30°D.如果∠CAD=150°,必有∠4=∠C11.如图,若直线MN∥PQ,∠ACB的顶点C在直线MN与PQ之间,若∠ACB=60°,∠CFQ=35°,则∠CEN的度数为()A.35°B.25°C.30°D.45°12.若∠A的两边与∠B的两边分别平行,且3∠A﹣∠B=80°,那么∠B的度数为()°140°或.°°或.B65115°°或.A80100C40D.°115°或4013.下列条件不能判定AB∥CD的是()第3页(共53页)A.∠3=∠4B.∠1=∠5C.∠1+∠2=180°D.∠3=∠514.如图,三角形ABC沿着由点B到点E的方向平移到三角形DEF的位置,已知BC=8,EC =5,那么平移的距离为()A.13B.8C.5D.315.如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是()A.∠A+∠C+∠D+∠E=360°B.∠A﹣∠C+∠D+∠E=180°D.∠A+∠°C C.∠E﹣∠+∠D﹣∠A=90D=∠C+∠E16.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l∥l的有()21A.5个B.4个C.3个D.2个17.如图,b∥c,a⊥b,∠1=130°,则∠2等于()B.40°C.50°D.A30°.60°18.如图,AB∥CD,BE⊥EF于E,∠B=25°,则∠EFD的度数是()第4页(共53页)30°°D.°A.80°B.65C.45)D的关系是(CDAB∥,BF平分∠ABE,且BF∥DE,则∠ABE与∠19.如图,90°B ABE=3∠D.∠ABE+∠D=A.∠D D.∠∠C.∠ABE+3D=180°ABE=2∠)°,∠AED=70°,则∠A的大小是(=20.如图,BC∥DE,∠111040°D.60°.A25°B.35°C.13小题)二.填空题(共的、分别在MN的交点为.把一张长方形纸片21ABCD沿EF折叠后ED与BCG,D、C.2=49°,则∠﹣∠1=EFG位置上,若∠.、∠C、∠P的关系为,则∠.如图,已知22AB∥CDA.ADC,⊥且112A,平分∠BDBCAD如图,23.已知∥,ABC∠=°,BDCD则∠=535第页(共页)°,则∠2 =度.,若∠24.如图,直线a∥b1=60.∠则∠1、2、∠3、∠4间的数量关系是P25.如图,若过点P,作直线m的平行线,21.相交,如果∠1=60°,那么∠2的度数26.如图,CD直线AB∥,EF分别与AB、CD作O,过点和∠ACB的平分线,且交于点.如图,OB,OOC分别是△ABC的∠ABC27.BC =2008,则△OEF的周长是BCBCOE∥AB交于点O,OF∥AC交于点F,的位置关系.与AB1,∠=∠2,试判断CDBC28.如图,已知DG⊥BC,⊥AC,EF⊥AB AC⊥(已知)⊥BC,BC解:∵DG90°(垂直的定义)=∴∠DGB=∠DG∴∥∴∠2=∠)已知∵∠1=(=∠∴∠1536第页(共页)∴EF∥)(∴∠AEF=∠∵EF⊥AB=90°∴∠AEF)°(∴∠ADC=90AB.即:CD⊥,,,若ABCBC=29.如图,将等腰直角△ABC沿BC方向平移得到△111.则BB=1已知这种红色地毯的售价准备在大厅的主楼梯上铺上红色地毯..某宾馆在重新装修后,30 米,其侧面如图所示,则购买地毯至少需要元.为每平方米32元,主楼道宽231.已知∠AOB=22.5°,分别以射线OA,OB为始边,在∠AOB的外部作∠AOC=∠AOB,∠BOD=2∠AOB,则OC与OD的位置关系是.32.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为cm;(2)如图2,若∠=∠,则AD∥BC;(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=度;第7页(共53页)度.=150°,∠D=145°,则∠C,∠33.如图,已知AB∥DEB=17小题)三.解答题(共90°.∠1=AFBC⊥于点C,∠A+34.如图1,;∥)求证:ABDE (1,ABPPE.则∠停止,连接AF运动到点FPB,,点(2)如图2P从点A出发,沿线段?C重合的情况)A与点,D,DEP∠,∠BPE三个角之间具有怎样的数量关系(不考虑点P并说明理由.有怎样的数量关系,并FA与∠D=110°,∠C=∠,试探索∠°,∠.如图,∠351=702说明理由.图中′,′CBABC在边长为如图,1个单位的正方形网格中,△经过平移后得到△A′.36′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的对应点B标出了点B:的问题(保留画图痕迹)538第页(共页)′(1)画出△A′BC′;(2)画出△ABC的高BD;,线段AC AA′与CC扫过的图形的面′的关系是′、(3)连接AACC′,那么积为.37.已知:∠MON=48°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=x°(1)如图1,若AB∥ON,则:①∠ABO的度数是°;②当∠BAD=∠ABD时,x=°;③当∠BAD=∠BDA时,x=°.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.38.如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.(1)∠BOD与∠DOF相等吗?请说明理由.(2)若∠DOF=∠BOE,求∠AOD的度数.第9页(共53页)的延长线在DE∥AC,点F上的点,E分别是三角形ABC的边AB,BCDE,39.如图,D A.上,且∠DFC=∠CF;)求证:AB∥1(的度数.BDE大40°,求∠(2)若∠ACF比∠BDE上一点,且ODF是,OE是CD上一点,∥40.已知:如图,FEOC,AC和BD相交于点.=∠A∠1DC;1()求证:AB∥的度数.65=°,求∠OFE2()若∠B=30°,∠1个单位长度.所在的网格图中,每个小正方形的边长均为1.如图,四边形41ABCD ABCD的面积;)求出四边形(1个单位长度后所得的25个单位长度,再向左平移ABCD(2)请画出将四边形向上平移′.C′′DBA四边形′5310第页(共页),D,∠=∠2C=∠DF上,BD,CE均与AF相交,∠1,42.如图所示,点BE分别在AC,.求证:∠A=∠F2,∠1=∠⊥.已知:如图,AEBC,FG⊥BC43CD)求证:AB∥(1°,求∠C的度数.=∠3+50°,∠CBD=70(2)若∠D经过一,在方格纸中将△ABC44.画图并填空:如图,方格纸中每个小正方形的边长都为1′.′、点C和它的对应点C,点次平移后得到△A′B′C′,图中标出来点AB′BC′;(1)请画出平移前后的△ABC和△A′AD;中2)利用网格画出△ABCBC边上的中线(;中AB边上的高CE)利用网格画出△(3ABC.′的面积为′′)△(4ABC5311第页(共页)分别平分、NO2,MO相交于点M、N,且∠1=∠AB45.如图,直线EF分别与直线、CD的形状,并说明理由.END,试判断△MON∠BMF和∠°,114AOC=,OF⊥OE,且∠O46.如图所示,直线AB,CD相交于点,OE平分∠BOC的度数.求∠BOF90°.,∠COE=CD47.已知如图,直线AB、相交于点O的度数;36°,求∠BOE(1)若∠AOC=AOE的度数;1:5,求∠BOC2()若∠BOD:∠=的度数.EOFOF作⊥AB,请直接写出∠O23()在()的条件下,过点5312第页(共页)48.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.(1)求∠AOE的度数;(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.49.如图,AB∥DG,∠1+∠2=180°,(1)求证:AD∥EF;(2)若DG是∠ADC的平分线,∠2=150°,求∠B的度数.50.如图,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.(1)求∠AON的度数;(2)求∠DON的余角.第13页(共53页)人教版七年级下册相交线与平行线培优50题参考答案与试题解析一.选择题(共20小题)1.如图:直线AB∥CD,直线EF分别与直线AB、CD相交于点G,H,若∠1=105°,则∠2的度数为()A.45°B.55°C.65°D.75°【分析】利用平行线的性质求出∠DHF即可.【解答】解:∵AB∥CD,∴∠1=∠DHF,∵∠1=105°,∴∠DHF=105°,∴∠2=180°﹣∠DHF=75°,故选:D.【点评】本题考查平行线的性质,邻补角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.2.如图,直线AB∥CD,EG平分∠AEF,EH⊥EG,且平移EH恰好到GF,则下列结论:①EH 平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°.其中正确的结论个数是()第14页(共53页)A.1个B.2个C.3个D.4个=∠AEF=∠GEF,根据余角的性质得到∠【分析】根据角平分线的定义得到∠AEGBEH=∠FEH,于是得到EH平分∠BEF;故①正确,根据平移的性质得到四边形EGFH是平行四边形,根据平行四边形的性质得到EG∥FH,EG=HF;故②正确;根据平行线的性质得到∠AEF=∠DFE,于是得到FH平分∠EFD;故③正确;根据矩形的性质得到∠GFH=90°,故④正确.【解答】解:∵EG平分∠AEF,=∠AEF,∴∠AEG=∠GEF∵HE⊥GE于E,∴∠GEH=90°,∴∠GEF+∠HEF=90°,∴∠AEG+∠BEH=90°,∴∠BEH=∠FEH,∴EH平分∠BEF;故①正确,∵平移EH恰好到GF,∴四边形EGFH是平行四边形,∴EG∥FH,EG=HF;故②正确;∴∠GEF=∠EFH,∵AB∥CD,∴∠AEF=∠DFE,=∠AEF∵∠GEF,=∠EFDEFH,∴∠∴FH平分∠EFD;故③正确;∵四边形EGFH是平行四边形,∠GEH=90°,∴四边形EGFH是矩形,∴∠GFH=90°,故④正确,∴正确的结论有4个,故选:D.第15页(共53页)【点评】本题考查了平移的性质,平行线的性质,角平分线的定义,平行四边形的判定和性质,矩形的判定和性质,熟练掌握平移的性质是解题的关键.3.如图,在△ABC中,已知∠1+∠2=180°,∠3=∠B=72°,∠AED=58°,则∠C=()A.32°B.58°C.72°D.108°【分析】首先根据∠1+∠EFD=180°和∠1+∠2=180°可以证明∠EFD=∠2,再根据内错角相等,两直线平行可得AB∥EF,进而得到∠ADE=∠3,再结合条件∠3=∠B可得∠ADE=∠B,进而得到DE∥BC,再由平行线的性质可得∠AED=∠C.【解答】解:∵∠1+∠2=180°(已知),∠1+∠EFD=180°(邻补角定义),∴∠2=∠EFD(同角的补角相等)∴AB∥EF(内错角相等,两直线平行)∴∠ADE=∠3=72°(两直线平行内错角相等)∵∠3=∠B(已知),∴∠ADE=∠3=72°(等量代换)∴DE∥BC(同位角相等,两直线平行)∴∠AED=∠C=58°(两直线平行同位角相等).故选:B.【点评】此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理和性质定理.4.将一副三角尺按如图的方式摆放,则∠α的度数是()第16页(共53页)A.45°B.60°C.75°D.105°【分析】根据平行线的性质和根据三角形的内角和计算即可.解:如图:【解答】90°,=∠ABE=∵∠DEC DE,∴AB∥30°,=∠D=∴∠AGD∴∠α=∠AHG=180°﹣∠A ﹣∠AGD=180°﹣45°﹣30°=105°,故选:D.【点评】本题考查的是平行线的判定和性质以及三角形的内角和的性质,掌握三角形的内角和是180°是解题的关键.5.如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,E交BC于点G,BG=4,EF=10,△BEG的面积为4,下列结论:①∠A=∠BED;②△ABC平移的距离是4;③BE=CF;④四边形GCFE的面积为16,正确的有()A.②③B.①②③C.①③④D.①②③④【分析】由平移的性质得到BE∥AC,AB∥DE,BC=EF,BE=CF,故③正确;根据平行四边形的性质得到∠A=∠BED,故①正确;根据直角三角形斜边大于直角边得到△ABC平移的距离>4,故②错误;根据三角形的面积公式得到GE=2,根据梯形的面积的面积=(6+10)×2=GCFE公式得到四边形16,故④正确.【解答】解:∵△DEF的是直角三角形ABC沿着斜边AC的方向平移后得到的,且A、D、C、F 四点在同一条直线上,∴BE∥AC,AB∥DE,BC=EF,BE=CF,故③正确;第17页(共53页)∴四边形ABED是平行四边形,∴∠A=∠BED,故①正确;∵BG=4,∴AD=BE>BG,∴△ABC平移的距离>4,故②正确;∵EF=10,∴CG=BC﹣BG=EF﹣BG=10﹣4=6,∵△BEG的面积等于4,∴BG?GE=4,∴GE=2,的面积=(6+10)×2=16,故④正确;∴四边形GCFE故选:C.【点评】本题考查了平移的性质,面积的计算,平行四边形的判定和性质,正确的识别图形是解题的关键.6.若a,b,c为同一平面内不同的三条直线,要使a∥b,则a,b,c应满足的条件是()A.a⊥b,b⊥c B.a∥c,b⊥c C.a⊥c,b∥c D.a∥c,b∥c【分析】根据在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行进行分析即可.【解答】解:A、a⊥b,a⊥c可判定b∥c,故此选项错误;B、a∥b,b⊥c可判定a⊥c,故此选项错误;C、a⊥c,b∥c可判定a⊥b,故此选项错误;D、根据在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行可得a∥b,故此选项正确;故选:D.【点评】此题主要考查了平行线的判定,关键是掌握平行线的判定定理.7.如图,AB∥DE,∠E=55°,则∠B+∠C=()第18页(共53页)45°°D.B.55°C.35.A125°【分析】利用平行线的性质结合三角形的外角的性质解决问题即可.DE,【解答】解:∵AB∥55°,=∠BFE=∴∠E,+∠CB∵∠BFE=∠°,C =55∴∠B+∠.故选:B本题考查平行线的性质,三角形的外角等知识,解题的关键是熟练掌握基本知【点评】识,属于中考常考题型.BA、,按如图所示方式放置,其中,将一块含30°角的直角三角板ABC.已知直线8m∥n)2的度数是(上,若∠m、n1=35°,则∠两点分别落在直线55°°D..30°A.35B.°C25即可解决问题.【分析】利用平行线的性质求出∠3解:如图,【解答】,m∵∥n5319第页(共页)∴∠1=∠3=35°,∵∠ABC=60°,∴∠2+∠3=60°,∴∠2=25°,故选:C.【点评】本题考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.9.已知直线l∥l,∠1和∠2互余,∠4=149°,则∠3的度数()21A.121°B.120°C.59°D.149°【分析】利用平行线的性质求出∠5即可解决问题.【解答】解:∵直线l∥l,21∴∠1+∠4=180°,∵∠4=149°,∴∠1=31°,∵∠1+∠2=90°,∴∠2=59°,∵直线l∥l,21∴∠5=∠2=59°,∴∠3=180°﹣∠5=121°,故选:A.【点评】本题考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.10.将一副三角板按如图的所示放置,下列结论中不正确的是()第20页(共53页)DE30°,则有AC∥A.若∠2=°CAD=180B.∠BAE+∠°2=30C.若BC∥AD,则有∠C°,必有∠1504=∠D.如果∠CAD=1根据已知可求出∠首先要知道一幅三角板中各角的度数;对于①【分析】要解答此题,的位置关系,即可判断;根据角的关系判断E°,结合∠1与∠的度数,再根据∠E=60;①的结论和平行线的性质定理判断④②,根据平行线的性质定理判断③,结合°,=302【解答】解:∵∠°,=60∴∠1°,=60又∠E,=∠E∴∠1正确;,故A∴AC∥DE90°,2+∠3=1+∵∠∠2=90°,∠正确;°,故°=180B2+∠3=90°+90∠即∠BAE+CAD=∠1+∠2+∠,BC∥AD∵°.=180∠∠2+∠3+C∴∠1+°,=90,∠1+∠2=∵∠C4545°,∴∠3=不正确;,故°=45C∴∠2=90°﹣45°,=150°,∠∵∠D=30CAD 180°,+D∠CAD=∴∵∠,AC∴∥DE D正确.C∴∠4∠=∠,故.故选:C5321第页(共页)本题侧重考查对知识点的应用能力,两直线平行,同旁内角互补;两直线平行,【点评】同错角相等;内错角相等,两直线平行;同角(等角)的余角相等°,=60PQ之间,若∠ACB在直线PQ,∠ACB的顶点CMN与11.如图,若直线MN∥)CEN的度数为(∠CFQ=35°,则∠°D.45C°.30°A.35°B.25即可解决问题.+∠CFQ∥MN,证明基本结论:∠ACB=∠CEN【分析】如图作CK,CK∥MN【解答】解:如图作,∥CKMN∥PQ,MN∵,∥CK∴PQ,=∠CFQ=∠ACK,∠FCK∴∠CEN CFQ,∠ACB=∠CEN+∴∠+35°,∴60°=∠CEN25°,∴∠CEN=B.故选:本题考查平行线的性质和判定等知识,解题的关键是学会添加常用辅助线,构【点评】造平行线解决问题.)(=80°,那么∠B 的度数为且12.若∠A的两边与∠B的两边分别平行,3∠A﹣∠B°140°或40.C°115°或°°或.A8010065.B.D115°或°40°,和已知组成方程组,求出方程组+或∠B=∠根据已知得出∠【分析】AAB∠=180第页(共2253页)的解即可.【解答】解:∵∠A的两边与∠B的两边分别平行,∴∠A=∠B或∠A+∠B=180°,∵3∠A﹣∠B=80°,∴∠A=40°,∠B=40°或∠A=65°,∠B=115°故选:D.【点评】本题考查了平行线的性质的应用,注意:如果两个角的两边互相平行,那么这两个角相等或互补,题目比较好,难度适中.13.下列条件不能判定AB∥CD的是()A.∠3=∠4B.∠1=∠5C.∠1+∠2=180°D.∠3=∠5【分析】分别利用平行线的判定方法,定理1:两条直线被第三条所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.定理2:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.定理3:两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行,分别判断得出即可.【解答】解:∵∠3=∠4,∴AB∥CD,∵∠1=∠5,∴AB∥CD,∵∠+∠2=180°,又∵∠2+∠5=180°,∴∠1=∠5,∴AB∥CD,∵∠3+∠5=180°,∴AB∥CD,故选:D.【点评】此题主要考查了平行线的判定,正确掌握平行线的判定方法是解题关键.14.如图,三角形ABC沿着由点B到点E的方向平移到三角形DEF的位置,已知BC=8,EC =5,那么平移的距离为()第23页(共53页).3.5D.13B.8CA对应,根据平移的性质,易得平、FE对应,CB【分析】观察图形,发现平移前后,、3,进而可得答案.﹣5=移的距离=BE=8【解答】解:根据平移的性质,3,﹣5=易得平移的距离=BE=8.D故选:本题考查平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平【点评】行且相等,对应角相等,本题关键要找到平移的对应点.)满足的数量关系是(、∠C、∠D、∠E15.如图,AB∥EF,则∠A°∠E=180D B°.∠A﹣∠C+∠+360C A.∠A+∠+∠D+∠E=D﹣∠A=90°∠ED=∠C+D.∠A+∠+.∠C E﹣∠C∠AB,利用平行线的性质即可解问题.,DN∥【分析】作CM∥AB,DN∥AB【解答】解:作CM∥AB,,AB∥EF∵,∥EFAB∥CM∥DN∴180°,+∠EDN=ACMA=∠,∠MCD=∠CDN,∠E∴∠CDE)=∠﹣∠ACM=∠﹣∠DCMCDE﹣(∠ACD=∠=∠∵∠EDNCDE﹣∠CDNCDE),﹣(∠ACD﹣∠A180°,A﹣∠CDEACD+∠=∠E∴∠+.故选:B5324第页(共页)【点评】本题考查平行线的性质,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.16.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l∥l的有()21A.5个B.4个C.3个D.2个【分析】根据平行线的判定定理,对各小题进行逐一判断即可.【解答】解:①∵∠1=∠2不能得到l∥l,故本条件不合题意;21②∵∠4=∠5,∴l∥l,故本条件符合题意;21③∵∠2+∠5=180°不能得到l∥l,故本条件不合题意;21④∵∠1=∠3,∴l∥l,故本条件符合题意;21⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l∥l,故本条件符合题意.21故选:C.【点评】本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.17.如图,b∥c,a⊥b,∠1=130°,则∠2等于()B.40°C.50°D°A.30.60°【分析】证明∠3=90°,利用三角形的外角的性质求出∠4即可解决问题.【解答】解:∵b∥c,a⊥b,第25页(共53页)∴a⊥c,∴∠3=90°,∵∠1=90°+∠4,∴130°=90°+∠4,∴∠4=40°,∴∠2=∠4=40°,故选:B.【点评】本题考查平行线的性质,垂线的性质,三角形的外角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.18.如图,AB∥CD,BE⊥EF于E,∠B=25°,则∠EFD的度数是()A.80°B.65°C.45°D.30°【分析】利用三角形的内角和定理求出∠1,再利用平行线的性质求出∠EFD即可.【解答】解:如图,∵BE⊥EF,∴∠E=90°,∵∠B=25°,∴∠1=65°,∵AB∥CD,∴∠EFD=∠1=65°,故选:B.【点评】本题考查平行线的性质,三角形的内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.第26页(共53页)19.如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是()A.∠ABE=3∠D B.∠ABE+∠D=90°D=180°D=2∠D.∠ABE C.∠ABE+3∠【分析】延长DE交AB的延长线于G,根据两直线平行,内错角相等可得∠D=∠G,再根据两直线平行,同位角相等可得∠G=∠ABF,然后根据角平分线的定义解答.【解答】证明:如图,延长DE交AB的延长线于G,∵AB∥CD,∴∠D=∠G,∵BF∥DE,∴∠G=∠ABF,∴∠D=∠ABF,∵BF平分∠ABE,∴∠ABE=2∠ABF=2∠D,即∠ABE=2∠D.故选:D.【点评】本题考查了平行线的性质,角平分线的定义,熟记性质并作辅助线是解题的关键.20.如图,BC∥DE,∠1=110°,∠AED=70°,则∠A的大小是()A.25°B.35°C.40°D.60°【分析】由DE∥BC,推出∠EDB=∠1=110°,根据∠EDB=∠A+∠AED,求出∠A即可.第27页(共53页)DE∥BC,【解答】解:∵=110°,∴∠EDB=∠1∠AED,∵∠EDB=∠A+A+70°,∴110°=∠=40°,∴∠A故选:C.本题考查平行线的性质,三角形的外角的性质等知识,解题的关键是熟练掌握【点评】基本知识,属于中考常考题型.13小题)二.填空题(共的、ND、C分别在MED21.把一张长方形纸片ABCD沿EF折叠后与BC的交点为G,.°=16=位置上,若∠EFG49°,则∠2﹣∠1°,再根据折叠的性49DEG=DEG,∠EFG=∠【分析】先利用平行线的性质得∠2=∠﹣,然后计算∠2=98°,接着利用互补计算出∠1GEF质得∠DEF=∠=49°,所以∠21.∠BC,解:∵AD∥【解答】°,49=∠DEG=∴∠2=∠DEG,∠EFG,BC的交点为GABCD沿EF折叠后ED与∵长方形纸片°,=49DEF∴∠=∠GEF°,°=98=2×492∴∠82°,180°﹣98°=∴∠1=°.82°=1698∴∠2﹣∠1=°﹣°.故答案为16本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角【点评】互补;两直线平行,内错角相等.也考查了折叠的性质.﹣∠P=180°.C+∠的关系为、∠、∠,则∠∥.如图,已知22ABCDACP A ∠第28页(共53页)AB=180°,而CD,根据两直线平行同旁内角互补可知∠C+∠CPE【分析】先作PE∥,再根据两直线平行内错角相∥AB∥CD,利用平行于同一直线的两条直线平行可得PE180°.∠C﹣∠P =+=∠APD,于是有∠A=∠APC∠CPE,即可求∠A+等可知∠A,PE【解答】解:如右图所示,作∥CD,∵PE∥CD°,+∠CPE=180∴∠C,又∵AB∥CD,∴PE∥AB A=∠APD,∴∠P=180°,∴∠A+∠C﹣∠=180°.故答案为:∠A+∠C﹣∠P【点评】本题考查了平行线的判定和性质.平行于同一直线的两条直线平行..°=则∠=A112°,且BD⊥CD,ADC124ABC,已知23.如图,AD∥BCBD平分∠,∠ABC112°,根据两直线平行,同旁内角互补,即可求得∠,∠A=∥【分析】由ADBC的度数,继而求得答案.,求得∠CCD平分∠ABC,BD⊥的度数,又由BD112°,BC,∠A=∥【解答】解:∵AD°,=68°﹣∠∴∠ABC=180A,BD平分∠ABC∵5329第页(共页)=∠ABCCBD=34°,∴∠∵BD⊥CD,=9056°,°﹣∠CBD=∴∠C124°.180°﹣∠C=∴∠ADC=124°.故答案为:此题考查了平行线的性质以及三角形内角和定理.注意掌握两直线平行,同旁【点评】内角互补定理的应用是解此题的关键.60度.=6024.如图,直线a ∥b,若∠1=°,则∠2【分析】根据两直线平行,同位角相等即可求解.【解答】解:∵a∥b,∴∠2=∠1,∵∠1=60°,∴∠2=60°.故答案为60.【点评】本题考查了平行线的性质,掌握两直线平行,同位角相等是解题的关键.25.如图,若过点P,P作直线m的平行线,则∠1、∠2、∠3、∠4间的数量关系是∠212+∠4=∠1+∠3.【分析】分别过点P1、P2作PC∥m,PD∥m,由平行线的性质可知,∠1=∠APC,121CPP=∠PPD,∠DPB=∠4,22112所以∠1+∠PPD+∠DPB=∠APC+∠CPP+∠4,即∠2+∠4=∠1+∠3.221112【解答】解:分别过点P、P作PC∥m,PD∥m,2121第30页(共53页)n,∵m∥,∥C∥PDm∥n∴P21,D,∠DPB=∠4=∠∴∠1=∠APC,CPPPP221112=∠1+∠.3+C∠CPP+∠4,即∠2+∠4∠1+∴∠∠PPD+DPB=∠AP212211.1+∠3故答案为:∠2+∠4=∠本题考查的是平行线的性质,即两直线平行,内错角相等.【点评】120°60°,那么∠2的度数.如果∠CD26.如图,直线AB∥,EF分别与AB、CD相交,1=【分析】先根据对顶角相等求出∠3的度数,再根据平行线的性质即可得出∠2的度数.【解答】解:∵∠1=60°,∠1与∠3是对顶角,∴∠3=∠1=60°,∵AB∥CD,∴∠2=180°﹣∠3=180°﹣60°=120°.故答案为:120°.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.27.如图,OB,OC分别是△ABC的∠ABC和∠ACB的平分线,且交于点O,过点O作OE∥AB 交于BC点O,OF∥AC交BC于点F,BC=2008,则△OEF的周长是2008.第31页(共53页)可ACAB和∠ACB的平分线和OE∥、OF∥ABC【分析】由OB,OC分别是△的∠ABC OF=CF,显然△OEF的长度.的周长即为BC=推出BEOE,ACB的平分线,ABC的∠ABC和∠OC【解答】解:OB,分别是△OCF,∠ACO=∠.∴∠ABO=∠OBF,ACOF∥∵OE∥AB=∠COF,∠∴∠ABO=∠BOEACO为等腰三角形OCF∴△BOE和△OF∴BE=EO,=CF∴△OEF的周长=BE.BC=2008+EF+CF=此题运用了平行线性质,和角平分线性质以及等腰三角形的性质,较为灵活,【点评】难度中等.,试判断的位置关系.CD与ABEFBC,⊥AC,⊥AB,∠1=∠2DG28.如图,已知⊥BC AC(已知)BC解:∵DG⊥,BC⊥=DGB∴∠BCA°(垂直的定义)=∠90DG∥AC∴∴∠2=∠DCA∵∠1=∠2(已知)∴∠1=∠DCA∴EF∥DC∴∠AEF=∠ADC(两直线平行,同位角相等)∵EF⊥AB(已知)∴∠AEF=90°(垂直定义)∴∠ADC=90°(等量代换)即:CD⊥AB.第32页(共53页),求出∠DCA,根据平行线的性质得出∠2=∠【分析】根据平行线的判定推出DG∥AC即ADC,根据平行线的性质得出∠AEF=∠1=∠DCA,根据平行线的判定得出EF∥DC可.⊥AC(已知)BC【解答】解:∵DG⊥,BC=90°(垂直的定义)∴∠DGB=∠BCA∥AC,∴DG=∠DCA,∴∠2),=∠2(已知∵∠1DCA,∴∠1=∠DC,∴EF∥(两直线平行,同位角相等),∴∠AEF=∠ADC(已知),∵EF⊥AB,AEF=90°(垂直定义)∴∠,ADC=90°(等量代换)∴∠,即:CD⊥AB,两直线平行,同位角相等,(已知)DC,DCA,,ADC,,故答案为:BCA,ACDCA,∠2(垂直定义),等量代换.本题考查了平行线的性质和判定,垂直定义的应用,能灵活运用平行线的性质【点评】和判定定理进行推理是解此题的关键.,,若BC,=C.如图,将等腰直角△29ABC沿BC方向平移得到△AB111.=则BB1【分析】先判断出△PBC是等腰直角三角形,再根据等腰直角三角形的性质利用面积列1式求出BC,然后根据BB=BC﹣BC代入数据计算即可得解.111【解答】解:∵△ABC是等腰直角三角形,∴平移后∠PBC=∠CB=45°,1∴△PBC是等腰直角三角形,1第33页(共53页))=2C?,(BC∴SB=11C1PB△2C解得B=,13=BB=BC﹣﹣B2C=.∴11故答案为:.本题考查了平移的性质,等腰直角三角形的判定与性质,利用等腰直角三角形【点评】的长度是解题的关键.B求出C1已知这种红色地毯的售价准备在大厅的主楼梯上铺上红色地毯.30.某宾馆在重新装修后,元.2512米,其侧面如图所示,则购买地毯至少需要为每平方米32元,主楼道宽根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得【分析】其面积,则购买地毯的钱数可求.解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为【解答】2.5米,米,5.516平方米,8×2=∴地毯的长度为2.5+5.5=8米,地毯的面积为512元.×32=16∴买地毯至少需要512.故答案为:本题考查平移性质的实际运用,难度不大.解决此题的关键是要利用平移的知【点评】识,把要求的所有线段平移到一条直线上进行计算.,AOB的外部作∠AOC=∠OA,OB为始边,在∠AOB.31已知∠AOB=22.5°,分别以射线OD的位置关系是垂直与.,则∠BOD=2∠AOBOC【分析】根据题意,结合图形,利用已知条件及角的和差关系,求∠COD度数.【解答】解:∵∠AOB=22.5°,∠AOC=∠AOB=22.5°,∠BOD=2∠AOB=45°,∴∠COD=∠AOC+∠AOB+∠BOD=22.5°+22.5°+45°=90°,∴OC与OD的位置关系是垂直.故填垂直.第34页(共53页)先利用角的和差关系求得这个角是90°,再由垂线的定义可得,两直线垂直.【点评】之间的距离为3cm,BC=2cm,则AB与CD2AB.32(1)如图1,在长方形ABCD中,=;cm;∥BC2,则AD2(2)如图,若∠1=∠度;EDC°,则∠=25BC,CD是∠ACB的平分线,∠ACB=503()如图3,DE∥1)夹在两条平行线间的垂线段的长度即为两平行线的距离.【分析】(2)运用的是平行线判定定理.(3)运用的是角平分线的定义和平行线的性质.(°.B=90C∥CD,∠=90°,∠1【解答】解:()已知四边形ABCD为长方形,则AB.2cm与cm,故ABCD之间的距离为又BC=2.故填22.BC,根据平行线的判定定理可得∠1=∠∥(2)要使AD2.故填∠1;∠,DE∥BC3()已知,=∠DCBEDC根据平行线判定定理可得∠ACB是∠的平分线,又CD DCB,∴∠ECD=∠°,ACB=50∵∠25°.EDC∴∠=.故填255335第页(共页)此类题考查的是平行线的性质以及平行线的判定定理,考生一定要熟记.【点评】=65=145°,则∠C度.D33.如图,已知AB∥DE,∠B=150°,∠【分析】过点C作CF平行于AB,再根据平行线的性质解答即可.【解答】解:过点C作CF平行于AB,如图:∵AB∥DE,∴AB∥CF∥ED.AB∥CF?∠1=180°﹣∠B=30°,CF∥ED?∠2=180°﹣∠D=35°,∴∠BCD=∠1+∠2=65°.故填65°.【点评】结合题意和图形作出正确的辅助线是解决本题的关键.三.解答题(共17小题)34.如图1,BC⊥AF于点C,∠A+∠1=90°.(1)求证:AB∥DE;(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.【分析】(1)根据∠A+∠B=90°,∠A+∠1=90°,即可得到∠B=∠1,进而得出AB第36页(共53页)∥DE.(2)分三种情况讨论:点P在A,D之间;点P在C,D之间;点P在C,F之间;分别过P 作PG∥AB,利用平行线的性质,即可得到∠ABP,∠DEP,∠BPE三个角之间的数量关系.【解答】解:(1)如图1,∵BC⊥AF于点C,∴∠A+∠B=90°,又∵∠A+∠1=90°,∴∠B=∠1,∴AB∥DE.(2)如图2,当点P在A,D之间时,过P作PG∥AB,∵AB∥DE,∴PG∥DE,∴∠ABP=∠GPB,∠DEP=∠GPE,∴∠BPE=∠BPG+∠EPG=∠ABP+∠DEP;如图所示,当点P在C,D之间时,过P作PG∥AB,∵AB∥DE,∴PG∥DE,第37页(共53页)∴∠ABP=∠GPB,∠DEP=∠GPE,∴∠BPE=∠BPG﹣∠EPG=∠ABP﹣∠DEP;如图所示,当点P在C,F之间时,过P作PG∥AB,∵AB∥DE,∴PG∥DE,∴∠ABP=∠GPB,∠DEP=∠GPE,∴∠BPE=∠EPG﹣∠BPG=∠DEP﹣∠ABP.【点评】本题主要考查了平行线的性质与判断的运用,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.35.如图,∠1=70°,∠2=110°,∠C=∠D,试探索∠A与∠F有怎样的数量关系,并说明理由.【分析】要找∠A与∠F的数量关系,根据平行线的判定,由已知可得∠1+∠2=180°,则CE ∥BD;根据平行线的性质,可得∠C=∠ABD,结合已知条件,得∠ABD=∠D,根据平行线的判定,得AC∥DF,从而求得结论.【解答】解:∠A=∠F.理由:∵∠1=70°,∠2=110°,∴∠1+∠2=180°,∴CE∥DB,∴∠C=∠ABD,∵∠C=∠D,第38页(共53页)ABD,=∠D∴∠,∥DF∴AC.=∠F∴∠A本题主要考查平行线的判定与性质,正确识别“三线八角”中的同位角、内错【点评】角、同旁内角是正确答题的关键.图中′,′ABC经过平移后得到△A′BC136.如图,在边长为个单位的正方形网格中,△′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关B标出了点B的对应点:的问题(保留画图痕迹)′AB′C′;(1)画出△ABC的高BD;)画出△(2平行且相等,线段CC′,那么AA′与CCAC扫过的′的关系是)连接(3AA′、图形的面积为10.【分析】(1)根据平移的定义和性质作出点A、C平移后的对应点,顺次连接即可得;(2)根据三角形高的定义作图即可得;(3)根据平移变换的性质可得,再利用割补法求出平行四边形的面积.【解答】解:(1)如图所示,△A′B′C′即为所求;第39页(共53页)BD即为所求;(2)如图所示,′的关系是平行且相等,)如图所示,(3AA′与CC,××6×1=线段AC扫过的图形的面积为10×2﹣2××4×1﹣210故答案为:平行且相等、10.此题主要考查了平移变换以及平行四边形面积求法等知识,根据题意正确把握【点评】平移的性质是解题关键.上的分别是射线OM、OE、ONMON.已知:∠MON=48°,OE平分∠,点A、B、C37°x.设∠OAC=B、C不与点O重合),连接AC交射线OE于点D、动点(A24°;的度数是)如图1,若AB∥ON,则:①∠ABO(1②当∠BAD=∠ABD时,x=108°;③当∠BAD=∠BDA时,x=54°.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.【分析】(1)①运用平行线的性质以及角平分线的定义,可得①∠ABO的度数;②根据∠ABO、∠BAD的度数以及△AOB的内角和,可得x的值;。
七年级数学.培优 专题24 相交线与平行线_答案

专题24 相交线与平行线例1 (1)40° 过点 C 作CF ∥AB ,则∠BCF =∠ABC =80°.∠DCF =180°—140°=40°,∴∠BCD =80°-40°=40°.(2)90° 过点E 作EM ∥AB ,∴AB ∥CD ,∴EM ∥CD ,∠AEM =180°−25°=155°. ∠CEM =180°−115°=65°,∴∠E =∠AEM −∠CEM =155°−65°=90°.例2 D 提示:原图可分解为8个基本图形.例3 提示:由DF ∥CE 得,∠BDF =∠BCE ,∠FDE =∠DEC ,AC ∥DE ,得∠DEC =∠ECA . 例4 过E 作EM ∥AB .∴AB ∥于CD ,∴EM ∥CD .∴∠AEC =∠AEM +∠CEM =∠EAB +∠ECD .同理:∠AFC =∠FAB +∠FCD .∴∠AEC =∠FAB +∠FCD +∠EAF +∠ECF =∠AFC +14∠EAB +14+∠ECD =∠AFC +14∠AEC .故∠AFC =34∠AEC .例5 提示:先证BD ∥CE ,再证DF ∥BC .例6 (1)直线a ,b ,c ,d 共有1个交点,理由如下:设直线a ,b ,c 的交点为P ,直线b ,c ,d 的交点为Q .这意味着点P 和点Q都是直线b 和c 的交点.而两条不同直线至多有一个交点.因此P 和Q 必为同一个点.即4条直线a ,b ,c 和d 相交于同一个点.因此这4条直线只有一个交点.(2)不妨设(1)中交点为O .因为作的第5条直线e 与(1)中的直线d 平行,所以直线e 和直线d 没有公共点,因此这些e 不过点O .而直线a ,b ,c 与直线e 必然都相交. 如图所示.设直线e 与直线a ,b ,c 分别相交于点A ,B ,C .这时有A ,B ,C ,O 共四个不同的点.可以连出OA ,OB ,OC ,AB ,AC ,BC 共6条不同的线段.A 级1.a 1∥a 102.20°3.①②③④4.90°5.D6.B7.C8.D 提示:m =5,n =6,m +n =5+6=11.9.60° 10.提示:过点E 作EF ∥AB . 11如图所示.12.作CK ∥FG ,延长GF ,CD 交于H 点,则∠1+∠2=∠ABC ,故∠ABC +∠BCK =180°,即CK ∥AB ,AB ∥GF .B 级1.120°2.72°3.50°4.30°5.C 提示:∠2=50°+d ,∠3=50°+2d ,∠4=50°+3d ,又∵∠3=50°+2d <90°,∴d <20°,∠4=50°+3d <110°.故∠4的最大整数值为109°.6.B7.D8.B 提示:由题意知每一个交点由a 上两点和b 上两点所确定.在a 上取两点有12×10×9=45种情况,在b 上取两点有12×9×8=36种情况,故交点个数为45×36=1620个.9.提示:过点O 作CD 的平行线.10.如图,设N 是AC 的中点,连接MN ,则MN ∥AB .又MF ∥AD ,∴∠FMN =∠BAD =∠DAC =∠MFN .∴FN =MN =12AB .因此FC =FN +NC =12AB +12AC =12(AB +AC )=12(7+11)=9. 11.提示:在平面上任取一点O ,将已知的七条直线平移过点O ,它们把以O 为圆心的圆周角分成14个彼此相邻的角a 1,a 2,……,a 14其中的每一个都和原来某两条直线交角中的一个相等,假设a i (i =1,2,……,14)都大于180°7,则a 1+a 2+……+a 14>14×180°7=360°,与a 1+a 2+……+a 14=360°矛盾,由此可推出结论.12.(1)180° 360° 540° 720° 证明略.(2)(n -1)180°(3)过F作FG∥AB,则AB∥FG∥CD.则∠BFD=1(∠ABE+∠CDE),又∠ABE+∠CDE+∠E=360°,得∠ABE+∠CDE=220°,故∠2BFD=110°。
相交线与平行线培优辅导

1、下列说法正确的有 。
①平面内,过直线上一点有且只有一条直线垂直于已知直线; ②平面内,过直线外一点有且只有一条直线垂直于已知直线;③不相交的两条直线是平行线; ④在平面内,有且只有一条直线垂直于已知直线. ⑤若线段AB 与CD 没有交点,则AB ∥CD; ⑥若a ∥b,b ∥c,则a 与c 不相交.2、如果两个角的两边分别垂直,而其中一个角比另一个角的4倍少30°,那么这两个角分别为 。
3、一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )A.第一次右拐50 ,第二次左拐130B.第一次左拐50 ,第二次右拐50 C .第一次左拐50 ,第二次左拐130 D .第一次右拐50 ,第二次右拐50 4、下面说法中正确的是____________________(填序号) (1)过已知直线外一点,有且只有一条直线与已知直线平行.(2) 平行于同一直线的两条直线互相平行.(3)垂直于同一直线的两条直线互相平行.(4)不相交的两条直线必平行.(5)两条直线被第三条直线所截,同位角相等.(6)两条平行线被第三条直线所截,一对内错角的平分线互相平行.5、如图,l ∥m ,等腰直角三角形ABC 的直角顶点C 在直线m 上,若∠β=30°,则∠α的度数为 。
6、如图,将长方形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C '处,折痕为EF 。
如果20ABE ∠=︒,那么EFB ∠= 度7、如图,将矩形纸片ABCD 折叠,使点A 与C 重合,折痕为EF ;且∠EFC=65°,则∠BEC=8、如图,已知: AC DE ⊥于E ,AC BC ⊥,AB FG ⊥于G ,21∠=∠。
求证:AB CD ⊥9、如下图所示,AB ∥DE ,若∠ABC=80°,∠CDE=140°,则BCD=_______度.10、如下图,AB ∥CD,由B 点出发作n 条直线1BB ,21B B ,32B B ,…,D B n 1-, 则∠1ABB -∠B 21B B +∠321B B B -…+∠D B n 1-C = .11、如图,已知∠1=∠2,∠3=∠4,CE//AB ,试说明:AD//BC.(8分)12、如图:已知∠BEF=∠CFE ,∠1=∠2,请指出AB 和CD 的位置关系并说明理由。
《易错题》初中七年级数学下册第五章《相交线与平行线》经典题(专题培优)

一、选择题1.下列语句不是命题的是( ).A .两直线平行,同位角相等B .作直线AB 垂直于直线CDC .若a b =,则22a b =D .等角的补角相等B解析:B【分析】根据“判断一件事情的语句叫做命题”进行判断即可得到答案.【详解】解:A 、两直线平行,同位角相等,是命题,不符合题意;B 、作直线AB 垂直于直线CD 是描述了一种作图的过程,故不是命题,符合题意;C 、正确,是判断语句,不符合题意;D 、正确,是判断语句,不符合题意.故选:B .【点睛】主要考查了命题的概念.判断一件事情的语句叫做命题.2.如图,下列条件中,不能判断直线a ∥b 的是( )A .∠1=∠3B .∠2=∠3C .∠4=∠5D .∠2+∠4=180°B解析:B【分析】 根据平行线的判定定理逐项判断即可.【详解】A 、当∠1=∠3时,a ∥b ,内错角相等,两直线平行,故正确;B 、∠2与∠3不是同位角,也不是内错角,无法判断,故错误;C 、当∠4=∠5时,a ∥b ,同位角相等,两直线平行,故正确;D 、当∠2+∠4=180°时,a ∥b ,同旁内角互补,两直线平行,故正确.故选:B .【点睛】本题考查了平行线的判定,熟记判定定理是解题的关键.3.下列所示的四个图形中,∠1和∠2是同位角的是( )A .②③B .①②③C .①②④D .①④C解析:C【分析】 根据同位角的定义逐一判断即得答案.【详解】图①中的∠1与∠2是同位角,图②中的∠1与∠2是同位角,图③中的∠1与∠2不是同位角,图④中的∠1与∠2是同位角,所以在如图所示的四个图形中,图①②④中的∠1和∠2是同位角.故选:C .【点睛】本题考查了同位角的定义,属于基础概念题型,熟知概念是关键.4.如图,1∠与2∠是同位角的共有( )个A .1个B .2个C .3个D .4个B解析:B【分析】 根据同位角的概念对每个图形一一判断,选出正确答案即可.【详解】图1:1∠与2∠是同位角;图2:1∠与2∠不是同位角;图3:1∠与2∠不是同位角;图4:1∠与2∠是同位角;只有图1、图4中1∠与2∠是同位角.故选:B .【点睛】本题主要考查同位角的概念,熟记同位角的概念是解题关键.5.已知//AB CD ,∠EAF=13∠EAB ,∠ECF=13∠ECD ,若∠E=66°,则∠F 为( )A .23°B .33°C .44°D .46°C解析:C【分析】 如图(见解析),先根据平行线的性质、角的和差可得66EAB EC C D AE ∠+∠=∠=︒,同样的方法可得F FAB FCD ∠=∠+∠,再根据角的倍分可得,2323FAB EAB FCD ECD ∠=∠∠=∠,由此即可得出答案. 【详解】如图,过点E 作//EG AB ,则////EG AB CD ,,EAB CE C A D G G E E ∴∠=∠∠∠=,66AEG EAB ECD CE A C G E ∴∠+=∠+=∠=∠∠︒,同理可得:F FAB FCD ∠=∠+∠,11,33EAF EAB ECF ECD ∠=∠∠=∠, ,2323FAB EAB FCD ECD ∴∠=∠∠=∠, ()266443333222F FAB FCD EAB ECD EAB ECD ∴∠=∠+∠=∠+∠=∠+∠=⨯︒=︒,故选:C .【点睛】本题考查了平行线的性质、角的和差倍分,熟练掌握平行线的性质是解题关键. 6.如图,△ABC 经平移得到△EFB ,则下列说法正确的有 ( )①线段AC的对应线段是线段EB;②点C的对应点是点B;③AC∥EB;④平移的距离等于线段BF的长度.A.1 B.2 C.3 D.4D解析:D【分析】根据平移的特点分别判断各选项即可.【详解】∵△ABC经平移得到△EFB∴点A、B、C的对应点分别为E、F、B,②正确∴BE是AC的对应线段,①正确∴AC∥EB,③正确平移距离为对应点连线的长度,即BF的长度,④正确故选:D【点睛】本题考查平移的特点,注意,在平移过程中,一定要把握住对应点,仅对应点的连线之间才有平行、相等的一些关系.7.下列命题是真命题的有()个①对顶角相等,邻补角互补②两条直线被第三条直线所截,同位角的平分线平行③垂直于同一条直线的两条直线互相平行④过一点有且只有一条直线与已知直线平行A.0 B.1 C.2 D.3B解析:B【分析】根据平行线的性质定理、平行公理、对顶角和邻补角的概念判断即可.【详解】解:对顶角相等,邻补角互补,故①是真命题;两条平行线被第三条直线所截,同位角的平分线平行,故②是假命题;在同一平面内,垂直于同一条直线的两条直线互相平行,故③是假命题;过直线外一点有且只有一条直线与已知直线平行,故④是假命题;故正确的个数只有1个,【点睛】本题考查的是平行的公理和应用,命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.8.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为()A.10°B.20°C.25°D.30°C解析:C【解析】分析:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∴∠ABC=60°.∵∠1=35°,∴∠AEC=∠ABC﹣∠1=25°.∵GH∥EF,∴∠2=∠AEC=25°.故选C.9.下列命题中,属于假命题的是()A.如果三角形三个内角的度数比是1:2:3,那么这个三角形是直角三角形B.内错角不一定相等C.平行于同一直线的两条直线平行>-,则a一定小于0DD.若数a使得a a解析:D【分析】利用三角形内角和对A进行判断;根据内错角的定义对B进行判断;根据平行线的判定方法对C进行判断;根据绝对值的意义对D进行判断.【详解】解:A、如果三角形三个内角的度数比是1:2:3,则三个角的度数分别为30°,60°,90°,所以这个三角形是直角三角形,所以A选项为真命题;B、内错角不一定相等,所以B选项为真命题;C、平行于同一直线的两条直线平行,所以C选项为真命题;D、若数a使得|a|>-a,则a为不等于0的实数,所以D选项为假命题.故选:D.本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.10.如图,将△ABE 向右平移50px 得到△DCF ,如果△ABE 的周长是400px(1px=0.04cm ),那么四边形ABFD 的周长是( )A .16cmB .18cmC .20cmD .21cm C解析:C【分析】 根据平移的性质可得DF=AE ,然后判断出四边形ABFD 的周长=△ABE 的周长+AD+EF ,然后代入数据计算即可得解.注意:1px = 0.04cm .【详解】∵1px = 0.04cm ,∴50px=2cm ,400px=16cm ,∵△ABE 向右平移2cm 得到△DCF ,∴DF=AE ,∴四边形ABFD 的周长=AB+BE+DF+AD+EF=AB+BE+AE+AD+EF=△ABE 的周长+AD+EF .∵平移距离为2cm ,∴AD=EF=2cm ,∵△ABE 的周长是16cm ,∴四边形ABFD 的周长=16+2+2=20cm .故选:C .【点睛】本题考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.二、填空题11.如图,直线AB ,CD 相交于点O ,AO 平分COE ∠,且50EOD ∠=︒,则DOB ∠的度数是________.【分析】根据求出利用AO 平分求得即可得到∠DOB=【详解】∵∴∵AO 平分∴∴∠DOB=故答案为:【点睛】此题考查求一个角的补角角平分线的性质对顶角相等正确理解补角定义求出是解题的关键解析:65︒【分析】根据180COE EOD ∠+∠=︒,50EOD ∠=︒,求出130COE ∠=︒,利用AO 平分COE ∠,求得65AOC ∠=︒,即可得到∠DOB=65AOC ∠=︒.【详解】∵180COE EOD ∠+∠=︒,50EOD ∠=︒,∴130COE ∠=︒,∵AO 平分COE ∠,∴65AOC ∠=︒,∴∠DOB=65AOC ∠=︒,故答案为:65︒.【点睛】此题考查求一个角的补角,角平分线的性质,对顶角相等,正确理解补角定义求出130COE ∠=︒是解题的关键.12.如图,直线AB 与CD 相交于点O ,EO ⊥CD 于点O ,OF 平分∠AOD ,且∠BOE =50°,则∠DOF 的度数为__.【分析】利用垂直定义可得∠COE =90°进而可得∠COB 的度数再利用对顶角相等可得∠AOD 再利用角平分线定义可得答案【详解】解:∵EO ⊥CD 于点O ∴∠COE =90°∵∠BOE =50°∴∠COB =90解析:70︒【分析】利用垂直定义可得∠COE =90°,进而可得∠COB 的度数,再利用对顶角相等可得∠AOD ,再利用角平分线定义可得答案.【详解】解:∵EO ⊥CD 于点O ,∴∠COE =90°,∵∠BOE =50°,∴∠COB =90°+50°=140°,∴∠AOD =140°,∵OF 平分∠AOD ,∴∠FOD =12∠AOD =70°, 故答案为:70°.【点睛】此题主要考查了垂直定义,关键是理清图中角之间的和差关系.13.两个角的两边两两互相平行,且一个角的12等于另一个角的13,则这两个角中较小角的度数为____︒.72【分析】如果两个角的两边互相平行则这两个角相等或互补根据题意这两个角只能互补然后列方程求解即可【详解】解:设其中一个角是x°则另一个角是(180-x)°根据题意得解得x=72∴180-x=108解析:72【分析】如果两个角的两边互相平行,则这两个角相等或互补.根据题意,这两个角只能互补,然后列方程求解即可.【详解】解:设其中一个角是x°,则另一个角是(180-x)°,根据题意,得11(180)23x x =-, 解得x=72,∴180-x=108°;∴较小角的度数为72°.故答案为:72.【点睛】本题考查了平行线的性质,一元一次方程的应用,运用“若两个角的两边互相平行,则两个角相等或互补”,而此题中显然没有两个角相等这一情况是解决此题的突破点. 14.阅读下面材料:在数学课上,老师提出如下问题:如图,需要在A 、B 两地和公路l 之间修地下管道.请你设计一种最节省材料的修路方案:小丽设计的方案如下:如图,(1)连接AB ;(2)过点A 画线段AC ⊥直线l 于点C ,所以线段BA 和线段AC 即为所求.老师说:“小丽的画法正确”请回答:小丽的画图依据是___.两点之间线段最短;直线外一点到这条直线上所有点连结的线段中垂线段最短(或垂线段最短)【分析】根据线段的概念和垂线的性质即可求解【详解】由垂线段最短可知点A 到直线l 的最短距离为AC 由两点之间线段最短可解析:两点之间线段最短;直线外一点到这条直线上所有点连结的线段中,垂线段最短(或垂线段最短)【分析】根据线段的概念和垂线的性质即可求解.【详解】由垂线段最短可知,点A 到直线l 的最短距离为AC ,由两点之间线段最短可知,点B 到点A 的最短距离为AB .故答案为:两点之间线段最短;直线外一点到这条直线上所有点连结的线段中,垂线段最短(或垂线段最短);【点睛】本题考察线段的概念和垂线的性质,熟练掌握其概念和性质是解题的关键.15.如图,//EF AD ,//AD BC ,CE 平分BCF ∠,120DAC ∠=︒,20ACF ∠=︒,FEC ∠为______°.20【分析】根据平行线的性质可得进而可得∠ACB =60°根据角平分线的性质和角的和差可得∠BCE 根据平行线的性质可得∠FEC 【详解】∵∴∵∴∵又∵∴∵平分∴∠BCE =∠ECF =∠BCF =20°∵∴∴解析:20【分析】根据平行线的性质可得180DAC ACB ∠+∠=︒,进而可得∠ACB =60°,根据角平分线的性质和角的和差可得∠BCE ,根据平行线的性质可得∠FEC .【详解】∵//AD BC ,∴180DAC ACB ∠+∠=︒.∵120DAC ∠=︒,∴180********ACB DAC ∠=︒-∠=︒-︒=︒.∵60BCF ACF ACB ∠+∠=∠=︒.又∵20ACF ∠=︒,∴602040BCF ACB ACF ∠=∠-∠=︒-︒=︒.∵CE 平分BCF ∠,∴∠BCE =∠ECF =12∠BCF =20° ∵//EF BC ,∴20FEC BCE ∠=∠=︒,∴20FEC ∠=︒.故答案为:20.【点睛】本题主要考查平行线的性质,涉及到角的和差,角平分线的性质,解题的关键是求得∠BCE .16.直线//,a b Rt ABC ∆的直角顶C 点在直线a 上,若135∠=︒,则2∠等于_______. 【分析】先根据直角为90°即可得到∠3的度数再根据平行线的性质即可得出∠2的度数【详解】解:∵Rt △ABC 的直角顶点C 在直线a 上∠1=35°∴∠3=90°-35°=55°又∵a ∥b ∴∠2=∠3=55解析:55【分析】先根据直角为90°,即可得到∠3的度数,再根据平行线的性质,即可得出∠2的度数.【详解】解:∵Rt △ABC 的直角顶点C 在直线a 上,∠1=35°,∴∠3=90°-35°=55°,又∵a ∥b ,∴∠2=∠3=55°,故答案为:55°.【点睛】本题主要考查了平行线的性质,直角三角形两个锐角互余的性质,解题时注意:两直线平行同位角相等.17.如图,AC ⊥AB ,AC ⊥CD ,垂足分别是点A 、C ,如果∠CDB=130°,那么直线AB 与BD 的夹角是________度.50【分析】先根据平行线的判定可得再根据平行线的性质两直线的夹角的定义即可得【详解】∵∴∵∴∴直线AB 与BD 的夹角是50度故答案为:50【点睛】本题考查了平行线的判定与性质两直线的夹角的定义熟练掌握解析:50【分析】先根据平行线的判定可得//AB CD ,再根据平行线的性质、两直线的夹角的定义即可得.【详解】∵AC AB ⊥,AC CD ⊥,∴//AB CD ,∵130CDB ∠=︒,∴18050ABD CDB ∠=︒-∠=︒,∴直线AB 与BD 的夹角是50度,故答案为:50.【点睛】本题考查了平行线的判定与性质、两直线的夹角的定义,熟练掌握平行线的判定与性质是解题关键.18.如图是某公园里一处矩形风景欣赏区ABCD ,长AB=50米,宽BC=30米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为______米.98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析水平距离等于AB铅直距离等于(AD-1)×2又∵长AB=50米宽BC=25米∴小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为50解析:98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析,水平距离等于AB,铅直距离等于(AD-1)×2,又∵长AB=50米,宽BC=25米,∴小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为50+(25-1)×2=98米,故答案为98.19.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOD=120°,则∠BOD=__________°.30°【分析】先利用补角的定义求出∠EOC=60°再根据角平分线的性质计算【详解】解:∵∠EOD=120°∴∠EOC=60°(邻补角定义)∵OA平分∠EOC∴∠AOC=∠EOC=30°(角平分线定义解析:30°【分析】先利用补角的定义求出∠EOC=60°,再根据角平分线的性质计算.【详解】解:∵∠EOD=120°,∴∠EOC=60°(邻补角定义).∠EOC=30°(角平分线定义),∵OA平分∠EOC,∴∠AOC=12∴∠BOD=30°(对顶角相等).故答案为:30.【点睛】本题考查由角平分线的定义,结合补角的性质,易求该角的度数.20.假设一家旅馆一共有30个房间,分别编以1~30三十个号码,现在要在每个房间的钥匙上刻上数字,要求所刻的数字必须使服务员很容易辨认是哪一个房间的钥匙,而使局外人不容易猜到.现在有一种编码的方法是:在每把钥匙上刻上两个数字,左边的一个数字是这把钥匙原来的房间号码除以5所得的余数,而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数.那么刻的数是25的钥匙所对应的原来房间应该是__________号.12【分析】根据编码的方法分析在1~30中除以5余2的数有712172227而其中除以7余5的数只有12故可求得答案【详解】解:∵1~30中除以5余2的数有712172227而其中除以7余5的数只有解析:12【分析】根据编码的方法分析,在1~30中,除以5余2的数有7,12,17,22,27,而其中除以7余5的数只有12,故可求得答案.【详解】解:∵1~30中,除以5余2的数有7,12,17,22,27,而其中除以7余5的数只有12,∴刻的数是25的钥匙所对应的原来房间应该是12,故答案为:12.【点睛】此题考查了带余数除法的知识.此题难度适中,解题的关键是理解题意,抓住1~30中,除以5余2的数有7,12,17,22,27,而其中除以7余5的数只有12.三、解答题21.如图,点D 、E 分别为AB 、AC 上的点,点F 、G 为BC 上的点,连接DE ,连接DG 、EF 交于点H .已知12180∠+∠=︒,3B ∠=∠,若66C ∠=︒,求DEC ∠的度数.请你将下面解答过程填写完整.解:∵12180∠+∠=︒∴//AB ________∴3ADE ∠=∠(________________________)∵3B ∠=∠∴_______B =∠∴//DE BC (____________________________)∴180C DEC ∠+∠=︒∵66C ∠=︒∴114DEC ∠=︒解析:见解析.【分析】先根据平行线的判定可得//AB EF ,再根据平行线的性质可得3ADE ∠=∠,从而可得ADE B ∠=∠,然后根据平行线的判定与性质可得.【详解】解:∵12180∠+∠=︒,∴//AB EF ,∴3ADE ∠=∠(两直线平行,内错角相等),∵3B ∠=∠,∴ADE B ∠=∠,∴//DE BC (同位角相等,两直线平行),∴180C DEC ∠+∠=︒,∵66C ∠=︒,∴114DEC ∠=︒.【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题关键.22.如图,直线AB ,CD 相交于点O ,OA 平分∠EOC .(1)∠AOC 的对顶角为______,∠AOC 的邻补角为______;(2)若∠EOC =70°,求∠BOD 的度数;(3)若∠EOC :∠EOD =2:3,求∠BOD 的度数.解析:(1)∠BOD ,∠BOC 或∠AOD ;(2)∠BOD =35°;(3)∠BOD =36°.【分析】(1)根据对顶角、邻补角的意义,结合图形即可得出答案;(2)根据角平分线的意义和对顶角的性质,即可得出答案;(3)根据平角、按比例分配,角平分线的意义、对顶角性质可得答案.【详解】(1)根据对顶角、邻补角的意义得:∠AOC 的对顶角为∠BOD , ∠AOC 的邻补角为∠BOC 或∠AOD ,故答案为:∠BOD ,∠BOC 或∠AOD(2)∵OA 平分∠EOC.∠EOC =70°,∴∠AOE =∠AOC 12=∠EOC =35°, ∵∠AOC =∠BOD ,∴∠BOD =35°,(3)∵∠EOC :∠EOD =2:3,∠EOC+∠EOD =180°,∴∠EOC =180°×25=72°,∠EOD =180°×35=108°, ∵OA 平分∠EOC , ∴∠AOE =∠AOC 12=∠EOC =36°, 又∵∠AOC =∠BOD ,∴∠BOD =36°.【点睛】本题考查对顶角、邻补角、角平分线、平角的意义和性质,通过图形具体理解这些角的意义是正确计算的前提.23.如图,直线AB ,CD 相交于点O ,EO AB ⊥,垂足为O ,35EOC ∠=︒,求AOD ∠的度数.解析:125°.【分析】由两直线垂直,求得∠AOE=90°;由∠AOC 与∠EOC 互余,∠EOC=35°,即可得到∠AOC 的度数;再由∠AOD 与∠AOC 互补,即可得出∠AOD 的度数.【详解】∵EO ⊥AB ,∴∠AOE=90°,又∵∠EOC=35°,∴∠AOC=∠AOE-∠EOC=90°-35°= 55°,∴∠AOD=180°-∠AOC=180°-55°=125°.【点睛】本题主要考查补角、余角和垂直的定义.解题的关键是熟练利用补角、余角关系求角的度数.24.如图,直线AB 、CD 相交于点O ,OE 平分BOD ∠,72AOC ∠=︒,OF CD ⊥.∠互余的角是______;(1)与BOF∠的度数.(2)求EOF解析:(1)∠BOD、∠AOC;(2)54°【分析】(1)根据垂直的定义得到∠FOD=90°,于是得到∠BOF+∠BOD=90°,根据对顶角的性质得到∠BOD=∠AOC,等量代换得到∠BOF+∠AOC=90°,即可得到结论.(2)根据已知条件得到∠BOF=90°﹣72°=18°,再由OE平分∠BOD,得出∠BOE=1∠BOD=36°,因此∠EOF=36°+18°=54°.2【详解】解:(1)∵OF⊥CD,∴∠FOD=90°,∴∠BOF+∠BOD=90°,∵∠BOD=∠AOC,∴∠BOF+∠AOC=90°,∴图中互余的角有∠BOF与∠BOD,∠BOF与∠AOC.故答案为:∠BOD、∠AOC;(2)∵直线AB和CD相交于点O,∴∠BOD=∠AOC=72°,∵OF⊥CD,∴∠BOF=90°﹣72°=18°,∵OE平分∠BOD,∠BOD=36°,∴∠BOE=12∴∠EOF=36°+18°=54°.【点睛】本题考查了对顶角、垂线以及角平分线的定义;弄清各个角之间的关系是解题的关键.25.已知:如图,DE∥BC,BE∥FG.求证:∠1=∠2.解析:证明见解析.【分析】由//DE BC ,利用“两直线平行,内错角相等”可得出1CBE ∠=∠,由//BE FG ,利用“两直线平行,同位角相等”可得出2CBE,进而可证出12∠=∠.【详解】 证明://DE BC ,1CBE ∴∠=∠.//BE FG ,2CBE ,12∠∠∴=.【点睛】 本题考查了平行线的性质,牢记平行线的各性质定理是解题的关键.26.如图,已知BC AE ⊥,DE AE ⊥,23180∠+∠=︒.(1)请你判断1∠与ABD ∠的数量关系,并说明理由;(2)若170∠=︒,BC 平分ABD ∠,试求ACF ∠的度数.解析:(1)∠1=∠ABD ,证明见解析;(2)∠ACF=55°.【分析】(1)先根据在平面内,垂直于同一条直线的两条直线互相平行得出BC ∥DE ,再根据平行线的性质结合23180∠+∠=︒可得∠2=∠CBD ,从而可得CF ∥DB 得出∠1=∠ABD ; (2)利用平行线的性质以及角平分线的定义,即可得出∠2的度数,再根据∠ACB 为直角,即可得出∠ACF .【详解】解:(1)∠1=∠ABD ,理由:∵BC ⊥AE ,DE ⊥AE ,∴BC ∥DE ,∴∠3+∠CBD=180°,又∵∠2+∠3=180°,∴∠2=∠CBD ,∴CF ∥DB ,∴∠1=∠ABD .(2)∵∠1=70°,CF ∥DB ,∴∠ABD=70°,又∵BC 平分∠ABD , ∴1352DBC ABD ︒∠=∠=, ∴∠2=∠DBC=35°,又∵BC ⊥AG , ∴∠ACF=90°-∠2=90°-35°=55°.【点睛】本题主要考查了平行线的判定与性质,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.27.试用举反例的方法说明下列命题是假命题.例如:如果ab <0,那么a +b <0.反例:设a =4,b =-3,ab =4⨯(-3)=-12<0,而a +b =4+(-3)=1>0,所以这个命题是假命题.(1)如果a +b >0,那么ab >0.(2)如果a 是无理数,b 也是无理数,那么a +b 也是无理数.解析:(1)见解析;(2)见解析.【分析】(1)此题是一道开放题,可举的例子多,但只举一例就可.如果a+b >0,那么ab >0;所举的反例就是,a 、b 一个为正数,一个为负数,且正数的绝对值大于负数.(2)可利用平方差公式找这样的无理数,比如【详解】解:(1)取a=2,b=-1,则a+b=1>0,但ab=-2<0.所以此命题是假命题.(2)取,,a 、b 均为无理数.但a+b=2是有理数,所以此命题是假命题.【点睛】本题主要锻炼了学生的逆向思维.在证明几何题的过程中,有时需从反例上先去判断,然后再证明.28.如图,已知直线AB 及直线AB 外一点P ,按下列要求完成画图和解答:(1)连接PA ,PB ,用量角器画出∠APB 的平分线PC ,交AB 于点C ;(2)过点P 作PD ⊥AB 于点D ;(3)用刻度尺取AB 中点E ,连接PE ;(4)根据图形回答:点P 到直线AB 的距离是线段 的长度.解析:(1)答案见解析;(2)答案见解析;(3)答案见解析;(4)PD.【详解】试题分析:(1)、用量角器量出∠APB的度数,然后求出一半的度数得出答案;(2)、根据垂线的作法得出答案;(3)、用刻度尺量出AB的长度,然后找出中点,从而得出答案;(4)、点到直线的距离是指点到直线垂线段的长度.试题(1)、如图所示;(2)、如图所示;(3)、如图所示;(4)、PD.。
数学第五章 相交线与平行线的专项培优练习题(含答案

,
,
,
本题的答案为:1, .
【点睛】
本题考查了平面内直线两两相交交点数的计算,涉及到一种很重要的数学方法数学归纳法的初步应用接触,此方法在推导证明中比较常用.
13.【解析】
【分析】
首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=25
13.如图, 平分 平分 ,则 ______.
14. 与 的两边互相垂直,且 ,则 的度数为_________.
15.如图,图①是长方形纸带,∠DEF=25°,将纸带沿EF折叠成图②,则图②中的∠CFG的度数是_____________.
16.两个角的两边分别平行,一个角是50°,那么另一个角是__________.
∴∠ABF+∠CDF= (∠ABE+∠CDE)=125°,
【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFE=∠DEF=26°,
∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,
故选:A.
【点睛】
本题考查了翻折变换(折叠问题)、矩形的性质、平行线的性质;熟练掌握翻折变换和矩形的性质,弄清各个角之间的关系是解决问题的关键.
17.如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
18.如图所示,AB∥CD,EC⊥CD.若∠BEC=30°,则∠ABE的度数为_____.
《易错题》初中七年级数学下册第五章《相交线与平行线》经典练习(培优练)

一、选择题1.如图,把一长方形纸片ABCD 沿EG 折叠后,AEG A EG '∠=∠,点A 、B 分别落在A '、B ′的位置,EA '与BC 相交于点F ,已知1125∠=︒,则2∠的度数是( )A .55°B .60°C .70°D .75°C解析:C【分析】 先根据平行线的性质可得55AEG ∠=︒,再根据平角的定义可得70∠︒=DEF ,然后根据平行线的性质即可得.【详解】由题意得://AD BC ,1125∠=︒,180155AEG ∴∠=︒-∠=︒,AEG A EG '∠=∠,55A EG '∴∠=︒,18070DEF AEG A EG '∴∠=︒-∠-∠=︒,又//AD BC ,270DEF ∴∠=∠=︒,故选:C .【点睛】本题考查了平角的定义、平行线的性质,熟练掌握平行线的性质是解题关键. 2.下列语句中不是命题的有( )(1)两点之间,线段最短;(2)连接A 、B 两点;(3)鸟是动物;(4)不相交的两条直线叫做平行线;(5)无论a 为怎样的有理数,式子a 2+1的值都是正数吗?A .1个B .2个C .3个D .4个C解析:C【分析】根据命题的定义对各语句进行判断.【详解】两点之间,线段最短,所以(1)为命题;连接A 、B 两点,它为描述性语言,所以(2)不是命题;鸟是动物,所以(3)为命题;不相交的两条直线叫做平行线,所以(4)为命题;无论a 为怎样的有理数,式子a 2+1的值都是正数吗?它为疑问句,所以(5)不是命题. 故选:C .【点睛】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.3.有下列命题:①两点之间,线段最短;②相等的角是对顶角;③当a ≥0时,|a |=a ;④内错角互补,两直线平行.其中是真命题的有( )A .1个B .2个C .3个D .4个B解析:B【分析】根据线段公理、对顶角、绝对值运算、平行线的判定逐个判断即可得.【详解】①两点之间,线段最短,是真命题;②相等的角不一定是对顶角,是假命题;③当0a ≥时,a a =,即非负数的绝对值等于它本身,是真命题;④内错角相等,两直线平行,是假命题;综上,真命题的个数是2个,故选:B .【点睛】本题考查了线段公理、对顶角、绝对值运算、平行线的判定,熟练掌握各判定定理与性质是解题关键.4.下列哪个图形是由图1平移得到的( )A .B .C .D . B解析:B【分析】根据平移的性质,结合图形,对选项进行一一分析,排除错误答案.【详解】A.不是由图1平移得到的,故错误;B.是由图1平移得到的,故正确;C.不是由图1平移得到的,故错误;D.不是由图1平移得到的,故错误;故选:B .【点睛】考查平移的性质,平移前后,图形的大小和形状没有变化.5.下列各命题中,属于假命题的是( )A .若0a b ->,则a b >B .若0a b -=,则0ab ≥C .若0a b -<,则a b <D .若0a b -≠,则0ab ≠ D解析:D【分析】根据不等式的性质对各选项进行逐一判断即可.【详解】A、正确,符合不等式的性质;B、正确,符合不等式的性质.C、正确,符合不等式的性质;D、错误,例如a=2,b=0;故选D.【点睛】考查了命题与定理的知识,解题的关键是了解不等式的性质,难度不大.6.如图,△ABC经平移得到△EFB,则下列说法正确的有()①线段AC的对应线段是线段EB;②点C的对应点是点B;③AC∥EB;④平移的距离等于线段BF的长度.A.1 B.2 C.3 D.4D解析:D【分析】根据平移的特点分别判断各选项即可.【详解】∵△ABC经平移得到△EFB∴点A、B、C的对应点分别为E、F、B,②正确∴BE是AC的对应线段,①正确∴AC∥EB,③正确平移距离为对应点连线的长度,即BF的长度,④正确故选:D【点睛】本题考查平移的特点,注意,在平移过程中,一定要把握住对应点,仅对应点的连线之间才有平行、相等的一些关系.7.下列命题是真命题的有()个①对顶角相等,邻补角互补②两条直线被第三条直线所截,同位角的平分线平行③垂直于同一条直线的两条直线互相平行④过一点有且只有一条直线与已知直线平行A.0 B.1 C.2 D.3B解析:B【分析】根据平行线的性质定理、平行公理、对顶角和邻补角的概念判断即可.【详解】解:对顶角相等,邻补角互补,故①是真命题;两条平行线被第三条直线所截,同位角的平分线平行,故②是假命题;在同一平面内,垂直于同一条直线的两条直线互相平行,故③是假命题;过直线外一点有且只有一条直线与已知直线平行,故④是假命题;故正确的个数只有1个,故选:B.【点睛】本题考查的是平行的公理和应用,命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.8.如图,直线a∥b,则∠A的度数是()A.28°B.31°C.39°D.42°C解析:C【解析】试题分析:根据平行线的性质可得∠1=70°,再根据三角形的一个外角等于和它不相邻的两个内角的和可得∠A=70°-31°=39°.故选C.考点:平行线的性质9.(2017•十堰)如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=()A.40°B.50°C.60°D.70°B解析:B【解析】试题分析:由AB ∥DE ,∠CDE=40°,∴∠B=∠CDE=40°,又∵FG ⊥BC ,∴∠FGB=90°﹣∠B=50°,故选B .考点:平行线的性质10.如图是一块长方形ABCD 的场地,长102AB m =,宽51AD m =,从A 、B 两处入口的中路宽都为1m ,两小路汇合处路宽为2m ,其余部分种植草坪,则草坪面积为( )A .5050m 2B .5000m 2C .4900m 2D .4998m 2B解析:B【详解】 解:由图可知:矩形ABCD 中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102-2)米,宽为(51-1)米.所以草坪的面积应该是长×宽=(102-2)(51-1)=5000(米2).故选B .二、填空题11.如图,点A 在直线m 上,点B 在直线l 上,点A 到直线l 的距离为a ,点B 到直线m 的距离为b ,线段AB 的长度为c ,通过测量等方法可以判断在a ,b ,c 三个数据中,最大的是_____________.【分析】过点A 作AD 垂直于垂足为D 过点B 作BH 垂直于垂足为H 连接AB 根据点到直线垂线段最短可知AB >ADAB >BH 可得最大【详解】过点A 作AD 垂直于垂足为D 过点B 作BH 垂直于垂足为H 连接AB 由题意得解析:c【分析】过点A作AD垂直于l垂足为D,过点B作BH垂直于m垂足为H,连接AB,根据点到直线垂线段最短,可知AB>AD,AB>BH,可得c最大.【详解】过点A作AD垂直于l垂足为D,过点B作BH垂直于m垂足为H,连接AB,由题意得:AD=a, BH=b,AB=c;根据点到直线垂线段最短,可知AB>AD,AB>BH∴c>a,c>b;∴c最大故答案:c【点睛】本题主要考查了垂线段最短的性质,熟记性质是解题的关键.12.高兴同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP=_____°.64【分析】由长方形直尺可得MP//OB再根据作图过程可知OP平分∠AOB进而可得∠AMP的度数【详解】解:∵OP平分∠AOB∴∠MOB=2∠BOP=64°由长方形直尺可知:MP//OB∴∠AMP=解析:64【分析】由长方形直尺可得MP //OB ,再根据作图过程可知OP 平分∠AOB ,进而可得∠AMP 的度数.【详解】解:∵OP 平分∠AOB ,∴∠MOB =2∠BOP =64°,由长方形直尺可知:MP //OB ,∴∠AMP =∠MOB =64°,故答案为:64.【点睛】此题主要考查了基本作图,关键是掌握角平分线的作法.13.如图,斜边长12cm ,∠A=30°的直角三角尺ABC 绕点C 顺时针方向旋转90°至''A B C 的位置,再沿CB 向左平移使点B'落在原三角尺ABC 的斜边AB 上,则三角尺向左平移的距离为_____.(结果保留根号)cm 【分析】作B′D//BC 与AB 交于点D 故三角板向左平移的距离为B′D 的长利用直角三角形的性质求出BC=B′C=6cmAC=cm 进而根据相似三角形对应线段成比例的性质即可求解【详解】如图作B′D/ 解析:(623-cm【分析】作B′D//BC 与AB 交于点D ,故三角板向左平移的距离为B′D 的长,利用直角三角形的性质求出BC=B′C=6cm ,AC=63,进而根据相似三角形对应线段成比例的性质即可求解.【详解】如图,作B′D//BC 与AB 交于点D ,故三角板向左平移的距离为B′D 的长.∵AB=12cm ,∠A=30°,∴BC=B′C=6cm ,AC=3cm ,∵B′D//BC , ∴AC D BC B AB ='',即(6636(623)63BC C B A AB D ⨯=='-'=cm , 故三角板向左平移的距离为(623-cm .【点睛】本题考查直角三角形的性质、相似三角形的性质,旋转和平移的性质,解题的关键是作辅助线构造相似三角形.14.如图,直线//m n ,点A B 、在直线n 上,点C F 、在直线m 上,连接,CA CB CD 、平分ACB ∠交AB 于点D ,平面内有点E ,连接,2180EC ECB BCF ︒∠+∠=,过点F 作//FG CE 交CD 于点,9,4G FGC ADC CAB ABC ︒∠-∠=∠=∠,则ACB =∠____________.【分析】根据条件找到等量关系计算即可;【详解】设∵∴∴∵∴∵ABD 在同一直线上∴∴在△ABC 中∴联立方程组:解得:度度度故答案是:【点睛】本题主要考查了平行线的综合应用结合三元一次方程组求解是解题的 解析:2707【分析】根据条件2180︒∠+∠=ECB BCF ,9︒∠-∠=FGC ADC ,4∠=∠CAB ABC 找到等量关系计算即可;【详解】设2ABC x ∠=∠,1ACE ∠=∠,∵//m n ,∴BCF ABC ∠=∠,12ECB ECA ACB x ∠=∠+∠=∠+∠,∴()212180x ABC ∠+∠+∠=︒,∵//FG CE ,∴1FGC ECD x ∠=∠=∠+∠,∵A ,B ,D 在同一直线上,∴ADC ABC DCB ABC x ∠=∠+∠=∠+∠,∴()1119x ABC x x ABC x ABC ∠+∠-∠+∠=∠+∠-∠-∠=∠-∠=︒, 在△ABC 中,1802CAB x ABC ∠=︒-∠-∠,∴18024x ABC ABC ︒-∠-∠=∠,联立方程组:()2121801918024x ABC ABC x ABC ABC ⎧∠+∠+∠=︒⎪∠-∠=︒⎨⎪︒-∠-∠=∠⎩, 解得:1987ABC ∠=度,26117∠=度,2707x ∠=度. 故答案是:2707. 【点睛】本题主要考查了平行线的综合应用,结合三元一次方程组求解是解题的关键. 15.“等腰三角形的两条边相等”的逆命题是________________.(填真命题或假命题)真命题【分析】交换命题的题设和结论即可得到该命题的逆命题根据等腰三角形的定义判断即可【详解】等腰三角形的两条边相等的逆命题是:两条边相等的三角形是等腰三角形;它是真命题故答案为:真命题【点睛】本题考 解析:真命题【分析】交换命题的题设和结论即可得到该命题的逆命题,根据等腰三角形的定义判断即可.【详解】“等腰三角形的两条边相等”的逆命题是:两条边相等的三角形是等腰三角形;它是真命题,故答案为:真命题.【点睛】本题考查了命题的真假判断、逆命题的概念,掌握等腰三角形的定义是解题的关键. 16.命题“若a 2>b 2则a >b ”是_____命题(填“真”或“假”),它的逆命题是_____.假若a >b 则a2>b2【分析】a2大于b2则a 不一定大于b 所以该命题是假命题它的逆命题是若a >b 则a2>b2【详解】①当a =-2b =1时满足a2>b2但不满足a >b 所以是假命题;②命题若a2>b2则解析:假 若a >b 则a 2>b 2【分析】a 2大于b 2则a 不一定大于b ,所以该命题是假命题,它的逆命题是“若a >b 则a 2>b 2”.【详解】①当a =-2,b =1时,满足a 2>b 2,但不满足a >b ,所以是假命题;②命题“若a 2>b 2则a >b ”的逆命题是若“a >b 则a 2>b 2”;故答案为:假;若a >b 则a 2>b 2.【点睛】本题主要考查判断命题真假、逆命题的概念以及平方的计算,熟记相关概念取特殊值代入是解题关键.17.如图,直线AB 、CD 相交于点O ,OE 平分∠AOC ,OF ⊥OE 于点O ,若∠AOD =70°,则∠AOF =______度.145【分析】由已知角平分线和垂直的定义可以得到∠AOE 和∠EOF 的大小从而得到∠AOF 的值【详解】解:∵∵OE 平分∠AOC ∴∵OF ⊥OE 于点O ∴∠EOF =90°∴∠AOF =∠AOE+∠EOF =55解析:145【分析】由已知、角平分线和垂直的定义可以得到∠AOE 和∠EOF 的大小,从而得到∠AOF 的值.【详解】解:∵70180110AOD AOC AOD ∠=︒∴∠=︒-∠=︒,,∵OE 平分∠AOC ,∴1552AOE AOC ∠=∠=︒, ∵OF ⊥OE 于点O ,∴∠EOF =90°,∴∠AOF =∠AOE+∠EOF =55°+90°=145°,故答案为145.【点睛】本题考查邻补角、角平分线和垂直以及角度的运算等知识,根据有关性质和定义灵活计算是解题关键.18.如图是某公园里一处矩形风景欣赏区ABCD ,长AB=50米,宽BC=30米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间出口A 到出口B 所走的路线(图中虚线)长为______米.98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析水平距离等于AB 铅直距离等于(AD-1)×2又∵长AB=50米宽BC=25米∴小明沿着小路的中间出口A 到出口B 所走的路线(图中虚线)长为50解析:98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析,水平距离等于AB ,铅直距离等于(AD -1)×2,又∵长AB =50米,宽BC =25米,∴小明沿着小路的中间出口A 到出口B 所走的路线(图中虚线)长为50+(25-1)×2=98米,故答案为98.19.如图,现给出下列条件:①1B ∠∠=,②25∠∠=,③34∠∠=,④1D ∠∠=,⑤B BCD 180∠∠+=︒.其中能够得到AB//CD 的条件是_______.(只填序号)①②⑤【分析】根据平行线的判定定理对各小题进行逐一判断即可【详解】解:①∵∠1=∠B ∴AB ∥CD 故本小题正确;②∵∠2=∠5∴AB ∥CD 故本小题正确;③∵∠3=∠4∴AD ∥BC 故本小题错误;④∵∠1解析:①②⑤【分析】根据平行线的判定定理对各小题进行逐一判断即可【详解】解:①∵∠1=∠B ,∴AB ∥CD ,故本小题正确;②∵∠2=∠5,∴AB ∥CD ,故本小题正确;③∵∠3=∠4,∴AD ∥BC ,故本小题错误;④∵∠1=∠D ,∴AD ∥BC ,故本小题错误;⑤∵∠B+∠BCD=180°,∴AB ∥CD ,故本小题正确.故答案为①②⑤.【点睛】本题考查的是平行线的判定,熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解答此题的关键.20.观察下列图形:已知a b ,在第一个图中,可得∠1+∠2=180°,则按照以上规律:112n P P ∠+∠+∠++∠=…_________度.(n ﹣1)×180【分析】分别过P1P2P3作直线AB 的平行线P1EP2FP3G 由平行线的性质可得出:∠1+∠3=180°∠5+∠6=180°∠7+∠8=180°∠4+∠2=180°于是得到∠1+∠ 解析:(n ﹣1)×180【分析】分别过P 1、P 2、P 3作直线AB 的平行线P 1E ,P 2F ,P 3G ,由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°于是得到∠1+∠2=10°,∠1+∠P 1+∠2=2×180,∠1+∠P 1+∠P 2+∠2=3×180°,∠1+∠P 1+∠P 2+∠P 3+∠2=4×180°,根据规律得到结果∠1+∠2+∠P 1+…+∠P n =(n+1)×180°.【详解】解:如图,分别过P 1、P 2、P 3作直线AB 的平行线P 1E ,P 2F ,P 3G ,∵AB ∥CD ,∴AB ∥P 1E ∥P 2F ∥P 3G .由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180° ∴(1)∠1+∠2=180°,(2)∠1+∠P 1+∠2=2×180,(3)∠1+∠P 1+∠P 2+∠2=3×180°,(4)∠1+∠P 1+∠P 2+∠P 3+∠2=4×180°,∴∠1+∠2+∠P 1+…+∠P n =(n+1)×180°.故答案为:(n+1)×180.【点睛】本题考查的是平行线的性质,根据题意作出辅助线,利用两直线平行,同旁内角互补是解答此题的关键.三、解答题21.如图,已知直线AB 与CD 相交于点40O OE CD AOC OF ︒⊥∠=,,,为AOD ∠的角平分线.(1)求EOB ∠的度数;(2)求EOF ∠的度数.解析:(1)50EOB ∠=︒;(2)160EOF ∠=︒【分析】(1)由对顶角相等的性质得40BOD AOC ∠=∠=︒,再由90EOD ∠=︒,即可求出EOB ∠的度数;(2)先求出AOD ∠的度数,再由角平分线的性质得到FOD ∠的度数,即可求出EOF ∠的度数.【详解】解:(1)OE CD ⊥,∴90EOD ∠=︒,∵40BOD AOC ∠=∠=︒,50EOB EOD BOD ∴∠=∠-∠=︒;(2)∵直线AB 与CD 相交于点O ,40AOC BOD ∴∠=∠=︒,∴180140AOD BOD =︒-=︒∠∠, OF 为AOD ∠的角平分线,70AOF FOD ∴∠=∠=︒,160EOF EOD FOD ∴∠=∠+∠=︒.【点睛】 本题考查角度求解,解题的关键是掌握对顶角的性质,垂直的性质,以及角平分线的性质.22.如图,直线AB ,CD 相交于点O ,OA 平分EOC ∠.(1)若70EOC ∠=︒,求BOD ∠的度数;(2)若:4:5∠∠=EOC EOD ,求BOC ∠的度数.解析:(1)35BOD ∠=︒;(2)140∠=︒BOC【分析】(1)首先根据角平分线的性质得出∠AOC ,然后利用对顶角相等即可得出∠BOD ; (2)首先设4EOC x ∠=,则5EOD x ∠=,然后根据平角的性质构建方程,得出∠EOC ,再利用角平分线的性质得出∠AOC ,最后由平角得旋转即可得出∠BOC 即可.【详解】()170,EOC OA ∠=︒平分EOC ∠, 1352AOC EOC ∴∠=∠=︒, 35BOD AOC ∴∠=∠=︒;()2设4EOC x ∠=,则5EOD x ∠=,,54180x x ∴+=︒,解得20x =︒,则80EOC ∠=︒,又OA 平分0E C ∠,40AOC ∴∠=︒,180********BOC AOC ∴∠=︒-∠=︒-︒=︒.【点睛】本题主要考查利用角平分线、对顶角以及平角的性质求解角的度数,熟练掌握,即可解题.23.ABC 在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.(1)ABC 关于x 轴对称图形为111A B C △,画出111A B C △的图形;(2)将ABC 向右平移4个单位,再向下平移3个单位,得到图形为222A B C △,画出222A B C △的图形;(3)求ABC 的面积.解析:(1)详见解析;(2)详见解析;(3)2.【分析】(1)分别作出A 、B 、C 关于对称轴x 的对应点A 1、B 1、C 1,再顺次连接即可得所求图形;(2)分别将A 、B 、C 三点向右平移4个单位,再向下平移3个单位,得到对应点A 2、B 2、C 2,再顺次连接即可得所求图形为222A B C △;(3)利用构图法即可求解;【详解】(1) ;(2) ;(3)ABC S =2×3-1112⨯⨯-1222⨯⨯-1132⨯⨯ 136222=--- 64=-2=.【点睛】本题考查作图—轴对称及平移变换,还涉及到三角形面积公式,解题的关键是熟练掌握轴对称的性质及平移的性质.24.如图,直线AB ∥CD ,EB 平分∠AED ,170∠=︒,求∠2的度数.解析:55︒.【分析】先根据对顶角相等可得170BAE ∠=∠=︒,再根据平行线的性质可得110AED ∠=︒,然后根据角平分线的定义可得55BED ∠=︒,最后根据平行线的性质即可得.【详解】170∠=︒,170BAE ∴∠=∠=︒,//AB CD ,180110AED BAE ∴∠=︒-∠=︒, EB 平分AED ∠, 1552BED AED ∴∠=∠=︒, 又//AB CD ,255BED ∴∠=∠=︒.【点睛】 本题考查了对顶角相等、平行线的性质、角平分线的定义,熟练掌握平行线的性质是解题关键.25.如图,直线AB 、CD 相交于点O ,OE 平分BOD ∠,72AOC ∠=︒,OF CD ⊥.(1)与BOF ∠互余的角是______;(2)求EOF ∠的度数.解析:(1)∠BOD 、∠AOC ;(2)54°【分析】(1)根据垂直的定义得到∠FOD =90°,于是得到∠BOF +∠BOD =90°,根据对顶角的性质得到∠BOD=∠AOC,等量代换得到∠BOF+∠AOC=90°,即可得到结论.(2)根据已知条件得到∠BOF=90°﹣72°=18°,再由OE平分∠BOD,得出∠BOE=1∠BOD=36°,因此∠EOF=36°+18°=54°.2【详解】解:(1)∵OF⊥CD,∴∠FOD=90°,∴∠BOF+∠BOD=90°,∵∠BOD=∠AOC,∴∠BOF+∠AOC=90°,∴图中互余的角有∠BOF与∠BOD,∠BOF与∠AOC.故答案为:∠BOD、∠AOC;(2)∵直线AB和CD相交于点O,∴∠BOD=∠AOC=72°,∵OF⊥CD,∴∠BOF=90°﹣72°=18°,∵OE平分∠BOD,∠BOD=36°,∴∠BOE=12∴∠EOF=36°+18°=54°.【点睛】本题考查了对顶角、垂线以及角平分线的定义;弄清各个角之间的关系是解题的关键.26.如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).(1)在平面直角坐标系中画出△ABC,作出△ABC向下平移3格后的△A1B1C1;(2)求△ABC的面积;(3)已知点Q为y轴上一点,若△ACQ的面积为8,求点Q的坐标.解析:(1)见解析;(2)4;(3)(0,5)或(0,-3).【分析】(1)先在平面直角坐标系中描点,再连接,然后分别作出平移后的对应点,再顺次连接即可得;(2)利用割补法求解可得;(3)根据三角形面积公式求出AQ的长,即可确定点Q的坐标.【详解】解:(1)如图所示,(2)△ABC 的面积=111342421234222⨯-⨯⨯-⨯⨯-⨯⨯= (3)∵Q 为y 轴上一点,△ACQ 的面积为8, ∴1||482AQ ⨯⨯=, ∴AQ=4 ∴点Q 的纵坐标为:4+1=5或1-4=-3,故Q 点坐标为:(0,5)或(0,-3).【点睛】本题主要考查的是作图-平移变换、点的坐标与图形的性质,明确△ABC 的面积=四边形的面积-3个直角三角形的面积是解题的关键.27.如图,已知BE 平分ABC ∠,点D 在射线BA 上,且ABE BED ∠=∠.判断BC 与DE 的位置关系,并说明理由.解析:BC ∥DE ;理由见解析【分析】根据角平分线的定义和已知条件可得∠CBE =∠BED ,再根据平行线的判定即得结论.【详解】解:BC ∥DE ;理由如下:因为BE 平分ABC ∠,所以∠ABE =∠CBE ,因为ABE BED ∠=∠,所以∠CBE =∠BED ,所以BC ∥DE .【点睛】本题考查了角平分线的定义和平行线的判定,属于基础题目,熟练掌握基本知识是解题的关键.28.如图:AD 是BAC ∠的角平分线,点E 是射线AC 上一点,延长ED 至点F ,180CAD ADF ︒∠+∠=.求证:(1)//AB EF ;(2)2ADE CEF ∠=∠解析:(1)证明见解析;(2)证明见解析.【分析】(1)根据角平分线和同旁内角互补两直线平行即可证得;(2)由(1)得2CEF EAB DAB ∠=∠=∠,又因为DAB ADE ∠=∠,即可证得.【详解】(1)AD 是BAC ∠的角平分线.CAD DAB ∴∠=∠ 又180CAD ADF ︒∠+∠=180DAB ADF ︒∠+∠=//AB EF ∴(2)//AB EF2CEF EAB DAB ∴∠=∠=∠又DAB ADE ∠=∠2ADE CEF ∴∠=∠【点睛】本题考查角平分线和平行线的证明与性质,掌握平行线证明方法是解题的关键.。
数学数学第五章 相交线与平行线的专项培优易错试卷练习题附解析

数学数学第五章 相交线与平行线的专项培优易错试卷练习题附解析一、选择题1.如图,∠1=20º,AO ⊥CO ,点B 、O 、D 在同一条直线上,则∠2的度数为( )A .70ºB .20ºC .110ºD .160º2.①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )A .、1个B .2个C .3个D .4个3.将一副三角板按如图放置,则下列结论①13∠=∠;②如果230∠=,则有//AC DE ;③如果245∠=,则有//BC AD ;④如果4C ∠=∠,必有230∠=,其中正确的有( )A .①②③B .①②④C .③④D .①②③④4.下列说法:①两点确定一条直线;②连接两点的线段叫做两点的距离;③两点之间,线段最短;④由两条射线组成的图形叫做角;⑤若AB =BC ,则点B 是线段AC 的中点.其中正确的有( )A .1个B .2个C .3个D .4个5.下列命题中,假命题的个数为( )(1)“是任意实数,”是必然事件; (2)抛物线的对称轴是直线;(3)若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为; (4)某件事情发生的概率是1,则它一定发生;(5)某彩票的中奖率为10%,则买100张彩票一定有1张会中奖;(6)函数与轴必有两个交点.A .2B .3C .4D .56.已知两个角的两边两两互相平行,则这两个角的关系是( )A .相等B .互补C .相等或互补D .相等且互补7.已知:点A ,B ,C 在同一条直线上,点M 、N 分别是AB 、BC 的中点,如果AB =10cm ,AC =8cm ,那么线段MN 的长度为( )A .6cmB .9cmC .3cm 或6cmD .1cm 或9cm8.下列图中的“笑脸”,由如图平移得到的是( )A .B .C .D .9.如图,△ABC 经平移得到△EFB ,则下列说法正确的有 ( )①线段AC 的对应线段是线段EB ;②点C 的对应点是点B ;③AC ∥EB ;④平移的距离等于线段BF 的长度.A .1B .2C .3D .410.下列命题中,是真命题的是( )A .在同一平面内,垂直于同一直线的两条直线平行B .相等的角是对顶角C .两条直线被第三条直线所截,同旁内角互补D .过一点有且只有一条直线与已知直线平行二、填空题11.如图,已知AB 、CD 相交于点O,OE ⊥AB 于O ,∠EOC=28°,则∠AOD=_____度;12.如图,//AB CD ,FN AB ⊥,垂足为点O ,EF 与CD 交于点G ,若130∠=︒,则2∠=______.13.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为_______.14.如图,请你添加一个条件....使得AD ∥BC ,所添的条件是__________.15.如图,把直角梯形ABCD 沿AD 方向平移到梯形EFGH ,28HG cm =,5MG cm =,4MC cm =,则阴影部分的面积是___16.如果一张长方形的纸条,如图所示折叠,那么∠α等于____.17.如图,AB ∥CD ,∠B =75°,∠E =27°,则∠D 的度数为_____.18.如图所示,AB ∥CD ,EC ⊥CD .若∠BEC =30°,则∠ABE 的度数为_____.19.如图,直线////a b c ,直角三角板的直角顶点落在直线b 上,若135∠=︒,则2∠等于_______.20.如图,直角△ABC 中,AC=3,BC=4,AB=5,则内部五个小直角三角形的周长为_____.三、解答题21.已知AB ∥CD(1)如图1,求证:∠ABE +∠DCE -∠BEC =180°(2)如图2,∠DCE 的平分线CG 的反向延长线交∠ABE 的平分线BF 于F①若BF ∥CE ,∠BEC =26°,求∠BFC②若∠BFC -∠BEC =74°,则∠BEC =________°22.问题情境(1)如图①,已知360B E D ∠+∠+∠=︒,试探究直线AB 与CD 有怎样的位置关系?并说明理由.小明给出下面正确的解法:直线AB 与CD 的位置关系是//AB CD .理由如下:过点E 作//EF AB (如图②所示)所以180B BEF ∠+∠=︒(依据1)因为360B BED D ∠+∠+∠=︒(已知)所以360B BEF FED D ∠+∠+∠+∠=︒所以180FED D ∠+∠=︒所以//EF CD (依据2)因为//EF AB所以//AB CD (依据3)交流反思上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?“依据1”:________________________________;“依据2”:________________________________;“依据3”:________________________________.类比探究(2)如图,当B 、E ∠、F ∠、D ∠满足条件________时,有//AB CD .拓展延伸(3)如图,当B 、E ∠、F ∠、D ∠满足条件_________时,有//AB CD .23.如图1,直线AB 与直线OC 交于点O ,()090BOC αα∠=︒<<.小明将一个含30的直角三角板PQD 如图1所示放置,使顶点P 落在直线AB 上,过点Q 作直线MN AB 交直线OC 于点H (点H 在Q 左侧).(1)若PD OC ∥,45NQD ∠=︒,则α=__________︒.(2)若PQH ∠的角平分线交直线AB 于点E ,如图2.①当QE OC ∥,60α=︒时,求证:OC PD .②小明将三角板保持PD OC ∥并向左平移,运动过程中,PEQ ∠=__________.(用α表示).24.AB ∥CD ,点P 为直线AB ,CD 所确定的平面内的一点.(1)如图1,写出∠APC 、∠A 、∠C 之间的数量关系,并证明;(2)如图2,写出∠APC 、∠A 、∠C 之间的数量关系,并证明;(3)如图3,点E 在射线BA 上,过点E 作EF ∥PC ,作∠PEG =∠PEF ,点G 在直线CD 上,作∠BEG 的平分线EH 交PC 于点H ,若∠APC =30°,∠PAB =140°,求∠PEH 的度数.25.直线AB ∥CD ,点M ,N 分别在直线AB ,CD 上,点E 为平面内一点.(1)如图①,探究∠AME ,∠MEN ,∠ENC 的数量关系,并说明理由;(2)如图②,∠AME =30°,EF 平分∠MEN ,NP 平分∠ENC ,EQ ∥NP ,求∠FEQ 的度数; (3)如图③,点G 为CD 上一点,∠AMN =m ∠EMN ,∠GEK =m ∠GEM ,EH ∥MN 交AB 于点H ,直接写出∠GEK ,∠BMN ,∠GEH 之间的数量关系(用含m 的式子表示).26.将一副三角板中的两个直角顶点C 叠放在一起(如图①),其中30A ∠=︒,60B ∠=︒,45D E ∠=∠=︒.(1)猜想BCD ∠与ACE ∠的数量关系,并说明理由;(2)若3BCD ACE ∠=∠,求BCD ∠的度数;等于多少度时(3)若按住三角板ABC不动,绕顶点C转动三角DCE,试探究BCDCE AB,并简要说明理由.//【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】由AO⊥CO和∠1=20º求得∠BOC=70º,再由邻补角的定义求得∠2的度数.【详解】∵AO⊥CO和∠1=20º,∴∠BOC=90 º-20 º=70º,又∵∠2+∠BOC=180 º(邻补角互补),∴∠2=110º.故选:C.【点睛】考查了邻补角和垂直的定义,解题关键是利用角的度数之间的和差的关系求未知的角的度数.2.C解析:C【详解】①如图1,过点E作EF∥AB,因为AB∥CD,所以AB∥EF∥CD,所以∠A+∠AEF=180°,∠C+∠CEF=180°,所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°,则①错误;②如图2,过点E作EF∥AB,因为AB∥CD,所以AB∥EF∥CD,所以∠A=∠AEF,∠C=∠CEF,所以∠A+∠C=∠AEC+∠AEF=∠AEC,则②正确;③如图3,过点E作EF∥AB,因为AB∥CD,所以AB∥EF∥CD,所以∠A+∠AEF=180°,∠1=∠CEF,所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°,则③正确;④如图4,过点P作PF∥AB,因为AB∥CD,所以AB∥PF∥CD,所以∠A=∠APF,∠C=∠CPF,所以∠A=∠CPF+∠APC=∠C+∠APC,则④正确;故选C.3.D解析:D【分析】根据∠1+∠2=∠3+∠2即可证得①;根据230∠=求出∠1与∠E 的度数大小即可判断②;利用∠2求出∠3,与∠B 的度数大小即可判断③;利用4C ∠=∠求出∠1,即可得到∠2的度数,即可判断④.【详解】∵∠1+∠2=∠3+∠2=90︒,∴∠1=∠3,故①正确;∵230∠=,∴190260∠=-∠=∠E=60︒,∴∠1=∠E ,∴AC ∥DE ,故②正确;∵245∠=,∴345∠=,∵45B ∠=,∴∠3=∠B,∴//BC AD ,故③正确;∵4C ∠=∠45=,∴∠CFE=∠C 45=,∵∠CFE+∠E=∠C+∠1,∴∠1=∠E=60,∴∠2=90︒-∠1=30,故④正确,故选:D.【点睛】此题考查互余角的性质,平行线的判定及性质,熟练运用解题是关键.4.B解析:B【解析】分析:根据直线公理对①进行判断;根据两点之间的距离的定义对②进行判断;根据线段公理对③进行判断;根据角的定义对④进行判断;根据线段的中点的定义对⑤进行判断.详解:根据直线公理:两点确定一条直线,所以①正确;连接两点的线段的长度叫做两点的距离,所以②错误;两点之间,线段最短,所以③正确;有一个公共端点的两条射线组成的图形叫做角,所以④错误;若AB=BC,且B点在AB上,则点B是AC的中点,所以⑤错误.故选B.点睛:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.5.C解析:C【解析】试题解析:(1)“a是任意实数,|a|-5>0”是不确定事件,是假命题;(2)抛物线y=(2x+1)2的对称轴是直线x=-,是假命题;(3)若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为,是假命题;(4)某件事情发生的概率是1,则它一定发生,是真命题;(5)某彩票的中奖率为10%,则买100张彩票中奖的可能性很大,但不是一定中奖,是假命题;(6)函数y=-9(x+2014)2+与x轴必有两个交点,是真命题,则假命题的个数是4;故选C.考点:命题与定理.6.C解析:C【解析】分类讨论:两个角的两边方向是否相同.若相同,则相等;否则互补.故选C. 7.D解析:D【解析】试题分析:有两种情况:①点C在AB上,②点C在AB的延长线上,这两种情况根据线段的中点的性质,可得BM、BN的长,再利用线段的和、差即可得出答案.解:(1)点C在线段AB上,如:点M是线段AB的中点,点N是线段BC的中点,MB=12AB=5,BN=12CB=4,MN=BM-BN=5-4=1cm;(2)点C在线段AB的延长线上,如:点M是线段AB的中点,点N是线段BC的中点,MB=12AB=5,BN=12CB=4,MN=MB+BN=5+4=9cm,故选D.点睛:本题考查了两点间的距离. 解题的关键在于要利用分类讨论思想结合线段中点的性质、线段的和差进行解答.8.D解析:D【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.【详解】解:A、B、C都是由旋转得到的,D是由平移得到的.故选:D.【点睛】本题考查平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.9.D解析:D【分析】根据平移的特点分别判断各选项即可.【详解】∵△ABC经平移得到△EFB∴点A、B、C的对应点分别为E、F、B,②正确∴BE是AC的对应线段,①正确∴AC∥EB,③正确平移距离为对应点连线的长度,即BF的长度,④正确故选:D【点睛】本题考查平移的特点,注意,在平移过程中,一定要把握住对应点,仅对应点的连线之间才有平行、相等的一些关系.10.A解析:A【解析】分析:根据平行线的判定与性质,对顶角的性质,平行线的作图,逐一判断即可.详解:根据平行公理的推论,可知:在同一平面内,垂直于同一直线的两条直线平行,故正确;根据对顶角的定义,可知相等的角不一定是对顶角,故不正确;根据两条平行的直线被第三条直线所截,同旁内角互补,故不正确;根据平行公理,可知过直线外一点有且只有一条直线与已知直线平行,故不正确. 故选A.点睛:此题主要考查了平行线的判定与性质,关键是熟记公理的内容和特点,找到反例说明即可.二、填空题11.62【详解】∵,,∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.解析:62【详解】∵OE AB ⊥,28EOC ∠=,∴∠BOC=90°-28°=62°∵∠BOC=∠AOD∴∠AOD=62°.12.120°【分析】过点F 作PT//AB ,则有PT//CD ,根据平行线的性质可得∠GFP=30゜,∠OFP=90゜,从而可求出∠2的度数.【详解】过点F 作PT//AB ,如图,∴∠OFP=∠N解析:120°【分析】过点F作PT//AB,则有PT//CD,根据平行线的性质可得∠GFP=30゜,∠OFP=90゜,从而可求出∠2的度数.【详解】过点F作PT//AB,如图,∴∠OFP=∠NOA⊥∵FN AB∴∠NOA=90゜∴∠OFP=90゜∵AB//CD∴CD//PT∴∠DGF=∠GFP∵∠DGF=∠1=30゜∴∠GFP=30゜∴∠2=∠OFP+∠GFP=90゜+30゜=120゜故答案为:120゜【点睛】此题主要考查了平行线的判定与性质,关键是掌握两直线平行,内错角相等,同位角相等.13.或【分析】由两角的两边互相平行可得出两角相等或互补,再由题意,其中一个角比另一个角的3倍少,可得出答案.【详解】解:设为x,则为,若两角互补,则,解得,;若两角相等,则,解得,.故答案解析:125︒或20︒【分析】由两角的两边互相平行可得出两角相等或互补,再由题意,其中一个角比另一个角的3倍少40︒,可得出答案.【详解】解:设β∠为x ,则α∠为340x -︒,若两角互补,则340180x x +-︒=︒,解得55x =︒,125α∠=︒;若两角相等,则340x x =-︒,解得20x =︒,20α∠=︒.故答案为:125︒或20︒.【点睛】本题考查了平行线的性质,解题的关键是注意若∠α与∠β的两边分别平行,即可得∠α与∠β相等或互补,注意方程思想与分类讨论思想的应用.14.∠EAD=∠B 或∠DAC=∠C【解析】当∠EAD=∠B 时,根据“同位角相等,两直线平行”可得AD//BC ;当∠DAC=∠C 时,根据“内错角相等,两直线平行”可得AD//BC ;当∠DAB+∠B解析:∠EAD =∠B 或∠DAC =∠C【解析】当∠EAD =∠B 时,根据“同位角相等,两直线平行”可得AD//BC ;当∠DAC =∠C 时,根据“内错角相等,两直线平行”可得AD//BC ;当∠DAB+∠B=180°时,根据“同旁内角互补,两直线平行”可得AD//BC ,故答案是:∠EAD =∠B 或∠DAC =∠C 或∠DAB+∠B=180°(答案不唯一).15.130cm2.【分析】根据平移的性质可知梯形EFGH≌梯形ABCD ,那么GH=CD ,BC=FG ,观察可知梯形EFMD 是两个梯形的公共部分,那么阴影部分的面积就等于梯形MGHD ,再根据梯形的面积计解析:130cm 2.【分析】根据平移的性质可知梯形EFGH ≌梯形ABCD ,那么GH=CD ,BC=FG ,观察可知梯形EFMD 是两个梯形的公共部分,那么阴影部分的面积就等于梯形MGHD ,再根据梯形的面积计算公式计算即可.【详解】解:∵直角梯形EFGH 是由直角梯形ABCD 平移得到的,∴梯形EFGH ≌梯形ABCD ,∴GH=CD ,BC=FG ,∵梯形EFMD 是两个梯形的公共部分,∴S 梯形ABCD -S 梯形EFMD =S 梯形EFGH -S 梯形EFMD ,∴S阴影=S梯形MGHD=12(DM+GH)•GM=12(28-4+28)×5=130(cm2).故答案是130cm2.【点睛】本题考查了图形的平移,解题的关键是知道平移前后的两个图形全等.16.70°.【分析】依据平行线的性质,可得∠BAE=∠DCE=140°,依据折叠即可得到∠α=70°.【详解】解:如图,∵AB∥CD,∴∠BAE=∠DCE=140°,由折叠可得:,∴∠解析:70°.【分析】依据平行线的性质,可得∠BAE=∠DCE=140°,依据折叠即可得到∠α=70°.【详解】解:如图,∵AB∥CD,∴∠BAE=∠DCE=140°,由折叠可得:12DCF DCE ∠=∠,∴∠α=70°.故答案为:70°.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.17.48°【分析】将BE与CD交点记为点F,由两直线平行同位角相等得出∠EFC度数,再利用三角形外角的性质可得答案.【详解】解:如图所示,将BE与CD交点记为点F,∵AB∥CD,∠B=75°解析:48°【分析】将BE与CD交点记为点F,由两直线平行同位角相等得出∠EFC度数,再利用三角形外角的性质可得答案.【详解】解:如图所示,将BE与CD交点记为点F,∵AB∥CD,∠B=75°,∴∠EFC=∠B=75°,又∵∠EFC=∠D+∠E,且∠E=27°,∴∠D=∠EFC﹣∠E=75°﹣27°=48°,故答案为:48°.【点睛】本题考查平行线的性质和三角形外角性质,解题的关键是掌握两直线平行,同位角相等这一性质.18.120°.【分析】先根据平行线的性质,得到∠GEC=90°,再根据垂线的定义以及平行线的性质进行计算即可.【详解】过点E作EG∥AB,则EG∥CD,由平行线的性质可得∠GEC=90°,解析:120°.【分析】先根据平行线的性质,得到∠GEC=90°,再根据垂线的定义以及平行线的性质进行计算即可.【详解】过点E作EG∥AB,则EG∥CD,由平行线的性质可得∠GEC =90°,所以∠GEB =90°﹣30°=60°,因为EG ∥AB ,所以∠ABE =180°﹣60°=120°.故答案为:120°.【点睛】本题主要考查了平行线的性质和垂直的概念等,解题时注意:两直线平行,同旁内角互补.19.【分析】如图,利用平行线的性质得出∠3=35°,然后进一步得出∠4的度数,从而再次利用平行线性质得出答案即可.【详解】如图所示,∵,,∴,∴∠4=90°−∠3=55°,∵,∴∠2解析:55︒【分析】如图,利用平行线的性质得出∠3=35°,然后进一步得出∠4的度数,从而再次利用平行线性质得出答案即可.【详解】如图所示,∵//a b ,135∠=︒,∴335∠=︒,∴∠4=90°−∠3=55°,∵////a b c,∴∠2=∠4=55°.故答案为:55°.【点睛】本题主要考查了平行线的性质,熟练掌握相关概念是解题关键.20.12【解析】分析:由图形可知,内部小三角形直角边是大三角形直角边平移得到的,故内部五个小直角三角形的周长为大直角三角形的周长.详解:由图形可以看出:内部小三角形直角边是大三角形直角边平移得到的解析:12【解析】分析:由图形可知,内部小三角形直角边是大三角形直角边平移得到的,故内部五个小直角三角形的周长为大直角三角形的周长.详解:由图形可以看出:内部小三角形直角边是大三角形直角边平移得到的,故内部五个小直角三角形的周长为AC+BC+AB=12.故答案为12.点睛:本题主要考查了平移的性质,需要注意的是:平移前后图形的大小、形状都不改变.三、解答题21.(1)详见解析;(2)①103°;②32°【分析】(1)过E作EF∥AB,根据平行线的性质可求∠B=∠BEF,∠C+∠CEF=180°,进而可证明结论;(2)①易求∠ABE=52°,根据(1)的结论可求解∠DCE=154°,根据角平分线的定义可得∠DCG=77°,过点F作FN∥AB,结合平行线的性质利用∠BFC=∠BFN+∠NFC可求解;②根据平行线的性质即角平分线的定义可求解∠BFC=∠FCE=180°-∠ECG=180°-(90°12∠BEC)=90°+12∠BEC,结合已知条件∠BFC-∠BEC=74°可求解∠BEC的度数.【详解】(1)证明:如图1,过E作EF∥AB,∵AB∥CD,∴DC∥EF,∴∠B=∠BEF,∠C+∠CEF=180°,∴∠C+∠B-∠BEC=180°,即:∠ABE+∠DCE-∠BEC=180°;(2)解:①∵FB∥CE,∴∠FBE=∠BEC=26°,∵BF平分∠ABE,∴∠ABE=2∠FBE=52°,由(1)得:∠DCE=180°-∠ABE+∠BEC=180°-52°+26°=154°,∵CG平分∠ECD,∴∠DCG=77°,过点F作FN∥AB,如图2,∵AB∥CD,∴FN∥CD,∴∠BFN=∠ABF=26°,∠NFC=∠DCG=77°,∴∠BFC=∠BFN+∠NFC=103°;②∵BF∥CE,∴∠BFC=∠ECF,∠FBE=∠BEC,∵BF平分∠ABE,∴∠ABE=2∠FBE=2∠BEC,由(1)知:∠ABE+∠DCE-∠BEC=180°,∴2∠BEC+∠DCE-∠BEC=180°,∴∠DCE=180°-∠BEC,∵CG平分∠DCE,∴∠ECG=12∠DCE=12(180°-∠BEC)=90°-12∠BEC,∴∠BFC=∠FCE=180°-∠ECG=180°-(90°-12∠BEC)=90°+12∠BEC,∵∠BFC-∠BEC=74°,∴∠BFC=74°+∠BEC,即74°+∠BEC=90°+12∠BEC,解得∠BEC=32°.故答案为:32°.【点睛】本题主要考查平行线的性质,角平分线的定义,灵活运用平行线的性质是解题的关键.22.(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)∠B+∠E+∠F+∠D=540°;(3)∠B +∠E+∠D-∠F=180°.【分析】(1)根据平行线的性质和判定,平行公理的推论回答即可;(2)过点E、F分别作GE∥HF∥CD,根据两直线平行,同旁内角互补及已知条件求得同旁内角∠ABE+∠BEG=180°,得到AB∥GE,再根据平行线的传递性来证得AB∥CD;(3)过点E、F分别作ME∥FN∥CD,根据两直线平行,内错角相等及已知条件求得同旁内角∠B+∠BEM=180°,得到AB∥ME,再根据平行线的传递性来证得AB∥CD.【详解】解:(1)由题意可知:“依据1”:两直线平行,同旁内角互补;“依据2”:同旁内角互补,两直线平行;“依据3”:如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.理由:如图,过点E、F分别作GE∥HF∥CD,则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,∴∠GEF+∠EFD+∠FDC=360°;又∵∠B+∠BEF+∠EFD+∠D=540°,∴∠ABE+∠BEG=180°,∴AB∥GE,∴AB∥CD;(3)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠D-∠F=180°时,有AB∥CD.如图,过点E、F分别作ME∥FN∥CD,则∠MEF=EFN,∠D=∠DFN,∵∠B+∠BEF+∠D-∠EFD=180°,∴∠B+∠BEM+∠MEF+∠D-∠EFN-∠DFN=180°,∴∠B+∠BEM=180°,∴AB∥ME,∴AB∥CD.【点睛】本题考查平行线的判定和性质的综合应用,作出合适的辅助线,灵活运用平行线的性质定理和判定定理是解题的关键.23.(1)45;(2)①详见解析;②302α︒+或602α︒-; 【分析】 (1)根据平行线性质可得180********BPD ∠=︒-︒-︒-︒=︒,再根据平行线性质得BOC BPD ∠=∠;(2)①根据平行线性质得160BOC ∠=∠=︒,2160∠=∠=︒,结合角平分线定义可证180DQE PDQ ∠+∠=︒,得PD QE ∥,根据平行线传递性可再证PD OC ∥; ②分两种情况分析:当Q 在H 的右侧时,根据平行线性质可得∠BPD=∠BOC=α,∠MQP=∠QPB=60°+α,根据角平分线性质∠MQE=12(60°+α),故∠PEQ=∠MQE ;当Q 在H 的右侧时,与上面同理,∠NQE=12(180°-60°-α),∠PEQ=∠NQE . 【详解】(1)由45NQD ∠=︒,MNAB ,可得180********BPD ∠=︒-︒-︒-︒=︒, 而PD OC ∥,则有BOC BPD ∠=∠.故45BPD α=∠=︒ (2)∵QE OC ∥,60BOC α∠==︒,∴160BOC ∠=∠=︒,又∵MN AB ,∴2160∠=∠=︒,又∵QE 平分PQH ∠,∴3260∠=∠=︒,又∵430∠=︒,∴4390DQE ∠=∠+∠=︒,且90PDQ ∠=︒,∴180DQE PDQ ∠+∠=︒,∴PD QE ∥,∵QE OC ∥,∴PD OC ∥.②当Q 在H 的右侧时,∵PD ∥OC∴∠BPD=∠BOC=α∵MN ∥AB∴∠MQP=∠QPB=60°+α又∵QE 平分∠MQP∴∠MQE=12(60°+α)=30°+12α ∴∠PEQ=∠MQE=30°+12α 当Q 在H 的左侧时∵PD ∥OC∴∠BPD=∠BOC=α∵MN ∥AB∴∠NQP=180°-60°-α又∵QE 平分∠NQP∠NQE=12(180°-60°-α)=60°-12α ∴∠PEQ=∠NQE=60°-12α∴302PEQ α∠=︒+或602α︒-.【点睛】 考核知识点:平移、平行线判定和性质综合运用.熟练运用平行线性质和判定,分类讨论问题是关键.24.(1)∠A +∠C +∠APC =360°,证明详见解析;(2)∠APC =∠A −∠C ,证明详见解析;(3)55°.【分析】(1)首先过点P 作PQ ∥AB ,结合题意得出AB ∥PQ ∥CD ,然后由“两直线平行,同旁内角互补”进一步分析即可证得∠A+∠C+∠APC =360°;(2)作PQ ∥AB ,结合题意得出AB ∥PQ ∥CD ,根据“两直线平行,内错角相等”进一步分析即可证得∠APC =∠A −∠C ;(3)由(2)知,∠APC =∠PAB −∠PCD ,先利用平行线性质得出∠BEF =∠PQB =110°,然后进一步得出∠PEG =12∠FEG ,∠GEH =12∠BEG ,最后根据∠PEH =∠PEG −∠GEH 即可得出答案.【详解】(1)∠A+∠C+∠APC =360°,证明如下:如图1所示,过点P 作PQ ∥AB ,∴∠A+∠APQ=180°,又∵AB∥CD,∴PQ∥CD,∴∠C+∠CPQ=180°,∴∠A+∠APQ+∠C+∠CPQ=360°,即∠A+∠C+∠APC=360°;(2)∠APC=∠A−∠C,证明如下:如图2所示,过点P作PQ∥AB,∴∠A=∠APQ,∵AB∥CD,∴PQ∥CD,∴∠C=∠CPQ,∵∠APC=∠APQ−∠CPQ,∴∠APC=∠A−∠C;(3)由(2)知,∠APC=∠PAB−∠PCD,∵∠APC=30°,∠PAB=140°,∴∠PCD=110°,∵AB∥CD,∴∠PQB=∠PCD=110°,∵EF∥PC,∴∠BEF=∠PQB=110°,∵∠PEG=∠PEF,∴∠PEG=12∠FEG,∵EH平分∠BEG,∴∠GEH=12∠BEG,∴∠PEH=∠PEG−∠GEH=12∠FEG−12∠BEG=12∠BEF=55°.【点睛】本题主要考查了利用平行线性质与角平分线性质求角度的综合运用,熟练掌握相关概念是解题关键.25.(1)∠MEN=∠AME+∠ENC,见解析;(2)∠FEQ=15°;(3)∠BMN+∠GEK-m∠GEH=180°.【分析】(1)过点E作l∥AB,利用平行线的性质可得∠1=∠BME,∠2=∠DNE,由∠MEN=∠1+∠2,等量代换可得结论;(2)利用角平分线的性质可得∠NEF=12∠MEN,∠ENP=12∠END,由EQ∥NP,可得∠QEN=∠ENP=12∠ENC,由(1)的结论可得∠MEN=∠AME+∠ENC,等量代换得出结论;(3)由已知可得∠EMN=1m∠BMN,∠GEN=1m∠GEK,由EH∥MN,可得∠HEM=∠ENM=1m∠AMN,因为∠GEH=∠GEM-∠HEM,等量代换得出结论.【详解】解:(1)过点E作l∥AB,∵AB∥CD,∴l∥AB∥CD∴∠1=∠AME,∠2=∠CNE.∵∠MEN=∠1+∠2,∴∠MEN=∠AME+∠ENC;(2)∵EF平分∠MEN,NP平分∠ENC,∴∠NEF=12∠MEN,∠ENP=12∠ENC.∵EQ∥NP,∴∠QEN=∠ENP=12∠ENC.由(1)可得∠MEN =∠AME +∠ENC ,∴∠MEN -∠ENC =∠AME =30°.∴∠FEQ =∠NEF -∠NEQ =12(∠MEN -∠ENC )=12×30°=15°; (3)∠BMN +∠GEK -m ∠GEH =180°.理由如下:∵∠AMN =m ∠EMN ,∠GEK =m ∠GEM , ∴∠EMN =1m ∠AMN ,∠GEM =1m∠GEK . ∵EH ∥MN ,∴∠HEM =∠EMN =1m ∠AMN . ∵∠GEH =∠GEM -∠HEM =1m ∠GEK -1m∠AMN , ∴m ∠GEH =∠GEK -∠AMN .∵∠BMN +∠AMN =180°,∴∠BMN +∠GEK -m ∠GEH =180°.【点睛】本题主要考查了平行线的性质,平行公理以及角平分线的定义等知识点,作出适当的辅助线,结合图形等量代换是解答此题的关键.26.(1)180BCD ACE ∠+∠=︒,理由详见解析;(2)135°;(3)BCD ∠等于150︒或30时,//CE AB .【分析】(1)依据∠BCD=∠ACB+∠ACD=90°+∠ACD ,即可得到∠BCD+∠ACE 的度数;(2)设∠ACE=α,则∠BCD=3α,依据∠BCD+∠ACE=180°,即可得到∠BCD 的度数; (3)分两种情况讨论,依据平行线的性质,即可得到当∠BCD 等于150°或30°时,CE//4B.【详解】解:(1)180BCD ACE ∠+∠=︒,理由如下:90BCD ACB ACD ACD ∠=∠+∠=︒+∠,∴90BCD ACE ACD ACE ∠+∠=︒+∠+∠9090180=︒+︒=︒;(2)如图①,设ACE α∠=,则3BCD α∠=,由(1)可得180BCD ACE ∠+∠=︒,∴3180αα+=︒,∴45α=,∴3135BCD α∠==︒;(3)分两种情况:①如图1所示,当//AB CE 时,180120BCE B ∠=︒-∠=︒, 又90DCE ∠=︒,∴36012090150BCD ∠=︒-︒-︒=︒;②如图2所示,当//AB CE 时,60BCE B ∠=∠=︒, 又90DCE ∠=︒,∴906030BCD ∠=︒-︒=︒.综上所述,BCD ∠等于150︒或30时,//CE AB .【点睛】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.熟练掌握定理并且能够准确识图是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一下数学寒假培优训练一(余角、补角以及三线八角、平行线的判定)一、考点讲解:1.余角:如果两个角的和是直角,那么称这两个角互为余角. 2.补角:如果两个角的和是平角,那.么称这两个角互为补角.3.对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角. 4.互为余角的有关性质:① ∠1+∠ 2=90°,则∠1、∠2互余.反过来,若∠1,∠2互余.则∠1+∠2=90○.②同角或等角的余角相等,如果∠l 十∠2=90○ ,∠1+∠ 3= 90○,则∠ 2= ∠ 3.5.互为补角的有关性质:①若∠A +∠B=180○则∠A 、∠B 互补,反过来,若∠A 、∠B 互补,则∠A+∠B =180○.②同角或等角的补角相等.如果∠A + ∠C=18 0○,∠A+∠B=18 0°,则∠B=∠C . 6.对顶角的性质:对顶角相等.项目定义性质图形互余角两个角和等于︒90(直角)︒=∠+∠9021同角或等角的余角相等互补角两个角和等于︒180(平角)︒=∠+∠18021同角或等角的补角相等对顶角两直线相交而成的一个角两边分别是另一角两边反向延长线对顶角相等21∠=∠三、经典例题题剖析:例1.已知一个角的余角比它的补角的135还少︒4,求这个角。
例2.如图所示,AOB 是一条直线,︒=∠︒=∠90,90DOE AOC ,问图中互余的角有哪几对?哪些角是相等的?例3.如图l -2-1,直线AB ,CD 相交于点O ,OE ⊥AB 于点O ,OF 平分∠AOE ,∠ 1=15○30’,则下列结论中不正确的是( )A .∠2 =45○B .∠1=∠3C .∠AOD 与∠1互为补角 D .∠1的余角等于75○30′ 解:D 点拨:此题考查了互为余角,互为补角和对顶角之间的综合运用知识. 四、巩固练习:1._______的余角相等,_______的补角相等.2.∠1和∠2互余,∠2和∠3互补,∠1=63○,∠3=__3.下列说法中正确的是( )A .两个互补的角中必有一个是钝角 B .一个角的补角一定比这个角大 C .互补的两个角中至少有一个角大于或等于直角 D .相等的角一定互余4.轮船航行到C 处测得小岛A 的方向为北偏东32○,那么从A 处观测到C 处的方向为( )121 212 ABEOCD12 3 4A .南偏西32○B .东偏南32○C .南偏西58○D .东偏南58○5.若∠l=2∠2,且∠1+∠2=90○则∠1=___,∠2=___.6.一个角的余角比它的补角的九分之二多1°,求这个角的度数.7.∠1和∠2互余,∠2和∠3互补,∠3=153○,∠l=_8.如果一个角的补角是150○,那么这个角的余角是_________ 9.一个角的余角( )A 、一定是钝角B 、一定是锐角C 、可能是锐角,也可能是钝角D 、以上答案都不对 10.若两个角互补,则( ) A 、这两个都是锐角 B 、这两个角都是钝角 C 、这两个角一个是锐角,一个是钝角 D 、以上结论都不对11.一个角等于它的余角的2倍,那么这个角等于它补角的( ) A 、2倍B 、21倍 C 、5倍 D 、51倍 12.下列说法中正确的是( ) A 、相等的角是对顶角B 、不是对顶角的角不相等C 、对顶角必相等D 、有公共顶点的角是对顶角13.三条直线相交于一点,所成对顶角有( ) A 、3对B 、4对C 、5对D 、6对14.下列说法正确的是( ) A 、不相等的角一定不是对顶角 B 、互补的两个角是邻补角C 、两条直线相交所成的角是对顶角D 、互补且有一条公共边的两个角是邻补角15.如图所示,AOE 是一条直线,︒=∠=∠90COD AOB ,则 (1)如果,301︒=∠那么=∠2 ,3∠= 。
(2)和1∠互为余角的角有 和1∠相等的角有 16.为下面推理填写理由。
(1)βα∠∠, 互为余角(已知),︒=∠+∠∴90βα( ) (2)如图所示, AB 、CD 相交于点O (已知),21∠=∠∴( ) (3)32,21∠=∠∠=∠ (已知),31∠=∠∴( )(4)︒=∠+∠90C A ,︒=∠+∠90C B (已知),∴∠A=∠B ( ) 五、关于同位角、内错角和同旁内角1.共同点:都是两条直线被第三条直线所截得到的不具有共公顶点的两个角之间的关系,这两个角有一条边在同一直线上。
2.不同点:同位角在两条直线的“同方”,第三条直线的“同侧”,(简称:位置相同的角,形状呈“F ”字形)。
内错角的两条直线“内侧”,第三条直线“两旁”(位置错开,形状呈“Z ”字形)。
同旁内角在两直线之间,第三条直线“同旁”(形状呈“C ”字形)。
A ED B C O32 4 1O 1 2A CBD另外注意:寻找“三线八角”关键是找准截线,截线是公共边所在的那条直线。
六、角位置的确定巩固练习:1.如图1所示,直线a、b、c两两相交,共构成对对顶角。
2.如图2,能与∠1构成同位角的角有()A、2个 B、3个 C、4个 D、5个3.如图2,能与∠1构成同旁内角的角有()A、2个 B、3个 C、4个 D、5个4.如图3所示,已知四条直线AB,BC,CD,DE。
问:①∠1,∠2是直线______和直线______被直线_____所截而成的____角.②∠1,∠3是直线_____和直线_____被直线_____所截而成的____角.③∠4,∠5是直线______和直线______被直线_____所截而成的____角.④∠2,∠5是直线______和直线______被直线_____所截而成的____角.5.如图4所示,下列各组判断错误的是【】.(A)∠2和∠3是同位角(B)∠1和∠3是内错角(C)∠2和∠4是同旁内角(D)∠1和∠2是内错角七、直线平行的条件(又叫平行线的判定);1.同位角相等,两直线平行; 2.内错角相等,两直线平行;3.同旁内角互补,两直线平行; 4.同时平行于第三条直线的两条直线也互相平行。
例1.如图所示,1∠和4∠是什么角?由哪两条直线被什么样的第三条直线所截?2∠和3∠呢?2∠和4∠呢?1∠和A∠呢?A∠和2∠呢?例2.如图所示,AB、CD两相交直线与EF、MN两平行直线与EF、MN两平行直线相交,试问一共可以得到同旁内角多少对?例3 (1) 如图所示,直线AB、CD被直线EF所截,如果∠1=∠2,∠CNF=∠BME,那么AB∥CD,MP∥NQ,请说明理由。
(2) 如图所示,直线ba,被直线c所截,1∠的3倍等于3,2∠∠是1∠的余角,求证:a∥b.(3)已知:如图,AD⊥BC,EF⊥BC,∠1=∠2,求证:AB∥GFAB CD1 234A CE FNMD BA BC DEFPQ12MN123 bacAB CD FEG12八、巩固练习1.给下列证明过程填写理由:已知:如图所示,AB ⊥BC 于B ,CD ⊥BC 于C ,∠1=∠2,求证:BE ∥CF .证明:∵AB ⊥BC 于B ,CD ⊥BC 于C,( ) ∴∠1+∠3=90°,∠2+∠4=90°( ) ∴∠1与∠3互余,∠2与∠4互余.( ) 又∵∠1=∠2,( ) ∴_______=_______.( )∴BE ∥CF .( ) 2.如图,已知∠B+∠C+∠D=360°,则AB ∥ED ,为什么?3.如图所示,已知︒=∠︒=∠︒=∠︒=∠10,30,45,25E CDE BCD B ,试说明,AB 与EF 有怎样的位置关系?并说说你判断的理由。
4.已知:如图,∠B 1+∠B 2=∠A 1+∠A 2+∠A 3 (即向左凸出的角的和等于向右凸出的角的和),求证:AA 1∥BA 35.下列说法正确的是( ) A 、同位角相等B 、同旁内角互补C 、若︒=∠+∠+∠180321,则3,2,1∠∠∠互补D 、对顶角相等 6.同一平面内有三条直线c b a ,,,若c b b a ⊥⊥,,则a 与c ( ) A 、平行B 、垂直C 、相交D 、重合7.一个人从A 点出发向北偏东︒60方向走了4m 到B 点,两从B 点向南偏西︒15的方向走了3m 到C 点,那么ABC ∠等于( ) A 、︒45 B 、︒75 C 、︒105 D 、︒1358.如图所示,根据下列条件:︒=∠+∠∠=∠∠=∠180,,B BED F ACB AOD A ,可以判定那两条直线平行,并说明判定的依据。
AB E13C DF 24ABCDEABECFO D ABCD EF AA 1 A 2A 3B 1 B 2B9.已知:如图,FE⊥AB,CD⊥AB,∠1=∠2,求证:∠AGD=∠ACB。
10.如图2-11,直线AB、CD相交于O点,∠AOD与∠BOD叫做______角;∠AOD与∠BOC叫______角;若∠AOD=2∠BOD,则∠BOD=______度,∠AOC=______度.11.如图2-14,直线AD、BC被CE所截,∠C的同位角是______,同旁内角是______;∠1与∠2是_____、____被____所截得的_____角;AB、CD被AD所截,∠A的内错角是______,∠A和∠ADC是______角;AB、CD被BD所截,_______和______是内错角.12.如图2-15,∵AO⊥OC,OB⊥OD∴∠1______∠2()13.已知:如图2-17,COD是直线,且∠1=∠3,说明A、O、B三点在一条直线的理由可以写成:∵COD是一条直线()∴∠1+∠2=______()∵∠1=∠3()∵∠______+∠3=______ ∴A、O、B在一条直线上.2.已知:如图2-18,直线AB、CD、EF交于点O,AB⊥CD,∠1=27°.求:∠2,∠FOB的度数.解:∵AB⊥CD,(已知)∴∠COB=______()∵∠1=27°(已知)∴∠3=______,∵∠3______∠2()∴∠2=______()∵∠2+∠FOB=______()∴∠FOB=______.(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
