《点直线平面投影》PPT课件
合集下载
工程制图(第四版)第3章 点、直线和平面的投影PPT

1.投影面平行线
平行于某一投影面,与另外两个投影面倾斜的直线
(1) 水平线 (2) 正平线 (3) 侧平线
2.投影面垂直线
垂直于某一投影面的直线
(1) 铅垂线 (2) 正垂线 (3) 侧垂线
3.一般位置直线
与三个投影面都倾斜的直线
水平线 — 平行于水平投影面的直线 z
Z
a b
a
b
a
b
A
a
X
O
YW
X
B O
b
a
a
b
Y
投影特性:1. ab OX ; ab OYW 3. 反映、 角的真实大小
b YH
2. ab=AB
正平线— 平行于正面投影面的直线
Z
Z
b
b
b
a
a
a
B
a
X
O
YW
A
b
X
O
a
b
a
b
Y
YH
投影特性: 1、ab OX ; a b OZ
2、a b=AB
3、反映、角的真实大小
侧平线— 平行于侧面投影面的直线
3、 a b = a b = AB
正垂线— 垂直于正面投影面的直线
ab
Z
z a
b
ab
A
a
X
O
YW
B
b
X
O
a
a b
b
Y
YH
投影特性: 1、 ab积聚 成一点
2 、 ab OX ; ab OZ
3 、 ab = ab =AB
侧垂线— 垂直于侧面投影面的直线
Z
a
b Z
ab
平行于某一投影面,与另外两个投影面倾斜的直线
(1) 水平线 (2) 正平线 (3) 侧平线
2.投影面垂直线
垂直于某一投影面的直线
(1) 铅垂线 (2) 正垂线 (3) 侧垂线
3.一般位置直线
与三个投影面都倾斜的直线
水平线 — 平行于水平投影面的直线 z
Z
a b
a
b
a
b
A
a
X
O
YW
X
B O
b
a
a
b
Y
投影特性:1. ab OX ; ab OYW 3. 反映、 角的真实大小
b YH
2. ab=AB
正平线— 平行于正面投影面的直线
Z
Z
b
b
b
a
a
a
B
a
X
O
YW
A
b
X
O
a
b
a
b
Y
YH
投影特性: 1、ab OX ; a b OZ
2、a b=AB
3、反映、角的真实大小
侧平线— 平行于侧面投影面的直线
3、 a b = a b = AB
正垂线— 垂直于正面投影面的直线
ab
Z
z a
b
ab
A
a
X
O
YW
B
b
X
O
a
a b
b
Y
YH
投影特性: 1、 ab积聚 成一点
2 、 ab OX ; ab OZ
3 、 ab = ab =AB
侧垂线— 垂直于侧面投影面的直线
Z
a
b Z
ab
第三章 点、直线、平面的投影

C b
O
|YA-YB| X
a b
ab
AB
a
|YA-YB|
|YA-YB|
ab
3 求直线的实长及对侧面投影面的夹角 角
Z
b b Z a
B
a X A a
b a X b a Y a YH O
O b
b YW
|XA-XB|
直线实长
直线实长
直线实长
△Z
△Y
△X
α
水平投影长
β
第三章 点、直线、平面的投影
第一节 点的投影 第二节 直线的投影 第三节 平面的投影
第三章 点、直线、平面的投影
3-1 点的投影
一、点的三面投影
二、点的投影与直角坐标的关系
三、点的投影规律
四、空间点的相对位置
一、点的三面投影
为了统一起见,规定空间点用大写字母表示,如A、B、C等; 水平投影用相应的小写字母表示,如a、b、c等;正面投影用 相应的小写字母加撇表示,如a′、b′、c′;侧面投影用相 应的小写字母加两撇表示,如a″、b″、c″。
b
d d c
b
a
d
A
b
a
例:判断图中两条直线是否平行。
①
a
a c c c d c b d a b a b b d c b d a c b d
AB与CD平行。
对于一般位置直线, 只要有两组同名投影互 相平行,空间两直线就 平行。
②
a
d
AB与CD不平行。
对于特殊位置直线, 只有两组同名投影互相 平行,空间直线不一定 平行。
a
X A a O bo b
机械制图(第四版)第2章 点、直线、平面的投影PPT课件
主视图、俯视图——长对正。
主视图、左视图——高平齐。
俯视图、左视图——宽相等。
上述关系统称为“三等关系”。 不论是整体还是局部,物体的
三视图都应符合三等关系,
图2-13 三视图度量的对应关系
在三等关系中,应注意理解俯视图和左视图“宽相等”的对应关系。
资讯
4. 视图间的方位对应关系 物体有上、下、前、后、左、右六个方位。 主视图反映了物体的上、下和左、右方位, 俯视图反映了左、右和前、后方位, 左视图则反映了上、下和前、后方位。
图2-14 补画左视图
图2-15 立体的空间形状与投影分析
(b) 三视图
图2-12 展开后的三投影面及物体的三视图
资讯
3.视图间的度量对应关系 根据三视图的形成可以分析出: 主视图反映物体长方向(OX)和高方向(OZ)的尺寸。 俯视图反映物体长方向(OX)和宽方向(OY)的尺寸。 左视图反映物体高方向(OZ)和宽方向(OY)的尺寸。
视图之间的度量关系为:
图2-9 三投影面体系
资讯
2.三视图的形成
如图2-10所示,将物体放在三投影面体系中用正投影方法将其向 各投影面投射,即可得到物体的三面视图。
画图时,需将相互垂直的三个投影面展平在同一平面上,规定:V 面保持不动,将H面绕OX轴向下旋转90°,W面绕OZ轴向后旋转 90°,如图2-11所示。
图2-10 三视图的形成
资讯
1. 三投影面体系
⑵ 三个投影轴
投影面之间的交线称为投影轴。
X投影轴:V与H面的交线,物体X轴方向的尺寸称为物体的长方向。 Y投影轴: H与W面的交线, 物体Y轴方向的尺寸称为物体的宽方向。 Z投影轴: V 与W面的交线,物体Z轴方向的尺寸称为物体的高方向。
教学课件PPT 点、直线、平面的投影
其投影特性取决于直线与三个投影 面间的相对位置
平行于某一投影面而 与其余两投影面倾斜
正平线(平行于V面)
投影面平行线 侧平线(平行于W面)
水平线(平行于H面)
统称特殊位置直线
正垂线(垂直于V面)
垂直于某一投影面 投影面垂直线 侧垂线(垂直于W面)
铅垂线(垂直于H面)
与三个投影面都倾斜的直线
一般位置直线
② 另外两个投影,反映线段实长,且垂直 于相应的投影轴。
⑶ 一般位置直线
V
b
B b
a
βγ
W
a
X
Ab
a
aH
a
投影特性
b Z b
a
O
Y
b
Y
三个投影都倾斜于投影轴,其与投影轴的夹角 并不反映空间线段与三个投影面夹角的大小。三个 投影的长度均比空间线段短,即都不反映空间线段 的实长。
二、直线与点的相对位置
a
a
三个投影都类似。
b
a
c
例:正垂面ABC与H面的夹角为45°,已知其水平投影 及顶点B的正面投影,求△ABC的正面投影及侧面 投影。
c
c
a
a
b ● 45°
b
a
c b
思考:此题有几个解?
三、平面上的直线和点
⒈ 平面上取任意直线
位于平面上的直线应满足的条件:
若一直线过平面上 的两点,则此直线 必在该平面内。
度量性较差。
平行投影法
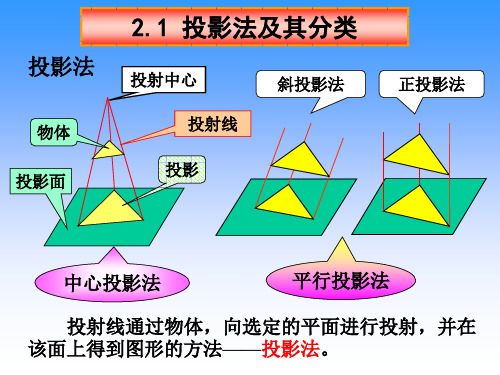
投影特性 投影大小与物体和投影面之间的距离无关。 度量性较好。 工程图样多数采用正投影法绘制。
画透视图
中心投影法
画斜轴测图
投影法
斜投影法
平行投影法
平行于某一投影面而 与其余两投影面倾斜
正平线(平行于V面)
投影面平行线 侧平线(平行于W面)
水平线(平行于H面)
统称特殊位置直线
正垂线(垂直于V面)
垂直于某一投影面 投影面垂直线 侧垂线(垂直于W面)
铅垂线(垂直于H面)
与三个投影面都倾斜的直线
一般位置直线
② 另外两个投影,反映线段实长,且垂直 于相应的投影轴。
⑶ 一般位置直线
V
b
B b
a
βγ
W
a
X
Ab
a
aH
a
投影特性
b Z b
a
O
Y
b
Y
三个投影都倾斜于投影轴,其与投影轴的夹角 并不反映空间线段与三个投影面夹角的大小。三个 投影的长度均比空间线段短,即都不反映空间线段 的实长。
二、直线与点的相对位置
a
a
三个投影都类似。
b
a
c
例:正垂面ABC与H面的夹角为45°,已知其水平投影 及顶点B的正面投影,求△ABC的正面投影及侧面 投影。
c
c
a
a
b ● 45°
b
a
c b
思考:此题有几个解?
三、平面上的直线和点
⒈ 平面上取任意直线
位于平面上的直线应满足的条件:
若一直线过平面上 的两点,则此直线 必在该平面内。
度量性较差。
平行投影法
投影特性 投影大小与物体和投影面之间的距离无关。 度量性较好。 工程图样多数采用正投影法绘制。
画透视图
中心投影法
画斜轴测图
投影法
斜投影法
平行投影法
土建工程制图第章点直线平面的投影_图文

已知
作图
直线的投影——两直线的相对位置
3.过E点作一直线与已知两交叉直线AB、C直线的相对位置
4.求作正平线MN与交叉三直线AB、CD、EF相交。
已知
作图
直线的投影——两直线的相对位置
5.作直线GH,使其与CD和EF相交且AB平行。
已知
作图
直线的投影——应用题
3.判断直线EF或点K是否在给定的平面上。
已知
作图
平面的投影——各种位置平面的投影
4.求平面内点的另一投影。
已知
作图
平面的投影——各种位置平面的投影
5.求平面ABC内直线EF的H面投影
(a)已知
(b)作图
分析:线段EF在平面ABC上,它一定通过平面上两个点, 作图过程及结果见上图(b)。
平面的投影——各种位置平面的投影
4.已知A、B、C三点的各一投影a、b′、c“,且Bb′=10, Aa=20,C c"=5。完成各点的三面投影,并用直线连接各同
面投影。
已知
点的投影
作图
点的投影
5.作出A、B两点的W面投影,并判断它 们的相对位置
A在B
A在B左前上方
已知
作图
分析:已知点的两投影可以求出点的第三投影,作图过程及 结果见上图(b)
1)过点A作正垂面P,其α为30° 2)过AB作铅垂面△ABC.
3) 过点A作一般面△ABC.
4) 过AB作一般面△ABC.
1)
2)
3)
4)
已知
平面的投影——各种位置平面的投影
3.过已知点、线作平面。
1)过点A作正垂面P,其α为30° 2)过AB作铅垂面△ABC.
3) 过点A作一般面△ABC.
机械制图与计算机绘图 PPT课件第4章 点、直线和平面的投影

e"( k")
YW
4.2.3 属于直线上的点
1. 从属性
V
直线上点的投影必在该直
Z b'
线的同面投影上,且符合点的
投影规律. b' Z b"
c'
c" X
c' a'
B Co
b"W c"
a'
X
o
b c
a YH
点C的三面投影必在
a" YW
A cb a
a" Y
2. 定比性
AC:CB=ac:cb=a′c′:c′b′ =a″c″:c″b″
b
小结
1、点与直线的投影特性,尤其是特殊位置直线 的投影特性。
2、点与直线及两直线的相对位置的判断方法及 投影特性。
3、定比定理。 4、平面的投影特性,尤其是特殊位置平的投影
特性。 5、如何在平面上确定直线和点。
c
YH
4.3.2 相交两直线
空间两直线 AB,CD相交 C 于点K,则交点K是两直线的 共有点。同时K要符合点的投
影规律。
c'
Z c"
c
a'
k'
b' b"
k" a"
B
K
bD A
kd a
X
d' O
d"
c
b
YW
kd a
YH
ab 、cd交于k a′b′、c′d′交于k′ a″b″、c″d″交于k″
4.3.3 交叉两直线
A点的Y坐标Ya=A点到V面的距离Aa ' ,表示宽度;
点直线平面的正投影(共9张PPT)
四. 点、直线、平面的正投影作图
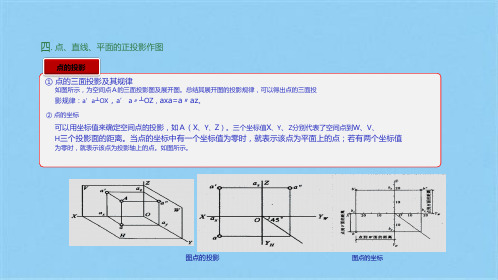
点的投影 ① 点的三面投影及其规律
如图所示,为空间点A的三面投影图及展开图。总结其展开图的投影规律,可以得出点的三面投
影规律:a’a┴OX,a’ a〃┴OZ,axa=a〃az。
② 点的坐标
可以用坐标值来确定空间点的投影,如A(X、Y、Z)。三个坐标值X、Y、Z分别代表了空间点到W、V、 H三个投影面的距离。当点的坐标中有一个坐标值为零时,就表示该点为平面上的点;若有两个坐标值
为零时,就表示该点为投影轴上的点。如图所示。
图点的投影
图点的坐标
四. 点、直线、平面的正投影作图
点的投影
③ 两点的相对位置
空间点的位置是根据它们对三个坐标轴的位置而定的。我们分别以 X轴,Y轴,Z轴的正向表示左、前、上方。依此规定,则 可确定两点的相对位置。,当空间两点位于同一投影线上,即该两点只有一个相对位置。同理可得C在D点的正前方 ,E在F点的正左方。如图(b)所示为重影点的正投影图。
图求平面上点M点及AB直线的投影
N直线平行AB,且➢过C直点线。通过平面上的两个点,则此直线在该平面上。
依N直此线规平定行,A则B可,确且➢定过两CN点点直。的线相平对行位A置B。,且过C点。N直线也在三角形ABC平面上。
➢ 若直线通过平面上的一点,且平行该平面上的 另一条直线,则此直线必在该平面上。
四. 点、直线、平面的正投影作图
表特殊位置直线的投影
四. 点、直线、平面的正投影作图
直线的投影 [例3]
如图(a)所示,已知E是CD线上的点,求e。
〔解法1〕:据已知条件,利用投影规律,先求出直线的 第三投影即W面投影c"d",再求出e"最后求出e点。如图所
示。
〔解法2〕:利用定比性,将直线的V面投影度量到H面投影 上,c、c’点重合,连接d、d’,过e点作dd’直线的平行线
点的投影 ① 点的三面投影及其规律
如图所示,为空间点A的三面投影图及展开图。总结其展开图的投影规律,可以得出点的三面投
影规律:a’a┴OX,a’ a〃┴OZ,axa=a〃az。
② 点的坐标
可以用坐标值来确定空间点的投影,如A(X、Y、Z)。三个坐标值X、Y、Z分别代表了空间点到W、V、 H三个投影面的距离。当点的坐标中有一个坐标值为零时,就表示该点为平面上的点;若有两个坐标值
为零时,就表示该点为投影轴上的点。如图所示。
图点的投影
图点的坐标
四. 点、直线、平面的正投影作图
点的投影
③ 两点的相对位置
空间点的位置是根据它们对三个坐标轴的位置而定的。我们分别以 X轴,Y轴,Z轴的正向表示左、前、上方。依此规定,则 可确定两点的相对位置。,当空间两点位于同一投影线上,即该两点只有一个相对位置。同理可得C在D点的正前方 ,E在F点的正左方。如图(b)所示为重影点的正投影图。
图求平面上点M点及AB直线的投影
N直线平行AB,且➢过C直点线。通过平面上的两个点,则此直线在该平面上。
依N直此线规平定行,A则B可,确且➢定过两CN点点直。的线相平对行位A置B。,且过C点。N直线也在三角形ABC平面上。
➢ 若直线通过平面上的一点,且平行该平面上的 另一条直线,则此直线必在该平面上。
四. 点、直线、平面的正投影作图
表特殊位置直线的投影
四. 点、直线、平面的正投影作图
直线的投影 [例3]
如图(a)所示,已知E是CD线上的点,求e。
〔解法1〕:据已知条件,利用投影规律,先求出直线的 第三投影即W面投影c"d",再求出e"最后求出e点。如图所
示。
〔解法2〕:利用定比性,将直线的V面投影度量到H面投影 上,c、c’点重合,连接d、d’,过e点作dd’直线的平行线
第2章--投影法及点、直线、平面的投影PPT课件
Y
a
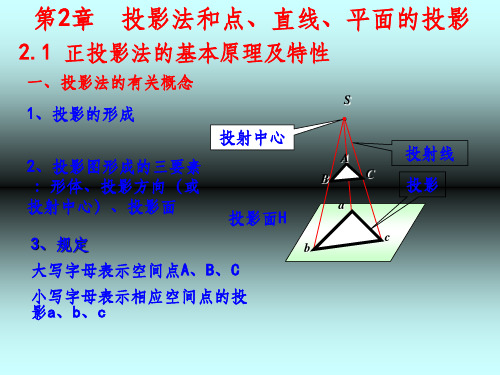
投影规律:
点的空间位置与投影的关系:
H
YH
aa′OX 长对正
点距H面的距离: a′ax和a〞ayw
aa〞OZ 高平齐
点距V面的距离:a ax和 a〞az
aax=a〞az 宽相等
点距W面的距离: a′az和 a ayH
举例:投影规律的应用
已知点A的正面投影a′和水平投影a,求其侧面投影a〞。
a'
相平行,但它们的第三组同面 三组同面投影相交,但它们的
投影是不平行的。
交点不符合点的投影规律。
例1:判断空间两直线AB、CD的相对位置。
1’
1 1′d′
1′c′
结论:
直线AB、CD是 两交叉直线。
例2 判断直线的空间相对位置
a’ c’
b’ c’
b’
d’
a’
d’
X
X
a d
d b a
c
b
c
( 交叉 ) ( 相交 )
一、三投影面体系的建立
B1
A
B2
V
b
a
H
单面投影:
点不定位,
体不定形。
三投影面体系
三个投影面:
V
水平投影面(H 面)
正立投影面(V 面)
侧立投影面(W 面)
X
三个投影轴:
两投影面相交,其交线称为投影轴。
H
V ∩ H = OX 轴
H ∩ W = OY 轴
V ∩ W = OZ 轴
Z W
O Y
二、立体三面投影的形成
a’
c’
c’
b’
d’
X
X
d
b a
点直线平面的投影课件

直线的投影
根据直线的方向和投影角度,确定 其在平面上的投影线。
点的轨迹
当点在直线上移动时,其在平面上 的投影点的轨迹形成一条直线。
直线与平面的投影问题解析
直线与平面的交点
根据直线的方向和平面的法线, 确定直线与平面的交点。
平面与直线的交线
根据平面的法线和直线的方向, 确定平面与直线的交线。
直线与平面的夹角
平行关系
如果直线与平面平行,则 它们的投影也平行。
点与平面的投影性 质
点与平面的相对位置关系
垂直关系
点与平面的相对位置关系可以通过其 投影在平面上的位置关系来反映。
如果点与平面垂直,则它们的投影也 垂直。
投影的特性
点与平面在空间中的位置关系,可以 通过其投影在平面上的位置关系来反 映。
03
点、直线和平面的投影应用
感谢观看
点在直线上的投影应用
确定点的投影
通过连接直线上的两个点,与投 影面交于一点,即为该点的投影。
判断点的位置
根据投影点和直线之间的关系, 判断点是否在直线上或与直线平行。
直线在平面上的投影应用
确定直线的投影
选择直线上的两个点,与投影面连接,得到直线的投影。
判断直线的位置
根据投影线与平面的交点或平行关系,判断直线是否在平面 上或与平面平行。
01
02
03
点的投影
点在空间中确定后,其投线在空间中确定后,其 投影在平面上也唯一确定。
投影的特性
点与直线在空间中的位置 关系,可以通过其投影在 平面上的位置关系来反映。
直线与平面的投影性质
平面的投影
平面在空间中确定后,其 投影在平面上也唯一确定。
投影的特性
