多属性决策的权重确定方法及matlab 程序

合集下载

多属性决策的权重确定方法及matlab 程序

多属性决策的权重确定方法及matlab 程序本文介绍11种多属性决策权重确定方法及matlab 程序。

目录1.列和求逆归一化方法（NHM ） ........................................................................................... 1 2.行和归一化方法（NRA ） ..................................................................................................... 1 3.和积法(ANC) .......................................................................................................................... 2 4.方根法（NGM ） ................................................................................................................... 2 5. 特征向量法（EM ） ............................................................................................................ 2 6.上三角梯度特征向量法HGEM ............................................................................................ 2 7.下三角梯度特征向量法LGEM ............................................................................................. 3 8.综合梯度特征向量法HLGEM ............................................................................................... 3 9.加权最小平方法WLSM ........................................................................................................ 3 10.几何最小二乘法GLSM ....................................................................................................... 3 11.最小平方几何距离方法（LSGM ） .................................................................................... 4 12. Matlab 程序 .. (5)1.列和求逆归一化方法（NHM ）()⨯=ij n n A a 为一致性判断矩阵的充分条件是=ωωiij ja ，由此可以得到如下等式，=,1,,，ωω=L j ij i a i j n ，两边关于i 求和化简得到列和求逆归一化的排序公式为，=11=,1,,ω=∑L j niji j n a如果A 为非一致性判断矩阵，则求得权重还要进行归一化处理。

基于CWAA算子(组合加权算术平均算子)的多属性决策方法及matlab应用

基于CWAA 算子（组合加权算术平均算子）的多属性决策方法及matlab 应用概念：CWAA 算子 11(,,)==∑L nn jjj CWAA a a w b其中，j b 是一组加权数据11(,,)ωωL n n t a t a 中第j 大的元素，1(,,)ωωL n 是数据1(,,)L n a a 的加权向量，t 是平衡因子。

特点：CWAA 算子不仅考虑了每个数据自身的重要性程度，而且还体现了该数据所在位置的重要程度。

决策步骤步骤1：设X 和U 分别为方案集和属性集。

1(,,)=L t D d d 是决策者集合，12(,,,)=L t w w w w 为CWAA 算子的权重向量，1(,,)ωωω=L k k nk 是指第k 个决策者对n个指标给出的指标权重。

对于方案i x ，按属性j u 测度，得到属性值ij a ，从而构成决策矩阵()⨯=ij n m A a ，如果属性量纲不一致，一般对矩阵A 进行规范化处理，得到规范化矩阵R 。

步骤2：利用W AA 算子对规范化矩阵R 中的第i 行元素进行集结，得出决策者d i 对方案i 的综合属性值()k i z 。

步骤3：利用CWAA 算子对t 位决策者给出的方案i 综合属性值()k i z 进行集结，得到方案i 的多人综合属性值i z 。

步骤4：利用方案i 的多人综合属性值对方案进行排序。

实例：步骤1：确定决策矩阵A ，这里不用进行数据的规范化处理。

步骤2：利用WAA 算子对矩阵A 中的第i 行进行集结，假设2位投资者分别对备选股票的6个指标的重要性进行赋权。

决策者d 1的权重为1=(0.4,0.05,0.1,0.05,0.05,0.35)ω，决策者d 2的权重为2=(0.1,0.3,0.3,0.1,0.1,0.1)ω，计算决策者d k 对方案i 的综合属性值()k i z ，假设两个投资者的重要性权重向量为(0.6,0.4)λ=d 。

步骤3：利用CWAA 算子的权重(0.5,0.5)=W ，对2位投资者所给出的方案i 综合属性值()k i z 进行集结，得到方案i 的多人综合属性值i z ：程序如下：clear;clc;R=[5.2 4.8 7.8 4.9 6.0 4.6 6 4.4 8.8 5.0 9.1 6.4 5.7 5.7 7.8 6.9 8.2 4.9 5.4 5 6.4 4.4 7.3 4.2]; rr=sort(R,2,'descend');omiga=[0.4 0.05 0.1 0.05 0.05 0.05 0.1 0.3 0.3 0.1 0.1 0.1]; Z=rr*omiga';Z1=2*0.6*Z(:,1); %对决策者1给出方案的综合属性值求解t*λ* Z1 Z2=2*0.4*Z(:,2); rr=[Z1 Z2]; % 合并 w=[0.5 0.5]; CWAA=rr*w';运行结果如下： CWAA=5.02106.0980 5.8490 4.9280 可以看到备选股票2为选择对象。

matlab信息熵方法确定权重

matlab信息熵方法确定权重Matlab是一种强大的数学建模和计算工具，可以用于解决各种实际问题。

信息熵是一种用于度量信息量和信息不确定性的方法，通过计算每个变量的信息熵，可以确定变量的权重。

在本文中，我们将介绍如何使用Matlab 的信息熵方法确定权重。

首先，我们需要明确问题的背景和目标。

假设我们有一个包含多个变量的数据集，我们希望确定每个变量对最终结果的影响程度，即各个变量的权重。

接下来，我们需要计算每个变量的信息熵。

信息熵的计算公式为：H(X) = - ΣP(x) log2(P(x))其中，H(X)表示变量X的信息熵，P(x)表示变量X取值为x的概率。

首先，我们需要对数据集进行预处理，以便计算每个变量的概率。

在Matlab中，我们可以使用histcounts函数来计算每个变量的概率分布。

例如，假设我们有一个包含n个样本的数据集，其中变量X有m个不同的取值。

我们可以使用以下代码计算变量X的概率分布：[counts, edges] = histcounts(X, 'Normalization', 'probability');在代码中，X表示待计算的变量，counts表示每个取值的频数，edges 表示每个取值的边界。

接下来，我们可以使用上述公式计算每个变量的信息熵。

在Matlab中，我们可以使用sum和log2函数来计算信息熵。

例如，假设我们有一个包含m个取值的变量X，我们可以使用以下代码计算变量X的信息熵：H = -sum(counts .* log2(counts));在代码中，counts表示变量X的概率分布，.*表示逐元素相乘操作。

计算完所有变量的信息熵后，我们可以将其归一化，以便比较各个变量的影响程度。

在Matlab中，我们可以使用normalize函数来实现归一化操作。

例如，假设我们有一个包含n个变量的信息熵向量H，我们可以使用以下代码将其归一化：normalized_H = normalize(H);在代码中，H表示信息熵向量，normalized_H表示归一化后的信息熵向量。

基于OWA算子和CWAA算子的多属性群决策方法及matlab应用

基于OWA 算子和CWAA 算子的多属性群决策方法及matlab 应用步骤1：对于某一多属性群决策问题，设X 和U 分别为方案集和属性集。

属性权重信息完全未知。

1(,,)=t D d d 是决策者集合，1(,,)λλ=t λ为决策者的权重向量，11λ==∑tk k 。

设决策者d k 给出方案i x 在属性j u 下的属性值()k ij a ，从而构成决策矩阵A k 。

如果属性量纲不一致，一般对矩阵A 进行规范化处理，得到规范化矩阵()()⨯=k k ij n m r R 。

步骤2：利用OWA 算子对决策矩阵k R 中的第i 行的属性值进行集结得到决策者d k 给出方案i x 的综合属性值()()k i z w 。

()()()()11()(,,)====∑mk k k k ii imj ij j zOWA r r w b w 12m (,,,)=w w w w 为OWA 算子的权重向量，()k ij b 是数据()()1(,,)k k i im r r 中第j 大的元素。

步骤3：利用CWAA 算子对t 位决策者给出方案i x 的综合属性值()()k i z w 进行集结，得到方案的群体综合属性值(,)'i z λw ，(1)()()1(,)((),,())=''==∑tt k i iiki k z CWAA z z w b λw w w 其中1(,,)'''=t w w w 是CWAA 算子的加权向量，满足权向量的条件。

()k i b 是一组加权数据(1)()1((),,())λλt i t i t z t z w w 中第k 大的元素，t 是平衡因子。

步骤4：利用(,)'i z λw 对方案进行排序。

该决策方法首先利用OWA 算子进行纵向集结（即对一个决策者所给定的某一方案所有属性值进行集结），然后利用CWAA 算子对纵向集结结果进行横向集结（即对由不同决策者得到的同一方案结合属性值进行集结）。

在Matlab中使用多目标优化进行多准则决策制定

在Matlab中使用多目标优化进行多准则决策制定随着社会的发展和科学技术的进步，人们在决策过程中需要考虑的因素越来越多，往往会涉及到多个准则。

面对这种情况，我们可以利用多目标优化算法来帮助决策者做出最佳的选择。

本文将介绍如何在Matlab中使用多目标优化进行多准则决策制定。

一个多准则决策问题通常涉及到多个决策变量和多个目标函数。

其中，决策变量是指需要决策者选择的决策因素，而目标函数是评价决策的准则。

多目标优化的目标是找到一组最优解，使得所有目标函数的值都能够达到最优。

在Matlab中，使用多目标优化算法进行多准则决策制定非常方便。

首先，我们需要定义决策变量和目标函数。

决策变量可以是连续的、离散的或者混合的。

而目标函数可以是线性的、非线性的、单目标的或者多目标的。

接下来，我们需要选择适合的多目标优化算法。

Matlab提供了多种多目标优化算法，包括非支配排序遗传算法（NSGA）、多目标遗传算法（MOGA）等。

根据具体情况选择合适的算法。

然后，我们需要定义问题的约束条件。

约束条件是指决策变量在决策空间中的限制条件。

约束条件可以是等式约束或者不等式约束。

在定义约束条件时，我们需要确保解空间的可行性。

在完成上述步骤后，我们可以使用Matlab中的优化函数进行多目标优化。

常用的优化函数有fmincon、gamultiobj等。

这些函数可以根据定义的决策变量、目标函数和约束条件，自动寻找最佳解集。

在进行多目标优化时，我们需要考虑目标之间的权重关系。

权重反映了各目标函数之间的重要性。

在Matlab中，可以通过设定权重向量来定义目标的优先级。

权重向量的选择需要根据具体情况来确定，可以根据专家知识或者利用模糊层次分析法等方法。

最后，我们需要根据优化结果进行决策制定。

在多目标优化中，我们通常得到一个解集，而不是单个最优解。

解集中的每个解都是一种最优解，并且在不同的权重下具有不同的优势。

决策者可以根据自己的需求和权衡来选择最终的决策。

多目标决策问题的多属性权重分配方法研究

多目标决策问题的多属性权重分配方法研究多属性权重分配是指根据不同属性的重要性，将权重适当地分配给多个目标，以便进行决策。

在多目标决策问题中，决策者需要考虑各个目标之间的权衡和权重。

多属性权重分配方法主要有层次分析法（Analytic Hierarchy Process，AHP）、主成分分析法（Principal Component Analysis，PCA）和熵权法（Entropy Weight Method，EWM）等。

首先，层次分析法是一种重要且经典的多属性权重分配方法。

该方法通过对比两两属性的相对重要性，按照一定的准则对属性进行排序，得到各个属性的权重。

层次分析法将复杂的决策问题层次化，减少了决策者的认知负担。

它将目标、准则和方案逐层分解，得出各层次之间的判断矩阵，并通过特征值法计算出最终权重。

其次，主成分分析法是一种通过线性变换将原始属性转化为新的属性，以最大限度地保留原始属性信息的方法。

主成分分析法的思想是通过将各个属性进行综合，得到一组新的属性，这些新属性能够更好地反映原始属性的特征。

在决策问题中，主成分分析法可以通过计算各个主成分的贡献率，得到每个属性的权重。

最后，熵权法是一种基于信息熵的多属性权重分配方法。

熵权法将信息熵应用于多属性决策问题中，通过计算各个属性的熵值和信息增益，得到各个属性的权重。

该方法充分考虑了属性之间的相互关系和信息量，对决策结果具有较好的解释性。

在实际应用中，选择适合的多属性权重分配方法需要考虑多个因素。

首先，需要根据具体的决策问题和决策者的需求，选择合适的方法。

其次，需要收集相关的决策数据，包括各个属性的权重和值。

然后，应根据所选方法进行计算和分析，得出最终权重。

最后，根据得到的最终权重对各个方案进行评估和排序，根据最终的决策目标进行选择。

综上所述，多目标决策问题的多属性权重分配方法包括层次分析法、主成分分析法和熵权法等。

这些方法在实践中具有一定的应用价值，可以帮助决策者在面对复杂的多目标决策问题时做出合理的决策。

基于正态分布的VIKOR多属性决策分析及matlab应用

基于正态分布的区间数VIKOR 多属性决策分析及matlab 应用1在已有的区间数的多属性决策方法的研究成果中大部分认为属性值在区间数内是服从均匀分布的，只有少部分文献认为是服从正态分布的．事实上认为其服从正态分布更加贴近实际，比如一个班级学生的期末考试成绩，高分和不及格的都占少数，大多数处于中间状态。

对已知属性权重取值范围及属性值为区间数的多属性决策问题进行了分析，利用线性规划模型求出属性权重的确定值，考虑了区间数正态分布，得到了基于正态分布的折中妥协(VIKOR)区间多属性决策法1.区间数的正态分布随机变量ξa 在区间数[],=a a a 服从正态分布，记2(,)ξμσ:a N ，根据正态分布的3σ原则()30.9973μσ-≤≈P a ，随机变量ξa 几乎可以肯定落在区间(3,3)μσμσ-+，故令3,3μσμσ=-=+a a ，解得[0,1],[0,1]26μσ+-=∈=∈a a a a a a 。

μa 可以表示[],a a 的中心，反映了信息的确定程度，σa 表示[],a a 的宽度，反映了信息的不确定程度。

定义：设区间数[,],[,]μσμσ==a a b b A B ，称22()μμσσ⎛⎫->=Φ ⎪-⎝⎭a b ab P A B 为>A B 的可能度。

2.决策方法有方案1,,L m A A ，共有m 个，1(,,)=L n u u u 为n 个属性，在方案(1,,)=L i i m A 在属性j u 下的决策值为,⎡⎤=⎣⎦ij ij ij a a a ，决策矩阵为()⨯=ijm n a A ，j w 为属性的权重，也为区间数，{1,,},{1,,}==L L M m N n 。

基于正态分布的折中妥协(VIKOR)决策法的具体步骤如下：步骤1用区间数规范化方法将原决策矩阵规范化处理得到矩阵,⨯⎡⎤=⎣⎦ij ij m n f f F效益型规范化 11==⎧=⎪⎪⎪⎨⎪=⎪⎪⎩∑∑ij ij m ij i ijijm ij i a f a a f a 成本型规范化1 Matlab 程序见文后的百度文库链接。

熵权法求权重matlab

熵权法求权重matlab
熵权法是一种多标准决策分析方法，其基本思想是通过计算各指标的信息熵，进而求得各指标的权重，从而进行综合评价或决策。

在Matlab 中，可以通过以下步骤实现熵权法求权重：
1. 收集各指标的数据，并将其组织成矩阵形式。

2. 对矩阵进行归一化处理，使得各指标的取值范围相同。

3. 计算各指标的信息熵。

对于第i个指标，其信息熵可以按照以下公式计算：
$E_i = -\sum_{j=1}^{n}s_{ij}\ln(s_{ij})$
其中，$s_{ij}$表示第i个指标在第j个样本中的归一化值，n表示样本数。

4. 计算各指标的权重。

对于第i个指标，其权重可以按照以下公式计算：
$w_i = \frac{1-E_i}{n-\sum_{j=1}^n E_j}$
其中，n表示指标数。

5. 对权重进行归一化，使得各权重之和为1。

以上就是使用熵权法求解指标权重的基本步骤，可以在Matlab中编写对应的代码来实现。

需要注意的是，在实际应用中，可能需要对不同指标的重要性进行调整，以更好地适应具体的决策问题。

基于模糊互补判断矩阵的多属性决策方法及matlab应用

基于模糊互补判断矩阵的多属性决策方法及matlab 应用目录一、模糊互补判断矩阵排序法 (1)1. 加型模糊互补判断矩阵排序的中转法 .............................................................................. 1 2.乘型模糊互补判断矩阵排序的和积法 ................................................................................ 2 二、模糊互补判断矩阵的最优化排序方法 .. (2)1. 加型模糊互补判断矩阵排序的最小方差法 ...................................................................... 2 2. 乘型模糊互补判断矩阵排序的最小平方法 ...................................................................... 3 3.模糊互补判断矩阵排序的幂法 ............................................................................................ 3 三、实例与matlab .. (4)决策者利用一定的标度对属性进行两两比较，并构造判断矩阵，然后按一定的排序方法计算判断矩阵的排序向量，从而获得属性权重，最后在根据各种算子进行多属性群决策。

一、模糊互补判断矩阵排序法1. 加型模糊互补判断矩阵排序的中转法判断矩阵的标度和含义如下表所示：按上述标度构成判断矩阵，=0.5ii b ，也满足其他条件。

设模糊判断矩阵()⨯=ij n n B b ，满足01<<ij b ，+1=ij ji b b ，若=+0.5-ij ik jk b b b ，则称矩阵B 为加型模糊一致互补判断矩阵。

各种多属性决策方法

j 人均专著生师比y2 科研经费逾期毕业
i
y1/(本/人)
y3/(万元/年) 率y4/(%)
1
0.1
5
5000
4.7
2
0.2
7
4000
2.2
3
0.6
10
1260
3.0
4
0.3
4
3000
3.9
5
2.8
2
284
1.2
2 数据预处理
数据预处理又称属性值的规范化，主要有三个作用：
(1)属性值有多种类型。有的属性值越大越好。有的属性值越小越好，有的属性值越接近于某个值越好。因此，需要对决策矩阵中的数据进行预处理，使表中任一属性下性能越优的方案变换后的属性值越大。
zij
yij y j
y max j
y
j
(1.00 M ) M
(7)
其中，
y j
1 m
m i 1
yij
是各方案属性j的均值，m为方案
个数，M的取值可在0.5-0.75之间。
６、专家打分数据的预处理
有时某些性能指标很难或根本不能用适当的统计数据来衡量其优劣。通常要请若干个同行专家对被评价对象按指标打分。再用各专家打分的平均值作为相应指标的属性并据此确定被评价对象的优劣。
0 j
,
则
理想解x
* j
mmiiianx
xij xij
j 为效益型属性 j 为成本型属性
j 1,, n (9.34)
负理想解x
0 j
mmiiianxxxiijj
j 为成本型属性 j 为效益型属性
j 1,, n (9.35)
(4)计算各方案到理想解与负理想解的距离。

熵值法确定权重matlab

熵值法（Entropy Method ）是一种确定权重的方法，通常应用于决策问题中。

这种方法的基本思想是，权重分配越分散，系统越复杂，其不确定性越大，因此可以通过计算每个指标的熵值来确定权重。

在Matlab 中，你可以使用以下步骤来实现熵值法确定权重：
1. 数据准备：准备数据矩阵，其中每行代表一个指标，每列代表一个样本。

2. 数据标准化：对数据进行标准化，确保不同指标的量纲一致。

3. 计算熵值：对每个指标计算熵值。

熵值的计算公式如下：
H j =−∑p ij n i=1⋅log(p ij ) 其中，H j 是指标 j 的熵值，p ij 是指标 j 在第 i 个样本中的相对权重。

4. 计算权重：计算每个指标的权重，使用熵值计算公式：
W j =1−H j m−∑H j m j=1 其中，W j 是指标 j 的权重，m 是指标的数量。

下面是一个简单的Matlab 示例代码，演示了如何实现熵值法确定权重：
这只是一个简单的示例代码，实际应用中需要根据具体情况进行调整和优化。

这个示例假设数据是已经标准化的，你可能需要根据实际情况修改标准化的方式。

Matlab中的多目标决策与多目标规划方法

Matlab中的多目标决策与多目标规划方法在工程和科学领域中，我们经常需要做出多个决策来解决一个问题。

而在现实中，这些决策可能有不同的目标或要求。

为了解决这个问题，我们可以利用Matlab中的多目标决策和多目标规划方法。

首先，让我们了解一下什么是多目标决策。

在传统的决策模型中，我们通常只有一个目标，在决策过程中我们优化这个目标。

然而，在实际问题中，往往存在多个目标，这些目标之间可能是相互矛盾的。

例如，在设计一个产品时，我们可能要同时考虑成本、品质和交货时间等多个目标。

这时，我们就需要多目标决策方法来找到一个最优解。

在Matlab中，我们可以利用多种多目标决策方法来解决这个问题。

其中一种常用的方法是多目标遗传算法（MOGA）。

遗传算法是一种模拟自然选择和遗传机制的优化算法。

它从一个初始的种群开始，通过模拟自然进化的过程，逐渐优化目标函数。

而多目标遗传算法则是在遗传算法的基础上进行了改进，使其能够同时优化多个目标。

多目标遗传算法的基本思想是通过保留当前种群中的一些非支配个体，并利用交叉和变异操作产生新的个体。

通过不断迭代，逐渐逼近最优解的非支配解集。

这样，我们就可以得到一系列的解，这些解都是在多个目标下都是最优的。

除了遗传算法外，Matlab还支持其他多目标决策方法，如多目标粒子群算法（MOPSO）和多目标蚁群算法（MOACO）。

这些方法在原理上有所不同，但都能够有效地解决多目标决策问题。

与多目标决策密切相关的是多目标规划。

多目标规划是一种数学优化方法，用于解决存在多个目标的问题。

在多目标规划中，我们需要同时优化多个目标函数，而不是简单地将它们合并成一个目标函数。

这使得我们可以获得一系列的最优解，而不是一个单一的最优解。

在Matlab中，我们可以使用多种多目标规划方法来解决这个问题。

其中一种常用的方法是帕累托前沿方法（Pareto Front）。

帕累托前沿是指在多目标问题中，不能通过改变一个目标而改善其他目标的解。

matlab信息熵方法确定权重 -回复

matlab信息熵方法确定权重-回复Matlab信息熵方法确定权重信息熵方法是一种常用的多准则决策方法，可用于确定权重。

在Matlab 中，我们可以利用该方法来解决多准则决策问题，帮助我们做出准确的权重确定。

本文将采用以下步骤来说明在Matlab中如何使用信息熵方法确定权重。

第一步：准备数据首先，我们需要准备准则矩阵数据。

准则矩阵包含n个准则和m个待评估的方案，我们需要将这些准则进行评分。

评分可以是数字或者是相对权重之间的比较，可以按照自己的需求进行选择。

例如，我们考虑了四个准则（A、B、C、D），并对三个方案（X、Y、Z）进行了评分，我们可以构建一个4×3的准则矩阵。

准则矩阵如下所示：X Y ZA 5 3 2B 4 2 1C 6 3 2D 3 1 1第二步：计算单个指标熵接下来，我们需要计算每个准则的熵。

熵是一种反映混乱程度的量化指标，可以用于衡量权重的不确定性。

准则熵越高，表示准则对决策结果的贡献越大。

在Matlab中，我们可以使用“entropy”函数来计算熵。

例如，我们可以计算准则A的熵：A = [5 4 6 3];entropy(A)计算结果为1.3863。

同样地，我们可以计算准则B、C和D的熵。

B = [3 2 3 1];C = [2 1 2 1];D = [2 1 2 1];entropy(B)entropy(C)entropy(D)计算结果分别为0.5623、0.5623和0。

第三步：计算熵权法得分熵权法是一种根据熵计算准则权重的方法，权重值越大表示准则对决策结果的贡献越大。

在Matlab中，我们可以使用以下公式来计算熵权法得分：权重= 1 - (准则熵/ 总准则熵)其中，总准则熵是所有准则的熵的和。

例如，我们可以计算准则A的权重：total_entropy = entropy(A) + entropy(B) + entropy(C) + entropy(D);weight_A = 1 - (entropy(A) / total_entropy);计算结果为0.4209。

基于离差最大化的区间多属性决策分析及matlab应用

基于离差最大化的区间多属性决策分析针对区间数多属性决策问题属性权重的确定，针对原属性权重已知且属性值为区间数的多属性决策问题，考虑到原属性值的差异及属性本身的重要度，采用EW 型区间距离，基于所有属性值的总离差和最大，建立了基于改进的离差最大线性分派(LA)多属性决策法。

1.离差最大化概念离差最大化确定权重的思想:在属性j u 下，如果所有决策方案的属性值差异很小，说明该属性对方案排序所起的作用越小；反之，方案的属性值差异很大，说明属性j u 对方案排序将起到重要作用.因此方案属性值离差越大，应赋予越大的权重，离差越小就赋予越小的权重。

如果所有决策方案在属性j u 下的属性值无差异，那么该属性对方案排序没有作用，其权重为零。

设属性权重为1(,,)ωω=n ω，0，ω≥∈j j N ，并满足单位化约束条件，设区间数决策矩阵为()(),⨯⨯⎡⎤==⎣⎦ijij ij m nm nR r r r ，则在属性j u 下，方案(1,,)=i a i m 与其他方案的离差用()ωij V 表示1/22211()=22322ωω=⎡⎤++--⎛⎫⎛⎫-+-⋅⎢⎥⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∑mij ij kj kj ij ij kj kj ij jk r r r r r r r r V根据上述分析，属性权重的选择应使所有方案对所有属性的总离差最大，因此通过如下最优化模型，1/2221111max ()=22322ω===⎡⎤++--⎛⎫⎛⎫-+-⋅⎢⎥⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∑∑∑nmmij ij kj kj ij ij kj kj jj i k r r r r r r r r V ω211..01,,，ωω=⎧=⎪⎨⎪≥=⎩∑n j j js t j n解此模型得到最优解，且对其进行归一化处理，可以得到:1/222111/222111122322=122322ω=====⎡⎤++--⎛⎫⎛⎫-+-⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎡⎤++--⎛⎫⎛⎫-+-⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∑∑∑∑∑mmij ij kj kj ij ij kj kj i k j n m m ij ijkj kj ij ij kj kj j i k r r r r r r r r r r r r r r r r （1）有方案1(,,)=m a a A ，属性权重为1(,,)=n u u u ，原属性权重为11(,,)0,1,==≥=∑nn j j j v v v v v ，j v 为实数，考虑区间离差最大及原属性权重，新得到的属性权重向量为11(,,)0,1,ωωωω==≥=∑nn j j j ω，ωj 为实数，在方案(1,,)=i a i m 在属性j u 下的决策值为,⎡⎤=⎣⎦ij ij ij a a a ，决策矩阵为()⨯=ij m na A ，设J 1和J 2分别表示效益型和成本型属性的下标集。

matlab极差法求权重

Matlab极差法求权重1. 引言在决策分析中，我们经常需要对不同因素或指标进行权重的确定。

权重反映了各个因素对决策结果的影响程度，是进行决策分析的基础。

Matlab提供了多种方法来计算权重，其中之一就是极差法。

极差法是一种常用的主观赋权方法，通过对指标值的范围进行归一化处理，得到各个指标的权重。

本文将详细介绍如何使用Matlab实现极差法求解权重。

2. 极差法原理极差法基于指标值的范围来确定权重。

具体步骤如下：1.确定评价指标：首先确定需要评价的指标集合，这些指标应该能够全面反映决策问题。

2.归一化处理：对每个指标的取值范围进行归一化处理，将其转换为0到1之间的数值。

3.计算极差：计算每个指标在评价对象中的取值范围。

4.计算权重：根据每个指标的极差大小计算其相对权重。

3. Matlab实现3.1 数据准备首先，我们需要准备评价指标的数据。

假设我们有n个评价指标，每个指标有m个评价对象。

可以将这些数据存储在一个n行m列的矩阵中，其中每一列代表一个评价对象的指标取值。

data = [1 2 3; 4 5 6; 7 8 9]; % 示例数据，3个指标，3个评价对象3.2 归一化处理归一化处理是将原始数据转换为0到1之间的数值。

常用的归一化方法有线性归一化和零均值归一化等。

在极差法中，我们使用线性归一化方法。

min_val = min(data,[],2); % 计算每个指标的最小值max_val = max(data,[],2); % 计算每个指标的最大值normalized_data = (data - min_val) ./ (max_val - min_val); % 线性归一化处理3.3 计算极差计算每个指标在评价对象中的取值范围。

range = max(normalized_data,[],2) - min(normalized_data,[],2); % 计算每个指标的极差3.4 计算权重根据每个指标的极差大小计算其相对权重。

对方案的偏好信息为效用值情形的多属性决策及matlab应用

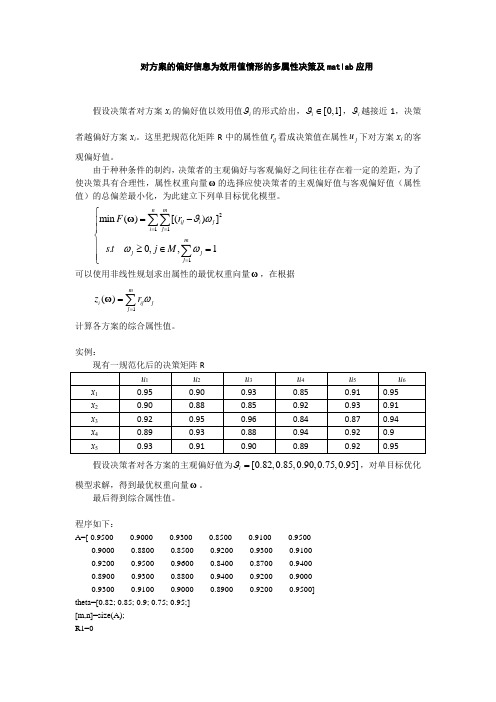
对方案的偏好信息为效用值情形的多属性决策及matlab 应用假设决策者对方案x i 的偏好值以效用值ϑi 的形式给出，[0,1]ϑ∈i ，ϑi 越接近1，决策者越偏好方案x i 。

这里把规范化矩阵R 中的属性值ij r 看成决策值在属性j u 下对方案x i 的客观偏好值。

由于种种条件的制约，决策者的主观偏好与客观偏好之间往往存在着一定的差距，为了使决策具有合理性，属性权重向量ω的选择应使决策者的主观偏好值与客观偏好值（属性值）的总偏差最小化，为此建立下列单目标优化模型。

2111min ()[()].0,,1ϑωωω===⎧=-⎪⎪⎨⎪≥∈=⎪⎩∑∑∑n mij i j i j mj jj F r s t j M ω 可以使用非线性规划求出属性的最优权重向量ω，在根据1()ω==∑mi ij j j z r ω计算各方案的综合属性值。

实例：假设决策者对各方案的主观偏好值为[0.82,0.85,0.90,0.75,0.95]ϑ=i ，对单目标优化模型求解，得到最优权重向量ω。

最后得到综合属性值。

程序如下：A=[ 0.9500 0.9000 0.9300 0.8500 0.9100 0.9500 0.9000 0.8800 0.8500 0.9200 0.9300 0.9100 0.9200 0.9500 0.9600 0.8400 0.8700 0.9400 0.8900 0.9300 0.8800 0.9400 0.9200 0.9000 0.9300 0.9100 0.9000 0.8900 0.9200 0.9500] theta=[0.82; 0.85; 0.9; 0.75; 0.95;] [m,n]=size(A); R1=0R2=0R3=0R4=0R5=0R6=0for i=1:mR1 = (A(i,1)-theta(i))^2+R1R2 = (A(i,2)-theta(i))^2+R2R3 = (A(i,3)-theta(i))^2+R3R4 = (A(i,4)-theta(i))^2+R4R5 = (A(i,5)-theta(i))^2+R5R6 = (A(i,6)-theta(i))^2+R6endR=[R1 R2 R3 R4 R5 R6]x=zeros(6,1)Aeq=[1 1 1 1 1 1];beq=1lb=zeros(6,1)x0=[1 1 1 1 1 1][x,y]=fmincon('fun2',x0,[],[],Aeq,beq,lb,[]) %非线性规划z=A*x'得到权重向量，x=0.1787 0.1622 0.2004 0.1429 0.1568 0.1591最终方案排序为z =0.91730.8959 0.9168 0.9079 0.9166可以看到方案1为最佳。

基于OWA算子的多属性决策方法及matlab应用

基于OWA 算子的多属性决策方法及matlab 应用概念1：AA 算术平均算子概念2：WAA 加权算术平均算子121(,,,)==∑L nn j j j WAA a a a w a其中w 是权重向量，权重小于1，和等于1.特点：对12(,,,)L n a a a 中对每个数据进行加权（即根据每个数据的重要性赋予适当的权重）。

概念3：有序加权几何平均OWA 算子121(,,,)==∑L nn j j j OWA a a a w b其中j b 是数据组12(,,,)L n a a a 中第j 大的元素。

特点：对数据12(,,,)L n a a a 按从大到小的顺序重新进行排序并通过加权集结。

而且元素i a 与i w 没有任何联系，只与第i 个位置有关。

如一权重(0.5,0.3,0.1,0.05,0.05)=W ，数据组12(,,,)=521863238469790（，，，，）L n a a a ，则OWA 加权几何平均值为，5218632384697900.5*863+0.3*790+0.1*521+0.05*469+0.05*238=755.95（，，，，）=OWA基于OWA 算子多属性决策方法步骤步骤1：设12=(,,,)L n X x x x 为方案集，12=(,,,)L m U u u u 为属性集，属性权重信息完全未知。

对于方案i x ，按属性j u 测度，得到属性值ij a ，从而构成决策矩阵()⨯=ij n m A a ，并经过规范化处理，得到规范化矩阵()⨯=ij n m R r 。

在多属性决策中，因为属性类型的不同，通常需要归一化处理。

• 效益型：属性值越大越好（比如利润）；• 成本型：属性值越小越好（比如成本价）；• 固定型：属性值越接近某个固定值α越好（生产标注宽度）； • 偏离型：属性值越偏离某个固定值β越好；• 区间型：属性值越接近某个固定区间[q 1,q 2]越好； •偏离区间型：属性值越偏离某个固定区间[q 1,q 2]越好；步骤2：利用OWA 算子对各方案i x 进行集结，求得其综合属性值()i z w11()=(,,)==∑L mi i im j j j z w OWA r r w b其中12(,,,)=L Tn W w w w 是权重，可以主观赋权、客观赋权或主客观赋权等。

matlab 熵值法

matlab 熵值法
熵值法是一种可以用来评估多属性决策问题的方法。

它可以帮助我们分析不同属性之间的相对重要性，并根据这些数据进行决策。

在MATLAB中，熵值法是一种非常有用的工具。

要使用熵值法，首先需要确定各个属性的权重。

这可以通过主观评价或客观统计方法来确定。

一旦确定了权重，就可以使用熵值法来进行决策。

在MATLAB中，使用熵值法进行多属性决策的步骤如下：
1. 输入数据。

将属性和每个属性的值输入MATLAB。

2. 计算归一化矩阵。

将每个属性值除以该属性的总和，这样可以将每个属性的值转换为百分比。

3. 计算熵值。

对于每个属性，计算其所有值的熵值。

熵值越高，不确定性就越大。

可以使用MATLAB中的熵函数来计算熵值。

4. 计算权重。

对于每个属性，计算其权重。

这可以通过将其熵值除以所有属性的熵值之和来实现。

5. 计算得分。

将每个属性的值乘以其相应的权重，然后将它们相加。

这将得到每个决策的得分，从而可以选择最佳决策。

总的来说，MATLAB中的熵值法可以帮助人们更好地了解多属性决策问题，从而做出更好的决策。

这是一个非常实用的工具，值得人们深入学习和研究。

不确定语言多属性群决策中属性权重确定方法_那迪

属性值的比重，
pkij=
bkij
m
，j∈n
Σbkij
i=1
（8）
第 3 步：计算属性 Cj 的熵值
m
Σ Qkj
=
1 In m i
=
pki·j Inpkij，j∈n
1
（9）
假设当 pkij=0 时，pki·j Inpkij=0 。
第 4 步：计算属性 Ci 的差异性系数： θki=1-Qki
（10）
第 5 步：确定个体属性权重
（1.Shenyang University of Technology, Information Science and Engineering, Shenyang Liaoning 110870, China; PC Northeast Refining & Chemical Engineering Company Limited, Shenyang Liaoning 110000, China）
射 χ 将 τ（l）转化为二元语义形式。
χ∶F（S）→[0，g]
（4）
设 S={S0，S1，...，Sg}是一个语言评语集，（Si，α）是一个二元语义，则
存在逆运算函数 △-1 将二元语义转换成相应的数值 β∈[0，g]，即：
χ（τ（l））=χ（F（S））=χ（{ Sj，ω）j }
g
Σjωj
=j = 0 g
1 0
0其＜它y＜。1 ，故由均匀分布
的定义知：Y 服从 U（0，1）.
例
6：若
X~F（2，2），证明
Y=
X 1+X
~U（0，1）。
证明：因为 X~F（2，2），故由 F 分布的定义（见文献[3]，p.146）知，X