Polyatomic Ions Writing Formulas Naming Compunds多原子离子的写作命名化合物公式

合集下载

化学物质解读

Ans: FeSO4
Ans: FeCl3
Ans: CaCl2
11
Common Monatomic Ions of Main-Group Elements
IA (1) IIA (2) IIIA (13) IVA
(14)
VA (15)
VIA (16)
VIIA (17)
1.
2. Li+ Be2+ B C N3O2-
1.
17
Group 7: fluorine fluoride F-; bromine bromide Br-; chlorine chloride Cl-; iodine iodide I-
Oxyanions Suffixes tell you the number of oxygen atoms in the anions = -ate e.g nitrate NO3-, sulfate SO42 = -ite e.g. nitrite NO2-, sulfite SO32-
Hydrogen sulfate (or bisulfate) (硫酸氫根) Thiosulfate (硫代硫硝根)
HSO3HSO4S2O3214
Permanganate (過錳酸根) MnO4-
Naming Simple Compounds

Systematic naming of chemical compounds Monoatomic ion = an ion formed from a single atom. e.g. Na+ Polyatomic ion = an ion of atoms chemically bonded together carrying net charges, e.g. SO42Naming: Cation + Anion (sodium chloride)

polynomials 词根

一、polynomials 词根的定义polynomial 是由两个词根组成的，分别是 poly 和 nomial。

其中，poly 源自希腊语，意为“多”，nomial 则来自拉丁语 nomen，意为“名称”或“命名”。

polynomial 这个词的字面意思是“有多个名称的”，在数学上指的是由多个项构成的代数式。

二、polynomial 的基本概念1. 代数式的构成在数学中，代数式由多个项以加减法连接而成。

而一个 polynomial 就是一个包含多个项的代数式，其中每一项都是一个系数与一个或多个变量的乘积。

3x^2 - 2x + 5 就是一个 polynomial。

2. polynomial 的次数一个 polynomial 的次数是指该 polynomial 中变量的最高次幂。

在代数式3x^2 - 2x + 5中，x^2 的次数是2，所以这个代数式的次数就是2。

次数为0的 polynomial 被称为常数。

3. polynomial 的系数在一个 polynomial 中，各个项的系数是指与变量相乘的常数。

在代数式3x^2 - 2x + 5中，3、-2 和5就分别是各个项的系数。

三、polynomial 在数学中的应用1. 代数方程的求解在数学中，polynomial 经常用来表示代数方程。

通过对 polynomial 的分解、化简和整理，可以帮助我们更好地理解和求解各种代数方程。

2. 描述多项式函数多项式函数是一种常见的数学函数形式，它们在数学和科学领域中有着广泛的应用。

通过对 polynomial 的研究，我们可以更好地理解多项式函数的性质和特点。

3. 数据拟合在统计学和数据分析中，polynomial 也常常被用来进行数据的拟合和预测。

通过拟合 polynomial 函数，可以帮助我们更好地理解数据的规律和趋势。

四、对 polynomial 的研究和发展1. polynomial 的历史对 polynomial 的研究可以追溯到古希腊时期。

唐山“PEP”2024年10版小学四年级下册J卷英语第4单元期末试卷

唐山“PEP”2024年10版小学四年级下册英语第4单元期末试卷考试时间：80分钟（总分:140）A卷考试人：_________题号一二三四五总分得分一、综合题(共计100题)1、What is the capital of the Czech Republic?A. PragueB. BratislavaC. BudapestD. Warsaw答案:A. Prague2、填空题：I love to play ________ (桌游) with my family.3、What is the process of changing from a liquid to a solid called?A. FreezingB. BoilingC. MeltingD. Evaporating答案: A4、听力题：The chemical formula for magnesium oxide is _______.5、What is the name of the imaginary line that divides the Earth into Eastern and Western Hemispheres?A. EquatorB. Prime MeridianC. Tropic of CancerD. Tropic of Capricorn答案: B6、听力题：She paints a _____ (画).A shooting star is actually a ______ entering the Earth's atmosphere.8、听力题：An experiment must be ______ (repeatable) to be scientifically valid.9、听力题：The chemical symbol for polonium is _______.10、填空题：My favorite subject in school is ______.11、What is the capital of Italy?A. ParisB. MadridC. RomeD. Berlin答案:C12、填空题：In my culture, we often greet each other with "Good morning, ."(在我的文化中，我们常常用“早上好，”互相问候。

计算器使用指南说明书

Candidates may use any calculator allowed by the regulations of theJoint Council for Qualifications. Calculators must not have the facilityfor symbolic algebra manipulation, differentiation and integration, orhave retrievable mathematical formulae stored in them.Instructionst Use black ink or ball-point pen.t I f pencil is used for diagrams/sketches/graphs it must be dark (HB or B).Coloured pencils and highlighter pens must not be used.t Fill in the boxes at the top of this page with your name,centre number and candidate number.t A n swer all questions and ensure that your answers to parts of questions areclearly labelled.t A nswer the questions in the spaces provided– there may be more space than you need.t Y ou should show sufficient working to make your methods clear. Answerswithout working may not gain full credit.t V alues from the statistical tables should be quoted in full. When a calculator is used, the answer should be given to an appropriate degree of accuracy.Informationt The total mark for this paper is 75.t T he marks for each question are shown in brackets– use this as a guide as to how much time to spend on each question.Advicet Read each question carefully before you start to answer it.t Try to answer every question.tCheck your answers if you have time at the end.*P44847A0124*Turn over P44847A©2015 Pearson Education Ltd.5/1/1/2*P44847A0224*3Turn over*P44847A0324*4*P44847A0424*5Turn over*P44847A0524*6*P44847A0624*7Turn over*P44847A0724*8*P44847A0824*9Turn over*P44847A0924*10*P44847A01024*21Turn over*P44847A02124*22*P44847A02224*23 *P44847A02324*24*P44847A02424*。

数学油画的英语作文

**Title: The Connection Between Mathematics and Oil Painting**Mathematics and art may seem like two completely different subjects, but they actually share a deep and fascinating connection. Oil painting, in particular, incorporates many mathematical concepts that help create beautiful and harmonious artworks. In this essay, I will explore how mathematics plays a vital role in oil painting.Firstly, geometry is essential in oil painting. Artists use geometric shapes to compose their works effectively. For instance, the principles of symmetry and balance help create a sense of harmony in a painting. When artists proportionate the size of different elements in their artwork, they often rely on geometric ratios. This technique ensures that the composition feels pleasing to the eye.Secondly, perspective is another important mathematical concept in oil painting. The use of linear perspective allows artists to create the illusion of depth and space in a two-dimensional artwork. By applying vanishing points and horizon lines, painters can depict objects that appear to recede into the background, making the scene more realistic. This technique requires a solid understanding of angles and proportions, showcasing the application of math in capturing three-dimensionality.Moreover, color theory, which involves understanding how colors interact, is also influenced by mathematics. Artists often use color wheels and value scales to determine which colors will complement each other. Mixing colors involves ratios, as artists must calculate how much of each color to combine to achieve the desired hue. This blending process illustrates how math is used even in the choice of colors.In conclusion, mathematics is an integral part of oil painting, influencing composition, perspective, and color theory. By understanding these mathematical principles, artists are able to create stunning works of art that captivate viewers. The connection between math and art enriches both fields, demonstrating that they are not as different as they may initially seem. Embracing this relationship allows us to appreciate the beauty of art in a new light.。

Polyatomic Ions Writing Formulas Naming Compounds多原子离子的写作命名化合物公式

• Name the compound. Potassium Chlorate
Mg3(SO4)2
• Name the metal. Magnesium
• Name the polyatomic ion from the ion chart. Sulfate
• Name the compound. Magnesium Sulfate
Polyatomic Ions
Writing Formulas / Naming Compounds
• A polyatomic ion is a covalent molecule that has an ionic charge. (As opposed to being a neutral molecule.)
Answers
• Li2SO4 • Ca(C2H3O2)2 • Al(NO3)3 • Mg3(PO4)2 • Na2CO3
Some Additional Examples
• Calcium Hydroxide
Ca+2
OH-1
• The least common factor is 2. Therefore, 1 calcium ion will bond with 2 hydroxide ions to form a neutral compound.
• Determine the common factor of the two oxidation numbers. In this case, 2.
• Decide how many of each ion is needed to equal the common factor. In this case, 2 sodium ions and 1 sulfate ion.

英语作文填充的废话翻译

英语作文填充的废话翻译Sure, here's a draft for you:---。

Title: The Art of Filling English Essays with Fluff。

When it comes to crafting English essays, one mightfind themselves grappling with the need to fill the pages with eloquent prose and insightful analysis. However, in the pursuit of verbosity, one must tread cautiously to avoid the pitfalls of banality. Herein lies the art of filling essays with fluff – the delicate balance between substance and style.First and foremost, it is imperative to establish a solid foundation of content. This entails thorough research and a comprehensive understanding of the topic at hand. Armed with a plethora of information, one can proceed to embellish their prose with carefully curated details andanecdotes. This not only adds depth to the narrative but also demonstrates the author's erudition and mastery of the subject matter.Moreover, the judicious use of literary devices can greatly enhance the richness of one's writing. Metaphors, similes, and personification serve as potent tools in the arsenal of the adept wordsmith, enabling them to paintvivid imagery and evoke visceral emotions in the reader. By imbuing their prose with such embellishments, the author transforms mundane ideas into captivating narratives that linger in the reader's mind long after the final paragraph.Furthermore, the art of filling essays with fluff extends beyond mere linguistic embellishments. Structural nuances such as parallelism, rhetorical questions, and thematic cohesion play a pivotal role in elevating the overall quality of the composition. By employing these techniques, the author not only captivates the reader's attention but also imbues their work with a sense of coherence and sophistication.However, it is crucial to exercise restraint in the pursuit of verbosity. Overindulgence in flowery languageand gratuitous embellishments can detract from the clarity and coherence of the essay, leaving the reader bewildered and disenchanted. Hence, it is incumbent upon the author to strike a delicate balance between eloquence and conciseness, ensuring that every word serves a purpose and contributesto the overarching narrative.In conclusion, the art of filling English essays with fluff is a nuanced endeavor that requires finesse, diligence, and a keen understanding of the intricacies of language. By judiciously employing literary devices, structural nuances, and thematic coherence, the author can elevate their prose to new heights of eloquence and sophistication. However, it is imperative to exercise restraint and avoid succumbing to the temptations of verbosity. Ultimately, it is the seamless integration of substance and style that distinguishes a truly exceptional essay from mere prose.--。

Numerical Recipes in C the art of scientific computing 2nd ed

(1.5) U0(x; a; b) = 1; U1(x; a; b) = x(1 + a); (1.6) Un+1(x; a; b) = x(1 + aqn)Un(x; a; b) ? bqn?1Un?1(x; a; b); n 1:
To indicate the dependence of Un(x; a; b) on q, when necessary we will use the notation Un(x; a; bjq). In accordance with the theory of orthogonal polynomials 4], the numerator polynomials fUn(x; a; b)g satisfy the recursion in (1.6) and the initial conditions (1.7) U0 (x; a; b) = 0; U1 (x; a; b) = 1 + a: Therefore (1.8) Un(x; a; b) = (1 + a)Un?1(x; qa; qb): Schur 8] actually considered the polynomials Un(1; 0; ?q) and Un(1; 0; ?q). In the notation of (1.2) and (1.3) we have (1.9) Dn = Un+1(1; 0; ?q); En = Un+1(1; 0; ?q) = Un(1; 0; ?q2):
(2.2) Schurn = Dn+m + En+m:
We can determine the parameters and using the initial conditions Schur0 = 1, Schur1 = 1 + q1+m, which leads to the evaluations

普林斯顿数学英文原文

普林斯顿数学英文原文The Mathematics of PrincetonPrinceton University has long been renowned for its excellence in mathematics. The institution has produced some of the most influential mathematicians and scientists in history, and its contributions to the field of mathematics are truly remarkable. In this essay, we will explore the rich history and legacy of mathematics at Princeton, examining the key figures, groundbreaking discoveries, and the enduring impact of this esteemed institution.One of the most significant figures in Princeton's mathematical history is John von Neumann, a Hungarian-American mathematician who made seminal contributions to a wide range of fields, including game theory, computer science, and quantum mechanics. Von Neumann's work on the theory of games and economic behavior laid the foundation for modern game theory, which has had far-reaching applications in economics, political science, and beyond. His contributions to the development of the modern computer, including his work on the von Neumann architecture, have had aprofound and lasting impact on the field of computer science.Another renowned mathematician associated with Princeton is Alan Turing, the British computer scientist and cryptanalyst who is widely regarded as the father of theoretical computer science and artificial intelligence. Turing's groundbreaking work on the concept of the "Turing machine," a theoretical model of computation, laid the foundation for the development of modern computers and algorithms. During World War II, Turing played a pivotal role in breaking the Nazi's Enigma code, a feat that is credited with shortening the war and saving countless lives.The legacy of mathematics at Princeton is also closely tied to the Institute for Advanced Study, a prestigious research institute located on the university's campus. The Institute has been a hub for some of the most brilliant minds in mathematics, physics, and other fields, attracting scholars from around the world to collaborate and push the boundaries of human knowledge. Many of the Institute's alumni and faculty have gone on to win the highest honors in their respective fields, including the Nobel Prize and the Fields Medal, the most prestigious award in mathematics.One of the most famous mathematicians associated with the Institute for Advanced Study is Albert Einstein, who spent the latter part of his career at the Institute. Einstein's groundbreaking work onthe theory of relativity, which revolutionized our understanding of the universe, is a testament to the intellectual rigor and creativity that has long been a hallmark of Princeton's mathematical community.Beyond the contributions of individual scholars, Princeton has also played a pivotal role in shaping the broader landscape of mathematical research and education. The university's mathematics department is consistently ranked among the best in the world, attracting top students and faculty from around the globe. The department's curriculum and research programs have had a profound influence on the way mathematics is taught and studied at institutions around the world.One of the key factors behind Princeton's enduring excellence in mathematics is its commitment to fostering a culture of collaboration and interdisciplinary research. The university's emphasis on cross-pollination between different fields of study has led to numerous groundbreaking discoveries and innovations, as researchers from diverse backgrounds come together to tackle complex problems.This spirit of collaboration is exemplified by the work of the renowned mathematician John Nash, whose contributions to game theory and the study of equilibria in complex systems earned him theNobel Prize in Economics. Nash's work, which has had far-reaching implications in fields ranging from economics to biology, is a testament to the power of interdisciplinary research and the value of bringing together diverse perspectives.Another key factor behind Princeton's success in mathematics is its commitment to nurturing the next generation of mathematical thinkers. The university's undergraduate and graduate programs in mathematics are widely regarded as among the best in the world, attracting top students from around the globe and providing them with the resources and support they need to thrive.The university's emphasis on hands-on research and collaborative learning has been particularly instrumental in shaping the careers of many of its most successful alumni. Many of Princeton's mathematics graduates have gone on to become leaders in their respective fields, taking their skills and knowledge to academia, industry, and beyond.Looking to the future, it is clear that Princeton's legacy in mathematics will continue to shape the course of the field for generations to come. The university's commitment to pushing the boundaries of human knowledge, fostering interdisciplinary collaboration, and nurturing the next generation of mathematical thinkers will undoubtedly continue to bear fruit in the years and decades ahead.Whether it is through groundbreaking discoveries, innovative teaching methods, or the cultivation of a vibrant intellectual community, Princeton's impact on the world of mathematics is undeniable. As the university continues to evolve and adapt to the changing needs of the 21st century, one thing is certain: its legacy as a bastion of mathematical excellence will endure, inspiring and shaping the field for years to come.。

Polynomials and Trigonometric Polynomials Orthogonal on the Unit Circle

POLYNOMIALS AND TRIGONOMETRIC POLYNOMIALSORTHOGONAL ON THE UNIT CIRCLEBARBARA ENGELHARDT‡Abstract.An orthonormal basis of L2( ,µ),µa nonnegative Borel measure on the unit circle ,consisting of trigonometric polynomials is presented which generalizes the basis{z n:n∈ }for Lebesgue measure and Euler’s formula.Key words.Trigonometric Polynomials,Orthogonal Polynomials and Special FunctionsAMS subject classiﬁcations.Primary42C05,42C30Consider a nonnegative Borel measureµon the unit circle :={z∈g:|z|=1} which has inﬁnite support.The corresponding system of orthonormal polynomi-als(ϕn)n∈x0with positive leading coeﬃcient (ϕn)can be generated from the set{z k,k∈x0}with the help of the Gram-Schmidt procedure w.r.t.the inner product f,g µ:= f¯g dµ.This system of functions may lack a crucial property.They span L2( ,µ)iﬀµdoes not fulﬁll Szeg¨o’s condition,i.e. lnµ (z)dz=−∞(compare[2],Ch.I.(15)or [3],3.3).Many interesting cases,e.g.that of the Lebesgue measure,fulﬁll this condition. Here already z−1cannot be approximated by linear combinations of theϕn so that trigonometric(or Laurent)polynomials are needed to obtain a basis of L2( ,µ).For this basis Szeg¨o’s condition is of no relevance.1.The Bases.First consider the following double system of trigonometric poly-nomials,which was introduced in[6].Theorem1.Deﬁne the double system of trigonometric polynomialsA n(z):=1√2d n e−iγ2n z−nϕ2n(z)+e iγ2n z n¯ϕ2n(¯z) ,n∈x0,(1)B n(z):=1i√2e n e−iγ2n z−nϕ2n(z)−e iγ2n z n¯ϕ2n(¯z) ,n∈x,where z∈g\{0},d n:= 1+|ϕ2n(0)|2n −12,e n:= 1−|ϕ2n(0)|2n −12,andγ2n such that e−2iγ2nϕ2n(0)∈ .Then{A n,n∈x0;B n,n∈x}is an orthonormal basis of L2( ,µ).Proof.The trigonometric polynomial z−nϕ2n(z)is orthogonal to any trigonomet-ric polynomial of lower degree sincez−nϕ2n,z k µ= ϕ2n,z n+k µ=0for any−n+1≤k≤n−1. Rotation,decomposition into real and imaginary parte−iγ2n z−nϕ2n(z)=f n(z)+ig n(z),‡Institute of Biomathematics and Biometry,GSF—National Research Center for Environment and Health,Ingolstaedter Landstraße1,D-85764Neuherberg,Germany,e-mail:engelhardt@gsf.de12 B.ENGELHARDTand normalization gives the system{A n,n∈x0;B n,n∈x},which is biorthogonal w.r.t.µ,i.e.A n,A m µ=δn,m,B n,B m µ=δn,m,and A n,B m µ=0.The orthogonality A n,B n µ=0is ensured by the rotation factor e−iγ2n.In fact we have for T n(z):=e−iγ2n z−nϕ2n(z)T n,T n µ=e−2iγ2n ϕ2n(z)z−2nϕ2n(0)dµ(z)=e−2iγ2nϕ2n(0)2n∈ . Hence,f n,g n µ=14iT n+T n,T n−T n =14i T n,T n − T n,T n + T n,T n − T n,T n=0.As A0,...,A n,B1,...,B n span the same set as z−n,...,z n for any n∈x,the double system{A n,n∈x0;B n,n∈x}is an orthonormal basis of L2( ,µ).In the special case of symmetricµthere is a connection between the orthogonal polynomials on the circle and two sets of associated polynomials orthogonal on[−1,1].A measureµis called symmetric ifµ(e−iA)=µ(e iA)for any Borel set A in[0,π].For any symmetric measure deﬁne two associated measuresνµand˜νµ:νµ(B):=µ(e i arccos B)for any Borel set B in(]−1,1[),νµ({1}):=12µ({1}),νµ({−1}):=12µ({−1}),and d˜νµ(x):=(1−x2)dνµ(x),two nonnegative Borel measures on[−1,1].If dνµ(x)=w(x)dx with a weight w on[−1,1]the corresponding measure on is dµ(e it)=w(cos t)|sin t|dt with an even weight function according toµ’s symmetry.For symmetricµthere is a connection between the three sequences of ortho normalpolynomials(ϕn)n∈x0w.r.t.µon ,(p n)n∈xw.r.t.νµ,and(q n)n∈xw.r.t.˜νµ,both on[−1,1](see[5]).For z=e it,n∈x,hold with d n and e n deﬁned as in Theorem1p n(cos t)=1√2πd n(z−nϕ2n(z)+z nϕ2n(¯z))=1√2πe n(z−n+1ϕ2n−1(z)+z n−1ϕ2n−1(¯z))andq n−1(cos t)= 2πe nz−nϕ2n(z)−z nϕ2n(¯z)z−¯z=πd nz−n+1ϕ2n−1(z)−z n−1ϕ2n−1(¯z)z−¯z, and vice versa(2)ϕ2n(z)=z n π 1np n(cos t)+i sin tnq n−1(cos t) andϕ2n−1(z)=z n−1 π2 1e np n(cos t)+i sin td nq n−1(cos t) .POLYNOMIALS AND TRIGONOMETRIC POLYNOMIALS ON THE UNIT CIRCLE3In particular,all coeﬃcients of ϕn ,n ∈x 0,are real.Hence,for symmetric µwe obtain with (2)and ϕ2n (0)∈ such that γ2n :=0for z =e it ∈ ,n ∈x 0A n (z )=1√2d n z −n ϕ2n (z )+z n ¯ϕ2n (¯z ) =√πp n (cos t ),(3)B n (z )=1i √2e n z −n ϕ2n (z )−z n ¯ϕ2n (¯z ) =√πsin t q n −1(cos t ),n =0.In the case of the normalized Lebesgue measure dt ,z =e it∈ ,p n (x )and q n (x )are the Chebychev polynomials of the ﬁrst and second kind,respectively.Hence,A n (z )=√2cos nt and B n (z )=√2sin nt (z =e it ∈ ).Generalizing Euler’s formulae int =cos |n |t +i sign n sin |n |t,a new trigonometric system is now deﬁned (without involving any symmetry of µ).Theorem 2.Let for n ∈ ,z ∈g \{0}ψn (z ):=1√2A |n |(z )+i sign nB |n |(z ) .(4)Then (ψn )n ∈ is an orthonormal basis of L 2( ,µ).Further holds for any n ∈¯ψ−n (¯z )=ψn (z )⇐⇒z ∈ ,and the ψn fulﬁll a six-term recurrence relationψn ψ±1=k ∈{−n −1,−n,−n +1,n −1,n,n +1}h (n,±1,k )ψkwith coeﬃcients h (n,±1,k )∈g ,n ∈ .Proof .Since (ψn )n ∈ is a hermitian image of the orthonormal basis {A n ,n ∈x 0;B n ,n ∈x },it is again an orthonormal bining (4)and (1)we get for n ∈ ,z ∈g \{0}ψn (z )=1√2A |n |(z )+i sign nB |n |(z )=12 e −iγ2|n |(d |n |+sign n e |n |)z −|n |ϕ2|n |(z )(5)+e iγ2|n |(d |n |−sign n e |n |)z |n |¯ϕ2|n |(¯z ),so that for any n ∈¯ψ−n (¯z )=ψn (z )⇐⇒z ∈ .The six-term recurrence relation is due to orthogonality.For normalized Lebesgue measure this new system is the classical basis ψn (z )=z n,n ∈ .4B.ENGELHARDTNow consider the trigonometric polynomials (ψn )n ∈ for symmetric µ.With (3)we obtain for z =e it ∈ ,n ∈ψn (e it )=π2p |n |(cos t )+i sign n sin t q |n |−1(cos t ) .(6)Again,the ψn have real coeﬃcients,so that p |n |and q |n |−1can be recovered from ψn p n (cos t )=πψn (e it ),q n (cos t )=π ψn +1(e it )sin t,n ∈x 0.(7)Moreover ψn (z )=ψ−n (¯z )iﬀz ∈ .Further,for symmetric µwe ﬁnd thatψn (z )=d n e n n n ϕ2n (z )+ϕ2n −1(z )for n ≥0(8)because with (2)ψn (e it )=d ne nd n +e nπ21d n p n (cos t )+i sin t e nq n −1(cos t )+ π2 1e n p n (cos t )+i sin t d nq n −1(cos t )=π2(p n (cos t )+i sin t q n −1(cos t )).Altogether we have the following connection between the diﬀerent systems of orthogonal functions?)(ϕn )n ∈x 0(ψn )n ∈ {A n ,n ∈x 0;B n ,n ∈x }(5)(1)(4)In the case of symmetric µthis corresponds to?6)-(ϕn )n ∈x 0(ψn )n ∈ (p n )n ∈x 0,(q n )n ∈x 0(8)(2)(6,7)2.Examples.Consider the Bernstein-Szeg¨o trigonometric polynomials,wheredµ(z )=dzρ(z )with a trigonometric polynomial ρof degree r ∈x 0with real coeﬃcientsPOLYNOMIALS AND TRIGONOMETRIC POLYNOMIALS ON THE UNIT CIRCLE5 such thatρ>0on .Due to the Theorem of Riesz-F´e jer(see e.g.[5],Theorem 1.2.2)there exists a root polynomial h(z)= r k=0αk z k of the same degree,ρ(e it)=|h(e it)|2.Asρhas no zeros on ,this polynomial is unique and h(z)=0for|z|≤1,h(0)>0.The polynomialsϕn are explicitly known for n≥r:ϕn(z)=z n¯h(z−1)=rk=0¯αk z n−k.Hence,for|n|>r/2we have d n=1=e n,γ2n:=0and someψn can also be given explicitly:ψn(z)=12(1+sign n)rk=0¯αk z n−k+(1−sign n)rk=0αk z k−n= r k=0¯αk z n−k=ϕn(z)for n≥r, r k=0αk z k−n=¯ϕ−n(¯z)for n≤−r.The measure is symmetric iﬀρ(z)=ρ(cos t)is a cosine polynomial and then all αk are real.Another example is given by the Jacobi weights,where forα,β>−1dµ(α,β)(e it):=12(1−cos t)α+12(1+cos t)β+12dt.To this symmetric measure correspond dνµ(x)(α,β)(x)=(1−x)α(1+x)βdx and d˜ν(α,β)µ(x)=(1−x)α+1(1+x)β+1dx so thatψ(α,β) n (z)= π2 p(α,β)|n|(cos t)+i sign n sin t p(α+1,β+1)|n|−1(cos t)where(p(α,β)n )n∈xdenote the normalized Jacobi polynomials.These trigonometric polynomials,although derived along a diﬀerent path,are exactly those considered in[4].In a diﬀerent normalization they can be used to obtain convolution structures on .This subject will be treated in a subsequent paper[1].REFERENCES[1] B.Engelhardt,Hypergroups on the Set of All Integers,Preprint.[2]Y.Geronimus,Polynomials Orthogonal on a Circle and Interval,Pergamon Press,1960.[3]U.Grenander and G.Szeg¨o,Toeplitz Forms and Their Applications,University of CaliforniaPress,1958.[4]M.R¨o sler,Trigonometric Convolution Structures on Derived from Jacobi Polynomials,Jour-nal of Computational and Applied Mathematics,65(1995),pp.357–368.[5]G.Szeg¨o,Orthogonal Polynomials,American Mathematical Society Colloquium Publications,New York,1959.[6],On Bi-Orthogonal Systems of Trigonometric Polynomials,in Gabor Szeg¨o:CollectedPapers,R.Askey,ed.,vol.3(1945-1972),Birkh¨a user,Boston,1982,pp.797–817.。

济宁2024年04版小学5年级上册第4次英语第1单元全练全测

济宁2024年04版小学5年级上册英语第1单元全练全测考试时间：90分钟（总分:120）A卷考试人：_________题号一二三四五总分得分一、综合题(共计100题)1、听力题：The tree is very ___. (tall)2、听力题：The capital of the United States is _______.3、填空题：The first animal in space was a dog named ______ (莱卡).4、Which animal is known for building dams?A. BeaverB. OtterC. FoxD. Squirrel5、填空题：The bat uses echolocation to find its _________. (食物)6、听力题：The chemical formula for silver sulfide is _______.7、听力题：The main gas involved in combustion is __________.8、听力题：The ______ is the center of an atom.9、填空题：The ________ has colorful petals that bloom in spring.10、填空题：I like to make up stories with my ________ (玩具名称).11、What do you call a baby chicken?A. DucklingB. PigletC. ChickD. Calf12、Which planet is known for its extreme winds?A. VenusB. SaturnC. NeptuneD. Jupiter13、填空题：The _____ (松树) stays green all year round. It is a symbol of strength.松树四季常绿，是力量的象征。

TaylorPolynomials（as.pdf）

plotting some Taylor polynomials and the function g(x) =
( Sin x g[x_] :=
Exp[Sin[x]] in Mathematica) together with the graph of g itself. Explain your
answer in complete sentences and make use of the error bounds in section
P 5, f, 0, x
x3 x5 x
6 120
P 6, f, Pi 2, x
1 1
2
Π
21
x
2
24
Π
41
x
2
720
Π
6
x
2
Notice that when a = Π/2, we get even powers of (x - a) = Π x rather
2
than odd powers. Do you see why? Let's plot these polynomials together with f(x):
QUESTION 1. i) Which of these two polynomials gives a more accurate value for sin(0.8)? For sin(2.1)? If we changed the polynomial about 0 from degree 5 to degree 7 would that alter your answers? ii) Suppose you want to approximate sin(2.3). What is the smallest degree for the polynomial around 0 that will result in an approximation comparably accurate to the approximation of sin(2.3) using the 6th degree Taylor polynomial about Π/2?

法布里珀罗基模共振英文

法布里珀罗基模共振英文The Fabryperot ResonanceOptics, the study of light and its properties, has been a subject of fascination for scientists and researchers for centuries. One of the fundamental phenomena in optics is the Fabry-Perot resonance, named after the French physicists Charles Fabry and Alfred Perot, who first described it in the late 19th century. This resonance effect has numerous applications in various fields, ranging from telecommunications to quantum physics, and its understanding is crucial in the development of advanced optical technologies.The Fabry-Perot resonance occurs when light is reflected multiple times between two parallel, partially reflective surfaces, known as mirrors. This creates a standing wave pattern within the cavity formed by the mirrors, where the light waves interfere constructively and destructively to produce a series of sharp peaks and valleys in the transmitted and reflected light intensity. The specific wavelengths at which the constructive interference occurs are known as the resonant wavelengths of the Fabry-Perot cavity.The resonant wavelengths of a Fabry-Perot cavity are determined bythe distance between the mirrors, the refractive index of the material within the cavity, and the wavelength of the incident light. When the optical path length, which is the product of the refractive index and the physical distance between the mirrors, is an integer multiple of the wavelength of the incident light, the light waves interfere constructively, resulting in a high-intensity transmission through the cavity. Conversely, when the optical path length is not an integer multiple of the wavelength, the light waves interfere destructively, leading to a low-intensity transmission.The sharpness of the resonant peaks in a Fabry-Perot cavity is determined by the reflectivity of the mirrors. Highly reflective mirrors result in a higher finesse, which is a measure of the ratio of the spacing between the resonant peaks to their width. This high finesse allows for the creation of narrow-linewidth, high-resolution optical filters and laser cavities, which are essential components in various optical systems.One of the key applications of the Fabry-Perot resonance is in the field of optical telecommunications. Fiber-optic communication systems often utilize Fabry-Perot filters to select specific wavelength channels for data transmission, enabling the efficient use of the available bandwidth in fiber-optic networks. These filters can be tuned by adjusting the mirror separation or the refractive index of the cavity, allowing for dynamic wavelength selection andreconfiguration of the communication system.Another important application of the Fabry-Perot resonance is in the field of laser technology. Fabry-Perot cavities are commonly used as the optical resonator in various types of lasers, providing the necessary feedback to sustain the lasing process. The high finesse of the Fabry-Perot cavity allows for the generation of highly monochromatic and coherent light, which is crucial for applications such as spectroscopy, interferometry, and precision metrology.In the realm of quantum physics, the Fabry-Perot resonance plays a crucial role in the study of cavity quantum electrodynamics (cQED). In cQED, atoms or other quantum systems are placed inside a Fabry-Perot cavity, where the strong interaction between the atoms and the confined electromagnetic field can lead to the observation of fascinating quantum phenomena, such as the Purcell effect, vacuum Rabi oscillations, and the generation of nonclassical states of light.Furthermore, the Fabry-Perot resonance has found applications in the field of optical sensing, where it is used to detect small changes in physical parameters, such as displacement, pressure, or temperature. The high sensitivity and stability of Fabry-Perot interferometers make them valuable tools in various sensing and measurement applications, ranging from seismic monitoring to the detection of gravitational waves.The Fabry-Perot resonance is a fundamental concept in optics that has enabled the development of numerous advanced optical technologies. Its versatility and importance in various fields of science and engineering have made it a subject of continuous research and innovation. As the field of optics continues to advance, the Fabry-Perot resonance will undoubtedly play an increasingly crucial role in shaping the future of optical systems and applications.。

五元氮杂环的芳香性和稳定性

五元氮杂环的芳香性和稳定性梁艳红【摘要】自然界中许多含有五元环的有机物都具有芳香性,其中这些五元环大部分是由(CH)单元和N原子组成的.(CH)单元和N原子是等电子体,笔者对一些五元杂环及其正负离子的稳定性和芳香性的规律进行了详细的研究.选用从头算和密度泛函理论方法,用cc-pVDZ基组对五元氮杂环及其正负离子的几何结构进行了优化,同时对它们的能量和频率进行了计算,得到了一些具有稳定平面结构的氮杂环和其正负离子.并在相同的计算水平下,对这些稳定结构的核独立化学位移(NICS)和谐振子模型的芳香性(HOMA)进行了计算,利用这两个判断标准对这些结构的芳香性进行了讨论,并得到了有关这些结构的稳定性和芳香性的一些规律.【期刊名称】《河北科技师范学院学报》【年(卷),期】2014(028)004【总页数】6页(P51-55,67)【关键词】氮杂环;芳香性;稳定性;从头计算;密度泛函理论【作者】梁艳红【作者单位】河北科技师范学院物理系,河北秦皇岛,066004【正文语种】中文【中图分类】TQ252氮的五元杂环在生物学上有很重要的地位，研究它们是否具有芳香性，对于探讨其结构的稳定性和在生物学上的应用是非常重要的。

现在化学家提出了很多芳香性的判断标准，这些标准基本上从物质能量，磁性和几何结构这三个方面来判定物质的芳香性，这是由于物质的芳香性对物质这三个方面有很明显的作用［1］。

其中，核独立化学位移(NICS)被化学家认为是一个简单而有效的芳香性判据［2］。

它主要是从磁性的角度来判定芳香性。

它是由Schleyer及其合作者提出的一个判据［3］，其定义是在平面环或原子簇的几何中心或中心之上计算的独立磁屏蔽系数的负值。

如果在这些位置计算的NICS值为负，表明分子具有芳香性;若这些位置的NICS值为正，表明分子是反芳香的;接近0，则是非芳香性分子［4］。

它的可靠性已经被一系列对二维和三维芳香化合物的研究所证明。

谐振子模型的芳香性(HOMA)是芳香性的另一个判断标准［5］。

Chem Formula Writing Worksheet ( ) ( )

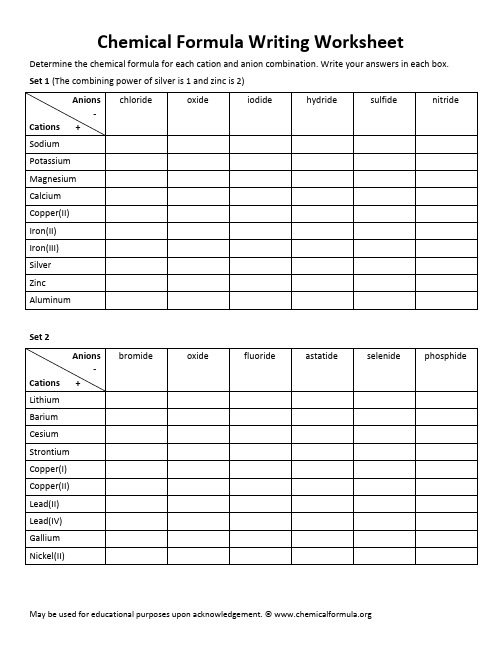
Chemical Formula Writing Worksheet
Determine the chemical formula for each cation and anion combination. Write your answers in each box. Brackets are only needed when the polyatomic group is greater than 1. Eg. Strontium phosphate, Sr3(PO4)2 Set 3 (The combining power of silver is 1 and zinc is 2. The formula for the ammonium ion is NH4+) Anions + nitrate NO3sulfate SO42hydroxide OHcarbonate CO32phosphate PO43hydrogen carbonate HCO3-
Anions + Li+ Ba2+ Cs+ Sr2+ Cu+ Cu2+ Pb2+ Pb4+ Ga3+ Ni2+
bromide BrLiBr BaBr2 CsBr SrBr2 CuBr CuBr2 PbBr2 PbBr4 GaBr3 NiBr2
oxide O2Li2O BaO Cs2O SrO Cu2O CuO Pb2O3 Pb2O Ga2O3 NiO
fluoride FLiF BaF2 CsF SrF2 CuF CuF2 PbF3 PbF4 GaF3 NiF2
Cations Sodium Potassium Calcium Copper(II) Iron(II) Iron(III) Silver Zinc Aluminum Set 2

Polynomialfunctions

Polynomial functionsMany common functions are polynomial functions.In this unit we describe polynomial functions and look at some of their properties.In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature.After reading this text,and/or viewing the video tutorial on this topic,you should be able to:•recognise when a rule describes a polynomial function,and write down the degree of the polynomial,•recognize the typical shapes of the graphs of polynomials,of degree up to4,•understand what is meant by the multiplicity of a root of a polynomial,•sketch the graph of a polynomial,given its expression as a product of linear factors.Contents1.Introduction22.What is a polynomial?23.Graphs of polynomial functions34.Turning points of polynomial functions65.Roots of polynomial functions71.IntroductionA polynomial function is a function such as a quadratic,a cubic,a quartic,and so on,involving only non-negative integer powers of x.We can give a general deﬁntion of a polynomial,and deﬁne its degree.2.What is a polynomial?A polynomial of degree n is a function of the formf(x)=a n x n+a n−1x n−1+...+a2x2+a1x+a0where the a’s are real numbers(sometimes called the coeﬃcients of the polynomial).Although this general formula might look quite complicated,particular examples are much simpler.For example,f(x)=4x3−3x2+2is a polynomial of degree3,as3is the highest power of x in the formula.This is called a cubic polynomial,or just a cubic.Andf(x)=x7−4x5+1is a polynomial of degree7,as7is the highest power of x.Notice here that we don’t need every power of x up to7:we need to know only the highest power of x toﬁnd out the degree.An example of a kind you may be familiar with isf(x)=4x2−2x−4which is a polynomial of degree2,as2is the highest power of x.This is called a quadratic. Functions containing other operations,such as square roots,are not polynomials.For example,√f(x)=4x3+3.Graphs of polynomial functionsWe have met some of the basic polynomials already.For example,f(x)=2is a constant function and f(x)=2x+1is a linear function.It is important to notice that the graphs of constant functions and linear functions are always straight lines.We have already said that a quadratic function is a polynomial of degree2.Here are some examples of quadratic functions:f(x)=x2,f(x)=2x2,f(x)=5x2.What is the impact of changing the coeﬃcient of x2as we have done in these examples?One way toﬁnd out is to sketch the graphs of the functions.You can see from the graph that,as the coeﬃcient of x2is increased,the graph is stretched vertically(that is,in the y direction).What will happen if the coeﬃcient is negative?This will mean that all of the positive f(x)values will now become negative.So what will the graphs of the functions look like?The functions are nowf(x)=−x2,f(x)=−2x2,f(x)=−5x2.−x22Notice here that all of these graphs have actually been reﬂected in the x-axis.This will always happen for functions of any degree if they are multiplied by−1.Now let us look at some other quadratic functions to see what happens when we vary the coeﬃcient of x,rather than the coeﬃcient of x2.We shall use a table of values in order to plot the graphs,but we shallﬁll in only those values near the turning points of the functions.x−5−3−112060−40−8−8You can see the symmetry in each row of the table,demonstrating that we have concentrated on the region around the turning point of each function.We can now use these values to plot the graphs.As you can see,increasing the positive coeﬃcient of x in this polynomial moves the graph down and to the left.What happens if the coeﬃcient of x is negative?x−1135602x2−4x−3−3−8−8−2022063177511−2−42Our table of values is particularly easy to complete since we can use our answers from the x2+x column toﬁnd everything else.We can use these tables of values to plot the graphs of the functions.x 2 + x + 5x 2 + x − 4x 2 + x + 1x 2 + x As we can see straight away,varying the constant term translates the x 2+x curve vertically.Furthermore,the value of the constant is the point at whichthe graph crosses the f (x )axis.4.T urning points of polynomial functionsA turning point of a function is apoint where the graph of the function changes from sloping downwards to sloping upwards,or vice versa.So the gradient changes from negative to positive,or from positive to negative.Generally speaking,curves ofdegree n can have up to (n −1)turning points.For instance,a quadratic has only one turning point.A cubic could have up to two turning points,and so would look something like this.However,some cubics have fewer turning points:for example f (x )=x 3.But no cubic has more than two turning points.In the same way,a quartic could have up tothree turning turning points,and so wouldlook something like this.Again,some quartics have fewer turning points,but none has more.Key PointA polynomial of degree n can have up to(n−1)turning points.5.Roots of polynomial functionsYou may recall that when(x−a)(x−b)=0,we know that a and b are roots of the function f(x)=(x−a)(x−b).Now we can use the converse of this,and say that if a and b are roots, then the polynomial function with these roots must be f(x)=(x−a)(x−b),or a multiple of this.For example,if a quadratic has roots x=3and x=−2,then the function must be f(x)= (x−3)(x+2),or a constant multiple of this.This can be extended to polynomials of any degree. For example,if the roots of a polynomial are x=1,x=2,x=3,x=4,then the function must bef(x)=(x−1)(x−2)(x−3)(x−4),or a constant multiple of this.Let us also think about the function f(x)=(x−2)2.We can see straight away that x−2=0, so that x=2.For this function we have only one root.This is what we call a repeated root, and a root can be repeated any number of times.For example,f(x)=(x−2)3(x+4)4has a repeated root x=2,and another repeated root x=−4.We say that the root x=2has multiplicity3,and that the root x=−4has multiplicity4.The useful thing about knowing the multiplicity of a root is that it helps us with sketching the graph of the function.If the multiplicity of a root is odd then the graph cuts through the x-axis at the point(x,0).But if the multiplicity is even then the graph just touches the x-axis at the point(x,0).For example,take the functionf(x)=(x−3)2(x+1)5(x−2)3(x+2)4.•The root x=3has multiplicity2,so the graph touches the x-axis at(3,0).•The root x=−1has multiplicity5,so the graph crosses the x-axis at(−1,0).•The root x=2has multiplicity3,so the graph crosses the x-axis at(2,0).•The root x=−2has multiplicity4,so the graph touches the x-axis at(−2,0).To take another example,suppose we have the function f(x)=(x−2)2(x+1).We can see that the largest power of x is3,and so the function is a cubic.We know the possible general shapes of a cubic,and as the coeﬃcient of x3is positive the curve must generally increase to the right and decrease to the left.We can also see that the roots of the function are x=2and x=−1.The root x=2has even multiplicity and so the curve just touches the x-axis here, whilst x=−1has odd multiplicity and so here the curve crosses the x-axis.This means we can sketch the graph as follows.Key PointThe number a is a root of the polynomial function f(x)if f(a)=0,and this occurs when (x−a)is a factor of f(x).If a is a root of f(x),and if(x−a)m is a factor of f(x)but(x−a)m+1is not a factor,then we say that the root has multiplicity m.At a root of odd multiplicity the graph of the function crosses the x-axis,whereas at a root of even multiplicity the graph touches the x-axis.Exercises1.What is a polynomial function?2.Which of the following functions are polynomial functions?(a)f(x)=4x2+2(b)f(x)=3x3−2x+√3.Write down one example of each of the following types of polynomial function:(a)cubic(b)linear(c)quartic(d)quadratic4.Sketch the graphs of the following functions on the same axes:(a)f(x)=x2(b)f(x)=4x2(c)f(x)=−x2(d)f(x)=−4x25.Consider a function of the form f(x)=x2+ax,where a represents a real number.The graph of this function is represented by a parabola.(a)When a>0,what happens to the parabola as a increases?(b)When a<0,what happens to the parabola as a decreases?6.Write down the maximum number of turning points on the graph of a polynomial function of degree:(a)2(b)3(c)12(d)n7.Write down a polynomial function with roots:(a)1,2,3,4(b)2,−4(c)12,−1,−68.Write down the roots and identify their multiplicity for each of the following functions:(a)f(x)=(x−2)3(x+4)4(b)f(x)=(x−1)(x+2)2(x−4)39.Sketch the following functions:(a)f(x)=(x−2)2(x+1)(b)f(x)=(x−1)2(x+3)Answers1.A polynomial function is a function that can be written in the formf(x)=a n x n+a n−1x n−1+a n−2x n−2+...+a2x2+a1x+a0,where each a0,a1,etc.represents a real number,and where n is a natural number(including 0).2.(a)f(x)=4x2+2is a polynomial(b)f(x)=3x3−2x+√x(c)f(x)=12−4x5+3x2is a polynomial(d)f(x)=sin x+1is not a polynomial,because of sin x(e)f(x)=3x12−2/x is not a polynomial,because of2/x(f)f(x)=3x11−2x12is a polynomial3.(a)The highest power of x must be3,so examples might be f(x)=x3−2x+1or f(x)=x3−2.(b)The highest power of x must be1,so examples might be f(x)=x or f(x)=6x−5.(c)The highest power of x must be4,so examples might be f(x)=x4−3x3+2x orf(x)=x4−x−5.(d)The highest power of x must be2,so examples might be f(x)=x2or f(x)=x2−5. 4.5.(a)When a>0,the parabola moves down and to the left as a increases.(b)When a<0,the parabola moves down and to the right as a decreases. 6.(a)1turning point(b)2turning points(c)11turning points (d)(n−1)turning points.7.(a)f(x)=(x−1)(x−2)(x−3)(x−4)or a multiple(b)f(x)=(x−2)(x+4)or a multiple(c)f(x)=(x−12)(x+1)(x+6)or a multiple.8.(a)x=2odd multiplicityx=−4even multiplicity(b)x=1odd multiplicityx=−2even multiplicityx=4odd multiplicity9)− 1)2(x + 3)x− 2)2(x + 1)11c math centre July18,2005。

empirical formula公式

empirical formula公式Empirical formula（实验式），这可是化学世界里的一个重要角色呢！咱先来说说啥是 empirical formula 。

简单讲，它就是用最简整数比来表示化合物中各元素原子个数的式子。

比如说，葡萄糖的化学式是C₆H₁₂O₆，那它的实验式就是 CH₂O ，是不是一下子就简洁明了多啦？我想起之前给学生们讲这部分内容的时候，有个特别好玩的事儿。

当时我在黑板上写下了一个复杂的化合物，然后让同学们试着写出它的实验式。

有个小调皮，皱着眉头，抓耳挠腮的，嘴里还嘟囔着：“这也太难了吧，老师您是不是故意为难我们呀！”我笑着告诉他：“别着急，咱们一步步来。

”然后带着他们从确定各元素的原子个数，到找出最大公约数，再化简，最后得出实验式。

看着他们恍然大悟的表情，我心里那叫一个满足。

那怎么求 empirical formula 呢？这就得先搞清楚化合物中各元素的质量分数。

假设我们知道一种化合物由碳、氢、氧三种元素组成，碳的质量分数是 40% ，氢是 6.7% ，氧是 53.3% 。

那第一步，咱假设化合物的质量是 100g ，这样碳的质量就是 40g ，氢是 6.7g ，氧是 53.3g 。

然后根据各元素的相对原子质量，碳是 12，氢是 1，氧是 16，算出各元素的物质的量。

碳就是40÷12 ≈ 3.33mol ，氢是 6.7÷1 = 6.7mol ，氧是53.3÷16 ≈ 3.33mol 。

接下来找出它们的最简整数比，约一下，就得到实验式啦。

再比如说，给你一个有机物燃烧生成二氧化碳和水的质量，让你求实验式，这时候就得根据质量守恒定律，算出碳和氢的质量，再按照上面的步骤来。

掌握了 empirical formula ，对于理解化合物的组成和性质那可是大有用处。

就像搭积木一样，实验式就是那最基础的几块积木，有了它，咱们才能搭建出更复杂、更精彩的化学结构。

College Chemistry Chapter 05

14
Practice—Determine the Total Number of Atoms or Ions in One Formula Unit of Each of the Following.
• Mg(C2H3O2)2 1 Mg + 4 C + 6 H + 4 O = 15
• (Hg2)3(PO4)2
Molecules or ions.
• Each element is represented by its letter symbol. • The number of atoms of each element is written to the right of the element as a subscript.
Introductory Chemistry, 3rd Edition Nivaldo Tro
Chapter 5 Molecules and Compounds
Roy Kennedy Massachusetts Bay Community College Wellesley Hills, MA
2009, Prentice Hall
composition = mass O : mass C
Sample 1 4.8 g O 2.7 1.8 g C
Sample 2 17.1 g O 2.7 6.4 g C
Compare:
Since both samples have the same proportion of elements, carbon dioxide shows constant composition.
3 4
• Acetone—Each molecule contains six hydrogen atoms, three carbon atoms, and one oxygen atom. C3H6O