频率特性的基本概念
精品文档-自动控制原理(第二版)(千博)-第5章

图 5-5 惯性环节的波德图
25
三、对数幅相图(Nichols图)
对数幅相图是以相角(°)为横坐标, 以对数幅频L(ω)(dB)
为纵坐标绘出的G(jω)曲线。频率ω为参变量。因此它与幅相
频率特性一样, 在曲线的适当位置上要标出ω的值, 并且要用
箭头表示ω增加的方向。
用对数幅频Hale Waihona Puke 性及相频特性取得数据来绘制对数幅相
第五章 频 域 分 析 法
第一节 第二节 第三节 第四节 第五节 第六节 第七节 第八节 关系 第九节 德图
频率特性的基本概念 频率特性的表示方法 典型环节的频率特性 系统开环频率特性 奈奎斯特稳定性判据和波德判据 稳定裕度 闭环频率特性 开环频率特性和系统阶跃响应的
利用MATLAB绘制奈奎斯特图和波
8
图 5-2 频率特性与系统描述之间的关系
9
利用频率特性曲线分析研究控制系统性能的方法称为频域 分析法。频域分析法主要有傅氏变换法和经典法。
(1) 傅氏变换法就是系统在输入信号r(t)的作用下,其输 出响应为
即把时间函数变换到频域进行计算并以此分析研究系统的方法。 (2) 经典法就是先求出系统的开环频率特性G(jω)并绘成
的对数频率
22
(1) 对数幅频特性曲线。通常用L(ω)简记对数幅频特性, 故
ω从0变化到∞时的对数幅频特性曲线如图5-3所示。
23
(2) 相频特性曲线。通常以j(ω)表示相频特性, 即 j (ω)=∠G(jω)。对于惯性环节, 有
j (ω)=-arctanTω 对不同ω值, 逐点求出相角值并绘成曲线即为相频特性曲线, 如图5-5所示。
45
图 5-11 振荡环节近似波德图
控制工程基础课件第六章 频率特性分析

G
j
arctan
1
n 2
n2
当=0时,G j 1,G j 0;
当=n时,G j 2,G j 90; 当=时,G j ,G j 180。
二阶微分环节的极坐标图也于阻尼比有关,对应不同的 ξ值,形成一簇坐标曲线,不论ξ值如何,当ω=0时,极 坐标曲线从(1,0)点开始,在ω=∞时指向无穷远处。
第6章 频率特性分析
本章介绍线性系统的频域分析方法。该方法是通 过控制系统对正弦函数的稳态响应来分析系统性能的。
频率特性不仅能反映系统的稳态性能,也可用来 研究系统的稳定性和动态性能。
6.2 频率响应与频率特性
一、频率特性的概念
1、频率响应:是系统对正弦输入的稳态响应。
2、频率特性:给线性系统输入某一频率的正弦波,
1 1 jT
G j 1 U jV
1 jT
1
1 T 22
j T 1 T 22
A e j
实频特性为U 虚频特性为V
1; 1+T 2 2
T。 1+T 2 2
幅频特性为A 1 ;
1 T 22
相频特性为 G j arctanT
特殊点:
当=0时,G j 1,G j 0; 当=1/T时,G j 1 ,G j 45;
取拉氏变换为: Xi s
A
s2
2
电路的输出为: X0 s G s Xi s 上式取拉氏反变换并整理得
1A Ts 1 s2 2
x0 t
AT 1 T2
e t/T
2
A sin t arctan T
1 T2 2
x0 t
AT 1 T2
e t/T
2
A sin t arctan T
自动控制原理与系统控制系统的频率特性

如图4-6所示。
12
四、惯性环节 传递函数 : G(s) C(s) 1
R(s) Ts 1
频率特性 : G( j) C( j) 1
R( j) jT 1
对数频率特性 : L() 20lg
1
20lg
(T)2 1
(T)2 1
Bode图 : arctanT
▪对数幅频特性L(ω)是一条曲线,逐点描绘很烦琐,通常采用近似的 绘制方法,用两条渐进线近似表示.
(极坐标表示法)
U () jV ()
(直角坐标表示法)
(A指(数表)e示j法 ())
图4-2
A() G(j) U 2 () V 2 ()
() G( j) arctan 1 V () U ()
6
例4-1 写出惯性环节的幅频特性、相频特性和频率特性。
解:惯性环节的传递函数为
G(s) 1 Ts 1
2
• 系统(或环节)输出量与输入量幅值之比为幅值频率特性, 简称幅频特性,它随角频率ω变化,常用M(ω)表示。
A()
A c
A r
• 输出量与输入量的相位差为相位频率特性,简称相频特性,它 也随角频率ω变化,常用φ(ω)表示,
c r
幅频特性和相频特性统称为频率特性,用G( jω)表示
3
频率特性就是线性系统(或环节)在正弦输入信号 作用下稳态时输出相量与输入相量之比。
G (j) G(j) G(j)
A() G(j)
() G(j)
幅频特性是输出量与输入量幅值之比M(ω),描述系统 对不同频率正弦输入信号在稳态时的放大(或衰减) 特性。
相频特性是输出稳态相对于正弦输入信号的相位差 φ(ω),描述系统稳态输出时对不同频率正弦输入信号 在相位上产生的相角迟后(或超前)的特性。
频率特性的基本概念

T = 0 T = 0.3 T = 0.8
() = 0° () = 16.7 ° () = 38.7 °
T = 1 T
Friday, May 15, 2020
() = 45°
() = 90°
37
37
5 一阶微分环节
Im =
频率特性 G(j) = 1 + jT
(1)极坐标图
0
=0 Re
幅频特性为 A() 1 2T 2
以横坐标(称为频率轴)上每一线性单位表示频率的十倍变化, 称为十倍频程(或十倍频),用Dec表示。如下图所示:
Friday, May 15, 2020
16
Dec Dec Dec Dec
... 2 1 0 1 2
0 0.01 0.1 1 10 100
log
由于 以对数分度,所以零频率线在 处。
特性表示在同一个复数平面上。
12
Friday, May 15, 2020
12
在一阶RC滤波电路中,系统是一个典型的 一阶惯性环节,其频率特性为:
G( j)
1
jT 1
在输入不同频率的正弦信号下,计算出幅值、相 位并列表如下:
根据该表格 可以绘制出 一阶惯性环 节的奈奎斯
特图。
Im
ω ∞0
-45
ω=0 Re
(渐进线)近似表示。 对实验所得的频率特性用对数坐标表示,并用分
段直线近似的方法,可以很容易的写出它的频率 特性表达式。
Friday, May 15, 2020
26
二、典型环节的频率特性
1 .比例环节
其传递函数为 G(s) = K
频率特性为 G(j ) = K
(1)幅相频率特性
频率特性理解
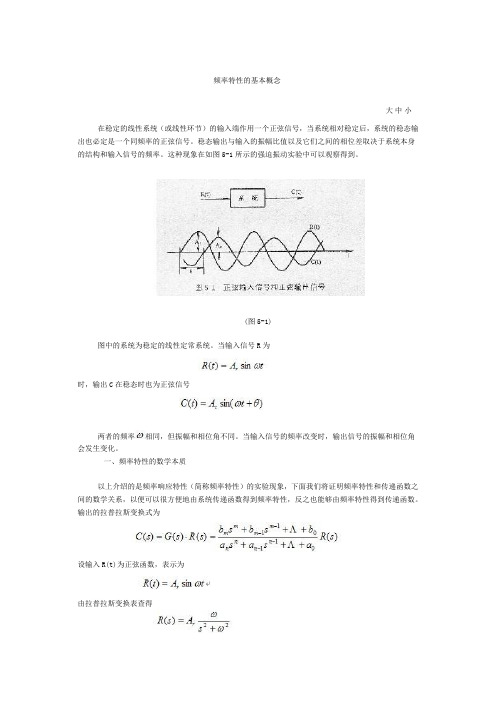
频率特性的基本概念大中小在稳定的线性系统(或线性环节)的输入端作用一个正弦信号,当系统相对稳定后,系统的稳态输出也必定是一个同频率的正弦信号。
稳态输出与输入的振幅比值以及它们之间的相位差取决于系统本身的结构和输入信号的频率。
这种现象在如图5-1所示的强迫振动实验中可以观察得到。
(图5-1)图中的系统为稳定的线性定常系统。
当输入信号R为时,输出C在稳态时也为正弦信号两者的频率相同,但振幅和相位角不同。
当输入信号的频率改变时,输出信号的振幅和相位角会发生变化。
一、频率特性的数学本质以上介绍的是频率响应特性(简称频率特性)的实验现象,下面我们将证明频率特性和传递函数之间的数学关系,以便可以很方便地由系统传递函数得到频率特性,反之也能够由频率特性得到传递函数。
输出的拉普拉斯变换式为设输入R(t)为正弦函数,表示为由拉普拉斯变换表查得故部分分式中及B、D均为待定系数。
对于一个稳定的系统,由于特征方程的所有特征根均具有负实数部分,的第一个分量总是随着t的增长逐渐消失,系统最终将以作稳态运动。
上式恰恰是我们需要求解的,其中系数由上式得到同理将系数B、D代入,则式中Im为G(jω)的虚部,Re为G(jω)的实部。
而输出端响应的振幅和输入端的振荡之比为输出端响应和输入端的相位差为由此可见,作用有正弦输入时的稳定线性定常系统,输出响应具有与输入同一频率的正弦稳定信号。
但是输出的振幅和相位角通常不等于输入量的振幅和相角,输出响应的振幅是输入量的倍,输出响应和输入量相位差为。
因此,系统的频率特性可以直接由G(jω)表示,系统的频率特性为式中是ω的函数,称为幅频特性,也是频率特性的模;是ω的函数,称为相频特性。
在上述数学推导中,我们可以清楚地看到所以,在已知系统或环节的传递函数时,只要令,就可以很方便地得到系统或环节的频率特性。
为了进一步说明频率特性的意义,现以图5-2所示的R-C电路为例。
图5-2频率特性可通过传递函数来求取,当电容两端电压uc为输出量,输入电压ui为输入量时,传递函数可用复阻抗串联的知识求取式中 T=RC频率特性只要将S以jω代替,频率特性为幅频特性(模)为相频特性(幅角)为当ui以低频信号输入时();这表明,当输入正弦电压ui的频率很低,则输出电压uc的振幅与的振幅几乎相等,相位近似同相。
放大电路的频率特性

(3)因各级均为共射放大电路,所以在中频段输出电压与输入 电压相位相反。则整个三级放大增益80dB,即放大倍数为 10000。
电压放大倍数
13 104
Au
1
10 jf
1
j
f 2 105
3
*2.7 电路仿真实例
【例2.8】分析共发射极放大电路
解:利用 Multisim 软件仿真如图2.61所示电路。
(3)高频段
耦合电容和旁路电容的容量较大,视为短路;
极间分布电容(含PN结结电容)容抗减小,不能视为开路。
高频源电压放大倍数为:
1
Aush
Uo Us
U
' s
Ub'e
Uo
Us
U
' s
Ub'e
Ri rb'e jRC'
Rs Ri
rbe
1
1 j RC'
gm RL'
Байду номын сангаас
Ausm
1
1 jRC
Ausm 1 1 j
f
fH
在高频段,电压放大倍数随频率升高而减小,相移也发生
变化。其幅频特性基本与低通电路幅频特性相同。
源电压放大倍数的全频率范围表达式为:
jf
Aus
Ausm 1
j
f fL
fL 1
j
f fL
Ausm 1
j
fL f
1
1
j
f fH
单管放大电路的波特图
综上所述,单管放大电路在低频段主要受耦合电容的影 响,表现在放大倍数随频率降低而降低,相移也增大;中频 段可认为其放大倍数和相移都基本为常数(这是放大电路工 作的频段)。在高频段其特性主要受极间电容的影响,表 现在放大倍数随频率升高而下降,相移也随之增大。
自动控制原理第5章频率特性

自动控制原理第5章频率特性频率特性是指系统对输入信号频率的响应特点。
在自动控制系统设计中,了解和分析系统的频率特性是非常重要的,因为它可以帮助工程师评估系统的稳定性,性能和稳定裕度。
本章主要介绍频率特性的相关概念和分析方法,包括频率响应函数、频率幅频特性、相频特性、对数坐标图等。
1.频率响应函数频率响应函数是描述系统在不同频率下的输出和输入之间的关系的函数。
在连续时间系统中,频率响应函数可以表示为H(jω),其中j是虚数单位,ω是频率。
频率响应函数通常是复数形式,它包含了系统的振幅和相位信息。
2.频率幅频特性频率幅频特性是频率响应函数的模的图形表示,通常用于表示系统的增益特性。
频率幅频特性通常用对数坐标图绘制,以便更好地显示系统在不同频率下的增益特性。
对数坐标图上,增益通常以分贝(dB)为单位表示。
3.相频特性相频特性是频率响应函数的相角的图形表示,通常用于表示系统的相位特性。
相频特性可以让我们了解系统对输入信号的相位延迟或提前情况。
在相频特性图上,频率通常是以对数坐标表示的。
4. Bode图Bode图是频率幅频特性和相频特性的综合图形表示。
它将频率幅频特性和相频特性分别绘制在纵轴和横轴上,因此可以直观地了解系统在不同频率下的增益和相位特性。
5.系统的稳定性分析频率特性可以帮助工程师判断系统的稳定性。
在Bode图上,当系统的相位角趋近于-180度,且增益在此处为0dB时,系统即将变得不稳定。
对于闭环控制系统,我们希望系统在特定频率范围内保持稳定,以便实现良好的控制性能。
6.频率特性的设计频率特性的设计是自动控制系统设计中的一个重要任务。
工程师需要根据系统对不同频率下的增益和相位的要求,设计出合适的控制器。
常见的设计方法包括校正器设计、分频补偿、频率域设计等。
总结:本章重点介绍了自动控制系统的频率特性,包括频率响应函数、频率幅频特性、相频特性和Bode图。
频率特性的分析和设计对于掌握自动控制系统的稳定性、性能和稳定裕度非常重要。
频率特性的基本概念

•表1-1 RC网络的幅频特性和相频0.707 0.45 0.196 0
() 0
45 63.4 78.69 90
图1-2 RC网络的幅频和相频特性 图1-3 RC网络频率特性的幅相曲线
对数频率特性图又称伯德图(Bode图),包括对数幅频特性 和对数相频特性两条曲线,其中,幅频特性曲线可以表示 一个线性系统或环节对不同频率正弦输入信号的稳态增益; 而相频特性曲线则可以表示一个线性系统或环节对不同频 率正弦输入信号的相位差。对数频率特性图通常绘制在半 对数坐标纸上,也称单对数坐标纸。
(3)利用对数运算可以将幅值的乘除运算化为加减运算, 并可以用简便的方法绘制近似的对数频率幅相特性,从而 大大简化系统频率特性的绘制过程。
自动控制原理
来求取。 (3)通过实验所测数据,进行分析求取。
G( j) G(s) s j
1.2频率特性的图形表示方法
频率特性函数最常用的两种图形表示 方法,分别为极坐标图和对数频率特 性图。
极坐标图,又称奈奎斯特图、幅相频 率特性图,其特点是将频率 作为参 变量。
当正弦信号的频率 由0 变化时, 系统频率特性向量的幅值和相位也随 之作相应的变化,其端点在复平面上 移动而形成的轨迹曲线称为幅相曲线, 其中曲线上的箭头表示频率增大的方 向。
自动控制原理
频率特性的基本概念
1.1频率特性的定义 频率特性反映了系统的频率响应与正弦
输入信号之间的关系。
图1-1 RC网络
控制系统频率特性的求解方法具有如下三种途径: (1)根据已知的系统方程,输入正弦函数求出其稳态解, 而后求解输出稳态分量和输入正弦信号的复数比。 (2)根椐系统传递函数,利用表达式
对数幅频特性图是表示环节的对数幅值 L() 20lg A()和频率 的关系曲线。
自动控制原理第5章_线性控制系统的频率特性分析法

5. 2控制系统开环传递函数的对数频率特性
5.2.2 系统伯德图的绘制
开环对数幅频渐近特性曲线的绘制步骤: (1)把系统开环传递函数化为标准形式,即化为典型环节的传递函
数乘积,分析它的组成环节; (2)确定一阶环节、二阶环节的转折频率,由小到大将各转折频率
标注在半对数坐标图的频率轴上; (3)绘制低频段渐近特性线; (4)以低频段为起始段,从它开始每到一个转折频率,折线发生转
开环极点的个数。
5. 4 频域稳定判据与系统稳定性
5.4.4 控制系统的相对稳定性
开环频率特性 G( j)H( j)在剪切频率 c处所对应的相角与 180 之差称为相角裕度,记为 ,按下式计算
(c ) (180 ) 180 (c )
开环频率特性 G( j)H的( 相j)角等于 时所1对80应的角频率称为相
闭环系统稳定的充要条件是,当 由 0 时0,开 环奈奎斯 特曲线逆时针方向包围( )点 周1, j。0 是具P有2 正实部P 的开 环极点的个数。 需注意,若开环传递函数含有 v 个积分环节,所谓 由 0 0 ,指的 是由 0 0 0 ,此时奈 奎斯特曲线需顺时针增补 v 角度的无穷大半径的圆弧。
5. 4 频域稳定判据与系统稳定性
5.4.1 奈奎斯特稳定判据
若闭环系统在[ s]右半平面上有 个P开环极点,当 从 变化到
时,奈奎斯特曲线 G( j对)H点( j) 的包围1周, j数0 为 ( 为逆时N针,
为顺N 时 0针),则系统N<在0[ ]右半平面上的闭环极点s的个数为 。
折,斜率变化规律取决于该转折频率对应的典型环节的种类; (5)如有必要,可对上述折线渐近线加以修正,一般在转折频率处
频率特性的基本概念

式中,kc1, kc2 分别为:
kc1
C(s)(s
j )
|s j
G(s) Rm(s (s j)(s
j ) j)
s j
RmG( 2j
j )
kc2
C(s)(s
j )
|s j
G(s) Rm(s (s j)(s
j ) j)
s j
RmG( j )
频率特性的基本概念
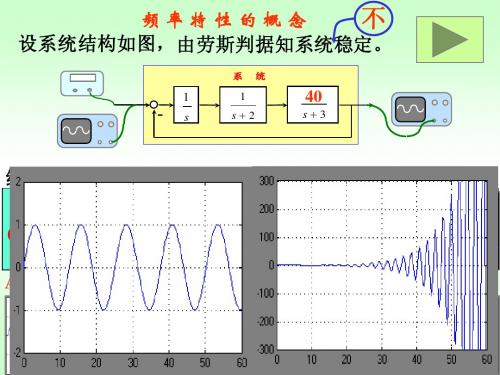
考察一个系统的好坏,通常用阶跃输入下系统的阶跃响应 来分析系统的动态性能和稳态性能。
有时也用正弦波输入时系统的响应来分析,但这种响应并 不是单看某一个频率正弦波输入时的瞬态响应,而是考察频率 由低到高无数个正弦波输入下所对应的每个输出的稳态响应。 因此,这种响应也叫频率响应。
频率响应尽管不如阶跃响应那样直观,但同样间接地表示 了系统的特性。频率响应法是分析和设计系统的一个既方便又 有效的工具。
2j
而 G( j ) G(s) |s j | G( j ) | e jG( j ) A( )e j ()
G( j ) G(s) |s j | G( j ) | e jG( j ) A( )e j ( )
kc1
Rm 2j
A( )e j ( ) , kc2
Rm 2j
A( )e j ( )
cs (t)
G( j ) G(s) |s j
由传递函数还是可以得到其频率特性。
定义稳态响应与正弦输入信号的相位差() G( j) 为系统
的相频特性,它描述系统的稳态响应对不同频率输入信号的相
位移特性;
幅频特性和相频特性可在复平面上构成一个完整的向量G( j),
G( j ) A( )e j() ,它也是 的函数。
第五章1 控制系统的频域分析(频率特性与BODE图)

自动控制原理
幅相频率特性画法举例
画出二阶系统 G ( s ) = 112
的幅相频率特性
s (1 + 0 .02 s )
自动控制原理
2. 伯德图(Bode图)
如将系统频率特性G(jω ) 的幅值和相角分别绘在半对数坐
标图上,分别得到对数幅频特性曲线(纵轴:对幅值取分贝数
自动控制原理
极坐标图(Polar plot),幅相频率特性曲线,幅相曲线 当ω在0~∞变化时,相量G(jω) 的幅值和相角随ω而变化,与 此对应的相量G(jω) 的端点在复平面 G(jω) 上的运动轨迹 就称为幅相频率特性曲线或 Nyqusit曲线。画有 Nyqusit曲 线的坐标图称为极坐标图或Nyqusit图。( ω在0~-∞变化 对称于实轴) 奈奎斯特(N.Nyquist)在1932年基于极坐标图阐述了反馈系统 稳定性
这些幅频特性曲线将通过点
自动控制原理
0dB,ω = 1
L(ω ) = 20 lg 1 = −20 lg ω (dB ) jω
ϕ (ω ) = −90°
Magnitude (dB)
Phas e (deg)
20 10
0 -10 -20 -30 -40 -89
-89.5
-90
-90.5
-91
-1
10
Bode Diagram of G(jw )=1/(jw )
(a) 幅频特性
自动控制原理
ϕ(ω) = −arctgTω
自动控制原理
输出与输入的相位之差
(b)相频特性
Uo (s) = G(s) = 1
Uo ( jω) = G( jω) = 1 = 1
[知识链接五]放大器的频率特性 (2)
![[知识链接五]放大器的频率特性 (2)](https://img.taocdn.com/s3/m/5de729392f60ddccda38a0d4.png)
一、频率特性的基本概念
1、 放大器的频率特性(又称频率响应):指电路的电压放大 倍数Au与频率f之间的关系,即:
2、 幅频特性│Au(f)│与相频特性
。 与频率f之间的关系。
(1)幅频特性:指放大倍数│Au│与频率f之间的关系;
(2)相频特性:是指放大器的相移
3、阻容耦合共射放大器的幅频特性曲线如图2-1-35所示,能 够得到有效放大的是中频区,两边的区域分别称为低频区和高频区。
4、上限频率fH和下限频率fL : 放大倍数│Au│下降到最大值 的0.707倍所对应的两个频率,分别称为通带上限频率fH和下限频 率fL。
5、通频带:上限频率fH和下限频率fL差值就是放大器的通频带 (又称带宽)BW,即:BW=fH-fL。
图2-1-35 阻容耦合共射放 大器 的幅频特性曲线
图2-1-36 直接耦合放大器的幅频特性曲 线
图-1-37 用扫频仪测试放大器的幅频特性 图2-1-38 用点频法测试放大器的幅频特性
2、 点频法:如图2-1-38所示,函数信号发生器为放大器提供正弦 信号,用示波器观测放大器的输出波形。保持放大器出入信号的有效值 (在放大器的中频区能有足够的不失真输出幅度,以便观测)不变,仅改 变正弦信号的频率,当输出波形的振幅下降到最大值的0.707倍时,便可 分别得到放大器的上限频率fH和下限频率fL,也就得到了通频带BW。若 用双踪示波器分别观测各频率点下的Uom和Uim(也可用交流毫伏表测 Uo和Ui),便可得到各频率点下的│Au│ (│Au│=Uo/Ui=Uom/Uim),从而在│Au│=f(f)的直角坐标系中 确定对应的点,描绘即得到放大器的幅频特性曲线。
6、直接耦合放大器的幅频特性曲线,如图2-1-36所示。其通带 频率由上限频率所决定,即:BW=fH 。
频率特性

RS
Vi +-
VDD
M2
RS
V1 Cgd1
M1
Vo
+ Vi - CL
Cgs1
Cgs2
gmb2Vo gm2Vo
gm1V1
Cdb1
Csb2
CL
gds2 Vo
共源级的频率响应
进一步简化,可得如图所示的等效电路。
RS
V1 Cgd1
基本概念
3 用分贝表示放大倍数 增益一般以分贝表示时,可以有两种形式,
即: 功率放大倍数:
AP
(dB)
10
lg
Po Pi
(dB)
电压放大倍数:
AV
(dB)
10
lg
Vo 2 Vi 2
20lg Vo Vi
(dB)
基本概念
4 对数频率特性 频率采用对数分度,而幅值(以分贝表示的
电压增益)或相角采用线性分度来表示放大 器的频率特性,这种以对数频率特性表示的 两条频率特性曲线,就称为对数频率特性, 也称为波特图。 对数频率特性一般是用折线近似表示的。
p2
C
G Cgd1
前一个极点称为输入极点,而后一个极点则为
输出极点。
共源级的频率响应
比较以上两种方法求出的零极点的值可以看出,零 点完全相等,而极点并不完全相同,比较两种方法 求得的极点,可以发现输入极点中的分母中多了一
项(Cgd1+C)/G,所以只要该项远小于式中分
母的前两项之和就可近似相等了。 即用密勒电容等效求出的输入极点是一种近似的方
为了获得相同的分母形式,上式除以ωP1ωP2就可得到:
第5章线性系统的频域分析法重点与难点一、基本概念1.频率特性的

·145·第5章 线性系统的频域分析法重点与难点一、基本概念 1. 频率特性的定义设某稳定的线性定常系统,在正弦信号作用下,系统输出的稳态分量为同频率的正弦函数,其振幅与输入正弦信号的振幅之比)(ωA 称为幅频特性,其相位与输入正弦信号的相位之差)(ωϕ称为相频特性。
系统频率特性与传递函数之间有着以下重要关系:ωωj s s G j G ==|)()(2. 频率特性的几何表示用曲线来表示系统的频率特性,常使用以下几种方法:(1)幅相频率特性曲线:又称奈奎斯特(Nyquist )曲线或极坐标图。
它是以ω为参变量,以复平面上的矢量表示)(ωj G 的一种方法。
(2)对数频率特性曲线:又称伯德(Bode )图。
这种方法用两条曲线分别表示幅频特性和相频特性。
横坐标为ω,按常用对数lg ω分度。
对数相频特性的纵坐标表示)(ωϕ,单位为“°”(度)。
而对数幅频特性的纵坐标为)(lg 20)(ωωA L =,单位为dB 。
(3)对数幅相频率特性曲线:又称尼柯尔斯曲线。
该方法以ω为参变量,)(ωϕ为横坐标,)(ωL 为纵坐标。
3. 典型环节的频率特性及最小相位系统 (1)惯性环节:惯性环节的传递函数为11)(+=Ts s G 其频率特性 11)()(+===j T s G j G j s ωωω·146·对数幅频特性 2211lg20)(ωωT L +=(5.1)其渐近线为⎩⎨⎧≥-<=1 )lg(2010)(ωωωωT T T L a (5.2) 在ωT =1处,渐近线与实际幅频特性曲线相差最大,为3dB 。
对数相频特性)(arctg )(ωωϕT -= (5.3)其渐近线为⎪⎩⎪⎨⎧≥︒-<≤+<=10 90101.0 )lg(1.0 0)(ωωωωωϕT T T b a T a (5.4)当ωT =0.1时,有b a b a -=+=1.0lg 0 (5.5)当ωT =10时,有b a b a +=+=︒-10lg 90 (5.6)由式(5.5)、式(5.6)得︒=︒-=45 45b a因此:⎪⎩⎪⎨⎧≥︒-<≤︒-<=10 90101.0 )10lg(451.0 0)(ωωωωωϕT T T T a (5.7)(2)振荡环节:振荡环节的传递函数为10 121)(22<<++=ξξTs S T s G·147·其频率特性)1(21|)()(22ωωξωωT j Ts s G j G j s -+=== 对数幅频特性2222224)1(lg 20)(ωξωωT T L +--= (5.8)其渐近线为⎩⎨⎧≥-<=1)lg(4010)(ωωωωT T T L a (5.9) 当707.0<ξ时,在221ξω-=T 处渐近线与实际幅频特性曲线相差最大,为2121lg20ξξ-。
自动控制原理第五章
均 匀 的
(lg ω)
0.1 0.2 0.3 … 1 2 3 … 10 20 30 … 100 200 …
ω
倍频程是均匀 均匀的 一倍频程是不均匀的, 十倍频程是均匀的! 倍频程是不均匀的 不均匀
§5.3 典型环节的频率特性
系统的传递函数可以看成是由若干个典型环节组成的. 系统的传递函数可以看成是由若干个典型环节组成的. 一,比例环节的频率特性 Y (s) = K 传递函数为 Φ ( s ) = R (s)
Im
ω =∞
(ω )
A(ω )
Re
ω =0
Φ( jω)
奈奎斯特 (N.Nyquist)在1932 年基于极坐标图 阐述了反馈系统 稳定性 奈奎斯特曲线, 简称奈氏图
2. 幅,相频率特性 它是将 A(ω) 和 (ω) 分别表示在以 为横坐标,以 A(ω) 分别表示在以ω 坐标, 坐标的平面上. 或 (ω) 为纵坐标的平面上.
A(ω)
ω单位为弧度/秒 单位为弧度 秒 单位为弧度
ω
(ω)
A(ω) 无量纲
ω
(ω) 单位为度 单位为度
3. 对数幅,相频率特性 对数幅,相频率特性——Bode图 图 纵坐标
幅频: L(ω ) = 20 lg A(ω ) 单位:分贝(dB) 单位:度 相频: (ω )
横坐标 以 lg ω 来分度,标注 ω ,单位:弧度 秒(rad/s) 分度, 单位:弧度/秒
本章需要掌握的主要内容:
典型环节 环节的频率特性 (1)典型环节的频率特性 系统开环频率特性的绘制 (2)系统开环频率特性的绘制 (3)利用频率特性分析系统的稳定性 利用频率特性分析系统的稳定性 (4)系统的稳态性能与动态性能分析 系统的稳态性能与动态性能分析 实验法求取元件或系统的 求取元件或系统的数学模型 (5)实验法求取元件或系统的数学模型
