2015届福建省宁德市高三普通高中毕业班5月质检数学文试卷
福建省宁德市2015届高三普通高中毕业班5月质检理综试卷 Word版含答案.pdf

过圆形轨道、水平轨道后压缩弹簧,并量m=1
kg,与PQ段间的动摩擦因数μ=0.4,轨道其部分摩擦不计。取g=10 m/s2。求:
1)物块圆轨道最高点B时对轨道的压力;
2)物块Q运动P的时间及弹簧获得的最大弹性势能;
H2O+H2OH3O++OH- K1=1.0×10-14
OH-+H2OH3O++O2- K2=1.0×10-36
水中c(O2-) =
mol·L-1(填数值)。
(2)水广泛应用于化学反应。将干燥的碘粉与铝粉混合未见反应,滴加一滴水后升起紫色的碘蒸气,最后得到白
色固体。有关该实验的解释合理的是
m,不计在流动中和管壁之间的阻力,重力加速度为g。则
A.泵体上表面应接电源负极
B.电磁泵
C.电源提供的电功率为
D.质量为m的离开泵时的动能为
19.(18分)
(1)如图为小球做自由落体运动验证机械能守恒的装置图O点是释放小球的初始位置光电门正方。已知小球的直径
为d。
①小球从光电门正中穿过,由数字计时器读出小球通过光电门的时间Δt,则小球通过光电门的速度大小约为v=。
(3)离子Q点到N板Q点距分界线高h
23.(15分)
甲、乙、丙是都含有同一种元素的不同物质,转化关系如下图:
(1)若甲是CO2。
①常用于泡沫灭火器的是
(填“乙”或“丙”,下同)。
②浓度均为0.01 mol·L-1的乙溶液和丙溶液中,水的电离程度较大的是
(2)若甲是Al。
9.利用下图所示装置进行实验,通入Cl2前装置Ⅰ中溶液呈红色。下列说法不合理的是 A.通入Cl2后,装置Ⅰ中发生了氧化还原反应 B.Cl2与Na2SO3溶液反应的离子方程式是:SO32-+Cl2+H2O=SO42-+2Cl-+2H+ C.通入Cl2后,装置Ⅰ中溶液不褪色 D.装置Ⅱ的作用是吸收尾气,防止污染空气 10.常温下,0.01 mol·L-1 NaHY(酸式盐,Y表示原子或原子团)溶液,下列说法正确的是 A.溶液一定呈酸性 B.溶液中一定存在:Y2-+H2OOH-+HY- C.溶液加水稀释,离子浓度都减小 D.溶液中:c(Na+)≥c(Y2-) 11.以二氧化碳和氢气为原料制取乙醇的反应为: 2CO2(g)+6H2(g)CH3CH2OH(g)+3H2O(g) △H<0 某压强下的密闭容器中,按CO2和H2的物质的量比为13 投料,不同温度下平衡体系中各物质的物质的量百分数(y%) 随温度变化如图所示。下列说法正确的是 A.a点的平衡常数小于b点 B.b点,v正(CO2)=v逆(H2O) C.a点,H2和H2O物质的量相等 D.其他条件恒定,充入更多H2,v(CO2)不变 12.电解降解法可用于治理水体硝酸盐污染,将NO3-降解成N2的电解装置如下图所示。下列说法正确的是 A.电源的正极为b B.电解时H+从膜右侧迁移到膜左侧 C.Ag Pt电极反应为:2H2O-4e-=4H++O2↑ D.若转移的电子数为1.204×1024,生成N2 5.6 g 13.下列光学现象说法正确的是 A.水中光的传播速度比红光 B.光纤由内芯和外套两层组成,内芯的折射率比外套的小 C.在岸边观察水中的鱼,看到的实际深 D.分别用光和红光在同一装置上做双缝干涉实验,用红光时得到的条纹间距更窄 14.理想变压器线圈的匝数为1100,线圈的匝数为25,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如 图乙所示,P为滑动变阻器的 A.副线圈输出电压的频率为100Hz B.副线圈输出电压的有效值为V C.P向左移动时,变压器原、副线圈的电流都 D.P向左移动时,变压器的输入功率增加 15.在某一均匀介质中由波源O发出的简谐横波x轴传播,某时刻的波形如图,其波速为5m/s,振幅为20cm下列说法 正确的是 A.波的频率与波源的频率无关 B.此时P、Q两点动方向相同 C.再经过0.5s波恰好传到(-5m,0)位置 D.能与该波发生干涉的横波的频率一定为3Hz 16.如图为高分一号卫星与北斗导航系统G1”卫星在空中某一面内绕地心O做匀速圆周运动的示意图。卫星G1”的 轨道半径为r,地球表面的重力加速度为g,地球半径为R万有引力常量为G。则 A.高分一号的加速度小于卫星G1”的加速度 B.高分一号的运行速度大于第一宇宙速度 C.地球的质量为 D.卫星G1”的周期为 17.真空中电量均为Q的两正点电荷一绝缘正方体框架的两侧面ABB1A1和DCC1D1中心连线方体中心 A.A、B、C、D电势相同 B.A、B、C、D电场强度相同
2015宁德5月质检 福建省宁德市2015届高三普通高中毕业班5月质检物理试卷 Word版含答案

-2s -乙 2015年宁德市普通高中毕业班质量检查理科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷。
第Ⅰ卷为必考题,第Ⅱ卷包括必考题和选考题两部分。
本试卷共12页,满分300分,考试时间150分钟。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2.考生作答时,请将答案答在答题卡上,在本试卷上答题无效;按照题号在各题的答题区域内作答,超出答题区域书写的答案无效。
3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
5.保持答题卡卡面清洁,不折叠,不破损;考试结束后,将答题卡交回。
所需相对原子质量:H 1 N 14 O 16 Fe 56 Cu 64第Ⅰ卷(选择题 共108分)本卷共18题,每小题6分,共108分。
在每小题给出的四个选项中,只有一个选项符合题目要求。
13.下列光学现象的说法正确的是A .在水中绿光的传播速度比红光的小B .光纤由内芯和外套两层组成,内芯的折射率比外套的小C .在岸边观察水中的鱼,看到的深度比实际的深D .分别用绿光和红光在同一装置上做双缝干涉实验,用红光时得到的条纹间距更窄14.理想变压器原线圈的匝数为1100匝,副线圈的匝数为25匝,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P 为滑动变阻器的滑片。
则A .副线圈输出电压的频率为100HzB .副线圈输出电压的有效值为7VC .P 向左移动时,变压器原、 副线圈的电流都减小D .P 向左移动时,变压器的输入 功率增加 15.在某一均匀介质中,由波源O 发出的简谐横波沿x 轴正负方向传播,某时刻的波形如图,其波速为5m/s ,振幅为20cm 。
下列说法正确的是A .波的频率与波源的频率无关B .此时P 、Q 两质点振动方向相同C .再经过0.5s ,波恰好传到坐标为(-5m ,0)的位置D .能与该波发生干涉的横波的频率一定为3Hz16.如图为“高分一号”卫星与北斗导航系统中的“G 1”卫星,在空中某一平面内绕地心O做匀速圆周运动的示意图。
福建省宁德市5月高三毕业班质量检查文数全word版

y 2,
x
1,
2x y 2 0,
B.
C.
(a)
8 ,则 a
C. 2
C. 1 3
C.
D.
D. 2 或 4
所表示的平面区域为 M ,O 为坐标原点,
文科数学试题 第 2 页 共 11 页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
福建省宁德市普通高中2015届高三英语毕业班5月质检试卷

2015年宁德市普通高中毕业班质量检查英语本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
第一卷1至12页,第二卷13至14页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2.考生作答时,请将答案答在答题卡上,请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
在草稿纸、试卷上答题无效。
3.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.保持答题卡卡面清洁,不折叠,不破损。
考试结束后,将本试卷和答题卡一并交回。
第一卷(选择题共115分)第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £ 19.15.B. £ 9.15.C. £ 9.18.答案是B。
1. Where does the conversation most probably take place?A. At the man’s house.B. In a restaurant.C. In an office.2. What is the relationship between May and Maria?A. Twin sisters.B. Close friends.C. Classmates.3. How will the woman go to the hotel?A. By taxi.B. By plane.C. By car.4. Why does the woman go to the post office?A. To post a letter.B. To send a telegraph.C. To meet a friend.5. Which subject does the woman think the boy is weak at?A. Physics.B. Math.C. Chemistry.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
文综宁德市2015届高三普通高中毕业班5月质检.
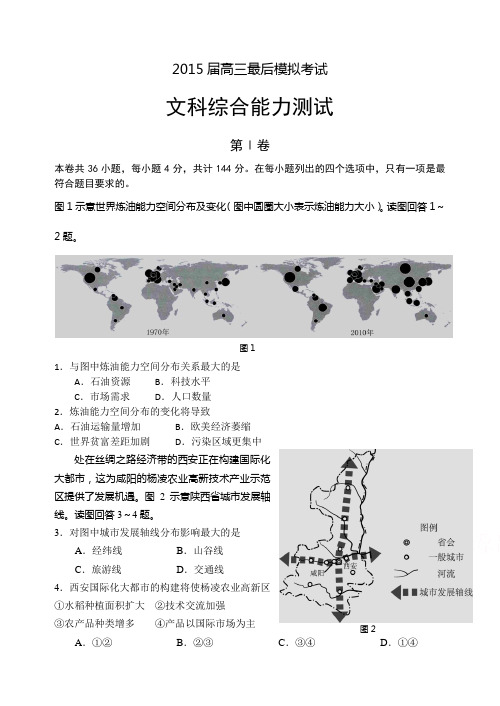
2015届高三最后模拟考试文科综合能力测试第Ⅰ卷本卷共36小题,每小题4分,共计144分。
在每小题列出的四个选项中,只有一项是最符合题目要求的。
图1示意世界炼油能力空间分布及变化(图中圆圈大小表示炼油能力大小)。
读图回答1~2题。
1.与图中炼油能力空间分布关系最大的是 A .石油资源 B .科技水平 C .市场需求 D .人口数量 2.炼油能力空间分布的变化将导致 A .石油运输量增加 B .欧美经济萎缩 C .世界贫富差距加剧 D .污染区域更集中处在丝绸之路经济带的西安正在构建国际化大都市,这为咸阳的杨凌农业高新技术产业示范区提供了发展机遇。
图2示意陕西省城市发展轴线。
读图回答3~4题。
3.对图中城市发展轴线分布影响最大的是 A .经纬线 B .山谷线C .旅游线D .交通线4.西安国际化大都市的构建将使杨凌农业高新区 ①水稻种植面积扩大 ②技术交流加强 ③农产品种类增多 ④产品以国际市场为主A .①②B .②③C .③④D .①④图1图2图3示意我国浙江、安徽、西藏三省区2005-2010年间迁移人口比重,迁移人口以青壮年为主。
读图回答5~6题。
5.据图推断A .①、②省区迁入人口数相同B .①省区经济较③省区发达C .人口迁移加剧①省区人口老龄化D .人口迁移导致①省区经济水平降低 6.②省区迁出、迁入人口比重低的主要原因是 A .地理环境独特 B .人口数量少7.该瀑布形成的地质作用过程是A .岩浆活动—固结成岩—地壳抬升—侵蚀作用B .岩浆活动—冷却凝固—地壳抬升—侵蚀作用C .沉积作用—固结成岩—地壳抬升—风化作用D .沉积作用—固结成岩—地壳抬升—侵蚀作用 8. 该瀑布可能会影响其下游河流的A .含沙量B .流量C .汛期D .结冰期图5示意我国某县年降水量及水系分布。
读图回答9~10题。
9. 影响该县年降水量空间分布的主要因素是A .河流B .海陆位置C .季风D .地形①③迁出人口比重(℅)10 8 6 4 2 ②20151050 迁入人口比重(℅) 图4图3(背面还有试题)10.据图推断,年平均气温A .N 地>M 地B .P 地>N 地C .Q 地>P 地D .Q 地>M 地一观测者在某日对当地的太阳方位和太阳高度进行观测,图6中a 、b 两点记录了该日两个不同时刻的太阳方位和太阳高度(同心圆上的数值表示太阳高度),其中a 点为北京时间19:00的观测记录。
福建省宁德市普通高中2015届高三语文毕业班5月质检试卷(DOC)

2015年宁德市普通高中毕业班质量检查语文本试卷分五大题,共12页。
满分150分,考试时间150分钟。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2.考生作答时,请将答案写在答题卡上,在本试卷上答题无效。
按照题号在各题的答题区域内作答,超出答题区域书写的答案无效。
3.答题使用O.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.做选考题时,考生按照题目要求作答,并在答题卡上填写所选题目的序号。
5.保持答题卡卡面清洁,不折叠,不破损。
考试结束后,将本试卷和答题卡一并交回。
一、古代诗文阅读(27分)(一)默写常见的名句名篇(6分)1.补写出下列名句名篇中的空缺部分。
(6分)(1)长太息以掩涕兮,。
(屈原《离骚》)(2)茕茕孑立,。
(李密《陈情表》)(3),都护在燕然。
(王维《使至塞上》)(4),相逢何必曾相识。
(白居易《琵琶行》)(5)无可奈何花落去,。
(晏殊《浣溪沙》)(6)箫鼓追随春社近,。
(陆游《游山西村》)(二)文言文阅读(15分)阅读下面文言文,完成2~5题。
(15分)赠郡侯郭文麓升副使序【明】唐顺之廉吏,自古难之。
虽然,今之所谓廉者,有之矣。
前有所慕于进而后有所惧于罪,是以虽其嗜利之心不胜其竞进之心,而其避罪之计有甚于忧贫之计,慕与惧相持于中,则势不得不矫强而为廉。
其幸而恒处于有可慕有可惧之地,则可以终其身而不至于坏,而世遂以全节归之。
其或权位渐以极,泄然志盈而气盛,则可慕者既已得之,而无复有惧于罪。
至如蹉跎沦落,不复自振,则可慕者既已绝望,萎然志销而气沮,且将甘心冒罪而不辞。
是故其始也,缩腹镂骨以自苦;而其后也,甚或出于饕餮之所不为。
人见其然,则曰:“若人也,而今乃若是!”而不知始终固此一人也。
虽然,此犹自其既坏言之也。
方其刻意为廉之时,而其萌芽固已露矣。
苟捐之足以为名而得之足以为罪,则千金有所必割;苟捐之不足以为名而得之不足以为罪,则锥刀①有所必算。
2015年福建省宁德市普通高中毕业班单科质量检查数学(文科)试卷

2015年福建省宁德市普通高中毕业班单科质量检查数学(文科)试卷本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分.本卷满分150分,考试时间120分钟.注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上.2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.4.保持答题卡卡面清楚,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回.参考公式:第I卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数i(12i)+(为虚数单位)等于A.2i-+B.2i+C.2i--D.2i-2.已知集合{}21xM x=>,若a M∉,则实数a可以是A.B.2C.D.1-3.已知sinα=α为第二象限角,则tanα的值是A.B.C.12-D.4.如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为A.4.7B.4.8C.1.2D.1.35.a b>>“”是的A.充分不必要条件B.必要不充分条件C .充要条件D .既不充分也不必要条件 6. 已知一个几何体的三视图如图所示,根据图中尺寸可得该几何体的体积为 A .36π B .24π C .15πD .12π7.要得到函数3sin(2)4y x π=-的图象,只需将函数3sin 2y x =的图象A .向右平移4π个单位B .向左平移4π个单位C .向右平移8π个单位8. 运行如图所示的程序框图,则输出的所有 实数对(,)x y 所对应的点都在函数 A .2()log (1)f x x =+的图像上 B .2()22f x x x =-+的图像上 C .4()3f x x =的图像上 D .1()2x f x -=的图像上9. 定义在R 上的函数()f x 满足()(),(2)()f x f x f x f x -=+=.当[0,1]x ∈时,2()2f x x =.若在区间[1,3]-上函数()()g x f x ax a =--有个零点,则实数a 的取值范围是 A .1(0,)2 B .1(0,]2C .1(,1)2D .1(,1]210. 若双曲线22221(0,0)x y a b a b-=>>的渐近线与圆22(2)1x y -+=有公共点,则此双曲线的离心率的取值范围是 A . B . C .)+∞ D .)+∞11.不等式组222,222x y x y -≤-≤⎧⎨-≤+≤⎩围成的区域为Ω,能够把区域Ω的周长和面积同时分为相等两部分的曲线为A .331y x x =-+B .sin 2y x x =C .2ln2x y x -=+ D .1(e e )4x x y -=+ 12.一数字游戏规则如下:第1次生成一个数a ,以后每次生成的结果均是由上一次生成的每一个数x 生成两个数,一个是x -,另一个是2x +.设前n 次生成的所有数...的和为n S ,若1a =,则6S = A .63 B .64 C .127 D .128第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡的相应位置.13.某校参加“数迷会”社团的学生中,高一年级有50名,高二年级有40名.现用分层抽样的方法在这90名学生中抽取一个容量为18的样本,则在高二年级的学生中应抽取的人数为 . 14.若向量(1,2)=-a ,(3,)y =-b ,且a ∥b ,则a +b = . 15.已知扇形的周长为4,则该扇形的面积的最大值为 .16.已知函数10,0()e ,0xx x f x x ⎧≥⎪=⎨<⎪⎩,若对于任意[12,12]x a a ∈-+,不等式()(2)f x a f x +≤恒成立,则实数a 的取值范围是 .三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,点(,)()n n S n *∈N 在函数2()f x x =的图象上. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设11n n n b a a +=⋅,求数列{}n b 的前n 项和n T .18.(本小题满分12分)某市一水电站的年发电量y (单位:亿千瓦时)与该市的年降雨量x (单位:毫米)有如下统计数据:(Ⅰ)若从统计的5年中任取2年,求这2年的发电量都低于8.0(亿千瓦时)的概率;(Ⅱ)由表中数据求得线性回归方程为ˆˆ0.004y x a =+.该水电站计划2015年的发电量不低于9.0亿千瓦时,现由气象部门获悉2015年的降雨量约为1800毫米,请你预测2015年能否完成发电任务,若不能,缺口约为多少亿千瓦时?19.(本小题满分12分)如图三棱柱ABC -A 1B 1C 1中,点M 为AB的中点. (Ⅰ)求证:BC 1∥平面A 1CM ;(Ⅱ)若CA=CB ,A 1在平面ABC 的射影为M , 求证: 平面A 1CM ⊥平面ABB 1 A 1.20.(本小题满分12分)已知函数()cos cos(2)3f x x x x ωωωπ=⋅++(0)ω>的最小正周期为2π.(Ⅰ)求函数()f x 的解析式;(Ⅱ)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,当x A =时函数()f x 取到最值,且ABC ∆,5b c +=,求a 的值.21.(本小题满分12分)已知函数()e x f x x =-.(Ⅰ)求函数()f x 的单调区间; (Ⅱ)求函数21()e 12x g x x =--在[0,)+∞上的最小值; (Ⅲ)求证:3e ln 2x x >+.22.(本小题满分14分)已知抛物线22(0)x py p =>的焦点F 与椭圆22143y x +=的一个焦点重合. (Ⅰ)求抛物线的方程;(Ⅱ)直线1y kx =+交抛物线于A ,B 两点,过A ,B 分别作抛物线的切线交于点P .B 1A 1ABC 1CM(ⅰ)探究PF AB ⋅是否为定值,若是,求出定值;若不是,请说明理由; (ⅱ)若直线PF 与抛物线交于C ,D2015年宁德市普通高中毕业班单科质量检查数学(文科)试题参考答案及评分标准说明:一、本解答指出了每题要考察的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考察内容比照评分标准指定相应的评分细则。
福建省宁德市普通高中2015届高三下学期毕业班第二次质量检查数学(文)试题Word版含解析

2015年福建省宁德市普通高中毕业班第二次质量检查数学(文科)试卷 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|320}M x x x =-+=,{2,1,1,2}N =--,则=N MA .{2,1}--B .{1,2}C .{2,1}-D .{2,1,1,2}-- 【答案】B 【解析】试题分析:{}{}2,1023|2==+-=x x x M ,{}{}2,1,1,22,1--=∴ N M {}2,1=,故答案为B.考点:集合的交集的运算.2.若x ∈R ,则“21x <”是“10x -<<”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B 【解析】试题分析:由12<x得0<x ,由0<x 不能推出01<<-x ,由01<<-x 能达到0<x ,因此12<x是01<<-x 的必要不充分条件,故答案为B. 考点:充分条件、必要条件的判断.3.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人. 现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取 A .55人,80人,45人 B .40人,100人,40人 C .60人,60人,60人 D .50人,100人,30人【答案】D 【解析】试题分析:专科生:本科生:研究生3:10:5900:3000:1500==,抽取的专科生人数50185180=⨯人, 抽取的本科生人数1001810180=⨯人,抽取的研究生人数30183180=⨯人,故答案为D. 考点:分层抽样的应用.4.经过圆22(2)1x y -+=的圆心且与直线210x y -+=平行的直线方程是 A .240x y --= B .240x y -+= C .220x y +-= D .220x y ++= 【答案】A考点:直线的方程.5.设m ,n 是两条不同的直线,α,β是两个不同的平面,下列正确的是A .若m ∥α,n ⊂α,则m ∥nB .若m ∥α,m ∥β,则α∥βC .若m ∥α,α⊥β,则m ⊥βD .若m ∥n ,m ⊥α,则n ⊥α 【答案】D 【解析】试题分析:对应A ,直线n m ,可能平行,可能异面直线;对应B ,平面βα,可能相交;对应C ,直线m 与平面α可能相交,也可能直线在平面内;对应D ,根据两条平行线中一条垂直这个平面,另一条也垂直这个平面,正确,故答案为D. 考点:空间中直线、平面的的位置关系.6.已知sin α,(0,)2απ∈,则tan2α= A .43- B .43 C .12- D .2【答案】A 【解析】试题分析:由552sin =α,⎪⎭⎫ ⎝⎛∈2,0πα得55sin 1cos 2=-=αα,2cos sin tan ==∴ααα,34tan 1tan 22tan 2-=-=∴ααα,故答案为A.考点:1、同角三角函数的基本关系;2、二倍角的正切公式. 7.下列函数中,既为奇函数又在(0,)+∞内单调递减的是A .()sin f x x x =B .12()f x x-=C .1()1x x e f x e -=+D .3()f x x x=-【答案】C考点:函数的奇偶性和单调性.8.运行如图所示的程序,若输出y 的值为1,则可输入x 的个数..为A .0B .1C .2D .3【答案】D 【解析】试题分析:当0≤x 时,12==xy ,得0=x 符合题意,当0>x 时,x x y 33+-=,由图象可知当0>x 时,x x y 33+-=与1=y 有两个交点,因此输出的x 个数为3,故答案为D.考点:1、程序的应用;2、分段函数求值.9.已知实数,x y 满足122x x y x y ≥⎧⎪+≤⎨⎪-≤⎩,若不等式3ax y -≤恒成立,则实数a 的取值范围为A .(,4]-∞B .3(,]2-∞ C .3[,2]2 D .[2,4]【答案】B 【解析】试题分析:不等式组表示的平面区域如图所示,不等式3≤-y ax 恒成立,即3-≥ax y 恒成立,平面区域ABC 在直线3-=ax y 上及上方,由图可知得()1,1A ,()0,2B ,()1,1-C 三点在直线上及上方,满足⎪⎩⎪⎨⎧≤+≤≤-313241a a a ,得23≤a ,故答案为B考点:线性规划的应用.10.已知四棱锥P ABCD -的三视图如图所示,则此四棱锥的侧面积为A.6+.9+ C.12+.20+【答案】C 【解析】试题分析:由三视图得几何体如图所示,平面⊥SAD 平面ABCD ,SF BC BC EF AD SE ⊥⊥⊥,,,侧视图俯视图第10题图又3==SD SA ,2===EF CD AB ,4==BC AD ,5=∴SE ,345=+=SF ,侧面SAD 的面积52,侧面SCD SAB ,的面积为3,侧面SBC 的面积63421=⋅⋅=S ,四棱锥的侧面积5212+,故答案为C.考点:由三视图求侧面积.11.已知点P 是ABC ∆所在平面上一点,AB 边的中点为D ,若23PD PA CB =+,则ABC ∆与ABP ∆的面积比为A .3B .2C .1D .12【答案】C 【解析】试题分析:由于点D 是AB 的中点,PD PB PA 2=+∴,因此CB PA PB PA +=+3,化简得PC PA =2,因此点A 是PC 的中点,ABC ∆的面积和ABP ∆的面积相等,故答案为C.考点:平面向量数量积的应用.12.O 为坐标原点,,A B 为曲线y =6OA OB ⋅=,则直线AB 与圆2249x y +=的位置关系是A. 相交B. 相离C. 相交或相切D. 相切或相离【答案】A 【解析】试题分析:设()121,t t A ,()222,t t B ,6212221=+=⋅t t t t ,解得221=t t (321-=t t 舍去),122122121t t t t t t k AB +=--=,直线AB 与y 轴的交点()b ,0,则2121110t t t b t +=--,解得2121t t t t b +=,直线AB 方程212121t t tt t t x y +++=,整理得()0221=++-y t t x ,圆心()0,0到直线AB 的距离 ()22112t t d ++=,由基本不等式得21212t t t t ≥+,由于B A ,是不同两点,因此等号不能成立,2221>+∴t t ,因此32812=+<d ,因此位置关系的相交,故答案为A. 考点:直线与圆的位置关系.第Ⅱ卷(共90分)二、填空题(每题4分,满分16分,将答案填在答题纸上) 13.复数()i i z 21+=(i 为虚数单位),则z = . 【答案】i --2 【解析】试题分析:()i i i z +-=+=221,i z --=∴2. 考点:共轭复数的概念.14.在区间(0,4)内任取一个实数x ,则使不等式2230x x --<成立的概率为 . 【答案】43. 【解析】试题分析:在区间()4,0内任取一个实数x ,试验全部结果构成的长度为4,不等式0322<--x x 得31<<-x ,满足题意的30<<x ,满足不等式的x 的长度是3,不等式0322<--x x 成立的概率为43=P . 考点:利用几何概型求随机事件的概率.15.关于x 的方程2log 0x a -=的两个根为1212,()x x x x <,则122x x +的最小值为 . 【答案】22【解析】试题分析:方程0log 2=-a x 的两个根()2121,x x x x <,则函数a y =与函数x y 2log =的交点有两个,由图可知,101<<x ,12>x ,因此a x -=12log ,ax -=∴21,a x =∴22log ,得ax 22=, 因此a ax x 222221+⋅=+-222222211=⋅≥+=--a a a a ,因此212x x +的最小值22.考点:1、方程的根和函数的零点;2、基本不等式的应用.16.已知函数()sin cos (22x xf x a a =+∈R),且()()3f x f 2π≤恒成立. 给出下列结论:①函数()y f x =在[0,]32π上单调递增; ②将函数()y f x =的图象向左平移3π个单位,所得图象对应的函数为偶函数; ③若2k ≥,则函数()(2)3g x kx f x π=--有且只有一个零点.其中正确的结论是 .(写出所有正确结论的序号) 【答案】①③ 【解析】试题分析:由于()⎪⎭⎫ ⎝⎛≤32πf x f ,得⎪⎭⎫⎝⎛32πf 为最大值,12123322+=+=⎪⎭⎫⎝⎛a a f π,平方化简得()032=-a ,得3=a ,因此()2cos 2sin3x x x f +=⎪⎭⎫⎝⎛+=62sin 2πx ,当320π≤≤x 时,2626πππ≤+≤x ,因此①对;将函数()y f x =的图象向左平移3π个单位,所得图象对应的函数为⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+=6321sin 2ππx y ⎪⎭⎫ ⎝⎛+=3221sin 2πx 不是偶函数,②错;当2≥k 时,()⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛--=63221sin 2ππx kx x g x kx sin 2-=,()0cos 2≥-='x k x g ,不恒等于0,函数()x kx x g sin 2-=在R 上单调递增,()00=g ,故③正确,答案为①③.考点:1、函数的单调性和奇偶性;2、函数的零点.三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分12分)已知等比数列{}n a 的前n 项和2n n S r =+. (1)求实数r 的值和{}n a 的通项公式;(2)若数列{}n b 满足11b =,121log n n n b b a ++-=,求n b .【答案】(1)()*12N n a n n ∈=-;(2)121212+-=n b n ()*N n ∈.又11b =符合上式,∴2111()22n b n n n *=-+∈N . ······················ 12分考点:1、由n S 得n a ;2、等差数列、等比数列的通项公式和前n 项和公式. 18.(本小题满分12分)某中学刚搬迁到新校区,学校考虑,若非住校生....上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课. 为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为[0,10),[10,20),[20,30),[30,40),[40,50].(1)求频率分布直方图中a 的值;(2)从统计学的角度说明学校是否需要推迟5分钟上课;(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在[40,50]上的概率.【答案】(1)015.0;(2)不需要推迟5分钟;(3)53=P . 【解析】试题分析:(1)解决频率分布直方图的问题,关键在于找出图中数据之间的关系,这些数据中,比较明显的有组距、组距频率,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)平均数是频率分布直方图的重心,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标;(3)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算,当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合. 试题解析:(1)时间分组为[0,10)的频率为110(0.060.020.0030.002)0.15-+++=, ················· 2分∴0.150.01510a ==, 所以所求的频率直方图中a 的值为0.015. ················· 3分 (2)100个非住校生上学路上单程所需时间的平均数:0.1550.6150.2250.03350.0245x =⨯+⨯+⨯+⨯+⨯ ············· 4分0.7595 1.050.9=++++16.7=. ······························· 5分 因为16.720<,所以该校不需要推迟5分钟上课. ···················· 6分 (3)依题意满足条件的单程所需时间在[30,40)中的有3人,不妨设为123,,a a a , 单程所需时间在[40,50]中的有2人,不妨设为12,b b , ··········· 7分 从单程所需时间不小于30分钟的5名学生中,随机抽取2人共有以下10种情况:12(,)a a ,13(,)a a ,11(,)a b ,12(,)a b ,23(,)a a ,21(,)a b ,22(,)a b ,31(,)a b ,32(,)a b ,12(,)b b ; ····················· 10分其中恰有一个学生的单程所需时间落在[40,50]中的有以下6种:11(,)a b ,12(,)a b ,21(,)a b ,22(,)a b ,31(,)a b ,32(,)a b ; ········ 11分故恰有一个学生的单程所需时间落在[40,50]中的概率63105P ==. ····· 12分 考点:1、频率分布直方图的应用;2、利用古典概型求随机事件的概率. 19.(本小题满分12分)已知函数()2sin()f x x ωϕ=+(0,)2ωϕπ><在一个周期内的图象如图所示,其中M (,2)12π,N (,0)3π.(1)求函数()f x 的解析式;(2)在ABC ∆中,角,,A B C 的对边分别是a,b,c,且3,()2Aa c f ===ABC∆的面积.【答案】(1)()⎪⎭⎫⎝⎛+=32sin 2πx x f ;(2)33.【解析】试题分析:(1)求函数()()()0,0sin >>+=ωϕωA x A x f 的解析式时,A 比较容易得出,困难的是确定待定系数ϕω和的值,常用如下方法;(2)一是由Tπω2=即可求出ω的值;确定ϕ的值,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标0x ,则令00=+ϕωx (或πϕω=+0x ),即可求出ϕ;(3)二是代入点的坐标,利用一些已知点坐标代入解析式,再结合图形解出ϕω和,若对ω,A 的符号或对ϕ的范围有要求,则可利用诱导公式进行变换使其符合要求;(4)在解决三角形的问题中,面积公式B ac A bc C ab S sin 21sin 21sin 21===最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来.试题解析:(1)由图像可知:函数()f x 的周期4()312T πππ=⨯-=, ····· 1分 ∴22ωπ==π. ···························· 2分 又()f x 过点(,2)12π,∴()2sin()2126f ππϕ=+=,sin()16πϕ+=, ················ 3分∵2πϕ<,2(,)633πππϕ+∈-, ∴62ππϕ+=,即3πϕ=. ························ 4分∴()2sin(2)3f x x π=+. ························· 5分(2)∵()2sin()23A f A π=+=即sin()3A π+又4(0,),(,)333A A ππππ∈+∈∴233A ππ+=,即3A π=. ······················· 7分在ABC ∆中,,33A a c π==,由余弦定理得 2222cos a b c bc A =+-, ················· 8分 ∴21393b b =+-,即2340b b --=,解得4b =或1b =-(舍去). ····················· 10分∴11sin 43sin 223ABC S bc A π∆==⨯⨯⨯=. ················ 12分考点:1、利用函数图象求函数解析式;2、三角形的面积. 20.(本小题满分12分)如图四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,//AB CD , 90ABC ︒∠=,且2,1CD AB BC PA ====,PD(1)求三棱锥A PCD -的体积;(2)问:棱PB 上是否存在点E ,使得//PD 平面ACE ?若存在,求出BEBP的值,并加以证明;若不存在,请说明理由.【答案】(1)31;(2)棱PB 上存在点E ,当13BE BP =时,//PD 平面ACE .【解析】试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键,利用棱锥的体积公式Sh V 31=求体积;(3))证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质.试题解析:(1)取CD 中点G ,连接AG ,2,//,CD AB AB CD =G//,,AB GC AB GC ∴=∴四边形AGCB 为平行四边形,090AGD DCB ABC ∴∠=∠=∠=在Rt AGD ∆中,11,1,2AG BC DG CD ====AD ∴=== ···················· 1分2223,123,PD PA AD ∴=+=+=222,PD PA AD =+090,PAD ∴∠= 即,PA AD ⊥ ······················ 2分平PAD ⊥面平ABCD 面,平PAD 面平ABCD AD =面PA ∴⊥平ABCD 面 ·························· 3分112ACD S CD AG ∆=⋅=, ························ 4分A PCD P ACD V V --∴= ··························· 5分13ACD S PA ∆=⋅⋅ 111133=⨯⨯=. ···························· 6分 (2)棱PB 上存在点E ,当13BE BP =时,//PD 平面ACE .·········· 7分证明:连结BD 交AC 于点O ,连结OE . ∵//,2AB CD CD AB = ∴1,2BO AB OD CD == ··························· 8分 ∴13BO BD =,又13BE BP = ∴BO BEBD BP=, ∴//,OE DP ····························· 10分又,OE ACE PD ACE ⊂⊄面,面//PD ACE ∴面.···························· 12分 考点:1、求三棱锥的体积;2、直线与平面平行的判定. 21.(本小题满分12分)已知点(A B ,动点E 满足直线EA 与直线EB 的斜率之积为12-.(1)求动点E 的轨迹C 的方程;(2)设过点()1,0F 的直线1l 与曲线C 交于点,P Q ,记点P 到直线2:2l x =的距离为d .①求PF d的值;②过点F 作直线1l 的垂线交直线2l 于点M ,求证:直线OM 平分线段PQ .【答案】(1)()21222±≠=+x y x ;(2)22=d PF ,证明略. 【解析】试题分析:(1)设E 点的坐标()y x ,,根据题意列方程找到y x ,之间的关系式,注意范围;(2)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出22,b a 的值,若不明确,需分焦点在x 轴和y 轴上两种情况讨论;(3)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式∆:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论. 试题解析:(1)设(,)E x y , 依题意得1,2EA EB k k ⋅==-(x ≠,············ 1分 整理得2212x y +=,∴动点E 的轨迹C 的方程为221(2x y x +=≠. ············ 3分(2)①(1,0)F ,设11(,),P x y 则 221112x y =-, ·············· 4分∴1||PF d =························ 5分1=1==. ······························· 7分②依题意,设直线22:1,(,)PQ x my Q x y =+,联立221,12x my x y =+⎧⎪⎨+=⎪⎩可得22(2)210m y my ++-=, ·············· 8分 显然12220,,2my y m ∆>+=-+ ······················ 9分 所以线段PQ 的中点T 坐标为222(,),22mm m -++··············· 10分 又因为1,FM l ⊥故直线FM 的方程为(1)y m x =--, 所以点M 的坐标为(2,)m -, 所以直线OM 的方程为:,2my x =- ··················· 11分 因为222(,)22m T m m -++满足方程,2my x =- 故OM 平分线段.PQ ························· 12分 考点:1、求轨迹方程;2、直线与椭圆的综合问题. 22.(本小题满分14分)已知函数1()ln (1)2f x x a x =--(a ∈R ).(1)若2a =-,求曲线()y f x =在点(1,(1))f 处的切线方程; (2)若不等式()0f x <对任意(1,)x ∈+∞恒成立.①求实数a 的取值范围;②试比较2a e -与2e a -的大小,并给出证明(e 为自然对数的底数, 2.71828e ≈).【答案】(1)22-=x y ;(2)2≥a ,22-->a a a e .【解析】试题分析:(1)利用导数的几何意义求曲线在点()()1,1f 处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率()1f k '=,从而求出直线方程;(2)若可导函数()x f 在指定的区间D 上单调递增(减),求参数问题,可转化为()0≥'x f ()()0≤'x f 恒成立,从而构建不等式,要注意“=”是否可以取到;(3)利用导数方法证明不等式()()x g x f >在区间D 上恒成立的基本方法是构造函数()()()x g x f x h -=,然后根据函数的单调性,或者函数的最值证明函数()0>x h ,其中一个重要的技巧就是找到函数()x h 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式. 试题解析:(1)2a =-时,()ln 1f x x x =+-,1()1,f x x'=+ ······· 1分 ∴切点为(1,0),(1)2k f '== ······················ 3分2a ∴=-时,曲线()y f x =在点(1,(1))f 处的切线方程为22y x =-. ······ 4分 (2)1()ln (1)2f x x a x =--,12()22a axf x x x-'∴=-=, ······················· 5分 ①当0a ≤时,(1,)x ∈+∞,()0f x '>,∴()f x 在(1,)+∞上单调递增, ()(1)0f x f >=,∴0a ≤不合题意. ·························· 6分②当2a ≥即201,a<≤时,2()2()022a x ax a f x x x --'==-<在(1,)+∞上恒成立, ()f x ∴在(1,)+∞上单调递减,有()(1)0f x f <=,∴2a ≥满足题意. ·························· 7分③若02a <<即21,a >时,由()0f x '>,可得21x a<<,由()0f x '<,可得2x a >, ∴()f x 在2(1,)a上单调递增,在2(,)a +∞上单调递减,∴2()(1)0f f a>=,∴02a <<不合题意. ························· 9分综上所述,实数a 的取值范围是[2,).+∞ ················· 10分 当2a ≥时,“比较2a e -与2e a -的大小”等价于“比较2a -与(2)ln e a -的大小” 设()2(2)ln (2)g x x e x x =---≥ 则2(2)()10,e x eg x x x-+-'=-=> ∴()g x 在[2,)+∞上单调递增, ····················· 12分 ()0,g e =当[2,)x e ∈时,()0,g x <即2(2)ln x e x -<-,22x e e x --∴< 当(,)x e ∈+∞时,()0g x >,即2(2)ln x e x ->-,22x e e x --∴> 综上所述,当[2,)a e ∈时,2a e -<2e a -; 当a e =时,2a e -=2e a -;当(,)a e ∈+∞时,2a e ->2e a -. ······················ 14分 考点:1、导数的几何意义;2、函数单调性的应用;3、利用导数证明不等式.。
福建省宁德市2015年5月普通高中毕业班质量试卷文科数学试卷及答案

D. { 2, 1,1,2}
2.若 x R ,则“ 2x 1”是“ 1 x 0”的
A .充分不必要条件
B.必要不充分条件
C .充要条件
D .既不充分也不必要条件
3.某全日制大学共有学生 5400 人,其中专科生有 1500 人,本科生有 3000 人,研究生有 900 人 . 现
采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为
20 分钟,则学
校推迟 5 分钟上课 . 为此,校方随机抽取 100 个非住校生,调查其上学路上单程所需时间 ( 单
位:分钟 ) ,根据所得数据绘制成如下频率分布直方图,其中时间分组为
[0,10) , [10,20) ,
[20,30) , [30,40) , [40,50] . (Ⅰ)求频率分布直方图中 a 的值;
2015 年宁德市普通高中毕业班第二次质量检查
数学(文科)试卷
本试卷分第 I 卷(选择题) 和第 Ⅱ卷(非选择题) 两部分. 本卷满分 150 分,考试时间 120 分钟. 注意事项 :
1.答题前,考生先将自己的姓名、准考证号填写在答题卡上.
2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超
PF
(ⅰ)求
的值;
d
(ⅱ)过点 F 作直线 l1 的垂线交直线 l 2 于点 M ,求证:直线 OM 平分线段 PQ .
22.(本小题满分 14 分)
已知函数 f (x)
ln x
1 a( x 1) ( a
R ).
2
(Ⅰ)若 a 2 ,求曲线 y f (x) 在点 (1, f (1)) 处的切线方程;
180 人,则应在专
科生、本科生与研究生这三类学生中分别抽取
福建省宁德市普通高中2015届高三下学期毕业班第二次质量检查数学(文)试题

2015年福建省宁德市普通高中毕业班第二次质量检查数学(文科)试卷 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|320}M x x x =-+=,{2,1,1,2}N =--,则=N MA .{2,1}--B .{1,2}C .{2,1}-D .{2,1,1,2}-- 【答案】B 【解析】试题分析:{}{}2,1023|2==+-=x x x M ,{}{}2,1,1,22,1--=∴ N M {}2,1=,故答案为B.考点:集合的交集的运算.2.若x ∈R ,则“21x <”是“10x -<<”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B 【解析】试题分析:由12<x得0<x ,由0<x 不能推出01<<-x ,由01<<-x 能达到0<x ,因此12<x是01<<-x 的必要不充分条件,故答案为B.考点:充分条件、必要条件的判断.3.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人. 现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取 A .55人,80人,45人 B .40人,100人,40人 C .60人,60人,60人 D .50人,100人,30人【答案】D 【解析】试题分析:专科生:本科生:研究生3:10:5900:3000:1500==,抽取的专科生人数50185180=⨯人, 抽取的本科生人数1001810180=⨯人,抽取的研究生人数30183180=⨯人,故答案为D. 考点:分层抽样的应用.4.经过圆22(2)1x y -+=的圆心且与直线210x y -+=平行的直线方程是 A .240x y --= B .240x y -+= C .220x y +-= D .220x y ++= 【答案】A考点:直线的方程.5.设m ,n 是两条不同的直线,α,β是两个不同的平面,下列正确的是A .若m ∥α,n ⊂α,则m ∥nB .若m ∥α,m ∥β,则α∥βC .若m ∥α,α⊥β,则m ⊥βD .若m ∥n ,m ⊥α,则n ⊥α 【答案】D 【解析】试题分析:对应A ,直线n m ,可能平行,可能异面直线;对应B ,平面βα,可能相交;对应C ,直线m 与平面α可能相交,也可能直线在平面内;对应D ,根据两条平行线中一条垂直这个平面,另一条也垂直这个平面,正确,故答案为D. 考点:空间中直线、平面的的位置关系.6.已知sin α=(0,)2απ∈,则tan 2α=A .43- B .43 C .12- D .2【答案】A 【解析】试题分析:由552sin =α,⎪⎭⎫ ⎝⎛∈2,0πα得55sin 1cos 2=-=αα,2cos sin tan ==∴ααα,34tan 1tan 22tan 2-=-=∴ααα,故答案为A.考点:1、同角三角函数的基本关系;2、二倍角的正切公式. 7.下列函数中,既为奇函数又在(0,)+∞内单调递减的是A .()sin f x x x =B .12()f x x-=C .1()1xxe f x e -=+ D .3()f x x x =-【答案】C考点:函数的奇偶性和单调性.8.运行如图所示的程序,若输出y 的值为1,则可输入x 的个数..为A .0B .1C .2D .3【答案】D 【解析】试题分析:当0≤x 时,12==xy ,得0=x 符合题意,当0>x 时,x x y 33+-=,由图象可知当0>x 时,x x y 33+-=与1=y 有两个交点,因此输出的x 个数为3,故答案为D.考点:1、程序的应用;2、分段函数求值.9.已知实数,x y 满足122x x y x y ≥⎧⎪+≤⎨⎪-≤⎩,若不等式3ax y -≤恒成立,则实数a 的取值范围为A .(,4]-∞B .3(,]2-∞ C .3[,2]2 D .[2,4]【答案】B 【解析】试题分析:不等式组表示的平面区域如图所示,不等式3≤-y ax 恒成立,即3-≥ax y 恒成立,平面区域ABC 在直线3-=ax y 上及上方,由图可知得()1,1A ,()0,2B ,()1,1-C 三点在直线上及上方,满足⎪⎩⎪⎨⎧≤+≤≤-313241a a a ,得23≤a ,故答案为B考点:线性规划的应用.10.已知四棱锥P ABCD -的三视图如图所示,则此四棱锥的侧面积为A.6+.9+ C.12+.20+【答案】C 【解析】试题分析:由三视图得几何体如图所示,平面⊥SAD 平面ABCD ,SF BC BC EF AD SE ⊥⊥⊥,,,侧视图俯视图第10题图又3==SD SA ,2===EF CD AB ,4==BC AD ,5=∴SE ,345=+=SF ,侧面SAD 的面积52,侧面SCD SAB ,的面积为3,侧面SBC 的面积63421=⋅⋅=S ,四棱锥的侧面积5212+,故答案为C.考点:由三视图求侧面积.11.已知点P 是ABC ∆所在平面上一点,AB 边的中点为D ,若23PD PA CB =+,则ABC ∆与ABP ∆的面积比为A .3B .2C .1D .12【答案】C 【解析】试题分析:由于点D 是AB 的中点,PD PB PA 2=+∴,因此CB PA PB PA +=+3,化简得PC PA =2,因此点A 是PC 的中点,ABC ∆的面积和ABP ∆的面积相等,故答案为C.考点:平面向量数量积的应用.12.O 为坐标原点,,A B 为曲线y 上的两个不同点,若6OA OB ⋅=,则直线AB 与圆2249x y +=的位置关系是A. 相交B. 相离C. 相交或相切D. 相切或相离【答案】A 【解析】试题分析:设()121,t t A ,()222,t t B ,6212221=+=⋅t t t t ,解得221=t t (321-=t t 舍去),122122121t t t t t t k AB +=--=,直线AB 与y 轴的交点()b ,0,则2121110t t t b t +=--,解得2121t t t t b +=,直线AB 方程212121t t tt t t x y +++=,整理得()0221=++-y t t x ,圆心()0,0到直线AB 的距离 ()22112t t d ++=,由基本不等式得21212t t t t ≥+,由于B A ,是不同两点,因此等号不能成立,2221>+∴t t ,因此32812=+<d ,因此位置关系的相交,故答案为A. 考点:直线与圆的位置关系.第Ⅱ卷(共90分)二、填空题(每题4分,满分16分,将答案填在答题纸上) 13.复数()i i z 21+=(i 为虚数单位),则z = . 【答案】i --2 【解析】试题分析:()i i i z +-=+=221,i z --=∴2. 考点:共轭复数的概念.14.在区间(0,4)内任取一个实数x ,则使不等式2230x x --<成立的概率为 . 【答案】43. 【解析】试题分析:在区间()4,0内任取一个实数x ,试验全部结果构成的长度为4,不等式0322<--x x 得31<<-x ,满足题意的30<<x ,满足不等式的x 的长度是3,不等式0322<--x x 成立的概率为43=P . 考点:利用几何概型求随机事件的概率.15.关于x 的方程2log 0x a -=的两个根为1212,()x x x x <,则122x x +的最小值为 . 【答案】22【解析】试题分析:方程0log 2=-a x 的两个根()2121,x x x x <,则函数a y =与函数x y 2log =的交点有两个,由图可知,101<<x ,12>x ,因此a x -=12log ,a x -=∴21,a x =∴22log ,得a x 22=,因此a a x x 222221+⋅=+-222222211=⋅≥+=--a a a a ,因此212x x +的最小值22.考点:1、方程的根和函数的零点;2、基本不等式的应用.16.已知函数()sin cos (22x xf x a a =+∈R),且()()3f x f 2π≤恒成立. 给出下列结论:①函数()y f x =在[0,]32π上单调递增; ②将函数()y f x =的图象向左平移3π个单位,所得图象对应的函数为偶函数; ③若2k ≥,则函数()(2)3g x kx f x π=--有且只有一个零点.其中正确的结论是 .(写出所有正确结论的序号) 【答案】①③ 【解析】试题分析:由于()⎪⎭⎫⎝⎛≤32πf x f ,得⎪⎭⎫⎝⎛32πf 为最大值,12123322+=+=⎪⎭⎫⎝⎛a a f π,平方化简得()032=-a ,得3=a ,因此()2cos 2sin3x x x f +=⎪⎭⎫⎝⎛+=62sin 2πx ,当320π≤≤x 时,2626πππ≤+≤x ,因此①对;将函数()y f x =的图象向左平移3π个单位,所得图象对应的函数为⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+=6321sin 2ππx y ⎪⎭⎫⎝⎛+=3221sin 2πx 不是偶函数,②错;当2≥k 时,()⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛--=63221sin 2ππx kx x g x kx sin 2-=,()0cos 2≥-='x k x g ,不恒等于0,函数()x kx x g sin 2-=在R 上单调递增,()00=g ,故③正确,答案为①③.考点:1、函数的单调性和奇偶性;2、函数的零点.三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分12分)已知等比数列{}n a 的前n 项和2n n S r =+. (1)求实数r 的值和{}n a 的通项公式;(2)若数列{}n b 满足11b =,121log n n n b b a ++-=,求n b . 【答案】(1)()*12N n a n n ∈=-;(2)121212+-=n b n ()*N n ∈.又11b =符合上式,∴2111()22n b n n n *=-+∈N . ······················ 12分考点:1、由n S 得n a ;2、等差数列、等比数列的通项公式和前n 项和公式. 18.(本小题满分12分)某中学刚搬迁到新校区,学校考虑,若非住校生....上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课. 为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为[0,10),[10,20),[20,30),[30,40),[40,50].(1)求频率分布直方图中a 的值;(2)从统计学的角度说明学校是否需要推迟5分钟上课;(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在[40,50]上的概率.【答案】(1)015.0;(2)不需要推迟5分钟;(3)53=P . 【解析】试题分析:(1)解决频率分布直方图的问题,关键在于找出图中数据之间的关系,这些数据中,比较明显的有组距、组距频率,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)平均数是频率分布直方图的重心,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标;(3)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算,当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合. 试题解析:(1)时间分组为[0,10)的频率为110(0.060.020.0030.002)0.15-+++=, ················· 2分∴0.150.01510a ==, 所以所求的频率直方图中a 的值为0.015. ················· 3分 (2)100个非住校生上学路上单程所需时间的平均数:0.1550.6150.2250.03350.0245x =⨯+⨯+⨯+⨯+⨯ ············· 4分0.7595 1.050.9=++++16.7=. ······························· 5分因为16.720<,所以该校不需要推迟5分钟上课. ···················· 6分 (3)依题意满足条件的单程所需时间在[30,40)中的有3人,不妨设为123,,a a a , 单程所需时间在[40,50]中的有2人,不妨设为12,b b , ··········· 7分 从单程所需时间不小于30分钟的5名学生中,随机抽取2人共有以下10种情况:12(,)a a ,13(,)a a ,11(,)a b ,12(,)a b ,23(,)a a ,21(,)a b ,22(,)a b ,31(,)a b ,32(,)a b ,12(,)b b ; ····················· 10分其中恰有一个学生的单程所需时间落在[40,50]中的有以下6种:11(,)a b ,12(,)a b ,21(,)a b ,22(,)a b ,31(,)a b ,32(,)a b ; ········ 11分故恰有一个学生的单程所需时间落在[40,50]中的概率63105P ==. ····· 12分 考点:1、频率分布直方图的应用;2、利用古典概型求随机事件的概率. 19.(本小题满分12分)已知函数()2sin()f x x ωϕ=+(0,)2ωϕπ><在一个周期内的图象如图所示,其中M (,2)12π,N (,0)3π.(1)求函数()f x 的解析式;(2)在ABC ∆中,角,,A B C 的对边分别是a,b,c,且3,()2Aa c f ==,求ABC∆的面积.【答案】(1)()⎪⎭⎫⎝⎛+=32sin 2πx x f ;(2)33.【解析】试题分析:(1)求函数()()()0,0sin >>+=ωϕωA x A x f 的解析式时,A 比较容易得出,困难的是确定待定系数ϕω和的值,常用如下方法;(2)一是由Tπω2=即可求出ω的值;确定ϕ的值,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标0x ,则令00=+ϕωx (或πϕω=+0x ),即可求出ϕ;(3)二是代入点的坐标,利用一些已知点坐标代入解析式,再结合图形解出ϕω和,若对ω,A 的符号或对ϕ的范围有要求,则可利用诱导公式进行变换使其符合要求;(4)在解决三角形的问题中,面积公式B ac A bc C ab S sin 21sin 21sin 21===最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来.试题解析:(1)由图像可知:函数()f x 的周期4()312T πππ=⨯-=, ····· 1分 ∴22ωπ==π. ···························· 2分 又()f x 过点(,2)12π,∴()2sin()2126f ππϕ=+=,sin()16πϕ+=, ················ 3分∵2πϕ<,2(,)633πππϕ+∈-, ∴62ππϕ+=,即3πϕ=. ························ 4分∴()2sin(2)3f x x π=+. ························· 5分(2)∵()2sin()23A f A π=+即sin()3A π+=又4(0,),(,)333A A ππππ∈+∈∴233A ππ+=,即3A π=. ······················· 7分在ABC ∆中,,33A a c π===,由余弦定理得 2222cos a b c bc A =+-, ················· 8分 ∴21393b b =+-,即2340b b --=,解得4b =或1b =-(舍去). ····················· 10分∴11sin 43sin 223ABC S bc A π∆==⨯⨯⨯=················ 12分考点:1、利用函数图象求函数解析式;2、三角形的面积. 20.(本小题满分12分)如图四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,//AB CD , 90ABC ︒∠=,且2,1CD AB BC PA ====,PD(1)求三棱锥A PCD -的体积;(2)问:棱PB 上是否存在点E ,使得//PD 平面ACE ?若存在,求出BEBP的值,并加以证明;若不存在,请说明理由.【答案】(1)31;(2)棱PB 上存在点E ,当13BE BP =时,//PD 平面ACE .【解析】试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键,利用棱锥的体积公式Sh V 31=求体积;(3))证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质.试题解析:(1)取CD 中点G ,连接AG ,2,//,CD AB AB CD =GC//,,AB GC AB GC ∴=∴四边形AGCB 为平行四边形,090AGD DCB ABC ∴∠=∠=∠=在Rt AGD ∆中,11,1,2AG BC DG CD ====AD ∴=···················· 1分 2223,123,PD PA AD ∴=+=+=222,PD PA AD =+090,PAD ∴∠= 即,PA AD ⊥ ······················ 2分平PAD ⊥面平ABCD 面,平PAD 面平ABCD AD =面PA ∴⊥平ABCD 面 ·························· 3分112ACD S CD AG ∆=⋅=, ························ 4分A PCD P ACD V V --∴= ··························· 5分13ACD S PA ∆=⋅⋅ 111133=⨯⨯=. ···························· 6分 (2)棱PB 上存在点E ,当13BE BP =时,//PD 平面ACE .·········· 7分证明:连结BD 交AC 于点O ,连结OE . ∵//,2AB CD CD AB = ∴1,2BO AB OD CD == ··························· 8分 ∴13BO BD =,又13BE BP = ∴BO BEBD BP=, ∴//,OE DP ····························· 10分又,OE ACE PD ACE ⊂⊄面,面//PD ACE ∴面. ···························· 12分考点:1、求三棱锥的体积;2、直线与平面平行的判定. 21.(本小题满分12分)已知点(A B ,动点E 满足直线EA 与直线EB 的斜率之积为12-.(1)求动点E 的轨迹C 的方程;(2)设过点()1,0F 的直线1l 与曲线C 交于点,P Q ,记点P 到直线2:2l x =的距离为d .①求PF d的值;②过点F 作直线1l 的垂线交直线2l 于点M ,求证:直线OM 平分线段PQ .【答案】(1)()21222±≠=+x y x ;(2)22=d PF ,证明略. 【解析】试题分析:(1)设E 点的坐标()y x ,,根据题意列方程找到y x ,之间的关系式,注意范围;(2)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出22,b a 的值,若不明确,需分焦点在x 轴和y 轴上两种情况讨论;(3)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式∆:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论. 试题解析:(1)设(,)E x y , 依题意得1,2EA EB k k ⋅==-(x ≠,············ 1分 整理得2212x y +=,∴动点E 的轨迹C 的方程为221(2x y x +=≠. ············ 3分(2)①(1,0)F ,设11(,),P x y 则 221112x y =-, ·············· 4分∴1||PF d = ························ 5分1=1=. ······························· 7分 ②依题意,设直线22:1,(,)PQ x my Q x y =+,联立221,12x my x y =+⎧⎪⎨+=⎪⎩可得22(2)210m y my ++-=, ·············· 8分 显然12220,,2my y m∆>+=-+ ······················ 9分 所以线段PQ 的中点T 坐标为222(,),22mm m-++ ··············· 10分 又因为1,FM l ⊥故直线FM 的方程为(1)y m x =--, 所以点M 的坐标为(2,)m -, 所以直线OM 的方程为:,2my x =- ··················· 11分 因为222(,)22m T m m -++满足方程,2my x =-故OM 平分线段.PQ ························· 12分 考点:1、求轨迹方程;2、直线与椭圆的综合问题. 22.(本小题满分14分)已知函数1()ln (1)2f x x a x =--(a ∈R ).(1)若2a =-,求曲线()y f x =在点(1,(1))f 处的切线方程; (2)若不等式()0f x <对任意(1,)x ∈+∞恒成立.①求实数a 的取值范围;②试比较2a e -与2e a -的大小,并给出证明(e 为自然对数的底数, 2.71828e ≈).【答案】(1)22-=x y ;(2)2≥a ,22-->a a a e .【解析】试题分析:(1)利用导数的几何意义求曲线在点()()1,1f 处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率()1f k '=,从而求出直线方程;(2)若可导函数()x f 在指定的区间D 上单调递增(减),求参数问题,可转化为()0≥'x f ()()0≤'x f 恒成立,从而构建不等式,要注意“=”是否可以取到;(3)利用导数方法证明不等式()()x g x f >在区间D 上恒成立的基本方法是构造函数()()()x g x f x h -=,然后根据函数的单调性,或者函数的最值证明函数()0>x h ,其中一个重要的技巧就是找到函数()x h 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式. 试题解析:(1)2a =-时,()ln 1f x x x =+-,1()1,f x x'=+ ······· 1分 ∴切点为(1,0),(1)2k f '== ······················ 3分 2a ∴=-时,曲线()y f x =在点(1,(1))f 处的切线方程为22y x =-. ······ 4分(2)1()ln (1)2f x x a x =--,12()22a axf x x x-'∴=-=, ······················· 5分 ①当0a ≤时,(1,)x ∈+∞,()0f x '>,∴()f x 在(1,)+∞上单调递增, ()(1)0f x f >=,∴0a ≤不合题意. ·························· 6分 ②当2a ≥即201,a <≤时,2()2()022a x ax a f x x x --'==-<在(1,)+∞上恒成立, ()f x ∴在(1,)+∞上单调递减,有()(1)0f x f <=,∴2a ≥满足题意. ·························· 7分③若02a <<即21,a >时,由()0f x '>,可得21x a<<,由()0f x '<,可得2x a >, ∴()f x 在2(1,)a上单调递增,在2(,)a +∞上单调递减,∴2()(1)0f f a>=,∴02a <<不合题意.························· 9分 综上所述,实数a 的取值范围是[2,).+∞ ················· 10分 当2a ≥时,“比较2a e -与2e a -的大小”等价于“比较2a -与(2)ln e a -的大小” 设()2(2)ln (2)g x x e x x =---≥ 则2(2)()10,e x e g x x x-+-'=-=> ∴()g x 在[2,)+∞上单调递增, ····················· 12分 ()0,g e =当[2,)x e ∈时,()0,g x <即2(2)ln x e x -<-,22x e e x --∴< 当(,)x e ∈+∞时,()0g x >,即2(2)ln x e x ->-,22x e e x --∴> 综上所述,当[2,)a e ∈时,2a e -<2e a -; 当a e =时,2a e -=2e a -;当(,)a e ∈+∞时,2a e ->2e a -. ······················ 14分 考点:1、导数的几何意义;2、函数单调性的应用;3、利用导数证明不等式.。
福建省宁德市2015届高三普通高中毕业班5月质检英语试卷 Word版含答案

2015年宁德市普通高中毕业班质量检查英语本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
第一卷1至12页,第二卷13至14页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2.考生作答时,请将答案答在答题卡上,请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
在草稿纸、试卷上答题无效。
3.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.保持答题卡卡面清洁,不折叠,不破损。
考试结束后,将本试卷和答题卡一并交回。
第一卷(选择题共115分)第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Where does the conversation most probably take place?A. At the man‟s house.B. In a restaurant.C. In an office.2. What is the relationship between May and Maria?A. Twin sisters.B. Close friends.C. Classmates.3. How will the woman go to the hotel?A. By taxi.B. By plane.C. By car.4. Why does the woman go to the post office?A. To post a letter.B. To send a telegraph.C. To meet a friend.5. Which subject does the woman think the boy is weak at?A. Physics.B. Math.C. Chemistry.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
福建省宁德市高三数学下学期第二次质量检查(5月)试题

参考答案评分说明:1、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考查内容比照评分标准指定相应的评分细则.2、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3、解答右端所注分数,表示考生正确做到这一步应得的累加分数.4、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分.1.C2. A3. B4. D5.B6.C7. B8. A9. C 10. B 11. D 12.C 二、填空题:本题考查基础知识和基本运算,每小题5分,满分20分.13.2π314.01a ≤≤三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程和演算步骤. 17.本小题主要考查正弦定理、余弦定理及两角和与差的三角函数公式等基础知识,考查运算求解能力,考查化归与转化思想、函数与方程思想等.满分12分. 解:(1)由正弦定理有:sin sin (sin cos )B A C C =+sin sin()sin cos cos sin =+=+B A C A C A C Q ··········· 2分 cos sin sin sin A C A C ∴= ···················· 3分 0sin 0c C π<<∴≠Q ····················· 4分 cos sin A A ∴= ························ 5分 tan 1A ∴= 0A π<<Q4A π∴=··························· 6分(2)4a b A π===Q由余弦定理有:2222cos a b c bc A =+- ····················· 8分2450c c ∴--=························ 9分 5c ∴=或1c =-(舍去) ···················· 10分sin BD c A ∴=5== ·················· 12分 18.本小题主要考查了概率、频率、平均数等概率、统计基础知识,考查数据处理能力、抽象概括能力、运算求解能力以及应用意识,考查或然与必然的思想、化归与转化思想等.满分12分. 解:(1)设“陈先生一次租用新能源租赁汽车的时间不低于30分钟”的事件为A则所求的概率为1219()1()15025P A P A =-=-=··········· 2分 所以陈先生一次租用新能源租赁汽车的时间不低于30分钟的概率为1925. 4分(2)每次开车所用的平均时间为122882253545553550505050⨯+⨯+⨯+⨯= ··· 6分每次租用新能源租赁汽车的平均费用为1120.1235=16.2⨯+⨯ ······ 8分每个月的费用为16.2222=712.8⨯⨯,712.8<800 ············ 10分 因此公车补贴够上下班租用新能源分时租赁汽车. ··········· 12分 19.本小题主要考查空间中直线与直线、直线与平面的位置关系、平面与平面位置关系,几何体的体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等.满分12分.证明:(1)取BD 中点O ,连接AO ,PO ················ 1分 AB AD =Q ,O 为BD 中点 AO BD ∴⊥又PB PD =,O 为BD 中点 PO BD ∴⊥ 又AO PO O =IBD ∴⊥面PAO············ 3分 又PA ⊂面PAOPA BD ∴⊥·············· 4分(2)(i)取PD 中点F ,连接CF ,EF ,则//CF BE ,CF 即为所作直线l ··· 5分 理由如下:Q 在PAD ∆中E 、F 分别为PA 、PD 中点//EF ∴AD ,且112EF AD ==又//AD BC Q ,112BC AD ==//EF BC ∴且=EF BC∴四边形BCFE 为平行四边形. ··················· 6分 //CF BE ∴ ···························· 7分 (ii)PA AB ⊥Q ,PA BD ⊥,AB BD B =IPA ∴⊥面ABD ·························· 8分 又在ABD ∆中,2AB AD ==,BD =,222AB AD BD +=AB AD ∴⊥又PA AB ⊥,PA AD A =IAB ∴⊥面PAD·························· 9分方法一:112232P ACD V -=⨯⨯⨯11(12)2C AEFD V -=⨯⨯+ ················· 10分P ECF V -∴= ····················· 11分 13P ECF C AEFD V V --∴= ························ 12分 方法二:Q 在PAD ∆中,EF 为中位线 14PEF PAD S S ∆∆∴=……………………………………………………………………………..10分113143PEF C PEF C PAD PAD S ABV V S AB ∆--∆⨯⨯∴==⨯⨯…………………………………………………………..11分 1=3P ECF C AEFD V V --∴....................................................................................................................12分方法三:12EF AD =Q113143PEC F PEC D PAC PAC S EFV V S AD ∆--∆⨯⨯∴==⨯⨯………………………………………………………..11分 1=3P ECF C AEFD V V --∴………………………………………………………………………….12分 20.本题主要考查椭圆的标准方程及其简单的几何性质,直线与圆锥曲线的位置关系等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、特殊与一般思想、函数与方程思想、化归与转化思想,考查考生分析问题和解决问题的能力,满分12分.解:(1)22221+=x y a b Q,1422∴=⨯==S ab ab,∴ab ① ···· 1分又2e =Q ②,联立①②得1a b ==.·········· 3分 ∴椭圆方程为2212x y +=. ················· 4分(2)由(1)得椭圆方程为2212x y +=,依题意,设直线l 的方程为2y x t =+,1122(,),(,)B x y C x y ,点12A (,)到直线l :2y x t =+的距离为d , 联立22212y x t x y =+⎧⎪⎨+=⎪⎩,,可得2298(22)0x tx t ++-=, 显然12212890,229t x x t x x ⎧+=-⎪⎪∆>⎨-⎪=⎪⎩ ···················· 6分BD ∴=7分d ∴== ························ 8分1122ABD S BD d ∆∴=⨯=·············· 9分290->tQ 22(9)-+∴=t t d t ··· 10分 ∴当且仅当292t =时,即t =,max ()ABD S ∆∴=, ····· 11分此时直线l 的方程为420x y ++或420x y +-=. ······· 12分 21.本小题主要考查导数及其应用、不等式等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等.满分12分.解:(1)2()36=3(2f x x ax x x a '=--) ……………………………………………………1分令()0f x '=,则=0x 或=2x a ,当0a =时,'()0f x ≥,()f x 在R 上是增函数; (2)分当0a >时,令'()0f x >,得0x <,2x a >,所以()f x 在(,0)-∞,(2,)a +∞上是增函数;令'()0f x <,得02x a <<,所以()f x 在(0,2)a 上是减函数…………………...……3分当0a <时,令'()0f x >,得2x a <,0x >,所以()f x 在(,2)a -∞,(0,)+∞上是增函数;令'()0f x <,得20a x <<,所以()f x 在(2,0)a 上是减函数…………………..…… 4分 综上所述:当0a =时,()f x 在R 上是增函数;当0a >时,()f x 在(,0)-∞,(2,)a +∞上是增函数,在(0,2)a 上是减函数. 当0a <时,()f x 在(,2)a -∞,(0,)+∞上是增函数,在(2,0)a 上是减函数.…………………………………….………5分(2)由(Ⅰ)可知:当0a =时,()f x 在R 上是增函数,∴函数()f x 不可能有三个零点;当0a <时,()f x 在(,2)a -∞,(0,)+∞上是增函数,在(2,0)a 上是减函数. ∴()f x 的极小值为(0)=40f >,∴函数()f x 不可能有三个零点 当0a >时,3min ()(2)44f x f a a ==-,要满足()f x 有三个零点,则需3440a -<,即1a >………………………..………6分 当0x >时,要证明:2()6()a f x a a e >-等价于要证明2min ()6()af x a a e >-即要证: 32446()a a a a e ->-………………………………………………………7分由于1a >,故等价于证明:2312a a a ae ++<,证明如下:法1:构造函数2()3222((1,))a g a ae a a a =---∈+∞………….…………………8分()(33)24a g a a e a '=+--……………………………………………………9分令()(33)24a h a a e a =+--()(63)40a h a a e '=+->Q ,∴函数()h a 在(1,)+∞单调递增min ()(1)660h a h e ∴==->,∴函数()g a 在(1,)+∞单调递增………….…10分min ()(1)360g a g e ∴==->,………………………………………………11分2312a a a ae ∴++≤ ∴2()6()a f x a a e >-.……………………………………………………12分法2:构造函数()1((1,))a g a e a a =--∈+∞…………………………………………8分∵()10a g a e '=->,∴函数()g a 在(1,)+∞单调递增………………………9分∴1a e a >+…………………………………………………………………10分 ∴2233(1)(1)(1)22a ae a a a a a a -++>+-++……………………………11分 231(1)(1)(2)022a ae a a a a -++>-+> ∴2()6()a f x a a e >-.……………………………………………………12分22.选修44-;坐标系与参数方程本小题考查直线和圆的极坐标方程、参数方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想等. 满分10分.解法一:(1)由1C :2(4cos )4r ρρθ-=-,得224cos 4r ρρθ-+=,即222440x y x r +-+-=, ………………………………………………………2分 曲线2C 化为一般方程为:222(4)3x y r -+=,即2228163x y x r +-+=,………4分 化为极坐标方程为:228cos 1630r ρρθ-+-=.……………………….………5分(2)由22244x y x r +-+=及2228163x y x r +-+=,消去2r ,得曲线3C 的直角坐标方程为2222x y x +-=. …………………………………7分设直线l的参数方程为1,2x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数),……………………………….…8分与2222x y x +-=联立得2213244t t t +-=,即220t t --=,………………………………………….…………………….9分故121t t +=,1220t t =-<, ∴121OA OB t t -=+=.………………………….………………………..…10分 解法二:(1)同解法一;(2)由224cos 4r ρρθ-+=及228cos 1630r ρρθ-+-=,消去2r ,得曲线3C 的极坐标方程为22cos 20()ρρθρ--=∈R . ………..….……………7分 将θπ=3代入曲线3C 的极坐标方程,可得220ρρ--=,…………………………8分 故121ρρ+=,1220ρρ=-<,……………………………..………………………9分 故121OA OB ρρ-=+=.…………………………………..……………………10分23.选修45-:不等式选讲本小题考查绝对值不等式的解法与性质等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、化归与转化思想等. 满分10分.解法一:(1)1,x y +=Q|2||1|5x x ∴-++≤,…………………………………………………………..1分当2x ≥时,原不等式化为215x -≤,解得3x ≤,∴23x ≤≤;……………………………………………………………………2分当12x -≤<时,原不等式化为215x x -++≤,∴12x -≤<;…………………………………………………………..………3分当1x <-时,原不等式化为215x -+≤,解得2x ≥-,∴21x -≤<-;…………………………………………………………………4分综上,不等式的解集为{}23x x -≤≤..…………………………...…………5分(2)1,x y +=Q 且0,0x y >>, 2222222211()()(1)(1)x y x x y y x y x y +-+-∴--=⋅………………………………7分 222222xy y xy x x y ++=⋅ 222222()()y y x x x x y y=++ 225x y y x=++………………………………………………………………8分59≥=. 当且仅当12x y ==时,取“=”. ……………………………….………………10分 解法二:(1)同解法一;(2)1,x y +=Q 且0,0x y >>,2222221111(1)(1)x y x y x y --∴--=⋅………………………………………………6分 22(1)(1)(1)(1)x x y y x y +-+-=⋅ 22(1)(1)x y y x x y ++=⋅………………………………………………..……………7分 1x y xy xy +++=…………………………………………………….……………8分 21xy =+2219()2x y ≥+=+ 当且仅当12x y ==时,取“=”. ……………………………….……………………10分。
福建省宁德市高三数学单科质量检测试题 文

2015年宁德市普通高中毕业班单科质量检查数学(文科)试卷本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.本卷满分150分,考试时间120分钟.注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上.2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚. 4.保持答题卡卡面清楚,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回. 参考公式:第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数i(12i)+(i 为虚数单位)等于A .2i -+B .2i +C .2i --D .2i - 2.已知集合{}21x M x =>,若a M ∉,则实数a 可以是A .3B .2C .1D .1-3.已知sin α=α为第二象限角,则tan α的值是A .B .C .12-D .4.如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆, 数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出 椭圆的面积约为A.4.7B.4.8C.1.2D.1.35.a b >>“”是的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6. 已知一个几何体的三视图如图所示, 根据图中尺寸可得该几何体的体积为 A .36π B .24π C .15π D .12π7.要得到函数3sin(2)4y x π=-的图象,只需将函数3sin 2y x =的图象 A .向右平移4π个单位 B .向左平移4π个单位 C .向右平移8π个单位 Dπ8. 运行如图所示的程序框图,则输出的所有 实数对(,)x y 所对应的点都在函数 A .2()log (1)f x x =+的图像上B .2()22f x x x =-+的图像上C .4()3f x x=的图像上 D .1()2x f x -=的图像上9. 定义在R 上的函数()f x 满足()(),(2)()f x f x f x f x -=+=.当[0,1]x ∈时,2()2f x x =.若在区间[1,3]-上函数()()g x f x ax a =--有3个零点,则实数a 的取值范围是A .1(0,)2B .1(0,]2 C .1(,1)2 D .1(,1]210. 若双曲线22221(0,0)x y a b a b -=>>的渐近线与圆22(2)1x y -+=有公共点,则此双曲线的离心率的取值范围是正视图侧视图俯视图A.B. C.)+∞ D.)+∞11.不等式组222,222x y x y -≤-≤⎧⎨-≤+≤⎩围成的区域为Ω,能够把区域Ω的周长和面积同时分为相等两部分的曲线为A .331y x x =-+ B .sin 2y x x = C .2ln2x y x -=+ D .1(e e )4x x y -=+12.一数字游戏规则如下:第1次生成一个数a ,以后每次生成的结果均是由上一次生成的每一个数x 生成两个数,一个是x -,另一个是2x +.设前n 次生成的所有数的和为n S ,若1a =,则6S =A .63B .64C .127D .128 第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡的相应位置. 13.某校参加“数迷会”社团的学生中,高一年级有50名,高二年级有40名.现用分层抽样的方法在这90名学生中抽取一个容量为18的样本,则在高二年级的学生中应抽取的人数为 .14.若向量(1,2)=-a ,(3,)y =-b ,且a ∥b ,则a +b= .15.已知扇形的周长为4,则该扇形的面积的最大值为 .16.已知函数10,0()e ,0x xx f x x ⎧≥⎪=⎨<⎪⎩,若对于任意[12,12]x a a ∈-+,不等式()(2)f x a f x +≤ 恒成立,则实数a 的取值范围是 .三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分) 已知数列{}n a 的前n 项和为n S ,点(,)()n n S n *∈N 在函数2()f x x =的图象上.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设11n n n b a a +=⋅,求数列{}n b的前n 项和n T .18.(本小题满分12分)某市一水电站的年发电量y (单位:亿千瓦时)与该市的年降雨量x (单位:毫米)有如下统(Ⅰ)若从统计的5年中任取2年,求这2年的发电量都低于8.0(亿千瓦时)的概率; (Ⅱ)由表中数据求得线性回归方程为ˆˆ0.004y x a =+.该水电站计划2015年的发电量不低于9.0亿千瓦时,现由气象部门获悉2015年的降雨量约为1800毫米,请你预测2015年能否完成发电任务,若不能,缺口约为多少亿千瓦时?19.(本小题满分12分)如图三棱柱ABC -A1B1C1中,点M为AB 的中点. (Ⅰ)求证:BC1∥平面A1CM ;(Ⅱ)若CA=CB ,A1在平面ABC 的射影为M , 求证: 平面A1CM ⊥平面ABB1 A1.20.(本小题满分12分)已知函数()cos cos(2)3f x x x x ωωωπ=⋅++(0)ω>的最小正周期为2π. (Ⅰ)求函数()f x 的解析式;(Ⅱ)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,当x A =时函数()f x 取到最值, 且ABC ∆的面积为,5b c +=,求a 的值.21.(本小题满分12分)已知函数()e xf x x =-. (Ⅰ)求函数()f x 的单调区间;B 1A 1 ABC 1C M(Ⅱ)求函数21()e 12x g x x =--在[0,)+∞上的最小值; (Ⅲ)求证:3e ln 2x x >+.22.(本小题满分14分)已知抛物线22(0)x py p =>的焦点F 与椭圆22143y x +=的一个焦点重合.(Ⅰ)求抛物线的方程;(Ⅱ)直线1y kx =+交抛物线于A,B 两点,过A,B 分别作抛物线的切线交于点P . (ⅰ)探究PF AB ⋅是否为定值,若是,求出定值;若不是,请说明理由; (ⅱ)若直线PF 与抛物线交于C,D ,求证:PC FD PD FC⋅=⋅.2015年宁德市普通高中毕业班单科质量检查 数学(文科)试题参考答案及评分标准 说明:一、本解答指出了每题要考察的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考察内容比照评分标准指定相应的评分细则。
【数学】福建省宁德市高三毕业班第二次(5月)质量检查考试试题(文)(解析版)

福建省宁德市高三毕业班第二次(5月)质量检查考试数学试题一、选择题.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则()A. B.C. D.【答案】A【解析】集合=,B={x|x2﹣2x<0}={x|0<x<2},则∪{x|0<x<2}=,故选:A.2.()A. B. C. D.【答案】B【解析】,故选:B3.若已知向量,,若,则的值为()A. B. C. D.【答案】D【解析】∵向量,,且,∴,即∴,故选:D4.在一组数据为,,…(,不全相等)的散点图中,若这组样本数据的相关系数为,则所有的样本点满足的方程可以是()A. B.C. D.【答案】A【解析】∵这组样本数据的相关系数为,∴这一组数据,,…线性相关,且是负相关,∴可排除D,B,C,故选:A5.我国古代数学家僧一行应用“九服晷(guǐ)影算法”在《大衍历》中建立了晷影长与太阳天顶距的对应数表,这是世界数学史上较早的一张正切函数表.根据三角学知识可知,晷影长度等于表高与太阳天顶距正切值的乘积,即.已知天顶距时,晷影长.现测得午中晷影长度,则天顶距为()(参考数据:,,,)A. B. C. D.【答案】B【解析】∵,且顶距时,晷影长.∴,当晷影长度,∴故选:B6.已知平面区域:,:,则点是的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】B【解析】平面区域,表示圆以及内部部分;的可行域如图三角形区域:则点P(x,y)∈Ω1是P(x,y)∈Ω2的必要不充分条件.故选:B.7.直三棱柱的所有棱长均为,则此三棱柱的外接球的表面积为()A. B. C. D. 【答案】C【解析】由直三棱柱的底面边长为,得底面所在平面截其外接球所成的圆O的半径r,又由直三棱柱的侧棱长为,则球心到圆O的球心距d,根据球心距,截面圆半径,球半径构成直角三角形,满足勾股定理,我们易得球半径R满足:R2=r2+d2,∴外接球的表面积S=4πR2.故选:C.8.若函数,则()A. 函数的最小正周期为B. 函数的最大值为C. 函数的一个对称中心为D. 函数在上是增函数【答案】D【解析】函数它的最小正周期为π,故排除A;函数的最大值为,故排除B;令x,求得f(x),故函数f(x)的图象不关于点对称;故排除C;,此时在上单调递增,∴函数在上是增函数故选:D9.如图,网格纸上小正方形的边长为,粗线画出的是某棱锥的三视图,则该棱锥中最长的棱长为()A. B. C. D.【答案】B【解析】作出四棱锥A﹣BCDE的直观图如图所示:由三视图可知底面BCDE是直角梯形,DE∥BC,BC⊥BE,DE⊥面ABE,AE⊥BE,且AE=BE=DE=4,BC=2,∴AD=AB=4,AC=6,CD,∴AC为四棱锥的最长棱.故选:B.10.若过抛物线:焦点的直线与相交于,两点,且,过线段的中点作轴的垂线交抛物线的准线于点,则的面积为()A. B. C. D.【答案】C【解析】抛物线:焦点为,设的方程为:,代入抛物线方程可得:,设A(,)、B(,),则+,,,∴,不妨取,则∴,∴的面积为故选:C11.函数的导函数满足在上恒成立,且,则下列判断一定正确的是()A. B. C. D.【答案】A【解析】令函数F(x),则F′(x),∵f′(x)>f(x),∴F′(x)>0,故函数F(x)是定义在R上的增函数,∴F(1)>F(0),即,故有f(1)>ef(0);又,∴,故选:A12.已知,则()A. B.C. D.【答案】B【解析】,∴∴而结合选项∴,故选:B二、填空题.13.复数的实部为__________.【答案】【解析】复数,则复数z的实部为.故答案为:.14.已知直线是双曲线:的一条渐近线,则双曲线的离心率为____.【答案】【解析】∵直线y=2x为双曲线C:1(a>0,b>0)的一条渐近线,∴2a=b,∴c a,∴e.故答案为:.15.海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径,两点间的距离,现在珊瑚群岛上取两点,,测得,,,,则,两点的距离为___.【答案】【解析】由已知,△ACD中,∠ACD=15°,∠ADC=150°,∴∠DAC=15°由正弦定理得,△BCD中,∠BDC=15°,∠BCD=135°,∴∠DBC=30°,由正弦定理,,所以BC;△ABC中,由余弦定理,AB2=AC2+BC2﹣2AC•BC•cos∠ACB=解得:AB,则两目标A,B间的距离为.故答案为:.16.若函数有最小值,则实数的取值范围为______.【答案】【解析】在上单调递增,∴,当时,,此时∴在上单调递减,在上单调递增,∴在上最小值为,若函数有最小值,的则,即,故答案为:三、解答题:解答须写出文字说明、证明过程和演算步骤.17.已知等比数列的各项均为正数,且,.(Ⅰ)求数列的通项公式;(Ⅱ)若数列满足,求数列的前项和.解:(Ⅰ)设数列的公比为,依题设有,因为,所以,,解得,,所以.(Ⅱ)由(Ⅰ)可得,从而,所以,.18.在三棱锥中,底面与侧面均为正三角形,,,为的中点.(Ⅰ)证明:平面平面;(Ⅱ)为线段上一点,且,求三棱锥的体积.解法一:(Ⅰ)因为是边长为的正三角形,为的中点,所以,同理,,又,因为,所以又,所以平面,又平面,所以平面平面.(Ⅱ)由(Ⅰ)得平面,所以,为直角三角形,所以,且,解得.在中,由,.解得,即即,,解法二: (Ⅰ)同解法一 (Ⅱ)由(Ⅰ)可得平面,所以, 即,, 所以, 得,则, 所以,又,所以平面,在中,,所以.19.党的十九大报告指出,要以创新理念提升农业发展新动力,引领经济发展走向更高形态.为进一步推进农村经济结构调整,某村举办水果观光采摘节,并推出配套乡村游项目现统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图:(Ⅰ)若将购买金额不低于元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取人,求这人中消费金额不低于元的人数;(Ⅱ)从(Ⅰ)中的人中抽取人作为幸运客户免费参加山村旅游项目,请列出所有的基本事件,并求人中至少有人购买金额不低于元的概率;(Ⅲ)为吸引顾客,该村特推出两种促销方案, 方案一:每满元可立减元;方案二:金额超过元但又不超过元的部分打折,金额超过元但又不超过元的部分打折,金额超过元的部分打折.若水果的价格为元/千克,某游客要购买千克,应该选择哪种方案.解:(Ⅰ)样本中“水果达人”的频率为所以样本中“水果达人”的人数为如图可知,消费金额在与的人数比为其中消费金额不低于元的人数为人所以,抽取的人中消费金额不低于元的人数(Ⅱ)由(Ⅰ)得,抽取的人中消费金额低于元的有人,记为,,消费金额不低于元的有人,记为,所有基本事件如下:,,,,,,,,,共有种,其中满足题意的有种所以(Ⅲ)依题意得,该游客要购买元的水果,若选择方案一,则需支付元选择方案二,则需支付元,所以选择方案二更优惠.20.已知椭圆:的左焦点为,且过点,为坐标原点.(Ⅰ)求椭圆的方程;(Ⅱ)点为椭圆上的动点,过点作平行于的直线交椭圆于,两点,求面积的取值范围.解:解法一:(Ⅰ)依题意得,左焦点,则右焦点即,且则得椭圆方程为(Ⅱ)当直线的斜率不存在时,,此时.当直线的斜率存在时,设直线的方程为.由消去得:.显然,设,,则故,.因为,所以点到直线的距离即为点到直线的距离,所以,,因为,所以,所以.综上,.21.若函数.(Ⅰ)讨论函数的单调性;(Ⅱ)若在上存在两个零点,求的取值范围.解:(Ⅰ)函数的定义域为,,当时,,在单调递减.当时,令,,其中舍去则当时,,则在上单调递减,当时,,则在上单调递增.所以在上单调递减,在上单调递增.综上所述,当时,在单调递减,当时,所以在上单调递减,在上单调递增.(Ⅱ)由(Ⅰ)得,当时,在单调递减,不合题意,舍去.当时,由于在上有两个零点,又因为,所以是的一个零点.因此问题等价于:在存在一个零点,又由(Ⅰ)得,当时,存在一个极值点,故,即.因此问题等价于:.因为,令,在恒成立,所以在单调递减,,所以成立,所以存在,.取,,,所以在存在一个零点.综上所述,.另解:当趋近于时,趋近于正无穷大,则.22.[选修4-4:坐标系与参数方程]在直角坐标系中,曲线的参数方程为(为参数),直线的方程为.(Ⅰ)以坐标原点为极点,轴的正半轴为极轴建立极坐标系,求曲线的极坐标方程和直线的极坐标方程;(Ⅱ)在(Ⅰ)的条件下,直线的极坐标方程为,设曲线与直线的交于点和点,曲线与直线的交于点和点,求的面积.解:(1)由,得曲线C的普通方程为,把,代入该式化简得曲线C的极坐标方程为:.因为直线:是过原点且倾斜角为的直线,所以直线的极坐标方程为:.(2)把代入得,故,把代入得,故,因为,所以的面积为.23.[选修4-5:不等式选讲]已知函数.(Ⅰ)求不等式的解集;(Ⅱ)若,且,求证:.解:解法一:(1)因,所以,由得:或或解得或或,所以不等式的解集为:.(2),又,,所以要证成立,只需证成立,即证,只需证成立,因为,,所以根据基本不等式成立,故命题得证.解法二:(1)因为,所以作出函数的图像(如下图)因为直线和函数图像的交点坐标为, . 所以不等式的解集为:(2),又,所以,,故所以成立.。
福建省宁德市2015年5月普通高中毕业班质量试卷英语试卷及答案

2015年宁德市普通高中毕业班质量检查英语本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
第一卷1至12页,第二卷13至14页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2.考生作答时,请将答案答在答题卡上,请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
在草稿纸、试卷上答题无效。
3.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.保持答题卡卡面清洁,不折叠,不破损。
考试结束后,将本试卷和答题卡一并交回。
第一卷(选择题共115分)第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Where does the conversation most probably take place?A. At the man’s house.B. In a restaurant.C. In an office.2. What is the relationship between May and Maria?A. Twin sisters.B. Close friends.C. Classmates.3. How will the woman go to the hotel?A. By taxi.B. By plane.C. By car.4. Why does the woman go to the post office?A. To post a letter.B. To send a telegraph.C. To meet a friend.5. Which subject does the woman think the boy is weak at?A. Physics.B. Math.C. Chemistry.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
高三数学月考试题及答案-宁德市2015届高中毕业班第二次质量检查(理)

2015年宁德市普通高中毕业班第二次质量检查(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题),第II 卷第(21)题为选考题,其它题为必考题.满分150分,考试时间120分钟. 参考公式:第I 卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若向量,,,则实数的值为( )A .B .C .2D .62.若集合,集合,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知等比数列的第项是二项式展开式的常数项,则( )A .B .C .D .4.若函数是定义在上的偶函数,则该函数的最大值为( ) A .5 B .4 C .3 D .25.阅读如图所示的程序框图,运行相应的程序.若该程序运行后输出的结果不大于20,则输入的整数的最大值为( )A .3B .4C .5D .6a (3,)m =b (2,1)=-//a b m 32-32{|21}x A x =>{|lg 0}B x x =>x A ∈x B ∈{}n a 541x x ⎛⎫+ ⎪⎝⎭37a a ⋅=61824362()1f x ax bx =++[1,2]a a --i6.已知某市两次数学测试的成绩和分别服从正态分布和,则以下结论正确的是( )A .第一次测试的平均分比第二次测试的平均分要高,也比第二次成绩稳定B .第一次测试的平均分比第二次测试的平均分要高,但不如第二次成绩稳定C .第二次测试的平均分比第一次测试的平均分要高,也比第一次成绩稳定D .第二次测试的平均分比第一次测试的平均分要高,但不如第一次成绩稳定7.已知双曲线的左、右焦点分别为,过点作直线轴交双曲线的渐近线于点.若以为直径的圆恰过点,则该双曲线的离心率为( )ABC .2D 8.某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天. 甲说:我在1日和3日都有值班; 乙说:我在8日和9日都有值班;丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是( ) A . 2日和5日 B . 5日和6日 C . 6日和11日 D . 2日和11日9.若关于的方程有三个实根,,,且满足,则的最小值为( )1ξ2ξ11(90,86)N ξ22(93,79)N ξ2222:1(0,0)x y C a b a b -=>>12,F F 1F l x ⊥C ,A B AB 2F x 320()x x x a a --+=∈R 1x 2x 3x 123x x x ≤≤1xA .B .C .D .010.如图所示为某几何体的正视图和侧视图,则该几何体体 积的所有可能取值的集合是( )A .B .C .D .第II 卷 (非选择题共100分)二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡相应位置. 11.复数(为虚数单位)在复平面上对应的点到原点的距离为__________. 12.设是抛掷一枚骰子得到的点数,则方程有两个不等实根的概率 为 .13.若关于x ,y 的不等式组 表示的平面区域是一个直角三角形,则k 的值为 .14.若在圆上有且仅有两个点到原点的距离为1,则实数的取值范围是 . 15.的中,.若点为边上的一点,且满足,则当取最小时,的长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分13分)2-1-13-12,33⎧⎫⎨⎬⎩⎭12,,336π⎧⎫⎨⎬⎩⎭1233V V ⎧⎫≤≤⎨⎬⎩⎭203V V ⎧⎫<≤⎨⎬⎩⎭1iiz +=i a 20x ax a ++=0,,10x y x kx y ≥⎧⎪≥⎨⎪-+≥⎩22:()4C x y a +-=O a ABC ∆3A π∠=D BC 2CD DB =AD BD将射线绕着原点逆时针旋转后所得的射线经过点. (Ⅰ)求点的坐标;(Ⅱ)若向量,,求函数,的值域.17.(本小题满分13分)某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数; (Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为,乙队猜对前两条的概率均为,猜对第3条的概率为.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?1(0)7y x x =≥4π(cos sin )A θθ,A (sin 2,2cos )x θ=m (3sin ,2cos2)x θ=n ()f x ⋅=m n [0,2x π∈]34451218. (本小题满分13分)如图,在四棱柱中,底面是矩形,且,,.若为的中点,且. (Ⅰ)求证:平面; (Ⅱ)线段上是否存在一点,使得二面角为? 若存在,求出的长;不存在,说明理由.19. (本小题满分13分)已知点,直线,直线于,连结,作线段的垂直平分线交直线于点.设点的轨迹为曲线.(Ⅰ)求曲线的方程;(Ⅱ)过点作曲线的两条切线,切点分别为, (ⅰ)求证:直线过定点;(ⅱ)若,过点作动直线交曲线于点,直线交于点,试探究是否为定值?若是,求出该定值;不是,说明理由.1111ABCD A B C D -ABCD 22AD CD ==12AA =13A AD π∠=O AD 1CD AO ⊥1AO ⊥ABCD BC P 1D A A P --6πBP (0,1)F 1:1l y =-21l l ⊥P PF PF 2l H H ΓΓP Γ,C D CD (1,1)P -P l Γ,A B CD l Q PQ PQ PAPB+20.(本小题满分14分)已知函数在点处的切线斜率为. (Ⅰ)求实数的值;(Ⅱ)设,若对恒成立,求的取值范围;(Ⅲ)已知数列满足,,求证:当时 (为自然对数的底数,).21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B 铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.(1)(本小题满分7分)选修4—2:矩阵与变换在平面直角坐标系中,矩阵对应的变换将平面上任意一点变换为点2()e ()x f x x ax -=+(0,(0))f 2a 3()(e g x x x t t =---∈R )()()()g x f x ≥[0,1]x ∈t {}n a 11a =11(1)n n a a n+=+2,n n ≥∈N 11213()()()62e n a a af f f n n nn -⎛⎫+++<⋅+ ⎪⎝⎭e e 2.71828≈M (,)P x y.(Ⅰ)求矩阵的逆矩阵;(Ⅱ)求曲线在矩阵的变换作用后得到的曲线的方程.(2)(本小题满分7分)选修4-4:坐标系与参数方程已知极坐标系的极点在直角坐标系的原点,极轴与轴的正半轴重合,直线的参数方程为(为参数), 圆的极坐标方程为.(Ⅰ)求直线的普通方程和圆的直角坐标方程;(Ⅱ)若圆上的点到直线的最大距离为,求的值.(3)(本小题满分7分)选修4—5:不等式选讲 已知函数. (Ⅰ)求函数的最小值;(Ⅱ)若正实数满足.(2,3)P x y x '+M 1M -410x y +-=M C 'x l x y ⎧=+⎪⎪⎨⎪=⎪⎩t C 222sin()1(0)4r r ρρθπ+++=>l C C l r ()|5||3|f x x x =-+-m ,a b 11a b +=2212m a b+≥2013年宁德市普通高中毕业班质量检查(理科)参考答案及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考查内容比照评分标准指定相应的评分细则.二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基础知识和基本运算,每小题5分,满分50分.1.A 2.B 3.D 4.A 5.B 6.C 7.D 8.C 9.B 10.D 二、填空题:本题考查基础知识和基本运算,每小题4分,满分20分.1112. 13.或14. 15三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程和演算步骤. 16.本题考查三角函数、平面向量等基础知识,考查运算求解能力,考查函数与方程的思想、数形结合的思想,满分13分. 解: (Ⅰ)设射线的倾斜角为,则,.……………1分 ∴,……………………………………………4分 ∴由解得……………………………………………6分∴点的坐标为.…………………………………………………………7分(Ⅱ)……………………………………8分…………………………………………………10分 131-0(3,1)(1,3)--1(0)7y x x =≥α1tan 7α=(0,)2απ∈1147tan tan()143117θα+π=+==-⨯22sin cos 1,sin 4,cos 3θθθθ⎧=⎪⎨=⎪⎩+4sin ,53cos .5θθ⎧=⎪⎪⎨⎪=⎪⎩A 3455⎛⎫⎪⎝⎭,()3sin sin 22cos 2cos2f x x x θθ⋅+⋅=1212sin 2cos255x x =+).4x π=+由,可得,∴,………………………………………………………12分 ∴函数的值域为.……………………………………………13分 17.本小题主要考查概率、概率与统计等基础知识,考查推理论证能力、数据处理能力、运算求解能力及应用意识,考查或然与必然的思想,满分13分. 解法一:(Ⅰ)设测试成绩的中位数为,由频率分布直方图得, ,解得:.……………………………2分 ∴测试成绩中位数为.进入第二阶段的学生人数为200×(0.003+0.0015)×20=18人.…………………4分 (Ⅱ)设最后抢答阶段甲、乙两队猜对灯谜的条数分别为、,则,……………………………5分∴.……………………………6分∴最后抢答阶段甲队得分的期望为,………………………8分∵,,,,∴, …………………………………………10分 ∴最后抢答阶段乙队得分的期望为.……………………12分∴,∴支持票投给甲队..……………………………13分 解法二:(Ⅰ)同解法一. ……………………………4分(Ⅱ)设最后抢答阶段甲队获得的分数为, 则所有可能的取值为,,,., , [0,2x π∈]2[,]444x ππ5π+∈2sin(2)[,1]42x π+∈-()f x 12[5-x (0.00150.019)20(140)0.0250.5x +⨯+-⨯=143.6x =143.6ξη3(3,)4B ξ39344E ξ=⨯=99[(3)]203044--⨯=2111(0)5250P η⎛⎫==⨯= ⎪⎝⎭2411119(1)25525250P η⎛⎫==⨯⨯⨯+⨯= ⎪⎝⎭24141112(2)25255225P η⎛⎫==⨯+⨯⨯⨯= ⎪⎝⎭24116(3)5250P η⎛⎫==⨯= ⎪⎝⎭9121621012350255010E η=+⨯+⨯+⨯=2121[(3)]20241010--⨯=1203012024+>+ξξ60-20-2060331(60)1464P ξ⎛⎫=-=-= ⎪⎝⎭213339(20)14464P C ξ⎛⎫=-=-=⎪⎝⎭,. ∴.……………………………8分 设最后抢答阶段乙队获得的分数为,则所有可能的取值为,,,. ∵,,,,∴,……………………………12分 ∵,∴支持票投给甲队.…………………………………………13分18.本小题主要考查直线与平面的位置关系,二面角的大小等基础知识,考查空间想象能力、推理论证能力和运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想,满分13分.(Ⅰ)证明:∵,且,, ∴…………………………………………2分 ∴ ∴.…………………………………………3分 又,且,∴平面.…………………………………………5分 (Ⅱ)解:过作,以为原点,建立空间直角坐标系(如图),3233327(20)14464P C ξ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭3327(60)464P ξ⎛⎫=== ⎪⎝⎭19276020206030646464E ξ=-⨯-⨯+⨯+=ηη60-20-20602111(60)5250P η⎛⎫=-=⨯= ⎪⎝⎭2411119(20)25525250P η⎛⎫=-=⨯⨯⨯+⨯= ⎪⎝⎭24141112(20)25255225P η⎛⎫==⨯+⨯⨯⨯= ⎪⎝⎭24116(60)5250P η⎛⎫==⨯= ⎪⎝⎭191216602020602450502550E η=-⨯-⨯+⨯+⨯=1203012024+>+13A AD π∠=12AA =1AO =1A O ==22211AO AD AA +=1AO AD ⊥1CD AO ⊥CD AD D =1AO ⊥ABCD O //Ox AB O O xyz -则,,……………………………6分 设,平面的法向量为=, ∵,,且 取,得=.……… ……………………8分又平面,且平面, ∴平面平面. 又,且平面平面∴平面.不妨设平面的法向量为=.………………………10分 由题意得,……………………12分解得或(舍去).∴当的长为时,二面角的值为.………………………13分 19.本题主要考查直线、抛物线、直线与抛物线的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、化归与转化思想,考查考生分析问题和解决问题的能力,满分13分.解法一: (Ⅰ)由题意可知,,(0,1,0)A-1A (1,,0)([1,1])P m m ∈-1A AP 1n (,,)x yz 1AA =(1,1,0)AP m =+1110,(1)0.AA y AP x m y ⋅⋅⎧=+=⎪⎨=++=⎪⎩n n 1z =1n 1),m +1AO ⊥ABCD 1AO ⊂11A ADD 11A ADD ⊥ABCD CD AD ⊥11A ADD ABCD AD =CD ⊥11A ADD 11A ADD 2n(1,0,0)12cos ,==n n 1m =3m =-BP 21D A A P --6πHF HP =∴点到点的距离与到直线的距离相等,……………………………2分 ∴点的轨迹是以点为焦点, 直线为准线的抛物线,………………3分 ∴点的轨迹方程为.…………………………………………4分 (Ⅱ)(ⅰ)证明:设,切点.由,得. ∴直线,…………………………………………5分又过点,,∴,∴,即.…………………………………………6分同理,∴直线的方程为,…………………………………………7分∴直线过定点.…………………………………………8分(ⅱ)由(Ⅱ)(ⅰ)得,直线的方程为.设,与方程联立,求得.……………………………………9分设,联立与,得 ,由根与系数的关系,得.…………………………………………10分 ∵同号, ∴ H (0,1)F 1:1l y =-H (0,1)F 1:1l y =-H 24x y =0(,1)P x -(,),(,)C C DD C x y D x y 214y x =12y x '=01:1()2C PC y x x x +=-PC C 214C C y x =2001111()222C C C C C y x x x x x x +=-=-01122C C C y y x x +=-01102C C x x y -+=01102D D x x y -+=CD 01102xx y -+=CD (0,1)CD 1102x y -+=:1(1)l y k x +=-1102x y -+=4221Q kx k +=-(,),(,)A A B B A x y B x y 1(1)y k x +=-24x y =24440x kx k -++=4,44A B A B x x k x x k +=⋅=+1,1,1Q A B x x x ---11PQ PQPQ PAPB PA PB ⎛⎫+=+⎪ ⎪⎝⎭11111Q A B x x x ⎛⎫-+⎪⎪--⎭…………………………………………11分, ∴为定值,定值为2.…………………………………………13分解法二: (Ⅰ)设,由题意可知, ,, ………………………………2分 ∴化简得,∴点的轨迹方程为.…………………………………………4分 (Ⅱ)(ⅰ)证明:设切点,直线的方程为. 联立与得,由根与系数的关系,得.…………………………………………5分由,得. ∴直线,又,所以.同理.…………………………………………6分联立两直线方程,解得,∴,即直线过定点.…………………………………………8分(ⅱ)由(Ⅱ)(ⅰ),解得,∴, ∴直线的方程为.以下同解法一.20.本题考查函数、导数等基础知识,考查推理论证能力和运算求解能力,考查函数与方程()11111Q A B x x x ⎛⎫=-⋅+ ⎪--⎝⎭()()24212111A B A B x x k k x x +-+⎛⎫=-⋅⎪---⎝⎭5422215k k -=⋅=-PQ PQ PAPB+(,)H x y HF HP =1y +24x y =H 24x y =(,),(,)C C D D C x y D x y CD y kx t =+y kx t =+24x y =2440x kx t --=4,4C D C D x x k x x t +=⋅=-214y x =12y x '=1:()2C C C PC y y x x x -=-214C C y x =211:24C C PC y x x x =-211:24D D PD y x x x =-1y t =-=-1t =CD (0,1)11()22C D x x k =+=12k =CD 1102x y -+=的思想、化归与转化的思想、数形结合的思想,考查运用数学知识分析和解决问题的能力,满分14分.解: (Ⅰ),…………………1分 由,得.…………………………………………3分 (Ⅱ).由,得,.当时,该不等式成立; …………………………………………4分当,不等式对恒成立,即.…………………………5分设,,,,∴在单调递增, ∴,∴在单调递增, …………………………………………………………7分∴,∴………………………………………………………………………………8分(Ⅲ)∵,∴,又, ∴时,,对也成立, ∴.……………………………10分 ∵当时,, ∴在上单调递增,且.22()e ()e (2)e (2)x x x f x x ax x a x ax x a ---'=-+++=-+--(0)()2f a '=--=2a =2()e (2)x f x x x -=+()()g x f x ≥23()e (2)ex x x t x x ----≥+[0,1]x ∈0x =(0,1]x ∈3e (2)ex x t x --++≥+(0,1]x ∈max 3e (2)e xt x x -⎡⎤≥++-⎢⎥⎣⎦3()e (2)ex h x x x -=++-(0,1]x ∈()e (2)e 1e (1)1x x x h x x x ---'=-+++=-++()e (1)e e 0x x xh x x x ---''⎡⎤=--++=⋅>⎣⎦()h x '(0,1]()(0)0h x h ''>=()h x (0,1]max 33()(1)11e eh x h ==+-=1.t ≥11(1)n n a a n+=+11n n a n a n++=11a =2n ≥321121231121n n n a a a na a n a a a n -=⋅⋅⋅⋅=⋅⋅⋅⋅=-1n =n a n =[0,1]x ∈2()e (2)0x f x x -'=-->()f x [0,1]()(0)0f x f ≥=又∵表示长为,宽为的小矩形的面积,∴, ∴.…… 12分又由(Ⅱ),取,得,∴, ∴, ∴.…………………………………………14分 21.(1)本题主要考查矩阵与变换等基础知识,考查运算求解能力及化归与转化思想.满分7分.解:(Ⅰ)设点在矩阵对应的变换作用下所得的点为, 则即, ∴.…………………………………………1分 又,∴.…………………………………………3分 (Ⅱ)设点在矩阵对应的变换作用下所得的点为, 则, 即…………………………………………5分1()i f n n ⋅(11,)i n i ≤≤-∈N ()i f n 1n11()()i n i nif f x dx n n +⋅<⎰(11,)i n i ≤≤-∈N 1112011121()()()()()()()n a aa n f f f f f f f x dx n n nn n n nn --⎡⎤⎡⎤+++=+++<⎢⎥⎢⎥⎣⎦⎣⎦⎰1t =23()()(1)ef xg x x x ≤=-++113210011313()()(1)32e62ef x dxg x dx x x ≤=-++=+⎰⎰112113()()()62en f f f n n n n -⎡⎤+++<+⎢⎥⎣⎦11213()()()62e n a a a f f f n n nn -⎛⎫+++<⋅+ ⎪⎝⎭(),P x y M (,)P x y '''2,3,x x y y x '=+⎧⎨'=⎩2130x x y y '⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪'⎝⎭⎝⎭⎝⎭2130M ⎛⎫= ⎪⎝⎭det()3M =-1103213M -⎛⎫- ⎪⎪= ⎪-- ⎪⎝⎭(),A x y M (,)A x y '''1103213x x x M y y y -⎛⎫- ⎪''⎛⎫⎛⎫⎛⎫ ⎪== ⎪ ⎪ ⎪'' ⎪⎝⎭⎝⎭⎝⎭-- ⎪⎝⎭1,32,3x y y x y ⎧'=-⎪⎪⎨⎪''=--⎪⎩∴代入,得,即变换后的曲线方程为.…………………………7分(2)本题主要考查直线的参数方程及极坐标方程等基础知识,考查运算求解能力及化归与转化思想.满分7分.解:(Ⅰ)直线的直角坐标方程为,………………………………………2分圆的直角坐标方程为.………………………… 4分 (Ⅱ)∵圆心,半径为,………………………………………5分 圆心到直线的距离为,………………………6分又∵圆上的点到直线的最大距离为3,即,∴.………………………………………7分(3)本题主要考查绝对值不等式和均值不等式等基础知识,考查运算求解能力,考查化归与转化思想.满分7分.解:(Ⅰ)∵,…………………………………2分 当且仅当时取最小值2,……………………3分 .…………………………………4分(Ⅱ), , ∴.…………………………………………7分410x y +-=241033y x y '⎛⎫''----= ⎪⎝⎭210x y ++=22222()()(0)x y r r +=>22(,)22C --C ()|5||3|532f x x x x x =-+-≥-+-=[3,5]x ∈2m ∴=22222121()[1](13a b a ++≥⨯+=222123()2a b ∴+⨯≥22122a b +≥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015届福建省宁德市高三普通高中毕业班5月质检数学文试卷数学(文科)试卷本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.本卷满分150分,考试时间120分钟. 注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上.2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.4.保持答题卡卡面清楚,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回. 参考公式:第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|320}M x x x =-+=,{2,1,1,2}N =--,则M N =IA .{2,1}--B .{1,2}C .{2,1}-D .{2,1,1,2}-- 2.若x ∈R ,则“21x <”是“10x -<<”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人. 现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取 A .55人,80人,45人 B .40人,100人,40人 C .60人,60人,60人D .50人,100人,30人4.经过圆22(2)1x y -+=的圆心且与直线210x y -+=平行的直线方程是,,(n x x ++-A .240x y --=B .240x y -+=C .220x y +-=D .220x y ++= 5.设m ,n 是两条不同的直线,α,β是两个不同的平面,下列正确的是A .若m ∥α,n ⊂α,则m ∥nB .若m ∥α,m ∥β,则α∥βC .若m ∥α,α⊥β,则m ⊥βD .若m ∥n ,m ⊥α,则n ⊥α 6.已知sin α=(0,)2απ∈,则tan 2α= A .43- B .43C .12-D .27.下列函数中,既为奇函数又在(0,)+∞内单调递减的是A .()sin f x x x =B .12()f x x -=C .1()1xxe f x e-=+ D .3()f x x x=-8.运行如图所示的程序,若输出y 的值为1, 则可输入x 的个数..为 A .0 B .1C .2D .39.已知实数,x y 满足122x x y x y ≥⎧⎪+≤⎨⎪-≤⎩,若不等式3ax y -≤恒成立,则实数a 的取值范围为A .(,4]-∞B .3(,]2-∞ C3[ D .[2,4]10.已知四棱锥P ABCD -的三视图如图所示,则此四棱锥的侧面积为A .6+B .9+C .12+D .20+11.已知点P 是ABC ∆所在平面上一点,AB 边的中点为D ,若23PD PA CB =+,则ABC ∆与ABP ∆的面积比为A .3B .2C .1D .1212. O 为坐标原点,,A B 为曲线y =上的两个不同点,若6OA OB ⋅=,则直线AB 与圆2249x y +=的位第8题图侧视图俯视图第10题图置关系是A. 相交B. 相离C. 相交或相切D. 相切或相离第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡的相应位置. 13.复数i(12i)z =+(i 为虚数单位),则z = .14.在区间(0,4)内任取一个实数x ,则使不等式2230x x --<成立的概率为 . 15.关于x 的方程2log 0x a -=的两个根为1212,()x x x x <,则122x x +的最小值为 .16.已知函数()sin cos (22x x f x a a =+∈R),且()()3f x f 2π≤恒成立. 给出下列结论:①函数()y f x =在[0,]32π上单调递增;②将函数()y f x =的图象向左平移3π个单位,所得图象对应的函数为偶函数;③若2k ≥,则函数()(2)3g x kx f x π=--有且只有一个零点.其中正确的结论是 .(写出所有正确结论的序号)三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知等比数列{}n a 的前n 项和2n n S r =+. (Ⅰ)求实数r 的值和{}n a 的通项公式;(Ⅱ)若数列{}n b 满足11b =,121log n n n b b a ++-=,求n b .18.(本小题满分12分)某中学刚搬迁到新校区,学校考虑,若非住校生....上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课. 为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为[0,10),[10,20),[20,30),[30,40),[40,50].(Ⅰ)求频率分布直方图中a 的值;(Ⅱ)从统计学的角度说明学校是否需要推迟5分钟上课; (Ⅲ)若从样本单程时间不小于30分钟的学生中, 随机抽取2人,求恰有一个学生的单程时间落在[40,50]上的概率.19.(本小题满分12分)已知函数()2sin()f x x ωϕ=+(0,)2ωϕπ><在一个周期内的图象如图所示,其中M (,2)12π,N (,0)3π.(Ⅰ)求函数()f x 的解析式;(Ⅱ)在ABC ∆中,角,,A B C 的对边分别是a,b,c且3,()2Aa c f ==ABC ∆的面积.20.(本小题满分12分)如图四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,//AB CD , 90ABC ︒∠=,且2,1CD AB BC PA ====,PD =(Ⅰ)求三棱锥A PCD -的体积;(Ⅱ)问:棱PB 上是否存在点E ,使得//PD 平面ACE ? 若存在,求出BEBP的值,并加以证明;若不存在,请说明理由.21.(本小题满分12分)已知点(A B ,动点E 满足直线EA 与直线EB 的斜率之积为12-.(Ⅰ)求动点E 的轨迹C 的方程;(Ⅱ)设过点()1,0F 的直线1l 与曲线C 交于点,P Q ,记点P 到直线2:2l x =的距离为d .(ⅰ)求PF d的值;(ⅱ)过点F 作直线1l 的垂线交直线2l 于点M ,求证:直线OM 平分线段PQ .22.(本小题满分14分)C已知函数1()ln (1)2f x x a x =--(a ∈R ).(Ⅰ)若2a =-,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)若不等式()0f x <对任意(1,)x ∈+∞恒成立.(ⅰ)求实数a 的取值范围;(ⅱ)试比较2a e -与2e a -的大小,并给出证明(e 为自然对数的底数, 2.71828e ≈).2015年宁德市普通高中毕业班第二次质量检查数学(文科)试题参考答案及评分标准说明:一、本解答指出了每题要考察的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考察内容比照评分标准指定相应的评分细则。
二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分。
一、选择题:本题考查基础知识和基本运算.本大题共12小题,每小题5分,共60分.1.B 2.B 3.D 4.A 5.D 6.A 7.C 8.D 9.B 10.C 11.C 12.A二、填空题:本题考查基础知识和基本运算.本大题共4小题,每小题4分,共16分.13.2i --; 14.34; 15.; 16.①③.三、解答题:本大题共6小题,共74分.17.本题主要考查等差数列、等比数列、数列求和等基础知识;考查推理论证与运算求解能力,满分12分.解:(Ⅰ)∵2n n S r =+,∴112a S r ==+,2212a S S =-=,3324a S S =-=. ············································ 3分 ∵数列{}n a 是等比数列,∴2213a a a =⋅,即224(2)r =+, ·········································································· 4分∴1r =- . ············································································································· 5分 ∴数列{}n a 是以1为首项,2为公比的等比数列, ·············································· 6分 ∴ 12()n n a n -*=∈N . ······························································································ 7分 (Ⅱ)∵12n n a +=,∴12log 2n n n b b n +-==, ······················································ 8分 当2n ≥时,121321()()()n n n b b b b b b b b -=+-+-++-112(1)n =++++- ···································································· 9分(1)12n n-=+211122n n =-+ ··············································································· 11分 又11b =符合上式,∴2111()22n b n n n *=-+∈N . ················································································· 12分18.本题主要考查概率、统计等基础知识,考查数据处理能力、抽象概括能力、运算求解能力以及应用意识,考查或然与必然思想、化归与转化思想.满分12分. 解:(Ⅰ)时间分组为[0,10)的频率为110(0.060.020.0030.002)0.15-+++=, ····························································· 2分∴0.150.01510a ==, 所以所求的频率直方图中a 的值为0.015. ···························································· 3分 (Ⅱ)100个非住校生上学路上单程所需时间的平均数: 0.1550.6150.2250.03350.0245x =⨯+⨯+⨯+⨯+⨯ ············································· 4分 0.7595 1.050.9=++++ 16.7=. ··················································································································· 5分 因为16.720<,所以该校不需要推迟5分钟上课. ······································································· 6分(Ⅲ)依题意满足条件的单程所需时间在[30,40)中的有3人,不妨设为123,,a a a , 单程所需时间在[40,50]中的有2人,不妨设为12,b b , ····································· 7分 从单程所需时间不小于30分钟的5名学生中,随机抽取2人共有以下10种情况:12(,)a a ,13(,)a a ,11(,)a b ,12(,)a b ,23(,)a a ,21(,)a b ,22(,)a b ,31(,)a b ,32(,)a b ,12(,)b b ;··············································································· 10分 其中恰有一个学生的单程所需时间落在[40,50]中的有以下6种:11(,)a b ,12(,)a b ,21(,)a b ,22(,)a b ,31(,)a b ,32(,)a b ; ···························· 11分 故恰有一个学生的单程所需时间落在[40,50]中的概率63105P ==. ··············· 12分 19.本题主要考查解三角形,三角函数的图象与性质等基础知识;考查运算求解能力,考查化归与转化思想、数形结合思想.满分12分. 解:(Ⅰ)由图像可知:函数()f x 的周期4()312T πππ=⨯-=, ································ 1分∴22ωπ==π.·········································································································· 2分 又()f x 过点(,2)12π,∴()2sin()2126f ππϕ=+=,sin()16πϕ+=, ························································ 3分∵2πϕ<,2(,)633πππϕ+∈-,∴62ππϕ+=,即3πϕ=. ························································································ 4分∴()2sin(2)3f x x π=+. ··························································································· 5分(Ⅱ)∵()2sin()23A f A π=+即sin()3A π+=,又4(0,),(,)333A A ππππ∈+∈∴233A ππ+=,即3A π=. ······················································································ 7分在ABC ∆中,,33A a c π===,由余弦定理得 2222cos a b c bc A =+-, ······························································· 8分 ∴21393b b =+-,即2340b b --=, 解得4b =或1b =-(舍去). ··············································································· 10分∴11sin 43sin 223ABC S bc A π∆==⨯⨯⨯=························································· 12分20.本题主要考查空间线与线、线与面的位置关系、体积的计算等基础知识;考查空间想象能力、运算求解能力及推理论证能力,满分12分.解:(Ⅰ)取CD 中点G ,连接AG ,2,//,CD AB AB CD = //,,AB GC AB GC ∴=∴四边形AGCB 为平行四边形,090AGD DCB ABC ∴∠=∠=∠=在Rt AGD ∆中,11,1,2AG BC DG CD ====AD ∴········································································ 1分 2223,123,PD PA AD ∴=+=+=222,PD PA AD =+090,PAD ∴∠= 即,PA AD ⊥ ················································································· 2分平PAD ⊥面平ABCD 面,平PAD 面平ABCD AD =面PA ∴⊥平ABCD 面································································································· 3分 112ACD S CD AG ∆=⋅=, ·························································································· 4分 A PCD P ACD V V --∴= ····································································································· 5分13ACD S PA ∆=⋅⋅ 111133=⨯⨯=. ····························································································· 6分 (II )棱PB 上存在点E ,当13BE BP =时,//PD 平面ACE .···································· 7分 证明:连结BD 交AC 于点O ,连结OE .∵//,2AB CD CD AB =∴1,2BO AB OD CD == ···················································· 8分 ∴13BO BD =,又13BE BP = ∴BO BEBD BP=, ∴//,OE DP ····························································· 10分 又,OE ACE PD ACE ⊂⊄面,面 //PD ACE ∴面.········································································································ 12分21.本题主要考查直线、椭圆、轨迹等基础知识及直线与圆锥曲线的位置关系;考查运算求解能力、推理论证能力;考查特殊与一般的思想、化归与转化思想.满分12分. 解法一:(Ⅰ)设(,)E x y ,依题意得 1,2EA EB k k ⋅==-(x ≠, ·········································· 1分 整理得2212xy +=,∴动点E 的轨迹C 的方程为 221(2x y x +=≠. ············································ 3分(Ⅱ)(ⅰ)(1,0)F ,设11(,),P x y 则 221112x y =-, ·············································· 4分∴1||PF d =······················································································· 5分1=1=. ········································································································ 7分 (说明:直接给出结论正确,没有过程得1分)(ⅱ)依题意,设直线22:1,(,)PQ x my Q x y =+,联立221,12x my x y =+⎧⎪⎨+=⎪⎩可得22(2)210m y my ++-=, ················································ 8分 显然12220,,2my y m ∆>+=-+ ··············································································· 9分 所以线段PQ 的中点T 坐标为222(,),22mm m -++ ·················································· 10分 又因为1,FM l ⊥故直线FM 的方程为(1)y m x =--, 所以点M 的坐标为(2,)m -,所以直线OM 的方程为:,2my x =-···································································· 11分 因为222(,)22m T m m -++满足方程,2my x =-故OM 平分线段.PQ ···························································································· 12分 解法二:(Ⅰ)(Ⅱ)(ⅰ)同解法一(ⅱ)当直线1l 的方程为1x =时,显然OM 平分线段PQ ; ···························· 8分当直线1l 的方程为(1)(0)y k x k =-≠时,设22(,)Q x y 联立22(1),12y k x x y =-⎧⎪⎨+=⎪⎩可得2222(21)4220k x k x k +-+-=, 显然212240,,21k x x k ∆>+=+·················································································· 9分 所以线段PQ 的中点坐标为2222(,)2121k kT k k -++ ················································· 10分 又因为1,FM l ⊥故直线FM 的方程为1(1)y x k=--,所以点M 的坐标为1(2,)k-,。
