补充教学:连接体问题
4连接体问题及解题方法

4连接体问题及处理方法一、连接体问题1.连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统.2.连接体题型(1)系统内所有物体相对静止,即运动情况相同,a 也相同------相对静止问题(2)系统内物体相对运动,运动情况不同,a 也不同------相对运动问题二、处理方法1整体法分析系统受力时只分析外力不必分析内力;在用隔离法解题时要注意判明隔离体的运动方向和加速度方向,同时为了方便解题,一般我们隔离受力个数少的物体.2.相对静止类:程。
(整体与隔离结合使用)例1.A 、B 两物体靠在一起,放在光滑水平面上,m B =6Kg ,今用水平力F A =6N 推A ,用水平力F B =3N 拉B ,A 、B 有多大?3.相对运动问题:例2.如图所示,光滑水平面上静止放着长L =1.6 m 、质量为M =3 kg 的木板.一个质量为m =1 kg 的小木块放在木板的最右端,m 与M 之间的动摩擦因数μ=0.1,今对木板施加一水平向右的拉力F ,若2s 时两者脱离,则F 为多大?4.判断相对静止还是相对运动:以最容易达到最大加速度的物体作为切入点,进入分析例3.如图所示,m 1=40 kg 的木板放在无摩擦的地板上,木板上又放m 2=10 kg 的石块,石块与木板间的动摩擦因数μ=0.6,试问(1)当水平力F =50 N 时,石块与木板间有无相对滑动?(2)当水平力F =100 N 时,石块与木板间有无相对滑动?(g =10 m/s 2)此时m 2的加速度为多大?5.方法总结①.当它们具有共同加速度时,一般是先整体列牛顿第二定律方程,再隔离受力个数少的物体分析列牛顿第二定律方程.②.当它们的加速度不同且涉及到相对运动问题,一般采用隔离法分别分析两个物体的运动情况,再找它们运动或受力的联系点列辅助条件方程.练习题1.两个物体A 和B ,质量分别为m 1和m 2,互相接触放在光滑水平面上,如图所示,对物体A 施以水平的推力F ,则物体A 对物体B 的作用力等于( )A .211m m m + FB .212m m m + FC .FD .21m m F 2.上题若m 1与m 2与水平面间有摩擦力且摩擦因数均为μ则A 对B 作用力等于为( )3.如图所示,光滑平面上以水平恒力F 拉动小车和木块,一起做无相对滑动的加速运动,若小车质量为M ,木块质量为m ,加速度大小为a ,木块和小车间的动摩擦因数为μ,对于这个过程某同学用以下四个式子来表示木块受到的摩擦力大小,正确的是() A.F-Ma B.μma C.μmg D.Ma4.如图所示,物体P置于水平面上,用轻细线跨过质量不计的光滑定滑轮连接一个重力G=10N的重物,物体P向右运动的加速度为a1;若细线下端不挂重物,而用F=10N的力竖直向下拉细线下端,这时物体P的加速度为a2,则( )A.a1>a2B.a1=a2C.a1<a2D.条件不足,无法判断5.如图所示,质量分别为M、m的滑块A、B叠放在固定的、倾角为θ的斜面上,A与斜面间、A与B之间的动摩擦因数分别为μ1,μ2,当A、B从静止开始以相同的加速度下滑时,B受到摩擦力()A.等于零B.方向平行于斜面向上C.大小为μ1mgcosθD.大小为μ2mgcosθ6.相同材料的物块m和M用轻绳连接,在M上施加恒力F,使两物块作匀加速直线运动,求在下列各种情况下绳中张力。
牛顿第二定律的应用——连接体问题

牛顿第二定律的应用――― 连接体问题一、连接体与隔离体两个或两个以上物体相连接组成的物体系统,称为 。
如果把其中某个物体隔离出来,该物体即为。
二、连接体问题的分析方法1.整体法:连接体中的各物体如果 ,求加速度时可以把连接体作为一个整体。
运用 列方程求解。
2.隔离法:如果要求连接体间的相互作用力,必须隔离其中一个物体,对该物体应用 求解,此法称为隔离法。
3.整体法与隔离法是相对统一,相辅相成的。
本来单用隔离法就可以解决的连接体问题,但如果这两种方法交叉使用,则处理问题就更加方便。
如当系统中各物体有相同的加速度,求系统中某两物体间的相互作用力时,往往是先用 法求出 ,再用 法求 。
【典型例题】例1.两个物体A 和B ,质量分别为m 1和m 2,互相接触放在光滑水平面上,如图所示,对物体A 施以水平的推力F ,则物体A 对物体B 的作用力等于( )A.F m m m 211+B.F m m m 212+C.FD.F m m 21 练习:1.若m 1与m 2与水平面间有摩擦力且摩擦因数均为μ则对B 作用力等于 。
2.如图右所示,质量为m 1、m 2的物块在F 1、F 2共同作用下向右运动。
已知m 1=3kg m 2=2kg F 1=14 N F 2=4N ,求m 1和m 2之间细绳的作用力F T 为多少?A B m 1 m 2 F3.如右图所示,物体m1、m2用一细绳连接,两者在竖直向上的力F的作用下向上加速运动,重力加速度为g,求细绳上的张力?例2:如图右,m1、m2用细线吊在光滑定滑轮,m1=3kg m2=2kg,当m1、m2开始运动时,求细线受到的张力?例3:如图所示,箱子的质量M=5.0kg,与水平地面的动摩擦因数μ=0.22。
在箱子顶板处系一细线,悬挂一个质量m=1.0kg的小球,箱子受到水平恒力F的作用,使小球的悬线偏离竖直方向θ=30°角,则F应为多少?(g=10m/s2)练习:如图所示,在前进的车厢的竖直后壁上放一个物体,物体与壁间的静摩擦因数μ=0.8,要使物体不致下滑,车厢至少应以多大的加速度前进?(g=10m/s2)例4:如图所示,质量分别为m 和2m 的两物体A 、B 叠放在一起,放在光滑的水平地面上,已知A 、B 间的最大摩擦力为A 物体重力的μ倍,若用水平力作用在B 上,使A 、B 保持相对静止做加速运动,则作用于B 的作用力为多少?练习.如图A 、B 、C 为三个完全相同的物体,当水平力F 作用于B 上,三物体可一起匀速运动。
高中物理连接体问题

牛顿第二定律——连接体问题(整体法与隔离法)一、连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统 二、处理方法——整体法与隔离法系统运动状态相同整体法问题不涉及物体间的内力 使用原则隔离法三、连接体题型:1【例1】A 、B 平力N F A 6=推A ,用水平力N F B 3=拉B ,A 、B【练1】如图所示,质量为M 的斜面A 在水平向左的推力F 作用下,A 与B 物体B 的质量为m ,则它们的加速度a A. ()(,sin μθ++==g m M F g a B. θθcos )(,cos g m M F g a +==C. ()(,tan μθ++==g m M F g a D. g m M F g a )(,cot +==μθ【练2】如图所示,质量为2m 的物体2滑定滑轮连接质量为1m 的物体,与物体1A. 车厢的加速度为θsin gB. 绳对物体1的拉力为θcos 1gmC. 底板对物体2的支持力为g m m )(12-D. 物体2所受底板的摩擦力为θtan 2g m2、连接体整体内部各部分有不同的加速度:【例2有一个环,箱和杆的总质量为M ,环的质量为m 加速度大小为a 时(a <g A. Mg + mg B. Mg —【练3】如图所示,一只质量为m 杆下降的加速度为( )A. gB. g M mC. g M m M +【练4个重4 N 的读数是(A.4 NB.23 NC.0 N【练5】如图所示,A 、B 的质量分别为m A =0.2kg ,m B =0.4kg ,盘C 的质量m C =0.6kg ,现悬挂于天花板O 处,处于静止状态。
当用火柴烧断O 处的细线瞬间,木块A 的加速度a A 多大?木块B 对盘C 的压力F BC 多大?(g 取10m/s 2)连接体作业1、如图所示,小车质量均为M ,光滑小球P 的质量为m ,绳的质量不计,水平地面光滑。
要使小球P 随车一起匀加速运动(相对位置如图所示),则施于小车的水平拉力F 各是多少?(θ已知)A BO球刚好离开斜面 球刚好离开槽底F= F= F= F=2、如图所示,A 、B 质量分别为m1,m2,它们在水平力F 的作用下均一起加速运动,甲、乙中水平面光滑,两物体间动摩擦因数为μ,丙中水平面光滑,丁中两物体与水平面间的动摩擦因数均为μ,求A 、B 间的摩擦力和弹力。
3.3连接体问题

两物体在F 3、如图所示,在光滑的水平面上,有A、B两物体在F1和 如图所示,在光滑的水平面上, 的作用下运动,已知F F2的作用下运动,已知F1 > F2, 则( 的加速度一定增大; A、若撤去F1,B的加速度一定增大; 若撤去F B、若撤去F1,B对A的作用力一定增大; 若撤去F 的作用力一定增大; 的加速度一定增大; C、若撤去F2,A的加速度一定增大; 若撤去F D、若撤去F2,A对B的作用力一定增大。 的作用力一定增大。 若撤去F
M m
θ
F`=mF(cosθ- µ sinθ)/(M+m)
拉力F 例4、地面光滑,两物块质量分别为m1、m2,拉力F1和F2 地面光滑,两物块质量分别为m 方向相反,与轻线沿同一水平直线, 方向相反,与轻线沿同一水平直线,且F1> F2,试求两 个物块运动过程中轻线的拉力F 个物块运动过程中轻线的拉力FT。 F1 FT F2
F1 m1 F2 m2
•备选题 备选题 1、如图所示,在光滑的水平面上,一个斜面被两个固定 如图所示,在光滑的水平面上, 挡住,然后在斜面上放一个物体, 在地面上的小桩 a和b挡住,然后在斜面上放一个物体, 下列说法正确的是( 下列说法正确的是( ) b a A、若物体加速下滑,则b受到挤压 若物体加速下滑, B、若物体减速下滑,则b受挤压 若物体减速下滑, C、若物体匀速下滑,则a受挤压 若物体匀速下滑, D、若物体静止在斜面上,则a受挤压 若物体静止在斜面上,
F合=(m1+m2+m3+m4+……+mn)a
例1、跨过定滑轮的绳的一端挂一吊板,另一端被吊板 跨过定滑轮的绳的一端挂一吊板, 上的人拉住,如图所示,已知人的质量为70kg, 上的人拉住,如图所示,已知人的质量为70kg,吊板的 70kg 质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计。 质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计。 10kg 取重力加速度g=10m/s 取重力加速度g=10m/s2。当人 g=10 以440N的力拉绳时,人与吊板 440N的力拉绳时, 的加速度α和人对吊板的压力 的加速度α F分别为多少? 分别为多少?
(精品讲义)新高一物理衔接课程 第16讲 连接体问题

第16讲 连接体问题一、连接体:运动中几个物体或叠放在一起,或并排挤放在一起,或用轻绳、轻杆、轻弹簧连接在一起的物体组。
常见的连接体一般具有速度、加速度大小相同的特点。
二、解决这类问题的基本方法:整体法和隔离法思考与练习:1.如图,不计绳的质量及绳与滑轮的摩擦,物体A 的质量为M ,水平面光滑,当在绳B 端挂一质量为m 的物体时,物体A 的加速度为a 1,当在绳B 端施以F =mg 的竖直向下的拉力作用时,A 的加速度为a 2,则a 1与a 2的大小关系是( 答案:C )A .a 1=a 2B .a 1>a 2C .a 1<a 2D .无法确定解析:挂m 时,mg =(m +M )a 1,a 1=m m +Mg ;用F =mg 拉时,mg =Ma 2,a 2=m M g 2. 如图,A 、B 两木块的质量分别为m A 、m B ,在水平推力F 作用下沿水平面匀加速向右运动,求下面几种情况下A 、B 间的弹力。
⑴ 水平面光滑⑵ 水平面摩擦系数μ⑶ 斜面光滑⑷ 斜面摩擦系数μ3. 如图,放在光滑水平面上的物体A和B质量分别为M和m,水平恒力F作用在A上,A、B间的作用力为F1;水平恒力F作用在B上,A、B间作用力为F2,则( AC ) A.F1+F2=F B.F1=F2C.F1/F2=m/M D.F1/F2=M/m4. 如图,五块完全相同的木块并排放在水平地面上,它们与地面间的摩擦不计.当用力F 推1使它们共同加速运动时,第2块木块对第3块木块的推力为___答案:F 53___.5.一根质量分布均匀的长绳AB ,在水平外力F 的作用下,沿光滑水平面做直线运动,如图甲所示.绳内距A 端x 处的张力F T 与x 的关系如图乙所示,由图可知(答案:AC )A .水平外力F =6 NB .绳子的质量m =3 kgC .绳子的长度l =2 mD .绳子的加速度a =2 m/s 2解析:取x =0,即A 端进行受力分析,F -F T =ma ,又A 端质量趋近于零,则F =F T =6 N ,A 正确;由于不知绳子的加速度,其质量也无法得知,B 、D 均错误;由图易知C 正确.6.如图,质量相同的物体1和2紧靠在一起放在光滑的水平面上,如果它们分别受到水平推力F 1和F 2作用,且F 1>F 2,则1施于2的作用力大小为( 答案:D )A .F 1B .F 1-F 2 C. 12(F 1-F 2) D. 12(F 1+F 2) 解析:因为F 1>F 2,物体1和2一起以相同的加速度a 向右做匀加速直线运动,将1和2作为一个整体,有:F 1-F 2=2ma ,∴ a =F 1-F 22m. 要求1施于2的作用力F N ,应将1和2隔离,对物体2, F N -F 2=ma ,∴ F N =F 2+ma =12(F 1+F 2). 7. 如图,物体abc 叠放在水平桌面上,水平力F b =5 N ,F c =10 N 分别作用于物体b 、c 上,abc 仍保持静止.以f 1、f 2、f 3分别表示a 与b 、b 与c 、c 与桌面间的静摩擦力的大小,则( 答案:C )A. f 1=5N ,f 2=0,f 3=5NB. f 1=5N ,f 2=5N ,f 3=0C. f 1=0,f 2=5N ,f 3=5ND. f 1=0,f 2=10N ,f 3=5N8.在光滑水平面上有一小车A ,质量m A =2.0 kg ,小车上放一个物体B ,质量m B =1.0 kg ,给B 一个水平推力F ,如图甲,当F 增大到稍大于3.0 N 时,A 、B 开始相对滑动.若撤去F ,对A 施加一水平推力F ′,如图乙,要使A 、B 不相对滑动,求F ′的最大值Fmax .解析:对甲图,F =(m A +m B )a ,F f max =m A a对乙图,F f max =m B a ′,F max =(m A +m B )a ′,得F max =6.0 N.9.如图,A 、B 质量分别为m A 和m B ,叠放在倾角为θ的斜面上以相同的速度匀速下滑,则( 答案:BCD )A .A 、B 间无摩擦力作用B .B 受到的滑动摩擦力大小为(m A +m B )g sin θC .B 受到的静摩擦力大小为m A g sin θD .取下A 物体后,B 物体仍能匀速下滑解析:对AB 整体,(m A +m B )g sin θ=μ(m A +m B )g ,B 正确.对A ,静摩擦力f =m A g sin θ,C 正确,A 错误。
连接体问题

(1)本题和课堂练习题有什么联系和区别?
(2)若两个固定斜面与水平方向的夹角不相等,又当如
何处理?
(3)你有几种方法寻找本题中的加速度之间的关系?
(图中 37 , 53, 重力加速度g=10m/s2)
B
C
AF
问题思考: (1)若各接触面光滑,不施加外力F,由静止释放A、
B、C,各物体的加速度各为多少? (2)若给C一个冲量I,不计所有摩擦,如何分析A、B
、C各物体的运动情况?
课堂练习:如图所示,斜劈A和圆柱体B的质量分别为mA
和mB,劈的倾角为 ,两个物体都只发生平动,由静止
巧思多变,一题多解
——连接体问题
基础知识回顾
1、连接体:两个或两个以上物体相互连接参与运动的系统称为连接 体。
2、质点系的牛顿第二定律:
F合x m1a1x m2 a2x mn anx
F合y m1a1y m2a2 y mnany
基础知识回顾
3、基本方法:
①隔离法:将各物体从系统中隔离出来, 单独考虑各物体的受力情况和运动情况。
状态释放系统,试求两个物体A和B的加速度(不计所有 摩擦)。
A
变式(课后练习):如图所示,一个圆柱体和一个楔子,
相互触及地沿着两个与地面成相等夹角 的固定斜面做无
摩擦的移动,圆柱体质量为m1,楔子的质量为m2。试求 楔子对圆柱体的压力。
答案 N 2m1m2 g tan
m1 m2
m1 m2
问题思考:
②整体法:将连接体系统看成一个整体, 分析整体所受外力的情况和运动情况。
基础知识回顾
4、注意事项:
①由约束条件准确找到各物体的加速度之间 的关系; ②注意各运动学参量所对应的参考系; ③非惯性系中的受力分析要考虑惯性力; ④整体法与隔离法相结合,灵活处理问题。
连接体问题

况由物体平衡条件得:
FNFfMg0 ② 由牛顿第三定律得:Ff Ff ③
联解得F :N(M m )g m aM g
由牛顿第三定律知,木箱对地面的
压力大小为F :N (M m )g m a M g
解法2:(整体法)
对于“一动一静”连接体,也可选取
整体为研究对象,根据牛顿第二定律得:
(M m )g F N M 0 m a
施于木板的摩擦力 应沿斜面向上,故人应加
速下跑,设人相对于斜面的加速度为 a 人 .现
分别对人和木板应用牛顿第二定律得:
对木板: M gsinf0
对人: mgsinf ma人
解得: a人Mmmgsin ,方向沿斜面向下.
(2)为了使人与斜面保持静止,必须满足人 在木板上所受合力为零,所以木板施于人的摩 擦力应沿斜面向上,故人相对木板向上跑,木 板相对斜面向下滑,但人对斜面静止不动.现 分别对人和木板应用牛顿第二定律,设木板对
解析:设绳上的拉力为T,由牛顿第二定律分
别对A、B列式得: TmAgmAa
①
联解得:
mBgTmBa
②
TmAmBgmAmBg1.4N
mAmB
〔拓展1〕 如图所示,质量为ml、m2的物体, 放在光滑水平面上,用仅能承受6N的拉力的线
相连.ml=2kg,m2=3kg.现用水平拉力F拉物体 ml或m2,要使系统得到最大加速度且不致把绳 拉断,则F的大小和方向应为(C )
了保持物块与斜面相对静止,可用一水平力
F推楔形木块,如图,求此水平力应等于多
少?
m
F
θ
M
μ
解析:由于物块与斜面相对静止,所以二者
的加速度大小相等,方向均为水平向左的方
连接体问题

两种方法都是根据牛顿第二定律列方程求解。
(接触连接)
1. 物体A和B的质量分别为1.0kg和2.0kg,用F=12N 的水平力推动A,使A和B一起沿着水平面运动,A和 B与水平面间的动摩擦因数均为0.2,求A对B的弹力。 (g取10m/s2) F
解:根据牛顿第二定律求出AB整体的加速度
A
B
F (mA mB ) g 2 a 2m / s ① mA mB
对B物体
FAB mB g mB a ② FAB mB (a g ) 8N
因此A对B的弹力
整体法求加速度,隔离法求相互作用力.
(弹簧连接)
2.如图所示,两个质量分别为m1=2 kg、m2=3 kg的物体置于光滑的水 平面上,中间用轻质弹簧秤连接.两个大小分别为F1=30 N、F2=20 N 的水平拉力分别作用在m1、m2上。当两物体以相同速度一起运动时,下 列说法正确的是()
A.弹簧秤Leabharlann 示数是30 N B.弹簧秤的示数是26 N C.在突然撤去F2的瞬间,m1的加速度大小为5 m/s2 D.在突然撤去F1的瞬间,m1的加速度大小为13 m/s2
(轻绳连接)
如图所示,在水平力F=12N的作用下,放在光滑水平面 上的,运动的位移x与时间t满足关系式:x=3t2+4t,该 物体运动的初速度 ,该物体的质量 m= 。若改用下图装置拉动,使m1的 运动状态与前面相同,则m2的质量应为 。(不计摩擦)
随堂练习:
1~5 11 13
6~10 12
1~5 11 13
6~10 12
1~5 11 13
6~10 12
例题:如图10所示,质量为M的长木板,静止放置在粗糙水平地面上,有 一个质量为m、可视为质点的物块,以某一水平初速度从左端冲上木 板.从物块冲上木板到物块和木板达到共同速度的过程中,物块和木板 的v-t图象分别如图中的折线acd和bcd所示,a、b、c、d点的坐标为a (0,10)、b(0,0)、c(4,4)、d(12,0).根据v-t图象,求:
连接体问题

A
练习2:如图,质量为m的木块在质量为M的长木 板上向右滑行,木块受到向右的拉力F的作用, 长木板处于静止状态,已知木块与长木板间的动 摩擦因数为μ1,长木板与地面间的动摩擦因数为 μ2,则 A.长木板受到地面的摩擦力的大小一定是μ1mg B.长木板受到地面的摩擦力的大小一定是μ2(m +M)g C.当F>μ2(m+M)g时,长木板便会开始运动 D.无论怎样改变F的大小,长木板都不可能运动
一、连接体问题
1、连接体
由相互作用的两个或两个以上的物体组成的系统。
2、连接体解题方法 整体法和隔离法交叉使用 3、解题步骤: ①求内力:先整体求a,再隔离求内力 ②求外力:先隔离求a,再整体求外力
例1:下图中所有摩擦不计、A中轻绳下挂一 质量为m的物体,B中用大小为mg拉轻绳,求A、 B两物体的加速度 A B
M B
变式:如图,一质量为m1的楔形木块放在水平桌 面上,两底角为α和β;a、b为两个位于斜面上 质量分别为m2和m3的小木块。已知两斜面都是光 滑的。现发现a、b沿斜面下滑,而楔形木块静止 不动,这时楔形木块对水平桌面的压力等于多少? 地面对斜面体的摩擦力为多大,方向怎样?
m1
例3:如图,光滑水平面上静止放着长L=1 m,质 量为M=3 kg的木板(厚度不计),一个质量为m=1 kg的小物体放在木板的最右端,m和M之间的动摩 擦因数μ=0.1,今对木板施加一水平向右的拉力 F.(g取10 m/s2) 4N (1)为使小物体不掉下去,F不能超过多少? (2)如果拉力F=10 N恒定不变,求小物体所能获得的 最大速率? 1m/s
m 2、结论:牵引力与质量成正比 T M m F
变式:
例2:光滑的水平面上,两物体叠放在一起,已知 两物体间的最大静摩擦力为fm,现在M上加一水 平恒力F,为使两者一起运动,求F的最大值
物理的连接体问题

物理的连接体问题
物理的连接体问题是指在物理学中探讨物体之间如何相互连接、交互作用以及受力等问题。
在物理学中,物体之间的连接常常涉及到物体之间的接触、插入、固定等方式。
例如,一个简单的连接体问题可以是两个弹簧的连接方式,或者两个物体之间的摩擦力如何影响它们的运动。
连接体问题可以通过分析物体之间的接触面积、形状、材质等因素来研究。
例如,接触面积的大小决定了接触力的大小,形状的不匹配可能导致接触面不完全,从而影响连接体的稳定性。
此外,连接体问题还涉及到物体之间的受力情况。
通过分析连接体上的受力情况,可以研究物体之间的力的平衡和不平衡情况,以及力的传递和转化等问题。
为了解决连接体问题,物理学采用了多种分析方法和工具,如力学、力的平衡和受力分析、力矩分析、静力学、材料力学等。
总之,连接体问题是物理学中研究物体之间连接、交互作用和受力等问题的重要内容,对于理解物体之间的相互作用和力的传递具有重要意义。
专题:连接体问题(整体法和隔离法)

专题:连接体问题(整体法和隔离法)一、什么是连接体问题特征:两物体紧靠着或者依靠一根细绳(一根弹簧)相连接后一起做匀加速运动(1)用细线连接的物体系(2)相互挤压在一起的物体系(3)用弹簧连接的物体系二、连接体问题如何处理1.对整体写牛顿第二定律2.把其中任意一个物体隔离写牛顿第二定律三、常见的连接体问题的类型1.计算连接体的加速度2.计算连接体之间的拉力大小3.根据绳子的最大拉力判断水平拉力F的大小4.放在不同平面上判断拉力的变化、加速度的变化5.两个相反方向的力作用与两个物体上,撤去其中一个力后判断物体加速度变化和绳子拉力变化6.在连接体上的某个物体上再放一个物体判断拉力的变化、加速度的变化7.三个物体的连接体问题【典型例题剖析】例1:如图所示,置于光滑水平面上的木块A和B,其质量为m A和m B。
当水平力F作用于A左端上时,两物体一起作加速运动,其A、B间相互作用力大小为N11计算:(1)计算N1的大小(2)若将F作用在物体B上,AB间的相互作用力N2变为多少?(3)计算N 1与N 2之和,N 1与N 2之比(4)若物体A 、B 与地面的动摩擦因数为μ,分析AB 的加速度如何变化,AB 之间相互作用力如何变化?例2:如图所示,置于水平地面上的相同材料的质量分别为m 和m 0的两物体用细绳连接,在m 0上施加一水平恒力F ,使两物体做匀加速直线运动,对两物体间细绳上的拉力,下列说法正确的是( )A .地面光滑时,绳子拉力大小等于mFm 0+mB .地面不光滑时,绳子拉力大小等于mFm 0+mC .地面不光滑时,绳子拉力大于mFm 0+mD .地面不光滑时,绳子拉力小于mFm 0+m答案 AB例3:(多选)如图所示,质量为ml 的物体和质量为m 2的物体,放在光滑水平面上,用仅能承受6N 的拉力的线相连。
m l =2kg ,m 2=3kg 。
现用水平拉力F 拉物体m l 或m 2,使物体运动起来且不致把绳拉断,则F 的大小和方向应为( ) A .10N ,水平向右拉物体m 2B .10N ,水平向左拉物体m 1C .15N ,水平向右拉物体m 2D .15N ,水平向左拉物体m 1 答案:BC例4:如图所示,在水平地面上有A 、B 两个小物体,质量分别为m A =3.0kg 、m B =2.0kg ,它们与地面间的动摩擦因数均为μ=0.10。
连接体问题

m2 N1 F m1 m2
1.传送带滑块模型
2.木板滑块模型
两类问题的共同点:
1. 相对运动 l 相对= s滑块-s板带 2. 摩擦力将两者联系起来 相对静止则可
以整体分析;相对运动需要隔离分析
3. 能量转化 相对静止时外力功使系统动 能增加;相对运动时,外力功减去磨擦 生热使系统动能增加。磨擦生热Q=fl
解:球与槽有共同加速度 由牛顿第二定律F=ma mgtanθ=ma tanθ=a/g =3/4 小球上升的高度h=R(1﹣cosθ)=0.2m
FN
F
mg
3.一质量为M,倾角为θ的楔形木块,静止在水平 桌面上,与桌面的动摩擦因数为μ ,一物块质量 为m,置于斜面上,物体与斜面的接触是光滑的, 为保持物体与斜面相对静止,可用多大的水平力F 推楔形木块。
传送带问题
1.传送带问题分类
按放置分: 水平、倾斜 、水平与倾斜交接 按转向分: 顺时针、逆时针。
2.传送带问题解题策略
(1)受力分析和运动分析是解题的基础。 首先根据初始条件比较 物体对地的速度 v物与v传 的大小与方向,明确物体受到的摩擦力的种类及其规 律,然后分析出物体受的合外力和加速度大小和方向, 再结合物体的初速度确定物体的运动性质。 受力分析的关键是摩擦力的分析。
各个物体分得的动力与自身的质量成正比,与两
物体的总质量成反比。
③条件:加速度相同;接触面相同
4. 物体M、N紧靠着置于摩擦因数为μ的斜面上,斜面 的 倾角θ,现施一水平力F作用于M,M、N共同加速 沿斜面向上运动,求它们之间的作用力大小。
解:对整体,根据牛顿第二定律 F
F cos (M m) g sin N (M m)a ①
牛顿第二定律典例(连接体)

牛顿第二定律是经典力学的基础和核心,是分析、研究和解决力学问题的三大法宝之一,同时也是高考考查的重点和热点。
因此,深刻理解和灵活应用牛顿第二定律是力学中非常重要的内容,下面阐述应用牛顿第二定律时的几类典型问题,供大家参考。
一、连接体问题两个或两个以上物体相互连接并参与运动的系统称为有相互作用力的系统, 即为连接体问题,处理非平衡状态下的有相互作用力的系统问题常常用整体法和隔离法。
当需要求内力时,常把某个物体从系统中“隔离”出来进行研究,当系统中各物体加速度相同时,可以把系统中的所有物体看成一个整体进行研究。
例 1:如图 1所示的三个物体质量分别为 m 1、 m 2和 m 3。
带有滑轮的物体放在光滑水平面上,滑轮和所有接触面的摩擦以及绳子的质量均不计。
为使三个物体无相对滑动,试求水平推力 F 的大小。
解答:本题是一道典型的连接体问题。
由题意可知,三个物体具有向右的相同的加速度,设为 a ,把它们三者看成一个整体,则这个整体在水平方向只受外力 F 的作用。
由牛顿第二定律,即:F=(m 1+m2+m3a ……①隔离 m 2,受力如图 2所示在竖直方向上,应有: T=m2g ……②隔离 m 1,受力如图 3所示在水平方向上,应有: T′=m1a ……③由牛顿第三定律T′=T ……④联立以上四式解得:点评:分析处理有相互作用力的系统问题时,首先遇到的关键问题就是研究对象的选取。
其方法一般采用隔离和整体的策略。
隔离法与整体法的策略,不是相互对立的, 在一般问题的求解中随着研究对象的转化,往往两种策略交叉运用,相辅相成,所以我们必须具体问题具体分析,做到灵活运用。
二、瞬时性问题当一个物体(或系统的受力情况出现变化时,由牛顿第二定律可知,其加速度也将出现变化,这样就将使物体的运动状态发生改变,从而导致该物体(或系统对和它有联系的物体(或系统的受力发生变化。
例 2:如图 4所示,木块 A 与 B 用一轻弹簧相连,竖直放在木块 C 上。
连接体问题专题详细讲解

连接体问题一、连接体与隔离体两个或两个以上物体相连接组成的物体系统,称为连接体。
如果把其中某个物体隔离出来,该物体即为隔离体。
二、外力和内力如果以物体系为研究对象,受到系统之外的作用力,这些力是系统受到的外力,而系统内各物体间的相互作用力为内力。
应用牛顿第二定律列方程不考虑内力。
如果把物体隔离出来作为研究对象,则这些内力将转换为隔离体的外力。
三、连接体问题的分析方法1.整体法连接体中的各物体如果加速度相同,求加速度时可以把连接体作为一个整体。
运用牛顿第二定律列方程求解。
2.隔离法如果要求连接体间的相互作用力,必须隔离其中一个物体,对该物体应用牛顿第二定律求解,此法称为隔离法。
3.整体法与隔离法是相对统一,相辅相成的。
本来单用隔离法就可以解决的连接体问题,但如果这两种方法交叉使用,则处理问题就更加方便。
如当系统中各物体有相同的加速度,求系统中某两物体间的相互作用力时,往往是先用整体法法求出加速度,再用隔离法法求物体受力。
简单连接体问题的分析方法1.连接体:两个(或两个以上)有相互作用的物体组成的具有相同大小加速度的整体。
2.“整体法”:把整个系统作为一个研究对象来分析(即当做一个质点来考虑)。
注意:此方法适用于系统中各部分物体的加速度大小方向相同情况。
3.“隔离法”:把系统中各个部分(或某一部分)隔离作为一个单独的研究对象来分析。
注意:此方法对于系统中各部分物体的加速度大小、方向相同或不相同情况均适用。
4.“整体法”和“隔离法”的选择求各部分加速度相同的连结体的加速度或合外力时,优选考虑“整体法”;如果还要求物体之间的作用力,再用“隔离法”,且一定是从要求作用力的那个作用面将物体进行隔离;如果连结体中各部分加速度不同,一般都是选用“隔离法”。
5.若题中给出的物体运动状态(或过程)有多个,应对不同状态(或过程)用“整体法”或“隔离法”进行受力分析,再列方程求解。
针对训练1.如图用轻质杆连接的物体AB沿斜面下滑,试分析在下列条件下,杆受到的力是拉力还是压力。
连接体问题

连接体问题1.连接体指运动中几个物体或叠放在一起,或并排挤放在一起,或用轻绳、轻杆、强弹簧联系在一起的物体系。
2.本质特征与解法(1)加速度相同的连接体:与运动方向、有无摩擦力、两物体放置的方式都无关,平面、斜面、竖直都一样,只要两物体保持相对静止,恒满足“合外力按质量均分”。
常见形式如下:……(2)加速度不同的连接体:常应用对系统的牛顿第二定律、图像法和分析推理法求解。
下面对系统的牛顿第二定律及其应用进行说明:对系统的牛顿第二定律:系统所受到的合外力等于系统中各物体的质量与自身对应加速度乘积之和。
表达式nnamamamamF+⋅⋅⋅⋅⋅⋅+++=∑332211分量式nxnxxxxamamamamF+⋅⋅⋅⋅⋅⋅+++=∑332211nynyyyyamamamamF+⋅⋅⋅⋅⋅⋅+++=∑332211应用对系统的牛顿第二定律求解组合体动力学问题的一般思路①弄清系统的构成和系统内各物体的状态②跟据题目所求建立坐标系,分解各物体的加速度③应用对系统的牛顿第二定律列方程,代值求解 使用要诀:分解物体加速度,选取系统来解求 常见形式举例:……加速度相同的连接体【例1】如图右所示,质量为m 1、m 2的物块在F 1、F 2共同作用下向右运动。
已知kg 31=m 、kg 22=m 、N 141=F 、N 42=F ,求m 1和m 2 之间的作用力F T 为多少?【引导】本题中物体系统水平方向,不仅受到外力1F 作用,还受到2F 作用,因此系统的合外力为两力的矢量和,然后再按照“合外力按质量均分”结论求解。
【解析】物体系的合外力∑==10N 4N -N 14F按照“合外力按质量来均分”知 m 1的合力 N 61=∑F m 2的合力 N 42=∑F由于 T 11F F F-=∑ 或2T 2F F F-=∑所以m 1和m 2之间的拉力8N 6N -N 1411T ==-=∑F F F也可以 8N 4N N 422T =+=+=∑FF F【答案】8N【品味】当系统所受外力不仅一个时,先求和力再分配,然后任意隔离一个物体进行分析就可求出物体间的“牵连力”。
15连接体问题及处理方法

15连接体问题及处理方法一、连接体问题1.连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统.2.连接体题型(1)系统内所有物体相对静止,即运动情况相同,a 也相同------相对静止问题(2)系统内物体相对运动,运动情况不同,a 也不同------相对运动问题二、处理方法1整体法分析系统受力时只分析外力不必分析内力;在用隔离法解题时要注意判明隔离体的运动方向和加速度方向,同时为了方便解题,一般我们隔离受力个数少的物体.2.相对静止类:程。
(整体与隔离结合使用)例1.A 、B 两物体靠在一起,放在光滑水平面上,m B =6Kg ,今用水平力F A =6N 推A ,用水平力F A =3N 拉B ,A 、B 有多大?3.相对运动问题:例2.如图所示,光滑水平面上静止放着长L =1.6 m 、质量为M =3 kg 的木板.一个质量为m =1 kg 的小木块放在木板的最右端,m 与M 之间的动摩擦因数μ=0.1,今对木板施加一水平向右的拉力F ,若2s 时两者脱离,则F 为多大?4.判断相对静止还是相对运动:例3.如图所示,m 1=40 kg 的木板放在无摩擦的地板上,木板上又放m 2=10 kg 的石块,石块与木板间的动摩擦因数μ=0.6,试问(1)当水平力F =50 N 时,石块与木板间有无相对滑动?(2)当水平力F =100 N 时,石块与木板间有无相对滑动?(g =10 m/s 2)此时m 2的加速度为多大?5.方法总结①.当它们具有共同加速度时,一般是先整体列牛顿第二定律方程,再隔离受力个数少的物体分析列牛顿第二定律方程.②.当它们的加速度不同且涉及到相对运动问题,一般采用隔离法分别分析两个物体的运动情况,再找它们运动或受力的联系点列辅助条件方程.练习题1.两个物体A 和B ,质量分别为m 1和m 2,互相接触放在光滑水平面上,如图所示,对物体A 施以水平的推力F ,则物体A 对物体B 的作用力等于( )A .211m m m +FB .212m m m + FC .FD .21m m F 2.上题若m 1与m 2与水平面间有摩擦力且摩擦因数均为μ则A 对B 作用力等于为( )3.如图所示,光滑平面上以水平恒力F 拉动小车和木块,一起做无相对滑动的加速运动,若小车质量为M ,木块质量为m ,加速度大小为a ,木块和小车间的动摩擦因数为μ,对于这个过程某同学用以下四个式子来表示木块受到的摩擦力大小,正确的是() A.F-Ma B.μma C.μmg D.Ma4.如图所示,物体P置于水平面上,用轻细线跨过质量不计的光滑定滑轮连接一个重力G=10N的重物,物体P向右运动的加速度为a1;若细线下端不挂重物,而用F=10N的力竖直向下拉细线下端,这时物体P的加速度为a2,则( )A.a1>a2B.a1=a2C.a1<a2D.条件不足,无法判断5.如图所示,质量分别为M、m的滑块A、B叠放在固定的、倾角为θ的斜面上,A与斜面间、A与B之间的动摩擦因数分别为μ1,μ2,当A、B从静止开始以相同的加速度下滑时,B受到摩擦力()(双选)A.等于零B.方向平行于斜面向上C.大小为μ1mgcosθD.大小为μ2mgcosθ6.相同材料的物块m和M用轻绳连接,在M上施加恒力F,使两物块作匀加速直线运动,求在下列各种情况下绳中张力。
高中物理:连接体问题

高中物理:连接体问题1、连接体与隔离体:两个或两个以上物体相连接组成的物体系统称为连接体。
如果把其中某个物体隔离出来,该物体即为隔离体。
2、外力和内力:一个物体系统受到的系统之外的作用力叫做该系统受到的外力。
而系统内各物体间的相互作用力叫内力。
需要强调的是牛顿第二定律方程中的力应是研究对象所受的合外力。
一个力是内力还是外力要根据研究对象而定。
3、连接体问题的处理方法①整体法:把整个连接体系统看做一个研究对象(或质点),根据整体所受的外力,运用牛顿第二定律的运动学公式列方程求解。
此方法适用于系统中的各物体加速度相同、不需要求内力的情况,其优点在于它不涉及系统内各物体之间的相互作用力。
②隔离法:把系统中某物体(或某一部分)隔离出来作为一个单独的研究对象,对其进行受力分析、列方程求解。
此方法对于系统中各部分物体的加速度相同或不相同的情况均适用。
隔离法的优点在于:它将系统内物体间相互作用的内力转化成了某研究对象的外力,可由此求出系统内物体间的相互作用力。
例1、如图1所示,两个质量相同的物体A和B紧靠在一起,放在光滑的水平面上,如果它们分别受到的水平推力,而且,则A施于B的作用力大小为()。
A.B.C.D.解析:物体A和B加速度相同,求它们之间的相互作用力,采取先整体后隔离的方法,先求出它们的共同加速度,然后再选取A或B 为研究对象,求出它们之间的相互作用力。
选取A和B整体为研究对象,共同加速度为再选取物体B为研究对象,受力分析如图2所示,根据牛顿第二定律,得另解:此题也可以对物体A进行隔离。
利用求解。
此题可以一开始就用隔离法:对于A:,①对于B:。
②联立①②两式解得从原则上讲,求内力可任意隔离与之相邻的物体均可求解。
但应注意尽量使过程简洁。
例2、甲、乙两人发生口角,甲打了乙的胸口一拳致使乙受伤,法院判决甲应支付乙医疗费。
甲狡辩说:我打了乙一拳,根据牛顿第三定律知,作用力与反作用力大小相等,乙对我也有相同大小的作用力,所以乙并没有吃亏。
2.连接体问题
③条件:加速度相同;接触面相同
m
F M F
m
M
Байду номын сангаас
F
F m M M m
F M
m
A
B:mg-T=ma
B
A:
T=Ma
M T mg M m
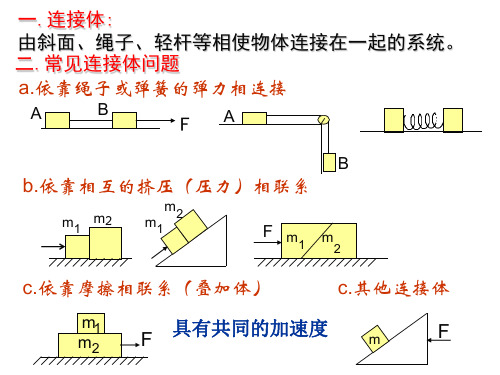
一.连接体: 由斜面、绳子、轻杆等相使物体连接在一起的系统。 二.常见连接体问题 a.依靠绳子或弹簧的弹力相连接
A B
F
A B
b.依靠相互的挤压(压力)相联系
m1 m2 m1 m2
F m 1
m
2
c.依靠摩擦相联系(叠加体)
m1 m2
c.其他连接体
m
F
具有共同的加速度
F
三、整体法与隔离法的综合应用
可用“整体法”也可用“隔离法”解,也有不少问题则
需要交替应用“整体法”与“隔离法”。因此,方法的选
用也应视具体问题而定。
A B
m1 m2
F
F m 1
m
2
1.求内力:先整体求加速度,后隔离求内力。 2.求外力:先隔离求加速度,后整体求外力。
例1、相同材料的物块m和M用轻绳连接,在M上施加恒 力 F,使两物块一起做匀加速直线运动,求: (1)地面光滑,T=? (2)地面粗糙,动摩擦因数为μ,T=?
m
M
F
(1)由牛顿第二定律,对整体可得:F=(M+m)a 隔离m可得:T=ma 联立解得:T=mF/(M+m)
(2) 由牛顿第二定律,对整体可得: F-μ(M+m)g=(M+m)a 隔离m可得:T-μmg =ma 联立解得:T=mF/(M+m)
(3)竖直加速上升,T=? 解:由牛顿第二定律,对整体可得:F- (M+m)g=(M+m)a 隔离m可得:T-mg=ma 联立解得:T=mF/(M+m)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F (m1 m2 mn )a
解题思路:
连 结 体 受 力 情 况
利用隔离法 单个体使用
F ma
整体使用
a
F ma
单 个 体 受 力 情 况
例题1.如图所示,质量为2m的物块A与质量 为m的物块B,放在光滑的水平地面上,在水 平推力F的作用下做加速运动,则A和B的相 互作用为____
高中一年级物理第三章
梧州一中 wenweicheng
一、连结体 把两个或两个以上的物体看成一个整 体,该整体就称为连结体。
二、把连结体作为研究对象时,牛顿 第二定律的表达式是
F m1a1 m2 a2 mn an
注意:若连结体是一起运动,各个物体的 加速度相同,则牛二律表达式变为:
F 3ቤተ መጻሕፍቲ ባይዱ
同步1.如图所示,质量为2kg的物块A与质量 为1Kg的物块B,A与地面μ=0, B与地面 μ=0.2,在水平推力F=8N的作用下做加速运 动,则A和B的相互作用为____N
