环形一级倒立摆设计
毕业设计毕业论文一阶倒立摆模糊控制系统[管理资料]
![毕业设计毕业论文一阶倒立摆模糊控制系统[管理资料]](https://img.taocdn.com/s3/m/cd451f987e21af45b307a8f7.png)
摘要一阶直线倒立摆是一个典型的“快速、多变量、非线性、自不稳定系统”,对一阶倒立摆系统的稳定性研究在理论上和方法上具有深远的意义。
对一阶倒立摆的研究可以归结为对非线性、多变量、不稳定系统的研究。
在应用上,一阶倒立摆广泛应用于控制理论研究、航空航天控制等领域,在自动化领域中具有重要的价值。
本文首先是建立一阶倒立摆的数学模型,并且采用的是双闭环控制系统,通过对一阶倒立摆的双闭环控制系统数学模型的分析,将模糊控制方法应用于一阶倒立摆的控制问题,其中,内环控制倒立摆的摆角,外环控制倒立摆的位置。
采用模糊控制器的设计包括隶属函数及模糊控制规则、解模糊,最后利用MATLAB软件进行仿真实验。
模糊控制方法应用于一阶倒立摆系统的控制中,能够发挥模糊控制在非线性系统的控制、复杂对象系统控制方面的优势,简化设计,提高系统的鲁棒性。
关键词:一阶倒立摆,数学模型,模糊控制,MATLABAbstractThe first-order linear inverted pendulum is a typical “fast, multivariable, nonlinear, unstable system”, for an inverted pendulum system stability research in theory and method has the profound significance. For an inverted pendulum can boil down to the research on nonlinear, multivariable, unstable system research. In application, an inverted pendulum is widely used in control theory, aerospace control and other fields, in the field of automation has important value.This paper is to establish a mathematical model of the inverted pendulum, and using the double closed-loop control system, through the inverted pendulum double closed-loop control mathematical model analysis, a fuzzy control method is applied to an inverted pendulum control, Wherein, the inner control of the inverted pendulum swing angle, the outer loop controls the position of inverted pendulum. Fuzzy controller design including the membership function and fuzzy control rule, fuzzy solution, finally using the Matlab software simulation. The fuzzy control method is applied to an inverted pendulum control system, fuzzy control can play in the control of nonlinear system, complex object systems control advantages, simplify the design, improve the stability of system.Key words: Inverted pendulum,Mathematical model,Fuzzy control,Matlab目录摘要 (I)Abstract.............................................................................................................................................. I I 1 绪论 (1)一阶倒立摆系统研究的意义 (1)一阶倒立摆系统在国内外研究综述 (1)本论文的研究内容和所用方法 (2)2 一阶倒立摆数学模型的建立与控制系统 (3)一阶倒立摆的数学模型 (3)一阶倒立摆系统的动力学分析 (4)系统微分方程的线性化 (5)系统微分方程状态空间表示 (6)一阶倒立摆定性分析 (7)系统的稳定性、能控性和能观测性判据 (7)基于状态方程的系统定性分析 (8)一阶倒立摆控制系统 (11)一阶倒立摆控制系统硬件 (11)一阶倒立摆系统总体控制框图 (11)3 模糊控制的基本原理 (15)模糊控制理论的基本概念 (15)模糊逻辑操作 (16)模糊规则与模糊推理 (16)模糊控制系统 (16)模糊控制系统的组成 (17)模糊控制系统的特点 (18)模糊控制器 (18)模糊控制器的组成 (18)模糊控制器的结构 (19)4 双闭环模糊控制系统设计 (21)建立双闭环模糊控制系统 (21)模糊控制器的设计 (21)隶属函数的确定 (21)模糊控制规则 (23)输出向量的解模糊 (24)建立模糊控制查询表 (25)5 一阶倒立摆系统仿真及其分析 (28)MATLAB及其模糊工具箱的介绍 (28)MATLAB的主要特点 (28)MATLAB的基本组成 (29)一阶倒立摆模糊控制系统仿真实验 (30)利用GUI编辑FIS结构文件,即设计模糊控制器 (30)建立一阶倒立摆模糊控制系统的仿真模型图 (33)6 结论与展望 (38)参考文献 (39)致谢 (40)系统总体框图 (41)系统总体原理图 (42)1 绪论一阶倒立摆系统研究的意义一阶倒立摆在稳定性控制问题中具有成本低廉,结构简单,形象直观,物理参数和结构易于调整的优点。
一级倒立摆【控制专区】系统设计
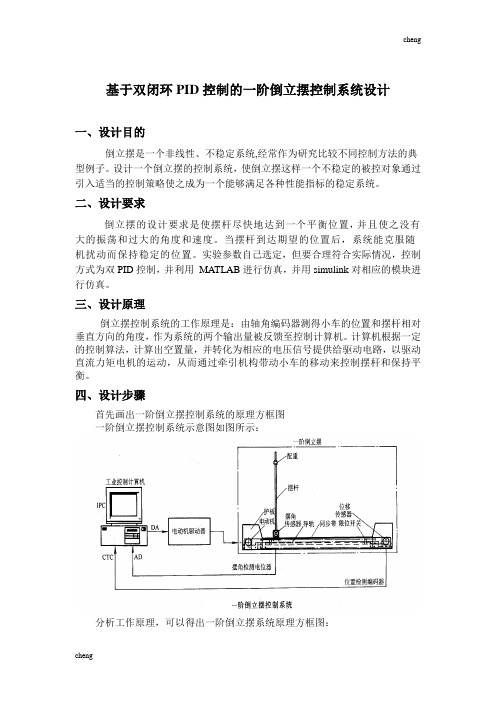
基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。
设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
二、设计要求倒立摆的设计要求是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
实验参数自己选定,但要合理符合实际情况,控制方式为双PID控制,并利用MATLAB进行仿真,并用simulink对相应的模块进行仿真。
三、设计原理倒立摆控制系统的工作原理是:由轴角编码器测得小车的位置和摆杆相对垂直方向的角度,作为系统的两个输出量被反馈至控制计算机。
计算机根据一定的控制算法,计算出空置量,并转化为相应的电压信号提供给驱动电路,以驱动直流力矩电机的运动,从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。
四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示:分析工作原理,可以得出一阶倒立摆系统原理方框图:一阶倒立摆控制系统动态结构图下面的工作是根据结构框图,分析和解决各个环节的传递函数!1.一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示,其中: M :小车质量 m :为摆杆质量 J :为摆杆惯量 F :加在小车上的力 x :小车位置θ:摆杆与垂直向上方向的夹角 l :摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律,可知: (1) 摆杆绕其重心的转动方程为(2) 摆杆重心的运动方程为得sin cos ..........(1)y x J F l F l θθθ=-2222(sin ) (2)(cos ) (3)x y d F m x l d td F mg m l d t θθ=+=-(3)小车水平方向上的运动为22..........(4)x d xF F M d t-=联列上述4个方程,可以得出一阶倒立精确气模型:()()()()()()()2222222222222222sin .sin cos cos cos .sin cos .lg sin cos J ml F ml J ml m l g x J ml M m m l ml F m l M m m m l M m J ml θθθθθθθθθθθθ⎧+++-⎪=++-⎪⎨+-+⎪=⎪-++⎩式中J 为摆杆的转动惯量:32ml J =若只考虑θ在其工作点附近θ0=0附近(︒︒≤≤-1010θ)的细微变化,则可以近似认为:⎪⎩⎪⎨⎧≈≈≈1cos sin 02θθθθ ⎪⎪⎩⎪⎪⎨⎧++-+=++-+=2..2222..)(lg )()()(Mml m M J mlF m m M Mml m M J g l m F ml J x θθθ 若取小车质量M=2kg,摆杆质量m=1kg,摆杆长度2 l =1m,重力加速度取g=2/10s m ,则可以得 一阶倒立摆简化模型:....0.44 3.330.412x F F θθθ⎧=-⎪⎨⎪=-+⎩即 G 1(s)= ; G 2(s)=一阶倒立摆环节问题解决!2.电动机驱动器选用日本松下电工MSMA021型小惯量交流伺服电动机,其有关参数如下:222()0.4()12() 1.110()s F s s x s s s s θθ-⎧=⎪-⎪⎨-+⎪=⎪⎩驱动电压:U=0~100V 额定功率:PN=200W 额定转速:n=3000r/min 转动惯量:J=3×10-6kg.m2 额定转矩:TN=0.64Nm 最大转矩:TM=1.91Nm 电磁时间常数:Tl=0.001s 电机时间常数:TM=0.003s经传动机构变速后输出的拖动力为:F=0~16N ;与其配套的驱动器为:MSDA021A1A ,控制电压:UDA=0~±10V 。
一级倒立摆控制系统设计
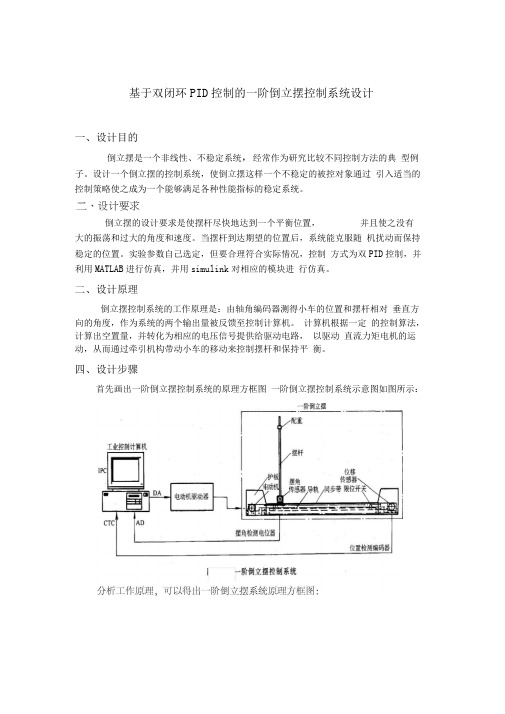
基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。
设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
、设计要求倒立摆的设计要求是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
实验参数自己选定,但要合理符合实际情况,控制方式为双PID控制,并利用MATLAB进行仿真,并用simulink对相应的模块进行仿真。
二、设计原理倒立摆控制系统的工作原理是:由轴角编码器测得小车的位置和摆杆相对垂直方向的角度,作为系统的两个输出量被反馈至控制计算机。
计算机根据一定的控制算法,计算出空置量,并转化为相应的电压信号提供给驱动电路,以驱动直流力矩电机的运动,从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。
四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示:工业控制计算机电动机驱动器一阶倒立摆一阶倒立摆控制系统动态结构图F面的工作是根据结构框图,分析和解决各个环节的传递函数!1. 一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示,其中:M小车质量m为摆杆质量J :为摆杆惯量F:加在小车上的力x :小车位置摆杆与垂直向上方向的夹角l :摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律,可知:(1) 摆杆绕其重心的转动方程为J鎳F y lsin 二- F x l cos: (1)(2) 摆杆重心的运动方程为F x d2(x l sin r)彳『=mg-m d2 d2t(3) 小车水平方向上的运动为-1-L+10-0一4即 G 1(s)=' ; G 2(s)='-一阶倒立摆环节问题解决!2. 电动机驱动器选用日本松下电工MSMA02型小惯量交流伺服电动机,其有关参数如下:F — F x 二 M d 2x联列上述4个方程,可以得出一阶倒立精确气模型:J ml 2F ml J ml 2sin u 2-m 2l 2gsin r COST2 2 2 2J ml j[ M m :-m l cos )mlcos v.F m 2l 2sin vcos m 2-<; M m mlg sin vm 2l 2cos 20—(M + m )(J +ml 2)式中J 为摆杆的转动惯量:J 』3若只考虑B 在其工作点附近B 0=0附近(-10 —”:10 )的细微变化,则可 以近似认为: 石2“* sin^比日 cos 日“若取小车质量M=2kg,摆杆质量 m=1kg,摆杆长度2 l =1m,重力加速度取g=10m/s 2,则可以得阶倒立摆简化模型:x =0.44F -3.33^ v - -0.4 F 12^拉氏变换=^>日(s)』F(s) x(s) ?(s)-0.42s-122 -1.1s 102 s2(J ml 2)F -m 2l 2g J J(M m) Mml (M m)mlg mlF J(M m) Mml电磁时间常数:Tl=0.001s电机时间常数:TM=0.003s经传动机构变速后输出的拖动力为: F=0~16N 与其配套的驱动器为:MSDA021A1A S 制电压:UDA=0± 10V 。
一阶倒立摆双闭环模糊控制

摘要本文讨论基于鲁棒性设计的一阶倒立摆双闭环控制问题。
以摆角为内环.以小车位置为外环利用鲁棒孔子系统理论进行模糊控制器设计及参数整定,使控制系统对于确定系统参数的变化具有较强的鲁棒性。
倒立摆系统的高阶次、不稳定、多变量、非线性和强耦合等特性使得许多现代控制理论的研究人员一直将它视为研究对象。
论文首先介绍了模糊系统的理论基础,和模糊控制器的分析和设计,充分的理解了倒立摆智能控制系统研究与设计所需要的理论知识。
然后通过对倒立摆系统的分析建模,采用模糊推理系统,设计相应的模糊控制器,对倒立摆进行控制,最后将控制过程在MATLAB上加以仿真。
在MATLAB仿真中,应用模糊逻辑工具箱来设计模糊逻辑控制器,然后通过Simulink来建立模糊系统,最后得到仿真结果。
关键词:倒立摆,模糊控制,双闭环模糊控制器,MATLAB仿真。
ABSTRACTThis article discusses the question of inverted pendulum double loop control that based on robust design. Take the pivot angle as the inner ring , the car position as the outer ring, Carries on the fuzzy controller design and the parameter installation by use robust control system theory, enable the control system to have strong robustness that determine changes in system parameters. As the inverted pendulum system is unstable,multivariable, nonlinear and strongly coupling and so on, many modern control theory researchers regard it as the object of study. The thesis introduced the Fuzzy systems theory ,the analysis and design of fuzzy controller , understand the theory knowledge that needed in study of intelligent control system of inverted pendulum . Then use fuzzy inference system and design corresponding fuzzy controller to control Inverted pendulum by making model of analysis of the inverted pndulum system.Finally,simulate the control processing in MATLAB.The simulation in MATLAB,design Fuzzy logic controller by applicating fuzzy logic toolbox,then set up fuzzy systems by use Simulink and at last obtained simulation results.Key word:Inverted pendulum, fuzzy control, double closed loop fuzzy controller, MATLAB simulation.目录第一章绪论 (4)1.1倒立摆系统稳定性研究 (4)1.1.1 倒立摆系统稳定性研究的意义 (4)1.1.2 倒立摆研究的发展状况 (5)1.2 模糊控制的研究现状 (6)1.2.1模糊控制理论的产生 (6)1.2.2模糊控制的数学基础 (7)1.2.3模糊控制的研究现状 (8)1.2.4模糊控制理论的发展前景 (9)1.3 论文主要工作 (10)第二章:单支点倒立摆系统数学模型的建立及系统分析 (11)2.1建模机理 (11)2.2系统建模 (11)2.3 模型简化 (13)第三章:模糊控制的基本原理 (16)3.1 模糊集合与隶属函数 (16)3.2 模糊逻辑操作 (16)3.3 模糊规则与模糊推理 (17)3.4 模糊推理系统 (17)第四章:一阶倒立摆系统的双闭环模糊控制器的设计与仿真 (19)4.1 一阶倒立摆系统的双闭环模糊控制方案 (19)4.1.1 问题的提出 (19)4.1.2 模糊控制器的设计 (20)4.2 仿真实验 (23)4.2.1 MATLAB模糊逻辑工具箱 (23)4.2.2 一阶倒立摆系统数字仿真模型的建立 (26)4.3仿真实验结果 (28)第五章结论 (33)致谢 (34)参考文献: (35)附录: (36)中文翻译: (41)第一章绪论1.1倒立摆系统稳定性研究倒立摆控制系统是应用于自动控制理论实验室的经典实验装置。
一级倒立摆LQR控制器的设计..

目录0.前言 (4)0.1倒立摆 (4)0.2LQR (7)0.3.最优控制(optimal control) (7)0.3.1数学角度 (8)0.3.2研究方法 (8)1.线性二次最优控制LQR基本理论 (8)1.1一级倒立摆建模 (8)1.2微分方程模型 (12)1.3传递函数模型 (12)1.4状态空间数学模型 (13)1.5LQR控制器的二次最优控制原理 (14)2. 方案设计 (16)3. 软件编程 (16)3.1求K值程序 (16)3.2系统的开环阶跃响应程序 (17)3.3小车的状态程序 (17)4. 系统调试和结果分析 (18)4.1得出K值 (18)4.2系统的开环阶跃响应结果 (19)4.3实际连接 (19)一级倒立摆LQR控制器的设计摘要:倒立摆控制系统是一个复杂的、不稳定的、非线性系统,是进行控制理论教学及开展各种控制实验的理想实验平台。
对倒立摆系统的研究能有效的反映控制中的许多典型问题。
从理论和实践上对线性一级倒立摆作了深入的研究。
首先,用拉格朗日方法建立了倒立摆的数学模型。
在此基础上采用线性二次型最优控制方法设计了倒立摆的控制器。
最后通过MATLAB仿真和实际系统实验,实现对倒立摆的稳定控制。
通过试验验证了设计结果并给出了控制器的性能评价。
建立模型,确定参数,进行控制算法设计、系统调试和分析等步骤实现。
关键词:倒立摆;建模,LQR控制器0.前言0.1倒立摆倒立摆系统是理想的自动控制教学实验设备,使用它能全方位的满足自动控制教学的要求。
许多抽象的控制概念如系统稳定性、可控性、系统收敛速度和系统抗干扰能力等,都可以通过倒立摆直观的表现出来。
倒立摆最初研究开始于20世纪50年代,麻省理工学院(MIT)的控制论专家根据火箭发射助推器原理设计出一级倒立摆实验设备,而后人们又参照双足机器人控制问题研制二级倒立摆控制设备,从而提高了检验控制理论或方法的能力,也拓宽了控制理论或方法的检验范围。
一阶倒立摆实验报告(实验)

一、实验介绍:1、背景介绍 (3)2、倒立摆简介 (3)3、实验目的 (5)4.预备知识 (5)二、实验内容:1.自学掌握MATLAB软件的基本使用方法 (6)2.自学掌握倒立摆的基本知识 (6)3.在MATLAB编程环境下完成以下实验操作 (6)4.在proteus环境下,完成倒立摆电机控制算法的仿真 (6)三、实验步骤:1.直线一阶倒立摆数学模型的推导‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥6 2.一阶倒立摆的微分方程模型‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥7 3.一阶倒立摆的传递函数模型‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥9 4.一阶倒立摆的状态空间模型‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥10 5.实际系统的传递函数与状态方程‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥12 6.用MATLAB的Simulink进行仿真‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥13四、实验总结:1、实验结论 (18)2、实验收获 (19)五、参考文献:一、实验介绍:1、背景介绍倒立摆装置被公认为自动控制理论中的典型实验设备,也是控制理论教学和科研中不可多得的典型物理模型。
它深刻揭示了自然界一种基本规律,即一个自然不稳定的被控对象,运用控制手段可使之具有良好的稳定性。
通过对倒立摆系统的研究,不仅可以解决控制中的理论问题,还能将控制理论所涉及的三个基础学科:力学、数学和电学(含计算机)有机的结合起来,在倒立摆系统中进行综合应用。
在多种控制理论与方法的研究和应用中,特别是在工程实践中,也存在一种可行性的试验问题,将其理论和方法得到有效的经验,倒立摆为此提供一个从控制理论通往实践的桥梁。
2、直线一阶倒立摆简介:倒立摆是进行控制理论研究的典型实验平台,可以作为一个典型的控制对象对其进行研究。
最初研究开始于二十世纪50 年代,麻省理工学院(MIT)的控制论专家根据火箭发射助推器原理设计出一级倒立摆实验设备。
近年来,新的控制方法不断出现,人们试图通过倒立摆这样一个典型的控制对象,检验新的控制方法是否有较强的处理多变量、非线性和绝对不稳定系统的能力,从而从中找出最优秀的控制方法。
倒立摆控制系统的设计

自动控制理论课程设计倒立摆系统的控制器设计学生姓名:指导教师:班级:二O一三课程设计指导教师评定成绩表:指导教师评定成绩:指导教师签名:年月日重庆大学本科学生课程设计任务书目录一、倒立摆控制系统概述倒立摆装置被公认为自动控制理论中的典型实验设备,也是控制理论教学和科研中控对象,运用控制手段可使之具有良好的稳定性。
通过对倒立摆系统的研究,不仅可以解决控制中的理论问题,还能将控制理论所涉与的三个基础学科:力学、数学和电学(含计算机)有机的结合起来,在倒立摆系统中进行综合应用。
在多种控制理论与方法的研究和应用中,特别是在工程实践中,也存在一种可行性的试验问题,将其理论和方法得到有效的经验,倒立摆为此提供一个从控制理论通往实践的桥梁。
在稳定性控制问题上,倒立摆既具有普遍性又具有典型性。
倒立摆系统作为一个控制装置,结构简单、价格低廉,便于模拟和数字实现多种不同的控制方法,作为一个被控对象,它是一个高阶次、不稳定、多变量、非线性、强耦合的快速系统,只有采用行之有效的控制策略,才能使其稳定。
倒立摆系统可以用多种理论和方法来实现其稳定控制,如、自适应、状态反馈、智能控制、模糊控制与人工神经元网络等多种理论和方法,都能在倒立摆系统控制上得到实现,而且当一种新的控制理论和方法提出以后,在不能用理论加以严格证明时,可以考虑通过倒立摆装置来验证其正确性和实用性。
倒立摆的种类:悬挂式、直线、环形、平面倒立摆等。
一级、二级、三级、四级乃至多级倒立摆。
倒立摆控制系统的组成:倒立摆系统由倒立摆本体,电控箱以与控制平台(包括运动控制卡和机)三大部分组成。
本次课程设计利用单级倒立摆,主要设计机内控制函数,减小超调量和调节时间!二、数学模型的建立系统建模可以分为两种:机理建模和实验建模。
对于倒立摆系统,由于其本身是自不稳定的系统,实验建模存在一定的困难。
机理建模就是在了解研究对象的运动规律基础上,通过物理、化学等学科的知识和数学手段建立起系统内部变量、输入变量以与输出变量之间的数学关系。
环形倒立摆说明书

目录序言 (2)第一章环形一级倒立摆的数学模型 (3)第二章环形二级倒立摆的数学模型 (5)第三章最优控制 (9)第四章环形倒立摆系统的硬件和软件 (10)4.1控制系统的硬件 (10)4.2控制系统软件 (10)4.2.1VC版控制系统软件说明 (11)4.2.2实时数据保存 (14)4.2.3 Matlab版软件说明 (15)第五章系统使用说明 (23)5.1 环形倒立摆系统的操作步骤 (23)5.2 注意事项 (25)5.3日常维护 (25)序言在控制理论发展的过程中某一理论的正确性及实际应用中的可行性需要一个按其理论设计的控制器去控制一个典型对象来验证.倒立摆就是这样一个被控制对象.倒立摆系统是进行控制理论教学及开展各种控制实验的理想平台,它具有成本低廉、结构简单、物理参数和结构易于调整的优点,倒立摆系统本身是一个典型的非线性、高阶次、多变量、强耦合和绝对不稳定系统,许多抽象的控制概念如系统的稳定性、可控性、系统的收敛速度和系统的抗干扰能力等,都可以通过倒立摆直观地表现出来.此外,通过倒立摆系统还可以研究结构控制、非线性观测器、摩擦补偿、目标定位控制、混合系统和混沌系统等.利用倒立摆系统研究产生的方法和技术在半导体及精密仪器加工、机器人控制技术、人工智能、导弹拦截控制系统、航空对接控制技术、火箭发射中的垂直度控制、卫星飞行中的姿态控制和一般工业应用等方面都具有广阔的利用开发前景.倒立摆系列产品包括直线运动型、圆周运动型和平面运动倒立摆几大系列,主要特点包括:开放性:采用二轴运动控制板卡,机械部分和电气部分非常容易扩展,可以根据用户需要进行配置.系统软件接口充分开放,用户不仅可以使用配套的实验软件,而且可以根据自己的实际需要扩展软件的功能.模块化:系统的机械部分可以选用直线或者旋转平台,根据实际需要配置成一级、二级或者三级倒立摆.而三级摆可以方便地改装成二级摆,二级摆可以改装成一级摆.系统实验软件同样是基于模块化的思想设计,用户可以根据需要增加或者修改相应的功能模块.简易安全:倒立摆实验系统包括运动控制卡、电控箱、机械本体和微型计算机几个部分组成,安装升级方便.同时在机械、运动控制板卡和实验软件上都采取了积极措施,保证实验时人员的安全可靠和仪器安全.方便性:倒立摆系统易于安装、升级,同时软件界面操作简单.先进性:采用工业级二轴运动控制板卡作为核心控制系统,先进的交流伺服电机作为驱动,检测元件使用高精度高性能光电码盘.系统设计符合当今先进的运动控制发展方向.实验软件多样化:用于实验的软件包括Windows界面(VC++),以及控制领域使用最多的仿真工具Matlab提供完备的设备接口和程序接口,方便用户进行实验和开发.倒立摆系统适应如下课程的实验:《自动控制原理》、《现代控制理论》、《现代控制工程》、《最优控制》、《非线性系统控制》、《智能控制》、《模糊控制》和《神经网络控制》等等.第一章 环形一级倒立摆的数学模型在忽略了空气阻力、各种摩擦之后,将环形倒立摆系统抽象成匀质摆杆和水平杆组成的刚体系统.环形一级倒立摆的结构如图所示:图1 环形一级倒立摆的结构图水平杆与x 的夹角:0θ,摆杆与垂直方向的夹角:1θ表1 环形一级倒立摆的物理参数水平杆的质量0m 0.308 kg 水平杆绕端点的转动惯量 0J 0.0042kg m ⋅摆杆的质量1m 0.1323 kg 摆杆绕质心的转动惯量1J 0.01152kg m⋅水平杆的长度0L 0.2535 m摆杆质心到转轴的距离1l 0.2433m系统的拉格朗日算子:(,)(,)(,)L q qT q q V q q =- ,其中L 为拉格朗日算子、q 为系统的广义坐标、T 为系统的总动能、V 为系统的总势能. 拉格朗日方程:()i i id L LQ dt q q ∂∂-=∂∂ (1.1) 其中,1,2,3,...,i n =、i Q 为系统沿广义坐标i q 方向上的外力.在环形一级倒立摆系统中广义坐标:000111,,q qq θθθθθθ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦环形一级倒立摆系统的动能T :01m m T T T =+ (1.2)其中,0m T 为水平杆的动能、1m T 为摆杆的动能. 水平杆的动能:020012m T J θ=在距摆杆转动中心距离l 处取一小段dl ,这一小段的坐标如下:000100011cos sin sin sin cos sin cos x L l y L l z l θθθθθθθ=-⎧⎪=+⎨⎪=⎩则,这一小段的动能:222111[()()()]22dl dx dy dz dT m l dt dt dt=++ 摆杆的动能: 1120l m T dT =⎰(1.3)以水平杆所在的水平面为零势能面,则系统的势能V 即为摆杆的重力势能:1111cos m V V m gl θ==(1.4) 则,拉格朗日方程:011()()0d LL u dt d L L dt θθθθ∂∂⎧-=⎪∂∂⎪⎨∂∂⎪-=⎪∂∂⎩ (1.5) 其中,u 为施加到水平杆上的控制力矩.在倒立摆实物控制中,我们采用水平杆的角加速度作为输入即:0u θ= 系统的状态变量:0101T x θθθθ⎡⎤=⎣⎦ ,在平衡位置[]0000T 对系统模型进行线性化即:2cos 1,sin ,0θθθθ≈≈≈系统的状态空间模型:xAx Bu y Cx=+⎧⎨=⎩ (1.6) 其中,A 为系统的状态矩阵、B 为控制矩阵、y 为系统的输出、C 为系统的输出矩阵 由上述(1.5)微分方程的:42400100000101000,,000010100000A B C a b ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦其中,04241133,44L ga b l l ==.第二章 环形二级倒立摆的数学模型在忽略了各种摩擦后,环形二级摆抽象成由两个摆杆和一个水平杆组成,系统结构如图所示:图2环形二级倒立摆的结构简化图水平杆与x 的夹角:0θ,下摆杆与垂直方向的夹角:1θ,上摆杆与垂直方向的夹角:2θ .表2环形二级倒立摆的物理参数水平杆的长度 0L 下摆杆绕质心的转动惯量 1J 下摆杆的长度1L 上摆杆绕质心的转动惯量 2J 下摆杆质心到转轴的距离 1l 下摆杆的质量 1m上摆杆质心到转轴的距离 2l 上摆杆的质量 2m水平杆绕端点的转动惯量0J系统的拉格朗日算子:(,)(,)(,)L q qT q q V q q =- ,其中L 为拉格朗日算子、q 为系统的广义坐标、T 为系统的总动能、V 为系统的总势能.拉格朗日方程:()i i i d L LQ dt qq ∂∂-=∂∂(2.1) 其中,1,2,3,...,i n =、i Q 为系统沿广义坐标i q 方向上的外力.在环形二级倒立摆系统中广义坐标:000111222,,q q q θθθθθθθθθ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦.环形二级倒立摆系统的动能T : 012m m m T T T T =++ (2.2)其中,0m T 为水平杆的动能、1m T 为下摆杆的动能、2m T 为上摆杆的动能. 水平杆的动能:020012m T J θ=(2.3)在距下摆杆转动中心距离l 处取一小段dl ,这一小段的坐标如下:100011000111cos sin sin sin cos sin cos x L l y L l z l θθθθθθθ=-⎧⎪=+⎨⎪=⎩ 则,这一小段的动能:1222111111[()()()]2m dx dy dz dldT m L dt dt dt=++ 下摆杆的动能:1110L m m T dT =⎰(2.4) 在距下摆杆转动中心距离h 处取一小段dh ,这一小段的坐标如下:20010102200101022112cos sin sin sin sin sin cos sin cos sin cos cos x L L h y L L h z L h θθθθθθθθθθθθ=--⎧⎪=++⎨⎪=+⎩ 则,这一小段的动能:2222222221[()()()]22m dx dy dz dhdT m l dt dt dt=++ 上摆杆的动能:22220l m m T dT =⎰(2.5) 以水平杆所在的水平面为零势能面,则系统的势能V 即为摆杆的重力势能11122211cos (cos cos )V m gl m g l L θθθ=++(2.6) 则,拉格朗日方程:001122()()0()0d L Lu dt d L Ldt d L Ldt θθθθθθ⎧∂∂-=⎪∂∂⎪⎪∂∂-=⎨∂∂⎪⎪∂∂-=⎪∂∂⎩(2.7) 其中,u 为施加到水平杆上的控制力矩. 将上述微分方程写成:(,)(,)()M q q q C q q q G q τ++= (2.8)由(2.7)可知:111213111213212223212223313233313233,,00m m m c c c u M m m m C c c c m m m c c c τ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦22110112201121210113002211222123011231133223332sin sin 2sin sin cos cos cos()m a a a b L m b L m b L m m m a m b L m m m m m a θθθθθθθθ⎧=+++⎪=⎪⎪=⎪=⎪⎪=⎨⎪=-⎪⎪=⎪=⎪⎪=⎩1112101101101012132020022010122110110101222230121231202201010sin 2sin 2cos sin sin 2sin 2sin cos sin cos cos sin 0sin()sin cos sin cos c c a b L b L c a b L b L c a b L c c b L c a b L θθθθθθθθθθθθθθθθθθθθθθθθθθθθθ==-+=-+=--==-=--2320111233sin()0c b L c θθθ⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪=--⎪=⎩ ,11020sin sin G b g b g θθ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦ 其中已置,22222001020111121222202211121,,,,a J m L m L a J m l m L a J m lb m l b m l m L ++++++在倒立摆实物控制中,我们采用水平杆的角加速度作为输入即:0u θ= 系统的状态变量:012012Tx θθθθθθ⎡⎤=⎣⎦,在平衡位置[]000000T对系统模型进行线性化即:2cos 1,sin ,0θθθθ≈≈≈系统的状态空间模型:xAx Bu =+ ,其中,A 为系统的状态矩阵、B 为控制矩阵 525356263600100000001000000010,000000100000000A B a a b a a b ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦其中,201215253222212011201011106263222212011201,()(),()()b L g a b ga a a ab L a a b L b b L g a b ga a a ab L a a b L -==-+-+-==-+-+,2012015221201001116221201()()()()L b a b L b a a b L b L b L a b a a b L -=-+--=-+表3环形二级倒立摆的物理参数:水平杆的长度0L 0.2135m 下摆杆绕质心的转动惯量1J 0.00332kg m ⋅ 下摆杆的长度1L 0.175m 上摆杆绕质心的转动惯量2J 0.00882kg m ⋅ 下摆杆质心到转轴的距离1l 0.1329m 下摆杆的质量1m 0.1617㎏ 上摆杆质心到转轴的距离 2l 0.221m 上摆杆的质量2m 0.1225 ㎏ 水平杆绕端点的转动惯量0J 0.0042kg m ⋅第三章 最优控制在经典控制理论中,设计控制系统的各种方法大多建立在试凑的基础上,设计结果与设计人员的经验有很大关系.对于多输入-多输出系统,或者要求较高精度的复杂系统,经典控制方法显得无能为力,迫切需要探索新的设计方法.20世纪60年代,由于空间技术的迅猛发展和计算机的广泛应用,动态系统的优化理论得到了迅速发展,形成了最优控制这一重要的学科分支,并在控制工程、经济管理与决策以及人口控制等领域得到了成功应用,取得了显著的成效.最优控制在被控对象已知的情况下,已经成为设计复杂系统的有效方法之一.最优控制是现代控制理论的核心.最优控制研究的主要问题是:根据已建立的被控对象的数学模型,选择一个容许的控制规律,使得被控对象按预定要求运行,并使某一性能指标达到极小值(或极大值).从数学观点来看,最优控制研究的问题是求解一类带有约束条件的泛函极值问题,属于变分学的范畴.然而经典的控制理论只能解决控制无约束,即容许控制属于开集的一类最优问题,而实际工程实践中所遇到的多为控制有约束,即容许控制属于闭集的一类最优控制问题.为了满足工程实践的需要,20世纪50年代中期,出现了变分理论,其中最常用的方法是动态规划和极小值原理.如果所研究的系统是线性的,且性能指标为状态变量和控制变量的二次型函数,则最优控制问题称为线性二次型问题.由于线性二次型问题的最优解具有统一的解析表达式,且可导致一个简单的线性状态反馈控制律,易于构成闭环最优反馈控制,便于工程实现,因而在实际工程中得到了广泛的应用.利用线性二次型性能指标设计的控制器称作LQR 控制器。
一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真

一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真倒立摆PID控制及其Matlab仿真学生姓名:学院:电气信息工程学院专业班级:专业课程:控制系统的MATLAB仿真与设计任课教师:2014 年 6 月 5 日倒立摆PID控制及其Matlab仿真Inverted Pendulum PID Control and ItsMatlab Simulation摘要倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,对倒立摆的控制研究无论在理论上和方法上都有深远的意义。
本论文以实验室原有的直线一级倒立摆实验装置为平台,重点研究其PID 控制方法,设计出相应的PID控制器,并将控制过程在MATLAB上加以仿真。
本文主要研究内容是:首先概述自动控制的发展和倒立摆系统研究的现状;介绍倒立摆系统硬件组成,对单级倒立摆模型进行建模,并分析其稳定性;研究倒立摆系统的几种控制策略,分别设计了相应的控制器,以MATLAB为基础,做了大量的仿真研究,比较了各种控制方法的效果;借助固高科技MATLAB实时控制软件实验平台;利用设计的控制方法对单级倒立摆系统进行实时控制,通过在线调整参数和突加干扰等,研究其实时性和抗千扰等性能;对本论文进行总结,对下一步研究作一些展望。
关键词:倒立摆;PID控制器;MATLAB仿真设计报告正文1.简述一级倒立摆系统的工作原理;倒立摆是一个数字式的闭环控制系统,其工作原理为:角度、位移信号检测电路获取后,由微分电路获取相应的微分信号。
这些信号经A/D转换器送入计算机,经过计算及内部的控制算法解算后得到相应的控制信号,该信号经过D/A变换、再经功率放大由执行电机带动皮带卷拖动小车在轨道上做往复运动,从而实现小车位移和倒立摆角位移的控制。
2.依据相关物理定理,列写倒立摆系统的运动方程;2lO1小车质量为M ,倒立摆的质量为m ,摆长为2l ,小车的位置为x ,摆的角度为θ,作用在小车水平方向上的力为F ,1O 为摆杆的质心。
(完整版)一级倒立摆系统分析
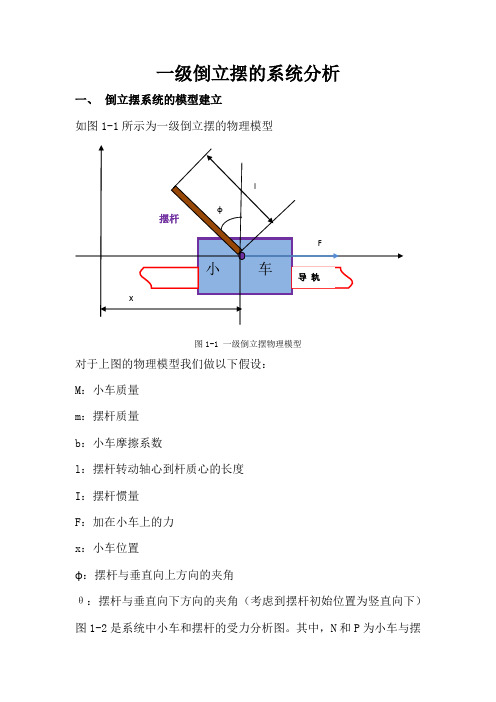
一级倒立摆的系统分析一、倒立摆系统的模型建立如图1-1所示为一级倒立摆的物理模型图1-1 一级倒立摆物理模型对于上图的物理模型我们做以下假设:M:小车质量m:摆杆质量b:小车摩擦系数l:摆杆转动轴心到杆质心的长度I:摆杆惯量F:加在小车上的力x:小车位置ɸ:摆杆与垂直向上方向的夹角θ:摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下)图1-2是系统中小车和摆杆的受力分析图。
其中,N和P为小车与摆杆相互作用力的水平和垂直方向的分量。
注意:实际倒立摆系统中的检测和执行装置的正负方向已经完全确定,因而矢量方向定义如图所示,图示方向为矢量正方向。
图1-2 小车及摆杆受力分析分析小车水平方向受力,可以得到以下方程:M ẍ=F-bẋ-N (1-1)由摆杆水平方向的受力进行分析可以得到以下方程:N =md 2dt 2(x +l sin θ) (1-2)即: N =mẍ+mlθcos θ−mlθ2sin θ (1-3)将这个等式代入式(1-1)中,可以得到系统的第一个运动方程: (M +m )ẍ+bẋ+mlθcos θ−mlθ2sin θ=F (1-4)为推出系统的第二个运动方程,我们对摆杆垂直方向上的合力进行分析,可以得出以下方程: P −mg =md 2dt 2(l cos θ) (1-5)P −mg =− mlθsin θ−mlθ2cos θ (1-6) 利用力矩平衡方程可以有:−Pl sinθ−Nl cosθ=Iθ (1-7)注意:此方程中的力矩方向,由于θ=π+ɸ,cosɸ=−cosθ,sinɸ=−sinθ,所以等式前面含有负号。
合并两个方程,约去P和N可以得到第二个运动方程:(I+ml2)θ+mgl sinθ=−mlẍcosθ (1-8)设θ=π+ɸ,假设ɸ与1(单位是弧度)相比很小,即ɸ<<1,则可以进行近似处理:cosθ=−1,sinθ=−ɸ,(dθdt )2=0。
用u来代表被控对象的输入力F,线性化后的两个运动方程如下:{(I+ml2)ɸ−mglɸ=mlẍ(M+m)ẍ+bẋ−mlɸ=u(1-9)假设初始条件为0,则对式(1-9)进行拉普拉斯变换,可以得到:{(I+ml2)Φ(s)s2−mglΦ(s)=mlX(s)s2(M+m)X(s)s2+bX(s)s−mlΦ(s)s2=U(s) (1-10) 由于输出为角度ɸ,求解方程组的第一个方程,可以得到:X(s)=[(I+ml2)ml −gs2]Φ(s) (1-11)或改写为:Φ(s)X(s)=mls2(I+ml2)s2−mgl(1-12)如果令v=ẍ,则有:Φ(s)V(s)=ml(I+ml2)s2−mgl(1-13)如果将上式代入方程组的第二个方程,可以得到:(M+m)[(I+ml2)ml −gs]Φ(s)s2+b[(I+ml2)ml+gs2]Φ(s)s−mlΦ(s)s2=U(s) (1-14) 整理后可得传递函数:Φ(s) U(s)=mlqs2s4+b(I+ml2)qs3−(M+m)mglqs2−bmglqs(1-15)其中q=[(M+m)(I+ml2)−(ml)2]假设系统状态空间方程为:X=AX+Buy=CX+Du (1-16) 方程组对ẍ,ɸ解代数方程,可以得到解如下:{ẋ=ẋẍ=−(I+ml2)bI(M+m)+Mml2ẋ+m2gl2I(M+m)+Mml2ɸ+(I+ml2)I(M+m)+Mml2uɸ=ɸɸ=−mlbI(M+m)+Mml2ẋ+mgl(M+m)I(M+m)+Mml2ɸ+mlI(M+m)+Mml2u(1-17)整理后可以得到系统状态空间方程:[ẋẍɸɸ]=[01000−(I+ml2)bI(M+m)+Mml2m2gl2I(M+m)+Mml200010−mlbI(M+m)+Mml2mgl(M+m)I(M+m)+Mml20][xẋɸɸ]+[(I+ml2)I(M+m)+Mml2mlI(M+m)+Mml2]uy=[xɸ]=[10000010][xẋɸɸ]+[0]u(1-18)由(1-9)的第一个方程为:(I+ml2)ɸ−mgl ɸ=mlẍ对于质量均匀分布的摆杆可以有:I=13ml2于是可以得到:(13ml2+ml2)ɸ−mgl ɸ=mlẍ化简可以得到:ɸ=3g4l ɸ+34lẍ(1-19)设X={x, ẋ, ɸ , ɸ},u=ẍ则有:[ẋẍɸɸ]=[010000000001003g4l0][xẋɸɸ]+[134l]uy=[xɸ]=[10000010][xẋɸɸ]+[0]u(1-20)以上公式推理是根据牛顿力学的微分方程验证的。
一阶倒立摆系统模型分析、状态反馈与观测器设计

u b +
x
+
y
A G
c
b
+ +
ˆ x
A-GC
ˆ x
K
5.仿真分析
• 基于全维状态观测器下的倒立摆控制系统仿真:
• 仿真结果
• 状态估计值与系统状态比较
• 从仿真结果看,控制性能满足系统要求的性能指 标。
• 全维观测器状态跟踪误差仿真结果:
降维观测器设计
• 在实际工程实践中,系统的输出是能够测量的, 因此可以考虑用输出量直接产生响应的部分状态 变量,其余状态变量则通过构造观测器来实现, 所构造的观测器为降维观测器。本实验的倒立摆 系统采用P变换方法设计降维观测器。
• 知系统是完全能控的,满足特征值可任意配置的 极点配置定理。
• (3)可观测性分析 • 由
1 0 0 C CA 0 rank rank 2 0 CA 3 CA 0 0 0
0 0 0 0 1 0 1 0 0 0 0 1 4 0 0 0 0 58.6118 0.6747 0 0 0 0 39.5454 59.067
• (2)取期望的特征值为 30,30 ,则特征多项 式为a (s) s 2 10s 37 ,解方程 det(sI A A K ) a (s) 0 • 得 K 30
T T 22 12
0
29.3253
• 进一步计算 • 30 LK
T
0
u x m gl sin c m l u cos J J J
• 根据以上系统方程可以看出倒立摆模型是非线性 的。为了应用线性系统理论,可在倒立摆平衡位 置附近对系统进行线性化,取 - ,令 • sin , cos 1 并忽略高次项,可得如下方程: u x • m gl c mlu J J J
一级倒立摆控制装置的设计与开发

得 到 了较 好 的控 制 效 角度 /i q
制 程 序编 制灵 活 的特 点 。用 于控制 技 术 的
实 验 教 学 . 在 实 验 课
嚣 ≥≤ ≤- 拦 ≯ 三
一
图 3电气 系统 的设计
i .h F g3T eDe i f lc r c l y t m s n g o e e ti a se s
置 保持 动 态 平衡 。根据 牛 顿一 拉方 法 可 建 立直 线 型 一 欧
收 稿 日期 :2 1 — 9 0 0 1 0 —2
『 『 0 0 1 X 1 1 0
y0= 1 = 【0 J 【J0 0
式 中 :M一小 车 质量 ;m一摆 杆质 量 ;b 小车 摩 擦 一 系数 ;l 一摆 杆转 动 轴心 到杆 质心 的长 度 ;I 一摆 杆惯 量 ;
A s at T e i l i e e edlm dv eicmp s f bt c: h n e n r dpn u ei o oe o r sg v t u c s d a
ecj cmpt cuio f edlm ag no ebc g a h o ue aq itno nu nl s sred a snl p r si p u ee f ki
K= 3 和 K = 5 以 I15 D7 ,
辨 率 为 8位 ,转 换 时 间
为 10x ) 0 1 ,最 终把 电压转 换 为 0 2 5的数 字量 。飞思卡 s —5
尔 H 桥 直 流 电机驱 动 器 ( 出功 率为 19 输 8 W,额定 输 入
电 压为 2 V,额定 输入 电流为 9 1 A)采 用 P WM 控 制方 式
程 的实 践学 习 ,丰 富了实 验 的手段 ,在 实 验课 中取 得 良
基于双闭环PID控制的一阶倒立摆控制系统设计

自动控制原理课程设计说明书基于双闭环PID控制的一阶倒立摆控制系统设计姓名:学号:学院:专业:指导教师:2018年 1月目录1 任务概述.......................................... 错误!未定义书签。
设计概述........................................ 错误!未定义书签。
要完成的设计任务:............................. 错误!未定义书签。
2系统建模.......................................... 错误!未定义书签。
对象模型....................................... 错误!未定义书签。
模型建立及封装................................. 错误!未定义书签。
3仿真验证.......................................... 错误!未定义书签。
实验设计....................................... 错误!未定义书签。
建立M文件编制绘图子程序....................... 错误!未定义书签。
4 双闭环PID控制器设计.............................. 错误!未定义书签。
内环控制器的设计................................ 错误!未定义书签。
外环控制器的设计................................ 错误!未定义书签。
5 仿真实验.......................................... 错误!未定义书签。
简化模型........................................ 错误!未定义书签。
仿真实验....................................... 错误!未定义书签。
毕业设计-一阶倒立摆最优控制器的设计

(二○○七 年 六 月本科毕业设计说明书 题 目:一阶倒立摆最优控制器的设计 学生姓名:xx 学 院:xx 系 别:xx 专 业:xx 班 级:xx 指导教师:xx摘要倒立摆系统的控制研究长期以来被认为是控制理论及其应用领域里能引起人们极大兴趣的问题。
它是检验各种新的控制理论和方法的有效性的著名实验装置。
作为一个高阶、非线性不稳定系统,倒立摆的稳定控制相当困难,对该领域的学者来说是一个极具挑战性的难题。
首先,本文阐述倒立摆系统控制的研究发展过程,介绍了倒立摆系统的结构,并详细推导了一级倒立摆的数学模型,为更高层次的控制规律的研究提供了一个途径。
其次,研究倒立摆系统的各种控制方法。
其中包括有经典控制理论中的PID控制方法和最优控制理论中的极点配置法、LQR法。
在MATLAB/SIMULINK的环境下,作了大量的系统仿真研究工作,比较了各种控制方法。
最后,发现经过最优控制方法校正后的系统的性能优于经典控制方法校正后的系统的性能,而且最优控制较易实现。
关键词:倒立摆系统;经典控制理论;最优控制理论;系统仿真AbstractThe control of inverted pendulum system has long been considered an intriguing problem for control theory and its applications. It is well known as a test bed for new control theory and techniques. As a highly nonlinear and unstable system, the stabilization control of inverted pendulum system is a primary challenge for researchers in this field because of the difficulty of the problem.Firstly, after introducing the development and current situation of inverted pendulum system research, the mechanism of inverted pendulum are presented. Mathematical model of the higher one level inverted pendulum is particularly educed in this chapter. Secondly, the thesis discusses mainly the control methods of inverted pendulum system based on the PID of classic control theories, the Pole arrangement and the LQR of modern control theories. And many system simulation researches on the stability of inverted pendulum have been done in the environment of MATLAB /SIMLTLINK. Finally, we will find that the performance of system which was adjusted by optimal control theory is better than the performance of system which was adjusted by classic control theory, and the optimal control is easier success than classic control.Keywords: Inverted pendulum system; Classic control theory; Optimal control theory;System simulation目录引言 (1)第一章绪论 (2)1.1 问题的提出及研究意义 (2)1.1.1 问题的提出 (2)1.1.2 研究意义 (2)1.2 本论文主要研究的内容 (2)第二章单级倒立摆数学模型 (4)2.1单级倒立摆数学模型的结构 (4)2.2系统的数学模型推导 (5)2.2.1 不考虑摩擦时的传递函数及状态方程 (5)2.2.2 考虑摩擦时的传递函数及状态方程 (8)第三章单级倒立摆PID控制器设计与仿真 (11)3.1理论分析 (11)3.2PID控制器的设计与仿真 (12)第四章现代控制理论在控制倒立摆系统中的应用 (20)4.1状态空间极点配置法 (20)4.1.1 理论分析 (20)4.1.2 状态空间极点配置法的设计及仿真 (20)4.2基于LQR的倒立摆最优控制系统研究 (24)4.2.1 理论分析 (24)4.2.2 LQR控制器的设计与仿真 (25)结论 (28)参考文献 (30)谢辞 (31)引言杂技顶杆表演之所以为人们熟悉,不仅是其技艺的精湛,更重要的是其物理与控制系统的稳定性密切相关。
环形一级倒立摆设计

1 绪论随着计算机技术和通信技术的飞速发展,控制理论的研究不断深入,自动控制技术在农业、工业、军队和家庭等社会各领域得到了广泛应用,对于提高劳动生产率做出了重要贡献。
倒立摆是一种理想的控制对象平台,它结构简单、成本较低,可以有效地检验众多控制方法的有效性。
对倒立摆系统这样一个典型的多变量、快速、非线性和自然不稳定系统的研究,无论在理论上和方法上都具有重要意义。
这不仅因为其级数增加而产生的控制难度是人类对其控制能力的有力挑战,更是因为在实现其稳定控制的过程中,众多的控制理论和方法被不断应用,新的控制理论和方法因而层出不穷。
各种控制理论和方法都可以在倒立摆这个控制对象平台上加以实现和检验,并可以促成控制理论和方法相互间的有机结合,进而使得这些新方法、新理论可以应用到更加广泛的受控对象中。
倒立摆系统的分类随着倒立摆系统控制方法研究的不断深入,倒立摆系统的种类也逐渐发展为多种形式。
目前研究的倒立摆大多为在二维空间仁即平面)内摆动的摆。
考虑倒立摆的不同结构形式,倒立摆系统可以分为以下几种类型1)小车倒立摆系统仁或称为“直线倒立摆系统”)小车倒立摆系统主要由小车和摆杆两部分构成。
其中,摆杆可以是一级、两级、三级、四级甚至多级。
摆杆的级数越多,控制难度越大,而摆杆的长度也可能是变化的。
控制目标一般是通过给小车施加一个水平方向的力,使小车在期望的位置上稳定,而摆杆达到竖直向上的动态平衡状态。
2)旋转倒立摆系统仁或称为“环形倒立摆系统”)旋转倒立摆系统是在小车倒立摆系统的基础上发展起来的。
与小车倒立摆不同,旋转倒立摆将摆杆安装在与电机转轴相连的水平旋臂上,通过电机带动旋臂在水平面的转动来控制摆杆的倒立,摆杆可以在垂直平面内旋转。
旋转倒立摆将小车倒立摆的平动控制改为旋转控制,使得整个系统更为复杂和不稳定,增加了控制的难度。
3)平面倒立摆系统在平面倒立摆系统中,匀质摆杆底端可以在平面内作二维自由运动,摆杆 可沿竖直平面内任一轴线转动。
(完整版)一阶环形倒立摆毕业论文

本文以利用电位器检测角度的一阶倒立摆系统作为研究对象,研究了其在摆角信号含有大噪声的情况下的平衡稳定控制问题,这对解决实际工程中的相关问题有一定的指导意义。本文首先设计了一阶环形倒立摆的模型。使用电位器作为姿态测量传感器不断测量摆杆的的姿态信息,通过转换这些模拟信息传送给作为控制核心的8位单片机,经过数据处理后,单片机通过驱动电路将控制信号以PWM方式去驱动直流电机的,达到调节摆杆姿态的目的。
现阶段检验某种控制方法或控制理论是否有较强的解决非线性和不稳定性问题的能力,一般都通过对倒立摆系统控制的研究来实现,倒立摆的研究不仅有其深刻的理论意义,同时还有重要的工程背景。从日常生活中所见到的空间飞行器和各种伺服云台的稳定,到任何重心在上、支点在下的控制问题,都类似于倒立摆的控制,故对倒立摆系统的稳定控制研究在实际中有很多应用,如火箭发射、海上钻井平台以及卫星发射架的稳定控制、化工过程控制、控制飞机安全着陆等都属于这类问题。由于其运动过程与人类的行走姿态相似,而其平衡控制又与火箭飞行的控制类似,致使倒立摆系统的研究在直升机的飞行控制、火箭发射过程中的姿态控制、双足机器人的直立行走控制等领域中具有重要的现实意义。随着现代控制理论的发展,倒立摆系统研究的相关科研成果己广泛应用于机器人、军工、航天科技及一般工业过程等诸多领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2设计内容及要求
设计内容:
1. 构建单级旋转倒立摆模型;;
2. 实现单级旋转倒立摆摆杆的稳定控制;;
3. 基于MATLAB完成稳定控制仿真;
基本要求:
1. 摆角稳定控制范围: ;
2. 旋臂转角可在 进行控制。
1.3课题研究的意义
倒立摆系统作为研究控制理论的一种典型的实验装置,具有较为简单的结构、可以有效地检验众多控制方法的有效性、参数和模型易于改变、相对低廉的成本等优点,研究控制理论的很多科研人员一直将它们视为主要的研究对象,用它们来描述线性控制领域中不稳定系统的稳定性以及在非线性控制领域中的无源性控制、变结构控制、非线性观测器、自由行走、非线性模型降阶、摩擦补偿等控制思想,且从中不断开发出新的控制方法和控制理论,所以倒立摆系统是研究智能控制方法较为理想的实验装置。不仅如此,倒立摆系统也是进行控制理论教学的理想平台。很显然,这种实验教学方法难以培养学生综合素质和实践能力。所以必须在实验环节的内容和形式上进行改革与创新,以培养学生的创新意识和实践动手能力。因此,进行设计性、开放性的综合实验具有极其重要的现实意义。
理论和方法因而层出不穷。各种控制理论和方法都可以在倒立摆这个控制对象
平台上加以实现和检验,并可以促成控制理论和方法相互间的有机结合,进而
使得这些新方法、新理论可以应用到更加广泛的受控对象中。
1.1 倒立摆系统的分类
随着倒立摆系统控制方法研究的不断深入,倒立摆系统的种类也逐渐发展
为多种形式。目前研究的倒立摆大多为在二维空间仁即平面)内摆动的摆。
为了简化旋转倒立摆系统的数学建模过程,本章采用了分析力学中的
Lagrange方程推导旋转倒立摆的系统模型,并对该系统的可控性进行了分析。首先,在第2.1节中分析了Lagrange方程的物理意义和特点;接下来,在第2.2节中讨论了旋转式倒立摆系统的特点,对倒立摆系统进行了动力学分析;然后,在第2.3节中根据Lagrange方程运用动力学理论对旋转倒立摆系统建立数学模型;随后,在第2.4节中分析了旋转倒立摆系统模型中的非线性因素以及局部线性化带来的问题;最后,在第2.5节中对旋转倒立摆系统的可控性进行了分析。
在期望的位置上稳定,而摆杆达到竖直向上的动态平衡状态。
2)旋转倒立摆系统仁或称为“环形倒立摆系统”)
旋转倒立摆系统是在小车倒立摆系统的基础上发展起来的。与小车倒立摆不同,旋转倒立摆将摆杆安装在与电机转轴相连的水平旋臂上,通过电机带动
旋臂在水平面的转动来控制摆杆的倒立,摆杆可以在垂直平面内旋转。旋转倒
设 为系统的广义坐标; 为系统的广义速度,即广义坐标对时间的导数;H是用广义坐标和广义速度表示的系统功能; 为对应于各个广义坐标的广义力,则系统的运动满足下列方程组:
1.4本人侧重点
本人主要工作是旋转倒立摆系统的lagrange方程建模及性能分析。倒立摆系统是一个异常复杂而又对准确性、快速性要求很高的非线性不稳定控制问题.显然一个典型的非线性、不稳定系统的研究成果无论在理论上或是在方法论上都有重要的意义.而倒立摆数学模型的建立对研究其稳定性具有指导作用.实验证明在此建模基础上采用状态反馈法对倒立摆系统的稳定控制相当成功,并可在此基础上对其进行分析,为计算机控制提供理论与实践的依据.
固定的运动轨迹,这也是它与前两种倒立摆的主要区别。
4)柔性倒立摆系统
在柔性倒立摆系统中,由于将匀质刚体摆杆换成了柔性摆杆,这种倒立摆
的摆杆本身已经变成了非线性分布参数系统。
5)直线柔性连接倒立摆系统
所谓直线柔性连接倒立摆系统,就是在直线刚性倒立摆的基础上,加入自
由弹簧系统:电机连接一个主动小车,而主动小车通过一根弹簧作用于从动小
考虑倒立摆的不同结构形式,倒立摆系统可以分为以下几种类型
1)小车倒立摆系统仁或称为“直线倒立摆系统”)
小车倒立摆系统主要由小车至多级。摆杆的级数越多,控制难度越大,而摆杆的长度
也可能是变化的。控制目标一般是通过给小车施加一个水平方向的力,使小车
环形一级倒立摆设计
———————————————————————————————— 作者:
———————————————————————————————— 日期:
ﻩ
1 绪论
随着计算机技术和通信技术的飞速发展,控制理论的研究不断深入,自动
控制技术在农业、工业、军队和家庭等社会各领域得到了广泛应用,对于提高
2 旋转倒立摆系统的Lagrange方程建模与可控性分析
在建立倒立摆系统的模型时,传统的方法一般采用牛顿运动定律来求解。但在用牛顿运动定律来求解质点组的运动问题时,常常要列解大量的微分方程组。在许多实际问题中,求解微分方程会遇到困难。特别是当质点组存在约束情况时,还需要确定各质点间的相互作用力、位移、速度、加速度关系,联立求解这些方程则更为困难。
立摆将小车倒立摆的平动控制改为旋转控制,使得整个系统更为复杂和不稳定,
增加了控制的难度。
3)平面倒立摆系统
在平面倒立摆系统中,匀质摆杆底端可以在平面内作二维自由运动,摆杆
可沿竖直平面内任一轴线转动。小车倒立摆的摆杆底端运动轨迹是直线,旋转
倒立摆的摆杆底端运动轨迹是圆周,而平面倒立摆的摆杆底端在二维平面内无
2.1 Lagrange方程及其特点
Lagrange方程是分析力学中的一个重要方程,它不仅在理论上揭示了系统的最小势能原理,在实用上也有很大价值。分析力学是理论力学的重要组成部分,主要从能量角度来研究力学体系的运动规律,把系统作为一个整体来考察,用动能和势能的标量函数来描述系统,使很多受理想约束的非自由质点系动力学问题的研究和求解过程大为简化。当系统的动能和势能的表达式可求的情况下,使用Lagrange方程可以使系统动力学方程的形式和求解变得很简单。
劳动生产率做出了重要贡献。
倒立摆是一种理想的控制对象平台,它结构简单、成本较低,可以有效地
检验众多控制方法的有效性。对倒立摆系统这样一个典型的多变量、快速、非
线性和自然不稳定系统的研究,无论在理论上和方法上都具有重要意义。这不
仅因为其级数增加而产生的控制难度是人类对其控制能力的有力挑战,更是因
为在实现其稳定控制的过程中,众多的控制理论和方法被不断应用,新的控制
