(全面突破)高考数学最新一轮复习必考题型巩固提升 4.2同角三角函数的基本关系与诱导公式学案

合集下载

高考数学一轮复习专题4.2同角三角函数的基本关系与诱导公式知识点讲解理科版含解析

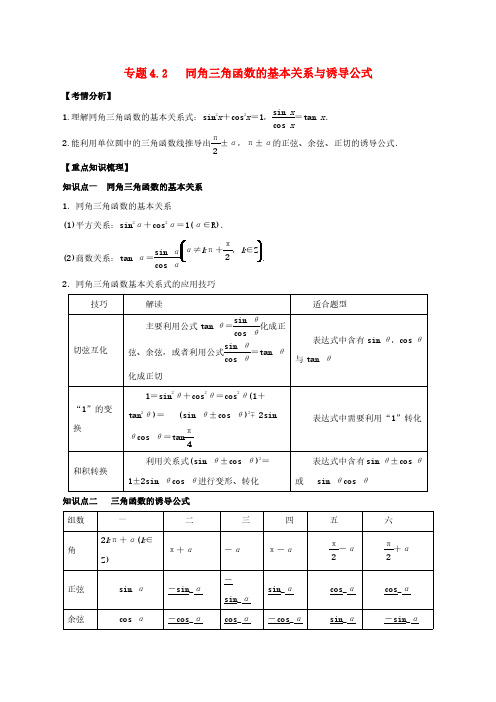
的值为________．
11π
9π
cos（－α）·sin（＋α）
2
2
3 【答案】－
4
（－sin α）sin α
【解析】原式＝
＝tan α，
（－sin α）cos α
3 根据三角函数的定义得 tan α＝－。
4
高频考点二同角三角函数的基本关系及应用
【例 2】（2020·新课标Ⅰ）已知 (0, π) ，且 3cos2 8cos 5 ，则 sin （）
5 ，
5
故选 B。
【方法技巧】同角三角函数关系式的应用方法
(1)利用
sin2α＋cos2α＝1
sinα 可实现α的正弦、余弦的互化，利用＝tanα可以实现角α的弦切互
cosα
化．
(2)由一个角的任一三角函数值可求出这个角的另外两个三角函数值，因为利用“平方关系”公式，需
求平方根，会出现两解，需根据角所在的象限判断符号，当角所在的象限不明确时，要进行分类讨论．
α＋3cos
α ＝5，则
cos2α＋1sin
2α的值
3cos α－sin α
2
是( )
3
3
A.
B．－
5
5
C．－3
D．3
【答案】A
sin 【解析】由
α＋3cos
α
tan
＝5 得
α＋3 ＝5，可得
tan
α＝2，则
cos2α＋1sin
2α＝cos2α＋sin
3cos α－sin α
3－tan α
2
cos2α＋sin αcos α 1＋tan α 3
sin α α≠kπ＋π，k∈Z

2025版高考数学一轮总复习第四章三角函数与解三角形4.2同角三角函数的基本关系及诱导公式课件

3
− ，且
5
∈
π 3π
( , )，则tan
2 2
√
4
A.
3
3
B.
4
3
5
=(
3
C.−
4
π 3π
2 2
)
3
D.±
4
4
5
解：因为sin = − ,且 ∈ ( , )，所以为第三象限角.所以cos = − .故
tan =
sin
cos
=
3
.故选B.
4
3.sin −
13π
6
=(
A.tan π + 1 = tan 1
√
sin π−
C.
cos π+
)
B.
√
= cos
cos π− tan −π−
D.
sin 2π−
= tan
=1
解：由诱导公式，知tan π + 1 = tan 1，故A正确.
sin −
tan 360∘ −
=
sin π−
cos π+
sin
A.−
√
1
2
1
2
B.
解：因为tan = −3，所以cos ≠
1
3
cos +sin
0.所以
cos −sin
)
C.−
1
3
1+ −3
1− −3
D.
=
1+tan
1−tan
=
1
2
= − .故选A.
（2）若tan = 3，则8cos2 + 2sin 2 =(

数学一轮复习第四章三角函数解三角形4.2同角三角函数的基本关系及诱导公式学案理

4。

2同角三角函数的基本关系及诱导公式必备知识预案自诊知识梳理1。

同角三角函数的基本关系（1）平方关系:sin2α+cos2α=。

(2)商数关系:sinαcosα=(α≠π2+kπ,k∈Z)。

2.三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)π+α-απ-απ2-απ2+α正弦sin α余弦cos α正切tan α续表公式一二三四五六口诀函数名不变,符号看象限函数名改变,符号看象限1。

特殊角的三角函数值2.同角三角函数基本关系式的常用变形(1)（sin α±cos α）2=1±2sin αcos α；（2)sin α=tan αcos αα≠π2+kπ,k∈Z；(3）sin2α=sin2αsin2α+cos2α=tan2αtan2α+1;（4）cos 2α=cos 2αsin 2α+cos 2α=1tan 2α+1。

考点自诊1.判断下列结论是否正确，正确的画“√”,错误的画“×”。

（1）对任意的角α，β有sin 2α+cos 2β=1。

( ）（2)若α∈R ，则tan α=sinαcosα恒成立.（）（3)sin （π+α）=-sin α成立的条件是α为锐角。

( )(4）若cos(n π—θ）=13(n ∈Z )，则cos θ=13.（）2。

(2020河北衡水中学模拟一,理3)已知cos α-π2=-2√55，α∈π，3π2,则tan α=（）A 。

2B 。

32C.1D.123。

(2020河北唐山模拟，理4）已知角α的顶点在原点,始边与x 轴的正半轴重合，终边上一点A (2sin α，3）（sin α≠0），则cos α=( ）A.12B 。

-12C 。

√32D.-√324。

函数f (x )=15sin x+π3+cos x —π6的最大值为（ ) A.65B.1C.35D.15关键能力学案突破考点同角三角函数基本关系式的应用【例1】（1)若tan(α-π）=12，则sin 2α+1cos 2α-sin 2α=( )A。

2022高考数学(文)一轮通用版讲义：4.2同角三角函数的基本关系与诱导公式

第二节同角三角函数的基本关系与诱导公式1理解同角三角函数的基本关系式：sin2＋cos2＝1，＝tan．±α，π±α的正弦、余弦、正切的诱导公式．突破点一同角三角函数的基本关系1．同角三角函数的基本关系1平方关系：sin2α＋cos2α＝1α∈R．2商数关系：tanα＝2．同角三角函数基本关系式的应用技巧技巧解读适合题型切弦互化主要利用公式tanθ＝化成正弦、余弦，或者利用公式＝tanθ化成正切表达式中含有sinθ，cosθ与tanθ“11＝sin2θ＋cos2θ＝表达式中需要利用一、判断题对的打“√”，错的打“×”1若α，β为锐角，则sin2α＋cos2β＝12若α∈R，则tanα＝恒成立．答案：1×2×二、填空题1．已知α∈，sinα＝，则tanα＝________解析：∵α∈，sinα＝，∴cosα＝－，于是tanα＝－答案：－2．已知tanα＝2，则的值为________．解析：原式＝＝＝3答案：3考法一知弦求弦、切或知切求弦利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．[例1] 12022·成都龙泉中学月考设cos－80°＝，那么tan100°等于B．－D．－22022·甘肃诊断已知tan＝，且角的终边落在第三象限，则cos＝B．－D．－[解析] 1∵cos－80°＝cos80°＝，∴sin80°＝＝，∴tan100°＝－tan80°＝－故选B2因为角的终边落在第三象限，所以cos<0，因为tan＝，所以解得cos＝－，故选D[答案] 1B 2D[易错提醒]知弦求弦、切或知切求弦时要注意判断角所在的象限，不要弄错切、弦的符号．考法二知切求f sinα、cosα的值[例2] 2022·保定三校联考已知tan3π＋α＝3，则＝D．2[解析] ∵tan3π＋α＝3，∴tanα＝3，∴＝＝＝故选B [答案] B[方法技巧]利用“切弦互化”的技巧1弦化切：把正弦、余弦化成切的结构形式，统一为“切”的表达式，进行求值．常见的结构有：①sinα，cosα的二次齐次式如a sin2α＋b sinαcosα＋c cos2α的问题常采用“切”代换法求解；②sinα，cosα的齐次分式的问题常采用分式的基本性质进行变形．2切化弦：利用公式tanα＝，把式子中的切化成弦．一般单独出现正切、余切的时候，采用此技巧．考法三sinα±cosα与sinαcosα关系的应用[例3] 1已知sinαcosα＝，且<α<，则cosα－sinα的值为B．±C．－D．－2已知－<α<0，sinα＋cosα＝，则＝[解析] 1因为sinαcosα＝，所以cosα－sinα2＝cos2α－2sinαcosα＋sin2α＝1－2sinαcosα＝1－2×＝，因为<α<，所以cosα<sinα，即cosα－sinα<0，所以cosα－sinα＝－2∵sinα＋cosα＝，∴1＋2sinαcosα＝，∴2sinαcosα＝－，cosα－sinα2＝1＋＝又∵－<α<0，∴cosα>0>sinα，∴cosα－sinα＝，∴＝＝＝[答案] 1D 2B[方法技巧]正弦、余弦“sinα±cosα，sinα·cosα”的应用sinα±cosα与sinα·cosα通过平方关系联系到一起，即sinα±cosα2＝1±2sinαcosα，sinαcosα＝，sinαcosα＝因此在解题中已知1个可求另外2个．已知α∈0，π，cosα＝－，则tanα＝B．－D．－解析：选D ∵cosα＝－且α∈0，π，∴sinα＝＝，∴tanα＝＝－故选D已知sinα＋cosα＝，则sinαcosα的值为________．解析：∵sinα＋cosα＝，∴sinα＋cosα2＝sin2α＋cos2α＋2sinαcosα＝1＋2sinαcosα＝，解得sinαcosα＝－答案：－已知tanα＝－，求：1的值；2的值；3sin2α＋2sinαcosα的值．解：1＝＝＝2＝＝＝＝＝－3sin2α＋2sinαcosα＝＝＝＝－突破点二三角函数的诱导公式组一二三四五六一、判断题对的打“√”，错的打“×”1sinπ＋α＝－sinα成立的条件是α为锐角．2诱导公式的记忆口诀中“奇变偶不变，符号看象限”，其中的奇、偶是指的奇数倍、偶数倍，变与不变指函数名称是否变化．答案：1×2√二、填空题1．已知cosπ＋α＝－，则sin等于________．解析：cosπ＋α＝－cosα＝－，则cosα＝，sin＝－sin ＝－cosα＝－答案：－2．已知sin＝，则sin等于________．解析：sin＝sin＝－sin＝－答案：－3．已知tan＝，则tan＝________解析：tan＝tan＝tanπ－－α＝－tan＝－答案：－1．利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤也就是：“负化正，大化小，化到锐角为终了．”2．利用诱导公式化简三角函数的要求1化简过程是恒等变形；2结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值．2022·武威六中第一次阶段性检测已知fα＝1化简fα；2若－<α<，且fα<，求α的取值范围．解：1fα＝＝＝＝－sinα2由已知得－sinα<，∴sinα>－，∴2π－<α<2π＋，∈Z∵－<α<，∴－<α<故α的取值范围为应用诱导公式化简求值的常见问题及注意事项1已知角求值问题．关键是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解．转化过程中注意口诀“奇变偶不变，符号看象限”的应用．2对给定的式子进行化简或求值问题．要注意给定的角之间存在的特定关系，充分利用给定的关系结合诱导公式将角进行转化．特别要注意每一个角所在的象限，防止符号及三角函数名出错．1．2022·玉林陆川中学期中sin570°的值是A．－D．－解析：选A sin570°＝sin720°－150°＝－sin150°＝－故选A2．2022·湖北八校联考已知sinπ＋α＝－，则tan＝A．2 B．－2D．±2解析：选D ∵sinπ＋α＝－，∴sinα＝，∴tan＝＝±2，故选D3．2022·南充模拟设f＝a sinπ＋α＋b cosπ＋β，其中a，b，α，β都是非零实数．若f2022＝－1，则f2022＝A．1 B．2C．0 D．－1解析：选A ∵f2022＝a sin2022π＋α＋b cos2022π＋β＝－a sinα－b cosβ＝－1，∴a sinα＋b cosβ＝1，∴f2022＝a sin2022π＋α＋b cos2022π＋β＝a sinα＋b cosβ＝4．化简：＝________解析：原式＝＝＝1答案：1[课时跟踪检测][A级基础题——基稳才能楼高]1．2022·新疆普通高中学业水平考试已知∈，cos＝，则tan的值为B．－D．－解析：选B 因为∈，所以sin＝－＝－，所以tan＝＝－故选B2．2022·淮南十校联考已知sin＝，则cos的值是A．－D．－解析：选A ∵sin＝，∴cos＝cos＝－sin＝－，故选A3．2022·重庆一模log2的值为A．－1 B．－解析：选B log2＝log2＝log2＝－故选B4．2022·遵义模拟若sin＝－，且α∈，π，则sinπ－2α＝A．－B．－解析：选A ∵sin＝cosα＝－，α∈，∴sinα＝，∴sinπ－2α＝sin2α＝2sinαcosα＝2××＝－故选A5．2022·沈阳模拟若＝2，则cosα－3sinα＝A．－3 B．3C．－解析：选C ∵＝2，∴cosα＝2sinα－1，又sin2α＋cos2α＝1，∴sin2α＋2sinα－12＝1,5sin2α－4sinα＝0，解得sinα＝或sinα＝0舍去，∴cosα－3sinα＝－sinα－1＝－故选C 6．2022·庄河高中期中已知sin＝，则cos等于C．－D．－解析：选A cos＝cos＝sin＝故选A[B级保分题——准做快做达标]1．2022·宝鸡金台区质检已知sin2α＝，则tanα＋＝C．3 D．2解析：选C tanα＋＝＋＝＝＝＝2．2022·常德一中月考已知α∈R，sinα＋2cosα＝，则tan2α＝C．－D．－解析：选C 因为sinα＋2cosα＝，sin2α＋cos2α＝1，解得或所以tanα＝3或－所以tan2α＝＝＝－或tan2α＝＝＝－故选C3．2022·株洲醴陵二中、四中期中联考已知2sinα－cosα＝0，则sin2α－2sinαcosα的值为A．－B．－解析：选A 由已知2sinα－cosα＝0得tanα＝，所以sin2α－2sinαcosα＝＝＝－故选A4．2022·大庆四地六校调研若α是三角形的一个内角，且sin＋cos＝，则tanα的值是A．－B．－C．－或－D．不存在解析：选A 由sin＋cos＝，得cosα＋sinα＝，∴2sinαcosα＝－<0∵α∈0，π，∴α∈，∴sinα－cosα＝＝，∴sinα＝，cosα＝－，∴tanα＝－，故选A5．2022·平顶山、许昌联考已知＝5，则cos2α＋sin2α的值是B．－C．－3 D．3解析：选A 由＝5，得＝5，解得tanα＝2，∴cos2α＋sin2α＝＝＝＝6．2022·河南中原名校联考已知θ为第二象限角，sinθ，cosθ是关于的方程22＋－1＋m＝0m∈R的两根，则sinθ－cosθ＝D．－解析：选B ∵sinθ，cosθ是方程22＋－1＋m＝0m∈R的两根，∴sinθ＋cosθ＝，sinθ·cosθ＝，可得sinθ＋cosθ2＝1＋2sinθ·cosθ＝1＋m＝，解得m＝－∵θ为第二象限角，∴sinθ>0，cosθ<0，即sinθ－cosθ>0，∵sinθ－cosθ2＝1－2sinθ·cosθ＝1－m＝1＋，∴sinθ－cosθ＝＝，故选B 7．2022·全国卷Ⅰ已知角α的顶点为坐标原点，始边与轴的非负半轴重合，终边上有两点A1，a，B2，b，且cos2α＝，则|a－b|＝D．1解析：选B 由cos2α＝，得cos2α－sin2α＝，∴＝，即＝，∴tanα＝±，即＝±，∴|a－b|＝故选B8．2022·武邑中学调研已知sinα＝，0<α<π，则sin＋cos＝________解析：2＝1＋sinα＝，又0<α<π，∴sin＋cos>0，∴sin ＋cos＝答案：9．2022·广西桂林等五市联考已知sinθ＋cosθ＝，θ∈，则tanθ＝________解析：∵sinθ＋cosθ＝，∴sinθ＋cosθ2＝sin2θ＋cos2θ＋2sinθcosθ＝1＋2sinθcosθ＝，∴sinθcosθ＝－，又<θ<π，∴sinθ－cosθ>0，∴sinθ－cosθ2＝sin2θ＋cos2θ－2sinθcosθ＝1－2sinθcosθ＝，∴sinθ－cosθ＝，由，解得∴tanθ＝＝－答案：－10．2022·浙江名校协作体检测已知sin·cos＝，且0<α<，则sinα＝________，cosα＝________解析：sincos＝－cosα－sinα＝sinαcosα＝又∵0<α<，∴0<sinα<得sinα＝，cosα＝答案：11．2022·惠安惠南中学月考已知cosα－sinα＝，α∈1求sinαcosα的值；2求的值．解：1∵cosα－sinα＝，α∈，平方可得1－2sinαcosα＝，∴sinαcosα＝2sinα＋cosα＝＝＝，∴原式＝＝＝cosα＋sinα＝12．在△ABC中，1求证：cos2＋cos2＝1；2若cossintan C－π＜0，求证：△ABC为钝角三角形．证明：1在△ABC中，A＋B＝π－C，所以＝－，所以cos＝cos＝sin，所以cos2＋cos2＝12因为cossintan C－π＜0，所以－sin A－cos B tan C＜0，即sin A cos B tan C＜0因为在△ABC中，0＜A＜π，0＜B＜π，0＜C＜π且sin A ＞0，所以或所以B为钝角或C为钝角，所以△ABC为钝角三角形。

高中数学(一轮复习)最基础考点系列考点4.4 同角三角函数的基本关系含解析

专题4 同角三角函数的基本关系同角三角函数的基本关系★★★○○○○1．同角三角函数的基本关系(1）平方关系：sin2α＋cos2α＝1（α∈R)．（2)商数关系：tan α＝错误!错误!.2．同角三角函数基本关系式的应用技巧技巧解读适合题型切弦互化主要利用公式tan θ＝错误!化成正弦、余弦，或者利用公式错误!＝tan θ化成正切表达式中含有sinθ,cos θ与tan θ“1”的变换1＝sin2θ＋cos2θ＝cos2θ（1＋tan2θ)＝（sin θ±cos θ）表达式中需要利用“1”转化2∓2sin θcos θ＝tan错误!和积转换利用关系式(sin θ±cos θ）2＝1±2sin θcos θ进行变形、转化表达式中含有sinθ±cos θ或sinθcosθ同角三角函数关系式应用的注意事项（1）同角并不拘泥于角的形式，如sin2错误!＋cos2错误!＝1，错误!＝tan 3x 错误!都成立，但是sin2α＋cos2β＝1就不一定成立．（2)对于含有sin α,cos α的齐次式，可根据同角三角函数商的关系，通过除以某一齐次项，转化为只含有正切的式子，即化弦为切，整体代入．［例] (2017·南京模拟）已知α为第二象限角，则cos α·错误!＋sin α错误!＝________。

［解析] 原式＝cos α错误!＋sin α错误!＝cos α·错误!＋sin α·错误!，因为α是第二象限角，所以sin α＞0, cos α＜0,所以cos α·错误!＋sin α·错误!＝－1＋1＝0,即原式等于0.［答案］01. 若tan α＝2，则(1)错误!＝________；(2)4sin2α－3sin αcos α－5cos2α＝________。

2。

已知x∈(－π，0),sin x＋cos x＝1 5 .(1)求sin x－cos x的值；（2)求sin 2x＋2sin2x1－tan x的值．［解］（1）由sin x＋cos x＝错误!，平方得sin2x＋2sin x cos x＋cos2x＝错误!，整理得2sin x cos x＝－24 25 .∴（sin x－cos x）2＝1－2sin x cos x＝错误!。

高三数学,一轮复习,人教A版, 4.2 ,同角三角函数,的基本关系,及诱导公式 , 课件 (1)

口诀函数名不变,符号看象限
函数名改变, 符号看象限
知识梳理知识梳理双击自测
规律总结
-5-
3.特殊角的三角函数值
角 α 0° 30° 45° 60° 90° 120° 150° 角α 的 �� 2�� 5�� 弧 0 6 4 3 2 3 6 度数 1 1 sin 2 3 3 0 1 α 2 2 2 2 2 1 1 cos 3 2 3 1 0 2 α 2 2 2 2 tan 3 3 0 1 - 3 3 α 3 3
2
知识梳理知识梳理双击自测
规律总结
-3-
1.同角三角函数的基本关系 (1)平方关系:sin2α+cos2α=1 .
(2)商数关系:
sin�� =tan α cos��
�� ≠ + ��π,��∈Z .
π 2
知识梳理知识梳理双击自测
规律总结
-4-
2.三角函数的诱导公式
180°
π
0 -1 0
知识梳理知识梳理双击自测
规律总结
-6-
1 2 3 4 5
1.下列结论正确的画“ ”,错误的画“×”. (1)若α,β为锐角,则sin2α+cos2β=1. ( × )
(2)若 α∈R,则 tan α= (3)已知 sin α= ,α∈
4 5
(4)sin(π+α)=-sin α 成立的条件是 α 为锐角. ( × ) (5)六组诱导公式中的角 α 可以是任意角. ( )
-1 1 =
4×4-3×2-5 4+1
=
4ta n 2 �� -3tan �� -5 ta n 2 �� +1

高考数学一轮复习4.2同角三角函数的基本关系及诱导公式课件理北师大版

A.2
B. 2
1
2π
2π
,cos
),即
3
3
1
1
√3
∴x= 2 ,y=-2,r=|OP|=1,∴sin(π-α)=sin α= =-2.
解析:∵角 α 的终边经过点 P(sin
1
π
√3
C.-2
D.- 2
√3 1
P( 2 ,-2),
π
4.函数 f(x)=5sin + 3 +cos - 6 的最大值为( A )
是
1
3
x-4
∈
π
0, 2
的最大值
.
3
4
解析:由题意可知 f(x)=1-cos2x+√3cos x=-cos2x+√3cos
π
2
1
x+ =4
cos-
√3
2
2
+1.
因为 x∈ 0, ,所以 cos x∈[0,1].
√3
所以当 cos x= 2 时,函数 f(x)取得最大值 1.
-7考点1
考点2
考点3
例 3(1)(2018 湖南长沙一模)化简:
=
π
1+sin 2+ tan
(2)设 f(α)=
2sin(π+)cos(π-)-cos(π+)
3π
1+sin2 +cos
+
√3
2
π
-sin2 +
(1+2sin α≠0),则 f -
2
.
sin(π-)+sincos
解析:(1)
π
1+sin 2+ tan

新高考数学一轮复习考点知识专题讲解与练习 24 同角三角函数的基本关系与诱导公式

考点知识总结24 同角三角函数的基本关系与诱导公式高考概览高考在本考点的常考题型为选择题、填空题，分值为5分，低、中等难度考纲研读1.理解同角三角函数的基本关系式：sin 2α＋cos 2α＝1，sin αcos α＝tan α 2．能推导出π2±α，π±α的正弦、余弦、正切的诱导公式一、基础小题1．cos ⎝ ⎛⎭⎪⎫－17π4－sin ⎝ ⎛⎭⎪⎫－17π4的值是( )A ．2B ．－2C ．0D ．22 答案 A解析原式＝cos ⎝ ⎛⎭⎪⎫－4π－π4－sin ⎝ ⎛⎭⎪⎫－4π－π4＝cos ⎝ ⎛⎭⎪⎫－π4－sin ⎝ ⎛⎭⎪⎫－π4＝cos π4＋sin π4＝2，故选A.2．若x 是第四象限角，且sin x ＝－45，则cos x ＝( ) A ．15 B ．－15 C ．35 D ．－35 答案 C解析因为x 是第四象限角，所以cos x ＞0，所以cos x ＝1－sin 2x ＝1－⎝ ⎛⎭⎪⎫－452＝35.故选C.3．直线y ＝2x 绕原点顺时针旋转45°得到直线l ，若l 的倾斜角为α，则cos2α的值为( )A ．8＋1010 B ．8－1010 C ．－45 D ．45答案 D解析由题意可知，tan (α＋45°)＝tan α＋11－tan α＝2，∴tan α＝13，∴cos 2α＝cos 2α－sin 2αcos 2α＋sin 2α＝1－tan 2α1＋tan 2α＝45，故选D. 4．已知sin θ＝－13，θ∈⎝ ⎛⎭⎪⎫－π2，π2，则sin(θ－5π)·sin ⎝ ⎛⎭⎪⎫3π2－θ的值是( )A ．229B ．－229C ．－19D ．19 答案 B解析因为sin θ＝－13，θ∈⎝ ⎛⎭⎪⎫－π2，π2，所以cos θ＝1－sin 2θ＝223，所以原式＝－sin (π－θ)·(－cos θ)＝sin θcos θ＝－13×223＝－229.故选B.5．若tan α＝2，则sin 2α＋3sin αcos αcos 2α＋1＝( )A ．53B ．54C ．52 D ．2答案 A解析 ∵tan α＝2，∴sin 2α＋3sin αcos αcos 2α＋1＝sin 2α＋3sin αcos α2cos 2α＋sin 2α＝tan 2α＋3tan α2＋tan 2α＝53.故选A.6．若tan α＝cos α，则1sin α＋cos 4α的值为( ) A ． 2 B ．2 C ．2 2 D ．4 答案 B解析由题意知，tan α＝cos α，则sin αcos α＝cos α，故sin α＝cos 2α，故1sin α＋cos 4α＝sin 2α＋cos 2αsin α＋sin 2α＝sin α＋cos 2αsin α＋1－cos 2α＝sin α＋sin αsin α＋1－sin α＝2.故选B.7．已知sin θ＋cos θ＝43⎝ ⎛⎭⎪⎫0<θ≤π4，则sin θ－cos θ＝( )A ．23B ．－23C ．13D ．－13 答案 B解析由(sin θ＋cos θ)2＝1＋2sin θcos θ＝169，得2sin θcos θ＝79，则(sin θ－cos θ)2＝1－2sin θcos θ＝29，又由于0<θ≤π4，知sin θ－cos θ≤0，所以sin θ－cos θ＝－23.8．已知sin (π＋θ)＝－3cos (2π－θ)，|θ|<π2，则θ＝( ) A ．－π6 B ．－π3 C ．π6 D ．π3 答案 D解析 ∵sin (π＋θ)＝－3cos (2π－θ)，∴－sin θ＝－3cos θ，∴tan θ＝3，∵|θ|<π2，∴θ＝π3.故选D.9．(多选)若sin α＝45，且α为锐角，则下列结论中正确的有( ) A ．tan α＝43 B ．cos α＝35 C ．sin α＋cos α＝85 D ．sin α－cos α＝－15 答案 AB解析 ∵sin α＝45，且α为锐角，∴cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫452＝35，故B 正确；∴tan α＝sin αcos α＝4535＝43，故A 正确；∴sin α＋cos α＝45＋35＝75≠85，故C 错误；∴sin α－cosα＝45－35＝15≠－15，故D 错误．故选AB.10．(多选)已知θ∈(0，π)，且sin θ＋cos θ＝m ，m ∈(0，1)，则tan θ可能的取值为( )A ．－3B ．－2C ．－13D ．13 答案 AB解析由m ∈(0，1)，得sin θ＋cos θ>0，所以θ∈⎝ ⎛⎭⎪⎫0，3π4.又因为(sin θ＋cos θ)2＝1＋2sin θcos θ＝m 2，m ∈(0，1)，从而得2sin θcos θ<0，得θ∈⎝ ⎛⎭⎪⎫π2，π.综上可得θ∈⎝ ⎛⎭⎪⎫π2，3π4，则tan θ<－1，所以tan θ可能的取值为－3和－2，故选AB.11．化简：sin 2（α＋π）cos （π＋α）cos （－α－2π）tan （π＋α）sin 3⎝ ⎛⎭⎪⎫π2＋αsin （－α－2π）＝________．答案 1解析原式＝sin 2α（－cos α）cos αtan αcos 3α（－sin α）＝sin 2αcos 2αsin 2αcos 2α＝1.12．若tan α＋1tan α＝3，则sin αcos α＝________，tan 2α＋1tan 2α＝________．答案137 解析 ∵tan α＋1tan α＝1cos αsin α＝3，∴sin αcos α＝13.又tan 2α＋1tan 2α＝⎝ ⎛⎭⎪⎫tan α＋1tan α2－2＝9－2＝7，∴tan 2α＋1tan 2α＝7.二、高考小题13．(2022·新高考Ⅰ卷)若tan θ＝－2，则sin θ（1＋sin 2θ）sin θ＋cos θ＝( )A ．－65B ．－25C ．25D ．65 答案 C解析解法一：因为tan θ＝－2，所以sin θ（1＋sin 2θ）sin θ＋cos θ＝sin θ（sin θ＋cos θ）2sin θ＋cos θ＝sin θ(sin θ＋cos θ)＝sin 2θ＋sin θcos θsin 2θ＋cos 2θ＝tan 2θ＋tan θ1＋tan 2θ＝4－21＋4＝25.故选C.解法二：sin θ（1＋sin 2θ）sin θ＋cos θ＝sin θ（sin 2θ＋2sin θcos θ＋cos 2θ）sin θ＋cos θ＝sin θ(sin θ＋cos θ)＝cos 2θ(tan 2θ＋tan θ).由tan θ＝sin θcos θ＝－2，sin 2θ＋cos 2θ＝1，解得cos 2θ＝15.所以sin θ（1＋sin 2θ）sin θ＋cos θ＝cos 2θ(tan 2θ＋tan θ)＝15×(4－2)＝25.故选C.14．(2022·全国Ⅰ卷)已知α∈(0，π)，且3cos 2α－8cos α＝5，则sin α＝( ) A ．53B ．23C ．13D ．59 答案 A解析由3cos 2α－8cos α＝5，得6cos 2α－8cos α－8＝0，解得cos α＝－23或cos α＝2(舍去).∵α∈(0，π)，∴sin α＝1－cos 2α＝53.故选A. 15．(2022·全国Ⅰ卷)tan255°＝( ) A ．－2－3B ．－2＋ 3 C ．2－3D ．2＋ 3 答案 D解析 tan 255°＝tan (180°＋75°)＝tan 75°＝tan (45°＋30°)＝tan 45°＋tan 30°1－tan 45°tan 30°＝1＋331－33＝2＋ 3.故选D.16．(2022·浙江高考)已知tan θ＝2，则cos 2θ＝________；tan ⎝ ⎛⎭⎪⎫θ－π4＝________．答案－3513解析 cos 2θ＝cos 2θ－sin 2θ＝cos 2θ－sin 2θcos 2θ＋sin 2θ＝1－tan 2θ1＋tan 2θ＝1－221＋22＝－35，tan ⎝ ⎛⎭⎪⎫θ－π4＝tan θ－11＋tan θ＝2－11＋2＝13.三、模拟小题17．(2022·河北省级联测高三第一次考试)若cos ⎝ ⎛⎭⎪⎫α－π7＝437，则sin ⎝ ⎛⎭⎪⎫α＋5π14＝( )A ．－17B ．17C ．－437D ．437 答案 D解析 sin ⎝ ⎛⎭⎪⎫α＋5π14＝sin ⎝ ⎛⎭⎪⎫α－π7＋π2＝cos ⎝ ⎛⎭⎪⎫α－π7＝437.故选D.18．(2022·兴安县兴安中学高三期中)若sin 2θ＋4cos θ＋1＝2，则(cos θ＋3)(sin θ＋1)的值为( )A ．0B ．2C ．4D ．0或4 答案 C解析 sin 2θ＋4cos θ＋1＝2，则sin 2θ＋2＝2cos θ，即1－cos 2θ＋2＝2cos θ，即(cos θ－1)(cos θ＋3)＝0，解得cos θ＝1或cos θ＝－3(舍去)，故有cos θ＝1，sin θ＝0.∴(cos θ＋3)(sin θ＋1)＝4×1＝4.故选C.19．(2022·淮北市树人高级中学月考)若sin (π＋α)＝35，且α是第三象限角，则sin ⎝ ⎛⎭⎪⎫π2＋α－cos ⎝ ⎛⎭⎪⎫π2＋αsin ⎝ ⎛⎭⎪⎫π2－α－cos ⎝ ⎛⎭⎪⎫π2－α＝( )A ．1B ．7C ．－7D ．－1 答案 B解析由sin (π＋α)＝－sin α＝35，则sin α＝－35.又α是第三象限角，所以cos α＝－1－sin 2α＝－45，所以sin ⎝ ⎛⎭⎪⎫π2＋α－cos ⎝ ⎛⎭⎪⎫π2＋αsin ⎝ ⎛⎭⎪⎫π2－α－cos ⎝ ⎛⎭⎪⎫π2－α＝cos α＋sin αcos α－sin α＝－45＋⎝ ⎛⎭⎪⎫－35－45－⎝ ⎛⎭⎪⎫－35＝7.故选B.20．(2022·广东茂名五校高三第一次联考)已知A 是△ABC 的内角，且sin A ＋3cos A ＝－2，则tan A 的值为( )A ．－1或7B ．－23或1 C ．－1 D ．－23 答案 C解析 ∵sin A ＋3cos A ＝－2，∴sin 2A ＋6sin A cos A ＋9cos 2A ＝2⇒8cos 2A ＋6sin A cos A ＝1⇒8cos 2A ＋6sin A cos A sin 2A ＋cos 2A ＝1⇒8＋6tan Atan 2A ＋1＝1⇒tan 2A －6tan A －7＝0⇒tan A ＝－1或tan A ＝7.∵0<A <π，且sin A ＋3cos A ＝－2，∴tan A <0，∴tan A ＝－1.故选C.21．(多选)(2022·湖南郴州高三模拟)已知θ∈(0，π)，sin θ＋cos θ＝15，则下列结论正确的是( )A ．θ∈⎝ ⎛⎭⎪⎫π2，π B ．cos θ＝－35C ．tan θ＝－34D ．sin θ－cos θ＝75 答案 ABD解析 ∵sin θ＋cos θ＝15①，∴(sin θ＋cos θ)2＝⎝ ⎛⎭⎪⎫152，即sin 2θ＋2sin θcos θ＋cos 2θ＝125，∴2sin θcos θ＝－2425，∵θ∈(0，π)，∴sin θ＞0，cos θ＜0，∴θ∈⎝ ⎛⎭⎪⎫π2，π，∴(sin θ－cos θ)2＝1－2sin θcos θ＝4925，∴sin θ－cos θ＝75②，由①＋②得sin θ＝45，①－②得cos θ＝－35，∴tan θ＝sin θcos θ＝45－35＝－43.综上可得，正确的有A ，B ，D.22．(多选)(2022·山东济南模拟)在△ABC 中，给出下列四个式子，其中为常数的是( )A ．sin (A ＋B )＋sinC B ．cos (A ＋B )＋cos C C ．sin (2A ＋2B )＋sin 2CD ．cos (2A ＋2B )＋cos 2C 答案 BC解析 sin (A ＋B )＋sin C ＝2sin C ；cos (A ＋B )＋cos C ＝－cos C ＋cos C ＝0；sin (2A ＋2B )＋sin 2C ＝sin [2(A ＋B )]＋sin 2C ＝sin [2(π－C )]＋sin 2C ＝sin (2π－2C )＋sin 2C ＝－sin 2C ＋sin 2C ＝0；cos (2A ＋2B )＋cos 2C ＝cos [2(A ＋B )]＋cos 2C ＝cos [2(π－C )]＋cos2C ＝cos (2π－2C )＋cos 2C ＝cos 2C ＋cos 2C ＝2cos 2C .故选BC.23．(2022·金华市江南中学月考)已知sin x ＋cos xsin x －cos x＝2，则tan x ＝________，sin x cosx ＝________．答案 3310 解析将sin x ＋cos x sin x －cos x ＝2左端分子分母同除以cos x ，得tan x ＋1tan x －1＝2，解得tan x ＝3，sin x cos x ＝sin x cos x sin 2x ＋cos 2x ＝tan x tan 2x ＋1＝332＋1＝310.24．(2022·珠海模拟)若方程cos 2x －sin x ＋a ＝0在⎝ ⎛⎦⎥⎤0，π2内有解，则a 的取值范围是________．答案 (－1，1]解析方程cos 2x －sin x ＋a ＝0，即sin 2x ＋sin x －a －1＝0.由于x ∈⎝ ⎛⎦⎥⎤0，π2，所以0<sinx ≤1.设sin x ＝t ∈(0，1]，则问题转化为方程t 2＋t －a －1＝0在(0，1]上有解．设y ＝f (t )＝t 2＋t －1－a ，其图象是开口向上的抛物线，对称轴直线t ＝－12在区间(0，1]的左侧，图象如图所示．因此f (t )＝0在(0，1]上有解，当且仅当⎩⎨⎧f （0）<0，f （1）≥0，即⎩⎨⎧－1－a <0，1－a ≥0，解得－1<a ≤1，故a 的取值范围是(－1，1].一、高考大题本考点在近三年高考中未涉及此题型．二、模拟大题1．(2022·河南三模)已知角α的终边经过点P (3m ，－6m )(m ≠0).(1)求sin （α＋π）＋cos （α－π）sin ⎝ ⎛⎭⎪⎫α＋π2＋2cos ⎝ ⎛⎭⎪⎫α－π2的值； (2)若α是第二象限角，求sin 2⎝ ⎛⎭⎪⎫α＋3π2＋sin (π－α)cos α－cos ⎝ ⎛⎭⎪⎫π2＋α的值. 解 (1)∵m ≠0，∴cos α≠0，即sin （α＋π）＋cos （α－π）sin ⎝ ⎛⎭⎪⎫α＋π2＋2cos ⎝ ⎛⎭⎪⎫α－π2＝－sin α－cos αcos α＋2sin α＝－tan α－11＋2tan α. 又角α的终边经过点P (3m ，－6m )(m ≠0)，∴tan α＝－6m 3m ＝－2，故sin （α＋π）＋cos （α－π）sin ⎝ ⎛⎭⎪⎫α＋π2＋2cos ⎝ ⎛⎭⎪⎫α－π2 ＝－tan α－11＋2tan α＝2－11＋2×（－2）＝－13. (2)∵α是第二象限角，∴m <0，则sin α＝－6m （3m ）2＋（－6m ）2＝－6m 35|m |＝255， cos α＝3m （3m ）2＋（－6m ）2＝3m 35|m |＝－55， ∴sin 2⎝ ⎛⎭⎪⎫α＋3π2＋sin (π－α)cos α－cos ⎝ ⎛⎭⎪⎫π2＋α ＝cos 2α＋sin αcos α＋sin α＝⎝ ⎛⎭⎪⎫－552＋255×⎝ ⎛⎭⎪⎫－55＋255 ＝－1＋255. 2．(2022·河南安阳林州市校级月考)已知函数f (x )＝cos ⎝ ⎛⎭⎪⎫x －π2cos （－x ）sin ⎝ ⎛⎭⎪⎫3π2＋x tan （π＋x ）. (1)若角x 的终边经过点(3，－4)，求f (x )的值；(2)若f (x )f ⎝ ⎛⎭⎪⎫x ＋π2＝－18，且角x 为第三象限角，求f ⎝ ⎛⎭⎪⎫x ＋π2－f (x )的值．解 (1)f (x )＝cos ⎝ ⎛⎭⎪⎫x －π2cos （－x ）sin ⎝ ⎛⎭⎪⎫3π2＋x tan （π＋x ）＝sin x cos x －cos x tan x＝－cos x . ∵角x 的终边经过点(3，－4)，∴cos x ＝332＋（－4）2＝35， ∴f (x )＝－35.(2)∵f (x )f ⎝ ⎛⎭⎪⎫x ＋π2＝－cos x sin x ＝－18， ∴sin x cos x ＝18，∵f ⎝ ⎛⎭⎪⎫x ＋π2－f (x )＝sin x ＋cos x ， ∴(cos x ＋sin x )2＝cos 2x ＋sin 2x ＋2cos x sin x ＝1＋14＝54，又角x 为第三象限角，∴sin x ＋cos x <0，∴sin x ＋cos x ＝－52，即f ⎝ ⎛⎭⎪⎫x ＋π2－f (x )的值为－52. 3．(2022·调兵山市第一高级中学月考)已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根为sin θ，cos θ，θ∈(0，2π).求：(1)cos 2⎝ ⎛⎭⎪⎫3π2－θcos ⎝ ⎛⎭⎪⎫π2－θ＋cos （－π－θ）＋sin ⎝ ⎛⎭⎪⎫π2＋θ1＋tan （π－θ）； (2)m 的值；(3)方程的两根及此时θ的值．解由根与系数的关系可得sin θ＋cos θ＝3＋12，sin θcos θ＝m 2.(1)原式＝sin 2θsin θ－cos θ＋cos θ1－tan θ＝sin 2θsin θ－cos θ－cos 2θsin θ－cos θ＝sin θ＋cos θ＝3＋12.(2)由sin θ＋cos θ＝3＋12，两边平方可得：1＋2sin θcos θ＝4＋234， ∵sin θcos θ＝m 2，∴1＋2×m 2＝1＋32，m ＝32. (3)由m ＝32可解方程2x 2－(3＋1)x ＋32＝0，得两根12和32. ∴⎩⎪⎨⎪⎧sin θ＝12，cos θ＝32．或⎩⎪⎨⎪⎧sin θ＝32，cos θ＝12．∵θ∈(0，2π)，∴θ＝π6或π3.4．(2022·浙江宁波二模)已知tan α＝－32，α为第二象限角.(1)求sin ⎝ ⎛⎭⎪⎫－α－π2cos ⎝ ⎛⎭⎪⎫3π2＋αtan （π－α）tan （－α－π）sin （－π－α）的值； (2)求1cos α1＋tan 2α＋1＋sin α1－sin α＋ 1－sin α1＋sin α的值．解 (1)原式＝－sin ⎝ ⎛⎭⎪⎫α＋π2sin α（－tan α）tan （－α）[－sin （π＋α）]＝－cos αsin α（－tan α）（－tan α）sin α＝－cos α.因为tan α＝－32，α为第二象限角，所以sin αcos α＝－32.又因为sin2α＋cos2α＝1，解得cosα＝－21313，故原式＝21313.(2)原式＝1cos α1＋sin2αcos2α＋（1＋sinα）2（1－sin α）（1＋sin α）＋（1－sin α）2（1－sin α）（1＋sin α）＝1 cos α·1|cos α|＋1＋sin α|cos α|＋1－sin α|cos α|＝|cos α|cos α＋2|cos α|，因为α为第二象限角，所以上式＝－1－2cos α＝－1－2－21313＝13－1.。

2025高考数学一轮复习-4.2-同角三角函数的基本关系式与诱导公式【课件】

(3)常见的互余和互补的角
互余的角
π3－α 与π6＋α；π3＋α 与π6－α；π4＋α 与π4－ α等
互补的角
π3＋θ 与23π－θ；4π＋θ 与34π－θ 等
考点二同角三角函数基本关系式的应用
角度 1：“知一求二”问题【例 1】 (1)已知 sinα＝13，且 α 为第二象限角，求 tanα. (2)已知 sinα＝13，求 tanα. (3)已知 sinα＝m(m≠0，m≠±1)，求 tanα.
易错易混 5．已知 θ∈(0，π)，sinθ＋cosθ＝ 32－1，则 tanθ 的值为__－___3___．
【解析】解法一：将 sinθ＋cosθ＝ 32－1两边平方，得 1＋2sinθcosθ＝1－ 23，即
sinθcosθ＝－ 43，易知 θ≠π2.
故 sinθcosθ＝sins2inθθ＋cocsoθs2θ＝1＋tatnaθn2θ＝－ 43，解得 tanθ＝－
cosα
－cosα □10 sinα □11 －sinα
□14 －tanα □15 －tanα
提醒：(1)诱导公式的记忆口诀 “奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化． (2)在利用同角三角函数的平方关系时，若开方，要特别注意判断符号．
『基础过关』思考辨析 1．判断下面结论是否正确(请在括号中打“√”或“×”) (1)若 α，β 为锐角，则 sin2α＋cos2β＝1.( × ) (2)若 α∈R，则 tanα＝csoinsαα恒成立．( × ) (3)sin(π＋α)＝－sinα 成立的条件是 α 为锐角．( × ) (4)若 sin(kπ－α)＝13(k∈Z)，则 sinα＝13.( × )

高三数学一轮复习 4.2 同角三角函数的基本关系及诱导公式

=-cos2x+
3cos x+14=-
cos��-
3 2
2
+1.
因为
x∈
0,
π 2
,所以
cos
x∈[0,1].
所以当 cos x= 23时,函数 f(x)取得最大值 1.
知识梳理双基自测自测点评
-12-
1.平方关系和商数关系中的角都是同一个角,且商数关系式中 α≠π2+kπ,k∈Z.
2.利用平方关系解决问题时,要注意开方运算结果的符号,需要根据角α的范围确定.
互化,利用 tan α=csoins��
��
≠
��π
+
π 2
,��∈Z
可以实现角 α 的弦切互化.
2.“1”的灵活代换:1=cos2α+sin2α=(sin
α+cos
α)2-2sin
αcos
��
α=tan 4 .
3.关于sin α,cos α的齐次式,往往化为关于tan α的式子.
∵α 是三角形的内角,
∴
sin�� cos��
= =
4 5
-
,
3 5
∴tan
,
α=-43.
sin2��+cos2��
(2)cos2��1-sin2��
=
scions22��+��-scions22��=
cos2�� cos2��-sin2��
口诀函数名不变,符号看象限

2025年高考数学一轮复习(新高考版)第4章 §4.2 同角三角函数基本关系式及诱导公式

第四章三角函数与解三角形
§4.2 同角三角函数基本关系式及诱导公式
考试要求
1.理解同角三角函数的基本关系式 sin2α＋cos2α＝1，csoins αα＝tan αα≠π2＋kπ，k∈Z. 2.掌握诱导公式，并会简单应用.
内容索引
第一部分
落实主干知识
第二部分
探究核心题型
第三部分
课时精练
第
(2)若 α∈(0，π)，sin(π－α)＋cos α＝ 32，则 sin α－cos α 的值为
2 A. 3
B.－
2 3
√C.43
D.－43
由诱导公式得，sin(π－α)＋cos α＝sin α＋cos α＝ 32，所以(sin α＋cos α)2＝1＋2sin αcos α＝29，则 2sin αcos α＝－79<0，
思维升华
(1)应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α， sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二. (2)注意公式逆用及变形应用：1＝sin2α＋cos2α，sin2α＝1－cos2α， cos2α＝1－sin2α.
αα－＋2cocos sαα＝3ttaannαα＋－12＝3×2＋2－1 2＝43.
23sin2α＋14cos2α＝23·sin2αsi＋n2cαos2α＋14·sin2αco＋s2cαos2α
＝23·tanta2nα2＋α 1＋14·tan21α＋1
＝23×222＋2 1＋14×22＋1 1＝172.
A.2110
B.32
C.
3 2
√D.2
由诱导公式可得，sin α＝sin32π－α＋cos(π－α)＝－2cos α，所以 tan α ＝－2. 因此，2sin2α－sin αcos α＝2sisni2nα2－α＋sincoαsc2oαs α

高考数学第一轮复习各个知识点攻破4-2 同角三角函数的基本关系式与诱导公式课件新人教B版

[ 拓展提升 ] 解决本题的关键在于如何处理已知条件，这需要一定的技巧．若由已知能得出 tanα＝ 2，则问题就转化为已知正切值求三角函数值的题型，所求的式子特征为分子与分母是关于 sinα、cosα 的齐次式，即 sinα、sinαcosα＋cos2α 则可以看作，那么 sinα、cosα 的 2 2 sin α＋cos α 次数均为二次．这类齐次式的求法，通常是将分子分母同除以 cosα 的最高次，将原式转化为 tanα 的表达式进行求解．
2
又 sinA>0，cosA<0，∴ sinA－cosA>0， 7 ∴sinA－cosA＝ 5② 4 3 ∴由①，②可得 sinA＝ 5，cosA＝－5， 4 sinA 5 4 ∴tanA＝＝＝－ . 3 3 cosA －5
• [拓展提升] 对于这类利用已知α的一个三角函数值或者几种三角函数值之间的关系及α所在的象限，求其他三角函数值的问题，我们可以利用平方关系和商数关系求解．其关键在于运用方程的思想及 (sinα±cosα)2＝1±2sinαcosα的等价转化，分析出解决问题的突破口．
• 第二节同角三角函数的基本关系式与诱导公式
考纲要求
1. 掌握同角三角函数的基本关系式． 2．掌握正弦、余弦的诱导公式． 3．能正确运用三角公式进行简单三角函数式的化简、求值和恒等式证明．
以选择题或填空题的形式，考查同角三角函数的基本关系式、诱导公式在三角函数求值问题和三角恒等变换中的应用.
• 如：sin( ＋θ)＝cosθ.若是偶数倍，则函数名称不变，符号看象限，若把α看作锐角，则270°－α，180°＋α 都看成是第三象限的角．值得注意的是，其中α为任意角，并不一定要为锐角，只不过是在运用的过程中把它 “看作”是锐角而已． • 利用诱导公式把任意的三角函数转化为锐角三角函数的基本步骤是：

2025版高考数学全程一轮复习第四章三角函数与解三角形第二节同角三角函数的基本关系式及诱导公式课件

5．(易错)已知sin αcos
________．
答案：
1
5π
3π
α＝，且 <α< ，则cos
8
4
2
3
2
5π
4
3π
2
2
2
解析：因为 <α< ，所以－ <cos α<0，
－1<sin α<－
又(cos α－sin
2
，则cos
2
α－sin α>0，
α)2＝cos2α＋sin2α－2sinαcos
3
2
sin α cos α
2
−
2 sin α−cos α
2 tan α−1 2×2−1 3
cos α cos α
所以
＝
＝
＝
＝ .故选C.
2 cos α+3 sin α 2cos α+3 sin α 2+3 tan α 2+3×2 8
cos α
cos α
(2)[2024·河北张家口模拟]已知sin α＝2sin
第二节
同角三角函数的基本关系式及诱导公式
课前自主预习案
课堂互动探究案
课前自主预习案
必备知识
1.同角三角函数的基本关系
sin2α＋cos2α＝1
(1)平方关系：________________(α∈R)．
(2)商数关系：tan
sin α
π
α＝________(α≠kπ＋
，k∈Z)．
cos
+
的值．
2
sin α
cos π−α
题后师说
(1)对于三角函数式sin θ±cos θ，sin θ·cos θ之间的关系，可以通过

核按钮(新课标)高考数学一轮复习第四章三角函数(基本初等函数(Ⅱ)) 4.2 同角三角函数的基本

§4.2 同角三角函数的基本关系及诱导公式1．同角三角函数的基本关系(1)由三角函数的定义，同角三角函数间有以下两个等式： ①____________________； ②____________________．(2)同角三角函数的关系式的基本用途：①根据一个角的某一三角函数值，求出该角的其他三角函数值；②化简同角的三角函数式；③证明同角的三角恒等式．2．三角函数的诱导公式 x函数sin x cos x tan x －α －sin αcos α－tan α π2±α∓cot α ※π±α3π2±α∓cot α ※2π±α(2)诱导公式的规律：三角函数的诱导公式可概括为：奇变偶不变，符号看象限．其中“奇变偶不变”中的奇、偶分别是指π2的奇数倍和偶数倍，变与不变是指函数名称的变化．若是奇数倍，则正、余弦互变，正、余切互变；若是偶数倍，则函数名称________．“符号看象限”是把α当成________时，原三角函数式中的角⎝ ⎛⎭⎪⎫如π2＋α 所在________原三角函数值的符号．注意：把α当成锐角是指α不一定是锐角，如sin(360°＋120°)＝sin120°，sin(270°＋120°)＝－cos120°，此时把120°当成了锐角来处理．“原三角函数”是指等号左边的函数．(3)诱导公式的作用：诱导公式可以将任意角的三角函数转化为________三角函数，因此常用于化简和求值，其一般步骤是：任意负角的三角函数――――――――――→去负（化负角为正角）任意正角的三角函数――――→脱周脱去k ·360°0°到360°的三角函数――――――――→化锐（把角化为锐角）锐角三角函数3．sin α＋cos α，sin αcos α，sin α－cos α三者之间的关系(sin α＋cos α)2＝________________； (sin α－cos α)2＝________________；(sin α＋cos α)2＋(sin α－cos α)2＝____________； (sin α＋cos α)2－(sin α－cos α)2＝___________.自查自纠1．(1)①sin 2α＋cos 2α＝1 ②sin αcos α＝tan α2．(1)x函数sin x cos x tan x －α －sin α cos α －tan α π2±α cos α ∓sin α ∓cot α ※ π±α ∓sin α －cos α ±tan α 3π2±α －cos α ±sin α ∓cot α ※ 2π±α ±sin αcos α±tan α(2)不变锐角象限 (3)锐角3．1＋sin2α 1－sin2α 2 2sin2α(2015·山东模拟)已知α为第二象限角，且sin α＝35，则tan (π＋α)的值是( )A.43B.34 C ．－43D ．－34解：∵α为第二象限角，∴cos α＝－1－⎝ ⎛⎭⎪⎫352＝－45，∴tan (π＋α)＝tan α＝sin αcos α＝－34.故选D .(2014·全国)设a ＝sin33°，b ＝cos55°，c ＝tan35°，则( ) A ．a ＞b ＞cB ．b ＞c ＞aC ．c ＞b ＞aD ．c ＞a ＞b解：∵a ＝sin33°，b ＝cos55°＝sin35°，c ＝tan35°，∴c ＞b ＞a .故选C . (2015·广东模拟)若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两根，则m 的值为( )A ．1＋ 5B ．1－ 5C ．1± 5D ．－1－ 5解：由题意知sin θ＋cos θ＝－m 2，sin θcos θ＝m4，又(sin θ＋cos θ)2＝1＋2sin θcos θ，∴m 24＝1＋m2，解得m ＝1± 5.又Δ＝4m 2－16m ≥0，∴m ≤0或m ≥4，∴m ＝1－ 5.故选B .已知sin αcos α＝18，且π4＜α＜π2，则cos α－sin α的值是________．解：∵π4＜α＜π2，∴sin α＞cos α.∵1－2sin αcos α＝(cos α－sin α)2＝34，∴cos α－sin α＝－32.故填－32. (2015·青海模拟)已知△ABC 中，tan A ＝－512，则cos A ＝________．解：在△ABC 中，由tan A ＝－512<0知∠A 为钝角，∴cos A <0，1＋tan 2A ＝sin 2A ＋cos 2A cos 2A＝1cos 2A ＝169144，得cos A ＝－1213.故填－1213.类型一利用同角三角函数的基本关系式进行化简和求值(1)已知sin α＝13，且α为第二象限角，求tan α；(2)已知sin α＝13，求tan α；(3)已知sin α＝m (m ≠0，m ≠±1)，求tan α.解：(1)∵sin α＝13，且α是第二象限角，∴cos α＝－1－sin 2α＝－1－⎝ ⎛⎭⎪⎫132＝－223. ∴tan α＝sin αcos α＝－24.(2)∵sin α＝13，∴α是第一或第二象限角．当α是第一象限角时，cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫132＝223， ∴tan α＝sin αcos α＝24；当α是第二象限角时，tan α＝－24. (3)∵sin α＝m (m ≠0，m ≠±1)，∴cos α＝±1－sin 2α＝±1－m 2(当α为第一、四象限角时取正号，当α为第二、三象限角时取负号)．∴当α为第一、四象限角时，tan α＝m1－m2；当α为第二、三象限角时，tan α＝－m1－m2.【点拨】解题时要注意角的取值范围，分类讨论，正确判断函数值的符号．(1)设sin α2＝45，且α是第二象限角，则tan α2的值为________．解：∵α是第二象限角，∴α2是第一或第三象限角．①当α2是第一象限角时，有cos α2＝1－sin2α2＝1－⎝ ⎛⎭⎪⎫452＝35， ∴tan α2＝sinα2cosα2＝43；②当α2是第三象限角时，与sin α2＝45矛盾，舍去．综上，tan α2＝43.故填43.(2)已知sin α－cos α＝2，α∈(0，π)，则tan α＝________. 解法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0，∴cos α＝－22.又α∈(0，π)，∴α＝3π4，tan α＝tan 3π4＝－1.解法二：∵sin α－cos α＝2，∴(sin α－cos α)2＝2，得sin2α＝－1.∵α∈(0，π)，∴2α∈(0，2π)，2α＝3π2，∴α＝3π4，tan α＝－1.故填－1.类型二诱导公式的运用(1)(2015·贵阳模拟)已知sin ⎝⎛⎭⎪⎫π3－α＝12，则cos ⎝ ⎛⎭⎪⎫π6＋α＝________. 解：∵⎝ ⎛⎭⎪⎫π3－α＋⎝ ⎛⎭⎪⎫π6＋α＝π2，∴cos ⎝ ⎛⎭⎪⎫π6＋α＝cos ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π3－α＝sin ⎝ ⎛⎭⎪⎫π3－α＝12.故填12.(2)化简sin （2π－α）cos （π＋α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫11π2－αcos （π－α）sin （3π－α）sin （－π－α）sin ⎝ ⎛⎭⎪⎫9π2＋α.解：原式＝（－sin α）（－cos α）（－sin α）（－sin α）（－cos α）·sin α·sin α·cos α＝－tan α.【点拨】①三角式的化简通常先用诱导公式，将角度统一后再用同角三角函数关系式，这可以避免交错使用公式时导致的混乱．②在运用公式时正确判断符号至关重要．③三角函数的化简、求值是三角函数中的基本问题，也是高考常考的问题，要予以重视．(1)化简sin 2(π＋α)－cos (π＋α)·cos(－α)＋1.解：原式＝sin 2α－(－cos α)·cos α＋1＝sin 2α＋cos 2α＋1＝2.(2)(2015·广西模拟)已知tan ⎝ ⎛⎭⎪⎫π6－α＝33，则tan ⎝ ⎛⎭⎪⎫56π＋α＝________.解：∵⎝ ⎛⎭⎪⎫π6－α＋⎝ ⎛⎭⎪⎫5π6＋α＝π，∴tan ⎝ ⎛⎭⎪⎫56π＋α＝－tan ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫56π＋α＝－tan ⎝ ⎛⎭⎪⎫π6－α＝－33.故填－33.类型三关于sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值．(1)sin α－3cos αsin α＋cos α； (2)sin 2α＋sin αcos α＋2.解：由已知得tan α＝12.(1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝ ⎛⎭⎪⎫122＋12⎝ ⎛⎭⎪⎫122＋1＋2＝135. 【点拨】(1)形如a sin α＋b cos α和a sin 2α＋b sin αcos α＋c cos 2α的式子分别称为关于sin α，cos α的一次齐次式和二次齐次式，对涉及它们的三角变换通常转化为正切(分子分母同除以cos α或cos 2α)求解．如果分母为1，可考虑将1写成sin 2α＋cos 2α.(2)已知tan α＝m 的条件下，求解关于sin α，cos α的齐次式问题，必须注意以下几点：①一定是关于sin α，cos α的齐次式(或能化为齐次式)的三角函数式．②因为cos α≠0，所以可以用cos n α(n ∈N *)除之，这样可以将被求式化为关于tan α的表示式，可整体代入tan α＝m 的值，从而完成被求式的求值运算．③注意1＝sin 2α＋cos 2α的运用．(2015·海南模拟)当0<x <π4时，函数f (x )＝cos 2xcos x sin x －sin 2x的最小值是( )A.14B.12C ．2D ．4 解：当0<x <π4时，0<tan x <1，f (x )＝cos 2x cos x sin x －sin 2x ＝1tan x －tan 2x ，设t ＝tan x ，则0<t <1，y ＝1t －t 2＝1t （1－t ）≥4，当且仅当t ＝1－t ，即t ＝12时等号成立．故选D .1．诱导公式用角度制和弧度制表示都可，运用时应注意函数名称是否要改变以及正负号的选取．2．已知一个角的某一个三角函数值，求这个角的其他三角函数值，这类问题用同角三角函数的基本关系式求解，一般分为三种情况：(1)一个角的某一个三角函数值和这个角所在的象限或终边所在的位置都是已知的，此类情况只有一组解．(2)一个角的某一个三角函数值是已知的，但这个角所在的象限或终边所在的位置没有给出，解答这类问题，首先要根据已知的三角函数值确定这个角所在的象限或终边所在的位置，然后分不同的情况求解．(3)一个角的某一个三角函数值是用字母给出的，此类情况须对字母进行讨论，并注意适当选取分类标准，一般有两组解．3．计算、化简三角函数式常用技巧(1)减少不同名的三角函数，或化切为弦，或化弦为切，如涉及sin α，cos α的齐次分式问题，常采用分子分母同除以cos n α(n ∈N *)，这样可以将被求式化为关于tan α的式子．※(2)巧用“1”进行变形，如1＝sin 2α＋cos 2α＝tan αcot α＝tan45°＝sec 2α－tan 2α等．(3)平方关系式需开方时，应慎重考虑符号的选取．(4)熟悉sin α＋cos α，sin α－cos α，sin αcos α三者之间的内在联系，利用(sin α±cos α)2＝1±2sin αcos α进行和积转换，可知一求二．1．sin585°的值为( )A ．－22 B.22 C ．－32 D.32解：sin585°＝sin ()90°×6＋45°＝－sin45°＝－22.故选A . 2．(2013·全国)已知α是第二象限角，sin α＝513，则cos α＝( )A ．－1213B ．－513 C.513 D.1213解：∵α是第二象限角，sin α＝513，∴cos α＝－1－sin 2α＝－1－⎝ ⎛⎭⎪⎫5132＝－1213.故选A .3．已知f (cos x )＝cos2x ，则f (sin15°)的值等于( ) A.12 B.－12 C.32 D.－32 解：f (sin15°)＝f (cos75°)＝cos150°＝－32.故选D . 4．(2015·深圳模拟)1＋2sin （π－3）cos （π＋3）化简的结果是( ) A ．sin3－cos3B ．cos3－sin3C ．±(sin3－cos3)D ．以上都不对解：∵sin (π－3)＝sin3，cos (π＋3)＝－cos3，∴原式＝1－2sin3·cos3＝（sin3－cos3）2＝|sin3－cos3|.∵π2＜3＜π，∴sin3＞0，cos3＜0.∴原式＝sin3－cos3.故选A .5．(2015·衡水模拟)已知α为锐角，且2tan (π－α)－3cos ⎝ ⎛⎭⎪⎫π2＋β＋5＝0，tan (π＋α)＋6sin (π＋β)＝1，则sin α的值是( )A.355B.377C.31010D.13解：由已知可得－2tan α＋3sin β＋5＝0，tan α－6sin β＝1，两式联立得tan α＝3，∴sin α＝31010.故选C .6．(2015·黑龙江模拟)若cos α＋2sin α＝－5，则tan α等于( ) A.12 B ．2 C ．－12D ．－2解：由cos α＋2sin α＝－5可知cos α≠0，两边同时除以cos α得1＋2tan α＝－5cos α，平方得(1＋2tan α)2＝5cos 2α＝5(1＋tan 2α)，∴tan 2α－4tan α＋4＝0，解得tan α＝2.故选B .7．(2015·湖北模拟)已知cos ⎝ ⎛⎭⎪⎫5π12＋α＝13，且－π<α<－π2，则cos ⎝ ⎛⎭⎪⎫π12－α＝________．解：∵－7π12<5π12＋α<－π12，cos ⎝ ⎛⎭⎪⎫5π12＋α＝13，∴sin ⎝ ⎛⎭⎪⎫5π12＋α＝－223，∴cos ⎝ ⎛⎭⎪⎫π12－α＝sin[π2－⎝ ⎛⎭⎪⎫π12－α]＝sin ⎝ ⎛⎭⎪⎫5π12＋α＝－223.故填－223. 8．(2015·上海模拟)若tan ⎝ ⎛⎭⎪⎫π4－θ＝12，则sin θcos θ＝________.解：由tan ⎝ ⎛⎭⎪⎫π4－θ＝1－tan θ1＋tan θ＝12，得tan θ＝13，∴sin θcos θ＝sin θcos θsin 2θ＋cos 2θ＝tan θtan 2θ＋1＝1319＋1＝310.故填310. 9．已知sin (3π＋θ)＝13，求cos （π＋θ）cos θ[cos （π－θ）－1]＋cos （θ－2π）sin ⎝ ⎛⎭⎪⎫θ－3π2cos （θ－π）－sin ⎝ ⎛⎭⎪⎫3π2＋θ的值．解：∵sin (3π＋θ)＝－sin θ＝13，∴sin θ＝－13.∴原式＝－cos θcos θ（－cos θ－1）＋cos θcos θ·（－cos θ）＋cos θ＝11＋cos θ＋11－cos θ＝21－cos 2θ＝2sin 2θ＝2⎝ ⎛⎭⎪⎫－132＝18.10．已知sin θ－cos θ＝12，求：(1)sin θcos θ； (2)sin 3θ－cos 3θ； (3)sin 4θ＋cos 4θ.解：(1)将sin θ－cos θ＝12两边平方得：1－2sin θcos θ＝14，sin θcos θ＝38.(2)sin 3θ－cos 3θ＝(sin θ－cos θ)(sin 2θ＋sin θcos θ＋cos 2θ)＝12×⎝ ⎛⎭⎪⎫1＋38＝1116. (3)sin 4θ＋cos 4θ＝(sin 2θ＋cos 2θ)2－2sin 2θcos 2θ＝1－2×⎝ ⎛⎭⎪⎫382＝2332.11．(1)已知tan α＝3，求23sin 2α＋14cos 2α的值．(2)已知1tan α－1＝1，求11＋sin αcos α的值．解：(1)23sin 2α＋14cos 2α＝23sin 2α＋14cos 2αsin 2α＋cos 2α＝23tan 2α＋14tan 2α＋1＝23×32＋1432＋1＝58. (2)由1tan α－1＝1得tan α＝2，11＋sin αcos α＝sin 2α＋cos 2αsin 2α＋cos 2α＋sin αcos α＝tan 2α＋1tan 2α＋tan α＋1 ＝22＋122＋2＋1＝57. 若A ，B 是锐角△ABC 的两个内角，则点P (cos B －sin A ，sin B －cos A )在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限解：∵A ＋B ＞π2，且A ，B 为锐角，∴π2＞A ＞π2－B ＞0， ∴sin A ＞sin ⎝ ⎛⎭⎪⎫π2－B ＝cos B ，cos A ＜cos ⎝ ⎛⎭⎪⎫π2－B ＝sin B ， ∴cos B －sin A ＜0，sin B －cos A ＞0，∴点P 在第二象限．故选B .。